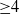The Nash problem asks about the existence of a correspondence between families of arcs through singularities of complex varieties and certain types of divisorial valuations. It has been positively settled in dimension 2 by Fernández de Bobadilla and Pe Pereira, and it was shown to have a negative answer in all dimensions ${\geq }4$ by Ishii and Kollár. In this note we discuss examples which show that the problem has a negative answer in dimension 3 as well. These examples also bring to light the different nature of the problem depending on whether it is formulated in the algebraic setting or in the analytic setting.

We compute the (generalized) Poincaré series of the multi-index filtration defined by a finite collection of divisorial valuations on the ring $\mathcal{O}_{\mathbb{C}^2,0}$ of germs of functions of two variables. We use the method initially elaborated by the authors and Campillo for computing the similar Poincaré series for the valuations defined by the irreducible components of a plane curve singularity. The method is essentially based on the notions of the so-called extended semigroup and of the integral with respect to the Euler characteristic over the projectivization of the space of germs of functions of two variables. The last notion is similar to (and inspired by) the notion of the motivic integration.

AMS 2000 Mathematics subject classification: Primary 14B05; 16W70