Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T23:02:59.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional counter-examples to the Nash problem

Part of: Birational geometry

Published online by Cambridge University Press:  13 August 2013

Tommaso de Fernex
Tommaso de Fernex*
Affiliation:
Department of Mathematics, University of Utah, 155 South 1400 East, Salt Lake City, UT 84112, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

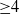The Nash problem asks about the existence of a correspondence between families of arcs through singularities of complex varieties and certain types of divisorial valuations. It has been positively settled in dimension 2 by Fernández de Bobadilla and Pe Pereira, and it was shown to have a negative answer in all dimensions ${\geq }4$ by Ishii and Kollár. In this note we discuss examples which show that the problem has a negative answer in dimension 3 as well. These examples also bring to light the different nature of the problem depending on whether it is formulated in the algebraic setting or in the analytic setting.

Keywords

arcsdivisorial valuationsresolution of singularities

MSC classification

Secondary: 14E05: Rational and birational maps 14E18: Arcs and motivic integration 14E15: Global theory and resolution of singularities
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 9 , September 2013 , pp. 1519 - 1534
Copyright
© The Author(s) 2013 

References

Abate, M., Bracci, F. and Tovena, F., Embeddings of submanifolds and normal bundles, Adv. Math. 220 (2009), 620–656.Google Scholar
Ambro, F., On minimal log discrepancies, Math. Res. Lett. 6 (1999), 573–580.Google Scholar
Cheltsov, I., Factorial threefold hypersurfaces, J. Algebraic Geom. 19 (2010), 781–791.Google Scholar
Ciliberto, C. and Di Gennaro, V., Factoriality of certain hypersurfaces of ${\mathbf{P} }^{4} $ with ordinary double points, in Algebraic transformation groups and algebraic varieties, Encyclopaedia of Mathematical Sciences, vol. 132 (Springer, Berlin, 2004), 1–7.Google Scholar
Cynk, S., Defect of a nodal hypersurface, Manuscripta Math. 104 (2001), 325–331.CrossRefGoogle Scholar
Denef, J. and Loeser, F., Germs of arcs on singular algebraic varieties and motivic integration, Invent. Math. 135 (1999), 201–232.Google Scholar
Ein, L., Lazarsfeld, R. and Mustaţǎ, M., Contact loci in arc spaces, Compositio Math. 140 (2004), 1229–1244.CrossRefGoogle Scholar
Ein, L. and Mustaţă, M., Jet schemes and singularities, in Algebraic geometry—Seattle 2005. Part 2, Proceedings of Symposia in Pure Mathematics, vol. 80 (American Mathematical Society, Providence, RI, 2009), 505–546.Google Scholar
Fernández de Bobadilla, J. and Pe Pereira, M., Nash problem for surfaces, Ann. of Math. (2), to appear, arXiv:1102.2212, also available on the journal webpage.Google Scholar
Fernández de Bobadilla, J. and Pe Pereira, M., Curve selection lemma in infinite-dimensional algebraic geometry and arc spaces, Preprint (2012), arXiv:1201.6310.Google Scholar
de Fernex, T., Ein, L. and Ishii, S., Divisorial valuations via arcs, Publ. Res. Inst. Math. Sci. 44 (2008), 425–448.Google Scholar
Greenberg, M. J., Rational points in Henselian discrete valuation rings, Publ. Math. Inst. Hautes Études Sci. 31 (1966), 59–64.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 255.Google Scholar
Ishii, S., Arcs, valuations and the Nash map, J. Reine Angew. Math. 588 (2005), 71–92.CrossRefGoogle Scholar
Ishii, S. and Kollár, J., The Nash problem on arc families of singularities, Duke Math. J. 120 (2003), 601–620.Google Scholar
Kollár, J., Arc spaces of $c{A}_{1} $singularities, Preprint (2012), arXiv:1207.5036.Google Scholar
Kollár, J. and Mori, S., Classification of three-dimensional flips, J. Amer. Math. Soc. 5 (1992), 533–703.CrossRefGoogle Scholar
Lejeune-Jalabert, M., Arcs analytiques et résolution minimale des surfaces quasihomogènes, in Séminaire sur les Singularités des Surfaces, Palaiseau, France, 1976/1977, Lecture Notes in Mathematics, vol. 777 (Springer, Berlin, 1980), 303–332; (in French).Google Scholar
Lejeune-Jalabert, M. and Reguera, A. J., Exceptional divisors that are not uniruled belong to the image of the Nash map, J. Inst. Math. Jussieu 11 (2012), 273–287.Google Scholar
Nash Jr, J. F., Arc structure of singularities, Duke Math. J. 81 (1996), 31–38 (A celebration of John F. Nash Jr).Google Scholar
Plénat, C. and Popescu-Pampu, P., Families of higher dimensional germs with bijective Nash map, Kodai Math. J. 31 (2008), 199–218.Google Scholar
Reguera, A. J., A curve selection lemma in spaces of arcs and the image of the Nash map, Compositio Math. 142 (2006), 119–130.Google Scholar