We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Minimax estimation procedures for the mean vector of a distribution on a compact set under squared error type loss functions are considered. In particular, a Dirichlet process prior is used to show that a linear function of 
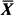is a minimax estimator in the class of all measurable estimators and all possible distributions. This effort extends some earlier work of Bühlmann to a more general setting.
