Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T05:12:25.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimax Estimation of a Mean Vector for Distributions on a Compact Set

Published online by Cambridge University Press:  29 August 2014

Richard Dykstra
Richard Dykstra*
Affiliation:
University of Iowa, USA
*
Department of Statistics and Actuarial Science, University of Iowa, Iowa City, IA 52242/, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Minimax estimation procedures for the mean vector of a distribution on a compact set under squared error type loss functions are considered. In particular, a Dirichlet process prior is used to show that a linear function of 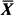is a minimax estimator in the class of all measurable estimators and all possible distributions. This effort extends some earlier work of Bühlmann to a more general setting.

Keywords

Minimax decision rulesquared error lossDirichlet processcompact setsBayes rulesisotonic regression
Type
Articles
Information
ASTIN Bulletin: The Journal of the IAA , Volume 20 , Issue 2 , November 1990 , pp. 173 - 179
Copyright
Copyright © International Actuarial Association 1990

References

Bühlmann, Hans (1976) Minimax Credibility. Scand. Actuarial J. 65–78.Google Scholar
Billingsley, Patrick (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Ferguson, T. S. (1973) A Bayesian Analysis of Some Nonparametric Problems. Ann. Statist. 1, 209–230.CrossRefGoogle Scholar
Hjort, N. L. (1976) Dirichletprosessen anvendt på noen ikke-parametriske estimeringsproblemer. Unpublished thesis from the University of Tromsø, Norway.Google Scholar
Phadia, E.G. (1973) Minimax estimation of a cumulative distribution function. Annals of Statistics, 1149–1157.Google Scholar
Robertson, Tim, Wright, F.T. and Dykstra, R. L. (1988) Order Restricted Statistical Inference. Wiley, Chichester.Google Scholar
Serfling, Robert J. (1980) Approximation Theorems of Mathematical Statistics. Wiley, New York.CrossRefGoogle Scholar