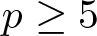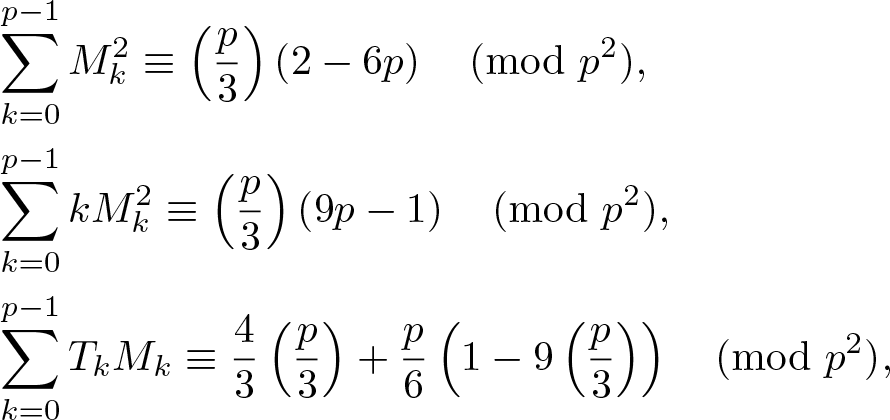1 results
Supercongruences involving Motzkin numbers and central trinomial coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
-
Let Mn and Tn denote the nth Motzkin number and the nth central trinomial coefficient respectively. We prove that for any prime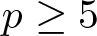
$p\ge 5$,
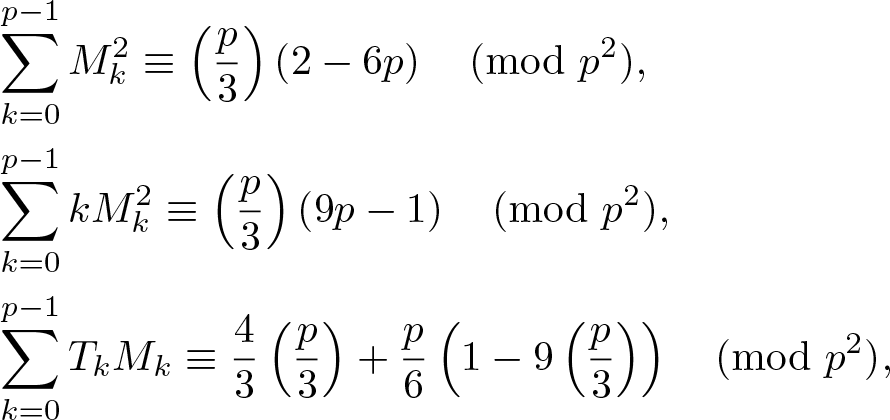\begin{equation*}\begin{aligned}\\[-22pt]&\sum_{k=0}^{p-1}M_k^2\equiv \left(\frac{p}{3}\right)\left(2-6p\right)\pmod{p^2},\\&\sum_{k=0}^{p-1}kM_k^2\equiv \left(\frac{p}{3}\right)\left(9p-1\right)\pmod{p^2},\\&\sum_{k=0}^{p-1}T_kM_k\equiv \frac{4}{3}\left(\frac{p}{3}\right)+\frac{p}{6}\left(1-9\left(\frac{p}{3}\right)\right)\pmod{p^2},\\[-6pt]\end{aligned}\end{equation*}where
$\left(-\right)$ is the Legendre symbol. These results confirm three supercongruences conjectured by Z.-W. Sun in 2010.
