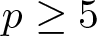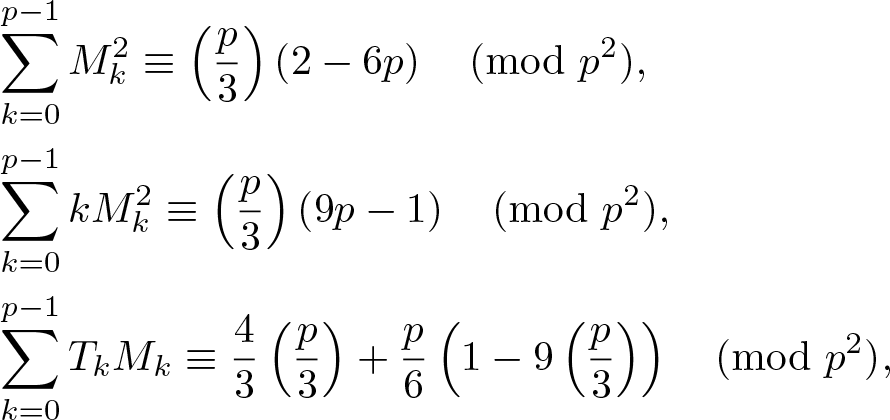1. Introduction
The Motzkin numbers ![]() $\{M_n\}_{n=0}^{\infty}=1, 1, 2, 4, 9, 21, 51, 127,\ldots$ first appeared in [Reference Motzkin6] in a circle chording setting, which count the number of ways of connecting a subset of n points on a circle by nonintersecting chords. The Motzkin number Mn also counts the number of lattice paths on the upper right quadrant of a grid from
$\{M_n\}_{n=0}^{\infty}=1, 1, 2, 4, 9, 21, 51, 127,\ldots$ first appeared in [Reference Motzkin6] in a circle chording setting, which count the number of ways of connecting a subset of n points on a circle by nonintersecting chords. The Motzkin number Mn also counts the number of lattice paths on the upper right quadrant of a grid from ![]() $(0,0)$ to
$(0,0)$ to ![]() $(n,0)$ if one is allowed to move by using only steps
$(n,0)$ if one is allowed to move by using only steps ![]() $(1,1),(1,0)$ and
$(1,1),(1,0)$ and ![]() $(1,-1)$ but forbidden from dipping below the y = 0 axis.
$(1,-1)$ but forbidden from dipping below the y = 0 axis.
The Motzkin numbers are named after Theodore Motzkin and naturally appear in various combinatorial objects. Fourteen different manifestations of Motzkin numbers in different branches of mathematics were enumerated by Donaghey and Shapiro [Reference Donaghey and Shapiro2] in their survey of Motzkin numbers. The interested readers may refer to [Reference Stanley11] for further information on Motzkin numbers.
The famous Catalan numbers  $C_n={2n\choose n}/(n+1)$ are closely related to Motzkin numbers. The Motzkin numbers can be expressed in terms of Catalan numbers:
$C_n={2n\choose n}/(n+1)$ are closely related to Motzkin numbers. The Motzkin numbers can be expressed in terms of Catalan numbers:
 \begin{align*}
M_n=\sum_{k=0}^{\lfloor n/2\rfloor}{n\choose 2k}C_k,
\end{align*}
\begin{align*}
M_n=\sum_{k=0}^{\lfloor n/2\rfloor}{n\choose 2k}C_k,
\end{align*}and inversely,
 \begin{align*}
C_{n+1}=\sum_{k=0}^n{n\choose k}M_k,
\end{align*}
\begin{align*}
C_{n+1}=\sum_{k=0}^n{n\choose k}M_k,
\end{align*} where ![]() $\lfloor x \rfloor$ denotes the integral part of real x.
$\lfloor x \rfloor$ denotes the integral part of real x.
Another sequence closely related to Motzkin numbers are the central trinomial coefficients. For ![]() $n\in \mathbb{N}$, the central trinomial coefficient Tn is given by the constant term in the expansion of
$n\in \mathbb{N}$, the central trinomial coefficient Tn is given by the constant term in the expansion of ![]() $(1+x+x^{-1})^n$, which can be expressed in terms of binomial coefficients:
$(1+x+x^{-1})^n$, which can be expressed in terms of binomial coefficients:
 \begin{align*}
T_n=\sum_{k=0}^{\lfloor n/2\rfloor}{n\choose 2k}{2k\choose k}.
\end{align*}
\begin{align*}
T_n=\sum_{k=0}^{\lfloor n/2\rfloor}{n\choose 2k}{2k\choose k}.
\end{align*} Note that ![]() $\{T_n\}_{n=0}^{\infty}=1, 1, 3, 7, 19, 51, 141, 393,\ldots$. We remark that the central trinomial coefficient Tn counts the number of lattice paths from
$\{T_n\}_{n=0}^{\infty}=1, 1, 3, 7, 19, 51, 141, 393,\ldots$. We remark that the central trinomial coefficient Tn counts the number of lattice paths from ![]() $(0,0)$ to
$(0,0)$ to ![]() $(n,0)$ if one is allowed to move by using only steps
$(n,0)$ if one is allowed to move by using only steps ![]() $(1,1),(1,0)$ and
$(1,1),(1,0)$ and ![]() $(1,-1)$.
$(1,-1)$.
Although Catalan numbers, Motzkin numbers and central trinomial coefficients naturally arise in combinatorics, they also possess rich arithmetic properties.
Throughout the paper, let ![]() $p\ge 5$ be a prime. Sun and Tauraso [Reference Sun and Tauraso16] showed that
$p\ge 5$ be a prime. Sun and Tauraso [Reference Sun and Tauraso16] showed that
 \begin{align*}
\sum_{k=0}^{p-1}C_k\equiv\frac{3}{2}\left(\frac{p}{3}\right)- \frac{1}{2}\pmod{p^2},
\end{align*}
\begin{align*}
\sum_{k=0}^{p-1}C_k\equiv\frac{3}{2}\left(\frac{p}{3}\right)- \frac{1}{2}\pmod{p^2},
\end{align*} where ![]() $\left(-\right)$ denotes the Legendre symbol.
$\left(-\right)$ denotes the Legendre symbol.
In 2014, Sun [Reference Sun12] proved that
 \begin{align*}
&\sum_{k=0}^{p-1}T_k^2\equiv \left(\frac{-1}{p}\right)\pmod{p},\\
&\sum_{k=0}^{p-1}T_kM_k\equiv \frac{4}{3}\left(\frac{p}{3}\right)\pmod{p}.
\end{align*}
\begin{align*}
&\sum_{k=0}^{p-1}T_k^2\equiv \left(\frac{-1}{p}\right)\pmod{p},\\
&\sum_{k=0}^{p-1}T_kM_k\equiv \frac{4}{3}\left(\frac{p}{3}\right)\pmod{p}.
\end{align*}By the telescoping method for double summations developed by Chen, Hou and Mu [Reference Chen, Hou and Mu1], Sun [Reference Sun14] recently established the following interesting supercongruence:
 \begin{align}
\sum_{k=0}^{p-1}(2k+1)M_k^2\equiv 12p\left(\frac{p}{3}\right)\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}(2k+1)M_k^2\equiv 12p\left(\frac{p}{3}\right)\pmod{p^2}.
\end{align}The motivation of the paper is the following three conjectural supercongruences of Sun [Reference Sun12, Conjecture 1.1]:
 \begin{align}
&\sum_{k=0}^{p-1}M_k^2\equiv \left(\frac{p}{3}\right)\left(2-6p\right)\pmod{p^2},
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}M_k^2\equiv \left(\frac{p}{3}\right)\left(2-6p\right)\pmod{p^2},
\end{align} \begin{align}
&\sum_{k=0}^{p-1}kM_k^2\equiv \left(\frac{p}{3}\right)\left(9p-1\right)\pmod{p^2},
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}kM_k^2\equiv \left(\frac{p}{3}\right)\left(9p-1\right)\pmod{p^2},
\end{align} \begin{align}
&\sum_{k=0}^{p-1}T_kM_k\equiv \frac{4}{3}\left(\frac{p}{3}\right)+\frac{p}{6}\left(1-9\left(\frac{p}{3}\right)\right)\pmod{p^2}.
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}T_kM_k\equiv \frac{4}{3}\left(\frac{p}{3}\right)+\frac{p}{6}\left(1-9\left(\frac{p}{3}\right)\right)\pmod{p^2}.
\end{align}‘The three supercongruences look curious and challenging’, as described by Sun [Reference Sun14] in his recent paper. Although the three supercongruence conjectures were officially announced by Sun [Reference Sun12] in 2014, they first appeared in arXiv version of Sun’s paper in 2010 (see https://arxiv.org/abs/1008.3887).
Note that (1.3) follows immediately from (1.1) and (1.2). In this paper, we aim to prove (1.2) and (1.4).
We remark that both Motzkin numbers and central trinomial coefficients have many different expressions (see A001006 and A002426 in [Reference Sloane10]). The following two expressions will be used in the proof of Theorem 1.1:
 \begin{align}
&M_n=\sum_{k=0}^n (-1)^{n+k}{n\choose k}C_{k+1},
\end{align}
\begin{align}
&M_n=\sum_{k=0}^n (-1)^{n+k}{n\choose k}C_{k+1},
\end{align} \begin{align}
&T_n=\sum_{k=0}^n (-1)^{n+k}{n\choose k}{2k\choose k}.
\end{align}
\begin{align}
&T_n=\sum_{k=0}^n (-1)^{n+k}{n\choose k}{2k\choose k}.
\end{align}The rest of the paper is organized as follows. Section 2 is devoted to proving some preliminary results. In § 3, we establish three congruences for triple sums which play an important role in the proof of Theorem 1.1. We show (1.2) in § 4, whereas (1.4) is proved in § 5.
2. Preliminaries
Let ![]() $p\ge 5$ be a prime. In the proof of Theorem 1.1, we will frequently use Wolstenholme’s theorem [Reference Wolstenholme19]:
$p\ge 5$ be a prime. In the proof of Theorem 1.1, we will frequently use Wolstenholme’s theorem [Reference Wolstenholme19]:
 \begin{align}
{2p-1\choose p-1}\equiv 1\pmod{p^3},
\end{align}
\begin{align}
{2p-1\choose p-1}\equiv 1\pmod{p^3},
\end{align}which is equivalent to
 \begin{align}
{2p\choose p}\equiv 2\pmod{p^3},
\end{align}
\begin{align}
{2p\choose p}\equiv 2\pmod{p^3},
\end{align}and Lehmer’s congruences [Reference Lehmer5]:
 \begin{align}
&H_{\lfloor p/6\rfloor}\equiv H_{\lfloor 5p/6\rfloor}\equiv -2q_p(2)-\frac{3}{2}q_p(3)\pmod{p},
\end{align}
\begin{align}
&H_{\lfloor p/6\rfloor}\equiv H_{\lfloor 5p/6\rfloor}\equiv -2q_p(2)-\frac{3}{2}q_p(3)\pmod{p},
\end{align} \begin{align}
&H_{\lfloor p/3\rfloor}\equiv H_{\lfloor 2p/3\rfloor}\equiv -\frac{3}{2}q_p(3)\pmod{p},
\end{align}
\begin{align}
&H_{\lfloor p/3\rfloor}\equiv H_{\lfloor 2p/3\rfloor}\equiv -\frac{3}{2}q_p(3)\pmod{p},
\end{align} where ![]() $q_p(a)$ denotes the Fermat quotient
$q_p(a)$ denotes the Fermat quotient ![]() $(a^{p-1}-1)/p$.
$(a^{p-1}-1)/p$.
In addition, we require some congruences related to central binomial coefficients and Catalan numbers.
Lemma 2.1. For any prime ![]() $p\ge 5$, we have
$p\ge 5$, we have
 \begin{align}
&\sum_{k=0}^{p-1}{2k\choose k}\equiv \left(\frac{p}{3}\right)\pmod{p^2},
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}{2k\choose k}\equiv \left(\frac{p}{3}\right)\pmod{p^2},
\end{align} \begin{align}
&\sum_{k=0}^{p-1}C_k\equiv\frac{3}{2}\left(\frac{p}{3}\right)- \frac{1}{2}\pmod{p^2},
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}C_k\equiv\frac{3}{2}\left(\frac{p}{3}\right)- \frac{1}{2}\pmod{p^2},
\end{align} \begin{align}
&\sum_{k=1}^{p-1}\frac{{2k\choose k}}{k}\equiv 0\pmod{p^2},
\end{align}
\begin{align}
&\sum_{k=1}^{p-1}\frac{{2k\choose k}}{k}\equiv 0\pmod{p^2},
\end{align} \begin{align}
&\sum_{k=0}^{p-1}k{2k\choose k}\equiv\frac{2}{3}\left(p-\left(\frac{p}{3}\right)\right)\pmod{p^2},
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}k{2k\choose k}\equiv\frac{2}{3}\left(p-\left(\frac{p}{3}\right)\right)\pmod{p^2},
\end{align} \begin{align}
&\sum_{k=0}^{p-2}\frac{{2k\choose k}}{(k+1)^2}\equiv 3\left(\frac{p}{3}\right)+1\pmod{p}.
\end{align}
\begin{align}
&\sum_{k=0}^{p-2}\frac{{2k\choose k}}{(k+1)^2}\equiv 3\left(\frac{p}{3}\right)+1\pmod{p}.
\end{align}Proof. Congruences (2.6)–(2.8) were proved by Sun and Tauraso (see [Reference Sun and Tauraso16, (1.7) and (1.9)] and [Reference Sun and Tauraso15, Theorem 1.3]). It is easily proved by induction on n that
 \begin{align}
\sum_{k=0}^{n-1}(3k+2){2k\choose k}=n{2n\choose n}.
\end{align}
\begin{align}
\sum_{k=0}^{n-1}(3k+2){2k\choose k}=n{2n\choose n}.
\end{align}Letting n = p in (2.11) and using (2.2) gives
 \begin{align}
\sum_{k=0}^{p-1}(3k+2){2k\choose k}\equiv 2p\pmod{p^4}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}(3k+2){2k\choose k}\equiv 2p\pmod{p^4}.
\end{align}Then the proof of (2.9) follows from (2.6) and (2.12).
From the following identity:
 \begin{align*}
{2k\choose k+1}=\frac{1}{2}{2k+2\choose k+1}-{2k\choose k},
\end{align*}
\begin{align*}
{2k\choose k+1}=\frac{1}{2}{2k+2\choose k+1}-{2k\choose k},
\end{align*}we deduce that
 \begin{align}
\sum_{k=0}^{p-2}\frac{{2k\choose k+1}}{k+1}&=\frac{1}{2}\sum_{k=1}^{p-1}\frac{{2k\choose k}}{k}
-\sum_{k=0}^{p-2}C_k\notag\\[7pt]
&\equiv \frac{1}{2}-\frac{3}{2}\left(\frac{p}{3}\right)+C_{p-1}\notag\\[7pt]
&\equiv -\frac{1}{2}-\frac{3}{2}\left(\frac{p}{3}\right)\pmod{p},
\end{align}
\begin{align}
\sum_{k=0}^{p-2}\frac{{2k\choose k+1}}{k+1}&=\frac{1}{2}\sum_{k=1}^{p-1}\frac{{2k\choose k}}{k}
-\sum_{k=0}^{p-2}C_k\notag\\[7pt]
&\equiv \frac{1}{2}-\frac{3}{2}\left(\frac{p}{3}\right)+C_{p-1}\notag\\[7pt]
&\equiv -\frac{1}{2}-\frac{3}{2}\left(\frac{p}{3}\right)\pmod{p},
\end{align}where we have used (2.7) and (2.8).
By (2.7), (2.13) and the identity  $C_k={2k\choose k}-{2k\choose k+1}$, we have
$C_k={2k\choose k}-{2k\choose k+1}$, we have
 \begin{align*}
\sum_{k=0}^{p-2}\frac{{2k\choose k}}{(k+1)^2}&=\sum_{k=0}^{p-2}C_k-\sum_{k=0}^{p-2}\frac{{2k\choose k+1}}{k+1}\\[7pt]
&\equiv 3\left(\frac{p}{3}\right)+1\pmod{p},
\end{align*}
\begin{align*}
\sum_{k=0}^{p-2}\frac{{2k\choose k}}{(k+1)^2}&=\sum_{k=0}^{p-2}C_k-\sum_{k=0}^{p-2}\frac{{2k\choose k+1}}{k+1}\\[7pt]
&\equiv 3\left(\frac{p}{3}\right)+1\pmod{p},
\end{align*}as desired.
We also need some congruences involving harmonic numbers ![]() $H_n=\sum_{k=1}^n 1/k$.
$H_n=\sum_{k=1}^n 1/k$.
Lemma 2.2 For any prime ![]() $p\ge 5$, we have
$p\ge 5$, we have
 \begin{align}
&\sum_{k=0}^{p-1}{2k\choose k}H_{k}\equiv -\left(\frac{p}{3}\right)q_p(3) \pmod{p},
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}{2k\choose k}H_{k}\equiv -\left(\frac{p}{3}\right)q_p(3) \pmod{p},
\end{align} \begin{align}
&\sum_{k=0}^{p-1}k{2k\choose k}H_{k}\equiv \frac{1}{3}\left(\frac{p}{3}\right)\left(\left(\frac{p}{3}\right)+2q_p(3)-1\right)\pmod{p},
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}k{2k\choose k}H_{k}\equiv \frac{1}{3}\left(\frac{p}{3}\right)\left(\left(\frac{p}{3}\right)+2q_p(3)-1\right)\pmod{p},
\end{align} \begin{align}
&\sum_{k=0}^{p-1}C_{k}H_k\equiv -\frac{3}{2}\left(\frac{p}{3}\right)q_p(3)\pmod{p}.
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}C_{k}H_k\equiv -\frac{3}{2}\left(\frac{p}{3}\right)q_p(3)\pmod{p}.
\end{align}Proof. Congruence (2.14) is a known result. We begin with the following congruence due to Tauraso [Reference Tauraso17, (9)]:
 \begin{align}
\sum_{k=0}^{p-1}{2k\choose k}H_k x^k\equiv -(1-4x)^{\frac{p-1}{2}}\sum_{j=1}^{p-1}{2j\choose j}\frac{y^j}{j}\pmod{p},
\end{align}
\begin{align}
\sum_{k=0}^{p-1}{2k\choose k}H_k x^k\equiv -(1-4x)^{\frac{p-1}{2}}\sum_{j=1}^{p-1}{2j\choose j}\frac{y^j}{j}\pmod{p},
\end{align} where ![]() $y=-x/(1-4x)$. Letting x = 1 in (2.17) and using the congruence [Reference Sun and Tauraso15, (1.13)], we arrive at
$y=-x/(1-4x)$. Letting x = 1 in (2.17) and using the congruence [Reference Sun and Tauraso15, (1.13)], we arrive at
 \begin{align*}
\sum_{k=0}^{p-1}{2k\choose k}H_{k}\equiv -(-3)^{\frac{p-1}{2}}\sum_{j=1}^{p-1}{2j\choose j}\frac{1}{j3^j}
\equiv -\left(\frac{p}{3}\right)q_p(3)\pmod{p},
\end{align*}
\begin{align*}
\sum_{k=0}^{p-1}{2k\choose k}H_{k}\equiv -(-3)^{\frac{p-1}{2}}\sum_{j=1}^{p-1}{2j\choose j}\frac{1}{j3^j}
\equiv -\left(\frac{p}{3}\right)q_p(3)\pmod{p},
\end{align*}which is (2.14).
By using the software package Sigma developed by Schneider [Reference Schneider9], we can automatically discover and prove the following three combinatorial identities:
 \begin{align}
&\sum_{k=0}^{n}(-4)^k {n\choose k}H_{k}=(-3)^n\left(H_n-\sum_{k=1}^n\frac{1}{k(-3)^k}\right),
\end{align}
\begin{align}
&\sum_{k=0}^{n}(-4)^k {n\choose k}H_{k}=(-3)^n\left(H_n-\sum_{k=1}^n\frac{1}{k(-3)^k}\right),
\end{align} \begin{align}
&\sum_{k=0}^{n}(-4)^k k{n\choose k}H_{k}=\frac{1-(-3)^n}{3}+\frac{4n(-3)^n}{3}\left(H_n-\sum_{k=1}^n
\frac{1}{k(-3)^k}\right),
\end{align}
\begin{align}
&\sum_{k=0}^{n}(-4)^k k{n\choose k}H_{k}=\frac{1-(-3)^n}{3}+\frac{4n(-3)^n}{3}\left(H_n-\sum_{k=1}^n
\frac{1}{k(-3)^k}\right),
\end{align}and
 \begin{align}
&\sum_{k=0}^n\frac{(-4)^k}{k+1}{n\choose k}H_k\notag\\
&=\frac{1}{4(n+1)}\left((-1+3(-3)^n)H_n-3(-3)^n
\sum_{k=1}^n\frac{1}{k(-3)^k}+\sum_{k=1}^n\frac{(-3)^k}{k}\right).
\end{align}
\begin{align}
&\sum_{k=0}^n\frac{(-4)^k}{k+1}{n\choose k}H_k\notag\\
&=\frac{1}{4(n+1)}\left((-1+3(-3)^n)H_n-3(-3)^n
\sum_{k=1}^n\frac{1}{k(-3)^k}+\sum_{k=1}^n\frac{(-3)^k}{k}\right).
\end{align}By (2.18), we can rewrite (2.19) and (2.20) as
 \begin{align}
\sum_{k=0}^{n}(-4)^k k{n\choose k}H_{k}=\frac{1-(-3)^n}{3}+\frac{4n}{3}\sum_{k=0}^{n}(-4)^k {n\choose k}H_{k},
\end{align}
\begin{align}
\sum_{k=0}^{n}(-4)^k k{n\choose k}H_{k}=\frac{1-(-3)^n}{3}+\frac{4n}{3}\sum_{k=0}^{n}(-4)^k {n\choose k}H_{k},
\end{align}and
 \begin{align}
&\sum_{k=0}^n\frac{(-4)^k}{k+1}{n\choose k}H_k\notag\\[7pt]
&=\frac{1}{4(n+1)}\left(\frac{3((-3)^n+1)}{(-3)^n}\sum_{k=0}^n(-4)^k{n\choose k}H_k\right)\notag\\[7pt]
&+\frac{1}{4(n+1)}\left(3\sum_{k=1}^n\frac{1}{k(-3)^k}+\sum_{k=1}^n\frac{(-3)^k}{k}-4H_n\right).
\end{align}
\begin{align}
&\sum_{k=0}^n\frac{(-4)^k}{k+1}{n\choose k}H_k\notag\\[7pt]
&=\frac{1}{4(n+1)}\left(\frac{3((-3)^n+1)}{(-3)^n}\sum_{k=0}^n(-4)^k{n\choose k}H_k\right)\notag\\[7pt]
&+\frac{1}{4(n+1)}\left(3\sum_{k=1}^n\frac{1}{k(-3)^k}+\sum_{k=1}^n\frac{(-3)^k}{k}-4H_n\right).
\end{align}Using Fermat’s little theorem, we obtain
 \begin{align*}
&\sum_{k=1}^{(p-1)/2}\frac{(-3)^k}{k}+3\sum_{k=1}^{(p-1)/2}\frac{1}{k(-3)^{k}}\\[7pt]
&\equiv \sum_{k=1}^{(p-1)/2}\frac{(-3)^k}{k}+\sum_{k=1}^{(p-1)/2}\frac{(-3)^{p-k}}{p-k}\\[7pt]
&=\sum_{k=1}^{p-1}\frac{(-3)^k}{k}\pmod{p}.
\end{align*}
\begin{align*}
&\sum_{k=1}^{(p-1)/2}\frac{(-3)^k}{k}+3\sum_{k=1}^{(p-1)/2}\frac{1}{k(-3)^{k}}\\[7pt]
&\equiv \sum_{k=1}^{(p-1)/2}\frac{(-3)^k}{k}+\sum_{k=1}^{(p-1)/2}\frac{(-3)^{p-k}}{p-k}\\[7pt]
&=\sum_{k=1}^{p-1}\frac{(-3)^k}{k}\pmod{p}.
\end{align*}From Granville’s congruence [Reference Granville4]:
 \begin{align*}
\sum_{j=1}^{p-1}\frac{x^j}{j}\equiv \frac{1-x^p+(x-1)^p}{p}\pmod{p},
\end{align*}
\begin{align*}
\sum_{j=1}^{p-1}\frac{x^j}{j}\equiv \frac{1-x^p+(x-1)^p}{p}\pmod{p},
\end{align*}we deduce that
 \begin{align*}
\sum_{k=1}^{p-1}\frac{(-3)^k}{k}\equiv 3q_p(3)-8q_p(2)\pmod{p},
\end{align*}
\begin{align*}
\sum_{k=1}^{p-1}\frac{(-3)^k}{k}\equiv 3q_p(3)-8q_p(2)\pmod{p},
\end{align*}which was also mentioned in the proof of [Reference Sun13, Lemma 3.3]. Thus,
 \begin{align}
\sum_{k=1}^{(p-1)/2}\frac{(-3)^k}{k}+3\sum_{k=1}^{(p-1)/2}\frac{1}{k(-3)^{k}}
\equiv 3q_p(3)-8q_p(2)\pmod{p}.
\end{align}
\begin{align}
\sum_{k=1}^{(p-1)/2}\frac{(-3)^k}{k}+3\sum_{k=1}^{(p-1)/2}\frac{1}{k(-3)^{k}}
\equiv 3q_p(3)-8q_p(2)\pmod{p}.
\end{align} Finally, letting ![]() $n=(p-1)/2$ in (2.21)–(2.22) and using (2.5), (2.14), (2.23) and the facts that
$n=(p-1)/2$ in (2.21)–(2.22) and using (2.5), (2.14), (2.23) and the facts that ![]() $H_{p-1}\equiv 0\pmod{p^2}$ and
$H_{p-1}\equiv 0\pmod{p^2}$ and
 \begin{align*}
&(-3)^{(p-1)/2}\equiv \left(\frac{p}{3}\right)\pmod{p},\\[7pt]
&{(p-1)/2\choose k}\equiv \frac{{2k\choose k}}{(-4)^k}\pmod{p},\\[7pt]
&{2k\choose k}\equiv 0\pmod{p}\quad\text{for } {(p+1)/2\le k\le p-1},
\end{align*}
\begin{align*}
&(-3)^{(p-1)/2}\equiv \left(\frac{p}{3}\right)\pmod{p},\\[7pt]
&{(p-1)/2\choose k}\equiv \frac{{2k\choose k}}{(-4)^k}\pmod{p},\\[7pt]
&{2k\choose k}\equiv 0\pmod{p}\quad\text{for } {(p+1)/2\le k\le p-1},
\end{align*}For an assertion A, we set
 \begin{align*}
[A]=\begin{cases}
1\quad&\text{if } A\ \text{holds,}\\
0\quad&\text{otherwise.}
\end{cases}
\end{align*}
\begin{align*}
[A]=\begin{cases}
1\quad&\text{if } A\ \text{holds,}\\
0\quad&\text{otherwise.}
\end{cases}
\end{align*}The following two known congruences play important roles in the proof of Theorem 1.1 (see [Reference Pan and Sun7, Theorem 1.2]).
Lemma 2.3. Let ![]() $p\ge 5$ be a prime. For
$p\ge 5$ be a prime. For ![]() $1\le k \le p$, we have
$1\le k \le p$, we have
 \begin{align}
&\sum_{i=0}^{p-1}{2i\choose i+k}\equiv \left(\frac{p-k}{3}\right)\pmod{p},
\end{align}
\begin{align}
&\sum_{i=0}^{p-1}{2i\choose i+k}\equiv \left(\frac{p-k}{3}\right)\pmod{p},
\end{align} \begin{align}
&\sum_{i=1}^{p-1}\frac{{2i\choose i+k}}{i}\equiv\frac{\alpha(k)-1}{k}\pmod{p},
\end{align}
\begin{align}
&\sum_{i=1}^{p-1}\frac{{2i\choose i+k}}{i}\equiv\frac{\alpha(k)-1}{k}\pmod{p},
\end{align} where ![]() $\alpha(k)=2(-1)^k+3[3\mid p-k])$.
$\alpha(k)=2(-1)^k+3[3\mid p-k])$.
Based on Lemma 2.3, we establish the following result which seems to be crude but useful in the proof of Theorem 1.1.
Lemma 2.4. Let ![]() $p\ge 5$ be a prime. For
$p\ge 5$ be a prime. For ![]() $1\le k \le p$, we have
$1\le k \le p$, we have
 \begin{align}
(-1)^k\sum_{i=1}^{p-2}\frac{{2i\choose i+k}}{i+1}
\equiv 2k+\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}+\sum_{i=1}^{k-1}\beta(i)
-k\sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\pmod{p},
\end{align}
\begin{align}
(-1)^k\sum_{i=1}^{p-2}\frac{{2i\choose i+k}}{i+1}
\equiv 2k+\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}+\sum_{i=1}^{k-1}\beta(i)
-k\sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\pmod{p},
\end{align} where ![]() $\beta(i)=(-1)^i(3[3\mid p-i]-1)$.
$\beta(i)=(-1)^i(3[3\mid p-i]-1)$.
Proof. By Pascal’s formula  ${n\choose m}={n-1\choose m}+{n-1\choose m-1}$, we have
${n\choose m}={n-1\choose m}+{n-1\choose m-1}$, we have
 \begin{align*}
{2i+2\choose i+1+k}&={2i+1\choose i+1+k}+{2i+1\choose i+k}\\[7pt]
&={2i \choose i+1+k}+2{2i\choose i+k}+{2i\choose i+k-1}.
\end{align*}
\begin{align*}
{2i+2\choose i+1+k}&={2i+1\choose i+1+k}+{2i+1\choose i+k}\\[7pt]
&={2i \choose i+1+k}+2{2i\choose i+k}+{2i\choose i+k-1}.
\end{align*}It follows that
 \begin{align}
\sum_{i=0}^{p-2}\frac{{2i \choose i+1+k}}{i+1}+2\sum_{i=0}^{p-2}\frac{{2i\choose i+k}}{i+1}+\sum_{i=0}^{p-2}\frac{{2i\choose i+k-1}}{i+1}
=\sum_{i=1}^{p-1}\frac{{2i\choose i+k}}{i}.
\end{align}
\begin{align}
\sum_{i=0}^{p-2}\frac{{2i \choose i+1+k}}{i+1}+2\sum_{i=0}^{p-2}\frac{{2i\choose i+k}}{i+1}+\sum_{i=0}^{p-2}\frac{{2i\choose i+k-1}}{i+1}
=\sum_{i=1}^{p-1}\frac{{2i\choose i+k}}{i}.
\end{align}Let
 \begin{align*}
&f(k)=(-1)^k\sum_{i=0}^{p-2}\frac{{2i\choose i+k}}{i+1},\\[7pt]
&g(k)=(-1)^{k+1}\sum_{i=1}^{p-1}\frac{{2i\choose i+k}}{i},\\[7pt]
&F(k)=f(k+1)-f(k).
\end{align*}
\begin{align*}
&f(k)=(-1)^k\sum_{i=0}^{p-2}\frac{{2i\choose i+k}}{i+1},\\[7pt]
&g(k)=(-1)^{k+1}\sum_{i=1}^{p-1}\frac{{2i\choose i+k}}{i},\\[7pt]
&F(k)=f(k+1)-f(k).
\end{align*}We rewrite (2.27) as
From (2.28), we deduce that
 \begin{align*}
F(k)=f(k+1)-f(k)=\sum_{j=1}^k g(j)+F(0),
\end{align*}
\begin{align*}
F(k)=f(k+1)-f(k)=\sum_{j=1}^k g(j)+F(0),
\end{align*}and so
 \begin{align}
f(k)&=\sum_{l=1}^{k-1}\sum_{j=1}^l g(j)+kF(0)+f(0)\notag\\[7pt]
&=\sum_{j=1}^{k-1}(k-j) g(j)+kf(1)+(1-k)f(0).
\end{align}
\begin{align}
f(k)&=\sum_{l=1}^{k-1}\sum_{j=1}^l g(j)+kF(0)+f(0)\notag\\[7pt]
&=\sum_{j=1}^{k-1}(k-j) g(j)+kf(1)+(1-k)f(0).
\end{align} By  ${2i\choose i+1}={2i\choose i}-{2i\choose i}/(i+1)$, we have
${2i\choose i+1}={2i\choose i}-{2i\choose i}/(i+1)$, we have
 \begin{align}
&kf(1)+(1-k)f(0)\notag\\[7pt]
&=-k\sum_{i=0}^{p-2}\frac{{2i\choose i+1}}{i+1}+(1-k)\sum_{i=0}^{p-2}\frac{{2i\choose i}}{i+1}\notag\\[7pt]
&=(1-2k)\sum_{i=0}^{p-2}C_i+k\sum_{i=0}^{p-2}\frac{{2i\choose i}}{(i+1)^2}\notag\\[7pt]
&\equiv \frac{3}{2}\left(\frac{p}{3}\right)+\frac{1}{2}\pmod{p},
\end{align}
\begin{align}
&kf(1)+(1-k)f(0)\notag\\[7pt]
&=-k\sum_{i=0}^{p-2}\frac{{2i\choose i+1}}{i+1}+(1-k)\sum_{i=0}^{p-2}\frac{{2i\choose i}}{i+1}\notag\\[7pt]
&=(1-2k)\sum_{i=0}^{p-2}C_i+k\sum_{i=0}^{p-2}\frac{{2i\choose i}}{(i+1)^2}\notag\\[7pt]
&\equiv \frac{3}{2}\left(\frac{p}{3}\right)+\frac{1}{2}\pmod{p},
\end{align}where we have used (2.7) and (2.10) in the last step.
Combining (2.25), (2.29) and (2.30) gives
 \begin{align*}
&(-1)^k\sum_{i=1}^{p-2}\frac{{2i\choose i+k}}{i+1}\\[7pt]
&\equiv -k\sum_{i=1}^{k-1}
\frac{(-1)^i(3[3\mid p-i]-1)+2}{i}+\sum_{i=1}^{k-1}(-1)^i(3[3\mid p-i]-1)
+2k+\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}\\[7pt]
&=2k+\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}+\sum_{i=1}^{k-1}\beta(i)
-k\sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\pmod{p},
\end{align*}
\begin{align*}
&(-1)^k\sum_{i=1}^{p-2}\frac{{2i\choose i+k}}{i+1}\\[7pt]
&\equiv -k\sum_{i=1}^{k-1}
\frac{(-1)^i(3[3\mid p-i]-1)+2}{i}+\sum_{i=1}^{k-1}(-1)^i(3[3\mid p-i]-1)
+2k+\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}\\[7pt]
&=2k+\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}+\sum_{i=1}^{k-1}\beta(i)
-k\sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\pmod{p},
\end{align*}as desired.
3. Three key triple sums
The main idea in the proof of Theorem 1.1 is to translate the left-hand sides of (1.2) and (1.4) into three triple sums, which can be determined modulo p by using Lemmas 2.3 and 2.4. The three congruences for triple sums are stated as follows.
Lemma 3.1. For any prime ![]() $p\ge 5$, we have
$p\ge 5$, we have
 \begin{align}
\sum_{k=1}^{p-2}\sum_{j=1}^{p-2}\sum_{i=1}^{p-1}\frac{(-1)^k}{i(j+1)}{2j\choose j+k}{2i\choose i+k}\equiv \left(\frac{p}{3}\right)\left(1-q_p(3)\right)-1\pmod{p}.
\end{align}
\begin{align}
\sum_{k=1}^{p-2}\sum_{j=1}^{p-2}\sum_{i=1}^{p-1}\frac{(-1)^k}{i(j+1)}{2j\choose j+k}{2i\choose i+k}\equiv \left(\frac{p}{3}\right)\left(1-q_p(3)\right)-1\pmod{p}.
\end{align}Proof. Substituting (2.25) and (2.26) into the left-hand side of (3.1) gives
 \begin{align}
&\sum_{k=1}^{p-2}(-1)^k\sum_{j=1}^{p-2}\frac{1}{j+1}{2j\choose j+k}\sum_{i=1}^{p-1}\frac{1}{i}{2i\choose i+k}\notag\\[7pt]
&\equiv \sum_{k=1}^{p-2} \left(1-\alpha(k)\right) \sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}
+\sum_{k=1}^{p-2} \frac{\alpha(k)-1}{k}\sum_{i=1}^{k-1}\beta(i)\notag\\[7pt]
&+2\sum_{k=1}^{p-2} \left(\alpha(k)-1\right)
+\left(\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}\right)\sum_{k=1}^{p-2} \frac{\alpha(k)-1}{k}\pmod{p}.
\end{align}
\begin{align}
&\sum_{k=1}^{p-2}(-1)^k\sum_{j=1}^{p-2}\frac{1}{j+1}{2j\choose j+k}\sum_{i=1}^{p-1}\frac{1}{i}{2i\choose i+k}\notag\\[7pt]
&\equiv \sum_{k=1}^{p-2} \left(1-\alpha(k)\right) \sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}
+\sum_{k=1}^{p-2} \frac{\alpha(k)-1}{k}\sum_{i=1}^{k-1}\beta(i)\notag\\[7pt]
&+2\sum_{k=1}^{p-2} \left(\alpha(k)-1\right)
+\left(\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}\right)\sum_{k=1}^{p-2} \frac{\alpha(k)-1}{k}\pmod{p}.
\end{align} We shall only prove the case ![]() $p\equiv 1\pmod{3}$ of (3.1). The proof of the case
$p\equiv 1\pmod{3}$ of (3.1). The proof of the case ![]() $p\equiv 2\pmod{3}$ runs analogously, and we omit the details.
$p\equiv 2\pmod{3}$ runs analogously, and we omit the details.
Suppose that ![]() $p\equiv 1\pmod{3}$. Let
$p\equiv 1\pmod{3}$. Let ![]() $n=\lfloor p/6\rfloor$. Then
$n=\lfloor p/6\rfloor$. Then ![]() $n\equiv -1/6\pmod{p}$. Since the sequences
$n\equiv -1/6\pmod{p}$. Since the sequences ![]() $\{\alpha(k)\}_{k\in \mathbb{N}}$ and
$\{\alpha(k)\}_{k\in \mathbb{N}}$ and ![]() $\{\beta(k)\}_{k\in \mathbb{N}}$ both have a period of 6, it is easy to check that
$\{\beta(k)\}_{k\in \mathbb{N}}$ both have a period of 6, it is easy to check that
 \begin{align*}
\Omega(k)=\sum_{i=1}^{k} \left(\alpha(i)-1\right)=
\begin{cases}
0\quad&\text{for } k\equiv 0,1\pmod{6},\\
1\quad&\text{for } k\equiv 2\pmod{6},\\
-2\quad&\text{for } k\equiv 3\pmod{6},\\
2\quad&\text{for } k\equiv 4\pmod{6},\\
-1\quad&\text{for } k\equiv 5\pmod{6},
\end{cases}
\end{align*}
\begin{align*}
\Omega(k)=\sum_{i=1}^{k} \left(\alpha(i)-1\right)=
\begin{cases}
0\quad&\text{for } k\equiv 0,1\pmod{6},\\
1\quad&\text{for } k\equiv 2\pmod{6},\\
-2\quad&\text{for } k\equiv 3\pmod{6},\\
2\quad&\text{for } k\equiv 4\pmod{6},\\
-1\quad&\text{for } k\equiv 5\pmod{6},
\end{cases}
\end{align*}and
 \begin{align*}
\left(\alpha(k)-1\right)\sum_{i=1}^{k-1}\beta(i)=
\begin{cases}
1\quad&\text{for }k\equiv 0\pmod{6},\\
0\quad&\text{for }k\equiv 1,5\pmod{6},\\
-2\quad&\text{for }k\equiv 2\pmod{6},\\
9\quad&\text{for }k\equiv 3\pmod{6},\\
-8\quad&\text{for }k\equiv 4\pmod{6}.
\end{cases}
\end{align*}
\begin{align*}
\left(\alpha(k)-1\right)\sum_{i=1}^{k-1}\beta(i)=
\begin{cases}
1\quad&\text{for }k\equiv 0\pmod{6},\\
0\quad&\text{for }k\equiv 1,5\pmod{6},\\
-2\quad&\text{for }k\equiv 2\pmod{6},\\
9\quad&\text{for }k\equiv 3\pmod{6},\\
-8\quad&\text{for }k\equiv 4\pmod{6}.
\end{cases}
\end{align*}It follows that
and
 \begin{align}
\sum_{k=1}^{p-2} \frac{\alpha(k)-1}{k}\sum_{i=1}^{k-1}\beta(i)
=\sum_{k=1}^{n-1}\frac{1}{6k}-2\sum_{k=1}^{n}\frac{1}{6k-4}
+9\sum_{k=1}^{n}\frac{1}{6k-3}-8\sum_{k=1}^{n}\frac{1}{6k-2}.
\end{align}
\begin{align}
\sum_{k=1}^{p-2} \frac{\alpha(k)-1}{k}\sum_{i=1}^{k-1}\beta(i)
=\sum_{k=1}^{n-1}\frac{1}{6k}-2\sum_{k=1}^{n}\frac{1}{6k-4}
+9\sum_{k=1}^{n}\frac{1}{6k-3}-8\sum_{k=1}^{n}\frac{1}{6k-2}.
\end{align}Furthermore, we have
 \begin{align*}
&\sum_{k=1}^{p-2} \left(1-\alpha(k)\right) \sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\\[7pt]
&=-\sum_{i=1}^{p-3}\frac{\beta(i)+2}{i} \sum_{k=i+1}^{p-2} \left(\alpha(k)-1\right)\\[7pt]
&=-\sum_{i=1}^{p-3}\frac{\left(\beta(i)+2\right)\left(\Omega(p-2)-\Omega(i)\right)}{i}\\[7pt]
&=\sum_{i=1}^{p-3}\frac{\left(\beta(i)+2\right)\left(1+\Omega(i)\right)}{i},
\end{align*}
\begin{align*}
&\sum_{k=1}^{p-2} \left(1-\alpha(k)\right) \sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\\[7pt]
&=-\sum_{i=1}^{p-3}\frac{\beta(i)+2}{i} \sum_{k=i+1}^{p-2} \left(\alpha(k)-1\right)\\[7pt]
&=-\sum_{i=1}^{p-3}\frac{\left(\beta(i)+2\right)\left(\Omega(p-2)-\Omega(i)\right)}{i}\\[7pt]
&=\sum_{i=1}^{p-3}\frac{\left(\beta(i)+2\right)\left(1+\Omega(i)\right)}{i},
\end{align*}where we have used (3.3) in the last step. It is also easy to check that
 \begin{align*}
\left(\beta(i)+2\right)\left(1+\Omega(i)\right)=
\begin{cases}
1\quad&\text{for }i\equiv 0\pmod{6},\\
0\quad&\text{for }i\equiv 1,5\pmod{6},\\
2\quad&\text{for }i\equiv 2\pmod{6},\\
-3\quad&\text{for }i\equiv 3\pmod{6},\\
12\quad&\text{for }i\equiv 4\pmod{6},
\end{cases}
\end{align*}
\begin{align*}
\left(\beta(i)+2\right)\left(1+\Omega(i)\right)=
\begin{cases}
1\quad&\text{for }i\equiv 0\pmod{6},\\
0\quad&\text{for }i\equiv 1,5\pmod{6},\\
2\quad&\text{for }i\equiv 2\pmod{6},\\
-3\quad&\text{for }i\equiv 3\pmod{6},\\
12\quad&\text{for }i\equiv 4\pmod{6},
\end{cases}
\end{align*}and so
 \begin{align}
&\sum_{k=1}^{p-2} \left(1-\alpha(k)\right) \sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\notag\\[7pt]
&=\sum_{k=1}^{n-1}\frac{1}{6k}+12\sum_{k=1}^{n}\frac{1}{6k-2}-3\sum_{k=1}^{n}\frac{1}{6k-3}
+2\sum_{k=1}^{n}\frac{1}{6k-4}.
\end{align}
\begin{align}
&\sum_{k=1}^{p-2} \left(1-\alpha(k)\right) \sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\notag\\[7pt]
&=\sum_{k=1}^{n-1}\frac{1}{6k}+12\sum_{k=1}^{n}\frac{1}{6k-2}-3\sum_{k=1}^{n}\frac{1}{6k-3}
+2\sum_{k=1}^{n}\frac{1}{6k-4}.
\end{align}Substituting (3.3)–(3.5) into the right-hand side of (3.2) gives
 \begin{align}
&\sum_{k=1}^{p-2}\sum_{j=1}^{p-2}\sum_{i=1}^{p-1}\frac{(-1)^k}{i(j+1)}{2j\choose j+k}{2i\choose i+k}\notag\\[7pt]
&\equiv 2\sum_{k=1}^{n-1}\frac{1}{6k}+4\sum_{k=1}^{n}\frac{1}{6k-2}+6\sum_{k=1}^{n}\frac{1}{6k-3}-2\notag\\[7pt]
&\equiv \frac{1}{3}\sum_{k=1}^n\frac{1}{k}+\frac{2}{3}\sum_{k=1}^n\frac{1}{k+2n}+\sum_{k=1}^n
\frac{1}{k+3n}\notag\\[7pt]
&=\frac{1}{3}H_n-\frac{2}{3}H_{2n}-\frac{1}{3}H_{3n}+H_{4n}\pmod{p}.
\end{align}
\begin{align}
&\sum_{k=1}^{p-2}\sum_{j=1}^{p-2}\sum_{i=1}^{p-1}\frac{(-1)^k}{i(j+1)}{2j\choose j+k}{2i\choose i+k}\notag\\[7pt]
&\equiv 2\sum_{k=1}^{n-1}\frac{1}{6k}+4\sum_{k=1}^{n}\frac{1}{6k-2}+6\sum_{k=1}^{n}\frac{1}{6k-3}-2\notag\\[7pt]
&\equiv \frac{1}{3}\sum_{k=1}^n\frac{1}{k}+\frac{2}{3}\sum_{k=1}^n\frac{1}{k+2n}+\sum_{k=1}^n
\frac{1}{k+3n}\notag\\[7pt]
&=\frac{1}{3}H_n-\frac{2}{3}H_{2n}-\frac{1}{3}H_{3n}+H_{4n}\pmod{p}.
\end{align} Finally, noting that for ![]() $p\equiv 1\pmod{3}$,
$p\equiv 1\pmod{3}$, ![]() $2n=\lfloor p/3\rfloor,3n=\lfloor p/2\rfloor, 4n=\lfloor 2p/3\rfloor$ and applying (2.3)–(2.5) to the right-hand side of (3.6), we arrive at the desired result:
$2n=\lfloor p/3\rfloor,3n=\lfloor p/2\rfloor, 4n=\lfloor 2p/3\rfloor$ and applying (2.3)–(2.5) to the right-hand side of (3.6), we arrive at the desired result:
 \begin{align*}
\sum_{k=1}^{p-2}\sum_{j=1}^{p-2}\sum_{i=1}^{p-1}\frac{(-1)^k}{i(j+1)}{2j\choose j+k}{2i\choose i+k}
\equiv -q_p(3)\pmod{p},
\end{align*}
\begin{align*}
\sum_{k=1}^{p-2}\sum_{j=1}^{p-2}\sum_{i=1}^{p-1}\frac{(-1)^k}{i(j+1)}{2j\choose j+k}{2i\choose i+k}
\equiv -q_p(3)\pmod{p},
\end{align*} which is the case ![]() $p\equiv 1\pmod{3}$ of (3.1).
$p\equiv 1\pmod{3}$ of (3.1).
Lemma 3.2. For any prime ![]() $p\ge 5$, we have
$p\ge 5$, we have
 \begin{align}
\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\equiv -\left(\frac{p}{3}\right)q_p(3)\pmod{p}.
\end{align}
\begin{align}
\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\equiv -\left(\frac{p}{3}\right)q_p(3)\pmod{p}.
\end{align}Proof. By (2.24) and (2.25), we have
 \begin{align}
\sum_{k=1}^{p-1}(-1)^k\sum_{i=1}^{p-1}\frac{1}{i}{2i\choose i+k}\sum_{j=0}^{p-1}{2j\choose j+k}
\equiv \sum_{k=1}^{p-1}\frac{(-1)^k(\alpha(k)-1)}{k}\left(\frac{p-k}{3}\right)\pmod{p}.
\end{align}
\begin{align}
\sum_{k=1}^{p-1}(-1)^k\sum_{i=1}^{p-1}\frac{1}{i}{2i\choose i+k}\sum_{j=0}^{p-1}{2j\choose j+k}
\equiv \sum_{k=1}^{p-1}\frac{(-1)^k(\alpha(k)-1)}{k}\left(\frac{p-k}{3}\right)\pmod{p}.
\end{align} We shall only prove the case ![]() $p\equiv 1\pmod{3}$, and the proof of the case
$p\equiv 1\pmod{3}$, and the proof of the case ![]() $p\equiv 2\pmod{3}$ runs similarly and the details are omitted.
$p\equiv 2\pmod{3}$ runs similarly and the details are omitted.
Suppose that ![]() $p\equiv 1\pmod{3}$. Let
$p\equiv 1\pmod{3}$. Let ![]() $n=\lfloor p/6\rfloor$. Then
$n=\lfloor p/6\rfloor$. Then ![]() $n\equiv -1/6\pmod{p}$. It is easy to check that
$n\equiv -1/6\pmod{p}$. It is easy to check that
 \begin{align*}
(-1)^k(\alpha(k)-1)\left(\frac{p-k}{3}\right)=
\begin{cases}
1\quad&\text{for }k\equiv 0\pmod{6},\\
0\quad&\text{for }k\equiv 1,4\pmod{6},\\
-1\quad&\text{for }k\equiv 2\pmod{6},\\
3\quad&\text{for }k\equiv 3\pmod{6},\\
-3\quad&\text{for }k\equiv 5\pmod{6}.
\end{cases}
\end{align*}
\begin{align*}
(-1)^k(\alpha(k)-1)\left(\frac{p-k}{3}\right)=
\begin{cases}
1\quad&\text{for }k\equiv 0\pmod{6},\\
0\quad&\text{for }k\equiv 1,4\pmod{6},\\
-1\quad&\text{for }k\equiv 2\pmod{6},\\
3\quad&\text{for }k\equiv 3\pmod{6},\\
-3\quad&\text{for }k\equiv 5\pmod{6}.
\end{cases}
\end{align*}It follows that
 \begin{align}
&\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\notag\\[7pt]
&\equiv\sum_{k=1}^n\frac{1}{6k}-\sum_{k=1}^n\frac{1}{6k-4}+3\sum_{k=1}^n\frac{1}{6k-3}-3\sum_{k=1}^n\frac{1}{6k-1}\notag\\[7pt]
&\equiv\frac{1}{6}\left(\sum_{k=1}^n\frac{1}{k}-\sum_{k=1}^n\frac{1}{k+4n}+3\sum_{k=1}^n\frac{1}{k+3n}
-3\sum_{k=1}^n\frac{1}{k+n}\right)\notag\\[7pt]
&=\frac{1}{6}\left(4H_{n}-3H_{2n}-3H_{3n}+4H_{4n}-H_{5n}\right)\pmod{p}.
\end{align}
\begin{align}
&\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\notag\\[7pt]
&\equiv\sum_{k=1}^n\frac{1}{6k}-\sum_{k=1}^n\frac{1}{6k-4}+3\sum_{k=1}^n\frac{1}{6k-3}-3\sum_{k=1}^n\frac{1}{6k-1}\notag\\[7pt]
&\equiv\frac{1}{6}\left(\sum_{k=1}^n\frac{1}{k}-\sum_{k=1}^n\frac{1}{k+4n}+3\sum_{k=1}^n\frac{1}{k+3n}
-3\sum_{k=1}^n\frac{1}{k+n}\right)\notag\\[7pt]
&=\frac{1}{6}\left(4H_{n}-3H_{2n}-3H_{3n}+4H_{4n}-H_{5n}\right)\pmod{p}.
\end{align} Finally, noting that for ![]() $p\equiv 1\pmod{3}$,
$p\equiv 1\pmod{3}$, ![]() $2n=\lfloor p/3\rfloor,3n=\lfloor p/2\rfloor, 4n=\lfloor 2p/3\rfloor, 5n=\lfloor 5p/6 \rfloor$ and applying (2.3)–(2.5) to the right-hand side of (3.9), we obtain
$2n=\lfloor p/3\rfloor,3n=\lfloor p/2\rfloor, 4n=\lfloor 2p/3\rfloor, 5n=\lfloor 5p/6 \rfloor$ and applying (2.3)–(2.5) to the right-hand side of (3.9), we obtain
 \begin{align*}
\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\equiv -q_p(3)\pmod{p},
\end{align*}
\begin{align*}
\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\equiv -q_p(3)\pmod{p},
\end{align*} which is the case ![]() $p\equiv 1\pmod{3}$ of (3.7).
$p\equiv 1\pmod{3}$ of (3.7).
Lemma 3.3. For any prime ![]() $p\ge 5$, we have
$p\ge 5$, we have
 \begin{align}
\sum_{k=1}^{p-1}\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}\equiv -\frac{1}{3}\left(2+\left(\frac{p}{3}\right)q_p(3)\right)\pmod{p}.
\end{align}
\begin{align}
\sum_{k=1}^{p-1}\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}\equiv -\frac{1}{3}\left(2+\left(\frac{p}{3}\right)q_p(3)\right)\pmod{p}.
\end{align}Proof. By (2.24) and (2.26), we have
 \begin{align}
&\sum_{k=1}^{p-1}(-1)^k\sum_{i=1}^{p-2}\frac{1}{i+1}{2i\choose i+k}\sum_{j=0}^{p-1}{2j\choose j+k}\notag\\[7pt]
&\equiv \sum_{k=1}^{p-1}\left(-k\sum_{i=1}^{k-1}
\frac{\beta(i)+2}{i}+\sum_{i=1}^{k-1}\beta(i)+2k
+\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}\right)\left(\frac{p-k}{3}\right)\notag\\[7pt]
&=-\sum_{k=1}^{p-1}k\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}
\frac{\beta(i)+2}{i}+\sum_{k=1}^{p-1}\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\beta(i)\notag\\[7pt]
&+2\sum_{k=1}^{p-1}k\left(\frac{p-k}{3}\right)+\left(\frac{3}{2}\left(\frac{p}{3}\right)
-\frac{3}{2}\right)\sum_{k=1}^{p-1}\left(\frac{p-k}{3}\right)\pmod{p}.
\end{align}
\begin{align}
&\sum_{k=1}^{p-1}(-1)^k\sum_{i=1}^{p-2}\frac{1}{i+1}{2i\choose i+k}\sum_{j=0}^{p-1}{2j\choose j+k}\notag\\[7pt]
&\equiv \sum_{k=1}^{p-1}\left(-k\sum_{i=1}^{k-1}
\frac{\beta(i)+2}{i}+\sum_{i=1}^{k-1}\beta(i)+2k
+\frac{3}{2}\left(\frac{p}{3}\right)-\frac{3}{2}\right)\left(\frac{p-k}{3}\right)\notag\\[7pt]
&=-\sum_{k=1}^{p-1}k\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}
\frac{\beta(i)+2}{i}+\sum_{k=1}^{p-1}\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\beta(i)\notag\\[7pt]
&+2\sum_{k=1}^{p-1}k\left(\frac{p-k}{3}\right)+\left(\frac{3}{2}\left(\frac{p}{3}\right)
-\frac{3}{2}\right)\sum_{k=1}^{p-1}\left(\frac{p-k}{3}\right)\pmod{p}.
\end{align} Similarly, we only prove the case ![]() $p\equiv 1\pmod{3}$. Suppose that
$p\equiv 1\pmod{3}$. Suppose that ![]() $p\equiv 1\pmod{3}$. It is easy to check that
$p\equiv 1\pmod{3}$. It is easy to check that
 \begin{align*}
k\left(\frac{p-k}{3}\right)=
\begin{cases}
k\quad&\text{for }k\equiv 0\pmod{3},\\
0\quad&\text{for }k\equiv 1\pmod{3},\\
-k\quad&\text{for }k\equiv 2\pmod{3},
\end{cases}
\end{align*}
\begin{align*}
k\left(\frac{p-k}{3}\right)=
\begin{cases}
k\quad&\text{for }k\equiv 0\pmod{3},\\
0\quad&\text{for }k\equiv 1\pmod{3},\\
-k\quad&\text{for }k\equiv 2\pmod{3},
\end{cases}
\end{align*}and
 \begin{align*}
\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\beta(i)=
\begin{cases}
1\quad&\text{for }k\equiv 0\pmod{6},\\
0\quad&\text{for }k\equiv 1,4,5\pmod{6},\\
2\quad&\text{for }k\equiv 2\pmod{6},\\
-3\quad&\text{for }k\equiv 3\pmod{6}.
\end{cases}
\end{align*}
\begin{align*}
\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\beta(i)=
\begin{cases}
1\quad&\text{for }k\equiv 0\pmod{6},\\
0\quad&\text{for }k\equiv 1,4,5\pmod{6},\\
2\quad&\text{for }k\equiv 2\pmod{6},\\
-3\quad&\text{for }k\equiv 3\pmod{6}.
\end{cases}
\end{align*}It follows that
 \begin{equation}
\begin{aligned}
\Psi(m)&=\sum_{k=1}^{m}k\left(\frac{p-k}{3}\right)\\[7pt]
&=\sum_{k=1}^{\lfloor m/3\rfloor}3k-\sum_{k=1}^{\lfloor (m+1)/3\rfloor}(3k-1)\\[7pt]
&=\left\lfloor \frac{m+1}{3}\right\rfloor-(m+1)[3\mid m-2],
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\Psi(m)&=\sum_{k=1}^{m}k\left(\frac{p-k}{3}\right)\\[7pt]
&=\sum_{k=1}^{\lfloor m/3\rfloor}3k-\sum_{k=1}^{\lfloor (m+1)/3\rfloor}(3k-1)\\[7pt]
&=\left\lfloor \frac{m+1}{3}\right\rfloor-(m+1)[3\mid m-2],
\end{aligned}
\end{equation}and
 \begin{align}
\sum_{k=1}^{p-1}\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\beta(i)=0.
\end{align}
\begin{align}
\sum_{k=1}^{p-1}\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\beta(i)=0.
\end{align}From (3.12), we deduce that
 \begin{align}
\Psi(p-1)\equiv -\frac{1}{3}\pmod{p}.
\end{align}
\begin{align}
\Psi(p-1)\equiv -\frac{1}{3}\pmod{p}.
\end{align}Furthermore, we have
 \begin{align}
&\sum_{k=1}^{p-1}k\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\notag\\[7pt]
&=\sum_{i=1}^{p-2}\frac{\beta(i)+2}{i}\sum_{k=i+1}^{p-1}k\left(\frac{p-k}{3}\right)\notag\\[7pt]
&=\sum_{i=1}^{p-2}\frac{\beta(i)+2}{i}\left(\Psi(p-1)-\Psi(i)\right)\notag\\[7pt]
&\equiv -\sum_{i=1}^{p-2}\frac{\beta(i)+2}{i}\left(\frac{1}{3}+\Psi(i)\right)\pmod{p},
\end{align}
\begin{align}
&\sum_{k=1}^{p-1}k\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\notag\\[7pt]
&=\sum_{i=1}^{p-2}\frac{\beta(i)+2}{i}\sum_{k=i+1}^{p-1}k\left(\frac{p-k}{3}\right)\notag\\[7pt]
&=\sum_{i=1}^{p-2}\frac{\beta(i)+2}{i}\left(\Psi(p-1)-\Psi(i)\right)\notag\\[7pt]
&\equiv -\sum_{i=1}^{p-2}\frac{\beta(i)+2}{i}\left(\frac{1}{3}+\Psi(i)\right)\pmod{p},
\end{align}where we have used (3.14) in the last step. It is easy to check that
 \begin{align}
\left(\beta(i)+2\right)\left(\frac{1}{3}+\Psi(i)\right)=
\begin{cases}
\frac{i+1}{3}\quad&\text{for }i\equiv 0\pmod{6},\\
0\quad&\text{for }i\equiv 1\pmod{6},\\
-\frac{2i+1}{3}\quad&\text{for }i\equiv 2\pmod{6},\\
i+1\quad&\text{for }i\equiv 3\pmod{6},\\
\frac{4i}{3}\quad&\text{for }i\equiv 4\pmod{6},\\
-(2i+1)\quad&\text{for }i\equiv 5\pmod{6}.
\end{cases}
\end{align}
\begin{align}
\left(\beta(i)+2\right)\left(\frac{1}{3}+\Psi(i)\right)=
\begin{cases}
\frac{i+1}{3}\quad&\text{for }i\equiv 0\pmod{6},\\
0\quad&\text{for }i\equiv 1\pmod{6},\\
-\frac{2i+1}{3}\quad&\text{for }i\equiv 2\pmod{6},\\
i+1\quad&\text{for }i\equiv 3\pmod{6},\\
\frac{4i}{3}\quad&\text{for }i\equiv 4\pmod{6},\\
-(2i+1)\quad&\text{for }i\equiv 5\pmod{6}.
\end{cases}
\end{align}Combining (3.15) and (3.16) yields
 \begin{align}
&\sum_{k=1}^{p-1}k\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\notag\\[7pt]
&\equiv -\frac{1}{3}\sum_{i=1}^{n-1}\frac{6i+1}{6i}+\frac{1}{3}\sum_{i=1}^{n}\frac{12i-7}{6i-4}
-\sum_{i=1}^{n}\frac{6i-2}{6i-3}-\frac{1}{3}\sum_{i=1}^{n}4
+\sum_{i=1}^{n}\frac{12i-1}{6i-1}\notag\\[7pt]
&=-\frac{1}{3}\sum_{i=1}^{n}\frac{1}{6i}+\frac{1}{3}\sum_{i=1}^{n}\frac{1}{6i-4}
-\sum_{i=1}^{n}\frac{1}{6i-3}+\sum_{i=1}^{n}\frac{1}{6i-1}+\frac{1}{3}+\frac{1}{18n}\notag\\[7pt]
&\equiv -\frac{1}{18}\sum_{i=1}^{n}\frac{1}{i}+\frac{1}{18}\sum_{i=1}^{n}\frac{1}{i+4n}
-\frac{1}{6}\sum_{i=1}^{n}\frac{1}{i+3n}+\frac{1}{6}\sum_{i=1}^{n}\frac{1}{i+n}\notag\\[7pt]
&=\frac{1}{6}\left(-\frac{4}{3}H_n+H_{2n}+H_{3n}-\frac{4}{3}H_{4n}+\frac{1}{3}H_{5n}\right)\notag\\[7pt]
&\equiv \frac{1}{3}q_p(3)\pmod{p},
\end{align}
\begin{align}
&\sum_{k=1}^{p-1}k\left(\frac{p-k}{3}\right)\sum_{i=1}^{k-1}\frac{\beta(i)+2}{i}\notag\\[7pt]
&\equiv -\frac{1}{3}\sum_{i=1}^{n-1}\frac{6i+1}{6i}+\frac{1}{3}\sum_{i=1}^{n}\frac{12i-7}{6i-4}
-\sum_{i=1}^{n}\frac{6i-2}{6i-3}-\frac{1}{3}\sum_{i=1}^{n}4
+\sum_{i=1}^{n}\frac{12i-1}{6i-1}\notag\\[7pt]
&=-\frac{1}{3}\sum_{i=1}^{n}\frac{1}{6i}+\frac{1}{3}\sum_{i=1}^{n}\frac{1}{6i-4}
-\sum_{i=1}^{n}\frac{1}{6i-3}+\sum_{i=1}^{n}\frac{1}{6i-1}+\frac{1}{3}+\frac{1}{18n}\notag\\[7pt]
&\equiv -\frac{1}{18}\sum_{i=1}^{n}\frac{1}{i}+\frac{1}{18}\sum_{i=1}^{n}\frac{1}{i+4n}
-\frac{1}{6}\sum_{i=1}^{n}\frac{1}{i+3n}+\frac{1}{6}\sum_{i=1}^{n}\frac{1}{i+n}\notag\\[7pt]
&=\frac{1}{6}\left(-\frac{4}{3}H_n+H_{2n}+H_{3n}-\frac{4}{3}H_{4n}+\frac{1}{3}H_{5n}\right)\notag\\[7pt]
&\equiv \frac{1}{3}q_p(3)\pmod{p},
\end{align} where we have used the fact that ![]() $2n=\lfloor p/3\rfloor,3n=\lfloor p/2\rfloor, 4n=\lfloor 2p/3\rfloor, 5n=\lfloor 5p/6 \rfloor$ for
$2n=\lfloor p/3\rfloor,3n=\lfloor p/2\rfloor, 4n=\lfloor 2p/3\rfloor, 5n=\lfloor 5p/6 \rfloor$ for ![]() $p\equiv 1\pmod{3}$ and (2.3)–(2.5) in the last step.
$p\equiv 1\pmod{3}$ and (2.3)–(2.5) in the last step.
Finally, substituting (3.13), (3.14) and (3.17) into the right-hand side of (3.11) gives
 \begin{align*}
\sum_{k=1}^{p-1}\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}
\equiv -\frac{1}{3}\left(q_p(3)+2\right)\pmod{p},
\end{align*}
\begin{align*}
\sum_{k=1}^{p-1}\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}
\equiv -\frac{1}{3}\left(q_p(3)+2\right)\pmod{p},
\end{align*} which is the case ![]() $p\equiv 1\pmod{3}$ of (3.10).
$p\equiv 1\pmod{3}$ of (3.10).
4. Proof of (1.2)
By (1.5), we have
 \begin{align}
\sum_{k=0}^{p-1}M_k^2&=\sum_{k=0}^{p-1}\sum_{i=0}^k \sum_{j=0}^k(-1)^{i+j}{k\choose i}{k\choose j}C_{i+1}C_{j+1}\notag\\
&=\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}(-1)^{i+j}C_{i+1}C_{j+1}\sum_{k=0}^{p-1}{k\choose i}{k\choose j}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}M_k^2&=\sum_{k=0}^{p-1}\sum_{i=0}^k \sum_{j=0}^k(-1)^{i+j}{k\choose i}{k\choose j}C_{i+1}C_{j+1}\notag\\
&=\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}(-1)^{i+j}C_{i+1}C_{j+1}\sum_{k=0}^{p-1}{k\choose i}{k\choose j}.
\end{align}From the identity [Reference Riordan8, (9), page 15]:
 \begin{align*}
{k\choose i}{k\choose j}=\sum_{l=0}^j
{l+i\choose j}{j\choose l}{k\choose l+i},
\end{align*}
\begin{align*}
{k\choose i}{k\choose j}=\sum_{l=0}^j
{l+i\choose j}{j\choose l}{k\choose l+i},
\end{align*}we deduce that
 \begin{align}
\sum_{k=0}^{p-1}{k\choose i}{k\choose j}
&=\sum_{l=0}^j
{l+i\choose j}{j\choose l}\sum_{k=0}^{p-1}{k\choose l+i}\notag\\
&=\sum_{l=0}^j
{i+l\choose j}{j\choose l}{p\choose i+l+1},
\end{align}
\begin{align}
\sum_{k=0}^{p-1}{k\choose i}{k\choose j}
&=\sum_{l=0}^j
{l+i\choose j}{j\choose l}\sum_{k=0}^{p-1}{k\choose l+i}\notag\\
&=\sum_{l=0}^j
{i+l\choose j}{j\choose l}{p\choose i+l+1},
\end{align} where we have utilized the hockey-stick identity in the last step. Letting ![]() $l\to k-i$ on the right-hand side of (4.2), we rewrite (4.2) as
$l\to k-i$ on the right-hand side of (4.2), we rewrite (4.2) as
 \begin{align*}
\sum_{k=0}^{p-1}{k\choose i}{k\choose j}=p\sum_{k=0}^{i+j}
\frac{1}{k+1}{k\choose j}{j\choose k-i}{p-1\choose k}.
\end{align*}
\begin{align*}
\sum_{k=0}^{p-1}{k\choose i}{k\choose j}=p\sum_{k=0}^{i+j}
\frac{1}{k+1}{k\choose j}{j\choose k-i}{p-1\choose k}.
\end{align*} Note that  ${k\choose j}{j\choose k-i}\equiv 0\pmod{p}$ for
${k\choose j}{j\choose k-i}\equiv 0\pmod{p}$ for ![]() $0\le i\le p-1,0\le j\le p-1$ and
$0\le i\le p-1,0\le j\le p-1$ and ![]() $p\le k \le 2p-2$, and
$p\le k \le 2p-2$, and
 \begin{align*}
\frac{p}{k+1}{p-1\choose k}\equiv \frac{p(-1)^k}{k+1}\pmod{p^2}
\end{align*}
\begin{align*}
\frac{p}{k+1}{p-1\choose k}\equiv \frac{p(-1)^k}{k+1}\pmod{p^2}
\end{align*} for ![]() $0\le k\le p-1$. It follows that
$0\le k\le p-1$. It follows that
 \begin{align}
\sum_{k=0}^{p-1}{k\choose i}{k\choose j}\equiv p\sum_{k=0}^{i+j}
\frac{(-1)^k}{k+1}{k\choose j}{j\choose k-i}\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}{k\choose i}{k\choose j}\equiv p\sum_{k=0}^{i+j}
\frac{(-1)^k}{k+1}{k\choose j}{j\choose k-i}\pmod{p^2}.
\end{align}Recall the following partial fraction decomposition:
 \begin{align}
\sum_{k=0}^{i+j}\frac{(-1)^{i+j+k}}{x+k}{k\choose j}{j\choose k-i}=
\frac{(x)_i (x)_j}{(x)_{i+j+1}},
\end{align}
\begin{align}
\sum_{k=0}^{i+j}\frac{(-1)^{i+j+k}}{x+k}{k\choose j}{j\choose k-i}=
\frac{(x)_i (x)_j}{(x)_{i+j+1}},
\end{align} where ![]() $(x)_0=1$ and
$(x)_0=1$ and ![]() $(x)_k=x(x+1)\cdots (x+k-1)$ for
$(x)_k=x(x+1)\cdots (x+k-1)$ for ![]() $k\ge 1$. Letting x = 1 in (4.4) gives
$k\ge 1$. Letting x = 1 in (4.4) gives
 \begin{align}
\sum_{k=0}^{i+j}\frac{(-1)^{k}}{k+1}{k\choose j}{j\choose k-i}=\frac{(-1)^{i+j}}{(i+j+1){i+j\choose j}}.
\end{align}
\begin{align}
\sum_{k=0}^{i+j}\frac{(-1)^{k}}{k+1}{k\choose j}{j\choose k-i}=\frac{(-1)^{i+j}}{(i+j+1){i+j\choose j}}.
\end{align}It follows from (4.3) and (4.5) that
 \begin{align}
\sum_{k=0}^{p-1}{k\choose i}{k\choose j}\equiv \frac{p(-1)^{i+j}}{(i+j+1){i+j\choose j}}\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}{k\choose i}{k\choose j}\equiv \frac{p(-1)^{i+j}}{(i+j+1){i+j\choose j}}\pmod{p^2}.
\end{align}Combining (4.1) and (4.6) gives
 \begin{align}
\sum_{k=0}^{p-1}M_k^2
\equiv p\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}\frac{C_{i+1}C_{j+1}}{(i+j+1){i+j\choose j}}\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}M_k^2
\equiv p\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}\frac{C_{i+1}C_{j+1}}{(i+j+1){i+j\choose j}}\pmod{p^2}.
\end{align}Let
 \begin{align*}
S(i,j)=\frac{{2i\choose i}{2j\choose j}}{{i+j\choose i}}.
\end{align*}
\begin{align*}
S(i,j)=\frac{{2i\choose i}{2j\choose j}}{{i+j\choose i}}.
\end{align*}From the identity due to Von Szily [Reference Von Szily18] (see also [Reference Gould3, (3.38)]):
 \begin{align}
S(i,j)=\sum_{k}(-1)^k{2i\choose i+k}{2j\choose j+k},
\end{align}
\begin{align}
S(i,j)=\sum_{k}(-1)^k{2i\choose i+k}{2j\choose j+k},
\end{align} we deduce that ![]() $S(i,j)$ is an integer. It is easy to verify that the numbers
$S(i,j)$ is an integer. It is easy to verify that the numbers ![]() $S(i,j)$ satisfy the recurrence:
$S(i,j)$ satisfy the recurrence:
Note that
 \begin{align}
\frac{C_{i+1}C_{j+1}}{(i+j+1){i+j\choose j}}=\frac{(i+j+2)S(i+1,j+1)}{(i+1)(j+1)(i+2)(j+2)}.
\end{align}
\begin{align}
\frac{C_{i+1}C_{j+1}}{(i+j+1){i+j\choose j}}=\frac{(i+j+2)S(i+1,j+1)}{(i+1)(j+1)(i+2)(j+2)}.
\end{align}It follows from (4.7) and (4.10) that
 \begin{align}
\sum_{k=0}^{p-1}M_k^2
&\equiv p\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}\frac{(i+j+2)S(i+1,j+1)}{(i+1)(j+1)(i+2)(j+2)}\notag\\
&=p\sum_{i=1}^{p} \sum_{j=1}^{p}\frac{(i+j)S(i,j)}{ij(i+1)(j+1)}\notag\\
&=2p\sum_{i=1}^{p} \sum_{j=1}^{p}\frac{S(i,j)}{i(i+1)(j+1)}\notag\\
&=2p\sum_{i=1}^{p} \sum_{j=1}^{p}\frac{S(i,j)}{i(j+1)}-2p\sum_{i=1}^{p} \sum_{j=1}^{p}\frac{S(i,j)}{(i+1)(j+1)}\pmod{p^2},
\end{align}
\begin{align}
\sum_{k=0}^{p-1}M_k^2
&\equiv p\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}\frac{(i+j+2)S(i+1,j+1)}{(i+1)(j+1)(i+2)(j+2)}\notag\\
&=p\sum_{i=1}^{p} \sum_{j=1}^{p}\frac{(i+j)S(i,j)}{ij(i+1)(j+1)}\notag\\
&=2p\sum_{i=1}^{p} \sum_{j=1}^{p}\frac{S(i,j)}{i(i+1)(j+1)}\notag\\
&=2p\sum_{i=1}^{p} \sum_{j=1}^{p}\frac{S(i,j)}{i(j+1)}-2p\sum_{i=1}^{p} \sum_{j=1}^{p}\frac{S(i,j)}{(i+1)(j+1)}\pmod{p^2},
\end{align}where we have used the symmetry with respect to i and j in the third step.
By (4.9), we have
 \begin{align}
&2p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{(i+1)(j+1)}\notag\\
&=\frac{p}{2}\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i+1,j)+S(i,j+1)}{(i+1)(j+1)}\notag\\
&=p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i+1,j)}{(i+1)(j+1)}\notag\\
&=p\sum_{i=2}^{p+1}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}\notag\\
&=p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}+p\sum_{j=1}^p\frac{S(p+1,j)}{(p+1)(j+1)}
-p\sum_{j=1}^p\frac{S(1,j)}{j+1}.
\end{align}
\begin{align}
&2p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{(i+1)(j+1)}\notag\\
&=\frac{p}{2}\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i+1,j)+S(i,j+1)}{(i+1)(j+1)}\notag\\
&=p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i+1,j)}{(i+1)(j+1)}\notag\\
&=p\sum_{i=2}^{p+1}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}\notag\\
&=p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}+p\sum_{j=1}^p\frac{S(p+1,j)}{(p+1)(j+1)}
-p\sum_{j=1}^p\frac{S(1,j)}{j+1}.
\end{align}Furthermore, by (2.2), we have
 \begin{align*}
&p\sum_{j=1}^p\frac{S(p+1,j)}{(p+1)(j+1)}\\[7pt]
&=\frac{2p(2p+1)}{(p+1)^2}{2p\choose p}\sum_{j=1}^p\frac{{2j\choose j}}{(j+1){p+1+j\choose j}}\\[7pt]
&\equiv \frac{4p(2p+1)}{(p+1)^2}\sum_{j=1}^p\frac{{2j\choose j}}{(j+1){p+1+j\choose j}}\pmod{p^2}.
\end{align*}
\begin{align*}
&p\sum_{j=1}^p\frac{S(p+1,j)}{(p+1)(j+1)}\\[7pt]
&=\frac{2p(2p+1)}{(p+1)^2}{2p\choose p}\sum_{j=1}^p\frac{{2j\choose j}}{(j+1){p+1+j\choose j}}\\[7pt]
&\equiv \frac{4p(2p+1)}{(p+1)^2}\sum_{j=1}^p\frac{{2j\choose j}}{(j+1){p+1+j\choose j}}\pmod{p^2}.
\end{align*} For ![]() $1\le j\le p-2$, we have
$1\le j\le p-2$, we have  ${p+1+j\choose j}\equiv j+1\pmod{p}$. It follows that
${p+1+j\choose j}\equiv j+1\pmod{p}$. It follows that
 \begin{align}
&p\sum_{j=1}^p\frac{S(p+1,j)}{(p+1)(j+1)}\notag\\[7pt]
&\equiv 4p\sum_{j=1}^{p-2}\frac{{2j\choose j}}{(j+1)^2}+\frac{2(2p+1)}{(p+1)(2p-1)}
+\frac{4p}{(p+1)^2}\notag\\[7pt]
&\equiv 12p\left(\frac{p}{3}\right)-2-2p\pmod{p^2},
\end{align}
\begin{align}
&p\sum_{j=1}^p\frac{S(p+1,j)}{(p+1)(j+1)}\notag\\[7pt]
&\equiv 4p\sum_{j=1}^{p-2}\frac{{2j\choose j}}{(j+1)^2}+\frac{2(2p+1)}{(p+1)(2p-1)}
+\frac{4p}{(p+1)^2}\notag\\[7pt]
&\equiv 12p\left(\frac{p}{3}\right)-2-2p\pmod{p^2},
\end{align}where we have used (2.10) in the last step.
On the other hand, we have
 \begin{align}
p\sum_{j=1}^p\frac{S(1,j)}{j+1}
&=2p\sum_{j=1}^p\frac{{2j\choose j}}{(j+1)^2}\notag\\[7pt]
&=2p\sum_{j=1}^{p-2}\frac{{2j\choose j}}{(j+1)^2}+\frac{2}{2p-1}{2p-1\choose p-1}+\frac{2p}{(p+1)^2}{2p\choose p}\notag\\[7pt]
&\equiv 6p\left(\frac{p}{3}\right)-2\pmod{p^2},
\end{align}
\begin{align}
p\sum_{j=1}^p\frac{S(1,j)}{j+1}
&=2p\sum_{j=1}^p\frac{{2j\choose j}}{(j+1)^2}\notag\\[7pt]
&=2p\sum_{j=1}^{p-2}\frac{{2j\choose j}}{(j+1)^2}+\frac{2}{2p-1}{2p-1\choose p-1}+\frac{2p}{(p+1)^2}{2p\choose p}\notag\\[7pt]
&\equiv 6p\left(\frac{p}{3}\right)-2\pmod{p^2},
\end{align}where we have used (2.1), (2.2) and (2.10) in the last step.
It follows from (4.12), (4.13) and (4.14) that
 \begin{align}
2p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{(i+1)(j+1)}-p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}
\equiv 2p\left(3\left(\frac{p}{3}\right)-1\right)\pmod{p^2}.
\end{align}
\begin{align}
2p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{(i+1)(j+1)}-p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}
\equiv 2p\left(3\left(\frac{p}{3}\right)-1\right)\pmod{p^2}.
\end{align}Combining (4.11) and (4.15) gives
 \begin{align}
\sum_{k=0}^{p-1}M_k^2\equiv p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}
-2p\left(3\left(\frac{p}{3}\right)-1\right)\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}M_k^2\equiv p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}
-2p\left(3\left(\frac{p}{3}\right)-1\right)\pmod{p^2}.
\end{align}Note that
 \begin{align}
&p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}\notag\\
&=p\sum_{i=1}^{p-1}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}+\sum_{j=1}^p\frac{S(p,j)}{j+1}\notag\\
&=p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{S(i,j)}{i(j+1)}+\sum_{j=1}^p\frac{S(p,j)}{j+1}
+\sum_{i=1}^{p-1}\frac{S(i,p-1)}{i}+p\sum_{i=1}^{p-1}\frac{S(i,p)}{i(p+1)}.
\end{align}
\begin{align}
&p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}\notag\\
&=p\sum_{i=1}^{p-1}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}+\sum_{j=1}^p\frac{S(p,j)}{j+1}\notag\\
&=p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{S(i,j)}{i(j+1)}+\sum_{j=1}^p\frac{S(p,j)}{j+1}
+\sum_{i=1}^{p-1}\frac{S(i,p-1)}{i}+p\sum_{i=1}^{p-1}\frac{S(i,p)}{i(p+1)}.
\end{align}Furthermore, we have
 \begin{align}
p\sum_{i=1}^{p-1}\frac{S(i,p)}{i(p+1)}\equiv 2p\sum_{i=1}^{p-1}\frac{{2i\choose i}}{i}\equiv 0\pmod{p^2},
\end{align}
\begin{align}
p\sum_{i=1}^{p-1}\frac{S(i,p)}{i(p+1)}\equiv 2p\sum_{i=1}^{p-1}\frac{{2i\choose i}}{i}\equiv 0\pmod{p^2},
\end{align} where we have used (2.2), (2.8) and the fact that  ${p+i\choose i}\equiv 1\pmod{p}$ for
${p+i\choose i}\equiv 1\pmod{p}$ for ![]() $1\le i\le p-1$.
$1\le i\le p-1$.
For ![]() $1\le i\le p-1$, we have
$1\le i\le p-1$, we have  $p/\left(i{i+p-1\choose i}\right)\equiv 1-pH_{i-1}\pmod{p^2}$, and so
$p/\left(i{i+p-1\choose i}\right)\equiv 1-pH_{i-1}\pmod{p^2}$, and so
 \begin{align}
\sum_{i=1}^{p-1}\frac{S(i,p-1)}{i}
&=\frac{p}{2p-1}{2p-1\choose p-1}\sum_{i=1}^{p-1}\frac{{2i\choose i}}{i{i+p-1\choose i}}\notag\\[7pt]
&\equiv -(2p+1)\sum_{i=1}^{p-1}{2i\choose i}+p\sum_{i=1}^{p-1}{2i\choose i}H_{i-1}\notag\\[7pt]
&=-(2p+1)\sum_{i=1}^{p-1}{2i\choose i}+p\sum_{i=1}^{p-1}{2i\choose i}H_{i}
-p\sum_{i=1}^{p-1}\frac{{2i\choose i}}{i}\notag\\[7pt]
&\equiv 2p+1-\left(\frac{p}{3}\right)\left(2p+3^{p-1}\right)\pmod{p^2},
\end{align}
\begin{align}
\sum_{i=1}^{p-1}\frac{S(i,p-1)}{i}
&=\frac{p}{2p-1}{2p-1\choose p-1}\sum_{i=1}^{p-1}\frac{{2i\choose i}}{i{i+p-1\choose i}}\notag\\[7pt]
&\equiv -(2p+1)\sum_{i=1}^{p-1}{2i\choose i}+p\sum_{i=1}^{p-1}{2i\choose i}H_{i-1}\notag\\[7pt]
&=-(2p+1)\sum_{i=1}^{p-1}{2i\choose i}+p\sum_{i=1}^{p-1}{2i\choose i}H_{i}
-p\sum_{i=1}^{p-1}\frac{{2i\choose i}}{i}\notag\\[7pt]
&\equiv 2p+1-\left(\frac{p}{3}\right)\left(2p+3^{p-1}\right)\pmod{p^2},
\end{align}where we have used (2.1), (2.6), (2.8) and (2.14).
For ![]() $1\le j\le p-1$, we have
$1\le j\le p-1$, we have  ${p+j\choose j}\equiv 1+pH_j \pmod{p^2}$, and so
${p+j\choose j}\equiv 1+pH_j \pmod{p^2}$, and so
 \begin{align}
\sum_{j=1}^p\frac{S(p,j)}{j+1}&=\frac{{2p\choose p}}{p+1}
+{2p\choose p}\sum_{j=1}^{p-1}\frac{{2j\choose j}}{(j+1){p+j\choose j}}\notag\\[7pt]
&\equiv 2-2p+2\sum_{j=1}^{p-1}C_j(1-pH_j)\notag\\[7pt]
&\equiv 3^p\left(\frac{p}{3}\right)-2p-1\pmod{p^2},
\end{align}
\begin{align}
\sum_{j=1}^p\frac{S(p,j)}{j+1}&=\frac{{2p\choose p}}{p+1}
+{2p\choose p}\sum_{j=1}^{p-1}\frac{{2j\choose j}}{(j+1){p+j\choose j}}\notag\\[7pt]
&\equiv 2-2p+2\sum_{j=1}^{p-1}C_j(1-pH_j)\notag\\[7pt]
&\equiv 3^p\left(\frac{p}{3}\right)-2p-1\pmod{p^2},
\end{align}where we have used (2.2), (2.7) and (2.16).
It follows from (4.17)–(4.20) that
 \begin{align}
p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}
\equiv p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{S(i,j)}{i(j+1)}
+2\left(\frac{p}{3}\right)\left(3^{p-1}-p\right)\pmod{p^2}.
\end{align}
\begin{align}
p\sum_{i=1}^{p}\sum_{j=1}^p\frac{S(i,j)}{i(j+1)}
\equiv p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{S(i,j)}{i(j+1)}
+2\left(\frac{p}{3}\right)\left(3^{p-1}-p\right)\pmod{p^2}.
\end{align}Combining (4.16) and (4.21) gives
 \begin{align}
\sum_{k=0}^{p-1}M_k^2\equiv p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{S(i,j)}{i(j+1)}
+2\left(\frac{p}{3}\right)\left(3^{p-1}-4p\right)+2p\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}M_k^2\equiv p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{S(i,j)}{i(j+1)}
+2\left(\frac{p}{3}\right)\left(3^{p-1}-4p\right)+2p\pmod{p^2}.
\end{align}By (4.8), we have
 \begin{align}
S(i,j)=2\sum_{k=1}^{j}(-1)^k{2i\choose i+k}{2j\choose j+k}+{2i\choose i}{2j\choose j}.
\end{align}
\begin{align}
S(i,j)=2\sum_{k=1}^{j}(-1)^k{2i\choose i+k}{2j\choose j+k}+{2i\choose i}{2j\choose j}.
\end{align}It follows that
 \begin{align}
&p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{S(i,j)}{i(j+1)}\notag\\[7pt]
&=2p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\sum_{k=1}^{j}\frac{(-1)^k}{i(j+1)}{2i\choose i+k}{2j\choose j+k}
+p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{{2i\choose i}{2j\choose j}}{i(j+1)}\notag\\[7pt]
&\equiv 2p\sum_{k=1}^{p-2}\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{(-1)^k}{i(j+1)}{2i\choose i+k}{2j\choose j+k}\pmod{p^2},
\end{align}
\begin{align}
&p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{S(i,j)}{i(j+1)}\notag\\[7pt]
&=2p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\sum_{k=1}^{j}\frac{(-1)^k}{i(j+1)}{2i\choose i+k}{2j\choose j+k}
+p\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{{2i\choose i}{2j\choose j}}{i(j+1)}\notag\\[7pt]
&\equiv 2p\sum_{k=1}^{p-2}\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{(-1)^k}{i(j+1)}{2i\choose i+k}{2j\choose j+k}\pmod{p^2},
\end{align}where we have used (2.8) in the last step.
Finally, combining (4.22) and (4.24) yields
 \begin{align}
\sum_{k=0}^{p-1}M_k^2&\equiv 2p\sum_{k=1}^{p-2}\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{(-1)^k}{i(j+1)}{2i\choose i+k}{2j\choose j+k}\notag\\[7pt]
&+2\left(\frac{p}{3}\right)\left(3^{p-1}-4p\right)+2p\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}M_k^2&\equiv 2p\sum_{k=1}^{p-2}\sum_{i=1}^{p-1}\sum_{j=1}^{p-2}\frac{(-1)^k}{i(j+1)}{2i\choose i+k}{2j\choose j+k}\notag\\[7pt]
&+2\left(\frac{p}{3}\right)\left(3^{p-1}-4p\right)+2p\pmod{p^2}.
\end{align}5. Proof of (1.4)
 \begin{align}
\sum_{k=0}^{p-1}T_kM_k&=\sum_{k=0}^{p-1}
\sum_{i=0}^k \sum_{j=0}^k(-1)^{i+j}{k\choose i}{k\choose j}{2j\choose j}C_{i+1}\notag\\[7pt]
&=\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}(-1)^{i+j}{2j\choose j}C_{i+1}\sum_{k=0}^{p-1}{k\choose i}{k\choose j}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}T_kM_k&=\sum_{k=0}^{p-1}
\sum_{i=0}^k \sum_{j=0}^k(-1)^{i+j}{k\choose i}{k\choose j}{2j\choose j}C_{i+1}\notag\\[7pt]
&=\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}(-1)^{i+j}{2j\choose j}C_{i+1}\sum_{k=0}^{p-1}{k\choose i}{k\choose j}.
\end{align}Applying (4.6) to the right-hand side of (5.1), we obtain
 \begin{align*}
\sum_{k=0}^{p-1}T_kM_k\equiv p\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}\frac{{2j\choose j}C_{i+1}}{(i+j+1){i+j\choose j}}\pmod{p^2}.
\end{align*}
\begin{align*}
\sum_{k=0}^{p-1}T_kM_k\equiv p\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}\frac{{2j\choose j}C_{i+1}}{(i+j+1){i+j\choose j}}\pmod{p^2}.
\end{align*}Noting that
 \begin{align*}
\frac{{2j\choose j}C_{i+1}}{(i+j+1){i+j\choose j}}=\frac{S(i+1,j)}{(i+1)(i+2)},
\end{align*}
\begin{align*}
\frac{{2j\choose j}C_{i+1}}{(i+j+1){i+j\choose j}}=\frac{S(i+1,j)}{(i+1)(i+2)},
\end{align*}we have
 \begin{align}
\sum_{k=0}^{p-1}T_kM_k&\equiv p\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}\frac{S(i+1,j)}{(i+1)(i+2)}\notag\\[7pt]
&=p\sum_{i=1}^{p} \sum_{j=0}^{p-1}\frac{S(i,j)}{i(i+1)}\notag\\[7pt]
&= p\sum_{i=1}^p\sum_{j=0}^{p-1}\frac{S(i,j)}{i}-p\sum_{i=1}^p\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}T_kM_k&\equiv p\sum_{i=0}^{p-1} \sum_{j=0}^{p-1}\frac{S(i+1,j)}{(i+1)(i+2)}\notag\\[7pt]
&=p\sum_{i=1}^{p} \sum_{j=0}^{p-1}\frac{S(i,j)}{i(i+1)}\notag\\[7pt]
&= p\sum_{i=1}^p\sum_{j=0}^{p-1}\frac{S(i,j)}{i}-p\sum_{i=1}^p\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}\pmod{p^2}.
\end{align}Note that
 \begin{align}
p\sum_{i=1}^p\sum_{j=0}^{p-1}\frac{S(i,j)}{i}=p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{S(i,j)}{i}
+\sum_{j=0}^{p-1}S(p,j),
\end{align}
\begin{align}
p\sum_{i=1}^p\sum_{j=0}^{p-1}\frac{S(i,j)}{i}=p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{S(i,j)}{i}
+\sum_{j=0}^{p-1}S(p,j),
\end{align}and
 \begin{align}
p\sum_{i=1}^p\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}=p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}
+\sum_{j=0}^{p-1}S(p-1,j)+p\sum_{j=0}^{p-1}\frac{S(p,j)}{p+1}.
\end{align}
\begin{align}
p\sum_{i=1}^p\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}=p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}
+\sum_{j=0}^{p-1}S(p-1,j)+p\sum_{j=0}^{p-1}\frac{S(p,j)}{p+1}.
\end{align} For ![]() $0\le j\le p-1$, we have
$0\le j\le p-1$, we have  ${p+j\choose j}\equiv 1+pH_j\pmod{p^2}$, and so
${p+j\choose j}\equiv 1+pH_j\pmod{p^2}$, and so
 \begin{align}
\sum_{j=0}^{p-1}S(p,j)&=
{2p\choose p}\sum_{j=0}^{p-1}\frac{{2j\choose j}}{{p+j\choose j}}\notag\\
&\equiv 2\sum_{j=0}^{p-1}{2j\choose j}(1-pH_j)\notag\\
&\equiv 2\left(\frac{p}{3}\right)3^{p-1}\pmod{p^2},
\end{align}
\begin{align}
\sum_{j=0}^{p-1}S(p,j)&=
{2p\choose p}\sum_{j=0}^{p-1}\frac{{2j\choose j}}{{p+j\choose j}}\notag\\
&\equiv 2\sum_{j=0}^{p-1}{2j\choose j}(1-pH_j)\notag\\
&\equiv 2\left(\frac{p}{3}\right)3^{p-1}\pmod{p^2},
\end{align}where we have used (2.2), (2.6) and (2.14).
By (5.5), we have
 \begin{align}
p\sum_{j=0}^{p-1}\frac{S(p,j)}{p+1}\equiv p\sum_{j=0}^{p-1}S(p,j)\equiv 2p\left(\frac{p}{3}\right)\pmod{p^2}.
\end{align}
\begin{align}
p\sum_{j=0}^{p-1}\frac{S(p,j)}{p+1}\equiv p\sum_{j=0}^{p-1}S(p,j)\equiv 2p\left(\frac{p}{3}\right)\pmod{p^2}.
\end{align} By (2.1) and  $p/{p+j-1\choose j}\equiv j(1-pH_{j-1})\pmod{p^2}$ for
$p/{p+j-1\choose j}\equiv j(1-pH_{j-1})\pmod{p^2}$ for ![]() $1\le j\le p-1$, we have
$1\le j\le p-1$, we have
 \begin{align}
\sum_{j=0}^{p-1}S(p-1,j)&=\frac{p}{2p-1}{2p-1\choose p-1}\sum_{j=0}^{p-1}\frac{{2j\choose j}}{{j+p-1\choose j}}\notag\\[7pt]
&\equiv -(2p+1)\sum_{j=0}^{p-1}j{2j\choose j}+p\sum_{j=0}^{p-1}j{2j\choose j}H_{j-1}\notag\\[7pt]
&=-(2p+1)\sum_{j=0}^{p-1}j{2j\choose j}+p\sum_{j=0}^{p-1}j{2j\choose j}H_{j}-p\sum_{j=0}^{p-1}{2j\choose j}\notag\\[7pt]
&\equiv -\frac{p}{3}+\frac{2}{3}\left(\frac{p}{3}\right)3^{p-1}\pmod{p^2},
\end{align}
\begin{align}
\sum_{j=0}^{p-1}S(p-1,j)&=\frac{p}{2p-1}{2p-1\choose p-1}\sum_{j=0}^{p-1}\frac{{2j\choose j}}{{j+p-1\choose j}}\notag\\[7pt]
&\equiv -(2p+1)\sum_{j=0}^{p-1}j{2j\choose j}+p\sum_{j=0}^{p-1}j{2j\choose j}H_{j-1}\notag\\[7pt]
&=-(2p+1)\sum_{j=0}^{p-1}j{2j\choose j}+p\sum_{j=0}^{p-1}j{2j\choose j}H_{j}-p\sum_{j=0}^{p-1}{2j\choose j}\notag\\[7pt]
&\equiv -\frac{p}{3}+\frac{2}{3}\left(\frac{p}{3}\right)3^{p-1}\pmod{p^2},
\end{align}where we have used (2.6), (2.9) and (2.15) in the last step.
It follows from (5.2)–(5.7) that
 \begin{align}
\sum_{k=0}^{p-1}T_kM_k&\equiv
p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{S(i,j)}{i}-p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}\notag\\[7pt]
&+\frac{p}{3}-2p\left(\frac{p}{3}\right)+\frac{4}{3}\left(\frac{p}{3}\right)3^{p-1}\pmod{p^2}.
\end{align}
\begin{align}
\sum_{k=0}^{p-1}T_kM_k&\equiv
p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{S(i,j)}{i}-p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}\notag\\[7pt]
&+\frac{p}{3}-2p\left(\frac{p}{3}\right)+\frac{4}{3}\left(\frac{p}{3}\right)3^{p-1}\pmod{p^2}.
\end{align}By (4.23), we have
 \begin{align}
&p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{S(i,j)}{i}\notag\\[7pt]
&=2p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\sum_{k=1}^{j}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k} +p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{{2i\choose i}{2j\choose j}}{i}\notag\\[7pt]
&\equiv 2p\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\pmod{p^2},
\end{align}
\begin{align}
&p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{S(i,j)}{i}\notag\\[7pt]
&=2p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\sum_{k=1}^{j}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k} +p\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{{2i\choose i}{2j\choose j}}{i}\notag\\[7pt]
&\equiv 2p\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\pmod{p^2},
\end{align}where we have used (2.8) in the last step.
On the other hand, we have
 \begin{align}
&p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}\notag\\[7pt]
&=2p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\sum_{k=1}^j\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}
+p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{{2i\choose i}{2j\choose j}}{i+1}\notag\\[7pt]
&\equiv 2p\sum_{k=1}^{p-1}\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}+\frac{p}{2}\left(3- \left(\frac{p}{3}\right)\right)\pmod{p^2},
\end{align}
\begin{align}
&p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{S(i,j)}{i+1}\notag\\[7pt]
&=2p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\sum_{k=1}^j\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}
+p\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{{2i\choose i}{2j\choose j}}{i+1}\notag\\[7pt]
&\equiv 2p\sum_{k=1}^{p-1}\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}+\frac{p}{2}\left(3- \left(\frac{p}{3}\right)\right)\pmod{p^2},
\end{align} where we have used (2.6), (2.7) and ![]() $C_{p-1}\equiv -1\pmod{p}$ in the last step.
$C_{p-1}\equiv -1\pmod{p}$ in the last step.
It follows from (5.8)–(5.10) that
 \begin{align}
&\sum_{k=0}^{p-1}T_kM_k\notag\\[7pt]
&\equiv2p\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\notag\\[7pt]
&-2p\sum_{k=1}^{p-1}\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}\notag\\[7pt]
&-\frac{7p}{6}-\frac{3p}{2}\left(\frac{p}{3}\right)+\frac{4}{3}\left(\frac{p}{3}\right)3^{p-1}\pmod{p^2}.
\end{align}
\begin{align}
&\sum_{k=0}^{p-1}T_kM_k\notag\\[7pt]
&\equiv2p\sum_{k=1}^{p-1}\sum_{i=1}^{p-1}\sum_{j=0}^{p-1}\frac{(-1)^k}{i}{2i\choose i+k}{2j\choose j+k}\notag\\[7pt]
&-2p\sum_{k=1}^{p-1}\sum_{i=1}^{p-2}\sum_{j=0}^{p-1}\frac{(-1)^k}{i+1}{2i\choose i+k}{2j\choose j+k}\notag\\[7pt]
&-\frac{7p}{6}-\frac{3p}{2}\left(\frac{p}{3}\right)+\frac{4}{3}\left(\frac{p}{3}\right)3^{p-1}\pmod{p^2}.
\end{align}Then the proof of (1.4) follows from (3.7), (3.10) and (5.11).
Acknowledgements
The author is grateful to the anonymous referee for both the careful reading of the manuscript, and also the valuable comments and suggestions, which well improve the exposition of the paper. This work was supported by the National Natural Science Foundation of China (grant 12171370).