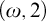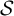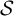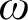3 results
DEFINABLE
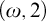 $(\omega ,2)$-THEOREM FOR FAMILIES WITH VC-CODENSITY LESS THAN
$(\omega ,2)$-THEOREM FOR FAMILIES WITH VC-CODENSITY LESS THAN 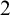 $2$
$2$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1659-1668
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THICKET DENSITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 110-127
- Print publication:
- March 2021
-
- Article
- Export citation
THE DP-RANK OF ABELIAN GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 957-986
- Print publication:
- September 2019
-
- Article
- Export citation