Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T20:25:56.628Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DP-RANK OF ABELIAN GROUPS

Published online by Cambridge University Press:  01 February 2019

YATIR HALEVI  and
DANIEL PALACÍN
YATIR HALEVI
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERUSALEM GIVAT RAM9190401, JERUSALEM, ISRAELE-mail: [email protected]
DANIEL PALACÍN
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERUSALEM GIVAT RAM9190401, JERUSALEM, ISRAELE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An equation to compute the dp-rank of any abelian group is given. It is also shown that its dp-rank, or more generally that of any one-based group, agrees with its Vapnik–Chervonenkis density. Furthermore, strong abelian groups are characterised to be precisely those abelian groups A such that there are only finitely many primes p such that the group A / pA is infinite and for every prime p, there are only finitely many natural numbers n such that 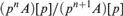$\left( {p^n A} \right)[p]/\left( {p^{n + 1} A} \right)[p]$ is infinite.

Finally, it is shown that an infinite stable field of finite dp-rank is algebraically closed.

Keywords

03C6003C4520K99abelian groupone-basedvc-densitydp-rank
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 957 - 986
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, H., Strong theories, burden, and weight, preprint, 2007.Google Scholar
Aschenbrenner, M., Dolich, A., Haskell, D., Macpherson, D., and Starchenko, S., Vapnik–Chervonenkis density in some theories without the independence property II. Notre Dame Journal of Formal Logic, vol. 54 (2013), no. 3–4, pp. 311–363.CrossRefGoogle Scholar
Aschenbrenner, M., Dolich, A., Haskell, D., Macpherson, D., and Starchenko, S., Vapnik–Chervonenkis density in some theories without the independence property I. Transactions of the American Mathematical Society, vol. 368 (2016), no. 8, pp. 5889–5949.CrossRefGoogle Scholar
Baur, W., Elimination of quantifiers for modules. Israel Journal of Mathematics, vol. 25 (1976), pp. 64–70.CrossRefGoogle Scholar
Buechler, S., Essential Stability Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar
Cherlin, G. and Shelah, S., Superstable fields and groups. Annals of Mathematical Logic, vol. 18 (1980), no. 3, pp. 227–270.CrossRefGoogle Scholar
Chernikov, A., Kaplan, I., and Simon, P., Groups and fields with NTP2. Proceedings of the American Mathematical Society, vol. 143 (2015), no. 1, pp. 395–406.CrossRefGoogle Scholar
Conant, G. and Pillay, A., Stable groups and expansions of $({\Bbb Z}, + ,0)$ . Fundamenta Mathematicae, vol. 242 (2018), no. 3, pp. 267–279.CrossRefGoogle Scholar
Eklof, P. C. and Fischer, E. R., The elementary theory of abelian groups. Annals of Mathematical Logic, vol. 4 (1972), no. 2, pp. 115–171.CrossRefGoogle Scholar
Farré, R., Strong ordered abelian groups and dp-rank, preprint, 2017.Google Scholar
Halevi, Y. and Hasson, A., Strongly dependent ordered abelian groups and henselian fields, preprint, 2017, arXiv:1706.03376.Google Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Hrushovski, E. and Pillay, A., Weakly normal groups, Logic colloquium ’85 (Orsay, 1985) (Paris Logic Group, editor), Studies in Logic and the Foundations of Mathematics, vol. 122, North-Holland, Amsterdam, 1987, pp. 233–244.CrossRefGoogle Scholar
Krupiński, K. and Pillay, A., On stable fields and weight. Journal of the Institute of Mathematics of Jussieu, vol. 10 (2011), no. 2, pp. 349–358.CrossRefGoogle Scholar
Monk, L. G., Elementary-recursive decision procedures, Ph.D. thesis, University of California, Berkeley, 1975.Google Scholar
Shelah, S., Strongly dependent theories. Israel Journal of Mathematics, vol. 204 (2014), no. 1, pp. 1–83.CrossRefGoogle Scholar
Simon, P., A Guide to NIP Theories, Lecture Notes in Logic, vol. 44, Cambridge University Press, Cambridge, 2015.CrossRefGoogle Scholar
Szmielew, W., Elementary properties of abelian groups. Fundamenta Mathematicae, vol. 41 (1995), no. 2, pp. 203–271.CrossRefGoogle Scholar
Wagner, F. O., Stable Groups, London Mathematical Society Lecture Note Series, vol. 240, Cambridge University Press, Cambridge, 1997.CrossRefGoogle Scholar