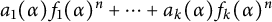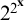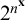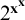3 results
On the Skolem problem and some related questions for parametric families of linear recurrence sequences
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 773-792
- Print publication:
- June 2022
-
- Article
- Export citation
ASYMPTOTIC ANALYSIS OF SKOLEM’S EXPONENTIAL FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 04 September 2020, pp. 758-782
- Print publication:
- June 2022
-
- Article
- Export citation
Problèmes de Skolem sur les champs algébriques
-
- Journal:
- Compositio Mathematica / Volume 125 / Issue 1 / January 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1-30
- Print publication:
- January 2001
-
- Article
-
- You have access
- Export citation