7 results
11 - Ramsey’s Theorem and Two-Player Deterministic Stopping Games
-
- Book:
- A Course in Stochastic Game Theory
- Published online:
- 05 May 2022
- Print publication:
- 26 May 2022, pp 195-210
-
- Chapter
- Export citation
Reverse mathematics and a Ramsey-type König's Lemma
-
- Journal:
- The Journal of Symbolic Logic / Volume 77 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1272-1280
- Print publication:
- December 2012
-
- Article
- Export citation
Term extraction and Ramsey's theorem for pairs
-
- Journal:
- The Journal of Symbolic Logic / Volume 77 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 12 March 2014, pp. 853-895
- Print publication:
- September 2012
-
- Article
- Export citation
RT22 does not imply WKL0
-
- Journal:
- The Journal of Symbolic Logic / Volume 77 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 March 2014, pp. 609-620
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On the strength of Ramsey's theorem for pairs
-
- Journal:
- The Journal of Symbolic Logic / Volume 66 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-55
- Print publication:
- March 2001
-
- Article
- Export citation
Effective versions of Ramsey's Theorem: Avoiding the cone above 0′
-
- Journal:
- The Journal of Symbolic Logic / Volume 59 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1301-1325
- Print publication:
- December 1994
-
- Article
- Export citation
A recursion theoretic analysis of the clopen Ramsey theorem
-
- Journal:
- The Journal of Symbolic Logic / Volume 49 / Issue 2 / June 1984
- Published online by Cambridge University Press:
- 12 March 2014, pp. 376-400
- Print publication:
- June 1984
-
- Article
- Export citation

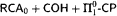 are primitive recursive. This also provides a uniform method to extract bounds from proofs that use these principles. As a consequence we obtain a new proof of the fact that
are primitive recursive. This also provides a uniform method to extract bounds from proofs that use these principles. As a consequence we obtain a new proof of the fact that 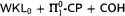 is
is 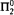 -conservative over PRA.
-conservative over PRA.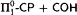 is equivalent to a weak variant of the Bolzano-Weierstraß principle. This makes it possible to use our results to analyze not only combinatorial but also analytical proofs.
is equivalent to a weak variant of the Bolzano-Weierstraß principle. This makes it possible to use our results to analyze not only combinatorial but also analytical proofs.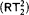 we obtain the upper bounded that the type 2 functional provable recursive relative to
we obtain the upper bounded that the type 2 functional provable recursive relative to 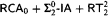 are in
are in 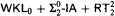 is
is 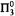 -conservative over
-conservative over 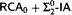 .
.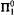 -comprehension. The comprehension is then eliminated in favor of induction using either elimination of monotone Skolem functions (for COH) or Howard's ordinal analysis of bar recursion (for
-comprehension. The comprehension is then eliminated in favor of induction using either elimination of monotone Skolem functions (for COH) or Howard's ordinal analysis of bar recursion (for 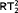 ).
).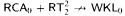 by showing that for any set
by showing that for any set 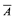 such that
such that 