Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Wei
2014.
Some logically weak Ramseyan theorems.
Advances in Mathematics,
Vol. 261,
Issue. ,
p.
1.
Wang, Wei
2014.
Cohesive sets and rainbows.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 2,
p.
389.
Liu, Lu
2014.
Cone avoiding closed sets.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 3,
p.
1609.
Kang, Xiaojun
2014.
Combinatorial principles between RRT 2 2 and RT 2 2.
Frontiers of Mathematics in China,
Vol. 9,
Issue. 6,
p.
1309.
Flood, Stephen
2015.
A packed Ramsey’s theorem and computability theory.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 7,
p.
4957.
Patey, Ludovic
2015.
Ramsey-type graph coloring and diagonal non-computability.
Archive for Mathematical Logic,
Vol. 54,
Issue. 7-8,
p.
899.
Rice, Brian
2015.
The Thin Set Theorem for Pairs Implies DNR.
Notre Dame Journal of Formal Logic,
Vol. 56,
Issue. 4,
Hirschfeldt, Denis R.
and
Jockusch, Carl G.
2016.
On notions of computability-theoretic reduction between Π21 principles.
Journal of Mathematical Logic,
Vol. 16,
Issue. 01,
p.
1650002.
PATEY, LUDOVIC
2016.
OPEN QUESTIONS ABOUT RAMSEY-TYPE STATEMENTS IN REVERSE MATHEMATICS.
The Bulletin of Symbolic Logic,
Vol. 22,
Issue. 2,
p.
151.
Patey, Ludovic
2016.
The weakness of being cohesive, thin or free in reverse mathematics.
Israel Journal of Mathematics,
Vol. 216,
Issue. 2,
p.
905.
Steila, Silvia
and
Yokoyama, Keita
2016.
Reverse mathematical bounds for the Termination Theorem.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 12,
p.
1213.
Flood, Stephen
and
Towsner, Henry
2016.
Separating principles below.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 6,
p.
507.
Dzhafarov, Damir D.
and
Patey, Ludovic
2017.
Coloring trees in reverse mathematics.
Advances in Mathematics,
Vol. 318,
Issue. ,
p.
497.
Bienvenu, Laurent
Patey, Ludovic
and
Shafer, Paul
2017.
On the logical strengths of partial solutions to mathematical problems.
Transactions of the London Mathematical Society,
Vol. 4,
Issue. 1,
p.
30.
Hirschfeldt, Denis R.
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
22.
Skrzypczak, Michał
2017.
Developments in Language Theory.
Vol. 10396,
Issue. ,
p.
75.
Eastaugh, Benedict
2017.
Book Reviews.
Studia Logica,
Vol. 105,
Issue. 4,
p.
873.
Patey, Ludovic
and
Yokoyama, Keita
2018.
The proof-theoretic strength of Ramsey's theorem for pairs and two colors.
Advances in Mathematics,
Vol. 330,
Issue. ,
p.
1034.
Monin, Benoit
and
Patey, Ludovic
2019.
Pigeons do not jump high.
Advances in Mathematics,
Vol. 352,
Issue. ,
p.
1066.
Chong, C.
Li, Wei
Wang, Wei
and
Yang, Yue
2019.
On the computability of perfect subsets of sets with positive measure.
Proceedings of the American Mathematical Society,
Vol. 147,
Issue. 9,
p.
4021.


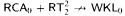 by showing that for any set
by showing that for any set 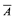 such that
such that 