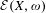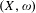6 results
WEAK GEODESIC RAYS IN THE SPACE OF KÄHLER POTENTIALS AND THE CLASS
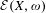 ${\mathcal{E}}(X,\unicode[STIX]{x1D714})$
${\mathcal{E}}(X,\unicode[STIX]{x1D714})$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 4 / September 2017
- Published online by Cambridge University Press:
- 03 September 2015, pp. 837-858
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
A NOTE ON THE MORSE–NOVIKOV COHOMOLOGY OF BLOW-UPS OF LOCALLY CONFORMAL KÄHLER MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 155-166
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
b-Stability and Blow-Ups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 23 December 2013, pp. 125-137
-
- Article
-
- You have access
- Export citation
On generalized Gauduchon metrics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 733-753
-
- Article
-
- You have access
- Export citation
On 4-dimensional generalized complex space forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 379-387
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
On Characterization of Hypersurfaces of Degrees 2 and 3 in the Complex Projective Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 1 / 01 March 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-78
- Print publication:
- 01 March 1986
-
- Article
-
- You have access
- Export citation