Using the Leray–Schauder degree, we study the existence of solutions for the following periodic differential equation with relativistic acceleration and singular nonlinearity:

where μ > 1 and the weight h: [0, T] → ℝ is a continuous sign-changing function. There are no a priori estimates on the set of positive solutions (a condition used in general to apply the Leray–Schauder degree), and we prove that no solution of the equation appears on the boundary of an unbounded open set during the deformation to an autonomous problem.

We characterize the centre variety of the eight-parameter families of real planar polynomial vector fields given, in complex notation, by 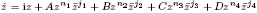, where A,B,C,D ∈ ℂ \{0}, (n1,j1) ≠ (n2,j2) ≠ (n3,j3) ≠ (n4,j4), nk + jk > 1 for k = 1,2,3,4, n1 + j1 = n2 + j2 = n3 + j3 = n4 + j4, |1 − n3 + j3| = |1 − n2 + j2| ≠ |1 − n1 + j1| and j4 = n4 − 1.

In this paper we establish a multiplicity result for a second-order non-autonomous system. Using a variational principle of Ricceri we prove that if the set of global minima of a certain function has at least $k$ connected components, then our problem has at least $k$ periodic solutions. Moreover, the existence of one more solution is investigated through a mountain-pass-like argument.