Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T04:35:12.168Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic solutions for indefinite singular perturbations of the relativistic acceleration

Part of: Boundary value problems Qualitative theory

Published online by Cambridge University Press:  22 June 2018

Cristian Bereanu  and
Manuel Zamora
Cristian Bereanu
Affiliation:
Faculty of Mathematics, University of Bucharest, 14 Academiei Street, 70190 Bucharest, Romania and Institute of Mathematics ‘Simion Stoilow’ of the Romanian Academy, 21 Calea Grivitei Street, 010702 Bucharest, Romania ([email protected])
Manuel Zamora
Affiliation:
Departamento de Matemática, Grupo de Investigación en Sistemas Dinámicos y Aplicaciones (GISDA), Universidad del Bío-Bío 5C, Concepción, Chile ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using the Leray–Schauder degree, we study the existence of solutions for the following periodic differential equation with relativistic acceleration and singular nonlinearity:

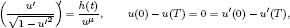
where μ > 1 and the weight h: [0, T] → ℝ is a continuous sign-changing function. There are no a priori estimates on the set of positive solutions (a condition used in general to apply the Leray–Schauder degree), and we prove that no solution of the equation appears on the boundary of an unbounded open set during the deformation to an autonomous problem.

Keywords

singular differential equationsindefinite singularityperiodic solutionsdegree theorycontinuation theorem

MSC classification

Secondary: 34C25: Periodic solutions 34B18: Positive solutions of nonlinear boundary value problems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 148 , Issue 4 , August 2018 , pp. 703 - 712
Copyright
Copyright © Royal Society of Edinburgh 2018 

Footnotes

*

Present address: Departamento de Matemàticas, Universidad de Oviedo, Calle Federico García Lorca 18, 33007 Oviedo, Spain ([email protected]).