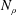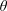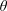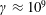35 results
A novel multi-shot target platform for laser-driven laboratory astrophysics experiments
-
- Journal:
- High Power Laser Science and Engineering / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 February 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Particle acceleration in explosive relativistic reconnection events and Crab Nebula gamma-ray flares
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 84 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 19 April 2018, 635840201
-
- Article
-
- You have access
- HTML
- Export citation
Particle acceleration in relativistic magnetic flux-merging events
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 12 December 2017, 635830602
-
- Article
- Export citation
Explosive X-point collapse in relativistic magnetically dominated plasma
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 12 December 2017, 635830601
-
- Article
-
- You have access
- HTML
- Export citation
Self-gravitational instability of dense degenerate viscous anisotropic plasma with rotation
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 06 November 2017, 905830601
-
- Article
- Export citation
Physics of ultimate detachment of a tokamak divertor plasma
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 27 September 2017, 155830501
-
- Article
-
- You have access
- HTML
- Export citation
Fast and spectrally accurate evaluation of gyroaverages in non-periodic gyrokinetic-Poisson simulations
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 22 August 2017, 905830407
-
- Article
- Export citation
Three-dimensional magnetohydrodynamic equilibria with continuous magnetic fields
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 27 July 2017, 715830403
-
- Article
-
- You have access
- HTML
- Export citation
Predictive simulations of operation scenarios for EAST with METIS code
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 24 July 2017, 905830404
-
- Article
- Export citation
Nonlinear interaction of intense left- and right-hand polarized laser pulse with hot magnetized plasma
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 11 July 2017, 655830401
-
- Article
- Export citation
Available energy and ground states of collisionless plasmas
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 06 July 2017, 715830401
-
- Article
- Export citation
GEMPIC: geometric electromagnetic particle-in-cell methods
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 03 July 2017, 905830401
-
- Article
-
- You have access
- HTML
- Export citation
Electromagnetic zonal flow residual responses
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 03 July 2017, 905830402
-
- Article
- Export citation
Spectral analysis of forced turbulence in a non-neutral plasma
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 21 June 2017, 705830303
-
- Article
- Export citation
A fully implicit numerical integration of the relativistic particle equation of motion
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 24 April 2017, 705830206
-
- Article
- Export citation
Kinetic inhibition of magnetohydrodynamics shocks in the vicinity of a parallel magnetic field
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 06 April 2017, 715830201
-
- Article
- Export citation
Generalized fluid theory including non-Maxwellian kinetic effects
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 29 March 2017, 595830201
-
- Article
- Export citation
Plasma turbulence at ion scales: a comparison between particle in cell and Eulerian hybrid-kinetic approaches
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 23 March 2017, 705830202
-
- Article
- Export citation
Plasma waves as a benchmark problem
- Part of
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 23 February 2017, 707830101
-
- Article
- Export citation
Jeans-Alfvén instability in quantum dusty magnetoplasmas
-
- Journal:
- Journal of Plasma Physics / Volume 83 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, 905830106
-
- Article
- Export citation