Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T05:34:47.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle acceleration in relativistic magnetic flux-merging events

Part of: Focus on Plasma Astrophysics Plasma Physics of Gamma Ray Emission

Published online by Cambridge University Press:  12 December 2017

Maxim Lyutikov ,
Lorenzo Sironi ,
Serguei S. Komissarov  and
Oliver Porth
Maxim Lyutikov*
Affiliation:
Department of Physics, Purdue University, 525 Northwestern Avenue, West Lafayette, IN 47907-2036, USA
Lorenzo Sironi
Affiliation:
Department of Astronomy, Columbia University, 550 W 120th St, New York, NY 10027, USA
Serguei S. Komissarov
Affiliation:
Department of Physics, Purdue University, 525 Northwestern Avenue, West Lafayette, IN 47907-2036, USA School of Mathematics, University of Leeds, LS29JT Leeds, UK
Oliver Porth
Affiliation:
School of Mathematics, University of Leeds, LS29JT Leeds, UK Institut für Theoretische Physik, J. W. Goethe-Universität, D-60438, Frankfurt am Main, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using analytical and numerical methods (fluid and particle-in-cell simulations) we study a number of model problems involving merger of magnetic flux tubes in relativistic magnetically dominated plasma. Mergers of current-carrying flux tubes (exemplified by the two-dimensional ‘ABC’ structures) and zero-total-current magnetic flux tubes are considered. In all cases regimes of spontaneous and driven evolution are investigated. We identify two stages of particle acceleration during flux mergers: (i) fast explosive prompt X-point collapse and (ii) ensuing island merger. The fastest acceleration occurs during the initial catastrophic X-point collapse, with the reconnection electric field of the order of the magnetic field. During the X-point collapse, particles are accelerated by charge-starved electric fields, which can reach (and even exceed) values of the local magnetic field. The explosive stage of reconnection produces non-thermal power-law tails with slopes that depend on the average magnetization $\unicode[STIX]{x1D70E}$. For plasma magnetization 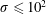$\unicode[STIX]{x1D70E}\leqslant 10^{2}$ the spectrum power-law index is 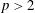$p>2$; in this case the maximal energy depends linearly on the size of the reconnecting islands. For higher magnetization, 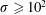$\unicode[STIX]{x1D70E}\geqslant 10^{2}$, the spectra are hard, 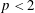$p<2$, yet the maximal energy 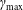$\unicode[STIX]{x1D6FE}_{\text{max}}$ can still exceed the average magnetic energy per particle, 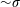${\sim}\unicode[STIX]{x1D70E}$, by orders of magnitude (if 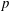$p$ is not too close to unity). The X-point collapse stage is followed by magnetic island merger that dissipates a large fraction of the initial magnetic energy in a regime of forced magnetic reconnection, further accelerating the particles, but proceeds at a slower reconnection rate.

Keywords

magnetized plasmasplasma nonlinear phenomenaspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 6 , December 2017 , 635830602
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdo, A. A., Ackermann, M., Ajello, M., Allafort, A., Baldini, L., Ballet, J., Barbiellini, G., Bastieri, D. et al. 2011 Gamma-ray flares from the crab nebula. Science 331, 739.CrossRefGoogle ScholarPubMed
Albright, B. J. 1999 The density and clustering of magnetic nulls in stochastic magnetic fields. Phys. Plasmas 6, 4222–4228.CrossRefGoogle Scholar
Amato, E. & Blasi, P. 2006 Non-linear particle acceleration at non-relativistic shock waves in the presence of self-generated turbulence. Mon. Not. R. Astron. Soc. 371, 1251–1258.CrossRefGoogle Scholar
Arnold, V. I. 1974 The asymptotic Hopf invariant and its applications (in Russian). In Proc. Summer School in Differential Equations, Erevan. Armenian SSR A d Sci.Google Scholar
Belyaev, M. A. 2015 PICsar: a 2.5D axisymmetric, relativistic, electromagnetic, particle in Cell code with a radiation absorbing boundary. New Astronomy 36, 37–49.CrossRefGoogle Scholar
Buehler, R., Scargle, J. D., Blandford, R. D., Baldini, L., Baring, M. G., Belfiore, A., Charles, E., Chiang, J., D’Ammando, F., Dermer, C. D. et al. 2012 Gamma-ray activity in the crab nebula: the exceptional flare of 2011 April. Astrophys. J. 749, 26.CrossRefGoogle Scholar
Buneman, O. 1993 Computer Space Plasma Physics, p. 67. Terra Scientific.Google Scholar
Cerutti, B., Uzdensky, D. A. & Begelman, M. C. 2012a Extreme particle acceleration in magnetic reconnection layers: application to the gamma-ray flares in the crab nebula. Astrophys. J. 746, 148.CrossRefGoogle Scholar
Cerutti, B., Werner, G. R., Uzdensky, D. A. & Begelman, M. C. 2012b Beaming and rapid variability of high-energy radiation from relativistic pair plasma reconnection. Astrophys. J. Lett. 754, L33.CrossRefGoogle Scholar
Cerutti, B., Werner, G. R., Uzdensky, D. A. & Begelman, M. C. 2013 Simulations of particle acceleration beyond the classical synchrotron burnoff limit in magnetic reconnection: an explanation of the crab flares. Astrophys. J. 770, 147.CrossRefGoogle Scholar
Cerutti, B., Werner, G. R., Uzdensky, D. A. & Begelman, M. C. 2014 Gamma-ray flares in the Crab Nebula: a case of relativistic reconnection?a). Phys. Plasmas 21 (5), 056501.CrossRefGoogle Scholar
Clausen-Brown, E. & Lyutikov, M. 2012 Crab nebula gamma-ray flares as relativistic reconnection minijets. Mon. Not. R. Astron. Soc. 426, 1374–1384.CrossRefGoogle Scholar
Drake, J. F. & Swisdak, M. 2012 Ion heating and acceleration during magnetic reconnection relevant to the corona. Space Sci. Rev. 172, 227–240.CrossRefGoogle Scholar
East, W. E., Zrake, J., Yuan, Y. & Blandford, R. D. 2015 Spontaneous decay of periodic magnetostatic equilibria. Phys. Rev. Lett. 115 (9), 095002.CrossRefGoogle ScholarPubMed
Green, R. M. 1965 Modes of annihilation and reconnection of magnetic fields. In Stellar and Solar Magnetic Fields (ed. Lust, R.), IAU Symposium, vol. 22, p. 398.Google Scholar
Guo, F., Liu, Y.-H., Daughton, W. & Li, H. 2015 Particle acceleration and plasma dynamics during magnetic reconnection in the magnetically dominated regime. Astrophys. J. 806, 167.CrossRefGoogle Scholar
Hoshino, M. 2012 Stochastic particle acceleration in multiple magnetic islands during reconnection. Phys. Rev. Lett. 108 (13), 135003.CrossRefGoogle ScholarPubMed
Keppens, R., Meliani, Z., van Marle, A. J., Delmont, P., Vlasis, A. & van der Holst, B. 2012 Parallel, grid-adaptive approaches for relativistic hydro and magnetohydrodynamics. J. Comput. Phys. 231 (3), 718–744.CrossRefGoogle Scholar
Komissarov, S. S. 1999 Numerical simulations of relativistic magnetized jets. Mon. Not. R. Astron. Soc. 308, 1069–1076.CrossRefGoogle Scholar
Komissarov, S. S. 2002 Time-dependent, force-free, degenerate electrodynamics. Mon. Not. R. Astron. Soc. 336, 759–766.CrossRefGoogle Scholar
Komissarov, S. S. 2012 Shock dissipation in magnetically dominated impulsive flows. Mon. Not. R. Astron. Soc. 422, 326–346.CrossRefGoogle Scholar
Komissarov, S. S., Barkov, M. & Lyutikov, M. 2007 Tearing instability in relativistic magnetically dominated plasmas. Mon. Not. R. Astron. Soc. 374, 415–426.CrossRefGoogle Scholar
Longcope, D. W. & Strauss, H. R. 1994 The form of ideal current layers in line-tied magnetic fields. Astrophys. J. 437, 851–859.CrossRefGoogle Scholar
Lyubarsky, Y. E. 2003 The termination shock in a striped pulsar wind. Mon. Not. R. Astron. Soc. 345, 153–160.CrossRefGoogle Scholar
Lyutikov, M. 2010 A high-sigma model of pulsar wind nebulae. Mon. Not. R. Astron. Soc. 405, 1809–1815.Google Scholar
Lyutikov, M., Sironi, L., Komissarov, S. S. & Porth, O. 2017 Explosive X-point collapse in relativistic magnetically-dominated plasma. J. Plasma Phys. 82.Google Scholar
Moffatt, H. K. 1986 Magnetostatic equilibria and analogous Euler flows of arbitrarily complex topology. II – stability considerations. J. Fluid Mech. 166, 359–378.CrossRefGoogle Scholar
Molodensky, M. M. 1974 Equilibrium and stability of force-free magnetic field. Solar Phys. 39, 393–404.CrossRefGoogle Scholar
Nalewajko, K., Zrake, J., Yuan, Y., East, W. E. & Blandford, R. D. 2016 Kinetic simulations of the lowest-order unstable mode of relativistic magnetostatic equilibria. Astrophys. J. 826, 115.CrossRefGoogle Scholar
Oka, M., Phan, T.-D., Krucker, S., Fujimoto, M. & Shinohara, I. 2010 Electron acceleration by multi-island coalescence. Astrophys. J. 714, 915–926.CrossRefGoogle Scholar
Parker, E. N. 1983 Magnetic neutral sheets in evolving fields. I – general theory. Astrophys. J. 264, 635–647.CrossRefGoogle Scholar
Pétri, J. & Lyubarsky, Y. 2007 Magnetic reconnection at the termination shock in a striped pulsar wind. Astron. Astrophys. 473, 683–700.CrossRefGoogle Scholar
Porth, O., Xia, C., Hendrix, T., Moschou, S. P. & Keppens, R. 2014 MPI-AMRVAC for solar and astrophysics. Astrophys. J. Suppl. 214, 4.CrossRefGoogle Scholar
Roberts, G. O. 1972 Dynamo action of fluid motions with two-dimensional periodicity. Phil. Trans. R. Soc. Lond. A 271, 411–454.Google Scholar
Sironi, L. & Spitkovsky, A. 2011 Acceleration of particles at the termination shock of a relativistic striped wind. Astrophys. J. 741, 39.CrossRefGoogle Scholar
Sironi, L. & Spitkovsky, A. 2014 Relativistic reconnection: an efficient source of non-thermal particles. Astrophys. J. Lett. 783, L21.CrossRefGoogle Scholar
Spitkovsky, A. 2005 Simulations of relativistic collisionless shocks: shock structure and particle acceleration. In Astrophysical Sources of High Energy Particles and Radiation (ed. Bulik, T., Rudak, B. & Madejski, G.), AIP Conf. Ser., vol. 801, p. 345.Google Scholar
Tanaka, K. G., Yumura, T., Fujimoto, M., Shinohara, I., Badman, S. V. & Grocott, A. 2010 Merging of magnetic islands as an efficient accelerator of electrons. Phys. Plasmas 17 (10), 102902.CrossRefGoogle Scholar
Tavani, M., Bulgarelli, A., Vittorini, V., Pellizzoni, A., Striani, E., Caraveo, P., Weisskopf, M. C., Tennant, A. et al. 2011 Discovery of powerful gamma-ray flares from the crab nebula. Science 331, 736.CrossRefGoogle ScholarPubMed
Taylor, J. B. 1974 Relaxation of toroidal plasma and generation of reverse magnetic fields. Phys. Rev. Lett. 33, 1139–1141.CrossRefGoogle Scholar
Uzdensky, D. A., Cerutti, B. & Begelman, M. C. 2011 Reconnection-powered linear accelerator and gamma-ray flares in the crab nebula. Astrophys. J. Lett. 737, L40.CrossRefGoogle Scholar
Uzdensky, D. A., Loureiro, N. F. & Schekochihin, A. A. 2010 Fast magnetic reconnection in the plasmoid-dominated regime. Phys. Rev. Lett. 105 (23), 235002.CrossRefGoogle ScholarPubMed
Voslamber, D. & Callebaut, D. K. 1962 Stability of force-free magnetic fields. Phys. Rev. 128, 2016–2021.CrossRefGoogle Scholar
Werner, G. R., Uzdensky, D. A., Cerutti, B., Nalewajko, K. & Begelman, M. C. 2016 The extent of power-law energy spectra in collisionless relativistic magnetic reconnection in pair plasmas. Astrophys. J. Lett. 816, L8.CrossRefGoogle Scholar
Woltier, L. 1958 Proc. Natl Acad. Sci. USA 44, 489.CrossRefGoogle Scholar
Zank, G. P., le Roux, J. A., Webb, G. M., Dosch, A. & Khabarova, O. 2014 Particle acceleration via reconnection processes in the supersonic solar wind. Astrophys. J. 797, 28.CrossRefGoogle Scholar
Zrake, J. 2014 Inverse cascade of nonhelical magnetic turbulence in a relativistic fluid. Astrophys. J. Lett. 794, L26.CrossRefGoogle Scholar