Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T20:36:50.046Z Has data issue: false hasContentIssue false
  • English
  • Français

Plasma turbulence at ion scales: a comparison between particle in cell and Eulerian hybrid-kinetic approaches

Part of: PLA The Vlasov Equation Focus on Space Plasmas

Published online by Cambridge University Press:  23 March 2017

S. S. Cerri ,
L. Franci ,
F. Califano ,
S. Landi  and
P. Hellinger Open the ORCID record for P. Hellinger [Opens in a new window]
S. S. Cerri*
Affiliation:
Physics Department ‘E. Fermi’, University of Pisa, Largo B. Pontecorvo 3, I-56127 Pisa, Italy
L. Franci*
Affiliation:
Dipartimento di Fisica e Astronomia, Università degli Studi di Firenze, Largo E. Fermi 2, I-50125 Firenze, Italy INFN – Sezione di Firenze, Via G. Sansone 1, I-50019 Sesto F.no (Firenze), Italy
F. Califano
Affiliation:
Physics Department ‘E. Fermi’, University of Pisa, Largo B. Pontecorvo 3, I-56127 Pisa, Italy
S. Landi
Affiliation:
Dipartimento di Fisica e Astronomia, Università degli Studi di Firenze, Largo E. Fermi 2, I-50125 Firenze, Italy INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, I-50125 Firenze, Italy
P. Hellinger
Affiliation:
Astronomical Institute, CAS, Bocni II/1401, CZ-14100 Prague, Czech Republic
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Kinetic-range turbulence in magnetized plasmas and, in particular, in the context of solar wind turbulence has been extensively investigated over the past decades via numerical simulations. Among others, one of the widely adopted reduced plasma models is the so-called hybrid-kinetic model, where the ions are fully kinetic and the electrons are treated as a neutralizing (inertial or massless) fluid. Within the same model, different numerical methods and/or approaches to turbulence development have been employed. In the present work, we present a comparison between two-dimensional hybrid-kinetic simulations of plasma turbulence obtained with two complementary approaches spanning approximately two decades in wavenumber – from the magnetohydrodynamics inertial range to scales well below the ion gyroradius – with a state-of-the-art accuracy. One approach employs hybrid particle-in-cell simulations of freely decaying Alfvénic turbulence, whereas the other consists of Eulerian hybrid Vlasov–Maxwell simulations of turbulence continuously driven with partially compressible large-scale fluctuations. Despite the completely different initialization and injection/drive at large scales, the same properties of turbulent fluctuations at 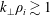$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gtrsim 1$ are observed, where 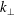$k_{\bot }$ is the fluctuations’ wavenumber perpendicular to the background magnetic field and 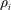$\unicode[STIX]{x1D70C}_{i}$ is the ion Larmor radius. The system indeed self-consistently ‘reprocesses’ the turbulent fluctuations while they are cascading towards smaller and smaller scales, in a way which actually depends on the plasma beta parameter (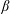$\unicode[STIX]{x1D6FD}$ is the ratio between the thermal and the magnetic pressures). Small-scale turbulence has been found to be mainly populated by kinetic Alfvén wave (KAW) fluctuations for 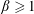$\unicode[STIX]{x1D6FD}\geqslant 1$, whereas KAW fluctuations are only sub-dominant for low-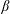$\unicode[STIX]{x1D6FD}$.

Keywords

astrophysical plasmasmagnetized plasmasspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 2 , April 2017 , 705830202
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S. J. & Robert, P. 2009 Universality of solar-wind turbulent spectrum from MHD to electron scales. Phys. Rev. Lett. 103 (16), 165003.CrossRefGoogle ScholarPubMed
Bale, S. D., Kellogg, P. J., Mozer, F. S., Horbury, T. S. & Reme, H. 2005 Measurement of the electric fluctuation spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 94 (21), 215002.Google Scholar
Biskamp, D. 2003 Magnetohydrodynamic Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Boldyrev, S., Chen, C. H. K., Xia, Q. & Zhdankin, V. 2015 Spectral breaks of Alfvénic turbulence in a collisionless plasma. Astrophys. J. 806, 238.CrossRefGoogle Scholar
Boldyrev, S., Horaites, K., Xia, Q. & Perez, J. C. 2013 Toward a theory of astrophysical plasma turbulence at subproton scales. Astrophys. J. 777, 41.CrossRefGoogle Scholar
Boldyrev, S. & Perez, J. C. 2012 Spectrum of kinetic-Alfvén turbulence. Astrophys. J. Lett. 758, L44.Google Scholar
Bruno, R. & Carbone, V. 2013 The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10, 2.CrossRefGoogle Scholar
Bruno, R., Trenchi, L. & Telloni, D. 2014 Spectral slope variation at proton scales from fast to slow solar wind. Astrophys. J. Lett. 793, L15.Google Scholar
Cerri, S. S. & Califano, F. 2017 Reconnection and small-scale fields in 2D-3V hybrid-kinetic driven turbulence simulations. New J. Phys. 19 (2), 025007.Google Scholar
Cerri, S. S., Califano, F., Jenko, F., Told, D. & Rincon, F. 2016 Subproton-scale cascades in solar wind turbulence: driven hybrid-kinetic simulations. Astrophys. J. Lett. 822, L12.Google Scholar
Chasapis, A., Retinò, A., Sahraoui, F., Vaivads, A., Khotyaintsev, Y. V., Sundkvist, D., Greco, A., Sorriso-Valvo, L. & Canu, P. 2015 Thin current sheets and associated electron heating in turbulent space plasma. Asotrophys. J. Lett. 804, L1.Google Scholar
Chen, C. H. K., Boldyrev, S., Xia, Q. & Perez, J. C. 2013 Nature of subproton scale turbulence in the solar wind. Phys. Rev. Lett. 110 (22), 225002.Google Scholar
Cheng, C. Z. & Knorr, G. 1976 The integration of the Vlasov equation in configuration space. J. Comput. Phys. 22, 330–351.CrossRefGoogle Scholar
Franci, L., Hellinger, P., Matteini, L., Verdini, A. & Landi, S. 2016a Two-dimensional Hybrid Simulations of Kinetic Plasma Turbulence: Current and Vorticity Versus Proton Temperature, American Institute of Physics Conference Series, vol. 1720, p. 040003.Google Scholar
Franci, L., Landi, S., Matteini, L., Verdini, A. & Hellinger, P. 2015a High-resolution hybrid simulations of kinetic plasma turbulence at proton scales. Astrophys. J. 812, 21.Google Scholar
Franci, L., Landi, S., Matteini, L., Verdini, A. & Hellinger, P. 2016b Plasma beta dependence of the ion-scale spectral break of solar wind turbulence: high-resolution 2D hybrid simulations. Astrophys. J. 833, 91.CrossRefGoogle Scholar
Franci, L., Verdini, A., Matteini, L., Landi, S. & Hellinger, P. 2015b Solar wind turbulence from MHD to sub-ion scales: high-resolution hybrid simulations. Astrophys. J. Lett. 804, L39.Google Scholar
Galtier, S. & Bhattacharjee, A. 2003 Anisotropic weak whistler wave turbulence in electron magnetohydrodynamics. Phys. Plasmas 10, 3065–3076.Google Scholar
Gary, S. P. & Smith, C. W. 2009 Short-wavelength turbulence in the solar wind: linear theory of whistler and kinetic Alfvén fluctuations. J. Geophys. Res. Space Phys. 114, A12105.Google Scholar
Greco, A., Perri, S., Servidio, S., Yordanova, E. & Veltri, P. 2016 The complex structure of magnetic field discontinuities in the turbulent solar wind. Astrophys. J. Lett. 823, L39.Google Scholar
Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E. & Schekochihin, A. A. 2008a A model of turbulence in magnetized plasmas: implications for the dissipation range in the solar wind. J. Geophys. Res. Space Phys. 113, A05103.Google Scholar
Howes, G. G., Dorland, W., Cowley, S. C., Hammett, G. W., Quataert, E., Schekochihin, A. A. & Tatsuno, T. 2008b Kinetic simulations of magnetized turbulence in astrophysical plasmas. Phys. Rev. Lett. 100 (6), 065004.CrossRefGoogle ScholarPubMed
Howes, G. G., Tenbarge, J. M., Dorland, W., Quataert, E., Schekochihin, A. A., Numata, R. & Tatsuno, T. 2011 Gyrokinetic simulations of solar wind turbulence from ion to electron scales. Phys. Rev. Lett. 107 (3), 035004.CrossRefGoogle ScholarPubMed
Karimabadi, H., Roytershteyn, V., Daughton, W. & Liu, Y.-H. 2013a Recent evolution in the theory of magnetic reconnection and its connection with turbulence. Space Sci. Rev. 178, 307–323.Google Scholar
Karimabadi, H., Roytershteyn, V., Wan, M., Matthaeus, W. H., Daughton, W., Wu, P., Shay, M., Loring, B., Borovsky, J., Leonardis, E. et al. 2013b Coherent structures, intermittent turbulence, and dissipation in high-temperature plasmas. Phys. Plasmas 20 (1), 012303.CrossRefGoogle Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.CrossRefGoogle Scholar
Li, T. C., Howes, G. G., Klein, K. G. & TenBarge, J. M. 2016 Energy dissipation and Landau damping in two- and three-dimensional plasma turbulence. Astrophys. J. Lett. 832, L24.Google Scholar
Lion, S., Alexandrova, O. & Zaslavsky, A. 2016 Coherent events and spectral shape at ion kinetic scales in the fast solar wind turbulence. Astrophys. J. 824, 47.CrossRefGoogle Scholar
Mangeney, A., Califano, F., Cavazzoni, C. & Travnicek, P. 2002 A numerical scheme for the integration of the Vlasov–Maxwell system of equations. J. Comput. Phys. 179, 495–538.CrossRefGoogle Scholar
Matthaeus, W. H. & Lamkin, S. L. 1986 Turbulent magnetic reconnection. Phys. Fluids 29, 2513–2534.Google Scholar
Matthews, A. P. 1994 Current advance method and cyclic leapfrog for 2D multispecies hybrid plasma simulations. J. Comput. Phys. 112, 102–116.CrossRefGoogle Scholar
Mininni, P. D. & Pouquet, A. 2009 Finite dissipation and intermittency in magnetohydrodynamics. Phys. Rev. E 80 (2), 025401.Google ScholarPubMed
Navarro, A. B., Teaca, B., Told, D., Groselj, D., Crandall, P. & Jenko, F. 2016 Structure of plasma heating in gyrokinetic Alfvénic turbulence. Phys. Rev. Lett. 117 (24), 245101.CrossRefGoogle ScholarPubMed
Parashar, T. N., Salem, C., Wicks, R. T., Karimabadi, H., Gary, S. P. & Matthaeus, W. H. 2015 Turbulent dissipation challenge: a community-driven effort. J. Plasma Phys. 81 (5), 905810513.Google Scholar
Parashar, T. N., Servidio, S., Breech, B., Shay, M. A. & Matthaeus, W. H. 2010 Kinetic driven turbulence: structure in space and time. Phys. Plasmas 17 (10), 102304.Google Scholar
Parashar, T. N., Servidio, S., Shay, M. A., Breech, B. & Matthaeus, W. H. 2011 Effect of driving frequency on excitation of turbulence in a kinetic plasma. Phys. Plasmas 18 (9), 092302.CrossRefGoogle Scholar
Passot, T., Henri, P., Laveder, D. & Sulem, P.-L. 2014 Fluid simulations of ion scale plasmas with weakly distorted magnetic fields. FLR-Landau fluid simulations. Eur. Phys. J. D 68, 207.Google Scholar
Passot, T. & Sulem, P. L. 2015 A model for the non-universal power law of the solar wind sub-ion-scale magnetic spectrum. Astrophys. J. Lett. 812, L37.Google Scholar
Perri, S., Goldstein, M. L., Dorelli, J. C. & Sahraoui, F. 2012 Detection of small-scale structures in the dissipation regime of solar-wind turbulence. Phys. Rev. Lett. 109 (19), 191101.Google Scholar
Perrone, D., Alexandrova, O., Mangeney, A., Maksimovic, M., Lacombe, C., Rakoto, V., Kasper, J. C. & Jovanovic, D. 2016 Compressive coherent structures at ion scales in the slow solar wind. Astrophys. J. 826, 196.Google Scholar
Perrone, D., Valentini, F., Servidio, S., Dalena, S. & Veltri, P. 2013 Vlasov simulations of multi-ion plasma turbulence in the solar wind. Astrophys. J. 762, 99.Google Scholar
Roberts, O. W., Li, X., Alexandrova, O. & Li, B. 2016 Observation of an MHD Alfvén vortex in the slow solar wind. J. Geophys. Res. Space Phys. 121, 3870–3881.Google Scholar
Roberts, O. W., Li, X. & Li, B. 2013 Kinetic plasma turbulence in the fast solar wind measured by cluster. Astrophys. J. 769, 58.Google Scholar
Sahraoui, F., Goldstein, M. L., Robert, P. & Khotyaintsev, Y. V. 2009 Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys. Rev. Lett. 102 (23), 231102.CrossRefGoogle ScholarPubMed
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. Series 182, 310–377.Google Scholar
Servidio, S., Dmitruk, P., Greco, A., Wan, M., Donato, S., Cassak, P. A., Shay, M. A., Carbone, V. & Matthaeus, W. H. 2011 Magnetic reconnection as an element of turbulence. Nonlinear Process. Geophys. 18, 675–695.CrossRefGoogle Scholar
Servidio, S., Osman, K. T., Valentini, F., Perrone, D., Califano, F., Chapman, S., Matthaeus, W. H. & Veltri, P. 2014 Proton kinetic effects in Vlasov and solar wind turbulence. Astrophys. J. Lett. 781, L27.Google Scholar
Servidio, S., Valentini, F., Califano, F. & Veltri, P. 2012 Local kinetic effects in two-dimensional plasma turbulence. Phys. Rev. Lett. 108 (4), 045001.CrossRefGoogle ScholarPubMed
Servidio, S., Valentini, F., Perrone, D., Greco, A., Califano, F., Matthaeus, W. H. & Veltri, P. 2015 A kinetic model of plasma turbulence. J. Plasma Phys. 81 (1), 325810107.CrossRefGoogle Scholar
Shaikh, D. & Zank, G. P. 2009 Spectral features of solar wind turbulent plasma. Mon. Not. R. Astron. Soc. 400, 1881–1891.CrossRefGoogle Scholar
Stawicki, O., Gary, S. P. & Li, H. 2001 Solar wind magnetic fluctuation spectra: dispersion versus damping. J. Geophys. Res. 106, 8273–8282.Google Scholar
Sulem, P. L., Passot, T., Laveder, D. & Borgogno, D. 2016 Influence of the nonlinearity parameter on the solar wind sub-ion magnetic energy spectrum: FLR-Landau fluid simulations. Astrophys. J. 818, 66.CrossRefGoogle Scholar
Told, D., Jenko, F., TenBarge, J. M., Howes, G. G. & Hammett, G. W. 2015 Multiscale nature of the dissipation range in gyrokinetic simulations of Alfvénic turbulence. Phys. Rev. Lett. 115 (2), 025003.Google Scholar
Valentini, F., Califano, F. & Veltri, P. 2010 Two-dimensional kinetic turbulence in the solar wind. Phys. Rev. Lett. 104 (20), 205002.Google Scholar
Valentini, F., Perrone, D., Stabile, S., Pezzi, O., Servidio, S., De Marco, R., Marcucci, F., Bruno, R., Lavraud, B., De Keyser, J. et al. 2016 Differential kinetic dynamics and heating of ions in the turbulent solar wind. New J. Phys. 18 (12), 125001.Google Scholar
Valentini, F., Servidio, S., Perrone, D., Califano, F., Matthaeus, W. H. & Veltri, P. 2014 Hybrid Vlasov–Maxwell simulations of two-dimensional turbulence in plasmas. Phys. Plasmas 21 (8), 082307.Google Scholar
Valentini, F., Trávníček, P., Califano, F., Hellinger, P. & Mangeney, A. 2007 A hybrid-Vlasov model based on the current advance method for the simulation of collisionless magnetized plasma. J. Comput. Phys. 225, 753–770.CrossRefGoogle Scholar
Wan, M., Matthaeus, W. H., Roytershteyn, V., Parashar, T. N., Wu, P. & Karimabadi, H. 2016 Intermittency, coherent structures and dissipation in plasma turbulence. Phys. Plasmas 23 (4), 042307.Google Scholar
Winske, D. 1985 Hybrid simulation codes with application to shocks and upstream waves. Space Sci. Rev. 42, 53–66.CrossRefGoogle Scholar