We consider a Poisson autoregressive process whose parameters depend on the past of the trajectory. We allow these parameters to take negative values, modelling inhibition. More precisely, the model is the stochastic process $(X_n)_{n\ge0}$ with parameters $a_1,\ldots,a_p \in \mathbb{R}$, $p\in\mathbb{N}$, and $\lambda \ge 0$, such that, for all $n\ge p$, conditioned on $X_0,\ldots,X_{n-1}$, $X_n$ is Poisson distributed with parameter $(a_1 X_{n-1} + \cdots + a_p X_{n-p} + \lambda)_+$. This process can be regarded as a discrete-time Hawkes process with inhibition and a memory of length p. In this paper we initiate the study of necessary and sufficient conditions of stability for these processes, which seems to be a hard problem in general. We consider specifically the case $p = 2$, for which we are able to classify the asymptotic behavior of the process for the whole range of parameters, except for boundary cases. In particular, we show that the process remains stochastically bounded whenever the solution to the linear recurrence equation $x_n = a_1x_{n-1} + a_2x_{n-2} + \lambda$ remains bounded, but the converse is not true. Furthermore, the criterion for stochastic boundedness is not symmetric in $a_1$ and $a_2$, in contrast to the case of non-negative parameters, illustrating the complex effects of inhibition.

We consider a variation of the processor-sharing (PS) queue, inspired by freelance job websites where multiple freelancers compete for a single job. We develop fluid limit approximations for the overloaded PS-model with multiple (possibly infinitely many) service stages. Based on this approximation, we estimate what proportion of freelancers get the job they apply for. In addition, the PS model studied here is an instance of PS with routing and impatience, for which no Lyapunov function is known, and we suggest some partial solutions.

This paper presents a practical approach for the point-to-point control of elastic-jointed robot manipulators. With the proposed approach only position and velocity feedback are referenced, as opposed to most of the existing control schemes of elastic-jointed manipulators which require additional acceleration and/or jerk feedback. To guarantee the robustness of the controller, it is designed on extreme parameter uncertainties due to highly elastic joints of manipulators and energy motivated Lyapunov functions are used to derive the control law. Four pertinent controller gains are chosen in light of the on-line position and velocity feedback of the links and joint sensors. Through a simulated experimental verification, it is demonstrated that the designed simple position and velocity feedback controller, similar to that used for rigid-jointed robots, can globally stabilize the elastic-jointed robot for a bounded reference position. In addition, the tracking performance of the controller reveals that this simple control algorithm is robust in terms of joint flexibility. And the simplicity of the presented control algorithm, as compared to other model-based techniques for flexiblejoint robots, is particularly advantageous. Even though the simulated experiments are conducted on a single-link flexible joint robot, control law derived in this paper has general meaning for multi-link flexible joint robots.

The stability analysis of active spatial mechanisms comprising both powered and unpowered joints is carried out for the first time using aggregation-decomposition method via Lyapunov vector functions. This method has already been used for analysis of mechanisms with all powered joints. To extend the application of the method to the stability analysis of mechanisms containing unpowered joints we developed modelling of special subsystem consisting of one powered and one unpowered joint. Then, we consider the stability of the complete system without neglecting any dynamic effect. The stability analysis is demonstrated by a numerical example of a particular biped system.

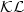We consider differential inclusions where a positive semidefinite function of the solutions satisfies a class-${\mathcal{KL}}$ estimate in terms of time and a second positive semidefinite function of the initial condition. We show that a smooth converse Lyapunov function, i.e., one whose derivative along solutions can be used to establish the class-${\mathcal{KL}}$ estimate, exists if and only if the class-${\mathcal{KL}}$ estimate is robust, i.e., it holds for a larger, perturbed differential inclusion. It remains an open question whether all class-${\mathcal{KL}}$ estimates are robust. One sufficient condition for robustness is that the original differential inclusion is locally Lipschitz. Another sufficient condition is that the two positive semidefinite functions agree and a backward completability condition holds. These special cases unify and generalize many results on converse Lyapunov theorems for differential equations and differential inclusions that have appeared in the literature.

We study stability and stabilizability properties of systems with discontinuous righthand side (with solutions intended in Filippov's sense) by means of locally Lipschitz continuous and regular Lyapunov functions. The stability result is obtained in the more general context of differential inclusions. Concerning stabilizability, we focus on systemsaffine with respect to the input: we give some sufficient conditions for a system to be stabilized by means of a feedback law of the Jurdjevic-Quinn type.


Some sufficient conditions for non-ergodicity are given for a Markov chain with denumerable state space. These conditions generalize Foster's results, in that unbounded Lyapunov functions are considered. Our criteria directly extend the conditions obtained in Kaplan (1979), in the sense that a class of Lyapunov functions is studied. Applications are presented through some examples; in particular, sufficient conditions for non-ergodicity of a multidimensional Markov chain are given.

A class of Lyapunov functions is used to demonstrate that strategy stability occurs in complex randomly mating diploid populations. Strategies close to the evolutionarily stable strategy tend to fare better than more remote strategies. If convergence in mean strategy to an evolutionarily stable strategy is not possible, evolution will continue until all strategies in use lie on a unique face of the convex hull of available strategies.

The results obtained are also relevant to the haploid parthenogenetic case.