Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Teel, A.R.
2000.
Lyapunov methods in nonsmooth optimization. Part II: Persistently exciting finite differences.
Vol. 1,
Issue. ,
p.
118.
Teel, A.R.
2000.
Lyapunov methods in nonsmooth optimization. Part I: Quasi-Newton algorithms for Lipschitz, regular functions.
Vol. 1,
Issue. ,
p.
112.
Camilli, Fabio
Grüne, Lars
and
Wirth, Fabian
2001.
A Generalization of Zubov's Method to Perturbed Systems.
SIAM Journal on Control and Optimization,
Vol. 40,
Issue. 2,
p.
496.
Karafyllis, I.
and
Tsinias, J.
2001.
Converse Lyapunov Theorems for Non-Uniform in Time Global Asymptotic Stability and Stabilization by Means of Time-Varying Feedback.
IFAC Proceedings Volumes,
Vol. 34,
Issue. 6,
p.
769.
Tsinias, J.
2001.
A converse Lyapunov theorem for, non-uniform in time, global exponential robust stability.
Systems & Control Letters,
Vol. 44,
Issue. 5,
p.
373.
Rifford, Ludovic
2001.
On the existence of nonsmooth control-Lyapunov functions in the sense of generalized gradients.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 6,
Issue. ,
p.
593.
Clarke, Francis
2001.
Nonsmooth Analysis in Control Theory: A Survey.
European Journal of Control,
Vol. 7,
Issue. 2-3,
p.
145.
Ingalls, B.P.
Sontag, E.D.
and
Yuan Wang
2002.
Measurement to error stability: a notion of partial detectability for nonlinear systems.
Vol. 4,
Issue. ,
p.
3946.
Efimov, D.V.
2002.
A condition of CLF existence for affine systems.
Vol. 2,
Issue. ,
p.
1882.
Kellett, C.M.
and
Teel, A.R.
2002.
On robustness of stability and Lyapunov functions for discontinuous difference equations.
Vol. 4,
Issue. ,
p.
4282.
Camilli, F.
Grune, L.
and
Wirth, F.
2002.
A generalization of Zubov's method to perturbed systems.
Vol. 3,
Issue. ,
p.
3518.
Skjetne, R.
Teel, A.R.
and
Kokotovic, P.V.
2002.
Nonlinear maneuvering with gradient optimization.
Vol. 4,
Issue. ,
p.
3926.
Angeli, D.
2002.
A Lyapunov approach to incremental stability properties.
IEEE Transactions on Automatic Control,
Vol. 47,
Issue. 3,
p.
410.
Karafyllis, I.
and
Tsinias, J.
2003.
A Converse Lyapunov Theorem for Nonuniform in Time Global Asymptotic Stability and Its Application to Feedback Stabilization.
SIAM Journal on Control and Optimization,
Vol. 42,
Issue. 3,
p.
936.
Nesic, D.
and
Teel, A.R.
2003.
A Matrosov theorem with an application to model reference adaptive control via approximate discrete-time models.
Vol. 2,
Issue. ,
p.
1556.
Clarke, F. H.
and
Stern, R. J.
2003.
State Constrained Feedback Stabilization.
SIAM Journal on Control and Optimization,
Vol. 42,
Issue. 2,
p.
422.
Astolfi, A.
and
Praly, L.
2003.
Global complete observability and output-to-state stability imply the existence of a globally convergent observer.
Vol. 2,
Issue. ,
p.
1562.
Chellaboina, V.
and
Haddad, W.M.
2003.
Feedback.
IEEE Control Systems,
Vol. 23,
Issue. 3,
p.
101.
Kellett, C.M.
and
Teel, A.R.
2003.
Results on discrete-time control-lyapunov functions.
Vol. 6,
Issue. ,
p.
5961.
Kellett, C.M.
and
Teel, A.R.
2003.
Results on converse Lyapunov theorems for difference inclusions.
p.
3627.
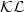 estimateinvolving two positive semidefinite functions
estimateinvolving two positive semidefinite functions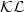 estimate
in terms of time and a second positive semidefinite function of the
initial condition.
We show that a smooth converse Lyapunov function, i.e., one whose
derivative along solutions can be
used to establish the class-${\mathcal{KL}}$
estimate
in terms of time and a second positive semidefinite function of the
initial condition.
We show that a smooth converse Lyapunov function, i.e., one whose
derivative along solutions can be
used to establish the class-${\mathcal{KL}}$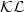 estimate, exists if and
only if the class-${\mathcal{KL}}$
estimate, exists if and
only if the class-${\mathcal{KL}}$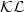 estimate
is robust, i.e., it holds for a larger, perturbed differential
inclusion.
It remains an open question whether all class-${\mathcal{KL}}$
estimate
is robust, i.e., it holds for a larger, perturbed differential
inclusion.
It remains an open question whether all class-${\mathcal{KL}}$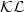 estimates are robust.
One sufficient condition for robustness is that the original
differential inclusion is locally Lipschitz.
Another sufficient condition is that the two positive semidefinite
functions agree and
a backward completability condition holds. These special cases unify
and generalize many results
on converse Lyapunov theorems for differential equations and
differential inclusions that have appeared in the literature.
estimates are robust.
One sufficient condition for robustness is that the original
differential inclusion is locally Lipschitz.
Another sufficient condition is that the two positive semidefinite
functions agree and
a backward completability condition holds. These special cases unify
and generalize many results
on converse Lyapunov theorems for differential equations and
differential inclusions that have appeared in the literature.


