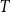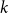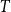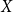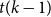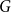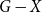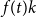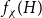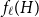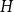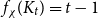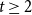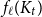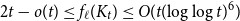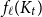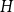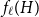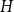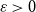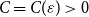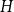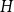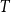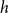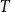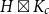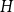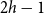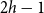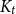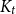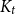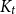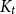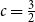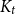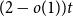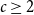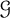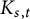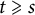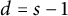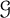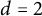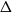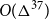8 results
Tight bound for the Erdős–Pósa property of tree minors
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 December 2024, pp. 321-325
-
- Article
-
- You have access
- HTML
- Export citation
On the choosability of
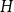 $H$-minor-free graphs
$H$-minor-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 129-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Excluded Tree Minor Theorem Revisited
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 85-90
-
- Article
-
- You have access
- HTML
- Export citation
Improved bound for improper colourings of graphs with no odd clique minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 September 2022, pp. 326-333
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved lower bound for the list chromatic number of graphs with no Kt minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1070-1075
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tree densities in sparse graph classes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 1385-1404
- Print publication:
- October 2022
-
- Article
- Export citation
Clustered 3-colouring graphs of bounded degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 June 2021, pp. 123-135
-
- Article
- Export citation
MINORS IN WEIGHTED GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 455-464
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation