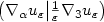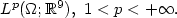3 results
Spatial heterogeneity in 3D-2D dimensional reduction
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 11 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 December 2004, pp. 139-160
- Print publication:
- January 2005
-
- Article
- Export citation
Equi-integrability results for 3D-2D dimension reduction problems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 7 / 2002
- Published online by Cambridge University Press:
- 15 September 2002, pp. 443-470
- Print publication:
- 2002
-
- Article
- Export citation
A-Quasiconvexity: Relaxation and Homogenization
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 5 / 2000
- Published online by Cambridge University Press:
- 15 August 2002, pp. 539-577
- Print publication:
- 2000
-
- Article
- Export citation