Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T10:29:18.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Equi-integrability results for 3D-2D dimension reduction problems

Published online by Cambridge University Press:  15 September 2002

Marian Bocea  and
Irene Fonseca
Marian Bocea
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA; [email protected].
Irene Fonseca
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA; [email protected].
Get access

Abstract

3D-2D asymptotic analysis for thin structures rests on the mastery of scaled gradients $\left( \nabla _{\alpha}u_\varepsilon\big| \frac{1}{\varepsilon}\nabla _3 u_\varepsilon\right) $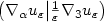 bounded in $L^p (\Omega; \mathbb{R}^9 ), \ 1 < p < +\infty .$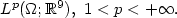 Here it is shown that, up to a subsequence, $u_\varepsilon$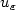 may be decomposed as $w_\varepsilon+ z_\varepsilon,$ 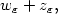where $z_\varepsilon$ 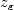carries all the concentration effects, i.e.$\left\{ \left| \left( \nabla _{\alpha }w_\varepsilon| \frac{1}{\varepsilon }\nabla _3 w_\varepsilon\right) \right| ^{p} \right\} $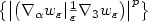 is equi-integrable, and $w_\varepsilon$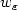 captures the oscillatory behavior, i.e.$z_\varepsilon\to 0$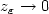 in measure. In addition, if $\{ u_\varepsilon\} $ 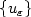is a recovering sequence then $z_\varepsilon= z_\varepsilon(x_\alpha )$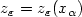 nearby $\partial \Omega.$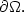

Keywords

Equi-integrabilitydimension reductionlower semicontinuitymaximal functionoscillationsconcentrationsquasiconvexity.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 7 , 2002 , pp. 443 - 470
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E. and Fusco, N., Semicontinuity problems in the calculus of variations. Arch. Rational. Mech. Anal. 86 (1984) 125-145. CrossRef
E. Acerbi and N. Fusco, An approximation lemma for W 1,p functions, in Material Instabilities in Continuum Mechanics and Related Mathematical Problems, edited by J.M. Ball. Heriot-Watt University, Oxford (1988).
Anzelotti, E., Baldo, S. and Percivale, D., Dimensional reduction in variational problems, asymptotic developments in $\Gamma $ -convergence, and thin structures in elasticity. Asymptot. Anal. 9 (1994) 61-100.
Balder, E.J., A general approach to lower semicontinuity and lower closure in optimal control theory. SIAM J. Control Optim. 22 (1984) 570-598. CrossRef
Ball, J.M., A version of the fundamental theorem for Young mesures, in PDE's and Continuum Models of Phase Transitions, edited by M. Rascle, D. Serre and M. Slemrod. Springer-Verlag, Berlin, Lecture Notes in Phys. 344 (1989) 207-215. CrossRef
Berliocchi, H. and Lasry, J.-M., Intégrands normales et mesures paramétrées en calcul des variations. Bull. Soc. Math. France 101 (1973) 129-184. CrossRef
K. Bhattacharya and A. Braides, Thin films with many small cracks. Preprint (2000).
Bhattacharya, K., Fonseca, I. and Francfort, G., An asymptotic study of the debonding of thin films. Arch. Rational. Mech. Anal. 161 (2002) 205-229. CrossRef
Bhattacharya, K. and James, R.D., A theory of thin films of martensitic materials with applications to microactuators. J. Mech. Phys. Solids 47 (1999) 531-576. CrossRef
A. Braides, Private communication.
Braides, A., Fonseca, I. and Francfort, G., 3D-2D asymptotic analysis for inhomogeneous thin films. Indiana Univ. Math. J. 49 (2000) 1367-1404.
Braides, A. and Fonseca, I., Brittle thin films. Appl. Math. Optim. 44 (2001) 299-323. CrossRef
S. Conti, I. Fonseca and G. Leoni, A $\Gamma $ -convergence result for the two-gradient theory of phase transitions, Preprint 01-CNA-008. Center for Nonlinear Analysis, Carnegie Mellon University (2001). Comm. Pure Applied Math. (to appear).
B. Dacorogna, Direct Methods in the Calculus of Variations. Springer-Verlag (1989).
Fonseca, I. and Francfort, G., On the inadequacy of scaling of linear elasticity for 3D-2D asymptotics in a nonlinear setting. J. Math. Pures Appl. 80 (2001) 547-562. CrossRef
I. Fonseca and G. Leoni, Modern Methods in the Calculus of Variations with Applications to Nonlinear Continuum Physics. Springer-Verlag (to appear).
Fonseca, I., Müller, S. and Pedregal, P., Analysis of concentration and oscillation effects generated by gradients. SIAM J. Math. Anal. 29 (1998) 736-756. CrossRef
Fox, D.D., Raoult, A. and Simo, J.C., A justification of nonlinear properly invariant plate theories. Arch. Rational. Mech. Anal. 124 (1993) 157-199. CrossRef
Iwaniec, T. and Sbordone, C., On the integrability of the Jacobian under minimal hypotheses. Arch. Rational. Mech. Anal. 119 (1992) 129-143. CrossRef
Kinderlehrer, D. and Pedregal, P., Characterizations of Young mesures generated by gradients. Arch. Rational. Mech. Anal. 115 (1991) 329-365. CrossRef
Kinderlehrer, D. and Pedregal, P., Gradient Young mesures generated by sequences in Sobolev spaces. J. Geom. Anal. 4 (1994) 59-90. CrossRef
J. Kristensen, Finite functionals and Young measures generated by gradients of Sobolev functions. Mathematical Institute, Technical University of Denmark, Mat-Report No. 1994-34 (1994).
Kristensen, J., Lower semicontinuity in spaces of weakly differentiable functions. Math. Ann. 313 (1999) 653-710. CrossRef
Le Dret, H. and Raoult, A., The nonlinear membrane model as variational limit of nonlinear three-dimensional elasticity. J. Math. Pures Appl. 74 (1995) 549-578.
Le Dret, H. and Raoult, A., Variational convergence for nonlinear shell models with directors and related semicontinuity and relaxation results. Arch. Rational. Mech. Anal. 154 (2000) 101-134. CrossRef
Liu, F.C., Luzin, A type property of Sobolev functions. Indiana Univ. Math. J. 26 (1997) 645-651. CrossRef
P. Pedregal, Parametrized mesures and Variational Principles. Birkhäuser, Boston (1997).
E.M. Stein, Singular integrals and differentiability properties of functions. Princeton University Press (1970).
Tartar, L., Compensated compactness and applications to partial differential equations, in Nonlinear Analysis and Mechanics: Heriot-Watt Symposium, edited by R. Knops. Longman, Harlow, Pitman Res. Notes Math. Ser. 39 (1979) 136-212.
L. Tartar, The compensated compactness method applied to systems of conservation laws, in Systems of Nonlinear Partial Differential Equations, edited by J.M. Ball. Riedel (1983).
Tartar, L., Étude des oscillations dans les équations aux dérivées partielles nonlinéaires. Springer-Verlag, Berlin, Lecture Notes in Phys. 195 (1994) 384-412. CrossRef
Shu, Y.C., Heterogeneous thin films of martensitic materials. Arch. Rational. Mech. Anal. 153 (2000) 39-90. CrossRef
L.C. Young, Generalized curves and the existence of an attained absolute minimum in the calculus of variations. C. R. Soc. Sci. Lettres de Varsovie, Classe III 30 (1937) 212-234.
L.C. Young, Lectures on the calculus of variations and optimal control theory. W.B. Saunders (1969).
W.P. Ziemer, Weakly Differentiable Functions. Sobolev spaces and functions of bounded variation. Springer-Verlag, Berlin (1989).