22 results
A classification of Shimura curves in
 $ \mathscr {A}_g$
$ \mathscr {A}_g$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
13 - Toroidal compactication
- from Part II - Extensions and applications
-
- Book:
- Modular Forms and String Theory
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024, pp 259-273
-
- Chapter
- Export citation
11 - Singular moduli and complex multiplication
- from Part II - Extensions and applications
-
- Book:
- Modular Forms and String Theory
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024, pp 208-222
-
- Chapter
- Export citation
There are at most finitely many singular moduli that are S-units
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 732-770
- Print publication:
- April 2024
-
- Article
- Export citation
BREUIL–KISIN–FARGUES MODULES WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 21 January 2020, pp. 1855-1904
- Print publication:
- November 2021
-
- Article
- Export citation
Binary quadratic forms and ray class groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 695-720
- Print publication:
- April 2020
-
- Article
- Export citation
Finiteness theorems for K3 surfaces and abelian varieties of CM type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1571-1592
- Print publication:
- August 2018
-
- Article
- Export citation
CM RELATIONS IN FIBERED POWERS OF ELLIPTIC FAMILIES – CORRIGENDUM
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 22 June 2018, p. 1029
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
CM Periods, CM Regulators, and Hypergeometric Functions, I
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 3 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-514
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 March 2018, pp. 175-208
- Print publication:
- January 2020
-
- Article
- Export citation
Corrigendum: Torsion points on abelian varieties of CM-type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 26 December 2017, p. 594
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
Bad reduction of genus
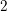 $2$ curves with CM jacobian varieties
$2$ curves with CM jacobian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 11 September 2017, pp. 2534-2576
- Print publication:
- December 2017
-
- Article
- Export citation
CM RELATIONS IN FIBERED POWERS OF ELLIPTIC FAMILIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 02 August 2017, pp. 941-956
- Print publication:
- September 2019
-
- Article
- Export citation
Height pairings on orthogonal Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 474-534
- Print publication:
- March 2017
-
- Article
- Export citation
On some Fricke families and application to the Lang–Schertz conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 18 May 2016, pp. 723-740
- Print publication:
- August 2016
-
- Article
- Export citation
Tate Cycles on Abelian Varieties with Complex Multiplication
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 1 / 01 February 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 198-213
- Print publication:
- 01 February 2015
-
- Article
-
- You have access
- Export citation
Twists of Shimura Curves
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 924-960
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF TORSION POINTS MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 339-347
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
INFINITUDE OF ELLIPTIC CARMICHAEL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 25 April 2012, pp. 45-60
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
MULTIPLICATIVE SUBGROUPS OF J0(N) AND APPLICATIONS TO ELLIPTIC CURVES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 4 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 08 March 2005, pp. 281-316
- Print publication:
- April 2005
-
- Article
- Export citation



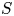
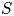
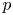
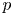
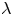
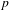
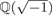
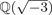
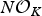
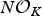
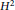
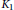
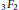
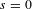





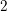
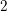
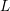
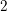
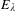

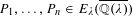

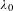
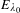
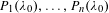
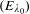
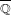
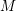
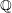
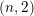

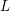
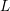
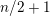
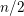

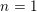
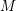
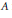
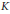
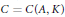
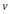
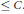
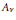
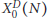
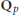
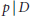
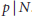
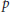
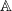 be a commutative algebraic group defined over a number field
be a commutative algebraic group defined over a number field 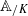 , we determine the average values of
, we determine the average values of 