Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T07:35:20.987Z Has data issue: false hasContentIssue false
  • English
  • Français

PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION

Part of: Arithmetic algebraic geometry Algebraic number theory: global fields Algebraic groups

Published online by Cambridge University Press:  20 March 2018

Urs Hartl  and
Rajneesh Kumar Singh
Urs Hartl
Affiliation:
Universität Münster, Mathematisches Institut, Einsteinstr. 62, D – 48149 Münster, GermanyURL: www.math.uni-muenster.de/u/urs.hartl/
Rajneesh Kumar Singh
Affiliation:
Ramakrishna Mission Vivekananda University, PO Belur Math, Dist Howrah 711202, West Bengal, India
Get access Rights & Permissions [Opens in a new window]

Abstract

Colmez [Périodes des variétés abéliennes a multiplication complexe, Ann. of Math. (2)138(3) (1993), 625–683; available at http://www.math.jussieu.fr/∼colmez] conjectured a product formula for periods of abelian varieties over number fields with complex multiplication and proved it in some cases. His conjecture is equivalent to a formula for the Faltings height of CM abelian varieties in terms of the logarithmic derivatives at 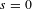$s=0$ of certain Artin $L$-functions. In a series of articles we investigate the analog of Colmez’s theory in the arithmetic of function fields. There abelian varieties are replaced by Drinfeld modules and their higher-dimensional generalizations, so-called $A$-motives. In the present article we prove the product formula for the Carlitz module and we compute the valuations of the periods of a CM $A$-motive at all finite places in terms of Artin $L$-series. The latter is achieved by investigating the local shtukas associated with the $A$-motive.

Keywords

Drinfeld moduleslocal shtukascomplex multiplicationArtin L-series

MSC classification

Primary: 11G09: Drinfel'd modules; higher-dimensional motives, etc.
Secondary: 11R42: Zeta functions and $L$-functions of number fields 11R58: Arithmetic theory of algebraic function fields 14L05: Formal groups, $p$-divisible groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 1 , January 2020 , pp. 175 - 208
Copyright
© The Author(s) 2018. Published by Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Both authors acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) in form of SFB 878.

References

Anderson, G., t-Motives, Duke Math. J. 53 (1986), 457–502.Google Scholar
Andreatta, F., Goren, E., Howard, B. and Madapusi Pera, K., Faltings heights of abelian varieties with complex multiplication, preprint, 2015, arXiv:math.NT/1508.00178.Google Scholar
Ax, J., Zero of polynomials over local fields – the Galois action, J. Algebra 15 (1970), 417–428.Google Scholar
Barquero-Sanchez, A. and Masri, R., On the Colmez conjecture for non-abelian CM fields, preprint, 2016, arXiv:math.NT/1604.01057.Google Scholar
Bhatt, B., Morrow, M. and Scholze, P., Integral p-adic Hodge theory – announcement, Math. Res. Lett. 22(6) (2015), 1601–1612; also available as arXiv:math.AG/1507.08129.Google Scholar
Bhatt, B., Morrow, M. and Scholze, P., Integral $p$ -adic Hodge theory, preprint, 2016, arXiv:math.AG/1602.03148.Google Scholar
Bornhofen, M. and Hartl, U., Pure Anderson motives over finite fields, J. Number Theory 129(2) (2009), 247–283; also available as arXiv:math.NT/0709.2815.Google Scholar
Bornhofen, M. and Hartl, U., Pure Anderson motives and abelian 𝜏-sheaves, Math. Z. 268 (2011), 67–100; also available as arXiv:math.NT/0709.2809.Google Scholar
Carlitz, L., On certain functions connected with polynomials in a Galois field, Duke Math. J. 1(2) (1935), 137–168.Google Scholar
Colmez, P., Périodes des variétés abéliennes a multiplication complexe, Ann. of Math. (2) 138(3) (1993), 625–683; available at http://www.math.jussieu.fr/∼colmez.Google Scholar
Drinfeld, V.G., Elliptic modules, Math. USSR-Sb. 23 (1976), 561–592.Google Scholar
Eisenbud, D., Commutative Algebra with a View Toward Algebraic Geometry, GTM, Volume 150 (Springer, Berlin, 1995).Google Scholar
Gardeyn, F., The structure of analytic 𝜏-sheaves, J. Number Theory 100 (2003), 332–362.Google Scholar
Goss, D., Basic Structures of Function Field Arithmetic, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), Volume 35 (Springer, Berlin–Heidelberg–New York, 1996).Google Scholar
Grothendieck, A., Élements de Géométrie Algébrique, Publ. Math. Inst. Hautes Études Sci. 4, 8, 11, 17, 20, 24, 28, 32; Bures-Sur-Yvette, 1960–1967; see also Grundlehren 166, Springer, Berlin etc 1971; also available at http://www.numdam.org/search/grothendieck-a.Google Scholar
Hartl, U., A dictionary between Fontaine-theory and its analogue in equal characteristic, J. Number Theory 129 (2009), 1734–1757; also available as arXiv:math.NT/0607182.Google Scholar
Hartl, U. and Juschka, A.-K., Pink’s theory of Hodge structures and the Hodge conjecture over function fields, in Proceedings of the Conference on ‘t-Motives: Hodge Structures, Transcendence and Other Motivic Aspects’, BIRS, Banff, Canada 2009 (ed. Böckle, G., Goss, D., Hartl, U. and Papanikolas, M.), (EMS, Zürich, 2018); also available as arXiv:math/1607.01412.Google Scholar
Hartl, U. and Kim, W., Local shtukas, Hodge–Pink structures and Galois representations, in Proceedings of the Conference on ‘t-Motives: Hodge Structures, Transcendence and Other Motivic Aspects’, BIRS, Banff, Canada 2009 (ed. Böckle, G., Goss, D., Hartl, U. and Papanikolas, M.), (EMS, Zürich, 2018), to appear; also available as arXiv:math/1512.05893.Google Scholar
Hartl, U. and Singh, R. K., Local shtukas and divisible local Anderson modules, preprint, 2015, arXiv:math/1511.03697.Google Scholar
Lubin, J. and Tate, J., Formal complex multiplication in local fields, Ann. of Math. (2) 81 (1965), 380–387; available at http://www.jstor.org/stable/1970622.Google Scholar
Obus, A., On Colmez’s product formula for periods of CM-abelian varieties, Math. Ann. 356(2) (2013), 401–418; also available as arXiv:math.NT/1107.0684.Google Scholar
Rosen, M., Number Theory in Function Fields, GTM, Volume 210 (Springer, New York, 2002).Google Scholar
Schindler, A., Anderson $A$ -Motive mit komplexer Multiplikation, Diploma thesis, University of Muenster, 2009; available at http://www.math.uni-muenster.de/u/urs.hartl/Publikat/Schindler_Diplomarbeit.pdf.Google Scholar
Scholze, P., Canonical $q$ -deformations in arithmetic geometry, preprint, 2016, arXiv:math.AG/1606.01796.Google Scholar
Serre, J.-P., Classes de corps cyclotomiques, d’après K. Iwasawa, Séminaire Bourbaki, Volume 5, Exp. No. 174 (1958–1960) pp. 83–93 (Soc. Math. France, Paris, 1995).Google Scholar
Serre, J.-P., Linear Representations of Finite Groups, GTM, Volume 42 (Springer, New York–Heidelberg, 1977).Google Scholar
Serre, J.-P., Local Fields, GTM, Volume 67 (Springer, New York–Berlin, 1979).Google Scholar
Silverman, J., The Arithmetic of Elliptic Curves, GTM, Volume 106 (Springer, New York, 1986).Google Scholar
Tate, J., Les conjectures de Stark sur les fonctions L d’Artin en s = 0 (ed. Bernardi, D. and Schappacher, N.), Progress in Mathematics, Volume 47 (Birkhäuser Boston, Inc., Boston, MA, 1984).Google Scholar
Weil, A., Sur les courbes algébriques et les variétés qui s’en déduisent, Actualités Sci. Ind. 1041 = Publ. Inst. Math. Univ. Strasbourg, Volume 7 (Hermann et Cie, Paris, 1948).Google Scholar
Yang, T., Arithmetic intersection on a Hilbert modular surface and the Faltings height, Asian J. Math. 17(2) (2013), 335–381; also available as arXiv:math.NT/1008.1854.Google Scholar
Yuan, X. and Zhang, S.-W., On the averaged Colmez conjecture, preprint, 2015, arXiv:math.NT/1507.06903.Google Scholar