 $\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
$\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
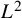 $L^2$-Bound of the Eisenstein series
$L^2$-Bound of the Eisenstein series
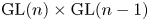 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
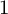 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 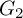 $G_2$
$G_2$
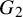 $G_2$
$G_2$
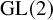 $\mathrm {GL}(2)$
$\mathrm {GL}(2)$