This journal utilises an Online Peer Review Service (OPRS) for submissions. By clicking "Continue" you will be taken to our partner site https://cup.msp.org/submit_new.php?jpath=pi. Please be aware that your Cambridge account is not valid for this OPRS and registration is required. We strongly advise you to read all "Author instructions" in the "Journal information" area prior to submitting.
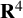 $\mathbf {R}^{4}$
$\mathbf {R}^{4}$
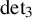 $\operatorname {det}_3$
$\operatorname {det}_3$
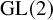 $\mathrm {GL}(2)$
$\mathrm {GL}(2)$