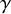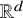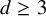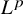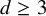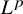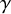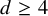Sharp smoothing properties of averages over curves

Abstract

We prove sharp smoothing properties of the averaging operator defined by convolution with a measure on a smooth nondegenerate curve $\gamma $ in $\mathbb R^d$ , $d\ge 3$ . Despite the simple geometric structure of such curves, the sharp smoothing estimates have remained largely unknown except for those in low dimensions. Devising a novel inductive strategy, we obtain the optimal $L^p$ Sobolev regularity estimates, which settle the conjecture raised by Beltran–Guo–Hickman–Seeger [1]. Besides, we show the sharp local smoothing estimates on a range of p for every $d\ge 3$ . As a result, we establish, for the first time, nontrivial $L^p$ boundedness of the maximal average over dilations of $\gamma $ for $d\ge 4$ .

1 Introduction

The regularity property of integral transforms defined by averages over submanifolds is a fundamental subject in harmonic analysis, which has been extensively studied since the 1970s. There is an immense body of literature devoted to the subject (see, for example, [33, 21, 32, 8] and references therein). However, numerous problems remain wide open. The regularity property is typically addressed in the frameworks of $L^p$ improving, $L^p$ Sobolev regularity, and local smoothing estimates, to which $L^p$ boundedness of the maximal average is also closely related. In this paper, we study the smoothing estimates for the averaging operator given by convolution with a measure supported on a curve.

Let $I=[-1,1]$ and $\gamma $ be a smooth curve from I to $\mathbb R^d$ . We define a measure $\mathfrak m_t$ supported on $t\gamma $ by

$$\begin{align*}\langle \mathfrak m_t , f \rangle = \int f(t\gamma(s)) \psi(s) ds, \end{align*}$$

where $\psi \in \mathrm C_c^\infty ((-1,1))$ . We are concerned with $d\ge 3$ since all the problems we address in the current paper are well understood when $d=2$ . We consider the averaging operator

$$\begin{align*}\mathcal A_t f(x)= f\ast \mathfrak m_t(x) \end{align*}$$

and study the above-mentioned regularity problems on $\mathcal A_t $ under the assumption that $\gamma $ is nondegenerate, that is to say,

(1.1) $$ \begin{align} \det( \gamma'(s), \dots, \gamma^{(d)}(s) )\neq0, \quad s\in I. \end{align} $$

The $L^p$ improving property of $ \mathcal A_t$ for a fixed $t\neq 0$ now has a complete characterization; see [7, 34] (also, see [36] for generalizations to variable coefficient settings). However, $L^p$ Sobolev and local smoothing estimates for $\mathcal A_t$ turned out to be more involved and are far less well understood. Recently, there has been progress in low dimensions $d= 3, 4$ ([24, 14, 1, 2]), but it does not seem feasible to extend the approaches in the recent works to higher dimensions. We discuss this matter in detail near the end of the introduction. By devising an inductive strategy, we prove the optimal $L^p$ Sobolev regularity and sharp local smoothing estimates in any dimension $d\ge 3$ . As a result, we also obtain $L^p$ boundedness of the associated maximal function which was unknown for $d\ge 4$ .

$L^p$ Sobolev regularity

Let $2\le p\le \infty $ . We set $ \mathcal A f=\mathcal A_1 f $ and consider the $L^p$ Sobolev regularity estimate

(1.2) $$ \begin{align} \| \mathcal A f\|_{L_\alpha^p(\mathbb R^d)} \le C \|f\|_{L^p(\mathbb R^d)}. \end{align} $$

When $d=2$ , the estimate holds if and only if $\alpha \le 1/p$ (e.g., see [6]). In higher dimensions, however, the problem of obtaining (1.2) with the sharp smoothing order $\alpha $ becomes highly nontrivial except for the $L^2\to L^2_{1/d}$ estimate which is an easy consequence of the decay property of the Fourier transform of ${\mathfrak m}_t$ :

(1.3) $$ \begin{align} |\widehat {\mathfrak m}_t(\xi)|\le C(1+|t\xi|)^{-1/d}\,.\end{align} $$

It was conjectured by Beltran, Guo, Hickman and Seeger [2, Conjecture 1] that the estimate (1.2) holds for $\alpha \le 1/p$ if $2d-2<p<\infty $ . When $d=3$ , the conjecture was verified by the conditional result of Pramanik and Seeger [24] and the decoupling inequality due to Bourgain and Demeter [4] (see [20, 35] for earlier results). The case $d=4$ was recently obtained by Beltran et al. [2]. Our first result proves the conjecture for every $d\ge 5$ .

Theorem 1.1. Let $d\ge 3$ . Suppose $\gamma $ is a smooth nondegenerate curve. Then, the estimate (1.2) holds for $\alpha \le 1/p$ if $p> 2(d-1)$ .

Interpolation with the $L^2\to L^2_{1/d}$ estimate gives (1.2) for $\alpha <(p+2)/(2dp)$ when $2< p \le 2(d-1)$ . It is also known that (1.2) fails if $\alpha> \alpha (p):=\min (1/p, (p+2)/(2dp)) $ (see [2, Proposition 1.2]). Thus, only the estimate (1.2) with $\alpha =\alpha (p) $ remains open for $2< p \le 2(d-1)$ . Those endpoint estimates seem to be a subtle problem. The argument in this paper provides simpler alternative proofs of the previous results for $d=3,4$ . Theorem 1.1 remains valid as long as $\gamma \in \mathrm C^{2d}(I)$ (see Theorem 4.1). However, we do not try to optimize the regularity assumption.

The result in Theorem 1.1 can be easily generalized to curves of different types. We say a smooth curve $\gamma $ from I to $\mathbb R^d$ is of finite type if there is an $ \ell $ such that $\operatorname {\mathrm {span}} \{ \gamma ^{(1)}(s), \dots , \gamma ^{( \ell )}(s)\}=\mathbb R^d$ for each $s\in I$ . The type at s is defined to be the smallest of such $ \ell $ and the maximal type is the supremum over $s \in I$ of the type at s. (See, e.g., [24, 12].) Using Theorem 1.1 and a rescaling argument ([24, 12]), one can obtain the following, which proves the Conjecture 2 in [2].

Corollary 1.2. Let $d\ge 3$ , $ \ell> d$ and $2 \le p <\infty $ . Suppose $\gamma $ is a curve of maximal type $ \ell $ . Then the estimate (1.2) holds for $\alpha \le \min \big (\alpha (p) , \,1/ \ell \big )$ if $p\neq \ell $ when $ \ell \ge 2d-2$ , and if $p\in [2, 2\ell /(2d-\ell ))\cup ( 2d-2, \infty )$ when $d< \ell < 2d-2$ .

By interpolation, (1.2) holds for $\alpha < \min \big (\alpha (p) , \,1/ \ell \big )$ if $p= \ell $ when $ \ell \ge 2d-2$ , and if ${2 \ell }/{(2d- \ell )} \le p \le 2d-2$ when $d< \ell < 2d-2$ . These estimates are sharp. Since a finite type curve contains a nondegenerate subcurve and the $L^2\to L^2_{1/ \ell }$ estimate is optimal, (1.2) fails if $\alpha> \min \big (\alpha (p) , \,1/ \ell \big )$ . In particular, when $ \ell \ge 2d-2$ , Corollary 1.2 resolves the problem of the Sobolev regularity estimate (1.2). In fact, failure of the $L^ \ell \to L^ \ell _{1/ \ell }$ bound was shown in [2] using Christ’s example [6]. By [28, Theorem 1.1], Corollary 1.2 also gives $H^1(\mathbb R^d)\to L^{1,\infty }(\mathbb R^d)$ bound on the lacunary maximal function $f\to \sup _{k\in \mathbb Z} |f\ast \mathfrak m_{2^k}|$ whenever $\gamma $ is of finite type.

Sharp local smoothing

We now consider the estimate

(1.4) $$ \begin{align} \| \chi(t) \mathcal A_t f\|_{L_\alpha^p(\mathbb R^{d+1})} \le C \|f\|_{L^p(\mathbb R^d)}, \end{align} $$

where $\chi $ is a smooth function supported in $(1/2,4)$ . Compared with the $L^p$ Sobolev estimate (1.2), the additional integration in t is expected to yield extra smoothing. Such a phenomenon is called local smoothing, which has been studied for the dispersive equations to a great extent (e.g., see [29, 9]). However, the local smoothing for the averaging operators exhibits considerably different nature.

In particular, there is no local smoothing when $p=2$ . Besides, a bump function example shows (1.4) holds only if $\alpha \le 1/d$ . As we shall see, the estimate (1.4) fails unless $\alpha \le 2/p$ (Proposition 3.9 below). So, it seems to be plausible to conjecture that (1.4) holds for $\alpha <\min (2/p, 1/d)$ if $2<p<\infty $ . For $d=2$ , the conjecture follows by the recent result on Sogge’s local smoothing conjecture for the wave operator ([30, 38, 16, 4]), which is due to Guth, Wang and Zhang [11]. When $d=3$ , some local smoothing estimates were utilized by Pramanik and Seeger [24] and Beltran et al. [1] to prove $L^p$ maximal bound.

Nevertheless, for $d\ge 3$ , no local smoothing estimate up to the sharp order $2/p$ has been known previously.

Theorem 1.3. Let $d\ge 3$ . Suppose $\gamma $ is a smooth nondegenerate curve. Then, if $p\ge 4d-2$ , the estimate (1.4) holds true for $\alpha <2/p$ .

Theorem 1.3 remains valid as far as $\gamma \in \mathrm C^{3d+1}(I)$ (see Theorem 2.2 below).

Maximal estimate

The local smoothing estimate (1.4) has been of particular interest in connection to $L^p$ boundedness of the maximal operator

$$ \begin{align*} M f(x)=\sup_{0<t} |\mathcal A_t f(x)| \end{align*} $$

([19, 27, 24, 1]) and problems in geometric measure theory (see, e.g., [38] and Corollary 1.6 below). If the estimate (1.4) holds for some $\alpha>1/p$ , $L^p$ boundedness of M follows by a standard argument relying on the Sobolev embedding ([24]).

The study of the maximal functions generated by dilations of submanifolds goes back to Stein’s spherical maximal theorem [31] (see, also, [32, Ch.10] and [13]). The circular maximal theorem was later proved by Bourgain [3] (also, see [30, 19, 26, 27, 15]). Afterwards, a natural question was whether the maximal operator M under consideration in the current paper is bounded on $L^p$ for some $p\neq \infty $ when $d\ge 3$ . In view of Stein’s interpolation argument based on $L^2$ estimate [31], proving $L^p$ boundedness of M becomes more challenging as d increases since the decay of the Fourier transform of $\mathfrak m_t$ gets weaker (see (1.3)). Though the question was raised as early as in the late 1980s, it remained open for any $d\ge 3$ until recently. In $\mathbb R^3$ , the first positive result was obtained by Pramanik and Seeger [24] and the range of p was further extended to $p>4$ thanks to the decoupling inequality for the cone [4]. Very recently, the authors [14] proved $L^p$ boundedness of M on the optimal range, that is, M is bounded on $L^p$ if and only if $p>3$ . The same result was independently obtained by Beltran et al. [1].

However, no nontrival $L^p$ bound on M has been known in higher dimensions. The following establishes existence of such maximal bounds for every $d\ge 4$ .

Theorem 1.4. Let $d\ge 4$ . Suppose $\gamma $ is a smooth nondegenerate curve. Then, for $p>2(d-1)$ we have

(1.5) $$ \begin{align} \| Mf \|_{L^p(\mathbb R^d)} \le C \|f\|_{L^p(\mathbb R^d)}. \end{align} $$

The result is a consequence of Theorem 1.3. Since the estimate (1.4) holds for $p=2$ and $\alpha =1/d$ , interpolation gives (1.4) for some $\alpha>1/p$ when $2d-2<p<\infty $ . So, the maximal estimate (1.5) follows, as mentioned before, by a standard argument. A natural conjecture is that M is bounded on $L^p$ if and only if $p>d$ . M cannot be bounded on $L^p$ if $p\le d$ , as can be seen by a simple adaptation of the argument in [14, Proposition 4.4]. Theorem 1.4 also extends to the finite type curves by the rescaling argument. The following result is sharp when $\ell \ge 2(d-1)$ .

Corollary 1.5. Let $d\ge 4$ and $\ell> d$ . Suppose $\gamma $ is a curve of maximal type $\ell $ . Then the estimate (1.5) holds if $p>\max (\ell ,2(d-1))$ .

Packing of curves in $\mathbb R^d$

The sharp local smoothing estimate (1.4) in Theorem 1.3 has interesting measure theoretic consequences concerning unions of curves generated by translation and dilation of a nondegenerate curve. The following generalizes Wolff’s result [38, Corollary 3], where unions of circles in $\mathbb R^2$ were considered (see also [17, 18, 37] for earlier results).

Corollary 1.6. Let $\gamma $ be a smooth nondegenerate curve in $\mathbb R^d$ , $d\ge 3$ , and let $E \subset \mathbb R^{d+1}$ be a set of Hausdorff dimension greater than $d-1$ . Suppose F is a set in $\mathbb R^d$ such that $(x+t\gamma (I))\cap F$ has positive one-dimensional outer measure for all $(x,t) \in E$ . Then F has positive outer measure.

Corollary 1.6 follows by Theorem 1.3 and the argument in [38]. The result does not hold in general without the nondegeneracy assumption on $\gamma $ as one can easily see considering a curve contained in a lower dimensional vector space. The same result continues to be valid for the finite type curves. Consequently, Corollary 1.6 implies the following.

Corollary 1.6^′. Let $\gamma $ be a smooth finite type curve in $\mathbb R^d$ , $d\ge 3$ , and let E and F be compact subsets in $\mathbb R^d$ . Suppose E has Hausdorff dimension greater than $d-1$ and for each $x \in E$ there is $t(x)> 0$ such that $x+t(x)\gamma (I)\subset F$ . Then, F has positive measure.

Our approach

To prove $L^p$ ( $p\neq 2$ ) smoothing properties of $\mathcal A_t$ , we need more than the decay of $\widehat {\mathfrak m}_t$ , that is, (1.3). When $d=2$ , we have rather a precise asymptotic expansion of $\widehat {\mathfrak m}_t$ , which makes it possible to relate $\mathcal A_t$ to other forms of operators. In fact, one can use the estimate for the wave operator (e.g., [27, 35, 15]) to obtain local smoothing estimate. However, in higher dimensions $d\ge 3$ , to compute $\widehat {\mathfrak m}_t$ explicitly is not a simple matter. Even worse, this becomes much more complicated as d increases since one has to take into account the derivatives $\gamma ^{(k)}(s)\cdot \xi $ , $k=2,\dots , d$ . The common approach in the previous works ([24, 1, 2]) to get around this difficulty was to use detailed decompositions (of various scales) on the Fourier side away from the conic sets where $\widehat {\mathfrak m}_t$ decays slowly. The consequent decompositions were then combined with the decoupling or square function estimate ([20, 23, 24, 25, 1, 2]). However, this type of approach based on fine scale decomposition becomes exceedingly difficult to manage as the dimension d gets larger and, consequently, does not seem to be tractable in higher dimensions.

To overcome the difficulty, we develop a new strategy which allows us to dispense with such sophisticated decomposition. Before closing the introduction, we briefly discuss the key ingredients of our approach.

• • The main novelty of this paper lies in an induction argument which we build on the local nondegeneracy assumption:

  (𝔑(L,B)) $$\begin{align} \sum_{\ell=1}^L |\langle \gamma^{(\ell)}(s), \xi\rangle| \ge B^{-1}|\xi| \end{align} $$
  for a constant $B\ge 1$ . To prove our results, we consider the operator $\mathcal A_t[\gamma , a]$ (see (2.2) below for its definition). Clearly, ${\mathfrak N({d}, {B'})}$ holds for a constant $B'>0$ if $\gamma $ satisfies the condition (1.1). However, instead of considering the case $L=d$ alone, we prove the estimate for all $L=2,\dots , d$ under the assumption that $\mathfrak N(L, B)$ holds on the support of a. See Theorem 2.2 and 4.1. A trivial (yet, important) observation is that ${\mathfrak N({L-1}, B)}$ implies ${\mathfrak N(L, B)}, $ so we may think of $\mathcal A_t[\gamma , a]$ as being more degenerate as L gets larger. Thanks to this hierarchical structure, we may use an inductive strategy along the number L. See Proposition 2.3 and 4.2 below.

• • We extend the rescaling [12, 14] and iteration [24] arguments. Roughly speaking, we combine the first with the induction assumption in Proposition 2.3 (or 4.2) to handle the less degenerate parts, and use the latter to deal with the remaining part. In order to generalize those arguments, we introduce a class of symbols which are naturally adjusted to a small subcurve (Definition 2.4). We also use the decoupling inequalities for the nondegenerate curves obtained by Beltran et al. [2] (Corollary 2.15). Their inequalities were deduced from those due to Bourgain, Demeter and Guth [5]. Instead of applying the inequalities directly, we use modified forms which are adjusted to the sharp smoothing orders of the specific estimates (see (2.40) and (2.41) below). This makes it possible to obtain the sharp estimates on extended ranges.

Organization of the paper. We first prove Theorem 1.3 whose proof is more involved than that of Theorem 1.1. In Section 2, the proof of Theorem 1.3 is reduced to that of Proposition 2.9, which we prove while assuming Proposition 2.10. The proof of Proposition 2.10 is given in Section 3. We prove Theorem 1.1 in Section 4.

2 Smoothing estimates with localized frequency

In this section, we consider an extension of Theorem 1.3 via microlocalization (see Theorem 2.2 below) so that we can prove it in an inductive manner. We then reduce the matter to proving Proposition 2.9, which we show by applying Proposition 2.10. We also obtain some preparatory results.

Let $1\le L \le d$ be a positive integer and $B\ge 1$ be a large number. For quantitative control of estimates we consider the following two conditions:

(2.1) $$ \begin{align} &\qquad \max_{0\le j\le 3d+1} |\gamma^{(j)}(s)|\,\le\, B, &&\quad s\in I, \end{align} $$

(𝔙(L,B)) $$\begin{align} &\operatorname{\mathrm{Vol}} \big( \gamma^{(1)}(s), \dots,\gamma^{(L)}(s) \big)\ge 1/B, &&s\in I, \end{align}$$

where $ \operatorname {\mathrm {Vol}} (v_1,\dots ,v_L)$ denotes the L-dimensional volume of the parallelepiped generated by $v_1,\dots , v_L$ . By finite decomposition and a standard reduction using rescaling and a change of variables, the constant B can be taken to be close to $1$ (see Section 2.2).

Notation. For nonnegative quantities A and $ D$ , we denote $A\lesssim D$ if there exists an independent positive constant C such that $A\le CD$ , but the constant C may differ at each occurrence depending on the context, and $A \lesssim _{B}\! D$ means the inequality holds with an implicit constant depending on B. Throughout the paper, the constant C mostly depends on B. However, we do not make it explicit every time since it is clear in the context. By $A=O(D)$ we denote $|A|\lesssim D$ .

Definition 2.1. For $k\ge 0$ , let $ \mathbb A_k=\{ \xi \in \mathbb R^d: 2^{k-1} \le |\xi | \le 2^{k+1}\}.$ We say $a\in \mathrm C^{d+L+2}(\mathbb R^{d+2})$ is a symbol of type $(k, L, B)$ relative to $\gamma $ if $\operatorname {\mathrm {supp}} a \subset I \times [2^{-1},4] \times \mathbb A_k$ , $\mathfrak N(L, B)$ holds for $\gamma $ whenever $(s,t,\xi )\in \operatorname {\mathrm {supp}} a$ for some t, and

$$ \begin{align*} |\partial_s^{j}\partial^{l}_t\partial_\xi^\alpha a(s,t,\xi)|\le B |\xi|^{-|\alpha|} \end{align*} $$

for $(j,l,\alpha )\in \mathcal I_L:=\{(j,l,\alpha ): 0\le j\le 1,\, 0\le l\le 2L,\, |\alpha |\le d+L+2\}$ .

We define an integral operator by

(2.2) $$ \begin{align} \mathcal A_t[\gamma, a]f(x)=(2\pi)^{-d}\iint_{\mathbb R} e^{i(x-t\gamma(s))\cdot\xi}\,a(s,t,\xi)ds \,\widehat f (\xi)\,d\xi. \end{align} $$

Note $\mathcal A_t f=\mathcal A_t[\gamma , \psi ]f$ . Theorem 1.3 is a consequence of the following.

Theorem 2.2. Let $\gamma \in \mathrm C^{3d+1}(I)$ satisfy (2.1) and $\mathfrak V(L,B)$ for some $B\ge 1$ . Suppose a is a symbol of type $(k, L, B)$ relative to $\gamma $ . Then, if $p\ge 4L-2$ , for $\epsilon>0$ there is a constant $C_\epsilon =C_\epsilon (B)$ such that

(2.3) $$ \begin{align} \| \mathcal A_t[\gamma, a]f\|_{L^p(\mathbb R^{d+1})}\le C_\epsilon 2^{(-\frac{2}p+\epsilon) k}\|f\|_{L^p(\mathbb R^d)}. \end{align} $$

Theorem 2.2 is easy to prove when $L=1$ . Indeed, (2.3) follows from the estimate

$$\begin{align*}|\mathcal A_t[\gamma, a]f(x)|\lesssim_B \int_I K\ast |f|(x-t\gamma(s)) \,ds,\end{align*}$$

where $K(x)= 2^{(d-1)k}(1+ |2^{k}x|)^{-d-3}.$ Note $|\gamma '(s)\cdot \xi |\sim 2^k$ if $(s,t,\xi )\in \operatorname {\mathrm {supp}} a$ for some t. By integration by parts in s, $\mathcal A_t[\gamma , a]=t^{-1}\mathcal A_t[\gamma , \tilde a]$ , where $\tilde a=i(\gamma '(s)\cdot \xi \, \partial _s a -\gamma "(s)\cdot \xi \, a)/(\gamma '(s)\cdot \xi )^2$ . Since $|\partial _\xi ^{\alpha } \tilde a|\lesssim |\xi |^{-|\alpha |-1}$ for $|\alpha |\le d+3$ , routine integration by parts in $\xi $ gives the desired estimate (e.g., see Proof of Lemma 2.7 below). When $L=2$ , Theorem 2.2 follows by the result in [24, Theorem 4.1] and the decoupling inequality in [4].

Once we have Theorem 2.2, the proof of Theorem 1.3 is straightforward. By the Littlewood–Paley decomposition it is sufficient to show the estimate (2.3) for $p\ge 4d-2$ with $a_k(s,t,\xi )=\psi (s) \chi (t) \beta (2^{-k}|\xi |)$ , where $\beta \in \mathrm C_c^\infty ((1/2,2))$ . This can be made rigorous using $\iint e^{-i t(\tau +\gamma (s)\cdot \xi )} \psi (s) \chi (t) dsdt =O((1+|\tau |)^{-N})$ for any N if $|\tau |\ge (1+\max _{s\in \operatorname {\mathrm {supp}} \psi } |\gamma (s)|)|\xi |$ . Since $\gamma $ satisfies the condition (1.1), $a_k$ is of type $(k, d, B)$ relative to $\gamma $ for a large B. Therefore, Theorem 1.3 follows from Theorem 2.2.

Theorem 2.2 is immediate from the next proposition, which places Theorem 2.2 in an inductive framework.

Proposition 2.3. Let $2 \le N \le d$ . Suppose Theorem 2.2 holds for $L=N-1$ . Then, Theorem 2.2 holds true with $L=N$ .

To prove Proposition 2.3, from this section to Section 3 we fix $N\in [2, d]$ , $\gamma $ satisfying ${\mathfrak V(N, B)}$ , and a symbol $ a$ of type $(k, N, B)$ relative to $\gamma $ .

One of the main ideas is that by a suitable decomposition of the symbol we can separate from $\mathcal A_t[\gamma ,a]$ the less degenerate part which corresponds to $L=N-1$ . To this part we apply the assumption combined with a rescaling argument. To do this, we introduce a class of symbols which are adjusted to short subcurves of $\gamma $ .

2.1 Symbols associated to subcurves

We begin with some notations. Let $N\ge 2$ , and let $\delta $ and $B'$ denote numbers such that

$$ \begin{align*} 2^{-k /N}\le \delta\le 2^{-7dN}B^{-6N}, \qquad B \le B' \le B^C \end{align*} $$

for a large constant $C\ge 3d+1$ . We note that ${\mathfrak V({N-1}, {B'})}$ holds for some $B'$ . In fact, ${\mathfrak V({N-1}, {B^2})}$ follows by (2.1) and ${\mathfrak V(N, B)}$ .

For $s\in I$ , we define a linear map $ \widetilde {\mathcal L}^\delta _s:\mathbb R^{d}\mapsto \mathbb R^{d}$ as follows:

(2.4) $$ \begin{align} \begin{aligned} (\widetilde{\mathcal L}_{s}^\delta)^\intercal \gamma^{(j)}(s) &=\delta^{N-j}\gamma^{(j)}(s), \qquad && j=1,\dots,N-1, \\ (\widetilde{\mathcal L}_{s}^\delta)^\intercal v &=v, \qquad \qquad \quad~ && v\in \big(\mathrm V_s^{\gamma,N-1}\big)^{\perp}, \end{aligned} \end{align} $$

where $\mathrm V_s^{\gamma ,\ell } = \operatorname {\mathrm {span}} \big \{ \gamma ^{(j)}(s) : j=1,\dots ,\ell \big \}$ . $\widetilde {\mathcal L}_{s}^\delta $ is well defined since ${\mathfrak V({N-1}, {B^2})}$ holds for $\gamma $ . The linear map $\widetilde {\mathcal L}_{s}^\delta $ naturally appears when we rescale a subcurve of length about $\delta $ (see the proofs of Lemma 2.7 and 2.8). We denote

(2.5) $$ \begin{align} \mathcal L_{s}^\delta(\tau, \xi)= \big(\delta^N \tau - \gamma(s)\cdot \widetilde{\mathcal L}_s^\delta \xi,\,\, \widetilde{\mathcal L}_s^\delta \xi\big), \qquad (\tau, \xi)\in \mathbb R\times \mathbb R^d. \end{align} $$

We set $G(s)=(1,\gamma (s))$ and define

$$ \begin{align*} \Lambda_k(s,\delta, B')= \bigcap_{0\le j\le N-1} \big\{(\tau,\xi) \in \mathbb R \times \mathbb A_k & : |\langle G^{(j)}(s),(\tau,\xi)\rangle| \le B'2^{k+5} \delta^{N-j} \big \}. \end{align*} $$

Definition 2.4. Let such that . Then, by we denote the set of $\mathfrak a \in \mathrm C^{d+N+2}(\mathbb R^{d+3})$ such that

(2.6)

(2.7)

We define $\operatorname {\mathrm {supp}}_{\xi } \mathfrak a=\bigcup _{s,t,\tau } \operatorname {\mathrm {supp}} \mathfrak a(s,t,\tau ,\cdot )$ and $\operatorname {\mathrm {supp}}_{s, \xi } \mathfrak a=\bigcup _{t,\tau } \operatorname {\mathrm {supp}} \mathfrak a(\cdot ,t,\tau ,\cdot )$ , and $\operatorname {\mathrm {supp}}_{s} \mathfrak a$ and $\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a$ are defined likewise. Note that a statement $S(s, \xi )$ , depending on $(s, \xi )$ , holds on $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$ if and only if $S(s,\xi )$ holds whenever $(s,t, \tau ,\xi ) \in \operatorname {\mathrm {supp}} \mathfrak a$ for some t, $\tau $ .

Denote $\mathrm V_s^{G,\ell } = \operatorname {\mathrm {span}} \{(1,0), G'(s), \dots , G^{(\ell )}(s) \}.$ We take a close look at the map ${\mathcal L}_s^\delta $ . By the equations (2.4) and (2.5) we have

(2.8) $$ \begin{align} \begin{cases} \begin{aligned} (\mathcal L_s^\delta)^\intercal G(s) &= \delta^{N}(1,0), \\[2pt] (\mathcal L_s^\delta)^\intercal G^{(j)}(s) &= \delta^{N-j}G^{(j)}(s), \qquad &&j=1,\dots, N-1, \\ ({\mathcal L}_s^\delta)^\intercal v &=v, \qquad&& v\in (\mathrm V_s^{G,N-1} )^\perp. \end{aligned} \end{cases} \end{align} $$

The first identity is clear since $(\mathcal L_s^\delta )^\intercal (\tau , \xi )=(\delta ^N \tau , (\widetilde {\mathcal L}_s^\delta )^\intercal \xi -\tau (\widetilde {\mathcal L}_s^\delta )^\intercal \gamma (s))$ . The second and the third follow from (2.4) since $G^{(j)}\in \{0\} \times \mathbb R^d$ , $1 \le j \le N-1$ , $\big ( \mathrm V_s^{G,N-1} \big )^\perp \subset \{0\} \times \mathbb R^d$ , and $(\mathcal L_s^\delta )^\intercal (0,\xi )=(0,(\widetilde {\mathcal L}_s^\delta )^\intercal \xi )$ . Furthermore, there is a constant $C=C(B)$ , independent of s and $\delta $ , such that

(2.9) $$ \begin{align} | \mathcal L_{s}^{\delta} (\tau, \xi)| \le C|(\tau,\xi)|. \end{align} $$

Note that (2.9) is equivalent to $ |( \mathcal L_{s}^{\delta })^\intercal (\tau , \xi )| \le C|(\tau ,\xi )|$ . The inequality is clear from (2.4) because ${\mathfrak V({N-1}, {B^2})}$ holds and all the eigenvalues of $(\widetilde {\mathcal L}_{s}^\delta )^\intercal $ are contained in the interval $(0,1]$ .

Lemma 2.5. Let $ \mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B')$ and ${\mathfrak V({N-1}, {B'})}$ hold for $\gamma $ . Then, there exists a constant $C=C(B')$ such that

(2.10) $$ \begin{align} C^{-1} |(\tau,\xi)|\le 2^k \le C|\xi|. \end{align} $$

Proof. Since $ \mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B')$ , by (2.5) we have $2^{k-1}\le |\widetilde {\mathcal L}_{s}^\delta \xi |\le 2^{k+1}$ . So, the second inequality in (2.10) is clear from (2.9) if we take $\tau =0$ .

To show the first inequality, from (2.8) we have $| \langle (1,0),(\tau ,\xi ) \rangle | \le B'2^{k+5}$ and $|\langle G^{(j)}(s),(\tau , \xi ) \rangle | \le B' 2^{k+5}$ , $1\le j\le N-1$ , because $\mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B').$ Also, if $v \in ( \mathrm V_s^{G,N-1} )^\perp $ and $|v|=1$ , by (2.8) we see $ |\langle v,(\tau ,\xi ) \rangle | =|\langle v, \mathcal L_{s}^\delta (\tau ,\xi ) \rangle |\le 2^{k+1}$ . Therefore, we get $|(\tau ,\xi )| \le C2^k$ for some $C=C(B')$ since ${\mathfrak V({N-1}, {B'})}$ holds and $\mathrm V_s^{G,N-1}\oplus ( \mathrm V_s^{G,N-1} )^\perp =\mathbb R^{d+1}$ .

The following shows the matrices $ \mathcal L_{s}^{\delta }$ , are close to each other if so are .

Lemma 2.6. Let and $\gamma $ satisfy ${\mathfrak V({N-1}, {B'})}$ . If , then there exists a constant $C=C(B')\ge 1$ such that

(2.11)

Proof. It suffices to prove that (2.11) holds if for a constant $c>0$ , independent of s and . Applying this finitely many times, we can remove the additional assumption. Moreover, it is enough to show

(2.12)

when . Here, $\| \cdot \|$ denotes a matrix norm. Taking $c>0$ sufficiently small, we get (2.11).

By (2.8),

for $j=1,\dots ,N-1$ . Let

, $|c'|\le c$ . Expanding $G^{(j)}$ in Taylor series at s, by the condition (2.1) we have

for $j=1,\dots ,N-1$ . By (2.8) and the mean value theorem, we get

From (2.8), we also have

. A similar argument also shows

.

Let $\{ v_N,\dots , v_d\}$ denote an orthonormal basis of . By ${\mathfrak V({N-1}, {B'})}$ and (2.1), it follows that , $j=1, \dots , N-1$ . Since , there is an orthonormal basis $\{v_N(s),\dots ,v_d(s)\}$ of $( \mathrm V_s^{G,N-1})^\perp $ such that $|v_j(s)-v_j| \lesssim _{B'}\! c\delta $ , $j=N,\dots ,d$ . So, we have $|(\mathcal L_{s}^\delta )^\intercal v_j -v_j|\lesssim _{B'}\! c\delta $ by (2.9). Since , it follows that , $j=N,\dots ,d$ .

We denote by $\mathrm M$ the matrix . Then, combining all together, we have . Note that ${\mathfrak V({N-1}, {B'})}$ gives $|\mathrm M^{-1} v| \lesssim _{B'}\! |v|$ for $v\in \mathbb R^{d+1}$ . Therefore, we obtain (2.12).

For a continuous function $\mathfrak a$ supported in $I\times [1/2, 4]\times \mathbb R\times \mathbb A_k$ , we set

(2.13) $$ \begin{align} m[\mathfrak a](\tau,\xi)&=\iint e^{-it'(\tau+ \gamma(s)\cdot \xi)}\mathfrak a(s,t',\tau,\xi)dsdt', \end{align} $$

(2.14) $$ \begin{align} \mathcal T[\mathfrak a]f(x,t)&=(2\pi)^{-d-1} \iint e^{i(x\cdot\xi+t\tau)}m[\mathfrak a](\tau,\xi) \widehat f (\xi)\,d\xi d\tau. \end{align} $$

Lemma 2.7. Suppose $\mathfrak a\in \mathrm{C}^{d+3}(\mathbb R^{d+3})$ satisfies (2.6) and (2.7) for $j=l=0$ and $|\alpha | \le d+3$ . Then, there is a constant $C=C(B)$ such that

(2.15) $$ \begin{align} \| \mathcal T[\mathfrak a]f\|_{L^\infty(\mathbb R^{d+1})} &\le C\delta \|f\|_{L^\infty(\mathbb R^d)}, \end{align} $$

(2.16) $$ \begin{align} \| (1-\tilde\chi)\mathcal T[\mathfrak a]f\|_{L^p(\mathbb R^{d+1})} &\le C2^{-k}\delta^{1-N} \|f\|_{L^p(\mathbb R^d)}, \quad p> 1, \end{align} $$

where $\tilde \chi \in \mathrm C_c^\infty ((2^{-2},2^3))$ such that $\tilde \chi =1$ on $[3^{-1},6]$ .

Proof. We first note

(2.17) $$ \begin{align} \mathcal T[\mathfrak a]f (x,t) = \int K[\mathfrak a](s,t, \cdot)\ast f(x) \,ds, \end{align} $$

where

(2.18) $$ \begin{align} K[\mathfrak a](s,t,x)=(2\pi)^{-d-1} \iiint e^{i(t-t',x-t'\gamma(s))\cdot (\tau, \xi)}\mathfrak a(s,t',\tau,\xi) \, d\xi d\tau dt'. \end{align} $$

Since , to prove the estimate (2.15) we need only to show

(2.19)

for some $C=C(B)>0$ . To this end, changing variables $(\tau ,\xi ) \rightarrow 2^k \mathcal L_{s}^{\delta }(\tau ,\xi )$ in the right-hand side of (2.18) and noting $|\!\det \mathcal L_{s}^{\delta }|= \delta ^N |\!\det \widetilde {\mathcal L}_{s}^\delta | =\delta ^{{N(N+1)}/2}$ , we get

$$ \begin{align*} K[\mathfrak a](s,t,x)=C_\ast \iiint e^{i 2^k(t-t',x-t\gamma(s))\cdot (\delta^N \tau,\, \widetilde{\mathcal L}_{s}^\delta \xi)} \mathfrak a(s,t',2^k\mathcal L_{s}^{\delta}(\tau,\xi)) \, d\xi d\tau dt', \end{align*} $$

where $C_\ast =(2\pi )^{-d-1} \delta ^{{N(N+1)}/2} 2^{k(d+1)}$ . Since $\mathfrak a$ satisfies (2.6), by (2.11) and Lemma 2.5 we have $\operatorname {\mathrm {supp}}\, \mathfrak a(s,t,2^k\mathcal L_{s}^\delta \cdot )\subset \{(\tau , \xi ): |(\tau ,\xi )| \lesssim _B\! 1\}$ . Besides, by (2.7) and (2.11) it follows that $|\partial _{\tau ,\xi }^{\alpha } \big (\mathfrak a(s,t, 2^k\mathcal L_{s}^\delta (\tau ,\xi ))\big )| \lesssim _B \!1 $ for $|\alpha |\le d+3$ . Thus, repeated integration by parts in $\tau ,\xi $ yields

$$\begin{align*}|K[\mathfrak a](s,t,x)| \lesssim C_\ast \int_{1/2}^{4} \Big(1+2^k \big|\big (\delta^N(t-t'), (\widetilde{\mathcal L}_{s}^\delta)^\intercal(x-t\gamma(s))\big)\big| \Big)^{-d-3}\,dt',\end{align*}$$

by which we obtain (2.19) as desired.

It is easy to show the estimate (2.16). The above estimate for $K[\mathfrak a]$ gives

$$\begin{align*}\|(1-\tilde\chi)K[\mathfrak a](s,t,\cdot)\|_{L^1_x} \lesssim \delta^{-N} 2^{-k}|t-1|^{-1}|1-\tilde\chi(t)|.\end{align*}$$

Since , (2.16) for $p>1$ follows by (2.17) and Minkowski’s and Young’s convolution inequalities.

2.2 Rescaling

Let . Suppose that

(2.20) $$ \begin{align} \sum_{j=1}^{N-1} \delta^{j} |\langle \gamma^{(j)}(s), \xi \rangle |\ge {2^k \delta^N}/{B'} \end{align} $$

holds on $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$ for some $B'>0$ . Then, via decomposition and rescaling, we can bound the $L^p$ norm of $\mathcal T[\mathfrak a]f$ by those of the operators given by symbols of type $(j, N-1, \tilde B)$ relative to a curve for some $\tilde B$ and j (see Lemma 2.8 below).

To do so, we define a rescaled curve by

(2.21)

As $\delta \to 0$ , the curves get close to a nondegenerate curve in an N-dimensional vector space, so the curves behave in a uniform manner. In particular, (2.1) and ${\mathfrak V(N, B)}$ hold for some B for if $\delta <\delta '$ for a constant $\delta '=\delta '(B)$ small enough.

Note

, $1\le j\le N-1$ , and

, $N+1\le j\le 3d+1$ . Thus, Taylor series expansion and (2.4) give

for $j=1, \dots , N-1$ . By (2.21), we have

. We write

, where

and

So,

. Since

and $|v'|\le B$ ,

for some $C=C(B)$ . Thus,

satisfies (2.1) with B replaced by $3B$ if $\delta <\delta '$ .

An elementary argument (elimination) shows

since

and

. Taking $\delta '$ small enough, from ${\mathfrak V(N, B)}$ for $\gamma $ we see that ${\mathfrak V({N}, {3B})}$ holds for

if $0<\delta <\delta '$ .

The next lemma (cf. [14, Lemma 2.9]) plays a crucial role in what follows.

Lemma 2.8. Let $2\le N\le d$ ,

, and $j_\ast =\log (2^k \delta ^N)$ . Suppose (2.20) holds on $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$ . Then, there exist constants $C, l_\ast $ , $\tilde B\ge 1$ and $\delta '>0$ depending on B, and symbols $a_{1}, \dots , a_{l_\ast }$ of type $(j, N-1, \tilde B)$ relative to

such that

$\|\tilde f_l\|_p= \|f\|_p$ , and $j\in [j_\ast -C, j_\ast +C]$ as long as $0<\delta <\delta '$ .

Proof. We set

Combining the identities (2.13) and (2.14), we write $\mathcal T[\mathfrak a] f$ as an integral (e.g., see (2.17) and (2.18)). Subsequently, the change of variables

and

gives

where

Let $\tilde f$ be given by

where $\mathcal F( \tilde f\,)$ denotes the Fourier transform of $ \tilde f.$ Then, $ \|\tilde f\|_p=\|f\|_p$ . Changing variables

gives

where

. This leads us to set

(2.22)

It is easy to check $\tilde a\in \mathrm{C}^{d+N+2}(\mathbb R^{d+2})$ , since so is $\mathfrak a$ and $\gamma \in \mathrm C^{3d+1}$ . By (2.21) and (2.5), we note

. Therefore,

and a change of variables gives

(2.23)

We shall obtain symbols of type $(j, N-1,\tilde B)$ from $\tilde a$ via decomposition and rescaling. To this end, we first note

(2.24) $$ \begin{align} \operatorname{\mathrm{supp}}_\xi \tilde a \subset \big\{ \xi \in \mathbb R^d: C^{-1}\delta^N 2^k \le |\xi | \le C \delta^N 2^{k} \big\} \end{align} $$

for a constant $C=C(B)\ge 1$ . This follows by Lemma 2.5 since there exists $\tau $ such that if $\xi \in \operatorname {\mathrm {supp}}_\xi \tilde a$ . We claim

(2.25) $$ \begin{align} |\partial_s^{j} \partial^{l}_t\partial_\xi^\alpha \tilde a(s,t,\xi) | \lesssim_B\! |\xi|^{-|\alpha|}, \qquad (j,l,\alpha)\in \mathcal I_{N-1}. \end{align} $$

To show (2.25), let us set

Note that $0\le j\le 1$ . Taking derivatives on both sides of the equation (2.22), we have

where

with $0 \le u_1 \le 1$ , $0 \le |\alpha _1| \le u_1$ , and constants $C_{\alpha , u}$ satisfying $|C_{\alpha , u}|=1$ . Integration by parts $u_1+|\alpha _2|$ times in $\tau $ gives $\partial _s^{j}\partial ^{l}_t\partial _\xi ^\alpha \tilde a=\mathcal I[\mathfrak b_2]$ , where

with constants $C_{\alpha , u}'$ satisfying $|C_{\alpha , u}'|=1$ . We decompose $\mathcal I[\mathfrak b_2]= \mathcal I[\chi _E \mathfrak b_2]+ \mathcal I[\chi _{E^c}\mathfrak b_2]$ , where

. Then, integrating by parts in $t'$ for $ \mathcal I[\chi _{E^c}\mathfrak b_2]$ , we obtain

Since

, $ |\partial _s^{j'} \partial _t^{l'} \partial _{\tau ,\xi }^{\alpha '} \mathfrak b| \lesssim _B\! |\xi |^{-|\alpha '|} $ for $(j', l', \alpha ')\in \mathcal I_N$ . It is also clear that

if $\delta < \delta ' $ . Thus, $|\mathfrak b_2|=O(|\xi |^{-|\alpha |})$ , and $|\partial _{t'}^2\mathfrak b_2|=O(|\xi |^{-|\alpha |})$ for $l\le 2(N-1) $ . Since $\partial _s^{j}\partial ^{l}_t\partial _\xi ^\alpha \tilde a=\mathcal I[\mathfrak b_2]$ , we obtain the inequality (2.25).

Now, we decompose $\tilde a$ . Let $\tilde \chi _1, \tilde \chi _2$ and $\tilde \chi _3\in \mathrm{C}_c^\infty (\mathbb R)$ such that $\tilde \chi _1 +\tilde \chi _2+\tilde \chi _3 =1 $ on $\operatorname {\mathrm {supp}} \tilde \chi $ and $\operatorname {\mathrm {supp}}\tilde \chi _\ell \subset [2^{\ell -3}, 2^{\ell }]$ for $\ell =1,2,3$ . Also, let $\beta \in \mathrm C_c^\infty ((2^{-1}, 2))$ such that $\sum \beta (2^{-k}\cdot ) =1$ on $\mathbb R_{+}$ . We set

$$\begin{align*}a_{\ell, j} (s,t,\xi) = \tilde \chi_\ell (t) \beta(2^{-j}|\xi|) \tilde a(s,t,\xi), \end{align*}$$

so $\sum _{\ell , j} a_{\ell , j}= \tilde a$ . By (2.24), $a_{\ell , j} =0$ if $|j-j_\ast |> C$ for some $C>0$ .

Denoting $(a)_\rho (s,t,\xi )=a(s,\rho t,\rho ^{-1}\xi )$ , via rescaling we observe

Thus, changes of variables yield

where $\tilde f_\ell = 2^{(\ell -2)d/p } \tilde f(2^{\ell -2}\cdot )$ . Since

, by (2.23) we get

To complete the proof, we only have to relabel $(a_{\ell , j})_{2^{\ell -2}}$ , $\ell =1,2,3$ , $j_\ast -C\le j\le j_\ast +C$ . Indeed, since $\tilde a\in \mathrm{C}^{d+N+2}$ , $(a_{\ell , j})_{2^{\ell -2}}\in \mathrm{C}^{d+N+2}$ , which is supported in $I \times [2^{-1},4] \times \mathbb A_{j+\ell -2}$ . Obviously, (2.25) holds for $\tilde a=(a_{\ell , j})_{2^{\ell -2}}$ because $\ell =1,2,3$ . Changing variables and in (2.20), by the identity (2.21) we see that (2.20) on $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$ is equivalent to for . Note that . So, the same holds on $\operatorname {\mathrm {supp}}_{s,\xi } \tilde a$ and hence on $\operatorname {\mathrm {supp}}_{s,\xi } (a_{\ell , j})_{2^{\ell -2}}$ if $B'$ replaced by $2B'$ . Therefore, $ C^{-1}(a_{\ell , j})_{2^{\ell -2}}$ is of type $(j+\ell -2, N-1, \tilde B)$ relative to for a large constant $C=C(B)$ .

2.3 Preliminary decomposition and reduction

For the proof of Proposition 2.3, we make some reductions by decomposing the symbol a. We fix a sufficiently small positive constant

(2.26) $$ \begin{align} \delta_*< \min \{ 2^{-10} B^{-3}\delta', \,\, (2^{7d}B^6)^{-N}\}, \end{align} $$

which is to be specified in what follows. Here, $\delta '$ is the number given in Lemma 2.8.

Recall $\gamma $ satisfies the condition (2.1), ${\mathfrak V(N, B)}$ and $ a$ is of type $(k, N, B)$ relative to $\gamma $ . We set

(2.27) $$ \begin{align} \eta_N(s,\xi)=\prod_{1\le j\le N-1} \beta_0 \Big( B2^{-k-1}\delta_*^{j-N} \langle\gamma^{(j)}(s),\, \xi \rangle \Big), \end{align} $$

where $\beta _0\in \mathrm C_c^\infty ((-1,1))$ such that $\beta _0= 1$ on $[-1/2,1/2]$ . It is easy to see $|\partial _s^{j} \partial ^{l}_t \partial _{\xi }^{\alpha } (a\eta _N)| \le C |\xi |^{-|\alpha |}$ for $(j,l,\alpha )\in \mathcal I_N$ , and the same holds for $a(1-\eta _N)$ .

Note $\sum _{j=1}^{N-1}|\gamma ^{(j)}(s)\cdot \xi |\ge (2B)^{-1} \delta _*^N|\xi |$ on $\operatorname {\mathrm {supp}}_{s,\xi }(a(1-\eta _N))$ . So, we see $a(1-\eta _N)$ is a symbol of type $(k, N-1, B')$ for $B'=CB^2 \delta _*^{-C}$ with a large C. Applying the assumption (Theorem 2.2 with $L=N-1$ and $B=B'$ ), we obtain

$$\begin{align*}\| \mathcal A_t[\gamma, a(1-\eta_N)]f\|_{L^p(\mathbb R^{d+1})}\le C 2^{(-\frac{2}p+\epsilon) k}\|f\|_{L^p(\mathbb R^d)}, \quad p\ge 4N-6. \end{align*}$$

Thus, it suffices to consider $\mathcal A_t[\gamma , a\eta _N]$ . Since ${\mathfrak N({N}, B)}$ holds on $\operatorname {\mathrm {supp}}_{s,\xi } a$ ,

(2.28) $$ \begin{align} | \gamma^{(N)}(s)\cdot \xi |\ge (2B)^{-1}|\xi| \end{align} $$

holds whenever $(s,t,\xi )\in \operatorname {\mathrm {supp}} a\eta _N$ for some t.

Basic assumption. Before we continue to prove the estimate for $\mathcal A_t[\gamma , a\eta _N]$ , we make several assumptions which are clearly permissible by elementary decompositions.

Decomposing a, we may assume that $\operatorname {\mathrm {supp}}_\xi a$ is contained in a narrow conic neighborhood and for some . Let us set

$$\begin{align*}\Gamma_k = \big\{\xi\in \mathbb A_k: \text{dist}\big( {|\xi|^{-1}}{\xi}, |\xi'|^{-1}{\xi'}\big)< \delta_\ast \ \text{ for some } \ \xi'\in \operatorname{\mathrm{supp}}_\xi (a\eta_N) \big\}. \end{align*}$$

We may also assume $\gamma ^{(N-1)}(s') \cdot \xi '=0$ for some . Otherwise, $|\gamma ^{(N-1)}(s) \cdot \xi |\gtrsim |\xi |$ on $\operatorname {\mathrm {supp}}_{s,\xi } a\eta _N$ and hence $a\eta _N=0$ if we take B large enough. By (2.28) and the implicit function theorem, there exists $\sigma $ such that

(2.29) $$ \begin{align} \gamma^{(N-1)}(\sigma(\xi)) \cdot \xi=0 \end{align} $$

on a narrow conic neighborhood of $\xi '$ where $\sigma \in \mathrm{C}^{2d+2}$ , since $\gamma \in \mathrm C^{3d+1}(I)$ . So, decomposing a further and taking $\delta _\ast $ small enough, we may assume that $\sigma \in \mathrm C^{2d+2}(\Gamma _k)$ and for $\xi \in \Gamma _k$ . Moreover, since $\sigma $ is homogeneous of degree zero, we have

(2.30) $$ \begin{align} |\partial_\xi^\alpha \sigma(\xi)| \le C |\xi|^{-|\alpha|}, \qquad \xi\in \Gamma_k \end{align} $$

for a constant $C=C(B)$ if $|\alpha |\le 2d+2$ . Any symbol which appears in what follows is to be given by decomposing the symbol a with appropriate cutoff functions. So, the $s,\xi $ -supports of the symbols are assumed to be contained in .

We break a to have further localization on the Fourier side. Let

$$ \begin{align*} \mathfrak a_1 (s,t,\tau,\xi)= a\eta_N \, \beta_0 \big( 2^{-2k}\delta_*^{-2N}|\tau+ \langle \gamma(s),\xi \rangle|^2\big) \end{align*} $$

and $\mathfrak a_0=a\eta _N-\mathfrak a_1$ . Then, by Fourier inversion

$$\begin{align*}\mathcal A_t[\gamma,a\eta_N]f=\mathcal T[ \mathfrak a_1] f+ \mathcal T [ \mathfrak a_0]f. \end{align*}$$

It is easy to show $ \| \mathcal T[ \mathfrak a_0]f \|_{p} \lesssim _B\! 2^{-2k} \|f\|_{p}$ for $1 \le p \le \infty .$ Indeed, we consider $ \tilde {\mathfrak a}_0 = -(\tau +\gamma (s)\cdot \xi )^{-2} {\partial _{t}^2\mathfrak a_0}. $ By (2.13) and integration by parts in $t'$ , $m[\mathfrak a_0]=m[\tilde {\mathfrak a}_0]$ and hence $\mathcal T [ \mathfrak a_0 ]= \mathcal T [\tilde {\mathfrak a}_0]$ . Thanks to (2.17), it is sufficient to show

$$ \begin{align*} | K [ \tilde{\mathfrak a}_0 ](s,t,x) \big| &\le C\, 2^{k(d-1)} \! \int \! \big(1+2^k |t-t'| +2^k |x-t'\gamma(s)|\big)^{-d-3}\,dt' \end{align*} $$

for a constant $C=C(B, \delta _\ast )$ . Note $|\tau +\langle \gamma (s),\xi \rangle |\gtrsim 2^k$ on $\operatorname {\mathrm {supp}} \tilde {\mathfrak a}_0$ , and recall (2.18). Rescaling and integration by parts in $\tau ,\xi $ , as in the proof of Lemma 2.7, show the estimate.

The difficult part is to obtain the estimate for $\mathcal T[\mathfrak a_1]$ . Since $\delta _*$ is a fixed constant, it is obvious that for some $C=C(B,\delta _\ast )$ . So, the desired estimate for $\mathcal T[\mathfrak a_1]$ follows once we have the next proposition.

Proposition 2.9. Let with $\operatorname {\mathrm {supp}}_{\xi } \mathfrak a \subset \Gamma _k$ . Suppose Theorem 2.2 holds for $L=N-1$ . Then, if $p\ge 4N-2$ , for $\epsilon>0$ , we have

$$\begin{align*}\big\| \mathcal T[\mathfrak a]f \big\|_{L^p(\mathbb R^{d+1})} \le C_\epsilon 2^{-\frac{2} pk+ \epsilon k}\|f\|_{L^p(\mathbb R^d)}. \end{align*}$$

Therefore, the proof of Proposition 2.3 is completed if we prove Proposition 2.9. For the purpose, we use Proposition 2.10 below, which allows us to decompose $ \mathcal T[\mathfrak a]$ into the operators given by symbols with smaller s-supports while the consequent minor parts have acceptable bounds. A similar argument was used in [24] when $L=2$ .

Let $\delta _0$ and $\delta _1$ be positive numbers such that

(2.31) $$ \begin{align} 2^{7d}B^6\delta_0^{(N+1)/N} \le \delta_1\le \delta_0 \le \delta_*, \qquad 2^{-k/N}\le \delta_1. \end{align} $$

Then, it is clear that

(2.32) $$ \begin{align} B^{6N}\delta_0^{j+1} \le 2^{-7dN} \delta_1^{j}, \qquad j=1,\dots, N. \end{align} $$

For $n\ge 0$ , we denote $ \mathfrak J_n^\mu =\{ \nu \in \mathbb Z: |2^n\delta _1 \nu - \delta _0 \mu | \le \delta _0\}. $

Proposition 2.10. For $\mu $ such that , let $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$ with . Suppose Theorem 2.2 holds for $L=N-1$ . Then, if $p\ge 4N-2$ , for $\epsilon>0$ there exist a constant $C_\epsilon =C_\epsilon (B) \ge 2$ and symbols $\mathfrak a_{\nu } \in \mathfrak A_k(\delta _1\nu ,\delta _1)$ with , $\nu \in \cup _\mu \mathfrak J_0^\mu $ , such that

$$ \begin{align*} \!\!\left( \sum_\mu \| \mathcal T[ \mathfrak a^\mu]f\|_p^p\right)^{\frac1p}\! \le C_\epsilon & \big({\delta_1}/{\delta_0} \big)^{\frac {2N}{p}-1-\epsilon} \left( \sum_\nu \| \mathcal T[\mathfrak a_{\nu}]f\|_p^p \right)^{\frac1p} \!+C_\epsilon \delta_0^{-\frac {2N}p +1+\epsilon } 2^{-\frac{2}pk+2\epsilon k}\|f\|_p. \end{align*} $$

Assuming Proposition 2.10, we prove Proposition 2.9.

2.4 Proof of Proposition 2.9

Let . We may assume for some $\mu \in \mathbb Z$ . To apply Proposition 2.10 iteratively, we need to choose an appropriate decreasing sequence of positive numbers since the decomposition is subject to the condition (2.31).

Let $\delta _0=\delta _*$ , so $(2^{7d}B^6)^{N}\delta _0< 1$ . Let J be the largest integer such that

$$\begin{align*}(2^{7d}B^6)^{N(\frac{N+1}N)^{J-1}-N} \delta_0^{(\frac{N+1}N)^{J-1}}>2^{-\frac kN}. \end{align*}$$

So, $ J \le C_1 \log k$ for a constant $C_1\ge 1$ . We set

(2.33) $$ \begin{align} \delta_{\!J}=2^{-\frac kN}, \qquad \delta_j=(2^{7d}B^6)^{N(\frac{N+1}N)^{j}-N} &\delta_0^{(\frac{N+1}N)^{j}} \end{align} $$

for $j=J-1,\dots ,1$ . Thus, it follows that

(2.34) $$ \begin{align} &2^{7d}B^6\delta_j^{(N+1)/N}\le \delta_{j+1} <\delta_j, \qquad \, j=0, \dots, J-1. \end{align} $$

For a given $\epsilon>0$ , let $\tilde \epsilon =\epsilon /4$ . Since $\mathfrak a\in \mathfrak A_k( \delta _0\mu ,\delta _0)$ and (2.31) holds for $\delta _0$ and $\delta _1$ , applying Proposition 2.10 to $\mathcal T[\mathfrak a]$ , we have

$$ \begin{align*} \| \mathcal T[\mathfrak a]f\|_p \le C_{\tilde \epsilon} & \big({\delta_1}/{\delta_0}\big)^{\frac {2N}{p}-1-\tilde \epsilon} \left(\sum_{\nu_1} \| \mathcal T[ \mathfrak a_{\nu_1}]f\|_p^p\,\right)^{\frac1p} +C_{\tilde \epsilon} \delta_0^{-\frac {2N}p+1 +\tilde \epsilon } 2^{-\frac{2}pk+2\tilde \epsilon k}\|f\|_p, \end{align*} $$

where $ \mathfrak a_{\nu _1} \in \mathfrak A_k(\delta _1\nu _1,\delta _1)$ , $\nu _1 \in \mathfrak J_0^\mu $ . Thanks to (2.34), we may again apply Proposition 2.10 to $\mathcal T[\mathfrak a_{\nu _1}]$ while $\delta _0$ , $\delta _1$ replaced by $\delta _1, \delta _2$ , respectively. Repeating this procedure up to J-th step yields symbols $\mathfrak a_\nu \in \mathfrak A_k(\delta _{\!J}\nu , \delta _{\!J})$ , $\delta _{\!J} \nu \in \delta _{\!J}\mathbb Z\cap I(\delta _0\mu , \delta _0)$ , such that

$$\begin{align*}\| \mathcal T[\mathfrak a]f\|_p \le C_{\tilde \epsilon}^J \delta_{\!J}^{\frac {2N}{p} -1-\tilde \epsilon} \left(\sum_\nu \|\mathcal T[\mathfrak a_\nu]f\|_p^p \,\right)^{\frac1p} +\sum_{0\le j\le J-1} C_{\tilde \epsilon}^{j+1} \delta_{0}^{-\frac{2N}p+1+\tilde \epsilon} 2^{-\frac{2} pk+ 2\tilde \epsilon k} \|f\|_p \end{align*}$$

for $p \ge 4N-2$ . Now, assuming

(2.35) $$ \begin{align} \left( \sum_\nu\| \mathcal T[ \mathfrak a_{\nu} ]f\|_p^p \,\right)^{1/p} \lesssim_B 2^{-k/N} \|f\|_p, \qquad 2\le p\le \infty \end{align} $$

for the moment, we can finish the proof of Proposition 2.9. Since $C_{\tilde \epsilon }\ge 2$ , combining the above inequalities, we get

$$\begin{align*}\| \mathcal T[\mathfrak a]f\|_p \lesssim_B \!C_{\tilde \epsilon}^{J+1} \big( 2^{-\frac 2p k+\frac{\tilde \epsilon }{N}k} +2^{-\frac{2} pk +2\tilde \epsilon k}\big) \|f\|_p. \end{align*}$$

Since $J \le C_1 \log k$ , $C_{\tilde \epsilon }^{J+1} \le C' 2^{\epsilon k/2}$ for some $C'$ if k is sufficiently large. Therefore, the right-hand side is bounded by $C 2^{- 2k/p+\epsilon k} \|f\|_p$ .

It remains to show the estimate (2.35) for $2\le p\le \infty $ . By interpolation, it is enough to obtain (2.35) for $p=\infty $ and $p=2$ . The case $p=\infty $ follows by (2.15) since $\mathfrak a_\nu \in \mathfrak A_k(\delta _{\!J}\nu ,\delta _{\!J})$ . So, we need only to prove the estimate (2.35) for $p=2$ . To do this, we first observe the following, which shows $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }$ are finitely overlapping.

Lemma 2.11. For $b\ge 1$ , and $0<\delta \le \delta _*$ , let us set

(2.36) $$ \begin{align} {\Lambda}^{\prime}_k(s,\delta, b) = \bigcap_{1\le j\le N-1} \big\{ \xi \in \Gamma_k : | \langle \gamma^{(j)}(s), \xi \rangle| \le b 2^{k} \delta^{N-j} \big \}. \end{align} $$

If ${\Lambda }^{\prime}_k(s_1, \delta , b) \cap {\Lambda }^{\prime}_k(s_2, \delta , b)\neq \emptyset $ for some , then there is a constant $C=C(B)$ such that $|s_1-s_2|\le Cb\delta $ .

Proof. Let $\xi \in \Lambda _k'(s_1,\delta ,b) \cap \Lambda _k'(s_2,\delta ,b)$ . Since $|\gamma ^{(N-1)}(s_j) \cdot \xi |\le b 2^k\delta $ , $j=1,2$ , by (2.29) and (2.28) we see $|s_j-\sigma (\xi )|\le 2^2bB \delta $ , $j=1,2$ , using the mean value theorem. This implies $|s_1-s_2|\le 2^3bB \delta $ .

We recall (2.13). Since (2.28) holds on $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_\nu $ , by van der Corput’s lemma (e.g., see [32, p. 334]) we have

$$ \begin{align*} |m[\mathfrak a_{\nu}](\tau,\xi)| \lesssim 2^{-k/N} \big( \| \mathfrak a_{\nu} (\cdot,t,\tau,\xi) \|_\infty +\| \partial_s \mathfrak a_{\nu} (\cdot, t,\tau,\xi) \|_1\big) \lesssim_B\! 2^{-k/N}. \end{align*} $$

The second inequality is clear since $\mathfrak a_{\nu } \in \mathfrak A_k(\delta _{\!J}\nu , \delta _{\!J})$ . From (2.14), note $\mathcal F(\mathcal T[\mathfrak a_{\nu }] f)= m[\mathfrak a_{\nu }]\widehat f$ . Since $\operatorname {\mathrm {supp}} \mathfrak a_{\nu }\subset \Lambda _k(\delta _{\!J}\nu , \delta _{\!J}, B)$ , $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }\subset S_\nu := {\Lambda }^{\prime}_k(\delta _{\!J}\nu , \delta _{\!J}, 2^5 B)$ . So, $\operatorname {\mathrm {supp}}_\xi \mathcal F(\mathcal T[\mathfrak a_{\nu }] f)\subset S_\nu $ (see (2.13)). By Lemma 2.11, it follows that the sets $S_\nu $ overlap at most $C=C(B)$ times. Therefore, Plancherel’s theorem and the estimate above give

$$\begin{align*}\| \sum_\nu \mathcal T[\mathfrak a_{\nu}] f\|_2^2 \lesssim_B\! 2^{-2k/N} \sum_\nu \int_{S_\nu}\int_{\{\tau: | \tau + \gamma(\delta_{\!J}\nu)\cdot \xi|\le 2^5 B\}} \,d\tau\, |\widehat f(\xi)|^2 \,d\xi, \end{align*}$$

by which we get (2.35) for $p=2$ .

2.5 Decoupling inequalities

We denote $\mathbf r_\circ ^N(s)=(s,s^2/2!,\,\dots, \, s^N/N!)$ and consider a collection of curves from I to $\mathbb R^N$ which are small perturbations of $\mathbf r_\circ ^N$ :

$$\begin{align*}\mathfrak C(\epsilon_\circ;N) =\{ \mathbf r \in \mathrm C^{2N+1}(I): \|\mathbf r-\mathbf r_\circ^N \|_{\mathrm C^{2N+1}(I)} < \epsilon_\circ\}. \end{align*}$$

For $\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $ and $s\in I$ , we define an anisotropic neighborhood by

$$\begin{align*}{\mathcal N}_{\mathbf r}(s,\delta)= \Big\{ \mathbf r(s)+ \sum_{1\le j\le N} u_j {{\mathbf r}^{(j)}(s)}: |u_j|\le \delta^j, \quad~j=1,\dots,N \Big\}. \end{align*}$$

Let $s_1, \dots , s_l\in I$ be $\delta $ -separated points, that is, $|s_n-s_j|\ge \delta $ if $n\neq j$ such that $\bigcup _{j=1}^l(s_j-\delta , s_j+\delta )\supset I$ . Then, we set

$$\begin{align*}\theta_j=\mathcal N_{\mathbf r}(s_j,\delta), \qquad 1\le j\le l. \end{align*}$$

The following is due to Bourgain, Demeter and Guth [5] (also see [10]).

Theorem 2.12. Let $0<\delta \ll 1$ . Suppose $\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $ for a small enough $\epsilon _\circ>0$ . Then, if $2 \le p\le N(N+1)$ , for $\epsilon>0$ we have

(2.37) $$ \begin{align} \big\| \sum_{1\le j\le l} f_j \big\|_{L^p(\mathbb R^{N})}\le C_\epsilon \delta^{-\epsilon} \left( \sum_{1\le j\le l}\|f_j \|_{L^p(\mathbb R^{N})}^2 \right)^{1/2} \end{align} $$

whenever $\operatorname {\mathrm {supp}} \widehat f_j \subset \theta _j$ for $1\le j\le l$ .

The constant $C_\epsilon $ can be taken to be independent of particular choices of the $\delta $ -separated points $s_1, \dots , s_l$ . One can obtain a conical extension of the inequality (2.37) by modifying the argument in [4] which deduces the decoupling inequality for the cone from that for the paraboloid (see [2, Proposition 7.7]). Let us consider the conical sets

$$\begin{align*}{\bar{\theta}}_j=\{ (\eta, \rho)\in \mathbb R^N\times [1,2]: \eta/\rho\in \theta_j\}, \quad 1\le j\le l.\end{align*}$$

Corollary 2.13. Let $0<\delta \le 1$ , and let $\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $ for a small enough $\epsilon _\circ>0$ . Then, if $2 \le p\le N(N+1)$ , for $\epsilon>0$ we have

(2.38) $$ \begin{align} \big\|\sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-\epsilon} \left(\sum_{1\le j\le l} \| F_j\|_{L^p(\mathbb R^{N+1})}^2 \,\right)^{1/2} \end{align} $$

whenever $\operatorname {\mathrm {supp}} \widehat F_j \subset {\bar {\theta }}_j$ for $1\le j\le l$ .

The inequality (2.38) does not fit with the symbols to appear when we decompose $\mathfrak a$ (see Section 3.1 and Section 4.2). As to be seen, those symbols are associated with the slabs of the following form.

Definition 2.14. Let $N\ge 2$ and $\tilde {\mathbf r}\in \mathfrak C(\epsilon _\circ ;N+1)$ . For $s\in I$ , we denote by $\mathbf S(s,\delta , \rho ;\tilde {\mathbf r})$ the set of $(\tau ,\eta ) \in \mathbb R\times \mathbb R^{N}$ which satisfies

$$ \begin{align*} & \rho^{-1}\le|\langle \tilde{\mathbf r}^{(N+1)}(s), (\tau,\eta) \rangle|\le 2\rho, \\[3pt] &\quad |\langle \tilde{\mathbf r}^{(j)}(s), (\tau,\eta) \rangle| \le \delta^{N+1-j}, \qquad \ \ j=N,\dots,1. \end{align*} $$

The same form of decoupling inequality remains valid for the slabs $\mathbf S(s_1,\delta ,1; \tilde {\mathbf r}), \dots , \mathbf S(s_l,\delta ,1; \tilde {\mathbf r})$ . Beltran et al. [2, Theroem 4.4] showed, using the Frenet–Serret formulas, that those slabs can be generated by conical extensions of the anisotropic neighborhoods given by a nondegenerate curve in $\mathbb R^N$ . Therefore, the following is a consequence of Corollary 2.13 and a simple manipulation using decomposition and rescaling.

Corollary 2.15. Let $0<\delta \le 1$ , $\rho \ge 1$ and $\tilde {\mathbf r} \in \mathfrak C(\epsilon _\circ ;N+1)$ for a small enough $\epsilon _\circ>0$ . Denote $\mathbf S_j=\mathbf S(s_j,\delta , \rho ;\tilde {\mathbf r})$ for $1\le j\le l$ . Then, if $2 \le p\le N(N+1)$ , for $\epsilon>0$ there is a constant $C_\epsilon =C_\epsilon (\rho )$ such that

(2.39) $$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^2 \right)^{1/2} \end{align} $$

whenever $\operatorname {\mathrm {supp}} \widehat {F_j} \subset \mathbf S_j$ for $1\le j\le l$ .

For our purpose of proving Proposition 2.10, we use a modified form. If $p_\ast \in [2 , N(N+1)] $ , then we have

$$\begin{align*}\big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-1+\frac{2+p_\ast}{2p}-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align*}$$

for $p\ge p_\ast $ . The case $p=p_\ast $ follows by the inequality (2.39) and Hölder’s inequality. Interpolation with the trivial $\ell ^\infty L^\infty $ – $L^\infty $ estimate gives the estimate for $p> p_\ast $ . One may choose different $p_\ast $ for the particular purposes. In fact, for the local smoothing estimate we take $p_\ast = 4N-2$ to get

(2.40) $$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-1+\frac{2N}{p}-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align} $$

for $p\ge 4N-2$ (see Section 3.2). For the $L^p$ Sobolev regularity estimate, we observe that

(2.41) $$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_{\epsilon_0} \delta^{-1+\frac{N+1}{p}+\epsilon_0} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align} $$

holds for some $\epsilon _0= \epsilon _0(p)>0$ if $2N<p<\infty $ . Indeed, we need only to take $p_\ast> 2N$ close enough to $2N$ . The presence of $\epsilon _0$ in (2.41) is crucial for proving the optimal Sobolev regularity estimate (see Proposition 4.5).

The inequalities (2.40) and (2.41) obviously extend to cylindrical forms via the Minkowski inequality. For example, set $ \tilde {\mathbf S}_j=\big \{ (\xi ,\eta )\in \mathbb R^{N+1}\times \mathbb R^M: \xi \in \mathbf S_j \big \}$ for $1\le j\le l$ . Using (2.40), we have

(2.42) $$ \begin{align} \big\| \sum_{1\le j\le l} G_j \big\|_{L^p(\mathbb R^{N+M+1})}\le C_\epsilon \delta^{-1+\frac{2N}{p}-\epsilon} \left( \sum_{1\le j\le l} \| G_j \|_{L^p(\mathbb R^{N+M+1})}^2 \right)^{1/2} \end{align} $$

whenever $\widehat {G}_j$ is supported in $\tilde {\mathbf S}_j$ . Clearly, we also have a similar extension of the inequality (2.41).

3 Decomposition of the symbols

In this section, we prove Proposition 2.10 by applying the decoupling inequality. Meanwhile, the induction assumption (Theorem 2.2 with $L=N-1$ ) plays an important role. We decompose a given symbol $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$ into the symbols with their s-supports contained in intervals of length about $\delta _1$ while the consequent minor contribution is controlled within an acceptable bound. To achieve it up to $\delta _1$ satisfying the condition (2.31), we approximate $\langle G(s), (\tau ,\xi ) \rangle $ in a local coordinate system near the set $\{(s,\xi ):\langle \gamma ^{(N-1)}(s),\xi \rangle =0\}$ .

3.1 Decomposition of the symbol $\mathfrak a^\mu $

We begin by introducing some notations.

Fixing $\mu \in \mathbb Z$ such that , we consider the linear maps

$$\begin{align*}y_\mu^j(\tau,\xi)= \langle G^{(j)}(\delta_0\mu ),(\tau,\xi)\rangle, \qquad j=0, 1,\dots,N. \end{align*}$$

In particular, $y_\mu ^j(\tau ,\xi )=\langle \gamma ^{(j)}(\delta _0\mu ),\xi \rangle $ if $1\le j\le N.$ By (2.28), it follows that

(3.1) $$ \begin{align} |y_\mu^N(\tau,\xi)| \ge (2B)^{-1}|\xi|. \end{align} $$

We denote

$$\begin{align*}\omega_\mu(\xi)=\frac{y_\mu^{N-1}(\tau,\xi)}{y_\mu^{N}(\tau,\xi)}, \end{align*}$$

which is close to $\delta _0\mu -\sigma (\xi )$ (see (3.5) below). Then, we define $\mathfrak g_\mu ^N, \mathfrak g_\mu ^{N-1},\dots , \mathfrak g_\mu ^{0}$ recursively, by setting $ \mathfrak g_\mu ^N=y_\mu ^N,$ and

(3.2) $$ \begin{align} \mathfrak g_\mu^{j}(\tau,\xi)=y^{j}_\mu(\tau,\xi)-\sum_{\ell=j+1}^{N}\frac{\mathfrak g^{\ell}_\mu(\tau,\xi)}{(\ell-j)!} (\omega_\mu(\xi))^{\ell-j}, \quad j=N-1, \dots, 0. \end{align} $$

Note that $\mathfrak g_\mu ^{N-1}=0$ and (3.2) can be rewritten as follows:

(3.3) $$ \begin{align} y^{m}_\mu(\tau,\xi) =\sum_{\ell=m}^{N}\frac{\mathfrak g^{\ell}_\mu(\tau,\xi)}{(\ell-m)!} (\omega_\mu(\xi))^{\ell-m}, \quad m=0,\dots,N. \end{align} $$

The identity continues to hold for $m=N$ since $\mathfrak g_\mu ^N=y_\mu ^N$ . Apparently, $\mathfrak g_\mu ^1,\dots , \mathfrak g_\mu ^N$ are independent of $\tau $ since so are $y_\mu ^1, \dots , y_\mu ^N$ .

For $j=1,\dots ,N$ , set

(3.4) $$ \begin{align} \mathcal E_j(\xi):=(y_\mu^N(\tau,\xi))^{-1}\int_{\sigma(\xi)}^{\delta_0\mu}\frac{\langle\gamma^{(N+1)}(r),\xi\rangle}{j!}(\sigma(\xi) -r)^{j}dr. \end{align} $$

By (3.4) with $j=1$ and integration by parts, we have

(3.5) $$ \begin{align} \mathcal E_1(\xi) = \sigma(\xi) -\delta_0\mu+\omega_\mu(\xi). \end{align} $$

Lemma 3.1. Let $0\le j\le N-1$ . Then, we have

(3.6) $$ \begin{align} \langle G^{(j)}(\sigma(\xi)),(\tau,&\xi) \rangle = \sum_{\ell=j}^{N}\frac{\,\, \mathfrak g^{\ell}_\mu\,\,(\mathcal E_1)^{\ell-j}}{(\ell-j)!} -y^N_\mu\mathcal E_{N-j}. \end{align} $$

Proof. When $j=N-1$ , the equation (3.6) is clear. To show (3.6) for $j=0,1,\dots ,N-2$ , by Taylor’s theorem with integral remainder we have

$$\begin{align*}\langle G^{(j)}(\sigma(\xi)),(\tau,\xi)\rangle =\sum_{m=j}^{N}y^{m}_\mu (\tau,\xi) \frac{(\sigma(\xi)-\delta_0\mu)^{m-j}}{(m-j)!}-y^N_\mu(\tau,\xi)\mathcal E_{N-j}(\xi).\end{align*}$$

Using (3.3) and then changing the order of the sums, we see

$$\begin{align*}\langle G^{(j)}(\sigma(\xi)),(\tau,\xi)\rangle= \sum_{\ell=j}^{N} \mathfrak g^{\ell}_\mu \left(\sum_{m=j}^{\ell} \frac{(\sigma(\xi)-\delta_0\mu)^{m-j}}{(\ell-m)!(m-j)!} (\omega_\mu)^{\ell-m} \right) -y^N_\mu\,\mathcal E_{N-j}. \end{align*}$$

The sum over m equals $(\sigma (\xi )-\delta _0\mu + \omega _\mu )^{\ell -j} /(\ell -j)!$ . So, (3.6) follows by (3.5).

We now decompose the symbol $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$ by making use of $\mathfrak g_\mu ^j$ , $j=0,\dots ,N-2$ . We define

$$\begin{align*}\mathfrak G_N^\mu(s,\tau,\xi)=\sum_{j=0}^{N-2}\big(2^{-k} \mathfrak g^{j}_\mu(\tau,\xi)\big)^{\frac{2N!}{N-j}}+(s-\sigma(\xi))^{2N!}. \end{align*}$$

Let $ \beta _N=\beta _0-\beta _0(2^{2N!}\cdot )$ , so we have $\sum _{\ell \in \mathbb Z}\beta _N(2^{2N!\ell }\cdot )=1$ on $\mathbb R_+$ . We also take $\zeta \in \mathrm C_c^\infty ((-1,1))$ such that $\sum _{\nu \in \mathbb Z} \zeta (\cdot -\nu )=1$ . For $n\ge 0$ and $\nu \in \mathfrak J_n^\mu $ , we set

$$\begin{align*}\mathfrak a_{\nu}^{\mu,n} = \mathfrak a^\mu \times \begin{cases} \beta_0 \big( \delta_1^{-2N!} \, \mathfrak G_N^\mu \big) \, \zeta(\delta_1^{-1}s-\nu), \quad & n=0, \\[4pt] \beta_N \big( (2^{n}\delta_1)^{-2N!} \, \mathfrak G_N^\mu \big) \, \zeta(2^{-n}\delta_1^{-1}s-\nu), \quad & n\ge 1. \end{cases} \end{align*}$$

Then, it follows that

(3.7) $$ \begin{align} \mathfrak a^\mu = \sum_{n\ge 0} \sum_{\nu \in \mathfrak J_n^\mu} \mathfrak a^{\mu,n}_{\nu}. \end{align} $$

Lemma 3.2. There is a constant $C=C(B)$ such that $C^{-1}\mathfrak a_{\nu }^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$ for $n\ge 0$ , $\mu $ and $\nu $ .

The proof of Lemma 3.2 is elementary though it is somewhat involved. We postpone the proof until Section 3.3.

We collect some elementary facts regarding $\mathfrak a_{\nu }^{\mu ,n}$ . First, we may assume

(3.8) $$ \begin{align} 2^n\delta_1\le 2^{10} B^3\delta_0 \end{align} $$

since, otherwise, $\mathfrak a_{\nu }^{\mu ,n}=0$ . To show this, we note $|\langle \gamma ^{(N-1)}(\delta _0\mu ),\xi \rangle |\le B2^{k+5}\delta _0$ if $\xi \in \operatorname {\mathrm {supp}}_{\xi } \mathfrak a^\mu $ . Thus, (2.28), (2.29), and the mean value theorem show that

(3.9) $$ \begin{align} |\sigma(\xi)-\delta_0\mu|\le B^22^{7}\delta_0 \end{align} $$

for $\xi \in \operatorname {\mathrm {supp}}_{\xi } \mathfrak a^\mu .$ If $(\tau , \xi )\in \operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a^\mu \subset \Lambda _k(\delta _0\mu , \delta _0, B)$ , $|y_\mu ^j(\tau ,\xi )|\le B2^{k+5}\delta _0^{N-j} $ for $0\le j\le N-1$ . Note $|\omega _\mu | \le B^22^7\delta _0$ and $|\mathfrak g_\mu ^N| \le B2^{k+1}$ . A routine computation using (3.2) gives $|\mathfrak g_\mu ^{j}| \le B2^{k-1}(B^22^8\delta _0)^{N-j} $ for $j=N-2, \dots , 0$ . Since $|s-\sigma (\xi )|\le (B^22^{7}+1)\delta _0$ , we have $ \mathfrak G_N^\mu \le 2(B^32^8)^{2N!} \delta _0^{2N!}$ on $\operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n}$ , and (3.8) follows.

Since $\mathfrak G_N^\mu \le (2^n\delta _1)^{2N!}$ on $\operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n}$ , the following hold:

(3.10) $$ \begin{align} |s-\sigma(&\xi)|\le 2^n\delta_1, \end{align} $$

(3.11) $$ \begin{align} 2^{-k}|\mathfrak g^{j}_\mu(\tau,\xi)&|\le (2^n\delta_1)^{N-j}, \qquad 0\le j \le N-1. \end{align} $$

Obviously, (3.11) holds true for $j=N-1$ since $\mathfrak g^{N-1}_\mu =0$ . We also have

(3.12) $$ \begin{align} &|\mathcal E_j(\xi)|\le B^2 (B^22^7\delta_0)^{j+1}, \end{align} $$

(3.13) $$ \begin{align} &|\sigma(\xi)-2^n\delta_1\nu| \le 2^{n+1}\delta_1 \end{align} $$

on $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }^{\mu ,n}$ . By using (3.4), (3.9) and (3.1), it is easy to show (3.12). Since $|s-2^n\delta _1\nu | \le 2^n\delta _1$ on $\operatorname {\mathrm {supp}}_s \mathfrak a_{\nu }^{\mu ,n}$ , (3.13) follows by (3.10).

3.2 Proof of Proposition 2.10

By (3.7) and the Minkowski inequality, we have

(3.14) $$ \begin{align} \begin{aligned} \left( \sum_\mu \big\| \mathcal T [\mathfrak a^\mu]f \big\|_p^p \,\right)^{1/p} \le \sum_{n\ge0} \left(\sum_{\mu} \big\| \sum_{\nu \in \mathfrak J_n^\mu} \mathcal T [ \mathfrak a^{\mu,n}_{\nu}]f \big\|_p^p\,\right)^{1/p}. \end{aligned} \end{align} $$

We use the inequality (2.40) for after a suitable linear change of variables. The symbols $\mathfrak a_{\nu }^{\mu ,0}$ are to constitute the set $\{\mathfrak a_\nu \}$ while the operators associated to $\mathfrak a_{\nu }^{\mu ,n}$ , $n\ge 1$ are to be handled similarly as in Section 2.

Applying the inequality (2.40). To prove Proposition 2.10, we first show

(3.15) $$ \begin{align} \big\| \sum_{\nu\in \mathfrak J_{n}^\mu} \mathcal T [\mathfrak a_{\nu}^{\mu,n}]f \big\|_p \le C_\epsilon \big({2^n\delta_1}/{\delta_0} \big)^{\frac {2N} {p}-1-\epsilon} \left(\sum_{\nu\in \mathfrak J_{n}^\mu} \big\| \mathcal T [\mathfrak a_{\nu}^{\mu,n}]f \big\|_p^p \,\right)^{1/p} \end{align} $$

for $p \ge 4N-2$ . To use (2.40), we consider $\operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a_{\nu }^{\mu ,n}$ , which contains the Fourier support of $ \mathcal T [\mathfrak a_{\nu }^{\mu ,n}]f$ as is clear from (2.13) and (2.14).

We set

$$\begin{align*}\mathbf y_\mu(\tau,\xi)=\big(y_\mu^0(\tau,\xi),\dots,y^{N}_\mu(\tau,\xi)\big). \end{align*}$$

Lemma 3.3. Let $\mathbf r =\mathbf r_{\circ }^{N+1}$ and $\mathcal D_\delta $ denote the matrix $ (\delta ^{-N} e_1, \delta ^{1-N} e_2, \dots , \delta ^0 e_{N+1})$ , where $e_j$ denotes the j-th standard unit vector in $\mathbb R^{N+1}$ . On $\operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a^{\mu ,n}_{\nu }$ , we have

(3.16) $$ \begin{align} \Big|\Big\langle \mathcal D_{\delta_0} \mathbf y_\mu(\tau,\xi), \mathbf r^{(j)}\Big(\frac{2^n\delta_1}{\delta_0}\nu-\mu\Big)\Big\rangle\Big| \lesssim &\, 2^k \Big(\frac{2^n\delta_1}{\delta_0}\Big)^{N+1-j}, \qquad 1 \le j \le N, \end{align} $$

(3.17) $$ \begin{align} (2B)^{-1} 2^{k-1} \le \big|\big\langle \mathbf y_\mu(\tau,\xi), \mathbf r^{(N+1)}& \big\rangle\big|\le B 2^{k+1}. \end{align} $$

Proof. We write $\mathbf r=(\mathbf r_1,\dots ,\mathbf r_{N+1})$ . Note $\mathbf r^{(j)}_m(s)=s^{m-j}/(m-j)!$ for $m\ge j$ . By the equation (3.3), we have

$$ \begin{align*} y^{m-1}_\mu \mathbf r^{(j)}_m(2^n\delta_1\nu-\delta_0\mu) &=\sum_{\ell=m-1}^{N}\mathfrak g^{\ell}_\mu\frac{(2^n\delta_1\nu-\delta_0\mu)^{m-j}}{(\ell+1-m)!(m-j)!}\,\omega_\mu^{\ell+1-m} \end{align*} $$

for $m\ge j$ . Since $\mathbf r^{(j)}_m(s)=0$ for $j>m$ , taking sum over m gives

$$ \begin{align*} \big\langle \mathbf y_\mu, \mathbf r^{(j)}(2^n\delta_1\nu-\delta_0\mu)\big\rangle =\sum_{\ell=j-1}^{N}\mathfrak g^{\ell}_\mu\frac{( 2^n\delta_1\nu-\delta_0\mu+ \omega_\mu)^{\ell+1-j}}{(\ell+1-j)!}. \end{align*} $$

From the equation (3.5), we note $2^n\delta _1\nu -\delta _0\mu +\omega _\mu =2^n\delta _1\nu -\sigma (\xi )+\mathcal E_1$ . Thus, (3.13), (3.12) with $j=1$ and (2.32) with $j=1$ show $|2^n\delta _1\nu -\delta _0\mu +\omega _\mu |\lesssim 2^n\delta _1$ . By (3.11), we obtain

$$\begin{align*}\big|\big\langle \mathbf y_\mu(\tau,\xi), \mathbf r^{(j)}(2^n\delta_1\nu-\delta_0\mu)\big\rangle\big| \lesssim 2^k (2^{n}\delta_1)^{N+1-j}, \qquad 1 \le j \le N. \end{align*}$$

By homogeneity, it follows that $\langle \eta , \mathbf r^{(j)}(\delta _0 s)\rangle =\delta _0^{N+1-j}\langle \mathcal D_{\delta _0} \eta , \mathbf r^{(j)}( s)\rangle $ for $\eta \in \mathbb R^{N+1}$ . Therefore, we get (3.16). For the inequality (3.17), note that $\mathbf r^{(N+1)}=(0,\dots , 0, 1)$ . Thus, $\langle \mathbf y_\mu , \mathbf r^{(N+1)}\rangle =y^{N}_\mu $ and (3.17) follows by (3.1).

Let $\mathrm V= \operatorname {\mathrm {span}}\{\gamma '(\delta _0\mu ),\dots ,\gamma ^{(N)}(\delta _0\mu )\}$ and $\{v_{N+1},\dots , v_d\}$ be an orthonormal basis of $\mathrm V^\perp $ . Since $\gamma $ satisfies ${\mathfrak V({N}, B)}$ , for each $\xi \in \mathbb R^d$ we can write

(3.18) $$ \begin{align} \xi= \overline \xi+\sum_{N+1\le j\le d}y_j(\xi) v_j, \end{align} $$

where $\overline \xi \in \mathrm V$ and $y_j(\xi ) \in \mathbb R$ , $N+1\le j\le d$ . We define a linear map by

$$\begin{align*}\mathrm Y_\mu^{\delta_0}(\tau,\xi)= \big( 2^{-k} \mathcal D_{\delta_0} \mathbf y_\mu(\tau, \xi),\, y_{N+1}(\xi),\dots,\,y_d(\xi)\big). \end{align*}$$

From (3.16) and (3.17), we see

(3.19) $$ \begin{align} \mathrm Y_\mu^{\delta_0} ( \operatorname{\mathrm{supp}}_{\tau,\xi} \mathfrak a_{\nu}^{\mu,n} ) \subset \mathbf S\Big(\frac{2^n\delta_1}{\delta_0}\nu-\mu, C\frac{2^n\delta_1}{\delta_0}, 2^2B; \mathbf r_\circ^{N+1}\Big) \times \mathbb R^{d-N} \end{align} $$

for some $C>1$ . We now have the inequality (2.40) for $\delta =C{2^n\delta _1}/{\delta _0}$ and the slabs $\mathbf S(2^n\delta _1\nu /\delta _0-\mu , C2^{n}\delta _1/\delta _0, 2^2B; \mathbf r_\circ ^{N+1}), \nu \in \mathfrak J_{n}^\mu $ . Therefore, by cylindrical extension in $y_{N+1},\dots ,y_d$ (see (2.42)) and the change of variables $(\tau ,\xi )\to \mathrm Y_\mu ^{\delta _0}(\tau ,\xi )$ , we obtain (3.15) since the decoupling inequality is not affected by an affine change of variables in the Fourier side.

Combining the inequalites (3.14) and (3.15), we obtain

$$ \begin{align*} \left(\sum_\mu \| \mathcal T[\mathfrak a^\mu]f\|_p^p\,\right)^{1/p} \le \sum_{n\ge 0}\, \mathbf E_n \end{align*} $$

for $p \ge 4N-2$ , where

$$ \begin{align*} \mathbf E_n= C_\epsilon \big({2^n\delta_1}/\delta_0\big)^{\frac {2N} {p}-1-\epsilon} \left(\sum_{\mu} \sum_{\nu\in \mathfrak J_n^\mu} \| \mathcal T[\mathfrak a^{\mu, n}_\nu]f\|_p^p\,\right)^{1/p}. \end{align*} $$

Since the intervals $I(\delta _0\mu ,\delta _0)$ overlap, there are at most three nonzero $\mathfrak a^{\mu , 0}_{\nu }$ for each $\nu $ . We take $\mathfrak a_\nu =\mathfrak a^{\mu , 0}_\nu $ which maximizes $\| \mathcal T[\mathfrak a^{\mu , 0}_\nu ]f\|_p$ . Then, it is clear that $\mathbf E_0\le 3^{1/p} C_\epsilon (\delta _1/\delta _0)^{\frac {2N} {p}-1-\epsilon } \left(\sum _{\nu } \| \mathcal T[\mathfrak a_\nu ]f\|_p^p\right)^{1/p}.$ By Lemma 3.2, $C^{-1}\mathfrak a_\nu \in \mathfrak A_k(\delta _1\nu , \delta _1)$ for a constant C. Thus, the proof of Proposition 2.10 is now reduced to showing

(3.20) $$ \begin{align} \sum_{n\ge1}\, \mathbf E_n \lesssim_B\! \delta_0^{-\frac{2N}p+1+\epsilon} 2^{-\frac 2pk +2\epsilon k} \|f\|_p, \quad p\ge 4N-2. \end{align} $$

Estimates for $\mathbf E_n$ when $n\ge 1$ . To prove the estimate (3.20), we decompose $\mathfrak a^{\mu , n}_\nu $ so that the inequalites (3.25) or (3.26) (see Lemma 3.5 below) holds on the $s,\xi $ -supports of the resulting symbols. If (3.25) holds, we use the assumption after rescaling, whereas we handle the other case using estimates for the kernels of the operators.

Let

(3.21) $$ \begin{align} \bar{\mathfrak G}_N^{\mu}(s,\xi) =\sum_{1\le j\le N-2}\big(2^{-k}\mathfrak g^{j}_\mu\big)^{\frac{2N!}{N-j}}+\big(s-\sigma(\xi)\big)^{2N!}. \end{align} $$

Note that the right-hand side is independent of $\tau $ since so are $\mathfrak g^{j}_\mu $ , $1\le j\le N-2$ .

Let $C_0=2^{2d}B$ . We set

(3.22) $$ \begin{align} \mathfrak a_{\nu,1}^{\mu,n} =\mathfrak a_{\nu}^{\mu,n} \, \beta_0 \Big({ (2^{-k}\mathfrak g_\mu^0)^{2(N-1)!}}/ ({C_0^{2N!} \bar{\mathfrak G}_N^{\mu}})\Big), \quad n\ge 1, \end{align} $$

and $\mathfrak a_{\nu ,2}^{\mu ,n}=\mathfrak a_{\nu }^{\mu ,n} -\mathfrak a_{\nu ,1}^{\mu ,n},$ so we have $ \mathfrak a_{\nu }^{\mu ,n} =\mathfrak a_{\nu ,1}^{\mu ,n}+\mathfrak a_{\nu ,2}^{\mu ,n}. $ Similarly as before, we have the following, which we prove in Section 3.4.

Lemma 3.4. There exists a constant $C=C(B)$ such that $C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}$ and $C^{-1} \mathfrak a_{\nu ,2}^{\mu ,n}$ are contained in $\mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$ for $n\ge 1$ .

The estimate (3.20) follows if we show

(3.23) $$ \begin{align} \left( \sum_{\mu} \sum_{\nu \in \mathfrak J_n^\mu} \|\mathcal T[\mathfrak a_{\nu,1}^{\mu,n}]f\|_p^p \right)^{1/p} \le C_\epsilon 2^{-\frac 2pk+\epsilon k} (2^n\delta_1)^{-\frac{2N}p+1+\epsilon} \|f\|_p, \, \quad p\ge 4N-6 \hspace{-4pt} \end{align} $$

for any $\epsilon>0$ , and

(3.24) $$ \begin{align} \left( \sum_\mu\sum_{\nu\in \mathfrak J_{n}^{\mu}}\| \mathcal T[\mathfrak a_{\nu,2}^{\mu,n}]f\|_p^p \right)^{1/p} \lesssim_B\! 2^{-\frac {(N+2)k} {2N}}(2^n\delta_1)^{-\frac N2}\|f\|_p, \quad 2\le p\le \infty \end{align} $$

when $n\ge 1$ . Thanks to the inequality (3.8), those estimates give

$$\begin{align*}\sum_{n\ge1} \mathbf E_n\,\le C_\epsilon \delta_0^{-\frac{2N}p+1+\epsilon} \! \sum_{1\le n\le \log_2 (C\delta_0/\delta_1)} \!\!\big(2^{-\frac {2}pk + \epsilon k} + 2^{-\frac {(N+2)k} {2N}}(2^n\delta_1)^{\frac{2N}p-\frac {N+2}2-\epsilon}\big) \|f\|_p \end{align*}$$

for $p\ge 4N-2$ . Note $ \log _2 (\delta _0/\delta _1)\le Ck $ from (2.31). So, the estimate (3.20) follows since $4N-2> 4N/(N+2)$ and $\delta _1\ge 2^{-k/N}$ .

In order to prove the estimates (3.23) and (3.24), we start with the next lemma.

Lemma 3.5. Let $n\ge 1$ . For a constant $C=C(B)>0$ , we have the following $:$

(3.25) $$ \begin{align} \sum_{1\le j\le N-1} (2^n\delta_1)^{-(N-j)} |\langle\gamma^{(j)}(s),\xi\rangle| \ge C 2^k, \qquad (s,\xi)\in \operatorname{\mathrm{supp}}_{s,\xi} \mathfrak a_{\nu,1}^{\mu,n}, \end{align} $$

(3.26) $$ \begin{align} (2^n\delta_1)^{-N} |\tau+\langle\gamma(s),\xi\rangle|\ge C 2^{k}, \qquad (s,\xi)\in \operatorname{\mathrm{supp}}_{s,\xi} \mathfrak a_{\nu,2}^{\mu,n}. \end{align} $$

Proof. We first prove (3.25). Since $\mathfrak G_N^\mu \ge 2^{-2N!-1}(2^n\delta _1)^{2N!}$ on $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_{\nu }^{\mu ,n}$ , one of the following holds on $\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,1}^{\mu ,n}$ :

(3.27) $$ \begin{align} |s-\sigma(\xi)|&\ge (2^{3}C_0B)^{-1}2^n\delta_1, \end{align} $$

(3.28) $$ \begin{align} 2^{-k}|\mathfrak g^{j}_\mu(\tau,\xi)| &\ge (2^2C_0)^{-(N-j)} (2^n\delta_1)^{N-j} \end{align} $$

for some $1\le j \le N-2$ , where $C_0=2^{2d}B$ (see (3.22)). If (3.27) holds, by (2.28) and (2.29) it follows that $ (2^n\delta _1)^{-1}|\langle \gamma ^{(N-1)}(s),\xi \rangle | \gtrsim 2^{k}.$ Thus, to show (3.25) we may assume the inequality (3.27) fails, that is, (3.28) holds for some $1\le j \le N-2$ . So, there is an integer $\ell \in [0, N-2]$ such that (3.28) fails for $\ell +1\le j \le N-2$ , whereas (3.28) holds for $j=\ell $ . By (3.6) and (3.12), we have

(3.29) $$ \begin{align} |\langle G^{(\ell)}(\sigma(\xi)),(\tau,\xi) \rangle| \ge |\mathfrak g_\mu^\ell| -\!\!\sum_{j=\ell+1}^N|\mathfrak g_\mu^j| \frac{(B^6 2^{14}\delta_0^2)^{j-\ell}}{(j-\ell)!} -2B^3 (B^2 2^7\delta_0)^{N+1-\ell}|\xi|. \end{align} $$

Thus, (2.32) gives $|\langle G^{(\ell )}(\sigma (\xi )),(\tau ,\xi ) \rangle | \ge (2^3C_0)^{-(N-\ell )} 2^k (2^n\delta _1)^{N-\ell }$ . Also, the equation (3.6) and our choice of $\ell $ yield $|\langle G^{(j)}(\sigma (\xi )),(\tau ,\xi ) \rangle | \le (2C_0)^{-(N-j)} 2^k (2^n\delta _1)^{N-j}$ for $\ell +1 \le j \le N-2$ . Combining this with $|s-\sigma (\xi )|< (2^3 C_0B)^{-1} 2^n\delta _1$ and expanding $G^{(\ell )}$ in Taylor series at $\sigma (\xi )$ , we see that $ |\langle G^{(\ell )}(s), (\tau ,\xi ) \rangle |\ge C 2^k (2^n\delta _1)^{N-\ell }$ for some $C=C(B)>0$ . This proves (3.25).

We now show (3.26), which is easier. On $\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,2}^{\mu ,n}$ , $2^{-k}|\mathfrak g_\mu ^0|\ge 2^{-N-1}(2^n\delta _1)^N$ and $2^{-k}|\mathfrak g_\mu ^j| \le 2C_0^{-(N-j)}(2^n\delta _1)^{N-j}$ for $j=1, \dots , N-2$ . Using (3.29) with $\ell =0$ , by (2.32) and (2.31) we get $ (2^n\delta _1)^{-N} |\tau +\langle \gamma (\sigma (\xi )),\xi \rangle | \ge 2^{-N-2}2^k$ . We also note that $|s-\sigma (\xi )| \le 2C_0^{-1} 2^n\delta _1$ and $|\langle G^{(j)}(\sigma (\xi )),(\tau ,\xi ) \rangle | \le C_0^{-1}2^k (2^n\delta _1)^{N-j}$ for $1 \le j \le N-2$ on $\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,2}^{\mu ,n}$ . Since $|\langle G^{(N)}(s),(\tau ,\xi ) \rangle | \le B2^{k+1}$ , using Taylor series expansion at $\sigma (\xi )$ as above, we see (3.26) holds true for some $C=C(B)>0$ .

Additionally, we make use of disjointness of $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }^{\mu ,n}$ by combining Lemma 2.11 and the next.

Lemma 3.6. There is a positive constant $C=C(B)$ such that

(3.30) $$ \begin{align} |( \widetilde{\mathcal L}_s^\delta)^{-1}\xi|\le Cb2^{k} \end{align} $$

whenever $\xi \in {\Lambda }^{\prime}_k(s,\delta ,b) ($ see (2.36) $)$ . If $\xi \in \Gamma _k$ and (3.30) holds with $C=1$ , then $\xi \in {\Lambda }^{\prime}_k(s,\delta , C_1b)$ for some $C_1=C_1(B)>0$ .

Proof. Let $\eta \in \mathbb R^d$ and $\{ v_{N}, \dots , v_d\}$ be an orthonormal basis of $(\operatorname {\mathrm {span}}\{ \gamma ^{(j)}(s): 1\le j\le N-1\})^\perp $ . We write $ \eta =\sum _{j=1}^{N-1} \mathbf c_j \gamma ^{(j)}(s) + \sum _{j=N}^d \mathbf c_j v_j.$ Since ${\mathfrak V(N, B)}$ holds for $\gamma $ , $|\eta |\sim |(\mathbf c_1, \cdots ,\mathbf c_d )|$ . Let $\xi \in {\Lambda }^{\prime}_k(s,\delta ,b) $ . Then, (2.4) gives

$$\begin{align*}\langle \eta, ( \widetilde{\mathcal L}_s^\delta)^{-1}\xi \rangle= \langle ( \widetilde{\mathcal L}_s^\delta)^{-\intercal} \eta, \xi \rangle= \sum_{j=1}^{N-1} \delta^{j-N} \mathbf c_j \langle\gamma^{(j)}(s), \xi\rangle + \sum_{j=N}^d \mathbf c_j \langle v_j,\xi\rangle. \end{align*}$$

Thus, by (2.36) we get $|\langle \eta , ( \widetilde {\mathcal L}_s^\delta )^{-1}\xi \rangle |\le Cb|\eta | 2^k $ , which shows (3.30).

By (2.4), $\langle \gamma ^{(j)}(s),\xi \rangle = \delta ^{N-j} \langle \gamma ^{(j)}(s), (\widetilde {\mathcal L}_s^\delta )^{-1}\xi \rangle $ for $1\le j\le N-1$ . Therefore, (3.30) with $C=1$ gives $|\langle \gamma ^{(j)}(s),\xi \rangle | \le C_1 b \delta ^{N-j} 2^k$ for a constant $C_1>0$ when $1\le j\le N-1$ . This proves the second statement.

Now, we are ready to prove the estimates (3.23) and (3.24).

Proof of (3.23).

By Lemma 3.4, $C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$ for some $C>0$ . Besides, (3.25) holds on $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_{\nu ,1}^{\mu ,n}$ , and we note $2^n\delta _1<\delta '$ from (3.8), (2.26), and (2.31). Thus, taking $\delta =2^n\delta _1$ and

, we may use Lemma 2.8 for $\tilde \chi \mathcal T [\mathfrak a_{\nu ,1}^{\mu ,n}] f$ to get

where $ \|\tilde f_l\|_p= \|f\|_p$ , $a_{l}$ are of type $(j, N-1, B')$ relative to

for some $B'>0$ , and $2^j\sim (2^n\delta _1)^N 2^k$ . As seen before,

satisfies ${\mathfrak V({N}, {3B})}$ and (2.1) with B replaced by $3B$ for $\delta \le \delta _*$ . So, ${\mathfrak V({N-1}, {B'})}$ with a large $B'$ holds for

.

Therefore, we may apply the assumption (Theorem 2.2 with $L=N-1$ ) to , which gives for a constant $C_\epsilon =C_\epsilon (B')$ . Consequently, we obtain

$$\begin{align*}\| \tilde\chi \mathcal T[\mathfrak a_{\nu,1}^{\mu,n}]f\|_p \le C_\epsilon 2^{-\frac 2pk+\epsilon k} (2^n\delta_1)^{1-\frac{2N}p+\epsilon}\|f\|_p\end{align*}$$

for $p\ge 4(N-1)-2$ . Besides, since $C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$ , by (2.16) we have $\| (1-\tilde \chi )\mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}]f\|_{L^p(\mathbb R^{d+1})} \lesssim _ B\!2^{-k}(2^n\delta _1)^{1-N} \|f\|_{L^p(\mathbb R^d)}$ for $p>1$ . Note $2^n\delta _1\gtrsim 2^{-k/N}$ . Combining those two estimates yields

(3.31) $$ \begin{align} \| \mathcal T[\mathfrak a_{\nu,1}^{\mu,n}]f\|_p \le C_\epsilon 2^{-\frac 2pk+\epsilon k} (2^n\delta_1)^{1-\frac{2N}p+\epsilon} \|f\|_p. \end{align} $$

To exploit disjointness of $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}$ , we define a multiplier operator by

$$\begin{align*}\mathcal F(P_s^\delta f)(\xi)= \beta_0\big(| (\widetilde {\mathcal L}_s^\delta)^{-1}\xi|/(C_12^k) \big)\widehat f(\xi)\end{align*}$$

for a constant $C_1>0$ . Since $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}\subset {\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, 2^5B)$ , by Lemma 3.6 we may choose $C_1$ large enough so that $\beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )=1 $ on $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}$ . Thus, $\mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}]f= \mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}] P_{2^n\delta _1\nu }^{2^n\delta _1} f $ . Combining this and (3.31), we obtain

$$\begin{align*}\left(\sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \| \mathcal T[\mathfrak a_{\nu,1}^{\mu,n}]f\|_p^p \,\right)^{1/p} \le C_\epsilon 2^{-\frac 2pk+\epsilon k} (2^n\delta_1)^{1-\frac{2N}p+\epsilon} \left( \sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \|P_{2^n\delta_1\nu}^{2^n\delta_1} f\|_p^p\, \right)^{1/p} \end{align*}$$

for a constant $C_\epsilon =C_\epsilon (B)$ if $p\ge 4N-6$ . Therefore, the estimate (3.23) follows if we show

(3.32) $$ \begin{align} \left( \sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \|P_{2^n\delta_1\nu}^{2^n\delta_1} f\|_p^p\,\right)^{1/p}\lesssim_B\! \|f\|_p, \qquad 2\le p\le\infty. \end{align} $$

By interpolation, it suffices to obtain (3.32) for $p=2, \infty $ . The case $p=\infty $ is trivial since $\|P_{2^n\delta _1\nu }^{2^n\delta _1} f\|_\infty \lesssim \|f\|_\infty $ . For $p=2$ , (3.32) follows by Plancherel’s theorem since $\operatorname {\mathrm {supp}} \beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )\widehat f$ , $\nu \in \mathfrak J_n^\mu $ are finitely overlapping. Indeed, by Lemma 3.6 we have $\operatorname {\mathrm {supp}} \beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )\widehat f\subset {\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, CB)$ for a constant C. It is clear from Lemma 2.11 that ${\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, C B)$ , $\nu \in \mathfrak J_n^\mu $ overlap at most $C(B)$ times.

The proof of the estimate (3.24) is much easier since we have a favorable estimate for the kernel of $\mathcal T[\mathfrak a_{\nu ,2}^{\mu ,n}]$ thanks to the inequality (3.26).

Proof of (3.24).

Let

$$\begin{align*}\mathfrak b(s,t,\tau,\xi)= i^{-1}(\tau+\langle\gamma(s),\xi\rangle)^{-1}\partial_t \mathfrak a_{\nu,2}^{\mu,n} (s,t,\tau,\xi). \end{align*}$$

Then, integration by parts in t shows $m[\mathfrak a_{\nu ,2}^{\mu ,n}]=m[\mathfrak b]$ . Note that (3.26) holds and $C^{-1}\mathfrak a_{\nu ,2}^{\mu ,n} \in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$ for a constant $C\ge 1$ . Thus, $\mathfrak a:=C^{-1}2^k (2^n\delta _1)^N \mathfrak b$ satisfies, with $\delta =2^n\delta _1$ and , (2.6) and (2.7) for $0\le j\le 1$ , $0\le l\le 2N-1$ , and $|\alpha |\le d+N+2$ . Applying the estimate (2.15), we obtain $ \|\mathcal T[\mathfrak a_{\nu ,2}^{\mu ,n}]f\|_\infty \lesssim _B\! 2^{-k}(2^n\delta _1)^{1-N}\|f\|_\infty. $ Since $\delta _1\ge 2^{-k/ N}$ , this gives

$$\begin{align*}\|\mathcal T[\mathfrak a_{\nu,2}^{\mu,n}]f\|_\infty \lesssim_B \! 2^{-\frac {(N+2)k} {2N}}(2^n\delta_1)^{-\frac N2}\|f\|_\infty. \end{align*}$$

By interpolation it is sufficient to show (3.24) for $p=2$ . Note that $\|b(\cdot ,t,\tau ,\xi )\|_\infty + \|\partial _s b(\cdot ,t,\tau ,\xi )\|_1\lesssim 2^{-k} (2^n\delta _1)^{-N}.$ Thus, (2.28) and using van der Corput’s lemma in s give $ |m[\mathfrak a_{\nu ,2}^{\mu ,n}](\tau ,\xi )| \lesssim 2^{-k(1+N)/N} (2^n\delta _1)^{-N}. $ Since $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,2}^{\mu ,n} \subset {\Lambda }^{\prime}_k ( 2^n\delta _1\nu , 2^n\delta _1, 2^5B)$ , as before, we have $\mathcal T[\mathfrak a^{\mu ,n}_{2,\nu }]f= \mathcal T[\mathfrak a^{\mu ,n}_{2,\nu }] P_{2^n\delta _1\nu }^{2^n\delta _1} f $ with a positive constant $C_1$ large enough. Thus, by Plancherel’s theorem

$$ \begin{align*} \| \mathcal T[\mathfrak a_{\nu,2}^{\mu,n}] f \|_{L^2}^2 \lesssim_B\! 2^{-\frac{2(1+N)}N k} (2^n\delta_1)^{-2N}\!\!\!\iint_{\{ \tau: |\mathfrak g_\mu^0(\tau,\xi)| \le 2^{k+1}(2^n\delta_1)^N \}}\!\!\!\!\! d\tau\, |\mathcal F(P_{2^n\delta_1\nu}^{2^n\delta_1} f)(\xi)|^2\, d\xi. \end{align*} $$

Combining this and (3.32) yields (3.24) for $p=2$ .

3.3 Proof of Lemma 3.2

To simplify notations, we denote

for the rest of this section. To prove Lemma 3.2, we verify the conditions (2.6) and (2.7) with $\mathfrak a=\mathfrak a_{\nu }^{\mu ,n}$ ,

and

. The first is easy. In fact, since $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$ and

, we only need to show

(3.33)

on $\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a_{\nu }^{\mu ,n}$ . Using (3.6) and (3.11) together with (2.32) and (3.12), one can easily obtain

(3.34)

on $\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a_{\nu }^{\mu ,n}$ . Expanding $\langle G^{(j)}(s),(\tau ,\xi )\rangle $ in Taylor’s series at $\sigma (\xi )$ gives (3.33) since (3.13) holds.

We now proceed to show (2.7) with $\mathfrak a=\mathfrak a_{\nu }^{\mu ,n}$ ,

and

. Since $\mathfrak a_{\nu }^{\mu ,n}$ consists of three factors $\mathfrak a^\mu $ ,

, and

, by Leibniz’s rule it is sufficient to consider the derivatives of each of them. The bounds on the derivatives of

are clear. So, it is enough to show (2.7) for

with

and

whenever

.

We handle $\mathfrak a^\mu $ first. That is to say, we show

(3.35)

for

. Since $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu , \delta _0)$ and

, we have

(3.36)

One can show this using (2.11). We consider

By (2.8), we have $|\,\mathcal U^\intercal z|\lesssim _B\! |z|$ because $|\delta _0^{-1} 2^n \delta _1| \lesssim _B 1$ . Thus, (3.36) gives

for

.

Let

. Then,

, so

by Lemma 2.5. This and (2.9) give

for

. Therefore, we obtain (3.35) since

.

We continue to show (2.7) for

. Note that $\delta _\ast ^{-2N!} \mathfrak G_N^\mu $ is a sum of

and

, $0\le j\le N-2$ . Since the exponents ${2N!}/{(N-j)}$ are even integers, for the desired bounds on

it suffices to show the same bounds on the derivatives of

The bound on

is a consequence of (2.10) and the following lemma. For simplicity, we denote

Lemma 3.7. If $\Xi \in \operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a_{\nu }^{\mu ,n}$ , then we have

(3.37)

Proof. By (2.29), $\gamma ^{(N-1)} ( \sigma (\tilde \Xi ) ) \cdot \tilde \Xi =0$ . Differentiation gives

(3.38)

Denote $s=\sigma (\tilde \Xi )$ . By (2.4),

. Since

, that is, (3.10), by Lemma 2.6 we have

. Besides, $|\gamma ^{(N)}(\sigma (\tilde \Xi )) \cdot \tilde \Xi | \gtrsim |\tilde \Xi | \sim 2^k$ (see (2.28)). Thus, (3.38) and (2.10) give

which proves (3.37) with $|\alpha |=1$ .

We show the bounds on the derivatives of higher orders by induction. Assume that (3.37) holds true for $|\alpha |\le L$ . Let $\alpha '$ be a multi-index such that $|\alpha '|=L+1$ . Then, differentiating the equation (3.38) and using the induction assumption, one can easily see , by which we get (3.37) for $|\alpha |=L+1$ . Since $\sigma \in \mathrm{C}^{2d+2}$ , one can continue this as far as $L\le 2d+1$ .

The proof of Lemma 3.2 is now completed if we show

(3.39)

for $0\le \ell \le N-2$ whenever $\Xi \in \operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n} (s,t,\cdot )$ . To this end, we use the following.

Lemma 3.8. For $ j=0,\dots ,N$ , set

If

, then for $ j=0,\dots ,N$ we have

(3.40) $$ \begin{align} |\partial_{\tau,\xi}^\alpha A_j| \lesssim_B\! |(\tau,\xi)|^{-|\alpha|}, \qquad 1\le |\alpha|\le 2d+2. \end{align} $$

Proof. When $j=N$ , the estimate (3.40) follows by Lemma 3.7 and (2.10). So, we may assume $j\le N-1$ . Differentiating $A_j$ , we have

$$\begin{align*}\nabla_{\tau,\xi}A_j= B_j+ D_j,\end{align*}$$

where

Note that

for $0\le j\le N-1$ . Since

, similarly as before, Lemma 2.6 and (2.8) give

(3.41)

By Lemma 3.7 and (3.34), $| B_j|\lesssim |\xi |^{-1}$ . Thus, for

, we have

$$\begin{align*}|\nabla_{\tau,\xi}A_j| \lesssim_B\! |\xi|^{-1}+2^{-k} \lesssim_B\! |(\tau,\xi)|^{-1}, \quad j=0,\dots,N-1. \end{align*}$$

For the second inequality we use (2.10). This gives the inequality (3.40) when $|\alpha |=1$ .

To show (3.40) for $2\le |\alpha |\le 2d+2$ , we use backward induction. By (2.29), we note $A_{N-1}=0$ , so (3.40) trivially holds when $j=N-1$ . We now assume that (3.40) holds true if $j_0+1\le j\le N-1$ for some $j_0\le N-2$ . Lemma 3.7, (2.10) and the induction assumption show $\partial ^{\alpha '}_{\tau , \xi } B_{j_0}=O(|(\tau ,\xi )|^{-1-|\alpha '|})$ for $1\le |\alpha '|\le 2d+1$ . Concerning $ D_{j_0}$ , observe that $\partial ^{\alpha '}_{\xi } ( G^{(j_0)}(\sigma (\tilde \Xi )))$ is given by a sum of the terms

$$\begin{align*}G^{(j)}(\sigma(\tilde \Xi ))\prod_{n=1}^{j-j_0}\partial^{\alpha^{\prime}_{n}}_{\xi}(\sigma(\tilde \Xi )), \end{align*}$$

where $j\ge j_0$ and $\alpha ^{\prime}_1+\cdots +\alpha ^{\prime}_{j-j_0}=\alpha '$ . Hence, Lemma 3.7, (3.41) and (2.10) give $\partial ^{\alpha '}_{ \xi } D_{j_0} =O(|(\tau ,\xi )|^{-1-|\alpha '|})$ for $1\le |\alpha '|\le 2d+1$ . Therefore, combining the estimates for $B_{j_0}$ and $D_{j_0}$ , we get $\partial ^{\alpha '}_{\tau , \xi } \nabla _{\tau ,\xi }A_{j_0}= O(|(\tau ,\xi )|^{-1-|\alpha '|})$ . This proves (3.40) for $j=j_0$ .

Before proving (3.39), we first note that

(3.42)

for $j=1, \dots , N$ . This can be shown by a routine computation. Indeed, differentiating (3.4) and using Lemma 3.7 and (2.32), one can easily see (3.42) holds since $|\sigma (\tilde \Xi )-\delta _0\mu |\lesssim \delta _0$ .

To show (3.39) for $0\le \ell \le N-2$ , we again use backward induction. Observe that (3.39) holds for $\ell =N,N-1$ . Then, we assume that (3.39) holds for $j+1\le \ell \le N$ for some $j\le N-2$ . By (3.6), we have

Thus, by Lemma 3.8 and (3.42), we get (3.39) with $\ell =j$ . This completes the proof of Lemma 3.2.

3.4 Proof of Lemma 3.4

Lemma 3.4 can be shown in the same manner as Lemma 3.2. So, we shall be brief.

By Lemma 3.2, we have

for a constant $C\ge 1$ , so it suffices to show

for some $C\ge 1$ . The support condition (2.6) is obvious, so we need only to show (2.7) with $\mathfrak a=\mathfrak a_{\nu ,1}^{\mu ,n}$ ,

, and

. Moreover, by recalling (3.22), it is enough to consider the additional factor only, that is, to show

for

. Since

on $\operatorname {\mathrm {supp}}_{s,\xi }\mathfrak a_{\nu ,1}^{\mu ,n}$ , one can obtain the estimate in the same way as in the proof of Lemma 3.2.

3.5 Sharpness of Theorem 1.3

Before closing this section, we show optimality of the regularity exponent $\alpha $ in Theorem 1.3.

Proposition 3.9. Suppose the estimate (1.4) holds for $\psi $ satisfying $\psi (0)\neq 0$ . Then $\alpha \le 2/p$ .

Proof. We write $\gamma =(\gamma _1, \dots , \gamma _d)$ . Via an affine change of variables, we may assume $\gamma _1(0)=0$ and $\gamma _1'(s) \neq 0$ on an interval $J=[-\delta _0,\delta _0] $ for $0<\delta _0\ll 1$ . Since $\psi (0)\neq 0$ , we may also assume $\psi \ge 1$ on J.

We choose $\zeta _0 \in \mathcal S(\mathbb R)$ such that $\operatorname {\mathrm {supp}} \widehat \zeta _0 \subset [-1,1]$ and $ \zeta _0 \ge 1$ on $[-r_1,r_1]$ , where $r_1=1+2\max \{ |\gamma (s)| : s \in J\}$ . Denoting $\bar x = (x_1,\dots ,x_{d-1})$ and $\bar \gamma (t)=(\gamma _1(t),\dots ,\gamma _{d-1}(t))$ , we define

$$ \begin{align*} \bar{\mathcal A}_t h(x) =\int e^{it\lambda \gamma_d(s)} \zeta_0(x_d-t\gamma_d(s)) h(\bar x - t \bar \gamma(s)) \psi(s)\,ds. \end{align*} $$

Let $\zeta \in \mathrm C_c^\infty ((-2,2))$ be a positive function such that $\zeta =1$ on $[-1,1]$ . For a positive constant $c\ll \delta _0$ , let $g_1(\bar x)=\sum _{\nu \in \lambda ^{-1}\mathbb Z \cap [-c,c]} \zeta (\lambda |\bar x+\bar \gamma (\nu )|)$ . We consider

$$\begin{align*}g(\bar x)=e^{-i\lambda \varphi(x_1)}g_1(\bar x), \end{align*}$$

where $\varphi (s)= \gamma _d \circ (- \gamma _1)^{-1}(s)$ . We claim that, if c is small enough,

(3.43) $$ \begin{align} |\bar{\mathcal A}_t g( x)| \gtrsim1, \qquad (x,t)\in S_c, \end{align} $$

where $S_c= \{ (x,t): |\bar x| \le c \lambda ^{-1}, \, |x_d| \le c, \, |t-1| \le c \lambda ^{-1}\}$ . To show this, note

$$ \begin{align*} \bar{\mathcal A}_t g(x) =\int e^{i\lambda ( t\gamma_d(s)- \varphi (x_1-t\gamma_1(s)))} \zeta_0(x_d-t\gamma_d(s)) g_1(\bar x - t \bar \gamma(s))\,\psi(s)\,ds. \end{align*} $$

Let $(x,t)\in S_c $ . Then, $\operatorname {\mathrm {supp}} g_1(\bar x - t \bar \gamma (\cdot )) \subset [-C_1c, C_1c]$ for some $C_1>0$ . Since $\varphi (s)= \gamma _d \circ (- \gamma _1)^{-1}(s)$ , by the mean value theorem we see $ |\varphi (x_1-t\gamma _1(s)) -\gamma _d(s)|\le 2r_0c\lambda ^{-1}, $ where $r_0=10 r_1\max \{ |\partial _s \varphi (s)| : \, s \in (-\gamma _1)(J_\ast )\} $ and $J_\ast =[-(C_1+1)c, (C_1+1)c]$ . Thus, we have

(3.44) $$ \begin{align} |t \gamma_d(s)- \varphi (x_1-t \gamma_1(s))| \le 3r_0c\lambda^{-1}. \end{align} $$

Besides, if $\lambda $ is sufficiently large, $ g_1(\bar x-t\bar \gamma (s))=\sum _{\nu \in \lambda ^{-1}\mathbb Z \cap [-c,c]} \zeta (\lambda |\bar x-(t-1) \bar \gamma (s)+\bar \gamma (\nu )-\bar \gamma (s)|) \gtrsim 1 $ if $s \in [-c/2, c/2]$ . Since $ \operatorname {\mathrm {supp}} g_1(\bar x - t \bar \gamma (\cdot ))\subset J$ with c small enough and $\zeta _0 (x_d-t\gamma _d(s))\ge 1$ , we get $\int \zeta _0 (x_d-t\gamma _d(s)) g_1(\bar x-t\bar \gamma (s)) \psi (s)\,ds \gtrsim 1. $ Therefore, (3.43) follows by (3.44) if c is small enough, that is, $c\ll 1/(3r_0)$ .

We set $f(x)=e^{-i\lambda x_d} \zeta _0(x_d) g(\bar x).$ Then, $ \chi (t) \mathcal A_t f(x)= e^{-i\lambda x_d} \chi (t) \bar {\mathcal A}_t g(x). $ By our choice of $\zeta _0$ , $\operatorname {\mathrm {supp}} \widehat f\subset \{\xi : |\xi _d+\lambda |\le 1\}$ , so $\operatorname {\mathrm {supp}} \mathcal F(\chi (t)\mathcal A_t f)\subset \{(\tau , \xi ): |\xi _d+\lambda |\le 1\}$ . This gives

(3.45) $$ \begin{align} \lambda^{\alpha}\| \chi(t) \mathcal A_t f\|_{L^p(\mathbb R^{d+1})} \lesssim \| \chi(t) \mathcal A_t f \|_{L_\alpha^p(\mathbb R^{d+1})}. \end{align} $$

Indeed, $ \lambda ^\alpha \| \chi (t) \mathcal A_t f \|_{L^p(\mathbb R^{d+1})} \lesssim \| \chi (t) \mathcal A_t f \|_{L^p( \mathbb R_{t,\bar x}; L_\alpha ^p(\mathbb R_{x_d}))}$ by Mihlin’s multiplier theorem in $x_d$ . Similarly, one also sees $ \|F \|_{L^p( \mathbb R_{t,\bar x}; L_\alpha ^p(\mathbb R_{x_d}))} \le C \|F \|_{L_\alpha ^p(\mathbb R^{d+1})} $ for $\alpha \ge 0$ and any F. Combining those inequalities gives (3.45).

From (3.43), we have $\|\chi (t) \mathcal A_t f\|_p= \| \chi (t) \bar {\mathcal A}_t g \|_{p} \ge C\lambda ^{-d/p}.$ Note that $\operatorname {\mathrm {supp}} g$ is contained in a $O(\lambda ^{-1})$ -neighborhood of $-\bar {\gamma }$ , so it follows that $\|f\|_p \lesssim \lambda ^{-(d-2)/p}$ . Therefore, by (3.45) the inequality (1.4) implies $\lambda ^\alpha \lambda ^{-d/p} \lesssim \lambda ^{-(d-2)/p}$ . Taking $\lambda \to \infty $ gives $\alpha \le 2/p$ .

4 $L^p$ Sobolev regularity

In this section, we prove Theorem 1.1, whose proof proceeds in a similar way as that of Theorem 1.3. However, we provide some details to make it clear how the optimal bounds are achieved. There are no t, $\tau $ variables appearing in the symbols, so the proof is consequently simpler but some modifications are necessary.

For a large $B\ge 1$ , we assume

(4.1) $$ \begin{align} \max_{0\le j\le 2d} |\gamma^{(j)}(s)|\,\le\, B, \qquad s\in I. \end{align} $$

Let $2 \le L \le d$ . For $\gamma $ satisfying $\mathfrak V(L,B)$ , we say $ \bar a \in \mathrm C^{d+1}(\mathbb R^{d+1})$ is a symbol of type $(k,L, B)$ relative to $\gamma $ if $ \operatorname {\mathrm {supp}} \bar a \subset I\times \mathbb A_k$ , $\mathfrak N(L, B)$ holds for $\gamma $ on $\operatorname {\mathrm {supp}} \bar a$ , and

(4.2) $$ \begin{align} |\partial_s^j \partial_\xi^\alpha \bar a (s,\xi) |\le B|\xi|^{-|\alpha|} \end{align} $$

for $0 \le j \le 1$ and $|\alpha | \le d+1$ . As before, Theorem 1.1 is a straightforward consequence of the following. We denote $\mathcal A[\gamma , \bar a ]=\mathcal A_1[\gamma , \bar a ]$ .

Theorem 4.1. Suppose $\gamma \in \mathrm C^{2d}(I)$ satisfies (4.1) and $\mathfrak V(L,B)$ for some $B\ge 1$ . Suppose $ \bar a $ is a symbol of type $(k,L,B)$ relative to $\gamma $ for some $B\ge 1$ . Then, if $p> 2(L-1)$ , for a constant $C=C(B)$

(4.3) $$ \begin{align} \| \mathcal A[\gamma, \bar a ]f \|_{L^p(\mathbb R^d)} \le C 2^{-k/p} \|f\|_{L^p(\mathbb R^d)}. \end{align} $$

In order to prove Theorem 1.1, we consider $ \bar a_k (s,\xi ):=\psi (s)\beta (2^{-k}|\xi |)$ , where $\beta \in \mathrm C_c^\infty ((1/2,4))$ . By the condition (1.1), $ \bar a_k $ is a symbol of type $(k,d, B)$ relative to $\gamma $ for some B, thus Theorem 4.1 gives (4.3) for $p> 2(d-1)$ . The estimate (4.3) for each dyadic pieces can be put together by the result in [22]. So, we get the estimate (1.2) for $\alpha =\alpha (p)$ if $p> 2(d-1)$ (e.g., see [2]).

Interpolation with $\| \mathcal A[\gamma , \bar a _k ] f\|_{2} \lesssim 2^{-k/d} \|f\|_{2}$ which follows from (1.3) gives $\| \mathcal A[\gamma ,\bar a _k ] f\|_{p} \lesssim _B\! 2^{-\alpha k } \|f\|_{p}$ for $\alpha \le \alpha (p)$ with strict inequality when $p\in (2, 2(d-1)]$ . Using those estimates, we can prove Corollary 1.2. Indeed, if $\gamma $ is a curve of maximal type $\ell>d$ , a typical anisotropic scaling argument gives $\| \mathcal A[\gamma ,\bar a _k ] f\|_{p} \lesssim _B\! 2^{-\min (\alpha (p), 1/\ell )k } \|f\|_{p}$ for $p\neq \ell $ when $ \ell \ge 2d-2$ , and for $p\in [2, 2\ell /(2d-\ell ))\cup ( 2d-2, \infty )$ when $d< \ell < 2d-2$ . As in the above, one can combine those estimates to get the estimate (1.2) ([22]).

4.1 Proof of Theorem 4.1

The case $L=2$ is easy. Since $ \bar a $ is a symbol of type $(k,2,B)$ relative to $\gamma $ , van der Corput’s lemma and Plancherel’s theorem give (4.3) for $p=2$ . Interpolation with the $L^\infty $ estimate shows (4.3) for $p\ge 2$ . When $L\ge 3$ , we have the following, which immediately yields Theorem 4.1.

Proposition 4.2. Let $3 \le N \le d$ . Suppose Theorem 4.1 holds for $L=N-1$ . Then, Theorem 4.1 holds true with $L=N$ .

To prove the proposition, we fix $N\in [3, d]$ and $\gamma $ satisfying ${\mathfrak V(N, B)}$ , and $\bar a$ of type $(k, N, B)$ relative to $\gamma $ . For

and $\delta>0$ such that

, let

By

we denote the collection of $ \bar {\mathfrak a} \in \mathrm C^{d+1}(\mathbb R^{d+1}) $ satisfying

and

for $0 \le j \le 1$ , $|\alpha | \le d+1$ .

The next lemma which plays the same role as Lemma 2.8 can be shown by routinely following the proof of Lemma 2.8.

Lemma 4.3. Let

and $j_\ast =\log (2^k \delta ^N)$ . Suppose (2.20) holds on $\operatorname {\mathrm {supp}} \bar {\mathfrak a}$ . Then, there exist constants $C, l_\ast $ , $\tilde B\ge 1$ , and $\delta '>0$ depending on B, and symbols $\bar {\mathfrak a}_{1}, \dots , \bar {\mathfrak a}_{l_\ast }$ of type $(j, N-1, \tilde B)$ relative to

such that

$ \|\tilde f_l\|_p= \|f\|_p$ , and $j\in [j_\ast -C, j_\ast +C]$ as long as $0<\delta <\delta '$ .

The required regularity order for $\gamma $ is reduced thanks to the fact that $\bar {\mathfrak a}$ is independent of $\tau , t$ . Actually, one may take when following the Proof of Lemma 2.8, since (4.2) clearly holds for $\bar a=\tilde a$ .

Using $\eta _N$ (see (2.27)), we break

$$\begin{align*}\mathcal A[\gamma,\bar a]=\mathcal A[\gamma, \bar a\eta_N]+ \mathcal A[\gamma, \bar a(1-\eta_N)].\end{align*}$$

Note that $C^{-1} \bar a(1-\eta _N)$ is of type $(k, N-1, B')$ relative to $\gamma $ for some large constants $B'$ and C, so we may apply the assumption to $\mathcal A[\gamma , \bar a(1-\eta _N)]f$ . Consequently, we have the estimate (4.3) for $\bar a=\bar a(1-\eta _N)$ if $ p> 2N-4$ .

To handle $\mathcal A[\gamma , \bar a\eta _N]$ , as before, we may assume that for some and a small $\delta _\ast $ . Here, $\bar \Gamma _k$ is defined in the same way as $\Gamma _k$ by replacing $a\eta _N$ by $\bar a\eta _N$ (see Section 2.3). Since (2.28) holds on $\operatorname {\mathrm {supp}} (\bar a\eta _N)$ , we may work under the same Basic assumption as in Section 2.3. That is to say, we have $\sigma $ on $\bar \Gamma _k$ satisfying (2.29) and for $\xi \in \bar \Gamma _k$ . Moreover, $\sigma \in \mathrm C^{d+1}$ since $\gamma \in \mathrm C^{2d}(I)$ , and (2.30) holds for $\xi \in \bar \Gamma _k$ and $|\alpha |\le d+1$ . Thus, (4.2) remains valid for the symbols to be given by decomposing $\bar a$ with cutoff functions associated with $\sigma $ and $\bar {\mathfrak G}_N^{\mu }.$

Apparently, for a constant $C=C(B, \delta _\ast )$ . Therefore, the proof of Proposition 4.2 is completed if we show the following.

Proposition 4.4. Let $3 \le N \le d$ and with $ \operatorname {\mathrm {supp}}_\xi \bar {\mathfrak a}\subset \bar \Gamma _k$ . Suppose Theorem 4.1 holds for $L=N-1$ . Then, if $p> 2(N-1)$ , we have the estimate (4.3).

We prove Proposition 4.4 using the next, which corresponds to Proposition 2.10. In what follows, we denote $\mathcal A[\bar {\mathfrak a}]=\mathcal A[\gamma , \bar {\mathfrak a}]$ .

Proposition 4.5. Let $\delta _0$ and $\delta _1$ satisfy (2.31). For $\mu $ such that , let $ \bar {\mathfrak a}^\mu \in \bar {\mathfrak A}_k(\delta _0\mu , \delta _0)$ with . Suppose Theorem 4.1 holds for $L=N-1$ . Then, if $p\in (2N-2, \infty )$ , there are constants $\epsilon _0>0$ , $C_0=C_0(\epsilon _0, B)\ge 2$ , and symbols $ \bar {\mathfrak a}_\nu \in \bar {\mathfrak A}_k( \delta _1\nu ,\delta _1)$ with , $\nu \in \cup _\mu \mathfrak J_0^\mu $ such that

$$ \begin{align*} \left(\sum_\mu \| \mathcal A[\bar{\mathfrak a} ^\mu] f \|_{p}^p \right)^{\frac1p} \le C_0 \big({\delta_1} / {\delta_0}\big)^{\frac Np-1+\epsilon_0} \left(\sum_{\nu} \| \mathcal A[\bar{\mathfrak a} _\nu]f \|_{p}^p \right)^{\frac1p} +C_0 \delta_0^{-\frac Np+1} 2^{-\frac kp}\|f\|_p. \end{align*} $$

Let $\delta '$ be the number given in Lemma 4.3. We choose a positive constant $\delta _\circ $ (cf. (2.26)) such that

(4.4) $$ \begin{align} \delta_\circ < \min \{ 2^{-10} B^{-3} \delta', \,(2^{7d}B^6)^{-N} C_0^{-2N/\epsilon_0}\}. \end{align} $$

Proof of Proposition 4.4.

Set $\delta _0=\delta _\circ $ , and let $\delta _1,\dots , \delta _J$ be given by (2.33). Then, applying Proposition 4.5 iteratively up to J-th step (cf. Section 2.4), we have symbols $ \bar {\mathfrak a}_\nu \in \bar {\mathfrak A}_k( \delta _{\!J}\nu , \delta _{\!J})$ , , such that

$$\begin{align*}\big\| \mathcal A[\bar{\mathfrak a} ]f \big\|_{p} \le C_0^J\delta_{\!J}^{\frac {N}{p}-1+\epsilon_0} \left(\sum_\nu \| \mathcal A[\bar{\mathfrak a} _{\nu}]f\|_p^p \right)^{1/p} \!+ 2^{-\frac{k}p} \delta_0^{-\frac Np+1-\epsilon_0}\! \sum_{0\le j\le J-1}C_0^{j+1} \delta_j^{\epsilon_0} \|f\|_p. \end{align*}$$

By (4.4) and (2.33), $ \delta _j \le C_0^{-2((N+1)/N)^jN/{\epsilon _0} }$ for $0 \le j \le J-1.$ So, $\sum _{j=0}^{J-1} C_0^{j+1} \delta _j^{\epsilon _0} \le C_1$ for a constant $C_1$ , and $C_0^J\delta _J^{\epsilon _0} \le C_1$ . Thus, the matter is now reduced to showing

$$\begin{align*}\left(\sum_{\nu} \| \mathcal A[\bar{\mathfrak a}_\nu] f\|_{L^p(\mathbb R^d)}^p \right)^{1/p} \lesssim_B\! 2^{-\frac kN}\|f\|_{L^p(\mathbb R^d)}, \qquad 2\le p\le \infty, \end{align*}$$

which corresponds to the estimate (2.35). The case $p=\infty $ follows from the estimate $\| \mathcal A[\bar {\mathfrak a} ]f\|_{L^\infty } \le C\delta \|f\|_{L^\infty }$ when for some (cf. (2.15)). One can obtain this in the same manner as in the proof of Lemma 2.7. The case $p=2$ can be handled similarly as before, using Plancherel’s theorem and van der Corput’s lemma combined with Lemma 2.11 and (2.28).

The proof of Proposition 4.5 is similar to that of Proposition 2.10. Instead of (2.40), we use the estimate (2.41), in which the exponent is adjusted to the sharp Sobolev regularity estimate. However, a similar approach breaks down if one tries to obtain the local smoothing estimate (1.4) with the optimal regularity $\alpha =2/p$ . To do so, we need the inequality (2.39) for $4N-2<p \le N(N+1)$ . However, there is no such estimate available when $N=2$ .

4.2 Proof of Proposition 4.5

Let $ \bar {\mathfrak a}^\mu \in \bar {\mathfrak A}_k(\delta _0\mu ,\delta _0)$ . For $\nu \in \mathfrak J_n^\mu $ , set

$$\begin{align*}\bar{\mathfrak a}_{\nu}^{\mu,n} = \bar{\mathfrak a}^\mu \times \begin{cases} \beta_0 \big( \delta_1^{-2N!} \, \bar{\mathfrak G}_N^{\mu} \big) \, \zeta(\delta_1^{-1}s-\nu), & \ n=0, \\[2pt] \beta_N \big( (2^{n}\delta_1)^{-2N!} \, \bar{\mathfrak G}_N^{\mu} \big) \, \zeta(2^{-n}\delta_1^{-1}s-\nu), & \ n\ge 1. \end{cases} \end{align*}$$

(See (3.21)). Let $\bar {\mathbf y}_\mu = (y_\mu ^1,\dots ,y^{N}_\mu )$ , and let $\bar {\mathcal D}_\delta $ denote the $N\times N$ matrix $(\delta ^{1-N} \bar e_1, \delta ^{2-N} \bar e_2, \dots , \delta ^0 \bar e_{N})$ where $\bar e_j$ is the j-th standard unit vector in $\mathbb R^{N}$ . Recalling (3.18), we consider a linear map

$$\begin{align*}\bar{\mathrm Y}_\mu^{\delta_0}(\xi)= \big( 2^{-k} \bar{\mathcal D}_{\delta_0} \bar{\mathbf y}_\mu,\, y_{N+1},\dots,\,y_d\big). \end{align*}$$

Let $\mathbf r$ denote the curve $\mathbf r_\circ ^N$ . Note that (3.10) and (3.11) hold on $\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$ . Similarly as in Proof of Lemma 3.3 , we see $ | \langle \bar {\mathbf y}_\mu , \mathbf r^{(j)}((2^n\delta _1/\delta _0)\nu -\mu ) \rangle | \lesssim 2^k (2^{n}\delta _1/\delta _0)^{N-j} $ for $1 \le j \le N-1$ and $2^{k-2}/B \le \big |\big \langle \bar {\mathbf y}_\mu , \mathbf r^{(N)} \big \rangle \big |\le CB 2^k$ on $\operatorname {\mathrm {supp}}_\xi \bar {\mathfrak a}_{\nu }^{\mu ,n}$ . Thus, as before (cf. (3.19)), we have

$$\begin{align*}\bar{\mathrm Y}_\mu^{\delta_0} ( \operatorname{\mathrm{supp}}_{\xi} \bar{\mathfrak a}_{\nu}^{\mu,n} ) \subset \mathbf S\Big(\frac{2^n\delta_1}{\delta_0}\nu-\mu, \, C\frac{2^n\delta_1}{\delta_0},\, CB; \, \mathbf r_\circ^N \Big) \times \mathbb R^{d-N} \end{align*}$$

for some $C>0$ . Note $\operatorname {\mathrm {supp}} \mathcal F( \mathcal A[\bar {\mathfrak a} _{\nu }^{\mu ,n}]f)\subset \operatorname {\mathrm {supp}}_{\xi } \bar {\mathfrak a}_{\nu }^{\mu ,n}$ . Therefore, using the change of variables $\xi \to \bar {\mathrm Y}_\mu ^{\delta _0} (\xi )$ , (2.41) with N replaced by $N-1$ and its cylindrical extension (e.g., (2.42)), we get

(4.5) $$ \begin{align} \big\| \sum_{\nu\in \mathfrak J_{n}^\mu} \mathcal A[\bar{\mathfrak a}_{\nu}^{\mu,n}]f \big\|_p \le C_0 \big( {2^n\delta_1} /{\delta_0}\big)^{\frac {N} {p}-1+\epsilon_0} \left(\sum_{\nu\in \mathfrak J_{n}^\mu} \big\|\mathcal A[\bar{\mathfrak a} _{\nu}^{\mu,n}]f \big\|_p^p\right)^{1/p} \end{align} $$

for $2N-2<p <\infty $ (cf. (3.15)). Since $\mathcal A [\bar {\mathfrak a}^\mu ]f=\sum _n \sum _{\nu \in \mathfrak J_n^\mu } \mathcal A[\bar {\mathfrak a}_{\nu }^{\mu ,n}]f$ , by Minkowski’s inequality and (4.5), we have $(\sum _\mu \| \mathcal A[\bar {\mathfrak a} ^\mu ]f\|_p^p\,)^{1/p}$ bounded by

$$ \begin{align*} \begin{aligned} \sum_{n\ge 0} \bar {\mathbf E}_n:= C_0 \sum_{n\ge 0} \big( {2^n\delta_1}/{\delta_0} \big)^{{\frac {N} {p}-1+\epsilon_0}} \left(\sum_{\mu} \sum_{\nu\in \mathfrak J_n^\mu} \| \mathcal A[\bar{\mathfrak a} ^{\mu,n}_{\nu}]f\|_p^p\right)^{1/p}. \end{aligned} \end{align*} $$

The proof of Lemma 3.2 also shows $C^{-1} \bar {\mathfrak a}_{\nu }^{\mu ,n}\in \bar {\mathfrak A}_k(2^n\delta _1\nu , 2^n\delta _1)$ for a positive constant C. The matter is reduced to obtaining

(4.6) $$ \begin{align} \left(\sum_{\mu} \sum_{\nu \in \mathfrak J_n^\mu} \|\mathcal A[\bar{\mathfrak a}_{\nu}^{\mu,n}] f\|_{L^p(\mathbb R^d)}^p \right)^{1/p} \lesssim_B\! (2^n\delta_1)^{1-\frac Np} 2^{-\frac kp} \|f\|_{L^p(\mathbb R^d)}, \qquad n\ge 1 \end{align} $$

for $p>2(N-2)$ . This gives $\sum _{n\ge 1} \bar {\mathbf E}_n \lesssim _B\! \delta _0^{-N/p+1} 2^{-k/p}\|f\|_p$ since $2^n\delta _1\le C\delta _0$ .

The proof of (4.6) is similar with that of (3.23). Since $C^{-1} \bar {\mathfrak a}_{\nu }^{\mu ,n}\in \bar {\mathfrak A}_k(2^n\delta _1\nu , 2^n\delta _1)$ , we have $\mathcal A[\bar {\mathfrak a} ^{\mu , n}_{\nu }]f= \mathcal A[\bar {\mathfrak a} ^{\mu , n}_{\nu }] P_{2^n\delta _1\nu }^{2^n\delta _1} f $ . Besides, (3.27) or (3.28) for some $1\le j\le N-2$ holds on $\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$ . Thus, we have (2.20) with $\delta =2^n\delta _1$ for some $B'$ on $\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$ for $n\ge 1$ (see Proof of Lemma 3.5 ). Therefore, applying Lemma 4.3 to $\mathcal A[\bar {\mathfrak a}_{\nu }^{\mu ,n}] f$ and then the assumption (Theorem 4.1 with $L=N-1$ ), we obtain

$$\begin{align*}\|\mathcal A[\bar{\mathfrak a}_{\nu}^{\mu,n}] f\|_{L^p}\lesssim_B\! (2^n\delta_1)^{1-\frac Np} 2^{-\frac kp} \|P_{2^n\delta_1\nu}^{2^n\delta_1} f\|_p.\end{align*}$$

This combined with (3.32) gives (4.6) as desired.