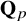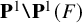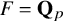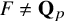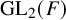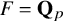Factorisation de la cohomologie étale p-adique de la tour de Drinfeld

Résumé

For a finite extension F of ${\mathbf Q}_p$ , Drinfeld defined a tower of coverings of (the Drinfeld half-plane). For $F = {\mathbf Q}_p$ , we describe a decomposition of the p-adic geometric étale cohomology of this tower analogous to Emerton’s decomposition of completed cohomology of the tower of modular curves. A crucial ingredient is a finiteness theorem for the arithmetic étale cohomology modulo p whose proof uses Scholze’s functor, global ingredients, and a computation of nearby cycles which makes it possible to prove that this cohomology has finite presentation. This last result holds for all F; for $F\neq {\mathbf Q}_p$ , it implies that the representations of $\mathrm{GL}_2(F)$ obtained from the cohomology of the Drinfeld tower are not admissible contrary to the case $F = {\mathbf Q}_p$ .

0 Introduction

Dans [16], nous avons calculé la multiplicité d’une représentation p-adique absolument irréductible du groupe de Galois absolu ${\cal G}_{\mathbf {Q}_p}$ de $\mathbf {Q}_p$ dans la cohomologie étale de la tour $({\cal M}_{n,\mathbf {C}_p})_{n\geq 0}$ des revêtements du demi-plan de Drinfeld (pour avoir une action de ${\cal G}_{\mathbf {Q}_p}$ et pas seulement du groupe de Weil $W_{\mathbf {Q}_p}$ , il faut remplacer ${\cal M}_{n,\mathbf {C}_p}$ par son quotient ¹ ${\cal M}_{n,\mathbf {C}_p}^p$ par ${\big (\begin {smallmatrix}p&0\\ 0&p\end {smallmatrix}\big )}\in G:={\mathrm{GL}}_2(\mathbf {Q}_p)$ ). La réponse fait intervenir la correspondance de Langlands locale p-adique pour G, ainsi que la correspondance de Jacquet-Langlands locale classique, cf. th. 0.14 ci-dessous.

Dans cet article, nous déterminons, pour ² $p>3$ , la structure complète de cette cohomologie en tant que ${\cal G}_{\mathbf {Q}_p}\times G\times \check G$ -module, où $\check G$ est le groupe des unités de l’algèbre des quaternions non déployée sur $\mathbf {Q}_p$ . La réponse (th. 0.1 ci-dessous) est similaire à la description d’Emerton [28] de la cohomologie complétée de la tour des courbes modulaires, les algèbres de Hecke dans la description d’Emerton étant remplacées par des anneaux de Kisin [46] paramétrant les représentations potentiellement cristallines, à poids de Hodge-Tate $0$ et $1$ , et type fixé (on fixe en fait la représentation de Weil-Deligne, pas seulement le type galoisien).

Plus précisément, l’objet que nous décrivons n’est pas la cohomologie de ${\cal M}_{n,\mathbf {C}_p}^p$ mais celle de ${\cal M}_{n,\overline {\mathbf {Q}}_p}^p$ (i.e. la cohomologie complétée ³ de la tour des ${\cal M}_{n,K}^p$ pour $[K:\mathbf {Q}_p]<\infty $ ); il est possible que le quotient de la cohomologie de ${\cal M}_{n,\mathbf {C}_p}^p$ par celle de ${\cal M}_{n,\overline {\mathbf {Q}}_p}^p$ soit du bruit sans signification arithmétique (en tout cas, nous avons échoué à lui trouver une interprétation).

Un rôle crucial est joué par un théorème de finitude pour la cohomologie arithmétique modulo p de la tour de Drinfeld (th. 0.2), dont la preuve (géométrique et très différente des méthodes utilisées dans [16], en particulier elle ne fait pas usage de [23]) occupe la majeure partie de l’article.

0.1 Les résultats principaux

Notre résultat principal (th. 5.15) s’énonce comme suit:

Théorème 0.1. Si L est une extension finie de $\mathbf {Q}_p$ assez grande ⁴ , on dispose d’un isomorphisme de $L[{\cal G}_{\mathbf {Q}_p}\times G\times \check G]$ -modules topologiques

$$ \begin{align*}H^1_{\operatorname{\acute{e}t} }({\mathcal{M}}^p_{n,\overline{\mathbf{Q}}_p},L(1))\simeq \oplus_M\big(\widehat{\oplus}_{\mathcal{ B}} \ {\boldsymbol\Pi}^{\boldsymbol *}(\rho_{\mathcal{B},M}) \otimes \rho_{\mathcal{B},M}\otimes \check{R}_{\mathcal{B},M}\big)\otimes_L{\mathrm{JL}}(M),\end{align*} $$

où $\check {R}_{{\cal B},M}$ est le L-dual continu de $R_{{\cal B},M}$ et les produits tensoriels sont au-dessus de $R_{{\cal B},M}$ .

Le lecteur trouvera des définitions précises ⁵ des objets intervenant ci-dessus dans la suite de cette introduction, bornons-nous ici à mettre en avant quelques points essentiels:

• • La première somme porte sur les types M de niveau $\leq n$ . Ces types sont en bijection avec les représentations irréductibles du groupe de Galois de ${\cal M}_{n,\mathbf {C}_p}^p$ par rapport au demi-plan de Drinfeld. Ce groupe est un quotient fini de $\check {G}$ . On note ${\mathrm{JL}}(M)$ la représentation irréductible (de dimension finie) de $\check G$ associée à M.

• • La somme directe complétée porte sur les blocs ${\cal B}$ de la catégorie des $k_L$ -représentations lisses de longueur finie de G. Ces blocs sont en bijection naturelle [54] avec les orbites sous ${\mathrm{Gal}}(\overline {\mathbf {F}}_p/k_L)$ des $\overline {\mathbf {F}}_p$ -représentations $\rho _{\cal B}$ de ${\cal G}_{\mathbf {Q}_p}$ , semi-simples, de dimension $2$ . La complétion intervenant dans la somme directe est p-adique. ⁶

• • $R_{{\cal B},M}$ est l’anneau de Kisin paramétrant les représentations de type M et réduction $\rho _{\cal B}$ , et $\rho _{{\cal B},M}$ est la représentation universelle associée. L’anneau $R_{{\cal B},M}$ est un quotient de la fibre générique de l’anneau des pseudo-caractères déformant la trace de $\rho _{\cal B}$ .

• • Le G-module topologique ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})$ interpole ⁷ les ${\boldsymbol \Pi }(\rho _x)^{\boldsymbol *}$ , pour $x\in {\mathrm{Spm}}(R_{{\cal B},M})$ , où $V\mapsto {\boldsymbol \Pi }(V)$ est la correspondance de Langlands locale p-adique, $\rho _x$ est la spécialisation de $\rho _{{\cal B},M}$ en x et tous les duaux sont topologiques ⁸ .

Un ingrédient crucial de la preuve (en dehors des résultats de [16] et [23], qui sont pleinement utilisés) est le théorème suivant (th. 4.1):

Théorème 0.2. Si $[K:\mathbf {Q}_p]<\infty $ , alors $H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,K}^p,{\boldsymbol \mu }_p)$ est la duale d’une représentation lisse admissible de G, de longueur finie comme $\mathbf {Z}_p[G]$ -module.

Le théorème ci-dessus couplé à des arguments globaux permet d’obtenir le résultat suivant (th. 4.23 et rem. 4.25), qui est un analogue modulo p du résultat principal de [16]. Si $\bar {\rho }: \mathcal {G}_{\mathbf {Q}_p}\to {\mathrm{GL}}_d(k_L)$ est une représentation continue, on pose:

$$ \begin{align*}{\boldsymbol\Pi}^{\mathrm{geo}}_n(\bar{\rho}):={\mathrm{Hom}}_{k_L[\mathcal{G}_{\mathbf{Q}_p}]}^{\mathrm{cont}}(\bar{\rho}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{p},k_L))^{\vee}.\end{align*} $$

Théorème 0.3. Soit $\bar {\rho }: \mathcal {G}_{\mathbf {Q}_p}\to {\mathrm{GL}}_d(k_L)$ une représentation continue.

1. a) ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })$ est une G-représentation lisse, de longueur finie.

2. b) Si $\bar {\rho }$ est absolument irréductible, alors ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })=0$ si $d>2$ et une extension successive de copies de ${\boldsymbol \Pi }(\bar {\rho })$ si $d=2$ , où ${\boldsymbol \Pi }(\bar {\rho })$ est la représentation supersingulière de G associée à $\bar {\rho }$ par la correspondance de Langlands locale modulo p.

On peut se demander ce qui reste vrai si on regarde la tour des revêtements du demi-plan de Drinfeld , où F est une extension finie de $\mathbf {Q}_p$ distincte de $\mathbf {Q}_p$ . Dans ce cas, nous prouvons le résultat suivant (th. 2.13 et 2.14), en utilisant un mélange d’arguments géométriques et de théorie des représentations de ${\mathrm{GL}}_2(F)$ , plus précisément les résultats de Hu [40], Schraen [66], Shotton [67], Vignéras [70] et Wu [71]:

Théorème 0.4. Soit F une extension finie de $\mathbf {Q}_p$ distincte de $\mathbf {Q}_p$ .

1. (i) Si K est une extension finie de F, alors $H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,K}^p,{\boldsymbol \mu }_p)^{\vee }$ est une représentation lisse de présentation finie de ${\mathrm{GL}}_2(F)$ . Si $n\geq 1$ et si K est assez grande, cette représentation n’est pas admissible.

2. (ii) Si $n\geq 1$ , il existe une représentation continue $\bar {\rho }:{\cal G}_{F}\to {\mathrm{GL}}_2(k_L)$ telle que ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })$ ne soit pas admissible.

Le théorème ci-dessus et sa forme précisée du th. 2.14 (complété par la rem. 2.15) posent des questions intéressantes sur la forme que doit prendre la correspondance de Langlands locale p-adique pour ${\mathrm{GL}}_2(F)$ , si $F\neq \mathbf {Q}_p$ : les problèmes rencontrés pour la classification des représentations modulo p de ${\mathrm{GL}}_2(F)$ se reflètent dans la cohomologie p-adique de la tour de Drinfeld (aucun de ces problèmes n’apparaît en $\ell $ -adique, avec $\ell \ne p$ ). Comme nous l’ont fait remarquer Dotto et Emerton, il est probable que les représentations lisses de présentation finie ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })$ (avec $\bar {\rho }: \mathcal {G}_F\to {\mathrm{GL}}_2(k_L)$ une représentation continue, et F non ramifié) aient un lien avec les représentations construites par Breuil et Paškūnas [12], ce qui fournirait une interprétation géométrique de ces dernières. Nous espérons revenir sur ce problème dans un travail ultérieur.

0.2 Finitude de la cohomologie de la tour de Drinfeld

Décrivons maintenant nos résultats plus en détail, en commençant par esquisser les preuves des th. 0.2, 0.3 et 0.4.

0.2.1 La tour de Drinfeld

Soient F une extension finie de $\mathbf {Q}_p$ , ${\cal O}_F$ l’anneau de ses entiers et l’idéal maximal de ${\cal O}_F$ . On définit les groupes:

• • $G={\mathrm{GL}}_2(F)$ , $G_0={\mathrm{GL}}_2({\cal O}_F)$ et si $n\geq 1$ .

• • $\check G=D^{\boldsymbol *}$ , où D est l’algèbre de quaternions non déployée de centre F, $\check {G}_0= {\cal O}_D^{\boldsymbol *}$ où ${\cal O}_D$ est l’ordre maximal de D, , si $n\geq 1$ et est l’idéal maximal de ${\cal O}_D$ .

Si $H=G,\check G,{\mathrm{W}}_F$ , on dispose d’un morphisme de groupes naturel $\nu _H:H{\hskip .5mm\to \hskip .5mm}F^{\boldsymbol *},$ où $\nu _G=\det $ , $\nu _{\check G}$ est la norme réduite, et $\nu _{{\mathrm{W}}_F}:{\mathrm{W}}_F\to {\mathrm{W}}_F^{\mathrm{ab}} \simeq F^{\boldsymbol *}$ est fourni par la théorie locale du corps de classes.

Le demi-plan p-adique (de Drinfeld) admet une structure naturelle d’espace analytique rigide $\Omega _{{\mathrm{Dr}},F}$ sur F, et une action de G par homographies, qui respecte cette structure. Drinfeld a défini [27] une tour de revêtements ${\cal M}_{n,\breve {F}}$ , pour $n\in \mathbf {N}$ , de ce demi-plan, vérifiant les propriétés suivantes:

• • ${\cal M}_{n,\breve {F}}$ est défini sur $\breve {F}=\widehat {F^{\mathrm{nr}}}$ et muni d’une action de ${\mathrm{W}}_F$ compatible avec l’action naturelle sur $\breve {F}$ .

• • ${\cal M}_{n,\breve {F}}$ est muni d’une action de $G\times \check G$ commutant avec l’action de ${\mathrm{W}}_F$ , et les flèches de transition ${\cal M}_{n+1,\breve {F}}\to {\cal M}_{n,\breve {F}}\to \Omega _{{\mathrm{Dr}},F}$ sont ${\mathrm{W}}_F\times \check G\times G$ -équivariantes (l’action de $\check G$ sur $\Omega _{{\mathrm{Dr}},F}$ étant l’action triviale).

• • ${\cal M}_{0,\breve {F}}=\mathbf {Z}\times \Omega _{{\mathrm{Dr}},\breve {F}}$ et, si $n\geq 1$ , alors ${\cal M}_{n,\breve {F}}$ est un revêtement galoisien de ${\cal M}_{0,\breve {F}}$ , de groupe de Galois $\check {G}_0/\check {G}_n$ .

• • L’ensemble $\pi _0({\cal M}_{n,\mathbf {C}_p})$ des composantes connexes de ${\cal M}_{n,\mathbf {C}_p}$ est un espace homogène principal sous l’action de et $H=G,\check G,{\mathrm{W}}_F$ agit sur $\pi _0({\cal M}_{n,\mathbf {C}_p})$ à travers $\nu _H:H\to F^{\boldsymbol *}$ .

Si $\varpi $ est une uniformisante de F, on note ${\cal M}_{n,\breve F}^{\varpi }$ le quotient de ${\cal M}_{n,\breve F}$ par ${\big (\begin {smallmatrix}\varpi &0\\ 0&\varpi \end {smallmatrix}\big )}\in G$ . On pose aussi

$$ \begin{align*}G':=G/{\big(\begin{smallmatrix}\varpi&0\\ 0&\varpi\end{smallmatrix}\big)}^{\mathbf{Z}}.\end{align*} $$

Alors ${\cal M}_{n,\breve F}^{\varpi }$ est l’extension des scalaires de F à $\breve F$ d’un espace analytique ${\cal M}_{n,F}^{\varpi }$ défini sur F et muni d’une action de $G'$ . Si K est une extension finie de F ou $\mathbf {C}_p$ , on note ${\cal M}_{n,K}^{\varpi }$ l’espace analytique sur K obtenu par extension des scalaires de F à K.

0.2.2 Résultats de finitude

Notre premier résultat (th. 2.1) est valable pour F quelconque:

Théorème 0.5. Si K est une extension finie de F et $k\geq 1$ alors $H^q_{\operatorname {\acute {e}t} }({\cal M}_{n,K}^{\varpi },{\cal O}_L/p^k)$ est un ${\cal O}_L$ -module profini, dont le dual de Pontryagin est une représentation lisse de G, de présentation finie.

En passant sous silence des contorsions topologiques un peu pénibles, la preuve de ce résultat utilise trois ingrédients:

• • l’existence [16] d’un modèle semi-stable G-équivariant pour ${\cal M}_{n,K}^{\varpi }$ (K assez grand),

• • la filtration de Bloch-Kato-Hyodo [9], [44] sur les cycles proches modulo p pour ramener le calcul de la cohomologie étale à celle de faisceaux cohérents sur la fibre spéciale,

• • les propriétés de la catégorie des représentations de présentation finie de $G'$ (en particulier le fait qu’elle est abélienne et stable par extensions d’après Shotton [67]).

Remarque 0.6.

1. (i) Si on disposait d’une dualité de Poincaré, on pourrait prouver la première partie du théorème de manière plus naturelle: les duaux de Pontryagin des $H^q_{\operatorname {\acute {e}t} }({\cal M}_{n,K}^{\varpi },{\cal O}_L/p^k)$ seraient les groupes de cohomologie à support compact, pour lesquels Berkovich [7] a établi la lissité de l’action de G. Malheureusement, l’existence d’une telle dualité pour des espaces analytiques comme ${\cal M}_{n,K}^{\varpi }$ n’est pas connue.

2. (ii) Il est probable qu’un tel énoncé reste valable pour la tour de Drinfeld associée à ${\mathrm{GL}}_d(F)$ avec $d>2$ , mais deux des ingrédients ci-dessus (le premier et le troisième) ne sont plus disponibles dans ce cadre.

3. (iii) Il n’est pas du tout clair si $H^1_{\operatorname {\acute {e}t} }({\cal M}_{n, \mathbf {C}_p}^{\varpi }, k_L)$ est profini. Les techniques utilisées ci-dessus utilisent de manière cruciale le fait que l’on travaille sur une extension finie de $\mathbf {Q}_p$ , pas sur $\mathbf {C}_p$ (la filtration du th. 2.4 utilise pleinement la finitude de la ramification).

Un autre résultat valable pour F quelconque est le suivant (th. 4.22):

Théorème 0.7. Si $\pi $ est un $k_L[{\mathrm{GL}}_2(F)]$ -module lisse, admissible, à caractère central, alors ${\mathrm{Hom}}_{k_L[{\mathrm{GL}}_2(F)]}^{\mathrm{cont}}(\pi ^{\vee },H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,\mathbf {C}_p},k_L))$ est de dimension finie sur $k_L$ .

Remarque 0.8.

1. (i) Pour $F=\mathbf {Q}_p$ , ce théorème est une version modulo p du th. 0.16 ci-dessous. Ce dernier se démontre par les méthodes de [16], mais il ne semble pas possible d’en déduire le th. 0.7 dans ce cas.

2. (ii) Il semble raisonnable de penser que le th. 0.7 s’étend à la tour de Drinfeld pour ${\mathrm{GL}}_d(F)$ sous la forme: les groupes ${\mathrm{Ext}}^i_{k_L[{\mathrm{GL}}_d(F)]}(\pi ^{\vee }, H^j_{\operatorname {\acute {e}t} }({\cal M}_{n,\mathbf {C}_p}, k_L))$ sont de dimension finie sur $k_L$ . Ce résultat (s’il est vrai) serait un analogue d’un résultat classique pour la cohomologie $\ell $ -adique, avec $\ell \ne p$ .

3. (iii) Si, dans l’énoncé, on remplace ${\cal M}_{n,\mathbf {C}_p}$ par ${\cal M}_{n, K}$ avec $[K:\mathbf {Q}_p]<\infty $ , le résultat est une conséquence immédiate du th. 0.5, mais il ne semble pas possible d’en tirer directement le th. 0.7.

Le résultat suivant (§4.2) est spécifique à $F=\mathbf {Q}_p$ , et nettement plus difficile à démontrer que les deux théorèmes ci-dessus:

Théorème 0.9. Si $[K:\mathbf {Q}_p]<\infty $ , alors ${\mathrm{Hom}}_{k_L[G']}^{\mathrm{cont}}(\pi ^{\vee },H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,K}^p,k_L))=0$ pour presque tout (i.e., sauf pour un nombre fini) $k_L[G']$ -module $\pi $ lisse, irréductible.

Remarque 0.10. Ce théorème implique (et est équivalent si on injecte un peu de théorie des représentations de G, cf. th. 1.24), via l’isomorphisme de Faltings entre les tours de Drinfeld et Lubin-Tate complétées, que les vecteurs lisses de ⁹ $H^1_{\operatorname {\acute {e}t} }({\mathrm{LT}}_{n,K}^p,k_L)$ pour l’action de $\check {G}$ sont de dimension finie (et proviennent des composantes connexes). On peut se demander s’il est possible de prouver ce résultat directement. S’il y a des vecteurs lisses ne provenant pas des composantes connexes, il y a des vecteurs invariants par $\check {G}_1\times {\big (\begin {smallmatrix}1+p\mathbf {Z}_p&\mathbf {Z}_p\\ p\mathbf {Z}_p&1+p\mathbf {Z}_p\end {smallmatrix}\big )}$ , et donc dans la cohomologie de ${\mathrm{LT}}_{1,K}$ , un espace dont les composantes connexes sont des couronnes ouvertes. Si on est très optimiste ¹⁰ , on peut espérer que, si H est un groupe de Lie compact agissant sur une couronne ouverte $C_K$ avec action non triviale sur , les vecteurs H-invariants de $H^1_{\operatorname {\acute {e}t} }(C_K,k_L)$ sont très petits.

Comme nous n’avons pas réussi à faire marcher les stratégies évoquées dans les rem. 0.8 et 0.10, notre preuve du th. 0.9 emprunte des chemins plus détournés. On suppose pour la suite de ce paragraphe que $F=\mathbf {Q}_p$ .

$\bullet $ Un ingrédient crucial est une suite spectrale (dont l’existence est démontrée dans le même degré de généralité que celui de l’article [61]) reliant les foncteurs de Scholze [61] $\pi \mapsto S^i(\pi )$ aux groupes qui nous intéressent. En injectant aussi le calcul de $H^i({\mathrm{SL}}_2(\mathbf {Q}_p),\pi )$ par Fust [34], cette suite spectrale permet de démontrer le résultat suivant (cor. 3.13):

Proposition 0.11. Soit $\pi $ un $k_L[G]$ -module lisse admissible, absolument irréductible. On dispose d’un morphisme naturel ¹¹

$$ \begin{align*}S^1(\pi) \to {\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty,\mathbf{C}_p}, k_L))\end{align*} $$

dont les noyau et conoyau sont de dimension finie sur $k_L$ , et qui est un isomorphisme si $\pi $ n’appartient pas à un twist $\{\chi ,{\mathrm{St}}\otimes \chi , I(\chi ,\chi \varepsilon )\}$ du bloc de la Steinberg.

L’admissibilité de $S^1(\pi )$ comme représentation de $\check G$ permet d’en déduire (via les résultats de Fust) le th. 0.7.

$\bullet $ Un autre ingrédient est une globalisation de la situation qui permet d’utiliser les résultats d’isotypie de Carayol et Scholze [61] pour analyser les représentations de ${\cal G}_{\mathbf {Q}_p}$ intervenant dans ${\mathrm{Hom}}_{k_L[G']}^{\mathrm{cont}}(\pi ^{\vee },H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,\mathbf {C}_p}^p,k_L))$ et en déduire le th. 0.9. Pour pouvoir bien globaliser on utilise des résultats de Gee et Kisin [36], et pour étudier la cohomologie complétée attachée aux algèbres de quaternions globales (déployées en toute place finie) issues de la globalisation nous utilisons les travaux de Paškūnas [55] et Paškūnas-Tung [56]. Ces arguments globaux permettent de contrôler l’action de $\mathcal {G}_{\mathbf {Q}_p}$ sur $S^1(\pi )$ , et en particulier de montrer que pour toute extension finie K de $\mathbf {Q}_p$ il n’y a qu’un nombre fini de $\pi $ comme dans le corollaire ci-dessus et tels que $S^1(\pi )^{\mathcal {G}_K}\ne 0$ .

En utilisant le fait (th. 1.21) qu’une représentation de type fini de G est de longueur finie si et seulement si son cosocle est de longueur finie (un résultat qui utilise pleinement la classification des représentations lisses irréductibles modulo p de G, classification non connue si $F\neq \mathbf {Q}_p$ , ainsi que les résultats de finitude pour les groupes d’extensions entre deux représentations lisses irréductibles de G), on déduit du th. 0.9 le résultat suivant.

Corollaire 0.12.

1. (i) Si $[K:\mathbf {Q}_p]<\infty $ , le dual de $H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,K}^p,k_L)$ est une représentation lisse de G, de longueur finie.

2. (ii) Si $\rho :{\cal G}_{\mathbf {Q}_p}\to {\mathrm{GL}}_2(k_L)$ est une représentation continue, le dual de ${\mathrm{Hom}}_{k_L[{\cal G}_{\mathbf {Q}_p}]}^{\mathrm{cont}}(\rho ,H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,\mathbf {C}_p}^p,k_L))$ est une représentation lisse de G, de longueur finie.

Remarque 0.13.

1. (i) Dans le cas $F=\mathbf {Q}_p$ , une $k_L$ -représentation de longueur finie de G est automatiquement admissible et de présentation finie.

2. (ii) Dans le cas $F\neq \mathbf {Q}_p$ , une $\overline {k}_L$ -représentation de présentation finie de G est admissible si et seulement si elle est de longueur finie, mais les $k_L$ -représentations irréductibles supersingulières de G ne sont pas forcément admissibles et ne sont pas de présentation finie [66], [71]; il existe même [48] de telles représentations qui deviennent de longueur infinie quand on étend les scalaires à $\overline {k}_L$ .

0.3 Multiplicités géométriques de représentations de ${\cal G}_{\mathbf {Q}_p}$ et G

Passons à la preuve du th. 0.1.

0.3.1 Types et objets associés

Soit F une extension finie de $\mathbf {Q}_p$ . Soit M un L- $(\varphi ,N,{\cal G}_F)$ -module (i.e. un $L\otimes \mathbf {Q}_p^{\mathrm{nr}}$ -module muni d’actions d’un frobenius semi-linéaire $\varphi $ , d’un opérateur N tel que $N\varphi =p\varphi N$ et d’une action semi-linéaire lisse de ${\cal G}_F$ ), de rang $2$ . On associe ¹² à M:

• • une L-représentation ${\mathrm{WD}}(M)$ de ${\mathrm{WD}}_{F}$ , de dimension $2$ ,

• • une L-représentation lisse irréductible ${\mathrm{LL}}(M)$ de G,

• • une L-représentation lisse irréductible (de dimension finie) ${\mathrm{JL}}(M)$ de $\check G$ .

Remarquons que, si ${\mathrm{WD}}(M)$ est irréductible, les pentes de $\varphi $ sont toutes égales à un même nombre rationnel appelé la pente de M. On dit que M est:

• • supercuspidal, si ${\mathrm{WD}}(M)$ est irréductible et de pente $\frac {1}{2}$ ,

• • spécial si ¹³ $N\neq 0$ et si les pentes de $\varphi $ sont $0$ et $1$ .

• • de niveau $\leq n$ si ${\mathrm{JL}}(M)$ se factorise à travers $\check G/\check G_n$ .

Supposons maintenant que $F=\mathbf {Q}_p$ . Si M est supercuspidal, on définit le L-module de rang $2$

$$ \begin{align*}M_{\mathrm{dR}}=(\overline{\mathbf{Q}}_p\otimes_{\mathbf{Q}_p^{\mathrm{nr}}}M)^{{\cal G}_{\mathbf{Q}_p}}.\end{align*} $$

Si ${\cal L}$ est une L-droite de $M_{\mathrm{dR}}$ , on définit la représentation $V_{M,{\cal L}}$ de ${\cal G}_{\mathbf {Q}_p}$ par

$$ \begin{align*}V_{M,{\cal L}}={\mathrm{Ker}}\big(({\mathrm{B}}_{{\mathrm{cris}}}^+\otimes_{\mathbf{Q}_p^{\mathrm{nr}}} M)^{\varphi=p}\to {\mathbf{C}_p}\otimes_{\mathbf{Q}_p} (M_{\mathrm{dR}}/{\cal L})\big).\end{align*} $$

Il résulte de [21] que $V_{M,{\cal L}}$ est une L-représentation de dimension $2$ , potentiellement semi-stable à poids $0$ et $1$ , dont le $D_{\mathrm{pst}}$ est M, et toute telle représentation est de la forme $V_{M,{\cal L}}$ . On note $\Pi _{M,{\cal L}}$ la représentation de G associée à $V_{M,{\cal L}}$ par la correspondance de Langlands locale p-adique: si $\Pi \mapsto \mathbf {V}(\Pi )$ est le foncteur réalisant la correspondance de Langlands locale p-adique [14, 20], on a

$$ \begin{align*}\mathbf{V}(\Pi_{M,{\cal L}})\simeq V_{M,{\cal L}}\end{align*} $$

On dit qu’une L-représentation V de ${\cal G}_{\mathbf {Q}_p}$ est de niveau $\leq n$ si $V\simeq V_{M,{\cal L}}$ pour un M supercuspidal de niveau $\leq n$ et une droite ${\cal L}$ de $M_{\mathrm{dR}}$ (en particulier, V est de dimension $2$ ).

0.3.2 Multiplicités individuelles

Le th. 0.14 ci-dessous est l’un des résultats principaux de [16].

Théorème 0.14. Si $V\in {\mathrm{Rep}}_L{\cal G}_{\mathbf {Q}_p}$ est absolument irréductible, de dimension $2$ , alors

$$ \begin{align*}{\mathrm{Hom}}_{{\mathrm{W}}_{\mathbf{Q}_p}}(V, H^1_{\mathrm{et}}(\mathcal{M}_{n, \mathbf{C}_p}, L(1)))\simeq \begin{cases}\Pi_{M,{\cal L}}^{\boldsymbol *}\otimes {\mathrm{JL}}(M) &{\text{si } V=V_{M,{\cal L}}, \text{ et } M \text{ de niveau } \leq n}\\ 0 &{\text{si } V \text{ n'est pas de niveau } \leq n.}\end{cases}\end{align*} $$

Remarque 0.15. On y prouve aussi que ${\mathrm{Hom}}_{{\mathrm{W}}_{\mathbf {Q}_p}}(V, H^1_{\mathrm{et}}(\mathcal {M}_{n, \mathbf {C}_p}, L(1)))=0$ si V est absolument irréductible, de dimension $\geq 3$ (ce résultat est un des plus délicats de [16]; voir le th. 5.10 pour une preuve nettement plus limpide). En résumé, $H^1_{\mathrm{et}}(\mathcal {M}_{n, \mathbf {C}_p}, L(1))$ contient exactement les représentations de ${\cal G}_{\mathbf {Q}_p}$ que l’on souhaite y voir, avec la multiplicité idéale pour une réalisation géométrique de la correspondance de Langlands locale p-adique pour ${\mathrm{GL}}_2(\mathbf {Q}_p)$ .

Les techniques utilisées dans la preuve du th. 0.14 permettent aussi de prouver le résultat suivant (th. 5.8) qui joue un grand rôle dans nos résultats en famille.

Théorème 0.16. Si $V\in {\mathrm{Rep}}_L{\cal G}_{\mathbf {Q}_p}$ est absolument irréductible, de dimension $2$ , alors

$$ \begin{align*}{\mathrm{Hom}}_G(\Pi(V)^{\boldsymbol *}, H^1_{\mathrm{et}}(\mathcal{M}_{n, \mathbf{C}_p}, L(1)))\simeq \begin{cases}V\otimes {\mathrm{JL}}(M) &\text{ si } V=V_{M,{\cal L}}, \text{ et } M \text{ de niveau} \leq n\\ 0 &\text{si } V \text{ n'est pas de niveau} \leq n. \end{cases}\end{align*} $$

0.3.3 Anneaux de Kisin

Soit M un $(\varphi ,N,{\cal G}_{\mathbf {Q}_p})$ -module spécial ou supercuspidal. Soit $\delta _M$ le caractère central de ${\mathrm{LL}}(M)$ . On note ${\mathrm{Rep}}^{\delta _M}\,G$ la catégorie des ${\cal O}_L[G]$ -modules lisses, de longueur finie, dont le caractère central est $\delta _M$ .

Il y a une bijection ${\cal B}\leftrightarrow \rho _{\cal B}$ entre blocs de ${\mathrm{Rep}}^{\delta _M}\,G$ et orbites sous ${\mathrm{Gal}}(\overline {\mathbf {F}}_p/k_L)$ de $\overline {\mathbf {F}}_p$ -représentations semi-simples de dimension $2$ de ${\cal G}_{\mathbf {Q}_p}$ , de déterminant $\delta _M\varepsilon $ , où $\varepsilon $ désigne le caractère cyclotomique. On note $R_{\cal B}^{{\mathrm{ps}},\delta _M}$ l’anneau des déformations universelles de déterminant $\delta _M\varepsilon $ du pseudo-caractère ${\mathrm{Tr}}\circ \rho _{\cal B}$ .

Si ${\cal B}$ est un bloc, on définit:

$$ \begin{align*} &P_{\cal B}=\oplus_{\pi\in{\cal B}} P_{\pi};&&P_{\pi}, \text{ enveloppe projective de } \pi^{\vee};\\ &E_{\cal B}={\mathrm{End}}_GP_{\cal B};&&Z_{\cal B}, \text{ centre de } E_{\cal B}. \end{align*} $$

On dispose du résultat fondamental suivant («théorème $R=T$ » local de Paškūnas [53] – et [56] pour les cas exceptionnels).

Théorème 0.17 (Paškūnas, Paškūnas-Tung; [53, 56]).

Il existe une flèche naturelle $R_{\cal B}^{{\mathrm{ps}},\delta _M}\to Z_{\cal B}$ , et cette flèche induit un isomorphisme

$$ \begin{align*}R_{\cal B}^{{\mathrm{ps}},\delta_M}[\tfrac{1}{p}]\simeq Z_{\cal B}[\tfrac{1}{p}]\end{align*} $$

• • Si $M={\mathrm{Sp}}\otimes \eta $ est spécial (note 0.3.1), on pose $R_{M,{\cal B}}=L$ . On pose aussi $\rho _{{\cal B},M}=0$ et ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})=0$ , sauf si ${\cal B}$ est le bloc de ${\mathrm{St}}\otimes \bar \eta $ , où $\bar \eta $ est la réduction modulo p de $\eta $ , auquel cas on pose $\rho _{{\cal B},M}=\eta $ (vu comme caractère de ${\cal G}_{\mathbf {Q}_p}$ via la théorie locale du corps de classes), et ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})=({\mathrm{St}}^{\mathrm{cont}}\otimes \eta )^{\boldsymbol *}$ .

• • Si M est supercuspidal, on note:

  • $\diamond \ \ R_{{\cal B},M}$ le quotient de $R_{\cal B}^{{\mathrm{ps}},\delta _M}[\tfrac {1}{p}]$ paramétrant les représentations de type M (i.e., potentiellement semi-stables, à poids $0$ et $1$ , dont le $D_{\mathrm{pst}}$ est isomorphe à M),

  • $\diamond \ \ \rho _{{\cal B},M}$ la $R_{{\cal B},M}$ -représentation de ${\cal G}_{\mathbf {Q}_p}$ de dimension $2$ interpolant les représentations de type M.(L’existence de $R_{{\cal B},M}$ et $\rho _{{\cal B},M}$ est due à Kisin [46] dans la plupart des cas; voir §5.2 pour des compléments. Notons que, via l’isomorphisme du th. 0.17, $R_{{\cal B},M}$ est aussi un quotient de $Z_{\cal B}[\frac {1}{p}]$ .)

  • $\diamond \ \ {\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})$ la représentation de G interpolant les ${\boldsymbol \Pi }(\rho _x)^{\boldsymbol *}$ pour $x\in {\mathrm{Spm}}(R_{{\cal B},M})$ : si $\rho ^{\diamond }_{{\cal B},M}$ est la $R_{{\cal B},M}$ -duale de $\rho _{{\cal B},M}$ , on a (cf. [14, §§ II.2.4 et II.3.1])

    $$ \begin{align*}{\boldsymbol\Pi}^{\boldsymbol *}(\rho_{{\cal B},M})=D^{\natural}(\rho^{\diamond}_{{\cal B},M}\otimes\varepsilon)\boxtimes\mathbf{P}^1\end{align*} $$

    Dans les deux cas,

    $$ \begin{align*}\check{\mathbf{V}}({\boldsymbol\Pi}^{\boldsymbol *}(\rho_{{\cal B},M}))\simeq\rho_{{\cal B},M} \end{align*} $$

0.3.4 Résultats en famille

On pose

$$ \begin{align*}H^1_{\operatorname{\acute{e}t} }({\cal M}^p_{n,\overline{\mathbf{Q}}_p},L(1)):=L\otimes_{{\cal O}_L}\big( {\varprojlim}_k\big({\varinjlim}_{[K:\mathbf{Q}_p]<\infty} H^1_{\operatorname{\acute{e}t} }({\cal M}^p_{n,K},({\cal O}_L/p^k)(1))\big)\big).\end{align*} $$

C’est un sous-objet de $H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\mathbf {C}_p},L(1))$ , stable par G, $\check G$ et ${\cal G}_{\mathbf {Q}_p}$ , nettement plus petit que le module initial.

On déduit du théorème de finitude (th. 0.2) et de la théorie de Gabriel [35], une décomposition en blocs des $H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,K},({\cal O}_L/p^n)(1))$ . Par passage à la limite, cela fournit une décomposition

où:

Le th. 0.1 est alors une conséquence directe du résultat suivant (th. 5.24):

Théorème 0.18.

1. (i) Le dual de est un $Z_{\cal B}[\frac {1}{p}]$ -module de type fini sur lequel $Z_{\cal B}[\frac {1}{p}]$ agit par son quotient $R_{{\cal B},M}$ .

2. (ii) Supposons ¹⁴ que $p>3$ . On a un isomorphisme de $E_{\cal B}^{\delta _M}[{\cal G}_{\mathbf {Q}_p}]$ -modules

   
   où les produits tensoriels sont au-dessus de $R_{{\cal B},M}$ .

Le premier énoncé du (i) résulte formellement du (i) du th. 0.9, le second énoncé est une conséquence du th. 0.16. La décomposition du (ii) est une interpolation de la décomposition en tout point fermé de ${\mathrm{Spec}}\,R_{{\cal B},M}$ fournie par le th. 0.16 (comme $R_{{\cal B},M}$ est un produit d’anneaux principaux, cette identification en tout point implique une identification globale).

1 Représentations de ${\mathrm{GL}}_2(F)$

Soient F une extension finie de $\mathbf {Q}_p$ , ${\cal O}_F$ l’anneau de ses entiers, $k_F$ son corps résiduel et $\varpi $ une uniformisante. On note:

• • G le groupe ${\mathrm{GL}}_2(F)$ ,

• • $Z=\big \{{\big (\begin {smallmatrix}a&0\\ 0&a\end {smallmatrix}\big )},\ a\in F^{\boldsymbol *}\big \}$ le centre de G,

• • $K={\mathrm{GL}}_2({\cal O}_F)$ le sous-groupe compact maximal standard de G,

• • $B={\big (\begin {smallmatrix}F^{\boldsymbol *}&F\\ 0&F^{\boldsymbol *}\end {smallmatrix}\big )}$ le borel supérieur,

• • $G'$ le groupe quotient $G/{\big (\begin {smallmatrix}\varpi &0\\ 0&\varpi \end {smallmatrix}\big )}^{\mathbf {Z}}$ .

1.1 Généralités

Soient L une extension finie de $\mathbf {Q}_p$ , ${\cal O}_L$ l’anneau de ses entiers, l’idéal maximal de ${\cal O}_L$ , et son corps résiduel.

1.1.1 Modules lisses de torsion

Soit H un groupe de Lie p-adique (dans les applications, H sera G ou $G'$ ). Un ${\cal O}_L[H]$ -module $\pi $ est dit:

• • de torsion si tout vecteur $v\in \pi $ est tué par $p^N$ , pour N assez grand;

• • lisse si $\pi $ est de torsion et si le stabilisateur dans H de tout $v\in \pi $ est ouvert.

On note ${\mathrm{Rep}}^{\mathrm{lisse}}\,H$ la catégorie des ${\cal O}_L[H]$ -modules lisses. On remarquera que les objets irréductibles de ${\mathrm{Rep}}^{\mathrm{lisse}}\,H$ sont tués par et donc sont des $k_L[H]$ -modules. Il n’est pas clair si une extension (dans la catégorie des ${\cal O}_L[H]$ -modules abstraits) de ${\cal O}_L[H]$ -modules lisses est encore un ${\cal O}_L[H]$ -module lisse. Le résultat beaucoup plus faible suivant nous sera cependant très utile par la suite.

Lemme 1.1. Soient U un sous-groupe ouvert de H et $0\to A\to B\to C\to 0$ une suite exacte de ${\cal O}_L[U]$ -modules. On suppose que $p^a$ tue A, et que U agit trivialement sur A et sur C. Alors H possède un sous-groupe ouvert agissant trivialement sur B.

Démonstration. Quitte à remplacer U par un sous-groupe ouvert, on peut supposer que U est un pro-p groupe uniforme, et alors $U_n=\{h^{p^n}|\,\, h\in U\}$ est un sous-groupe ouvert de U pour tout $n\geq 1$ . Nous allons montrer que $U_{a}$ agit trivialement sur B, ce qui permettra de conclure. Notons que $(h-1)^2\cdot v=0$ pour tout $h\in U$ et $v\in B$ . Il s’ensuit que $h^{p^a}\cdot v=v+p^a(h-1)\cdot v$ pour $h\in U$ et $v\in B$ , et comme $(h-1)\cdot v$ est tué par $p^a$ puisqu’il appartient à A, on a $h^{p^a}\cdot v=v$ , d’où le résultat.

Soit K un sous-groupe ouvert compact de H. Le ${\cal O}_L[H]$ -module

$$ \begin{align*}{\cal O}_L\langle H\rangle:={\cal O}_L[H]\otimes_{{\cal O}_L[K]} {\cal O}_L[[K]]\end{align*} $$

est muni [67, prop. 3.2] de l’unique structure de ${\cal O}_L$ -algèbre telle que les morphismes naturels ${\cal O}_L[H]\to {\cal O}_L\langle H\rangle $ et ${\cal O}_L[[K]]\to {\cal O}_L\langle H\rangle $ soient des morphismes de ${\cal O}_L$ -algèbres, et cette structure est indépendante (à isomorphisme canonique près) du choix du sous-groupe ouvert compact K de H utilisé pour la définir. De plus, par [67, lemme 3.5] la structure de ${\cal O}_L[H]$ -module de tout objet de ${\mathrm{Rep}}^{\mathrm{lisse}}\,H$ s’étend de manière unique en une structure de ${\cal O}_L\langle H\rangle $ -module.

1.1.2 Admissibilité, finitude

On dit que $\pi \in {\mathrm{Rep}}^{\mathrm{lisse}}\,H$ est:

• • admissible si est de longueur finie sur ${\cal O}_L$ , pour tout sous-groupe ouvert compact K de H et tout $j\geq 1$ .

• • localement admissible si ${\cal O}_L[H]\cdot v\subset \pi $ est admissible pour tout $v\in \pi $ , ou, de manière équivalente, si $\pi $ peut s’écrire comme une limite inductive de représentations lisses admissibles.

• • de longueur finie si $\pi $ est de longueur finie comme ${\cal O}_L[H]$ -module.

• • de type fini si $\pi $ est de type fini comme ${\cal O}_L[H]$ -module. Les conditions suivantes sont équivalentes [67, lemmas 2.4, 3.6]:

  1. (i) $\pi $ est de type fini;

  2. (ii) $\pi $ est quotient d’une induite compacte c- ${\mathrm{Ind}}_K^H(\sigma )$ pour une ${\cal O}_L$ -représentation lisse $\sigma $ , de longueur finie, d’un sous-groupe ouvert compact K de H;

  3. (iii) $\pi $ est un ${\cal O}_L\langle H\rangle $ -module de type fini.

• • de présentation finie s’il existe une suite exacte de ${\cal O}_L[H]$ -modules

  $$ \begin{align*}\text{c-}{\mathrm{Ind}}_{K_1}^H(\sigma_1)\to \text{c-}{\mathrm{Ind}}_{K_2}^H (\sigma_2)\to \pi\to 0\end{align*} $$
  où $K_1$ , $K_2$ sont des sous-groupes ouverts compacts de H et $\sigma _i$ est une ${\cal O}_L$ -représentation lisse de $K_i$ , de longueur finie sur ${\cal O}_L$ . Cela n’est pas équivalent à ce que $\pi $ soit un ${\cal O}_L[H]$ -module de présentation finie, mais plutôt [67, prop. 3.8] à ce que $\pi $ soit un ${\cal O}_L\langle H\rangle $ -module de présentation finie.

On note

$$ \begin{align*}{\mathrm{Rep}}^{\mathrm{adm}}\,H,\quad {\mathrm{Rep}}^{\mathrm{ladm}}\,H,\quad {\mathrm{Rep}}^{\mathrm{\ell f}}\,H,\quad {\mathrm{Rep}}^{\mathrm{tf}}\,H,\quad {\mathrm{Rep}}^{\mathrm{pf}}\,H\end{align*} $$

les sous-catégories pleines de ${\mathrm{Rep}}^{\mathrm{lisse}}\,H$ des représentations admissibles, localement admissibles, de longueur finie, de type fini et de présentation finie, respectivement. Si $\delta : H\to {\cal O}_L^{{\boldsymbol *}}$ est un caractère lisse, on rajoute $\delta $ en exposant pour indiquer la sous-catégorie pleine des représentations de caractère central $\delta $ .

Le résultat suivant découle directement de la discussion ci-dessus et des propriétés usuelles des modules de type fini et de présentation finie sur un anneau, mais il peut aussi être démontré directement (et pour des groupes plus généraux que les groupes de Lie p-adiques), voir [67, lemmes 2.6, 2.7]:

Proposition 1.2 (Shotton).

Soit $0\to \pi _1\to \pi \to \pi _2\to 0$ une suite exacte dans ${\mathrm{Rep}}^{\mathrm{lisse}}\,H$ .

1. a) Si $\pi _1, \pi _2$ sont de type fini (resp. de présentation finie), il en est de même de $\pi $ .

2. b) Si $\pi $ est de présentation finie et $\pi _1$ est de type fini, $\pi _2$ est de présentation finie.

Un des résultats principaux de l’article [67] de Shotton est le suivant:

Proposition 1.3 [67, cor. 4.4].

Si H est un groupe de Lie p-adique qui est un produit amalgamé de deux sous-groupes ouverts compacts, alors ${\cal O}_L\langle H\rangle $ est un anneau cohérent, et donc ${\mathrm{Rep}}^{\mathrm{pf}}\,H$ est une sous-catégorie abélienne de ${\mathrm{Rep}}^{\mathrm{lisse}}\,H$ (i.e. le noyau et le conoyau d’un morphisme entre des représentations de présentation finie sont encore de présentation finie).

(C’est immédiat pour le conoyau, mais pas du tout clair pour le noyau!)

Remarque 1.4.

1. (i) ${\mathrm{SL}}_2(F)$ et $\{g\in {\mathrm{GL}}_2(F),\ \det g\in {\cal O}_F^{\boldsymbol *}\}$ sont des produits amalgamés de deux sous-groupes ouverts compacts, d’après le théorème d’Ihara; le résultat ci-dessus s’applique donc à ces groupes.

2. (ii) Si H est un sous-groupe ouvert de $G'$ , d’indice fini, alors une représentation lisse de $G'$ est de type fini (resp. de présentation finie) si et seulement si sa restriction à H l’est [67, lemme 2.8].

Nous allons utiliser cette remarque pour le groupe $H=\{g\in {\mathrm{GL}}_2(F),\ \det g\in {\cal O}_F^{\boldsymbol *}\}$ vu comme sous-groupe ouvert d’indice fini de .

1.2 Représentations irréductibles de ${\mathrm{GL}}_2(F)$

Les objets irréductibles de ${\mathrm{Rep}}^{\mathrm{lisse}}\,G$ sont tués par , et donc sont des $k_L$ -modules.

1.2.1 Représentations absolument irréductibles

Appelons poids de Serre un $KZ$ -module lisse irréductible sur $\overline {\mathbf {F}}_p$ , le centre Z agissant par un caractère (la restriction à K se factorise alors par le quotient $ {\mathrm{GL}}_2(k_F)$ ).

Si $\sigma $ est un poids de Serre, on note

$$ \begin{align*}I(\sigma)=\text{c-}{\mathrm{Ind}}_{KZ}^G(\sigma)\end{align*} $$

l’induite compacte de $\sigma $ . On dispose d’un isomorphisme [3, prop. 8] de $\overline {\mathbf {F}}_p$ -algèbres

(1.5) $$ \begin{align} {\mathrm{End}}_G (I(\sigma))\simeq \overline{\mathbf{F}}_p[T], \end{align} $$

pour un certain opérateur de Hecke T. De plus, $I(\sigma )$ est un module libre sur $\overline {\mathbf {F}}_p[T]$ d’après [3, th. 19].

Le théorème de classification de Barthel-Livné [2, 3] montre que les représentations lisses irréductibles de G sur $\overline {\mathbf {F}}_p$ , avec un caractère central, sont les suivantes:

• • les $\chi \circ \det $ (notées simplement $\chi $ ), avec $\chi : G\to \overline {\mathbf {F}}_p^{\boldsymbol *}$ un caractère lisse.

• • les ${\mathrm{Ind}}_B^G(\chi _1\otimes \chi _2)$ , où $\chi _1,\chi _2$ sont des caractères lisses distincts de $F^{\boldsymbol *}$ .

• • les ${\mathrm{St}}\otimes \chi $ , où ${\mathrm{St}}$ est la steinberg, quotient de ${\mathrm{Ind}}_B^G(1\otimes 1)$ par la représentation triviale.

• • les supersingulières, i.e. les quotients irréductibles des $I(\sigma )/(T)$ , avec $\sigma $ un poids de Serre.

Les représentations irréductibles non supersingulières sont dites ordinaires; les représentations ordinaires sont donc les composantes de Jordan-Hölder des représentations de la série principale.

1.2.2 Questions de rationalité

Le lemme suivant de Paškūnas ([53, lemma 5.1]) nous sera très utile.

Lemme 1.6. Soit H un groupe, $L/K$ une extension de corps et soient $V,W$ de $K[H]$ -modules, V étant de type fini. Alors

$$ \begin{align*}{\mathrm{Hom}}_{K[H]}(V, W)\otimes_K L\simeq {\mathrm{Hom}}_{L[H]}(V\otimes_K L, W\otimes_K L).\end{align*} $$

Lemme 1.7. Soit $\pi \in {\mathrm{Rep}}^{\mathrm{adm}}\,G$ , irréductible. Si $k={\mathrm{End}}_{k_L[G]}\pi $ , alors:

1. (i) k est une extension finie de $k_L$ .

2. (ii) $\pi $ est absolument irréductible vue comme $k[G]$ -module.

3. (iii) $k\otimes _{k_L}\pi =\oplus _{\sigma \in {\mathrm{Hom}}(k,k)}k\otimes _{k,\sigma }\pi $ , et les $k\otimes _{k,\sigma }\pi $ sont deux à deux non isomorphes comme $k[G]$ -modules mais sont toutes isomorphes comme $k_L[G]$ -modules.

Démonstration. k est une algèbre à division, de dimension finie sur le corps fini $k_L$ (car $\pi $ est irréductible et admissible, donc si l’on fixe $v\in \pi ^{K_1}$ non nul, la flèche $f\mapsto f(v)$ induit une injection de k dans le $k_L$ -espace de dimension finie $\pi ^{K_1}$ ). Il s’ensuit que k est une extension finie de $k_L$ , ce qui prouve le (i).

Si $k'$ est une extension de k et si $\pi ':=k'\otimes _k\pi $ , alors d’après le lemme 1.6,

$$ \begin{align*}{\mathrm{End}}_{k'[G]}(\pi')= k'\otimes_k{\mathrm{End}}_{k[G]}(\pi)=k'\end{align*} $$

Si $\pi $ n’est pas absolument irréductible vue comme $k[G]$ -module, on peut trouver une extension finie $k'$ de k et un sous $k'[G]$ -module propre $\tau \subset \pi '$ . Comme $\pi '$ est admissible, on peut supposer que $\tau $ est irréductible ¹⁵ . Le groupe $\Gamma ={\mathrm{Gal}}(k'/k)$ agit sur $\pi '$ et $X:=\sum _{h\in \Gamma } h\cdot \tau $ est $G\times \Gamma $ -stable dans $\pi '$ . Par descente galoisienne $X^{\Gamma }$ est non nul et G-stable dans $\pi $ , donc $X^{\Gamma }=\pi $ (car $\pi $ est irréductible comme $k_L[G]$ -module et donc, a fortiori, comme $k[G]$ -module), ce qui exhibe $\pi '$ comme un quotient d’une somme directe finie $\oplus _{h\in \Gamma } h\cdot \tau $ de représentations irréductibles. Donc $\pi '$ est semi-simple et comme ses endomorphismes sont $k'$ , elle est irréductible contrairement à l’hypothèse. Ceci prouve le (ii).

Enfin la décomposition $k\otimes _{k_L}k=\prod _{\sigma \in {\mathrm{Hom}}(k,k)} k$ fournit celle du (iii); le fait que les $k\otimes _{k,\sigma }\pi $ sont deux à deux non isomorphes comme $k[G]$ -modules résulte de ce que ${\mathrm{End}}_{k[G]}(k\otimes _{k_L}\pi )=k\otimes _{k_L}k$ (d’après le lemme 1.6) est un produit de corps; qu’elles soient toutes isomorphes comme $k_L[G]$ -modules est évident.

Remarque 1.8. L’irréductibilité sans l’admissibilité n’est pas suffisante pour impliquer les conclusions du lemme 1.7: Le [48, th. 1.2] a construit une $\mathbf {F}_{p^3}$ -représentation supersingulière $\pi $ de ${\mathrm{GL}}_2(\mathbf {Q}_{p^3})$ , telle que ${\mathrm{End}}_{G}\,\pi =\overline {\mathbf {F}}_{p}$ , ce qui implique que $\mathbf {F}_{p^{3n}}\otimes \pi $ a n composantes irréductibles, pour tout n, et aucune n’est absolument irréductible.

1.2.3 Le cas $F=\mathbf {Q}_p$

La classification des représentations irréductibles est nettement mieux comprise dans le cas $F=\mathbf {Q}_p$ :

• • Breuil [11] a montré que les $I(\sigma )/(T)$ sont irréductibles et donc les supersingulières sont les $I(\sigma )/(T)$ (il a aussi déterminé dans quels cas $I(\sigma _1)/(T)\simeq I(\sigma _2)/(T)$ ).

• • Berger [4] a montré que l’existence d’un caractère central est en fait une conséquence de l’irréductibilité.

• • Il est facile de vérifier que les représentations ordinaires sont admissibles et de présentation finie (cela est vrai même pour $F\ne \mathbf {Q}_p$ ). La preuve de Breuil permet de vérifier que les supersingulières le sont aussi (on obtient des résultats plus fins en combinant les th. IV.2.1 et IV.4.7 de [14]). Il en résulte que tout $\pi \in {\mathrm{Rep}}^{\mathrm{lisse}}\,G$ irréductible est admissible et de présentation finie, et donc (en utilisant la stabilité de ces deux propriétés par extensions) que

  $$ \begin{align*}{\mathrm{Rep}}^{\mathrm\ell f}\,G\subset {\mathrm{Rep}}^{\mathrm{adm}}\,G\cap {\mathrm{Rep}}^{\mathrm{pf}} \, G\end{align*} $$
  (Voir le th. 1.26 pour une inclusion dans l’autre sens.)

• • Il résulte de la classification de Barthel-Livné et Breuil des $\overline {\mathbf {F}}_p$ -représentations irréductibles de G que, si $\pi $ est une telle représentation, il existe un corps fini k tel que $\pi $ soit obtenue par extension des scalaires d’une représentation définie sur k. Il s’ensuit que l’orbite de $\pi $ sous l’action de ${\mathrm{Gal}}(\overline {\mathbf {F}}_p/k_L)$ est finie ¹⁶ . Si H est le fixateur de $\pi $ dans ${\mathrm{Gal}}(\overline {\mathbf {F}}_p/k_L)$ , et si $k=\overline {\mathbf {F}}_p^H$ , alors $\pi $ est l’extension des scalaires d’une représentation $\pi _k$ définie sur k, telle que ${\mathrm{End}}_G\pi _k=k$ . Les $\pi _k^{\sigma }$ , vues comme $k_L$ -représentations de G, sont alors toutes isomorphes, et on note $\pi _L$ la classe d’isomorphisme de $K_L$ -représentations ainsi définie.

L’application $\pi \mapsto \pi _L$ induit une bijection naturelle entre les orbites sous ${\mathrm{Gal}}(\overline {\mathbf {F}}_p/k_L)$ de l’ensemble des $\overline {\mathbf {F}}_p$ -représentations irréductibles de G et les $k_L$ -représentations irréductibles de G, la bijection réciproque envoyant $\pi $ sur l’ensemble des composantes de Jordan-Hölder de $\overline {\mathbf {F}}_p\otimes _{k_L}\pi $ (que celles-ci forment une orbite sous ${\mathrm{Gal}}(\overline {\mathbf {F}}_p/k_L)$ se déduit du (iii) du lemme 1.7).

1.3 Représentations de ${\mathrm{GL}}_2(\mathbf {Q}_p)$ et représentations de ${\cal G}_{\mathbf {Q}_p}$

On suppose $F=\mathbf {Q}_p$ dans ce paragraphe. Si $\delta :\mathbf {Q}_p^{\boldsymbol *}\to {\cal O}_L^{\boldsymbol *}$ est un caractère continu, on note ${\mathrm{Rep}}^{\delta }\,G$ la sous-catégorie de ${\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ des objets de caractère central $\delta $ .

1.3.1 La correspondance de Langlands locale p-adique

Rappelons que l’on dispose d’un foncteur covariant exact $\Pi \mapsto \mathbf {V}(\Pi )$ de ${\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ (plus précisément de la sous-catégorie des objets à caractère central) dans la catégorie des ${\cal O}_L$ -représentations continues de ${\cal G}_{\mathbf {Q}_p}$ , de longueur finie sur ${\cal O}_L$ .

On étend ce foncteur par limite projective et tensorisation par L aux L-représentations de Banach unitaires de G, résiduellement de longueur finie (i.e. dont la réduction modulo est de longueur finie; une telle représentation est automatiquement admissible et tout L-banach admissible, de longueur finie est résiduellement de longueur finie – un des résultats principaux de [20]) et avec un caractère central. Si $\Pi $ est une telle L-représentation, $\mathbf {V}(\Pi )$ est une L-représentation de ${\cal G}_{\mathbf {Q}_p}$ , de dimension finie.

Réciproquement, si V est une L-représentation de ${\cal G}_{\mathbf {Q}_p}$ , de dimension $2$ , il existe [14, 20] une plus grande représentation ${\boldsymbol \Pi }(V)$ de G, unitaire, résiduellement de longueur finie telle que $\mathbf {V}({\boldsymbol \Pi }(V))=V$ et ${\boldsymbol \Pi }(V)^{{\mathrm{SL}}_2(\mathbf {Q}_p)}=0$ (cette dernière condition est nécessaire pour assurer l’unicité car $\mathbf {V}$ tue $\Pi ^{{\mathrm{SL}}_2(\mathbf {Q}_p)}$ ). La correspondance $V\mapsto {\boldsymbol \Pi }(V)$ est la correspondance de Langlands locale p-adique.

La représentation $\mathbf {V}(\Pi )$ n’est pas toujours de dimension $2$ , mais est toujours «de type ${\mathrm{GL}}_2$ » (cf. th. 1.16 pour un énoncé précis: l’expression $g+\delta \varepsilon (g)g^{-1}$ qui apparaît dans l’énoncé de ce théorème est la trace de g si g agit sur un module de rang $2$ et le déterminant de g est $\delta \varepsilon (g)$ ).

1.3.2 Les représentations $I(\chi _1,\chi _2)$

On voit les caractères continus de $\mathbf {Q}_p^{\boldsymbol *}$ comme des caractères de $\mathcal {G}_{\mathbf {Q}_p}$ par la théorie locale du corps de classes ¹⁷ et aussi comme des caractères de G en composant avec le déterminant.

Soit $\varepsilon $ la réduction modulo p du caractère $x\to x|x|$ de $\mathbf {Q}_p^{{\boldsymbol *}}$ ; vu comme caractère de ${\mathcal {G}}_{\mathbf {Q}_p}$ , c’est la réduction du caractère cyclotomique. On dit qu’un couple de caractères $\chi _1, \chi _2: \mathbf {Q}_p^{{\boldsymbol *}}\to \overline {\mathbf {F}}_p^{{\boldsymbol *}}$ continus (et donc lisses) est générique si $\chi _1\chi _2^{-1}\ne 1,\varepsilon ^{\pm 1}$ .

Soit $(\chi _1,\chi _2)$ générique, et soient $I(\chi _1, \chi _2)$ et $I(\chi _2,\chi _1)$ les représentations absolument irréductibles de G

$$ \begin{align*}I(\chi_1, \chi_2):={\mathrm{Ind}}_B^G(\chi_2\otimes \chi_1\varepsilon^{-1}), \quad I(\chi_2,\chi_1)={\mathrm{Ind}}_B^G(\chi_1\otimes \chi_2\varepsilon^{-1}).\end{align*} $$

Leur caractère central est $\chi _1\chi _2\varepsilon ^{-1}$ , et il existe une unique extension non triviale

$$ \begin{align*}0\to I(\chi_1,\chi_2)\to\Pi_{\chi_1,\chi_2}\to I(\chi_2,\chi_1)\to 0\end{align*} $$

Les représentations $I(\chi _1,\chi _2)$ , $I(\chi _2,\chi _1)$ et $\Pi _{\chi _1,\chi _2}$ ont des modèles sur $k_L(\chi _1,\chi _2)$ qui, comme dans le $\mathrm{n}^{\mathrm{o}}$ 1.2.3, peuvent être considérées comme des représentations sur $k_L$ . On a alors

$$ \begin{align*}\mathbf{V}(I(\chi_1,\chi_2))=\chi_1,\quad \mathbf{V}(I(\chi_2,\chi_1))=\chi_2, \quad \mathbf{V}(\Pi_{\chi_1,\chi_2})=\bar{r}_{\chi_1,\chi_2}\end{align*} $$

où $\chi _1$ et $\chi _2$ sont les $k_L(\chi _1,\chi _2)$ -représentations de ${\cal G}_{\mathbf {Q}_p}$ de dimension $1$ associées à $\chi _1$ et $\chi _2$ , vues comme des $k_L$ -représentations (de dimension $[k_L(\chi _1,\chi _2):k_L]$ ) et $\bar {r}_{\chi _1,\chi _2}$ l’unique $k_L(\chi _1,\chi _2)$ -représentation de $\mathcal {G}_{\mathbf {Q}_p}$ extension nontriviale de $\chi _2$ par $\chi _1$ (vue comme une $k_L$ -représentation)

$$ \begin{align*}0\to \chi_1\to \bar{r}_{\chi_1,\chi_2}\to \chi_2\to 0\end{align*} $$

Remarque 1.9. Soit $\delta : Z\to \overline {\mathbf {F}}_p^{{\boldsymbol *}}$ un caractère lisse. La classification de Barthel-Livné et Breuil montre qu’il n’y a qu’un nombre fini de $\pi \in {\mathrm{Rep}}^{\delta }\,G$ , irréductibles, qui ne sont pas de la forme $I(\chi _1,\chi _2)$ , avec $(\chi _1,\chi _2)$ générique.

1.3.3 Généralités sur les blocs

On met une relation d’équivalence sur les représentations irréductibles définie par $\pi \sim \pi '$ si et seulement si il existe une suite $\pi =\pi _0,\pi _1,\dots ,\pi _r=\pi '$ telle que $\pi _{i+1}=\pi _i$ ou ${\mathrm{Ext}}^1(\pi _i,\pi _{i+1})\neq 0$ ou ${\mathrm{Ext}}^1(\pi _{i+1},\pi _i)\neq 0$ (ces conditions ne sont pas exclusives). Une classe d’équivalence est un bloc. Si ${\cal B}$ est un bloc, on note ${\mathrm{Rep}}_{\cal B}\,G$ la sous-catégorie de ${\mathrm{Rep}}^{\mathrm{\ell f}}\, G$ des objets dont toutes les composantes de Jordan-Hölder appartiennent à ${\cal B}$ .

Proposition 1.10 (Paškūnas).

Les blocs de ${\mathrm{Rep}}_{\overline {\mathbf {F}}_p}\,G$ sont les:

• • $\{\pi \}$ , où $\pi $ est supersingulière.

• • $\{I(\chi _1,\chi _2),I(\chi _2,\chi _1)\}$ , où $\chi _1\chi _2^{-1}\neq \varepsilon ^{\pm }, 1$ .

• • $\{I(\chi ,\chi )\}$ , si $p\neq 2$ . (Si $p=2$ , ce bloc devient $\{\chi , {\mathrm{St}}\otimes \chi \}$ .)

• • $\{\chi , {\mathrm{St}}\otimes \chi , I(\chi ,\chi \varepsilon )\}$ , si $p\neq 3$ . (Si $p=3$ , ce bloc devient $\{\chi , {\mathrm{St}}\otimes \chi , \chi \varepsilon , {\mathrm{St}}\otimes \chi \varepsilon \}$ .)

Remarque 1.11. On peut utiliser le lemme 1.6 et le $\mathrm {n}^{\mathrm{o}} $ 1.2.3 pour en déduire une description des blocs de ${\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ : ceux-ci sont en bijection naturelle avec les orbites des blocs de ${\mathrm{Rep}}_{\overline {\mathbf {F}}_p}\,G$ sous l’action de ${\mathrm{Gal}}(\overline {\mathbf {F}}_p/k_L)$ .

Si $\pi \in {\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ est irréductible, on note $P_{\pi }$ le dual de Pontryagin d’une enveloppe injective de $\pi $ dans ${\mathrm{Rep}}^{\mathrm{ladm}} G$ . Alors $P_{\pi }$ est un ${\cal O}_L[G]$ -module compact sans p-torsion, limite projective de ${\cal O}_L[G]$ -modules compacts et de longueur finie. Si ${\cal B}$ est un bloc, on pose

$$ \begin{align*}P_{\cal B}:=\oplus_{\pi\in {\cal B}} P_{\pi}\quad E_{\cal B}:={\mathrm{End}}_G(P_{\cal B}),\quad Z_{\cal B}:= \text{centre de } E_{\cal B}.\end{align*} $$

La théorie générale de Gabriel [35] fournit le résultat suivant:

Proposition 1.12.

1. (i) Les foncteurs

   
   sont inverses l’un de l’autre et fournissent une équivalence de catégories entre ${\mathrm{Rep}}_{\cal B}\,G$ et la catégorie des modules de longueur finie sur $E_{\cal B}$ .

2. (ii) Si $\Pi \in {\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ , alors

   

Remarque 1.13.

1. (i) On a les mêmes résultats pour ${\mathrm{Rep}}^{\delta }\,G$ ; les blocs sont les mêmes que pour ${\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ en rajoutant la condition que le caractère central soit $\delta $ (ce qui se traduit par $\chi _1\chi _2\varepsilon ^{-1}=\delta $ pour $I(\chi _1,\chi _2)$ , et par $\chi ^2=\delta $ pour le bloc contenant $\chi $ ). Si ${\cal B}$ est un bloc, on définit $P_{\cal B}^{\delta }$ , $E_{\cal B}^{\delta }$ , $Z_{\cal B}^{\delta }$ , comme ci-dessus, mais en prenant les enveloppes projectives dans la catégorie des représentations de caractère central $\delta ^{-1}$ (dualiser change le caractère central en son inverse).

2. (ii) Si $\pi \in {\mathrm{Rep}}^{\delta }_{\cal B}\, G$ , alors $Z_{\cal B}^{\delta }$ agit sur $\pi $ ainsi que, par fonctorialité, sur $\mathbf {V}(\pi )$ .

Remarque 1.14. Si ${\cal B}$ est un bloc de ${\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ et si $\pi \in {\cal B}$ , alors ${\mathrm{End}}_{k_L[G]}\pi $ ne dépend pas de $\pi $ ; notons le $k({\cal B})$ et notons $L({\cal B})$ l’extension non ramifiée de L de corps résiduel $k({\cal B})$ . Les composantes irréductibles des $k({\cal B})\otimes _k\pi $ , pour $\pi \in {\cal B}$ , se répartissent dans des types ${\cal B}^{\sigma }$ de ${\mathrm{Rep}}^{\mathrm{\ell f}}_{{\cal O}_{L({\cal B})}}\,G$ formant une orbite sous l’action de ${\mathrm{Gal}}(k({\cal B})/k_L)$ et les ${\cal B}^{\sigma }$ sont formés de représentations absolument irréductibles. L’oubli de l’action de ${\cal O}_{L({\cal B})}$ induit une équivalence entre ${\mathrm{Rep}}_{{\cal O}_{L({\cal B})},{\cal B}^{\sigma }}\,G$ et ${\mathrm{Rep}}_{\cal B}\,G$ . On en déduit, pour tout $\sigma $ , des isomorphismes:

$$ \begin{align*}E_{\cal B}\simeq E_{{\cal O}_{L({\cal B})},{\cal B}^{\sigma}},\quad Z_{\cal B}\simeq Z_{{\cal O}_{L({\cal B})},{\cal B}^{\sigma}}\end{align*} $$

et de même pour $E_{\cal B}^{\delta },Z_{\cal B}^{\delta }$ .

1.3.4 Blocs et représentations galoisiennes modulo p

Remarque 1.15. (i) Il y a [54] une bijection ${\cal B}\leftrightarrow \rho _{\cal B}$ entre $\overline {\mathbf {F}}_p$ -blocs et $\overline {\mathbf {F}}_p$ -représentations de $G_{\mathbf {Q}_p}$ , semi-simples, de dimension $2$ . Cette bijection envoie un bloc ${\cal B}$ sur la représentation semi-simple dont l’ensemble des sous-représentations irréductibles est $\{\mathbf {V}(\pi ),\ \pi \in {\cal B}\}$ . Donc:

• • $\rho _{\cal B}$ est irréductible, de dimension $2$ , si ${\cal B}=\{\pi \}$ , avec $\pi $ supersingulière.

• • $\rho _{\cal B}=\chi _1\oplus \chi _2$ , si ${\cal B}=\{I(\chi _1,\chi _2),I(\chi _2,\chi _1)\}$ et $\chi _1 \chi _2^{-1}\neq 1, \varepsilon ^{\pm 1}$ .

• • $\rho _{\cal B}=\chi \oplus \chi $ , si ${\cal B}=\{I(\chi ,\chi )\}$ .

• • $\rho _{\cal B}=\chi \oplus \chi \varepsilon $ , si ${\cal B}=\{\chi ,{\mathrm{St}}\otimes \chi ,I(\chi ,\chi \varepsilon )\}$ .

Dans tous les cas, $(\det \rho _{\cal B})\varepsilon ^{-1}$ est égal au caractère central des éléments de ${\cal B}$ .

(ii) On déduit de ce résultat une bijection naturelle entre les blocs de ${\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ (resp. ${\mathrm{Rep}}^{\delta }\,G$ ) et les orbites sous l’action de ${\mathrm{Gal}}(\overline {\mathbf {F}}_p/k_L)$ des $\overline {\mathbf {F}}_p$ -représentations de ${\cal G}_{\mathbf {Q}_p}$ , semi-simples, de dimension $2$ (resp. et dont le déterminant est $\delta \varepsilon $ ).

Plus précisément, si ${\cal B}$ est un bloc de ${\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ et si $\pi \in {\cal B}$ , alors ${\mathrm{End}}_{k_L[G]}\pi $ ne dépend pas de $\pi $ ; notons le $k({\cal B})$ . Alors ${\mathrm{Tr}}\rho _{\cal B}$ est à valeurs dans $k({\cal B})$ et donc $\rho _{\cal B}$ est définie sur $k({\cal B})$ . Les $\rho _{\cal B}^{\sigma }$ , pour $\sigma \in {\mathrm{Gal}}(k({\cal B})/k_L)$ , sont deux à deux non isomorphes comme $k({\cal B})$ -représentations de ${\cal G}_{\mathbf {Q}_p}$ mais sont toutes isomorphes comme $k_L$ -représentations (de dimension $[k({\cal B}):k_L]$ ).

Soit ${\cal B}$ un bloc de ${\mathrm{Rep}}^{\delta }\,G$ . Notons $R_{\cal B}^{{\mathrm{ps}},\delta }$ l’anneau des déformations universelles du pseudo-caractère ${\mathrm{Tr}}\circ \rho _{\cal B}$ (vu comme pseudo-caractère de dimension $2$ à valeurs dans $k({\cal B})$ , cf. (ii) de la rem. 1.15), de déterminant $\delta \varepsilon $ , et

$$ \begin{align*}T_{\cal B}^{\delta}:{\cal G}_{\mathbf{Q}_p}\to R_{\cal B}^{{\mathrm{ps}},\delta}\end{align*} $$

le pseudo-caractère universel. On a alors le «théorème» $R=T$ local suivant ¹⁸ (cf. (ii) de la rem. 1.13 pour l’action de $Z_{\cal B}^{\delta }$ ).

Théorème 1.16 (Paškūnas [53], Paškūnas-Tung [56]).

Il existe un unique morphisme

$$ \begin{align*}\iota_{\cal B}^{\delta}:R_{\cal B}^{{\mathrm{ps}},\delta}\to Z_{\cal B}^{\delta}\end{align*} $$

tel que, pour tout $\pi \in {\mathrm{Rep}}^{\delta }_{\cal B} G$ et tout $g\in {\mathrm{Gal}}_{\mathbf {Q}_p}$ , on ait

$$ \begin{align*}\iota_{\cal B}^{\delta}(T_{\cal B}^{\delta}(g))=g+\delta\varepsilon(g)g^{-1} \quad \text{dans End} (\mathbf{V}(\pi)).\end{align*} $$

De plus:

• • Si $p\geq 5$ , $\iota _{\cal B}^{\delta }$ est un isomorphisme.

• • Dans le cas général $L\otimes _{{\cal O}_L}\iota _{\cal B}^{\delta }$ est un isomorphisme, $Z_{\cal B}^{\delta }=R_{\cal B}^{{\mathrm{ps}},\delta }/{\cal O}_L\mathrm{-torsion}$ si $p=3$ et le conoyau de $R_{\cal B}^{{\mathrm{ps}},\delta }/{\cal O}_L\mathrm {-torsion}\to Z_{\cal B}^{\delta }$ est tué par $2$ si $p=2$ .

1.4 Critères de finitude

On suppose $F=\mathbf {Q}_p$ dans ce paragraphe. Le th. 1.21 ci-dessous joue un rôle important dans la preuve du cor. 0.12.

1.4.1 Quotients de $I(\sigma )$

Si $\sigma $ est un poids de Serre, la représentation $I(\sigma )$ n’est pas de longueur finie mais on dispose du résultat de rigidité suivant, spécifique à notre groupe G et découlant des résultats de Barthel-Livné et Breuil.

Proposition 1.17. Soit $\sigma $ un poids de Serre et soit $\pi $ un quotient nontrivial de $I(\sigma )$ . Alors $\pi $ est de longueur finie.

Démonstration. Ce résultat est “standard”, mais nous allons en donner la preuve pour le confort du lecteur. Soit $\pi '=\ker (I(\sigma )\to \pi )$ et soit $I_1$ le pro-p Iwahori de G. La prop. 18 de [3] montre que $(\pi ')^{I_1}$ est de co-dimension finie dans $I(\sigma )^{I_1}$ . De plus ${\mathrm{End}}_{k_L[G]}(I(\sigma ))\simeq k_L[T]$ (cf. relation (1.5)). Soit $f\in I(\sigma )$ une fonction de support $KZ$ , telle que $f(1)$ engendre la droite $\sigma ^{I_1}$ . Puisque $\dim I(\sigma )^{I_1}/(\pi ')^{I_1}<\infty $ , il existe un polynôme non nul P tel que $P(T)f\in \pi '$ . Mais alors la surjection $I(\sigma )\to \pi $ se factorise par $I(\sigma )/(P(T))$ , et cette dernière représentation est de longueur finie d’après les résultats de Barthel-Livné et Breuil. Voir aussi le cor. 2.1.4 de [26] pour un autre argument, utilisant la classification (due à Barthel-Livné) des morphismes G-équivariants $I(\sigma )\to I(\sigma ')$ , pour $\sigma , \sigma '$ poids de Serre.

Remarque 1.18. Emerton conjecture [29, conj. 2.3.7] que la proposition admet la version suivante pour ${\mathrm{GL}}_2(F)$ (avec $F/\mathbf {Q}_p$ une extension finie arbitraire): un quotient nontrivial admissible de $I(\sigma )$ est de longueur finie. Plus généralement, il conjecture que, pour un groupe réductif p-adique quelconque, une représentation admissible et de type fini est de longueur finie.

1.4.2 Finitude et finitude du cosocle

Soit $G':=G/p^{\mathbf {Z}}$ , p étant vu comme l’élément ${\big (\begin {smallmatrix}p&0\\ 0&p\end {smallmatrix}\big )}$ de Z. On identifie K à un sous-groupe de $G'$ . Si $\sigma $ est un poids de Serre, on pose

$$ \begin{align*}I_{G'}(\sigma):={\mathrm{c}\mbox{-}\mathrm{Ind}}_{K}^{G'}(\sigma).\end{align*} $$

Si l’on munit $\sigma $ de sa structure de $KZ$ -module obtenue en faisant agir p trivialement, alors $I_{G'}(\sigma )$ s’identifie à $I(\sigma )$ .

Proposition 1.19. Les $k_L[G']$ -modules lisses de type fini sont précisément les $k_L[G']$ -modules lisses $\pi $ tels qu’il existe une filtration

$$ \begin{align*}0=\pi_0\subset...\subset \pi_r=\pi\end{align*} $$

et des surjections $G'$ -équivariantes $I(\sigma _i)\to \pi _i/\pi _{i-1}$ pour $1\leq i\leq r$ et pour certains poids de Serre $\sigma _i$ .

Démonstration. Une implication découle du fait que $I(\sigma _i)$ (et donc tout quotient de $I(\sigma _i)$ ) est de type fini et la stabilité des représentations de type fini par extensions.

Réciproquement, supposons que $\pi $ est une représentation lisse de type fini de $G'$ . Soit $v_1,\dots ,v_n$ une famille de vecteurs qui engendre $\pi $ en tant que $k_L[G']$ -module. Soit W le $k_L[K]$ sous-module de $\pi $ engendré par $v_1,\dots ,v_n$ . Alors $\dim _{k_L}(W)<\infty $ et l’on dispose d’une surjection naturelle ${\mathrm{c}\mbox{-}\mathrm{Ind}}_{K}^{G'}(W)\to \pi $ . Prenons une filtration $0=W_0\subset \dots \subset W_r=W$ avec $\sigma _i:=W_i/W_{i-1}$ irréductible, et notons $\pi _i$ l’image de ${\mathrm{c}\mbox{-}\mathrm{Ind}}_{K}^{G'}(W_i)$ dans $\pi $ par la surjection ci-dessus. Alors $\pi _i/\pi _{i-1}$ est un quotient de ${\mathrm{c}\mbox{-}\mathrm{Ind}}_{K}^{G'}(W_i)/{\mathrm{c}\mbox{-}\mathrm{Ind}}_{K}^{G'}(W_{i-1})\simeq {\mathrm{c}\mbox{-}\mathrm{Ind}}_{K}^{G'} (\sigma _i)$ , ce que l’on voulait.

Le résultat ci-dessus reste valable, avec la même preuve, pour $F\ne \mathbf {Q}_p$ , mais la proposition ci-dessous est très spécifique au cas $F=\mathbf {Q}_p$ .

Proposition 1.20. Tout $k_L[G]$ -module lisse de type fini de $G'$ est de présentation finie.

Démonstration. Soit $0=\pi _n\subset \pi _{n-1}\subset ...\subset \pi _0=\pi $ une filtration de $\pi $ telle qu’il existe des poids de Serre $\sigma _i$ et des surjections $I_{G'}(\sigma _i)\to \pi _{i-1}/\pi _i$ . Comme les représentations de présentation finie sont stables par extensions, il suffit de voir que chaque $\pi _{i-1}/\pi _i$ est de présentation finie. Or $\pi _{i-1}/\pi _i$ est soit de longueur finie (prop. 1.17), auquel cas on peut conclure par le $\mathrm {n}^{\mathrm{o}}$ 1.2.3, ou isomorphe à $I_{G'}(\sigma _i)$ , qui est clairement de présentation finie.

Théorème 1.21. Soit $\pi $ un $k_L[G']$ -module lisse de type fini, dont le cosocle est admissible (ou, de manière équivalente, de longueur finie). Alors $\pi $ est de longueur finie.

Démonstration. Soit $0=\pi _n\subset \pi _{n-1}\subset ...\subset \pi _0=\pi $ une filtration de $\pi $ telle qu’il existe des poids de Serre $\sigma _i$ et des surjections $I_{G'}(\sigma _i)\to \pi _{i-1}/\pi _i$ . Nous allons montrer que $\pi _{i-1}/\pi _i$ est de longueur finie pour tout i, ce qui permettra de conclure.

Puisque le cosocle de $I_{G'}(\sigma _1)$ est de longueur infinie (conséquence de [3]) et celui de $\pi $ est de longueur finie, la surjection $I_{G'}(\sigma _1)\to \pi _0/\pi _1$ n’est pas un isomorphisme, et la prop. 1.17 montre que $\pi _0/\pi _1$ est de longueur finie. Il suffit de montrer que le cosocle de $\pi _1$ est de longueur finie, car on peut alors conclure par récurrence sur la longueur de la filtration.

On veut donc montrer que ${\mathrm{Hom}}_{G'}(\pi _1, \pi ')={\mathrm{Hom}}_{G}(\pi _1, \pi ')$ est de dimension finie sur $k_L$ pour tout $k_L[G']$ -module lisse irréductible $\pi '$ , et nul pour presque tout $\pi '$ (i.e. tous sauf un nombre fini). La suite exacte

$$ \begin{align*}0\to \pi_1\to \pi_0\to \pi_0/\pi_1\to 0\end{align*} $$

en induit une autre

$$ \begin{align*}0\to {\mathrm{Hom}}_G(\pi_0/\pi_1, \pi')\to {\mathrm{Hom}}_G(\pi_0, \pi')\to {\mathrm{Hom}}_G(\pi_1, \pi')\to {\mathrm{Ext}}^1_G(\pi_0/\pi_1, \pi').\end{align*} $$

Puisque $\pi _0/\pi _1$ est de longueur finie, les lemmes 1.23 et 1.22 ci-dessous montrent que les termes extrêmes de la suite exacte ci-dessus sont de dimension finie, et nuls pour presque tout $\pi '$ . Comme il en est de même du terme ${\mathrm{Hom}}_G(\pi _0, \pi ')$ (puisque le cosocle de $\pi _0=\pi $ est de longueur finie), cela permet de conclure.

Le résultat suivant est une adaptation directe d’un résultat analogue dans [4]:

Lemme 1.22. Tout $k_L[G']$ -module lisse irréductible $\pi $ possède un caractère central.

Démonstration. Comme $\pi $ est lisse et irréductible, le pro-p sous-groupe central $1+p\mathbf {Z}_p$ de $G'$ agit trivialement sur $\pi $ , donc l’action du centre de $G'$ se factorise par $\mathbf {F}_p^{\boldsymbol *}$ . Si x est un générateur de ce dernier groupe, alors $0=x^{p-1}-1=\prod _{i=1}^{p-1}(x-i)$ en tant qu’endomorphismes de $\pi $ , donc par irréductibilité il existe i tel que $x=i$ sur $\pi $ . Cela permet de conclure.

Lemme 1.23. Soit $\pi $ un $k_L[G]$ -module lisse, de longueur finie, avec un caractère central. Alors ${\mathrm{Ext}}^1_G(\pi , \pi ')$ est de dimension finie sur $k_L$ pour tout $k_L[G]$ -module lisse irréductible $\pi '$ , avec un caractère central, et nul pour presque tout $\pi '$ .

Démonstration. Soit $\delta $ (resp. $\delta '$ ) le caractère central de $\pi $ (resp. $\pi '$ ). On peut supposer que $\pi $ est irréductible. Soit $\overline {\pi }=\overline {\mathbf {F}}_p\otimes _{k_L} \pi $ et $\overline {\pi '}=\overline {\mathbf {F}}_p\otimes _{k_L} \pi '$ . Écrivons $\overline {\pi }=\oplus _{i=1}^n \pi _i$ et $\overline {\pi '}=\oplus _{j=1}^m \pi ^{\prime }_j$ , les représentations $\pi _i$ et $\pi ^{\prime }_j$ étant irréductibles (cf. (ii) et (iii) du lemme 1.7).

Le lemme 1.6 montre que la flèche

$$ \begin{align*}{\mathrm{Ext}}^1_G(\pi,\pi')\otimes_{k_L} \overline{\mathbf{F}}_p\to {\mathrm{Ext}}^1_G(\overline{\pi}, \overline{\pi'})\simeq \bigoplus_{1\leq i\leq n, 1\leq j\leq m} {\mathrm{Ext}}^1_G(\pi_i, \pi^{\prime}_j)\end{align*} $$

est injective, il suffit donc de s’assurer que ce dernier espace est de dimension finie, et nul pour presque tout $\pi '$ .

La prop. 8.1 de [52] montre que ${\mathrm{Ext}}^1_G(\pi _i, \pi ^{\prime }_j)=0$ pour tout $i,j$ si $\delta \neq \delta '$ , et si $\delta =\delta '$ , on a une suite exacte

$$ \begin{align*}0\to {\mathrm{Ext}}^1_{G,\delta}(\pi_i, \pi^{\prime}_j)\to {\mathrm{Ext}}^1_G(\pi_i, \pi^{\prime}_j)\to X_{ij}\to 0,\end{align*} $$

avec $X_{ij}=0$ si $\pi _i$ n’est pas isomorphe à $\pi ^{\prime }_j$ et $X_{ij}={\mathrm{Hom}}(Z, \overline {\mathbf {F}}_p)$ dans le cas contraire. Notons que si $\pi _i\simeq \pi ^{\prime }_j$ , alors ${\mathrm{Hom}}_G(\overline {\pi }, \overline {\pi '})\ne 0$ et le lemme 1.6 montre que ${\mathrm{Hom}}_G(\pi ,\pi ')\ne 0$ , donc $\pi '\simeq \pi $ . Comme ${\mathrm{Hom}}(Z, \overline {\mathbf {F}}_p)$ est de dimension finie, il suffit donc de montrer que les ${\mathrm{Ext}}^1_{G,\delta }(\pi _i, \pi ^{\prime }_j)$ sont de dimension finie, et nuls pour presque tout $\pi '$ . Cela est classique (cf. [52, 54]).

1.4.3 Finitude des vecteurs lisses de $\pi ^{\vee }$

Pour les applications à la cohomologie de la tour de Lubin-Tate nous aurons aussi besoin du résultat suivant:

Théorème 1.24. Soit $\pi $ un $k_L[G']$ -module lisse de type fini. Alors $\pi $ est de longueur finie si et seulement si l’espace des vecteurs lisses de $\pi ^{\vee }$ est de dimension finie sur $k_L$ .

Démonstration. Supposons que $\pi $ est de longueur finie et montrons que $\dim (\pi ^{\vee })^{\mathrm{lisse}}<\infty $ . Par dévissage on peut supposer que $\pi $ est irréductible, auquel cas le résultat est bien connu (on a même $(\pi ^{\vee })^{\mathrm{lisse}}=0$ sauf si $\pi $ est de dimension finie, cf. [47, prop. 3.9]).

L’autre implication est plus délicate. Nous allons commencer par montrer:

Lemme 1.25. Si $\pi $ est un $k_L[G']$ -module lisse de type fini et de longueur infinie, alors il existe un poids de Serre $\sigma $ tel que ${\mathrm{Hom}}_{G}(\pi , I_{G'}(\sigma ))\ne 0$ .

Démonstration. Soit $0=\pi _n\subset \pi _{n-1}\subset ...\subset \pi _0=\pi $ une filtration de $\pi $ telle qu’il existe des poids de Serre $\sigma _i$ et des surjections $I_{G'}(\sigma _i)\to \pi _{i-1}/\pi _i$ . Si la surjection $I_{G'}(\sigma _1)\to \pi /\pi _1$ est un isomorphisme, on peut conclure, supposons donc que ce n’est pas le cas, donc (prop. 1.17) $\pi /\pi _1$ est de longueur finie. Alors $\pi _1$ est de type fini et de longueur infinie, donc par récurrence sur la longueur de la filtration on dispose d’un poids de Serre $\sigma $ tel que ${\mathrm{Hom}}_G(\pi _1, I_{G'}(\sigma ))\ne 0$ . En appliquant le foncteur ${\mathrm{Hom}}_{G}(-, I_{G'}(\sigma ))$ à la suite exacte $0\to \pi _1\to \pi \to \pi /\pi _1\to 0$ on obtient une suite exacte

$$ \begin{align*}{\mathrm{Hom}}_G(\pi, I_{G'}(\sigma))\to {\mathrm{Hom}}_G(\pi_1, I_{G'}(\sigma))\to {\mathrm{Ext}}^1(\pi/\pi_1, I_{G'}(\sigma)).\end{align*} $$

Comme $\pi /\pi _1$ est de longueur finie, un résultat de Dotto-Emerton-Gee [26] montre que ${\mathrm{Ext}}^1(\pi /\pi _1, I_{G'}(\sigma ))$ est de dimension finie. ¹⁹ Supposons que ${\mathrm{Hom}}_G(\pi , I_{G'}(\sigma ))$ , donc ${\mathrm{Hom}}_G(\pi _1, I_{G'}(\sigma ))$ est de dimension finie sur $k_L$ . D’autre part ${\mathrm{Hom}}_G(\pi _1, I_{G'}(\sigma ))$ est un $k_L[T]={\mathrm{End}}_{G}(I_{G'}(\sigma ))$ -module, donc il existe $P\in k_L[T]$ non nul tel qui tue ${\mathrm{Hom}}_G(\pi _1, I_{G'}(\sigma ))$ mais, comme $I_{G'}(\sigma )$ est libre sur $k_L[T]$ , la multiplication par $P(T)$ est injective sur ${\mathrm{Hom}}_G(\pi _1, I_{G'}(\sigma ))$ , une contradiction.

Revenons à la preuve du th. 1.24. Supposons que $(\pi ^{\vee })^{\mathrm{lisse}}$ est de dimension finie sur $k_L$ et montrons que $\pi $ est de longueur finie. Si ce n’est pas le cas, le lemme fournit un poids de Serre $\sigma $ et un morphisme G-équivariant continu non nul $f: I_{G'}(\sigma )^{\vee }\to \pi ^{\vee }$ . Comme $(\pi ^{\vee })^{\mathrm{lisse}}$ est de dimension finie sur $k_L$ , il est fermé dans $\pi ^{\vee }$ , donc $f^{-1}((\pi ^{\vee })^{\mathrm{lisse}})$ est fermé dans $I_{G'}(\sigma )^{\vee }$ . D’autre part, $f^{-1}((\pi ^{\vee })^{\mathrm{lisse}})$ contient $(I_{G'}(\sigma )^{\vee })^{\mathrm{lisse}}$ , qui est dense dans $I_{G'}(\sigma )^{\vee }$ , donc $f^{-1}((\pi ^{\vee })^{\mathrm{lisse}})= I_{G'}(\sigma )^{\vee }$ ; ainsi l’image de f est incluse dans $(\pi ^{\vee })^{\mathrm{lisse}}$ et donc est de dimension finie, ce qui fournit une sous-représentation $({\mathrm{Im}}(f))^{\vee }$ de dimension finie de $I_{G'}(\sigma )$ , non nulle puisque $f\neq 0$ . Cela est impossible.

1.5 Représentations admissibles de présentation finie de ${\mathrm{GL}}_2(F)$

Soit

$$ \begin{align*}\mathcal{C}={\mathrm{Rep}}^{\mathrm{adm}}\,G\cap {\mathrm{Rep}}^{\mathrm{pf}}\,G\end{align*} $$

la sous-catégorie de ${\mathrm{Rep}}^{\mathrm{lisse}}\,G$ des représentations admissibles et de présentation finie. Cette catégorie a été étudiée par Hu [40] et Vignéras [70].

Théorème 1.26.

1. (i) $\mathcal {C}$ est une sous-catégorie de ${\mathrm{Rep}}^{\mathrm{\ell f}}\,G$ .

2. (ii) ${\cal C}$ est stable par sous-quotients et extensions.

Démonstration. Le point (i) découle directement de la proposition $5.6\, (i)$ de [70]. La stabilité de ${\cal C}$ par extensions découle de la proposition 1.2 (une extension lisse de représentations lisses admissibles est trivialement admissible). Soit $V\in {\cal C}$ et soit $V_1$ un sous-objet de V. Par la proposition $5.5\, (i)$ de [70] (noter que l’hypothèse est satisfaite grâce à la proposition $5.6$ de loc.cit.) on a $V_1\in \mathcal {C}$ . Si $V_2$ est un quotient de $V_1$ , alors $V_2$ est admissible (tout quotient d’une représentation lisse admissible est encore lisse admissible) et $V_2$ est de présentation finie par la proposition 1.2 (noter que le noyau de la surjection $V_1\to V_2$ est dans $\mathcal {C}$ , en particulier de type fini, d’après ce que l’on vient de faire).

Si $F=\mathbf {Q}_p$ , les représentations irréductibles de G sont admissibles et de présentation finie, donc

$$ \begin{align*} {\cal C}={\mathrm{Rep}}^{\mathrm{\ell f}}\,G,\quad \text{ si } F = \mathbf{Q}_p. \end{align*} $$

Ce n’est plus du tout le cas pour $F\ne \mathbf {Q}_p$ , comme le montre le résultat suivant:

Théorème 1.27 (Schraen [66], Wu [71]).

Si $F\neq \mathbf {Q}_p$ , les représentations supersingulières de ${\mathrm{GL}}_2(F)$ sur $\overline {\mathbf {F}}_p$ ne sont pas de présentation finie.

Remarque 1.28. Le [48] a construit des $k_L$ -représentations de ${\mathrm{GL}}_2(\mathbf {Q}_{p^3})$ qui sont lisses, irréductibles, mais pas admissibles.

Nous allons décrire ${\cal C}$ dans le cas $F\neq \mathbf {Q}_p$ via le foncteur «partie ordinaire» d’Emerton.

Nous supposons $F\neq \mathbf {Q}_p$ dans le reste de ce paragraphe.

1.5.1 Composantes de Jordan-Hölder

Si k est une extension finie de $k_L$ , on note $\mathcal {C}_k^{\mathrm{ord}}$ la catégorie des $k[G]$ -modules lisses, de longueur finie, dont tous les sous-quotients irréductibles sont de la forme $\chi \circ \det , {\mathrm{St}}\otimes \chi \circ \det $ ou ${\mathrm{Ind}}_B^G (\chi _1\otimes \chi _2)$ , avec $\chi , \chi _1,\chi _2: F^{{\boldsymbol *}}\to k^{{\boldsymbol *}}$ des caractères lisses. Ainsi $\mathcal {C}_{k_L}^{\mathrm{ord}}$ est une sous-catégorie de $\mathcal {C}$ .

Lemme 1.29. Pour tout $\pi \in \mathcal {C}$ tué par il existe une extension finie k de $k_L$ telle que $\pi \otimes _{k_L} k\in \mathcal {C}_k^{\mathrm{ord}}$ .

Démonstration. On peut supposer que $\pi $ est irréductible. Prenons une extension k de $k_L$ et des $\pi _i$ comme dans le (iii) du lemme 1.7. Notons que chaque $\pi _i$ est aussi de présentation finie, donc $\pi _i\otimes _k \overline {\mathbf {F}}_p$ aussi. De plus, par construction les endomorphismes de $\pi _i\otimes _k \overline {\mathbf {F}}_p$ sont scalaires, donc cette reprèsentation possède un caractère central. Le th. 1.27 montre alors que $\pi _i\otimes _k \overline {\mathbf {F}}_p$ n’est pas supersingulière, et la classification de Barthel-Livné [2] permet de conclure que $\pi _i\otimes _k \overline {\mathbf {F}}_p$ est un caractère lisse, une tordue de la Steinberg ou une série principale. Dans tous les cas on trouve une extension finie $k'$ de k et une représentation $\sigma $ définie sur $k'$ , qui est un caractère, une tordue de la Steinberg ou une série principale et telle que $\pi _i\otimes _k \overline {\mathbf {F}}_p\simeq \sigma \otimes _{k'} \overline {\mathbf {F}}_p$ . Le lemme 1.6 montre alors que $\pi _i\otimes _{k} k'$ est isomorphe à $\sigma $ , ce qui permet de conclure.

1.5.2 Le foncteur «partie ordinaire»

Soit $\bar {B}$ le Borel inférieur de G et soit A le tore diagonal de G. Le foncteur $U\mapsto {\mathrm{Ind}}_{\bar {B}}^G(U)$ de ${\mathrm{Rep}}(A)$ dans ${\mathrm{Rep}}(G)$ est exact et préserve l’admissibilité [29, prop. 4.1.5, 4.1.7], donc induit un foncteur

$$ \begin{align*}{\mathrm{Ind}}_{\bar{B}}^G: {\mathrm{Rep}}(A)^{\mathrm{adm}}\to {\mathrm{Rep}}(G)^{\mathrm{adm}}\end{align*} $$

Emerton a montré [29, th. 4.4.6] que ce dernier foncteur possède un adjoint à droite, le foncteur partie ordinaire

$$ \begin{align*}{\mathrm{Ord}}={\mathrm{Ord}}_B: {\mathrm{Rep}}(G)^{\mathrm{adm}}\to {\mathrm{Rep}}(A)^{\mathrm{adm}}\end{align*} $$

Ainsi le passage à la partie ordinaire induit une identification

$$ \begin{align*}{\mathrm{Hom}}_G({\mathrm{Ind}}_{\bar{B}}^G(U), V)\simeq {\mathrm{Hom}}_{A}(U, {\mathrm{Ord}}(V))\end{align*} $$

pour des représentations lisses admissibles U et V de A, respectivement G. En particulier l’identité de ${\mathrm{Ord}}(V)$ induit un morphisme canonique

$$ \begin{align*}\iota_V: {\mathrm{Ind}}_{\bar{B}}^G( {\mathrm{Ord}}(V))\to V,\end{align*} $$

tel que ${\mathrm{Ord}}(\ker \iota _V)=0$ et ${\mathrm{Ord}}(V^{\mathrm{ord}})={\mathrm{Ord}}(V)$ si l’on note $V^{\mathrm{ord}}$ l’image de $\iota _V$ . On se propose de montrer (prop. 1.33) que, si $V\in \mathcal {C}$ , alors $\iota _V$ est presqu’un isomorphisme, i.e. son noyau et son conoyau sont de type fini sur $\mathcal {O}_L$ . L’argument qui suit est inspiré des lemme 5.4 et 5.11 de [41], et demande quelques préliminaires.

Proposition 1.30.

1. a) Si $U\in {\mathrm{Rep}}^{\mathrm{adm}}(A)$ alors

   $$ \begin{align*}{\mathrm{Ord}}({\mathrm{Ind}}_{\bar{B}}^G(U))\simeq U,\,\, R^1{\mathrm{Ord}}({\mathrm{Ind}}_{\bar{B}}^G(U))=0.\end{align*} $$

2. b) On a ${\mathrm{Ord}}({\mathrm{St}}\otimes \chi \circ \det )\simeq \chi \otimes \chi $ et $ R^1{\mathrm{Ord}}({\mathrm{St}}\otimes \chi \circ \det )=0$ .

3. c) Si $\pi =\chi \circ \det $ alors ${\mathrm{Ord}}(\pi )=R^1{\mathrm{Ord}}(\pi )=0$ .

Démonstration.

1. a) Le premier est le contenu de [29, lemma 2.3.4, prop. 4.3.4], le second est démontré dans [39, cor. 4.2.4].

2. b) Cela découle de [30, th. 4.2.12].

3. c) Il suffit d’utiliser a) et b) et la suite exacte évidente.

1.5.3 Description de ${\cal C}$

Lemme 1.31. Le foncteur ${\mathrm{Ord}}$ est exact sur $\mathcal {C}$ et ${\mathrm{Ord}}(\pi )$ est un $\mathcal {O}_L$ -module de type fini pour $\pi \in \mathcal {C}$ .

Démonstration. Il suffit de montrer que ${\mathrm{R}^1\mathrm{Ord}}$ est nul sur $\mathcal {C}$ , et par dévissage il suffit de voir que ${\mathrm{R}^1\mathrm{Ord}}(\pi )=0$ pour un objet irréductible $\pi $ de $\mathcal {C}$ . Un tel $\pi $ est tué par , et il existe une extension finie k de $k_L$ telle que $\pi \otimes _k k_L\in \mathcal {C}_k^{\mathrm{ord}}$ (lemme 1.29). Comme le foncteur ${\mathrm{Ind}}_{\bar B}^G$ est compatible avec les extensions finies du corps des coefficients, il en est de même du foncteur ${\mathrm{Ord}}$ et de ses foncteurs dérivés. Il suffit donc de voir que ${\mathrm{R}^1\mathrm{Ord}}$ est nul sur $\mathcal {C}_k^{\mathrm{ord}}$ , et encore par dévissage on se ramène à l’annulation de ${\mathrm{R}^1\mathrm{Ord}}$ sur $\chi \circ \det , {\mathrm{St}}\otimes \chi \circ \det $ ou ${\mathrm{Ind}}_B^G (\chi _1\otimes \chi _2)$ , qui découle de la prop. 1.30.

Pour le deuxième point, on sait que ${\mathrm{Ord}}(\pi )$ est un $\mathcal {O}_L[A]$ -module de torsion, lisse, admissible, et que ${\mathrm{Ord}}(\pi )\otimes _{\mathcal {O}_L} k_L={\mathrm{Ord}}(\pi \otimes _{\mathcal {O}_L} k_L)$ d’après ce que l’on vient de démontrer. Il suffit de montrer que ${\mathrm{Ord}}(\pi \otimes _{\mathcal {O}_L} k_L)$ est de dimension finie sur $k_L$ . Cela se fait encore par dévissage en utilisant le lemme 1.29 et la compatibilité du foncteur partie ordinaire avec le changement du corps des coefficients, et le calcul de ${\mathrm{Ord}}$ sur les objets irréductibles de $\mathcal {C}_k^{\mathrm{ord}}$ fourni par la prop. 1.30.

Lemme 1.32. Soit $\pi \in \mathcal {C}$ tel que ${\mathrm{Ord}}(\pi )=0$ . Alors $\pi $ est un $\mathcal {O}_L$ -module de type fini.

Démonstration. Soit $\pi '$ un sous-objet irréductible de $\pi $ , alors ${\mathrm{Ord}}(\pi ')=0$ et donc ${\mathrm{Ord}}(\pi '\otimes _{k_L} k)=0$ pour toute extension finie k de $k_L$ . Comme ${\mathrm{Ord}}$ est exact sur $\mathcal {C}_k^{\mathrm{ord}}$ et prend des valeurs non nulles sur les tordus de la Steinberg et les séries principales, le lemme 1.29 montre que $\pi '$ est de dimension finie sur $k_L$ . Comme ${\mathrm{Ord}}$ est exact sur $\mathcal {C}$ , on a ${\mathrm{Ord}}(\pi /\pi ')=0$ et une récurrence sur la longueur montre que tous les sous-quotients irréductibles de $\pi $ sont de dimension finie sur $k_L$ , ce qui permet de conclure.

Proposition 1.33. Pour tout $\pi \in \mathcal {C}$ le noyau et le conoyau de la flèche naturelle $\iota _V: {\mathrm{Ind}}_{\bar {B}}^G({\mathrm{Ord}}(\pi ))\to \pi $ sont de type fini sur $\mathcal {O}_L$ .

Démonstration. Soit $\pi ^{\mathrm{ord}}$ l’image de $\iota _V$ , alors par construction ${\mathrm{Ord}}(\pi ^{\mathrm{ord}})={\mathrm{Ord}}(\pi )$ et $\pi /\pi ^{\mathrm{ord}}, \pi ^{\mathrm{ord}}\in \mathcal {C}$ donc par le lemme 1.31 on a ${\mathrm{Ord}}(\pi /\pi ^{\mathrm{ord}})=0$ et donc le conoyau de $\iota _V$ est de type fini sur $\mathcal {O}_L$ par le lemme 1.32. Soit $X=\ker (\iota _V)$ . Alors ${\mathrm{Ord}}(X)=0$ , donc par le lemme 1.32 il suffit de montrer que $X\in \mathcal {C}$ . Comme X est un sous-objet de ${\mathrm{Ind}}_{\bar {B}}^G ({\mathrm{Ord}}(\pi ))$ , il suffit de voir que ce dernier est dans $\mathcal {C}$ , ce qui découle facilement du fait que ${\mathrm{Ord}}(\pi )$ est de type fini sur $\mathcal {O}_L$ (lemme 1.31).

Corollaire 1.34. Soit $\Theta $ un réseau dans un L-Banach unitaire admissible $\Pi $ de G tel que $\Theta /\varpi _L\Theta \in \mathcal {C}$ . Il existe alors une représentation $\sigma $ de A, de type fini sur $\mathcal {O}_L$ , et un morphisme ${\mathrm{Ind}}_{\bar {B}}^G(\sigma )\to \Theta $ dont le noyau et le conoyau sont de type fini sur $\mathcal {O}_L$ .

Démonstration. Il suffit d’appliquer le résultat ci-dessus avec $\pi _n=\Theta /\varpi _L^n\Theta $ , en remarquant que ${\mathrm{Ord}}(\pi _{n+1})\otimes _{\mathcal {O}_L/\varpi _L^{n+1}} \mathcal {O}_L/\varpi _L^n={\mathrm{Ord}}(\pi _n)$ par exactitude de ${\mathrm{Ord}}$ sur $\mathcal {C}$ , et un résultat semblable pour l’induite parabolique.

2 Coprésentation finie

Soit F une extension finie de $\mathbf {Q}_p$ . Le but de ce chapitre est de démontrer le résultat suivant:

Théorème 2.1. Soient K une extension finie de F et $k\geq 1$ , $q\geq 0$ . Le $G^{\prime }$ -module $H^q_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K}^{\varpi }, {\cal O}_L/p^k)$ est le dual de Pontryagin d’une représentation lisse, de présentation finie de $G^{\prime }$ , en particulier c’est un ${\cal O}_L$ -module profini.

Remarque 2.2. Si $F=\mathbf {Q}_p$ , nous montrons au chap. 4 que $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K}^{\varpi }, k_L)^{\vee }$ est de longueur finie et donc admissible. Par contraste, si $F\neq \mathbf {Q}_p$ , le th. 2.1 implique que $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K}^{\varpi }, k_L)^{\vee }$ n’est pas admissible si K est assez grand. (cf. th. 2.13).

Remarque 2.3. Il est fort probable qu’en dimension arbitraire on dispose encore du résultat suivant: $H^i_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K}^{\varpi }, k_L)^{\vee }$ est un $G^{\prime }$ -module lisse, de type fini.

2.1 Préliminaires

La preuve du théorème est purement géométrique et demande quelques préliminaires. Dans beaucoup des énoncés qui suivent, il est plus naturel de travailler avec $\mathbf {Z}_p/p^k$ plutôt que ${\cal O}_L/p^k$ ; on obtient le résultat pour ${\cal O}_L/p^k$ en appliquant $\otimes _{\mathbf {Z}_p}{\cal O}_L$ .

2.1.1 La filtration de Bloch–Kato-Hyodo sur les cycles proches

Nous allons étendre aux schémas formels la filtration de Bloch-Kato-Hyodo sur les faisceaux de cycles proches pour les schémas et l’identification du gradué; que ce soit possible est «bien connu» des experts mais nous n’avons pas trouvé de référence où ceci est fait.

Soient K une extension finie de $\mathbf {Q}_p$ , $\varpi $ une uniformisante, et k le corps résiduel de ${\cal O}_K$ . Soit X un schéma formel semistable sur ${\cal O}_K$ ou le changement de base d’un tel schéma sur l’anneau des entiers d’un sous-corps de K. On munit X de la log-structure induite par la fibre spéciale. Soit M le faisceau en monoïdes sur X définissant la log-structure, $M^{\operatorname {gp} }$ le faisceau en groupes associé. Cette log-structure est canonique, dans la terminologie de Berkovich [8, 2.3], i.e., $M(U)=\{x\in {\cal O}_X(U)| x_K\in {\cal O}^{{\boldsymbol *}}_{X_K}(U_K)\}$ , cf. [8, Theorem 2.3.1]. Il s’ensuit que $M^{\operatorname {gp} }(U)={\cal O}(U_K)^{\boldsymbol *}$ .

Soit i l’inclusion de la fibre spéciale $X_0$ dans X. Soit $\mathrm {R} ^i\Psi \mathbf {Z}/p^n(j)$ le faisceau sur $X_{0,\operatorname {\acute {e}t} }$ associé au préfaisceau ${U}_0\to H^i_{\operatorname {\acute {e}t} }({U}_K,\mathbf {Z}/p^n(j))$ , où U décrit les schémas formels, étales au-dessus de X. C’est le i-ième foncteur dérivé du foncteur $\Psi $ des cycles proches de [7, Prop. 4.1] (où il est noté $\Theta $ ) mais nous n’utiliserons pas $\Psi $ lui-même.

Pour U comme ci-dessus, la suite exacte de Kummer fournit une flèche

$$ \begin{align*}i^{\boldsymbol *} M^{\mathrm{gp}}(U_0)=M^{\mathrm{gp}}(U)={\cal O}(U_K)^{\boldsymbol *}\stackrel{\partial}{\to} \mathbf{Z}/p^n(1)(U_K)[1], \end{align*} $$

qui se faisceautise en une application “symbole”

$$ \begin{align*}i^{\boldsymbol *} M^{\mathrm{gp}}\to \mathrm {R} ^1\Psi\mathbf{Z}/p^n(1). \end{align*} $$

En utilisant le cup-produit, cela induit une flèche symbole

$$ \begin{align*}i^{\boldsymbol *}(M^{\mathrm{gp}})^{\otimes q}\to \mathrm {R} ^q\Psi\mathbf{Z}/p^n(q).\end{align*} $$

Soit $(X_2, M_2)$ la réduction modulo $p^2$ de $(X,M)$ . On munit $(M_2^{\mathrm{gp}})^{\otimes q}$ d’une filtration

$$ \begin{align*}...\subset U^2\subset V^1\subset U^1\subset V^0\subset U^0=(M_2^{\mathrm{gp}})^{\otimes q},\end{align*} $$

définie comme suit. Si $q=0$ on pose

$$ \begin{align*}U^{m+1}=V^m=0 \,\, \text{si}\,\, m\geq 0;\end{align*} $$

si $q=1$ on pose

$$ \begin{align*}V^0=(1+\varpi \mathcal{O}_{X_2}) \varpi^{\mathbf{Z}}, U^m=1+\varpi^m \mathcal{O}_{X_2}, V^m=U^{m+1}, \, m\geq 1;\end{align*} $$

et, enfin, si $q\geq 2$ on note $U^m$ l’image de $U^m(M_2^{\mathrm{gp}})\otimes (M_2^{\mathrm{gp}})^{\otimes (q-1)}$ et $V^m$ l’image de

$$ \begin{align*}U^m(M_2^{\mathrm{gp}})\otimes (M_2^{\mathrm{gp}})^{\otimes (q-2)}\otimes \varpi^{\mathbf{Z}}+ U^{m+1}.\end{align*} $$

En utilisant la flèche symbole, cela permet de définir une filtration sur $ \mathrm {R} ^q\Psi \mathbf {Z}/p(q)$ . Si $a_i\in i^{\boldsymbol *}(M^{\mathrm{gp}}_2)$ , on note $\{a_1,...,a_q\}$ l’image de $a_1\otimes ...\otimes a_q\in (i^{\boldsymbol *}(M^{\mathrm{gp}}_2))^{\otimes q}$ dans $\mathrm {R} ^q\Psi \mathbf {Z}/p(q)$ par l’application symbole.

Soit $Y:=X_0$ avec la log-structure induite, et soit $\Omega ^{q}_{Y/k}$ le faisceau des q-différentielles logarithmiques sur Y relativement à la log-structure sur k induite par $1\mapsto 0$ . Posons

$$ \begin{align*}B^q_{Y/k}=d \Omega^{q-1}_{Y/k}\subset \Omega^q_{Y/k},\,\, Z^{q}_{Y/k}=\ker(d: \Omega^q_{Y/k}\to \Omega^{q+1}_{Y/k}).\end{align*} $$

Enfin, notons $\Omega ^q_{Y/k,{\mathrm{log}}}$ le sous-faisceau abélien de $\Omega ^q_{Y/k}$ engendré par les $\wedge _{i=1}^q d\log a_i$ pour $a_i\in M_Y$ .

Le théorème suivant est un simple corollaire de l’analogue algébrique prouvé par Bloch–Kato-Hyodo dans [9], [44] (voir aussi [69, Th. 3.3.1])

Théorème 2.4. Si e est l’indice de ramification absolu de K, les gradués de la filtration sur $ \mathrm {R} ^q\Psi \mathbf {Z}/p(q)$ sont décrits comme suit:

1. (1) On a des isomorphismes

   $$ \begin{align*}U^0/V^0\simeq \Omega^q_{Y/k, \mathrm{log}}, \quad V^0/U^1\simeq \Omega^{q-1}_{Y/k, \mathrm{log}},\end{align*} $$
   induits respectivement par
   $$ \begin{align*}\{a_1,...,a_q\}\mapsto \wedge_{i=1}^q \operatorname{dlog} \overline{a_i},\quad \{a_1,...,a_{q-1},\varpi\}\mapsto \wedge_{i=1}^{q-1} \operatorname{dlog} \overline{a_i}\end{align*} $$

2. (2) Si $m\in ]0, pe/(p-1)[$ est premier à p, on a des isomorphismes

   $$ \begin{align*}U^m/V^m\simeq \Omega^{q-1}_{Y/k}/B_{Y/k}^{q-1}, \quad V^m/U^{m+1}\simeq \Omega_{Y/k}^{q-2}/Z_{Y/k}^{q-2}\end{align*} $$
   induits respectivement par
   $$ \begin{align*}\{1{+}\varpi^m x, a_1,...,a_{q-1}\}\mapsto \bar{x}\wedge_{i=1}^{q-1} \operatorname{dlog} \overline{a_i},\quad \{1{+}\varpi^m x, a_1,...,a_{q-2}, \varpi\}\mapsto \bar{x}\wedge_{i=1}^{q-2} \operatorname{dlog} \overline{a_i}\end{align*} $$

3. (3) Si $m\in ]0, pe/(p-1)[$ est un multiple de p, on a des isomorphismes

   $$ \begin{align*}U^m/V^m\simeq \Omega^{q-1}_{Y/k}/Z^{q-1}_{Y/k}, \quad V^m/U^{m+1}\simeq \Omega_{Y/k}^{q-2}/Z_{Y/k}^{q-2}\end{align*} $$
   induits respectivement par
   $$ \begin{align*}\{1{+}\varpi^m x, a_1,...,a_{q-1}\}\mapsto \bar{x}\wedge_{i=1}^{q-1} \operatorname{dlog} \overline{a_i}, \ \ \{1{+}\varpi^m x, a_1,...,a_{q-2}, \varpi\}\mapsto \bar{x}\wedge_{i=1}^{q-2} \operatorname{dlog} \overline{a_i}\end{align*} $$

4. (4) Si $m\geq pe/(p-1)$ alors $U^m=0$ .

Démonstration. Commençons par l’isomorphisme $U^0/V^0\simeq \Omega ^q_{Y/k,\log }$ . Considérons les flèches:

où nous avons ajouté des indices pour indiquer où se trouvent les filtrations. Il s’agit de prouver que $f_X$ est un isomorphisme.

Le problème est local et nous pouvons supposer que X est algébrisable, i.e., que X est la complétion $X=\widehat {T}$ d’un schéma semistable T over ${\cal O}_K$ . Par [7, Th. 5.1], la complétion induit un isomorphisme naturel:

(2.5) $$ \begin{align} i^{\boldsymbol *}\mathrm {R} ^qj_* \mathbf{Z}/p(q) \stackrel{\sim}{\to }\mathrm {R} ^q\Psi \mathbf{Z}/p(q), \quad j: T_K\hookrightarrow T. \end{align} $$

Le faisceau des cycles proches algébrique $ i^{\boldsymbol *}\mathrm {R} ^qj_* \mathbf {Z}/p(q) $ possède une filtration $U^{\bullet }_T,V^{\bullet }_T$ analogue à celle de son analogue formel et on a un diagramme commutatif:

La flèche $f_T$ est un isomorphisme d’après le théorème de Bloch–Kato–Hyodo. Une chasse au diagramme prouve que $f_X$ est un isomorphisme. Cela signifie aussi que la flèche verticale est un isomorphisme qui, combiné avec l’isomorphisme $U^0_T\stackrel {\sim }{\to } U^0_X$ de la formule (2.5), montre que la flèche naturelle $V^0_T\to V^0_X$ est aussi un isomorphisme. En résumé, nous avons établi les isomorphismes

$$ \begin{align*}U^0_X/V^0_X\simeq \Omega^q_{Y/k,\log}, \quad V^0_T\stackrel{\sim}{\to} V^0_X. \end{align*} $$

Maintenant, partant du dernier isomorphisme, on prouve de manière analogue les isomorphismes

$$ \begin{align*} & V^0_X/U^1_X\simeq \Omega^{q-1}_{Y/k,\log}, \quad U^1_T\stackrel{\sim}{\to }U^1_X, \\ & U^1_X/V^1_X\simeq \Omega^{q-1}_{Y/k}/B^{q-1}_{Y/k},\quad V^1_T\stackrel{\sim}{\to }V^1_X, \end{align*} $$

etc. Puisque, pour $m\geq pe/(p-1)$ , on a $U_T^m=0$ , cela suffit à prouver le théorème.

Remarque 2.6. En particulier, pour $q=1$ , on obtient les résultats suivants pour $\mathrm {R} ^1\Psi \mathbf {Z}/p(1)$ .

1. 1. On construit une extension

   $$ \begin{align*}0\to \mathbf{F}_p\to U^0/U^1\to \Omega^{1}_{Y/k, \mathrm{log}}\to 0,\end{align*} $$

   à partir des isomorphismes

   $$ \begin{align*}U^0/V^0\simeq \Omega^{1}_{Y/k, \mathrm{log}},\ a\mapsto \operatorname{dlog} \bar{a}, \quad V^0/U^1\simeq \mathbf{F}_p, \ \varpi^n \mapsto n\ ({\mathrm{mod}}\, p).\end{align*} $$

2. 2. De plus $U^m=0$ si $m\geq pe/(p-1)$ , et pour $m\in ]0, pe/(p-1)[$

   $$ \begin{align*}U^m/U^{m+1}\simeq \begin{cases} \mathcal{O}_Y, & m \notin p\mathbf{Z},\\ \mathcal{O}_Y/Z^0_{Y/k}, & m\in p\mathbf{Z}, \end{cases}\end{align*} $$

   l’isomorphisme étant induit par $1+\varpi ^m a\mapsto \bar {a}$ .

3. 3. Comme Y est log-lisse et de type Cartier, on a un isomorphisme

   $$ \begin{align*}\mathcal{O}_Y\simeq Z^0_{Y/k}, \,\, a\mapsto a^p.\end{align*} $$

2.1.2 Modèles semistables

Si K est une extension finie de $\mathbf {Q}_p$ , un schéma formel sur ${\cal O}_K$ est dit semistable si, localement pour la topologie de Zariski, il admet une flèche étale vers le spectre formel

$$ \begin{align*}\operatorname{Spf} ({\cal O}_K\{X_1,\ldots,X_n\}/(X_1\cdots X_r-\varpi_K)), \quad 1\leq r\leq n, \end{align*} $$

où $\varpi _K$ est une uniformisante de K.

Les courbes $\mathcal {M}_n^{\varpi }$ ne sont pas quasi-compactes, donc l’existence d’un modèle semi-stable défini sur une extension finie de $\mathbf {Q}_p$ n’est pas automatique. Cependant, on dispose du résultat suivant, essentiellement prouvé dans l’appendice de [16]. Il est valable pour ${\mathrm{GL}}_2(F)$ , mais pas pour ${\mathrm{GL}}_n(F)$ .

Proposition 2.7. L’espace $\mathcal {M}_n^{\varpi }$ possède un modèle formel semi-stable $G\times \check {G}\times \mathcal {G}_F$ -équivariant, défini sur une extension finie de F. Les composantes irréductibles de la fibre spéciale de ce modèle forment un nombre fini d’orbites sous l’action de G, et chacune de ces composantes irréductibles est fixée par un sous-groupe ouvert de G.

Démonstration. Le premier point est établi dans la prop. A.1 de [16].

Pour le second point, considérons les diagrammes commutatifs G-équivariants suivants de morphismes de courbes E-analytiques et de schémas formels, respectivement, qui apparaissent dans la preuve de [16, prop. A.1].

• – $\Omega _{\mathrm{Dr}}$ est le demi-plan de Drinfeld sur F, $\Omega _{\mathrm{Dr}}^{+}$ est son modèle semistable standard;

• – $\Gamma \subset G/\varpi ^{\mathbf {Z}}$ est un sous-groupe cocompact assez petit pour que l’action de $\Gamma $ sur l’arbre de Bruhat-Tits soit libre;

• – $X:=\Gamma \backslash \Omega _{\mathrm{Dr}}$ est une courbe propre et lisse; $X^+:=\Gamma \backslash \Omega ^+_{\mathrm{Dr}}$ – le modèle stable (et aussi le modèle semistable minimal) de X;

• – $X_n:=\Gamma \backslash \mathcal {M}_n^{\varpi }$ ; E est une extension finie de F telle que $X_n$ possède un modèle stable $X_{n,E}^+$ ;

• – $X_{n,E}^{\circ }$ est le modèle minimal semistable de $X_{n,E}$ obtenu à partir de $X_{n,E}^+$ en commençant par éclater les points singuliers puis en éclatant les points d’auto-intersection.

Les diagrammes ci-dessus sont cartésiens et $({\cal M}^{\varpi }_{n,E})^{\circ }$ est un modèle semistable de ${\cal M}^{\varpi }_{n,E}$ . De plus, la triangulation $S(X_{n,E}^{+})$ associée est le quotient de la triangulation $S(({\cal M}^{\varpi }_{n,E})^{+} )$ par $\Gamma $ . Comme $S(X_{n,E}^{+})$ et $S(({\cal M}^{\varpi }_{n,E})^{+} )$ sont toutes les deux les ensembles des préimages (par spécialisation), dans $X_{n,E}$ et ${\cal M}^{\varpi }_{n,E}$ respectivement, des points génériques des composantes irréductibles de leurs fibres spéciales respectives, la fibre spéciale de $({\cal M}^{\varpi }_{n,E})^{+} $ a un nombre fini de $\Gamma $ -orbites (et donc de G-orbites) de composantes irreductibles. Il en est donc de même, pour le modèle semistable $({\cal M}^{\varpi }_{n,E})^{\circ } $ (essentiellement par sa définition).

De plus, la fibre spéciale est munie de la topologie discrète; il en résulte que l’orbite sous l’action de ${\mathrm{GL}}_2({\cal O}_F)$ d’une composante irréductible est finie (car ${\mathrm{GL}}_2({\cal O}_F)$ est profini) et donc que le stabilisateur d’une composante est d’indice fini et ouvert (car fermé) et agit à travers un quotient fini sur la composante (qui est donc fixée par un sous-groupe ouvert). Ceci permet de conclure.

2.1.3 Faisceaux cohomologiquement profinis de coprésentation finie

Ce numéro contient quelques préliminaires de nature topologique, qui seront utilisés dans la preuve du théorème principal de ce chapitre.

Rappelons quelques sorites sur les pro-objets d’une catégorie, en suivant [58]. Soit $\mathcal {A}$ une catégorie abélienne. La catégorie ${\mathrm{Pro}}(\mathcal {A})$ des systèmes projectifs (ou prosystèmes) d’objets de $\mathcal {A}$ est aussi abélienne. Soit $\mathcal {A}_1$ une sous-catégorie épaisse de $\mathcal {A}$ , i.e. pour toute suite exacte $0\to A\to B\to C\to 0$ dans $\mathcal {A}$ , B est un objet de $\mathcal {A}_1$ si et seulement si A et C sont des objets de $\mathcal {A}_1$ . Notons $E(\mathcal {A}_1)$ la sous-catégorie pleine de ${\mathrm{Pro}}(\mathcal {A})$ formée des prosystèmes isomorphes dans ${\mathrm{Pro}}(\mathcal {A})$ à un prosystème d’objets de $\mathcal {A}_1$ . Alors $E(\mathcal {A}_1)$ est aussi une sous-catégorie épaisse de la catégorie ${\mathrm{Pro}}(\mathcal {A})$ (prop. 2.9 de [58]).

Nous allons travailler avec la catégorie $\mathcal {A}={\mathrm{Mod}}_{{\cal O}_L}$ des ${\cal O}_L$ -modules (discrets) et avec sa sous-catégorie épaisse $\mathcal {A}_1={\mathrm{Mod}}_{{\cal O}_L}^{\mathrm{\ell f}}$ des ${\cal O}_L$ -modules de longueur finie. Les objets de la sous-catégorie épaisse $E({\mathrm{Mod}}_{{\cal O}_L}^{\mathrm{\ell f}})$ de ${\mathrm{Pro}}({\mathrm{Mod}}_{{\cal O}_L})$ seront appelés des prosystèmes profinis. Le critère de Mittag-Leffler combiné avec la prop. 2.3 de [58] montrent que le foncteur limite projective de $E({\mathrm{Mod}}_{{\cal O}_L}^{\mathrm{\ell f}})$ dans la catégorie des ${\cal O}_L$ -modules topologiques profinis est exact.

Soit maintenant Y un ${\cal O}_L$ -schéma et soit $\{U_s\}_{s\geq 1}$ un recouvrement croissant de Y par des ouverts quasi-compacts. Soit ${\mathrm{Mod}}_{{\cal O}_L}(Y_{\operatorname {\acute {e}t} })$ la catégorie des faisceaux de ${\cal O}_L$ -modules sur $Y_{\operatorname {\acute {e}t} }$ . On dispose de foncteurs

$$ \begin{align*}{\mathrm{SP}}^i: {\mathrm{Mod}}_{{\cal O}_L}(Y_{\operatorname{\acute{e}t} })\to {\mathrm{Pro}}({\mathrm{Mod}}_{{\cal O}_L}), \quad {\mathrm{SP}}^i(\mathcal{F}):=\{H^i_{\operatorname{\acute{e}t} }(U_s, \mathcal{F}|_{U_s})\}_s.\end{align*} $$

On dit que $\mathcal {F}\in {\mathrm{Mod}}_{{\cal O}_L}(Y_{\operatorname {\acute {e}t} })$ est cohomologiquement profini si ${\mathrm{SP}}^i(\mathcal {F})\in E({\mathrm{Mod}}_{{\cal O}_L}^{\mathrm{\ell f}})$ pour tout $i\geq 0$ . La discussion ci-dessus montre que si $\mathcal {F}$ est cohomologiquement profini, alors $H^i_{\operatorname {\acute {e}t} }(Y, \mathcal {F})$ est isomorphe à $\varprojlim _{s} H^i_{\operatorname {\acute {e}t} }(U_s, \mathcal {F}|_{U_s})$ , et donc est un ${\cal O}_L$ -module profini, pour tout $i\geq 0$ . En effet, dans la suite exacte de Milnor

$$ \begin{align*}0\to {\mathrm{R}^1}\varprojlim_{s} H^{i-1}_{\operatorname{\acute{e}t} }(U_s, \mathcal{F}|_{U_s})\to H^i_{\operatorname{\acute{e}t} }(Y, \mathcal{F})\to \varprojlim_{s} H^i_{\operatorname{\acute{e}t} }(U_s, \mathcal{F}|_{U_s})\to 0\end{align*} $$

le terme à gauche est nul par le critère de Mittag-Leffler.

Soit $G'$ un groupe de Lie p-adique pour lequel la catégorie des ${\cal O}_L$ -représentations lisses de présentation finie est abélienne. On suppose que $G'$ agit sur Y de telle sorte que chaque $U_s$ est fixé par un sous-groupe ouvert de $G'$ . Soit ${\mathrm{Mod}}_{{\cal O}_L}^{G'}(Y_{\operatorname {\acute {e}t} })$ la catégorie des faisceaux $G'$ -équivariants de ${\cal O}_L$ -modules sur $Y_{\operatorname {\acute {e}t} }$ . On dit que $\mathcal {F}\in {\mathrm{Mod}}^{G'}_{{\cal O}_L}(Y_{\operatorname {\acute {e}t} })$ est $G'$ -continu si pour tous $i\geq 0$ et $s\geq 1$ le ${\cal O}_L$ -module $H^i_{\operatorname {\acute {e}t} }(U_s, \mathcal {F}):=H^i_{\operatorname {\acute {e}t} }(U_s, \mathcal {F}|_{U_s})$ est tué par une puissance de p et fixé par un sous-groupe ouvert compact de $G'$ . Si $\mathcal {F}$ est cohomologiquement profini et $G'$ -continu, l’action de $G'$ sur le ${\cal O}_L$ -module profini $H^i_{\operatorname {\acute {e}t} }(Y,\mathcal {F})$ est continue pour tout $i\geq 0$ , et donc $H^i_{\operatorname {\acute {e}t} }(Y,\mathcal {F})^{\vee }$ (dual de Pontryagin) est une représentation lisse de $G'$ sur ${\cal O}_L$ . On dit que $\mathcal {F}$ est cohomologiquement profini de coprésentation finie (abrégé en cpcf) si $\mathcal {F}$ est cohomologiquement profini, $G'$ -continu, et si les $H^i_{\operatorname {\acute {e}t} }(Y, \mathcal {F})^{\vee }$ , $i\geq 0$ , sont des représentations lisses de présentation finie de $G'$ .

Lemme 2.8. Soit $0\to {\mathcal {F}}_1\to {\mathcal {F}}\to {\mathcal {F}}_2\to 0$ une suite exacte dans ${\mathrm{Mod}}_{{\cal O}_L}^{G'}(Y_{\operatorname {\acute {e}t} })$ .

1. (i) Si deux des trois faisceaux sont cohomologiquement profinis, il en est de même du troisième.

2. (ii) Si deux des trois faisceaux sont $G'$ -continus, il en est de même du troisième.

3. (iii) Si les trois faisceaux sont cohomologiquement profinis et $G'$ -continus, et si deux des trois faisceaux sont cpcf, il en est de même du troisième.

Démonstration. Le (i) résulte de la suite exacte longue dans ${\mathrm{Pro}}({\mathrm{Mod}}_{{\cal O}_L})$

$$ \begin{align*}\cdots\to {\mathrm{SP}}^{i-1}(\mathcal{F}_1)\to {\mathrm{SP}}^{i-1}(\mathcal{F})\to {\mathrm{SP}}^{i-1}(\mathcal{F}_2)\to {\mathrm{SP}}^{i}(\mathcal{F}_1)\to {\mathrm{SP}}^{i}(\mathcal{F})\to {\mathrm{SP}}^{i}(\mathcal{F}_2)\to\cdots\end{align*} $$

et du fait que $E({\mathrm{Mod}}^{\mathrm{\ell f}}_{{\cal O}_L})$ est épaisse dans ${\mathrm{Pro}}({\mathrm{Mod}}_{{\cal O}_L})$ .

Passons au (ii), et supposons que $\mathcal {F}_1$ et $\mathcal {F}_2$ sont $G'$ -continus (la preuve des deux autres cas est identique). Fixons $s\geq 1$ . Par hypothèse il existe un sous-groupe ouvert K de $G'$ qui agit trivialement sur $U_s$ et sur $H^i_{\operatorname {\acute {e}t} }(U_s, \mathcal {F}_1)$ et $H^i_{\operatorname {\acute {e}t} }(U_s, \mathcal {F}_2)$ . On peut supposer que K est pro-p et uniforme. Soit $N\geq 1$ un entier tel que $p^N$ tue $H^i_{\operatorname {\acute {e}t} }(U_s, \mathcal {F}_1)$ et $H^i_{\operatorname {\acute {e}t} }(U_s, \mathcal {F}_2)$ . La suite longue de cohomologie et le lemme 1.1 montrent qu’un sous-groupe ouvert de K (donc de $G'$ ) agit trivialement sur $H^i_{\operatorname {\acute {e}t} }(U_s, \mathcal {F})$ , donc $\mathcal {F}$ est $G'$ -continu.

Pour le (iii), supposons que ${\mathcal {F}}_1, {\mathcal {F}}_2$ sont cpcf, et montrons qu’il en est de même de ${\mathcal {F}}$ (la preuve des autres cas est identique). On a une suite exacte

$$ \begin{align*}H^{i-1}_{\operatorname{\acute{e}t} }(Y, {\mathcal{F}}_2)\to H^i_{\operatorname{\acute{e}t} }(Y, {\mathcal{F}}_1)\to H^i_{\operatorname{\acute{e}t} }(Y,{\mathcal{F}})\to H^i_{\operatorname{\acute{e}t} }(Y, {\mathcal{F}}_2)\to H^{i+1}_{\operatorname{\acute{e}t} }(Y, {\mathcal{F}}_1).\end{align*} $$

Par (i) et (ii) $\mathcal {F}$ est cohomologiquement profini et $G'$ -continu, on a donc une suite exacte

$$ \begin{align*}H^{i+1}_{\operatorname{\acute{e}t} }(Y, {\mathcal{F}}_1)^{\vee}\to H^i_{\operatorname{\acute{e}t} }(Y, {\mathcal{F}}_2)^{\vee}\to H^i_{\operatorname{\acute{e}t} }(Y,{\mathcal{F}})^{\vee}\to H^i_{\operatorname{\acute{e}t} }(Y, {\mathcal{F}}_1)^{\vee}\to H^{i-1}_{\operatorname{\acute{e}t} }(Y, {\mathcal{F}}_2)^{\vee}\end{align*} $$

de ${\cal O}_L[G']$ -modules lisses. Par hypothèse tous les termes sauf celui du milieu sont de présentation finie. On conclut grâce au lemme suivant.

Lemme 2.9. Si $A\to B\to C\to D\to E$ est une suite exacte de ${\cal O}_L[G']$ -modules lisses, avec $A,B,D,E$ de présentation finie, alors C l’est aussi.

Démonstration. Soit $\delta : D\to E$ et $\alpha : A\to B$ , alors on a une suite exacte

$$ \begin{align*}0\to \operatorname{coker} (\alpha)\to C\to \ker(\delta)\to 0.\end{align*} $$

D’après le §1.1.2, $\operatorname {coker} (\alpha )$ et $\ker (\delta )$ sont lisses de présentation finie. Comme les représentations lisses de présentation finie sont stables par extension, C est lisse de présentation finie, ce qui permet de conclure.

2.2 Preuve du Théorème 2.1

Passons à la preuve du Théorème 2.1.

$\bullet $ Préliminaires.— Soit $X'$ un modèle formel semi-stable de $\mathcal {M}_n^{\varpi }$ , défini sur une extension finie $F'$ de F (un tel modèle existe d’après le §2.1.2). Soit $K'$ une extension finie de $\mathbf {Q}_p$ contenant $F'$ , K et les racines p-ièmes de l’unité, et telle que $K'/K$ soit galoisienne. Soit $k'$ le corps résiduel de $K'$ . Soient $X:=X'\otimes _{{\cal O}_{F^{\prime }}} \mathcal {O}_{K'}$ et Y sa fibre spéciale. Il existe une suite de sous-schémas fermés (resp. ouverts) $Y_s, s\in \mathbf {N},$ (resp. $U_s, s\in \mathbf {N}$ ) de Y telle que:

1. (i) $Y_s$ est une réunion finie de composantes irréductibles,

2. (ii) $Y_s\subset U_s\subset Y_{s+1}$ et leur réunion est $Y,$

3. (iii) les tubes $\{U_{s,\eta }:=]U_{s}[_{X}\},s\in \mathbf {N},$ forment un recouvrement Stein de $X_{K'}$ .

(Il suffit de prendre pour $Y_0$ une composante irréductible, de définir $Y_{s+1}$ comme la réunion de $Y_s$ et des composantes irréductibles d’intersection non vide avec $Y_s$ , et de prendre pour $U_{s-1}$ le complémentaire dans $Y_s$ des composantes de $Y_{s+1}$ non incluses dans $Y_s$ .)

On voit X comme un log-schéma formel muni de la log-structure venant de Y. On munit $Y, U_s, Y_s$ de la log-structure induite.

$\bullet $ Étape 1.— Montrons que le faisceau $\Omega ^t_{Y/k'}$ est cpcf pour tout $t\geq 0$ . Il est $G'$ -continu, car il existe un sous-groupe ouvert de $G'$ qui fixe $U_s$ , et ce sous-groupe agit trivialement sur $H^i_{\operatorname {\acute {e}t} }(U_s, \Omega ^t_{Y/k'}|_{U_s})$ pour tout i. Il est cohomologiquement profini car le prosystème $\{H^i_{\operatorname {\acute {e}t} }(U_s, \Omega ^t_{Y/k'}|U_s)\}_s$ est isomorphe au prosystème des $H^i(Y_s, \Omega ^t_{Y/k'}\otimes _{{\cal O}_Y}{\cal O}_{Y_s})$ et ces groupes sont finis car $Y_s$ est propre et le faisceau $\Omega ^t_{Y/k'}\otimes _{{\cal O}_Y}{\cal O}_{Y_s}$ est localement libre de rang fini.

Il nous reste à montrer que le ${\cal O}_L[G']$ -module $H^s_{\operatorname {\acute {e}t} }(Y, \Omega ^t_{Y/k'})^{\vee }$ (lisse, d’après ce que l’on vient de démontrer) est de présentation finie pour tout s. Soit $\{C_j\}_{j\in J}$ l’ensemble des composantes irréductibles de Y. Par Mayer-Vietoris fermé, on a une suite exacte, avec $C_{i,j}:=C_i\cap C_j$

(2.10)

où l’on a posé $\Omega ^t_{C_{j}}:=\Omega ^t_{Y/k'}\otimes {\cal O}_{C_j}$ et $\Omega ^t_{C_{i,j}}:=\Omega ^t_{Y/k'}\otimes {\cal O}_{C_{i,j}}$ .

Il suffit de montrer que les $G^{\prime }$ -modules $\prod _{j}H^*_{\operatorname {\acute {e}t} }(C_{j},\Omega ^t_{C_{j}})$ and $\prod _{i<j}H^*_{\operatorname {\acute {e}t} }(C_{i,j},\Omega ^t_{C_{i,j}})$ sont isomorphes à $I(W)^{\vee }\simeq {\mathrm{Ind}}_{H}^{G^{\prime }}(W^{\vee })$ pour un sous-groupe ouvert compact H de $G'$ et une représentation de dimension finie W de H. En effet, si c’est le cas la suite exacte ci-dessus est automatiquement stricte (tous les objets intervenant sont profinis), on peut donc la dualiser et conclure en utilisant le lemme 2.9.

Dans le cas de $\prod _{j}H^*_{\operatorname {\acute {e}t} }(C_{j},\Omega ^t_{C_{j}})$ , chaque schéma $C_j$ est propre et lisse et les faisceaux $\Omega ^t_{C_j}$ sont des ${\cal O}_{C_j}$ -modules localement libres de rang fini, donc les $H^*_{\operatorname {\acute {e}t} }(C_j, \Omega ^t_{C_j})$ sont de dimension finie sur $k'$ . Comme les $C_j$ ne forment qu’un nombre fini d’orbites sous l’action de $G^{\prime }$ (on choisit un système J de représentants), et comme le stabilisateur $K_j$ de chaque $C_j$ est ouvert dans $G^{\prime }$ (prop. 2.7) et donc est conjugué à un sous-groupe d’indice fini dans ${\mathrm{GL}}_2({\cal O}_F)$ , on peut supposer, en remplaçant $C_j$ par un translaté, que $K_j$ est d’indice fini dans ${\mathrm{GL}}_2({\cal O}_F)$ . Alors

$$ \begin{align*}\prod_{j\in I} H^*_{\operatorname{\acute{e}t} }(C_j, \Omega^t_{C_j})\simeq {\mathrm{Ind}}_{{\mathrm{GL}}_2({\cal O}_F)}^{G^{\prime}}W,\quad {\text{o\`u }} W=\bigoplus_{j\in J}{\mathrm{Ind}}_{K_j}^{{\mathrm{GL}}_2({\cal O}_F)}H^*_{\operatorname{\acute{e}t} }(C_j, \Omega^t_{C_j})\end{align*} $$

est de dimension finie sur $k'$ .

Pour traiter le cas de $\prod _{i<j}H^*_{\operatorname {\acute {e}t} }(C_{i,j},\Omega ^t_{C_{i,j}})$ , on peut raisonner de même en remplaçant ${\mathrm{GL}}_2({\cal O}_F)$ par le sous-groupe d’Iwahori I (qui est le sous-groupe de ${\mathrm{GL}}_2({\cal O}_F)$ stabilisant l’arête évidente en niveau $0$ ).

$\bullet $ Étape 2.— Montrons que le faisceau $\mathrm {R} ^j\Psi \mathbf {F}_p$ , ainsi que ceux intervenant dans la filtration de Bloch-Kato-Hyodo sont cpcf.

Puisque $K'$ contient les racines p-ièmes de l’unité, on a $\mathbf {F}_p(j)\simeq \mathbf {F}_p$ . D’après le th. 2.4, le faisceau étale $\mathcal {F}^j:=\mathrm {R} ^j\Psi \mathbf {F}_p(j)$ sur Y possède une filtration finie

$$ \begin{align*}0=\mathcal{F}_d\subset...\subset \mathcal{F}_1\subset \mathcal{F}_0=\mathcal{F}^j,\end{align*} $$

dont les quotients successifs $\mathcal {F}_r/\mathcal {F}_{r+1}$ sont de la forme ²⁰

$$ \begin{align*}\Omega^m_{Y/k',\log}, \quad \Omega^m_{Y/k'}/B^m_{Y/k},\quad \Omega^m_{Y/k'}/Z^m_{Y/k'}. \end{align*} $$

Considérons les suites exactes de faisceaux

$$ \begin{align*} & 0\to \Omega^m_{Y/k',{\mathrm{log}}}\to Z^m_{Y/k'}\stackrel{C-1}{\longrightarrow}\Omega^m_{Y/k'}\to 0,\\ & 0\to B^m_{Y/k'}\to Z^m_{Y/k'}\stackrel{C}{\to} \Omega^m_{Y/k'}\to 0,\\ & 0\to Z^m_{Y/k'}\to \Omega^m_{Y/k'}\stackrel{d}{\to} B^{m+1}_{Y/k'}\to 0. \end{align*} $$

Tous les faisceaux intervenant dans ces suites exactes sont nuls pour m assez grand (en fait pour $m>1$ puisque Y est une courbe). En utilisant cette observation, l’étape $1$ et le lemme 2.8, on montre par récurrence descendante sur m que $B^m_{Y/k'}, Z^m_{Y/k'}, \Omega ^m_{Y/k',{\mathrm{log}}}$ sont cpcf, et deux nouvelles applications du lemme 2.8 montrent que $\Omega ^m_{Y/k'}/B^m_{Y/k}$ , $\Omega ^m_{Y/k'}/Z^m_{Y/k'}$ et enfin chaque $\mathcal {F}_k$ est aussi cpcf. En particulier $\mathrm {R} ^j\Psi \mathbf {F}_p$ est cpcf.

$\bullet $ Étape 3.— Montrons que le prosystème $\{H^{q}_{\operatorname {\acute {e}t} }(U_{s,\eta }, \mathbf {Z}/p^k)\}_s$ est profini pour tous q et k, et que l’action de $G'$ y est continue, i.e. chaque $H^{q}_{\operatorname {\acute {e}t} }(U_{s,\eta }, \mathbf {Z}/p^k)$ est fixé par un sous-groupe ouvert compact de $G'$ . On a une suite exacte de prosystèmes

$$ \begin{align*}\{H^{q}_{\operatorname{\acute{e}t} }(U_{s,\eta}, \mathbf{Z}/p^{k-1})\}_s\to \{H^{q}_{\operatorname{\acute{e}t} }(U_{s,\eta}, \mathbf{Z}/p^k)\}_s\to \{H^{q}_{\operatorname{\acute{e}t} }(U_{s,\eta}, \mathbf{Z}/p)\}_s\end{align*} $$

Si le résultat est connu pour les deux termes extrêmes, il s’obtient pour le terme au milieu en utilisant le fait que les prosystèmes profinis forment une sous-catégorie épaisse de ${\mathrm{Pro}}({\mathrm{Mod}}_{{\cal O}_L})$ et le lemme 1.1. On peut donc supposer que $k=1$ .

D’après [7, cor. 4.2], on dispose, pour tout s, d’une suite spectrale

$$ \begin{align*}E_2^{i,j}=H^i_{\operatorname{\acute{e}t} }(U_s, \mathrm {R} ^j\Psi \mathbf{F}_p)\Longrightarrow H^{i+j}_{\operatorname{\acute{e}t} }(U_{s,\eta}, \mathbf{F}_p).\end{align*} $$

Comme les prosystèmes $\{H^i_{\operatorname {\acute {e}t} }(U_s, \mathrm {R} ^j\Psi \mathbf {F}_p)\}_s$ (pour $i,j\geq 0$ ) sont profinis (étape $2$ ), il en résulte que le prosystème $\{H^{q}_{\operatorname {\acute {e}t} }(U_{s,\eta }, \mathbf {F}_p)\}_s$ est finiment filtré par des prosystèmes dont les gradués associés sont dans $E({\mathrm{Mod}}^{\mathrm{\ell f}}_{{\cal O}_L})$ , et donc est profini car $E({\mathrm{Mod}}^{\mathrm{\ell f}}_{{\cal O}_L})$ est une sous-catégorie épaisse de ${\mathrm{Pro}}({\mathrm{Mod}}_{{\cal O}_L})$ . Le même argument couplé au lemme 1.1 fournit la continuité de l’action de $G'$ .

$\bullet $ Étape 4.— Montrons que $H^{q}_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K'}^{\varpi }, \mathbf {Z}/p^k)$ est profini, dual d’une représentation lisse de présentation finie de $G'$ . Le caractère profini et la continuité de l’action de $G'$ sur $H^{q}_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K'}^{\varpi }, \mathbf {Z}/p^k)$ découlent directement de l’étape $3$ , qui montre que

$$ \begin{align*}H^{q}_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,K'}^{\varpi}, \mathbf{Z}/p^k)\simeq \varprojlim_{s} H^{q}_{\operatorname{\acute{e}t} }(U_{s,\eta}, \mathbf{Z}/p^k).\end{align*} $$

En particulier $H^{q}_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K'}^{\varpi }, \mathbf {Z}/p^k)^{\vee }$ est bien un ${\cal O}_L[G']$ -module lisse. Il reste à voir qu’il est de présentation finie. Les suites exactes

réduisent le problème au cas $k=1$ (cela utilise implicitement le fait que tous les objets sont profinis, comme on vient de le voir, donc on peut dualiser ces suites exactes et ensuite appliquer le lemme 2.9). Mais ce cas découle du fait que les $\mathrm {R} ^j\Psi \mathbf {F}_p$ sont cpcf (étape $2$ ), de la suite spectrale

$$ \begin{align*}E_2^{i,j}=H^i_{\operatorname{\acute{e}t} }(Y, \mathrm {R} ^j\Psi \mathbf{F}_p)\Longrightarrow H^{i+j}_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,K'}^{\varpi}, \mathbf{F}_p)\end{align*} $$

et d’un raisonnement comme dans l’étape $3$ (remplacer l’usage du lemme 1.1 par celui de la prop. 1.2).

Remarque 2.11. Les arguments ci-dessus prouvent en fait le résultat suivant:

Si X est un schéma formel semistable sur ${\cal O}_K$ dont la fibre spéciale a une stratification comme celle de la preuve du th.2.1, alors les $H^q_{\operatorname {\acute {e}t} }(X_K,{\mathbf F}_p)$ , pour $q\geq 0$ , sont profinis.

$\bullet $ Étape 5.—Nous venons de démontrer l’existence d’une extension finie galoisienne $K'$ de K telle que $H^i_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K'}^{\varpi },{\cal O}_L/p^k)$ , $i,k\geq 0$ , est co-lisse, de coprésentation finie. Il reste à expliquer comment descendre à K.

Soit $H:={\mathrm{Gal}}(K^{\prime }/K)$ et soit $\{V_s\}_{s}$ un recouvrement Stein de $X:=\mathcal {M}_{n,K}^{\varpi }$ , donc les $V^{\prime }_s:=V_s\otimes _K K'$ fournissent un recouvrement Stein de $\mathcal {M}_{n,K'}^{\varpi }$ . On a des suites spectrales de Hochschild-Serre [43, prop. 2.6.12]

$$ \begin{align*}E^{i,j}_2=H^i(H, H^j_{\operatorname{\acute{e}t} }(V^{\prime}_s,{\cal O}_L/p^k))\Rightarrow H^{i+j}_{\operatorname{\acute{e}t} }(V_s,{\cal O}_L/p^k). \end{align*} $$

Comme les prosystèmes $\{H^j_{\operatorname {\acute {e}t} }(V^{\prime }_s,{\cal O}_L/p^k)\}_s$ sont profinis (étape $3$ ) et H est fini, le complexe calculant la cohomologie de H est formé de prosystèmes profinis. Donc les prosystèmes $\{H^i(H, H^j_{\operatorname {\acute {e}t} }(V^{\prime }_s,{\cal O}_L/p^k))\}_s$ sont profinis. A partir de là, on peut conclure comme dans l’étape 1 que les prosystèmes $\{H^{q}_{\operatorname {\acute {e}t} }(V_s,{\cal O}_L/p^k)\}_s$ , pour $q\geq 0$ , sont profinis. De plus, nous avons vu que l’action de $G'$ sur $\{H^j_{\operatorname {\acute {e}t} }(V^{\prime }_s,{\cal O}_L/p^k)\}_s$ est continue, donc il en est de même de celle sur $E^{i,j}_2$ , et le lemme 1.1 couplé à la suite spectrale ci-dessus permettent de déduire la continuité de l’action de $G'$ sur $\{H^{q}_{\operatorname {\acute {e}t} }(V_s,{\cal O}_L/p^k)\}_s$ .

On a donc une suite spectrale

$$ \begin{align*}E^{i,j}_2=H^i(H, H^j_{\operatorname{\acute{e}t} }(X_{K'},{\cal O}_L/p^k))\Rightarrow H^{i+j}_{\operatorname{\acute{e}t} }(X,{\cal O}_L/p^k) \end{align*} $$

avec des objets profinis sur toutes les pages et aboutissement profini. De plus, tous les objets sont munis d’une action continue de $G'$ . Dualiser ne pose donc pas de problème donc on peut argumenter comme ci-dessus: en partant du fait que les $H^j_{\operatorname {\acute {e}t} }(X_{K'},{\cal O}_L/p^k)$ sont co-lisses de coprésentation finie, on en déduit que l’aboutissement $H^{q}_{\operatorname {\acute {e}t} }(X,{\cal O}_L/p^k)$ est aussi co-lisse, de coprésentation finie, comme on le voulait.

Corollaire 2.12. Pour toute représentation continue $\bar {\rho }: \mathcal {G}_{F}\to {\mathrm{GL}}_d(k_L)$ le ${\mathrm{GL}}_2(F)$ -module ${\mathrm{Hom}}_{k_L[\mathcal {G}_{F}]}(\bar {\rho }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,\mathbf {C}_p}^{\varpi },k_L))^{\vee }$ est lisse, de présentation finie.

Démonstration. Soit $F'$ une extension galoisienne finie de F telle que $\bar {\rho }$ se factorise par $H:={\mathrm{Gal}}(F'/F)$ . Alors

$$ \begin{align*}{\mathrm{Hom}}_{k_L[\mathcal{G}_{F}]}(\bar{\rho}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{\varpi},k_L))^{\vee}\simeq{\mathrm{Hom}}_H(\bar{\rho}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{\varpi},k_L)^{\mathcal{G}_{F'}}).\end{align*} $$

Si l’on montre que $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,\mathbf {C}_p}^{\varpi },k_L)^{\mathcal {G}_{F'}}\simeq \pi ^{\vee }$ pour une représentation lisse de présentation finie $\pi $ , alors

$$ \begin{align*}{\mathrm{Hom}}_{H} (\bar{\rho}, \pi^{\vee})\simeq(\bar{\rho}^{\vee}\otimes_{k_L} \pi^{\vee})^H\simeq((\bar{\rho}\otimes_{k_L} \pi)_H)^{\vee},\end{align*} $$

et $(\bar {\rho }\otimes _{k_L}\pi )_H$ est lisse, de présentation finie d’après la prop. 1.3 (car $\bar {\rho }$ est de dimension finie et H est fini), ce qui permet de conclure.

Pour montrer l’existence d’une représentation $\pi $ comme ci-dessus, prenons un recouvrement Stein $\{V_s\}$ de ${\mathcal M}^{\varpi }_{n,F^{\prime }}$ . D’après [22, cor. 3.7.5], on dispose de suites spectrales de Hochschild-Serre pour les revêtements $V_{s,\mathbf {C}_p}/V_s$ , ce qui fournit des suites exactes

Un passage à la limite sur s fournit la suite exacte

Notons que $H^0(\mathcal {M}_{n,\mathbf {C}_p}^{\varpi },k_L)$ est de dimension finie, donc les termes extrèmes de cette suite exacte sont de dimension finie. Un raisonnement comme dans la preuve du théorème ci-dessus montre que tous les termes sont profinis et munis d’une action continue de $G'$ . Comme tous les termes à l’exception de $ H^1(\mathcal {M}_{n,\mathbf {C}_p}^{\varpi },k_L)^{\mathcal {G}_{F'}}$ sont des duaux de représentations lisses de présentation finie, il en est de même de $ H^1(\mathcal {M}_{n,\mathbf {C}_p}^{\varpi },k_L)^{\mathcal {G}_{F'}}$ , ce qui permet de conclure.

2.3 Non admissibilité pour $F\ne \mathbf {Q}_p$

On suppose $F\neq \mathbf {Q}_p$ dans ce qui suit. On a alors le résultat suivant qui contraste avec la situation dans le cas $F=\mathbf {Q}_p$ .

Théorème 2.13. Si $F\ne \mathbf {Q}_p$ et $n>0$ , alors $H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,K}^{\varpi }, k_L)^{\vee }$ n’est pas admissible si K est une extension finie, assez grande, de F.

Nous allons prouver le résultat plus précis du th. 2.14 ci-dessous (le th. 2.13 est une conséquence de la non-admissibilité de $\Pi _M(V^+_1)$ dans les notations du th. 2.14).

Soient M un $(\varphi ,N,{\cal G}_F)$ -module supercuspidal et ${\mathrm{JL}}(M)^+$ un réseau de ${\mathrm{JL}}(M)$ stable par $\check G$ . Si V une L-représentation de ${\cal G}_F$ , de dimension finie, et $V^+$ est un réseau de V stable par ${\cal G}_F$ , on pose

et:

(L-dual pour le premier, ${\cal O}_L$ -dual pour le second et

-dual pour le dernier).

Théorème 2.14. Si $\Pi _M(V)\neq 0$ , alors pour tout $k\geq 1$ , $\Pi _M(V^+_k)$ est une représentation lisse de G, non admissible.

Démonstration. $\Pi _M(V)$ est un G-banach unitaire (lemme 2.16) et, s’il existe $k\geq 1$ tel que $\Pi _M(V^+_k)$ est admissible, alors $\Pi _M(V)$ possède un réseau dont la réduction modulo est un objet de ${\cal C}$ (lemme 2.17). La prop. 2.18 implique alors que ${\mathrm{Hom}}_G(\widehat {\mathrm{LL}}(M),\Pi _M(V))=0$ .

Par ailleurs, en passant aux vecteurs G-bornés dans la première ligne du diagramme de [16, th. 0.8] (après avoir appliqué ${\mathrm{Hom}}_{{\cal G}_F}(V,-)$ ) on obtient une injection de $\Pi _M(V)^{\boldsymbol *}$ dans $H(V)\otimes \widehat {\mathrm{LL}}(M)^{\boldsymbol *}$ , où $H(V):={\mathrm{Hom}}_{{\cal G}_F}(V,X_{\mathrm{st}}(M))$ est un L-module de rang fini, avec action triviale de G. Par dualité, cela fournit une flèche de $H(V)\otimes \widehat {\mathrm{LL}}(M)$ dans $\Pi _M(V)$ , d’image dense. Comme cette image est nulle d’après ce qui précède, on a $\Pi _M(V)=0$ , ce qui prouve, par l’absurde, le th. 2.14.

Remarque 2.15.

1. (i) Si $F=\mathbf {Q}_p$ , alors $\Pi _M(V)$ et $\Pi _M(V^+_k)$ , pour tout k, sont admissibles.

2. (ii) Pour tout M supercuspidal tel que $\varpi $ agit trivialement sur ${\mathrm{JL}}(M)$ on peut trouver V telle que $\Pi _M(V)\neq 0$ . On prend $\Gamma \subset G'$ , cocompact et on définit la courbe analytique $X_n:={\cal M}_{n,F}^{\varpi }/\Gamma $ . Alors $X_n$ est l’analytifiée d’une courbe algébrique définie sur F. On suppose $\Gamma $ assez petit pour que $X_0$ soit de genre $\geq 2$ . Alors, d’après Nakajima [51, th. 4], toute représentation de ${\mathrm{Gal}}(X_n/X_0)=\check G_0/\check G_n$ a une multiplicité non nulle dans $\Omega ^1(X_n)$ , et donc aussi dans $H^1_{\mathrm{dR}}(X_n)$ et dans $H^1_{\operatorname {\acute {e}t} }(X_{n,\mathbf {C}_p},L(1))$ par le théorème de comparaison étale–de Rham. Autrement dit, $V_M:=H^1_{\operatorname {\acute {e}t} }(X_{n,\mathbf {C}_p},L(1))[M]$ est non nul, pour tout M de niveau $\leq n$ . On peut alors prendre pour V n’importe quel sous-L-module de $V_M$ stable par ${\cal G}_F$ (par exemple $V_M$ ).

3. (iii) Il ne semble pas possible de déduire du théorème que $\Pi _M(V)$ est non admissible. La question de son admissibilité reste donc en suspens.

4. (iv) On peut définir un $L[G]$ -module

   $$ \begin{align*}\Pi_M^{\mathrm{an}}(V):={\mathrm{Hom}}_{{\cal G}_F\times\check G} \big(V\otimes {\mathrm{JL}}(M),H^1_{\operatorname{pro\acute{e}t} }({\cal M}^{\varpi}_{n,\mathbf{C}_p},L(1))\big)^{\boldsymbol *}\end{align*} $$
   En combinant les résultats de [16] avec ceux de Patel-Schmidt-Strauch [57] et Ardakov-Wadsley [1], on peut montrer que, si $n=1$ , alors $\Pi _M^{\mathrm{an}}(V)$ est une représentation localement analytique coadmissible, de longueur finie de G. Il est probable que cela reste vrai pour tout n.

Lemme 2.16. $\Pi _M(V)$ est une représentation unitaire de G dont $\Pi _M(V)^+$ est un réseau stable par G, et est un quotient de $\Pi _M({V}^+_k)$ .

Démonstration. Soient X, $X^+$ et $X_k^+$ les duaux respectifs de $\Pi _M(V)$ , $\Pi _M(V^+)$ et $\Pi _M(V^+_k)$ . Alors $X^+$ est sans p-torsion (puisque $H^1_{\operatorname {\acute {e}t} }({\cal M}_{n,\mathbf {C}_p}, \mathcal {O}_L(1))$ l’est). On va montrer que $X^+$ est profini, ce qui prouve que $\Pi _M(V^+)$ est un réseau dans un banach, et que $\Pi _M(V)$ est un banach. On a

Il suffit de voir que chaque

est profini, et par l’argument usuel de descente (via la suite spectrale de Hochschild-Serre) il suffit de voir que pour toute extension finie K de F le groupe

est profini pour tout $k\geq 1$ , or cela est garanti par le th. 2.1.

La flèche naturelle est injective. Comme et $X^+_k$ sont compacts, cette injection est un homéomorphisme de sur son image qui est fermée dans $X^+_k$ . Par dualité, cela fournit une surjection de $\Pi _M({V}_k^+)$ sur .

Lemme 2.17. S’il existe $k\geq 1$ tel que $\Pi _M(V^+_k)$ soit admissible, alors $k_L\otimes \Pi _M(V^+)$ est un objet de ${\cal C}$ .

Démonstration. Il résulte du th. 2.1 que $\Pi _M(V^+_k)$ est un objet de ${\cal C}$ . Il en est de même de (et donc aussi de $k_L\otimes \Pi _M(V^+)$ ) puisque c’est un quotient de $\Pi _M(V^+_k)$ .

Proposition 2.18. Soient $\pi $ une L-représentation lisse supercuspidale de G et $\widehat \pi $ son complété universel, et soit $\Pi $ une L-représentation de Banach unitaire de G qui possède un réseau G-invariant dont la réduction modulo est dans $\mathcal {C}$ . Alors ${\mathrm{Hom}}_G(\widehat {\pi }, \Pi )=0$ .

Démonstration. D’après le cor. 1.34, il existe une L-représentation unitaire W de A, de dimension finie, et un morphisme G-équivariant $\iota =\iota _{\Pi }: {\mathrm{Ind}}_{\bar {B}}^G(W)\to \Pi $ dont le noyau et le conoyau sont de dimension finie sur L. Supposons qu’il existe une application G-équivariante non nulle $\alpha : \hat {\pi }\to \Pi $ . La composée $\hat {\pi }\to \Pi \to {\mathrm{coker}}(\iota )$ est forcément nulle car $\pi $ est dense dans $\hat {\pi }$ et n’a pas de quotient de dimension finie. Donc on peut supposer que $\Pi \simeq {\mathrm{Ind}}_{\bar {B}}^G(W)/W'$ pour une représentation de dimension finie $W'$ . Quitte à remplacer L par une extension finie, on peut supposer que W et $W'$ sont des extensions successives de caractères et donc que ${\mathrm{Ind}}_{\bar {B}}^G(W)/W'$ est une extension successive finie de représentations de la forme ${\mathrm{Ind}}_{\bar {B}}^G (\chi _1\otimes \chi _2)$ , ${\mathrm{St}}\otimes \chi \circ \det $ ou $\chi \circ \det $ avec $\chi , \chi _1,\chi _2: F^{{\boldsymbol *}}\to L^{{\boldsymbol *}}$ des caractères continus. Mais $\hat {\pi }$ n’a pas de morphisme G-équivariant non nul vers une de ces représentations: il suffit en effet de voir que $\pi $ s’envoie sur $0$ , ce qui est clair car $\pi $ est cuspidale et l’espace des vecteurs lisses d’une de ces représentations est de la série principale. Donc tout morphisme G-équivariant de $\hat {\pi }$ vers une extension successive finie de représentations de la forme ci-dessus est nul, ce qui permet de conclure.

3 Une suite spectrale pour le foncteur de Scholze

Le but de ce chapitre est de démontrer l’existence d’une suite spectrale reliant les foncteurs de Scholze [61] et la cohomologie des espaces de Drinfeld. L’étude de cette suite spectrale dans le cas particulier du groupe ${\mathrm{GL}}_2(\mathbf {Q}_p)$ est un ingrédient important de la preuve du théorème de finitude (th. 0.2), mais cette suite spectrale a sans doute un intérêt en soi, et donc nous l’établirons dans la généralité de [61].

3.1 Rappels concernant le foncteur de Scholze

Soit F une extension finie de $\mathbf {Q}_p$ et soit $\breve {F}\subset {\mathbf {C}_p}$ le complété de l’extension maximale non ramifiée de F. Soit $\mathcal {G}_F={\mathrm{Gal}}(\bar {F}/F)$ .

On fixe un entier $n\geq 1$ et une algèbre centrale à division $D_p$ sur F, d’invariant $1/n$ . On note $(\mathcal {M}_{\mathrm{LT, K}})_{K}$ la tour de Lubin-Tate, une famille d’espaces rigides analytiques sur $\breve {F}$ , indexée par les sous-groupes ouverts compacts K de ${\mathrm{GL}}_n(F)$ . Le groupe $D_p^{{\boldsymbol *}}$ agit sur chaque étage de la tour et le groupe ${\mathrm{GL}}_n(F)$ agit sur la tour, un élément g de ${\mathrm{GL}}_n(F)$ transformant $\mathcal {M}_{\mathrm{LT, K}}$ en $\mathcal {M}_{\mathrm{LT, g}^{-1}\mathrm{Kg}}$ . On dispose d’applications de périodes

qui sont étales surjectives (de fibres ${\mathrm{GL}}_n(F)/K$ ), $D_p^{{\boldsymbol *}}$ -équivariantes ( $D_p^{{\boldsymbol *}}$ agissant sur

via l’identification de cet espace avec la variété de Brauer-Severi associée à $D_p$ ). De plus, tous ces espaces sont munis de données de descente à la Weil et $\pi _{\mathrm{GH}}$ respectent ces données.

La tour $(\mathcal {M}_{\mathrm{LT, K}})_{K}$ possède une limite, qui est un espace perfectoïde $\mathcal {M}_{\mathrm{LT}, \infty ,\breve {\mathrm{F}}}$ sur $\breve {F}$ (cf. [63]) et les applications des périodes $\pi _{\mathrm{GH}}$ ci-dessus induisent un morphisme

faisant de $\mathcal {M}_{\mathrm{LT}, \infty ,\breve {\mathrm{F}}}$ un ${\mathrm{GL}}_n(F)$ -torseur proétale. Si $\pi $ est un ${\mathrm{GL}}_n(F)$ -module muni de la topologie discrète, on note $\underline {\pi }$ le faisceau constant sur le site étale de $\mathcal {M}_{\mathrm{LT}, \infty ,\breve {\mathrm{F}}}$ et

$$ \begin{align*}\mathcal{F}_{\pi}:=(\pi_{\mathrm{GH}, *}(\underline{\pi}))^{{\mathrm{GL}}_n(F)},\end{align*} $$

un faisceau étale $D_p^{{\boldsymbol *}}$ et Weil-équivariant sur

. Concrètement, pour tout morphisme étale

on a $\mathcal {F}_{\pi }(U)= \mathcal {C}^0_{{\mathrm{GL}}_n(F)}(|U_{\infty }|, \pi )$ , où

est le pullback de U en niveau infini. Si $\pi $ est lisse (i.e. le stabilisateur de tout vecteur de $\pi $ est ouvert), alors les fibres géométriques de $\mathcal {F}_{\pi }$ s’identifient à $\pi $ (cf. la preuve de la prop 3.1 de [61]). Cette identification dépend du choix d’un relèvement du point géométrique de

à $\mathcal {M}_{\mathrm{LT}, \infty ,\breve {\mathrm{F}}}$ , mais une fois un tel choix fait elle est fonctorielle par rapport à $\pi $ . On posera

Soit $(A, \mathfrak {m})$ un anneau local, noethérien, complet, de corps résiduel une extension finie de $\mathbf {F}_p$ et soit H un groupe de Lie p-adique. On dit qu’un $A[H]$ -module $\pi $ est admissible si

$$ \begin{align*}\pi=\bigcup_{K, n} \pi^{K}[\mathfrak{m}^n],\end{align*} $$

la réunion étant prise sur les sous-groupes ouverts compacts K de H et sur les entiers $n\geq 1$ , et si les $\pi ^K[\mathfrak {m}^n]$ sont des $A/\mathfrak {m}^n$ -modules de type fini (et donc finis tous court).

Le résultat suivant résume les propriétés locales des foncteurs $\pi \mapsto S^i(\pi )$ , établies dans [61].

Théorème 3.1 (Scholze).

Soit $(A,\mathfrak {m})$ comme ci-dessus et soit $\pi $ un $A[{\mathrm{GL}}_n(F)]$ -module admissible.

1. (1) $S^i(\pi )$ est un $A[D_p^{{\boldsymbol *}}]$ -module admissible et le morphisme naturel

   
   est un presqu’isomorphisme.

2. (2) On a $S^i(\pi )=0$ pour $i>2(n-1)$ .

3. (3) L’action ²¹ du groupe de Weil $W_F$ sur $S^i(\pi )$ s’étend par continuité en une action de $\mathcal {G}_F$ .

4. (4) On a $S^0(\pi ^{ {\mathrm{SL}}_n(F)})=S^0(\pi )$ , l’action de ${\mathrm{GL}}_n(F)$ s’y factorise par $\det : {\mathrm{GL}}_n(F)\to F^{{\boldsymbol *}}$ et celle de $W_F\times D_p^{{\boldsymbol *}}$ par le morphisme $W_F\times D^{{\boldsymbol *}}\to F^{{\boldsymbol *}}$ , inverse du produit de l’application d’Artin (envoyant des Frobenius géométriques sur des uniformisantes) et de la norme réduite.

Démonstration. Les deux premiers points (et les plus délicats) sont le th. 4.4 de [61], le troisième et le quatrième sont les prop. 4.6 et 4.7 de loc. cit.

3.2 Foncteur de Scholze et cohomologie de la tour de Drinfeld

Le but de ce paragraphe est de démontrer le théorème de comparaison 3.2 ci-dessous. On reprend les notations du paragraphe ci-dessus, en particulier soit $\pi $ un $A[{\mathrm{GL}}_n(F)]$ -module lisse admissible. Supposons aussi qu’il existe $k\geq 1$ tel que $p^k\pi =0$ . Alors $\pi ^{\vee }$ (dual de Pontryagin de $\pi $ ) est un $\mathbf {Z}_p$ -module profini, limite inverse des $\mathbf {Z}_p$ -modules de longueur finie $(\pi ^{K}[\mathfrak {m}^i])^{\vee }$ (pour $i\geq 1$ et K des sous-groupes ouverts compacts de ${\mathrm{GL}}_n(F)$ ).

L’espace $\mathcal {M}_{\infty }:=\mathcal {M}_{\mathrm{LT}, \infty ,{\mathbf {C}_{\mathrm{p}}}}$ possède un recouvrement affinoïde perfectoïde Stein $\{U_i\}_{i\geq 1}$ et on a des suites exactes

$$ \begin{align*}0\to \mathrm {R} ^1\lim_{i} H^{q-1}_{\operatorname{\acute{e}t} }(U_i, \mathbf{Z}/p^k)\to H^q_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \mathbf{Z}/p^k)\to \lim_{i} H^q_{\operatorname{\acute{e}t} }(U_i, \mathbf{Z}/p^k)\to 0.\end{align*} $$

On verra ci-dessous que $\mathrm {R} ^1\lim _{i} H^{q-1}_{\operatorname {\acute {e}t} }(U_i, \mathbf {Z}/p^k)=0$ , donc $H^q_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }, \mathbf {Z}/p^k)$ est aussi un $\mathbf {Z}_p$ -module prodiscret. Si $U=\lim _i U_i$ et $V=\lim _j V_j$ sont des $\mathbf {Z}_p$ -modules prodiscrets, alors

$$ \begin{align*}{\mathrm{Hom}}_{\mathbf{Z}_p}^{\mathrm{cont}}(U, V)=\lim_{j}(\operatorname{colim}_{i} {\mathrm{Hom}}_{\mathbf{Z}_p}(U_i, V_j))\end{align*} $$

en est aussi un, en munissant les ${\mathrm{Hom}}_{\mathbf {Z}_p}(U_i, V_j)$ de la topologie discrète.

Soit $G={\mathrm{GL}}_n(F)$ . La cohomologie (continue) de G à coefficients dans un module prodiscret M est par définition la cohomologie du complexe des cochaînes continues sur G à valeurs dans M.

Théorème 3.2. Soit $\pi $ un $A[G]$ -module lisse admissible, tué par $p^k$ . Il existe une suite spectrale de $D_p^{{\boldsymbol *}}\times W_F$ -modules

(3.3) $$ \begin{align} E_2^{i,j}=H^i(G,H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi}))\Longrightarrow S^{i+j}(\pi). \end{align} $$

De plus $H^j_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }, \underline {\pi })=0$ pour $j\geq 2$ .

Démonstration. Considérons le morphisme des périodes . C’est un G-torseur proétale. La suite spectrale (3.3) à établir est une suite de type Cartan-Leray pour le recouvrement proétale . Pour la construire, considérons la suite spectrale de Čech pour la projection ,

(3.4)

où $\widetilde {\mathcal {F}}_{\pi }:=\nu ^{\boldsymbol *}{\mathcal {F}}_{\pi }$ . La dernière égalité dans (3.4) est une conséquence de [62, prop. 14.8].

Il suffit de prouver que l’on a un isomorphisme naturel

$$ \begin{align*}\check{H}^i(\mathcal{U}, \underline{H}^j(\widetilde{\mathcal{F}}_{\pi}))\simeq H^i(G, H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi})).\end{align*} $$

Pour ce faire, rappelons que $E_2^{i,j}$ est la cohomologie en degré i du complexe

Puisque $\pi _{\mathrm{GH}}$ est un G-torseur proétale, on a un isomorphisme de diamants ²²

Cela implique que (le membre de gauche a $k+1$ facteurs $\mathcal {M}_{\infty }$ )

De plus, par cet isomorphisme, $\widetilde {{\mathcal {F}}}_{\pi }\simeq {\mathrm{pr}}^{\boldsymbol *}_{1}\widetilde {\underline {\pi }}$ , où ${\mathrm{pr}}_1: \mathcal {M}_{\infty }\times \underline {G}^k\to \mathcal {M}_{\infty }$ est la projection canonique et $\widetilde {\underline {\pi }}=\nu ^{\boldsymbol *} \underline {\pi }$ . Il s’ensuit que l’on a un quasi-isomorphisme

(3.5) $$ \begin{align} C^j\simeq (H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi})\to H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}\times \underline{G}, \underline{\pi})\to...) \end{align} $$

Il suffit maintenant de montrer que l’on a un quasi-isomorphisme

(3.6) $$ \begin{align} C^j\simeq (\mathcal{C}^0(G^0, H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi}))\to \mathcal{C}^0(G^1, H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi}))\to \cdots) \end{align} $$

Commençons par montrer que, pour $t\geq 1$ , on a un isomorphisme

(3.7) $$ \begin{align} H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}\times \underline{G}^t, \underline{\pi}) & \simeq \mathcal{C}^0(G^t, H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi})). \end{align} $$

Soit $\{U_s\}_{s\in \mathbf {N}}$ un recouvrement Stein affinoïde perfectoïde de $\mathcal {M}_{\infty }$ . Soit $\{S^t_q\}_{q\in \mathbf {N}}$ une suite croissante de sous-ensembles compacts ouverts de $G^t$ , dont la réunion est $G^t$ . On obtient alors un recouvrement

$$ \begin{align*}U_s\times \underline{S^t_s}={\mathrm{Spa}}( \mathcal{C}^0(S^t_s, \mathcal{O}(U_s)), \mathcal{C}^0(S^t_s, \mathcal{O}^+(U_s)))\end{align*} $$

de $\mathcal {M}_{\infty }\times \underline {G}^t$ par une suite croissante d’ouverts affinoïdes perfectoïdes.

Le lemme 23.6 de [62] montre que

$$ \begin{align*}H^i_{\operatorname{\acute{e}t} }(U_s\times \underline{S^t_s}, \underline{\pi})=H^i_{\operatorname{\acute{e}t} }(U_s, \mathcal{C}^0(S^t_s, \mathbf{Z}/p^k)\otimes_{\mathbf{Z}/p^k} \underline{\pi}).\end{align*} $$

Puisque $U_s$ est qcqs et $\pi $ est une limite inductive de $\mathbf {Z}/p^k$ -modules finis, le dernier groupe de cohomologie n’est rien d’autre que $\mathcal {C}^0(S^t_s, \mathbf {Z}/p^k)\otimes _{\mathbf {Z}/p^k} \pi \otimes _{\mathbf {Z}/p^k} H^i_{\operatorname {\acute {e}t} }(U_s, \mathbf {Z}/p^k)$ . Le lemme 3.10 ci-dessous montre que pour tout i le système projectif $\{H^i_{\operatorname {\acute {e}t} }(U_s, \mathbf {Z}/p^k)\}_{s}$ est Mittag-Leffler. Puisque les $S^t_s$ forment une suite croissante d’ensembles profinis, le système projectif $\{\mathcal {C}^0(S^t_s, \mathbf {Z}/p^k)\}_{q}$ est Mittag-Leffler (en fait $\mathcal {C}^0(S^t_{s+1}, \mathbf {Z}/p^k)\to \mathcal {C}^0(S^t_s, \mathbf {Z}/p^k)$ est surjective). On en déduit que le système projectif $\{H^i_{\operatorname {\acute {e}t} }(U_s\times \underline {S^t_s}, \underline {\pi })\}_{s}$ est aussi Mittag-Leffler, et donc que

(3.8) $$ \begin{align} H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}\times \underline{G}^t, \underline{\pi})\simeq \lim_{s} \big(\mathcal{C}^0(S^t_s, \mathbf{Z}/p^k)\otimes_{\mathbf{Z}/p^k} \pi\otimes_{\mathbf{Z}/p^k} H^i_{\operatorname{\acute{e}t} }(U_s, \mathbf{Z}/p^k)\big). \end{align} $$

Par ailleurs, on a

(3.9) $$ \begin{align} \mathcal{C}^0(G^t, H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi})) & \stackrel{\sim}{\to} \lim_{s} \mathcal{C}^0(S^t_s, H^i_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi}))\\ & \stackrel{\sim}{\to}\lim_{q,s} \big(\mathcal{C}^0(S^t_s, \mathbf{Z}/p^k)\otimes_{\mathbf{Z}/p^k} \pi\otimes_{\mathbf{Z}/p^k} H^i_{\operatorname{\acute{e}t} }(U_{s}, \mathbf{Z}/p^k)\big)\notag \end{align} $$

Combiné avec l’isomorphisme (3.8), cela fournit l’isomorphisme (3.7) que l’on voulait.

Il reste à vérifier que les isomorphismes (3.7) sont compatibles avec les différentielles dans les complexes apparaissant dans (3.5) et (3.6). Pour cela, prenons un recouvrement $\{S_q\}_{q}$ de G et recouvrons $G^t$ par les $S^t_q$ . Cela fournit des complexes à partir des objets intervenant dans (3.8) et (3.9) et les flèches qui s’en déduisent sont des morphismes de complexes: les différentielles sont des sommes alternées faisant intervenir des projections (qui ne posent pas de problèmes grâce à notre choix de recouvrement de $G^t$ ), des multiplications $S_a\times S_b\mapsto S_{c(a,b)}$ induites par la multiplication $\mu : G\times G\mapsto G$ , et les actions $\underline {S_a}\times U_b\mapsto U_{c(a,b)}$ induites par l’action $\underline {G}\times {\mathcal {M}}_{\infty }\mapsto {\mathcal {M}}_{\infty }$ (l’existence de $c(a,b)$ dans les deux cas vient de ce que les $S_a$ sont compacts et les $U_b$ quasi-compacts).

Lemme 3.10. Soit $\{U_s\}_{s\in \mathbf {N}}$ un recouvrement Stein affinoïde perfectoïde de $\mathcal {M}_{\infty }$ . Le système projectif $\{H^i_{\operatorname {\acute {e}t} }(U_s, \mathbf {Z}/p^k)\}_s$ est Mittag-Leffler pour tout i.

Démonstration. Par dévissage on se ramène au cas $k=1$ . Supposons d’abord que $i\geq 1$ . Alors

$$ \begin{align*}H^i_{\operatorname{\acute{e}t} }(U_s,\mathbf{F}_p)\simeq H^i_{\operatorname{\acute{e}t} }(U_s^{\flat},\mathbf{F}_p)\end{align*} $$

et $U_s^{\flat }$ est un affinoïde perfectoïde. La suite d’Artin-Schreier

$$ \begin{align*}0\to\mathbf{F}_p\to \mathcal{O}_{U_s^{\flat}}\to \mathcal{O}_{U_s^{\flat}}\to 0\end{align*} $$

et l’annulation de $H^i_{\operatorname {\acute {e}t} }(U_s^{\flat }, \mathcal {O}_{U_j^{\flat }})$ pour $i\geq 1$ montrent que $H^i_{\operatorname {\acute {e}t} }(U_s,\mathbf {F}_p)=0$ pour $i\geq 2$ et

$$ \begin{align*}H^1_{\operatorname{\acute{e}t} }(U_s,\mathbf{F}_p)\simeq \mathcal{O}(U_s^{\flat})/(1-\varphi).\end{align*} $$

Il suffit donc de prouver que la flèche naturelle $\mathcal {O}(U_{s+1}^{\flat })\to \mathcal {O}(U_s^{\flat })$ est d’image dense. Par [45, th. 2.4.3], cela suit du même énoncé pour les débasculés, qui est standard.

Il reste à traiter le cas $i=0$ . On peut supposer que les $U_s$ sont les images inverses du recouvrement standard $\{V_s\}_s$ de l’espace en niveau $0$ (qui est un disque ouvert). Alors $U_s\to V_s$ est un K-torseur proétale, donc K agit transitivement sur $\pi _0(U_s)$ . L’inclusion $U_s\to U_{s+1}$ correspond sur les $\pi _0$ à une flèche $K/\Gamma _s\to K/\Gamma _{s+1}$ , avec $\Gamma _s\subset \Gamma _{s+1}$ des sous-groupes fermés de K, et, sur les $H^0$ , à l’application naturelle $\operatorname {Hom} _{\mathrm{cont}}(K/\Gamma _{s+1},\mathbf {F}_p)\to \operatorname {Hom} _{\mathrm{cont}}(K/\Gamma _s,\mathbf {F}_p)$ .

Il suffit donc de prouver que le prosystème $\{ \operatorname {Hom} _{\mathrm{cont}}(K/\Gamma _s,\mathbf {F}_p)\}_s$ est Mittag-Leffler. Or d’après [37, prop 2.4], K contient un sous-groupe ouvert $K'$ tel que toute suite croissante de sous-groupes fermés soit stationnaire. Mais alors K a la même propriété puisque $K'$ est d’indice fini dans K. Il s’ensuit que notre système est en fait constant pour s assez grand, et donc, a fortiori, Mittag-Leffler.

Corollaire 3.11. Soit $\pi $ un $A[G]$ -module lisse admissible, tué par $p^k$ . Il existe une suite spectrale de $D_p^{{\boldsymbol *}}\times W_{F}$ -modules

(3.12) $$ \begin{align} E_2^{i,j}=H^i(G, {\mathrm{Hom}}_{\mathbf{Z}_p}^{\mathrm{cont}}(\pi^{\vee}, H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \mathbf{Z}/p^k)))\Longrightarrow S^{i+j}(\pi). \end{align} $$

De plus $H^j_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }, \mathbf {Z}/p^k)=0$ pour $j\geq 2$ .

Démonstration. Compte-tenu du th. 3.2, il suffit de vérifier que

$$ \begin{align*}H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi})\simeq {\mathrm{Hom}}_{\mathbf{Z}_p}^{\mathrm{cont}}(\pi^{\vee}, H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \mathbf{Z}/p^k)). \end{align*} $$

En raisonnant comme dans la preuve dudit théorème et en reprenant ses notations, on obtient:

$$ \begin{align*} H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \underline{\pi}) & \stackrel{\sim}{\to} \lim_{s} (\pi\otimes H^j_{\operatorname{\acute{e}t} }(U_s, \mathbf{Z}/p^k))\simeq \lim_{s} {\mathrm{Hom}}_{\mathbf{Z}_p}^{\mathrm{cont}}(\pi^{\vee}, H^j_{\operatorname{\acute{e}t} }(U_s, \mathbf{Z}/p^k))\\ & \simeq {\mathrm{Hom}}_{\mathbf{Z}_p}^{\mathrm{cont}}(\pi^{\vee}, H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, \mathbf{Z}/p^k)).\Box \end{align*} $$

Pour $G={\mathrm{GL}}_2(\mathbf {Q}_p)$ on obtient le résultat suivant:

Corollaire 3.13. Soit $\pi $ un $k_L[G]$ -module lisse admissible, irréductible. On dispose d’un morphisme naturel

$$ \begin{align*}S^1(\pi) \to {\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L))\end{align*} $$

qui est un isomorphisme si $\pi $ n’appartient pas à un twist $\{\chi ,{\mathrm{St}}\otimes \chi , I({\chi ,\chi \varepsilon })\}$ du bloc de la Steinberg, et dont les noyau et conoyau sont de dimension finie sur $k_L$ si $\pi $ appartient à un twist du bloc de la Steinberg.

Démonstration. La suite spectrale (3.12) fournit une suite exacte

(3.14) $$ \begin{align} 0 \to H^1(G, {\mathrm{Hom}}_{\mathbf{Z}_p}^{\mathrm{cont}}(\pi^{\vee}, & H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L))) \stackrel{f_{\pi}}{\to} S^1(\pi) \to {\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L))\\ & \to H^2(G, {\mathrm{Hom}}_{\mathbf{Z}_p}^{\mathrm{cont}}(\pi^{\vee}, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L))).\notag \end{align} $$

On a un isomorphisme

$$ \begin{align*}{\mathrm{Hom}}_{k_L}^{\mathrm{cont}}(\pi^{\vee}, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L)) \simeq {\mathrm{Ind}}_{{\mathrm{SL}}_2(\mathbf{Q}_p)}^{G} (\pi).\end{align*} $$

Le lemme de Shapiro [10, prop. IX.2.3] (notons que le déterminant $G\to \mathbf {Q}_p^{{\boldsymbol *}}$ a une section continue) montre alors que

$$ \begin{align*}V_i(\pi):=H^i(G, {\mathrm{Hom}}_{k_L}^{\mathrm{cont}}(\pi^{\vee}, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L)))\simeq H^i({\mathrm{SL}}_2(\mathbf{Q}_p), \pi).\end{align*} $$

L’énoncé du corollaire (i.e. la finitude des $V_i(\pi )$ et leur nullité si $\pi $ n’appartient pas à un twist du bloc de la Steinberg) est donc une conséquence de résultats de Fust [34, th. 1.2, lemma 6.3] (utiliser le lemme 1.7 pour se ramener au cas absolument irréductible et noter qu’une représentation admissible de G avec un caractère central est déjà admissible en tant que représentation de ${\mathrm{SL}}_2(\mathbf {Q}_p)$ ).

4 Longueur finie

Dans ce chapitre, on suppose que $F=\mathbf {Q}_p$ , avec ²³ $p>2$ et on prend $\varpi =p$ . Notre but est de prouver le résultat de finitude suivant.

Théorème 4.1. Pour toute extension finie K de $\mathbf {Q}_p$ , le G-module $H^1_{\operatorname {\acute {e}t} }( \mathcal {M}_{n,K}^{ p}, k_L)$ est le dual d’une représentation lisse de G, de longueur finie.

Remarque 4.2. On a bien sûr un énoncé analogue avec des coefficients , qui se déduit formellement du théorème ci-dessus et du th. 2.1. En combinant cela avec le $\mathrm {n}^{\mathrm{o}}$ 1.2.3, on obtient (par voie assez détournée ²⁴ ) l’admissibilité des G-modules lisses $H^1_{\operatorname {\acute {e}t} }( \mathcal {M}_{n,K}^{ p}, {\cal O}_L/\varpi _L^k)^{\vee }$ .

4.1 Compatibilité local-global

Le but de ce paragraphe est de démontrer la prop. 4.3 ci-dessous, qui joue un rôle clé dans la preuve du théorème de longueur finie. Les ingrédients de la preuve sont les travaux de Scholze [61], Ludwig [49] et Paškūnas [55].

Proposition 4.3. Soit $(\chi _1, \chi _2)$ un couple de caractères lisses $\mathbf {Q}_p^{{\boldsymbol *}}\to \overline {\mathbf {F}}_p^{{\boldsymbol *}}$ , générique. Si K est une extension finie de $\mathbf {Q}_p$ telle que ²⁵ $S^1(I(\chi _1,\chi _2))^{\mathcal {G}_K}\ne 0$ , alors $\chi _1$ ou $\chi _2$ se factorise par ${\mathrm{Gal}}(K/\mathbf {Q}_p)$ .

Remarque 4.4. Nous renvoyons le lecteur au chapitre 8 de [42] pour des résultats plus fins concernant la structure de $S^1(I(\chi _1,\chi _2))$ .

Même si la prop. 4.3 est purement locale, nous aurons besoin d’un certain nombre d’objets de nature globale pour la prouver. Nous supposerons ²⁶ que $[k_L:\mathbf {F}_p]\geq 3$ .

4.1.1 Globalisation

Soit $\bar {r}: \mathcal {G}_{\mathbf {Q}_p}\to {\mathrm{GL}}_2(k_L)$ une représentation continue. Le résultat suivant [25, prop. 8.1] est une conséquence directe de [36, cor. A.3]:

Proposition 4.5. Il existe un corps totalement réel E, de degré pair sur $\mathbf {Q}$ , dans lequel p est totalement décomposé, ainsi qu’une représentation automorphe cuspidale régulière, algébrique, de poids $0$ de ${\mathrm{GL}}_2(\mathbf {A}_E)$ , telle que:

• • la représentation galoisienne $\rho _{\pi }: \mathcal {G}_E\to {\mathrm{GL}}_2(\overline {\mathbf {Q}}_p)$ associée à $\pi $ est non ramifiée en dehors de p;

• • on a ${\mathrm{SL}}_2(k_L)\subset {\mathrm{Im}}(\overline {\rho }_{\pi })\subset {\mathrm{GL}}_2(k_L)$ (en particulier $\overline {\rho }_{\pi }$ est absolument irréductible) et $ \overline {\rho }_{\pi ,v}:=\overline {\rho }_{\pi }|_{\mathcal {G}_{E_v}}$ est isomorphe à $\bar {r}$ pour toute place v de E divisant p.

Fixons pour toute la suite E et $\pi $ comme dans la proposition ci-dessus. Notons simplement $\mathbf {A}$ l’anneau des adèles de E, $\mathbf {A}_f$ les adèles finis, et

$$ \begin{align*}\bar{\rho}:=\bar{\rho}_{\pi}: \mathcal{G}_E\to {\mathrm{GL}}_2(k_L), \quad \rho=\rho_{\pi}: \mathcal{G}_E\to {\mathrm{GL}}_2(\overline{\mathbf{Q}}_p).\end{align*} $$

Quitte à remplacer L par une extension finie et à conjuguer $\rho $ , on peut supposer que $\rho (\mathcal {G}_{E})\subset {\mathrm{GL}}_2(\mathcal {O}_L)$ .

On regarde le caractère unitaire

$$ \begin{align*}\psi:=\chi_{\mathrm{cyc}}\cdot \det \rho: \mathcal{G}_{E}\to \mathcal{O}_L^{{\boldsymbol *}}\end{align*} $$

comme un caractère continu de $\mathbf {A}_{f}^{{\boldsymbol *}}/E^{{\boldsymbol *}}$ , par la théorie du corps de classes (normalisée de telle sorte que les uniformisantes s’envoient sur des frobenius géométriques). On note $\psi _v$ la restriction de $\psi $ à un sous-groupe de décomposition en v, et on considère $\psi _v$ comme un caractère de $E_v^{{\boldsymbol *}}$ .

Fixons enfin une place

de E divisant p (on a donc

) ainsi qu’une place infinie $\infty _{0}$ de E, et notons

On considère aussi $ \zeta $ comme un caractère de G.

4.1.2 Groupes quaternioniques

Soit $D_0$ une algèbre de quaternions sur E, compacte (modulo le centre) en toute place infinie de E et déployée en toute place finie de E. Soit $\mathcal {O}_{D_0}$ un ordre maximal de $D_0$ , et fixons des isomorphismes $(\mathcal {O}_{D_0})_v\simeq M_2(\mathcal {O}_{E_v})$ pour toute place finie v. Soit D l’algèbre de quaternions sur E obtenue à partir de $D_0$ en échangeant les invariants en et $\infty _{0}$ . On fixe un isomorphisme

(4.6)

Notons

et

les groupes algébriques associés à $D^{\boldsymbol *} $ et $D_0^{\boldsymbol *}$ , i.e.

et

pour toute E-algèbre R. En particulier

où $\check G$ est le groupe des unités de l’algèbre de quaternions non déployée sur $\mathbf {Q}_p$ . On identifie $\mathbf {A}_f^{{\boldsymbol *}}$ aux centres de

et

.

On peut décomposer comme une réunion disjointe finie de doubles classes , le groupe $U_{\mathrm{max}}:=\prod _{v\nmid \infty } {\mathrm{GL}}_2(\mathcal {O}_{E_v})$ étant identifié (par les choix faits ci-dessus) à un sous-groupe ouvert compact de . Les sont des groupes finis, et on note N le produit des cardinaux de ces groupes finis. Le lemme 8.2 de [25] montre l’existence d’une place finie $w_1$ de E telle que $\mathbf {N}(w_1)$ soit premier avec $2Np$ et non congru à $1$ modulo p, et telle que le quotient des valeurs propres de $\bar {\rho }({\mathrm{Frob}}_{w_1})$ ne soit pas $1$ ou $\mathbf {N}(w_1)^{\pm 1}$ . On fixe une telle place $w_1$ et on définit un sous-groupe ouvert compact U de par

$$ \begin{align*}U=\prod_{v\nmid \infty} U_v,\end{align*} $$

avec $U_v={\mathrm{GL}}_2(\mathcal {O}_{E_v})$ pour $v\ne w_1$ et

$$ \begin{align*}U_{w_1}=\{g\in {\mathrm{GL}}_2(\mathcal{O}_{E_{w_1}})|\,\, g\equiv {\big(\begin{smallmatrix}1&*\\ 0&1\end{smallmatrix}\big)} \pmod{\varpi_{w_1}}\}.\end{align*} $$

Le sous-groupe U de

donne naissance à un sous-groupe ouvert compact

de

, que l’on identifie aussi à un sous-groupe ouvert compact de

par l’isomorphisme

induit par (4.6). Posons

4.1.3 Formes automorphes et opérateurs de Hecke

Soit A un $\mathcal {O}_L$ -module topologique. Le $\mathcal {O}_L$ -module

est une représentation de

(agissant par translation à droite). On note $S_{\psi }(U^p, A)$ le sous-espace $\psi $ -isotypique (pour l’action de $\mathbf {A}_{f}^{{\boldsymbol *}}$ ) de $S(U^p,A)$ . Si $\lambda $ est une representation continue de

sur un $\mathcal {O}_L$ -module libre de type fini, telle que

agisse à travers $\psi $ , on dispose du G-module

Soit S un ensemble fini de places de E, contenant $w_1$ , les places divisant p et les places infinies de E. L’algèbre

de polynômes en les variables indiquées agit ²⁷ sur $S(U^p, A)$ , et cette action commute avec celle de

. Ainsi $S(U^p, A)$ devient un

-module et $S_{\psi }(U^p, A)$ devient un

-module.

La représentation $\rho : \mathcal {G}_E\to {\mathrm{GL}}_2(\mathcal {O}_L)$ est non ramifiée en dehors de S et induit un morphisme

envoyant $T_v$ (respectivement $S_v$ ) sur ${\mathrm{tr}}(\bar {\rho }({\mathrm{Frob}}_v))$ (respectivement $\mathbf {N}(v)^{-1}\det (\bar {\rho }({\mathrm{Frob}}_v))$ ). On note

le noyau de ce morphisme, c’est donc un idéal maximal $\mathfrak {m}$ de

, de corps résiduel $k_L$ , tel que $\psi ({\mathrm{Frob}}_v)\equiv S_v\pmod {\mathfrak {m}}$ pour $v\notin S$ .

Proposition 4.7.

1. a) Le localisé $S_{\psi }(U^p, L/\mathcal {O}_L)_{\mathfrak {m}}$ est non nul, admissible et injectif dans ${\mathrm{Rep}}^{\mathrm{lisse}, \psi_{\mathrm{p}}}\, U_p$ , où $\psi _p$ est le caractère du centre de $U_p=\prod _{v\mid p} {\mathrm{GL}}_2(\mathbf {Z}_p)$ induit par $\psi $ .

2. b) On peut choisir $\lambda $ de la forme , de telle sorte que $\lambda _v$ ait $\psi _v$ pour caractère central et .

Démonstration. Le premier point est le contenu de [25, prop. 8.4] et le second est démontré dans le lemme 8.6 de loc.cit.

On fixe par la suite une représentation $\lambda $ comme dans la proposition ci-dessus et on note pour simplifier

Proposition 4.8. Soit $\mathcal {B}$ le bloc associé à $\bar {r}^{\mathrm{ss}}$ . Alors $S_{\psi ,\lambda , \mathfrak {m}}$ est un objet admissible de ${\mathrm{Rep}}_{\mathcal {B}}^{\zeta }\, G$ , dont la restriction à $K={\mathrm{GL}}_2(\mathbf {Z}_p)$ est injective dans ${\mathrm{Rep}}^{\zeta }\, K$ .

Démonstration. Toutes les références ci-dessous sont par rapport à l’article de Paškūnas [55]. Le premier point est établi dans les lemmes 5.1, 5.3 et la prop. 5.4, pour le second voir les lemmes 5.2 et 5.3.

Remarque 4.9. Si l’on munit

de la topologie p-adique, alors

est un $\mathcal {O}_L$ -module compact pour la topologie de la convergence simple et on dispose d’un isomorphisme naturel (combiner la relation $(27)$ dans [55] avec la dualité de Schikhof)

Proposition 4.10. Le G-module

$$ \begin{align*}M_{\psi,\lambda, \mathfrak{m}}=(k_L\otimes_{R^{{\mathrm{ps}}, \zeta}_{\mathcal{B}}} S_{\psi,\lambda, \mathfrak{m}}^{\vee})^{\vee}\end{align*} $$

est un objet de longueur finie de ${\mathrm{Rep}}_{\mathcal {B}}^{\zeta }\, G$ , et tout $\pi \in \mathcal {B}$ est un sous-quotient irréductible de $M_{\psi ,\lambda , \mathfrak {m}}$ .

Démonstration. Notons que $M_{\psi ,\lambda , \mathfrak {m}}$ a bien un sens grâce à la prop. 4.8. Le fait que $M_{\psi ,\lambda , \mathfrak {m}}$ est de longueur finie est une conséquence de l’admissibilité de $S_{\psi ,\lambda , \mathfrak {m}}^{\vee }$ (prop. 4.8) et du cor. 6.7 de [56].

Supposons qu’il existe $\pi \in \mathcal {B}$ qui n’est pas un sous-quotient irréductible de $M_{\psi ,\lambda , \mathfrak {m}}$ . Soit $S=S_{\psi ,\lambda , \mathfrak {m}}$ et $M=M_{\psi ,\lambda , \mathfrak {m}}$ , et soit $m_{{\mathrm{ps}}}$ l’idéal maximal de $R^{{\mathrm{ps}}, \zeta }_{\mathcal {B}}$ . Comme $\pi ^{\vee }$ n’intervient pas dans $M^{\vee }\simeq S^{\vee }/m_{{\mathrm{ps}}} S^{\vee }$ , il n’intervient pas non plus dans $S^{\vee }/m_{{\mathrm{ps}}}^j S^{\vee }$ pour tout $j\geq 1$ . Si P est une enveloppe projective de $\pi ^{\vee }$ dans ${\mathrm{Rep}}^{{\mathrm{ladm}}, \zeta } \, G$ , on a donc ${\mathrm{Hom}}_G(P, S^{\vee }/m_{{\mathrm{ps}}}^j S^{\vee })=0$ pour tout j, et donc ${\mathrm{Hom}}_G(P, \varprojlim _{j} S^{\vee }/m_{{\mathrm{ps}}}^j S^{\vee })=0$ . Comme $S^{\vee }$ est la limite inverse de ses quotients de longueur finie, et chacun est tué par une puissance de $m_{{\mathrm{ps}}}$ , on a $ \varprojlim _{j} S^{\vee }/m_{{\mathrm{ps}}}^j S^{\vee }\simeq S^{\vee }$ . Par projectivité de P, on en déduit que ${\mathrm{Hom}}_G(P, \Theta ^d)=0$ pour tout réseau G-stable $\Theta $ de $\Pi _x:=S^{\vee }[1/p]/\ker (x)$ , et tout morphisme $x: R^{{\mathrm{ps}}, \zeta }_{\mathcal {B}}\to \overline {\mathbf {Q}}_p$ (avec comme d’habitude $\Theta ^d:={\mathrm{Hom}}_{\mathcal {O}_L}^{\mathrm{cont}}(\Theta , \mathcal {O}_L)$ ).

On va voir ci-dessous qu’il existe un morphisme $x: R^{{\mathrm{ps}}, \zeta }_{\mathcal {B}}\to \overline {\mathbf {Q}}_p$ tel que la spécialisation du pseudo-caractère universel en x soit la trace d’une représentation absolument irréductible (quitte à remplacer L par une extension finie) et tel que $\Pi _x$ soit non nul. Alors $\Pi _x\simeq \Pi ^{\oplus d}$ pour un $d\geq 1$ et une représentation absolument irréductible non ordinaire $\Pi $ de G (cela suit de [56, cor. 6.16]). Mais la compatibilité entre les correspondances de Langlands p-adique et modulo p ([5] et [15, prop. III.55, rem. III.56]) montre que $\pi $ intervient dans la réduction modulo $\varpi $ d’un réseau G-stable de $\Pi $ , une contradiction.

Pour finir, il reste à justifier l’existence d’un tel x. L’argument est identique à celui utilisé dans la preuve du th. 6.5 de [55], avec à la place de $S_{\psi ,\lambda }(U^p, \mathcal {O}_L)_{\mathfrak {m}}[1/p]$ . Plus précisément, comme dans loc.cit. on peut construire un pro- sous-groupe ouvert de et une représentation $\gamma $ de de dimension finie sur L telle que tout vecteur propre pour les opérateurs de Hecke agissant sur l’espace de dimension finie induit une forme automorphe qui est supercuspidale en , et donc la représentation galoisienne associée est absolument irréductible en restriction à . Enfin, le fait que l’espace est non nul est expliqué à la fin du deuxième paragraphe dans la preuve de loc.cit.

4.1.4 Cohomologie complétée et compatibilité local-global

Soit l’algèbre de quaternions non déployée sur . Si V est un sous-groupe ouvert de , notons ${\mathrm{Sh}}_{VU^p}$ la courbe de Shimura définie sur E, associée à $VU^p$ .

Le $\mathcal {O}_L$ -module ²⁸

$$ \begin{align*}\widehat{H}^1(U^p, \mathcal{O}_L/\varpi_L^n):=\varinjlim_{V} H^1_{\operatorname{\acute{e}t} }({\mathrm{Sh}}_{VU^{p}, \bar{E}}, \mathcal{O}_L/\varpi_L^n)\end{align*} $$

est naturellement un

-module. Soit $\widehat {H}^1_{\psi }(U^p, \mathcal {O}_L/\varpi _L^n)_{\mathfrak {m}}$ la partie $\psi $ -isotypique (pour l’action de $\mathbf {A}_{f}^{{\boldsymbol *}}$ ) du localisé $\widehat {H}^1(U^p, \mathcal {O}_L/\varpi _L^n)_{\mathfrak {m}}$ et soit

Posons

les applications de transition étant induites par celles qui fournissent l’isomorphisme usuel $\varinjlim _{n} \mathcal {O}_L/\varpi _L^n\simeq L/\mathcal {O}_L$ .

Le résultat de compatibilité local-global suivant est obtenu dans [55, lemma 6.2], en utilisant les résultats de Scholze [61].

Proposition 4.11. Il existe un isomorphisme naturel de -modules

$$ \begin{align*}S^1(S_{\psi,\lambda, \mathfrak{m}})\simeq \widehat{H}^1_{\psi, \lambda, \mathfrak{m}}.\end{align*} $$

En munissant

de la topologie p-adique et

de la topologie de la convergence simple (pour laquelle il est compact), on obtient un isomorphisme de

-modules

La représentation $\bar {\rho }$ se déforme en une représentation

telle que le polynôme caractéristique de $\rho _{\mathfrak {m}}({\mathrm{Frob}}_v)$ soit $X^2-T_v X+N(v)S_v$ pour $v\notin S$ (cf. prop. 5.7 de [61]).

Proposition 4.12. Si

, alors le morphisme naturel

est un isomorphisme.

Démonstration. Combiner les prop. 5.3, 5.4, 5.8 de l’article de Scholze [61].

4.1.5 Preuve de la prop. 4.3

On suppose que $\bar {r}=\bar {r}_{\chi _1,\chi _2}$ , avec $(\chi _1, \chi _2)$ générique. Notons pour simplifier $V=V_{\psi ,\lambda , \mathfrak {m}}$ , $A=R^{{\mathrm{ps}}, \zeta }_{\mathcal {B}}$ et $M=M_{\psi ,\lambda , \mathfrak {m}}=(k_L\otimes _{A} S_{\psi ,\lambda , \mathfrak {m}}^{\vee })^{\vee }$ . Alors M est un $k_L[G]$ -module lisse, de longueur finie, dont l’ensemble des sous-quotients irréductibles est $\{I(\chi _1,\chi _2), I(\chi _2,\chi _1)\}$ , d’après la prop. 4.10.

Le théorème d’annulation de Ludwig (résultat principal de [49]) affirme que $S^2(I(\chi _1,\chi _2))=0=S^2(I(\chi _2,\chi _1))$ . Comme de plus $S^0(I(\chi _1,\chi _2))=0=S^0(I(\chi _2,\chi _1))$ (utiliser la prop. 4.7 de [61] et le fait que $I(\chi _1, \chi _2)$ et $I(\chi _2, \chi _1)$ n’ont pas d’invariants non nuls sous ${\mathrm{SL}}_2(\mathbf {Q}_p)$ ), on en déduit que $S^1(M)$ est une extension successive de copies de $S^1(I(\chi _1,\chi _2))$ et $S^1(I(\chi _2,\chi _1))$ . D’autre part, la prop. 4.11 combinée avec le lemme 6.1 de [55] montrent que

On conclut que $S^1(I(\chi _1,\chi _2))$ est un sous-quotient de

en tant que $\mathcal {G}_{\mathbf {Q}_p}$ -module.

Puisque $\bar {\rho }$ est une globalisation de $\bar {r}$ , la prop. 4.12 montre que est de la forme $\bar {r}\otimes _{k_L} N'$ pour un $k_L$ -espace vectoriel $N'$ muni de l’action triviale de $\mathcal {G}_{\mathbf {Q}_p}$ . Ainsi, $S^1(I(\chi _1,\chi _2))$ est un sous-quotient de $\bar {r}\otimes _{k_L} N'$ en tant que $\mathcal {G}_{\mathbf {Q}_p}$ -module. En utilisant la suite exacte

$$ \begin{align*}0\to \chi_1\otimes_{k_L} N'\to \bar{r}\otimes_{k_L} N'\to \chi_2\otimes_{k_L} N'\to 0\end{align*} $$

on voit que tout sous-quotient de $\bar {r}\otimes _{k_L} N'$ contient une copie de $\chi _1$ ou de $\chi _2$ , et donc si $S^1(I(\chi _1,\chi _2))^{\mathcal {G}_K}\ne 0$ alors $\chi _1$ ou $\chi _2$ se factorise par ${\mathrm{Gal}}(K/\mathbf {Q}_p)$ , ce qui permet de conclure.

4.2 Preuve du théorème de longueur finie

Dans ce paragraphe nous mettons ensemble les résultats établis ci-dessus pour démontrer le théorème de finitude (th. 4.1 ci-dessus).

Démonstration (Du th.4.1).

Puisque $\mathcal {M}_{n,K}^{ p}$ n’a qu’un nombre fini de composantes connexes, $H^0_{\operatorname {\acute {e}t} }({\cal M}^{ p}_{n,K'},L)$ est un groupe fini pour tout $K'$ avec $[K':K]<\infty $ , et une application de la suite de Hochschild-Serre permet de déduire le résultat pour K du résultat pour $K'$ . L’argument est analogue (mais plus simple) à celui utilisé dans la preuve du th. 2.1. Il suffit donc de démontrer le théorème pour K assez grand.

D’après le th. 2.1, pour une telle extension K, le G-module

$$ \begin{align*}V:=H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,K}^{ p}, k_L)^{\vee}\end{align*} $$

est lisse, de type fini. Comme V est un $G'$ -module ²⁹ , par le th. 1.21, il suffit de montrer que le cosocle de V est de longueur finie, autrement dit que, pour tout $k_L[G']$ -module lisse irréductible $\pi $ , l’espace

$$ \begin{align*}{\mathrm{Hom}}_{k_L[G']}(V, \pi)\simeq {\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G']}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,K}^{ p}, k_L))\end{align*} $$

est de dimension finie sur $k_L$ , nul pour presque tout $\pi $ (i.e. sauf un nombre fini).

Notons que par la preuve du lemme 1.22 le caractère central d’un $k_L[G']$ -module lisse et irréductible $\pi $ ne prend qu’un nombre fini de valeurs, on peut donc supposer le caractère central de tous les $\pi $ fixé, égal à $\delta $ .

La preuve consiste à suivre le diagramme suivant d’espaces:

1. 1. On monte de ${\mathcal {M}}_{n,K}^{p}$ au niveau infini ${\mathcal {M}}_{{\mathrm{Dr}},\infty } $ de la tour de Drinfeld, ce qui remplace ${\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G']}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K}^{{p}}, k_L))$ par ${\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G]}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{{\mathrm{Dr}},\infty }, k_L))^{W_K\times \check {G}_n}$ .

2. 2. On passe du côté Lubin-Tate, où est défini le foncteur de Scholze, via l’isomorphisme $ {\mathcal {M}}_{{\mathrm{Dr}},\infty }\simeq {\mathcal {M}}_{{\mathrm{LT}},\infty }:={\cal M}_{\infty }$ de Faltings [31].

3. 3. Le cor. 3.13 permet de remplacer ${\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G]}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }, k_L))^{\mathcal {G}_K\times \check {G}_n}$ par $S^1(\pi )^{W_K\times \check {G}_n}$

4. 4. On étudie $S^1(\pi )^{\mathcal {G}_K\times \check {G}_n}$ par des méthodes globales.

On dit qu’un foncteur $\pi \mapsto V(\pi )$ en $k_L$ -modules est d’image finie si $V(\pi )$ est de dimension finie sur $k_L$ pour tout $k_L[G']$ -module lisse irréductible $\pi $ , et nul pour presque tout tel $\pi $ . On cherche à prouver que $\pi \mapsto {\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G']}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,K}^{{p}}, k_L))$ est d’image finie.

$\bullet $ Montée en niveau infini.

Lemme 4.13. Il suffit de prouver que le foncteur

$$ \begin{align*}\pi\mapsto Y(\pi): ={\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G]}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L))^{{W}_K\times \check{G}_n}\end{align*} $$

est d’image finie.

Démonstration. On part du $k_L$ -module

$$ \begin{align*}{\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G']}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,K}^{{p}}, k_L)) \end{align*} $$

et on monte de $\mathcal {M}_{n,K}^{{p}}$ à $\mathcal {M}_{\infty }$ en trois étapes.

$\bullet $ Étape 1: de $\mathcal {M}_{n,K}^{{p}}$ à $\mathcal {M}_{n,\mathbf {C}_p}^{{p}}$ . On a une suite exacte

(4.14) $$ \begin{align} 0\to H^1({\mathcal{G}}_K, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{{p}}, k_L))\to H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,K}^{{p}}, k_L)\to H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{{p}}, k_L)^{\mathcal{G}_K}. \end{align} $$

Les flèches dans la suite ci-dessus sont continues et la suite est strictement exacte. Cela se voit par les mêmes arguments que dans l’étape $3$ de la preuve du th. 2.1:

• – On écrit des suites exactes analogues pour les ouverts d’un recouvrement Stein de $\mathcal {M}^p_{n,K}$ ; elles existent par le corollaire $3.7.5$ de [22] et sont strictement exactes car tous les termes sont naturellement munis de la topologie discrète.

• – Comme le premier terme ne dépend pas de l’ouvert et donc est Mittag-Leffler, on voit que la suite exacte (4.14) est la limite des suites exactes pour les ouverts; c’est donc une suite strictement exacte de modules prodiscrets.

En appliquant ${\mathrm{Ho}}(-):={\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G]}(\pi ^{\vee },-)$ à (4.14), on obtient donc une suite exacte

$$ \begin{align*} 0\to {\mathrm{Ho}}( H^1({\mathcal{G}}_K, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{{p}}, k_L)))\to {\mathrm{Ho}}(H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,K}^{{p}}, k_L)) \to {\mathrm{Ho}}(H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{{p}}, k_L))^{\mathcal{G}_K}. \end{align*} $$

Puisque $\mathcal {M}_{n,\mathbf {C}_p}^{{p}}$ n’a qu’un nombre fini de composantes connexes, il suffit de montrer que $\pi \mapsto {\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G']}(\pi ^{\vee },H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_n^{{p}}, k_L))^{\mathcal {G}_K}$ est d’image finie.

$\bullet $ Étape 2: de $\mathcal {M}_{n,\mathbf {C}_p}^{{p}}$ à $\mathcal {M}_{{\mathrm{Dr}},\infty }^{{p}}$ . Nous allons maintenant utiliser un argument similaire pour le $\check {G}_n$ -torseur proétale $\mathcal {M}_{{\mathrm{Dr}},\infty }^{{p}}\to \mathcal {M}_{n,\mathbf {C}_p}^{{p}}$ . En utilisant un argument analogue à celui de la preuve du th. 3.2, on obtient une suite spectrale

$$ \begin{align*}E_2^{i,j}=H^i(\check{G}_n, H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}^{{p}}, k_L))\Longrightarrow H^{i+j}_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{{p}}, k_L).\end{align*} $$

Celle-ci fournit une suite strictement exacte (même argument que dans l’étape $1$ )

$$ \begin{align*}0\to H^1(\check{G}_n, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}^{{p}}, k_L))\to H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{{p}}, k_L)\to H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}^{{p}}, k_L)^{\check{G}_n}.\end{align*} $$

En appliquant ${\mathrm{Ho}}(-):={\mathrm{Hom}}^{\mathrm{cont}}_{k_L[G']}(\pi ^{\vee },-)^{{\mathcal {G}}_K}$ , on obtient une suite exacte

$$ \begin{align*} 0\to {\mathrm{Ho}}(H^1(\check{G}_n, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}^{{p}}, k_L)))^{{\mathcal{G}}_K}\to {\mathrm{Ho}}(H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{{p}}, k_L))^{{\mathcal{G}}_K} \to {\mathrm{Ho}}(H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}^{{p}}, k_L))^{\mathcal{G}_K\times\check{G}_n}. \end{align*} $$

Contrairement à $\pi _0(\mathcal {M}_{n,\mathbf {C}_p}^{{p}})$ , l’espace $\pi _0(\mathcal {M}_{{\mathrm{Dr}},\infty }^{{p}})$ est infini, donc on doit faire plus attention. La description des composantes connexes géométriques de la tour de Lubin-Tate [68] montre que $\pi _0(\mathcal {M}_{{\mathrm{Dr}},\infty })\simeq \mathbf {Q}_p^{{\boldsymbol *}}$ , les groupes $\check {G}$ et G agissant par la norme réduite et le déterminant, respectivement. En prenant les invariants par $p\in Z(G)$ , on voit que $\pi _0(\mathcal {M}_{{\mathrm{Dr}},\infty }^{{p}})\simeq \mathbf {Q}_p^{{\boldsymbol *}}/p^{\mathbf {Z}}$ . Donc

(4.15) $$ \begin{align} H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}, k_L)\simeq \mathcal{C}^0(\mathbf{Q}_p^{{\boldsymbol *}}, k_L),\quad H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}^{{p}}, k_L)\simeq \mathcal{C}^0(\mathbf{Q}_p^{{\boldsymbol *}}/p^{\mathbf{Z}}, k_L). \end{align} $$

Comme $\mathcal {C}^0(\mathbf {Q}_p^{{\boldsymbol *}}/p^{\mathbf {Z}}, k_L)$ est une représentation lisse admissible de $\check {G}_n$ , et comme $\check {G}_n$ est un groupe de Lie p-adique compact, sans torsion, les $ H^i(\check {G}_n, H^0_{\operatorname {\acute {e}t} }(\mathcal {M}_{{\mathrm{Dr}},\infty }^{{p}}, k_L))$ sont de dimension finie sur $k_L$ , pour tout $i\geq 0$ (cf. [61, lemma 3.13]).

Il suffit donc de vérifier que $\pi \mapsto {\mathrm{Hom}}_{k_L[G']}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{{\mathrm{Dr}},\infty }^{{p}}, k_L))^{\mathcal {G}_K\times \check {G}_n}$ est d’image finie.

$\bullet $ Étape 3: de $\mathcal {M}_{{\mathrm{Dr}},\infty }^{{p}}$ à $\mathcal {M}_{\infty }$ . Enfin, on utilise un argument similaire pour le $p^{\mathbf {Z}}$ -torseur étale $\mathcal {M}_{{\mathrm{Dr}},\infty }\to \mathcal {M}_{{\mathrm{Dr}},\infty }^{{p}}$ . En utilisant un argument analogue à celui de la preuve du th. 3.2 (notons que $p^{\mathbf {Z}}$ est un groupe localement profini), on obtient une suite spectrale

$$ \begin{align*}E_2^{i,j}=H^i(p^{\mathbf{Z}}, H^j_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}, k_L))\Longrightarrow H^{i+j}_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}^{{p}}, k_L).\end{align*} $$

Celle-ci fournit une suite strictement exacte (même argument que dans l’étape $1$ )

(4.16) $$ \begin{align}0\to H^1(p^{\mathbf{Z}}, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}, k_L))\to H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}^{{p}}, k_L)\to H^0(p^{\mathbf{Z}},H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}, k_L))\to 0 \end{align} $$

Notons que

$$ \begin{align*} H^1(p^{\mathbf{Z}}, H^0_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}, k_L))) &\simeq H^1(p^{\mathbf{Z}},\mathcal{C}^0(\mathbf{Q}_p^{{\boldsymbol *}}, k_L))\\ &\simeq H^1(p^{\mathbf{Z}}, {\mathrm{Ind}}^{p^{\mathbf{Z}}}_{\{1\}} \mathcal{C}^0(\mathbf{Z}_p^{{\boldsymbol *}}, k_L)) \simeq H^1(\{1\},\mathcal{C}^0(\mathbf{Z}_p^{{\boldsymbol *}}, k_L))=0, \end{align*} $$

où le premier isomorphisme vient de (4.15) et le troisième du lemme de Shapiro [10, prop. IX.2.3].

La seconde flèche dans (4.16) est donc un isomorphisme, et comme $p^{\mathbf {Z}}$ agit trivialement sur $\pi ^{\vee }$ , on a

$$ \begin{align*}{\mathrm{Hom}}_{k_L[G]}(\pi^{\vee}, H^0(p^{\mathbf{Z}},H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{{\mathrm{Dr}},\infty}, k_L))) ={\mathrm{Hom}}_{k_L[G]}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}^p_{{\mathrm{Dr}},\infty}, k_L)).\end{align*} $$

On peut remplacer $\mathcal {M}_{{\mathrm{Dr}},\infty }$ par ${\mathcal {M}}_{\infty }$ grâce à l’isomorphisme de Faltings, ce qui permet de conclure.

$\bullet $ Passage au foncteur de Scholze.— Nous allons étudier l’espace $Y(\pi )$ via la suite spectrale 3.11.

Lemme 4.17. Il suffit de démontrer que le foncteur $\pi \mapsto S^1(\pi )^{\mathcal {G}_K\times \check {G}_n}$ est d’image finie.

Démonstration. On suppose que $\pi \mapsto S^1(\pi )^{\mathcal {G}_K\times \check {G}_n}$ est d’image finie; on va montrer qu’il en est de même de $\pi \mapsto Y(\pi )$ .

La suite exacte (3.14) de la preuve du cor. 3.13 s’écrit

(4.18) $$ \begin{align} 0 \to V_1(\pi) \stackrel{f_{\pi}}{\to} S^1(\pi) {\to} {\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty},k_L))\to V_2(\pi) \end{align} $$

où $\pi \mapsto V_1(\pi )$ et $\pi \mapsto V_2(\pi )$ , définis dans la preuve du cor. 3.13, sont d’images finies. Soit $A(\pi )$ le conoyau de la flèche $f_{\pi }$ de (4.18). On a une suite exacte

$$ \begin{align*} 0\to & H^0(W_K\times \check{G}_n,V_1(\pi))\to H^0(W_K\times \check{G}_n,S^1(\pi))\stackrel{f_{\pi}}{\to} H^0(W_K\times \check{G}_n,A(\pi))\\ & \to H^1(W_K\times \check{G}_n,V_1(\pi)). \end{align*} $$

Nous prétendons que $\pi \mapsto H^0(W_K\times \check {G}_n,A(\pi ))$ est d’image finie. En effet, ceci est, par hypothèse, vrai pour $\pi \mapsto H^0(W_K\times \check {G}_n,S^1(\pi ))$ . Il suffit donc de vérifier que c’est vrai aussi pour $H^1(W_K\times \check {G}_n,V_1(\pi ))$ , ce qui est clair car $ \check {G}_n$ est un groupe de Lie p-adique compact et $\pi \mapsto V_1(\pi )$ est d’image finie.

La suite exacte

$$ \begin{align*}0\to H^0(W_K\times \check{G}_n,A(\pi))\to Y(\pi)\to H^0(W_K\times \check{G}_n,V_2(\pi))\end{align*} $$

ce que l’on sait de $V_2(\pi )$ , et ce que l’on vient de démontrer sur $H^0(W_K\times \check {G}_n,A(\pi ))$ , impliquent que $\pi \mapsto Y(\pi )$ est d’image finie, ce que l’on voulait.

$\bullet $ Analyse de $S^1(\pi )^{\mathcal {G}_K\times \check {G}_n}$ . Soit $\pi $ un $k_L[G']$ -module, lisse irréductible. Il résulte du lemme 1.22 et du $\mathrm {n}^{\mathrm{o}}$ 1.2.3 que le G-module $\pi $ est admissible, et donc le théorème de finitude de Scholze 3.1 permet de conclure que $S^1(\pi )^{\mathcal {G}_K\times \check {G}_n}$ est bien de dimension finie sur $k_L$ .

Il reste à prouver que $S^1(\pi )^{\mathcal {G}_K\times \check {G}_n}\neq 0$ pour seulement un nombre fini de $k_L[G']$ -modules $\pi $ , lisses et irréductibles. Pour tout tel $\pi $ , posons

$$ \begin{align*}\bar{\pi}=\overline{\mathbf{F}}_p\otimes_{k_L} \pi.\end{align*} $$

Le morphisme naturel $\overline {\mathbf {F}}_p\otimes _{k_L} \mathcal {F}_{\pi }\to \mathcal {F}_{\bar {\pi }}$ est un isomorphisme (cela peut se tester sur les fibres géométriques) et on a un isomorphisme équivariant

(4.19) $$ \begin{align} S^1(\bar{\pi}) \simeq \overline{\mathbf{F}}_p\otimes_{k_L} S^1(\pi) \end{align} $$

obtenu en composant les isomorphismes équivariants

(pour le troisième isomorphisme on a utilisé le fait que,

étant quasi-compact, la cohomologie de

commute aux limites inductives filtrantes).

Soit M l’ensemble des (classes d’isomorphisme de) $k_L[G']$ -modules lisses irréductibles $\pi $ pour lesquels $S^1(\pi )^{\mathcal {G}_K\times \check {G}_n}\ne 0$ et soit T l’ensemble des (classes d’isomorphisme de) $\overline {\mathbf {F}}_p[G']$ -modules lisses irréductibles $\pi $ tels que $S^1(\pi )^{\mathcal {G}_K}\ne 0$ . La prop. 4.3 combinée avec la rem. 1.9 montrent que T est fini.

Si $\pi \in M$ , l’isomorphisme (4.19) montre que $\bar {\pi }$ possède un facteur irréductible dans T. Si M est infini, il existe $\pi _1,\pi _2\in M$ non isomorphes et tels que $\overline {\pi }_1$ et $\overline {\pi }_2$ possèdent un facteur irréductible commun. Comme $\overline {\pi }_1$ et $\overline {\pi }_2$ sont semi-simples (lemme 1.7), il s’ensuit que ${\mathrm{Hom}}_{\overline {\mathbf {F}}_p[G]}(\bar {\pi }_1, \bar {\pi }_2)\ne 0$ . Le lemme 1.6 montre que ${\mathrm{Hom}}_{k_L[G]}({\pi }_1, {\pi }_2)\ne 0$ , une contradiction. Donc M est fini, ce qui finit la preuve du théorème.

Remarque 4.20. Dans la preuve du th. 4.1, on n’a utilisé l’action de ${\cal G}_K$ que pour montrer la nullité de ${\mathrm{Hom}}_{k_L[G']}^{\mathrm{cont}}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }({\mathcal {M}}_{n,K}^p,k_L))$ pour presque tout $\pi $ , pas pour la finitude de ce module. La même preuve (partant de ${\mathcal {M}}_{n,\mathbf {C}_p}^p$ au lieu de ${\mathcal {M}}_{n,K}^p$ ) permet donc de montrer que:

Corollaire 4.21. ${\mathrm{Hom}}_{k_L[G']}^{\mathrm{cont}}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }({\mathcal {M}}_{n,\mathbf {C}_p}^p,k_L))$ est de dimension finie pour tout $k_L[G']$ -module $\pi $ lisse et admissible.

4.3 Compléments

La preuve du théorème de finitude a d’autres applications; nous en donnons trois ci-dessous.

4.3.1 Multiplicités des représentations de G

La première application est valable pour F quelconque:

Théorème 4.22. Si $\pi $ est une $k_L$ -représentation lisse admissible de ${\mathrm{GL}}_2(F)$ , à caractère central, alors ${\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,\mathbf {C}_p},k_L))$ est de dimension finie sur $k_L$ .

Démonstration. L’argument utilisé dans la preuve du cor. 3.13 n’utilise pas l’hypothèse $F=\mathbf {Q}_p$ implicite dans ce corollaire, et fournit une suite exacte

$$ \begin{align*}0\to H^1({\mathrm{SL}}_2(F), \pi)\to S^1(\pi)\to {\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi^{\vee}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L))\to H^2({\mathrm{SL}}_2(F), \pi).\end{align*} $$

Puisque $\pi $ est admissible en tant que ${\mathrm{GL}}_2(F)$ -représentation et possède un caractère central (forcément trivial sur un sous-groupe ouvert de $F^{{\boldsymbol *}}$ ), $\pi $ est admissible en tant que ${\mathrm{SL}}_2(F)$ -représentation lisse. Le lemme 6.3 de [34] montre alors que $H^i({\mathrm{SL}}_2(F), \pi )$ est de dimension finie sur $k_L$ pour tout i. Puisque $S^1(\pi )$ est admissible en tant que $\check {G}$ -représentation par le théorème de finitude de Scholze, on en déduit que ${\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }, k_L))^{\check {G}_n}$ est de dimension finie sur $k_L$ . D’autre part, les arguments (purement géométriques et donc valables aussi quand $F\ne \mathbf {Q}_p$ ) utilisés dans les étapes $1-3$ de la preuve du lemme 4.13 fournissent une suite exacte

$$ \begin{align*}0\to H^1(\check{G}_n, \mathcal{C}^0(F^{\times}, k_L))\to H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p},k_L)\to H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L)^{\check{G}_n}.\end{align*} $$

En appliquant le foncteur ${\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi ^{\vee }, -)$ à cette suite exacte et en tenant compte de ce que l’on vient de démontrer, il suffit de vérifier que

$$ \begin{align*}\dim_{k_L} {\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi^{\vee}, H^1(\check{G}_n, \mathcal{C}^0(F^{\times}, k_L)))<\infty.\end{align*} $$

Le $k_L$ -espace vectoriel $W=H^1(\check {G}_n, \mathcal {C}^0(\mathcal {O}_F^{\times }, k_L))$ est de dimension finie (par admissibilité de la $\check {G}$ -représentation $\mathcal {C}^0(\mathcal {O}_F^{\times }, k_L)$ ) et si $\varpi $ est une uniformisante de F,

$$ \begin{align*}H^1(\check{G}_n, \mathcal{C}^0(F^{\times}, k_L))=H^1(\check{G}_n, {\mathrm{Ind}}_{\{1\}}^{\varpi^{\mathbf{Z}}} \mathcal{C}^0(\mathcal{O}_F^{\times}, k_L))={\mathrm{Ind}}_{\{1\}}^{\varpi^{\mathbf{Z}}} W.\end{align*} $$

On en déduit une injection

$$ \begin{align*}{\mathrm{Hom}}_{k_L[G]}^{\mathrm{cont}}(\pi^{\vee}, H^1(\check{G}_n, \mathcal{C}^0(F^{\times}, k_L))) \hookrightarrow (\pi\otimes_{k_L} W)^{{\mathrm{SL}}_2(F)},\end{align*} $$

et le membre de droite est de dimension finie sur $k_L$ car $\pi $ est admissible en tant que ${\mathrm{SL}}_2(F)$ -représentation et W est de dimension finie sur $k_L$ .

4.3.2 Multiplicité des représentations de ${\cal G}_{\mathbf {Q}_p}$

Si $\bar {\rho }: \mathcal {G}_{\mathbf {Q}_p}\to {\mathrm{GL}}_d(k_L)$ est une représentation continue, on pose

$$ \begin{align*}{\boldsymbol\Pi}^{\mathrm{geo}}_n(\bar{\rho}):={\mathrm{Hom}}_{k_L[\mathcal{G}_{\mathbf{Q}_p}]}(\bar{\rho}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}^{p},k_L))^{\vee}.\end{align*} $$

Le reste de ce numéro est consacré à la preuve du résultat suivant:

Théorème 4.23. Soit $\bar {\rho }: \mathcal {G}_{\mathbf {Q}_p}\to {\mathrm{GL}}_d(k_L)$ une représentation continue.

1. a) ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })$ est un G-module lisse, de longueur finie.

2. b) Si $d>2$ et si $\bar {\rho }$ est absolument irréductible, alors ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })=0$ .

Démonstration. a) Analogue à la preuve du cor. 2.12, grâce au th. 4.1.

b) Supposons que ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })\neq 0$ , et prenons un quotient irréductible $\pi $ de ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })$ . Alors $\pi ^{\vee }$ s’injecte dans ${\mathrm{Hom}}_{k_L[\mathcal {G}_{\mathbf {Q}_p}]}(\bar {\rho }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,\mathbf {C}_p}^{p},k_L))$ et donc $\bar {\rho }$ s’injecte dans ${\mathrm{Hom}}_G(\pi ^{\vee }, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,\mathbf {C}_p}^{p},k_L))$ . Les mêmes arguments que dans la preuve du lemme 4.13 combinés au fait que $\bar {\rho }$ ne peut pas intervenir dans $H^0_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }, k_L)$ et à la suite exacte 3.14 montrent que ${\mathrm{Hom}}_{k_L[\mathcal {G}_{\mathbf {Q}_p}]}(\bar {\rho }, S^1(\pi ))\ne 0$ .

Notons que $\pi $ n’est pas un caractère, car $S^1$ tue les caractères. Quitte à remplacer L par une extension finie, on peut supposer que $\pi $ est absolument irréductible. Soit $\mathcal {B}$ le bloc contenant $\pi $ et soit $\bar {r}$ la représentation semi-simple de dimension $2$ associée à $\mathcal {B}$ . On globalise $\bar {r}$ comme au début de ce chapitre et on considère le module $M=M_{\psi , \lambda , \mathfrak {m}}$ introduit dans la prop. 4.10.

Supposons que $\pi $ est supersingulière. Alors $\mathcal {B}=\{\pi \}$ et la prop. 4.10 montre que l’on dispose d’une suite exacte

$$ \begin{align*}0\to \pi\to M\to \pi'\to 0,\end{align*} $$

$\pi '$ étant une extension successive de copies de $\pi $ . En particulier $(\pi ')^{{\mathrm{SL}}_2(\mathbf {Q}_p)}=0$ , donc $S^0(\pi ')=0$ et $S^1(\pi )$ s’injecte dans $S^1(M)$ , qui lui-même s’injecte dans un $\mathcal {G}_{\mathbf {Q}_p}$ -module $\bar {r}$ -isotypique (prop. 4.12 et 4.11). On en déduit (via la prop. 5.4 de [61]) que $S^1(\pi )$ est $\bar {r}$ -isotypique, ce qui contredit le fait que ${\mathrm{Hom}}_{k_L[\mathcal {G}_{\mathbf {Q}_p}]}(\bar {\rho }, S^1(\pi ))\ne 0$ .

Le cas où $\pi $ n’est pas supersingulière est plus pénible. Dans ce cas on peut écrire $\bar {r}=\chi _1\oplus \chi _2$ pour deux caractères galoisiens $\chi _1, \chi _2$ .

Lemme 4.24. Soit Z un sous G-module de M et soit H un sous-groupe ouvert compact de $D_p^{{\boldsymbol *}}$ . Si $\mathcal {E}\in \{S^1(Z)^H, H^1(H, S^1(Z))\}$ , alors $\mathcal {E}$ est une représentation de dimension finie de $\mathcal {G}_{\mathbf {Q}_p}$ , dont les sous-quotients irréductibles sont de dimension $1$ .

Démonstration. Le fait que $\dim \mathcal {E}<\infty $ est une conséquence de l’admissibilité de $S^1(Z)$ . Soit $\alpha : S^1(Z)\to S^1(M)$ la flèche induite par l’inclusion $Z\subset M$ . On a une suite exacte

$$ \begin{align*}0\to (\ker(\alpha))^H\to S^1(Z)^H\to ({\mathrm{Im}}(\alpha))^H\to H^1(H, \ker(\alpha))\to H^1(H, S^1(Z))\to H^1(H, {\mathrm{Im}}(\alpha))\end{align*} $$

de représentations de dimension finie de $\mathcal {G}_{\mathbf {Q}_p}$ . La suite exacte

$$ \begin{align*}S^0(M/Z)\to S^1(Z)\to S^1(M)\end{align*} $$

montre que $\ker (\alpha )$ est un quotient de $S^0(M/Z)=S^0((M/Z)^{{\mathrm{SL}}_2(\mathbf {Q}_p)})$ en tant que $D^{{\boldsymbol *}}\times \mathcal {G}_{\mathbf {Q}_p}$ -module. Mais $(M/Z)^{{\mathrm{SL}}_2(\mathbf {Q}_p)}$ est une extension successive de caractères (quitte à remplacer L par une extension finie), donc $S^0((M/Z)^{{\mathrm{SL}}_2(\mathbf {Q}_p)})$ est une extension successive finie de caractères en tant que $D^{{\boldsymbol *}}$ -module et en tant que $\mathcal {G}_{\mathbf {Q}_p}$ -module. On en déduit que $(\ker (\alpha ))^H$ et $H^1(H, \ker (\alpha ))$ sont des extensions successives de caractères galoisiens.

Soit $T={\mathrm{Im}}(\alpha )$ , alors T est un sous $D^{{\boldsymbol *}}\times \mathcal {G}_{\mathbf {Q}_p}$ -module de $S^1(M)$ . On sait (prop. 4.12 et 4.11) que l’on dispose d’une injection $D^{{\boldsymbol *}}\times \mathcal {G}_{\mathbf {Q}_p}$ -équivariante $S^1(M)\subset \bar {r}\otimes _{k_L} U$ pour un $D^{{\boldsymbol *}}$ -module lisse admissible U avec action triviale de $\mathcal {G}_{\mathbf {Q}_p}$ . On a donc une injection $D^{{\boldsymbol *}}\times \mathcal {G}_{\mathbf {Q}_p}$ -équivariante $T\subset \bar {r}\otimes _{k_L} U$ . On a une suite exacte $D^{{\boldsymbol *}}\times \mathcal {G}_{\mathbf {Q}_p}$ -équivariante

$$ \begin{align*}0\to \chi_1\otimes U\to \bar{r}\otimes U\to \chi_2\otimes U\to 0\end{align*} $$

et donc une suite exacte $D^{{\boldsymbol *}}\times \mathcal {G}_{\mathbf {Q}_p}$ -équivariante

$$ \begin{align*}0\to \chi_1\otimes U_1\to T\to \chi_2\otimes U_2\to 0,\end{align*} $$

avec $U_i$ des sous $D^{{\boldsymbol *}}$ -modules de U. En passant à la H-cohomologie continue on voit que $T^H$ et $H^1(T,H)$ sont des extensions successives de $\chi _1$ et $\chi _2$ , ce qui permet de conclure.

Revenons à la preuve du théorème. Soit H un sous-groupe ouvert pro-p de $D^{{\boldsymbol *}}$ . Comme ${\mathrm{Hom}}_{k_L[\mathcal {G}_{\mathbf {Q}_p}]}(\bar {\rho }, S^1(\pi ))$ est lisse et non nulle, ${\mathrm{Hom}}_{k_L[\mathcal {G}_{\mathbf {Q}_p}]}(\bar {\rho }, S^1(\pi )^H)\ne 0$ . D’autre part, on dispose (prop. 4.10) d’une suite exacte de G-modules

$$ \begin{align*}0\to X\to Y\to \pi\to 0,\end{align*} $$

avec $X,Y$ des sous G-modules de M. Comme $\pi $ n’est pas un caractère (donc $\pi ^{{\mathrm{SL}}_2(\mathbf {Q}_p)}=0$ ) on a $S^0(\pi )=0$ , d’où une suite exacte

$$ \begin{align*}0\to S^1(X)\to S^1(Y)\to S^1(\pi)\to S^2(X),\end{align*} $$

ou encore

$$ \begin{align*}0\to (S^1(Y)/S^1(X))^H\to S^1(\pi)^H\to S^2(X)^H.\end{align*} $$

Pour arriver à une contradiction il suffit de montrer que ${\mathrm{Hom}}_{k_L[\mathcal {G}_{\mathbf {Q}_p}]}(\bar {\rho }, \mathcal {E})=0$ pour $\mathcal {E}\in \{(S^1(Y)/S^1(X))^H, S^2(X)^H\}$ . Si $\mathcal {E}=(S^1(Y)/S^1(X))^H$ cela suit du lemme 4.24, supposons donc que $\mathcal {E}=S^2(X)^H$ . Comme X est une extension successive de représentations qui sont soit des steinberg, soit des induites paraboliques, soit des caractères, et comme $S^2$ tue la steinberg et les induites (par le théorème de Ludwig) et transforme les caractères en des caractères, il s’ensuit que $S^2(X)^H$ est une extension successive de caractères en tant que $\mathcal {G}_{\mathbf {Q}_p}$ -module, ce qui permet de conclure.

Remarque 4.25. Si $d=2$ et $\bar {\rho }$ est absolument irréductible, alors on peut montrer (avec des arguments semblables à ceux utilisés ci-dessus) que ${\boldsymbol \Pi }^{\mathrm{geo}}_n(\bar {\rho })$ est dans le bloc de ${\mathrm{Rep}}^{{\mathrm{ladm}}}\, G$ découpé par $\bar {\rho }$ . Ce résultat n’est pas vrai quand $\bar {\rho }$ est réductible car un morphisme $\bar \rho \to H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\mathbf {C}_p},k_L)$ peut se factoriser par un quotient strict de $\bar \rho $ . Il est possible qu’il reste valable si on impose que $\bar \rho \to H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\mathbf {C}_p},k_L)$ soit injectif.

4.3.3 Vecteurs lisses du côté Lubin-Tate

Soit ${\mathrm{LT}}_{n,\mathbf {C}_p}:=\mathcal {M}_{\mathrm{LT}, \mathrm{G}_{\mathrm{n}}}\otimes _{\breve {\mathbf {Q}}_p} {\mathbf {C}_p}$ le n-ème étage de la tour de Lubin-Tate, et soit ${\mathrm{LT}}_{n,\mathbf {C}_p}^{p}$ le quotient par l’action de $p^{\mathbf {Z}}$ , p étant vu comme élément du centre de $\check {G}$ . Alors ${\mathrm{LT}}_{n,\mathbf {C}_p}^{p}$ est défini sur F, ce qui permet de définir ${\mathrm{LT}}_{n,K}^{p}$ pour toute extension finie K de F.

Théorème 4.26. On suppose que $F=\mathbf {Q}_p$ . Si K est une extension finie de $\mathbf {Q}_p$ , l’espace des vecteurs $\check {G}$ -lisses de $H^1_{\operatorname {\acute {e}t} }({\mathrm{LT}}^p_{n,K}, k_L)$ est de dimension finie sur $k_L$ .

Démonstration. Comme dans l’étape $1$ de la preuve du lemme 4.13, il suffit de voir que l’espace des vecteurs lisses de $H^1_{\operatorname {\acute {e}t} }({\mathrm{LT}}_{n,\mathbf {C}_p}^p, k_L)^{\mathcal {G}_K}$ est de dimension finie. Comme dans l’étape $2$ de la même preuve on obtient une suite exacte $0\to A\to H^1_{\operatorname {\acute {e}t} }({\mathrm{LT}}_{n,\mathbf {C}_p}^p, k_L)\to H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }^p, k_L)^{G_n}$ avec A de dimension finie, donc il suffit de voir que $\varinjlim _{j} H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }^p, k_L)^{G_n\times \mathcal {G}_K\times \check {G}_j}$ est de dimension finie. On va montrer que cet espace est nul.

Lemme 4.27. L’espace des vecteurs G-lisses de $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }^p, k_L)^{\mathcal {G}_K\times \check {G}_j}$ est de dimension finie.

Démonstration. Les suites spectrales usuelles (voir la preuve du lemme 4.13) montrent que l’on dispose d’une flèche $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{j,K}^p, k_L)\to H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }^p, k_L)^{\mathcal {G}_K\times \check {G}_j}$ dont le noyau et le conoyau sont de dimension finie sur $k_L$ . Si $f: A\to B$ est un morphisme G-équivariant entre des $k_L[G]$ -modules, dont le noyau et le conoyau sont de dimension finie sur $k_L$ , et si $A^{G-{\mathrm{lisse}}}$ est de dimension finie, alors $B^{G-{\mathrm{lisse}}}$ est aussi de dimension finie. Il suffit donc de voir que $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{j,K}^p, k_L)^{G-{\mathrm{lisse}}}$ est de dimension finie, ce qui découle du fait que $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{j,K}^p, k_L)$ est le dual d’une représentation lisse admissible de G.

Lemme 4.28. L’espace $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }^p, k_L)$ ne contient pas de sous-G-module non nul, de dimension finie sur $k_L$ .

Démonstration. Puisque L est arbitraire, il suffit de voir que $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }^p, k_L)$ ne contient pas de caractère lisse de G. Par l’étape $3$ de la preuve du lemme 4.13 il suffit de montrer la même assertion pour $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }, k_L)$ . On veut donc montrer que ${\mathrm{Hom}}_G^{\mathrm{cont}}(\delta , H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }, k_L))=0$ pour tout caractère lisse $\delta $ de G. Comme dans la preuve du cor. 3.13 on a une suite exacte

$$ \begin{align*}S^1(\delta^{-1})\to {\mathrm{Hom}}_G^{\mathrm{cont}}(\delta, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{\infty}, k_L))\to H^2({\mathrm{SL}}_2(\mathbf{Q}_p), \delta^{-1}).\end{align*} $$

Le lemme 7.4 de [25] combiné avec la trivialité de $S^1(1)$ (qui vient simplement du fait que le faisceau associé à la représentation triviale est le faisceau constant, qui a une cohomologie nulle en degré $1$ sur $\mathbf {P}^1$ ) montre que le terme à gauche est nul. Celui à droite l’est aussi: il suffit de voir que $H^2({\mathrm{SL}}_2(\mathbf {Q}_p), \mathbf {F}_p)=0$ . En utilisant la suite exacte $0\to \mathbf {F}_p\to \mathbf {Q}/\mathbf {Z}\to \mathbf {Q}/\mathbf {Z}\to 0$ et le fait que l’abélianisé de ${\mathrm{SL}}_2(\mathbf {Q}_p)$ est trivial, il suffit de voir que la p-torsion de $H^2({\mathrm{SL}}_2(\mathbf {Q}_p), \mathbf {Q}/\mathbf {Z})$ est nulle. Mais on voit facilement que $H^2({\mathrm{SL}}_2(\mathbf {Q}_p), \mathbf {Q}/\mathbf {Z})\simeq H^2({\mathrm{SL}}_2(\mathbf {Q}_p), \mathbf {R}/\mathbf {Z})$ et ce dernier groupe a été calculé par Moore [50], et il vaut le dual de Pontryagin du groupe des racines de l’unité dans $\mathbf {Q}_p$ . Le résultat s’en déduit.

Si l’on combine les deux lemmes on voit que l’espace des vecteurs G-lisses de $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }^p, k_L)^{\mathcal {G}_K\times \check {G}_j}$ est nul pour tout j, et donc $\varinjlim _{j} H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{\infty }^p, k_L)^{G_n\times \mathcal {G}_K\times \check {G}_j}=0$ .

Remarque 4.29. Le th. 1.24 combiné avec l’argument ci-dessus montre que les th. 4.26 et 4.1 sont en fait équivalents. Il semble raisonnable de penser que le th. 4.26 reste valable pour $F\ne \mathbf {Q}_p$ (alors que nous avons vu que le th. 4.1 est bien spécifique à $F=\mathbf {Q}_p$ ).

5 Factorisation de $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,\overline {\mathbf {Q}}_p}, L(1))$

Dans ce chapitre, on démontre notre résultat principal, à savoir la factorisation à la Emerton de la cohomologie étale géométrique de ${\cal M}_{n}^p$ (th. 5.15 ci-dessous).

Dans tout le chapitre, M désigne un $(\varphi ,N,{\cal G}_{\mathbf {Q}_p})$ -module, et nous renvoyons au $\mathrm {n}^{\mathrm{o}}$ 0.3.1 pour les définitions des objets qui lui sont associés: ${\mathrm{LL}}(M)$ , ${\mathrm{JL}}(M)$ , $M_{\mathrm{dR}}$ , ${\cal L}$ , $V_{M,{\cal L}}$ , $\Pi _{M,{\cal L}}$ ainsi que pour les notions de «supercuspidal», «spécial» et «de niveau $\leq n$ ».

On note $\Phi {\mathrm{N}}$ l’ensemble des M spéciaux ou supercuspidaux, $\Phi {\mathrm{N}}^p\subset \Phi {\mathrm{N}}$ le sous-ensemble des M tels que $p\in Z(\check G)$ agit trivialement sur ${\mathrm{JL}}(M)$ , et on rajoute un n en indice (i.e. $\Phi {\mathrm{N}}_n$ et $\Phi {\mathrm{N}}^p_n$ ) pour indiquer le sous-ensemble des M de niveau $\leq n$ . Si X est un $L[\check G]$ -module lisse avec action triviale de $p\in Z(\check G)$ , alors X a une décomposition

$$ \begin{align*}X=\oplus_MX[M]\otimes_L {\mathrm{JL}}(M),\end{align*} $$

où $\check {G}$ agit trivialement sur $X[M]$ . On pose aussi, pour alléger un peu les notations,

$$ \begin{align*}H^1_{\operatorname{pro\acute{e}t} }(-):=H^1_{\operatorname{pro\acute{e}t} }(-,L(1)),\quad H^1_{\operatorname{\acute{e}t} }(-):=H^1_{\operatorname{\acute{e}t} }(-,L(1)), \quad H^1_{\operatorname{\acute{e}t} }(-)^+:=H^1_{\operatorname{\acute{e}t} }(-,{\cal O}_L(1)).\end{align*} $$

5.1 Compléments à [16]

5.1.1 Multiplicités des représentations de ${\cal G}_{\mathbf {Q}_p}$

Le résultat suivant est l’un des résultats principaux de [16]. (Si $\delta $ est un caractère de $\mathbf {Q}_p^{\boldsymbol *}$ , on note

$$ \begin{align*}\delta_G:=\delta\circ\nu_G\quad{\mathrm{et}}\quad \delta_{\check G}:=\delta\circ\nu_{\check G}\end{align*} $$

les caractères de G et $\check G$ , et simplement $\delta $ le caractère de ${\mathrm{W}}_{\mathbf {Q}_p}$ qui lui sont associés.)

Théorème 5.1. Si $V\in {\mathrm{Rep}}_L{\cal G}_{\mathbf {Q}_p}$ est absolument irréductible, de dimension $\leq 2$ , alors

$$ \begin{align*}{\mathrm{Hom}}_{{\mathrm{W}}_{\mathbf{Q}_p}}(V, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p}))\simeq \begin{cases}\Pi_{M,{\cal L}}^{\boldsymbol *}\otimes_L {\mathrm{JL}}(M) &\text{si } V=V_{M,{\cal L}} \text{ et } M \text{de niveau} \leq n,\\ ({\mathrm{St}}^{\mathrm{cont}}\otimes\delta_G)^{\boldsymbol *} \otimes\delta_{\check G} &\text{si } V=\delta \text{ et } \delta \text{ est de niveau} \leq n,\\ 0 &\text{si } V \text{ n'est pas de niveau} \leq n. \end{cases} \end{align*} $$

Remarque 5.2.

1. (i) Dans [16], le cas des caractères n’est pas traité, mais il se prouve facilement en remarquant que, si M est supercuspidal, $X_{\mathrm{st}}(M)$ n’a pas de sous- ${\cal G}_{\mathbf {Q}_p}$ -représentation de dimension $1$ (cf. (i) de [16, prop. 2.5]), et donc que les caractères de ${\cal G}_{\mathbf {Q}_p}$ vivent dans les $[M]$ -composantes, pour M spécial. Comme celles-ci proviennent, par torsion par un caractère, de la cohomologie du demi-plan de Drinfeld, on conclut en utilisant [16, th. 1.7].

2. (ii) Dans [16], on prouve aussi que ${\mathrm{Hom}}_{{\mathrm{W}}_{\mathbf {Q}_p}}(V, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n,\mathbf {C}_p}))=0$ si V est absolument irréductible, de dimension $\geq 3$ . La preuve qui y est donnée est combinatoirement assez pénible. Le lecteur trouvera une preuve plus naturelle de cet énoncé un peu plus loin (th. 5.10).

5.1.2 Considérations topologiques

Si $\mathcal {F}$ est un L-espace vectoriel localement convexe muni d’une action continue de G, on note $\mathcal {F}^b$ l’espace des vecteurs G-bornés de $\mathcal {F}$ , i.e. les $v\in \mathcal {F}$ pour lesquels $\{g\cdot v,\ g\in G\}$ est borné dans $\mathcal {F}$ .

Lemme 5.3.

1. a) Si $\Pi $ est une L-représentation de Banach unitaire de G, alors $(\Pi ^{\boldsymbol *})^b=\Pi ^{\boldsymbol *}$ .

2. b) Si $\pi $ est une L-représentation lisse admissible de G, de longueur finie, alors $(\pi ^{\boldsymbol *})^b\simeq \widehat {\pi }^{\boldsymbol *}$ , où $\widehat {\pi }$ est le complété unitaire universel de $\pi $ .

3. c) Si $\Pi $ est une représentation unitaire admissible de G, de longueur finie, alors $(\Pi ^{\mathrm{an},*})^b=\Pi ^{\boldsymbol *}$ .

Démonstration. D’après le théorème de Banach-Steinhaus, si $\Pi $ est un fréchet (en particulier, si $\Pi $ est un banach), $\mu \in \Pi ^{\boldsymbol *}$ est G-borné si et seulement si $\{\langle \mu ,g^{-1}\cdot v\rangle ,\ g\in G\}$ est borné, pour tout $v\in G$ . On en déduit facilement que, si $\Pi $ est un banach unitaire, tout $\mu $ est G-borné, ce qui prouve le a).

Pour prouver le b), il suffit de remarquer que $\widehat {\pi }$ est le complété par la norme définie par ${\cal O}_L[G]\cdot v_1+\cdots +{\cal O}_L[G]\cdot v_r$ , pour tous $v_1,\dots ,v_r$ tels que ce module soit un réseau de $\pi $ . Un élément de $\widehat {\pi }^{\boldsymbol *}$ est donc un élément de $\pi ^{\boldsymbol *}$ borné sur ${\cal O}_L[G]\cdot v_1+\cdots +{\cal O}_L[G]\cdot v_r$ , pour tous les $v_1,\dots ,v_r$ comme ci-dessus; c’est donc un élément G-borné de $\pi ^{\boldsymbol *}$ d’après le théorème de Banach-Steinhaus.

Enfin, le c) est [15, th. 0.2].

Si $X,Y$ sont des L-espaces vectoriels localement convexes, on écrit ${\mathrm{Hom}}(X,Y)$ pour l’espace des applications L-linéaires continues de X dans Y, muni de la topologie forte (i.e. de la convergence sur les parties bornées de X), et on note simplement $X'={\mathrm{Hom}}(X,L)$ le dual fort de X.

Lemme 5.4. Soit E un L-fréchet nucléaire et soient $F,D$ des L-fréchets. Il existe un isomorphisme naturel

$$ \begin{align*}{\mathrm{Hom}}(E, F\widehat{\otimes}_L D)\simeq {\mathrm{Hom}}(E, F)\widehat{\otimes}_L D.\end{align*} $$

Démonstration. Comme E est un L-fréchet nucléaire, il est bornologique et semi-réflexif, donc par [64, prop. 18.8], on a un isomorphisme naturel $E'\widehat {\otimes }_{L} X\simeq {\mathrm{Hom}}(E, X)$ pour tout L-fréchet X. On a donc

$$ \begin{align*}{\mathrm{Hom}}(E, F\widehat{\otimes}_L D)\simeq E'\widehat{\otimes}_{L} ( F\widehat{\otimes}_L D)\simeq (E'\widehat{\otimes}_{L} F)\widehat{\otimes}_{L} D\simeq {\mathrm{Hom}}(E, F)\widehat{\otimes}_{L} D,\end{align*} $$

ce qui permet de conclure.

Lemme 5.5. Si X est un L-espace localement convexe séparé muni d’une action continue de G, et si B est un L-banach muni de l’action triviale de G, alors on a un isomorphisme naturel $(X\widehat {\otimes }_L B)^G\simeq X^G\widehat {\otimes }_L B$ .

Démonstration. Si $(e_i)_{i\in I}$ est une base orthonormale de B, alors $X\widehat {\otimes }_L B=\ell ^{\infty }_0(I,X)$ (suites tendant vers $0$ suivant le filtre des complémentaires des parties finies), et $(X\widehat {\otimes }_L B)^G=\ell ^{\infty }_0(I,X^G)=X^G\widehat {\otimes }_L B$ .

Rappelons que $H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}_{n, \mathbf {C}_p})$ est un espace de Fréchet, en tant que limite inverse des espaces de Banach $H^1_{\operatorname {\acute {e}t} }(U_i)$ (de boule unité $H^1_{\operatorname {\acute {e}t} }(U_i)^+$ ), si $\{U_i\}_{i\geq 1}$ est un recouvrement Stein de $\mathcal {M}_{n, \mathbf {C}_p}$ . Le résultat suivant est [16, prop. 2.12].

Proposition 5.6. L’application naturelle $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}_{n, \mathbf {C}_p})\to H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}_{n, \mathbf {C}_p})$ est injective et induit un isomorphisme

$$ \begin{align*}H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n, \mathbf{C}_p})\simeq H^1_{\operatorname{pro\acute{e}t} }(\mathcal{M}_{n, \mathbf{C}_p})^b_.\end{align*} $$

5.1.3 Multiplicités de représentations de G

Proposition 5.7. Soit $\Pi $ une L-représentation de Banach unitaire, admissible, absolument irréductible de G. Alors

$$ \begin{align*}{\mathrm{Hom}}_G(\Pi^{\boldsymbol *}, L\otimes \Omega^1(\mathcal{M}^p_{n,\mathbf{Q}_p}))\simeq \begin{cases}\mathcal{L}\otimes_L {\mathrm{JL}}(M) &\text{si } \Pi=\Pi_{M,{\cal L}} \text{ et } M \text{ de niveau} \leq n,\\ \delta_{\check G} &\text{si } \Pi={\mathrm{St}}^{\mathrm{cont}}\otimes \delta_{G}, \delta \text{ de niveau} \leq n ,\\ 0 &{\text{sinon.}}\end{cases}\end{align*} $$

Démonstration. D’après la discussion ci-dessus il suffit de comprendre la multiplicité de $\Pi ^{\boldsymbol *}$ dans $(L\otimes \Omega ^1(\mathcal {M}^p_{n,\mathbf {Q}_p}))[M]$ pour tout $M\in \Phi {\mathrm{N}}^p$ .

Si M est spécial, on se ramène, par torsion, à $M={\mathrm{Sp}}$ , et $(L\otimes \Omega ^1(\mathcal {M}_{n,\mathbf {Q}_p}^p))[M]$ est alors l’espace des formes différentielles sur le demi-plan de Drinfeld, dont la structure est très simple, voir [16, prop. 1.6]. Le résultat s’en déduit aisement dans ce cas.

On suppose dans ce qui suit que M est supercuspidal. Le théorème principal de [23] fournit un isomorphisme ³⁰

$$ \begin{align*}j: (L\otimes H^1_{\mathrm{dR}}(\mathcal{M}^p_{n,\mathbf{Q}_p}))[M]\simeq M_{\mathrm{dR}}\otimes_L {\mathrm{LL}}(M)^{\boldsymbol *}\end{align*} $$

et, pour chaque $\mathcal {L}$ , une suite exacte

$$ \begin{align*}0\to (\Pi_{M,\mathcal{L}}^{\mathrm{an}})^{\boldsymbol *}\to (L\otimes\Omega^1(\mathcal{M}^p_{n,\mathbf{Q}_p}))[M]\to (M_{\mathrm{dR}}/\mathcal{L})\otimes_{L} {\mathrm{LL}}(M)^{\boldsymbol *}\to 0,\end{align*} $$

la flèche $(L\otimes \Omega ^1(\mathcal {M}^p_{n,\mathbf {Q}_p}))[M]\to (M_{\mathrm{dR}}/\mathcal {L})\otimes _{L} {\mathrm{LL}}(M)^{\boldsymbol *}$ étant induite par la flèche naturelle $\Omega ^1(\mathcal {M}^p_{n,\mathbf {Q}_p})\to H^1_{\mathrm{dR}}(\mathcal {M}^p_{n,\mathbf {Q}_p})$ et par l’isomorphisme j. Distinguons deux cas:

• • $\Pi $ est une série principale ou une tordue de la Steinberg. Dans ce cas, ${\mathrm{Hom}}_G (\Pi ^{\boldsymbol *}, (\Pi _{M,\mathcal {L}}^{\mathrm{an}})^{\boldsymbol *})=0$ et ${\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, {\mathrm{LL}}(M)^{\boldsymbol *})=0$ (le premier point découle du point c) du lemme 5.3, le second résulte de ce que ${\mathrm{LL}}(M)$ est supercuspidale, alors que les vecteurs lisses de $\Pi $ sont de la série principale).

• • $\Pi ={\boldsymbol \Pi }(V)$ avec V irréductible de dimension $2$ .

  • $\diamond $ Si V n’est pas de type M, alors ${\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, (\Pi _{M,\mathcal {L}}^{\mathrm{an}})^{\boldsymbol *})=0$ (par le point c) du lemme 5.3 et l’injectivité de la correspondance $V\mapsto {\boldsymbol \Pi }(V)$ pour V irréductible de dimension $2$ ), et ${\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, {\mathrm{LL}}(M)^{\boldsymbol *})=0$ (par la compatibilité de la correspondance de Langlands locale p-adique avec la classique), donc ${\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, (L\otimes \Omega ^1(\mathcal {M}^p_{n,\mathbf {Q}_p}))[M])=0$ dans ce cas.

  • $\diamond $ Si V est de type M, disons $V=V_{M, \mathcal {L}}$ , en appliquant ${\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, -)$ à la suite exacte ci-dessus on voit que ${\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, (L\otimes \Omega ^1(\mathcal {M}^p_{n,\mathbf {Q}_p}))[M])\ne 0$ . En appliquant le même foncteur à une suite exacte du type ci-dessus, mais avec un autre $\mathcal {L}'\subset M_{\mathrm{dR}}$ (et en utilisant le fait que ${\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, (\Pi _{M, \mathcal {L'}}^{\mathrm{an}, *}))=0$ , qui découle encore du lemme 5.3), on en déduit que ${\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, (L\otimes \Omega ^1(\mathcal {M}^p_{n,\mathbf {Q}_p}))[M])$ est de dimension au plus $1$ et s’injecte dans $\mathcal {L}$ , ce qui permet de conclure.

Théorème 5.8. Soit $\Pi $ une L-représentation de Banach unitaire, admissible, absolument irréductible de G. Alors

$$ \begin{align*}{\mathrm{Hom}}_G(\Pi^{\boldsymbol *}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}^p_{n, \mathbf{C}_p}))\simeq \begin{cases}V_{M,{\cal L}}\otimes_L {\mathrm{JL}}(M) &\text{si } \Pi=\Pi_{M,{\cal L}}, \text{ et } M \text{ de niveau} \leq n,\\ \delta\otimes \delta_{\check G} &\text{si } \Pi={\mathrm{St}}^{\mathrm{cont}}\otimes \delta_G, \delta \text{ de niveau} \leq n ,\\ 0 &{\text{sinon}}.\end{cases}\end{align*} $$

Démonstration. On décompose $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ selon les divers $M\in \Phi {\mathrm{N}}^p_n$ . Si M est spécial, par torsion on se ramène au cas $M={\mathrm{Sp}}$ , et alors

$$ \begin{align*}H^1_{\operatorname{\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p})[M]\simeq ({\mathrm{St}}^{\mathrm{cont}})^{\boldsymbol *},\end{align*} $$

par [16], ce qui permet de conclure.

On suppose par la suite que M est supercuspidal. Nous allons montrer d’abord que l’on peut remplacer $\Pi $ par $\Pi ^{\mathrm{an}}$ et $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ par $H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ sans changer les multiplicités. (Le passage de $\Pi $ à $\Pi ^{\mathrm{an}}$ va nous permettre d’utiliser le lemme 5.4.)

Lemme 5.9. Les injections $\Pi ^{\boldsymbol *}\to (\Pi ^{\mathrm{an}})^{\boldsymbol *}$ et $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})\to H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ induisent un isomorphisme

$$ \begin{align*}{\mathrm{Hom}}_G((\Pi^{\mathrm{an}})^{\boldsymbol *}, H^1_{\operatorname{pro\acute{e}t} }(\mathcal{M}^p_{n, \mathbf{C}_p})) \overset{\sim}{\to} {\mathrm{Hom}}_G(\Pi^{\boldsymbol *}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}^p_{n, \mathbf{C}_p})).\end{align*} $$

Démonstration. Tout morphisme G-équivariant $f: (\Pi ^{\mathrm{an}})^{\boldsymbol *}\to H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ doit envoyer $\Pi ^{\boldsymbol *}$ dans $H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})^b$ , qui s’identifie à $H^1_{\operatorname {\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ par la prop. 5.6. Cela fournit une flèche

$$ \begin{align*}\iota: {\mathrm{Hom}}_G((\Pi^{\mathrm{an}})^{\boldsymbol *}, H^1_{\operatorname{pro\acute{e}t} }(\mathcal{M}^p_{n, \mathbf{C}_p})) \to {\mathrm{Hom}}_G(\Pi^{\boldsymbol *}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}^p_{n, \mathbf{C}_p})),\end{align*} $$

dont l’injectivité est une conséquence de la densité de $\Pi ^{\boldsymbol *}$ dans $(\Pi ^{\mathrm{an}})^{\boldsymbol *}$ .

Soit $f: \Pi ^{\boldsymbol *}\to H^1_{\operatorname {\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ une flèche G-équivariante continue. Soit K un sous-groupe ouvert compact de G et soit $D(K)$ (resp. $\Lambda (K)$ ) l’algèbre des distributions (resp. des mesures) sur K à valeurs dans L. Le G-Fréchet $H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ est un $D(K)$ -module, car il s’identifie à un sous-fréchet K-stable de $\Omega ^1(\mathcal {M}^p_{n, \mathbf {C}_p})= \Omega ^1(\mathcal {M}_{n,\mathbf {Q}_p}^p)\widehat {\otimes }_{\mathbf {Q}_p} \mathbf {C}_p$ , et ce dernier est un $D(K)$ -module topologique par le th. 3.2 de [23]. Donc f se prolonge en une application $f: \Pi ^{\boldsymbol *}\otimes _{\Lambda (K)} D(K)\to H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ . Par le théorème de Schneider et Teitelbaum (th. 7.1 de [65]) le terme de gauche s’identifie à $(\Pi ^{\mathrm{an}})^{\boldsymbol *}$ , et l’application qui s’en déduit $\tilde {f}: (\Pi ^{\mathrm{an}})^{\boldsymbol *}\to H^1_{\operatorname {pro\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p})$ est G-équivariante, continue et un antécédent de f, ce qui montre que $\iota $ est bien un isomorphisme.

Soit $M\in \Phi {\mathrm{N}}^p_{n}$ supercuspidal. Le th. 5.11 de [16] montre l’existence d’un diagramme commutatif de G-fréchets

les flèches verticales étant injectives (car M est de pente $1/2$ , et $X^+_{\mathrm{st}}(M)\to {\mathbf {C}_p}\otimes _{\mathbf {Q}_p}M_{\mathrm{dR}}$ est injective), d’image fermée (comme le montre le th. 1.8 de [17]). On en déduit une suite exacte de G-fréchets

$$ \begin{align*}0\to H^1_{\operatorname{pro\acute{e}t} }(\mathcal{M}^p_{n,\mathbf{C}_p})[M]\to (L\otimes\Omega^1(\mathcal{M}^p_{n, \mathbf{C}_p}))[M] \to \tfrac{M_{\mathrm{dR}}\otimes {\mathbf{C}_p}}{X_{\mathrm{st}}^+(M)}\widehat{\otimes}_L {\mathrm{LL}}(M)^{\boldsymbol *}\to 0.\end{align*} $$

En appliquant ${\mathrm{H}}(-):={\mathrm{Hom}}_G((\Pi ^{\mathrm{an}})^{\boldsymbol *},-)$ , et en tenant compte des résultats ci-dessus, on obtient

$$ \begin{align*} {\mathrm{H}}\big(H^1_{\operatorname{\acute{e}t} }(\mathcal{M}^p_{n, \mathbf{C}_p})[M]\big)&\simeq {\mathrm{H}}\big(H^1_{\operatorname{pro\acute{e}t} }(\mathcal{M}_{n,\mathbf{C}_p})[M]\big)\\ &\simeq{\mathrm{Ker}}\big[\, {\mathrm{H}}\big((L\otimes\Omega^1(\mathcal{M}_{n,\mathbf{Q}_p}))[M]\widehat{\otimes}_{\mathbf{Q}_p} \mathbf{C}_p\big) \to {\mathrm{H}}\big(\tfrac{M_{\mathrm{dR}}\otimes {\mathbf{C}_p}}{X_{\mathrm{st}}^+(M)}\widehat{\otimes}_L {\mathrm{LL}}(M)^{\boldsymbol *}\big)\,\big]\\ & \simeq {\mathrm{Ker}}\big[\, {\mathrm{H}}\big((L\otimes\Omega^1(\mathcal{M}_{n,\mathbf{Q}_p}))[M]\big)\widehat{\otimes}_{\mathbf{Q}_p} \mathbf{C}_p\to \tfrac{M_{\mathrm{dR}}\otimes {\mathbf{C}_p}}{X_{\mathrm{st}}^+(M)}\widehat{\otimes}_L {\mathrm{H}}\big({\mathrm{LL}}(M)^{\boldsymbol *}\big)\,\big] \end{align*} $$

On a ${\mathrm{Hom}}_G((\Pi ^{\mathrm{an}})^{\boldsymbol *}, (L\otimes \Omega ^1(\mathcal {M}_{n,\mathbf {Q}_p}))[M])=0$ , par la prop. 5.7 et un argument comme dans le lemme 5.9, sauf si $\Pi =\Pi _{M, \mathcal {L}}$ , auquel cas l’espace en question est $\mathcal {L}$ . On peut donc supposer que $\Pi =\Pi _{M, \mathcal {L}}$ , et alors $ {\mathrm{Hom}}_G((\Pi ^{\mathrm{an}})^{\boldsymbol *}, {\mathrm{LL}}(M)^{\boldsymbol *})\simeq {\cal L}$ , donc

$$ \begin{align*} {\mathrm{Hom}}_G(\Pi^{\boldsymbol *}, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}^p_{n, \mathbf{C}_p}))&\simeq {\mathrm{Ker}}\big(\mathcal{L}\otimes_{\mathbf{Q}_p} \mathbf{C}_p\to \tfrac{M_{\mathrm{dR}}\otimes {\mathbf{C}_p}}{X_{\mathrm{st}}^+(M)}\big)\\ &\simeq X_{\mathrm{st}}^+(M)\cap (\mathcal{L}\otimes_{\mathbf{Q}_p} \mathbf{C}_p)\simeq V_{M,\mathcal{L}}, \end{align*} $$

ce qui permet de conclure.

Le théorème de finitude 4.1 combiné au résultat ci-dessus permet d’obtenir une preuve nettement plus naturelle (mais pas forcément plus simple…) du résultat suivant, un des plus délicats de [16].

Théorème 5.10. Si V est une L-représentation absolument irréductible de ${\cal G}_{\mathbf {Q}_p}$ , de dimension $\geq 3$ , alors

$$ \begin{align*}{\mathrm{Hom}}_{{\cal G}_{\mathbf{Q}_p}}(V, H^1_{\operatorname{\acute{e}t} }(\mathcal{M}^p_{n, \mathbf{C}_p}))=0.\end{align*} $$

Démonstration. Si ce n’est pas le cas, la G-représentation $\Pi (V)={\mathrm{Hom}}_{{\cal G}_{\mathbf {Q}_p}}(V, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p}))^{\boldsymbol *}$ est une L-représentation de Banach (lemme 2.16) qui possède un réseau $\Pi (V^+)$ dont la réduction modulo est de longueur finie (par le théorème de finitude), donc admissible. Ainsi $\Pi (V)$ est une L-représentation de Banach unitaire, admissible, de longueur finie. Par une conséquence du lemme de Schur [24, lemme 3.14], quitte à remplacer L par une extension finie, on peut supposer que $\Pi (V)$ contient une L-représentation de Banach unitaire, admissible, absolument irréductible $\Pi $ . Mais alors on obtient une injection $V\to {\mathrm{Hom}}_G(\Pi ^{\boldsymbol *}, H^1_{\operatorname {\acute {e}t} }(\mathcal {M}^p_{n, \mathbf {C}_p}))$ , ce qui contredit le th. 5.8.

5.2 Familles de représentations potentiellement semi-stables

Si $M={\mathrm{Sp}}\otimes \eta $ est spécial (note 0.3.1), on pose $R_{M,{\cal B}}=L$ . On pose aussi $\rho _{{\cal B},M}=0$ et ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})=0$ , sauf si ${\cal B}$ est le bloc de ${\mathrm{St}}\otimes \bar \eta $ , où $\bar \eta $ est la réduction modulo p de $\eta $ , auquel cas on pose $\rho _{{\cal B},M}=\eta $ (vu comme caractère de ${\cal G}_{\mathbf {Q}_p}$ via la théorie locale du corps de classes), et ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})=({\mathrm{St}}^{\mathrm{cont}}\otimes \eta )^{\boldsymbol *}$ .

Supposons maintenant que M est supercuspidal et fixons un bloc $\cal B$ . Soit $I_{M, \cal B}$ l’intersection des idéaux maximaux de $R_{\cal B}^{{\mathrm{ps}},\delta _M}[1/p]$ tels que la spécialisation en du pseudo-caractère universel soit la trace d’une représentation de de Rham à poids $0$ et $1$ , et de type M (et donc de déterminant $\delta _M\varepsilon $ ). L’anneau

$$ \begin{align*}R_{{\cal B},M}:=R_{\cal B}^{{\mathrm{ps}},\delta_M}[1/p]/I_{\cal B, M}\end{align*} $$

est alors réduit, de Jacobson, et on note $R^+_{{\cal B},M}$ l’image de $R_{\cal B}^{{\mathrm{ps}},\delta _M}$ dans $R_{{\cal B},M}$ . On a donc $R_{{\cal B},M}:=R^+_{{\cal B},M}[\tfrac {1}{p}]$ .

Théorème 5.11. L’anneau $R_{{\cal B},M}$ s’identifie à l’anneau des fonctions analytiques bornées sur un ouvert de $\mathbf {P}^1$ , est un produit fini d’anneaux principaux, et il existe une unique (à isomorphisme près) représentation

$$ \begin{align*}\rho_{{\cal B},M}:{\cal G}_{\mathbf{Q}_p}\to{\mathrm{GL}}_2(R_{{\cal B},M})\end{align*} $$

telle que

$$ \begin{align*}{\mathrm{Tr}}\circ \rho_{{\cal B},M}=\alpha_{{\cal B},M}\circ T_{\cal B}^{\delta_M}.\end{align*} $$

Démonstration. L’unicité de $\rho _{{\cal B},M}$ est une conséquence du lemme 5.12 ci-dessous et de l’irréductibilité des $V_{M,{\cal L}}$ (conséquence de celle de M). L’existence de $\rho _{{\cal B},M}$ et les autres propriétés de $R_{{\cal B},M}$ sont établies dans [19, th. 0.1].

Lemme 5.12. Soit A un anneau principal ayant une infinité d’idéaux premiers (ou un produit de tels anneaux), et soient $V,W$ des représentations de $\mathcal {G}_{\mathbf {Q}_p}$ localement libres de type fini sur A et dont les spécialisations en tout point fermé de ${\mathrm{Spec}}(A)$ sont absolument irréductibles. Si ces spécialisations sont isomorphes pour tout point fermé, alors V et W sont isomorphes.

Démonstration. Supposons A principal (donc intègre). Les représentations ont même trace modulo tout idéal maximal, et donc ont même trace. Elles sont irréductibles sur le corps des fractions K de A car, sinon, elles seraient réductibles modulo presque tout idéal maximal de A; il s’ensuit qu’elles sont isomorphes sur K. Si $V_{\sigma }$ et $W_{\sigma }$ désignent les matrices de $\sigma \in {\cal G}_{\mathbf {Q}_p}$ dans des bases de V et W sur A, il existe $M\in {\mathrm{GL}}_d(K)$ telle que $V_{\sigma }=M^{-1}W_{\sigma } M$ , pour tout $\sigma $ .

La théorie des diviseurs élémentaires permet d’écrire M sous la forme $PDQ$ , avec $P,Q\in {\mathrm{GL}}_d(A)$ et D diagonale de $(\lambda _1,\dots ,\lambda _d)$ et $\lambda _i\mid \lambda _{i+1}$ . Changer de bases permet de supposer que $P=Q=1$ , et quitte à multiplier M par une matrice scalaire, on peut supposer que $\lambda _1$ est une unité. Il s’agit de prouver que tous les $\lambda _i$ sont des unités. Dans le cas contraire, il y a un i minimum qui n’est pas une unité, et la relation $V_{\sigma }=D^{-1}W_{\sigma } D$ implique que V et W ne sont pas irréductibles modulo les idéaux maximaux divisant $\lambda _i$ , contrairement à l’hypothèse.

Ceci permet de conclure dans le cas A principal. Le cas général s’en déduit en décomposant tout via les idempotents de A correspondant à chaque facteur de A.

Remarque 5.13. Pour la plupart des blocs $\mathcal {B}$ le th. 5.11 découle facilement des résultats de Kisin [46] et de l’observation [59] que l’espace rigide associé à $R_{{\cal B},M}$ s’identifie à un ouvert de la droite projective analytique (en utilisant la filtration de Hodge des diverses représentations interpolées par cet anneau), ce qui permet de montrer que cet anneau est un produit fini d’anneaux principaux. Les blocs délicats sont ceux correspondant à un twist des représentations $1\oplus 1$ et $1\oplus \varepsilon $ (cette dernière seulement pour $p=3$ ). L’approche de [19] permet de traiter tous les blocs sur le même pied.

Si x est un idéal maximal de $R_{{\cal B},M}$ on note $\kappa (x)$ son corps résiduel (une extension finie de L) et $\rho _x$ la spécialisation de $\rho _{{\cal B},M}$ en x.

Définition 5.14. On définit un $R_{{\cal B},M}[G]$ -module ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})$ de telle sorte que pour tout idéal maximal x de $R_{{\cal B},M}$ on ait

$$ \begin{align*}\kappa(x)\otimes_{R_{{\cal B},M}} {\boldsymbol\Pi}^{\boldsymbol *}(\rho_{{\cal B},M})={\boldsymbol\Pi}(\rho_x)^{\boldsymbol *}.\end{align*} $$

Pour cela, on part d’un $R^+_{{\cal B},M}$ -réseau $\mathcal {G}_{\mathbf {Q}_p}$ -stable $\rho _{{\cal B},M}^{\diamond ,+}$ du $R_{{\cal B},M}$ -dual de $\rho _{{\cal B},M}$ . Le dual de Pontryagin de $\rho _{{\cal B},M}^{\diamond ,+}$ est une limite inductive $\varinjlim _i V_i$ de représentations de dimension $2$ sur des quotients de $R_{{\cal B},M}^+$ et on pose ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})=L\otimes _{{\cal O}_L}\varprojlim _i{\boldsymbol \Pi }(V_i)^{\vee }$ . On a aussi ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})=\mathbf {D}(\rho _{{\cal B},M}^{\diamond ,+})^{\natural }\boxtimes \mathbf {P}^1$ ou encore ${\boldsymbol \Pi }^{\boldsymbol *}(\rho _{{\cal B},M})={\mathrm{Hom}}_{R_{{\cal B},M}}({\mathrm{LL}}_{M,{\cal B}}^{[0,1]},R_{{\cal B},M})$ , où ${\mathrm{LL}}_{M,{\cal B}}^{[0,1]}$ est la complétée ${\cal B}$ -adique de ${\mathrm{LL}}(M)$ (cf. [19]) et on ne considère que les morphismes continus.

5.3 Factorisation en niveau fini

Ce paragraphe est consacré à la preuve du résultat suivant (l’espace $H^1_{\operatorname {\acute {e}t} }({\mathcal {M}}^p_{n,\overline {\mathbf {Q}}_p})$ est défini dans l’introduction, voir aussi le numéro ci-dessous, et la complétion est p-adique).

Théorème 5.15. Si L est assez grand pour que tous les ${\mathrm{JL}}(M)$ soient définis sur L, on a une décomposition

$$ \begin{align*}H^1_{\operatorname{\acute{e}t} }({\mathcal{M}}^p_{n,\overline{\mathbf{Q}}_p})\simeq \oplus_M\big(\widehat{\oplus}_{\cal B} \ {\boldsymbol\Pi}^{\boldsymbol *}(\rho_{{\cal B},M}) \otimes \rho_{{\cal B},M}\otimes \check{R}_{{\cal B},M}\big)\otimes_L{\mathrm{JL}}(M),\end{align*} $$

où les produits tensoriels non spécifiés sont au-dessus de $R_{{\cal B},M}$ et $\check {R}_{{\cal B},M}={\mathrm{Hom}}(\check {R}_{{\cal B},M},L)$ .

Démonstration. C’est une conséquence de la prop. 5.21, de la rem. 5.23, et du (ii) du th. 5.24.

5.3.1 Extension des scalaires à $\overline {\mathbf {Q}}_p$ ou à $\mathbf {C}_p$

On pose

$$ \begin{align*}H^{i,+}_{\overline{\mathbf{Q}}_p}:=H^i_{\operatorname{\acute{e}t} }({\cal M}^p_{n,\overline{\mathbf{Q}}_p})^+=\varprojlim\nolimits_k\big(\varinjlim\nolimits_{[K:\mathbf{Q}_p]<\infty} H^i_{\operatorname{\acute{e}t} }({\cal M}^p_{n,K},({\cal O}_L/{p^k})(1))\big),\end{align*} $$

i.e. la cohomologie complétée de la tour $({\cal M}^p_{n,K})_{[K:\mathbf {Q}_p]<\infty }$ (noter que n est fixé ici). Soit $H^{i}_{\overline {\mathbf {Q}}_p}=L\otimes _{\mathcal {O}_L} H^{i,+}_{\overline {\mathbf {Q}}_p}$ .

Pour simplifier les notations, posons pour $i\geq 0$ et $?\in \{\mathbf {C}_p, K\}$ , avec $[K:\mathbf {Q}_p]<\infty $ ,

$$ \begin{align*}H^i_{k,?}:=H_{\operatorname{\acute{e}t} }^i({\cal M}^p_{n,?}, ({\cal O}_L/{p^k})(1)), \quad H^{i,+}_{?}:=H_{\operatorname{\acute{e}t} }^i({\cal M}^p_{n,?})^+,\quad H^i_{k,\overline{\mathbf{Q}}_p}:=\varinjlim_K H^i_{k,K}.\end{align*} $$

On a donc $H^{i,+}_{?}\simeq \varprojlim _k H^i_{k,?}$ pour $i\leq 1$ (seuls cas dont nous aurons besoin) et $H^{i,+}_{\overline {\mathbf {Q}}_p}\simeq \varprojlim _{k} H^i_{k,\overline {\mathbf {Q}}_p}$ .

Proposition 5.16. L’application naturelle

$$ \begin{align*}H^{1,+}_{\overline{\mathbf{Q}}_p}\to H^{1,+}_{\mathbf{C}_p}\end{align*} $$

est injective et identifie $H^{1,+}_{\overline {\mathbf {Q}}_p}$ à l’ensemble des $x\in H^{1,+}_{\mathbf {C}_p}$ presque lisses sous l’action de ${\cal G}_{\mathbf {Q}_p}$ (i.e. qui, pour pour tout $k\geq 1$ , sont fixes modulo $p^k$ par un sous-groupe ouvert de ${\cal G}_{\mathbf {Q}_p}$ ).

Démonstration. La suite de Hochschild-Serre fournit des suites exactes

$$ \begin{align*}0\to H_{\operatorname{\acute{e}t} }^1({\mathcal{G}}_K, H^0_{k,\mathbf{C}_p})\to H^1_{k,K}\to (H^1_{k,\mathbf{C}_p})^{{\mathcal{G}}_K} \to H^2({\mathcal{G}}_K, H^0_{k,\mathbf{C}_p})\end{align*} $$

Or $H^0_{k,\mathbf {C}_p}$ est un groupe fini car ${\cal M}^p_{n,\mathbf {C}_p}$ n’a qu’un nombre fini de composantes connexes. Il s’ensuit que $\varinjlim _K H^j({\mathcal {G}}_K, H^0_{k,\mathbf {C}_p})=0$ pour $j\in \{1,2\}$ et donc

$$ \begin{align*}H^1_{k,\overline{\mathbf{Q}}_p}=\varinjlim\nolimits_{K} H^1_{k,K}\simeq (H^1_{k,\mathbf{C}_p})^{{\mathcal{G}}_{\mathbf{Q}_p}{\text{-lisse}}}.\end{align*} $$

En particulier la flèche $H^1_{k,\overline {\mathbf {Q}}_p}\to H^1_{k,\mathbf {C}_p}$ est injective et on obtient l’injectivité de l’application naturelle $H^{1,+}_{\overline {\mathbf {Q}}_p}\to H^{1,+}_{\mathbf {C}_p}$ en passant à la limite sur k.

Le morphisme évident $\gamma _k: H^{1,+}_{\mathbf {C}_p}\to H^1_{k, \mathbf {C}_p}$ se factorise $\gamma _k=\alpha _k\circ \beta _k$ , où $\beta _k: H^{1,+}_{\mathbf {C}_p}\to H^{1,+}_{\mathbf {C}_p}/p^k$ est la projection canonique et $\alpha _k: H^{1,+}_{\mathbf {C}_p}/p^k\to H^1_{k, \mathbf {C}_p}$ est ${\mathcal {G}}_{\mathbf {Q}_p}$ -équivariante et injective. En particulier pour tout $z\in H^{1,+}_{\mathbf {C}_p}$ et tout $k\geq 1$ les deux assertions suivantes sont équivalentes:

• • $\beta _k(z)$ est fixe par un sous-groupe ouvert de $\mathcal {G}_{\mathbf {Q}_p}$ .

• • $\gamma _k(z)$ est fixe par un sous-groupe ouvert de $\mathcal {G}_{\mathbf {Q}_p}$ .

La seconde se traduit par $\gamma _k(z)\in (H^1_{k,\mathbf {C}_p})^{{\mathcal {G}}_{\mathbf {Q}_p}{\text {-lisse}}}\simeq H^1_{k,\overline {\mathbf {Q}}_p}$ . En passant à la limite sur k, on voit que l’ensemble des $x\in H^{1,+}_{\mathbf {C}_p}$ presque lisses sous l’action de ${\cal G}_{\mathbf {Q}_p}$ s’identifie à $\varprojlim _k (H^1_{k,\mathbf {C}_p})^{{\mathcal {G}}_{\mathbf {Q}_p}{\text {-lisse}}}\simeq \varprojlim _k H^1_{k,\overline {\mathbf {Q}}_p}=H^{1,+}_{\overline {\mathbf {Q}}_p}$ .

Corollaire 5.17.

1. a) $H^{1,+}_{\overline {\mathbf {Q}}_p}$ est sans p-torsion, p-adiquement complet et p-saturé dans $H^{1,+}_{\mathbf {C}_p}$ .

2. b) Pour tout $k\geq 1$ le $\mathcal {G}_{\mathbf {Q}_p}$ -module $H^{1,+}_{\overline {\mathbf {Q}}_p}/p^k$ est lisse.

Démonstration.

1. a) C’est une conséquence directe de la proposition ci-dessus et du fait que $H^{1,+}_{\mathbf {C}_p}$ est sans p-torsion et p-adiquement complet.

2. b) Soit $x\in H^{1,+}_{\overline {\mathbf {Q}}_p}$ et soit K tel que $gx-x\in p^k H^{1,+}_{\mathbf {C}_p}$ pour $g\in \mathcal {G}_K$ . Par a) on a $gx-x\in p^k H^{1,+}_{\overline {\mathbf {Q}}_p}$ pour $g\in \mathcal {G}_K$ , ce qui montre que $H^{1,+}_{\overline {\mathbf {Q}}_p}/p^k=\varinjlim _{K} (H^{1,+}_{\overline {\mathbf {Q}}_p}/p^k )^{\mathcal {G}_K}$ .

Question 5.18. $H^{1,+}_{\overline {\mathbf {Q}}_p}$ est-il dense dans $H^{1,+}_{\mathbf {C}_p}$ ?

5.3.2 Décomposition suivant les blocs

Le but de ce numéro est de démontrer l’existence d’une décomposition au niveau entier, de la forme

la complétion étant p-adique et

étant un ${\cal O}_L$ -module sans torsion, séparé et complet pour la topologie p-adique, dont le ${\cal O}_L$ -dual continu est de type fini sur $R_{\cal B}^{\mathrm{ps}}$ . Le numéro suivant décrit la fibre générique de

(il ne semble pas facile de décrire le module

lui-même).

Proposition 5.19. $(H^{1,+}_{\overline {\mathbf {Q}}_p}/p^k)^{\mathcal {G}_K}$ est le dual d’un ${\cal O}_L[G']$ -module lisse de longueur finie pour tous $k\geq 1$ et $[K:\mathbf {Q}_p]<\infty $ .

Démonstration. Notons pour simplifier $Y=(H^{1,+}_{\overline {\mathbf {Q}}_p}/p^k)^{\mathcal {G}_K}$ , muni de la topologie induite par celle de $H^{1,+}_{\overline {\mathbf {Q}}_p}$ . On dispose d’une injection continue $\iota : Y\to Z:=(H^1_{k, \mathbf {C}_p})^{\mathcal {G}_K}$ , composée des injections $Y\to (H^{1,+}_{\mathbf {C}_p}/p^k)^{\mathcal {G}_K}$ et $(H^{1,+}_{\mathbf {C}_p}/p^k)^{\mathcal {G}_K}\to Z$ (cf. cor. 5.17 pour la première).

Par le théorème de finitude, Z est un ${\cal O}_L$ -module profini, dual d’une représentation lisse de longueur finie, donc admissible, de G. En particulier la topologie sur Y est séparée. Soit H un sous-groupe ouvert compact de G. Par le théorème de finitude l’action de H sur chaque $H^1_{k,K}$ se prolonge en une structure de ${\cal O}_L[[H]]$ -module topologique, donc l’action de H sur Y se prolonge en une structure de ${\cal O}_L[[H]]$ -module topologique, et $\iota $ est ${\cal O}_L[[H]]$ -linéaire (car H-équivariante et continue). On en déduit que Y est de type fini comme ${\cal O}_L[[H]]$ -module, puisque Z l’est. Comme Y est aussi séparé, la topologie sur Y définie par sa structure de ${\cal O}_L[[H]]$ -module de type fini (pour laquelle il est profini) est la même que sa topologie de départ, donc Y est profini et $\iota $ est un homéomorphisme sur son image, ce qui permet de conclure.

Remarque 5.20. Indiquons une autre preuve de la proposition ci-dessus. Si $X=\varprojlim _k X_k$ où les $X_k$ sont des espaces topologiques, et si $Y_k={\mathrm{Im}}(X\to X_k)$ est muni de la topologie induite par celle de $X_k$ , alors $X\hookrightarrow \prod _k X_k$ se factorise par $X\hookrightarrow \prod _k Y_k\hookrightarrow \prod _k X_k$ et $\prod _kY_k\subset \prod _k X_k$ est muni de la topologie induite, et donc $X=\varprojlim Y_k$ comme espace topologique. On va utiliser ce qui précède pour $X_k=H^{1}_{k,\overline {\mathbf {Q}}_p}$ (et alors $Y_k= H^{1,+}_{\overline {\mathbf {Q}}_p}/p^k$ ).

Montrons maintenant que si K est une extension finie de $\mathbf {Q}_p$ , alors $Y_k\cap H^1_{k,K}$ est un module compact, topologiquement de longueur finie comme ${\cal O}_L[G]$ -module. Il suffit de prouver que $Y_k\cap H^1_{k,K}$ est fermé dans $H^1_{k,K}$ puisque ce dernier est compact, topologiquement de longueur finie comme ${\cal O}_L[G]$ -module.

Soit $(v_i)_{i\in I}$ une famille finie d’éléments de $H^{1,+}_{\overline {\mathbf {Q}}_p}$ dont les images modulo $p^k$ appartiennent à $Y_k\cap H^1_{k,K}$ . Si $j\geq k$ , soit $\Pi _j$ l’adhérence dans $H^1_{j,\mathbf {C}_p}$ du sous- ${\cal O}_L[G\times {\cal G}_{\mathbf {Q}_p}]$ -module engendré par les images des $v_i$ . Comme la famille est finie, il existe une extension finie $K_j$ de $\mathbf {Q}_p$ telle que $\Pi _j\subset H^1_{j,K_j}$ , et comme $H^1_{j,K_j}$ est topologiquement de longueur finie et $\Pi _j$ fermé par hypothèse, on en déduit que $\Pi _j$ est compact et topologiquement de longueur finie. La flèche naturelle $\Pi _{j+1}\to \Pi _j$ est surjective car l’image est compacte et donc fermée, stable par G et ${\cal G}_{\mathbf {Q}_p}$ , et contient les images des $v_i$ . La limite projective $\Pi $ des $\Pi _j$ est compacte et donc s’identifie à un sous-module fermé de $H^{1,+}_{\mathbf {C}_p}$ contenu dans $H^{1,+}_{\overline {\mathbf {Q}}_p}$ , stable par G et ${\cal G}_{\mathbf {Q}_p}$ ; c’est donc l’adhérence dans $H^{1,+}_{\overline {\mathbf {Q}}_p}$ du sous- ${\cal O}_L[G\times {\cal G}_{\mathbf {Q}_p}]$ -module engendré par les $v_i$ . La flèche $\Pi \to \Pi _k$ est surjective puisque toutes les flèches de transition sont surjectives. On a donc démontré que $\Pi _k\subset Y_k\cap H^1_{k,K}$ . Comme $H^1_{k,K}$ est de longueur finie, il en est de même de $\Pi _k$ et la longueur de $\Pi _k$ est bornée indépendamment de $(v_i)_{i\in I}$ . Si la famille $(v_i)_{i\in I}$ est choisie pour que la longueur de $\Pi _k$ soit maximale, on a $\Pi _k=Y_k\cap H^1_{k,K}$ , ce qui permet de conclure puisque $\Pi _k$ est fermé par définition.

Proposition 5.21. Soit

L’application naturelle

identifie $H^{1,+}_{\overline {\mathbf {Q}}_p}$ au complété p-adique de

.

Démonstration. Notons pour simplifier $X=H^{1,+}_{\overline {\mathbf {Q}}_p}$ et $X_{k,K}=(X/p^k)^{\mathcal {G}_K}$ . Par la prop. 5.19 on peut décomposer $X_{k,K}$ suivant les blocs:

est un $E_{\cal B}$ -module compact, de longueur finie comme ${\cal O}_L$ -module. Le cor. 5.17 permet de déduire que

Puisque ${P}_{\mathcal {B}}$ est compact et les $X_{k,K}$ sont profinis, on a

Pour conclure, il nous reste à démontrer que

. Comme X est sans p-torsion, on a bien une injection

. Comme X est p-adiquement complet, pour montrer que cette injection est surjective, il suffit de montrer que les flèches

sont surjectives pour tout j, ou encore que

est surjective.

Fixons K et notons $f: X/p^{j+1}\to X/p^j$ la projection canonique. Alors $\cup _{[L:\mathbf {Q}_p]<\infty } f(X_{j+1,L})=f(X/p^{j+1})=X/p^j$ , donc $X_{j,K}$ est la réunion des $f(X_{j+1,L})\cap X_{j,K}$ . Comme $X_{j,K}$ est de longueur finie, on en déduit qu’il existe L tel que $f(X_{j+1,L})$ contienne $X_{j,K}$ . Comme $X_{j+1,L}$ est de longueur finie, tout morphisme G-équivariant $u: {P}_{\mathcal {B}}\to X_{j,K}$ se relève en un morphisme G-équivariant ${P}_{\mathcal {B}}\to X_{j+1,L}$ , ce qui permet de conclure.

Posons simplement

Alors

est un ${\cal O}_L$ -module sans torsion, séparé et complet pour la topologie p-adique, tandis que

est un ${\cal O}_L$ -module compact, sans torsion.

Théorème 5.22. est un $R_{\cal B}^{\mathrm{ps}}$ -module de type fini.

Démonstration. Soit

l’idéal maximal de $R_{\cal B}^{\mathrm{ps}}$ . Par le lemme de Nakayama topologique il suffit de voir que

est de dimension finie sur $k_L$ , autrement dit que

. On a une injection

et donc une injection

Le cor. 6.7 de [56] montre que $k_L\otimes _{R_{\cal B}^{\mathrm{ps}}} {P}_{\mathcal {B}}=\pi ^{\vee } $ pour une représentation lisse, admissible (en fait de longueur finie) $\pi $ , et on conclut en utilisant le cor. 4.21.

5.3.3 Structure de comme $R_{\cal B}^{\mathrm{ps}}$ -module

Nous allons maintenant rendre p inversible pour pouvoir décomposer notre module en composantes isotypiques pour les représentations de dimension finie de $\check G$ . Si X est un G-module topologique on pose . On a donc par compacité de ${P}_{\mathcal {B}}$ .

Remarque 5.23. (i) Puisque $H^{1}_{\overline {\mathbf {Q}}_p}$ s’injecte dans $H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\mathbf {C}_p})$ , sur lequel l’action de $\check {G}$ se factorise par un quotient fini, il n’y a qu’un nombre fini de M tels que $H^{1}_{\overline {\mathbf {Q}}_p}[M]$ soit non nul, et on a

$$ \begin{align*}H^{1}_{\overline{\mathbf{Q}}_p}=\oplus_M \big(H^{1}_{\overline{\mathbf{Q}}_p}[M]\otimes_L {\mathrm{JL}}(M)\big)\end{align*} $$

et donc on dispose d’une décomposition

avec

Le module

ne dépend pas du choix de n supérieur ou égal au niveau de M car $H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\overline {\mathbf {Q}}_p})$ est le sous-espace des $\check {G}_n$ -invariants de $\varinjlim _n H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\overline {\mathbf {Q}}_p})$ (comme on a inversé p, on peut fabriquer des projecteurs $\check {G}$ -équivariants en composant restrictions et corestrictions).

(ii) Sur $H^{1}_{\overline {\mathbf {Q}}_p}[M]$ et donc aussi sur le centre de G agit par un caractère $\delta _M$ puisque c’est le cas de celui de $\check G$ et que les actions des deux centres sont inverses l’une de l’autre sur $H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\mathbf {C}_p})$ , qui contient $H^{1}_{\overline {\mathbf {Q}}_p}$ .

Le point (ii) de la remarque ci-dessus va nous permettre d’utiliser le th. 1.16 pour analyser le module .

Théorème 5.24.

1. (i) $R_{\cal B}^{{\mathrm{ps}},\delta _M}$ agit sur à travers son quotient $R_{{\cal B},M}$ .

2. (ii) On a un isomorphisme de $E_{\cal B}^{\delta _M}[{\cal G}_{\mathbf {Q}_p}]$ -modules

   
   où $\check {R}_{{\cal B},M}$ est le L-dual de $R_{{\cal B},M}$ et les produits tensoriels sont au-dessus de $R_{{\cal B},M}$ .

Démonstration. Le cas M spécial est immédiat. Supposons donc M supercuspidal dans ce qui suit.

1. (i) On veut montrer que $I:=\ker (R_{\cal B}^{{\mathrm{ps}}, \delta _M}[1/p]\to R_{{\cal B},M})$ tue , et il suffit de voir que I tue ${\mathrm{Hom}}_{G} ({P}_{\mathcal {B}}, H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\mathbf {C}_p})[M])$ . Puisque $p>2$ , on a une identification $Z_{\mathcal {B}}^{\delta _M}\simeq R_{\cal B}^{{\mathrm{ps}}, \delta _M}/\mathcal {O}_L{\mathrm{-tors}}$ , ce qui permet de voir $Z_{\mathcal {B}}^{\delta _M}$ comme un $\mathcal {O}_L$ -réseau de $R_{\cal B}^{{\mathrm{ps}}, \delta _M}[1/p]$ . Soit $J=Z_{\mathcal {B}}^{\delta _M}\cap I$ , donc $I=J[1/p]$ .

   Comme les fonctions bornées sur ${\cal M}^p_{n,\mathbf {C}_p}$ sont constantes ³¹ et comme ${\cal M}^p_{n,\mathbf {C}_p}$ possède un ouvert affinoïde dont les translatés sous l’action de G recouvrent ${\cal M}^p_{n,\mathbf {C}_p}$ , on a $\mathcal {O}({\cal M}^p_{n,\mathbf {C}_p})[M]^b=0$ . En passant aux vecteurs G-bornés dans la suite exacte (th. 5.11 de [16])

   $$ \begin{align*}0 \to \mathcal{O}({\cal M}^p_{n, \mathbf{C}_p})[M]\to H^1_{\operatorname{pro\acute{e}t} }({\cal M}^p_{n, \mathbf{C}_p})[M]\to X_{\mathrm{st}}^+(M)\widehat{\otimes}_L{\mathrm{LL}}(M)^{\boldsymbol *}\to 0\end{align*} $$
   et en utilisant la prop. 5.6 et le lemme 5.3 on voit que $H^1_{\operatorname {\acute {e}t} }({\cal M}^p_{n,\mathbf {C}_p})[M]$ s’injecte dans $X_{\mathrm{st}}^+(M)\widehat {\otimes }_L \widehat {{\mathrm{LL}}}(M)^{\boldsymbol *}$ . Il suffit donc de montrer que I tue ${\mathrm{Hom}}_{G} ({P}_{\mathcal {B}}, \widehat {{\mathrm{LL}}}(M)^{\boldsymbol *})$ .

   Soit ${\mathrm{LL}}(M)^+$ un $\mathcal {O}_L$ -réseau G-stable dans ${\mathrm{LL}}(M)$ (un tel réseau existe car ${\mathrm{LL}}(M)$ est supercuspidale, à caractère central unitaire) et soit Y son complété p-adique. On a donc $\widehat {{\mathrm{LL}}}(M)^{\boldsymbol *}=Y^d[1/p]$ , avec $Y^d:={\mathrm{Hom}}_{\mathcal {O}_L}^{\mathrm{cont}}(Y, \mathcal {O}_L)\simeq \varprojlim _{n} (Y/p^nY)^{\vee }$ (un $\mathcal {O}_L$ -module compact). Par compacité de ${P}_{\mathcal {B}}$ on a ${\mathrm{Hom}}_{G} ({P}_{\mathcal {B}}, \widehat {{\mathrm{LL}}}(M)^{\boldsymbol *})={\mathrm{Hom}}_G({P}_{\mathcal {B}}, Y^d)[1/p]$ . Il suffit donc de montrer que $J=Z_{\mathcal {B}}^{\delta _M}\cap I$ tue

   $$ \begin{align*}{\mathrm{Hom}}_G({P}_{\mathcal{B}}, Y^d)\simeq \varprojlim_{n} {\mathrm{Hom}}_G({P}_{\mathcal{B}}, (Y/p^nY)^{\vee}).\end{align*} $$

   Fixons n par la suite, et montrons que J tue ${\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y/p^nY)^{\vee })$ .

   Soit S l’ensemble des quotients du $\mathcal {O}_L[G]$ -module ${\mathrm{LL}}(M)^+$ qui sont des objets de ${\mathrm{Rep}}_{\mathcal {B}}^{\delta _M} G$ , i.e. des représentations lisses de longueur finie de G, dans la catégorie découpée par le bloc $\mathcal {B}$ . Alors S est au plus dénombrable, et puisque tout objet de ${\mathrm{Rep}}_{\mathcal {B}}^{\delta _M} G$ est tué par une puissance de p, le morphisme naturel ${\mathrm{LL}}(M)^+\to Y$ identifie S à l’ensemble des quotients de Y appartenant à ${\mathrm{Rep}}_{\mathcal {B}}^{\delta _M} G$ . Le $\mathcal {O}_L[G]$ -module prodiscret

   $$ \begin{align*}Y_{\mathcal{B}}:=\varprojlim\nolimits_{\sigma\in S} \sigma\end{align*} $$
   possède un morphisme naturel d’image dense $\iota : Y\to Y_{\mathcal {B}}$ . Il est montré dans [19, cor. 3.12] que $Y_{\mathcal {B}}$ est sans p-torsion, p-adiquement complet et que $\iota $ induit une surjection de $Y/p^n Y$ sur $Y_{\mathcal {B}}/p^n Y_{\mathcal {B}}$ pour tout n. Nous allons montrer que l’injection ${\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y_{\mathcal {B}}/p^nY_{\mathcal {B}})^{\vee })\to {\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y/p^nY)^{\vee })$ induite par le plongement $(Y_{\mathcal {B}}/p^n Y_{\mathcal {B}})^{\vee }\to (Y/p^n Y)^{\vee }$ est un isomorphisme, et que J tue ${\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y_{\mathcal {B}}/p^nY_{\mathcal {B}})^{\vee })$ , ce qui permettra de conclure.

   Soit donc $\varphi : {P}_{\mathcal {B}}\to (Y/p^nY)^{\vee }$ un morphisme continu G-équivariant et soit $\sigma :=\varphi ({P}_{\mathcal {B}})^{\vee }$ . Alors $\sigma $ est un quotient de $Y/p^nY\simeq {\mathrm{LL}}(M)^+/p^n {\mathrm{LL}}(M)^+ $ et $\sigma $ s’injecte dans ${P}_{\mathcal {B}}^{\vee }$ , qui est une limite inductive de représentations dans ${\mathrm{Rep}}_{\mathcal {B}}^{\delta _M} G$ , donc $\sigma $ est la réunion de ses sous-représentations appartenant à ${\mathrm{Rep}}_{\mathcal {B}}^{\delta _M} G$ . Puisque $\sigma $ est un quotient de ${\mathrm{LL}}(M)^+/p^n {\mathrm{LL}}(M)^+$ , qui est de type fini comme $\mathcal {O}_L[G]$ -module, on en déduit que $\sigma \in {\mathrm{Rep}}_{\mathcal {B}}^{\delta _M} G$ et $\varphi $ se factorise par $\sigma ^{\vee }$ , qui se plonge dans $(Y_{\mathcal {B}}/p^nY_{\mathcal {B}})^{\vee }$ . Donc l’injection ${\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y_{\mathcal {B}}/p^nY_{\mathcal {B}})^{\vee })\subset {\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y/p^nY)^{\vee })$ est aussi surjective.

   Il reste à expliquer pourquoi J tue ${\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y_{\mathcal {B}}/p^nY_{\mathcal {B}})^{\vee })$ . Pour cela, notons que $Y_{\mathcal {B}}$ possède une structure naturelle de $Z_{\mathcal {B}}^{\delta _M}$ -module, puisque chaque $\sigma \in S$ en a une. Il est montré dans [19] que J tue $Y_{\mathcal {B}}$ . On dispose de deux structures de $Z_{\mathcal {B}}^{\delta _M}$ -module sur ${\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y_{\mathcal {B}}/p^nY_{\mathcal {B}})^{\vee }))$ : une à partir de la structure de $Z_{\mathcal {B}}^{\delta _M}$ -module de ${P}_{\mathcal {B}}$ et l’autre à partir de la structure de $Z_{\mathcal {B}}^{\delta _M}$ -module de $Y_{\mathcal {B}}$ . Puisque $Z_{\mathcal {B}}^{\delta _M}$ est le centre de ${\mathrm{Rep}}_{\mathcal {B}}^{\delta _M} G$ , ces deux structures sont les mêmes et donc J tue ${\mathrm{Hom}}_G({P}_{\mathcal {B}}, (Y_{\mathcal {B}}/p^nY_{\mathcal {B}})^{\vee })$ , ce qui finit la preuve du point (i).

2. (ii) Posons $X:={\mathrm{Spm}}(R_{\cal B}^{{\mathrm{ps}},\delta _M}[\frac {1}{p}])$ , et $X_M:={\mathrm{Spm}}(R_{{\cal B},M})$ et écrivons pour l’idéal maximal correspondant à $x\in X$ .

Si $x\in X$ , alors

est le dual de

. Mais

(On passe de la première à la seconde ligne en utilisant la prop. 1.12 (et la rem. 1.13), et de la seconde à la troisième en utilisant le th. 5.8.)

On en déduit que les L-duaux des deux membres de (ii) ont la même spécialisation en tout point. Comme ces L-duaux sont des $R_{{\cal B},M}$ -modules localement libres, de type fini, et que $R_{{\cal B},M}$ est un produit d’anneaux principaux, le résultat s’en déduit en adaptant ³² le lemme 5.12 pour inclure l’action de $E_{{\cal B},M}:=R_{{\cal B},M}\otimes _{R^{{\mathrm{ps}},\delta _M}_{\cal B}} E_{\cal B}^{\delta _M}$ .