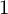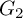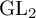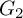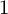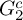1 Introduction
1.1 Context
This work first develops an ‘explicit’ trace formula (1) to study so-called quaternionic automorphic representations in general and then specializes it to describe level-
![]() $1$
, discrete, quaternionic automorphic representations on
$1$
, discrete, quaternionic automorphic representations on
![]() $G_2$
. Let
$G_2$
. Let
![]() $\mathcal {Q}_1(k)$
be the set of such representations of weight k counted with multiplicity. For each
$\mathcal {Q}_1(k)$
be the set of such representations of weight k counted with multiplicity. For each
![]() $k>2$
, we give a formula, (11), for
$k>2$
, we give a formula, (11), for
![]() $|\mathcal {Q}_1(k)|$
in terms of counts of automorphic representations on the compact-at-infinity inner form
$|\mathcal {Q}_1(k)|$
in terms of counts of automorphic representations on the compact-at-infinity inner form
![]() $G_2^c$
that were calculated by Chenevier and Renard in [Reference Chenevier and RenardCR15] (In case the use of counts on
$G_2^c$
that were calculated by Chenevier and Renard in [Reference Chenevier and RenardCR15] (In case the use of counts on
![]() $G_2^c$
is bothersome, Section 9.4 also gives a relatively short closed-form formula, though this is less conceptually enlightening). We also give a Jacquet–Langlands-style result (Corollary 8.2.1) describing all elements of
$G_2^c$
is bothersome, Section 9.4 also gives a relatively short closed-form formula, though this is less conceptually enlightening). We also give a Jacquet–Langlands-style result (Corollary 8.2.1) describing all elements of
![]() $\mathcal {Q}_1(k)$
in terms of certain automorphic representations on
$\mathcal {Q}_1(k)$
in terms of certain automorphic representations on
![]() $G_2^c$
and certain pairs of classical modular forms.
$G_2^c$
and certain pairs of classical modular forms.
Quaternionic automorphic representations are one way to generalize to other groups the special place holomorphic modular forms have among automorphic representations of
![]() $\mathrm {GL}_2$
. Just like holomorphic modular forms, they are characterized by their infinite component being in a particular nice class of discrete series representations: the quaternionic discrete series of [Reference Gross and WallachGW96]. Just like modular forms, they also have many unexpected applications and connections to other areas of mathematics. For example, they have a nice theory of Fourier expansions with interesting arithmetic content – this was described for
$\mathrm {GL}_2$
. Just like holomorphic modular forms, they are characterized by their infinite component being in a particular nice class of discrete series representations: the quaternionic discrete series of [Reference Gross and WallachGW96]. Just like modular forms, they also have many unexpected applications and connections to other areas of mathematics. For example, they have a nice theory of Fourier expansions with interesting arithmetic content – this was described for
![]() $G_2$
in [Reference Gan, Gross and SavinGGS02] and generalized to all exceptional groups in [Reference PollackPol20]. They also somehow appear in certain string theory computations involving black holes – see the end of chapter 15 in [Reference Fleig, Gustafsson, Kleinschmidt and PerssonFGKP18] for example. Quaternionic forms have been studied a lot by Pollack: See [Reference PollackPol21] for an introductory article on them and [Reference PollackPol18] for good exposition specifically on
$G_2$
in [Reference Gan, Gross and SavinGGS02] and generalized to all exceptional groups in [Reference PollackPol20]. They also somehow appear in certain string theory computations involving black holes – see the end of chapter 15 in [Reference Fleig, Gustafsson, Kleinschmidt and PerssonFGKP18] for example. Quaternionic forms have been studied a lot by Pollack: See [Reference PollackPol21] for an introductory article on them and [Reference PollackPol18] for good exposition specifically on
![]() $G_2$
-quaternionic forms.
$G_2$
-quaternionic forms.
We study discrete, quaternionic representations in general using the trace formula: Arthur’s invariant trace formula, as in [Reference ArthurArt89], lets us analyze automorphic representations with infinite component contained in a fixed discrete series L-packet. However, quaternionic discrete series appear in L-packets with nonquaternionic members and therefore cannot be isolated within the packet without further techniques. A previous work, [Reference DalalDal22], uses the stabilization of the trace formula to abstractly isolate members of the L-packet and prove general asymptotic bounds. Here, we demonstrate that the same techniques suffice for computing more explicit information.
As one technical point of interest, there is a particular miracle about quaternionic discrete series that crucially underpins the result. A priori, quaternionic discrete series are not regular, implying that there may not be a compact test function at infinity whose trace picks out exactly a quaternionic discrete series without also picking up some unwanted contributions from nontempered representations. This would preclude the use of easy trace formula arguments. However, it turns out that specifically quaternionic discrete series don’t get entangled in this way, even though other members of their L-packet do. The proof is a computation in real representation theory.
Applying these generalities to
![]() $G_2$
lets us develop an ‘Eicher–Selberg’-style trace formula for quaternionic discrete series there. The counts of level-
$G_2$
lets us develop an ‘Eicher–Selberg’-style trace formula for quaternionic discrete series there. The counts of level-
![]() $1$
forms and Jacquet–Langlands-style results come from computations with it. The level-
$1$
forms and Jacquet–Langlands-style results come from computations with it. The level-
![]() $1$
computation in particular also relies heavily on powerful shortcuts developed in [Reference Chenevier and RenardCR15] and [Reference TaïbiTaï17] to get exact counts of level-
$1$
computation in particular also relies heavily on powerful shortcuts developed in [Reference Chenevier and RenardCR15] and [Reference TaïbiTaï17] to get exact counts of level-
![]() $1$
automorphic representations on classical groups.
$1$
automorphic representations on classical groups.
This work can be be compared to the much more difficult aforementioned papers of Chenevier, Renard and Taïbi counting level-
![]() $1$
representations with arbitrary discrete series at infinity on classical groups. Those avoided needing our real representation theory miracle by using the extremely powerful endoscopic classification of [Reference ArthurArt13] which, in essence, gave a finer decomposition of the trace formula than pure stabilization. In particular, it allowed the isolation of summands in the trace formula that did not contain any contributions from automorphic representations with nontempered local components through a far more complicated inductive procedure. Unfortunately, there is no endoscopic classification currently available for
$1$
representations with arbitrary discrete series at infinity on classical groups. Those avoided needing our real representation theory miracle by using the extremely powerful endoscopic classification of [Reference ArthurArt13] which, in essence, gave a finer decomposition of the trace formula than pure stabilization. In particular, it allowed the isolation of summands in the trace formula that did not contain any contributions from automorphic representations with nontempered local components through a far more complicated inductive procedure. Unfortunately, there is no endoscopic classification currently available for
![]() $G_2$
.
$G_2$
.
The methods here should be able to also compute averages of Hecke eigenvalues. We also hope that the computation highlights enough general methods and shortcuts to be helpful for people interested in doing explicit computations with discrete-at-infinity automorphic representations whenever an endoscopic classification might either be unavailable or be too complicated to use. See the end of Section 3.3 for some comments on this. In particular, a very similar method, albeit with more complicated computation at infinity, should be able to ‘quickly’ count the quaternionic forms on type
![]() $D_4$
studied by Martin Weissman in [Reference WeissmanWei06].
$D_4$
studied by Martin Weissman in [Reference WeissmanWei06].
1.2 Summary
We start with the case of general groups with quaternionic discrete series at infinity. Section 2 discusses quaternionic discrete series and their properties, culminating in Proposition 2.3.3 showing that they satisfy a property of being ‘trace-distinguishable’. This is used in Theorem 3.1.1 to show that the spectral side of Arthur’s invariant trace formula can be made equal to the trace of any desired finite-place test function against the space of all quaternionic representations of a fixed weight.
The second part of Section 3 uses ‘hyperendoscopy’ from [Reference FerrariFer07] to simplify the geometric side and develops an expression (1) for this trace that is explicit up to computing endoscopic transfers and orbital integrals. We conclude with some remarks on how to do the necessary computations and outline how they simplify in the special case of level-
![]() $1$
on
$1$
on
![]() $G_2$
. This special case of
$G_2$
. This special case of
![]() $G_2$
then takes up the rest of the paper.
$G_2$
then takes up the rest of the paper.
Specifically, after some setup work in Section 4, we work out what formula (1) reduces to in the unramified case for
![]() $G_2$
in Section 5 using a computation of the endoscopy of
$G_2$
in Section 5 using a computation of the endoscopy of
![]() $G_2$
. Instead of using formula (1) directly, we compare its application to
$G_2$
. Instead of using formula (1) directly, we compare its application to
![]() $G_2$
to its application to the compact real form
$G_2$
to its application to the compact real form
![]() $G_2^c$
to construct a formula for
$G_2^c$
to construct a formula for
![]() $I_{\mathrm {spec}}^{G_2}$
involving just
$I_{\mathrm {spec}}^{G_2}$
involving just
![]() $I_{\mathrm {spec}}^{G_2^c}$
- and
$I_{\mathrm {spec}}^{G_2^c}$
- and
![]() $I_{\mathrm {spec}}^H$
-terms. Here, H is the endoscopic group
$I_{\mathrm {spec}}^H$
-terms. Here, H is the endoscopic group
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2/\pm 1$
of
$\mathrm {SL}_2 \times \mathrm {SL}_2/\pm 1$
of
![]() $G_2$
.
$G_2$
.
Section 6 then tells us which exact
![]() $I_{\mathrm {spec}}^{G_2^c}$
- and
$I_{\mathrm {spec}}^{G_2^c}$
- and
![]() $I_{\mathrm {spec}}^H$
-terms appear by computing endoscopic transfers at infinity. The difficult part of this computation is pinning down various signs coming from transfer factors. We present a shortcut to make it more manageable. The final result should be thought of as an ‘Eichler–Selberg’ trace formula for quaternionic automorphic representations on
$I_{\mathrm {spec}}^H$
-terms appear by computing endoscopic transfers at infinity. The difficult part of this computation is pinning down various signs coming from transfer factors. We present a shortcut to make it more manageable. The final result should be thought of as an ‘Eichler–Selberg’ trace formula for quaternionic automorphic representations on
![]() $G_2$
. As a last piece of the puzzle, Section 7 uses results about level-
$G_2$
. As a last piece of the puzzle, Section 7 uses results about level-
![]() $1$
forms from [Reference Chenevier and RenardCR15] to reduce counts of forms on H to counts of classical modular forms.
$1$
forms from [Reference Chenevier and RenardCR15] to reduce counts of forms on H to counts of classical modular forms.
Section 8 uses all these formulas to characterize representations in
![]() $\mathcal {Q}_k(1)$
with
$\mathcal {Q}_k(1)$
with
![]() $k>2$
in terms of automorphic representations on
$k>2$
in terms of automorphic representations on
![]() $G_2^c$
and certain pairs of classical modular forms. We substitute in values for the
$G_2^c$
and certain pairs of classical modular forms. We substitute in values for the
![]() $I_{\mathrm {spec}}^{G_2^c}$
-terms from [Reference Chenevier and RenardCR15] and present a final table of dimensions: table 1, in Section 9. Finally, building off an impressive undergraduate thesis [Reference SullivanSul13] of Sullivan, we give a relatively simple closed-form formula for the
$I_{\mathrm {spec}}^{G_2^c}$
-terms from [Reference Chenevier and RenardCR15] and present a final table of dimensions: table 1, in Section 9. Finally, building off an impressive undergraduate thesis [Reference SullivanSul13] of Sullivan, we give a relatively simple closed-form formula for the
![]() $G_2^c$
-term and present the resulting closed-form formula for
$G_2^c$
-term and present the resulting closed-form formula for
![]() $|\mathcal {Q}_k(1)|$
in Section 9.4.
$|\mathcal {Q}_k(1)|$
in Section 9.4.
1.3 Notation
Here is a list of notation used throughout:
The group
![]() $G_2$
$G_2$
-
•
 $G_2$
is the standard exceptional Chevalley group defined over
$G_2$
is the standard exceptional Chevalley group defined over
 ${\mathbb Z}$
.
${\mathbb Z}$
. -
•
 $G_2^c$
is the unique inner form of
$G_2^c$
is the unique inner form of
 $G_2$
over
$G_2$
over
 $\mathbb Q$
. Recall that
$\mathbb Q$
. Recall that
 $(G_2^c)_{\mathbb R}$
is the compact real form.
$(G_2^c)_{\mathbb R}$
is the compact real form. -
•
 $\alpha _i, \epsilon _i, \lambda _i$
are particular roots and coroots of
$\alpha _i, \epsilon _i, \lambda _i$
are particular roots and coroots of
 $G_2$
defined in Section 4.1.
$G_2$
defined in Section 4.1. -
•
 $s_\lambda $
is the simple reflection associated to root or coroot
$s_\lambda $
is the simple reflection associated to root or coroot
 $\lambda $
.
$\lambda $
. -
•
 $\rho $
is half the sum of the positive roots of
$\rho $
is half the sum of the positive roots of
 $G_2$
.
$G_2$
. -
•
 $V_\lambda $
is the finite-dimensional representation of
$V_\lambda $
is the finite-dimensional representation of
 $G_2$
of highest weight
$G_2$
of highest weight
 $\lambda $
.
$\lambda $
. -
• K is a choice of maximal compact subgroup
 $\mathrm {SU}(2) \times \mathrm {SU}(2)/\pm 1$
of
$\mathrm {SU}(2) \times \mathrm {SU}(2)/\pm 1$
of
 $G_2(\mathbb R)$
.
$G_2(\mathbb R)$
. -
•
 $K^\infty $
is the product of maximal compact subgroups
$K^\infty $
is the product of maximal compact subgroups
 $G_2(\mathbb Z_p)$
over all p.
$G_2(\mathbb Z_p)$
over all p. -
•
 $\Omega = \Omega _{\mathbb C}$
is the Weyl group of
$\Omega = \Omega _{\mathbb C}$
is the Weyl group of
 $G_2$
.
$G_2$
. -
•
 $\Omega _{\mathbb R}$
is the Weyl group of K as a subset of
$\Omega _{\mathbb R}$
is the Weyl group of K as a subset of
 $\Omega $
.
$\Omega $
. -
• H will often refer to the specific endoscopic group
 $\mathrm {SL}_2 \times \mathrm {SL}_2/\pm 1$
of
$\mathrm {SL}_2 \times \mathrm {SL}_2/\pm 1$
of
 $G_2$
.
$G_2$
. -
•
 $\mathcal {Q}_k(1)$
is the set of discrete, quaternionic automorphic representations of
$\mathcal {Q}_k(1)$
is the set of discrete, quaternionic automorphic representations of
 $G_2$
of weight k and level
$G_2$
of weight k and level
 $1$
(see Section 4.2).
$1$
(see Section 4.2). -
•
 $\pi _k$
is the weight k quaternionic discrete series of
$\pi _k$
is the weight k quaternionic discrete series of
 $G_2$
(see Section 4.2).
$G_2$
(see Section 4.2).
General groups
-
•
 $G_\infty = \operatorname {\mathrm {Res}}^F_{\mathbb Q} G(\mathbb R)$
for G a reductive group over number field F. Since most groups here are over
$G_\infty = \operatorname {\mathrm {Res}}^F_{\mathbb Q} G(\mathbb R)$
for G a reductive group over number field F. Since most groups here are over
 $\mathbb Q$
,
$\mathbb Q$
,
 $G_\infty $
is usually
$G_\infty $
is usually
 $G(\mathbb R)$
.
$G(\mathbb R)$
. -
•
 $G^S, G_S$
are more generally the standard upper- and lower-index notation for
$G^S, G_S$
are more generally the standard upper- and lower-index notation for
 $G(\mathbb A^S), G(\mathbb A_S)$
– leaving out the places in S or only including the places in S, respectively.
$G(\mathbb A^S), G(\mathbb A_S)$
– leaving out the places in S or only including the places in S, respectively. -
•
 $\Omega (G)$
is the absolute Weyl group of G.
$\Omega (G)$
is the absolute Weyl group of G. -
•
 $\Omega _{\mathbb R}(G)$
is the subset of the Weyl group of
$\Omega _{\mathbb R}(G)$
is the subset of the Weyl group of
 $G_\infty $
with respect to an elliptic maximal torus (if one exists) generated by elements of
$G_\infty $
with respect to an elliptic maximal torus (if one exists) generated by elements of
 $G_\infty $
.
$G_\infty $
. -
•
 $K_G$
is a maximal compact subgroup of
$K_G$
is a maximal compact subgroup of
 $G_\infty $
.
$G_\infty $
. -
•
 $K^\infty _G$
for unramified G is the product of chosen hyperspecial subgroups at all finite places.
$K^\infty _G$
for unramified G is the product of chosen hyperspecial subgroups at all finite places. -
•
 $\rho _G$
is half the sum of the positive roots of G.
$\rho _G$
is half the sum of the positive roots of G. -
•
 $[G(F)], [G(F)]_{\mathrm {ss}}, [G(F)]_{\mathrm {st}}, [G(F)]_{\mathrm {ell}}$
are the (semisimple, stable, elliptic) conjugacy classes of
$[G(F)], [G(F)]_{\mathrm {ss}}, [G(F)]_{\mathrm {st}}, [G(F)]_{\mathrm {ell}}$
are the (semisimple, stable, elliptic) conjugacy classes of
 $G(F)$
.
$G(F)$
.
Real test functions
-
•
 $\varphi _\pi $
for
$\varphi _\pi $
for
 $\pi $
a discrete series representation of
$\pi $
a discrete series representation of
 $G_\infty $
is the pseudocoefficient defined in the corollary to Proposition 4 in [Reference Clozel and DelormeCD90].
$G_\infty $
is the pseudocoefficient defined in the corollary to Proposition 4 in [Reference Clozel and DelormeCD90]. -
•
 $\Pi _{\mathrm {disc}}(\lambda )$
is the discrete series L-packet corresponding to dominant weight
$\Pi _{\mathrm {disc}}(\lambda )$
is the discrete series L-packet corresponding to dominant weight
 $\lambda $
.
$\lambda $
. -
•
 $\eta _\lambda $
is the Euler–Poincaré function from [Reference Clozel and DelormeCD90] for
$\eta _\lambda $
is the Euler–Poincaré function from [Reference Clozel and DelormeCD90] for
 $\Pi _{\mathrm {disc}}(\lambda )$
. We normalize it to be the average of the pseudocoefficients for
$\Pi _{\mathrm {disc}}(\lambda )$
. We normalize it to be the average of the pseudocoefficients for
 $\pi \in \Pi _{\mathrm {disc}}(\lambda )$
instead of their sum.
$\pi \in \Pi _{\mathrm {disc}}(\lambda )$
instead of their sum.
Trace formula
-
•
 $\mathcal {AR}(G)$
,
$\mathcal {AR}(G)$
,
 $\mathcal {AR}_{\mathrm {disc}}(G)$
is the set of (discrete) automorphic representations on G.
$\mathcal {AR}_{\mathrm {disc}}(G)$
is the set of (discrete) automorphic representations on G. -
•
 $\mathcal {AR}_{\mathrm {ur}}(G)$
for G unramified is the space of unramified automorphic representations of G.
$\mathcal {AR}_{\mathrm {ur}}(G)$
for G unramified is the space of unramified automorphic representations of G. -
•
 $m_{\mathrm {disc}}(\pi ), m_{\mathrm {cusp}}(\pi )$
are the multiplicities of automorphic representation
$m_{\mathrm {disc}}(\pi ), m_{\mathrm {cusp}}(\pi )$
are the multiplicities of automorphic representation
 $\pi $
in the discrete (cuspidal) subspace.
$\pi $
in the discrete (cuspidal) subspace. -
•
 $I^G_{\mathrm {spec}}, I^G_{\mathrm {geom}}, I^G_{\mathrm {disc}}$
are the distributions from Arthur’s invariant trace formula on G.
$I^G_{\mathrm {spec}}, I^G_{\mathrm {geom}}, I^G_{\mathrm {disc}}$
are the distributions from Arthur’s invariant trace formula on G. -
•
 $S^G = S^G_{\mathrm {geom}}$
is the stable distribution defined in Theorem 3.2.1.
$S^G = S^G_{\mathrm {geom}}$
is the stable distribution defined in Theorem 3.2.1.
Miscellaneous
-
•
 ${\mathbf {1}}_S$
is the indicator function of set S.
${\mathbf {1}}_S$
is the indicator function of set S. -
•
 ${\mathbf {1}}_G$
is the trivial representation on group G.
${\mathbf {1}}_G$
is the trivial representation on group G. -
•
 $\mathcal {S}_k(1)$
is the set of normalized, classical, cuspidal eigenforms on
$\mathcal {S}_k(1)$
is the set of normalized, classical, cuspidal eigenforms on
 $\mathrm {GL}_2$
of level
$\mathrm {GL}_2$
of level
 $1$
and weight k.
$1$
and weight k.
2 Quaternionic discrete series
2.1 Discrete series
2.1.1 Parametrization
For this section, let G be a reductive group over
![]() $\mathbb R$
and K a maximal compact of
$\mathbb R$
and K a maximal compact of
![]() $G(\mathbb R)$
. Assume G has elliptic torus T so that
$G(\mathbb R)$
. Assume G has elliptic torus T so that
![]() $G(\mathbb R)$
has discrete series. Without loss of generality,
$G(\mathbb R)$
has discrete series. Without loss of generality,
![]() $T \subseteq K$
. Recall the notation from [Reference DalalDal22, §2.2.1] to discuss discrete series. In particular, recall the two parametrizations of discrete series on
$T \subseteq K$
. Recall the notation from [Reference DalalDal22, §2.2.1] to discuss discrete series. In particular, recall the two parametrizations of discrete series on
![]() $G(\mathbb R)$
:
$G(\mathbb R)$
:
for
![]() $\lambda $
a dominant (but possibly irregular) weight of T and
$\lambda $
a dominant (but possibly irregular) weight of T and
![]() $\omega $
a Weyl-element that takes a chosen
$\omega $
a Weyl-element that takes a chosen
![]() $\Omega _G$
dominant chamber into a chosen
$\Omega _G$
dominant chamber into a chosen
![]() $\Omega _K$
-dominant one. Note that
$\Omega _K$
-dominant one. Note that
![]() $\pi ^G_{\lambda , \omega }$
has infinitesimal character
$\pi ^G_{\lambda , \omega }$
has infinitesimal character
![]() $\lambda + \rho _{G}$
. Recall that
$\lambda + \rho _{G}$
. Recall that
![]() $\omega (\lambda + \rho _{G})$
is called the Harish–Chandra parameter of this discrete series.
$\omega (\lambda + \rho _{G})$
is called the Harish–Chandra parameter of this discrete series.
2.1.2 Their pseudocoefficients
Recall from the corollary on page 213 in [Reference Clozel and DelormeCD90] the notion of pseudocoefficients
![]() $\varphi _\pi $
for discrete series
$\varphi _\pi $
for discrete series
![]() $\pi $
. They are defined by their traces against standard modules
$\pi $
. They are defined by their traces against standard modules
![]() $\rho $
:
$\rho $
:
 $$\begin{align*}\operatorname{\mathrm{tr}}_\rho(\varphi_\pi) = \begin{cases} 1 & \rho = \pi \\ 0 & \rho \text{ standard, } \sigma \neq \pi \end{cases}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{tr}}_\rho(\varphi_\pi) = \begin{cases} 1 & \rho = \pi \\ 0 & \rho \text{ standard, } \sigma \neq \pi \end{cases}. \end{align*}$$
Here, a standard module is a parabolic induction of a discrete series or limit of discrete series.
Note. By the Langlands classification, every irreducible representation has a character formula writing it as a linear combination of standard modules in the Grothendieck group. By linearity of trace, if
![]() $\sigma $
is an irreducible representation, then
$\sigma $
is an irreducible representation, then
![]() $\operatorname {\mathrm {tr}}_\sigma (\varphi _\pi )$
is the coefficient of
$\operatorname {\mathrm {tr}}_\sigma (\varphi _\pi )$
is the coefficient of
![]() $\pi $
in its character formula.
$\pi $
in its character formula.
Recall also the Euler–Poincaré functions
![]() $\eta _\lambda $
that we normalize to be the average of pseudocoefficients over an L-packet of infinitesimal character
$\eta _\lambda $
that we normalize to be the average of pseudocoefficients over an L-packet of infinitesimal character
![]() $\lambda + \rho _G$
. For a quick summary of relevant properties of these functions in the notation used here, see [Reference DalalDal22, §2.2.2].
$\lambda + \rho _G$
. For a quick summary of relevant properties of these functions in the notation used here, see [Reference DalalDal22, §2.2.2].
2.2 Trace distinguishability
A priori, the trace against
![]() $\varphi _\pi $
may be nonzero for certain nontempered representations in addition to just
$\varphi _\pi $
may be nonzero for certain nontempered representations in addition to just
![]() $\pi $
. This could make
$\pi $
. This could make
![]() $\varphi _k$
unusable as a test function to pick out just automorphic representations
$\varphi _k$
unusable as a test function to pick out just automorphic representations
![]() $\pi $
with
$\pi $
with
![]() $\pi _\infty = \pi $
. We analyze when this happens.
$\pi _\infty = \pi $
. We analyze when this happens.
Definition. Call discrete series
![]() $\pi $
on group
$\pi $
on group
![]() $G(\mathbb R)$
trace-distinguishable if for all unitary representations
$G(\mathbb R)$
trace-distinguishable if for all unitary representations
![]() $\sigma $
of
$\sigma $
of
![]() $G(\mathbb R)$
$G(\mathbb R)$
 $$\begin{align*}\operatorname{\mathrm{tr}}_\sigma(\varphi_k) = \begin{cases} 1 & \sigma = \pi_k \\ 0 & \text{else} \end{cases}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{tr}}_\sigma(\varphi_k) = \begin{cases} 1 & \sigma = \pi_k \\ 0 & \text{else} \end{cases}. \end{align*}$$
To motivate this definition, the Paley–Weiner theorem of [Reference Clozel and DelormeCD90] shows that
![]() $\varphi _\pi $
is the only compactly supported function that could have the property of isolating
$\varphi _\pi $
is the only compactly supported function that could have the property of isolating
![]() $\pi $
in the unitary dual in this way – there are none if
$\pi $
in the unitary dual in this way – there are none if
![]() $\pi $
isn’t trace-distinguishable.
$\pi $
isn’t trace-distinguishable.
Proposition 2.2.1. Let discrete series
![]() $\pi $
on
$\pi $
on
![]() $G(\mathbb R)$
have Harish–Chandra parameter
$G(\mathbb R)$
have Harish–Chandra parameter
![]() $\xi $
. Define
$\xi $
. Define
where
![]() $\Phi _G$
is the set of roots of
$\Phi _G$
is the set of roots of
![]() $(G, T)$
for T elliptic. Then
$(G, T)$
for T elliptic. Then
![]() $\pi $
is trace-distinguishable if and only if
$\pi $
is trace-distinguishable if and only if
![]() $\pi $
contains no noncompact roots.
$\pi $
contains no noncompact roots.
Proof. The following proof was described to me by David Vogan. Choose simple roots so that
![]() $\xi $
is dominant. By the same argument of Vogan described in [Reference DalalDal22, lem. 6.3.1],
$\xi $
is dominant. By the same argument of Vogan described in [Reference DalalDal22, lem. 6.3.1],
![]() $\operatorname {\mathrm {tr}}_\sigma (\varphi _\pi ) = 0$
unless
$\operatorname {\mathrm {tr}}_\sigma (\varphi _\pi ) = 0$
unless
![]() $\operatorname {\mathrm {tr}}_\sigma (\eta _{\xi - \rho _G}) \neq 0$
for
$\operatorname {\mathrm {tr}}_\sigma (\eta _{\xi - \rho _G}) \neq 0$
for
![]() $\eta _{\xi - \rho _G}$
the Euler–Poincaré function at infinitesimal character
$\eta _{\xi - \rho _G}$
the Euler–Poincaré function at infinitesimal character
![]() $\xi $
. If
$\xi $
. If
![]() $\sigma $
is unitary, this is only possible if
$\sigma $
is unitary, this is only possible if
![]() $\sigma $
has nonzero
$\sigma $
has nonzero
![]() $(\mathfrak {g},K)$
-cohomology with respect to the irreducible finite-dimensional representation of infinitesimal character
$(\mathfrak {g},K)$
-cohomology with respect to the irreducible finite-dimensional representation of infinitesimal character
![]() $\xi $
.
$\xi $
.
By the main classification result of [Reference Vogan and ZuckermanVZ84], the only representations that do so are the discrete-series packet
![]() $\Pi _\lambda (\xi - \rho _G)$
and certain cohomological inductions
$\Pi _\lambda (\xi - \rho _G)$
and certain cohomological inductions
![]() $A_{\mathfrak {q}}(\lambda )$
for
$A_{\mathfrak {q}}(\lambda )$
for
![]() $\theta $
-stable parabolic subalgebras
$\theta $
-stable parabolic subalgebras
![]() $\mathfrak {q}$
of
$\mathfrak {q}$
of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\lambda $
a character of the Levi algebra
$\lambda $
a character of the Levi algebra
![]() $\mathfrak {l}$
associated to
$\mathfrak {l}$
associated to
![]() $\mathfrak {q}$
(see, for example, [Reference Adams and JohnsonAJ87, §2.1] for a definition of
$\mathfrak {q}$
(see, for example, [Reference Adams and JohnsonAJ87, §2.1] for a definition of
![]() $A_{\mathfrak {q}}(\lambda )$
). It therefore suffices to show that none of these except
$A_{\mathfrak {q}}(\lambda )$
). It therefore suffices to show that none of these except
![]() $\pi $
itself have
$\pi $
itself have
![]() $\pi $
appearing in their character formulas.
$\pi $
appearing in their character formulas.
The only nontrivial case to check is that of nondiscrete-series
![]() $A_{\mathfrak {q}}(\lambda )$
. Theorem 8.2 in [Reference Adams and JohnsonAJ87] provides its character formula and shows that the discrete series that appear are exactly those with Harish–Chandra parameters of the form
$A_{\mathfrak {q}}(\lambda )$
. Theorem 8.2 in [Reference Adams and JohnsonAJ87] provides its character formula and shows that the discrete series that appear are exactly those with Harish–Chandra parameters of the form
![]() $\lambda + \omega \rho _{\mathfrak {l}}$
, where
$\lambda + \omega \rho _{\mathfrak {l}}$
, where
![]() $\omega $
ranges over the Weyl group of
$\omega $
ranges over the Weyl group of
![]() $\mathfrak {l}$
. For each
$\mathfrak {l}$
. For each
![]() $\omega $
, pick a set of simple roots of
$\omega $
, pick a set of simple roots of
![]() $\mathfrak {l}$
so that
$\mathfrak {l}$
so that
![]() $\omega \rho _l$
is dominant. Then for simple root
$\omega \rho _l$
is dominant. Then for simple root
![]() $\alpha $
of
$\alpha $
of
![]() $\mathfrak {l}$
,
$\mathfrak {l}$
,
In particular, if
![]() $\pi $
appears in the character formula for
$\pi $
appears in the character formula for
![]() $A_{\mathfrak {q}}(\lambda )$
, then there is a choice of simple roots of
$A_{\mathfrak {q}}(\lambda )$
, then there is a choice of simple roots of
![]() $\mathfrak {l}$
that are in
$\mathfrak {l}$
that are in
![]() $S_\xi $
.
$S_\xi $
.
Finally, since
![]() $\lambda $
is regular, for any root
$\lambda $
is regular, for any root
![]() $\alpha $
of G,
$\alpha $
of G,
![]() $|\langle \lambda , \alpha ^\vee \rangle | \geq 1$
. Therefore,
$|\langle \lambda , \alpha ^\vee \rangle | \geq 1$
. Therefore,
![]() $S_\xi $
needs to be a subset our simple roots chosen to make
$S_\xi $
needs to be a subset our simple roots chosen to make
![]() $\lambda G$
-dominant. Let
$\lambda G$
-dominant. Let
![]() $\mathfrak {l}_\xi $
be the associated Levi subalgebra. If
$\mathfrak {l}_\xi $
be the associated Levi subalgebra. If
![]() $\pi $
appears in the character formula for
$\pi $
appears in the character formula for
![]() $A_{\mathfrak {q}}(\lambda )$
, the above gives that
$A_{\mathfrak {q}}(\lambda )$
, the above gives that
![]() $\mathfrak {l} \subseteq \mathfrak {l}_\xi $
. Therefore, if
$\mathfrak {l} \subseteq \mathfrak {l}_\xi $
. Therefore, if
![]() $S_\xi $
has no noncompact roots, then
$S_\xi $
has no noncompact roots, then
![]() $\mathfrak {l}$
is compact, so our condition on
$\mathfrak {l}$
is compact, so our condition on
![]() $\mathfrak {l}$
implies that
$\mathfrak {l}$
implies that
![]() $A_{\mathfrak {q}}(\lambda )$
is discrete series (see, for example, the bottom of [Reference Adams and JohnsonAJ87, pg. 272]) and therefore equal to
$A_{\mathfrak {q}}(\lambda )$
is discrete series (see, for example, the bottom of [Reference Adams and JohnsonAJ87, pg. 272]) and therefore equal to
![]() $\pi $
. In total,
$\pi $
. In total,
![]() $\pi $
cannot appear in other character formulas completing one direction.
$\pi $
cannot appear in other character formulas completing one direction.
In the other direction, if
![]() $S_\xi $
has a noncompact root, then this can be used to construct a rank-
$S_\xi $
has a noncompact root, then this can be used to construct a rank-
![]() $1$
Levi subalgebra
$1$
Levi subalgebra
![]() $\mathfrak {l}$
that isn’t compact. Pick corresponding
$\mathfrak {l}$
that isn’t compact. Pick corresponding
![]() $\mathfrak {q}$
, and choose chamber for
$\mathfrak {q}$
, and choose chamber for
![]() $\mathfrak {l}$
so that
$\mathfrak {l}$
so that
![]() $\lambda $
is
$\lambda $
is
![]() $\mathfrak {l}$
-dominant. Then
$\mathfrak {l}$
-dominant. Then
![]() $\pi $
will appear in the character formula of
$\pi $
will appear in the character formula of
![]() $A_{\mathfrak {q}}(\lambda - \rho _{\mathfrak {l}})$
which isn’t discrete series.
$A_{\mathfrak {q}}(\lambda - \rho _{\mathfrak {l}})$
which isn’t discrete series.
2.3 Quaternionic discrete series
Quaternionic discrete series are a special class of discrete series picked out in [Reference Gross and WallachGW96]. We recall some needed definitions and properties:
Definition. Call
![]() $G(\mathbb R)$
quaternionic if K is isogenous to a group of the form
$G(\mathbb R)$
quaternionic if K is isogenous to a group of the form
![]() $\mathrm {SU}_2(\mathbb R) \times L$
(that has the same rank as G).
$\mathrm {SU}_2(\mathbb R) \times L$
(that has the same rank as G).
Definition. If
![]() $G(\mathbb R)$
is quaternionic, call discrete series
$G(\mathbb R)$
is quaternionic, call discrete series
![]() $\pi $
quaternionic if its minimal K type lifts to a representation of the form
$\pi $
quaternionic if its minimal K type lifts to a representation of the form
![]() $V \boxtimes {\mathbf {1}}_L$
on
$V \boxtimes {\mathbf {1}}_L$
on
![]() $\mathrm {SU}_2(\mathbb R) \times L$
. Let the weight of
$\mathrm {SU}_2(\mathbb R) \times L$
. Let the weight of
![]() $\pi $
be
$\pi $
be
![]() $(\dim V -1)/2$
.
$(\dim V -1)/2$
.
By looking at extended root diagrams:
Lemma 2.3.1. Group
![]() $G(\mathbb R)$
is quaternionic if and only if there is a choice of simple roots of
$G(\mathbb R)$
is quaternionic if and only if there is a choice of simple roots of
![]() $(G(\mathbb R),T)$
such that there is a is unique noncompact simple root that is also the unique simple root not perpendicular to the highest root.
$(G(\mathbb R),T)$
such that there is a is unique noncompact simple root that is also the unique simple root not perpendicular to the highest root.
Then, by Blattner’s formula for minimal K-types:
Lemma 2.3.2. Let G have quaternionic discrete series with simple roots chosen as in the previous lemma. Then all quaternionic discrete series have Harish–Chandra parameter of the form
![]() $n \beta ' + \rho _G$
for
$n \beta ' + \rho _G$
for
![]() $n \in \mathbb Z_{\geq 0}$
and
$n \in \mathbb Z_{\geq 0}$
and
![]() $\beta '$
the highest root.
$\beta '$
the highest root.
Miraculously, almost all quaternionic discrete series are trace distinguishable:
Proposition 2.3.3. Let
![]() $\pi $
be a quaternionic discrete series of
$\pi $
be a quaternionic discrete series of
![]() $G(\mathbb R)$
with infinitesimal character not equal to
$G(\mathbb R)$
with infinitesimal character not equal to
![]() $\rho _G$
. Then
$\rho _G$
. Then
![]() $\pi $
is trace-distinguishable.
$\pi $
is trace-distinguishable.
3 Trace formula
Let G be a reductive group over number field F such that
![]() $G_\infty $
is quaternionic.
$G_\infty $
is quaternionic.
Definition. A quaternionic automorphic representation on G is an automorphic representation
![]() $\pi $
such that
$\pi $
such that
![]() $\pi _\infty $
is quaternionic.
$\pi _\infty $
is quaternionic.
In this section, we construct an ‘explicit’ trace formula for studying almost all quaternionic automorphic representations.
3.1 Spectral side
The previous discussion on quaternionic discrete series shows:
Theorem 3.1.1. Let
![]() $G_\infty $
have quaternionic discrete series, and let
$G_\infty $
have quaternionic discrete series, and let
![]() $\pi _0$
be a quaternionic discrete series of
$\pi _0$
be a quaternionic discrete series of
![]() $G_\infty $
with infinitesimal character not equal to
$G_\infty $
with infinitesimal character not equal to
![]() $\rho _G$
. Then
$\rho _G$
. Then
 $$ \begin{align*} I_{\mathrm{spec}}(\varphi_{\pi_0} \otimes f^\infty) & = \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}}(G_2)} m_{\mathrm{disc}}(\pi) \delta_{\pi_\infty = \pi_0} \operatorname{\mathrm{tr}}_{\pi^\infty} (f^\infty) \\ &= \sum_{\pi \in \mathcal{AR}_{\mathrm{cusp}}(G_2)} m_{\mathrm{cusp}}(\pi) \delta_{\pi_\infty = \pi_0} \operatorname{\mathrm{tr}}_{\pi^\infty} (f^\infty). \end{align*} $$
$$ \begin{align*} I_{\mathrm{spec}}(\varphi_{\pi_0} \otimes f^\infty) & = \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}}(G_2)} m_{\mathrm{disc}}(\pi) \delta_{\pi_\infty = \pi_0} \operatorname{\mathrm{tr}}_{\pi^\infty} (f^\infty) \\ &= \sum_{\pi \in \mathcal{AR}_{\mathrm{cusp}}(G_2)} m_{\mathrm{cusp}}(\pi) \delta_{\pi_\infty = \pi_0} \operatorname{\mathrm{tr}}_{\pi^\infty} (f^\infty). \end{align*} $$
Proof. The statement for discrete representations is the same argument as [Reference DalalDal22, prop. 6.3.3] after we know Proposition 2.3.3 that these quaternionic discrete series are trace-distinguishable. Since
![]() $\pi _\infty = \pi _0$
is necessarily discrete series for the nonzero terms, the main result of [Reference WallachWal84] shows that
$\pi _\infty = \pi _0$
is necessarily discrete series for the nonzero terms, the main result of [Reference WallachWal84] shows that
![]() $m_{\mathrm {cusp}}(\pi ) = m_{\mathrm {disc}}(\pi )$
.
$m_{\mathrm {cusp}}(\pi ) = m_{\mathrm {disc}}(\pi )$
.
Note. Of course, this theorem holds more generally for
![]() $\pi _0$
an arbitrary trace-distinguishable discrete series.
$\pi _0$
an arbitrary trace-distinguishable discrete series.
3.2 Geometric side/the hyperendoscopy formula
3.2.1 Notation
We will need to recall some extra notation related to general reductive group H over F to understand the geometric side
-
•
 $\Omega ^c_H$
is the Weyl group generated by compact roots at infinity.
$\Omega ^c_H$
is the Weyl group generated by compact roots at infinity. -
•
 $d(H_\infty )$
is the size of the discrete series L-packets of
$d(H_\infty )$
is the size of the discrete series L-packets of
 $H_\infty $
. Alternatively,
$H_\infty $
. Alternatively,
 $d(H_\infty ) = |\Omega _H|/|\Omega ^c_H|$
.
$d(H_\infty ) = |\Omega _H|/|\Omega ^c_H|$
. -
•
 $k(H_\infty )$
is the size of the group
$k(H_\infty )$
is the size of the group
 $\mathfrak {K} = \ker (H^1(\mathbb R, T_{\mathrm {ell}}) \to H^1(\mathbb R, G_\infty ))$
that appears in the theory of endoscopy for
$\mathfrak {K} = \ker (H^1(\mathbb R, T_{\mathrm {ell}}) \to H^1(\mathbb R, G_\infty ))$
that appears in the theory of endoscopy for
 $G_\infty $
.
$G_\infty $
. -
•
 $q(H_\infty ) = \dim (H_\infty /K_\infty Z_{H_\infty })$
where
$q(H_\infty ) = \dim (H_\infty /K_\infty Z_{H_\infty })$
where
 $K_\infty $
is a maximal compact subgroup of
$K_\infty $
is a maximal compact subgroup of
 $H_\infty $
.
$H_\infty $
. -
•
 $H_\infty ^*$
is the quasisplit inner form of
$H_\infty ^*$
is the quasisplit inner form of
 $H_\infty $
.
$H_\infty $
. -
•
 $\bar H_\infty $
is the compact form. If
$\bar H_\infty $
is the compact form. If
 $H_\infty $
has an elliptic maximal torus, this is inner.
$H_\infty $
has an elliptic maximal torus, this is inner. -
•
 $e(H_\infty )$
is the Kottwitz sign
$e(H_\infty )$
is the Kottwitz sign
 $(-1)^{q(H^*_\infty ) - q(H_\infty )}$
.
$(-1)^{q(H^*_\infty ) - q(H_\infty )}$
. -
•
 $[H:M] = [H:M]_F = \dim (A_M/A_G)$
, where
$[H:M] = [H:M]_F = \dim (A_M/A_G)$
, where
 $A_\star $
is the maximal F-split torus in the center of
$A_\star $
is the maximal F-split torus in the center of
 $\star $
. We call this the index of M in H.
$\star $
. We call this the index of M in H. -
•
 $\tau (H)$
is the Tamagawa number of H.
$\tau (H)$
is the Tamagawa number of H. -
•
 $\mathrm {Mot}_H$
is the Gross motive for H.
$\mathrm {Mot}_H$
is the Gross motive for H. -
•
 $L(\mathrm {Mot}_H)$
is the value of the corresponding L-function at
$L(\mathrm {Mot}_H)$
is the value of the corresponding L-function at
 $0$
(or residue of the pole).
$0$
(or residue of the pole). -
•
 $\iota ^H(\gamma ) = \iota _F^H(\gamma )$
for
$\iota ^H(\gamma ) = \iota _F^H(\gamma )$
for
 $\gamma \in H(F)$
is the number of connected components of
$\gamma \in H(F)$
is the number of connected components of
 $H_\gamma $
that have an F-point.
$H_\gamma $
that have an F-point.
3.2.2 Preliminaries
Let
![]() $\pi _0$
be a quaternionic discrete series on
$\pi _0$
be a quaternionic discrete series on
![]() $G_\infty $
. We will use the hyperendoscopy formula of [Reference FerrariFer07] to compute
$G_\infty $
. We will use the hyperendoscopy formula of [Reference FerrariFer07] to compute
![]() $I_{\mathrm {geom}}(\varphi _{\pi _0} \otimes f^\infty )$
. We need to apply the general case of [Reference DalalDal22, Thm. 4.2.3] since G might have endoscopy without simply connected derived subgroup. We use notation from [Reference DalalDal22, §3,4] to discuss endoscopy and hyperendoscopy. See [Reference Kottwitz and ShelstadKS99] for a full reference to the theory of endoscopy and [Reference LabesseLab11] for a course-notes-style introduction.
$I_{\mathrm {geom}}(\varphi _{\pi _0} \otimes f^\infty )$
. We need to apply the general case of [Reference DalalDal22, Thm. 4.2.3] since G might have endoscopy without simply connected derived subgroup. We use notation from [Reference DalalDal22, §3,4] to discuss endoscopy and hyperendoscopy. See [Reference Kottwitz and ShelstadKS99] for a full reference to the theory of endoscopy and [Reference LabesseLab11] for a course-notes-style introduction.
Let
![]() $\eta $
be the Euler–Poincaré function for the L-packet
$\eta $
be the Euler–Poincaré function for the L-packet
![]() $\Pi _{\mathrm {disc}}(\lambda )$
that conatins
$\Pi _{\mathrm {disc}}(\lambda )$
that conatins
![]() $\pi _0$
. Let
$\pi _0$
. Let
![]() $\mathcal {HE}_{\mathrm {ell}}(G)$
be the set of nontrivial hyperendoscopic paths for G. Then, in the notation of [Reference DalalDal22, §4],
$\mathcal {HE}_{\mathrm {ell}}(G)$
be the set of nontrivial hyperendoscopic paths for G. Then, in the notation of [Reference DalalDal22, §4],
 $$\begin{align*}I^{G_2}_{\mathrm{geom}}(\varphi_{\pi_0} \otimes f^\infty) = I^{G_2}_{\mathrm{geom}}(\eta_k \otimes f^\infty) + \sum_{H \in \mathcal{HE}_{\mathrm{ell}}(G_2)} \iota(G, \mathcal{H}) I^{\tilde{\mathcal{H}}}_{\mathrm{geom}}(((\eta - \varphi_{\pi_0}) \otimes f^\infty)^{\tilde{\mathcal{H}}}), \end{align*}$$
$$\begin{align*}I^{G_2}_{\mathrm{geom}}(\varphi_{\pi_0} \otimes f^\infty) = I^{G_2}_{\mathrm{geom}}(\eta_k \otimes f^\infty) + \sum_{H \in \mathcal{HE}_{\mathrm{ell}}(G_2)} \iota(G, \mathcal{H}) I^{\tilde{\mathcal{H}}}_{\mathrm{geom}}(((\eta - \varphi_{\pi_0}) \otimes f^\infty)^{\tilde{\mathcal{H}}}), \end{align*}$$
where the
![]() $\tilde {\mathcal {H}}$
are choices of z-pair paths when they are needed.
$\tilde {\mathcal {H}}$
are choices of z-pair paths when they are needed.
3.2.3 Telescoping
Next, an unpublished result of Kottwitz summarized in [Reference MorelMor10, §5.4] and proved by other methods in [Reference PengPen19] stabilizes
![]() $I_{\mathrm {geom}}(\varphi \otimes f^\infty )$
when
$I_{\mathrm {geom}}(\varphi \otimes f^\infty )$
when
![]() $\varphi $
satisfies a technical property of being stable-cuspidal (as EP-functions are but pseudocoefficients are not):
$\varphi $
satisfies a technical property of being stable-cuspidal (as EP-functions are but pseudocoefficients are not):
Theorem 3.2.1. Let
![]() $\varphi $
be stable cuspidal (e.g., an EP-function, but not a pseudocoefficient) on
$\varphi $
be stable cuspidal (e.g., an EP-function, but not a pseudocoefficient) on
![]() $G_\infty $
and
$G_\infty $
and
![]() $f^\infty $
a test function on
$f^\infty $
a test function on
![]() $G(\mathbb A^\infty )$
. Then
$G(\mathbb A^\infty )$
. Then
 $$\begin{align*}I^{G}_{\mathrm{geom}}(\varphi \otimes f^\infty) = \sum_{H \in \mathcal{E}_{\mathrm{ell}}(G)} \iota(G,H) S^{\tilde{H}}_{\mathrm{geom}}((\varphi \otimes f^\infty)^{\tilde{H}}), \end{align*}$$
$$\begin{align*}I^{G}_{\mathrm{geom}}(\varphi \otimes f^\infty) = \sum_{H \in \mathcal{E}_{\mathrm{ell}}(G)} \iota(G,H) S^{\tilde{H}}_{\mathrm{geom}}((\varphi \otimes f^\infty)^{\tilde{H}}), \end{align*}$$
where
![]() $\mathcal {E}_{\mathrm {ell}}(G)$
is the set of elliptic endoscopic groups for G and the
$\mathcal {E}_{\mathrm {ell}}(G)$
is the set of elliptic endoscopic groups for G and the
![]() $\tilde {H}$
are z-extensions if necessary. The transfers
$\tilde {H}$
are z-extensions if necessary. The transfers
![]() $(\varphi \otimes f^\infty )^{\tilde {H}}$
depend on choices of measures for G and H.
$(\varphi \otimes f^\infty )^{\tilde {H}}$
depend on choices of measures for G and H.
The
![]() $S_{\mathrm {geom}}$
terms are defined by their values on Euler–Poincaré functions:
$S_{\mathrm {geom}}$
terms are defined by their values on Euler–Poincaré functions:
 $$ \begin{align*} S^H_{\mathrm{geom}}(\eta_\lambda \otimes f^\infty) &= \sum_{M \in \mathcal{L}^{\mathrm{cusp}}(H)} (-1)^{[H : M]} \frac{|\Omega_{M,F}|}{|\Omega_{H,F}|} \tau(M) \\ &\quad \times \sum_{\gamma \in [M(\mathbb Q)]_{{\mathrm{st}}, \mathrm{ell}^\infty}} |\iota^M(\gamma)|^{-1} \frac{e(\bar M_{\gamma, \infty})}{ \operatorname{\mathrm{vol}}(\bar M_{\gamma, \infty}/A_{\bar M_\gamma, \infty})} \frac{k(M_\infty)}{k(H_\infty)} \Phi^H_M(\gamma, \lambda) SO_\gamma^\infty((f^\infty)_M), \end{align*} $$
$$ \begin{align*} S^H_{\mathrm{geom}}(\eta_\lambda \otimes f^\infty) &= \sum_{M \in \mathcal{L}^{\mathrm{cusp}}(H)} (-1)^{[H : M]} \frac{|\Omega_{M,F}|}{|\Omega_{H,F}|} \tau(M) \\ &\quad \times \sum_{\gamma \in [M(\mathbb Q)]_{{\mathrm{st}}, \mathrm{ell}^\infty}} |\iota^M(\gamma)|^{-1} \frac{e(\bar M_{\gamma, \infty})}{ \operatorname{\mathrm{vol}}(\bar M_{\gamma, \infty}/A_{\bar M_\gamma, \infty})} \frac{k(M_\infty)}{k(H_\infty)} \Phi^H_M(\gamma, \lambda) SO_\gamma^\infty((f^\infty)_M), \end{align*} $$
choosing Tamagawa globally measure on all centralizers. The volume on
![]() $\bar M_{\gamma , \infty }$
is transferred from that on
$\bar M_{\gamma , \infty }$
is transferred from that on
![]() $M_{\gamma , \infty }$
in the standard way for inner forms so that the entire term doesn’t depend on a choice of measure at infinity.
$M_{\gamma , \infty }$
in the standard way for inner forms so that the entire term doesn’t depend on a choice of measure at infinity.
There’s an alternating sign in the hyperendoscopy formula: If
![]() $\mathcal {H}$
is a hyperendoscopic path, then
$\mathcal {H}$
is a hyperendoscopic path, then
![]() $-\iota (G, \mathcal {H}) \iota (\mathcal {H}, H) = \iota (G, (\mathcal {H}, H))$
for H any endoscopic group of
$-\iota (G, \mathcal {H}) \iota (\mathcal {H}, H) = \iota (G, (\mathcal {H}, H))$
for H any endoscopic group of
![]() $\mathcal {H}$
. Here,
$\mathcal {H}$
. Here,
![]() $(\mathcal {H}, H)$
represents the concatenation and
$(\mathcal {H}, H)$
represents the concatenation and
![]() $\mathcal {H}$
is overloaded to also refer to the last group in
$\mathcal {H}$
is overloaded to also refer to the last group in
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
In particular, substituting in the stabilization telescopes the hyperendoscopy formula.
3.3 Final formula and usage notes
3.3.1 Formula
Telescoping together with Theorem 3.1.1 produces the final formula for quaternionic discrete series
![]() $\pi _0$
of
$\pi _0$
of
![]() $G_\infty $
that has infinitesimal character not equal to
$G_\infty $
that has infinitesimal character not equal to
![]() $\rho _G$
:
$\rho _G$
:
 $$ \begin{align} \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}}(G)}& m_{\mathrm{disc}}(\pi) \delta_{\pi_\infty = \pi_0} \operatorname{\mathrm{tr}}_{\pi^\infty} (f^\infty) \nonumber\\ &\quad= S^{G}_{\mathrm{geom}}(\eta \otimes f^\infty) + \sum_{\substack{H \in \mathcal{E}_{\mathrm{ell}}(G) \\ H \neq G}} \iota(G, H) S^{\tilde{H}}_{\mathrm{geom}}((\varphi_{\pi_0} \otimes f^\infty)^{\tilde{H}}). \end{align} $$
$$ \begin{align} \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}}(G)}& m_{\mathrm{disc}}(\pi) \delta_{\pi_\infty = \pi_0} \operatorname{\mathrm{tr}}_{\pi^\infty} (f^\infty) \nonumber\\ &\quad= S^{G}_{\mathrm{geom}}(\eta \otimes f^\infty) + \sum_{\substack{H \in \mathcal{E}_{\mathrm{ell}}(G) \\ H \neq G}} \iota(G, H) S^{\tilde{H}}_{\mathrm{geom}}((\varphi_{\pi_0} \otimes f^\infty)^{\tilde{H}}). \end{align} $$
The right side can be evaluated with Theorem 3.2.1.
We recall
 $$\begin{align*}\iota(G,H) = |\Lambda(H, \mathcal{H}, s, \eta)|^{-1} \frac{\tau(G)}{\tau(H)}, \end{align*}$$
$$\begin{align*}\iota(G,H) = |\Lambda(H, \mathcal{H}, s, \eta)|^{-1} \frac{\tau(G)}{\tau(H)}, \end{align*}$$
where
![]() $\Lambda (H, \mathcal {H}, s, \eta )$
is the image in
$\Lambda (H, \mathcal {H}, s, \eta )$
is the image in
![]() $\operatorname {\mathrm {Out}}(\widehat H)$
of the automorphisms of the endoscopic quadruple.
$\operatorname {\mathrm {Out}}(\widehat H)$
of the automorphisms of the endoscopic quadruple.
While getting a formula in terms of the distributions
![]() $S_{\mathrm {geom}}$
on smaller endoscopic groups comes immediately from stabilization, the above telescoping argument seems to be necessary to get explicit formulas for the
$S_{\mathrm {geom}}$
on smaller endoscopic groups comes immediately from stabilization, the above telescoping argument seems to be necessary to get explicit formulas for the
![]() $S_{\mathrm {geom}}$
when using a test factor at infinity that is just cuspidal instead of a stable cuspidal.
$S_{\mathrm {geom}}$
when using a test factor at infinity that is just cuspidal instead of a stable cuspidal.
3.3.2 Usage
There are two possible methods to compute terms here. If we were interested in working with more general groups or at more general level, something like method 1 would have been necessary. However, our application case of level-
![]() $1$
representations on
$1$
representations on
![]() $G_2$
allows us to use the much easier method 2. Method 2 in fact does not even need an explicit expansion for
$G_2$
allows us to use the much easier method 2. Method 2 in fact does not even need an explicit expansion for
![]() $S_{\mathrm {geom}}$
.
$S_{\mathrm {geom}}$
.
Method 1:
We can try calculate the
![]() $S_{\mathrm {geom}}$
terms directly from their formula in Theorem 3.2.1. We will need to choose Euler–Poincaré measure at
$S_{\mathrm {geom}}$
terms directly from their formula in Theorem 3.2.1. We will need to choose Euler–Poincaré measure at
![]() $\bar M_\gamma $
times canonical measure for the orbital integrals (canonical measure is the same for all inner forms). This adds an extra factor of
$\bar M_\gamma $
times canonical measure for the orbital integrals (canonical measure is the same for all inner forms). This adds an extra factor of
 $$\begin{align*}d(\bar M_{\gamma, \infty}) \frac{L(\mathrm{Mot}_{M_{\gamma}})}{e(\bar M_{\gamma, \infty}) 2^{\operatorname{\mathrm{rank}}(M_{\gamma, \infty})}} \end{align*}$$
$$\begin{align*}d(\bar M_{\gamma, \infty}) \frac{L(\mathrm{Mot}_{M_{\gamma}})}{e(\bar M_{\gamma, \infty}) 2^{\operatorname{\mathrm{rank}}(M_{\gamma, \infty})}} \end{align*}$$
by [Reference Shin and TemplierST16, lem. 6.2]. Since
![]() $d(H_\infty ) = 1$
and
$d(H_\infty ) = 1$
and
![]() $\operatorname {\mathrm {vol}}_{EP}(H_\infty /A_{H_\infty }) = 1$
for H compact, this expands the terms in Equation (1) as
$\operatorname {\mathrm {vol}}_{EP}(H_\infty /A_{H_\infty }) = 1$
for H compact, this expands the terms in Equation (1) as
 $$ \begin{align*} &S^H_{\mathrm{geom}}(\eta_\lambda \otimes f^\infty) = \sum_{M \in \mathcal{L}^{\mathrm{cusp}}(H)} \left( (-1)^{[H : M]} \frac{|\Omega_{M,F}|}{|\Omega_{H,F}|} \right) \left( \tau(M) \frac{k(M_\infty)}{k(H_\infty)} \right) \\ &\qquad\times \sum_{\gamma \in [M(\mathbb Q)]_{{\mathrm{st}}, \mathrm{ell}^\infty}} 2^{-\operatorname{\mathrm{rank}}(M_{\gamma, \infty})} \Phi^H_M(\gamma, \lambda) \left( L(\mathrm{Mot}_{M_{\gamma}}) |\iota^M(\gamma)|^{-1} SO_\gamma^\infty((f^\infty)_M) \right), \end{align*} $$
$$ \begin{align*} &S^H_{\mathrm{geom}}(\eta_\lambda \otimes f^\infty) = \sum_{M \in \mathcal{L}^{\mathrm{cusp}}(H)} \left( (-1)^{[H : M]} \frac{|\Omega_{M,F}|}{|\Omega_{H,F}|} \right) \left( \tau(M) \frac{k(M_\infty)}{k(H_\infty)} \right) \\ &\qquad\times \sum_{\gamma \in [M(\mathbb Q)]_{{\mathrm{st}}, \mathrm{ell}^\infty}} 2^{-\operatorname{\mathrm{rank}}(M_{\gamma, \infty})} \Phi^H_M(\gamma, \lambda) \left( L(\mathrm{Mot}_{M_{\gamma}}) |\iota^M(\gamma)|^{-1} SO_\gamma^\infty((f^\infty)_M) \right), \end{align*} $$
where the stable orbital integrals are now computed using canonical measure on centralizers.
The hardest terms here are the stable orbital integrals, the L-values and the characters
![]() $\Phi $
. The constant terms
$\Phi $
. The constant terms
![]() $(f^\infty )_M$
are explicit integrals.
$(f^\infty )_M$
are explicit integrals.
The L-values may be computed as products of values of Artin L-functions by explicitly describing the motives from [Reference GrossGro97]. The terms
![]() $\Phi $
can be reduced to linear combinations of traces of
$\Phi $
can be reduced to linear combinations of traces of
![]() $\gamma $
against finite-dimensional representations of G by the algorithm on [Reference ArthurArt89, pg. 273]. These can be computed by the Weyl character formula and its extension to irregular elements stated in, for example, [Reference Chenevier and RenardCR15, prop. 2.3].
$\gamma $
against finite-dimensional representations of G by the algorithm on [Reference ArthurArt89, pg. 273]. These can be computed by the Weyl character formula and its extension to irregular elements stated in, for example, [Reference Chenevier and RenardCR15, prop. 2.3].
The stable orbital integrals unfortunately cause far more difficulty. For specific groups, including our eventual application case of
![]() $G_2$
, they are computed and listed in tables in [Reference Gross and PollackGP05, pg. 159]. First, they are interpreted as orbital integrals on compact-at-infinity form
$G_2$
, they are computed and listed in tables in [Reference Gross and PollackGP05, pg. 159]. First, they are interpreted as orbital integrals on compact-at-infinity form
![]() $G^c$
by endoscopic transfer. The spectral side of the trace formula on
$G^c$
by endoscopic transfer. The spectral side of the trace formula on
![]() $G^c$
is then possible to compute, allowing the orbital integrals to be solved for once the coefficients in terms of L-values are known. Alternatively, [Reference Chenevier and TaïbiCT20] uses another trick, inputting vanishing results for small weight automorphic representations to solve for unstable orbital integrals in the resulting system of linear equations.
$G^c$
is then possible to compute, allowing the orbital integrals to be solved for once the coefficients in terms of L-values are known. Alternatively, [Reference Chenevier and TaïbiCT20] uses another trick, inputting vanishing results for small weight automorphic representations to solve for unstable orbital integrals in the resulting system of linear equations.
They can also be computed directly from unstable orbital integrals: [Reference KottwitzKot77] and [Reference TaïbiTaï17] use Bruhat–Tits theory to do this for
![]() $\mathrm {GL}_3$
and some classical groups respectively. Either way, all currently known methods are not fully general and extremely complicated.
$\mathrm {GL}_3$
and some classical groups respectively. Either way, all currently known methods are not fully general and extremely complicated.
Method 2:
Fortunately, there is a much simpler way to compute for our desired application of level-
![]() $1$
representations on
$1$
representations on
![]() $G_2$
. Recalling that
$G_2$
. Recalling that
![]() $I^{G_2^c}$
is known from [Reference Chenevier and RenardCR15], we can compare the expansions (1) for
$I^{G_2^c}$
is known from [Reference Chenevier and RenardCR15], we can compare the expansions (1) for
![]() $G_2$
and
$G_2$
and
![]() $G_2^c$
. The term for
$G_2^c$
. The term for
![]() $S^{G_2}$
a appears in the expansion for
$S^{G_2}$
a appears in the expansion for
![]() $I^{G_2^c}$
and can therefore be solved for and substituted in the expansion for
$I^{G_2^c}$
and can therefore be solved for and substituted in the expansion for
![]() $I^{G_2}$
. In total, we get a formula
$I^{G_2}$
. In total, we get a formula
where the corrections are in terms of
![]() $S^H$
for smaller endoscopic H.
$S^H$
for smaller endoscopic H.
In the next section, we will see that there aren’t actually that many H appearing. Finally, Section 7 will show that the terms for these H are easily computed through another trick in the case of level-
![]() $1$
. Method 2 also gives in Section 8 a Jacquet–Langlands-style result comparing quaternionic representations on
$1$
. Method 2 also gives in Section 8 a Jacquet–Langlands-style result comparing quaternionic representations on
![]() $G_2$
to representations on
$G_2$
to representations on
![]() $G_2^c$
.
$G_2^c$
.
Note. We comment on possible extensions of method 2. The comparison to a compact form would work for any group with a form that is compact at infinity and unramified at all finite places. These appear in types,
![]() $G_2, B_3, D_4, B_4, F_4, B_7, D_8, B_8$
and
$G_2, B_3, D_4, B_4, F_4, B_7, D_8, B_8$
and
![]() $E_8$
as enumerated in [Reference GrossGro96].
$E_8$
as enumerated in [Reference GrossGro96].
Being able to easily count the endoscopic terms spectrally is more rare and requires some kind of recursive expansion down to only terms of Lie type
![]() $A_1^n$
. This in particular works out for type
$A_1^n$
. This in particular works out for type
![]() $D_4$
, so level-
$D_4$
, so level-
![]() $1$
forms on type
$1$
forms on type
![]() $D_4$
should be countable analogously to method 2.
$D_4$
should be countable analogously to method 2.
In another direction, plugging in other unramified test functions could compute counts weighted by Hecke eigenvalues. These would be in terms of the same weighted counts on
![]() $G_2^c$
and certain other weighted counts of classical modular forms that are determined by combinatorial formulas for unramified transfers as explained in [Reference DalalDal22, §5.4].
$G_2^c$
and certain other weighted counts of classical modular forms that are determined by combinatorial formulas for unramified transfers as explained in [Reference DalalDal22, §5.4].
4
 $G_2$
computation setup
$G_2$
computation setup
From now on, we specialize to
![]() $G = G_2$
and discuss how to apply the previous theory to count
$G = G_2$
and discuss how to apply the previous theory to count
![]() $|\mathcal {Q}_k(1)|$
.
$|\mathcal {Q}_k(1)|$
.
4.1 Root system of
 $G_2$
$G_2$
4.1.1 Roots
We use notation from [Reference Li and SchwermerLS93] to specify the root system of
![]() $G_2$
. Let K be the maximal compact
$G_2$
. Let K be the maximal compact
![]() $\mathrm {SU}(2) \times \mathrm {SU}(2)/\pm 1$
of
$\mathrm {SU}(2) \times \mathrm {SU}(2)/\pm 1$
of
![]() $G_2(\mathbb R)$
, and choose a maximal torus
$G_2(\mathbb R)$
, and choose a maximal torus
![]() $T(\mathbb R)$
that is inside K. Make a choice of simple roots of
$T(\mathbb R)$
that is inside K. Make a choice of simple roots of
![]() $G_2(\mathbb R)$
that are noncompact; in this case determining a unique dominant chamber with respect to both
$G_2(\mathbb R)$
that are noncompact; in this case determining a unique dominant chamber with respect to both
![]() $G_2$
and K. Let
$G_2$
and K. Let
![]() $\beta $
be the highest root of
$\beta $
be the highest root of
![]() $G_2$
with respect to the choice of simple roots and note that it is long.
$G_2$
with respect to the choice of simple roots and note that it is long.
We now give explicit coordinates. As a mnemonic convention, roots indexed
![]() $1$
will be short and roots indexed
$1$
will be short and roots indexed
![]() $2$
will be long. Figure 1 displays all the roots and shades our choices of dominant Weyl chambers for both
$2$
will be long. Figure 1 displays all the roots and shades our choices of dominant Weyl chambers for both
![]() $G_2$
and K. The compact roots at infinity are the four along the
$G_2$
and K. The compact roots at infinity are the four along the
![]() $\epsilon _i$
-coordinate axes.
$\epsilon _i$
-coordinate axes.

Figure 1 Character lattice, roots and choices of dominant chamber for
![]() $G_2$
.
$G_2$
.
If the roots of the short and long
![]() $\mathrm {SU}_2$
are
$\mathrm {SU}_2$
are
![]() $2\epsilon _1$
and
$2\epsilon _1$
and
![]() $2\epsilon _2$
respectively, then the simple roots of
$2\epsilon _2$
respectively, then the simple roots of
![]() $G_2$
are
$G_2$
are
The other positive roots are
 $$ \begin{gather*} \text{(short) } 2 \epsilon_1 = \alpha_1 + \alpha_2, \qquad \epsilon_1 + \epsilon_2 = 2 \alpha_1 + \alpha_2, \\ \text{(long) } 2 \epsilon_2 = 3 \alpha_1 + \alpha_2, \qquad 3 \epsilon_1 + \epsilon_2 = 3 \alpha_2 + 2 \alpha_2. \end{gather*} $$
$$ \begin{gather*} \text{(short) } 2 \epsilon_1 = \alpha_1 + \alpha_2, \qquad \epsilon_1 + \epsilon_2 = 2 \alpha_1 + \alpha_2, \\ \text{(long) } 2 \epsilon_2 = 3 \alpha_1 + \alpha_2, \qquad 3 \epsilon_1 + \epsilon_2 = 3 \alpha_2 + 2 \alpha_2. \end{gather*} $$
The fundamental weights are
Of course
![]() $\beta = \lambda _2$
.
$\beta = \lambda _2$
.
The Weyl group is generated by simple reflections
 $$\begin{align*}s_{\alpha_1} \begin{pmatrix} 2\epsilon_1 \\ 2\epsilon_2 \end{pmatrix} = \begin{pmatrix} \epsilon_1 + \epsilon_2 \\ 3\epsilon_1 - \epsilon_2 \end{pmatrix}, \qquad s_{\alpha_2} \begin{pmatrix} 2\epsilon_1 \\ 2\epsilon_2 \end{pmatrix} = \begin{pmatrix} -\epsilon_1 + \epsilon_2 \\ 3\epsilon_1 + \epsilon_2 \end{pmatrix}. \end{align*}$$
$$\begin{align*}s_{\alpha_1} \begin{pmatrix} 2\epsilon_1 \\ 2\epsilon_2 \end{pmatrix} = \begin{pmatrix} \epsilon_1 + \epsilon_2 \\ 3\epsilon_1 - \epsilon_2 \end{pmatrix}, \qquad s_{\alpha_2} \begin{pmatrix} 2\epsilon_1 \\ 2\epsilon_2 \end{pmatrix} = \begin{pmatrix} -\epsilon_1 + \epsilon_2 \\ 3\epsilon_1 + \epsilon_2 \end{pmatrix}. \end{align*}$$
Finally,
 $$ \begin{gather*} \rho_K = \epsilon_1 + \epsilon_2 = 2 \alpha_1 + \alpha_2, \\ \rho_G = 4 \epsilon_1 + 2 \epsilon_2 = 5 \alpha_1 + 3 \alpha_2. \end{gather*} $$
$$ \begin{gather*} \rho_K = \epsilon_1 + \epsilon_2 = 2 \alpha_1 + \alpha_2, \\ \rho_G = 4 \epsilon_1 + 2 \epsilon_2 = 5 \alpha_1 + 3 \alpha_2. \end{gather*} $$
4.1.2 Coroots
Coroots will follow the opposite mnemonic: Coroots indexed
![]() $1$
are long, and coroots indexed
$1$
are long, and coroots indexed
![]() $2$
are short.
$2$
are short.
Since
![]() $G_2$
has trivial center,
$G_2$
has trivial center,
![]() $X^*(T)$
is the root lattice, which is exactly
$X^*(T)$
is the root lattice, which is exactly
Let
![]() $(\delta _1, \delta _2)$
be the dual basis to
$(\delta _1, \delta _2)$
be the dual basis to
![]() $(2\epsilon _1, 2\epsilon _2)$
: that is,
$(2\epsilon _1, 2\epsilon _2)$
: that is,
![]() $(\delta _i, \epsilon _j) = 1/2 {\mathbf {1}}_{i=j}$
. Then
$(\delta _i, \epsilon _j) = 1/2 {\mathbf {1}}_{i=j}$
. Then
Since
![]() $\epsilon _1$
and
$\epsilon _1$
and
![]() $\epsilon _2$
are perpendicular,
$\epsilon _2$
are perpendicular,
 $$ \begin{gather*} (2 \epsilon_1)^\vee = 2\delta_1, \\ (2 \epsilon_2)^\vee = 2\delta_2. \end{gather*} $$
$$ \begin{gather*} (2 \epsilon_1)^\vee = 2\delta_1, \\ (2 \epsilon_2)^\vee = 2\delta_2. \end{gather*} $$
More generally, the Weyl action gives
 $$ \begin{gather*} (\alpha_1^\vee, 2 \epsilon_1) = -1, \qquad (\alpha_1^\vee, 2\epsilon_2) = 3,\\ (\alpha_2^\vee, 2 \epsilon_1) = 1, \qquad (\alpha_2^\vee, 2\epsilon_2) = - 1, \end{gather*} $$
$$ \begin{gather*} (\alpha_1^\vee, 2 \epsilon_1) = -1, \qquad (\alpha_1^\vee, 2\epsilon_2) = 3,\\ (\alpha_2^\vee, 2 \epsilon_1) = 1, \qquad (\alpha_2^\vee, 2\epsilon_2) = - 1, \end{gather*} $$
so we get simple coroots
 $$ \begin{gather*} \alpha_1^\vee = -\delta_1 + 3\delta_2, \\ \alpha_2^\vee = \delta_1 - \delta_2. \end{gather*} $$
$$ \begin{gather*} \alpha_1^\vee = -\delta_1 + 3\delta_2, \\ \alpha_2^\vee = \delta_1 - \delta_2. \end{gather*} $$
This reproduces that the coroot lattice is
![]() $X_*(T)$
, implying that
$X_*(T)$
, implying that
![]() $G_2$
is simply connected. For completeness,
$G_2$
is simply connected. For completeness,
 $$ \begin{gather*} \lambda_1^\vee = \delta_1 + 3 \delta_2,\\ \lambda_2^\vee = \delta_1 + \delta_2. \end{gather*} $$
$$ \begin{gather*} \lambda_1^\vee = \delta_1 + 3 \delta_2,\\ \lambda_2^\vee = \delta_1 + \delta_2. \end{gather*} $$
4.2 Quaternionic discrete series for
 $G_2$
$G_2$
The quaternionic discrete series on
![]() $G_2$
of weight k for
$G_2$
of weight k for
![]() $k \geq 2$
lies in the L-packet
$k \geq 2$
lies in the L-packet
The members of this L-packet have Harish–Chandra parameters:
As in [Reference Gan, Gross and SavinGGS02], the quaternionic member is the one with minimal K-type
![]() $\lambda _B = 2k\epsilon _2$
. We know that the discrete series
$\lambda _B = 2k\epsilon _2$
. We know that the discrete series
![]() $\pi (\omega , \lambda )$
has minimal K-type
$\pi (\omega , \lambda )$
has minimal K-type
by the Blattner formula [Reference KnappKna01, Thm. 9.20]. Therefore, the weight-k quaternionic discrete series
![]() $\pi _k$
is specifically
$\pi _k$
is specifically
![]() $\pi (s_{\alpha _2}, (k-2)\beta )$
– computing,
$\pi (s_{\alpha _2}, (k-2)\beta )$
– computing,
![]() $s_{\alpha _2}$
fixes
$s_{\alpha _2}$
fixes
![]() $\rho _K$
so
$\rho _K$
so
This is the discrete series with Harish–Chandra parameter
Call it
![]() $\pi _k$
and its pseudocoefficient
$\pi _k$
and its pseudocoefficient
![]() $\varphi _k$
.
$\varphi _k$
.
Theorem 3.1.1 then gives that for
![]() $k> 2$
,
$k> 2$
,
if we choose measures so that
![]() $\operatorname {\mathrm {vol}} G_2(\widehat {\mathbb {Z}}) = 1$
. Note again that this heavily depends on the miracle of Proposition 2.3.3 and a similar result does not hold either for pseudocofficients for the other members of
$\operatorname {\mathrm {vol}} G_2(\widehat {\mathbb {Z}}) = 1$
. Note again that this heavily depends on the miracle of Proposition 2.3.3 and a similar result does not hold either for pseudocofficients for the other members of
![]() $\Pi _{\mathrm {disc}}((k-2)\beta )$
or for the Euler–Poincaré function.
$\Pi _{\mathrm {disc}}((k-2)\beta )$
or for the Euler–Poincaré function.
Note. Theorem 3.1.1 for just the case of
![]() $G_2$
can be produced much more easily by the computation in [Reference MundyMun20] of the A-packets of infinitesimal character
$G_2$
can be produced much more easily by the computation in [Reference MundyMun20] of the A-packets of infinitesimal character
![]() $(k-2)\beta + \rho _G$
for
$(k-2)\beta + \rho _G$
for
![]() $k>2$
. Mundy found that
$k>2$
. Mundy found that
![]() $\pi _k$
appears in all of them. Therefore, trace-distinguishability follows immediately from [Reference Adams and JohnsonAJ87, Lemma 8.8] that a given discrete series appears in the character formula of exactly one element of such an A-packet.
$\pi _k$
appears in all of them. Therefore, trace-distinguishability follows immediately from [Reference Adams and JohnsonAJ87, Lemma 8.8] that a given discrete series appears in the character formula of exactly one element of such an A-packet.
5 Groups contributing and related constants
5.1 Elliptic endoscopy of
 $G_2$
$G_2$
The elliptic endoscopic groups of
![]() $G_2$
are
$G_2$
are
![]() $G_2$
,
$G_2$
,
![]() $\mathrm {PGL}_3$
and
$\mathrm {PGL}_3$
and
![]() $\mathrm {SO}_4$
. This is stated in a thesis [Reference AltschulAlt13] but not fully explained, so we fill in some details here for reader convenience. We use notational conventions for endoscopy as in [Reference DalalDal22, §3]. We compute the possible endoscopic pairs
$\mathrm {SO}_4$
. This is stated in a thesis [Reference AltschulAlt13] but not fully explained, so we fill in some details here for reader convenience. We use notational conventions for endoscopy as in [Reference DalalDal22, §3]. We compute the possible endoscopic pairs
![]() $(s, \rho )$
.
$(s, \rho )$
.
Since
![]() $G_2$
has trivial center, the cohomology condition on s is always satisfied so we don’t bother checking it. Trivial center further gives that the isomorphism class of the pair only depends on s through its centralizer. Next, we note a result that we thank a referee for pointing out:
$G_2$
has trivial center, the cohomology condition on s is always satisfied so we don’t bother checking it. Trivial center further gives that the isomorphism class of the pair only depends on s through its centralizer. Next, we note a result that we thank a referee for pointing out:
Lemma 5.1.1. Let G be a split, adjoint and simply connected group over number field F. Then all its endoscopic groups are split.
Proof. Since G is simply connected, there is an L-embedding
![]() ${}^L\!{H} \hookrightarrow {}^L\!{G}$
. Since G is split, there is a projection
${}^L\!{H} \hookrightarrow {}^L\!{G}$
. Since G is split, there is a projection
![]() ${}^L\!{G} \twoheadrightarrow \widehat G$
. By inspecting the reconstruction of
${}^L\!{G} \twoheadrightarrow \widehat G$
. By inspecting the reconstruction of
![]() ${}^L\!{H}$
from
${}^L\!{H}$
from
![]() $(s, \rho )$
, the image of
$(s, \rho )$
, the image of
![]() ${}^L\!{H}$
in
${}^L\!{H}$
in
![]() $\widehat G$
is connected if and only if
$\widehat G$
is connected if and only if
![]() $\rho $
is trivial.
$\rho $
is trivial.
However, since
![]() $\widehat G$
also has trivial center, s is fixed by
$\widehat G$
also has trivial center, s is fixed by
![]() $\rho $
which implies that the image of
$\rho $
which implies that the image of
![]() ${}^L\!{H}$
in
${}^L\!{H}$
in
![]() $\widehat G$
is the centralizer of s. It is therefore necessarily connected since s is semisimple and
$\widehat G$
is the centralizer of s. It is therefore necessarily connected since s is semisimple and
![]() $\widehat G$
is simply connected.
$\widehat G$
is simply connected.
In particular,
![]() $\rho $
is always trivial and we can always find a valid s for any possible centralizer
$\rho $
is always trivial and we can always find a valid s for any possible centralizer
![]() $\widehat H$
. The possible elliptic
$\widehat H$
. The possible elliptic
![]() $\widehat H$
with trivial
$\widehat H$
with trivial
![]() $\rho $
are
$\rho $
are
![]() $G_2, \mathrm {SL}_3$
and
$G_2, \mathrm {SL}_3$
and
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2/\{\pm 1\}$
corresponding to split endoscopic groups
$\mathrm {SL}_2 \times \mathrm {SL}_2/\{\pm 1\}$
corresponding to split endoscopic groups
![]() $G_2, \mathrm {PGL}_3$
, and
$G_2, \mathrm {PGL}_3$
, and
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2/\{\pm 1\}$
. In each of these cases,
$\mathrm {SL}_2 \times \mathrm {SL}_2/\{\pm 1\}$
. In each of these cases,
![]() $\Lambda = 1$
.
$\Lambda = 1$
.
If a group contributes to the stabilization applied to our test function, then by the fundamental lemma, it needs to be unramified away from infinity. By formulas for transfers of pseudocoefficients (see [Reference DalalDal22, lem. 5.6.1]), it also needs to have an elliptic maximal torus at infinity. The only groups contributing are therefore the
![]() $G_2$
and the
$G_2$
and the
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2/\{\pm 1\}$
.
$\mathrm {SL}_2 \times \mathrm {SL}_2/\{\pm 1\}$
.
5.2 Endoscopic constants and normalizations
5.2.1 The
 $\iota $
$\iota $
Let
![]() $H = \mathrm {SL}_2 \times \mathrm {SL}_2/\pm 1$
, and let
$H = \mathrm {SL}_2 \times \mathrm {SL}_2/\pm 1$
, and let
![]() $G_2^c$
be the unique nonsplit inner form of
$G_2^c$
be the unique nonsplit inner form of
![]() $G_2$
over
$G_2$
over
![]() $\mathbb Q$
which is compact at infinity. Then,
$\mathbb Q$
which is compact at infinity. Then,
 $$ \begin{gather*} \iota(G_2^c, H) = \iota(G_2, H) = |\Lambda(H, \mathcal{H}, s, \eta)|^{-1} \frac{\tau(G)}{\tau(H)} = 1 \cdot \frac12, \\ \iota(G_2^c, G_2) = 1, \end{gather*} $$
$$ \begin{gather*} \iota(G_2^c, H) = \iota(G_2, H) = |\Lambda(H, \mathcal{H}, s, \eta)|^{-1} \frac{\tau(G)}{\tau(H)} = 1 \cdot \frac12, \\ \iota(G_2^c, G_2) = 1, \end{gather*} $$
by Kottwitz’s formula for Tamagawa numbers (note that
![]() $\ker ^1(\mathbb Q, Z_H) = \ker ^1(\mathbb Q, \{\pm 1\}) =1$
).
$\ker ^1(\mathbb Q, Z_H) = \ker ^1(\mathbb Q, \{\pm 1\}) =1$
).
5.2.2 The transfer factors
We also need to fix transfer factors at all places for both
![]() $G_2$
and
$G_2$
and
![]() $G_2^c$
to compute transfers. The computations in [Reference TaïbiTaï17] demonstrate how to do so explicitly. First, they can be chosen consistently by fixing a global Whittaker datum. The corresponding local Whittaker datum determines the local transfer factors on
$G_2^c$
to compute transfers. The computations in [Reference TaïbiTaï17] demonstrate how to do so explicitly. First, they can be chosen consistently by fixing a global Whittaker datum. The corresponding local Whittaker datum determines the local transfer factors on
![]() $G_2$
as in [Reference Kottwitz and ShelstadKS99]. Since
$G_2$
as in [Reference Kottwitz and ShelstadKS99]. Since
![]() $G_2$
is defined over
$G_2$
is defined over
![]() $\mathbb Z$
, we can choose global data that are unramified/admissible at all finite places with respect to the
$\mathbb Z$
, we can choose global data that are unramified/admissible at all finite places with respect to the
![]() $G_2(\mathbb Z_p)$
so we can use the fundamental lemma at all finite places as in [Reference HalesHal93, §7]. By [Reference KalethaKal18, §4.4], the Whittaker datum on
$G_2(\mathbb Z_p)$
so we can use the fundamental lemma at all finite places as in [Reference HalesHal93, §7]. By [Reference KalethaKal18, §4.4], the Whittaker datum on
![]() $G_2$
also gives compatible local transfer factors on
$G_2$
also gives compatible local transfer factors on
![]() $G_2^c$
(note that
$G_2^c$
(note that
![]() $G_2$
is simply connected for applying Theorem 4.4.1). These allow us to use the fundamental lemma at finite places since transfer factors there stay the same as our choices for
$G_2$
is simply connected for applying Theorem 4.4.1). These allow us to use the fundamental lemma at finite places since transfer factors there stay the same as our choices for
![]() $G_2$
.
$G_2$
.
We need to know two things about the Archimedean transfer factors. First, Whittaker normalization lets us use the formulas for discrete transfer from [Reference ShelstadShe10] on both
![]() $G_2$
and
$G_2$
and
![]() $G_2^c$
. Note here that
$G_2^c$
. Note here that
![]() $G_2^c$
is in particular a pure inner form since
$G_2^c$
is in particular a pure inner form since
![]() $G_2$
is adjoint. This formula is stated in a slightly easier to use form in [Reference LabesseLab11, §IV.3] for our case of
$G_2$
is adjoint. This formula is stated in a slightly easier to use form in [Reference LabesseLab11, §IV.3] for our case of
![]() $\rho _G - \rho _H \in X^*(T)$
(the
$\rho _G - \rho _H \in X^*(T)$
(the
![]() $\mathrm {inv}(\pi (1), \pi (w))$
of Shelstad is the
$\mathrm {inv}(\pi (1), \pi (w))$
of Shelstad is the
![]() $\kappa \cdot \epsilon $
term of Labesse).
$\kappa \cdot \epsilon $
term of Labesse).
Second, we need to know which element of
![]() $\Pi _{\mathrm {disc}}((k-2)\beta )$
our Archimedean Whittaker datum makes Whittaker-generic. This will have to be
$\Pi _{\mathrm {disc}}((k-2)\beta )$
our Archimedean Whittaker datum makes Whittaker-generic. This will have to be
![]() $\pi _{(k-2)\beta , 1}$
since our choice of dominant Weyl chamber has all simple roots noncompact and is the only possible such choice up to
$\pi _{(k-2)\beta , 1}$
since our choice of dominant Weyl chamber has all simple roots noncompact and is the only possible such choice up to
![]() $\Omega _K$
(see the discussion before Lemma 4.2.1 in [Reference TaïbiTaï17]. In fact, there is only one possible conjugacy class of Whittaker datum at infinity by considerations explained there).
$\Omega _K$
(see the discussion before Lemma 4.2.1 in [Reference TaïbiTaï17]. In fact, there is only one possible conjugacy class of Whittaker datum at infinity by considerations explained there).
5.2.3 The stabilizations
We fix canonical measure at finite places so that the fundamental lemma directly gives
![]() ${\mathbf {1}}_{K^\infty _{G_2}}^H = {\mathbf {1}}_{K^\infty _H}$
. Recall that EP-functions and pseudocoefficients are defined depending on measure so we don’t need to fix measure at infinity.
${\mathbf {1}}_{K^\infty _{G_2}}^H = {\mathbf {1}}_{K^\infty _H}$
. Recall that EP-functions and pseudocoefficients are defined depending on measure so we don’t need to fix measure at infinity.
Then, Equation (1) gives
 $$ \begin{align} I^{G_2}(\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)} \otimes &{\mathbf{1}}_{K^\infty_{G_2}}) \nonumber\\&= S^{G_2}(\eta^{G_2}_{(k-2)\beta} \otimes {\mathbf{1}}_{K^\infty_{G_2}}) + \frac12 S^H((\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)})^H \otimes {\mathbf{1}}_{K^\infty_{H}}). \end{align} $$
$$ \begin{align} I^{G_2}(\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)} \otimes &{\mathbf{1}}_{K^\infty_{G_2}}) \nonumber\\&= S^{G_2}(\eta^{G_2}_{(k-2)\beta} \otimes {\mathbf{1}}_{K^\infty_{G_2}}) + \frac12 S^H((\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)})^H \otimes {\mathbf{1}}_{K^\infty_{H}}). \end{align} $$
A simple case of the discrete transfer formula in [Reference LabesseLab11, §IV.3] computes that
![]() $(\eta ^{G_2^c}_{(k-2)\beta })^{G_2} = \eta ^{G_2}_{(k-2)\beta }$
(note that
$(\eta ^{G_2^c}_{(k-2)\beta })^{G_2} = \eta ^{G_2}_{(k-2)\beta }$
(note that
![]() $\Omega _{\mathbb R}(G_2^c) \backslash \Omega _{\mathbb C}(G_2^c)$
is trivial so
$\Omega _{\mathbb R}(G_2^c) \backslash \Omega _{\mathbb C}(G_2^c)$
is trivial so
![]() $\kappa $
is too), so
$\kappa $
is too), so
Since type
![]() $A_1 \times A_1$
has no nontrivial centralizer of full semisimple rank, all elliptic endoscopy of
$A_1 \times A_1$
has no nontrivial centralizer of full semisimple rank, all elliptic endoscopy of
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2/\pm 1$
is nonsplit. Therefore, it is ramified at some prime, so the transfers of
$\mathrm {SL}_2 \times \mathrm {SL}_2/\pm 1$
is nonsplit. Therefore, it is ramified at some prime, so the transfers of
![]() ${\mathbf {1}}_{K^\infty _H}$
vanish, implying that
${\mathbf {1}}_{K^\infty _H}$
vanish, implying that
![]() $S^H = I^H$
on our test functions. Substituting one stabilization into another finally gives
$S^H = I^H$
on our test functions. Substituting one stabilization into another finally gives
 $$ \begin{align} I^{G_2}(\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)} &\otimes {\mathbf{1}}_{K^\infty_{G_2}}) = I^{G_2^c}(\eta^{G_2^c}_{(k-2)\beta} \otimes {\mathbf{1}}_{K^\infty_{G_2^c}}) \nonumber\\&- \frac12 I^H ((\eta^{G^c_2}_{(k-2)\beta})^H \otimes {\mathbf{1}}_{K^\infty_{H}}) + \frac12 I^H((\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)})^H \otimes {\mathbf{1}}_{K^\infty_{H}}) \end{align} $$
$$ \begin{align} I^{G_2}(\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)} &\otimes {\mathbf{1}}_{K^\infty_{G_2}}) = I^{G_2^c}(\eta^{G_2^c}_{(k-2)\beta} \otimes {\mathbf{1}}_{K^\infty_{G_2^c}}) \nonumber\\&- \frac12 I^H ((\eta^{G^c_2}_{(k-2)\beta})^H \otimes {\mathbf{1}}_{K^\infty_{H}}) + \frac12 I^H((\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)})^H \otimes {\mathbf{1}}_{K^\infty_{H}}) \end{align} $$
under canonical measure at finite places.
This is our realization of method 2. There are three steps remaining to get counts:
-
1. Compute the transfers of EP-functions to H.
-
2. Write the resulting
 $I^H(\eta _\lambda \otimes {\mathbf {1}}_{K_H})$
terms in terms of counts of level-
$I^H(\eta _\lambda \otimes {\mathbf {1}}_{K_H})$
terms in terms of counts of level-
 $1$
, classical modular forms.
$1$
, classical modular forms. -
3. Look up values for the
 $G_2^c$
-term from [Reference Chenevier and RenardCR15].
$G_2^c$
-term from [Reference Chenevier and RenardCR15].
6 Real endoscopic transfers
Let H again be the one endoscopic group we care about:
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2/\{\pm 1\}$
. We want to compute
$\mathrm {SL}_2 \times \mathrm {SL}_2/\{\pm 1\}$
. We want to compute
![]() $(\varphi _{\pi _{G_2}(s_{\alpha _2}, (k-2) \beta )})^H$
and
$(\varphi _{\pi _{G_2}(s_{\alpha _2}, (k-2) \beta )})^H$
and
![]() $(\eta ^{G_2^c}_{(k-2)\beta })^H$
. By the choices of transfer factors in Section 5.2.2, we may do so by the formulas in [Reference LabesseLab11, §IV.3].
$(\eta ^{G_2^c}_{(k-2)\beta })^H$
. By the choices of transfer factors in Section 5.2.2, we may do so by the formulas in [Reference LabesseLab11, §IV.3].
As a choice for computation that doesn’t affect the final result, we realize the roots of H as
![]() $2 \epsilon _1$
and
$2 \epsilon _1$
and
![]() $2 \epsilon _2$
. Orient
$2 \epsilon _2$
. Orient
![]() $X^*(T)$
by setting the first quadrant in
$X^*(T)$
by setting the first quadrant in
![]() $\epsilon _1$
and
$\epsilon _1$
and
![]() $\epsilon _2$
to be H-dominant. The Weyl elements
$\epsilon _2$
to be H-dominant. The Weyl elements
![]() $\Omega (G, H)$
that send the G-dominant chamber to an H-dominant one are
$\Omega (G, H)$
that send the G-dominant chamber to an H-dominant one are
![]() $\{1, s_{\alpha _1}, s_{\alpha _2}\}$
.
$\{1, s_{\alpha _1}, s_{\alpha _2}\}$
.
6.1 Root combinatorics
Since
![]() $\rho _G - \rho _H \in X^*(T)$
, [Reference LabesseLab11, §IV.3] gives the transfer of the pseudocoefficient of the quaternionic discrete series to H:
$\rho _G - \rho _H \in X^*(T)$
, [Reference LabesseLab11, §IV.3] gives the transfer of the pseudocoefficient of the quaternionic discrete series to H:
 $$ \begin{align} &(\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)})^H= \nonumber\\&\quad \kappa^H(s_{\alpha_2}^{-1}) \eta^H_{(k-2)\beta + \rho_G - \rho_H} - \kappa^H(s_{\alpha_1} s_{\alpha_2}^{-1}) \eta^H_{s_{\alpha_1}((k-2)\beta + \rho_G) - \rho_H} - \eta^H_{s_{\alpha_2}((k-2)\beta + \rho_G) - \rho_H} \end{align} $$
$$ \begin{align} &(\varphi_{\pi_{G_2}(s_{\alpha_2}, (k-2) \beta)})^H= \nonumber\\&\quad \kappa^H(s_{\alpha_2}^{-1}) \eta^H_{(k-2)\beta + \rho_G - \rho_H} - \kappa^H(s_{\alpha_1} s_{\alpha_2}^{-1}) \eta^H_{s_{\alpha_1}((k-2)\beta + \rho_G) - \rho_H} - \eta^H_{s_{\alpha_2}((k-2)\beta + \rho_G) - \rho_H} \end{align} $$
for some signs
![]() $\kappa ^H(\cdot )$
.
$\kappa ^H(\cdot )$
.
We compute that
![]() $\rho _H = \epsilon _1 + \epsilon _2$
. Then
$\rho _H = \epsilon _1 + \epsilon _2$
. Then
In addition,
 $$ \begin{align*} s_{\alpha_1} \rho_G = 5\epsilon_1 + \epsilon_2, &\qquad s_{\alpha_1} \beta = \beta, \\ s_{\alpha_2} \rho_G = \epsilon_1 + 3\epsilon_2, &\qquad s_{\alpha_2} \beta = 2 \epsilon_2, \end{align*} $$
$$ \begin{align*} s_{\alpha_1} \rho_G = 5\epsilon_1 + \epsilon_2, &\qquad s_{\alpha_1} \beta = \beta, \\ s_{\alpha_2} \rho_G = \epsilon_1 + 3\epsilon_2, &\qquad s_{\alpha_2} \beta = 2 \epsilon_2, \end{align*} $$
so
and
6.2 Endoscopic characters
6.2.1 Setup
It remains to compute the
![]() $\kappa $
terms in Equation (5). These signs depend in a very complicated way on the realization of H and the exact transfer factors chosen. We will therefore use an indirect trick to compute them more easily.
$\kappa $
terms in Equation (5). These signs depend in a very complicated way on the realization of H and the exact transfer factors chosen. We will therefore use an indirect trick to compute them more easily.
Let
![]() $\psi _H$
be a (discrete in our case) L-parameter for
$\psi _H$
be a (discrete in our case) L-parameter for
![]() $H(\mathbb R)$
and
$H(\mathbb R)$
and
![]() $\psi _G$
the composition with
$\psi _G$
the composition with
![]() ${}^L\!{H} \hookrightarrow {}^L\!{G}_2$
. Then we have an identity of traces over L-packets:
${}^L\!{H} \hookrightarrow {}^L\!{G}_2$
. Then we have an identity of traces over L-packets:
 $$\begin{align*}S \Theta_{\psi_H}(f^H) = \sum_{\pi \in \Pi_{\psi_G}} \langle s_H, \pi \rangle \Theta_\pi(f), \end{align*}$$
$$\begin{align*}S \Theta_{\psi_H}(f^H) = \sum_{\pi \in \Pi_{\psi_G}} \langle s_H, \pi \rangle \Theta_\pi(f), \end{align*}$$
where
![]() $f^H$
is a transfer of f,
$f^H$
is a transfer of f,
![]() $\Theta _\pi $
is the Harish–Chandra character,
$\Theta _\pi $
is the Harish–Chandra character,
![]() $S\Theta _{\psi _H}$
is the stable character corresponding to the L-packet,
$S\Theta _{\psi _H}$
is the stable character corresponding to the L-packet,
![]() $\Pi _{\psi _G}$
is the L-packet corresponding to the L-parameter, and
$\Pi _{\psi _G}$
is the L-packet corresponding to the L-parameter, and
![]() $\langle s_H, \pi \rangle $
is shorthand for a sign depending on
$\langle s_H, \pi \rangle $
is shorthand for a sign depending on
![]() $\pi $
and the choice of Whittaker data. This sign comes from pairing an element
$\pi $
and the choice of Whittaker data. This sign comes from pairing an element
![]() $s_H$
of the centralizer of
$s_H$
of the centralizer of
![]() $\psi _G$
determined by H with a character associated to
$\psi _G$
determined by H with a character associated to
![]() $\pi $
through the Whittaker datum. See [Reference KalethaKal16, §1] for an exposition of how this works in general.
$\pi $
through the Whittaker datum. See [Reference KalethaKal16, §1] for an exposition of how this works in general.
If
![]() $\pi $
on
$\pi $
on
![]() $G_2$
is discrete series, Labesse’s formula tells us that we can choose
$G_2$
is discrete series, Labesse’s formula tells us that we can choose
for some signs
![]() $\epsilon $
that depend on the transfer factor and some set of weights
$\epsilon $
that depend on the transfer factor and some set of weights
![]() $\lambda $
that only depends on the infinitesimal character of
$\lambda $
that only depends on the infinitesimal character of
![]() $\pi $
.
$\pi $
.
Let
![]() $\psi _\lambda $
be the L-parameter corresponding to weight-
$\psi _\lambda $
be the L-parameter corresponding to weight-
![]() $\mu $
discrete series on H. Plugging this formula for
$\mu $
discrete series on H. Plugging this formula for
![]() $\varphi ^{G_2}_\pi $
into the trace identity for
$\varphi ^{G_2}_\pi $
into the trace identity for
![]() $\psi _\lambda $
gives that
$\psi _\lambda $
gives that
 $$\begin{align*}\epsilon(\lambda, \pi) = \sum_\mu \epsilon(\mu, \pi) S \Theta_{\psi_\lambda}(\eta_\mu^H) = \sum_{\pi' \in \Pi_{\psi_G}} \langle s_H, \pi' \rangle \Theta_{\pi'}(\varphi^{G_2}_\pi) = \begin{cases} \langle s_H, \pi \rangle & \pi \in \Pi_{\psi_G} \\ 0 & \text{else} \end{cases}, \end{align*}$$
$$\begin{align*}\epsilon(\lambda, \pi) = \sum_\mu \epsilon(\mu, \pi) S \Theta_{\psi_\lambda}(\eta_\mu^H) = \sum_{\pi' \in \Pi_{\psi_G}} \langle s_H, \pi' \rangle \Theta_{\pi'}(\varphi^{G_2}_\pi) = \begin{cases} \langle s_H, \pi \rangle & \pi \in \Pi_{\psi_G} \\ 0 & \text{else} \end{cases}, \end{align*}$$
where
![]() $\psi _G$
is the pushforward of
$\psi _G$
is the pushforward of
![]() $\psi _\lambda $
. The last equality is the definition of pseudocoefficient since all
$\psi _\lambda $
. The last equality is the definition of pseudocoefficient since all
![]() $\pi $
in a packet for an L-parameter should be tempered. This computation shows that
$\pi $
in a packet for an L-parameter should be tempered. This computation shows that
![]() $\psi _\lambda $
is required to push forward to the parameter for
$\psi _\lambda $
is required to push forward to the parameter for
![]() $\pi $
and that
$\pi $
and that
![]() $\epsilon (\lambda , \pi ) = \langle s_H, \pi \rangle $
.
$\epsilon (\lambda , \pi ) = \langle s_H, \pi \rangle $
.
6.2.2 The trick
Now, we are ready to compute the signs. Instead of doing the hard work of figuring out how the transfer factor directly affects the signs in Labesse’s formulation, we will use the key fact that
![]() $\epsilon (\lambda , \pi ) = \langle s_H, \pi \rangle = 1$
whenever
$\epsilon (\lambda , \pi ) = \langle s_H, \pi \rangle = 1$
whenever
![]() $\pi $
is the Whittaker-generic member of its L-packet. Therefore, in Labesse’s formula for the generic member
$\pi $
is the Whittaker-generic member of its L-packet. Therefore, in Labesse’s formula for the generic member
![]() $\pi _{1, (k-2)\beta }$
,
$\pi _{1, (k-2)\beta }$
,
 $$ \begin{align*} &(\varphi_{\pi_{G_2}(1, (k-2) \beta)})^H = \eta^H_{(k-2)\beta + \rho_G - \rho_H} + \kappa^H(s_{\alpha_1}) \operatorname{\mathrm{sgn}}(s_{\alpha_1}) \eta^H_{s_{\alpha_1}((k-2)\beta + \rho_G) - \rho_H}\\ &+ \kappa^H(s_{\alpha_2}) \operatorname{\mathrm{sgn}}(s_{\alpha_2}) \eta^H_{s_{\alpha_2}((k-2)\beta + \rho_G) - \rho_H}, \end{align*} $$
$$ \begin{align*} &(\varphi_{\pi_{G_2}(1, (k-2) \beta)})^H = \eta^H_{(k-2)\beta + \rho_G - \rho_H} + \kappa^H(s_{\alpha_1}) \operatorname{\mathrm{sgn}}(s_{\alpha_1}) \eta^H_{s_{\alpha_1}((k-2)\beta + \rho_G) - \rho_H}\\ &+ \kappa^H(s_{\alpha_2}) \operatorname{\mathrm{sgn}}(s_{\alpha_2}) \eta^H_{s_{\alpha_2}((k-2)\beta + \rho_G) - \rho_H}, \end{align*} $$
all the coefficients need to be
![]() $1$
. The allows to solve
$1$
. The allows to solve
for our choice of transfer factors. Right-
![]() $\Omega _{\mathbb R}$
-invariance of Labesse’s
$\Omega _{\mathbb R}$
-invariance of Labesse’s
![]() $\kappa $
then also gives that
$\kappa $
then also gives that
6.3 Final formulas for transfers
Therefore, our final transfer is
Transfers from
![]() $G_2^c$
are easier. Here,
$G_2^c$
are easier. Here,
![]() $\Omega _{\mathbb R}(G_2^c) \backslash \Omega _{\mathbb C}(G_2^c)$
is trivial so the average value of
$\Omega _{\mathbb R}(G_2^c) \backslash \Omega _{\mathbb C}(G_2^c)$
is trivial so the average value of
![]() $\kappa $
is
$\kappa $
is
![]() $1$
. Averaging Labesse’s formula as in [Reference DalalDal22, cor. 5.1.5] therefore gives
$1$
. Averaging Labesse’s formula as in [Reference DalalDal22, cor. 5.1.5] therefore gives
7 The
 $H = \mathrm {SL}_2 \times \mathrm {SL}_2 / \pm 1$
term
$H = \mathrm {SL}_2 \times \mathrm {SL}_2 / \pm 1$
term
Here, we compute the terms
![]() $I^H(\eta _\lambda \otimes {\mathbf {1}}_{K_H})$
for Euler–Poincaré functions
$I^H(\eta _\lambda \otimes {\mathbf {1}}_{K_H})$
for Euler–Poincaré functions
![]() $\eta _\lambda $
. Any
$\eta _\lambda $
. Any
![]() $\lambda = a \epsilon _1 + b \epsilon _2$
is a weight of H if
$\lambda = a \epsilon _1 + b \epsilon _2$
is a weight of H if
![]() $a+b$
is even. Note first that
$a+b$
is even. Note first that
 $$\begin{align*}I^H(\eta^H_\lambda \otimes {\mathbf{1}}_{K_H}) = \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}}(H)} \operatorname{\mathrm{tr}}_{\pi_\infty}(\eta^H_\lambda) \operatorname{\mathrm{tr}}_{\pi^\infty}({\mathbf{1}}_{K_H}) = \sum_{\substack{\pi \in \mathcal{AR}_{\mathrm{disc}}(H) \\ \pi \text{ unram.}}} \operatorname{\mathrm{tr}}_{\pi_\infty}(\eta^H_\lambda), \end{align*}$$
$$\begin{align*}I^H(\eta^H_\lambda \otimes {\mathbf{1}}_{K_H}) = \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}}(H)} \operatorname{\mathrm{tr}}_{\pi_\infty}(\eta^H_\lambda) \operatorname{\mathrm{tr}}_{\pi^\infty}({\mathbf{1}}_{K_H}) = \sum_{\substack{\pi \in \mathcal{AR}_{\mathrm{disc}}(H) \\ \pi \text{ unram.}}} \operatorname{\mathrm{tr}}_{\pi_\infty}(\eta^H_\lambda), \end{align*}$$
by Arthur’s simple trace formula and using our choice of canonical measure at finite places.
To move forward, we need to understand automorphic reps on H by relating them to other groups. Consider the sequence
It induces on local or global F
using that
![]() $H^1(F, \pm 1) = F^\times /(F^\times )^2$
and
$H^1(F, \pm 1) = F^\times /(F^\times )^2$
and
![]() $H^1(F, \mathrm {SL}_2) = 1$
for the F we care about (the
$H^1(F, \mathrm {SL}_2) = 1$
for the F we care about (the
![]() $\mathbb R$
case of the second equality comes from the determinant exact sequence on
$\mathbb R$
case of the second equality comes from the determinant exact sequence on
![]() $\mathrm {GL}_2$
). The image of
$\mathrm {GL}_2$
). The image of
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2(F)$
is the connected component
$\mathrm {SL}_2 \times \mathrm {SL}_2(F)$
is the connected component
![]() $H(F)^0$
.
$H(F)^0$
.
Note. As pointed out by a referee, we may also think of H as
![]() $(\mathrm {GL}_2 \times \mathrm {GL}_2)^{\det }/Z$
, where the superscript
$(\mathrm {GL}_2 \times \mathrm {GL}_2)^{\det }/Z$
, where the superscript
![]() $\det $
signifies that the two coordinates have the same determinant and the Z is the center of
$\det $
signifies that the two coordinates have the same determinant and the Z is the center of
![]() $\mathrm {GL}_2$
embedded diagonally. Then, since
$\mathrm {GL}_2$
embedded diagonally. Then, since
![]() $\mathbb G_m$
has trivial cohomology,
$\mathbb G_m$
has trivial cohomology,
![]() $H(F) = (\mathrm {GL}_2(F) \times \mathrm {GL}_2(F))^{\det }/F^\times $
. This suggests an alternate way to perform the ensuing computations that may be conceptually clearer.
$H(F) = (\mathrm {GL}_2(F) \times \mathrm {GL}_2(F))^{\det }/F^\times $
. This suggests an alternate way to perform the ensuing computations that may be conceptually clearer.
7.1 Cohomological representations of
 $H(\mathbb R)$
$H(\mathbb R)$
Next, we recall that the infinite trace measures an Euler characteristic against
![]() $(\mathfrak {h}, K_{H,\infty })$
-cohomology:
$(\mathfrak {h}, K_{H,\infty })$
-cohomology:
where
![]() $\mathfrak {h}$
is the Lie algebra of
$\mathfrak {h}$
is the Lie algebra of
![]() $H_\infty $
and
$H_\infty $
and
![]() $V_\lambda $
is the finite-dimensional representation of weight
$V_\lambda $
is the finite-dimensional representation of weight
![]() $\lambda $
of
$\lambda $
of
![]() $H^0_\infty $
pulled back to
$H^0_\infty $
pulled back to
![]() $H_\infty $
. Using the definition from [Reference Borel and WallachBW00, §5.1],
$H_\infty $
. Using the definition from [Reference Borel and WallachBW00, §5.1],
it suffices to consider the
![]() $\pi _\infty $
whose restrictions to
$\pi _\infty $
whose restrictions to
![]() $H_\infty ^0$
contain a component that is cohomological when pulled back to
$H_\infty ^0$
contain a component that is cohomological when pulled back to
![]() $[\mathrm {SL}_2 \times \mathrm {SL}_2](\mathbb R)$
. By Frobenius reciprocity and semisimplicity of inductions, these are exactly the irreducible constituents of
$[\mathrm {SL}_2 \times \mathrm {SL}_2](\mathbb R)$
. By Frobenius reciprocity and semisimplicity of inductions, these are exactly the irreducible constituents of
![]() $\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi '$
for
$\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi '$
for
![]() $\pi '$
cohomological of
$\pi '$
cohomological of
![]() $H_\infty ^0$
.
$H_\infty ^0$
.
Next,
![]() $H_\infty ^0$
is index
$H_\infty ^0$
is index
![]() $2$
in
$2$
in
![]() $H_\infty $
. Pick
$H_\infty $
. Pick
![]() $h \in H_\infty - H_\infty ^0$
, and let
$h \in H_\infty - H_\infty ^0$
, and let
![]() $\pi ^{\prime (h)}$
be the representation
$\pi ^{\prime (h)}$
be the representation
![]() $\gamma \mapsto \pi '(h^{-1} \gamma h)$
. Define character
$\gamma \mapsto \pi '(h^{-1} \gamma h)$
. Define character
As noted in the proof of Lemma 2.5 in [Reference Labesse and LanglandsLL79], there are two cases for
![]() $H_\infty ^0$
-representations
$H_\infty ^0$
-representations
![]() $\pi '$
:
$\pi '$
:
-
1.
 $\pi ' \neq \pi ^{\prime (h)}$
: Then
$\pi ' \neq \pi ^{\prime (h)}$
: Then
 $\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi '$
is irreducible and
$\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi '$
is irreducible and
 $\operatorname {\mathrm {Res}}_{H_\infty ^0}^{H_\infty }\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi ' = \pi ' \oplus \pi ^{\prime (h)}$
.
$\operatorname {\mathrm {Res}}_{H_\infty ^0}^{H_\infty }\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi ' = \pi ' \oplus \pi ^{\prime (h)}$
. -
2.
 $\pi ' = \pi ^{\prime (h)}$
: Then
$\pi ' = \pi ^{\prime (h)}$
: Then
 $\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi ' = V \oplus (V \otimes \chi )$
for some irreducible V. Also,
$\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi ' = V \oplus (V \otimes \chi )$
for some irreducible V. Also,
 $\operatorname {\mathrm {Res}}_{H_\infty ^0}^{H_\infty }\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi ' = \pi ' \oplus \pi '$
$\operatorname {\mathrm {Res}}_{H_\infty ^0}^{H_\infty }\operatorname {\mathrm {Ind}}_{H_\infty ^0}^{H_\infty } \pi ' = \pi ' \oplus \pi '$
Recalling a standard result, the cohomological representations of
![]() $\mathrm {SL}_2(\mathbb R)$
with respect to
$\mathrm {SL}_2(\mathbb R)$
with respect to
![]() $\lambda $
are:
$\lambda $
are:
-
• A discrete series L-packet
 $\{\pi _{\lambda ,1}$
,
$\{\pi _{\lambda ,1}$
,
 $\pi _{\lambda , s}\}$
(where
$\pi _{\lambda , s}\}$
(where
 $\Omega _{\mathrm {SL}_2} = \{1, s\}$
),
$\Omega _{\mathrm {SL}_2} = \{1, s\}$
), -
• The trivial representation
 ${\mathbf {1}}_{\mathrm {SL}_2}$
if
${\mathbf {1}}_{\mathrm {SL}_2}$
if
 $\lambda = 0$
.
$\lambda = 0$
.
By the Künneth rule, cohomological representations of
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb R)$
are exactly products of those on
$\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb R)$
are exactly products of those on
![]() $\mathrm {SL}_2(\mathbb R)$
. Those of
$\mathrm {SL}_2(\mathbb R)$
. Those of
![]() $H_\infty ^0$
are exactly those of
$H_\infty ^0$
are exactly those of
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb R)$
that are trivial on
$\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb R)$
that are trivial on
![]() $\pm 1$
– in other words, with
$\pm 1$
– in other words, with
![]() $\lambda = a\epsilon _1+b\epsilon _2$
and
$\lambda = a\epsilon _1+b\epsilon _2$
and
![]() $a+b$
even.
$a+b$
even.
Consider such
![]() $\lambda $
. There are three cases of inductions to consider to compute the cohomological representations of
$\lambda $
. There are three cases of inductions to consider to compute the cohomological representations of
![]() $H_\infty $
. Note that conjugation by
$H_\infty $
. Note that conjugation by
![]() $h \in H_\infty -H_\infty ^0$
swaps the two members of a discrete-series L-packet of an embedded
$h \in H_\infty -H_\infty ^0$
swaps the two members of a discrete-series L-packet of an embedded
![]() $\mathrm {SL}_2$
factor and fixes the trivial representation.
$\mathrm {SL}_2$
factor and fixes the trivial representation.
-
•
 $a,b \neq 0$
: We look at the inductions of products of discrete series. This is case (1) so the
$a,b \neq 0$
: We look at the inductions of products of discrete series. This is case (1) so the
 $4$
products pair up in sums that are
$4$
products pair up in sums that are
 $2$
members of an L-packet. These are of course
$2$
members of an L-packet. These are of course
 $\pi ^H_{\lambda ,1}$
and
$\pi ^H_{\lambda ,1}$
and
 $\pi ^H_{\lambda , s}$
, where s is a length-
$\pi ^H_{\lambda , s}$
, where s is a length-
 $1$
element of
$1$
element of
 $\Omega _H$
:
$\Omega _H$
:  $$ \begin{align*} \pi^H_{\lambda,1}|_{H_\infty^0} &= (\pi_{a \epsilon_1,1} \boxtimes \pi_{b \epsilon_2,1}) \oplus (\pi_{a \epsilon_1,s} \boxtimes \pi_{b \epsilon_2,s}), \\ \pi^H_{\lambda,s}|_{H_\infty^0} &= (\pi_{a \epsilon_1,1} \boxtimes \pi_{b \epsilon_2,s}) \oplus (\pi_{a \epsilon_1,s} \boxtimes \pi_{b \epsilon_2,1}). \end{align*} $$
$$ \begin{align*} \pi^H_{\lambda,1}|_{H_\infty^0} &= (\pi_{a \epsilon_1,1} \boxtimes \pi_{b \epsilon_2,1}) \oplus (\pi_{a \epsilon_1,s} \boxtimes \pi_{b \epsilon_2,s}), \\ \pi^H_{\lambda,s}|_{H_\infty^0} &= (\pi_{a \epsilon_1,1} \boxtimes \pi_{b \epsilon_2,s}) \oplus (\pi_{a \epsilon_1,s} \boxtimes \pi_{b \epsilon_2,1}). \end{align*} $$
-
• Without loss of generality,
 $a = 0, b \neq 0$
: We also need to consider inductions of
$a = 0, b \neq 0$
: We also need to consider inductions of
 ${\mathbf {1}} \boxtimes \pi _{b \epsilon _2, \star }$
. This is case (1), and both induce to a single irreducible
${\mathbf {1}} \boxtimes \pi _{b \epsilon _2, \star }$
. This is case (1), and both induce to a single irreducible
 $\sigma ^H_{\lambda }$
:
$\sigma ^H_{\lambda }$
:  $$\begin{align*}\sigma^H_\lambda|_{H_\infty^0} = ({\mathbf{1}} \boxtimes \pi_{b \epsilon_2,1}) \oplus ({\mathbf{1}} \boxtimes \pi_{b \epsilon_2, s}). \end{align*}$$
$$\begin{align*}\sigma^H_\lambda|_{H_\infty^0} = ({\mathbf{1}} \boxtimes \pi_{b \epsilon_2,1}) \oplus ({\mathbf{1}} \boxtimes \pi_{b \epsilon_2, s}). \end{align*}$$
-
•
 $a = b = 0$
: In addition to both the above, we need to consider the induction of
$a = b = 0$
: In addition to both the above, we need to consider the induction of
 ${\mathbf {1}}_{\mathrm {SL}_2} \boxtimes {\mathbf {1}}_{\mathrm {SL}_2}$
. This is case (2). This trivial representation induces to
${\mathbf {1}}_{\mathrm {SL}_2} \boxtimes {\mathbf {1}}_{\mathrm {SL}_2}$
. This is case (2). This trivial representation induces to
 ${\mathbf {1}}_{H_\infty } \oplus \chi $
on
${\mathbf {1}}_{H_\infty } \oplus \chi $
on
 $H_\infty $
. Both factors are cohomological.
$H_\infty $
. Both factors are cohomological.
Grothendieck group relations stay true restricted to
![]() $H_\infty ^0$
, so we can compute traces against
$H_\infty ^0$
, so we can compute traces against
![]() $\eta _\lambda $
. Recall that in
$\eta _\lambda $
. Recall that in
![]() $\mathrm {SL}_2(\mathbb R)$
$\mathrm {SL}_2(\mathbb R)$
where I is some parabolically induced representation with trivial trace against
![]() $\eta ^{\mathrm {SL}_2}_0$
.
$\eta ^{\mathrm {SL}_2}_0$
.
First, by our normalization
Next, working in
![]() $H_\infty ^0$
and for
$H_\infty ^0$
and for
![]() $\lambda = b \epsilon _2$
,
$\lambda = b \epsilon _2$
,
so
implying
Finally,
 $$ \begin{align*} {\mathbf{1}} \boxtimes {\mathbf{1}} &= ( I - \pi_{0, 1} - \pi_{0,s}) \boxtimes ( I - \pi_{0, 1} - \pi_{0,s}) \\ &= I \boxtimes I - I \boxtimes (\pi_{0,1} + \pi_{0,s}) - (\pi_{0,1} + \pi_{0,s}) \boxtimes I + \pi^H_{0 + 0, 1} + \pi^H_{0+ 0, s}, \end{align*} $$
$$ \begin{align*} {\mathbf{1}} \boxtimes {\mathbf{1}} &= ( I - \pi_{0, 1} - \pi_{0,s}) \boxtimes ( I - \pi_{0, 1} - \pi_{0,s}) \\ &= I \boxtimes I - I \boxtimes (\pi_{0,1} + \pi_{0,s}) - (\pi_{0,1} + \pi_{0,s}) \boxtimes I + \pi^H_{0 + 0, 1} + \pi^H_{0+ 0, s}, \end{align*} $$
so
Since
![]() $\eta _\lambda $
is supported on
$\eta _\lambda $
is supported on
![]() $H^0_\infty $
, we similarly have
$H^0_\infty $
, we similarly have
In total, our H-term becomes a count
 $$ \begin{align} I^H(\eta^H_\lambda \otimes {\mathbf{1}}_{K_H}) = \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}, \mathrm{ur}}(H)} m_{\mathrm{disc}}^H(\pi) w^H(\pi_\infty), \end{align} $$
$$ \begin{align} I^H(\eta^H_\lambda \otimes {\mathbf{1}}_{K_H}) = \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}, \mathrm{ur}}(H)} m_{\mathrm{disc}}^H(\pi) w^H(\pi_\infty), \end{align} $$
where
![]() $w^H$
is a weight
$w^H$
is a weight
 $$\begin{align*}w^H(\pi_\infty) = \begin{cases} 0 & \pi_\infty \text{ not cohomological of weight } \lambda \\ 1/2 & \pi_\infty \text{ one of the } \pi^H_{\lambda, *} \\ -1 & \pi_\infty = \sigma^H_\lambda \\ 1 & \pi_\infty \text{ trivial or }\chi\text{ and } \lambda = 0 \end{cases}. \end{align*}$$
$$\begin{align*}w^H(\pi_\infty) = \begin{cases} 0 & \pi_\infty \text{ not cohomological of weight } \lambda \\ 1/2 & \pi_\infty \text{ one of the } \pi^H_{\lambda, *} \\ -1 & \pi_\infty = \sigma^H_\lambda \\ 1 & \pi_\infty \text{ trivial or }\chi\text{ and } \lambda = 0 \end{cases}. \end{align*}$$
Call the cohomological cases type I, II and III in order.
7.2 Reduction to modular form counts
We now recall two results from [Reference Chenevier and RenardCR15]. Consider central isogeny
![]() $G \to G'$
of semisimple algebraic groups over
$G \to G'$
of semisimple algebraic groups over
![]() $\mathbb Z$
. If
$\mathbb Z$
. If
![]() $\pi ' = \pi ^{\prime }_\infty \otimes \pi ^{\prime \infty }$
is an unramified, discrete automorphic representation of
$\pi ' = \pi ^{\prime }_\infty \otimes \pi ^{\prime \infty }$
is an unramified, discrete automorphic representation of
![]() $G'$
, let
$G'$
, let
![]() $R(\pi ')$
be the set of unitary, admissible representations
$R(\pi ')$
be the set of unitary, admissible representations
![]() $\pi = \pi _\infty \otimes \pi ^\infty $
of
$\pi = \pi _\infty \otimes \pi ^\infty $
of
![]() $G(\mathbb A)$
that satisfy:
$G(\mathbb A)$
that satisfy:
-
•
 $\pi ^\infty $
is unramified with set of Satake parameters
$\pi ^\infty $
is unramified with set of Satake parameters
 $c^\infty (\pi ^\infty )$
induced from that of
$c^\infty (\pi ^\infty )$
induced from that of
 $\pi ^{\prime \infty }$
through
$\pi ^{\prime \infty }$
through
 $T_{G'}^G : \widehat G' \to \widehat G$
.
$T_{G'}^G : \widehat G' \to \widehat G$
. -
•
 $\pi _\infty $
is a constituent of the restriction of
$\pi _\infty $
is a constituent of the restriction of
 $\pi ^{\prime }_\infty $
through
$\pi ^{\prime }_\infty $
through
 $G(\mathbb R) \to G'(\mathbb R)$
.
$G(\mathbb R) \to G'(\mathbb R)$
.
Note that the size of
![]() $R(\pi ')$
is the number of constituents of the restriction
$R(\pi ')$
is the number of constituents of the restriction
![]() $\pi ^{\prime }_\infty |_{G(\mathbb R)}$
.
$\pi ^{\prime }_\infty |_{G(\mathbb R)}$
.
Theorem 7.2.1 [Reference Chenevier and RenardCR15, prop. 4.7]
Let
![]() $\pi $
be an automorphic representation of G. Then
$\pi $
be an automorphic representation of G. Then
 $$\begin{align*}m_{\mathrm{disc}}^G(\pi) = \sum_{\pi' : \pi \in R(\pi')} m_{\mathrm{disc}}^{G'}(\pi') [\pi_\infty, \pi^{\prime}_\infty], \end{align*}$$
$$\begin{align*}m_{\mathrm{disc}}^G(\pi) = \sum_{\pi' : \pi \in R(\pi')} m_{\mathrm{disc}}^{G'}(\pi') [\pi_\infty, \pi^{\prime}_\infty], \end{align*}$$
where
![]() $[\pi _\infty , \pi ^{\prime }_\infty ]$
is the multiplicity of
$[\pi _\infty , \pi ^{\prime }_\infty ]$
is the multiplicity of
![]() $\pi _\infty $
in
$\pi _\infty $
in
![]() $\pi ^{\prime }_\infty |_{G(\mathbb R)}$
.
$\pi ^{\prime }_\infty |_{G(\mathbb R)}$
.
We will apply this with
![]() $G = H$
and
$G = H$
and
![]() $G' = \mathrm {PGL}_2 \times \mathrm {PGL}_2$
. Make similar definitions of type I, II and III for representations of
$G' = \mathrm {PGL}_2 \times \mathrm {PGL}_2$
. Make similar definitions of type I, II and III for representations of
![]() $[\mathrm {PGL}_2 \times \mathrm {PGL}_2](\mathbb R)$
. Type I on
$[\mathrm {PGL}_2 \times \mathrm {PGL}_2](\mathbb R)$
. Type I on
![]() $\mathrm {PGL}_2 \times \mathrm {PGL}_2$
restricts to the sum over a discrete L-packet on
$\mathrm {PGL}_2 \times \mathrm {PGL}_2$
restricts to the sum over a discrete L-packet on
![]() $H_\infty $
. Type II and III on
$H_\infty $
. Type II and III on
![]() $\mathrm {PGL}_2 \times \mathrm {PGL}_2$
have irreducible restrictions. These restrictions partition the cohomological representations of H except for
$\mathrm {PGL}_2 \times \mathrm {PGL}_2$
have irreducible restrictions. These restrictions partition the cohomological representations of H except for
![]() $\chi $
so
$\chi $
so
 $$\begin{align*}m_{\mathrm{disc}}^H(\pi_\infty \otimes \pi^\infty) = \sum_{c^\infty({\pi'}^\infty) \in (T_{G'}^H)^{-1}(c^\infty(\pi^\infty))} m_{\mathrm{disc}}^{G'}(\pi^{\prime}_\infty \oplus {\pi'}^\infty) \end{align*}$$
$$\begin{align*}m_{\mathrm{disc}}^H(\pi_\infty \otimes \pi^\infty) = \sum_{c^\infty({\pi'}^\infty) \in (T_{G'}^H)^{-1}(c^\infty(\pi^\infty))} m_{\mathrm{disc}}^{G'}(\pi^{\prime}_\infty \oplus {\pi'}^\infty) \end{align*}$$
when
![]() $\pi _\infty \subseteq \pi ^{\prime }_\infty |_{H_\infty }$
and the multiplicity is
$\pi _\infty \subseteq \pi ^{\prime }_\infty |_{H_\infty }$
and the multiplicity is
![]() $0$
when
$0$
when
![]() $\pi _\infty = \chi $
. Now, we sum over the constituents of
$\pi _\infty = \chi $
. Now, we sum over the constituents of
![]() $\pi ^{\prime }_\infty |_{H_\infty }$
and the possible values of
$\pi ^{\prime }_\infty |_{H_\infty }$
and the possible values of
![]() $c^\infty (\pi ^\infty )$
, noting that
$c^\infty (\pi ^\infty )$
, noting that
![]() $T_{G'}^H$
is surjective. This gives
$T_{G'}^H$
is surjective. This gives
Corollary 7.2.2.
 $$\begin{align*}\sum_{\pi \in \mathcal{AR}_{\mathrm{disc}, \mathrm{ur}}(H)} m_{\mathrm{disc}}^H(\pi) w^H(\pi_\infty) = \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}, \mathrm{ur}}(G')} m_{\mathrm{disc}}^{G'}(\pi) w^{G'}(\pi_\infty), \end{align*}$$
$$\begin{align*}\sum_{\pi \in \mathcal{AR}_{\mathrm{disc}, \mathrm{ur}}(H)} m_{\mathrm{disc}}^H(\pi) w^H(\pi_\infty) = \sum_{\pi \in \mathcal{AR}_{\mathrm{disc}, \mathrm{ur}}(G')} m_{\mathrm{disc}}^{G'}(\pi) w^{G'}(\pi_\infty), \end{align*}$$
where
![]() $w^{G'}$
is the weight
$w^{G'}$
is the weight
 $$\begin{align*}w^{\mathrm{PGL}_2 \times \mathrm{PGL}_2}(\pi_\infty) = \begin{cases} 1 & \pi_\infty \text{ type I}\\ -1 & \pi_\infty \text{ type II}\\ 1 & \pi_\infty \text{ type III} \end{cases} \end{align*}$$
$$\begin{align*}w^{\mathrm{PGL}_2 \times \mathrm{PGL}_2}(\pi_\infty) = \begin{cases} 1 & \pi_\infty \text{ type I}\\ -1 & \pi_\infty \text{ type II}\\ 1 & \pi_\infty \text{ type III} \end{cases} \end{align*}$$
that only differs from
![]() $w^H$
by multiplying the type I case by two.
$w^H$
by multiplying the type I case by two.
Let
![]() $\mathcal {S}_k(1)$
be the set of normalized, level-
$\mathcal {S}_k(1)$
be the set of normalized, level-
![]() $1$
, weight-k cuspidal (new)eigenforms. If
$1$
, weight-k cuspidal (new)eigenforms. If
![]() $\lambda = a\epsilon _1 + b \epsilon _2$
, then type I representations on
$\lambda = a\epsilon _1 + b \epsilon _2$
, then type I representations on
![]() $\mathrm {PGL}_2 \times \mathrm {PGL}_2$
correspond to pairs in
$\mathrm {PGL}_2 \times \mathrm {PGL}_2$
correspond to pairs in
![]() $S_{a+2}(1) \times S_{b+2}(1)$
. Type II is a single form times the trivial representation, and type III is only the trivial representation.
$S_{a+2}(1) \times S_{b+2}(1)$
. Type II is a single form times the trivial representation, and type III is only the trivial representation.
7.3 Final formula for
 $S^H$
$S^H$
Therefore, if
we get:
using canonical measure at finite places. By a classical formula ([Reference Diamond and ShurmanDS05, Thm. 3.5.2], for example),
 $$ \begin{align*} S_{a+2} &= \begin{cases} 0 & a+2 = 2 \text{ or } a+2 \text{ odd}\\ \lfloor \frac{a+2}{12} \rfloor - 1 & a+2 \equiv 2\quad \pmod{12} \\ \lfloor \frac{a+2}{12} \rfloor & \text{else} \\ \end{cases}. \end{align*} $$
$$ \begin{align*} S_{a+2} &= \begin{cases} 0 & a+2 = 2 \text{ or } a+2 \text{ odd}\\ \lfloor \frac{a+2}{12} \rfloor - 1 & a+2 \equiv 2\quad \pmod{12} \\ \lfloor \frac{a+2}{12} \rfloor & \text{else} \\ \end{cases}. \end{align*} $$
8 A Jacquet–Langlands-style result
8.1 First form
Generalizing Equation (4) slightly and substituting in Equations (6) and (7) gives
 $$ \begin{align} I^{G_2}(\varphi_{\pi_k} \otimes f^\infty) &= I^{G_2^c}(\eta^{G_2^c}_{(k-2)\beta} \otimes f^\infty) - I^H (\eta^H_{(3k-3)\epsilon_1+ (k-1)\epsilon_2} \otimes (f^\infty)^H) \nonumber\\ &\quad+ I^H (\eta^H_{(3k-2)\epsilon_1 + (k-2)\epsilon_2} \otimes (f^\infty)^H) \end{align} $$
$$ \begin{align} I^{G_2}(\varphi_{\pi_k} \otimes f^\infty) &= I^{G_2^c}(\eta^{G_2^c}_{(k-2)\beta} \otimes f^\infty) - I^H (\eta^H_{(3k-3)\epsilon_1+ (k-1)\epsilon_2} \otimes (f^\infty)^H) \nonumber\\ &\quad+ I^H (\eta^H_{(3k-2)\epsilon_1 + (k-2)\epsilon_2} \otimes (f^\infty)^H) \end{align} $$
for any unramified function
![]() $f^\infty $
(we use here that
$f^\infty $
(we use here that
![]() $(G_2^c)^\infty =(G_2)^\infty $
). This will let us describe the set
$(G_2^c)^\infty =(G_2)^\infty $
). This will let us describe the set
![]() $\mathcal {Q}_k(1)$
for
$\mathcal {Q}_k(1)$
for
![]() $k> 2$
in terms of certain representations of
$k> 2$
in terms of certain representations of
![]() $G_2^c$
and H.
$G_2^c$
and H.
Choose
![]() $\pi = \pi _k \otimes \pi ^\infty \in \mathcal {Q}_k(1)$
. Since
$\pi = \pi _k \otimes \pi ^\infty \in \mathcal {Q}_k(1)$
. Since
![]() $\pi ^\infty $
is unramified, it can be described by a sequence of Satake parameters: For each prime p, a semisimple conjugacy class
$\pi ^\infty $
is unramified, it can be described by a sequence of Satake parameters: For each prime p, a semisimple conjugacy class
![]() $c_p(\pi ^\infty ) \in [\widehat {G_2}]_{\mathrm {ss}}$
(note that
$c_p(\pi ^\infty ) \in [\widehat {G_2}]_{\mathrm {ss}}$
(note that
![]() $G_2$
is split so we don’t need to worry about the full Langlands dual and see [Reference Shin and TemplierST16, §3.2] for full background).
$G_2$
is split so we don’t need to worry about the full Langlands dual and see [Reference Shin and TemplierST16, §3.2] for full background).
The endoscopic datum for H also gives an embedding
![]() $\widehat H \hookrightarrow \widehat {G_2}$
(noting again that everything is split) whose image contains a chosen maximal torus and therefore induces a map
$\widehat H \hookrightarrow \widehat {G_2}$
(noting again that everything is split) whose image contains a chosen maximal torus and therefore induces a map
The fibers of this map are
![]() $\Omega _{G_2}$
-orbits of conjugacy classes in H and have size
$\Omega _{G_2}$
-orbits of conjugacy classes in H and have size
![]() $3$
at
$3$
at
![]() $G_2$
-regular elements.
$G_2$
-regular elements.
Proposition 8.1.1. Let
![]() $k> 2$
and
$k> 2$
and
![]() $\pi ^\infty $
an unramified representation of
$\pi ^\infty $
an unramified representation of
![]() $(G_2)^\infty $
. Then
$(G_2)^\infty $
. Then
 $$ \begin{align*} m^{G_2}_{\mathrm{disc}}(\pi_k \otimes \pi^\infty) &= m^{G_2^c}_{\mathrm{disc}}(V_{(k-2)\beta} \otimes \pi^\infty) - \frac12 |S^H(\pi^\infty, (3k-3)\epsilon_1+ (k-1)\epsilon_2)| \\ &\quad + \frac12 |S^H(\pi^\infty, (3k-2)\epsilon_1+ (k-2)\epsilon_2)|. \end{align*} $$
$$ \begin{align*} m^{G_2}_{\mathrm{disc}}(\pi_k \otimes \pi^\infty) &= m^{G_2^c}_{\mathrm{disc}}(V_{(k-2)\beta} \otimes \pi^\infty) - \frac12 |S^H(\pi^\infty, (3k-3)\epsilon_1+ (k-1)\epsilon_2)| \\ &\quad + \frac12 |S^H(\pi^\infty, (3k-2)\epsilon_1+ (k-2)\epsilon_2)|. \end{align*} $$
Recall here that
![]() $V_\lambda $
is the finite-dimensional representation of
$V_\lambda $
is the finite-dimensional representation of
![]() $G_2^c$
with highest weight
$G_2^c$
with highest weight
![]() $\lambda $
. Also,
$\lambda $
. Also,
![]() $S^H(\pi ^\infty , \lambda )$
is the multiset of
$S^H(\pi ^\infty , \lambda )$
is the multiset of
![]() $\pi _\infty \otimes \pi _1^\infty \in \mathcal {AR}_{\mathrm {disc}}(H)$
with multiplicity such that
$\pi _\infty \otimes \pi _1^\infty \in \mathcal {AR}_{\mathrm {disc}}(H)$
with multiplicity such that
-
•
 $\pi _\infty \in \Pi ^H_{\mathrm {disc}}(\lambda )$
,
$\pi _\infty \in \Pi ^H_{\mathrm {disc}}(\lambda )$
, -
• For all p,
 $c_p(\pi _1^\infty ) \in (T^{G_2}_H)^{-1}(c_p(\pi ^\infty ))$
.
$c_p(\pi _1^\infty ) \in (T^{G_2}_H)^{-1}(c_p(\pi ^\infty ))$
.
Proof. This is a standard Jacquet–Langlands-style argument. Through the Satake isomorphism, each
![]() $f_p$
can be thought of as a function
$f_p$
can be thought of as a function
![]() $[\widehat {G_2}]_{\mathrm {ss}} \to \mathbb C$
through
$[\widehat {G_2}]_{\mathrm {ss}} \to \mathbb C$
through
![]() $f_p(c_p(\pi )) = \operatorname {\mathrm {tr}}_{\pi _p}(f_p)$
. It is in fact a Weyl-invariant regular function on a maximal torus in
$f_p(c_p(\pi )) = \operatorname {\mathrm {tr}}_{\pi _p}(f_p)$
. It is in fact a Weyl-invariant regular function on a maximal torus in
![]() $\widehat {G_2}$
. The full version of the fundamental lemma (see the introduction to [Reference HalesHal95], for example) shows that
$\widehat {G_2}$
. The full version of the fundamental lemma (see the introduction to [Reference HalesHal95], for example) shows that
for all
![]() $c_p \in \widehat H$
.
$c_p \in \widehat H$
.
There are only finitely many sequences
![]() $c_p(\pi _1^\infty )$
and
$c_p(\pi _1^\infty )$
and
![]() $T^{G_2}_H(c_p(\pi _1^\infty ))$
for
$T^{G_2}_H(c_p(\pi _1^\infty ))$
for
![]() $\pi _1^\infty $
the unramified finite component of an automorphic representation either:
$\pi _1^\infty $
the unramified finite component of an automorphic representation either:
-
• of
 $G_2$
with infinite part
$G_2$
with infinite part
 $\pi _k$
,
$\pi _k$
, -
• of
 $G_2^c$
with infinite part
$G_2^c$
with infinite part
 $V_{(k-2)\beta }$
,
$V_{(k-2)\beta }$
, -
• or of H with infinite part in
 $\Pi _{\mathrm {disc}}((3k-3)\epsilon _1+ (k-1)\epsilon _2)$
or
$\Pi _{\mathrm {disc}}((3k-3)\epsilon _1+ (k-1)\epsilon _2)$
or
 $\Pi _{\mathrm {disc}}((3k-2)\epsilon _1+ (k-2)\epsilon _2)$
.
$\Pi _{\mathrm {disc}}((3k-2)\epsilon _1+ (k-2)\epsilon _2)$
.
Therefore, we can choose an
![]() $f^\infty $
that is
$f^\infty $
that is
![]() $0$
on all of these sequences
$0$
on all of these sequences
![]() $c_p(\pi _1^\infty )$
except
$c_p(\pi _1^\infty )$
except
![]() $1$
on exactly the sequence
$1$
on exactly the sequence
![]() $c_p(\pi ^\infty )$
(this reduces to finding Weyl-invariant polynomials on
$c_p(\pi ^\infty )$
(this reduces to finding Weyl-invariant polynomials on
![]() $(\mathbb C^\times )^2$
that take specified values on certain Weyl orbits). The result follows from plugging this
$(\mathbb C^\times )^2$
that take specified values on certain Weyl orbits). The result follows from plugging this
![]() $f^\infty $
into Equation (10), noting that the
$f^\infty $
into Equation (10), noting that the
![]() $w^H$
from Equation (8) is always
$w^H$
from Equation (8) is always
![]() $1/2$
in the relevant cases.
$1/2$
in the relevant cases.
8.2 In terms of modular forms
We can use the argument from Section 7.2 to reduce the H-multiplicity terms to
![]() $\mathrm {PGL}_2$
-multiplicity ones.
$\mathrm {PGL}_2$
-multiplicity ones.
First, we have a map on conjugacy classes
Since the first group is
![]() $\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb C)$
, the fibers of this map are of the form
$\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb C)$
, the fibers of this map are of the form
![]() $\{c, -c\}$
for some
$\{c, -c\}$
for some
![]() $c \in [\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb C)]_{\mathrm {ss}}$
. Composing then gives map
$c \in [\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb C)]_{\mathrm {ss}}$
. Composing then gives map
This allows us to define
![]() $S^{\mathrm {PGL}_2 \times \mathrm {PGL}_2}(\pi ^\infty , \lambda )$
analogous to
$S^{\mathrm {PGL}_2 \times \mathrm {PGL}_2}(\pi ^\infty , \lambda )$
analogous to
![]() $S^H(\pi ^\infty , \lambda )$
for all
$S^H(\pi ^\infty , \lambda )$
for all
![]() $\lambda = a \epsilon _1 + b \epsilon _2$
with both a and b even. For indexing purposes, set it to be empty when a and b aren’t even.
$\lambda = a \epsilon _1 + b \epsilon _2$
with both a and b even. For indexing purposes, set it to be empty when a and b aren’t even.
Formula (9) also gives us that
![]() $S^H(\pi ^\infty , a \epsilon _1 + b \epsilon _2) = \emptyset $
when a and b aren’t both even. Recall from §7.2 that the restriction of discrete series
$S^H(\pi ^\infty , a \epsilon _1 + b \epsilon _2) = \emptyset $
when a and b aren’t both even. Recall from §7.2 that the restriction of discrete series
![]() $\pi ^{\mathrm {PGL}_2 \times \mathrm {PGL}_2}_\lambda $
to
$\pi ^{\mathrm {PGL}_2 \times \mathrm {PGL}_2}_\lambda $
to
![]() $H(\mathbb R)$
has as components the two members of the L-packet
$H(\mathbb R)$
has as components the two members of the L-packet
![]() $\Pi _{\mathrm {disc}}^H(\lambda )$
. Therefore, a similar analysis using Theorem 7.2.1 shows that
$\Pi _{\mathrm {disc}}^H(\lambda )$
. Therefore, a similar analysis using Theorem 7.2.1 shows that
Finally,
![]() $\mathrm {PGL}_2$
is a quotient of
$\mathrm {PGL}_2$
is a quotient of
![]() $\mathrm {GL}_2$
by a central torus with trivial Galois cohomology, so automorphic representations on
$\mathrm {GL}_2$
by a central torus with trivial Galois cohomology, so automorphic representations on
![]() $\mathrm {PGL}_2$
are just those on
$\mathrm {PGL}_2$
are just those on
![]() $\mathrm {GL}_2$
with all components having trivial central character. Recalling injection
$\mathrm {GL}_2$
with all components having trivial central character. Recalling injection
this gives:
Corollary 8.2.1. Let
![]() $k> 2$
and
$k> 2$
and
![]() $\pi ^\infty $
an unramified representation of
$\pi ^\infty $
an unramified representation of
![]() $(G_2)^\infty $
. Then
$(G_2)^\infty $
. Then
 $$ \begin{align*} m^{G_2}_{\mathrm{disc}}(\pi_k \otimes \pi^\infty) = m^{G_2^c}_{\mathrm{disc}}(V_{(k-2)\beta} \otimes \pi^\infty) - |S^{\mathrm{GL}_2 \times \mathrm{GL}_2}(\pi^\infty, (3k-3)\epsilon_1+ (k-1)\epsilon_2)| \\ + |S^{\mathrm{GL}_2 \times \mathrm{GL}_2}(\pi^\infty, (3k-2)\epsilon_1+ (k-2)\epsilon_2)|. \end{align*} $$
$$ \begin{align*} m^{G_2}_{\mathrm{disc}}(\pi_k \otimes \pi^\infty) = m^{G_2^c}_{\mathrm{disc}}(V_{(k-2)\beta} \otimes \pi^\infty) - |S^{\mathrm{GL}_2 \times \mathrm{GL}_2}(\pi^\infty, (3k-3)\epsilon_1+ (k-1)\epsilon_2)| \\ + |S^{\mathrm{GL}_2 \times \mathrm{GL}_2}(\pi^\infty, (3k-2)\epsilon_1+ (k-2)\epsilon_2)|. \end{align*} $$
Recall here that
![]() $V_\lambda $
is the finite-dimensional representation of
$V_\lambda $
is the finite-dimensional representation of
![]() $G_2^c$
with highest weight
$G_2^c$
with highest weight
![]() $\lambda $
. Also,
$\lambda $
. Also,
![]() $S^{\mathrm {GL}_2 \times \mathrm {GL}_2}(\pi ^\infty , \lambda )$
is the set of
$S^{\mathrm {GL}_2 \times \mathrm {GL}_2}(\pi ^\infty , \lambda )$
is the set of
![]() $\pi _\infty \otimes \pi _1^\infty \in \mathcal {AR}_{\mathrm {disc}}(\mathrm {GL}_2 \times \mathrm {GL}_2)$
such that
$\pi _\infty \otimes \pi _1^\infty \in \mathcal {AR}_{\mathrm {disc}}(\mathrm {GL}_2 \times \mathrm {GL}_2)$
such that
-
•
 $\pi _\infty $
is the discrete series
$\pi _\infty $
is the discrete series
 $\pi ^{\mathrm {GL}_2 \times \mathrm {GL}_2}_\lambda $
,
$\pi ^{\mathrm {GL}_2 \times \mathrm {GL}_2}_\lambda $
, -
• For all p,
 $c_p(\pi _1^\infty ) = \iota (c^{\prime }_p)$
for some
$c_p(\pi _1^\infty ) = \iota (c^{\prime }_p)$
for some
 $c^{\prime }_p \in (T^{G_2}_{\mathrm {PGL}_2 \times \mathrm {PGL}_2})^{-1}(c_p(\pi ^\infty ))$
. Here
$c^{\prime }_p \in (T^{G_2}_{\mathrm {PGL}_2 \times \mathrm {PGL}_2})^{-1}(c_p(\pi ^\infty ))$
. Here
 $\iota $
is the map
$\iota $
is the map
 $ [\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb C)]_{\mathrm {ss}} \hookrightarrow [\mathrm {GL}_2 \times \mathrm {GL}_2(\mathbb C)]_{\mathrm {ss}}$
.
$ [\mathrm {SL}_2 \times \mathrm {SL}_2(\mathbb C)]_{\mathrm {ss}} \hookrightarrow [\mathrm {GL}_2 \times \mathrm {GL}_2(\mathbb C)]_{\mathrm {ss}}$
.
Of course, since all infinite factors in sight are discrete series, we may again replace the
![]() $m_{\mathrm {disc}}$
by
$m_{\mathrm {disc}}$
by
![]() $m_{\mathrm {cusp}}$
using [Reference WallachWal84].
$m_{\mathrm {cusp}}$
using [Reference WallachWal84].
Note of course that
![]() $S^{\mathrm {GL}_2 \times \mathrm {GL}_2}(\pi ^\infty , a\epsilon _1 + b \epsilon _2) = \emptyset $
unless both a and b are even. Therefore, we can interpret this as, for
$S^{\mathrm {GL}_2 \times \mathrm {GL}_2}(\pi ^\infty , a\epsilon _1 + b \epsilon _2) = \emptyset $
unless both a and b are even. Therefore, we can interpret this as, for
![]() $k> 2$
:
$k> 2$
:
-
• If k is even:
 $\mathcal {Q}_k(1)$
is the corresponding set of representations transferred from
$\mathcal {Q}_k(1)$
is the corresponding set of representations transferred from
 $G_2^c$
in addition to representations transferred from pairs of cuspidal eigenforms in
$G_2^c$
in addition to representations transferred from pairs of cuspidal eigenforms in
 $\mathcal {S}_{3k}(1) \times \mathcal {S}_{k}(1)$
.
$\mathcal {S}_{3k}(1) \times \mathcal {S}_{k}(1)$
. -
• If k is odd:
 $\mathcal {Q}_k(1)$
is the corresponding set of representations transferred from
$\mathcal {Q}_k(1)$
is the corresponding set of representations transferred from
 $G_2^c$
except for representations that are also transferred from pairs of cuspidal eigenforms in
$G_2^c$
except for representations that are also transferred from pairs of cuspidal eigenforms in
 $\mathcal {S}_{3k-1}(1) \times \mathcal {S}_{k+1}(1)$
.
$\mathcal {S}_{3k-1}(1) \times \mathcal {S}_{k+1}(1)$
.
Results for level
![]() $>1$
would be a lot more complicated since formula (4) would have many further hyperendoscopic terms and the comparison to
$>1$
would be a lot more complicated since formula (4) would have many further hyperendoscopic terms and the comparison to
![]() $\mathrm {GL}_2 \times \mathrm {GL}_2$
would not work as nicely.
$\mathrm {GL}_2 \times \mathrm {GL}_2$
would not work as nicely.
9 Counts of forms
9.1 Formula in terms of
 $I^{G_2^c}$
$I^{G_2^c}$
To get counts instead of a list, combining formulas (2),(10) and (9) gives that
 $$ \begin{align} |\mathcal{Q}_k(1)| &= I^{G_2^c}(\eta^{G_2^c}_\lambda \otimes {\mathbf{1}}_{K^\infty_{G_2^c}}) - (S_{3k-1} -{\mathbf{1}}_{3k-3 = 0})(S_{k+1} -{\mathbf{1}}_{k-1 = 0}) \nonumber\\&\quad+ (S_{3k} -{\mathbf{1}}_{3k-2 = 0})(S_{k} -{\mathbf{1}}_{k-2 = 0}), \end{align} $$
$$ \begin{align} |\mathcal{Q}_k(1)| &= I^{G_2^c}(\eta^{G_2^c}_\lambda \otimes {\mathbf{1}}_{K^\infty_{G_2^c}}) - (S_{3k-1} -{\mathbf{1}}_{3k-3 = 0})(S_{k+1} -{\mathbf{1}}_{k-1 = 0}) \nonumber\\&\quad+ (S_{3k} -{\mathbf{1}}_{3k-2 = 0})(S_{k} -{\mathbf{1}}_{k-2 = 0}), \end{align} $$
where
![]() $S_k$
as before represents the count of classical modular forms of weight k.
$S_k$
as before represents the count of classical modular forms of weight k.
Substituting in the formulas for
![]() $S_k$
, for
$S_k$
, for
![]() $k> 2$
:
$k> 2$
:
 $$ \begin{align*} |\mathcal{Q}_k(1)| &= I^{G_2^c}(\eta_\lambda \otimes {\mathbf{1}}_{K^\infty_{G_2^c}}) \\ &\qquad + \begin{cases} \lfloor \frac k4 \rfloor \left( \lfloor \frac k{12} \rfloor - 1 \right) & k \equiv 2\quad \pmod{12} \\ \lfloor \frac k4 \rfloor \lfloor \frac k{12} \rfloor & k \equiv 0,4,6,8,10\quad \pmod{12} \\ -\left(\lfloor \frac {3k-1}{12} \rfloor - 1\right) \left( \lfloor \frac {k+1}{12} \rfloor - 1 \right) & k \equiv 1\quad \pmod{12} \\ -\left(\lfloor \frac {3k-1}{12} \rfloor - 1\right) \lfloor \frac {k+1}{12} \rfloor & k \equiv 5,9\quad \pmod{12} \\ -\lfloor \frac {3k-1}{12} \rfloor \lfloor \frac {k+1}{12} \rfloor & k \equiv 3,7,11\quad \pmod{12} \\ \end{cases}. \end{align*} $$
$$ \begin{align*} |\mathcal{Q}_k(1)| &= I^{G_2^c}(\eta_\lambda \otimes {\mathbf{1}}_{K^\infty_{G_2^c}}) \\ &\qquad + \begin{cases} \lfloor \frac k4 \rfloor \left( \lfloor \frac k{12} \rfloor - 1 \right) & k \equiv 2\quad \pmod{12} \\ \lfloor \frac k4 \rfloor \lfloor \frac k{12} \rfloor & k \equiv 0,4,6,8,10\quad \pmod{12} \\ -\left(\lfloor \frac {3k-1}{12} \rfloor - 1\right) \left( \lfloor \frac {k+1}{12} \rfloor - 1 \right) & k \equiv 1\quad \pmod{12} \\ -\left(\lfloor \frac {3k-1}{12} \rfloor - 1\right) \lfloor \frac {k+1}{12} \rfloor & k \equiv 5,9\quad \pmod{12} \\ -\lfloor \frac {3k-1}{12} \rfloor \lfloor \frac {k+1}{12} \rfloor & k \equiv 3,7,11\quad \pmod{12} \\ \end{cases}. \end{align*} $$
9.2 Computing
 $I^{G_2^c}$
$I^{G_2^c}$
The group
![]() $G_2^c(\mathbb R)$
is compact, so the
$G_2^c(\mathbb R)$
is compact, so the
![]() $I^{G_2^c}$
term takes a very simple form:
$I^{G_2^c}$
term takes a very simple form:
![]() $L^2(G_2^c(\mathbb Q) \backslash G_2^c(\mathbb A))$
decomposes as a direct sum of automorphic representations and the EP-functions
$L^2(G_2^c(\mathbb Q) \backslash G_2^c(\mathbb A))$
decomposes as a direct sum of automorphic representations and the EP-functions
![]() $\eta _\lambda $
are just scaled matrix coefficients of the finite-dimensional representations
$\eta _\lambda $
are just scaled matrix coefficients of the finite-dimensional representations
![]() $V_\lambda $
with highest weight
$V_\lambda $
with highest weight
![]() $\lambda $
on
$\lambda $
on
![]() $G_2^c(\mathbb R)$
. Therefore,
$G_2^c(\mathbb R)$
. Therefore,
 $$\begin{align*}I^{G_2^c}(\eta_\lambda \otimes {\mathbf{1}}_{K^\infty_{G_2^c}}) = \sum_{\pi \in \mathcal{AR}(G_2^c)} {\mathbf{1}}_{\pi_\infty = V_\lambda} \operatorname{\mathrm{tr}}_{\pi^\infty}({\mathbf{1}}_{K^\infty_{G_2^c}}), \end{align*}$$
$$\begin{align*}I^{G_2^c}(\eta_\lambda \otimes {\mathbf{1}}_{K^\infty_{G_2^c}}) = \sum_{\pi \in \mathcal{AR}(G_2^c)} {\mathbf{1}}_{\pi_\infty = V_\lambda} \operatorname{\mathrm{tr}}_{\pi^\infty}({\mathbf{1}}_{K^\infty_{G_2^c}}), \end{align*}$$
which is just counting the number of unramifed automorphic reps of
![]() $G_2^c$
that have infinite component
$G_2^c$
that have infinite component
![]() $V_\lambda $
.
$V_\lambda $
.
For reader convenience, we now explain in detail an argument well known to experts. Since unramified representations have one-dimensional spaces of
![]() $K^\infty $
-fixed vectors, taking
$K^\infty $
-fixed vectors, taking
![]() $K^\infty _{G_2^c}$
invariants sends each such
$K^\infty _{G_2^c}$
invariants sends each such
![]() $\pi $
to a linearly independent copy of
$\pi $
to a linearly independent copy of
![]() $V_\lambda $
that together span the
$V_\lambda $
that together span the
![]() $V_\lambda $
-isotypic component of
$V_\lambda $
-isotypic component of
By Peter–Weyl,
![]() $L^2(G_2^c(\mathbb R))$
has
$L^2(G_2^c(\mathbb R))$
has
![]() $V_\lambda $
-isotypic component
$V_\lambda $
-isotypic component
![]() $V_\lambda ^{\oplus \dim V_\lambda }$
. In fact, this component for both the left and right actions is the same subspace. Therefore, the number of copies of
$V_\lambda ^{\oplus \dim V_\lambda }$
. In fact, this component for both the left and right actions is the same subspace. Therefore, the number of copies of
![]() $V_\lambda \subseteq L^2(G_2^c(\mathbb Z) \backslash G_2^c(\mathbb R))$
is
$V_\lambda \subseteq L^2(G_2^c(\mathbb Z) \backslash G_2^c(\mathbb R))$
is
![]() $\dim \left (V_\lambda ^{G_2^c(\mathbb Z)}\right )$
by a dimension count.
$\dim \left (V_\lambda ^{G_2^c(\mathbb Z)}\right )$
by a dimension count.
Summarizing:
A PARI/GP 2.5.0 program in the online appendix to [Reference Chenevier and RenardCR15] computes this for all
![]() $\lambda $
by pairing the trace character of
$\lambda $
by pairing the trace character of
![]() $V_\lambda |_{G_2(\mathbb Z)}$
with the trivial character.
$V_\lambda |_{G_2(\mathbb Z)}$
with the trivial character.
An explicit paper formula for this computation is more-or-less written out in an honors thesis of Steven Sullivan [Reference SullivanSul13]. Sullivan writes out the traces of all
![]() $16$
conjugacy classes in
$16$
conjugacy classes in
![]() $G_2^c(\mathbb Z)$
against
$G_2^c(\mathbb Z)$
against
![]() $V_{(k-2) \beta }$
as polynomials of k with coefficients that are sums of kth powers of
$V_{(k-2) \beta }$
as polynomials of k with coefficients that are sums of kth powers of
![]() $7$
th,
$7$
th,
![]() $8$
th and
$8$
th and
![]() $12$
th roots of unity. This gets a polynomial expression for the trace character pairing and therefore
$12$
th roots of unity. This gets a polynomial expression for the trace character pairing and therefore
![]() $I^{G_2^c}(\eta _\lambda \otimes {\mathbf {1}}_{K^\infty _{G_2^c}})$
in cases
$I^{G_2^c}(\eta _\lambda \otimes {\mathbf {1}}_{K^\infty _{G_2^c}})$
in cases
![]() $\pmod {168}$
. Simplifications in Mathematica give a reasonable closed-form version in Section 9.4.
$\pmod {168}$
. Simplifications in Mathematica give a reasonable closed-form version in Section 9.4.
It is important to note here that getting the explicit descriptions and sizes of the conjugacy classes in
![]() $G_2^c(\mathbb Z)$
was nontrivial and required some trickery in both Sullivan’s and Chenevier-Taïbi’s computations. This step would be an obstacle to any generalizations.
$G_2^c(\mathbb Z)$
was nontrivial and required some trickery in both Sullivan’s and Chenevier-Taïbi’s computations. This step would be an obstacle to any generalizations.
9.3 Table of counts
Table 1 gives values of
![]() $|\mathcal {Q}_k(1)|$
for
$|\mathcal {Q}_k(1)|$
for
![]() $k=3$
to
$k=3$
to
![]() $52$
produced by formula (11) and [Reference Chenevier and RenardCR15]’s table for formula (12). The lowest-weight example is bolded, although this work does not rule out the existence of an example with weight
$52$
produced by formula (11) and [Reference Chenevier and RenardCR15]’s table for formula (12). The lowest-weight example is bolded, although this work does not rule out the existence of an example with weight
![]() $2$
or weight
$2$
or weight
![]() $1$
(as defined by [Reference PollackPol20, §1.1]).
$1$
(as defined by [Reference PollackPol20, §1.1]).
Table 1 Counts of discrete, quaternionic automorphic representations of level
![]() $1$
on
$1$
on
![]() $G_2$
.
$G_2$
.

9.4 Explicit formula
For the reader’s amusement, we build off the work of [Reference SullivanSul13] to present a closed-form formula for
![]() $|\mathcal {Q}_k(1)|$
that fits in a few lines:
$|\mathcal {Q}_k(1)|$
that fits in a few lines:
 $$ \begin{align*} &|\mathcal{Q}_{n+2}(1)| = \\ & \frac1{12096} \frac1{120}(n+1)(3n+4)(n+2)(3n+5)(2n+3) + \frac1{216}\frac16 (n+1) (n+ 2 ) (2 n+3) \\ &+ \frac5{192}\frac18 \begin{cases} (n+2) ( 3 n+4) & n = 0\quad \pmod 2 \\ -(n+1) (3 n+5)& n = 1 \quad\pmod 2 \\ \end{cases} + \frac1{18}\begin{cases} \frac{2n}3 + 1& n = 0 \quad\pmod 3 \\ - \lfloor \frac n3 \rfloor - 1 & n = 1,2 \quad\pmod 3 \end{cases} \\ &+ \frac1{32}\begin{cases} \frac{3n}2 + 10& n = 0 \quad\pmod 4 \\ 6\lfloor \frac{n}4 \rfloor - 4 & n = 1 \quad\pmod 4 \\ - 2\lfloor \frac{n}4 \rfloor - 2 & n = 2,3 \quad\pmod 4 \end{cases} + \frac1{24} \begin{cases} 3\lfloor \frac{n}6 \rfloor+ 5& n = 0,1 \quad\pmod 6 \\ 3 \lfloor \frac{n}6 \rfloor -2 & n = 2,3 \quad\pmod 6 \\ 3 \lfloor \frac{n}6 \rfloor +3 & n = 4,5 \quad\pmod 6 \end{cases} \\ &+ \frac17 \begin{cases} 1 & n = 0 \quad\pmod 7 \\ -1 & n = 4 \quad\pmod 7 \\ 0 & n = 1,2,3,5,6 \quad\pmod 7 \end{cases} + \frac14\begin{cases} 1 & n = 0 \quad\pmod 8 \\ -1 & n = 5 \quad\pmod 8 \\ 0 & n = 1,2,3,4,6,7 \quad\pmod 8 \end{cases} \\ &+ \begin{cases} \lfloor \frac {n+2}4 \rfloor \left( \lfloor \frac {n+2}{12} \rfloor - 1 \right) & n = 0 \quad\pmod{12} \\ \lfloor \frac {n+2}4 \rfloor \lfloor \frac {n+2}{12} \rfloor & n = 2,4,6,8,10 \quad\pmod{12} \\ -\left(\lfloor \frac {3n+5}{12} \rfloor - 1\right) \left( \lfloor \frac {n+3}{12} \rfloor - 1 \right) & n = 11 \quad\pmod{12} \\ -\left(\lfloor \frac {3n+5}{12} \rfloor - 1\right) \lfloor \frac {n+3}{12} \rfloor & n = 3,7 \quad\pmod{12} \\ -\lfloor \frac {3n + 5}{12} \rfloor \lfloor \frac {n+3}{12} \rfloor & n = 1,5,9 \quad\pmod{12} \\ \end{cases}. \end{align*} $$
$$ \begin{align*} &|\mathcal{Q}_{n+2}(1)| = \\ & \frac1{12096} \frac1{120}(n+1)(3n+4)(n+2)(3n+5)(2n+3) + \frac1{216}\frac16 (n+1) (n+ 2 ) (2 n+3) \\ &+ \frac5{192}\frac18 \begin{cases} (n+2) ( 3 n+4) & n = 0\quad \pmod 2 \\ -(n+1) (3 n+5)& n = 1 \quad\pmod 2 \\ \end{cases} + \frac1{18}\begin{cases} \frac{2n}3 + 1& n = 0 \quad\pmod 3 \\ - \lfloor \frac n3 \rfloor - 1 & n = 1,2 \quad\pmod 3 \end{cases} \\ &+ \frac1{32}\begin{cases} \frac{3n}2 + 10& n = 0 \quad\pmod 4 \\ 6\lfloor \frac{n}4 \rfloor - 4 & n = 1 \quad\pmod 4 \\ - 2\lfloor \frac{n}4 \rfloor - 2 & n = 2,3 \quad\pmod 4 \end{cases} + \frac1{24} \begin{cases} 3\lfloor \frac{n}6 \rfloor+ 5& n = 0,1 \quad\pmod 6 \\ 3 \lfloor \frac{n}6 \rfloor -2 & n = 2,3 \quad\pmod 6 \\ 3 \lfloor \frac{n}6 \rfloor +3 & n = 4,5 \quad\pmod 6 \end{cases} \\ &+ \frac17 \begin{cases} 1 & n = 0 \quad\pmod 7 \\ -1 & n = 4 \quad\pmod 7 \\ 0 & n = 1,2,3,5,6 \quad\pmod 7 \end{cases} + \frac14\begin{cases} 1 & n = 0 \quad\pmod 8 \\ -1 & n = 5 \quad\pmod 8 \\ 0 & n = 1,2,3,4,6,7 \quad\pmod 8 \end{cases} \\ &+ \begin{cases} \lfloor \frac {n+2}4 \rfloor \left( \lfloor \frac {n+2}{12} \rfloor - 1 \right) & n = 0 \quad\pmod{12} \\ \lfloor \frac {n+2}4 \rfloor \lfloor \frac {n+2}{12} \rfloor & n = 2,4,6,8,10 \quad\pmod{12} \\ -\left(\lfloor \frac {3n+5}{12} \rfloor - 1\right) \left( \lfloor \frac {n+3}{12} \rfloor - 1 \right) & n = 11 \quad\pmod{12} \\ -\left(\lfloor \frac {3n+5}{12} \rfloor - 1\right) \lfloor \frac {n+3}{12} \rfloor & n = 3,7 \quad\pmod{12} \\ -\lfloor \frac {3n + 5}{12} \rfloor \lfloor \frac {n+3}{12} \rfloor & n = 1,5,9 \quad\pmod{12} \\ \end{cases}. \end{align*} $$
Acknowledgements
This work was done under the support of NSF RTG grant DMS-1646385. I would like to thank Kimball Martin and Aaron Pollack for discussions at conferences that eventually led to the consideration of this problem. The key idea that something like Theorem 3.1.1 could hold for
![]() $G_2$
, thereby making this problem solvable, grew out of email conversations with Sam Mundy. I thank Jeffrey Adams and David Vogan for the full argument of Equation 3.1.1. Olivier Taïbi provided a great deal of help in pointing out many, many tricks and previous results I could use to keep computations reasonably simple and actually feasible. In particular, I am grateful for the suggestion to use ‘method 2’ described in Section 3.3 that he passed on from Gaëtan Chenevier. I also thank Gordan Savin for pointing out the thesis of Sullivan which saved a lot of work in producing the closed-form formula. Finally, Alexander Bertoloni-Meli provided much help in teaching me things about transfer factors. The root system picture for
$G_2$
, thereby making this problem solvable, grew out of email conversations with Sam Mundy. I thank Jeffrey Adams and David Vogan for the full argument of Equation 3.1.1. Olivier Taïbi provided a great deal of help in pointing out many, many tricks and previous results I could use to keep computations reasonably simple and actually feasible. In particular, I am grateful for the suggestion to use ‘method 2’ described in Section 3.3 that he passed on from Gaëtan Chenevier. I also thank Gordan Savin for pointing out the thesis of Sullivan which saved a lot of work in producing the closed-form formula. Finally, Alexander Bertoloni-Meli provided much help in teaching me things about transfer factors. The root system picture for
![]() $G_2$
was heavily modified from an answer by user Heiko Oberdiek on TeX Stack Exchange.
$G_2$
was heavily modified from an answer by user Heiko Oberdiek on TeX Stack Exchange.
Competing interests
The authors have no competing interest to declare.