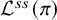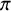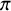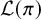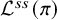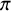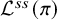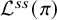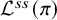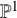1 Introduction
Let G be a connected reductive group over a nonarchimedean local field F and let
![]() $\pi $
be an irreducible smooth representation of
$\pi $
be an irreducible smooth representation of
![]() $G(F)$
. The local Langlands conjecture (LLC) posits that to such a
$G(F)$
. The local Langlands conjecture (LLC) posits that to such a
![]() $\pi $
can be attached an L-parameter
$\pi $
can be attached an L-parameter
which is an admissible homomorphism from the Weil-Deligne group
![]() $WD_F = W_F \times SL_2(C)$
with values in the Langlands L-group
$WD_F = W_F \times SL_2(C)$
with values in the Langlands L-group
![]() ${}^LG$
over an appropriate algebraically closed field C of characteristic
${}^LG$
over an appropriate algebraically closed field C of characteristic
![]() $0$
. In what follows, we take
$0$
. In what follows, we take
![]() $C = {\overline {\mathbb Q}_{\ell }}$
with
$C = {\overline {\mathbb Q}_{\ell }}$
with
![]() $\ell $
different from
$\ell $
different from
![]() $\mathrm {char}(F)$
. One condition of being admissible is that
$\mathrm {char}(F)$
. One condition of being admissible is that
![]() ${\mathcal {L}}(\pi )$
should be semisimple, in the sense that if
${\mathcal {L}}(\pi )$
should be semisimple, in the sense that if
![]() ${\mathcal {L}}(\pi )(WD_F) \cap \hat {G}(C)$
(where
${\mathcal {L}}(\pi )(WD_F) \cap \hat {G}(C)$
(where
![]() $\hat {G}(C)$
is the Langlands dual group of G) is contained in a parabolic subgroup
$\hat {G}(C)$
is the Langlands dual group of G) is contained in a parabolic subgroup
![]() $P \subset \hat {G}(C)$
, then it is contained in a Levi subgroup of P. Such L-parameters can also be described in the language of semisimple Weil-Deligne parameters
$P \subset \hat {G}(C)$
, then it is contained in a Levi subgroup of P. Such L-parameters can also be described in the language of semisimple Weil-Deligne parameters
![]() $(\rho , N)$
, as we recall in §3.
$(\rho , N)$
, as we recall in §3.
However, when F is of positive characteristic p, Genestier and Lafforgue [Reference Genestier and LafforgueGLa] have defined a semisimple Weil parameterFootnote 1
This semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
should be related to
${\mathcal {L}}^{ss}(\pi )$
should be related to
![]() ${\mathcal {L}}(\pi )$
via
${\mathcal {L}}(\pi )$
via
 $$ \begin{align} {\mathcal{L}}^{ss}(\pi) (w) = {\mathcal{L}}(\pi) \left( w, \left( \begin{array}{cc} |w|^{1/2} & \\ & |w|^{-1/2} \end{array} \right) \right). \end{align} $$
$$ \begin{align} {\mathcal{L}}^{ss}(\pi) (w) = {\mathcal{L}}(\pi) \left( w, \left( \begin{array}{cc} |w|^{1/2} & \\ & |w|^{-1/2} \end{array} \right) \right). \end{align} $$
A natural question is then as follows: can the semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
of Genestier-Lafforgue be enriched to give the true L-parameter
${\mathcal {L}}^{ss}(\pi )$
of Genestier-Lafforgue be enriched to give the true L-parameter
![]() ${\mathcal {L}}(\pi )$
?
${\mathcal {L}}(\pi )$
?
By the properties of the Genestier-Lafforgue construction (recalled in §2), it suffices to address this question for (essentially) discrete series representations. For such a
![]() $\pi $
, one desiderata of the LLC is that
$\pi $
, one desiderata of the LLC is that
![]() ${\mathcal {L}}(\pi )$
should be irreducible (or elliptic) – its image is contained in no proper parabolic P, and in particular is essentially tempered (or equivalently pure). It is not hard to see (cf. Lemma 3.5) that for any semisimple parameter
${\mathcal {L}}(\pi )$
should be irreducible (or elliptic) – its image is contained in no proper parabolic P, and in particular is essentially tempered (or equivalently pure). It is not hard to see (cf. Lemma 3.5) that for any semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
, there is at most one essentially tempered L-parameter that could give rise to it via (1.1). The first result of this paper is the following theorem:
${\mathcal {L}}^{ss}(\pi )$
, there is at most one essentially tempered L-parameter that could give rise to it via (1.1). The first result of this paper is the following theorem:
Theorem 1.2. Let G be a connected reductive group over a local function field F of positive characteristic p. Let
![]() $\pi $
be an irreducible discrete series representation of
$\pi $
be an irreducible discrete series representation of
![]() $G(F)$
. Then there exists a (necessarily unique) essentially tempered L-parameter
$G(F)$
. Then there exists a (necessarily unique) essentially tempered L-parameter
![]() ${\mathcal {L}}(\pi )$
whose associated semisimple parameter (via (1.1)) is the Genestier-Lafforgue parameter
${\mathcal {L}}(\pi )$
whose associated semisimple parameter (via (1.1)) is the Genestier-Lafforgue parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
.
${\mathcal {L}}^{ss}(\pi )$
.
In particular, for a discrete series
![]() $\pi $
, we have a unique candidate
$\pi $
, we have a unique candidate
![]() ${\mathcal {L}}(\pi )$
for its L-parameter. As a consequence, we have the following:
${\mathcal {L}}(\pi )$
for its L-parameter. As a consequence, we have the following:
Corollary 1.3. There is a well-defined
refining the construction of Genestier-Lafforgue, where
![]() $\mathcal {T}(G(F))$
is the set of equivalence classes of irreducible essentially tempered representations of
$\mathcal {T}(G(F))$
is the set of equivalence classes of irreducible essentially tempered representations of
![]() $G(F)$
.
$G(F)$
.
Unfortunately, we are not quite able to show that the image of a discrete series representation under
![]() ${\mathcal {L}}$
is irreducible (or elliptic).
${\mathcal {L}}$
is irreducible (or elliptic).
Assume now that G is an unramified reductive group. Our second result concerns the ramification property of the semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
of a supercuspidal representation
${\mathcal {L}}^{ss}(\pi )$
of a supercuspidal representation
![]() $\pi $
. If the Frobenius eigenvalues of
$\pi $
. If the Frobenius eigenvalues of
![]() ${\mathcal {L}}^{ss}(\pi )$
are pure in an appropriate sense, then the LLC asserts that
${\mathcal {L}}^{ss}(\pi )$
are pure in an appropriate sense, then the LLC asserts that
![]() ${\mathcal {L}}^{ss}(\pi )$
itself is, in fact, irreducible. In particular, unless G is a torus, one expects that
${\mathcal {L}}^{ss}(\pi )$
itself is, in fact, irreducible. In particular, unless G is a torus, one expects that
![]() ${\mathcal {L}}^{ss}(\pi )$
is ramified. More precisely, we show the following:
${\mathcal {L}}^{ss}(\pi )$
is ramified. More precisely, we show the following:
Theorem 1.4. Suppose F is the nonarchimedean local field
![]() $k(\!(t)\!)$
, where
$k(\!(t)\!)$
, where
![]() $k = {{\mathbb F}_q}$
is a finite field of order
$k = {{\mathbb F}_q}$
is a finite field of order
![]() $q = p^m> 5$
for some prime p. Let G be an unramified connected reductive group over F which is not a torus. Assume that
$q = p^m> 5$
for some prime p. Let G be an unramified connected reductive group over F which is not a torus. Assume that
![]() $\pi $
is an irreducible supercuspidal representation of
$\pi $
is an irreducible supercuspidal representation of
![]() $G(F)$
of the form
$G(F)$
of the form
for some (irreducible) smooth representation
![]() $\tau $
of a compact open (modulo center) subgroup U with coefficients in
$\tau $
of a compact open (modulo center) subgroup U with coefficients in
![]() ${\overline {\mathbb Q}_{\ell }}$
.
${\overline {\mathbb Q}_{\ell }}$
.
(i) Suppose that
![]() ${\mathcal {L}}^{ss}(\pi )$
is pure: if
${\mathcal {L}}^{ss}(\pi )$
is pure: if
![]() $\mathrm {Frob}_F \in W_F$
is any Frobenius element, then the eigenvalues of
$\mathrm {Frob}_F \in W_F$
is any Frobenius element, then the eigenvalues of
![]() ${\mathcal {L}}^{ss}(\pi )(\mathrm {Frob}_F)$
are all Weil q-numbers of the same weight (in which case we say that
${\mathcal {L}}^{ss}(\pi )(\mathrm {Frob}_F)$
are all Weil q-numbers of the same weight (in which case we say that
![]() $\pi $
is a pure supercuspidal representation). Then
$\pi $
is a pure supercuspidal representation). Then
![]() ${\mathcal {L}}^{ss}(\pi ) = {\mathcal {L}}(\pi )$
is ramified: it is nontrivial on the inertia subgroup
${\mathcal {L}}^{ss}(\pi ) = {\mathcal {L}}(\pi )$
is ramified: it is nontrivial on the inertia subgroup
![]() $I_F \subset W_F$
.
$I_F \subset W_F$
.
(ii) Suppose that U is sufficiently small. Then
![]() ${\mathcal {L}}^{ss}(\pi )$
(and hence
${\mathcal {L}}^{ss}(\pi )$
(and hence
![]() ${\mathcal {L}}(\pi )$
) is wildly ramified: it is nontrivial on the wild inertia subgroup of
${\mathcal {L}}(\pi )$
) is wildly ramified: it is nontrivial on the wild inertia subgroup of
![]() $W_F$
.
$W_F$
.
Let us make a few remarks:
-
○ Conjecturally, every
 $\pi $
is compactly induced in the above sense. This property was recently proved by Fintzen to be true as long as p does not divide the order of the Weyl group of G [Reference FintzenFi]. Moreover, when p is odd and G is a classical group – that is, a unitary, symplectic, or special orthogonal group – Shaun Stevens proved in [Reference StevensSt] that every supercuspidal representation is compactly induced. These cases can eventually be treated by comparison to GL(n), but the necessary methods, especially those involving the trace formula, are not yet available.
$\pi $
is compactly induced in the above sense. This property was recently proved by Fintzen to be true as long as p does not divide the order of the Weyl group of G [Reference FintzenFi]. Moreover, when p is odd and G is a classical group – that is, a unitary, symplectic, or special orthogonal group – Shaun Stevens proved in [Reference StevensSt] that every supercuspidal representation is compactly induced. These cases can eventually be treated by comparison to GL(n), but the necessary methods, especially those involving the trace formula, are not yet available. -
○ It would be good to produce some examples of supercuspidal representations whose Genestier-Lafforgue parameter
 ${\mathcal {L}}^{ss}(\pi )$
is pure. This does not seem so simple to do. The Kloosterman representations used in §3.3 in the proof of Theorem 1.2 have irreducible parameters and are therefore pure. In §9, we describe a strategy to produce more examples of depth 0 generic supercuspidal representations.
${\mathcal {L}}^{ss}(\pi )$
is pure. This does not seem so simple to do. The Kloosterman representations used in §3.3 in the proof of Theorem 1.2 have irreducible parameters and are therefore pure. In §9, we describe a strategy to produce more examples of depth 0 generic supercuspidal representations. -
○ The precise definition of ‘sufficiently small’ in (ii) above is given at the beginning of §8.
As an immediate application of Theorem 1.4, we have the following corollary:
Theorem 1.5. Let
![]() $F = k((t))$
and let
$F = k((t))$
and let
![]() $\sigma $
be an irreducible representation of
$\sigma $
be an irreducible representation of
![]() $G(F)$
, with G unramified reductive over F. Suppose the Genestier-Lafforgue parameter
$G(F)$
, with G unramified reductive over F. Suppose the Genestier-Lafforgue parameter
![]() ${\mathcal {L}}^{ss}(\sigma )$
is pure and unramified. Suppose every supercuspidal representation of every Levi factor of
${\mathcal {L}}^{ss}(\sigma )$
is pure and unramified. Suppose every supercuspidal representation of every Levi factor of
![]() $G(F)$
contains an
$G(F)$
contains an
![]() $\mathfrak {s}$
-type. This is true in particular in the following cases:
$\mathfrak {s}$
-type. This is true in particular in the following cases:
-
○ p does not divide the order of the Weyl group of G [Reference FintzenFi];
-
○ p is odd and G is an unramified classical group (unitary, symplectic, or special orthogonal) [Reference StevensSt].
Then
![]() $\sigma $
is an irreducible constituent of an unramified principal series representation of
$\sigma $
is an irreducible constituent of an unramified principal series representation of
![]() $G(F)$
.
$G(F)$
.
When
![]() $G = \mathrm {GL}(n)$
, our three theorems are part of the local Langlands correspondence (LLC) proved by Laumon, Rapoport and Stuhler [Reference Laumon, Rapoport and StuhlerLRS93]. When G is a split classical group, the results were proved in most cases by Ganapathy and Varma by comparison with Arthur’s LLC over p-adic fields, via the method of close local fields [Reference Ganapathy and VarmaGV, Reference ArthurA13]. Thus, the novelty of this paper is that, like the Genestier-Lafforgue result, Theorems 1.2 and 1.4 are valid uniformly for all (unramified) reductive groups, including exceptional groups.
$G = \mathrm {GL}(n)$
, our three theorems are part of the local Langlands correspondence (LLC) proved by Laumon, Rapoport and Stuhler [Reference Laumon, Rapoport and StuhlerLRS93]. When G is a split classical group, the results were proved in most cases by Ganapathy and Varma by comparison with Arthur’s LLC over p-adic fields, via the method of close local fields [Reference Ganapathy and VarmaGV, Reference ArthurA13]. Thus, the novelty of this paper is that, like the Genestier-Lafforgue result, Theorems 1.2 and 1.4 are valid uniformly for all (unramified) reductive groups, including exceptional groups.
Of course, Theorem 1.4(i) is a much weaker statement than the expected local Langlands correspondence, which not only asserts that
![]() ${\mathcal {L}}^{ss}(\pi )$
is irreducible when
${\mathcal {L}}^{ss}(\pi )$
is irreducible when
![]() $\pi $
is pure but gives a complete description of the L-packet of representations with the given local parameter. However, all proofs of the local Langlands correspondence for
$\pi $
is pure but gives a complete description of the L-packet of representations with the given local parameter. However, all proofs of the local Langlands correspondence for
![]() $\mathrm {GL}(n)$
begin with the observation that a supercuspidal representation
$\mathrm {GL}(n)$
begin with the observation that a supercuspidal representation
![]() $\pi $
of
$\pi $
of
![]() $\mathrm {GL}(n,F)$
is not incorrigible [Reference HarrisH19] – that it becomes a constituent of a principal series representation after a finite series of base changes corresponding to cyclic extensions
$\mathrm {GL}(n,F)$
is not incorrigible [Reference HarrisH19] – that it becomes a constituent of a principal series representation after a finite series of base changes corresponding to cyclic extensions
![]() $F_{i+1}/F_i$
,
$F_{i+1}/F_i$
,
![]() $i = 0, \dots , n$
, where
$i = 0, \dots , n$
, where
![]() $F_0 = F$
. Since one can choose the
$F_0 = F$
. Since one can choose the
![]() $F_i$
so that the Galois parameter restricted to
$F_i$
so that the Galois parameter restricted to
![]() $W_{F_{n+1}}$
is unramified, this is obvious if we know that
$W_{F_{n+1}}$
is unramified, this is obvious if we know that
-
(1) no supercuspidal representation of any Levi factor of
 $\mathrm {GL}(n,F)$
other than
$\mathrm {GL}(n,F)$
other than
 $\mathrm {GL}(1)^n$
has an unramified parameter, and
$\mathrm {GL}(1)^n$
has an unramified parameter, and -
(2) the parametrization is compatible with cyclic stable base change.
In the proofs of the LLC in [Reference Laumon, Rapoport and StuhlerLRS93, Reference Harris and TaylorHT01, Reference HenniartHe00], point (1) is proved by reference to Henniart’s numerical local correspondence [Reference HenniartHe88], whereas point (2) is proved by a global method. In Scholze’s proof of the LLC for
![]() $\mathrm {GL}(n)$
[Reference ScholzeSch13], point (1) is proved by a geometric argument using a study of nearby cycles in an integral model of the Lubin-Tate local moduli space.
$\mathrm {GL}(n)$
[Reference ScholzeSch13], point (1) is proved by a geometric argument using a study of nearby cycles in an integral model of the Lubin-Tate local moduli space.
Starting with point (1), the LLC is deduced by a study of the fibers of (stable) base change for cyclic extensions of p-adic fields. This is ultimately a consequence of deep properties – the ‘advanced theory’ – of the Arthur-Selberg trace formula that are established by Arthur and Clozel in [Reference Arthur and ClozelAC]. For
![]() $\mathrm {GL}(n)$
over a number field, the trace formula and its twisted analogue are automatically stable, but there is as yet no stable trace formula for general groups over function fields. If and when a stable trace formula is developed in this generality, it is likely that Theorem 1.4(i) will provide the starting point for an inductive proof of the LLC, at least for pure supercuspidal representations.
$\mathrm {GL}(n)$
over a number field, the trace formula and its twisted analogue are automatically stable, but there is as yet no stable trace formula for general groups over function fields. If and when a stable trace formula is developed in this generality, it is likely that Theorem 1.4(i) will provide the starting point for an inductive proof of the LLC, at least for pure supercuspidal representations.
The proofs of both Theorems 1.2 and 1.4 proceed via global-to-local arguments and thus involve globalizing a given supercuspidal (or discrete series) representation. For a supercuspidal representation, this globalization is achieved by an adaptation of the method of [Reference Gan and LomelíGLo] which involves a delicate construction of Poincaré series with precise control on ramification. Let us elaborate on the proof of Theorem 1.4(i) as an example.
Take the base curve to be
![]() $Y = {\mathbb {P}}^1$
and let K denote the global function field
$Y = {\mathbb {P}}^1$
and let K denote the global function field
![]() $k(Y) = k(t)$
. By the method of Poincaré series used in [Reference Gan and LomelíGLo], we construct a cuspidal automorphic representation
$k(Y) = k(t)$
. By the method of Poincaré series used in [Reference Gan and LomelíGLo], we construct a cuspidal automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $G({\mathbf A}_K)$
that is unramified outside the set of places of K corresponding to the set
$G({\mathbf A}_K)$
that is unramified outside the set of places of K corresponding to the set
![]() $Y(k)$
of k-rational points of Y. At the points
$Y(k)$
of k-rational points of Y. At the points
![]() $v = 0$
and
$v = 0$
and
![]() $v = \infty $
, we arrange for the local components of
$v = \infty $
, we arrange for the local components of
![]() $\Pi $
to be tamely ramified, with
$\Pi $
to be tamely ramified, with
![]() $\Pi _\infty ^{I_-(p)} \neq 0$
and
$\Pi _\infty ^{I_-(p)} \neq 0$
and
![]() $\Pi _0^{I^+(p)} \neq 0$
; here
$\Pi _0^{I^+(p)} \neq 0$
; here
![]() $I_-$
and
$I_-$
and
![]() $I^+$
denote opposite Iwahori subgroups of
$I^+$
denote opposite Iwahori subgroups of
![]() $G(k(\frac {1}{t}))$
and
$G(k(\frac {1}{t}))$
and
![]() $G(k(t))$
, respectively, and
$G(k(t))$
, respectively, and
![]() $I_-(p) \subset I_-$
and
$I_-(p) \subset I_-$
and
![]() $I^+(p) \subset I^+$
are the corresponding maximal pro-p subgroups. At the other rational points v, we assume
$I^+(p) \subset I^+$
are the corresponding maximal pro-p subgroups. At the other rational points v, we assume
![]() $\Pi _v$
to be isomorphic to the fixed supercuspidal
$\Pi _v$
to be isomorphic to the fixed supercuspidal
![]() $\pi $
in the context of Theorem 1.4(i). Moreover, we assume
$\pi $
in the context of Theorem 1.4(i). Moreover, we assume
![]() $\Pi _0$
contains a sufficiently regular character
$\Pi _0$
contains a sufficiently regular character
![]() $\alpha $
of the Iwahori subgroup
$\alpha $
of the Iwahori subgroup
![]() $I^+$
. V. Lafforgue has attached to such a
$I^+$
. V. Lafforgue has attached to such a
![]() $\Pi $
a local system
$\Pi $
a local system
![]() ${\mathcal {L}}(\Pi )$
over
${\mathcal {L}}(\Pi )$
over
![]() $Y \setminus {\mathbb {P}}^1(k)$
. Supposing that
$Y \setminus {\mathbb {P}}^1(k)$
. Supposing that
![]() ${\mathcal {L}}^{ss}(\Pi )$
is pure and unramified, it follows by Deligne [Reference DeligneDe80] that
${\mathcal {L}}^{ss}(\Pi )$
is pure and unramified, it follows by Deligne [Reference DeligneDe80] that
![]() ${\mathcal {L}}(\Pi )$
extends to a local system over
${\mathcal {L}}(\Pi )$
extends to a local system over
![]() ${\mathbb G}_m$
. Provided
${\mathbb G}_m$
. Provided
![]() $q> 5$
, we can then choose
$q> 5$
, we can then choose
![]() $\alpha $
to obtain a contradiction.
$\alpha $
to obtain a contradiction.
We conclude the introduction with a brief summary of the sections that follow. After recalling the results of V. Lafforgue and Genestier-Lafforgue in §2, and basic properties about Weil-Deligne parameters in §3, we complete the proof of Theorem 1.2 at the end of §3. We then lay the groundwork for the proof of Theorem 1.4(i). In §4, we establish some preparatory results about local systems on open subsets of
![]() ${\mathbb {P}}^1$
, and in §5, we prove a useful result (Lemma 5.1) about parahoric subgroups of unramified groups. In §6, we construct some open compact subgroups of
${\mathbb {P}}^1$
, and in §5, we prove a useful result (Lemma 5.1) about parahoric subgroups of unramified groups. In §6, we construct some open compact subgroups of
![]() $G(\mathbb {A}_K)$
via building theoretic considerations and use these for the construction of appropriate Poincaré series. Using this Poincaré series construction and our earlier results about local systems on
$G(\mathbb {A}_K)$
via building theoretic considerations and use these for the construction of appropriate Poincaré series. Using this Poincaré series construction and our earlier results about local systems on
![]() ${\mathbb {P}}^1$
, we prove Theorem 1.4(i) in §7. The proof of Theorem 1.4(ii) is given in §8: this requires yet another Poincaré series construction. We then highlight some natural questions suggested by our results in §9. An example is whether one can show that a generic supercuspidal representation is pure. We show this for certain generic supercuspidal representations of depth 0. In §10, we explain the implications of our results for incorrigible representations and prove a weak version of the local Langlands correspondance for
${\mathbb {P}}^1$
, we prove Theorem 1.4(i) in §7. The proof of Theorem 1.4(ii) is given in §8: this requires yet another Poincaré series construction. We then highlight some natural questions suggested by our results in §9. An example is whether one can show that a generic supercuspidal representation is pure. We show this for certain generic supercuspidal representations of depth 0. In §10, we explain the implications of our results for incorrigible representations and prove a weak version of the local Langlands correspondance for
![]() $GL(n)$
: all supercuspidal representations of
$GL(n)$
: all supercuspidal representations of
![]() $GL(n,F)$
are either pure with ramified Galois parameters or have wildly ramified parameters. The purpose of this is to provide a sufficently general template that has the potential of being extended to general G. Finally, in §11, we propose the obvious conjecture linking the Fargues-Scholze parametrization of representations of groups over p-adic fields to the Genestier-Lafforgue parametrization, by means of the Deligne-Kazhdan method of close local fields.
$GL(n,F)$
are either pure with ramified Galois parameters or have wildly ramified parameters. The purpose of this is to provide a sufficently general template that has the potential of being extended to general G. Finally, in §11, we propose the obvious conjecture linking the Fargues-Scholze parametrization of representations of groups over p-adic fields to the Genestier-Lafforgue parametrization, by means of the Deligne-Kazhdan method of close local fields.
2 Global and local Langlands-Lafforgue parameters
We begin by reviewing the global results of V. Lafforgue and the local results of Genestier-Lafforgue.
2.1 The global results of V. Lafforgue
Let Y be a smooth projective curve over k and
![]() $K = k(Y)$
be its global function field. Let G be a connected reductive algebraic group over K. Let
$K = k(Y)$
be its global function field. Let G be a connected reductive algebraic group over K. Let
![]() ${\hat {G}}$
be the Langlands dual group of G with coefficients in
${\hat {G}}$
be the Langlands dual group of G with coefficients in
![]() ${\overline {\mathbb Q}_{\ell }}$
and let
${\overline {\mathbb Q}_{\ell }}$
and let
![]() ${}^LG = {\hat {G}} \rtimes Gal(K^{sep}/K)$
be the Langlands L-group of G (in the Galois form).
${}^LG = {\hat {G}} \rtimes Gal(K^{sep}/K)$
be the Langlands L-group of G (in the Galois form).
Let
![]() ${\mathcal {A}}_0(G) = {\mathcal {A}}_0(G,Y)$
denote the set of cuspidal automorphic representations of G with central character of finite order. We let
${\mathcal {A}}_0(G) = {\mathcal {A}}_0(G,Y)$
denote the set of cuspidal automorphic representations of G with central character of finite order. We let
![]() ${\mathcal {G}}^{ss}(G)$
denote the set of equivalence classes of compatible families of semisimple
${\mathcal {G}}^{ss}(G)$
denote the set of equivalence classes of compatible families of semisimple
![]() $\ell $
-adic homomorphisms, for
$\ell $
-adic homomorphisms, for
![]() $\ell \neq p$
:
$\ell \neq p$
:
The term semisimple is understood to mean that if
![]() $\rho _\ell (Gal(K^{sep}/K))\cap {\hat {G}}$
is contained in a parabolic subgroup
$\rho _\ell (Gal(K^{sep}/K))\cap {\hat {G}}$
is contained in a parabolic subgroup
![]() $P \subset {\hat {G}}$
, then it is contained in a Levi subgroup of P.
$P \subset {\hat {G}}$
, then it is contained in a Levi subgroup of P.
If
![]() $\nu : G {~\rightarrow ~} {\mathbb G}_m$
is an algebraic character, with
$\nu : G {~\rightarrow ~} {\mathbb G}_m$
is an algebraic character, with
![]() ${\mathbb G}_m$
here designating the split
${\mathbb G}_m$
here designating the split
![]() $1$
-dimensional torus over K, the theory of L-groups provides a dual character
$1$
-dimensional torus over K, the theory of L-groups provides a dual character
![]() $\hat {\nu }: {\mathbb G}_m {~\rightarrow ~} {\hat {G}} \subset {}^LG$
. If Z is the center of G, and if
$\hat {\nu }: {\mathbb G}_m {~\rightarrow ~} {\hat {G}} \subset {}^LG$
. If Z is the center of G, and if
![]() $c: {\mathbb G}_m {~\rightarrow ~} Z \subset G$
is a homomorphism, then the theory of L-groups provides an algebraic character
$c: {\mathbb G}_m {~\rightarrow ~} Z \subset G$
is a homomorphism, then the theory of L-groups provides an algebraic character
![]() ${}^Lc: {}^LG {~\rightarrow ~} {\mathbb G}_m$
.
${}^Lc: {}^LG {~\rightarrow ~} {\mathbb G}_m$
.
We state Lafforgue’s theorem for general reductive groups over general global function fields, but we will mainly be applying it to
![]() $K = k({\mathbb {P}}^1)$
. In what follows, a representation of G over a local field F is ‘unramified’ if it contains a vector invariant under a hyperspecial maximal compact subgroup, in which case the group itself is assumed to be unramified over F.
$K = k({\mathbb {P}}^1)$
. In what follows, a representation of G over a local field F is ‘unramified’ if it contains a vector invariant under a hyperspecial maximal compact subgroup, in which case the group itself is assumed to be unramified over F.
Theorem 2.1. Let K be any global function field and G a connected reductive algebraic group over K.
(i) [Reference LafforgueLaf18][Théorème 0.1] There is a map
with the following property: if v is a place of K and
![]() $\Pi \in {\mathcal {A}}_0(G)$
is a cuspidal automorphic representation such that
$\Pi \in {\mathcal {A}}_0(G)$
is a cuspidal automorphic representation such that
![]() $\Pi _v$
is unramified, then
$\Pi _v$
is unramified, then
![]() ${\mathcal {L}}(\Pi )$
is unramified at v, and
${\mathcal {L}}(\Pi )$
is unramified at v, and
![]() ${\mathcal {L}}^{ss}(\Pi ) ~|_{W_{K_v}}$
is the Satake parameter of
${\mathcal {L}}^{ss}(\Pi ) ~|_{W_{K_v}}$
is the Satake parameter of
![]() $\Pi _v$
.Footnote
2
$\Pi _v$
.Footnote
2
(ii) Suppose
![]() $\nu : G {~\rightarrow ~} {\mathbb G}_m$
is an algebraic character and
$\nu : G {~\rightarrow ~} {\mathbb G}_m$
is an algebraic character and
is a continuous character of finite order. For any
![]() $\Pi \in {\mathcal {G}}_0(G)$
, let
$\Pi \in {\mathcal {G}}_0(G)$
, let
![]() $\Pi \otimes \chi \circ \nu $
denote the twist of
$\Pi \otimes \chi \circ \nu $
denote the twist of
![]() $\Pi $
by the character
$\Pi $
by the character
![]() $\chi \circ \nu $
of
$\chi \circ \nu $
of
![]() $G({\mathbf A})$
. Then
$G({\mathbf A})$
. Then
where
![]() $\hat {\nu }$
is as above and where
$\hat {\nu }$
is as above and where
![]() $\hat {\chi }: Gal(K^{sep}/K)^{ab} {~\rightarrow ~} GL(1,{\overline {\mathbb Q}_{\ell }})$
is the character corresponding to
$\hat {\chi }: Gal(K^{sep}/K)^{ab} {~\rightarrow ~} GL(1,{\overline {\mathbb Q}_{\ell }})$
is the character corresponding to
![]() $\chi $
by class field theory.
$\chi $
by class field theory.
(iii) [Reference Genestier and LafforgueGLa][Théorème 0.1] Let v be a place of K and let
![]() $F = K_v$
. Then the semisimplification of the restriction of
$F = K_v$
. Then the semisimplification of the restriction of
![]() ${\mathcal {L}}(\Pi )$
to
${\mathcal {L}}(\Pi )$
to
![]() $W_{K_v}$
depends only on F and the local component
$W_{K_v}$
depends only on F and the local component
![]() $\Pi _v$
of
$\Pi _v$
of
![]() $\Pi $
, which is an irreducible admissible representation of
$\Pi $
, which is an irreducible admissible representation of
![]() $G(F)$
, and not on the rest of the automorphic representation
$G(F)$
, and not on the rest of the automorphic representation
![]() $\Pi $
, nor on the global field K. We denote this parameter
$\Pi $
, nor on the global field K. We denote this parameter
![]() ${\mathcal {L}}^{ss}(\Pi _v)$
.
${\mathcal {L}}^{ss}(\Pi _v)$
.
2.2 The local results of Genestier-Lafforgue
Now let F be a nonarchimedean local field of characteristic p, so that
![]() $F {~\overset \sim \longrightarrow ~} k'(\!(t)\!)$
for some finite extension
$F {~\overset \sim \longrightarrow ~} k'(\!(t)\!)$
for some finite extension
![]() $k'$
of
$k'$
of
![]() ${{\mathbb F}_p}$
. Let
${{\mathbb F}_p}$
. Let
![]() ${\mathcal {A}}(G,F)$
denote the set of equivalence classes of irreducible admissible representations of
${\mathcal {A}}(G,F)$
denote the set of equivalence classes of irreducible admissible representations of
![]() $G(F)$
and let
$G(F)$
and let
![]() ${\mathcal {G}}^{ss}(G,F)$
denote the set of equivalence classes of semisimple
${\mathcal {G}}^{ss}(G,F)$
denote the set of equivalence classes of semisimple
![]() $\ell $
-adic homomorphisms
$\ell $
-adic homomorphisms
By (iii) above, we thus obtain a (semisimple) parametrization of
![]() ${\mathcal {A}}(G,F)$
:
${\mathcal {A}}(G,F)$
:
Of course, the theorem quoted above only constructs
![]() ${\mathcal {L}}^{ss}(\pi )$
when
${\mathcal {L}}^{ss}(\pi )$
when
![]() $\pi $
can be realized as the local component
$\pi $
can be realized as the local component
![]() $\Pi _v$
of a global cuspidal automorphic representation
$\Pi _v$
of a global cuspidal automorphic representation
![]() $\Pi $
, but the statement of Théorème 0.1 of [Reference Genestier and LafforgueGLa] includes the extension to a (semisimple) parametrization of all members of
$\Pi $
, but the statement of Théorème 0.1 of [Reference Genestier and LafforgueGLa] includes the extension to a (semisimple) parametrization of all members of
![]() ${\mathcal {A}}(G,F)$
. Theorem 2.1 continues:
${\mathcal {A}}(G,F)$
. Theorem 2.1 continues:
Theorem 2.3 ([Reference Genestier and LafforgueGLa],Théorème 0.1).
(iv) The local parametrization
![]() ${\mathcal {L}}^{ss}$
is compatible with parabolic induction in the following sense: Let
${\mathcal {L}}^{ss}$
is compatible with parabolic induction in the following sense: Let
![]() $P \subset G$
be an F-rational parabolic subgroup with Levi factor M and let
$P \subset G$
be an F-rational parabolic subgroup with Levi factor M and let
![]() $\sigma \in {\mathcal {A}}(M,F)$
. If
$\sigma \in {\mathcal {A}}(M,F)$
. If
![]() $\pi \in {\mathcal {A}}(G,F)$
is an irreducible constituent of
$\pi \in {\mathcal {A}}(G,F)$
is an irreducible constituent of
![]() $Ind_{P(F)}^{G(F)} \sigma $
(normalized induction) and
$Ind_{P(F)}^{G(F)} \sigma $
(normalized induction) and
![]() $i_M: {}^LM {~\rightarrow ~} {}^LG$
is the inclusion of the L-group of M as a Levi factor of a parabolic subgroup in the L-group of G, then
$i_M: {}^LM {~\rightarrow ~} {}^LG$
is the inclusion of the L-group of M as a Levi factor of a parabolic subgroup in the L-group of G, then
(v) In particular, suppose G is quasi-split over F with Borel subgroup B,
![]() $T \subset B$
is a maximal torus,
$T \subset B$
is a maximal torus,
![]() $I \subset G(F)$
is an Iwahori subgroup, and
$I \subset G(F)$
is an Iwahori subgroup, and
![]() $I(p) \subset I$
is its maximal pro-p subgroup. Suppose
$I(p) \subset I$
is its maximal pro-p subgroup. Suppose
![]() $\pi ^{I(p)} \neq 0$
. Then
$\pi ^{I(p)} \neq 0$
. Then
![]() ${\mathcal {L}}^{ss}(\pi )$
takes values in the L-group of T.
${\mathcal {L}}^{ss}(\pi )$
takes values in the L-group of T.
(vi) The local and global parametrizations
![]() ${\mathcal {L}}$
and
${\mathcal {L}}$
and
![]() ${\mathcal {L}}^{ss}$
are compatible with homomorphisms
${\mathcal {L}}^{ss}$
are compatible with homomorphisms
of reductive groups where the image of
![]() $\Upsilon $
is a normal subgroup, in the following sense. Let
$\Upsilon $
is a normal subgroup, in the following sense. Let
![]() ${}^L\Upsilon : {^L}G_2 {~\rightarrow ~} {^L}G_1$
be the homomorphism of L-groups corresponding to
${}^L\Upsilon : {^L}G_2 {~\rightarrow ~} {^L}G_1$
be the homomorphism of L-groups corresponding to
![]() $\Upsilon $
. Then for any cuspidal automorphic (resp. admissible irreducible) representation
$\Upsilon $
. Then for any cuspidal automorphic (resp. admissible irreducible) representation
![]() $\pi $
of
$\pi $
of
![]() $G_2$
over K (resp. over F),
$G_2$
over K (resp. over F),
(resp.
This applies in particular if
![]() $\Upsilon $
is an isogeny of semisimple groups.
$\Upsilon $
is an isogeny of semisimple groups.
Proof. In the situation of (v), the condition
![]() $\pi ^{I(p)} \neq 0$
implies that
$\pi ^{I(p)} \neq 0$
implies that
![]() $\pi $
contains an eigenvector for I and thus is a constituent of a principal series representation. The assertion (v) then follows from (iv). Assertion (vi) in the local setting is the last assertion of [Reference Genestier and LafforgueGLa, Théorème 0.1]; in the global setting, it is [Reference LafforgueLaf18, Proposition 12.5].
$\pi $
contains an eigenvector for I and thus is a constituent of a principal series representation. The assertion (v) then follows from (iv). Assertion (vi) in the local setting is the last assertion of [Reference Genestier and LafforgueGLa, Théorème 0.1]; in the global setting, it is [Reference LafforgueLaf18, Proposition 12.5].
Corollary 2.4. Let
![]() $\Pi \in {\mathcal {A}}_0(G)$
and suppose
$\Pi \in {\mathcal {A}}_0(G)$
and suppose
![]() $|X| \subset Y$
is the largest closed subset such that
$|X| \subset Y$
is the largest closed subset such that
![]() $\Pi _v$
is unramified for
$\Pi _v$
is unramified for
![]() $v \notin |X|$
.
$v \notin |X|$
.
(i) The parametrization of Theorem 2.1 defines a symmetric monoidal functor from the category
![]() $Rep({}^LG)$
of finite-dimensional algebraic representations of
$Rep({}^LG)$
of finite-dimensional algebraic representations of
![]() ${}^LG$
to the category of completely reducible local systems on
${}^LG$
to the category of completely reducible local systems on
![]() $Y \setminus |X|$
: to any
$Y \setminus |X|$
: to any
![]() $\tau : {}^LG {~\rightarrow ~} GL(N)$
, one attaches the N-dimensional local system attached to the representation
$\tau : {}^LG {~\rightarrow ~} GL(N)$
, one attaches the N-dimensional local system attached to the representation
of
![]() $\pi _1(Y \setminus |X|)$
(any base point).
$\pi _1(Y \setminus |X|)$
(any base point).
(ii) Similarly, let
![]() $\sigma \in {\mathcal {A}}(G,F)$
. The local parametrization
$\sigma \in {\mathcal {A}}(G,F)$
. The local parametrization
![]() ${\mathcal {L}}^{ss}$
of (2.2) defines a symmetric monoidal functor from the category
${\mathcal {L}}^{ss}$
of (2.2) defines a symmetric monoidal functor from the category
![]() $Rep({}^LG)$
of finite-dimensional algebraic representations of
$Rep({}^LG)$
of finite-dimensional algebraic representations of
![]() ${}^LG$
to the category of completely reducible representations of
${}^LG$
to the category of completely reducible representations of
![]() $W_F$
:
$W_F$
:
(iii) Suppose
![]() $\Pi $
has the property that
$\Pi $
has the property that
![]() ${\mathcal {V}}(\Pi ,\tau )$
is abelian and semisimple for some faithful representation
${\mathcal {V}}(\Pi ,\tau )$
is abelian and semisimple for some faithful representation
![]() $\tau $
. Then the image of
$\tau $
. Then the image of
![]() ${\mathcal {L}}(\Pi )$
, intersected with
${\mathcal {L}}(\Pi )$
, intersected with
![]() ${\hat {G}}$
, lies in a maximal torus of
${\hat {G}}$
, lies in a maximal torus of
![]() ${\hat {G}}$
.
${\hat {G}}$
.
Proof. The first two assertions express the standard characterization of
![]() ${\hat {G}}$
-local systems as symmetric monoidal functors (see, for example, the discussion on p. 52 of [Reference SimpsonSi]); the third assertion is obvious.
${\hat {G}}$
-local systems as symmetric monoidal functors (see, for example, the discussion on p. 52 of [Reference SimpsonSi]); the third assertion is obvious.
We conclude this section with the following definition.
Definition 2.5. With notation as in Theorem 2.3, let
![]() $\sigma \in {\mathcal {A}}(G,F)$
. We say
$\sigma \in {\mathcal {A}}(G,F)$
. We say
![]() $\sigma $
is pure if, for some (equivalently, for all) faithful representations
$\sigma $
is pure if, for some (equivalently, for all) faithful representations
![]() $\tau : {}^LG {~\rightarrow ~} GL(N)$
,
$\tau : {}^LG {~\rightarrow ~} GL(N)$
,
![]() ${\mathcal {L}}^{ss}(\sigma ,\tau )$
has the property that, for any Frobenius element
${\mathcal {L}}^{ss}(\sigma ,\tau )$
has the property that, for any Frobenius element
![]() $Frob_F \in W_F$
, the eigenvalues of
$Frob_F \in W_F$
, the eigenvalues of
![]() ${\mathcal {L}}^{ss}(\sigma ,\tau )(Frob)$
are all Weil q-numbers of the same weight.
${\mathcal {L}}^{ss}(\sigma ,\tau )(Frob)$
are all Weil q-numbers of the same weight.
3 Pure Weil-Deligne parameters
This section is devoted to the proof of Theorem 1.2. We shall begin with some background material on tempered L–parameters or their equivalent incarnation as pure Weil-Deligne parameters.
3.1 Tempered parameters and pure Weil-Deligne parameters
Let F be a nonarchimedean local field.
Definition 3.1. A Weil-Deligne parameter for F with values in
![]() ${}^LG(C)$
is a pair
${}^LG(C)$
is a pair
![]() $(\rho ,N)$
, where
$(\rho ,N)$
, where
![]() $\rho : W_F {~\rightarrow ~} {}^LG(C)$
is a continuous homomorphism (for the discrete topology on C) and
$\rho : W_F {~\rightarrow ~} {}^LG(C)$
is a continuous homomorphism (for the discrete topology on C) and
![]() $N \in Lie(\hat {G})(C)$
is a nilpotent element such that
$N \in Lie(\hat {G})(C)$
is a nilpotent element such that
![]() $(Ad\circ \rho ,N)$
is a homomorphism from the Weil-Deligne group of F to
$(Ad\circ \rho ,N)$
is a homomorphism from the Weil-Deligne group of F to
![]() $Aut(Lie(\hat {G}))(C)$
.
$Aut(Lie(\hat {G}))(C)$
.
Without loss of generality, we may assume
![]() $C = {\mathbb C}$
. There is a simple recipe for converting a Weil-Deligne parameter
$C = {\mathbb C}$
. There is a simple recipe for converting a Weil-Deligne parameter
![]() $(\rho ,N)$
for F with values in
$(\rho ,N)$
for F with values in
![]() ${}^LG({\mathbb C})$
to an L-parameter
${}^LG({\mathbb C})$
to an L-parameter
which is algebraic in the second factor, and vice versa. This recipe (and the proof that it gives an equivalence between the two notions) is given in [Reference Gross and ReederGR, §2.1 and Prop. 2.2].
We define a couple of properties of Weil-Deligne parameters.
Definition 3.2. The Weil-Deligne parameter
![]() $(\rho ,N)$
is tempered if the restriction of
$(\rho ,N)$
is tempered if the restriction of
![]() $\varphi _{\rho ,N}$
to
$\varphi _{\rho ,N}$
to
![]() $W_F \times SU(2)$
has bounded image after projection to
$W_F \times SU(2)$
has bounded image after projection to
![]() $\hat {G}({\mathbb C})$
. The parameter
$\hat {G}({\mathbb C})$
. The parameter
![]() $(\rho ,N)$
is essentially tempered if its image in
$(\rho ,N)$
is essentially tempered if its image in
![]() $\hat {G}^{ad}$
is bounded.
$\hat {G}^{ad}$
is bounded.
Definition 3.3. (a) The Weil-Deligne representation
![]() $(\rho ,N)$
with values in
$(\rho ,N)$
with values in
![]() $GL(V)$
is pure if there is a complex number t such that
$GL(V)$
is pure if there is a complex number t such that
-
(i) The eigenvalues of
 $\rho _t(Frob_F) := \rho (Frob_F)q^t$
are all q-numbers of integer weight.
$\rho _t(Frob_F) := \rho (Frob_F)q^t$
are all q-numbers of integer weight. -
(ii) The subspace
 $W_aV \subset V$
of eigenvectors for
$W_aV \subset V$
of eigenvectors for
 $\rho _t(Frob_F)$
with eigenvalues of weight
$\rho _t(Frob_F)$
with eigenvalues of weight
 $\leq a$
is invariant under
$\leq a$
is invariant under
 $(\rho ,N)$
;
$(\rho ,N)$
; -
(iii) Letting
 $gr_aV = W_aV/W_{a-1}V$
, there is an integer w such that, for all
$gr_aV = W_aV/W_{a-1}V$
, there is an integer w such that, for all
 $i \geq 0$
, the map is an isomorphism.
$i \geq 0$
, the map is an isomorphism. $$ \begin{align*}N: gr_{w+i}V {~\rightarrow~} gr_{w-i}V\end{align*} $$
$$ \begin{align*}N: gr_{w+i}V {~\rightarrow~} gr_{w-i}V\end{align*} $$
The integer w in (iii) is then called the weight of
 $(\rho ,N)$
(twisted by t).
$(\rho ,N)$
(twisted by t).
(b) Let G be a connected reductive group over F. The Weil-Deligne parameter
![]() $(\rho ,N)$
with values in
$(\rho ,N)$
with values in
![]() ${}^LG({\mathbb C})$
is pure if
${}^LG({\mathbb C})$
is pure if
![]() $(\sigma \circ \rho ,N)$
is pure of some weight for some (equivalently every) faithful representation
$(\sigma \circ \rho ,N)$
is pure of some weight for some (equivalently every) faithful representation
![]() $\sigma $
of
$\sigma $
of
![]() ${}^LG$
.
${}^LG$
.
In particular, if
![]() $N = 0$
, then the Weil-Deligne parameter
$N = 0$
, then the Weil-Deligne parameter
![]() $(\rho ,N)$
is pure if and only if the Weil group parameter
$(\rho ,N)$
is pure if and only if the Weil group parameter
![]() $\rho $
is pure (in the usual sense) of some weight (up to twist by a power of the norm). We distinguish the two notions of purity by referring to ‘pure Weil-Deligne parameters’ and ‘pure Weil parameters’, or ‘pure semisimple parameters’, respectively. In [Reference Taylor and YoshidaTY], pure Weil parameters are called strictly pure.
$\rho $
is pure (in the usual sense) of some weight (up to twist by a power of the norm). We distinguish the two notions of purity by referring to ‘pure Weil-Deligne parameters’ and ‘pure Weil parameters’, or ‘pure semisimple parameters’, respectively. In [Reference Taylor and YoshidaTY], pure Weil parameters are called strictly pure.
Remark 3.4. The local parameters
![]() ${\mathcal {L}}^{ss}(\pi )$
attached by Genestier and Lafforgue are
${\mathcal {L}}^{ss}(\pi )$
attached by Genestier and Lafforgue are
![]() $\ell $
-adic. In order to define what it means for them to be pure (as Weil or Weil-Deligne parameters), one usually chooses an isomorphism
$\ell $
-adic. In order to define what it means for them to be pure (as Weil or Weil-Deligne parameters), one usually chooses an isomorphism
![]() $\iota : {\overline {\mathbb Q}_{\ell }} {~\overset \sim \longrightarrow ~} {\mathbb C}$
(or more sensibly, an isomorphism between the algebraic closures of
$\iota : {\overline {\mathbb Q}_{\ell }} {~\overset \sim \longrightarrow ~} {\mathbb C}$
(or more sensibly, an isomorphism between the algebraic closures of
![]() ${\mathbb Q}$
in the two fields) and declares them to be
${\mathbb Q}$
in the two fields) and declares them to be
![]() $\iota $
-pure if they are pure in the above sense after composing with
$\iota $
-pure if they are pure in the above sense after composing with
![]() $\iota $
. For this purpose, one would want to replace the complex number t in Definition 3.3 by an
$\iota $
. For this purpose, one would want to replace the complex number t in Definition 3.3 by an
![]() $\ell $
-adic number. In practice, the parameters that arise in the automorphic theory are
$\ell $
-adic number. In practice, the parameters that arise in the automorphic theory are
![]() $\iota $
-pure for every
$\iota $
-pure for every
![]() $\iota $
.
$\iota $
.
The following facts are well known and in any case are easy to verify.
Lemma 3.5.
(a) The Weil-Deligne parameter
![]() $(\rho ,N)$
is pure if and only if
$(\rho ,N)$
is pure if and only if
![]() $\varphi _{\rho , N}$
is essentially tempered.
$\varphi _{\rho , N}$
is essentially tempered.
(b) Let
![]() $\rho : W_F {~\rightarrow ~} {}^LG(C)$
be a semisimple parameter. There is at most one way (up to equivalence) to complete
$\rho : W_F {~\rightarrow ~} {}^LG(C)$
be a semisimple parameter. There is at most one way (up to equivalence) to complete
![]() $\rho $
to a pure Weil-Deligne parameter
$\rho $
to a pure Weil-Deligne parameter
![]() $(\rho ,N)$
. If it exists, we call it the pure completion of
$(\rho ,N)$
. If it exists, we call it the pure completion of
![]() $\rho $
. Equivalently, there is at most one essentially tempered L-parameter
$\rho $
. Equivalently, there is at most one essentially tempered L-parameter
![]() $\varphi $
whose associated semisimple parameter (via (1.1)) is
$\varphi $
whose associated semisimple parameter (via (1.1)) is
![]() $\rho $
.
$\rho $
.
Proof. Both conditions in (a) are checked by composition with a faithful representation
![]() $\sigma $
of
$\sigma $
of
![]() ${}^LG$
. This reduces the verification of (a) to the case of
${}^LG$
. This reduces the verification of (a) to the case of
![]() $GL(n)$
, which is verified in [Reference Taylor and YoshidaTY, Lemma 1.4(3)]. Part (b) for
$GL(n)$
, which is verified in [Reference Taylor and YoshidaTY, Lemma 1.4(3)]. Part (b) for
![]() $GL(n)$
is [Reference Taylor and YoshidaTY, Lemma 1.4(4)]. For general groups G, one can cite the argument on p. 10 of [Reference ArthurA84]; Arthur is there classifying Arthur parameters, rather than Weil-Deligne parameters, of real groups, but the proof of uniqueness is the same. More precisely, suppose
$GL(n)$
is [Reference Taylor and YoshidaTY, Lemma 1.4(4)]. For general groups G, one can cite the argument on p. 10 of [Reference ArthurA84]; Arthur is there classifying Arthur parameters, rather than Weil-Deligne parameters, of real groups, but the proof of uniqueness is the same. More precisely, suppose
![]() $\rho $
can be completed to a pure Weil-Deligne parameter
$\rho $
can be completed to a pure Weil-Deligne parameter
![]() $(\rho ,N)$
, and let
$(\rho ,N)$
, and let
![]() $\varphi _{\rho ,N}: W_F \times SL(2)$
be as above. Let
$\varphi _{\rho ,N}: W_F \times SL(2)$
be as above. Let
![]() $\varphi $
be the restriction of
$\varphi $
be the restriction of
![]() $\varphi _{\rho ,N}$
to the
$\varphi _{\rho ,N}$
to the
![]() $W_F$
factor. Since the image of
$W_F$
factor. Since the image of
![]() $\varphi $
is bounded and consists only of semisimple elements, its centralizer
$\varphi $
is bounded and consists only of semisimple elements, its centralizer
![]() $C_\varphi \subset {}^LG$
is reductive. We need to show that the restriction of
$C_\varphi \subset {}^LG$
is reductive. We need to show that the restriction of
![]() $\varphi _{\rho ,N}$
to
$\varphi _{\rho ,N}$
to
![]() $SL(2)$
, whose image lies in
$SL(2)$
, whose image lies in
![]() $C_\varphi $
, is unique up to
$C_\varphi $
, is unique up to
![]() $C_\varphi $
-conjugacy, but this is exactly what Arthur shows in his situation.
$C_\varphi $
-conjugacy, but this is exactly what Arthur shows in his situation.
3.2 An application of the purity of the monodromy weight filtration
The parametrization of Genestier-Lafforgue only attaches a semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
to a local representation
${\mathcal {L}}^{ss}(\pi )$
to a local representation
![]() $\pi $
. But when
$\pi $
. But when
![]() $\pi $
is realized as a local component of a cuspidal automorphic representation
$\pi $
is realized as a local component of a cuspidal automorphic representation
![]() $\Pi $
of G over some global function field K – say
$\Pi $
of G over some global function field K – say
![]() $\pi = \Pi _x$
for some place x of K – then the restriction
$\pi = \Pi _x$
for some place x of K – then the restriction
![]() ${\mathcal {L}}(\Pi )_x$
to the decomposition group
${\mathcal {L}}(\Pi )_x$
to the decomposition group
![]() $\Gamma _x$
at x need not be semisimple. We let
$\Gamma _x$
at x need not be semisimple. We let
denote the Weil-Deligne parameter associated to the Galois parameter
![]() ${\mathcal {L}}(\Pi )_x$
.
${\mathcal {L}}(\Pi )_x$
.
The following result of Sawin and Templier generalizes Deligne’s theorem on the purity of the monodromy weight filtration to G-local systems:
Lemma 3.6. [Reference Sawin and TemplierST, Lemma 11.4] Let X be a smooth projective curve over a finite field k, with function field
![]() $K = k(X)$
and let
$K = k(X)$
and let
![]() $\rho : Gal(K^{sep}/K) {~\rightarrow ~} {}^LG(C)$
be an irreducible homomorphism (with image not contained in a proper parabolic subgroup, where a parabolic subgroup is defined in the ‘dynamic’ way [Reference Conrad, Gabber and PrasaCGP, Definition 2.2.1] as, for any homomorphism
$\rho : Gal(K^{sep}/K) {~\rightarrow ~} {}^LG(C)$
be an irreducible homomorphism (with image not contained in a proper parabolic subgroup, where a parabolic subgroup is defined in the ‘dynamic’ way [Reference Conrad, Gabber and PrasaCGP, Definition 2.2.1] as, for any homomorphism
![]() $\lambda \colon \mathbb G_m \to {}^L G$
, the subgroup of
$\lambda \colon \mathbb G_m \to {}^L G$
, the subgroup of
![]() $g \in {}^L G$
such that
$g \in {}^L G$
such that
![]() $\lim _{t\to 0} \lambda (t) g \lambda (t)^{-1}$
exists). Let z be any place of K and let
$\lim _{t\to 0} \lambda (t) g \lambda (t)^{-1}$
exists). Let z be any place of K and let
![]() $(\rho ^{ss}_z,N_z)$
be the Weil-Deligne parameter associated to the restriction
$(\rho ^{ss}_z,N_z)$
be the Weil-Deligne parameter associated to the restriction
![]() $\rho _z$
of
$\rho _z$
of
![]() $\rho $
to a decomposition group at z. Then
$\rho $
to a decomposition group at z. Then
![]() $(\rho ^{ss}_z,N_z)$
is a pure Weil-Deligne parameter.
$(\rho ^{ss}_z,N_z)$
is a pure Weil-Deligne parameter.
Proof. We explain how to deduce this from [Reference Sawin and TemplierST, Lemma 11.4] since this result is not explicitly stated there. Under the irreducibility hypothesis, [Reference Sawin and TemplierST, Lemma 11.4] states that the composition of
![]() $\rho $
with any representation of
$\rho $
with any representation of
![]() ${}^L G(C)$
is pure of some weight w as a local system on an open subset of X. (The mixedness property assumed in [Reference Sawin and TemplierST] is a consequence of [Reference LafforgueLaf02].) It then follows from [Reference DeligneDe80, Theorem 1.8.4] that the i’th associated graded of the monodromy filtration of the composition of
${}^L G(C)$
is pure of some weight w as a local system on an open subset of X. (The mixedness property assumed in [Reference Sawin and TemplierST] is a consequence of [Reference LafforgueLaf02].) It then follows from [Reference DeligneDe80, Theorem 1.8.4] that the i’th associated graded of the monodromy filtration of the composition of
![]() $\rho _z$
with the same representation is pure of weight
$\rho _z$
with the same representation is pure of weight
![]() $w+i$
. In particular, all the Frobenius eigenvalues are q-numbers, and the sum of eigenspaces of Frobenius associated to eigenvalues of size
$w+i$
. In particular, all the Frobenius eigenvalues are q-numbers, and the sum of eigenspaces of Frobenius associated to eigenvalues of size
![]() $\leq q^{ \frac {w+i}{2}}$
is the ith member of the monodromy filtration. Part (iii) of the definition of pure Weil-Deligne parameter then follows from the defining property [Reference DeligneDe80, Proposition 1.6.13].
$\leq q^{ \frac {w+i}{2}}$
is the ith member of the monodromy filtration. Part (iii) of the definition of pure Weil-Deligne parameter then follows from the defining property [Reference DeligneDe80, Proposition 1.6.13].
Remark 3.7. The lemma is stated in [Reference Sawin and TemplierST] when G is split semisimple, but the proof is valid for any reductive G, since it is easy to see that the limit
![]() $\lim _{t\to \infty } \alpha (t) g \alpha (t)^{-1}$
exists if and only if g preserves the filtration into weight spaces of
$\lim _{t\to \infty } \alpha (t) g \alpha (t)^{-1}$
exists if and only if g preserves the filtration into weight spaces of
![]() $\alpha $
on a faithful representation.
$\alpha $
on a faithful representation.
Corollary 3.8. Let
![]() $\pi $
be an irreducible admissible representation of
$\pi $
be an irreducible admissible representation of
![]() $G(F)$
. Suppose
$G(F)$
. Suppose
-
○ X is a smooth projective curve over a finite field k
-
○ z is a place of the function field
 $K = k(X)$
such that
$K = k(X)$
such that
 $K_z {~\overset \sim \longrightarrow ~} F$
.
$K_z {~\overset \sim \longrightarrow ~} F$
. -
○ there is a cuspidal automorphic representation
 $\Pi $
of
$\Pi $
of
 $G_K$
, with
$G_K$
, with
 $\Pi _z {~\overset \sim \longrightarrow ~} \pi $
, such that the global parameter
$\Pi _z {~\overset \sim \longrightarrow ~} \pi $
, such that the global parameter
 ${\mathcal {L}}(\Pi )$
is irreducible.
${\mathcal {L}}(\Pi )$
is irreducible.
Then the Weil-Deligne parameter
![]() ${\mathcal {L}}_\Pi (\pi )$
is pure. Moreover, it is the unique pure completion of the semisimple parameter
${\mathcal {L}}_\Pi (\pi )$
is pure. Moreover, it is the unique pure completion of the semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
.
${\mathcal {L}}^{ss}(\pi )$
.
Not every semisimple parameter admits a completion to a pure Weil-Deligne parameter. Corollary 3.8 asserts that
![]() ${\mathcal {L}}^{ss}(\pi )$
does admit a pure completion provided
${\mathcal {L}}^{ss}(\pi )$
does admit a pure completion provided
![]() $\pi $
can be realized as a local component of a cuspidal automorphic representation whose global parameter is irreducible in the indicated sense.
$\pi $
can be realized as a local component of a cuspidal automorphic representation whose global parameter is irreducible in the indicated sense.
3.3 Proof of Theorem 1.2
We are now ready to prove Theorem 1.2. In view of Corollary 3.8, it suffices to construct cuspidal globalizations of any essentially discrete series representation
![]() $\pi $
whose global parameter is irreducible. The following proposition achieves this when
$\pi $
whose global parameter is irreducible. The following proposition achieves this when
![]() $\pi $
is supercuspidal.
$\pi $
is supercuspidal.
Proposition 3.9. Let G be a reductive group over F. Let
![]() $\pi $
be a supercuspidal representation of
$\pi $
be a supercuspidal representation of
![]() $G(F)$
. Let X be a smooth projective curve over a finite field k and let z be a place of the function field
$G(F)$
. Let X be a smooth projective curve over a finite field k and let z be a place of the function field
![]() $K = k(X)$
such that
$K = k(X)$
such that
![]() $K_z {~\overset \sim \longrightarrow ~} F$
. Then there exist infinitely many cuspidal automorphic representations
$K_z {~\overset \sim \longrightarrow ~} F$
. Then there exist infinitely many cuspidal automorphic representations
![]() $\Pi $
of
$\Pi $
of
![]() $G_K$
, such that
$G_K$
, such that
-
○
 $\Pi _z {~\overset \sim \longrightarrow ~} \pi $
;
$\Pi _z {~\overset \sim \longrightarrow ~} \pi $
; -
○ the global parameter
 ${\mathcal {L}}(\Pi )$
is irreducible.
${\mathcal {L}}(\Pi )$
is irreducible.
In particular, the semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
admits a completion to a pure Weil-Deligne parameter that is realized as the specialization at z of the global parameter
${\mathcal {L}}^{ss}(\pi )$
admits a completion to a pure Weil-Deligne parameter that is realized as the specialization at z of the global parameter
![]() ${\mathcal {L}}(\Pi )$
, for any such
${\mathcal {L}}(\Pi )$
, for any such
![]() $\Pi $
.
$\Pi $
.
Proof. We shall use the results of [Reference Gan and LomelíGLo] to produce the desired globalizations. Let
![]() $x \neq z$
be any other place of K such that
$x \neq z$
be any other place of K such that
![]() $G(K_x)$
is a split reductive group. There are infinitely many such x – just take any x that splits completely in a finite cover of X over which G splits. Thus, it suffices to show
$G(K_x)$
is a split reductive group. There are infinitely many such x – just take any x that splits completely in a finite cover of X over which G splits. Thus, it suffices to show
-
(i) There is a supercuspidal representation
 $\pi '$
of
$\pi '$
of
 $G(K_x)$
such that
$G(K_x)$
such that
 ${\mathcal {L}}^{ss}(\pi ')$
is irreducible, and
${\mathcal {L}}^{ss}(\pi ')$
is irreducible, and -
(ii) There is an automorphic representation
 $\Pi $
of
$\Pi $
of
 $G_K$
with
$G_K$
with
 $\Pi _x {~\overset \sim \longrightarrow ~} \pi '$
and
$\Pi _x {~\overset \sim \longrightarrow ~} \pi '$
and
 $\Pi _z {~\overset \sim \longrightarrow ~} \pi $
, and with
$\Pi _z {~\overset \sim \longrightarrow ~} \pi $
, and with
 $\Pi _y$
tamely ramified for all
$\Pi _y$
tamely ramified for all
 $y \neq x, z$
.
$y \neq x, z$
.
Once (i) is given, the existence of
![]() $\Pi $
as in (ii) is proved in [Reference Gan and LomelíGLo] by a Poincaré series construction. It thus remains to produce a supercuspidal representation
$\Pi $
as in (ii) is proved in [Reference Gan and LomelíGLo] by a Poincaré series construction. It thus remains to produce a supercuspidal representation
![]() $\pi '$
as in (i).
$\pi '$
as in (i).
We let
![]() $k' = k(x)$
denote the residue field at x and construct the Kloosterman sheaf
$k' = k(x)$
denote the residue field at x and construct the Kloosterman sheaf
![]() $\mathrm {Kl}_{\hat {G}}(\phi ,\chi )$
of [Reference Heinloth, Ngô and YunHNY] over
$\mathrm {Kl}_{\hat {G}}(\phi ,\chi )$
of [Reference Heinloth, Ngô and YunHNY] over
![]() $\mathbb {P}^1_{k'}$
. Let
$\mathbb {P}^1_{k'}$
. Let
![]() $\pi '$
be the local component at
$\pi '$
be the local component at
![]() $\infty $
of the corresponding automorphic representation
$\infty $
of the corresponding automorphic representation
![]() $\pi (\phi ,\chi )$
. Theorem 2 of [Reference Heinloth, Ngô and YunHNY] implies that the restriction to the inertia group at
$\pi (\phi ,\chi )$
. Theorem 2 of [Reference Heinloth, Ngô and YunHNY] implies that the restriction to the inertia group at
![]() $\infty $
of the local monodromy representation of
$\infty $
of the local monodromy representation of
![]() $\mathrm {Kl}_{\hat {G}}(\phi ,\chi )$
is irreducible. The statement in [Reference Heinloth, Ngô and YunHNY] includes slightly restrictive hypotheses on the prime p for non-simply laced groups, but these hypotheses have since been removed by Xu and Zhu in [Reference Xu and ZhuXZ, Corollary 4.5.8, Remark 4.5.10], under the hypothesis that
$\mathrm {Kl}_{\hat {G}}(\phi ,\chi )$
is irreducible. The statement in [Reference Heinloth, Ngô and YunHNY] includes slightly restrictive hypotheses on the prime p for non-simply laced groups, but these hypotheses have since been removed by Xu and Zhu in [Reference Xu and ZhuXZ, Corollary 4.5.8, Remark 4.5.10], under the hypothesis that
![]() $G(K_x)$
is split, which we are assuming. However, it follows from construction that
$G(K_x)$
is split, which we are assuming. However, it follows from construction that
![]() $\mathrm {Kl}_{\hat {G}}(\phi ,\chi )$
is the global parameter attached by [Reference LafforgueLaf18] to
$\mathrm {Kl}_{\hat {G}}(\phi ,\chi )$
is the global parameter attached by [Reference LafforgueLaf18] to
![]() $\pi (\phi ,\chi )$
. More precisely, [Reference Heinloth, Ngô and YunHNY, Reference Xu and ZhuXZ] computes the local monodromy of
$\pi (\phi ,\chi )$
. More precisely, [Reference Heinloth, Ngô and YunHNY, Reference Xu and ZhuXZ] computes the local monodromy of
![]() $\mathrm { Kl}_{\hat {G}}(\phi ,\chi )$
at unramified places and identifies it with that obtained from the Satake parameters of
$\mathrm { Kl}_{\hat {G}}(\phi ,\chi )$
at unramified places and identifies it with that obtained from the Satake parameters of
![]() $\pi (\phi ,\chi )$
. (The construction of
$\pi (\phi ,\chi )$
. (The construction of
![]() $\pi (\phi ,\chi )$
is made explicit in [Reference YunY16] but its existence is implicit in [Reference Heinloth, Ngô and YunHNY].) It then follows that
$\pi (\phi ,\chi )$
is made explicit in [Reference YunY16] but its existence is implicit in [Reference Heinloth, Ngô and YunHNY].) It then follows that
![]() ${\mathcal {L}}^{ss}(\pi ')$
is irreducible, as desired.
${\mathcal {L}}^{ss}(\pi ')$
is irreducible, as desired.
Remark 3.10. The paper [Reference Heinloth, Ngô and YunHNY] was written before [Reference LafforgueLaf18], but the
![]() ${}^LG$
-valued parameters attached to the automorphic representations constructed in [Reference Heinloth, Ngô and YunHNY] coincide at all unramified places with those obtained by Lafforgue, because both are given by the Satake correspondence. It follows by Chebotarev density that the semisimple
${}^LG$
-valued parameters attached to the automorphic representations constructed in [Reference Heinloth, Ngô and YunHNY] coincide at all unramified places with those obtained by Lafforgue, because both are given by the Satake correspondence. It follows by Chebotarev density that the semisimple
![]() $\ell $
-adic local systems obtained by composing the
$\ell $
-adic local systems obtained by composing the
![]() ${}^LG$
-valued parameters of [Reference Heinloth, Ngô and YunHNY] and [Reference LafforgueLaf18] with any representation of
${}^LG$
-valued parameters of [Reference Heinloth, Ngô and YunHNY] and [Reference LafforgueLaf18] with any representation of
![]() ${}^LG$
are identical. In particular, the irreducibility property proved by [Reference Heinloth, Ngô and YunHNY, Reference Xu and ZhuXZ] implies that Lafforgue’s
${}^LG$
are identical. In particular, the irreducibility property proved by [Reference Heinloth, Ngô and YunHNY, Reference Xu and ZhuXZ] implies that Lafforgue’s
![]() ${\mathcal {L}}^{ss}(\pi ')$
, composed with the adjoint representation, is irreducible.
${\mathcal {L}}^{ss}(\pi ')$
, composed with the adjoint representation, is irreducible.
For essentially discrete series but not supercuspidal representations, we have a weaker globalization result which is nonetheless sufficient for our applications.
Proposition 3.11. Assume the notation and hypotheses of Proposition 3.9 but let
![]() $\pi $
be an essentially discrete series representation. Then there exists a cuspidal automorphic representation
$\pi $
be an essentially discrete series representation. Then there exists a cuspidal automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $G_K$
such that
$G_K$
such that
-
○
 ${\mathcal {L}}^{ss}(\Pi _z) = {\mathcal {L}}^{ss}(\pi )$
;
${\mathcal {L}}^{ss}(\Pi _z) = {\mathcal {L}}^{ss}(\pi )$
; -
○ the global parameter
 ${\mathcal {L}}(\Pi )$
is irreducible.
${\mathcal {L}}(\Pi )$
is irreducible.
In particular, the semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
admits a completion to a pure Weil-Deligne parameter
${\mathcal {L}}^{ss}(\pi )$
admits a completion to a pure Weil-Deligne parameter
![]() ${\mathcal {L}}(\pi )$
that is realized as the specialization at z of the global parameter
${\mathcal {L}}(\pi )$
that is realized as the specialization at z of the global parameter
![]() ${\mathcal {L}}(\Pi )$
, for any such
${\mathcal {L}}(\Pi )$
, for any such
![]() $\Pi $
.
$\Pi $
.
Proof. Let
![]() $f_{\pi }$
be a pseudo-coefficient of
$f_{\pi }$
be a pseudo-coefficient of
![]() $\pi $
, whose properties are recalled in [Reference Gan and LomelíGLo, §8.1]. In [Reference Gan and LomelíGLo, §8.2], a version of the simple trace formula was formulated as a working hypothesis. Applying Lemma A.1 in the appendix by R. Beuzart-Plessis, it follows as in the proof of [Reference Gan and LomelíGLo, Proposition 8.2] that there is a cuspidal
$\pi $
, whose properties are recalled in [Reference Gan and LomelíGLo, §8.1]. In [Reference Gan and LomelíGLo, §8.2], a version of the simple trace formula was formulated as a working hypothesis. Applying Lemma A.1 in the appendix by R. Beuzart-Plessis, it follows as in the proof of [Reference Gan and LomelíGLo, Proposition 8.2] that there is a cuspidal
![]() $\Pi $
with
$\Pi $
with
![]() $\Pi _x {~\overset \sim \longrightarrow ~} \pi '$
(with
$\Pi _x {~\overset \sim \longrightarrow ~} \pi '$
(with
![]() $\pi '$
as in Proposition 3.9) for some place x and
$\pi '$
as in Proposition 3.9) for some place x and
![]() $Tr(\Pi _z)(f_\pi ) \neq 0$
. This implies (by [Reference Gan and LomelíGLo, Lemma 8.1]) that
$Tr(\Pi _z)(f_\pi ) \neq 0$
. This implies (by [Reference Gan and LomelíGLo, Lemma 8.1]) that
![]() $\Pi _z$
has the same cuspidal support as
$\Pi _z$
has the same cuspidal support as
![]() $\pi $
, and therefore that
$\pi $
, and therefore that
since the semisimple Genestier-Lafforgue parameter is compatible with parabolic induction. Now we do not know, nor care, whether
![]() $\Pi _z$
is isomorphic to the discrete series
$\Pi _z$
is isomorphic to the discrete series
![]() $\pi $
or not. Since
$\pi $
or not. Since
![]() ${\mathcal {L}}^{ss}(\Pi _x) = {\mathcal {L}}^{ss}(\pi ')$
is irreducible, so is the global parameter
${\mathcal {L}}^{ss}(\Pi _x) = {\mathcal {L}}^{ss}(\pi ')$
is irreducible, so is the global parameter
![]() ${\mathcal {L}}(\Pi )$
, and we have produced the desired
${\mathcal {L}}(\Pi )$
, and we have produced the desired
![]() $\Pi $
.
$\Pi $
.
Using Corollary 3.8, Proposition 3.9 and Proposition 3.11, the proof of Theorem 1.2 is now complete.
We note that the idea behind Corollary 3.8 and Proposition 3.9 was already applied in the case of classical groups in the proof of [Reference Gan and LomelíGLo, Proposition 7.3]. Instead of using the Kloosterman representations of [Reference Heinloth, Ngô and YunHNY] to establish irreducibility, [Reference Gan and LomelíGLo] used depth zero supercuspidal representations, but introduced a hypothesis because the irreducibility of the corresponding L-parameter has not (yet) been established for local fields of positive characteristic.
Corollary 3.12. Under the hypotheses of Theorem 1.2, suppose G is semisimple. Then the composition of the adjoint representation of
![]() ${}^LG$
with the Weil-Deligne parameter
${}^LG$
with the Weil-Deligne parameter
![]() ${\mathcal {L}}(\pi )$
of
${\mathcal {L}}(\pi )$
of
![]() $\pi $
is pure of weight
$\pi $
is pure of weight
![]() $0$
.
$0$
.
Proof. It follows from Proposition 3.11 that
![]() $Ad\circ {\mathcal {L}}(\pi )$
is a pure Weil-Deligne representation of some weight w. But since G, and therefore
$Ad\circ {\mathcal {L}}(\pi )$
is a pure Weil-Deligne representation of some weight w. But since G, and therefore
![]() $\hat {G}$
, is semisimple, the determinant of
$\hat {G}$
, is semisimple, the determinant of
![]() $Ad\circ {\mathcal {L}}(\pi )$
is pure of weight
$Ad\circ {\mathcal {L}}(\pi )$
is pure of weight
![]() $0$
. It follows that w must equal
$0$
. It follows that w must equal
![]() $0$
.
$0$
.
Remark 3.13. The proof actually shows that
![]() ${\mathcal {L}}(\pi )$
is
${\mathcal {L}}(\pi )$
is
![]() $\iota $
-pure, in the sense of Remark 3.4, for every
$\iota $
-pure, in the sense of Remark 3.4, for every
![]() $\iota $
.
$\iota $
.
4 Local systems on open subsets of
 ${\mathbb {P}}^1$
${\mathbb {P}}^1$
The rest of the paper is devoted to establishing more refined properties of the semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
of a supercuspidal representation
${\mathcal {L}}^{ss}(\pi )$
of a supercuspidal representation
![]() $\pi $
and, in particular, proving Theorem 1.4. For this, we shall need to appeal to a global argument which necessitates the construction of appropriate globalizations of supercuspidal representations by Poincaré series. Unlike the previous section, these globalizations will have to be constructed over the function field of
$\pi $
and, in particular, proving Theorem 1.4. For this, we shall need to appeal to a global argument which necessitates the construction of appropriate globalizations of supercuspidal representations by Poincaré series. Unlike the previous section, these globalizations will have to be constructed over the function field of
![]() $\mathbb {P}^1$
, so that we may appeal to special properties of local systems on open subsets of
$\mathbb {P}^1$
, so that we may appeal to special properties of local systems on open subsets of
![]() $\mathbb {P}^1$
. In this section, we shall discuss the requisite results about local systems on open subsets of
$\mathbb {P}^1$
. In this section, we shall discuss the requisite results about local systems on open subsets of
![]() ${\mathbb {P}}^1$
.
${\mathbb {P}}^1$
.
4.1 Purity
Let
![]() $k = {{\mathbb F}_q}$
be a finite field of characteristic p. Let
$k = {{\mathbb F}_q}$
be a finite field of characteristic p. Let
![]() $Z, X \subset {\mathbb {P}}^1(k)$
be disjoint finite subsets, let
$Z, X \subset {\mathbb {P}}^1(k)$
be disjoint finite subsets, let
![]() $|Z|$
and
$|Z|$
and
![]() $|X|$
be the corresponding reduced subschemes of
$|X|$
be the corresponding reduced subschemes of
![]() ${\mathbb {P}}^1(k)$
and let
${\mathbb {P}}^1(k)$
and let
![]() $Y = {\mathbb {P}}^1_k \setminus |X| \cup |Z|$
, viewed as a scheme over
$Y = {\mathbb {P}}^1_k \setminus |X| \cup |Z|$
, viewed as a scheme over
![]() $Spec(k)$
. Let L be a finite extension of
$Spec(k)$
. Let L be a finite extension of
![]() ${\mathbb Q}_{\ell }$
and consider a local system
${\mathbb Q}_{\ell }$
and consider a local system
![]() ${\mathcal {V}}$
over Y with coefficients in L (a lisse
${\mathcal {V}}$
over Y with coefficients in L (a lisse
![]() $\ell $
-adic sheaf). Picking a point y of Y (the generic point, for example), and letting V denote the finite-dimensional vector space
$\ell $
-adic sheaf). Picking a point y of Y (the generic point, for example), and letting V denote the finite-dimensional vector space
![]() ${\mathcal {V}}_y$
over L, we can identify
${\mathcal {V}}_y$
over L, we can identify
![]() ${\mathcal {V}}$
with a representation
${\mathcal {V}}$
with a representation
Let
![]() $F_z = k(Y)_z$
be the completion of
$F_z = k(Y)_z$
be the completion of
![]() $k(Y)$
at the point
$k(Y)$
at the point
![]() $z \in Z$
. The monodromy of
$z \in Z$
. The monodromy of
![]() ${\mathcal {V}}$
at z is the restriction of
${\mathcal {V}}$
at z is the restriction of
![]() $\rho $
(up to conjugation) to a homomorphism
$\rho $
(up to conjugation) to a homomorphism
Let
![]() $I_z \subset Gal(F_z^{sep}/F_z)$
denote the inertia group and let
$I_z \subset Gal(F_z^{sep}/F_z)$
denote the inertia group and let
![]() $Frob_z \in Gal(F_z^{sep}/F_z)$
denote any geometric Frobenius element (i.e., any lift to an automorphism of
$Frob_z \in Gal(F_z^{sep}/F_z)$
denote any geometric Frobenius element (i.e., any lift to an automorphism of
![]() $F_z^{sep}$
of the automorphism
$F_z^{sep}$
of the automorphism
![]() $x \mapsto x^{\frac {1}{q}}$
of
$x \mapsto x^{\frac {1}{q}}$
of
![]() $\bar {k}$
).
$\bar {k}$
).
If
![]() $\Gamma $
is a topological group and
$\Gamma $
is a topological group and
![]() $\rho : \Gamma {~\rightarrow ~} Aut(V)$
is a continuous homomorphism, we let
$\rho : \Gamma {~\rightarrow ~} Aut(V)$
is a continuous homomorphism, we let
![]() $\rho ^{ss}$
denote its semisimplification – the sum of its Jordan-Hölder constituents.
$\rho ^{ss}$
denote its semisimplification – the sum of its Jordan-Hölder constituents.
Theorem 4.2 ([Reference DeligneDe80], Corollary 1.7.6).
Suppose that Z is not empty and, for all
![]() $z \in Z$
, the following conditions are satisfied:
$z \in Z$
, the following conditions are satisfied:
-
○
 $\rho _z^{ss}$
is unramified;
$\rho _z^{ss}$
is unramified; -
○ the Frobenius eigenvalues
 $\rho _z(Frob_z)$
are all Weil q-numbers of the same weight.
$\rho _z(Frob_z)$
are all Weil q-numbers of the same weight.
Then
![]() ${\mathcal {V}}$
extends to a local system over
${\mathcal {V}}$
extends to a local system over
![]() ${\mathbb {P}}^1_k \setminus |X|$
.
${\mathbb {P}}^1_k \setminus |X|$
.
Proof. In fact, Deligne’s result only requires the Frobenius eigenvalues to have the same weight for a single complex embedding; under this condition,
![]() $\rho _z(I_z)$
is a finite group. But we have assumed that
$\rho _z(I_z)$
is a finite group. But we have assumed that
![]() $\rho _z^{ss}$
is unramified; thus,
$\rho _z^{ss}$
is unramified; thus,
![]() $\rho _z(I_z)$
is unipotent. It follows that
$\rho _z(I_z)$
is unipotent. It follows that
![]() $\rho _z(I_z)$
must be trivial.
$\rho _z(I_z)$
must be trivial.
Corollary 4.3. Under the hypotheses of Theorem 4.2, suppose
![]() $X = \{0,\infty \}$
and
$X = \{0,\infty \}$
and
![]() ${\mathcal {V}}$
is a semisimple local system on Y with associated monodromy representation
${\mathcal {V}}$
is a semisimple local system on Y with associated monodromy representation
Suppose moreover that
-
(a) the local monodromy representation of
 ${\mathcal {V}}$
at
${\mathcal {V}}$
at
 $0$
and
$0$
and
 $\infty $
is tame,
$\infty $
is tame, -
(b) the semisimplification of the local monodromy representation at
 $0$
or
$0$
or
 $\infty $
is abelian and Frobenius-semisimple.
$\infty $
is abelian and Frobenius-semisimple.
Then, possibly after replacing L by a finite extension
![]() $L'$
,
$L'$
,
![]() ${\mathcal {V}}$
breaks up as the sum of
${\mathcal {V}}$
breaks up as the sum of
![]() $1$
-dimensional local systems.
$1$
-dimensional local systems.
Proof. Theorem 4.2 implies that
![]() ${\mathcal {V}}$
extends to a tame local system, also called
${\mathcal {V}}$
extends to a tame local system, also called
![]() ${\mathcal {V}}$
, over
${\mathcal {V}}$
, over
![]() ${\mathbb G}_m$
. By [Reference LafforgueLaf02], Corollary VII.8,
${\mathbb G}_m$
. By [Reference LafforgueLaf02], Corollary VII.8,
![]() ${\mathcal {V}}$
can be written as a (finite) direct sum
${\mathcal {V}}$
can be written as a (finite) direct sum
where each
![]() ${\mathcal {V}}_\chi $
is a mixed local system and
${\mathcal {V}}_\chi $
is a mixed local system and
![]() $\chi $
is the pullback to
$\chi $
is the pullback to
![]() ${\mathbb {P}}^1\setminus |X|$
of a rank
${\mathbb {P}}^1\setminus |X|$
of a rank
![]() $1\ \ell $
-adic local system over
$1\ \ell $
-adic local system over
![]() $Spec(k)$
– in other words, a continuous
$Spec(k)$
– in other words, a continuous
![]() $\ell $
-adic character of
$\ell $
-adic character of
![]() $Gal(\bar {k}/k)$
. We thus reduce to the case where
$Gal(\bar {k}/k)$
. We thus reduce to the case where
![]() ${\mathcal {V}}$
is a mixed
${\mathcal {V}}$
is a mixed
![]() $\ell $
-adic local system, and since
$\ell $
-adic local system, and since
![]() ${\mathcal {V}}$
is assumed semisimple, we may assume
${\mathcal {V}}$
is assumed semisimple, we may assume
![]() ${\mathcal {V}}$
to be irreducible.
${\mathcal {V}}$
to be irreducible.
Then the purity hypothesis at the points z in the nonempty set Z implies that
![]() ${\mathcal {V}}$
is itself pure. Since the tame fundamental group of
${\mathcal {V}}$
is itself pure. Since the tame fundamental group of
![]() ${\mathbb G}_{m,\bar {k}}$
is just
${\mathbb G}_{m,\bar {k}}$
is just
![]() $\prod _{p' \neq p} {\mathbb Z}_{p'}(1)$
, it follows from the purity that the image J under
$\prod _{p' \neq p} {\mathbb Z}_{p'}(1)$
, it follows from the purity that the image J under
![]() $\rho $
of the geometric fundamental group of
$\rho $
of the geometric fundamental group of
![]() ${\mathbb G}_m$
is finite and necessarily abelian.
${\mathbb G}_m$
is finite and necessarily abelian.
Now one knows that the image of the tame inertia group
![]() $I_0$
at
$I_0$
at
![]() $0$
in the tame fundamental group of
$0$
in the tame fundamental group of
![]() ${\mathbb G}_{m,k}$
is equal to the tame fundamental group of
${\mathbb G}_{m,k}$
is equal to the tame fundamental group of
![]() ${\mathbb G}_{m, \bar {k}}$
(i.e., the tame geometric fundamental group of
${\mathbb G}_{m, \bar {k}}$
(i.e., the tame geometric fundamental group of
![]() ${\mathbb G}_{m,k}$
). The same is true for the tame inertia group at
${\mathbb G}_{m,k}$
). The same is true for the tame inertia group at
![]() $\infty $
. Hence, the hypothesis (b) on the local monodromy at
$\infty $
. Hence, the hypothesis (b) on the local monodromy at
![]() $0$
or
$0$
or
![]() $\infty $
implies that the conjugation action of
$\infty $
implies that the conjugation action of
![]() $Gal(\bar {k}/k)$
on J is trivial, and thus, the image under
$Gal(\bar {k}/k)$
on J is trivial, and thus, the image under
![]() $\rho $
of the arithmetic fundamental group
$\rho $
of the arithmetic fundamental group
![]() $\pi _1({\mathbb {P}}^1 \setminus |X|,y)$
is also abelian; moreover, the image of
$\pi _1({\mathbb {P}}^1 \setminus |X|,y)$
is also abelian; moreover, the image of
![]() $Gal(\bar {k}/k)$
is semisimple by hypothesis. This completes the proof.
$Gal(\bar {k}/k)$
is semisimple by hypothesis. This completes the proof.
4.2 Kummer theory
Let
![]() $K = k({\mathbb {P}}^1) = k(T)$
be the global function field of
$K = k({\mathbb {P}}^1) = k(T)$
be the global function field of
![]() ${\mathbb {P}}^1$
and let
${\mathbb {P}}^1$
and let
![]() $K'$
denote the union of all abelian extensions of K of degree dividing
$K'$
denote the union of all abelian extensions of K of degree dividing
![]() $q - 1$
, which is the order of the group of roots of unity in K. Homomorphisms
$q - 1$
, which is the order of the group of roots of unity in K. Homomorphisms
are classified by Kummer theory:
Let
![]() $C_T \subset K^\times /(K^\times )^{q-1}$
be the subgroup generated by
$C_T \subset K^\times /(K^\times )^{q-1}$
be the subgroup generated by
![]() $k^\times $
and the parameter T and let
$k^\times $
and the parameter T and let
![]() $X_T = \psi (C_T)$
. We also consider Kummer theory for the constant field k:
$X_T = \psi (C_T)$
. We also consider Kummer theory for the constant field k:
where
![]() $k'$
is the cyclic extension of k of order
$k'$
is the cyclic extension of k of order
![]() $q^{q-1}$
. For
$q^{q-1}$
. For
![]() $b \in k^\times $
,
$b \in k^\times $
,
![]() $\beta \in Gal(k'/k)$
, let us write
$\beta \in Gal(k'/k)$
, let us write
Any
![]() $z \in k^\times $
defines a closed point
$z \in k^\times $
defines a closed point
![]() $z \in {\mathbb G}_{m,k}$
; let
$z \in {\mathbb G}_{m,k}$
; let
![]() $\Gamma _z \subset Gal(K'/K)$
denote its decomposition group and
$\Gamma _z \subset Gal(K'/K)$
denote its decomposition group and
![]() $I_z$
its inertia group. An element
$I_z$
its inertia group. An element
![]() $\alpha \in X_T$
is unramified at such a point z and thus defines a homomorphism
$\alpha \in X_T$
is unramified at such a point z and thus defines a homomorphism
For
![]() $a = 1, \dots , q-1$
, we let
$a = 1, \dots , q-1$
, we let
![]() $\alpha _a = \psi (T^a)$
. Then we have the following reciprocity law:
$\alpha _a = \psi (T^a)$
. Then we have the following reciprocity law:
Lemma 4.6. For
![]() $z \in {\mathbb G}_{m}(k)$
and
$z \in {\mathbb G}_{m}(k)$
and
![]() $a = 1, \dots , q-1$
, we have
$a = 1, \dots , q-1$
, we have
Proof. Let
![]() $K_z$
denote the completion of K at z,
$K_z$
denote the completion of K at z,
![]() ${\mathcal {O}}_z$
its integer ring,
${\mathcal {O}}_z$
its integer ring,
![]() $k_z$
its residue field, which the inclusion of k in K canonically identifies with k. The image of the element
$k_z$
its residue field, which the inclusion of k in K canonically identifies with k. The image of the element
![]() $T \in {\mathcal {O}}_z$
in
$T \in {\mathcal {O}}_z$
in
![]() $k_z$
is identified with the element
$k_z$
is identified with the element
![]() $z \in k^\times $
, so the residue field of the unramified extension
$z \in k^\times $
, so the residue field of the unramified extension
![]() ${\mathcal {O}}_z[T^{1/(q-1)}]$
is just
${\mathcal {O}}_z[T^{1/(q-1)}]$
is just
![]() $k(z^{1/(q-1)})$
. Both sides of the identity are defined by taking an element of the Galois group, observing that it acts on
$k(z^{1/(q-1)})$
. Both sides of the identity are defined by taking an element of the Galois group, observing that it acts on
![]() $T^{1/(q-1)} = z^{1/(q-1)}$
by multiplication by a
$T^{1/(q-1)} = z^{1/(q-1)}$
by multiplication by a
![]() $(q-1)$
st root of unity and then composing with a fixed embedding of the
$(q-1)$
st root of unity and then composing with a fixed embedding of the
![]() $(q-1)$
st roots of unity into
$(q-1)$
st roots of unity into
![]() ${\overline {\mathbb Q}_{\ell }}^\times $
. The only difference is that
${\overline {\mathbb Q}_{\ell }}^\times $
. The only difference is that
![]() $(\alpha _a)^{(z)}$
is calculated by first considering the action of the Galois group of K, restricting to the decomposition group, and observing that it factors through the Galois group of the residue field, while
$(\alpha _a)^{(z)}$
is calculated by first considering the action of the Galois group of K, restricting to the decomposition group, and observing that it factors through the Galois group of the residue field, while
![]() $\psi _k(az)$
is calculated by considering the action of the Galois group of the residue field directly, but these agree since the homomorphism from the decomposition group to the Galois group of the residue field is defined to be compatible with the action on elements of the residue field.
$\psi _k(az)$
is calculated by considering the action of the Galois group of the residue field directly, but these agree since the homomorphism from the decomposition group to the Galois group of the residue field is defined to be compatible with the action on elements of the residue field.
Lemma 4.7. Let
![]() $\mathcal L$
be a rank one local system on
$\mathcal L$
be a rank one local system on
![]() $\mathbb G_{m,k}$
and
$\mathbb G_{m,k}$
and
![]() $z \in k^{\times }$
. Then
$z \in k^{\times }$
. Then
where
![]() $m_z$
is the element of the inertia group
$m_z$
is the element of the inertia group
![]() $I_0$
which acts by multiplication by z on the
$I_0$
which acts by multiplication by z on the
![]() $(q-1)$
st root of T.
$(q-1)$
st root of T.
Proof. We give two proofs of the lemma.
(i) (Class field theory) It suffices to show that
![]() $\operatorname {Frob}_z = \operatorname {Frob}_1 \cdot m_z^{-1} $
in the abelianization of the tame fundamental group of
$\operatorname {Frob}_z = \operatorname {Frob}_1 \cdot m_z^{-1} $
in the abelianization of the tame fundamental group of
![]() $\mathbb G_m$
. Class field theory gives an isomorphism between this abelianization and the profinite completion of
$\mathbb G_m$
. Class field theory gives an isomorphism between this abelianization and the profinite completion of
 $$\begin{align*}K^\times \backslash \mathbb A_K^\times / \left( \prod_{\substack{ y \in |\mathbb P^1_k|\\ y \notin \{0,\infty|}} \mathcal O_{K_y}^\times \times \prod_{y \in \{0,\infty\}} U_{K_y, 1} \right), \end{align*}$$
$$\begin{align*}K^\times \backslash \mathbb A_K^\times / \left( \prod_{\substack{ y \in |\mathbb P^1_k|\\ y \notin \{0,\infty|}} \mathcal O_{K_y}^\times \times \prod_{y \in \{0,\infty\}} U_{K_y, 1} \right), \end{align*}$$
where
![]() $U_{K_y, 1}$
denotes the units of
$U_{K_y, 1}$
denotes the units of
![]() $\mathcal O_{K_y}$
that are congruent to
$\mathcal O_{K_y}$
that are congruent to
![]() $1$
modulo the maximal ideal. Moreover,
$1$
modulo the maximal ideal. Moreover,
-
○
 $\operatorname {Frob}_z$
corresponds to the idèle which is a uniformizer at z and the identity at all other places,
$\operatorname {Frob}_z$
corresponds to the idèle which is a uniformizer at z and the identity at all other places, -
○
 $\operatorname {Frob}_1$
corresponds to the idèle which is a uniformizer at
$\operatorname {Frob}_1$
corresponds to the idèle which is a uniformizer at
 $1$
and the identity at all other places, and
$1$
and the identity at all other places, and -
○
 $m_z$
corresponds to the idele which is z at
$m_z$
corresponds to the idele which is z at
 $0$
and the identity at all other places.
$0$
and the identity at all other places.
So it suffices to check that the first idèle class is the product of the other two idèle classes. This can be checked by multiplying by
![]() $\frac {T- z}{T-1} \in K^\times $
, which is a uniformizer at z, the inverse of a uniformizer at
$\frac {T- z}{T-1} \in K^\times $
, which is a uniformizer at z, the inverse of a uniformizer at
![]() $1$
, and z at
$1$
, and z at
![]() $0$
.
$0$
.
(ii) (Kummer theory) We can construct a one-dimensional representation of
![]() $Gal(\overline {k}/k)$
on which
$Gal(\overline {k}/k)$
on which
![]() $\operatorname {Frob}_q$
acts by multiplication by
$\operatorname {Frob}_q$
acts by multiplication by
![]() $ \operatorname {tr}(\operatorname {Frob}_1 , \mathcal L)$
. On tensoring
$ \operatorname {tr}(\operatorname {Frob}_1 , \mathcal L)$
. On tensoring
![]() $\mathcal L$
with the inverse representation, we reduce to the case where
$\mathcal L$
with the inverse representation, we reduce to the case where
![]() $\operatorname {Frob}_1$
acts trivially on
$\operatorname {Frob}_1$
acts trivially on
![]() $\mathcal L$
. Since the tame fundamental group of
$\mathcal L$
. Since the tame fundamental group of
![]() $\mathbb G_m$
is generated by the geometric tame fundamental group and Frobenius, the image of the Galois group acting on
$\mathbb G_m$
is generated by the geometric tame fundamental group and Frobenius, the image of the Galois group acting on
![]() $\mathcal L$
must equal the image of the geometric tame fundamental group. The action of the geometric tame fundamental group on
$\mathcal L$
must equal the image of the geometric tame fundamental group. The action of the geometric tame fundamental group on
![]() $\mathcal L$
must be by a
$\mathcal L$
must be by a
![]() $\operatorname {Frob}_q$
-invariant character, which means it factors through the
$\operatorname {Frob}_q$
-invariant character, which means it factors through the
![]() $\operatorname {Frob}_q$
-coinvariant of the abelianization of the tame geometric fundamental group, which is
$\operatorname {Frob}_q$
-coinvariant of the abelianization of the tame geometric fundamental group, which is
![]() $\mathbb Z/(q-1)$
. So the action of the geometric fundamental group is by a character of order
$\mathbb Z/(q-1)$
. So the action of the geometric fundamental group is by a character of order
![]() $q-1$
. The result now follows from Lemma 4.6.
$q-1$
. The result now follows from Lemma 4.6.
5 Unramified Reductive Groups
We continue to assume that
![]() $K = k({\mathbb {P}}^1)$
, with
$K = k({\mathbb {P}}^1)$
, with
![]() $k = \mathbb {F}_q$
. In this section, we establish some structural results for an unramified connected reductive group G over K. In particular, we establish a useful result (Lemma 5.1) which gives congruence conditions on the matrix entries of a parahoric subgroup of G (at a place of K) under a faithful algebraic representation. This parahoric entry inequality will be crucially used in the next few sections.
$k = \mathbb {F}_q$
. In this section, we establish some structural results for an unramified connected reductive group G over K. In particular, we establish a useful result (Lemma 5.1) which gives congruence conditions on the matrix entries of a parahoric subgroup of G (at a place of K) under a faithful algebraic representation. This parahoric entry inequality will be crucially used in the next few sections.
5.1 Unramified groups
By definition, a connected reductive group over K is unramified if it is quasi-split and split by an unramified extension of K. Such a G can, in fact, be defined over the finite field k. Hence, we assume that G is defined over k, with Z the identity component of its center and
![]() $B = T \cdot N$
a fixed Borel k-subgroup. Let
$B = T \cdot N$
a fixed Borel k-subgroup. Let
![]() $S \subset T$
be the maximal k-split subtorus in T, so that S is a maximal split torus of G over k.
$S \subset T$
be the maximal k-split subtorus in T, so that S is a maximal split torus of G over k.
Let
be a faithful algebraic representation of G defined over k and let
![]() $e_1,\dots , e_n$
be a basis of V on which S acts diagonally via the eigencharacter
$e_1,\dots , e_n$
be a basis of V on which S acts diagonally via the eigencharacter
![]() $\lambda _i \in X^* (S)$
on
$\lambda _i \in X^* (S)$
on
![]() $e_i$
.
$e_i$
.
By base change, we obtain from the above the analogous objects over any k-algebra. In particular, we have
-
○
 $S_K \subset B_K = T_K \cdot N_K \subset G_K$
over
$S_K \subset B_K = T_K \cdot N_K \subset G_K$
over
 $K = k({\mathbb {P}}^1) = k(t)$
; to simplify notation, we shall suppress the subscript K. Note that S is still a maximal K-split torus in G.
$K = k({\mathbb {P}}^1) = k(t)$
; to simplify notation, we shall suppress the subscript K. Note that S is still a maximal K-split torus in G. -
○ At each place y of K, with associated local completion
 $K_y$
and ring of integers
$K_y$
and ring of integers
 $\mathcal {O}_y \subset K_y$
, we have the
$\mathcal {O}_y \subset K_y$
, we have the
 $\mathcal {O}_y$
-group schemes Note, however, that
$\mathcal {O}_y$
-group schemes Note, however, that $$\begin{align*}S_y \subset B_y = T_y\cdot N_y \subset G_y. \end{align*}$$
$$\begin{align*}S_y \subset B_y = T_y\cdot N_y \subset G_y. \end{align*}$$
 $S_y$
need no longer be a maximal
$S_y$
need no longer be a maximal
 $K_y$
-spit torus in
$K_y$
-spit torus in
 $G_y$
; we let
$G_y$
; we let
 $A_y \supset S_y$
be a maximal split torus over
$A_y \supset S_y$
be a maximal split torus over
 $\mathcal {O}_y$
. For
$\mathcal {O}_y$
. For
 $y \in {\mathbb {P}}^1(k)$
, we have
$y \in {\mathbb {P}}^1(k)$
, we have
 $A_y = S_y$
.
$A_y = S_y$
.
-
○ At each place y of K,
 $G(\mathcal {O}_y)$
is a hyperspecial maximal compact subgroup of
$G(\mathcal {O}_y)$
is a hyperspecial maximal compact subgroup of
 $G(K_y)$
. One has the reduction-mod-p map where
$G(K_y)$
. One has the reduction-mod-p map where $$\begin{align*}G(\mathcal{O}_y) \longrightarrow G(k_y), \end{align*}$$
$$\begin{align*}G(\mathcal{O}_y) \longrightarrow G(k_y), \end{align*}$$
 $k_y$
is the residue field of
$k_y$
is the residue field of
 $K_y$
. The preimage of
$K_y$
. The preimage of
 $B(k_y) \subset G(k_y)$
in
$B(k_y) \subset G(k_y)$
in
 $G(\mathcal {O}_y)$
is an Iwahori subgroup
$G(\mathcal {O}_y)$
is an Iwahori subgroup
 $I_y$
of
$I_y$
of
 $G(K_y)$
. Its pro-p radical
$G(K_y)$
. Its pro-p radical
 $I(p)$
is the preimage of the unipotent radical
$I(p)$
is the preimage of the unipotent radical
 $N(k_y)$
of
$N(k_y)$
of
 $B(k_y)$
.
$B(k_y)$
.
-
○ For each place y of K, we have a faithful algebraic representation
 $\rho _y \colon G_y \to \operatorname {Aut}(V_y)$
. If
$\rho _y \colon G_y \to \operatorname {Aut}(V_y)$
. If
 $y \in {\mathbb {P}}^1(k)$
, then the basis
$y \in {\mathbb {P}}^1(k)$
, then the basis
 $\{e_i \}$
is a basis of eigenvectors for the maximal
$\{e_i \}$
is a basis of eigenvectors for the maximal
 $K_y$
-split torus
$K_y$
-split torus
 $S_y = A_y$
.
$S_y = A_y$
.
5.2 Buildings
For each place y of K, consider the (extended) Bruhat-Tits building
![]() $\mathcal {B}(G_y)$
which contains the apartment
$\mathcal {B}(G_y)$
which contains the apartment
![]() $\mathcal {A}(A_y)$
associated to the maximal
$\mathcal {A}(A_y)$
associated to the maximal
![]() $K_y$
-split torus
$K_y$
-split torus
![]() $A_y$
. The hyperspecial maximal compact subgroup
$A_y$
. The hyperspecial maximal compact subgroup
![]() $G(\mathcal {O}_y)$
determines a basepoint in
$G(\mathcal {O}_y)$
determines a basepoint in
![]() $\mathcal {A}(A_y)$
, giving an identification
$\mathcal {A}(A_y)$
, giving an identification
with
![]() $G(\mathcal {O}_y)$
the stabilizer of the origin
$G(\mathcal {O}_y)$
the stabilizer of the origin
![]() $0 \in X_*(A_y)$
. For places
$0 \in X_*(A_y)$
. For places
![]() $y \notin {\mathbb {P}}^1(k)$
, we shall only need to consider this basepoint
$y \notin {\mathbb {P}}^1(k)$
, we shall only need to consider this basepoint
![]() $0$
and its stabilizer
$0$
and its stabilizer
![]() $G(\mathcal {O}_y)$
.
$G(\mathcal {O}_y)$
.
Now consider only those
![]() $y \in {\mathbb {P}}^1(k)$
, so that
$y \in {\mathbb {P}}^1(k)$
, so that
![]() $A_y = S_y$
. In this case, one has a natural identification of the apartment
$A_y = S_y$
. In this case, one has a natural identification of the apartment
![]() $\mathcal {A}(A_y)$
with
$\mathcal {A}(A_y)$
with
![]() $X_*(S) \otimes {\mathbb R}$
. In particular, the apartments
$X_*(S) \otimes {\mathbb R}$
. In particular, the apartments
![]() $\mathcal {A}(A_y)$
are naturally identified with each other as y varies in
$\mathcal {A}(A_y)$
are naturally identified with each other as y varies in
![]() ${\mathbb {P}}^1(k)$
.
${\mathbb {P}}^1(k)$
.
5.3 Parahoric entry inequality
In this section, we prove a technical lemma on the matrix entries of elements of parahoric subgroups of G over the local field
![]() $K_y= k((t))$
(for
$K_y= k((t))$
(for
![]() $y \in {\mathbb {P}}^1(k)$
) that will be useful for us later on.
$y \in {\mathbb {P}}^1(k)$
) that will be useful for us later on.
Lemma 5.1. Fix a local field
![]() $F= k((t))$
(which we may think of as
$F= k((t))$
(which we may think of as
![]() $K_y$
for
$K_y$
for
![]() $y \in {\mathbb {P}}^1(k)$
) and let
$y \in {\mathbb {P}}^1(k)$
) and let
-
○ G be an unramified semisimple group (as introduced above), with maximal F-split torus S contained in a Borel subgroup
 $B = TN$
, all defined over k;
$B = TN$
, all defined over k; -
○ c be a point in the apartment of S in the Bruhat-Tits building
 $\mathcal {B}(G)$
with associated parahoric subgroup
$\mathcal {B}(G)$
with associated parahoric subgroup
 $G_c$
;
$G_c$
; -
○
 $\rho \colon G \to \operatorname {Aut}(V) $
be a faithful algebraic representation of G defined over k, with S-eigenbasis
$\rho \colon G \to \operatorname {Aut}(V) $
be a faithful algebraic representation of G defined over k, with S-eigenbasis
 $e_1,\dots , e_n$
with associated eigencharacters
$e_1,\dots , e_n$
with associated eigencharacters
 $\lambda _i \in X^* (S)$
on
$\lambda _i \in X^* (S)$
on
 $e_i$
.
$e_i$
.
Then for any
![]() $g \in G_c \subset G(F)$
, we have
$g \in G_c \subset G(F)$
, we have
where
![]() $v: F \to {\mathbb Z}$
is the normalized valuation on F and
$v: F \to {\mathbb Z}$
is the normalized valuation on F and
![]() $\rho _{ij}(g)$
denotes the
$\rho _{ij}(g)$
denotes the
![]() $(i,j)$
-th entry of the matrix of
$(i,j)$
-th entry of the matrix of
![]() $\rho (g)$
relative to the basis
$\rho (g)$
relative to the basis
![]() $\{e_i\}$
.
$\{e_i\}$
.
More generally, if g lies in the Moy-Prasad subgroup
![]() $G_{c,r+}$
for some
$G_{c,r+}$
for some
![]() $r \geq 0$
, then we have
$r \geq 0$
, then we have
Proof. We give the proof in the
![]() $G_c$
case and then describe the modifications necessary for
$G_c$
case and then describe the modifications necessary for
![]() $G_{c,r+}$
.
$G_{c,r+}$
.
If (5.2) holds for
![]() $g_1$
and
$g_1$
and
![]() $g_2$
, then it holds for
$g_2$
, then it holds for
![]() $g_1g_2$
, so that it suffices to verify (5.2) for a set of generators of the parahoric
$g_1g_2$
, so that it suffices to verify (5.2) for a set of generators of the parahoric
![]() $G_c$
. The parahoric
$G_c$
. The parahoric
![]() $G_c$
is generated by the subgroups
$G_c$
is generated by the subgroups
![]() $U_\psi $
for those affine functions
$U_\psi $
for those affine functions
![]() $\psi $
on the apartment of S such that
$\psi $
on the apartment of S such that
Here,
![]() $\psi $
is an affine function of the form
$\psi $
is an affine function of the form
![]() $\psi (w) = b \cdot w -s$
for a root
$\psi (w) = b \cdot w -s$
for a root
![]() $b \in X^*(S)$
and a real number s. If
$b \in X^*(S)$
and a real number s. If
![]() $U_b \subset G$
is the (restricted) root group associated to b, then one has an isomorphism over k:
$U_b \subset G$
is the (restricted) root group associated to b, then one has an isomorphism over k:
where
![]() $k_b$
is the field of definition of the root b and
$k_b$
is the field of definition of the root b and
![]() $\mathbb G_a$
is the additive group, and the subgroup
$\mathbb G_a$
is the additive group, and the subgroup
![]() $U_\psi $
can be described as
$U_\psi $
can be described as
where v is the unique extension of v to
![]() $k_b$
.
$k_b$
.
To obtain (5.2), it suffices to check that the following two statements hold for
![]() $g\in U_b$
:
$g\in U_b$
:
-
(a) If
 $\rho _{ij} (g) \neq 0$
, then
$\rho _{ij} (g) \neq 0$
, then
 $\lambda _i -\lambda _j = n b$
for some
$\lambda _i -\lambda _j = n b$
for some
 $n\geq 0$
;
$n\geq 0$
; -
(b)
 $\rho _{ij}(g)$
is a homogeneous polynomial function on
$\rho _{ij}(g)$
is a homogeneous polynomial function on
 $U_b$
defined over k of degree n.
$U_b$
defined over k of degree n.
Indeed, if (a) and (b) hold, then we have, for
![]() $g \in U_{\psi}$
$g \in U_{\psi}$
as desired.
To prove (a) and (b), we use lifting to characteristic
![]() $0$
. The group G (which is defined over k) has a lift from the field k to the Witt vectors
$0$
. The group G (which is defined over k) has a lift from the field k to the Witt vectors
![]() $W(k)$
, unique up to not-necessarily-unique isomorphism. Since irreducible algebraic representations of G are classified by Galois orbits of highest weights, and the Galois action for k and
$W(k)$
, unique up to not-necessarily-unique isomorphism. Since irreducible algebraic representations of G are classified by Galois orbits of highest weights, and the Galois action for k and
![]() $W(k)$
are the same, we may lift the representation V from the field k to its ring of Witt vectors
$W(k)$
are the same, we may lift the representation V from the field k to its ring of Witt vectors
![]() $W(k)$
. Both properties in (a) and (b) are preserved by reduction mod p and thus may be checked over the fraction field of
$W(k)$
. Both properties in (a) and (b) are preserved by reduction mod p and thus may be checked over the fraction field of
![]() $W(k)$
, where
$W(k)$
, where
![]() $U_b$
is obtained by exponentiating the root subspace of b. In characteristic
$U_b$
is obtained by exponentiating the root subspace of b. In characteristic
![]() $0$
, both (a) and (b) follow readily from the representation theory of
$0$
, both (a) and (b) follow readily from the representation theory of
![]() $SL_2$
.
$SL_2$
.
We now indicate the modifications needed for the statement for
![]() $G_{c, r^+}$
. The inequality (5.3) is also stable under matrix multiplication since
$G_{c, r^+}$
. The inequality (5.3) is also stable under matrix multiplication since
![]() $r \geq 0$
. Because the subgroups
$r \geq 0$
. Because the subgroups
![]() $G_{c,r+}$
are generated by
$G_{c,r+}$
are generated by
![]() $U_\psi $
for those
$U_\psi $
for those
![]() $\psi $
with
$\psi $
with
![]() $\psi (c)> r$
and the subgroups
$\psi (c)> r$
and the subgroups
![]() $T^a_{n \delta }$
for the maximal torus T containing S, for
$T^a_{n \delta }$
for the maximal torus T containing S, for
![]() $n> r$
, it suffices to verify (5.3) for these subgroups. Here, a is an (absolute) simple root of T (over
$n> r$
, it suffices to verify (5.3) for these subgroups. Here, a is an (absolute) simple root of T (over
![]() $\overline {k}$
), with associated root subgroup
$\overline {k}$
), with associated root subgroup
![]() $SL_2$
(over
$SL_2$
(over
![]() $\overline {k}$
),
$\overline {k}$
),
![]() $T^a$
is the 1-dimensional torus (over
$T^a$
is the 1-dimensional torus (over
![]() $\overline {k}$
) which is the image of the coroot
$\overline {k}$
) which is the image of the coroot
and
We begin with the elements of
![]() $U_{\psi }$
as above. That the elements of such
$U_{\psi }$
as above. That the elements of such
![]() $U_\psi $
satisfy (5.3) follow from (a) and (b) above and the additional fact that
$U_\psi $
satisfy (5.3) follow from (a) and (b) above and the additional fact that
![]() $\rho _{ij}$
is the constant function
$\rho _{ij}$
is the constant function
![]() $1$
on
$1$
on
![]() $U_b$
if
$U_b$
if
![]() $n=0$
. Indeed, these imply that
$n=0$
. Indeed, these imply that
if
![]() $n>0$
and
$n>0$
and
![]() $v (\rho _{ij}(g)-1) = \infty $
if
$v (\rho _{ij}(g)-1) = \infty $
if
![]() $n=0$
.
$n=0$
.
Hence, it remains to show that elements
![]() $g\in T^a_{n \delta }$
satisfy (5.3). Because T is the centralizer of S in G, we see that
$g\in T^a_{n \delta }$
satisfy (5.3). Because T is the centralizer of S in G, we see that
Thus, it suffices to show
Now the action of the elements
![]() $g \in T^a$
and therefore the matrix entries
$g \in T^a$
and therefore the matrix entries
![]() $\rho _{ij}$
(restricted to
$\rho _{ij}$
(restricted to
![]() $T^a$
) are given by polynomial functions on
$T^a$
) are given by polynomial functions on
![]() $\mathbb G_m$
over
$\mathbb G_m$
over
![]() $\overline {k}$
, which are equal to
$\overline {k}$
, which are equal to
![]() $\delta _{ij}$
at the identity element
$\delta _{ij}$
at the identity element
![]() $1$
. Thus, the difference between
$1$
. Thus, the difference between
![]() $\rho _{ij}(g)$
and
$\rho _{ij}(g)$
and
![]() $\delta_{ij}$
has valuation at least n for
$\delta_{ij}$
has valuation at least n for
![]() $g \in T^a_{n \delta }$
, as desired.
$g \in T^a_{n \delta }$
, as desired.
6 Open compact subgroups of
 $G(\mathbb {A}_K)$
$G(\mathbb {A}_K)$
After the preparatory local lemma above, we return to the global setting of §5.1 where G is an unramified semisimple group over
![]() $K = k(t)$
. We will thus use the notation of §5.1 and §5.2. Our goal is to construct some open compact subgroups of
$K = k(t)$
. We will thus use the notation of §5.1 and §5.2. Our goal is to construct some open compact subgroups of
![]() $G(\mathbb {A}_K)$
with desirable properties.
$G(\mathbb {A}_K)$
with desirable properties.
With
![]() $F = k((t))$
, let
$F = k((t))$
, let
![]() $U^* \subset G(F)$
be a fixed maximal compact subgroup. We choose an open compact subgroup of
$U^* \subset G(F)$
be a fixed maximal compact subgroup. We choose an open compact subgroup of
![]() $G({\mathbb A}_{k(t)})$
of the form
$G({\mathbb A}_{k(t)})$
of the form
![]() $U = \prod _x U_x$
, where x runs over the places of K, with the following properties.
$U = \prod _x U_x$
, where x runs over the places of K, with the following properties.
-
(a) At every
 $z \in {\mathbb G}_m(k) \subset {\mathbb {P}}^1(k)$
,
$z \in {\mathbb G}_m(k) \subset {\mathbb {P}}^1(k)$
,
 $U_z$
equals the fixed
$U_z$
equals the fixed
 $U^*$
, with respect to a chosen isomorphism
$U^*$
, with respect to a chosen isomorphism  $$ \begin{align*}G(K_z) {~\overset\sim\longrightarrow~} G(F);\end{align*} $$
$$ \begin{align*}G(K_z) {~\overset\sim\longrightarrow~} G(F);\end{align*} $$
-
(b) For
 $x \notin |{\mathbb {P}}^1(k)|$
,
$x \notin |{\mathbb {P}}^1(k)|$
,
 $U_x$
is the hyperspecial maximal compact subgroup
$U_x$
is the hyperspecial maximal compact subgroup
 $G({\mathcal {O}}_x)$
;
$G({\mathcal {O}}_x)$
; -
(c) The subgroups
 $U_0$
and
$U_0$
and
 $U_\infty $
are parahoric subgroups that remain to be chosen.
$U_\infty $
are parahoric subgroups that remain to be chosen.
Proposition 6.1. Let G be unramified and simply-connected. The subgroups
![]() $U_0$
and
$U_0$
and
![]() $U_\infty $
can be chosen in such a way that
$U_\infty $
can be chosen in such a way that
Proof. Let
![]() $\Lambda = X_*(S)$
be the cocharacter lattice of S. We have remarked that for
$\Lambda = X_*(S)$
be the cocharacter lattice of S. We have remarked that for
![]() $z \in {\mathbb {P}}^1(k)$
, we have a natural identification of
$z \in {\mathbb {P}}^1(k)$
, we have a natural identification of
![]() $\Lambda \otimes {\mathbb R}$
as an apartment in the Bruhat-Tits building of
$\Lambda \otimes {\mathbb R}$
as an apartment in the Bruhat-Tits building of
![]() $G_z$
. Let
$G_z$
. Let
![]() $c \in \Lambda \otimes {\mathbb R}$
be the fixed point of
$c \in \Lambda \otimes {\mathbb R}$
be the fixed point of
![]() $U^* \subset G(F) \cong G(K_z)$
; because G is simply-connected,
$U^* \subset G(F) \cong G(K_z)$
; because G is simply-connected,
![]() $U^*$
is the parahoric subgroup
$U^*$
is the parahoric subgroup
![]() $G_c$
. For
$G_c$
. For
![]() $y \notin \mathbb{P}^1(k)$
, we also have a natural inclusion
$y \notin \mathbb{P}^1(k)$
, we also have a natural inclusion
![]() $\Lambda \otimes {\mathbb R} \hookrightarrow \mathcal {A}(A_y)$
. Choose
$\Lambda \otimes {\mathbb R} \hookrightarrow \mathcal {A}(A_y)$
. Choose
![]() $a, b \in \Lambda \otimes {\mathbb R}$
such that
$a, b \in \Lambda \otimes {\mathbb R}$
such that
and such that a is sufficiently generic in the sense that
![]() $a \cdot v$
is not an integer for all v in a finite set of nonzero elements of
$a \cdot v$
is not an integer for all v in a finite set of nonzero elements of
![]() $X^*(S)$
to be chosen later.
$X^*(S)$
to be chosen later.
For a place v of K, define
![]() $f(v)$
by
$f(v)$
by
 $$\begin{align*}\begin{cases} f(0) = a, \\ f(\infty) = b \\ f(z) = c \text{ for } z \in {\mathbb G}_m(k), \\ f(x) = 0, \text{ for } x \notin |{\mathbb{P}}^1(k)|. \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} f(0) = a, \\ f(\infty) = b \\ f(z) = c \text{ for } z \in {\mathbb G}_m(k), \\ f(x) = 0, \text{ for } x \notin |{\mathbb{P}}^1(k)|. \end{cases} \end{align*}$$
Under this definition, we take
![]() $U_v $
to be the parahoric subgroup
$U_v $
to be the parahoric subgroup
![]() $G_{f(v)}$
associated to
$G_{f(v)}$
associated to
![]() $f(v)$
.
$f(v)$
.
We are now ready to prove that
![]() $G(K) \cap U = T(k)$
. To do this, we use the faithful algebraic representation
$G(K) \cap U = T(k)$
. To do this, we use the faithful algebraic representation
![]() $(\rho , V)$
fixed in §5.1, equipped with a basis
$(\rho , V)$
fixed in §5.1, equipped with a basis
![]() $e_1,\dots , e_n$
, where
$e_1,\dots , e_n$
, where
![]() $e_i$
is an eigenvector of S with eigencharacter
$e_i$
is an eigenvector of S with eigencharacter
![]() $\lambda _i \in X^*(S)$
. Applying Lemma 5.1, we see that for
$\lambda _i \in X^*(S)$
. Applying Lemma 5.1, we see that for
![]() $g \in U \cap G( K)$
with
$g \in U \cap G( K)$
with
![]() $\rho _{ij}(g) \neq 0$
(for a fixed pair
$\rho _{ij}(g) \neq 0$
(for a fixed pair
![]() $(i,j)$
), we have
$(i,j)$
), we have
Because both sides are
![]() $0$
, the inequality is sharp, so
$0$
, the inequality is sharp, so
for all v. This implies that
![]() $f(v) \cdot (\lambda _i - \lambda _j)$
is an integer, and, in particular, that
$f(v) \cdot (\lambda _i - \lambda _j)$
is an integer, and, in particular, that
![]() $a \cdot (\lambda _i -\lambda _j)$
is an integer. However, for our genericity assumption on a, we may assume that
$a \cdot (\lambda _i -\lambda _j)$
is an integer. However, for our genericity assumption on a, we may assume that
![]() $ a \cdot (\lambda _i -\lambda _j)$
is not an integer for any pair
$ a \cdot (\lambda _i -\lambda _j)$
is not an integer for any pair
![]() $(i,j)$
for which
$(i,j)$
for which
![]() $\lambda _i \ne \lambda _j$
.
$\lambda _i \ne \lambda _j$
.
We conclude that, for
![]() $g \in U$
,
$g \in U$
,
![]() $\rho _{ij}(g) =0$
unless
$\rho _{ij}(g) =0$
unless
![]() $\lambda _i = \lambda _j$
. In other words,
$\lambda _i = \lambda _j$
. In other words,
![]() $\rho (g)$
commutes with
$\rho (g)$
commutes with
![]() $\rho (S)$
, and thus,
$\rho (S)$
, and thus,
![]() $g \in T(K)$
. Furthermore, for a pair
$g \in T(K)$
. Furthermore, for a pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $\rho _{ij}(g) \neq 0$
, we have
$\rho _{ij}(g) \neq 0$
, we have
for all v. This shows that
![]() $\rho _{ij}(g) \in k$
, and so
$\rho _{ij}(g) \in k$
, and so
![]() $g \in T(k)$
. We have thus shown that
$g \in T(k)$
. We have thus shown that
![]() $U \cap G(K) = T(k)$
, as desired.
$U \cap G(K) = T(k)$
, as desired.
The following is then obvious.
Corollary 6.2. Under the hypotheses of Proposition 6.1, one can choose Iwahori subgroups
![]() $I_0 \subset U_0$
and
$I_0 \subset U_0$
and
![]() $I_\infty \subset U_\infty $
such that, if
$I_\infty \subset U_\infty $
such that, if
![]() $I_\infty (p) \subset I_\infty $
is the maximal pro-p subgroup, then
$I_\infty (p) \subset I_\infty $
is the maximal pro-p subgroup, then
Remark 6.3. Suppose
![]() $U_z = G({\mathcal {O}}_z)$
for
$U_z = G({\mathcal {O}}_z)$
for
![]() $z \in {\mathbb G}_m(k)$
. Then in Proposition 6.1, we can take
$z \in {\mathbb G}_m(k)$
. Then in Proposition 6.1, we can take
![]() $U_0 = I^+$
and
$U_0 = I^+$
and
![]() $U_\infty = I^-$
to be respectively the upper and lower Iwahori subgroups; by this, we mean that
$U_\infty = I^-$
to be respectively the upper and lower Iwahori subgroups; by this, we mean that
![]() $U_0$
(resp.
$U_0$
(resp.
![]() $U_\infty $
) is the Iwahori subgroup corresponding to the positive (resp. negative) root system corresponding to our fixed Borel subgroup B. Then
$U_\infty $
) is the Iwahori subgroup corresponding to the positive (resp. negative) root system corresponding to our fixed Borel subgroup B. Then
The right-hand side is the group of global maps from
![]() ${\mathbb {P}}^1_k$
to the affine group
${\mathbb {P}}^1_k$
to the affine group
![]() $G_k$
. Any such map must be constant because
$G_k$
. Any such map must be constant because
![]() ${\mathbb {P}}^1$
is projective and thus must belong to
${\mathbb {P}}^1$
is projective and thus must belong to
![]() $G(k)$
because it is defined over k. Thus,
$G(k)$
because it is defined over k. Thus,
The open compact subgroups of
![]() $G(\mathbb {A}_K)$
built in this section will be used in the next section to constuct some Poincaré series.
$G(\mathbb {A}_K)$
built in this section will be used in the next section to constuct some Poincaré series.
7 Proof of Theorem 1.4(i)
This section is devoted to the proof of Theorem 1.4(i). In fact, we prove the following slightly stronger statement.
Theorem 7.1. Suppose F is the nonarchimedean local field
![]() $k(\!(t)\!)$
, where
$k(\!(t)\!)$
, where
![]() $k = {{\mathbb F}_q}$
is a finite field of order
$k = {{\mathbb F}_q}$
is a finite field of order
![]() $q = p^m$
for some prime p. Let G be an unramified connected reductive group over F which is not a torus. Assume
$q = p^m$
for some prime p. Let G be an unramified connected reductive group over F which is not a torus. Assume
![]() $q> 5$
and
$q> 5$
and
![]() $\pi $
is an irreducible supercuspidal representation of
$\pi $
is an irreducible supercuspidal representation of
![]() $G(F)$
that can be obtained as the induction of a representation of a compact open (modulo center) subgroup
$G(F)$
that can be obtained as the induction of a representation of a compact open (modulo center) subgroup
![]() $U \subset G(F)$
:
$U \subset G(F)$
:
for some (irreducible) smooth representation
![]() $\tau $
of U with coefficients in
$\tau $
of U with coefficients in
![]() ${\overline {\mathbb Q}_{\ell }}$
.
${\overline {\mathbb Q}_{\ell }}$
.
Then we have
where
![]() $f: {^L}G \longrightarrow {^L}G / Z(\hat {G})$
is the natural projection map.
$f: {^L}G \longrightarrow {^L}G / Z(\hat {G})$
is the natural projection map.
Because
![]() ${^L}G / Z(\hat {G})$
is the L-group of the simply-connected cover
${^L}G / Z(\hat {G})$
is the L-group of the simply-connected cover
![]() $G_{sc}$
of the derived group
$G_{sc}$
of the derived group
![]() $G_{der}$
of G, Theorem 2.3(vi) implies (by applying it to the natural maps
$G_{der}$
of G, Theorem 2.3(vi) implies (by applying it to the natural maps
![]() $G_{sc} \to G_{der} \to G$
) that it suffices to prove the above theorem under the additional hypothesis that G is k-simple and simply-connected.
$G_{sc} \to G_{der} \to G$
) that it suffices to prove the above theorem under the additional hypothesis that G is k-simple and simply-connected.
7.1 Purity and ramification
We shall prove Theorem 1.4(i) by a global argument. Hence, we assume the setup and notation from §5.1. In particular,
![]() $K = k({\mathbb {P}}^1) = k(t)$
and G is an unramified simply connected simple group over k.
$K = k({\mathbb {P}}^1) = k(t)$
and G is an unramified simply connected simple group over k.
Before stating the theorem below, we choose a special character of T. The adjoint representation of
![]() $\hat {G}$
splits as a sum of irreducible representations, each corresponding to a simple factor, up to isogeny, of
$\hat {G}$
splits as a sum of irreducible representations, each corresponding to a simple factor, up to isogeny, of
![]() $G_{\overline {k}}$
. The group
$G_{\overline {k}}$
. The group
![]() $W_k$
acts on these irreducible representations. Let
$W_k$
acts on these irreducible representations. Let
![]() ${\mathfrak {v}}_1,\dots , {\mathfrak {v}}_n$
be an orbit of this action. Let
${\mathfrak {v}}_1,\dots , {\mathfrak {v}}_n$
be an orbit of this action. Let
![]() $\hat {\alpha }_i $
be the highest weight of
$\hat {\alpha }_i $
be the highest weight of
![]() ${\mathfrak {v}}_i$
, a coroot of G, and let
${\mathfrak {v}}_i$
, a coroot of G, and let
![]() $\alpha _i$
be the corresponding root of G. Let
$\alpha _i$
be the corresponding root of G. Let
![]() $\alpha \in X^* (T) $
be given by
$\alpha \in X^* (T) $
be given by
![]() $\alpha = \sum _{i=1}^n \alpha _i$
. Then since the action of
$\alpha = \sum _{i=1}^n \alpha _i$
. Then since the action of
![]() $W_i$
permutes the
$W_i$
permutes the
![]() ${\mathfrak {v}}_i$
s, it permutes the
${\mathfrak {v}}_i$
s, it permutes the
![]() $\hat {\alpha }_i$
s, and thus the
$\hat {\alpha }_i$
s, and thus the
![]() $\alpha _i$
s, so
$\alpha _i$
s, so
![]() $\alpha $
is
$\alpha $
is
![]() $W_k$
-invariant.
$W_k$
-invariant.
The following theorem is the key step in proving Theorem 1.4(i).
Theorem 7.2. Let
![]() $F = k(\!(t)\!)$
with
$F = k(\!(t)\!)$
with
![]() $k = \mathbb {F}_q$
and
$k = \mathbb {F}_q$
and
![]() $q> 5$
, and let
$q> 5$
, and let
![]() $\sigma $
be a supercuspidal representation of
$\sigma $
be a supercuspidal representation of
![]() $G(F)$
(with G unramified over k). Let
$G(F)$
(with G unramified over k). Let
![]() $K = k({\mathbb {P}}^1)$
and suppose there exists a cuspidal automorphic representation
$K = k({\mathbb {P}}^1)$
and suppose there exists a cuspidal automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $G({\mathbb A}_K)$
, with the following properties:
$G({\mathbb A}_K)$
, with the following properties:
-
(a) At every
 $z \in {\mathbb G}_m(k) \subset {\mathbb {P}}^1(k)$
,
$z \in {\mathbb G}_m(k) \subset {\mathbb {P}}^1(k)$
,
 $\Pi _z {~\overset \sim \longrightarrow ~} \sigma $
.
$\Pi _z {~\overset \sim \longrightarrow ~} \sigma $
. -
(b) The representation
 $\Pi _\infty $
has a vector invariant under the pro-p Iwahori subgroup
$\Pi _\infty $
has a vector invariant under the pro-p Iwahori subgroup
 $I_{\infty }(p)$
in Corollary 6.2.
$I_{\infty }(p)$
in Corollary 6.2. -
(c) The representation
 $\Pi _0$
is a constituent of a principal series
$\Pi _0$
is a constituent of a principal series
 $Ind_{B(F)}^{G(F)} \chi $
, where
$Ind_{B(F)}^{G(F)} \chi $
, where
 $\chi $
is a tame (i.e., depth 0) character of
$\chi $
is a tame (i.e., depth 0) character of
 $T(F)$
, whose restriction
$T(F)$
, whose restriction
 $\chi _k$
to the subgroup
$\chi _k$
to the subgroup
 $T(k) \subset T(F)$
arises in the following way: where
$T(k) \subset T(F)$
arises in the following way: where
 $\mu $
is a faithful character of
$\mu $
is a faithful character of
 $k^{\times }$
.
$k^{\times }$
.
-
(d) The local components
 $\Pi _y$
of
$\Pi _y$
of
 $\Pi $
for all
$\Pi $
for all
 $y \notin {\mathbb {P}}^1(k)$
are
$y \notin {\mathbb {P}}^1(k)$
are
 $G(\mathcal {O}_y)$
-unramified.
$G(\mathcal {O}_y)$
-unramified.
Then
Proof. Assume
![]() ${\mathcal {L}}^{ss}(\sigma )$
is unramified; we shall derive a contradiction.
${\mathcal {L}}^{ss}(\sigma )$
is unramified; we shall derive a contradiction.
Applying Lafforgue, let
be the global Galois representation associated to
![]() $\Pi $
as in Theorem 2.1. By property (d),
$\Pi $
as in Theorem 2.1. By property (d),
![]() ${\mathcal {L}}(\Pi )_x$
is unramified for all places x of
${\mathcal {L}}(\Pi )_x$
is unramified for all places x of
![]() ${\mathbb {P}}^1$
outside of
${\mathbb {P}}^1$
outside of
![]() ${\mathbb {P}}^1(k)$
. However, by property (b) and (c), it follows by Theorem 2.3 (iv) that
${\mathbb {P}}^1(k)$
. However, by property (b) and (c), it follows by Theorem 2.3 (iv) that
![]() ${\mathcal {L}}(\Pi )^{ss}_0$
and
${\mathcal {L}}(\Pi )^{ss}_0$
and
![]() ${\mathcal {L}}(\Pi )^{ss}_{\infty }$
are tamely ramified. For
${\mathcal {L}}(\Pi )^{ss}_{\infty }$
are tamely ramified. For
![]() $z \in {\mathbb G}_m(k)$
, with decomposition group
$z \in {\mathbb G}_m(k)$
, with decomposition group
![]() $\Gamma _z \subset \pi _1({\mathbb {P}}^1 \setminus |{\mathbb {P}}^1(k)|)$
, it follows by property (a) and Theorem 2.1(iii) that
$\Gamma _z \subset \pi _1({\mathbb {P}}^1 \setminus |{\mathbb {P}}^1(k)|)$
, it follows by property (a) and Theorem 2.1(iii) that
By our hypothesis,
![]() ${\mathcal {L}}(\Pi )^{ss}_z$
is thus unramified for all
${\mathcal {L}}(\Pi )^{ss}_z$
is thus unramified for all
![]() $z \in \mathbb {G}_m(k) = k^{\times }$
.
$z \in \mathbb {G}_m(k) = k^{\times }$
.
We shall now examine in greater detail the restriction of
![]() ${\mathcal {L}}(\Pi )$
to the local decomposition group
${\mathcal {L}}(\Pi )$
to the local decomposition group
![]() $\Gamma _0$
at
$\Gamma _0$
at
![]() $0 \in k$
. By property (c) and Theorem 2.3 (iv), one has
$0 \in k$
. By property (c) and Theorem 2.3 (iv), one has
where the first map is the L-parameter of the character
![]() $\chi $
of
$\chi $
of
![]() $T(F)$
. By the discussion in [Reference Debacker and ReederDR, §4.3], one has
$T(F)$
. By the discussion in [Reference Debacker and ReederDR, §4.3], one has
where
![]() $k_n = \mathbb {F}_{q^n}$
is the splitting field of T over k,
$k_n = \mathbb {F}_{q^n}$
is the splitting field of T over k,
![]() $I_t$
is the tame inertia group of
$I_t$
is the tame inertia group of
![]() $\Gamma _0$
and
$\Gamma _0$
and
![]() ${\mathrm {Hom}}_{\mathrm {Frob}}$
stands for Frobenius-equivariant homomorphisms. Hence, the restriction of
${\mathrm {Hom}}_{\mathrm {Frob}}$
stands for Frobenius-equivariant homomorphisms. Hence, the restriction of
![]() ${\mathcal {L}}(\Pi )^{ss}_0$
to the inertia group (which factors to the tame inertia group) determines and is determined by the restriction
${\mathcal {L}}(\Pi )^{ss}_0$
to the inertia group (which factors to the tame inertia group) determines and is determined by the restriction
![]() $\chi _k$
of
$\chi _k$
of
![]() $\chi $
to
$\chi $
to
![]() $T(k)$
. The special form of
$T(k)$
. The special form of
![]() $\chi _k$
given in property (c) and the fact that
$\chi _k$
given in property (c) and the fact that
![]() $\alpha $
is fixed by
$\alpha $
is fixed by
![]() ${\mathrm {Frob}}$
thus imply that the restriction of
${\mathrm {Frob}}$
thus imply that the restriction of
![]() $ {\mathcal {L}}(\Pi )^{ss}_0 $
to
$ {\mathcal {L}}(\Pi )^{ss}_0 $
to
![]() $I_t$
factors as
$I_t$
factors as
Let
![]() $V= \otimes _{i=1}^n {\mathfrak {v}}_i$
be the representation of
$V= \otimes _{i=1}^n {\mathfrak {v}}_i$
be the representation of
![]() ${^L}G = {\hat {G}} \rtimes W_{k}$
where
${^L}G = {\hat {G}} \rtimes W_{k}$
where
![]() $\hat {G}$
acts on each
$\hat {G}$
acts on each
![]() ${\mathfrak {v}}_i$
and
${\mathfrak {v}}_i$
and
![]() $W_i$
permutes the factors. The composite
$W_i$
permutes the factors. The composite
![]() $V \circ {\mathcal {L}}(\Pi )^{ss}$
gives rise to a (semisimple) local system
$V \circ {\mathcal {L}}(\Pi )^{ss}$
gives rise to a (semisimple) local system
![]() ${\mathcal {V}}(\Pi ,V)$
on
${\mathcal {V}}(\Pi ,V)$
on
![]() ${\mathbb {P}}^1 \setminus |{\mathbb {P}}^1(k)|$
over k. However, since
${\mathbb {P}}^1 \setminus |{\mathbb {P}}^1(k)|$
over k. However, since
![]() $ {\mathcal {L}}(\Pi )^{ss}_z$
is unramified, the purity of
$ {\mathcal {L}}(\Pi )^{ss}_z$
is unramified, the purity of
![]() ${\mathcal {L}}^{ss}(\sigma )$
and Theorem 4.2 then imply that
${\mathcal {L}}^{ss}(\sigma )$
and Theorem 4.2 then imply that
![]() ${\mathcal {V}}(\Pi ,V)$
extends to a local system on
${\mathcal {V}}(\Pi ,V)$
extends to a local system on
![]() ${\mathbb {G}}_m$
over k.
${\mathbb {G}}_m$
over k.
The representation V is obtained as a tensor product of the representations
![]() ${\mathfrak {v}}_i$
of
${\mathfrak {v}}_i$
of
![]() $\hat {G}$
, which do not extend to representations of
$\hat {G}$
, which do not extend to representations of
![]() $\hat {G} \rtimes W_k$
, but do extend to representations of
$\hat {G} \rtimes W_k$
, but do extend to representations of
![]() $\hat {G} \rtimes W_{k_n}$
for
$\hat {G} \rtimes W_{k_n}$
for
![]() $k_n$
the degree n extension, since the stabilizer of
$k_n$
the degree n extension, since the stabilizer of
![]() ${\mathfrak {v}}_i$
in the action of
${\mathfrak {v}}_i$
in the action of
![]() $W_k$
on irreducible factors of the adjoint representation of
$W_k$
on irreducible factors of the adjoint representation of
![]() $\hat {G}$
is
$\hat {G}$
is
![]() $W_{k_n}$
. Thus, we similarly have that the composite
$W_{k_n}$
. Thus, we similarly have that the composite
![]() ${\mathfrak {v}}_i \circ {\mathcal {L}}(\Pi )^{ss}\mid _{ \mathrm {Gal} (K^{sep} / k_n( t))}$
gives rise to a (semisimple) local system
${\mathfrak {v}}_i \circ {\mathcal {L}}(\Pi )^{ss}\mid _{ \mathrm {Gal} (K^{sep} / k_n( t))}$
gives rise to a (semisimple) local system
![]() ${\mathcal {V}}(\Pi ,{\mathfrak {v}}_i)$
on
${\mathcal {V}}(\Pi ,{\mathfrak {v}}_i)$
on
![]() ${\mathbb {P}}^1 \setminus |{\mathbb {P}}^1(k)|$
over
${\mathbb {P}}^1 \setminus |{\mathbb {P}}^1(k)|$
over
![]() $k_n$
, which extends to a local system on
$k_n$
, which extends to a local system on
![]() ${\mathbb G}_m$
over
${\mathbb G}_m$
over
![]() $k_n$
.
$k_n$
.
The above discussion shows that the local system
![]() ${\mathcal {V}}(\Pi ,{\mathfrak {v}}_i)$
on
${\mathcal {V}}(\Pi ,{\mathfrak {v}}_i)$
on
![]() ${\mathbb {G}}_m$
over
${\mathbb {G}}_m$
over
![]() $k_n$
satisfies the hypotheses of Corollary 4.3. In particular,
$k_n$
satisfies the hypotheses of Corollary 4.3. In particular,
-
(a) the local monodromy representations at
 $0$
and
$0$
and
 $\infty $
are tamely ramified;
$\infty $
are tamely ramified; -
(b) the local monodromy representation at
 $0$
has abelian image.
$0$
has abelian image.
Corollary 4.3 thus implies that
![]() ${\mathcal {V}}(\Pi ,{\mathfrak {v}}_i )$
breaks up as the sum of rank 1 local systems
${\mathcal {V}}(\Pi ,{\mathfrak {v}}_i )$
breaks up as the sum of rank 1 local systems
![]() ${\mathcal {L}}_1, \dots , {\mathcal {L}}_N$
over
${\mathcal {L}}_1, \dots , {\mathcal {L}}_N$
over
![]() $k_n$
.
$k_n$
.
Applying Lemma 4.7 to the
![]() ${\mathcal {L}}_i$
’s, and a standard formula for the trace on a tensor product representation of an operator that permutes the tensor factors, one sees that for each
${\mathcal {L}}_i$
’s, and a standard formula for the trace on a tensor product representation of an operator that permutes the tensor factors, one sees that for each
![]() $z \in \mathbb {G}_m(k)$
,
$z \in \mathbb {G}_m(k)$
,
 $$ \begin{align} \operatorname{tr}(\operatorname{Frob}_z, {\mathcal{V}}(\Pi,V)) = \operatorname{tr}(\operatorname{Frob}_z^n, {\mathcal{V}}(\Pi,{\mathfrak{v}}_1)) = \sum_{j=1}^N \operatorname{tr}(\operatorname{Frob}_z^n, \mathcal L_j) = \sum_{j=1}^N \operatorname{tr}(\operatorname{Frob}_1^n, \mathcal L_j) \cdot \operatorname{tr}(m_z^{-n} , \mathcal L_j).\end{align} $$
$$ \begin{align} \operatorname{tr}(\operatorname{Frob}_z, {\mathcal{V}}(\Pi,V)) = \operatorname{tr}(\operatorname{Frob}_z^n, {\mathcal{V}}(\Pi,{\mathfrak{v}}_1)) = \sum_{j=1}^N \operatorname{tr}(\operatorname{Frob}_z^n, \mathcal L_j) = \sum_{j=1}^N \operatorname{tr}(\operatorname{Frob}_1^n, \mathcal L_j) \cdot \operatorname{tr}(m_z^{-n} , \mathcal L_j).\end{align} $$
Here, it is crucial that we consider the tensor induction instead of the usual induction because the trace of
![]() $\operatorname {Frob}_z$
on the usual induction would be identically zero as soon as
$\operatorname {Frob}_z$
on the usual induction would be identically zero as soon as
![]() $n>1$
, and so studying this trace would not be helpful. We take
$n>1$
, and so studying this trace would not be helpful. We take
![]() $i=1$
without loss of generality because
$i=1$
without loss of generality because
![]() $\operatorname {tr}(\operatorname {Frob}_z^n, {\mathcal {V}}(\Pi ,{\mathfrak {v}}_i))$
is independent of i.
$\operatorname {tr}(\operatorname {Frob}_z^n, {\mathcal {V}}(\Pi ,{\mathfrak {v}}_i))$
is independent of i.
Let us now evaluate
![]() $ \operatorname {tr}(m_z , \mathcal L_j)$
. By (7.4), and observing that the eigenvalues of
$ \operatorname {tr}(m_z , \mathcal L_j)$
. By (7.4), and observing that the eigenvalues of
![]() $\hat {T}$
on
$\hat {T}$
on
![]() ${\mathfrak {v}}_1 $
are the roots of
${\mathfrak {v}}_1 $
are the roots of
![]() $({\hat {G}}, \hat {T})$
contained in the simple factor corresponding to
$({\hat {G}}, \hat {T})$
contained in the simple factor corresponding to
![]() ${\mathfrak {v}}_1$
, we see that
${\mathfrak {v}}_1$
, we see that
where
![]() $\beta _j$
is either a root of
$\beta _j$
is either a root of
![]() ${\hat {G}}$
(or equivalently a coroot of G) contained in
${\hat {G}}$
(or equivalently a coroot of G) contained in
![]() ${\mathfrak {v}}_1$
or the zero element in
${\mathfrak {v}}_1$
or the zero element in
![]() $X^*(\hat {T})$
.
$X^*(\hat {T})$
.
Now note that
-
(a)
 $\mu $
is a character of order
$\mu $
is a character of order
 $q-1$
of
$q-1$
of
 $k^{\times }$
;
$k^{\times }$
; -
(b) the function
is a constant function of z, since the local representation at each $$\begin{align*}z \mapsto \operatorname{tr}(\operatorname{Frob}_z, {\mathcal{V}}(\Pi,{V})) \end{align*}$$
$$\begin{align*}z \mapsto \operatorname{tr}(\operatorname{Frob}_z, {\mathcal{V}}(\Pi,{V})) \end{align*}$$
 $z \in \mathbb {G}_m(k)$
is just
$z \in \mathbb {G}_m(k)$
is just
 ${\mathcal {L}}^{ss}(\sigma )$
.
${\mathcal {L}}^{ss}(\sigma )$
.
By orthogonality of characters (of
![]() $k^{\times }$
) and (7.5), we thus have
$k^{\times }$
) and (7.5), we thus have
 $$ \begin{align} 0 &= \sum_{z \in k^\times} \mu(z)^{-2} \cdot \operatorname{tr}(\operatorname{Frob}_z, {\mathcal{V}}(\Pi,{V})) \notag \\ &= \sum_{z \in k^\times} \mu(z)^{-2} \cdot \sum_{j=1}^N \operatorname{tr}(\operatorname{Frob}_1^n, \mathcal L_j) \cdot \mu(z)^{ \langle \alpha, \beta_j \rangle } \notag \\ &= \sum_{j=1}^N \operatorname{tr}(\operatorname{Frob}_1^n, \mathcal L_j) \cdot \sum_{z \in k^\times} \mu(z)^{-2} \cdot \mu(z)^{ \langle \alpha, \beta_j \rangle } \notag \\ &= (q-1) \cdot \sum_{\substack{ j: \\ \langle \alpha, \beta_j \rangle \equiv 2\quad \mod (q-1) }} \operatorname{tr}(\operatorname{Frob}_1^n, \mathcal L_j). \end{align} $$
$$ \begin{align} 0 &= \sum_{z \in k^\times} \mu(z)^{-2} \cdot \operatorname{tr}(\operatorname{Frob}_z, {\mathcal{V}}(\Pi,{V})) \notag \\ &= \sum_{z \in k^\times} \mu(z)^{-2} \cdot \sum_{j=1}^N \operatorname{tr}(\operatorname{Frob}_1^n, \mathcal L_j) \cdot \mu(z)^{ \langle \alpha, \beta_j \rangle } \notag \\ &= \sum_{j=1}^N \operatorname{tr}(\operatorname{Frob}_1^n, \mathcal L_j) \cdot \sum_{z \in k^\times} \mu(z)^{-2} \cdot \mu(z)^{ \langle \alpha, \beta_j \rangle } \notag \\ &= (q-1) \cdot \sum_{\substack{ j: \\ \langle \alpha, \beta_j \rangle \equiv 2\quad \mod (q-1) }} \operatorname{tr}(\operatorname{Frob}_1^n, \mathcal L_j). \end{align} $$
Furthermore, we have
 $$\begin{align*}\langle \alpha, \beta_j \rangle = \langle \sum_{i=1}^n \alpha_i, \beta_j \rangle =\sum_{i=1}^n \langle \alpha_i,\beta_j\rangle = \langle \alpha_1,\beta_j \rangle \end{align*}$$
$$\begin{align*}\langle \alpha, \beta_j \rangle = \langle \sum_{i=1}^n \alpha_i, \beta_j \rangle =\sum_{i=1}^n \langle \alpha_i,\beta_j\rangle = \langle \alpha_1,\beta_j \rangle \end{align*}$$
since for
![]() $i \neq 1$
,
$i \neq 1$
,
![]() $\alpha _i$
is a root of a different simple factor from
$\alpha _i$
is a root of a different simple factor from
![]() $\beta _j$
and thus is orthogonal to
$\beta _j$
and thus is orthogonal to
![]() $\beta _j$
.
$\beta _j$
.
Now one of the
![]() $\beta _j$
’s is the highest weight
$\beta _j$
’s is the highest weight
![]() $\alpha _1^\vee $
of
$\alpha _1^\vee $
of
![]() ${\mathfrak {v}}_1$
, for which one has
${\mathfrak {v}}_1$
, for which one has
![]() $\langle \alpha , \alpha _1^{\vee } \rangle = \langle \alpha _1,\alpha _1^\vee \rangle =2$
. For all other
$\langle \alpha , \alpha _1^{\vee } \rangle = \langle \alpha _1,\alpha _1^\vee \rangle =2$
. For all other
![]() $\beta _j$
, one has
$\beta _j$
, one has
Hence, since
![]() $\langle \alpha , \beta _j \rangle \in \mathbb {Z}$
, we have
$\langle \alpha , \beta _j \rangle \in \mathbb {Z}$
, we have
Since we have assumed
![]() $q> 5$
, this implies that there is only one term appearing in the sum in (7.7) – namely, the term corresponding to the highest root
$q> 5$
, this implies that there is only one term appearing in the sum in (7.7) – namely, the term corresponding to the highest root
![]() $\alpha _1^{\vee }$
of
$\alpha _1^{\vee }$
of
![]() ${\hat {G}}$
. Hence, we deduce the desired contradiction
${\hat {G}}$
. Hence, we deduce the desired contradiction
which is impossible as
![]() $\mathcal L_j$
is a one-dimensional representation.
$\mathcal L_j$
is a one-dimensional representation.
We have thus completed the proof of Theorem 7.2.
7.2 Poincare series I
We continue with the proof of Theorem 1.4(i), under the hypothesis that G is semisimple and simply-connected. Let
![]() $F = k(\!(t)\!)$
and let
$F = k(\!(t)\!)$
and let
![]() $\sigma $
be a supercuspidal representation of
$\sigma $
be a supercuspidal representation of
![]() $G(F)$
. We say
$G(F)$
. We say
![]() $\sigma $
contains an
$\sigma $
contains an
![]() $\mathfrak {s}$
-type if there is an open compact subgroup
$\mathfrak {s}$
-type if there is an open compact subgroup
![]() $U^* \subset G(F)$
and an irreducible representation
$U^* \subset G(F)$
and an irreducible representation
![]() $\rho $
of
$\rho $
of
![]() $U^*$
such that
$U^*$
such that
Theorem 7.9. Let
![]() $K = k({\mathbb {P}}^1)$
. Let
$K = k({\mathbb {P}}^1)$
. Let
![]() $F = k(\!(t)\!)$
and let
$F = k(\!(t)\!)$
and let
![]() $\sigma $
be a supercuspidal representation of
$\sigma $
be a supercuspidal representation of
![]() $G(F)$
. Suppose
$G(F)$
. Suppose
Then there exists a cuspidal automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $G(K)$
satisfying the conditions (a)–(d) of Theorem 7.2.
$G(K)$
satisfying the conditions (a)–(d) of Theorem 7.2.
Proof. The construction follows the method of [Reference Gan and LomelíGLo]. Hypothesis (7.10) implies that
![]() $\sigma $
has a matrix coefficient
$\sigma $
has a matrix coefficient
![]() $\varphi ^*$
with support in
$\varphi ^*$
with support in
![]() $U^*$
, with the property that
$U^*$
, with the property that
![]() $\varphi ^*(1) = 1$
. Using this
$\varphi ^*(1) = 1$
. Using this
![]() $U^*$
, let
$U^*$
, let
![]() $U = \prod _x U_x \subset G({\mathbb A}_K)$
be the open compact subgroup constructed in Proposition 6.1. Define a function
$U = \prod _x U_x \subset G({\mathbb A}_K)$
be the open compact subgroup constructed in Proposition 6.1. Define a function
![]() $\varphi = \prod _x \varphi _x: G({\mathbb A}_K) {~\rightarrow ~} {\mathbb C}$
as follows:
$\varphi = \prod _x \varphi _x: G({\mathbb A}_K) {~\rightarrow ~} {\mathbb C}$
as follows:
-
(a) At every
 $z \in {\mathbb G}_m(k) \subset {\mathbb {P}}^1(k)$
,
$z \in {\mathbb G}_m(k) \subset {\mathbb {P}}^1(k)$
,
 $\varphi _z = \varphi ^*$
;
$\varphi _z = \varphi ^*$
; -
(b)
 $\varphi _\infty $
is the characteristic function of the group
$\varphi _\infty $
is the characteristic function of the group
 $I_\infty (p)$
of Corollary 6.2;
$I_\infty (p)$
of Corollary 6.2; -
(c)
 $\varphi _0$
is the character
$\varphi _0$
is the character
 $\chi _k: I_0/I_0(p) \cong T(k) {~\rightarrow ~} {\mathbb C}^\times $
, where
$\chi _k: I_0/I_0(p) \cong T(k) {~\rightarrow ~} {\mathbb C}^\times $
, where
 $\chi _k$
is as in the proof of Theorem 7.2;
$\chi _k$
is as in the proof of Theorem 7.2; -
(d) For
 $x \notin |{\mathbb {P}}^1(k)|$
,
$x \notin |{\mathbb {P}}^1(k)|$
,
 $\varphi _x$
is the characteristic function of the hyperspecial maximal compact subgroup
$\varphi _x$
is the characteristic function of the hyperspecial maximal compact subgroup
 $G({\mathcal {O}}_x)$
;
$G({\mathcal {O}}_x)$
;
Now define the Poincaré series
![]() $P_\varphi : G(K)\backslash G({\mathbf A}_K) {~\rightarrow ~} {\mathbb C}$
:
$P_\varphi : G(K)\backslash G({\mathbf A}_K) {~\rightarrow ~} {\mathbb C}$
:
 $$ \begin{align*}P_\varphi(g) = \sum_{\gamma \in G(K)} \varphi(\gamma\cdot g).\end{align*} $$
$$ \begin{align*}P_\varphi(g) = \sum_{\gamma \in G(K)} \varphi(\gamma\cdot g).\end{align*} $$
The sum converges absolutely, as in [Reference Gan and LomelíGLo]. It follows from Corollary 6.2 that
In particular,
![]() $P_\varphi \neq 0$
. The spectral decomposition of
$P_\varphi \neq 0$
. The spectral decomposition of
![]() $P_{\varphi }$
yields the desired cuspidal automorphic representation
$P_{\varphi }$
yields the desired cuspidal automorphic representation
![]() $\Pi $
.
$\Pi $
.
Corollary 7.11. Let G be an unramified reductive group over a nonarchimedean local field F of characteristic p, with constant field k of order
![]() $q> 5$
. Suppose that G is not a torus and p does not divide the order of the Weyl group of G. Then if
$q> 5$
. Suppose that G is not a torus and p does not divide the order of the Weyl group of G. Then if
![]() $\sigma $
is pure,
$\sigma $
is pure,
![]() $f \circ {\mathcal {L}}^{ss}(\sigma )$
is ramified (where
$f \circ {\mathcal {L}}^{ss}(\sigma )$
is ramified (where
![]() $f: {^L}G \to {^L}G/Z(\hat {G})$
). In particular, Theorem 1.4(i) holds.
$f: {^L}G \to {^L}G/Z(\hat {G})$
). In particular, Theorem 1.4(i) holds.
Proof. As mentioned at the beginning of the section, we may assume G is simply-connected. Thanks to the results of [Reference FintzenFi], the supercuspidal representation
![]() $\sigma $
of
$\sigma $
of
![]() $G(F)$
contains an
$G(F)$
contains an
![]() $\mathfrak {s}$
-type by our hypothesis on p. The claim now follows immediately from Theorems 7.2 and 7.9.
$\mathfrak {s}$
-type by our hypothesis on p. The claim now follows immediately from Theorems 7.2 and 7.9.
Theorem 7.12. Let
![]() $F = k((t))$
and let
$F = k((t))$
and let
![]() $\sigma $
be an irreducible representation of
$\sigma $
be an irreducible representation of
![]() $G(F)$
, with G unramified reductive over F. Suppose the Genestier-Lafforgue parameter
$G(F)$
, with G unramified reductive over F. Suppose the Genestier-Lafforgue parameter
![]() ${\mathcal {L}}^{ss}(\sigma )$
is pure and unramified. Suppose every supercuspidal representation of every Levi factor of
${\mathcal {L}}^{ss}(\sigma )$
is pure and unramified. Suppose every supercuspidal representation of every Levi factor of
![]() $G(F)$
contains an
$G(F)$
contains an
![]() $\mathfrak {s}$
-type. This is true in particular in the following cases:
$\mathfrak {s}$
-type. This is true in particular in the following cases:
-
○ p does not divide the order of the Weyl group of G [Reference FintzenFi];
-
○ p is odd and G is an unramified classical group (unitary, symplectic or special orthogonal) [Reference StevensSt].
Then
![]() $\sigma $
is an irreducible constituent of an unramified principal series representation of
$\sigma $
is an irreducible constituent of an unramified principal series representation of
![]() $G(F)$
.
$G(F)$
.
Proof. In any case,
![]() $\sigma $
is an irreducible constituent of a representation of the form
$\sigma $
is an irreducible constituent of a representation of the form
![]() $Ind_{P(F)}^{G(F)} \tau $
for some parabolic subgroup
$Ind_{P(F)}^{G(F)} \tau $
for some parabolic subgroup
![]() $P(F) = L(F)\cdot N(F) \subset G(F)$
, where
$P(F) = L(F)\cdot N(F) \subset G(F)$
, where
![]() $L(F)$
is a Levi subgroup of
$L(F)$
is a Levi subgroup of
![]() $P(F)$
,
$P(F)$
,
![]() $N(F)$
its unipotent radical, and
$N(F)$
its unipotent radical, and
![]() $\tau $
is a supercuspidal representation of
$\tau $
is a supercuspidal representation of
![]() $L(F)$
. Since the Genestier-Lafforgue parametrization is compatible with parabolic induction by Theorem 2.3, it follows that
$L(F)$
. Since the Genestier-Lafforgue parametrization is compatible with parabolic induction by Theorem 2.3, it follows that
![]() ${\mathcal {L}}^{ss}(\tau )$
is unramified. Since
${\mathcal {L}}^{ss}(\tau )$
is unramified. Since
![]() $\tau $
is supercuspidal, it follows from Theorems 7.9 and 7.2 (or more simply Corollary 7.11) that L must be a torus and
$\tau $
is supercuspidal, it follows from Theorems 7.9 and 7.2 (or more simply Corollary 7.11) that L must be a torus and
![]() $\tau $
an unramified character of
$\tau $
an unramified character of
![]() $L(F)$
.
$L(F)$
.
8 Proof of Theorem 1.4(ii): wild ramification
The goal of this section is to prove Theorem 1.4(ii). For the convenience of the reader, we restate the result here:
Theorem 8.1. Let G be an unramified reductive group over a local field
![]() $F= k((t))$
of equal characteristic p, and J an open subgroup of a parahoric subgroup
$F= k((t))$
of equal characteristic p, and J an open subgroup of a parahoric subgroup
![]() $G_a$
. Let
$G_a$
. Let
![]() $\sigma $
be a representation of J such that
$\sigma $
be a representation of J such that
![]() $\pi = \operatorname {c-Ind}_J^{G( F)} \sigma $
is irreducible.
$\pi = \operatorname {c-Ind}_J^{G( F)} \sigma $
is irreducible.
If J is sufficiently small and
![]() $|k| = q>5$
, then
$|k| = q>5$
, then
![]() $f\circ {\mathcal {L}}^{ss}(\pi )$
(and hence,
$f\circ {\mathcal {L}}^{ss}(\pi )$
(and hence,
![]() $f \circ {\mathcal {L}}(\pi )$
) is wildly ramified (where
$f \circ {\mathcal {L}}(\pi )$
) is wildly ramified (where
![]() $f: {^L}G \to {^L}G/Z(\hat {G})$
).
$f: {^L}G \to {^L}G/Z(\hat {G})$
).
8.1 Sufficiently small subgroups
Let us first give the precise definition of being ‘sufficiently small’, recalling that G is defined over k.
Definition 8.2. (i) A finite subgroup H of
![]() $G(k)$
is sufficiently small if there is a Borel k-subgroup B of G such that
$G(k)$
is sufficiently small if there is a Borel k-subgroup B of G such that
![]() $B(k) \cap H$
is trivial.
$B(k) \cap H$
is trivial.
(ii) For a parahoric subgroup
![]() $G_a$
of
$G_a$
of
![]() $G(F)$
, we say
$G(F)$
, we say
![]() $J \subseteq G_a$
is sufficiently small if its projection to the reductive group
$J \subseteq G_a$
is sufficiently small if its projection to the reductive group
![]() $G_a/G_{a,0+}$
is sufficiently small.
$G_a/G_{a,0+}$
is sufficiently small.
For example, the maximal unipotent subgroup of a Borel subgroup is a sufficiently small subgroup of
![]() $G(k)$
(by the Bruhat decomposition), and
$G(k)$
(by the Bruhat decomposition), and
![]() $G_{a,0+}$
is a sufficiently small subgroup of
$G_{a,0+}$
is a sufficiently small subgroup of
![]() $G(F)$
.
$G(F)$
.
8.2 An open compact subgroup of
 $G(\mathbb {A}_K)$
$G(\mathbb {A}_K)$
As for Theorem 1.4(i), we may and shall assume that G is simply-connected when proving Theorem 8.1. The proof will be via a global argument. Hence, we will be working over
![]() $K = k({\mathbb {P}}^1)$
and make use of the notation of §5.1. We will need to construct appropriate globalizations of
$K = k({\mathbb {P}}^1)$
and make use of the notation of §5.1. We will need to construct appropriate globalizations of
![]() $\pi $
by Poincaré series, and the purpose of this section is to construct appropriate open compact subgroups of
$\pi $
by Poincaré series, and the purpose of this section is to construct appropriate open compact subgroups of
![]() $G(\mathbb {A}_K)$
.
$G(\mathbb {A}_K)$
.
Recall from §5.2 that for
![]() $z \in {\mathbb {P}}^1(k)$
, the apartments
$z \in {\mathbb {P}}^1(k)$
, the apartments
![]() $\mathcal {A}(S_z)$
in the buildings
$\mathcal {A}(S_z)$
in the buildings
![]() $\mathcal {B}(G_z)$
can be naturally identified with
$\mathcal {B}(G_z)$
can be naturally identified with
![]() $X_*(S) \otimes {\mathbb R}$
and hence with each other. Without loss of generality, we may assume that the parahoric subgroup
$X_*(S) \otimes {\mathbb R}$
and hence with each other. Without loss of generality, we may assume that the parahoric subgroup
![]() $G_a$
in Theorem 8.1 is associated to a point
$G_a$
in Theorem 8.1 is associated to a point
![]() $a \in \mathcal {A}(S_0) = X_*(S) \otimes {\mathbb R}$
. Let b be a small perturbation of the point
$a \in \mathcal {A}(S_0) = X_*(S) \otimes {\mathbb R}$
. Let b be a small perturbation of the point
![]() $-a$
in
$-a$
in
![]() $\mathcal {A}(S_{\infty })$
. Specifically, we choose b so that
$\mathcal {A}(S_{\infty })$
. Specifically, we choose b so that
![]() $a+b$
is a small rational multiple of a cocharacter which lies in the interior of the positive Weyl chamber of
$a+b$
is a small rational multiple of a cocharacter which lies in the interior of the positive Weyl chamber of
![]() $X_*(S) \otimes {\mathbb R}$
. Because
$X_*(S) \otimes {\mathbb R}$
. Because
![]() $a+b$
does not lie on the walls of the Weyl chamber, b does not lie on any wall of the apartment that also contains
$a+b$
does not lie on the walls of the Weyl chamber, b does not lie on any wall of the apartment that also contains
![]() $-a$
, and because
$-a$
, and because
![]() $a+b$
is small, b does not lie on any wall of the apartment that does not contain
$a+b$
is small, b does not lie on any wall of the apartment that does not contain
![]() $-a$
. So b lies in the interior of a Weyl alcove and thus gives rise to an Iwahori subgroup
$-a$
. So b lies in the interior of a Weyl alcove and thus gives rise to an Iwahori subgroup
![]() $G_b \subset G(K_{\infty })$
.
$G_b \subset G(K_{\infty })$
.
For each place v of K, set
 $$\begin{align*}f(v) = \begin{cases} a, \text{ if } v = 0; \\ b, \text{ if } v = \infty; \\ 0, \text{ for all other } v. \end{cases} \end{align*}$$
$$\begin{align*}f(v) = \begin{cases} a, \text{ if } v = 0; \\ b, \text{ if } v = \infty; \\ 0, \text{ for all other } v. \end{cases} \end{align*}$$
Let
be the associated compact open subgroup of
![]() $G( \mathbb A_K ) $
and write
$G( \mathbb A_K ) $
and write
![]() $C_v = G_{f(v)}$
, so that for
$C_v = G_{f(v)}$
, so that for
![]() $v \notin \{0, \infty \}$
,
$v \notin \{0, \infty \}$
,
![]() $C_v$
is the standard hyperspecial maximal compact subgroup
$C_v$
is the standard hyperspecial maximal compact subgroup
![]() $G(\mathcal {O}_v)$
.
$G(\mathcal {O}_v)$
.
We now note the following:
Lemma 8.3. The natural map
is injective with image contained in a Borel subgroup of
![]() $G_a/ G_{a,0+}$
.
$G_a/ G_{a,0+}$
.
Proof. Let
![]() $\lambda \colon \mathbb G_m \to S$
be a cocharacter which is a negative multiple of
$\lambda \colon \mathbb G_m \to S$
be a cocharacter which is a negative multiple of
![]() $a+b$
. (This exists because
$a+b$
. (This exists because
![]() $a+b$
is a small rational multiple of a cocharacter, and we may multiply by any negative integer that cancels the denominator of that rational to obtain a cocharacter.) The image of
$a+b$
is a small rational multiple of a cocharacter, and we may multiply by any negative integer that cancels the denominator of that rational to obtain a cocharacter.) The image of
![]() $\lambda $
in
$\lambda $
in
![]() $G_{a}/G_{a,0+}$
continues to define a cocharacter of the maximal split torus of
$G_{a}/G_{a,0+}$
continues to define a cocharacter of the maximal split torus of
![]() $G_{a}/G_{a, 0+}$
. Since
$G_{a}/G_{a, 0+}$
. Since
![]() $\lambda $
lies in the interior of a Weyl chamber, it defines a Borel subgroup
$\lambda $
lies in the interior of a Weyl chamber, it defines a Borel subgroup
![]() $B_{\lambda }$
over k (under the ‘dynamical’ definition of parabolic subgroups). We shall show that the image of
$B_{\lambda }$
over k (under the ‘dynamical’ definition of parabolic subgroups). We shall show that the image of
![]() $C \cap G(K)$
in
$C \cap G(K)$
in
![]() $G_a/G_{a,0+}$
belongs to
$G_a/G_{a,0+}$
belongs to
![]() $B_{\lambda }$
. For this, we need to show that for any
$B_{\lambda }$
. For this, we need to show that for any
![]() $g \in C \cap G(K)$
,
$g \in C \cap G(K)$
,
To verify this, we shall apply Lemma 5.1 to the faithful algebraic representation
![]() $\rho \colon G \to \operatorname {Aut}(V)$
of G over k that was fixed in §5.1. Recall that V is equipped with a k-basis
$\rho \colon G \to \operatorname {Aut}(V)$
of G over k that was fixed in §5.1. Recall that V is equipped with a k-basis
![]() $e_1,\dots , e_n$
of V, where
$e_1,\dots , e_n$
of V, where
![]() $e_i$
is an eigenvector of S with eigencharacter
$e_i$
is an eigenvector of S with eigencharacter
![]() $\lambda _i$
. For any
$\lambda _i$
. For any
![]() $g \in C \cap G(K)$
and
$g \in C \cap G(K)$
and
![]() $(i,j)$
such that
$(i,j)$
such that
![]() $\rho _{ij}(g) \ne 0$
, we deduce by the product formula, Lemma 5.1, and the definition of
$\rho _{ij}(g) \ne 0$
, we deduce by the product formula, Lemma 5.1, and the definition of
![]() $f(v)$
, that
$f(v)$
, that
Now since b is a small perturbation of
![]() $-a$
, (8.4) can only be satisfied if
$-a$
, (8.4) can only be satisfied if
![]() $ a \cdot (\lambda _i - \lambda _j) $
is an integer and
$ a \cdot (\lambda _i - \lambda _j) $
is an integer and
![]() $b \cdot (\lambda _i -\lambda _j) \leq -a \cdot (\lambda _i - \lambda _j)$
. Indeed, b is a small perturbation of
$b \cdot (\lambda _i -\lambda _j) \leq -a \cdot (\lambda _i - \lambda _j)$
. Indeed, b is a small perturbation of
![]() $-a$
, so we may assume that
$-a$
, so we may assume that
![]() $b \cdot (\lambda _i-\lambda _j)$
is arbitrarily close to
$b \cdot (\lambda _i-\lambda _j)$
is arbitrarily close to
![]() $-a \cdot (\lambda _i - \lambda _j)$
. In particular, if
$-a \cdot (\lambda _i - \lambda _j)$
. In particular, if
![]() $a \cdot (\lambda _i-\lambda _j)$
lies in the interval
$a \cdot (\lambda _i-\lambda _j)$
lies in the interval
![]() $(n,n+1)$
for some integer n, then
$(n,n+1)$
for some integer n, then
![]() $b \cdot (\lambda _i-\lambda _j)$
lies in the interval
$b \cdot (\lambda _i-\lambda _j)$
lies in the interval
![]() $(-n-1,-n)$
, and so the sum of their ceilings is
$(-n-1,-n)$
, and so the sum of their ceilings is
![]() $ n+1 + (-n) = 1>0$
.
$ n+1 + (-n) = 1>0$
.
With
![]() $\lambda $
chosen as in the beginning of the proof, we thus deduce that for
$\lambda $
chosen as in the beginning of the proof, we thus deduce that for
![]() $g\in C \cap G(K)$
such that
$g\in C \cap G(K)$
such that
![]() $\rho _{ij}(g) \neq 0$
, we have
$\rho _{ij}(g) \neq 0$
, we have
![]() $(a+b) \cdot (\lambda _i - \lambda _j ) \leq 0$
, and thus,
$(a+b) \cdot (\lambda _i - \lambda _j ) \leq 0$
, and thus,
It follows that
![]() $\lambda (t) g \lambda (t)^{-1}$
is bounded as
$\lambda (t) g \lambda (t)^{-1}$
is bounded as
![]() $t \to 0$
, since all the nonvanishing coordinates
$t \to 0$
, since all the nonvanishing coordinates
![]() $\rho _{ij}$
of g are eigenvectors under the conjugation action by
$\rho _{ij}$
of g are eigenvectors under the conjugation action by
![]() $\lambda (t)$
with eigenvalue a positive power of t. This implies that the image of g in
$\lambda (t)$
with eigenvalue a positive power of t. This implies that the image of g in
![]() $G_{a}/G_{a,0+}$
lies in the Borel subgroup
$G_{a}/G_{a,0+}$
lies in the Borel subgroup
![]() $B_{\lambda }$
, as desired.
$B_{\lambda }$
, as desired.
It remains to show that if
![]() $g \in C \cap G(K)$
has trivial image in
$g \in C \cap G(K)$
has trivial image in
![]() $G_a/ G_{a, 0+}$
, then g is the identity element. If
$G_a/ G_{a, 0+}$
, then g is the identity element. If
![]() $\rho _{ij}(g) \neq 0$
, then because
$\rho _{ij}(g) \neq 0$
, then because
![]() $ a \cdot (\lambda _i - \lambda _j) $
is an integer and
$ a \cdot (\lambda _i - \lambda _j) $
is an integer and
![]() $b \cdot (\lambda _i -\lambda _j) \leq -a \cdot (\lambda _i - \lambda _j)$
, the right side of (8.4) is
$b \cdot (\lambda _i -\lambda _j) \leq -a \cdot (\lambda _i - \lambda _j)$
, the right side of (8.4) is
![]() $0$
. So every inequality is sharp; that is,
$0$
. So every inequality is sharp; that is,
However, by Lemma 5.1(ii), if
![]() $g \in G_{a, 0+}$
, then
$g \in G_{a, 0+}$
, then
Thus, if
![]() $i \neq j$
, we obtain a contradiction from the assumption
$i \neq j$
, we obtain a contradiction from the assumption
![]() $\rho _{ij}(g) \neq 0$
. Hence,
$\rho _{ij}(g) \neq 0$
. Hence,
![]() $\rho _{ij}(g) =0$
for
$\rho _{ij}(g) =0$
for
![]() $i \ne j$
. However, if
$i \ne j$
. However, if
![]() $i=j$
, then
$i=j$
, then
![]() $\rho _{ij}(g) \in \mathcal {O}_v$
for every place of K, and thus lies in k, but since
$\rho _{ij}(g) \in \mathcal {O}_v$
for every place of K, and thus lies in k, but since
![]() $v_0(\rho _{ii}(g) -1)> 0$
, we see that
$v_0(\rho _{ii}(g) -1)> 0$
, we see that
![]() $\rho _{ii}(g) =1$
. Thus, if
$\rho _{ii}(g) =1$
. Thus, if
![]() $g \in G_{0,a+}$
, then
$g \in G_{0,a+}$
, then
![]() $\rho (g)$
is the identity, so that g is the identity since
$\rho (g)$
is the identity, so that g is the identity since
![]() $\rho $
is faithful.
$\rho $
is faithful.
8.3 Poincaré series II
Using the above lemma, we will construct two different Poincaré series for G which are unramified outside
![]() $\{0,\infty \}$
and whose local representation at
$\{0,\infty \}$
and whose local representation at
![]() $0$
is
$0$
is
![]() $\pi $
, but with different local representations at
$\pi $
, but with different local representations at
![]() $\infty $
.
$\infty $
.
Let
![]() $B_{\lambda }$
be a Borel subgroup of
$B_{\lambda }$
be a Borel subgroup of
![]() $G_a/G_{a,0+}$
containing the image of
$G_a/G_{a,0+}$
containing the image of
![]() $C \cap G(K)$
. Let H be the image of J in
$C \cap G(K)$
. Let H be the image of J in
![]() $G_a/G_{a,0+}$
. Since we are assuming that J is sufficiently small, there exists g in
$G_a/G_{a,0+}$
. Since we are assuming that J is sufficiently small, there exists g in
![]() $G_a/G_{a,0+}$
with
$G_a/G_{a,0+}$
with
![]() $J \cap g B_{\lambda } g^{-1}$
trivial. By conjugating J by a lift of g, we may assume
$J \cap g B_{\lambda } g^{-1}$
trivial. By conjugating J by a lift of g, we may assume
![]() $g=1$
. Set
$g=1$
. Set
Then the previous lemma implies that natural map
![]() $C' \cap G(K) \to G_a / G_{a,0+}$
is injective with image contained in
$C' \cap G(K) \to G_a / G_{a,0+}$
is injective with image contained in
![]() $H \cap B =\{1\}$
. Hence,
$H \cap B =\{1\}$
. Hence,
![]() $C' \cap G(K)$
is trivial.
$C' \cap G(K)$
is trivial.
Recall that
![]() $G_b \subset G(K_{\infty })$
is an Iwahori subgroup, so that the quotient
$G_b \subset G(K_{\infty })$
is an Iwahori subgroup, so that the quotient
![]() $G_{b} / G_{b,0+}$
is a torus of rank
$G_{b} / G_{b,0+}$
is a torus of rank
![]() $r \geq \dim S$
and hence has at least
$r \geq \dim S$
and hence has at least
![]() $(q-1)^r$
points. It thus has a nontrivial character
$(q-1)^r$
points. It thus has a nontrivial character
![]() $\chi $
because
$\chi $
because
![]() $q> 2$
. We can view
$q> 2$
. We can view
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma \otimes \chi $
as representations of
$\sigma \otimes \chi $
as representations of
![]() $C'$
by projection onto the components at
$C'$
by projection onto the components at
![]() $0$
and
$0$
and
![]() $\infty $
. Now apply the Poincaré series construction to obtain
$\infty $
. Now apply the Poincaré series construction to obtain
-
○ an automorphic function
 $f_1$
created from a matrix coefficient of
$f_1$
created from a matrix coefficient of
 $\sigma $
,
$\sigma $
, -
○ an automorphic function
 $f_2$
created from a matrix coefficient of
$f_2$
created from a matrix coefficient of
 $\sigma \otimes \chi $
.
$\sigma \otimes \chi $
.
These Poincaré series are nonzero because
![]() $C' \cap G(K)$
is trivial, so that the sum defining the series has only one nonzero term. From the spectral expansion of
$C' \cap G(K)$
is trivial, so that the sum defining the series has only one nonzero term. From the spectral expansion of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
, we obtain two cuspidal automorphic representations
$f_2$
, we obtain two cuspidal automorphic representations
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
which are unramified outside
$\Pi _2$
which are unramified outside
![]() $\{0,\infty \}$
and such that
$\{0,\infty \}$
and such that
-
○ at
 $0$
, the local components of
$0$
, the local components of
 $\Pi _1$
and
$\Pi _1$
and
 $\Pi _2$
are both isomorphic to
$\Pi _2$
are both isomorphic to
 $\pi $
;
$\pi $
; -
○ at
 $\infty $
,
$\infty $
,
 $\Pi _{1,\infty }$
has nonzero Iwahori-fixed vectors, whereas
$\Pi _{1,\infty }$
has nonzero Iwahori-fixed vectors, whereas
 $\Pi _{2,\infty }$
does not. Indeed, both these representations are subquotients of principal series representations induced from characters of
$\Pi _{2,\infty }$
does not. Indeed, both these representations are subquotients of principal series representations induced from characters of
 $T(K)$
whose restrictions to
$T(K)$
whose restrictions to
 $T(k)$
are
$T(k)$
are
 $1$
and
$1$
and
 $\chi $
, respectively.
$\chi $
, respectively.
8.4 Proof of Theorem 8.1
We can now conclude the proof of Theorem 8.1. Consider the global parameters
![]() $\mathcal {L}(\Pi _1)$
and
$\mathcal {L}(\Pi _1)$
and
![]() $\mathcal {L}(\Pi _2)$
associated to
$\mathcal {L}(\Pi _2)$
associated to
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
above. These are both unramified outside
$\Pi _2$
above. These are both unramified outside
![]() $\{0, \infty \}$
. Moreover,
$\{0, \infty \}$
. Moreover,
Indeed, at
![]() $\infty $
, the associated local Genestier-Lafforgue parameters are tame, and their restrictions to the tame inertia group at
$\infty $
, the associated local Genestier-Lafforgue parameters are tame, and their restrictions to the tame inertia group at
![]() $\infty $
correspond under class field theory to
$\infty $
correspond under class field theory to
![]() $1$
and
$1$
and
![]() $\chi \ne 1$
(up to semisimplification).
$\chi \ne 1$
(up to semisimplification).
Now suppose, for the sake of contradiction, that the local Genestier-Lafforgue parameter of
![]() $\pi $
is tame. Thus,
$\pi $
is tame. Thus,
![]() $\mathcal L(\Pi _1)$
and
$\mathcal L(\Pi _1)$
and
![]() $\mathcal L(\Pi _2)$
factor through the tame fundamental group of
$\mathcal L(\Pi _2)$
factor through the tame fundamental group of
![]() $\mathbb G_{m, k}$
. In the tame fundamental group of
$\mathbb G_{m, k}$
. In the tame fundamental group of
![]() $\mathbb G_{m, k}$
, the inertia subgroups at
$\mathbb G_{m, k}$
, the inertia subgroups at
![]() $0$
and
$0$
and
![]() $\infty $
are the same subgroup, both being equal to the tame geometric fundamental group. Since
$\infty $
are the same subgroup, both being equal to the tame geometric fundamental group. Since
![]() $\mathcal L(\Pi _1)$
and
$\mathcal L(\Pi _1)$
and
![]() $\mathcal L(\Pi _2)$
are isomorphic when restricted to the tame inertia group at
$\mathcal L(\Pi _2)$
are isomorphic when restricted to the tame inertia group at
![]() $0$
and semisimplified, they must also be isomorphic when restricted to the tame inertia group at
$0$
and semisimplified, they must also be isomorphic when restricted to the tame inertia group at
![]() $\infty $
and semisimplified. This contradicts what we showed above: that
$\infty $
and semisimplified. This contradicts what we showed above: that
![]() $\mathcal L(\Pi _1)$
is trivial while
$\mathcal L(\Pi _1)$
is trivial while
![]() $\mathcal L(\Pi _2)$
is nontrivial when restricted to the tame inertia group at
$\mathcal L(\Pi _2)$
is nontrivial when restricted to the tame inertia group at
![]() $\infty $
and semisimplified. This gives the desired contradiction and completes the proof of Theorem 8.1.
$\infty $
and semisimplified. This gives the desired contradiction and completes the proof of Theorem 8.1.
8.5 A special case
When the group J is contained in the principal congruence subgroup of a hyperspecial maximal compact, there is a shorter argument, though it requires the purity of
![]() ${\mathcal {L}}^{ss}(\pi )$
as a hypothesis and appeals to Theorem 7.2.
${\mathcal {L}}^{ss}(\pi )$
as a hypothesis and appeals to Theorem 7.2.
Proposition 8.5. Under the hypotheses of Proposition 8.1, suppose
![]() $G_a$
is a hyperspecial maximal compact and J is contained in its principal congruence subgroup
$G_a$
is a hyperspecial maximal compact and J is contained in its principal congruence subgroup
![]() $G_{a,0+}$
. Let
$G_{a,0+}$
. Let
![]() $\pi $
be a pure supercuspidal representation of
$\pi $
be a pure supercuspidal representation of
![]() $G(K)$
compactly induced from an irreducible representation
$G(K)$
compactly induced from an irreducible representation
![]() $\sigma $
of J. Then
$\sigma $
of J. Then
![]() $\mathcal {L}^{ss}(\pi )$
is wildly ramified.
$\mathcal {L}^{ss}(\pi )$
is wildly ramified.
Proof. We construct a Poincaré series as in Theorem 7.9 using a function
![]() $\varphi $
which at
$\varphi $
which at
![]() $\infty $
is a matrix coefficient of
$\infty $
is a matrix coefficient of
![]() $\sigma $
and is a characteristic function of the standard hyperspecial maximal compact
$\sigma $
and is a characteristic function of the standard hyperspecial maximal compact
![]() $U_v = G(\mathcal {O}_v)$
at all other places v. Now the support of
$U_v = G(\mathcal {O}_v)$
at all other places v. Now the support of
![]() $\varphi _\infty $
is contained in J, and
$\varphi _\infty $
is contained in J, and
![]() $J \times \otimes _{v \neq \infty }U_v \cap G(K) = \{1\}$
. Thus, the Poincaré series
$J \times \otimes _{v \neq \infty }U_v \cap G(K) = \{1\}$
. Thus, the Poincaré series
![]() $P_\varphi $
does not vanish at
$P_\varphi $
does not vanish at
![]() $1$
, and the space of cusp forms it generates contains a cuspidal automorphic representation
$1$
, and the space of cusp forms it generates contains a cuspidal automorphic representation
![]() $\Pi $
that is unramified except at
$\Pi $
that is unramified except at
![]() $\infty $
. So
$\infty $
. So
![]() ${\mathcal {L}}(\Pi )$
is a parameter with values in
${\mathcal {L}}(\Pi )$
is a parameter with values in
![]() ${^L}G$
that is unramified away from
${^L}G$
that is unramified away from
![]() $\infty $
. However, by Theorem 7.2,
$\infty $
. However, by Theorem 7.2,
![]() ${\mathcal {L}}^{ss}(\pi )$
is ramified. Since a tamely ramified local system on
${\mathcal {L}}^{ss}(\pi )$
is ramified. Since a tamely ramified local system on
![]() $\mathbb {A}^1$
is unramified, it follows that the ramification at
$\mathbb {A}^1$
is unramified, it follows that the ramification at
![]() $\infty $
must be wild.
$\infty $
must be wild.
9 Questions
In this section, we raise a number of natural questions which are suggested by our results.
9.1 Positive depth representations
In the context of Theorem 8.1, for a given reductive group G over a local field F, one may ask for a better understanding (or even a classification) of all supercuspidal representations satisfying the condition of Theorem 8.1 (i.e., that can be induced from a sufficiently small open compact (modulo center) subgroup J). In particular, one may ask if they can be understood in the framework of J. K. Yu’s construction of supercuspidal representations. For example, one might hope that if the smallest twisted Levi subgroup in the twisted Levi sequence in a Yu datum is a torus, then the resulting supercuspidal representation should satisfy the condition of Theorem 8.1 or a slightly modified version of it.
9.2 Examples of pure supercuspidals
Theorem 1.4(i) has the serious condition that
![]() $\pi $
is a pure supercuspidal representation. It will be good to have some examples of pure supercuspidal representations in addition to the ones used in §3.3. For example, the desiderata of the LLC suggests that if
$\pi $
is a pure supercuspidal representation. It will be good to have some examples of pure supercuspidal representations in addition to the ones used in §3.3. For example, the desiderata of the LLC suggests that if
![]() $\pi $
is a generic supercuspidal representation of a quasi-split G, then
$\pi $
is a generic supercuspidal representation of a quasi-split G, then
![]() $\pi $
is pure. In the rest of this section, we show this for certain generic supercuspidal representations of depth 0, conditionally on the independence of
$\pi $
is pure. In the rest of this section, we show this for certain generic supercuspidal representations of depth 0, conditionally on the independence of
![]() $\ell $
result assumed in [Reference Dat and LanardDL].
$\ell $
result assumed in [Reference Dat and LanardDL].
9.3 Poincaré series III
We begin by giving yet another construction of Poincaré series. Let us work in the context of §5.1 again, so that G is an unramified semisimple group over k.
Proposition 9.1. Let
![]() $\pi $
be a depth 0 generic supercuspidal representation of
$\pi $
be a depth 0 generic supercuspidal representation of
![]() $G(F)$
(with
$G(F)$
(with
![]() $F = k((t))$
) of the form
$F = k((t))$
) of the form
where
![]() $\sigma $
is a generic cuspidal representation of the finite reductive group
$\sigma $
is a generic cuspidal representation of the finite reductive group
![]() $G(k)$
. There is a globally generic representation
$G(k)$
. There is a globally generic representation
![]() $\Pi $
of G such that
$\Pi $
of G such that
-
○
 $\Pi _0 \cong \pi $
and
$\Pi _0 \cong \pi $
and
 $ \Pi _{\infty } \cong \pi ^{\vee }$
;
$ \Pi _{\infty } \cong \pi ^{\vee }$
; -
○ for all other places v of
 $K = k(t)$
,
$K = k(t)$
,
 $\Pi _v$
is
$\Pi _v$
is
 $G(\mathcal {O}_v)$
-unramified.
$G(\mathcal {O}_v)$
-unramified.
Proof. Since
![]() $\sigma $
is a generic representation of
$\sigma $
is a generic representation of
![]() $G(k)$
, one can find a generic character
$G(k)$
, one can find a generic character
such that the
![]() $(N(k), \psi )$
-eigenspace of
$(N(k), \psi )$
-eigenspace of
![]() $\sigma $
is nonzero, in which case it is 1-dimensional. Let us fix a nonzero vector w such that
$\sigma $
is nonzero, in which case it is 1-dimensional. Let us fix a nonzero vector w such that
Fixing a
![]() $G(k)$
-invariant inner product
$G(k)$
-invariant inner product
![]() $\langle -, -\rangle $
on
$\langle -, -\rangle $
on
![]() $\sigma $
, we may assume that
$\sigma $
, we may assume that
![]() $\langle w,w \rangle =1$
.
$\langle w,w \rangle =1$
.
Now we may consider the function on
![]() $G(K_0)$
defined by
$G(K_0)$
defined by
 $$\begin{align*}f_0(g) =\begin{cases} \langle \sigma(g )\cdot w , w \rangle , \quad \text{ if } g \in G(\mathcal{O}_0); \\ 0, \quad \text{ if } g \notin G(\mathcal{O}_0). \end{cases} \end{align*}$$
$$\begin{align*}f_0(g) =\begin{cases} \langle \sigma(g )\cdot w , w \rangle , \quad \text{ if } g \in G(\mathcal{O}_0); \\ 0, \quad \text{ if } g \notin G(\mathcal{O}_0). \end{cases} \end{align*}$$
This is a matrix coefficient of
![]() $\pi $
, which is built out of a matrix coefficient of
$\pi $
, which is built out of a matrix coefficient of
![]() $\sigma $
supported on
$\sigma $
supported on
![]() $G(\mathcal {O}_0)$
. Likewise, we define a function on
$G(\mathcal {O}_0)$
. Likewise, we define a function on
![]() $G(K_{\infty })$
by
$G(K_{\infty })$
by
 $$\begin{align*}f_{\infty}(g) = \begin{cases} \langle w, \sigma(g)\cdot w \rangle, \quad \text{ if } g \in G(\mathcal{O}_{\infty}); \\ 0, \quad \text{ if } g \notin G(\mathcal{O}_{\infty}), \end{cases} \end{align*}$$
$$\begin{align*}f_{\infty}(g) = \begin{cases} \langle w, \sigma(g)\cdot w \rangle, \quad \text{ if } g \in G(\mathcal{O}_{\infty}); \\ 0, \quad \text{ if } g \notin G(\mathcal{O}_{\infty}), \end{cases} \end{align*}$$
which is a matrix coefficient of
![]() $\overline {\pi } \cong \pi ^{\vee }$
. Define a locally constant compactly supported function
$\overline {\pi } \cong \pi ^{\vee }$
. Define a locally constant compactly supported function
![]() $f = \prod _v f_v$
on
$f = \prod _v f_v$
on
![]() $G(\mathbb {A}_K)$
by requiring that
$G(\mathbb {A}_K)$
by requiring that
![]() $f_0$
and
$f_0$
and
![]() $f_{\infty }$
are as defined above and
$f_{\infty }$
are as defined above and
![]() $f_v$
is the characteristic function of
$f_v$
is the characteristic function of
![]() $G(\mathcal {O}_v)$
for all other v. Then consider the Poincaré series
$G(\mathcal {O}_v)$
for all other v. Then consider the Poincaré series
 $$\begin{align*}P_f(g) = \sum_{\gamma \in G(K)} f(\gamma g). \end{align*}$$
$$\begin{align*}P_f(g) = \sum_{\gamma \in G(K)} f(\gamma g). \end{align*}$$
Because of the support conditions on f, one has
 $$\begin{align*}P_f(1) = \sum_{\gamma \in G(k)} f_0(\gamma) \cdot f_{\infty}(\gamma) = \sum_{\gamma \in G(k)} | \langle \sigma(\gamma) \cdot w, w \rangle|^2. \end{align*}$$
$$\begin{align*}P_f(1) = \sum_{\gamma \in G(k)} f_0(\gamma) \cdot f_{\infty}(\gamma) = \sum_{\gamma \in G(k)} | \langle \sigma(\gamma) \cdot w, w \rangle|^2. \end{align*}$$
This sum is certainly nonzero, so that
![]() $P_f$
is nonzero.
$P_f$
is nonzero.
To see if
![]() $P_f$
is globally generic, let us first construct an appropriate automorphic generic character
$P_f$
is globally generic, let us first construct an appropriate automorphic generic character
Note that one has
where
![]() $\widehat {O} = \prod _v \mathcal {O}_v$
. We define
$\widehat {O} = \prod _v \mathcal {O}_v$
. We define
![]() $\Psi $
by requiring that
$\Psi $
by requiring that
-
○
 $\Psi _v =1$
on
$\Psi _v =1$
on
 $N(\mathcal {O}_v)$
for all
$N(\mathcal {O}_v)$
for all
 $v \ne 0$
or
$v \ne 0$
or
 $\infty $
,
$\infty $
, -
○ the restriction of
 $\Psi _0$
to
$\Psi _0$
to
 $N(\mathcal {O}_0)$
is obtained as
$N(\mathcal {O}_0)$
is obtained as 
-
○ likewise, the restriction of
 $\Psi _{\infty }$
to
$\Psi _{\infty }$
to
 $N(\mathcal {O}_{\infty })$
is obtained as
$N(\mathcal {O}_{\infty })$
is obtained as 
Hence, for
![]() $n \in N(\widehat {O})$
, one has
$n \in N(\widehat {O})$
, one has
so that
![]() $\Psi $
is indeed trivial on the diagonally embedded
$\Psi $
is indeed trivial on the diagonally embedded
![]() $N(k) \hookrightarrow N(\widehat {O})$
.
$N(k) \hookrightarrow N(\widehat {O})$
.
We can now compute the
![]() $(N, \Psi )$
-Whittaker-Fourier coefficient of
$(N, \Psi )$
-Whittaker-Fourier coefficient of
![]() $P_f$
:
$P_f$
:
 $$ \begin{align*} &\int_{N(K) \backslash N(\mathbb{A}_K)} \overline{\Psi(n)} \cdot P_f(n) \, dn \notag \\ =&\int_{N(k)\backslash N(\widehat{\mathcal{O})}} \overline{\Psi(n)} \cdot \sum_{\gamma \in G(K)} f(\gamma n) \, dn. \notag \end{align*} $$
$$ \begin{align*} &\int_{N(K) \backslash N(\mathbb{A}_K)} \overline{\Psi(n)} \cdot P_f(n) \, dn \notag \\ =&\int_{N(k)\backslash N(\widehat{\mathcal{O})}} \overline{\Psi(n)} \cdot \sum_{\gamma \in G(K)} f(\gamma n) \, dn. \notag \end{align*} $$
For
![]() $n \in N(\widehat {O})$
,
$n \in N(\widehat {O})$
,
Moreover, with
![]() $n \in N(\widehat {O})$
, one deduces by (9.2) that
$n \in N(\widehat {O})$
, one deduces by (9.2) that
Hence, one has
 $$ \begin{align*} &\int_{N(K) \backslash N(\mathbb{A}_K)} \overline{\Psi(n)} \cdot P_f(n) \, dn \notag \\ =& \int_{N(k)\backslash N(\widehat{\mathcal{O})}} \overline{\psi(n_0)} \cdot \psi(n_{\infty}) \cdot \sum_{\gamma \in G(k)} \psi(n_0) \cdot \overline{\psi(n_{\infty})} \cdot | \langle \sigma(\gamma) w,w \rangle|^2 \, dn. \notag \\ =& \mathrm{Vol}(N(k) \backslash N(\widehat{O})) \cdot \sum_{\gamma \in G(k)} | \langle \sigma(\gamma) w,w \rangle|^2, \notag \end{align*} $$
$$ \begin{align*} &\int_{N(K) \backslash N(\mathbb{A}_K)} \overline{\Psi(n)} \cdot P_f(n) \, dn \notag \\ =& \int_{N(k)\backslash N(\widehat{\mathcal{O})}} \overline{\psi(n_0)} \cdot \psi(n_{\infty}) \cdot \sum_{\gamma \in G(k)} \psi(n_0) \cdot \overline{\psi(n_{\infty})} \cdot | \langle \sigma(\gamma) w,w \rangle|^2 \, dn. \notag \\ =& \mathrm{Vol}(N(k) \backslash N(\widehat{O})) \cdot \sum_{\gamma \in G(k)} | \langle \sigma(\gamma) w,w \rangle|^2, \notag \end{align*} $$
which is nonzero. Thus,
![]() $P_f$
is
$P_f$
is
![]() $(N,\Psi )$
-generic.
$(N,\Psi )$
-generic.
9.4 Purity of generic depth zero representations
Now we can sketch our strategy for showing that a depth
![]() $0$
generic supercuspidal representation is pure. We use the following:
$0$
generic supercuspidal representation is pure. We use the following:
Expected Theorem 9.3 (Dat-Lanard).
Let
![]() $\pi \in {\mathcal {A}}(G,F)$
be a depth
$\pi \in {\mathcal {A}}(G,F)$
be a depth
![]() $0$
supercuspidal representation of
$0$
supercuspidal representation of
![]() $G(F)$
(in the sense of [Reference Debacker and ReederDR]). Then the semisimple parameter
$G(F)$
(in the sense of [Reference Debacker and ReederDR]). Then the semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
is (at most) tamely ramified.
${\mathcal {L}}^{ss}(\pi )$
is (at most) tamely ramified.
Dat and Lanard prove this in [Reference Dat and LanardDL], conditionally on the independence of
![]() $\ell $
of the
$\ell $
of the
![]() $\ell $
-adic parameter
$\ell $
-adic parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
.Footnote
3
${\mathcal {L}}^{ss}(\pi )$
.Footnote
3
Using this, we can now show the following:
Theorem 9.4. Assume that G is semisimple over k and
![]() $p = \mathrm {char}(k)$
is a good prime for G. Then for any depth 0 generic supercuspidal representation of
$p = \mathrm {char}(k)$
is a good prime for G. Then for any depth 0 generic supercuspidal representation of
![]() $G(F)$
, the associated semisimple parameter
$G(F)$
, the associated semisimple parameter
![]() ${\mathcal {L}}^{ss}(\pi )$
is pure.
${\mathcal {L}}^{ss}(\pi )$
is pure.
Proof. Consider the global Lafforgue parameter
![]() ${\mathcal {L}}(\Pi )$
associated to the globally generic cuspidal representation
${\mathcal {L}}(\Pi )$
associated to the globally generic cuspidal representation
![]() $\Pi $
of Proposition 9.1. Since
$\Pi $
of Proposition 9.1. Since
![]() $\Pi $
is unramified outside
$\Pi $
is unramified outside
![]() $0$
and
$0$
and
![]() $\infty $
, it gives rise to a semisimple local system
$\infty $
, it gives rise to a semisimple local system
![]() ${\mathcal {L}}(\Pi ,Ad)$
on
${\mathcal {L}}(\Pi ,Ad)$
on
![]() ${\mathbb G}_m/k$
, where
${\mathbb G}_m/k$
, where
![]() $Ad$
is the adjoint representation of
$Ad$
is the adjoint representation of
![]() ${}^LG$
. Expected Theorem 9.3 implies that
${}^LG$
. Expected Theorem 9.3 implies that
![]() ${\mathcal {L}}(\Pi ,Ad)$
is tamely ramified. It follows that, for a finite extension
${\mathcal {L}}(\Pi ,Ad)$
is tamely ramified. It follows that, for a finite extension
![]() $k'/k$
of the constant field, the restriction
$k'/k$
of the constant field, the restriction
![]() ${\mathcal {L}}(\Pi ,Ad)_{k'}$
of
${\mathcal {L}}(\Pi ,Ad)_{k'}$
of
![]() ${\mathcal {L}}(\Pi ,Ad)^{ss}$
to
${\mathcal {L}}(\Pi ,Ad)^{ss}$
to
![]() ${\mathbb G}_m/k'$
is a sum of
${\mathbb G}_m/k'$
is a sum of
![]() $1$
-dimensional tamely ramified
$1$
-dimensional tamely ramified
![]() $\ell $
-adic local systems:
$\ell $
-adic local systems:
where each
![]() $L_i$
is pure of weight
$L_i$
is pure of weight
![]() $w_i$
. Let
$w_i$
. Let
![]() $\Omega $
be the set of weights
$\Omega $
be the set of weights
![]() $w_i$
that occur.
$w_i$
that occur.
Now suppose
![]() ${\mathcal {L}}^{ss}(\pi )$
is not pure. Since
${\mathcal {L}}^{ss}(\pi )$
is not pure. Since
![]() $\pi $
belongs to the discrete series, G is semisimple and p is good for G, it follows from Theorem 1.2 and Corollary 3.12 that the weights that occur in
$\pi $
belongs to the discrete series, G is semisimple and p is good for G, it follows from Theorem 1.2 and Corollary 3.12 that the weights that occur in
![]() ${\mathcal {L}}(\pi )^{ss}$
are integral and two of them differ by at least
${\mathcal {L}}(\pi )^{ss}$
are integral and two of them differ by at least
![]() $2$
.
$2$
.
Thus, there are two weights
![]() $w_i$
and
$w_i$
and
![]() $w_j$
in
$w_j$
in
![]() $\Omega $
with
$\Omega $
with
![]() $|w_i - w_j| \geq 2$
. This would imply that for
$|w_i - w_j| \geq 2$
. This would imply that for
![]() $z \in {\mathbb G}_m(k)$
, the Satake parameter of the unramified representation
$z \in {\mathbb G}_m(k)$
, the Satake parameter of the unramified representation
![]() $\Pi _z$
also has at least two weights that differ by at least
$\Pi _z$
also has at least two weights that differ by at least
![]() $2$
. But
$2$
. But
![]() $\Pi _z$
is unitary and generic because
$\Pi _z$
is unitary and generic because
![]() $\Pi $
is cuspidal and globally generic. The existence of two distinct integral weights that differ by at least 2 is then ruled out by the main theorem of [Reference Ciubotaru and HarrisCH].
$\Pi $
is cuspidal and globally generic. The existence of two distinct integral weights that differ by at least 2 is then ruled out by the main theorem of [Reference Ciubotaru and HarrisCH].
10 Base change and incorrigible representations
As we mentioned in the introduction, though our ramification result in Theorem 1.4 may seem rather weak, it could, in fact, serve as a starting point, in conjunction with the global input of automorphic base change, in the (long) journey towards establishing the local Langlands correspondence for a general reductive group G over local function fields. In this section, we would like to elaborate on this.
10.1 Tempered base change
Let
![]() $E = k((t))$
for a finite field k and let G be a connected reductive group over E. For any finite separable field extension F of E, let
$E = k((t))$
for a finite field k and let G be a connected reductive group over E. For any finite separable field extension F of E, let
![]() ${\mathcal {T}}(G,F) \subset {\mathcal {A}}(G,F)$
denote the set of irreducible tempered (admissible) representations of
${\mathcal {T}}(G,F) \subset {\mathcal {A}}(G,F)$
denote the set of irreducible tempered (admissible) representations of
![]() $G(F)$
with coefficients in C and let
$G(F)$
with coefficients in C and let
![]() $P({\mathcal {T}}(G,F))$
be the set of nonempty subsets of
$P({\mathcal {T}}(G,F))$
be the set of nonempty subsets of
![]() ${\mathcal {T}}(G,F)$
. We write
${\mathcal {T}}(G,F)$
. We write
![]() ${\mathcal {L}}^{ss}_F$
for the semisimple Langlands parametrization of (2.2) for
${\mathcal {L}}^{ss}_F$
for the semisimple Langlands parametrization of (2.2) for
![]() ${\mathcal {A}}(G,F)$
, with a subscript to indicate the base field.
${\mathcal {A}}(G,F)$
, with a subscript to indicate the base field.
Definition 10.1. Say G admits tempered base change if, for every pair
![]() $F \subset F'$
of finite extensions of E, with
$F \subset F'$
of finite extensions of E, with
![]() $F'/F$
a cyclic extension of prime order, there is a map
$F'/F$
a cyclic extension of prime order, there is a map
so that for any
![]() $\pi \in {\mathcal {T}}(G,F)$
and any
$\pi \in {\mathcal {T}}(G,F)$
and any
![]() $\pi ' \in BC_{F'/F}(\pi )$
,
$\pi ' \in BC_{F'/F}(\pi )$
,
We may naturally regard
![]() $BC_{F'/F}$
as a map from
$BC_{F'/F}$
as a map from
![]() $P(\mathcal{T}(G,F))$
to
$P(\mathcal{T}(G,F))$
to
![]() $P(\mathcal{T}(G,F'))$
. Of course, it is expected that every G admits tempered base change and that the set
$P(\mathcal{T}(G,F'))$
. Of course, it is expected that every G admits tempered base change and that the set
![]() $BC(\pi )$
is characterized intrinsically inside
$BC(\pi )$
is characterized intrinsically inside
![]() ${\mathcal {A}}(G,F)$
in terms of
${\mathcal {A}}(G,F)$
in terms of
![]() $\pi $
by relations of distribution characters. It is also assumed that
$\pi $
by relations of distribution characters. It is also assumed that
![]() $BC(\pi )$
is always a finite set, but we do not make that assumption. There is a brief discussion of the existence of tempered base change at the end of this section.
$BC(\pi )$
is always a finite set, but we do not make that assumption. There is a brief discussion of the existence of tempered base change at the end of this section.
Definition 10.3. Suppose G admits tempered base change. The supercuspidal representation
![]() $\pi $
of
$\pi $
of
![]() $G(F)$
is incorrigible if for any sequence
$G(F)$
is incorrigible if for any sequence
of extensions, where
![]() $F_i/F_{i-1}$
is cyclic of prime order for all
$F_i/F_{i-1}$
is cyclic of prime order for all
![]() $i \geq 1$
, the set
$i \geq 1$
, the set
contains a supercuspidal member.
Proposition 10.5. Assume G admits tempered base change and
![]() $p \nmid |W|$
. Then for any extension
$p \nmid |W|$
. Then for any extension
![]() $F/E$
, no pure supercuspidal representation of
$F/E$
, no pure supercuspidal representation of
![]() $G(F)$
is incorrigible. More generally, suppose G has the property that, for every Levi subgroup
$G(F)$
is incorrigible. More generally, suppose G has the property that, for every Levi subgroup
![]() $L(F)$
of
$L(F)$
of
![]() $G(F)$
, every supercuspidal representation of
$G(F)$
, every supercuspidal representation of
![]() $L(F)$
contains an
$L(F)$
contains an
![]() $\mathfrak {s}$
-type. Then no pure supercuspidal representation of
$\mathfrak {s}$
-type. Then no pure supercuspidal representation of
![]() $G(F)$
is incorrigible.
$G(F)$
is incorrigible.
Proof. Let
![]() $\pi $
be a pure supercuspidal representation of
$\pi $
be a pure supercuspidal representation of
![]() $G(F)$
. The image of the inertia group under
$G(F)$
. The image of the inertia group under
![]() ${\mathcal {L}}^{ss}_F(\pi )$
is finite, so there is a sequence of cyclic extensions of prime order, as in (10.4), such that, if
${\mathcal {L}}^{ss}_F(\pi )$
is finite, so there is a sequence of cyclic extensions of prime order, as in (10.4), such that, if
![]() $\pi _r$
is any member of
$\pi _r$
is any member of
![]() $BC_{F_r/F}(\pi )$
, we have
$BC_{F_r/F}(\pi )$
, we have
is unramified. It then follows from Corollary 7.12 that
![]() $\pi _r$
is a constituent of an unramified principal series representation. In particular, no member of
$\pi _r$
is a constituent of an unramified principal series representation. In particular, no member of
![]() $BC_{F_r/F}(\pi )$
can be supercuspidal.
$BC_{F_r/F}(\pi )$
can be supercuspidal.
10.2 Existence of tempered base change
Suppose for the moment that F is a p-adic field. A procedure for defining cyclic base change can be constructed using the methods of [Reference LabesseLab99]. Suppose first that
![]() $\pi $
is supercuspidal with central character of finite order. Then there is
$\pi $
is supercuspidal with central character of finite order. Then there is
-
(i) A totally real number field K with a local place w such that
 $K_w {~\overset \sim \longrightarrow ~} F$
;
$K_w {~\overset \sim \longrightarrow ~} F$
; -
(ii) A totally real cyclic extension
 $K'/K$
with
$K'/K$
with
 $K^{\prime }_w = K' \otimes _K F {~\overset \sim \longrightarrow ~} F'$
,
$K^{\prime }_w = K' \otimes _K F {~\overset \sim \longrightarrow ~} F'$
, -
(iii) A connected reductive group
 ${\mathcal {G}}$
over K, with
${\mathcal {G}}$
over K, with
 ${\mathcal {G}}(K_w) {~\overset \sim \longrightarrow ~} G(F)$
and
${\mathcal {G}}(K_w) {~\overset \sim \longrightarrow ~} G(F)$
and -
(iv)
 ${\mathcal {G}}(K_\sigma )$
compact modulo center for all archimedean places
${\mathcal {G}}(K_\sigma )$
compact modulo center for all archimedean places
 $\sigma $
of K,
$\sigma $
of K, -
(v) And an automorphic representation
 $\Pi $
such that
$\Pi $
such that
 $\Pi _w {~\overset \sim \longrightarrow ~} \pi $
and
$\Pi _w {~\overset \sim \longrightarrow ~} \pi $
and -
(vi)
 $\Pi _{v_i}$
isomorphic to a Steinberg representation at any chosen finite set of places
$\Pi _{v_i}$
isomorphic to a Steinberg representation at any chosen finite set of places
 $v_i$
.
$v_i$
.
Then it is proved in [Reference LabesseLab99], using the stable twisted trace formula, that there is a nonempty collection
![]() $\{\Pi '\}$
of automorphic representations of
$\{\Pi '\}$
of automorphic representations of
![]() ${\mathcal {G}}_{K'}$
such that, at every place u at which
${\mathcal {G}}_{K'}$
such that, at every place u at which
![]() $\Pi $
and
$\Pi $
and
![]() $K'/K$
are unramified,
$K'/K$
are unramified,
![]() $\Pi ^{\prime }_u$
is the unramified base change of
$\Pi ^{\prime }_u$
is the unramified base change of
![]() $\Pi _u$
. We can then define
$\Pi _u$
. We can then define
![]() $BC(\pi )$
to be the collection of
$BC(\pi )$
to be the collection of
![]() $\Pi ^{\prime }_w$
for all such
$\Pi ^{\prime }_w$
for all such
![]() $K, K', {\mathcal {G}}, \Pi $
. The stable twisted characters of such collections of
$K, K', {\mathcal {G}}, \Pi $
. The stable twisted characters of such collections of
![]() $\Pi ^{\prime }_w$
are related to the stable character of
$\Pi ^{\prime }_w$
are related to the stable character of
![]() $\pi $
, but in the absence of a canonical notion of L-packet, we omit the precise statement.
$\pi $
, but in the absence of a canonical notion of L-packet, we omit the precise statement.
When Labesse defined his construction in [Reference LabesseLab99], the stabilization of the trace formula had not yet been established in either the twisted or the untwisted setting. Arthur reduced the stabilization to the fundamental lemma in a series of papers shortly thereafter, and a few years later, the main step in the proof of the fundamental lemma was completed by Ngô. The stabilization of the twisted trace formula is contained in [Reference Moeglin and WaldspurgerMW]; see also [Reference Clozel, Harris, Labesse and NgôCHLN] for references for the untwisted case. Labesse needed hypothesis (vi) in the above list in order to work with a simplified version of the trace formula. In principle, (vi) is no longer necessary, but the necessary consequences of the full stabilized trace formula have not yet been established (see [Reference Clozel, Harris, Labesse and NgôCHLN, §CHL.IV.B] for an example of the kind of work required). Thus for practical purposes, the construction in [Reference LabesseLab99] still provides the most complete definition of local supercuspidal base change in general.
Since we are only looking for semisimple Langlands parameters, we can reduce a general tempered
![]() $\pi $
to the supercuspidal case by means of parabolic induction. Unfortunately, although Fargues and Scholze have defined a semisimple parametrization of all irreducible admissible representations of
$\pi $
to the supercuspidal case by means of parabolic induction. Unfortunately, although Fargues and Scholze have defined a semisimple parametrization of all irreducible admissible representations of
![]() $G(F)$
, when F is a p-adic field, there is no way to relate the parameter attached to
$G(F)$
, when F is a p-adic field, there is no way to relate the parameter attached to
![]() $\pi $
to that attached to the elements of the set
$\pi $
to that attached to the elements of the set
![]() $BC(\pi )$
defined by Labesse’s construction, unless we know how to attach Galois parameters to the globalizations
$BC(\pi )$
defined by Labesse’s construction, unless we know how to attach Galois parameters to the globalizations
![]() $\Pi $
as in (v). If we could do that, then the relation between the parameters of
$\Pi $
as in (v). If we could do that, then the relation between the parameters of
![]() $\Pi _u$
and
$\Pi _u$
and
![]() $\Pi ^{\prime }_u$
at unramified places would suffice, by Chebotarev density, to establish the relation (10.2) at the place of interest. This reasoning has, in fact, been applied for most classical groups, and for
$\Pi ^{\prime }_u$
at unramified places would suffice, by Chebotarev density, to establish the relation (10.2) at the place of interest. This reasoning has, in fact, been applied for most classical groups, and for
![]() $G_2$
, but it is not available in general.
$G_2$
, but it is not available in general.
Now suppose
![]() $F = k((t))$
as above. We can certainly globalize
$F = k((t))$
as above. We can certainly globalize
![]() $\pi $
as in the number field case, and then [Reference LafforgueLaf18] supplies the necessary global parametrization that is missing in the setting of number fields. However, the stable twisted trace formula is lacking for function fields, so for most G, tempered base change is not (yet) available. It should nevertheless be (relatively) straightforward, although time-consuming, for specialists to prove the necessary statements, starting with the construction of the non-invariant trace formula by Labesse and Lemaire [Reference Labesse and LemaireLL], when p is large relative to the group G.
$\pi $
as in the number field case, and then [Reference LafforgueLaf18] supplies the necessary global parametrization that is missing in the setting of number fields. However, the stable twisted trace formula is lacking for function fields, so for most G, tempered base change is not (yet) available. It should nevertheless be (relatively) straightforward, although time-consuming, for specialists to prove the necessary statements, starting with the construction of the non-invariant trace formula by Labesse and Lemaire [Reference Labesse and LemaireLL], when p is large relative to the group G.
10.3 Base change of large prime degree and fields of small order
Let
![]() $\pi $
be a supercuspidal representation as in Theorems 7.1 and 7.2. Those theorems are stated under the hypothesis
$\pi $
be a supercuspidal representation as in Theorems 7.1 and 7.2. Those theorems are stated under the hypothesis
![]() $q = |k|> 5$
, which concerns the size of the residue field k rather than the characteristic. Theorem 7.2 of [Reference Böckle, Feng, Harris, Khare and ThorneBFHKT] asserts that there is a constant
$q = |k|> 5$
, which concerns the size of the residue field k rather than the characteristic. Theorem 7.2 of [Reference Böckle, Feng, Harris, Khare and ThorneBFHKT] asserts that there is a constant
![]() $c(\pi )$
such that, if
$c(\pi )$
such that, if
![]() $m> c(\pi )$
, and
$m> c(\pi )$
, and
![]() $F'/F$
is cyclic of prime degree m, then there exists a base change
$F'/F$
is cyclic of prime degree m, then there exists a base change
![]() $\pi '$
of
$\pi '$
of
![]() $\pi $
to
$\pi $
to
![]() $F'$
, in the sense that the
$F'$
, in the sense that the
![]() ${\mathcal {L}}^{ss}(\pi ')$
is the restriction of
${\mathcal {L}}^{ss}(\pi ')$
is the restriction of
![]() ${\mathcal {L}}^{ss}(\pi )$
to the Weil group of
${\mathcal {L}}^{ss}(\pi )$
to the Weil group of
![]() $F'$
. In particular, we may assume
$F'$
. In particular, we may assume
![]() $F' = k'((t))$
is an unramified extension, where
$F' = k'((t))$
is an unramified extension, where
![]() $[k':k] = m$
and therefore
$[k':k] = m$
and therefore
![]() $|k'| = q^m$
. In particular, the hypotheses on q are satisfied for
$|k'| = q^m$
. In particular, the hypotheses on q are satisfied for
![]() $\pi '$
. Write
$\pi '$
. Write
![]() $\pi _{m}$
instead of
$\pi _{m}$
instead of
![]() $\pi '$
. Then
$\pi '$
. Then
![]() ${\mathcal {L}}^{ss}(\pi )$
is unramified if and only if
${\mathcal {L}}^{ss}(\pi )$
is unramified if and only if
![]() ${\mathcal {L}}^{ss}(\pi _m)$
is unramified. We thus have the following alternative:
${\mathcal {L}}^{ss}(\pi _m)$
is unramified. We thus have the following alternative:
-
(i) For some
 $m \geq \sup (3,c(\pi ))$
,
$m \geq \sup (3,c(\pi ))$
,
 $\pi _m$
is supercuspidal, and then the results of Theorems 7.1 and 7.2 remain valid for
$\pi _m$
is supercuspidal, and then the results of Theorems 7.1 and 7.2 remain valid for
 $\pi $
, without any hypothesis on q;
$\pi $
, without any hypothesis on q; -
(ii) Or else, for all
 $m \geq \sup (3,c(\pi ))$
,
$m \geq \sup (3,c(\pi ))$
,
 $\pi _m$
is not supercuspidal.
$\pi _m$
is not supercuspidal.
Although the second alternative is clearly absurd, we do not see how to exclude it by available means. At least for the toral supercuspidals considered by Chan and Oi, the results of [Reference Böckle, Feng, Harris, Khare and ThorneBFHKT, §8] show that
![]() $\pi _m$
remains supercuspidal for almost all prime m. However, we have not proved that their parameters are pure.
$\pi _m$
remains supercuspidal for almost all prime m. However, we have not proved that their parameters are pure.
The above alternatives do seem to provide a route to proving that a given pure supercuspidal
![]() $\pi $
is not incorrigible, even when
$\pi $
is not incorrigible, even when
![]() $|k| \leq 5$
. If we are in the first alternative, then the residue field satisfies the hypotheses of Theorems 7.1 and 7.2. We can then define what it means for
$|k| \leq 5$
. If we are in the first alternative, then the residue field satisfies the hypotheses of Theorems 7.1 and 7.2. We can then define what it means for
![]() $\pi $
to be incorrigible if we have access to cyclic base change of all prime degrees – not just those guaranteed by [Reference Böckle, Feng, Harris, Khare and ThorneBFHKT] – and argue as in the previous sections. Under the second (absurd) alternative, we have already reduced the supercuspidality by base change, and we can then argue by induction on the size of the cuspidal support.
$\pi $
to be incorrigible if we have access to cyclic base change of all prime degrees – not just those guaranteed by [Reference Böckle, Feng, Harris, Khare and ThorneBFHKT] – and argue as in the previous sections. Under the second (absurd) alternative, we have already reduced the supercuspidality by base change, and we can then argue by induction on the size of the cuspidal support.
Too much attention should not be given to these remarks, however. The restriction on
![]() $|k|$
is only relevant when the residue characteristic is
$|k|$
is only relevant when the residue characteristic is
![]() $2, 3$
or
$2, 3$
or
![]() $5$
. These are the primes that tend to divide the order of Weyl groups. So it would be unnatural to try to formulate unconditional results based on these observations.
$5$
. These are the primes that tend to divide the order of Weyl groups. So it would be unnatural to try to formulate unconditional results based on these observations.
10.4 The case of
 $GL(n)$
$GL(n)$
We again assume F is a local field of positive characteristic. We shall illustrate the strategy discussed above for
![]() $G = GL(n)$
. It has been proved by Henniart and Lemaire in [Reference Henniart and LemaireHeLe] that
$G = GL(n)$
. It has been proved by Henniart and Lemaire in [Reference Henniart and LemaireHeLe] that
![]() $G = GL(n)$
admits tempered base change; they even prove that
$G = GL(n)$
admits tempered base change; they even prove that
![]() $BC_{F'/F}(\pi )$
is a singleton for any
$BC_{F'/F}(\pi )$
is a singleton for any
![]() $\pi $
. Moreover, every supercuspidal representation of every Levi subgroup of
$\pi $
. Moreover, every supercuspidal representation of every Levi subgroup of
![]() $G(F)$
contains an
$G(F)$
contains an
![]() $\mathfrak {s}$
-type [Reference Bushnell and KutzkoBK]. Thus, the above discussion applies. Before drawing the relevant conclusion, we make the following observation.
$\mathfrak {s}$
-type [Reference Bushnell and KutzkoBK]. Thus, the above discussion applies. Before drawing the relevant conclusion, we make the following observation.
The following lemma may be derived from the work of Bushnell and Kutzko.
Lemma 10.6. Let
![]() $\pi $
be a supercuspidal representation of
$\pi $
be a supercuspidal representation of
![]() $GL(n,F)$
for F a local field. One of the following is true:
$GL(n,F)$
for F a local field. One of the following is true:
(a) There exists a principal hereditary order
![]() $\mathfrak A \subset M_n(F)$
, a field
$\mathfrak A \subset M_n(F)$
, a field
![]() $E \subset M_n(F)$
which is an extension of F of degree
$E \subset M_n(F)$
which is an extension of F of degree
![]() $>1$
, such that
$>1$
, such that
![]() $E^\times $
normalizes
$E^\times $
normalizes
![]() $\mathfrak A$
, and, writing
$\mathfrak A$
, and, writing
![]() $\mathfrak B$
for the centralizer of E in
$\mathfrak B$
for the centralizer of E in
![]() $\mathfrak A$
and
$\mathfrak A$
and
![]() $\mathfrak P$
for the maximal ideal of
$\mathfrak P$
for the maximal ideal of
![]() $\mathfrak A$
, a representation
$\mathfrak A$
, a representation
![]() $\Lambda $
of
$\Lambda $
of
![]() $ E^\times \cdot (\mathfrak A^\times \cap (\mathfrak B + \mathfrak P) )$
such that
$ E^\times \cdot (\mathfrak A^\times \cap (\mathfrak B + \mathfrak P) )$
such that
![]() $\pi $
is the induced representation of
$\pi $
is the induced representation of
![]() $\Lambda $
.
$\Lambda $
.
(b) There exists a representation
![]() $\Lambda $
of
$\Lambda $
of
![]() $ F^\times GL_n (\mathcal O_F)$
such that
$ F^\times GL_n (\mathcal O_F)$
such that
![]() $\pi $
is the induced representation of
$\pi $
is the induced representation of
![]() $\Lambda $
.
$\Lambda $
.
Proof. By [Reference Bushnell and KutzkoBK, Theorem 8.4.1], there exists a simple type
![]() $(J, \lambda )$
in G such that
$(J, \lambda )$
in G such that
![]() $\pi \mid J$
contains
$\pi \mid J$
contains
![]() $\lambda $
. The definition [Reference Bushnell and KutzkoBK, Definition 5.5.10] of simple type splits into two cases, (a) and (b).
$\lambda $
. The definition [Reference Bushnell and KutzkoBK, Definition 5.5.10] of simple type splits into two cases, (a) and (b).
The case (b) will be easier to handle – so much so that it is not even necessary to give the definition of this case. Instead, we note that in this case, by [Reference Bushnell and KutzkoBK, Theorem 8.4.1(iii)], there exists a representation
![]() $\Lambda $
of
$\Lambda $
of
![]() $F^\times \mathbf U( \mathfrak A)$
, where
$F^\times \mathbf U( \mathfrak A)$
, where
![]() $\mathbf U( \mathfrak A)$
is the unit group of a hereditary order
$\mathbf U( \mathfrak A)$
is the unit group of a hereditary order
![]() $\mathfrak A$
, such that
$\mathfrak A$
, such that
![]() $\pi = \operatorname {Ind} (\Lambda )$
. Because
$\pi = \operatorname {Ind} (\Lambda )$
. Because
![]() $\mathfrak A$
is a hereditary order,
$\mathfrak A$
is a hereditary order,
![]() $\mathbf U(\mathfrak A)$
is a compact open subgroup of
$\mathbf U(\mathfrak A)$
is a compact open subgroup of
![]() $GL(n, F)$
and thus, up to conjugation, is contained in the maximal compact
$GL(n, F)$
and thus, up to conjugation, is contained in the maximal compact
![]() $GL_n(\mathcal O_F)$
, By first inducing
$GL_n(\mathcal O_F)$
, By first inducing
![]() $\Lambda $
from
$\Lambda $
from
![]() $F^\times \mathbf U( \mathfrak A)$
to
$F^\times \mathbf U( \mathfrak A)$
to
![]() $F^\times GL_n(\mathcal O_F)$
, we obtain case (b) above.
$F^\times GL_n(\mathcal O_F)$
, we obtain case (b) above.
Now we turn to case (a). Let A be the algebra of
![]() $n \times n$
matrices over F. In this case,
$n \times n$
matrices over F. In this case,
![]() $\mathfrak A$
is a principal
$\mathfrak A$
is a principal
![]() $\mathcal O_F$
-order in A and
$\mathcal O_F$
-order in A and
![]() $[\mathfrak A, n, 0, \beta ]$
is a simple stratum. Let us unpack this definition. The order
$[\mathfrak A, n, 0, \beta ]$
is a simple stratum. Let us unpack this definition. The order
![]() $\mathfrak A$
is a compact open
$\mathfrak A$
is a compact open
![]() $\mathcal O_F$
-subalgebra of A. We write
$\mathcal O_F$
-subalgebra of A. We write
![]() $\mathfrak P$
for the Jacobson radical of
$\mathfrak P$
for the Jacobson radical of
![]() $\mathfrak A$
. We let
$\mathfrak A$
. We let
![]() $\beta $
be an element of A and take n to be a positive integer. We define
$\beta $
be an element of A and take n to be a positive integer. We define
![]() $E = F[\beta ]$
,
$E = F[\beta ]$
,
![]() $\mathfrak B $
the centralizer of E in
$\mathfrak B $
the centralizer of E in
![]() $\mathfrak A$
, and
$\mathfrak A$
, and
![]() $\mathfrak P$
the maximal ideal of
$\mathfrak P$
the maximal ideal of
![]() $\mathfrak A$
. We set [Reference Bushnell and KutzkoBK, Definitions 1.4.3 and 1.4.5]
$\mathfrak A$
. We set [Reference Bushnell and KutzkoBK, Definitions 1.4.3 and 1.4.5]
Then the assumption that
![]() $[\mathfrak A, n, 0, \beta ]$
is a simple stratum means that
$[\mathfrak A, n, 0, \beta ]$
is a simple stratum means that
![]() $\mathfrak A$
is hereditary,
$\mathfrak A$
is hereditary,
![]() $E^\times $
normalizes
$E^\times $
normalizes
![]() $\mathfrak A$
,
$\mathfrak A$
,
![]() $v_{\mathfrak A}(\beta ) =-n$
, and
$v_{\mathfrak A}(\beta ) =-n$
, and
![]() $0< - k_0(\beta , \mathfrak A)$
[Reference Bushnell and KutzkoBK, Definition 1.5.5].
$0< - k_0(\beta , \mathfrak A)$
[Reference Bushnell and KutzkoBK, Definition 1.5.5].
In this context, [Reference Bushnell and KutzkoBK, Definition 3.1.8] defines an algebra
![]() $\mathfrak J(\beta )$
by an inductive procedure. For us, the only relevant feature of this definition is that it is contained in
$\mathfrak J(\beta )$
by an inductive procedure. For us, the only relevant feature of this definition is that it is contained in
![]() $\mathfrak B + \beta ^{ [\frac {r+1}{2} ]}$
where
$\mathfrak B + \beta ^{ [\frac {r+1}{2} ]}$
where
![]() $r = - k_0(\beta , \mathfrak A)>0$
([Reference Bushnell and KutzkoBK, 3.1.6]), and thus,
$r = - k_0(\beta , \mathfrak A)>0$
([Reference Bushnell and KutzkoBK, 3.1.6]), and thus,
![]() $\mathfrak J \subseteq \mathfrak B + \mathfrak P$
. We can next define [Reference Bushnell and KutzkoBK, (3.1.14)] a group
$\mathfrak J \subseteq \mathfrak B + \mathfrak P$
. We can next define [Reference Bushnell and KutzkoBK, (3.1.14)] a group
![]() $J( \beta , \mathfrak A)$
as the intersection of
$J( \beta , \mathfrak A)$
as the intersection of
![]() $\mathfrak J$
with the group of units
$\mathfrak J$
with the group of units
![]() $\mathbf U^0 (\mathfrak A) = \mathfrak A^\times $
.
$\mathbf U^0 (\mathfrak A) = \mathfrak A^\times $
.
We can finally state the conclusion of [Reference Bushnell and KutzkoBK, Theorem 8.4.1(ii)] in this case, which is that there is a representation
![]() $\Lambda $
of
$\Lambda $
of
![]() $E^\times J(\beta , \mathfrak A)$
such that
$E^\times J(\beta , \mathfrak A)$
such that
![]() $\pi = \operatorname {Ind}(\Lambda )$
. We will use only this structure and will not concern ourselves with the exact construction of
$\pi = \operatorname {Ind}(\Lambda )$
. We will use only this structure and will not concern ourselves with the exact construction of
![]() $\Lambda $
. If
$\Lambda $
. If
![]() $E=F$
, then, because
$E=F$
, then, because
![]() $J(\beta , \mathfrak A)$
is contained in a maximal compact subgroup, we are again in case (b), so we may assume
$J(\beta , \mathfrak A)$
is contained in a maximal compact subgroup, we are again in case (b), so we may assume
![]() $E \neq F$
.
$E \neq F$
.
Since
![]() $J(\beta , \mathfrak A)$
is contained in
$J(\beta , \mathfrak A)$
is contained in
![]() $\mathfrak A^\times \cap (\mathfrak B + \mathfrak P)$
, we can induce
$\mathfrak A^\times \cap (\mathfrak B + \mathfrak P)$
, we can induce
![]() $\Lambda $
from
$\Lambda $
from
![]() $E^\times J(\beta , \mathfrak A)$
to
$E^\times J(\beta , \mathfrak A)$
to
![]() $E^\times \cdot (\mathfrak A^\times \cap (\mathfrak B + \mathfrak P))$
, and we are in case (a) above.
$E^\times \cdot (\mathfrak A^\times \cap (\mathfrak B + \mathfrak P))$
, and we are in case (a) above.
Lemma 10.7. If
![]() $\pi $
satisfies case (b) of Lemma 10.6, then
$\pi $
satisfies case (b) of Lemma 10.6, then
![]() $\pi $
is pure and ramified.
$\pi $
is pure and ramified.
Proof. The determinants of elements of
![]() $GL_n(\mathcal O_F)$
must have zero valuation, and because
$GL_n(\mathcal O_F)$
must have zero valuation, and because
![]() $F^\times $
consists of scalars, the determinants of its elements must have valuation divisible by n. It follows that, if
$F^\times $
consists of scalars, the determinants of its elements must have valuation divisible by n. It follows that, if
![]() $\alpha $
is the character of
$\alpha $
is the character of
![]() $GL(n,F)$
defined by
$GL(n,F)$
defined by
![]() $\alpha (g) = e^{ \frac { 2 \pi i}{n} v( \det (g))}$
, then
$\alpha (g) = e^{ \frac { 2 \pi i}{n} v( \det (g))}$
, then
By [Reference Genestier and LafforgueGLa, Remarque 0.2], it follows that the Genestier-Lafforgue parameter
![]() $\sigma _\pi $
is stable under tensor-product with the one-dimensional unramified representation of
$\sigma _\pi $
is stable under tensor-product with the one-dimensional unramified representation of
![]() $W_F$
sending Frobenius to
$W_F$
sending Frobenius to
![]() $e^{ 2\pi i/n}$
. Let a be a matrix representing that isomorphism. Then
$e^{ 2\pi i/n}$
. Let a be a matrix representing that isomorphism. Then
![]() $\sigma _{\pi } (\operatorname {Frob}_q) \circ a = e^{ 2\pi i/n} a \circ \sigma _\pi (\operatorname {Frob}_q)$
, so a is conjugate to
$\sigma _{\pi } (\operatorname {Frob}_q) \circ a = e^{ 2\pi i/n} a \circ \sigma _\pi (\operatorname {Frob}_q)$
, so a is conjugate to
![]() $e^{2 \pi i/n }a$
. Thus, the set of eigenvalues of a is stable under multiplication by
$e^{2 \pi i/n }a$
. Thus, the set of eigenvalues of a is stable under multiplication by
![]() $e^{ 2\pi i/n}$
, so a has n distinct eigenvalues, and thus, a has a one-dimensional eigenspace. This one-dimensional eigenspace is a one-dimensional representation
$e^{ 2\pi i/n}$
, so a has n distinct eigenvalues, and thus, a has a one-dimensional eigenspace. This one-dimensional eigenspace is a one-dimensional representation
![]() $\chi $
of the subgroup of
$\chi $
of the subgroup of
![]() $W_F$
corresponding to the degree n unramified extension
$W_F$
corresponding to the degree n unramified extension
![]() $F_n$
of F, which, because Frobenius permutes the eigenspaces, gives an isomorphism
$F_n$
of F, which, because Frobenius permutes the eigenspaces, gives an isomorphism
![]() $\operatorname {Ind}_{ W_{F_n}}^{W_F} \chi \cong \sigma _\pi $
. Since
$\operatorname {Ind}_{ W_{F_n}}^{W_F} \chi \cong \sigma _\pi $
. Since
![]() $\chi $
is a one-dimensional representation, it is automatically pure of some weight (possibly non-integral), so
$\chi $
is a one-dimensional representation, it is automatically pure of some weight (possibly non-integral), so
![]() $\sigma _\pi $
is pure. By Theorem 1.4(i),
$\sigma _\pi $
is pure. By Theorem 1.4(i),
![]() $\sigma _\pi $
is ramified.
$\sigma _\pi $
is ramified.
We now assume given
![]() $\pi $
in case (a) of Lemma 10.6, and prepare for the construction of a Poincairé series by choosing compact subgroups at each place.
$\pi $
in case (a) of Lemma 10.6, and prepare for the construction of a Poincairé series by choosing compact subgroups at each place.
It follows from an elementary calculation or [Reference Bushnell and KutzkoBK, p. 76 and p. 183] that a principal hereditary order
![]() $\mathfrak A$
, after choosing a basis, can be put into the following form: We choose a divisor e of n, and then we take all
$\mathfrak A$
, after choosing a basis, can be put into the following form: We choose a divisor e of n, and then we take all
![]() $n\times n$
matrices decomposed into
$n\times n$
matrices decomposed into
![]() $n/e \times n/e$
blocks of size
$n/e \times n/e$
blocks of size
![]() $e \times e$
, where all the blocks on the diagonal and above have entries in the ring of integers
$e \times e$
, where all the blocks on the diagonal and above have entries in the ring of integers
![]() $\mathcal O_F$
, and all the the blocks below the diagonal have entries in the maximal ideal of
$\mathcal O_F$
, and all the the blocks below the diagonal have entries in the maximal ideal of
![]() $\mathcal O_F$
. We fix for the remainder of this argument a basis where
$\mathcal O_F$
. We fix for the remainder of this argument a basis where
![]() $\mathfrak A$
has this form.
$\mathfrak A$
has this form.
We can choose a finite field
![]() $\mathbb F_q$
such that
$\mathbb F_q$
such that
![]() $F \cong \mathbb F_q((t))$
and fix such an isomorphism. This identifies F with the local field
$F \cong \mathbb F_q((t))$
and fix such an isomorphism. This identifies F with the local field
![]() $\mathbb F_q(t)_0$
of
$\mathbb F_q(t)_0$
of
![]() $\mathbb P^1_{\mathbb F_q}$
at
$\mathbb P^1_{\mathbb F_q}$
at
![]() $0$
. We now define subgroups
$0$
. We now define subgroups
![]() $U_x$
of
$U_x$
of
![]() $GL_n(\mathbb F_q(t)_x)$
for each place x of
$GL_n(\mathbb F_q(t)_x)$
for each place x of
![]() $\mathbb F_q(t)$
. For
$\mathbb F_q(t)$
. For
![]() $x\neq 0,\infty $
, we take
$x\neq 0,\infty $
, we take
![]() $U_x$
to be the standard maximal compact subgroup. We take
$U_x$
to be the standard maximal compact subgroup. We take
![]() $U_\infty $
to consist of block-diagonal matrices in
$U_\infty $
to consist of block-diagonal matrices in
![]() $GL_n(\mathbb F_q((t^{-1})))$
where all the blocks on the diagonal and below are in
$GL_n(\mathbb F_q((t^{-1})))$
where all the blocks on the diagonal and below are in
![]() $M_e (\mathbb F_q[[t^{-1}]])$
, all the blocks above the diagonal are in
$M_e (\mathbb F_q[[t^{-1}]])$
, all the blocks above the diagonal are in
![]() $M_e ( t^{-1} \mathbb F_q[[t^{-1}]])$
, and all the diagonal blocks, modulo
$M_e ( t^{-1} \mathbb F_q[[t^{-1}]])$
, and all the diagonal blocks, modulo
![]() $t^{-1}$
are in
$t^{-1}$
are in
![]() $n/e$
fixed Borel subgroups of
$n/e$
fixed Borel subgroups of
![]() $GL_n$
, to be chosen in Lemma 10.8. We take
$GL_n$
, to be chosen in Lemma 10.8. We take
![]() $U_0$
to be
$U_0$
to be
![]() $ E^\times (\beta , \mathfrak A)$
.
$ E^\times (\beta , \mathfrak A)$
.
Let
![]() $ S= GL_n(\mathbb F_q(t)) \cap \prod _x U_x$
.
$ S= GL_n(\mathbb F_q(t)) \cap \prod _x U_x$
.
Lemma 10.8. For a suitable choice of Borel subgroups, the group S is contained in a maximal torus T of
![]() $GL_n(\mathbb F_q)$
, and furthermore, the n-dimensional vector space, when viewed as a representation of S, is a sum of
$GL_n(\mathbb F_q)$
, and furthermore, the n-dimensional vector space, when viewed as a representation of S, is a sum of
![]() $n/k$
characters each repeated k times for some
$n/k$
characters each repeated k times for some
![]() $k>1$
a divisor of n.
$k>1$
a divisor of n.
Proof. First observe that the valuation of the determinant of any element of
![]() $U_x$
for any
$U_x$
for any
![]() $x \neq 0$
is
$x \neq 0$
is
![]() $0$
. It follows that for
$0$
. It follows that for
![]() $g \in S$
,
$g \in S$
,
![]() $\det g$
has valuation
$\det g$
has valuation
![]() $0$
at every place away from
$0$
at every place away from
![]() $0$
and thus by the product formula has valuation
$0$
and thus by the product formula has valuation
![]() $0$
at
$0$
at
![]() $0$
as well. The valuation of the determinant of every element of
$0$
as well. The valuation of the determinant of every element of
![]() $\mathfrak A^\times $
is
$\mathfrak A^\times $
is
![]() $0$
, so g must be the product of an element of
$0$
, so g must be the product of an element of
![]() $\mathfrak A^\times \cap (\mathfrak B + \mathfrak P)$
with a unit
$\mathfrak A^\times \cap (\mathfrak B + \mathfrak P)$
with a unit
![]() $u \in E^\times $
. Now every unit of
$u \in E^\times $
. Now every unit of
![]() $E^\times $
is contained in
$E^\times $
is contained in
![]() $\mathfrak A^\times $
by [Reference Bushnell and KutzkoBK, Proposition 1.2.1(i)]. Because
$\mathfrak A^\times $
by [Reference Bushnell and KutzkoBK, Proposition 1.2.1(i)]. Because
![]() $u \in E^\times $
and thus u commutes with
$u \in E^\times $
and thus u commutes with
![]() $\beta $
, we have
$\beta $
, we have
![]() $u \in \mathfrak B$
. Thus,
$u \in \mathfrak B$
. Thus,
In particular, g, at
![]() $0$
, is contained in
$0$
, is contained in
![]() $\mathfrak A$
. Together with our assumptions at other places, we conclude that every matrix entry of g is integral at each place of
$\mathfrak A$
. Together with our assumptions at other places, we conclude that every matrix entry of g is integral at each place of
![]() $\mathbb F_q(t)$
and hence, in fact, lies in
$\mathbb F_q(t)$
and hence, in fact, lies in
![]() $\mathbb F_q$
, so
$\mathbb F_q$
, so
![]() $g \in GL_n(\mathbb F_q)$
. Furthermore, by the integrality conditions at
$g \in GL_n(\mathbb F_q)$
. Furthermore, by the integrality conditions at
![]() $0$
, we see that every
$0$
, we see that every
![]() $e \times e$
block of g below the diagonal vanishes, and by the integrality conditions at
$e \times e$
block of g below the diagonal vanishes, and by the integrality conditions at
![]() $\infty $
, every
$\infty $
, every
![]() $e \times e$
block of g above the diagonal vanishes. So g is a block-diagonal matrix (i.e.,
$e \times e$
block of g above the diagonal vanishes. So g is a block-diagonal matrix (i.e.,
![]() $g \in (GL_e(\mathbb F_q))^{n/e} $
). Furthermore, each of the diagonal matrices must be contained in some fixed Borel, to be chosen later.
$g \in (GL_e(\mathbb F_q))^{n/e} $
). Furthermore, each of the diagonal matrices must be contained in some fixed Borel, to be chosen later.
We now use the fact that
![]() $E/F$
is a nontrivial extension. Thus, it either ramifies or contains an extension of the residue field.
$E/F$
is a nontrivial extension. Thus, it either ramifies or contains an extension of the residue field.
We handle the case when E is ramified first. In this case, E contains an element x whose determinant does not have valuation divisible by n, and thus the action of x on
![]() $\mathfrak A$
must permute the
$\mathfrak A$
must permute the
![]() $n/e$
diagonal blocks. The action on the blocks divides them into
$n/e$
diagonal blocks. The action on the blocks divides them into
![]() $n/(ek)$
orbits of size k for some
$n/(ek)$
orbits of size k for some
![]() $k>1$
dividing
$k>1$
dividing
![]() $n/e$
. Because elements of
$n/e$
. Because elements of
![]() $\mathfrak B$
commute with E, and thus in particular with x, their value mod
$\mathfrak B$
commute with E, and thus in particular with x, their value mod
![]() $\mathfrak p_F$
on one block in the orbit determines their value on every other block in the orbit. So, mod
$\mathfrak p_F$
on one block in the orbit determines their value on every other block in the orbit. So, mod
![]() $\mathfrak P$
, the elements of
$\mathfrak P$
, the elements of
![]() $\mathfrak B$
lie in
$\mathfrak B$
lie in
![]() $M_e(\mathbb F_q)^{n/(ek)}$
, and the units of
$M_e(\mathbb F_q)^{n/(ek)}$
, and the units of
![]() $\mathfrak B$
lie in
$\mathfrak B$
lie in
![]() $GL_e(\mathbb F_q)^{n/(ek)}$
. To define
$GL_e(\mathbb F_q)^{n/(ek)}$
. To define
![]() $U_{\infty }$
, we choose
$U_{\infty }$
, we choose
![]() $n/e$
Borel subgroups of
$n/e$
Borel subgroups of
![]() $GL_e(\mathbb F_q)$
such that, in each orbit, at least one of the Borel subgroups is sent by x to a Borel in general position with respect to the next Borel in the orbit. It follows that each element of
$GL_e(\mathbb F_q)$
such that, in each orbit, at least one of the Borel subgroups is sent by x to a Borel in general position with respect to the next Borel in the orbit. It follows that each element of
![]() $S \subset GL_e(\mathbb F_q)^{n/(ek)}$
lies in the intersection of two Borels in general position and thus lies in the maximal torus, which is contained in a maximal torus of
$S \subset GL_e(\mathbb F_q)^{n/(ek)}$
lies in the intersection of two Borels in general position and thus lies in the maximal torus, which is contained in a maximal torus of
![]() $GL_n$
. Furthermore, the n-dimensional representation of S is the restriction of the n-dimensional representation of
$GL_n$
. Furthermore, the n-dimensional representation of S is the restriction of the n-dimensional representation of
![]() $GL_e(\mathbb F_q)^{n/(ek)}$
, which is the sum of
$GL_e(\mathbb F_q)^{n/(ek)}$
, which is the sum of
![]() $n/(ek)$
standard representations, each repeated k times, so as a representation of S, it is the sum of
$n/(ek)$
standard representations, each repeated k times, so as a representation of S, it is the sum of
![]() $n/k$
characters, each repeated k times, as desired.
$n/k$
characters, each repeated k times, as desired.
We handle the case when E contains a residue field extension
![]() $\mathbb F_{q^k}$
next. In this case, E contains an element x which generates the residue field extension. Because x is a unit, x lies in
$\mathbb F_{q^k}$
next. In this case, E contains an element x which generates the residue field extension. Because x is a unit, x lies in
![]() $\mathfrak A$
. Restricting to each of the
$\mathfrak A$
. Restricting to each of the
![]() $n/e$
diagonal blocks and modding out by
$n/e$
diagonal blocks and modding out by
![]() $\mathfrak p_F$
, the element x satisfies the characteristic polynomial of a generator of
$\mathfrak p_F$
, the element x satisfies the characteristic polynomial of a generator of
![]() $\mathbb F_{q^k}$
and thus generates a subfield isomorphic to
$\mathbb F_{q^k}$
and thus generates a subfield isomorphic to
![]() $\mathbb F_{q^k}$
. Thus, the centralizer of x in each block is isomorphic to
$\mathbb F_{q^k}$
. Thus, the centralizer of x in each block is isomorphic to
![]() $GL_{e/k}(\mathbb F_{q^k})$
, and every unit in
$GL_{e/k}(\mathbb F_{q^k})$
, and every unit in
![]() $\mathfrak B + \mathfrak P$
, restricted to each diagonal block and reduced modulo
$\mathfrak B + \mathfrak P$
, restricted to each diagonal block and reduced modulo
![]() $\mathfrak p_F$
, must lie in this
$\mathfrak p_F$
, must lie in this
![]() $GL_{e/k}(\mathbb F_{q^k})$
.
$GL_{e/k}(\mathbb F_{q^k})$
.
We choose a Borel as follows: Fix a
![]() $\mathbb F_{q^k}$
-basis of the e-dimensional vector space
$\mathbb F_{q^k}$
-basis of the e-dimensional vector space
![]() $v_1,\dots , v_{e/k}$
, and then extend the sequence
$v_1,\dots , v_{e/k}$
, and then extend the sequence
arbitrarily to an
![]() $\mathbb F_q$
-basis of this space. For each block, choose a Borel consisting of linear transformations which are upper-triangular with respect to this basis, and use these to define
$\mathbb F_q$
-basis of this space. For each block, choose a Borel consisting of linear transformations which are upper-triangular with respect to this basis, and use these to define
![]() $U_{\infty }$
. Then every
$U_{\infty }$
. Then every
![]() $g \in S$
, restricted to this block, will lie in the intersection of
$g \in S$
, restricted to this block, will lie in the intersection of
![]() $GL_{e/k}( \mathbb F_{q^k})$
with this Borel. Hence, g will be upper-triangular with respect to the
$GL_{e/k}( \mathbb F_{q^k})$
with this Borel. Hence, g will be upper-triangular with respect to the
![]() $\mathbb F_{q^k}$
-basis
$\mathbb F_{q^k}$
-basis
![]() $v_1,\dots , v_k$
and upper-triangular with respect to the
$v_1,\dots , v_k$
and upper-triangular with respect to the
![]() $\mathbb F_{q^k}$
-basis
$\mathbb F_{q^k}$
-basis
![]() $xv_{e/k}, x v_{e/k-1},\dots , xv_1$
, and thus
$xv_{e/k}, x v_{e/k-1},\dots , xv_1$
, and thus
![]() $\mathbb F_{q^k}$
-diagonal with respect to the basis
$\mathbb F_{q^k}$
-diagonal with respect to the basis
![]() $v_1,\dots , v_k$
. Furthermore, g must act on
$v_1,\dots , v_k$
. Furthermore, g must act on
![]() $v_1,\dots , v_k$
by multiplication by elements of
$v_1,\dots , v_k$
by multiplication by elements of
![]() $\mathbb F_q$
, since otherwise it would not preserve the
$\mathbb F_q$
, since otherwise it would not preserve the
![]() $\mathbb F_q$
-subspace generated by
$\mathbb F_q$
-subspace generated by
![]() $v_1,\dots , v_k$
. So, in fact, g is contained in the diagonal of
$v_1,\dots , v_k$
. So, in fact, g is contained in the diagonal of
![]() $GL_{e/k}(\mathbb F_q)$
inside
$GL_{e/k}(\mathbb F_q)$
inside
![]() $GL_{e/k}(\mathbb F_{q^k}) $
inside
$GL_{e/k}(\mathbb F_{q^k}) $
inside
![]() $GL_e(\mathbb F_q)$
. Passing from
$GL_e(\mathbb F_q)$
. Passing from
![]() $GL_{e/k}(\mathbb F_q)$
to
$GL_{e/k}(\mathbb F_q)$
to
![]() $GL_e(\mathbb F_q)$
in this way sends the maximal torus to a subset of the maximal torus, as desired, and expresses the e-dimensional standard representation of
$GL_e(\mathbb F_q)$
in this way sends the maximal torus to a subset of the maximal torus, as desired, and expresses the e-dimensional standard representation of
![]() $GL_e$
as a sum of k copies of the
$GL_e$
as a sum of k copies of the
![]() $e/k$
-dimensional standard representation of
$e/k$
-dimensional standard representation of
![]() $GL_{e/k}$
. Hence, the sum of k copies of
$GL_{e/k}$
. Hence, the sum of k copies of
![]() $e/k$
characters of S, as desired.
$e/k$
characters of S, as desired.
Note that
![]() $U_\infty $
is an Iwahori subgroup of
$U_\infty $
is an Iwahori subgroup of
![]() $GL_n ( \mathbb F_q((t^{-1})))$
and thus surjects onto
$GL_n ( \mathbb F_q((t^{-1})))$
and thus surjects onto
![]() $((\mathbb F_q)^\times )^n$
.
$((\mathbb F_q)^\times )^n$
.
Lemma 10.9. If
![]() $q>2$
, any (one-dimensional) character of S may be extended to a nontrivial character of
$q>2$
, any (one-dimensional) character of S may be extended to a nontrivial character of
![]() $U_\infty $
.
$U_\infty $
.
Furthermore, if
![]() $q>3$
, any character of S may be extended to two characters,
$q>3$
, any character of S may be extended to two characters,
![]() $\chi _a,\chi _b$
, both pulled back from
$\chi _a,\chi _b$
, both pulled back from
![]() $((\mathbb F_q)^\times )^n$
, where
$((\mathbb F_q)^\times )^n$
, where
![]() $\chi _a$
is trivial on at least one copy of
$\chi _a$
is trivial on at least one copy of
![]() $\mathbb F_q^\times $
and
$\mathbb F_q^\times $
and
![]() $\chi _b$
is trivial on no copies of
$\chi _b$
is trivial on no copies of
![]() $\mathbb F_q^\times $
.
$\mathbb F_q^\times $
.
Proof. For each case, note that the subgroup
![]() $U_{\infty }$
is an Iwahori subgroup of
$U_{\infty }$
is an Iwahori subgroup of
![]() $GL_n ( \mathbb F_q((t^{-1})))$
, so its quotient by its maximal pro-p subgroup is
$GL_n ( \mathbb F_q((t^{-1})))$
, so its quotient by its maximal pro-p subgroup is
![]() $((\mathbb F_q)^\times )^n$
. Since S is a subgroup of the maximal torus of
$((\mathbb F_q)^\times )^n$
. Since S is a subgroup of the maximal torus of
![]() $GL_n(\mathbb F_q)$
by Lemma 10.8, its order is prime to p, and so the quotient of
$GL_n(\mathbb F_q)$
by Lemma 10.8, its order is prime to p, and so the quotient of
![]() $U_{\infty }$
by its maximal pro-p subgroup is faithful. Thus,
$U_{\infty }$
by its maximal pro-p subgroup is faithful. Thus,
![]() $\chi _S$
is a character of the image of S inside
$\chi _S$
is a character of the image of S inside
![]() $((\mathbb F_q)^\times )^n$
.
$((\mathbb F_q)^\times )^n$
.
For the first case, it suffices to extend
![]() $\chi _S^{-1}$
to a nontrivial character of
$\chi _S^{-1}$
to a nontrivial character of
![]() $(\mathbb F_q^\times )^n$
and inflate to
$(\mathbb F_q^\times )^n$
and inflate to
![]() $U_{\infty }$
. We can do this unless
$U_{\infty }$
. We can do this unless
![]() $\chi _S$
is trivial and
$\chi _S$
is trivial and
![]() $S = ((\mathbb F_q)^\times )^n$
, which contradicts our claim that the characters of S are repeated unless
$S = ((\mathbb F_q)^\times )^n$
, which contradicts our claim that the characters of S are repeated unless
![]() $\mathbb F_q^\times $
is trivial, which implies
$\mathbb F_q^\times $
is trivial, which implies
![]() $q=2$
.
$q=2$
.
For the second case, if
![]() $q>3$
, note that since the standard representation of S is the sum of
$q>3$
, note that since the standard representation of S is the sum of
![]() $n/k$
characters repeated k times, the image of S inside
$n/k$
characters repeated k times, the image of S inside
![]() $(\mathbb F_q^\times )^n$
is contained in
$(\mathbb F_q^\times )^n$
is contained in
![]() $(\mathbb F_q^\times )^{n/k}$
, repeated k times. It follows that when we extend
$(\mathbb F_q^\times )^{n/k}$
, repeated k times. It follows that when we extend
![]() $\chi _S^{-1}$
to a character
$\chi _S^{-1}$
to a character
![]() $\chi $
of
$\chi $
of
![]() $(\mathbb F_q^\times )^n$
, which can be viewed as a tuple of n characters
$(\mathbb F_q^\times )^n$
, which can be viewed as a tuple of n characters
![]() $\chi _1,\dots , \chi _n$
of
$\chi _1,\dots , \chi _n$
of
![]() $\mathbb F_q$
, we can choose any tuple of characters as long as the product of k characters in each of
$\mathbb F_q$
, we can choose any tuple of characters as long as the product of k characters in each of
![]() $n/k$
orbits takes some fixed value depending on the orbit. So we can certainly choose
$n/k$
orbits takes some fixed value depending on the orbit. So we can certainly choose
![]() $k-1$
of the characters in each orbit to be trivial, and the last one to take the fixed value, to produce
$k-1$
of the characters in each orbit to be trivial, and the last one to take the fixed value, to produce
![]() $\chi _a$
. To produce
$\chi _a$
. To produce
![]() $\chi _b$
, we choose
$\chi _b$
, we choose
![]() $k-2$
of the characters in each orbit to be an arbitrary nontrivial character. The product of the two remaining characters is then determined. Since
$k-2$
of the characters in each orbit to be an arbitrary nontrivial character. The product of the two remaining characters is then determined. Since
![]() $q>3$
, there are more than two characters, and so we can choose the next character to be a character which is neither trivial nor the determined product. It follows that the last character is nontrivial, so
$q>3$
, there are more than two characters, and so we can choose the next character to be a character which is neither trivial nor the determined product. It follows that the last character is nontrivial, so
![]() $\chi _b$
indeed contains no trivial characters.
$\chi _b$
indeed contains no trivial characters.
We are now ready to construct our Poincaré series. Since S is a finite abelian group,
![]() $\lambda $
restricted to
$\lambda $
restricted to
![]() $S \subset E^\times J(\beta , \mathfrak A)$
is a sum of one-dimensional characters. Let
$S \subset E^\times J(\beta , \mathfrak A)$
is a sum of one-dimensional characters. Let
![]() $\chi _S$
be one of these.
$\chi _S$
be one of these.
Proposition 10.10. Assume the residue field of F has more than
![]() $2$
elements. Then every supercuspidal representation of
$2$
elements. Then every supercuspidal representation of
![]() $GL(n,F)$
is ramified. Moreover, if the residue field of F has more than
$GL(n,F)$
is ramified. Moreover, if the residue field of F has more than
![]() $3$
elements, then every supercuspidal representation of
$3$
elements, then every supercuspidal representation of
![]() $GL(n,F)$
is either ramified and pure or wildly ramified.
$GL(n,F)$
is either ramified and pure or wildly ramified.
Proof. Let
![]() $F = \mathbb F_q((t))$
. Fix a supercuspidal rerpesentation
$F = \mathbb F_q((t))$
. Fix a supercuspidal rerpesentation
![]() $\pi $
. We apply Lemma 10.6. In case (b),
$\pi $
. We apply Lemma 10.6. In case (b),
![]() $\pi $
is pure and ramified by Lemma 10.7, so we may reduce to case (a), where we will prove that
$\pi $
is pure and ramified by Lemma 10.7, so we may reduce to case (a), where we will prove that
![]() $\pi $
is ramified if
$\pi $
is ramified if
![]() $q>2$
and wildly ramified if
$q>2$
and wildly ramified if
![]() $q>3$
.
$q>3$
.
To do this, we construct a Poincaré series, using all the notation above. Since S is a finite abelian group,
![]() $\lambda $
restricted to
$\lambda $
restricted to
![]() $S \subset E^\times J(\beta , \mathfrak A)$
is a sum of one-dimensional characters. Let
$S \subset E^\times J(\beta , \mathfrak A)$
is a sum of one-dimensional characters. Let
![]() $\chi _S$
be one of these. We extend
$\chi _S$
be one of these. We extend
![]() $\chi _S^{-1}$
to a nontrivial character
$\chi _S^{-1}$
to a nontrivial character
![]() $\chi $
of
$\chi $
of
![]() $U_\infty $
using Lemma 10.9. We take the representation
$U_\infty $
using Lemma 10.9. We take the representation
![]() $\lambda \otimes \chi $
of
$\lambda \otimes \chi $
of
![]() $\prod _x U_x$
, which is trivial by construction on
$\prod _x U_x$
, which is trivial by construction on
![]() $S =GL_n(F) \cap \prod _x U_x$
. Using a matrix coefficient of this representation, we can construct a Poincaré series. After decomposing into Hecke eigenforms, this series generates an automorphic representation
$S =GL_n(F) \cap \prod _x U_x$
. Using a matrix coefficient of this representation, we can construct a Poincaré series. After decomposing into Hecke eigenforms, this series generates an automorphic representation
![]() $\Pi $
which is unramified outside of
$\Pi $
which is unramified outside of
![]() $0$
and
$0$
and
![]() $\infty $
, of type
$\infty $
, of type
![]() $\operatorname {Ind} (\lambda ) = \pi $
at
$\operatorname {Ind} (\lambda ) = \pi $
at
![]() $0$
, and whose local factor at
$0$
, and whose local factor at
![]() $\infty $
contains a vector that transforms according to
$\infty $
contains a vector that transforms according to
![]() $\chi $
under
$\chi $
under
![]() $U_{\infty }$
. By Lafforgue, associated to this representation is a global parameter
$U_{\infty }$
. By Lafforgue, associated to this representation is a global parameter
![]() $\sigma _\Pi $
which matches
$\sigma _\Pi $
which matches
![]() $\sigma _\pi $
at
$\sigma _\pi $
at
![]() $0$
, and is unramified away from
$0$
, and is unramified away from
![]() $0$
and
$0$
and
![]() $\infty $
.
$\infty $
.
Furthermore, at
![]() $\infty $
, the local factor of
$\infty $
, the local factor of
![]() $\Pi $
is contained in a parabolic induction from the Borel of a tamely ramified character of the maximal torus, which, restricted to the
$\Pi $
is contained in a parabolic induction from the Borel of a tamely ramified character of the maximal torus, which, restricted to the
![]() $\mathbb F_q$
-points of the maximal torus, is
$\mathbb F_q$
-points of the maximal torus, is
![]() $\chi $
. Thus, by the compatibility of Genestier-Lafforgue with parabolic induction and the local Langlands correspondence for
$\chi $
. Thus, by the compatibility of Genestier-Lafforgue with parabolic induction and the local Langlands correspondence for
![]() $GL_1$
, the Genestier-Lafforgue parameter at
$GL_1$
, the Genestier-Lafforgue parameter at
![]() $\infty $
is a sum of n tamely ramified characters whose restriction to the inertia group is trivial if and only if the restriction of
$\infty $
is a sum of n tamely ramified characters whose restriction to the inertia group is trivial if and only if the restriction of
![]() $\chi $
to the corresponding copy of
$\chi $
to the corresponding copy of
![]() $ \mathbb F_q^\times $
is trivial. Thus, the restriction of the global parameter
$ \mathbb F_q^\times $
is trivial. Thus, the restriction of the global parameter
![]() $\sigma _\Pi $
to
$\sigma _\Pi $
to
![]() $\infty $
is tamely ramified and is unipotent if and only if
$\infty $
is tamely ramified and is unipotent if and only if
![]() $\chi $
is trivial.
$\chi $
is trivial.
If
![]() $\pi $
is unramified, then
$\pi $
is unramified, then
![]() $\sigma _\Pi $
is unramified away from
$\sigma _\Pi $
is unramified away from
![]() $0$
and
$0$
and
![]() $\infty $
and has at worst unipotent ramification at
$\infty $
and has at worst unipotent ramification at
![]() $0$
. Because
$0$
. Because
![]() $\sigma _\Pi $
is unramified away from
$\sigma _\Pi $
is unramified away from
![]() $0$
and
$0$
and
![]() $\infty $
and tamely ramified at
$\infty $
and tamely ramified at
![]() $0$
and
$0$
and
![]() $\infty $
, the restrictions of
$\infty $
, the restrictions of
![]() $\sigma _\Pi $
to the inertia groups at
$\sigma _\Pi $
to the inertia groups at
![]() $0$
and
$0$
and
![]() $\infty $
are isomorphic, which contradicts the fact that
$\infty $
are isomorphic, which contradicts the fact that
![]() $\sigma _\Pi $
is unipotent at
$\sigma _\Pi $
is unipotent at
![]() $0$
and
$0$
and
![]() $\sigma _\Pi $
is non-unipotent at
$\sigma _\Pi $
is non-unipotent at
![]() $\infty $
. So, in fact,
$\infty $
. So, in fact,
![]() $\sigma _\pi $
is ramified.
$\sigma _\pi $
is ramified.
If
![]() $q>3$
and
$q>3$
and
![]() $\pi $
is tamely ramified, then we apply the second case of Lemma 10.9 to produce two characters,
$\pi $
is tamely ramified, then we apply the second case of Lemma 10.9 to produce two characters,
![]() $\chi _a$
and
$\chi _a$
and
![]() $\chi _b$
, and follow the same procedure above to produce two globalizations
$\chi _b$
, and follow the same procedure above to produce two globalizations
![]() $\Pi _a, \Pi _b$
. Again,
$\Pi _a, \Pi _b$
. Again,
![]() $\sigma _{\Pi _a},\sigma _{\Pi _b}$
are tame at
$\sigma _{\Pi _a},\sigma _{\Pi _b}$
are tame at
![]() $0$
and
$0$
and
![]() $\infty $
, so the restrictions of
$\infty $
, so the restrictions of
![]() $\sigma _{\Pi _a}$
to the inertia subgroup at
$\sigma _{\Pi _a}$
to the inertia subgroup at
![]() $\infty $
is isomorphic to its restriction to the inertia subgroup at
$\infty $
is isomorphic to its restriction to the inertia subgroup at
![]() $0$
and thus isomorphic, up to semisimplification, to
$0$
and thus isomorphic, up to semisimplification, to
![]() $\sigma _\pi $
. The same is true for
$\sigma _\pi $
. The same is true for
![]() $\sigma _{\Pi _b}$
, so
$\sigma _{\Pi _b}$
, so
![]() $\sigma _{\Pi _a}$
and
$\sigma _{\Pi _a}$
and
![]() $\sigma _{\Pi _b}$
are isomorphic up to semisimplification. However, the semisimplification of
$\sigma _{\Pi _b}$
are isomorphic up to semisimplification. However, the semisimplification of
![]() $\sigma _{\Pi _a}$
is a sum of one-dimensional characters, at least one trivial, whereas the semisimplification of
$\sigma _{\Pi _a}$
is a sum of one-dimensional characters, at least one trivial, whereas the semisimplification of
![]() $\sigma _{\Pi _b}$
is a sum of one-dimesional characters, all nontrivial, so they cannot be isomorphic. This is a contradiction; hence,
$\sigma _{\Pi _b}$
is a sum of one-dimesional characters, all nontrivial, so they cannot be isomorphic. This is a contradiction; hence,
![]() $\pi $
is wildly ramified in this case.
$\pi $
is wildly ramified in this case.
Corollary 10.11. Let
![]() $\pi $
be a supercuspidal representation of
$\pi $
be a supercuspidal representation of
![]() $GL(n,F)$
. Then there is a sequence of cyclic extensions as in (10.4) such that
$GL(n,F)$
. Then there is a sequence of cyclic extensions as in (10.4) such that
![]() $BC_{F_r/F}(\pi )$
is an irreducible constituent of an unramified principal series representation.
$BC_{F_r/F}(\pi )$
is an irreducible constituent of an unramified principal series representation.
Proof. By 7.12 and induction, we know that we can find a sequence of cyclic extensions as in (10.4) such that
![]() $BC_{F_r/F}(\pi )$
is an irreducible constituent of a principal series representation whose parameter is unramified. By Proposition 10.10, such a principal series must be a parabolic induction from the Borel, as a supercuspidal on any Levi except the maximal torus would have a ramified Langlands parameter. By the local Langlands conjecture for
$BC_{F_r/F}(\pi )$
is an irreducible constituent of a principal series representation whose parameter is unramified. By Proposition 10.10, such a principal series must be a parabolic induction from the Borel, as a supercuspidal on any Levi except the maximal torus would have a ramified Langlands parameter. By the local Langlands conjecture for
![]() $GL_1$
, it must be an induction of an unramified representation of the maximal torus (i.e., an unramified principal series).
$GL_1$
, it must be an induction of an unramified representation of the maximal torus (i.e., an unramified principal series).
Corollary 10.11 is the key point in (almost) every proof of the local Langlands correspondence for
![]() $GL(n)$
. It was already mentioned in the introduction that in [Reference Laumon, Rapoport and StuhlerLRS93, Reference Harris and TaylorHT01, Reference HenniartHe00], this result is obtained as a consequence of Henniart’s numerical correspondence, whereas in [Reference ScholzeSch13], it is proved by a geometric argument involving nearby cycles in the local model. Starting with Corollary 10.11, one obtains the full local correspondence by an inductive study of the fibers of local base change.
$GL(n)$
. It was already mentioned in the introduction that in [Reference Laumon, Rapoport and StuhlerLRS93, Reference Harris and TaylorHT01, Reference HenniartHe00], this result is obtained as a consequence of Henniart’s numerical correspondence, whereas in [Reference ScholzeSch13], it is proved by a geometric argument involving nearby cycles in the local model. Starting with Corollary 10.11, one obtains the full local correspondence by an inductive study of the fibers of local base change.
Here, we obtain Corollary 10.11 by a completely different argument, based on the geometric considerations of [Reference LafforgueLaf18], the global base change of [Reference Henniart and LemaireHeLe] and the existence of types for supercuspidal representations [Reference Bushnell and KutzkoBK]. It is questionable whether this argument is genuinely new because the existence of the global parametrization in [Reference LafforgueLaf18], combined with the converse theorem as in [Reference LafforgueLaf02], already suffices to prove the local as well as the global correspondence. However, the reasoning used here can be applied to any G for which global base change and the existence of types is known.
11 Applications to groups over p-adic fields
In this final section, we speculate on how our results in positive characteristic could have impact on analogous questions in characteristic zero local fields, via the principle of close local fields.
Let
![]() $F = k((t))$
be a local field of characteristic p as before and let
$F = k((t))$
be a local field of characteristic p as before and let
![]() $F^\sharp $
be a p-adic field. We write
$F^\sharp $
be a p-adic field. We write
![]() ${\mathcal {O}}_F, {\mathcal {O}}_{F^\sharp }$
for their integer rings, and
${\mathcal {O}}_F, {\mathcal {O}}_{F^\sharp }$
for their integer rings, and
![]() $m_F$
,
$m_F$
,
![]() $m_{F^\sharp }$
for the corresponding maximal ideals.
$m_{F^\sharp }$
for the corresponding maximal ideals.
Definition 11.1. Let n be a positive integer. We say that F and
![]() $F^\sharp $
are
$F^\sharp $
are
![]() ${n}$
-close if
${n}$
-close if
as rings.
We write
![]() $F^?$
for either F or
$F^?$
for either F or
![]() $F^\sharp $
. Let G be a connected reductive group over
$F^\sharp $
. Let G be a connected reductive group over
![]() $F^?$
. The depth of a parameter
$F^?$
. The depth of a parameter
![]() $\phi \in {\mathcal {G}}^{ss}(G,F)$
is defined to be the maximum n such that
$\phi \in {\mathcal {G}}^{ss}(G,F)$
is defined to be the maximum n such that
![]() $\phi $
is trivial on the subgroup
$\phi $
is trivial on the subgroup
![]() $I_{F^?}^n$
of the inertia group
$I_{F^?}^n$
of the inertia group
![]() $I_{F^?}$
, where we are using the upper numbering. Let
$I_{F^?}$
, where we are using the upper numbering. Let
![]() ${\mathcal {G}}^{ss,n}(G,F) \subset {\mathcal {G}}^{ss}(G,F)$
denote the subset of parameters of depth at most n.
${\mathcal {G}}^{ss,n}(G,F) \subset {\mathcal {G}}^{ss}(G,F)$
denote the subset of parameters of depth at most n.
Theorem 11.2 (Deligne).
If F and
![]() $F^\sharp $
are n-close, then there is a natural bijection
$F^\sharp $
are n-close, then there is a natural bijection
Assume now that G is split and let
![]() $I_n(F^?) \subset G({\mathcal {O}}_{F^?})$
denote the n-th Iwahori filtration subgroup, as defined in [Reference GanapathyG, §3]; thus,
$I_n(F^?) \subset G({\mathcal {O}}_{F^?})$
denote the n-th Iwahori filtration subgroup, as defined in [Reference GanapathyG, §3]; thus,
![]() $I = I_0$
is the usual Iwahori subgroup, and
$I = I_0$
is the usual Iwahori subgroup, and
![]() $I_n$
is the kernel of the reduction map
$I_n$
is the kernel of the reduction map
![]() $\mathbf {I}({\mathcal {O}}_{F^?}) {~\rightarrow ~} \mathbf {I}({\mathcal {O}}_{F^?}/m_{F^?}^n).$
Let
$\mathbf {I}({\mathcal {O}}_{F^?}) {~\rightarrow ~} \mathbf {I}({\mathcal {O}}_{F^?}/m_{F^?}^n).$
Let
![]() $H(G(F^?),I_n)$
denote the Hecke algebra of
$H(G(F^?),I_n)$
denote the Hecke algebra of
![]() $I_n(F^?)$
-biinvariant functions on
$I_n(F^?)$
-biinvariant functions on
![]() $G(F^?)$
with coefficients in the algebraically closed field C. Let
$G(F^?)$
with coefficients in the algebraically closed field C. Let
![]() ${\mathcal {A}}^n(G,F^?) \subset {\mathcal {A}}(G,F)$
denote the subset of equivalence classes of irreducible admissible representations generated by vectors fixed under
${\mathcal {A}}^n(G,F^?) \subset {\mathcal {A}}(G,F)$
denote the subset of equivalence classes of irreducible admissible representations generated by vectors fixed under
![]() $I_n(F^?)$
. Any
$I_n(F^?)$
. Any
![]() $\pi \in {\mathcal {A}}^n(G,F^?)$
is then determined up to isomorphism by the representation of
$\pi \in {\mathcal {A}}^n(G,F^?)$
is then determined up to isomorphism by the representation of
![]() $H(G(F^?),I_n)$
on its invariant subspace
$H(G(F^?),I_n)$
on its invariant subspace
![]() $\pi ^{I_n(F^?)}$
. The following is Ganapathy’s refinement of a theorem of Kazhdan:
$\pi ^{I_n(F^?)}$
. The following is Ganapathy’s refinement of a theorem of Kazhdan:
Theorem 11.4 (Ganapathy-Kazhdan, [Reference GanapathyG]).
If
![]() $F^\sharp $
and F are n-close, then there is a natural isomorphism
$F^\sharp $
and F are n-close, then there is a natural isomorphism
of finitely-generated C-algebras. Moreover, there is a bijection
with the property that, if
![]() $\pi \in {\mathcal {A}}^n(G,F)$
corresponds to
$\pi \in {\mathcal {A}}^n(G,F)$
corresponds to
![]() $\pi ^\sharp \in {\mathcal {A}}^n(G,F^\sharp )$
, then the invariant subspaces
$\pi ^\sharp \in {\mathcal {A}}^n(G,F^\sharp )$
, then the invariant subspaces
![]() $\pi ^{I_n(F)}$
and
$\pi ^{I_n(F)}$
and
![]() $\pi ^{\sharp ,I_n(F^\sharp )}$
are isomorphic as modules with respect to the isomorphism (11.5).
$\pi ^{\sharp ,I_n(F^\sharp )}$
are isomorphic as modules with respect to the isomorphism (11.5).
In view of these results, it would be unnatural not to make the following conjecture:
Conjecture 11.7. For any positive integer n, the following diagram commutes:

Here, the top line is the parametrization of Genestier and Lafforgue (Theorem 2.1 (iii)), while the bottom line is the parametrization defined by Fargues and Scholze in [Reference Fargues and ScholzeFS] for groups over p-adic fields. Fargues and Scholze have also constructed a semisimple parametrization for groups over local fields of positive characteristic. Li Huerta has shown in [Reference Li HuertaLH23] that this latter parametrization is compatible with Lafforgue’s global parametrization and therefore coincides with the Genestier-Lafforgue parametrization. Thus, Conjecture 11.7 also asserts that the two Fargues-Scholze parametrizations are compatible with the Deligne-Kazhdan correspondence.
The following corollary is an immediate consequence of the conjecture and the results of the previous sections.
Corollary 11.8. Let
![]() $F^\sharp $
be a finite extension of
$F^\sharp $
be a finite extension of
![]() ${{\mathbb Q}_p}$
with residue field k of characteristic p. Let
${{\mathbb Q}_p}$
with residue field k of characteristic p. Let
![]() $n \geq 0$
and assume there is a local field F of characteristic p such that
$n \geq 0$
and assume there is a local field F of characteristic p such that
![]() $F^\sharp $
and F are n-close. Let G be a split semisimple group over F. Suppose
$F^\sharp $
and F are n-close. Let G be a split semisimple group over F. Suppose
![]() $|k|> 5$
and p does not divide the order of the Weyl group of G. Finally, suppose Conjecture 11.7 holds for the p-adic field
$|k|> 5$
and p does not divide the order of the Weyl group of G. Finally, suppose Conjecture 11.7 holds for the p-adic field
![]() $F^\sharp $
.
$F^\sharp $
.
Let
![]() $\sigma $
be a supercuspidal representation of
$\sigma $
be a supercuspidal representation of
![]() $G(F^\sharp )$
. Suppose the semisimple Fargues-Scholze parameter
$G(F^\sharp )$
. Suppose the semisimple Fargues-Scholze parameter
![]() ${\mathcal {L}}^{ss}(\sigma )$
attached to
${\mathcal {L}}^{ss}(\sigma )$
attached to
![]() $\sigma $
is pure. Then
$\sigma $
is pure. Then
![]() ${\mathcal {L}}^{ss}(\sigma )$
is ramified.
${\mathcal {L}}^{ss}(\sigma )$
is ramified.
More generally, let
![]() $\sigma $
be any pure irreducible representation of
$\sigma $
be any pure irreducible representation of
![]() $G(F^\sharp )$
with unramified Fargues-Scholze parameter. Then
$G(F^\sharp )$
with unramified Fargues-Scholze parameter. Then
![]() $\sigma $
is an irreducible constituent of an unramified principal series representation.
$\sigma $
is an irreducible constituent of an unramified principal series representation.
Since every p-adic field has a local field F of characteristic p that is
![]() $0$
-close to
$0$
-close to
![]() $F^\sharp $
, we have the following special case of Corollary 11.8
$F^\sharp $
, we have the following special case of Corollary 11.8
Corollary 11.9. Let
![]() $F^\sharp $
be a finite extension of
$F^\sharp $
be a finite extension of
![]() ${{\mathbb Q}_p}$
with residue field k of characteristic p. Let G be a split semisimple group over F. Suppose
${{\mathbb Q}_p}$
with residue field k of characteristic p. Let G be a split semisimple group over F. Suppose
![]() $|k|> 5$
and p does not divide the order of the Weyl group of G. Finally, suppose Conjecture 11.7 holds for the p-adic field
$|k|> 5$
and p does not divide the order of the Weyl group of G. Finally, suppose Conjecture 11.7 holds for the p-adic field
![]() $F^\sharp $
. Then any pure depth zero supercuspidal representation of
$F^\sharp $
. Then any pure depth zero supercuspidal representation of
![]() $G(F^\sharp )$
has ramified Fargues-Scholze parameter.
$G(F^\sharp )$
has ramified Fargues-Scholze parameter.
One can hope to derive consequences of Conjecture 11.7 for general supercuspidal representations of a general p-adic field
![]() $F^\sharp $
, replacing
$F^\sharp $
, replacing
![]() $F^\sharp $
by a Galois extension
$F^\sharp $
by a Galois extension
![]() $F'$
with an n-close F for any n. This is the strategy followed by Henniart in his proof of the numerical local correspondence for p-adic fields in [Reference HenniartHe88]; the Galois extension
$F'$
with an n-close F for any n. This is the strategy followed by Henniart in his proof of the numerical local correspondence for p-adic fields in [Reference HenniartHe88]; the Galois extension
![]() $F'$
in his construction was obtained by applying the results of [Reference Arthur and ClozelAC] on cyclic base change. For general groups over p-adic fields, one can define a version of local cyclic base change using the global methods of [Reference LabesseLab99], as explained in §10.2. In order to apply this to prove results about purity, we need to know the answers to the following questions:
$F'$
in his construction was obtained by applying the results of [Reference Arthur and ClozelAC] on cyclic base change. For general groups over p-adic fields, one can define a version of local cyclic base change using the global methods of [Reference LabesseLab99], as explained in §10.2. In order to apply this to prove results about purity, we need to know the answers to the following questions:
Question 11.10. Does the Fargues-Scholze parametrization commute with cyclic base change, as described in §10.2?
Question 11.11. Let
![]() $F'/F^\sharp $
be a cyclic extension of prime order. Suppose
$F'/F^\sharp $
be a cyclic extension of prime order. Suppose
![]() $\pi \in {\mathcal {A}}^n(G/F^\sharp )$
, and
$\pi \in {\mathcal {A}}^n(G/F^\sharp )$
, and
![]() $\pi '$
belongs to the base change of
$\pi '$
belongs to the base change of
![]() $\pi $
to
$\pi $
to
![]() $G(F')$
. Is
$G(F')$
. Is
![]() $\pi ' \in {\mathcal {A}}^n(G/F')$
?
$\pi ' \in {\mathcal {A}}^n(G/F')$
?
A Globalization of discrete series, by Raphaël Beuzart-Plessis
Let X be a smooth proper algebraic curve X over
![]() $\mathbb {F}_q$
, with function field
$\mathbb {F}_q$
, with function field
![]() $K = \mathbb {F}_q(X)$
. Let G be a connected reductive group over K and let
$K = \mathbb {F}_q(X)$
. Let G be a connected reductive group over K and let
![]() $Z^0$
be the neutral component of its center. Recall that for
$Z^0$
be the neutral component of its center. Recall that for
![]() $v\in \lvert X\rvert $
and
$v\in \lvert X\rvert $
and
![]() $\pi _v$
a discrete series of
$\pi _v$
a discrete series of
![]() $G(K_v)$
a pseudo-coefficient of
$G(K_v)$
a pseudo-coefficient of
![]() $\pi _v$
is a function
$\pi _v$
is a function
![]() $\varphi _{\pi _v}\in C_c^\infty (G(K_v)/Z^0(K_v),\xi ^{-1}_v)$
, where
$\varphi _{\pi _v}\in C_c^\infty (G(K_v)/Z^0(K_v),\xi ^{-1}_v)$
, where
![]() $\xi _v$
denotes the restriction of the central character of
$\xi _v$
denotes the restriction of the central character of
![]() $\pi _v$
to
$\pi _v$
to
![]() $Z^0(K_v)$
, such that for every tempered irreducible representation
$Z^0(K_v)$
, such that for every tempered irreducible representation
![]() $\pi ^{\prime }_v$
of
$\pi ^{\prime }_v$
of
![]() $G(K_v)$
on which
$G(K_v)$
on which
![]() $Z^0(K_v)$
acts through the character
$Z^0(K_v)$
acts through the character
![]() $\xi _v$
, we have
$\xi _v$
, we have
 $$ \begin{align*}\displaystyle \mathrm{Trace}\; \pi^{\prime}_v(\varphi_{\pi_v})=\left\{\begin{array}{ll} 1 & \text{ if } \pi^{\prime}_v\simeq \pi_v; \\ 0 & \text{ if } \pi^{\prime}_v\not\simeq \pi_v. \end{array} \right.\end{align*} $$
$$ \begin{align*}\displaystyle \mathrm{Trace}\; \pi^{\prime}_v(\varphi_{\pi_v})=\left\{\begin{array}{ll} 1 & \text{ if } \pi^{\prime}_v\simeq \pi_v; \\ 0 & \text{ if } \pi^{\prime}_v\not\simeq \pi_v. \end{array} \right.\end{align*} $$
The existence of pseudo-coefficients can be deduced from the Trace Paley-Wiener theorem [Reference Bernstein, Deligne and KazhdanBDK]. Moreover, it follows from Langlands classification that if
![]() $\pi ^{\prime }_v$
is an arbitrary smooth irreducible representation of
$\pi ^{\prime }_v$
is an arbitrary smooth irreducible representation of
![]() $G(K_v)$
, on which
$G(K_v)$
, on which
![]() $Z^0(K_v)$
acts through the character
$Z^0(K_v)$
acts through the character
![]() $\xi _v$
, if
$\xi _v$
, if
![]() $\mathrm {Trace}\; \pi ^{\prime }_v(\varphi _{\pi _v})\neq 0$
, then
$\mathrm {Trace}\; \pi ^{\prime }_v(\varphi _{\pi _v})\neq 0$
, then
![]() $\pi ^{\prime }_v$
has the same cuspidal support as
$\pi ^{\prime }_v$
has the same cuspidal support as
![]() $\pi _v$
.
$\pi _v$
.
Let
![]() $\xi : Z^0(K)\backslash Z^0(\mathbf {A}_K)\to \mathbf {C}^\times $
be a continuous character.
$\xi : Z^0(K)\backslash Z^0(\mathbf {A}_K)\to \mathbf {C}^\times $
be a continuous character.
Let T be the universal Cartan of G (i.e., the torus quotient of a Borel subgroup in any quasi-split inner form of G). Let
![]() $S_{ram}\subset |X|$
be the finite subset of places where G or
$S_{ram}\subset |X|$
be the finite subset of places where G or
![]() $\xi $
is ramified and choose for every
$\xi $
is ramified and choose for every
![]() $v\in |X|\setminus S_{ram}$
a hyperspecial maximal compact subgroup
$v\in |X|\setminus S_{ram}$
a hyperspecial maximal compact subgroup
![]() $J_v\subset G(K_v)$
such that
$J_v\subset G(K_v)$
such that
![]() $J_v=G(\mathcal {O}_v)$
for almost all v. By the Satake isomorphism, (
$J_v=G(\mathcal {O}_v)$
for almost all v. By the Satake isomorphism, (
![]() $J_v$
-)unramified irreducible representations of
$J_v$
-)unramified irreducible representations of
![]() $G(K_v)$
are parametrized by
$G(K_v)$
are parametrized by
![]() $\widehat {T}_v//W_v$
, where
$\widehat {T}_v//W_v$
, where
![]() $\widehat {T}_v$
denotes the complex torus of unramified characters of
$\widehat {T}_v$
denotes the complex torus of unramified characters of
![]() $T(K_v)$
and
$T(K_v)$
and
![]() $W_v=Norm_{G(K_v)}(T)/T(K_v)$
the Weyl group. We denote by
$W_v=Norm_{G(K_v)}(T)/T(K_v)$
the Weyl group. We denote by
![]() $(\widehat {T}_v//W_v)_{\xi _v}$
the subvariety of unramified characters
$(\widehat {T}_v//W_v)_{\xi _v}$
the subvariety of unramified characters
![]() $\chi \in \widehat {T}_v$
such that
$\chi \in \widehat {T}_v$
such that
![]() $\chi \mid _{Z^0(K_v)}=\xi _v$
.
$\chi \mid _{Z^0(K_v)}=\xi _v$
.
The purpose of this appendix is to prove the following lemma.
Lemma A.1. Let
![]() $S, S' \subset |X|$
be disjoint subsets of places of X with
$S, S' \subset |X|$
be disjoint subsets of places of X with
![]() $S'\cap S_{ram}=\emptyset $
. For each
$S'\cap S_{ram}=\emptyset $
. For each
![]() $v \in S$
, let
$v \in S$
, let
![]() $\pi _v$
be a discrete series representation whose central character restricted to
$\pi _v$
be a discrete series representation whose central character restricted to
![]() $Z^0(K_v)$
equals
$Z^0(K_v)$
equals
![]() $\xi _v$
, with at least one
$\xi _v$
, with at least one
![]() $v_0 \in S$
such that
$v_0 \in S$
such that
![]() $\pi _{v_0}$
is supercuspidal. Also, for
$\pi _{v_0}$
is supercuspidal. Also, for
![]() $v\in S'$
, let
$v\in S'$
, let
![]() $X_v\subset (\widehat {T}_v//W_v)_{\xi _v}$
be a proper closed subset for the Zariski topology. Then there exists a (necessarily cuspidal) automorphic representation
$X_v\subset (\widehat {T}_v//W_v)_{\xi _v}$
be a proper closed subset for the Zariski topology. Then there exists a (necessarily cuspidal) automorphic representation
![]() $\Pi \simeq \bigotimes ^{\prime }_{x \in |X|} \Pi _x$
of
$\Pi \simeq \bigotimes ^{\prime }_{x \in |X|} \Pi _x$
of
![]() $G(\mathbf {A}_K)$
, on which
$G(\mathbf {A}_K)$
, on which
![]() $Z^0(\mathbf {A})$
acts through the character
$Z^0(\mathbf {A})$
acts through the character
![]() $\xi $
, such that
$\xi $
, such that
-
(i) For all
 $v \in S$
,
$v \in S$
,
 $\Pi _v$
has nonzero trace against a pseudo-coefficient for
$\Pi _v$
has nonzero trace against a pseudo-coefficient for
 $\pi _v$
(in particular,
$\pi _v$
(in particular,
 $\Pi _v$
and
$\Pi _v$
and
 $\pi _v$
have the same cuspidal support),
$\pi _v$
have the same cuspidal support), -
(ii) For all
 $v\in S'$
,
$v\in S'$
,
 $\Pi _{v}$
is an unramified representation with Satake parameter in
$\Pi _{v}$
is an unramified representation with Satake parameter in
 $(\widehat {T}_v//W_v)_{\xi _v}\setminus X_v$
.
$(\widehat {T}_v//W_v)_{\xi _v}\setminus X_v$
.
Proof. This follows from an application of the Deligne-Kazhdan simple trace formula [Reference Deligne, Kazhdan and VignérasDKV, §A.1 p.41]. More precisely, we consider test functions
![]() $f=\otimes _v f_v\in C_c^\infty (G(\mathbf {A}_K)/Z^0(\mathbf {A}_K),\xi ^{-1})$
satisfying
$f=\otimes _v f_v\in C_c^\infty (G(\mathbf {A}_K)/Z^0(\mathbf {A}_K),\xi ^{-1})$
satisfying
-
(i) For each
 $v\in S$
,
$v\in S$
,
 $f_v=\varphi _{\pi _v}$
is a pseudo-coefficient of
$f_v=\varphi _{\pi _v}$
is a pseudo-coefficient of
 $\pi _v$
. Moreover, for
$\pi _v$
. Moreover, for
 $v=v_0$
we assume, as we may, that
$v=v_0$
we assume, as we may, that
 $f_{v_0}$
is a matrix coefficient of
$f_{v_0}$
is a matrix coefficient of
 $\pi _{v_0}^\vee $
;
$\pi _{v_0}^\vee $
; -
(ii) For each
 $v\in S'$
,
$v\in S'$
,
 $f_v(g)=\int _{Z^0(K_v)} f^{\prime }_v(z^{-1}g) \xi _v(z)dz$
, where
$f_v(g)=\int _{Z^0(K_v)} f^{\prime }_v(z^{-1}g) \xi _v(z)dz$
, where
 $f^{\prime }_v\in \mathcal {H}(G(K_v),J_v)$
is a
$f^{\prime }_v\in \mathcal {H}(G(K_v),J_v)$
is a
 $J_v$
-spherical function whose Satake transform (a regular function on
$J_v$
-spherical function whose Satake transform (a regular function on
 $\widehat {T}_v//W_v$
) vanishes identically on
$\widehat {T}_v//W_v$
) vanishes identically on
 $X_v$
but not on
$X_v$
but not on
 $(\widehat {T}_v//W_v)_{\xi _v}$
;
$(\widehat {T}_v//W_v)_{\xi _v}$
; -
(iii) For almost all v,
 $f_v$
equals the function
$f_v$
equals the function
 $f^0_v$
which coincides with
$f^0_v$
which coincides with
 $zk\mapsto \xi _v(z)^{-1}$
on
$zk\mapsto \xi _v(z)^{-1}$
on
 $Z^0(K_v)J_v$
and is zero outside;
$Z^0(K_v)J_v$
and is zero outside; -
(iv) For all
 $\delta \in G(K)$
, if the
$\delta \in G(K)$
, if the
 $G(\mathbf {A}_K)$
-conjugacy class of
$G(\mathbf {A}_K)$
-conjugacy class of
 $\delta $
intersects the support of f, then
$\delta $
intersects the support of f, then
 $\delta $
is regular elliptic.
$\delta $
is regular elliptic.
Then the Deligne-Kazhdan simple trace formula can be applied to f yielding the following identity:
where the left sum runs over cuspidal automorphic representations
![]() $\Pi $
of
$\Pi $
of
![]() $G(\mathbf {A}_K)$
with central character
$G(\mathbf {A}_K)$
with central character
![]() $\xi $
, the right sum runs over elliptic regular conjugacy classes in
$\xi $
, the right sum runs over elliptic regular conjugacy classes in
![]() $G(K)/Z^0(K)$
,
$G(K)/Z^0(K)$
,
![]() $G_\delta $
(resp.
$G_\delta $
(resp.
![]() $G_\delta ^+$
) denotes the centralizer of
$G_\delta ^+$
) denotes the centralizer of
![]() $\delta $
(resp.
$\delta $
(resp.
![]() $Z^0 \delta $
) in G,
$Z^0 \delta $
) in G,
![]() $\iota (\delta )=[G_\delta ^+(K):G_\delta (K)]$
and
$\iota (\delta )=[G_\delta ^+(K):G_\delta (K)]$
and
 $$ \begin{align*}\displaystyle O_\delta(f)=\prod_v \underbrace{\int_{G_\delta(K_v)\backslash G(K_v)} f_v(g_v^{-1}\delta g_v) dg_v}_{=: O_\delta(f_v)}\end{align*} $$
$$ \begin{align*}\displaystyle O_\delta(f)=\prod_v \underbrace{\int_{G_\delta(K_v)\backslash G(K_v)} f_v(g_v^{-1}\delta g_v) dg_v}_{=: O_\delta(f_v)}\end{align*} $$
stands for the orbital integral of f at
![]() $\delta $
. Moreover, both sums are finite.
$\delta $
. Moreover, both sums are finite.
The choice of the test functions
![]() $f_v$
for
$f_v$
for
![]() $v\in S\cup S'$
implies that the only nonzero contributions to the left-hand side of (A.2) come from cuspidal representations satisfying the conclusion of the lemma. Thus, it suffices to see that f can be arranged so that the right-hand side of (A.2) is nonzero. For this, we need an auxiliary lemma.
$v\in S\cup S'$
implies that the only nonzero contributions to the left-hand side of (A.2) come from cuspidal representations satisfying the conclusion of the lemma. Thus, it suffices to see that f can be arranged so that the right-hand side of (A.2) is nonzero. For this, we need an auxiliary lemma.
Lemma A.3. We can find local test functions
![]() $f_v$
, for
$f_v$
, for
![]() $v\in S\cup S'$
, satisfying conditions (i) and (ii) above as well as a regular elliptic element
$v\in S\cup S'$
, satisfying conditions (i) and (ii) above as well as a regular elliptic element
![]() $\delta \in G(K)$
such that
$\delta \in G(K)$
such that
![]() $G_\delta ^+=G_\delta $
and
$G_\delta ^+=G_\delta $
and
![]() $O_\delta (f_v)\neq 0$
for every
$O_\delta (f_v)\neq 0$
for every
![]() $v\in S\cup S'$
.
$v\in S\cup S'$
.
Proof. If weak approximation holds for the inclusion
![]() $G(K)\hookrightarrow \prod _{v\in S\cup S'} G(K_v)$
, then the argument is pretty standard. More precisely, we can choose any set of test functions
$G(K)\hookrightarrow \prod _{v\in S\cup S'} G(K_v)$
, then the argument is pretty standard. More precisely, we can choose any set of test functions
![]() $(f_v)_{v\in S\cup S'}$
satisfying (i) and (ii). Indeed, by definition of the Satake transform, for every
$(f_v)_{v\in S\cup S'}$
satisfying (i) and (ii). Indeed, by definition of the Satake transform, for every
![]() $v\in S'$
, the hyperbolic regular orbital integrals of
$v\in S'$
, the hyperbolic regular orbital integrals of
![]() $f_v$
are not identically zero (where by hyperbolic regular orbital integral we mean one that is associated to a regular element in the maximal torus of a Borel subgroup), whereas by [Reference Beuzart-PlessisBP], for each
$f_v$
are not identically zero (where by hyperbolic regular orbital integral we mean one that is associated to a regular element in the maximal torus of a Borel subgroup), whereas by [Reference Beuzart-PlessisBP], for each
![]() $v\in S$
, the elliptic regular orbital integrals of
$v\in S$
, the elliptic regular orbital integrals of
![]() $f_v$
are not identically zero. From this, weak approximation and the local constancy of regular semisimple orbital integrals, we deduce the existence of
$f_v$
are not identically zero. From this, weak approximation and the local constancy of regular semisimple orbital integrals, we deduce the existence of
![]() $\delta \in G(K)$
that is elliptic regular in
$\delta \in G(K)$
that is elliptic regular in
![]() $G(K_v)$
for every
$G(K_v)$
for every
![]() $v\in S$
(hence, in particular,
$v\in S$
(hence, in particular,
![]() $\delta $
is regular elliptic in
$\delta $
is regular elliptic in
![]() $G(K)$
since
$G(K)$
since
![]() $S\neq \emptyset $
) and such that
$S\neq \emptyset $
) and such that
![]() $O_\delta (f_v)\neq 0$
for every
$O_\delta (f_v)\neq 0$
for every
![]() $v\in S\cup S'$
. Moreover, we can also certainly arrange to have
$v\in S\cup S'$
. Moreover, we can also certainly arrange to have
![]() $G_\delta ^+=G_\delta $
as the subset of regular semisimple elements
$G_\delta ^+=G_\delta $
as the subset of regular semisimple elements
![]() $\delta _v\in G(K_v)$
satisfying
$\delta _v\in G(K_v)$
satisfying
![]() $G_{\delta _v}^+=G_{\delta _v}$
is open and dense.
$G_{\delta _v}^+=G_{\delta _v}$
is open and dense.
To deal with the general case (that is including the case where weak approximation fails), we introduce the closure
![]() $\overline {G(K)}$
of
$\overline {G(K)}$
of
![]() $G(K)$
in
$G(K)$
in
![]() $G(K_{S\cup S'})=\prod _{v\in S\cup S'} G(K_v)$
. According to the argument at the beginning of [Reference Platonov and RapinchukPR, Proof of Proposition 7.9 p.419] (which is valid regardless of the characteristic of the global field),
$G(K_{S\cup S'})=\prod _{v\in S\cup S'} G(K_v)$
. According to the argument at the beginning of [Reference Platonov and RapinchukPR, Proof of Proposition 7.9 p.419] (which is valid regardless of the characteristic of the global field),
![]() $\overline {G(K)}$
is an open subgroup of finite index in
$\overline {G(K)}$
is an open subgroup of finite index in
![]() $G(K_{S\cup S'})$
. Let
$G(K_{S\cup S'})$
. Let
![]() $v\in S\cup S'$
and let
$v\in S\cup S'$
and let
![]() $H_v$
be a normal open subgroup of finite index of
$H_v$
be a normal open subgroup of finite index of
![]() $G(K_v)$
contained in
$G(K_v)$
contained in
![]() $\overline {G(K)}\cap G(K_v)$
. Then we just need to check the existence of a test function
$\overline {G(K)}\cap G(K_v)$
. Then we just need to check the existence of a test function
![]() $f_v$
satisfying condition (i) or (ii) above (according to whether
$f_v$
satisfying condition (i) or (ii) above (according to whether
![]() $v\in S$
or
$v\in S$
or
![]() $v\in S'$
) and a regular semisimple element
$v\in S'$
) and a regular semisimple element
![]() $\delta \in H_v$
such that
$\delta \in H_v$
such that
![]() $O_\delta (f_v)\neq 0$
. First we consider the case
$O_\delta (f_v)\neq 0$
. First we consider the case
![]() $v\in S'$
. Then the image of
$v\in S'$
. Then the image of
![]() $H_v\cap T(K_v)$
in
$H_v\cap T(K_v)$
in
![]() $T(K_v)/T(\mathcal {O}_v)$
is a subgroup of finite index corresponding to a finite quotient
$T(K_v)/T(\mathcal {O}_v)$
is a subgroup of finite index corresponding to a finite quotient
![]() $\widehat {T}^{\prime }_v$
of
$\widehat {T}^{\prime }_v$
of
![]() $\widehat {T}_v$
. Then we look for a regular function on
$\widehat {T}_v$
. Then we look for a regular function on
![]() $\widehat {T}_v//W_v$
vanishing identically on
$\widehat {T}_v//W_v$
vanishing identically on
![]() $X_v$
but not on
$X_v$
but not on
![]() $(\widehat {T}_v//W_v)_{\xi _v}$
and whose push forward to
$(\widehat {T}_v//W_v)_{\xi _v}$
and whose push forward to
![]() $\widehat {T}^{\prime }_v$
via the projection
$\widehat {T}^{\prime }_v$
via the projection
![]() $\widehat {T}_v\to \widehat {T}^{\prime }_v$
is nonzero. Such a function is readily seen to exist. Consider now the case
$\widehat {T}_v\to \widehat {T}^{\prime }_v$
is nonzero. Such a function is readily seen to exist. Consider now the case
![]() $v\in S$
and let
$v\in S$
and let
![]() $f_v$
be a pseudo-coefficient of
$f_v$
be a pseudo-coefficient of
![]() $\pi _v$
. By [Reference Beuzart-PlessisBP], it suffices to show that the restriction of the Harish-Chandra character
$\pi _v$
. By [Reference Beuzart-PlessisBP], it suffices to show that the restriction of the Harish-Chandra character
![]() $\Theta _{\pi _v}$
of
$\Theta _{\pi _v}$
of
![]() $\pi _v$
to the subset
$\pi _v$
to the subset
![]() $H_{v,ell-rs}$
of elliptic regular semisimple relements in
$H_{v,ell-rs}$
of elliptic regular semisimple relements in
![]() $H_v$
is nonzero. For
$H_v$
is nonzero. For
![]() $\delta $
a finite dimensional representation of
$\delta $
a finite dimensional representation of
![]() $G(K_v)/H_v$
,
$G(K_v)/H_v$
,
![]() $\pi _v\otimes \delta $
is a direct sum of discrete series with Harish-Chandra character
$\pi _v\otimes \delta $
is a direct sum of discrete series with Harish-Chandra character
![]() $\Theta _{\pi _v\otimes \delta }=\Theta _{\pi _v}\Theta _\delta $
where
$\Theta _{\pi _v\otimes \delta }=\Theta _{\pi _v}\Theta _\delta $
where
![]() $\Theta _\delta $
denotes the usual character of
$\Theta _\delta $
denotes the usual character of
![]() $\delta $
. Then if
$\delta $
. Then if
![]() $\Theta _{\pi _v}\mid _{H_{v,ell-rs}}=0$
, the restriction of
$\Theta _{\pi _v}\mid _{H_{v,ell-rs}}=0$
, the restriction of
![]() $\sum _{\delta } \frac {1}{\dim \delta }\Theta _{\pi _v\otimes \delta }$
to the elliptic regular semisimple locus of
$\sum _{\delta } \frac {1}{\dim \delta }\Theta _{\pi _v\otimes \delta }$
to the elliptic regular semisimple locus of
![]() $G(K_v)$
would be zero, and this would contradict the elliptic orthogonality relations of [Reference Beuzart-PlessisBP] on Harish-Chandra characters of discrete series.
$G(K_v)$
would be zero, and this would contradict the elliptic orthogonality relations of [Reference Beuzart-PlessisBP] on Harish-Chandra characters of discrete series.
Let
![]() $(f_v)_{v\in S\cup S'}$
and
$(f_v)_{v\in S\cup S'}$
and
![]() $\delta \in G(K)$
as in the above lemma. Then we choose the functions
$\delta \in G(K)$
as in the above lemma. Then we choose the functions
![]() $f_v\in C_c^\infty (G(K_v)/Z^0(K_v),\xi _v^{-1})$
for
$f_v\in C_c^\infty (G(K_v)/Z^0(K_v),\xi _v^{-1})$
for
![]() $v\notin S\cup S'$
such that
$v\notin S\cup S'$
such that
![]() $O_\delta (f_v)\neq 0$
for all v and
$O_\delta (f_v)\neq 0$
for all v and
![]() $f_v=f^0_v$
for almost all v (this is certainly possible thanks to the condition
$f_v=f^0_v$
for almost all v (this is certainly possible thanks to the condition
![]() $G_\delta ^+=G_\delta $
). Then the set of semisimple conjugacy classes of
$G_\delta ^+=G_\delta $
). Then the set of semisimple conjugacy classes of
![]() $G(K)$
whose
$G(K)$
whose
![]() $G(\mathbf {A}_K)$
-conjugacy classes meet the support of f is finite. Hence, up to shrinking the support of
$G(\mathbf {A}_K)$
-conjugacy classes meet the support of f is finite. Hence, up to shrinking the support of
![]() $f_v$
at some auxiliary place
$f_v$
at some auxiliary place
![]() $v\notin S\cup S'$
, we may assume that this set only consists in the orbit of
$v\notin S\cup S'$
, we may assume that this set only consists in the orbit of
![]() $\delta $
. The function f then satisfies condition (iii) above and the right-hand side of the trace formula (A.2) is reduced to the term corresponding to
$\delta $
. The function f then satisfies condition (iii) above and the right-hand side of the trace formula (A.2) is reduced to the term corresponding to
![]() $\delta $
. As
$\delta $
. As
![]() $O_\delta (f)\neq 0$
by construction, this implies that the left-hand side does not vanish either, and we are done.
$O_\delta (f)\neq 0$
by construction, this implies that the left-hand side does not vanish either, and we are done.
Acknowledgements
The authors thank Hélène Esnault, Tony Feng, Jessica Fintzen, Dennis Gaitsgory, Guy Henniart, Tasho Kaletha, Jean-Pierre Labesse, Bertrand Lemaire and Zhiwei Yun for helpful discussions of various aspects of the paper. We benefited from exchanges with Laurent Fargues and Peter Scholze regarding the material in the final section. We thank Xinwen Zhu for directing our attention to his article [Reference Xu and ZhuXZ] with Daxin Xu, which allowed us to remove a restriction in the statement of Theorem 1.2. We are especially grateful to Luis Lomelí for his role, in collaboration with one of us, in developing the main techniques on which our results are based, and for his comments in the early stages of this project. Finally, we thank Raphael Beuzart-Plessis for providing us with the appendix, allowing us to prove Theorem 1.2 for discrete series representations.
Competing interests
The authors have no competing interest to declare.
Financial support
The work of Beuzart-Plessis was funded by the European Union ERC Consolidator Grant, RELANTRA, project number 101044930. Views and opinions expressed are however those of the authors only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
W. T. Gan was partially supported by a Singapore government MOE Tier 1 grant R-146-000-320-114.
M. Harris was partially supported by NSF Grant DMS-2001369 and by a Simons Foundation Fellowship, Award number 663678.
W. Sawin was partially supported by NSF grant DMS-2101491 and served as a Clay Research Fellow.