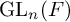1. Introduction
Let
![]() $\mathcal {M}_k(q,\chi )$
denote the finite-dimensional vector space of holomorphic modular forms of weight k, level q and nebentypus
$\mathcal {M}_k(q,\chi )$
denote the finite-dimensional vector space of holomorphic modular forms of weight k, level q and nebentypus
![]() $\chi $
, where
$\chi $
, where
![]() $\chi $
is a primitive Dirichlet character of conductor
$\chi $
is a primitive Dirichlet character of conductor
![]() $q_{\chi } \mid q$
. The classical theory of newforms due to Atkin and Lehner [Reference Atkin and LehnerAL70] states that for each
$q_{\chi } \mid q$
. The classical theory of newforms due to Atkin and Lehner [Reference Atkin and LehnerAL70] states that for each
![]() $q' \mid q$
with
$q' \mid q$
with
![]() $q' \neq q$
and
$q' \neq q$
and
![]() $q' \equiv 0\ \pmod {q_{\chi }}$
and for each
$q' \equiv 0\ \pmod {q_{\chi }}$
and for each
![]() $\ell \mid \frac {q}{q'}$
, the function
$\ell \mid \frac {q}{q'}$
, the function ![]() defines an element of
defines an element of
![]() $\mathcal {M}_k(q,\chi )$
whenever
$\mathcal {M}_k(q,\chi )$
whenever
![]() $f \in \mathcal {M}_k(q',\chi )$
. We call
$f \in \mathcal {M}_k(q',\chi )$
. We call
![]() $\iota _{\ell } f$
an oldform. Moreover, the orthogonal complement with respect to the Petersson inner product of the vector subspace of oldforms has an orthonormal basis consisting of newforms, which are eigenfunctions of the n-th Hecke operator not just for each positive integer n for which
$\iota _{\ell } f$
an oldform. Moreover, the orthogonal complement with respect to the Petersson inner product of the vector subspace of oldforms has an orthonormal basis consisting of newforms, which are eigenfunctions of the n-th Hecke operator not just for each positive integer n for which
![]() $(n,q) = 1$
but for all
$(n,q) = 1$
but for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Casselman [Reference CasselmanCas73], building on the seminal work of Jacquet and Langlands [Reference Jacquet and LanglandsJL70], gave an adèlic reformulation of the Atkin–Lehner theory of newforms. Because automorphic representations
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
have a tensor product factorisation in terms of representations of
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
have a tensor product factorisation in terms of representations of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$
for each prime p, this reformulation is purely local and is in terms of distinguished vectors in certain classes of representations of
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$
for each prime p, this reformulation is purely local and is in terms of distinguished vectors in certain classes of representations of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$
determined in terms of congruence subgroups. Such a theory of newforms has been extended to the setting of generic irreducible admissible smooth representations of
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$
determined in terms of congruence subgroups. Such a theory of newforms has been extended to the setting of generic irreducible admissible smooth representations of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, where F is a nonarchimedean local field [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81]. This allows one to generalise Atkin–Lehner theory to automorphic representations of
$\operatorname {\mathrm {GL}}_n(F)$
, where F is a nonarchimedean local field [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81]. This allows one to generalise Atkin–Lehner theory to automorphic representations of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {A}_E)$
for any number field E. Furthermore, this theory has blossomed to include a well-developed theory of oldforms and conductor exponents associated to such representations, coupled with the local theory of test vectors for certain families of
$\operatorname {\mathrm {GL}}_n(\mathbb {A}_E)$
for any number field E. Furthermore, this theory has blossomed to include a well-developed theory of oldforms and conductor exponents associated to such representations, coupled with the local theory of test vectors for certain families of
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals [Reference JacquetJac12, Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81, Reference MatringeMat13, Reference ReederRee91].
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals [Reference JacquetJac12, Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81, Reference MatringeMat13, Reference ReederRee91].
Although this nonarchimedean aspect of the adèlic theory of newforms has been well understood since the seminal work of Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81], there has been little development – indeed, little even in the way of a conjectural formulation – of the corresponding archimedean theory beyond the case
![]() $n = 2$
. For
$n = 2$
. For
![]() $n = 2$
, the archimedean aspect of the adèlic theory of newforms, due to Popa [Reference PopaPop08], concerns distinguished vectors in certain classes of representations of
$n = 2$
, the archimedean aspect of the adèlic theory of newforms, due to Popa [Reference PopaPop08], concerns distinguished vectors in certain classes of representations of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {C})$
determined in terms of the restrictions to the maximal compact subgroups
$\operatorname {\mathrm {GL}}_2(\mathbb {C})$
determined in terms of the restrictions to the maximal compact subgroups
![]() $\operatorname {\mathrm {O}}(2)$
and
$\operatorname {\mathrm {O}}(2)$
and
![]() $\operatorname {\mathrm {U}}(2)$
. In the classical language of holomorphic modular forms and Maaß forms on the upper half-plane, this translates to prescribed automorphic forms determined in terms of Maaß raising and lowering operators, which raise and lower the weight of the automorphic form.
$\operatorname {\mathrm {U}}(2)$
. In the classical language of holomorphic modular forms and Maaß forms on the upper half-plane, this translates to prescribed automorphic forms determined in terms of Maaß raising and lowering operators, which raise and lower the weight of the automorphic form.
In this article, we put the archimedean setting on an equal footing with the nonarchimedean setting by developing such a theory for
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
. We summarise our main results concerning generic irreducible Casselman–Wallach representations
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
. We summarise our main results concerning generic irreducible Casselman–Wallach representations
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n$
as follows; precise statements are given in more detail in Section 4.
$\operatorname {\mathrm {GL}}_n$
as follows; precise statements are given in more detail in Section 4.
-
• Among the
 $K_n$
-types
$K_n$
-types
 $\tau $
of
$\tau $
of
 $\pi $
whose restriction to
$\pi $
whose restriction to
 $K_{n - 1}$
contains the trivial representation, there exists a unique
$K_{n - 1}$
contains the trivial representation, there exists a unique
 $K_n$
-type
$K_n$
-type
 $\tau ^{\circ }$
of lowest Howe degree, which occurs with multiplicity one in
$\tau ^{\circ }$
of lowest Howe degree, which occurs with multiplicity one in
 $\pi $
; moreover, the subspace of
$\pi $
; moreover, the subspace of
 $K_{n - 1}$
-invariant
$K_{n - 1}$
-invariant
 $\tau ^{\circ }$
-isotypic vectors in
$\tau ^{\circ }$
-isotypic vectors in
 $\pi $
is one-dimensional (Theorem 4.7). We call the distinguished nonzero vector lying in this subspace, unique up to scalar multiplication, the newform of
$\pi $
is one-dimensional (Theorem 4.7). We call the distinguished nonzero vector lying in this subspace, unique up to scalar multiplication, the newform of
 $\pi $
, and we define the conductor exponent
$\pi $
, and we define the conductor exponent
 $c(\pi )$
of
$c(\pi )$
of
 $\pi $
to be the Howe degree of
$\pi $
to be the Howe degree of
 $\tau ^{\circ }$
(Definition 4.8).
$\tau ^{\circ }$
(Definition 4.8). -
• For each nonnegative integer
 $m \geq c(\pi )$
, the dimension of the subspace of
$m \geq c(\pi )$
, the dimension of the subspace of
 $K_{n - 1}$
-invariant vectors in
$K_{n - 1}$
-invariant vectors in
 $\pi $
that are
$\pi $
that are
 $\tau $
-isotypic for some
$\tau $
-isotypic for some
 $K_n$
-type
$K_n$
-type
 $\tau $
of Howe degree m is given explicitly as a certain binomial coefficient (Theorem 4.12). We call vectors of this form oldforms.
$\tau $
of Howe degree m is given explicitly as a certain binomial coefficient (Theorem 4.12). We call vectors of this form oldforms. -
• The epsilon factor
 $\varepsilon (s,\pi ,\psi )$
of
$\varepsilon (s,\pi ,\psi )$
of
 $\pi $
is equal to
$\pi $
is equal to
 $i^{-c(\pi )}$
(Theorem 4.14); additionally, the conductor exponent
$i^{-c(\pi )}$
(Theorem 4.14); additionally, the conductor exponent
 $c(\pi )$
of
$c(\pi )$
of
 $\pi $
is additive with respect to isobaric sums of representations (Theorem 4.15) and is inductive (Theorem 4.16).
$\pi $
is additive with respect to isobaric sums of representations (Theorem 4.15) and is inductive (Theorem 4.16). -
• When viewed in the Whittaker model and appropriately normalised, the newform is a test vector for the
 $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
(Theorem 4.17) and
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
(Theorem 4.17) and
 $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
(Theorem 4.18) Rankin–Selberg integrals whenever the second representation is spherical.
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
(Theorem 4.18) Rankin–Selberg integrals whenever the second representation is spherical. -
• The newform is a test vector for the Godement–Jacquet zeta integral (Theorem 4.23).
As we explain in Sections 3 and 4, each of these results parallels an analogous result in the nonarchimedean setting.
Some aspects of this archimedean theory have long been expected. In particular, there has been a flurry of work in recent years studying the problem of finding test vectors for local
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals involving ramified representations over archimedean fields; see, for example, [Reference Hirano, Ishii, Miyazaki, Hamahata, Ichikawa, Murase and SuganoHIM12, Reference Hirano, Ishii and MiyazakiHIM16, Reference Hirano, Ishii and MiyazakiHIM22, Reference Ishii and MiyazakiIM22, Reference MiyazakiMiy18, Reference PopaPop08]. With the exception of [Reference PopaPop08], previous work has invariably involved choosing test vectors that are associated in some way to the minimal K-type (in the sense of Vogan [Reference VoganVog81]), whereas we propose a theory of newforms without such a direct relation to minimal K-types. Apart from the recent work [Reference Ishii and MiyazakiIM22], these results have also been confined to low rank – namely,
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals involving ramified representations over archimedean fields; see, for example, [Reference Hirano, Ishii, Miyazaki, Hamahata, Ichikawa, Murase and SuganoHIM12, Reference Hirano, Ishii and MiyazakiHIM16, Reference Hirano, Ishii and MiyazakiHIM22, Reference Ishii and MiyazakiIM22, Reference MiyazakiMiy18, Reference PopaPop08]. With the exception of [Reference PopaPop08], previous work has invariably involved choosing test vectors that are associated in some way to the minimal K-type (in the sense of Vogan [Reference VoganVog81]), whereas we propose a theory of newforms without such a direct relation to minimal K-types. Apart from the recent work [Reference Ishii and MiyazakiIM22], these results have also been confined to low rank – namely,
![]() $n \leq 3$
and
$n \leq 3$
and
![]() $m \leq 2$
.
$m \leq 2$
.
A key part of this archimedean theory is the introduction of a new invariant, a nonnegative integer that we call the conductor exponent, associated to a generic irreducible Casselman–Wallach representation of
![]() $\operatorname {\mathrm {GL}}_n(F)$
that in a certain sense quantifies the extent of ramification of such a representation. Somewhat surprisingly, there seems to have been no previous considerations in the literature of such a theory of the conductor exponent, despite that it has many properties that mirror those of the nonarchimedean conductor exponent introduced by Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81].
$\operatorname {\mathrm {GL}}_n(F)$
that in a certain sense quantifies the extent of ramification of such a representation. Somewhat surprisingly, there seems to have been no previous considerations in the literature of such a theory of the conductor exponent, despite that it has many properties that mirror those of the nonarchimedean conductor exponent introduced by Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81].
The structure of this article is the following. Section 2 contains a brief review of the theory of induced representations of Whittaker and Langlands types,
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals, Godement–Jacquet zeta integrals and L-functions and epsilon factors. We survey the nonarchimedean theory of newforms, oldforms, conductor exponents and test vectors for Rankin–Selberg integrals and Godement–Jacquet zeta integrals in Section 3. This serves to motivate the results stated in Section 4, where we present an analogous theory in the archimedean setting; these results are all essentially new, although several of the results for
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals, Godement–Jacquet zeta integrals and L-functions and epsilon factors. We survey the nonarchimedean theory of newforms, oldforms, conductor exponents and test vectors for Rankin–Selberg integrals and Godement–Jacquet zeta integrals in Section 3. This serves to motivate the results stated in Section 4, where we present an analogous theory in the archimedean setting; these results are all essentially new, although several of the results for
![]() $n = 2$
are implicit in the work of Popa [Reference PopaPop08]. We discuss this theory further in Section 5. The remaining sections are devoted to the proofs of the theorems stated in Section 4.
$n = 2$
are implicit in the work of Popa [Reference PopaPop08]. We discuss this theory further in Section 5. The remaining sections are devoted to the proofs of the theorems stated in Section 4.
2. Preliminaries
2.1. Groups and Haar measures
2.1.1. Local fields and absolute values
Let F be a local field, and denote by
![]() $|\cdot |_F$
the absolute value on F: for nonarchimedean F with ring of integers
$|\cdot |_F$
the absolute value on F: for nonarchimedean F with ring of integers
![]() $\mathcal {O}$
, maximal ideal
$\mathcal {O}$
, maximal ideal
![]() $\mathfrak {p}$
and uniformiser
$\mathfrak {p}$
and uniformiser
![]() $\varpi $
, so that
$\varpi $
, so that
![]() $\varpi \mathcal {O} = \mathfrak {p}$
and
$\varpi \mathcal {O} = \mathfrak {p}$
and
![]() $\mathcal {O} / \mathfrak {p} \cong \mathbb {F}_q$
for some finite field of order q, this absolute value is normalised such that
$\mathcal {O} / \mathfrak {p} \cong \mathbb {F}_q$
for some finite field of order q, this absolute value is normalised such that
![]() $|\varpi |_F = q^{-1}$
, whereas for archimedean F, this is normalised such that
$|\varpi |_F = q^{-1}$
, whereas for archimedean F, this is normalised such that
 $$\begin{align*}|x|_F = \begin{cases} \max\{x,-x\} & \text{if }F = \mathbb{R}, \\ x \overline{x} & \text{if }F = \mathbb{C}. \end{cases}\end{align*}$$
$$\begin{align*}|x|_F = \begin{cases} \max\{x,-x\} & \text{if }F = \mathbb{R}, \\ x \overline{x} & \text{if }F = \mathbb{C}. \end{cases}\end{align*}$$
When the local field is clear from context, we write
![]() $|\cdot |$
in place of
$|\cdot |$
in place of
![]() $|\cdot |_F$
. We also let
$|\cdot |_F$
. We also let ![]() denote the standard modulus on
denote the standard modulus on
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
2.1.2. Haar measures on F and
 $F^{\times }$
$F^{\times }$
We let
![]() $dx$
denote the Haar measure on F normalised such that it is self-dual with respect to a fixed nontrivial additive character
$dx$
denote the Haar measure on F normalised such that it is self-dual with respect to a fixed nontrivial additive character
![]() $\psi = \psi _F$
of F. For
$\psi = \psi _F$
of F. For
![]() $F = \mathbb {R}$
, we choose
$F = \mathbb {R}$
, we choose ![]() , so that
, so that
![]() $dx$
is the Lebesgue measure; for
$dx$
is the Lebesgue measure; for
![]() $F = \mathbb {C}$
, we choose
$F = \mathbb {C}$
, we choose ![]() , so that
, so that
![]() $dx$
is twice the Lebesgue measure; finally, we choose
$dx$
is twice the Lebesgue measure; finally, we choose
![]() $\psi $
to be unramified when F is nonarchimedean, in which case
$\psi $
to be unramified when F is nonarchimedean, in which case
![]() $dx$
gives
$dx$
gives
![]() $\mathcal {O}$
volume
$\mathcal {O}$
volume
![]() $1$
. The multiplicative Haar measure
$1$
. The multiplicative Haar measure
![]() $d^{\times } x$
for
$d^{\times } x$
for
![]() $F^{\times }$
is defined to be
$F^{\times }$
is defined to be
![]() $\zeta _F(1) |x|^{-1} \, dx$
, where
$\zeta _F(1) |x|^{-1} \, dx$
, where

2.1.3. Subgroups of
 $\operatorname {\mathrm {GL}}_n(F)$
and the Iwasawa decomposition
$\operatorname {\mathrm {GL}}_n(F)$
and the Iwasawa decomposition
For each r-tuple of positive integers
![]() $(n_1,\ldots ,n_r) \in \mathbb {N}^r$
for which
$(n_1,\ldots ,n_r) \in \mathbb {N}^r$
for which
![]() $n_1 + \cdots + n_r = n$
, let
$n_1 + \cdots + n_r = n$
, let
![]() $\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)$
denote the associated standard upper parabolic subgroup of
$\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)$
denote the associated standard upper parabolic subgroup of
![]() $\operatorname {\mathrm {GL}}_n(F)$
containing the standard Borel subgroup of upper triangular matrices. This has the Levi decomposition
$\operatorname {\mathrm {GL}}_n(F)$
containing the standard Borel subgroup of upper triangular matrices. This has the Levi decomposition
![]() $\mathrm {P}(F) = \mathrm {N}_{\mathrm {P}}(F) \mathrm {M}_{\mathrm {P}}(F)$
, where the block-diagonal Levi subgroup
$\mathrm {P}(F) = \mathrm {N}_{\mathrm {P}}(F) \mathrm {M}_{\mathrm {P}}(F)$
, where the block-diagonal Levi subgroup
![]() $\mathrm {M}_{\mathrm {P}}(F)$
is isomorphic to
$\mathrm {M}_{\mathrm {P}}(F)$
is isomorphic to
![]() $\operatorname {\mathrm {GL}}_{n_1}(F) \times \cdots \times \operatorname {\mathrm {GL}}_{n_r}(F)$
, while the unipotent radical
$\operatorname {\mathrm {GL}}_{n_1}(F) \times \cdots \times \operatorname {\mathrm {GL}}_{n_r}(F)$
, while the unipotent radical
![]() $\mathrm {N}_{\mathrm {P}}(F)$
of
$\mathrm {N}_{\mathrm {P}}(F)$
of
![]() $\mathrm {P}(F)$
consists of upper triangular matrices with block-diagonal entries
$\mathrm {P}(F)$
consists of upper triangular matrices with block-diagonal entries
![]() $(1_{n_1},\ldots ,1_{n_r})$
; here we have written
$(1_{n_1},\ldots ,1_{n_r})$
; here we have written
![]() $1_n$
to denote the
$1_n$
to denote the
![]() $n \times n$
identity matrix. When
$n \times n$
identity matrix. When
![]() $\mathrm {P}(F)$
is the standard Borel (and minimal parabolic) subgroup
$\mathrm {P}(F)$
is the standard Borel (and minimal parabolic) subgroup
![]() $\mathrm {P}_{(1,\ldots ,1)}(F)$
, we write
$\mathrm {P}_{(1,\ldots ,1)}(F)$
, we write ![]() , the subgroup of unipotent upper triangular matrices, and
, the subgroup of unipotent upper triangular matrices, and ![]() , the subgroup of diagonal matrices.
, the subgroup of diagonal matrices.
The maximal compact subgroup
![]() $K_n$
of
$K_n$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, unique up to conjugacy, is
$\operatorname {\mathrm {GL}}_n(F)$
, unique up to conjugacy, is
 $$\begin{align*}K_n = \begin{cases} \operatorname{\mathrm{O}}(n) & \text{if }F = \mathbb{R}, \\ \operatorname{\mathrm{U}}(n) & \text{if }F = \mathbb{C}, \\ \operatorname{\mathrm{GL}}_n(\mathcal{O}) & \text{if }F\text{ is nonarchimedean}. \end{cases}\end{align*}$$
$$\begin{align*}K_n = \begin{cases} \operatorname{\mathrm{O}}(n) & \text{if }F = \mathbb{R}, \\ \operatorname{\mathrm{U}}(n) & \text{if }F = \mathbb{C}, \\ \operatorname{\mathrm{GL}}_n(\mathcal{O}) & \text{if }F\text{ is nonarchimedean}. \end{cases}\end{align*}$$
When the context is clear, we write K in place of
![]() $K_n$
. Given a standard parabolic subgroup
$K_n$
. Given a standard parabolic subgroup
![]() $\mathrm {P}(F)$
, we have the Iwasawa decomposition
$\mathrm {P}(F)$
, we have the Iwasawa decomposition
![]() $\operatorname {\mathrm {GL}}_n(F) = \mathrm {P}(F) K_n = \mathrm {N}_{\mathrm {P}}(F) \mathrm {M}_{\mathrm {P}}(F) K_n$
. Note that the Iwasawa decomposition is not unique since
$\operatorname {\mathrm {GL}}_n(F) = \mathrm {P}(F) K_n = \mathrm {N}_{\mathrm {P}}(F) \mathrm {M}_{\mathrm {P}}(F) K_n$
. Note that the Iwasawa decomposition is not unique since
![]() $\mathrm {M}_{\mathrm {P}}(F)$
intersects
$\mathrm {M}_{\mathrm {P}}(F)$
intersects
![]() $K_n$
nontrivially.
$K_n$
nontrivially.
2.1.4. Haar measures on
 $\operatorname {\mathrm {GL}}_n(F)$
and its subgroups
$\operatorname {\mathrm {GL}}_n(F)$
and its subgroups
We normalise the Haar measure
![]() $dg$
on
$dg$
on
![]() $\operatorname {\mathrm {GL}}_n(F) \ni g$
via the Iwasawa decomposition
$\operatorname {\mathrm {GL}}_n(F) \ni g$
via the Iwasawa decomposition
![]() $g = uak$
for the standard Borel subgroup, so that
$g = uak$
for the standard Borel subgroup, so that
![]() $dg = \delta _n^{-1}(a) \, du \, d^{\times } a \, dk$
. Here,
$dg = \delta _n^{-1}(a) \, du \, d^{\times } a \, dk$
. Here,
![]() $du = \prod _{j = 1}^{n - 1} \prod _{\ell = j + 1}^{n} du_{j,\ell }$
for
$du = \prod _{j = 1}^{n - 1} \prod _{\ell = j + 1}^{n} du_{j,\ell }$
for
![]() $u \in \mathrm {N}_n(F)$
with upper triangular entries
$u \in \mathrm {N}_n(F)$
with upper triangular entries
![]() $u_{j,\ell } \in F$
,
$u_{j,\ell } \in F$
,
![]() $d^{\times } a = \prod _{j = 1}^{n} d^{\times } a_j$
for
$d^{\times } a = \prod _{j = 1}^{n} d^{\times } a_j$
for
![]() $a \in \mathrm {A}_n(F)$
with diagonal entries
$a \in \mathrm {A}_n(F)$
with diagonal entries
![]() $a_j \in F^{\times }$
,
$a_j \in F^{\times }$
,
![]() $\delta _n(a) = \prod _{j = 1}^{n} |a_j|^{n - 2j + 1}$
denotes the modulus character of the Borel subgroup, and
$\delta _n(a) = \prod _{j = 1}^{n} |a_j|^{n - 2j + 1}$
denotes the modulus character of the Borel subgroup, and
![]() $dk$
is the Haar measure on the compact group
$dk$
is the Haar measure on the compact group
![]() $K_n \ni k$
normalised to give
$K_n \ni k$
normalised to give
![]() $K_n$
volume
$K_n$
volume
![]() $1$
(so that when
$1$
(so that when
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $n = 1$
, in which case
$n = 1$
, in which case
![]() $K_1 = \operatorname {\mathrm {O}}(1) = \{\pm 1\} \cong \mathbb {Z}/2\mathbb {Z}$
, this is just half the counting measure).
$K_1 = \operatorname {\mathrm {O}}(1) = \{\pm 1\} \cong \mathbb {Z}/2\mathbb {Z}$
, this is just half the counting measure).
More generally, given a standard parabolic subgroup
![]() $\mathrm {P}(F) = \mathrm {N}_{\mathrm {P}}(F) \mathrm {M}_{\mathrm {P}}(F)$
of
$\mathrm {P}(F) = \mathrm {N}_{\mathrm {P}}(F) \mathrm {M}_{\mathrm {P}}(F)$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, the Haar measure
$\operatorname {\mathrm {GL}}_n(F)$
, the Haar measure
![]() $dg$
on
$dg$
on
![]() $\operatorname {\mathrm {GL}}_n(F) \ni g$
is given by
$\operatorname {\mathrm {GL}}_n(F) \ni g$
is given by
![]() $dg = \delta _{\mathrm {P}}^{-1}(m) \, du \, d^{\times } m \, dk$
with respect to the Iwasawa decomposition
$dg = \delta _{\mathrm {P}}^{-1}(m) \, du \, d^{\times } m \, dk$
with respect to the Iwasawa decomposition
![]() $g = umk$
, where for
$g = umk$
, where for
![]() $m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r)$
, the modulus character is
$m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r)$
, the modulus character is
 $$\begin{align*}\delta_{\mathrm{P}}(m) = \prod_{j = 1}^{r} \left|\det m_j\right|{}^{n - 2(n_1 + \cdots + n_{j - 1}) - n_j}\end{align*}$$
$$\begin{align*}\delta_{\mathrm{P}}(m) = \prod_{j = 1}^{r} \left|\det m_j\right|{}^{n - 2(n_1 + \cdots + n_{j - 1}) - n_j}\end{align*}$$
and
![]() $d^{\times } m = \prod _{j = 1}^{r} dm_j$
with
$d^{\times } m = \prod _{j = 1}^{r} dm_j$
with
![]() $dm_j$
the Haar measure on
$dm_j$
the Haar measure on
![]() $\operatorname {\mathrm {GL}}_{n_j}(F) \ni m_j$
normalised via the Iwasawa decomposition for the standard Borel subgroup of
$\operatorname {\mathrm {GL}}_{n_j}(F) \ni m_j$
normalised via the Iwasawa decomposition for the standard Borel subgroup of
![]() $\operatorname {\mathrm {GL}}_{n_j}(F)$
.
$\operatorname {\mathrm {GL}}_{n_j}(F)$
.
2.2. Representations
2.2.1. Isobaric sums
Given representations
![]() $(\pi _1,V_{\pi _1}), \ldots , (\pi _r,V_{\pi _r})$
of
$(\pi _1,V_{\pi _1}), \ldots , (\pi _r,V_{\pi _r})$
of
![]() $\operatorname {\mathrm {GL}}_{n_1}(F), \ldots , \operatorname {\mathrm {GL}}_{n_r}(F)$
, where F is a local field and
$\operatorname {\mathrm {GL}}_{n_1}(F), \ldots , \operatorname {\mathrm {GL}}_{n_r}(F)$
, where F is a local field and
![]() $n_1 + \cdots + n_r = n$
, we form the representation
$n_1 + \cdots + n_r = n$
, we form the representation
![]() $\pi _1 \boxtimes \cdots \boxtimes \pi _r$
of
$\pi _1 \boxtimes \cdots \boxtimes \pi _r$
of
![]() $\mathrm {M}_{\mathrm {P}}(F)$
, where
$\mathrm {M}_{\mathrm {P}}(F)$
, where
![]() $\boxtimes $
denotes the outer tensor product and
$\boxtimes $
denotes the outer tensor product and
![]() $\mathrm {M}_{\mathrm {P}}(F)$
denotes the block-diagonal Levi subgroup of the standard (upper) parabolic subgroup
$\mathrm {M}_{\mathrm {P}}(F)$
denotes the block-diagonal Levi subgroup of the standard (upper) parabolic subgroup
![]() $\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)$
of
$\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. We then extend this representation trivially to a representation of
$\operatorname {\mathrm {GL}}_n(F)$
. We then extend this representation trivially to a representation of
![]() $\mathrm {P}(F)$
. By normalised parabolic induction, we obtain an induced representation
$\mathrm {P}(F)$
. By normalised parabolic induction, we obtain an induced representation
![]() $(\pi ,V_{\pi })$
of
$(\pi ,V_{\pi })$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
,
$\operatorname {\mathrm {GL}}_n(F)$
,

where
![]() $V_{\pi }$
denotes the space of smooth functions
$V_{\pi }$
denotes the space of smooth functions
![]() $f : \operatorname {\mathrm {GL}}_n(F) \to V_{\pi _1} \otimes \cdots \otimes V_{\pi _r}$
that satisfy
$f : \operatorname {\mathrm {GL}}_n(F) \to V_{\pi _1} \otimes \cdots \otimes V_{\pi _r}$
that satisfy
for any
![]() $u \in \mathrm {N}_{\mathrm {P}}(F)$
,
$u \in \mathrm {N}_{\mathrm {P}}(F)$
,
![]() $m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r) \in \mathrm {M}_{\mathrm {P}}(F)$
, and
$m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r) \in \mathrm {M}_{\mathrm {P}}(F)$
, and
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
, and the action of
$g \in \operatorname {\mathrm {GL}}_n(F)$
, and the action of
![]() $\pi $
on
$\pi $
on
![]() $V_{\pi }$
is by right translation – namely,
$V_{\pi }$
is by right translation – namely, ![]() . We call
. We call
![]() $\pi $
the isobaric sum of
$\pi $
the isobaric sum of
![]() $\pi _1,\ldots ,\pi _r$
, which we denote by
$\pi _1,\ldots ,\pi _r$
, which we denote by

2.2.2. Induced representations of Whittaker and Langlands types
A representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
is said to be an induced representation of Whittaker type if it is the isobaric sum of
$\operatorname {\mathrm {GL}}_n(F)$
is said to be an induced representation of Whittaker type if it is the isobaric sum of
![]() $\pi _1,\ldots ,\pi _r$
and each
$\pi _1,\ldots ,\pi _r$
and each
![]() $\pi _j$
is irreducible and essentially square-integrable. Such a representation is admissible and smooth; moreover, if F is archimedean, then it is a Fréchet representation of moderate growth and of finite length. The contragredient of an induced representation of Whittaker type
$\pi _j$
is irreducible and essentially square-integrable. Such a representation is admissible and smooth; moreover, if F is archimedean, then it is a Fréchet representation of moderate growth and of finite length. The contragredient of an induced representation of Whittaker type
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
is
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
is
![]() $\widetilde {\pi } = \widetilde {\pi _1} \boxplus \cdots \boxplus \widetilde {\pi _r}$
, which is again an induced representation of Whittaker type. If each
$\widetilde {\pi } = \widetilde {\pi _1} \boxplus \cdots \boxplus \widetilde {\pi _r}$
, which is again an induced representation of Whittaker type. If each
![]() $\pi _j$
is additionally of the form
$\pi _j$
is additionally of the form
![]() $\sigma _j \otimes \left |\det \right |{}^{t_j}$
, where
$\sigma _j \otimes \left |\det \right |{}^{t_j}$
, where
![]() $\sigma _j$
is irreducible, unitary and square-integrable, and
$\sigma _j$
is irreducible, unitary and square-integrable, and
![]() $\Re (t_1) \geq \cdots \geq \Re (t_r)$
, then
$\Re (t_1) \geq \cdots \geq \Re (t_r)$
, then
![]() $\pi $
is said to be an induced representation of Langlands type.
$\pi $
is said to be an induced representation of Langlands type.
2.2.3. Whittaker models
A Whittaker functional
![]() $\Lambda : V_{\pi } \to \mathbb {C}$
of an admissible smooth representation
$\Lambda : V_{\pi } \to \mathbb {C}$
of an admissible smooth representation
![]() $(\pi ,V_{\pi })$
of
$(\pi ,V_{\pi })$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
is a continuous linear functional that satisfies
$\operatorname {\mathrm {GL}}_n(F)$
is a continuous linear functional that satisfies
for all
![]() $v \in V_{\pi }$
and
$v \in V_{\pi }$
and
![]() $u \in \mathrm {N}_n(F)$
; here,
$u \in \mathrm {N}_n(F)$
; here,

If
![]() $\pi $
is additionally irreducible, then the space of Whittaker functionals of
$\pi $
is additionally irreducible, then the space of Whittaker functionals of
![]() $\pi $
is at most one-dimensional. If this space is indeed one-dimensional, so that there exists a unique such functional up to scalar multiplication, then
$\pi $
is at most one-dimensional. If this space is indeed one-dimensional, so that there exists a unique such functional up to scalar multiplication, then
![]() $\pi $
is said to be generic. Every induced representation of Langlands type
$\pi $
is said to be generic. Every induced representation of Langlands type
![]() $(\pi ,V_{\pi })$
admits a nontrivial Whittaker functional
$(\pi ,V_{\pi })$
admits a nontrivial Whittaker functional
![]() $\Lambda $
; moreover,
$\Lambda $
; moreover,
![]() $\pi $
is isomorphic to its unique Whittaker model
$\pi $
is isomorphic to its unique Whittaker model
![]() $\mathcal {W}(\pi ,\psi )$
, which is the image of
$\mathcal {W}(\pi ,\psi )$
, which is the image of
![]() $V_{\pi }$
under the map
$V_{\pi }$
under the map
![]() $v \mapsto \Lambda (\pi (\cdot ) \cdot v)$
, so that
$v \mapsto \Lambda (\pi (\cdot ) \cdot v)$
, so that
![]() $\mathcal {W}(\pi ,\psi )$
consists of Whittaker functions on
$\mathcal {W}(\pi ,\psi )$
consists of Whittaker functions on
![]() $\operatorname {\mathrm {GL}}_n(F)$
of the form
$\operatorname {\mathrm {GL}}_n(F)$
of the form ![]() . An induced representation of Whittaker type
. An induced representation of Whittaker type
![]() $\pi $
also has a one-dimensional space of Whittaker functionals, but the map
$\pi $
also has a one-dimensional space of Whittaker functionals, but the map
![]() $v \mapsto \Lambda (\pi (\cdot ) \cdot v)$
need not be injective, so that the Whittaker model may only be a model of a quotient of
$v \mapsto \Lambda (\pi (\cdot ) \cdot v)$
need not be injective, so that the Whittaker model may only be a model of a quotient of
![]() $\pi $
.
$\pi $
.
2.2.4. Irreducible representations
For nonarchimedean F, every irreducible admissible smooth representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
is isomorphic to the unique irreducible quotient of some induced representation of Langlands type. If
$\operatorname {\mathrm {GL}}_n(F)$
is isomorphic to the unique irreducible quotient of some induced representation of Langlands type. If
![]() $\pi $
is also generic, then it is isomorphic to some (necessarily irreducible) induced representation of Langlands type [Reference Casselman and ShahidiCS98].
$\pi $
is also generic, then it is isomorphic to some (necessarily irreducible) induced representation of Langlands type [Reference Casselman and ShahidiCS98].
For archimedean F, we recall that a Casselman–Wallach representation of
![]() $\operatorname {\mathrm {GL}}_n(F)$
is an admissible smooth Fréchet representation of moderate growth and of finite length [Reference WallachWal92; Reference Bernstein and KrötzBK14]; in particular, induced representations of Whittaker type are Casselman–Wallach representations. Every irreducible Casselman–Wallach representation
$\operatorname {\mathrm {GL}}_n(F)$
is an admissible smooth Fréchet representation of moderate growth and of finite length [Reference WallachWal92; Reference Bernstein and KrötzBK14]; in particular, induced representations of Whittaker type are Casselman–Wallach representations. Every irreducible Casselman–Wallach representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
is isomorphic to the unique irreducible quotient of some induced representation of Langlands type. Again, if
$\operatorname {\mathrm {GL}}_n(F)$
is isomorphic to the unique irreducible quotient of some induced representation of Langlands type. Again, if
![]() $\pi $
is additionally generic, then it is isomorphic to some (necessarily irreducible) induced representation of Langlands type.
$\pi $
is additionally generic, then it is isomorphic to some (necessarily irreducible) induced representation of Langlands type.
2.2.5. Spherical Representations
An induced representation of Whittaker type
![]() $\pi $
is said to be spherical if it has a K-fixed vector. Such a spherical representation
$\pi $
is said to be spherical if it has a K-fixed vector. Such a spherical representation
![]() $\pi $
must then be a principal series representation of the form
$\pi $
must then be a principal series representation of the form
![]() $|\cdot |^{t_1} \boxplus \cdots \boxplus |\cdot |^{t_n}$
; furthermore, the subspace of K-fixed vectors must be one-dimensional. This K-fixed vector, which is unique up to scalar multiplication, is called the spherical vector of
$|\cdot |^{t_1} \boxplus \cdots \boxplus |\cdot |^{t_n}$
; furthermore, the subspace of K-fixed vectors must be one-dimensional. This K-fixed vector, which is unique up to scalar multiplication, is called the spherical vector of
![]() $\pi $
. For a spherical representation of Langlands type
$\pi $
. For a spherical representation of Langlands type
![]() $\pi $
, the spherical Whittaker function
$\pi $
, the spherical Whittaker function
![]() $W^{\circ }$
in the Whittaker model
$W^{\circ }$
in the Whittaker model
![]() $\mathcal {W}(\pi ,\psi )$
is given by the Jacquet integral
$\mathcal {W}(\pi ,\psi )$
is given by the Jacquet integral

where ![]() is the long Weyl element and
is the long Weyl element and
![]() $f^{\circ }$
is the canonically normalised spherical vector in the induced model: the unique smooth function
$f^{\circ }$
is the canonically normalised spherical vector in the induced model: the unique smooth function
![]() ${f^{\circ } : \operatorname {\mathrm {GL}}_n(F) \to \mathbb {C}}$
satisfying
${f^{\circ } : \operatorname {\mathrm {GL}}_n(F) \to \mathbb {C}}$
satisfying
 $$\begin{align*}f^{\circ}(1_n) = \prod_{j = 1}^{n - 1} \prod_{\ell = j + 1}^{n} \zeta_F(1 + t_j - t_{\ell}),\!\!\qquad f^{\circ}(uag) = f^{\circ}(g) \delta_n^{1/2}(a) \prod_{j = 1}^{n} |a_j|^{t_j}, \qquad\!\! f^{\circ}(gk) = f^{\circ}(g)\end{align*}$$
$$\begin{align*}f^{\circ}(1_n) = \prod_{j = 1}^{n - 1} \prod_{\ell = j + 1}^{n} \zeta_F(1 + t_j - t_{\ell}),\!\!\qquad f^{\circ}(uag) = f^{\circ}(g) \delta_n^{1/2}(a) \prod_{j = 1}^{n} |a_j|^{t_j}, \qquad\!\! f^{\circ}(gk) = f^{\circ}(g)\end{align*}$$
for all
![]() $u \in \mathrm {N}_n(F)$
,
$u \in \mathrm {N}_n(F)$
,
![]() $a = \operatorname {\mathrm {diag}}(a_1,\ldots ,a_n) \in \mathrm {A}_n(F)$
,
$a = \operatorname {\mathrm {diag}}(a_1,\ldots ,a_n) \in \mathrm {A}_n(F)$
,
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
, and
$g \in \operatorname {\mathrm {GL}}_n(F)$
, and
![]() $k \in K$
. The Jacquet integral of
$k \in K$
. The Jacquet integral of
![]() $f^{\circ }$
converges absolutely when
$f^{\circ }$
converges absolutely when
![]() $\Re (t_1)> \cdots > \Re (t_n)$
and extends holomorphically to all of
$\Re (t_1)> \cdots > \Re (t_n)$
and extends holomorphically to all of
![]() $\mathbb {C}^n \ni (t_1,\ldots ,t_n)$
(cf. Section 9.1). For nonarchimedean F, the normalisation of
$\mathbb {C}^n \ni (t_1,\ldots ,t_n)$
(cf. Section 9.1). For nonarchimedean F, the normalisation of
![]() $W^{\circ }$
is such that
$W^{\circ }$
is such that
![]() $W^{\circ }(1_n) = 1$
.
$W^{\circ }(1_n) = 1$
.
2.3. Integral representations of L-functions
2.3.1. Rankin–Selberg integrals
We recall the definition of Rankin–Selberg integrals over a local field F; see [Reference Cogdell, Cogdell, Kim and MurtyCog04] for further details. Given induced representations of Whittaker type
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_m(F)$
with
$\operatorname {\mathrm {GL}}_m(F)$
with
![]() $m \leq n$
, we take Whittaker functions
$m \leq n$
, we take Whittaker functions
![]() $W \in \mathcal {W}(\pi ,\psi )$
and
$W \in \mathcal {W}(\pi ,\psi )$
and
![]() $W' \in \mathcal {W}\left (\pi ',\overline {\psi }\right )$
and form the local
$W' \in \mathcal {W}\left (\pi ',\overline {\psi }\right )$
and form the local
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integral defined by
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integral defined by


where
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
is a Schwartz–Bruhat function and
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
is a Schwartz–Bruhat function and ![]() . These integrals converge absolutely for
. These integrals converge absolutely for
![]() $\Re (s)$
sufficiently large and extend meromorphically to the entire complex plane via the local functional equation.
$\Re (s)$
sufficiently large and extend meromorphically to the entire complex plane via the local functional equation.
2.3.2. Godement–Jacquet zeta integrals
Following [Reference Godement and JacquetGJ72; Reference JacquetJac79], we define Godement–Jacquet zeta integrals over a local field F. Given an induced representation of Whittaker type
![]() $(\pi ,V_{\pi })$
of
$(\pi ,V_{\pi })$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, we take
$\operatorname {\mathrm {GL}}_n(F)$
, we take
![]() $v_1 \in V_{\pi }$
,
$v_1 \in V_{\pi }$
,
![]() $\widetilde {v_2} \in V_{\widetilde {\pi }}$
, with associated matrix coefficient
$\widetilde {v_2} \in V_{\widetilde {\pi }}$
, with associated matrix coefficient ![]() of
of
![]() $\pi $
, and form the local Godement–Jacquet zeta integral defined by
$\pi $
, and form the local Godement–Jacquet zeta integral defined by

where
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is a Schwartz–Bruhat function. This integral converges absolutely for
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is a Schwartz–Bruhat function. This integral converges absolutely for
![]() $\Re (s)$
sufficiently large and extends meromorphically to the entire complex plane via the local functional equation.
$\Re (s)$
sufficiently large and extends meromorphically to the entire complex plane via the local functional equation.
2.4. L-functions and epsilon factors
2.4.1. Rankin–Selberg L-functions and standard L-functions
For nonarchimedean F, the Rankin–Selberg L-function
![]() $L(s,\pi \times \pi ')$
is the generator of the
$L(s,\pi \times \pi ')$
is the generator of the
![]() $\mathbb {C}[q^s,q^{-s}]$
-fractional ideal of
$\mathbb {C}[q^s,q^{-s}]$
-fractional ideal of
![]() $\mathbb {C}(q^{-s})$
generated by the family of Rankin–Selberg integrals
$\mathbb {C}(q^{-s})$
generated by the family of Rankin–Selberg integrals
![]() $\Psi (s,W,W')$
(or
$\Psi (s,W,W')$
(or
![]() $\Psi (s,W,W',\Phi )$
if
$\Psi (s,W,W',\Phi )$
if
![]() $m = n$
) with
$m = n$
) with
![]() $W \in \mathcal {W}(\pi ,\psi )$
and
$W \in \mathcal {W}(\pi ,\psi )$
and
![]() $W' \in \mathcal {W}\left (\pi ',\overline {\psi }\right )$
(and
$W' \in \mathcal {W}\left (\pi ',\overline {\psi }\right )$
(and
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
if
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
if
![]() $m = n$
) with
$m = n$
) with
![]() $L(s,\pi \times \pi ')$
normalised to be of the form
$L(s,\pi \times \pi ')$
normalised to be of the form
![]() $P(q^{-s})^{-1}$
for some
$P(q^{-s})^{-1}$
for some
![]() $P(q^{-s}) \in \mathbb {C}[q^{-s}]$
whose constant term is
$P(q^{-s}) \in \mathbb {C}[q^{-s}]$
whose constant term is
![]() $1$
. For archimedean F, the Rankin–Selberg L-function
$1$
. For archimedean F, the Rankin–Selberg L-function
![]() $L(s,\pi \times \pi ')$
is defined via the local Langlands correspondence as explicated in [Reference Knapp, Jannsen, Kleiman and SerreKna94].
$L(s,\pi \times \pi ')$
is defined via the local Langlands correspondence as explicated in [Reference Knapp, Jannsen, Kleiman and SerreKna94].
Similarly, for nonarchimedean F, the standard L-function
![]() $L(s,\pi )$
is the generator of the
$L(s,\pi )$
is the generator of the
![]() $\mathbb {C}[q^s,q^{-s}]$
-fractional ideal of
$\mathbb {C}[q^s,q^{-s}]$
-fractional ideal of
![]() $\mathbb {C}(q^{-s})$
generated by the family of Godement–Jacquet zeta integrals
$\mathbb {C}(q^{-s})$
generated by the family of Godement–Jacquet zeta integrals
![]() $Z(s,\beta ,\Phi )$
with
$Z(s,\beta ,\Phi )$
with
![]() $v_1 \in V_{\pi }$
,
$v_1 \in V_{\pi }$
,
![]() $\widetilde {v_2} \in V_{\widetilde {\pi }}$
, and
$\widetilde {v_2} \in V_{\widetilde {\pi }}$
, and
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
, with
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
, with
![]() $L(s,\pi )$
normalised to be of the form
$L(s,\pi )$
normalised to be of the form
![]() $P(q^{-s})^{-1}$
for some
$P(q^{-s})^{-1}$
for some
![]() $P(q^{-s}) \in \mathbb {C}[q^{-s}]$
whose constant term is
$P(q^{-s}) \in \mathbb {C}[q^{-s}]$
whose constant term is
![]() $1$
. For archimedean F, the standard L-function
$1$
. For archimedean F, the standard L-function
![]() $L(s,\pi )$
is defined via the local Langlands correspondence as explicated in [Reference Knapp, Jannsen, Kleiman and SerreKna94].
$L(s,\pi )$
is defined via the local Langlands correspondence as explicated in [Reference Knapp, Jannsen, Kleiman and SerreKna94].
In both settings, upon decomposing
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
as isobaric sums
$\pi '$
as isobaric sums

we have the identities
 $$ \begin{align} L(s,\pi) = \prod_{j = 1}^{r} L(s,\pi_j), \qquad L(s,\pi \times \pi') = \prod_{j = 1}^{r} \prod_{j' = 1}^{r'} L(s,\pi_j \times \pi_{j'}^{\prime}). \end{align} $$
$$ \begin{align} L(s,\pi) = \prod_{j = 1}^{r} L(s,\pi_j), \qquad L(s,\pi \times \pi') = \prod_{j = 1}^{r} \prod_{j' = 1}^{r'} L(s,\pi_j \times \pi_{j'}^{\prime}). \end{align} $$
Moreover, Rankin–Selberg L-functions involving twists by a character are related to standard L-functions via the identity
2.4.2. L-functions for representations of
 $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
Essentially square-integrable representations of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
exist only for
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
exist only for
![]() $n = 1$
, in which case the representation must be a character of the form
$n = 1$
, in which case the representation must be a character of the form
![]() $\pi (z) = \chi ^{\kappa }(z) |z|_{\mathbb {C}}^t$
for some
$\pi (z) = \chi ^{\kappa }(z) |z|_{\mathbb {C}}^t$
for some
![]() $\kappa \in \mathbb {Z}$
and
$\kappa \in \mathbb {Z}$
and
![]() $t \in \mathbb {C}$
, where
$t \in \mathbb {C}$
, where
![]() $z \in \operatorname {\mathrm {GL}}_1(\mathbb {C}) = \mathbb {C}^{\times }$
and
$z \in \operatorname {\mathrm {GL}}_1(\mathbb {C}) = \mathbb {C}^{\times }$
and
![]() $\chi $
is the canonical character
$\chi $
is the canonical character

The L-function of
![]() $\pi $
is
$\pi $
is
 $$ \begin{align} L(s,\pi) = \zeta_{\mathbb{C}}\left(s + t + \frac{\|\kappa\|}{2}\right), \end{align} $$
$$ \begin{align} L(s,\pi) = \zeta_{\mathbb{C}}\left(s + t + \frac{\|\kappa\|}{2}\right), \end{align} $$
where
This integral representation of
![]() $\zeta _{\mathbb {C}}(s)$
converges absolutely for
$\zeta _{\mathbb {C}}(s)$
converges absolutely for
![]() $\Re (s)> 0$
and extends meromorphically to the entire complex plane with poles at nonpositive integers. The contragredient of
$\Re (s)> 0$
and extends meromorphically to the entire complex plane with poles at nonpositive integers. The contragredient of
![]() $\pi $
is
$\pi $
is
![]() $\widetilde {\pi } = \chi ^{-\kappa } |\cdot |_{\mathbb {C}}^{-t}$
, so that
$\widetilde {\pi } = \chi ^{-\kappa } |\cdot |_{\mathbb {C}}^{-t}$
, so that
 $$ \begin{align} L(s,\widetilde{\pi}) = \zeta_{\mathbb{C}}\left(s - t + \frac{\|\kappa\|}{2}\right). \end{align} $$
$$ \begin{align} L(s,\widetilde{\pi}) = \zeta_{\mathbb{C}}\left(s - t + \frac{\|\kappa\|}{2}\right). \end{align} $$
2.4.3. L-functions for representations of
 $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
Essentially square-integrable representations of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
exist only for
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
exist only for
![]() $n \in \{1,2\}$
. An essentially square-integrable representation of
$n \in \{1,2\}$
. An essentially square-integrable representation of
![]() $\operatorname {\mathrm {GL}}_1(\mathbb {R})$
must be a character of the form
$\operatorname {\mathrm {GL}}_1(\mathbb {R})$
must be a character of the form
![]() $\pi (x) = \chi ^{\kappa }(x) |x|_{\mathbb {R}}^t$
for some
$\pi (x) = \chi ^{\kappa }(x) |x|_{\mathbb {R}}^t$
for some
![]() $\kappa \in \{0,1\}$
and
$\kappa \in \{0,1\}$
and
![]() $t \in \mathbb {C}$
, where
$t \in \mathbb {C}$
, where
![]() $x \in \operatorname {\mathrm {GL}}_1(\mathbb {R}) = \mathbb {R}^{\times }$
and
$x \in \operatorname {\mathrm {GL}}_1(\mathbb {R}) = \mathbb {R}^{\times }$
and
![]() $\chi $
is the canonical character
$\chi $
is the canonical character
The L-function of
![]() $\pi $
is
$\pi $
is
where
This integral representation of
![]() $\zeta _{\mathbb {R}}(s)$
converges absolutely for
$\zeta _{\mathbb {R}}(s)$
converges absolutely for
![]() $\Re (s)> 0$
and extends meromorphically to the entire complex plane with poles at nonpositive even integers. The contragredient is
$\Re (s)> 0$
and extends meromorphically to the entire complex plane with poles at nonpositive even integers. The contragredient is
![]() $\widetilde {\pi } = \chi ^{\kappa } |\cdot |_{\mathbb {R}}^{-t}$
, so that
$\widetilde {\pi } = \chi ^{\kappa } |\cdot |_{\mathbb {R}}^{-t}$
, so that
For
![]() $n = 2$
, we note that
$n = 2$
, we note that
where
![]() $\operatorname {\mathrm {GL}}_1(\mathbb {C})$
is viewed as a subgroup of
$\operatorname {\mathrm {GL}}_1(\mathbb {C})$
is viewed as a subgroup of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
via the identification
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
via the identification ![]() . For
. For
![]() $\kappa \neq 0$
, the essentially discrete series representation of weight
$\kappa \neq 0$
, the essentially discrete series representation of weight
![]() $\|\kappa \| + 1$
,
$\|\kappa \| + 1$
,
is essentially square-integrable, and every essentially square-integrable representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
is of the form
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
is of the form
![]() $\pi = D_{\kappa } \otimes \left |\det \right |{}_{\mathbb {R}}^t$
for some integer
$\pi = D_{\kappa } \otimes \left |\det \right |{}_{\mathbb {R}}^t$
for some integer
![]() $\kappa \geq 2$
and
$\kappa \geq 2$
and
![]() $t \in \mathbb {C}$
. The L-function of
$t \in \mathbb {C}$
. The L-function of
![]() $\pi $
is
$\pi $
is
 $$ \begin{align} L(s,\pi) = \zeta_{\mathbb{C}}\left(s + t + \frac{\kappa - 1}{2}\right) = \zeta_{\mathbb{R}}\left(s + t + \frac{\kappa - 1}{2}\right) \zeta_{\mathbb{R}}\left(s + t + \frac{\kappa + 1}{2}\right). \end{align} $$
$$ \begin{align} L(s,\pi) = \zeta_{\mathbb{C}}\left(s + t + \frac{\kappa - 1}{2}\right) = \zeta_{\mathbb{R}}\left(s + t + \frac{\kappa - 1}{2}\right) \zeta_{\mathbb{R}}\left(s + t + \frac{\kappa + 1}{2}\right). \end{align} $$
The contragredient of
![]() $\pi $
is
$\pi $
is
![]() $\widetilde {\pi } = D_{\kappa } \otimes \left |\det \right |{}_{\mathbb {R}}^{-t}$
, so that
$\widetilde {\pi } = D_{\kappa } \otimes \left |\det \right |{}_{\mathbb {R}}^{-t}$
, so that
 $$ \begin{align} L(s,\widetilde{\pi}) = \zeta_{\mathbb{C}}\left(s - t + \frac{\kappa - 1}{2}\right) = \zeta_{\mathbb{R}}\left(s - t + \frac{\kappa - 1}{2}\right) \zeta_{\mathbb{R}}\left(s - t + \frac{\kappa + 1}{2}\right). \end{align} $$
$$ \begin{align} L(s,\widetilde{\pi}) = \zeta_{\mathbb{C}}\left(s - t + \frac{\kappa - 1}{2}\right) = \zeta_{\mathbb{R}}\left(s - t + \frac{\kappa - 1}{2}\right) \zeta_{\mathbb{R}}\left(s - t + \frac{\kappa + 1}{2}\right). \end{align} $$
2.4.4. Epsilon factors
To any induced representations of Whittaker type
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_m(F)$
and any nontrivial additive character
$\operatorname {\mathrm {GL}}_m(F)$
and any nontrivial additive character
![]() $\psi $
of F, one can associate the epsilon factor
$\psi $
of F, one can associate the epsilon factor
![]() $\varepsilon (s,\pi ,\psi )$
of
$\varepsilon (s,\pi ,\psi )$
of
![]() $\pi $
,
$\pi $
,
![]() $\varepsilon (s,\pi ',\psi )$
of
$\varepsilon (s,\pi ',\psi )$
of
![]() $\pi '$
, and
$\pi '$
, and
![]() $\varepsilon (s,\pi \times \pi ',\psi )$
of
$\varepsilon (s,\pi \times \pi ',\psi )$
of
![]() $\pi \times \pi '$
, which arise via the local functional equations for the Godement–Jacquet zeta integral and
$\pi \times \pi '$
, which arise via the local functional equations for the Godement–Jacquet zeta integral and
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integral, respectively. In particular, the local functional equation for the Godement–Jacquet zeta integral is
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integral, respectively. In particular, the local functional equation for the Godement–Jacquet zeta integral is
 $$ \begin{align} \frac{Z(1 - s,\widetilde{\beta},\widehat{\Phi})}{L(1 - s,\widetilde{\pi})} = \varepsilon(s,\pi,\psi) \frac{Z(s,\beta,\Phi)}{L(s,\pi)}, \end{align} $$
$$ \begin{align} \frac{Z(1 - s,\widetilde{\beta},\widehat{\Phi})}{L(1 - s,\widetilde{\pi})} = \varepsilon(s,\pi,\psi) \frac{Z(s,\beta,\Phi)}{L(s,\pi)}, \end{align} $$
where ![]() with
with ![]() denoting the transpose of g, while the Fourier transform
denoting the transpose of g, while the Fourier transform
![]() $\widehat {\Phi }$
is
$\widehat {\Phi }$
is

Note that this normalisation of the Fourier transform differs from that in [Reference Godement and JacquetGJ72] and that the epsilon factor is dependent on this normalisation. For the local functional equation for the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integral, see, for example, [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Theorem 2.1].
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integral, see, for example, [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Theorem 2.1].
Upon decomposing
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
as isobaric sums as in (2.4), we have the identities
$\pi '$
as isobaric sums as in (2.4), we have the identities
 $$ \begin{align} \varepsilon(s,\pi,\psi) = \prod_{j = 1}^{r} \varepsilon(s,\pi_j,\psi), \qquad \varepsilon(s,\pi \times \pi',\psi) = \prod_{j = 1}^{r} \prod_{j' = 1}^{r'} \varepsilon(s,\pi_j \times \pi_{j'}^{\prime},\psi) \end{align} $$
$$ \begin{align} \varepsilon(s,\pi,\psi) = \prod_{j = 1}^{r} \varepsilon(s,\pi_j,\psi), \qquad \varepsilon(s,\pi \times \pi',\psi) = \prod_{j = 1}^{r} \prod_{j' = 1}^{r'} \varepsilon(s,\pi_j \times \pi_{j'}^{\prime},\psi) \end{align} $$
by [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS83, Theorem (3.1), Proposition (8.4), Proposition (9.4)] for nonarchimedean F and via the local Langlands correspondence for archimedean F. When
![]() $\pi '$
is the trivial representation of
$\pi '$
is the trivial representation of
![]() $\operatorname {\mathrm {GL}}_1(F)$
, we have the equality
$\operatorname {\mathrm {GL}}_1(F)$
, we have the equality
![]() $\varepsilon (s,\pi ,\psi ) = \varepsilon (s,\pi \times \pi ',\psi )$
between the epsilon factor of
$\varepsilon (s,\pi ,\psi ) = \varepsilon (s,\pi \times \pi ',\psi )$
between the epsilon factor of
![]() $\pi $
defined via the Godement–Jacquet zeta integral and the epsilon factor of
$\pi $
defined via the Godement–Jacquet zeta integral and the epsilon factor of
![]() $\pi \times \pi '$
defined via the
$\pi \times \pi '$
defined via the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_1$
Rankin–Selberg integral.
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_1$
Rankin–Selberg integral.
For nonarchimedean F, the epsilon factors
![]() $\varepsilon (s,\pi ,\psi )$
and
$\varepsilon (s,\pi ,\psi )$
and
![]() $\varepsilon (s,\pi \times \pi ',\psi )$
are units in
$\varepsilon (s,\pi \times \pi ',\psi )$
are units in
![]() $\mathbb {C}[q^s,q^{-s}]$
of the form
$\mathbb {C}[q^s,q^{-s}]$
of the form
 $$ \begin{align} \varepsilon(s,\pi,\psi) = \varepsilon\left(\frac{1}{2},\pi,\psi\right) q^{-c(\pi) \left(s - \frac{1}{2}\right)}, \qquad \varepsilon(s,\pi \times \pi',\psi) = \varepsilon\left(\frac{1}{2},\pi \times \pi',\psi\right) q^{-c(\pi \times \pi') \left(s - \frac{1}{2}\right)} \end{align} $$
$$ \begin{align} \varepsilon(s,\pi,\psi) = \varepsilon\left(\frac{1}{2},\pi,\psi\right) q^{-c(\pi) \left(s - \frac{1}{2}\right)}, \qquad \varepsilon(s,\pi \times \pi',\psi) = \varepsilon\left(\frac{1}{2},\pi \times \pi',\psi\right) q^{-c(\pi \times \pi') \left(s - \frac{1}{2}\right)} \end{align} $$
for some nonnegative integers
![]() $c(\pi )$
and
$c(\pi )$
and
![]() $c(\pi \times \pi ')$
.
$c(\pi \times \pi ')$
.
For archimedean F, we have that
 $$ \begin{align} \varepsilon(s,\pi,\psi) = \begin{cases} i^{-\kappa} &\text{if }F = \mathbb{R}\text{ and }\pi = \chi^{\kappa} |\cdot|_{\mathbb{R}}^t\text{ for }\kappa \in \{0,1\}, \\ i^{-\kappa} &\text{if }F = \mathbb{R}\text{ and }\pi = D_{\kappa} \otimes \left|\det\right|{}_{\mathbb{R}}^t\text{ for }\kappa \geq 2, \\ i^{-\|\kappa\|} &\text{if }F = \mathbb{C}\text{ and }\pi = \chi^{\kappa} |\cdot|_{\mathbb{C}}^t\text{ for }\kappa \in \mathbb{Z}, \end{cases} \end{align} $$
$$ \begin{align} \varepsilon(s,\pi,\psi) = \begin{cases} i^{-\kappa} &\text{if }F = \mathbb{R}\text{ and }\pi = \chi^{\kappa} |\cdot|_{\mathbb{R}}^t\text{ for }\kappa \in \{0,1\}, \\ i^{-\kappa} &\text{if }F = \mathbb{R}\text{ and }\pi = D_{\kappa} \otimes \left|\det\right|{}_{\mathbb{R}}^t\text{ for }\kappa \geq 2, \\ i^{-\|\kappa\|} &\text{if }F = \mathbb{C}\text{ and }\pi = \chi^{\kappa} |\cdot|_{\mathbb{C}}^t\text{ for }\kappa \in \mathbb{Z}, \end{cases} \end{align} $$
which, via (2.15), may be used to determine
![]() $\varepsilon (s,\pi ,\psi )$
and
$\varepsilon (s,\pi ,\psi )$
and
![]() $\varepsilon (s,\pi \times \pi ',\psi )$
for any induced representations of Whittaker type
$\varepsilon (s,\pi \times \pi ',\psi )$
for any induced representations of Whittaker type
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
, not just for essentially square-integrable representations.
$\pi '$
, not just for essentially square-integrable representations.
3. Nonarchimedean Newform Theory
We now detail the theory of the conductor exponent, newforms and oldforms associated to generic irreducible admissible smooth representations of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with F nonarchimedean (or more generally associated to induced representations of Whittaker or Langlands type; cf. Section 2.2.4), as well as the relation between newforms and test vectors for
$\operatorname {\mathrm {GL}}_n(F)$
with F nonarchimedean (or more generally associated to induced representations of Whittaker or Langlands type; cf. Section 2.2.4), as well as the relation between newforms and test vectors for
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals and test vectors for Godement–Jacquet zeta integrals. The results herein are for the most part well known; we recall them as motivation for Section 4, in which we discuss analogous yet new results for archimedean F.
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals and test vectors for Godement–Jacquet zeta integrals. The results herein are for the most part well known; we recall them as motivation for Section 4, in which we discuss analogous yet new results for archimedean F.
3.1. The conductor exponent, the newform, and the newform K-type
Let F be a nonarchimedean local field, and let
![]() $K = \operatorname {\mathrm {GL}}_n(\mathcal {O})$
be the maximal compact subgroup of
$K = \operatorname {\mathrm {GL}}_n(\mathcal {O})$
be the maximal compact subgroup of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, unique up to conjugation. For a nonnegative integer m, we define the following finite index subgroup of K:
$\operatorname {\mathrm {GL}}_n(F)$
, unique up to conjugation. For a nonnegative integer m, we define the following finite index subgroup of K:
(This is not to be confused with ![]() , the maximal compact subgroup of
, the maximal compact subgroup of
![]() $\operatorname {\mathrm {GL}}_1(F) = F^{\times }$
.) Given an induced representation of Langlands type
$\operatorname {\mathrm {GL}}_1(F) = F^{\times }$
.) Given an induced representation of Langlands type
![]() $(\pi ,V_{\pi })$
of
$(\pi ,V_{\pi })$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, we define the vector subspace
$\operatorname {\mathrm {GL}}_n(F)$
, we define the vector subspace
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
of
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
of
![]() $V_{\pi }$
consisting of
$V_{\pi }$
consisting of
![]() $K_1(\mathfrak {p}^m)$
-fixed vectors:
$K_1(\mathfrak {p}^m)$
-fixed vectors:
The following theorem is due to Casselman [Reference CasselmanCas73, Theorem 1] for
![]() $n = 2$
and Jacquet, Piatetski-Shapiro and Shalika for arbitrary n (though cf. Remark 3.15).
$n = 2$
and Jacquet, Piatetski-Shapiro and Shalika for arbitrary n (though cf. Remark 3.15).
Theorem 3.1 (Jacquet–Piatetski-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81, Théorème (5)])
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Langlands type of
$(\pi ,V_{\pi })$
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. There exists a minimal nonnegative integer m for which
$\operatorname {\mathrm {GL}}_n(F)$
. There exists a minimal nonnegative integer m for which
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
is nontrivial. For this minimal value of m,
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
is nontrivial. For this minimal value of m,
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
is one-dimensional.
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
is one-dimensional.
Definition 3.2. We define the conductor exponent of
![]() $\pi $
to be this minimal nonnegative integer m and denote it by
$\pi $
to be this minimal nonnegative integer m and denote it by
![]() $c(\pi )$
; we then call the ideal
$c(\pi )$
; we then call the ideal
![]() $\mathfrak {p}^{c(\pi )}$
the conductor of
$\mathfrak {p}^{c(\pi )}$
the conductor of
![]() $\pi $
. The newform of
$\pi $
. The newform of
![]() $\pi $
is defined to be the nonzero vector
$\pi $
is defined to be the nonzero vector
![]() $v^{\circ } \in V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}$
, unique up to scalar multiplication.
$v^{\circ } \in V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}$
, unique up to scalar multiplication.
The uniqueness of the newform may be thought of as being a multiplicity-one theorem for newforms. The reason for naming this distinguished vector a newform is due to its relation to the classical theory of modular forms: as shown by Casselman [Reference CasselmanCas73, Section 3], an automorphic form on
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
whose associated Whittaker function is a pure tensor composed of newforms in the Whittaker model is the adèlic lift of a classical newform in the sense of Atkin and Lehner [Reference Atkin and LehnerAL70].
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
whose associated Whittaker function is a pure tensor composed of newforms in the Whittaker model is the adèlic lift of a classical newform in the sense of Atkin and Lehner [Reference Atkin and LehnerAL70].
Remark 3.3. There is no consensus on the name of this distinguished vector: Casselman [Reference CasselmanCas73] leaves it unnamed; Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81] name it the essential vector, whereas Reeder [Reference ReederRee91] calls it the new vector; and Schmidt [Reference SchmidtSch02], regarding
![]() $\pi $
as being the local component of an automorphic representation, refers to it as the local newform. When viewed in the Whittaker model, this vector is referred to by Popa [Reference PopaPop08] as the Whittaker newform, whereas Matringe [Reference MatringeMat13] calls it the essential Whittaker function. Similarly, some authors instead call
$\pi $
as being the local component of an automorphic representation, refers to it as the local newform. When viewed in the Whittaker model, this vector is referred to by Popa [Reference PopaPop08] as the Whittaker newform, whereas Matringe [Reference MatringeMat13] calls it the essential Whittaker function. Similarly, some authors instead call
![]() $c(\pi )$
the conductor of
$c(\pi )$
the conductor of
![]() $\pi $
, whereas others yet refer to
$\pi $
, whereas others yet refer to
![]() $q^{c(\pi )}$
as the conductor of
$q^{c(\pi )}$
as the conductor of
![]() $\pi $
. Perhaps a more apt name for
$\pi $
. Perhaps a more apt name for
![]() $q^{c(\pi )}$
is the absolute conductor of
$q^{c(\pi )}$
is the absolute conductor of
![]() $\pi $
, being the absolute norm of the ideal
$\pi $
, being the absolute norm of the ideal
![]() $\mathfrak {p}^{c(\pi )}$
.
$\mathfrak {p}^{c(\pi )}$
.
Remark 3.4. Under the local Langlands correspondence, which gives a bijection between irreducible admissible smooth representations
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and n-dimensional Frobenius semisimple Weil–Deligne representations
$\operatorname {\mathrm {GL}}_n(F)$
and n-dimensional Frobenius semisimple Weil–Deligne representations
![]() $\rho $
of F, the conductor exponent
$\rho $
of F, the conductor exponent
![]() $c(\pi )$
is equal to the Artin exponent
$c(\pi )$
is equal to the Artin exponent
![]() $a(\rho )$
.
$a(\rho )$
.
If
![]() $c(\pi ) = 0$
, so that
$c(\pi ) = 0$
, so that
![]() $K_1(\mathfrak {p}^{c(\pi )}) = K$
, then
$K_1(\mathfrak {p}^{c(\pi )}) = K$
, then
![]() $\pi $
must be a spherical representation, and we say that
$\pi $
must be a spherical representation, and we say that
![]() $\pi $
is unramified. If
$\pi $
is unramified. If
![]() $c(\pi )> 0$
, then
$c(\pi )> 0$
, then
![]() $\pi $
is said to be ramified. In this sense, the conductor exponent is a measure of the extent of ramification of
$\pi $
is said to be ramified. In this sense, the conductor exponent is a measure of the extent of ramification of
![]() $\pi $
: it quantifies how ramified
$\pi $
: it quantifies how ramified
![]() $\pi $
may be.
$\pi $
may be.
Since
![]() $\pi $
is admissible,
$\pi $
is admissible,
![]() $\operatorname {\mathrm {Hom}}_K(\tau ,\pi |_K)$
is finite-dimensional for each irreducible smooth representation
$\operatorname {\mathrm {Hom}}_K(\tau ,\pi |_K)$
is finite-dimensional for each irreducible smooth representation
![]() $\tau $
of K. We say that such a representation
$\tau $
of K. We say that such a representation
![]() $\tau $
is a K-type of
$\tau $
is a K-type of
![]() $\pi $
if
$\pi $
if
![]() $\operatorname {\mathrm {Hom}}_K(\tau ,\pi |_K)$
is nontrivial, and we call
$\operatorname {\mathrm {Hom}}_K(\tau ,\pi |_K)$
is nontrivial, and we call
![]() $\dim \operatorname {\mathrm {Hom}}_K(\tau ,\pi |_K)$
the multiplicity of
$\dim \operatorname {\mathrm {Hom}}_K(\tau ,\pi |_K)$
the multiplicity of
![]() $\tau $
in
$\tau $
in
![]() $\pi $
. The complexity of an irreducible smooth representation
$\pi $
. The complexity of an irreducible smooth representation
![]() $\tau $
of K can be measured by its level m, which is the least nonnegative integer m for which
$\tau $
of K can be measured by its level m, which is the least nonnegative integer m for which
![]() $\tau $
factors through the finite group
$\tau $
factors through the finite group
![]() $\operatorname {\mathrm {GL}}_n(\mathcal {O}/\mathfrak {p}^m)$
. In [Reference HumphriesHum22], the author proved the existence of a distinguished K-type of
$\operatorname {\mathrm {GL}}_n(\mathcal {O}/\mathfrak {p}^m)$
. In [Reference HumphriesHum22], the author proved the existence of a distinguished K-type of
![]() $\pi $
that occurs with multiplicity one and is closely associated to the newform and the conductor exponent.
$\pi $
that occurs with multiplicity one and is closely associated to the newform and the conductor exponent.
Theorem 3.5 [Reference HumphriesHum22, Theorem 4.11]
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Langlands type of
$(\pi ,V_{\pi })$
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. Among the K-types of
$\operatorname {\mathrm {GL}}_n(F)$
. Among the K-types of
![]() $\pi $
whose restriction to
$\pi $
whose restriction to

contains the trivial representation, there exists a unique K-type
![]() $\tau ^{\circ }$
of minimal level. Furthermore,
$\tau ^{\circ }$
of minimal level. Furthermore,
![]() $\tau ^{\circ }$
occurs with multiplicity one in
$\tau ^{\circ }$
occurs with multiplicity one in
![]() $\pi $
, the level of
$\pi $
, the level of
![]() $\tau ^{\circ }$
is equal to the conductor exponent
$\tau ^{\circ }$
is equal to the conductor exponent
![]() $c(\pi )$
, and the subspace of
$c(\pi )$
, and the subspace of
![]() $V_{\pi }$
of
$V_{\pi }$
of
![]() $\tau ^{\circ }$
-isotypic
$\tau ^{\circ }$
-isotypic
![]() $K_{n - 1,1}$
-invariant vectors is equal to the one-dimensional subspace
$K_{n - 1,1}$
-invariant vectors is equal to the one-dimensional subspace
![]() $V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}$
spanned by the newform
$V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}$
spanned by the newform
![]() $v^{\circ }$
.
$v^{\circ }$
.
Definition 3.6. We call the distinguished K-type
![]() $\tau ^{\circ }$
the newform K-type.
$\tau ^{\circ }$
the newform K-type.
3.2. Oldforms
Although Jacquet, Piatetski-Shapiro and Shalika merely show that
![]() $V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}$
is one-dimensional, one can also calculate the dimension of
$V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}$
is one-dimensional, one can also calculate the dimension of
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
for all
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
for all
![]() $m \geq c(\pi )$
in terms of a binomial coefficient; for
$m \geq c(\pi )$
in terms of a binomial coefficient; for
![]() $n = 2$
, this is due to Casselman [Reference CasselmanCas73, Corollary to the Proof], while Reeder has proven this result for arbitrary n.
$n = 2$
, this is due to Casselman [Reference CasselmanCas73, Corollary to the Proof], while Reeder has proven this result for arbitrary n.
Theorem 3.7 (Reeder [Reference ReederRee91, Theorem 1])
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Langlands type of
$(\pi ,V_{\pi })$
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with
$\operatorname {\mathrm {GL}}_n(F)$
with
![]() $n \geq 2$
. We have that
$n \geq 2$
. We have that
 $$\begin{align*}\dim V_{\pi}^{K_1(\mathfrak{p}^m)} = \begin{cases} \binom{m - c(\pi) + n - 1}{n - 1} & \text{if }m \geq c(\pi), \\ 0 & \text{otherwise}. \end{cases}\end{align*}$$
$$\begin{align*}\dim V_{\pi}^{K_1(\mathfrak{p}^m)} = \begin{cases} \binom{m - c(\pi) + n - 1}{n - 1} & \text{if }m \geq c(\pi), \\ 0 & \text{otherwise}. \end{cases}\end{align*}$$
Casselman and Reeder also give a basis for each of these spaces in terms of the action of certain Hecke operators on the newform. For
![]() $m> c(\pi )$
, we call
$m> c(\pi )$
, we call
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
the space of oldforms of exponent m. Once again, the reason for naming these distinguished vectors oldforms is due to their relation to the classical theory of modular forms: an automorphic form on
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
the space of oldforms of exponent m. Once again, the reason for naming these distinguished vectors oldforms is due to their relation to the classical theory of modular forms: an automorphic form on
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
whose associated Whittaker function is a pure tensor composed of Whittaker newforms at all but finitely many places and of Whittaker oldforms at the remaining places corresponds to an oldform in the sense of Atkin and Lehner [Reference Atkin and LehnerAL70].
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
whose associated Whittaker function is a pure tensor composed of Whittaker newforms at all but finitely many places and of Whittaker oldforms at the remaining places corresponds to an oldform in the sense of Atkin and Lehner [Reference Atkin and LehnerAL70].
In [Reference HumphriesHum22], the author showed that spaces of oldforms can be described in terms of distinguished K-types.
Theorem 3.8 [Reference HumphriesHum22, Theorem 4.11]
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Langlands type of
$(\pi ,V_{\pi })$
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. For each
$\operatorname {\mathrm {GL}}_n(F)$
. For each
![]() $m \geq c(\pi )$
, there exists a unique K-type
$m \geq c(\pi )$
, there exists a unique K-type
![]() $\tau _m$
of
$\tau _m$
of
![]() $\pi $
of level m whose restriction to
$\pi $
of level m whose restriction to
![]() $K_{n - 1,1}$
contains the trivial representation. Furthermore, this K-type occurs with multiplicity
$K_{n - 1,1}$
contains the trivial representation. Furthermore, this K-type occurs with multiplicity
 $$\begin{align*}\binom{m - c(\pi) + n - 2}{n - 2},\end{align*}$$
$$\begin{align*}\binom{m - c(\pi) + n - 2}{n - 2},\end{align*}$$
and the direct sum indexed by nonnegative integers
![]() $\ell \in \{c(\pi ),\ldots ,m\}$
of the subspaces of
$\ell \in \{c(\pi ),\ldots ,m\}$
of the subspaces of
![]() $V_{\pi }$
of
$V_{\pi }$
of
![]() $\tau _{\ell }$
-isotypic
$\tau _{\ell }$
-isotypic
![]() $K_{n - 1,1}$
-invariant vectors is equal to
$K_{n - 1,1}$
-invariant vectors is equal to
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
, the space of oldforms of exponent m.
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
, the space of oldforms of exponent m.
3.3. Additivity and inductivity of the conductor exponent
Associated to any induced representation of Langlands type
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
is an integer
$\operatorname {\mathrm {GL}}_n(F)$
is an integer
![]() $c(\pi )$
defined via the epsilon factor as in (2.17).
$c(\pi )$
defined via the epsilon factor as in (2.17).
Theorem 3.9 (Jacquet–Piateski-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS83, Section 5])
Let
![]() $\pi $
be an induced representation of Langlands type of
$\pi $
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. The integer
$\operatorname {\mathrm {GL}}_n(F)$
. The integer
![]() $c(\pi )$
appearing in the epsilon factor
$c(\pi )$
appearing in the epsilon factor
![]() $\varepsilon (s,\pi ,\psi )$
as in (2.17) is equal to the conductor exponent of
$\varepsilon (s,\pi ,\psi )$
as in (2.17) is equal to the conductor exponent of
![]() $\pi $
.
$\pi $
.
From the multiplicativity of epsilon factors (2.16), we have the following.
Theorem 3.10 (Jacquet–Piateski-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS83, Theorem (3.1)])
For an induced representation of Langlands type
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, we have that
$\operatorname {\mathrm {GL}}_n(F)$
, we have that
 $$\begin{align*}c(\pi) = \sum_{j = 1}^{r} c(\pi_j).\end{align*}$$
$$\begin{align*}c(\pi) = \sum_{j = 1}^{r} c(\pi_j).\end{align*}$$
Thus, the conductor exponent
![]() $c(\pi )$
is additive with respect to isobaric sums; equivalently, the conductor
$c(\pi )$
is additive with respect to isobaric sums; equivalently, the conductor
![]() $\mathfrak {p}^{c(\pi )}$
is multiplicative.
$\mathfrak {p}^{c(\pi )}$
is multiplicative.
Remark 3.11. In the classical setting of automorphic forms on the upper half-plane, Theorem 3.10 manifests itself via the conductor of an Eisenstein newform: an Eisenstein newform, in the sense of [Reference YoungYou19], is associated to a pair of primitive Dirichlet characters, and the conductor of such a newform is the product of the conductors of the two Dirichlet characters.
Finally, the epsilon factor is inductive in degree zero: if
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are induced representations of Langlands type of
$\pi '$
are induced representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(E)$
, where E is a finite cyclic extension of F of degree
$\operatorname {\mathrm {GL}}_n(E)$
, where E is a finite cyclic extension of F of degree
![]() $m \geq 2$
, and
$m \geq 2$
, and
![]() $\mathcal {AI}_{E/F} \pi $
and
$\mathcal {AI}_{E/F} \pi $
and
![]() $\mathcal {AI}_{E/F} \pi '$
denote the induced representations of Langlands type of
$\mathcal {AI}_{E/F} \pi '$
denote the induced representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_{mn}(F)$
obtained by induction [Reference Henniart and HerbHH95], then
$\operatorname {\mathrm {GL}}_{mn}(F)$
obtained by induction [Reference Henniart and HerbHH95], then
 $$\begin{align*}\frac{\varepsilon\left(s,\mathcal{AI}_{E/F} \pi, \psi\right)}{\varepsilon\left(s,\mathcal{AI}_{E/F} \pi',\psi\right)} = \frac{\varepsilon\left(s,\pi,\psi \circ \operatorname{\mathrm{Tr}}_{E/F}\right)}{\varepsilon\left(s,\pi',\psi \circ \operatorname{\mathrm{Tr}}_{E/F}\right)}.\end{align*}$$
$$\begin{align*}\frac{\varepsilon\left(s,\mathcal{AI}_{E/F} \pi, \psi\right)}{\varepsilon\left(s,\mathcal{AI}_{E/F} \pi',\psi\right)} = \frac{\varepsilon\left(s,\pi,\psi \circ \operatorname{\mathrm{Tr}}_{E/F}\right)}{\varepsilon\left(s,\pi',\psi \circ \operatorname{\mathrm{Tr}}_{E/F}\right)}.\end{align*}$$
Taking
![]() $\pi '$
to be the isobaric sum of n copies of the trivial representation, we deduce the following.
$\pi '$
to be the isobaric sum of n copies of the trivial representation, we deduce the following.
Theorem 3.12. For an induced representation of Langlands type
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(E)$
, where E is a finite cyclic extension of F of degree
$\operatorname {\mathrm {GL}}_n(E)$
, where E is a finite cyclic extension of F of degree
![]() $m \geq 2$
, we have that
$m \geq 2$
, we have that
where
![]() $f_{E/F}$
denotes the residual degree of
$f_{E/F}$
denotes the residual degree of
![]() $E/F$
and
$E/F$
and
![]() $d_{E/F}$
denotes the valuation of the discriminant of
$d_{E/F}$
denotes the valuation of the discriminant of
![]() $E/F$
.
$E/F$
.
Remark 3.13. This result also has a classical manifestation. Let
![]() $\psi $
be a Hecke Größencharakter of a quadratic extension E of
$\psi $
be a Hecke Größencharakter of a quadratic extension E of
![]() $\mathbb {Q}$
with conductor
$\mathbb {Q}$
with conductor
![]() $\mathfrak {q} \subset \mathcal {O}_E$
. By automorphic induction, one can associate to
$\mathfrak {q} \subset \mathcal {O}_E$
. By automorphic induction, one can associate to
![]() $\psi $
a classical newform
$\psi $
a classical newform
![]() $f_{\psi } : \mathbb {H} \to \mathbb {C}$
of conductor
$f_{\psi } : \mathbb {H} \to \mathbb {C}$
of conductor
![]() $\operatorname {\mathrm {N}}(\mathfrak {q}) D_{E/\mathbb {Q}}$
, where
$\operatorname {\mathrm {N}}(\mathfrak {q}) D_{E/\mathbb {Q}}$
, where ![]() is the absolute norm of the integral ideal
is the absolute norm of the integral ideal
![]() $\mathfrak {q}$
and
$\mathfrak {q}$
and
![]() $D_{E/\mathbb {Q}}$
is the absolute discriminant of
$D_{E/\mathbb {Q}}$
is the absolute discriminant of
![]() $E/\mathbb {Q}$
.
$E/\mathbb {Q}$
.
3.4. Test vectors for Rankin–Selberg integrals
Next, we discuss the relation between newforms and test vectors for Rankin–Selberg integrals. We first recall the test vector problem for
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals.
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals.
Test Vector Problem. Given induced representations of Langlands type
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_m(F)$
with
$\operatorname {\mathrm {GL}}_m(F)$
with
![]() $n \geq m$
, determine the existence of right
$n \geq m$
, determine the existence of right
![]() $K_n$
- and
$K_n$
- and
![]() $K_m$
-finite Whittaker functions
$K_m$
-finite Whittaker functions
![]() $W \in \mathcal {W}(\pi ,\psi )$
and
$W \in \mathcal {W}(\pi ,\psi )$
and
![]() $W' \in \mathcal {W}(\pi ',\overline {\psi })$
, and additionally, a right
$W' \in \mathcal {W}(\pi ',\overline {\psi })$
, and additionally, a right
![]() $K_n$
-finite Schwartz–Bruhat function
$K_n$
-finite Schwartz–Bruhat function
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F)) = \mathscr {S}(F^n)$
should m be equal to n, such that
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F)) = \mathscr {S}(F^n)$
should m be equal to n, such that
 $$\begin{align*}L(s,\pi \times \pi') = \begin{cases} \Psi(s,W,W') & \text{if }m < n, \\ \Psi(s,W,W',\Phi) & \text{if }m = n. \end{cases}\end{align*}$$
$$\begin{align*}L(s,\pi \times \pi') = \begin{cases} \Psi(s,W,W') & \text{if }m < n, \\ \Psi(s,W,W',\Phi) & \text{if }m = n. \end{cases}\end{align*}$$
In full generality, this problem remains unresolved. For
![]() $m = n - 1$
,
$m = n - 1$
,
![]() $\pi '$
a spherical representation of Langlands type, and
$\pi '$
a spherical representation of Langlands type, and
![]() $W' = W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
the spherical vector normalised as in Section 2.2.5, this has been solved by Jacquet, Piatetski-Shapiro and Shalika.
$W' = W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
the spherical vector normalised as in Section 2.2.5, this has been solved by Jacquet, Piatetski-Shapiro and Shalika.
Theorem 3.14 (Jacquet–Piatetski-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81, Théorème (4)], Jacquet [Reference JacquetJac12], Matringe [Reference MatringeMat13, Corollary 3.3])
For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi $
be an induced representation of Langlands type of
$\pi $
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. There exists a Whittaker function
$\operatorname {\mathrm {GL}}_n(F)$
. There exists a Whittaker function
![]() $W \in \mathcal {W}(\pi ,\psi )$
such that for any spherical representation of Langlands type
$W \in \mathcal {W}(\pi ,\psi )$
such that for any spherical representation of Langlands type
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
with spherical Whittaker function
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
with spherical Whittaker function
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
,
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
,
for
![]() $\Re (s)$
sufficiently large.
$\Re (s)$
sufficiently large.
Moreover, there exists a unique such function
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
that additionally satisfies
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
that additionally satisfies
 $$\begin{align*}W^{\circ}\left(g\begin{pmatrix} k & 0 \\ 0 & 1 \end{pmatrix}\right) = W^{\circ}(g)\end{align*}$$
$$\begin{align*}W^{\circ}\left(g\begin{pmatrix} k & 0 \\ 0 & 1 \end{pmatrix}\right) = W^{\circ}(g)\end{align*}$$
for all
![]() $k \in K_{n - 1}$
. Up to multiplication by a scalar, this function is the newform
$k \in K_{n - 1}$
. Up to multiplication by a scalar, this function is the newform
![]() ${v^{\circ } \in V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}}$
viewed in the Whittaker model.
${v^{\circ } \in V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}}$
viewed in the Whittaker model.
That is,
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
is a right
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
is a right
![]() $K_{n - 1}$
-invariant test vector for the
$K_{n - 1}$
-invariant test vector for the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral for all spherical representations
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral for all spherical representations
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
. We call
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
. We call
![]() $W^{\circ }$
the Whittaker newform of
$W^{\circ }$
the Whittaker newform of
![]() $\pi $
.
$\pi $
.
Remark 3.15. The proof of [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81, Théorème (4)] is in fact incomplete, as was observed by Matringe; correct proofs have subsequently independently been given by Jacquet [Reference JacquetJac12, Theorem 1] and Matringe [Reference MatringeMat13, Corollary 3.3].
Remark 3.16. The normalisation of the Whittaker newform is such that
![]() $W^{\circ }(1_n) = 1$
.
$W^{\circ }(1_n) = 1$
.
The Whittaker newform is a test vector for more than just the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral for all spherical representations
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral for all spherical representations
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
.
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
.
Theorem 3.17 (Kim [Reference KimKim10, Theorem 2.2.1], Matringe [Reference MatringeMat13, Corollary 3.3])
Let
![]() $\pi $
be an induced representation of Langlands type of
$\pi $
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with
$\operatorname {\mathrm {GL}}_n(F)$
with
![]() $n \geq 2$
. For
$n \geq 2$
. For
![]() $m \in \{1, \ldots , n - 2\}$
and for every spherical representation of Langlands type
$m \in \{1, \ldots , n - 2\}$
and for every spherical representation of Langlands type
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_m(F)$
with spherical Whittaker function
$\operatorname {\mathrm {GL}}_m(F)$
with spherical Whittaker function
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
, the Whittaker newform
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
, the Whittaker newform
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
of
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
of
![]() $\pi $
satisfies
$\pi $
satisfies
for
![]() $\Re (s)$
sufficiently large.
$\Re (s)$
sufficiently large.
Miyauchi also gave a proof when
![]() $m = 1$
[Reference MiyauchiMiy14, Theorem 5.1] by a different method that generalises easily to prove the result for
$m = 1$
[Reference MiyauchiMiy14, Theorem 5.1] by a different method that generalises easily to prove the result for
![]() $m \in \{2, \ldots , n - 1\}$
.
$m \in \{2, \ldots , n - 1\}$
.
A similar theory also holds for the case
![]() $m = n$
.
$m = n$
.
Theorem 3.18 (Kim [Reference KimKim10, Theorem 2.1.1])
Let
![]() $\pi $
be an induced representation of Langlands type of
$\pi $
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. Then for every spherical representation of Langlands type
$\operatorname {\mathrm {GL}}_n(F)$
. Then for every spherical representation of Langlands type
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with spherical Whittaker function
$\operatorname {\mathrm {GL}}_n(F)$
with spherical Whittaker function
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
, the Whittaker newform
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
, the Whittaker newform
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
of
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
of
![]() $\pi $
satisfies
$\pi $
satisfies
for
![]() $\Re (s)$
sufficiently large, where
$\Re (s)$
sufficiently large, where
![]() $\Phi ^{\circ } \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
is given by
$\Phi ^{\circ } \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
is given by

if
![]() $c(\pi )> 0$
, where
$c(\pi )> 0$
, where
![]() $\omega _{\pi }$
denotes the central character of
$\omega _{\pi }$
denotes the central character of
![]() $\pi $
and
$\pi $
and
while for
![]() $c(\pi ) = 0$
,
$c(\pi ) = 0$
,

Again, this can also be proven via the method of Miyauchi [Reference MiyauchiMiy14].
Remark 3.19. Little is known about test vectors for Rankin–Selberg integrals when
![]() $\pi '$
is ramified. Kim [Reference KimKim10, Proposition 2.2.2] has shown that Whittaker newforms are not test vectors when
$\pi '$
is ramified. Kim [Reference KimKim10, Proposition 2.2.2] has shown that Whittaker newforms are not test vectors when
![]() $\pi '$
is ramified: if
$\pi '$
is ramified: if
![]() $\pi '$
is a ramified representation of
$\pi '$
is a ramified representation of
![]() $\operatorname {\mathrm {GL}}_m(F)$
with
$\operatorname {\mathrm {GL}}_m(F)$
with
![]() $m < n$
and
$m < n$
and
![]() $W^{\circ },W^{\prime \circ }$
are newforms of
$W^{\circ },W^{\prime \circ }$
are newforms of
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
, respectively, then
$\pi '$
, respectively, then
![]() $\Psi \left (s,W^{\circ },W^{\prime \circ }\right ) = 0$
for all
$\Psi \left (s,W^{\circ },W^{\prime \circ }\right ) = 0$
for all
![]() $s \in \mathbb {C}$
. For
$s \in \mathbb {C}$
. For
![]() $n = m = 2$
, Kim has determined test vectors for certain pairs of representations
$n = m = 2$
, Kim has determined test vectors for certain pairs of representations
![]() $\pi ,\pi '$
[Reference KimKim10]. Recently, Kurinczuk and Matringe have explicitly determined test vectors for
$\pi ,\pi '$
[Reference KimKim10]. Recently, Kurinczuk and Matringe have explicitly determined test vectors for
![]() $n = m$
arbitrary
$n = m$
arbitrary
![]() $\pi $
supercuspidal, and
$\pi $
supercuspidal, and
![]() $\pi ' = \widetilde {\pi } \otimes \chi $
for some unramified character
$\pi ' = \widetilde {\pi } \otimes \chi $
for some unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
[Reference Kurinczuk and MatringeKM19]. Booker, Krishnamurthy and Lee have resolved a weakened version of the test vector problem in [Reference Booker, Krishnamurthy and LeeBKL20] when
$F^{\times }$
[Reference Kurinczuk and MatringeKM19]. Booker, Krishnamurthy and Lee have resolved a weakened version of the test vector problem in [Reference Booker, Krishnamurthy and LeeBKL20] when
![]() $m < n$
: they construct vectors
$m < n$
: they construct vectors
![]() $W \in \mathcal {W}(\pi ,\psi )$
and
$W \in \mathcal {W}(\pi ,\psi )$
and
![]() $W' \in \mathcal {W}(\pi ',\overline {\psi })$
for which
$W' \in \mathcal {W}(\pi ',\overline {\psi })$
for which
![]() $\Psi (s,W,W')$
is a multiple of
$\Psi (s,W,W')$
is a multiple of
![]() $L(s,\pi \times \pi ')$
by a nonzero polynomial in
$L(s,\pi \times \pi ')$
by a nonzero polynomial in
![]() $q^{-s}$
; an analogous result when
$q^{-s}$
; an analogous result when
![]() $m = n$
is due to Jo [Reference JoJo23, Theorem 1.1]. Finally, Jacquet, Piatetski-Shapiro and Shalika have shown that for each pair of representations
$m = n$
is due to Jo [Reference JoJo23, Theorem 1.1]. Finally, Jacquet, Piatetski-Shapiro and Shalika have shown that for each pair of representations
![]() $\pi ,\pi '$
of
$\pi ,\pi '$
of
![]() $\operatorname {\mathrm {GL}}_n(F),\operatorname {\mathrm {GL}}_m(F)$
with
$\operatorname {\mathrm {GL}}_n(F),\operatorname {\mathrm {GL}}_m(F)$
with
![]() $n> m$
, there exist finite collections
$n> m$
, there exist finite collections
![]() $\{W_j\} \subset \mathcal {W}(\pi ,\psi )$
and
$\{W_j\} \subset \mathcal {W}(\pi ,\psi )$
and
![]() $\{W_j^{\prime }\} \subset \mathcal {W}(\pi ',\overline {\psi })$
of right
$\{W_j^{\prime }\} \subset \mathcal {W}(\pi ',\overline {\psi })$
of right
![]() $K_n$
- and
$K_n$
- and
![]() $K_m$
-finite Whittaker functions for which
$K_m$
-finite Whittaker functions for which
![]() $\sum _j \Psi (s,W_j,W_j^{\prime }) = L(s,\pi \times \pi ')$
[Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS83, Theorem (2.7)]; a similar result (additionally involving Schwartz–Bruhat functions
$\sum _j \Psi (s,W_j,W_j^{\prime }) = L(s,\pi \times \pi ')$
[Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS83, Theorem (2.7)]; a similar result (additionally involving Schwartz–Bruhat functions
![]() $\{\Phi _j\} \subset \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
) also holds for
$\{\Phi _j\} \subset \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
) also holds for
![]() $m = n$
.
$m = n$
.
3.5. Test Vectors for Godement–Jacquet Zeta Integrals
Finally, we mention the relation between newforms and test vectors for Godement–Jacquet zeta integrals. The test vector problem for the Godement–Jacquet zeta integral is the following.
Test Vector Problem. Given an induced representation of Langlands type
![]() $(\pi ,V_{\pi })$
of
$(\pi ,V_{\pi })$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, determine the existence of K-finite vectors
$\operatorname {\mathrm {GL}}_n(F)$
, determine the existence of K-finite vectors
![]() $v_1 \in V_{\pi }$
,
$v_1 \in V_{\pi }$
,
![]() $\widetilde {v_2} \in V_{\widetilde {\pi }}$
, and a bi-K-finite Schwartz–Bruhat function
$\widetilde {v_2} \in V_{\widetilde {\pi }}$
, and a bi-K-finite Schwartz–Bruhat function
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
such that
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
such that
This has been solved for spherical representations by Godement and Jacquet and for nonspherical representations by the author.
Theorem 3.20 (Godement–Jacquet [Reference Godement and JacquetGJ72, Lemma 6.10], Humphries [Reference HumphriesHum21, Theorem 1.2])
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Langlands type of
$(\pi ,V_{\pi })$
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. Let
$\operatorname {\mathrm {GL}}_n(F)$
. Let
![]() $\beta (g)$
denote the matrix coefficient
$\beta (g)$
denote the matrix coefficient
![]() $\langle \pi (g) \cdot v^{\circ }, \widetilde {v}^{\circ } \rangle $
, where
$\langle \pi (g) \cdot v^{\circ }, \widetilde {v}^{\circ } \rangle $
, where
![]() $v^{\circ } \in V_{\pi }$
denotes the newform and
$v^{\circ } \in V_{\pi }$
denotes the newform and
![]() $\widetilde {v}^{\circ } \in V_{\widetilde {\pi }}$
is the corresponding newform normalised such that
$\widetilde {v}^{\circ } \in V_{\widetilde {\pi }}$
is the corresponding newform normalised such that
![]() $\beta (1_n) = 1$
. Then
$\beta (1_n) = 1$
. Then
for
![]() $\Re (s)$
sufficiently large, where
$\Re (s)$
sufficiently large, where
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is given by
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is given by

if
![]() $c(\pi )> 0$
, while for
$c(\pi )> 0$
, while for
![]() $c(\pi ) = 0$
,
$c(\pi ) = 0$
,

4. Archimedean Newform Theory
4.1. Analogues of nonarchimedean results
For an induced representation of Whittaker type
![]() $(\pi ,V_{\pi })$
of
$(\pi ,V_{\pi })$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with F archimedean, it is not so clear what the definition of the conductor exponent and the newform of
$\operatorname {\mathrm {GL}}_n(F)$
with F archimedean, it is not so clear what the definition of the conductor exponent and the newform of
![]() $\pi $
ought to be. When F is nonarchimedean, the conductor exponent may be defined either as the least nonnegative integer m for which
$\pi $
ought to be. When F is nonarchimedean, the conductor exponent may be defined either as the least nonnegative integer m for which
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
is nonempty or as the exponent appearing in the epsilon factor
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
is nonempty or as the exponent appearing in the epsilon factor
![]() $\varepsilon (s,\pi ,\psi )$
. Neither of these properties, however, can be easily imported to the archimedean setting. Indeed, there is no obvious analogue of the congruence subgroup
$\varepsilon (s,\pi ,\psi )$
. Neither of these properties, however, can be easily imported to the archimedean setting. Indeed, there is no obvious analogue of the congruence subgroup
![]() $K_1(\mathfrak {p}^m)$
(though cf. [Reference Jana and NelsonJN19]), while the epsilon factor
$K_1(\mathfrak {p}^m)$
(though cf. [Reference Jana and NelsonJN19]), while the epsilon factor
![]() $\varepsilon (s,\pi ,\psi )$
is an integral power of i for all
$\varepsilon (s,\pi ,\psi )$
is an integral power of i for all
![]() $s \in \mathbb {C}$
; this integer is therefore only determined modulo
$s \in \mathbb {C}$
; this integer is therefore only determined modulo
![]() $4$
, and so cannot be directly used to define the conductor exponent.
$4$
, and so cannot be directly used to define the conductor exponent.
Our starting observation that leads us to define the conductor exponent and newform in the archimedean setting is that the key property shared by the newform defined in terms of the congruence subgroup
![]() $K_1(\mathfrak {p}^{c(\pi )})$
in Theorem 3.1 and the Whittaker newform defined in terms of a test vector for the
$K_1(\mathfrak {p}^{c(\pi )})$
in Theorem 3.1 and the Whittaker newform defined in terms of a test vector for the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral in Theorem 3.14 is its invariance under the action of the subgroup
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral in Theorem 3.14 is its invariance under the action of the subgroup
![]() $K_{n - 1} \ni k'$
embedded in
$K_{n - 1} \ni k'$
embedded in
![]() $\operatorname {\mathrm {GL}}_n(F)$
via the map
$\operatorname {\mathrm {GL}}_n(F)$
via the map ![]() . Moreover, Theorem 3.1 essentially states that the newform is the ‘simplest’ such vector for which this is so, in the sense that
. Moreover, Theorem 3.1 essentially states that the newform is the ‘simplest’ such vector for which this is so, in the sense that
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
is trivial for
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
is trivial for
![]() $m < c(\pi )$
. The following lemma exemplifies the necessity of
$m < c(\pi )$
. The following lemma exemplifies the necessity of
![]() $K_{n - 1}$
-invariance for the Whittaker newform.
$K_{n - 1}$
-invariance for the Whittaker newform.
Lemma 4.1. Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Langlands type of
$(\pi ,V_{\pi })$
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with
$\operatorname {\mathrm {GL}}_n(F)$
with
![]() $n \geq 2$
, and let
$n \geq 2$
, and let
![]() $W \in \mathcal {W}(\pi ,\psi )$
be a right
$W \in \mathcal {W}(\pi ,\psi )$
be a right
![]() $K_n$
-finite Whittaker function, so that the action of
$K_n$
-finite Whittaker function, so that the action of ![]() on W for
on W for
![]() $k' \in K_{n - 1}$
generates a finite-dimensional representation
$k' \in K_{n - 1}$
generates a finite-dimensional representation
![]() $\tau '$
of
$\tau '$
of
![]() $K_{n - 1}$
. If
$K_{n - 1}$
. If
![]() $\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1,\tau ')$
is trivial, then the
$\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1,\tau ')$
is trivial, then the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
![]() $\Psi \left (s,W,W^{\prime \circ }\right )$
is identically equal to zero for every spherical representation of Langlands type
$\Psi \left (s,W,W^{\prime \circ }\right )$
is identically equal to zero for every spherical representation of Langlands type
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
with spherical Whittaker function
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
with spherical Whittaker function
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
.
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
.
Proof. We may write
![]() $W(g) = \Lambda (\pi (g) \cdot v)$
for some
$W(g) = \Lambda (\pi (g) \cdot v)$
for some
![]() $v \in V_{\pi }$
. Via the Iwasawa decomposition with respect to the standard Borel subgroup and the fact that
$v \in V_{\pi }$
. Via the Iwasawa decomposition with respect to the standard Borel subgroup and the fact that
![]() $W^{\prime \circ }$
is the spherical Whittaker function, the Rankin–Selberg integral
$W^{\prime \circ }$
is the spherical Whittaker function, the Rankin–Selberg integral
![]() $\Psi \left (s,W,W^{\prime \circ }\right )$
, defined in (2.1), is equal to
$\Psi \left (s,W,W^{\prime \circ }\right )$
, defined in (2.1), is equal to
 $$\begin{align*}\int_{\mathrm{A}_{n - 1}(F)} W^{\prime\circ}(a') \left|\det a'\right|{}^{s - \frac{1}{2}} \delta_{n - 1}^{-1}(a') \Lambda\left(\pi\begin{pmatrix} a' & 0 \\ 0 & 1 \end{pmatrix} \cdot \int_{K_{n - 1}} \pi\begin{pmatrix} k' & 0 \\ 0 & 1 \end{pmatrix} \cdot v \, dk'\right) \, d^{\times} a',\end{align*}$$
$$\begin{align*}\int_{\mathrm{A}_{n - 1}(F)} W^{\prime\circ}(a') \left|\det a'\right|{}^{s - \frac{1}{2}} \delta_{n - 1}^{-1}(a') \Lambda\left(\pi\begin{pmatrix} a' & 0 \\ 0 & 1 \end{pmatrix} \cdot \int_{K_{n - 1}} \pi\begin{pmatrix} k' & 0 \\ 0 & 1 \end{pmatrix} \cdot v \, dk'\right) \, d^{\times} a',\end{align*}$$
and the integral over
![]() $K_{n - 1}$
vanishes whenever
$K_{n - 1}$
vanishes whenever
![]() $\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1,\tau ')$
is trivial.
$\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1,\tau ')$
is trivial.
This leads us to search for vectors
![]() $v \in V_{\pi }$
that are invariant under the action of
$v \in V_{\pi }$
that are invariant under the action of
![]() $K_{n - 1}$
and to define the newform of
$K_{n - 1}$
and to define the newform of
![]() $\pi $
to be the ‘simplest’ such vector. A natural way to interpret ‘simplest’ is to search for vectors in K-types of
$\pi $
to be the ‘simplest’ such vector. A natural way to interpret ‘simplest’ is to search for vectors in K-types of
![]() $\pi $
that are ‘small’ in a sense that we make precise. Once we have located the newform of
$\pi $
that are ‘small’ in a sense that we make precise. Once we have located the newform of
![]() $\pi $
, we show that, when viewed in the Whittaker model, it is a Whittaker newform in the sense of Theorem 3.14. In this way, we work in the reverse direction of the nonarchimedean setting, where Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81] first prove Theorem 3.14 and then use this to deduce Theorem 3.1.
$\pi $
, we show that, when viewed in the Whittaker model, it is a Whittaker newform in the sense of Theorem 3.14. In this way, we work in the reverse direction of the nonarchimedean setting, where Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81] first prove Theorem 3.14 and then use this to deduce Theorem 3.1.
4.2. K-Types
The representation
![]() $\pi $
being admissible means that
$\pi $
being admissible means that
![]() $\operatorname {\mathrm {Hom}}_K \left (\tau , \pi |_K\right )$
is finite-dimensional for any
$\operatorname {\mathrm {Hom}}_K \left (\tau , \pi |_K\right )$
is finite-dimensional for any
![]() $\tau $
in
$\tau $
in
![]() $\widehat {K}$
, the set of equivalence classes of irreducible representations of K. We call
$\widehat {K}$
, the set of equivalence classes of irreducible representations of K. We call
![]() $\tau $
a K-type of
$\tau $
a K-type of
![]() $\pi $
should the vector space
$\pi $
should the vector space
![]() $\operatorname {\mathrm {Hom}}_K \left (\tau , \pi |_K\right )$
be nontrivial. To each
$\operatorname {\mathrm {Hom}}_K \left (\tau , \pi |_K\right )$
be nontrivial. To each
![]() $\tau \in \widehat {K}$
, one can associate a nonnegative integer
$\tau \in \widehat {K}$
, one can associate a nonnegative integer
![]() $\deg \tau $
called the Howe degree of
$\deg \tau $
called the Howe degree of
![]() $\tau $
[Reference HoweHow89]; this is the archimedean analogue of the level of an irreducible smooth representation of
$\tau $
[Reference HoweHow89]; this is the archimedean analogue of the level of an irreducible smooth representation of
![]() $\operatorname {\mathrm {GL}}_n(\mathcal {O})$
. In order to define this, we first recall the theory of highest weights for the two groups
$\operatorname {\mathrm {GL}}_n(\mathcal {O})$
. In order to define this, we first recall the theory of highest weights for the two groups
![]() $\operatorname {\mathrm {U}}(n)$
and
$\operatorname {\mathrm {U}}(n)$
and
![]() $\operatorname {\mathrm {O}}(n)$
, then explain how the Howe degree of an irreducible representation is defined in terms of the highest weight.
$\operatorname {\mathrm {O}}(n)$
, then explain how the Howe degree of an irreducible representation is defined in terms of the highest weight.
4.2.1. Highest weight theory for
 $\operatorname {\mathrm {U}}(n)$
$\operatorname {\mathrm {U}}(n)$
The equivalence classes of finite-dimensional irreducible representations of the unitary group
are parametrised by the set of highest weights, which we may identify with n-tuples of integers that are nonincreasing:
We denote by
![]() $\tau _{\mu }$
an irreducible representation of
$\tau _{\mu }$
an irreducible representation of
![]() $\operatorname {\mathrm {U}}(n)$
with highest weight
$\operatorname {\mathrm {U}}(n)$
with highest weight
![]() $\mu \in \Lambda _n$
. The Howe degree of
$\mu \in \Lambda _n$
. The Howe degree of
![]() $\tau _{\mu }$
is given by
$\tau _{\mu }$
is given by
 $$ \begin{align} \deg \tau_{\mu} = \sum_{j = 1}^{n} \|\mu_j\|. \end{align} $$
$$ \begin{align} \deg \tau_{\mu} = \sum_{j = 1}^{n} \|\mu_j\|. \end{align} $$
Remark 4.3. There is another natural invariant that one associates to an irreducible representation
![]() $\tau _{\mu }$
– namely, its Vogan norm
$\tau _{\mu }$
– namely, its Vogan norm
![]() $\|\tau _{\mu }\|_{\mathrm {V}}$
[Reference VoganVog81], which is
$\|\tau _{\mu }\|_{\mathrm {V}}$
[Reference VoganVog81], which is
 $$\begin{align*}\|\tau_{\mu}\|_{\mathrm{V}}^2 = \sum_{j = 1}^{n} \left(\mu_j + n + 1 - 2j\right)^2.\end{align*}$$
$$\begin{align*}\|\tau_{\mu}\|_{\mathrm{V}}^2 = \sum_{j = 1}^{n} \left(\mu_j + n + 1 - 2j\right)^2.\end{align*}$$
4.2.2. Highest weight theory for
 $\operatorname {\mathrm {O}}(n)$
$\operatorname {\mathrm {O}}(n)$
The equivalence classes of finite-dimensional irreducible representations
![]() $\tau _{\mu }$
of the orthogonal group
$\tau _{\mu }$
of the orthogonal group
are parametrised by an n-tuple of integers
![]() $\mu $
, which we again call highest weights (though unlike
$\mu $
, which we again call highest weights (though unlike
![]() $\operatorname {\mathrm {U}}(n)$
, the compact Lie group
$\operatorname {\mathrm {U}}(n)$
, the compact Lie group
![]() $\operatorname {\mathrm {O}}(n)$
is not connected). These highest weights
$\operatorname {\mathrm {O}}(n)$
is not connected). These highest weights
![]() $\mu $
are precisely those for which the highest weight vector of the irreducible representation of
$\mu $
are precisely those for which the highest weight vector of the irreducible representation of
![]() $\operatorname {\mathrm {U}}(n)$
with highest weight
$\operatorname {\mathrm {U}}(n)$
with highest weight
![]() $\mu $
generates
$\mu $
generates
![]() $\tau _{\mu }$
when restricted to
$\tau _{\mu }$
when restricted to
![]() $\operatorname {\mathrm {O}}(n)$
, and are of the form
$\operatorname {\mathrm {O}}(n)$
, and are of the form
where
![]() $m \in \{0,\ldots ,\lfloor \frac {n}{2}\rfloor \}$
,
$m \in \{0,\ldots ,\lfloor \frac {n}{2}\rfloor \}$
,
![]() $\mu _1 \geq \cdots \geq \mu _m \geq 1$
,
$\mu _1 \geq \cdots \geq \mu _m \geq 1$
,
![]() $\eta \in \{0,1\}$
and
$\eta \in \{0,1\}$
and ![]() . We again let
. We again let
![]() $\Lambda _n$
denote the set of highest weights; note, in particular, that
$\Lambda _n$
denote the set of highest weights; note, in particular, that
![]() $\Lambda _1 = \{0,1\}$
. We denote by
$\Lambda _1 = \{0,1\}$
. We denote by
![]() $\tau _{\mu }$
an irreducible representation of
$\tau _{\mu }$
an irreducible representation of
![]() $\operatorname {\mathrm {O}}(n)$
with highest weight
$\operatorname {\mathrm {O}}(n)$
with highest weight
![]() $\mu \in \Lambda _n$
. The Howe degree of
$\mu \in \Lambda _n$
. The Howe degree of
![]() $\tau _{\mu }$
is
$\tau _{\mu }$
is
 $$ \begin{align} \deg \tau_{\mu} = \sum_{j = 1}^{n} \mu_j. \end{align} $$
$$ \begin{align} \deg \tau_{\mu} = \sum_{j = 1}^{n} \mu_j. \end{align} $$
Remark 4.5. The Vogan norm
![]() $\|\tau _{\mu }\|_{\mathrm {V}}$
of
$\|\tau _{\mu }\|_{\mathrm {V}}$
of
![]() $\tau _{\mu }$
is
$\tau _{\mu }$
is
 $$\begin{align*}\|\tau_{\mu}\|_{\mathrm{V}}^2 = \sum_{j = 1}^{m} \left(\mu_j + n - 2j\right)^2 + \sum_{j = m + 1}^{\left\lfloor \frac{n}{2} \right\rfloor} (n - 2j)^2.\end{align*}$$
$$\begin{align*}\|\tau_{\mu}\|_{\mathrm{V}}^2 = \sum_{j = 1}^{m} \left(\mu_j + n - 2j\right)^2 + \sum_{j = m + 1}^{\left\lfloor \frac{n}{2} \right\rfloor} (n - 2j)^2.\end{align*}$$
4.3. The conductor exponent, the newform, and the newform K-type
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Whittaker type of
$(\pi ,V_{\pi })$
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. We define the projection map
$\operatorname {\mathrm {GL}}_n(F)$
. We define the projection map
![]() $\Pi ^{K_{n - 1}} : V_{\pi } \to V_{\pi }$
given by
$\Pi ^{K_{n - 1}} : V_{\pi } \to V_{\pi }$
given by

whose image is the subspace of
![]() $K_{n - 1}$
-invariant vectors; for the sake of consistency and completeness, we define
$K_{n - 1}$
-invariant vectors; for the sake of consistency and completeness, we define
![]() $\Pi ^{K_0}$
to be the identity when
$\Pi ^{K_0}$
to be the identity when
![]() $n = 1$
. We also define the projection map
$n = 1$
. We also define the projection map
for each irreducible representation
![]() $\tau \in \widehat {K_n}$
, where
$\tau \in \widehat {K_n}$
, where
is the elementary idempotent associated to
![]() $\tau $
. The image of
$\tau $
. The image of
![]() $V_{\pi }$
under
$V_{\pi }$
under
![]() $\Pi ^{\tau }$
is the
$\Pi ^{\tau }$
is the
![]() $\tau $
-isotypic subspace
$\tau $
-isotypic subspace
![]() $V_{\pi }^{\tau }$
of
$V_{\pi }^{\tau }$
of
![]() $V_{\pi }$
, which is finite-dimensional since
$V_{\pi }$
, which is finite-dimensional since
![]() $\pi $
is admissible and is trivial unless
$\pi $
is admissible and is trivial unless
![]() $\tau $
is a K-type of
$\tau $
is a K-type of
![]() $\pi $
. The composition of these two projections is the projection
$\pi $
. The composition of these two projections is the projection
onto the subspace of
![]() $K_{n - 1}$
-invariant
$K_{n - 1}$
-invariant
![]() $\tau $
-isotypic vectors
$\tau $
-isotypic vectors

Here,

Note that
![]() $\xi ^{\tau ,K_{n - 1}}$
is identically equal to zero if and only if
$\xi ^{\tau ,K_{n - 1}}$
is identically equal to zero if and only if
![]() $\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1,\tau |_{K_{n - 1}})$
is trivial. Finally, for any nonnegative integer m, we set
$\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1,\tau |_{K_{n - 1}})$
is trivial. Finally, for any nonnegative integer m, we set

the subspace of
![]() $K_{n - 1}$
-invariant vectors that are
$K_{n - 1}$
-invariant vectors that are
![]() $\tau $
-isotypic for some
$\tau $
-isotypic for some
![]() $\tau \in \widehat {K_n}$
of degree m. We prove the following.
$\tau \in \widehat {K_n}$
of degree m. We prove the following.
Theorem 4.7 (Cf. Theorems 3.1 and 3.5)
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Whittaker type of
$(\pi ,V_{\pi })$
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. There exists a minimal nonnegative integer m for which
$\operatorname {\mathrm {GL}}_n(F)$
. There exists a minimal nonnegative integer m for which
![]() $V_{\pi }(m)^{K_{n - 1}}$
is nontrivial. For this minimal value of m,
$V_{\pi }(m)^{K_{n - 1}}$
is nontrivial. For this minimal value of m,
![]() $V_{\pi }(m)^{K_{n - 1}}$
is one-dimensional.
$V_{\pi }(m)^{K_{n - 1}}$
is one-dimensional.
That is, we show that among the K-types
![]() $\tau \in \widehat {K_n}$
of
$\tau \in \widehat {K_n}$
of
![]() $\pi $
for which
$\pi $
for which
![]() $V_{\pi }^{\tau ,K_{n - 1}}$
is nontrivial, there exists a unique such K-type
$V_{\pi }^{\tau ,K_{n - 1}}$
is nontrivial, there exists a unique such K-type
![]() $\tau ^{\circ }$
minimising
$\tau ^{\circ }$
minimising
![]() $\deg \tau $
; moreover,
$\deg \tau $
; moreover,
![]() $V_{\pi }^{\tau ^{\circ },K_{n - 1}}$
is one-dimensional.
$V_{\pi }^{\tau ^{\circ },K_{n - 1}}$
is one-dimensional.
Definition 4.8 (Cf. Definitions 3.2 and 3.6)
We call
![]() $\deg \tau ^{\circ }$
the conductor exponent of
$\deg \tau ^{\circ }$
the conductor exponent of
![]() $\pi $
and denote it by
$\pi $
and denote it by
![]() $c(\pi )$
, and the nonzero vector
$c(\pi )$
, and the nonzero vector
![]() $v^{\circ } \in V_{\pi }(c(\pi ))^{K_{n - 1}} = V_{\pi }^{\tau ^{\circ },K_{n - 1}}$
, unique up to scalar multiplication, is called the newform of
$v^{\circ } \in V_{\pi }(c(\pi ))^{K_{n - 1}} = V_{\pi }^{\tau ^{\circ },K_{n - 1}}$
, unique up to scalar multiplication, is called the newform of
![]() $\pi $
. The K-type
$\pi $
. The K-type
![]() $\tau ^{\circ }$
containing the newform is called the newform K-type of
$\tau ^{\circ }$
containing the newform is called the newform K-type of
![]() $\pi $
.
$\pi $
.
Analogously to the nonarchimedean theory of the conductor exponent, we regard
![]() $c(\pi )$
as quantifying the extent to which
$c(\pi )$
as quantifying the extent to which
![]() $\pi $
is ramified; once again, the conductor exponent
$\pi $
is ramified; once again, the conductor exponent
![]() $c(\pi )$
is zero if and only if
$c(\pi )$
is zero if and only if
![]() $\pi $
is unramified, so that
$\pi $
is unramified, so that
![]() $\pi $
is a spherical representation. Moreover, the fact that
$\pi $
is a spherical representation. Moreover, the fact that
![]() $v^{\circ }$
is unique up to scalar multiplication may be thought of as a multiplicity-one theorem for newforms.
$v^{\circ }$
is unique up to scalar multiplication may be thought of as a multiplicity-one theorem for newforms.
Remark 4.9. In general, the newform K-type
![]() $\tau ^{\circ }$
is not equal to the minimal K-type (in the sense of Vogan [Reference VoganVog81]) of
$\tau ^{\circ }$
is not equal to the minimal K-type (in the sense of Vogan [Reference VoganVog81]) of
![]() $\pi $
, and
$\pi $
, and
![]() $\deg \tau ^{\circ }$
is not equal to the Vogan norm of the minimal K-type. However, we shall see that the Howe degree of the minimal K-type is equal to
$\deg \tau ^{\circ }$
is not equal to the Vogan norm of the minimal K-type. However, we shall see that the Howe degree of the minimal K-type is equal to
![]() $\deg \tau ^{\circ } = c(\pi )$
. This gives another way to define the conductor exponent, albeit with the downside that the connection between the minimal K-type and the newform is unclear.
$\deg \tau ^{\circ } = c(\pi )$
. This gives another way to define the conductor exponent, albeit with the downside that the connection between the minimal K-type and the newform is unclear.
Remark 4.10. The conductor exponent and newform K-type of an induced representation of Whittaker type
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
remain unchanged when
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
remain unchanged when
![]() $\pi $
is replaced by
$\pi $
is replaced by
![]() $\pi _{\sigma (1)} \boxplus \cdots \boxplus \pi _{\sigma (r)}$
for any permutation
$\pi _{\sigma (1)} \boxplus \cdots \boxplus \pi _{\sigma (r)}$
for any permutation
![]() $\sigma \in S_r$
.
$\sigma \in S_r$
.
4.4. Oldforms
We also define oldforms in the archimedean setting.
Definition 4.11. The space of oldforms of exponent
![]() $m> c(\pi )$
is
$m> c(\pi )$
is
![]() $V_{\pi }(m)^{K_{n - 1}}$
.
$V_{\pi }(m)^{K_{n - 1}}$
.
Theorem 4.12 (Cf. Theorems 3.7 and 3.8)
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Whittaker type of
$(\pi ,V_{\pi })$
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with
$\operatorname {\mathrm {GL}}_n(F)$
with
![]() $n \geq 2$
. We have that
$n \geq 2$
. We have that
 $$\begin{align*}\dim V_{\pi}(m)^{K_{n - 1}} = \begin{cases} \binom{\frac{m - c(\pi)}{2} + n - 2}{n - 2} & \text{if }m \geq c(\pi)\text{ and }m \equiv c(\pi)\quad \pmod{2}, \\ 0 & \text{otherwise}. \end{cases}\end{align*}$$
$$\begin{align*}\dim V_{\pi}(m)^{K_{n - 1}} = \begin{cases} \binom{\frac{m - c(\pi)}{2} + n - 2}{n - 2} & \text{if }m \geq c(\pi)\text{ and }m \equiv c(\pi)\quad \pmod{2}, \\ 0 & \text{otherwise}. \end{cases}\end{align*}$$
More precisely, we prove that when
![]() $m \geq c(\pi )$
with
$m \geq c(\pi )$
with
![]() $m \equiv c(\pi )\ \pmod {2}$
, either
$m \equiv c(\pi )\ \pmod {2}$
, either
![]() $\operatorname {\mathrm {Hom}}_{K_n}(\tau , \pi |_{K_n})$
or
$\operatorname {\mathrm {Hom}}_{K_n}(\tau , \pi |_{K_n})$
or
![]() $\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1,\tau |_{K_{n - 1}})$
is trivial for all but one K-type
$\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1,\tau |_{K_{n - 1}})$
is trivial for all but one K-type
![]() $\tau $
with
$\tau $
with
![]() $\deg \tau = m$
, and for this particular K-type,
$\deg \tau = m$
, and for this particular K-type,
 $$ \begin{align*} \dim \operatorname{\mathrm{Hom}}_{K_n}\left(\tau, \pi|_{K_n}\right) & = \binom{\frac{m - c(\pi)}{2} + n - 2}{n - 2}, \\ \dim \operatorname{\mathrm{Hom}}_{K_{n - 1}}\left(1,\tau|_{K_{n - 1}}\right) & = 1. \end{align*} $$
$$ \begin{align*} \dim \operatorname{\mathrm{Hom}}_{K_n}\left(\tau, \pi|_{K_n}\right) & = \binom{\frac{m - c(\pi)}{2} + n - 2}{n - 2}, \\ \dim \operatorname{\mathrm{Hom}}_{K_{n - 1}}\left(1,\tau|_{K_{n - 1}}\right) & = 1. \end{align*} $$
The fact that
![]() $V_{\pi }(m)^{K_{n - 1}}$
is trivial when
$V_{\pi }(m)^{K_{n - 1}}$
is trivial when
![]() $m \equiv c(\pi ) + 1\ \pmod {2}$
follows more generally from a result of Fan [Reference FanFan18] – namely, that for
$m \equiv c(\pi ) + 1\ \pmod {2}$
follows more generally from a result of Fan [Reference FanFan18] – namely, that for
![]() $\tau \in \widehat {K_n}$
,
$\tau \in \widehat {K_n}$
,
![]() $V_{\pi }^{\tau }$
is trivial whenever
$V_{\pi }^{\tau }$
is trivial whenever
![]() $\deg \tau \equiv c(\pi ) + 1\ \pmod {2}$
.
$\deg \tau \equiv c(\pi ) + 1\ \pmod {2}$
.
We may think of
![]() $\bigoplus _{j = 0}^{m} V_{\pi }(j)^{K_{n - 1}}$
as being the archimedean analogue of
$\bigoplus _{j = 0}^{m} V_{\pi }(j)^{K_{n - 1}}$
as being the archimedean analogue of
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
. This space has dimension
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
. This space has dimension
![]() $\binom {\lfloor \frac {m - c(\pi )}{2} \rfloor + n - 1}{n - 1}$
if
$\binom {\lfloor \frac {m - c(\pi )}{2} \rfloor + n - 1}{n - 1}$
if
![]() $m \geq c(\pi )$
and dimension zero otherwise. This aligns closely with the dimension of
$m \geq c(\pi )$
and dimension zero otherwise. This aligns closely with the dimension of
![]() $V_{\pi }^{K_1(\mathfrak {p}^m)}$
as in Theorem 3.7 – namely,
$V_{\pi }^{K_1(\mathfrak {p}^m)}$
as in Theorem 3.7 – namely,
![]() $\binom {m - c(\pi ) + n - 1}{n - 1}$
if
$\binom {m - c(\pi ) + n - 1}{n - 1}$
if
![]() $m \geq c(\pi )$
and zero otherwise.
$m \geq c(\pi )$
and zero otherwise.
Remark 4.13. For nonarchimedean F, Reeder [Reference ReederRee91] explicitly describes the space of oldforms as the image of the space of newforms under the action of certain elements of the Hecke algebra. It would be of interest to generalise this to the archimedean setting. In particular, when viewed in the Whittaker model, it would be of interest to describe oldforms in terms of the action of certain differential operators on the newform. For
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
, these are simply the Maaß raising and lowering operators, while the theory for
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
, these are simply the Maaß raising and lowering operators, while the theory for
![]() $\operatorname {\mathrm {GL}}_3(\mathbb {R})$
is explored in [Reference Buttcane, Miller, Miller and YauBM19].
$\operatorname {\mathrm {GL}}_3(\mathbb {R})$
is explored in [Reference Buttcane, Miller, Miller and YauBM19].
4.5. Additivity and inductivity of the conductor exponent
Associated to any induced representation of Whittaker type
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
is the epsilon factor
$\operatorname {\mathrm {GL}}_n(F)$
is the epsilon factor
![]() $\varepsilon (s,\pi ,\psi )$
; with
$\varepsilon (s,\pi ,\psi )$
; with
![]() $\psi $
chosen as in Section 2.1.2, the epsilon factor is an integral power of i via (2.16) and (2.18). This integer is only determined modulo
$\psi $
chosen as in Section 2.1.2, the epsilon factor is an integral power of i via (2.16) and (2.18). This integer is only determined modulo
![]() $4$
, in contrast to the nonarchimedean setting. In this regard, the following theorem is not so instructive as Theorem 3.9.
$4$
, in contrast to the nonarchimedean setting. In this regard, the following theorem is not so instructive as Theorem 3.9.
Theorem 4.14 (Cf. Theorem 3.9)
Let
![]() $\pi $
be an induced representation of Whittaker type of
$\pi $
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. The epsilon factor
$\operatorname {\mathrm {GL}}_n(F)$
. The epsilon factor
![]() $\varepsilon (s,\pi ,\psi )$
is equal to
$\varepsilon (s,\pi ,\psi )$
is equal to
![]() $i^{-c(\pi )}$
, where
$i^{-c(\pi )}$
, where
![]() $c(\pi )$
denotes the conductor exponent of
$c(\pi )$
denotes the conductor exponent of
![]() $\pi $
.
$\pi $
.
Upon decomposing
![]() $\pi $
as the isobaric sums
$\pi $
as the isobaric sums
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
, we have the identity
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
, we have the identity
 $$\begin{align*}i^{-c(\pi)} = \varepsilon(s,\pi,\psi) = \prod_{j = 1}^{r} \varepsilon(s,\pi_j,\psi) = i^{-c(\pi_1) - \cdots - c(\pi_r)}\end{align*}$$
$$\begin{align*}i^{-c(\pi)} = \varepsilon(s,\pi,\psi) = \prod_{j = 1}^{r} \varepsilon(s,\pi_j,\psi) = i^{-c(\pi_1) - \cdots - c(\pi_r)}\end{align*}$$
via (2.18). This is only enough to conclude that
![]() $c(\pi )$
is congruent to
$c(\pi )$
is congruent to
![]() $c(\pi _1) + \cdots + c(\pi _r)$
modulo
$c(\pi _1) + \cdots + c(\pi _r)$
modulo
![]() $4$
, rather than an equality of conductor exponents. Nonetheless, we still prove by different means that the conductor exponent is additive with respect to isobaric sums.
$4$
, rather than an equality of conductor exponents. Nonetheless, we still prove by different means that the conductor exponent is additive with respect to isobaric sums.
Theorem 4.15 (Cf. Theorem 3.10)
For an induced representation of Whittaker type
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, we have that
$\operatorname {\mathrm {GL}}_n(F)$
, we have that
 $$\begin{align*}c(\pi) = \sum_{j = 1}^{r} c(\pi_j).\end{align*}$$
$$\begin{align*}c(\pi) = \sum_{j = 1}^{r} c(\pi_j).\end{align*}$$
The epsilon factor is again inductive in degree zero, so that if
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are induced representations of Whittaker type of
$\pi '$
are induced representations of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
and
![]() $\mathcal {AI}_{\mathbb {C}/\mathbb {R}} \pi $
and
$\mathcal {AI}_{\mathbb {C}/\mathbb {R}} \pi $
and
![]() $\mathcal {AI}_{\mathbb {C}/\mathbb {R}} \pi '$
denote the induced representation of Whittaker type of
$\mathcal {AI}_{\mathbb {C}/\mathbb {R}} \pi '$
denote the induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_{2n}(\mathbb {R})$
obtained by induction [Reference HenniartHen10], then
$\operatorname {\mathrm {GL}}_{2n}(\mathbb {R})$
obtained by induction [Reference HenniartHen10], then
 $$\begin{align*}\frac{\varepsilon\left(s,\mathcal{AI}_{\mathbb{C}/\mathbb{R}} \pi, \psi\right)}{\varepsilon\left(s,\mathcal{AI}_{\mathbb{C}/\mathbb{R}} \pi',\psi\right)} = \frac{\varepsilon\left(s,\pi,\psi \circ \operatorname{\mathrm{Tr}}_{\mathbb{C}/\mathbb{R}}\right)}{\varepsilon\left(s,\pi',\psi \circ \operatorname{\mathrm{Tr}}_{\mathbb{C}/\mathbb{R}}\right)}.\end{align*}$$
$$\begin{align*}\frac{\varepsilon\left(s,\mathcal{AI}_{\mathbb{C}/\mathbb{R}} \pi, \psi\right)}{\varepsilon\left(s,\mathcal{AI}_{\mathbb{C}/\mathbb{R}} \pi',\psi\right)} = \frac{\varepsilon\left(s,\pi,\psi \circ \operatorname{\mathrm{Tr}}_{\mathbb{C}/\mathbb{R}}\right)}{\varepsilon\left(s,\pi',\psi \circ \operatorname{\mathrm{Tr}}_{\mathbb{C}/\mathbb{R}}\right)}.\end{align*}$$
Taking
![]() $\pi '$
to be the isobaric sum of n copies of the trivial representation, we find that
$\pi '$
to be the isobaric sum of n copies of the trivial representation, we find that
We prove by different means that this congruence can be replaced by an equality.
Theorem 4.16 (Cf. Theorem 3.12)
For an induced representation of Whittaker type
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
, we have that
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
, we have that
4.6. Test vectors for Rankin–Selberg integrals
One can once again ask about the existence of test vectors for
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals. This is known for spherical representations
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals. This is known for spherical representations
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
with
$\pi '$
with
![]() $m \in \{n - 1,n\}$
, due to Stade [Reference StadeSta01, Theorem 3.4], [Reference StadeSta02, Theorem 1.1] (see also [Reference Gerasimov, Lebedev and OblezinGLO08, Lemma 4.2] and [Reference Ishii and StadeIsSt13, Theorem 3.1]), while recent work of Ishii and Miyazaki deals with the case of pairs of principal series representations of certain specific forms [Reference Ishii and MiyazakiIM22, Theorem 2.5]. We prove the existence of a test vector for nonspherical representations
$m \in \{n - 1,n\}$
, due to Stade [Reference StadeSta01, Theorem 3.4], [Reference StadeSta02, Theorem 1.1] (see also [Reference Gerasimov, Lebedev and OblezinGLO08, Lemma 4.2] and [Reference Ishii and StadeIsSt13, Theorem 3.1]), while recent work of Ishii and Miyazaki deals with the case of pairs of principal series representations of certain specific forms [Reference Ishii and MiyazakiIM22, Theorem 2.5]. We prove the existence of a test vector for nonspherical representations
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
provided that
$\operatorname {\mathrm {GL}}_n(F)$
provided that
![]() $\pi '$
is a spherical representation of Langlands type of
$\pi '$
is a spherical representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
and
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
and
![]() $W' = W^{\prime \circ } \in \mathcal {W}\left (\pi ',\overline {\psi }\right )$
is the spherical vector normalised as in Section 2.2.5.
$W' = W^{\prime \circ } \in \mathcal {W}\left (\pi ',\overline {\psi }\right )$
is the spherical vector normalised as in Section 2.2.5.
Theorem 4.17 (Cf. Theorem 3.14)
Let
![]() $\pi $
be an induced representation of Langlands type of
$\pi $
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with
$\operatorname {\mathrm {GL}}_n(F)$
with
![]() $n \geq 2$
. There exists a Whittaker function
$n \geq 2$
. There exists a Whittaker function
![]() $W \in \mathcal {W}(\pi ,\psi )$
such that for any spherical representation of Langlands type
$W \in \mathcal {W}(\pi ,\psi )$
such that for any spherical representation of Langlands type
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
with spherical Whittaker function
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
with spherical Whittaker function
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
,
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
,
for
![]() $\Re (s)$
sufficiently large.
$\Re (s)$
sufficiently large.
Moreover, there exists a unique such function
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
that additionally satisfies
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
that additionally satisfies
 $$\begin{align*}W^{\circ}\left(g\begin{pmatrix} k & 0 \\ 0 & 1 \end{pmatrix}\right) = W^{\circ}(g)\end{align*}$$
$$\begin{align*}W^{\circ}\left(g\begin{pmatrix} k & 0 \\ 0 & 1 \end{pmatrix}\right) = W^{\circ}(g)\end{align*}$$
for all
![]() $k \in K_{n - 1}$
. Up to multiplication by a scalar, this function is the newform
$k \in K_{n - 1}$
. Up to multiplication by a scalar, this function is the newform
![]() ${v^{\circ } \in V_{\pi }(c(\pi ))^{K_{n - 1}}}$
viewed in the Whittaker model.
${v^{\circ } \in V_{\pi }(c(\pi ))^{K_{n - 1}}}$
viewed in the Whittaker model.
We again call
![]() $W^{\circ }$
the Whittaker newform. The normalisation of the Whittaker newform is specified in Definition 9.2.
$W^{\circ }$
the Whittaker newform. The normalisation of the Whittaker newform is specified in Definition 9.2.
Stade [Reference StadeSta02, Theorem 1.1] has shown that for all spherical representations
![]() $\pi ,\pi '$
of
$\pi ,\pi '$
of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
,
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
,
where
![]() $\Phi ^{\circ } \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {R}))$
is given by
$\Phi ^{\circ } \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {R}))$
is given by ![]() ; see also [Reference Gerasimov, Lebedev and OblezinGLO08, Lemma 4.1] and [Reference Ishii and StadeIsSt13, Theorem 3.1]. We extend this to nonspherical representations
; see also [Reference Gerasimov, Lebedev and OblezinGLO08, Lemma 4.1] and [Reference Ishii and StadeIsSt13, Theorem 3.1]. We extend this to nonspherical representations
![]() $\pi $
.
$\pi $
.
Theorem 4.18 (Cf. Theorem 3.18)
Let
![]() $\pi $
be an induced representation of Langlands type of
$\pi $
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. For every spherical representation of Langlands type
$\operatorname {\mathrm {GL}}_n(F)$
. For every spherical representation of Langlands type
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with spherical Whittaker function
$\operatorname {\mathrm {GL}}_n(F)$
with spherical Whittaker function
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
, the Whittaker newform
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
, the Whittaker newform
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
of
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
of
![]() $\pi $
satisfies
$\pi $
satisfies
for
![]() $\Re (s)$
sufficiently large, where
$\Re (s)$
sufficiently large, where
![]() $\Phi ^{\circ } \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
is given by
$\Phi ^{\circ } \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
is given by

with
![]() $P^{\circ }$
a homogeneous harmonic polynomial that depends only on the newform K-type
$P^{\circ }$
a homogeneous harmonic polynomial that depends only on the newform K-type
![]() $\tau ^{\circ }$
of
$\tau ^{\circ }$
of
![]() $\pi $
.
$\pi $
.
We discuss this distinguished polynomial
![]() $P^{\circ }$
in further detail in Section 7; it is the unique homogeneous harmonic polynomial that is right
$P^{\circ }$
in further detail in Section 7; it is the unique homogeneous harmonic polynomial that is right
![]() $K_{n - 1}$
-invariant and satisfies
$K_{n - 1}$
-invariant and satisfies
![]() $P^{\circ }(e_n) = 1$
in the vector space of such polynomials that forms a model of
$P^{\circ }(e_n) = 1$
in the vector space of such polynomials that forms a model of
![]() $\tau ^{\circ }$
.
$\tau ^{\circ }$
.
In the nonarchimedean setting, it is not only the case that the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
![]() $\Psi (s,W^{\circ },W^{\prime \circ })$
is equal to
$\Psi (s,W^{\circ },W^{\prime \circ })$
is equal to
![]() $L(s,\pi \times \pi ')$
for all spherical representations
$L(s,\pi \times \pi ')$
for all spherical representations
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
, but also for all spherical representations
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
, but also for all spherical representations
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_m(F)$
and all
$\operatorname {\mathrm {GL}}_m(F)$
and all
![]() $m \in \{1, \ldots , n - 1\}$
; see Theorem 3.17. In the archimedean setting, however, it is widely believed (see, for example, [Reference Bump, Aubert, Bombieri and GoldfeldBum89, Section 2.6]) that
$m \in \{1, \ldots , n - 1\}$
; see Theorem 3.17. In the archimedean setting, however, it is widely believed (see, for example, [Reference Bump, Aubert, Bombieri and GoldfeldBum89, Section 2.6]) that
![]() $\Psi (s,W,W')$
is never equal to
$\Psi (s,W,W')$
is never equal to
![]() $L(s,\pi \times \pi ')$
when
$L(s,\pi \times \pi ')$
when
![]() $\pi '$
is an induced representation of Whittaker type of
$\pi '$
is an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_m(F)$
with
$\operatorname {\mathrm {GL}}_m(F)$
with
![]() $m \in \{1, \ldots , n - 2\}$
and the Whittaker functions
$m \in \{1, \ldots , n - 2\}$
and the Whittaker functions
![]() $W \in \mathcal {W}(\pi ,\psi )$
and
$W \in \mathcal {W}(\pi ,\psi )$
and
![]() $W' \in \mathcal {W}(\pi ',\overline {\psi })$
are right
$W' \in \mathcal {W}(\pi ',\overline {\psi })$
are right
![]() $K_n$
- and
$K_n$
- and
![]() $K_m$
-finite, respectively.
$K_m$
-finite, respectively.
Notably, Ishii and Stade [Reference Ishii and StadeIsSt13, Theorem 3.2], furthering the work of Hoffstein and Murty [Reference Hoffstein, Murty, de Koninck and LevesqueHM89], have shown that for all spherical representations
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
,
$\operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
,
 $$ \begin{align} \Psi(s,W^{\circ},W^{\prime\circ}) = L(s,\pi \times \pi') \frac{1}{2\pi i} \int_{\sigma - i\infty}^{\sigma + i\infty} \frac{L\left(w,\widetilde{\pi}\right)}{2 L(s + w,\pi')} \, dw \end{align} $$
$$ \begin{align} \Psi(s,W^{\circ},W^{\prime\circ}) = L(s,\pi \times \pi') \frac{1}{2\pi i} \int_{\sigma - i\infty}^{\sigma + i\infty} \frac{L\left(w,\widetilde{\pi}\right)}{2 L(s + w,\pi')} \, dw \end{align} $$
for some sufficiently large
![]() $\sigma $
. Though we do not include a proof, our methods may also be used to show the identity (4.20) when
$\sigma $
. Though we do not include a proof, our methods may also be used to show the identity (4.20) when
![]() $\pi $
is a ramified induced representation of Langlands type and
$\pi $
is a ramified induced representation of Langlands type and
![]() $W^{\circ }$
is the Whittaker newform.
$W^{\circ }$
is the Whittaker newform.
Remark 4.21. Just as in the nonarchimedean setting, little is known about test vectors for archimedean Rankin–Selberg integrals when
![]() $\pi '$
is ramified. The nonarchimedean method of Kim [Reference KimKim10, Proposition 2.2.2] remains valid in the archimedean setting in showing that Whittaker newforms are not test vectors when
$\pi '$
is ramified. The nonarchimedean method of Kim [Reference KimKim10, Proposition 2.2.2] remains valid in the archimedean setting in showing that Whittaker newforms are not test vectors when
![]() $\pi '$
is ramified: if
$\pi '$
is ramified: if
![]() $\pi '$
is a ramified representation of
$\pi '$
is a ramified representation of
![]() $\operatorname {\mathrm {GL}}_m(F)$
with
$\operatorname {\mathrm {GL}}_m(F)$
with
![]() $m < n$
and
$m < n$
and
![]() $W^{\circ },W^{\prime \circ }$
are newforms of
$W^{\circ },W^{\prime \circ }$
are newforms of
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
, respectively, then
$\pi '$
, respectively, then
![]() $\Psi \left (s,W^{\circ },W^{\prime \circ }\right ) = 0$
for all
$\Psi \left (s,W^{\circ },W^{\prime \circ }\right ) = 0$
for all
![]() $s \in \mathbb {C}$
. The test vector problem has been resolved for
$s \in \mathbb {C}$
. The test vector problem has been resolved for
![]() $m = n = 2$
by Miyazaki [Reference MiyazakiMiy18, Theorem 6.1] and Hirano, Ishii and Miyazaki [Reference Hirano, Ishii and MiyazakiHIM22, Appendix A] and for
$m = n = 2$
by Miyazaki [Reference MiyazakiMiy18, Theorem 6.1] and Hirano, Ishii and Miyazaki [Reference Hirano, Ishii and MiyazakiHIM22, Appendix A] and for
![]() $m = 2$
and
$m = 2$
and
![]() $n = 3$
by Hirano, Ishii and Miyazaki [Reference Hirano, Ishii and MiyazakiHIM16, Reference Hirano, Ishii and MiyazakiHIM22]. Ishii and Miyazaki have also resolved this problem for n arbitrary and
$n = 3$
by Hirano, Ishii and Miyazaki [Reference Hirano, Ishii and MiyazakiHIM16, Reference Hirano, Ishii and MiyazakiHIM22]. Ishii and Miyazaki have also resolved this problem for n arbitrary and
![]() $m \in \{n,n - 1\}$
when both
$m \in \{n,n - 1\}$
when both
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are principal series representations [Reference Ishii and MiyazakiIM22, Theorems 2.5 and 2.9]. Akin to the nonarchimedean work of Jo [Reference JoJo23], the author and Jo have resolved a weakened version of the test vector problem in [Reference Humphries and JoHJ24] when
$\pi '$
are principal series representations [Reference Ishii and MiyazakiIM22, Theorems 2.5 and 2.9]. Akin to the nonarchimedean work of Jo [Reference JoJo23], the author and Jo have resolved a weakened version of the test vector problem in [Reference Humphries and JoHJ24] when
![]() $m = n$
, where it is shown that there exists an explicit right
$m = n$
, where it is shown that there exists an explicit right
![]() $K_n$
-finite Schwartz–Bruhat function
$K_n$
-finite Schwartz–Bruhat function
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
for which
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
for which
![]() $\Psi (s,W^{\circ },W^{\prime \circ },\Phi )$
is a multiple of
$\Psi (s,W^{\circ },W^{\prime \circ },\Phi )$
is a multiple of
![]() $L(s,\pi \times \pi ')$
by a nonzero polynomial in s.
$L(s,\pi \times \pi ')$
by a nonzero polynomial in s.
4.7. Test vectors for Godement–Jacquet zeta integrals
Test vectors for archimedean Godement–Jacquet zeta integrals are known to exist; see [Reference LinLin18] for
![]() $F = \mathbb {R}$
and [Reference IshiiIsh19] for the case
$F = \mathbb {R}$
and [Reference IshiiIsh19] for the case
![]() $F = \mathbb {C}$
. We give a new resolution of the test vector problem via newforms.
$F = \mathbb {C}$
. We give a new resolution of the test vector problem via newforms.
Remark 4.22. We were unable to verify certain aspects of [Reference LinLin18]; cf. [Reference HumphriesHum21, Footnote †].
Theorem 4.23 (Cf. Theorem 3.20)
Let
![]() $(\pi ,V_{\pi })$
be an induced representation of Whittaker type of
$(\pi ,V_{\pi })$
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. Let
$\operatorname {\mathrm {GL}}_n(F)$
. Let
![]() $\beta (g)$
denote the matrix coefficient
$\beta (g)$
denote the matrix coefficient
![]() $\langle \pi (g) \cdot v^{\circ }, \widetilde {v}^{\circ } \rangle $
, where
$\langle \pi (g) \cdot v^{\circ }, \widetilde {v}^{\circ } \rangle $
, where
![]() $v^{\circ } \in V_{\pi }$
denotes the newform and
$v^{\circ } \in V_{\pi }$
denotes the newform and
![]() $\widetilde {v}^{\circ } \in V_{\widetilde {\pi }}$
is the corresponding newform normalised such that
$\widetilde {v}^{\circ } \in V_{\widetilde {\pi }}$
is the corresponding newform normalised such that
![]() $\beta (1_n) = 1$
. Then
$\beta (1_n) = 1$
. Then
for
![]() $\Re (s)$
sufficiently large, where
$\Re (s)$
sufficiently large, where
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is given by
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is given by
with
![]() $P^{\circ }$
a homogeneous harmonic polynomial that depends only on the newform K-type
$P^{\circ }$
a homogeneous harmonic polynomial that depends only on the newform K-type
![]() $\tau ^{\circ }$
of
$\tau ^{\circ }$
of
![]() $\pi $
.
$\pi $
.
The homogeneous harmonic polynomial
![]() $P^{\circ }$
appearing in Theorem 4.23 is the same as that appearing in Theorem 4.18.
$P^{\circ }$
appearing in Theorem 4.23 is the same as that appearing in Theorem 4.18.
5. Further Discussion
5.1. Previous results
Previous cases of test vectors for
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
and
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
and
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integrals over archimedean fields with n arbitrary were only known when either both representations are unramified – see [Reference StadeSta01, Theorem 3.4], [Reference Gerasimov, Lebedev and OblezinGLO08, Lemma 4.2] and [Reference Ishii and StadeIsSt13, Theorem 3.2] — or when both representations are principal series representations of certain specific forms, due to recent work of Ishii and Miyazaki [Reference Ishii and MiyazakiIM22, Theorems 2.5 and 2.9]. Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Theorem 2.7] has shown that for each pair
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integrals over archimedean fields with n arbitrary were only known when either both representations are unramified – see [Reference StadeSta01, Theorem 3.4], [Reference Gerasimov, Lebedev and OblezinGLO08, Lemma 4.2] and [Reference Ishii and StadeIsSt13, Theorem 3.2] — or when both representations are principal series representations of certain specific forms, due to recent work of Ishii and Miyazaki [Reference Ishii and MiyazakiIM22, Theorems 2.5 and 2.9]. Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Theorem 2.7] has shown that for each pair
![]() $\pi ,\pi '$
of generic irreducible Casselman–Wallach representations of
$\pi ,\pi '$
of generic irreducible Casselman–Wallach representations of
![]() $\operatorname {\mathrm {GL}}_n(F),\operatorname {\mathrm {GL}}_{n - 1}(F)$
, there exists a finite collection
$\operatorname {\mathrm {GL}}_n(F),\operatorname {\mathrm {GL}}_{n - 1}(F)$
, there exists a finite collection
![]() $\{W_j\} \subset \mathcal {W}(\pi ,\psi )$
and
$\{W_j\} \subset \mathcal {W}(\pi ,\psi )$
and
![]() $\{W_j^{\prime }\} \subset \mathcal {W}(\pi ',\overline {\psi })$
of right
$\{W_j^{\prime }\} \subset \mathcal {W}(\pi ',\overline {\psi })$
of right
![]() $K_n$
- and
$K_n$
- and
![]() $K_{n - 1}$
-finite Whittaker functions for which
$K_{n - 1}$
-finite Whittaker functions for which
![]() $\sum _j \Psi (s,W_j,W_j^{\prime }) = L(s,\pi \times \pi ')$
; a similar result (additionally involving Schwartz functions
$\sum _j \Psi (s,W_j,W_j^{\prime }) = L(s,\pi \times \pi ')$
; a similar result (additionally involving Schwartz functions
![]() $\{\Phi _j\} \subset \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
) also holds for pairs of representations of
$\{\Phi _j\} \subset \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
) also holds for pairs of representations of
![]() $\operatorname {\mathrm {GL}}_n(F)$
.
$\operatorname {\mathrm {GL}}_n(F)$
.
Explicit descriptions of specific Whittaker functions for ramified principal series representations of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
are given in [Reference Ishii and OdaIO14] and of
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
are given in [Reference Ishii and OdaIO14] and of
![]() $\operatorname {\mathrm {GL}}_3(\mathbb {C})$
in [Reference Hirano and OdaHO09], while recursive formulæ for specific Whittaker functions for principal series representations of
$\operatorname {\mathrm {GL}}_3(\mathbb {C})$
in [Reference Hirano and OdaHO09], while recursive formulæ for specific Whittaker functions for principal series representations of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
are given in [Reference Ishii and MiyazakiIM22]. In all three cases, these are Whittaker functions in the minimal K-type; as observed in [Reference Hirano, Ishii, Miyazaki, Hamahata, Ichikawa, Murase and SuganoHIM12, Theorem 6.1], such a Whittaker function W is generally not a test vector for Rankin–Selberg integrals
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
are given in [Reference Ishii and MiyazakiIM22]. In all three cases, these are Whittaker functions in the minimal K-type; as observed in [Reference Hirano, Ishii, Miyazaki, Hamahata, Ichikawa, Murase and SuganoHIM12, Theorem 6.1], such a Whittaker function W is generally not a test vector for Rankin–Selberg integrals
![]() $\Psi (s,W,W^{\prime \circ })$
when
$\Psi (s,W,W^{\prime \circ })$
when
![]() $W^{\prime \circ }$
is the spherical vector of a spherical representation.
$W^{\prime \circ }$
is the spherical vector of a spherical representation.
For
![]() $n \leq 3$
and
$n \leq 3$
and
![]() $m \leq 2$
, the state of affairs of test vectors for
$m \leq 2$
, the state of affairs of test vectors for
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals is in much better shape. In particular, the existence of the Whittaker newform for
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_m$
Rankin–Selberg integrals is in much better shape. In particular, the existence of the Whittaker newform for
![]() $\operatorname {\mathrm {GL}}_2(F)$
has previously been proven by Popa [Reference PopaPop08], though in a slightly different formulation that we now describe.
$\operatorname {\mathrm {GL}}_2(F)$
has previously been proven by Popa [Reference PopaPop08], though in a slightly different formulation that we now describe.
Let
![]() $\pi $
be a generic irreducible Casselman–Wallach representation of
$\pi $
be a generic irreducible Casselman–Wallach representation of
![]() $\operatorname {\mathrm {GL}}_2(F)$
with central character
$\operatorname {\mathrm {GL}}_2(F)$
with central character
![]() $\omega _{\pi }$
, let T denote the diagonal torus embedded in
$\omega _{\pi }$
, let T denote the diagonal torus embedded in
![]() $\operatorname {\mathrm {GL}}_2(F)$
, and let
$\operatorname {\mathrm {GL}}_2(F)$
, and let
![]() $\chi _T$
be a character of T whose restriction to the centre of
$\chi _T$
be a character of T whose restriction to the centre of
![]() $\operatorname {\mathrm {GL}}_2(F)$
is
$\operatorname {\mathrm {GL}}_2(F)$
is
![]() $\omega _{\pi }^{-1}$
. Given
$\omega _{\pi }^{-1}$
. Given
![]() $\tau \in \widehat {K_2}$
, we define
$\tau \in \widehat {K_2}$
, we define
![]() $\mathcal {W}^{\tau ,T}$
to be the subspace of the
$\mathcal {W}^{\tau ,T}$
to be the subspace of the
![]() $\tau $
-isotypic subspace
$\tau $
-isotypic subspace
![]() $\mathcal {W}^{\tau }$
of
$\mathcal {W}^{\tau }$
of
![]() $\mathcal {W}(\pi ,\psi )$
for which
$\mathcal {W}(\pi ,\psi )$
for which
![]() $\pi |_{K_2 \cap T}$
acts by
$\pi |_{K_2 \cap T}$
acts by
![]() $\chi _T^{-1}$
.
$\chi _T^{-1}$
.
Theorem 5.1 (Popa [Reference PopaPop08, Proposition 1, Theorem 1])
The space
![]() $\mathcal {W}^{\tau ,T}$
is at most one-dimensional. Furthermore, if
$\mathcal {W}^{\tau ,T}$
is at most one-dimensional. Furthermore, if
![]() $\chi _T(\operatorname {\mathrm {diag}}(a_1,a_2)) = |a_1|^{s - 1/2} |a_2|^{1/2 - s} \omega _{\pi }^{-1}(a_2)$
and
$\chi _T(\operatorname {\mathrm {diag}}(a_1,a_2)) = |a_1|^{s - 1/2} |a_2|^{1/2 - s} \omega _{\pi }^{-1}(a_2)$
and
![]() $\tau = \tau ^{\circ }$
is the K-type of lowest degree for which
$\tau = \tau ^{\circ }$
is the K-type of lowest degree for which
![]() $\mathcal {W}^{\tau ,T}$
is nontrivial, then there exists
$\mathcal {W}^{\tau ,T}$
is nontrivial, then there exists
![]() $W^{\circ } \in \mathcal {W}^{\tau ^{\circ },T}$
for which
$W^{\circ } \in \mathcal {W}^{\tau ^{\circ },T}$
for which
While this superficially appears to be different than the definition of the Whittaker newform, it is readily checked that
 $$\begin{align*}\mathcal{W}^{\tau,T} = \left\{W \in \mathcal{W}^{\tau} : W\left(g \begin{pmatrix} k & 0 \\ 0 & 1 \end{pmatrix}\right) = W(g) \text{ for all }g \in \operatorname{\mathrm{GL}}_2(F)\text{ and }k \in K_1\right\},\end{align*}$$
$$\begin{align*}\mathcal{W}^{\tau,T} = \left\{W \in \mathcal{W}^{\tau} : W\left(g \begin{pmatrix} k & 0 \\ 0 & 1 \end{pmatrix}\right) = W(g) \text{ for all }g \in \operatorname{\mathrm{GL}}_2(F)\text{ and }k \in K_1\right\},\end{align*}$$
and so the Whittaker function
![]() $W^{\circ }$
is indeed the Whittaker newform and
$W^{\circ }$
is indeed the Whittaker newform and
![]() $\mathcal {W}^{\tau ^{\circ },T}$
is equal to the space
$\mathcal {W}^{\tau ^{\circ },T}$
is equal to the space
![]() $V_{\pi }^{K_1(c(\pi ))} = V_{\pi }^{\tau ^{\circ }|_{K_1}}$
when viewed in the Whittaker model.
$V_{\pi }^{K_1(c(\pi ))} = V_{\pi }^{\tau ^{\circ }|_{K_1}}$
when viewed in the Whittaker model.
Jacquet [Reference JacquetJac72, Theorem 17.2] has previously determined, in several cases, explicit right
![]() $K_2$
-finite test vectors
$K_2$
-finite test vectors
![]() $W \in \mathcal {W}(\pi ,\psi )$
and
$W \in \mathcal {W}(\pi ,\psi )$
and
![]() $W' \in \mathcal {W}(\pi ',\overline {\psi })$
and Schwartz functions
$W' \in \mathcal {W}(\pi ',\overline {\psi })$
and Schwartz functions
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times 2}(F))$
for the
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times 2}(F))$
for the
![]() $\operatorname {\mathrm {GL}}_2 \times \operatorname {\mathrm {GL}}_2$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_2 \times \operatorname {\mathrm {GL}}_2$
Rankin–Selberg integral
![]() $\Psi (s,W,W',\Phi )$
when
$\Psi (s,W,W',\Phi )$
when
![]() $F = \mathbb {R}$
; moreover, this includes cases involving generic irreducible Casselman–Wallach representations
$F = \mathbb {R}$
; moreover, this includes cases involving generic irreducible Casselman–Wallach representations
![]() $\pi ,\pi '$
of
$\pi ,\pi '$
of
![]() $\operatorname {\mathrm {GL}}_2(F)$
for which
$\operatorname {\mathrm {GL}}_2(F)$
for which
![]() $\pi '$
need not be spherical. Further results along these lines have been proven by Zhang [Reference ZhangZha01, Proposition 2.5.2] and extended to
$\pi '$
need not be spherical. Further results along these lines have been proven by Zhang [Reference ZhangZha01, Proposition 2.5.2] and extended to
![]() $F = \mathbb {C}$
by Miyazaki [Reference MiyazakiMiy18, Theorem 6.1]; see also [Reference Hirano, Ishii and MiyazakiHIM22, Appendix A].
$F = \mathbb {C}$
by Miyazaki [Reference MiyazakiMiy18, Theorem 6.1]; see also [Reference Hirano, Ishii and MiyazakiHIM22, Appendix A].
For
![]() $n = 3$
, Hirano, Ishii and Miyazaki [Reference Hirano, Ishii and MiyazakiHIM16, Reference Hirano, Ishii and MiyazakiHIM22] have given an explicit description of right
$n = 3$
, Hirano, Ishii and Miyazaki [Reference Hirano, Ishii and MiyazakiHIM16, Reference Hirano, Ishii and MiyazakiHIM22] have given an explicit description of right
![]() $K_3$
- and
$K_3$
- and
![]() $K_2$
-finite Whittaker functions
$K_2$
-finite Whittaker functions
![]() $W \in \mathcal {W}(\pi ,\psi )$
and
$W \in \mathcal {W}(\pi ,\psi )$
and
![]() $W' \in \mathcal {W}(\pi ',\overline {\psi })$
for which
$W' \in \mathcal {W}(\pi ',\overline {\psi })$
for which
![]() $\Psi (s,W,W') = L(s,\pi \times \pi ')$
, where
$\Psi (s,W,W') = L(s,\pi \times \pi ')$
, where
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are any generic irreducible Casselman–Wallach representations of
$\pi '$
are any generic irreducible Casselman–Wallach representations of
![]() $\operatorname {\mathrm {GL}}_3(F)$
and
$\operatorname {\mathrm {GL}}_3(F)$
and
![]() $\operatorname {\mathrm {GL}}_2(F)$
, respectively; in particular,
$\operatorname {\mathrm {GL}}_2(F)$
, respectively; in particular,
![]() $\pi '$
need not be spherical.
$\pi '$
need not be spherical.
5.2. Examples and applications
5.2.1. The conductor exponent for essentially square-integrable representations
For
![]() $\pi = \chi ^{\kappa } |\cdot |^t$
, where
$\pi = \chi ^{\kappa } |\cdot |^t$
, where
![]() $\kappa \in \{0,1\}$
for
$\kappa \in \{0,1\}$
for
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\kappa \in \mathbb {Z}$
for
$\kappa \in \mathbb {Z}$
for
![]() $F = \mathbb {C}$
, the conductor exponent is
$F = \mathbb {C}$
, the conductor exponent is
![]() $c(\pi ) = \|\kappa \|$
. For
$c(\pi ) = \|\kappa \|$
. For
![]() $\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, where
$\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, where
![]() $\kappa \geq 2$
, the conductor exponent is
$\kappa \geq 2$
, the conductor exponent is
![]() $c(\pi ) = \kappa $
. Via Theorem 4.15, this allows one to calculate the conductor exponent of any induced representation of Whittaker type.
$c(\pi ) = \kappa $
. Via Theorem 4.15, this allows one to calculate the conductor exponent of any induced representation of Whittaker type.
5.2.2.
 $\operatorname {\mathrm {GL}}_2$
Examples
$\operatorname {\mathrm {GL}}_2$
Examples
Let us consider the classical setting of automorphic forms on the upper half-plane.
Example 5.2. Let f be a holomorphic cuspidal newform of weight
![]() $\kappa \geq 2$
, level
$\kappa \geq 2$
, level
![]() $q \in \mathbb {N}$
and nebentypus
$q \in \mathbb {N}$
and nebentypus
![]() $\psi $
modulo q, where
$\psi $
modulo q, where
![]() $\psi (-1) = (-1)^{\kappa }$
. Then the underlying automorphic representation of
$\psi (-1) = (-1)^{\kappa }$
. Then the underlying automorphic representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
, as described in [Reference CasselmanCas73, Section 3], has as its archimedean component a discrete series of weight
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
, as described in [Reference CasselmanCas73, Section 3], has as its archimedean component a discrete series of weight
![]() $\kappa $
,
$\kappa $
,
![]() $D_{\kappa }$
. In particular, the conductor exponent of this archimedean component is simply the weight
$D_{\kappa }$
. In particular, the conductor exponent of this archimedean component is simply the weight
![]() $\kappa $
.
$\kappa $
.
Example 5.3. Let f be a Maaß cuspidal newform of weight
![]() $\kappa \in \{0,1\}$
, level
$\kappa \in \{0,1\}$
, level
![]() $q \in \mathbb {N}$
and nebentypus
$q \in \mathbb {N}$
and nebentypus
![]() $\psi $
, where
$\psi $
, where
![]() $\psi (-1) = (-1)^{\kappa }$
. The archimedean component of the underlying automorphic representation of
$\psi (-1) = (-1)^{\kappa }$
. The archimedean component of the underlying automorphic representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
is one of three possible representations:
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$
is one of three possible representations:
-
• If
 $\kappa = 1$
, then the archimedean component is a principal series representation of the form
$\kappa = 1$
, then the archimedean component is a principal series representation of the form
 $|\cdot |^{it_f} \boxplus \chi |\cdot |^{-it_f}$
or
$|\cdot |^{it_f} \boxplus \chi |\cdot |^{-it_f}$
or
 $\chi |\cdot |^{it_f} \boxplus |\cdot |^{-it_f}$
, where
$\chi |\cdot |^{it_f} \boxplus |\cdot |^{-it_f}$
, where
 $t_f \in \mathbb {R}$
is the spectral parameter of f. The conductor exponent is
$t_f \in \mathbb {R}$
is the spectral parameter of f. The conductor exponent is
 $1$
.
$1$
. -
• If
 $\kappa = 0$
and f is even, so that
$\kappa = 0$
and f is even, so that
 $f(-\overline {z}) = f(z)$
, then the archimedean component is of the form
$f(-\overline {z}) = f(z)$
, then the archimedean component is of the form
 $|\cdot |^{it_f} \boxplus |\cdot |^{-it_f}$
, where
$|\cdot |^{it_f} \boxplus |\cdot |^{-it_f}$
, where
 $t_f \in \mathbb {R} \cup i(-1/2,1/2)$
. The conductor exponent is
$t_f \in \mathbb {R} \cup i(-1/2,1/2)$
. The conductor exponent is
 $0$
.
$0$
. -
• If
 $\kappa = 0$
and f is odd, so that
$\kappa = 0$
and f is odd, so that
 $f(-\overline {z}) = -f(z)$
, then the archimedean component is of the form
$f(-\overline {z}) = -f(z)$
, then the archimedean component is of the form
 $\chi |\cdot |^{it_f} \boxplus \chi |\cdot |^{-it_f}$
, where again
$\chi |\cdot |^{it_f} \boxplus \chi |\cdot |^{-it_f}$
, where again
 $t_f \in \mathbb {R} \cup i(-1/2,1/2)$
. The conductor exponent is
$t_f \in \mathbb {R} \cup i(-1/2,1/2)$
. The conductor exponent is
 $2$
.
$2$
.
Remark 5.4. The newform K-type of the archimedean component of the automorphic representation associated to an odd Maaß form of weight zero is not its minimal K-type: the newform K-type is
![]() $\tau _{(2,0)}$
, whereas the minimal K-type is the determinant representation
$\tau _{(2,0)}$
, whereas the minimal K-type is the determinant representation
![]() $\tau _{(1,1)}$
. Classically, this manifests itself via the fact that an odd Maaß form f of weight zero is not a test vector for the Rankin–Selberg integral
$\tau _{(1,1)}$
. Classically, this manifests itself via the fact that an odd Maaß form f of weight zero is not a test vector for the Rankin–Selberg integral
 $$\begin{align*}\int_{0}^{\infty} f(iy) y^{s - \frac{1}{2}} \, \frac{dy}{y}.\end{align*}$$
$$\begin{align*}\int_{0}^{\infty} f(iy) y^{s - \frac{1}{2}} \, \frac{dy}{y}.\end{align*}$$
Instead, one must use Maaß raising and lowering operators on such a Maaß form to obtain a test vector.
5.2.3. A non-application: the analytic conductor and analytic newvector
We have introduced in Section 4.3 the notion of the conductor exponent of a generic irreducible Casselman–Wallach representation
![]() $\pi $
as a measure of the extent of ramification. This can also be thought of as quantifying the (representation-theoretic) complexity of
$\pi $
as a measure of the extent of ramification. This can also be thought of as quantifying the (representation-theoretic) complexity of
![]() $\pi $
.
$\pi $
.
There is another well-known quantification of the complexity of
![]() $\pi $
: the analytic conductor. First introduced by Iwaniec and Sarnak [Reference Iwaniec, Sarnak, Alon, Bourgain, Connes, Gromov and MilmanIwSa00, (31)], this is defined on essentially square-integrable representations
$\pi $
: the analytic conductor. First introduced by Iwaniec and Sarnak [Reference Iwaniec, Sarnak, Alon, Bourgain, Connes, Gromov and MilmanIwSa00, (31)], this is defined on essentially square-integrable representations
![]() $\pi $
by
$\pi $
by

and extended to arbitrary induced representations of Whittaker type
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
via multiplicativity:
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
via multiplicativity:

One can relate this to the asymptotic behaviour of the local
![]() $\gamma $
-factor
$\gamma $
-factor
![]() $\gamma (s,\pi ,\psi )$
as s tends to
$\gamma (s,\pi ,\psi )$
as s tends to
![]() $1/2$
; see, in particular, [Reference Jana and NelsonJN19, Lemma 3.1 (1)] and also [Reference Conrey, Farmer, Keating, Rubinstein and SnaithCFKRS05, Section 3.1] (the latter also alludes to how this similarly encompasses the conductor at the nonarchimedean places).
$1/2$
; see, in particular, [Reference Jana and NelsonJN19, Lemma 3.1 (1)] and also [Reference Conrey, Farmer, Keating, Rubinstein and SnaithCFKRS05, Section 3.1] (the latter also alludes to how this similarly encompasses the conductor at the nonarchimedean places).
These two quantifications are entirely distinct. This can be seen most clearly for spherical representations
![]() $\pi = |\cdot |^{it_f} \boxplus |\cdot |^{-it_f}$
of
$\pi = |\cdot |^{it_f} \boxplus |\cdot |^{-it_f}$
of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
occurring as the archimedean component of an automorphic representation associated to an even Maaß form f of weight zero. As discussed in Example 5.3, the conductor exponent of such a representation
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
occurring as the archimedean component of an automorphic representation associated to an even Maaß form f of weight zero. As discussed in Example 5.3, the conductor exponent of such a representation
![]() $\pi $
is
$\pi $
is
![]() $c(\pi ) = 0$
; however, the analytic conductor is
$c(\pi ) = 0$
; however, the analytic conductor is
![]() $\mathfrak {q}(\pi ) = (1 + \|t_f\|)^2$
. This distinction boils down to the fact that the analytic conductor
$\mathfrak {q}(\pi ) = (1 + \|t_f\|)^2$
. This distinction boils down to the fact that the analytic conductor
![]() $\mathfrak {q}(\pi )$
is better thought of as being a measure of the size of the L-function
$\mathfrak {q}(\pi )$
is better thought of as being a measure of the size of the L-function
![]() $L(s,\pi )$
rather than a measure of the complexity of the representation itself.
$L(s,\pi )$
rather than a measure of the complexity of the representation itself.
Similarly, the newform is unrelated to the analytic newvectors introduced by Jana and Nelson in [Reference Jana and NelsonJN19]. Analytic newvectors are a different archimedean analogue of newforms; they are a family of vectors in a generic irreducible unitary Casselman–Wallach representation that are almost invariant under certain subsets (but not subgroups) of
![]() $\operatorname {\mathrm {GL}}_n(F)$
that are archimedean analogues of the congruence subgroups
$\operatorname {\mathrm {GL}}_n(F)$
that are archimedean analogues of the congruence subgroups
![]() $K_1(\mathfrak {p}^m)$
. Notably, analytic newvectors are not necessarily
$K_1(\mathfrak {p}^m)$
. Notably, analytic newvectors are not necessarily
![]() $K_n$
-finite, though they are
$K_n$
-finite, though they are
![]() $K_{n - 1}$
-invariant; in particular, they lie in the subspace spanned by the newform and all oldforms. Note that Jana and Nelson call the newform an ‘algebraic newvector’.
$K_{n - 1}$
-invariant; in particular, they lie in the subspace spanned by the newform and all oldforms. Note that Jana and Nelson call the newform an ‘algebraic newvector’.
5.2.4. Global Eulerian integrals
We mention a global application of the resolution of the test vector problem for Rankin–Selberg integrals. In order to do so, we require some discussion of global automorphic forms.
Let
![]() $\psi _{\mathbb {A}_{\mathbb {Q}}}$
denote the standard additive character of
$\psi _{\mathbb {A}_{\mathbb {Q}}}$
denote the standard additive character of
![]() $\mathbb {A}_{\mathbb {Q}}$
that is unramified at every place of
$\mathbb {A}_{\mathbb {Q}}$
that is unramified at every place of
![]() $\mathbb {Q}$
. Given a global number field F, define the additive character
$\mathbb {Q}$
. Given a global number field F, define the additive character ![]() of
of
![]() $\mathbb {A}_F$
. The conductor of
$\mathbb {A}_F$
. The conductor of
![]() $\psi _{\mathbb {A}_F}$
is the inverse different
$\psi _{\mathbb {A}_F}$
is the inverse different
![]() $\mathfrak {d}^{-1}$
of F; furthermore, there is a finite idèle
$\mathfrak {d}^{-1}$
of F; furthermore, there is a finite idèle
![]() $d \in \mathbb {A}_F^{\times }$
representing
$d \in \mathbb {A}_F^{\times }$
representing
![]() $\mathfrak {d}$
such that
$\mathfrak {d}$
such that
![]() $\psi _{\mathbb {A}_F} = \bigotimes _v \psi _v^{d_v}$
, where the additive character
$\psi _{\mathbb {A}_F} = \bigotimes _v \psi _v^{d_v}$
, where the additive character
![]() $\psi _v^{d_v}$
of
$\psi _v^{d_v}$
of
![]() $F_v$
of conductor
$F_v$
of conductor
![]() $\mathfrak {d}_v^{-1}$
is defined by
$\mathfrak {d}_v^{-1}$
is defined by ![]() with
with
![]() $\psi _v$
an unramified additive character of
$\psi _v$
an unramified additive character of
![]() $F_v$
as in Section 2.1.2.
$F_v$
as in Section 2.1.2.
Let
![]() $(\pi ,V_{\pi })$
be a cuspidal automorphic representation of
$(\pi ,V_{\pi })$
be a cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
with
$\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
with
![]() $n \geq 2$
, where
$n \geq 2$
, where
![]() $V_{\pi }$
is a space of automorphic forms on
$V_{\pi }$
is a space of automorphic forms on
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
. Let
$\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
. Let
![]() $W_{\varphi } \in \mathcal {W}(\pi ,\psi _{\mathbb {A}_F})$
denote the Whittaker function of
$W_{\varphi } \in \mathcal {W}(\pi ,\psi _{\mathbb {A}_F})$
denote the Whittaker function of
![]() $\varphi \in V_{\pi }$
, so that
$\varphi \in V_{\pi }$
, so that

where
![]() $du$
denotes the Tamagawa measure. If
$du$
denotes the Tamagawa measure. If
![]() $W_{\varphi }$
is a pure tensor, we may write
$W_{\varphi }$
is a pure tensor, we may write
![]() $W_{\varphi } = \prod _v W_{\varphi ,v}$
with
$W_{\varphi } = \prod _v W_{\varphi ,v}$
with
![]() $W_{\varphi ,v} \in \mathcal {W}(\pi _v,\psi _v^{d_v})$
, where the generic irreducible admissible smooth representations
$W_{\varphi ,v} \in \mathcal {W}(\pi _v,\psi _v^{d_v})$
, where the generic irreducible admissible smooth representations
![]() $\pi _v$
are the local components of the automorphic representation
$\pi _v$
are the local components of the automorphic representation
![]() $\pi = \bigotimes _v \pi _v$
. We define the global newform
$\pi = \bigotimes _v \pi _v$
. We define the global newform
![]() $\varphi ^{\circ } \in V_{\pi }$
to be such that at each place v of F, we have that
$\varphi ^{\circ } \in V_{\pi }$
to be such that at each place v of F, we have that ![]() with
with
![]() $W_v \in \mathcal {W}(\pi _v,\psi _v)$
the (local) Whittaker newform as in Theorems 3.14 and 4.17.
$W_v \in \mathcal {W}(\pi _v,\psi _v)$
the (local) Whittaker newform as in Theorems 3.14 and 4.17.
Proposition 5.5. Let F be a global number field of absolute discriminant
![]() $D_{F/\mathbb {Q}}$
, and let
$D_{F/\mathbb {Q}}$
, and let
![]() $(\pi ,V_{\pi })$
be a cuspidal automorphic representation of
$(\pi ,V_{\pi })$
be a cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
with
$\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
with
![]() $n \geq 2$
. Then the global newform
$n \geq 2$
. Then the global newform
![]() $\varphi ^{\circ } \in V_{\pi }$
is such that for all cuspidal automorphic representations
$\varphi ^{\circ } \in V_{\pi }$
is such that for all cuspidal automorphic representations
![]() $(\pi ',V_{\pi '})$
of
$(\pi ',V_{\pi '})$
of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {A}_F)$
that are everywhere unramified with global newforms
$\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {A}_F)$
that are everywhere unramified with global newforms
![]() $\varphi ^{\prime \circ } \in V_{\pi '}$
and for
$\varphi ^{\prime \circ } \in V_{\pi '}$
and for
![]() $\Re (s)$
sufficiently large, the global
$\Re (s)$
sufficiently large, the global
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral

with
![]() $dg$
the Tamagawa measure is equal, up to multiplication by a constant dependent only on F, to the product of
$dg$
the Tamagawa measure is equal, up to multiplication by a constant dependent only on F, to the product of
![]() $\omega _{\pi '}^{-1}(d) D_{F/\mathbb {Q}}^{\frac {n(n - 1)s}{2}}$
, where
$\omega _{\pi '}^{-1}(d) D_{F/\mathbb {Q}}^{\frac {n(n - 1)s}{2}}$
, where
![]() $\omega _{\pi '}$
denotes the central character of
$\omega _{\pi '}$
denotes the central character of
![]() $\pi '$
, and of the global completed Rankin–Selberg L-function
$\pi '$
, and of the global completed Rankin–Selberg L-function ![]() .
.
Remark 5.6. Via a regularisation process due to Ichino and Yamana [Reference Ichino and YamanaIY15, Theorem 1.1], a suitably modified version of this result still holds even if either
![]() $\pi $
or
$\pi $
or
![]() $\pi '$
(or both) is not cuspidal.
$\pi '$
(or both) is not cuspidal.
Proof. By unfolding,
 $$ \begin{align*} I(s,\varphi^{\circ},\varphi^{\prime\circ}) & = \int\limits_{\mathrm{N}_{n - 1}(\mathbb{A}_F) \backslash \operatorname{\mathrm{GL}}_{n - 1}(\mathbb{A}_F)} W_{\varphi^{\circ}}\begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} W_{\varphi^{\prime\circ}}(g) \left|\det g\right|{}_{\mathbb{A}_F}^{s - \frac{1}{2}} \, dg \\ & = c_{F/\mathbb{Q}} \prod_v \Psi(s,W_{\varphi^{\circ},v},W_{\varphi^{\prime\circ},v}), \end{align*} $$
$$ \begin{align*} I(s,\varphi^{\circ},\varphi^{\prime\circ}) & = \int\limits_{\mathrm{N}_{n - 1}(\mathbb{A}_F) \backslash \operatorname{\mathrm{GL}}_{n - 1}(\mathbb{A}_F)} W_{\varphi^{\circ}}\begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} W_{\varphi^{\prime\circ}}(g) \left|\det g\right|{}_{\mathbb{A}_F}^{s - \frac{1}{2}} \, dg \\ & = c_{F/\mathbb{Q}} \prod_v \Psi(s,W_{\varphi^{\circ},v},W_{\varphi^{\prime\circ},v}), \end{align*} $$
where the local Rankin–Selberg integrals
![]() $\Psi (s,W_{\varphi ^{\circ },v},W_{\varphi ^{\prime \circ },v})$
are as in (2.1), and
$\Psi (s,W_{\varphi ^{\circ },v},W_{\varphi ^{\prime \circ },v})$
are as in (2.1), and
![]() ${c_{F/\mathbb {Q}}> 0}$
is an absolute constant dependent only on F that arises from the compatibility of the global Tamagawa measure on
${c_{F/\mathbb {Q}}> 0}$
is an absolute constant dependent only on F that arises from the compatibility of the global Tamagawa measure on
![]() $\mathrm {N}_{n - 1}(\mathbb {A}_F) \backslash \operatorname {\mathrm {GL}}_{n - 1}(\mathbb {A}_F)$
compared to the local Haar measure on
$\mathrm {N}_{n - 1}(\mathbb {A}_F) \backslash \operatorname {\mathrm {GL}}_{n - 1}(\mathbb {A}_F)$
compared to the local Haar measure on
![]() $\mathrm {N}_{n - 1}(F_v) \backslash \operatorname {\mathrm {GL}}_{n - 1}(F_v)$
as normalised in Section 2.1. Upon making the change of variables
$\mathrm {N}_{n - 1}(F_v) \backslash \operatorname {\mathrm {GL}}_{n - 1}(F_v)$
as normalised in Section 2.1. Upon making the change of variables
![]() $g_v^{\prime } \mapsto \operatorname {\mathrm {diag}}(d_v^{1 - n},\ldots ,d_v^{-1}) g_v^{\prime }$
and using the fact that
$g_v^{\prime } \mapsto \operatorname {\mathrm {diag}}(d_v^{1 - n},\ldots ,d_v^{-1}) g_v^{\prime }$
and using the fact that
![]() $W_v^{\prime }(\operatorname {\mathrm {diag}}(d_v^{-1},\ldots ,d_v^{-1}) g_v^{\prime }) = \omega _{\pi _v^{\prime }}^{-1}(d_v) W_v^{\prime }(g_v^{\prime })$
, we see that
$W_v^{\prime }(\operatorname {\mathrm {diag}}(d_v^{-1},\ldots ,d_v^{-1}) g_v^{\prime }) = \omega _{\pi _v^{\prime }}^{-1}(d_v) W_v^{\prime }(g_v^{\prime })$
, we see that
A similar result holds for global
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integrals via Theorems 3.18 and 4.18. These involve an Eisenstein series
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integrals via Theorems 3.18 and 4.18. These involve an Eisenstein series
 $$\begin{align*}E(g,s;\Phi,\eta) = \left|\det g\right|{}_{\mathbb{A}_F}^s \int_{F^{\times} \backslash \mathbb{A}_F^{\times}} \Theta_{\Phi}^{\prime}(a,g) \eta(a) |a|_{\mathbb{A}_F}^{ns} \, d^{\times} a,\end{align*}$$
$$\begin{align*}E(g,s;\Phi,\eta) = \left|\det g\right|{}_{\mathbb{A}_F}^s \int_{F^{\times} \backslash \mathbb{A}_F^{\times}} \Theta_{\Phi}^{\prime}(a,g) \eta(a) |a|_{\mathbb{A}_F}^{ns} \, d^{\times} a,\end{align*}$$
where
![]() $\eta : F^{\times } \backslash \mathbb {A}_F^{\times } \to \mathbb {C}^{\times }$
is a Hecke character,
$\eta : F^{\times } \backslash \mathbb {A}_F^{\times } \to \mathbb {C}^{\times }$
is a Hecke character,
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {A}_F))$
is a Schwartz–Bruhat function, and
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {A}_F))$
is a Schwartz–Bruhat function, and

Proposition 5.7. Let F be a number field of absolute discriminant
![]() $D_{F/\mathbb {Q}}$
, and let
$D_{F/\mathbb {Q}}$
, and let
![]() $(\pi ,V_{\pi })$
and
$(\pi ,V_{\pi })$
and
![]() $(\pi ',V_{\pi '})$
be automorphic representations of
$(\pi ',V_{\pi '})$
be automorphic representations of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
with central characters
$\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
with central characters
![]() $\omega _{\pi }$
and
$\omega _{\pi }$
and
![]() $\omega _{\pi '}$
. Suppose that at least one of
$\omega _{\pi '}$
. Suppose that at least one of
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
is cuspidal and that
$\pi '$
is cuspidal and that
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
have disjoint ramification. Then there exists a right K-finite Schwartz–Bruhat function
$\pi '$
have disjoint ramification. Then there exists a right K-finite Schwartz–Bruhat function
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {A}_F))$
such that for
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {A}_F))$
such that for
![]() $\Re (s)$
sufficiently large, the global
$\Re (s)$
sufficiently large, the global
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral

with
![]() $dg$
the Tamagawa measure is equal, up to multiplication by a constant dependent only on F, to the product of
$dg$
the Tamagawa measure is equal, up to multiplication by a constant dependent only on F, to the product of
![]() $D_{F/\mathbb {Q}}^{\frac {n(n - 1)s}{2}}$
and of the global completed Rankin–Selberg L-function
$D_{F/\mathbb {Q}}^{\frac {n(n - 1)s}{2}}$
and of the global completed Rankin–Selberg L-function ![]() .
.
Remark 5.8. When both
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are noncuspidal, it ought to be possible to prove a suitably modified version of this result by extending to
$\pi '$
are noncuspidal, it ought to be possible to prove a suitably modified version of this result by extending to
![]() $\operatorname {\mathrm {GL}}_n$
a regularisation process due to Zagier [Reference ZagierZag82, Theorem] for
$\operatorname {\mathrm {GL}}_n$
a regularisation process due to Zagier [Reference ZagierZag82, Theorem] for
![]() $\operatorname {\mathrm {GL}}_2$
.
$\operatorname {\mathrm {GL}}_2$
.
We also may show the existence of a test vector for the global Godement–Jacquet zeta integral via Theorems 3.20 and 4.23.
Proposition 5.9. Let F be a number field, and let
![]() $(\pi ,V_{\pi })$
be an automorphic representation of
$(\pi ,V_{\pi })$
be an automorphic representation of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
. Then there exists a matrix coefficient
$\operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
. Then there exists a matrix coefficient ![]() and a bi-K-finite Schwartz–Bruhat function
and a bi-K-finite Schwartz–Bruhat function
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(\mathbb {A}_F))$
such that for
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(\mathbb {A}_F))$
such that for
![]() $\Re (s)$
sufficiently large, the global Godement–Jacquet zeta integral
$\Re (s)$
sufficiently large, the global Godement–Jacquet zeta integral

with
![]() $dg$
the Tamagawa measure is equal, up to multiplication by a constant dependent only on F, to the global completed standard L-function
$dg$
the Tamagawa measure is equal, up to multiplication by a constant dependent only on F, to the global completed standard L-function ![]() .
.
A similar result also holds for the Piatetski-Shapiro–Rallis integral [Reference Piatetski-Shapiro and RallisP-SR87], since this doubling integral is equal to the Godement–Jacquet zeta integral [Reference Piatetski-Shapiro and RallisP-SR87, Proposition 3.2].
Remark 5.10. In fact, we show something slightly stronger – namely, that
 $$\begin{align*}\int_{\operatorname{\mathrm{GL}}_n(\mathbb{A}_F)} \varphi^{\circ}(hg) \Phi(g) \left|\det g\right|{}_{\mathbb{A}_F}^{s + \frac{n - 1}{2}} \, dg\end{align*}$$
$$\begin{align*}\int_{\operatorname{\mathrm{GL}}_n(\mathbb{A}_F)} \varphi^{\circ}(hg) \Phi(g) \left|\det g\right|{}_{\mathbb{A}_F}^{s + \frac{n - 1}{2}} \, dg\end{align*}$$
is equal, up to multiplication by a constant dependent only on F, to
![]() $\Lambda (s,\pi ) \varphi ^{\circ }(h)$
for all
$\Lambda (s,\pi ) \varphi ^{\circ }(h)$
for all
![]() $h \in \operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
.
$h \in \operatorname {\mathrm {GL}}_n(\mathbb {A}_F)$
.
5.3. Strategy of the proofs
5.3.1. Nonarchimedean strategies
As discussed in Section 3, there are several approaches towards developing nonarchimedean newform theory for
![]() $\operatorname {\mathrm {GL}}_n$
. We briefly examine the challenges in transporting each of these methods to the archimedean setting.
$\operatorname {\mathrm {GL}}_n$
. We briefly examine the challenges in transporting each of these methods to the archimedean setting.
Matringe [Reference MatringeMat13] uses the nonarchimedean theory of Bernstein–Zelevinsky derivatives to explicitly construct the Whittaker newform. The archimedean theory of Bernstein–Zelevinsky derivatives is less well-developed (though see [Reference Aizenbud, Gourevitch and SahiAGS15] and [Reference ChaiCha15] for two different approaches), and it does not seem straightforward to transport Matringe’s proof to this setting.
The method of Jacquet [Reference JacquetJac12] does not use Bernstein–Zelevinsky derivatives; the proof, however, is nonconstructive and only shows the existence of a
![]() $K_{n - 1}$
-invariant test vector for
$K_{n - 1}$
-invariant test vector for
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integrals. In the archimedean setting, it seems difficult to describe the newform K-type when one only knows of the existence of such a test vector.
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integrals. In the archimedean setting, it seems difficult to describe the newform K-type when one only knows of the existence of such a test vector.
Finally, the method of Miyauchi [Reference MiyauchiMiy14] assumes the existence of the newform in
![]() $V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}$
and uses the action of certain Hecke operators to derive a recursive relation between certain values of the newform in the Whittaker model; using this, one can then show that the newform in the Whittaker model is a test vector for Rankin–Selberg integrals. The archimedean analogue of this is to assume the existence of the newform in the newform K-type and use the action of certain differential operators (arising from elements of the centre of the universal enveloping algebra) to derive systems of partial differential equations satisfied by the newform in the Whittaker model. This is essentially the approach undertaken in [Reference Hirano and OdaHO09] and [Reference Ishii and OdaIO14] (where the Whittaker function studied lies in the minimal K-type, not the newform K-type); already for
$V_{\pi }^{K_1(\mathfrak {p}^{c(\pi )})}$
and uses the action of certain Hecke operators to derive a recursive relation between certain values of the newform in the Whittaker model; using this, one can then show that the newform in the Whittaker model is a test vector for Rankin–Selberg integrals. The archimedean analogue of this is to assume the existence of the newform in the newform K-type and use the action of certain differential operators (arising from elements of the centre of the universal enveloping algebra) to derive systems of partial differential equations satisfied by the newform in the Whittaker model. This is essentially the approach undertaken in [Reference Hirano and OdaHO09] and [Reference Ishii and OdaIO14] (where the Whittaker function studied lies in the minimal K-type, not the newform K-type); already for
![]() $\operatorname {\mathrm {GL}}_3(\mathbb {C})$
, however, this leads to immense combinatorial difficulties in solving these systems of partial differential equations.
$\operatorname {\mathrm {GL}}_3(\mathbb {C})$
, however, this leads to immense combinatorial difficulties in solving these systems of partial differential equations.
5.3.2. The archimedean strategy
We take a different path. To prove the existence of the newform and newform K-type, we use Frobenius reciprocity to reduce the problem to branching rules on the associated maximal compact subgroups. Here, we benefit from the fact that, unlike in the nonarchimedean setting, irreducible representations of K and explicit branching rules are well understood, and the induced representations of Whittaker type are particularly easy to describe, since essentially square-integrable representations do not exist for
![]() $\operatorname {\mathrm {GL}}_n(F)$
with
$\operatorname {\mathrm {GL}}_n(F)$
with
![]() $n \geq 3$
. This approach also determines the dimension of spaces of oldforms and yields the additivity and inductivity of the conductor exponent. All of this is proven in Section 6.
$n \geq 3$
. This approach also determines the dimension of spaces of oldforms and yields the additivity and inductivity of the conductor exponent. All of this is proven in Section 6.
To study the newform in more detail, with an eye towards formulæ for the Whittaker newform that are beneficial for evaluating
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
and
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
and
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integrals, we require additional knowledge, given in Section 7, of a particular model of the newform K-type – namely, a space of homogeneous harmonic polynomials. Using this, we explicitly construct the newform in the induced model of
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integrals, we require additional knowledge, given in Section 7, of a particular model of the newform K-type – namely, a space of homogeneous harmonic polynomials. Using this, we explicitly construct the newform in the induced model of
![]() $\pi $
in Section 8.
$\pi $
in Section 8.
We give three different constructions of the newform in the induced model: via the Iwasawa decomposition, via convolution sections and via Godement sections. Each construction has its advantages and disadvantages. The construction via the Iwasawa decomposition is straightforward but lacks a direct relation to Whittaker functions. The construction via convolution sections, following work of Jacquet [Reference Jacquet, Hida, Ramakrishnan and ShahidiJac04], gives a recursive formula for the newform in terms of a convolution of the newform itself with an explicit standard Schwartz function; this gives an immediate resolution of the test vector problem for archimedean Godement–Jacquet integrals. Finally, following Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09], the newform is shown to be given as an element of a Godement section, which gives a recursive formula for the newform in terms of an integral of a distinguished newform of a representation of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
against a particular standard Schwartz function; this is limited to certain induced representations of Whittaker type, but is invaluable as an inductive step.
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
against a particular standard Schwartz function; this is limited to certain induced representations of Whittaker type, but is invaluable as an inductive step.
With these formulæ in hand, we then express the newform in the Whittaker model via the Jacquet integral in Section 9. The usage of convolution sections and Godement sections gives us recursive formulæ for the Whittaker newform. The latter, in particular, gives what we call a propagation formula: this is a recursive formula for
![]() $\operatorname {\mathrm {GL}}_n(F)$
Whittaker functions in terms of
$\operatorname {\mathrm {GL}}_n(F)$
Whittaker functions in terms of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
Whittaker functions.
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
Whittaker functions.
Our expression for the newform via convolution sections gives a quick resolution of the test vector problem for the Godement–Jacquet zeta integral. Our strategy for resolving the test vector problems for
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
and
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
and
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integrals follows an approach pioneered by Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09] (which is also followed in [Reference Ishii and MiyazakiIM22]). We employ a double induction argument presented in Section 10. This type of argument is due to Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09] (who, in turn, attributes this strategy to Shalika): it expresses the
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integrals follows an approach pioneered by Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09] (which is also followed in [Reference Ishii and MiyazakiIM22]). We employ a double induction argument presented in Section 10. This type of argument is due to Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09] (who, in turn, attributes this strategy to Shalika): it expresses the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral as the product of a
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral as the product of a
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral and a
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral and a
![]() $\operatorname {\mathrm {GL}}_n$
Godement–Jacquet zeta integral, and similarly expresses the
$\operatorname {\mathrm {GL}}_n$
Godement–Jacquet zeta integral, and similarly expresses the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral as a product of a
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral as a product of a
![]() $\operatorname {\mathrm {GL}}_{n - 1} \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral and a
$\operatorname {\mathrm {GL}}_{n - 1} \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral and a
![]() $\operatorname {\mathrm {GL}}_{n - 1}$
Godement–Jacquet zeta integral. (In fact, we find a slightly more direct approach via convolution sections that masks the presence of Godement–Jacquet zeta integrals.)
$\operatorname {\mathrm {GL}}_{n - 1}$
Godement–Jacquet zeta integral. (In fact, we find a slightly more direct approach via convolution sections that masks the presence of Godement–Jacquet zeta integrals.)
5.3.3. Additional remarks on the proofs
We emphasise that the proofs of Theorems 4.17 and 4.18, given in Section 10, are independent of the proofs in [Reference Gerasimov, Lebedev and OblezinGLO08, Reference Ishii and StadeIsSt13, Reference StadeSta01, Reference StadeSta02] of the unramified cases. Although our proofs are somewhat involved when ramification is present, they are particularly simple for spherical representations. In particular, these give proofs of Stade’s formulæ – namely, the unramified cases of Theorems 4.17 and 4.18. These reproofs of Stade’s formulæ also follow from the proofs of [Reference Ishii and MiyazakiIM22, Theorems 2.5 and 2.9]; they are essentially implicit in the work of Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09].
Notably, we do not explicitly make use of the action of the universal enveloping algebra of the complexified Lie algebra of
![]() $\operatorname {\mathrm {GL}}_n(F)$
as differential operators on Whittaker functions, nor do we require any calculations involving Mellin transforms. In this regard, our construction of Whittaker functions is entirely distinct to that of much previous work on archimedean Whittaker functions [Reference Hirano, Ishii, Miyazaki, Hamahata, Ichikawa, Murase and SuganoHIM12, Reference Hirano, Ishii and MiyazakiHIM16; Reference Hirano and OdaHO09, Reference Ishii and OdaIO14, Reference Ishii and StadeIsSt13, Reference PopaPop08, Reference StadeSta90, Reference StadeSta95, Reference StadeSta01, Reference StadeSta02]. In particular, our proofs of Theorems 4.17 and 4.18 demonstrate that the Jacquet integral is adequate for the direct computation of archimedean Rankin–Selberg integrals, contrary to an assertion of Ishii and Oda [Reference Ishii and OdaIO14, p. 1288], provided one couples this with the usage of convolution sections and Godement sections.
$\operatorname {\mathrm {GL}}_n(F)$
as differential operators on Whittaker functions, nor do we require any calculations involving Mellin transforms. In this regard, our construction of Whittaker functions is entirely distinct to that of much previous work on archimedean Whittaker functions [Reference Hirano, Ishii, Miyazaki, Hamahata, Ichikawa, Murase and SuganoHIM12, Reference Hirano, Ishii and MiyazakiHIM16; Reference Hirano and OdaHO09, Reference Ishii and OdaIO14, Reference Ishii and StadeIsSt13, Reference PopaPop08, Reference StadeSta90, Reference StadeSta95, Reference StadeSta01, Reference StadeSta02]. In particular, our proofs of Theorems 4.17 and 4.18 demonstrate that the Jacquet integral is adequate for the direct computation of archimedean Rankin–Selberg integrals, contrary to an assertion of Ishii and Oda [Reference Ishii and OdaIO14, p. 1288], provided one couples this with the usage of convolution sections and Godement sections.
6. The Newform K-Type
To study the newform K-type of an induced representation of Whittaker type
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, as well as determine the dimension of spaces of oldforms, we must determine the dimension of
$\operatorname {\mathrm {GL}}_n(F)$
, as well as determine the dimension of spaces of oldforms, we must determine the dimension of
![]() $\operatorname {\mathrm {Hom}}_{K_n}(\tau , \pi |_{K_n})$
for each
$\operatorname {\mathrm {Hom}}_{K_n}(\tau , \pi |_{K_n})$
for each
![]() $\tau \in \widehat {K_n}$
for which
$\tau \in \widehat {K_n}$
for which
![]() $\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1, \tau |_{K_{n - 1}})$
is nontrivial. This is achieved via branching rules.
$\operatorname {\mathrm {Hom}}_{K_{n - 1}}(1, \tau |_{K_{n - 1}})$
is nontrivial. This is achieved via branching rules.
6.1. Branching from
 $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
to
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
to
 $\operatorname {\mathrm {U}}(n)$
$\operatorname {\mathrm {U}}(n)$
Let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _n$
be an induced representation of Whittaker type of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _n$
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
, so that for each
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
, so that for each
![]() $j \in \{1,\ldots ,n\}$
,
$j \in \{1,\ldots ,n\}$
,
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
for some
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
for some
![]() $\kappa _j \in \mathbb {Z}$
and
$\kappa _j \in \mathbb {Z}$
and
![]() $t_j \in \mathbb {C}$
.
$t_j \in \mathbb {C}$
.
Lemma 6.1. For
![]() $\tau \in \widehat {\operatorname {\mathrm {U}}(n)}$
, we have that
$\tau \in \widehat {\operatorname {\mathrm {U}}(n)}$
, we have that

Here, we view
![]() $\operatorname {\mathrm {U}}(1)^n$
as the subgroup of diagonal matrices in
$\operatorname {\mathrm {U}}(1)^n$
as the subgroup of diagonal matrices in
![]() $\operatorname {\mathrm {U}}(n)$
; it is the maximal compact subgroup of the Levi subgroup
$\operatorname {\mathrm {U}}(n)$
; it is the maximal compact subgroup of the Levi subgroup
![]() $\mathrm {M}_{(1,\ldots ,1)}(\mathbb {C}) \cong \operatorname {\mathrm {GL}}_1(\mathbb {C})^n$
of the standard parabolic subgroup
$\mathrm {M}_{(1,\ldots ,1)}(\mathbb {C}) \cong \operatorname {\mathrm {GL}}_1(\mathbb {C})^n$
of the standard parabolic subgroup
![]() $\mathrm {P}(\mathbb {C}) = \mathrm {P}_{(1,\ldots ,1)}(\mathbb {C})$
of
$\mathrm {P}(\mathbb {C}) = \mathrm {P}_{(1,\ldots ,1)}(\mathbb {C})$
of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
from which
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
from which
![]() $\pi $
is induced.
$\pi $
is induced.
Proof. Mackey’s restriction-induction formula implies that
and so by the Frobenius reciprocity theorem,
It remains to note that

The right-hand side of (6.2) is a branching from
![]() $\operatorname {\mathrm {U}}(n)$
to
$\operatorname {\mathrm {U}}(n)$
to
![]() $\operatorname {\mathrm {U}}(1)^n$
. This can be understood via iterating the following branching rule from
$\operatorname {\mathrm {U}}(1)^n$
. This can be understood via iterating the following branching rule from
![]() $\operatorname {\mathrm {U}}(n)$
to
$\operatorname {\mathrm {U}}(n)$
to
![]() $\operatorname {\mathrm {U}}(n - 1) \times \operatorname {\mathrm {U}}(1)$
.
$\operatorname {\mathrm {U}}(n - 1) \times \operatorname {\mathrm {U}}(1)$
.
Lemma 6.3 [Reference ProctorPro94, Proposition 10.1]
For
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {U}}(n)}$
of highest weight
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {U}}(n)}$
of highest weight
![]() $\mu = (\mu _1,\ldots ,\mu _n) \in \Lambda _n$
,
$\mu = (\mu _1,\ldots ,\mu _n) \in \Lambda _n$
,
 $$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{U}}(n - 1) \times \operatorname{\mathrm{U}}(1)} \cong \bigoplus_{\lambda \in \Lambda_1} \bigoplus_{\substack{\nu = (\nu_1,\ldots,\nu_{n - 1}) \in \Lambda_{n - 1} \\ \mu_1 \geq \nu_1 \geq \mu_2 \geq \cdots \geq \nu_{n - 1} \geq \mu_n \\ \sum_{j = 1}^{n - 1} \nu_j = \sum_{j = 1}^{n} \mu_j - \lambda}} \tau_{\nu} \boxtimes \tau_{\lambda}.\end{align*}$$
$$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{U}}(n - 1) \times \operatorname{\mathrm{U}}(1)} \cong \bigoplus_{\lambda \in \Lambda_1} \bigoplus_{\substack{\nu = (\nu_1,\ldots,\nu_{n - 1}) \in \Lambda_{n - 1} \\ \mu_1 \geq \nu_1 \geq \mu_2 \geq \cdots \geq \nu_{n - 1} \geq \mu_n \\ \sum_{j = 1}^{n - 1} \nu_j = \sum_{j = 1}^{n} \mu_j - \lambda}} \tau_{\nu} \boxtimes \tau_{\lambda}.\end{align*}$$
In particular,
 $$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{U}}(n - 1)} \cong \bigoplus_{\substack{\nu = (\nu_1,\ldots,\nu_{n - 1}) \in \Lambda_{n - 1} \\ \mu_1 \geq \nu_1 \geq \mu_2 \geq \cdots \geq \nu_{n - 1} \geq \mu_n}} \tau_{\nu}.\end{align*}$$
$$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{U}}(n - 1)} \cong \bigoplus_{\substack{\nu = (\nu_1,\ldots,\nu_{n - 1}) \in \Lambda_{n - 1} \\ \mu_1 \geq \nu_1 \geq \mu_2 \geq \cdots \geq \nu_{n - 1} \geq \mu_n}} \tau_{\nu}.\end{align*}$$
Corollary 6.4. The restriction to
![]() $\operatorname {\mathrm {U}}(n - 1)$
of the irreducible representation
$\operatorname {\mathrm {U}}(n - 1)$
of the irreducible representation
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {U}}(n)}$
of highest weight
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {U}}(n)}$
of highest weight
![]() $\mu = (\mu _1, \ldots , \mu _n) \in \Lambda _n$
contains the trivial representation if and only if
$\mu = (\mu _1, \ldots , \mu _n) \in \Lambda _n$
contains the trivial representation if and only if
![]() $\mu _1 \geq 0$
,
$\mu _1 \geq 0$
,
![]() $\mu _2 = \cdots = \mu _{n - 1} = 0$
, and
$\mu _2 = \cdots = \mu _{n - 1} = 0$
, and
![]() $\mu _n \leq 0$
, in which case the trivial representation occurs with multiplicity one.
$\mu _n \leq 0$
, in which case the trivial representation occurs with multiplicity one.
We now iterate the branching rule in Lemma 6.3 to determine the multiplicity of a representation
![]() $\tau _{\lambda _1} \boxtimes \cdots \boxtimes \tau _{\lambda _n}$
of
$\tau _{\lambda _1} \boxtimes \cdots \boxtimes \tau _{\lambda _n}$
of
![]() $\operatorname {\mathrm {U}}(1)^n$
in a given representation
$\operatorname {\mathrm {U}}(1)^n$
in a given representation
![]() $\tau _{\mu }$
of
$\tau _{\mu }$
of
![]() $\operatorname {\mathrm {U}}(n)$
.
$\operatorname {\mathrm {U}}(n)$
.
Lemma 6.5. For
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {U}}(n)}$
of highest weight
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {U}}(n)}$
of highest weight
![]() $\mu = (\mu _1,0,\ldots ,0,\mu _n) \in \Lambda _n$
and for any
$\mu = (\mu _1,0,\ldots ,0,\mu _n) \in \Lambda _n$
and for any
![]() $\lambda _1,\ldots ,\lambda _n \in \Lambda _1$
,
$\lambda _1,\ldots ,\lambda _n \in \Lambda _1$
,

Proof. We take
![]() $\mu = (\mu _1,0,\ldots ,0,\mu _n)$
in Lemma 6.3 and then iterate this branching rule in order to find that
$\mu = (\mu _1,0,\ldots ,0,\mu _n)$
in Lemma 6.3 and then iterate this branching rule in order to find that

where we define ![]() ,
, ![]() and
and ![]() . By induction, the condition
. By induction, the condition
![]() $\nu _{j,1} + \nu _{j,n - j} = \nu _{j - 1,1} + \nu _{j - 1,n - j + 1} - \lambda _j$
implies that
$\nu _{j,1} + \nu _{j,n - j} = \nu _{j - 1,1} + \nu _{j - 1,n - j + 1} - \lambda _j$
implies that
 $$\begin{align*}\mu_1 + \mu_n - \sum_{k = 1}^{j} \lambda_k = \begin{cases} \nu_{j,1} + \nu_{j,n - j} &\text{for }j \in \{1, \ldots, n - 2\}, \\ \nu_{n - 1,1} & \text{for }j = n - 1, \\ 0 & \text{for }j = n. \end{cases}\end{align*}$$
$$\begin{align*}\mu_1 + \mu_n - \sum_{k = 1}^{j} \lambda_k = \begin{cases} \nu_{j,1} + \nu_{j,n - j} &\text{for }j \in \{1, \ldots, n - 2\}, \\ \nu_{n - 1,1} & \text{for }j = n - 1, \\ 0 & \text{for }j = n. \end{cases}\end{align*}$$
The multiplicity of
![]() $\tau _{\lambda _1} \boxtimes \cdots \boxtimes \tau _{\lambda _n}$
in
$\tau _{\lambda _1} \boxtimes \cdots \boxtimes \tau _{\lambda _n}$
in
![]() $\tau _{\mu }$
is thereby equal to
$\tau _{\mu }$
is thereby equal to
– namely, the number of
![]() $(n - 2)$
-tuples
$(n - 2)$
-tuples
![]() $(\nu _{1,1},\ldots ,\nu _{n - 2,1})$
for which the system of inequalities
$(\nu _{1,1},\ldots ,\nu _{n - 2,1})$
for which the system of inequalities
 $$\begin{align*}\mu_1 \geq \nu_{1,1} + \max\{\lambda_1,0\} \geq \cdots \geq \nu_{n - 2,1} + \sum_{j = 1}^{n - 2} \max\{\lambda_j,0\} \geq \sum_{j = 1}^{n} \max\{\lambda_j,0\}\end{align*}$$
$$\begin{align*}\mu_1 \geq \nu_{1,1} + \max\{\lambda_1,0\} \geq \cdots \geq \nu_{n - 2,1} + \sum_{j = 1}^{n - 2} \max\{\lambda_j,0\} \geq \sum_{j = 1}^{n} \max\{\lambda_j,0\}\end{align*}$$
holds. This is zero unless there exists some
![]() $\ell \in \mathbb {N}_0$
such that
$\ell \in \mathbb {N}_0$
such that
 $$\begin{align*}\mu_1 = \sum_{j = 1}^{n} \max\{\lambda_j,0\} + \ell, \qquad \mu_n = \sum_{j = 1}^{n} \min\{\lambda_j,0\} - \ell,\end{align*}$$
$$\begin{align*}\mu_1 = \sum_{j = 1}^{n} \max\{\lambda_j,0\} + \ell, \qquad \mu_n = \sum_{j = 1}^{n} \min\{\lambda_j,0\} - \ell,\end{align*}$$
in which case the multiplicity is precisely the number of ordered
![]() $(n - 2)$
-tuples taking values between
$(n - 2)$
-tuples taking values between
![]() $0$
and
$0$
and
![]() $\ell $
, which is
$\ell $
, which is
 $$\begin{align*}\binom{\ell + n - 2}{n - 2}.\\[-40pt]\end{align*}$$
$$\begin{align*}\binom{\ell + n - 2}{n - 2}.\\[-40pt]\end{align*}$$
With this in hand, we can now explicitly determine the right-hand side of (6.2).
Lemma 6.6. Suppose that the restriction of
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {U}}(n)}$
to
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {U}}(n)}$
to
![]() $\operatorname {\mathrm {U}}(n - 1)$
contains the trivial representation. Then the highest weight of
$\operatorname {\mathrm {U}}(n - 1)$
contains the trivial representation. Then the highest weight of
![]() $\tau _{\mu }$
is of the form
$\tau _{\mu }$
is of the form
![]() $\mu = (\mu _1,0,\ldots ,0,\mu _n) \in \Lambda _n$
, the trivial representation occurs with multiplicity one, and
$\mu = (\mu _1,0,\ldots ,0,\mu _n) \in \Lambda _n$
, the trivial representation occurs with multiplicity one, and

Proofs of Theorems 4.7, 4.12, 4.14 and 4.15 for
 $F = \mathbb {C}$
$F = \mathbb {C}$
Lemmata 6.1 and 6.6 combine to complete the proofs of Theorems 4.7 and 4.12 for
![]() $F = \mathbb {C}$
, noting that for
$F = \mathbb {C}$
, noting that for
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _n$
with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _n$
with
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, the newform K-type
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, the newform K-type
![]() $\tau ^{\circ } = \tau _{\mu ^{\circ }}$
has highest weight
$\tau ^{\circ } = \tau _{\mu ^{\circ }}$
has highest weight
 $$\begin{align*}\mu^{\circ} = \left(\sum_{j = 1}^{n} \max\{\kappa_j,0\},0,\ldots,0,\sum_{j = 1}^{n} \min\{\kappa_j,0\}\right),\end{align*}$$
$$\begin{align*}\mu^{\circ} = \left(\sum_{j = 1}^{n} \max\{\kappa_j,0\},0,\ldots,0,\sum_{j = 1}^{n} \min\{\kappa_j,0\}\right),\end{align*}$$
so that, recalling the definition (4.2) of
![]() $\deg \tau ^{\circ }$
,
$\deg \tau ^{\circ }$
,

Theorem 4.14 then holds for
![]() $F = \mathbb {C}$
via the fact that
$F = \mathbb {C}$
via the fact that
 $$\begin{align*}\varepsilon(s,\pi,\psi) = \prod_{j = 1}^{n} \varepsilon(s,\pi_j,\psi) = \prod_{j = 1}^{n} i^{-\|\kappa_j\|} = i^{-\|\kappa_1\| - \cdots - \|\kappa_n\|} = i^{-c(\pi)},\end{align*}$$
$$\begin{align*}\varepsilon(s,\pi,\psi) = \prod_{j = 1}^{n} \varepsilon(s,\pi_j,\psi) = \prod_{j = 1}^{n} i^{-\|\kappa_j\|} = i^{-\|\kappa_1\| - \cdots - \|\kappa_n\|} = i^{-c(\pi)},\end{align*}$$
recalling (2.18), while the case
![]() $n = 1$
implies Theorem 4.15 for
$n = 1$
implies Theorem 4.15 for
![]() $F = \mathbb {C}$
.
$F = \mathbb {C}$
.
Remark 6.7. Note that
![]() $\deg \tau _{\mu (\ell )} = \deg \tau ^{\circ } + 2\ell $
for
$\deg \tau _{\mu (\ell )} = \deg \tau ^{\circ } + 2\ell $
for

and, in particular, that
![]() $\deg \tau _{\mu (\ell )} \equiv \deg \tau ^{\circ }\ \pmod {2}$
. This congruence holds not just for a K-type
$\deg \tau _{\mu (\ell )} \equiv \deg \tau ^{\circ }\ \pmod {2}$
. This congruence holds not just for a K-type
![]() $\tau $
of
$\tau $
of
![]() $\pi $
for which
$\pi $
for which
![]() $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {U}}(n - 1)}(1,\tau |_{\operatorname {\mathrm {U}}(n - 1)})$
is nontrivial, but for any K-type of
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {U}}(n - 1)}(1,\tau |_{\operatorname {\mathrm {U}}(n - 1)})$
is nontrivial, but for any K-type of
![]() $\pi $
; see [Reference FanFan18, Theorem 2.1].
$\pi $
; see [Reference FanFan18, Theorem 2.1].
Remark 6.8. The minimal K-type of
![]() $\pi $
has highest weight
$\pi $
has highest weight
where
![]() $\sigma $
is a permutation for which
$\sigma $
is a permutation for which
![]() $\kappa _{\sigma (1)} \geq \cdots \geq \kappa _{\sigma (n)}$
. The corresponding Vogan norm is
$\kappa _{\sigma (1)} \geq \cdots \geq \kappa _{\sigma (n)}$
. The corresponding Vogan norm is
 $$\begin{align*}\|\tau_{\mu}\|_{\mathrm{V}}^2 = \sum_{j = 1}^{n} \left(\kappa_{\sigma(j)} + n + 1 - 2j\right)^2.\end{align*}$$
$$\begin{align*}\|\tau_{\mu}\|_{\mathrm{V}}^2 = \sum_{j = 1}^{n} \left(\kappa_{\sigma(j)} + n + 1 - 2j\right)^2.\end{align*}$$
This minimal K-type is the newform K-type
![]() $\tau ^{\circ }$
if and only if
$\tau ^{\circ }$
if and only if
![]() $\kappa _{\sigma (2)} = \cdots = \kappa _{\sigma (n - 1)} = 0$
.
$\kappa _{\sigma (2)} = \cdots = \kappa _{\sigma (n - 1)} = 0$
.
In general, the Vogan norm of the minimal K-type is not equal to
![]() $c(\pi )$
. However, the same cannot be said for the Howe degree: the Howe degree of the minimal K-type is
$c(\pi )$
. However, the same cannot be said for the Howe degree: the Howe degree of the minimal K-type is
 $$\begin{align*}\sum_{j = 1}^{n} \left\|\kappa_{\sigma(j)}\right\| = \deg \tau^{\circ} = c(\pi).\end{align*}$$
$$\begin{align*}\sum_{j = 1}^{n} \left\|\kappa_{\sigma(j)}\right\| = \deg \tau^{\circ} = c(\pi).\end{align*}$$
6.2. Branching from
 $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
to
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
to
 $\operatorname {\mathrm {O}}(n)$
$\operatorname {\mathrm {O}}(n)$
Let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
. This is induced from a standard parabolic subgroup
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
. This is induced from a standard parabolic subgroup
![]() $\mathrm {P}(\mathbb {R}) = \mathrm {P}_{(n_1,\ldots ,n_r)}(\mathbb {R})$
of
$\mathrm {P}(\mathbb {R}) = \mathrm {P}_{(n_1,\ldots ,n_r)}(\mathbb {R})$
of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
; when
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
; when
![]() $n_j = 1$
,
$n_j = 1$
,
![]() $\pi _j$
is of the form
$\pi _j$
is of the form
![]() $\chi ^{\kappa _j} |\cdot |^{t_j}$
for some
$\chi ^{\kappa _j} |\cdot |^{t_j}$
for some
![]() $\kappa _j \in \{0,1\}$
and
$\kappa _j \in \{0,1\}$
and
![]() $t_j \in \mathbb {C}$
, while when
$t_j \in \mathbb {C}$
, while when
![]() $n_j = 2$
,
$n_j = 2$
,
![]() $\pi _j$
is of the form
$\pi _j$
is of the form
![]() $D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
for some
$D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
for some
![]() $\kappa _j \geq 2$
and
$\kappa _j \geq 2$
and
![]() $t_j \in \mathbb {C}$
.
$t_j \in \mathbb {C}$
.
Lemma 6.9. For
![]() $\tau \in \widehat {\operatorname {\mathrm {O}}(n)}$
, the vector space
$\tau \in \widehat {\operatorname {\mathrm {O}}(n)}$
, the vector space
![]() $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {O}}(n)} \left (\tau , \pi |_{\operatorname {\mathrm {O}}(n)}\right )$
is isomorphic to
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {O}}(n)} \left (\tau , \pi |_{\operatorname {\mathrm {O}}(n)}\right )$
is isomorphic to

Here, we view
![]() $\operatorname {\mathrm {O}}(n_1) \times \cdots \times \operatorname {\mathrm {O}}(n_r)$
as a subgroup of block-diagonal matrices in
$\operatorname {\mathrm {O}}(n_1) \times \cdots \times \operatorname {\mathrm {O}}(n_r)$
as a subgroup of block-diagonal matrices in
![]() $\operatorname {\mathrm {O}}(n)$
; it is the maximal compact subgroup of the Levi subgroup
$\operatorname {\mathrm {O}}(n)$
; it is the maximal compact subgroup of the Levi subgroup
![]() $\mathrm {M}_{\mathrm {P}}(\mathbb {R}) \cong \operatorname {\mathrm {GL}}_{n_1}(\mathbb {R}) \times \cdots \times \operatorname {\mathrm {GL}}_{n_r}(\mathbb {R})$
of the parabolic subgroup
$\mathrm {M}_{\mathrm {P}}(\mathbb {R}) \cong \operatorname {\mathrm {GL}}_{n_1}(\mathbb {R}) \times \cdots \times \operatorname {\mathrm {GL}}_{n_r}(\mathbb {R})$
of the parabolic subgroup
![]() $\mathrm {P}(\mathbb {R}) = \mathrm {P}_{(n_1,\ldots ,n_r)}(\mathbb {R})$
.
$\mathrm {P}(\mathbb {R}) = \mathrm {P}_{(n_1,\ldots ,n_r)}(\mathbb {R})$
.
Proof. Mackey’s restriction-induction formula implies that
and
![]() $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {O}}(n)} \left (\tau , \pi |_{\operatorname {\mathrm {O}}(n)}\right )$
is isomorphic to
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {O}}(n)} \left (\tau , \pi |_{\operatorname {\mathrm {O}}(n)}\right )$
is isomorphic to
by the Frobenius reciprocity theorem. Note that if
![]() $n_j = 1$
, so that
$n_j = 1$
, so that
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, then
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, then
![]() $\pi _j |_{\operatorname {\mathrm {O}}(1)} \cong \tau _{\kappa _j}$
, while if
$\pi _j |_{\operatorname {\mathrm {O}}(1)} \cong \tau _{\kappa _j}$
, while if
![]() $n_j = 2$
, so that
$n_j = 2$
, so that
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
, then
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
, then
 $$\begin{align*}\pi_j |_{\operatorname{\mathrm{O}}(2)} \cong \bigoplus_{\substack{\ell_j = \kappa_j \\ \ell_j \equiv \kappa_j \ \pmod{2}}}^{\infty} \tau_{(\ell_j,0)},\end{align*}$$
$$\begin{align*}\pi_j |_{\operatorname{\mathrm{O}}(2)} \cong \bigoplus_{\substack{\ell_j = \kappa_j \\ \ell_j \equiv \kappa_j \ \pmod{2}}}^{\infty} \tau_{(\ell_j,0)},\end{align*}$$
from which it follows that

By restricting in stages and using the fact that
![]() $\#\{j : n_j = 1\} = 2r - n$
and
$\#\{j : n_j = 1\} = 2r - n$
and
![]() $\#\{j : n_j = 2\} = n - r$
, we deduce the following.
$\#\{j : n_j = 2\} = n - r$
, we deduce the following.
Corollary 6.10. For
![]() $\tau \in \widehat {\operatorname {\mathrm {O}}(n)}$
,
$\tau \in \widehat {\operatorname {\mathrm {O}}(n)}$
,
![]() $\dim \operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {O}}(n)} \left (\tau , \pi |_{\operatorname {\mathrm {O}}(n)}\right )$
is equal to
$\dim \operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {O}}(n)} \left (\tau , \pi |_{\operatorname {\mathrm {O}}(n)}\right )$
is equal to

To understand (6.11), which involves branching from
![]() $\operatorname {\mathrm {O}}(n)$
to various subgroups, we make use of the following branching rule from
$\operatorname {\mathrm {O}}(n)$
to various subgroups, we make use of the following branching rule from
![]() $\operatorname {\mathrm {O}}(n)$
to
$\operatorname {\mathrm {O}}(n)$
to
![]() $\operatorname {\mathrm {O}}(n - 1) \times \operatorname {\mathrm {O}}(1)$
.
$\operatorname {\mathrm {O}}(n - 1) \times \operatorname {\mathrm {O}}(1)$
.
Lemma 6.12 [Reference ProctorPro94, Proposition 10.1]
For
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
of highest weight
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
of highest weight
![]() $\mu = (\mu _1,\ldots ,\mu _n) \in \Lambda _n$
,
$\mu = (\mu _1,\ldots ,\mu _n) \in \Lambda _n$
,
 $$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{O}}(n - 1) \times \operatorname{\mathrm{O}}(1)} \cong \bigoplus_{\lambda \in \Lambda_1} \bigoplus_{\substack{\nu = (\nu_1,\ldots,\nu_{n - 1}) \in \Lambda_{n - 1} \\ \mu_1 \geq \nu_1 \geq \mu_2 \geq \cdots \geq \nu_{n - 1} \geq \mu_n \\ \sum_{j = 1}^{n - 1} \nu_j \equiv \sum_{j = 1}^{n} \mu_j - \lambda \ \pmod{2}}} \tau_{\nu} \boxtimes \tau_{\lambda}.\end{align*}$$
$$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{O}}(n - 1) \times \operatorname{\mathrm{O}}(1)} \cong \bigoplus_{\lambda \in \Lambda_1} \bigoplus_{\substack{\nu = (\nu_1,\ldots,\nu_{n - 1}) \in \Lambda_{n - 1} \\ \mu_1 \geq \nu_1 \geq \mu_2 \geq \cdots \geq \nu_{n - 1} \geq \mu_n \\ \sum_{j = 1}^{n - 1} \nu_j \equiv \sum_{j = 1}^{n} \mu_j - \lambda \ \pmod{2}}} \tau_{\nu} \boxtimes \tau_{\lambda}.\end{align*}$$
In particular,
 $$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{O}}(n - 1)} \cong \bigoplus_{\substack{\nu = (\nu_1,\ldots,\nu_{n - 1}) \in \Lambda_{n - 1} \\ \mu_1 \geq \nu_1 \geq \mu_2 \geq \cdots \geq \nu_{n - 1} \geq \mu_n}} \tau_{\nu}.\end{align*}$$
$$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{O}}(n - 1)} \cong \bigoplus_{\substack{\nu = (\nu_1,\ldots,\nu_{n - 1}) \in \Lambda_{n - 1} \\ \mu_1 \geq \nu_1 \geq \mu_2 \geq \cdots \geq \nu_{n - 1} \geq \mu_n}} \tau_{\nu}.\end{align*}$$
Corollary 6.13. The restriction to
![]() $\operatorname {\mathrm {O}}(n - 1)$
of the irreducible representation
$\operatorname {\mathrm {O}}(n - 1)$
of the irreducible representation
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
of highest weight
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
of highest weight
![]() $\mu = (\mu _1, \ldots , \mu _n) \in \Lambda _n$
contains the trivial representation if and only if
$\mu = (\mu _1, \ldots , \mu _n) \in \Lambda _n$
contains the trivial representation if and only if
![]() $\mu _1 \geq 0$
and
$\mu _1 \geq 0$
and
![]() $\mu _2 = \cdots = \mu _n = 0$
, in which case the trivial representation occurs with multiplicity one.
$\mu _2 = \cdots = \mu _n = 0$
, in which case the trivial representation occurs with multiplicity one.
Now we iterate the branching rule in Lemma 6.12.
Lemma 6.14. For
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
of highest weight
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
of highest weight
![]() $\mu = (\mu _1,0,\ldots ,0) \in \Lambda _n$
, and for
$\mu = (\mu _1,0,\ldots ,0) \in \Lambda _n$
, and for
![]() $\lambda _1,\ldots ,\lambda _{2r - n} \in \Lambda _1$
and
$\lambda _1,\ldots ,\lambda _{2r - n} \in \Lambda _1$
and
![]() $\nu _{2(n - r)} \in \Lambda _{2(n - r)}$
,
$\nu _{2(n - r)} \in \Lambda _{2(n - r)}$
,

is equal to
 $$\begin{align*}\begin{cases} 1 & \text{if }\nu_{2(n - r)} = (\mu_1 - \lambda_1 - 2\ell,0,\ldots,0)\text{ for some }\ell \in \mathbb{N}_0, \\ 0 & \text{otherwise} \end{cases}\end{align*}$$
$$\begin{align*}\begin{cases} 1 & \text{if }\nu_{2(n - r)} = (\mu_1 - \lambda_1 - 2\ell,0,\ldots,0)\text{ for some }\ell \in \mathbb{N}_0, \\ 0 & \text{otherwise} \end{cases}\end{align*}$$
if
![]() $\#\{j : n_j = 1\} = 1$
, while if
$\#\{j : n_j = 1\} = 1$
, while if
![]() $\#\{j : n_j = 1\} \geq 2$
, this is equal to
$\#\{j : n_j = 1\} \geq 2$
, this is equal to
 $$\begin{align*}\begin{cases} \binom{\ell + n' - 1}{n' - 1} & \text{if } \nu_{2(n - r)} = \left(\mu_1 - \sum_{j = 1}^{2r - n} \lambda_j - 2\ell,0,\ldots,0\right)\text{ for some }\ell \in \mathbb{N}_0, \\ 0 & \text{otherwise}. \end{cases}\end{align*}$$
$$\begin{align*}\begin{cases} \binom{\ell + n' - 1}{n' - 1} & \text{if } \nu_{2(n - r)} = \left(\mu_1 - \sum_{j = 1}^{2r - n} \lambda_j - 2\ell,0,\ldots,0\right)\text{ for some }\ell \in \mathbb{N}_0, \\ 0 & \text{otherwise}. \end{cases}\end{align*}$$
Proof. We take
![]() $\mu = (\mu _1,0,\ldots ,0)$
in Lemma 6.12; the case
$\mu = (\mu _1,0,\ldots ,0)$
in Lemma 6.12; the case
![]() $\#\{j : n_j = 1\} = 1$
is then immediate, while if
$\#\{j : n_j = 1\} = 1$
is then immediate, while if
![]() $\#\{j : n_j = 1\} \geq 2$
, we iterate this branching rule in order to find that
$\#\{j : n_j = 1\} \geq 2$
, we iterate this branching rule in order to find that

where we set ![]() . It follows that for fixed
. It follows that for fixed
![]() $\mu = (\mu _1,0,\ldots ,0) \in \Lambda _n$
,
$\mu = (\mu _1,0,\ldots ,0) \in \Lambda _n$
,
![]() $\lambda _1,\ldots ,\lambda _{2r - n} \in \Lambda _1$
, and
$\lambda _1,\ldots ,\lambda _{2r - n} \in \Lambda _1$
, and
![]() $\nu _{2(n - r)} \in \Lambda _{2(n - r)}$
, the multiplicity of
$\nu _{2(n - r)} \in \Lambda _{2(n - r)}$
, the multiplicity of
![]() $\tau _{\nu _{2(n - r)}} \boxtimes \tau _{\lambda _1} \boxtimes \cdots \boxtimes \tau _{\lambda _{2r - n}}$
in
$\tau _{\nu _{2(n - r)}} \boxtimes \tau _{\lambda _1} \boxtimes \cdots \boxtimes \tau _{\lambda _{2r - n}}$
in
![]() $\tau _{\mu }$
is zero unless
$\tau _{\mu }$
is zero unless
![]() $\nu _{2(n - r)}$
is of the form
$\nu _{2(n - r)}$
is of the form
![]() $(\nu _{n',1},0,\ldots ,0)$
for some
$(\nu _{n',1},0,\ldots ,0)$
for some
![]() $\nu _{n',1} \in \mathbb {N}_0$
, in which case it is equal to
$\nu _{n',1} \in \mathbb {N}_0$
, in which case it is equal to
– namely, the number of
![]() $(n' - 1)$
-tuples
$(n' - 1)$
-tuples
![]() $(\nu _{1,1},\ldots ,\nu _{n' - 1,1})$
for which the system of inequalities
$(\nu _{1,1},\ldots ,\nu _{n' - 1,1})$
for which the system of inequalities
 $$\begin{align*}\mu_1 \geq \nu_{1,1} + \lambda_1 \geq \cdots \geq \nu_{n',1} + \sum_{j = 1}^{2r - n} \lambda_j\end{align*}$$
$$\begin{align*}\mu_1 \geq \nu_{1,1} + \lambda_1 \geq \cdots \geq \nu_{n',1} + \sum_{j = 1}^{2r - n} \lambda_j\end{align*}$$
holds with each quantity being of the same parity. This is zero unless
 $$\begin{align*}\mu_1 = \nu_{n',1} + \sum_{j = 1}^{2r - n} \lambda_j + 2\ell\end{align*}$$
$$\begin{align*}\mu_1 = \nu_{n',1} + \sum_{j = 1}^{2r - n} \lambda_j + 2\ell\end{align*}$$
for some
![]() $\ell \in \mathbb {N}_0$
, in which case the multiplicity is precisely the number of ordered
$\ell \in \mathbb {N}_0$
, in which case the multiplicity is precisely the number of ordered
![]() $(n' - 1)$
-tuples taking values between
$(n' - 1)$
-tuples taking values between
![]() $0$
and
$0$
and
![]() $\ell $
, which is
$\ell $
, which is
 $$\begin{align*}\binom{\ell + n' - 2}{n' - 2}.\\[-40pt]\end{align*}$$
$$\begin{align*}\binom{\ell + n' - 2}{n' - 2}.\\[-40pt]\end{align*}$$
We also require a special case of the branching rule from
![]() $\operatorname {\mathrm {O}}(n)$
to
$\operatorname {\mathrm {O}}(n)$
to
![]() $\operatorname {\mathrm {O}}(n - 2) \times \operatorname {\mathrm {O}}(2)$
.
$\operatorname {\mathrm {O}}(n - 2) \times \operatorname {\mathrm {O}}(2)$
.
Lemma 6.15 [Reference ProctorPro94, Proposition 10.3]
For
![]() $n \geq 3$
and
$n \geq 3$
and
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
of highest weight
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
of highest weight
![]() $\mu = (\mu _1,0,\ldots ,0) \in \Lambda _n$
,
$\mu = (\mu _1,0,\ldots ,0) \in \Lambda _n$
,
 $$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{O}}(n - 2) \times \operatorname{\mathrm{O}}(2)} \cong \bigoplus_{\substack{\lambda = (\lambda_1,0) \in \Lambda_2 \\ \lambda_1 \leq \mu_1}} \bigoplus_{\substack{\nu = (\nu_1,0,\ldots,0) \in \Lambda_{n - 2} \\ \nu_1 \leq \mu_1 - \lambda_1 \\ \nu_1 \equiv \mu_1 - \lambda_1 \ \pmod{2}}} \tau_{\nu} \boxtimes \tau_{\lambda}.\end{align*}$$
$$\begin{align*}\tau_{\mu}|_{\operatorname{\mathrm{O}}(n - 2) \times \operatorname{\mathrm{O}}(2)} \cong \bigoplus_{\substack{\lambda = (\lambda_1,0) \in \Lambda_2 \\ \lambda_1 \leq \mu_1}} \bigoplus_{\substack{\nu = (\nu_1,0,\ldots,0) \in \Lambda_{n - 2} \\ \nu_1 \leq \mu_1 - \lambda_1 \\ \nu_1 \equiv \mu_1 - \lambda_1 \ \pmod{2}}} \tau_{\nu} \boxtimes \tau_{\lambda}.\end{align*}$$
We again iterate this branching rule.
Lemma 6.16. For
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(2(n - r))}$
of highest weight
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(2(n - r))}$
of highest weight
![]() $\mu = (\mu _1,0,\ldots ,0) \in \Lambda _{2(n - r)}$
and for
$\mu = (\mu _1,0,\ldots ,0) \in \Lambda _{2(n - r)}$
and for
![]() $(\lambda _{j,1},\lambda _{j,2}) \in \Lambda _2$
with
$(\lambda _{j,1},\lambda _{j,2}) \in \Lambda _2$
with
![]() $j \in \{1,\ldots ,n - r\}$
,
$j \in \{1,\ldots ,n - r\}$
,

Proof. The result follows from Schur’s lemma if
![]() $\#\{j : n_j = 2\} = 1$
. If
$\#\{j : n_j = 2\} = 1$
. If
![]() $\#\{j : n_j = 2\} \geq 2$
, iterating Lemma 6.15 yields
$\#\{j : n_j = 2\} \geq 2$
, iterating Lemma 6.15 yields

where we again set ![]() . So the multiplicity of
. So the multiplicity of
![]() $\tau _{(\lambda _{1,1},\lambda _{1,2})} \boxtimes \cdots \boxtimes \tau _{(\lambda _{n - r,1},\lambda _{n - r,2})}$
in
$\tau _{(\lambda _{1,1},\lambda _{1,2})} \boxtimes \cdots \boxtimes \tau _{(\lambda _{n - r,1},\lambda _{n - r,2})}$
in
![]() $\tau _{\mu }$
is equal to the number of
$\tau _{\mu }$
is equal to the number of
![]() $(n - r - 1)$
-tuples
$(n - r - 1)$
-tuples
![]() $(\nu _{1,1}, \ldots , \nu _{n - r - 1})$
for which the system of inequalities
$(\nu _{1,1}, \ldots , \nu _{n - r - 1})$
for which the system of inequalities
 $$\begin{align*}\mu_1 \geq \nu_{1,1} + \lambda_{1,1} \geq \nu_{2,1} + \lambda_{1,1} + \lambda_{2,1} \geq \cdots \geq \nu_{n - r - 1,1} + \sum_{j = 1}^{n - r - 1} \lambda_{j,1} \geq \sum_{j = 1}^{n - r} \lambda_{j,1}\end{align*}$$
$$\begin{align*}\mu_1 \geq \nu_{1,1} + \lambda_{1,1} \geq \nu_{2,1} + \lambda_{1,1} + \lambda_{2,1} \geq \cdots \geq \nu_{n - r - 1,1} + \sum_{j = 1}^{n - r - 1} \lambda_{j,1} \geq \sum_{j = 1}^{n - r} \lambda_{j,1}\end{align*}$$
holds with each quantity being of the same parity. This is zero unless
 $$\begin{align*}\mu_1 = \sum_{j = 1}^{n - r} \lambda_{j,1} + 2\ell\end{align*}$$
$$\begin{align*}\mu_1 = \sum_{j = 1}^{n - r} \lambda_{j,1} + 2\ell\end{align*}$$
for some
![]() $\ell \in \mathbb {N}_0$
, in which case the multiplicity is precisely the number of ordered
$\ell \in \mathbb {N}_0$
, in which case the multiplicity is precisely the number of ordered
![]() $(n - r - 2)$
-tuples taking values between
$(n - r - 2)$
-tuples taking values between
![]() $0$
and
$0$
and
![]() $\ell $
, which is
$\ell $
, which is
 $$\begin{align*}\binom{\ell + n - r - 2}{n - r - 2}.\\[-42pt]\end{align*}$$
$$\begin{align*}\binom{\ell + n - r - 2}{n - r - 2}.\\[-42pt]\end{align*}$$
Shortly, we shall require the following combinatorial identity involving binomial coefficients.
Lemma 6.17. For
![]() $k,m,n \in \mathbb {N}_0$
, we have that
$k,m,n \in \mathbb {N}_0$
, we have that
 $$\begin{align*}\sum_{j = 0}^{k} \binom{j + m}{m} \binom{k - j + n}{n} = \binom{k + m + n + 1}{m + n + 1}.\end{align*}$$
$$\begin{align*}\sum_{j = 0}^{k} \binom{j + m}{m} \binom{k - j + n}{n} = \binom{k + m + n + 1}{m + n + 1}.\end{align*}$$
Proof. Such an identity begs for a proof via a generating series:
 $$ \begin{align*} \sum_{k = 0}^{\infty} \binom{k + m + n + 1}{m + n + 1} x^k & = \frac{1}{(1 - x)^{m + n + 2}} \\ & = \frac{1}{(1 - x)^{m + 1}} \frac{1}{(1 - x)^{n + 1}} \\ & = \sum_{k_1 = 0}^{\infty} \binom{k_1 + m}{m} x^{k_1} \sum_{k_2 = 0}^{\infty} \binom{k_2 + n}{n} x^{k_2} \\ & = \sum_{k = 0}^{\infty} \sum_{j = 0}^{k} \binom{j + m}{m} \binom{k - j + n}{n} x^k.\\[-42pt] \end{align*} $$
$$ \begin{align*} \sum_{k = 0}^{\infty} \binom{k + m + n + 1}{m + n + 1} x^k & = \frac{1}{(1 - x)^{m + n + 2}} \\ & = \frac{1}{(1 - x)^{m + 1}} \frac{1}{(1 - x)^{n + 1}} \\ & = \sum_{k_1 = 0}^{\infty} \binom{k_1 + m}{m} x^{k_1} \sum_{k_2 = 0}^{\infty} \binom{k_2 + n}{n} x^{k_2} \\ & = \sum_{k = 0}^{\infty} \sum_{j = 0}^{k} \binom{j + m}{m} \binom{k - j + n}{n} x^k.\\[-42pt] \end{align*} $$
With these results in hand, we can now explicitly determine (6.11).
Lemma 6.18. Suppose that the restriction of
![]() $\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
to
$\tau _{\mu } \in \widehat {\operatorname {\mathrm {O}}(n)}$
to
![]() $\operatorname {\mathrm {O}}(n - 1)$
contains the trivial representation. Then the highest weight of
$\operatorname {\mathrm {O}}(n - 1)$
contains the trivial representation. Then the highest weight of
![]() $\tau _{\mu }$
is of the form
$\tau _{\mu }$
is of the form
![]() $\mu = (\mu _1,0,\ldots ,0)$
, the trivial representation occurs with multiplicity one, and
$\mu = (\mu _1,0,\ldots ,0)$
, the trivial representation occurs with multiplicity one, and

Proof. The first claim two claims are Corollary 6.13. To prove the identity (6.19), we first note that if
![]() $\#\{j : n_j = 2\} = 0$
, Lemma 6.14 implies the result upon replacing
$\#\{j : n_j = 2\} = 0$
, Lemma 6.14 implies the result upon replacing
![]() $2r - n$
with
$2r - n$
with
![]() $2r - n - 1$
. If
$2r - n - 1$
. If
![]() $\#\{j : n_j = 2\} \geq 1$
, we combine Lemmata 6.14 and 6.16 to see that the inner sum over
$\#\{j : n_j = 2\} \geq 1$
, we combine Lemmata 6.14 and 6.16 to see that the inner sum over
![]() $\nu _{2(n - r)} \in \Lambda _{2(n - r)}$
in the left-hand side of (6.19) is equal to zero unless
$\nu _{2(n - r)} \in \Lambda _{2(n - r)}$
in the left-hand side of (6.19) is equal to zero unless
 $$\begin{align*}\mu_1 = \sum_{\substack{j = 1 \\ n_j = 1}}^{r} \kappa_j + \sum_{\substack{j = 1 \\ n_j = 2}}^{r} \ell_j + 2\ell\end{align*}$$
$$\begin{align*}\mu_1 = \sum_{\substack{j = 1 \\ n_j = 1}}^{r} \kappa_j + \sum_{\substack{j = 1 \\ n_j = 2}}^{r} \ell_j + 2\ell\end{align*}$$
for some
![]() $\ell \in \mathbb {N}_0$
, so that
$\ell \in \mathbb {N}_0$
, so that
 $$\begin{align*}\nu_{2(n - r)} = \left(\sum_{\substack{j = 1 \\ n_j = 2}}^{r} \ell_j + 2(\ell - \ell'),0,\ldots,0\right)\end{align*}$$
$$\begin{align*}\nu_{2(n - r)} = \left(\sum_{\substack{j = 1 \\ n_j = 2}}^{r} \ell_j + 2(\ell - \ell'),0,\ldots,0\right)\end{align*}$$
for some
![]() $\ell ' \in \{0, \ldots , \ell \}$
, in which case this inner sum is equal to
$\ell ' \in \{0, \ldots , \ell \}$
, in which case this inner sum is equal to
 $$\begin{align*}\sum_{\ell' = 0}^{\ell} \binom{\ell' + n' - 2}{n' - 2} \binom{\ell - \ell' + n - r - 2}{n - r - 2}.\end{align*}$$
$$\begin{align*}\sum_{\ell' = 0}^{\ell} \binom{\ell' + n' - 2}{n' - 2} \binom{\ell - \ell' + n - r - 2}{n - r - 2}.\end{align*}$$
Coupled with Corollary 6.10, we find that the left-hand side of (6.19) is equal to zero unless
 $$\begin{align*}\mu_1 = \sum_{j = 1}^{r} \kappa_j + 2\ell\end{align*}$$
$$\begin{align*}\mu_1 = \sum_{j = 1}^{r} \kappa_j + 2\ell\end{align*}$$
for some
![]() $\ell \in \mathbb {N}_0$
, in which case it is equal to
$\ell \in \mathbb {N}_0$
, in which case it is equal to
 $$\begin{align*}\sum_{i = 1}^{n - r} \sum_{\alpha_i = 0}^{\infty} \sum_{\ell' = 0}^{\ell - \sum_{i = 1}^{n - r} \alpha_i} \binom{\ell' + 2r - n - 1}{2r - n - 1} \binom{\ell - \ell' - \sum_{i = 1}^{n - r} \alpha_i + n - r - 2}{n - r - 2}\end{align*}$$
$$\begin{align*}\sum_{i = 1}^{n - r} \sum_{\alpha_i = 0}^{\infty} \sum_{\ell' = 0}^{\ell - \sum_{i = 1}^{n - r} \alpha_i} \binom{\ell' + 2r - n - 1}{2r - n - 1} \binom{\ell - \ell' - \sum_{i = 1}^{n - r} \alpha_i + n - r - 2}{n - r - 2}\end{align*}$$
upon defining
![]() $\alpha _i$
such that there is an equality of the sets
$\alpha _i$
such that there is an equality of the sets
![]() $\{\alpha _i\}$
and
$\{\alpha _i\}$
and
![]() $\{(\ell _j - \kappa _j)/2 : n_j = 2\}$
. Interchanging the order of summation, this becomes
$\{(\ell _j - \kappa _j)/2 : n_j = 2\}$
. Interchanging the order of summation, this becomes
 $$ \begin{align} \sum_{\ell' = 0}^{\ell} \binom{\ell' + 2r - n - 1}{2r - n - 1} \sum_{i = 1}^{n - r} \sum_{\alpha_i = 0}^{\ell - \ell' - \sum_{m = 1}^{i - 1} \alpha_m} \binom{\ell - \ell' - \sum_{i = 1}^{n - r} \alpha_i + n - r - 2}{n - r - 2}. \end{align} $$
$$ \begin{align} \sum_{\ell' = 0}^{\ell} \binom{\ell' + 2r - n - 1}{2r - n - 1} \sum_{i = 1}^{n - r} \sum_{\alpha_i = 0}^{\ell - \ell' - \sum_{m = 1}^{i - 1} \alpha_m} \binom{\ell - \ell' - \sum_{i = 1}^{n - r} \alpha_i + n - r - 2}{n - r - 2}. \end{align} $$
Using the fact that
![]() $\binom {n - 1}{k - 1} = \binom {n}{k} - \binom {n - 1}{k}$
, the sum over
$\binom {n - 1}{k - 1} = \binom {n}{k} - \binom {n - 1}{k}$
, the sum over
![]() $\alpha _{n - r}$
telescopes to
$\alpha _{n - r}$
telescopes to
 $$\begin{align*}\binom{\ell - \ell' - \sum_{i = 1}^{n - r - 1} \alpha_i + n - r - 1}{n - r - 1},\end{align*}$$
$$\begin{align*}\binom{\ell - \ell' - \sum_{i = 1}^{n - r - 1} \alpha_i + n - r - 1}{n - r - 1},\end{align*}$$
and so upon iterating this process, we find that the inner double sum in (6.20) is equal to
 $$\begin{align*}\binom{\ell - \ell' + 2n - r - 2}{2n - r - 2},\end{align*}$$
$$\begin{align*}\binom{\ell - \ell' + 2n - r - 2}{2n - r - 2},\end{align*}$$
at which point Lemma 6.17 completes the proof.
Proofs of Theorems 4.7, 4.12, 4.14, 4.15 and 4.16 for
 $F = \mathbb {R}$
$F = \mathbb {R}$
Lemmata 6.9 and 6.18 combine to complete the proofs of Theorems 4.7 and 4.12 for
![]() $F = \mathbb {R}$
: for
$F = \mathbb {R}$
: for
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
when
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
when
![]() $n_j = 1$
and
$n_j = 1$
and
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
when
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
when
![]() $n_j = 2$
, the newform K-type
$n_j = 2$
, the newform K-type
![]() $\tau ^{\circ } = \tau _{\mu ^{\circ }}$
has highest weight
$\tau ^{\circ } = \tau _{\mu ^{\circ }}$
has highest weight
 $$\begin{align*}\mu^{\circ} = \left(\sum_{j = 1}^{r} \kappa_j,0,\ldots,0\right),\end{align*}$$
$$\begin{align*}\mu^{\circ} = \left(\sum_{j = 1}^{r} \kappa_j,0,\ldots,0\right),\end{align*}$$
so that, recalling the definition (4.4) of
![]() $\deg \tau ^{\circ }$
,
$\deg \tau ^{\circ }$
,

Theorem 4.14 then holds for
![]() $F = \mathbb {R}$
via the fact that
$F = \mathbb {R}$
via the fact that
 $$\begin{align*}\varepsilon(s,\pi,\psi) = \prod_{j = 1}^{r} \varepsilon(s,\pi_j,\psi) = \prod_{j = 1}^{r} i^{-\kappa_j} = i^{-\kappa_1 - \cdots - \kappa_r} = i^{-c(\pi)},\end{align*}$$
$$\begin{align*}\varepsilon(s,\pi,\psi) = \prod_{j = 1}^{r} \varepsilon(s,\pi_j,\psi) = \prod_{j = 1}^{r} i^{-\kappa_j} = i^{-\kappa_1 - \cdots - \kappa_r} = i^{-c(\pi)},\end{align*}$$
while the cases
![]() $n = \#\{j : n_j = 1\} = 1$
, so that
$n = \#\{j : n_j = 1\} = 1$
, so that
![]() $\pi = \chi ^{\kappa } |\cdot |^t$
, and
$\pi = \chi ^{\kappa } |\cdot |^t$
, and
![]() $n = 2\#\{j : n_j = 2\} = 2$
, so that
$n = 2\#\{j : n_j = 2\} = 2$
, so that
![]() $\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, imply Theorem 4.15 for
$\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, imply Theorem 4.15 for
![]() $F = \mathbb {R}$
. Finally, for an induced representation of Whittaker type of
$F = \mathbb {R}$
. Finally, for an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {C})$
of the form
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$
of the form
![]() $\pi = \chi ^{\kappa _1} |\cdot |_{\mathbb {C}}^{t_1} \boxplus \cdots \boxplus \chi ^{\kappa _n} |\cdot |_{\mathbb {C}}^{t_n}$
, the induced representation
$\pi = \chi ^{\kappa _1} |\cdot |_{\mathbb {C}}^{t_1} \boxplus \cdots \boxplus \chi ^{\kappa _n} |\cdot |_{\mathbb {C}}^{t_n}$
, the induced representation
![]() $\mathcal {AI}_{\mathbb {C}/\mathbb {R}} \pi $
is isomorphic to the isobaric sum
$\mathcal {AI}_{\mathbb {C}/\mathbb {R}} \pi $
is isomorphic to the isobaric sum

and
 $$\begin{align*}\operatorname{\mathrm{Ind}}_{\operatorname{\mathrm{GL}}_1(\mathbb{C})}^{\operatorname{\mathrm{GL}}_2(\mathbb{R})} \chi^{\kappa} |\cdot|_{\mathbb{C}}^t \cong \begin{cases} |\cdot|_{\mathbb{R}}^t \boxplus \chi |\cdot|_{\mathbb{R}}^t & \text{if }\kappa = 0, \\ D_{\|\kappa\| + 1} \otimes \left|\det\right|{}_{\mathbb{R}}^t & \text{if }\kappa \neq 0, \end{cases}\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Ind}}_{\operatorname{\mathrm{GL}}_1(\mathbb{C})}^{\operatorname{\mathrm{GL}}_2(\mathbb{R})} \chi^{\kappa} |\cdot|_{\mathbb{C}}^t \cong \begin{cases} |\cdot|_{\mathbb{R}}^t \boxplus \chi |\cdot|_{\mathbb{R}}^t & \text{if }\kappa = 0, \\ D_{\|\kappa\| + 1} \otimes \left|\det\right|{}_{\mathbb{R}}^t & \text{if }\kappa \neq 0, \end{cases}\end{align*}$$
so that
 $$\begin{align*}c\left(\mathcal{AI}_{\mathbb{C}/\mathbb{R}} \pi\right) = \sum_{j = 1}^{n} \left(\|\kappa_j\| + 1\right) = c(\pi) + n,\end{align*}$$
$$\begin{align*}c\left(\mathcal{AI}_{\mathbb{C}/\mathbb{R}} \pi\right) = \sum_{j = 1}^{n} \left(\|\kappa_j\| + 1\right) = c(\pi) + n,\end{align*}$$
thereby proving Theorem 4.16.
Remark 6.21. Just as was observed in Remark 6.7 for
![]() $F = \mathbb {C}$
, the Howe degree of a K-type of
$F = \mathbb {C}$
, the Howe degree of a K-type of
![]() $\pi $
is always congruent to
$\pi $
is always congruent to
![]() $\deg \tau ^{\circ }$
modulo
$\deg \tau ^{\circ }$
modulo
![]() $2$
.
$2$
.
Remark 6.22. From [Reference LinLin18, Proposition 4.3], the minimal K-type of
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
has highest weight
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
has highest weight
 $$\begin{align*}\mu = \left(\kappa_{\sigma(1)},\ldots,\kappa_{\sigma(r)},\underbrace{0,\ldots,0}_{n - r \text{ times}}\right),\end{align*}$$
$$\begin{align*}\mu = \left(\kappa_{\sigma(1)},\ldots,\kappa_{\sigma(r)},\underbrace{0,\ldots,0}_{n - r \text{ times}}\right),\end{align*}$$
where
![]() $\sigma $
is a permutation for which
$\sigma $
is a permutation for which
![]() $\kappa _{\sigma (1)} \geq \cdots \geq \kappa _{\sigma (r)}$
. This minimal K-type is
$\kappa _{\sigma (1)} \geq \cdots \geq \kappa _{\sigma (r)}$
. This minimal K-type is
![]() $\tau ^{\circ }$
if and only if
$\tau ^{\circ }$
if and only if
![]() $r = n - 1$
and
$r = n - 1$
and
![]() $\kappa _j = 0$
whenever
$\kappa _j = 0$
whenever
![]() $n_j = 1$
or
$n_j = 1$
or
![]() $r = n$
and
$r = n$
and
![]() $\kappa _j \neq 0$
for at most one j.
$\kappa _j \neq 0$
for at most one j.
Once again, the Howe degree of the minimal K-type is
 $$\begin{align*}\sum_{j = 1}^{n} \kappa_{\sigma(j)} = \deg \tau^{\circ} = c(\pi).\end{align*}$$
$$\begin{align*}\sum_{j = 1}^{n} \kappa_{\sigma(j)} = \deg \tau^{\circ} = c(\pi).\end{align*}$$
7. Homogeneous Harmonic Polynomials
Having identified the newform K-type, we now study a particular model, a space of homogeneous harmonic polynomials, of this representation of K. This allows us to explicitly describe the matrix coefficients of this representation, which are used to construct the explicit Schwartz functions
![]() $\Phi ^{\circ } \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
and
$\Phi ^{\circ } \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
and
![]() $\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
given in (4.19) and (4.24).
$\Phi \in \mathscr {S}(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
given in (4.19) and (4.24).
7.1. Homogeneous harmonic polynomials and representations of
 $\operatorname {\mathrm {U}}(n)$
$\operatorname {\mathrm {U}}(n)$
For nonnegative integers
![]() $p,q$
, let
$p,q$
, let
![]() $\mathcal {H}_{p,q}(\mathbb {C}^n)$
denote the vector space consisting of harmonic polynomials that are homogeneous of bidegree
$\mathcal {H}_{p,q}(\mathbb {C}^n)$
denote the vector space consisting of harmonic polynomials that are homogeneous of bidegree
![]() $(p,q)$
– namely, the set of polynomials
$(p,q)$
– namely, the set of polynomials
![]() $P(z) = P(z_1,\ldots ,z_n,\overline {z_1},\ldots ,\overline {z_n})$
in
$P(z) = P(z_1,\ldots ,z_n,\overline {z_1},\ldots ,\overline {z_n})$
in
![]() $z \in \operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {C}) = \mathbb {C}^n$
that are annihilated by the Laplacian
$z \in \operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {C}) = \mathbb {C}^n$
that are annihilated by the Laplacian
 $$\begin{align*}\Delta = 4 \sum_{j = 1}^{n} \frac{\partial^2}{\partial z_j \partial \overline{z_j}}\end{align*}$$
$$\begin{align*}\Delta = 4 \sum_{j = 1}^{n} \frac{\partial^2}{\partial z_j \partial \overline{z_j}}\end{align*}$$
and satisfy
for all
![]() $\lambda \in \mathbb {C}$
. The dimension of
$\lambda \in \mathbb {C}$
. The dimension of
![]() $\mathcal {H}_{p,q}(\mathbb {C}^n)$
is
$\mathcal {H}_{p,q}(\mathbb {C}^n)$
is
![]() $1$
for
$1$
for
![]() $n = 1$
and
$n = 1$
and
 $$\begin{align*}\frac{(p + q + n - 1) (p + n - 2)! (q + n - 2)!}{p! q! (n - 2)! (n - 1)!} = \frac{p + q + n - 1}{n - 1} \binom{p + n - 2}{n - 2} \binom{q + n - 2}{n - 2}\end{align*}$$
$$\begin{align*}\frac{(p + q + n - 1) (p + n - 2)! (q + n - 2)!}{p! q! (n - 2)! (n - 1)!} = \frac{p + q + n - 1}{n - 1} \binom{p + n - 2}{n - 2} \binom{q + n - 2}{n - 2}\end{align*}$$
for
![]() $n \geq 2$
.
$n \geq 2$
.
Let
![]() $\tau $
be an irreducible representation of
$\tau $
be an irreducible representation of
![]() $\operatorname {\mathrm {U}}(n)$
of highest weight
$\operatorname {\mathrm {U}}(n)$
of highest weight
![]() $\mu = (p,0,\ldots ,0,-q)$
; note that for
$\mu = (p,0,\ldots ,0,-q)$
; note that for
![]() $n = 1$
, either p or q must be zero. Then
$n = 1$
, either p or q must be zero. Then
![]() $\mathcal {H}_{p,q}(\mathbb {C}^n)$
is a model of
$\mathcal {H}_{p,q}(\mathbb {C}^n)$
is a model of
![]() $\tau $
, where the group
$\tau $
, where the group
![]() $\operatorname {\mathrm {U}}(n) \ni k$
acts on
$\operatorname {\mathrm {U}}(n) \ni k$
acts on
![]() $\mathcal {H}_{p,q}(\mathbb {C}^n) \ni P$
via right translation – namely,
$\mathcal {H}_{p,q}(\mathbb {C}^n) \ni P$
via right translation – namely,
that is, ![]() . We define a
. We define a
![]() $\operatorname {\mathrm {U}}(n)$
-invariant inner product on
$\operatorname {\mathrm {U}}(n)$
-invariant inner product on
![]() $\mathcal {H}_{p,q}(\mathbb {C}^n) \ni P,Q$
by
$\mathcal {H}_{p,q}(\mathbb {C}^n) \ni P,Q$
by

From the branching rule in Lemma 6.3, there is a one-dimensional subspace of
![]() $\mathcal {H}_{p,q}(\mathbb {C}^n)$
that is invariant under the action of
$\mathcal {H}_{p,q}(\mathbb {C}^n)$
that is invariant under the action of
![]() $\operatorname {\mathrm {U}}(n - 1) \ni k'$
embedded in
$\operatorname {\mathrm {U}}(n - 1) \ni k'$
embedded in
![]() $\operatorname {\mathrm {U}}(n)$
via
$\operatorname {\mathrm {U}}(n)$
via ![]() , which we can describe explicitly.
, which we can describe explicitly.
Lemma 7.1 [Reference RudinRud08, Proposition 12.2.6]
There exists a unique homogeneous harmonic polynomial
![]() $P^{\circ } \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
satisfying
$P^{\circ } \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
satisfying
![]() $P^{\circ }(e_n) = 1$
and
$P^{\circ }(e_n) = 1$
and ![]() for all
for all
![]() $k' \in \operatorname {\mathrm {U}}(n - 1)$
– namely,
$k' \in \operatorname {\mathrm {U}}(n - 1)$
– namely,

In particular, for
![]() $n = 1$
, so that either p or q is equal to
$n = 1$
, so that either p or q is equal to
![]() $0$
,
$0$
,
 $$ \begin{align} P^{\circ}(z_1) = \begin{cases} z_1^p & \text{for }p \in \mathbb{N}_0\text{ and }q = 0, \\ \overline{z_1}^q & \text{for }p = 0\text{ and }q \in \mathbb{N}_0. \end{cases} \end{align} $$
$$ \begin{align} P^{\circ}(z_1) = \begin{cases} z_1^p & \text{for }p \in \mathbb{N}_0\text{ and }q = 0, \\ \overline{z_1}^q & \text{for }p = 0\text{ and }q \in \mathbb{N}_0. \end{cases} \end{align} $$
Remark 7.4. When restricted to the unit sphere in
![]() $\mathbb {C}^n$
, this polynomial is sometimes referred to as the zonal spherical harmonic of bidegree
$\mathbb {C}^n$
, this polynomial is sometimes referred to as the zonal spherical harmonic of bidegree
![]() $(p,q)$
in dimension n. When
$(p,q)$
in dimension n. When
![]() $z_1 \overline {z_1} + \cdots + z_{n - 1} \overline {z_{n - 1}} = 1 - z_n \overline {z_n}$
,
$z_1 \overline {z_1} + \cdots + z_{n - 1} \overline {z_{n - 1}} = 1 - z_n \overline {z_n}$
,
![]() $P^{\circ }(z_1,\ldots ,z_n,\overline {z_1},\ldots ,\overline {z_n})$
is a polynomial in
$P^{\circ }(z_1,\ldots ,z_n,\overline {z_1},\ldots ,\overline {z_n})$
is a polynomial in
![]() $z_n,\overline {z_n}$
and can be expressed in terms of the generalised Zernike polynomial
$z_n,\overline {z_n}$
and can be expressed in terms of the generalised Zernike polynomial
![]() $P_{q,p}^{n - 2}$
(also called a generalised disc polynomial) or the Jacobi polynomial
$P_{q,p}^{n - 2}$
(also called a generalised disc polynomial) or the Jacobi polynomial
![]() $P_q^{(n - 2,p - q)}$
.
$P_q^{(n - 2,p - q)}$
.
We make crucial use of the fact that for all
![]() $P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
and
$P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
and
![]() $k \in \operatorname {\mathrm {U}}(n)$
,
$k \in \operatorname {\mathrm {U}}(n)$
,
![]() $P(e_n k)$
is equal to a matrix coefficient of
$P(e_n k)$
is equal to a matrix coefficient of
![]() $\tau $
. This can be thought of as an explicit form of Schur orthogonality.
$\tau $
. This can be thought of as an explicit form of Schur orthogonality.
Lemma 7.5 [Reference RudinRud08, Theorem 12.2.5]
The reproducing kernel for
![]() $\mathcal {H}_{p,q}(\mathbb {C}^n)$
is
$\mathcal {H}_{p,q}(\mathbb {C}^n)$
is
![]() $(\dim \tau ) P^{\circ }$
, so that for all
$(\dim \tau ) P^{\circ }$
, so that for all
![]() $P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
and
$P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
and
![]() $k \in \operatorname {\mathrm {U}}(n)$
,
$k \in \operatorname {\mathrm {U}}(n)$
,
In particular,
![]() $\langle P^{\circ }, P^{\circ } \rangle = (\dim \tau )^{-1}$
. Moreover, for all
$\langle P^{\circ }, P^{\circ } \rangle = (\dim \tau )^{-1}$
. Moreover, for all
![]() $P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
and
$P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
and
![]() $z \in \mathbb {C}^n$
,
$z \in \mathbb {C}^n$
,
 $$\begin{align*}P(z) = \dim \tau \int_{\operatorname{\mathrm{U}}(n)} P(e_n k^{-1}) P^{\circ}(zk) \, dk.\end{align*}$$
$$\begin{align*}P(z) = \dim \tau \int_{\operatorname{\mathrm{U}}(n)} P(e_n k^{-1}) P^{\circ}(zk) \, dk.\end{align*}$$
Finally, we also require the following identity, which states that homogeneous harmonic polynomials
![]() $P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
are eigenfunctions of the Fourier transform.
$P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
are eigenfunctions of the Fourier transform.
Lemma 7.6 (Hecke’s Identity; cf. [Reference Stein and WeissSW71, Chapter IV, Theorem 3.4])
For any homogeneous harmonic polynomial
![]() $P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
and
$P \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
and
![]() $w \in \mathbb {C}^n$
, we have that
$w \in \mathbb {C}^n$
, we have that
Proof. First, we prove this for
![]() $P(z) = z_1^p \overline {z_n}^q$
, the highest weight vector of
$P(z) = z_1^p \overline {z_n}^q$
, the highest weight vector of
![]() $\tau $
. In this case,
$\tau $
. In this case,

For any other
![]() $Q \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
, we may write
$Q \in \mathcal {H}_{p,q}(\mathbb {C}^n)$
, we may write
![]() $Q(z)$
as a linear combination of elements of the form
$Q(z)$
as a linear combination of elements of the form
![]() $P(zk)$
with
$P(zk)$
with
![]() $k \in \operatorname {\mathrm {U}}(n)$
, and so using the above calculation with w replaced by
$k \in \operatorname {\mathrm {U}}(n)$
, and so using the above calculation with w replaced by
![]() $wk$
and making the change of variables
$wk$
and making the change of variables
![]() $z \mapsto zk$
yields the result upon recalling that
$z \mapsto zk$
yields the result upon recalling that ![]() .
.
7.2. Homogeneous harmonic polynomials and representations of
 $\operatorname {\mathrm {O}}(n)$
$\operatorname {\mathrm {O}}(n)$
Similarly, for a nonnegative integer p, let
![]() $\mathcal {H}_p(\mathbb {R}^n)$
denote the vector space consisting of homogeneous harmonic polynomials of degree p – namely, the set of polynomials
$\mathcal {H}_p(\mathbb {R}^n)$
denote the vector space consisting of homogeneous harmonic polynomials of degree p – namely, the set of polynomials
![]() $P(x) = P(x_1,\ldots ,x_n)$
in
$P(x) = P(x_1,\ldots ,x_n)$
in
![]() $x \in \operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {R}) = \mathbb {R}^n$
that are annihilated by the Laplacian
$x \in \operatorname {\mathrm {Mat}}_{1 \times n}(\mathbb {R}) = \mathbb {R}^n$
that are annihilated by the Laplacian
 $$\begin{align*}\Delta = \sum_{j = 1}^{n} \frac{\partial^2}{\partial x_j^2}\end{align*}$$
$$\begin{align*}\Delta = \sum_{j = 1}^{n} \frac{\partial^2}{\partial x_j^2}\end{align*}$$
and satisfy
![]() $P(\lambda x) = \lambda ^p P(x)$
for all
$P(\lambda x) = \lambda ^p P(x)$
for all
![]() $\lambda \in \mathbb {R}$
. This space has dimension
$\lambda \in \mathbb {R}$
. This space has dimension
![]() $1$
for
$1$
for
![]() $n = 1$
and
$n = 1$
and
![]() $p \in \{0,1\}$
and has dimension
$p \in \{0,1\}$
and has dimension
 $$\begin{align*}\binom{p + n - 2}{n - 2} + \binom{p + n - 3}{n - 3} = \frac{(2p + n - 2) (p + n - 3)!}{p!(n - 2)!} = \frac{2p + n - 2}{p + n - 2} \binom{p + n - 2}{n - 2}\end{align*}$$
$$\begin{align*}\binom{p + n - 2}{n - 2} + \binom{p + n - 3}{n - 3} = \frac{(2p + n - 2) (p + n - 3)!}{p!(n - 2)!} = \frac{2p + n - 2}{p + n - 2} \binom{p + n - 2}{n - 2}\end{align*}$$
for
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $p \in \mathbb {N}_0$
.
$p \in \mathbb {N}_0$
.
Let
![]() $\tau $
be an irreducible representation of
$\tau $
be an irreducible representation of
![]() $\operatorname {\mathrm {O}}(n)$
of highest weight
$\operatorname {\mathrm {O}}(n)$
of highest weight
![]() $\mu = (p,0,\ldots ,0)$
, where p is a nonnegative integer; note that
$\mu = (p,0,\ldots ,0)$
, where p is a nonnegative integer; note that
![]() $p \in \{0,1\}$
for
$p \in \{0,1\}$
for
![]() $n = 1$
. Then
$n = 1$
. Then
![]() $\mathcal {H}_p(\mathbb {R}^n)$
is a model of
$\mathcal {H}_p(\mathbb {R}^n)$
is a model of
![]() $\tau $
, where the group
$\tau $
, where the group
![]() $\operatorname {\mathrm {O}}(n) \ni k$
acts on the space
$\operatorname {\mathrm {O}}(n) \ni k$
acts on the space
![]() $\mathcal {H}_p(\mathbb {R}^n) \ni P$
via right translation – namely,
$\mathcal {H}_p(\mathbb {R}^n) \ni P$
via right translation – namely, ![]() . We define an
. We define an
![]() $\operatorname {\mathrm {O}}(n)$
-invariant inner product on
$\operatorname {\mathrm {O}}(n)$
-invariant inner product on
![]() $\mathcal {H}_p(\mathbb {R}^n) \ni P,Q$
by
$\mathcal {H}_p(\mathbb {R}^n) \ni P,Q$
by

We record the following results, all of which are analogous to those for
![]() $\mathcal {H}_{p,q}(\mathbb {C}^n)$
in Section 7.1.
$\mathcal {H}_{p,q}(\mathbb {C}^n)$
in Section 7.1.
Lemma 7.7 [Reference Atkinson and HanAH12, Section 2.1.2]
There exists a unique homogeneous harmonic polynomial
![]() $P^{\circ } \in \mathcal {H}_p(\mathbb {R}^n)$
satisfying
$P^{\circ } \in \mathcal {H}_p(\mathbb {R}^n)$
satisfying
![]() $P^{\circ }(e_n) = 1$
and
$P^{\circ }(e_n) = 1$
and ![]() for all
for all
![]() $k' \in \operatorname {\mathrm {O}}(n - 1)$
– namely,
$k' \in \operatorname {\mathrm {O}}(n - 1)$
– namely,

In particular, for
![]() $n = 1$
, so that
$n = 1$
, so that
![]() $p \in \{0,1\}$
,
$p \in \{0,1\}$
,
while for
![]() $n = 2$
, so that
$n = 2$
, so that
![]() $p \in \mathbb {N}_0$
,
$p \in \mathbb {N}_0$
,
 $$ \begin{align} P^{\circ}(x_1,x_2) = \frac{1}{2} \left(x_2 - i x_1\right)^p + \frac{1}{2} \left(x_2 + i x_1\right)^p = \sum_{\substack{\nu = 0 \\ \nu \equiv 0 \ \pmod{2}}}^{p} \binom{p}{\nu} (ix_1)^{\nu} x_2^{p - \nu}. \end{align} $$
$$ \begin{align} P^{\circ}(x_1,x_2) = \frac{1}{2} \left(x_2 - i x_1\right)^p + \frac{1}{2} \left(x_2 + i x_1\right)^p = \sum_{\substack{\nu = 0 \\ \nu \equiv 0 \ \pmod{2}}}^{p} \binom{p}{\nu} (ix_1)^{\nu} x_2^{p - \nu}. \end{align} $$
Remark 7.11. Atkinson and Han name
![]() $P^{\circ }$
the Legendre polynomial of degree p in n dimensions [Reference Atkinson and HanAH12, Section 2.1.2]; when restricted to the unit sphere in
$P^{\circ }$
the Legendre polynomial of degree p in n dimensions [Reference Atkinson and HanAH12, Section 2.1.2]; when restricted to the unit sphere in
![]() $\mathbb {R}^n$
, this polynomial is also referred to as the zonal spherical harmonic. When
$\mathbb {R}^n$
, this polynomial is also referred to as the zonal spherical harmonic. When
![]() $x_1^2 + \cdots + x_{n - 1}^2 = 1 - x_n^2$
,
$x_1^2 + \cdots + x_{n - 1}^2 = 1 - x_n^2$
,
![]() $P^{\circ }(x_1,\ldots ,x_n)$
is a polynomial in
$P^{\circ }(x_1,\ldots ,x_n)$
is a polynomial in
![]() $x_n$
and can be expressed in terms of the Gegenbauer polynomial
$x_n$
and can be expressed in terms of the Gegenbauer polynomial
![]() $C_p^{\frac {n - 2}{2}}$
(also called an ultraspherical polynomial) or the Jacobi polynomial
$C_p^{\frac {n - 2}{2}}$
(also called an ultraspherical polynomial) or the Jacobi polynomial
![]() $P_p^{\left (\frac {n - 3}{2},\frac {n - 3}{2}\right )}$
; in particular, when
$P_p^{\left (\frac {n - 3}{2},\frac {n - 3}{2}\right )}$
; in particular, when
![]() $n = 2$
, this is just the usual Legendre polynomial of degree p.
$n = 2$
, this is just the usual Legendre polynomial of degree p.
Lemma 7.12 [Reference Atkinson and HanAH12, Section 2.2]
The reproducing kernel for
![]() $\mathcal {H}_p(\mathbb {R}^n)$
is
$\mathcal {H}_p(\mathbb {R}^n)$
is
![]() $(\dim \tau ) P^{\circ }$
, so that for all
$(\dim \tau ) P^{\circ }$
, so that for all
![]() $P \in \mathcal {H}_p(\mathbb {R}^n)$
and
$P \in \mathcal {H}_p(\mathbb {R}^n)$
and
![]() $k \in \operatorname {\mathrm {O}}(n)$
,
$k \in \operatorname {\mathrm {O}}(n)$
,
In particular,
![]() $\langle P^{\circ }, P^{\circ } \rangle = (\dim \tau )^{-1}$
. Moreover, for all
$\langle P^{\circ }, P^{\circ } \rangle = (\dim \tau )^{-1}$
. Moreover, for all
![]() $P \in \mathcal {H}_p(\mathbb {R}^n)$
and
$P \in \mathcal {H}_p(\mathbb {R}^n)$
and
![]() $x \in \mathbb {R}^n$
,
$x \in \mathbb {R}^n$
,
 $$\begin{align*}P(x) = \dim \tau \int_{\operatorname{\mathrm{O}}(n)} P(e_n k^{-1}) P^{\circ}(xk) \, dk.\end{align*}$$
$$\begin{align*}P(x) = \dim \tau \int_{\operatorname{\mathrm{O}}(n)} P(e_n k^{-1}) P^{\circ}(xk) \, dk.\end{align*}$$
Lemma 7.13 (Hecke’s Identity [Reference Stein and WeissSW71, Chapter IV, Theorem 3.4])
For any homogeneous harmonic polynomial
![]() $P \in \mathcal {H}_p(\mathbb {R}^n)$
and
$P \in \mathcal {H}_p(\mathbb {R}^n)$
and
![]() $\xi \in \mathbb {R}^n$
, we have that
$\xi \in \mathbb {R}^n$
, we have that
8. The Newform in the Induced Model
8.1. The induced model
Let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type. Let
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type. Let
![]() $V_{\pi _j}$
be the space of
$V_{\pi _j}$
be the space of
![]() $\pi _j$
; the space
$\pi _j$
; the space
![]() $V_{\pi }$
of
$V_{\pi }$
of
![]() $\pi $
may then be viewed as the space of smooth functions
$\pi $
may then be viewed as the space of smooth functions
![]() $f : \operatorname {\mathrm {GL}}_n(F) \to V_{\pi _1} \otimes \cdots \otimes V_{\pi _r}$
that satisfy
$f : \operatorname {\mathrm {GL}}_n(F) \to V_{\pi _1} \otimes \cdots \otimes V_{\pi _r}$
that satisfy
for any
![]() $u \in \mathrm {N}_{\mathrm {P}}(F)$
,
$u \in \mathrm {N}_{\mathrm {P}}(F)$
,
![]() $m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r) \in \mathrm {M}_{\mathrm {P}}(F)$
, and
$m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r) \in \mathrm {M}_{\mathrm {P}}(F)$
, and
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
, where
$g \in \operatorname {\mathrm {GL}}_n(F)$
, where
![]() ${\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)}$
. The action of
${\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)}$
. The action of
![]() $\pi $
on
$\pi $
on
![]() $V_{\pi }$
is via right translation – namely,
$V_{\pi }$
is via right translation – namely, ![]() .
.
To make this more explicit, we first describe the space
![]() $V_{\pi _j}$
of the essentially square-integrable representation
$V_{\pi _j}$
of the essentially square-integrable representation
![]() $\pi _j$
of
$\pi _j$
of
![]() $\operatorname {\mathrm {GL}}_{n_j}(F)$
. The following result is well-known; see, for example, [Reference Goldfeld and HundleyGH11, Chapter 7].
$\operatorname {\mathrm {GL}}_{n_j}(F)$
. The following result is well-known; see, for example, [Reference Goldfeld and HundleyGH11, Chapter 7].
Lemma 8.1.
-
(1) Let
 $\pi = \chi ^{\kappa } |\cdot |^{t}$
be a character of
$\pi = \chi ^{\kappa } |\cdot |^{t}$
be a character of
 $\operatorname {\mathrm {GL}}_1(F) = F^{\times }$
. The space
$\operatorname {\mathrm {GL}}_1(F) = F^{\times }$
. The space
 $V_{\pi }$
of
$V_{\pi }$
of
 $\pi $
is simply the one-dimensional vector space spanned by the function
$\pi $
is simply the one-dimensional vector space spanned by the function
 $\chi ^{\kappa }(x) |x|^{t}$
.
$\chi ^{\kappa }(x) |x|^{t}$
. -
(2) Let
 $\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
be an essentially discrete series representation of
$\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
be an essentially discrete series representation of
 $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
. Then
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
. Then
 $\pi $
is a subrepresentation of the reducible principal series representation
$\pi $
is a subrepresentation of the reducible principal series representation  of
of
 $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
. Moreover, if
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
. Moreover, if
 $V_{\pi ^{\sharp }}$
denotes the induced model of
$V_{\pi ^{\sharp }}$
denotes the induced model of
 $\pi ^{\sharp }$
consisting of smooth functions
$\pi ^{\sharp }$
consisting of smooth functions
 $f : \operatorname {\mathrm {GL}}_2(\mathbb {R}) \to \mathbb {C}$
that satisfy for all
$f : \operatorname {\mathrm {GL}}_2(\mathbb {R}) \to \mathbb {C}$
that satisfy for all $$\begin{align*}f(uag) = |a_1|^{t + \frac{\kappa}{2}} \chi^{\kappa}(a_2) |a_2|^{t - \frac{\kappa}{2}} f(g)\end{align*}$$
$$\begin{align*}f(uag) = |a_1|^{t + \frac{\kappa}{2}} \chi^{\kappa}(a_2) |a_2|^{t - \frac{\kappa}{2}} f(g)\end{align*}$$
 $u \in \mathrm {N}_2(\mathbb {R})$
,
$u \in \mathrm {N}_2(\mathbb {R})$
,
 $a = \operatorname {\mathrm {diag}}(a_1,a_2) \in \mathrm {A}_2(\mathbb {R})$
and
$a = \operatorname {\mathrm {diag}}(a_1,a_2) \in \mathrm {A}_2(\mathbb {R})$
and
 $g \in \operatorname {\mathrm {GL}}_2(\mathbb {R})$
, where
$g \in \operatorname {\mathrm {GL}}_2(\mathbb {R})$
, where
 $\pi ^{\sharp }$
acts on
$\pi ^{\sharp }$
acts on
 $V_{\pi ^{\sharp }}$
via right translation, then the induced model of
$V_{\pi ^{\sharp }}$
via right translation, then the induced model of
 $\pi $
is precisely the subspace of
$\pi $
is precisely the subspace of
 $V_{\pi ^{\sharp }}$
, where
$V_{\pi ^{\sharp }}$
, where
 $\Pi ^{\tau }$
denotes the projection of
$\Pi ^{\tau }$
denotes the projection of
 $V_{\pi ^{\sharp }}$
onto the
$V_{\pi ^{\sharp }}$
onto the
 $\tau $
-isotypic component
$\tau $
-isotypic component
 $V_{\pi ^{\sharp }}^{\tau }$
.
$V_{\pi ^{\sharp }}^{\tau }$
.
Corollary 8.2. Let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type. Then the induced model of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type. Then the induced model of
![]() $\pi $
may be taken to be the space
$\pi $
may be taken to be the space
![]() $V_{\pi }$
of smooth functions
$V_{\pi }$
of smooth functions
![]() $f : \operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F) \to \mathbb {C}$
satisfying
$f : \operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F) \to \mathbb {C}$
satisfying
for all
![]() $u \in \mathrm {N}_{\mathrm {P}}(F)$
,
$u \in \mathrm {N}_{\mathrm {P}}(F)$
,
![]() $m,m' \in \mathrm {M}_{\mathrm {P}}(F)$
and
$m,m' \in \mathrm {M}_{\mathrm {P}}(F)$
and
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
and such that for each
$g \in \operatorname {\mathrm {GL}}_n(F)$
and such that for each
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
,
$g \in \operatorname {\mathrm {GL}}_n(F)$
,
![]() $f(g;\cdot ) : \mathrm {M}_{\mathrm {P}}(F) \to \mathbb {C}$
is an element of
$f(g;\cdot ) : \mathrm {M}_{\mathrm {P}}(F) \to \mathbb {C}$
is an element of
![]() $V_{\pi _1} \otimes \cdots \otimes V_{\pi _r}$
with
$V_{\pi _1} \otimes \cdots \otimes V_{\pi _r}$
with
![]() $V_{\pi _j}$
as in Lemma 8.1.
$V_{\pi _j}$
as in Lemma 8.1.
For
![]() $f \in V_{\pi }$
, we write
$f \in V_{\pi }$
, we write
![]() $f(g)$
to denote
$f(g)$
to denote
![]() $f(g;1_n)$
.
$f(g;1_n)$
.
Example 8.4. Suppose that
![]() $\pi = \chi ^{\kappa _1} |\cdot |^{t_1} \boxplus \cdots \boxplus \chi ^{\kappa _n} |\cdot |^{t_n}$
is a principal series representation, so that
$\pi = \chi ^{\kappa _1} |\cdot |^{t_1} \boxplus \cdots \boxplus \chi ^{\kappa _n} |\cdot |^{t_n}$
is a principal series representation, so that
![]() $\kappa _j \in \mathbb {Z}$
for
$\kappa _j \in \mathbb {Z}$
for
![]() $F = \mathbb {C}$
for
$F = \mathbb {C}$
for
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\kappa _j \in \{0,1\}$
. The induced model of
$\kappa _j \in \{0,1\}$
. The induced model of
![]() $\pi $
is the vector space
$\pi $
is the vector space
![]() $V_{\pi }$
of smooth functions
$V_{\pi }$
of smooth functions
![]() $f : \operatorname {\mathrm {GL}}_n(F) \to \mathbb {C}$
that satisfy
$f : \operatorname {\mathrm {GL}}_n(F) \to \mathbb {C}$
that satisfy
 $$\begin{align*}f(uag) = f(g) \delta_n^{1/2}(a) \prod_{j = 1}^{n} \chi^{\kappa_j}(a_j) |a_j|^{t_j}\end{align*}$$
$$\begin{align*}f(uag) = f(g) \delta_n^{1/2}(a) \prod_{j = 1}^{n} \chi^{\kappa_j}(a_j) |a_j|^{t_j}\end{align*}$$
for all
![]() $u \in \mathrm {N}_n(F)$
,
$u \in \mathrm {N}_n(F)$
,
![]() $a = \operatorname {\mathrm {diag}}(a_1,\ldots ,a_n) \in \mathrm {A}_n(F)$
, and
$a = \operatorname {\mathrm {diag}}(a_1,\ldots ,a_n) \in \mathrm {A}_n(F)$
, and
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
.
$g \in \operatorname {\mathrm {GL}}_n(F)$
.
Our goal now is to explicitly describe the newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
of an induced representation of Whittaker type
$V_{\pi }$
of an induced representation of Whittaker type
![]() $\pi $
. We give three different explicit constructions: via the Iwasawa decomposition, via convolution sections and via Godement sections. Initially, we define the newform in the induced model only up to multiplication by a nonzero constant; eventually in Definitions 8.10 and 9.2, we specify a normalisation that is particularly useful when proceeding to study the newform in the Whittaker model.
$\pi $
. We give three different explicit constructions: via the Iwasawa decomposition, via convolution sections and via Godement sections. Initially, we define the newform in the induced model only up to multiplication by a nonzero constant; eventually in Definitions 8.10 and 9.2, we specify a normalisation that is particularly useful when proceeding to study the newform in the Whittaker model.
8.2. The newform via the Iwasawa decomposition
8.2.1. Essentially square-integrable representations
We first describe the newform in the induced model of essentially square-integrable representations.
Lemma 8.5.
-
(1) For
 $\pi = \chi ^{\kappa } |\cdot |^t$
, the newform in the induced model is simply (8.6)for any
$\pi = \chi ^{\kappa } |\cdot |^t$
, the newform in the induced model is simply (8.6)for any $$ \begin{align} f^{\circ}(x) = c^{\circ} \chi^{\kappa}(x) |x|^t \end{align} $$
$$ \begin{align} f^{\circ}(x) = c^{\circ} \chi^{\kappa}(x) |x|^t \end{align} $$
 $c^{\circ } \in \mathbb {C}^{\times }$
.
$c^{\circ } \in \mathbb {C}^{\times }$
.
-
(2) For
 $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
 $\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, the newform in the induced model of
$\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, the newform in the induced model of
 $\pi $
is (8.7)for any
$\pi $
is (8.7)for any $$ \begin{align} f^{\circ}(g) = c^{\circ} |a_1|^{t + \frac{\kappa}{2}} \chi^{\kappa}(a_2) |a_2|^{t - \frac{\kappa}{2}} \overline{P^{\circ}}(e_2 k^{-1}) \end{align} $$
$$ \begin{align} f^{\circ}(g) = c^{\circ} |a_1|^{t + \frac{\kappa}{2}} \chi^{\kappa}(a_2) |a_2|^{t - \frac{\kappa}{2}} \overline{P^{\circ}}(e_2 k^{-1}) \end{align} $$
 $c^{\circ } \in \mathbb {C}^{\times }$
and
$c^{\circ } \in \mathbb {C}^{\times }$
and
 $g \in \operatorname {\mathrm {GL}}_2(\mathbb {R})$
having the Iwasawa decomposition
$g \in \operatorname {\mathrm {GL}}_2(\mathbb {R})$
having the Iwasawa decomposition
 $g = uak$
with
$g = uak$
with
 $u \in \mathrm {N}_2(\mathbb {R})$
,
$u \in \mathrm {N}_2(\mathbb {R})$
,
 $a = \operatorname {\mathrm {diag}}(a_1,a_2) \in \mathrm {A}_2(\mathbb {R})$
and
$a = \operatorname {\mathrm {diag}}(a_1,a_2) \in \mathrm {A}_2(\mathbb {R})$
and
 $k \in \operatorname {\mathrm {O}}(2)$
, where
$k \in \operatorname {\mathrm {O}}(2)$
, where
 $P^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
$P^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
 $\tau ^{\circ }$
given by (7.10).
$\tau ^{\circ }$
given by (7.10).
Remark 8.8. Strictly speaking, there is no need to write
![]() $\overline {P^{\circ }}$
instead of
$\overline {P^{\circ }}$
instead of
![]() $P^{\circ }$
, since this is real-valued; we do this simply to ensure notational consistency when later treating the cases
$P^{\circ }$
, since this is real-valued; we do this simply to ensure notational consistency when later treating the cases
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $F = \mathbb {C}$
simultaneously, for the distinction is no longer moot in the latter case.
$F = \mathbb {C}$
simultaneously, for the distinction is no longer moot in the latter case.
Proof. This is clear for
![]() $\pi = \chi ^{\kappa } |\cdot |^t$
. For
$\pi = \chi ^{\kappa } |\cdot |^t$
. For
![]() $\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, we must first check that
$\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, we must first check that
![]() $f^{\circ }$
is well defined, for the Iwasawa decomposition is not unique as
$f^{\circ }$
is well defined, for the Iwasawa decomposition is not unique as
![]() $\mathrm {A}_2(\mathbb {R})$
and
$\mathrm {A}_2(\mathbb {R})$
and
![]() $\operatorname {\mathrm {O}}(2)$
intersect nontrivially. If
$\operatorname {\mathrm {O}}(2)$
intersect nontrivially. If
![]() $a' = \operatorname {\mathrm {diag}}(a_1^{\prime },a_2^{\prime }) \in \mathrm {A}_2(\mathbb {R}) \cap \operatorname {\mathrm {O}}(2)$
, so that
$a' = \operatorname {\mathrm {diag}}(a_1^{\prime },a_2^{\prime }) \in \mathrm {A}_2(\mathbb {R}) \cap \operatorname {\mathrm {O}}(2)$
, so that
![]() $a_1^{\prime },a_2^{\prime } \in \{1,-1\}$
, then on the one hand,
$a_1^{\prime },a_2^{\prime } \in \{1,-1\}$
, then on the one hand,
since
![]() $a' \in \mathrm {A}_2(\mathbb {R})$
with
$a' \in \mathrm {A}_2(\mathbb {R})$
with
![]() $|a_1^{\prime }| = |a_2^{\prime }| = 1$
, while on the other hand,
$|a_1^{\prime }| = |a_2^{\prime }| = 1$
, while on the other hand,
since
![]() $a' \in \operatorname {\mathrm {O}}(2)$
, and these are equal since
$a' \in \operatorname {\mathrm {O}}(2)$
, and these are equal since
![]() $e_2 a' = a_2^{\prime } e_2$
,
$e_2 a' = a_2^{\prime } e_2$
,
![]() $P^{\circ }$
is homogeneous of degree
$P^{\circ }$
is homogeneous of degree
![]() $\kappa $
as
$\kappa $
as
![]() $\tau ^{\circ } = \tau _{(\kappa ,0)}$
, so that
$\tau ^{\circ } = \tau _{(\kappa ,0)}$
, so that
![]() $P^{\circ } \in \mathcal {H}_{\kappa }(\mathbb {R}^2)$
, and
$P^{\circ } \in \mathcal {H}_{\kappa }(\mathbb {R}^2)$
, and
![]() $a_2^{\prime \kappa } = \chi ^{\kappa }(a_2^{\prime })$
as
$a_2^{\prime \kappa } = \chi ^{\kappa }(a_2^{\prime })$
as
![]() $a_2^{\prime } \in \{1,-1\}$
.
$a_2^{\prime } \in \{1,-1\}$
.
Next, Schur orthogonality shows that
![]() $f^{\circ } \in \ker \Pi ^{\tau _{(\mu _1,0)}}$
for
$f^{\circ } \in \ker \Pi ^{\tau _{(\mu _1,0)}}$
for
![]() $0 \leq \mu _1 \leq \kappa - 2$
with
$0 \leq \mu _1 \leq \kappa - 2$
with
![]() $\mu _1 \equiv \kappa\ \pmod {2}$
since
$\mu _1 \equiv \kappa\ \pmod {2}$
since
![]() $P^{\circ } \in \mathcal {H}_{\kappa }(\mathbb {R}^2)$
, and so
$P^{\circ } \in \mathcal {H}_{\kappa }(\mathbb {R}^2)$
, and so
![]() $f^{\circ }$
is indeed an element of the induced model
$f^{\circ }$
is indeed an element of the induced model
![]() $V_{\pi }$
of
$V_{\pi }$
of
![]() $\pi $
as defined in Lemma 8.1.
$\pi $
as defined in Lemma 8.1.
Finally, to prove that
![]() $f^{\circ }$
is the newform, we must show that
$f^{\circ }$
is the newform, we must show that
 $$\begin{align*}\int_{\operatorname{\mathrm{O}}(2)} \xi^{\tau^{\circ}|_{\operatorname{\mathrm{O}}(1)}}(k) (\pi(k) \cdot f^{\circ})(g) \, dk = f^{\circ}(g).\end{align*}$$
$$\begin{align*}\int_{\operatorname{\mathrm{O}}(2)} \xi^{\tau^{\circ}|_{\operatorname{\mathrm{O}}(1)}}(k) (\pi(k) \cdot f^{\circ})(g) \, dk = f^{\circ}(g).\end{align*}$$
From the definition (8.7) of
![]() $f^{\circ }$
, it suffices to show that
$f^{\circ }$
, it suffices to show that
 $$ \begin{align} \int_{\operatorname{\mathrm{O}}(2)} \xi^{\tau^{\circ}|_{\operatorname{\mathrm{O}}(1)}}(k) \overline{P^{\circ}}\left(e_2 k^{-1} k^{\prime -1}\right) \, dk = \overline{P^{\circ}}\left(e_2 k^{\prime -1}\right) \end{align} $$
$$ \begin{align} \int_{\operatorname{\mathrm{O}}(2)} \xi^{\tau^{\circ}|_{\operatorname{\mathrm{O}}(1)}}(k) \overline{P^{\circ}}\left(e_2 k^{-1} k^{\prime -1}\right) \, dk = \overline{P^{\circ}}\left(e_2 k^{\prime -1}\right) \end{align} $$
for any
![]() $k' \in \operatorname {\mathrm {O}}(2)$
. We note that
$k' \in \operatorname {\mathrm {O}}(2)$
. We note that
 $$\begin{align*}\xi^{\tau^{\circ}|_{\operatorname{\mathrm{O}}(1)}}(k) = (\dim \tau^{\circ}) \frac{\left\langle \tau^{\circ}(k^{-1}) \cdot P^{\circ}, P^{\circ} \right\rangle}{\left\langle P^{\circ}, P^{\circ} \right\rangle} = (\dim \tau^{\circ}) P^{\circ}(e_2 k^{-1}),\end{align*}$$
$$\begin{align*}\xi^{\tau^{\circ}|_{\operatorname{\mathrm{O}}(1)}}(k) = (\dim \tau^{\circ}) \frac{\left\langle \tau^{\circ}(k^{-1}) \cdot P^{\circ}, P^{\circ} \right\rangle}{\left\langle P^{\circ}, P^{\circ} \right\rangle} = (\dim \tau^{\circ}) P^{\circ}(e_2 k^{-1}),\end{align*}$$
where the first equality follows from the definitions (4.6) of
![]() $\xi ^{\tau ^{\circ }|_{\operatorname {\mathrm {O}}(1)}}$
and (7.10) of
$\xi ^{\tau ^{\circ }|_{\operatorname {\mathrm {O}}(1)}}$
and (7.10) of
![]() $P^{\circ }$
, while the second follows from Lemma 7.12. The equality (8.9) then follows from one more application of Lemma 7.12.
$P^{\circ }$
, while the second follows from Lemma 7.12. The equality (8.9) then follows from one more application of Lemma 7.12.
For our applications, we require explicit choices of the constants
![]() $c^{\circ }$
appearing in (8.6) and (8.7).
$c^{\circ }$
appearing in (8.6) and (8.7).
Definition 8.10. Let
![]() $\pi $
be an essentially square-integrable representation of
$\pi $
be an essentially square-integrable representation of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, and let
$\operatorname {\mathrm {GL}}_n(F)$
, and let
![]() $f^{\circ }$
denote the newform in the induced model, which is given by (8.6) if
$f^{\circ }$
denote the newform in the induced model, which is given by (8.6) if
![]() $n = 1$
, so that
$n = 1$
, so that
![]() $\pi = \chi ^{\kappa } |\cdot |^t$
, and by (8.7) if
$\pi = \chi ^{\kappa } |\cdot |^t$
, and by (8.7) if
![]() $n = 2$
, so that
$n = 2$
, so that
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
. We say that
$\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
. We say that
![]() $f^{\circ }$
is canonically normalised if
$f^{\circ }$
is canonically normalised if
 $$ \begin{align} c^{\circ} = \begin{cases} 1 & \text{if }\pi = \chi^{\kappa} |\cdot|^t, \\ i^{\kappa} \zeta_{\mathbb{R}}(\kappa) \zeta_{\mathbb{R}}(\kappa + 1) & \text{if }\pi = D_{\kappa} \otimes \left|\det\right|{}^t. \end{cases} \end{align} $$
$$ \begin{align} c^{\circ} = \begin{cases} 1 & \text{if }\pi = \chi^{\kappa} |\cdot|^t, \\ i^{\kappa} \zeta_{\mathbb{R}}(\kappa) \zeta_{\mathbb{R}}(\kappa + 1) & \text{if }\pi = D_{\kappa} \otimes \left|\det\right|{}^t. \end{cases} \end{align} $$
8.2.2. Induced representations of Whittaker type
We now give an explicit construction of the newform
![]() $f^{\circ } : \operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F) \to \mathbb {C}$
in the induced model of an induced representation of Whittaker type
$f^{\circ } : \operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F) \to \mathbb {C}$
in the induced model of an induced representation of Whittaker type
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
of
![]() $\operatorname {\mathrm {GL}}_n(F)$
when
$\operatorname {\mathrm {GL}}_n(F)$
when
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
is written in terms of its Iwasawa decomposition.
$g \in \operatorname {\mathrm {GL}}_n(F)$
is written in terms of its Iwasawa decomposition.
This description involves a distinguished homogeneous harmonic polynomial
![]() $P_{(n_1,\ldots ,n_r)}^{\circ }$
that is defined in terms of polynomials
$P_{(n_1,\ldots ,n_r)}^{\circ }$
that is defined in terms of polynomials
![]() $P_j^{\circ }$
in the following way. To each essentially square-integrable representation
$P_j^{\circ }$
in the following way. To each essentially square-integrable representation
![]() $\pi _j$
of
$\pi _j$
of
![]() $\operatorname {\mathrm {GL}}_{n_j}(F)$
with newform K-type
$\operatorname {\mathrm {GL}}_{n_j}(F)$
with newform K-type
![]() $\tau _j^{\circ }$
, we associate a distinguished homogeneous harmonic polynomial
$\tau _j^{\circ }$
, we associate a distinguished homogeneous harmonic polynomial
![]() $P_j^{\circ }$
.
$P_j^{\circ }$
.
-
• For
 $F = \mathbb {R}$
,
$F = \mathbb {R}$
,
 $n_j = 1$
,
$n_j = 1$
,
 $\pi _j = \chi ^{\kappa _j} |\cdot |_{\mathbb {R}}^{t_j}$
and
$\pi _j = \chi ^{\kappa _j} |\cdot |_{\mathbb {R}}^{t_j}$
and
 $\tau _j^{\circ }$
the one-dimensional representation of
$\tau _j^{\circ }$
the one-dimensional representation of
 $\operatorname {\mathrm {O}}(1)$
of highest weight
$\operatorname {\mathrm {O}}(1)$
of highest weight
 $\kappa _j \in \{0,1\}$
,
$\kappa _j \in \{0,1\}$
,
 $P_j^{\circ } \in \mathcal {H}_p(\mathbb {R})$
is the homogeneous harmonic polynomial associated to
$P_j^{\circ } \in \mathcal {H}_p(\mathbb {R})$
is the homogeneous harmonic polynomial associated to
 $\tau = \tau _j^{\circ }$
given by (7.9) with
$\tau = \tau _j^{\circ }$
given by (7.9) with
 $p = \kappa _j$
.
$p = \kappa _j$
. -
• For
 $F = \mathbb {R}$
,
$F = \mathbb {R}$
,
 $n_j = 2$
,
$n_j = 2$
,
 $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}_{\mathbb {R}}^{t_j}$
and
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}_{\mathbb {R}}^{t_j}$
and
 $\tau _j^{\circ }$
the two-dimensional representation of
$\tau _j^{\circ }$
the two-dimensional representation of
 $\operatorname {\mathrm {O}}(2)$
of highest weight
$\operatorname {\mathrm {O}}(2)$
of highest weight
 $(\kappa _j,0)$
with
$(\kappa _j,0)$
with
 $\kappa _j \geq 2$
a positive integer,
$\kappa _j \geq 2$
a positive integer,
 $P_j^{\circ } \in \mathcal {H}_p(\mathbb {R}^2)$
is the homogeneous harmonic polynomial associated to
$P_j^{\circ } \in \mathcal {H}_p(\mathbb {R}^2)$
is the homogeneous harmonic polynomial associated to
 $\tau = \tau _j^{\circ }$
given by (7.10) with
$\tau = \tau _j^{\circ }$
given by (7.10) with
 $p = \kappa _j$
.
$p = \kappa _j$
. -
• For
 $F = \mathbb {C}$
, so that
$F = \mathbb {C}$
, so that
 $n_j = 1$
,
$n_j = 1$
,
 $\pi _j = \chi ^{\kappa _j} |\cdot |_{\mathbb {C}}^{t_j}$
and
$\pi _j = \chi ^{\kappa _j} |\cdot |_{\mathbb {C}}^{t_j}$
and
 $\tau _j^{\circ }$
the one-dimensional representation of
$\tau _j^{\circ }$
the one-dimensional representation of
 $\operatorname {\mathrm {U}}(1)$
of highest weight
$\operatorname {\mathrm {U}}(1)$
of highest weight
 $\kappa _j \in \mathbb {Z}$
,
$\kappa _j \in \mathbb {Z}$
,
 $P_j^{\circ } \in \mathcal {H}_{p,q}(\mathbb {C})$
is the homogeneous harmonic polynomial associated to
$P_j^{\circ } \in \mathcal {H}_{p,q}(\mathbb {C})$
is the homogeneous harmonic polynomial associated to
 $\tau = \tau _j^{\circ }$
given by (7.3) with
$\tau = \tau _j^{\circ }$
given by (7.3) with
 $p = \max \{\kappa _j,0\}$
and
$p = \max \{\kappa _j,0\}$
and
 $q = -\min \{\kappa _j,0\}$
.
$q = -\min \{\kappa _j,0\}$
.
We then define

for
![]() $F = \mathbb {R}$
, while for
$F = \mathbb {R}$
, while for
![]() $F = \mathbb {C}$
, we define
$F = \mathbb {C}$
, we define

It is straightforward to see that the polynomials
![]() $P_{(n_1,\ldots ,n_r)}^{\circ }(x)$
and
$P_{(n_1,\ldots ,n_r)}^{\circ }(x)$
and
![]() $P_{(n_1,\ldots ,n_r)}^{\circ }(z)$
are elements of
$P_{(n_1,\ldots ,n_r)}^{\circ }(z)$
are elements of
![]() $\mathcal {H}_{\mu _1^{\circ }}(\mathbb {R}^n)$
and
$\mathcal {H}_{\mu _1^{\circ }}(\mathbb {R}^n)$
and
![]() $\mathcal {H}_{\mu _1^{\circ },-\mu _n^{\circ }}(\mathbb {C}^n)$
, respectively, where
$\mathcal {H}_{\mu _1^{\circ },-\mu _n^{\circ }}(\mathbb {C}^n)$
, respectively, where
![]() $\mu ^{\circ } = (\mu _1^{\circ },\ldots ,\mu _n^{\circ })$
is the highest weight of the newform K-type
$\mu ^{\circ } = (\mu _1^{\circ },\ldots ,\mu _n^{\circ })$
is the highest weight of the newform K-type
![]() $\tau ^{\circ } = \tau _{\mu ^{\circ }}$
of
$\tau ^{\circ } = \tau _{\mu ^{\circ }}$
of
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
.
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
.
The description of the newform
![]() $f^{\circ }$
in the induced model of
$f^{\circ }$
in the induced model of
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
also involves the canonically normalised newforms
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
also involves the canonically normalised newforms
![]() $f_1^{\circ },\ldots ,f_r^{\circ }$
of the essentially square-integrable representations
$f_1^{\circ },\ldots ,f_r^{\circ }$
of the essentially square-integrable representations
![]() $\pi _1,\ldots ,\pi _r$
.
$\pi _1,\ldots ,\pi _r$
.
Proposition 8.14. Let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type with
![]() $r \geq 2$
. For
$r \geq 2$
. For
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
having the Iwasawa decomposition
$g \in \operatorname {\mathrm {GL}}_n(F)$
having the Iwasawa decomposition
![]() $g = umk$
with respect to the parabolic subgroup
$g = umk$
with respect to the parabolic subgroup
![]() $\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)$
, so that
$\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)$
, so that
![]() $u \in \mathrm {N}_{\mathrm {P}}(F)$
,
$u \in \mathrm {N}_{\mathrm {P}}(F)$
,
![]() $m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r) \in \mathrm {M}_{\mathrm {P}}(F)$
, and
$m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r) \in \mathrm {M}_{\mathrm {P}}(F)$
, and
![]() $k \in K$
, and for
$k \in K$
, and for
![]() $m' = \operatorname {\mathrm {blockdiag}}(m_1^{\prime },\ldots ,m_r^{\prime }) \in \mathrm {M}_{\mathrm {P}}(F)$
, the newform
$m' = \operatorname {\mathrm {blockdiag}}(m_1^{\prime },\ldots ,m_r^{\prime }) \in \mathrm {M}_{\mathrm {P}}(F)$
, the newform
![]() $f^{\circ } : \operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F) \to \mathbb {C}$
in the induced model
$f^{\circ } : \operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F) \to \mathbb {C}$
in the induced model
![]() $V_{\pi }$
of
$V_{\pi }$
of
![]() $\pi $
is of the form
$\pi $
is of the form

for some constant
![]() $c^{\circ } \in \mathbb {C}^{\times }$
, where each
$c^{\circ } \in \mathbb {C}^{\times }$
, where each
![]() $f_j^{\circ }$
is the canonically normalised newform of
$f_j^{\circ }$
is the canonically normalised newform of
![]() $\pi _j$
and
$\pi _j$
and
![]() $\tau _j^{\circ }$
is the newform
$\tau _j^{\circ }$
is the newform
![]() $K_{n_j}$
-type of
$K_{n_j}$
-type of
![]() $\pi _j$
.
$\pi _j$
.
Proof. Since the Iwasawa decomposition is not unique as
![]() $\mathrm {M}_{\mathrm {P}}(F)$
and K intersect nontrivially, our first task is to show that
$\mathrm {M}_{\mathrm {P}}(F)$
and K intersect nontrivially, our first task is to show that
![]() $f^{\circ }(umm"k;m')$
is well defined for
$f^{\circ }(umm"k;m')$
is well defined for
![]() $m" = \operatorname {\mathrm {blockdiag}}(m_1^{\prime \prime },\ldots ,m_r^{\prime \prime }) \in \mathrm {M}_{\mathrm {P}}(F) \cap K$
. On the one hand, this is
$m" = \operatorname {\mathrm {blockdiag}}(m_1^{\prime \prime },\ldots ,m_r^{\prime \prime }) \in \mathrm {M}_{\mathrm {P}}(F) \cap K$
. On the one hand, this is
 $$ \begin{align*} c^{\circ} \dim \tau_1^{\circ} \cdots \dim \tau_r^{\circ} \delta_{\mathrm{P}}^{1/2}(m) \int_{K_{n_1}} \cdots \int_{K_{n_r}} &f_1^{\circ}\left(m_1^{\prime} m_1 m_1^{\prime\prime} k_1\right) \cdots f_r^{\circ}\left(m_r^{\prime} m_r m_r^{\prime\prime} k_r\right) \\ &\times \overline{P_{(n_1,\ldots,n_r)}^{\circ}}\left(e_n k^{-1} \operatorname{\mathrm{blockdiag}}\left(k_1,\ldots,k_r\right)\kern-1pt\right) \,\kern-1pt dk_r \cdots dk_1 \end{align*} $$
$$ \begin{align*} c^{\circ} \dim \tau_1^{\circ} \cdots \dim \tau_r^{\circ} \delta_{\mathrm{P}}^{1/2}(m) \int_{K_{n_1}} \cdots \int_{K_{n_r}} &f_1^{\circ}\left(m_1^{\prime} m_1 m_1^{\prime\prime} k_1\right) \cdots f_r^{\circ}\left(m_r^{\prime} m_r m_r^{\prime\prime} k_r\right) \\ &\times \overline{P_{(n_1,\ldots,n_r)}^{\circ}}\left(e_n k^{-1} \operatorname{\mathrm{blockdiag}}\left(k_1,\ldots,k_r\right)\kern-1pt\right) \,\kern-1pt dk_r \cdots dk_1 \end{align*} $$
since
![]() $m" \in \mathrm {M}_{\mathrm {P}}(F)$
, noting that
$m" \in \mathrm {M}_{\mathrm {P}}(F)$
, noting that
![]() $\delta _{\mathrm {P}}(m") = 1$
as
$\delta _{\mathrm {P}}(m") = 1$
as
![]() $m" \in K$
. On the other hand, this is
$m" \in K$
. On the other hand, this is
 $$ \begin{align*} c^{\circ} \dim \tau_1^{\circ} \cdots \dim \tau_r^{\circ} \delta_{\mathrm{P}}^{1/2}(m) \int_{K_{n_1}} \cdots \int_{K_{n_r}} &f_1^{\circ}\left(m_1^{\prime} m_1 k_1\right) \cdots f_r^{\circ}\left(m_r^{\prime} m_r k_r\right) \\ &\times \overline{P_{(n_1,\ldots,n_r)}^{\circ}}\left(e_n k^{-1} {m"}^{-1} \operatorname{\mathrm{blockdiag}}\left(k_1, \ldots, k_r\right)\right) \, dk_r \cdots dk_1 \end{align*} $$
$$ \begin{align*} c^{\circ} \dim \tau_1^{\circ} \cdots \dim \tau_r^{\circ} \delta_{\mathrm{P}}^{1/2}(m) \int_{K_{n_1}} \cdots \int_{K_{n_r}} &f_1^{\circ}\left(m_1^{\prime} m_1 k_1\right) \cdots f_r^{\circ}\left(m_r^{\prime} m_r k_r\right) \\ &\times \overline{P_{(n_1,\ldots,n_r)}^{\circ}}\left(e_n k^{-1} {m"}^{-1} \operatorname{\mathrm{blockdiag}}\left(k_1, \ldots, k_r\right)\right) \, dk_r \cdots dk_1 \end{align*} $$
since
![]() $m" \in K$
; as
$m" \in K$
; as
![]() $m_j^{\prime \prime } \in K_{n_j}$
, this is seen to be equal to the first expression upon making the change of variables
$m_j^{\prime \prime } \in K_{n_j}$
, this is seen to be equal to the first expression upon making the change of variables
![]() $k_j \mapsto m_j^{\prime \prime } k_j$
.
$k_j \mapsto m_j^{\prime \prime } k_j$
.
Next, we confirm that this is an element of the induced model
![]() $V_{\pi }$
of
$V_{\pi }$
of
![]() $\pi $
. It is clear that
$\pi $
. It is clear that
![]() $f^{\circ }$
is a smooth function from
$f^{\circ }$
is a smooth function from
![]() $\operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F)$
to
$\operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F)$
to
![]() $\mathbb {C}$
that satisfies (8.3). Moreover,
$\mathbb {C}$
that satisfies (8.3). Moreover,
![]() $f^{\circ }(g;\cdot )$
is indeed an element of
$f^{\circ }(g;\cdot )$
is indeed an element of
![]() $V_{\pi _1} \otimes \cdots \otimes V_{\pi _r}$
for each
$V_{\pi _1} \otimes \cdots \otimes V_{\pi _r}$
for each
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
, since upon writing
$g \in \operatorname {\mathrm {GL}}_n(F)$
, since upon writing
![]() $P_{(n_1,\ldots ,n_r)}^{\circ } = \prod _{j = 1}^{r} P_j^{\circ }$
, the integrals over
$P_{(n_1,\ldots ,n_r)}^{\circ } = \prod _{j = 1}^{r} P_j^{\circ }$
, the integrals over
![]() $K_{n_j} \ni k_j$
are either trivial if
$K_{n_j} \ni k_j$
are either trivial if
![]() $n_j = 1$
, or lead to
$n_j = 1$
, or lead to
![]() $f_j^{\circ } \overline {P_j^{\circ }}$
being replaced with the sum of two such products of elements of
$f_j^{\circ } \overline {P_j^{\circ }}$
being replaced with the sum of two such products of elements of
![]() $V_{\pi _j}$
and homogeneous harmonic polynomials, for we may use Schur orthogonality for the two-dimensional representation
$V_{\pi _j}$
and homogeneous harmonic polynomials, for we may use Schur orthogonality for the two-dimensional representation
![]() $\tau _j^{\circ } = \tau _{(\kappa _j,0)}$
for
$\tau _j^{\circ } = \tau _{(\kappa _j,0)}$
for
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
Finally, we show that this is the newform, which requires confirming that
From the definition (8.15) of
![]() $f^{\circ }$
together with the Iwasawa decomposition, it suffices to show that for each
$f^{\circ }$
together with the Iwasawa decomposition, it suffices to show that for each
![]() $k' \in K_n$
,
$k' \in K_n$
,
We note that
 $$\begin{align*}\xi^{\tau^{\circ},K_{n - 1}}(k) = (\dim \tau^{\circ}) \frac{\left\langle \tau^{\circ}(k^{-1}) \cdot P^{\circ}, P^{\circ} \right\rangle}{\left\langle P^{\circ}, P^{\circ} \right\rangle} = (\dim \tau^{\circ}) P^{\circ}(e_n k^{-1}),\end{align*}$$
$$\begin{align*}\xi^{\tau^{\circ},K_{n - 1}}(k) = (\dim \tau^{\circ}) \frac{\left\langle \tau^{\circ}(k^{-1}) \cdot P^{\circ}, P^{\circ} \right\rangle}{\left\langle P^{\circ}, P^{\circ} \right\rangle} = (\dim \tau^{\circ}) P^{\circ}(e_n k^{-1}),\end{align*}$$
where the first equality follows from the definitions (4.6) of
![]() $\xi ^{\tau ^{\circ },K_{n - 1}}$
and (7.2) and (7.8) of
$\xi ^{\tau ^{\circ },K_{n - 1}}$
and (7.2) and (7.8) of
![]() $P^{\circ }$
, while the second follows from Lemmata 7.5 and 7.12. The equality (8.16) then follows from one more application of Lemmata 7.5 and 7.12.
$P^{\circ }$
, while the second follows from Lemmata 7.5 and 7.12. The equality (8.16) then follows from one more application of Lemmata 7.5 and 7.12.
Proposition 8.14 completely prescribes the behaviour of the newform ![]() when
when
![]() $g = uak$
is given by the Iwasawa decomposition with respect to the standard Borel subgroup.
$g = uak$
is given by the Iwasawa decomposition with respect to the standard Borel subgroup.
Corollary 8.17. For
![]() $u \in \mathrm {N}_n(F)$
,
$u \in \mathrm {N}_n(F)$
,
![]() $a = \operatorname {\mathrm {diag}}(a_1,\ldots ,a_n) \in \mathrm {A}_n(F)$
and
$a = \operatorname {\mathrm {diag}}(a_1,\ldots ,a_n) \in \mathrm {A}_n(F)$
and
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
, the newform in the induced model satisfies
$g \in \operatorname {\mathrm {GL}}_n(F)$
, the newform in the induced model satisfies
 $$ \begin{align} f^{\circ}(uag) = f^{\circ}(g) \delta_n^{1/2}(a) \prod_{j = 1}^{r} \begin{cases} \chi^{\kappa_j}(a_{\ell}) |a_{\ell}|^{t_j} & \text{if }\ell = n_1 + \cdots + n_j\text{ and }\\&\pi_j = \chi^{\kappa_j} |\cdot|^{t_j}, \\ \chi^{\kappa_j}(a_{\ell + 1}) |a_{\ell}|^{t_j + \frac{\kappa_j - 1}{2}} |a_{\ell + 1}|^{t_j - \frac{\kappa_j - 1}{2}} & \text{if }\ell = n_1 + \cdots + n_j - 1\\&\text{and }\pi_j = D_{\kappa_j} \otimes \left|\det\right|{}^{t_j}, \end{cases} \end{align} $$
$$ \begin{align} f^{\circ}(uag) = f^{\circ}(g) \delta_n^{1/2}(a) \prod_{j = 1}^{r} \begin{cases} \chi^{\kappa_j}(a_{\ell}) |a_{\ell}|^{t_j} & \text{if }\ell = n_1 + \cdots + n_j\text{ and }\\&\pi_j = \chi^{\kappa_j} |\cdot|^{t_j}, \\ \chi^{\kappa_j}(a_{\ell + 1}) |a_{\ell}|^{t_j + \frac{\kappa_j - 1}{2}} |a_{\ell + 1}|^{t_j - \frac{\kappa_j - 1}{2}} & \text{if }\ell = n_1 + \cdots + n_j - 1\\&\text{and }\pi_j = D_{\kappa_j} \otimes \left|\det\right|{}^{t_j}, \end{cases} \end{align} $$
and for
![]() $k \in K_n$
,
$k \in K_n$
,
 $$ \begin{align} f^{\circ}(k) & = c^{\circ} c_1^{\circ} \cdots c_r^{\circ} \overline{P_{(n_1,\ldots,n_r)}^{\circ}}(e_n k^{-1}) \nonumber\\ & = c^{\circ} \prod_{j = 1}^{r} \begin{cases} \overline{P_j^{\circ}}\left(\overline{k_{\ell,n}}\right) & \text{if }\ell = n_1 + \cdots + n_j\text{ and }\pi_j =\\& \chi^{\kappa_j} |\cdot|^{t_j}, \\ i^{\kappa_j} \zeta_{\mathbb{R}}(\kappa_j) \zeta_{\mathbb{R}}(\kappa_j + 1) \overline{P_j^{\circ}}\left(\overline{k_{\ell,n}}, \overline{k_{\ell + 1,n}}\right) & \text{if }\ell = n_1 + \cdots + n_j - 1\text{ and }\pi_j =\\& D_{\kappa_j} \otimes \left|\det\right|{}^{t_j}. \end{cases} \end{align} $$
$$ \begin{align} f^{\circ}(k) & = c^{\circ} c_1^{\circ} \cdots c_r^{\circ} \overline{P_{(n_1,\ldots,n_r)}^{\circ}}(e_n k^{-1}) \nonumber\\ & = c^{\circ} \prod_{j = 1}^{r} \begin{cases} \overline{P_j^{\circ}}\left(\overline{k_{\ell,n}}\right) & \text{if }\ell = n_1 + \cdots + n_j\text{ and }\pi_j =\\& \chi^{\kappa_j} |\cdot|^{t_j}, \\ i^{\kappa_j} \zeta_{\mathbb{R}}(\kappa_j) \zeta_{\mathbb{R}}(\kappa_j + 1) \overline{P_j^{\circ}}\left(\overline{k_{\ell,n}}, \overline{k_{\ell + 1,n}}\right) & \text{if }\ell = n_1 + \cdots + n_j - 1\text{ and }\pi_j =\\& D_{\kappa_j} \otimes \left|\det\right|{}^{t_j}. \end{cases} \end{align} $$
Proof. Via the Iwasawa decomposition, it suffices to prove (8.18) for
![]() $g = k \in K$
. We write
$g = k \in K$
. We write
![]() $u \in \mathrm {N}_n(F)$
as
$u \in \mathrm {N}_n(F)$
as
![]() $u' u"$
with
$u' u"$
with
![]() $u' \in \mathrm {N}_{\mathrm {P}}(F)$
and
$u' \in \mathrm {N}_{\mathrm {P}}(F)$
and
![]() $u" = \operatorname {\mathrm {blockdiag}}(u_1^{\prime \prime },\ldots ,u_r^{\prime \prime }) \in \mathrm {M}_{\mathrm {P}}(F)$
with
$u" = \operatorname {\mathrm {blockdiag}}(u_1^{\prime \prime },\ldots ,u_r^{\prime \prime }) \in \mathrm {M}_{\mathrm {P}}(F)$
with
![]() $u_j^{\prime \prime } \in \mathrm {N}_{n_j}(F)$
, so that
$u_j^{\prime \prime } \in \mathrm {N}_{n_j}(F)$
, so that
![]() $u" a \in \mathrm {M}_{\mathrm {P}}(F)$
whenever
$u" a \in \mathrm {M}_{\mathrm {P}}(F)$
whenever
![]() $a \in \mathrm {A}_n(F)$
. We then take
$a \in \mathrm {A}_n(F)$
. We then take
![]() $g = uak = u' u"a k$
and
$g = uak = u' u"a k$
and
![]() $m' = 1_n$
in (8.15) and apply (8.6) and (8.7) to deduce (8.18). The identity (8.19) then follows upon taking
$m' = 1_n$
in (8.15) and apply (8.6) and (8.7) to deduce (8.18). The identity (8.19) then follows upon taking
![]() $u = a = 1_n$
, writing
$u = a = 1_n$
, writing
![]() $P_{(n_1,\ldots ,n_r)}^{\circ } = \prod _{j = 1}^{r} P_j^{\circ }$
and invoking Lemmata 7.5 and 7.12 to evaluate the integrals over
$P_{(n_1,\ldots ,n_r)}^{\circ } = \prod _{j = 1}^{r} P_j^{\circ }$
and invoking Lemmata 7.5 and 7.12 to evaluate the integrals over
![]() $K_{n_j} \ni k_j$
.
$K_{n_j} \ni k_j$
.
8.3. The newform via convolution sections
We now give a different description of the newform in the induced model. This description is a recursive formula for
![]() $f^{\circ }$
as an integral over
$f^{\circ }$
as an integral over
![]() $\operatorname {\mathrm {GL}}_n(F)$
involving
$\operatorname {\mathrm {GL}}_n(F)$
involving
![]() $f^{\circ }$
itself and a distinguished standard Schwartz function
$f^{\circ }$
itself and a distinguished standard Schwartz function
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
, where the space of standard Schwartz functions
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
, where the space of standard Schwartz functions
![]() $\mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
consists of functions
$\mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
consists of functions
![]() $\Phi : \operatorname {\mathrm {Mat}}_{n \times n}(F) \to \mathbb {C}$
of the form
$\Phi : \operatorname {\mathrm {Mat}}_{n \times n}(F) \to \mathbb {C}$
of the form
with P a polynomial in the entries of x and
![]() $\overline {x}$
and
$\overline {x}$
and ![]() as in (4.19). When
as in (4.19). When
![]() $\pi $
is a spherical representation and f is the spherical vector, such a formula is known by the work of Gerasimov, Lebedev and Oblezin [Reference Gerasimov, Lebedev and OblezinGLO08, Theorem 5.1] and Ishii and Stade [Reference Ishii and StadeIsSt13, Proposition 2.6] (with the latter expressed in terms of the Mellin transform of the Whittaker function); see also [Reference Ishii and StadeIsSt13, Section 5].
$\pi $
is a spherical representation and f is the spherical vector, such a formula is known by the work of Gerasimov, Lebedev and Oblezin [Reference Gerasimov, Lebedev and OblezinGLO08, Theorem 5.1] and Ishii and Stade [Reference Ishii and StadeIsSt13, Proposition 2.6] (with the latter expressed in terms of the Mellin transform of the Whittaker function); see also [Reference Ishii and StadeIsSt13, Section 5].
Proposition 8.20. Let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with newform
$\operatorname {\mathrm {GL}}_n(F)$
with newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
. Then for all
$V_{\pi }$
. Then for all
![]() $h \in \operatorname {\mathrm {GL}}_n(F)$
and for
$h \in \operatorname {\mathrm {GL}}_n(F)$
and for
![]() $\Re (s)$
sufficiently large,
$\Re (s)$
sufficiently large,
 $$ \begin{align} \int_{\operatorname{\mathrm{GL}}_n(F)} f^{\circ}(hg) \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg = L(s,\pi) f^{\circ}(h), \end{align} $$
$$ \begin{align} \int_{\operatorname{\mathrm{GL}}_n(F)} f^{\circ}(hg) \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg = L(s,\pi) f^{\circ}(h), \end{align} $$
where
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is the standard Schwartz function
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is the standard Schwartz function
with
![]() $P^{\circ }$
the homogeneous harmonic polynomial associated to the newform K-type
$P^{\circ }$
the homogeneous harmonic polynomial associated to the newform K-type
![]() $\tau ^{\circ }$
of
$\tau ^{\circ }$
of
![]() $\pi $
via (7.2) and (7.8).
$\pi $
via (7.2) and (7.8).
In particular, the integral (8.21) converges absolutely if
![]() $\Re (s)> -\Re (t_j)$
for each
$\Re (s)> -\Re (t_j)$
for each
![]() ${j \in \{1,\ldots ,r\}}$
for which
${j \in \{1,\ldots ,r\}}$
for which
![]() $n_j = 1$
, so that
$n_j = 1$
, so that
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
![]() $\Re (s)> -\Re (t_j) + (\kappa _j - 1)/2$
for each
$\Re (s)> -\Re (t_j) + (\kappa _j - 1)/2$
for each
![]() $j \in \{1,\ldots ,r\}$
for which
$j \in \{1,\ldots ,r\}$
for which
![]() $n_j = 2$
, so that
$n_j = 2$
, so that
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
We may think of the integral (8.21) as defining a convolution section of
![]() $V_{\pi }$
in the sense of Jacquet [Reference Jacquet, Hida, Ramakrishnan and ShahidiJac04], where the convolution is with respect to the function
$V_{\pi }$
in the sense of Jacquet [Reference Jacquet, Hida, Ramakrishnan and ShahidiJac04], where the convolution is with respect to the function ![]() . (Note that Jacquet deals only with functions
. (Note that Jacquet deals only with functions
![]() $\phi : \operatorname {\mathrm {GL}}_n(F) \to \mathbb {C}$
that are smooth and compactly supported.) Alternatively, the identity (8.21) may be thought of as a Pieri-type formula, generalising [Reference IshiiIsh18, Theorem 3.8].
$\phi : \operatorname {\mathrm {GL}}_n(F) \to \mathbb {C}$
that are smooth and compactly supported.) Alternatively, the identity (8.21) may be thought of as a Pieri-type formula, generalising [Reference IshiiIsh18, Theorem 3.8].
Proof. Via the Iwasawa decomposition with respect to the standard Borel subgroup and (8.18), it suffices to show the identity (8.21) for
![]() $h = k \in K_n$
. We make the change of variables
$h = k \in K_n$
. We make the change of variables
![]() $g \mapsto k^{-1} g$
, then use the Iwasawa decomposition
$g \mapsto k^{-1} g$
, then use the Iwasawa decomposition
![]() $g = umk'$
with respect to the parabolic subgroup
$g = umk'$
with respect to the parabolic subgroup
![]() $\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)$
; the Haar measure becomes
$\mathrm {P}(F) = \mathrm {P}_{(n_1,\ldots ,n_r)}(F)$
; the Haar measure becomes
![]() $dg = \delta _{\mathrm {P}}^{-1}(m) \, du \, d^{\times }m \, dk'$
. We see that the left-hand side of (8.21) is
$dg = \delta _{\mathrm {P}}^{-1}(m) \, du \, d^{\times }m \, dk'$
. We see that the left-hand side of (8.21) is
 $$ \begin{align} \int_{\mathrm{M}_{\mathrm{P}}(F)} \left|\det m\right|{}^{s + \frac{n - 1}{2}} \delta_{\mathrm{P}}^{-1}(m) \int_{\mathrm{N}_{\mathrm{P}}(F)} \int_{K_n} f^{\circ}(umk') \Phi(k^{-1} umk') \, dk' \, du \, d^{\times} m. \end{align} $$
$$ \begin{align} \int_{\mathrm{M}_{\mathrm{P}}(F)} \left|\det m\right|{}^{s + \frac{n - 1}{2}} \delta_{\mathrm{P}}^{-1}(m) \int_{\mathrm{N}_{\mathrm{P}}(F)} \int_{K_n} f^{\circ}(umk') \Phi(k^{-1} umk') \, dk' \, du \, d^{\times} m. \end{align} $$
The absolute convergence of this integral for
![]() $\Re (s)$
sufficiently large is not difficult; it follows directly from the definitions (8.15) of the newform in the induced model and (8.22) of the standard Schwartz function
$\Re (s)$
sufficiently large is not difficult; it follows directly from the definitions (8.15) of the newform in the induced model and (8.22) of the standard Schwartz function
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
together with the bounds from [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Lemma 3.3 (ii)].
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
together with the bounds from [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Lemma 3.3 (ii)].
We may evaluate the integral over
![]() $K_n \ni k'$
in (8.23) by inserting (8.15) and (8.22) and using Lemmata 7.5 and 7.12. We subsequently make the change of variables
$K_n \ni k'$
in (8.23) by inserting (8.15) and (8.22) and using Lemmata 7.5 and 7.12. We subsequently make the change of variables
![]() $m_j \mapsto m_j k_j^{-1}$
, where
$m_j \mapsto m_j k_j^{-1}$
, where
![]() $m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r)$
, to trivially evaluate the integrals over
$m = \operatorname {\mathrm {blockdiag}}(m_1,\ldots ,m_r)$
, to trivially evaluate the integrals over
![]() $K_{n_j} \ni k_j$
, leading to
$K_{n_j} \ni k_j$
, leading to

We evaluate the integrals over
![]() $\mathrm {M}_{\mathrm {P}}(F) \ni m$
and
$\mathrm {M}_{\mathrm {P}}(F) \ni m$
and
![]() $\mathrm {N}_{\mathrm {P}}(F) \ni u$
in (8.24) by breaking these integrals up into parts, where this decomposition is dependent on the size of
$\mathrm {N}_{\mathrm {P}}(F) \ni u$
in (8.24) by breaking these integrals up into parts, where this decomposition is dependent on the size of
![]() $n_j \in \{1,2\}$
for
$n_j \in \{1,2\}$
for
![]() $j \in \{1,\ldots ,r\}$
. In doing so, we use the fact that
$j \in \{1,\ldots ,r\}$
. In doing so, we use the fact that ![]() and recall the definitions (8.13) and (8.12) of the polynomial
and recall the definitions (8.13) and (8.12) of the polynomial
![]() $P_{(n_1,\ldots ,n_r)}^{\circ }$
in order to write
$P_{(n_1,\ldots ,n_r)}^{\circ }$
in order to write
 $$\begin{align*}\dim \tau_1^{\circ} \cdots \dim \tau_r^{\circ} \overline{P_{(n_1,\ldots,n_r)}^{\circ}}(e_n g) = \prod_{j = 1}^{r} \dim \tau_j^{\circ} \begin{cases} \overline{P_j^{\circ}}(g_{n,\ell}) & \text{if }\ell = n_1 + \cdots + n_j\text{ and }\\&\pi_j = \chi^{\kappa_j} |\cdot|^{t_j}, \\ \overline{P_j^{\circ}}(g_{n,\ell},g_{n,\ell + 1}) & \text{if }\ell = n_1 + \cdots + n_j - 1\\&\text{and }\pi_j = D_{\kappa_j} \otimes \left|\det\right|{}^{t_j}. \end{cases}\end{align*}$$
$$\begin{align*}\dim \tau_1^{\circ} \cdots \dim \tau_r^{\circ} \overline{P_{(n_1,\ldots,n_r)}^{\circ}}(e_n g) = \prod_{j = 1}^{r} \dim \tau_j^{\circ} \begin{cases} \overline{P_j^{\circ}}(g_{n,\ell}) & \text{if }\ell = n_1 + \cdots + n_j\text{ and }\\&\pi_j = \chi^{\kappa_j} |\cdot|^{t_j}, \\ \overline{P_j^{\circ}}(g_{n,\ell},g_{n,\ell + 1}) & \text{if }\ell = n_1 + \cdots + n_j - 1\\&\text{and }\pi_j = D_{\kappa_j} \otimes \left|\det\right|{}^{t_j}. \end{cases}\end{align*}$$
We first deal with the case of
![]() $n_j = 1$
, so that
$n_j = 1$
, so that
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
; in this case, we evaluate the integrals over
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
; in this case, we evaluate the integrals over
![]() $F^{\times } \ni m_j$
and
$F^{\times } \ni m_j$
and
![]() $F \ni u_{i,\ell }$
with
$F \ni u_{i,\ell }$
with
![]() $i \in \{1,\ldots ,\ell - 1\}$
for
$i \in \{1,\ldots ,\ell - 1\}$
for
![]() $\ell = n_1 + \cdots + n_j$
. After making the change of variables
$\ell = n_1 + \cdots + n_j$
. After making the change of variables
![]() $u_{i,\ell } \mapsto m_j^{-1} u_{i,\ell }$
, recalling the definitions (8.6) of the newform in the induced model
$u_{i,\ell } \mapsto m_j^{-1} u_{i,\ell }$
, recalling the definitions (8.6) of the newform in the induced model
![]() $f_j^{\circ }$
and (7.3) and (7.9) of the polynomial
$f_j^{\circ }$
and (7.3) and (7.9) of the polynomial
![]() $P_j^{\circ }$
, and expanding this polynomial via the multinomial theorem, we are left with evaluating
$P_j^{\circ }$
, and expanding this polynomial via the multinomial theorem, we are left with evaluating
 $$ \begin{align*} &c_j^{\circ} \sum_{\nu_1 + \cdots + \nu_{\ell} = \|\kappa_j\|} \binom{\|\kappa_j\|}{\nu_1, \ldots, \nu_{\ell}} \prod_{i = 1}^{\ell} k_{i,n}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_i,0\}} \overline{k_{i,n}}^{-\min\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_i,0\}} \\ &\quad\times \int_{F^{\times}} \overline{m_j}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_{\ell},0\}} m_j^{- \min\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_{\ell},0\}} \chi^{\kappa_j}(m_j) |m_j|^{s + t_j} \exp\left(-d_F \pi m_j \overline{m_j}\right) \, dm_j \\ &\qquad\qquad\times \prod_{i = 1}^{\ell - 1} \int_F \overline{u_{i,\ell}}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_i,0\}} u_{i,\ell}^{-\min\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_i,0\}} \exp\left(-d_F \pi u_{i,\ell} \overline{u_{i,\ell}}\right) \, du_{i,\ell}. \end{align*} $$
$$ \begin{align*} &c_j^{\circ} \sum_{\nu_1 + \cdots + \nu_{\ell} = \|\kappa_j\|} \binom{\|\kappa_j\|}{\nu_1, \ldots, \nu_{\ell}} \prod_{i = 1}^{\ell} k_{i,n}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_i,0\}} \overline{k_{i,n}}^{-\min\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_i,0\}} \\ &\quad\times \int_{F^{\times}} \overline{m_j}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_{\ell},0\}} m_j^{- \min\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_{\ell},0\}} \chi^{\kappa_j}(m_j) |m_j|^{s + t_j} \exp\left(-d_F \pi m_j \overline{m_j}\right) \, dm_j \\ &\qquad\qquad\times \prod_{i = 1}^{\ell - 1} \int_F \overline{u_{i,\ell}}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_i,0\}} u_{i,\ell}^{-\min\{\operatorname{\mathrm{sgn}}(\kappa_j) \nu_i,0\}} \exp\left(-d_F \pi u_{i,\ell} \overline{u_{i,\ell}}\right) \, du_{i,\ell}. \end{align*} $$
Here,

denotes the multinomial coefficient for
![]() $\kappa ,\nu _1,\ldots ,\nu _{\ell } \in \mathbb {N}_0$
with
$\kappa ,\nu _1,\ldots ,\nu _{\ell } \in \mathbb {N}_0$
with
![]() $\nu _1 + \cdots + \nu _{\ell } = \kappa $
. The integral over
$\nu _1 + \cdots + \nu _{\ell } = \kappa $
. The integral over
![]() $F \ni u_{i,\ell }$
vanishes unless
$F \ni u_{i,\ell }$
vanishes unless
![]() $\nu _i = 0$
, in which case it is
$\nu _i = 0$
, in which case it is
![]() $1$
, upon applying Hecke’s identity, Lemmata 7.6 and 7.13. All that remains is the integral over
$1$
, upon applying Hecke’s identity, Lemmata 7.6 and 7.13. All that remains is the integral over
![]() $F^{\times } \ni m_j$
, which is equal to
$F^{\times } \ni m_j$
, which is equal to
having used the fact that
and recalling the definitions (7.3) and (7.9) of the polynomial
![]() $P_j^{\circ }$
, (2.7) and (2.10) of the L-function
$P_j^{\circ }$
, (2.7) and (2.10) of the L-function
![]() $L(s,\pi _j)$
in terms of
$L(s,\pi _j)$
in terms of
![]() $\zeta _F(s)$
, and (2.8) and (2.11) of the zeta function
$\zeta _F(s)$
, and (2.8) and (2.11) of the zeta function
![]() $\zeta _F(s)$
as an integral over
$\zeta _F(s)$
as an integral over
![]() $F^{\times }$
.
$F^{\times }$
.
Next, we deal with the case of
![]() $n_j = 2$
, so that
$n_j = 2$
, so that
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
; we evaluate the integrals over
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
; we evaluate the integrals over
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {R}) \ni m_j$
and
$\operatorname {\mathrm {GL}}_2(\mathbb {R}) \ni m_j$
and
![]() $\mathbb {R}^2 \ni (u_{i,\ell }, u_{i,\ell + 1})$
with
$\mathbb {R}^2 \ni (u_{i,\ell }, u_{i,\ell + 1})$
with
![]() $i \in \{1,\ldots ,\ell - 1\}$
for
$i \in \{1,\ldots ,\ell - 1\}$
for
![]() $\ell = n_1 + \cdots + n_j - 1$
. We write
$\ell = n_1 + \cdots + n_j - 1$
. We write ![]() for
for
![]() $u_{\ell ,\ell + 1} \in \mathbb {R}$
,
$u_{\ell ,\ell + 1} \in \mathbb {R}$
,
![]() $a_{\ell },a_{\ell + 1} \in \mathbb {R}^{\times }$
, and
$a_{\ell },a_{\ell + 1} \in \mathbb {R}^{\times }$
, and
![]() ${k' \in \operatorname {\mathrm {O}}(2)}$
; the Haar measure becomes
${k' \in \operatorname {\mathrm {O}}(2)}$
; the Haar measure becomes
![]() $dm_j = |a_{\ell }|^{-1} |a_{\ell + 1}| \, du_{\ell ,\ell + 1} \, d^{\times }a_{\ell } \, d^{\times }a_{\ell + 1} \, dk'$
. We use Schur orthogonality to evaluate the integral over
$dm_j = |a_{\ell }|^{-1} |a_{\ell + 1}| \, du_{\ell ,\ell + 1} \, d^{\times }a_{\ell } \, d^{\times }a_{\ell + 1} \, dk'$
. We use Schur orthogonality to evaluate the integral over
![]() $\operatorname {\mathrm {O}}(2) \ni k'$
and then make the change of variables
$\operatorname {\mathrm {O}}(2) \ni k'$
and then make the change of variables
![]() $u_{\ell ,\ell + 1} \mapsto a_{\ell + 1}^{-1} u_{\ell ,\ell + 1}$
,
$u_{\ell ,\ell + 1} \mapsto a_{\ell + 1}^{-1} u_{\ell ,\ell + 1}$
,
![]() $u_{i,\ell } \mapsto a_{\ell }^{-1} u_{i,\ell }$
, and
$u_{i,\ell } \mapsto a_{\ell }^{-1} u_{i,\ell }$
, and
![]() $u_{i,\ell + 1} \mapsto a_{\ell + 1}^{-1} u_{i,\ell + 1} - u_{\ell ,\ell + 1} u_{i,\ell }$
for
$u_{i,\ell + 1} \mapsto a_{\ell + 1}^{-1} u_{i,\ell + 1} - u_{\ell ,\ell + 1} u_{i,\ell }$
for
![]() $i \in \{1,\ldots ,\ell - 1\}$
. Recalling the definitions (8.7) of
$i \in \{1,\ldots ,\ell - 1\}$
. Recalling the definitions (8.7) of
![]() $f_j^{\circ }$
and (7.10) of
$f_j^{\circ }$
and (7.10) of
![]() $P_j^{\circ }$
, and expanding this polynomial via the multinomial theorem, we are led to
$P_j^{\circ }$
, and expanding this polynomial via the multinomial theorem, we are led to
 $$ \begin{align*} &\frac{c_j^{\circ}}{2} \sum_{\pm} \sum_{\nu_1 + \cdots + \nu_{\ell + 1} = \kappa_j} \binom{\kappa_j}{\nu_1, \ldots, \nu_{\ell + 1}} \prod_{i = 1}^{\ell + 1} k_{i,n}^{\nu_i} \\ &\qquad\qquad\qquad\quad\times \int_{\mathbb{R}^{\times}} a_{\ell + 1}^{\nu_{\ell + 1}} \chi^{\kappa_j}(a_{\ell + 1}) |a_{\ell + 1}|^{s + t_j - \frac{\kappa_j - 1}{2}} \exp\left(-\pi a_{\ell + 1}^2\right) d^{\times} a_{\ell + 1} \\ &\quad\times \int_{\mathbb{R}^{\times}} |a_{\ell}|^{s + t_j + \frac{\kappa_j - 1}{2}} \exp\left(-\pi a_{\ell}^2\right) \int_{\mathbb{R}} \left(u_{\ell,\ell + 1} \mp i a_{\ell}\right)^{\nu_{\ell}} \exp\left(-\pi u_{\ell,\ell + 1}^2\right) \, du_{\ell,\ell + 1} \, d^{\times} a_{\ell} \\ &\qquad\qquad\qquad\qquad\times \prod_{i = 1}^{\ell - 1} \int_{\mathbb{R}^2} \left(u_{i, \ell + 1} \mp i u_{i,\ell}\right)^{\nu_i} \exp\left(-\pi \left(u_{i,\ell}^2 + u_{i,\ell + 1}^2\right)\right) \, du_{i,\ell} \, du_{i,\ell + 1}. \end{align*} $$
$$ \begin{align*} &\frac{c_j^{\circ}}{2} \sum_{\pm} \sum_{\nu_1 + \cdots + \nu_{\ell + 1} = \kappa_j} \binom{\kappa_j}{\nu_1, \ldots, \nu_{\ell + 1}} \prod_{i = 1}^{\ell + 1} k_{i,n}^{\nu_i} \\ &\qquad\qquad\qquad\quad\times \int_{\mathbb{R}^{\times}} a_{\ell + 1}^{\nu_{\ell + 1}} \chi^{\kappa_j}(a_{\ell + 1}) |a_{\ell + 1}|^{s + t_j - \frac{\kappa_j - 1}{2}} \exp\left(-\pi a_{\ell + 1}^2\right) d^{\times} a_{\ell + 1} \\ &\quad\times \int_{\mathbb{R}^{\times}} |a_{\ell}|^{s + t_j + \frac{\kappa_j - 1}{2}} \exp\left(-\pi a_{\ell}^2\right) \int_{\mathbb{R}} \left(u_{\ell,\ell + 1} \mp i a_{\ell}\right)^{\nu_{\ell}} \exp\left(-\pi u_{\ell,\ell + 1}^2\right) \, du_{\ell,\ell + 1} \, d^{\times} a_{\ell} \\ &\qquad\qquad\qquad\qquad\times \prod_{i = 1}^{\ell - 1} \int_{\mathbb{R}^2} \left(u_{i, \ell + 1} \mp i u_{i,\ell}\right)^{\nu_i} \exp\left(-\pi \left(u_{i,\ell}^2 + u_{i,\ell + 1}^2\right)\right) \, du_{i,\ell} \, du_{i,\ell + 1}. \end{align*} $$
We use Hecke’s identity, Lemma 7.13, to see that the integral over
![]() $\mathbb {R}^2 \ni (u_{i,\ell },u_{i,\ell + 1})$
vanishes unless
$\mathbb {R}^2 \ni (u_{i,\ell },u_{i,\ell + 1})$
vanishes unless
![]() $\nu _i = 0$
, in which case it is
$\nu _i = 0$
, in which case it is
![]() $1$
; consequently, the only nonzero summands are those for which
$1$
; consequently, the only nonzero summands are those for which ![]() . For the integral over
. For the integral over
![]() $\mathbb {R} \ni u_{\ell ,\ell + 1}$
, we make the change of variables
$\mathbb {R} \ni u_{\ell ,\ell + 1}$
, we make the change of variables
![]() $u_{\ell ,\ell + 1} \mapsto u_{\ell ,\ell + 1} \pm ia_{\ell }$
and shift the contour of integration back to the line
$u_{\ell ,\ell + 1} \mapsto u_{\ell ,\ell + 1} \pm ia_{\ell }$
and shift the contour of integration back to the line
![]() $\Im (u_{\ell ,\ell + 1}) = 0$
via Cauchy’s integral theorem, for the integrand extends holomorphically to an entire function of the complex variable
$\Im (u_{\ell ,\ell + 1}) = 0$
via Cauchy’s integral theorem, for the integrand extends holomorphically to an entire function of the complex variable
![]() $u_{\ell ,\ell + 1}$
. Since
$u_{\ell ,\ell + 1}$
. Since
we arrive at
 $$ \begin{align*} &\ c_j^{\circ} \sum_{\substack{\nu = 0 \\ \nu \equiv 0 \ \pmod{2}}}^{\kappa_j} \binom{\kappa_j}{\nu} \left(i k_{\ell,n}\right)^{\nu} k_{\ell + 1,n}^{\kappa_j - \nu} \\ &\times (2\pi)^{-\nu} \int_{\mathbb{R}^{\times}} |a_{\ell + 1}|^{s + t_j + \frac{\kappa_j + 1}{2} - \nu} \exp\left(-\pi a_{\ell + 1}^2\right) d^{\times} a_{\ell + 1} \int_{\mathbb{R}^{\times}} |a_{\ell}|^{s + t_j + \frac{\kappa_j - 1}{2}} \frac{\partial^{\nu}}{\partial a_{\ell}^{\nu}} \exp\left(-\pi a_{\ell}^2\right) \, d^{\times} a_{\ell}, \end{align*} $$
$$ \begin{align*} &\ c_j^{\circ} \sum_{\substack{\nu = 0 \\ \nu \equiv 0 \ \pmod{2}}}^{\kappa_j} \binom{\kappa_j}{\nu} \left(i k_{\ell,n}\right)^{\nu} k_{\ell + 1,n}^{\kappa_j - \nu} \\ &\times (2\pi)^{-\nu} \int_{\mathbb{R}^{\times}} |a_{\ell + 1}|^{s + t_j + \frac{\kappa_j + 1}{2} - \nu} \exp\left(-\pi a_{\ell + 1}^2\right) d^{\times} a_{\ell + 1} \int_{\mathbb{R}^{\times}} |a_{\ell}|^{s + t_j + \frac{\kappa_j - 1}{2}} \frac{\partial^{\nu}}{\partial a_{\ell}^{\nu}} \exp\left(-\pi a_{\ell}^2\right) \, d^{\times} a_{\ell}, \end{align*} $$
having observed the vanishing of the integral over
![]() $\mathbb {R}^{\times } \ni a_{\ell + 1}$
for odd
$\mathbb {R}^{\times } \ni a_{\ell + 1}$
for odd
![]() $\nu $
. We integrate by parts
$\nu $
. We integrate by parts
![]() $\nu $
times with respect to
$\nu $
times with respect to
![]() $a_{\ell }$
and then integrate by parts
$a_{\ell }$
and then integrate by parts
![]() $\nu /2$
times with respect to
$\nu /2$
times with respect to
![]() $a_{\ell }$
, differentiating
$a_{\ell }$
, differentiating
![]() $\exp (-\pi a_{\ell }^2)$
, and
$\exp (-\pi a_{\ell }^2)$
, and
![]() $\nu /2$
times with respect to
$\nu /2$
times with respect to
![]() $a_{\ell + 1}$
, differentiating
$a_{\ell + 1}$
, differentiating
![]() $\exp (-\pi a_{\ell + 1}^2)$
. We end up at
$\exp (-\pi a_{\ell + 1}^2)$
. We end up at
 $$ \begin{align*} c_j^{\circ} &\sum_{\substack{\nu = 0 \\ \nu \equiv 0 \ \pmod{2}}}^{\kappa_j} \binom{\kappa_j}{\nu} \left(i k_{\ell,n}\right)^{\nu} k_{\ell + 1,n}^{\kappa_j - \nu} \\ &\times \int_{\mathbb{R}^{\times}} |a_{\ell + 1}|^{s + t_j + \frac{\kappa_j + 1}{2}} \exp\left(-\pi a_{\ell + 1}^2\right) d^{\times} a_{\ell + 1} \int_{\mathbb{R}^{\times}} |a_{\ell}|^{s + t_j + \frac{\kappa_j - 1}{2}} \exp\left(-\pi a_{\ell}^2\right) \, d^{\times} a_{\ell} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= c_j^{\circ} L(s,\pi_j) \overline{P_j^{\circ}}\left(\overline{k_{\ell,n}}, \overline{k_{\ell + 1,n}}\right), \end{align*} $$
$$ \begin{align*} c_j^{\circ} &\sum_{\substack{\nu = 0 \\ \nu \equiv 0 \ \pmod{2}}}^{\kappa_j} \binom{\kappa_j}{\nu} \left(i k_{\ell,n}\right)^{\nu} k_{\ell + 1,n}^{\kappa_j - \nu} \\ &\times \int_{\mathbb{R}^{\times}} |a_{\ell + 1}|^{s + t_j + \frac{\kappa_j + 1}{2}} \exp\left(-\pi a_{\ell + 1}^2\right) d^{\times} a_{\ell + 1} \int_{\mathbb{R}^{\times}} |a_{\ell}|^{s + t_j + \frac{\kappa_j - 1}{2}} \exp\left(-\pi a_{\ell}^2\right) \, d^{\times} a_{\ell} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= c_j^{\circ} L(s,\pi_j) \overline{P_j^{\circ}}\left(\overline{k_{\ell,n}}, \overline{k_{\ell + 1,n}}\right), \end{align*} $$
again recalling the definitions (7.10) of
![]() $P_j^{\circ }$
, (2.13) of
$P_j^{\circ }$
, (2.13) of
![]() $L(s,\pi _j)$
in terms of products of
$L(s,\pi _j)$
in terms of products of
![]() $\zeta _F(s)$
, and (2.11) of
$\zeta _F(s)$
, and (2.11) of
![]() $\zeta _F(s)$
as an integral over
$\zeta _F(s)$
as an integral over
![]() $F^{\times }$
.
$F^{\times }$
.
Combining these calculations, we find that
 $$ \begin{align*} &\int_{\operatorname{\mathrm{GL}}_n(F)} f^{\circ}(kg) \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg \\ &\qquad = c^{\circ} \prod_{j = 1}^{r} c_j^{\circ} L(s,\pi_j) \begin{cases} \overline{P_j^{\circ}}(\overline{k_{\ell,n}}) & \text{if }\ell = n_1 + \cdots + n_j\text{ and }\pi_j = \chi^{\kappa_j} |\cdot|^{t_j}, \\ \overline{P_j^{\circ}}(\overline{k_{\ell,n}},\overline{k_{\ell + 1,n}}) & \text{if }\ell = n_1 + \cdots + n_j - 1\text{ and }\pi_j = D_{\kappa_j} \otimes \left|\det\right|{}^{t_j}, \end{cases} \end{align*} $$
$$ \begin{align*} &\int_{\operatorname{\mathrm{GL}}_n(F)} f^{\circ}(kg) \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg \\ &\qquad = c^{\circ} \prod_{j = 1}^{r} c_j^{\circ} L(s,\pi_j) \begin{cases} \overline{P_j^{\circ}}(\overline{k_{\ell,n}}) & \text{if }\ell = n_1 + \cdots + n_j\text{ and }\pi_j = \chi^{\kappa_j} |\cdot|^{t_j}, \\ \overline{P_j^{\circ}}(\overline{k_{\ell,n}},\overline{k_{\ell + 1,n}}) & \text{if }\ell = n_1 + \cdots + n_j - 1\text{ and }\pi_j = D_{\kappa_j} \otimes \left|\det\right|{}^{t_j}, \end{cases} \end{align*} $$
which is precisely
![]() $L(s,\pi ) f^{\circ }(k)$
via the isobaric decomposition (2.5) of
$L(s,\pi ) f^{\circ }(k)$
via the isobaric decomposition (2.5) of
![]() $L(s,\pi )$
and the identity (8.19) for
$L(s,\pi )$
and the identity (8.19) for
![]() $f^{\circ }(k)$
.
$f^{\circ }(k)$
.
Finally, an inspection of the proof above shows that the integral (8.24) converges absolutely if
![]() $\Re (s)> -\Re (t_j)$
for each
$\Re (s)> -\Re (t_j)$
for each
![]() $j \in \{1,\ldots ,r\}$
for which
$j \in \{1,\ldots ,r\}$
for which
![]() $n_j = 1$
and
$n_j = 1$
and
![]() $\Re (s)> -\Re (t_j) + (\kappa _j - 1)/2$
for each
$\Re (s)> -\Re (t_j) + (\kappa _j - 1)/2$
for each
![]() $j \in \{1,\ldots ,r\}$
for which
$j \in \{1,\ldots ,r\}$
for which
![]() $n_j = 2$
.
$n_j = 2$
.
We may use the identity (8.21) to prove Theorem 4.23, thereby resolving the test vector problem for archimedean Godement–Jacquet zeta integrals.
Proof of Theorem 4.23
From the definition (2.3) of the Godement–Jacquet zeta integral and Proposition 8.20, we have that
 $$ \begin{align*} Z(s,\beta,\Phi) & = \int_{\operatorname{\mathrm{GL}}_n(F)} \left\langle \pi(g) \cdot v^{\circ}, \widetilde{v}^{\circ} \right\rangle \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg \\ & = \left\langle \int_{\operatorname{\mathrm{GL}}_n(F)} \left(\pi(g) \cdot v^{\circ}\right) \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg, \widetilde{v}^{\circ} \right\rangle \\ & = \left\langle L(s,\pi) v^{\circ}, \widetilde{v}^{\circ} \right\rangle \\ & = L(s,\pi) \left\langle v^{\circ}, \widetilde{v}^{\circ} \right\rangle \\ & = L(s,\pi).\\[-36pt] \end{align*} $$
$$ \begin{align*} Z(s,\beta,\Phi) & = \int_{\operatorname{\mathrm{GL}}_n(F)} \left\langle \pi(g) \cdot v^{\circ}, \widetilde{v}^{\circ} \right\rangle \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg \\ & = \left\langle \int_{\operatorname{\mathrm{GL}}_n(F)} \left(\pi(g) \cdot v^{\circ}\right) \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg, \widetilde{v}^{\circ} \right\rangle \\ & = \left\langle L(s,\pi) v^{\circ}, \widetilde{v}^{\circ} \right\rangle \\ & = L(s,\pi) \left\langle v^{\circ}, \widetilde{v}^{\circ} \right\rangle \\ & = L(s,\pi).\\[-36pt] \end{align*} $$
A similar calculation to that of the proof of Proposition 8.20 yields the following.
Proposition 8.26. Let
![]() $\pi $
be an induced representation of Whittaker type of
$\pi $
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with newform
$\operatorname {\mathrm {GL}}_n(F)$
with newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
. Define
$V_{\pi }$
. Define ![]() . Then for all
. Then for all
![]() $h \in \operatorname {\mathrm {GL}}_n(F)$
and for
$h \in \operatorname {\mathrm {GL}}_n(F)$
and for
![]() $\Re (s)$
sufficiently large,
$\Re (s)$
sufficiently large,
 $$ \begin{align} \int_{\operatorname{\mathrm{GL}}_n(F)} \widetilde{f}^{\circ}(hg) \widetilde{\Phi}(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg = L(s,\widetilde{\pi}) \widetilde{f}^{\circ}(h), \end{align} $$
$$ \begin{align} \int_{\operatorname{\mathrm{GL}}_n(F)} \widetilde{f}^{\circ}(hg) \widetilde{\Phi}(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg = L(s,\widetilde{\pi}) \widetilde{f}^{\circ}(h), \end{align} $$
where
![]() $\widetilde {\Phi } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is the standard Schwartz function
$\widetilde {\Phi } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is the standard Schwartz function
with
![]() $P^{\circ }$
the homogeneous harmonic polynomial associated to the newform K-type
$P^{\circ }$
the homogeneous harmonic polynomial associated to the newform K-type
![]() $\tau ^{\circ }$
of
$\tau ^{\circ }$
of
![]() $\pi $
via (7.2) and (7.8).
$\pi $
via (7.2) and (7.8).
In particular, the integral (8.27) converges absolutely if
![]() $\Re (s)> \Re (t_j)$
for each
$\Re (s)> \Re (t_j)$
for each
![]() $j \in \{1,\ldots ,r\}$
for which
$j \in \{1,\ldots ,r\}$
for which
![]() $n_j = 1$
, so that
$n_j = 1$
, so that
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
![]() $\Re (s)> \Re (t_j) + (\kappa _j - 1)/2$
for each
$\Re (s)> \Re (t_j) + (\kappa _j - 1)/2$
for each
![]() ${j \in \{1,\ldots ,r\}}$
for which
${j \in \{1,\ldots ,r\}}$
for which
![]() $n_j = 2$
, so that
$n_j = 2$
, so that
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
Remark 8.29. From (8.27), we see that
![]() $Z(s,\widetilde {\beta },\widetilde {\Phi }) = L(s,\widetilde {\pi })$
, where
$Z(s,\widetilde {\beta },\widetilde {\Phi }) = L(s,\widetilde {\pi })$
, where ![]() . This is in perfect accordance with the local functional equation (2.15) upon noting that
. This is in perfect accordance with the local functional equation (2.15) upon noting that
![]() ${\widetilde {\Phi } = i^{c(\pi )} \widehat {\Phi }}$
via Hecke’s identity, Lemmata 7.6 and 7.13.
${\widetilde {\Phi } = i^{c(\pi )} \widehat {\Phi }}$
via Hecke’s identity, Lemmata 7.6 and 7.13.
8.4. The newform via Godement sections
Our third description of the newform in the induced model is via Godement sections. This is a recursive formula for the newform
![]() $f^{\circ }$
of
$f^{\circ }$
of
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
in terms of an integral involving the newform
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
in terms of an integral involving the newform
![]() $f_0^{\circ }$
of
$f_0^{\circ }$
of ![]() and a distinguished standard Schwartz function. Unlike our earlier descriptions of
and a distinguished standard Schwartz function. Unlike our earlier descriptions of
![]() $f^{\circ }$
via the Iwasawa decomposition and via convolution sections, this description via Godement sections is only valid for certain induced representations of Whittaker type; we require the parameter
$f^{\circ }$
via the Iwasawa decomposition and via convolution sections, this description via Godement sections is only valid for certain induced representations of Whittaker type; we require the parameter
![]() $t_1$
associated to
$t_1$
associated to
![]() $\pi _1$
to have sufficiently large real part. When we proceed to studying the Whittaker newform, we remove this condition via analytic continuation.
$\pi _1$
to have sufficiently large real part. When we proceed to studying the Whittaker newform, we remove this condition via analytic continuation.
8.4.1. The case
 $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
We first consider the case for which
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
![]() $n_1 = 1$
, so that
$n_1 = 1$
, so that
![]() $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
. We begin with a simple modification of Proposition 8.14.
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
. We begin with a simple modification of Proposition 8.14.
Lemma 8.30. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Whittaker type of
be induced representations of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
with
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
with
![]() $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
. Let
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
. Let
![]() $f_0^{\circ }$
be the newform of
$f_0^{\circ }$
be the newform of
![]() $\pi _0$
in the induced model
$\pi _0$
in the induced model
![]() $V_{\pi _0}$
. Then for
$V_{\pi _0}$
. Then for
![]() $v \in \operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F)$
,
$v \in \operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F)$
,
![]() $x \in F^{\times }$
,
$x \in F^{\times }$
,
![]() $h \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
and
$h \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
and
![]() $k \in K_n$
, the newform
$k \in K_n$
, the newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
satisfies
$V_{\pi }$
satisfies
 $$\begin{align} &f^{\circ}\left(\begin{pmatrix} 1 & v \\ 0 & 1_{n - 1} \end{pmatrix} \begin{pmatrix} x & 0 \\ 0 & h \end{pmatrix} k\right) = \frac{c^{\circ}}{c_0^{\circ}} (\dim \tau_0^{\circ}) |x|^{\frac{n - 1}{2}} \left|\det h\right|{}^{-\frac{1}{2}} \nonumber\\ &\qquad\qquad\qquad \times \int_{K_1} \int_{K_{n - 1}} \chi^{\kappa_1}(x k_1) |x k_1|^{t_1} f_0^{\circ}(h k_2) \overline{P_{(1,n - 1)}^{\circ}}\left(e_n k^{-1} \begin{pmatrix} k_1 & 0 \\ 0 & k_2 \end{pmatrix}\right) \, dk_2 \, dk_1. \end{align} $$
$$\begin{align} &f^{\circ}\left(\begin{pmatrix} 1 & v \\ 0 & 1_{n - 1} \end{pmatrix} \begin{pmatrix} x & 0 \\ 0 & h \end{pmatrix} k\right) = \frac{c^{\circ}}{c_0^{\circ}} (\dim \tau_0^{\circ}) |x|^{\frac{n - 1}{2}} \left|\det h\right|{}^{-\frac{1}{2}} \nonumber\\ &\qquad\qquad\qquad \times \int_{K_1} \int_{K_{n - 1}} \chi^{\kappa_1}(x k_1) |x k_1|^{t_1} f_0^{\circ}(h k_2) \overline{P_{(1,n - 1)}^{\circ}}\left(e_n k^{-1} \begin{pmatrix} k_1 & 0 \\ 0 & k_2 \end{pmatrix}\right) \, dk_2 \, dk_1. \end{align} $$
Here, the constants
![]() $c^{\circ }$
and
$c^{\circ }$
and
![]() $c_0^{\circ }$
are those associated to
$c_0^{\circ }$
are those associated to
![]() $f^{\circ }$
and
$f^{\circ }$
and
![]() $f_0^{\circ }$
via (8.15), while
$f_0^{\circ }$
via (8.15), while
where
![]() $P_1^{\circ }$
and
$P_1^{\circ }$
and
![]() $P_0^{\circ }$
are the homogeneous harmonic polynomials associated to the newform K-types
$P_0^{\circ }$
are the homogeneous harmonic polynomials associated to the newform K-types
![]() $\tau _1^{\circ }$
and
$\tau _1^{\circ }$
and
![]() $\tau _0^{\circ }$
of
$\tau _0^{\circ }$
of
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _0$
, respectively, via (7.2) and (7.8).
$\pi _0$
, respectively, via (7.2) and (7.8).
Proof. We show that (8.31) reproduces Corollary 8.17, which determines
![]() $f^{\circ }$
completely. Writing
$f^{\circ }$
completely. Writing
![]() $P_{(1,n - 1)}^{\circ } = P_1^{\circ } P_0^{\circ }$
, we see that the integral over
$P_{(1,n - 1)}^{\circ } = P_1^{\circ } P_0^{\circ }$
, we see that the integral over
![]() $K_1 \ni k_1$
is trivial by the homogeneity of
$K_1 \ni k_1$
is trivial by the homogeneity of
![]() $P_1^{\circ }$
and (8.25). We then use the Iwasawa decomposition
$P_1^{\circ }$
and (8.25). We then use the Iwasawa decomposition
![]() $h = u' a' k'$
with respect to the standard Borel subgroup, so that
$h = u' a' k'$
with respect to the standard Borel subgroup, so that
![]() $u' \in \mathrm {N}_{n - 1}(F)$
,
$u' \in \mathrm {N}_{n - 1}(F)$
,
![]() $a' = \operatorname {\mathrm {diag}}(a_1^{\prime },\ldots ,a_{n - 1}^{\prime }) \in \mathrm {A}_{n - 1}(F)$
and
$a' = \operatorname {\mathrm {diag}}(a_1^{\prime },\ldots ,a_{n - 1}^{\prime }) \in \mathrm {A}_{n - 1}(F)$
and
![]() $k' \in K_{n - 1}$
, and we apply Corollary 8.17 in order to rewrite
$k' \in K_{n - 1}$
, and we apply Corollary 8.17 in order to rewrite
![]() $f_0^{\circ }(hk_2)$
. The integral over
$f_0^{\circ }(hk_2)$
. The integral over
![]() $K_{n - 1} \ni k_2$
may then be evaluated via Lemmata 7.5 and 7.12. The resulting expression for
$K_{n - 1} \ni k_2$
may then be evaluated via Lemmata 7.5 and 7.12. The resulting expression for
![]() $f^{\circ }$
is then precisely that given in Corollary 8.17 with
$f^{\circ }$
is then precisely that given in Corollary 8.17 with ![]() ,
,
![]() $a = \operatorname {\mathrm {diag}}(x,a_1^{\prime },\ldots ,a_{n - 1}^{\prime }) \in \mathrm {A}_n(F)$
and
$a = \operatorname {\mathrm {diag}}(x,a_1^{\prime },\ldots ,a_{n - 1}^{\prime }) \in \mathrm {A}_n(F)$
and ![]() in place of k.
in place of k.
We now use the identity (8.31) in conjunction with the convolution section (8.27) in order to prove that
![]() $f^{\circ }$
may be written as a Godement section.
$f^{\circ }$
may be written as a Godement section.
Proposition 8.32. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Whittaker type of
be induced representations of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
with
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
with
![]() $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
. Let
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
. Let
![]() $f_0^{\circ }$
be the newform of
$f_0^{\circ }$
be the newform of
![]() $\pi _0$
in the induced model
$\pi _0$
in the induced model
![]() $V_{\pi _0}$
. Let
$V_{\pi _0}$
. Let
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(F))$
be the standard Schwartz function of the form
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(F))$
be the standard Schwartz function of the form

where
![]() $P_1^{\circ }$
and
$P_1^{\circ }$
and
![]() $P_0^{\circ }$
are the homogeneous harmonic polynomials associated to the newform K-types
$P_0^{\circ }$
are the homogeneous harmonic polynomials associated to the newform K-types
![]() $\tau _1^{\circ }$
and
$\tau _1^{\circ }$
and
![]() $\tau _0^{\circ }$
of
$\tau _0^{\circ }$
of
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _0$
, respectively, via (7.2) and (7.8). Then if
$\pi _0$
, respectively, via (7.2) and (7.8). Then if
![]() $\Re (t_1)$
is sufficiently large, the newform
$\Re (t_1)$
is sufficiently large, the newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
satisfies the identity
$V_{\pi }$
satisfies the identity
 $$ \begin{align} &f^{\circ}(g) = \frac{c^{\circ} (-1)^{\kappa_1(n - 1)}}{c_0^{\circ} L\left(1 + t_1 + \frac{\|\kappa_1\|}{d_F}, \widetilde{\pi_0}\right)} \chi^{\kappa_1}(\det g) \left|\det g\right|{}^{t_1 + \frac{n - 1}{2}} \nonumber\\ &\qquad\qquad\qquad\times \int_{\operatorname{\mathrm{GL}}_{n - 1}(F)} f_0^{\circ}(h) \Phi\left(h^{-1} \begin{pmatrix} 0 & 1_{n - 1} \end{pmatrix} g\right) \chi^{-\kappa_1}(\det h) \left|\det h\right|{}^{-t_1 - \frac{n}{2}} \, dh, \end{align} $$
$$ \begin{align} &f^{\circ}(g) = \frac{c^{\circ} (-1)^{\kappa_1(n - 1)}}{c_0^{\circ} L\left(1 + t_1 + \frac{\|\kappa_1\|}{d_F}, \widetilde{\pi_0}\right)} \chi^{\kappa_1}(\det g) \left|\det g\right|{}^{t_1 + \frac{n - 1}{2}} \nonumber\\ &\qquad\qquad\qquad\times \int_{\operatorname{\mathrm{GL}}_{n - 1}(F)} f_0^{\circ}(h) \Phi\left(h^{-1} \begin{pmatrix} 0 & 1_{n - 1} \end{pmatrix} g\right) \chi^{-\kappa_1}(\det h) \left|\det h\right|{}^{-t_1 - \frac{n}{2}} \, dh, \end{align} $$
where the constants
![]() $c^{\circ }$
and
$c^{\circ }$
and
![]() $c_0^{\circ }$
are those associated to
$c_0^{\circ }$
are those associated to
![]() $f^{\circ }$
and
$f^{\circ }$
and
![]() $f_0^{\circ }$
via (8.15).
$f_0^{\circ }$
via (8.15).
In particular, the integral (8.33) converges absolutely if
![]() $\Re (t_1)> \Re (t_j) - 1 - \|\kappa _1\|/d_F$
for each
$\Re (t_1)> \Re (t_j) - 1 - \|\kappa _1\|/d_F$
for each
![]() $j \in \{2,\ldots ,r\}$
for which
$j \in \{2,\ldots ,r\}$
for which
![]() $n_j = 1$
, so that
$n_j = 1$
, so that
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
![]() $\Re (t_1)> \Re (t_j) + (\kappa _j - 1)/2 - 1 - \kappa _1$
for each
$\Re (t_1)> \Re (t_j) + (\kappa _j - 1)/2 - 1 - \kappa _1$
for each
![]() $j \in \{2,\ldots ,r\}$
for which
$j \in \{2,\ldots ,r\}$
for which
![]() $n_j = 2$
, so that
$n_j = 2$
, so that
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
Proof. We take
![]() $s = 1 + t_1 + \|\kappa _1\|/d_F$
in the convolution section identity (8.27), so that
$s = 1 + t_1 + \|\kappa _1\|/d_F$
in the convolution section identity (8.27), so that

with
![]() $\widetilde {\Phi }$
as in (8.28). We make the change of variables
$\widetilde {\Phi }$
as in (8.28). We make the change of variables ![]() and use the Iwasawa decomposition
and use the Iwasawa decomposition
![]() $g' = umk$
with respect to the parabolic subgroup
$g' = umk$
with respect to the parabolic subgroup
![]() $\mathrm {P}(F) = \mathrm {P}_{(1,n - 1)}(F)$
, where
$\mathrm {P}(F) = \mathrm {P}_{(1,n - 1)}(F)$
, where ![]() with
with
![]() $v \in \operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F)$
,
$v \in \operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F)$
, ![]() with
with
![]() $x \in F^{\times }$
and
$x \in F^{\times }$
and
![]() $h \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
, and
$h \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
, and
![]() $k \in K_n$
; the Haar measure is
$k \in K_n$
; the Haar measure is
![]() $dg' = |x|^{1 - n} \left |\det h\right | \, dv \, d^{\times }x \, dh \, dk$
. We may now insert the identity (8.31) for
$dg' = |x|^{1 - n} \left |\det h\right | \, dv \, d^{\times }x \, dh \, dk$
. We may now insert the identity (8.31) for
![]() $f^{\circ }$
. Next, we make the change of variables
$f^{\circ }$
. Next, we make the change of variables
![]() $x \mapsto x k_1^{-1}$
,
$x \mapsto x k_1^{-1}$
,
![]() $h \mapsto h k_2^{-1}$
, and
$h \mapsto h k_2^{-1}$
, and ![]() , so that the integrals over
, so that the integrals over
![]() $K_1 \ni k_1$
and
$K_1 \ni k_1$
and
![]() $K_{n - 1} \ni k_2$
are trivial; subsequently, the integral over
$K_{n - 1} \ni k_2$
are trivial; subsequently, the integral over
![]() $K_n \ni k$
may be evaluated via Lemmata 7.5 and 7.12 after inserting the definition (8.28) of
$K_n \ni k$
may be evaluated via Lemmata 7.5 and 7.12 after inserting the definition (8.28) of
![]() $\widetilde {\Phi }$
. After making the change of variables
$\widetilde {\Phi }$
. After making the change of variables
![]() $v \mapsto -xv$
and
$v \mapsto -xv$
and
![]() $x \mapsto x^{-1}$
, we write
$x \mapsto x^{-1}$
, we write ![]() , so that
, so that
![]() $dv' = \zeta _F(1)^{-1} |x| \, d^{\times }x \, dv$
, and we make the change of variables
$dv' = \zeta _F(1)^{-1} |x| \, d^{\times }x \, dv$
, and we make the change of variables
![]() $v' \mapsto v' g^{-1}$
. Finally, we use (8.25) in conjunction with the homogeneity of
$v' \mapsto v' g^{-1}$
. Finally, we use (8.25) in conjunction with the homogeneity of
![]() $P_1^{\circ }$
and the fact that
$P_1^{\circ }$
and the fact that
 $$\begin{align*}L\left(1 + t_1 + \frac{\|\kappa_1\|}{d_F}, \widetilde{\pi}\right) = \zeta_F\left(1 + \frac{2\|\kappa_1\|}{d_F}\right) L\left(1 + t_1 + \frac{\|\kappa_1\|}{d_F}, \widetilde{\pi_0}\right)\end{align*}$$
$$\begin{align*}L\left(1 + t_1 + \frac{\|\kappa_1\|}{d_F}, \widetilde{\pi}\right) = \zeta_F\left(1 + \frac{2\|\kappa_1\|}{d_F}\right) L\left(1 + t_1 + \frac{\|\kappa_1\|}{d_F}, \widetilde{\pi_0}\right)\end{align*}$$
via (2.5), (2.9) and (2.12). We arrive at the identity

having recalled that the adjugate of g is ![]() . To evaluate the last line of (8.34), we expand
. To evaluate the last line of (8.34), we expand
![]() $\overline {P_1^{\circ }}$
as a polynomial in
$\overline {P_1^{\circ }}$
as a polynomial in
![]() $v_1^{\prime },\ldots ,v_n^{\prime }$
via the multinomial theorem, yielding
$v_1^{\prime },\ldots ,v_n^{\prime }$
via the multinomial theorem, yielding
 $$ \begin{align*} &\frac{\zeta_F(1)}{\zeta_F\left(1 + \frac{2\|\kappa_1\|}{d_F}\right)} (\overline{\det h^{-1}})^{\max\{\kappa_1,0\}} (\det h^{-1})^{-\min\{\kappa_1,0\}} \sum_{\nu_1 + \cdots + \nu_n = \|\kappa_1\|} \binom{\|\kappa_1\|}{\nu_1, \ldots, \nu_n} \\ &\qquad\qquad\quad\times \prod_{i = 1}^{n} (\overline{\operatorname{\mathrm{adj}}(g)_{i,1}})^{\max\{\operatorname{\mathrm{sgn}}(\kappa_1) \nu_i,0\}} (\operatorname{\mathrm{adj}}(g)_{i,1})^{-\min\{\operatorname{\mathrm{sgn}}(\kappa_1) \nu_i,0\}} \\ &\qquad\times \prod_{i = 1}^{n - 1} \int_F \overline{v_i^{\prime}}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_1) \nu_i,0\}} {v_i^{\prime}}^{- \min\{\operatorname{\mathrm{sgn}}(\kappa_1) \nu_i,0\}} \exp\left(-d_F \pi v_i^{\prime} \overline{v_i^{\prime}}\right) \, dv_i^{\prime} \\ &\quad\times \int_F \overline{v_n^{\prime}}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_1)\nu_n,0\} - \min\{\kappa_1,0\}} {v_n^{\prime}}^{-\min\{\operatorname{\mathrm{sgn}}(\kappa_1)\nu_n,0\} + \max\{\kappa_1,0\}} \exp\left(-d_F \pi v_n^{\prime} \overline{v_n^{\prime}}\right) \, dv_n^{\prime}. \end{align*} $$
$$ \begin{align*} &\frac{\zeta_F(1)}{\zeta_F\left(1 + \frac{2\|\kappa_1\|}{d_F}\right)} (\overline{\det h^{-1}})^{\max\{\kappa_1,0\}} (\det h^{-1})^{-\min\{\kappa_1,0\}} \sum_{\nu_1 + \cdots + \nu_n = \|\kappa_1\|} \binom{\|\kappa_1\|}{\nu_1, \ldots, \nu_n} \\ &\qquad\qquad\quad\times \prod_{i = 1}^{n} (\overline{\operatorname{\mathrm{adj}}(g)_{i,1}})^{\max\{\operatorname{\mathrm{sgn}}(\kappa_1) \nu_i,0\}} (\operatorname{\mathrm{adj}}(g)_{i,1})^{-\min\{\operatorname{\mathrm{sgn}}(\kappa_1) \nu_i,0\}} \\ &\qquad\times \prod_{i = 1}^{n - 1} \int_F \overline{v_i^{\prime}}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_1) \nu_i,0\}} {v_i^{\prime}}^{- \min\{\operatorname{\mathrm{sgn}}(\kappa_1) \nu_i,0\}} \exp\left(-d_F \pi v_i^{\prime} \overline{v_i^{\prime}}\right) \, dv_i^{\prime} \\ &\quad\times \int_F \overline{v_n^{\prime}}^{\max\{\operatorname{\mathrm{sgn}}(\kappa_1)\nu_n,0\} - \min\{\kappa_1,0\}} {v_n^{\prime}}^{-\min\{\operatorname{\mathrm{sgn}}(\kappa_1)\nu_n,0\} + \max\{\kappa_1,0\}} \exp\left(-d_F \pi v_n^{\prime} \overline{v_n^{\prime}}\right) \, dv_n^{\prime}. \end{align*} $$
Via Hecke’s identity, Lemmata 7.6 and 7.13, the integral over
![]() $F \ni v_n^{\prime }$
vanishes unless
$F \ni v_n^{\prime }$
vanishes unless
![]() $\nu _1 = \cdots = \nu _{n - 1} = 0$
and
$\nu _1 = \cdots = \nu _{n - 1} = 0$
and
![]() $\nu _n = \|\kappa _1\|$
, in which case the integral over
$\nu _n = \|\kappa _1\|$
, in which case the integral over
![]() $F \ni v_i^{\prime }$
for
$F \ni v_i^{\prime }$
for
![]() $i \in \{1,\ldots ,n - 1\}$
is equal to
$i \in \{1,\ldots ,n - 1\}$
is equal to
![]() $1$
. Via (8.25) and the fact that
$1$
. Via (8.25) and the fact that
![]() $\zeta _F(1) |v_n^{\prime }|^{-1} \, dv_n^{\prime } = d^{\times }v_n^{\prime }$
, we are left with
$\zeta _F(1) |v_n^{\prime }|^{-1} \, dv_n^{\prime } = d^{\times }v_n^{\prime }$
, we are left with
 $$\begin{align*}\frac{\overline{P_1^{\circ}}\left((\det h^{-1}) \operatorname{\mathrm{adj}}(g)_{n,1}\right)}{\zeta_F\left(1 + \frac{2\|\kappa_1\|}{d_F}\right)} \int_{F^{\times}} |v_n^{\prime}|^{1 + \frac{2\|\kappa_1\|}{d_F}} \exp\left(-d_F \pi v_n^{\prime} \overline{v_n^{\prime}}\right) \, d^{\times}v_n^{\prime} = \overline{P_1^{\circ}}\left((\det h^{-1}) \operatorname{\mathrm{adj}}(g)_{n,1}\right)\end{align*}$$
$$\begin{align*}\frac{\overline{P_1^{\circ}}\left((\det h^{-1}) \operatorname{\mathrm{adj}}(g)_{n,1}\right)}{\zeta_F\left(1 + \frac{2\|\kappa_1\|}{d_F}\right)} \int_{F^{\times}} |v_n^{\prime}|^{1 + \frac{2\|\kappa_1\|}{d_F}} \exp\left(-d_F \pi v_n^{\prime} \overline{v_n^{\prime}}\right) \, d^{\times}v_n^{\prime} = \overline{P_1^{\circ}}\left((\det h^{-1}) \operatorname{\mathrm{adj}}(g)_{n,1}\right)\end{align*}$$
 $$\begin{align*}\operatorname{\mathrm{adj}}(g)_{n,1} = (-1)^{n - 1} \det \left(\begin{pmatrix} 0 & 1_{n - 1}\end{pmatrix} g \begin{pmatrix} 1_{n - 1} \\ 0 \end{pmatrix}\right),\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{adj}}(g)_{n,1} = (-1)^{n - 1} \det \left(\begin{pmatrix} 0 & 1_{n - 1}\end{pmatrix} g \begin{pmatrix} 1_{n - 1} \\ 0 \end{pmatrix}\right),\end{align*}$$
the result then follows from (8.34) and the homogeneity of
![]() $P_1^{\circ }$
.
$P_1^{\circ }$
.
8.4.2. The case
 $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
Next, we give a description of the newform in the induced model when
![]() $F = \mathbb {R}$
,
$F = \mathbb {R}$
,
![]() $n_1 = 2$
and
$n_1 = 2$
and
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
is an essentially discrete series representation. We do this first when
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
is an essentially discrete series representation. We do this first when
![]() $n = 2$
, so that
$n = 2$
, so that
![]() $\pi = \pi _1$
.
$\pi = \pi _1$
.
Proposition 8.35. Let
![]() $\pi = D_{\kappa } \otimes \left |\det \right |{}^{t}$
be an essentially discrete series representation of
$\pi = D_{\kappa } \otimes \left |\det \right |{}^{t}$
be an essentially discrete series representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {R})$
. Let
$\operatorname {\mathrm {GL}}_2(\mathbb {R})$
. Let
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times 2}(\mathbb {R}))$
be the standard Schwartz function of the form
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times 2}(\mathbb {R}))$
be the standard Schwartz function of the form
where
![]() $P^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
$P^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
![]() $\tau ^{\circ } = \tau _{(\kappa ,0)}$
of
$\tau ^{\circ } = \tau _{(\kappa ,0)}$
of
![]() $\pi $
via (7.8). Then the canonically normalised newform
$\pi $
via (7.8). Then the canonically normalised newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
satisfies the identity
$V_{\pi }$
satisfies the identity
Remark 8.38. The integral over
![]() $\mathbb {R} \ni v$
in (8.36) may be expressed in terms of Hermite polynomials, though we do not make direct use of this fact.
$\mathbb {R} \ni v$
in (8.36) may be expressed in terms of Hermite polynomials, though we do not make direct use of this fact.
Proof. We take
![]() $s = 1 + t + (\kappa - 1)/2$
in the convolution section identity (8.27), so that
$s = 1 + t + (\kappa - 1)/2$
in the convolution section identity (8.27), so that

with
![]() $\widetilde {\Phi }$
as in (8.28). We make the change of variables
$\widetilde {\Phi }$
as in (8.28). We make the change of variables ![]() and use the Iwasawa decomposition
and use the Iwasawa decomposition
![]() $g' = uak$
with respect to the standard Borel subgroup, where
$g' = uak$
with respect to the standard Borel subgroup, where ![]() with
with
![]() $v \in \mathbb {R}$
,
$v \in \mathbb {R}$
,
![]() $a = \operatorname {\mathrm {diag}}(a_1,a_2) \in \mathrm {A}_2(\mathbb {R})$
with
$a = \operatorname {\mathrm {diag}}(a_1,a_2) \in \mathrm {A}_2(\mathbb {R})$
with
![]() $a_1,a_2 \in \mathbb {R}^{\times }$
, and
$a_1,a_2 \in \mathbb {R}^{\times }$
, and
![]() $k \in \operatorname {\mathrm {O}}(2)$
; the Haar measure is
$k \in \operatorname {\mathrm {O}}(2)$
; the Haar measure is
![]() $dg' = |a_1|^{-1} |a_2| \, dv \, d^{\times }a_1 \, d^{\times }a_2 \, dk$
. We may now insert the identity (8.7) for
$dg' = |a_1|^{-1} |a_2| \, dv \, d^{\times }a_1 \, d^{\times }a_2 \, dk$
. We may now insert the identity (8.7) for
![]() $f^{\circ }$
, at which point Lemma 7.12 allows us to evaluate the integral over
$f^{\circ }$
, at which point Lemma 7.12 allows us to evaluate the integral over
![]() $\operatorname {\mathrm {O}}(2) \ni k$
. Next, we make the change of variables
$\operatorname {\mathrm {O}}(2) \ni k$
. Next, we make the change of variables
![]() $a_1 \mapsto a_1^{-1}$
,
$a_1 \mapsto a_1^{-1}$
,
![]() $v \mapsto -a_1^{-1} v$
and
$v \mapsto -a_1^{-1} v$
and
![]() $\begin {pmatrix} a_1 & v \end {pmatrix} \mapsto \begin {pmatrix} a_1 & v \end {pmatrix} g^{-1}$
, noting that
$\begin {pmatrix} a_1 & v \end {pmatrix} \mapsto \begin {pmatrix} a_1 & v \end {pmatrix} g^{-1}$
, noting that
![]() $d^{\times }a_1 = |a_1|^{-1} \, da_1$
as
$d^{\times }a_1 = |a_1|^{-1} \, da_1$
as
![]() $\zeta _{\mathbb {R}}(1) = 1$
. Finally, we use the fact that
$\zeta _{\mathbb {R}}(1) = 1$
. Finally, we use the fact that
 $$\begin{align*}L\left(1 + t + \frac{\kappa - 1}{2}, \widetilde{\pi}\right) = \zeta_{\mathbb{R}}(\kappa) \zeta_{\mathbb{R}}(\kappa + 1)\end{align*}$$
$$\begin{align*}L\left(1 + t + \frac{\kappa - 1}{2}, \widetilde{\pi}\right) = \zeta_{\mathbb{R}}(\kappa) \zeta_{\mathbb{R}}(\kappa + 1)\end{align*}$$
via (2.14). In this way, we find that

It remains to note that the integral over
![]() $\mathbb {R} \ni a_1$
is equal to
$\mathbb {R} \ni a_1$
is equal to
![]() $1$
and to recall the definition (8.11) of the normalising constant
$1$
and to recall the definition (8.11) of the normalising constant
![]() $c^{\circ }$
.
$c^{\circ }$
.
Finally, we consider the more general case for which
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
![]() $n_1 = 2$
and
$n_1 = 2$
and
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
. We first require a simple modification of Proposition 8.14 akin to Lemma 8.30.
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
. We first require a simple modification of Proposition 8.14 akin to Lemma 8.30.
Lemma 8.39. For
![]() $n \geq 3$
, let
$n \geq 3$
, let
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Whittaker type of
be induced representations of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
with
$\operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
with
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
. Let
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
. Let
![]() $f_0^{\circ }$
be the newform of
$f_0^{\circ }$
be the newform of
![]() $\pi _0$
in the induced model
$\pi _0$
in the induced model
![]() $V_{\pi _0}$
. Then for
$V_{\pi _0}$
. Then for
![]() $v_1,v_2 \in \operatorname {\mathrm {Mat}}_{1 \times (n - 2)}(\mathbb {R})$
,
$v_1,v_2 \in \operatorname {\mathrm {Mat}}_{1 \times (n - 2)}(\mathbb {R})$
,
![]() $v_3 \in \mathbb {R}$
,
$v_3 \in \mathbb {R}$
,
![]() $a_1,a_2 \in \mathbb {R}^{\times } h \in \operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
, and
$a_1,a_2 \in \mathbb {R}^{\times } h \in \operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
, and
![]() $k \in \operatorname {\mathrm {O}}(n)$
, the newform
$k \in \operatorname {\mathrm {O}}(n)$
, the newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
satisfies
$V_{\pi }$
satisfies
 $$ \begin{align} &f^{\circ}\left(\!\begin{pmatrix} 1 & v_1 & v_2 \\ 0 & 1 & v_3 \\ 0 & 0 & 1_{n - 2} \end{pmatrix} \begin{pmatrix} a_1 & 0 & 0 \\ 0 & a_2 & 0 \\ 0 & 0 & h \end{pmatrix} \!k\right) = \frac{c^{\circ} c_1^{\circ}}{c_0^{\circ}} |a_1|^{t_1 + \frac{\kappa_1 - 1}{2} + \frac{n - 1}{2}} \chi^{\kappa_1}(a_2) |a_2|^{t_1 - \frac{\kappa_1 - 1}{2} + \frac{n - 3}{2}} \left|\det h\right|{}^{-1} \nonumber\\ &\qquad\qquad\quad\times \dim \tau_0^{\circ} \int_{\operatorname{\mathrm{O}}(n - 2)} f_0^{\circ}(hk_2) \overline{P_{(2,n - 2)}^{\circ}}\left(e_n k^{-1} \begin{pmatrix} 1_2 & 0 \\ 0 & k_2 \end{pmatrix}\right) \, dk_2. \end{align} $$
$$ \begin{align} &f^{\circ}\left(\!\begin{pmatrix} 1 & v_1 & v_2 \\ 0 & 1 & v_3 \\ 0 & 0 & 1_{n - 2} \end{pmatrix} \begin{pmatrix} a_1 & 0 & 0 \\ 0 & a_2 & 0 \\ 0 & 0 & h \end{pmatrix} \!k\right) = \frac{c^{\circ} c_1^{\circ}}{c_0^{\circ}} |a_1|^{t_1 + \frac{\kappa_1 - 1}{2} + \frac{n - 1}{2}} \chi^{\kappa_1}(a_2) |a_2|^{t_1 - \frac{\kappa_1 - 1}{2} + \frac{n - 3}{2}} \left|\det h\right|{}^{-1} \nonumber\\ &\qquad\qquad\quad\times \dim \tau_0^{\circ} \int_{\operatorname{\mathrm{O}}(n - 2)} f_0^{\circ}(hk_2) \overline{P_{(2,n - 2)}^{\circ}}\left(e_n k^{-1} \begin{pmatrix} 1_2 & 0 \\ 0 & k_2 \end{pmatrix}\right) \, dk_2. \end{align} $$
Here, the constants
![]() $c^{\circ }$
,
$c^{\circ }$
,
![]() $c_1^{\circ }$
and
$c_1^{\circ }$
and
![]() $c_0^{\circ }$
are those associated to
$c_0^{\circ }$
are those associated to
![]() $f^{\circ }$
,
$f^{\circ }$
,
![]() $f_1^{\circ }$
and
$f_1^{\circ }$
and
![]() $f_0^{\circ }$
via (8.15) and (8.7), while
$f_0^{\circ }$
via (8.15) and (8.7), while
where
![]() $P_1^{\circ }$
and
$P_1^{\circ }$
and
![]() $P_0^{\circ }$
are the homogeneous harmonic polynomials associated to the newform K-types
$P_0^{\circ }$
are the homogeneous harmonic polynomials associated to the newform K-types
![]() $\tau _1^{\circ }$
and
$\tau _1^{\circ }$
and
![]() $\tau _0^{\circ }$
of
$\tau _0^{\circ }$
of
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _0$
, respectively, via (7.8).
$\pi _0$
, respectively, via (7.8).
Proof. The proof is essentially identical to that of Lemma 8.30.
We now use the identity (8.40) in conjunction with the convolution section (8.27) in order to prove that
![]() $f^{\circ }$
may be written as a Godement section.
$f^{\circ }$
may be written as a Godement section.
Proposition 8.41. For
![]() $n \geq 3$
, let
$n \geq 3$
, let
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Whittaker type of
be induced representations of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
with
$\operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
with
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
. Let
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
. Let
![]() $f_0^{\circ }$
be the newform of
$f_0^{\circ }$
be the newform of
![]() $\pi _0$
in the induced model
$\pi _0$
in the induced model
![]() $V_{\pi _0}$
. Let
$V_{\pi _0}$
. Let
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(\mathbb {R}))$
be the standard Schwartz function of the form
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(\mathbb {R}))$
be the standard Schwartz function of the form

where
![]() $P_1^{\circ }$
and
$P_1^{\circ }$
and
![]() $P_0^{\circ }$
are the homogeneous harmonic polynomials associated to the newform K-types
$P_0^{\circ }$
are the homogeneous harmonic polynomials associated to the newform K-types
![]() $\tau _1^{\circ }$
and
$\tau _1^{\circ }$
and
![]() $\tau _0^{\circ }$
of
$\tau _0^{\circ }$
of
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _0$
, respectively, via (7.8). Then if
$\pi _0$
, respectively, via (7.8). Then if
![]() $\Re (t_1)$
is sufficiently large, the newform
$\Re (t_1)$
is sufficiently large, the newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
satisfies the identity
$V_{\pi }$
satisfies the identity
 $$ \begin{align} &f^{\circ}(g) = \frac{c^{\circ} i^{\kappa_1}}{c_0^{\circ} L\left(1 + t_1 + \frac{\kappa_1 - 1}{2},\widetilde{\pi_0}\right)} \left|\det g\right|{}^{t_1 + \frac{\kappa_1 - 1}{2} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 2}(\mathbb{R})} f_0^{\circ}(h) \left|\det h\right|{}^{-t_1 - \frac{\kappa_1 - 1}{2} - \frac{n - 1}{2}} \\\nonumber &\qquad\qquad\qquad\times \int_{\mathbb{R}^{\times}} a_2^{-\kappa_1} \int\limits_{\operatorname{\mathrm{Mat}}_{1 \times (n - 2)}(\mathbb{R})} \Phi\left(\begin{pmatrix} a_2^{-1} & v_3 \\ 0 & h^{-1} \end{pmatrix} \begin{pmatrix} 0 & 1_{n - 1}\end{pmatrix} g\right) \, dv_3 \, d^{\times}a_2 \, dh, \end{align} $$
$$ \begin{align} &f^{\circ}(g) = \frac{c^{\circ} i^{\kappa_1}}{c_0^{\circ} L\left(1 + t_1 + \frac{\kappa_1 - 1}{2},\widetilde{\pi_0}\right)} \left|\det g\right|{}^{t_1 + \frac{\kappa_1 - 1}{2} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 2}(\mathbb{R})} f_0^{\circ}(h) \left|\det h\right|{}^{-t_1 - \frac{\kappa_1 - 1}{2} - \frac{n - 1}{2}} \\\nonumber &\qquad\qquad\qquad\times \int_{\mathbb{R}^{\times}} a_2^{-\kappa_1} \int\limits_{\operatorname{\mathrm{Mat}}_{1 \times (n - 2)}(\mathbb{R})} \Phi\left(\begin{pmatrix} a_2^{-1} & v_3 \\ 0 & h^{-1} \end{pmatrix} \begin{pmatrix} 0 & 1_{n - 1}\end{pmatrix} g\right) \, dv_3 \, d^{\times}a_2 \, dh, \end{align} $$
where the constants
![]() $c^{\circ }$
and
$c^{\circ }$
and
![]() $c_0^{\circ }$
are those associated to
$c_0^{\circ }$
are those associated to
![]() $f^{\circ }$
and
$f^{\circ }$
and
![]() $f_0^{\circ }$
via (8.15).
$f_0^{\circ }$
via (8.15).
In particular, the integral (8.42) converges absolutely if
![]() $\Re (t_1)> \Re (t_j) - 1 - (\kappa _1 - 1)/2$
for each
$\Re (t_1)> \Re (t_j) - 1 - (\kappa _1 - 1)/2$
for each
![]() $j \in \{2,\ldots ,r\}$
for which
$j \in \{2,\ldots ,r\}$
for which
![]() $n_j = 1$
, so that
$n_j = 1$
, so that
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
![]() $\Re (t_1)> \Re (t_j) + (\kappa _j - 1)/2 - 1 - (\kappa _1 - 1)/2$
for each
$\Re (t_1)> \Re (t_j) + (\kappa _j - 1)/2 - 1 - (\kappa _1 - 1)/2$
for each
![]() $j \in \{2,\ldots ,r\}$
for which
$j \in \{2,\ldots ,r\}$
for which
![]() $n_j = 2$
, so that
$n_j = 2$
, so that
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
Proof. We take
![]() $s = 1 + t_1 + (\kappa _1 - 1)/2$
in the convolution section identity (8.27), so that
$s = 1 + t_1 + (\kappa _1 - 1)/2$
in the convolution section identity (8.27), so that

with
![]() $\widetilde {\Phi }$
as in (8.28). We make the change of variables
$\widetilde {\Phi }$
as in (8.28). We make the change of variables ![]() and then use the Iwasawa decomposition
and then use the Iwasawa decomposition
![]() $g' = umk$
with respect to the parabolic subgroup
$g' = umk$
with respect to the parabolic subgroup
![]() ${\mathrm {P}(\mathbb {R}) = \mathrm {P}_{(1,1,n - 2)}(\mathbb {R})}$
, where
${\mathrm {P}(\mathbb {R}) = \mathrm {P}_{(1,1,n - 2)}(\mathbb {R})}$
, where  with
with
![]() $v_1 \in \mathbb {R}$
,
$v_1 \in \mathbb {R}$
,
![]() $v_2,v_3 \in \operatorname {\mathrm {Mat}}_{1 \times (n - 2)}(\mathbb {R})$
,
$v_2,v_3 \in \operatorname {\mathrm {Mat}}_{1 \times (n - 2)}(\mathbb {R})$
, ![]() with
with
![]() $a_1,a_2 \in \mathbb {R}^{\times }$
and
$a_1,a_2 \in \mathbb {R}^{\times }$
and
![]() $h \in \operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
, and
$h \in \operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
, and
![]() $k \in \operatorname {\mathrm {O}}(n)$
; the Haar measure is
$k \in \operatorname {\mathrm {O}}(n)$
; the Haar measure is
We may now insert the identity (8.40) for
![]() $f^{\circ }$
. Next, we make the change of variables
$f^{\circ }$
. Next, we make the change of variables
![]() ${h \mapsto h k_2^{-1}}$
and
${h \mapsto h k_2^{-1}}$
and ![]() , so that the integral over
, so that the integral over
![]() $\operatorname {\mathrm {O}}(n - 2) \ni k_2$
is trivial; subsequently, the integral over
$\operatorname {\mathrm {O}}(n - 2) \ni k_2$
is trivial; subsequently, the integral over
![]() $\operatorname {\mathrm {O}}(n) \ni k$
may be evaluated via Lemma 7.12. Next, we make the change of variables
$\operatorname {\mathrm {O}}(n) \ni k$
may be evaluated via Lemma 7.12. Next, we make the change of variables
![]() $v_1 \mapsto -a_1 v_1$
,
$v_1 \mapsto -a_1 v_1$
,
![]() $v_2 \mapsto -a_1 v_2 - v_1 v_3$
,
$v_2 \mapsto -a_1 v_2 - v_1 v_3$
,
![]() $v_3 \mapsto -a_2 v_3$
,
$v_3 \mapsto -a_2 v_3$
,
![]() $a_1 \mapsto a_1^{-1}$
, and
$a_1 \mapsto a_1^{-1}$
, and
![]() $\begin {pmatrix} a_1 & v_1 & v_2 \end {pmatrix} \mapsto \begin {pmatrix} a_1 & v_1 & v_2 \end {pmatrix} g^{-1}$
, noting that
$\begin {pmatrix} a_1 & v_1 & v_2 \end {pmatrix} \mapsto \begin {pmatrix} a_1 & v_1 & v_2 \end {pmatrix} g^{-1}$
, noting that
![]() $d^{\times }a_1 = |a_1|^{-1} \, da_1$
as
$d^{\times }a_1 = |a_1|^{-1} \, da_1$
as
![]() $\zeta _{\mathbb {R}}(1) = 1$
. Finally, we use the fact that
$\zeta _{\mathbb {R}}(1) = 1$
. Finally, we use the fact that
 $$\begin{align*}L\left(1 + t_1 + \frac{\kappa_1 - 1}{2},\widetilde{\pi}\right) = \zeta_{\mathbb{R}}(\kappa_1) \zeta_{\mathbb{R}}(\kappa_1 + 1) L\left(1 + t_1 + \frac{\kappa_1 - 1}{2},\widetilde{\pi_0}\right)\end{align*}$$
$$\begin{align*}L\left(1 + t_1 + \frac{\kappa_1 - 1}{2},\widetilde{\pi}\right) = \zeta_{\mathbb{R}}(\kappa_1) \zeta_{\mathbb{R}}(\kappa_1 + 1) L\left(1 + t_1 + \frac{\kappa_1 - 1}{2},\widetilde{\pi_0}\right)\end{align*}$$
via (2.5) and (2.14). In this way, we find that

It remains to note that the integrals over
![]() $\mathbb {R} \ni a_1$
,
$\mathbb {R} \ni a_1$
,
![]() $\mathbb {R} \ni v_1$
and
$\mathbb {R} \ni v_1$
and
![]() $\mathbb {R} \ni v_{2,i}$
for
$\mathbb {R} \ni v_{2,i}$
for
![]() $i \in \{1,\ldots ,n - 3\}$
are trivial and to recall the definition (8.11) of the normalising constant
$i \in \{1,\ldots ,n - 3\}$
are trivial and to recall the definition (8.11) of the normalising constant
![]() $c_1^{\circ }$
.
$c_1^{\circ }$
.
In order to prove a recursive formula for the newform in the Whittaker model, we require a similar identity to (8.42) for a slightly modified induced representation of Whittaker type.
Lemma 8.43. For
![]() $n \geq 3$
, let
$n \geq 3$
, let
![]() $\pi ^{\ast } = \pi _1^{\ast } \boxplus \pi _2^{\ast } \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi ^{\ast } = \pi _1^{\ast } \boxplus \pi _2^{\ast } \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Whittaker type of
be induced representations of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
with
$\operatorname {\mathrm {GL}}_{n - 2}(\mathbb {R})$
with
![]() $\pi _1^{\ast } = |\cdot |^{t_1^{\ast }}$
and
$\pi _1^{\ast } = |\cdot |^{t_1^{\ast }}$
and
![]() $\pi _2^{\ast } = |\cdot |^{t_2^{\ast }}$
. Let
$\pi _2^{\ast } = |\cdot |^{t_2^{\ast }}$
. Let
![]() $f_0^{\circ }$
be the newform of
$f_0^{\circ }$
be the newform of
![]() $\pi _0$
in the induced model
$\pi _0$
in the induced model
![]() $V_{\pi _0}$
. Let
$V_{\pi _0}$
. Let
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(\mathbb {R}))$
be the standard Schwartz function of the form
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(\mathbb {R}))$
be the standard Schwartz function of the form

where
![]() $P_0^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
$P_0^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
![]() $\tau _0^{\circ }$
of
$\tau _0^{\circ }$
of
![]() $\pi _0$
via (7.8). Then if
$\pi _0$
via (7.8). Then if
![]() $\Re (t_1^{\ast })$
is sufficiently large, the newform
$\Re (t_1^{\ast })$
is sufficiently large, the newform
![]() $f^{\ast \circ }$
in the induced model
$f^{\ast \circ }$
in the induced model
![]() $V_{\pi ^{\ast }}$
satisfies the identity
$V_{\pi ^{\ast }}$
satisfies the identity
 $$ \begin{align} f^{\ast\circ}(g) = &\frac{c^{\ast\circ}}{c_0^{\circ} \zeta_{\mathbb{R}}(1 + t_1^{\ast} - t_2^{\ast}) L\left(1 + t_1^{\ast},\widetilde{\pi_0}\right)} \left|\det g\right|{}^{t_1^{\ast} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 2}(\mathbb{R})} f_0^{\circ}(h) \left|\det h\right|{}^{-t_1^{\ast} - \frac{n - 1}{2}} \\\nonumber &\quad\times \int_{\mathbb{R}^{\times}} |a_2|^{-1 - t_1^{\ast} + t_2^{\ast}} \int\limits_{\operatorname{\mathrm{Mat}}_{1 \times (n - 2)}(\mathbb{R})} \Phi\left(\begin{pmatrix} a_2^{-1} & v_3 \\ 0 & h^{-1} \end{pmatrix} \begin{pmatrix} 0 & 1_{n - 1}\end{pmatrix} g\right) \, dv_3 \, d^{\times}a_2 \, dh, \end{align} $$
$$ \begin{align} f^{\ast\circ}(g) = &\frac{c^{\ast\circ}}{c_0^{\circ} \zeta_{\mathbb{R}}(1 + t_1^{\ast} - t_2^{\ast}) L\left(1 + t_1^{\ast},\widetilde{\pi_0}\right)} \left|\det g\right|{}^{t_1^{\ast} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 2}(\mathbb{R})} f_0^{\circ}(h) \left|\det h\right|{}^{-t_1^{\ast} - \frac{n - 1}{2}} \\\nonumber &\quad\times \int_{\mathbb{R}^{\times}} |a_2|^{-1 - t_1^{\ast} + t_2^{\ast}} \int\limits_{\operatorname{\mathrm{Mat}}_{1 \times (n - 2)}(\mathbb{R})} \Phi\left(\begin{pmatrix} a_2^{-1} & v_3 \\ 0 & h^{-1} \end{pmatrix} \begin{pmatrix} 0 & 1_{n - 1}\end{pmatrix} g\right) \, dv_3 \, d^{\times}a_2 \, dh, \end{align} $$
where the constants
![]() $c^{\ast \circ }$
and
$c^{\ast \circ }$
and
![]() $c_0^{\circ }$
are those associated to
$c_0^{\circ }$
are those associated to
![]() $f^{\ast \circ }$
and
$f^{\ast \circ }$
and
![]() $f_0^{\circ }$
via (8.15).
$f_0^{\circ }$
via (8.15).
In particular, the integral (8.44) converges absolutely if
![]() $\Re (t_1^{\ast })> \Re (t_2^{\ast }) - 1$
,
$\Re (t_1^{\ast })> \Re (t_2^{\ast }) - 1$
,
![]() $\Re (t_1^{\ast })> \Re (t_j) - 1$
for each
$\Re (t_1^{\ast })> \Re (t_j) - 1$
for each
![]() $j \in \{2,\ldots ,r\}$
for which
$j \in \{2,\ldots ,r\}$
for which
![]() $n_j = 1$
, so that
$n_j = 1$
, so that
![]() $\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
$\pi _j = \chi ^{\kappa _j} |\cdot |^{t_j}$
, and
![]() $\Re (t_1^{\ast })> \Re (t_j) + (\kappa _j - 1)/2 - 1$
for each
$\Re (t_1^{\ast })> \Re (t_j) + (\kappa _j - 1)/2 - 1$
for each
![]() $j \in \{2,\ldots ,r\}$
for which
$j \in \{2,\ldots ,r\}$
for which
![]() $n_j = 2$
, so that
$n_j = 2$
, so that
![]() $\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
$\pi _j = D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
.
Proof. This follows via the same method as the proof of Proposition 8.41.
9. The Newform in the Whittaker Model
9.1. The Jacquet integral
Let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Whittaker type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, so that each
$\operatorname {\mathrm {GL}}_n(F)$
, so that each
![]() $\pi _j$
is of the form
$\pi _j$
is of the form
![]() $\chi ^{\kappa _j} |\cdot |^{t_j}$
or
$\chi ^{\kappa _j} |\cdot |^{t_j}$
or
![]() $D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
. Given an element f of the induced model
$D_{\kappa _j} \otimes \left |\det \right |{}^{t_j}$
. Given an element f of the induced model
![]() $V_{\pi }$
of
$V_{\pi }$
of
![]() $\pi $
, we define the Jacquet integral
$\pi $
, we define the Jacquet integral

This integral converges absolutely if
![]() $\Re (t_1)> \cdots > \Re (t_r)$
and defines a Whittaker function
$\Re (t_1)> \cdots > \Re (t_r)$
and defines a Whittaker function
![]() $W = W_f \in \mathcal {W}(\pi ,\psi )$
; that is, as a function of
$W = W_f \in \mathcal {W}(\pi ,\psi )$
; that is, as a function of
![]() $f \in V_{\pi }$
,
$f \in V_{\pi }$
, ![]() defines a Whittaker functional, which is therefore unique up to scalar multiplication.
defines a Whittaker functional, which is therefore unique up to scalar multiplication.
Wallach [Reference WallachWal92] has shown that the Jacquet integral gives a Whittaker functional for all induced representations of Whittaker type, and not just those for which
![]() ${\Re (t_1)> \cdots > \Re (t_r)}$
, via analytic continuation in the following way. Write
${\Re (t_1)> \cdots > \Re (t_r)}$
, via analytic continuation in the following way. Write
![]() $\pi = \pi _{t_1,\ldots ,t_r}$
for such a representation, and let
$\pi = \pi _{t_1,\ldots ,t_r}$
for such a representation, and let
![]() $V_{\pi } = V_{\pi _{t_1,\ldots ,t_r}}$
denote its induced model. Fixing each
$V_{\pi } = V_{\pi _{t_1,\ldots ,t_r}}$
denote its induced model. Fixing each
![]() $\chi ^{\kappa _j}$
and
$\chi ^{\kappa _j}$
and
![]() $D_{\kappa _j}$
but regarding
$D_{\kappa _j}$
but regarding
![]() $t_j$
as a complex variable, we may view the space
$t_j$
as a complex variable, we may view the space
![]() $V_{\pi _{t_1,\ldots ,t_r}}$
as a holomorphic fibre bundle. A section
$V_{\pi _{t_1,\ldots ,t_r}}$
as a holomorphic fibre bundle. A section
![]() $f_{t_1,\ldots ,t_r}(g;m')$
is a map from
$f_{t_1,\ldots ,t_r}(g;m')$
is a map from
![]() $\operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F) \times \mathbb {C}^r$
to
$\operatorname {\mathrm {GL}}_n(F) \times \mathrm {M}_{\mathrm {P}}(F) \times \mathbb {C}^r$
to
![]() $\mathbb {C}$
such that
$\mathbb {C}$
such that
![]() $f_{t_1,\ldots ,t_r}(\cdot ;\cdot )$
is an element of
$f_{t_1,\ldots ,t_r}(\cdot ;\cdot )$
is an element of
![]() $V_{\pi _{t_1,\ldots ,t_r}}$
for each fixed
$V_{\pi _{t_1,\ldots ,t_r}}$
for each fixed
![]() $(t_1,\ldots ,t_r) \in \mathbb {C}^r$
; a standard section (or flat section) is a section for which
$(t_1,\ldots ,t_r) \in \mathbb {C}^r$
; a standard section (or flat section) is a section for which
![]() $f_{t_1,\ldots ,t_r}(k;1_n)$
is independent of
$f_{t_1,\ldots ,t_r}(k;1_n)$
is independent of
![]() $(t_1,\ldots ,t_r) \in \mathbb {C}^r$
for all
$(t_1,\ldots ,t_r) \in \mathbb {C}^r$
for all
![]() $k \in K$
. From [Reference WallachWal92, Theorem 15.4.1], the Jacquet integral (9.1) evaluated on a standard section extends holomorphically as a function of
$k \in K$
. From [Reference WallachWal92, Theorem 15.4.1], the Jacquet integral (9.1) evaluated on a standard section extends holomorphically as a function of
![]() $(t_1,\ldots ,t_r) \in \mathbb {C}^r$
with
$(t_1,\ldots ,t_r) \in \mathbb {C}^r$
with
![]() $\Re (t_1)> \cdots > \Re (t_r)$
to all of
$\Re (t_1)> \cdots > \Re (t_r)$
to all of
![]() $\mathbb {C}^r$
, and hence via analytic continuation defines an equivariant map from
$\mathbb {C}^r$
, and hence via analytic continuation defines an equivariant map from
![]() $V_{\pi _{t_1,\ldots ,t_r}}$
to
$V_{\pi _{t_1,\ldots ,t_r}}$
to
![]() $\mathcal {W}(\pi _{t_1,\ldots ,t_r},\psi )$
.
$\mathcal {W}(\pi _{t_1,\ldots ,t_r},\psi )$
.
From this, we see that the newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
defined via the Iwasawa decomposition (8.15) gives a standard section of newforms
$V_{\pi }$
defined via the Iwasawa decomposition (8.15) gives a standard section of newforms
![]() $f_{t_1,\ldots ,t_r}^{\circ }$
provided that we choose the normalising constant
$f_{t_1,\ldots ,t_r}^{\circ }$
provided that we choose the normalising constant
![]() $c^{\circ }$
to be independent of
$c^{\circ }$
to be independent of
![]() $(t_1,\ldots ,t_r) \in \mathbb {C}^r$
. The corresponding Whittaker function is then given via the analytic continuation of the Jacquet integral (9.1). Furthermore, we may choose the normalising constant
$(t_1,\ldots ,t_r) \in \mathbb {C}^r$
. The corresponding Whittaker function is then given via the analytic continuation of the Jacquet integral (9.1). Furthermore, we may choose the normalising constant
![]() $c^{\circ }$
to be dependent on
$c^{\circ }$
to be dependent on
![]() $(t_1,\ldots ,t_r) \in \mathbb {C}^r$
and still obtain the corresponding Whittaker function via the analytic continuation of the Jacquet integral so long as
$(t_1,\ldots ,t_r) \in \mathbb {C}^r$
and still obtain the corresponding Whittaker function via the analytic continuation of the Jacquet integral so long as
![]() $c^{\circ }$
is holomorphic as a function of
$c^{\circ }$
is holomorphic as a function of
![]() $(t_1,\ldots ,t_r) \in \mathbb {C}^r$
.
$(t_1,\ldots ,t_r) \in \mathbb {C}^r$
.
With this in mind, we may now define the canonically normalised newform in the induced and Whittaker models.
Definition 9.2. Let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Langlands type of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
. The canonically normalised newform
$\operatorname {\mathrm {GL}}_n(F)$
. The canonically normalised newform
![]() $f^{\circ }$
in the induced model
$f^{\circ }$
in the induced model
![]() $V_{\pi }$
is defined via (8.6) and (8.7) with normalising constant (8.11) if
$V_{\pi }$
is defined via (8.6) and (8.7) with normalising constant (8.11) if
![]() $r = 1$
, while for
$r = 1$
, while for
![]() $r \geq 2$
, it is defined via (8.15) with normalising constant
$r \geq 2$
, it is defined via (8.15) with normalising constant

The canonically normalised newform
![]() $W^{\circ }$
in the Whittaker model
$W^{\circ }$
in the Whittaker model
![]() $\mathcal {W}(\pi ,\psi )$
is given by the analytic continuation of the Jacquet integral (9.1) of the canonically normalised newform
$\mathcal {W}(\pi ,\psi )$
is given by the analytic continuation of the Jacquet integral (9.1) of the canonically normalised newform
![]() $f^{\circ }$
. We call
$f^{\circ }$
. We call
![]() $W^{\circ }$
the Whittaker newform.
$W^{\circ }$
the Whittaker newform.
Remark 9.3. When
![]() $\pi $
is spherical, some authors refer to the canonically normalised Whittaker function as the completed Whittaker function; see, for example, [Reference Blomer, Harcos and MagaBHM20, Section 2.1]. We follow the nomenclature of [Reference Goldfeld, Miller and WoodburyGMW21, Section 8].
$\pi $
is spherical, some authors refer to the canonically normalised Whittaker function as the completed Whittaker function; see, for example, [Reference Blomer, Harcos and MagaBHM20, Section 2.1]. We follow the nomenclature of [Reference Goldfeld, Miller and WoodburyGMW21, Section 8].
Recalling the identities (2.9), (2.12) and (2.14) relating L-functions to zeta functions, we observe that the normalising constant
![]() $c^{\circ }$
is well defined since
$c^{\circ }$
is well defined since
![]() $\zeta _F(s)$
is holomorphic for
$\zeta _F(s)$
is holomorphic for
![]() $\Re (s)> 0$
and
$\Re (s)> 0$
and
![]() $\pi $
being an induced representation of Langlands type means that
$\pi $
being an induced representation of Langlands type means that
![]() ${\Re (t_1) \geq \cdots \geq \Re (t_r)}$
. We also note that if
${\Re (t_1) \geq \cdots \geq \Re (t_r)}$
. We also note that if
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() , then the associated normalising constants satisfy the relation
, then the associated normalising constants satisfy the relation
 $$ \begin{align} c^{\circ} = \begin{cases} i^{c(\pi_0)} L\left(1 + t_1 + \frac{\|\kappa_1\|}{d_F}, \widetilde{\pi_0}\right) c_0^{\circ} & \text{if }\pi_1 = \chi^{\kappa_1} |\cdot|^{t_1}, \\ i^{c(\pi_0)} L\left(1 + t_1 + \frac{\kappa_1 - 1}{2}, \widetilde{\pi_0}\right) L\left(1 + t_1 + \frac{\kappa_1 + 1}{2}, \widetilde{\pi_0}\right) c_0^{\circ} & \text{if }\pi_1 = D_{\kappa_1} \otimes \left|\det\right|{}^{t_1}. \end{cases} \end{align} $$
$$ \begin{align} c^{\circ} = \begin{cases} i^{c(\pi_0)} L\left(1 + t_1 + \frac{\|\kappa_1\|}{d_F}, \widetilde{\pi_0}\right) c_0^{\circ} & \text{if }\pi_1 = \chi^{\kappa_1} |\cdot|^{t_1}, \\ i^{c(\pi_0)} L\left(1 + t_1 + \frac{\kappa_1 - 1}{2}, \widetilde{\pi_0}\right) L\left(1 + t_1 + \frac{\kappa_1 + 1}{2}, \widetilde{\pi_0}\right) c_0^{\circ} & \text{if }\pi_1 = D_{\kappa_1} \otimes \left|\det\right|{}^{t_1}. \end{cases} \end{align} $$
This is a consequence of Definition 9.2, Theorem 4.15 and (2.5).
Remark 9.5. While we do not prove this, our methods below can be extended to show that not only is the Whittaker newform well defined for induced representations of Langlands type, it is also well defined for induced representations of Whittaker type, including those for which
![]() $c^{\circ }$
is not well defined (note that in these cases, the Whittaker model is a model for a quotient of
$c^{\circ }$
is not well defined (note that in these cases, the Whittaker model is a model for a quotient of
![]() $\pi $
rather than for
$\pi $
rather than for
![]() $\pi $
itself). Furthermore, one can show that the Whittaker newform of
$\pi $
itself). Furthermore, one can show that the Whittaker newform of
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
remains unchanged when
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
remains unchanged when
![]() $\pi $
is replaced by
$\pi $
is replaced by
![]() $\pi _{\sigma (1)} \boxplus \cdots \boxplus \pi _{\sigma (r)}$
for any permutation
$\pi _{\sigma (1)} \boxplus \cdots \boxplus \pi _{\sigma (r)}$
for any permutation
![]() $\sigma \in S_r$
(cf. Remark 4.10). When
$\sigma \in S_r$
(cf. Remark 4.10). When
![]() $\pi $
is a spherical induced representation of Whittaker type, these claims follow from the work of Jacquet [Reference JacquetJac67, Théorème (8.6)].
$\pi $
is a spherical induced representation of Whittaker type, these claims follow from the work of Jacquet [Reference JacquetJac67, Théorème (8.6)].
9.2. The newform via convolution sections
We now use the convolution section identity (8.21) for the newform in the induced model together with the Jacquet integral (9.1) in order to give a convolution section identity for the Whittaker newform. This is a recursive formula for
![]() $W^{\circ }$
as an integral over
$W^{\circ }$
as an integral over
![]() $\operatorname {\mathrm {GL}}_n(F)$
involving
$\operatorname {\mathrm {GL}}_n(F)$
involving
![]() $W^{\circ }$
and the distinguished standard Schwartz function
$W^{\circ }$
and the distinguished standard Schwartz function
![]() $\Phi $
given by (8.22).
$\Phi $
given by (8.22).
Lemma 9.6. Let
![]() $\pi $
be an induced representation of Langlands type of
$\pi $
be an induced representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
with Whittaker newform
$\operatorname {\mathrm {GL}}_n(F)$
with Whittaker newform
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
. Then for all
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
. Then for all
![]() $h \in \operatorname {\mathrm {GL}}_n(F)$
and for
$h \in \operatorname {\mathrm {GL}}_n(F)$
and for
![]() $\Re (s)$
sufficiently large,
$\Re (s)$
sufficiently large,
 $$ \begin{align} \int_{\operatorname{\mathrm{GL}}_n(F)} W^{\circ}(hg) \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg = L(s,\pi) W^{\circ}(h), \end{align} $$
$$ \begin{align} \int_{\operatorname{\mathrm{GL}}_n(F)} W^{\circ}(hg) \Phi(g) \left|\det g\right|{}^{s + \frac{n - 1}{2}} \, dg = L(s,\pi) W^{\circ}(h), \end{align} $$
where
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is the standard Schwartz function given by (8.22).
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is the standard Schwartz function given by (8.22).
Proof. We show this initially for
![]() $\Re (t_1)> \cdots > \Re (t_r)$
with
$\Re (t_1)> \cdots > \Re (t_r)$
with
![]() $\Re (t_1)$
sufficiently large; this identity then extends via analytic continuation to all induced representations of Langlands type, for the left-hand side is absolutely convergent for
$\Re (t_1)$
sufficiently large; this identity then extends via analytic continuation to all induced representations of Langlands type, for the left-hand side is absolutely convergent for
![]() $\Re (s)$
sufficiently large by [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Lemma 3.2 (ii) and Proposition 3.3].
$\Re (s)$
sufficiently large by [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Lemma 3.2 (ii) and Proposition 3.3].
We replace h with
![]() $w_n uh$
in the convolution section identity (8.21) for
$w_n uh$
in the convolution section identity (8.21) for
![]() $f^{\circ }$
and insert this identity into the Jacquet integral (9.1). The result then follows upon interchanging the order of integration, which is justified by the absolute convergence of the Jacquet integral together with the absolute convergence of the integral (8.21).
$f^{\circ }$
and insert this identity into the Jacquet integral (9.1). The result then follows upon interchanging the order of integration, which is justified by the absolute convergence of the Jacquet integral together with the absolute convergence of the integral (8.21).
9.3. The newform via Godement sections
Next, we use Godement section identities for the newform in the induced model together with the Jacquet integral (9.1) in order to give a Godement section identity for the Whittaker newform. This is a propagation formula: a recursive formula for
![]() $W^{\circ }$
in terms of an integral over
$W^{\circ }$
in terms of an integral over
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
involving a
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
involving a
![]() $\operatorname {\mathrm {GL}}_{n - 1}$
Whittaker function and a distinguished standard Schwartz function.
$\operatorname {\mathrm {GL}}_{n - 1}$
Whittaker function and a distinguished standard Schwartz function.
9.3.1. The case
 $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
As in Section 8.4, we first treat the case for which
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
![]() $n_1 = 1$
, so that
$n_1 = 1$
, so that
![]() $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
.
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
.
Lemma 9.8. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Langlands type of
be induced representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
with
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
with
![]() $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
. Let
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
. Let
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
and
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
and
![]() $W_0^{\circ } \in \mathcal {W}(\pi _0,\psi )$
be the Whittaker newforms of
$W_0^{\circ } \in \mathcal {W}(\pi _0,\psi )$
be the Whittaker newforms of
![]() $\pi $
and
$\pi $
and
![]() $\pi _0$
. Then for
$\pi _0$
. Then for
![]() $g \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
,
$g \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
,
 $$ \begin{align} W^{\circ} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = \left|\det g\right|{}^{t_1 + \frac{\|\kappa_1\|}{d_F} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 1}(F)} W_0^{\circ}(h) \Phi_1(h^{-1} g) \Phi_0^{\circ}(e_{n - 1} h) \left|\det h\right|{}^{-t_1 - \frac{\|\kappa_1\|}{d_F} - \frac{n}{2} + 1} \, dh, \end{align} $$
$$ \begin{align} W^{\circ} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = \left|\det g\right|{}^{t_1 + \frac{\|\kappa_1\|}{d_F} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 1}(F)} W_0^{\circ}(h) \Phi_1(h^{-1} g) \Phi_0^{\circ}(e_{n - 1} h) \left|\det h\right|{}^{-t_1 - \frac{\|\kappa_1\|}{d_F} - \frac{n}{2} + 1} \, dh, \end{align} $$
with the standard Schwartz functions
![]() $\Phi _1 \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times (n - 1)}(F))$
and
$\Phi _1 \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times (n - 1)}(F))$
and
![]() $\Phi _0^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F))$
given by
$\Phi _0^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F))$
given by
where
![]() $P_0^{\circ }$
is the homogeneous harmonic polynomial associated to the newform
$P_0^{\circ }$
is the homogeneous harmonic polynomial associated to the newform
![]() $K_{n - 1}$
-type
$K_{n - 1}$
-type
![]() $\tau _0^{\circ }$
of
$\tau _0^{\circ }$
of
![]() $\pi _0$
via (7.2) and (7.8).
$\pi _0$
via (7.2) and (7.8).
Remark 9.12. When
![]() $n = 2$
, so that
$n = 2$
, so that
![]() $\pi = \chi ^{\kappa _1} |\cdot |^{t_1} \boxplus \chi ^{\kappa _2} |\cdot |^{t_2}$
, the integral over
$\pi = \chi ^{\kappa _1} |\cdot |^{t_1} \boxplus \chi ^{\kappa _2} |\cdot |^{t_2}$
, the integral over
![]() $\operatorname {\mathrm {GL}}_1(F) = F^{\times } \ni h$
in (9.9) may be explicitly evaluated in order to show that
$\operatorname {\mathrm {GL}}_1(F) = F^{\times } \ni h$
in (9.9) may be explicitly evaluated in order to show that
 $$\begin{align*}W^{\circ}\begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = \begin{cases} 2 |g|^{\frac{t_1 + t_2 + 1 + \kappa_1 + \kappa_2}{2}} K_{\frac{t_1 - t_2 + \kappa_1 - \kappa_2}{2}}(2\pi|g|) & \text{if }F = \mathbb{R}, \\ 4 |g|^{\frac{t_1 + t_2 + 1}{2} + \frac{\|\kappa_1\| + \|\kappa_2\|}{4}} K_{t_1 - t_2 + \frac{\|\kappa_1\| - \|\kappa_2\|}{2}}(4\pi|g|^{1/2}) & \text{if }F = \mathbb{C}, \end{cases}\end{align*}$$
$$\begin{align*}W^{\circ}\begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = \begin{cases} 2 |g|^{\frac{t_1 + t_2 + 1 + \kappa_1 + \kappa_2}{2}} K_{\frac{t_1 - t_2 + \kappa_1 - \kappa_2}{2}}(2\pi|g|) & \text{if }F = \mathbb{R}, \\ 4 |g|^{\frac{t_1 + t_2 + 1}{2} + \frac{\|\kappa_1\| + \|\kappa_2\|}{4}} K_{t_1 - t_2 + \frac{\|\kappa_1\| - \|\kappa_2\|}{2}}(4\pi|g|^{1/2}) & \text{if }F = \mathbb{C}, \end{cases}\end{align*}$$
where
![]() $K_{\nu }(z)$
denotes the modified Bessel function of the second kind.
$K_{\nu }(z)$
denotes the modified Bessel function of the second kind.
Proof. We show this initially for
![]() $\Re (t_1)> \cdots > \Re (t_r)$
with
$\Re (t_1)> \cdots > \Re (t_r)$
with
![]() $\Re (t_1)$
sufficiently large; from [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Proposition 7.2], this identity then extends via analytic continuation to all induced representations of Langlands type (note that Jacquet instead works with representations that are induced from a lower parabolic subgroup rather than an upper parabolic subgroup). We may write
$\Re (t_1)$
sufficiently large; from [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Proposition 7.2], this identity then extends via analytic continuation to all induced representations of Langlands type (note that Jacquet instead works with representations that are induced from a lower parabolic subgroup rather than an upper parabolic subgroup). We may write
 $$\begin{align*}&W^{\circ} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} \\&\quad= \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 1) \times 1}(F)} \int_{\mathrm{N}_{n - 1}(F)} f^{\circ}\left(\begin{pmatrix} 0 & 1 \\ w_{n - 1} & 0 \end{pmatrix} \begin{pmatrix} u & v \\ 0 & 1 \end{pmatrix} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix}\right) \overline{\psi_{n - 1}}(u) \overline{\psi}(e_{n - 1} v) \, du \, dv\end{align*}$$
$$\begin{align*}&W^{\circ} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} \\&\quad= \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 1) \times 1}(F)} \int_{\mathrm{N}_{n - 1}(F)} f^{\circ}\left(\begin{pmatrix} 0 & 1 \\ w_{n - 1} & 0 \end{pmatrix} \begin{pmatrix} u & v \\ 0 & 1 \end{pmatrix} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix}\right) \overline{\psi_{n - 1}}(u) \overline{\psi}(e_{n - 1} v) \, du \, dv\end{align*}$$
from the definition (9.1) of the Jacquet integral. We insert the Godement section identity (8.33) for
![]() $f^{\circ }$
with g replaced by
$f^{\circ }$
with g replaced by ![]() into this expression, additionally inserting the identity (9.4) for the normalising constant
into this expression, additionally inserting the identity (9.4) for the normalising constant
![]() $c^{\circ }$
. As explicated in [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Section 7.2], the ensuing double integral is absolutely convergent, so that we can make the change of variables
$c^{\circ }$
. As explicated in [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Section 7.2], the ensuing double integral is absolutely convergent, so that we can make the change of variables
![]() $h \mapsto w_{n - 1} u h$
and
$h \mapsto w_{n - 1} u h$
and
![]() $v \mapsto uhv$
; we find that
$v \mapsto uhv$
; we find that ![]() is equal to
is equal to

The integral over
![]() $\operatorname {\mathrm {Mat}}_{(n - 1) \times 1}(F) \ni v$
is equal to
$\operatorname {\mathrm {Mat}}_{(n - 1) \times 1}(F) \ni v$
is equal to
via Hecke’s identity, Lemmata 7.6 and 7.13, while the integral over
![]() $\mathrm {N}_{n - 1}(F) \ni u$
is equal to
$\mathrm {N}_{n - 1}(F) \ni u$
is equal to
![]() $W_0^{\circ }(h)$
via (9.1). It remains to use (8.25) in conjunction with the definition of
$W_0^{\circ }(h)$
via (9.1). It remains to use (8.25) in conjunction with the definition of
![]() $P_1^{\circ }$
as well as to note that
$P_1^{\circ }$
as well as to note that
![]() $\det w_n \det w_{n - 1} = (-1)^{n - 1}$
, so that
$\det w_n \det w_{n - 1} = (-1)^{n - 1}$
, so that
![]() $\chi ^{\kappa _1}(\det w_n) \chi ^{-\kappa _1}(\det w_{n - 1}) = (-1)^{\kappa _1(n - 1)}$
.
$\chi ^{\kappa _1}(\det w_n) \chi ^{-\kappa _1}(\det w_{n - 1}) = (-1)^{\kappa _1(n - 1)}$
.
Remark 9.13. For spherical Whittaker functions, such a propagation formula (in a slightly modified form) is due to Gerasimov, Lebedev and Oblezin [Reference Gerasimov, Lebedev and OblezinGLO08, Proposition 4.1] and Ishii and Stade [Reference Ishii and StadeIsSt13, Proposition 2.1] (cf. [Reference Ishii and MiyazakiIM22, Appendix A]); iterating this propagation formula gives a recursive formula for
![]() $\operatorname {\mathrm {GL}}_n(F)$
Whittaker functions in terms of
$\operatorname {\mathrm {GL}}_n(F)$
Whittaker functions in terms of
![]() $\operatorname {\mathrm {GL}}_2(F)$
and
$\operatorname {\mathrm {GL}}_2(F)$
and
![]() $\operatorname {\mathrm {GL}}_{n - 2}(F)$
Whittaker functions known earlier by the work of Stade [Reference StadeSta90, Theorem 2.1].
$\operatorname {\mathrm {GL}}_{n - 2}(F)$
Whittaker functions known earlier by the work of Stade [Reference StadeSta90, Theorem 2.1].
We also require the following propagation formula for
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
when
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
when
![]() $\pi '$
is spherical, which follows analogously to Lemma 9.8.
$\pi '$
is spherical, which follows analogously to Lemma 9.8.
Lemma 9.14. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi ' = |\cdot |^{t_1^{\prime }} \boxplus |\cdot |^{t_2^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_n^{\prime }}$
and
$\pi ' = |\cdot |^{t_1^{\prime }} \boxplus |\cdot |^{t_2^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_n^{\prime }}$
and ![]() be spherical representations of Langlands type of
be spherical representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
. Let
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
. Let
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
and
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
and
![]() $W_0^{\prime \circ } \in \mathcal {W}(\pi _0^{\prime },\overline {\psi })$
be the spherical Whittaker functions of
$W_0^{\prime \circ } \in \mathcal {W}(\pi _0^{\prime },\overline {\psi })$
be the spherical Whittaker functions of
![]() $\pi '$
and
$\pi '$
and
![]() $\pi _0^{\prime }$
. Then for
$\pi _0^{\prime }$
. Then for
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
,
$g \in \operatorname {\mathrm {GL}}_n(F)$
,
 $$ \begin{align} W^{\prime\circ}(g) = \left|\det g\right|{}^{t_1^{\prime} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 1}(F)} &W_0^{\prime\circ}(h) \left|\det h\right|{}^{-t_1^{\prime} - \frac{n}{2}} \nonumber\\ &\times \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 1) \times 1}(F)} \Phi'\left(h^{-1} \begin{pmatrix} 1_{n - 1} & v \end{pmatrix} g\right) \psi(e_{n - 1} v) \, dv \, dh, \end{align} $$
$$ \begin{align} W^{\prime\circ}(g) = \left|\det g\right|{}^{t_1^{\prime} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 1}(F)} &W_0^{\prime\circ}(h) \left|\det h\right|{}^{-t_1^{\prime} - \frac{n}{2}} \nonumber\\ &\times \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 1) \times 1}(F)} \Phi'\left(h^{-1} \begin{pmatrix} 1_{n - 1} & v \end{pmatrix} g\right) \psi(e_{n - 1} v) \, dv \, dh, \end{align} $$
with the standard Schwartz function
![]() $\Phi ' \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(F))$
given by
$\Phi ' \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(F))$
given by
9.3.2. The case
 $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
We next treat the case for which
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
![]() $n_1 = 2$
, so that
$n_1 = 2$
, so that
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
.
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
.
Lemma 9.17. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Langlands type of
be induced representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
with
$\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
with
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
and
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
and ![]() . Let
. Let
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
and
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
and
![]() $W_0^{\ast \circ } \in \mathcal {W}(\pi _0^{\ast },\psi )$
be the Whittaker newforms of
$W_0^{\ast \circ } \in \mathcal {W}(\pi _0^{\ast },\psi )$
be the Whittaker newforms of
![]() $\pi $
and
$\pi $
and
![]() $\pi _0^{\ast }$
. Then for
$\pi _0^{\ast }$
. Then for
![]() $g \in \operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
,
$g \in \operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
,
 $$ \begin{align} W^{\circ} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = \left|\det g\right|{}^{t_1 + \frac{\kappa_1 - 1}{2} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 1}(\mathbb{R})} W_0^{\ast\circ}(h) \Phi_1(h^{-1} g) \Phi_0^{\circ}(e_{n - 1} h) \left|\det h\right|{}^{-t_1 - \frac{\kappa_1 - 1}{2} - \frac{n}{2} + 1} \, dh, \end{align} $$
$$ \begin{align} W^{\circ} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = \left|\det g\right|{}^{t_1 + \frac{\kappa_1 - 1}{2} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 1}(\mathbb{R})} W_0^{\ast\circ}(h) \Phi_1(h^{-1} g) \Phi_0^{\circ}(e_{n - 1} h) \left|\det h\right|{}^{-t_1 - \frac{\kappa_1 - 1}{2} - \frac{n}{2} + 1} \, dh, \end{align} $$
with the standard Schwartz functions
![]() $\Phi _1 \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times (n - 1)}(\mathbb {R}))$
as in (9.10) and
$\Phi _1 \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times (n - 1)}(\mathbb {R}))$
as in (9.10) and
![]() $\Phi _0^{\ast \circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(\mathbb {R}))$
given by
$\Phi _0^{\ast \circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(\mathbb {R}))$
given by
where
![]() $P_0^{\ast \circ }$
is the homogeneous harmonic polynomial associated to the newform
$P_0^{\ast \circ }$
is the homogeneous harmonic polynomial associated to the newform
![]() $\operatorname {\mathrm {O}}(n - 1)$
-type
$\operatorname {\mathrm {O}}(n - 1)$
-type
![]() $\tau _0^{\ast \circ }$
of
$\tau _0^{\ast \circ }$
of
![]() $\pi _0^{\ast }$
via (7.8).
$\pi _0^{\ast }$
via (7.8).
Remark 9.20. When
![]() $n = 2$
, so that
$n = 2$
, so that
![]() $\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, the integral over
$\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
, the integral over
![]() $\operatorname {\mathrm {GL}}_1(\mathbb {R}) = \mathbb {R}^{\times } \ni h$
in (9.18) may be explicitly evaluated in order to show that
$\operatorname {\mathrm {GL}}_1(\mathbb {R}) = \mathbb {R}^{\times } \ni h$
in (9.18) may be explicitly evaluated in order to show that
 $$\begin{align*}W^{\circ}\begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = |g|^{t + \frac{\kappa}{2}} \exp(-2\pi|g|).\end{align*}$$
$$\begin{align*}W^{\circ}\begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = |g|^{t + \frac{\kappa}{2}} \exp(-2\pi|g|).\end{align*}$$
Proof. First, we consider the case
![]() $n = 2$
, so that
$n = 2$
, so that
![]() $\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
and
$\pi = D_{\kappa } \otimes \left |\det \right |{}^t$
and
![]() $\pi _0^{\ast } = |\cdot |^{t + \frac {\kappa + 1}{2}}$
. We insert the Godement section identity (8.37) for
$\pi _0^{\ast } = |\cdot |^{t + \frac {\kappa + 1}{2}}$
. We insert the Godement section identity (8.37) for
![]() $f^{\circ }$
with g replaced by
$f^{\circ }$
with g replaced by ![]() into the Jacquet integral (9.1), and we then interchange the order of integration and make the change of variables
into the Jacquet integral (9.1), and we then interchange the order of integration and make the change of variables
![]() $v' \mapsto a_2 v'$
, yielding
$v' \mapsto a_2 v'$
, yielding
 $$ \begin{align*} W^{\circ}\begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = i^{\kappa} |g|^{t + \frac{\kappa}{2}} \int_{\mathbb{R}^{\times}} |a_2| a_2^{-\kappa} &\exp\left(-\pi (a_2^{-1} g)^2\right) \\ &\!\!\times \int_{\mathbb{R}} \int_{\mathbb{R}} \overline{P^{\circ}}(v,v') \exp\left(-\pi\left(v^2 + v^{\prime 2}\right)\right) \overline{\psi}(a_2 v') \, dv \, dv' \, d^{\times}a_2. \end{align*} $$
$$ \begin{align*} W^{\circ}\begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} = i^{\kappa} |g|^{t + \frac{\kappa}{2}} \int_{\mathbb{R}^{\times}} |a_2| a_2^{-\kappa} &\exp\left(-\pi (a_2^{-1} g)^2\right) \\ &\!\!\times \int_{\mathbb{R}} \int_{\mathbb{R}} \overline{P^{\circ}}(v,v') \exp\left(-\pi\left(v^2 + v^{\prime 2}\right)\right) \overline{\psi}(a_2 v') \, dv \, dv' \, d^{\times}a_2. \end{align*} $$
Via Hecke’s identity, Lemma 7.13, the integral over
![]() $\mathbb {R}^2 \ni (v,v')$
is
$\mathbb {R}^2 \ni (v,v')$
is
and so we obtain the identity (9.18) upon relabelling
![]() $a_2$
as h.
$a_2$
as h.
Now we consider the case
![]() $n \geq 3$
. We again show this initially for
$n \geq 3$
. We again show this initially for
![]() $\Re (t_1)> \cdots > \Re (t_r)$
with
$\Re (t_1)> \cdots > \Re (t_r)$
with
![]() $\Re (t_1)$
sufficiently large; from [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Proposition 7.2], this identity then extends via analytic continuation to all induced representations of Langlands type. The derivation of the identity (9.18) is somewhat indirect: we first determine an alternate expression for the right-hand side of (9.18) and then show that the left-hand side is equal to this expression.
$\Re (t_1)$
sufficiently large; from [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Proposition 7.2], this identity then extends via analytic continuation to all induced representations of Langlands type. The derivation of the identity (9.18) is somewhat indirect: we first determine an alternate expression for the right-hand side of (9.18) and then show that the left-hand side is equal to this expression.
To begin, let ![]() and
and ![]() be induced representations of Langlands type of
be induced representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
with
$\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
with
![]() $\pi _1^{\ast } = |\cdot |^{t_1^{\ast }}$
and
$\pi _1^{\ast } = |\cdot |^{t_1^{\ast }}$
and
![]() $\pi _2^{\ast } = |\cdot |^{t_2^{\ast }}$
, and let
$\pi _2^{\ast } = |\cdot |^{t_2^{\ast }}$
, and let
![]() $W^{\ast \circ } \in \mathcal {W}(\pi ^{\ast },\psi )$
and
$W^{\ast \circ } \in \mathcal {W}(\pi ^{\ast },\psi )$
and
![]() $W_0^{\ast \circ } \in \mathcal {W}(\pi _0^{\ast },\psi )$
be the Whittaker newforms of
$W_0^{\ast \circ } \in \mathcal {W}(\pi _0^{\ast },\psi )$
be the Whittaker newforms of
![]() $\pi ^{\ast }$
and
$\pi ^{\ast }$
and
![]() $\pi _0^{\ast }$
.
$\pi _0^{\ast }$
.
On the one hand, we have from (9.9) that ![]() is equal to
is equal to
 $$ \begin{align} \left|\det g\right|{}^{t_1^{\ast} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 1}(\mathbb{R})} W_0^{\ast\circ}(h) \Phi_1(h^{-1} g) \Phi_0^{\ast\circ}(e_{n - 1} h) \left|\det h\right|{}^{-t_1^{\ast} - \frac{n}{2} + 1} \, dh, \end{align} $$
$$ \begin{align} \left|\det g\right|{}^{t_1^{\ast} + \frac{n - 1}{2}} \int_{\operatorname{\mathrm{GL}}_{n - 1}(\mathbb{R})} W_0^{\ast\circ}(h) \Phi_1(h^{-1} g) \Phi_0^{\ast\circ}(e_{n - 1} h) \left|\det h\right|{}^{-t_1^{\ast} - \frac{n}{2} + 1} \, dh, \end{align} $$
with
![]() $\Phi _1$
as in (9.10) and
$\Phi _1$
as in (9.10) and
![]() $\Phi _0^{\ast \circ }$
as in (9.19).
$\Phi _0^{\ast \circ }$
as in (9.19).
On the other hand, for
![]() $\Re (t_1^{\ast })$
sufficiently large,
$\Re (t_1^{\ast })$
sufficiently large, ![]() is equal to
is equal to
 $$ \begin{align*} \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 2) \times 1}(\mathbb{R})} \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 2) \times 1}(\mathbb{R})} \int_{\mathbb{R}} \int_{\mathrm{N}_{n - 2}(\mathbb{R})} f^{\ast\circ}&\left(\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ w_{n - 2} & 0 & 0 \end{pmatrix} \begin{pmatrix} u' & v_1^{\prime} & v_2^{\prime} \\ 0 & 1 & v_3^{\prime} \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix}\right) \\ &\qquad\qquad\!\!\times \overline{\psi_{n - 2}}(u) \overline{\psi}(e_{n - 2} v_1^{\prime}) \overline{\psi}(v_3^{\prime}) \, du \, dv_3^{\prime} \, dv_2^{\prime} \, dv_1^{\prime}. \end{align*} $$
$$ \begin{align*} \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 2) \times 1}(\mathbb{R})} \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 2) \times 1}(\mathbb{R})} \int_{\mathbb{R}} \int_{\mathrm{N}_{n - 2}(\mathbb{R})} f^{\ast\circ}&\left(\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ w_{n - 2} & 0 & 0 \end{pmatrix} \begin{pmatrix} u' & v_1^{\prime} & v_2^{\prime} \\ 0 & 1 & v_3^{\prime} \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix}\right) \\ &\qquad\qquad\!\!\times \overline{\psi_{n - 2}}(u) \overline{\psi}(e_{n - 2} v_1^{\prime}) \overline{\psi}(v_3^{\prime}) \, du \, dv_3^{\prime} \, dv_2^{\prime} \, dv_1^{\prime}. \end{align*} $$
We insert the Godement section identity (8.44) for
![]() $f^{\ast \circ }$
into this expression, additionally inserting the identity (9.4) for the normalising constant
$f^{\ast \circ }$
into this expression, additionally inserting the identity (9.4) for the normalising constant
![]() $c^{\ast \circ }$
. By a straightforward extension of [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Proposition 7.2], the ensuing multiple integral is absolutely convergent, so that we can make the change of variables
$c^{\ast \circ }$
. By a straightforward extension of [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Proposition 7.2], the ensuing multiple integral is absolutely convergent, so that we can make the change of variables
![]() $h \mapsto w_{n - 2} u' h$
,
$h \mapsto w_{n - 2} u' h$
,
![]() $v_1^{\prime } \mapsto u' v_1^{\prime }$
,
$v_1^{\prime } \mapsto u' v_1^{\prime }$
,
![]() $v_2^{\prime } \mapsto u' hv_2^{\prime }$
,
$v_2^{\prime } \mapsto u' hv_2^{\prime }$
,
![]() $v_3 \mapsto u^{\prime -1} w_{n - 2}$
and
$v_3 \mapsto u^{\prime -1} w_{n - 2}$
and
![]() $v_3^{\prime } \mapsto a_2 (v_3^{\prime } - v_3 hv_2^{\prime })$
. Using the definition of the Jacquet integral, (9.1), to evaluate the ensuing integral over
$v_3^{\prime } \mapsto a_2 (v_3^{\prime } - v_3 hv_2^{\prime })$
. Using the definition of the Jacquet integral, (9.1), to evaluate the ensuing integral over
![]() $\mathrm {N}_{n - 2}(\mathbb {R}) \ni u'$
and Hecke’s identity, Lemma 7.13, to evaluate the ensuing integrals over
$\mathrm {N}_{n - 2}(\mathbb {R}) \ni u'$
and Hecke’s identity, Lemma 7.13, to evaluate the ensuing integrals over
![]() $\operatorname {\mathrm {Mat}}_{(n - 2) \times 1}(\mathbb {R}) \ni v_2^{\prime }$
and
$\operatorname {\mathrm {Mat}}_{(n - 2) \times 1}(\mathbb {R}) \ni v_2^{\prime }$
and
![]() $\mathbb {R} \ni v_3^{\prime }$
, we find that
$\mathbb {R} \ni v_3^{\prime }$
, we find that

Here,
![]() $W_0^{\circ }$
is the Whittaker newform for
$W_0^{\circ }$
is the Whittaker newform for ![]() and
and
![]() $P_0^{\circ }$
is the homogeneous harmonic polynomial associated to the newform
$P_0^{\circ }$
is the homogeneous harmonic polynomial associated to the newform
![]() $\operatorname {\mathrm {O}}(n - 2)$
-type
$\operatorname {\mathrm {O}}(n - 2)$
-type
![]() $\tau _0^{\circ }$
of
$\tau _0^{\circ }$
of
![]() $\pi ^{\circ }$
via (7.8), and we have used Theorem 4.15 to write
$\pi ^{\circ }$
via (7.8), and we have used Theorem 4.15 to write
![]() $c(\pi _0^{\ast }) = c(\pi _2^{\ast }) + c(\pi _0) = c(\pi _0)$
.
$c(\pi _0^{\ast }) = c(\pi _2^{\ast }) + c(\pi _0) = c(\pi _0)$
.
Next, we note that the identities (9.21) and (9.22) for ![]() both extend holomorphically to
both extend holomorphically to
![]() $t_1^{\ast } = t_1 + (\kappa _1 - 1)/2$
and
$t_1^{\ast } = t_1 + (\kappa _1 - 1)/2$
and
![]() $t_2^{\ast } = t_1 + (\kappa _1 + 1)/2$
. From this, we see that the right-hand side of (9.18) is equal to
$t_2^{\ast } = t_1 + (\kappa _1 + 1)/2$
. From this, we see that the right-hand side of (9.18) is equal to

Now we show that ![]() is equal to (9.23) when
is equal to (9.23) when
![]() $\Re (t_1)$
is sufficiently large, from which the result shall follow via analytic continuation. We begin by noting that it is equal to
$\Re (t_1)$
is sufficiently large, from which the result shall follow via analytic continuation. We begin by noting that it is equal to
 $$ \begin{align*} \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 2) \times 1}(\mathbb{R})} \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 2) \times 1}(\mathbb{R})} \int_{\mathbb{R}} \int_{\mathrm{N}_{n - 2}(\mathbb{R})} f^{\circ}&\left(\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ w_{n - 2} & 0 & 0 \end{pmatrix} \begin{pmatrix} u' & v_1^{\prime} & v_2^{\prime} \\ 0 & 1 & v_3^{\prime} \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix}\right) \\ &\qquad\qquad\times \overline{\psi_{n - 2}}(u) \overline{\psi}(e_{n - 2} v_1^{\prime}) \overline{\psi}(v_3^{\prime}) \, du \, dv_3^{\prime} \, dv_2^{\prime} \, dv_1^{\prime}. \end{align*} $$
$$ \begin{align*} \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 2) \times 1}(\mathbb{R})} \int\limits_{\operatorname{\mathrm{Mat}}_{(n - 2) \times 1}(\mathbb{R})} \int_{\mathbb{R}} \int_{\mathrm{N}_{n - 2}(\mathbb{R})} f^{\circ}&\left(\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ w_{n - 2} & 0 & 0 \end{pmatrix} \begin{pmatrix} u' & v_1^{\prime} & v_2^{\prime} \\ 0 & 1 & v_3^{\prime} \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix}\right) \\ &\qquad\qquad\times \overline{\psi_{n - 2}}(u) \overline{\psi}(e_{n - 2} v_1^{\prime}) \overline{\psi}(v_3^{\prime}) \, du \, dv_3^{\prime} \, dv_2^{\prime} \, dv_1^{\prime}. \end{align*} $$
We insert the Godement section identity (8.42) for
![]() $f^{\circ }$
into this expression, additionally inserting the identity (9.4) for the normalising constant
$f^{\circ }$
into this expression, additionally inserting the identity (9.4) for the normalising constant
![]() $c^{\circ }$
. The ensuing multiple integral is again absolutely convergent, so that we can make the change of variables
$c^{\circ }$
. The ensuing multiple integral is again absolutely convergent, so that we can make the change of variables
![]() $h \mapsto w_{n - 2} u' h$
,
$h \mapsto w_{n - 2} u' h$
,
![]() $v_1^{\prime } \mapsto u' v_1^{\prime }$
,
$v_1^{\prime } \mapsto u' v_1^{\prime }$
,
![]() $v_2^{\prime } \mapsto u' hv_2^{\prime }$
,
$v_2^{\prime } \mapsto u' hv_2^{\prime }$
,
![]() $v_3 \mapsto u^{\prime -1} w_{n - 2}$
and
$v_3 \mapsto u^{\prime -1} w_{n - 2}$
and
![]() $v_3^{\prime } \mapsto a_2 (v_3^{\prime } - v_3 hv_2^{\prime })$
. We again evaluate the ensuing integral over
$v_3^{\prime } \mapsto a_2 (v_3^{\prime } - v_3 hv_2^{\prime })$
. We again evaluate the ensuing integral over
![]() $\mathrm {N}_{n - 2}(\mathbb {R}) \ni u'$
via the definition of the Jacquet integral and use Hecke’s identity, Lemma 7.13, to evaluate the integrals over
$\mathrm {N}_{n - 2}(\mathbb {R}) \ni u'$
via the definition of the Jacquet integral and use Hecke’s identity, Lemma 7.13, to evaluate the integrals over
![]() $\operatorname {\mathrm {Mat}}_{(n - 2) \times 1}(\mathbb {R}) \ni v_2^{\prime }$
and
$\operatorname {\mathrm {Mat}}_{(n - 2) \times 1}(\mathbb {R}) \ni v_2^{\prime }$
and
![]() $\mathbb {R}^2 \ni (v_3,v_3^{\prime })$
. The latter integral is equal to
$\mathbb {R}^2 \ni (v_3,v_3^{\prime })$
. The latter integral is equal to
The resulting expression is precisely (9.23).
10. Rankin–Selberg Integrals
It is time to put the propagation formulæ (9.9), (9.15) and (9.18) for
![]() $W^{\circ }$
and
$W^{\circ }$
and
![]() $W^{\prime \circ }$
to good use. Following the method of Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Section 8], we use these formulæ to express the
$W^{\prime \circ }$
to good use. Following the method of Jacquet [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Section 8], we use these formulæ to express the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral as the product of a
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral as the product of a
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral and a
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral and a
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_1$
Rankin–Selberg L-function, and similarly express the
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_1$
Rankin–Selberg L-function, and similarly express the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral as a product of a
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral as a product of a
![]() $\operatorname {\mathrm {GL}}_{n - 1} \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral and a
$\operatorname {\mathrm {GL}}_{n - 1} \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral and a
![]() $\operatorname {\mathrm {GL}}_1 \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg L-function.
$\operatorname {\mathrm {GL}}_1 \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg L-function.
10.1.
 $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integrals
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integrals
We first consider the
![]() $\operatorname {\mathrm {GL}}_1 \times \operatorname {\mathrm {GL}}_1$
Rankin–Selberg integral defined by (2.2); this is simply the Tate zeta integral.
$\operatorname {\mathrm {GL}}_1 \times \operatorname {\mathrm {GL}}_1$
Rankin–Selberg integral defined by (2.2); this is simply the Tate zeta integral.
Proposition 10.1. Let
![]() $\pi = \chi ^{\kappa } |\cdot |^t$
be a character of
$\pi = \chi ^{\kappa } |\cdot |^t$
be a character of
![]() $F^{\times }$
, and let
$F^{\times }$
, and let
![]() $\pi ' = |\cdot |^{t'}$
be a spherical character of
$\pi ' = |\cdot |^{t'}$
be a spherical character of
![]() $F^{\times }$
. Let
$F^{\times }$
. Let
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
be the Whittaker newform of
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
be the Whittaker newform of
![]() $\pi $
and let
$\pi $
and let
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
be the spherical Whittaker function of
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
be the spherical Whittaker function of
![]() $\pi '$
. Then for
$\pi '$
. Then for
![]() $\Re (s)$
sufficiently large, the
$\Re (s)$
sufficiently large, the
![]() $\operatorname {\mathrm {GL}}_1 \times \operatorname {\mathrm {GL}}_1$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_1 \times \operatorname {\mathrm {GL}}_1$
Rankin–Selberg integral
![]() $\Psi (s,W^{\circ },W^{\prime \circ },\Phi ^{\circ })$
is equal to
$\Psi (s,W^{\circ },W^{\prime \circ },\Phi ^{\circ })$
is equal to
![]() $L(s,\pi \times \pi ')$
with the standard Schwartz function
$L(s,\pi \times \pi ')$
with the standard Schwartz function
![]() $\Phi ^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times 1}(F))$
given by
$\Phi ^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times 1}(F))$
given by
where
![]() $P^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
$P^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
![]() $\tau ^{\circ }$
of
$\tau ^{\circ }$
of
![]() $\pi $
via (7.2) and (7.8).
$\pi $
via (7.2) and (7.8).
Proof. By definition,
![]() $W^{\circ }(g) = \chi ^{\kappa }(g) |g|^t$
and
$W^{\circ }(g) = \chi ^{\kappa }(g) |g|^t$
and
![]() $W^{\prime \circ }(g) = |g|^{t'}$
. We then use (8.25) in conjunction with the definition of
$W^{\prime \circ }(g) = |g|^{t'}$
. We then use (8.25) in conjunction with the definition of
![]() $P^{\circ }$
in order to see that
$P^{\circ }$
in order to see that
By the identities (2.8) and (2.11) relating the integral to zeta functions, the identities (2.7) and (2.10) relating zeta functions to L-functions, and the identity (2.6) relating Rankin–Selberg L-functions involving twists by a character to standard L-functions, this is precisely
![]() $L(s, \pi \times \pi ')$
.
$L(s, \pi \times \pi ')$
.
Next, we prove a recursive formula for the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral for
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral for
![]() $n \geq 2$
.
$n \geq 2$
.
Proposition 10.2. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representations of Langlands type of
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
be an induced representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
, and let
$\operatorname {\mathrm {GL}}_n(F)$
, and let
![]() $\pi ' = |\cdot |^{t_1^{\prime }} \boxplus |\cdot |^{t_2^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_n^{\prime }}$
and
$\pi ' = |\cdot |^{t_1^{\prime }} \boxplus |\cdot |^{t_2^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_n^{\prime }}$
and ![]() be spherical representations of Langlands type of
be spherical representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
. Let
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
. Let
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
be the Whittaker newform of
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
be the Whittaker newform of
![]() $\pi $
, and let
$\pi $
, and let
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
and
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
and
![]() $W_0^{\prime \circ } \in \mathcal {W}(\pi _0^{\prime },\overline {\psi })$
be the spherical Whittaker functions of
$W_0^{\prime \circ } \in \mathcal {W}(\pi _0^{\prime },\overline {\psi })$
be the spherical Whittaker functions of
![]() $\pi '$
and
$\pi '$
and
![]() $\pi _0^{\prime }$
. Then for
$\pi _0^{\prime }$
. Then for
![]() $\Re (s)$
sufficiently large, the
$\Re (s)$
sufficiently large, the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
Rankin–Selberg integral
![]() $\Psi (s,W^{\circ },W^{\prime \circ },\Phi ^{\circ })$
is equal to
$\Psi (s,W^{\circ },W^{\prime \circ },\Phi ^{\circ })$
is equal to
with the standard Schwartz function
![]() $\Phi ^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
given by
$\Phi ^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times n}(F))$
given by
where
![]() $P^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
$P^{\circ }$
is the homogeneous harmonic polynomial associated to the newform K-type
![]() $\tau ^{\circ }$
of
$\tau ^{\circ }$
of
![]() $\pi $
via (7.2) and (7.8).
$\pi $
via (7.2) and (7.8).
Proof. Just as in [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Equation (8.1)], we insert the propagation formula (9.15) for
![]() $W^{\prime \circ }(g)$
into the definition (2.2) of
$W^{\prime \circ }(g)$
into the definition (2.2) of
![]() $\Psi (s,W^{\circ },W^{\prime \circ },\Phi ^{\circ })$
; the absolute convergence of the triple integral is shown in [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Section 8.2]. We replace h with
$\Psi (s,W^{\circ },W^{\prime \circ },\Phi ^{\circ })$
; the absolute convergence of the triple integral is shown in [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Section 8.2]. We replace h with
![]() $uh$
, where now
$uh$
, where now
![]() $u \in \mathrm {N}_{n - 1}(F)$
and
$u \in \mathrm {N}_{n - 1}(F)$
and
![]() $h \in \mathrm {N}_{n - 1}(F) \backslash \operatorname {\mathrm {GL}}_{n - 1}(F)$
, make the change of variables
$h \in \mathrm {N}_{n - 1}(F) \backslash \operatorname {\mathrm {GL}}_{n - 1}(F)$
, make the change of variables
![]() $u \mapsto u^{-1}$
and
$u \mapsto u^{-1}$
and
![]() $v \mapsto u^{-1} v$
, then replace
$v \mapsto u^{-1} v$
, then replace ![]() with g, where now
with g, where now
![]() $g \in \operatorname {\mathrm {GL}}_n(F)$
; in doing so, we use the fact that
$g \in \operatorname {\mathrm {GL}}_n(F)$
; in doing so, we use the fact that
![]() $W^{\prime \circ }(uh) = \overline {\psi _{n - 1}}(u) W^{\prime \circ }(h)$
and that
$W^{\prime \circ }(uh) = \overline {\psi _{n - 1}}(u) W^{\prime \circ }(h)$
and that ![]() . We then make the change of variables
. We then make the change of variables ![]() . In this way, we find that
. In this way, we find that
![]() $\Psi (s,W^{\circ },W^{\prime \circ },\Phi ^{\circ })$
is equal to
$\Psi (s,W^{\circ },W^{\prime \circ },\Phi ^{\circ })$
is equal to
 $$\begin{align*}\int\limits_{\mathrm{N}_{n - 1}(F) \backslash \operatorname{\mathrm{GL}}_{n - 1}(F)} W_0^{\prime\circ}(h) \left|\det h\right|{}^{s - \frac{1}{2}} \int_{\operatorname{\mathrm{GL}}_n(F)} W^{\circ}\left(\begin{pmatrix} h & 0 \\ 0 & 1 \end{pmatrix} g\right) \Phi(g) \left|\det g\right|{}^{s + t_1^{\prime} + \frac{n - 1}{2}} \, dg \, dh,\end{align*}$$
$$\begin{align*}\int\limits_{\mathrm{N}_{n - 1}(F) \backslash \operatorname{\mathrm{GL}}_{n - 1}(F)} W_0^{\prime\circ}(h) \left|\det h\right|{}^{s - \frac{1}{2}} \int_{\operatorname{\mathrm{GL}}_n(F)} W^{\circ}\left(\begin{pmatrix} h & 0 \\ 0 & 1 \end{pmatrix} g\right) \Phi(g) \left|\det g\right|{}^{s + t_1^{\prime} + \frac{n - 1}{2}} \, dg \, dh,\end{align*}$$
where we have defined ![]() , where
, where
![]() $\Phi ' \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(F))$
is as in (9.16). Since the standard Schwartz function
$\Phi ' \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times n}(F))$
is as in (9.16). Since the standard Schwartz function
![]() $\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is as in (8.22), the integral over
$\Phi \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{n \times n}(F))$
is as in (8.22), the integral over
![]() $\operatorname {\mathrm {GL}}_n(F) \ni g$
is equal to
$\operatorname {\mathrm {GL}}_n(F) \ni g$
is equal to ![]() from (9.7). This yields the desired identity upon recalling the definition (2.1) of
from (9.7). This yields the desired identity upon recalling the definition (2.1) of
![]() $\Psi (s,W^{\circ },W_0^{\prime \circ })$
and the identity (2.6) relating Rankin–Selberg L-functions involving twists by a character to standard L-functions.
$\Psi (s,W^{\circ },W_0^{\prime \circ })$
and the identity (2.6) relating Rankin–Selberg L-functions involving twists by a character to standard L-functions.
10.2.
 $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integrals
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integrals
10.2.1. The case
 $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
We now prove a recursive formula for the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral. As in Sections 8.4 and 9.3, we first treat the case for which
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral. As in Sections 8.4 and 9.3, we first treat the case for which
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
![]() $n_1 = 1$
, so that
$n_1 = 1$
, so that
![]() $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
.
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
.
Proposition 10.3. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Langlands type of
be induced representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(F)$
and
$\operatorname {\mathrm {GL}}_n(F)$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
with
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
with
![]() $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
a character of
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
a character of
![]() $F^{\times }$
, and let
$F^{\times }$
, and let
![]() $\pi ' = |\cdot |^{t_1^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_{n - 1}^{\prime }}$
be a spherical representation of Langlands type of
$\pi ' = |\cdot |^{t_1^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_{n - 1}^{\prime }}$
be a spherical representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
. Let
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
. Let
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
and
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
and
![]() $W_0^{\circ } \in \mathcal {W}(\pi _0,\psi )$
be the Whittaker newforms of
$W_0^{\circ } \in \mathcal {W}(\pi _0,\psi )$
be the Whittaker newforms of
![]() $\pi $
and
$\pi $
and
![]() $\pi _0$
, and let
$\pi _0$
, and let
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
be the spherical Whittaker function of
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
be the spherical Whittaker function of
![]() $\pi '$
. Then for
$\pi '$
. Then for
![]() $\Re (s)$
sufficiently large, the
$\Re (s)$
sufficiently large, the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
![]() $\Psi (s,W^{\circ },W^{\prime \circ })$
is equal to
$\Psi (s,W^{\circ },W^{\prime \circ })$
is equal to
with the standard Schwartz function
![]() $\Phi _0^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F))$
given by
$\Phi _0^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F))$
given by
where
![]() $P_0^{\circ }$
is the homogeneous harmonic polynomial associated to the newform
$P_0^{\circ }$
is the homogeneous harmonic polynomial associated to the newform
![]() $K_{n - 1}$
-type
$K_{n - 1}$
-type
![]() $\tau _0^{\circ }$
of
$\tau _0^{\circ }$
of
![]() $\pi _0$
via (7.2) and (7.8).
$\pi _0$
via (7.2) and (7.8).
Proof. Just as in [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Equation (8.3)], we insert the propagation formula (9.9) for ![]() into the definition (2.1) of
into the definition (2.1) of
![]() $\Psi (s,W^{\circ },W^{\prime \circ })$
; the absolute convergence of the ensuing double integral is justified in [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Section 8.3]. We replace h with
$\Psi (s,W^{\circ },W^{\prime \circ })$
; the absolute convergence of the ensuing double integral is justified in [Reference Jacquet, Ginzburg, Lapid and SoudryJac09, Section 8.3]. We replace h with
![]() $uh$
, where now
$uh$
, where now
![]() $u \in \mathrm {N}_{n - 1}(F)$
and
$u \in \mathrm {N}_{n - 1}(F)$
and
![]() $h \in \mathrm {N}_{n - 1}(F) \backslash \operatorname {\mathrm {GL}}_{n - 1}(F)$
, make the change of variables
$h \in \mathrm {N}_{n - 1}(F) \backslash \operatorname {\mathrm {GL}}_{n - 1}(F)$
, make the change of variables
![]() $u \mapsto u^{-1}$
, and then replace
$u \mapsto u^{-1}$
, and then replace
![]() $ug$
with g, where now
$ug$
with g, where now
![]() $g \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
; in doing so, we use the fact that
$g \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
; in doing so, we use the fact that
![]() $W_0^{\circ }(uh) = \psi _{n - 1}(u) W_0^{\circ }(h)$
and that
$W_0^{\circ }(uh) = \psi _{n - 1}(u) W_0^{\circ }(h)$
and that
![]() $\overline {\psi _{n - 1}}(u) W^{\prime \circ }(g) = W^{\prime \circ }(ug)$
. We then make the change of variables
$\overline {\psi _{n - 1}}(u) W^{\prime \circ }(g) = W^{\prime \circ }(ug)$
. We then make the change of variables
![]() $g \mapsto hg$
, leading to the identity
$g \mapsto hg$
, leading to the identity
 $$ \begin{align*} \Psi(s,W^{\circ},W^{\prime\circ}) = \int\limits_{\mathrm{N}_{n - 1}(F) \backslash \operatorname{\mathrm{GL}}_{n - 1}(F)} &W_0^{\circ}(h) \Phi_0^{\circ}(e_{n - 1} h) \left|\det h\right|{}^s \\ &\!\!\quad\times \int_{\operatorname{\mathrm{GL}}_{n - 1}(F)} W^{\prime\circ}(hg) \Phi_1(g) \left|\det g\right|{}^{s + t_1 + \frac{\|\kappa_1\|}{d_F} + \frac{n}{2} - 1} \, dg \, dh, \end{align*} $$
$$ \begin{align*} \Psi(s,W^{\circ},W^{\prime\circ}) = \int\limits_{\mathrm{N}_{n - 1}(F) \backslash \operatorname{\mathrm{GL}}_{n - 1}(F)} &W_0^{\circ}(h) \Phi_0^{\circ}(e_{n - 1} h) \left|\det h\right|{}^s \\ &\!\!\quad\times \int_{\operatorname{\mathrm{GL}}_{n - 1}(F)} W^{\prime\circ}(hg) \Phi_1(g) \left|\det g\right|{}^{s + t_1 + \frac{\|\kappa_1\|}{d_F} + \frac{n}{2} - 1} \, dg \, dh, \end{align*} $$
where the standard Schwartz functions
![]() $\Phi _1 \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times (n - 1)}(F))$
and
$\Phi _1 \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{(n - 1) \times (n - 1)}(F))$
and
![]() ${\Phi _0^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F))}$
are as in (9.10) and (9.11). From (9.7), the integral over
${\Phi _0^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(F))}$
are as in (9.10) and (9.11). From (9.7), the integral over
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F) \ni g$
is equal to
$\operatorname {\mathrm {GL}}_{n - 1}(F) \ni g$
is equal to
 $$\begin{align*}L\left(s + t_1 + \frac{\|\kappa_1\|}{d_F},\pi'\right) W^{\prime\circ}(h).\end{align*}$$
$$\begin{align*}L\left(s + t_1 + \frac{\|\kappa_1\|}{d_F},\pi'\right) W^{\prime\circ}(h).\end{align*}$$
From (2.5), (2.6), (2.7) and (2.10), we have that
 $$\begin{align*}L\left(s + t_1 + \frac{\|\kappa_1\|}{d_F},\pi'\right) = L(s,\pi_1 \times \pi').\end{align*}$$
$$\begin{align*}L\left(s + t_1 + \frac{\|\kappa_1\|}{d_F},\pi'\right) = L(s,\pi_1 \times \pi').\end{align*}$$
This yields the desired identity upon recalling the definition (2.2) of
![]() $\Psi (s,W_0^{\circ },W^{\prime \circ },\Phi _0^{\circ })$
.
$\Psi (s,W_0^{\circ },W^{\prime \circ },\Phi _0^{\circ })$
.
10.2.2. The case
 $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
We next treat the case for which
![]() $\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
$\pi = \pi _1 \boxplus \cdots \boxplus \pi _r$
with
![]() $n_1 = 2$
, so that
$n_1 = 2$
, so that
![]() $F = \mathbb {R}$
and
$F = \mathbb {R}$
and
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
.
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
.
Proposition 10.4. For
![]() $n \geq 2$
, let
$n \geq 2$
, let
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() be induced representations of Langlands type of
be induced representations of Langlands type of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
with
$\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
with
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
and
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
and
![]() $\pi _1^{\ast } = |\cdot |^{t_1 + \frac {\kappa _1 + 1}{2}}$
, and let
$\pi _1^{\ast } = |\cdot |^{t_1 + \frac {\kappa _1 + 1}{2}}$
, and let
![]() $\pi ' = |\cdot |^{t_1^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_{n - 1}^{\prime }}$
be a spherical representation of Langlands type of
$\pi ' = |\cdot |^{t_1^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_{n - 1}^{\prime }}$
be a spherical representation of Langlands type of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
. Let
$\operatorname {\mathrm {GL}}_{n - 1}(\mathbb {R})$
. Let
![]() $W^{\circ } \in \mathcal {W}(\pi ,\psi )$
and
$W^{\circ } \in \mathcal {W}(\pi ,\psi )$
and
![]() $W_0^{\ast \circ } \in \mathcal {W}(\pi _0^{\ast },\psi )$
be the Whittaker newforms of
$W_0^{\ast \circ } \in \mathcal {W}(\pi _0^{\ast },\psi )$
be the Whittaker newforms of
![]() $\pi $
and
$\pi $
and
![]() $\pi _0^{\ast }$
, and let
$\pi _0^{\ast }$
, and let
![]() $W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
be the spherical Whittaker function of
$W^{\prime \circ } \in \mathcal {W}(\pi ',\overline {\psi })$
be the spherical Whittaker function of
![]() $\pi '$
. Then for
$\pi '$
. Then for
![]() $\Re (s)$
sufficiently large, the
$\Re (s)$
sufficiently large, the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral
![]() $\Psi (s,W^{\circ },W^{\prime \circ })$
is equal to
$\Psi (s,W^{\circ },W^{\prime \circ })$
is equal to
 $$\begin{align*}\Psi(s,W_0^{\ast\circ},W^{\prime\circ},\Phi_0^{\ast\circ}) L\left(s + t_1 + \frac{\kappa_1 - 1}{2}, \pi'\right),\end{align*}$$
$$\begin{align*}\Psi(s,W_0^{\ast\circ},W^{\prime\circ},\Phi_0^{\ast\circ}) L\left(s + t_1 + \frac{\kappa_1 - 1}{2}, \pi'\right),\end{align*}$$
with the standard Schwartz function
![]() $\Phi _0^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(\mathbb {R}))$
given by
$\Phi _0^{\circ } \in \mathscr {S}_0(\operatorname {\mathrm {Mat}}_{1 \times (n - 1)}(\mathbb {R}))$
given by
where
![]() $P_0^{\ast \circ }$
is the homogeneous harmonic polynomial associated to the newform
$P_0^{\ast \circ }$
is the homogeneous harmonic polynomial associated to the newform
![]() $\operatorname {\mathrm {O}}(n - 1)$
-type
$\operatorname {\mathrm {O}}(n - 1)$
-type
![]() $\tau _0^{\ast \circ }$
of
$\tau _0^{\ast \circ }$
of
![]() $\pi _0^{\ast }$
via (7.8).
$\pi _0^{\ast }$
via (7.8).
10.3. Proofs of Theorems 4.17 and 4.18
We first record the following uniqueness principle.
Lemma 10.5. Suppose that W is a smooth function on
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
of moderate growth that satisfies
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
of moderate growth that satisfies
![]() $W(ugk) = \psi _{n - 1}(u) W(g)$
for all
$W(ugk) = \psi _{n - 1}(u) W(g)$
for all
![]() $u \in \mathrm {N}_{n - 1}(F)$
,
$u \in \mathrm {N}_{n - 1}(F)$
,
![]() $g \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
and
$g \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
and
![]() $k \in K_{n - 1}$
. Then if
$k \in K_{n - 1}$
. Then if
 $$\begin{align*}\int\limits_{\mathrm{N}_{n - 1}(F) \backslash \operatorname{\mathrm{GL}}_{n - 1}(F)} W(g) W^{\prime\circ}(g) \left|\det g\right|{}^{s - \frac{1}{2}} \, dg = 0\end{align*}$$
$$\begin{align*}\int\limits_{\mathrm{N}_{n - 1}(F) \backslash \operatorname{\mathrm{GL}}_{n - 1}(F)} W(g) W^{\prime\circ}(g) \left|\det g\right|{}^{s - \frac{1}{2}} \, dg = 0\end{align*}$$
for all
![]() $s \in \mathbb {C}$
and spherical representations
$s \in \mathbb {C}$
and spherical representations
![]() $\pi '$
of
$\pi '$
of
![]() $\operatorname {\mathrm {GL}}_{n - 1}(F)$
, we must have that
$\operatorname {\mathrm {GL}}_{n - 1}(F)$
, we must have that
![]() $W(g) = 0$
for all
$W(g) = 0$
for all
![]() $g \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
.
$g \in \operatorname {\mathrm {GL}}_{n - 1}(F)$
.
Proof. This is proved by Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetski-Shapiro and ShalikaJP-SS81, Lemme (3.5)] when F is nonarchimedean; the same proof holds for archimedean F with minimal modifications. Alternatively, one can show this via the Whittaker–Plancherel theorem [Reference WallachWal92, Chapter 15].
With these results in hand, we may complete the proofs of Theorems 4.17 and 4.18.
Proofs of Theorems 4.17 and 4.18
We prove these theorems by double induction. The base case is the case
![]() $n = 1$
of Theorem 4.18, which is precisely Proposition 10.1.
$n = 1$
of Theorem 4.18, which is precisely Proposition 10.1.
Suppose by induction that Theorem 4.18 holds with
![]() $n - 1$
in place in n. If
$n - 1$
in place in n. If
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() with
with
![]() $\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
, then Proposition 10.3 and the induction hypothesis imply that
$\pi _1 = \chi ^{\kappa _1} |\cdot |^{t_1}$
, then Proposition 10.3 and the induction hypothesis imply that
By (2.5), this is precisely
![]() $L(s,\pi \times \pi ')$
. Similarly, if
$L(s,\pi \times \pi ')$
. Similarly, if
![]() $\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and
$\pi = \pi _1 \boxplus \pi _2 \boxplus \cdots \boxplus \pi _r$
and ![]() with
with
![]() $\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
and
$\pi _1 = D_{\kappa _1} \otimes \left |\det \right |{}^{t_1}$
and ![]() , then Proposition 10.4 and the induction hypothesis imply that
, then Proposition 10.4 and the induction hypothesis imply that
 $$\begin{align*}\Psi(s,W^{\circ},W^{\prime\circ}) = L(s,\pi_0^{\ast} \times \pi') L\left(s + t_1 + \frac{\kappa_1 - 1}{2},\pi'\right).\end{align*}$$
$$\begin{align*}\Psi(s,W^{\circ},W^{\prime\circ}) = L(s,\pi_0^{\ast} \times \pi') L\left(s + t_1 + \frac{\kappa_1 - 1}{2},\pi'\right).\end{align*}$$
 $$\begin{align*}L\left(s + t_1 + \frac{\kappa_1 - 1}{2},\pi'\right) L\left(s + t_1 + \frac{\kappa_1 + 1}{2},\pi'\right) \prod_{j = 2}^{r} L(s,\pi_j \times \pi'),\end{align*}$$
$$\begin{align*}L\left(s + t_1 + \frac{\kappa_1 - 1}{2},\pi'\right) L\left(s + t_1 + \frac{\kappa_1 + 1}{2},\pi'\right) \prod_{j = 2}^{r} L(s,\pi_j \times \pi'),\end{align*}$$
which by (2.10), (2.13) and (2.5) is again
![]() $L(s,\pi \times \pi ')$
.
$L(s,\pi \times \pi ')$
.
Next, suppose by induction that Theorem 4.17 holds. Then Proposition 10.2 and the induction hypothesis imply that for
![]() $\pi ' = |\cdot |^{t_1^{\prime }} \boxplus |\cdot |^{t_2^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_n^{\prime }}$
and
$\pi ' = |\cdot |^{t_1^{\prime }} \boxplus |\cdot |^{t_2^{\prime }} \boxplus \cdots \boxplus |\cdot |^{t_n^{\prime }}$
and ![]() ,
,
By (2.5), this is precisely
![]() $L(s,\pi \times \pi ')$
.
$L(s,\pi \times \pi ')$
.
Finally, Lemma 10.5 implies the uniqueness of
![]() $W^{\circ }$
as a right
$W^{\circ }$
as a right
![]() $K_{n - 1}$
-invariant test function for the
$K_{n - 1}$
-invariant test function for the
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral.
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_{n - 1}$
Rankin–Selberg integral.
Acknowledgements
I would like to thank Hervé Jacquet and Akshay Venkatesh for their encouragement as well as useful discussions. Thanks are also owed to Subhajit Jana for helpful clarifications regarding the theory of analytic newvectors.
Competing interests
The authors have no competing interest to declare.