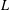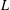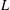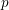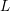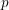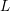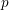7 results
KERNEL FUNCTIONS OF THE TWISTED SYMMETRIC SQUARE OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 130-131
- Print publication:
- 2019
-
- Article
-
- You have access
- HTML
- Export citation
KERNEL FUNCTIONS OF THE TWISTED SYMMETRIC SQUARE OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 07 February 2018, pp. 184-210
- Print publication:
- 2018
-
- Article
- Export citation
ANDRÉ–OORT CONJECTURE AND NONVANISHING OF CENTRAL
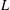 $L$ -VALUES OVER HILBERT CLASS FIELDS
$L$ -VALUES OVER HILBERT CLASS FIELDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 20 July 2016, e20
-
- Article
-
- You have access
- Open access
- Export citation
The
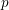 $p$-adic
$p$-adic 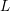 $L$-functions of evil Eisenstein series
$L$-functions of evil Eisenstein series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 13 January 2015, pp. 999-1040
- Print publication:
- June 2015
-
- Article
- Export citation
On mean values and non-vanishing of derivatives of L-functions in a nonlinear family
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 20 April 2010, pp. 19-34
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
The exceptional zero conjecture for Hilbert modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 1-55
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
Saito–Kurokawa lifts and applications to the Bloch–Kato conjecture
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 2 / March 2007
- Published online by Cambridge University Press:
- 26 March 2007, pp. 290-322
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation