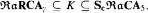Research Article
A power function with a fixed finite gap everywhere
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 361-417
-
- Article
- Export citation
Asymptotic classes of finite structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 418-438
-
- Article
- Export citation
The basic intuitionistic logic of proofs
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 439-451
-
- Article
- Export citation
Δ3O-determinacy, comprehension and induction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 452-462
-
- Article
- Export citation
Sublocales in formal topology
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 463-482
-
- Article
- Export citation
On sets not belonging to algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 483-500
-
- Article
- Export citation
Ideal convergence of bounded sequences
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 501-512
-
- Article
- Export citation
An analysis of the W*-hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 513-534
-
- Article
- Export citation
Connecting many-sorted theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 535-583
-
- Article
- Export citation
Simplicial structures in MV-algebras and logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 584-600
-
- Article
- Export citation
Successor-invariant first-order logic on finite structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 601-618
-
- Article
- Export citation
Burgess’ PV is Robinson’s Q
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 619-624
-
- Article
- Export citation
Transfer principle in quantum set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 625-648
-
- Article
- Export citation
NP search problems in low fragments of bounded arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 649-672
-
- Article
- Export citation
Relation algebra reducts of cylindric algebras and complete representations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 673-703
-
- Article
- Export citation
Assignment of ordinals to patterns of resemblance
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 704-720
-
- Article
- Export citation
Front matter
JSL volume 72 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JSL volume 72 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation

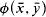 in the language of rings, there are finitely many pairs (
in the language of rings, there are finitely many pairs (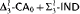 and
and 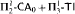 proves
proves 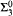 -Det and that neither
-Det and that neither 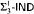 nor
nor 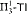 can be dropped. We also show that neither
can be dropped. We also show that neither 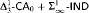 nor
nor 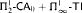 proves
proves 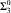 -Det. Moreover, we prove that none of
-Det. Moreover, we prove that none of 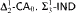 and
and 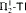 is provable in
is provable in 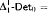
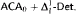
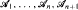 be a finite sequence of algebras of sets given on a set
be a finite sequence of algebras of sets given on a set 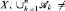
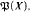 with more than
with more than 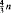 pairwise disjoint sets not belonging to
pairwise disjoint sets not belonging to 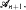 It was shown in [4] and [5] that in this case
It was shown in [4] and [5] that in this case 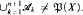 Let us consider, instead
Let us consider, instead 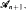 a finite sequence of algebras
a finite sequence of algebras 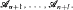 It turns out that if for each natural
It turns out that if for each natural 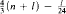 pairwise disjoint sets not belonging to
pairwise disjoint sets not belonging to 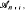 then
then 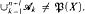 But if
But if 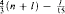 pairwise disjoint sets not belonging to
pairwise disjoint sets not belonging to 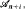 then
then 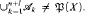 After consideration of finite sequences of algebras, it is natural to consider countable sequences of algebras. We obtained two essentially important theorems on a countable sequence of almost σ-algebras (the concept of almost σ-algebra was introduced in [4]).
After consideration of finite sequences of algebras, it is natural to consider countable sequences of algebras. We obtained two essentially important theorems on a countable sequence of almost σ-algebras (the concept of almost σ-algebra was introduced in [4]).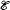 -connection approach for combining modal logics to an algebraic setting.
-connection approach for combining modal logics to an algebraic setting.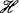 via the axioms and rules of inference, while the latter just says that every evaluation that “satisfies” all the members of
via the axioms and rules of inference, while the latter just says that every evaluation that “satisfies” all the members of 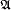 ,
, 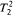 and
and 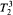 .
.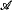 with countably many atoms, that
with countably many atoms, that