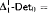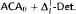Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nemoto, Takako
2008.
Logic and Theory of Algorithms.
Vol. 5028,
Issue. ,
p.
457.
Welch, P. D.
2009.
Games for Truth.
The Bulletin of Symbolic Logic,
Vol. 15,
Issue. 4,
p.
410.
Nemoto, Takako
2009.
Determinacy of Wadge classes and subsystems of second order arithmetic.
Mathematical Logic Quarterly,
Vol. 55,
Issue. 2,
p.
154.
Shore, Richard A.
2010.
Reverse Mathematics: The Playground of Logic.
The Bulletin of Symbolic Logic,
Vol. 16,
Issue. 3,
p.
378.
Heinatsch, Christoph
and
Möllerfeld, Michael
2010.
The determinacy strength of Π21-comprehension.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 12,
p.
1462.
Montalbán, Antonio
2011.
Open Questions in Reverse Mathematics.
The Bulletin of Symbolic Logic,
Vol. 17,
Issue. 3,
p.
431.
Yoshii, Keisuke
and
Tanaka, Kazuyuki
2012.
How the World Computes.
Vol. 7318,
Issue. ,
p.
374.
Kołodziejczyk, Leszek Aleksander
and
Michalewski, Henryk
2016.
How unprovable is Rabin's decidability theorem?.
p.
788.
Montalbán, Antonio
2017.
Fraïssé’s conjecture in Π11-comprehension.
Journal of Mathematical Logic,
Vol. 17,
Issue. 02,
p.
1750006.
YOSHII, Keisuke
2017.
A Survey of Determinacy of Infinite Games in Second Order Arithmetic.
Annals of the Japan Association for Philosophy of Science,
Vol. 25,
Issue. 0,
p.
35.
Li, Wenjuan
and
Tanaka, Kazuyuki
2017.
The determinacy strength of pushdownω-languages.
RAIRO - Theoretical Informatics and Applications,
Vol. 51,
Issue. 1,
p.
29.
FUCHINO, Sakaé
2017.
A Reflection Principle As a Reverse-mathematical Fixed Point over the Base Theory ZFC.
Annals of the Japan Association for Philosophy of Science,
Vol. 25,
Issue. 0,
p.
67.
Normann, Dag
and
Sanders, Sam
2019.
The strength of compactness in Computability Theory and Nonstandard Analysis.
Annals of Pure and Applied Logic,
Vol. 170,
Issue. 11,
p.
102710.


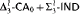 and
and 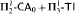 proves
proves 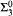 -Det and that neither
-Det and that neither 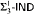 nor
nor 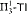 can be dropped. We also show that neither
can be dropped. We also show that neither 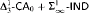 nor
nor 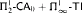 proves
proves 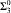 -Det. Moreover, we prove that none of
-Det. Moreover, we prove that none of 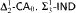 and
and 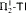 is provable in
is provable in