Article contents
QUANTIFIED MODAL RELEVANT LOGICS
Published online by Cambridge University Press: 23 April 2021
Abstract
Here, I combine the semantics of Mares and Goldblatt [20] and Seki [29, 30] to develop a semantics for quantified modal relevant logics extending
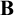 ${\bf B}$
. The combination requires demonstrating that the Mares–Goldblatt approach is apt for quantified extensions of
${\bf B}$
. The combination requires demonstrating that the Mares–Goldblatt approach is apt for quantified extensions of
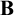 ${\bf B}$
and other relevant logics, but no significant bridging principles are needed. The result is a single semantic approach for quantified modal relevant logics. Within this framework, I discuss the requirements a quantified modal relevant logic must satisfy to be “sufficiently classical” in its modal fragment, where frame conditions are given that work for positive fragments of logics. The roles of the Barcan formula and its converse are also investigated.
${\bf B}$
and other relevant logics, but no significant bridging principles are needed. The result is a single semantic approach for quantified modal relevant logics. Within this framework, I discuss the requirements a quantified modal relevant logic must satisfy to be “sufficiently classical” in its modal fragment, where frame conditions are given that work for positive fragments of logics. The roles of the Barcan formula and its converse are also investigated.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
BIBLIOGRAPHY
- 6
- Cited by



