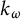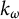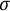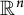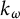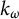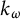1 Introduction
A
![]() $k_{\omega }$
-space—or a hemicompact k-space—is a Hausdorff space which is the image of a locally compact,
$k_{\omega }$
-space—or a hemicompact k-space—is a Hausdorff space which is the image of a locally compact,
![]() $\sigma $
-compact Hausdorff space under a quotient map. The class of
$\sigma $
-compact Hausdorff space under a quotient map. The class of
![]() $k_{\omega }$
-spaces was extensively studied from the 1940s and the literature of the subject (see [Reference Franklin and Smith Thomas10] for a useful summary) contains some famous names: R. Arens, M. Graev, E. Michael, J. Milnor, K. Morita, N. Steenrod, and others. Since then
$k_{\omega }$
-spaces was extensively studied from the 1940s and the literature of the subject (see [Reference Franklin and Smith Thomas10] for a useful summary) contains some famous names: R. Arens, M. Graev, E. Michael, J. Milnor, K. Morita, N. Steenrod, and others. Since then
![]() $k_{\omega }$
-spaces have become a standard tool (like locally compact Hausdorff spaces).
$k_{\omega }$
-spaces have become a standard tool (like locally compact Hausdorff spaces).
For general topologists, the class of
![]() $k_{\omega }$
-spaces has good closure properties (under quotients, closed subspaces, and finite products). In the study of spaces of continuous functions, the
$k_{\omega }$
-spaces has good closure properties (under quotients, closed subspaces, and finite products). In the study of spaces of continuous functions, the
![]() $k_{\omega }$
-spaces are those for which the space
$k_{\omega }$
-spaces are those for which the space
![]() $C_k(X)$
of continuous real-valued functions on X, with the compact-open topology, is completely metrizable (see [Reference McDougle16] for example). In C
$C_k(X)$
of continuous real-valued functions on X, with the compact-open topology, is completely metrizable (see [Reference McDougle16] for example). In C
![]() $^*$
-algebras (the authors’ interest) the Glimm spaces of
$^*$
-algebras (the authors’ interest) the Glimm spaces of
![]() $\sigma $
-unital C
$\sigma $
-unital C
![]() $^*$
-algebras belong to this class [Reference Lazar14, Theorem 2.6]. In topological algebras, the spectrum of a Fréchet algebra is usually (but not always) a
$^*$
-algebras belong to this class [Reference Lazar14, Theorem 2.6]. In topological algebras, the spectrum of a Fréchet algebra is usually (but not always) a
![]() $k_{\omega }$
-space; and
$k_{\omega }$
-space; and
![]() $k_{\omega }$
-spaces crop up, too, in the study of topological groups and semi-groups, and in mathematical economics, see [Reference Caterino, Ceppitelli and Maccarino7] for example.
$k_{\omega }$
-spaces crop up, too, in the study of topological groups and semi-groups, and in mathematical economics, see [Reference Caterino, Ceppitelli and Maccarino7] for example.
A
![]() $k_{\omega }$
-space is paracompact and normal [Reference Morita20, Lemma 5], but can be nowhere first countable, even when it is the quotient of a second countable space. The standard example is the countable space
$k_{\omega }$
-space is paracompact and normal [Reference Morita20, Lemma 5], but can be nowhere first countable, even when it is the quotient of a second countable space. The standard example is the countable space
![]() $S_{\omega }$
introduced by Arkhangel’skii and Franklin [Reference Arkhangel’skii and Franklin6]. One well-known weakening of first countability is the Fréchet-Urysohn property: a topological space X is Fréchet-Urysohn at
$S_{\omega }$
introduced by Arkhangel’skii and Franklin [Reference Arkhangel’skii and Franklin6]. One well-known weakening of first countability is the Fréchet-Urysohn property: a topological space X is Fréchet-Urysohn at
![]() $x\in X$
if
$x\in X$
if
![]() $A\subseteq X$
and
$A\subseteq X$
and
![]() $x\in \overline A$
implies the existence of a sequence
$x\in \overline A$
implies the existence of a sequence
![]() $(x_n)_{n\ge 1}\subseteq A$
with
$(x_n)_{n\ge 1}\subseteq A$
with
![]() $\lim _n x_x=x$
. If X is Fréchet-Urysohn at each point then X is a Fréchet-Urysohn space. The sequential fan (consisting of countably many convergent sequences with the non-isolated points identified to a single point) is a countable Fréchet-Urysohn
$\lim _n x_x=x$
. If X is Fréchet-Urysohn at each point then X is a Fréchet-Urysohn space. The sequential fan (consisting of countably many convergent sequences with the non-isolated points identified to a single point) is a countable Fréchet-Urysohn
![]() $k_{\omega }$
-space with first countability failing at a single point. Attempts to build more complicated examples run into difficulties, however, and in 2010, in exhibiting “a countable Tychonoff Fréchet-Urysohn space which is nowhere first countable,” Arkhangel’skii raised the question of whether a quotient of a locally compact second countable metric space could be found with all these features [Reference Arkhangel’skii5]. In point of fact this question had already been answered negatively by Siwiec in 1976 [Reference Siwiec22], but the fact that the question was even asked is significant because it highlights a basic gap in the understanding of
$k_{\omega }$
-space with first countability failing at a single point. Attempts to build more complicated examples run into difficulties, however, and in 2010, in exhibiting “a countable Tychonoff Fréchet-Urysohn space which is nowhere first countable,” Arkhangel’skii raised the question of whether a quotient of a locally compact second countable metric space could be found with all these features [Reference Arkhangel’skii5]. In point of fact this question had already been answered negatively by Siwiec in 1976 [Reference Siwiec22], but the fact that the question was even asked is significant because it highlights a basic gap in the understanding of
![]() $k_{\omega }$
-spaces.
$k_{\omega }$
-spaces.
The general picture is as follows. Recall that a point x in a topological space X is a k-point if
![]() $E\subseteq X$
and
$E\subseteq X$
and
![]() $x\in \overline E$
implies that there is a compact set K such that
$x\in \overline E$
implies that there is a compact set K such that
![]() $x\in \overline {E\cap K}$
. Clearly every point with a compact neighborhood is a k-point. As temporary notation, for a
$x\in \overline {E\cap K}$
. Clearly every point with a compact neighborhood is a k-point. As temporary notation, for a
![]() $k_{\omega }$
-space X, let L denote the set of points with compact neighborhood, F the set of k-points without compact neighborhood, and N the set of non-k-points. Then L is obviously an open set, and Morita and Arkhangel’skii (Theorems 2.1 and 2.3) showed that if X is the image of a closed quotient map then L is dense, F is discrete, and N is empty. Furthermore, the points of L are characterized by the fact that their inverse images have compact boundary.
$k_{\omega }$
-space X, let L denote the set of points with compact neighborhood, F the set of k-points without compact neighborhood, and N the set of non-k-points. Then L is obviously an open set, and Morita and Arkhangel’skii (Theorems 2.1 and 2.3) showed that if X is the image of a closed quotient map then L is dense, F is discrete, and N is empty. Furthermore, the points of L are characterized by the fact that their inverse images have compact boundary.
When a
![]() $k_{\omega }$
-space X is the image of a general (nonclosed) quotient map q, the set L can still be characterized by the biquotient property and
$k_{\omega }$
-space X is the image of a general (nonclosed) quotient map q, the set L can still be characterized by the biquotient property and
![]() $L\cup F$
by pseudo-openness (definitions below), but there is no explicit extension of Morita’s theorem relating these properties to q being locally closed or attempting to describe the sets F and N.
$L\cup F$
by pseudo-openness (definitions below), but there is no explicit extension of Morita’s theorem relating these properties to q being locally closed or attempting to describe the sets F and N.
In this paper, we introduce pure quotients maps—a partial generalization of closed quotient maps—and show that whenever X is the image of a quotient map q from a locally compact
![]() $\sigma $
-compact Hausdorff space Y, there is a corresponding pure quotient map
$\sigma $
-compact Hausdorff space Y, there is a corresponding pure quotient map
![]() $q_*:Y_*\to X$
where
$q_*:Y_*\to X$
where
![]() $Y_*$
is a locally compact
$Y_*$
is a locally compact
![]() $\sigma $
-compact Hausdorff space derived from Y using Fell’s topology on closed sets. Thus, every
$\sigma $
-compact Hausdorff space derived from Y using Fell’s topology on closed sets. Thus, every
![]() $k_{\omega }$
-space is the image of a pure quotient map.
$k_{\omega }$
-space is the image of a pure quotient map.
For pure quotient maps, N is precisely the set of points at which the map is not locally closed, and we extend Morita’s theorem by showing that F is contained in the set of P-points of
![]() $N\cup F$
and is thus a P-space with empty interior in X (Theorem 4.5). Thus a general
$N\cup F$
and is thus a P-space with empty interior in X (Theorem 4.5). Thus a general
![]() $k_{\omega }$
-space X decomposes as the disjoint union
$k_{\omega }$
-space X decomposes as the disjoint union
![]() $L\cup F\cup N$
where L is open and F has empty interior and is contained in the set of P-points of the closed set
$L\cup F\cup N$
where L is open and F has empty interior and is contained in the set of P-points of the closed set
![]() $F\cup N$
. If X is countably tight (in particular if X is a quotient of a locally compact subset of
$F\cup N$
. If X is countably tight (in particular if X is a quotient of a locally compact subset of
![]() ${\mathbb {R}}^n$
) then the P-points of
${\mathbb {R}}^n$
) then the P-points of
![]() $F\cup N$
are isolated points of
$F\cup N$
are isolated points of
![]() $F\cup N$
, lying in the closure of L; so N is closed,
$F\cup N$
, lying in the closure of L; so N is closed,
![]() $L\cup F$
is open with L dense, and F is discrete (Corollary 4.6). For general X, however, F need not be discrete, nor N closed, nor F lie in the closure of L; and we show by example that
$L\cup F$
is open with L dense, and F is discrete (Corollary 4.6). For general X, however, F need not be discrete, nor N closed, nor F lie in the closure of L; and we show by example that
![]() $F\cup N$
can be any compact Hausdorff space with F as its set of P-points (Example 4.7). A Fréchet-Urysohn space is countably tight with N empty, so the answer to Arkhangel’skii’s question quickly follows from the description just given (see Corollary 5.3 and Theorem 5.4, where more general results are obtained).
$F\cup N$
can be any compact Hausdorff space with F as its set of P-points (Example 4.7). A Fréchet-Urysohn space is countably tight with N empty, so the answer to Arkhangel’skii’s question quickly follows from the description just given (see Corollary 5.3 and Theorem 5.4, where more general results are obtained).
The authors encountered pure quotient maps in work on Glimm spaces of C
![]() $^*$
-algebras, where they occur naturally (indeed Theorem 4.5, in the second countable case, was originally proved entirely using C
$^*$
-algebras, where they occur naturally (indeed Theorem 4.5, in the second countable case, was originally proved entirely using C
![]() $^*$
-algebras). They look less obvious when translated into a topological context, but perhaps that is part of their wider interest.
$^*$
-algebras). They look less obvious when translated into a topological context, but perhaps that is part of their wider interest.
2 Morita’s theorem and locally closed maps
Let Y be a locally compact,
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff. Then, we can write
$q:Y\to X$
a quotient map with X Hausdorff. Then, we can write
![]() $Y=\bigcup _{i\ge 1} Y_i$
where each
$Y=\bigcup _{i\ge 1} Y_i$
where each
![]() $Y_i$
is compact and is contained in the interior of its successor. We will say that
$Y_i$
is compact and is contained in the interior of its successor. We will say that
![]() $\{Y_i: i\ge 1\}$
is a compact decomposition for Y, while the compact sets
$\{Y_i: i\ge 1\}$
is a compact decomposition for Y, while the compact sets
![]() $\{ q(Y_i): i\ge 1\}$
are a
$\{ q(Y_i): i\ge 1\}$
are a
![]() $k_{\omega }$
-decomposition for X. The space X is hemicompact with regard to a
$k_{\omega }$
-decomposition for X. The space X is hemicompact with regard to a
![]() $k_{\omega }$
-decompositon; that is, for any compact
$k_{\omega }$
-decompositon; that is, for any compact
![]() $K\subseteq X$
, eventually
$K\subseteq X$
, eventually
![]() $K\subseteq q(Y_i)$
for some i (see [Reference Franklin and Smith Thomas10, p. 113]).
$K\subseteq q(Y_i)$
for some i (see [Reference Franklin and Smith Thomas10, p. 113]).
One of the central results on
![]() $k_{\omega }$
-spaces is due to Morita [Reference Morita19, Theorem 4].
$k_{\omega }$
-spaces is due to Morita [Reference Morita19, Theorem 4].
Theorem 2.1 (Morita, 1956)
Let Y be a locally compact,
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff. If q is closed then X is locally compact except at a closed discrete set of exceptional points, namely those points x for which the fiber
$q:Y\to X$
a quotient map with X Hausdorff. If q is closed then X is locally compact except at a closed discrete set of exceptional points, namely those points x for which the fiber
![]() $q^{-1}(x)$
has noncompact boundary.
$q^{-1}(x)$
has noncompact boundary.
As Morita observes, the discrete set of exceptional points is in fact contained in a larger discrete set of points with noncompact fiber. For all other points, the fiber is compact.
If q is not closed, the situation becomes more complicated, and to discuss this the following definition is useful. Let X and Y be topological spaces. A map
![]() $q:Y\to X$
is locally closed at a point
$q:Y\to X$
is locally closed at a point
![]() $x\in X$
if for every closed set
$x\in X$
if for every closed set
![]() $W\subseteq Y$
,
$W\subseteq Y$
,
![]() $x\in \overline {q(W)}$
implies
$x\in \overline {q(W)}$
implies
![]() $x\in q(W)$
[Reference Kuratowski13, Section 13.XIV]. Clearly if q is surjective then q is closed if and only q is locally closed at each point of x. One basic result is as follows.
$x\in q(W)$
[Reference Kuratowski13, Section 13.XIV]. Clearly if q is surjective then q is closed if and only q is locally closed at each point of x. One basic result is as follows.
Proposition 2.2 Let Y be a locally compact Hausdorff space and
![]() $q:Y\to X$
a continuous surjective map with X Hausdorff. Let
$q:Y\to X$
a continuous surjective map with X Hausdorff. Let
![]() $x\in X$
and suppose that q is locally closed at x and that the boundary of
$x\in X$
and suppose that q is locally closed at x and that the boundary of
![]() $q^{-1}(x)$
is compact. Then x has a compact neighborhood in X.
$q^{-1}(x)$
is compact. Then x has a compact neighborhood in X.
Proof If the boundary of
![]() $q^{-1}(x)$
is compact then it is contained in an open subset O of Y whose closure is compact. The set
$q^{-1}(x)$
is compact then it is contained in an open subset O of Y whose closure is compact. The set
![]() $U:=q^{-1}(x)\cup O$
is open and the map q is locally closed at x. Thus
$U:=q^{-1}(x)\cup O$
is open and the map q is locally closed at x. Thus
![]() $V:=X\setminus \overline {q(Y\setminus U)}$
is an open neighborhood of x. We have
$V:=X\setminus \overline {q(Y\setminus U)}$
is an open neighborhood of x. We have
![]() $q^{-1}(x)\subseteq q^{-1}(V)$
, hence
$q^{-1}(x)\subseteq q^{-1}(V)$
, hence
![]() $\overline V\subseteq \overline {q(U)}=\{x\}\cup \overline {q(O)}= \{x\}\cup q(\overline O)$
, and thus
$\overline V\subseteq \overline {q(U)}=\{x\}\cup \overline {q(O)}= \{x\}\cup q(\overline O)$
, and thus
![]() $\overline V$
is compact.▪
$\overline V$
is compact.▪
In general, there seems to be little relation between the compactness of the fiber and “local closedness” of the quotient map on the one hand, and the local compactness of the image on the other. The following example is typical. Let
![]() $Y=\bigcup _{n\ge 0} L_n$
where
$Y=\bigcup _{n\ge 0} L_n$
where
![]() $L_n$
is the line
$L_n$
is the line
![]() $y=n$
in
$y=n$
in
![]() $ {\mathbb {R}}^2$
, and let
$ {\mathbb {R}}^2$
, and let
![]() $q:Y\to X$
be the projection of Y onto the x-axis, which is a quotient map. Then X is locally compact and Hausdorff but q is nowhere locally closed and
$q:Y\to X$
be the projection of Y onto the x-axis, which is a quotient map. Then X is locally compact and Hausdorff but q is nowhere locally closed and
![]() $q^{-1}(x)$
has noncompact boundary for every
$q^{-1}(x)$
has noncompact boundary for every
![]() $x\in X$
.
$x\in X$
.
A rather similar definition to “locally closed” was introduced independently by various authors, the earliest of whom seems to have been McDougle [Reference Malyhin17]. Let X and Y be topological spaces. A surjective map
![]() $f:Y\to X$
is pseudo-open at
$f:Y\to X$
is pseudo-open at
![]() $x\in X$
if whenever U is an open subset of Y containing
$x\in X$
if whenever U is an open subset of Y containing
![]() $f^{-1}(x)$
,
$f^{-1}(x)$
,
![]() $f(U)$
is a neighborhood of x. If f is pseudo-open at every point of X then f is said to be pseudo-open. A pseudo-open map is easily seen to be a quotient map, and if f is locally closed at x then f is pseudo-open at x. The example above, with q open but nowhere locally closed, shows that the converse is not true. We will see, however, that the two conditions are equivalent if the quotient map q is pure.
$f(U)$
is a neighborhood of x. If f is pseudo-open at every point of X then f is said to be pseudo-open. A pseudo-open map is easily seen to be a quotient map, and if f is locally closed at x then f is pseudo-open at x. The example above, with q open but nowhere locally closed, shows that the converse is not true. We will see, however, that the two conditions are equivalent if the quotient map q is pure.
The next theorem was essentially proved in [Reference Arkhangel’skii2, Theorems 3.3 and 3.4] (see also [Reference Arkhangel’skii1]) but our statement of it is somewhat different, so we include the short proof here.
Theorem 2.3 (Arkhangel’skii, 1963)
Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff. Let
$q:Y\to X$
a quotient map with X Hausdorff. Let
![]() $x\in X$
. Then x is a k-point if and only if q is pseudo-open at x.
$x\in X$
. Then x is a k-point if and only if q is pseudo-open at x.
Proof Suppose first that q is pseudo-open at x (this does not use the
![]() $\sigma $
-compactness of Y). Let
$\sigma $
-compactness of Y). Let
![]() $E\subseteq X$
with
$E\subseteq X$
with
![]() $x\in \overline E$
, and set
$x\in \overline E$
, and set
![]() $F=q^{-1}(E)$
. Then
$F=q^{-1}(E)$
. Then
![]() $\overline F$
meets
$\overline F$
meets
![]() $q^{-1}(x)$
, at y say, because q is pseudo-open (for otherwise there is an open set U containing
$q^{-1}(x)$
, at y say, because q is pseudo-open (for otherwise there is an open set U containing
![]() $q^{-1}(x)$
and disjoint from F, and then
$q^{-1}(x)$
and disjoint from F, and then
![]() $q(U)$
is a neighborhood of x disjoint from E). Let L be a compact neighborhood of y and set
$q(U)$
is a neighborhood of x disjoint from E). Let L be a compact neighborhood of y and set
![]() $K=q(L)$
. Then
$K=q(L)$
. Then
![]() $y\in \overline {F\cap L}$
and
$y\in \overline {F\cap L}$
and
![]() $x\in \overline {E\cap K}$
.
$x\in \overline {E\cap K}$
.
Conversely, suppose that x is a k-point and let U be an open subset of Y containing
![]() $f^{-1}(x)$
. Let
$f^{-1}(x)$
. Let
![]() $E=X\setminus q(U)$
and
$E=X\setminus q(U)$
and
![]() $F=q^{-1}(E)$
. Then F does not meet U. If
$F=q^{-1}(E)$
. Then F does not meet U. If
![]() $x\in \overline E$
then there exists a compact set K such that
$x\in \overline E$
then there exists a compact set K such that
![]() $x\in \overline {E\cap K}$
. By hemicompactness, there exists compact L in Y such
$x\in \overline {E\cap K}$
. By hemicompactness, there exists compact L in Y such
![]() $q(L)=K$
. Then
$q(L)=K$
. Then
![]() $\overline {F\cap L}$
is compact and
$\overline {F\cap L}$
is compact and
![]() $x\in q(\overline {F\cap L})$
. Hence,
$x\in q(\overline {F\cap L})$
. Hence,
![]() $\overline F$
meets
$\overline F$
meets
![]() $q^{-1}(x)$
, contradicting the fact that F does not meet U. Thus
$q^{-1}(x)$
, contradicting the fact that F does not meet U. Thus
![]() $x\notin \overline E$
, and
$x\notin \overline E$
, and
![]() $q(U)$
is a neighborhood of x.▪
$q(U)$
is a neighborhood of x.▪
For a quotient map
![]() $q: Y\to X$
, let
$q: Y\to X$
, let
![]() $H_q$
be the set of points in X at which q is pseudo-open. Theorem 1.3 shows that if Y is a locally compact
$H_q$
be the set of points in X at which q is pseudo-open. Theorem 1.3 shows that if Y is a locally compact
![]() $\sigma $
-compact Hausdorff space and X is Hausdorff then
$\sigma $
-compact Hausdorff space and X is Hausdorff then
![]() $H_q$
is the set of k-points in X.
$H_q$
is the set of k-points in X.
Among the k-points, the points x of local compactness in a
![]() $k_{\omega }$
-space (and more generally) can be characterized as those which satisfy the biquotient property: every open cover
$k_{\omega }$
-space (and more generally) can be characterized as those which satisfy the biquotient property: every open cover
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $q^{-1}(x)$
has a finite subset
$q^{-1}(x)$
has a finite subset
![]() $\{U_1, \ldots , U_n\}\subseteq \mathcal {U}$
such that
$\{U_1, \ldots , U_n\}\subseteq \mathcal {U}$
such that
![]() $\{ q(U_1), \ldots , q(U_n)\}$
covers a neighborhood of x (see [Reference Michael18, Reference Stone23]). While the characterizations given by the biquotient property and by pseudo-openness are elegant and versatile, they do not seem to lead to a structure theory for general
$\{ q(U_1), \ldots , q(U_n)\}$
covers a neighborhood of x (see [Reference Michael18, Reference Stone23]). While the characterizations given by the biquotient property and by pseudo-openness are elegant and versatile, they do not seem to lead to a structure theory for general
![]() $k_{\omega }$
-spaces along the lines of Morita’s theorem. Something is needed to bring the ideas together.
$k_{\omega }$
-spaces along the lines of Morita’s theorem. Something is needed to bring the ideas together.
3 Pure quotient maps
In this section, we introduce pure quotient maps. They are weaker than closed quotient maps in one important aspect, but with a compensatory strengthening in another direction; and while they retain some of the nice properties of closed quotient maps, they are much more general. We begin with a preparatory lemma.
Lemma 3.1 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff space. Then the following are equivalent:
$q:Y\to X$
a quotient map with X Hausdorff space. Then the following are equivalent:
-
(i) q is not closed;
-
(ii) there are nets
 $(y_{\alpha })$
(with the points
$(y_{\alpha })$
(with the points
 $y_{\alpha }$
from distinct fibers) and
$y_{\alpha }$
from distinct fibers) and
 $(z_{\alpha })$
in Y with
$(z_{\alpha })$
in Y with
 $y_{\alpha }\to \infty $
and
$y_{\alpha }\to \infty $
and
 $z_{\alpha }\not \to \infty $
such that
$z_{\alpha }\not \to \infty $
such that
 $q(y_{\alpha })=q(z_{\alpha })$
for all
$q(y_{\alpha })=q(z_{\alpha })$
for all
 $\alpha $
; and
$\alpha $
; and -
(iii) there are sequences
 $(y_n)$
(with the points
$(y_n)$
(with the points
 $y_n$
from distinct fibers) and
$y_n$
from distinct fibers) and
 $(z_n)$
in Y with
$(z_n)$
in Y with
 $y_n\to \infty $
and
$y_n\to \infty $
and
 $(z_n)$
contained in a compact set such that
$(z_n)$
contained in a compact set such that
 $q(y_n)=q(z_n)$
for all n.
$q(y_n)=q(z_n)$
for all n.
Proof (i)
![]() $\Rightarrow $
(ii). Let W be a closed subset of Y such that
$\Rightarrow $
(ii). Let W be a closed subset of Y such that
![]() $q(W)$
is not closed. Then the saturation
$q(W)$
is not closed. Then the saturation
![]() $W_0$
of W is not closed, so there is a net
$W_0$
of W is not closed, so there is a net
![]() $(z_{\alpha })$
in
$(z_{\alpha })$
in
![]() $W_0$
, which can be chosen from distinct fibers, such that
$W_0$
, which can be chosen from distinct fibers, such that
![]() $z_{\alpha }\to w\notin W_0$
. Let
$z_{\alpha }\to w\notin W_0$
. Let
![]() $(y_{\alpha })$
be a corresponding net in W with
$(y_{\alpha })$
be a corresponding net in W with
![]() $y_{\alpha }$
and
$y_{\alpha }$
and
![]() $z_{\alpha }$
from the same fiber for each
$z_{\alpha }$
from the same fiber for each
![]() $\alpha $
. Then if
$\alpha $
. Then if
![]() $(y_{\alpha })$
had any convergent subnet
$(y_{\alpha })$
had any convergent subnet
![]() $(y_{\beta })$
with limit
$(y_{\beta })$
with limit
![]() $y\in W$
, y and w would lie in the same fiber so w would belong to
$y\in W$
, y and w would lie in the same fiber so w would belong to
![]() $W_0$
, a contradiction. Hence
$W_0$
, a contradiction. Hence
![]() $y_{\alpha }\to \infty $
.
$y_{\alpha }\to \infty $
.
(ii)
![]() $\Rightarrow $
(iii). If (ii) holds, then
$\Rightarrow $
(iii). If (ii) holds, then
![]() $(z_{\alpha })$
is frequently in some compact set K, so for each
$(z_{\alpha })$
is frequently in some compact set K, so for each
![]() $n\ge 1$
, we may choose
$n\ge 1$
, we may choose
![]() $z_n$
from the set
$z_n$
from the set
![]() $\{ z_{\alpha }\}$
such the corresponding
$\{ z_{\alpha }\}$
such the corresponding
![]() $y_n\in \{ y_{\alpha }\}$
does not belong to
$y_n\in \{ y_{\alpha }\}$
does not belong to
![]() $K_n$
(where
$K_n$
(where
![]() $Y=\bigcup _{n\ge 1} K_n$
is a compact decomposition for Y). Then
$Y=\bigcup _{n\ge 1} K_n$
is a compact decomposition for Y). Then
![]() $y_n\to \infty $
while
$y_n\to \infty $
while
![]() $(z_n)$
is contained in K.
$(z_n)$
is contained in K.
(iii)
![]() $\Rightarrow $
(i). If (iii) holds, let K be the compact set containing
$\Rightarrow $
(i). If (iii) holds, let K be the compact set containing
![]() $(z_n)$
. Then
$(z_n)$
. Then
![]() $(z_n)$
has subnet converging to some
$(z_n)$
has subnet converging to some
![]() $y\in K$
, so
$y\in K$
, so
![]() $q(y)$
lies in the closure of the set
$q(y)$
lies in the closure of the set
![]() $\{q(z_n): n\ge 1\}$
. But
$\{q(z_n): n\ge 1\}$
. But
![]() $\{q(z_n):n\ge 1\}=q(\{y_n: n\ge 1\})$
, the image of a closed set, so q is not a closed map.▪
$\{q(z_n):n\ge 1\}=q(\{y_n: n\ge 1\})$
, the image of a closed set, so q is not a closed map.▪
Definition Let Y be a locally compact
![]() $\sigma $
-compact space and
$\sigma $
-compact space and
![]() $q:Y\to X$
a quotient map with X Hausdorff. We say that q is pure if there is a subset D of Y such that (i) D is dense in Y and the restriction of q to D is injective, and (ii) for every net
$q:Y\to X$
a quotient map with X Hausdorff. We say that q is pure if there is a subset D of Y such that (i) D is dense in Y and the restriction of q to D is injective, and (ii) for every net
![]() $(d_{\alpha })$
in D, if
$(d_{\alpha })$
in D, if
![]() $d_{\alpha }\to \infty $
(i.e., eventually escapes from every compact set in Y) then
$d_{\alpha }\to \infty $
(i.e., eventually escapes from every compact set in Y) then
![]() $e_{\alpha }\to \infty $
for any other net
$e_{\alpha }\to \infty $
for any other net
![]() $(e_{\alpha })$
for which
$(e_{\alpha })$
for which
![]() $q(d_{\alpha })=q(e_{\alpha })$
for all
$q(d_{\alpha })=q(e_{\alpha })$
for all
![]() $\alpha $
.
$\alpha $
.
Condition (ii) is equivalent to requiring that if
![]() $d_{\alpha }\to \infty $
then the net
$d_{\alpha }\to \infty $
then the net
![]() $q^{-1}(q(d_{\alpha }))$
converges to infinity in the Fell topology. Lemma 3.1 shows that condition (ii) is automatically satisfied whenever q is a closed quotient map.
$q^{-1}(q(d_{\alpha }))$
converges to infinity in the Fell topology. Lemma 3.1 shows that condition (ii) is automatically satisfied whenever q is a closed quotient map.
On the other hand, condition (i) implies that for every
![]() $x\in X$
, the interior of
$x\in X$
, the interior of
![]() $q^{-1}(x)$
is either empty or consists of an isolated point. In fact, condition (i) is equivalent to this when Y is second countable. To see this, let
$q^{-1}(x)$
is either empty or consists of an isolated point. In fact, condition (i) is equivalent to this when Y is second countable. To see this, let
![]() $D_0$
be the (countable) set of isolated points in Y and fix a countable base
$D_0$
be the (countable) set of isolated points in Y and fix a countable base
![]() $\{U_i\}_{i\ge 1}$
for
$\{U_i\}_{i\ge 1}$
for
![]() $Y\setminus \overline {D_0}$
. Inductively chose a point from each
$Y\setminus \overline {D_0}$
. Inductively chose a point from each
![]() $U_i$
which does not belong to any fiber with nonempty interior or any fiber previously chosen. This is possible because
$U_i$
which does not belong to any fiber with nonempty interior or any fiber previously chosen. This is possible because
![]() $U_i$
contains no isolated point and hence is an uncountable Baire space, and every fiber intersects
$U_i$
contains no isolated point and hence is an uncountable Baire space, and every fiber intersects
![]() $U_i$
in a closed set with empty interior. Let
$U_i$
in a closed set with empty interior. Let
![]() $D_1$
be the set thus obtained, and set
$D_1$
be the set thus obtained, and set
![]() $D=D_0\cup D_1$
. Then D is dense in Y and q restricted to D is injective.
$D=D_0\cup D_1$
. Then D is dense in Y and q restricted to D is injective.
Here is an alternative description of pure quotient maps that will be useful later.
Lemma 3.2 Let Y be a locally compact,
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff. Then the following are equivalent:
$q:Y\to X$
a quotient map with X Hausdorff. Then the following are equivalent:
-
(a) q is pure and
-
(b) there is a subset D in Y such that (i) D is dense and the restriction of q to D is injective, and (ii) whenever
 $Y=\bigcup _{i\ge 1} Y_i$
is a compact decomposition of Y, the sets
$Y=\bigcup _{i\ge 1} Y_i$
is a compact decomposition of Y, the sets
 $D_i:=\{ d\in D: q(d)\in q(Y_i)\}$
have compact closure in Y.
$D_i:=\{ d\in D: q(d)\in q(Y_i)\}$
have compact closure in Y.
Proof (a)
![]() $\Rightarrow $
(b). Let W be the closure of
$\Rightarrow $
(b). Let W be the closure of
![]() $D_i$
. If W is not compact, then there is a sequence
$D_i$
. If W is not compact, then there is a sequence
![]() $(d_j)$
in
$(d_j)$
in
![]() $D_i$
with
$D_i$
with
![]() $d_j\to \infty $
as
$d_j\to \infty $
as
![]() $j\to \infty $
. But for each j, there exists
$j\to \infty $
. But for each j, there exists
![]() $y_j\in Y_i$
such that
$y_j\in Y_i$
such that
![]() $q(y_j)=q(d_j)$
. Since
$q(y_j)=q(d_j)$
. Since
![]() $Y_i$
is compact,
$Y_i$
is compact,
![]() $y_j\not \to \infty $
, contradicting condition (ii) for pure quotient maps.
$y_j\not \to \infty $
, contradicting condition (ii) for pure quotient maps.
(b)
![]() $\Rightarrow $
(a). Let
$\Rightarrow $
(a). Let
![]() $(d_{\alpha })$
be a net in D with
$(d_{\alpha })$
be a net in D with
![]() $d_{\alpha }\to \infty $
. Let
$d_{\alpha }\to \infty $
. Let
![]() $(y_{\alpha })$
be any net in Y such that
$(y_{\alpha })$
be any net in Y such that
![]() $q(y_{\alpha })=q(d_{\alpha })$
for each
$q(y_{\alpha })=q(d_{\alpha })$
for each
![]() $\alpha $
. Then for any
$\alpha $
. Then for any
![]() $Y_i$
, if
$Y_i$
, if
![]() $(y_{\alpha })$
were frequently in
$(y_{\alpha })$
were frequently in
![]() $Y_i$
then
$Y_i$
then
![]() $(d_{\alpha })$
would frequently be in the compact closure of
$(d_{\alpha })$
would frequently be in the compact closure of
![]() $D_i$
, contradicting the convergence of
$D_i$
, contradicting the convergence of
![]() $(d_{\alpha })$
to infinity. Hence,
$(d_{\alpha })$
to infinity. Hence,
![]() $(y_{\alpha })$
is eventually outside each compact set
$(y_{\alpha })$
is eventually outside each compact set
![]() $Y_i$
, so
$Y_i$
, so
![]() $y_{\alpha }\to \infty $
.▪
$y_{\alpha }\to \infty $
.▪
Thus, if q is a pure quotient map and
![]() $Y=\bigcup _{i\ge 1} Y_i$
is a compact decomposition of Y, then for each
$Y=\bigcup _{i\ge 1} Y_i$
is a compact decomposition of Y, then for each
![]() $Y_i$
we may find
$Y_i$
we may find
![]() $Y_{d(i)}$
with
$Y_{d(i)}$
with
![]() $d(i)\ge i$
such that
$d(i)\ge i$
such that
![]() $D_i\subseteq Y_{d(i)}$
.
$D_i\subseteq Y_{d(i)}$
.
The usefulness of pure quotient maps appears in the following converse to Proposition 2.2 (note that because a fiber of a pure quotient map has at most a singleton as its interior, the fiber is compact if and only if its boundary is compact).
Theorem 3.3 Let Y be a locally compact,
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q: Y\to X$
a pure quotient map with X Hausdorff. If
$q: Y\to X$
a pure quotient map with X Hausdorff. If
![]() $x\in X$
has a compact neighborhood then q is locally closed at x and
$x\in X$
has a compact neighborhood then q is locally closed at x and
![]() $q^{-1}(x)$
is compact.
$q^{-1}(x)$
is compact.
Proof If Y is compact then q is closed and
![]() $q^{-1}(x)$
is compact for all
$q^{-1}(x)$
is compact for all
![]() $x\in X$
, so we may suppose that Y is noncompact. Let
$x\in X$
, so we may suppose that Y is noncompact. Let
![]() $Y=\bigcup _{i\ge 1} Y_i$
be a compact decomposition for Y. Suppose first that q is not locally closed at x. Let W be a closed subset of Y such that
$Y=\bigcup _{i\ge 1} Y_i$
be a compact decomposition for Y. Suppose first that q is not locally closed at x. Let W be a closed subset of Y such that
![]() $x\in \overline {q(W)}$
but W does not meet
$x\in \overline {q(W)}$
but W does not meet
![]() $q^{-1}(x)$
. Then for any neighborhood U of x,
$q^{-1}(x)$
. Then for any neighborhood U of x,
![]() $q(W)\cap U$
is not closed in U, so
$q(W)\cap U$
is not closed in U, so
![]() $W\cap q^{-1}(U)$
is not contained in any of the compact sets
$W\cap q^{-1}(U)$
is not contained in any of the compact sets
![]() $Y_i$
. Thus for each i, there exists
$Y_i$
. Thus for each i, there exists
![]() $w_i\in (W\cap q^{-1}(U))\setminus Y_i$
. By the density of D, there exists
$w_i\in (W\cap q^{-1}(U))\setminus Y_i$
. By the density of D, there exists
![]() $d_i\in (D\cap q^{-1}(U))\setminus Y_i$
. Then the set
$d_i\in (D\cap q^{-1}(U))\setminus Y_i$
. Then the set
![]() $F=\bigcup _i q^{-1}(q(d_i))$
is a saturated subset of Y, and F is closed by condition (ii) for pure quotient maps. Hence
$F=\bigcup _i q^{-1}(q(d_i))$
is a saturated subset of Y, and F is closed by condition (ii) for pure quotient maps. Hence
![]() $q(F)$
is an infinite closed discrete subset of U, so U is not countably compact.
$q(F)$
is an infinite closed discrete subset of U, so U is not countably compact.
Now suppose instead that
![]() $q^{-1}(x)$
is noncompact, and let U be a neighborhood of x. Then for each
$q^{-1}(x)$
is noncompact, and let U be a neighborhood of x. Then for each
![]() $i\ge 1$
, there exists
$i\ge 1$
, there exists
![]() $y_i\in q^{-1}(x)\setminus Y_i$
, so by the density of D, there exists
$y_i\in q^{-1}(x)\setminus Y_i$
, so by the density of D, there exists
![]() $d_i\in q^{-1}(U)\setminus Y_i$
. Then again the set
$d_i\in q^{-1}(U)\setminus Y_i$
. Then again the set
![]() $F=\bigcup _i q^{-1}(q(d_i))$
is a saturated subset of Y, and F is closed by condition (ii) for pure quotient maps. Hence
$F=\bigcup _i q^{-1}(q(d_i))$
is a saturated subset of Y, and F is closed by condition (ii) for pure quotient maps. Hence
![]() $q(F)$
is an infinite closed discrete subset of U, so again U is not countably compact.▪
$q(F)$
is an infinite closed discrete subset of U, so again U is not countably compact.▪
Pure quotient maps are not uncommon. Clearly, every locally compact
![]() $\sigma $
-compact Hausdorff space X admits the trivial pure quotient, taking
$\sigma $
-compact Hausdorff space X admits the trivial pure quotient, taking
![]() $Y=X$
and q as the identity map, and we now show that every
$Y=X$
and q as the identity map, and we now show that every
![]() $k_{\omega }$
-space X admits a pure quotient. Specifically, we show that if Y is a locally compact,
$k_{\omega }$
-space X admits a pure quotient. Specifically, we show that if Y is a locally compact,
![]() $\sigma $
-compact Hausdorff space, and
$\sigma $
-compact Hausdorff space, and
![]() $q:Y\to X$
a quotient map with X Hausdorff, then q can be “purified”: that is, a locally compact
$q:Y\to X$
a quotient map with X Hausdorff, then q can be “purified”: that is, a locally compact
![]() $\sigma $
-compact space
$\sigma $
-compact space
![]() $Y_*$
can be derived from Y such that the quotient map
$Y_*$
can be derived from Y such that the quotient map
![]() $q_*:Y_*\to X$
is pure (and induces the same topology on X as q).
$q_*:Y_*\to X$
is pure (and induces the same topology on X as q).
For a topological space X, let
![]() $\operatorname {Cl}(X)$
be the hyperspace of closed subsets of X with the Fell topology. A base for the Fell topology consists of the family of all sets
$\operatorname {Cl}(X)$
be the hyperspace of closed subsets of X with the Fell topology. A base for the Fell topology consists of the family of all sets
where K is a compact subset of X and
![]() $\Phi $
is a finite family of open subsets of X. Then
$\Phi $
is a finite family of open subsets of X. Then
![]() $\operatorname {Cl}(X)$
is a compact space [Reference Fell9, Lemma 1], and is Hausdorff if X is locally compact [Reference Fell9, Theorem 1]. The next lemma is presumably standard.
$\operatorname {Cl}(X)$
is a compact space [Reference Fell9, Lemma 1], and is Hausdorff if X is locally compact [Reference Fell9, Theorem 1]. The next lemma is presumably standard.
Lemma 3.4 Let X be a locally compact
![]() $\sigma $
-compact space. Then
$\sigma $
-compact space. Then
![]() $\operatorname {Cl}(X)\setminus \{\emptyset \}$
is
$\operatorname {Cl}(X)\setminus \{\emptyset \}$
is
![]() $\sigma $
-compact.
$\sigma $
-compact.
Proof We may write
![]() $X=\bigcup _i X_i$
where each
$X=\bigcup _i X_i$
where each
![]() $X_i$
is compact. For each i, set
$X_i$
is compact. For each i, set
![]() $K_i=\{K\in \operatorname {Cl}(X): K\cap X_i\ne \emptyset \}$
. Let
$K_i=\{K\in \operatorname {Cl}(X): K\cap X_i\ne \emptyset \}$
. Let
![]() $(K_{\alpha })$
be a net in
$(K_{\alpha })$
be a net in
![]() $K_i$
. Then by the compactness of
$K_i$
. Then by the compactness of
![]() $\operatorname {Cl}(X)$
,
$\operatorname {Cl}(X)$
,
![]() $(K_{\alpha })$
has a convergent subnet
$(K_{\alpha })$
has a convergent subnet
![]() $(K_{\beta })$
with limit W. But
$(K_{\beta })$
with limit W. But
![]() $W\cap X_i$
must be nonempty, since each
$W\cap X_i$
must be nonempty, since each
![]() $K_{\beta }$
meets
$K_{\beta }$
meets
![]() $X_i$
and hence
$X_i$
and hence
![]() $W\in K_i$
. Thus
$W\in K_i$
. Thus
![]() $K_i$
is compact, and
$K_i$
is compact, and
![]() $\operatorname {Cl}(X)\setminus \{\emptyset \}=\bigcup _i K_i$
is
$\operatorname {Cl}(X)\setminus \{\emptyset \}=\bigcup _i K_i$
is
![]() $\sigma $
-compact.▪
$\sigma $
-compact.▪
Lemma 3.5 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff. Let
$q:Y\to X$
a quotient map with X Hausdorff. Let
![]() $\operatorname {Cl}(Y)$
be the hyperspace of closed subsets of Y with the Fell topology, and let
$\operatorname {Cl}(Y)$
be the hyperspace of closed subsets of Y with the Fell topology, and let
![]() $Y_*$
be the closure of the set
$Y_*$
be the closure of the set
![]() $D=\{q^{-1}(x): x\in X\}$
in
$D=\{q^{-1}(x): x\in X\}$
in
![]() $\operatorname {Cl}(Y)\setminus \{\emptyset \}$
. Then for each
$\operatorname {Cl}(Y)\setminus \{\emptyset \}$
. Then for each
![]() $F\in Y_*$
there exists
$F\in Y_*$
there exists
![]() $F'\in D$
such that
$F'\in D$
such that
![]() $F\subseteq F'$
.
$F\subseteq F'$
.
Proof Let
![]() $(F_{\alpha })$
be a net in D with limit
$(F_{\alpha })$
be a net in D with limit
![]() $F\ne \emptyset $
in
$F\ne \emptyset $
in
![]() $\operatorname {Cl}(Y)$
. Let
$\operatorname {Cl}(Y)$
. Let
![]() $y\in F$
and set
$y\in F$
and set
![]() $F'=q^{-1}(q(y))$
. Then there is a net
$F'=q^{-1}(q(y))$
. Then there is a net
![]() $(y_{\alpha })$
with
$(y_{\alpha })$
with
![]() $y_{\alpha }\in F_{\alpha }$
such that
$y_{\alpha }\in F_{\alpha }$
such that
![]() $y_{\alpha }\to y$
. Hence,
$y_{\alpha }\to y$
. Hence,
![]() $q(y_{\alpha })\to q(y)$
. Let
$q(y_{\alpha })\to q(y)$
. Let
![]() $y'\in F$
. Then there is another net
$y'\in F$
. Then there is another net
![]() $(y^{\prime }_{\alpha })$
with
$(y^{\prime }_{\alpha })$
with
![]() $y^{\prime }_{\alpha }\in F_{\alpha }$
such that
$y^{\prime }_{\alpha }\in F_{\alpha }$
such that
![]() $y^{\prime }_{\alpha }\to y'$
. Hence,
$y^{\prime }_{\alpha }\to y'$
. Hence,
![]() $q(y_{\alpha })=q(y^{\prime }_{\alpha })\to q(y')$
, so
$q(y_{\alpha })=q(y^{\prime }_{\alpha })\to q(y')$
, so
![]() $y'\in F'$
. Thus
$y'\in F'$
. Thus
![]() $F\subseteq F'$
.▪
$F\subseteq F'$
.▪
It follows from Lemma 3.5 that, in the context of the lemma, we may consistently define a map
![]() $q_*: Y_*\to X$
by
$q_*: Y_*\to X$
by
![]() $q_*(F)=q(y) (y\in F)$
.
$q_*(F)=q(y) (y\in F)$
.
Theorem 3.6 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff. Let
$q:Y\to X$
a quotient map with X Hausdorff. Let
![]() $\operatorname {Cl}(Y)$
be the hyperspace of closed subsets of Y with the Fell topology, and let
$\operatorname {Cl}(Y)$
be the hyperspace of closed subsets of Y with the Fell topology, and let
![]() $Y_*$
be the closure of the set
$Y_*$
be the closure of the set
![]() $D=\{q^{-1}(x): x\in X\}$
in
$D=\{q^{-1}(x): x\in X\}$
in
![]() $\operatorname {Cl}(Y)\setminus \{\emptyset \}$
. Then
$\operatorname {Cl}(Y)\setminus \{\emptyset \}$
. Then
![]() $Y_*$
is a locally compact,
$Y_*$
is a locally compact,
![]() $\sigma $
-compact Hausdorff and the map
$\sigma $
-compact Hausdorff and the map
![]() $q_*: Y_*\to X$
is a pure quotient map inducing the same topology on X as q.
$q_*: Y_*\to X$
is a pure quotient map inducing the same topology on X as q.
Proof It follows from Lemma 3.4 that
![]() $Y_*$
is
$Y_*$
is
![]() $\sigma $
-compact.
$\sigma $
-compact.
Let C be a subset of X. We must show that
![]() $q_*^{-1}(C)$
is closed if and only if
$q_*^{-1}(C)$
is closed if and only if
![]() $q^{-1}(C)$
is closed. Suppose first that
$q^{-1}(C)$
is closed. Suppose first that
![]() $q^{-1}(C)$
is closed, and let
$q^{-1}(C)$
is closed, and let
![]() $F\in Y_*$
with
$F\in Y_*$
with
![]() $q_*(F)=y\notin C$
. Then the complement of
$q_*(F)=y\notin C$
. Then the complement of
![]() $q^{-1}(C)$
defines an open subset of
$q^{-1}(C)$
defines an open subset of
![]() $Y_*$
containing
$Y_*$
containing
![]() $F$
, and thus no net in
$F$
, and thus no net in
![]() $q_*^{-1}(C)$
can converge to F. Thus
$q_*^{-1}(C)$
can converge to F. Thus
![]() $q_*^{-1}(C)$
is closed. Conversely, suppose that
$q_*^{-1}(C)$
is closed. Conversely, suppose that
![]() $q_*^{-1}(C)$
is closed. Let
$q_*^{-1}(C)$
is closed. Let
![]() $(y_{\alpha })$
be a net in
$(y_{\alpha })$
be a net in
![]() $q^{-1}(C)$
with limit y. Set
$q^{-1}(C)$
with limit y. Set
![]() $F_{\alpha }=q_*^{-1}(q(y_{\alpha }))$
. Then
$F_{\alpha }=q_*^{-1}(q(y_{\alpha }))$
. Then
![]() $F_{\alpha }\not \to \infty $
, so by local compactness of
$F_{\alpha }\not \to \infty $
, so by local compactness of
![]() $Y_*$
there exists a convergent subnet of
$Y_*$
there exists a convergent subnet of
![]() $(F_{\alpha })$
with limit
$(F_{\alpha })$
with limit
![]() $F\in Y_*$
, and
$F\in Y_*$
, and
![]() $y\in F$
. Then
$y\in F$
. Then
![]() $F\in q_*^{-1}(C)$
by assumption, and
$F\in q_*^{-1}(C)$
by assumption, and
![]() $q_*(F)=q(y)\in C$
. Thus
$q_*(F)=q(y)\in C$
. Thus
![]() $y\in q^{-1}(C)$
as required.
$y\in q^{-1}(C)$
as required.
Finally, it is immediate that the restriction of
![]() $q_*$
to D is injective, while condition (ii) of pure quotient maps follows from Lemma 3.5.▪
$q_*$
to D is injective, while condition (ii) of pure quotient maps follows from Lemma 3.5.▪
Note that
![]() $q_*^{-1}(x)$
is the set consisting of
$q_*^{-1}(x)$
is the set consisting of
![]() $q^{-1}(x)$
and a family of closed subsets of the boundary of
$q^{-1}(x)$
and a family of closed subsets of the boundary of
![]() $q^{-1}(x)$
, obtained as limits of nets of fibers; see Lemma 3.5. (Thus in the example after Proposition 2.2, D is homeomorphic to
$q^{-1}(x)$
, obtained as limits of nets of fibers; see Lemma 3.5. (Thus in the example after Proposition 2.2, D is homeomorphic to
![]() ${\mathbb {R}}$
and is closed in
${\mathbb {R}}$
and is closed in
![]() $\operatorname {Cl}(Y)\setminus \{\emptyset \}$
). If the boundary of
$\operatorname {Cl}(Y)\setminus \{\emptyset \}$
). If the boundary of
![]() $q^{-1}(x)$
is compact then
$q^{-1}(x)$
is compact then
![]() $q_*^{-1}(x)$
is also compact because
$q_*^{-1}(x)$
is also compact because
![]() $Y_*$
is the closure of D in
$Y_*$
is the closure of D in
![]() $\operatorname {Cl}(Y)\setminus \{\emptyset \}$
. On the other hand, if the boundary of
$\operatorname {Cl}(Y)\setminus \{\emptyset \}$
. On the other hand, if the boundary of
![]() $q^{-1}(x)$
is noncompact then a net of its closed subsets might converge to
$q^{-1}(x)$
is noncompact then a net of its closed subsets might converge to
![]() $\emptyset $
in the Fell topology, so
$\emptyset $
in the Fell topology, so
![]() $q_*^{-1}(x)$
might be compact or noncompact.
$q_*^{-1}(x)$
might be compact or noncompact.
Apart from the fact that its fibers are more likely to be compact (or to have compact boundary) than those of q, a further advantage that
![]() $q_*$
has over q is that it is more likely to be locally closed.
$q_*$
has over q is that it is more likely to be locally closed.
Proposition 3.7 Let Y be a locally compact,
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() ${q:Y\to X}$
a quotient map with X Hausdorff. Let
${q:Y\to X}$
a quotient map with X Hausdorff. Let
![]() $q_*$
be the pure quotient constructed in Theorem
3.6
, and let
$q_*$
be the pure quotient constructed in Theorem
3.6
, and let
![]() $x\in X$
. If q is locally closed at x, then so is
$x\in X$
. If q is locally closed at x, then so is
![]() $q_*$
.
$q_*$
.
Proof Suppose that q is locally closed at x and let C be a closed subset of
![]() $Y_*$
disjoint from
$Y_*$
disjoint from
![]() $q_*^{-1}(x)$
. Set
$q_*^{-1}(x)$
. Set
![]() $W=\bigcup _{K\in C}K$
. Then W is disjoint from
$W=\bigcup _{K\in C}K$
. Then W is disjoint from
![]() $q^{-1}(x)$
. Let
$q^{-1}(x)$
. Let
![]() $(y_{\alpha })$
be a net in W with limit
$(y_{\alpha })$
be a net in W with limit
![]() $y\in Y$
. Then there is a net
$y\in Y$
. Then there is a net
![]() $(K_{\alpha })$
in C with
$(K_{\alpha })$
in C with
![]() $y_{\alpha }\in K_{\alpha }$
for each
$y_{\alpha }\in K_{\alpha }$
for each
![]() $\alpha $
, and
$\alpha $
, and
![]() $K_{\alpha }\not \to \infty $
, so by the local compactness of
$K_{\alpha }\not \to \infty $
, so by the local compactness of
![]() $Y_*$
there is a net
$Y_*$
there is a net
![]() $(K_{\beta })$
converging to some K, which belongs to C since C is closed. Since
$(K_{\beta })$
converging to some K, which belongs to C since C is closed. Since
![]() $y\in K$
, it follows that
$y\in K$
, it follows that
![]() $y\in W$
, and hence that W is closed. Since
$y\in W$
, and hence that W is closed. Since
![]() $q(W)=q_*(C)$
, it follows that
$q(W)=q_*(C)$
, it follows that
![]() $x\notin \overline {q_*(C)} $
.▪
$x\notin \overline {q_*(C)} $
.▪
In particular, if q is closed then
![]() $q_*$
is closed. Note, however, that in this case if the boundary of
$q_*$
is closed. Note, however, that in this case if the boundary of
![]() $q^{-1}(x)$
is noncompact then x does not have a compact neighborhood in X by Theorem 2.1, and hence
$q^{-1}(x)$
is noncompact then x does not have a compact neighborhood in X by Theorem 2.1, and hence
![]() $q_*^{-1}(x)$
is noncompact by Proposition 2.2 applied to
$q_*^{-1}(x)$
is noncompact by Proposition 2.2 applied to
![]() $q_*$
.
$q_*$
.
Proposition 3.7 raises the question of whether
![]() $q_{**}$
might be locally closed at even more points of X than
$q_{**}$
might be locally closed at even more points of X than
![]() $q_*$
is, but we will see in the next section that
$q_*$
is, but we will see in the next section that
![]() $q_*$
already reaches the limit.
$q_*$
already reaches the limit.
4 An extension of Morita’s theorem
In this section, we use pure quotient maps to extend Morita’s theorem to general
![]() $k_{\omega }$
-spaces.
$k_{\omega }$
-spaces.
Given a quotient map q from a locally compact
![]() $\sigma $
-compact Hausdorff space Y onto a Hausdorff space X, we partition X into three sets as follows:
$\sigma $
-compact Hausdorff space Y onto a Hausdorff space X, we partition X into three sets as follows:
(i)
![]() $L_q=\{x\in X: q$
is locally closed at x and
$L_q=\{x\in X: q$
is locally closed at x and
![]() $q^{-1}(x)$
has compact boundary};
$q^{-1}(x)$
has compact boundary};
(ii)
![]() $F_q=\{ x\in X: q$
is locally closed at x and
$F_q=\{ x\in X: q$
is locally closed at x and
![]() $q^{-1}(x)$
has noncompact boundary}; and (iii)
$q^{-1}(x)$
has noncompact boundary}; and (iii)
![]() $N_q=\{ x\in X: q$
is not locally closed at x}.
$N_q=\{ x\in X: q$
is not locally closed at x}.
We saw in Proposition 2.2 that if
![]() $x\in L_q$
then x has a compact neighborhood in X, and in Theorem 3.3 that if q is a pure quotient map then
$x\in L_q$
then x has a compact neighborhood in X, and in Theorem 3.3 that if q is a pure quotient map then
![]() $L_q$
is precisely the set of points in X which have a compact neighborhood. We now show that if q is a pure quotient map, the sets
$L_q$
is precisely the set of points in X which have a compact neighborhood. We now show that if q is a pure quotient map, the sets
![]() $F_q$
and
$F_q$
and
![]() $N_q$
can similarly be characterized in terms of the topology of X.
$N_q$
can similarly be characterized in terms of the topology of X.
Theorem 4.1 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q: Y\to X$
a pure quotient map with X Hausdorff. Then q is locally closed at
$q: Y\to X$
a pure quotient map with X Hausdorff. Then q is locally closed at
![]() $x\in X$
if and only if x is a k-point.
$x\in X$
if and only if x is a k-point.
Proof We have seen that if q is locally closed at x then it is pseudo-open at x, and hence x is a k-point by Theorem 2.3.
Conversely, suppose that q is not locally closed at x, and let N be a closed subset of Y disjoint from
![]() $q^{-1}(x)$
with
$q^{-1}(x)$
with
![]() $x\in \overline {q(N)}$
. Let W be a closed subset of Y disjoint from
$x\in \overline {q(N)}$
. Let W be a closed subset of Y disjoint from
![]() $q^{-1}(x)$
with N in its interior. Let D be the dense subset of Y from the pure quotient property, and set
$q^{-1}(x)$
with N in its interior. Let D be the dense subset of Y from the pure quotient property, and set
![]() $M=W\cap D$
and
$M=W\cap D$
and
![]() $E=q(M)$
. Then
$E=q(M)$
. Then
![]() $\overline M\supseteq N$
, so
$\overline M\supseteq N$
, so
![]() $x\in \overline {E}\setminus E$
. Let
$x\in \overline {E}\setminus E$
. Let
![]() $Y=\bigcup _i Y_i$
be a compact decomposition for Y and set
$Y=\bigcup _i Y_i$
be a compact decomposition for Y and set
![]() $K_i=q(Y_i)$
. Then for any i,
$K_i=q(Y_i)$
. Then for any i,
![]() $q^{-1}(K_i\cap E)=\{ d\in M: q(d)\in K_i\}$
so
$q^{-1}(K_i\cap E)=\{ d\in M: q(d)\in K_i\}$
so
![]() $q^{-1}(K_i\cap E)\subseteq Y_{d(i)}$
(in the terminology introduced after Lemma 3.2). Thus
$q^{-1}(K_i\cap E)\subseteq Y_{d(i)}$
(in the terminology introduced after Lemma 3.2). Thus
and this latter set is compact and does not contain x. Since every compact subset of X is contained in some
![]() $K_i$
by hemicompactness, it follows that there does not exist compact K with
$K_i$
by hemicompactness, it follows that there does not exist compact K with
![]() $x\in \overline {E\cap K}$
. Hence x is not a k-point.▪
$x\in \overline {E\cap K}$
. Hence x is not a k-point.▪
Thus if q is a pure quotient map, q is locally closed at x if and only if q is pseudo-open at x. The following corollary is immediate from Theorem 4.1.
Corollary 4.2 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q: Y\to X$
a pure quotient map with X Hausdorff. Let
$q: Y\to X$
a pure quotient map with X Hausdorff. Let
![]() $x\in X$
. Then
$x\in X$
. Then
(i)
![]() $x\in L_q$
if and only if x has a compact neighborhood in X;
$x\in L_q$
if and only if x has a compact neighborhood in X;
(ii)
![]() $x\in F_q$
if and only if x is a k-point without a compact neighborhood in X; and
$x\in F_q$
if and only if x is a k-point without a compact neighborhood in X; and
(iii)
![]() $x\in N_q$
if and only if x is not a k-point.
$x\in N_q$
if and only if x is not a k-point.
In particular, for any quotient map with domain a locally compact,
![]() $\sigma $
-compact Hausdorff space and Hausdorff range,
$\sigma $
-compact Hausdorff space and Hausdorff range,
![]() $N_{q_{**}}=N_{q_*}$
, answering the question raised in Section 3. It follows from Corollary 4.2 that for a
$N_{q_{**}}=N_{q_*}$
, answering the question raised in Section 3. It follows from Corollary 4.2 that for a
![]() $k_{\omega }$
-space X, the sets
$k_{\omega }$
-space X, the sets
![]() $L_{q_*}$
,
$L_{q_*}$
,
![]() $F_{q_*}$
, and
$F_{q_*}$
, and
![]() $N_{q_*}$
are independent of the original quotient map q, and in future we may use this notation even when there is no particular original quotient map in mind.
$N_{q_*}$
are independent of the original quotient map q, and in future we may use this notation even when there is no particular original quotient map in mind.
The next corollary is also immediate from Theorem 4.1 (applied to
![]() $q_*$
) and Theorem 2.3 (applied to q). Recall that
$q_*$
) and Theorem 2.3 (applied to q). Recall that
![]() $H_q$
denotes the set of points of X at which q is pseudo-open.
$H_q$
denotes the set of points of X at which q is pseudo-open.
Corollary 4.3 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q: Y\to X$
a quotient map with X Hausdorff. For
$q: Y\to X$
a quotient map with X Hausdorff. For
![]() $x\in X$
,
$x\in X$
,
![]() $x\in H_q$
if and only if
$x\in H_q$
if and only if
![]() $q_*$
is locally closed at x. Hence, q is pseudo-open if and only if
$q_*$
is locally closed at x. Hence, q is pseudo-open if and only if
![]() $q_*$
is closed.
$q_*$
is closed.
We turn now to consider the topology of the sets
![]() $L_{q}$
,
$L_{q}$
,
![]() $F_{q}$
, and
$F_{q}$
, and
![]() $N_{q}$
when q is pure (in which case
$N_{q}$
when q is pure (in which case
![]() $H_q=L_q\cup F_q$
by Corollary 4.3). It follows from Corollary 4.2 that
$H_q=L_q\cup F_q$
by Corollary 4.3). It follows from Corollary 4.2 that
![]() $L_q$
is open, and hence that
$L_q$
is open, and hence that
![]() $F_q\cup N_q$
is closed in X.
$F_q\cup N_q$
is closed in X.
Recall that a point x in a Tychonoff space X is a P-point if the intersection of any countable family of neighborhoods of x is a neighborhood of x. If every point is a P-point then X is a P-space. If U is an open subset of X and x is a P-point in U then x is P-point in X. Conversely, a P-point in X is a P-point in any subspace of X, and hence the set of P-points of X forms a P-space. If X is a compact P-space then X is finite [Reference Gillman and Jerison11, 4K]. The next theorem shows that
![]() $F_q$
is contained in the set of P-points of
$F_q$
is contained in the set of P-points of
![]() $F_q\cup N_q$
. For this, we need the following observation.
$F_q\cup N_q$
. For this, we need the following observation.
Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q: Y\to X$
a quotient map with X Hausdorff. Then q extends to a continuous map
$q: Y\to X$
a quotient map with X Hausdorff. Then q extends to a continuous map
![]() $\overline q: \beta Y\to \beta X$
, and
$\overline q: \beta Y\to \beta X$
, and
![]() $\overline q$
is continuous and surjective from a compact Hausdorff space, and is therefore also a quotient map. If
$\overline q$
is continuous and surjective from a compact Hausdorff space, and is therefore also a quotient map. If
![]() $x\in X$
and q is not locally closed at x, then there is a closed set
$x\in X$
and q is not locally closed at x, then there is a closed set
![]() $N\subseteq Y$
disjoint from
$N\subseteq Y$
disjoint from
![]() $q^{-1}(x)$
such that
$q^{-1}(x)$
such that
![]() $x\in \overline {q(N)}$
. Hence, there is a point
$x\in \overline {q(N)}$
. Hence, there is a point
![]() $y\in \overline {N}^{\beta Y}$
such that
$y\in \overline {N}^{\beta Y}$
such that
![]() $\overline q(y)=x$
.
$\overline q(y)=x$
.
Lemma 4.4 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q: Y\to X$
a pure quotient map with X Hausdorff. Let
$q: Y\to X$
a pure quotient map with X Hausdorff. Let
![]() $x\in N_q$
and let
$x\in N_q$
and let
![]() $y\in \beta Y\setminus Y$
such that
$y\in \beta Y\setminus Y$
such that
![]() $\overline q(y)=x$
. Let V be any neighborhood of x in X. Then Y has a zero set
$\overline q(y)=x$
. Let V be any neighborhood of x in X. Then Y has a zero set
![]() $Z\subseteq q^{-1}(V)$
with
$Z\subseteq q^{-1}(V)$
with
![]() $y\in \overline {Z}^{\beta Y}$
.
$y\in \overline {Z}^{\beta Y}$
.
Proof Let
![]() $U\subseteq V$
be a cozero set containing x with complement W in X. Then
$U\subseteq V$
be a cozero set containing x with complement W in X. Then
![]() $q^{-1}(W)$
is a saturated zero subset in Y. If Z is a zero set in Y contained in
$q^{-1}(W)$
is a saturated zero subset in Y. If Z is a zero set in Y contained in
![]() $q^{-1}(W)$
then
$q^{-1}(W)$
then
![]() $q(Z)$
is contained in W, so
$q(Z)$
is contained in W, so
![]() $y\notin \overline {Z}^{\beta Y}$
. Hence, by the z-ultrafilter property [Reference Gillman and Jerison11, 2.6 Theorem], there is a zero set Z in Y with
$y\notin \overline {Z}^{\beta Y}$
. Hence, by the z-ultrafilter property [Reference Gillman and Jerison11, 2.6 Theorem], there is a zero set Z in Y with
![]() $y\in \overline {Z}^{\beta Y}$
such that
$y\in \overline {Z}^{\beta Y}$
such that
![]() $Z\cap q^{-1}(W)$
is empty.▪
$Z\cap q^{-1}(W)$
is empty.▪
Theorem 4.5 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q: Y\to X$
a pure quotient map with X Hausdorff.
$q: Y\to X$
a pure quotient map with X Hausdorff.
(i) If
![]() $x\in X$
is a P-point then q is locally closed at x.
$x\in X$
is a P-point then q is locally closed at x.
(ii) Let W be the set of P-points in
![]() $ F_q\cup N_q$
and V the interior of
$ F_q\cup N_q$
and V the interior of
![]() $F_q\cup N_q$
in X. Then
$F_q\cup N_q$
in X. Then
(iii)
![]() $F_q$
is a P-space and has empty interior in X.
$F_q$
is a P-space and has empty interior in X.
Proof (i) (This does not require q to be pure). Let C be a closed subset of Y disjoint from
![]() $q^{-1}(x)$
. Then
$q^{-1}(x)$
. Then
where
![]() $Y=\bigcup _{n\ge 1} K_n$
is a compact decomposition for Y, so
$Y=\bigcup _{n\ge 1} K_n$
is a compact decomposition for Y, so
![]() $q(C)=\bigcup _{n\ge 1} q(C\cap K_n)$
. Since
$q(C)=\bigcup _{n\ge 1} q(C\cap K_n)$
. Since
![]() $q(C\cap K_n)$
is compact, hence closed in X, the P-point x does not lie in
$q(C\cap K_n)$
is compact, hence closed in X, the P-point x does not lie in
![]() $\overline {q(C)}$
. Thus q is locally closed at x.
$\overline {q(C)}$
. Thus q is locally closed at x.
(ii) It follows from (i) that
![]() $F_q\supseteq V\cap W$
. Now suppose that
$F_q\supseteq V\cap W$
. Now suppose that
![]() $x_0\in F_q\cup N_q$
is not a P-point of
$x_0\in F_q\cup N_q$
is not a P-point of
![]() $F_q\cup N_q$
. Let
$F_q\cup N_q$
. Let
![]() $\{E_i: i\ge 1\}$
be a countable family of closed sets in
$\{E_i: i\ge 1\}$
be a countable family of closed sets in
![]() $F_q\cup N_q\setminus \{ x_0\}$
with
$F_q\cup N_q\setminus \{ x_0\}$
with
![]() $x_0\in \overline {\bigcup _i E_i}$
. Fix i, and let
$x_0\in \overline {\bigcup _i E_i}$
. Fix i, and let
![]() $U_i$
be a closed neighborhood of
$U_i$
be a closed neighborhood of
![]() $x_0$
in X that does not meet
$x_0$
in X that does not meet
![]() $E_i$
. For each
$E_i$
. For each
![]() $x\in E_i$
choose
$x\in E_i$
choose
![]() $y\in q^{-1}(x)$
with
$y\in q^{-1}(x)$
with
![]() $y\notin Y_{i+1}$
if this is possible (as it is for each
$y\notin Y_{i+1}$
if this is possible (as it is for each
![]() $x\in F_q$
since
$x\in F_q$
since
![]() $q^{-1}(x)$
is noncompact). Otherwise, by the observation preceding Lemma 4.4, there exists
$q^{-1}(x)$
is noncompact). Otherwise, by the observation preceding Lemma 4.4, there exists
![]() $y\in \beta Y\setminus Y$
such that
$y\in \beta Y\setminus Y$
such that
![]() $\overline q(y)=x$
. By Lemma 4.4, there is a zero set Z in Y with
$\overline q(y)=x$
. By Lemma 4.4, there is a zero set Z in Y with
![]() $y\in \overline Z^{\beta Y}$
and
$y\in \overline Z^{\beta Y}$
and
![]() $Z\cap q^{-1}(U_i)$
empty, and we may also arrange that
$Z\cap q^{-1}(U_i)$
empty, and we may also arrange that
![]() $Z\cap Y_{i+1}$
is empty.
$Z\cap Y_{i+1}$
is empty.
Let
![]() $N_i'$
be the union of the collection of elements y and zero sets Z thus obtained, and let
$N_i'$
be the union of the collection of elements y and zero sets Z thus obtained, and let
![]() $N_i$
be the closure of
$N_i$
be the closure of
![]() $N_i'$
in Y. Then
$N_i'$
in Y. Then
![]() $N_i$
does not meet
$N_i$
does not meet
![]() $Y_i$
since
$Y_i$
since
![]() $Y_i$
is contained in the interior of
$Y_i$
is contained in the interior of
![]() $Y_{i+1}$
, and
$Y_{i+1}$
, and
![]() $\overline {q(N_i)}\supseteq E_i$
, but
$\overline {q(N_i)}\supseteq E_i$
, but
![]() $q(N_i)\cap U_i$
is empty (so in particular
$q(N_i)\cap U_i$
is empty (so in particular
![]() $x_0\notin q(N_i)$
). Set
$x_0\notin q(N_i)$
). Set
![]() $N=\bigcup N_i$
. Then N does not meet
$N=\bigcup N_i$
. Then N does not meet
![]() $q^{-1}(x_0)$
, and N is closed in Y because, for any
$q^{-1}(x_0)$
, and N is closed in Y because, for any
![]() $Y_j$
, only finitely many of the sets
$Y_j$
, only finitely many of the sets
![]() $N_i$
meet
$N_i$
meet
![]() $Y_j$
, so
$Y_j$
, so
![]() $N\cap Y_j$
is closed. But
$N\cap Y_j$
is closed. But
![]() $\overline {q(N)}\supseteq \bigcup _i E_i$
, so
$\overline {q(N)}\supseteq \bigcup _i E_i$
, so
![]() $x_0\in \overline {q(N)}\setminus q(N)$
. Hence,
$x_0\in \overline {q(N)}\setminus q(N)$
. Hence,
![]() $x_0\in N_q$
, so
$x_0\in N_q$
, so
![]() $F_q\subseteq W$
.
$F_q\subseteq W$
.
(iii)
![]() $F_q$
is a P-space by (ii). Let U be the interior of
$F_q$
is a P-space by (ii). Let U be the interior of
![]() $F_q$
in
$F_q$
in
![]() $F_q\cup N_q$
. Then
$F_q\cup N_q$
. Then
![]() $O:=q^{-1}(U)$
is open in Y, hence a locally compact Hausdorff space, and
$O:=q^{-1}(U)$
is open in Y, hence a locally compact Hausdorff space, and
![]() $q|_O$
is a quotient map. Thus U is a k-space, so a subset of U is closed if and only if its intersection with every compact subset of U is closed. But U is P-space, so compact subsets are finite [Reference Gillman and Jerison11, 4K]. Thus, every subset of U is closed, so U is discrete. Hence, each point in U lies in the closure of
$q|_O$
is a quotient map. Thus U is a k-space, so a subset of U is closed if and only if its intersection with every compact subset of U is closed. But U is P-space, so compact subsets are finite [Reference Gillman and Jerison11, 4K]. Thus, every subset of U is closed, so U is discrete. Hence, each point in U lies in the closure of
![]() $L_q$
(for otherwise it would be an isolated point of X and would belong to
$L_q$
(for otherwise it would be an isolated point of X and would belong to
![]() $L_q$
itself). Thus,
$L_q$
itself). Thus,
![]() $F_q$
has empty interior in X.▪
$F_q$
has empty interior in X.▪
Theorem 4.5 is an extension of Morita’s theorem (1.1) because if q is a closed quotient map then
![]() $q_*$
is closed (Proposition 3.7), so
$q_*$
is closed (Proposition 3.7), so
![]() $N_q$
and
$N_q$
and
![]() $N_{q_*}$
are both empty. Furthermore
$N_{q_*}$
are both empty. Furthermore
![]() $F_q=F_{q_*}$
by the remark after Proposition 3.7, so
$F_q=F_{q_*}$
by the remark after Proposition 3.7, so
![]() $F_{q}$
is closed, and thus
$F_{q}$
is closed, and thus
![]() $\sigma $
-compact. Being a P-space by Theorem 4.5,
$\sigma $
-compact. Being a P-space by Theorem 4.5,
![]() $F_{q}$
must be a countable discrete set in the closure of
$F_{q}$
must be a countable discrete set in the closure of
![]() $L_q$
, and thus we recover Morita’s theorem.
$L_q$
, and thus we recover Morita’s theorem.
In some cases, we can go further. Recall that a topological space X has countable tightness at
![]() $x\in X$
if for each
$x\in X$
if for each
![]() $A\subseteq X$
with
$A\subseteq X$
with
![]() $x\in \overline A$
, there is a countable subset
$x\in \overline A$
, there is a countable subset
![]() $B\subseteq A$
with
$B\subseteq A$
with
![]() $x\in \overline B$
; and X is countably tight if it is has countable tightness at every point. Clearly every metric space is countably tight.
$x\in \overline B$
; and X is countably tight if it is has countable tightness at every point. Clearly every metric space is countably tight.
Corollary 4.6 Let Y be a locally compact
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q: Y\to X$
a pure quotient map with X Hausdorff.
$q: Y\to X$
a pure quotient map with X Hausdorff.
(i) If
![]() $x\in F_q$
is a point of countable tightness in X then x is isolated in
$x\in F_q$
is a point of countable tightness in X then x is isolated in
![]() $F_q\cup N_q$
and lies in the closure of
$F_q\cup N_q$
and lies in the closure of
![]() $L_q$
.
$L_q$
.
(ii) If X is countably tight then
![]() $N_q$
is closed in X, and
$N_q$
is closed in X, and
![]() $F_q$
is discrete and lies in the closure of
$F_q$
is discrete and lies in the closure of
![]() $L_q$
.
$L_q$
.
Proof (i) follows immediately from the fact that x is a P-point in
![]() $F_q\cup N_q$
, and (ii) follows from (i).▪
$F_q\cup N_q$
, and (ii) follows from (i).▪
Corollary 4.6 seems to be new even for quotients of locally compact subsets of
![]() ${\mathbb {R}}^n$
.
${\mathbb {R}}^n$
.
We have just seen that if X is countably tight then there are no points of
![]() $F_q$
in the interior of
$F_q$
in the interior of
![]() $N_q\cup F_q$
, but if X is not countably tight, such points may occur. For example, let X be the quotient of
$N_q\cup F_q$
, but if X is not countably tight, such points may occur. For example, let X be the quotient of
![]() $\omega _1+1\times S_{\omega }$
(where
$\omega _1+1\times S_{\omega }$
(where
![]() $S_{\omega }$
is the Arkhangel’skii–Franklin space [Reference Arkhangel’skii and Franklin6] obtained by identifying
$S_{\omega }$
is the Arkhangel’skii–Franklin space [Reference Arkhangel’skii and Franklin6] obtained by identifying
![]() $\{\omega _1\}\times S_{\omega }$
to a point
$\{\omega _1\}\times S_{\omega }$
to a point
![]() $x_0$
. Then
$x_0$
. Then
![]() $L_q$
is empty and
$L_q$
is empty and
![]() $F_q=\{x_0\}$
.
$F_q=\{x_0\}$
.
Not every P-point of
![]() $F_q\cup N_q$
need belong to
$F_q\cup N_q$
need belong to
![]() $F_q$
. For example, let
$F_q$
. For example, let
![]() $Y={\mathbb {R}}$
and for
$Y={\mathbb {R}}$
and for
![]() $n\ge 1$
, identify the pairs of points n and
$n\ge 1$
, identify the pairs of points n and
![]() $1/n$
. Let X be the resulting quotient space and
$1/n$
. Let X be the resulting quotient space and
![]() $q:Y\to X$
the quotient map, which is obviously pure. Then
$q:Y\to X$
the quotient map, which is obviously pure. Then
![]() $F_q\cup N_q$
consists of the singleton
$F_q\cup N_q$
consists of the singleton
![]() $\{ q(0)\}$
, but
$\{ q(0)\}$
, but
![]() $F_q$
is empty. The following example, however, has the satisfying feature that
$F_q$
is empty. The following example, however, has the satisfying feature that
![]() $F_q$
consists precisely of the P-points in
$F_q$
consists precisely of the P-points in
![]() $F_q\cup N_q$
.
$F_q\cup N_q$
.
Example 4.7 Let Z be a locally compact
![]() $\sigma $
-compact Hausdorff space and V a closed subset with empty interior (so that
$\sigma $
-compact Hausdorff space and V a closed subset with empty interior (so that
![]() $V\subseteq \overline {Z\setminus V}$
). We shall find a locally compact
$V\subseteq \overline {Z\setminus V}$
). We shall find a locally compact
![]() $\sigma $
-compact Hausdorff space Y and a pure quotient map
$\sigma $
-compact Hausdorff space Y and a pure quotient map
![]() $q: Y\to X$
with X Hausdorff such that V is homeomorphic to
$q: Y\to X$
with X Hausdorff such that V is homeomorphic to
![]() $F_q\cup N_q$
, with
$F_q\cup N_q$
, with
![]() $F_q$
corresponding to the P-points in V.
$F_q$
corresponding to the P-points in V.
Let
![]() $Y=\bigcup _i Z_i$
be the disjoint union of countably many copies of Z. Set
$Y=\bigcup _i Z_i$
be the disjoint union of countably many copies of Z. Set
![]() $W=\bigcup _i V_i$
, and for each i let
$W=\bigcup _i V_i$
, and for each i let
![]() $\phi _i$
be a homeomorphism from V to
$\phi _i$
be a homeomorphism from V to
![]() $V_i$
. Let O be the complement of W in Y. Let
$V_i$
. Let O be the complement of W in Y. Let
![]() $\sim $
be the equivalence relation defined on points
$\sim $
be the equivalence relation defined on points
![]() $y\in Y$
by
$y\in Y$
by
![]() $y\sim y'$
if and only if either (i)
$y\sim y'$
if and only if either (i)
![]() $y=y'$
; or (ii)
$y=y'$
; or (ii)
![]() $y, y'\in W$
and there exists
$y, y'\in W$
and there exists
![]() $v\in V$
such that
$v\in V$
such that
![]() $\phi _i(v)=y$
and
$\phi _i(v)=y$
and
![]() $\phi _j(v)=y'$
for some i and j. Set
$\phi _j(v)=y'$
for some i and j. Set
![]() $X=Y/\sim $
and let q be the quotient map. Then q is pure because V has empty interior in Z. Note that
$X=Y/\sim $
and let q be the quotient map. Then q is pure because V has empty interior in Z. Note that
![]() $q(W)$
is homeomorphic to V, and that
$q(W)$
is homeomorphic to V, and that
![]() $q|_{V_i}$
is a homeomorphism from
$q|_{V_i}$
is a homeomorphism from
![]() $V_i$
onto
$V_i$
onto
![]() $q(W)$
for each i. For ease of notation, we will identify
$q(W)$
for each i. For ease of notation, we will identify
![]() $q(W)$
with V, so that
$q(W)$
with V, so that
![]() $\phi _i: V\to V_i$
is the inverse of
$\phi _i: V\to V_i$
is the inverse of
![]() $q|_{V_i}$
.
$q|_{V_i}$
.
Clearly
![]() $q|_O$
is a homeomorphism from O onto
$q|_O$
is a homeomorphism from O onto
![]() $q(O)$
, so if
$q(O)$
, so if
![]() $x\in q(O)$
then x is a point of local compactness. Now let
$x\in q(O)$
then x is a point of local compactness. Now let
![]() $x\in V$
and suppose first that x is not a P-point in V. Let
$x\in V$
and suppose first that x is not a P-point in V. Let
![]() $\{N_i\}$
be a countable family of closed subsets of V such that
$\{N_i\}$
be a countable family of closed subsets of V such that
![]() $x\notin N_i$
for all i but
$x\notin N_i$
for all i but
![]() $x\in \overline {\bigcup _i N_i}$
. Set
$x\in \overline {\bigcup _i N_i}$
. Set
![]() $N=\bigcup _i \phi _i(N_i)$
. Then N is a closed subset of Y disjoint from
$N=\bigcup _i \phi _i(N_i)$
. Then N is a closed subset of Y disjoint from
![]() $q^{-1}(x)$
, but
$q^{-1}(x)$
, but
![]() $x\in \overline {q(N)}$
. Hence
$x\in \overline {q(N)}$
. Hence
![]() $x\in N_q$
.
$x\in N_q$
.
Now suppose that that x is a P-point in V. Let N be a closed subset of Y not meeting
![]() $q^{-1}(x)$
. Then the sets
$q^{-1}(x)$
. Then the sets
![]() $q(N\cap V_i)$
are a countable family of closed set in V (since
$q(N\cap V_i)$
are a countable family of closed set in V (since
![]() $q|_{V_i}$
is a homeomorphism), and they each miss x, so
$q|_{V_i}$
is a homeomorphism), and they each miss x, so
![]() $M:=\overline {\bigcup _i q(N\cap V_i)}$
also misses x. Set
$M:=\overline {\bigcup _i q(N\cap V_i)}$
also misses x. Set
![]() $N'=N\cup \bigcup _i \phi _i(M)$
. Then
$N'=N\cup \bigcup _i \phi _i(M)$
. Then
![]() $N'$
is a closed saturated set in Y containing N and missing
$N'$
is a closed saturated set in Y containing N and missing
![]() $q^{-1}(x)$
, so
$q^{-1}(x)$
, so
![]() $x\notin \overline {q(N)}$
. Hence
$x\notin \overline {q(N)}$
. Hence
![]() $x\in F_q$
.
$x\in F_q$
.
Thus in Example 4.7,
![]() $N_q$
is closed in X if and only if every P-point in V is an isolated point of V. If V has a nonisolated P-point, for example, if
$N_q$
is closed in X if and only if every P-point in V is an isolated point of V. If V has a nonisolated P-point, for example, if
![]() $V=\omega _1+1$
(and Z is the cone over V), then
$V=\omega _1+1$
(and Z is the cone over V), then
![]() $N_q$
is not closed. If
$N_q$
is not closed. If
![]() $Z= \beta {\mathbb {N}}$
and
$Z= \beta {\mathbb {N}}$
and
![]() $V=\beta {\mathbb {N}}\setminus {\mathbb {N}}$
, then it depends on the set theoretic axioms adopted as to whether
$V=\beta {\mathbb {N}}\setminus {\mathbb {N}}$
, then it depends on the set theoretic axioms adopted as to whether
![]() $F_q$
is empty or dense in
$F_q$
is empty or dense in
![]() $F_q\cup N_q$
.
$F_q\cup N_q$
.
5 Arkhangelskii’s question and Fréchet-Urysohn spaces
Finally, we turn to consider first countable and Fréchet-Urysohn spaces and Arkhangel’skii’s question (for a vast amount of information on this whole area, see [Reference Siwiec21]).
As mentioned in the Introduction, a point x in a topological space X is a Fréchet-Urysohn point if whenever
![]() $E\subseteq X$
with
$E\subseteq X$
with
![]() $x\in \overline E$
there is a sequence
$x\in \overline E$
there is a sequence
![]() $(v_n)$
in E with
$(v_n)$
in E with
![]() $v_n\to x$
. Clearly, every point of first countability is a Fréchet-Urysohn point. If every point is a Fréchet-Urysohn point then X is a Fréchet-Urysohn space. A Fréchet-Urysohn point in a
$v_n\to x$
. Clearly, every point of first countability is a Fréchet-Urysohn point. If every point is a Fréchet-Urysohn point then X is a Fréchet-Urysohn space. A Fréchet-Urysohn point in a
![]() $k_{\omega }$
-space is easily seen to be a a k-point (Proposition 5.1(ii)) and thus belongs either to
$k_{\omega }$
-space is easily seen to be a a k-point (Proposition 5.1(ii)) and thus belongs either to
![]() $L_{q_*}$
or to
$L_{q_*}$
or to
![]() $F_{q_*}$
. Ordman showed that a point of first countability must belong to
$F_{q_*}$
. Ordman showed that a point of first countability must belong to
![]() $L_{q_*}$
(see [Reference Franklin and Smith Thomas10, p. 113]) but a general Fréchet-Urysohn point may belong to
$L_{q_*}$
(see [Reference Franklin and Smith Thomas10, p. 113]) but a general Fréchet-Urysohn point may belong to
![]() $F_{q_*}$
. Being a point of countable tightness, however, it must belong to the closure of
$F_{q_*}$
. Being a point of countable tightness, however, it must belong to the closure of
![]() $L_{q_*}$
, and the set of such points must be countable (Corollary 4.6(i)).
$L_{q_*}$
, and the set of such points must be countable (Corollary 4.6(i)).
The importance of Fréchet-Urysohn spaces is that every quotient of a compact first countable (or Fréchet-Urysohn) space is Fréchet-Urysohn (see Corollary 5.2). For example, let
![]() $Y=[0,1]\times [0,1]$
with the order topology of the lexicographic order and let
$Y=[0,1]\times [0,1]$
with the order topology of the lexicographic order and let
![]() $V=[0,1]\times \{0,1\}$
. Let
$V=[0,1]\times \{0,1\}$
. Let
![]() $q:Y\to X$
be the quotient map that takes V to a point
$q:Y\to X$
be the quotient map that takes V to a point
![]() $x_0$
. Then Y is compact, Hausdorff, and first countable, and V is closed but not a zero-set, so X is compact, Hausdorff and Fréchet-Urysohn but not first countable at
$x_0$
. Then Y is compact, Hausdorff, and first countable, and V is closed but not a zero-set, so X is compact, Hausdorff and Fréchet-Urysohn but not first countable at
![]() $x_0$
.
$x_0$
.
Recall that a topological space X is sequential if every sequentially closed subset of X is closed. Every Fréchet-Urysohn space is sequential, but there are compact Hausdorff sequential spaces which are not Fréchet-Urysohn. More generally, every sequential space has countable tightness; and the famous Moore-Mrowka problem—shown by Ostaszewski et al. to depend on set-theoretic axioms—was whether there exists a compact Hausdorff space of countable tightness which is not sequential.
If Y is a second countable locally compact Hausdorff then
![]() $\operatorname {Cl}(Y)$
is also second countable [Reference Fell9, Remark 3, p. 474], but the same does not hold for first countability. Indeed, if Y is a locally compact Hausdorff space, then the following three conditions are equivalent: (a)
$\operatorname {Cl}(Y)$
is also second countable [Reference Fell9, Remark 3, p. 474], but the same does not hold for first countability. Indeed, if Y is a locally compact Hausdorff space, then the following three conditions are equivalent: (a)
![]() $\operatorname {Cl}(Y)\setminus \{\emptyset \}$
is first countable; (b) Y is both hereditarily Lindelof and hereditary separable (for a locally compact space, first countability is a consequence of being hereditarily Lindelof); and (c)
$\operatorname {Cl}(Y)\setminus \{\emptyset \}$
is first countable; (b) Y is both hereditarily Lindelof and hereditary separable (for a locally compact space, first countability is a consequence of being hereditarily Lindelof); and (c)
![]() $\operatorname {Cl}(Y)\setminus \{\emptyset \}$
is countably tight [Reference Hou12], [Reference Costatini, Hola and Vitolo8, Corollary 2.16]. The unit square with the lexicographic order (above) is neither separable nor hereditarily Lindelof. The passage from Y to
$\operatorname {Cl}(Y)\setminus \{\emptyset \}$
is countably tight [Reference Hou12], [Reference Costatini, Hola and Vitolo8, Corollary 2.16]. The unit square with the lexicographic order (above) is neither separable nor hereditarily Lindelof. The passage from Y to
![]() $Y_*$
in Theorem 3.6 thus preserves second countability but it is not clear that it will preserve first countability or the Fréchet-Urysohn property (although we do not have specific counter-examples). This problem, however, is easily circumvented.
$Y_*$
in Theorem 3.6 thus preserves second countability but it is not clear that it will preserve first countability or the Fréchet-Urysohn property (although we do not have specific counter-examples). This problem, however, is easily circumvented.
Proposition 5.1 Let Y be a locally compact,
![]() $\sigma $
-compact Hausdorff space and
$\sigma $
-compact Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff.
$q:Y\to X$
a quotient map with X Hausdorff.
(i) If Y is a Fréchet-Urysohn space and
![]() $q_*$
is locally closed at x then x is a Fréchet-Urysohn point.
$q_*$
is locally closed at x then x is a Fréchet-Urysohn point.
(ii) Suppose that q is pure. If
![]() $x\in X$
is a Fréchet-Urysohn point then q is locally closed at x.
$x\in X$
is a Fréchet-Urysohn point then q is locally closed at x.
Proof (i) Let V be a subset of X and suppose that
![]() $x\in \overline V$
. With
$x\in \overline V$
. With
![]() $E:=q_*^{-1}(V)$
, we have
$E:=q_*^{-1}(V)$
, we have
![]() $\overline E \cap q_*^{-1}(x)\ne \emptyset $
because
$\overline E \cap q_*^{-1}(x)\ne \emptyset $
because
![]() $q_*$
is locally closed at x. Let
$q_*$
is locally closed at x. Let
![]() $(C_{\alpha })$
be a net of points in E converging to some
$(C_{\alpha })$
be a net of points in E converging to some
![]() $C\in q_*^{-1}(x)$
. Let
$C\in q_*^{-1}(x)$
. Let
![]() $y\in C$
. Then there exists a net
$y\in C$
. Then there exists a net
![]() $(y_{\alpha })$
, with
$(y_{\alpha })$
, with
![]() $y_{\alpha }\in C_{\alpha }$
for each
$y_{\alpha }\in C_{\alpha }$
for each
![]() $\alpha $
, such that
$\alpha $
, such that
![]() $\lim _{\alpha } y_{\alpha }=y$
. Then the set
$\lim _{\alpha } y_{\alpha }=y$
. Then the set
![]() $\{y_{\alpha }\}\subseteq q^{-1}(V)$
, and hence
$\{y_{\alpha }\}\subseteq q^{-1}(V)$
, and hence
![]() $ \overline {q^{-1}(V)}\cap q^{-1}(x)\supseteq \{y\}$
. Since Y is a Fréchet-Urysohn space, there is a sequence
$ \overline {q^{-1}(V)}\cap q^{-1}(x)\supseteq \{y\}$
. Since Y is a Fréchet-Urysohn space, there is a sequence
![]() $(y_n)$
in
$(y_n)$
in
![]() $\overline {q^{-1}(V)}$
converging to y. Thus
$\overline {q^{-1}(V)}$
converging to y. Thus
![]() $(q(y_n))$
gives the required sequence in V converging to x.
$(q(y_n))$
gives the required sequence in V converging to x.
(ii) Let
![]() $x\in X$
be a Fréchet-Urysohn point and let
$x\in X$
be a Fréchet-Urysohn point and let
![]() $E\subseteq X$
with
$E\subseteq X$
with
![]() $x\in \overline E$
. Then by assumption there is a sequence
$x\in \overline E$
. Then by assumption there is a sequence
![]() $(x_n)$
in E such that
$(x_n)$
in E such that
![]() $x_n\to x$
. Let K be the compact set
$x_n\to x$
. Let K be the compact set
![]() $\{x\}\cup \{x_i: i\ge 1\}$
. Then
$\{x\}\cup \{x_i: i\ge 1\}$
. Then
![]() $x\in \overline {E\cap K}$
, so x is a k-point, and hence q is locally closed at x by Theorem 4.1.▪
$x\in \overline {E\cap K}$
, so x is a k-point, and hence q is locally closed at x by Theorem 4.1.▪
Corollary 5.2 Let Y be a Fréchet-Urysohn locally compact,
![]() $\sigma $
-compact, Hausdorff space and
$\sigma $
-compact, Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff.
$q:Y\to X$
a quotient map with X Hausdorff.
(i) The open set
![]() $H_{q_*}=L_{q_*}\cup F_{q_*}$
is the set of Fréchet-Urysohn points of X.
$H_{q_*}=L_{q_*}\cup F_{q_*}$
is the set of Fréchet-Urysohn points of X.
(ii) X is a Fréchet-Urysohn space if and only if
![]() $q_*$
is closed.
$q_*$
is closed.
(iii) If X is locally compact then X is a Fréchet-Urysohn space.
Proof (i) follows from Proposition 5.1 and Corollary 4.6; (ii) from Proposition 5.1; and (iii) from Proposition 5.1 and Theorem 3.3.▪
Corollary 5.3 Let Y be a locally compact,
![]() $\sigma $
-compact, Hausdorff space and
$\sigma $
-compact, Hausdorff space and
![]() $q:Y\to X$
a quotient map with X Hausdorff and a Fréchet-Urysohn space. Then
$q:Y\to X$
a quotient map with X Hausdorff and a Fréchet-Urysohn space. Then
(i)
![]() $q_*$
is closed and
$q_*$
is closed and
![]() $L_{q_*}$
is a dense open subset of X with discrete complement and
$L_{q_*}$
is a dense open subset of X with discrete complement and
(ii) if Y is hereditarily Lindelof then X is first countable at each point of
![]() $L_{q_*}$
.
$L_{q_*}$
.
Proof (i) The first statement follows from Theorems 2.1 and 3.6 and Proposition 5.1(ii).
(ii) For second statement, note (as already mentioned) that a locally compact hereditarily Lindelof space is first countable. Furthermore, the property of being hereditarily Lindelof is equivalent, in the presence of local compactness, to every open subset being
![]() $\sigma $
-compact. The set
$\sigma $
-compact. The set
![]() $L_{q_*}$
is locally compact and open, and each open subset of
$L_{q_*}$
is locally compact and open, and each open subset of
![]() $L_{q_*}$
inherits the property of
$L_{q_*}$
inherits the property of
![]() $\sigma $
-compactness from its inverse image under q. Hence,
$\sigma $
-compactness from its inverse image under q. Hence,
![]() $L_{q_*}$
is first countable.▪
$L_{q_*}$
is first countable.▪
Arkhangel’skii’s question. In [Reference Arkhangel’skii5, Problems 5.14 and 5.15], Arkhangel’skii asked for a Hausdorff quotient of a locally compact second countable Hausdorff space which is (countable and) Fréchet-Urysohn but nowhere first countable. A locally compact second countable Hausdorff space is perfectly normal (i.e., every open set is an
![]() $F_{\sigma }$
), and the same is true in every Hausdorff quotient, so every point in a quotient is a
$F_{\sigma }$
), and the same is true in every Hausdorff quotient, so every point in a quotient is a
![]() $G_{\delta }$
, and it is well known that a
$G_{\delta }$
, and it is well known that a
![]() $G_{\delta }$
point with a compact neighborhood is first countable. Thus, the required example had to have
$G_{\delta }$
point with a compact neighborhood is first countable. Thus, the required example had to have
![]() $L_{q_*}$
empty and
$L_{q_*}$
empty and
![]() $F_{q_*}\cup N_{q_*}$
as a Fréchet-Urysohn space, along the lines of the space
$F_{q_*}\cup N_{q_*}$
as a Fréchet-Urysohn space, along the lines of the space
![]() $S_{\omega }$
mentioned in Section 1.
$S_{\omega }$
mentioned in Section 1.
In the absence of a structure theory for
![]() $k_{\omega }$
-spaces, Arkhangel’skii’s question is very pertinent, but in the course of this paper, we have seen multiple reasons why such an example cannot exist: for instance, every Fréchet-Urysohn point in a
$k_{\omega }$
-spaces, Arkhangel’skii’s question is very pertinent, but in the course of this paper, we have seen multiple reasons why such an example cannot exist: for instance, every Fréchet-Urysohn point in a
![]() $k_{\omega }$
-space lies in the closure of
$k_{\omega }$
-space lies in the closure of
![]() $L_{q_*}$
(Corollary 4.6(ii)). As we have mentioned, the question had, in fact, already been answered negatively by Siwiec in 1976 [Reference Siwiec22] who showed (among other things) that if a
$L_{q_*}$
(Corollary 4.6(ii)). As we have mentioned, the question had, in fact, already been answered negatively by Siwiec in 1976 [Reference Siwiec22] who showed (among other things) that if a
![]() $k_{\omega }$
-space is Fréchet-Urysohn and has a
$k_{\omega }$
-space is Fréchet-Urysohn and has a
![]() $k_{\omega }$
-decomposition of compact metric spaces then it is the closed image of a locally compact separable metric space (and hence Morita’s theorem implies that
$k_{\omega }$
-decomposition of compact metric spaces then it is the closed image of a locally compact separable metric space (and hence Morita’s theorem implies that
![]() $L_{q_*}$
is dense).
$L_{q_*}$
is dense).
Since a locally compact second countable space is hereditarily Lindelof, Corollary 5.3(i) and (ii) gives a more general negative answer to Arkhangel’skii’s question. If the Continuum Hypothesis is assumed, a still more general answer can be given.
Theorem 5.4 (CH)
Let X be a sequential
![]() $k_{\omega }$
-space. Then X is first countable at a dense subset of points if and only if the set of non-k-points of X has empty interior.
$k_{\omega }$
-space. Then X is first countable at a dense subset of points if and only if the set of non-k-points of X has empty interior.
Proof The set
![]() $L_{q_*}$
of points with compact neighborhoods is open and hence sequential. Since X is sequential it is countably tight, so it follows from Corollary 4.6(ii) that
$L_{q_*}$
of points with compact neighborhoods is open and hence sequential. Since X is sequential it is countably tight, so it follows from Corollary 4.6(ii) that
![]() $N_{q_*}$
has empty interior if and only
$N_{q_*}$
has empty interior if and only
![]() $L_{q_*}$
is dense. If X is first countable at
$L_{q_*}$
is dense. If X is first countable at
![]() $x\in X$
then
$x\in X$
then
![]() $x\in L_{q_*}$
, see [Reference Franklin and Smith Thomas10, p. 113]. Thus if X is first countable at a dense subset of points,
$x\in L_{q_*}$
, see [Reference Franklin and Smith Thomas10, p. 113]. Thus if X is first countable at a dense subset of points,
![]() $N_{q_*}$
has empty interior. Conversely, if
$N_{q_*}$
has empty interior. Conversely, if
![]() $N_{q_*}$
has empty interior, then
$N_{q_*}$
has empty interior, then
![]() $L_{q_*}$
is dense in X, and Arkhangelski showed in 1970 ([Reference Arkhangel’skii3]; see also [Reference Arkhangel’skii4, p. 381]) that under (CH) every (locally) compact Hausdorff sequential space is first countable at a dense subset of points.▪
$L_{q_*}$
is dense in X, and Arkhangelski showed in 1970 ([Reference Arkhangel’skii3]; see also [Reference Arkhangel’skii4, p. 381]) that under (CH) every (locally) compact Hausdorff sequential space is first countable at a dense subset of points.▪
In particular, under (CH), every Fréchet-Urysohn
![]() $k_{\omega }$
-space is first countable at a dense subset of points. On the other hand, in 1987 Malyhin used the method of forcing to exhibit a compact Hausdorff Fréchet-Urysohn which is nowhere first countable [Reference McCoy and Ntantu15]. Thus Corollary 5.3 may be about as far as one can go in ZFC in answer to Arkhangel’skii’s question.
$k_{\omega }$
-space is first countable at a dense subset of points. On the other hand, in 1987 Malyhin used the method of forcing to exhibit a compact Hausdorff Fréchet-Urysohn which is nowhere first countable [Reference McCoy and Ntantu15]. Thus Corollary 5.3 may be about as far as one can go in ZFC in answer to Arkhangel’skii’s question.
Acknowledgment
We are grateful to Eric Wofsey and Henno Brandsma for help on Math Stack Exchange at early stages of this enquiry.