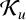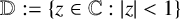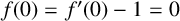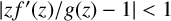1 Introduction
Let
![]() $\mathcal {H}$
be the class of all analytic functions in the unit disk
$\mathcal {H}$
be the class of all analytic functions in the unit disk
![]() $\mathbb {D}:=\{z\in \mathbb {C}:\, |z|<1\}$
. Let
$\mathbb {D}:=\{z\in \mathbb {C}:\, |z|<1\}$
. Let
![]() $\mathcal {B}$
be the subclass of
$\mathcal {B}$
be the subclass of
![]() $\mathcal {H}$
consisting of all functions f in
$\mathcal {H}$
consisting of all functions f in
![]() $\mathcal {H}$
with
$\mathcal {H}$
with
![]() $|f(z)|<1$
for all
$|f(z)|<1$
for all
![]() $z\in \mathbb {D}$
,
$z\in \mathbb {D}$
,
![]() $\mathcal {B}_0$
be the subclass of
$\mathcal {B}_0$
be the subclass of
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $f(0)=0$
and
$f(0)=0$
and
![]() $\mathcal {A}$
be the subclass of
$\mathcal {A}$
be the subclass of
![]() $\mathcal {H}$
consisting of all functions f normalised by
$\mathcal {H}$
consisting of all functions f normalised by
![]() $f(0)=f'(0)-1=0$
with the Taylor series expansion
$f(0)=f'(0)-1=0$
with the Taylor series expansion
 $$ \begin{align} f(z)= z+\sum_{n=2}^{\infty}a_n z^n. \end{align} $$
$$ \begin{align} f(z)= z+\sum_{n=2}^{\infty}a_n z^n. \end{align} $$
Further, let
![]() $\mathcal {S}$
be the subclass of
$\mathcal {S}$
be the subclass of
![]() $\mathcal {A}$
that are univalent (that is, one-to-one) in
$\mathcal {A}$
that are univalent (that is, one-to-one) in
![]() $\mathbb {D}$
. A function
$\mathbb {D}$
. A function
![]() $f\in \mathcal {A}$
is called starlike (respectively, convex) if
$f\in \mathcal {A}$
is called starlike (respectively, convex) if
![]() $f(\mathbb {D})$
is a starlike domain (respectively, a convex domain) with respect to the origin. The set of all starlike functions and convex functions in
$f(\mathbb {D})$
is a starlike domain (respectively, a convex domain) with respect to the origin. The set of all starlike functions and convex functions in
![]() $\mathcal {S}$
are denoted by
$\mathcal {S}$
are denoted by
![]() $\mathcal {S}^*$
and
$\mathcal {S}^*$
and
![]() $\mathcal {C}$
, respectively. It is well known that a function f in
$\mathcal {C}$
, respectively. It is well known that a function f in
![]() $\mathcal {A}$
is starlike (respectively, convex) if and only if
$\mathcal {A}$
is starlike (respectively, convex) if and only if
![]() $\mathrm {Re\,} zf'(z)/f(z)>0$
(respectively,
$\mathrm {Re\,} zf'(z)/f(z)>0$
(respectively,
![]() $\mathrm {Re\,} (1+zf"(z)/f'(z))>0$
) for
$\mathrm {Re\,} (1+zf"(z)/f'(z))>0$
) for
![]() $z\in \mathbb {D}$
. For further information about these classes, we refer to [Reference Duren5, Reference Goodman7].
$z\in \mathbb {D}$
. For further information about these classes, we refer to [Reference Duren5, Reference Goodman7].
A function
![]() $f\in \mathcal {A}$
is said to be close-to-convex if the complement of the image-domain
$f\in \mathcal {A}$
is said to be close-to-convex if the complement of the image-domain
![]() $f(\mathbb {D})$
in
$f(\mathbb {D})$
in
![]() $\mathbb {C}$
is the union of rays that are disjoint (except that the origin of one ray may lie on another one of the rays) and the class of all close-to-convex functions is denoted by
$\mathbb {C}$
is the union of rays that are disjoint (except that the origin of one ray may lie on another one of the rays) and the class of all close-to-convex functions is denoted by
![]() $\mathcal {K}$
. This class was introduced by Kaplan [Reference Kaplan10]. A function
$\mathcal {K}$
. This class was introduced by Kaplan [Reference Kaplan10]. A function
![]() $f\in \mathcal {A}$
is close-to-convex if and only if there exists a starlike function
$f\in \mathcal {A}$
is close-to-convex if and only if there exists a starlike function
![]() $g\in \mathcal {S}^*$
and a real number
$g\in \mathcal {S}^*$
and a real number
![]() $\alpha \in (-\pi /2,\pi /2)$
such that (see [Reference Duren5, Reference Kaplan10])
$\alpha \in (-\pi /2,\pi /2)$
such that (see [Reference Duren5, Reference Kaplan10])
 $$ \begin{align*} \mathrm{Re\,} \bigg(e^{i\alpha}\frac{zf'(z)}{g(z)}\bigg)>0,\quad z\in\mathbb{D}. \end{align*} $$
$$ \begin{align*} \mathrm{Re\,} \bigg(e^{i\alpha}\frac{zf'(z)}{g(z)}\bigg)>0,\quad z\in\mathbb{D}. \end{align*} $$
In 1968, Singh [Reference Singh16] introduced and studied the class
![]() $\mathcal {S}_u^*$
consisting of functions f in
$\mathcal {S}_u^*$
consisting of functions f in
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
 $$ \begin{align*} \bigg|\frac{zf'(z)}{f(z)}-1\bigg|<1\quad \text{for}~z\in\mathbb{D}. \end{align*} $$
$$ \begin{align*} \bigg|\frac{zf'(z)}{f(z)}-1\bigg|<1\quad \text{for}~z\in\mathbb{D}. \end{align*} $$
It is easy to see that every function in
![]() $\mathcal {S}_u^*$
also belongs to
$\mathcal {S}_u^*$
also belongs to
![]() $\mathcal {S}^*$
. Singh [Reference Singh16] obtained the distortion theorem, coefficient estimate and radius of convexity for the class
$\mathcal {S}^*$
. Singh [Reference Singh16] obtained the distortion theorem, coefficient estimate and radius of convexity for the class
![]() $\mathcal {S}_u^*$
. Recently, Allu
$\mathcal {S}_u^*$
. Recently, Allu
![]() $et~ al.$
[Reference Allu, Sokól and Thomas1] introduced a close-to-convex analogue of the class
$et~ al.$
[Reference Allu, Sokól and Thomas1] introduced a close-to-convex analogue of the class
![]() $\mathcal {S}_u^*$
denoted by
$\mathcal {S}_u^*$
denoted by
![]() $\mathcal {K}_u$
. A function f in
$\mathcal {K}_u$
. A function f in
![]() $\mathcal {A}$
belongs to
$\mathcal {A}$
belongs to
![]() $\mathcal {K}_u$
if there exists a starlike function
$\mathcal {K}_u$
if there exists a starlike function
![]() $g\in \mathcal {S}^*$
such that
$g\in \mathcal {S}^*$
such that
 $$ \begin{align*} \bigg|\frac{zf'(z)}{g(z)}-1\bigg|<1\quad \text{for } z\in\mathbb{D}. \end{align*} $$
$$ \begin{align*} \bigg|\frac{zf'(z)}{g(z)}-1\bigg|<1\quad \text{for } z\in\mathbb{D}. \end{align*} $$
Clearly, every function in
![]() $\mathcal {K}_u$
is close-to-convex.
$\mathcal {K}_u$
is close-to-convex.
It is well known that if
![]() $f\in \mathcal {S}$
is of the form (1.1), then
$f\in \mathcal {S}$
is of the form (1.1), then
![]() $|a_n|\le n$
for all
$|a_n|\le n$
for all
![]() $n\geq 2$
, and equality holds for the rotations of the Koebe function
$n\geq 2$
, and equality holds for the rotations of the Koebe function
![]() $k(z)=z/(1- z)^2$
. Singh [Reference Singh16] proved that if
$k(z)=z/(1- z)^2$
. Singh [Reference Singh16] proved that if
![]() $f\in \mathcal {S}_u^*$
, then
$f\in \mathcal {S}_u^*$
, then
![]() $|a_n|\le 1/(n-1)$
for all
$|a_n|\le 1/(n-1)$
for all
![]() $~n\geq 2$
, and this inequality is sharp. In 2020, Allu
$~n\geq 2$
, and this inequality is sharp. In 2020, Allu
![]() $et~al.$
[Reference Allu, Sokól and Thomas1] studied coefficient bounds for the functions
$et~al.$
[Reference Allu, Sokól and Thomas1] studied coefficient bounds for the functions
![]() $f(z)$
of the form (1.1) in the class
$f(z)$
of the form (1.1) in the class
![]() $\mathcal {K}_{u}$
and obtained the sharp bounds
$\mathcal {K}_{u}$
and obtained the sharp bounds
![]() $|a_2|\le 3/2$
and
$|a_2|\le 3/2$
and
![]() $|a_3|\leq 5/3$
and proposed a conjecture that
$|a_3|\leq 5/3$
and proposed a conjecture that
![]() $|a_n|\le (2n-1)/n$
for
$|a_n|\le (2n-1)/n$
for
![]() $n\ge 4$
.
$n\ge 4$
.
The Fekete–Szegö problem is to find the maximum value of the coefficient functional
when f of the form (1.1) varies over a class of functions
![]() $\mathcal {F}$
. In 1933, Fekete–Szegö [Reference Fekete and Szegö6] used the Löwner differential method to prove that
$\mathcal {F}$
. In 1933, Fekete–Szegö [Reference Fekete and Szegö6] used the Löwner differential method to prove that
 $$ \begin{align*} \max\limits_{f\in\mathcal{S}} \Phi_\mu(f)= \begin{cases} 1+2e^{-{2\mu}/{(1-\mu)}} &\text{for }0\leq\mu<1, \\ 1 &\text{for } \mu=1. \end{cases} \end{align*} $$
$$ \begin{align*} \max\limits_{f\in\mathcal{S}} \Phi_\mu(f)= \begin{cases} 1+2e^{-{2\mu}/{(1-\mu)}} &\text{for }0\leq\mu<1, \\ 1 &\text{for } \mu=1. \end{cases} \end{align*} $$
In 1987, Koepf [Reference Koepf12] obtained the sharp bound of
![]() $\Phi _\mu (f)$
for any
$\Phi _\mu (f)$
for any
![]() $\mu \in \mathbb {R}$
for the class
$\mu \in \mathbb {R}$
for the class
![]() $\mathcal {K}$
:
$\mathcal {K}$
:
 $$ \begin{align*} \max\limits_{f\in\mathcal{K}} \Phi_\mu(f)=\begin{cases} |3-4\mu| &\text{if } \mu\in\bigg(-\infty,\dfrac{1}{3}\bigg]\cup[1,\infty),\\[6pt] \dfrac{1}{3}+\dfrac{4}{9\mu} &\text{if } \mu\in\bigg[\dfrac{1}{3},\dfrac{2}{3}\bigg],\\[6pt] 1 &\text{if } \mu\in\bigg[\dfrac{2}{3},1\bigg]. \end{cases} \end{align*} $$
$$ \begin{align*} \max\limits_{f\in\mathcal{K}} \Phi_\mu(f)=\begin{cases} |3-4\mu| &\text{if } \mu\in\bigg(-\infty,\dfrac{1}{3}\bigg]\cup[1,\infty),\\[6pt] \dfrac{1}{3}+\dfrac{4}{9\mu} &\text{if } \mu\in\bigg[\dfrac{1}{3},\dfrac{2}{3}\bigg],\\[6pt] 1 &\text{if } \mu\in\bigg[\dfrac{2}{3},1\bigg]. \end{cases} \end{align*} $$
The Fekete–Szegö problem has been studied for different subclasses of
![]() $\mathcal {S}$
(see [Reference Kanas and Lecko9, Reference Koepf13–Reference London15, Reference Singh and Singh17]). Allu
$\mathcal {S}$
(see [Reference Kanas and Lecko9, Reference Koepf13–Reference London15, Reference Singh and Singh17]). Allu
![]() $et~ al.$
[Reference Allu, Sokól and Thomas1] considered the class
$et~ al.$
[Reference Allu, Sokól and Thomas1] considered the class
![]() $\mathcal {K}_{u}$
and obtained an estimate of the Fekete–Szegö functional
$\mathcal {K}_{u}$
and obtained an estimate of the Fekete–Szegö functional
![]() $|a_3-\mu a_2^2|$
with
$|a_3-\mu a_2^2|$
with
![]() $\mu \in \mathbb {R}$
. However, they were only able to show sharpness when
$\mu \in \mathbb {R}$
. However, they were only able to show sharpness when
![]() $\mu \leq 0,~2/3\leq \mu \leq 1~\text {and}~\mu \geq 10/9$
.
$\mu \leq 0,~2/3\leq \mu \leq 1~\text {and}~\mu \geq 10/9$
.
Let
![]() $\mathcal {LU}$
denote the subclass of
$\mathcal {LU}$
denote the subclass of
![]() $\mathcal {H}$
consisting of all locally univalent functions in
$\mathcal {H}$
consisting of all locally univalent functions in
![]() $\mathbb {D}$
, that is,
$\mathbb {D}$
, that is,
![]() $\mathcal {LU}:=\{f\in \mathcal {H}:f'(z)\ne 0\text { for all }z\in \mathbb {D}\}$
. For a locally univalent function
$\mathcal {LU}:=\{f\in \mathcal {H}:f'(z)\ne 0\text { for all }z\in \mathbb {D}\}$
. For a locally univalent function
![]() $f\in \mathcal {LU}$
, the pre-Schwarzian derivative is defined by
$f\in \mathcal {LU}$
, the pre-Schwarzian derivative is defined by
 $$ \begin{align*}P_f(z)=\frac{f"(z)}{f'(z)},\end{align*} $$
$$ \begin{align*}P_f(z)=\frac{f"(z)}{f'(z)},\end{align*} $$
and the pre-Schwarzian norm (the hyperbolic sup-norm) is defined by
This norm has significant meaning in the theory of Teichmüller spaces. For a univalent function f, it is well known that
![]() $\|P_f\|\leq 6$
and the estimate is sharp. However, if
$\|P_f\|\leq 6$
and the estimate is sharp. However, if
![]() $\|P_f\|\leq 1$
, then f is univalent in
$\|P_f\|\leq 1$
, then f is univalent in
![]() $\mathbb {D}$
(see [Reference Becker2, Reference Becker and Pommerenke3]). In 1976, Yamashita [Reference Yamashita18] proved that
$\mathbb {D}$
(see [Reference Becker2, Reference Becker and Pommerenke3]). In 1976, Yamashita [Reference Yamashita18] proved that
![]() $\|P_f \|$
is finite if and only if f is uniformly locally univalent in
$\|P_f \|$
is finite if and only if f is uniformly locally univalent in
![]() $\mathbb {D}$
. Moreover, if
$\mathbb {D}$
. Moreover, if
![]() $\|P_f\|<2$
, then f is bounded in
$\|P_f\|<2$
, then f is bounded in
![]() $\mathbb {D}$
(see [Reference Kim and Sugawa11]). We will obtain results related to the pre-Schwarzian norm for functions
$\mathbb {D}$
(see [Reference Kim and Sugawa11]). We will obtain results related to the pre-Schwarzian norm for functions
![]() $f\in \mathcal {K}_u$
.
$f\in \mathcal {K}_u$
.
We first prove the conjecture
![]() $|a_n|\le (2n-1)/n$
for
$|a_n|\le (2n-1)/n$
for
![]() $n\ge 2$
for functions in
$n\ge 2$
for functions in
![]() $\mathcal {K}_u$
as proposed by Allu
$\mathcal {K}_u$
as proposed by Allu
![]() $et~ al.$
[Reference Allu, Sokól and Thomas1]. We next obtain the sharp estimate of the Fekete–Szegö functional
$et~ al.$
[Reference Allu, Sokól and Thomas1]. We next obtain the sharp estimate of the Fekete–Szegö functional
![]() $\Phi _\mu (f)$
for the class
$\Phi _\mu (f)$
for the class
![]() $\mathcal {K}_u$
for any
$\mathcal {K}_u$
for any
![]() $\mu \in \mathbb {R}$
. Finally, we obtain estimates of the pre-Schwarzian norm for functions in
$\mu \in \mathbb {R}$
. Finally, we obtain estimates of the pre-Schwarzian norm for functions in
![]() $\mathcal {K}_u$
.
$\mathcal {K}_u$
.
2 Main results
Before stating our main results, we will discuss some preliminaries which will help us to prove our results. The first lemma is part of a result proved by Choi
![]() $et~al.$
[Reference Choi, Kim and Sugawa4].
$et~al.$
[Reference Choi, Kim and Sugawa4].
Lemma 2.1. For
![]() $A, B\in \mathbb {C}$
and
$A, B\in \mathbb {C}$
and
![]() $K, L, M\in \mathbb {R}$
, let
$K, L, M\in \mathbb {R}$
, let
 $$ \begin{align*} \Omega_(A, B, K, L, M)=\max_{\substack{|u_1\leq 1\\ |v_1|\leq 1}}(|A|(1-|u_1|^2)+|B|(1-|v_1|^2)+|Ku_1^2+Lv_1^2+2Mu_1v_1|). \end{align*} $$
$$ \begin{align*} \Omega_(A, B, K, L, M)=\max_{\substack{|u_1\leq 1\\ |v_1|\leq 1}}(|A|(1-|u_1|^2)+|B|(1-|v_1|^2)+|Ku_1^2+Lv_1^2+2Mu_1v_1|). \end{align*} $$
Further consider the following four conditions involving
![]() $A, B, K, L, M$
:
$A, B, K, L, M$
:
-
(A1)
 $|A|\geq \max \bigg \{|K|\sqrt {1-\dfrac {M^2}{KL}},|M|-|K|\bigg \}$
;
$|A|\geq \max \bigg \{|K|\sqrt {1-\dfrac {M^2}{KL}},|M|-|K|\bigg \}$
; -
(A2)
 $|K|+|M|\leq |A| <|K|\sqrt {1-\dfrac {M^2}{KL}}$
;
$|K|+|M|\leq |A| <|K|\sqrt {1-\dfrac {M^2}{KL}}$
; -
(B1)
 $|B|\geq \max \bigg \{|L|\sqrt {1-\dfrac {M^2}{KL}},|M|-|L|\bigg \}$
;
$|B|\geq \max \bigg \{|L|\sqrt {1-\dfrac {M^2}{KL}},|M|-|L|\bigg \}$
; -
(B2)
 $|L|+|M|\leq |B| <|L|\sqrt {1-\dfrac {M^2}{KL}}$
.
$|L|+|M|\leq |B| <|L|\sqrt {1-\dfrac {M^2}{KL}}$
.
If
![]() $KL\geq 0$
and
$KL\geq 0$
and
![]() $D=(|K|-|A|)(|L|-|B|)-M^2$
, then
$D=(|K|-|A|)(|L|-|B|)-M^2$
, then
 $$ \begin{align*} \Omega(A, B, K, L, M)= \begin{cases} |A|+|L|-\dfrac{M^2}{|K|-|L|} &\text{if } |A|> |M|+|K|~\text{and}~D<0,\\ |B|+|K|-\dfrac{M^2}{|L|-|B|} &\text{if } |B|> |M|+|L|~\text{and}~D<0,\\ |K|+2|M|+|L| &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \Omega(A, B, K, L, M)= \begin{cases} |A|+|L|-\dfrac{M^2}{|K|-|L|} &\text{if } |A|> |M|+|K|~\text{and}~D<0,\\ |B|+|K|-\dfrac{M^2}{|L|-|B|} &\text{if } |B|> |M|+|L|~\text{and}~D<0,\\ |K|+2|M|+|L| &\text{otherwise}. \end{cases} \end{align*} $$
If
![]() $KL<0$
, then
$KL<0$
, then
![]() $\Omega (A, B, K, L, M)=|A|+|B|+\max \{0,R\},$
where
$\Omega (A, B, K, L, M)=|A|+|B|+\max \{0,R\},$
where
 $$ \begin{align*} R=\begin{cases} |K|-|A|+\dfrac{M^2}{|B|+|L|}, &\text{when (B1) holds but (A1) and (A2) do not hold}, \\ |L|-|B|+\dfrac{M^2}{|A|+|K|} , &\text{when (A1) holds but (B1) and (B2) do not hold}. \end{cases} \end{align*} $$
$$ \begin{align*} R=\begin{cases} |K|-|A|+\dfrac{M^2}{|B|+|L|}, &\text{when (B1) holds but (A1) and (A2) do not hold}, \\ |L|-|B|+\dfrac{M^2}{|A|+|K|} , &\text{when (A1) holds but (B1) and (B2) do not hold}. \end{cases} \end{align*} $$
For two functions f and g in
![]() $\mathcal {H}$
, we say that
$\mathcal {H}$
, we say that
![]() $f(z)$
is majorised by
$f(z)$
is majorised by
![]() $g(z)$
if
$g(z)$
if
![]() $|f(z)|\leq |g(z)|$
for all
$|f(z)|\leq |g(z)|$
for all
![]() $z\in \mathbb {D}$
or equivalently, if there exists
$z\in \mathbb {D}$
or equivalently, if there exists
![]() $\omega \in \mathcal {B}$
such that
$\omega \in \mathcal {B}$
such that
![]() ${f(z)=\omega (z)g(z)}$
. Let
${f(z)=\omega (z)g(z)}$
. Let
![]() $f(z)=\sum _{n=0}^\infty a_nz^n$
and
$f(z)=\sum _{n=0}^\infty a_nz^n$
and
![]() $F(z)=\sum _{n=0}^\infty A_nz^n$
be two power series convergent in some disk
$F(z)=\sum _{n=0}^\infty A_nz^n$
be two power series convergent in some disk
![]() $E_R=\{z:|z|<R,~R>0\}$
. We say that
$E_R=\{z:|z|<R,~R>0\}$
. We say that
![]() $f(z)$
is dominated by
$f(z)$
is dominated by
![]() $F(z)$
and we write
$F(z)$
and we write
![]() $f(z)\ll F(z)$
if for any integer
$f(z)\ll F(z)$
if for any integer
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $|a_n|\leq |A_n|.$
$|a_n|\leq |A_n|.$
Lemma 2.2 [Reference Hallenbeck and Macgregor8, Theorem 6.7].
If
![]() $f(z)=\sum _{n=1}^\infty a_nz^n$
,
$f(z)=\sum _{n=1}^\infty a_nz^n$
,
![]() $z\in \mathbb {D}$
, is majorised by g and
$z\in \mathbb {D}$
, is majorised by g and
![]() $g\in \mathcal {S}^*$
, then
$g\in \mathcal {S}^*$
, then
![]() $|a_n|\le n$
for all
$|a_n|\le n$
for all
![]() $n\ge 1$
, that is,
$n\ge 1$
, that is,
![]() $f(z)\ll k(z)$
, where
$f(z)\ll k(z)$
, where
![]() $k(z)=z/(1-z)^2$
is the Koebe function.
$k(z)=z/(1-z)^2$
is the Koebe function.
Our first result confirms the conjecture of Allu
![]() $et~al.$
in [Reference Allu, Sokól and Thomas1].
$et~al.$
in [Reference Allu, Sokól and Thomas1].
Theorem 2.3. Let
![]() $f\in \mathcal {K}_{u}$
be of the form (1.1). Then,
$f\in \mathcal {K}_{u}$
be of the form (1.1). Then,
Moreover, the estimate is sharp.
Proof. Let
![]() $f\in \mathcal {K}_{u}$
be of the form (1.1). Then there exists a starlike function
$f\in \mathcal {K}_{u}$
be of the form (1.1). Then there exists a starlike function
![]() $g\in \mathcal {S}^*$
such that
$g\in \mathcal {S}^*$
such that
 $$ \begin{align*}\bigg|\frac{zf'(z)}{g(z)}-1\bigg|<1.\end{align*} $$
$$ \begin{align*}\bigg|\frac{zf'(z)}{g(z)}-1\bigg|<1.\end{align*} $$
Further, there exists a function
![]() $\omega (z)\in \mathcal {B}_{0}$
such that
$\omega (z)\in \mathcal {B}_{0}$
such that
that is,
for some
![]() $\omega _1(z)\in \mathcal {B}$
. Since,
$\omega _1(z)\in \mathcal {B}$
. Since,
![]() $g(z)\omega _1(z)$
is majorised by
$g(z)\omega _1(z)$
is majorised by
![]() $g(z)$
and
$g(z)$
and
![]() $g\in \mathcal {S}^*$
, by Lemma 2.2, the function
$g\in \mathcal {S}^*$
, by Lemma 2.2, the function
![]() $g(z)\omega _1(z)$
is dominated by
$g(z)\omega _1(z)$
is dominated by
![]() $k(z)$
, that is,
$k(z)$
, that is,
![]() $g(z)\omega _1(z)\ll k(z)$
. Thus, from (2.1),
$g(z)\omega _1(z)\ll k(z)$
. Thus, from (2.1),
and consequently,
The estimate is sharp for the function
![]() $f_1\in \mathcal {K}_{u}$
given by
$f_1\in \mathcal {K}_{u}$
given by
For functions in
![]() $\mathcal {K}_{u}$
, Allu
$\mathcal {K}_{u}$
, Allu
![]() $et~ al.$
[Reference Allu, Sokól and Thomas1] obtained an estimate of the Fekete–Szegö functional
$et~ al.$
[Reference Allu, Sokól and Thomas1] obtained an estimate of the Fekete–Szegö functional
![]() $|a_3-\mu a_2^2|$
with
$|a_3-\mu a_2^2|$
with
![]() $\mu \in \mathbb {R}$
. The result is sharp only when
$\mu \in \mathbb {R}$
. The result is sharp only when
![]() $\mu \leq 0,~2/3\leq \mu \leq ~1~\text {and}~\mu \geq 10/9$
. In the next theorem, we will give the sharp bounds of
$\mu \leq 0,~2/3\leq \mu \leq ~1~\text {and}~\mu \geq 10/9$
. In the next theorem, we will give the sharp bounds of
![]() $|a_3-\mu a_2^2|$
for all values of
$|a_3-\mu a_2^2|$
for all values of
![]() $\mu \in \mathbb {R}$
. Our proof is completely different from that in [Reference Allu, Sokól and Thomas1]. Our main tool to get the sharp bound is Lemma 2.1.
$\mu \in \mathbb {R}$
. Our proof is completely different from that in [Reference Allu, Sokól and Thomas1]. Our main tool to get the sharp bound is Lemma 2.1.
Theorem 2.4. Let
![]() $f\in \mathcal {K}_{u}$
be given by (1.1). Then for every
$f\in \mathcal {K}_{u}$
be given by (1.1). Then for every
![]() $\mu \in \mathbb {R}$
,
$\mu \in \mathbb {R}$
,
 $$ \begin{align*} |a_3-\mu a_2^2|\leq \begin{cases} \dfrac{5}{3}-\dfrac{9}{4}\mu &\text{if}\ \mu\leq0,\\[2mm] \dfrac{4(5-3\mu)}{3(4+3\mu)} &\text{if}\ 0\leq \mu \leq \dfrac{2}{3},\\[3mm] \dfrac{2}{3} &\text{if}\ \dfrac{2}{3}\leq \mu \leq 1,\\[1.5mm] \dfrac{3\mu-5}{3(3\mu-4)} &\text{if}\ 1\leq \mu \leq \dfrac{10}{9},\\[3mm] \dfrac{9}{4}\mu-\dfrac{5}{3} &\text{if}\ \mu\geq \dfrac{10}{9}. \end{cases} \end{align*} $$
$$ \begin{align*} |a_3-\mu a_2^2|\leq \begin{cases} \dfrac{5}{3}-\dfrac{9}{4}\mu &\text{if}\ \mu\leq0,\\[2mm] \dfrac{4(5-3\mu)}{3(4+3\mu)} &\text{if}\ 0\leq \mu \leq \dfrac{2}{3},\\[3mm] \dfrac{2}{3} &\text{if}\ \dfrac{2}{3}\leq \mu \leq 1,\\[1.5mm] \dfrac{3\mu-5}{3(3\mu-4)} &\text{if}\ 1\leq \mu \leq \dfrac{10}{9},\\[3mm] \dfrac{9}{4}\mu-\dfrac{5}{3} &\text{if}\ \mu\geq \dfrac{10}{9}. \end{cases} \end{align*} $$
Moreover, all the inequalities are sharp.
Proof. Let
![]() $f\in \mathcal {K}_{u}$
be of the form (1.1). Then there exists a starlike function
$f\in \mathcal {K}_{u}$
be of the form (1.1). Then there exists a starlike function
![]() $g(z)=z+\sum _{n=2}^{\infty }b_nz^n$
in
$g(z)=z+\sum _{n=2}^{\infty }b_nz^n$
in
![]() $\mathcal {S}^* $
such that
$\mathcal {S}^* $
such that
 $$ \begin{align*} \bigg|\frac{zf'(z)}{g(z)}-1\bigg|<1. \end{align*} $$
$$ \begin{align*} \bigg|\frac{zf'(z)}{g(z)}-1\bigg|<1. \end{align*} $$
Thus, there exists
![]() $\omega (z)=\sum _{n=1}^{\infty }c_nz^n$
in
$\omega (z)=\sum _{n=1}^{\infty }c_nz^n$
in
![]() $\mathcal {B}_0$
such that
$\mathcal {B}_0$
such that
From (2.2), comparing the coefficients of
![]() $z^2$
and
$z^2$
and
![]() $z^3$
on both sides,
$z^3$
on both sides,
Since
![]() $g\in \mathcal {S}^*$
, it follows that there exists another
$g\in \mathcal {S}^*$
, it follows that there exists another
![]() $\rho \in \mathcal {B}_0$
of the form
$\rho \in \mathcal {B}_0$
of the form
![]() $\rho (z)=\sum _{n=1}^{\infty }d_nz^n$
such that
$\rho (z)=\sum _{n=1}^{\infty }d_nz^n$
such that
 $$ \begin{align} \frac{zg'(z)}{g(z)}= \frac{1+ \rho(z)}{1- \rho(z)}. \end{align} $$
$$ \begin{align} \frac{zg'(z)}{g(z)}= \frac{1+ \rho(z)}{1- \rho(z)}. \end{align} $$
On comparing the coefficients of
![]() $z^2$
and
$z^2$
and
![]() $z^3$
on both sides,
$z^3$
on both sides,
Therefore, for any
![]() $\mu \in \mathbb {R}$
,
$\mu \in \mathbb {R}$
,
where
Thus,
 $$ \begin{align*} |a_3-\mu a_2^2|&\leq |A\|c_2|+|B\|d_2|+|Kc_1^2+Ld_1^2+2Mc_1d_1|\\ &\leq |A|(1-|c_1|^2)+|B|(1-|d_1|^2)+|Kc_1^2+Ld_1^2+2Mc_1d_1|.\nonumber \end{align*} $$
$$ \begin{align*} |a_3-\mu a_2^2|&\leq |A\|c_2|+|B\|d_2|+|Kc_1^2+Ld_1^2+2Mc_1d_1|\\ &\leq |A|(1-|c_1|^2)+|B|(1-|d_1|^2)+|Kc_1^2+Ld_1^2+2Mc_1d_1|.\nonumber \end{align*} $$
Now, we have to find the maximum value of
![]() $|a_3-\mu a_2^2|$
when
$|a_3-\mu a_2^2|$
when
![]() $|c_1|\leq 1,~ |d_1|\leq 1$
. To do this, we will use Lemma 2.1 and consider the following five cases.
$|c_1|\leq 1,~ |d_1|\leq 1$
. To do this, we will use Lemma 2.1 and consider the following five cases.
Case 1: Let
![]() $\mu \leq 0$
. A simple calculation shows that
$\mu \leq 0$
. A simple calculation shows that
Therefore, from Lemma 2.1,
The inequality is sharp and the equality holds for the function
![]() $f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
$f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
![]() $\omega (z)=z$
and
$\omega (z)=z$
and
![]() $\rho (z)=z$
, that is,
$\rho (z)=z$
, that is,
Case 2: Let
![]() $0\leq \mu \leq 2/3$
. A simple calculation shows that
$0\leq \mu \leq 2/3$
. A simple calculation shows that
Thus, from Lemma 2.1,
where R can be obtained from Lemma 2.1. For
![]() $0\leq \mu \leq \tfrac 23$
,
$0\leq \mu \leq \tfrac 23$
,
and
 $$ \begin{align*} |K|\sqrt{1-\dfrac{M^2}{KL}}\leq|A|&\iff\dfrac{\mu}{4}\sqrt{1+\dfrac{(2-3\mu)^2}{9\mu(1-\mu)}} \le\frac{1}{3}\\ &\iff 3\mu^2-20\mu+16\geq0, \end{align*} $$
$$ \begin{align*} |K|\sqrt{1-\dfrac{M^2}{KL}}\leq|A|&\iff\dfrac{\mu}{4}\sqrt{1+\dfrac{(2-3\mu)^2}{9\mu(1-\mu)}} \le\frac{1}{3}\\ &\iff 3\mu^2-20\mu+16\geq0, \end{align*} $$
which is true for all
![]() $\mu \in [0,~2/3]$
. Thus, the condition (A1) of Lemma 2.1 is satisfied.
$\mu \in [0,~2/3]$
. Thus, the condition (A1) of Lemma 2.1 is satisfied.
Again, for
![]() $0\leq \mu \leq 2/3$
,
$0\leq \mu \leq 2/3$
,
and
 $$ \begin{align*} |L|\sqrt{1-\dfrac{M^2}{KL}}\leq|B|&\iff(1-\mu)\sqrt{1+\dfrac{(2-3\mu)^2}{9\mu(1-\mu)}}\leq\frac{1}{3}\\ &\iff 3\mu^2-8\mu+4\leq 0, \end{align*} $$
$$ \begin{align*} |L|\sqrt{1-\dfrac{M^2}{KL}}\leq|B|&\iff(1-\mu)\sqrt{1+\dfrac{(2-3\mu)^2}{9\mu(1-\mu)}}\leq\frac{1}{3}\\ &\iff 3\mu^2-8\mu+4\leq 0, \end{align*} $$
which is not true for any
![]() $\mu \in [0,~2/3]$
. Thus, the condition (B1) of Lemma 2.1 is not satisfied. Further, for
$\mu \in [0,~2/3]$
. Thus, the condition (B1) of Lemma 2.1 is not satisfied. Further, for
![]() $0\leq \mu \leq 2/3$
,
$0\leq \mu \leq 2/3$
,
and so, the condition (B2) of Lemma 2.1 is not satisfied.
Therefore, by Lemma 2.1,
 $$ \begin{align*}R=|L|-|B|+\dfrac{M^2}{|A|+|K|}=\dfrac{2}{3}-\mu+\dfrac{(2-3\mu)^2}{4(4+3\mu)}\end{align*} $$
$$ \begin{align*}R=|L|-|B|+\dfrac{M^2}{|A|+|K|}=\dfrac{2}{3}-\mu+\dfrac{(2-3\mu)^2}{4(4+3\mu)}\end{align*} $$
and consequently, from (2.6),
 $$ \begin{align*} |a_3-\mu a_2^2|\leq\frac{4(5-3\mu)}{3(4+3\mu)}. \end{align*} $$
$$ \begin{align*} |a_3-\mu a_2^2|\leq\frac{4(5-3\mu)}{3(4+3\mu)}. \end{align*} $$
The inequality is sharp and the equality holds for the function
![]() $f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
$f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
where
 $$ \begin{align*} v_1=\frac{2(2-3\mu)}{4+3\mu}\quad\text{and}\quad a=\frac{v_2}{1-v_1^2}\quad\text{with}\quad v_1^2+v_2=1,\end{align*} $$
$$ \begin{align*} v_1=\frac{2(2-3\mu)}{4+3\mu}\quad\text{and}\quad a=\frac{v_2}{1-v_1^2}\quad\text{with}\quad v_1^2+v_2=1,\end{align*} $$
that is,
 $$ \begin{align*}f(z)=\int_0^z\frac{1+(a\bar{v_1}+v_1)t+at^2}{(1-t)^2(1+a\bar{v_1}t)}\,dt=z+\frac{6}{4+3\mu}z^2+\frac{80+120\mu-36\mu^2}{3(4+3\mu)^2}z^3+\cdots.\end{align*} $$
$$ \begin{align*}f(z)=\int_0^z\frac{1+(a\bar{v_1}+v_1)t+at^2}{(1-t)^2(1+a\bar{v_1}t)}\,dt=z+\frac{6}{4+3\mu}z^2+\frac{80+120\mu-36\mu^2}{3(4+3\mu)^2}z^3+\cdots.\end{align*} $$
Case 3: Let
![]() $2/3\leq \mu \leq 1$
. It is easy to show that
$2/3\leq \mu \leq 1$
. It is easy to show that
![]() $KL= -\tfrac 14\mu (1-\mu )<0$
. So, from Lemma 2.1,
$KL= -\tfrac 14\mu (1-\mu )<0$
. So, from Lemma 2.1,
where R can be obtained from Lemma 2.1. Proceeding as in Case 2, we can verify that the condition (A1) holds but (B1) and (B2) of Lemma 2.1 do not hold. Therefore,
 $$ \begin{align*}R=|K|-|A|+\dfrac{M^2}{|B|+|L|}=\frac{\mu-1}{4-3\mu}\leq0\quad\text{for}~ \frac{2}{3}\leq\mu\leq 1\end{align*} $$
$$ \begin{align*}R=|K|-|A|+\dfrac{M^2}{|B|+|L|}=\frac{\mu-1}{4-3\mu}\leq0\quad\text{for}~ \frac{2}{3}\leq\mu\leq 1\end{align*} $$
and consequently, from (2.7),
The inequality is sharp and the equality holds for the function
![]() $f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
$f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
![]() $\omega (z)=z^2$
and
$\omega (z)=z^2$
and
![]() $\rho (z)=z^2,$
that is,
$\rho (z)=z^2,$
that is,
Case 4: Let
![]() $1\leq \mu \leq 10/9$
. A simple calculation shows that
$1\leq \mu \leq 10/9$
. A simple calculation shows that
Thus, from Lemma 2.1,
 $$ \begin{align*}|a_3-\mu a_2^2|\leq|B|+|K|-\frac{M^2}{|L|-|B|}=\frac{5-3\mu}{3(4-3\mu)}.\end{align*} $$
$$ \begin{align*}|a_3-\mu a_2^2|\leq|B|+|K|-\frac{M^2}{|L|-|B|}=\frac{5-3\mu}{3(4-3\mu)}.\end{align*} $$
The inequality is sharp and the equality holds for the function
![]() $f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
$f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
where
 $$ \begin{align*} v_1=\frac{3\mu-2}{8-6\mu}\quad \text{and} \quad a=-\frac{v_2}{1-v_1^2}\quad\text{with}\quad v_1^2+v_2=1,\end{align*} $$
$$ \begin{align*} v_1=\frac{3\mu-2}{8-6\mu}\quad \text{and} \quad a=-\frac{v_2}{1-v_1^2}\quad\text{with}\quad v_1^2+v_2=1,\end{align*} $$
that is,
 $$ \begin{align*} \frac{g(z)}{z}=\exp\bigg( \int_0^z\frac{2(v_1+at)}{1+a\bar{v_1}t-v_1t-at^2}\,dt\bigg)=1+2v_1z+(4v_1^2-1)z^2+\cdots\end{align*} $$
$$ \begin{align*} \frac{g(z)}{z}=\exp\bigg( \int_0^z\frac{2(v_1+at)}{1+a\bar{v_1}t-v_1t-at^2}\,dt\bigg)=1+2v_1z+(4v_1^2-1)z^2+\cdots\end{align*} $$
and
 $$ \begin{align*}f(z)=\int_0^z\frac{g(t)}{t}(1+t)\,dt=z+\frac{1}{4-3\mu}z^2+\frac{30\mu-20-9\mu^2}{3(4-3\mu)^2}z^3+\cdots.\end{align*} $$
$$ \begin{align*}f(z)=\int_0^z\frac{g(t)}{t}(1+t)\,dt=z+\frac{1}{4-3\mu}z^2+\frac{30\mu-20-9\mu^2}{3(4-3\mu)^2}z^3+\cdots.\end{align*} $$
Case 5: Let
![]() $\mu \geq 10/9$
. A simple calculation shows that
$\mu \geq 10/9$
. A simple calculation shows that
Thus, from Lemma 2.1,
The inequality is sharp and the equality holds for the function
![]() $f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
$f\in \mathcal {K}_{u}$
given by (2.2) and (2.4) with
![]() $\omega (z)=z$
and
$\omega (z)=z$
and
![]() $\rho (z)=z$
, that is,
$\rho (z)=z$
, that is,
Finally, we establish a result related to the pre-Schwarzian norm for functions in
![]() $\mathcal {K}_{u}$
. We first note that a function f in
$\mathcal {K}_{u}$
. We first note that a function f in
![]() $\mathcal {A}$
belongs to
$\mathcal {A}$
belongs to
![]() $\mathcal {K}_{u}$
if there exists a function
$\mathcal {K}_{u}$
if there exists a function
![]() $g\in \mathcal {S}^*$
such that
$g\in \mathcal {S}^*$
such that
![]() $|zf'(z)/g(z)-1|<1.$
In other words, if there exists a convex function
$|zf'(z)/g(z)-1|<1.$
In other words, if there exists a convex function
![]() $h\in \mathcal {C}$
with
$h\in \mathcal {C}$
with
![]() $g(z)=zh'(z)$
such that
$g(z)=zh'(z)$
such that
 $$ \begin{align*}\bigg|\frac{f'(z)}{h'(z)}-1\bigg|<1.\end{align*} $$
$$ \begin{align*}\bigg|\frac{f'(z)}{h'(z)}-1\bigg|<1.\end{align*} $$
Theorem 2.5. Let
![]() $f\in \mathcal {K}_{u}$
and
$f\in \mathcal {K}_{u}$
and
![]() $h\in \mathcal {C}$
be the associated convex function. Then,
$h\in \mathcal {C}$
be the associated convex function. Then,
and the estimate is sharp. Further,
![]() $\|P_f\|\le 6$
.
$\|P_f\|\le 6$
.
Proof. Let
![]() $f\in \mathcal {K}_{u}$
and
$f\in \mathcal {K}_{u}$
and
![]() $h\in \mathcal {C}$
be the associated convex function such that
$h\in \mathcal {C}$
be the associated convex function such that
 $$ \begin{align*}\bigg|\frac{f'(z)}{h'(z)}-1\bigg|<1.\end{align*} $$
$$ \begin{align*}\bigg|\frac{f'(z)}{h'(z)}-1\bigg|<1.\end{align*} $$
Then there exists a function
![]() $\omega (z)\in \mathcal {B}_{0}$
such that
$\omega (z)\in \mathcal {B}_{0}$
such that
 $$ \begin{align*}\frac{f'(z)}{h'(z)}=1+\omega(z).\end{align*} $$
$$ \begin{align*}\frac{f'(z)}{h'(z)}=1+\omega(z).\end{align*} $$
Taking the logarithmic derivative on both sides,
 $$ \begin{align*} \frac{f"(z)}{f'(z)}-\frac{h"(z)}{h'(z)}=\frac{\omega'(z)}{1+\omega(z)} \end{align*} $$
$$ \begin{align*} \frac{f"(z)}{f'(z)}-\frac{h"(z)}{h'(z)}=\frac{\omega'(z)}{1+\omega(z)} \end{align*} $$
and so,
 $$ \begin{align*} \left|\frac{f"(z)}{f'(z)}\right|-\left|\frac{h"(z)}{h'(z)}\right| \leq\left|\frac{f"(z)}{f'(z)}-\frac{h"(z)}{h'(z)}\right| =\left|\frac{\omega'(z)}{1+\omega(z)}\right|. \end{align*} $$
$$ \begin{align*} \left|\frac{f"(z)}{f'(z)}\right|-\left|\frac{h"(z)}{h'(z)}\right| \leq\left|\frac{f"(z)}{f'(z)}-\frac{h"(z)}{h'(z)}\right| =\left|\frac{\omega'(z)}{1+\omega(z)}\right|. \end{align*} $$
Thus,
 $$ \begin{align*} |\, \|P_f\|-\|P_h\| \,|&=\bigg|\sup\limits_{z\in\mathbb{D}}(1-|z|^2)\bigg|\frac{f"(z)}{f'(z)}\bigg| -\sup\limits_{z\in\mathbb{D}}(1-|z|^2)\bigg|\frac{h"(z)}{h'(z)}\bigg|\,\bigg|\\&\le\sup\limits_{z\in\mathbb{D}}(1-|z|^2)\bigg|\bigg(\bigg|\frac{f"(z)}{f'(z)}\bigg|-\bigg|\frac{h"(z)}{h'(z)}\bigg|\bigg)\bigg| \\&\leq\sup\limits_{z\in\mathbb{D}}(1-|z|^2)\bigg|\frac{f"(z)}{f'(z)}-\frac{h"(z)}{h'(z)}\bigg| \\&= \sup\limits_{z\in\mathbb{D}}(1-|z|^2)\frac{|\omega'(z)|}{|1+\omega(z)|}. \end{align*} $$
$$ \begin{align*} |\, \|P_f\|-\|P_h\| \,|&=\bigg|\sup\limits_{z\in\mathbb{D}}(1-|z|^2)\bigg|\frac{f"(z)}{f'(z)}\bigg| -\sup\limits_{z\in\mathbb{D}}(1-|z|^2)\bigg|\frac{h"(z)}{h'(z)}\bigg|\,\bigg|\\&\le\sup\limits_{z\in\mathbb{D}}(1-|z|^2)\bigg|\bigg(\bigg|\frac{f"(z)}{f'(z)}\bigg|-\bigg|\frac{h"(z)}{h'(z)}\bigg|\bigg)\bigg| \\&\leq\sup\limits_{z\in\mathbb{D}}(1-|z|^2)\bigg|\frac{f"(z)}{f'(z)}-\frac{h"(z)}{h'(z)}\bigg| \\&= \sup\limits_{z\in\mathbb{D}}(1-|z|^2)\frac{|\omega'(z)|}{|1+\omega(z)|}. \end{align*} $$
Since
![]() $\omega (z)\in \mathcal {B}_0$
, by the Schwarz–Pick lemma,
$\omega (z)\in \mathcal {B}_0$
, by the Schwarz–Pick lemma,
 $$ \begin{align*} |\omega'(z)|\le\frac{1-|\omega(z)|^2}{1-|z|^2}. \end{align*} $$
$$ \begin{align*} |\omega'(z)|\le\frac{1-|\omega(z)|^2}{1-|z|^2}. \end{align*} $$
Therefore,
 $$ \begin{align*} |\, \|P_f\|-\|P_h\| \,|\le \sup\limits_{z\in\mathbb{D}}\frac{1-|\omega(z)|^2}{|1+\omega(z)|}\le 2. \end{align*} $$
$$ \begin{align*} |\, \|P_f\|-\|P_h\| \,|\le \sup\limits_{z\in\mathbb{D}}\frac{1-|\omega(z)|^2}{|1+\omega(z)|}\le 2. \end{align*} $$
The above inequality is sharp for the functions
It is well known that
![]() $\|P_h\|\le 4$
for
$\|P_h\|\le 4$
for
![]() $f\in \mathcal {C}$
(see [Reference Yamashita19]), and so
$f\in \mathcal {C}$
(see [Reference Yamashita19]), and so
![]() $\|P_f\|\le 6$
.
$\|P_f\|\le 6$
.