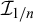1 Introduction
For more than 20 years, many mathematicians have been examining sequentially compact spaces that are, in a sense, topological counterparts of some combinatorial theorems, for instance, Ramsey’s theorem for coloring graphs, Hindman’s finite sums theorem, and van der Waerden’s arithmetical progressions theorem [Reference Bergelson and Zelada5, Reference Bojańczyk, Kopczyński and Toruńczyk6, Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20–Reference Filipów22, Reference Filipów, Kowitz, Kwela and Tryba24, Reference Filipów, Mrożek, Recław and Szuca26–Reference Filipów and Tryba28, Reference Flašková30, Reference Furstenberg35, Reference Furstenberg and Weiss36, Reference Jones52, Reference Kojman57–Reference Kwela and Tryba63, Reference Shi73]. These spaces are defined with the aid of different kinds of convergences: IP-convergence, R-convergence, and ordinary convergence.
We start our brief overview of these spaces with the ones defined using ordinary convergence. A topological space X is called:
-
• van der Waerden [Reference Kojman58] if for every sequence
 $\langle x_n\rangle _{n\in \mathbb {N}}$
in X there exists a convergent subsequence
$\langle x_n\rangle _{n\in \mathbb {N}}$
in X there exists a convergent subsequence
 $\langle x_{n}\rangle _{n\in A}$
with A being an AP-set (i.e., A contains arithmetic progressions of arbitrary finite length);
$\langle x_{n}\rangle _{n\in A}$
with A being an AP-set (i.e., A contains arithmetic progressions of arbitrary finite length); -
• an
 $\mathcal {I}_{1/n}$
-space [Reference Flašková30] if for every sequence
$\mathcal {I}_{1/n}$
-space [Reference Flašková30] if for every sequence
 $\langle x_n\rangle _{n\in \mathbb {N}}$
in X there exists a convergent subsequence
$\langle x_n\rangle _{n\in \mathbb {N}}$
in X there exists a convergent subsequence
 $\langle x_{n}\rangle _{n\in A}$
with A having the property that the series of reciprocals of elements of A diverges.
$\langle x_{n}\rangle _{n\in A}$
with A having the property that the series of reciprocals of elements of A diverges.
In fact both mentioned classes of spaces are special cases of a more general notion. A nonempty family
![]() $\mathcal {I}\subseteq \mathcal {P}(\mathbb {N})$
of subsets of
$\mathcal {I}\subseteq \mathcal {P}(\mathbb {N})$
of subsets of
![]() $\mathbb {N}$
is an ideal on
$\mathbb {N}$
is an ideal on
![]() $\mathbb {N}$
if it is closed under taking subsets and finite unions of its elements,
$\mathbb {N}$
if it is closed under taking subsets and finite unions of its elements,
![]() $\mathbb {N}\notin {\mathcal {I}}$
and
$\mathbb {N}\notin {\mathcal {I}}$
and
![]() $\mathcal {I}$
contains all finite subsets of
$\mathcal {I}$
contains all finite subsets of
![]() $\mathbb {N}$
(it is easy to see that the family
$\mathbb {N}$
(it is easy to see that the family
![]() $\mathcal {I}_{1/n}=\{A\subseteq {\mathbb {N}}: \sum _{n\in A} 1/n<\infty \}$
is an ideal on
$\mathcal {I}_{1/n}=\{A\subseteq {\mathbb {N}}: \sum _{n\in A} 1/n<\infty \}$
is an ideal on
![]() ${\mathbb {N}}$
, and it follows from van der Waerden’s theorem [Reference van der Waerden75] that the family
${\mathbb {N}}$
, and it follows from van der Waerden’s theorem [Reference van der Waerden75] that the family
![]() $\mathcal {W} = \{A\subseteq {\mathbb {N}}: A\text { is not an AP-set}\}$
is an ideal on
$\mathcal {W} = \{A\subseteq {\mathbb {N}}: A\text { is not an AP-set}\}$
is an ideal on
![]() $\mathbb {N}$
). If
$\mathbb {N}$
). If
![]() $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
![]() $\mathbb {N}$
then a topological space X is called an
$\mathbb {N}$
then a topological space X is called an
![]() $\mathcal {I}$
-space [Reference Flašková30] if for every sequence
$\mathcal {I}$
-space [Reference Flašková30] if for every sequence
![]() $\langle x_n\rangle _{n\in {\mathbb {N}}}$
in X there exists a converging subsequence
$\langle x_n\rangle _{n\in {\mathbb {N}}}$
in X there exists a converging subsequence
![]() $\langle x_{n}\rangle _{n\in A}$
with
$\langle x_{n}\rangle _{n\in A}$
with
![]() $A\notin {\mathcal {I}}$
. In particular, van der Waerden spaces coincide with
$A\notin {\mathcal {I}}$
. In particular, van der Waerden spaces coincide with
![]() $\mathcal {W}$
-spaces.
$\mathcal {W}$
-spaces.
Now we want to turn our attention to spaces defined with the aid of different kinds of convergences. We start with Hindman spaces. A set
![]() $A\subseteq \mathbb {N}$
is an IP-set [Reference Furstenberg and Weiss36] if there exists an infinite set
$A\subseteq \mathbb {N}$
is an IP-set [Reference Furstenberg and Weiss36] if there exists an infinite set
![]() $D\subseteq \mathbb {N}$
such that
$D\subseteq \mathbb {N}$
such that
![]() $\operatorname {\mathrm {FS}}(D)\subseteq A$
where
$\operatorname {\mathrm {FS}}(D)\subseteq A$
where
![]() $\operatorname {\mathrm {FS}}(D)$
denotes the set of all finite sums of distinct elements of D. The family
$\operatorname {\mathrm {FS}}(D)$
denotes the set of all finite sums of distinct elements of D. The family
![]() $\mathcal {H} = \{A\subseteq \mathbb {N}: A\text { is not an IP-set}\}$
is an ideal on
$\mathcal {H} = \{A\subseteq \mathbb {N}: A\text { is not an IP-set}\}$
is an ideal on
![]() $\mathbb {N}$
(it follows from Hindman’s theorem [Reference Hindman44]).
$\mathbb {N}$
(it follows from Hindman’s theorem [Reference Hindman44]).
An IP-sequence in X is a sequence indexed by
![]() $\operatorname {\mathrm {FS}}(D)$
for some infinite
$\operatorname {\mathrm {FS}}(D)$
for some infinite
![]() $D\subseteq \mathbb {N}$
. An IP-sequence
$D\subseteq \mathbb {N}$
. An IP-sequence
![]() $\langle x_n\rangle _{n\in \operatorname {\mathrm {FS}}(D)}$
in a topological space X is IP-convergent [Reference Furstenberg and Weiss36] to a point
$\langle x_n\rangle _{n\in \operatorname {\mathrm {FS}}(D)}$
in a topological space X is IP-convergent [Reference Furstenberg and Weiss36] to a point
![]() $x\in X$
if for every neighborhood U of x there exists
$x\in X$
if for every neighborhood U of x there exists
![]() $m\in \mathbb {N}$
so that
$m\in \mathbb {N}$
so that
![]() $x_n \in U$
for every
$x_n \in U$
for every
![]() $n\in \operatorname {\mathrm {FS}}(D\setminus \{0,1,\dots ,m\})$
(then x is called the IP-limit of the sequence).
$n\in \operatorname {\mathrm {FS}}(D\setminus \{0,1,\dots ,m\})$
(then x is called the IP-limit of the sequence).
Since only finite spaces are
![]() $\mathcal {H}$
-spaces [Reference Kojman57], Kojman replaced the ordinary convergence with IP-convergence (introduced by Furstenberg and Weiss [Reference Furstenberg and Weiss36]) to define a meaningful topological counterpart of Hindman’s finite sums theorem. Namely, a topological space X is called Hindman [Reference Kojman57] if for every sequence
$\mathcal {H}$
-spaces [Reference Kojman57], Kojman replaced the ordinary convergence with IP-convergence (introduced by Furstenberg and Weiss [Reference Furstenberg and Weiss36]) to define a meaningful topological counterpart of Hindman’s finite sums theorem. Namely, a topological space X is called Hindman [Reference Kojman57] if for every sequence
![]() $\langle x_n\rangle _{n\in \mathbb {N}}$
in X there exists an infinite set
$\langle x_n\rangle _{n\in \mathbb {N}}$
in X there exists an infinite set
![]() $D\subseteq \mathbb {N}$
such that the subsequence
$D\subseteq \mathbb {N}$
such that the subsequence
![]() $\langle x_n\rangle _{n\in \operatorname {\mathrm {FS}}(D)}$
IP-converges to some
$\langle x_n\rangle _{n\in \operatorname {\mathrm {FS}}(D)}$
IP-converges to some
![]() $x\in X$
.
$x\in X$
.
We finish our brief overview of classes of sequentially compact spaces with Ramsey spaces. Let
![]() $[A]^2$
denote the set of all pairs of elements of A. A sequence
$[A]^2$
denote the set of all pairs of elements of A. A sequence
![]() $\langle x_n\rangle _{n\in [D]^2}$
in X (indexed by pairs of natural numbers from some infinite set
$\langle x_n\rangle _{n\in [D]^2}$
in X (indexed by pairs of natural numbers from some infinite set
![]() $D\subseteq \mathbb {N}$
) R-converges [Reference Bergelson and Zelada5, Reference Bojańczyk, Kopczyński and Toruńczyk6] to a point
$D\subseteq \mathbb {N}$
) R-converges [Reference Bergelson and Zelada5, Reference Bojańczyk, Kopczyński and Toruńczyk6] to a point
![]() $x\in X$
if for every neighborhood U of x there is a finite set F such that
$x\in X$
if for every neighborhood U of x there is a finite set F such that
![]() $x_{\{a,b\}} \in U$
for all distinct
$x_{\{a,b\}} \in U$
for all distinct
![]() $a,b\in D\setminus F$
. A topological space X is called Ramsey [Reference Kubiś and Szeptycki61] if for every sequence
$a,b\in D\setminus F$
. A topological space X is called Ramsey [Reference Kubiś and Szeptycki61] if for every sequence
![]() $\langle x_n\rangle _{n\in [\mathbb {N}]^2}$
in X there exists an infinite set
$\langle x_n\rangle _{n\in [\mathbb {N}]^2}$
in X there exists an infinite set
![]() $D\subseteq \mathbb {N}$
such that the subsequence
$D\subseteq \mathbb {N}$
such that the subsequence
![]() $\langle x_n\rangle _{n\in [D]^2}$
R-converges to some
$\langle x_n\rangle _{n\in [D]^2}$
R-converges to some
![]() $x\in X$
.
$x\in X$
.
We say that an ideal
![]() $\mathcal {I}$
(on
$\mathcal {I}$
(on
![]() $\mathbb {N}$
) is below an ideal
$\mathbb {N}$
) is below an ideal
![]() $\mathcal {J}$
in the Katětov order [Reference Katětov55] if there is a function
$\mathcal {J}$
in the Katětov order [Reference Katětov55] if there is a function
![]() $f:\mathbb {N}\to \mathbb {N}$
such that
$f:\mathbb {N}\to \mathbb {N}$
such that
![]() $f^{-1}[A]\in \mathcal {J}$
for every
$f^{-1}[A]\in \mathcal {J}$
for every
![]() $A\in \mathcal {I}$
. Note that Katětov order has been extensively examined (even in its own right) for many years so far [Reference Barbarski, Filipów, Mrożek and Szuca2, Reference Baumgartner3, Reference Brendle and Flašková8, Reference Cancino-Manríquez10, Reference Das, Filipów, Gła̧b and Tryba12, Reference Grebík and Hrušák41, Reference Guzmán-González and Meza-Alcántara42, Reference Hrušák45, Reference Hrušák47–Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui50, Reference Meza-Alcántara67, Reference Minami and Sakai68, Reference Mrożek70, Reference Sakai72, Reference Zhang and Zhang76].
$A\in \mathcal {I}$
. Note that Katětov order has been extensively examined (even in its own right) for many years so far [Reference Barbarski, Filipów, Mrożek and Szuca2, Reference Baumgartner3, Reference Brendle and Flašková8, Reference Cancino-Manríquez10, Reference Das, Filipów, Gła̧b and Tryba12, Reference Grebík and Hrušák41, Reference Guzmán-González and Meza-Alcántara42, Reference Hrušák45, Reference Hrušák47–Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui50, Reference Meza-Alcántara67, Reference Minami and Sakai68, Reference Mrożek70, Reference Sakai72, Reference Zhang and Zhang76].
There are three objectives of this paper. The first aim is to present a unified approach to these various types of convergences and spaces. This is achieved in sections in Part 1 with the aid of partition regular functions (Definition 3.1), a convergence with respect to partition regular functions (Definition 9.1), and a subclass of sequentially compact spaces defined using this new kind of convergence (see Definition 10.1). Then using this approach, we prove some general theorems about those classes of spaces (Theorem 10.5) and show that all results obtained so far in this subject can be derived from our theorems (see sections in Parts 2 and 3).
The second aim of this paper is to obtain new results concerning specific types of these spaces: Ramsey spaces, Hindman spaces, van der Waerden spaces, and
![]() $\mathcal {I}_{1/n}$
-spaces. For instance, we construct a Hausdorff Hindman space that is not an
$\mathcal {I}_{1/n}$
-spaces. For instance, we construct a Hausdorff Hindman space that is not an
![]() $\mathcal {I}_{1/n}$
-space (Corollary 14.10(2))—this gives a positive answer to a question posed by Flašková [Reference Flašková29] (so far only non-Hausdorff answer to this question was known [Reference Filipów, Kowitz, Kwela and Tryba24, Theorem 2.5]). We also construct a Hausdorff so-called differentially compact space that is not Hindman (Corollary 14.9(3)) which yields the negative answer to a question posed by Shi [Reference Shi73, Question 4.2.2] and other authors [Reference Filipów22, Problem 1], [Reference Kowitz60, Question 3]. Moreover, we compare Ramsey spaces with other types of spaces (so far Ramsey spaces were only examined in their own right without comparing them with other kinds of spaces [Reference Bojańczyk, Kopczyński and Toruńczyk6, Reference Corral, Guzmán and López-Callejas11, Reference Kubiś and Szeptycki61]). For instance, we construct a Ramsey space that is not Hindman and a Hindman space that is not Ramsey (Corollary 14.9).
$\mathcal {I}_{1/n}$
-space (Corollary 14.10(2))—this gives a positive answer to a question posed by Flašková [Reference Flašková29] (so far only non-Hausdorff answer to this question was known [Reference Filipów, Kowitz, Kwela and Tryba24, Theorem 2.5]). We also construct a Hausdorff so-called differentially compact space that is not Hindman (Corollary 14.9(3)) which yields the negative answer to a question posed by Shi [Reference Shi73, Question 4.2.2] and other authors [Reference Filipów22, Problem 1], [Reference Kowitz60, Question 3]. Moreover, we compare Ramsey spaces with other types of spaces (so far Ramsey spaces were only examined in their own right without comparing them with other kinds of spaces [Reference Bojańczyk, Kopczyński and Toruńczyk6, Reference Corral, Guzmán and López-Callejas11, Reference Kubiś and Szeptycki61]). For instance, we construct a Ramsey space that is not Hindman and a Hindman space that is not Ramsey (Corollary 14.9).
The final aim of this paper is to provide a characterization that shows when there exists a space of one considered type that is not of the other type (Theorem 16.1 and other results in Part 4). This characterization is expressed in purely combinatorial manner with the aid of the Katětov order or its counterpart in the realm of partition regular functions (Definition 7.3).
2 Preliminaries
In the paper we are exclusively interested in Hausdorff topological spaces with one exception (Sections 17 and 18) where we were unable to obtain results for Hausdorff spaces but succeeded in constructing a topological space with unique limits of sequences.
Following von Neumann, we identify an ordinal number
![]() $\alpha $
with the set of all ordinal numbers less than
$\alpha $
with the set of all ordinal numbers less than
![]() $\alpha $
. In particular, the smallest infinite ordinal number
$\alpha $
. In particular, the smallest infinite ordinal number
![]() $\omega =\{0,1,\dots \}$
is equal to the set
$\omega =\{0,1,\dots \}$
is equal to the set
![]() $\mathbb {N}$
of all natural numbers, and each natural number
$\mathbb {N}$
of all natural numbers, and each natural number
![]() $n = \{0,\dots ,n-1\}$
is equal to the set of all natural numbers less than n. Using this identification, we can, for instance, write
$n = \{0,\dots ,n-1\}$
is equal to the set of all natural numbers less than n. Using this identification, we can, for instance, write
![]() $n\in k$
instead of
$n\in k$
instead of
![]() $n<k$
and
$n<k$
and
![]() $n<\omega $
instead of
$n<\omega $
instead of
![]() $n\in \omega $
or
$n\in \omega $
or
![]() $A\cap n$
instead of
$A\cap n$
instead of
![]() $A\cap \{0,1,\dots ,n-1\}$
.
$A\cap \{0,1,\dots ,n-1\}$
.
If
![]() $A\subseteq \omega $
and
$A\subseteq \omega $
and
![]() $n\in \omega $
, we write
$n\in \omega $
, we write
![]() $A+n = \{a+n:a\in A\}$
and
$A+n = \{a+n:a\in A\}$
and
![]() $A-n=\{a-n:a\in A, a>n\}$
.
$A-n=\{a-n:a\in A, a>n\}$
.
We write
![]() $[A]^2$
to denote the set of all unordered pairs of elements of A,
$[A]^2$
to denote the set of all unordered pairs of elements of A,
![]() $[A]^{<\omega }$
to denote the family of all finite subsets of A,
$[A]^{<\omega }$
to denote the family of all finite subsets of A,
![]() $[A]^\omega $
to denote the family of all infinite countable subsets of A, and
$[A]^\omega $
to denote the family of all infinite countable subsets of A, and
![]() $\mathcal {P}(A)$
to denote the family of all subsets of A.
$\mathcal {P}(A)$
to denote the family of all subsets of A.
We say that a family
![]() $\mathcal {A}$
of subsets of a set
$\mathcal {A}$
of subsets of a set
![]() $\Lambda $
is an almost disjoint family on
$\Lambda $
is an almost disjoint family on
![]() $\Lambda $
if
$\Lambda $
if
-
(1)
 $|A|=|\Lambda |$
for every
$|A|=|\Lambda |$
for every
 $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and -
(2)
 $|A\cap B|<|\Lambda |$
for all distinct elements
$|A\cap B|<|\Lambda |$
for all distinct elements
 $A,B\in \mathcal {A}$
.
$A,B\in \mathcal {A}$
.
By
![]() $A \sqcup B$
we denote the disjoint union of sets A and B:
$A \sqcup B$
we denote the disjoint union of sets A and B:
For families of sets
![]() $\mathcal {A}\subseteq \mathcal {P}(\Lambda )$
and
$\mathcal {A}\subseteq \mathcal {P}(\Lambda )$
and
![]() $\mathcal {B}\subseteq \mathcal {P}(\Sigma )$
, we write
$\mathcal {B}\subseteq \mathcal {P}(\Sigma )$
, we write
![]() $\mathcal {A} \oplus \mathcal {B} =\{ A\sqcup B:A\in \mathcal {A},B\in \mathcal {B}\}.$
$\mathcal {A} \oplus \mathcal {B} =\{ A\sqcup B:A\in \mathcal {A},B\in \mathcal {B}\}.$
A nonempty family
![]() $\mathcal {I}\subseteq \mathcal {P}(\Lambda )$
of subsets of
$\mathcal {I}\subseteq \mathcal {P}(\Lambda )$
of subsets of
![]() $\Lambda $
is an ideal on
$\Lambda $
is an ideal on
![]() $\Lambda $
if it is closed under taking subsets and finite unions of its elements,
$\Lambda $
if it is closed under taking subsets and finite unions of its elements,
![]() $\Lambda \notin \mathcal {I}$
and
$\Lambda \notin \mathcal {I}$
and
![]() $\mathcal {I}$
contains all finite subsets of
$\mathcal {I}$
contains all finite subsets of
![]() $\Lambda $
. By
$\Lambda $
. By
![]() $\mathrm {Fin}(\Lambda )$
we denote the family of all finite subsets of
$\mathrm {Fin}(\Lambda )$
we denote the family of all finite subsets of
![]() $\Lambda $
. For
$\Lambda $
. For
![]() $\Lambda =\omega $
, we write
$\Lambda =\omega $
, we write
![]() $\mathrm {Fin}$
instead of
$\mathrm {Fin}$
instead of
![]() $\mathrm {Fin}(\omega )$
. For an ideal
$\mathrm {Fin}(\omega )$
. For an ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\Lambda $
, we write
$\Lambda $
, we write
![]() $\mathcal {I}^+=\{A\subseteq \Lambda : A\notin \mathcal {I}\}$
and call it the coideal of
$\mathcal {I}^+=\{A\subseteq \Lambda : A\notin \mathcal {I}\}$
and call it the coideal of
![]() $\mathcal {I}$
, and we write
$\mathcal {I}$
, and we write
![]() $\mathcal {I}^*=\{\Lambda \setminus A: A\in \mathcal {I}\}$
and call it the filter dual to
$\mathcal {I}^*=\{\Lambda \setminus A: A\in \mathcal {I}\}$
and call it the filter dual to
![]() $\mathcal {I}$
. For an ideal
$\mathcal {I}$
. For an ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\Lambda $
and
$\Lambda $
and
![]() $A\in \mathcal {I}^+$
, it is easy to see that
$A\in \mathcal {I}^+$
, it is easy to see that
![]() $\mathcal {I}\restriction A=\{A\cap B:B\in \mathcal {I}\}$
is an ideal on A.
$\mathcal {I}\restriction A=\{A\cap B:B\in \mathcal {I}\}$
is an ideal on A.
In our research the following ideal on
![]() $\omega ^2$
plays an important role:
$\omega ^2$
plays an important role:
We say that a function
![]() $f:\Lambda \to \Sigma $
is
$f:\Lambda \to \Sigma $
is
![]() $\mathcal {I}$
-to-one if
$\mathcal {I}$
-to-one if
![]() $f^{-1}(\sigma )\in \mathcal {I}$
for every
$f^{-1}(\sigma )\in \mathcal {I}$
for every
![]() $\sigma \in \Sigma $
.
$\sigma \in \Sigma $
.
A set
![]() $A\subseteq X$
is
$A\subseteq X$
is
![]() $F_\sigma $
(
$F_\sigma $
(
![]() $G_\delta $
,
$G_\delta $
,
![]() $F_{\sigma \delta }$
, etc., resp.) in a topological space X if A is a union of a countable family of closed sets (A is an intersection of a countable family of open sets, A is an intersection of a countable family of
$F_{\sigma \delta }$
, etc., resp.) in a topological space X if A is a union of a countable family of closed sets (A is an intersection of a countable family of open sets, A is an intersection of a countable family of
![]() $F_\sigma $
sets, etc., resp.).
$F_\sigma $
sets, etc., resp.).
For a function
![]() $f:X\to Y$
and a set
$f:X\to Y$
and a set
![]() $A\subseteq X$
, we write
$A\subseteq X$
, we write
![]() $f\restriction A$
to denote the restriction of f to the set A.
$f\restriction A$
to denote the restriction of f to the set A.
Part 1. Partition regular operations
3 Partition regular operations and ideals associated with them
Below we introduce a notion that proved to be a convenient tool allowing to grasp the common feature of different kinds of convergences related to Hindman, Ramsey, and van der Waerden spaces.
Definition 3.1. Let
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Omega $
be countable infinite sets. Let
$\Omega $
be countable infinite sets. Let
![]() $\mathcal {F}$
be a nonempty family of infinite subsets of
$\mathcal {F}$
be a nonempty family of infinite subsets of
![]() $\Omega $
such that
$\Omega $
such that
![]() $F\setminus K\in \mathcal {F}$
for every
$F\setminus K\in \mathcal {F}$
for every
![]() $F\in \mathcal {F}$
and a finite set
$F\in \mathcal {F}$
and a finite set
![]() $K\subseteq \Omega $
. We say that a function
$K\subseteq \Omega $
. We say that a function
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
is partition regular if:
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
is partition regular if:
-
(M):
 $\forall E,F\in \mathcal {F}\, \left ( E\subseteq F \implies \rho (E)\subseteq \rho (F)\right )$
,
$\forall E,F\in \mathcal {F}\, \left ( E\subseteq F \implies \rho (E)\subseteq \rho (F)\right )$
, -
(R):
 $\forall F\in \mathcal {F}\,\forall A,B \subseteq \Lambda \,\left (\rho (F) = A\cup B\hspace{-1pt}\implies\hspace{-1pt} \exists E\in \mathcal {F} \,(\rho (E)\hspace{-0.5pt}\subseteq\hspace{-0.5pt} A\hspace{-0.5pt} \lor\hspace{-0.5pt} \rho (E)\hspace{-0.5pt}\subseteq\hspace{-0.5pt} B) \right ),$
$\forall F\in \mathcal {F}\,\forall A,B \subseteq \Lambda \,\left (\rho (F) = A\cup B\hspace{-1pt}\implies\hspace{-1pt} \exists E\in \mathcal {F} \,(\rho (E)\hspace{-0.5pt}\subseteq\hspace{-0.5pt} A\hspace{-0.5pt} \lor\hspace{-0.5pt} \rho (E)\hspace{-0.5pt}\subseteq\hspace{-0.5pt} B) \right ),$
-
(S):
 $\forall F\in \mathcal {F}\,\exists E\in \mathcal {F}\,(E\subseteq F \land \forall a\in \rho (E)\,\exists K\in [\Omega ]^{<\omega }(a\notin \rho (E\setminus K)))$
.
$\forall F\in \mathcal {F}\,\exists E\in \mathcal {F}\,(E\subseteq F \land \forall a\in \rho (E)\,\exists K\in [\Omega ]^{<\omega }(a\notin \rho (E\setminus K)))$
.
In our considerations, we use the following easy observation concerning condition (S) of Definition 3.1.
Proposition 3.2. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega (with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
be a partition regular function. Then for every
$\rho :\mathcal {F}\to [\Lambda ]^\omega (with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
be a partition regular function. Then for every
![]() $F\in \mathcal {F}$
there is
$F\in \mathcal {F}$
there is
![]() $E\in \mathcal {F}$
such that
$E\in \mathcal {F}$
such that
![]() $E\subseteq F$
and for every finite set
$E\subseteq F$
and for every finite set
![]() $L\subseteq \Lambda $
there exists a finite set
$L\subseteq \Lambda $
there exists a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $\rho (E\setminus K)\subseteq \rho (E)\setminus L$
.
$\rho (E\setminus K)\subseteq \rho (E)\setminus L$
.
Proof For
![]() $F\in \mathcal {F}$
, let
$F\in \mathcal {F}$
, let
![]() $E\in \mathcal {F}$
be as in condition (S) of Definition 3.1. Let
$E\in \mathcal {F}$
be as in condition (S) of Definition 3.1. Let
![]() $L\subseteq \Lambda $
be a finite set. For every
$L\subseteq \Lambda $
be a finite set. For every
![]() $a\in \rho (E)$
, we take a finite set
$a\in \rho (E)$
, we take a finite set
![]() $K_a$
such that
$K_a$
such that
![]() $a\notin \rho (E\setminus K_a)$
. Then
$a\notin \rho (E\setminus K_a)$
. Then
![]() $K=\bigcup \{K_a:a\in \rho (E)\cap L\}$
is finite and
$K=\bigcup \{K_a:a\in \rho (E)\cap L\}$
is finite and
![]() $\rho (E\setminus K)\subseteq \rho (E)\setminus L$
.
$\rho (E\setminus K)\subseteq \rho (E)\setminus L$
.
The following easy proposition reveals basic relationships between partition regular functions and ideals.
Proposition 3.3.
-
(1) If
 $\rho :\mathcal {F}\to [\Lambda ]^\omega $
is partition regular, then
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
is partition regular, then  $$ \begin{align*}\mathcal{I}_{\rho} = \{A\subseteq \Lambda: \forall F\in \mathcal{F}\, (\rho(F)\not\subseteq A)\}.\end{align*} $$
$$ \begin{align*}\mathcal{I}_{\rho} = \{A\subseteq \Lambda: \forall F\in \mathcal{F}\, (\rho(F)\not\subseteq A)\}.\end{align*} $$
is an ideal on
 $\Lambda $
.
$\Lambda $
. -
(2) If
 $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
 $\Lambda $
, then the function
$\Lambda $
, then the function  $$ \begin{align*}\rho_{\mathcal{I}}:\mathcal{I}^+\to[\Lambda]^\omega \text{\ \ \ given by \ \ } \rho_{\mathcal{I}}(A)=A\end{align*} $$
$$ \begin{align*}\rho_{\mathcal{I}}:\mathcal{I}^+\to[\Lambda]^\omega \text{\ \ \ given by \ \ } \rho_{\mathcal{I}}(A)=A\end{align*} $$
is partition regular and
 $\mathcal {I}=\mathcal {I}_{\rho _{\mathcal {I}}}.$
$\mathcal {I}=\mathcal {I}_{\rho _{\mathcal {I}}}.$
Remark. If
![]() $\rho $
is partition regular and
$\rho $
is partition regular and
![]() $\tau =\rho _{\mathcal {I}_\rho }$
, then
$\tau =\rho _{\mathcal {I}_\rho }$
, then
![]() $\mathcal {I}_{\tau } = \mathcal {I}_\rho $
, but, as we will see, in general,
$\mathcal {I}_{\tau } = \mathcal {I}_\rho $
, but, as we will see, in general,
![]() $\rho \neq \tau $
. More important,
$\rho \neq \tau $
. More important,
![]() $\tau $
may miss some crucial properties which
$\tau $
may miss some crucial properties which
![]() $\rho $
possesses (e.g., P-like properties—see Proposition 6.5(3) and (4)).
$\rho $
possesses (e.g., P-like properties—see Proposition 6.5(3) and (4)).
Below we present the most important examples of partition regular functions that were our prototypes while we were thinking on a unified approach to Hindman, Ramsey, and van der Waerden spaces.
3.1 Hindman’s finite sums theorem
Let the function
![]() $\operatorname {\mathrm {FS}} :[\omega ]^\omega \to [\omega ]^\omega $
be given by
$\operatorname {\mathrm {FS}} :[\omega ]^\omega \to [\omega ]^\omega $
be given by
 $$ \begin{align*}\operatorname{\mathrm{FS}}(D) = \left\{ \sum_{n\in \alpha} n : \alpha\in [D]^{<\omega}\setminus\{\emptyset\}\right\},\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{FS}}(D) = \left\{ \sum_{n\in \alpha} n : \alpha\in [D]^{<\omega}\setminus\{\emptyset\}\right\},\end{align*} $$
i.e.,
![]() $\operatorname {\mathrm {FS}}(D)$
is the set of all finite non-empty sums of distinct elements of D.
$\operatorname {\mathrm {FS}}(D)$
is the set of all finite non-empty sums of distinct elements of D.
A set
![]() $D \subseteq \omega $
is sparse [Reference Kojman57, p. 1598] if for each
$D \subseteq \omega $
is sparse [Reference Kojman57, p. 1598] if for each
![]() $n\in \operatorname {\mathrm {FS}}(D)$
there exists the unique set
$n\in \operatorname {\mathrm {FS}}(D)$
there exists the unique set
![]() $\alpha \subseteq D$
such that
$\alpha \subseteq D$
such that
![]() $n = \sum _{i\in \alpha } i$
. This unique set will be denoted by
$n = \sum _{i\in \alpha } i$
. This unique set will be denoted by
![]() $\alpha _D(n)$
. For instance, the set
$\alpha _D(n)$
. For instance, the set
![]() $E = \{2^i:i\in \omega \}$
is sparse, and in the sequel, we write
$E = \{2^i:i\in \omega \}$
is sparse, and in the sequel, we write
![]() $\alpha (n)$
instead of
$\alpha (n)$
instead of
![]() $\alpha _E(n)$
.
$\alpha _E(n)$
.
A sparse set
![]() $D\subseteq \omega $
is very sparse [Reference Filipów, Kowitz, Kwela and Tryba24, p. 894] if
$D\subseteq \omega $
is very sparse [Reference Filipów, Kowitz, Kwela and Tryba24, p. 894] if
![]() $\alpha _D(x)\cap \alpha _D(y)\neq \emptyset $
implies
$\alpha _D(x)\cap \alpha _D(y)\neq \emptyset $
implies
![]() $x+y\notin \operatorname {\mathrm {FS}}(D)$
for every
$x+y\notin \operatorname {\mathrm {FS}}(D)$
for every
![]() $x,y\in \operatorname {\mathrm {FS}}(D)$
.
$x,y\in \operatorname {\mathrm {FS}}(D)$
.
Theorem 3.4 (Hindman).
The function
![]() $\operatorname {\mathrm {FS}}$
is partition regular and the family
$\operatorname {\mathrm {FS}}$
is partition regular and the family
is an ideal on
![]() $\omega $
. The ideal
$\omega $
. The ideal
![]() $\mathcal {H}$
is called the Hindman ideal [Reference Flašková30, p. 109].
$\mathcal {H}$
is called the Hindman ideal [Reference Flašková30, p. 109].
Proof It is easy to see that condition (M) of Definition 3.1 is satisfied for
![]() $\operatorname {\mathrm {FS}}$
. Condition (R) of Definition 3.1 holds for
$\operatorname {\mathrm {FS}}$
. Condition (R) of Definition 3.1 holds for
![]() $\operatorname {\mathrm {FS}}$
as in this case it is the well-known Hindman’s finite sums theorem [Reference Hindman44, Theorem 3.1], [Reference Bergelson4, Theorem 3.5]. To see that condition (S) of Definition 3.1 holds for
$\operatorname {\mathrm {FS}}$
as in this case it is the well-known Hindman’s finite sums theorem [Reference Hindman44, Theorem 3.1], [Reference Bergelson4, Theorem 3.5]. To see that condition (S) of Definition 3.1 holds for
![]() $\operatorname {\mathrm {FS}}$
, it is enough to notice [Reference Kojman57, p. 1598] that every infinite set
$\operatorname {\mathrm {FS}}$
, it is enough to notice [Reference Kojman57, p. 1598] that every infinite set
![]() $F\subseteq \omega $
has an infinite sparse subset
$F\subseteq \omega $
has an infinite sparse subset
![]() $G\subseteq F$
which obviously satisfies condition (S). Finally, Proposition 3.3(1) shows that
$G\subseteq F$
which obviously satisfies condition (S). Finally, Proposition 3.3(1) shows that
![]() $\mathcal {H}$
is an ideal on
$\mathcal {H}$
is an ideal on
![]() $\omega $
.
$\omega $
.
Remark. It is known that sets from
![]() $\mathcal {H}^+$
(that are called IP-sets) are examples of so-called Poincaré sequencesFootnote
1
that play an important role in the study of recurrences in topological dynamics [Reference Furstenberg35, p. 74].
$\mathcal {H}^+$
(that are called IP-sets) are examples of so-called Poincaré sequencesFootnote
1
that play an important role in the study of recurrences in topological dynamics [Reference Furstenberg35, p. 74].
The following lemma will be used in some proofs regarding properties of the function
![]() $\operatorname {\mathrm {FS}}$
.
$\operatorname {\mathrm {FS}}$
.
Lemma 3.5 [Reference Kojman57, Lemma 7].
If D is an infinite sparse set, then there exists a set
![]() $S=\{s_i:i\in \omega \}\subseteq \operatorname {\mathrm {FS}}(D)$
such that for every
$S=\{s_i:i\in \omega \}\subseteq \operatorname {\mathrm {FS}}(D)$
such that for every
![]() $i\in \omega $
we have
$i\in \omega $
we have
![]() $s_i<s_{i+1}$
and
$s_i<s_{i+1}$
and
3.2 Ramsey’s theorem for coloring graphs
Theorem 3.6 (Ramsey).
Let
![]() $r:[\omega ]^\omega \to \left [[\omega ]^2\right ]^\omega $
be given by
$r:[\omega ]^\omega \to \left [[\omega ]^2\right ]^\omega $
be given by
i.e.,
![]() $r(H)$
is the set of all unordered pairs of elements of H. Then r is partition regular and the family
$r(H)$
is the set of all unordered pairs of elements of H. Then r is partition regular and the family
is an ideal on
![]() $[\omega ]^2$
. The ideal
$[\omega ]^2$
. The ideal
![]() $\mathcal {R}$
is called the Ramsey ideal [Reference Hrušák and Meza-Alcántara49, Reference Meza-Alcántara67]. (If we identify a set
$\mathcal {R}$
is called the Ramsey ideal [Reference Hrušák and Meza-Alcántara49, Reference Meza-Alcántara67]. (If we identify a set
![]() $A\subseteq [\omega ]^2$
with a graph
$A\subseteq [\omega ]^2$
with a graph
![]() $G_A=(\omega ,A)$
, the ideal
$G_A=(\omega ,A)$
, the ideal
![]() $\mathcal {R}$
can be seen as an ideal consisting of graphs without infinite complete subgraphs.)
$\mathcal {R}$
can be seen as an ideal consisting of graphs without infinite complete subgraphs.)
Proof It is easy to see that condition (M) of Definition 3.1 is satisfied for r. Condition (R) of Definition 3.1 holds for r as in this case it is the well-known Ramsey’s theorem for coloring graphs [Reference Ramsey71, Theorem A], [Reference Graham, Rothschild and Spencer40, Theorem 1.5]. To see that condition (S) of Definition 3.1 holds for r, it is enough to notice that for every
![]() $\{a,b\}\in [F]^2$
we have
$\{a,b\}\in [F]^2$
we have
![]() $\{a,b\}\notin [F\setminus \{a,b\}]^2$
. Finally, Proposition 3.3(1) shows that
$\{a,b\}\notin [F\setminus \{a,b\}]^2$
. Finally, Proposition 3.3(1) shows that
![]() $\mathcal {R}$
is an ideal on
$\mathcal {R}$
is an ideal on
![]() $[\omega ]^2$
.
$[\omega ]^2$
.
3.3 The positive differences and the associated ideal
Let the function
![]() $\Delta :[\omega ]^\omega \to [\omega ]^\omega $
be given by
$\Delta :[\omega ]^\omega \to [\omega ]^\omega $
be given by
i.e.,
![]() $\Delta (E)$
is the set of all positive differences of distinct elements of E.
$\Delta (E)$
is the set of all positive differences of distinct elements of E.
We say that a set
![]() $E\subseteq \omega $
is
$E\subseteq \omega $
is
![]() $\mathcal {D}$
-sparse [Reference Filipów22, p. 2009] if for every
$\mathcal {D}$
-sparse [Reference Filipów22, p. 2009] if for every
![]() $a\in \Delta (E)$
there are unique elements
$a\in \Delta (E)$
there are unique elements
![]() $b,c\in E$
such that
$b,c\in E$
such that
![]() $a = b-c$
.
$a = b-c$
.
Proposition 3.7. The function
![]() $\Delta $
is partition regular and the family
$\Delta $
is partition regular and the family
is an ideal on
![]() $\omega $
such that
$\omega $
such that
![]() $\mathcal {D}\subsetneq \mathcal {H}$
. It is known that sets from
$\mathcal {D}\subsetneq \mathcal {H}$
. It is known that sets from
![]() $\mathcal {D}^+$
are examples of so-called Poincaré sequences [Reference Furstenberg35, p. 74].
$\mathcal {D}^+$
are examples of so-called Poincaré sequences [Reference Furstenberg35, p. 74].
Proof It is easy to see that condition (M) of Definition 3.1 is satisfied for
![]() $\Delta $
. It is known [Reference Filipów22, Proposition 4.1] that condition (R) of Definition 3.1 holds for
$\Delta $
. It is known [Reference Filipów22, Proposition 4.1] that condition (R) of Definition 3.1 holds for
![]() $\Delta $
. To see that condition (S) of Definition 3.1 holds for
$\Delta $
. To see that condition (S) of Definition 3.1 holds for
![]() $\Delta $
, it is enough to notice [Reference Filipów22, Proposition 4.3(2)] that every infinite set
$\Delta $
, it is enough to notice [Reference Filipów22, Proposition 4.3(2)] that every infinite set
![]() $F\subseteq \omega $
has an infinite
$F\subseteq \omega $
has an infinite
![]() $\mathcal {D}$
-sparse subset
$\mathcal {D}$
-sparse subset
![]() $G\subseteq F$
which obviously satisfies condition (S). Finally, Proposition 3.3(1) shows that
$G\subseteq F$
which obviously satisfies condition (S). Finally, Proposition 3.3(1) shows that
![]() $\mathcal {D}$
is an ideal on
$\mathcal {D}$
is an ideal on
![]() $\omega $
and it is known [Reference Shi73, Proposition 4.2.1], [Reference Filipów22, Proposition 4.1] that
$\omega $
and it is known [Reference Shi73, Proposition 4.2.1], [Reference Filipów22, Proposition 4.1] that
![]() $\mathcal {D}\subsetneq \mathcal {H}$
.
$\mathcal {D}\subsetneq \mathcal {H}$
.
3.4 The summable ideal
Proposition 3.8. The family
 $$ \begin{align*}\mathcal{I}_{1/n}=\left\{A\subseteq\omega: \sum_{n\in A}\frac{1}{n+1}<\infty\right\}\end{align*} $$
$$ \begin{align*}\mathcal{I}_{1/n}=\left\{A\subseteq\omega: \sum_{n\in A}\frac{1}{n+1}<\infty\right\}\end{align*} $$
is an ideal on
![]() $\omega $
. The ideal
$\omega $
. The ideal
![]() $\mathcal {I}_{1/n}$
is called the summable ideal [Reference Mazur66, Definition 1.6], [Reference Mathias64, Example 3], [Reference van Douwen, Monk and Rubin15, p. 238], [Reference Just and Krawczyk53, p. 411]. The function
$\mathcal {I}_{1/n}$
is called the summable ideal [Reference Mazur66, Definition 1.6], [Reference Mathias64, Example 3], [Reference van Douwen, Monk and Rubin15, p. 238], [Reference Just and Krawczyk53, p. 411]. The function
![]() $\rho _{\mathcal {I}_{1/n}}:\mathcal {I}_{1/n}^+\to [\omega ]^\omega $
given by
$\rho _{\mathcal {I}_{1/n}}:\mathcal {I}_{1/n}^+\to [\omega ]^\omega $
given by
![]() $\rho _{\mathcal {I}_{1/n}}(A)=A$
is partition regular and
$\rho _{\mathcal {I}_{1/n}}(A)=A$
is partition regular and
![]() $\mathcal {I}_{1/n} = \mathcal {I}_{\rho _{\mathcal {I}_{1/n}}}$
.
$\mathcal {I}_{1/n} = \mathcal {I}_{\rho _{\mathcal {I}_{1/n}}}$
.
Proof It is easy to show that
![]() $\mathcal {I}_{1/n}$
is an ideal on
$\mathcal {I}_{1/n}$
is an ideal on
![]() $\omega $
, whereas Proposition 3.3(2) gives the required properties of
$\omega $
, whereas Proposition 3.3(2) gives the required properties of
![]() $\rho _{\mathcal {I}_{1/n}}$
.
$\rho _{\mathcal {I}_{1/n}}$
.
3.5 van der Waerden’s arithmetical progressions theorem
Theorem 3.9 (van der Waerden).
A set
![]() $A\subseteq \omega $
is called an AP-set if it contains an arithmetic progressions of arbitrary finite length. The family
$A\subseteq \omega $
is called an AP-set if it contains an arithmetic progressions of arbitrary finite length. The family
is an ideal on
![]() $\omega $
. The ideal
$\omega $
. The ideal
![]() $\mathcal {W}$
is called the van der Waerden ideal [Reference Flašková30, p. 107]. The function
$\mathcal {W}$
is called the van der Waerden ideal [Reference Flašková30, p. 107]. The function
![]() $\rho _{\mathcal {W}}:\mathcal {W}^+\to [\omega ]^\omega $
given by
$\rho _{\mathcal {W}}:\mathcal {W}^+\to [\omega ]^\omega $
given by
![]() $\rho _{\mathcal {W}}(A)=A$
is partition regular and
$\rho _{\mathcal {W}}(A)=A$
is partition regular and
![]() $\mathcal {W} = \mathcal {I}_{\rho _{\mathcal {W}}}$
.
$\mathcal {W} = \mathcal {I}_{\rho _{\mathcal {W}}}$
.
Proof It is easy to see that all conditions from the definition of an ideal but additivity are satisfied, whereas additivity is the well-known van der Waerden’s arithmetical progressions theorem [Reference van der Waerden75], [Reference Graham, Rothschild and Spencer40, Theorem 2.1]. Finally, Proposition 3.3(2) gives the required properties of
![]() $\rho _{\mathcal {W}}$
.
$\rho _{\mathcal {W}}$
.
3.6 Ideals on directed sets
Finally, we introduce a class of partition regular functions which are connected with ideals on directed sets [Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos19, Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20]. Recall that
![]() $(\Lambda ,<)$
is a directed set if the relation
$(\Lambda ,<)$
is a directed set if the relation
![]() $<$
is an upward directed strict partial order on
$<$
is an upward directed strict partial order on
![]() $\Lambda $
.
$\Lambda $
.
Let
![]() $(\Lambda ,<)$
be a directed set such that
$(\Lambda ,<)$
be a directed set such that
![]() $\Lambda $
is infinite countable. A set
$\Lambda $
is infinite countable. A set
![]() $B\subseteq \Lambda $
is cofinal in
$B\subseteq \Lambda $
is cofinal in
![]() $(\Lambda ,<)$
if for every
$(\Lambda ,<)$
if for every
![]() $\lambda \in \Lambda $
there is
$\lambda \in \Lambda $
there is
![]() $b\in B$
with
$b\in B$
with
![]() $\lambda < b$
. A family
$\lambda < b$
. A family
![]() $\mathcal {I}$
of subsets of
$\mathcal {I}$
of subsets of
![]() $\Lambda $
is an ideal on
$\Lambda $
is an ideal on
![]() $(\Lambda ,<)$
[Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, Definition 2.2] if
$(\Lambda ,<)$
[Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, Definition 2.2] if
![]() $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mathcal {I}$
contains all sets which are not cofinal. A family
$\mathcal {I}$
contains all sets which are not cofinal. A family
![]() $\mathcal {B}$
of subsets of
$\mathcal {B}$
of subsets of
![]() $\Lambda $
is a coideal basis on
$\Lambda $
is a coideal basis on
![]() $(\Lambda ,<)$
[Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, Definition 2.4] if
$(\Lambda ,<)$
[Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, Definition 2.4] if
![]() $\mathcal {B}\neq \emptyset $
, all sets in
$\mathcal {B}\neq \emptyset $
, all sets in
![]() $\mathcal {B}$
are cofinal and if
$\mathcal {B}$
are cofinal and if
![]() $C\cup D\in \mathcal {B}$
, then there exists
$C\cup D\in \mathcal {B}$
, then there exists
![]() $B\in \mathcal {B}$
such that
$B\in \mathcal {B}$
such that
![]() $B\subseteq C$
or
$B\subseteq C$
or
![]() $B\subseteq D$
. In particular, for every ideal
$B\subseteq D$
. In particular, for every ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $(\Lambda ,<)$
the family
$(\Lambda ,<)$
the family
![]() $\mathcal {I}^+$
is a coideal basis on
$\mathcal {I}^+$
is a coideal basis on
![]() $(\Lambda ,<)$
. It is known [Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos19, Proposition 2.7] that
$(\Lambda ,<)$
. It is known [Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos19, Proposition 2.7] that
![]() $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
![]() $(\Lambda ,<)$
if and only if there exists a coideal basis
$(\Lambda ,<)$
if and only if there exists a coideal basis
![]() $\mathcal {B}$
on
$\mathcal {B}$
on
![]() $(\Lambda ,<)$
such that
$(\Lambda ,<)$
such that
![]() $\mathcal {I}=\{A\subseteq \Lambda : \forall B\in \mathcal {B}\,(B\not \subseteq A)\}$
.
$\mathcal {I}=\{A\subseteq \Lambda : \forall B\in \mathcal {B}\,(B\not \subseteq A)\}$
.
The following easy proposition reveals basic relationships between partition regular functions and ideals on directed sets.
Proposition 3.10. Let
![]() $(\Lambda ,<)$
be a directed set.
$(\Lambda ,<)$
be a directed set.
-
(1) If
 $\rho :\mathcal {F}\to [\Lambda ]^\omega $
is a partition regular function such that
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
is a partition regular function such that
 $\rho (F)$
is cofinal for every
$\rho (F)$
is cofinal for every
 $F\in \mathcal {F}$
, then
$F\in \mathcal {F}$
, then  $$ \begin{align*}\mathcal{I}_{\rho} = \{A\subseteq \Lambda: \forall F\in \mathcal{F}\, (\rho(F)\not\subseteq A)\}\end{align*} $$
$$ \begin{align*}\mathcal{I}_{\rho} = \{A\subseteq \Lambda: \forall F\in \mathcal{F}\, (\rho(F)\not\subseteq A)\}\end{align*} $$
is an ideal on
 $(\Lambda ,<)$
.
$(\Lambda ,<)$
. -
(2) For a coideal basis
 $\mathcal {B}$
on
$\mathcal {B}$
on
 $(\Lambda ,<) \ (in particular for\ \mathcal {B}=\mathcal {I}^+$
, where
$(\Lambda ,<) \ (in particular for\ \mathcal {B}=\mathcal {I}^+$
, where
 $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
 $(\Lambda ,<))$
, we define
$(\Lambda ,<))$
, we define  $$ \begin{align*} \widehat{\mathcal{B}} = \{B\setminus K:B\in \mathcal{B}, K\in[\Lambda]^{<\omega}\}.\end{align*} $$
$$ \begin{align*} \widehat{\mathcal{B}} = \{B\setminus K:B\in \mathcal{B}, K\in[\Lambda]^{<\omega}\}.\end{align*} $$
Then the function
 $\rho _{\mathcal {B}}:\widehat {\mathcal {B}}\oplus \mathrm {Fin}(\Lambda )^*\to [\Lambda ]^\omega $
given by
$\rho _{\mathcal {B}}:\widehat {\mathcal {B}}\oplus \mathrm {Fin}(\Lambda )^*\to [\Lambda ]^\omega $
given by  $$ \begin{align*}\rho_{\mathcal{B}}((B\setminus K)\sqcup C)=(B\setminus K)\cap\{\lambda\in\Lambda:\forall \lambda'\in (\Lambda\setminus C)\, (\lambda'<\lambda)\}\end{align*} $$
$$ \begin{align*}\rho_{\mathcal{B}}((B\setminus K)\sqcup C)=(B\setminus K)\cap\{\lambda\in\Lambda:\forall \lambda'\in (\Lambda\setminus C)\, (\lambda'<\lambda)\}\end{align*} $$
is a partition regular function such that
 $\rho _{\mathcal {B}}((B\setminus K)\sqcup C)$
is cofinal for every
$\rho _{\mathcal {B}}((B\setminus K)\sqcup C)$
is cofinal for every
 $(B\setminus K)\sqcup C\in \widehat {\mathcal {B}}\oplus \mathrm {Fin}(\Lambda )^*$
and
$(B\setminus K)\sqcup C\in \widehat {\mathcal {B}}\oplus \mathrm {Fin}(\Lambda )^*$
and
 $\mathcal {I}_{\rho _{\mathcal {B}}} = \{A\subseteq \Lambda : \forall B\in \mathcal {B}\,(B\not \subseteq A)\}.$
$\mathcal {I}_{\rho _{\mathcal {B}}} = \{A\subseteq \Lambda : \forall B\in \mathcal {B}\,(B\not \subseteq A)\}.$
4 Restrictions and small accretions
4.1 Restrictions of partition regular operations
For
![]() $B\notin \mathcal {I}_\rho $
, we define a family
$B\notin \mathcal {I}_\rho $
, we define a family
![]() $\mathcal {F}\restriction B = \{E\in \mathcal {F}: \rho (E)\subseteq B\}$
and a function
$\mathcal {F}\restriction B = \{E\in \mathcal {F}: \rho (E)\subseteq B\}$
and a function
![]() $\rho \restriction B :\mathcal {F}\restriction B\to [B]^\omega $
by
$\rho \restriction B :\mathcal {F}\restriction B\to [B]^\omega $
by
![]() $(\rho \restriction B)(E) = \rho (E)$
(i.e.,
$(\rho \restriction B)(E) = \rho (E)$
(i.e.,
![]() $\rho \restriction B = \rho \restriction (\mathcal {F}\restriction B)$
). The following easy proposition reveals relationships between restriction of a function
$\rho \restriction B = \rho \restriction (\mathcal {F}\restriction B)$
). The following easy proposition reveals relationships between restriction of a function
![]() $\rho $
and restriction of an ideal
$\rho $
and restriction of an ideal
![]() $\mathcal {I}_\rho $
.
$\mathcal {I}_\rho $
.
Proposition 4.1. If
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
is partition regular and
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
is partition regular and
![]() $B\notin \mathcal {I}_\rho $
, then
$B\notin \mathcal {I}_\rho $
, then
![]() $\rho \restriction B$
is partition regular and
$\rho \restriction B$
is partition regular and
![]() $\mathcal {I}_{\rho \restriction B} = \mathcal {I}_{\rho }\restriction B$
.
$\mathcal {I}_{\rho \restriction B} = \mathcal {I}_{\rho }\restriction B$
.
4.2 Small accretions of partition regular operations
We will need the following notion in the last part of the paper for characterization that shows when there exists a space of one considered type that is not of the other type (Theorem 16.1).
Definition 4.2. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
(with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
(with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
) be a partition regular function.
$\mathcal {F}\subseteq [\Omega ]^\omega $
) be a partition regular function.
-
(1) A set
 $F\in \mathcal {F}$
has small accretions if
$F\in \mathcal {F}$
has small accretions if
 $\rho (F)\setminus \rho (F\setminus K)\in \mathcal {I}_\rho $
for every finite set K.
$\rho (F)\setminus \rho (F\setminus K)\in \mathcal {I}_\rho $
for every finite set K. -
(2)
 $\rho $
has small accretions if for every
$\rho $
has small accretions if for every
 $E\in \mathcal {F}$
there is
$E\in \mathcal {F}$
there is
 $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
 $F\subseteq E$
and F has small accretions.
$F\subseteq E$
and F has small accretions.
Proposition 4.3. If
![]() $\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}\cup \{\rho _{\mathcal {I}}:\mathcal {I}\text { is an ideal}\}$
, then
$\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}\cup \{\rho _{\mathcal {I}}:\mathcal {I}\text { is an ideal}\}$
, then
![]() $\rho $
has small accretions.
$\rho $
has small accretions.
Proof for
 $\rho = \rho _{\mathcal {I}}$
where
$\rho = \rho _{\mathcal {I}}$
where
 $\mathcal {I}$
is an ideal
$\mathcal {I}$
is an ideal
The function
![]() $\rho $
has small accretions, since for every
$\rho $
has small accretions, since for every
![]() $A\in \mathcal {I}^+$
and finite
$A\in \mathcal {I}^+$
and finite
![]() $K\subseteq \Lambda $
we have
$K\subseteq \Lambda $
we have
![]() $\rho _{\mathcal {I}}(A)\setminus \rho _{\mathcal {I}}(A\setminus K)=A\setminus (A\setminus K) \subseteq K \in \mathcal {I}$
.
$\rho _{\mathcal {I}}(A)\setminus \rho _{\mathcal {I}}(A\setminus K)=A\setminus (A\setminus K) \subseteq K \in \mathcal {I}$
.
Proof for
 $\rho = \operatorname {\mathrm {FS}}$
$\rho = \operatorname {\mathrm {FS}}$
It is known [Reference Filipów, Kowitz, Kwela and Tryba24, Lemma 2.2] that every infinite set
![]() $E\subseteq \omega $
has an infinite very sparse subset
$E\subseteq \omega $
has an infinite very sparse subset
![]() $F\subseteq E$
, so if we show that every very sparse set has small accretions, the proof will be finished.
$F\subseteq E$
, so if we show that every very sparse set has small accretions, the proof will be finished.
Let
![]() $F\subseteq \omega $
be an infinite very sparse set and
$F\subseteq \omega $
be an infinite very sparse set and
![]() $K\subseteq \omega $
be a finite set. Assume towards contradiction that
$K\subseteq \omega $
be a finite set. Assume towards contradiction that
![]() $\operatorname {\mathrm {FS}}(D)\subseteq \operatorname {\mathrm {FS}}(F)\setminus \operatorname {\mathrm {FS}}(F\setminus K)=\{x\in \operatorname {\mathrm {FS}}(F):\ \alpha _{F}(x)\cap K\neq \emptyset \}$
for some
$\operatorname {\mathrm {FS}}(D)\subseteq \operatorname {\mathrm {FS}}(F)\setminus \operatorname {\mathrm {FS}}(F\setminus K)=\{x\in \operatorname {\mathrm {FS}}(F):\ \alpha _{F}(x)\cap K\neq \emptyset \}$
for some
![]() $D\in [\omega ]^\omega $
. Since K is finite, we can find
$D\in [\omega ]^\omega $
. Since K is finite, we can find
![]() $x,y\in D$
,
$x,y\in D$
,
![]() $x\neq y$
, such that
$x\neq y$
, such that
![]() $\alpha _{F}(x)\cap \alpha _{F}(y)\neq \emptyset $
. But then
$\alpha _{F}(x)\cap \alpha _{F}(y)\neq \emptyset $
. But then
![]() $x+y\in \operatorname {\mathrm {FS}}(D )\setminus \operatorname {\mathrm {FS}}(F)$
, a contradiction.
$x+y\in \operatorname {\mathrm {FS}}(D )\setminus \operatorname {\mathrm {FS}}(F)$
, a contradiction.
Proof for
 $\rho = r$
$\rho = r$
The function r has small accretions, since for every
![]() $A\in [\omega ]^\omega $
and finite
$A\in [\omega ]^\omega $
and finite
![]() $K\subseteq \omega $
we have
$K\subseteq \omega $
we have
![]() $r(A)\setminus r(A\setminus K) = [A]^2\setminus [A\setminus K]^2=\{\{i,j\}:\ i\in A\cap K,j\in A\}\in \mathcal {R}$
.
$r(A)\setminus r(A\setminus K) = [A]^2\setminus [A\setminus K]^2=\{\{i,j\}:\ i\in A\cap K,j\in A\}\in \mathcal {R}$
.
Proof for
 $\rho = \Delta $
$\rho = \Delta $
It is known [Reference Filipów22, Proposition 4.3(2)] that every infinite set
![]() $E\subseteq \omega $
has an infinite
$E\subseteq \omega $
has an infinite
![]() $\mathcal {D}$
-sparse subset
$\mathcal {D}$
-sparse subset
![]() $F\subseteq E$
, so if we show that every
$F\subseteq E$
, so if we show that every
![]() $\mathcal {D}$
-sparse set has small accretions, the proof will be finished.
$\mathcal {D}$
-sparse set has small accretions, the proof will be finished.
Let
![]() $F\subseteq \omega $
be an infinite
$F\subseteq \omega $
be an infinite
![]() $\mathcal {D}$
-sparse set and
$\mathcal {D}$
-sparse set and
![]() $K\subseteq \omega $
be a finite set. It is known [Reference Filipów22, Proposition 4.3(1)] that then
$K\subseteq \omega $
be a finite set. It is known [Reference Filipów22, Proposition 4.3(1)] that then
![]() $F-n\in \mathcal {D}$
for every
$F-n\in \mathcal {D}$
for every
![]() $n<\min F$
, and consequently,
$n<\min F$
, and consequently,
![]() $\{a-b:a\in F\setminus K,b\in F\cap K\}\cap \omega \in \mathcal {D}$
. Thus,
$\{a-b:a\in F\setminus K,b\in F\cap K\}\cap \omega \in \mathcal {D}$
. Thus,
![]() $\Delta (F)\setminus \Delta (F\setminus K)= \{a-b:a\in F\cap K, b\in F, a>b\}\cup (\{a-b:a\in F\setminus K,b\in F\cap K\}\cap \omega )\in \mathcal {D}$
as a finite union of sets from
$\Delta (F)\setminus \Delta (F\setminus K)= \{a-b:a\in F\cap K, b\in F, a>b\}\cup (\{a-b:a\in F\setminus K,b\in F\cap K\}\cap \omega )\in \mathcal {D}$
as a finite union of sets from
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
5 Topological complexity of partition regular operations
If
![]() $\Lambda $
is a countable infinite set, then we consider
$\Lambda $
is a countable infinite set, then we consider
![]() $2^\Lambda =\{0,1\}^\Lambda $
as a product (with the product topology) of countably many copies of a discrete topological space
$2^\Lambda =\{0,1\}^\Lambda $
as a product (with the product topology) of countably many copies of a discrete topological space
![]() $\{0,1\}$
. Since
$\{0,1\}$
. Since
![]() $2^\Lambda $
is a Polish space [Reference Kechris56, p. 13] and
$2^\Lambda $
is a Polish space [Reference Kechris56, p. 13] and
![]() $[\Lambda ]^\omega $
is a
$[\Lambda ]^\omega $
is a
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $2^\Lambda $
, we obtain that
$2^\Lambda $
, we obtain that
![]() $[\Lambda ]^\omega $
is a Polish space as well [Reference Kechris56, Theorem 3.11]. In particular, if
$[\Lambda ]^\omega $
is a Polish space as well [Reference Kechris56, Theorem 3.11]. In particular, if
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Omega $
are countable infinite and
$\Omega $
are countable infinite and
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
, we say that a partition regular function
$\mathcal {F}\subseteq [\Omega ]^\omega $
, we say that a partition regular function
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
is continuous if
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
is continuous if
![]() $\rho $
is a continuous function from a topological subspace
$\rho $
is a continuous function from a topological subspace
![]() $\mathcal {F}$
into a topological space
$\mathcal {F}$
into a topological space
![]() $[\Lambda ]^\omega $
.
$[\Lambda ]^\omega $
.
By identifying subsets of
![]() $\Lambda $
with their characteristic functions, we equip
$\Lambda $
with their characteristic functions, we equip
![]() $\mathcal {P}(\Lambda )$
with the topology of the space
$\mathcal {P}(\Lambda )$
with the topology of the space
![]() $2^\Lambda $
and therefore we can assign topological notions to ideals on
$2^\Lambda $
and therefore we can assign topological notions to ideals on
![]() $\Lambda $
. In particular, an ideal
$\Lambda $
. In particular, an ideal
![]() $\mathcal {I}$
is Borel (analytic, coanalytic, resp.) if
$\mathcal {I}$
is Borel (analytic, coanalytic, resp.) if
![]() $\mathcal {I}$
is a Borel (analytic, coanalytic, resp.) subset of
$\mathcal {I}$
is a Borel (analytic, coanalytic, resp.) subset of
![]() $2^\Lambda $
. Recall, a set
$2^\Lambda $
. Recall, a set
![]() $A\subseteq X$
is analytic if there is a Polish space Y and a Borel set
$A\subseteq X$
is analytic if there is a Polish space Y and a Borel set
![]() $B\subseteq X\times Y$
such that A is a projection of B onto the first coordinate [Reference Kechris56, Exercise 14.3], and a set
$B\subseteq X\times Y$
such that A is a projection of B onto the first coordinate [Reference Kechris56, Exercise 14.3], and a set
![]() $C\subseteq X$
is coanalytic if
$C\subseteq X$
is coanalytic if
![]() $X\setminus C$
is an analytic set.
$X\setminus C$
is an analytic set.
Proposition 5.1. If a partition regular function
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega (with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
is continuous and
$\rho :\mathcal {F}\to [\Lambda ]^\omega (with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
is continuous and
![]() $\mathcal {F}$
is a closed subset of
$\mathcal {F}$
is a closed subset of
![]() $[\Omega ]^\omega $
, then the ideal
$[\Omega ]^\omega $
, then the ideal
![]() $\mathcal {I}_\rho $
is coanalytic.
$\mathcal {I}_\rho $
is coanalytic.
Proof We will show that
![]() $\mathcal {I}_\rho ^+ = \mathcal {P}(\Lambda )\setminus \mathcal {I}_\rho $
is an analytic set. Let
$\mathcal {I}_\rho ^+ = \mathcal {P}(\Lambda )\setminus \mathcal {I}_\rho $
is an analytic set. Let
![]() $B = \{(A,F)\in \mathcal {P}(\Lambda )\times \mathcal {F}: \rho (F)\subseteq A\}.$
Since
$B = \{(A,F)\in \mathcal {P}(\Lambda )\times \mathcal {F}: \rho (F)\subseteq A\}.$
Since
![]() $B\subseteq \mathcal {P}(\Lambda )\times [\Omega ]^\omega $
and
$B\subseteq \mathcal {P}(\Lambda )\times [\Omega ]^\omega $
and
![]() $\mathcal {I}_\rho ^+$
is a projection of B onto the first coordinate, we only need to show that B is a Borel set. It suffices to show that
$\mathcal {I}_\rho ^+$
is a projection of B onto the first coordinate, we only need to show that B is a Borel set. It suffices to show that
![]() $C = (\mathcal {P}(\Lambda )\times [\Omega ]^\omega ) \setminus B$
is an open set, since
$C = (\mathcal {P}(\Lambda )\times [\Omega ]^\omega ) \setminus B$
is an open set, since
Let
![]() $(A,F)\in C$
. We have two cases: (1)
$(A,F)\in C$
. We have two cases: (1)
![]() $F\notin \mathcal {F}$
or (2)
$F\notin \mathcal {F}$
or (2)
![]() $F\in \mathcal {F}$
.
$F\in \mathcal {F}$
.
Case (1). Since
![]() $\mathcal {F}$
is closed, there is an open set
$\mathcal {F}$
is closed, there is an open set
![]() $U\subseteq [\Omega ]^\omega $
with
$U\subseteq [\Omega ]^\omega $
with
![]() $F\in U$
and
$F\in U$
and
![]() $U\cap \mathcal {F}=\emptyset $
. Then
$U\cap \mathcal {F}=\emptyset $
. Then
![]() $W = \mathcal {P}(\Lambda ) \times U$
is open and
$W = \mathcal {P}(\Lambda ) \times U$
is open and
![]() $(A,F)\in W \subseteq C$
.
$(A,F)\in W \subseteq C$
.
Case (2). Since
![]() $\rho (F)\not \subseteq A$
, there is
$\rho (F)\not \subseteq A$
, there is
![]() $a\in \rho (F)\setminus A$
. Let
$a\in \rho (F)\setminus A$
. Let
![]() $V=\{D\in \mathcal {P}(\Lambda ): a\in D\}$
. Then V is an open and closed set,
$V=\{D\in \mathcal {P}(\Lambda ): a\in D\}$
. Then V is an open and closed set,
![]() $A\notin V$
, and
$A\notin V$
, and
![]() $\rho (F)\in V$
. Since
$\rho (F)\in V$
. Since
![]() $\rho $
is continuous at the point F, there is an open set
$\rho $
is continuous at the point F, there is an open set
![]() $U\subseteq [\Omega ]^\omega $
such that
$U\subseteq [\Omega ]^\omega $
such that
![]() $F\in U$
and
$F\in U$
and
![]() $\rho [U]\subseteq V $
. Then
$\rho [U]\subseteq V $
. Then
![]() $W = (\mathcal {P}(\Lambda )\setminus V)\times U$
is open and
$W = (\mathcal {P}(\Lambda )\setminus V)\times U$
is open and
![]() $(A,F)\in W \subseteq C$
.
$(A,F)\in W \subseteq C$
.
Proposition 5.2.
-
(1) The ideals
 $\mathcal {I}_{1/n}$
and
$\mathcal {I}_{1/n}$
and
 $\mathcal {W}$
are
$\mathcal {W}$
are
 $F_\sigma $
.
$F_\sigma $
. -
(2) The functions
 $\operatorname {\mathrm {FS}}$
and r are continuous.
$\operatorname {\mathrm {FS}}$
and r are continuous. -
(3) The function
 $\Delta $
is not continuous. In fact, the function
$\Delta $
is not continuous. In fact, the function
 $\Delta $
is discontinuous at every point A such that
$\Delta $
is discontinuous at every point A such that
 $\Delta (A)\neq \omega $
.
$\Delta (A)\neq \omega $
. -
(4) If
 $\mathcal {L} = \{A\in [\omega ]^{\omega }: \forall n\in \omega \,(e_A(n+1)-e_A(n)>e_A(n))\}$
where
$\mathcal {L} = \{A\in [\omega ]^{\omega }: \forall n\in \omega \,(e_A(n+1)-e_A(n)>e_A(n))\}$
where
 $e_A : \omega \to A$
is the increasing enumeration of a set
$e_A : \omega \to A$
is the increasing enumeration of a set
 $A\subseteq \omega $
, then
$A\subseteq \omega $
, then
 $\mathcal {I}_{\Delta }=\mathcal {I}_{\Delta \restriction \mathcal {L}}$
,
$\mathcal {I}_{\Delta }=\mathcal {I}_{\Delta \restriction \mathcal {L}}$
,
 $\mathcal {L}$
is closed and
$\mathcal {L}$
is closed and
 $\Delta \restriction \mathcal {L}$
is continuous.
$\Delta \restriction \mathcal {L}$
is continuous. -
(5) The ideals
 $\mathcal {H}$
,
$\mathcal {H}$
,
 $\mathcal {R}$
, and
$\mathcal {R}$
, and
 $\mathcal {D}$
are coanalytic.
$\mathcal {D}$
are coanalytic.
Proof (1) It is known that
![]() $\mathcal {I}_{1/n}$
and
$\mathcal {I}_{1/n}$
and
![]() $\mathcal {W}$
are
$\mathcal {W}$
are
![]() $F_\sigma $
[Reference Mazur66, Example 1.5], [Reference Filipów, Kwela and Tryba25, Example 4.12].
$F_\sigma $
[Reference Mazur66, Example 1.5], [Reference Filipów, Kwela and Tryba25, Example 4.12].
(2) Case of
![]() $\operatorname {\mathrm {FS}}$
. Let
$\operatorname {\mathrm {FS}}$
. Let
![]() $D\in [\omega ]^\omega $
and let U be an open basic neighborhood of
$D\in [\omega ]^\omega $
and let U be an open basic neighborhood of
![]() $\operatorname {\mathrm {FS}}(D)$
. Then there exists a finite set
$\operatorname {\mathrm {FS}}(D)$
. Then there exists a finite set
![]() $G\subseteq \omega $
such that
$G\subseteq \omega $
such that
![]() $U = \{B\in [\omega ]^\omega : B\cap \{0,1,\dots ,\max G\} = G\}$
. Let
$U = \{B\in [\omega ]^\omega : B\cap \{0,1,\dots ,\max G\} = G\}$
. Let
![]() $F = D \cap \{0,1,\dots ,\max G\}$
. Then
$F = D \cap \{0,1,\dots ,\max G\}$
. Then
![]() $V = \{A\in [\omega ]^\omega : A\cap \{0,1,\dots ,\max G\}=F\}$
is an open neighborhood of D and
$V = \{A\in [\omega ]^\omega : A\cap \{0,1,\dots ,\max G\}=F\}$
is an open neighborhood of D and
![]() $\operatorname {\mathrm {FS}}[V]\subseteq U$
.
$\operatorname {\mathrm {FS}}[V]\subseteq U$
.
Case of r. Let
![]() $D\in [\omega ]^\omega $
and let U be an open basic neighborhood of
$D\in [\omega ]^\omega $
and let U be an open basic neighborhood of
![]() $[D]^2$
. There exists a finite set
$[D]^2$
. There exists a finite set
![]() $G\subseteq [\omega ]^2$
such that
$G\subseteq [\omega ]^2$
such that
![]() $U = \{B\in \left [[\omega ]^2\right ]^\omega : B\cap [N]^2 = G\}$
, where
$U = \{B\in \left [[\omega ]^2\right ]^\omega : B\cap [N]^2 = G\}$
, where
![]() $N=\max \{\max \{p,q\}:\{p,q\}\in G\}$
. Then
$N=\max \{\max \{p,q\}:\{p,q\}\in G\}$
. Then
![]() $V = \{A\in [\omega ]^\omega : A\cap N=D\}$
is an open neighborhood of D and
$V = \{A\in [\omega ]^\omega : A\cap N=D\}$
is an open neighborhood of D and
![]() $r[V]\subseteq U$
.
$r[V]\subseteq U$
.
(3) Let
![]() $A\subseteq \omega $
be such that
$A\subseteq \omega $
be such that
![]() $b\notin \Delta (A)$
for some
$b\notin \Delta (A)$
for some
![]() $b\in \omega $
. Then
$b\in \omega $
. Then
![]() $U=\{B\subseteq \omega : b\notin B\}$
is an open neighborhood of
$U=\{B\subseteq \omega : b\notin B\}$
is an open neighborhood of
![]() $\Delta (A)$
. Let V be an open basic neighborhood of A. There is
$\Delta (A)$
. Let V be an open basic neighborhood of A. There is
![]() $N\in \omega $
such that
$N\in \omega $
such that
![]() $V=\{C\subseteq \omega : C\cap N=A\cap N\}$
. Then
$V=\{C\subseteq \omega : C\cap N=A\cap N\}$
. Then
![]() $C=(A\cap N)\cup (\omega \setminus N)\in V$
and
$C=(A\cap N)\cup (\omega \setminus N)\in V$
and
![]() $\Delta (C)=\omega \notin U$
. Hence the function
$\Delta (C)=\omega \notin U$
. Hence the function
![]() $\Delta $
is discontinuous at the point A.
$\Delta $
is discontinuous at the point A.
(4) It is obvious that
![]() $\mathcal {I}_{\Delta }=\mathcal {I}_{\Delta \restriction \mathcal {L}}$
. To show that
$\mathcal {I}_{\Delta }=\mathcal {I}_{\Delta \restriction \mathcal {L}}$
. To show that
![]() $\mathcal {L}$
is closed, notice that
$\mathcal {L}$
is closed, notice that
![]() $[\omega ]^\omega \setminus \mathcal {L}$
is open as for each
$[\omega ]^\omega \setminus \mathcal {L}$
is open as for each
![]() $A\in [\omega ]^\omega \setminus \mathcal {L}$
there is
$A\in [\omega ]^\omega \setminus \mathcal {L}$
there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $e_A(n+1)-e_A(n)\leq e_A(n)$
and
$e_A(n+1)-e_A(n)\leq e_A(n)$
and
![]() $U=\{C\in [\omega ]^\omega :C\cap (e_A(n+1)+1)=A\cap (e_A(n+1)+1)\}$
is an open neighborhood of A disjoint with
$U=\{C\in [\omega ]^\omega :C\cap (e_A(n+1)+1)=A\cap (e_A(n+1)+1)\}$
is an open neighborhood of A disjoint with
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Below we show that
![]() $\Delta \restriction \mathcal {L}$
is continuous. Let
$\Delta \restriction \mathcal {L}$
is continuous. Let
![]() $A\in \mathcal {L}$
. We are going to show that the function
$A\in \mathcal {L}$
. We are going to show that the function
![]() $\Delta \restriction \mathcal {L}$
is continuous at the point A. Let U be a neighborhood of
$\Delta \restriction \mathcal {L}$
is continuous at the point A. Let U be a neighborhood of
![]() $\Delta (A)$
. Without loss of generality, we can assume that there is
$\Delta (A)$
. Without loss of generality, we can assume that there is
![]() $N\in \omega $
such that
$N\in \omega $
such that
![]() $U=\{B\in [\omega ]^{\omega }: B\cap N=\Delta (A)\cap N\}$
. There exists
$U=\{B\in [\omega ]^{\omega }: B\cap N=\Delta (A)\cap N\}$
. There exists
![]() $M\in \omega $
such that
$M\in \omega $
such that
![]() $e_A(M)>N$
. Then
$e_A(M)>N$
. Then
![]() $V=\{C\in [\omega ]^{\omega }: C\cap (e_A(M)+1)=A\cap (e_A(M)+1)\}$
is an open neighborhood of A. Once we show that
$V=\{C\in [\omega ]^{\omega }: C\cap (e_A(M)+1)=A\cap (e_A(M)+1)\}$
is an open neighborhood of A. Once we show that
![]() $\Delta [V\cap \mathcal {L}]\subseteq U$
, the proof will be finished. Let
$\Delta [V\cap \mathcal {L}]\subseteq U$
, the proof will be finished. Let
![]() $C\in V\cap \mathcal {L}$
. Since
$C\in V\cap \mathcal {L}$
. Since
![]() $A,C\in \mathcal {L}$
, we obtain
$A,C\in \mathcal {L}$
, we obtain
![]() $\Delta (C)\cap (e_A(M)+1)=\Delta (C\cap (e_A(M)+1))=\Delta (A\cap (e_A(M)+1))= \Delta (A)\cap (e_A(M)+1)$
. But
$\Delta (C)\cap (e_A(M)+1)=\Delta (C\cap (e_A(M)+1))=\Delta (A\cap (e_A(M)+1))= \Delta (A)\cap (e_A(M)+1)$
. But
![]() $N<e_A(M)$
, hence
$N<e_A(M)$
, hence
![]() $\Delta (C)\cap N=\Delta (A)\cap N$
and consequently
$\Delta (C)\cap N=\Delta (A)\cap N$
and consequently
![]() $\Delta (C)\in U$
.
$\Delta (C)\in U$
.
(5) It is known that
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {R}$
are coanalytic [Reference Filipów, Kwela and Tryba25, Example 4.11], [Reference Meza-Alcántara67, Lemma 1.6.24] (but it also follows from item (2) and Proposition 5.1). It follows from item (4) and Proposition 5.1 that
$\mathcal {R}$
are coanalytic [Reference Filipów, Kwela and Tryba25, Example 4.11], [Reference Meza-Alcántara67, Lemma 1.6.24] (but it also follows from item (2) and Proposition 5.1). It follows from item (4) and Proposition 5.1 that
![]() $\mathcal {D}$
is coanalytic.
$\mathcal {D}$
is coanalytic.
6 P-like properties
6.1 P-like properties of ideals
For
![]() $A,B\subseteq \Lambda $
, we write
$A,B\subseteq \Lambda $
, we write
![]() $A\subseteq ^* B$
if there is a finite set
$A\subseteq ^* B$
if there is a finite set
![]() $K\subseteq \Lambda $
with
$K\subseteq \Lambda $
with
![]() $A\setminus K \subseteq B$
.
$A\setminus K \subseteq B$
.
Let us recall definitions of P-like properties of ideals that are considered in the literature [Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui50, p. 2030]. An ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\Lambda $
is:
$\Lambda $
is:
-
•
 $P^-(\Lambda )$
if for every
$P^-(\Lambda )$
if for every
 $\subseteq $
-decreasing sequence
$\subseteq $
-decreasing sequence
 $A_n\in \mathcal {I}^+$
with
$A_n\in \mathcal {I}^+$
with
 $A_0=\Lambda $
and
$A_0=\Lambda $
and
 $A_n\setminus A_{n+1}\in \mathcal {I}$
for each
$A_n\setminus A_{n+1}\in \mathcal {I}$
for each
 $n\in \omega $
there exists
$n\in \omega $
there exists
 $B\in \mathcal {I}^+$
such that
$B\in \mathcal {I}^+$
such that
 $B \subseteq ^* A_n$
for each
$B \subseteq ^* A_n$
for each
 $n\in \omega $
;
$n\in \omega $
; -
•
 $P^-$
if for every
$P^-$
if for every
 $\subseteq $
-decreasing sequence
$\subseteq $
-decreasing sequence
 $A_n\in \mathcal {I}^+$
with
$A_n\in \mathcal {I}^+$
with
 $A_n\setminus A_{n+1}\in \mathcal {I}$
for each
$A_n\setminus A_{n+1}\in \mathcal {I}$
for each
 $n\in \omega $
there exists
$n\in \omega $
there exists
 $B\in \mathcal {I}^+$
such that
$B\in \mathcal {I}^+$
such that
 $B \subseteq ^* A_n$
for each
$B \subseteq ^* A_n$
for each
 $n\in \omega $
;
$n\in \omega $
; -
•
 $P^+$
if for every
$P^+$
if for every
 $\subseteq $
-decreasing sequence
$\subseteq $
-decreasing sequence
 $A_n\in \mathcal {I}^+$
there exists
$A_n\in \mathcal {I}^+$
there exists
 $B\in \mathcal {I}^+$
such that
$B\in \mathcal {I}^+$
such that
 $B \subseteq ^* A_n$
for each
$B \subseteq ^* A_n$
for each
 $n\in \omega $
.
$n\in \omega $
.
The following proposition reveals some implications between P-like properties and provides equivalent forms of the properties
![]() $P^-(\Lambda )$
and
$P^-(\Lambda )$
and
![]() $P^-$
that were considered in the literature [Reference Kwela62] under the names weak P-ideals and hereditary weak P-ideals, where the author used them for in-depth research on
$P^-$
that were considered in the literature [Reference Kwela62] under the names weak P-ideals and hereditary weak P-ideals, where the author used them for in-depth research on
![]() $\mathcal {I}$
-spaces.
$\mathcal {I}$
-spaces.
Proposition 6.1. Let
![]() $\mathcal {I}$
be an ideal on an infinite countable set
$\mathcal {I}$
be an ideal on an infinite countable set
![]() $\Lambda $
.
$\Lambda $
.
-
(1)
 $\mathcal {I}\text { is }P^+\implies \mathcal {I}\text { is }P^-\implies \mathcal {I}\text { is }P^-(\Lambda )$
.
$\mathcal {I}\text { is }P^+\implies \mathcal {I}\text { is }P^-\implies \mathcal {I}\text { is }P^-(\Lambda )$
. -
(2) The implications from item (1) cannot be reversed.
-
(3) The following conditions are equivalent.
-
(a)
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^-(\Lambda ) (\mathcal {I}$
is
$P^-(\Lambda ) (\mathcal {I}$
is
 $P^-, resp.)$
.
$P^-, resp.)$
. -
(b) For every partition
 $\mathcal {A}$
of
$\mathcal {A}$
of
 $\Lambda $
(of any set
$\Lambda $
(of any set
 $C\in \mathcal {I}^+$
, resp.
$C\in \mathcal {I}^+$
, resp.
 $)$
into sets from
$)$
into sets from
 $\mathcal {I}$
there exists
$\mathcal {I}$
there exists
 $B\in \mathcal {I}^+$
such that
$B\in \mathcal {I}^+$
such that
 $B\subseteq \Lambda (B\subseteq C, resp.)$
and
$B\subseteq \Lambda (B\subseteq C, resp.)$
and
 $B\cap A$
is finite for each
$B\cap A$
is finite for each
 $A\in \mathcal {A}$
.
$A\in \mathcal {A}$
. -
(c)
 $\mathcal {I}$
is a weak P-ideal
$\mathcal {I}$
is a weak P-ideal
 $($
hereditary weak P-ideal, resp.
$($
hereditary weak P-ideal, resp.
 $)$
i.e., for every countable family
$)$
i.e., for every countable family
 $\mathcal {A}\subseteq \mathcal {I}$
of subsets of
$\mathcal {A}\subseteq \mathcal {I}$
of subsets of
 $\Lambda\ (subsets\ of any\ C\in \mathcal {I}^+, resp.)$
there exists
$\Lambda\ (subsets\ of any\ C\in \mathcal {I}^+, resp.)$
there exists
 $B\in \mathcal {I}^+$
such that
$B\in \mathcal {I}^+$
such that
 $B\subseteq \Lambda (B\subseteq C,\ resp.)$
and
$B\subseteq \Lambda (B\subseteq C,\ resp.)$
and
 $B\cap A$
is finite for each
$B\cap A$
is finite for each
 $A\in \mathcal {A}$
.
$A\in \mathcal {A}$
.
-
Proof (1) Straightforward.
(2) The ideal
![]() $\mathrm {Fin}\oplus \mathrm {Fin}^2 $
is
$\mathrm {Fin}\oplus \mathrm {Fin}^2 $
is
![]() $P^-(\omega \sqcup \omega ^2)$
(the set
$P^-(\omega \sqcup \omega ^2)$
(the set
![]() $B=\omega \sqcup \emptyset $
works for every sequence) but not
$B=\omega \sqcup \emptyset $
works for every sequence) but not
![]() $P^-$
(as witnessed by the sets
$P^-$
(as witnessed by the sets
![]() $A_n=\emptyset \sqcup ((\omega \setminus n)\times \omega )$
).
$A_n=\emptyset \sqcup ((\omega \setminus n)\times \omega )$
).
Below we show an example of a
![]() $P^-$
ideal that is not
$P^-$
ideal that is not
![]() $P^+$
. For a set
$P^+$
. For a set
![]() $A\subseteq \omega $
, we define the asymptotic density of A by
$A\subseteq \omega $
, we define the asymptotic density of A by
![]() $\overline {d}(A)=\limsup _{n\to \infty } |A\cap n|/n$
. Then the ideal
$\overline {d}(A)=\limsup _{n\to \infty } |A\cap n|/n$
. Then the ideal
![]() $\mathcal {I}_d=\{A\subseteq \omega :\overline {d}(A)=0\}$
is
$\mathcal {I}_d=\{A\subseteq \omega :\overline {d}(A)=0\}$
is
![]() $P^-$
(see, e.g., [Reference Buck9, Corollary 1.1]). Now we show that
$P^-$
(see, e.g., [Reference Buck9, Corollary 1.1]). Now we show that
![]() $\mathcal {I}_d$
is not
$\mathcal {I}_d$
is not
![]() $P^+$
. Take a decreasing sequence
$P^+$
. Take a decreasing sequence
![]() $B_n\subseteq \omega $
such that
$B_n\subseteq \omega $
such that
![]() $0<\overline {d}(B_n)< 1/n$
for each
$0<\overline {d}(B_n)< 1/n$
for each
![]() $n\in \omega $
. If
$n\in \omega $
. If
![]() $C\subseteq \omega $
is such that
$C\subseteq \omega $
is such that
![]() $C\subseteq ^* B_n$
for all
$C\subseteq ^* B_n$
for all
![]() $n\in \omega $
, then
$n\in \omega $
, then
![]() $\overline {d}(C)\leq \overline {d}(B_n)\to 0$
as
$\overline {d}(C)\leq \overline {d}(B_n)\to 0$
as
![]() $n\to \infty $
. Hence
$n\to \infty $
. Hence
![]() $C\in \mathcal {I}_d$
. This shows that
$C\in \mathcal {I}_d$
. This shows that
![]() $\mathcal {I}_d$
is not
$\mathcal {I}_d$
is not
![]() $P^+$
.
$P^+$
.
(3) Straightforward.
There are known relationships between topological complexity and P-like properties.
Theorem 6.2 [Reference Kwela62, Proposition 4.9], [Reference Just and Krawczyk53, Lemma 1.2], [Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui50, Theorem 3.7].
-
(1) Each
 $G_{\delta \sigma \delta }\ (in particular, F_{\sigma \delta })$
ideal is
$G_{\delta \sigma \delta }\ (in particular, F_{\sigma \delta })$
ideal is
 $P^- (hence\ P^-(\Lambda ))$
.
$P^- (hence\ P^-(\Lambda ))$
. -
(2) Each
 $F_\sigma $
ideal is
$F_\sigma $
ideal is
 $P^+ (hence\ P^-$
and
$P^+ (hence\ P^-$
and
 $P^-(\Lambda ))$
.
$P^-(\Lambda ))$
. -
(3) If
 $\mathcal {I}$
is an analytic ideal, then the following conditions are equivalent.
$\mathcal {I}$
is an analytic ideal, then the following conditions are equivalent.-
(a) There exists a
 $P^+$
ideal
$P^+$
ideal
 $\mathcal {J}$
with
$\mathcal {J}$
with
 $\mathcal {I}\subseteq \mathcal {J}$
.
$\mathcal {I}\subseteq \mathcal {J}$
. -
(b) There exists an
 $F_\sigma $
ideal
$F_\sigma $
ideal
 $\mathcal {K}$
with
$\mathcal {K}$
with
 $\mathcal {I}\subseteq \mathcal {K}$
.
$\mathcal {I}\subseteq \mathcal {K}$
.
-
6.2 P-like properties of partition regular operations
Definition 6.3. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular. For sets
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular. For sets
![]() $F\in \mathcal {F}$
and
$F\in \mathcal {F}$
and
![]() $B\subseteq \Lambda $
, we write
$B\subseteq \Lambda $
, we write
![]() $\rho (F)\subseteq ^\rho B$
if there is a finite set
$\rho (F)\subseteq ^\rho B$
if there is a finite set
![]() $K\subseteq \Omega $
with
$K\subseteq \Omega $
with
![]() $\rho (F\setminus K)\subseteq B$
.
$\rho (F\setminus K)\subseteq B$
.
Remark. We want to stress here that the relation “
![]() $\rho (F)\subseteq ^\rho B$
” is in fact a relation between F and B and not between
$\rho (F)\subseteq ^\rho B$
” is in fact a relation between F and B and not between
![]() $\rho (F)$
and B because it can happen that
$\rho (F)$
and B because it can happen that
![]() $\rho (F)=\rho (G)$
and
$\rho (F)=\rho (G)$
and
![]() $\rho (F)\subseteq ^\rho B$
but
$\rho (F)\subseteq ^\rho B$
but
![]() $\rho (G)\not \subseteq ^\rho B$
. We decided that we write
$\rho (G)\not \subseteq ^\rho B$
. We decided that we write
![]() $\rho (F)\subseteq ^\rho B$
instead of
$\rho (F)\subseteq ^\rho B$
instead of
![]() $F\subseteq ^\rho B$
as the former seems more natural for us. The same remark applies to other notions involving “
$F\subseteq ^\rho B$
as the former seems more natural for us. The same remark applies to other notions involving “
![]() $\rho (F)$
” we defined earlier or we define later (e.g., Definitions 6.4 and 9.1).
$\rho (F)$
” we defined earlier or we define later (e.g., Definitions 6.4 and 9.1).
The following properties will prove useful in the studies of classes of sequentially compact spaces defined with the aid of partition regular functions.
Definition 6.4. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular. We say that
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular. We say that
![]() $\rho $
is:
$\rho $
is:
-
(1)
 $P^-(\Lambda )$
if for every
$P^-(\Lambda )$
if for every
 $\subseteq $
-decreasing sequence
$\subseteq $
-decreasing sequence
 $A_n\in \mathcal {I}_{\rho }^+$
with
$A_n\in \mathcal {I}_{\rho }^+$
with
 $A_0=\Lambda $
and
$A_0=\Lambda $
and
 $A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
$A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
 $n\in \omega $
there exists
$n\in \omega $
there exists
 $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
 $\rho (F)\subseteq ^\rho A_n$
for each
$\rho (F)\subseteq ^\rho A_n$
for each
 $n\in \omega $
;
$n\in \omega $
; -
(2)
 $P^-$
if for every
$P^-$
if for every
 $\subseteq $
-decreasing sequence
$\subseteq $
-decreasing sequence
 $A_n\in \mathcal {I}_{\rho }^+$
with
$A_n\in \mathcal {I}_{\rho }^+$
with
 $A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
$A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
 $n\in \omega $
there exists
$n\in \omega $
there exists
 $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
 $\rho (F)\subseteq ^\rho A_n$
for each
$\rho (F)\subseteq ^\rho A_n$
for each
 $n\in \omega $
;
$n\in \omega $
; -
(3)
 $P^+$
if for every
$P^+$
if for every
 $\subseteq $
-decreasing sequence
$\subseteq $
-decreasing sequence
 $A_n\in \mathcal {I}_{\rho }^+$
there exists
$A_n\in \mathcal {I}_{\rho }^+$
there exists
 $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
 $\rho (F)\subseteq ^\rho A_n$
for each
$\rho (F)\subseteq ^\rho A_n$
for each
 $n\in \omega $
;
$n\in \omega $
; -
(4) weak
 $P^+$
if for every
$P^+$
if for every
 $E\in \mathcal {F}$
there exists
$E\in \mathcal {F}$
there exists
 $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
 $\rho (F)\subseteq \rho (E)$
and for every sequence
$\rho (F)\subseteq \rho (E)$
and for every sequence
 $\{F_n: n\in \omega \}\subseteq \mathcal {F}$
such that
$\{F_n: n\in \omega \}\subseteq \mathcal {F}$
such that
 $\rho (F) \supseteq \rho (F_n)\supseteq \rho (F_{n+1})$
for each
$\rho (F) \supseteq \rho (F_n)\supseteq \rho (F_{n+1})$
for each
 $n\in \omega $
there exists
$n\in \omega $
there exists
 $G\in \mathcal {F}$
such that
$G\in \mathcal {F}$
such that
 $\rho (G)\subseteq ^\rho \rho (F_n)$
for each
$\rho (G)\subseteq ^\rho \rho (F_n)$
for each
 $n\in \omega $
.
$n\in \omega $
.
The following result reveals basic properties of the above defined notions and their connections with P-like properties of ideals.
Proposition 6.5. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\Lambda $
.
$\Lambda $
.
-
(1)
 $\rho \text { is }P^+\implies \rho \text { is weak }P^+\implies \rho \text { is }P^-\implies \rho \text { is }P^-(\Lambda )$
.
$\rho \text { is }P^+\implies \rho \text { is weak }P^+\implies \rho \text { is }P^-\implies \rho \text { is }P^-(\Lambda )$
. -
(2)
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^+ \iff \rho _{\mathcal {I}}$
is
$P^+ \iff \rho _{\mathcal {I}}$
is
 $P^+$
, for every ideal
$P^+$
, for every ideal
 $\mathcal {I}$
. Similar equivalences hold for
$\mathcal {I}$
. Similar equivalences hold for
 $P^-$
and
$P^-$
and
 $P^-(\Lambda )$
, resp.
$P^-(\Lambda )$
, resp. -
(3) The implications from item (1) cannot be reversed.
-
(4) If
 $\mathcal {I}_\rho $
is
$\mathcal {I}_\rho $
is
 $P^-(\Lambda ) (P^-, P^+,\ resp.)$
, then
$P^-(\Lambda ) (P^-, P^+,\ resp.)$
, then
 $\rho $
is
$\rho $
is
 $P^-(\Lambda ) (P^-, P^+, resp.)$
.
$P^-(\Lambda ) (P^-, P^+, resp.)$
. -
(5) The implications from item (4) cannot be reversed in case of
 $P^-(\Lambda )$
and
$P^-(\Lambda )$
and
 $P^-$
properties.
$P^-$
properties.
Proof (1) Below we only show that if
![]() $\rho $
is weak
$\rho $
is weak
![]() $P^+$
then it is
$P^+$
then it is
![]() $P^-$
since other implications are straightforward.
$P^-$
since other implications are straightforward.
Let
![]() $A_n\in \mathcal {I}_{\rho }^+$
be a
$A_n\in \mathcal {I}_{\rho }^+$
be a
![]() $\subseteq $
-decreasing sequence with
$\subseteq $
-decreasing sequence with
![]() $A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
$A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $A_0\in \mathcal {I}_{\rho }^+$
, there is
$A_0\in \mathcal {I}_{\rho }^+$
, there is
![]() $E\in \mathcal {F}$
such that
$E\in \mathcal {F}$
such that
![]() $\rho (E)\subseteq A_0$
. Using the fact that
$\rho (E)\subseteq A_0$
. Using the fact that
![]() $\rho $
is weak
$\rho $
is weak
![]() $P^+$
we can find
$P^+$
we can find
![]() $F\in \mathcal {F}$
with
$F\in \mathcal {F}$
with
![]() $\rho (F)\subseteq \rho (E)$
and such as in the definition of weak
$\rho (F)\subseteq \rho (E)$
and such as in the definition of weak
![]() $P^+$
property.
$P^+$
property.
We will show that there is a sequence
![]() $\{F_n: n\in \omega \}\subseteq \mathcal {F}$
such that
$\{F_n: n\in \omega \}\subseteq \mathcal {F}$
such that
![]() $\rho (F_0)\subseteq \rho (F)$
and
$\rho (F_0)\subseteq \rho (F)$
and
![]() $\rho (F_{n+1})\subseteq \rho (F_n)\cap A_{n+1}$
for each
$\rho (F_{n+1})\subseteq \rho (F_n)\cap A_{n+1}$
for each
![]() $n\in \omega $
. Indeed, since
$n\in \omega $
. Indeed, since
![]() $\rho (F)\subseteq A_0$
, it suffices to put
$\rho (F)\subseteq A_0$
, it suffices to put
![]() $F_0=F$
. Suppose now that
$F_0=F$
. Suppose now that
![]() $F_i$
have been constructed for
$F_i$
have been constructed for
![]() $i\leq n$
. Since
$i\leq n$
. Since
![]() $\rho (F_n)\cap A_{n+1} = \rho (F_n) \setminus (A_n\setminus A_{n+1}) \in \mathcal {I}^+_\rho $
, there is
$\rho (F_n)\cap A_{n+1} = \rho (F_n) \setminus (A_n\setminus A_{n+1}) \in \mathcal {I}^+_\rho $
, there is
![]() $F_{n+1}\in \mathcal {F}$
with
$F_{n+1}\in \mathcal {F}$
with
![]() $\rho (F_{n+1})\subseteq \rho (F_n)\cap A_{n+1}$
.
$\rho (F_{n+1})\subseteq \rho (F_n)\cap A_{n+1}$
.
Since F is as in the definition of weak
![]() $P^+$
property, there exists
$P^+$
property, there exists
![]() $G\in \mathcal {F}$
such that
$G\in \mathcal {F}$
such that
![]() $\rho (G)\subseteq ^\rho \rho (F_n)$
for each
$\rho (G)\subseteq ^\rho \rho (F_n)$
for each
![]() $n\in \omega $
. Thus,
$n\in \omega $
. Thus,
![]() $\rho (G)\subseteq ^\rho A_n$
for each
$\rho (G)\subseteq ^\rho A_n$
for each
![]() $n\in \omega $
.
$n\in \omega $
.
(2) Straightforward.
(3) The cases of the second and third implications follow from Proposition 6.1(2) and item (2), where the proof of the fact that
![]() $\rho _{\mathcal {I}_d}$
is not weak
$\rho _{\mathcal {I}_d}$
is not weak
![]() $P^+$
is just a slight modification of the proof that
$P^+$
is just a slight modification of the proof that
![]() $\mathcal {I}_d$
is not
$\mathcal {I}_d$
is not
![]() $P^+$
.
$P^+$
.
Now we show that the first implication cannot be reversed. Consider the ideal
![]() $\mathcal {I}= \{A\subseteq \omega \times \omega $
:
$\mathcal {I}= \{A\subseteq \omega \times \omega $
:
![]() $A\cap (\{n\}\times \omega )$
is finite for every
$A\cap (\{n\}\times \omega )$
is finite for every
![]() $n\in {\omega }\}$
. Then
$n\in {\omega }\}$
. Then
![]() $\mathcal {I}$
is not
$\mathcal {I}$
is not
![]() $P^+$
as witnessed by
$P^+$
as witnessed by
![]() $A_n=(\omega \setminus n)\times \omega $
, so
$A_n=(\omega \setminus n)\times \omega $
, so
![]() $\rho _{\mathcal {I}}$
is not
$\rho _{\mathcal {I}}$
is not
![]() $P^+$
(by item (2)). However, we will show that
$P^+$
(by item (2)). However, we will show that
![]() $\rho _{\mathcal {I}}$
is weak
$\rho _{\mathcal {I}}$
is weak
![]() $P^+$
. Let
$P^+$
. Let
![]() $E\in \mathcal {I}^+$
. Then there is
$E\in \mathcal {I}^+$
. Then there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $F=E\cap (\{n\}\times \omega )$
is infinite. Then
$F=E\cap (\{n\}\times \omega )$
is infinite. Then
![]() $F\in \mathcal {I}^+$
and it is easy to see that if
$F\in \mathcal {I}^+$
and it is easy to see that if
![]() $F_n\in \mathcal {I}^+$
are such that
$F_n\in \mathcal {I}^+$
are such that
![]() $F\supseteq F_n\supseteq F_{n+1}$
then one can pick
$F\supseteq F_n\supseteq F_{n+1}$
then one can pick
![]() $x_n\in F_n$
for each
$x_n\in F_n$
for each
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $G=\{x_n:n\in \omega \}\in \mathcal {I}^+$
is such that
$G=\{x_n:n\in \omega \}\in \mathcal {I}^+$
is such that
![]() $G\setminus \{x_i:i<n\}\subseteq F_n$
for all
$G\setminus \{x_i:i<n\}\subseteq F_n$
for all
![]() $n\in \omega $
.
$n\in \omega $
.
(4) Proofs in all cases are very similar, so we only present a proof for the property
![]() $P^-(\Lambda )$
. Let
$P^-(\Lambda )$
. Let
![]() $A_n\in \mathcal {I}_{\rho }^+$
be a
$A_n\in \mathcal {I}_{\rho }^+$
be a
![]() $\subseteq $
-decreasing sequence with
$\subseteq $
-decreasing sequence with
![]() $A_0=\Lambda $
and
$A_0=\Lambda $
and
![]() $A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
$A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $\mathcal {I}_{\rho }$
is
$\mathcal {I}_{\rho }$
is
![]() $P^-(\Lambda )$
, there is
$P^-(\Lambda )$
, there is
![]() $B\not \in \mathcal {I}_{\rho }$
such that for every
$B\not \in \mathcal {I}_{\rho }$
such that for every
![]() $n\in \omega $
one can find a finite set
$n\in \omega $
one can find a finite set
![]() $K_n\subseteq \Omega $
such that
$K_n\subseteq \Omega $
such that
![]() $B\setminus K_n\subseteq A_n$
. From the fact that
$B\setminus K_n\subseteq A_n$
. From the fact that
![]() $B\not \in \mathcal {I}_{\rho }$
, there is
$B\not \in \mathcal {I}_{\rho }$
, there is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq B$
. Using Proposition 3.2, we can find
$\rho (F)\subseteq B$
. Using Proposition 3.2, we can find
![]() $E\in \mathcal {F}$
such that
$E\in \mathcal {F}$
such that
![]() $E\subseteq F$
and for every
$E\subseteq F$
and for every
![]() $K_n$
there exists a finite set
$K_n$
there exists a finite set
![]() $L_n\subseteq \Omega $
such that
$L_n\subseteq \Omega $
such that
![]() $\rho (E\setminus L_n)\subseteq \rho (E)\setminus K_n$
. Then
$\rho (E\setminus L_n)\subseteq \rho (E)\setminus K_n$
. Then
![]() $\rho (E\setminus L_n)\subseteq \rho (E)\setminus K_n \subseteq B\setminus K_n\subseteq A_n$
, so
$\rho (E\setminus L_n)\subseteq \rho (E)\setminus K_n \subseteq B\setminus K_n\subseteq A_n$
, so
![]() $\rho $
is
$\rho $
is
![]() $P^-(\Lambda )$
.
$P^-(\Lambda )$
.
(5) In Proposition 6.7(3) and (4) we will show that
![]() $\rho =\operatorname {\mathrm {FS}}$
is weak
$\rho =\operatorname {\mathrm {FS}}$
is weak
![]() $P^+$
, but
$P^+$
, but
![]() $\mathcal {I}_\rho = \mathcal {H}$
is not
$\mathcal {I}_\rho = \mathcal {H}$
is not
![]() $P^-(\omega )$
.
$P^-(\omega )$
.
We will need the following lemma to show that
![]() $FS$
, r, and
$FS$
, r, and
![]() $\Delta $
are not
$\Delta $
are not
![]() $P^+$
.
$P^+$
.
Lemma 6.6. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega\ (with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
be a partition regular function such that there exists a function
$\rho :\mathcal {F}\to [\Lambda ]^\omega\ (with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
be a partition regular function such that there exists a function
![]() $\tau :[\Omega ]^{<\omega }\to \Lambda $
such that:
$\tau :[\Omega ]^{<\omega }\to \Lambda $
such that:
-
(1)
 $\forall F\in \mathcal {F}\, \forall \{a,b\}\in [F]^2 \, (\tau \left (\{a,b\}\right )\in \rho (F))$
,
$\forall F\in \mathcal {F}\, \forall \{a,b\}\in [F]^2 \, (\tau \left (\{a,b\}\right )\in \rho (F))$
, -
(2)
 $\forall F\in \mathcal {F}\, \forall c\in \rho (F)\, \exists S\in [F]^{<\omega }\,(\tau (S)=c)$
,
$\forall F\in \mathcal {F}\, \forall c\in \rho (F)\, \exists S\in [F]^{<\omega }\,(\tau (S)=c)$
, -
(3) there exists a pairwise disjoint family
 $\{P_n: n\in \omega \}\subseteq \mathcal {F}$
such that the family
$\{P_n: n\in \omega \}\subseteq \mathcal {F}$
such that the family
 $\{\rho (P_n):n\in \omega \}$
is also pairwise disjoint and the restriction
$\{\rho (P_n):n\in \omega \}$
is also pairwise disjoint and the restriction
 $\tau \restriction \left [\bigcup \{P_n:n\in \omega \}\right ]^{<\omega }$
is one-to-one.
$\tau \restriction \left [\bigcup \{P_n:n\in \omega \}\right ]^{<\omega }$
is one-to-one.
Then
![]() $\rho $
is not
$\rho $
is not
![]() $P^+$
.
$P^+$
.
Proof Let
![]() $\{P_n:n\in \omega \}$
be as in item (3) of the lemma. For each
$\{P_n:n\in \omega \}$
be as in item (3) of the lemma. For each
![]() $n\in \omega $
, we define
$n\in \omega $
, we define
![]() $B_n = \bigcup \{\rho (P_i): i\geq n\}.$
Then
$B_n = \bigcup \{\rho (P_i): i\geq n\}.$
Then
![]() $B_n\in \mathcal {I}_{\rho }^+$
and
$B_n\in \mathcal {I}_{\rho }^+$
and
![]() $B\supseteq B_n\supseteq B_{n+1}$
for each
$B\supseteq B_n\supseteq B_{n+1}$
for each
![]() $n\in \omega $
. If we show that there is no
$n\in \omega $
. If we show that there is no
![]() $G\in \mathcal {F}$
such that
$G\in \mathcal {F}$
such that
![]() $\rho (G)\subseteq ^\rho B_n$
for every
$\rho (G)\subseteq ^\rho B_n$
for every
![]() $n\in \omega $
, the proof will be finished. Suppose for the sake of contradiction that there exists
$n\in \omega $
, the proof will be finished. Suppose for the sake of contradiction that there exists
![]() $G\in \mathcal {F}$
such that for every
$G\in \mathcal {F}$
such that for every
![]() $n\in \omega $
there exists a finite set
$n\in \omega $
there exists a finite set
![]() $K_n\subseteq \Omega $
with
$K_n\subseteq \Omega $
with
![]() $\rho (G\setminus K_n)\subseteq B_n$
. We have two cases:
$\rho (G\setminus K_n)\subseteq B_n$
. We have two cases:
-
(1)
 $|G\cap P_{n_0}|=\omega $
for some
$|G\cap P_{n_0}|=\omega $
for some
 $n_0\in \omega $
,
$n_0\in \omega $
, -
(2)
 $|G\cap P_{n}|<\omega $
for all
$|G\cap P_{n}|<\omega $
for all
 $n\in \omega $
.
$n\in \omega $
.
Case (1). We take distinct
![]() $a,b\in (G\cap P_{n_0})\setminus K_{n_0+1}$
. Since
$a,b\in (G\cap P_{n_0})\setminus K_{n_0+1}$
. Since
![]() $a,b\in P_{n_0}\in \mathcal {F}$
, we have
$a,b\in P_{n_0}\in \mathcal {F}$
, we have
![]() $\tau \left (\{a,b\}\right )\in \rho (P_{n_0})$
. On the other hand,
$\tau \left (\{a,b\}\right )\in \rho (P_{n_0})$
. On the other hand,
![]() $a,b\in G\setminus K_{n_0+1}\in \mathcal {F}$
, so
$a,b\in G\setminus K_{n_0+1}\in \mathcal {F}$
, so
![]() $\tau \left (\{a,b\}\right )\in \rho (G\setminus K_{n_0+1}) \subseteq B_{n_0+1}$
. Hence, there exists
$\tau \left (\{a,b\}\right )\in \rho (G\setminus K_{n_0+1}) \subseteq B_{n_0+1}$
. Hence, there exists
![]() $i\geq n_0+1$
such that
$i\geq n_0+1$
such that
![]() $\tau \left (\{a,b\}\right )\in \rho (P_i)$
. A contradiction with
$\tau \left (\{a,b\}\right )\in \rho (P_i)$
. A contradiction with
![]() $\rho (P_i)\cap \rho (P_{n_0})=\emptyset $
.
$\rho (P_i)\cap \rho (P_{n_0})=\emptyset $
.
Case (2). In this case, there exists a strictly increasing sequence
![]() $\{k_n : n\in \omega \}$
such that we can choose an element
$\{k_n : n\in \omega \}$
such that we can choose an element
![]() $x_{k_n}\in G\cap P_{k_n}$
for each
$x_{k_n}\in G\cap P_{k_n}$
for each
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $x_{k_n}$
are pairwise distinct, there is
$x_{k_n}$
are pairwise distinct, there is
![]() $N\in \omega $
such that
$N\in \omega $
such that
![]() $x_{k_n}\in G\setminus K_0$
for every
$x_{k_n}\in G\setminus K_0$
for every
![]() $n\geq N$
. In particular,
$n\geq N$
. In particular,
![]() $\tau \left (\{x_{k_N},x_{k_{N+1}}\}\right )\in \rho (G\setminus K_0)\subseteq B_0$
, and consequently there exists
$\tau \left (\{x_{k_N},x_{k_{N+1}}\}\right )\in \rho (G\setminus K_0)\subseteq B_0$
, and consequently there exists
![]() $i\in \omega $
such that
$i\in \omega $
such that
![]() $\tau \left (\{x_{k_N},x_{k_{N+1}}\}\right )\in \rho (P_i)$
. Therefore there is a finite set
$\tau \left (\{x_{k_N},x_{k_{N+1}}\}\right )\in \rho (P_i)$
. Therefore there is a finite set
![]() $S\subseteq P_i$
such that
$S\subseteq P_i$
such that
![]() $\tau (S)=\tau \left (\{x_{k_N},x_{k_{N+1}}\}\right )$
. Since
$\tau (S)=\tau \left (\{x_{k_N},x_{k_{N+1}}\}\right )$
. Since
![]() $P_n$
are pairwise disjoint and
$P_n$
are pairwise disjoint and
![]() $x_{k_n}\in P_n$
, we obtain that
$x_{k_n}\in P_n$
, we obtain that
![]() $x_{k_N}\notin P_i$
or
$x_{k_N}\notin P_i$
or
![]() $x_{k_N+1}\notin P_i$
. Consequently,
$x_{k_N+1}\notin P_i$
. Consequently,
![]() $\{x_{k_N},x_{k_{N+1}}\} \neq S$
, so
$\{x_{k_N},x_{k_{N+1}}\} \neq S$
, so
![]() $\tau \restriction \left [\bigcup \{P_n:n\in \omega \}\right ]^{<\omega }$
is not one-to-one, a contradiction.
$\tau \restriction \left [\bigcup \{P_n:n\in \omega \}\right ]^{<\omega }$
is not one-to-one, a contradiction.
Proposition 6.7.
-
(1) The ideals
 $\mathcal {W}$
and
$\mathcal {W}$
and
 $\mathcal {I}_{1/n}$
are
$\mathcal {I}_{1/n}$
are
 $P^+ (hence, P^- and\ P^-(\omega ))$
while
$P^+ (hence, P^- and\ P^-(\omega ))$
while
 $\rho _{\mathcal {W}}$
and
$\rho _{\mathcal {W}}$
and
 $\rho _{\mathcal {I}_{1/n}}$
are
$\rho _{\mathcal {I}_{1/n}}$
are
 $P^+$
, weak
$P^+$
, weak
 $P^+$
,
$P^+$
,
 $P^-$
and
$P^-$
and
 $P^-(\omega )$
.
$P^-(\omega )$
. -
(2) If
 $\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
, then
$\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
, then
 $\rho $
is not
$\rho $
is not
 $P^+$
,
$P^+$
, -
(3) If
 $\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
, then
$\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
, then
 $\rho $
is weak
$\rho $
is weak
 $P^+ (hence\ P^-$
and
$P^+ (hence\ P^-$
and
 $P^-(\Lambda ))$
.
$P^-(\Lambda ))$
. -
(4) If
 $\mathcal {I}\in \{\mathcal {H},\mathcal {R},\mathcal {D}\}$
, then
$\mathcal {I}\in \{\mathcal {H},\mathcal {R},\mathcal {D}\}$
, then
 $\mathcal {I}$
is not
$\mathcal {I}$
is not
 $P^-(\Lambda ) (hence\ not\ P^+$
and not
$P^-(\Lambda ) (hence\ not\ P^+$
and not
 $P^-)$
.
$P^-)$
.
Proof (1) It follows from Theorem 6.2(2) and the fact that
![]() $\mathcal {W}$
and
$\mathcal {W}$
and
![]() $\mathcal {I}_{1/n}$
are
$\mathcal {I}_{1/n}$
are
![]() $F_{\sigma }$
ideals (see Proposition 5.2(1)). The “hence” part follows from Proposition 6.5.
$F_{\sigma }$
ideals (see Proposition 5.2(1)). The “hence” part follows from Proposition 6.5.
(2) Below we show that
![]() $\rho $
is not
$\rho $
is not
![]() $P^+$
separately for each
$P^+$
separately for each
![]() $\rho $
.
$\rho $
.
Case of
![]() $\rho =FS$
. We define a function
$\rho =FS$
. We define a function
![]() $\tau :[\omega ]^{<\omega }\to \omega $
by
$\tau :[\omega ]^{<\omega }\to \omega $
by
![]() $\tau (S) =\sum _{i\in S}i$
. Then we take an infinite sparse set P and a partition
$\tau (S) =\sum _{i\in S}i$
. Then we take an infinite sparse set P and a partition
![]() $\{P_n:n\in \omega \}$
of P into infinite sets. Lemma 6.6 shows that
$\{P_n:n\in \omega \}$
of P into infinite sets. Lemma 6.6 shows that
![]() $\operatorname {\mathrm {FS}}$
is not
$\operatorname {\mathrm {FS}}$
is not
![]() $P^+$
.
$P^+$
.
Case of
![]() $\rho =r$
. Let
$\rho =r$
. Let
![]() $A\subseteq \omega $
be such that both A and
$A\subseteq \omega $
be such that both A and
![]() $\omega \setminus A$
are infinite. Let
$\omega \setminus A$
are infinite. Let
![]() $f:[\omega ]^{<\omega }\to [\omega \setminus A]^2$
be any bijection. We define a function
$f:[\omega ]^{<\omega }\to [\omega \setminus A]^2$
be any bijection. We define a function
![]() $\tau :[\omega ]^{<\omega }\to [\omega ]^2$
by
$\tau :[\omega ]^{<\omega }\to [\omega ]^2$
by
![]() $\tau (\{a,b\}) = \{a,b\}$
for distinct
$\tau (\{a,b\}) = \{a,b\}$
for distinct
![]() $a,b\in \omega $
and
$a,b\in \omega $
and
![]() $\tau (S) = f(S)$
for
$\tau (S) = f(S)$
for
![]() $S\in [\omega ]^{<\omega }\setminus [\omega ]^2$
. Then we take a partition
$S\in [\omega ]^{<\omega }\setminus [\omega ]^2$
. Then we take a partition
![]() $\{P_n:n\in \omega \}$
of A into infinite sets. Lemma 6.6 shows that r is not
$\{P_n:n\in \omega \}$
of A into infinite sets. Lemma 6.6 shows that r is not
![]() $P^+$
.
$P^+$
.
Case of
![]() $\rho =\Delta $
. We define a function
$\rho =\Delta $
. We define a function
![]() $\tau :[\omega ]^{<\omega }\to \omega $
by
$\tau :[\omega ]^{<\omega }\to \omega $
by
![]() $\tau (\{a,b\}) = a-b$
for distinct
$\tau (\{a,b\}) = a-b$
for distinct
![]() $a>b$
and
$a>b$
and
![]() $\tau (S) = 0$
otherwise. Then we take an infinite
$\tau (S) = 0$
otherwise. Then we take an infinite
![]() $\mathcal {D}$
-sparse set P and a partition
$\mathcal {D}$
-sparse set P and a partition
![]() $\{P_n:n\in \omega \}$
of P into infinite sets. Lemma 6.6 shows that
$\{P_n:n\in \omega \}$
of P into infinite sets. Lemma 6.6 shows that
![]() $\Delta $
is not
$\Delta $
is not
![]() $P^+$
.
$P^+$
.
(3) The “hence” part follows from Proposition 6.5(1). Below we show that
![]() $\rho $
is weak
$\rho $
is weak
![]() $P^+$
separately for each
$P^+$
separately for each
![]() $\rho $
.
$\rho $
.
Case of
![]() $\rho =\operatorname {\mathrm {FS}}$
. It is proved in [Reference Filipów, Kowitz, Kwela and Tryba24, Lemma 2.3] (see also [Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, Example 2.9(2)]).
$\rho =\operatorname {\mathrm {FS}}$
. It is proved in [Reference Filipów, Kowitz, Kwela and Tryba24, Lemma 2.3] (see also [Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, Example 2.9(2)]).
Case of
![]() $\rho =r$
. For any
$\rho =r$
. For any
![]() $E\in [\omega ]^\omega $
we take
$E\in [\omega ]^\omega $
we take
![]() $F=E$
. Let
$F=E$
. Let
![]() $F_n\in [\omega ]^\omega $
be such that
$F_n\in [\omega ]^\omega $
be such that
![]() $[F]^2\supseteq [F_n]^2\supseteq [F_{n+1}]^2$
for each
$[F]^2\supseteq [F_n]^2\supseteq [F_{n+1}]^2$
for each
![]() $n\in \omega $
. We pick
$n\in \omega $
. We pick
![]() $x_n\in F_n\setminus \{x_i:i<n\}$
for each
$x_n\in F_n\setminus \{x_i:i<n\}$
for each
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $G=\{x_n:n\in \omega \}\in [\omega ]^\omega $
and
$G=\{x_n:n\in \omega \}\in [\omega ]^\omega $
and
![]() $[G]^2\subseteq ^r[F_n]^2$
for each
$[G]^2\subseteq ^r[F_n]^2$
for each
![]() $n\in \omega $
.
$n\in \omega $
.
Case of
![]() $\rho =\Delta $
. Fix any
$\rho =\Delta $
. Fix any
![]() $F\in [\omega ]^\omega $
. Inductively pick a sequence
$F\in [\omega ]^\omega $
. Inductively pick a sequence
![]() $(x_i)_{i\in \omega }\subseteq \omega $
such that
$(x_i)_{i\in \omega }\subseteq \omega $
such that
![]() $x_i\in F$
,
$x_i\in F$
,
![]() $x_i<x_{i+1}$
, and
$x_i<x_{i+1}$
, and
![]() $x_{i+1}-x_i>x_i-x_0$
for all
$x_{i+1}-x_i>x_i-x_0$
for all
![]() $i\in \omega $
. Let
$i\in \omega $
. Let
![]() $E=\{x_i:\ i\in \omega \}\in [F]^{\omega }$
.
$E=\{x_i:\ i\in \omega \}\in [F]^{\omega }$
.
Define
![]() $a_i=x_{i+1}-x_i$
for all
$a_i=x_{i+1}-x_i$
for all
![]() $i\in \omega $
and observe that
$i\in \omega $
and observe that
![]() $a_i=x_{i+1}-x_i>x_i-x_0=\sum _{j<i}a_j$
. Put
$a_i=x_{i+1}-x_i>x_i-x_0=\sum _{j<i}a_j$
. Put
![]() $A=\{a_i:\ i\in \omega \}$
. By [Reference Filipów, Kowitz, Kwela and Tryba24, proof of Lemma 2.2] the set A is very sparse, i.e., A is sparse and if
$A=\{a_i:\ i\in \omega \}$
. By [Reference Filipów, Kowitz, Kwela and Tryba24, proof of Lemma 2.2] the set A is very sparse, i.e., A is sparse and if
![]() $\alpha _{A}(x)\cap \alpha _{A}(y)\neq \emptyset $
then
$\alpha _{A}(x)\cap \alpha _{A}(y)\neq \emptyset $
then
![]() $x+y\notin \operatorname {\mathrm {FS}}(A)$
. Note that
$x+y\notin \operatorname {\mathrm {FS}}(A)$
. Note that
![]() $\Delta (E)=\{\sum _{i\in I}a_i:\ I\text { is a finite interval in }\omega \}\subseteq \operatorname {\mathrm {FS}}(A)$
.
$\Delta (E)=\{\sum _{i\in I}a_i:\ I\text { is a finite interval in }\omega \}\subseteq \operatorname {\mathrm {FS}}(A)$
.
Observe that if
![]() $\Delta (\{y_n:\ n\in \omega \})\subseteq \Delta (E)$
, where
$\Delta (\{y_n:\ n\in \omega \})\subseteq \Delta (E)$
, where
![]() $y_n<y_{n+1}$
for all
$y_n<y_{n+1}$
for all
![]() $n\in \omega $
, then there is a partition of
$n\in \omega $
, then there is a partition of
![]() $\omega $
into finite intervals
$\omega $
into finite intervals
![]() $(I_n)_{n\in \omega }$
such that
$(I_n)_{n\in \omega }$
such that
![]() $\max I_n<\min I_{n+1}$
and
$\max I_n<\min I_{n+1}$
and
![]() $y_{n+1}-y_n=\sum _{i\in I_n}a_i$
. Indeed, as
$y_{n+1}-y_n=\sum _{i\in I_n}a_i$
. Indeed, as
![]() $y_{n+1}-y_n\in \Delta (\{y_n:\ n\in \omega \})\subseteq \Delta (E)\subseteq \operatorname {\mathrm {FS}}(A)$
, for each
$y_{n+1}-y_n\in \Delta (\{y_n:\ n\in \omega \})\subseteq \Delta (E)\subseteq \operatorname {\mathrm {FS}}(A)$
, for each
![]() $n\in \omega $
there is a finite interval
$n\in \omega $
there is a finite interval
![]() $I_n$
such that
$I_n$
such that
![]() $y_{n+1}-y_n=\sum _{i\in I_n}a_i$
(because A is sparse, we get
$y_{n+1}-y_n=\sum _{i\in I_n}a_i$
(because A is sparse, we get
![]() $I_n=\alpha _{A}(y_{n+1}-y_n)$
). We need to show that the intervals
$I_n=\alpha _{A}(y_{n+1}-y_n)$
). We need to show that the intervals
![]() $I_n$
are pairwise disjoint and cover
$I_n$
are pairwise disjoint and cover
![]() $\omega $
. Suppose first that
$\omega $
. Suppose first that
![]() $\sup I_n+1<\inf I_{n+1}$
for some
$\sup I_n+1<\inf I_{n+1}$
for some
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $y_{n+2}-y_n=(y_{n+2}-y_{n+1})+(y_{n+1}-y_{n})=\sum _{i\in I_n\cup I_{n+1}}a_i$
. On the other hand,
$y_{n+2}-y_n=(y_{n+2}-y_{n+1})+(y_{n+1}-y_{n})=\sum _{i\in I_n\cup I_{n+1}}a_i$
. On the other hand,
![]() $y_{n+2}-y_n\in \Delta (\{y_n:\ n\in \omega \})\subseteq \Delta (E)$
, so
$y_{n+2}-y_n\in \Delta (\{y_n:\ n\in \omega \})\subseteq \Delta (E)$
, so
![]() $y_{n+2}-y_n=\sum _{i\in I}a_i$
for some interval I. This contradicts uniqueness of
$y_{n+2}-y_n=\sum _{i\in I}a_i$
for some interval I. This contradicts uniqueness of
![]() $\alpha _{A}(y_{n+2}-y_n)$
(because A is sparse). Suppose now that
$\alpha _{A}(y_{n+2}-y_n)$
(because A is sparse). Suppose now that
![]() $I_n\cap I_{n+1}\neq \emptyset $
. Then
$I_n\cap I_{n+1}\neq \emptyset $
. Then
![]() $y_{n+2}-y_n=(y_{n+2}-y_{n+1})+(y_{n+1}-y_{n})\notin \operatorname {\mathrm {FS}}(A)$
(because A is very sparse), which contradicts
$y_{n+2}-y_n=(y_{n+2}-y_{n+1})+(y_{n+1}-y_{n})\notin \operatorname {\mathrm {FS}}(A)$
(because A is very sparse), which contradicts
![]() $\Delta (\{y_n:\ n\in \omega \})\subseteq \Delta (E)\subseteq FS(A)$
.
$\Delta (\{y_n:\ n\in \omega \})\subseteq \Delta (E)\subseteq FS(A)$
.
Fix any sequence
![]() $(F_k)_{k\in \omega }\subseteq [\omega ]^\omega $
such that
$(F_k)_{k\in \omega }\subseteq [\omega ]^\omega $
such that
![]() $\Delta (F_{k+1})\subseteq \Delta (F_k)\subseteq \Delta (E)$
for all
$\Delta (F_{k+1})\subseteq \Delta (F_k)\subseteq \Delta (E)$
for all
![]() ${k\in \omega }$
. By the previous paragraph, with each
${k\in \omega }$
. By the previous paragraph, with each
![]() $k\in \omega $
we can associate a partition of
$k\in \omega $
we can associate a partition of
![]() $\omega $
into finite intervals
$\omega $
into finite intervals
![]() $I^k_n$
, i.e.,
$I^k_n$
, i.e.,
![]() $\Delta (F_k)=\{\sum _{i\in I}a_i:\ I=I^k_j\cup I^k_{j+1}\cup \ldots \cup I^k_{j'}\text { for some } j\,{<}\,j'\}$
.
$\Delta (F_k)=\{\sum _{i\in I}a_i:\ I=I^k_j\cup I^k_{j+1}\cup \ldots \cup I^k_{j'}\text { for some } j\,{<}\,j'\}$
.
Observe that actually for each
![]() $n,k\in \omega $
we have that
$n,k\in \omega $
we have that
![]() $I^{k+1}_n=\bigcup _{i\in I}I^k_i$
for some interval I. Indeed, otherwise for some
$I^{k+1}_n=\bigcup _{i\in I}I^k_i$
for some interval I. Indeed, otherwise for some
![]() $n,k\in \omega $
we would have
$n,k\in \omega $
we would have
![]() $x=\sum _{i\in I^{k+1}_n}a_i\in \Delta (F_{k+1})\subseteq \Delta (F_k)$
, so
$x=\sum _{i\in I^{k+1}_n}a_i\in \Delta (F_{k+1})\subseteq \Delta (F_k)$
, so
![]() $x=\sum _{i\in I}a_i$
for some
$x=\sum _{i\in I}a_i$
for some
![]() $I=I^k_j\cup I^k_{j+1}\cup \cdots \cup I^k_{j'}$
, which contradicts that A is sparse.
$I=I^k_j\cup I^k_{j+1}\cup \cdots \cup I^k_{j'}$
, which contradicts that A is sparse.
Inductively pick a sequence
![]() $(n_k)_{k\in \omega }\subseteq \omega $
such that for each
$(n_k)_{k\in \omega }\subseteq \omega $
such that for each
![]() $k\in \omega $
we have
$k\in \omega $
we have
![]() $n_{k+1}>n_k$
(so also
$n_{k+1}>n_k$
(so also
![]() $a_{n_{k+1}}>a_{n_k}$
) and
$a_{n_{k+1}}>a_{n_k}$
) and
![]() $n_k=\min I^k_j$
for some
$n_k=\min I^k_j$
for some
![]() $j\in \omega $
. Define
$j\in \omega $
. Define
![]() $E'=\{x_{n_k}:\ k\in \omega \}$
. Notice that
$E'=\{x_{n_k}:\ k\in \omega \}$
. Notice that
![]() $x_{n_{k+1}}-x_{n_k}=\sum _{i\in [n_k,n_{k+1})} a_i$
. Then for each
$x_{n_{k+1}}-x_{n_k}=\sum _{i\in [n_k,n_{k+1})} a_i$
. Then for each
![]() $k\in \omega $
we have
$k\in \omega $
we have
 $\Delta (E'\setminus [0,x_{n_k}))=\Delta (\{x_{n_i}:\ i\geq k\})\subseteq \{\sum _{i\in I}a_i:\ I=I^k_j\cup I^k_{j+1}\cup \cdots \cup I^k_{j'}\text { for some }j<j'\}=\Delta (F_k)$
.
$\Delta (E'\setminus [0,x_{n_k}))=\Delta (\{x_{n_i}:\ i\geq k\})\subseteq \{\sum _{i\in I}a_i:\ I=I^k_j\cup I^k_{j+1}\cup \cdots \cup I^k_{j'}\text { for some }j<j'\}=\Delta (F_k)$
.
(4) The “hence” part follows from Proposition 6.1. Below we show that
![]() $\mathcal {I}$
is not
$\mathcal {I}$
is not
![]() $P^-(\Lambda )$
separately for each
$P^-(\Lambda )$
separately for each
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Case of
![]() $\mathcal {I}=\mathcal {H}$
. Let
$\mathcal {I}=\mathcal {H}$
. Let
![]() $A_k=\{2^k(2n+1): n\in \omega \}$
for each
$A_k=\{2^k(2n+1): n\in \omega \}$
for each
![]() $k\in \omega $
. In [Reference Filipów, Kowitz, Kwela and Tryba24, item (2) in the proof of Proposition 1.1], the authors showed that
$k\in \omega $
. In [Reference Filipów, Kowitz, Kwela and Tryba24, item (2) in the proof of Proposition 1.1], the authors showed that
![]() $A_k\in \mathcal {H}$
for every
$A_k\in \mathcal {H}$
for every
![]() $k\in \omega $
, whereas in [Reference Filipów, Kowitz, Kwela and Tryba24, item (1) in the proof of Proposition 1.1] it is shown that for every
$k\in \omega $
, whereas in [Reference Filipów, Kowitz, Kwela and Tryba24, item (1) in the proof of Proposition 1.1] it is shown that for every
![]() $B\notin \mathcal {H}$
there is
$B\notin \mathcal {H}$
there is
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $B\cap A_k$
is infinite. Thus, the family
$B\cap A_k$
is infinite. Thus, the family
![]() $\{A_k:k\in \omega \}$
witnesses the fact that
$\{A_k:k\in \omega \}$
witnesses the fact that
![]() $\mathcal {H}$
is not
$\mathcal {H}$
is not
![]() $P^-(\omega )$
.
$P^-(\omega )$
.
Case of
![]() $\mathcal {I}=\mathcal {R}$
. Let
$\mathcal {I}=\mathcal {R}$
. Let
![]() $A_n = \{\{k,i\}: i>k\geq n\}$
for every
$A_n = \{\{k,i\}: i>k\geq n\}$
for every
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $A_n\notin \mathcal {R}$
,
$A_n\notin \mathcal {R}$
,
![]() $A_0=[\omega ]^2$
, and
$A_0=[\omega ]^2$
, and
![]() $A_n\setminus A_{n+1} = \{\{n,i\}: i> n\}\in \mathcal {R}$
. Suppose, for the sake of contradiction, that there is
$A_n\setminus A_{n+1} = \{\{n,i\}: i> n\}\in \mathcal {R}$
. Suppose, for the sake of contradiction, that there is
![]() $B\notin \mathcal {R}$
such that
$B\notin \mathcal {R}$
such that
![]() $B\subseteq ^* A_n$
for every
$B\subseteq ^* A_n$
for every
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $H=\{h_n:n\in \omega \}$
be an infinite set such that
$H=\{h_n:n\in \omega \}$
be an infinite set such that
![]() $[H]^2\subseteq B$
and
$[H]^2\subseteq B$
and
![]() $h_n<h_{n+1}$
for every
$h_n<h_{n+1}$
for every
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $[H]^2\subseteq ^*A_{h_1}$
, there is a finite set F such that
$[H]^2\subseteq ^*A_{h_1}$
, there is a finite set F such that
![]() $[H]^2\setminus F\subseteq A_{h_1}$
. Since F is finite, there is
$[H]^2\setminus F\subseteq A_{h_1}$
. Since F is finite, there is
![]() $k>0$
such that
$k>0$
such that
![]() $\{h_0,h_n\}\notin F$
for every
$\{h_0,h_n\}\notin F$
for every
![]() $n\geq k$
. Then
$n\geq k$
. Then
![]() $\{\{h_0,h_n\}:n\geq k\}\subseteq [H]^2\setminus F$
and
$\{\{h_0,h_n\}:n\geq k\}\subseteq [H]^2\setminus F$
and
![]() $\{\{h_0,h_n\}:n\geq k\}\cap A_{h_1}=\emptyset $
, a contradiction.
$\{\{h_0,h_n\}:n\geq k\}\cap A_{h_1}=\emptyset $
, a contradiction.
Case of
![]() $\mathcal {I}=\mathcal {D}$
. Let
$\mathcal {I}=\mathcal {D}$
. Let
![]() $A_k=\{2^k(2n+1): n\in \omega \}$
for each
$A_k=\{2^k(2n+1): n\in \omega \}$
for each
![]() $k\in \omega $
. In [Reference Kowitz60, item (2) in the proof of Theorem 2.1], the author showed that
$k\in \omega $
. In [Reference Kowitz60, item (2) in the proof of Theorem 2.1], the author showed that
![]() $A_k\in \mathcal {D}$
for every
$A_k\in \mathcal {D}$
for every
![]() $k\in \omega $
, whereas in [Reference Kowitz60, item (1) in the proof of Theorem 2.1] it is shown that for every
$k\in \omega $
, whereas in [Reference Kowitz60, item (1) in the proof of Theorem 2.1] it is shown that for every
![]() $B\notin \mathcal {D}$
there is
$B\notin \mathcal {D}$
there is
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $B\cap A_k$
is infinite. Thus, the family
$B\cap A_k$
is infinite. Thus, the family
![]() $\{A_k:k\in \omega \}$
witnesses the fact that
$\{A_k:k\in \omega \}$
witnesses the fact that
![]() $\mathcal {D}$
is not
$\mathcal {D}$
is not
![]() $P^-(\omega )$
.
$P^-(\omega )$
.
The following easy observation will be useful in our considerations.
Proposition 6.8. If
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
is partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
is partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
, then the following conditions are equivalent.
$\mathcal {F}\subseteq [\Omega ]^\omega $
, then the following conditions are equivalent.
-
(1)
 $\rho $
is
$\rho $
is
 $P^- (P^-(\Lambda ), resp.)$
.
$P^- (P^-(\Lambda ), resp.)$
. -
(2) For every countable family
 $\mathcal {B}\subseteq \mathcal {I}_\rho $
with
$\mathcal {B}\subseteq \mathcal {I}_\rho $
with
 $\bigcup \mathcal {B}\notin \mathcal {I}_\rho\ (\bigcup \mathcal {B} = \Lambda ,\ resp.)$
there exists
$\bigcup \mathcal {B}\notin \mathcal {I}_\rho\ (\bigcup \mathcal {B} = \Lambda ,\ resp.)$
there exists
 $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
 $\rho (F) \subseteq \bigcup \mathcal {B}$
and for every finite subfamily
$\rho (F) \subseteq \bigcup \mathcal {B}$
and for every finite subfamily
 $\mathcal {C}\subseteq \mathcal {B}$
there is a finite
$\mathcal {C}\subseteq \mathcal {B}$
there is a finite
 $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
 $\rho (F\setminus K) \cap \bigcup \mathcal {C} =\emptyset $
.
$\rho (F\setminus K) \cap \bigcup \mathcal {C} =\emptyset $
.
Proof We will assume that
![]() $\rho $
is
$\rho $
is
![]() $P^-$
, as the proof in the case of
$P^-$
, as the proof in the case of
![]() $P^-(\Lambda )$
is similar.
$P^-(\Lambda )$
is similar.
![]() $(1)\implies (2)$
. Let
$(1)\implies (2)$
. Let
![]() $\mathcal {B}=\{B_n:n\in \omega \}$
, where
$\mathcal {B}=\{B_n:n\in \omega \}$
, where
![]() $\bigcup \mathcal {B}\notin \mathcal {I}_\rho $
and
$\bigcup \mathcal {B}\notin \mathcal {I}_\rho $
and
![]() $B_n\in \mathcal {I}_{\rho }$
for every
$B_n\in \mathcal {I}_{\rho }$
for every
![]() $n\in \omega $
. For each
$n\in \omega $
. For each
![]() $n\in \omega $
, we define
$n\in \omega $
, we define
![]() $A_n = \bigcup \mathcal {B}\setminus \bigcup \{B_i:i<n\}$
. Since
$A_n = \bigcup \mathcal {B}\setminus \bigcup \{B_i:i<n\}$
. Since
![]() $\rho $
is
$\rho $
is
![]() $P^-$
, there exists
$P^-$
, there exists
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq ^\rho A_n$
for each
$\rho (F)\subseteq ^\rho A_n$
for each
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\mathcal {C}\subseteq \mathcal {B}$
be a finite subfamily. Let
$\mathcal {C}\subseteq \mathcal {B}$
be a finite subfamily. Let
![]() $n\in \omega $
be such that
$n\in \omega $
be such that
![]() $\mathcal {C}\subseteq \{B_i:i<n\}$
. Then
$\mathcal {C}\subseteq \{B_i:i<n\}$
. Then
![]() $\bigcup \mathcal {C} \subseteq \bigcup \{B_i:i<n\}$
. Let
$\bigcup \mathcal {C} \subseteq \bigcup \{B_i:i<n\}$
. Let
![]() $K\subseteq \Omega $
be a finite set such that
$K\subseteq \Omega $
be a finite set such that
![]() $\rho (F\setminus K)\subseteq A_n$
. Then
$\rho (F\setminus K)\subseteq A_n$
. Then
![]() $\rho (F\setminus K)\cap \bigcup \{B_i:i<n\}=\emptyset $
, so
$\rho (F\setminus K)\cap \bigcup \{B_i:i<n\}=\emptyset $
, so
![]() $\rho (F\setminus K)\cap \bigcup \mathcal {C}=\emptyset $
.
$\rho (F\setminus K)\cap \bigcup \mathcal {C}=\emptyset $
.
![]() $(2)\implies (1)$
. Let
$(2)\implies (1)$
. Let
![]() $A_n\in \mathcal {I}_{\rho }^+$
be such that
$A_n\in \mathcal {I}_{\rho }^+$
be such that
![]() $A_n\supseteq A_{n+1}$
and
$A_n\supseteq A_{n+1}$
and
![]() $A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
$A_n\setminus A_{n+1}\in \mathcal {I}_{\rho }$
for each
![]() $n\in \omega $
. For each
$n\in \omega $
. For each
![]() $n\in \omega $
we define
$n\in \omega $
we define
![]() $B_n=A_n\setminus A_{n+1}$
. Let
$B_n=A_n\setminus A_{n+1}$
. Let
![]() $\mathcal {B}=\{B_n:n\in \omega \}$
. Then there exists
$\mathcal {B}=\{B_n:n\in \omega \}$
. Then there exists
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F) \subseteq \bigcup \mathcal {B}$
and for every finite subfamily
$\rho (F) \subseteq \bigcup \mathcal {B}$
and for every finite subfamily
![]() $\mathcal {C}\subseteq \mathcal {B}$
there is a finite
$\mathcal {C}\subseteq \mathcal {B}$
there is a finite
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $\rho (F\setminus K) \cap \bigcup \mathcal {C} =\emptyset $
. Thus for any
$\rho (F\setminus K) \cap \bigcup \mathcal {C} =\emptyset $
. Thus for any
![]() $n\in \omega $
, we find a finite set
$n\in \omega $
, we find a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $\rho (F\setminus K) \cap \bigcup \{B_i:i<n\} =\emptyset $
. Hence
$\rho (F\setminus K) \cap \bigcup \{B_i:i<n\} =\emptyset $
. Hence
![]() $\rho (F\setminus K)\subseteq \bigcup \{B_i:i\geq n\}=A_n$
, so
$\rho (F\setminus K)\subseteq \bigcup \{B_i:i\geq n\}=A_n$
, so
![]() $\rho (F)\subseteq ^\rho A_n$
.
$\rho (F)\subseteq ^\rho A_n$
.
7 Katětov order
7.1 Katětov order between ideals
We say that an ideal
![]() $\mathcal {I}_1$
on
$\mathcal {I}_1$
on
![]() $\Lambda _1$
is above an ideal
$\Lambda _1$
is above an ideal
![]() $\mathcal {I}_2$
on
$\mathcal {I}_2$
on
![]() $\Lambda _2$
in the Katětov order (in short:
$\Lambda _2$
in the Katětov order (in short:
![]() $\mathcal {I}_2\leq _K \mathcal {I}_1$
) [Reference Katětov55] if there exists a function
$\mathcal {I}_2\leq _K \mathcal {I}_1$
) [Reference Katětov55] if there exists a function
![]() $\phi :\Lambda _1\to \Lambda _2$
such that
$\phi :\Lambda _1\to \Lambda _2$
such that
![]() $\phi [A]\notin \mathcal {I}_2$
for each
$\phi [A]\notin \mathcal {I}_2$
for each
![]() $A\notin \mathcal {I}_1$
. If
$A\notin \mathcal {I}_1$
. If
![]() $\Lambda _1=\Lambda _2$
and
$\Lambda _1=\Lambda _2$
and
![]() $\mathcal {I}_2\subseteq \mathcal {I}_1$
, then obviously the identity function on
$\mathcal {I}_2\subseteq \mathcal {I}_1$
, then obviously the identity function on
![]() $\Lambda _1$
witnesses that
$\Lambda _1$
witnesses that
![]() $\mathcal {I}_2\leq _K\mathcal {I}_1$
.
$\mathcal {I}_2\leq _K\mathcal {I}_1$
.
There are known relationships between Katětov order, P-like properties, and topological complexity.
Proposition 7.1 [Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui50, Theorem 3.8].
Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\Lambda $
.
$\Lambda $
.
-
(1)
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^-\ (\Lambda ) \iff \mathrm {Fin}^2 \not \leq _K \mathcal {I}$
.
$P^-\ (\Lambda ) \iff \mathrm {Fin}^2 \not \leq _K \mathcal {I}$
. -
(2)
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^- \iff \mathrm {Fin}^2\not \leq _K \mathcal {I}\restriction A$
for every
$P^- \iff \mathrm {Fin}^2\not \leq _K \mathcal {I}\restriction A$
for every
 $A\in \mathcal {I}^+$
.
$A\in \mathcal {I}^+$
.
Proposition 7.2.
-
(1)
 $\mathrm {Fin}^2\leq _K\mathcal {I}$
for
$\mathrm {Fin}^2\leq _K\mathcal {I}$
for
 $\mathcal {I}\in \{\mathcal {D},\mathcal {H},\mathcal {R}\}$
.
$\mathcal {I}\in \{\mathcal {D},\mathcal {H},\mathcal {R}\}$
. -
(2) If
 $\mathcal {I}$
is a
$\mathcal {I}$
is a
 $G_{\delta \sigma \delta }$
ideal, then
$G_{\delta \sigma \delta }$
ideal, then
 $\mathrm {Fin}^2 \not \leq _K \mathcal {I}\restriction A$
for every
$\mathrm {Fin}^2 \not \leq _K \mathcal {I}\restriction A$
for every
 $A\in \mathcal {I}^+$
In particular,
$A\in \mathcal {I}^+$
In particular,
 $\mathrm {Fin}^2 \not \leq _K \mathcal {W}$
and
$\mathrm {Fin}^2 \not \leq _K \mathcal {W}$
and
 $\mathrm {Fin}^2 \not \leq _K \mathcal {I}_{1/n}$
.
$\mathrm {Fin}^2 \not \leq _K \mathcal {I}_{1/n}$
.
Proof (1) Using Proposition 7.1(1), we need to show that
![]() $\mathcal {D}$
,
$\mathcal {D}$
,
![]() $\mathcal {H}$
, and
$\mathcal {H}$
, and
![]() $\mathcal {R}$
are not
$\mathcal {R}$
are not
![]() $P^-(\Lambda )$
ideals, but this follows from Proposition 6.7(4). (For
$P^-(\Lambda )$
ideals, but this follows from Proposition 6.7(4). (For
![]() $\mathcal {I} =\mathcal {R}$
, this item was earlier proved by Meza-Alcántara [Reference Meza-Alcántara67, Lemma 1.6.25].)
$\mathcal {I} =\mathcal {R}$
, this item was earlier proved by Meza-Alcántara [Reference Meza-Alcántara67, Lemma 1.6.25].)
(2) It follows from Theorem 6.2(1) and Propositions 7.1(2) and 6.7(1).
7.2 Katětov order between partition regular operations
The following notion will be crucial for showing when a class of sequentially compact spaces defined by
![]() $\rho _1$
is contained in a class of sequentially compact spaces defined by
$\rho _1$
is contained in a class of sequentially compact spaces defined by
![]() $\rho _2$
.
$\rho _2$
.
Definition 7.3. Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular (with
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular (with
![]() $\mathcal {F}_i\subseteq [\Omega _i]^\omega $
) for each
$\mathcal {F}_i\subseteq [\Omega _i]^\omega $
) for each
![]() $i=1,2$
. We say that
$i=1,2$
. We say that
![]() $\rho _1$
is above
$\rho _1$
is above
![]() $\rho _2$
in the Katětov order (in short:
$\rho _2$
in the Katětov order (in short:
![]() $\rho _2\leq _K \rho _1$
) if there is a function
$\rho _2\leq _K \rho _1$
) if there is a function
![]() $\phi :\Lambda _1\to \Lambda _2$
such that
$\phi :\Lambda _1\to \Lambda _2$
such that
or equivalently:
The following proposition reveals some basic properties of this new order on partition regular functions.
Proposition 7.4.
-
(1) The relation
 $\leq _K$
is a preorder
$\leq _K$
is a preorder
 $($
a.k.a. quasi order
$($
a.k.a. quasi order
 $)$
, i.e., it is reflexive and transitive.
$)$
, i.e., it is reflexive and transitive. -
(2) The preorder
 $\leq _K$
is upward and downward directed.
$\leq _K$
is upward and downward directed. -
(3) Let
 $\rho :\mathcal {F}\to [\Lambda ]^\omega (with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
be partition regular.
$\rho :\mathcal {F}\to [\Lambda ]^\omega (with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
be partition regular.-
(a)
 $\rho \leq _K \rho \restriction \rho (F)$
for every
$\rho \leq _K \rho \restriction \rho (F)$
for every
 $F\in \mathcal {F}$
.
$F\in \mathcal {F}$
. -
(b)
 $\rho _{\mathrm {Fin}(\Lambda )}\leq _K\rho $
.
$\rho _{\mathrm {Fin}(\Lambda )}\leq _K\rho $
.
-
Proof (1) Reflexivity of
![]() $\leq _K$
is obvious. To show transitivity, fix
$\leq _K$
is obvious. To show transitivity, fix
![]() $\mathcal {F}_i\subseteq [\Omega _i]^\omega $
and
$\mathcal {F}_i\subseteq [\Omega _i]^\omega $
and
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
,
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
,
![]() $i=1,2,3$
, and suppose that
$i=1,2,3$
, and suppose that
![]() $\rho _1\leq _K\rho _2$
is witnessed by f and
$\rho _1\leq _K\rho _2$
is witnessed by f and
![]() $\rho _2\leq _K\rho _3$
is witnessed by g. We claim that
$\rho _2\leq _K\rho _3$
is witnessed by g. We claim that
![]() $\rho _1\leq _K\rho _3$
is witnessed by
$\rho _1\leq _K\rho _3$
is witnessed by
![]() $h:\Lambda _3\to \Lambda _1$
given by
$h:\Lambda _3\to \Lambda _1$
given by
![]() $h(x)=f(g(x))$
for all
$h(x)=f(g(x))$
for all
![]() $x\in \Lambda _3$
. Let
$x\in \Lambda _3$
. Let
![]() $F_3\in \mathcal {F}_3$
. Then we can find
$F_3\in \mathcal {F}_3$
. Then we can find
![]() $F_2\in \mathcal {F}_2$
such that for every
$F_2\in \mathcal {F}_2$
such that for every
![]() $K\in [\Omega _3]^{<\omega }$
there exists
$K\in [\Omega _3]^{<\omega }$
there exists
![]() $L_K\in [\Omega _2]^{<\omega }$
such that
$L_K\in [\Omega _2]^{<\omega }$
such that
![]() $\rho _2(F_2\setminus L_K)\subseteq g\left [\rho _3(F_3\setminus K)\right ].$
Then for
$\rho _2(F_2\setminus L_K)\subseteq g\left [\rho _3(F_3\setminus K)\right ].$
Then for
![]() $F_2$
we can find
$F_2$
we can find
![]() $F_1\in \mathcal {F}_1$
such that for every
$F_1\in \mathcal {F}_1$
such that for every
![]() $L\in [\Omega _2]^{<\omega }$
there exists
$L\in [\Omega _2]^{<\omega }$
there exists
![]() $M_L\in [\Omega _1]^{<\omega }$
such that
$M_L\in [\Omega _1]^{<\omega }$
such that
![]() $\rho _1(F_1\setminus M_L)\subseteq f\left [\rho _2(F_2\setminus L)\right ].$
Now for a given
$\rho _1(F_1\setminus M_L)\subseteq f\left [\rho _2(F_2\setminus L)\right ].$
Now for a given
![]() $K\in [\Omega _3]^{<\omega }$
we have
$K\in [\Omega _3]^{<\omega }$
we have
![]() $\rho _1(F_1\setminus M_{L_K})\subseteq f\left [\rho _2(F_2\setminus L_K)\right ]\subseteq f\left [g\left [\rho _3(F_3\setminus K)\right ]\right ]=h\left [\rho _3(F_3\setminus K)\right ],$
so the proof is finished.
$\rho _1(F_1\setminus M_{L_K})\subseteq f\left [\rho _2(F_2\setminus L_K)\right ]\subseteq f\left [g\left [\rho _3(F_3\setminus K)\right ]\right ]=h\left [\rho _3(F_3\setminus K)\right ],$
so the proof is finished.
(2) Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
with
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
with
![]() $\mathcal {F}_i\subseteq [\Omega _i]^\omega $
be partition regular for
$\mathcal {F}_i\subseteq [\Omega _i]^\omega $
be partition regular for
![]() $i=0,1$
. We define the following partition regular functions
$i=0,1$
. We define the following partition regular functions
![]() $\pi : \{F_0\times F_1: F_0\in \mathcal {F}_0, F_1\in \mathcal {F}_1\}\to [\Lambda _0\times \Lambda _1]^{\omega }$
by
$\pi : \{F_0\times F_1: F_0\in \mathcal {F}_0, F_1\in \mathcal {F}_1\}\to [\Lambda _0\times \Lambda _1]^{\omega }$
by
![]() $\pi (F_0\times F_1)=\rho _0(F_0)\times \rho _1(F_1)$
and
$\pi (F_0\times F_1)=\rho _0(F_0)\times \rho _1(F_1)$
and
![]() $\sigma : \mathcal {F}_0\oplus \mathcal {F}_1 \to [\Lambda _0\oplus \Lambda _1]^{\omega }$
by
$\sigma : \mathcal {F}_0\oplus \mathcal {F}_1 \to [\Lambda _0\oplus \Lambda _1]^{\omega }$
by
![]() $\sigma ((F_0\times \{0\}) \cup (F_1\times \{1\}))= (\rho _0(F_0)\times \{0\}) \cup (\rho _1(F_1)\times \{1\}).$
$\sigma ((F_0\times \{0\}) \cup (F_1\times \{1\}))= (\rho _0(F_0)\times \{0\}) \cup (\rho _1(F_1)\times \{1\}).$
Then
![]() $\sigma \leq _K \rho _i$
(
$\sigma \leq _K \rho _i$
(
![]() $i=0,1$
) is witnessed by a function
$i=0,1$
) is witnessed by a function
![]() $\phi _i:\Lambda _i\to \Lambda _0\oplus \Lambda _1$
given by
$\phi _i:\Lambda _i\to \Lambda _0\oplus \Lambda _1$
given by
![]() $\phi _i(x) = (x,i)$
, whereas
$\phi _i(x) = (x,i)$
, whereas
![]() $\rho _i\leq _K \pi $
(
$\rho _i\leq _K \pi $
(
![]() $i=0,1$
) is witness by a function
$i=0,1$
) is witness by a function
![]() $\psi _i:\Lambda _0\times \Lambda _1\to \Lambda _i$
given by
$\psi _i:\Lambda _0\times \Lambda _1\to \Lambda _i$
given by
![]() $\psi _i(x_0,x_1) = x_i$
.
$\psi _i(x_0,x_1) = x_i$
.
(3a) Let
![]() $F\in \mathcal {F}$
. We claim that
$F\in \mathcal {F}$
. We claim that
![]() $\phi : \rho (F)\to \Lambda $
given by
$\phi : \rho (F)\to \Lambda $
given by
![]() $\phi (\lambda )=\lambda $
is a witness for
$\phi (\lambda )=\lambda $
is a witness for
![]() $\rho \leq _K \rho \restriction \rho (F)$
. Let
$\rho \leq _K \rho \restriction \rho (F)$
. Let
![]() $F_1\in \mathcal {F}\restriction \rho (F)$
. Then
$F_1\in \mathcal {F}\restriction \rho (F)$
. Then
![]() $F_2=F_1$
is such that for every finite set
$F_2=F_1$
is such that for every finite set
![]() $K_1\subseteq \Omega $
we take
$K_1\subseteq \Omega $
we take
![]() $K_2=K_1$
and see that
$K_2=K_1$
and see that
![]() $\rho (F_2\setminus K_2)\subseteq \phi (\rho (F_1\setminus K_1))$
.
$\rho (F_2\setminus K_2)\subseteq \phi (\rho (F_1\setminus K_1))$
.
(3b) We claim that
![]() $\phi :\Lambda \to \Lambda $
given by
$\phi :\Lambda \to \Lambda $
given by
![]() $\phi (\lambda )=\lambda $
is a witness for
$\phi (\lambda )=\lambda $
is a witness for
![]() $\rho _{\mathrm {Fin}(\Lambda )}\leq _K \rho $
. Let
$\rho _{\mathrm {Fin}(\Lambda )}\leq _K \rho $
. Let
![]() $F\in \mathcal {F}$
. Let
$F\in \mathcal {F}$
. Let
![]() $\Omega =\{o_n:n\in \omega \}$
. Since
$\Omega =\{o_n:n\in \omega \}$
. Since
![]() $\rho (F\setminus \{o_i:i<n\})$
is infinite for every
$\rho (F\setminus \{o_i:i<n\})$
is infinite for every
![]() $n\in \omega $
, we can pick a one-to-one sequence
$n\in \omega $
, we can pick a one-to-one sequence
![]() $(a_n:n\in \omega )$
such that
$(a_n:n\in \omega )$
such that
![]() $a_n\in \rho (F\setminus \{o_i:i<n\})$
for every
$a_n\in \rho (F\setminus \{o_i:i<n\})$
for every
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $A=\{a_n:n\in \omega \}\in \mathrm {Fin}(\Lambda )^+$
is an infinite set. For a finite set
$A=\{a_n:n\in \omega \}\in \mathrm {Fin}(\Lambda )^+$
is an infinite set. For a finite set
![]() $K\subseteq \Omega $
there is
$K\subseteq \Omega $
there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $K\subseteq \{o_i:i<n\}$
. Then
$K\subseteq \{o_i:i<n\}$
. Then
![]() $L=\{a_i:i<n\}$
is finite subset of
$L=\{a_i:i<n\}$
is finite subset of
![]() $\Lambda $
and
$\Lambda $
and
![]() $A\setminus L \subseteq \rho (F\setminus \{o_i:i<n\})\subseteq \rho (F\setminus K)$
.
$A\setminus L \subseteq \rho (F\setminus \{o_i:i<n\})\subseteq \rho (F\setminus K)$
.
Now we compare the relation
![]() $\leq _K$
between partition regular operations with the relation
$\leq _K$
between partition regular operations with the relation
![]() $\leq _K$
between ideals.
$\leq _K$
between ideals.
Proposition 7.5. Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
for each
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
for each
![]() $i=1,2$
and
$i=1,2$
and
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular. Let
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular. Let
![]() $\mathcal {I}$
be ideal.
$\mathcal {I}$
be ideal.
-
(1)
 $\rho _2\leq _K\rho _1 \implies \mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
with the same witnessing function.
$\rho _2\leq _K\rho _1 \implies \mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
with the same witnessing function. -
(2)
-
(a) If
 $\rho _2$
is
$\rho _2$
is
 $P^+ (in particular,\ \textit{if}\ \rho _2=\rho _{\mathcal {I}}$
and
$P^+ (in particular,\ \textit{if}\ \rho _2=\rho _{\mathcal {I}}$
and
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^+)$
, then
$P^+)$
, then
 $\rho _2\leq _K\rho _1 \iff \mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
.
$\rho _2\leq _K\rho _1 \iff \mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
. -
(b)
 $\rho \leq _K\rho _{\mathcal {I}} \iff \mathcal {I}_{\rho }\leq _K\mathcal {I}$
.
$\rho \leq _K\rho _{\mathcal {I}} \iff \mathcal {I}_{\rho }\leq _K\mathcal {I}$
.
-
Proof (1) Let
![]() $\mathcal {F}_i\subseteq [\Omega _i]^\omega $
for
$\mathcal {F}_i\subseteq [\Omega _i]^\omega $
for
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $\phi $
be a witness for
$\phi $
be a witness for
![]() $\rho _2\leq _K\rho _1$
. We claim that
$\rho _2\leq _K\rho _1$
. We claim that
![]() $\phi $
is also a witness for
$\phi $
is also a witness for
![]() $ \mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
. Let
$ \mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
. Let
![]() $A\notin \mathcal {I}_{\rho _1}$
. Then there is
$A\notin \mathcal {I}_{\rho _1}$
. Then there is
![]() $F_1\in \mathcal {F}_1$
with
$F_1\in \mathcal {F}_1$
with
![]() $\rho _1(F_1)\subseteq A$
. Since
$\rho _1(F_1)\subseteq A$
. Since
![]() $\rho _2\leq _K\rho _1$
, there is
$\rho _2\leq _K\rho _1$
, there is
![]() $F_2\in \mathcal {F}_2$
and a finite set
$F_2\in \mathcal {F}_2$
and a finite set
![]() $K_2\subseteq \Omega _2$
such that
$K_2\subseteq \Omega _2$
such that
![]() $\rho _2(F_2\setminus K_2)\subseteq \phi [\rho _1(F_1\setminus \emptyset )]=\phi [\rho _1(F_1)]$
. Since
$\rho _2(F_2\setminus K_2)\subseteq \phi [\rho _1(F_1\setminus \emptyset )]=\phi [\rho _1(F_1)]$
. Since
![]() $F_2\setminus K_2\in \mathcal {F}_2$
and
$F_2\setminus K_2\in \mathcal {F}_2$
and
![]() $\rho _2(F_2\setminus K_2)\subseteq \phi [A]$
, we obtain that
$\rho _2(F_2\setminus K_2)\subseteq \phi [A]$
, we obtain that
![]() $\phi [A]\notin \mathcal {I}_{\rho _2}$
. Thus the proof of this item is finished.
$\phi [A]\notin \mathcal {I}_{\rho _2}$
. Thus the proof of this item is finished.
(2a) The “in particular” part follows from Propositions 3.3(2) and 6.5(2).
We only have to show the implication “
![]() $\impliedby $
,” because the reversed implication is true by item (1). Let
$\impliedby $
,” because the reversed implication is true by item (1). Let
![]() $\phi :\Lambda _1\to \Lambda _2$
be a witness for
$\phi :\Lambda _1\to \Lambda _2$
be a witness for
![]() $\mathcal {I}_{\rho _2}\leq _K \mathcal {I}_{\rho _1}$
. We claim that
$\mathcal {I}_{\rho _2}\leq _K \mathcal {I}_{\rho _1}$
. We claim that
![]() $\phi $
is also a witness for
$\phi $
is also a witness for
![]() $\rho _2\leq _K\rho _1$
. Let
$\rho _2\leq _K\rho _1$
. Let
![]() $F_1\in \mathcal {F}_1$
,
$F_1\in \mathcal {F}_1$
,
![]() $\Omega _1=\{o_n:n\in \omega \}$
and
$\Omega _1=\{o_n:n\in \omega \}$
and
![]() $B_n = \phi [\rho _1(F_1\setminus \{o_i:i<n\})]$
for each
$B_n = \phi [\rho _1(F_1\setminus \{o_i:i<n\})]$
for each
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $B_n\notin \mathcal {I}_{\rho _2}$
,
$B_n\notin \mathcal {I}_{\rho _2}$
,
![]() $B_n\supseteq B_{n+1}$
for each
$B_n\supseteq B_{n+1}$
for each
![]() $n\in \omega $
, and since
$n\in \omega $
, and since
![]() $\mathcal {I}_{\rho _2}$
is
$\mathcal {I}_{\rho _2}$
is
![]() $P^+$
, there is
$P^+$
, there is
![]() $F_2\in \mathcal {F}_2$
such that for each
$F_2\in \mathcal {F}_2$
such that for each
![]() $n\in \omega $
there is a finite set
$n\in \omega $
there is a finite set
![]() $L_n\subseteq \Omega _2$
with
$L_n\subseteq \Omega _2$
with
![]() $\rho _2(F_2\setminus L_n)\subseteq B_n$
. Now, for any finite set
$\rho _2(F_2\setminus L_n)\subseteq B_n$
. Now, for any finite set
![]() $K_1\subseteq \Omega _1$
there is
$K_1\subseteq \Omega _1$
there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $K_1\subseteq \{o_i:i<n\}$
. Let
$K_1\subseteq \{o_i:i<n\}$
. Let
![]() $K_2=L_n$
. Then
$K_2=L_n$
. Then
![]() $\rho _2(F_2\setminus K_2) \subseteq B_n \subseteq \phi [\rho _1(F_1\setminus K_1)] $
. Thus the proof of this item is finished.
$\rho _2(F_2\setminus K_2) \subseteq B_n \subseteq \phi [\rho _1(F_1\setminus K_1)] $
. Thus the proof of this item is finished.
(2b) The implication “
![]() $\implies $
” follows from item (1) and Proposition 3.3(2), so below we show the reverse implication.
$\implies $
” follows from item (1) and Proposition 3.3(2), so below we show the reverse implication.
Suppose that
![]() $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
![]() $\phi :\Lambda \to \Lambda $
be a witness of
$\phi :\Lambda \to \Lambda $
be a witness of
![]() $\mathcal {I}_{\rho }\leq _K\mathcal {I}$
. We claim that the same
$\mathcal {I}_{\rho }\leq _K\mathcal {I}$
. We claim that the same
![]() $\phi $
is also a witness for
$\phi $
is also a witness for
![]() $\rho \leq _K\rho _{\mathcal {I}}$
. Indeed, for
$\rho \leq _K\rho _{\mathcal {I}}$
. Indeed, for
![]() $A\notin \mathcal {I}$
we find
$A\notin \mathcal {I}$
we find
![]() $E\in \mathcal {F}$
such that
$E\in \mathcal {F}$
such that
![]() $\rho (E)\subseteq \phi [A]$
. Using Proposition 3.2, we can find a set
$\rho (E)\subseteq \phi [A]$
. Using Proposition 3.2, we can find a set
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $F\subseteq E$
and for any finite set
$F\subseteq E$
and for any finite set
![]() $K\subseteq \Lambda _1$
there exists a finite set
$K\subseteq \Lambda _1$
there exists a finite set
![]() $L\subseteq \Omega $
with
$L\subseteq \Omega $
with
![]() $\rho (F\setminus L)\subseteq \rho (F)\setminus \phi [K]$
. Consequently,
$\rho (F\setminus L)\subseteq \rho (F)\setminus \phi [K]$
. Consequently,
![]() $\rho (F\setminus L)\subseteq \phi [A]\setminus \phi [K] \subseteq \phi [A\setminus K]$
.
$\rho (F\setminus L)\subseteq \phi [A]\setminus \phi [K] \subseteq \phi [A\setminus K]$
.
The following example shows that in general
![]() $\rho _2\leq _K\rho _1$
and
$\rho _2\leq _K\rho _1$
and
![]() $\mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
are not equivalent.
$\mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
are not equivalent.
Example 7.6.
![]() $\mathrm {Fin}^2\leq _K\mathcal {H}$
, but
$\mathrm {Fin}^2\leq _K\mathcal {H}$
, but
![]() $\rho _{\mathrm {Fin}^2}\not \leq _K\operatorname {\mathrm {FS}}$
.
$\rho _{\mathrm {Fin}^2}\not \leq _K\operatorname {\mathrm {FS}}$
.
Proof By Proposition 7.2(1) we know that
![]() $\mathcal {I}_{\rho _{\mathrm {Fin}^2}}=\mathrm {Fin}^2\leq _K\mathcal {H} = \mathcal {I}_{\operatorname {\mathrm {FS}}}$
. Thus, we only need to show that
$\mathcal {I}_{\rho _{\mathrm {Fin}^2}}=\mathrm {Fin}^2\leq _K\mathcal {H} = \mathcal {I}_{\operatorname {\mathrm {FS}}}$
. Thus, we only need to show that
![]() $\rho _{\mathrm {Fin}^2}\not \leq _K\operatorname {\mathrm {FS}}$
.
$\rho _{\mathrm {Fin}^2}\not \leq _K\operatorname {\mathrm {FS}}$
.
Suppose that
![]() $\rho _{\mathrm {Fin}^2}\leq _K \operatorname {\mathrm {FS}}$
and let
$\rho _{\mathrm {Fin}^2}\leq _K \operatorname {\mathrm {FS}}$
and let
![]() $\phi :\omega \to \omega ^2$
be a witness for this. For each
$\phi :\omega \to \omega ^2$
be a witness for this. For each
![]() $n\in \omega $
, we define
$n\in \omega $
, we define
![]() $A_n = \phi ^{-1}[(\omega \setminus n)\times \omega ]$
. Then
$A_n = \phi ^{-1}[(\omega \setminus n)\times \omega ]$
. Then
![]() $A_0=\omega $
,
$A_0=\omega $
,
![]() $A_n\supseteq A_{n+1}$
, and
$A_n\supseteq A_{n+1}$
, and
![]() $A_n\setminus A_{n+1}\subseteq \phi ^{-1}[\{n\}\times \omega ]\in \mathcal {H}$
for each
$A_n\setminus A_{n+1}\subseteq \phi ^{-1}[\{n\}\times \omega ]\in \mathcal {H}$
for each
![]() $n\in \omega $
by Proposition 7.5(1). Since
$n\in \omega $
by Proposition 7.5(1). Since
![]() $\operatorname {\mathrm {FS}}$
is
$\operatorname {\mathrm {FS}}$
is
![]() $P^-(\omega )$
by Proposition 6.7(3), there is
$P^-(\omega )$
by Proposition 6.7(3), there is
![]() $F\in [\omega ]^\omega $
such that for every
$F\in [\omega ]^\omega $
such that for every
![]() $n\in \omega $
there is a finite set
$n\in \omega $
there is a finite set
![]() $K_n\subseteq \omega $
with
$K_n\subseteq \omega $
with
![]() $\operatorname {\mathrm {FS}}(F\setminus K_n) \subseteq A_n$
. Now, using the fact that
$\operatorname {\mathrm {FS}}(F\setminus K_n) \subseteq A_n$
. Now, using the fact that
![]() $\rho _{\mathrm {Fin}^2}\leq _K\operatorname {\mathrm {FS}}$
, we find
$\rho _{\mathrm {Fin}^2}\leq _K\operatorname {\mathrm {FS}}$
, we find
![]() $B\notin \mathrm {Fin}^2$
such that for every
$B\notin \mathrm {Fin}^2$
such that for every
![]() $n\in \omega $
there is a finite set
$n\in \omega $
there is a finite set
![]() $L_n\subseteq \omega ^2$
with
$L_n\subseteq \omega ^2$
with
![]() $B\setminus L_n\subseteq \phi [\operatorname {\mathrm {FS}}(F\setminus K_n)] \subseteq \phi [A_n] \subseteq (\omega \setminus n)\times \omega $
. In particular, sets
$B\setminus L_n\subseteq \phi [\operatorname {\mathrm {FS}}(F\setminus K_n)] \subseteq \phi [A_n] \subseteq (\omega \setminus n)\times \omega $
. In particular, sets
![]() $B\cap (\{n\}\times \omega )$
are finite for every n, so
$B\cap (\{n\}\times \omega )$
are finite for every n, so
![]() $B\in \mathrm {Fin}^2$
, a contradiction.
$B\in \mathrm {Fin}^2$
, a contradiction.
Remark. The partition regular function
![]() $\rho _{\mathrm {Fin}^2}$
from Example 7.6 is not
$\rho _{\mathrm {Fin}^2}$
from Example 7.6 is not
![]() $P^-$
. In Example 15.5 we will show that there are partition regular functions
$P^-$
. In Example 15.5 we will show that there are partition regular functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
which are
$\rho _2$
which are
![]() $P^-$
and have small accretions such that
$P^-$
and have small accretions such that
![]() $\mathcal {I}_{\rho _2}\subseteq \mathcal {I}_{\rho _1}$
(in particular,
$\mathcal {I}_{\rho _2}\subseteq \mathcal {I}_{\rho _1}$
(in particular,
![]() $\mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
), but
$\mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
), but
![]() $\rho _2\not \leq _K\rho _1$
.
$\rho _2\not \leq _K\rho _1$
.
7.3 Katětov order between
 $\operatorname {\mathrm {FS}}, r, \Delta , \mathcal {W}, \text { and } \mathcal {I}_{1/n}$
$\operatorname {\mathrm {FS}}, r, \Delta , \mathcal {W}, \text { and } \mathcal {I}_{1/n}$
Theorem 7.7.
-
(1)
 $\mathcal {H} \not \leq _K \mathcal {R}$
. In particular,
$\mathcal {H} \not \leq _K \mathcal {R}$
. In particular,
 $\operatorname {\mathrm {FS}}\not \leq _K r$
.
$\operatorname {\mathrm {FS}}\not \leq _K r$
. -
(2)
 $\mathcal {R} \not \leq _K \mathcal {H}$
. In particular,
$\mathcal {R} \not \leq _K \mathcal {H}$
. In particular,
 $r\not \leq _K\operatorname {\mathrm {FS}}$
.
$r\not \leq _K\operatorname {\mathrm {FS}}$
. -
(3)
 $\Delta \leq _K \operatorname {\mathrm {FS}}$
and
$\Delta \leq _K \operatorname {\mathrm {FS}}$
and
 $\mathcal {D}\subseteq \mathcal {H}$
. In particular,
$\mathcal {D}\subseteq \mathcal {H}$
. In particular,
 $\mathcal {D}\leq _K\mathcal {H}$
.
$\mathcal {D}\leq _K\mathcal {H}$
. -
(4)
 $\Delta \leq _K r$
. In particular,
$\Delta \leq _K r$
. In particular,
 $\mathcal {D}\leq _K\mathcal {R}$
.
$\mathcal {D}\leq _K\mathcal {R}$
. -
(5)
 $\mathcal {R}\not \leq _K \mathcal {D}$
. In particular,
$\mathcal {R}\not \leq _K \mathcal {D}$
. In particular,
 $r\not \leq _K \Delta $
.
$r\not \leq _K \Delta $
. -
(6)
 $\mathcal {H}\not \leq _K \mathcal {D}$
. In particular,
$\mathcal {H}\not \leq _K \mathcal {D}$
. In particular,
 $\operatorname {\mathrm {FS}}\not \leq _K \Delta $
.
$\operatorname {\mathrm {FS}}\not \leq _K \Delta $
. -
(7)
 $\mathcal {I}_{1/n} \not \leq _K \mathcal {R}$
. In particular,
$\mathcal {I}_{1/n} \not \leq _K \mathcal {R}$
. In particular,
 $\rho _{\mathcal {I}_{1/n}} \not \leq _K r$
.
$\rho _{\mathcal {I}_{1/n}} \not \leq _K r$
. -
(8)
 $\mathcal {I}_{1/n} \not \leq _K \mathcal {H}$
. In particular,
$\mathcal {I}_{1/n} \not \leq _K \mathcal {H}$
. In particular,
 $\rho _{\mathcal {I}_{1/n}} \not \leq _K \operatorname {\mathrm {FS}}$
.
$\rho _{\mathcal {I}_{1/n}} \not \leq _K \operatorname {\mathrm {FS}}$
. -
(9)
 $\mathcal {I}_{1/n} \not \leq _K \mathcal {D}$
. In particular,
$\mathcal {I}_{1/n} \not \leq _K \mathcal {D}$
. In particular,
 $\rho _{\mathcal {I}_{1/n}} \not \leq _K \Delta $
.
$\rho _{\mathcal {I}_{1/n}} \not \leq _K \Delta $
. -
(10)
 $\mathcal {I}_{1/n} \not \leq _K \mathcal {W}$
. In particular,
$\mathcal {I}_{1/n} \not \leq _K \mathcal {W}$
. In particular,
 $\rho _{\mathcal {I}_{1/n}} \not \leq _K \rho _{\mathcal {W}}$
.
$\rho _{\mathcal {I}_{1/n}} \not \leq _K \rho _{\mathcal {W}}$
. -
(11)
 $\mathcal {D} \not \leq _K \mathcal {I}_{1/n}$
. In particular,
$\mathcal {D} \not \leq _K \mathcal {I}_{1/n}$
. In particular,
 $\Delta \not \leq _K \rho _{\mathcal {I}_{1/n}}$
.
$\Delta \not \leq _K \rho _{\mathcal {I}_{1/n}}$
. -
(12)
 $\mathcal {H} \not \leq _K \mathcal {I}_{1/n}$
. In particular,
$\mathcal {H} \not \leq _K \mathcal {I}_{1/n}$
. In particular,
 $\operatorname {\mathrm {FS}} \not \leq _K \rho _{\mathcal {I}_{1/n}}$
.
$\operatorname {\mathrm {FS}} \not \leq _K \rho _{\mathcal {I}_{1/n}}$
. -
(13)
 $\mathcal {R} \not \leq _K \mathcal {I}_{1/n}$
. In particular,
$\mathcal {R} \not \leq _K \mathcal {I}_{1/n}$
. In particular,
 $r \not \leq _K \rho _{\mathcal {I}_{1/n}}$
.
$r \not \leq _K \rho _{\mathcal {I}_{1/n}}$
. -
(14)
 $\mathcal {D}\not \leq _K\mathcal {W}$
. In particular,
$\mathcal {D}\not \leq _K\mathcal {W}$
. In particular,
 $\Delta \not \leq _K \rho _{\mathcal {W}}$
.
$\Delta \not \leq _K \rho _{\mathcal {W}}$
. -
(15)
 $\mathcal {H}\not \leq _K\mathcal {W}$
. In particular,
$\mathcal {H}\not \leq _K\mathcal {W}$
. In particular,
 $\operatorname {\mathrm {FS}} \not \leq _K \rho _{\mathcal {W}}$
.
$\operatorname {\mathrm {FS}} \not \leq _K \rho _{\mathcal {W}}$
. -
(16)
 $\mathcal {R}\not \leq _K\mathcal {W}$
. In particular,
$\mathcal {R}\not \leq _K\mathcal {W}$
. In particular,
 $r\not \leq _K \rho _{\mathcal {W}}$
.
$r\not \leq _K \rho _{\mathcal {W}}$
.
Proof The “in particular” parts follow from Proposition 7.5(1).
The proofs of items (1), (2), (7), and (8) can be found in [Reference Filipów, Kowitz and Kwela23] (item (8) is also proved in [Reference Filipów, Kowitz, Kwela and Tryba24, Theorem 3.2(1)]). Item (10) can be found in [Reference Flašková30, Lemma 3.1].
(3) The inclusion is proved in [Reference Shi73, Proposition 4.2.1] (see also [Reference Filipów22, Propositions 4.2]). Below, we show that
![]() $\Delta \leq _K \operatorname {\mathrm {FS}}$
.
$\Delta \leq _K \operatorname {\mathrm {FS}}$
.
We claim that the identity function
![]() $\phi :\omega \to \omega $
,
$\phi :\omega \to \omega $
,
![]() $\phi (n)=n$
for every
$\phi (n)=n$
for every
![]() $n\in \omega $
is a witness for
$n\in \omega $
is a witness for
![]() $\Delta \leq _K \operatorname {\mathrm {FS}}$
.
$\Delta \leq _K \operatorname {\mathrm {FS}}$
.
For any infinite set
![]() $A\subseteq \omega $
, we define an infinite set
$A\subseteq \omega $
, we define an infinite set
![]() $B=\{\sum _{i\leq n}a_i:n\in \omega \}$
, where
$B=\{\sum _{i\leq n}a_i:n\in \omega \}$
, where
![]() $\{a_n:n\in \omega \}$
is the increasing enumeration of A. Next, for any finite set K, we define a finite set
$\{a_n:n\in \omega \}$
is the increasing enumeration of A. Next, for any finite set K, we define a finite set
![]() $L=\{0,1,\dots ,\sum _{i\leq k}a_i\}$
, where
$L=\{0,1,\dots ,\sum _{i\leq k}a_i\}$
, where
![]() $k = \max \{i\in \omega :a_i\in K\}$
(for
$k = \max \{i\in \omega :a_i\in K\}$
(for
![]() $K=\emptyset $
we take
$K=\emptyset $
we take
![]() $k=0$
). Finally, we observe that
$k=0$
). Finally, we observe that
![]() $\Delta (B\setminus L)\subseteq \operatorname {\mathrm {FS}}(A\setminus K) = \phi [\operatorname {\mathrm {FS}}(A\setminus K)]$
, so the proof is finished.
$\Delta (B\setminus L)\subseteq \operatorname {\mathrm {FS}}(A\setminus K) = \phi [\operatorname {\mathrm {FS}}(A\setminus K)]$
, so the proof is finished.
(4) We claim that
![]() $\phi : [\omega ]^2\to \omega $
given by the formula
$\phi : [\omega ]^2\to \omega $
given by the formula
![]() $\phi (\{n,k\})=n-k$
, where
$\phi (\{n,k\})=n-k$
, where
![]() $n>k$
, is a witness for
$n>k$
, is a witness for
![]() $\Delta \leq _K r$
. For any infinite set
$\Delta \leq _K r$
. For any infinite set
![]() $A\subseteq \omega $
, we take
$A\subseteq \omega $
, we take
![]() $B = A$
. Then for any finite set
$B = A$
. Then for any finite set
![]() $K\subseteq \omega $
, we take
$K\subseteq \omega $
, we take
![]() $L=K$
. Next, we notice that
$L=K$
. Next, we notice that
![]() $\Delta (B\setminus L) = \Delta (A\setminus K) = \phi [[A\setminus K]^2] = \phi [r(A\setminus K)]$
, so the proof is finished.
$\Delta (B\setminus L) = \Delta (A\setminus K) = \phi [[A\setminus K]^2] = \phi [r(A\setminus K)]$
, so the proof is finished.
(5) It follows from items (3) and (2).
(6) It follows from items (4) and (1).
(9) It follows from items (8) and (3).
(11) Suppose otherwise:
![]() $\mathcal {D}\leq _K\mathcal {I}_{1/n}$
. By Proposition 7.2(1)
$\mathcal {D}\leq _K\mathcal {I}_{1/n}$
. By Proposition 7.2(1)
![]() $\mathrm {Fin}^2\leq _K \mathcal {D}$
, so
$\mathrm {Fin}^2\leq _K \mathcal {D}$
, so
![]() $\mathrm {Fin}^2\leq _K\mathcal {I}_{1/n}$
. By Proposition 7.1(1), we obtain that
$\mathrm {Fin}^2\leq _K\mathcal {I}_{1/n}$
. By Proposition 7.1(1), we obtain that
![]() $\mathcal {I}_{1/n}$
is not a
$\mathcal {I}_{1/n}$
is not a
![]() $P^-(\omega )$
ideal, a contradiction with Proposition 6.7(1).
$P^-(\omega )$
ideal, a contradiction with Proposition 6.7(1).
(12) It follows from items (3) and (11).
(13) It follows from items (4) and (11).
(14) Suppose otherwise:
![]() $\mathcal {D}\leq _K\mathcal {W}$
. Using Proposition 7.2(1) we get that
$\mathcal {D}\leq _K\mathcal {W}$
. Using Proposition 7.2(1) we get that
![]() $\mathrm {Fin}^2\leq _K \mathcal {D}$
, so
$\mathrm {Fin}^2\leq _K \mathcal {D}$
, so
![]() $\mathrm {Fin}^2\leq _K\mathcal {W}$
. However, since
$\mathrm {Fin}^2\leq _K\mathcal {W}$
. However, since
![]() $\mathcal {W}$
is
$\mathcal {W}$
is
![]() $F_\sigma $
(see [Reference Filipów, Kwela and Tryba25, Example 4.12]),
$F_\sigma $
(see [Reference Filipów, Kwela and Tryba25, Example 4.12]),
![]() $\mathrm {Fin}^2\not \leq _K\mathcal {W}$
by [Reference Debs and Raymond13, Theorems 7.5 and 9.1]. A contradiction.
$\mathrm {Fin}^2\not \leq _K\mathcal {W}$
by [Reference Debs and Raymond13, Theorems 7.5 and 9.1]. A contradiction.
(15) The proof can be found in [Reference Kojman and Shelah59, Lemma 1], but it also follows from items (3) and (14).
(16) It follows from items (3) and (14).
Question 7.8. Is
![]() $\mathcal {W} \leq _K \mathcal {I}$
for
$\mathcal {W} \leq _K \mathcal {I}$
for
![]() $\mathcal {I}\in \{\mathcal {I}_{1/n},\mathcal {H}, \mathcal {R},\mathcal {D}\}$
?
$\mathcal {I}\in \{\mathcal {I}_{1/n},\mathcal {H}, \mathcal {R},\mathcal {D}\}$
?
Remark. The positive answer to Question 7.8 for
![]() $\mathcal {I}=\mathcal {I}_{1/n}$
is implied by the inclusion
$\mathcal {I}=\mathcal {I}_{1/n}$
is implied by the inclusion
![]() $\mathcal {W}\subseteq \mathcal {I}_{1/n}$
that is known as the Erdős conjecture on arithmetic progressions (a.k.a. the Erdős–Turán conjecture) which can be rephrased in the following manner: if the sum of the reciprocals of the elements of a set
$\mathcal {W}\subseteq \mathcal {I}_{1/n}$
that is known as the Erdős conjecture on arithmetic progressions (a.k.a. the Erdős–Turán conjecture) which can be rephrased in the following manner: if the sum of the reciprocals of the elements of a set
![]() $A\subseteq \omega $
diverges, then A contains arbitrarily long finite arithmetic progressions.
$A\subseteq \omega $
diverges, then A contains arbitrarily long finite arithmetic progressions.
8 Tallness and homogeneity
8.1 Tallness of partition regular functions
An ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\Lambda $
is tall if for every infinite set
$\Lambda $
is tall if for every infinite set
![]() $A\subseteq \Lambda $
there exists an infinite set
$A\subseteq \Lambda $
there exists an infinite set
![]() $B\subseteq A$
such that
$B\subseteq A$
such that
![]() $B\in \mathcal {I}$
[Reference Mathias64, p. 210] (see also [Reference Mathias65, Definition 0.6]). It is not difficult to see that
$B\in \mathcal {I}$
[Reference Mathias64, p. 210] (see also [Reference Mathias65, Definition 0.6]). It is not difficult to see that
![]() $\mathcal {I}$
is not tall
$\mathcal {I}$
is not tall
![]() $\iff \mathcal {I}\leq _K\mathcal {J}$
for every ideal
$\iff \mathcal {I}\leq _K\mathcal {J}$
for every ideal
![]() $\mathcal {J} \iff \mathcal {I}\leq _K\mathrm {Fin} \iff \mathcal {I}\restriction A=\mathrm {Fin}(A)$
for some
$\mathcal {J} \iff \mathcal {I}\leq _K\mathrm {Fin} \iff \mathcal {I}\restriction A=\mathrm {Fin}(A)$
for some
![]() $A\in \mathcal {I}^+$
.
$A\in \mathcal {I}^+$
.
The following proposition characterizes tallness of the ideal
![]() $\mathcal {I}_\rho $
in terms of
$\mathcal {I}_\rho $
in terms of
![]() $\rho $
and serves as a definition of tallness of partition regular functions.
$\rho $
and serves as a definition of tallness of partition regular functions.
Proposition 8.1. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular
![]() $(with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
. The following conditions are equivalent.
$(with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
. The following conditions are equivalent.
-
(1)
 $\mathcal {I}_{\rho }$
is tall.
$\mathcal {I}_{\rho }$
is tall. -
(2) There exists a partition regular function
 $\tau $
such that
$\tau $
such that
 $\rho \not \leq _K \tau $
.
$\rho \not \leq _K \tau $
. -
(3)
 $\mathcal {I}_{\rho }\restriction \rho (F) \neq \mathrm {Fin}(\rho (F))$
for every
$\mathcal {I}_{\rho }\restriction \rho (F) \neq \mathrm {Fin}(\rho (F))$
for every
 $F\in \mathcal {F}$
.
$F\in \mathcal {F}$
. -
(4)
 $\rho \not \leq _K\rho _{\mathrm {Fin}(\Lambda )}$
.
$\rho \not \leq _K\rho _{\mathrm {Fin}(\Lambda )}$
.
Proof (1)
![]() $\implies $
(2) If
$\implies $
(2) If
![]() $\mathcal {I}_\rho $
is tall, there is an ideal
$\mathcal {I}_\rho $
is tall, there is an ideal
![]() $\mathcal {J}$
such that
$\mathcal {J}$
such that
![]() $\mathcal {I}_\rho \not \leq _K\mathcal {J}$
. Then
$\mathcal {I}_\rho \not \leq _K\mathcal {J}$
. Then
![]() $\rho \not \leq _K\rho _{\mathcal {J}}$
by Proposition 7.5(1).
$\rho \not \leq _K\rho _{\mathcal {J}}$
by Proposition 7.5(1).
(2)
![]() $\implies $
(3) Suppose that there is
$\implies $
(3) Suppose that there is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\mathcal {I}_{\rho }\restriction \rho (F) = \mathrm {Fin}(\rho (F))$
. We will show that
$\mathcal {I}_{\rho }\restriction \rho (F) = \mathrm {Fin}(\rho (F))$
. We will show that
![]() $\rho \leq _K \tau $
for every partition regular function
$\rho \leq _K \tau $
for every partition regular function
![]() $\tau $
.
$\tau $
.
Take any partition regular function
![]() $\tau :\mathcal {G}\to [\Sigma ]^\omega $
with
$\tau :\mathcal {G}\to [\Sigma ]^\omega $
with
![]() $\mathcal {G}\subseteq [\Gamma ]^\omega $
.
$\mathcal {G}\subseteq [\Gamma ]^\omega $
.
Let
![]() $\phi :\Sigma \to \Lambda $
be a one-to-one function such that
$\phi :\Sigma \to \Lambda $
be a one-to-one function such that
![]() $\phi [\Sigma ]=\rho (F)$
. We claim that
$\phi [\Sigma ]=\rho (F)$
. We claim that
![]() $\phi $
is a witness for
$\phi $
is a witness for
![]() $\rho \leq _K\tau $
.
$\rho \leq _K\tau $
.
Let
![]() $G\in \mathcal {G}$
and
$G\in \mathcal {G}$
and
![]() $\Gamma =\{\gamma _n:n\in \omega \}$
. Since
$\Gamma =\{\gamma _n:n\in \omega \}$
. Since
![]() $\phi [\tau (G\setminus \{\gamma _i:i<n\})]$
is infinite for every
$\phi [\tau (G\setminus \{\gamma _i:i<n\})]$
is infinite for every
![]() $n\in \omega $
, we can pick a one-to-one sequence
$n\in \omega $
, we can pick a one-to-one sequence
![]() $(b_n:n\in \omega )$
such that
$(b_n:n\in \omega )$
such that
![]() $b_n\in \phi [\tau (G\setminus \{\gamma _i:i<n\})]$
for each
$b_n\in \phi [\tau (G\setminus \{\gamma _i:i<n\})]$
for each
![]() $n\in \omega $
. Define
$n\in \omega $
. Define
![]() $B=\{b_n:n\in \omega \}$
. Since B is infinite,
$B=\{b_n:n\in \omega \}$
. Since B is infinite,
![]() $B\subseteq \rho (F)$
, and
$B\subseteq \rho (F)$
, and
![]() $\mathcal {I}_{\rho }\restriction \rho (F)=\mathrm {Fin}(\rho (F))$
, there is
$\mathcal {I}_{\rho }\restriction \rho (F)=\mathrm {Fin}(\rho (F))$
, there is
![]() $H\in \mathcal {F}$
such that
$H\in \mathcal {F}$
such that
![]() $\rho (H)\subseteq B$
. Using Proposition 3.2, there is
$\rho (H)\subseteq B$
. Using Proposition 3.2, there is
![]() $E\in \mathcal {F}$
with
$E\in \mathcal {F}$
with
![]() $E\subseteq H$
such that for any
$E\subseteq H$
such that for any
![]() $n\in \omega $
there is a finite set
$n\in \omega $
there is a finite set
![]() $L\subseteq \Omega $
such that
$L\subseteq \Omega $
such that
![]() $\rho (E\setminus L)\subseteq \rho (E)\setminus \{b_i:i<n\}$
. Consequently, for any finite set
$\rho (E\setminus L)\subseteq \rho (E)\setminus \{b_i:i<n\}$
. Consequently, for any finite set
![]() $K\subseteq \Gamma $
there is
$K\subseteq \Gamma $
there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $K\subseteq \{\gamma _i:i<n\}$
, so we can find a finite set
$K\subseteq \{\gamma _i:i<n\}$
, so we can find a finite set
![]() $L\subseteq \Omega $
such that
$L\subseteq \Omega $
such that
![]() $\rho (E\setminus L) \subseteq \rho (E)\setminus \{b_i:i<n\} \subseteq B\setminus \{b_i:i<n\} \subseteq \phi [\tau (G\setminus \{\gamma _i:i<n\})] \subseteq \phi [\tau (G\setminus K)] $
.
$\rho (E\setminus L) \subseteq \rho (E)\setminus \{b_i:i<n\} \subseteq B\setminus \{b_i:i<n\} \subseteq \phi [\tau (G\setminus \{\gamma _i:i<n\})] \subseteq \phi [\tau (G\setminus K)] $
.
(3)
![]() $\implies $
(4) Let
$\implies $
(4) Let
![]() $\phi :\Lambda \to \Lambda $
be a witness for
$\phi :\Lambda \to \Lambda $
be a witness for
![]() $\rho \leq _K\rho _{\mathrm {Fin}(\Lambda )}$
. Since
$\rho \leq _K\rho _{\mathrm {Fin}(\Lambda )}$
. Since
![]() $\phi ^{-1}[\{\lambda \}]\in \mathrm {Fin}(\Lambda )$
for every
$\phi ^{-1}[\{\lambda \}]\in \mathrm {Fin}(\Lambda )$
for every
![]() $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
![]() $\phi [\Lambda ]$
is infinite, there is an infinite set
$\phi [\Lambda ]$
is infinite, there is an infinite set
![]() $A\subseteq \Lambda $
, such that
$A\subseteq \Lambda $
, such that
![]() $\phi \restriction A$
is one-to-one. Then we can find
$\phi \restriction A$
is one-to-one. Then we can find
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq \phi [A]$
. We claim that
$\rho (F)\subseteq \phi [A]$
. We claim that
![]() $\mathcal {I}_{\rho }\restriction \rho (F) = \mathrm {Fin}(\rho (F))$
. Indeed, let
$\mathcal {I}_{\rho }\restriction \rho (F) = \mathrm {Fin}(\rho (F))$
. Indeed, let
![]() $B\subseteq \rho (F)$
be infinite and observe that
$B\subseteq \rho (F)$
be infinite and observe that
![]() $\phi ^{-1}[B]$
is infinite, so
$\phi ^{-1}[B]$
is infinite, so
![]() $B=\phi [\phi ^{-1}[B]]\notin \mathcal {I}_\rho $
.
$B=\phi [\phi ^{-1}[B]]\notin \mathcal {I}_\rho $
.
(4)
![]() $\implies $
(1) If
$\implies $
(1) If
![]() $\rho \not \leq _K\rho _{\mathrm {Fin}(\Lambda )}$
then by Proposition 7.5(2b),
$\rho \not \leq _K\rho _{\mathrm {Fin}(\Lambda )}$
then by Proposition 7.5(2b),
![]() $\mathcal {I}_\rho \not \leq _K\mathrm {Fin}(\Lambda )$
, and consequently
$\mathcal {I}_\rho \not \leq _K\mathrm {Fin}(\Lambda )$
, and consequently
![]() $\mathcal {I}_\rho $
is tall.
$\mathcal {I}_\rho $
is tall.
Definition 8.2. We say that a partition regular function
![]() $\rho $
is tall if any item of Proposition 8.1 holds.
$\rho $
is tall if any item of Proposition 8.1 holds.
Proposition 8.3. The ideals
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
![]() $\mathcal {R}$
,
$\mathcal {R}$
,
![]() $\mathcal {D}$
,
$\mathcal {D}$
,
![]() $\mathcal {W}$
, and
$\mathcal {W}$
, and
![]() $\mathcal {I}_{1/n}$
are tall
$\mathcal {I}_{1/n}$
are tall
![]() $($
hence,
$($
hence,
![]() $FS$
, r,
$FS$
, r,
![]() $\Delta $
,
$\Delta $
,
![]() $\rho _{\mathcal {W}}$
, and
$\rho _{\mathcal {W}}$
, and
![]() $\rho _{\mathcal {I}_{1/n}}$
are tall
$\rho _{\mathcal {I}_{1/n}}$
are tall
![]() $)$
.
$)$
.
Proof For the case of
![]() $\mathcal {W}$
and
$\mathcal {W}$
and
![]() $\mathcal {I}_{1/n}$
, see [Reference Brendle, Farkas and Verner7, p. 3–4]. For other cases, see [Reference Meza-Alcántara67, under Lemma 1.6.24] and [Reference Filipów22, Proposition 4.3 and text above Lemma 3.2]. Tallness of the listed partition regular functions follows then from Proposition 8.1.
$\mathcal {I}_{1/n}$
, see [Reference Brendle, Farkas and Verner7, p. 3–4]. For other cases, see [Reference Meza-Alcántara67, under Lemma 1.6.24] and [Reference Filipów22, Proposition 4.3 and text above Lemma 3.2]. Tallness of the listed partition regular functions follows then from Proposition 8.1.
8.2 Homogeneity of partition regular functions
Let
![]() $\mathcal {I}_i$
be an ideal on
$\mathcal {I}_i$
be an ideal on
![]() $\Lambda _i$
for each
$\Lambda _i$
for each
![]() $i=1,2$
. Ideals
$i=1,2$
. Ideals
![]() $\mathcal {I}_1$
and
$\mathcal {I}_1$
and
![]() $\mathcal {I}_2$
are isomorphic (in short:
$\mathcal {I}_2$
are isomorphic (in short:
![]() $\mathcal {I}_1\approx \mathcal {I}_2$
) if there exists a bijection
$\mathcal {I}_1\approx \mathcal {I}_2$
) if there exists a bijection
![]() $\phi :\Lambda _1\to \Lambda _2$
such that
$\phi :\Lambda _1\to \Lambda _2$
such that
![]() $ A\in \mathcal {I}_1 \iff \phi [A] \in \mathcal {I}_2$
for each
$ A\in \mathcal {I}_1 \iff \phi [A] \in \mathcal {I}_2$
for each
![]() $A\subseteq \Lambda _1$
. An ideal
$A\subseteq \Lambda _1$
. An ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\Lambda $
is homogeneous if the ideals
$\Lambda $
is homogeneous if the ideals
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {I}\restriction A$
are isomorphic for every
$\mathcal {I}\restriction A$
are isomorphic for every
![]() $A\in \mathcal {I}^+$
[Reference Kwela and Tryba63, Definition 1.3] (see also [Reference Fremlin34]). We say that
$A\in \mathcal {I}^+$
[Reference Kwela and Tryba63, Definition 1.3] (see also [Reference Fremlin34]). We say that
![]() $\mathcal {I}$
is K-homogeneous if
$\mathcal {I}$
is K-homogeneous if
![]() $\mathcal {I}\restriction A \leq _K \mathcal {I}$
for every
$\mathcal {I}\restriction A \leq _K \mathcal {I}$
for every
![]() $A\in \mathcal {I}^+$
(in [Reference Hrušák45, p. 37], the author uses the name K-uniform in this case). Note that we always have
$A\in \mathcal {I}^+$
(in [Reference Hrušák45, p. 37], the author uses the name K-uniform in this case). Note that we always have
![]() $\mathcal {I}\leq _K \mathcal {I}\restriction A$
for every
$\mathcal {I}\leq _K \mathcal {I}\restriction A$
for every
![]() $A\in \mathcal {I}^+$
(see, e.g., [Reference Hrušák45, p. 46]).
$A\in \mathcal {I}^+$
(see, e.g., [Reference Hrušák45, p. 46]).
Definition 8.4. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular. We say that
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular. We say that
![]() $\rho $
is K-homogeneous if
$\rho $
is K-homogeneous if
![]() $\rho \restriction A \leq _K \rho $
for every
$\rho \restriction A \leq _K \rho $
for every
![]() $A\in \mathcal {I}_\rho ^+$
(note that we always have
$A\in \mathcal {I}_\rho ^+$
(note that we always have
![]() $\rho \leq _K \rho \restriction A$
for every
$\rho \leq _K \rho \restriction A$
for every
![]() $A\in \mathcal {I}_\rho ^+$
by Proposition 7.4(3a)).
$A\in \mathcal {I}_\rho ^+$
by Proposition 7.4(3a)).
Proposition 8.5.
-
(1) If a partition regular function
 $\rho $
is K-homogeneous then
$\rho $
is K-homogeneous then
 $\mathcal {I}_\rho $
is K-homogeneous.
$\mathcal {I}_\rho $
is K-homogeneous. -
(2) An ideal
 $\mathcal {I}$
is K-homogeneous
$\mathcal {I}$
is K-homogeneous
 $\iff \rho _{\mathcal {I}}$
is K-homogeneous.
$\iff \rho _{\mathcal {I}}$
is K-homogeneous.
Proof (1) It follows from Propositions 7.5(1) and 4.1.
(2) Observe that if
![]() $A\in \mathcal {I}^+$
then
$A\in \mathcal {I}^+$
then
![]() $\rho _{\mathcal {I}\restriction A}=\rho _{\mathcal {I}}\restriction A$
. Thus, it follows from Propositions 7.5(2b) and 4.1.
$\rho _{\mathcal {I}\restriction A}=\rho _{\mathcal {I}}\restriction A$
. Thus, it follows from Propositions 7.5(2b) and 4.1.
We need the following lemma to show that
![]() $FS$
and r are K-homogeneous.
$FS$
and r are K-homogeneous.
Lemma 8.6. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular
![]() $(with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
. If
$(with\ \mathcal {F}\subseteq [\Omega ]^\omega )$
. If
![]() $\mathcal {I}_\rho $
is homogeneous and
$\mathcal {I}_\rho $
is homogeneous and
![]() $\rho $
is
$\rho $
is
![]() $P^-$
and has small accretions then
$P^-$
and has small accretions then
![]() $\rho $
is K-homogeneous.
$\rho $
is K-homogeneous.
Proof Let
![]() $A\in \mathcal {I}_\rho ^+$
. Since
$A\in \mathcal {I}_\rho ^+$
. Since
![]() $\mathcal {I}_\rho $
is homogeneous,
$\mathcal {I}_\rho $
is homogeneous,
![]() $\mathcal {I}_\rho \restriction A$
and
$\mathcal {I}_\rho \restriction A$
and
![]() $\mathcal {I}_\rho $
are isomorphic. Let
$\mathcal {I}_\rho $
are isomorphic. Let
![]() $f:\Lambda \to A$
be a bijection witnessing it. We claim that f witnesses
$f:\Lambda \to A$
be a bijection witnessing it. We claim that f witnesses
![]() $\rho \restriction A\leq _K\rho $
.
$\rho \restriction A\leq _K\rho $
.
Let
![]() $F\in \mathcal {F}$
. Since
$F\in \mathcal {F}$
. Since
![]() $\rho $
has small accretions, there is
$\rho $
has small accretions, there is
![]() $G\in \mathcal {F}$
such that
$G\in \mathcal {F}$
such that
![]() $G\subseteq F$
and G has small accretions. Enumerate
$G\subseteq F$
and G has small accretions. Enumerate
![]() $\Omega =\{o_n:n\in \omega \}$
and define
$\Omega =\{o_n:n\in \omega \}$
and define
![]() $K_n=\{o_i:i\leq n\}$
and
$K_n=\{o_i:i\leq n\}$
and
![]() $A_n=f[\rho (G\setminus K_n)]$
for all
$A_n=f[\rho (G\setminus K_n)]$
for all
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $A_n\supseteq A_{n+1}$
. Since G has small accretions and f is a bijection and witnesses that
$A_n\supseteq A_{n+1}$
. Since G has small accretions and f is a bijection and witnesses that
![]() $\mathcal {I}_\rho \restriction A$
and
$\mathcal {I}_\rho \restriction A$
and
![]() $\mathcal {I}_\rho $
are isomorphic,
$\mathcal {I}_\rho $
are isomorphic,
![]() $A_n\in (\mathcal {I}_\rho \restriction A)^+$
and
$A_n\in (\mathcal {I}_\rho \restriction A)^+$
and
![]() $A_n\setminus A_{n+1}\subseteq f[\rho (G\setminus K_n)\setminus \rho (G\setminus K_{n+1})]\subseteq f[\rho (G)\setminus \rho (G\setminus K_{n+1})]\in \mathcal {I}_\rho \restriction A$
. Using the fact that
$A_n\setminus A_{n+1}\subseteq f[\rho (G\setminus K_n)\setminus \rho (G\setminus K_{n+1})]\subseteq f[\rho (G)\setminus \rho (G\setminus K_{n+1})]\in \mathcal {I}_\rho \restriction A$
. Using the fact that
![]() $\rho $
is
$\rho $
is
![]() $P^-$
, we can find
$P^-$
, we can find
![]() $H\in \mathcal {F}\restriction A$
such that
$H\in \mathcal {F}\restriction A$
such that
![]() $\rho (H)\subseteq ^\rho A_n=f[\rho (G\setminus K_n)]$
for all
$\rho (H)\subseteq ^\rho A_n=f[\rho (G\setminus K_n)]$
for all
![]() $n\in \omega $
. Hence, given any finite set
$n\in \omega $
. Hence, given any finite set
![]() $K\subseteq \Omega $
there are
$K\subseteq \Omega $
there are
![]() $n\in \omega $
and finite
$n\in \omega $
and finite
![]() $L\subseteq \Omega $
such that
$L\subseteq \Omega $
such that
![]() $K\subseteq K_n$
and
$K\subseteq K_n$
and
![]() $\rho (H\setminus L)\subseteq A_n=f[\rho (G\setminus K_n)]\subseteq f[\rho (G\setminus K)]$
.
$\rho (H\setminus L)\subseteq A_n=f[\rho (G\setminus K_n)]\subseteq f[\rho (G\setminus K)]$
.
Proposition 8.7.
-
(1) The ideals
 $\mathcal {H}$
,
$\mathcal {H}$
,
 $\mathcal {R}$
, and
$\mathcal {R}$
, and
 $\mathcal {W}$
are homogeneous
$\mathcal {W}$
are homogeneous
 $($
hence, K-homogeneous
$($
hence, K-homogeneous
 $)$
.
$)$
. -
(2) The functions
 $\operatorname {\mathrm {FS}}$
and r are K-homogeneous.
$\operatorname {\mathrm {FS}}$
and r are K-homogeneous.
Proof (1) See [Reference Kwela and Tryba63, Examples 2.5 and 2.6].
(2) It follows from item (1), Lemma 8.6, and Propositions 6.7(3) and 4.3.
Question 8.8.
-
(1) Is the function
 $\Delta $
K-homogeneous?
$\Delta $
K-homogeneous? -
(2) Is the ideal
 $\mathcal {I}_{1/n}$
K-homogeneous?
$\mathcal {I}_{1/n}$
K-homogeneous?
Part 2.
![]() $\mathbf {\operatorname {\mathrm {FinBW}}}$
spaces
$\mathbf {\operatorname {\mathrm {FinBW}}}$
spaces
In this part we define the main object of our studies—classes of sequentially compact spaces defined with the aid of partition regular functions (Definition 10.1). Next, we prove some general results about those classes of spaces (Theorem 10.5).
9 A convergence with respect to partition regular functions
Definition 9.1. Let X be a topological space. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
.
$\mathcal {F}\subseteq [\Omega ]^\omega $
.
-
(1) For
 $F\in \mathcal {F}$
, a function
$F\in \mathcal {F}$
, a function
 $f: \rho (F) \to X$
is called a
$f: \rho (F) \to X$
is called a
 $\rho $
-sequence in X.
$\rho $
-sequence in X. -
(2) A
 $\rho $
-sequence
$\rho $
-sequence
 $f:\rho (F) \to X$
is
$f:\rho (F) \to X$
is
 $\rho $
-convergent to a point
$\rho $
-convergent to a point
 $x\in X$
if for every neighbourhood U of x there is a finite set
$x\in X$
if for every neighbourhood U of x there is a finite set
 $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that  $$ \begin{align*}f[\rho(F\setminus K)] \subseteq U.\end{align*} $$
$$ \begin{align*}f[\rho(F\setminus K)] \subseteq U.\end{align*} $$
Remark. Various kinds of convergences considered in the literature can be described in terms of
![]() $\rho $
-convergence.
$\rho $
-convergence.
-
(1) If
 $\rho =\operatorname {\mathrm {FS}}$
, then
$\rho =\operatorname {\mathrm {FS}}$
, then
 $\rho $
-convergence coincides with
$\rho $
-convergence coincides with
 $IP$
-convergence (see [Reference Furstenberg35], [Reference Furstenberg and Weiss36], or [Reference Kojman57]).
$IP$
-convergence (see [Reference Furstenberg35], [Reference Furstenberg and Weiss36], or [Reference Kojman57]). -
(2) If
 $\rho =r$
, then
$\rho =r$
, then
 $\rho $
-convergence coincides with the
$\rho $
-convergence coincides with the
 $\mathcal {R}$
-convergence (see [Reference Bergelson and Zelada5], [Reference Bojańczyk, Kopczyński and Toruńczyk6], or [Reference Kubiś and Szeptycki61, Definition 2.1]).
$\mathcal {R}$
-convergence (see [Reference Bergelson and Zelada5], [Reference Bojańczyk, Kopczyński and Toruńczyk6], or [Reference Kubiś and Szeptycki61, Definition 2.1]). -
(3) If
 $\rho =\Delta $
, then
$\rho =\Delta $
, then
 $\rho $
-convergence coincides with the differential convergence (see [Reference Shi73, Definition 4.2.4] or [Reference Filipów22, p. 2010]).
$\rho $
-convergence coincides with the differential convergence (see [Reference Shi73, Definition 4.2.4] or [Reference Filipów22, p. 2010]). -
(4) If
 $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
 $\Lambda $
and
$\Lambda $
and
 $\rho _{\mathcal {I}}$
is defined as in Proposition 3.3(2), then
$\rho _{\mathcal {I}}$
is defined as in Proposition 3.3(2), then
 $\rho _{\mathcal {I}}$
-convergence coincides with the ordinary convergence.
$\rho _{\mathcal {I}}$
-convergence coincides with the ordinary convergence.
The following proposition reveals relationships between
![]() $\rho $
-convergence and convergence.
$\rho $
-convergence and convergence.
Proposition 9.2.
-
(1) Let
 $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
 $\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
 $F\in \mathcal {F}$
and
$F\in \mathcal {F}$
and
 $f:\rho (F)\to X$
.
$f:\rho (F)\to X$
.-
(a) If f is convergent to L, then
 $f\restriction \rho (E)$
is
$f\restriction \rho (E)$
is
 $\rho $
-convergent to L for some
$\rho $
-convergent to L for some
 $E\in \mathcal {F}\restriction \rho (F)$
.
$E\in \mathcal {F}\restriction \rho (F)$
. -
(b) If f is
 $\rho $
-convergent to L, then
$\rho $
-convergent to L, then
 $f\restriction A$
is convergent to L for some infinite set
$f\restriction A$
is convergent to L for some infinite set
 $A \subseteq \rho (F)$
.
$A \subseteq \rho (F)$
.
-
-
(2) Let
 $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
 $\Lambda $
and
$\Lambda $
and
 $f:A\to X$
for some
$f:A\to X$
for some
 $A\in \mathcal {I}^+$
. Then f is convergent to
$A\in \mathcal {I}^+$
. Then f is convergent to
 $L \iff f$
is
$L \iff f$
is
 $\rho _{\mathcal {I}}$
-convergent to L.
$\rho _{\mathcal {I}}$
-convergent to L.
Proof (1a) Let
![]() $E\in \mathcal {F}$
with
$E\in \mathcal {F}$
with
![]() $E\subseteq F$
be as in Proposition 3.2 and let U be a neighborhood of L. Then there exists a finite set K such that
$E\subseteq F$
be as in Proposition 3.2 and let U be a neighborhood of L. Then there exists a finite set K such that
![]() $f(n)\in U$
for every
$f(n)\in U$
for every
![]() $n\in \rho (F)\setminus K$
. There is a finite set L such that
$n\in \rho (F)\setminus K$
. There is a finite set L such that
![]() $\rho (E\setminus L)\subseteq \rho (E)\setminus K\subseteq \rho (F)\setminus K$
. Consequently,
$\rho (E\setminus L)\subseteq \rho (E)\setminus K\subseteq \rho (F)\setminus K$
. Consequently,
![]() $f(n)\in U$
for every
$f(n)\in U$
for every
![]() $n\in \rho (E\setminus L)$
.
$n\in \rho (E\setminus L)$
.
(1b) Let
![]() $\Omega =\{o_n:n\in \omega \}$
. For each
$\Omega =\{o_n:n\in \omega \}$
. For each
![]() $n\in \omega $
, we pick
$n\in \omega $
, we pick
![]() $\lambda _n \in \rho (F\setminus \{o_i:i<n\})\setminus \{\lambda _i:i<n\}$
. Let
$\lambda _n \in \rho (F\setminus \{o_i:i<n\})\setminus \{\lambda _i:i<n\}$
. Let
![]() $A=\{\lambda _n:n\in \omega \}$
. We claim that
$A=\{\lambda _n:n\in \omega \}$
. We claim that
![]() $f\restriction A$
is convergent to L. Indeed, if U is a neighborhood of L, then there is a finite set
$f\restriction A$
is convergent to L. Indeed, if U is a neighborhood of L, then there is a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $f[\rho (F\setminus K)]\subseteq U$
. Let
$f[\rho (F\setminus K)]\subseteq U$
. Let
![]() $n\in \omega $
be such that
$n\in \omega $
be such that
![]() $K\subseteq \{o_i:i<n\}$
. Then
$K\subseteq \{o_i:i<n\}$
. Then
![]() $ f[A\setminus \{\lambda _i:i<n\}] \subseteq f[\rho (F\setminus \{o_i:i<n\})] \subseteq f[\rho (F\setminus K)] \subseteq U $
.
$ f[A\setminus \{\lambda _i:i<n\}] \subseteq f[\rho (F\setminus \{o_i:i<n\})] \subseteq f[\rho (F\setminus K)] \subseteq U $
.
(2) It is straightforward.
10
 $\operatorname {\mathrm {FinBW}}$
spaces
$\operatorname {\mathrm {FinBW}}$
spaces
Let
![]() $\mathcal {I}$
be an ideal on a countable infinite set
$\mathcal {I}$
be an ideal on a countable infinite set
![]() $\Lambda $
. The following classes of topological spaces were extensively examined in the literature (see, e.g., [Reference Filipów, Mrożek, Recław and Szuca26, Reference Flašková30, Reference Kwela62]):
$\Lambda $
. The following classes of topological spaces were extensively examined in the literature (see, e.g., [Reference Filipów, Mrożek, Recław and Szuca26, Reference Flašková30, Reference Kwela62]):
-
(1)
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
is the class of all topological spaces X such that for every sequence
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
is the class of all topological spaces X such that for every sequence
 $f:\Lambda \to X$
there exists
$f:\Lambda \to X$
there exists
 $A\in \mathcal {I}^+$
such that
$A\in \mathcal {I}^+$
such that
 $f\restriction A$
converges (in [Reference Flašková30], spaces from
$f\restriction A$
converges (in [Reference Flašková30], spaces from
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
are called
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
are called
 $\mathcal {I}$
-spaces).
$\mathcal {I}$
-spaces). -
(2)
 $\operatorname {\mathrm {hFinBW}}(\mathcal {I})$
is the class of all topological spaces X such that for every
$\operatorname {\mathrm {hFinBW}}(\mathcal {I})$
is the class of all topological spaces X such that for every
 $B\in \mathcal {I}^+$
and every sequence
$B\in \mathcal {I}^+$
and every sequence
 $f:B\to X$
there exists
$f:B\to X$
there exists
 $A\in \mathcal {I}^+$
such that
$A\in \mathcal {I}^+$
such that
 $A\subseteq B$
and
$A\subseteq B$
and
 $f\restriction A$
converges.
$f\restriction A$
converges.
Remark. The classes
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I}_{\rho })$
for
$\operatorname {\mathrm {FinBW}}(\mathcal {I}_{\rho })$
for
![]() $\rho \in \{\mathcal {W},\mathcal {I}_{1/n}\}$
were examined in the literature under other names:
$\rho \in \{\mathcal {W},\mathcal {I}_{1/n}\}$
were examined in the literature under other names:
-
(1) In [Reference Kojman58, Definition 3], spaces from
 $\operatorname {\mathrm {FinBW}}(\mathcal {W})$
are called van der Waerden spaces.
$\operatorname {\mathrm {FinBW}}(\mathcal {W})$
are called van der Waerden spaces. -
(2) In [Reference Flašková30, Definition 2.1], spaces from
 $\operatorname {\mathrm {FinBW}}(\mathcal {I}_{1/n})$
are called
$\operatorname {\mathrm {FinBW}}(\mathcal {I}_{1/n})$
are called
 $\mathcal {I}_{1/n}$
-spaces.
$\mathcal {I}_{1/n}$
-spaces.
Definition 10.1. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be a partition regular function.
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be a partition regular function.
-
(1)
 $\operatorname {\mathrm {FinBW}}(\rho )$
is the class of all topological spaces X such that for every sequence
$\operatorname {\mathrm {FinBW}}(\rho )$
is the class of all topological spaces X such that for every sequence
 $f:\Lambda \to X$
there exists
$f:\Lambda \to X$
there exists
 $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
 $f\restriction \rho\ (F)\ \rho$
-converges.
$f\restriction \rho\ (F)\ \rho$
-converges. -
(2)
 $\operatorname {\mathrm {hFinBW}}(\rho )$
is the class of all topological spaces X such that for every
$\operatorname {\mathrm {hFinBW}}(\rho )$
is the class of all topological spaces X such that for every
 $\rho $
-sequence
$\rho $
-sequence
 $f:\rho (E)\to X$
there exists
$f:\rho (E)\to X$
there exists
 $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
 $\rho (F)\subseteq \rho (E)$
and
$\rho (F)\subseteq \rho (E)$
and
 $f\restriction \rho (F)\ \rho $
-converges.
$f\restriction \rho (F)\ \rho $
-converges.
Remark. The classes
![]() $\operatorname {\mathrm {FinBW}}(\rho )$
for
$\operatorname {\mathrm {FinBW}}(\rho )$
for
![]() $\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
were examined in the literature under other names:
$\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
were examined in the literature under other names:
-
(1) In [Reference Kojman57, Definition 4], spaces from
 $\operatorname {\mathrm {FinBW}}(\operatorname {\mathrm {FS}})$
are called Hindman spaces.
$\operatorname {\mathrm {FinBW}}(\operatorname {\mathrm {FS}})$
are called Hindman spaces. -
(2) In [Reference Bojańczyk, Kopczyński and Toruńczyk6] (see also [Reference Kubiś and Szeptycki61, Definition 2.1]), spaces from
 $\operatorname {\mathrm {FinBW}}(r)$
are called spaces with the Ramsey property, and we will call them Ramsey spaces in short.
$\operatorname {\mathrm {FinBW}}(r)$
are called spaces with the Ramsey property, and we will call them Ramsey spaces in short. -
(3) In [Reference Shi73, Definition 4.2.4] (see also [Reference Filipów22, p. 2010]), spaces in
 $\operatorname {\mathrm {FinBW}}(\Delta )$
are called differentially compact spaces.
$\operatorname {\mathrm {FinBW}}(\Delta )$
are called differentially compact spaces.
Remark. Recall that if
![]() $(\Lambda ,<)$
is a directed set, then any function
$(\Lambda ,<)$
is a directed set, then any function
![]() $f:\Lambda \to X$
is called a net in X. A net
$f:\Lambda \to X$
is called a net in X. A net
![]() $f:\Lambda \to X$
in a topological space X converges to
$f:\Lambda \to X$
in a topological space X converges to
![]() $x\in X$
if for every neighborhood U of x there is
$x\in X$
if for every neighborhood U of x there is
![]() $\lambda _0\in \Lambda $
such that
$\lambda _0\in \Lambda $
such that
![]() $f(\lambda )\in U$
for every
$f(\lambda )\in U$
for every
![]() $\lambda>\lambda _0$
(see, e.g., [Reference Engelking17, p. 49]). In [Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, Remark 2.6], the authors notice that if
$\lambda>\lambda _0$
(see, e.g., [Reference Engelking17, p. 49]). In [Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, Remark 2.6], the authors notice that if
![]() $\mathcal {B}$
is a coideal basis on
$\mathcal {B}$
is a coideal basis on
![]() $(\Lambda ,<)$
, then
$(\Lambda ,<)$
, then
![]() $(B,<\cap (B\times B))$
is a directed set and
$(B,<\cap (B\times B))$
is a directed set and
![]() $f\restriction B$
is a subnet of f for every
$f\restriction B$
is a subnet of f for every
![]() $B\in \mathcal {B}$
. Furthermore, they examine topological spaces X having the property that every net
$B\in \mathcal {B}$
. Furthermore, they examine topological spaces X having the property that every net
![]() $f:\Lambda \to X$
has a convergent subnet
$f:\Lambda \to X$
has a convergent subnet
![]() $f\restriction B$
with some
$f\restriction B$
with some
![]() $B\in \mathcal {B}$
[Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, p. 418]. It is not difficult to see that the class of spaces they examine coincides with the class
$B\in \mathcal {B}$
[Reference Farmaki, Karageorgos, Koutsogiannis and Mitropoulos20, p. 418]. It is not difficult to see that the class of spaces they examine coincides with the class
![]() $\operatorname {\mathrm {FinBW}}(\rho _{\mathcal {B}})$
with
$\operatorname {\mathrm {FinBW}}(\rho _{\mathcal {B}})$
with
![]() $\rho _{\mathcal {B}}$
defined as in Proposition 3.10(2).
$\rho _{\mathcal {B}}$
defined as in Proposition 3.10(2).
The following proposition reveals relationships between
![]() $\operatorname {\mathrm {FinBW}}$
-like spaces defined with the aid of partition regular functions and ideals.
$\operatorname {\mathrm {FinBW}}$
-like spaces defined with the aid of partition regular functions and ideals.
Proposition 10.2. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\Lambda $
.
$\Lambda $
.
-
(1)
-
(a)
 $\operatorname {\mathrm {hFinBW}}(\rho ) = \bigcap \{\operatorname {\mathrm {FinBW}}(\rho \restriction \rho (F)):F\in \mathcal {F}\}$
.
$\operatorname {\mathrm {hFinBW}}(\rho ) = \bigcap \{\operatorname {\mathrm {FinBW}}(\rho \restriction \rho (F)):F\in \mathcal {F}\}$
. -
(b)
 $\operatorname {\mathrm {hFinBW}}(\mathcal {I}) = \bigcap \{\operatorname {\mathrm {FinBW}}(\mathcal {I}\restriction A):A\in \mathcal {I}^+\}$
.
$\operatorname {\mathrm {hFinBW}}(\mathcal {I}) = \bigcap \{\operatorname {\mathrm {FinBW}}(\mathcal {I}\restriction A):A\in \mathcal {I}^+\}$
.
-
-
(2)
-
(a)
 $\operatorname {\mathrm {hFinBW}}(\rho ) \subseteq \operatorname {\mathrm {FinBW}}(\rho )$
.
$\operatorname {\mathrm {hFinBW}}(\rho ) \subseteq \operatorname {\mathrm {FinBW}}(\rho )$
. -
(b)
 $\operatorname {\mathrm {hFinBW}}(\mathcal {I}) \subseteq \operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {hFinBW}}(\mathcal {I}) \subseteq \operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
-
-
(3)
 $\operatorname {\mathrm {FinBW}}(\mathcal {I}_\rho ) \subseteq \operatorname {\mathrm {FinBW}}(\rho )$
and
$\operatorname {\mathrm {FinBW}}(\mathcal {I}_\rho ) \subseteq \operatorname {\mathrm {FinBW}}(\rho )$
and
 $\operatorname {\mathrm {hFinBW}}(\mathcal {I}_\rho ) \subseteq \operatorname {\mathrm {hFinBW}}(\rho )$
.
$\operatorname {\mathrm {hFinBW}}(\mathcal {I}_\rho ) \subseteq \operatorname {\mathrm {hFinBW}}(\rho )$
. -
(4)
 $\operatorname {\mathrm {FinBW}}(\mathcal {I}) = \operatorname {\mathrm {FinBW}}(\rho _{\mathcal {I}})$
and
$\operatorname {\mathrm {FinBW}}(\mathcal {I}) = \operatorname {\mathrm {FinBW}}(\rho _{\mathcal {I}})$
and
 $\operatorname {\mathrm {hFinBW}}(\mathcal {I}) = \operatorname {\mathrm {hFinBW}}(\rho _{\mathcal {I}})$
.
$\operatorname {\mathrm {hFinBW}}(\mathcal {I}) = \operatorname {\mathrm {hFinBW}}(\rho _{\mathcal {I}})$
. -
(5)
-
(a) If
 $\rho $
is K-homogeneous, then
$\rho $
is K-homogeneous, then
 $\operatorname {\mathrm {hFinBW}}(\rho )=\operatorname {\mathrm {FinBW}}(\rho )$
.
$\operatorname {\mathrm {hFinBW}}(\rho )=\operatorname {\mathrm {FinBW}}(\rho )$
. -
(b) If
 $\mathcal {I}$
is K-homogeneous, then
$\mathcal {I}$
is K-homogeneous, then
 $\operatorname {\mathrm {hFinBW}}(\mathcal {I})=\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {hFinBW}}(\mathcal {I})=\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
-
Proof (1) and (2) Straightforward.
(3) It follows from Proposition 9.2(1a) (the other inclusion does not follow from Proposition 9.2(1b) as it gives us only an infinite set A, not necessarily
![]() $A\in \mathcal {I}_\rho ^+$
).
$A\in \mathcal {I}_\rho ^+$
).
(4) It follows from Proposition 9.2(2).
(5a) We only need to show
![]() $\operatorname {\mathrm {FinBW}}(\rho )\subseteq \operatorname {\mathrm {hFinBW}}(\rho )$
. Let
$\operatorname {\mathrm {FinBW}}(\rho )\subseteq \operatorname {\mathrm {hFinBW}}(\rho )$
. Let
![]() $X\in \operatorname {\mathrm {FinBW}}(\rho )$
and
$X\in \operatorname {\mathrm {FinBW}}(\rho )$
and
![]() $f:\rho (E)\to X$
be a
$f:\rho (E)\to X$
be a
![]() $\rho $
-sequence in X for some
$\rho $
-sequence in X for some
![]() $E\in \mathcal {F}$
. Let
$E\in \mathcal {F}$
. Let
![]() $\phi :\Lambda \to \rho (E)$
be a witness for
$\phi :\Lambda \to \rho (E)$
be a witness for
![]() $\rho \restriction (\mathcal {F}\restriction \rho (E))\leq _K \rho $
. Since
$\rho \restriction (\mathcal {F}\restriction \rho (E))\leq _K \rho $
. Since
![]() $f\circ \phi :\Lambda \to X$
, there is
$f\circ \phi :\Lambda \to X$
, there is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $f\circ \phi \restriction \rho (F)$
is
$f\circ \phi \restriction \rho (F)$
is
![]() $\rho $
-convergent to some
$\rho $
-convergent to some
![]() $x\in X$
. Since
$x\in X$
. Since
![]() $\rho \restriction (\mathcal {F}\restriction \rho (E))\leq _K \rho $
, there is
$\rho \restriction (\mathcal {F}\restriction \rho (E))\leq _K \rho $
, there is
![]() $G\in \mathcal {F}\restriction \rho (E)$
such that for every finite set
$G\in \mathcal {F}\restriction \rho (E)$
such that for every finite set
![]() $K\subseteq \Omega $
there is a finite set
$K\subseteq \Omega $
there is a finite set
![]() $L\subseteq \Omega $
with
$L\subseteq \Omega $
with
![]() $\rho (G\setminus L) \subseteq \phi [\rho (F\setminus K)]$
. We claim that
$\rho (G\setminus L) \subseteq \phi [\rho (F\setminus K)]$
. We claim that
![]() $f\restriction \rho (G)$
is
$f\restriction \rho (G)$
is
![]() $\rho $
-convergent to x. Let U be a neighborhood of x. Then there is a finite set
$\rho $
-convergent to x. Let U be a neighborhood of x. Then there is a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $(f\circ \phi )[\rho (F\setminus K)]\subseteq U$
. We pick a finite set
$(f\circ \phi )[\rho (F\setminus K)]\subseteq U$
. We pick a finite set
![]() $L\subseteq \Omega $
such that
$L\subseteq \Omega $
such that
![]() $\rho (G\setminus L) \subseteq \phi [\rho (F\setminus K)]$
. Then
$\rho (G\setminus L) \subseteq \phi [\rho (F\setminus K)]$
. Then
![]() $f[\rho (G\setminus L)] \subseteq f[\phi [\rho (F\setminus K)]] \subseteq U$
, so the proof is finished.
$f[\rho (G\setminus L)] \subseteq f[\phi [\rho (F\setminus K)]] \subseteq U$
, so the proof is finished.
(5b) It follows from items (5a) and (4) and Proposition 8.5(2).
Remark. In Theorem 10.2(3), we cannot replace inclusion with equality in general because in [Reference Kojman57, Theorems 3 and 10] the author proved that
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {H})$
contains only finite Hausdorff spaces, whereas
$\operatorname {\mathrm {FinBW}}(\mathcal {H})$
contains only finite Hausdorff spaces, whereas
![]() $\operatorname {\mathrm {FinBW}}(\operatorname {\mathrm {FS}})$
contains infinite (even uncountable) ones.
$\operatorname {\mathrm {FinBW}}(\operatorname {\mathrm {FS}})$
contains infinite (even uncountable) ones.
Corollary 10.3.
-
(1) [Reference Kojman58, Proposition 4]
 $\operatorname {\mathrm {hFinBW}}(\mathcal {W})=\operatorname {\mathrm {FinBW}}(\mathcal {W})$
, and consequently the product of two van der Waerden spaces is van der Waerden.
$\operatorname {\mathrm {hFinBW}}(\mathcal {W})=\operatorname {\mathrm {FinBW}}(\mathcal {W})$
, and consequently the product of two van der Waerden spaces is van der Waerden. -
(2) [Reference Kojman57, Lemma 8]
 $\operatorname {\mathrm {hFinBW}}(\operatorname {\mathrm {FS}})=\operatorname {\mathrm {FinBW}}(\operatorname {\mathrm {FS}})$
, and consequently the product of two Hindman spaces is Hindman.
$\operatorname {\mathrm {hFinBW}}(\operatorname {\mathrm {FS}})=\operatorname {\mathrm {FinBW}}(\operatorname {\mathrm {FS}})$
, and consequently the product of two Hindman spaces is Hindman. -
(3) [Reference Kubiś and Szeptycki61, Theorem 3.4]
 $\operatorname {\mathrm {hFinBW}}(r)=\operatorname {\mathrm {FinBW}}(r)$
, and consequently the product of two Ramsey spaces is Ramsey.
$\operatorname {\mathrm {hFinBW}}(r)=\operatorname {\mathrm {FinBW}}(r)$
, and consequently the product of two Ramsey spaces is Ramsey.
Question 10.4 [Reference Flašková31, Reference Flašková32] and [Reference Shi73, Question 4.2.3].
-
(1)
-
(a) Does
 $\operatorname {\mathrm {FinBW}}(\mathcal {I}_{1/n})=\operatorname {\mathrm {hFinBW}}(\mathcal {I}_{1/n})$
?
$\operatorname {\mathrm {FinBW}}(\mathcal {I}_{1/n})=\operatorname {\mathrm {hFinBW}}(\mathcal {I}_{1/n})$
? -
(b) Is the product of two
 $\mathcal {I}_{1/n}$
-spaces an
$\mathcal {I}_{1/n}$
-spaces an
 $\mathcal {I}_{1/n}$
-space?
$\mathcal {I}_{1/n}$
-space?
-
-
(2)
-
(a) Does
 $\operatorname {\mathrm {FinBW}}(\Delta )=\operatorname {\mathrm {hFinBW}}(\Delta )$
?
$\operatorname {\mathrm {FinBW}}(\Delta )=\operatorname {\mathrm {hFinBW}}(\Delta )$
? -
(b) Is the product of two differentially compact spaces a differentially compact space?
-
Note that the positive answer to the question in item (1a) gives the positive answer to the question in item (1b), and similarly for the questions in the second item. Moreover, the positive answer to the Question 8.8(1) (Question 8.8(2), resp.) gives the positive answer to Question 10.4(2a) (Question 10.4(1a), resp.).
Let us now turn to one of the main results of this paper.
Theorem 10.5. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
.
$\mathcal {F}\subseteq [\Omega ]^\omega $
.
-
(1)
 $\operatorname {\mathrm {FinBW}}(\rho )$
contains all finite spaces and is a subclass of the class of all sequentially compact spaces.
$\operatorname {\mathrm {FinBW}}(\rho )$
contains all finite spaces and is a subclass of the class of all sequentially compact spaces. -
(2)
 $\rho $
is not tall
$\rho $
is not tall
 $\iff \operatorname {\mathrm {FinBW}}(\rho )$
coincides with the class of all sequentially compact spaces.
$\iff \operatorname {\mathrm {FinBW}}(\rho )$
coincides with the class of all sequentially compact spaces. -
(3) The following conditions are equivalent.
-
(a)
 $\rho $
is
$\rho $
is
 $P^-(\Lambda )$
.
$P^-(\Lambda )$
. -
(b) There are Hausdorff compact spaces of arbitrary cardinality that belong to
 $\operatorname {\mathrm {FinBW}}(\rho )$
.
$\operatorname {\mathrm {FinBW}}(\rho )$
. -
(c) There exists an infinite Hausdorff topological space
 $X\in \operatorname {\mathrm {FinBW}}(\rho )$
.
$X\in \operatorname {\mathrm {FinBW}}(\rho )$
.
-
-
(4) The following conditions are equivalent.
-
(a)
 $\rho $
is
$\rho $
is
 $P^-$
.
$P^-$
. -
(b) There are Hausdorff compact spaces of arbitrary cardinality that belong to
 $\operatorname {\mathrm {hFinBW}}(\rho )$
.
$\operatorname {\mathrm {hFinBW}}(\rho )$
. -
(c) There exists an infinite Hausdorff topological space
 $X\in \operatorname {\mathrm {hFinBW}}(\rho )$
.
$X\in \operatorname {\mathrm {hFinBW}}(\rho )$
.
-
-
(5) If
 $\rho $
is
$\rho $
is
 $P^-$
, then
$P^-$
, then-
(a) the uncountable non-compact Hausdorff space
 $X=\omega _1$
with the order topology belongs to
$X=\omega _1$
with the order topology belongs to
 $\operatorname {\mathrm {FinBW}}(\rho )$
,
$\operatorname {\mathrm {FinBW}}(\rho )$
, -
(b) assuming Continuum Hypothesis (CH) there are Hausdorff compact and separable spaces of cardinality
 $\mathfrak {c}$
that belong to
$\mathfrak {c}$
that belong to
 $\operatorname {\mathrm {FinBW}}(\rho )$
.
$\operatorname {\mathrm {FinBW}}(\rho )$
.
-
-
(6) If
 $\rho $
is weak
$\rho $
is weak
 $P^+$
, then every compact metric space is in
$P^+$
, then every compact metric space is in
 $\operatorname {\mathrm {hFinBW}}(\rho )$
.
$\operatorname {\mathrm {hFinBW}}(\rho )$
. -
(7) If
 $\rho $
is
$\rho $
is
 $P^+$
, then every Hausdorff topological space with the property
$P^+$
, then every Hausdorff topological space with the property
 $(*)$
belongs to
$(*)$
belongs to
 $\operatorname {\mathrm {hFinBW}}(\rho )$
.
$\operatorname {\mathrm {hFinBW}}(\rho )$
. $($
A topological space X has the property (*) if for every countable set
$($
A topological space X has the property (*) if for every countable set
 $D\subseteq X$
the closure
$D\subseteq X$
the closure
 $\operatorname {\mathrm {cl}}_X(D)$
is compact and first-countable—see [Reference Kojman58].
$\operatorname {\mathrm {cl}}_X(D)$
is compact and first-countable—see [Reference Kojman58].
 $)$
$)$
Proof (1) It follows from Proposition 9.2(1b).
(2) The implication “
![]() $\impliedby $
” will follow from Theorem 13.2(1). To prove the implication “
$\impliedby $
” will follow from Theorem 13.2(1). To prove the implication “
![]() $\implies $
” we only need to show that every sequentially compact space belongs to
$\implies $
” we only need to show that every sequentially compact space belongs to
![]() $\operatorname {\mathrm {FinBW}}(\rho )$
. Fix a sequentially compact space X and
$\operatorname {\mathrm {FinBW}}(\rho )$
. Fix a sequentially compact space X and
![]() $f:\Lambda \to X$
. Let
$f:\Lambda \to X$
. Let
![]() $\phi :\Lambda \to \Lambda $
be a witness for
$\phi :\Lambda \to \Lambda $
be a witness for
![]() $\rho \leq _K \rho _{\mathrm {Fin}(\Lambda )}$
. Since
$\rho \leq _K \rho _{\mathrm {Fin}(\Lambda )}$
. Since
![]() $f\circ \phi :\Lambda \to X$
, there is an infinite set
$f\circ \phi :\Lambda \to X$
, there is an infinite set
![]() $A\subseteq \Lambda $
such that
$A\subseteq \Lambda $
such that
![]() $(f\circ \phi )\restriction A$
is convergent to some
$(f\circ \phi )\restriction A$
is convergent to some
![]() $x\in X$
. Then there is
$x\in X$
. Then there is
![]() $F\in \mathcal {F}$
with
$F\in \mathcal {F}$
with
![]() $\rho (F)\subseteq \phi [A]$
. We claim that
$\rho (F)\subseteq \phi [A]$
. We claim that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to x. Let U be any neighbourhood of x. Then there is a finite set
$\rho $
-convergent to x. Let U be any neighbourhood of x. Then there is a finite set
![]() $L\subseteq \Lambda $
such that
$L\subseteq \Lambda $
such that
![]() $f[\phi [A\setminus L]] \subseteq U$
. Now, we can find a finite set
$f[\phi [A\setminus L]] \subseteq U$
. Now, we can find a finite set
![]() $K \subseteq \Omega $
such that
$K \subseteq \Omega $
such that
![]() $\rho (F\setminus K) \subseteq \phi [A\setminus L]$
. Thus,
$\rho (F\setminus K) \subseteq \phi [A\setminus L]$
. Thus,
![]() $f[\rho (F\setminus K)]\subseteq U$
.
$f[\rho (F\setminus K)]\subseteq U$
.
(3) (a)
![]() $\implies $
(b) Let
$\implies $
(b) Let
![]() $\kappa $
be an infinite cardinal number. Let
$\kappa $
be an infinite cardinal number. Let
![]() $X = \kappa \cup \{\infty \}$
be the Alexandroff one-point compactification of the discrete space
$X = \kappa \cup \{\infty \}$
be the Alexandroff one-point compactification of the discrete space
![]() $\kappa $
. Then X is Hausdorff, compact, and has cardinality
$\kappa $
. Then X is Hausdorff, compact, and has cardinality
![]() $\kappa $
. Moreover, open neighborhoods of
$\kappa $
. Moreover, open neighborhoods of
![]() $\infty $
are of the form
$\infty $
are of the form
![]() $X \setminus S$
where S is a compact (hence finite) subset of
$X \setminus S$
where S is a compact (hence finite) subset of
![]() $\kappa $
. We show that X is in
$\kappa $
. We show that X is in
![]() $\operatorname {\mathrm {FinBW}}(\rho )$
. Let
$\operatorname {\mathrm {FinBW}}(\rho )$
. Let
![]() $f:\Lambda \to X$
. If there is
$f:\Lambda \to X$
. If there is
![]() $x\in X$
with
$x\in X$
with
![]() $f^{-1}[\{x\}]\notin \mathcal {I}_\rho $
, then we take
$f^{-1}[\{x\}]\notin \mathcal {I}_\rho $
, then we take
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq f^{-1}[\{x\}]$
and see that
$\rho (F)\subseteq f^{-1}[\{x\}]$
and see that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to x. Now, we assume that
$\rho $
-convergent to x. Now, we assume that
![]() $f^{-1}[\{x\}]\in \mathcal {I}_\rho $
for every
$f^{-1}[\{x\}]\in \mathcal {I}_\rho $
for every
![]() $x\in X$
. By Proposition 6.8, there is
$x\in X$
. By Proposition 6.8, there is
![]() $F\in \mathcal {F}$
such that for every finite set
$F\in \mathcal {F}$
such that for every finite set
![]() $S\subseteq X$
there is a finite set
$S\subseteq X$
there is a finite set
![]() $K_S$
such that
$K_S$
such that
![]() $\rho (F\setminus K_S)\cap f^{-1}[S]=\emptyset $
. We claim that
$\rho (F\setminus K_S)\cap f^{-1}[S]=\emptyset $
. We claim that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to
$\rho $
-convergent to
![]() $\infty $
. Let U be an open neighborhood of
$\infty $
. Let U be an open neighborhood of
![]() $\infty $
. Let
$\infty $
. Let
![]() $S\subseteq \kappa $
be a finite set with
$S\subseteq \kappa $
be a finite set with
![]() $U=X\setminus S$
. Then
$U=X\setminus S$
. Then
![]() $f[\rho (F\setminus K_S)] \subseteq X\setminus S=U$
.
$f[\rho (F\setminus K_S)] \subseteq X\setminus S=U$
.
(b)
![]() $\implies $
(c) Obvious.
$\implies $
(c) Obvious.
(c)
![]() $\implies $
(a) Suppose that
$\implies $
(a) Suppose that
![]() $\rho $
is not
$\rho $
is not
![]() $P^-(\Lambda )$
and let
$P^-(\Lambda )$
and let
![]() $A_n\in \mathcal {I}^+_\rho $
be the witnessing sequence, i.e.,
$A_n\in \mathcal {I}^+_\rho $
be the witnessing sequence, i.e.,
![]() $A_0=\Lambda $
,
$A_0=\Lambda $
,
![]() $A_{n+1}\subseteq A_n$
,
$A_{n+1}\subseteq A_n$
,
![]() $A_n\setminus A_{n+1}\in \mathcal {I}_\rho $
and for each
$A_n\setminus A_{n+1}\in \mathcal {I}_\rho $
and for each
![]() $F\in \mathcal {F}$
there is
$F\in \mathcal {F}$
there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $\rho (F)\not \subseteq ^\rho A_n$
. Note that
$\rho (F)\not \subseteq ^\rho A_n$
. Note that
![]() $\bigcap _{n\in \omega }A_n\in \mathcal {I}_\rho $
.
$\bigcap _{n\in \omega }A_n\in \mathcal {I}_\rho $
.
Let X be an infinite Hausdorff topological space. We will show that
![]() $X\notin \operatorname {\mathrm {FinBW}}(\rho )$
. If X is not sequentially compact, then
$X\notin \operatorname {\mathrm {FinBW}}(\rho )$
. If X is not sequentially compact, then
![]() $X\notin \operatorname {\mathrm {FinBW}}(\rho )$
by item (1). If X is sequentially compact, then find any one-to-one sequence
$X\notin \operatorname {\mathrm {FinBW}}(\rho )$
by item (1). If X is sequentially compact, then find any one-to-one sequence
![]() $\{x_n:n\in \omega \}$
in X converging to some
$\{x_n:n\in \omega \}$
in X converging to some
![]() $x\in X$
. Without loss of generality we may assume that
$x\in X$
. Without loss of generality we may assume that
![]() $x\neq x_n$
for all
$x\neq x_n$
for all
![]() $n\in \omega $
. Define
$n\in \omega $
. Define
![]() $f:\Lambda \to X$
by
$f:\Lambda \to X$
by
![]() $f\restriction \bigcap _{n\in \omega }A_n=x_0$
and
$f\restriction \bigcap _{n\in \omega }A_n=x_0$
and
![]() $f(\lambda )=x_{n+1}$
, where n is such that
$f(\lambda )=x_{n+1}$
, where n is such that
![]() $\lambda \in A_n\setminus A_{n+1}$
. Suppose for the sake of contradiction that there are
$\lambda \in A_n\setminus A_{n+1}$
. Suppose for the sake of contradiction that there are
![]() $L\in X$
and
$L\in X$
and
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $f\restriction \rho (F)\ \rho $
-converges to L. By Proposition 9.2(1b) we get that either
$f\restriction \rho (F)\ \rho $
-converges to L. By Proposition 9.2(1b) we get that either
![]() $L=x_n$
for some
$L=x_n$
for some
![]() $n\in \omega $
or
$n\in \omega $
or
![]() $L=x$
.
$L=x$
.
If
![]() $L=x_n$
for some
$L=x_n$
for some
![]() $n\in \omega $
, find open U and V such that
$n\in \omega $
, find open U and V such that
![]() $x_n\in U$
,
$x_n\in U$
,
![]() $x\in V$
, and
$x\in V$
, and
![]() $U\cap V=\emptyset $
. Since
$U\cap V=\emptyset $
. Since
![]() $x_m\in V$
(so
$x_m\in V$
(so
![]() $x_m\notin U$
) for almost all
$x_m\notin U$
) for almost all
![]() $m\in \omega $
and
$m\in \omega $
and
![]() $f^{-1}[\{x_m\}]\in \mathcal {I}_\rho $
for all
$f^{-1}[\{x_m\}]\in \mathcal {I}_\rho $
for all
![]() $m\in \omega $
,
$m\in \omega $
,
![]() $f^{-1}[U]\in \mathcal {I}_\rho $
. Hence,
$f^{-1}[U]\in \mathcal {I}_\rho $
. Hence,
![]() $f\restriction \rho (F)$
cannot
$f\restriction \rho (F)$
cannot
![]() $\rho $
-converge to
$\rho $
-converge to
![]() $x_n$
.
$x_n$
.
If
![]() $L=x$
, we can find
$L=x$
, we can find
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $\rho (F)\not \subseteq ^\rho A_n$
. Since X is Hausdorff, there is an open neighbourhood U of L such that
$\rho (F)\not \subseteq ^\rho A_n$
. Since X is Hausdorff, there is an open neighbourhood U of L such that
![]() $x_{i+1}\notin U$
for all
$x_{i+1}\notin U$
for all
![]() $i<n$
. Since
$i<n$
. Since
![]() $f\restriction \rho (F)\ \rho $
-converges to L, there should be a finite
$f\restriction \rho (F)\ \rho $
-converges to L, there should be a finite
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $f[\rho (F\setminus K)]\subseteq U$
; however,
$f[\rho (F\setminus K)]\subseteq U$
; however,
![]() $\rho (F\setminus K)\setminus A_n\neq \emptyset $
(by
$\rho (F\setminus K)\setminus A_n\neq \emptyset $
(by
![]() $\rho (F)\not \subseteq ^\rho A_n$
), so
$\rho (F)\not \subseteq ^\rho A_n$
), so
![]() $f[\rho (F\setminus K)]\cap \{x_{i+1}:i<n\}\neq \emptyset $
, which contradicts
$f[\rho (F\setminus K)]\cap \{x_{i+1}:i<n\}\neq \emptyset $
, which contradicts
![]() $x_{i+1}\notin U$
for all
$x_{i+1}\notin U$
for all
![]() $i<n$
.
$i<n$
.
(4) (a)
![]() $\implies $
(b) Notice that if X is the space defined in the proof of the implication
$\implies $
(b) Notice that if X is the space defined in the proof of the implication
![]() $(3a)\implies (3b)$
then
$(3a)\implies (3b)$
then
![]() $X\in \operatorname {\mathrm {FinBW}}(\rho )$
for every
$X\in \operatorname {\mathrm {FinBW}}(\rho )$
for every
![]() $\rho $
that is
$\rho $
that is
![]() $P^-(\Lambda )$
(the definition of X did not depend on
$P^-(\Lambda )$
(the definition of X did not depend on
![]() $\rho $
). Thus, if
$\rho $
). Thus, if
![]() $\rho $
is
$\rho $
is
![]() $P^-$
then
$P^-$
then
![]() $\rho \restriction \rho (F)$
is
$\rho \restriction \rho (F)$
is
![]() $P^-(\rho (F))$
for every
$P^-(\rho (F))$
for every
![]() $F\in \mathcal {F}$
and consequently
$F\in \mathcal {F}$
and consequently
![]() $X\in \bigcap _{F\in \mathcal {F}}\operatorname {\mathrm {FinBW}}(\rho \restriction \rho (F))=\operatorname {\mathrm {hFinBW}}(\rho )$
(by Proposition 10.2(1a)).
$X\in \bigcap _{F\in \mathcal {F}}\operatorname {\mathrm {FinBW}}(\rho \restriction \rho (F))=\operatorname {\mathrm {hFinBW}}(\rho )$
(by Proposition 10.2(1a)).
(b)
![]() $\implies $
(c) Obvious.
$\implies $
(c) Obvious.
(c)
![]() $\implies $
(a) If
$\implies $
(a) If
![]() $\rho $
is not
$\rho $
is not
![]() $P^-$
then
$P^-$
then
![]() $\rho \restriction \rho (F)$
is not
$\rho \restriction \rho (F)$
is not
![]() $P^-(\rho (F))$
for some
$P^-(\rho (F))$
for some
![]() $F\in \mathcal {F}$
. Hence, by item (3),
$F\in \mathcal {F}$
. Hence, by item (3),
![]() $\operatorname {\mathrm {FinBW}}(\rho \restriction \rho (F))$
contains only finite Hausdorff spaces. Since
$\operatorname {\mathrm {FinBW}}(\rho \restriction \rho (F))$
contains only finite Hausdorff spaces. Since
![]() $\operatorname {\mathrm {hFinBW}}(\rho )\subseteq \operatorname {\mathrm {FinBW}}(\rho \restriction \rho (F))$
by Proposition 10.2(1a),
$\operatorname {\mathrm {hFinBW}}(\rho )\subseteq \operatorname {\mathrm {FinBW}}(\rho \restriction \rho (F))$
by Proposition 10.2(1a),
![]() $\operatorname {\mathrm {hFinBW}}(\rho )$
also contains only finite Hausdorff spaces.
$\operatorname {\mathrm {hFinBW}}(\rho )$
also contains only finite Hausdorff spaces.
(5a) Let
![]() $f:\Lambda \to \omega _1$
. If there is
$f:\Lambda \to \omega _1$
. If there is
![]() $\alpha <\omega _1$
with
$\alpha <\omega _1$
with
![]() $f^{-1}[\{\alpha \}]\notin \mathcal {I}_\rho $
, then we take
$f^{-1}[\{\alpha \}]\notin \mathcal {I}_\rho $
, then we take
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq f^{-1}[\{\alpha \}]$
and see that
$\rho (F)\subseteq f^{-1}[\{\alpha \}]$
and see that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to
$\rho $
-convergent to
![]() $\alpha $
. Now, we assume that
$\alpha $
. Now, we assume that
![]() $f^{-1}[\{\alpha \}]\in \mathcal {I}_\rho $
for every
$f^{-1}[\{\alpha \}]\in \mathcal {I}_\rho $
for every
![]() $\alpha <\omega _1$
. Since
$\alpha <\omega _1$
. Since
![]() $\Lambda $
is countable and the cofinality of
$\Lambda $
is countable and the cofinality of
![]() $\omega _1$
is uncountable, there is
$\omega _1$
is uncountable, there is
![]() $\alpha <\omega _1$
with
$\alpha <\omega _1$
with
![]() $f^{-1}[\alpha ]\notin \mathcal {I}_\rho $
. Let
$f^{-1}[\alpha ]\notin \mathcal {I}_\rho $
. Let
![]() $\alpha _0$
be the smallest
$\alpha _0$
be the smallest
![]() $\alpha $
such that
$\alpha $
such that
![]() $f^{-1}[\alpha ]\notin \mathcal {I}_\rho $
. Note that
$f^{-1}[\alpha ]\notin \mathcal {I}_\rho $
. Note that
![]() $\alpha _0$
is a limit ordinal. Indeed, if
$\alpha _0$
is a limit ordinal. Indeed, if
![]() $\alpha _0=\alpha +1$
, then
$\alpha _0=\alpha +1$
, then
![]() $\alpha <\alpha _0$
and
$\alpha <\alpha _0$
and
![]() $f^{-1}[\alpha ] = f^{-1}[\alpha _0]\setminus f^{-1}[\{\alpha \}]\notin \mathcal {I}_\rho $
, a contradiction. Since
$f^{-1}[\alpha ] = f^{-1}[\alpha _0]\setminus f^{-1}[\{\alpha \}]\notin \mathcal {I}_\rho $
, a contradiction. Since
![]() $\alpha _0$
is a countable limit ordinal, there is an increasing sequence
$\alpha _0$
is a countable limit ordinal, there is an increasing sequence
![]() $\{\beta _n:n\in \omega \}$
such that
$\{\beta _n:n\in \omega \}$
such that
![]() $\sup \{\beta _n:n\in \omega \}=\alpha _0$
. By Proposition 6.8, there is
$\sup \{\beta _n:n\in \omega \}=\alpha _0$
. By Proposition 6.8, there is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq f^{-1}[\alpha _0]$
and for each
$\rho (F)\subseteq f^{-1}[\alpha _0]$
and for each
![]() $n\in \omega $
there is a finite set
$n\in \omega $
there is a finite set
![]() $K_n$
such that
$K_n$
such that
![]() $\rho (F\setminus K_n)\cap f^{-1}[\beta _n]=\emptyset $
. We claim that
$\rho (F\setminus K_n)\cap f^{-1}[\beta _n]=\emptyset $
. We claim that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to
$\rho $
-convergent to
![]() $\alpha _0$
. Indeed, let U be a neighborhood of
$\alpha _0$
. Indeed, let U be a neighborhood of
![]() $\alpha _0$
. Without loss of generality, we can assume that
$\alpha _0$
. Without loss of generality, we can assume that
![]() $U = (\alpha _0+1)\setminus \beta _n$
for some
$U = (\alpha _0+1)\setminus \beta _n$
for some
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $f[\rho (F\setminus K_n)] \subseteq \alpha _0\setminus \beta _n \subseteq U$
.
$f[\rho (F\setminus K_n)] \subseteq \alpha _0\setminus \beta _n \subseteq U$
.
(5b) Spaces with these properties are constructed in Theorem 14.5.
(6) Let
![]() $f:\rho (E)\to X$
be a
$f:\rho (E)\to X$
be a
![]() $\rho $
-sequence in a metric compact space X.
$\rho $
-sequence in a metric compact space X.
Since
![]() $\rho $
is weak
$\rho $
is weak
![]() $P^+$
, there exists
$P^+$
, there exists
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq \rho (E)$
and for every sequence
$\rho (F)\subseteq \rho (E)$
and for every sequence
![]() $\{F_n: n\in \omega \}\subseteq \mathcal {F}$
such that
$\{F_n: n\in \omega \}\subseteq \mathcal {F}$
such that
![]() $\rho (F) \supseteq \rho (F_n)\supseteq \rho (F_{n+1})$
for each
$\rho (F) \supseteq \rho (F_n)\supseteq \rho (F_{n+1})$
for each
![]() $n\in \omega $
there exists
$n\in \omega $
there exists
![]() $G\in \mathcal {F}$
such that
$G\in \mathcal {F}$
such that
![]() $\rho (G)\subseteq \rho (F)$
and
$\rho (G)\subseteq \rho (F)$
and
![]() $\rho (G)\subseteq ^\rho \rho (F_n)$
for each
$\rho (G)\subseteq ^\rho \rho (F_n)$
for each
![]() $n\in \omega $
.
$n\in \omega $
.
For
![]() $x\in X$
and
$x\in X$
and
![]() $r>0$
we write
$r>0$
we write
![]() $B(x,r)$
and
$B(x,r)$
and
![]() $\overline {B}(x,r)$
to denote an open and closed ball of radius r centered at a point x, respectively.
$\overline {B}(x,r)$
to denote an open and closed ball of radius r centered at a point x, respectively.
Since X is compact metric, there are finitely many
![]() $x_i^0\in X$
,
$x_i^0\in X$
,
![]() $i<n_0$
such that
$i<n_0$
such that
![]() $X=\bigcup \{B(x_i^0,1):i<n_0\}$
. Then there exists
$X=\bigcup \{B(x_i^0,1):i<n_0\}$
. Then there exists
![]() $i_0<n_0$
such that
$i_0<n_0$
such that
![]() $\rho (F)\cap f^{-1}[B(x^0_{i_0},1)] \notin \mathcal {I}_{\rho }$
, and consequently there is
$\rho (F)\cap f^{-1}[B(x^0_{i_0},1)] \notin \mathcal {I}_{\rho }$
, and consequently there is
![]() $F_0\in \mathcal {F}$
such that
$F_0\in \mathcal {F}$
such that
![]() $\rho (F_0)\subseteq \rho (F)\cap f^{-1}[B(x^0_{i_0},1)]$
.
$\rho (F_0)\subseteq \rho (F)\cap f^{-1}[B(x^0_{i_0},1)]$
.
Since
![]() $\overline {B}(x^0_{i_0},1)$
is compact metric, there are finitely many
$\overline {B}(x^0_{i_0},1)$
is compact metric, there are finitely many
![]() $x_i^1\in X$
,
$x_i^1\in X$
,
![]() $i<n_1$
such that
$i<n_1$
such that
![]() $\overline {B}(x^0_{i_0},1)\subseteq \bigcup \{B(x_i^1,\frac {1}{2}):i<n_1\}$
. Then there exists
$\overline {B}(x^0_{i_0},1)\subseteq \bigcup \{B(x_i^1,\frac {1}{2}):i<n_1\}$
. Then there exists
![]() $i_1<n_1$
such that
$i_1<n_1$
such that
![]() $\rho (F_0)\cap f^{-1}[B(x^1_{i_1},\frac {1}{2})] \notin \mathcal {I}_{\rho }$
, and consequently there is
$\rho (F_0)\cap f^{-1}[B(x^1_{i_1},\frac {1}{2})] \notin \mathcal {I}_{\rho }$
, and consequently there is
![]() $F_1\in \mathcal {F}$
such that
$F_1\in \mathcal {F}$
such that
![]() $\rho (F_1)\subseteq \rho (F_0)\cap f^{-1}[B(x^1_{i_1},\frac {1}{2})]$
.
$\rho (F_1)\subseteq \rho (F_0)\cap f^{-1}[B(x^1_{i_1},\frac {1}{2})]$
.
If we continue the above procedure, we obtain
![]() $F_n\in \mathcal {F}$
and
$F_n\in \mathcal {F}$
and
![]() $x^n_{i_n}\in X$
such that
$x^n_{i_n}\in X$
such that
![]() $\rho (F_{n})\subseteq \rho (F_{n-1}) \cap f^{-1}[B(x^n_{i_n},\frac {1}{n+1})]$
for each
$\rho (F_{n})\subseteq \rho (F_{n-1}) \cap f^{-1}[B(x^n_{i_n},\frac {1}{n+1})]$
for each
![]() $n\in \omega $
(assuming that
$n\in \omega $
(assuming that
![]() $F_{-1}=F$
).
$F_{-1}=F$
).
Let
![]() $x\in \bigcap \{\overline {B}(x^n_{i_n},\frac {1}{n+1}):n\in \omega \}$
.
$x\in \bigcap \{\overline {B}(x^n_{i_n},\frac {1}{n+1}):n\in \omega \}$
.
Since
![]() $\rho $
is weak
$\rho $
is weak
![]() $P^+$
, we have
$P^+$
, we have
![]() $G\in \mathcal {F}$
such that
$G\in \mathcal {F}$
such that
![]() $\rho (G)\subseteq \rho (F)$
and
$\rho (G)\subseteq \rho (F)$
and
![]() $\rho (G)\subseteq ^\rho \rho (F_n)$
for each
$\rho (G)\subseteq ^\rho \rho (F_n)$
for each
![]() $n\in \omega $
.
$n\in \omega $
.
We claim that
![]() $f\restriction \rho (G)$
is
$f\restriction \rho (G)$
is
![]() $\rho $
-convergent to x. Let U be a neighborhood of x. Since the sequence
$\rho $
-convergent to x. Let U be a neighborhood of x. Since the sequence
![]() $(x^n_{i_n})_{n\in \omega }$
is convergent to x, there is
$(x^n_{i_n})_{n\in \omega }$
is convergent to x, there is
![]() $n_0\in \omega $
such that
$n_0\in \omega $
such that
![]() $B(x^n_{i_n},\frac {1}{n+1})\subseteq U$
for every
$B(x^n_{i_n},\frac {1}{n+1})\subseteq U$
for every
![]() $n\geq n_0$
. Consequently, there is
$n\geq n_0$
. Consequently, there is
![]() $n\in \omega $
with
$n\in \omega $
with
![]() $B(x^n_{i_n},\frac {1}{n+1})\subseteq U$
. Let
$B(x^n_{i_n},\frac {1}{n+1})\subseteq U$
. Let
![]() $K\subseteq \Omega $
be a finite set such that
$K\subseteq \Omega $
be a finite set such that
![]() $\rho (G\setminus K)\subseteq \rho (F_n)$
. Then
$\rho (G\setminus K)\subseteq \rho (F_n)$
. Then
![]() $f[\rho (G\setminus K)]\subseteq f[\rho (F_n)] \subseteq B(x^n_{i_n},\frac {1}{n+1}) \subseteq U,$
so the proof is finished.
$f[\rho (G\setminus K)]\subseteq f[\rho (F_n)] \subseteq B(x^n_{i_n},\frac {1}{n+1}) \subseteq U,$
so the proof is finished.
(7) Let
![]() $E\in \mathcal {F}$
and
$E\in \mathcal {F}$
and
![]() $f:\rho (E)\to X$
be a sequence in a Hausdorff topological space X having the property
$f:\rho (E)\to X$
be a sequence in a Hausdorff topological space X having the property
![]() $(*)$
. Since the set
$(*)$
. Since the set
![]() $D=\{f(\lambda ):\lambda \in \rho (E)\}$
is countable, the closure
$D=\{f(\lambda ):\lambda \in \rho (E)\}$
is countable, the closure
![]() $\operatorname {\mathrm {cl}}_X(D)$
is compact and first-countable. We claim that there exists
$\operatorname {\mathrm {cl}}_X(D)$
is compact and first-countable. We claim that there exists
![]() $L\in \operatorname {\mathrm {cl}}_X(D)$
such that
$L\in \operatorname {\mathrm {cl}}_X(D)$
such that
![]() $f^{-1}[U] \in \mathcal {I}_{\rho }^+$
for every neighborhood U of L.
$f^{-1}[U] \in \mathcal {I}_{\rho }^+$
for every neighborhood U of L.
Suppose, for the sake of contradiction, that for every
![]() $x\in \operatorname {\mathrm {cl}}_X(D)$
there is a neighborhood
$x\in \operatorname {\mathrm {cl}}_X(D)$
there is a neighborhood
![]() $U_x$
of x such that
$U_x$
of x such that
![]() $f^{-1}[U_x]\in \mathcal {I}_{\rho }$
. Since
$f^{-1}[U_x]\in \mathcal {I}_{\rho }$
. Since
![]() $\operatorname {\mathrm {cl}}_X(D)$
is compact, there are finitely many
$\operatorname {\mathrm {cl}}_X(D)$
is compact, there are finitely many
![]() $x_i\in \operatorname {\mathrm {cl}}_X(D)$
for
$x_i\in \operatorname {\mathrm {cl}}_X(D)$
for
![]() $i<n$
with
$i<n$
with
![]() $\operatorname {\mathrm {cl}}_X(D) \subseteq \bigcup \{ U_{x_i} : i<n\}.$
Then
$\operatorname {\mathrm {cl}}_X(D) \subseteq \bigcup \{ U_{x_i} : i<n\}.$
Then
![]() $\rho (E) = \bigcup \{f^{-1}[U_{x_i}]:i<n\} \in \mathcal {I}_{\rho },$
a contradiction, so the claim is proved.
$\rho (E) = \bigcup \{f^{-1}[U_{x_i}]:i<n\} \in \mathcal {I}_{\rho },$
a contradiction, so the claim is proved.
Let
![]() $\{U_n:n\in \omega \}$
be a base at L. Without loss of generality, we can assume that
$\{U_n:n\in \omega \}$
be a base at L. Without loss of generality, we can assume that
![]() $U_n\supseteq U_{n+1}$
for each
$U_n\supseteq U_{n+1}$
for each
![]() $n\in \omega $
. For each
$n\in \omega $
. For each
![]() $n\in \omega $
, we define
$n\in \omega $
, we define
![]() $A_n=\{\lambda \in \rho (E): f(\lambda )\in U_n\}$
. Since
$A_n=\{\lambda \in \rho (E): f(\lambda )\in U_n\}$
. Since
![]() $A_n\in \mathcal {I}_{\rho }^+$
and
$A_n\in \mathcal {I}_{\rho }^+$
and
![]() $A_n\supseteq A_{n+1}$
for each
$A_n\supseteq A_{n+1}$
for each
![]() $n\in \omega $
, using the fact that
$n\in \omega $
, using the fact that
![]() $\rho $
is
$\rho $
is
![]() $P^+$
, there exists
$P^+$
, there exists
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq \rho (E)$
and
$\rho (F)\subseteq \rho (E)$
and
![]() $\rho (F)\subseteq ^\rho A_n$
for each
$\rho (F)\subseteq ^\rho A_n$
for each
![]() $n\in \omega $
. We claim that
$n\in \omega $
. We claim that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to L.
$\rho $
-convergent to L.
Take any neighborhood U of L. Then there exists
![]() $n_0\in \omega $
with
$n_0\in \omega $
with
![]() $U_{n_0}\subseteq U$
. Since
$U_{n_0}\subseteq U$
. Since
![]() $\rho (F)\subseteq ^\rho A_{n_0}$
, there exists a finite set
$\rho (F)\subseteq ^\rho A_{n_0}$
, there exists a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $\rho (F\setminus K) \subseteq A_{n_0}$
. Thus
$\rho (F\setminus K) \subseteq A_{n_0}$
. Thus
![]() $f[\rho (F\setminus K)] \subseteq U_{n_0}\subseteq U$
, so the proof is finished.
$f[\rho (F\setminus K)] \subseteq U_{n_0}\subseteq U$
, so the proof is finished.
The following series of corollaries shows that many known earlier results can be easily derived from Theorem 10.5.
Corollary 10.6 [Reference Filipów and Tryba28, Proposition 2.4].
If an ideal
![]() $\mathcal {I}$
is not tall, then
$\mathcal {I}$
is not tall, then
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
coincides with the class of all sequentially compact spaces.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
coincides with the class of all sequentially compact spaces.
Corollary 10.7 [Reference Kwela62, Theorem 6.5].
![]() $\mathrm {Fin}^2\leq _K\mathcal {I} \iff \operatorname {\mathrm {FinBW}}(\mathcal {I})$
coincides with the class of all finite spaces in the realm of Hausdorff spaces.
$\mathrm {Fin}^2\leq _K\mathcal {I} \iff \operatorname {\mathrm {FinBW}}(\mathcal {I})$
coincides with the class of all finite spaces in the realm of Hausdorff spaces.
Corollary 10.8. Every metric compact space belongs to
![]() $\operatorname {\mathrm {hFinBW}}(\rho )$
in case when
$\operatorname {\mathrm {hFinBW}}(\rho )$
in case when
![]() $:$
$:$
-
(1)
 $\rho =\rho _{\mathcal {I}}$
and
$\rho =\rho _{\mathcal {I}}$
and
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^+$
ideal,
$P^+$
ideal, -
(2) [Reference Flašková30, Theorem 2.3]
 $\rho =\rho _{\mathcal {I}}$
and
$\rho =\rho _{\mathcal {I}}$
and
 $\mathcal {I}$
is an
$\mathcal {I}$
is an
 $F_\sigma $
ideal,
$F_\sigma $
ideal, -
(3) [Reference Kojman58, Theorem 10]
 $\rho =\rho _{\mathcal {I}}$
and
$\rho =\rho _{\mathcal {I}}$
and
 $\mathcal {I} = \mathcal {W}$
,
$\mathcal {I} = \mathcal {W}$
, -
(4) [Reference Flašková30, Theorem 2.3]
 $\rho =\rho _{\mathcal {I}}$
and
$\rho =\rho _{\mathcal {I}}$
and
 $\mathcal {I} = \mathcal {I}_{1/n}$
,
$\mathcal {I} = \mathcal {I}_{1/n}$
, -
(5) [Reference Furstenberg and Weiss36, Theorem 2.5]
 $\rho =\operatorname {\mathrm {FS}}$
,
$\rho =\operatorname {\mathrm {FS}}$
, -
(6) [Reference Bojańczyk, Kopczyński and Toruńczyk6, Theorem 1] (see also [Reference Bergelson and Zelada5, Theorem 1.16])
 $\rho = r$
,
$\rho = r$
, -
(7) [Reference Filipów22, Corollary 4.8]
 $\rho = \Delta $
.
$\rho = \Delta $
.
Corollary 10.9. Every Hausdorff space with the property
![]() $(*)$
belongs to
$(*)$
belongs to
![]() $\operatorname {\mathrm {hFinBW}}(\rho )$
in case when
$\operatorname {\mathrm {hFinBW}}(\rho )$
in case when
![]() $:$
$:$
-
(1)
 $\rho =\rho _{\mathcal {I}}$
and
$\rho =\rho _{\mathcal {I}}$
and
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^+$
ideal,
$P^+$
ideal, -
(2) [Reference Flašková30, Theorem 2.3]
 $\rho =\rho _{\mathcal {I}}$
and
$\rho =\rho _{\mathcal {I}}$
and
 $\mathcal {I}$
is an
$\mathcal {I}$
is an
 $F_\sigma $
ideal,
$F_\sigma $
ideal, -
(3) [Reference Kojman58, Theorem 10]
 $\rho =\rho _{\mathcal {I}}$
and
$\rho =\rho _{\mathcal {I}}$
and
 $\mathcal {I} = \mathcal {W}$
,
$\mathcal {I} = \mathcal {W}$
, -
(4) [Reference Flašková30, Theorem 2.3]
 $\rho =\rho _{\mathcal {I}}$
and
$\rho =\rho _{\mathcal {I}}$
and
 $\mathcal {I} = \mathcal {I}_{1/n}$
.
$\mathcal {I} = \mathcal {I}_{1/n}$
.
In [Reference Kojman57, Theorem 11] ([Reference Kubiś and Szeptycki61, Corollary 3.2], resp.), the authors proved that every Hausdorff space with the property
![]() $(*)$
belongs to
$(*)$
belongs to
![]() $\operatorname {\mathrm {hFinBW}}(\operatorname {\mathrm {FS}})$
(
$\operatorname {\mathrm {hFinBW}}(\operatorname {\mathrm {FS}})$
(
![]() $\operatorname {\mathrm {hFinBW}}(r)$
, resp.). However, their proofs use properties very specific to
$\operatorname {\mathrm {hFinBW}}(r)$
, resp.). However, their proofs use properties very specific to
![]() $\operatorname {\mathrm {FS}}$
and r. For instance, the proof for
$\operatorname {\mathrm {FS}}$
and r. For instance, the proof for
![]() $\operatorname {\mathrm {FS}}$
uses idempotent ultrafilters, whereas the proof for r uses the bounding number
$\operatorname {\mathrm {FS}}$
uses idempotent ultrafilters, whereas the proof for r uses the bounding number
![]() $\mathfrak {b}$
.
$\mathfrak {b}$
.
Problem 10.10. Find a property W of partition regular functions such that both
![]() $\operatorname {\mathrm {FS}}$
and r have the property W and if
$\operatorname {\mathrm {FS}}$
and r have the property W and if
![]() $\rho $
has the property W then every Hausdorff space with the property
$\rho $
has the property W then every Hausdorff space with the property
![]() $(*)$
belongs to
$(*)$
belongs to
![]() $\operatorname {\mathrm {hFinBW}}(\rho )$
.
$\operatorname {\mathrm {hFinBW}}(\rho )$
.
In [Reference Filipów22, Corollary 4.8], the author proved that every Hausdorff space with the property
![]() $(*)$
belongs to
$(*)$
belongs to
![]() $\operatorname {\mathrm {FinBW}}(\Delta )$
.
$\operatorname {\mathrm {FinBW}}(\Delta )$
.
Question 10.11. Does every Hausdorff space with the property
![]() $(*)$
belong to
$(*)$
belong to
![]() $\operatorname {\mathrm {hFinBW}}(\Delta )$
?
$\operatorname {\mathrm {hFinBW}}(\Delta )$
?
Note that the positive answer to Question 10.4(2a) gives the positive answer to Question 10.11.
11 Inclusions between
 $\operatorname {\mathrm {FinBW}}$
classes
$\operatorname {\mathrm {FinBW}}$
classes
Theorem 11.1. Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular with
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular with
![]() $\mathcal {F}_i\subseteq [\Omega _i]^\omega $
for each
$\mathcal {F}_i\subseteq [\Omega _i]^\omega $
for each
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\Lambda $
.
$\Lambda $
.
-
(1)
 $\rho _2\leq _K \rho _1 \implies \operatorname {\mathrm {FinBW}}(\rho _1) \subseteq \operatorname {\mathrm {FinBW}}(\rho _2)$
.
$\rho _2\leq _K \rho _1 \implies \operatorname {\mathrm {FinBW}}(\rho _1) \subseteq \operatorname {\mathrm {FinBW}}(\rho _2)$
. -
(2)
-
(a) If
 $\rho _2$
is
$\rho _2$
is
 $P^+$
, then
$P^+$
, then  $$ \begin{align*}\mathcal{I}_{\rho_2}\leq_K \mathcal{I}_{\rho_1} \implies \operatorname{\mathrm{FinBW}}(\rho_1) \subseteq \operatorname{\mathrm{FinBW}}(\rho_2).\end{align*} $$
$$ \begin{align*}\mathcal{I}_{\rho_2}\leq_K \mathcal{I}_{\rho_1} \implies \operatorname{\mathrm{FinBW}}(\rho_1) \subseteq \operatorname{\mathrm{FinBW}}(\rho_2).\end{align*} $$
-
(b)
 $\mathcal {I}_{\rho _2}\leq _K \mathcal {I} \implies \operatorname {\mathrm {FinBW}}(\mathcal {I})\subseteq \operatorname {\mathrm {FinBW}}(\rho _2)$
.
$\mathcal {I}_{\rho _2}\leq _K \mathcal {I} \implies \operatorname {\mathrm {FinBW}}(\mathcal {I})\subseteq \operatorname {\mathrm {FinBW}}(\rho _2)$
.
-
Proof (1) Let
![]() $\phi :\Lambda _1\to \Lambda _2$
be a witness for
$\phi :\Lambda _1\to \Lambda _2$
be a witness for
![]() $\rho _2\leq _K \rho _1$
. Let
$\rho _2\leq _K \rho _1$
. Let
![]() $X\in \operatorname {\mathrm {FinBW}}(\rho _1)$
. If
$X\in \operatorname {\mathrm {FinBW}}(\rho _1)$
. If
![]() $f:\Lambda _2\to X$
, then
$f:\Lambda _2\to X$
, then
![]() $f\circ \phi : \Lambda _1\to X$
, so there is
$f\circ \phi : \Lambda _1\to X$
, so there is
![]() $F_1\in \mathcal {F}_1$
such that
$F_1\in \mathcal {F}_1$
such that
![]() $\rho _1(F_1)\subseteq \Lambda _1$
and
$\rho _1(F_1)\subseteq \Lambda _1$
and
![]() $(f\circ \phi )\restriction \rho _1(F_1)$
is
$(f\circ \phi )\restriction \rho _1(F_1)$
is
![]() $\rho _1$
-convergent to some
$\rho _1$
-convergent to some
![]() $x\in X$
.
$x\in X$
.
Let
![]() $F_2\in \mathcal {F}_2$
be such that for every finite
$F_2\in \mathcal {F}_2$
be such that for every finite
![]() $K_1\subseteq \Omega _1$
there is a finite
$K_1\subseteq \Omega _1$
there is a finite
![]() $K_2\subseteq \Omega _2$
with
$K_2\subseteq \Omega _2$
with
![]() $\rho _2(F_2\setminus K_2)\subseteq \phi [\rho _1(F_1\setminus K_1)]$
.
$\rho _2(F_2\setminus K_2)\subseteq \phi [\rho _1(F_1\setminus K_1)]$
.
We claim that
![]() $f\restriction \rho _2(F_2)$
is
$f\restriction \rho _2(F_2)$
is
![]() $\rho _2$
-convergent to x. Let U be a neighborhood of x. Since
$\rho _2$
-convergent to x. Let U be a neighborhood of x. Since
![]() $(f\circ \phi )\restriction \rho _1(F_1)$
is
$(f\circ \phi )\restriction \rho _1(F_1)$
is
![]() $\rho _1$
-convergent to x, then there is a finite set
$\rho _1$
-convergent to x, then there is a finite set
![]() $K_1\subseteq \Omega _1$
such that
$K_1\subseteq \Omega _1$
such that
![]() $(f\circ \phi )[\rho _1(F_1\setminus K_1)]\subseteq U$
. Hence, we can find a finite
$(f\circ \phi )[\rho _1(F_1\setminus K_1)]\subseteq U$
. Hence, we can find a finite
![]() $K_2\subseteq \Omega _2$
with
$K_2\subseteq \Omega _2$
with
![]() $\rho _2(F_2\setminus K_2)\subseteq \phi [\rho _1(F_1\setminus K_1)]$
. Then
$\rho _2(F_2\setminus K_2)\subseteq \phi [\rho _1(F_1\setminus K_1)]$
. Then
![]() $f[\rho _2(F_2\setminus K_2)] \subseteq f[\phi [\rho _1(F_1\setminus K_1)]] \subseteq U$
. That finishes the proof.
$f[\rho _2(F_2\setminus K_2)] \subseteq f[\phi [\rho _1(F_1\setminus K_1)]] \subseteq U$
. That finishes the proof.
(2a) It follows from Proposition 7.5(2a) and item (1).
(2b) It follows from item (1) and Propositions 7.5(2b) and 10.2(4).
The following series of corollaries shows that many known earlier results as well as some new one can be easily derived from Theorem 11.1.
Corollary 11.2.
-
(1) [Reference Shi73, p. 39] Every Hindman space is differentially compact.
-
(2) Every Ramsey space is differentially compact.
-
(3) Let
 $\mathcal {I}$
be a
$\mathcal {I}$
be a
 $P^+$
ideal.
$P^+$
ideal.-
(a) [Reference Filipów, Kowitz, Kwela and Tryba24, Proposition 2.6] If
 $\mathcal {I}\leq _K\mathcal {H}$
then every Hindman space is in
$\mathcal {I}\leq _K\mathcal {H}$
then every Hindman space is in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
. -
(b) If
 $\mathcal {I}\leq _K\mathcal {R}$
then every Ramsey space is in
$\mathcal {I}\leq _K\mathcal {R}$
then every Ramsey space is in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
. -
(c) If
 $\mathcal {I}\leq _K\mathcal {D}$
then every differentially compact space is in
$\mathcal {I}\leq _K\mathcal {D}$
then every differentially compact space is in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
-
-
(4) [Reference Kwela62, Corollary 10.2(a)] If
 $\mathcal {I}_i$
are ideals for
$\mathcal {I}_i$
are ideals for
 $i=1,2$
and
$i=1,2$
and
 $\mathcal {I}_2\leq _K\mathcal {I}_1$
, then
$\mathcal {I}_2\leq _K\mathcal {I}_1$
, then
 $\operatorname {\mathrm {FinBW}}(\mathcal {I}_1)\subseteq \operatorname {\mathrm {FinBW}}(\mathcal {I}_2)$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I}_1)\subseteq \operatorname {\mathrm {FinBW}}(\mathcal {I}_2)$
.
Proof (1) It follows from Theorems 11.1(1) and 7.7(3).
(2) It follows from Theorems 11.1(1) and 7.7(4).
(3) It follows from Theorem 11.1(2a) and Propositions 6.5(2) and 10.2(4).
(4) It follows from Theorem 11.1(2b) and Proposition 10.2(4).
Corollary 11.3.
-
(1) Let
 $\rho :\mathcal {F}_i\to [\Lambda ]^\omega $
be a partition regular function.
$\rho :\mathcal {F}_i\to [\Lambda ]^\omega $
be a partition regular function.-
(a) If
 $\rho \leq _K\rho '$
for some weak
$\rho \leq _K\rho '$
for some weak
 $P^+$
partition regular function
$P^+$
partition regular function
 $\rho '$
, then every compact metric space belongs to
$\rho '$
, then every compact metric space belongs to
 $\operatorname {\mathrm {FinBW}}(\rho )$
.
$\operatorname {\mathrm {FinBW}}(\rho )$
. -
(b) If
 $\rho \leq _K\rho '$
for some
$\rho \leq _K\rho '$
for some
 $P^+$
partition regular function
$P^+$
partition regular function
 $\rho '$
, then every Hausdorff topological space with the property
$\rho '$
, then every Hausdorff topological space with the property
 $(*)$
belongs to
$(*)$
belongs to
 $\operatorname {\mathrm {FinBW}}(\rho )$
.
$\operatorname {\mathrm {FinBW}}(\rho )$
.
-
-
(2) Let
 $\mathcal {I}$
be an ideal. If an ideal
$\mathcal {I}$
be an ideal. If an ideal
 $\mathcal {I}$
can be extended to a
$\mathcal {I}$
can be extended to a
 $P^+$
ideal, then
$P^+$
ideal, then
 $:$
$:$
-
(a) every compact metric space belongs to
 $\operatorname {\mathrm {FinBW}}(\mathcal {I});$
$\operatorname {\mathrm {FinBW}}(\mathcal {I});$
-
(b) [Reference Filipów, Mrożek, Recław and Szuca27, Corollary 5.6] every Hausdorff topological space with the property
 $(*)$
belongs to
$(*)$
belongs to
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
-
Proof (1) It follows from Theorems 11.1(1) and 10.5(6) and (7) and Proposition 10.2(2).
(2) It follows from item (1) and Propositions 6.5(2), 7.5(2b), and 10.2(4).
The following proposition shows that when comparing classes
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)$
and
$\operatorname {\mathrm {FinBW}}(\rho _1)$
and
![]() $\operatorname {\mathrm {FinBW}}(\rho _2)$
for distinct functions
$\operatorname {\mathrm {FinBW}}(\rho _2)$
for distinct functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
we can in fact assume that both
$\rho _2$
we can in fact assume that both
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
“live” on the same sets
$\rho _2$
“live” on the same sets
![]() $\Omega $
and
$\Omega $
and
![]() $\Lambda $
.
$\Lambda $
.
Proposition 11.4. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. Suppose that
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Suppose that
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Sigma $
are countable infinite sets and
$\Sigma $
are countable infinite sets and
![]() $\phi :\Omega \to \Gamma $
and
$\phi :\Omega \to \Gamma $
and
![]() $\psi :\Lambda \to \Sigma $
are bijections. Let
$\psi :\Lambda \to \Sigma $
are bijections. Let
![]() $\mathcal {G}=\{\phi [F]:F\in \mathcal {F}\}$
and
$\mathcal {G}=\{\phi [F]:F\in \mathcal {F}\}$
and
![]() $\tau :\mathcal {G}\to [\Sigma ]^\omega $
be given by
$\tau :\mathcal {G}\to [\Sigma ]^\omega $
be given by
![]() $\tau (G) = \psi [\rho (\phi ^{-1}[G])]$
. Then
$\tau (G) = \psi [\rho (\phi ^{-1}[G])]$
. Then
![]() $:$
$:$
-
(1)
 $\tau $
is partition regular,
$\tau $
is partition regular, -
(2)
 $\rho $
and
$\rho $
and
 $\tau $
are Katětov equivalent:
$\tau $
are Katětov equivalent:
 $\rho \leq _K\tau $
and
$\rho \leq _K\tau $
and
 $\tau \leq _K\rho $
,
$\tau \leq _K\rho $
, -
(3)
 $\rho $
and
$\rho $
and
 $\tau $
are hereditary Katětov equivalent
$\tau $
are hereditary Katětov equivalent
 $:$
$:$
-
(a)
 $\forall F\in \mathcal {F}\, \exists G\in \mathcal {G} \, (\rho \restriction \rho (F) \leq _K \tau \restriction \tau (G)),$
$\forall F\in \mathcal {F}\, \exists G\in \mathcal {G} \, (\rho \restriction \rho (F) \leq _K \tau \restriction \tau (G)),$
-
(b)
 $\forall G\in \mathcal {G}\, \exists F\in \mathcal {F} \, (\tau \restriction \tau (G) \leq _K \rho \restriction \rho (F)),$
$\forall G\in \mathcal {G}\, \exists F\in \mathcal {F} \, (\tau \restriction \tau (G) \leq _K \rho \restriction \rho (F)),$
-
-
(4)
 $\operatorname {\mathrm {FinBW}}(\tau )=\operatorname {\mathrm {FinBW}}(\rho )$
and
$\operatorname {\mathrm {FinBW}}(\tau )=\operatorname {\mathrm {FinBW}}(\rho )$
and
 $\operatorname {\mathrm {hFinBW}}(\tau )=\operatorname {\mathrm {hFinBW}}(\rho )$
.
$\operatorname {\mathrm {hFinBW}}(\tau )=\operatorname {\mathrm {hFinBW}}(\rho )$
.
Proof Items (1)–(3) are straightforward, whereas item (4) follows from previous items and Proposition 11.1.
Part 3. Distinguishing between
![]() $\mathbf {\operatorname {\mathrm {FinBW}}}$
classes
$\mathbf {\operatorname {\mathrm {FinBW}}}$
classes
In this part we are interested in finding spaces that are in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)$
, but are not in
$\operatorname {\mathrm {FinBW}}(\rho _1)$
, but are not in
![]() $\operatorname {\mathrm {FinBW}}(\rho _2)$
. Similar investigations concerning the classes
$\operatorname {\mathrm {FinBW}}(\rho _2)$
. Similar investigations concerning the classes
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
were conducted in [Reference Kwela62]. In that paper all the examples (showing that under some set-theoretic assumption
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
were conducted in [Reference Kwela62]. In that paper all the examples (showing that under some set-theoretic assumption
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})\setminus \operatorname {\mathrm {FinBW}}(\mathcal {J})\neq \emptyset $
for some ideals
$\operatorname {\mathrm {FinBW}}(\mathcal {I})\setminus \operatorname {\mathrm {FinBW}}(\mathcal {J})\neq \emptyset $
for some ideals
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
) were inspired by [Reference Kojman and Shelah59] and are of one specific type—they are defined using maximal almost disjoint families. It turns out (see Theorem 13.2) that, in general, we cannot use maximal almost disjoint families to distinguish between
$\mathcal {J}$
) were inspired by [Reference Kojman and Shelah59] and are of one specific type—they are defined using maximal almost disjoint families. It turns out (see Theorem 13.2) that, in general, we cannot use maximal almost disjoint families to distinguish between
![]() $\operatorname {\mathrm {FinBW}}(\rho )$
classes with the aid of spaces defined as in [Reference Kwela62]. Fortunately, we managed to use not necessary maximal almost disjoint families to prove two main results of this part (Theorems 14.3 and 15.2), which give us
$\operatorname {\mathrm {FinBW}}(\rho )$
classes with the aid of spaces defined as in [Reference Kwela62]. Fortunately, we managed to use not necessary maximal almost disjoint families to prove two main results of this part (Theorems 14.3 and 15.2), which give us
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)\neq \emptyset $
for certain
$\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)\neq \emptyset $
for certain
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
. Our methods were inspired by [Reference Kubiś and Szeptycki61].
$\rho _2$
. Our methods were inspired by [Reference Kubiś and Szeptycki61].
12 Mrówka spaces and their compactifications
For an infinite almost disjoint family
![]() $\mathcal {A}$
on a countable set
$\mathcal {A}$
on a countable set
![]() $\Lambda $
, we define a set
$\Lambda $
, we define a set
and introduce a topology on
![]() $\Psi (\mathcal {A})$
as follows: the points of
$\Psi (\mathcal {A})$
as follows: the points of
![]() $\Lambda $
are isolated and a basic neighborhood of
$\Lambda $
are isolated and a basic neighborhood of
![]() $A\in \mathcal {A}$
has the form
$A\in \mathcal {A}$
has the form
![]() $\{A\}\cup (A\setminus F)$
with F finite.
$\{A\}\cup (A\setminus F)$
with F finite.
Topological spaces of the form
![]() $\Psi (\mathcal {A})$
were introduced by Alexandroff and Urysohn in [Reference Alexandroff and Urysohn1, Chapter V, paragraph 1.3] (as noted in [Reference Engelking17, p. 182], [Reference Dow and Vaughan16, p. 1380], and [Reference Hrušák46, p. 605]) and its topology is known as the rational sequence topology (see [Reference Steen and Seebach74, Example 65]; the same topology was later described by Katětov in [Reference Katětov54, p. 74]). Spaces
$\Psi (\mathcal {A})$
were introduced by Alexandroff and Urysohn in [Reference Alexandroff and Urysohn1, Chapter V, paragraph 1.3] (as noted in [Reference Engelking17, p. 182], [Reference Dow and Vaughan16, p. 1380], and [Reference Hrušák46, p. 605]) and its topology is known as the rational sequence topology (see [Reference Steen and Seebach74, Example 65]; the same topology was later described by Katětov in [Reference Katětov54, p. 74]). Spaces
![]() $\Psi (\mathcal {A})$
with maximal (with respect to the inclusion) almost disjoint families
$\Psi (\mathcal {A})$
with maximal (with respect to the inclusion) almost disjoint families
![]() $\mathcal {A}$
were first examined by Mrówka (see [Reference Mrówka69]) and Isbell (as noted in [Reference Gillman and Jerison39, p. 269]). It seems that the notation
$\mathcal {A}$
were first examined by Mrówka (see [Reference Mrówka69]) and Isbell (as noted in [Reference Gillman and Jerison39, p. 269]). It seems that the notation
![]() $\Psi $
for these kinds of spaces was used for the first time in [Reference Gillman and Jerison39, Problem 5I, p. 79].
$\Psi $
for these kinds of spaces was used for the first time in [Reference Gillman and Jerison39, Problem 5I, p. 79].
Spaces of the form
![]() $\Psi (\mathcal {A})$
are known under many names, including
$\Psi (\mathcal {A})$
are known under many names, including
![]() $\Psi $
-spaces, Isbell–Mrówka spaces, and Mrówka spaces. Recent surveys on these spaces and their numerous applications can be found in [Reference Hernández-Hernández and Hrušák43, Reference Hrušák46].
$\Psi $
-spaces, Isbell–Mrówka spaces, and Mrówka spaces. Recent surveys on these spaces and their numerous applications can be found in [Reference Hernández-Hernández and Hrušák43, Reference Hrušák46].
It is known that
![]() $\Psi (\mathcal {A})$
is Hausdorff, regular, locally compact, first countable, and separable, but it is not compact nor sequentially compact (see [Reference Mrówka69] or [Reference van Douwen14, Section 11]). It is not difficult to see that
$\Psi (\mathcal {A})$
is Hausdorff, regular, locally compact, first countable, and separable, but it is not compact nor sequentially compact (see [Reference Mrówka69] or [Reference van Douwen14, Section 11]). It is not difficult to see that
![]() $A\cup \{A\}$
is compact in
$A\cup \{A\}$
is compact in
![]() $\Psi (\mathcal {A})$
for every
$\Psi (\mathcal {A})$
for every
![]() $A\in \mathcal {A}$
and for every compact set
$A\in \mathcal {A}$
and for every compact set
![]() $K\subseteq \Psi (\mathcal {A})$
both sets
$K\subseteq \Psi (\mathcal {A})$
both sets
![]() $K\cap \mathcal {A}$
and
$K\cap \mathcal {A}$
and
![]() $(K \cap \Lambda ) \setminus \bigcup \{A : A\in K\cap \mathcal {A}\}$
are finite. In particular, for every compact set
$(K \cap \Lambda ) \setminus \bigcup \{A : A\in K\cap \mathcal {A}\}$
are finite. In particular, for every compact set
![]() $K\subseteq \Psi (\mathcal {A})$
there are finitely many sets
$K\subseteq \Psi (\mathcal {A})$
there are finitely many sets
![]() $A_i\in \mathcal {A}$
and a finite set F such that
$A_i\in \mathcal {A}$
and a finite set F such that
![]() $ K\subseteq \{A_i:i<n\}\cup \bigcup \{ A_i \cup F: i<n\}$
.
$ K\subseteq \{A_i:i<n\}\cup \bigcup \{ A_i \cup F: i<n\}$
.
Let
be the Alexandroff one-point compactification of
![]() $\Psi (\mathcal {A})$
(recall that open neighborhoods of
$\Psi (\mathcal {A})$
(recall that open neighborhoods of
![]() $\infty $
are of the form
$\infty $
are of the form
![]() $\Phi (\mathcal {A})\setminus K$
for compact sets
$\Phi (\mathcal {A})\setminus K$
for compact sets
![]() $K\subseteq \Psi (\mathcal {A})$
). It is not difficult to see that
$K\subseteq \Psi (\mathcal {A})$
). It is not difficult to see that
![]() $\Phi (\mathcal {A})$
is Hausdorff, compact, sequentially compact, separable, and first countable at every point of
$\Phi (\mathcal {A})$
is Hausdorff, compact, sequentially compact, separable, and first countable at every point of
![]() $\Phi (\mathcal {A})\setminus \{\infty \}$
.
$\Phi (\mathcal {A})\setminus \{\infty \}$
.
Topological spaces of the form
![]() $\Phi (\mathcal {A})$
with maximal almost disjoint families
$\Phi (\mathcal {A})$
with maximal almost disjoint families
![]() $\mathcal {A}$
were first used by Franklin [Reference Franklin33, Example 7.1] where the author used the notation
$\mathcal {A}$
were first used by Franklin [Reference Franklin33, Example 7.1] where the author used the notation
![]() $\Psi ^*$
instead of
$\Psi ^*$
instead of
![]() $\Phi $
. Later, these spaces were considered in [Reference García-Ferreira and Szeptycki38] where the authors use the notation
$\Phi $
. Later, these spaces were considered in [Reference García-Ferreira and Szeptycki38] where the authors use the notation
![]() $\mathcal {F}(\mathcal {A})$
and call them the Franklin compact spaces associated with
$\mathcal {F}(\mathcal {A})$
and call them the Franklin compact spaces associated with
![]() $\mathcal {A}$
, whereas in [Reference Garcia-Ferreira and Guzmán37] the authors use the notation
$\mathcal {A}$
, whereas in [Reference Garcia-Ferreira and Guzmán37] the authors use the notation
![]() $Fr(\mathcal {A})$
and call them the Franklin spaces of
$Fr(\mathcal {A})$
and call them the Franklin spaces of
![]() $\mathcal {A}$
. The notation
$\mathcal {A}$
. The notation
![]() $\Phi (\mathcal {A})$
for these spaces is used in the following papers [Reference Filipów22, Reference Filipów, Kowitz, Kwela and Tryba24, Reference Kowitz60, Reference Kwela62]. Recently, spaces of the form
$\Phi (\mathcal {A})$
for these spaces is used in the following papers [Reference Filipów22, Reference Filipów, Kowitz, Kwela and Tryba24, Reference Kowitz60, Reference Kwela62]. Recently, spaces of the form
![]() $\Phi (\mathcal {A})$
were also considered for non-maximal almost disjoint families [Reference Corral, Guzmán and López-Callejas11, Reference Kubiś and Szeptycki61].
$\Phi (\mathcal {A})$
were also considered for non-maximal almost disjoint families [Reference Corral, Guzmán and López-Callejas11, Reference Kubiś and Szeptycki61].
It also makes sense to define
![]() $\Phi (\mathcal {A})$
for infinite families
$\Phi (\mathcal {A})$
for infinite families
![]() $\mathcal {A}$
that are not almost disjoint, but then
$\mathcal {A}$
that are not almost disjoint, but then
![]() $\Phi (\mathcal {A})$
is no longer Hausdorff (almost disjointness of
$\Phi (\mathcal {A})$
is no longer Hausdorff (almost disjointness of
![]() $\mathcal {A}$
is a necessary and sufficient condition for a space
$\mathcal {A}$
is a necessary and sufficient condition for a space
![]() $\Phi (\mathcal {A})$
to be Hausdorff).
$\Phi (\mathcal {A})$
to be Hausdorff).
The following lemma (which will be used repeatedly in the sequel) shows that a sequence in a space
![]() $\Phi (\mathcal {A})$
may fail to have a
$\Phi (\mathcal {A})$
may fail to have a
![]() $\rho $
-convergent
$\rho $
-convergent
![]() $\rho $
-subsequence only in one specific case. Hence, checking whether
$\rho $
-subsequence only in one specific case. Hence, checking whether
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho )$
will be reduced to considering only sequences of this one specific kind.
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho )$
will be reduced to considering only sequences of this one specific kind.
Lemma 12.1. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
![]() $\mathcal {A}$
be an infinite almost disjoint family on
$\mathcal {A}$
be an infinite almost disjoint family on
![]() $\Lambda $
. For every sequence
$\Lambda $
. For every sequence
![]() $f:\Lambda \to \Phi (\mathcal {A})$
, the following five cases can only occur
$f:\Lambda \to \Phi (\mathcal {A})$
, the following five cases can only occur
![]() $:$
$:$
-
(1)
 $f^{-1}(\infty )\notin \mathcal {I}_{\rho }$
,
$f^{-1}(\infty )\notin \mathcal {I}_{\rho }$
, -
(2)
 $f^{-1}[\mathcal {A}] \notin \mathcal {I}_{\rho }$
,
$f^{-1}[\mathcal {A}] \notin \mathcal {I}_{\rho }$
, -
(3)
 $f^{-1}(\infty )\in \mathcal {I}_{\rho }$
,
$f^{-1}(\infty )\in \mathcal {I}_{\rho }$
,
 $f^{-1}[\mathcal {A}] \in \mathcal {I}_{\rho }$
,
$f^{-1}[\mathcal {A}] \in \mathcal {I}_{\rho }$
,
 $f^{-1}[\Lambda ]\in \mathcal {I}_{\rho }^*$
and
$f^{-1}[\Lambda ]\in \mathcal {I}_{\rho }^*$
and-
(a)
 $f^{-1}(\lambda )\notin \mathcal {I}_{\rho }$
for some
$f^{-1}(\lambda )\notin \mathcal {I}_{\rho }$
for some
 $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
, -
(b)
 $f^{-1}(\lambda )\in \mathcal {I}_{\rho }$
for every
$f^{-1}(\lambda )\in \mathcal {I}_{\rho }$
for every
 $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
 $f^{-1}[A]\notin \mathcal {I}_{\rho }$
for some
$f^{-1}[A]\notin \mathcal {I}_{\rho }$
for some
 $A \in \mathcal {A}$
,
$A \in \mathcal {A}$
, -
(c)
 $f^{-1}(\lambda )\in \mathcal {I}_{\rho }$
for every
$f^{-1}(\lambda )\in \mathcal {I}_{\rho }$
for every
 $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
 $f^{-1}[A]\in \mathcal {I}_{\rho }$
for every
$f^{-1}[A]\in \mathcal {I}_{\rho }$
for every
 $A \in \mathcal {A}$
.
$A \in \mathcal {A}$
.
-
If
![]() $\rho $
is
$\rho $
is
![]() $P^-$
, then in cases (1), (2), (3a), and (3b) there is
$P^-$
, then in cases (1), (2), (3a), and (3b) there is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent.
$\rho $
-convergent.
Proof
Case (1). There is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $f\restriction \rho (F)$
is constant (with the value
$f\restriction \rho (F)$
is constant (with the value
![]() $\infty $
); hence, it is
$\infty $
); hence, it is
![]() $\rho $
-convergent.
$\rho $
-convergent.
Case (2). We find
![]() $F\in \mathcal {F}$
with
$F\in \mathcal {F}$
with
![]() $\rho (F)\subseteq f^{-1}[\mathcal {A}]$
. Then we enumerate
$\rho (F)\subseteq f^{-1}[\mathcal {A}]$
. Then we enumerate
![]() $f[\rho (F)] = \{A_{n} : n \in \omega \}$
and define
$f[\rho (F)] = \{A_{n} : n \in \omega \}$
and define
![]() $E_n = f^{-1}[\{A_{n}\}]$
for each
$E_n = f^{-1}[\{A_{n}\}]$
for each
![]() $n\in \omega $
.
$n\in \omega $
.
If there is
![]() $n_0\in \omega $
such that
$n_0\in \omega $
such that
![]() $E_{n_0}\notin \mathcal {I}_{\rho }$
, then we find
$E_{n_0}\notin \mathcal {I}_{\rho }$
, then we find
![]() $F'\in \mathcal {F}$
with
$F'\in \mathcal {F}$
with
![]() $\rho (F')\subseteq E_{n_0}$
, and we see that
$\rho (F')\subseteq E_{n_0}$
, and we see that
![]() $f\restriction \rho (F')$
is constant, so it is
$f\restriction \rho (F')$
is constant, so it is
![]() $\rho $
-convergent.
$\rho $
-convergent.
Now assume that
![]() $E_n\in \mathcal {I}_{\rho }$
for each
$E_n\in \mathcal {I}_{\rho }$
for each
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $\rho (F)\subseteq \bigcup \{E_n:n\in \omega \}$
, we can use Proposition 6.8 to find
$\rho (F)\subseteq \bigcup \{E_n:n\in \omega \}$
, we can use Proposition 6.8 to find
![]() $E\in \mathcal {F}$
such that for each
$E\in \mathcal {F}$
such that for each
![]() $n\in \omega $
there is a finite set
$n\in \omega $
there is a finite set
![]() $K\subseteq \Omega $
with
$K\subseteq \Omega $
with
![]() $\rho (E\setminus K) \subseteq \rho (F) \cap \bigcup \{ E_i: i\geq n\}$
. We claim that
$\rho (E\setminus K) \subseteq \rho (F) \cap \bigcup \{ E_i: i\geq n\}$
. We claim that
![]() $f\restriction \rho (E)$
is
$f\restriction \rho (E)$
is
![]() $\rho $
-convergent to
$\rho $
-convergent to
![]() $\infty $
. Let U be a neighborhood of
$\infty $
. Let U be a neighborhood of
![]() $\infty $
. Without loss of generality, we can assume that
$\infty $
. Without loss of generality, we can assume that
![]() $U = \Phi (\mathcal {A})\setminus (\{A_{i}:i<n\}\cup \bigcup _{i<n}A_{i})$
for some
$U = \Phi (\mathcal {A})\setminus (\{A_{i}:i<n\}\cup \bigcup _{i<n}A_{i})$
for some
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $K\subseteq \Omega $
be a finite set such that
$K\subseteq \Omega $
be a finite set such that
![]() $\rho (E\setminus K) \subseteq \rho (F)\cap \bigcup \{ E_i: i\geq n\}$
. Then
$\rho (E\setminus K) \subseteq \rho (F)\cap \bigcup \{ E_i: i\geq n\}$
. Then
![]() $f[\rho (E\setminus K)] \cap \{A_{i}:i<n\}=\emptyset $
, and consequently
$f[\rho (E\setminus K)] \cap \{A_{i}:i<n\}=\emptyset $
, and consequently
![]() $f[\rho (E\setminus K)] \subseteq U$
.
$f[\rho (E\setminus K)] \subseteq U$
.
Case (3a). There is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $f\restriction \rho _1(F)$
is constant; hence, it is
$f\restriction \rho _1(F)$
is constant; hence, it is
![]() $\rho $
-convergent.
$\rho $
-convergent.
Case (3b). Let
![]() $A\in \mathcal {A}$
be such that
$A\in \mathcal {A}$
be such that
![]() $f^{-1}[A]\notin \mathcal {I}_{\rho }$
. Using Proposition 6.8, we find
$f^{-1}[A]\notin \mathcal {I}_{\rho }$
. Using Proposition 6.8, we find
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq f^{-1}[A]$
and for every finite
$\rho (F)\subseteq f^{-1}[A]$
and for every finite
![]() $S\subseteq A$
there is a finite set
$S\subseteq A$
there is a finite set
![]() $K\subseteq \Omega $
with
$K\subseteq \Omega $
with
![]() $\rho (F\setminus K)\subseteq f^{-1}[A]\setminus f^{-1}[S]=f^{-1}[A\setminus S]$
. We claim that
$\rho (F\setminus K)\subseteq f^{-1}[A]\setminus f^{-1}[S]=f^{-1}[A\setminus S]$
. We claim that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to A. Indeed, let U be a neighborhood of A. Without loss of generality, we can assume that
$\rho $
-convergent to A. Indeed, let U be a neighborhood of A. Without loss of generality, we can assume that
![]() $U=\{A\}\cup (A\setminus S)$
where S is a finite subset of A. Then we take a finite
$U=\{A\}\cup (A\setminus S)$
where S is a finite subset of A. Then we take a finite
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $\rho (F\setminus K)\subseteq f^{-1}[A\setminus S]$
, so
$\rho (F\setminus K)\subseteq f^{-1}[A\setminus S]$
, so
![]() $f[\rho (F\setminus K)]\subseteq A\setminus S \subseteq U$
.
$f[\rho (F\setminus K)]\subseteq A\setminus S \subseteq U$
.
Proposition 12.2. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
![]() $\mathcal {A}$
be an infinite almost disjoint family of infinite subsets of
$\mathcal {A}$
be an infinite almost disjoint family of infinite subsets of
![]() $\Lambda $
. If
$\Lambda $
. If
![]() $\rho $
is
$\rho $
is
![]() $P^-$
and
$P^-$
and
![]() $\mathcal {A}$
is countable, then
$\mathcal {A}$
is countable, then
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho )$
.
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho )$
.
Proof Let
![]() $f:\Lambda \to \Phi (\mathcal {A})$
. By Lemma 12.1, we can assume that
$f:\Lambda \to \Phi (\mathcal {A})$
. By Lemma 12.1, we can assume that
![]() $f^{-1}(\infty )\in \mathcal {I}_{\rho }$
,
$f^{-1}(\infty )\in \mathcal {I}_{\rho }$
,
![]() $f^{-1}[\mathcal {A}] \in \mathcal {I}_{\rho }$
,
$f^{-1}[\mathcal {A}] \in \mathcal {I}_{\rho }$
,
![]() $f^{-1}[\Lambda ]\in \mathcal {I}_{\rho }^*$
,
$f^{-1}[\Lambda ]\in \mathcal {I}_{\rho }^*$
,
![]() $f^{-1}(\lambda )\in \mathcal {I}_{\rho }$
for every
$f^{-1}(\lambda )\in \mathcal {I}_{\rho }$
for every
![]() $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
![]() $f^{-1}[A]\in \mathcal {I}_{\rho }$
for every
$f^{-1}[A]\in \mathcal {I}_{\rho }$
for every
![]() $A \in \mathcal {A}$
.
$A \in \mathcal {A}$
.
Since
![]() $f^{-1}[A]\in \mathcal {I}_\rho $
for every
$f^{-1}[A]\in \mathcal {I}_\rho $
for every
![]() $A\in \mathcal {A}$
, we can use Proposition 6.8 to find
$A\in \mathcal {A}$
, we can use Proposition 6.8 to find
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq f^{-1}[\Lambda ]$
and for any finite set
$\rho (F)\subseteq f^{-1}[\Lambda ]$
and for any finite set
![]() $\mathcal {A}'\subseteq \mathcal {A}$
there is a finite set
$\mathcal {A}'\subseteq \mathcal {A}$
there is a finite set
![]() $K\subseteq \Omega $
with
$K\subseteq \Omega $
with
 $$ \begin{align*} \rho(F\setminus K) \cap f^{-1}\left[\bigcup \mathcal{A}'\right] = \rho(F\setminus K) \cap \left( \bigcup_{A\in \mathcal{A}'} f^{-1}[A] \right) = \emptyset .\end{align*} $$
$$ \begin{align*} \rho(F\setminus K) \cap f^{-1}\left[\bigcup \mathcal{A}'\right] = \rho(F\setminus K) \cap \left( \bigcup_{A\in \mathcal{A}'} f^{-1}[A] \right) = \emptyset .\end{align*} $$
We claim that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to
$\rho $
-convergent to
![]() $\infty $
. Indeed, let U be a neighborhood of
$\infty $
. Indeed, let U be a neighborhood of
![]() $\infty $
. Without loss of generality, we can assume that there is a finite set
$\infty $
. Without loss of generality, we can assume that there is a finite set
![]() $\mathcal {A}' \subseteq \mathcal {A}$
such that
$\mathcal {A}' \subseteq \mathcal {A}$
such that
![]() $U = \Phi (\mathcal {A})\setminus \left ( \mathcal {A}' \cup \bigcup \mathcal {A}'\right ).$
Then we have a finite set
$U = \Phi (\mathcal {A})\setminus \left ( \mathcal {A}' \cup \bigcup \mathcal {A}'\right ).$
Then we have a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $\rho (F\setminus K) \cap f^{-1}\left [\bigcup \mathcal {A}'\right ] = \emptyset $
, and consequently
$\rho (F\setminus K) \cap f^{-1}\left [\bigcup \mathcal {A}'\right ] = \emptyset $
, and consequently
![]() $f[\rho (F\setminus K)] \subseteq U$
, so the proof is finished.
$f[\rho (F\setminus K)] \subseteq U$
, so the proof is finished.
13 Mrówka spaces for maximal almost disjoint families
In [Reference Kwela62] the author extensively studied
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
spaces. In particular, for a large class of ideals, assuming the continuum hypothesis, he characterized in terms of Katětov order when there is a space in
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
spaces. In particular, for a large class of ideals, assuming the continuum hypothesis, he characterized in terms of Katětov order when there is a space in
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not in
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not in
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {J})$
. In his proofs the right space is always of the form
$\operatorname {\mathrm {FinBW}}(\mathcal {J})$
. In his proofs the right space is always of the form
![]() $\Phi (\mathcal {A})$
for some maximal almost disjoint family. In our paper we want to generalize results of [Reference Kwela62] so that they will apply also for Hindman spaces, Ramsey spaces, and differentially compact spaces. As we will see at the end of this section, our generalization requires going beyond maximal almost disjoint families (as always
$\Phi (\mathcal {A})$
for some maximal almost disjoint family. In our paper we want to generalize results of [Reference Kwela62] so that they will apply also for Hindman spaces, Ramsey spaces, and differentially compact spaces. As we will see at the end of this section, our generalization requires going beyond maximal almost disjoint families (as always
![]() $\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\rho )$
for maximal
$\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\rho )$
for maximal
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\rho \in \{FS,r,\Delta \}$
—see Corollary 13.3) and working with almost disjoint families that are not necessarily maximal.
$\rho \in \{FS,r,\Delta \}$
—see Corollary 13.3) and working with almost disjoint families that are not necessarily maximal.
Lemma 13.1. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
![]() $\mathcal {A}$
be an almost disjoint family on
$\mathcal {A}$
be an almost disjoint family on
![]() $\Lambda $
.
$\Lambda $
.
-
(1) If
 $\mathcal {A}\subseteq \mathcal {I}_\rho $
and then
$\mathcal {A}\subseteq \mathcal {I}_\rho $
and then $$ \begin{align*}\forall F\in \mathcal{F}\,\exists A\in \mathcal{A}\,\forall K\in [\Omega]^{<\omega}\,(A\cap \rho(F\setminus K)\neq\emptyset),\end{align*} $$
$$ \begin{align*}\forall F\in \mathcal{F}\,\exists A\in \mathcal{A}\,\forall K\in [\Omega]^{<\omega}\,(A\cap \rho(F\setminus K)\neq\emptyset),\end{align*} $$
 $\Phi (\mathcal {A}) \notin \operatorname {\mathrm {FinBW}}(\rho ).$
$\Phi (\mathcal {A}) \notin \operatorname {\mathrm {FinBW}}(\rho ).$
-
(2) If
 $\mathcal {A}\subseteq \mathcal {I}_\rho $
and
$\mathcal {A}\subseteq \mathcal {I}_\rho $
and
 $\mathcal {A}$
is a maximal almost disjoint family, then
$\mathcal {A}$
is a maximal almost disjoint family, then
 $\Phi (\mathcal {A}) \notin \operatorname {\mathrm {FinBW}}(\rho ).$
$\Phi (\mathcal {A}) \notin \operatorname {\mathrm {FinBW}}(\rho ).$
Proof (1) Let
![]() $f:\Lambda \to \Phi (\mathcal {A})$
be given by
$f:\Lambda \to \Phi (\mathcal {A})$
be given by
![]() $f(\lambda )=\lambda $
. We claim that there is no
$f(\lambda )=\lambda $
. We claim that there is no
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent. Assume, for the sake of contradiction, that there is
$\rho $
-convergent. Assume, for the sake of contradiction, that there is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to some
$\rho $
-convergent to some
![]() $L\in \Phi (\mathcal {A})$
. We have three cases: (1)
$L\in \Phi (\mathcal {A})$
. We have three cases: (1)
![]() $L\in \Lambda $
, (2)
$L\in \Lambda $
, (2)
![]() $L\in \mathcal {A}$
, and (3)
$L\in \mathcal {A}$
, and (3)
![]() $L=\infty $
.
$L=\infty $
.
Case (1). The set
![]() $U=\{L\}$
is a neighborhood of L. But for any finite set
$U=\{L\}$
is a neighborhood of L. But for any finite set
![]() $K\subseteq \Omega $
we have
$K\subseteq \Omega $
we have
![]() $f[\rho (F\setminus K)] = \rho (F\setminus K) \not \subseteq \{L\}=U.$
Thus,
$f[\rho (F\setminus K)] = \rho (F\setminus K) \not \subseteq \{L\}=U.$
Thus,
![]() $f\restriction \rho (F)$
is not
$f\restriction \rho (F)$
is not
![]() $\rho $
-convergent to L, a contradiction.
$\rho $
-convergent to L, a contradiction.
Case (2). The set
![]() $U=L \cup \{L \}$
is a neighborhood of L. Since
$U=L \cup \{L \}$
is a neighborhood of L. Since
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to L, there is a finite set
$\rho $
-convergent to L, there is a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $\rho (F\setminus K)=f[\rho (F\setminus K)]\subseteq U$
. Thus,
$\rho (F\setminus K)=f[\rho (F\setminus K)]\subseteq U$
. Thus,
![]() $\rho (F\setminus K)\subseteq L$
, so
$\rho (F\setminus K)\subseteq L$
, so
![]() $L\notin \mathcal {I}_{\rho }$
, but
$L\notin \mathcal {I}_{\rho }$
, but
![]() $\mathcal {A}\subseteq \mathcal {I}_{\rho }$
, a contradiction.
$\mathcal {A}\subseteq \mathcal {I}_{\rho }$
, a contradiction.
Case (3). Let
![]() $A\in \mathcal {A}$
be such that
$A\in \mathcal {A}$
be such that
![]() $A\cap \rho (F\setminus K)\neq \emptyset $
for every finite set
$A\cap \rho (F\setminus K)\neq \emptyset $
for every finite set
![]() $K\subseteq \Omega $
. The set
$K\subseteq \Omega $
. The set
![]() $U = \Phi (\mathcal {A})\setminus (A\cup \{A\})$
is a neighborhood of
$U = \Phi (\mathcal {A})\setminus (A\cup \{A\})$
is a neighborhood of
![]() $\infty $
. Since
$\infty $
. Since
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to L, there is a finite set
$\rho $
-convergent to L, there is a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $ \rho (F\setminus K) = f[\rho (F\setminus K)]\subseteq U$
. Hence,
$ \rho (F\setminus K) = f[\rho (F\setminus K)]\subseteq U$
. Hence,
![]() $A\cap \rho (F\setminus K)=\emptyset $
, a contradiction.
$A\cap \rho (F\setminus K)=\emptyset $
, a contradiction.
(2) Let
![]() $F\in \mathcal {F}$
and enumerate
$F\in \mathcal {F}$
and enumerate
![]() $\Omega =\{o_n:n\in \omega \}$
. We pick inductively a point
$\Omega =\{o_n:n\in \omega \}$
. We pick inductively a point
![]() $b_{n}\in \rho (F\setminus \{o_j:j<n\})\setminus \{b_j:j<n\}$
for each
$b_{n}\in \rho (F\setminus \{o_j:j<n\})\setminus \{b_j:j<n\}$
for each
![]() $n\in \omega $
. Then using maximality of
$n\in \omega $
. Then using maximality of
![]() $\mathcal {A}$
we can find
$\mathcal {A}$
we can find
![]() $A\in \mathcal {A}$
such that
$A\in \mathcal {A}$
such that
![]() $A\cap \{b_n:n\in \omega \}$
is infinite. Thus, the condition for item (1) is satisfied, so the proof is finished.
$A\cap \{b_n:n\in \omega \}$
is infinite. Thus, the condition for item (1) is satisfied, so the proof is finished.
Theorem 13.2. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
.
$\mathcal {F}\subseteq [\Omega ]^\omega $
.
-
(1) If
 $\rho $
is tall
$\rho $
is tall
 $($
equivalently,
$($
equivalently,
 $\mathcal {I}_\rho $
is a tall ideal
$\mathcal {I}_\rho $
is a tall ideal
 $)$
, then there exists an infinite
$)$
, then there exists an infinite
 $(even\ \textit{of}\ cardinality\ \mathfrak {c})$
maximal almost disjoint family
$(even\ \textit{of}\ cardinality\ \mathfrak {c})$
maximal almost disjoint family
 $\mathcal {A}$
on
$\mathcal {A}$
on
 $\Lambda $
such that
$\Lambda $
such that
 $\Phi (\mathcal {A}) \notin \operatorname {\mathrm {FinBW}}(\rho ).$
$\Phi (\mathcal {A}) \notin \operatorname {\mathrm {FinBW}}(\rho ).$
-
(2) If
 $\mathcal {I}_\rho $
is not
$\mathcal {I}_\rho $
is not
 $P^-(\Lambda)\ (equivalently, \mathrm {Fin}^2\leq _K\mathcal {I}_\rho )$
, then
$P^-(\Lambda)\ (equivalently, \mathrm {Fin}^2\leq _K\mathcal {I}_\rho )$
, then
 $\Phi (\mathcal {A}) \notin \operatorname {\mathrm {FinBW}}(\rho )$
for every infinite maximal almost disjoint family
$\Phi (\mathcal {A}) \notin \operatorname {\mathrm {FinBW}}(\rho )$
for every infinite maximal almost disjoint family
 $\mathcal {A}$
on
$\mathcal {A}$
on
 $\Lambda $
.
$\Lambda $
.
Proof (1) It follows from Lemma 13.1(2), because in [Reference Filipów and Tryba28, Proposition 2.2], the authors proved that if an ideal
![]() $\mathcal {I}$
is tall, then there exists an infinite maximal almost disjoint family
$\mathcal {I}$
is tall, then there exists an infinite maximal almost disjoint family
![]() $\mathcal {A}$
of infinite subsets of
$\mathcal {A}$
of infinite subsets of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\mathcal {A}\subseteq \mathcal {I}$
. If necessary, we can make
$\mathcal {A}\subseteq \mathcal {I}$
. If necessary, we can make
![]() $\mathcal {A}$
to be of cardinality
$\mathcal {A}$
to be of cardinality
![]() $\mathfrak {c}$
(just take one set
$\mathfrak {c}$
(just take one set
![]() $A\in \mathcal {A}$
, construct your favourite almost disjoint family
$A\in \mathcal {A}$
, construct your favourite almost disjoint family
![]() $\mathcal {B}$
of cardinality
$\mathcal {B}$
of cardinality
![]() $\mathfrak {c}$
on A, then any maximal almost disjoint family extending
$\mathfrak {c}$
on A, then any maximal almost disjoint family extending
![]() $\mathcal {A}\cup \mathcal {B}$
is the required family). The equivalence of
$\mathcal {A}\cup \mathcal {B}$
is the required family). The equivalence of
![]() $\rho $
being tall and
$\rho $
being tall and
![]() $\mathcal {I}_\rho $
being a tall ideal follows from Proposition 8.1.
$\mathcal {I}_\rho $
being a tall ideal follows from Proposition 8.1.
(2) The equivalence of
![]() $\mathcal {I}_\rho $
not being
$\mathcal {I}_\rho $
not being
![]() $P^-(\Lambda )$
and
$P^-(\Lambda )$
and
![]() $\mathrm {Fin}^2\leq _K\mathcal {I}_\rho $
follows from Proposition 7.1(1).
$\mathrm {Fin}^2\leq _K\mathcal {I}_\rho $
follows from Proposition 7.1(1).
Let
![]() $\phi :\Lambda \to \omega ^2$
be a witness for
$\phi :\Lambda \to \omega ^2$
be a witness for
![]() $\mathrm {Fin}^2\leq _K\mathcal {I}_\rho $
. In [Reference Barbarski, Filipów, Mrożek and Szuca2], the authors proved that we can assume that
$\mathrm {Fin}^2\leq _K\mathcal {I}_\rho $
. In [Reference Barbarski, Filipów, Mrożek and Szuca2], the authors proved that we can assume that
![]() $\phi $
is a bijection. For each
$\phi $
is a bijection. For each
![]() $n\in \omega $
, we define
$n\in \omega $
, we define
![]() $P_n=\phi ^{-1}[\{n\}\times \omega ]$
. Then
$P_n=\phi ^{-1}[\{n\}\times \omega ]$
. Then
![]() $\{P_n:n\in \omega \}$
is a partition of
$\{P_n:n\in \omega \}$
is a partition of
![]() $\Lambda $
and
$\Lambda $
and
![]() $P_n\in \mathcal {I}_\rho \cap [\Lambda ]^\omega $
for each
$P_n\in \mathcal {I}_\rho \cap [\Lambda ]^\omega $
for each
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\mathcal {A}=\{A_\alpha :\alpha <|\mathcal {A}|\}$
. Since
$\mathcal {A}=\{A_\alpha :\alpha <|\mathcal {A}|\}$
. Since
![]() $\mathcal {A}$
is infinite,
$\mathcal {A}$
is infinite,
![]() $|\mathcal {A}|\geq \omega $
. Let
$|\mathcal {A}|\geq \omega $
. Let
![]() $f:\Lambda \to \Phi (\mathcal {A})$
be a bijection such that
$f:\Lambda \to \Phi (\mathcal {A})$
be a bijection such that
![]() $f[P_n]=A_n \setminus \bigcup \{ A_i:i<n\}$
for each
$f[P_n]=A_n \setminus \bigcup \{ A_i:i<n\}$
for each
![]() $n\in \omega .$
We claim that f does not have a
$n\in \omega .$
We claim that f does not have a
![]() $\rho $
-convergent subsequence. Assume, for the sake of contradiction, that
$\rho $
-convergent subsequence. Assume, for the sake of contradiction, that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to some
$\rho $
-convergent to some
![]() $L\in \Phi (\mathcal {A})$
for some
$L\in \Phi (\mathcal {A})$
for some
![]() $F\in \mathcal {F}$
. We have three cases: (1)
$F\in \mathcal {F}$
. We have three cases: (1)
![]() $L\in \Lambda $
, (2)
$L\in \Lambda $
, (2)
![]() $L\in \mathcal {A}$
, and (3)
$L\in \mathcal {A}$
, and (3)
![]() $L=\infty $
.
$L=\infty $
.
Case (1). The set
![]() $U=\{L\}$
is a neighborhood of L. But for any finite set
$U=\{L\}$
is a neighborhood of L. But for any finite set
![]() $K\subseteq \Omega $
we have
$K\subseteq \Omega $
we have
![]() $f[\rho (F\setminus K)] \not \subseteq \{L\}=U.$
Thus,
$f[\rho (F\setminus K)] \not \subseteq \{L\}=U.$
Thus,
![]() $f\restriction \rho (F)$
is not
$f\restriction \rho (F)$
is not
![]() $\rho $
-convergent to L, a contradiction.
$\rho $
-convergent to L, a contradiction.
Case (2). We have two subcases: (2a)
![]() $\exists n\in \omega \, (L=A_n)$
and (2b)
$\exists n\in \omega \, (L=A_n)$
and (2b)
![]() $\exists \alpha \in |\mathcal {A}|\setminus \omega \, (L=A_\alpha )$
.
$\exists \alpha \in |\mathcal {A}|\setminus \omega \, (L=A_\alpha )$
.
Case (2a). The set
![]() $U=\{A_n\}\cup A_n$
is a neighborhood of L, so there is a finite set
$U=\{A_n\}\cup A_n$
is a neighborhood of L, so there is a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $f[\rho (F\setminus K)] \subseteq U$
. Then
$f[\rho (F\setminus K)] \subseteq U$
. Then
![]() $f[\rho (F\setminus K)] \subseteq A_n$
, so
$f[\rho (F\setminus K)] \subseteq A_n$
, so
![]() $\rho (F\setminus K) \subseteq f^{-1}[A_n]\subseteq \bigcup _{i\leq n}P_i\in \mathcal {I}_\rho $
, a contradiction.
$\rho (F\setminus K) \subseteq f^{-1}[A_n]\subseteq \bigcup _{i\leq n}P_i\in \mathcal {I}_\rho $
, a contradiction.
Case (2b). The set
![]() $U=A_\alpha \cup \{A_\alpha \}$
is a neighborhood of L, so there is a finite set
$U=A_\alpha \cup \{A_\alpha \}$
is a neighborhood of L, so there is a finite set
![]() $K\subseteq \Omega $
such that
$K\subseteq \Omega $
such that
![]() $f[\rho (F\setminus K)] \subseteq U$
. Then
$f[\rho (F\setminus K)] \subseteq U$
. Then
![]() $f[\rho (F\setminus K)] \subseteq A_\alpha $
, so
$f[\rho (F\setminus K)] \subseteq A_\alpha $
, so
![]() $\rho (F\setminus K) \subseteq f^{-1}[A_\alpha ]$
. Thus
$\rho (F\setminus K) \subseteq f^{-1}[A_\alpha ]$
. Thus
![]() $f^{-1}[A_\alpha ]\notin \mathcal {I}_\rho $
, and consequently
$f^{-1}[A_\alpha ]\notin \mathcal {I}_\rho $
, and consequently
![]() $\phi [f^{-1}[A_\alpha ]]\notin \mathrm {Fin}^2$
. On the other hand,
$\phi [f^{-1}[A_\alpha ]]\notin \mathrm {Fin}^2$
. On the other hand,
![]() $A_\alpha \cap A_n$
is finite for each
$A_\alpha \cap A_n$
is finite for each
![]() $n\in \omega $
, so
$n\in \omega $
, so
![]() $f^{-1}[A_\alpha \cap A_n]$
is finite, and consequently
$f^{-1}[A_\alpha \cap A_n]$
is finite, and consequently
![]() $f^{-1}[A_\alpha ]\cap P_n$
is finite for every
$f^{-1}[A_\alpha ]\cap P_n$
is finite for every
![]() $n\in \omega $
. Thus,
$n\in \omega $
. Thus,
![]() $\phi [f^{-1}[A_\alpha ]]\in \mathrm {Fin}^2$
, a contradiction.
$\phi [f^{-1}[A_\alpha ]]\in \mathrm {Fin}^2$
, a contradiction.
Case (3). Using Proposition 9.2(1b) we find an infinite set
![]() $B\subseteq \Lambda $
such that
$B\subseteq \Lambda $
such that
![]() $f\restriction B$
is convergent to
$f\restriction B$
is convergent to
![]() $\infty $
. Since f is a bijection,
$\infty $
. Since f is a bijection,
![]() $f[B]$
is infinite. Thus, using maximality of
$f[B]$
is infinite. Thus, using maximality of
![]() $\mathcal {A}$
, we find
$\mathcal {A}$
, we find
![]() $\alpha $
such that
$\alpha $
such that
![]() $A_\alpha \cap f[B]$
is infinite. Since
$A_\alpha \cap f[B]$
is infinite. Since
![]() $U=\Phi (\mathcal {A})\setminus (\{A_\alpha \}\cup A_\alpha )$
is a neighborhood of
$U=\Phi (\mathcal {A})\setminus (\{A_\alpha \}\cup A_\alpha )$
is a neighborhood of
![]() $\infty $
, there is a finite set
$\infty $
, there is a finite set
![]() $K\subseteq \Lambda $
such that
$K\subseteq \Lambda $
such that
![]() $f[B\setminus K] \subseteq U$
. Then
$f[B\setminus K] \subseteq U$
. Then
![]() $A_\alpha \cap f[B \setminus K] = \emptyset $
, a contradiction.
$A_\alpha \cap f[B \setminus K] = \emptyset $
, a contradiction.
Corollary 13.3. Let
![]() $\mathcal {A}$
be an infinite maximal almost disjoint family.
$\mathcal {A}$
be an infinite maximal almost disjoint family.
-
(1) Hindman spaces.
-
(a) [Reference Kojman57, Theorem 10] If
 $\mathcal {A}\subseteq \mathcal {H}$
, then
$\mathcal {A}\subseteq \mathcal {H}$
, then
 $\Phi (\mathcal {A})$
is not a Hindman space.
$\Phi (\mathcal {A})$
is not a Hindman space. -
(b) [Reference Filipów, Kowitz, Kwela and Tryba24, Proposition 1.1]
 $\Phi (\mathcal {A})$
is not a Hindman space.
$\Phi (\mathcal {A})$
is not a Hindman space.
-
-
(1) Ramsey spaces.
-
(a) [Reference Kubiś and Szeptycki61, Example 4.1] If
 $\{\{n,k\}: k\in \omega \setminus \{n\}\}\in \mathcal {A}$
for every
$\{\{n,k\}: k\in \omega \setminus \{n\}\}\in \mathcal {A}$
for every
 $n\in \omega $
, then
$n\in \omega $
, then
 $\Phi (\mathcal {A})$
is not a Ramsey space.
$\Phi (\mathcal {A})$
is not a Ramsey space. -
(b)
 $\Phi (\mathcal {A})$
is not a Ramsey space.
$\Phi (\mathcal {A})$
is not a Ramsey space.
-
-
(3) Differentially compact spaces.
-
(a) [Reference Shi73, Theorem 4.2.2] or [Reference Filipów22, Theorem 4.9] If
 $\mathcal {A}\subseteq \mathcal {D}$
, then
$\mathcal {A}\subseteq \mathcal {D}$
, then
 $\Phi (\mathcal {A})$
is not a differentially compact space.
$\Phi (\mathcal {A})$
is not a differentially compact space. -
(b) [Reference Kowitz60, Theorem 2.1]
 $\Phi (\mathcal {A})$
is not a differentially compact space.
$\Phi (\mathcal {A})$
is not a differentially compact space.
-
-
(4) van der Waerden spaces.
-
(a) [Reference Kojman58, Theorem 6] If
 $\mathcal {A}\subseteq \mathcal {W}$
, then
$\mathcal {A}\subseteq \mathcal {W}$
, then
 $\Phi (\mathcal {A})$
is not a van der Waerden space.
$\Phi (\mathcal {A})$
is not a van der Waerden space.
-
-
(5)
 $\mathcal {I}_{1/n}$
-spaces.
$\mathcal {I}_{1/n}$
-spaces.-
(a) [Reference Flašková30, Proposition 2.2] If
 $\mathcal {A}\subseteq \mathcal {I}_{1/n}$
, then
$\mathcal {A}\subseteq \mathcal {I}_{1/n}$
, then
 $\Phi (\mathcal {A})$
is not a
$\Phi (\mathcal {A})$
is not a
 $\mathcal {I}_{1/n}$
-space.
$\mathcal {I}_{1/n}$
-space.
-
-
(6)
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.-
(a) [Reference Flašková30, Proposition 2.2] If
 $\mathcal {I}$
is a tall
$\mathcal {I}$
is a tall
 $F_\sigma $
-ideal on
$F_\sigma $
-ideal on
 $\Lambda $
and
$\Lambda $
and
 $\mathcal {A}\subseteq \mathcal {I}$
, then
$\mathcal {A}\subseteq \mathcal {I}$
, then
 $\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\mathcal {I})$
. -
(b) [Reference Filipów and Tryba28, Proposition 2.3] If
 $\mathcal {I}$
is a tall ideal and
$\mathcal {I}$
is a tall ideal and
 $\mathcal {A}\subseteq \mathcal {I}$
, then
$\mathcal {A}\subseteq \mathcal {I}$
, then
 $\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
-
14 Distinguishing between FinBW classes via Katětov order on ideals
In this section we prove first of the two main results of this part and show its various particular cases and consequences. We will need the following two lemmas.
Lemma 14.1. Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
$\mathcal {F}\subseteq [\Omega ]^\omega $
. Let
![]() $\mathcal {A}$
be an infinite almost disjoint family on
$\mathcal {A}$
be an infinite almost disjoint family on
![]() $\Lambda $
such that for every
$\Lambda $
such that for every
![]() $\mathcal {I}_\rho $
-to-one function
$\mathcal {I}_\rho $
-to-one function
![]() $f:\Lambda \to \Lambda $
there is
$f:\Lambda \to \Lambda $
there is
![]() $E\in \mathcal {F}$
such that the family
$E\in \mathcal {F}$
such that the family
is at most countable. If
![]() $\rho $
is
$\rho $
is
![]() $P^-$
, then
$P^-$
, then
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho ).$
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho ).$
Proof Let
![]() $f:\Lambda \to \Phi (\mathcal {A})$
. By Lemma 12.1, we can assume that
$f:\Lambda \to \Phi (\mathcal {A})$
. By Lemma 12.1, we can assume that
![]() $f^{-1}(\infty )\in \mathcal {I}_{\rho }$
,
$f^{-1}(\infty )\in \mathcal {I}_{\rho }$
,
![]() $f^{-1}[\mathcal {A}] \in \mathcal {I}_{\rho }$
,
$f^{-1}[\mathcal {A}] \in \mathcal {I}_{\rho }$
,
![]() $f^{-1}[\Lambda ]\in \mathcal {I}_{\rho }^*$
,
$f^{-1}[\Lambda ]\in \mathcal {I}_{\rho }^*$
,
![]() $f^{-1}(\lambda )\in \mathcal {I}_{\rho }$
for every
$f^{-1}(\lambda )\in \mathcal {I}_{\rho }$
for every
![]() $\lambda \in \Lambda $
, and
$\lambda \in \Lambda $
, and
![]() $f^{-1}[A]\in \mathcal {I}_{\rho }$
for every
$f^{-1}[A]\in \mathcal {I}_{\rho }$
for every
![]() $A\in \mathcal {A}$
. Then
$A\in \mathcal {A}$
. Then
![]() $B = f^{-1}[\Lambda ]\in \mathcal {I}^*_{\rho }$
and
$B = f^{-1}[\Lambda ]\in \mathcal {I}^*_{\rho }$
and
![]() $f\restriction B :B\to \Lambda $
is
$f\restriction B :B\to \Lambda $
is
![]() $\mathcal {I}_\rho $
-to-one.
$\mathcal {I}_\rho $
-to-one.
We fix an element
![]() $\lambda _0\in \Lambda $
and define
$\lambda _0\in \Lambda $
and define
![]() $g:\Lambda \to \Lambda $
by
$g:\Lambda \to \Lambda $
by
![]() $g(\lambda )=f(\lambda )$
for
$g(\lambda )=f(\lambda )$
for
![]() $\lambda \in B$
and
$\lambda \in B$
and
![]() $g(\lambda )=\lambda _0$
otherwise. Then g is
$g(\lambda )=\lambda _0$
otherwise. Then g is
![]() $\mathcal {I}_\rho $
-to-one, so there is
$\mathcal {I}_\rho $
-to-one, so there is
![]() $E\in \mathcal {F}$
such that the family
$E\in \mathcal {F}$
such that the family
is at most countable.
Since
![]() $\rho (E)\cap B\notin \mathcal {I}_\rho $
and
$\rho (E)\cap B\notin \mathcal {I}_\rho $
and
![]() $\rho $
is
$\rho $
is
![]() $P^-$
, we can use Proposition 6.8 to find
$P^-$
, we can use Proposition 6.8 to find
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\rho (F)\subseteq \rho (E)\cap B$
and for any finite sets
$\rho (F)\subseteq \rho (E)\cap B$
and for any finite sets
![]() $S\subseteq \Lambda $
and
$S\subseteq \Lambda $
and
![]() $\mathcal {T}\subseteq \mathcal {C}$
there is a finite set
$\mathcal {T}\subseteq \mathcal {C}$
there is a finite set
![]() $L\subseteq \Omega $
with
$L\subseteq \Omega $
with
We claim that
![]() $f\restriction \rho (F)$
is
$f\restriction \rho (F)$
is
![]() $\rho $
-convergent to
$\rho $
-convergent to
![]() $\infty $
. Indeed, let U be a neighborhood of
$\infty $
. Indeed, let U be a neighborhood of
![]() $\infty $
. Without loss of generality, we can assume that there is a finite set
$\infty $
. Without loss of generality, we can assume that there is a finite set
![]() $\Gamma \subseteq \mathcal {A}$
such that
$\Gamma \subseteq \mathcal {A}$
such that
![]() $U = \Phi (\mathcal {A})\setminus \left (\{A: A\in \Gamma \} \cup \bigcup \{A:A\in \Gamma \}\right ).$
$U = \Phi (\mathcal {A})\setminus \left (\{A: A\in \Gamma \} \cup \bigcup \{A:A\in \Gamma \}\right ).$
For each
![]() $A\in \Gamma \setminus \mathcal {C}$
, there is a finite set
$A\in \Gamma \setminus \mathcal {C}$
, there is a finite set
![]() $K_A\subseteq \Omega $
such that
$K_A\subseteq \Omega $
such that
![]() $A\cap f[\rho (F\setminus K_A)] = A\cap g[\rho (F\setminus K_A)]$
is finite. Then
$A\cap f[\rho (F\setminus K_A)] = A\cap g[\rho (F\setminus K_A)]$
is finite. Then
![]() $K=\bigcup \{K_A:A\in \Gamma \setminus \mathcal {C}\}\subseteq \Omega $
is a finite set such that
$K=\bigcup \{K_A:A\in \Gamma \setminus \mathcal {C}\}\subseteq \Omega $
is a finite set such that
![]() $A\cap f[\rho (F\setminus K)]$
is finite for every
$A\cap f[\rho (F\setminus K)]$
is finite for every
![]() $A\in \Gamma \setminus \mathcal {C}$
.
$A\in \Gamma \setminus \mathcal {C}$
.
Then both
![]() $S = f[\rho (F\setminus K)]\cap \bigcup \{A: A \in \Gamma \setminus \mathcal {C}\}$
and
$S = f[\rho (F\setminus K)]\cap \bigcup \{A: A \in \Gamma \setminus \mathcal {C}\}$
and
![]() $\mathcal {T} = \Gamma \cap \mathcal {C}$
are finite, so we can find a finite set
$\mathcal {T} = \Gamma \cap \mathcal {C}$
are finite, so we can find a finite set
![]() $L\subseteq \Omega $
such that
$L\subseteq \Omega $
such that
and consequently we obtain a finite set
![]() $K\cup L$
such that
$K\cup L$
such that
That finishes the proof.
Recall that
![]() $\mathfrak {p}$
is the smallest cardinality of a family
$\mathfrak {p}$
is the smallest cardinality of a family
![]() $\mathcal {F}$
of infinite subsets of
$\mathcal {F}$
of infinite subsets of
![]() $\omega $
with the strong finite intersection property (i.e., intersection of finitely many sets from
$\omega $
with the strong finite intersection property (i.e., intersection of finitely many sets from
![]() $\mathcal {F}$
is infinite) that does not have a pseudointersection (i.e., there is no infinite set
$\mathcal {F}$
is infinite) that does not have a pseudointersection (i.e., there is no infinite set
![]() $A\subseteq \omega $
such that
$A\subseteq \omega $
such that
![]() $A\setminus F$
is finite for each
$A\setminus F$
is finite for each
![]() $F\in \mathcal {F}$
; see, e.g., [Reference van Douwen14]).
$F\in \mathcal {F}$
; see, e.g., [Reference van Douwen14]).
Lemma 14.2 (Assume
 $\mathfrak {p}=\mathfrak {c}$
).
$\mathfrak {p}=\mathfrak {c}$
).
Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular with
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular with
![]() $\mathcal {F}_i\subseteq [\Omega _i]^\omega $
for each
$\mathcal {F}_i\subseteq [\Omega _i]^\omega $
for each
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $\{f_\alpha : \alpha <\mathfrak {c}\}$
be an enumeration of all functions
$\{f_\alpha : \alpha <\mathfrak {c}\}$
be an enumeration of all functions
![]() $f:\Lambda _1\to \Lambda _2$
and
$f:\Lambda _1\to \Lambda _2$
and
![]() $\mathcal {F}_2=\{F_\alpha :\alpha <\mathfrak {c}\}$
.
$\mathcal {F}_2=\{F_\alpha :\alpha <\mathfrak {c}\}$
.
If
![]() $\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, then there exist families
$\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, then there exist families
![]() $\mathcal {A} = \{A_\alpha :\alpha <\mathfrak {c}\}$
and
$\mathcal {A} = \{A_\alpha :\alpha <\mathfrak {c}\}$
and
![]() $\mathcal {C}=\{C_\alpha : \alpha <\mathfrak {c}\}$
such that for every
$\mathcal {C}=\{C_\alpha : \alpha <\mathfrak {c}\}$
such that for every
![]() $\alpha <\mathfrak {c}:$
$\alpha <\mathfrak {c}:$
-
(1)
 $C_\alpha \in \mathcal {F}_1$
,
$C_\alpha \in \mathcal {F}_1$
, -
(2)
 $f_\alpha [\rho _1(C_\alpha )]\in \mathcal {I}_{\rho _2}$
,
$f_\alpha [\rho _1(C_\alpha )]\in \mathcal {I}_{\rho _2}$
, -
(3)
 $A_\alpha \in \mathcal {I}_{\rho _2}\cap [\Lambda _2]^\omega $
,
$A_\alpha \in \mathcal {I}_{\rho _2}\cap [\Lambda _2]^\omega $
, -
(4)
 $\forall \beta <\alpha \, (|A_\alpha \cap A_\beta |<\omega )$
,
$\forall \beta <\alpha \, (|A_\alpha \cap A_\beta |<\omega )$
, -
(5)
 $\forall \gamma>\alpha \, (|A_\gamma \cap f_\alpha [\rho _1(C_\alpha )]|<\omega )$
,
$\forall \gamma>\alpha \, (|A_\gamma \cap f_\alpha [\rho _1(C_\alpha )]|<\omega )$
, -
(6)
 $\forall L\in [\Omega _2]^{<\omega }\, (A_\alpha \subseteq ^* \rho _2(F_\alpha \setminus L))$
.
$\forall L\in [\Omega _2]^{<\omega }\, (A_\alpha \subseteq ^* \rho _2(F_\alpha \setminus L))$
.
Proof Suppose that
![]() $A_\beta $
and
$A_\beta $
and
![]() $C_\beta $
have been constructed for
$C_\beta $
have been constructed for
![]() $\beta <\alpha $
and satisfy items (1)-(6).
$\beta <\alpha $
and satisfy items (1)-(6).
First, we construct the set
![]() $C_\alpha $
. Since
$C_\alpha $
. Since
![]() $\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, there is a set
$\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, there is a set
![]() $C_\alpha \in \mathcal {F}_1$
such that
$C_\alpha \in \mathcal {F}_1$
such that
![]() $f_\alpha [\rho _1(C_\alpha )]\in \mathcal {I}_{\rho _2}$
.
$f_\alpha [\rho _1(C_\alpha )]\in \mathcal {I}_{\rho _2}$
.
Now, we turn to the construction of the set
![]() $A_\alpha $
. Let
$A_\alpha $
. Let
Since
![]() $\bigcap \{\rho _2(F_\alpha \setminus L_i):i<n\} \in \mathcal {I}_{\rho _2}^+$
for every
$\bigcap \{\rho _2(F_\alpha \setminus L_i):i<n\} \in \mathcal {I}_{\rho _2}^+$
for every
![]() $n\in \omega $
and finite sets
$n\in \omega $
and finite sets
![]() $L_i\subseteq \Omega $
, and
$L_i\subseteq \Omega $
, and
![]() $\Lambda _2\setminus f_\beta [\rho _1(C_\beta )]\in \mathcal {I}_{\rho _2}^*$
and
$\Lambda _2\setminus f_\beta [\rho _1(C_\beta )]\in \mathcal {I}_{\rho _2}^*$
and
![]() $\Lambda _2\setminus A_\beta \in \mathcal {I}_{\rho _2}^*$
for every
$\Lambda _2\setminus A_\beta \in \mathcal {I}_{\rho _2}^*$
for every
![]() $\beta <\alpha $
, we obtain that the intersection of finitely many sets from
$\beta <\alpha $
, we obtain that the intersection of finitely many sets from
![]() $\mathcal {D}$
is in
$\mathcal {D}$
is in
![]() $\mathcal {I}_{\rho _2}^+$
. In particular, this intersection is infinite, so
$\mathcal {I}_{\rho _2}^+$
. In particular, this intersection is infinite, so
![]() $\mathcal {D}$
has the strong finite intersection property. Since
$\mathcal {D}$
has the strong finite intersection property. Since
![]() $|\mathcal {D}|<\mathfrak {c}=\mathfrak {p}$
, there exists an infinite set
$|\mathcal {D}|<\mathfrak {c}=\mathfrak {p}$
, there exists an infinite set
![]() $A\subseteq \Lambda _2$
such that
$A\subseteq \Lambda _2$
such that
![]() $A\subseteq ^* D$
for every
$A\subseteq ^* D$
for every
![]() $D\in \mathcal {D}$
. Since
$D\in \mathcal {D}$
. Since
![]() $\mathcal {I}_{\rho _2}\not \leq _K\mathcal {I}_{\rho _1}$
, we obtain that the ideal
$\mathcal {I}_{\rho _2}\not \leq _K\mathcal {I}_{\rho _1}$
, we obtain that the ideal
![]() $\mathcal {I}_{\rho _2}$
is tall, and consequently there is an infinite set
$\mathcal {I}_{\rho _2}$
is tall, and consequently there is an infinite set
![]() $A_\alpha \subseteq A$
such that
$A_\alpha \subseteq A$
such that
![]() $A_\alpha \in \mathcal {I}_{\rho _2}$
.
$A_\alpha \in \mathcal {I}_{\rho _2}$
.
It is not difficult to see that the sets
![]() $A_\alpha $
and
$A_\alpha $
and
![]() $C_\alpha $
satisfy all the required conditions, so the proof of the lemma is finished.
$C_\alpha $
satisfy all the required conditions, so the proof of the lemma is finished.
We are ready for the main result of this section.
Theorem 14.3 (Assume CH).
Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular for each
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular for each
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
and
$P^-$
and
![]() $\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, then there exists an almost disjoint family
$\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, then there exists an almost disjoint family
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $|\mathcal {A}|=\mathfrak {c}$
and
$|\mathcal {A}|=\mathfrak {c}$
and
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
In particular, there is a Hausdorff compact and separable space of cardinality
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
In particular, there is a Hausdorff compact and separable space of cardinality
![]() $\mathfrak {c}$
in
$\mathfrak {c}$
in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
$\operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
Proof Using Proposition 11.4 we can assume that
![]() $\Lambda _1=\Lambda _2=\Lambda $
.
$\Lambda _1=\Lambda _2=\Lambda $
.
Let
![]() $\{f_\alpha : \alpha <\mathfrak {c}\}$
be an enumeration of all functions
$\{f_\alpha : \alpha <\mathfrak {c}\}$
be an enumeration of all functions
![]() $f:\Lambda \to \Lambda $
and
$f:\Lambda \to \Lambda $
and
![]() $\mathcal {F}_2=\{F_\alpha :\alpha <\mathfrak {c}\}$
. By Lemma 14.2, there exist families
$\mathcal {F}_2=\{F_\alpha :\alpha <\mathfrak {c}\}$
. By Lemma 14.2, there exist families
![]() $\mathcal {A} = \{A_\alpha :\alpha <\mathfrak {c}\}$
and
$\mathcal {A} = \{A_\alpha :\alpha <\mathfrak {c}\}$
and
![]() $\mathcal {C}=\{C_\alpha : \alpha <\mathfrak {c}\}$
such that for every
$\mathcal {C}=\{C_\alpha : \alpha <\mathfrak {c}\}$
such that for every
![]() $\alpha <\mathfrak {c}$
all conditions of Lemma 14.2 are satisfied. We claim that
$\alpha <\mathfrak {c}$
all conditions of Lemma 14.2 are satisfied. We claim that
![]() $\mathcal {A}$
is the required family.
$\mathcal {A}$
is the required family.
First, we see that
![]() $\mathcal {A}$
is an almost disjoint family on
$\mathcal {A}$
is an almost disjoint family on
![]() $\Lambda $
by item (4) of Lemma 14.2,
$\Lambda $
by item (4) of Lemma 14.2,
![]() $|\mathcal {A}|=\mathfrak {c}$
and
$|\mathcal {A}|=\mathfrak {c}$
and
![]() $\mathcal {A}\subseteq \mathcal {I}_{\rho _2}$
. Second, CH together with item (5) of Lemma 14.2 ensures that
$\mathcal {A}\subseteq \mathcal {I}_{\rho _2}$
. Second, CH together with item (5) of Lemma 14.2 ensures that
for each
![]() $\alpha <\mathfrak {c}$
, so knowing that
$\alpha <\mathfrak {c}$
, so knowing that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
we can use Lemma 14.1 to see that
$P^-$
we can use Lemma 14.1 to see that
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1)$
. Third, we use item (6) of Lemma 14.2 and Lemma 13.1(1) to see that
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1)$
. Third, we use item (6) of Lemma 14.2 and Lemma 13.1(1) to see that
![]() $\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\rho _2)$
.
$\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\rho _2)$
.
Now we want to show various applications of Theorem 14.3. Those applications can be divided into three parts. The first part concerns existence of a Hausdorff compact and separable space in
![]() $\operatorname {\mathrm {FinBW}}(\rho )$
. Before applying Theorem 14.3, we need to prove one more result.
$\operatorname {\mathrm {FinBW}}(\rho )$
. Before applying Theorem 14.3, we need to prove one more result.
Proposition 14.4. For every ideal
![]() $\mathcal {I}$
there is an ideal
$\mathcal {I}$
there is an ideal
![]() $\mathcal {J}$
such that
$\mathcal {J}$
such that
![]() $\mathcal {J}\not \leq _K\mathcal {I}$
.
$\mathcal {J}\not \leq _K\mathcal {I}$
.
Proof Suppose for the sake of contradiction that there is an ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\mathcal {J}\leq _K\mathcal {I}$
for every ideal
$\mathcal {J}\leq _K\mathcal {I}$
for every ideal
![]() $\mathcal {J}$
. Then for every maximal (with respect to inclusion) ideal
$\mathcal {J}$
. Then for every maximal (with respect to inclusion) ideal
![]() $\mathcal {J}$
on
$\mathcal {J}$
on
![]() $\omega $
there exists a function
$\omega $
there exists a function
![]() $f_{\mathcal {J}}:\Lambda \to \omega $
such that
$f_{\mathcal {J}}:\Lambda \to \omega $
such that
![]() $f_{\mathcal {J}}^{-1}[A]\in \mathcal {I}$
for every
$f_{\mathcal {J}}^{-1}[A]\in \mathcal {I}$
for every
![]() $A\in \mathcal {J}$
. Let
$A\in \mathcal {J}$
. Let
![]() $\mathcal {K}(f_{\mathcal {J}}) = \{A\subseteq \omega : f_{\mathcal {J}}^{-1}[A]\in \mathcal {I}\}$
. Then
$\mathcal {K}(f_{\mathcal {J}}) = \{A\subseteq \omega : f_{\mathcal {J}}^{-1}[A]\in \mathcal {I}\}$
. Then
![]() $\mathcal {K}(f_{\mathcal {J}})$
is an ideal and
$\mathcal {K}(f_{\mathcal {J}})$
is an ideal and
![]() $\mathcal {J}\subseteq \mathcal {K}(f_{\mathcal {J}})$
. Since
$\mathcal {J}\subseteq \mathcal {K}(f_{\mathcal {J}})$
. Since
![]() $\mathcal {J}$
is maximal,
$\mathcal {J}$
is maximal,
![]() $\mathcal {K}(f_{\mathcal {J}})=\mathcal {J}$
. There are
$\mathcal {K}(f_{\mathcal {J}})=\mathcal {J}$
. There are
![]() $2^{\mathfrak {c}}$
pairwise distinct ultrafilters on
$2^{\mathfrak {c}}$
pairwise distinct ultrafilters on
![]() $\omega $
(see, e.g., [Reference Jech51, Theorem 7.6]), so there are
$\omega $
(see, e.g., [Reference Jech51, Theorem 7.6]), so there are
![]() $2^{\mathfrak {c}}$
pairwise distinct maximal ideals on
$2^{\mathfrak {c}}$
pairwise distinct maximal ideals on
![]() $\omega $
(given an ultrafilter
$\omega $
(given an ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\omega $
, the family
$\omega $
, the family
![]() $\{A\subseteq \omega :A\notin \mathcal {U}\}$
is a maximal ideal). However, there are only
$\{A\subseteq \omega :A\notin \mathcal {U}\}$
is a maximal ideal). However, there are only
![]() $\mathfrak {c}$
many functions from
$\mathfrak {c}$
many functions from
![]() $\omega $
into
$\omega $
into
![]() $\omega $
, a contradiction.
$\omega $
, a contradiction.
Theorem 14.5 (Assume CH).
Let
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
be partition regular with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
. If
$\mathcal {F}\subseteq [\Omega ]^\omega $
. If
![]() $\rho $
is
$\rho $
is
![]() $P^-$
, then there exists an almost disjoint family
$P^-$
, then there exists an almost disjoint family
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $|\mathcal {A}|=\mathfrak {c}$
and
$|\mathcal {A}|=\mathfrak {c}$
and
![]() $ \Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho ).$
In particular, there is a Hausdorff compact and separable space of cardinality
$ \Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho ).$
In particular, there is a Hausdorff compact and separable space of cardinality
![]() $\mathfrak {c}$
in
$\mathfrak {c}$
in
![]() $\operatorname {\mathrm {FinBW}}(\rho )$
.
$\operatorname {\mathrm {FinBW}}(\rho )$
.
Proof By Proposition 14.4 there is an ideal
![]() $\mathcal {J}$
such that
$\mathcal {J}$
such that
![]() $\mathcal {J}\not \leq _K\mathcal {I}_\rho $
, so Theorem 14.3 gives us an almost disjoint family
$\mathcal {J}\not \leq _K\mathcal {I}_\rho $
, so Theorem 14.3 gives us an almost disjoint family
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $|\mathcal {A}|=\mathfrak {c}$
and
$|\mathcal {A}|=\mathfrak {c}$
and
![]() $ \Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho )\setminus \operatorname {\mathrm {FinBW}}(\rho _{\mathcal {J}})$
.
$ \Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho )\setminus \operatorname {\mathrm {FinBW}}(\rho _{\mathcal {J}})$
.
Corollary 14.6 (Assume CH).
There exists
![]() $($
for each item distinct
$($
for each item distinct
![]() $)$
an almost disjoint family
$)$
an almost disjoint family
![]() $\mathcal {A}$
for which
$\mathcal {A}$
for which
![]() $\Phi (\mathcal {A})$
is a Hausdorff compact and separable space of cardinality
$\Phi (\mathcal {A})$
is a Hausdorff compact and separable space of cardinality
![]() $\mathfrak {c}$
such that:
$\mathfrak {c}$
such that:
-
(1)
 $\Phi (\mathcal {A})$
is a Hindman space,
$\Phi (\mathcal {A})$
is a Hindman space, -
(2) [Reference Kubiś and Szeptycki61, Theorem 4.7]
 $\Phi (\mathcal {A})$
is a Ramsey space,
$\Phi (\mathcal {A})$
is a Ramsey space, -
(3)
 $\Phi (\mathcal {A})$
is a differentially compact space,
$\Phi (\mathcal {A})$
is a differentially compact space, -
(4) [Reference Kwela62, Theorem 5.3]
 $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\mathcal {I})$
, where
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\mathcal {I})$
, where
 $\mathcal {I}$
is a
$\mathcal {I}$
is a
 $P^-$
ideal
$P^-$
ideal
 $($
in particular, if
$($
in particular, if
 $\mathcal {I}$
is a
$\mathcal {I}$
is a
 $G_{\delta \sigma \delta }$
ideal
$G_{\delta \sigma \delta }$
ideal
 $)$
.
$)$
.
Proof Items (1), (2), and (3) follow from Theorem 14.5 and Proposition 6.7(3). Item (4) follows from Theorem 14.5 and Propositions 6.5(2) and 10.2(4), and the “in particular” part follows from Proposition 6.2(1).
The second part of applications of Theorem 14.3 concerns a special case when
![]() $\mathcal {I}_{\rho _1}$
is
$\mathcal {I}_{\rho _1}$
is
![]() $P^-(\Lambda _1)$
while
$P^-(\Lambda _1)$
while
![]() $\mathcal {I}_{\rho _2}$
is not
$\mathcal {I}_{\rho _2}$
is not
![]() $P^-(\Lambda _2)$
.
$P^-(\Lambda _2)$
.
Theorem 14.7 (Assume CH).
Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular functions for each
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular functions for each
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
,
$P^-$
,
![]() $\mathcal {I}_{\rho _1}$
is
$\mathcal {I}_{\rho _1}$
is
![]() $P^-(\Lambda _1)\ (equivalently, \mathrm {Fin}^2\not \leq _K\mathcal {I}_{\rho _1})$
and
$P^-(\Lambda _1)\ (equivalently, \mathrm {Fin}^2\not \leq _K\mathcal {I}_{\rho _1})$
and
![]() $\mathcal {I}_{\rho _2}$
is not
$\mathcal {I}_{\rho _2}$
is not
![]() $P^-(\Lambda _2)\ (equivalently, \mathrm {Fin}^2\leq _K \mathcal {I}_{\rho _2})$
, then there exists an infinite almost disjoint family
$P^-(\Lambda _2)\ (equivalently, \mathrm {Fin}^2\leq _K \mathcal {I}_{\rho _2})$
, then there exists an infinite almost disjoint family
![]() $\mathcal {A}$
of cardinality
$\mathcal {A}$
of cardinality
![]() $\mathfrak {c}$
such that
$\mathfrak {c}$
such that
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
In particular, there is a Hausdorff compact and separable space of cardinality
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
In particular, there is a Hausdorff compact and separable space of cardinality
![]() $\mathfrak {c}$
in
$\mathfrak {c}$
in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
$\operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
Proof The equivalence of
![]() $\mathcal {I}_{\rho _1}$
being
$\mathcal {I}_{\rho _1}$
being
![]() $P^-(\Lambda _1)$
and
$P^-(\Lambda _1)$
and
![]() $\mathrm {Fin}^2\not \leq _K\mathcal {I}_{\rho _1}$
follows from Proposition 7.1(1).
$\mathrm {Fin}^2\not \leq _K\mathcal {I}_{\rho _1}$
follows from Proposition 7.1(1).
Since
![]() $\mathrm {Fin}^2\leq _K \mathcal {I}_{\rho _2}$
and
$\mathrm {Fin}^2\leq _K \mathcal {I}_{\rho _2}$
and
![]() $\mathrm {Fin}^2\not \leq _K\mathcal {I}_{\rho _1}$
, we know that
$\mathrm {Fin}^2\not \leq _K\mathcal {I}_{\rho _1}$
, we know that
![]() $\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, so Theorem 14.3 finishes the proof.
$\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, so Theorem 14.3 finishes the proof.
Corollary 14.8 (Assume CH).
There exists
![]() $($
for each item distinct
$($
for each item distinct
![]() $)$
an almost disjoint family
$)$
an almost disjoint family
![]() $\mathcal {A}$
for which
$\mathcal {A}$
for which
![]() $\Phi (\mathcal {A})$
is a Hausdorff compact and separable space of cardinality
$\Phi (\mathcal {A})$
is a Hausdorff compact and separable space of cardinality
![]() $\mathfrak {c}$
and the following holds.
$\mathfrak {c}$
and the following holds.
-
(1)
 $\Phi (\mathcal {A})$
is in
$\Phi (\mathcal {A})$
is in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
, where
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
, where
 $\mathcal {I}$
is a
$\mathcal {I}$
is a
 $P^-$
ideal
$P^-$
ideal
 $($
in particular, if
$($
in particular, if
 $\mathcal {I}$
is a
$\mathcal {I}$
is a
 $G_{\delta \sigma \delta }$
ideal
$G_{\delta \sigma \delta }$
ideal
 $)$
, but
$)$
, but
 $\Phi (\mathcal {A})$
is not a
$\Phi (\mathcal {A})$
is not a
 $:$
$:$
-
(a) [Reference Kwela62, Corollary 11.5] Hindman space,
-
(b) Ramsey space,
-
(c) differentially compact space.
-
-
(2)
-
(a) [Reference Kojman and Shelah59, Theorem 3]
 $\Phi (\mathcal {A})$
is a van der Waerden space that is not a Hindman space.
$\Phi (\mathcal {A})$
is a van der Waerden space that is not a Hindman space. -
(b) [Reference Flašková30, Theorem 4.4]
 $\Phi (\mathcal {A})$
is an
$\Phi (\mathcal {A})$
is an
 $\mathcal {I}_{1/n}$
-space that is not a Hindman space.
$\mathcal {I}_{1/n}$
-space that is not a Hindman space.
-
-
(3)
-
(a) [Reference Shi73, Theorem 4.2.2]
 $\Phi (\mathcal {A})$
is a van der Waerden space that is not a differentially compact space.
$\Phi (\mathcal {A})$
is a van der Waerden space that is not a differentially compact space. -
(b) [Reference Kowitz60, Theorem 3.5]
 $\Phi (\mathcal {A})$
is in
$\Phi (\mathcal {A})$
is in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
but it is not a differentially compact space for any
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
but it is not a differentially compact space for any
 $P^+$
ideal
$P^+$
ideal
 $\mathcal {I}\ (in\ particular,\ \textit{for}\ any\ F_\sigma $
ideal
$\mathcal {I}\ (in\ particular,\ \textit{for}\ any\ F_\sigma $
ideal
 $)$
. For instance,
$)$
. For instance,
 $\Phi (\mathcal {A})$
is an
$\Phi (\mathcal {A})$
is an
 $\mathcal {I}_{1/n}$
-space that is not a differentially compact space.
$\mathcal {I}_{1/n}$
-space that is not a differentially compact space.
-
Proof Item (1) follows from Theorem 14.7 and Propositions 7.2(2), 10.2(4), 6.5(2), and 6.1(1). Other items follow from item (1), Theorem 6.2(2), and Propositions 6.7(1) and 6.1(1).
Now we deal with the third part of applications of Theorems 14.3, in which we need to use its full strength.
Corollary 14.9 (Assume CH).
There exists
![]() $($
for each item distinct
$($
for each item distinct
![]() $)$
an almost disjoint family
$)$
an almost disjoint family
![]() $\mathcal {A}$
for which
$\mathcal {A}$
for which
![]() $\Phi (\mathcal {A})$
is a Hausdorff compact and separable space of cardinality
$\Phi (\mathcal {A})$
is a Hausdorff compact and separable space of cardinality
![]() $\mathfrak {c}$
such that
$\mathfrak {c}$
such that
![]() $:$
$:$
-
(1)
 $\Phi (\mathcal {A})$
is a Ramsey space that is not a Hindman space;
$\Phi (\mathcal {A})$
is a Ramsey space that is not a Hindman space; -
(2)
 $\Phi (\mathcal {A})$
is a Hindman space that is not a Ramsey space;
$\Phi (\mathcal {A})$
is a Hindman space that is not a Ramsey space; -
(3)
 $\Phi (\mathcal {A})$
is a differentially compact space that is not a Hindman space;
$\Phi (\mathcal {A})$
is a differentially compact space that is not a Hindman space; -
(4)
 $\Phi (\mathcal {A})$
is a differentially compact space that is not a Ramsey space.
$\Phi (\mathcal {A})$
is a differentially compact space that is not a Ramsey space.
Remark. The space from Corollary 14.9(3) yields the negative answer to [Reference Shi73, Question 4.2.2] (see also [Reference Filipów22, Problem 1] and [Reference Kowitz60, Question 3]).
Corollary 14.10 (Assume CH).
-
(1) If
 $\mathcal {I}$
is an ideal such that
$\mathcal {I}$
is an ideal such that
 $\mathcal {I}\not \leq _K\mathcal {H}\ (\mathcal {I}\not \leq _K\mathcal {R}, \mathcal {I}\not \leq _K\mathcal {D}, resp.)$
, then there exists an almost disjoint family
$\mathcal {I}\not \leq _K\mathcal {H}\ (\mathcal {I}\not \leq _K\mathcal {R}, \mathcal {I}\not \leq _K\mathcal {D}, resp.)$
, then there exists an almost disjoint family
 $\mathcal {A}$
such that the Hausdorff compact and separable space
$\mathcal {A}$
such that the Hausdorff compact and separable space
 $\Phi (\mathcal {A})$
of cardinality
$\Phi (\mathcal {A})$
of cardinality
 $\mathfrak {c}$
is a Hindman
$\mathfrak {c}$
is a Hindman
 $($
Ramsey, differentially compact, resp.
$($
Ramsey, differentially compact, resp.
 $)$
space that is not in
$)$
space that is not in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
. -
(2) There exists an almost disjoint family
 $\mathcal {A}$
such that the Hausdorff compact and separable space
$\mathcal {A}$
such that the Hausdorff compact and separable space
 $\Phi (\mathcal {A})$
of cardinality
$\Phi (\mathcal {A})$
of cardinality
 $\mathfrak {c}$
is a Hindman
$\mathfrak {c}$
is a Hindman
 $($
Ramsey, differentially compact, resp.
$($
Ramsey, differentially compact, resp.
 $)$
space that is not an
$)$
space that is not an
 $\mathcal {I}_{1/n}$
-space.
$\mathcal {I}_{1/n}$
-space.
Proof (1) It follows from Theorem 14.3 and Propositions 6.7(3) and 10.2(4).
(2) It follows from item (1) and Theorem 7.7.
Remark. In [Reference Filipów, Kowitz, Kwela and Tryba24, Theorem 2.5], the authors constructed, assuming CH and
![]() $\mathcal {I}\not \leq _K\mathcal {H}$
, a non-Hausdorff Hindman space that is not in
$\mathcal {I}\not \leq _K\mathcal {H}$
, a non-Hausdorff Hindman space that is not in
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
. Corollary 14.10(1) strengthens this result to the case of Hausdorff spaces. Taking
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
. Corollary 14.10(1) strengthens this result to the case of Hausdorff spaces. Taking
![]() $\mathcal {I}=\mathcal {I}_{1/n}$
, they obtained a positive answer to the question posed in [Reference Flašková29], namely they constructed a (non-Hausdorff) Hindman space which is not
$\mathcal {I}=\mathcal {I}_{1/n}$
, they obtained a positive answer to the question posed in [Reference Flašková29], namely they constructed a (non-Hausdorff) Hindman space which is not
![]() $\mathcal {I}_{1/n}$
-space. In Corollary 14.10(2), we obtained a Hausdorff answer to the above mentioned question.
$\mathcal {I}_{1/n}$
-space. In Corollary 14.10(2), we obtained a Hausdorff answer to the above mentioned question.
Corollary 14.11 (Assume CH).
-
(1) [Reference Kwela62, Theorem 9.3] If
 $\mathcal {I}_1$
and
$\mathcal {I}_1$
and
 $\mathcal {I}_2$
are ideals such that
$\mathcal {I}_2$
are ideals such that
 $\mathcal {I}_1$
is
$\mathcal {I}_1$
is
 $P^-\ (in particular,\ \textit{if}\ \mathcal {I}_1$
is a
$P^-\ (in particular,\ \textit{if}\ \mathcal {I}_1$
is a
 $G_{\delta \sigma \delta }$
ideal
$G_{\delta \sigma \delta }$
ideal
 $)$
and
$)$
and
 $\mathcal {I}_{2}\not \leq _K \mathcal {I}_{1}$
, then there exists an almost disjoint family
$\mathcal {I}_{2}\not \leq _K \mathcal {I}_{1}$
, then there exists an almost disjoint family
 $\mathcal {A}$
such that the Hausdorff compact and separable space
$\mathcal {A}$
such that the Hausdorff compact and separable space
 $\Phi (\mathcal {A})$
of cardinality
$\Phi (\mathcal {A})$
of cardinality
 $\mathfrak {c}$
belongs to
$\mathfrak {c}$
belongs to
 $\operatorname {\mathrm {FinBW}}(\mathcal {I}_1) \setminus \operatorname {\mathrm {FinBW}}(\mathcal {I}_2).$
$\operatorname {\mathrm {FinBW}}(\mathcal {I}_1) \setminus \operatorname {\mathrm {FinBW}}(\mathcal {I}_2).$
-
(2) [Reference Flašková30, Theorem 3.3] There exists an almost disjoint family
 $\mathcal {A}$
such that the Hausdorff compact and separable space
$\mathcal {A}$
such that the Hausdorff compact and separable space
 $\Phi (\mathcal {A})$
of cardinality
$\Phi (\mathcal {A})$
of cardinality
 $\mathfrak {c}$
is a van der Waerden space that is not an
$\mathfrak {c}$
is a van der Waerden space that is not an
 $\mathcal {I}_{1/n}$
-space.
$\mathcal {I}_{1/n}$
-space.
15 Distinguishing between
 $\operatorname {\mathrm {FinBW}}$
classes via Katětov order on partition regular functions
$\operatorname {\mathrm {FinBW}}$
classes via Katětov order on partition regular functions
In this section we prove the second of the main results of Part 3. Then we compare it with Theorem 14.3 and show that none of them can be derived from the other one. We start with a technical lemma.
Lemma 15.1 (Assume CH).
Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular with
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular with
![]() $\mathcal {F}_i\subseteq [\Omega _i]^\omega $
for each
$\mathcal {F}_i\subseteq [\Omega _i]^\omega $
for each
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $\{f_\alpha : \alpha <\mathfrak {c}\}$
be an enumeration of all functions
$\{f_\alpha : \alpha <\mathfrak {c}\}$
be an enumeration of all functions
![]() $f:\Lambda _1\to \Lambda _2$
and
$f:\Lambda _1\to \Lambda _2$
and
![]() $\{F_\alpha :\alpha <\mathfrak {c}\}$
be an enumeration of all sets
$\{F_\alpha :\alpha <\mathfrak {c}\}$
be an enumeration of all sets
![]() $F\in \mathcal {F}_2$
having small accretions.
$F\in \mathcal {F}_2$
having small accretions.
If
![]() $\rho _2$
is
$\rho _2$
is
![]() $P^-$
and
$P^-$
and
![]() $\rho _2\not \leq _K \rho _1$
, then there exist families
$\rho _2\not \leq _K \rho _1$
, then there exist families
![]() $\mathcal {A} = \{A_\alpha :\alpha <\mathfrak {c}\}$
and
$\mathcal {A} = \{A_\alpha :\alpha <\mathfrak {c}\}$
and
![]() $\mathcal {C}=\{C_\alpha : \alpha <\mathfrak {c}\}$
such that for every
$\mathcal {C}=\{C_\alpha : \alpha <\mathfrak {c}\}$
such that for every
![]() $\alpha <\mathfrak {c}:$
$\alpha <\mathfrak {c}:$
-
(1)
 $A_\alpha =\emptyset \lor A_\alpha \in \mathcal {I}_{\rho _2}\cap [\Lambda _2]^\omega $
,
$A_\alpha =\emptyset \lor A_\alpha \in \mathcal {I}_{\rho _2}\cap [\Lambda _2]^\omega $
, -
(2)
 $\forall \beta <\alpha \, (|A_\alpha \cap A_\beta |<\omega )$
,
$\forall \beta <\alpha \, (|A_\alpha \cap A_\beta |<\omega )$
, -
(3)
 $C_\alpha \in \mathcal {F}_1$
,
$C_\alpha \in \mathcal {F}_1$
, -
(4)
 $\forall F\in \mathcal {F}_2\,\exists K\in [\Omega _1]^{<\omega }\, \forall L\in [\Omega _2]^{<\omega }\, (\rho _2(F\setminus L) \not \subseteq f_\alpha [\rho _1(C_\alpha \setminus K)])$
,
$\forall F\in \mathcal {F}_2\,\exists K\in [\Omega _1]^{<\omega }\, \forall L\in [\Omega _2]^{<\omega }\, (\rho _2(F\setminus L) \not \subseteq f_\alpha [\rho _1(C_\alpha \setminus K)])$
, -
(5)
 $\forall \gamma> \alpha \, \exists K\in [\Omega _1]^{<\omega } \,(|A_\gamma \cap f_\alpha [\rho _1(C_\alpha \setminus K)]|<\omega )$
,
$\forall \gamma> \alpha \, \exists K\in [\Omega _1]^{<\omega } \,(|A_\gamma \cap f_\alpha [\rho _1(C_\alpha \setminus K)]|<\omega )$
, -
(6)
 $\exists \beta \leq \alpha \, \forall L\in [\Omega _2]^{<\omega }\, (A_\beta \cap \rho _2(F_\alpha \setminus L)\neq \emptyset )$
.
$\exists \beta \leq \alpha \, \forall L\in [\Omega _2]^{<\omega }\, (A_\beta \cap \rho _2(F_\alpha \setminus L)\neq \emptyset )$
.
Proof Suppose that
![]() $A_\beta $
and
$A_\beta $
and
![]() $C_\beta $
have been constructed for
$C_\beta $
have been constructed for
![]() $\beta <\alpha $
and satisfy all the required conditions.
$\beta <\alpha $
and satisfy all the required conditions.
First, we construct a set
![]() $C_\alpha $
. Since
$C_\alpha $
. Since
![]() $\rho _2 \not \leq _K \rho _1$
, there is a set
$\rho _2 \not \leq _K \rho _1$
, there is a set
![]() $C_\alpha \in \mathcal {F}_1$
such that
$C_\alpha \in \mathcal {F}_1$
such that
Now, we turn to the construction of a set
![]() $A_\alpha $
. We have two cases:
$A_\alpha $
. We have two cases:
-
(1)
 $\exists \beta < \alpha \, \forall L\in [\Omega _2]^{<\omega }\, (A_\beta \cap \rho _2(F_\alpha \setminus L)\neq \emptyset )$
.
$\exists \beta < \alpha \, \forall L\in [\Omega _2]^{<\omega }\, (A_\beta \cap \rho _2(F_\alpha \setminus L)\neq \emptyset )$
. -
(2)
 $\forall \beta < \alpha \, \exists L_\beta \in [\Omega _2]^{<\omega }\, (A_\beta \cap \rho _2(F_\alpha \setminus L_\beta ) = \emptyset )$
.
$\forall \beta < \alpha \, \exists L_\beta \in [\Omega _2]^{<\omega }\, (A_\beta \cap \rho _2(F_\alpha \setminus L_\beta ) = \emptyset )$
.
Case (1). We put
![]() $A_\alpha =\emptyset $
. Then the sets
$A_\alpha =\emptyset $
. Then the sets
![]() $A_\alpha $
and
$A_\alpha $
and
![]() $C_\alpha $
satisfy all the required conditions, so the proof of the lemma is finished in this case.
$C_\alpha $
satisfy all the required conditions, so the proof of the lemma is finished in this case.
Case (2). Let
![]() $\alpha =\{\beta _n:n\in \omega \}$
. Let
$\alpha =\{\beta _n:n\in \omega \}$
. Let
![]() $\{L_n:n\in \omega \}$
be an increasing sequence of finite subsets of
$\{L_n:n\in \omega \}$
be an increasing sequence of finite subsets of
![]() $\Omega _2$
such that
$\Omega _2$
such that
![]() $\bigcup \{L_{\beta _i}:i<n\} \subseteq L_n$
and
$\bigcup \{L_{\beta _i}:i<n\} \subseteq L_n$
and
![]() $\bigcup \{L_n:n\in \omega \} = \Omega _2$
. Notice that
$\bigcup \{L_n:n\in \omega \} = \Omega _2$
. Notice that
![]() $\rho _2(F_\alpha \setminus L_n)\cap \bigcup \{A_{\beta _i}:i<n\} = \emptyset $
for every
$\rho _2(F_\alpha \setminus L_n)\cap \bigcup \{A_{\beta _i}:i<n\} = \emptyset $
for every
![]() $n\in \omega $
.
$n\in \omega $
.
We define inductively sequences
![]() $\{E_n:n\in \omega \} \subseteq \mathcal {F}_2$
,
$\{E_n:n\in \omega \} \subseteq \mathcal {F}_2$
,
![]() $\{K_n:n\in \omega \}\subseteq [\Omega _1]^{<\omega }$
and
$\{K_n:n\in \omega \}\subseteq [\Omega _1]^{<\omega }$
and
![]() $\{a_n:n\in \omega \}\subseteq \Lambda _2$
such that for every
$\{a_n:n\in \omega \}\subseteq \Lambda _2$
such that for every
![]() $n\in \omega $
the following conditions hold:
$n\in \omega $
the following conditions hold:
-
(i)
 $\rho _2(E_{n+1})\subseteq \rho _2(E_n)\subseteq \rho _2(F_\alpha )$
,
$\rho _2(E_{n+1})\subseteq \rho _2(E_n)\subseteq \rho _2(F_\alpha )$
, -
(ii)
 $\rho _2(E_n) \subseteq \rho _2(F_\alpha \setminus L_n)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K_n)]$
,
$\rho _2(E_n) \subseteq \rho _2(F_\alpha \setminus L_n)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K_n)]$
, -
(iii)
 $a_n\in \rho _2(E_n) \setminus \{a_i:i<n\}$
.
$a_n\in \rho _2(E_n) \setminus \{a_i:i<n\}$
.
Suppose that
![]() $E_i$
,
$E_i$
,
![]() $K_i$
, and
$K_i$
, and
![]() $a_i$
have been constructed for
$a_i$
have been constructed for
![]() $i<n$
and satisfy all the required conditions.
$i<n$
and satisfy all the required conditions.
Since
![]() $F_\alpha $
has small accretions, we obtain
$F_\alpha $
has small accretions, we obtain
![]() $\rho _2(F_\alpha \setminus L_{n-1})\setminus \rho _2(F_\alpha \setminus L_n)\in \mathcal {I}_{\rho _2}$
, and consequently
$\rho _2(F_\alpha \setminus L_{n-1})\setminus \rho _2(F_\alpha \setminus L_n)\in \mathcal {I}_{\rho _2}$
, and consequently
![]() $\rho _2(E_{n-1})\cap \rho _2(F_\alpha \setminus L_{n})\notin \mathcal {I}_{\rho _2}$
(in the case of
$\rho _2(E_{n-1})\cap \rho _2(F_\alpha \setminus L_{n})\notin \mathcal {I}_{\rho _2}$
(in the case of
![]() $n=0$
we put
$n=0$
we put
![]() $L_{-1}=\emptyset $
and
$L_{-1}=\emptyset $
and
![]() $E_{-1}=F_\alpha $
). Let
$E_{-1}=F_\alpha $
). Let
![]() $E\in \mathcal {F}_2$
be such that
$E\in \mathcal {F}_2$
be such that
![]() $\rho _2(E)\subseteq \rho _2(E_{n-1})\cap \rho _2(F_\alpha \setminus L_{n})$
. We have 2 subcases:
$\rho _2(E)\subseteq \rho _2(E_{n-1})\cap \rho _2(F_\alpha \setminus L_{n})$
. We have 2 subcases:
-
(2a)
 $\exists K_n\in [\Omega _1]^{<\omega }\,(\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K_n)]\notin \mathcal {I}_{\rho _2}),$
$\exists K_n\in [\Omega _1]^{<\omega }\,(\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K_n)]\notin \mathcal {I}_{\rho _2}),$
-
(2b)
 $\forall K\in [\Omega _1]^{<\omega }\,(\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]\in \mathcal {I}_{\rho _2}).$
$\forall K\in [\Omega _1]^{<\omega }\,(\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]\in \mathcal {I}_{\rho _2}).$
Case (2a). We take
![]() $E_n\in \mathcal {F}_2$
such that
$E_n\in \mathcal {F}_2$
such that
![]() $\rho _2(E_n)\subseteq \rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K_n)]$
and pick any
$\rho _2(E_n)\subseteq \rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K_n)]$
and pick any
![]() $a_n\in \rho _2(E_n) \setminus \{a_i:i<n\}$
. Then
$a_n\in \rho _2(E_n) \setminus \{a_i:i<n\}$
. Then
![]() $E_n$
,
$E_n$
,
![]() $K_n$
, and
$K_n$
, and
![]() $a_n$
satisfy all the required conditions.
$a_n$
satisfy all the required conditions.
Case (2b). It will turn out that this subcase is impossible. Let
![]() $\{M_i:i\in \omega \}$
be an increasing sequence of finite subsets of
$\{M_i:i\in \omega \}$
be an increasing sequence of finite subsets of
![]() $\Omega _1$
such that
$\Omega _1$
such that
![]() $\bigcup \{M_i:i\in \omega \} = \Omega _1$
.
$\bigcup \{M_i:i\in \omega \} = \Omega _1$
.
We have two further subcases:
-
(2b-1)
 $\bigcup \{\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \}\notin \mathcal {I}_{\rho _2}$
,
$\bigcup \{\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \}\notin \mathcal {I}_{\rho _2}$
, -
(2b-2)
 $\bigcup \{\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \}\in \mathcal {I}_{\rho _2}$
.
$\bigcup \{\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \}\in \mathcal {I}_{\rho _2}$
.
Case (2b-1). Since
![]() $\rho _2$
is
$\rho _2$
is
![]() $P^-$
, there is
$P^-$
, there is
![]() $G\in \mathcal {F}_2$
such that
$G\in \mathcal {F}_2$
such that
![]() $\rho _2(G)\subseteq \bigcup \{\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \}$
and for every
$\rho _2(G)\subseteq \bigcup \{\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \}$
and for every
![]() $i\in \omega $
there is a finite set
$i\in \omega $
there is a finite set
![]() $L\subseteq \Omega _2$
such that
$L\subseteq \Omega _2$
such that
![]() $\rho _2(G\setminus L)\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]$
. On the other hand, from the inductive assumptions (more precisely: since
$\rho _2(G\setminus L)\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]$
. On the other hand, from the inductive assumptions (more precisely: since
![]() $C_{\beta _n}$
satisfies item 4), we know that there is a finite set K such that
$C_{\beta _n}$
satisfies item 4), we know that there is a finite set K such that
![]() $\rho _2(G\setminus L)\not \subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]$
for any finite set L. Let
$\rho _2(G\setminus L)\not \subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]$
for any finite set L. Let
![]() $i\in \omega $
be such that
$i\in \omega $
be such that
![]() $K\subseteq M_i$
. Then there is a finite set
$K\subseteq M_i$
. Then there is a finite set
![]() $L\subseteq \Omega _2$
such that
$L\subseteq \Omega _2$
such that
![]() $\rho _2(G\setminus L)\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]$
, a contradiction.
$\rho _2(G\setminus L)\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]$
, a contradiction.
Case (2b-2). In this case, there is
![]() $G\in \mathcal {F}_2$
such that
$G\in \mathcal {F}_2$
such that
![]() $\rho _2(G)\subseteq \rho _2(E)\setminus \bigcup \{\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \} = \rho _2(E)\cap \bigcap \{f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \}$
. From the inductive assumptions, we know that there is a finite set K such that
$\rho _2(G)\subseteq \rho _2(E)\setminus \bigcup \{\rho _2(E)\setminus f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \} = \rho _2(E)\cap \bigcap \{f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]: i\in \omega \}$
. From the inductive assumptions, we know that there is a finite set K such that
![]() $\rho _2(G\setminus L)\not \subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]$
for any finite set L. Let
$\rho _2(G\setminus L)\not \subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]$
for any finite set L. Let
![]() $i\in \omega $
be such that
$i\in \omega $
be such that
![]() $K\subseteq M_i$
. Then
$K\subseteq M_i$
. Then
![]() $\rho _2(G)\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]$
, a contradiction.
$\rho _2(G)\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus M_i)]\subseteq f_{\beta _n}[\rho _1(C_{\beta _n}\setminus K)]$
, a contradiction.
The construction of
![]() $E_n$
,
$E_n$
,
![]() $K_n$
and
$K_n$
and
![]() $a_n$
is finished.
$a_n$
is finished.
We define
![]() $A = \{a_n:n\in \omega \}$
. Since
$A = \{a_n:n\in \omega \}$
. Since
![]() $\rho _2\not \leq _K\rho _1$
, we obtain that
$\rho _2\not \leq _K\rho _1$
, we obtain that
![]() $\rho _2$
is tall. Thus
$\rho _2$
is tall. Thus
![]() $\mathcal {I}_{\rho _2}$
is a tall ideal (by Proposition 8.1). Since A is infinite, there is an infinite set
$\mathcal {I}_{\rho _2}$
is a tall ideal (by Proposition 8.1). Since A is infinite, there is an infinite set
![]() $A_\alpha \subseteq A$
such that
$A_\alpha \subseteq A$
such that
![]() $A_\alpha \in \mathcal {I}_{\rho _2}$
.
$A_\alpha \in \mathcal {I}_{\rho _2}$
.
It is not difficult to see that the sets
![]() $A_\alpha $
and
$A_\alpha $
and
![]() $C_\alpha $
satisfy all the required conditions, so the proof of the lemma is finished.
$C_\alpha $
satisfy all the required conditions, so the proof of the lemma is finished.
The main result of this section is as follows.
Theorem 15.2 (Assume CH).
Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular for each
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular for each
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
are
$\rho _2$
are
![]() $P^-$
,
$P^-$
,
![]() $\rho _2$
has small accretions, and
$\rho _2$
has small accretions, and
![]() $\rho _2\not \leq _K \rho _1$
, then there exists an almost disjoint family
$\rho _2\not \leq _K \rho _1$
, then there exists an almost disjoint family
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $|\mathcal {A}|=\mathfrak {c}$
,
$|\mathcal {A}|=\mathfrak {c}$
,
![]() $\mathcal {A}\subseteq \mathcal {I}_{\rho _2}$
, and
$\mathcal {A}\subseteq \mathcal {I}_{\rho _2}$
, and
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
In particular, there is a Hausdorff compact and separable space of cardinality
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
In particular, there is a Hausdorff compact and separable space of cardinality
![]() $\mathfrak {c}$
in
$\mathfrak {c}$
in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
$\operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
Proof Using Proposition 11.4 we can assume that
![]() $\Lambda _1=\Lambda _2=\Lambda $
. Let
$\Lambda _1=\Lambda _2=\Lambda $
. Let
![]() $\{f_\alpha : \alpha <\mathfrak {c}\}$
be an enumeration of all functions
$\{f_\alpha : \alpha <\mathfrak {c}\}$
be an enumeration of all functions
![]() $f:\Lambda _1\to \Lambda _2$
and
$f:\Lambda _1\to \Lambda _2$
and
![]() $\{F_\alpha :\alpha <\mathfrak {c}\}$
be an enumeration of all sets
$\{F_\alpha :\alpha <\mathfrak {c}\}$
be an enumeration of all sets
![]() $F\in \mathcal {F}_2$
having small accretions. By Lemma 15.1, there exist families
$F\in \mathcal {F}_2$
having small accretions. By Lemma 15.1, there exist families
![]() $\mathcal {A} = \{A_\alpha :\alpha <\mathfrak {c}\}$
and
$\mathcal {A} = \{A_\alpha :\alpha <\mathfrak {c}\}$
and
![]() $\mathcal {C}=\{C_\alpha : \alpha <\mathfrak {c}\}$
such that for every
$\mathcal {C}=\{C_\alpha : \alpha <\mathfrak {c}\}$
such that for every
![]() $\alpha <\mathfrak {c}$
all the required conditions of Lemma 15.1 are satisfied. We claim that
$\alpha <\mathfrak {c}$
all the required conditions of Lemma 15.1 are satisfied. We claim that
![]() $\mathcal {A}\setminus \{\emptyset \}$
is the required family.
$\mathcal {A}\setminus \{\emptyset \}$
is the required family.
First, we see that
![]() $\mathcal {A}\setminus \{\emptyset \}$
is an almost disjoint family on
$\mathcal {A}\setminus \{\emptyset \}$
is an almost disjoint family on
![]() $\Lambda _2$
(by item (2) of Lemma 15.1) and
$\Lambda _2$
(by item (2) of Lemma 15.1) and
![]() $\mathcal {A}\setminus \{\emptyset \}\subseteq \mathcal {I}_{\rho _2}$
.
$\mathcal {A}\setminus \{\emptyset \}\subseteq \mathcal {I}_{\rho _2}$
.
Second, let CH together with item (5) of Lemma 15.1 ensures that
for each
![]() $\alpha <\mathfrak {c}$
, so knowing that
$\alpha <\mathfrak {c}$
, so knowing that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
we can use Lemma 14.1 to see that
$P^-$
we can use Lemma 14.1 to see that
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1)$
.
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\rho _1)$
.
Third, we use Lemma 13.1(1) along with item (6) of Lemma 15.1 and the fact that
![]() $\rho _2$
has small accretions to see that
$\rho _2$
has small accretions to see that
![]() $\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\rho _2)$
.
$\Phi (\mathcal {A})\notin \operatorname {\mathrm {FinBW}}(\rho _2)$
.
Finally, using Proposition 12.2 we know that
![]() $\mathcal {A}$
cannot be countable, so
$\mathcal {A}$
cannot be countable, so
![]() $|\mathcal {A}\setminus \{\emptyset \}|=\mathfrak {c}$
.
$|\mathcal {A}\setminus \{\emptyset \}|=\mathfrak {c}$
.
Now we want to compare Theorem 15.2 with Theorem 14.3. Next two examples show that there are partition regular functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
satisfying the assumptions of Theorem 14.3 (so it gives us, under CH, a space in
$\rho _2$
satisfying the assumptions of Theorem 14.3 (so it gives us, under CH, a space in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
), but not satisfying assumptions of Theorem 15.2 (i.e., we cannot apply it).
$\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
), but not satisfying assumptions of Theorem 15.2 (i.e., we cannot apply it).
Example 15.3. There exist partition regular functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
such that
$\rho _2$
such that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
,
$P^-$
,
![]() $\rho _2$
is not
$\rho _2$
is not
![]() $P^-$
(so we cannot apply Theorem 15.2) and
$P^-$
(so we cannot apply Theorem 15.2) and
![]() $\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
.
$\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
.
Proof Let
![]() $\rho _1=\rho _{\mathcal {I}_{1/n}}$
and
$\rho _1=\rho _{\mathcal {I}_{1/n}}$
and
![]() $\rho _2=\rho _{\mathcal {H}}$
. By Theorem 6.7,
$\rho _2=\rho _{\mathcal {H}}$
. By Theorem 6.7,
![]() $\mathcal {I}_{1/n}$
is
$\mathcal {I}_{1/n}$
is
![]() $P^+$
(hence,
$P^+$
(hence,
![]() $P^-$
) and
$P^-$
) and
![]() $\mathcal {H}$
is not
$\mathcal {H}$
is not
![]() $P^-(\omega )$
(hence, not
$P^-(\omega )$
(hence, not
![]() $P^-$
). Applying Proposition 6.5(2), we see that
$P^-$
). Applying Proposition 6.5(2), we see that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
and
$P^-$
and
![]() $\rho _2$
is not
$\rho _2$
is not
![]() $P^-$
. By Theorem 7.7(12),
$P^-$
. By Theorem 7.7(12),
![]() $\mathcal {H}\not \leq _K \mathcal {I}_{1/n}$
.
$\mathcal {H}\not \leq _K \mathcal {I}_{1/n}$
.
The above example may not be satisfactory as all Hausdorff spaces from the class
![]() $\operatorname {\mathrm {FinBW}}(\rho _2)$
are finite (by Theorem 10.5(3) and Proposition 10.2(4)), so one could just use Theorem 10.5(3) instead of Theorem 14.3. The next example is more sophisticated.
$\operatorname {\mathrm {FinBW}}(\rho _2)$
are finite (by Theorem 10.5(3) and Proposition 10.2(4)), so one could just use Theorem 10.5(3) instead of Theorem 14.3. The next example is more sophisticated.
Example 15.4. There exist partition regular functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
such that
$\rho _2$
such that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
,
$P^-$
,
![]() $\rho _2$
is not
$\rho _2$
is not
![]() $P^-$
(so we cannot apply Theorem 15.2),
$P^-$
(so we cannot apply Theorem 15.2),
![]() $\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, and under CH there is a Hausdorff compact separable space of cardinality
$\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
, and under CH there is a Hausdorff compact separable space of cardinality
![]() $\mathfrak {c}$
in
$\mathfrak {c}$
in
![]() $\operatorname {\mathrm {FinBW}}(\rho _2)$
.
$\operatorname {\mathrm {FinBW}}(\rho _2)$
.
Proof Let
![]() $\rho _1=\rho _{\mathcal {I}_{1/n}}$
and
$\rho _1=\rho _{\mathcal {I}_{1/n}}$
and
![]() $\rho _2=\rho _{\mathrm {conv}}$
, where
$\rho _2=\rho _{\mathrm {conv}}$
, where
![]() $\mathrm {conv}$
is an ideal on
$\mathrm {conv}$
is an ideal on
![]() $\mathbb {Q}\cap [0,1]$
consisting of those subsets of
$\mathbb {Q}\cap [0,1]$
consisting of those subsets of
![]() $\mathbb {Q}\cap [0,1]$
that have only finitely many cluster points in
$\mathbb {Q}\cap [0,1]$
that have only finitely many cluster points in
![]() $[0,1]$
. Then,
$[0,1]$
. Then,
![]() $\operatorname {\mathrm {FinBW}}(\rho _2)=\operatorname {\mathrm {FinBW}}(\mathrm {conv})$
(Proposition 10.2(4)). Applying [Reference Kwela62, Definition 4.3, Proposition 4.6, and Theorem 6.6], assuming CH, there is a Hausdorff compact separable space of cardinality
$\operatorname {\mathrm {FinBW}}(\rho _2)=\operatorname {\mathrm {FinBW}}(\mathrm {conv})$
(Proposition 10.2(4)). Applying [Reference Kwela62, Definition 4.3, Proposition 4.6, and Theorem 6.6], assuming CH, there is a Hausdorff compact separable space of cardinality
![]() $\mathfrak {c}$
in
$\mathfrak {c}$
in
![]() $\operatorname {\mathrm {FinBW}}(\rho _2)$
. Moreover,
$\operatorname {\mathrm {FinBW}}(\rho _2)$
. Moreover,
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
and
$P^-$
and
![]() $\rho _2$
is not
$\rho _2$
is not
![]() $P^-$
(by Proposition 6.5(2), Theorem 6.7, and [Reference Kwela62, proof of Proposition 4.10(b)]). Finally,
$P^-$
(by Proposition 6.5(2), Theorem 6.7, and [Reference Kwela62, proof of Proposition 4.10(b)]). Finally,
![]() $\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
[Reference Hrušák47, Section 2].
$\mathcal {I}_{\rho _2}\not \leq _K \mathcal {I}_{\rho _1}$
[Reference Hrušák47, Section 2].
Next example shows that there are partition regular functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
satisfying the assumptions of Theorem 15.2 (so it gives us, under CH, a space in
$\rho _2$
satisfying the assumptions of Theorem 15.2 (so it gives us, under CH, a space in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
), but not satisfying assumptions of Theorem 14.3 (i.e., we cannot apply it).
$\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
), but not satisfying assumptions of Theorem 14.3 (i.e., we cannot apply it).
Example 15.5. There exist partition regular functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
with small accretions which are
$\rho _2$
with small accretions which are
![]() $P^-$
and such that
$P^-$
and such that
![]() $\mathcal {I}_{\rho _2} \subseteq \mathcal {I}_{\rho _1}$
(in particular,
$\mathcal {I}_{\rho _2} \subseteq \mathcal {I}_{\rho _1}$
(in particular,
![]() $\mathcal {I}_{\rho _2} \leq _K \mathcal {I}_{\rho _1}$
, so we cannot apply Theorem 14.3), but
$\mathcal {I}_{\rho _2} \leq _K \mathcal {I}_{\rho _1}$
, so we cannot apply Theorem 14.3), but
![]() $\rho _2\not \leq _K\rho _1$
.
$\rho _2\not \leq _K\rho _1$
.
Proof Consider the ideal
![]() $\mathrm {nwd}=\{A\subseteq \mathbb {Q}\cap [0,1]:\ \overline {A}\text { is meager}\}$
. Let
$\mathrm {nwd}=\{A\subseteq \mathbb {Q}\cap [0,1]:\ \overline {A}\text { is meager}\}$
. Let
![]() $\rho _2=\rho _{\mathrm {nwd}}$
.
$\rho _2=\rho _{\mathrm {nwd}}$
.
Fix an almost disjoint family
![]() $\mathcal {A}$
of cardinality
$\mathcal {A}$
of cardinality
![]() $\mathfrak {c}$
, enumerate it as
$\mathfrak {c}$
, enumerate it as
![]() $\mathcal {A}=\{A_\alpha :\ \alpha <\mathfrak {c}\}$
and denote
$\mathcal {A}=\{A_\alpha :\ \alpha <\mathfrak {c}\}$
and denote
![]() $\mathcal {A}'=\{A\setminus K:\ A\in \mathcal {A},\ K\in [\omega ]^{<\omega }\}$
. Let
$\mathcal {A}'=\{A\setminus K:\ A\in \mathcal {A},\ K\in [\omega ]^{<\omega }\}$
. Let
![]() $I_n=[\frac {1}{n+2},\frac {1}{n+1})$
for all
$I_n=[\frac {1}{n+2},\frac {1}{n+1})$
for all
![]() $n\in \omega $
. Enumerate also the set
$n\in \omega $
. Enumerate also the set
![]() $\mathcal {B}=\{B\subseteq \mathbb {Q}\cap [0,1]:\ B\cap I_n\notin \mathrm {nwd}\text { for infinitely many }n\in \omega \}$
as
$\mathcal {B}=\{B\subseteq \mathbb {Q}\cap [0,1]:\ B\cap I_n\notin \mathrm {nwd}\text { for infinitely many }n\in \omega \}$
as
![]() $\{B_\alpha :\ \alpha <\mathfrak {c}\}$
. Let
$\{B_\alpha :\ \alpha <\mathfrak {c}\}$
. Let
![]() $\rho _1:\mathcal {A}'\to [\mathbb {Q}\cap [0,1]]^\omega $
be given by
$\rho _1:\mathcal {A}'\to [\mathbb {Q}\cap [0,1]]^\omega $
be given by
![]() $\rho _1(A_\alpha \setminus K)=B_\alpha \setminus \bigcup _{n\in K}I_n$
.
$\rho _1(A_\alpha \setminus K)=B_\alpha \setminus \bigcup _{n\in K}I_n$
.
Observe that
![]() $\mathcal {I}_{\rho _1}=\{A\subseteq \mathbb {Q}\cap [0,1]:\ \exists _{K\in \mathrm {Fin}}\ \overline {A}\setminus \bigcup _{n\in K}I_n\text { is meager}\}$
. Thus,
$\mathcal {I}_{\rho _1}=\{A\subseteq \mathbb {Q}\cap [0,1]:\ \exists _{K\in \mathrm {Fin}}\ \overline {A}\setminus \bigcup _{n\in K}I_n\text { is meager}\}$
. Thus,
![]() $\mathrm {nwd}\subseteq \mathcal {I}_{\rho _1}$
and
$\mathrm {nwd}\subseteq \mathcal {I}_{\rho _1}$
and
![]() $\mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
. Moreover, it is easy to see that
$\mathcal {I}_{\rho _2}\leq _K\mathcal {I}_{\rho _1}$
. Moreover, it is easy to see that
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
both have small accretions (in the case of
$\rho _2$
both have small accretions (in the case of
![]() $\rho _2$
just apply Proposition 4.3). Since
$\rho _2$
just apply Proposition 4.3). Since
![]() $\mathrm {nwd}$
is
$\mathrm {nwd}$
is
![]() $F_{\sigma \delta }$
(see [Reference Farah and Solecki18, Theorem 3]), it is
$F_{\sigma \delta }$
(see [Reference Farah and Solecki18, Theorem 3]), it is
![]() $P^-$
(by Proposition 6.2(1)) and consequently
$P^-$
(by Proposition 6.2(1)) and consequently
![]() $\rho _2$
is
$\rho _2$
is
![]() $P^-$
(by Proposition 6.5(2)).
$P^-$
(by Proposition 6.5(2)).
Now we show that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
. Suppose that
$P^-$
. Suppose that
![]() $\{C_n: n\in \omega \}\subseteq \mathcal {I}^+_{\rho _1}$
is decreasing and such that
$\{C_n: n\in \omega \}\subseteq \mathcal {I}^+_{\rho _1}$
is decreasing and such that
![]() $C_n\setminus C_{n+1}\in \mathcal {I}_{\rho _1}$
for all
$C_n\setminus C_{n+1}\in \mathcal {I}_{\rho _1}$
for all
![]() $n\in \omega $
. For each
$n\in \omega $
. For each
![]() $n\in \omega $
let
$n\in \omega $
let
![]() $T_n=\{i\in \omega :\ C_n\cap I_i\notin \mathrm {nwd}\}$
.
$T_n=\{i\in \omega :\ C_n\cap I_i\notin \mathrm {nwd}\}$
.
Assume first that
![]() $T=\bigcap _{n\in \omega }T_n$
is infinite. Since
$T=\bigcap _{n\in \omega }T_n$
is infinite. Since
![]() $\mathrm {nwd}$
is
$\mathrm {nwd}$
is
![]() $P^-$
, for each
$P^-$
, for each
![]() $i\in T$
we can find
$i\in T$
we can find
![]() $D_i\notin \mathrm {nwd}$
,
$D_i\notin \mathrm {nwd}$
,
![]() $D_i\subseteq I_i$
with
$D_i\subseteq I_i$
with
![]() $D_i\subseteq ^*C_n$
for all
$D_i\subseteq ^*C_n$
for all
![]() $n\in \omega $
. Then for
$n\in \omega $
. Then for
![]() $E=\bigcup _{i\in T}D_i\cap C_i$
we have
$E=\bigcup _{i\in T}D_i\cap C_i$
we have
![]() $E\in \mathcal {B}$
(as
$E\in \mathcal {B}$
(as
![]() $D_i\notin \mathrm {nwd}$
and
$D_i\notin \mathrm {nwd}$
and
![]() $D_i\setminus C_i$
is finite for all
$D_i\setminus C_i$
is finite for all
![]() $i\in T$
). Hence,
$i\in T$
). Hence,
![]() $E=B_\alpha $
for some
$E=B_\alpha $
for some
![]() $\alpha <\mathfrak {c}$
. Moreover, for each
$\alpha <\mathfrak {c}$
. Moreover, for each
![]() $n\in \omega $
we have
$n\in \omega $
we have
![]() $\rho _1(A_\alpha \setminus n)=E\setminus \bigcup _{i<n}I_i=\bigcup _{i\in T,i\geq n}D_i\cap C_i\subseteq C_n$
.
$\rho _1(A_\alpha \setminus n)=E\setminus \bigcup _{i<n}I_i=\bigcup _{i\in T,i\geq n}D_i\cap C_i\subseteq C_n$
.
Assume now that T is finite. Inductively pick
![]() $i_n\in \omega $
and
$i_n\in \omega $
and
![]() $D_n\notin \mathrm {nwd}$
such that
$D_n\notin \mathrm {nwd}$
such that
![]() $i_{n+1}>i_n$
and
$i_{n+1}>i_n$
and
![]() $D_n\subseteq I_{i_n}\cap C_n$
for all
$D_n\subseteq I_{i_n}\cap C_n$
for all
![]() $n\in \omega $
. Define
$n\in \omega $
. Define
![]() $E=\bigcup _{n\in \omega }D_n$
and note that
$E=\bigcup _{n\in \omega }D_n$
and note that
![]() $E\in \mathcal {B}$
. Hence,
$E\in \mathcal {B}$
. Hence,
![]() $E=B_\alpha $
for some
$E=B_\alpha $
for some
![]() $\alpha <\mathfrak {c}$
. Moreover, for each
$\alpha <\mathfrak {c}$
. Moreover, for each
![]() $n\in \omega $
we have
$n\in \omega $
we have
![]() $\rho _1(A_\alpha \setminus i_n)=E\setminus \bigcup _{i<i_n}I_i=\bigcup _{i\geq n}D_i\subseteq C_n$
.
$\rho _1(A_\alpha \setminus i_n)=E\setminus \bigcup _{i<i_n}I_i=\bigcup _{i\geq n}D_i\subseteq C_n$
.
Finally, we will show that
![]() $\rho _2\not \leq _K\rho _1$
. Fix any
$\rho _2\not \leq _K\rho _1$
. Fix any
![]() $f:\mathbb {Q}\cap [0,1]\to \mathbb {Q}\cap [0,1]$
. For each
$f:\mathbb {Q}\cap [0,1]\to \mathbb {Q}\cap [0,1]$
. For each
![]() $n\in \omega $
find
$n\in \omega $
find
![]() $r_n\in \mathbb {Q}\cap [0,1]$
such that
$r_n\in \mathbb {Q}\cap [0,1]$
such that
![]() $f^{-1}[(r_n-\frac {1}{2^n},r_n+\frac {1}{2^n})]\cap I_n\notin \mathrm {nwd}$
. This is possible as
$f^{-1}[(r_n-\frac {1}{2^n},r_n+\frac {1}{2^n})]\cap I_n\notin \mathrm {nwd}$
. This is possible as
![]() $[0,1]$
can be covered by finitely many intervals of the form
$[0,1]$
can be covered by finitely many intervals of the form
![]() $(r-\frac {1}{2^n},r+\frac {1}{2^n})$
and
$(r-\frac {1}{2^n},r+\frac {1}{2^n})$
and
![]() $I_n\cap (\mathbb {Q}\cap [0,1])\notin \mathrm {nwd}$
. Since
$I_n\cap (\mathbb {Q}\cap [0,1])\notin \mathrm {nwd}$
. Since
![]() $[0,1]$
is sequentially compact, there is an infinite
$[0,1]$
is sequentially compact, there is an infinite
![]() $S\subseteq \omega $
such that
$S\subseteq \omega $
such that
![]() $(r_n)_{n\in S}$
converges to some
$(r_n)_{n\in S}$
converges to some
![]() $x\in [0,1]$
. Put
$x\in [0,1]$
. Put
![]() $F=\bigcup _{n\in S}f^{-1}[(r_n-\frac {1}{2^n},r_n+\frac {1}{2^n})]\cap I_n$
. Then
$F=\bigcup _{n\in S}f^{-1}[(r_n-\frac {1}{2^n},r_n+\frac {1}{2^n})]\cap I_n$
. Then
![]() $F\in \mathcal {B}$
(in particular,
$F\in \mathcal {B}$
(in particular,
![]() $F\in \mathcal {I}_{\rho _1}^+$
), so
$F\in \mathcal {I}_{\rho _1}^+$
), so
![]() $F=B_\alpha $
for some
$F=B_\alpha $
for some
![]() $\alpha <\mathfrak {c}$
. Fix any
$\alpha <\mathfrak {c}$
. Fix any
![]() $E\in \mathrm {nwd}^+$
and enumerate
$E\in \mathrm {nwd}^+$
and enumerate
![]() $S=\{s_i:\ i\in \omega \}$
in such a way that
$S=\{s_i:\ i\in \omega \}$
in such a way that
![]() $s_i<s_j$
whenever
$s_i<s_j$
whenever
![]() $i<j$
. Observe that
$i<j$
. Observe that
![]() $E\cap ((r_{s_i}-\frac {1}{2^{s_i}},r_{s_i}+\frac {1}{2^{s_i}})\setminus \bigcup _{j>i}(r_{s_{j}}-\frac {1}{2^{s_{j}}},r_{s_{j}}+\frac {1}{2^{s_{j}}}))$
is infinite for some
$E\cap ((r_{s_i}-\frac {1}{2^{s_i}},r_{s_i}+\frac {1}{2^{s_i}})\setminus \bigcup _{j>i}(r_{s_{j}}-\frac {1}{2^{s_{j}}},r_{s_{j}}+\frac {1}{2^{s_{j}}}))$
is infinite for some
![]() $i\in \omega $
as otherwise E would converge to x, so
$i\in \omega $
as otherwise E would converge to x, so
![]() $E\in \mathrm {nwd}$
.
$E\in \mathrm {nwd}$
.
We claim that for every finite set
![]() $L\subseteq \mathbb {Q}\cap [0,1]$
we have
$L\subseteq \mathbb {Q}\cap [0,1]$
we have
 $$ \begin{align*} E\setminus L &= \rho_1(E\setminus L)\not\subseteq f[\rho_2(A_\alpha\setminus(s_i+1))] \\&=f\left[F\setminus\bigcup_{j\leq i}(f^{-1}[(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}})]\cap I_{s_j})\right]. \end{align*} $$
$$ \begin{align*} E\setminus L &= \rho_1(E\setminus L)\not\subseteq f[\rho_2(A_\alpha\setminus(s_i+1))] \\&=f\left[F\setminus\bigcup_{j\leq i}(f^{-1}[(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}})]\cap I_{s_j})\right]. \end{align*} $$
Let
![]() $L\subseteq \mathbb {Q}\cap [0,1]$
be a finite set. We will show that
$L\subseteq \mathbb {Q}\cap [0,1]$
be a finite set. We will show that
![]() $E\setminus L\not \subseteq f[F\setminus \bigcup _{j\leq i}(f^{-1}[(r_{s_j}-\frac {1}{2^{s_j}},r_{s_j}+\frac {1}{2^{s_j}})]$
. Suppose that
$E\setminus L\not \subseteq f[F\setminus \bigcup _{j\leq i}(f^{-1}[(r_{s_j}-\frac {1}{2^{s_j}},r_{s_j}+\frac {1}{2^{s_j}})]$
. Suppose that
![]() $E\setminus L\subseteq f[F\setminus \bigcup _{j\leq i}(f^{-1}[(r_{s_j}-\frac {1}{2^{s_j}},r_{s_j}+\frac {1}{2^{s_j}})]$
. Let
$E\setminus L\subseteq f[F\setminus \bigcup _{j\leq i}(f^{-1}[(r_{s_j}-\frac {1}{2^{s_j}},r_{s_j}+\frac {1}{2^{s_j}})]$
. Let
 $$ \begin{align*}x\in E\cap\left(\left(r_{s_i}-\frac{1}{2^{s_i}},r_{s_i}+\frac{1}{2^{s_i}}\right)\setminus \bigcup_{j>i}\left(r_{s_{j}}-\frac{1}{2^{s_{j}}},r_{s_{j}}+\frac{1}{2^{s_{j}}}\right)\right)\setminus L\subseteq E\setminus L.\end{align*} $$
$$ \begin{align*}x\in E\cap\left(\left(r_{s_i}-\frac{1}{2^{s_i}},r_{s_i}+\frac{1}{2^{s_i}}\right)\setminus \bigcup_{j>i}\left(r_{s_{j}}-\frac{1}{2^{s_{j}}},r_{s_{j}}+\frac{1}{2^{s_{j}}}\right)\right)\setminus L\subseteq E\setminus L.\end{align*} $$
Then
 $$ \begin{align*} x &\in f\left[F\setminus\bigcup_{j\leq i}\left(f^{-1}\left[\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right)\right]\cap I_{s_j}\right)\right] \\&=f\left[\bigcup_{j> i}\left(f^{-1}\left[\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right)\right]\cap I_{s_j}\right)\right] \\&\subseteq f\left[\bigcup_{j> i}\left(f^{-1}\left[\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right)\right]\right)\right] \\&=f\left[f^{-1}\left[\bigcup_{j> i}\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right)\right]\right] \\&\subseteq \bigcup_{j> i}\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right). \end{align*} $$
$$ \begin{align*} x &\in f\left[F\setminus\bigcup_{j\leq i}\left(f^{-1}\left[\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right)\right]\cap I_{s_j}\right)\right] \\&=f\left[\bigcup_{j> i}\left(f^{-1}\left[\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right)\right]\cap I_{s_j}\right)\right] \\&\subseteq f\left[\bigcup_{j> i}\left(f^{-1}\left[\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right)\right]\right)\right] \\&=f\left[f^{-1}\left[\bigcup_{j> i}\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right)\right]\right] \\&\subseteq \bigcup_{j> i}\left(r_{s_j}-\frac{1}{2^{s_j}},r_{s_j}+\frac{1}{2^{s_j}}\right). \end{align*} $$
A contradiction.
Part 4. Characterizations
In the final part we want to characterize when
![]() $\operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2) \neq \emptyset $
in the cases of
$\operatorname {\mathrm {FinBW}}(\rho _1) \setminus \operatorname {\mathrm {FinBW}}(\rho _2) \neq \emptyset $
in the cases of
![]() $\rho _1\in \{FS, r, \Delta \}\cup \{\rho _{\mathcal {I}}:\mathcal {I}\text { is an ideal}\}$
. In the realm of partition regular functions that are
$\rho _1\in \{FS, r, \Delta \}\cup \{\rho _{\mathcal {I}}:\mathcal {I}\text { is an ideal}\}$
. In the realm of partition regular functions that are
![]() $P^-$
and have small accretions we were able to obtain a full characterization (Theorem 16.1(1)) using Theorem 15.2. If
$P^-$
and have small accretions we were able to obtain a full characterization (Theorem 16.1(1)) using Theorem 15.2. If
![]() $\rho _1=\rho _{\mathcal {I}}$
for some
$\rho _1=\rho _{\mathcal {I}}$
for some
![]() $P^-$
ideal
$P^-$
ideal
![]() $\mathcal {I}$
, then Theorem 14.3 gives us a complete characterization (Theorem 16.1(2b)) and this problem for
$\mathcal {I}$
, then Theorem 14.3 gives us a complete characterization (Theorem 16.1(2b)) and this problem for
![]() $\rho _1=\rho _{\mathcal {I}}$
in the case of non-
$\rho _1=\rho _{\mathcal {I}}$
in the case of non-
![]() $P^-$
ideals
$P^-$
ideals
![]() $\mathcal {I}$
is rather complicated (see [Reference Kwela62] and Example 16.3). However, for instance, in the case of
$\mathcal {I}$
is rather complicated (see [Reference Kwela62] and Example 16.3). However, for instance, in the case of
![]() $\rho _1=FS$
and
$\rho _1=FS$
and
![]() $\rho _2$
not being
$\rho _2$
not being
![]() $P^-$
, we needed another construction—we were able to obtain a characterization (Theorem 17.2), but only in the realm of spaces with unique limits of sequences (which are not necessarily Hausdorff).
$P^-$
, we needed another construction—we were able to obtain a characterization (Theorem 17.2), but only in the realm of spaces with unique limits of sequences (which are not necessarily Hausdorff).
16 Characterizations of distinguishness between FinBW classes via Katětov order
Theorem 16.1 (Assume CH).
Let
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
be partition regular functions. Let
$\rho _2$
be partition regular functions. Let
![]() $\mathcal {I}_1$
be an ideal.
$\mathcal {I}_1$
be an ideal.
-
(1) If
 $\rho _1$
is
$\rho _1$
is
 $P^-$
and
$P^-$
and
 $\rho _2$
is
$\rho _2$
is
 $P^-$
with small accretions, then
$P^-$
with small accretions, then  $$ \begin{align*} \rho_2 \not\leq_K \rho_1 \iff \operatorname{\mathrm{FinBW}}(\rho_1) \setminus \operatorname{\mathrm{FinBW}}(\rho_2) \neq\emptyset.\end{align*} $$
$$ \begin{align*} \rho_2 \not\leq_K \rho_1 \iff \operatorname{\mathrm{FinBW}}(\rho_1) \setminus \operatorname{\mathrm{FinBW}}(\rho_2) \neq\emptyset.\end{align*} $$
-
(2)
-
(a) If
 $\rho _1$
is
$\rho _1$
is
 $P^-$
and
$P^-$
and
 $\rho _2$
is
$\rho _2$
is
 $P^+$
, then
$P^+$
, then  $$ \begin{align*} \mathcal{I}_{\rho_2}\not\leq_K \mathcal{I}_{\rho_1} \iff \operatorname{\mathrm{FinBW}}(\rho_1) \setminus \operatorname{\mathrm{FinBW}}(\rho_2) \neq\emptyset.\end{align*} $$
$$ \begin{align*} \mathcal{I}_{\rho_2}\not\leq_K \mathcal{I}_{\rho_1} \iff \operatorname{\mathrm{FinBW}}(\rho_1) \setminus \operatorname{\mathrm{FinBW}}(\rho_2) \neq\emptyset.\end{align*} $$
-
(b) If
 $\mathcal {I}_1$
is
$\mathcal {I}_1$
is
 $P^-$
, then
$P^-$
, then  $$ \begin{align*} \mathcal{I}_{\rho_2}\not\leq_K \mathcal{I}_1 \iff \operatorname{\mathrm{FinBW}}(\mathcal{I}_1) \setminus \operatorname{\mathrm{FinBW}}(\rho_2) \neq\emptyset.\end{align*} $$
$$ \begin{align*} \mathcal{I}_{\rho_2}\not\leq_K \mathcal{I}_1 \iff \operatorname{\mathrm{FinBW}}(\mathcal{I}_1) \setminus \operatorname{\mathrm{FinBW}}(\rho_2) \neq\emptyset.\end{align*} $$
-
Moreover, in every item an example showing that the above difference between
![]() $\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
$\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
![]() $\Phi (\mathcal {A})$
with
$\Phi (\mathcal {A})$
with
![]() $\mathcal {A}$
being almost disjoint and of cardinality
$\mathcal {A}$
being almost disjoint and of cardinality
![]() $\mathfrak {c}$
(in particular, these examples are Hausdorff, compact, separable, and of cardinality
$\mathfrak {c}$
(in particular, these examples are Hausdorff, compact, separable, and of cardinality
![]() $\mathfrak {c})$
.
$\mathfrak {c})$
.
Proof (1) The implication “
![]() $\implies $
” follows from Theorem 15.2, whereas the implication “
$\implies $
” follows from Theorem 15.2, whereas the implication “
![]() $\impliedby $
” follows from Theorem 11.1(1).
$\impliedby $
” follows from Theorem 11.1(1).
(2a) The implication “
![]() $\implies $
” follows from Theorem 14.3, whereas the implication “
$\implies $
” follows from Theorem 14.3, whereas the implication “
![]() $\impliedby $
” follows from Theorem 11.1(2a).
$\impliedby $
” follows from Theorem 11.1(2a).
(2b) It follows from Theorems 14.3, 11.1(2b), and 10.2(4) and Proposition 6.5(2).
Next two examples show that in Theorem 16.1 we cannot drop the assumption that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
and obtain a characterization in the realm of Hausdorff spaces.
$P^-$
and obtain a characterization in the realm of Hausdorff spaces.
Example 16.2. There exist partition regular functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
with small accretions such that:
$\rho _2$
with small accretions such that:
-
(1)
 $\rho _1$
is not
$\rho _1$
is not
 $P^-$
and
$P^-$
and
 $\rho _2$
is
$\rho _2$
is
 $P^+$
,
$P^+$
, -
(2)
 $\rho _{2}\not \leq _K\rho _{1}$
,
$\rho _{2}\not \leq _K\rho _{1}$
, -
(3) there is no Hausdorff space in
 $\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
.
$\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
.
Proof Let
![]() $\rho _1=\rho _{\mathcal {H}}$
and
$\rho _1=\rho _{\mathcal {H}}$
and
![]() $\rho _2=\rho _{\mathcal {I}_{1/n}}$
. Then
$\rho _2=\rho _{\mathcal {I}_{1/n}}$
. Then
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
have small accretions (by Proposition 4.3). By Theorem 6.7,
$\rho _2$
have small accretions (by Proposition 4.3). By Theorem 6.7,
![]() $\mathcal {I}_{1/n}$
is
$\mathcal {I}_{1/n}$
is
![]() $P^+$
and
$P^+$
and
![]() $\mathcal {H}$
is not
$\mathcal {H}$
is not
![]() $P^-(\omega )$
(hence, not
$P^-(\omega )$
(hence, not
![]() $P^-$
). Applying Proposition 6.5(2), we see that
$P^-$
). Applying Proposition 6.5(2), we see that
![]() $\rho _1$
is not
$\rho _1$
is not
![]() $P^-$
and
$P^-$
and
![]() $\rho _2$
is
$\rho _2$
is
![]() $P^+$
. By Theorem 7.7(8),
$P^+$
. By Theorem 7.7(8),
![]() $\mathcal {I}_2\not \leq _K\mathcal {I}_1$
, so
$\mathcal {I}_2\not \leq _K\mathcal {I}_1$
, so
![]() $\rho _{2}\not \leq _K\rho _{1}$
(by Proposition 7.5(2b)).
$\rho _{2}\not \leq _K\rho _{1}$
(by Proposition 7.5(2b)).
By Theorem 10.5(3),
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {H})$
contains only finite Hausdorff spaces. On the other hand,
$\operatorname {\mathrm {FinBW}}(\mathcal {H})$
contains only finite Hausdorff spaces. On the other hand,
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I}_2)$
contains all finite spaces (Theorem 10.5(1)), so there is no Hausdorff space
$\operatorname {\mathrm {FinBW}}(\mathcal {I}_2)$
contains all finite spaces (Theorem 10.5(1)), so there is no Hausdorff space
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {H})\setminus \operatorname {\mathrm {FinBW}}(\mathcal {I}_{1/n})$
. Applying Proposition 10.2(4), we obtain that there is no Hausdorff space in
$\operatorname {\mathrm {FinBW}}(\mathcal {H})\setminus \operatorname {\mathrm {FinBW}}(\mathcal {I}_{1/n})$
. Applying Proposition 10.2(4), we obtain that there is no Hausdorff space in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
.
$\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
.
The above example may not be satisfactory as all Hausdorff spaces from
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)$
are finite. The next example is more sophisticated.
$\operatorname {\mathrm {FinBW}}(\rho _1)$
are finite. The next example is more sophisticated.
Example 16.3. There exist partition regular functions
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
with small accretions such that:
$\rho _2$
with small accretions such that:
-
(1)
 $\rho _1$
is not
$\rho _1$
is not
 $P^-$
and
$P^-$
and
 $\rho _2$
is
$\rho _2$
is
 $P^-$
,
$P^-$
, -
(2) assuming CH, there is a Hausdorff, compact, separable space of cardinality
 $\mathfrak {c}$
in
$\mathfrak {c}$
in
 $\operatorname {\mathrm {FinBW}}(\rho _1)$
,
$\operatorname {\mathrm {FinBW}}(\rho _1)$
, -
(3)
 $\rho _{2}\not \leq _K\rho _{1}$
,
$\rho _{2}\not \leq _K\rho _{1}$
, -
(4) there is no Hausdorff space in
 $\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
.
$\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
.
Proof Let
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
be the ideals from [Reference Kwela62, Example 8.9] and define
$\mathcal {J}$
be the ideals from [Reference Kwela62, Example 8.9] and define
![]() $\rho _1=\rho _{\mathcal {I}}$
and
$\rho _1=\rho _{\mathcal {I}}$
and
![]() $\rho _2=\rho _{\mathcal {J}}$
. Then
$\rho _2=\rho _{\mathcal {J}}$
. Then
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
have small accretions (by Proposition 4.3) and
$\rho _2$
have small accretions (by Proposition 4.3) and
![]() $\mathcal {J}\not \leq _K\mathcal {I}$
, so
$\mathcal {J}\not \leq _K\mathcal {I}$
, so
![]() $\rho _{2}\not \leq _K\rho _{1}$
(by Proposition 7.5(2b)). By [Reference Kwela62, Example 10.6] and Proposition 10.2(4), there is no Hausdorff space in
$\rho _{2}\not \leq _K\rho _{1}$
(by Proposition 7.5(2b)). By [Reference Kwela62, Example 10.6] and Proposition 10.2(4), there is no Hausdorff space in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
. Applying [Reference Kwela62, Theorem 6.6] and Proposition 10.2(4) we see that, assuming CH, there is a Hausdorff, compact, separable space of cardinality
$\operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2)$
. Applying [Reference Kwela62, Theorem 6.6] and Proposition 10.2(4) we see that, assuming CH, there is a Hausdorff, compact, separable space of cardinality
![]() $\mathfrak {c}$
in
$\mathfrak {c}$
in
![]() $\operatorname {\mathrm {FinBW}}(\rho _1)$
. Since
$\operatorname {\mathrm {FinBW}}(\rho _1)$
. Since
![]() $\mathcal {J}$
is
$\mathcal {J}$
is
![]() $P^-$
,
$P^-$
,
![]() $\rho _2$
is
$\rho _2$
is
![]() $P^-$
(by Proposition 6.5(2)) and
$P^-$
(by Proposition 6.5(2)) and
![]() $\rho _1$
cannot be
$\rho _1$
cannot be
![]() $P^-$
as it would contradict Theorem 16.1(1).
$P^-$
as it would contradict Theorem 16.1(1).
Question 16.4. Can we drop the assumption that
![]() $\rho _2$
is
$\rho _2$
is
![]() $P^-$
in Theorem 16.1 and obtain the characterization in the realm of Hausdorff spaces?
$P^-$
in Theorem 16.1 and obtain the characterization in the realm of Hausdorff spaces?
In Theorem 17.2, we show that we can drop the assumption that
![]() $\rho _2$
is
$\rho _2$
is
![]() $P^-$
in Theorem 16.1(1) and obtain a characterization in the realm of non-Hausdorff spaces with unique limits of sequences, but at the cost of requiring that
$P^-$
in Theorem 16.1(1) and obtain a characterization in the realm of non-Hausdorff spaces with unique limits of sequences, but at the cost of requiring that
![]() $\rho _1$
is weak
$\rho _1$
is weak
![]() $P^+$
instead of
$P^+$
instead of
![]() $P^-$
.
$P^-$
.
Now we present some applications of Theorem 16.1.
Corollary 16.5 [Reference Kwela62, Theorem 10.4].
Assume CH. Let
![]() $\mathcal {I}_1$
and
$\mathcal {I}_1$
and
![]() $\mathcal {I}_2$
be ideals. If
$\mathcal {I}_2$
be ideals. If
![]() $\mathcal {I}_1$
is
$\mathcal {I}_1$
is
![]() $P^-$
, then the following are equivalent
$P^-$
, then the following are equivalent
![]() $:$
$:$
-
(1)
 $\mathcal {I}_{2}\not \leq _K \mathcal {I}_{1}$
.
$\mathcal {I}_{2}\not \leq _K \mathcal {I}_{1}$
. -
(2)
 $\operatorname {\mathrm {FinBW}}(\mathcal {I}_1) \setminus \operatorname {\mathrm {FinBW}}(\mathcal {I}_2)\neq \emptyset $
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I}_1) \setminus \operatorname {\mathrm {FinBW}}(\mathcal {I}_2)\neq \emptyset $
.
Moreover, an example showing that the above difference between
![]() $\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
$\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
![]() $\Phi (\mathcal {A})$
with
$\Phi (\mathcal {A})$
with
![]() $\mathcal {A}$
being almost disjoint and of cardinality
$\mathcal {A}$
being almost disjoint and of cardinality
![]() $\mathfrak {c}$
(in particular, these examples are Hausdorff, compact, separable, and of cardinality
$\mathfrak {c}$
(in particular, these examples are Hausdorff, compact, separable, and of cardinality
![]() $\mathfrak {c})$
.
$\mathfrak {c})$
.
Question 16.6. Is every
![]() $\mathcal {I}_{1/n}$
-space (Hindman space, Ramsey space) a van der Waerden space?
$\mathcal {I}_{1/n}$
-space (Hindman space, Ramsey space) a van der Waerden space?
Note that under CH Theorem 16.1 reduces the above question to Question 7.8.
Corollary 16.7 (Assume CH).
Let
![]() $\mathcal {I}$
be an ideal.
$\mathcal {I}$
be an ideal.
-
(1) If
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^-$
, then the following conditions are equivalent
$P^-$
, then the following conditions are equivalent
 $:$
$:$
-
(a)
 $\rho _{\mathcal {I}}\not \leq _K\operatorname {\mathrm {FS}}\ (\rho _{\mathcal {I}}\not \leq _K r, \rho _{\mathcal {I}}\not \leq _K\Delta ,\ resp.)$
.
$\rho _{\mathcal {I}}\not \leq _K\operatorname {\mathrm {FS}}\ (\rho _{\mathcal {I}}\not \leq _K r, \rho _{\mathcal {I}}\not \leq _K\Delta ,\ resp.)$
. -
(b) There exists a Hindman
 $($
Ramsey, differentially compact, resp.
$($
Ramsey, differentially compact, resp.
 $)$
space that is not in
$)$
space that is not in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
Moreover, if
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^+$
then the above are equivalent to
$P^+$
then the above are equivalent to
 $\mathcal {I}\not \leq _K\mathcal {H}$
.
$\mathcal {I}\not \leq _K\mathcal {H}$
. -
-
(2) If
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $P^-$
, then the following conditions are equivalent
$P^-$
, then the following conditions are equivalent
 $:$
$:$
-
(a)
 $\mathcal {H}\not \leq _K\mathcal {I}\ (\mathcal {R}\not \leq _K\mathcal {I}, \mathcal {D}\not \leq _K\mathcal {I},\ resp.)$
.
$\mathcal {H}\not \leq _K\mathcal {I}\ (\mathcal {R}\not \leq _K\mathcal {I}, \mathcal {D}\not \leq _K\mathcal {I},\ resp.)$
. -
(b)
 $\operatorname {\mathrm {FS}}\not \leq _K\rho _{\mathcal {I}}\ (r\not \leq _K\rho _{\mathcal {I}}, \Delta \not \leq _K\rho _{\mathcal {I}},\ resp.)$
.
$\operatorname {\mathrm {FS}}\not \leq _K\rho _{\mathcal {I}}\ (r\not \leq _K\rho _{\mathcal {I}}, \Delta \not \leq _K\rho _{\mathcal {I}},\ resp.)$
. -
(c) There exists a space in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not a Hindman
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not a Hindman
 $($
Ramsey, differentially compact, resp.
$($
Ramsey, differentially compact, resp.
 $)$
space.
$)$
space.
Moreover, in every item an example showing that the above difference between
 $\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
$\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
 $\Phi (\mathcal {A})$
with
$\Phi (\mathcal {A})$
with
 $\mathcal {A}$
being almost disjoint and of cardinality
$\mathcal {A}$
being almost disjoint and of cardinality
 $\mathfrak {c}$
(in particular, these examples are Hausdorff, compact, separable and of cardinality
$\mathfrak {c}$
(in particular, these examples are Hausdorff, compact, separable and of cardinality
 $\mathfrak {c})$
.
$\mathfrak {c})$
. -
Proof It follows from Theorem 16.1(1) and Propositions 4.3, 6.5(2), 6.7(3), 7.5(2a) and (2b), and 10.2(4).
Remark. In [Reference Filipów, Kowitz, Kwela and Tryba24, Corollary 2.8], the authors obtained Corollary 16.7(1) in the case of Hindman spaces and
![]() $P^+$
ideals but in the realm of non-Hausdorff spaces.
$P^+$
ideals but in the realm of non-Hausdorff spaces.
Corollary 16.8 (Assume CH).
Let
![]() $\mathcal {I}$
be an ideal.
$\mathcal {I}$
be an ideal.
-
(1) The following conditions are equivalent
 $:$
$:$
-
(a)
 $\mathcal {I}\not \leq _K\mathcal {W}\ (\mathcal {I}\not \leq _K\mathcal {I}_{1/n},\ resp.)$
.
$\mathcal {I}\not \leq _K\mathcal {W}\ (\mathcal {I}\not \leq _K\mathcal {I}_{1/n},\ resp.)$
. -
(b)
 $\rho _{\mathcal {I}}\not \leq _K\rho _{\mathcal {W}}\ (\rho _{\mathcal {I}}\not \leq _K\rho _{\mathcal {I}_{1/n}},\ resp.)$
.
$\rho _{\mathcal {I}}\not \leq _K\rho _{\mathcal {W}}\ (\rho _{\mathcal {I}}\not \leq _K\rho _{\mathcal {I}_{1/n}},\ resp.)$
. -
(c) There exists a van der Waerden space
 $(\mathcal {I}_{1/n}{-}space)$
that is not in
$(\mathcal {I}_{1/n}{-}space)$
that is not in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
-
-
(2) If
 $\mathcal {I}$
is a
$\mathcal {I}$
is a
 $P^-$
ideal, then the following conditions are equivalent:
$P^-$
ideal, then the following conditions are equivalent:-
(1)
 $\mathcal {W}\not \leq _K\mathcal {I}\ (\mathcal {I}_{1/n}\not \leq _K\mathcal {I},\ resp.)$
.
$\mathcal {W}\not \leq _K\mathcal {I}\ (\mathcal {I}_{1/n}\not \leq _K\mathcal {I},\ resp.)$
. -
(2)
 $\rho _{\mathcal {W}}\not \leq _K\rho _{\mathcal {I}}\ (\rho _{\mathcal {I}_{1/n}}\not \leq _K\rho _{\mathcal {I}},\ resp.)$
.
$\rho _{\mathcal {W}}\not \leq _K\rho _{\mathcal {I}}\ (\rho _{\mathcal {I}_{1/n}}\not \leq _K\rho _{\mathcal {I}},\ resp.)$
. -
(3) There exists a space in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not a van der Waerden space
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not a van der Waerden space
 $(\mathcal {I}_{1/n}{-}space)$
.
$(\mathcal {I}_{1/n}{-}space)$
.
-
Moreover, in every item an example showing that the above difference between
![]() $\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
$\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
![]() $\Phi (\mathcal {A})$
with
$\Phi (\mathcal {A})$
with
![]() $\mathcal {A}$
being almost disjoint and of cardinality
$\mathcal {A}$
being almost disjoint and of cardinality
![]() $\mathfrak {c}$
(in particular, these examples are Hausdorff, compact, separable, and of cardinality
$\mathfrak {c}$
(in particular, these examples are Hausdorff, compact, separable, and of cardinality
![]() $\mathfrak {c})$
.
$\mathfrak {c})$
.
17 Non-Hausdorff world
Proposition 17.1. The following conditions are equivalent for every topological space X.
-
(1) X has unique limits of sequences.
-
(2)
 $\rho $
-limits of sequences in X are unique for every
$\rho $
-limits of sequences in X are unique for every
 $\rho $
.
$\rho $
.
Proof Since
![]() $\rho _{\mathrm {Fin}}$
-convergence is convergence, (2)
$\rho _{\mathrm {Fin}}$
-convergence is convergence, (2)
![]() $\implies $
(1) is obvious.
$\implies $
(1) is obvious.
(1)
![]() $\implies $
(2): We will show that the negation of (2) implies the negation of (1). Suppose that there are partition regular
$\implies $
(2): We will show that the negation of (2) implies the negation of (1). Suppose that there are partition regular
![]() $\rho :\mathcal {F}\to [\Lambda ]^\omega $
with
$\rho :\mathcal {F}\to [\Lambda ]^\omega $
with
![]() $\mathcal {F}\subseteq [\Omega ]^\omega $
,
$\mathcal {F}\subseteq [\Omega ]^\omega $
,
![]() $F\in \mathcal {F}$
, and
$F\in \mathcal {F}$
, and
![]() $\{x_n: n\in \rho (F)\}\subseteq X$
which
$\{x_n: n\in \rho (F)\}\subseteq X$
which
![]() $\rho $
-converges to x and to y, for some
$\rho $
-converges to x and to y, for some
![]() $x,y\in X$
,
$x,y\in X$
,
![]() $x\neq y$
. Let
$x\neq y$
. Let
![]() $\{K_n: n\in \omega \}\subseteq [\Omega ]^{<\omega }$
be nondecreasing and such that
$\{K_n: n\in \omega \}\subseteq [\Omega ]^{<\omega }$
be nondecreasing and such that
![]() $\bigcup _{n\in \omega } K_n=\Omega $
. For each
$\bigcup _{n\in \omega } K_n=\Omega $
. For each
![]() $n\in \omega $
inductively find any
$n\in \omega $
inductively find any
![]() $m_n\in \rho (F\setminus K_n)\setminus \{m_i:\ i<n\}$
(this is possible as
$m_n\in \rho (F\setminus K_n)\setminus \{m_i:\ i<n\}$
(this is possible as
![]() $\rho (F\setminus K_n)$
is infinite). Observe that the sequence
$\rho (F\setminus K_n)$
is infinite). Observe that the sequence
![]() $(x_{m_n})_{n\in \omega }$
is convergent to x and to y.
$(x_{m_n})_{n\in \omega }$
is convergent to x and to y.
The main result of this section is as follows.
Theorem 17.2 (Assume CH).
Let
![]() $\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular for each
$\rho _i:\mathcal {F}_i\to [\Lambda _i]^\omega $
be partition regular for each
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $\rho _1$
is weak
$\rho _1$
is weak
![]() $P^+$
and has small accretions, then the following conditions are equivalent.
$P^+$
and has small accretions, then the following conditions are equivalent.
-
(1)
 $\rho _2\not \leq _K\rho _1$
.
$\rho _2\not \leq _K\rho _1$
. -
(2) There exists a separable space X with unique limits of sequences such that
 $X\in \operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
$X\in \operatorname {\mathrm {FinBW}}(\rho _1)\setminus \operatorname {\mathrm {FinBW}}(\rho _2).$
Proof
![]() $(2)\implies (1)$
. It follows from Theorem 11.1(1).
$(2)\implies (1)$
. It follows from Theorem 11.1(1).
![]() $(1)\implies (2)$
. Fix a list
$(1)\implies (2)$
. Fix a list
![]() $\{f_\alpha :\alpha <\mathfrak {c}\}$
of all
$\{f_\alpha :\alpha <\mathfrak {c}\}$
of all
![]() $\mathcal {I}_{\rho _1}$
-to-one functions
$\mathcal {I}_{\rho _1}$
-to-one functions
![]() $f:\Lambda _1\to \Lambda _2$
.
$f:\Lambda _1\to \Lambda _2$
.
We will construct a sequence
![]() $\{D_\alpha : \alpha <\mathfrak {c}\}\subseteq \mathcal {F}_1$
such that for every
$\{D_\alpha : \alpha <\mathfrak {c}\}\subseteq \mathcal {F}_1$
such that for every
![]() $\alpha <\mathfrak {c}$
we have
$\alpha <\mathfrak {c}$
we have
and one of the following conditions holds:
or
 $$ \begin{align} \exists \beta<\alpha \, \forall K\in[\Omega_1]^{<\omega} \, \forall M\in[\Lambda_2]^{<\omega} \, &\exists L\in[\Omega_1]^{<\omega} \\& \, \nonumber (f_\alpha[\rho_1(D_\alpha\setminus L) ]\subseteq f_\beta[\rho_1(D_\beta\setminus K)]\setminus M). \end{align} $$
$$ \begin{align} \exists \beta<\alpha \, \forall K\in[\Omega_1]^{<\omega} \, \forall M\in[\Lambda_2]^{<\omega} \, &\exists L\in[\Omega_1]^{<\omega} \\& \, \nonumber (f_\alpha[\rho_1(D_\alpha\setminus L) ]\subseteq f_\beta[\rho_1(D_\beta\setminus K)]\setminus M). \end{align} $$
Suppose that
![]() $\alpha <\mathfrak {c}$
and that
$\alpha <\mathfrak {c}$
and that
![]() $D_\beta $
have been chosen for all
$D_\beta $
have been chosen for all
![]() $\beta <\alpha $
. Since
$\beta <\alpha $
. Since
![]() $\rho _2\not \leq _K\rho _1$
, there is
$\rho _2\not \leq _K\rho _1$
, there is
![]() $D^0\in \mathcal {F}_1$
such that
$D^0\in \mathcal {F}_1$
such that
Since
![]() $\rho _1$
has small accretions, there is
$\rho _1$
has small accretions, there is
![]() $D^1\in \mathcal {F}_1$
,
$D^1\in \mathcal {F}_1$
,
![]() $D^1\subseteq D^0$
, such that for every
$D^1\subseteq D^0$
, such that for every
![]() $K\in [\Omega _1]^{<\omega }$
we have
$K\in [\Omega _1]^{<\omega }$
we have
![]() $\rho _1(D^1)\setminus \rho _1(D^1\setminus K)\in \mathcal {I}_{\rho _1}$
. Observe that
$\rho _1(D^1)\setminus \rho _1(D^1\setminus K)\in \mathcal {I}_{\rho _1}$
. Observe that
![]() $D^1$
also has the property (A1) as
$D^1$
also has the property (A1) as
![]() $f_\alpha [\rho _1(D^0\setminus K)]\supseteq f_\alpha [\rho _1(D^1\setminus K)]$
for every
$f_\alpha [\rho _1(D^0\setminus K)]\supseteq f_\alpha [\rho _1(D^1\setminus K)]$
for every
![]() $K\in [\Omega _1]^{<\omega }$
.
$K\in [\Omega _1]^{<\omega }$
.
Since
![]() $\rho _1$
is weak
$\rho _1$
is weak
![]() $P^+$
, there is
$P^+$
, there is
![]() $D\in \mathcal {F}_1$
such that
$D\in \mathcal {F}_1$
such that
![]() $\rho _1(D)\subseteq \rho _1(D^1)$
and satisfying property:
$\rho _1(D)\subseteq \rho _1(D^1)$
and satisfying property:
 $$ \begin{align} &\forall \{F_n: n\in \omega\}\subseteq\mathcal{F}_1 \, (\forall n\in\omega \, (\rho_1(F_{n+1})\subseteq\rho_1(F_n)\subseteq\rho_1(D) ) \\ \nonumber & \implies \exists E'\in\mathcal{F}_1 \, \forall n\in\omega \, \exists K\in[\Omega_1]^{<\omega} \, (\rho_1(E'\setminus K)\subseteq\rho_1(F_n)). \end{align} $$
$$ \begin{align} &\forall \{F_n: n\in \omega\}\subseteq\mathcal{F}_1 \, (\forall n\in\omega \, (\rho_1(F_{n+1})\subseteq\rho_1(F_n)\subseteq\rho_1(D) ) \\ \nonumber & \implies \exists E'\in\mathcal{F}_1 \, \forall n\in\omega \, \exists K\in[\Omega_1]^{<\omega} \, (\rho_1(E'\setminus K)\subseteq\rho_1(F_n)). \end{align} $$
Now we have two cases:
 $$ \begin{align} & \forall D'\in\mathcal{F}_1\, \forall \beta<\alpha \, (\rho_1(D')\subseteq \rho_1(D) \\ \nonumber &\implies \exists K\in[\Omega_1]^{<\omega}\, ( \rho_1(D')\setminus f_\alpha^{-1}[ f_\beta[\rho_1(D_\beta\setminus K)]]\notin \mathcal{I}_{\rho_1}) \end{align} $$
$$ \begin{align} & \forall D'\in\mathcal{F}_1\, \forall \beta<\alpha \, (\rho_1(D')\subseteq \rho_1(D) \\ \nonumber &\implies \exists K\in[\Omega_1]^{<\omega}\, ( \rho_1(D')\setminus f_\alpha^{-1}[ f_\beta[\rho_1(D_\beta\setminus K)]]\notin \mathcal{I}_{\rho_1}) \end{align} $$
or
 $$ \begin{align} & \exists D'\in\mathcal{F}_1 \, \exists \beta<\alpha \, (\rho_1(D')\subseteq \rho_1(D) \\& \nonumber \land \forall K\in[\Omega_1]^{<\omega} \, ( \rho_1(D')\setminus f_\alpha^{-1}[f_\beta[\rho_1(D_\beta\setminus K)]]\in \mathcal{I}_{\rho_1}). \end{align} $$
$$ \begin{align} & \exists D'\in\mathcal{F}_1 \, \exists \beta<\alpha \, (\rho_1(D')\subseteq \rho_1(D) \\& \nonumber \land \forall K\in[\Omega_1]^{<\omega} \, ( \rho_1(D')\setminus f_\alpha^{-1}[f_\beta[\rho_1(D_\beta\setminus K)]]\in \mathcal{I}_{\rho_1}). \end{align} $$
In the first case, let
![]() $\{K_n:n\in \omega \}\subseteq [\Omega _1]^{<\omega }$
be such that
$\{K_n:n\in \omega \}\subseteq [\Omega _1]^{<\omega }$
be such that
![]() $\bigcup _{n\in \omega } K_n=\Omega _1$
and let
$\bigcup _{n\in \omega } K_n=\Omega _1$
and let
![]() $\alpha \times [\Lambda _2]^{<\omega } =\{(\beta _n,M_n): n\in \omega \}$
, taking into account that
$\alpha \times [\Lambda _2]^{<\omega } =\{(\beta _n,M_n): n\in \omega \}$
, taking into account that
![]() $\alpha $
is countable (as we assumed CH). Using condition (P1) repeatedly and the facts that
$\alpha $
is countable (as we assumed CH). Using condition (P1) repeatedly and the facts that
![]() $f_\alpha ^{-1}[\{\lambda \}]\in \mathcal {I}_{\rho _1}$
, for every
$f_\alpha ^{-1}[\{\lambda \}]\in \mathcal {I}_{\rho _1}$
, for every
![]() $\lambda \in \Lambda _2$
, and
$\lambda \in \Lambda _2$
, and
![]() $\rho _1(D^1)\setminus \rho _1(D^1\setminus K)\in \mathcal {I}_{\rho _1}$
, for all
$\rho _1(D^1)\setminus \rho _1(D^1\setminus K)\in \mathcal {I}_{\rho _1}$
, for all
![]() $K\in [\Omega _1]^{<\omega }$
, one can easily construct a sequence
$K\in [\Omega _1]^{<\omega }$
, one can easily construct a sequence
![]() $\{E_n: n\in \omega \}\subseteq \mathcal {F}_1$
such that
$\{E_n: n\in \omega \}\subseteq \mathcal {F}_1$
such that
-
(1)
 $\rho _1(E_0)\subseteq \rho _1(D)$
,
$\rho _1(E_0)\subseteq \rho _1(D)$
, -
(2)
 $\forall {n\in \omega }\, (\rho _1(E_{n+1})\subseteq \rho _1(E_{n}))$
,
$\forall {n\in \omega }\, (\rho _1(E_{n+1})\subseteq \rho _1(E_{n}))$
, -
(3)
 $\forall {n\in \omega } \, \exists {K\in [\Omega _1]^{<\omega }} \left (\rho _1(E_n) \cap f_\alpha ^{-1}[M_n\cup f_{\beta _n}[\rho _1(D_{\beta _n}\setminus K)]] = \emptyset \right )$
,
$\forall {n\in \omega } \, \exists {K\in [\Omega _1]^{<\omega }} \left (\rho _1(E_n) \cap f_\alpha ^{-1}[M_n\cup f_{\beta _n}[\rho _1(D_{\beta _n}\setminus K)]] = \emptyset \right )$
, -
(4)
 $\forall {n\in \omega } \, \rho _1(E_n)\cap \rho _1(D^1)\setminus \rho _1(D^1\setminus K_n)=\emptyset $
.
$\forall {n\in \omega } \, \rho _1(E_n)\cap \rho _1(D^1)\setminus \rho _1(D^1\setminus K_n)=\emptyset $
.
Now using property (A2) we find
![]() $E'\in \mathcal {F}_1$
such that
$E'\in \mathcal {F}_1$
such that
![]() $\rho _1(E')\subseteq \rho _1(D)\subseteq \rho _1(D^1)$
and for every
$\rho _1(E')\subseteq \rho _1(D)\subseteq \rho _1(D^1)$
and for every
![]() $n\in \omega $
there is
$n\in \omega $
there is
![]() $K\in [\Omega _1]^{<\omega }$
with
$K\in [\Omega _1]^{<\omega }$
with
![]() $\rho _1(E'\setminus K) \subseteq \rho _1(E_n)$
.
$\rho _1(E'\setminus K) \subseteq \rho _1(E_n)$
.
It is not difficult to see that
![]() $D_\alpha = E'$
satisfies (A1) and (W1), i.e., it is as needed.
$D_\alpha = E'$
satisfies (A1) and (W1), i.e., it is as needed.
Consider the second case. Let
![]() $D'\in \mathcal {F}_1$
and
$D'\in \mathcal {F}_1$
and
![]() $\beta <\alpha $
be such that
$\beta <\alpha $
be such that
![]() $\rho _1(D')\subseteq \rho _1(D)$
and
$\rho _1(D')\subseteq \rho _1(D)$
and
![]() $\rho _1(D')\setminus f_\alpha ^{-1}[f_\beta [\rho _1(D_\beta \setminus K)]]\in \mathcal {I}_{\rho _1}$
for each
$\rho _1(D')\setminus f_\alpha ^{-1}[f_\beta [\rho _1(D_\beta \setminus K)]]\in \mathcal {I}_{\rho _1}$
for each
![]() $K\in [\Omega _1]^{<\omega }$
. Since
$K\in [\Omega _1]^{<\omega }$
. Since
![]() $f_\alpha ^{-1}[\{\lambda \}]\in \mathcal {I}_{\rho _1}$
for every
$f_\alpha ^{-1}[\{\lambda \}]\in \mathcal {I}_{\rho _1}$
for every
![]() $\lambda \in \Lambda _2$
, we also have
$\lambda \in \Lambda _2$
, we also have
![]() $\rho _1(D')\setminus f_\alpha ^{-1}[f_\beta [\rho _1(D_\beta \setminus K)]\setminus M]\in \mathcal {I}_{\rho _1}$
for each
$\rho _1(D')\setminus f_\alpha ^{-1}[f_\beta [\rho _1(D_\beta \setminus K)]\setminus M]\in \mathcal {I}_{\rho _1}$
for each
![]() $K\in [\Omega _1]^{<\omega }$
and
$K\in [\Omega _1]^{<\omega }$
and
![]() $M\in [\Lambda _2]^{<\omega }$
. Recall also that
$M\in [\Lambda _2]^{<\omega }$
. Recall also that
![]() $\rho _1(D^1)\setminus \rho _1(D^1\setminus K)\in \mathcal {I}_{\rho _1}$
, for all
$\rho _1(D^1)\setminus \rho _1(D^1\setminus K)\in \mathcal {I}_{\rho _1}$
, for all
![]() $K\in [\Omega _1]^{<\omega }$
. Since
$K\in [\Omega _1]^{<\omega }$
. Since
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
(by Proposition 6.5(1), as
$P^-$
(by Proposition 6.5(1), as
![]() $\rho _1$
is weak
$\rho _1$
is weak
![]() $P^+$
), we find an infinite set
$P^+$
), we find an infinite set
![]() $D"\in \mathcal {F}_1$
such that:
$D"\in \mathcal {F}_1$
such that:
-
•
 $\rho _1(D")\subseteq \rho _1(D')$
,
$\rho _1(D")\subseteq \rho _1(D')$
, -
• for every
 $K\in [\Omega _1]^{<\omega }$
there is
$K\in [\Omega _1]^{<\omega }$
there is
 $L\in [\Omega _1]^{<\omega }$
with
$L\in [\Omega _1]^{<\omega }$
with
 $\rho _1(D"\setminus L)\subseteq \rho _1(D^1\setminus K)$
,
$\rho _1(D"\setminus L)\subseteq \rho _1(D^1\setminus K)$
, -
• for every
 $K\in [\Omega _1]^{<\omega }$
and
$K\in [\Omega _1]^{<\omega }$
and
 $M\in [\Lambda _2]^{<\omega }$
there is
$M\in [\Lambda _2]^{<\omega }$
there is
 $L\in [\Omega _1]^{<\omega }$
with
$L\in [\Omega _1]^{<\omega }$
with
 $\rho _1(D"\setminus L)\cap (\rho _1(D')\setminus f_\alpha ^{-1}[f_\beta [\rho _1(D_\beta \setminus K)]\setminus M]) = \emptyset $
.
$\rho _1(D"\setminus L)\cap (\rho _1(D')\setminus f_\alpha ^{-1}[f_\beta [\rho _1(D_\beta \setminus K)]\setminus M]) = \emptyset $
.
It is not difficult to see that
![]() $D_\alpha = D"$
satisfies (A1) and (W2).
$D_\alpha = D"$
satisfies (A1) and (W2).
The construction of sets
![]() $D_\alpha $
is finished.
$D_\alpha $
is finished.
We are ready to define the required space. Let
![]() $T=\{\alpha <\mathfrak {c}:D_\alpha\ \text {satisfies}\ (W1)\}$
and
$T=\{\alpha <\mathfrak {c}:D_\alpha\ \text {satisfies}\ (W1)\}$
and
For every
![]() $x\in X$
we define the family
$x\in X$
we define the family
![]() $\mathcal {B}(x)\subseteq \mathcal {P}(X)$
as follows:
$\mathcal {B}(x)\subseteq \mathcal {P}(X)$
as follows:
-
•
 $\mathcal {B}(\lambda )=\{\{\lambda \}\}$
for
$\mathcal {B}(\lambda )=\{\{\lambda \}\}$
for
 $\lambda \in \Lambda _2$
,
$\lambda \in \Lambda _2$
, -
•
 $\mathcal {B}(\rho _1(D_\alpha ))= \{\{\rho _1(D_\alpha )\}\cup f_\alpha [\rho _1(D_\alpha \setminus K)]\setminus M:K\in [\Omega _1]^{<\omega },M\in [\Lambda _2]^{<\omega }\}$
for
$\mathcal {B}(\rho _1(D_\alpha ))= \{\{\rho _1(D_\alpha )\}\cup f_\alpha [\rho _1(D_\alpha \setminus K)]\setminus M:K\in [\Omega _1]^{<\omega },M\in [\Lambda _2]^{<\omega }\}$
for
 $\alpha \in T$
,
$\alpha \in T$
, -
•
 $\mathcal {B}(\infty )\kern1.4pt{=}\kern1.4pt\{\{\infty \}\cup \bigcup _{\alpha \in T\setminus F}U_\alpha : F\kern1.4pt{\in}\kern1.4pt [T]^{<\omega } \kern1.4pt{\land}\kern1.4pt U_\alpha \kern1.4pt{\in}\kern1.4pt \mathcal {B}(\rho _1(D_\alpha )) \text { for } \alpha \kern1.4pt{\in}\kern1.4pt T\setminus F\}$
.
$\mathcal {B}(\infty )\kern1.4pt{=}\kern1.4pt\{\{\infty \}\cup \bigcup _{\alpha \in T\setminus F}U_\alpha : F\kern1.4pt{\in}\kern1.4pt [T]^{<\omega } \kern1.4pt{\land}\kern1.4pt U_\alpha \kern1.4pt{\in}\kern1.4pt \mathcal {B}(\rho _1(D_\alpha )) \text { for } \alpha \kern1.4pt{\in}\kern1.4pt T\setminus F\}$
.
It is not difficult to check that the family
![]() $\mathcal {N} = \{\mathcal {B}(x):x\in X\}$
is a neighborhood system (see, e.g., [Reference Engelking17, Proposition 1.2.3]). We claim that X with the topology generated by
$\mathcal {N} = \{\mathcal {B}(x):x\in X\}$
is a neighborhood system (see, e.g., [Reference Engelking17, Proposition 1.2.3]). We claim that X with the topology generated by
![]() $\mathcal {N}$
is a topological space that we are looking for.
$\mathcal {N}$
is a topological space that we are looking for.
First we will show that X has unique limits of sequences. It is not difficult to see that
![]() $X\setminus \{\infty \}$
is Hausdorff. Thus, it suffices to check that if
$X\setminus \{\infty \}$
is Hausdorff. Thus, it suffices to check that if
![]() $\{x_n: n\in \omega \}\subseteq X$
converges to
$\{x_n: n\in \omega \}\subseteq X$
converges to
![]() $\infty $
then it cannot converge to any other point in X. Indeed, if
$\infty $
then it cannot converge to any other point in X. Indeed, if
![]() $\{x_n: n\in \omega \}$
would converge to some
$\{x_n: n\in \omega \}$
would converge to some
![]() $\lambda \in \Lambda _2$
then it would have to be constant from some point on, so
$\lambda \in \Lambda _2$
then it would have to be constant from some point on, so
![]() $\{\infty \}\cup \bigcup _{\alpha \in T}(\{\rho _1(D_\alpha )\}\cup f_\alpha [\rho _1(D_\alpha )]\setminus \{\lambda \})$
would be an open neighborhood of
$\{\infty \}\cup \bigcup _{\alpha \in T}(\{\rho _1(D_\alpha )\}\cup f_\alpha [\rho _1(D_\alpha )]\setminus \{\lambda \})$
would be an open neighborhood of
![]() $\infty $
omitting almost all
$\infty $
omitting almost all
![]() $x_n$
’s. On the other hand, if
$x_n$
’s. On the other hand, if
![]() $(x_n)_{n\in \omega }$
would converge to some
$(x_n)_{n\in \omega }$
would converge to some
![]() $\rho _1(D_\alpha )$
for
$\rho _1(D_\alpha )$
for
![]() $\alpha \in T$
then using (W1) for each
$\alpha \in T$
then using (W1) for each
![]() $\beta \in T\setminus \{\alpha \}$
we could find
$\beta \in T\setminus \{\alpha \}$
we could find
![]() $K_\beta \in [\Omega ]^{<\omega }$
with
$K_\beta \in [\Omega ]^{<\omega }$
with
![]() $f_\alpha [\rho _1(D_\alpha \setminus K_\beta ) ]\cap f_\beta [\rho _1(D_\beta \setminus K_\beta )]=\emptyset $
. Then, denoting
$f_\alpha [\rho _1(D_\alpha \setminus K_\beta ) ]\cap f_\beta [\rho _1(D_\beta \setminus K_\beta )]=\emptyset $
. Then, denoting
![]() $M_\beta =\{x_n: n\in \omega \}\setminus f_\alpha [\rho _1(D_\alpha \setminus K_\beta ) ]$
(which is a finite set, as
$M_\beta =\{x_n: n\in \omega \}\setminus f_\alpha [\rho _1(D_\alpha \setminus K_\beta ) ]$
(which is a finite set, as
![]() $\{\rho _1(D_\alpha )\}\cup f_\alpha [\rho _1(D_\alpha \setminus K_\beta ) ]$
is an open neighborhood of
$\{\rho _1(D_\alpha )\}\cup f_\alpha [\rho _1(D_\alpha \setminus K_\beta ) ]$
is an open neighborhood of
![]() $\rho _1(D_\alpha )$
and
$\rho _1(D_\alpha )$
and
![]() $(x_n)_{n\in \omega }$
converges to
$(x_n)_{n\in \omega }$
converges to
![]() $\rho _1(D_\alpha )$
), the set
$\rho _1(D_\alpha )$
), the set
![]() $\{\infty \}\cup \bigcup _{\beta \in T\setminus \{\alpha \}}(\{\rho _1(D_\beta )\}\cup f_\beta [\rho _1(D_\beta \setminus K_\beta )]\setminus M_\beta )$
would be an open neighborhood of
$\{\infty \}\cup \bigcup _{\beta \in T\setminus \{\alpha \}}(\{\rho _1(D_\beta )\}\cup f_\beta [\rho _1(D_\beta \setminus K_\beta )]\setminus M_\beta )$
would be an open neighborhood of
![]() $\infty $
omitting all
$\infty $
omitting all
![]() $x_n$
’s. Hence, X has unique limits of sequences.
$x_n$
’s. Hence, X has unique limits of sequences.
Now we show that
![]() $X\in \operatorname {\mathrm {FinBW}}(\rho _1)$
. Fix any
$X\in \operatorname {\mathrm {FinBW}}(\rho _1)$
. Fix any
![]() $f:\Lambda _1\to X$
. If there is
$f:\Lambda _1\to X$
. If there is
![]() $x\in X$
with
$x\in X$
with
![]() $f^{-1}[\{x\}]\notin \mathcal {I}_{\rho _1}$
then find
$f^{-1}[\{x\}]\notin \mathcal {I}_{\rho _1}$
then find
![]() $F\in \mathcal {F}_1$
with
$F\in \mathcal {F}_1$
with
![]() $\rho _1(F)\subseteq f^{-1}[\{x\}]$
and observe that
$\rho _1(F)\subseteq f^{-1}[\{x\}]$
and observe that
![]() $(f(n))_{n\in \rho _1(F)}$
is
$(f(n))_{n\in \rho _1(F)}$
is
![]() $\rho _1$
-convergent to x. Thus, we can assume that
$\rho _1$
-convergent to x. Thus, we can assume that
![]() $f^{-1}[\{x\}]\in \mathcal {I}_{\rho _1}$
for all
$f^{-1}[\{x\}]\in \mathcal {I}_{\rho _1}$
for all
![]() $x\in X$
. There are two possible cases:
$x\in X$
. There are two possible cases:
![]() $f^{-1}[X\setminus \Lambda _2]\notin \mathcal {I}_{\rho _1}$
or
$f^{-1}[X\setminus \Lambda _2]\notin \mathcal {I}_{\rho _1}$
or
![]() $f^{-1}[X\setminus \Lambda _2]\in \mathcal {I}_{\rho _1}$
.
$f^{-1}[X\setminus \Lambda _2]\in \mathcal {I}_{\rho _1}$
.
If
![]() $f^{-1}[X\setminus \Lambda _2]\notin \mathcal {I}_{\rho _1}$
then we find
$f^{-1}[X\setminus \Lambda _2]\notin \mathcal {I}_{\rho _1}$
then we find
![]() $F\in \mathcal {F}_1$
with
$F\in \mathcal {F}_1$
with
![]() $\rho _1(F)\subseteq f^{-1}[X\setminus \Lambda _2]$
. As
$\rho _1(F)\subseteq f^{-1}[X\setminus \Lambda _2]$
. As
![]() $f^{-1}[\{x\}]\in \mathcal {I}_{\rho _1}$
for all
$f^{-1}[\{x\}]\in \mathcal {I}_{\rho _1}$
for all
![]() $x\in X$
and
$x\in X$
and
![]() $f^{-1}[\{x\}] \neq \emptyset $
only for countably many
$f^{-1}[\{x\}] \neq \emptyset $
only for countably many
![]() $x\in X$
, using the fact that
$x\in X$
, using the fact that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
(by Proposition 6.5(1)) we can find
$P^-$
(by Proposition 6.5(1)) we can find
![]() $E\in \mathcal {F}_1$
with
$E\in \mathcal {F}_1$
with
![]() $\rho _1(E)\subseteq \rho _1(F)$
and such that for each
$\rho _1(E)\subseteq \rho _1(F)$
and such that for each
![]() $x\in X\setminus \Lambda _2$
there is
$x\in X\setminus \Lambda _2$
there is
![]() $K\in [\Omega _1]^{<\omega }$
with
$K\in [\Omega _1]^{<\omega }$
with
![]() $\rho _1(E\setminus K)\cap f^{-1}[\{x\}]=\emptyset $
. Since for each
$\rho _1(E\setminus K)\cap f^{-1}[\{x\}]=\emptyset $
. Since for each
![]() $U\in \mathcal {B}(\infty )$
there are only finitely many
$U\in \mathcal {B}(\infty )$
there are only finitely many
![]() $\alpha \in T$
with
$\alpha \in T$
with
![]() $\rho _1(D_\alpha )\notin U$
,
$\rho _1(D_\alpha )\notin U$
,
![]() $(f(n))_{n\in \rho _1(E)} \rho _1$
-converges to
$(f(n))_{n\in \rho _1(E)} \rho _1$
-converges to
![]() $\infty $
.
$\infty $
.
If
![]() $f^{-1}[X\setminus \Lambda _2]\in \mathcal {I}_{\rho _1}$
then define
$f^{-1}[X\setminus \Lambda _2]\in \mathcal {I}_{\rho _1}$
then define
![]() $g:\Lambda _1\to \Lambda _2$
by
$g:\Lambda _1\to \Lambda _2$
by
![]() $g(\lambda )=f(\lambda )$
for all
$g(\lambda )=f(\lambda )$
for all
![]() $\lambda \in \Lambda _1\setminus f^{-1}[X\setminus \Lambda _2]$
and
$\lambda \in \Lambda _1\setminus f^{-1}[X\setminus \Lambda _2]$
and
![]() $g(\lambda )=x$
for all
$g(\lambda )=x$
for all
![]() $\lambda \in f^{-1}[X\setminus \Lambda _2]$
, where
$\lambda \in f^{-1}[X\setminus \Lambda _2]$
, where
![]() $x\in \Lambda _2$
is a fixed point. Then there is
$x\in \Lambda _2$
is a fixed point. Then there is
![]() $\alpha <\mathfrak {c}$
with
$\alpha <\mathfrak {c}$
with
![]() $f_\alpha =g$
. We have two subcases:
$f_\alpha =g$
. We have two subcases:
![]() $\alpha \in T$
and
$\alpha \in T$
and
![]() $\alpha \notin T$
.
$\alpha \notin T$
.
Assume
![]() $\alpha \in T$
. Since
$\alpha \in T$
. Since
![]() $\rho _1$
has small accretions, there is
$\rho _1$
has small accretions, there is
![]() $E\subseteq D_\alpha $
,
$E\subseteq D_\alpha $
,
![]() $E\in \mathcal {F}_1$
such that
$E\in \mathcal {F}_1$
such that
![]() $\rho _1(E)\setminus \rho _1(E\setminus K)\in \mathcal {I}_{\rho _1}$
for all
$\rho _1(E)\setminus \rho _1(E\setminus K)\in \mathcal {I}_{\rho _1}$
for all
![]() $K\in [\Omega _1]^{<\omega }$
. Using that
$K\in [\Omega _1]^{<\omega }$
. Using that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
(by Proposition 6.5(1)), we find
$P^-$
(by Proposition 6.5(1)), we find
![]() $D\in \mathcal {F}_1$
such that:
$D\in \mathcal {F}_1$
such that:
-
•
 $\rho _1(D)\subseteq \rho _1(E)\setminus f^{-1}[X\setminus \Lambda _2]$
,
$\rho _1(D)\subseteq \rho _1(E)\setminus f^{-1}[X\setminus \Lambda _2]$
, -
• for each
 $K\in [\Omega _1]^{<\omega }$
there is
$K\in [\Omega _1]^{<\omega }$
there is
 $L\in [\Omega _1]^{<\omega }$
with
$L\in [\Omega _1]^{<\omega }$
with
 $\rho _1(D\setminus L)\subseteq \rho _1(E\setminus K)\subseteq \rho _1(D_\alpha \setminus K)$
,
$\rho _1(D\setminus L)\subseteq \rho _1(E\setminus K)\subseteq \rho _1(D_\alpha \setminus K)$
, -
• for each
 $M\in [\Lambda _2]^{<\omega }$
there is
$M\in [\Lambda _2]^{<\omega }$
there is
 $L\in [\Omega _1]^{<\omega }$
with
$L\in [\Omega _1]^{<\omega }$
with
 $\rho _1(D\setminus L)\cap f^{-1}[M] = \emptyset $
.
$\rho _1(D\setminus L)\cap f^{-1}[M] = \emptyset $
.
Since each
![]() $U\in \mathcal {B}(\rho _1(D_\alpha ))$
is of the form
$U\in \mathcal {B}(\rho _1(D_\alpha ))$
is of the form
![]() $\{\rho _1(D_\alpha )\}\cup f_\alpha [\rho _1(D_\alpha \setminus K)]\setminus M$
for some
$\{\rho _1(D_\alpha )\}\cup f_\alpha [\rho _1(D_\alpha \setminus K)]\setminus M$
for some
![]() $K\in [\Omega _1]^{<\omega }$
and
$K\in [\Omega _1]^{<\omega }$
and
![]() $M\in [\Lambda _2]^{<\omega }$
, the subsequence
$M\in [\Lambda _2]^{<\omega }$
, the subsequence
![]() $(f(n))_{n\in \rho _1(D)}\ \rho _1$
-converges to
$(f(n))_{n\in \rho _1(D)}\ \rho _1$
-converges to
![]() $\rho _1(D_\alpha )$
.
$\rho _1(D_\alpha )$
.
Assume
![]() $\alpha \notin T$
. Then there is
$\alpha \notin T$
. Then there is
![]() $\beta <\alpha $
,
$\beta <\alpha $
,
![]() $\beta \in T$
such that
$\beta \in T$
such that
(we take the minimal
![]() $\beta <\alpha $
satisfying property (W2)). Since each open neighborhood of
$\beta <\alpha $
satisfying property (W2)). Since each open neighborhood of
![]() $\rho _1(D_\beta )$
is of the form
$\rho _1(D_\beta )$
is of the form
![]() $\{\rho _1(D_\beta )\}\cup f_\beta [\rho _1(D_\beta \setminus K)]\setminus M$
for some
$\{\rho _1(D_\beta )\}\cup f_\beta [\rho _1(D_\beta \setminus K)]\setminus M$
for some
![]() $K\in [\Omega _1]^{<\omega }$
and
$K\in [\Omega _1]^{<\omega }$
and
![]() $M\in [\Lambda _2]^{<\omega }$
,
$M\in [\Lambda _2]^{<\omega }$
,
![]() $(f_\alpha (n))_{n\in \rho _1(D_\alpha )} \rho _1$
-converges to
$(f_\alpha (n))_{n\in \rho _1(D_\alpha )} \rho _1$
-converges to
![]() $\rho _1(D_\beta )\in X$
. Since
$\rho _1(D_\beta )\in X$
. Since
![]() $\rho _1$
has small accretions, there is
$\rho _1$
has small accretions, there is
![]() $E\subseteq D_\alpha $
,
$E\subseteq D_\alpha $
,
![]() $E\in \mathcal {F}_1$
such that
$E\in \mathcal {F}_1$
such that
![]() $\rho _1(E)\setminus \rho _1(E\setminus K)\in \mathcal {I}_{\rho _1}$
for all
$\rho _1(E)\setminus \rho _1(E\setminus K)\in \mathcal {I}_{\rho _1}$
for all
![]() $K\in [\Omega _1]^{<\omega }$
. Then also
$K\in [\Omega _1]^{<\omega }$
. Then also
![]() $(f_\alpha (n))_{n\in \rho _1(E)}\ \rho _1$
-converges to
$(f_\alpha (n))_{n\in \rho _1(E)}\ \rho _1$
-converges to
![]() $\rho _1(D_\beta )\in X$
. Finally, since
$\rho _1(D_\beta )\in X$
. Finally, since
![]() $f^{-1}[X\setminus \Lambda _2]\in \mathcal {I}_{\rho _1}$
, using that
$f^{-1}[X\setminus \Lambda _2]\in \mathcal {I}_{\rho _1}$
, using that
![]() $\rho _1$
is
$\rho _1$
is
![]() $P^-$
(by Proposition 6.5(1)), we get
$P^-$
(by Proposition 6.5(1)), we get
![]() $E'\in \mathcal {F}_1$
such that
$E'\in \mathcal {F}_1$
such that
![]() $\rho _1(E')\subseteq \rho _1(E)\setminus f^{-1}[X\setminus \Lambda _2]$
and for each
$\rho _1(E')\subseteq \rho _1(E)\setminus f^{-1}[X\setminus \Lambda _2]$
and for each
![]() $K\in [\Omega _1]^{<\omega }$
there is
$K\in [\Omega _1]^{<\omega }$
there is
![]() $L\in [\Omega _1]^{<\omega }$
with
$L\in [\Omega _1]^{<\omega }$
with
![]() $\rho _1(E'\setminus L)\subseteq \rho _1(E\setminus K)$
. It is easy to see that
$\rho _1(E'\setminus L)\subseteq \rho _1(E\setminus K)$
. It is easy to see that
![]() $f_\alpha \restriction \rho _1(E')=f\restriction \rho _1(E')$
and
$f_\alpha \restriction \rho _1(E')=f\restriction \rho _1(E')$
and
![]() $(f_\alpha (n))_{n\in \rho _1(E')} \rho _1$
-converges to
$(f_\alpha (n))_{n\in \rho _1(E')} \rho _1$
-converges to
![]() $\rho _1(D_\beta )\in X$
.
$\rho _1(D_\beta )\in X$
.
Finally, we check that
![]() $X\notin \operatorname {\mathrm {FinBW}}(\rho _2)$
. Define
$X\notin \operatorname {\mathrm {FinBW}}(\rho _2)$
. Define
![]() $f:\Lambda _2\to X$
by
$f:\Lambda _2\to X$
by
![]() $f(\lambda )=\lambda $
for all
$f(\lambda )=\lambda $
for all
![]() $\lambda \in \Lambda _2$
and fix any
$\lambda \in \Lambda _2$
and fix any
![]() $E\in \mathcal {F}_2$
. We claim that
$E\in \mathcal {F}_2$
. We claim that
![]() $(f(n))_{n\in \rho _2(E)}$
does not
$(f(n))_{n\in \rho _2(E)}$
does not
![]() $\rho _2$
-converge. Clearly, it cannot converge to any
$\rho _2$
-converge. Clearly, it cannot converge to any
![]() $x\in \Lambda _2$
. Moreover, it cannot converge to any
$x\in \Lambda _2$
. Moreover, it cannot converge to any
![]() $\rho _1(D_\alpha )$
for
$\rho _1(D_\alpha )$
for
![]() $\alpha \in T$
as property (A1) guarantees that for some
$\alpha \in T$
as property (A1) guarantees that for some
![]() $K\in [\Omega _1]^{<\omega }$
we have
$K\in [\Omega _1]^{<\omega }$
we have
![]() $\rho _2(E\setminus L)\not \subseteq f_\alpha [\rho _1(D_\alpha \setminus K)]$
for all
$\rho _2(E\setminus L)\not \subseteq f_\alpha [\rho _1(D_\alpha \setminus K)]$
for all
![]() $L\in [\Omega _2]^{<\omega }$
, so
$L\in [\Omega _2]^{<\omega }$
, so
![]() $U=\{\rho _1(D_\alpha )\}\cup f_\alpha [ \rho _1(D_\alpha \setminus K)]$
would be an open neighborhood of
$U=\{\rho _1(D_\alpha )\}\cup f_\alpha [ \rho _1(D_\alpha \setminus K)]$
would be an open neighborhood of
![]() $\rho _1(D_\alpha )$
such that
$\rho _1(D_\alpha )$
such that
![]() $\rho _2(E\setminus L)\subseteq U$
for no
$\rho _2(E\setminus L)\subseteq U$
for no
![]() $L\in [\Omega _2]^{<\omega }$
.
$L\in [\Omega _2]^{<\omega }$
.
We will show that
![]() $(f(n))_{n\in \rho _2(E)}$
cannot
$(f(n))_{n\in \rho _2(E)}$
cannot
![]() $\rho _2$
-converge to
$\rho _2$
-converge to
![]() $\infty $
. Suppose otherwise, let
$\infty $
. Suppose otherwise, let
![]() $\{L_n: n\in \omega \}\subseteq [\Omega _2]^{<\omega }$
be such that
$\{L_n: n\in \omega \}\subseteq [\Omega _2]^{<\omega }$
be such that
![]() $\bigcup _{n\in \omega } L_n=\Omega _2$
and inductively pick
$\bigcup _{n\in \omega } L_n=\Omega _2$
and inductively pick
![]() $m_n\in \rho _2(E\setminus L_n)\setminus \{m_i:i<n\}$
. Then
$m_n\in \rho _2(E\setminus L_n)\setminus \{m_i:i<n\}$
. Then
![]() $(f(m_n))_{n\in \omega }$
is convergent to
$(f(m_n))_{n\in \omega }$
is convergent to
![]() $\infty $
. However, if
$\infty $
. However, if
![]() $g:\Lambda _1\to \{f(m_n): n\in \omega \}$
is any bijection (the set
$g:\Lambda _1\to \{f(m_n): n\in \omega \}$
is any bijection (the set
![]() $\{f(m_n): n\in \omega \}$
is infinite since f is one-to-one) then
$\{f(m_n): n\in \omega \}$
is infinite since f is one-to-one) then
![]() $g=f_\alpha $
for some
$g=f_\alpha $
for some
![]() $\alpha $
. If
$\alpha $
. If
![]() $\alpha \in T$
then in
$\alpha \in T$
then in
![]() $(f(m_n))_{n\in \omega }$
we could find a subsequence converging to
$(f(m_n))_{n\in \omega }$
we could find a subsequence converging to
![]() $\rho _1(D_\alpha )$
(in the same way as above when showing that
$\rho _1(D_\alpha )$
(in the same way as above when showing that
![]() $X\in \operatorname {\mathrm {FinBW}}(\rho _1)$
in the case of
$X\in \operatorname {\mathrm {FinBW}}(\rho _1)$
in the case of
![]() $\alpha \in T$
) which contradicts that X has unique limits of sequences. If
$\alpha \in T$
) which contradicts that X has unique limits of sequences. If
![]() $\alpha \notin T$
then in
$\alpha \notin T$
then in
![]() $(f(m_n))_{n\in \omega }$
we could find a subsequence converging to
$(f(m_n))_{n\in \omega }$
we could find a subsequence converging to
![]() $\rho _1(D_\beta )$
for some
$\rho _1(D_\beta )$
for some
![]() $\beta <\alpha $
,
$\beta <\alpha $
,
![]() $\beta \in T$
(in the same way as above when showing that
$\beta \in T$
(in the same way as above when showing that
![]() $X\in \operatorname {\mathrm {FinBW}}(\rho _1)$
in the case of
$X\in \operatorname {\mathrm {FinBW}}(\rho _1)$
in the case of
![]() $\alpha \notin T$
) which also contradicts that X has unique limits of sequences.
$\alpha \notin T$
) which also contradicts that X has unique limits of sequences.
18 Hindman (Ramsey, differentially compact) spaces that are not in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
and vice versa
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
and vice versa
Now we turn our attention to the question when there is a space in
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not Hindman (Ramsey, differentially compact, resp.) and vice versa in the case when
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not Hindman (Ramsey, differentially compact, resp.) and vice versa in the case when
![]() $\mathcal {I}$
is an arbitrary ideal.
$\mathcal {I}$
is an arbitrary ideal.
Corollary 18.1 (Assume CH).
For each ideal
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
the following conditions are equivalent.
$\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
the following conditions are equivalent.
-
(1)
 $\rho _{\mathcal {I}}\not \leq _K\rho $
.
$\rho _{\mathcal {I}}\not \leq _K\rho $
. -
(2) There exists a Hindman
 $($
Ramsey, differentially compact, resp.
$($
Ramsey, differentially compact, resp.
 $)$
space that is not in
$)$
space that is not in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
.
Moreover, an example showing that the above difference between
![]() $\operatorname {\mathrm {FinBW}}$
classes is nonempty is separable and has unique limits of sequences. If
$\operatorname {\mathrm {FinBW}}$
classes is nonempty is separable and has unique limits of sequences. If
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $P^-$
, then this example is of the form
$P^-$
, then this example is of the form
![]() $\Phi (\mathcal {A})$
with
$\Phi (\mathcal {A})$
with
![]() $\mathcal {A}$
being almost disjoint of cardinality
$\mathcal {A}$
being almost disjoint of cardinality
![]() $\mathfrak {c}$
(in particular, it is Hausdorff, compact, separable, and of cardinality
$\mathfrak {c}$
(in particular, it is Hausdorff, compact, separable, and of cardinality
![]() $\mathfrak {c})$
.
$\mathfrak {c})$
.
Proof It follows from Theorem 17.2 and Proposition 10.2(4) as each
![]() $\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
is weak
$\rho \in \{\operatorname {\mathrm {FS}},r,\Delta \}$
is weak
![]() $P^+$
(by Theorem 6.7(3)) and has small accretions (by Proposition 4.3). The case of
$P^+$
(by Theorem 6.7(3)) and has small accretions (by Proposition 4.3). The case of
![]() $P^-$
ideals
$P^-$
ideals
![]() $\mathcal {I}$
follows from Corollary 16.7(1).
$\mathcal {I}$
follows from Corollary 16.7(1).
In [Reference Kwela62, Definition 4.1], the author introduced the following ideal:
where
![]() $A_{(i)}=\{(x,y)\in \omega ^2: (i,x,y)\in A\}$
. The ideal
$A_{(i)}=\{(x,y)\in \omega ^2: (i,x,y)\in A\}$
. The ideal
![]() $\mathcal {BI}$
proved to be useful in research of
$\mathcal {BI}$
proved to be useful in research of
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
spaces (see [Reference Kwela62] for more details).
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
spaces (see [Reference Kwela62] for more details).
Corollary 18.2 (Assume CH).
For each ideal
![]() $\mathcal {I}$
, the following conditions are equivalent.
$\mathcal {I}$
, the following conditions are equivalent.
-
(1)
 $\mathcal {BI}\not \leq _K\mathcal {I}$
.
$\mathcal {BI}\not \leq _K\mathcal {I}$
. -
(2) There exists a space in
 $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not a Hindman
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
that is not a Hindman
 $($
Ramsey, differentially compact, resp.
$($
Ramsey, differentially compact, resp.
 $)$
space.
$)$
space.
Moreover, an example showing that the above difference between
![]() $\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
$\operatorname {\mathrm {FinBW}}$
classes is nonempty is of the form
![]() $\Phi (\mathcal {A})$
with
$\Phi (\mathcal {A})$
with
![]() $\mathcal {A}$
being infinite maximal almost disjoint
$\mathcal {A}$
being infinite maximal almost disjoint
![]() $($
in particular, it is Hausdorff, compact, separable, and of cardinality
$($
in particular, it is Hausdorff, compact, separable, and of cardinality
![]() $\mathfrak {c})$
.
$\mathfrak {c})$
.
Proof
![]() $(1)\implies (2)$
In [Reference Kwela62, Theorem 5.3], the author proved that if
$(1)\implies (2)$
In [Reference Kwela62, Theorem 5.3], the author proved that if
![]() $\mathcal {BI}\not \leq _K\mathcal {I}$
then there exists an infinite maximal almost disjoint family
$\mathcal {BI}\not \leq _K\mathcal {I}$
then there exists an infinite maximal almost disjoint family
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\mathcal {I})$
. Then Corollary 13.3 shows that
$\Phi (\mathcal {A})\in \operatorname {\mathrm {FinBW}}(\mathcal {I})$
. Then Corollary 13.3 shows that
![]() $\Phi (\mathcal {A})$
is not Hindman (Ramsey nor differentially compact).
$\Phi (\mathcal {A})$
is not Hindman (Ramsey nor differentially compact).
![]() $(2)\implies (1)$
Using [Reference Kwela62, Proposition 6.3 and Lemma 3.2(ii)], it is not difficult to see that if
$(2)\implies (1)$
Using [Reference Kwela62, Proposition 6.3 and Lemma 3.2(ii)], it is not difficult to see that if
![]() $\mathcal {BI}\leq _K\mathcal {I}$
then each space in
$\mathcal {BI}\leq _K\mathcal {I}$
then each space in
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
satisfies property
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
satisfies property
![]() $(*)$
. On the other hand, we know that spaces with
$(*)$
. On the other hand, we know that spaces with
![]() $(*)$
property are Hindman, Ramsey, and differentially compact (see [Reference Kojman57, Theorem 11], [Reference Kubiś and Szeptycki61, Corollary 3.2], and [Reference Filipów22, Corollary 4.8], resp.).
$(*)$
property are Hindman, Ramsey, and differentially compact (see [Reference Kojman57, Theorem 11], [Reference Kubiś and Szeptycki61, Corollary 3.2], and [Reference Filipów22, Corollary 4.8], resp.).
Corollary 18.3 (Assume CH).
If
![]() $\rho \in \{FS, r, \Delta \}$
then
$\rho \in \{FS, r, \Delta \}$
then
![]() $\operatorname {\mathrm {FinBW}}(\rho )\neq \operatorname {\mathrm {FinBW}}(\mathcal {I})$
for every ideal
$\operatorname {\mathrm {FinBW}}(\rho )\neq \operatorname {\mathrm {FinBW}}(\mathcal {I})$
for every ideal
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Proof Let
![]() $\rho \in \{FS, r, \Delta \}$
and
$\rho \in \{FS, r, \Delta \}$
and
![]() $\mathcal {I}$
be an ideal. If
$\mathcal {I}$
be an ideal. If
![]() $\mathcal {BI}\not \leq _K\mathcal {I}$
then
$\mathcal {BI}\not \leq _K\mathcal {I}$
then
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})\setminus \operatorname {\mathrm {FinBW}}(\rho )\neq \emptyset $
by Corollary 18.2. On the other hand, if
$\operatorname {\mathrm {FinBW}}(\mathcal {I})\setminus \operatorname {\mathrm {FinBW}}(\rho )\neq \emptyset $
by Corollary 18.2. On the other hand, if
![]() $\mathcal {BI}\leq _K\mathcal {I}$
then the interval
$\mathcal {BI}\leq _K\mathcal {I}$
then the interval
![]() $[0,1]$
is in
$[0,1]$
is in
![]() $\operatorname {\mathrm {FinBW}}(\rho )$
(by Theorem 10.5(6) and Propositions 10.2(2) and 6.7(3)) and it is not in
$\operatorname {\mathrm {FinBW}}(\rho )$
(by Theorem 10.5(6) and Propositions 10.2(2) and 6.7(3)) and it is not in
![]() $\operatorname {\mathrm {FinBW}}(\mathcal {I})$
(by [Reference Kwela62, Proposition 4.6], [Reference Barbarski, Filipów, Mrożek and Szuca2, Example 4.1], and [Reference Meza-Alcántara67, Section 2.7]).
$\operatorname {\mathrm {FinBW}}(\mathcal {I})$
(by [Reference Kwela62, Proposition 4.6], [Reference Barbarski, Filipów, Mrożek and Szuca2, Example 4.1], and [Reference Meza-Alcántara67, Section 2.7]).