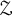1 Introduction
Approximate intertwinings have played a significant role in the classification theory of C
![]() $^*$
-algebras (e.g., [Reference Bratteli7, Reference Dadarlat and Eilers20, Reference Elliott24, Reference Elliott25, Reference Elliott and Evans27, Reference Elliott, Gong and Li28, Reference Elliott, Gong, Lin and Niu30, Reference Elliott and Loring32, Reference Gong34–Reference Gong, Lin and Niu37, Reference Kirchberg and Phillips40, Reference Lin42, Reference Lin43, Reference Phillips50, Reference Pimsner and Voiculescu51]). A related notion called n-colored isomorphism, which specializes to an approximate intertwining in the case of a single color, was considered by Castillejos in [Reference Castillejos10]. There it is shown that any two (unital) classifiable C
$^*$
-algebras (e.g., [Reference Bratteli7, Reference Dadarlat and Eilers20, Reference Elliott24, Reference Elliott25, Reference Elliott and Evans27, Reference Elliott, Gong and Li28, Reference Elliott, Gong, Lin and Niu30, Reference Elliott and Loring32, Reference Gong34–Reference Gong, Lin and Niu37, Reference Kirchberg and Phillips40, Reference Lin42, Reference Lin43, Reference Phillips50, Reference Pimsner and Voiculescu51]). A related notion called n-colored isomorphism, which specializes to an approximate intertwining in the case of a single color, was considered by Castillejos in [Reference Castillejos10]. There it is shown that any two (unital) classifiable C
![]() $^*$
-algebras (i.e., those satisfying the hypotheses of Theorem 4.5) with at most one trace are two-colored isomorphic, and it is posed as a question whether any two such C
$^*$
-algebras (i.e., those satisfying the hypotheses of Theorem 4.5) with at most one trace are two-colored isomorphic, and it is posed as a question whether any two such C
![]() $^*$
-algebras with isomorphic tracial simplices are n-colored isomorphic. We show that this question has an affirmative answer using a somewhat modified notion, which we shall simply refer to as colored isomorphism.
$^*$
-algebras with isomorphic tracial simplices are n-colored isomorphic. We show that this question has an affirmative answer using a somewhat modified notion, which we shall simply refer to as colored isomorphism.
Theorem 4.5 Any two unital, simple,
![]() $\mathcal Z$
-stable, separable amenable C
$\mathcal Z$
-stable, separable amenable C
![]() $^*$
-algebras satisfying the universal coefficient theorem (UCT) with isomorphic tracial simplices are colored isomorphic.
$^*$
-algebras satisfying the universal coefficient theorem (UCT) with isomorphic tracial simplices are colored isomorphic.
Let us begin by giving context for the notion from [Reference Castillejos10] and comparing the approaches taken there and here. In fact, much of the original strategy is retained in this paper, so let us outline the proof of the main result, the finite case considered in Theorem 4.5, and mention the differences with [Reference Castillejos10] along the way. Throughout, let
![]() $\omega $
be a fixed free ultrafilter on the natural numbers. Two unital C
$\omega $
be a fixed free ultrafilter on the natural numbers. Two unital C
![]() $^*$
-algebras A and B were said in [Reference Castillejos10] to be n-colored isomorphic if there exist c.p.c. order zero maps
$^*$
-algebras A and B were said in [Reference Castillejos10] to be n-colored isomorphic if there exist c.p.c. order zero maps
![]() $\varphi \,{\colon}\, A \to B$
and
$\varphi \,{\colon}\, A \to B$
and
![]() $\psi \,{\colon}\, B \to A$
, and unitaries
$\psi \,{\colon}\, B \to A$
, and unitaries
![]() $u_1, \ldots , u_n \in A_{\omega }$
and
$u_1, \ldots , u_n \in A_{\omega }$
and
![]() $v_1, \ldots , v_n \in B_{\omega }$
, such that
$v_1, \ldots , v_n \in B_{\omega }$
, such that
 $$\begin{align*}\sum_{k=1}^n u_k \psi \varphi(a) u_k^* = a \hspace{15 pt} \text{ and } \hspace{15 pt} \sum_{k=1}^n v_k \varphi \psi(b) v_k^* = b \end{align*}$$
$$\begin{align*}\sum_{k=1}^n u_k \psi \varphi(a) u_k^* = a \hspace{15 pt} \text{ and } \hspace{15 pt} \sum_{k=1}^n v_k \varphi \psi(b) v_k^* = b \end{align*}$$
for all
![]() $a \in A$
and all
$a \in A$
and all
![]() $b \in B$
. The present notion, colored isomorphism, on the other hand, has order zero maps at the level of ultrapowers
$b \in B$
. The present notion, colored isomorphism, on the other hand, has order zero maps at the level of ultrapowers
![]() $A_{\omega }$
and
$A_{\omega }$
and
![]() $B_{\omega }$
(and so includes the case that the ultrapower maps are induced by a sequence of order zero maps at the level of the algebras A and B); and the
$B_{\omega }$
(and so includes the case that the ultrapower maps are induced by a sequence of order zero maps at the level of the algebras A and B); and the
![]() $u_i$
(resp.
$u_i$
(resp.
![]() $v_i$
) are contractions (not just unitaries) such that the absolute values squared add up to the identity of
$v_i$
) are contractions (not just unitaries) such that the absolute values squared add up to the identity of
![]() $A_{\omega }$
(resp.
$A_{\omega }$
(resp.
![]() $B_{\omega }$
) (rather than a multiple of this). (We also assume that traces on the ultrapower determined by a single trace on the algebra are preserved.)
$B_{\omega }$
) (rather than a multiple of this). (We also assume that traces on the ultrapower determined by a single trace on the algebra are preserved.)
While the earlier notion, n-colored isomorphism, preserves the tracial cone, up to isomorphism, the present notion preserves the tracial simplex, up to isomorphism (Theorem 4.1). We note that isomorphism of tracial cones coincides with (a multiple of) tracial simplex isomorphism in the cases considered in [Reference Castillejos10] (at most one trace). Our definition is formulated in terms of colored equivalence for order zero maps, which has its origins in the
![]() $\mathcal Z$
-stable implies finite nuclear dimension direction of the Toms–Winter conjecture, having first appeared in [Reference Matui and Sato45] and later more definitively in [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Reference Sato, White and Winter59]. (That of [Reference Castillejos10] is not explicitly based on colored equivalence of maps.)
$\mathcal Z$
-stable implies finite nuclear dimension direction of the Toms–Winter conjecture, having first appeared in [Reference Matui and Sato45] and later more definitively in [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Reference Sato, White and Winter59]. (That of [Reference Castillejos10] is not explicitly based on colored equivalence of maps.)
Now let A and B be finite classifiable C
![]() $^*$
-algebras with isomorphic tracial simplices. In order to show that A and B are colored isomorphic, we must construct order zero maps
$^*$
-algebras with isomorphic tracial simplices. In order to show that A and B are colored isomorphic, we must construct order zero maps
![]() $\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
$\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
![]() $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
![]() $\psi \varphi \iota _A$
is colored equivalent to
$\psi \varphi \iota _A$
is colored equivalent to
![]() $\iota _A,$
where
$\iota _A,$
where
![]() $\iota _A$
is the canonical embedding of A into
$\iota _A$
is the canonical embedding of A into
![]() $A_{\omega }$
, and likewise for
$A_{\omega }$
, and likewise for
![]() $\varphi \psi \iota _B$
and
$\varphi \psi \iota _B$
and
![]() $\iota _B$
. By the finite order zero uniqueness theorem of [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6], which was later extended to remove restrictions on the tracial simplices in [Reference Castillejos, Evington, Tikuisis, White and Winter11], it is sufficient to show that (in the notation of Corollary 2.3)
$\iota _B$
. By the finite order zero uniqueness theorem of [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6], which was later extended to remove restrictions on the tracial simplices in [Reference Castillejos, Evington, Tikuisis, White and Winter11], it is sufficient to show that (in the notation of Corollary 2.3)
![]() $\tau (\psi \varphi )^n = \tau $
for all
$\tau (\psi \varphi )^n = \tau $
for all
![]() $n \in \mathbb N$
and all
$n \in \mathbb N$
and all
![]() $\tau \in T(A_{\omega })$
, and that
$\tau \in T(A_{\omega })$
, and that
![]() $\tau (\varphi \psi )^n = \tau $
for all
$\tau (\varphi \psi )^n = \tau $
for all
![]() $n \in \mathbb N$
and all
$n \in \mathbb N$
and all
![]() $\tau \in T(B_{\omega })$
. Since
$\tau \in T(B_{\omega })$
. Since
![]() $(\psi \varphi )^n = \psi ^n \varphi ^n$
and
$(\psi \varphi )^n = \psi ^n \varphi ^n$
and
![]() $(\varphi \psi )^n = \varphi ^n \psi ^n$
, by Corollary 2.4, these tracial identities imply that
$(\varphi \psi )^n = \varphi ^n \psi ^n$
, by Corollary 2.4, these tracial identities imply that
![]() $\varphi ^n$
and
$\varphi ^n$
and
![]() $\psi ^n$
also (for each n) induce mutually inverse isomorphisms of
$\psi ^n$
also (for each n) induce mutually inverse isomorphisms of
![]() $T(A_{\omega })$
and
$T(A_{\omega })$
and
![]() $T(B_{\omega })$
. In fact, the order zero maps we construct will induce the same mutually inverse isomorphisms of tracial simplices for each n.
$T(B_{\omega })$
. In fact, the order zero maps we construct will induce the same mutually inverse isomorphisms of tracial simplices for each n.
Roughly speaking,
![]() $\varphi $
is constructed with a sequence of maps at the level of the algebras A and B which factor through a fixed AF algebra D via a fixed embedding
$\varphi $
is constructed with a sequence of maps at the level of the algebras A and B which factor through a fixed AF algebra D via a fixed embedding
![]() $\alpha _A$
. Furthermore,
$\alpha _A$
. Furthermore,
![]() $\alpha _A$
is chosen so that it induces an isomorphism of the tracial simplices
$\alpha _A$
is chosen so that it induces an isomorphism of the tracial simplices
![]() $T(D)$
and
$T(D)$
and
![]() $T(A)$
. This is obtained from the recently established homomorphism theorem of [Reference Gong, Lin and Niu37]. Such embeddings are now also known to exist outside the classification setting (i.e., without the assumption of
$T(A)$
. This is obtained from the recently established homomorphism theorem of [Reference Gong, Lin and Niu37]. Such embeddings are now also known to exist outside the classification setting (i.e., without the assumption of
![]() $\mathcal Z$
-stability), building on ideas from [Reference Schafhauser60, Reference Schafhauser61]. Lastly, the maps
$\mathcal Z$
-stability), building on ideas from [Reference Schafhauser60, Reference Schafhauser61]. Lastly, the maps
![]() $\varphi _k$
into B from the AF algebra D are chosen to have prescribed tracial data. More specifically, given a faithful trace
$\varphi _k$
into B from the AF algebra D are chosen to have prescribed tracial data. More specifically, given a faithful trace
![]() $\mu _k$
on
$\mu _k$
on
![]() $C_0(0,1]$
and an affine map
$C_0(0,1]$
and an affine map
![]() $\Phi \,{\colon}\, T(B) \to T(D)$
,
$\Phi \,{\colon}\, T(B) \to T(D)$
,
![]() $\varphi _k$
is an order zero map satisfying the identity
$\varphi _k$
is an order zero map satisfying the identity
for each
![]() $k, n \in \mathbb N$
and each
$k, n \in \mathbb N$
and each
![]() $\tau \in T(B)$
, where t denotes the identity map on
$\tau \in T(B)$
, where t denotes the identity map on
![]() $(0,1]$
. (But, for obvious reasons, with
$(0,1]$
. (But, for obvious reasons, with
![]() $\mu _k(t^n) \to 1$
for each n.) This is the content of Theorem 4.3.
$\mu _k(t^n) \to 1$
for each n.) This is the content of Theorem 4.3.
Let us show how the desired order zero maps
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
can be constructed from here. Let
$\psi $
can be constructed from here. Let
![]() $\Phi $
be an isomorphism of the tracial simplices
$\Phi $
be an isomorphism of the tracial simplices
![]() $T(B)$
and
$T(B)$
and
![]() $T(D)$
, which exists since
$T(D)$
, which exists since
![]() $T(A)$
is assumed to be isomorphic to
$T(A)$
is assumed to be isomorphic to
![]() $T(B)$
, by hypothesis, and D was chosen so that
$T(B)$
, by hypothesis, and D was chosen so that
![]() $T(D)$
is isomorphic to
$T(D)$
is isomorphic to
![]() $T(A)$
; and let
$T(A)$
; and let
![]() $\mu _k$
be a sequence of faithful traces on
$\mu _k$
be a sequence of faithful traces on
![]() $C_0(0,1]$
such that
$C_0(0,1]$
such that
![]() $\lim _{k \to \omega } \mu _k(t^n) = 1$
for each
$\lim _{k \to \omega } \mu _k(t^n) = 1$
for each
![]() $n \in \mathbb N$
. (It is enough that
$n \in \mathbb N$
. (It is enough that
![]() $\lim _{k \to \infty } \mu _k(t) = 1$
.) Then with
$\lim _{k \to \infty } \mu _k(t) = 1$
.) Then with
![]() $\varphi _k \,{\colon}\, D \to B$
satisfying
$\varphi _k \,{\colon}\, D \to B$
satisfying
![]() $(*)$
, and with
$(*)$
, and with
![]() $\varphi : A_{\omega } \to B_{\omega }$
the order zero map induced by the sequence
$\varphi : A_{\omega } \to B_{\omega }$
the order zero map induced by the sequence
![]() $(\varphi _k \alpha _A)$
, we have
$(\varphi _k \alpha _A)$
, we have
for each
![]() $n \in \mathbb N$
and for each trace
$n \in \mathbb N$
and for each trace
![]() $\tau \in T(B_{\omega })$
with Corollary 2.4 having been used at the last equality. In order to make use of the fact that
$\tau \in T(B_{\omega })$
with Corollary 2.4 having been used at the last equality. In order to make use of the fact that
![]() $\mu _k$
levels out moments, we will need a reduction which was observed in [Reference Ozawa47]. The limit traces in
$\mu _k$
levels out moments, we will need a reduction which was observed in [Reference Ozawa47]. The limit traces in
![]() $T(B_{\omega })$
(i.e., those which are induced by a sequence of traces in
$T(B_{\omega })$
(i.e., those which are induced by a sequence of traces in
![]() $T(B)$
) are weak
$T(B)$
) are weak
![]() $^*$
dense in
$^*$
dense in
![]() $T(B_{\omega })$
(Theorem 2.7). Therefore, it suffices to check that the desired tracial identities (see the next paragraph) hold for such traces. Let a trace
$T(B_{\omega })$
(Theorem 2.7). Therefore, it suffices to check that the desired tracial identities (see the next paragraph) hold for such traces. Let a trace
![]() $\tau $
of the form
$\tau $
of the form
![]() $\lim _{k \to \omega } \tau _k$
in
$\lim _{k \to \omega } \tau _k$
in
![]() $T(B_{\omega })$
be given. Then
$T(B_{\omega })$
be given. Then
 $$ \begin{align*} \tau(\varphi_k^n \alpha_A) & = \lim_{k \to \omega} \tau_k \varphi_k^n \alpha_A = \lim_{k \to \omega} \alpha_A^* \tau_k \varphi_k^n = \alpha_A^* \lim_{k \to \omega} \tau_k \varphi_k^n \\ &\stackrel{(*)}{=} \alpha_A^* \lim_{k \to \omega} \mu_k(t^n) \Phi(\tau_k) = \alpha_A^* \lim_{k \to \omega} \Phi(\tau_k) = \lim_{k \to \omega} \alpha_A^* \Phi(\tau_k) \end{align*} $$
$$ \begin{align*} \tau(\varphi_k^n \alpha_A) & = \lim_{k \to \omega} \tau_k \varphi_k^n \alpha_A = \lim_{k \to \omega} \alpha_A^* \tau_k \varphi_k^n = \alpha_A^* \lim_{k \to \omega} \tau_k \varphi_k^n \\ &\stackrel{(*)}{=} \alpha_A^* \lim_{k \to \omega} \mu_k(t^n) \Phi(\tau_k) = \alpha_A^* \lim_{k \to \omega} \Phi(\tau_k) = \lim_{k \to \omega} \alpha_A^* \Phi(\tau_k) \end{align*} $$
for each
![]() $k, n \in \mathbb N$
. The second to last equality uses the fact that
$k, n \in \mathbb N$
. The second to last equality uses the fact that
![]() $\lim _{k \to \omega } \mu _k(t^n) = 1$
and continuity of
$\lim _{k \to \omega } \mu _k(t^n) = 1$
and continuity of
![]() $\alpha _A^*$
is used for the third equality and the last two.
$\alpha _A^*$
is used for the third equality and the last two.
The remaining map
![]() $\psi $
is constructed in a similar way. Let
$\psi $
is constructed in a similar way. Let
![]() $\alpha _B \,{\colon}\, B \to E$
be an AF embedding which induces a tracial simplex isomorphism
$\alpha _B \,{\colon}\, B \to E$
be an AF embedding which induces a tracial simplex isomorphism
![]() $T(E) \to T(B)$
, and let
$T(E) \to T(B)$
, and let
![]() $\psi _k \,{\colon}\, E \to A$
be order zero maps satisfying the identity
$\psi _k \,{\colon}\, E \to A$
be order zero maps satisfying the identity
for each
![]() $k, n \in \mathbb N$
and each
$k, n \in \mathbb N$
and each
![]() $\tau \in T(A)$
, where
$\tau \in T(A)$
, where
![]() $\Psi $
is the tracial simplex isomorphism
$\Psi $
is the tracial simplex isomorphism
![]() $(\alpha _A^* \Phi \alpha _B^*) ^{-1}$
. Let
$(\alpha _A^* \Phi \alpha _B^*) ^{-1}$
. Let
![]() $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
denote the order zero map induced by the sequence
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
denote the order zero map induced by the sequence
![]() $(\psi _k \alpha _B)$
. Then for each limit trace
$(\psi _k \alpha _B)$
. Then for each limit trace
![]() $\tau = \lim _{k \to \omega } \tau _k$
in
$\tau = \lim _{k \to \omega } \tau _k$
in
![]() $T(A_{\omega })$
,
$T(A_{\omega })$
,
for each
![]() $n \in \mathbb N$
. Therefore (see the proof of Theorem 4.5 for more details),
$n \in \mathbb N$
. Therefore (see the proof of Theorem 4.5 for more details),
for each
![]() $n \in \mathbb N$
and each limit trace
$n \in \mathbb N$
and each limit trace
![]() $\tau \in T(A_{\omega })$
. By Theorem 2.7, the above identity holds for all
$\tau \in T(A_{\omega })$
. By Theorem 2.7, the above identity holds for all
![]() $\tau \in T(A_{\omega })$
. A symmetric argument shows that
$\tau \in T(A_{\omega })$
. A symmetric argument shows that
![]() $\tau (\varphi \psi )^n = \tau $
for each
$\tau (\varphi \psi )^n = \tau $
for each
![]() $n \in \mathbb N$
and each
$n \in \mathbb N$
and each
![]() $\tau \in T(B_{\omega })$
. Therefore,
$\tau \in T(B_{\omega })$
. Therefore,
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
determine a colored isomorphism of A and B. (To simplify the discussion, we omit the question of preserving constant limit traces and defer to the proof of Theorem 4.5.)
$\psi $
determine a colored isomorphism of A and B. (To simplify the discussion, we omit the question of preserving constant limit traces and defer to the proof of Theorem 4.5.)
Since the n-colored isomorphism of [Reference Castillejos10] requires unitaries rather than contractions, a different uniqueness theorem is developed for order zero maps in the unique trace case (see [Reference Castillejos10, Lemma 5.6.2]). It provides a stronger statement than [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Theorem 5.5] (in the unique trace case) since it is applicable to pairs of order zero maps (rather than one
![]() $*$
-homomorphism and one order zero map) and because it provides unitary equivalence of the order zero maps involved rather than after tensoring the order zero maps with a positive element
$*$
-homomorphism and one order zero map) and because it provides unitary equivalence of the order zero maps involved rather than after tensoring the order zero maps with a positive element
![]() $h \in \mathcal Z$
with full spectrum. Let h be such an element with the additional stipulation that
$h \in \mathcal Z$
with full spectrum. Let h be such an element with the additional stipulation that
![]() $\tau _{\mathcal Z}(h^n) = \tau _{\mathcal Z}( (1_{\mathcal Z}-h)^n) = 1/(n+1)$
for each
$\tau _{\mathcal Z}(h^n) = \tau _{\mathcal Z}( (1_{\mathcal Z}-h)^n) = 1/(n+1)$
for each
![]() $n \in \mathbb N$
where
$n \in \mathbb N$
where
![]() $\tau _{\mathcal Z}$
denotes the unique trace of
$\tau _{\mathcal Z}$
denotes the unique trace of
![]() $\mathcal Z$
. Because the scaling factors introduced by the unitaries differ from those introduced by contractions under traces, the compositions of the order zero maps
$\mathcal Z$
. Because the scaling factors introduced by the unitaries differ from those introduced by contractions under traces, the compositions of the order zero maps
![]() $\varphi : A \to B$
and
$\varphi : A \to B$
and
![]() $\psi \,{\colon}\, B \to A$
implementing the n-colored equivalence are compared with the contractive order zero maps
$\psi \,{\colon}\, B \to A$
implementing the n-colored equivalence are compared with the contractive order zero maps
![]() ${\rho _{A,h}:= \sigma _1(\text {id}_A \otimes h)}$
and
${\rho _{A,h}:= \sigma _1(\text {id}_A \otimes h)}$
and
![]() $\rho _{A,h}:= \sigma _2(\text {id}_B \otimes h$
) under traces where
$\rho _{A,h}:= \sigma _2(\text {id}_B \otimes h$
) under traces where
![]() $\sigma _1\,{\colon}\, A \otimes \mathcal Z \to A$
and
$\sigma _1\,{\colon}\, A \otimes \mathcal Z \to A$
and
![]() $\sigma _2\,{\colon}\, B \otimes \mathcal Z \to B$
are isomorphisms whose inverses are approximately unitarily equivalent to the first factor embeddings. The moment problem in this setting is more complicated than the one in ours because the order zero maps involved in the uniqueness theorem are induced by constant sequences of maps, and therefore the moments need to match up on the dot rather than only approximately. Moreover, the target moments of
$\sigma _2\,{\colon}\, B \otimes \mathcal Z \to B$
are isomorphisms whose inverses are approximately unitarily equivalent to the first factor embeddings. The moment problem in this setting is more complicated than the one in ours because the order zero maps involved in the uniqueness theorem are induced by constant sequences of maps, and therefore the moments need to match up on the dot rather than only approximately. Moreover, the target moments of
![]() $\psi \varphi $
and
$\psi \varphi $
and
![]() $\varphi \psi $
actually depend on
$\varphi \psi $
actually depend on
![]() $n \in \mathbb N$
, as
$n \in \mathbb N$
, as
where
![]() $\tau _A$
and
$\tau _A$
and
![]() $\tau _B$
denote the unique trace of A and B (see [Reference Castillejos10, Theorem 5.6.8]).
$\tau _B$
denote the unique trace of A and B (see [Reference Castillejos10, Theorem 5.6.8]).
The main step in constructing
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
(in [Reference Castillejos10]) is the construction of maps out of unital, simple, separable AF algebras with unique trace into
$\psi $
(in [Reference Castillejos10]) is the construction of maps out of unital, simple, separable AF algebras with unique trace into
![]() $\mathcal Z$
realizing specific moments. Let us outline the construction of
$\mathcal Z$
realizing specific moments. Let us outline the construction of
![]() $\varphi $
using this result. By [Reference Schafhauser60, Theorem A], A embeds into a simple, separable, unital AF algebra D with unique trace via a map
$\varphi $
using this result. By [Reference Schafhauser60, Theorem A], A embeds into a simple, separable, unital AF algebra D with unique trace via a map
![]() $\alpha _A$
which induces an isomorphism of tracial simplices. Then an order zero map
$\alpha _A$
which induces an isomorphism of tracial simplices. Then an order zero map
![]() $\phi \,{\colon}\, D \to \mathcal Z$
is constructed, using a measure
$\phi \,{\colon}\, D \to \mathcal Z$
is constructed, using a measure
![]() $\mu $
on the unit interval with the very specific moments
$\mu $
on the unit interval with the very specific moments
![]() $\mu (t^n) = 1/\sqrt {n+1}$
, where t denotes the identity map on
$\mu (t^n) = 1/\sqrt {n+1}$
, where t denotes the identity map on
![]() $(0,1]$
, such that
$(0,1]$
, such that
for each
![]() $n \in \mathbb N$
(see [Reference Castillejos10, Lemma 5.6.5]). The order zero map
$n \in \mathbb N$
(see [Reference Castillejos10, Lemma 5.6.5]). The order zero map
![]() $\varphi $
is then given by the composition
$\varphi $
is then given by the composition
Apart from
![]() $\phi $
, each of the above maps is a trace-preserving
$\phi $
, each of the above maps is a trace-preserving
![]() $*$
-homomorphism, and so by Corollary 2.4, the moments of
$*$
-homomorphism, and so by Corollary 2.4, the moments of
![]() $\varphi $
are
$\varphi $
are
for each
![]() $n \in \mathbb N$
. The second order zero map
$n \in \mathbb N$
. The second order zero map
![]() $\psi $
is constructed in a similar way so that
$\psi $
is constructed in a similar way so that
for each
![]() $n \in \mathbb N$
. The appropriate uniqueness theorem (see [Reference Castillejos10, Lemma 5.6.2]) is then applied twice with
$n \in \mathbb N$
. The appropriate uniqueness theorem (see [Reference Castillejos10, Lemma 5.6.2]) is then applied twice with
![]() $\psi \varphi $
: once with
$\psi \varphi $
: once with
![]() $\rho _{A,h}$
, and once more with
$\rho _{A,h}$
, and once more with
![]() $\rho _{A,1-h}$
, and similarly for
$\rho _{A,1-h}$
, and similarly for
![]() $\varphi \psi $
, in order to obtain a two-colored isomorphism of A and B.
$\varphi \psi $
, in order to obtain a two-colored isomorphism of A and B.
All that remains to be outlined in the construction of order zero maps, either in our setting or in that of [Reference Castillejos10], is how to ensure the prescribed tracial data. Let us begin with the approach taken in [Reference Castillejos10]. Let D be a simple, separable, unital AF algebra with unique trace
![]() $\tau $
and let
$\tau $
and let
![]() $\nu $
be a fully supported Borel measure on
$\nu $
be a fully supported Borel measure on
![]() $[0,1]$
. Recall (e.g., from [Reference Elliott, Robert and Santiago33]) that
$[0,1]$
. Recall (e.g., from [Reference Elliott, Robert and Santiago33]) that
![]() $\tau $
induces a functional
$\tau $
induces a functional
![]() $d_{\tau } \,{\colon}\, \operatorname {Cu}(D) \to [0,\infty ]$
. It is stated in [Reference Castillejos10, Proposition 1.10.12] that the map
$d_{\tau } \,{\colon}\, \operatorname {Cu}(D) \to [0,\infty ]$
. It is stated in [Reference Castillejos10, Proposition 1.10.12] that the map
![]() $\sigma : \text {Lsc}([0,1],\operatorname {Cu} (D)) \to \operatorname {Cu} (\mathcal Z)$
determined by the rule
$\sigma : \text {Lsc}([0,1],\operatorname {Cu} (D)) \to \operatorname {Cu} (\mathcal Z)$
determined by the rule
for each
![]() $f \in \text {Lsc}([0,1],\operatorname {Cu} (D))$
is a Cuntz category morphism. Since
$f \in \text {Lsc}([0,1],\operatorname {Cu} (D))$
is a Cuntz category morphism. Since
![]() $\mathcal Z$
has unique trace,
$\mathcal Z$
has unique trace,
![]() $\sigma $
maps into
$\sigma $
maps into
![]() $\operatorname {Cu} (\mathcal Z)$
(which is naturally isomorphic to
$\operatorname {Cu} (\mathcal Z)$
(which is naturally isomorphic to
![]() $V(D) \sqcup (0,\infty ]$
, by [Reference Elliott, Robert and Santiago33, Corollary 6.8]). By [Reference Antoine, Perera and Santiago4, Theorem 2.6], the natural map
$V(D) \sqcup (0,\infty ]$
, by [Reference Elliott, Robert and Santiago33, Corollary 6.8]). By [Reference Antoine, Perera and Santiago4, Theorem 2.6], the natural map
![]() $\operatorname {Cu}(C([0,1],D)) \to \text {Lsc}([0,1],\operatorname {Cu} (D))$
is a Cuntz category isomorphism. Combining this isomorphism with
$\operatorname {Cu}(C([0,1],D)) \to \text {Lsc}([0,1],\operatorname {Cu} (D))$
is a Cuntz category isomorphism. Combining this isomorphism with
![]() $\sigma $
, one has a Cuntz category morphism from
$\sigma $
, one has a Cuntz category morphism from
![]() $\operatorname {Cu}(C([0,1],D)) \to \operatorname {Cu}(\mathcal Z)$
. This induces a Cuntz category morphism between
$\operatorname {Cu}(C([0,1],D)) \to \operatorname {Cu}(\mathcal Z)$
. This induces a Cuntz category morphism between
![]() $C_0(0,1] \otimes D$
and
$C_0(0,1] \otimes D$
and
![]() $\mathcal Z$
of the augmented invariant of [Reference Robert54] and by [Reference Robert54, Theorem 1.0.1], there exists a
$\mathcal Z$
of the augmented invariant of [Reference Robert54] and by [Reference Robert54, Theorem 1.0.1], there exists a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi \,{\colon}\, C_0(0,1] \otimes D \to \mathcal Z$
which then induces an order zero map
$\pi \,{\colon}\, C_0(0,1] \otimes D \to \mathcal Z$
which then induces an order zero map
![]() $\rho \,{\colon}\, D \to \mathcal Z$
, by [Reference Winter and Zacharias68, Corollary 4.1]. It is then checked that
$\rho \,{\colon}\, D \to \mathcal Z$
, by [Reference Winter and Zacharias68, Corollary 4.1]. It is then checked that
![]() $\rho $
satisfies the desired tracial identity in [Reference Castillejos10, Lemma 5.6.5].
$\rho $
satisfies the desired tracial identity in [Reference Castillejos10, Lemma 5.6.5].
In order to move beyond the unique trace case in Theorem 4.5, the order zero maps implementing a colored equivalence cannot be made with a sequence of maps that factor through
![]() $\mathcal Z$
, as that would collapse the trace space to a single point (such maps necessarily preserve the trace space up to isomorphism, by Theorem 4.1). Hence, a replacement for [Reference Castillejos10, Lemma 5.6.5] is needed. Our formulation of the order zero map realizing prescribed tracial data maps directly into a unital, simple, separable, exact,
$\mathcal Z$
, as that would collapse the trace space to a single point (such maps necessarily preserve the trace space up to isomorphism, by Theorem 4.1). Hence, a replacement for [Reference Castillejos10, Lemma 5.6.5] is needed. Our formulation of the order zero map realizing prescribed tracial data maps directly into a unital, simple, separable, exact,
![]() $\mathcal Z$
-stable C
$\mathcal Z$
-stable C
![]() $^*$
-algebra B with stable rank one whose tracial simplex is isomorphic to that of an AF algebra D (no longer assumed to have unique trace) instead of
$^*$
-algebra B with stable rank one whose tracial simplex is isomorphic to that of an AF algebra D (no longer assumed to have unique trace) instead of
![]() $\mathcal Z$
. This order zero map is constructed by showing that the map
$\mathcal Z$
. This order zero map is constructed by showing that the map
![]() $\sigma \,{\colon}\, \operatorname {Cu}(C_0(0,1] \otimes D) \to \text {LAff}_+(TB)$
determined by the rule
$\sigma \,{\colon}\, \operatorname {Cu}(C_0(0,1] \otimes D) \to \text {LAff}_+(TB)$
determined by the rule
for each
![]() $[d] \in \operatorname {Cu}(C_0(0,1] \otimes D)$
is a Cuntz category morphism, where
$[d] \in \operatorname {Cu}(C_0(0,1] \otimes D)$
is a Cuntz category morphism, where
![]() $\mu $
is a faithful densely defined lower semicontinuous trace on
$\mu $
is a faithful densely defined lower semicontinuous trace on
![]() $C_0(0,1]$
. Since
$C_0(0,1]$
. Since
![]() $\operatorname {LAff}_+(TB)$
is a subobject of
$\operatorname {LAff}_+(TB)$
is a subobject of
![]() $\operatorname {Cu}(B)$
(Lemma 2.12),
$\operatorname {Cu}(B)$
(Lemma 2.12),
![]() $\sigma $
extends to a Cuntz category morphism into
$\sigma $
extends to a Cuntz category morphism into
![]() $\operatorname {Cu}(B)$
.
$\operatorname {Cu}(B)$
.
In fact, we could not figure out how to use the characterization of compact containment given in [Reference Antoine, Perera and Santiago4] to work directly at the level of the cone over the AF algebra and so it is established that
![]() $\sigma $
is a Cuntz category morphism by showing that it is the inductive limit of Cuntz category morphisms
$\sigma $
is a Cuntz category morphism by showing that it is the inductive limit of Cuntz category morphisms
![]() $\sigma _i$
at the finite stages of the AF algebra inductive limit decomposition. That
$\sigma _i$
at the finite stages of the AF algebra inductive limit decomposition. That
![]() $\sigma _i$
is a generalized Cuntz morphism follows from [Reference Elliott, Robert and Santiago33]. To show that compact containment is preserved by
$\sigma _i$
is a generalized Cuntz morphism follows from [Reference Elliott, Robert and Santiago33]. To show that compact containment is preserved by
![]() $\sigma _i$
, we show (in the proof of Theorem 4.3) that
$\sigma _i$
, we show (in the proof of Theorem 4.3) that
![]() $\sigma _i$
is a weighted direct sum of copies of the functional
$\sigma _i$
is a weighted direct sum of copies of the functional
![]() $d_{\mu } \,{\colon}\, \operatorname {Cu}(C_0(0,1]) \to [0,\infty ]$
. This reduces the problem of showing that
$d_{\mu } \,{\colon}\, \operatorname {Cu}(C_0(0,1]) \to [0,\infty ]$
. This reduces the problem of showing that
![]() $\sigma _i$
preserves compact containment to showing that the functional
$\sigma _i$
preserves compact containment to showing that the functional
![]() $d_{\mu }$
preserves compact containment. This is done in Section 3, where we give a topological characterization of when functionals arising from a faithful densely defined lower semicontinuous trace preserve compact containment. In particular, an essential property of the half open interval is that it does not contain nonempty compact open sets. (At the end of the section, we give a sufficient condition for when nonfaithful densely defined lower semicontinuous traces induce functionals which preserve compact containment.) In Theorem 4.3, it is shown that the morphisms
$d_{\mu }$
preserves compact containment. This is done in Section 3, where we give a topological characterization of when functionals arising from a faithful densely defined lower semicontinuous trace preserve compact containment. In particular, an essential property of the half open interval is that it does not contain nonempty compact open sets. (At the end of the section, we give a sufficient condition for when nonfaithful densely defined lower semicontinuous traces induce functionals which preserve compact containment.) In Theorem 4.3, it is shown that the morphisms
![]() $\sigma _i$
give rise to a one-sided intertwining at the level of the Cuntz category. By the classification theorem (of [Reference Ciuperca and Elliott14]) for
$\sigma _i$
give rise to a one-sided intertwining at the level of the Cuntz category. By the classification theorem (of [Reference Ciuperca and Elliott14]) for
![]() $*$
-homomorphisms out of cones, this then gives rise to an approximate one-sided intertwining at the level of C
$*$
-homomorphisms out of cones, this then gives rise to an approximate one-sided intertwining at the level of C
![]() $^*$
-algebras. The inductive limit
$^*$
-algebras. The inductive limit
![]() $*$
-homomorphism
$*$
-homomorphism
![]() ${\pi : C_0(0,1] \otimes D \to B}$
then induces the desired order zero map.
${\pi : C_0(0,1] \otimes D \to B}$
then induces the desired order zero map.
The outline of the paper is as follows: In Section 2, we introduce basic notions and terminology along with important results that are essential for the main results. We also include statements which are likely known to experts, but possibly not spelled out in literature. In Section 3, we give a characterization for when a trace
![]() $\tau $
on a C
$\tau $
on a C
![]() $^*$
-algebra A induces a functional
$^*$
-algebra A induces a functional
![]() $d_{\tau }$
on
$d_{\tau }$
on
![]() $\operatorname {Cu}(A)$
which preserves compact containment. In Section 4, we prove the main results and discuss some consequences and questions.
$\operatorname {Cu}(A)$
which preserves compact containment. In Section 4, we prove the main results and discuss some consequences and questions.
2 Preliminaries
2.1 Order zero maps
Let A and B be C
![]() $^*$
-algebras, and let
$^*$
-algebras, and let
![]() $\varphi \,{\colon}\, A \to B$
be a completely positive (c.p.) map (c.p.c. if the map is contractive). The map
$\varphi \,{\colon}\, A \to B$
be a completely positive (c.p.) map (c.p.c. if the map is contractive). The map
![]() $\varphi $
is said to have order zero if it preserves orthogonality (see [Reference Winter and Zacharias68, Definition 1.3]). Examples of such maps include
$\varphi $
is said to have order zero if it preserves orthogonality (see [Reference Winter and Zacharias68, Definition 1.3]). Examples of such maps include
![]() $*$
-homomorphisms and more generally, the product of a
$*$
-homomorphisms and more generally, the product of a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi \,{\colon}\, A \to B$
with a positive element
$\pi \,{\colon}\, A \to B$
with a positive element
![]() $h \in B$
which commutes with the image of
$h \in B$
which commutes with the image of
![]() $\pi $
. The following structure theorem shows that all order zero maps admit such a decomposition. The
$\pi $
. The following structure theorem shows that all order zero maps admit such a decomposition. The
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi _{\varphi }$
which appears below is called the support
$\pi _{\varphi }$
which appears below is called the support
![]() $*$
-homomorphism of
$*$
-homomorphism of
![]() $\varphi $
.
$\varphi $
.
Theorem 2.1 [Reference Winter and Zacharias68, Theorem 2.3]
Let A and B be C
![]() $^*$
-algebras, and let
$^*$
-algebras, and let
![]() $\varphi \,{\colon}\, A \to B$
be a c.p. order zero map. Define
$\varphi \,{\colon}\, A \to B$
be a c.p. order zero map. Define
![]() $C:= \text {C}^*(\varphi (A)) \subseteq B$
(and denote the multiplier algebra of C by
$C:= \text {C}^*(\varphi (A)) \subseteq B$
(and denote the multiplier algebra of C by
![]() $\mathcal M(C)$
). Then there exist a unique positive element
$\mathcal M(C)$
). Then there exist a unique positive element
![]() $h_{\varphi }$
in the center of
$h_{\varphi }$
in the center of
![]() $\mathcal M(C)$
and a
$\mathcal M(C)$
and a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi _{\varphi } \,{\colon}\, A \to \mathcal M(C)$
such that
$\pi _{\varphi } \,{\colon}\, A \to \mathcal M(C)$
such that
for all
![]() $a \in A$
. Necessarily,
$a \in A$
. Necessarily,
![]() $\|h_{\varphi }\| = \|\varphi \|$
, and if A is unital, then
$\|h_{\varphi }\| = \|\varphi \|$
, and if A is unital, then
![]() $h_{\varphi } = \varphi (1_A) \in B$
.
$h_{\varphi } = \varphi (1_A) \in B$
.
Corollary 2.2 [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Proposition 1.4]
Let
![]() $\varphi \,{\colon}\, A \to B$
be a c.p.c. order zero map between C
$\varphi \,{\colon}\, A \to B$
be a c.p.c. order zero map between C
![]() $^*$
-algebras where A is unital. Then
$^*$
-algebras where A is unital. Then
![]() $\varphi $
is a
$\varphi $
is a
![]() $*$
-homomorphism if, and only if,
$*$
-homomorphism if, and only if,
![]() $\varphi (1_A)$
is a projection.
$\varphi (1_A)$
is a projection.
Proof This follows immediately from Theorem 2.1.
The next corollary is known as the order zero functional calculus. To avoid ambiguity with the notation introduced below, we will never use
![]() $\varphi ^n$
to mean iterated composition.
$\varphi ^n$
to mean iterated composition.
Corollary 2.3 [Reference Winter and Zacharias68, Corollary 3.2]
Let
![]() $\varphi : A \to B$
be a c.p.c. order zero map, and let the notation be as in Theorem 2.1. Then, for any positive function f in
$\varphi : A \to B$
be a c.p.c. order zero map, and let the notation be as in Theorem 2.1. Then, for any positive function f in
![]() $C_0((0,1])$
, the map
$C_0((0,1])$
, the map
defined by
is a well-defined c.p. order zero map taking values in C. If f has norm at most one, then the map
![]() $f(\varphi )$
is contractive.
$f(\varphi )$
is contractive.
Let
![]() $\varphi \,{\colon}\, A \to B$
and
$\varphi \,{\colon}\, A \to B$
and
![]() $\psi \,{\colon}\, B \to C$
be c.p.c. order zero maps between unital C
$\psi \,{\colon}\, B \to C$
be c.p.c. order zero maps between unital C
![]() $^*$
-algebras, and let the notation be as in Theorem 2.1. The following statement concerning the composition
$^*$
-algebras, and let the notation be as in Theorem 2.1. The following statement concerning the composition
![]() $\psi \varphi $
is established in [Reference Castillejos10] by proving that the support
$\psi \varphi $
is established in [Reference Castillejos10] by proving that the support
![]() $*$
-homomorphism of a composition is essentially the composition of the the individual support
$*$
-homomorphism of a composition is essentially the composition of the the individual support
![]() $*$
-homomorphisms (more precisely, it is shown that
$*$
-homomorphisms (more precisely, it is shown that
![]() $h_{\psi \varphi }\pi _{\psi \varphi } = h_{\psi \varphi } \pi _{\psi } \pi _{\varphi }$
[Reference Castillejos10, Corollary 1.4.14]. We give a slightly more direct proof.
$h_{\psi \varphi }\pi _{\psi \varphi } = h_{\psi \varphi } \pi _{\psi } \pi _{\varphi }$
[Reference Castillejos10, Corollary 1.4.14]. We give a slightly more direct proof.
Corollary 2.4 [Reference Castillejos10, Section 5.6]
Suppose
![]() $\varphi \,{\colon}\, A \to B$
and
$\varphi \,{\colon}\, A \to B$
and
![]() $\psi \,{\colon}\, B \to C$
are c.p.c. order zero maps between C
$\psi \,{\colon}\, B \to C$
are c.p.c. order zero maps between C
![]() $^*$
-algebras. Then
$^*$
-algebras. Then
for each
![]() $n \in \mathbb N$
(excluding
$n \in \mathbb N$
(excluding
![]() $n = 0$
). If
$n = 0$
). If
![]() $\varphi $
is a
$\varphi $
is a
![]() $*$
-homomorphism, then
$*$
-homomorphism, then
![]() $\varphi ^n = \varphi $
.
$\varphi ^n = \varphi $
.
Proof By [Reference Winter and Zacharias68, Proposition 2.2], we may suppose, without loss of generality, that A is unital. Let the notation be as in Theorem 2.1 for
![]() $\varphi $
,
$\varphi $
,
![]() $\psi $
and
$\psi $
and
![]() $\psi \varphi $
. Then we have
$\psi \varphi $
. Then we have
using that A is unital for the first two equalities. Now, for fixed
![]() $n \in \mathbb N$
, we have
$n \in \mathbb N$
, we have
 $$ \begin{align*} (\psi \varphi)^{n+1} & \stackrel{(2.2)}{=} h_{\psi \varphi}^{n+1} \pi_{\psi \varphi} = h_{\psi \varphi}^n h_{\psi \varphi} \pi_{\psi \varphi} \stackrel{(2.4)}{=} h_{\psi}^n \pi_{\psi}(h_{\varphi}^n) h_{\psi \varphi} \pi_{\psi \varphi} \\ & \stackrel{(2.1)}{=} h_{\psi}^n \pi_{\psi}(h_{\varphi}^n) \psi \varphi \stackrel{(2.1)}{=} (h_{\psi}^{n+1} \pi_{\psi}(h_{\varphi}^n)\pi_{\psi})(h_{\varphi} \pi_{\varphi}) \\ & = (h_{\psi}^{n+1} \pi_{\psi})(h_{\varphi}^{n+1} \pi_{\varphi}) \stackrel{(2.2)}{=} \psi^{n+1} \varphi^{n+1}. \end{align*} $$
$$ \begin{align*} (\psi \varphi)^{n+1} & \stackrel{(2.2)}{=} h_{\psi \varphi}^{n+1} \pi_{\psi \varphi} = h_{\psi \varphi}^n h_{\psi \varphi} \pi_{\psi \varphi} \stackrel{(2.4)}{=} h_{\psi}^n \pi_{\psi}(h_{\varphi}^n) h_{\psi \varphi} \pi_{\psi \varphi} \\ & \stackrel{(2.1)}{=} h_{\psi}^n \pi_{\psi}(h_{\varphi}^n) \psi \varphi \stackrel{(2.1)}{=} (h_{\psi}^{n+1} \pi_{\psi}(h_{\varphi}^n)\pi_{\psi})(h_{\varphi} \pi_{\varphi}) \\ & = (h_{\psi}^{n+1} \pi_{\psi})(h_{\varphi}^{n+1} \pi_{\varphi}) \stackrel{(2.2)}{=} \psi^{n+1} \varphi^{n+1}. \end{align*} $$
If
![]() $\varphi $
is a
$\varphi $
is a
![]() $*$
-homomorphism, then
$*$
-homomorphism, then
![]() $h_{\varphi } = \varphi (1_A)$
is a projection and so
$h_{\varphi } = \varphi (1_A)$
is a projection and so
![]() $\varphi ^n = \varphi $
.
$\varphi ^n = \varphi $
.
The following correspondence between c.p.c. order zero maps and
![]() $*$
-homomorphisms out of cones is from [Reference Winter and Zacharias68], but the formulation presented here is that of [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Proposition 1.3]. Both Corollary 2.5 and Lemma 2.6 will be used in the proof of Theorem 4.5.
$*$
-homomorphisms out of cones is from [Reference Winter and Zacharias68], but the formulation presented here is that of [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Proposition 1.3]. Both Corollary 2.5 and Lemma 2.6 will be used in the proof of Theorem 4.5.
Corollary 2.5 [Reference Winter and Zacharias68, Corollary 3.1]
Let A and B be C
![]() $^*$
-algebras. There is a one-to-one correspondence between c.p.c. order zero maps
$^*$
-algebras. There is a one-to-one correspondence between c.p.c. order zero maps
![]() $\varphi \,{\colon}\, A \to B$
and
$\varphi \,{\colon}\, A \to B$
and
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\pi : C_0(0,1] \otimes A \to B$
where
$\pi : C_0(0,1] \otimes A \to B$
where
![]() $\varphi $
and
$\varphi $
and
![]() $\pi $
are related by the commuting diagram
$\pi $
are related by the commuting diagram

and
![]() $t \in C_0(0,1]$
denotes the identity function.
$t \in C_0(0,1]$
denotes the identity function.
Lemma 2.6 The order zero functional calculus can be recovered from the identity
where f is a positive function in
![]() $C_0(0,1]$
,
$C_0(0,1]$
,
![]() $a \in A$
, and
$a \in A$
, and
![]() $\varphi $
and
$\varphi $
and
![]() $\pi $
are as in the corollary above.
$\pi $
are as in the corollary above.
Proof We may again, by [Reference Winter and Zacharias68, Proposition 2.2], suppose without loss of generality that A is unital. Let the notation be as in Theorem 2.1, and let
![]() $f \in C_0(0,1]_+$
be given. By Theorem 2.1 and Corollary 2.5,
$f \in C_0(0,1]_+$
be given. By Theorem 2.1 and Corollary 2.5,
![]() $h_{\varphi } = \varphi (1_A) = \pi (t \otimes 1_A)$
. So for fixed
$h_{\varphi } = \varphi (1_A) = \pi (t \otimes 1_A)$
. So for fixed
![]() $n \in \mathbb N$
and
$n \in \mathbb N$
and
![]() $a \in A$
,
$a \in A$
,
 $$ \begin{align*} \varphi^{n+1}(a) & \stackrel{(2.2)}{=} h_{\varphi}^{n+1} \pi_{\varphi}(a) = h_{\varphi}^n (h_{\varphi} \pi_{\varphi}(a)) \stackrel{(2.1)}{=} h_{\varphi}^n \varphi(a) \\ & \stackrel{(2.5)}{=} \pi(t^n \otimes 1_A) \pi(t \otimes a) = \pi(t^{n+1} \otimes a). \end{align*} $$
$$ \begin{align*} \varphi^{n+1}(a) & \stackrel{(2.2)}{=} h_{\varphi}^{n+1} \pi_{\varphi}(a) = h_{\varphi}^n (h_{\varphi} \pi_{\varphi}(a)) \stackrel{(2.1)}{=} h_{\varphi}^n \varphi(a) \\ & \stackrel{(2.5)}{=} \pi(t^n \otimes 1_A) \pi(t \otimes a) = \pi(t^{n+1} \otimes a). \end{align*} $$
It is readily seen from this calculation and approximating f by polynomials in
![]() $C_0(0,1]$
that
$C_0(0,1]$
that
![]() $f(\varphi )(a) = \pi (f \otimes a)$
.
$f(\varphi )(a) = \pi (f \otimes a)$
.
2.2 Ultrapowers
Let A be a C
![]() $^*$
-algebra. The bounded sequence algebra of A, denoted by
$^*$
-algebra. The bounded sequence algebra of A, denoted by
![]() $l^{\infty }(A)$
, is defined to be the collection of all norm-bounded sequences of elements from A. The ideal of elements in
$l^{\infty }(A)$
, is defined to be the collection of all norm-bounded sequences of elements from A. The ideal of elements in
![]() $l^{\infty }(A)$
which go to zero along the ultrafilter
$l^{\infty }(A)$
which go to zero along the ultrafilter
![]() $\omega $
is denoted by
$\omega $
is denoted by
![]() $c_{\omega }(A)$
. The ultrapower of A is the quotient C
$c_{\omega }(A)$
. The ultrapower of A is the quotient C
![]() $^*$
-algebra
$^*$
-algebra
![]() $A_{\omega }:= l^{\infty }(A)/c_{\omega }(A)$
. We shall write
$A_{\omega }:= l^{\infty }(A)/c_{\omega }(A)$
. We shall write
![]() $(a_n)_{n=1}^{\infty }$
for an element in
$(a_n)_{n=1}^{\infty }$
for an element in
![]() $A_{\omega }$
rather than the class it belongs to. We will occasionally write a to refer to the image of a under the canonical embedding of A into
$A_{\omega }$
rather than the class it belongs to. We will occasionally write a to refer to the image of a under the canonical embedding of A into
![]() $A_{\omega }$
. A sequence
$A_{\omega }$
. A sequence
![]() $\varphi _n \,{\colon}\, A \to B$
of c.p.c. order zero maps between C
$\varphi _n \,{\colon}\, A \to B$
of c.p.c. order zero maps between C
![]() $^*$
-algebras induces a c.p.c order zero map
$^*$
-algebras induces a c.p.c order zero map
![]() $\varphi : A_{\omega } \to B_{\omega }$
between ultrapowers. We denote the induced map by
$\varphi : A_{\omega } \to B_{\omega }$
between ultrapowers. We denote the induced map by
![]() $\varphi := (\varphi _n)_{n = 1}^{\infty }$
. If A is unital, then, with notation as in Theorem 2.1, we see that
$\varphi := (\varphi _n)_{n = 1}^{\infty }$
. If A is unital, then, with notation as in Theorem 2.1, we see that
![]() $h_{\varphi } = (h_{\varphi _n})_{n=1}^{\infty }$
and so the order zero functional calculus for
$h_{\varphi } = (h_{\varphi _n})_{n=1}^{\infty }$
and so the order zero functional calculus for
![]() $\varphi $
can be realized by applying positive functions in
$\varphi $
can be realized by applying positive functions in
![]() $C_0(0,1]$
componentwise to
$C_0(0,1]$
componentwise to
![]() $\varphi _n$
.
$\varphi _n$
.
2.3 Traces and finiteness
Let A be a C
![]() $^*$
-algebra. By a trace on
$^*$
-algebra. By a trace on
![]() $A,$
we will mean a lower semicontinuous function
$A,$
we will mean a lower semicontinuous function
![]() $\tau : A_+ \to [0,\infty ]$
that is additive, preserves zero, is positively homogeneous, and satisfies the trace identity
$\tau : A_+ \to [0,\infty ]$
that is additive, preserves zero, is positively homogeneous, and satisfies the trace identity
![]() $\tau (a^*a) = \tau (aa^*)$
for all
$\tau (a^*a) = \tau (aa^*)$
for all
![]() $a \in A$
. We will denote by
$a \in A$
. We will denote by
![]() $N_{\tau }$
the ideal of elements
$N_{\tau }$
the ideal of elements
![]() $a \in A$
such that
$a \in A$
such that
![]() $\tau (a^*a) = 0$
. A trace
$\tau (a^*a) = 0$
. A trace
![]() $\tau $
is said to be faithful if
$\tau $
is said to be faithful if
![]() $\tau (a^*a) = 0$
implies
$\tau (a^*a) = 0$
implies
![]() $a = 0$
. We will use the notation
$a = 0$
. We will use the notation
![]() $T(A)$
(or simply
$T(A)$
(or simply
![]() $TA$
) to denote the collection of all tracial states on A—a Choquet simplex if A is unital. The limit traces of
$TA$
) to denote the collection of all tracial states on A—a Choquet simplex if A is unital. The limit traces of
![]() $A_{\omega }$
are the tracial states on
$A_{\omega }$
are the tracial states on
![]() $A_{\omega }$
which are equal to
$A_{\omega }$
which are equal to
![]() $\lim _{n \to \omega } \tau _n$
where
$\lim _{n \to \omega } \tau _n$
where
![]() $(\tau _n)$
is some sequence of tracial states on A. We will denote the collection of limit traces on
$(\tau _n)$
is some sequence of tracial states on A. We will denote the collection of limit traces on
![]() $A_{\omega }$
by
$A_{\omega }$
by
![]() $T_{\omega }(A_{\omega })$
. We will occasionally not make a notational distinction between a trace in
$T_{\omega }(A_{\omega })$
. We will occasionally not make a notational distinction between a trace in
![]() $T(A)$
and (what we will refer to as) the constant limit trace in
$T(A)$
and (what we will refer to as) the constant limit trace in
![]() $T(A_{\omega })$
induced by it.
$T(A_{\omega })$
induced by it.
By [Reference Winter and Zacharias68, Corollary 3.4], a c.p.c. order zero map
![]() $\varphi \,{\colon}\, A \to B$
induces a mapping of bounded traces
$\varphi \,{\colon}\, A \to B$
induces a mapping of bounded traces
![]() $\varphi ^*\,{\colon}\, \mathbb R_+ T(B) \to \mathbb R_+ T(A)$
. We would be be interested in the case that
$\varphi ^*\,{\colon}\, \mathbb R_+ T(B) \to \mathbb R_+ T(A)$
. We would be be interested in the case that
![]() $\varphi ^*$
is an isomorphism of tracial simplices, but this hope turns out not to be realistic. Rather, considering a sequence of c.p.c. order zero maps
$\varphi ^*$
is an isomorphism of tracial simplices, but this hope turns out not to be realistic. Rather, considering a sequence of c.p.c. order zero maps
![]() $\varphi _k \,{\colon}\, A \to B$
, we will be interested in the case that the c.p.c. order zero map
$\varphi _k \,{\colon}\, A \to B$
, we will be interested in the case that the c.p.c. order zero map
![]() $\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
induced by
$\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
induced by
![]() $(\varphi _k)$
preserves constant limit traces (i.e., takes constant limit traces on
$(\varphi _k)$
preserves constant limit traces (i.e., takes constant limit traces on
![]() $B_{\omega }$
to constant limit traces on
$B_{\omega }$
to constant limit traces on
![]() $A_{\omega }$
), and furthermore, the map
$A_{\omega }$
), and furthermore, the map
![]() $ \tau \mapsto \lim _{k \to \omega } \tau \varphi _k$
,
$ \tau \mapsto \lim _{k \to \omega } \tau \varphi _k$
,
![]() $\tau \in T(B)$
, is an isomorphism of the simplices
$\tau \in T(B)$
, is an isomorphism of the simplices
![]() $T(B)$
and
$T(B)$
and
![]() $T(A)$
. (Note that requiring the sequence
$T(A)$
. (Note that requiring the sequence
![]() $(\varphi _k)$
to preserve constant limit traces is equivalent to requiring the sequence
$(\varphi _k)$
to preserve constant limit traces is equivalent to requiring the sequence
![]() $(\tau \varphi _k)$
to be norm convergent for every
$(\tau \varphi _k)$
to be norm convergent for every
![]() $\tau \in T(B)$
.) More generally, we shall be interested in the condition that a constant limit trace preserving c.p.c. order zero map
$\tau \in T(B)$
.) More generally, we shall be interested in the condition that a constant limit trace preserving c.p.c. order zero map
![]() $\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
(not necessarily arising from a sequence
$\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
(not necessarily arising from a sequence
![]() $(\varphi _k)$
as above) induces an isomorphism
$(\varphi _k)$
as above) induces an isomorphism
![]() ${T(B) \to T(A)}$
of tracial simplices via the composed map
${T(B) \to T(A)}$
of tracial simplices via the composed map
![]() $\iota _A^* \varphi ^* c_B$
where
$\iota _A^* \varphi ^* c_B$
where
![]() $c_B \,{\colon}\, T(B) \to T(B_{\omega })$
denotes the embedding of
$c_B \,{\colon}\, T(B) \to T(B_{\omega })$
denotes the embedding of
![]() $T(B)$
as constant limit traces on
$T(B)$
as constant limit traces on
![]() $T(B_{\omega })$
. (One might also consider the tracial cones, instead, and ask when they are isomorphic.)
$T(B_{\omega })$
. (One might also consider the tracial cones, instead, and ask when they are isomorphic.)
Calculations involving traces on
![]() $A_{\omega }$
will often be reduced to the case of limit traces by using the following fact about weak
$A_{\omega }$
will often be reduced to the case of limit traces by using the following fact about weak
![]() $^*$
density of limit traces. Generalizations of the statement presented here can be found in [Reference Ng and Robert46, Reference Ozawa47, Reference Rørdam57].
$^*$
density of limit traces. Generalizations of the statement presented here can be found in [Reference Ng and Robert46, Reference Ozawa47, Reference Rørdam57].
Theorem 2.7 [Reference Ozawa47, Theorem 8]
Let A be a separable, exact, and
![]() $\mathcal Z$
-stable C
$\mathcal Z$
-stable C
![]() $^*$
-algebra (where
$^*$
-algebra (where
![]() $\mathcal Z$
denotes the Jiang–Su algebra [Reference Jiang and Su39]). Then
$\mathcal Z$
denotes the Jiang–Su algebra [Reference Jiang and Su39]). Then
![]() $T_{\omega }(A)$
is weak
$T_{\omega }(A)$
is weak
![]() $^*$
dense in
$^*$
dense in
![]() $T(A_{\omega })$
.
$T(A_{\omega })$
.
Let A be a C
![]() $^*$
-algebra with nonempty tracial state space. We define the seminorm
$^*$
-algebra with nonempty tracial state space. We define the seminorm
![]() $\| \cdot \|_{2, T(A)}$
by
$\| \cdot \|_{2, T(A)}$
by
for each
![]() $a \in A$
. The trace-kernel ideal of
$a \in A$
. The trace-kernel ideal of
![]() $A_{\omega }$
is the set
$A_{\omega }$
is the set
and the quotient of
![]() $A_{\omega }$
by
$A_{\omega }$
by
![]() $J_A$
is called the uniform tracial ultrapower of A, and it is denoted by
$J_A$
is called the uniform tracial ultrapower of A, and it is denoted by
![]() $A^{\omega }$
. More details about these notions can be found in [Reference Castillejos, Evington, Tikuisis, White and Winter11, Section 1] and [Reference Kirchberg and Rørdam41, Section 4].
$A^{\omega }$
. More details about these notions can be found in [Reference Castillejos, Evington, Tikuisis, White and Winter11, Section 1] and [Reference Kirchberg and Rørdam41, Section 4].
Warning: In literature,
![]() $A^{\omega }$
has sometimes been used for the ultrapower of
$A^{\omega }$
has sometimes been used for the ultrapower of
![]() $A,$
while
$A,$
while
![]() $A_{\omega }$
has sometimes been used for the central sequence algebra of A. We remind the reader that
$A_{\omega }$
has sometimes been used for the central sequence algebra of A. We remind the reader that
![]() $A_{\omega }$
denotes the ultrapower of A and that
$A_{\omega }$
denotes the ultrapower of A and that
![]() $A^{\omega }$
denotes the uniform tracial ultrapower of A.
$A^{\omega }$
denotes the uniform tracial ultrapower of A.
Lemma 2.8 Let A be a C
![]() $^*$
-algebra, and let B be a C
$^*$
-algebra, and let B be a C
![]() $^*$
-algebra with
$^*$
-algebra with
![]() $T(B)$
nonempty such that the limit traces of
$T(B)$
nonempty such that the limit traces of
![]() $B_{\omega }$
are dense in
$B_{\omega }$
are dense in
![]() $T(B_{\omega })$
(e.g., C
$T(B_{\omega })$
(e.g., C
![]() $^*$
-algebras as in Theorem 2.7
$^*$
-algebras as in Theorem 2.7
![]() $),$
and let
$),$
and let
![]() $\varphi , \psi : A \to B_{\omega }$
be c.p.c. order zero maps. Then
$\varphi , \psi : A \to B_{\omega }$
be c.p.c. order zero maps. Then
![]() $\tau \varphi = \tau \psi $
for all
$\tau \varphi = \tau \psi $
for all
![]() $\tau \in T(B_{\omega })$
if, and only if,
$\tau \in T(B_{\omega })$
if, and only if,
![]() $\varphi $
agrees with
$\varphi $
agrees with
![]() $\psi $
in the uniform tracial ultrapower
$\psi $
in the uniform tracial ultrapower
![]() $B^{\omega }$
.
$B^{\omega }$
.
Proof Let
![]() $\pi \,{\colon}\, B_{\omega } \to B^{\omega }$
denote the canonical quotient map. It is enough to show that an element of
$\pi \,{\colon}\, B_{\omega } \to B^{\omega }$
denote the canonical quotient map. It is enough to show that an element of
![]() $B_{\omega }$
is in the kernel of every trace in
$B_{\omega }$
is in the kernel of every trace in
![]() $T(B_{\omega })$
exactly when it belongs to the trace-kernel ideal of
$T(B_{\omega })$
exactly when it belongs to the trace-kernel ideal of
![]() $B_{\omega }$
. Suppose
$B_{\omega }$
. Suppose
![]() $(b_n) \in \ker \tau $
for every
$(b_n) \in \ker \tau $
for every
![]() $\tau \in T(B_{\omega })$
. For each
$\tau \in T(B_{\omega })$
. For each
![]() $n \in \mathbb N$
, there exists a trace
$n \in \mathbb N$
, there exists a trace
![]() $\tau _n \in T(B)$
such that
$\tau _n \in T(B)$
such that
![]() $\tau _n(b_n^*b_n)$
is within
$\tau _n(b_n^*b_n)$
is within
![]() $1/n$
of
$1/n$
of
![]() $\|b_n\|_{2,T(B)}^2$
. By assumption,
$\|b_n\|_{2,T(B)}^2$
. By assumption,
![]() $(b_n)$
is in the kernel of the limit trace
$(b_n)$
is in the kernel of the limit trace
![]() $\lim _{n \to \omega } \tau _n$
on
$\lim _{n \to \omega } \tau _n$
on
![]() $T(B_{\omega })$
. Since the kernel of a trace is a left ideal, it follows that
$T(B_{\omega })$
. Since the kernel of a trace is a left ideal, it follows that
Conversely, suppose
![]() $b = (b_n)$
is in the trace-kernel ideal of
$b = (b_n)$
is in the trace-kernel ideal of
![]() $B_{\omega }$
. Since the limit traces of
$B_{\omega }$
. Since the limit traces of
![]() $B_{\omega }$
are weak
$B_{\omega }$
are weak
![]() $^*$
dense in
$^*$
dense in
![]() $T(B_{\omega })$
, it is enough to show that
$T(B_{\omega })$
, it is enough to show that
![]() $\tau (b) = 0$
for every limit trace
$\tau (b) = 0$
for every limit trace
![]() $\tau = \lim _{n \to \omega } \tau _n \in T(B_{\omega })$
. This follows from the computation
$\tau = \lim _{n \to \omega } \tau _n \in T(B_{\omega })$
. This follows from the computation
The first and second inequalities follow from [Reference Choi12, Theorem 2.7] and [Reference Choi12, Corollary 2.8], respectively.
The following statement holds somewhat more generally (see [Reference Rørdam57, Corollary 5.1]), but this is the setting which will be relevant for us in Theorem 4.5.
Theorem 2.9 [Reference Rørdam57, Corollary 5.1]
Let A be a (nonzero) unital, simple, exact,
![]() $\mathcal {Z}$
-stable C
$\mathcal {Z}$
-stable C
![]() $^*$
-algebra. Then A is either purely infinite or finite.
$^*$
-algebra. Then A is either purely infinite or finite.
Remark 2.10 When A is unital, simple, and
![]() $\mathcal Z$
-stable, the proof of the preceding theorem shows that the statement of [Reference Rørdam57, Theorem 6.7] can be slightly strengthened to say that the following three statements are equivalent:
$\mathcal Z$
-stable, the proof of the preceding theorem shows that the statement of [Reference Rørdam57, Theorem 6.7] can be slightly strengthened to say that the following three statements are equivalent:
-
(1) A is finite.
-
(2) A has stable rank one.
-
(3) A is stably finite.
2.4 The Cuntz category
If a and b are elements of an ordered set M, we will say that a is (countably) compactly contained in b, and we write
![]() $a \ll b$
, if for any increasing sequence
$a \ll b$
, if for any increasing sequence
![]() $(b_k) _{k=1}^{\infty }$
in M with
$(b_k) _{k=1}^{\infty }$
in M with
![]() $\sup _k b_k \geq b$
(or such that every upper bound of the sequence majorizes b), eventually
$\sup _k b_k \geq b$
(or such that every upper bound of the sequence majorizes b), eventually
![]() $b_k \geq a$
. An increasing sequence with each term compactly contained in the next is called rapidly increasing. An element which is compactly contained in itself is called compact (more precisely, countably compact).
$b_k \geq a$
. An increasing sequence with each term compactly contained in the next is called rapidly increasing. An element which is compactly contained in itself is called compact (more precisely, countably compact).
Cuntz category semigroups are ordered abelian semigroups with an additive identity with the following four properties:
-
(O1) Every increasing sequence in S has a supremum in S.
-
(O2) Any element of S is the supremum of a rapidly increasing sequence.
-
(O3) If
 $a_i$
and
$a_i$
and
 $b_i$
are elements of S such that
$b_i$
are elements of S such that
 $a_i \ll b_i$
for
$a_i \ll b_i$
for
 $i = 1,2$
, then
$i = 1,2$
, then
 $a_1 + a_2 \ll b_1 + b_2$
.
$a_1 + a_2 \ll b_1 + b_2$
. -
(O4) If
 $(a_n)$
and
$(a_n)$
and
 $(b_n)$
are increasing sequences in S, then
$(b_n)$
are increasing sequences in S, then
 $\sup _n (a_n + b_n) = \sup _n a_n + \sup _n b_n$
.
$\sup _n (a_n + b_n) = \sup _n a_n + \sup _n b_n$
.
Cuntz category morphisms
![]() $f \,{\colon}\, S \to T$
are ordered semigroup maps (i.e., preserving order, addition, and the additive identity) which preserve suprema of increasing sequences and compact containment. A generalized Cuntz category morphism is a Cuntz category morphism which does not necessarily preserve compact containment. The Cuntz category has as objects the ordered semigroups and ordered semigroup maps with the properties stipulated above (see ([Reference Coward, Elliott and Ivanescu18, Reference Elliott, Robert and Santiago33, Reference Robert54]). It is easily checked, and it will be used without mention that Cartesian products and direct sums exist in this category.
$f \,{\colon}\, S \to T$
are ordered semigroup maps (i.e., preserving order, addition, and the additive identity) which preserve suprema of increasing sequences and compact containment. A generalized Cuntz category morphism is a Cuntz category morphism which does not necessarily preserve compact containment. The Cuntz category has as objects the ordered semigroups and ordered semigroup maps with the properties stipulated above (see ([Reference Coward, Elliott and Ivanescu18, Reference Elliott, Robert and Santiago33, Reference Robert54]). It is easily checked, and it will be used without mention that Cartesian products and direct sums exist in this category.
It was shown in [Reference Coward, Elliott and Ivanescu18] that there is a functor
![]() $\operatorname {Cu}(\cdot )$
from the category of C
$\operatorname {Cu}(\cdot )$
from the category of C
![]() $^*$
-algebras to the Cuntz category. Recall that, for a C
$^*$
-algebras to the Cuntz category. Recall that, for a C
![]() $^*$
-algebra A,
$^*$
-algebra A,
![]() $\operatorname {Cu}(A)$
is the ordered semigroup of Cuntz equivalence classes of positive elements in the stabilization of A and is a Cuntz category semigroup. We shall denote by
$\operatorname {Cu}(A)$
is the ordered semigroup of Cuntz equivalence classes of positive elements in the stabilization of A and is a Cuntz category semigroup. We shall denote by
![]() $[a]$
the Cuntz equivalence class of a positive element a of
$[a]$
the Cuntz equivalence class of a positive element a of
![]() $A \otimes \mathcal K$
. We shall denote by
$A \otimes \mathcal K$
. We shall denote by
![]() $V(A)$
the semigroup of Murray–von Neumann equivalence classes of projections in the stabilization of A. For a compact convex subset K of a locally convex topological vector space, we shall denote by
$V(A)$
the semigroup of Murray–von Neumann equivalence classes of projections in the stabilization of A. For a compact convex subset K of a locally convex topological vector space, we shall denote by
![]() $\operatorname {LAff}_+(K)$
the collection of lower semicontinuous extended positive real-valued affine functions on K which are strictly positive, except for the zero function which we include in
$\operatorname {LAff}_+(K)$
the collection of lower semicontinuous extended positive real-valued affine functions on K which are strictly positive, except for the zero function which we include in
![]() $\operatorname {LAff}_+(K)$
, and are the pointwise supremum of an increasing sequence of continuous and finite-valued such functions. If K is metrizable, then the latter condition is automatic. It was observed in Section 2 of [Reference Elliott, Ivanescu and Kucerovsky31] (and in Section 3 of [Reference Thiel62]) that
$\operatorname {LAff}_+(K)$
, and are the pointwise supremum of an increasing sequence of continuous and finite-valued such functions. If K is metrizable, then the latter condition is automatic. It was observed in Section 2 of [Reference Elliott, Ivanescu and Kucerovsky31] (and in Section 3 of [Reference Thiel62]) that
![]() $\operatorname {LAff}_+(K)$
, equipped with pointwise order and addition, is a Cuntz category semigroup. The addition and order structure defined on the disjoint union decomposition appearing in the following important computation can be found in Section 6 of [Reference Elliott, Robert and Santiago33]. Related work on the unstabilized Cuntz semigroup that was done prior to the result stated here can be found in [Reference Brown, Perera and Toms9, Reference Dadarlat and Toms21, Reference Perera and Toms49]. Recent developments that go well beyond what is needed in this paper include [Reference Antoine, Perera, Robert and Thiel3, Theorem 7.15] and [Reference Thiel62, Theorem 8.11].
$\operatorname {LAff}_+(K)$
, equipped with pointwise order and addition, is a Cuntz category semigroup. The addition and order structure defined on the disjoint union decomposition appearing in the following important computation can be found in Section 6 of [Reference Elliott, Robert and Santiago33]. Related work on the unstabilized Cuntz semigroup that was done prior to the result stated here can be found in [Reference Brown, Perera and Toms9, Reference Dadarlat and Toms21, Reference Perera and Toms49]. Recent developments that go well beyond what is needed in this paper include [Reference Antoine, Perera, Robert and Thiel3, Theorem 7.15] and [Reference Thiel62, Theorem 8.11].
Theorem 2.11 [Reference Elliott, Robert and Santiago33, Corollary 6.8]
Let A be a unital, simple, separable, exact,
![]() $\mathcal Z$
-stable, and finite C
$\mathcal Z$
-stable, and finite C
![]() $^*$
-algebra. Then, in a natural way,
$^*$
-algebra. Then, in a natural way,
Lemma 2.12 We note that
![]() $\operatorname {LAff}_+(TA)$
is a subobject of
$\operatorname {LAff}_+(TA)$
is a subobject of
![]() $\operatorname {Cu}(A)$
in the setting of Theorem 2.11, according to the embedding there.
$\operatorname {Cu}(A)$
in the setting of Theorem 2.11, according to the embedding there.
Proof Since the elements of
![]() $V(A)$
are compact in
$V(A)$
are compact in
![]() $\operatorname {Cu}(A)$
(by Corollary 5 of [Reference Coward, Elliott and Ivanescu18]; this statement does not use stable rank one), it is clear that the embedding of
$\operatorname {Cu}(A)$
(by Corollary 5 of [Reference Coward, Elliott and Ivanescu18]; this statement does not use stable rank one), it is clear that the embedding of
![]() $\operatorname {LAff}_+(TA)$
into
$\operatorname {LAff}_+(TA)$
into
![]() $\operatorname {Cu}(A)$
is a generalized Cuntz category morphism. To show that compact containment is preserved, let
$\operatorname {Cu}(A)$
is a generalized Cuntz category morphism. To show that compact containment is preserved, let
![]() $f \ll g$
in
$f \ll g$
in
![]() $\operatorname {LAff}_+(TA)$
and let
$\operatorname {LAff}_+(TA)$
and let
![]() $(g_n) _{n=1}^{\infty }$
be an increasing sequence in
$(g_n) _{n=1}^{\infty }$
be an increasing sequence in
![]() $\operatorname {Cu}(A)$
such that
$\operatorname {Cu}(A)$
such that
![]() $\sup _n g_n$
majorizes g. Passing to a subsequence, we may suppose that the sequence
$\sup _n g_n$
majorizes g. Passing to a subsequence, we may suppose that the sequence
![]() $(g_n) _{n=1}^{\infty }$
is composed entirely of projections or entirely of affine functions. In the latter case, since the embedding of
$(g_n) _{n=1}^{\infty }$
is composed entirely of projections or entirely of affine functions. In the latter case, since the embedding of
![]() $\operatorname {LAff}_+(TA)$
in
$\operatorname {LAff}_+(TA)$
in
![]() $\operatorname {Cu}(A)$
preserves increasing sequential suprema, we have
$\operatorname {Cu}(A)$
preserves increasing sequential suprema, we have
![]() $\sup _n g_n \in \operatorname {LAff}_+(TA)$
and so there is, by assumption, some
$\sup _n g_n \in \operatorname {LAff}_+(TA)$
and so there is, by assumption, some
![]() $g_n$
which majorizes f. Let us now consider the former case. Denote by
$g_n$
which majorizes f. Let us now consider the former case. Denote by
![]() $\widehat g_k$
the rank of
$\widehat g_k$
the rank of
![]() $g_k$
—the element of
$g_k$
—the element of
![]() $\operatorname {LAff}_+(TA)$
gotten by evaluation of traces in
$\operatorname {LAff}_+(TA)$
gotten by evaluation of traces in
![]() $TA$
at the projection
$TA$
at the projection
![]() $g_k$
.
$g_k$
.
By the characterization of compact containment in
![]() $\operatorname {LAff}_+(TA)$
in Section 2 of [Reference Elliott, Ivanescu and Kucerovsky31] (or [Reference Thiel62, Lemma 3.6]), there exists an
$\operatorname {LAff}_+(TA)$
in Section 2 of [Reference Elliott, Ivanescu and Kucerovsky31] (or [Reference Thiel62, Lemma 3.6]), there exists an
![]() $h \in \operatorname {LAff}_+(TA)$
which is continuous and finite-valued and an
$h \in \operatorname {LAff}_+(TA)$
which is continuous and finite-valued and an
![]() $\varepsilon> 0$
such that
$\varepsilon> 0$
such that
![]() $f \leq h < (1 + \varepsilon ) h \leq g$
. Since
$f \leq h < (1 + \varepsilon ) h \leq g$
. Since
![]() $0 \notin \operatorname {LAff}_+(TA)$
, h is strictly positive. It follows that there is, for each
$0 \notin \operatorname {LAff}_+(TA)$
, h is strictly positive. It follows that there is, for each
![]() $\tau \in TA$
, a neighbourhood of
$\tau \in TA$
, a neighbourhood of
![]() $\tau $
on which f is strictly majorized by some
$\tau $
on which f is strictly majorized by some
![]() $\widehat {g_k}$
. By compactness of
$\widehat {g_k}$
. By compactness of
![]() $TA$
and the fact that
$TA$
and the fact that
![]() $(g_n) _{n=1}^{\infty }$
is increasing, f is majorized by some
$(g_n) _{n=1}^{\infty }$
is increasing, f is majorized by some
![]() $\widehat {g_n}$
on all of
$\widehat {g_n}$
on all of
![]() $TA$
. This shows
$TA$
. This shows
![]() $f \ll g$
in
$f \ll g$
in
![]() $\operatorname {Cu}(A)$
.
$\operatorname {Cu}(A)$
.
To check that
![]() $\operatorname {LAff}_+(TA)$
is a subobject, it remains to note that
$\operatorname {LAff}_+(TA)$
is a subobject, it remains to note that
![]() $f \ll g$
holds in
$f \ll g$
holds in
![]() $\operatorname {LAff}_+(TA)$
if it holds in
$\operatorname {LAff}_+(TA)$
if it holds in
![]() $\operatorname {Cu}(A)$
. This follows immediately from the fact that increasing sequential suprema in
$\operatorname {Cu}(A)$
. This follows immediately from the fact that increasing sequential suprema in
![]() $\operatorname {LAff}_+(TA)$
are the same in
$\operatorname {LAff}_+(TA)$
are the same in
![]() $\operatorname {Cu} (A)$
(see above).
$\operatorname {Cu} (A)$
(see above).
Examples of Cuntz category semigroups not explicitly involving a C
![]() $^*$
-algebra include
$^*$
-algebra include
![]() $\overline {\mathbb N}:= \{0, 1, 2, \ldots , \infty \} $
and
$\overline {\mathbb N}:= \{0, 1, 2, \ldots , \infty \} $
and
![]() $[0,\infty ]$
with the usual order and addition taken from
$[0,\infty ]$
with the usual order and addition taken from
![]() $\mathbb R$
. In fact, these Cuntz objects both arise from C
$\mathbb R$
. In fact, these Cuntz objects both arise from C
![]() $^*$
-algebras. Let
$^*$
-algebras. Let
![]() $\text {Lsc}(X,M)$
denote the collection of lower semicontinuous functions from a space X to a Cuntz category semigroup M, equipped with pointwise order and addition. Then
$\text {Lsc}(X,M)$
denote the collection of lower semicontinuous functions from a space X to a Cuntz category semigroup M, equipped with pointwise order and addition. Then
![]() $\text {Lsc}(X,M)$
is a Cuntz category semigroup whenever X is a second-countable compact Hausdorff space with finite covering dimension and M is countably based (see [Reference Antoine, Perera and Santiago4, Theorem 5.17]). It was also shown in [Reference Vilalta66, Corollary 4.22] that
$\text {Lsc}(X,M)$
is a Cuntz category semigroup whenever X is a second-countable compact Hausdorff space with finite covering dimension and M is countably based (see [Reference Antoine, Perera and Santiago4, Theorem 5.17]). It was also shown in [Reference Vilalta66, Corollary 4.22] that
![]() $\text {Lsc}(X,\overline {\mathbb N})$
is a Cuntz category object when X is a compact metric space. It was proved in [Reference Ciuperca and Elliott14, Theorem 10.1] and [Reference Ivanescu38, Theorem 6.11] that
$\text {Lsc}(X,\overline {\mathbb N})$
is a Cuntz category object when X is a compact metric space. It was proved in [Reference Ciuperca and Elliott14, Theorem 10.1] and [Reference Ivanescu38, Theorem 6.11] that
![]() $\operatorname {Cu}(C_0(X)) \cong \text {Lsc}(X,\overline {\mathbb N})$
, via the rank map, if X is
$\operatorname {Cu}(C_0(X)) \cong \text {Lsc}(X,\overline {\mathbb N})$
, via the rank map, if X is
![]() $[0,1]$
or
$[0,1]$
or
![]() $(0,1]$
. More generally, if X is a locally compact Hausdorff space with covering dimension at most two and
$(0,1]$
. More generally, if X is a locally compact Hausdorff space with covering dimension at most two and
![]() $\check H_2(K) = 0$
(Cěch cohomology with integer coefficients) for every compact subset K of X, then again (via the rank map)
$\check H_2(K) = 0$
(Cěch cohomology with integer coefficients) for every compact subset K of X, then again (via the rank map)
![]() $\operatorname {Cu}(C_0(X)) \cong \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
, the ordered semigroup of lower semicontinuous extended positive integer-valued functions f such that
$\operatorname {Cu}(C_0(X)) \cong \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
, the ordered semigroup of lower semicontinuous extended positive integer-valued functions f such that
![]() $f ^{-1} (k,\infty ]$
is
$f ^{-1} (k,\infty ]$
is
![]() $\sigma $
-compact for each
$\sigma $
-compact for each
![]() $k \in \mathbb N$
(see [Reference Robert55, Theorem 1.1]). If
$k \in \mathbb N$
(see [Reference Robert55, Theorem 1.1]). If
![]() $C_0(X)$
is separable, these are the exact conditions needed on X for
$C_0(X)$
is separable, these are the exact conditions needed on X for
![]() $\operatorname {Cu}(C_0(X))$
to be isomorphic (via the rank map) to
$\operatorname {Cu}(C_0(X))$
to be isomorphic (via the rank map) to
![]() $\text {Lsc}(X,\overline {\mathbb N})$
(see [Reference Robert55, Theorem 1.3]). Note that X is a hereditarily Lindelöf locally compact Hausdorff space (as is the case when
$\text {Lsc}(X,\overline {\mathbb N})$
(see [Reference Robert55, Theorem 1.3]). Note that X is a hereditarily Lindelöf locally compact Hausdorff space (as is the case when
![]() $C_0(X)$
is separable) if, and only if,
$C_0(X)$
is separable) if, and only if,
![]() $\text {Lsc}_{\sigma }(X,\overline {\mathbb N}) = \text {Lsc}(X,\overline {\mathbb N})$
. In general,
$\text {Lsc}_{\sigma }(X,\overline {\mathbb N}) = \text {Lsc}(X,\overline {\mathbb N})$
. In general,
![]() $\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
is a Cuntz category object, and in fact (Theorem 3 of [Reference Elliott26]) a subobject of
$\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
is a Cuntz category object, and in fact (Theorem 3 of [Reference Elliott26]) a subobject of
![]() $\operatorname {Cu}(C_0(X))$
(this is noted in [Reference Thiel and Vilalta63, Corollary 4.8] in the case that X is metrizable and compact).
$\operatorname {Cu}(C_0(X))$
(this is noted in [Reference Thiel and Vilalta63, Corollary 4.8] in the case that X is metrizable and compact).
Proposition 2.13 Let X be a locally compact Hausdorff space. Then
![]() $\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
is a Cuntz category object.
$\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
is a Cuntz category object.
Proof Let us first recall a characterization of compact containment for
![]() $\sigma $
-compact elements in the lattice of open subsets of X, ordered by inclusion. If there is a compact subset K of X sitting in between open sets U and V, then U is compactly contained in V. For the converse, suppose U is compactly contained in V and that V is
$\sigma $
-compact elements in the lattice of open subsets of X, ordered by inclusion. If there is a compact subset K of X sitting in between open sets U and V, then U is compactly contained in V. For the converse, suppose U is compactly contained in V and that V is
![]() $\sigma $
-compact. Since X is locally compact Hausdorff, V is locally compact and by assumption, V is
$\sigma $
-compact. Since X is locally compact Hausdorff, V is locally compact and by assumption, V is
![]() $\sigma $
-compact so there exist an increasing sequence of open sets
$\sigma $
-compact so there exist an increasing sequence of open sets
![]() $(V_k) _{k=1}^{\infty }$
and an increasing sequence of compact sets
$(V_k) _{k=1}^{\infty }$
and an increasing sequence of compact sets
![]() $(K_k)_{k=1}^{\infty }$
such that
$(K_k)_{k=1}^{\infty }$
such that
![]() $V_k \subseteq K_k \subseteq V_{k+1}$
for each k and
$V_k \subseteq K_k \subseteq V_{k+1}$
for each k and
![]() $\sup _k K_k = V$
. Since U is compactly contained in V, there exists a k such that
$\sup _k K_k = V$
. Since U is compactly contained in V, there exists a k such that
![]() $U \subseteq V_k \subseteq K_k \subseteq V$
.
$U \subseteq V_k \subseteq K_k \subseteq V$
.
In the latter construction, we claim each
![]() $V_k$
can be chosen to be
$V_k$
can be chosen to be
![]() $\sigma $
-compact. Set
$\sigma $
-compact. Set
![]() $V_1:= \varnothing $
. By Urysohn’s lemma, there exists a continuous function
$V_1:= \varnothing $
. By Urysohn’s lemma, there exists a continuous function
![]() $f_{k+1}$
from X into
$f_{k+1}$
from X into
![]() $[0,1]$
which is equal to 1 on
$[0,1]$
which is equal to 1 on
![]() $K_k$
and is equal to 0 on
$K_k$
and is equal to 0 on
![]() $X \backslash V_{k+1}$
. The open support of
$X \backslash V_{k+1}$
. The open support of
![]() $f_{k+1}$
, with which we replace
$f_{k+1}$
, with which we replace
![]() $V_{k+1}$
, is an
$V_{k+1}$
, is an
![]() $F_{\sigma }$
-set sitting in between
$F_{\sigma }$
-set sitting in between
![]() $K_k$
and
$K_k$
and
![]() $K_{k+1}$
, and is therefore
$K_{k+1}$
, and is therefore
![]() $\sigma $
-compact.
$\sigma $
-compact.
(O1) Let
![]() $(f_n) _{n=1}^{\infty }$
be an increasing sequence in
$(f_n) _{n=1}^{\infty }$
be an increasing sequence in
![]() $\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
and denote by
$\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
and denote by
![]() ${f:= \sup _n f_n}$
. Then for each
${f:= \sup _n f_n}$
. Then for each
![]() $k \in \mathbb N$
,
$k \in \mathbb N$
,
![]() $\{f> k\} = \bigcup _{n=1}^{\infty } \{f_n > k\}$
. (Abbreviated notation.) Since
$\{f> k\} = \bigcup _{n=1}^{\infty } \{f_n > k\}$
. (Abbreviated notation.) Since
![]() $f_n$
is lower semicontinuous, each
$f_n$
is lower semicontinuous, each
![]() $\{f_n> k\}$
is open and so f is lower semicontinuous. Since each
$\{f_n> k\}$
is open and so f is lower semicontinuous. Since each
![]() $\{f_n> k\}$
is
$\{f_n> k\}$
is
![]() $\sigma $
-compact, a diagonalization argument shows
$\sigma $
-compact, a diagonalization argument shows
![]() $\{f> k\}$
is
$\{f> k\}$
is
![]() $\sigma $
-compact. This shows
$\sigma $
-compact. This shows
![]() $\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
is closed under suprema of increasing sequences.
$\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
is closed under suprema of increasing sequences.
(O4) is easily verified. It is also easy to see that if
![]() $\chi _U$
and
$\chi _U$
and
![]() $\chi _V$
are characteristic functions in
$\chi _V$
are characteristic functions in
![]() $\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
, then
$\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
, then
![]() $\chi _U \ll \chi _V$
if, and only if,
$\chi _U \ll \chi _V$
if, and only if,
![]() $U \ll V$
. We will now show that if
$U \ll V$
. We will now show that if
![]() $f, g \in \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
, then
$f, g \in \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
, then
![]() $f \ll g$
if, and only if, f is bounded and
$f \ll g$
if, and only if, f is bounded and
![]() $\{f> k\} \ll \{g > k\}$
for each k. Suppose f is compactly contained in g. Each
$\{f> k\} \ll \{g > k\}$
for each k. Suppose f is compactly contained in g. Each
![]() $\{g>k\}$
is the supremum of a rapidly increasing sequence of
$\{g>k\}$
is the supremum of a rapidly increasing sequence of
![]() $\sigma $
-compact open sets
$\sigma $
-compact open sets
![]() $(U_{k,i})_{i=0}^{\infty }$
and so there exist compact sets
$(U_{k,i})_{i=0}^{\infty }$
and so there exist compact sets
![]() $K_{k,i}$
such that
$K_{k,i}$
such that
![]() $U_{k,i} \subseteq K_{k,i} \subseteq U_{k+1,i}$
for each i. Moreover, by taking finite unions we may choose
$U_{k,i} \subseteq K_{k,i} \subseteq U_{k+1,i}$
for each i. Moreover, by taking finite unions we may choose
![]() $U_{k,i}$
and
$U_{k,i}$
and
![]() $K_{k,i}$
so that
$K_{k,i}$
so that
![]() $U_{k,i} \supseteq U_{k+1,i}$
and
$U_{k,i} \supseteq U_{k+1,i}$
and
![]() $K_{k,i} \supseteq K_{k+1,i}$
whenever
$K_{k,i} \supseteq K_{k+1,i}$
whenever
![]() $k \leq i$
. This gives the following inclusions:
$k \leq i$
. This gives the following inclusions:

The supremum of the increasing sequence of functions
![]() $(\sum _{k=0}^i \chi _{U_{k,i}}) _{i=0}^{\infty }$
is g. Since f is compactly contained in g, f is majorized by
$(\sum _{k=0}^i \chi _{U_{k,i}}) _{i=0}^{\infty }$
is g. Since f is compactly contained in g, f is majorized by
![]() $\sum _{k=0}^n \chi _{U_{k,n}}$
for some n and so f is bounded. By construction,
$\sum _{k=0}^n \chi _{U_{k,n}}$
for some n and so f is bounded. By construction,
![]() $\{f> k\} \subseteq U_{k,n} \subseteq K_{k,n} \subseteq \{g > k\}$
for
$\{f> k\} \subseteq U_{k,n} \subseteq K_{k,n} \subseteq \{g > k\}$
for
![]() $k \leq n$
(and if
$k \leq n$
(and if
![]() $k> n$
, then
$k> n$
, then
![]() $\{f> k\} = \varnothing \ll \{g > k\}$
). This shows
$\{f> k\} = \varnothing \ll \{g > k\}$
). This shows
![]() $\{f> k\}$
is compactly contained in
$\{f> k\}$
is compactly contained in
![]() $\{g> k\}$
for each k.
$\{g> k\}$
for each k.
Conversely, suppose f is bounded and that
![]() $\{f> k\} \ll \{g > k\}$
for each k. Let an increasing sequence
$\{f> k\} \ll \{g > k\}$
for each k. Let an increasing sequence
![]() $(g_i) _{i=1}^{\infty } $
whose supremum majorizes g be given. Since f is bounded,
$(g_i) _{i=1}^{\infty } $
whose supremum majorizes g be given. Since f is bounded,
![]() $f = \sum _{k=0}^n \chi _{\{f> k\}}$
for some n. Since
$f = \sum _{k=0}^n \chi _{\{f> k\}}$
for some n. Since
![]() $\{f> k\} \ll \{g > k\}$
for each k, there exists a compact set
$\{f> k\} \ll \{g > k\}$
for each k, there exists a compact set
![]() $K_k$
which sits in between
$K_k$
which sits in between
![]() $\{f> k\}$
and
$\{f> k\}$
and
![]() $\{g> k\}$
. Using that
$\{g> k\}$
. Using that
![]() $(g_i) _{i=1}^{\infty }$
is increasing, and that
$(g_i) _{i=1}^{\infty }$
is increasing, and that
![]() $g_i$
is extended positive integer-valued and lower semicontinuous, by compactness of each
$g_i$
is extended positive integer-valued and lower semicontinuous, by compactness of each
![]() $K_k$
,
$K_k$
,
![]() $g_i$
eventually majorizes
$g_i$
eventually majorizes
![]() $\sum _{k=0}^n \chi _{K_k}$
and therefore
$\sum _{k=0}^n \chi _{K_k}$
and therefore
![]() $g_i$
eventually majorizes f. This shows f is compactly contained in g.
$g_i$
eventually majorizes f. This shows f is compactly contained in g.
(O3) Suppose
![]() $f_i \ll g_i$
for
$f_i \ll g_i$
for
![]() $i = 1, 2$
. Then
$i = 1, 2$
. Then
![]() $f_1 + f_2$
is bounded (since
$f_1 + f_2$
is bounded (since
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are bounded). There is, for each k, a compact set
$f_2$
are bounded). There is, for each k, a compact set
![]() $K_{i,k}$
sitting in between
$K_{i,k}$
sitting in between
![]() $\{f_i> k\}$
and
$\{f_i> k\}$
and
![]() $\{g_i> k\}$
for
$\{g_i> k\}$
for
![]() $i = 1, 2$
. Taking the convention that
$i = 1, 2$
. Taking the convention that
![]() $K_{i,-1} = X$
, we have
$K_{i,-1} = X$
, we have
 $$ \begin{align*} \{f_1 + f_2> k\} & = \bigcup_{i=0}^{k+1} \{f_1 > k-i\} \cap \{f_2 > i-1\} \\ & \subseteq \bigcup_{i=0}^{k+1} \left ( K_{1,k-i} \cap K_{2,i-1} \right) \\ & \subseteq \bigcup_{i=0}^{k+1} \{g_1 > k-i\} \cap \{g_2 > i-1\} = \{g_1 + g_2 > k\}. \end{align*} $$
$$ \begin{align*} \{f_1 + f_2> k\} & = \bigcup_{i=0}^{k+1} \{f_1 > k-i\} \cap \{f_2 > i-1\} \\ & \subseteq \bigcup_{i=0}^{k+1} \left ( K_{1,k-i} \cap K_{2,i-1} \right) \\ & \subseteq \bigcup_{i=0}^{k+1} \{g_1 > k-i\} \cap \{g_2 > i-1\} = \{g_1 + g_2 > k\}. \end{align*} $$
This shows that
![]() $\{f_1 + f_2> k\} \ll \{g_1 + g_2 > k\}$
for each k, so (see the proof of (O4) above)
$\{f_1 + f_2> k\} \ll \{g_1 + g_2 > k\}$
for each k, so (see the proof of (O4) above)
![]() $f_1 + f_2$
is compactly contained in
$f_1 + f_2$
is compactly contained in
![]() $g_1 + g_2$
.
$g_1 + g_2$
.
(O2) Let
![]() $g \in \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
be given. Each
$g \in \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
be given. Each
![]() $\{g> k\}$
is the supremum of a rapidly increasing sequence of open sets
$\{g> k\}$
is the supremum of a rapidly increasing sequence of open sets
![]() $(U_{k,i})_{i=0}^{\infty }$
and so g is the supremum of the increasing sequence
$(U_{k,i})_{i=0}^{\infty }$
and so g is the supremum of the increasing sequence
![]() $(\sum _{k=0}^n \chi _{U_{k,n}})_{n=0}^{\infty }$
. By (O3), this sequence is rapidly increasing.
$(\sum _{k=0}^n \chi _{U_{k,n}})_{n=0}^{\infty }$
. By (O3), this sequence is rapidly increasing.
Theorem 2.14 [Reference Robert55, Theorem 1.1]
Let X be a locally compact Hausdorff space of covering dimension at most two with
![]() $\check H_2(K) = 0$
for every compact subset K of X. Then
$\check H_2(K) = 0$
for every compact subset K of X. Then
![]() $\operatorname {Cu}(C_0(X)) \cong \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
, the isomorphism being given by the rank map.
$\operatorname {Cu}(C_0(X)) \cong \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
, the isomorphism being given by the rank map.
In order to lift Cuntz category morphisms to
![]() $*$
-homomorphisms, we will need the following classification theorem of [Reference Ciuperca and Elliott14]. Further developments in this direction include [Reference Ciuperca, Elliott and Santiago15, Theorem 1], [Reference Robert54, Theorem 1.0.1], and [Reference Robert and Santiago56, Theorem 2].
$*$
-homomorphisms, we will need the following classification theorem of [Reference Ciuperca and Elliott14]. Further developments in this direction include [Reference Ciuperca, Elliott and Santiago15, Theorem 1], [Reference Robert54, Theorem 1.0.1], and [Reference Robert and Santiago56, Theorem 2].
Theorem 2.15 [Reference Ciuperca and Elliott14, Theorem 4.1 and remark page 29]
Let B be a stable rank one C
![]() $^*$
-algebra, and let
$^*$
-algebra, and let
![]() $s_B$
be a strictly positive element of B. If
$s_B$
be a strictly positive element of B. If
![]() $\sigma : \operatorname {Cu}(C_0(0,1]) \to \operatorname {Cu}(B)$
is a Cuntz category morphism taking
$\sigma : \operatorname {Cu}(C_0(0,1]) \to \operatorname {Cu}(B)$
is a Cuntz category morphism taking
![]() $[t]$
(where t denotes the identity map on
$[t]$
(where t denotes the identity map on
![]() $(0,1]$
) into
$(0,1]$
) into
![]() $[s_B]$
, or into
$[s_B]$
, or into
![]() $g \leq [s_B]$
, then there is a
$g \leq [s_B]$
, then there is a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi \,{\colon}\, C_0(0,1] \to B$
, which is unique up to approximate unitary equivalence, such that
$\pi \,{\colon}\, C_0(0,1] \to B$
, which is unique up to approximate unitary equivalence, such that
![]() $\operatorname {Cu}(\pi ) = \sigma $
.
$\operatorname {Cu}(\pi ) = \sigma $
.
2.5 Embedding theorems
Theorem 2.16 [Reference Kirchberg and Phillips40, Theorem 2.8]
If A is a unital, separable, and exact C
![]() $^*$
-algebra, then there exists a unital embedding of A into
$^*$
-algebra, then there exists a unital embedding of A into
![]() $\mathcal O_2$
.
$\mathcal O_2$
.
Theorem 2.17 If A is a unital, finite,
![]() $\mathcal Z$
-stable, simple, separable amenable C
$\mathcal Z$
-stable, simple, separable amenable C
![]() $^*$
-algebra satisfying the UCT), then there is a unital embedding of A into a unital, simple, separable AF algebra D giving rise to an isomorphism of tracial simplices.
$^*$
-algebra satisfying the UCT), then there is a unital embedding of A into a unital, simple, separable AF algebra D giving rise to an isomorphism of tracial simplices.
Proof Let
![]() $\mathcal Q$
denote the universal UHF algebra. Since there is an embedding of A into
$\mathcal Q$
denote the universal UHF algebra. Since there is an embedding of A into
![]() $A \otimes \mathcal Q$
which induces an isomorphism of tracial simplices, we may suppose, without loss of generality, that A is
$A \otimes \mathcal Q$
which induces an isomorphism of tracial simplices, we may suppose, without loss of generality, that A is
![]() $\mathcal Q$
-stable. (This will be used in applying [Reference Gong, Lin and Niu37] below.)
$\mathcal Q$
-stable. (This will be used in applying [Reference Gong, Lin and Niu37] below.)
Let
![]() $\rho \,{\colon}\, K_0(A) \to \text {Aff}(T(A))$
denote the map associated with the canonical pairing of
$\rho \,{\colon}\, K_0(A) \to \text {Aff}(T(A))$
denote the map associated with the canonical pairing of
![]() $K_0(A)$
with
$K_0(A)$
with
![]() $T(A)$
. Choose a countable dense subgroup G of
$T(A)$
. Choose a countable dense subgroup G of
![]() $\text {Aff}(T(A))$
containing the image of
$\text {Aff}(T(A))$
containing the image of
![]() $\rho $
. By [Reference Andô2, Reference Lindenstrauss44],
$\rho $
. By [Reference Andô2, Reference Lindenstrauss44],
![]() $\text {Aff}(T(A))$
with the strict pointwise order has the Riesz interpolation property, and therefore G does also. By [Reference Effros, Handelman and Shen23], there exists a unital, simple, separable AF algebra D with
$\text {Aff}(T(A))$
with the strict pointwise order has the Riesz interpolation property, and therefore G does also. By [Reference Effros, Handelman and Shen23], there exists a unital, simple, separable AF algebra D with
![]() $K_0(D) = G$
. Since
$K_0(D) = G$
. Since
![]() $K_0(D)$
is dense in
$K_0(D)$
is dense in
![]() $\text {Aff}(T(A))$
, the map
$\text {Aff}(T(A))$
, the map
![]() $T(A) \to S(K_0(D))$
is an isomorphism. Since D is an AF algebra,
$T(A) \to S(K_0(D))$
is an isomorphism. Since D is an AF algebra,
![]() $T(D) = S(K_0(D))$
, and so we have an isomorphism
$T(D) = S(K_0(D))$
, and so we have an isomorphism
![]() $\Phi \,{\colon}\, T(D) \to T(A)$
. We now have compatible maps
$\Phi \,{\colon}\, T(D) \to T(A)$
. We now have compatible maps
![]() $\rho : K_0(A) \to K_0(D)$
and
$\rho : K_0(A) \to K_0(D)$
and
![]() $\Phi \,{\colon}\, T(D) \to T(A)$
. Furthermore, A and we may suppose also D are
$\Phi \,{\colon}\, T(D) \to T(A)$
. Furthermore, A and we may suppose also D are
![]() $\mathcal Q$
-stable. By [Reference Castillejos, Evington, Tikuisis, White and Winter11, Theorem A], [Reference Elliott, Gong, Lin and Niu29, Theorem 1.1], and [Reference Tikuisis, White and Winter64, Theorem A],
$\mathcal Q$
-stable. By [Reference Castillejos, Evington, Tikuisis, White and Winter11, Theorem A], [Reference Elliott, Gong, Lin and Niu29, Theorem 1.1], and [Reference Tikuisis, White and Winter64, Theorem A],
![]() $A \otimes \mathcal Q$
has generalized tracial rank at most one—and therefore, A does too as it is
$A \otimes \mathcal Q$
has generalized tracial rank at most one—and therefore, A does too as it is
![]() $\mathcal Q$
-stable. The only additional constituent of the invariant (see [Reference Gong, Lin and Niu37, Definition 2.4]) used in the homomorphism theorem [Reference Gong, Lin and Niu37, Corollary 21.11] is a
$\mathcal Q$
-stable. The only additional constituent of the invariant (see [Reference Gong, Lin and Niu37, Definition 2.4]) used in the homomorphism theorem [Reference Gong, Lin and Niu37, Corollary 21.11] is a
![]() $K_1$
-map which we can take to be zero. The corresponding algebra map is the desired embedding.
$K_1$
-map which we can take to be zero. The corresponding algebra map is the desired embedding.
2.6 Uniqueness theorems
A couple of the key technical ingredients used in the proof of Theorem 4.5 are the following uniqueness theorems for maps from unital, separable amenable C
![]() $^*$
-algebras into unital, simple, separable,
$^*$
-algebras into unital, simple, separable,
![]() $\mathcal Z$
-stable C
$\mathcal Z$
-stable C
![]() $^*$
-algebras. These results were developed in [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6] with certain restrictions on the trace space. These tracial assumptions were removed in [Reference Castillejos, Evington, Tikuisis, White and Winter11]. For the statement involving a Kirchberg algebra (i.e., a unital, purely infinite, simple, separable amenable C
$^*$
-algebras. These results were developed in [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6] with certain restrictions on the trace space. These tracial assumptions were removed in [Reference Castillejos, Evington, Tikuisis, White and Winter11]. For the statement involving a Kirchberg algebra (i.e., a unital, purely infinite, simple, separable amenable C
![]() $^*$
-algebra) as the codomain, we specialize to the case that the maps are injective
$^*$
-algebra) as the codomain, we specialize to the case that the maps are injective
![]() $*$
-homomorphisms. Such maps
$*$
-homomorphisms. Such maps
![]() $\varphi $
induce injective c.p.c. order zero maps
$\varphi $
induce injective c.p.c. order zero maps
![]() $(\varphi -t)_+$
for each
$(\varphi -t)_+$
for each
![]() $t \in [0,1)$
and so [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Corollary 9.11] is applicable to them. (To see this, it suffices to show that
$t \in [0,1)$
and so [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Corollary 9.11] is applicable to them. (To see this, it suffices to show that
![]() $(h_{\varphi }-t)_+$
is a nonzero scalar multiple of the projection
$(h_{\varphi }-t)_+$
is a nonzero scalar multiple of the projection
![]() $\pi (1_A),$
where notation is as in Theorem 2.1 (note that, here,
$\pi (1_A),$
where notation is as in Theorem 2.1 (note that, here,
![]() $\pi _{\varphi } = \varphi $
). Since
$\pi _{\varphi } = \varphi $
). Since
![]() $h_{\varphi }$
is a projection (namely,
$h_{\varphi }$
is a projection (namely,
![]() $\pi _{\varphi }(1_A)$
),
$\pi _{\varphi }(1_A)$
),
![]() $(h_{\varphi } -t)_+ = (1-t) h_{\varphi }$
.)
$(h_{\varphi } -t)_+ = (1-t) h_{\varphi }$
.)
Theorem 2.18 [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Corollary 9.11]
Let A be a unital, separable, amenable C
![]() $^*$
-algebra, and let B be a Kirchberg algebra. Let
$^*$
-algebra, and let B be a Kirchberg algebra. Let
![]() $\phi _1, \phi _2 \,{\colon}\, A \to B_{\omega }$
be a pair of injective
$\phi _1, \phi _2 \,{\colon}\, A \to B_{\omega }$
be a pair of injective
![]() $*$
-homomorphisms. Then, there exist contractions
$*$
-homomorphisms. Then, there exist contractions
![]() $v_i, w_i \in B_{\omega }$
for
$v_i, w_i \in B_{\omega }$
for
![]() $i = 1, 2$
, such that
$i = 1, 2$
, such that
 $$ \begin{align*} \phi_1(a) & = w_1 \phi_2(a) w_1^* + w_2 \phi_2(a) w_2^*, \\ \phi_2(a) & = v_1 \phi_1(a) v_1^* + v_2 \phi_1(a) v_2^*, \end{align*} $$
$$ \begin{align*} \phi_1(a) & = w_1 \phi_2(a) w_1^* + w_2 \phi_2(a) w_2^*, \\ \phi_2(a) & = v_1 \phi_1(a) v_1^* + v_2 \phi_1(a) v_2^*, \end{align*} $$
for all
![]() $a \in A$
, and
$a \in A$
, and
with
![]() $w_i^*w_i \in \phi _2(A)'$
and
$w_i^*w_i \in \phi _2(A)'$
and
![]() $v_i^*v_i \in \phi _1(A)'$
for
$v_i^*v_i \in \phi _1(A)'$
for
![]() $i=1,2$
.
$i=1,2$
.
Definition 2.19 Let A and B be unital C
![]() $^*$
-algebras. Any two order zero maps
$^*$
-algebras. Any two order zero maps
![]() $\phi _1, \phi _2 \,{\colon}\, A \to B_{\omega }$
satisfying the conclusion of Theorem 2.18 will be said to be colored equivalent (see [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Section 6]).
$\phi _1, \phi _2 \,{\colon}\, A \to B_{\omega }$
satisfying the conclusion of Theorem 2.18 will be said to be colored equivalent (see [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Section 6]).
For the statement involving a finite algebra as the codomain, only one map is assumed to be a homomorphism.
Theorem 2.20 [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Theorem 6.6], [Reference Castillejos, Evington, Tikuisis, White and Winter11]
Let A be a unital, separable amenable C
![]() $^*$
-algebra, and let B be a unital, finite,
$^*$
-algebra, and let B be a unital, finite,
![]() $\mathcal Z$
-stable, simple, separable amenable C
$\mathcal Z$
-stable, simple, separable amenable C
![]() $^*$
-algebra. Let
$^*$
-algebra. Let
![]() $\phi _1 \,{\colon}\, A \to B_{\omega }$
be a totally full
$\phi _1 \,{\colon}\, A \to B_{\omega }$
be a totally full
![]() $*$
-homomorphism (i.e.,
$*$
-homomorphism (i.e.,
![]() $\phi _1(a)$
generates
$\phi _1(a)$
generates
![]() $B_{\omega }$
as a closed two-sided ideal for every nonzero
$B_{\omega }$
as a closed two-sided ideal for every nonzero
![]() $a \in A$
), and let
$a \in A$
), and let
![]() $\phi _2 \,{\colon}\, A \to B_{\omega }$
be a c.p.c. order zero map with
$\phi _2 \,{\colon}\, A \to B_{\omega }$
be a c.p.c. order zero map with
for all
![]() $\tau \in T(B_{\omega })$
and all
$\tau \in T(B_{\omega })$
and all
![]() $m \in \mathbb N$
. Then,
$m \in \mathbb N$
. Then,
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
are colored equivalent.
$\phi _2$
are colored equivalent.
Proof By [Reference Castillejos, Evington, Tikuisis, White and Winter11, Theorem I], B has complemented partitions of unity. Now the proof is exactly as in [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Theorem 6.6] using [Reference Castillejos, Evington, Tikuisis, White and Winter11, Lemma 4.8] in place of [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Theorem 5.5]. The same lemma also permits relaxing the tracial extreme boundary hypothesis in [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Theorem 6.2].
In practice, the
![]() $*$
-homomorphism typically used in Theorem 2.20 is essentially the canonical embedding
$*$
-homomorphism typically used in Theorem 2.20 is essentially the canonical embedding
![]() $\iota _A: A \to A_{\omega }$
(e.g., [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Corollary 6.5 and Theorem 7.5]), which is totally full if A is simple. To see this, let a nonzero element
$\iota _A: A \to A_{\omega }$
(e.g., [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Corollary 6.5 and Theorem 7.5]), which is totally full if A is simple. To see this, let a nonzero element
![]() $a \in A$
be given. If A is unital,
$a \in A$
be given. If A is unital,
![]() $\iota _A(a)$
can be cut down to any coordinate with a projection. In the nonunital case, the coordinate projection can be replaced with an approximate unit in a coordinate. Since A is simple, a copy of A is generated in each coordinate of
$\iota _A(a)$
can be cut down to any coordinate with a projection. In the nonunital case, the coordinate projection can be replaced with an approximate unit in a coordinate. Since A is simple, a copy of A is generated in each coordinate of
![]() $A_{\omega }$
. This shows
$A_{\omega }$
. This shows
![]() $\iota _A$
is totally full.
$\iota _A$
is totally full.
2.7 Colored isomorphism
We introduce two notions of colored isomorphism. The first one (Definition 2.21) is symmetrically formulated, but it is a little long. A weaker notion (Definition 2.23) is all that’s needed to establish Theorem 4.1. Together with Theorem 4.5, it follows that these two notions coincide in the classifiable setting.
Definition 2.21 Unital C
![]() $^*$
-algebras A and B will be said to be colored isomorphic if there exist c.p.c. order zero maps
$^*$
-algebras A and B will be said to be colored isomorphic if there exist c.p.c. order zero maps
![]() $\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
$\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
![]() $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
![]() $\psi \varphi \iota _A$
is colored equivalent to
$\psi \varphi \iota _A$
is colored equivalent to
![]() $\iota _A$
(see Definition 2.19) and
$\iota _A$
(see Definition 2.19) and
![]() $\varphi \psi \iota _B$
is colored equivalent to
$\varphi \psi \iota _B$
is colored equivalent to
![]() $\iota _B$
; and
$\iota _B$
; and
![]() $\varphi ^*$
and
$\varphi ^*$
and
![]() $\psi ^*$
preserve constant limit traces.
$\psi ^*$
preserve constant limit traces.
Remark 2.22 Colored isomorphism is reflexive and symmetric. It follows from Corollary 4.6 that transitivity holds for classifiable C
![]() $^*$
-algebras (cf. [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Section 6]), but transitivity is not clear in general.
$^*$
-algebras (cf. [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Section 6]), but transitivity is not clear in general.
Definition 2.23 Unital C
![]() $^*$
-algebras A and B will be said to be minimalist colored isomorphic if there exist constant limit trace preserving c.p.c. order zero maps
$^*$
-algebras A and B will be said to be minimalist colored isomorphic if there exist constant limit trace preserving c.p.c. order zero maps
![]() $\varphi : A_{\omega } \to B_{\omega }$
and
$\varphi : A_{\omega } \to B_{\omega }$
and
![]() $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
, and contractions
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
, and contractions
![]() $u_1, \ldots , u_m \in A_{\omega }$
and
$u_1, \ldots , u_m \in A_{\omega }$
and
![]() $v_1, \ldots , v_n \in B_{\omega }$
, such that
$v_1, \ldots , v_n \in B_{\omega }$
, such that
 $$ \begin{align} \sum_{i=1}^m u_i \psi \varphi(a) u_i^* = a \hspace{10 pt} \text{ and } \hspace{10 pt} \sum_{j=1}^n v_j \varphi \psi (b) v_j^* = b \end{align} $$
$$ \begin{align} \sum_{i=1}^m u_i \psi \varphi(a) u_i^* = a \hspace{10 pt} \text{ and } \hspace{10 pt} \sum_{j=1}^n v_j \varphi \psi (b) v_j^* = b \end{align} $$
for all
![]() $a \in A$
and for all
$a \in A$
and for all
![]() $b \in B$
, and, in addition,
$b \in B$
, and, in addition,
 $$ \begin{align} \sum_{i=1}^m u_i^* u_i = 1_{A_{\omega}}, \hspace{10 pt} \sum_{j=1}^n v_j^* v_j = 1_{B_{\omega}}. \end{align} $$
$$ \begin{align} \sum_{i=1}^m u_i^* u_i = 1_{A_{\omega}}, \hspace{10 pt} \sum_{j=1}^n v_j^* v_j = 1_{B_{\omega}}. \end{align} $$
We note that (2.7) is weaker than requiring that
![]() $\psi \varphi \iota _A$
and
$\psi \varphi \iota _A$
and
![]() $\iota _A$
are colored equivalent (and requiring that
$\iota _A$
are colored equivalent (and requiring that
![]() $\psi \varphi \iota _B$
and
$\psi \varphi \iota _B$
and
![]() $\iota _B$
are colored equivalent), as required by Definition 2.21. It follows from Theorems 4.1 and 4.5 that
$\iota _B$
are colored equivalent), as required by Definition 2.21. It follows from Theorems 4.1 and 4.5 that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
can be chosen so that the maps
$\psi $
can be chosen so that the maps
![]() $\psi \varphi \iota _A$
and
$\psi \varphi \iota _A$
and
![]() $\iota _A$
are colored equivalent (and likewise for
$\iota _A$
are colored equivalent (and likewise for
![]() $\psi \varphi \iota _B$
and
$\psi \varphi \iota _B$
and
![]() $\iota _B$
) in the classifiable setting.
$\iota _B$
) in the classifiable setting.
The identity (2.7) implies that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are injective; furthermore, the commutation relations coming from the colored equivalences of maps—the symmetrized form of colored isomorphism holding automatically in the classifiable case—guarantee that
$\psi $
are injective; furthermore, the commutation relations coming from the colored equivalences of maps—the symmetrized form of colored isomorphism holding automatically in the classifiable case—guarantee that
![]() $u_i \psi \varphi (\cdot ) u_i^*$
and
$u_i \psi \varphi (\cdot ) u_i^*$
and
![]() $v_j \varphi \psi (\cdot ) v_j^*$
are order zero for
$v_j \varphi \psi (\cdot ) v_j^*$
are order zero for
![]() $i = 1, \ldots , m$
and for
$i = 1, \ldots , m$
and for
![]() $j = 1, \ldots , n$
.
$j = 1, \ldots , n$
.
3 Functionals preserving compact containment
The main result of this section characterizes when a functional on the Cuntz semigroup
![]() $\operatorname {Cu}(A)$
arising from a faithful densely defined lower semicontinuous traces on a commutative C
$\operatorname {Cu}(A)$
arising from a faithful densely defined lower semicontinuous traces on a commutative C
![]() $^*$
-algebra, A, with the property that the rank map gives rise to an isomorphism
$^*$
-algebra, A, with the property that the rank map gives rise to an isomorphism
![]() $\operatorname {Cu}(A) \cong \text {Lsc}_{\sigma }(\widehat A,\overline {\mathbb N})$
, preserves compact containment. Let us first establish some necessary conditions for a functional to preserve compact containment in a more general context. Suppose
$\operatorname {Cu}(A) \cong \text {Lsc}_{\sigma }(\widehat A,\overline {\mathbb N})$
, preserves compact containment. Let us first establish some necessary conditions for a functional to preserve compact containment in a more general context. Suppose
![]() $\lambda $
is a functional (i.e., a generalized Cuntz category morphism into
$\lambda $
is a functional (i.e., a generalized Cuntz category morphism into
![]() $[0,\infty ]$
) on a positive Cuntz category object M. In order for
$[0,\infty ]$
) on a positive Cuntz category object M. In order for
![]() $\lambda $
to preserve compact containment,
$\lambda $
to preserve compact containment,
![]() $\lambda $
must be finite on any element that is compactly contained in some element of M. Moreover,
$\lambda $
must be finite on any element that is compactly contained in some element of M. Moreover,
![]() $\lambda $
must be finite on any element that is majorized by a finite sum of such elements. It is also necessary that
$\lambda $
must be finite on any element that is majorized by a finite sum of such elements. It is also necessary that
![]() $\lambda $
vanish on compact elements. Now recall, for instance from [Reference Elliott, Robert and Santiago33, Proposition 4.2], that a lower semicontinuous trace
$\lambda $
vanish on compact elements. Now recall, for instance from [Reference Elliott, Robert and Santiago33, Proposition 4.2], that a lower semicontinuous trace
![]() $\tau $
on a C
$\tau $
on a C
![]() $^*$
-algebra induces a functional
$^*$
-algebra induces a functional
![]() $d_{\tau }$
on
$d_{\tau }$
on
![]() $\operatorname {Cu}(A)$
(the trace of the range projection of a positive element). (In later sections, we will not make a distinction between
$\operatorname {Cu}(A)$
(the trace of the range projection of a positive element). (In later sections, we will not make a distinction between
![]() $\tau $
and
$\tau $
and
![]() $d_{\tau }$
.) The finiteness condition requires
$d_{\tau }$
.) The finiteness condition requires
![]() $d_{\tau }$
to be finite-valued on the Pedersen ideal of
$d_{\tau }$
to be finite-valued on the Pedersen ideal of
![]() $A \otimes \mathcal K$
. If
$A \otimes \mathcal K$
. If
![]() $\tau $
is faithful, the latter condition requires
$\tau $
is faithful, the latter condition requires
![]() $\operatorname {Cu}(A)$
to have no nonzero compact elements. If A is stably finite, then, by [Reference Brown and Ciuperca8, Corollary 3.6], this is equivalent to A being stably projectionless. If A is, moreover, commutative, this is equivalent to the spectrum of A not containing any nonempty compact open subsets. To see this, suppose K is a nonempty compact open subset of the spectrum of A. Then
$\operatorname {Cu}(A)$
to have no nonzero compact elements. If A is stably finite, then, by [Reference Brown and Ciuperca8, Corollary 3.6], this is equivalent to A being stably projectionless. If A is, moreover, commutative, this is equivalent to the spectrum of A not containing any nonempty compact open subsets. To see this, suppose K is a nonempty compact open subset of the spectrum of A. Then
![]() $[\chi _K \otimes p]$
is a nonzero compact element of
$[\chi _K \otimes p]$
is a nonzero compact element of
![]() $\operatorname {Cu}(A)$
for any nonzero projection
$\operatorname {Cu}(A)$
for any nonzero projection
![]() $p \in \mathcal K$
. Conversely, suppose
$p \in \mathcal K$
. Conversely, suppose
![]() $A \otimes \mathcal K$
contains a nonzero projection p. Then the map
$A \otimes \mathcal K$
contains a nonzero projection p. Then the map
![]() $\eta \,{\colon}\, \widehat A \ni x \mapsto \|p(x)\| \in \mathbb C$
is continuous. Since p vanishes at infinity and is a nonzero projection, the same is true of
$\eta \,{\colon}\, \widehat A \ni x \mapsto \|p(x)\| \in \mathbb C$
is continuous. Since p vanishes at infinity and is a nonzero projection, the same is true of
![]() $\eta $
. This shows A contains a nonzero projection.
$\eta $
. This shows A contains a nonzero projection.
Theorem 3.1 Suppose that
![]() $\mu $
is a faithful densely defined lower semicontinuous trace on a commutative C
$\mu $
is a faithful densely defined lower semicontinuous trace on a commutative C
![]() $^*$
-algebra,
$^*$
-algebra,
![]() $C_0(X)$
, with the property that
$C_0(X)$
, with the property that
![]() $\operatorname {Cu}( C_0(X) ) \cong \text {Lsc}_{\sigma } (X,\overline {\mathbb N})$
(the isomorphism being given by the rank map) (for example, X is as in Theorem 2.14). Then the functional
$\operatorname {Cu}( C_0(X) ) \cong \text {Lsc}_{\sigma } (X,\overline {\mathbb N})$
(the isomorphism being given by the rank map) (for example, X is as in Theorem 2.14). Then the functional
![]() $d_{\mu }: \operatorname {Cu}(C_0(X)) \to [0,\infty ]$
preserves compact containment if, and only if, X does not contain any nonempty compact open sets.
$d_{\mu }: \operatorname {Cu}(C_0(X)) \to [0,\infty ]$
preserves compact containment if, and only if, X does not contain any nonempty compact open sets.
Proof Denote by
![]() $\iota $
the natural set-theoretical mapping of
$\iota $
the natural set-theoretical mapping of
![]() $\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
into
$\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
into
![]() $\operatorname {Cu}(C_0(X))$
:
$\operatorname {Cu}(C_0(X))$
:
 $$\begin{align*}f = \sum_{k=0}^{\infty} \chi_{\{f> k\}} \mapsto \sum_{k=0}^{\infty} [f_k \otimes p_k], \end{align*}$$
$$\begin{align*}f = \sum_{k=0}^{\infty} \chi_{\{f> k\}} \mapsto \sum_{k=0}^{\infty} [f_k \otimes p_k], \end{align*}$$
where
![]() $f_k$
is a positive function in
$f_k$
is a positive function in
![]() $C_0(X)$
with open support equal to
$C_0(X)$
with open support equal to
![]() $\{f> k\}$
and
$\{f> k\}$
and
![]() $(p_k) _{k=0}^{\infty }$
is a family of mutually orthogonal rank-one projections in
$(p_k) _{k=0}^{\infty }$
is a family of mutually orthogonal rank-one projections in
![]() $\mathcal K$
. By hypothesis,
$\mathcal K$
. By hypothesis,
![]() $\text {rank} \,{\colon}\, \operatorname {Cu}(C_0(X)) \to \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
is an isomorphism. It follows, since as easily checked,
$\text {rank} \,{\colon}\, \operatorname {Cu}(C_0(X)) \to \text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
is an isomorphism. It follows, since as easily checked,
![]() $\text {rank} \circ \iota = \text {id}_{\text {Lsc}_{\sigma }(X,\overline {\mathbb N})}$
, that
$\text {rank} \circ \iota = \text {id}_{\text {Lsc}_{\sigma }(X,\overline {\mathbb N})}$
, that
![]() $\iota $
is an isomorphism. Denote by
$\iota $
is an isomorphism. Denote by
![]() $\mu : \text {Lsc}_{\sigma }(X,\overline {\mathbb N}) \to [0,\infty ]$
the functional
$\mu : \text {Lsc}_{\sigma }(X,\overline {\mathbb N}) \to [0,\infty ]$
the functional
![]() $d_{\mu } \circ \iota $
and denote also by
$d_{\mu } \circ \iota $
and denote also by
![]() $\mu $
the locally finite (as the Pedersen ideal of
$\mu $
the locally finite (as the Pedersen ideal of
![]() $C_0(X)$
is
$C_0(X)$
is
![]() $C_c(X)$
and by [Reference Pedersen48, Theorem 1.3]) extended Radon measure induced by the densely defined lower semicontinuous trace
$C_c(X)$
and by [Reference Pedersen48, Theorem 1.3]) extended Radon measure induced by the densely defined lower semicontinuous trace
![]() $\mu $
. Since
$\mu $
. Since
![]() $d_{\mu } = \mu \circ \operatorname {rank}$
, to show that
$d_{\mu } = \mu \circ \operatorname {rank}$
, to show that
![]() $d_{\mu }$
preserves compact containment, it suffices to show that
$d_{\mu }$
preserves compact containment, it suffices to show that
![]() $\mu $
preserves compact containment. Suppose f and g are elements of
$\mu $
preserves compact containment. Suppose f and g are elements of
![]() $\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
and that
$\text {Lsc}_{\sigma }(X,\overline {\mathbb N})$
and that
![]() $f \ll g$
. If
$f \ll g$
. If
![]() $\mu (f) = 0$
, then
$\mu (f) = 0$
, then
![]() $\mu (f) \ll \mu (g)$
because
$\mu (f) \ll \mu (g)$
because
![]() $0$
is compactly contained in every element of
$0$
is compactly contained in every element of
![]() $[0,\infty ]$
. Let us now consider the case where
$[0,\infty ]$
. Let us now consider the case where
![]() $\mu (f)> 0$
. Since f is compactly contained in g, by the proof of (O4) in Proposition 2.13,
$\mu (f)> 0$
. Since f is compactly contained in g, by the proof of (O4) in Proposition 2.13,
![]() $f = \sum _{k=0}^n \chi _{\{f> k\}}$
for some n and there exists a compact set
$f = \sum _{k=0}^n \chi _{\{f> k\}}$
for some n and there exists a compact set
![]() $K \subseteq X$
such that (with abbreviated notation)
$K \subseteq X$
such that (with abbreviated notation)
![]() $\{f> 0\} \subseteq K \subseteq \{g > 0\}$
, and so
$\{f> 0\} \subseteq K \subseteq \{g > 0\}$
, and so
![]() $\mu (f) \leq (n+1)\mu (K)< \infty $
. Now suppose
$\mu (f) \leq (n+1)\mu (K)< \infty $
. Now suppose
![]() $\mu (f) = \mu (g)$
, i.e.,
$\mu (f) = \mu (g)$
, i.e.,
![]() $\sum _{k=0}^{\infty } \mu ( \{f> k\}) = \sum _{k=0}^{\infty } \mu ( \{g > k\})$
. Since
$\sum _{k=0}^{\infty } \mu ( \{f> k\}) = \sum _{k=0}^{\infty } \mu ( \{g > k\})$
. Since
![]() $f \leq g$
and since
$f \leq g$
and since
![]() $\mu (f)$
is finite, we have
$\mu (f)$
is finite, we have
![]() ${\mu (\{f> k\}) = \mu (\{g >k\})}$
for each k. If
${\mu (\{f> k\}) = \mu (\{g >k\})}$
for each k. If
![]() $K = \{g> 0\}$
, then since X contains no nonempty compact open sets,
$K = \{g> 0\}$
, then since X contains no nonempty compact open sets,
![]() $\{g> 0\}$
is empty. This implies g is zero and hence f is zero, which is a contradiction. In other words, K is properly contained in
$\{g> 0\}$
is empty. This implies g is zero and hence f is zero, which is a contradiction. In other words, K is properly contained in
![]() $\{g> 0\}$
, and so there is a nonempty open subset of
$\{g> 0\}$
, and so there is a nonempty open subset of
![]() $\{g> 0\}$
which is disjoint from K and therefore disjoint from
$\{g> 0\}$
which is disjoint from K and therefore disjoint from
![]() $\{f> 0\}$
as well. Since
$\{f> 0\}$
as well. Since
![]() $\mu $
is faithful,
$\mu $
is faithful,
![]() $\mu (\{f> 0\}) < \mu (\{g> 0\})$
and so (since
$\mu (\{f> 0\}) < \mu (\{g> 0\})$
and so (since
![]() $f \leq g$
and
$f \leq g$
and
![]() $\mu (f)$
is finite)
$\mu (f)$
is finite)
![]() $\mu (f) < \mu (g)$
.
$\mu (f) < \mu (g)$
.
Remark 3.2 A different proof of Theorem 3.1, in the case of the half-open interval (the case pertinent to this paper), using the characterization of compact containment given in [Reference Antoine, Perera and Santiago4] is possible.
Proof Suppose
![]() $f, g \in \text {Lsc}((0,1],\overline {\mathbb N})$
are such that
$f, g \in \text {Lsc}((0,1],\overline {\mathbb N})$
are such that
![]() $f \ll g$
. Let
$f \ll g$
. Let
![]() $\mu $
be as in the proof of Theorem 3.1 and suppose f is nonzero. Extend both f and g to be zero at zero and call these extensions
$\mu $
be as in the proof of Theorem 3.1 and suppose f is nonzero. Extend both f and g to be zero at zero and call these extensions
![]() $\widetilde f$
and
$\widetilde f$
and
![]() $\widetilde g$
. It is easily checked that these extensions are lower semicontinuous and that
$\widetilde g$
. It is easily checked that these extensions are lower semicontinuous and that
![]() $\widetilde f$
remains compactly contained in
$\widetilde f$
remains compactly contained in
![]() $\widetilde g$
in
$\widetilde g$
in
![]() $\text {Lsc}([0,1],\overline {\mathbb N})$
(one could also use [Reference Ciuperca and Elliott14, Theorem 10.1], [Reference Ciuperca, Robert and Santiago16, Theorem 5], and [Reference Ivanescu38, Theorem 6.11]). An application of [Reference Antoine, Perera and Santiago4, Proposition 5.5] at the point zero shows that
$\text {Lsc}([0,1],\overline {\mathbb N})$
(one could also use [Reference Ciuperca and Elliott14, Theorem 10.1], [Reference Ciuperca, Robert and Santiago16, Theorem 5], and [Reference Ivanescu38, Theorem 6.11]). An application of [Reference Antoine, Perera and Santiago4, Proposition 5.5] at the point zero shows that
![]() $\widetilde f$
is zero on a neighbourhood of zero because
$\widetilde f$
is zero on a neighbourhood of zero because
![]() $\widetilde g(0) = 0$
. This shows f is compactly supported, and since f is bounded,
$\widetilde g(0) = 0$
. This shows f is compactly supported, and since f is bounded,
![]() $\mu (f)$
is finite. Since f is nonzero and extended positive integer-valued, its extension
$\mu (f)$
is finite. Since f is nonzero and extended positive integer-valued, its extension
![]() $\widetilde f$
is necessarily discontinuous. Its first point of discontinuity,
$\widetilde f$
is necessarily discontinuous. Its first point of discontinuity,
![]() $x_0$
, must occur within
$x_0$
, must occur within
![]() $(0,1)$
. By [Reference Antoine, Perera and Santiago4, Proposition 5.5] applied to the point
$(0,1)$
. By [Reference Antoine, Perera and Santiago4, Proposition 5.5] applied to the point
![]() $x_0$
, there exists a neighbourhood U of
$x_0$
, there exists a neighbourhood U of
![]() $x_0$
which is contained in
$x_0$
which is contained in
![]() $(0,1)$
and a nonzero constant
$(0,1)$
and a nonzero constant
![]() $c \in \overline {\mathbb N}$
such that
$c \in \overline {\mathbb N}$
such that
![]() $\widetilde f \leq c \ll \widetilde g$
on U. Since
$\widetilde f \leq c \ll \widetilde g$
on U. Since
![]() $\widetilde f$
is zero to the left of
$\widetilde f$
is zero to the left of
![]() $x_0$
, and since
$x_0$
, and since
![]() $\widetilde f \leq \widetilde g$
, the integral of f on U is strictly less than the integral of c on U, and hence also of g. This implies
$\widetilde f \leq \widetilde g$
, the integral of f on U is strictly less than the integral of c on U, and hence also of g. This implies
![]() $\mu (f) < \mu (g)$
.
$\mu (f) < \mu (g)$
.
Remark 3.3 The characterization of compact containment in [Reference Coward, Elliott and Ivanescu18] can be used to show that if
![]() $\tau $
is a faithful densely defined lower semicontinuous trace on a C
$\tau $
is a faithful densely defined lower semicontinuous trace on a C
![]() $^*$
-algebra A, then
$^*$
-algebra A, then
![]() $d_{\tau }$
preserves compact containment if, and only if,
$d_{\tau }$
preserves compact containment if, and only if,
![]() $\operatorname {Cu}(A)$
does not contain nonzero compact elements. Since the only case of interest in this paper is covered by Theorem 3.1, we will not prove this.
$\operatorname {Cu}(A)$
does not contain nonzero compact elements. Since the only case of interest in this paper is covered by Theorem 3.1, we will not prove this.
Remark 3.4 A simple reduction to the faithful case shows that if
![]() $\tau $
is a (not necessarily faithful) densely defined lower semicontinuous trace on A and
$\tau $
is a (not necessarily faithful) densely defined lower semicontinuous trace on A and
![]() $\operatorname {Cu}(A/N_{\tau })$
does not contain nonzero compact elements, where
$\operatorname {Cu}(A/N_{\tau })$
does not contain nonzero compact elements, where
![]() $N_{\tau }$
denotes the kernel of
$N_{\tau }$
denotes the kernel of
![]() $\tau $
, then
$\tau $
, then
![]() $d_{\tau }$
preserves compact containment.
$d_{\tau }$
preserves compact containment.
Proof Denote by
![]() $\pi _{N_{\tau }} \,{\colon}\, A \to A/N_{\tau }$
the canonical quotient map and let
$\pi _{N_{\tau }} \,{\colon}\, A \to A/N_{\tau }$
the canonical quotient map and let
![]() $\eta \,{\colon}\, (A/N_{\tau })_+ \to [0,\infty ]$
be the faithful densely defined lower semicontinuous trace induced by
$\eta \,{\colon}\, (A/N_{\tau })_+ \to [0,\infty ]$
be the faithful densely defined lower semicontinuous trace induced by
![]() $\tau $
. Suppose
$\tau $
. Suppose
![]() $\operatorname {Cu}(A/N_{\tau })$
contains no nonzero compact elements. Then, by Remark 3.3, the functional
$\operatorname {Cu}(A/N_{\tau })$
contains no nonzero compact elements. Then, by Remark 3.3, the functional
![]() $d_{\eta } \,{\colon}\, \operatorname {Cu}(A/N_{\tau }) \to [0,\infty ]$
preserves compact containment and by [Reference Coward, Elliott and Ivanescu18, Theorem 2],
$d_{\eta } \,{\colon}\, \operatorname {Cu}(A/N_{\tau }) \to [0,\infty ]$
preserves compact containment and by [Reference Coward, Elliott and Ivanescu18, Theorem 2],
![]() $\pi _{N_{\tau }}$
induces a Cuntz category morphism
$\pi _{N_{\tau }}$
induces a Cuntz category morphism
![]() $\operatorname {Cu}(\pi _{N_{\tau }}) \,{\colon}\, \operatorname {Cu}(A) \to \operatorname {Cu}(A/N_{\tau })$
. Since the functional
$\operatorname {Cu}(\pi _{N_{\tau }}) \,{\colon}\, \operatorname {Cu}(A) \to \operatorname {Cu}(A/N_{\tau })$
. Since the functional
![]() $d_{\tau }$
factors through
$d_{\tau }$
factors through
![]() $\operatorname {Cu}(A/N_{\tau })$
, via the commutative diagram
$\operatorname {Cu}(A/N_{\tau })$
, via the commutative diagram

it preserves compact containment.
Remark 3.5 It is possible for the functional
![]() $d_{\tau }$
induced by a lower semicontinuous trace
$d_{\tau }$
induced by a lower semicontinuous trace
![]() $\tau $
on a C
$\tau $
on a C
![]() $^*$
-algebra A to fail to preserve compact containment even if
$^*$
-algebra A to fail to preserve compact containment even if
![]() $d_{\tau }$
is assumed to vanish on every compact element of
$d_{\tau }$
is assumed to vanish on every compact element of
![]() $\operatorname {Cu}(A)$
. For example, let
$\operatorname {Cu}(A)$
. For example, let
![]() $\mu $
be the trace induced by the measure on
$\mu $
be the trace induced by the measure on
![]() $(0,1]$
which is the Lebesgue measure on
$(0,1]$
which is the Lebesgue measure on
![]() $(1/2,1]$
and zero on
$(1/2,1]$
and zero on
![]() $(0,1/2]$
. The condition that
$(0,1/2]$
. The condition that
![]() $d_{\mu }$
vanishes on every compact element of
$d_{\mu }$
vanishes on every compact element of
![]() $\operatorname {Cu}(C_0(0,1])$
is automatic since
$\operatorname {Cu}(C_0(0,1])$
is automatic since
![]() $C_0(0,1]$
is stably projectionless.
$C_0(0,1]$
is stably projectionless.
To show that
![]() $d_{\mu }$
fails to preserve compact containment, it suffices, by the proof of Theorem 3.1, to show that
$d_{\mu }$
fails to preserve compact containment, it suffices, by the proof of Theorem 3.1, to show that
![]() $\mu $
fails to preserve compact containment. By a characterization of compact containment in the proof of Proposition 2.13,
$\mu $
fails to preserve compact containment. By a characterization of compact containment in the proof of Proposition 2.13,
![]() $\chi _{(1/2,1]}$
is compactly contained in
$\chi _{(1/2,1]}$
is compactly contained in
![]() $\chi _{(0,1]}$
, but
$\chi _{(0,1]}$
, but
![]() $\mu ((1/2,1]) = \mu ((0,1])$
.
$\mu ((1/2,1]) = \mu ((0,1])$
.
4 Colored classification of C
 $^*$
-algebras
$^*$
-algebras
Theorem 4.1 Any two unital C
![]() $^*$
-algebras which are colored isomorphic have isomorphic tracial simplices. Moreover, the order zero maps implementing a colored isomorphism induce mutually inverse isomorphisms of tracial simplices (as described in Section 2.3).
$^*$
-algebras which are colored isomorphic have isomorphic tracial simplices. Moreover, the order zero maps implementing a colored isomorphism induce mutually inverse isomorphisms of tracial simplices (as described in Section 2.3).
Proof The same conclusion holds with the weaker hypothesis that A and B are unital C
![]() $^*$
-algebras which are minimalist colored isomorphic, so this is what we prove. Let the notation be as in Definition 2.23. Since
$^*$
-algebras which are minimalist colored isomorphic, so this is what we prove. Let the notation be as in Definition 2.23. Since
![]() $\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
$\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
![]() $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
are c.p.c. order zero maps, they induce mappings of bounded traces
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
are c.p.c. order zero maps, they induce mappings of bounded traces
![]() $\varphi ^*: \mathbb R_+ T(B_{\omega }) \to \mathbb R_+T(A_{\omega })$
and
$\varphi ^*: \mathbb R_+ T(B_{\omega }) \to \mathbb R_+T(A_{\omega })$
and
![]() $\psi ^*: \mathbb R_+ T(A_{\omega }) \to \mathbb R_+T (B_{\omega })$
(see [Reference Winter and Zacharias68, Corollary 3.4]). In fact,
$\psi ^*: \mathbb R_+ T(A_{\omega }) \to \mathbb R_+T (B_{\omega })$
(see [Reference Winter and Zacharias68, Corollary 3.4]). In fact,
![]() $\varphi ^*$
and
$\varphi ^*$
and
![]() $\psi ^*$
are mutually inverse affine isomorphisms of the cones of bounded traces. To see this, let
$\psi ^*$
are mutually inverse affine isomorphisms of the cones of bounded traces. To see this, let
![]() $\tau \in T(A_{\omega })$
and
$\tau \in T(A_{\omega })$
and
![]() $a \in A_{\omega }$
be given. Then
$a \in A_{\omega }$
be given. Then
 $$ \begin{align*} \tau(a) & \stackrel{(2.7)}{=} \tau \left ( \sum_{i=1}^m u_i \psi \varphi(a) u_i^* \right) = \sum_{i=1}^m \tau(u_i \psi \varphi (a) u_i^*) \\ &\ \ \,= \sum_{i=1}^m \tau(\psi \varphi (a) u_i^* u_i) \stackrel{(2.8)}{=} \tau(\psi \varphi (a)) = \varphi^* \psi^*(\tau)(a). \end{align*} $$
$$ \begin{align*} \tau(a) & \stackrel{(2.7)}{=} \tau \left ( \sum_{i=1}^m u_i \psi \varphi(a) u_i^* \right) = \sum_{i=1}^m \tau(u_i \psi \varphi (a) u_i^*) \\ &\ \ \,= \sum_{i=1}^m \tau(\psi \varphi (a) u_i^* u_i) \stackrel{(2.8)}{=} \tau(\psi \varphi (a)) = \varphi^* \psi^*(\tau)(a). \end{align*} $$
A symmetric calculation shows
![]() $\psi ^* \varphi ^* (\tau ) =\tau $
for each
$\psi ^* \varphi ^* (\tau ) =\tau $
for each
![]() $\tau \in T(B_{\omega })$
.
$\tau \in T(B_{\omega })$
.
Let us now show that the cones of bounded traces on A and B are affinely isomorphic. Denote by
![]() $c_B \,{\colon}\, \mathbb R_+T(B) \to \mathbb R_+T(B_{\omega })$
the embedding of bounded traces on B as bounded limit traces on
$c_B \,{\colon}\, \mathbb R_+T(B) \to \mathbb R_+T(B_{\omega })$
the embedding of bounded traces on B as bounded limit traces on
![]() $B_{\omega }$
and by
$B_{\omega }$
and by
![]() $\iota _A \,{\colon}\, A \to A_{\omega }$
the canonical embedding of A into
$\iota _A \,{\colon}\, A \to A_{\omega }$
the canonical embedding of A into
![]() $A_{\omega }$
. Denote by
$A_{\omega }$
. Denote by
![]() $\iota _A^*$
the dual map induced on bounded traces and define
$\iota _A^*$
the dual map induced on bounded traces and define
![]() $\Phi : \mathbb R_+T(B) \to \mathbb R_+T(A)$
to be the composition
$\Phi : \mathbb R_+T(B) \to \mathbb R_+T(A)$
to be the composition
and define
![]() $c_A \,{\colon}\, \mathbb R_+T(A) \to \mathbb R_+T(A_{\omega })$
,
$c_A \,{\colon}\, \mathbb R_+T(A) \to \mathbb R_+T(A_{\omega })$
,
![]() $\iota _B: B \to B_{\omega }$
, and
$\iota _B: B \to B_{\omega }$
, and
![]() $\Psi \,{\colon}\, \mathbb R_+T(A) \to \mathbb R_+T(B)$
similarly. Then
$\Psi \,{\colon}\, \mathbb R_+T(A) \to \mathbb R_+T(B)$
similarly. Then
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are weak
$\Psi $
are weak
![]() $^*$
continuous and affine, and for
$^*$
continuous and affine, and for
![]() $\tau \in \mathbb R_+T(B)$
,
$\tau \in \mathbb R_+T(B)$
,
 $$ \begin{align*} \Psi \Phi (\tau) & = \iota_B^* \psi^* c_A \iota_A^* \varphi^* c_B (\tau) \\ & = \iota_B^* \psi^* \varphi^* c_B(\tau) = \iota_B^* c_B(\tau) = \tau. \end{align*} $$
$$ \begin{align*} \Psi \Phi (\tau) & = \iota_B^* \psi^* c_A \iota_A^* \varphi^* c_B (\tau) \\ & = \iota_B^* \psi^* \varphi^* c_B(\tau) = \iota_B^* c_B(\tau) = \tau. \end{align*} $$
The second equality follows from the assumption that
![]() $\varphi ^*$
takes constant limit traces to constant limit traces so that
$\varphi ^*$
takes constant limit traces to constant limit traces so that
![]() $c_A \iota _A^* \varphi ^* c_B (\tau ) = \varphi ^* c_B(\tau )$
. The third equality follows from the previous paragraph. A symmetric calculation shows that
$c_A \iota _A^* \varphi ^* c_B (\tau ) = \varphi ^* c_B(\tau )$
. The third equality follows from the previous paragraph. A symmetric calculation shows that
![]() $\Phi \Psi (\tau ) = \tau $
for
$\Phi \Psi (\tau ) = \tau $
for
![]() ${\tau \in \mathbb R_+T(A)}$
. This shows
${\tau \in \mathbb R_+T(A)}$
. This shows
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are mutually inverse isomorphisms of the topological convex cones
$\Psi $
are mutually inverse isomorphisms of the topological convex cones
![]() $\mathbb R_+ T(A)$
and
$\mathbb R_+ T(A)$
and
![]() $\mathbb R_+ T(B)$
.
$\mathbb R_+ T(B)$
.
To see that
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
preserve the tracial simplices, i.e., are isometries, note that they are contractions since they are the compositions of contractions. By the preceding paragraph,
$\Psi $
preserve the tracial simplices, i.e., are isometries, note that they are contractions since they are the compositions of contractions. By the preceding paragraph,
![]() $\Phi \Psi = \text {id}_{T(A)}$
and so we have
$\Phi \Psi = \text {id}_{T(A)}$
and so we have
![]() $1 = \|\Phi \Psi \| \leq \|\Phi \| \|\Psi \| \leq 1$
which implies that the norms of
$1 = \|\Phi \Psi \| \leq \|\Phi \| \|\Psi \| \leq 1$
which implies that the norms of
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are both one so these maps are isometries and therefore constitute an isomorphism of the tracial simplices.
$\Psi $
are both one so these maps are isometries and therefore constitute an isomorphism of the tracial simplices.
Remark 4.2 Colored isomorphism (as defined in Section 2.7), extended in a natural way to the nonunital case, also preserves, up to isometric isomorphism, the topological convex cone of lower semicontinuous traces of [Reference Elliott, Robert and Santiago33]. To see this, we will need to know that c.p.c. order zero maps induce mappings of lower semicontinuous traces. This follows from [Reference Winter and Zacharias68, Corollary 3.4]. The result now follows by extending the maps considered in the proof of Theorem 4.1 to the cone of lower semicontinuous traces rather than just the cone of bounded traces.
From this one can deduce that colored isomorphism, in the present sense, preserves ideal lattices, up to isomorphism (cf. [Reference Castillejos10, Theorem 5.4.9]). Let the notation be as in the proof of Theorem 4.1 with
![]() $\Psi $
assumed to be an isomorphism of cones of lower semicontinuous traces. Recall, from [Reference Elliott, Robert and Santiago33], that there is an order-reversing bijection
$\Psi $
assumed to be an isomorphism of cones of lower semicontinuous traces. Recall, from [Reference Elliott, Robert and Santiago33], that there is an order-reversing bijection
![]() $\alpha _A$
between closed two-sided ideals I of A and lower semicontinuous traces on A taking only the values 0 and
$\alpha _A$
between closed two-sided ideals I of A and lower semicontinuous traces on A taking only the values 0 and
![]() $\infty $
given by
$\infty $
given by
 $$\begin{align*}I \mapsto \tau_I(x):= \begin{cases} 0, & \text{if} \hspace{5 pt} x \in I_+,\\ \infty, & \text{if} \hspace{5 pt} x \notin I_+. \end{cases} \end{align*}$$
$$\begin{align*}I \mapsto \tau_I(x):= \begin{cases} 0, & \text{if} \hspace{5 pt} x \in I_+,\\ \infty, & \text{if} \hspace{5 pt} x \notin I_+. \end{cases} \end{align*}$$
Such traces are characterized by the property
![]() $\tau + \tau = \tau $
, and so
$\tau + \tau = \tau $
, and so
![]() $\Psi $
restricts to a mapping between these traces. Therefore, the composition
$\Psi $
restricts to a mapping between these traces. Therefore, the composition
![]() $\alpha _B ^{-1} \circ \Psi \circ \alpha _A$
gives an order-preserving bijection of ideal lattices. If the prime ideals of A and B are primitive, as is the case with separable or postliminary C
$\alpha _B ^{-1} \circ \Psi \circ \alpha _A$
gives an order-preserving bijection of ideal lattices. If the prime ideals of A and B are primitive, as is the case with separable or postliminary C
![]() $^*$
-algebras (see [Reference Dixmier22, Theorems 4.3.5 and 4.4.5] and [Reference Raeburn and Williams52, Theorem A.50]), then the primitive ideal spaces of A and B are homeomorphic. By Gelfand duality, it follows that colored isomorphism (in the present sense) is a rigid notion for commutative C
$^*$
-algebras (see [Reference Dixmier22, Theorems 4.3.5 and 4.4.5] and [Reference Raeburn and Williams52, Theorem A.50]), then the primitive ideal spaces of A and B are homeomorphic. By Gelfand duality, it follows that colored isomorphism (in the present sense) is a rigid notion for commutative C
![]() $^*$
-algebras (i.e., if A is a commutative C
$^*$
-algebras (i.e., if A is a commutative C
![]() $^*$
-algebra which is colored isomorphic, in the present sense, to a C
$^*$
-algebra which is colored isomorphic, in the present sense, to a C
![]() $^*$
-algebra B, then A is isomorphic to B) (cf. [Reference Castillejos10, Proposition 5.4.13]). It is easily seen that colored isomorphism, in the present sense, is also a rigid notion for finite-dimensional C
$^*$
-algebra B, then A is isomorphic to B) (cf. [Reference Castillejos10, Proposition 5.4.13]). It is easily seen that colored isomorphism, in the present sense, is also a rigid notion for finite-dimensional C
![]() $^*$
-algebras (cf. [Reference Castillejos10, Proposition 5.4.12]).
$^*$
-algebras (cf. [Reference Castillejos10, Proposition 5.4.12]).
Theorem 4.3 Let B be a unital, simple, separable, exact,
![]() $\mathcal Z$
-stable C
$\mathcal Z$
-stable C
![]() $^*$
-algebra with stable rank one, and let D be a simple, unital AF algebra. Let
$^*$
-algebra with stable rank one, and let D be a simple, unital AF algebra. Let
![]() $\mu $
be a faithful trace on
$\mu $
be a faithful trace on
![]() $C_0(0,1]$
with norm at most one, and let
$C_0(0,1]$
with norm at most one, and let
![]() $\Phi \,{\colon}\, T(B) \to T(D)$
be a continuous affine map of simplices. There exists a c.p.c. order zero map
$\Phi \,{\colon}\, T(B) \to T(D)$
be a continuous affine map of simplices. There exists a c.p.c. order zero map
![]() $\varphi \,{\colon}\, D \to B$
which satisfies the identity
$\varphi \,{\colon}\, D \to B$
which satisfies the identity
for all
![]() $n \in \mathbb N$
and for all
$n \in \mathbb N$
and for all
![]() $\tau \in T(B)$
, where t denotes the identity map on
$\tau \in T(B)$
, where t denotes the identity map on
![]() $(0,1]$
.
$(0,1]$
.
Proof Let
![]() $(D_i)_{i=1}^{\infty }$
be an increasing sequence of finite-dimensional C
$(D_i)_{i=1}^{\infty }$
be an increasing sequence of finite-dimensional C
![]() $^*$
-subalgebras of D such that
$^*$
-subalgebras of D such that
![]() $\bigcup _{i=1}^{\infty } D_i$
is dense in D. Denote by
$\bigcup _{i=1}^{\infty } D_i$
is dense in D. Denote by
![]() $\iota _i$
the embedding of
$\iota _i$
the embedding of
![]() $D_i$
into D. We claim that the map
$D_i$
into D. We claim that the map
determined by the rule
is a Cuntz category morphism.
We first show that
![]() $\sigma _i$
in fact maps into
$\sigma _i$
in fact maps into
![]() $\operatorname {LAff}_+(TB)$
. The image of
$\operatorname {LAff}_+(TB)$
. The image of
![]() $[d] \in \operatorname {Cu} (C_0(0,1] \otimes D_i)$
is clearly a positive real-valued affine function on
$[d] \in \operatorname {Cu} (C_0(0,1] \otimes D_i)$
is clearly a positive real-valued affine function on
![]() $TB$
. By Section 5 of [Reference Elliott, Robert and Santiago33],
$TB$
. By Section 5 of [Reference Elliott, Robert and Santiago33],
![]() $\sigma _i([d])$
is lower semicontinuous. By assumption,
$\sigma _i([d])$
is lower semicontinuous. By assumption,
![]() $\mu $
is faithful and
$\mu $
is faithful and
![]() $\iota _i^* \circ \Phi (\tau )$
, being the restriction of a faithful trace on D (as D is simple), is also faithful for each
$\iota _i^* \circ \Phi (\tau )$
, being the restriction of a faithful trace on D (as D is simple), is also faithful for each
![]() $\tau \in TD_i$
. Therefore,
$\tau \in TD_i$
. Therefore,
![]() $(\mu \otimes (\iota _i^* \circ \Phi (\cdot )))[d]$
is (pointwise) strictly positive whenever
$(\mu \otimes (\iota _i^* \circ \Phi (\cdot )))[d]$
is (pointwise) strictly positive whenever
![]() $[d]$
is nonzero. Since B is unital and separable,
$[d]$
is nonzero. Since B is unital and separable,
![]() $TB$
is metrizable. Therefore, by [Reference Alfsen1, Corollary I.1.4] and [Reference Thiel62, Lemma 3.6],
$TB$
is metrizable. Therefore, by [Reference Alfsen1, Corollary I.1.4] and [Reference Thiel62, Lemma 3.6],
![]() $\sigma _i([d])$
is the pointwise supremum of an increasing sequence of continuous finite-valued functions in
$\sigma _i([d])$
is the pointwise supremum of an increasing sequence of continuous finite-valued functions in
![]() $\operatorname {LAff}_+(TB)$
. This shows that
$\operatorname {LAff}_+(TB)$
. This shows that
![]() $\sigma _i([d])$
is an element of
$\sigma _i([d])$
is an element of
![]() $\operatorname {LAff}_+(TB)$
.
$\operatorname {LAff}_+(TB)$
.
That
![]() $\sigma _i$
is a generalized Cuntz category morphism follows from Section 4 of [Reference Elliott, Robert and Santiago33], so all that remains is to show
$\sigma _i$
is a generalized Cuntz category morphism follows from Section 4 of [Reference Elliott, Robert and Santiago33], so all that remains is to show
![]() $\sigma _i$
preserves compact containment. Since
$\sigma _i$
preserves compact containment. Since
![]() $D_i$
is a finite-dimensional C
$D_i$
is a finite-dimensional C
![]() $^*$
-algebra, we may identify it with a finite direct sum of matrix algebras,
$^*$
-algebra, we may identify it with a finite direct sum of matrix algebras,
![]() $\bigoplus _{j=1}^k M_{n_j}$
. Using that
$\bigoplus _{j=1}^k M_{n_j}$
. Using that
![]() $C_0(0,1] \otimes (\bigoplus _{j=1}^k M_{n_j})$
is isomorphic to
$C_0(0,1] \otimes (\bigoplus _{j=1}^k M_{n_j})$
is isomorphic to
![]() $\bigoplus _{j=1}^k (C_0(0,1] \otimes M_{n_j})$
, we make the identification
$\bigoplus _{j=1}^k (C_0(0,1] \otimes M_{n_j})$
, we make the identification
![]() $\operatorname {Cu}(C_0(0,1] \otimes D_i) = \bigoplus _{j=1}^k \operatorname {Cu}(C_0(0,1] \otimes M_{n_j})$
. By [Reference Coward, Elliott and Ivanescu18, Appendix 6], the embedding of
$\operatorname {Cu}(C_0(0,1] \otimes D_i) = \bigoplus _{j=1}^k \operatorname {Cu}(C_0(0,1] \otimes M_{n_j})$
. By [Reference Coward, Elliott and Ivanescu18, Appendix 6], the embedding of
![]() $C_0(0,1]$
into the upper-left corner of
$C_0(0,1]$
into the upper-left corner of
![]() $C_0(0,1] \otimes M_{n_j}$
induces an isomorphism at the level of the Cuntz category. For each j, we denote by
$C_0(0,1] \otimes M_{n_j}$
induces an isomorphism at the level of the Cuntz category. For each j, we denote by
![]() $e_j$
the nonzero minimal projection in the upper-left corner of
$e_j$
the nonzero minimal projection in the upper-left corner of
![]() $M_{n_j}$
, and we denote by
$M_{n_j}$
, and we denote by
![]() $\rho _j$
the trace on
$\rho _j$
the trace on
![]() $M_{n_j}$
. These maps induce an isomorphism
$M_{n_j}$
. These maps induce an isomorphism
![]() $\bigoplus _{j=1}^k \operatorname {Cu}(C_0(0,1] \otimes M_{n_j}) \cong \bigoplus _{j=1}^k \operatorname {Cu} (C_0(0,1])$
. By Theorem 2.14,
$\bigoplus _{j=1}^k \operatorname {Cu}(C_0(0,1] \otimes M_{n_j}) \cong \bigoplus _{j=1}^k \operatorname {Cu} (C_0(0,1])$
. By Theorem 2.14,
![]() $\operatorname {Cu}(C_0(0,1]) \cong \text {Lsc}((0,1],\overline {\mathbb N})$
and so under these isomorphisms, an arbitrary element
$\operatorname {Cu}(C_0(0,1]) \cong \text {Lsc}((0,1],\overline {\mathbb N})$
and so under these isomorphisms, an arbitrary element
![]() $[d] \in \operatorname {Cu}(C_0(0,1] \otimes D_i)$
is a direct sum of elements
$[d] \in \operatorname {Cu}(C_0(0,1] \otimes D_i)$
is a direct sum of elements
![]() $d_1, \ldots , d_k$
of
$d_1, \ldots , d_k$
of
![]() $\text {Lsc}((0,1],\overline {\mathbb N})$
. Pick
$\text {Lsc}((0,1],\overline {\mathbb N})$
. Pick
![]() $d_j^i \in C_0(0,1]$
to have open support exactly
$d_j^i \in C_0(0,1]$
to have open support exactly
![]() $\{d_j> i\}$
(
$\{d_j> i\}$
(
![]() $j = 1, \ldots , k$
and
$j = 1, \ldots , k$
and
![]() $i \in \mathbb N$
). Let
$i \in \mathbb N$
). Let
![]() $(p_i)_{i=0}^{\infty }$
be a sequence of mutually orthogonal rank-one projections and let
$(p_i)_{i=0}^{\infty }$
be a sequence of mutually orthogonal rank-one projections and let
![]() $\iota : \text {Lsc}((0,1],\overline {\mathbb N}) \to \operatorname {Cu} (C_0(0,1])$
and
$\iota : \text {Lsc}((0,1],\overline {\mathbb N}) \to \operatorname {Cu} (C_0(0,1])$
and
![]() $\mu \,{\colon}\, \text {Lsc}((0,1],\overline {\mathbb N}) \to [0,\infty ]$
be as in the proof of Theorem 3.1. The direct sum of copies of
$\mu \,{\colon}\, \text {Lsc}((0,1],\overline {\mathbb N}) \to [0,\infty ]$
be as in the proof of Theorem 3.1. The direct sum of copies of
![]() $\iota $
gives an isomorphism
$\iota $
gives an isomorphism
![]() $\bigoplus _{j=1}^k \text {Lsc}((0,1],\overline {\mathbb N}) \to \bigoplus _{j=1}^k\operatorname {Cu}(C_0(0,1])$
. Under the aforementioned isomorphisms, we have
$\bigoplus _{j=1}^k \text {Lsc}((0,1],\overline {\mathbb N}) \to \bigoplus _{j=1}^k\operatorname {Cu}(C_0(0,1])$
. Under the aforementioned isomorphisms, we have
 $$\begin{align*}[d] = \sum_{j=1}^k \sum_{i=0}^{\infty} [d_j^i \otimes e_j \otimes p_i]. \end{align*}$$
$$\begin{align*}[d] = \sum_{j=1}^k \sum_{i=0}^{\infty} [d_j^i \otimes e_j \otimes p_i]. \end{align*}$$
Therefore,
 $$ \begin{align*} \sigma_i([d]) & = \sum_{j=1}^k \sum_{i=0}^{\infty} \mu(d_j^i) (\iota_i^* \circ \Phi(\cdot))(e_j) \text{Tr} (p_i) \\ & = \sum_{j=1}^k \sum_{i=0}^{\infty} \mu(d_j^i) (\iota_i^* \circ \Phi(\cdot))(e_j) \\ & = \sum_{j=1}^k \mu(d_j) (\iota_i^* \circ \Phi(\cdot))(e_j). \end{align*} $$
$$ \begin{align*} \sigma_i([d]) & = \sum_{j=1}^k \sum_{i=0}^{\infty} \mu(d_j^i) (\iota_i^* \circ \Phi(\cdot))(e_j) \text{Tr} (p_i) \\ & = \sum_{j=1}^k \sum_{i=0}^{\infty} \mu(d_j^i) (\iota_i^* \circ \Phi(\cdot))(e_j) \\ & = \sum_{j=1}^k \mu(d_j) (\iota_i^* \circ \Phi(\cdot))(e_j). \end{align*} $$
Let us use the above calculation to show that
![]() $\sigma _i([d])$
is continuous. If
$\sigma _i([d])$
is continuous. If
![]() $\sigma _i([d])$
is bounded, then
$\sigma _i([d])$
is bounded, then
![]() $\sigma _i([d])$
is an affine extension of the continuous function taking on the real values
$\sigma _i([d])$
is an affine extension of the continuous function taking on the real values
![]() $\mu (d_j)$
at the extreme points
$\mu (d_j)$
at the extreme points
![]() $\rho _j$
of
$\rho _j$
of
![]() $TD_i$
. Since
$TD_i$
. Since
![]() $D_i$
is finite-dimensional,
$D_i$
is finite-dimensional,
![]() $TD_i$
is a Bauer simplex and so
$TD_i$
is a Bauer simplex and so
![]() $\sigma _i([d])$
is continuous. If
$\sigma _i([d])$
is continuous. If
![]() $\sigma _i([d])$
is not bounded, then
$\sigma _i([d])$
is not bounded, then
![]() $\mu (d_j)$
must be equal to
$\mu (d_j)$
must be equal to
![]() $\infty $
for some j. Since
$\infty $
for some j. Since
![]() $\iota _i^* \circ \Phi (\cdot )$
maps into the faithful part of
$\iota _i^* \circ \Phi (\cdot )$
maps into the faithful part of
![]() $TD_i$
,
$TD_i$
,
![]() $\sigma _i([d])$
is the continuous function which is constant and equal to
$\sigma _i([d])$
is the continuous function which is constant and equal to
![]() $\infty $
.
$\infty $
.
Suppose
![]() $[f] \ll [g]$
in
$[f] \ll [g]$
in
![]() $\operatorname {Cu}(C_0(0,1] \otimes D_i)$
. Let the notation be as in the preceding two paragraphs for both
$\operatorname {Cu}(C_0(0,1] \otimes D_i)$
. Let the notation be as in the preceding two paragraphs for both
![]() $[f]$
and
$[f]$
and
![]() $[g]$
. If
$[g]$
. If
![]() $[f]$
is equal to zero, then
$[f]$
is equal to zero, then
![]() $\sigma _i([f])$
is also equal to zero and it is compactly contained in every element of
$\sigma _i([f])$
is also equal to zero and it is compactly contained in every element of
![]() $\operatorname {LAff}_+( TB)$
(and in particular,
$\operatorname {LAff}_+( TB)$
(and in particular,
![]() $\sigma _i([g])$
). If
$\sigma _i([g])$
). If
![]() $[f]$
is nonzero, then
$[f]$
is nonzero, then
![]() $f_j \ll g_j$
for each j and
$f_j \ll g_j$
for each j and
![]() $f_j$
must be nonzero for some j. For this particular j,
$f_j$
must be nonzero for some j. For this particular j,
![]() $\mu (f_j) < \mu (g_j)$
, by faithfulness of
$\mu (f_j) < \mu (g_j)$
, by faithfulness of
![]() $\mu $
, and for each j,
$\mu $
, and for each j,
![]() $\mu (f_j)$
is finite and
$\mu (f_j)$
is finite and
![]() $\mu (f_j) \leq \mu (g_j)$
(these facts are established in the proof of Theorem 3.1). It follows from the above computation and the fact that
$\mu (f_j) \leq \mu (g_j)$
(these facts are established in the proof of Theorem 3.1). It follows from the above computation and the fact that
![]() $\iota _i^* \circ \Phi (\tau )> 0$
(
$\iota _i^* \circ \Phi (\tau )> 0$
(
![]() $\tau \in TB$
) that
$\tau \in TB$
) that
![]() $\sigma _i([f]) < \sigma _i([g])$
. By the previous paragraph, this also shows that
$\sigma _i([f]) < \sigma _i([g])$
. By the previous paragraph, this also shows that
![]() $\sigma _i([f])$
is continuous and finite-valued. Since lower semicontinuous functions attain their infima on compact sets, it follows from the characterization of compact containment in Section 2 of [Reference Elliott, Robert and Santiago33] (or [Reference Thiel62, Lemma 3.6]) that
$\sigma _i([f])$
is continuous and finite-valued. Since lower semicontinuous functions attain their infima on compact sets, it follows from the characterization of compact containment in Section 2 of [Reference Elliott, Robert and Santiago33] (or [Reference Thiel62, Lemma 3.6]) that
![]() $\sigma _i([f])$
is compactly contained in
$\sigma _i([f])$
is compactly contained in
![]() $\sigma _i([g])$
. This shows
$\sigma _i([g])$
. This shows
![]() $\sigma _i$
is a Cuntz category morphism.
$\sigma _i$
is a Cuntz category morphism.
Since
![]() $\operatorname {LAff}_+(TB)$
is (in a natural way) a subobject of
$\operatorname {LAff}_+(TB)$
is (in a natural way) a subobject of
![]() $\operatorname {Cu}(B)$
(Lemma 2.12),
$\operatorname {Cu}(B)$
(Lemma 2.12),
![]() $\sigma _i$
extends to a Cuntz category morphism into
$\sigma _i$
extends to a Cuntz category morphism into
![]() $\operatorname {Cu}(B)$
which we denote again by
$\operatorname {Cu}(B)$
which we denote again by
![]() $\sigma _i$
. In order to lift
$\sigma _i$
. In order to lift
![]() $\sigma _i$
to a
$\sigma _i$
to a
![]() $*$
-homomorphism, let us check that
$*$
-homomorphism, let us check that
![]() $\sigma _i$
takes a strictly positive element into an element majorized by a strictly positive element:
$\sigma _i$
takes a strictly positive element into an element majorized by a strictly positive element:
 $$ \begin{align*} \sigma_i([t \otimes 1_{D_i}]) & = \sum_{j=1}^k \mu(\chi_{(0,1]})(\iota_i^* \circ \Phi(\cdot))[1_{M_{n_j}}] \leq \sum_{j=1}^k (\iota_i^* \circ \Phi(\cdot))[1_{M_{n_j}}] \\ & = \sum_{j=1}^k \Phi(\cdot)[\iota_i(1_{M_{n_j}})] = \Phi(\cdot) [\iota_i(1_{D_i})] \leq \widehat{[1_B]}. \end{align*} $$
$$ \begin{align*} \sigma_i([t \otimes 1_{D_i}]) & = \sum_{j=1}^k \mu(\chi_{(0,1]})(\iota_i^* \circ \Phi(\cdot))[1_{M_{n_j}}] \leq \sum_{j=1}^k (\iota_i^* \circ \Phi(\cdot))[1_{M_{n_j}}] \\ & = \sum_{j=1}^k \Phi(\cdot)[\iota_i(1_{M_{n_j}})] = \Phi(\cdot) [\iota_i(1_{D_i})] \leq \widehat{[1_B]}. \end{align*} $$
In the first inequality, we have used that
![]() $\mu $
is of norm at most one. By Theorem 2.15, i.e., by [Reference Ciuperca and Elliott14, Theorem 4.1], as modified in the remark on page 29 of [Reference Ciuperca and Elliott14] (to replace
$\mu $
is of norm at most one. By Theorem 2.15, i.e., by [Reference Ciuperca and Elliott14, Theorem 4.1], as modified in the remark on page 29 of [Reference Ciuperca and Elliott14] (to replace
![]() $[0,1]$
with
$[0,1]$
with
![]() $(0,1]$
), for each i there exists a
$(0,1]$
), for each i there exists a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi _i \,{\colon}\, C_0(0,1] \otimes D_i \to B$
, which is unique up to approximate unitary equivalence, such that
$\pi _i \,{\colon}\, C_0(0,1] \otimes D_i \to B$
, which is unique up to approximate unitary equivalence, such that
![]() $\operatorname {Cu} (\pi _i) = \sigma _i$
. Let us now denote by
$\operatorname {Cu} (\pi _i) = \sigma _i$
. Let us now denote by
![]() $\iota _i$
the embedding of
$\iota _i$
the embedding of
![]() $C_0(0,1] \otimes D_i$
into
$C_0(0,1] \otimes D_i$
into
![]() $C_0(0,1] \otimes D_{i+1}$
. Then with the embeddings
$C_0(0,1] \otimes D_{i+1}$
. Then with the embeddings
![]() $\operatorname {Cu}(\iota _i)$
on the top row and the identity map
$\operatorname {Cu}(\iota _i)$
on the top row and the identity map
![]() $\operatorname {Cu}(\text {id}_B)$
on the bottom row, we have the following one-sided intertwining at the level of the Cuntz category:
$\operatorname {Cu}(\text {id}_B)$
on the bottom row, we have the following one-sided intertwining at the level of the Cuntz category:

The
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\pi _i \,{\colon}\, C_0(0,1] \otimes D_i \to B$
may be corrected by inner automorphisms to obtain the following one-sided approximate intertwining (in the sense of [Reference Elliott25, Section 2]):
$\pi _i \,{\colon}\, C_0(0,1] \otimes D_i \to B$
may be corrected by inner automorphisms to obtain the following one-sided approximate intertwining (in the sense of [Reference Elliott25, Section 2]):

By [Reference Elliott25, Remark 2.3], there exists a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi : C_0(0,1] \otimes D \to B$
as in the above diagram and the map
$\pi : C_0(0,1] \otimes D \to B$
as in the above diagram and the map
![]() $\varphi \,{\colon}\, D \to B$
determined by the rule
$\varphi \,{\colon}\, D \to B$
determined by the rule
![]() $\varphi (d):= \pi (t \otimes d)$
is c.p.c. order zero, by Corollary 2.5. Let us now verify that
$\varphi (d):= \pi (t \otimes d)$
is c.p.c. order zero, by Corollary 2.5. Let us now verify that
![]() $\varphi $
satisfies the required tracial identity. By continuity, it suffices to check that the the tracial identity holds at the finite stages. Let
$\varphi $
satisfies the required tracial identity. By continuity, it suffices to check that the the tracial identity holds at the finite stages. Let
![]() $d \in D_i,$
and let
$d \in D_i,$
and let
![]() $\tau \in TB$
be given. Then
$\tau \in TB$
be given. Then
 $$ \begin{align*} \tau \varphi^n(d) & \stackrel{(2.6)}{=} \tau \pi(t^n \otimes d) = \tau \lim_{i \to \infty} \pi_i(t^n \otimes d) \\ & \ \ \,= \lim_{i \to \infty} (\mu \otimes (\iota_i^* \circ \Phi)(\tau))(t^n \otimes d) \\ & \ \ \,= \mu(t^n) \Phi(\tau) (d). \end{align*} $$
$$ \begin{align*} \tau \varphi^n(d) & \stackrel{(2.6)}{=} \tau \pi(t^n \otimes d) = \tau \lim_{i \to \infty} \pi_i(t^n \otimes d) \\ & \ \ \,= \lim_{i \to \infty} (\mu \otimes (\iota_i^* \circ \Phi)(\tau))(t^n \otimes d) \\ & \ \ \,= \mu(t^n) \Phi(\tau) (d). \end{align*} $$
The second equality follows from the one-sided approximate intertwining, and the third equality follows from continuity of
![]() $\tau $
and by definition of
$\tau $
and by definition of
![]() $\sigma _i$
. (Note that
$\sigma _i$
. (Note that
![]() $\operatorname {Cu}(\pi ) = \lim _{i\to \infty } \sigma _i$
, but we do not actually use this.)
$\operatorname {Cu}(\pi ) = \lim _{i\to \infty } \sigma _i$
, but we do not actually use this.)
Lemma 4.4 There exists a sequence of fully supported Radon measures
![]() $\mu _k$
on
$\mu _k$
on
![]() $(0,1]$
with total mass one such that
$(0,1]$
with total mass one such that
where t denotes the identity map on
![]() $(0,1]$
. Necessarily, this holds also for
$(0,1]$
. Necessarily, this holds also for
![]() $t^n$
, rather than just t, for each
$t^n$
, rather than just t, for each
![]() $n \in \mathbb N$
.
$n \in \mathbb N$
.
Proof Pick measures which are increasingly weighted to the right.
Theorem 4.5 Any two unital, simple,
![]() $\mathcal Z$
-stable, separable amenable C
$\mathcal Z$
-stable, separable amenable C
![]() $^*$
-algebras satisfying the UCT with isomorphic tracial simplices are colored isomorphic.
$^*$
-algebras satisfying the UCT with isomorphic tracial simplices are colored isomorphic.
Proof We first consider the purely infinite case. This part of the theorem holds without assuming the UCT. Let A and B be Kirchberg algebras. By [Reference Choi and Effros13, Theorem 3.1], [Reference Connes17, Corollary 2], and [Reference Wassermann67, Proposition 7], separable amenable C
![]() $^*$
-algebras are exact. Hence by Theorem 2.16, there is a unital embedding of A into
$^*$
-algebras are exact. Hence by Theorem 2.16, there is a unital embedding of A into
![]() $\mathcal O_2$
. Since B is purely infinite,
$\mathcal O_2$
. Since B is purely infinite,
![]() $K_0(B)$
consists of the Murray–von Neumann equivalence classes of nonzero properly infinite projections in B (see [Reference Cuntz19, Theorem 1.4]). In particular, there is a nonzero properly infinite projection
$K_0(B)$
consists of the Murray–von Neumann equivalence classes of nonzero properly infinite projections in B (see [Reference Cuntz19, Theorem 1.4]). In particular, there is a nonzero properly infinite projection
![]() $p \in B$
whose
$p \in B$
whose
![]() $K_0$
-class is equal to zero. It follows from [Reference Rørdam and Størmer58, Proposition 4.2.3] that there exists a unital embedding of
$K_0$
-class is equal to zero. It follows from [Reference Rørdam and Størmer58, Proposition 4.2.3] that there exists a unital embedding of
![]() $\mathcal O_2$
into
$\mathcal O_2$
into
![]() $pBp$
and therefore a (possibly) nonunital embedding into B. Denote by
$pBp$
and therefore a (possibly) nonunital embedding into B. Denote by
![]() $\varphi \,{\colon}\, A \to B$
the composition of these embeddings and construct
$\varphi \,{\colon}\, A \to B$
the composition of these embeddings and construct
![]() $\psi \,{\colon}\, B \to A$
symmetrically. Then since
$\psi \,{\colon}\, B \to A$
symmetrically. Then since
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are injective and therefore isometric
$\psi $
are injective and therefore isometric
![]() $*$
-homomorphisms, the ultrapower maps
$*$
-homomorphisms, the ultrapower maps
![]() $\psi \varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
$\psi \varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
![]() $\varphi \psi : B_{\omega } \to A_{\omega }$
induced by their compositions are also isometric and in particular injective. By two applications of Theorem 2.18, the pairs
$\varphi \psi : B_{\omega } \to A_{\omega }$
induced by their compositions are also isometric and in particular injective. By two applications of Theorem 2.18, the pairs
![]() $\psi \varphi \iota _A$
and
$\psi \varphi \iota _A$
and
![]() $\iota _A$
; and
$\iota _A$
; and
![]() $\varphi \psi \iota _B$
and
$\varphi \psi \iota _B$
and
![]() $\iota _B$
are each colored equivalent, where
$\iota _B$
are each colored equivalent, where
![]() $\iota _A$
(resp.
$\iota _A$
(resp.
![]() $\iota _B$
) denote the canonical embedding of A (resp. B) into its ultrapower.
$\iota _B$
) denote the canonical embedding of A (resp. B) into its ultrapower.
Now (as we may, in view of Theorem 2.9), suppose that A and B are two finite C
![]() $^*$
-algebras satisfying the hypotheses. By Theorem 2.17, there exists a unital embedding
$^*$
-algebras satisfying the hypotheses. By Theorem 2.17, there exists a unital embedding
![]() $\alpha _A$
of A into a separable, unital, simple AF algebra D such that the induced map
$\alpha _A$
of A into a separable, unital, simple AF algebra D such that the induced map
![]() $\alpha _A^*: T(D) \to T(A)$
is an isomorphism of tracial simplices. This, combined with an isomorphism
$\alpha _A^*: T(D) \to T(A)$
is an isomorphism of tracial simplices. This, combined with an isomorphism
![]() $T(B) \to T(A)$
(assumed to exist), yields an isomorphism
$T(B) \to T(A)$
(assumed to exist), yields an isomorphism
![]() $\Phi \,{\colon}\, T(B) \to T(D)$
. Pairing this with the faithful tracial states
$\Phi \,{\colon}\, T(B) \to T(D)$
. Pairing this with the faithful tracial states
![]() $\mu _k$
on
$\mu _k$
on
![]() $C_0(0,1]$
of Lemma 4.4, one obtains by Theorem 4.3 a sequence of c.p.c. order zero maps
$C_0(0,1]$
of Lemma 4.4, one obtains by Theorem 4.3 a sequence of c.p.c. order zero maps
![]() $\varphi _k \,{\colon}\, D \to B$
satisfying the identity
$\varphi _k \,{\colon}\, D \to B$
satisfying the identity
for every
![]() $k,n \in \mathbb N$
and each
$k,n \in \mathbb N$
and each
![]() $\tau \in T(B)$
. Denote by
$\tau \in T(B)$
. Denote by
![]() $\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
the c.p.c. order zero map induced between the ultrapowers by the maps
$\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
the c.p.c. order zero map induced between the ultrapowers by the maps
![]() $\varphi _k \alpha _A \,{\colon}\, A \to B$
. As above, by [Reference Winter and Zacharias68, Corollary 3.4],
$\varphi _k \alpha _A \,{\colon}\, A \to B$
. As above, by [Reference Winter and Zacharias68, Corollary 3.4],
![]() $\varphi $
induces a mapping
$\varphi $
induces a mapping
![]() $\varphi ^*$
of bounded traces on
$\varphi ^*$
of bounded traces on
![]() $B_{\omega }$
into bounded traces on
$B_{\omega }$
into bounded traces on
![]() $A_{\omega }$
. Then we have
$A_{\omega }$
. Then we have
 $$ \begin{align} \begin{aligned} \tau\varphi^n & \stackrel{(2.3)}{=} \lim_{k \to \omega} \tau_k (\varphi_k^n \alpha_A) \\ & \stackrel{(4.3)}{=} \alpha_A^* (\lim_{k \to \omega} (\mu_k(t^n) \Phi(\tau_k))) \stackrel{(4.2)}{=} \lim_{k \to \omega} (\alpha_A^* \Phi)(\tau_k) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \tau\varphi^n & \stackrel{(2.3)}{=} \lim_{k \to \omega} \tau_k (\varphi_k^n \alpha_A) \\ & \stackrel{(4.3)}{=} \alpha_A^* (\lim_{k \to \omega} (\mu_k(t^n) \Phi(\tau_k))) \stackrel{(4.2)}{=} \lim_{k \to \omega} (\alpha_A^* \Phi)(\tau_k) \end{aligned} \end{align} $$
for each
![]() $n \in \mathbb N$
and limit trace
$n \in \mathbb N$
and limit trace
![]() $\tau = \lim _{k \to \omega } \tau _k \in T_{\omega }(B_{\omega })$
.
$\tau = \lim _{k \to \omega } \tau _k \in T_{\omega }(B_{\omega })$
.
Symmetrically, there is, again by Theorem 2.17, a unital embedding
![]() $\alpha _B$
of B into a unital, simple, separable AF algebra E such that the induced map
$\alpha _B$
of B into a unital, simple, separable AF algebra E such that the induced map
![]() $\alpha _B^* \,{\colon}\, T(E) \to T(B)$
is an isomorphism of tracial simplices. Using as above the isomorphism
$\alpha _B^* \,{\colon}\, T(E) \to T(B)$
is an isomorphism of tracial simplices. Using as above the isomorphism
![]() $\Psi := (\alpha _A^* \Phi \alpha _B^*) ^{-1} \,{\colon}\, T(A) \to T(E)$
and the faithful tracial states
$\Psi := (\alpha _A^* \Phi \alpha _B^*) ^{-1} \,{\colon}\, T(A) \to T(E)$
and the faithful tracial states
![]() $\mu _k$
, we obtain a c.p.c. order zero map
$\mu _k$
, we obtain a c.p.c. order zero map
![]() $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
for each
![]() $n \in \mathbb N$
and limit trace
$n \in \mathbb N$
and limit trace
![]() $\tau = \lim _{k \to \omega } \tau _k\in T_{\omega }(A_{\omega })$
. So for all limit traces
$\tau = \lim _{k \to \omega } \tau _k\in T_{\omega }(A_{\omega })$
. So for all limit traces
![]() $\tau = \lim _{k \to \omega } \tau _k \in T_{\omega }(A_{\omega })$
, we have
$\tau = \lim _{k \to \omega } \tau _k \in T_{\omega }(A_{\omega })$
, we have
 $$ \begin{align} \begin{aligned} \tau (\psi \varphi)^n & \stackrel{(2.3)}{=} \tau \psi^n \varphi^n \stackrel{(4.5)}{=} (\varphi^n)^* (\lim_{k \to \omega}(\alpha _B^* \Psi)(\tau_k)) \\ & \stackrel{(4.4)}{=} \alpha_A^* \Phi (\lim_{k \to \omega} (\alpha_B^* \Psi)(\tau_k)) = \lim_{k \to \omega} \alpha_A^* \Phi\alpha_B^* \Psi(\tau_k) = \tau, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \tau (\psi \varphi)^n & \stackrel{(2.3)}{=} \tau \psi^n \varphi^n \stackrel{(4.5)}{=} (\varphi^n)^* (\lim_{k \to \omega}(\alpha _B^* \Psi)(\tau_k)) \\ & \stackrel{(4.4)}{=} \alpha_A^* \Phi (\lim_{k \to \omega} (\alpha_B^* \Psi)(\tau_k)) = \lim_{k \to \omega} \alpha_A^* \Phi\alpha_B^* \Psi(\tau_k) = \tau, \end{aligned} \end{align} $$
where the last equality follows from the definition of
![]() $\Psi $
.
$\Psi $
.
Weak
![]() $^*$
density of
$^*$
density of
![]() $T_{\omega }(A)$
in
$T_{\omega }(A)$
in
![]() $T(A_{\omega })$
(Theorem 2.7) extends the identity (4.6) to all tracial states on
$T(A_{\omega })$
(Theorem 2.7) extends the identity (4.6) to all tracial states on
![]() $A_{\omega }$
. Since A is simple, the canonical embedding of A into
$A_{\omega }$
. Since A is simple, the canonical embedding of A into
![]() $A_{\omega }$
is totally full. Hence by Theorem 2.20,
$A_{\omega }$
is totally full. Hence by Theorem 2.20,
![]() $\psi \varphi \iota _A$
and
$\psi \varphi \iota _A$
and
![]() $\iota _A$
are colored equivalent. By a symmetric argument,
$\iota _A$
are colored equivalent. By a symmetric argument,
![]() $\varphi \psi \iota _B$
and
$\varphi \psi \iota _B$
and
![]() $\iota _B$
are colored equivalent. It follows immediately from (4.4) and (4.5) that
$\iota _B$
are colored equivalent. It follows immediately from (4.4) and (4.5) that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
preserve constant limit traces. This shows A is colored isomorphic to B (with m and n of (2.7) equal to two).
$\psi $
preserve constant limit traces. This shows A is colored isomorphic to B (with m and n of (2.7) equal to two).
Corollary 4.6 Let A and B be classifiable C
![]() $^*$
-algebras (i.e., ones satisfying the hypotheses of Theorem 4.5). Then the following statements are equivalent:
$^*$
-algebras (i.e., ones satisfying the hypotheses of Theorem 4.5). Then the following statements are equivalent:
-
(1) There exist constant limit trace preserving c.p.c. order zero maps
 $\varphi : A_{\omega } \to B_{\omega }$
and
$\varphi : A_{\omega } \to B_{\omega }$
and
 $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
 $\varphi ^n$
and
$\varphi ^n$
and
 $\psi ^n$
induce mutually inverse isomorphisms of
$\psi ^n$
induce mutually inverse isomorphisms of
 $T(A_{\omega })$
and
$T(A_{\omega })$
and
 $T(B_{\omega })$
for each
$T(B_{\omega })$
for each
 $n \in \mathbb N$
.
$n \in \mathbb N$
. -
(2) There exist constant limit trace preserving c.p.c. order zero maps
 $\varphi :A_{\omega } \to B_{\omega }$
and
$\varphi :A_{\omega } \to B_{\omega }$
and
 $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
such that
 $\varphi ^n$
and
$\varphi ^n$
and
 $\psi ^n$
induce mutually inverse isomorphisms of
$\psi ^n$
induce mutually inverse isomorphisms of
 $T(A_{\omega })$
and
$T(A_{\omega })$
and
 $T(B_{\omega })$
for some
$T(B_{\omega })$
for some
 $n \in \mathbb N$
.
$n \in \mathbb N$
. -
(3) A and B are colored isomorphic (Definition 2.21).
-
(4) A and B are minimalist colored isomorphic (Definition 2.23).
-
(5)
 $T(A)$
is isomorphic to
$T(A)$
is isomorphic to
 $T(B)$
.
$T(B)$
.
Every isomorphism of
![]() $T(A)$
with
$T(A)$
with
![]() $T(B)$
arises from a colored isomorphism of A and B.
$T(B)$
arises from a colored isomorphism of A and B.
Proof (1)
![]() $\Longrightarrow $
(2) is clear. (2)
$\Longrightarrow $
(2) is clear. (2)
![]() $\Longrightarrow $
(1) Let
$\Longrightarrow $
(1) Let
![]() $\pi \,{\colon}\, A_{\omega } \to A^{\omega }$
denote the canonical quotient map. By assumption, there exists an
$\pi \,{\colon}\, A_{\omega } \to A^{\omega }$
denote the canonical quotient map. By assumption, there exists an
![]() $n \in \mathbb N$
such that
$n \in \mathbb N$
such that
![]() $\tau \psi ^n \varphi ^n = \tau $
for all
$\tau \psi ^n \varphi ^n = \tau $
for all
![]() $\tau \in T(A_{\omega })$
. By Lemma 2.8, this implies
$\tau \in T(A_{\omega })$
. By Lemma 2.8, this implies
![]() $\pi \psi ^n \varphi ^n = \pi \text {id}_{A_{\omega }}$
. In particular, we will use that
$\pi \psi ^n \varphi ^n = \pi \text {id}_{A_{\omega }}$
. In particular, we will use that
![]() $\pi \psi ^n \varphi ^n(1_{A_{\omega }}) = \pi (1_{A_{\omega }})$
below. Since
$\pi \psi ^n \varphi ^n(1_{A_{\omega }}) = \pi (1_{A_{\omega }})$
below. Since
is a projection, it then follows from Corollary 2.2 that
![]() $\pi \psi \varphi $
is a
$\pi \psi \varphi $
is a
![]() $*$
-homomorphism. We have used Corollaries 2.3 and 2.4 for the second and third equalities. Therefore,
$*$
-homomorphism. We have used Corollaries 2.3 and 2.4 for the second and third equalities. Therefore,
![]() $ \pi \psi ^k \varphi ^k = \pi (\psi \varphi )^k = (\pi \psi \varphi )^k = \pi \psi \varphi $
for each
$ \pi \psi ^k \varphi ^k = \pi (\psi \varphi )^k = (\pi \psi \varphi )^k = \pi \psi \varphi $
for each
![]() $k \in \mathbb N$
. By Lemma 2.8 again, this implies
$k \in \mathbb N$
. By Lemma 2.8 again, this implies
![]() $\tau \psi ^k \varphi ^k = \tau $
for each
$\tau \psi ^k \varphi ^k = \tau $
for each
![]() $\tau \in T(A_{\omega })$
and each
$\tau \in T(A_{\omega })$
and each
![]() $k \in \mathbb N$
. A symmetric argument shows that
$k \in \mathbb N$
. A symmetric argument shows that
![]() $\varphi ^k$
and
$\varphi ^k$
and
![]() $\psi ^k$
induce mutually inverse isomorphisms of
$\psi ^k$
induce mutually inverse isomorphisms of
![]() $T(A_{\omega })$
and
$T(A_{\omega })$
and
![]() $T(B_{\omega })$
.
$T(B_{\omega })$
.
(1)
![]() $\Longrightarrow $
(3) follows (without the UCT assumption) from two applications of Theorem 2.20: once with
$\Longrightarrow $
(3) follows (without the UCT assumption) from two applications of Theorem 2.20: once with
![]() $\psi \varphi \iota _A$
and
$\psi \varphi \iota _A$
and
![]() $\iota _A$
where
$\iota _A$
where
![]() $\iota _A$
is the constant sequence embedding of A into
$\iota _A$
is the constant sequence embedding of A into
![]() $A_{\omega }$
and once more with
$A_{\omega }$
and once more with
![]() $\varphi \psi \iota _B$
and
$\varphi \psi \iota _B$
and
![]() $\iota _B$
. (3)
$\iota _B$
. (3)
![]() $\Longrightarrow $
(4) is immediate. (4)
$\Longrightarrow $
(4) is immediate. (4)
![]() $\Longrightarrow $
(5) as mentioned in the proof of Theorem 4.1, the same conclusion holds with the weaker hypothesis that the two C
$\Longrightarrow $
(5) as mentioned in the proof of Theorem 4.1, the same conclusion holds with the weaker hypothesis that the two C
![]() $^*$
-algebras are minimalist colored isomorphic. (5)
$^*$
-algebras are minimalist colored isomorphic. (5)
![]() $\Longrightarrow $
(1) is given by (4.6) in the proof of Theorem 4.5 (along with the analogous statement for
$\Longrightarrow $
(1) is given by (4.6) in the proof of Theorem 4.5 (along with the analogous statement for
![]() $(\varphi \psi )^n$
) and Corollary 2.4.
$(\varphi \psi )^n$
) and Corollary 2.4.
The last statement follows from the proof of Theorem 4.5, which constructs a colored isomorphism using a given isomorphism of
![]() $T(A)$
with
$T(A)$
with
![]() $T(B)$
, and the proof of Theorem 4.1, which recovers the given isomorphism of
$T(B)$
, and the proof of Theorem 4.1, which recovers the given isomorphism of
![]() $T(A)$
with
$T(A)$
with
![]() $T(B)$
from the constructed colored isomorphism.
$T(B)$
from the constructed colored isomorphism.
We are not sure to what extent the c.p.c. order zero maps involved in a colored isomorphism are unique.
Corollary 4.7 Let A be a classifiable C
![]() $^*$
-algebra. If
$^*$
-algebra. If
![]() $T(A) = \varnothing $
, then A is colored isomorphic to
$T(A) = \varnothing $
, then A is colored isomorphic to
![]() $\mathcal O_2$
. If
$\mathcal O_2$
. If
![]() $T(A) \neq \varnothing $
, then A is colored isomorphic to a unital simple AF algebra.
$T(A) \neq \varnothing $
, then A is colored isomorphic to a unital simple AF algebra.
Proof If
![]() $T(A) = \varnothing $
, then by Theorem 4.5, A is colored isomorphic to
$T(A) = \varnothing $
, then by Theorem 4.5, A is colored isomorphic to
![]() $\mathcal O_2$
. If
$\mathcal O_2$
. If
![]() $T(A) \neq \varnothing $
, by [Reference Blackadar5, Theorem 3.10], there exists a unital AF algebra B whose tracial simplex isomorphic to
$T(A) \neq \varnothing $
, by [Reference Blackadar5, Theorem 3.10], there exists a unital AF algebra B whose tracial simplex isomorphic to
![]() $T(A)$
. The conclusion now follows from Theorem 4.5.
$T(A)$
. The conclusion now follows from Theorem 4.5.
The existence step in establishing finite nuclear dimension from
![]() $\mathcal Z$
-stability (see [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Lemma 7.4] and [Reference Castillejos, Evington, Tikuisis, White and Winter11, Lemma 5.2]) is the construction of a sequence of c.p.c. maps
$\mathcal Z$
-stability (see [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Lemma 7.4] and [Reference Castillejos, Evington, Tikuisis, White and Winter11, Lemma 5.2]) is the construction of a sequence of c.p.c. maps
![]() $\phi _i \,{\colon}\, A \to A$
, where A is a finite, unital, simple,
$\phi _i \,{\colon}\, A \to A$
, where A is a finite, unital, simple,
![]() $\mathcal Z$
-stable, separable amenable C
$\mathcal Z$
-stable, separable amenable C
![]() $^*$
-algebra, which factorize through finite-dimensional C
$^*$
-algebra, which factorize through finite-dimensional C
![]() $^*$
-algebras
$^*$
-algebras
![]() $F_i$
as
$F_i$
as

with
![]() $\theta _i$
c.p.c. and
$\theta _i$
c.p.c. and
![]() $\eta _i$
c.p.c. order zero, such that the induced maps
$\eta _i$
c.p.c. order zero, such that the induced maps
![]() $(\theta _i)_{i=1}^{\infty } \,{\colon}\, A \to \prod _{\omega } F_i$
and
$(\theta _i)_{i=1}^{\infty } \,{\colon}\, A \to \prod _{\omega } F_i$
and
![]() $\Phi = (\phi _i)_{i=1}^{\infty } \,{\colon}\, A \to A_{\omega }$
are order zero and
$\Phi = (\phi _i)_{i=1}^{\infty } \,{\colon}\, A \to A_{\omega }$
are order zero and
for each
![]() $a \in A$
and each
$a \in A$
and each
![]() $\tau \in T(A_{\omega })$
.
$\tau \in T(A_{\omega })$
.
More precisely, the conclusion in [Reference Castillejos, Evington, Tikuisis, White and Winter11, Lemma 5.2] is that
![]() $\Phi $
agrees with the canonical embedding
$\Phi $
agrees with the canonical embedding
![]() $\iota _A$
of A into
$\iota _A$
of A into
![]() $A_{\omega }$
in the uniform tracial ultrapower
$A_{\omega }$
in the uniform tracial ultrapower
![]() $A^{\omega },$
whereas the conclusion in [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Lemma 7.4] is that
$A^{\omega },$
whereas the conclusion in [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6, Lemma 7.4] is that
![]() $\tau \Phi = \tau \iota _A$
for each
$\tau \Phi = \tau \iota _A$
for each
![]() $\tau \in T(A_{\omega })$
. These conclusions are equivalent by Lemma 2.8 and Theorem 2.7.
$\tau \in T(A_{\omega })$
. These conclusions are equivalent by Lemma 2.8 and Theorem 2.7.
In the presence of the UCT, a one-sided formulation of Theorem 4.5 (Corollary 4.8) can be viewed as a generalization of the existence step mentioned earlier since the conclusion follows from the special case that B is an AF algebra. Since the nuclear dimension of B is zero (see [Reference Winter and Zacharias69, Remark 2.2(iii)]), there exist finite-dimensional C
![]() $^*$
-algebras
$^*$
-algebras
![]() $F_i$
and c.p.c. maps
$F_i$
and c.p.c. maps
![]() $\rho _i \,{\colon}\, B \to F_i$
and c.p.c. order zero maps
$\rho _i \,{\colon}\, B \to F_i$
and c.p.c. order zero maps
![]() $\sigma _i: F_i \to B$
such that the triangle below commutes approximately.
$\sigma _i: F_i \to B$
such that the triangle below commutes approximately.

The maps
![]() $\theta _i: A \to F_i$
on the left side of the diagram and the maps
$\theta _i: A \to F_i$
on the left side of the diagram and the maps
![]() $\eta _i \,{\colon}\, F_i \to A$
on the right side of the diagram satisfy the conclusion of the aforementioned existence step.
$\eta _i \,{\colon}\, F_i \to A$
on the right side of the diagram satisfy the conclusion of the aforementioned existence step.
Corollary 4.8 Let A and B be finite classifiable C
![]() $^*$
-algebras with isomorphic tracial simplices. Then there exist sequences of c.p.c. order zero maps
$^*$
-algebras with isomorphic tracial simplices. Then there exist sequences of c.p.c. order zero maps
![]() $\varphi _i \,{\colon}\, A \to B$
and
$\varphi _i \,{\colon}\, A \to B$
and
![]() $\psi _i \,{\colon}\, B \to A$
for
$\psi _i \,{\colon}\, B \to A$
for
![]() $i \in \mathbb N$
, such that the induced c.p.c. order zero maps
$i \in \mathbb N$
, such that the induced c.p.c. order zero maps
![]() $\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
$\varphi \,{\colon}\, A_{\omega } \to B_{\omega }$
and
![]() $\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
induce mutually inverse isomorphisms of
$\psi \,{\colon}\, B_{\omega } \to A_{\omega }$
induce mutually inverse isomorphisms of
![]() $T(A_{\omega })$
and
$T(A_{\omega })$
and
![]() $T(B_{\omega })$
. In particular,
$T(B_{\omega })$
. In particular,
for each
![]() $a \in A$
and each
$a \in A$
and each
![]() $\tau \in T(A_{\omega })$
.
$\tau \in T(A_{\omega })$
.
Proof This is a special case of Corollary 4.6.
Corollary 4.8 gives rise to the completely positive approximation property below. The nuclear dimension calculation in Corollary 4.9 is not new—in fact, it holds without the UCT assumption and without unitality (see [Reference Castillejos, Evington, Tikuisis, White and Winter11, Reference Ciuperca and Elliott14]), and our proof of it using the UCT still relies on the main technical results of [Reference Bosa, Brown, Sato, Tikuisis, White and Winter6] and [Reference Castillejos, Evington, Tikuisis, White and Winter11] that were used in establishing finite nuclear dimension from
![]() $\mathcal Z$
-stability in the context of the Toms–Winter conjecture (see [Reference Castillejos, Evington, Tikuisis, White and Winter11, Reference Ciuperca and Elliott14]).
$\mathcal Z$
-stability in the context of the Toms–Winter conjecture (see [Reference Castillejos, Evington, Tikuisis, White and Winter11, Reference Ciuperca and Elliott14]).
Corollary 4.9 Let A and B be finite classifiable C
![]() $^*$
-algebras with isomorphic tracial simplices. Then there exist a sequence
$^*$
-algebras with isomorphic tracial simplices. Then there exist a sequence
![]() $\varphi _i \,{\colon}\, A \to B$
of c.p.c. order zero maps and a sequence
$\varphi _i \,{\colon}\, A \to B$
of c.p.c. order zero maps and a sequence
![]() $\xi _i \,{\colon}\, B \to A$
such that
$\xi _i \,{\colon}\, B \to A$
such that
![]() $\xi _i$
is a sum of two c.p.c. order zero maps from B to A for
$\xi _i$
is a sum of two c.p.c. order zero maps from B to A for
![]() $i \in \mathbb N$
, and such that the following diagram approximately commutes.
$i \in \mathbb N$
, and such that the following diagram approximately commutes.

Since a possible choice for B is an AF algebra, it follows that the nuclear dimension of A is at most one. If A is not an AF algebra, then the nuclear dimension of A is exactly one.
Proof Let the notation for
![]() $\varphi _i$
,
$\varphi _i$
,
![]() $\psi _i$
,
$\psi _i$
,
![]() $\varphi $
, and
$\varphi $
, and
![]() $\psi $
be as in Corollary 4.8, and let h be a positive element with full spectrum in
$\psi $
be as in Corollary 4.8, and let h be a positive element with full spectrum in
![]() $\mathcal Z$
. Then since
$\mathcal Z$
. Then since
![]() $\iota _A$
is totally full and since
$\iota _A$
is totally full and since
![]() $\iota _A$
and
$\iota _A$
and
![]() $\psi \varphi \iota _A$
agree on traces,
$\psi \varphi \iota _A$
agree on traces,
![]() $\iota _A \otimes h$
and
$\iota _A \otimes h$
and
![]() $\psi \varphi \iota _A \otimes h$
are approximately unitarily equivalent, by [Reference Castillejos, Evington, Tikuisis, White and Winter11, Lemma 4.8]. Since
$\psi \varphi \iota _A \otimes h$
are approximately unitarily equivalent, by [Reference Castillejos, Evington, Tikuisis, White and Winter11, Lemma 4.8]. Since
![]() $1_{\mathcal Z} - h$
is also a positive element of
$1_{\mathcal Z} - h$
is also a positive element of
![]() $\mathcal Z$
with full spectrum,
$\mathcal Z$
with full spectrum,
![]() $\iota _A \otimes (1_{\mathcal Z} - h)$
and
$\iota _A \otimes (1_{\mathcal Z} - h)$
and
![]() $\psi \varphi \iota \otimes (1_{\mathcal Z} - h)$
are also approximately unitarily equivalent. Therefore, there exist unitaries
$\psi \varphi \iota \otimes (1_{\mathcal Z} - h)$
are also approximately unitarily equivalent. Therefore, there exist unitaries
![]() $u_1$
and
$u_1$
and
![]() $u_2 \in (A \otimes \mathcal Z)_{\omega }$
such that
$u_2 \in (A \otimes \mathcal Z)_{\omega }$
such that
![]() $a \otimes h = {u_1} (\psi \varphi (a) \otimes h) u_1^*$
and
$a \otimes h = {u_1} (\psi \varphi (a) \otimes h) u_1^*$
and
![]() $a \otimes (1_{\mathcal Z} - h) = {u_2} (\psi \varphi (a) \otimes (1_{\mathcal Z} - h)) u_2^*$
. Since
$a \otimes (1_{\mathcal Z} - h) = {u_2} (\psi \varphi (a) \otimes (1_{\mathcal Z} - h)) u_2^*$
. Since
![]() $\mathcal Z$
is strongly self-absorbing (see [Reference Jiang and Su39, Theorem 8.7]) and therefore
$\mathcal Z$
is strongly self-absorbing (see [Reference Jiang and Su39, Theorem 8.7]) and therefore
![]() $K_1$
-injective ((see [Reference Rieffel53, Theorem 10.12] and [Reference Rørdam57, Theorem 6.7]), [Reference Rørdam57, Theorem 6.7]), there is a
$K_1$
-injective ((see [Reference Rieffel53, Theorem 10.12] and [Reference Rørdam57, Theorem 6.7]), [Reference Rørdam57, Theorem 6.7]), there is a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\theta \,{\colon}\, A \otimes \mathcal Z \to A_{\omega }$
such that
$\theta \,{\colon}\, A \otimes \mathcal Z \to A_{\omega }$
such that
![]() $\theta (a \otimes 1_{\mathcal Z}) = a$
for each
$\theta (a \otimes 1_{\mathcal Z}) = a$
for each
![]() $a \in A$
, by [Reference Toms and Winter65, Theorem 2.3]. Let
$a \in A$
, by [Reference Toms and Winter65, Theorem 2.3]. Let
![]() $h_1:= h$
and
$h_1:= h$
and
![]() $h_2:= 1_{\mathcal Z}-h$
. Taking representative sequences of
$h_2:= 1_{\mathcal Z}-h$
. Taking representative sequences of
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\theta _i \,{\colon}\, A \otimes \mathcal Z \to A$
(which exist by the proof of [Reference Toms and Winter65, Theorem 2.3]) and of unitaries
$\theta _i \,{\colon}\, A \otimes \mathcal Z \to A$
(which exist by the proof of [Reference Toms and Winter65, Theorem 2.3]) and of unitaries
![]() $(u_1^{(i)})_{i=1}^{\infty }$
and
$(u_1^{(i)})_{i=1}^{\infty }$
and
![]() $(u_2^{(i)})_{i=1}^{\infty }$
in
$(u_2^{(i)})_{i=1}^{\infty }$
in
![]() $A \otimes \mathcal Z$
corresponding to
$A \otimes \mathcal Z$
corresponding to
![]() $u_1$
and
$u_1$
and
![]() $u_2$
, we have the following approximately commutative diagram.
$u_2$
, we have the following approximately commutative diagram.

The maps
![]() $\varphi _i \,{\colon}\, A \to B$
and the maps
$\varphi _i \,{\colon}\, A \to B$
and the maps
![]() $\xi _i \,{\colon}\, B \to A$
which factor though A and
$\xi _i \,{\colon}\, B \to A$
which factor though A and
![]() $A \otimes \mathcal Z$
give the desired completely positive approximation property.
$A \otimes \mathcal Z$
give the desired completely positive approximation property.
Let us now specialize to the case that B is an AF algebra with
![]() $T(B) \cong T(A)$
, which exists by [Reference Blackadar5, Theorem 3.10]. Since the nuclear dimension of B is zero (see [Reference Winter and Zacharias69, Remark 2.2(iii)]), there exist c.p.c. maps
$T(B) \cong T(A)$
, which exists by [Reference Blackadar5, Theorem 3.10]. Since the nuclear dimension of B is zero (see [Reference Winter and Zacharias69, Remark 2.2(iii)]), there exist c.p.c. maps
![]() $\rho _i \,{\colon}\, B \to F_i$
into finite-dimensional C
$\rho _i \,{\colon}\, B \to F_i$
into finite-dimensional C
![]() $^*$
-algebras
$^*$
-algebras
![]() $F_i$
and c.p.c. order zero maps
$F_i$
and c.p.c. order zero maps
![]() $\sigma _i: F_i \to B$
which make the following diagram approximately commute
$\sigma _i: F_i \to B$
which make the following diagram approximately commute

Since the maps
![]() $\rho _i \varphi _i \,{\colon}\, A \to F_i$
are and the maps
$\rho _i \varphi _i \,{\colon}\, A \to F_i$
are and the maps
![]() $\xi _i \sigma _i \,{\colon}\, F_i \to A$
are c.p. and since
$\xi _i \sigma _i \,{\colon}\, F_i \to A$
are c.p. and since
![]() $\xi _i \sigma _i$
is a sum of two c.p.c. order zero maps, A has nuclear dimension at most one (see [Reference Castillejos, Evington, Tikuisis, White and Winter11, Section 1.1]). If A is not an AF algebra, then the nuclear dimension of A is exactly 1 (see [Reference Winter and Zacharias69, Remark 2.2(iii)]).
$\xi _i \sigma _i$
is a sum of two c.p.c. order zero maps, A has nuclear dimension at most one (see [Reference Castillejos, Evington, Tikuisis, White and Winter11, Section 1.1]). If A is not an AF algebra, then the nuclear dimension of A is exactly 1 (see [Reference Winter and Zacharias69, Remark 2.2(iii)]).
Question All that is used about the (multiplicative) AF embeddings in Theorem 4.5 is that they are c.p.c. order zero maps which induce isomorphisms of simplices. In fact, it would be enough for each AF embedding to be replaced by a sequence of order zero maps which induce an isomorphism of tracial simplices in the sense described in Section 2.3. If this could be done without the UCT, then one would have Theorem 4.5 for classifiable C
![]() $^*$
-algebras not necessarily satisfying the UCT, as the UCT assumption is only used to produce AF embeddings. If A and B are unital, simple, exact,
$^*$
-algebras not necessarily satisfying the UCT, as the UCT assumption is only used to produce AF embeddings. If A and B are unital, simple, exact,
![]() $\mathcal Z$
-stable, separable C
$\mathcal Z$
-stable, separable C
![]() $^*$
-algebras with stable rank one, is there an order zero map
$^*$
-algebras with stable rank one, is there an order zero map
![]() $\varphi \,{\colon}\, A \to B$
realizing prescribed tracial data as in Theorem 4.3?
$\varphi \,{\colon}\, A \to B$
realizing prescribed tracial data as in Theorem 4.3?
Acknowledgment
J.I. would like to thank Jorge Castillejos, Christopher Schafhauser, Aaron Tikuisis, and Stuart White for suggestions and encouragement; Chris Phillips for detailed comments on an earlier draft of this paper; and the anonymous reviewer for helpful comments.