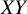1 Introduction
The homogeneous
![]() $XY$
model is an exactly solvable quantum spin chain going back to the pioneering work of Lieb, Schultz and Mattis [Reference Lieb, Schultz and MattisLSM61]. Its inhomogeneous isotropic variants, often referred to as
$XY$
model is an exactly solvable quantum spin chain going back to the pioneering work of Lieb, Schultz and Mattis [Reference Lieb, Schultz and MattisLSM61]. Its inhomogeneous isotropic variants, often referred to as
![]() $XX$
chains in the literature, serve as models for the transfer of qubit states through quantum wires [Reference BoseB07, Reference Bossé and VinetBV17, Reference KayK10]. The computation of the spectrum and eigenstates of such isotropic
$XX$
chains in the literature, serve as models for the transfer of qubit states through quantum wires [Reference BoseB07, Reference Bossé and VinetBV17, Reference KayK10]. The computation of the spectrum and eigenstates of such isotropic
![]() $XY$
chains is achieved through the diagonalization of the underlying Jacobi matrix of coupling constants (representing the one-particle Hamiltonian), cf., for example, [Reference Albanese, Christandl, Datta and EkertA-E04, Reference Chakrabarti and Van der JeugtCV10, Reference Hamza, Sims and StolzHSS12]. It is well known, cf., for example, [Reference WilfW78, Chapter 2], that both the eigenbasis and spectrum of a Jacobi matrix can be conveniently computed by means of orthogonal polynomials and their zero loci. For particular Jacobi matrices stemming from the hypergeometric orthogonal polynomials in Askey’s scheme [Reference Koekoek, Lesky and SwarttouwKLS10] the construction of the spectrum via the zero locus becomes explicit, thus giving rise to a rich family of corresponding inhomogeneous isotropic XY chains for which spectrum and eigenstates can be determined in closed form [Reference Albanese, Christandl, Datta and EkertA-E04, Reference Bossé and VinetBV17, Reference Chakrabarti and Van der JeugtCV10, Reference Crampé, Nepomechie and VinetCNV19, Reference Finkel and González-LópezFG20, Reference Genest, Vinet and ZhedanovGVZ16, Reference Grünbaum, Vinet and ZhedanovGVZ13, Reference Jafarov and Van der JeugtJV10, Reference Stoilova and Van der JeugtSV11, Reference Vinet and ZhedanovVZ12].
$XY$
chains is achieved through the diagonalization of the underlying Jacobi matrix of coupling constants (representing the one-particle Hamiltonian), cf., for example, [Reference Albanese, Christandl, Datta and EkertA-E04, Reference Chakrabarti and Van der JeugtCV10, Reference Hamza, Sims and StolzHSS12]. It is well known, cf., for example, [Reference WilfW78, Chapter 2], that both the eigenbasis and spectrum of a Jacobi matrix can be conveniently computed by means of orthogonal polynomials and their zero loci. For particular Jacobi matrices stemming from the hypergeometric orthogonal polynomials in Askey’s scheme [Reference Koekoek, Lesky and SwarttouwKLS10] the construction of the spectrum via the zero locus becomes explicit, thus giving rise to a rich family of corresponding inhomogeneous isotropic XY chains for which spectrum and eigenstates can be determined in closed form [Reference Albanese, Christandl, Datta and EkertA-E04, Reference Bossé and VinetBV17, Reference Chakrabarti and Van der JeugtCV10, Reference Crampé, Nepomechie and VinetCNV19, Reference Finkel and González-LópezFG20, Reference Genest, Vinet and ZhedanovGVZ16, Reference Grünbaum, Vinet and ZhedanovGVZ13, Reference Jafarov and Van der JeugtJV10, Reference Stoilova and Van der JeugtSV11, Reference Vinet and ZhedanovVZ12].
Recently, the method of orthogonal polynomials was employed to construct the eigenvectors of a tridiagonal matrix obtained by truncating a discrete variant of the difference Lamé operator [Reference van Diejen and GörbeDG21], but detailed insight into the pertinent zero locus yielding the spectrum has unfortunately remained somewhat elusive so far. The difference Lamé operator itself had emerged previously as a rank-one elliptic quantum Ruijsenaars–Schneider Hamiltonian [Reference RuijsenaarsR90, Reference RuijsenaarsR99a] that turns out to be deeply connected to both the representation theory of the Sklyanin algebra [Reference Krichever and ZabrodinKZ95, Reference RosengrenR04, Reference SklyaninS83] and to the representation theory of elliptic quantum groups [Reference Felder and VarchenkoFV96]. An in-depth spectral analysis of the difference Lamé equation was performed in [Reference RuijsenaarsR99b] for a dense parameter regime of positive values for the coupling parameter. Like in the case of the classical Lamé differential equation, at the single-gap integral value of the coupling parameter this spectral analysis simplifies and the eigensolutions can be expressed compactly in terms of Jacobi theta functions [Reference RuijsenaarsR99c]. This opens the way to achieve the main goal of this note: To compute the spectrum of the truncated discrete Lamé equation of [Reference van Diejen and GörbeDG21] at the single-gap integral value of the coupling parameter and therewith solve the spectral problem for the isotropic
![]() $XY$
chain associated with the corresponding Jacobi matrix.
$XY$
chain associated with the corresponding Jacobi matrix.
Specifically, we will consider an open chain of m quantum spins placed on the finite integer lattice
![]() $\{ 1,2,\ldots ,m\}$
that is characterized by a Hamiltonian of the form
$\{ 1,2,\ldots ,m\}$
that is characterized by a Hamiltonian of the form

where
![]() $g>0$
and
$g>0$
and
![]() $\alpha = \frac {2\pi }{2g+m-1}$
. Here,
$\alpha = \frac {2\pi }{2g+m-1}$
. Here,
![]() $\vartheta _1 (\cdot ;p)$
refers to Jacobi’s theta function (2.3) and
$\vartheta _1 (\cdot ;p)$
refers to Jacobi’s theta function (2.3) and
![]() $ \sigma _l^{\mathrm {x}} $
,
$ \sigma _l^{\mathrm {x}} $
,
![]() $ \sigma _l^{\mathrm {y}} $
denote the corresponding local spin-
$ \sigma _l^{\mathrm {y}} $
denote the corresponding local spin-
![]() $\frac {1}{2}$
operators at site l (cf. Equations (4.3a), (4.3b)). Below, the spectrum and eigenfunctions of this open inhomogeneous isotropic
$\frac {1}{2}$
operators at site l (cf. Equations (4.3a), (4.3b)). Below, the spectrum and eigenfunctions of this open inhomogeneous isotropic
![]() $XY$
model will be computed at the single-gap value
$XY$
model will be computed at the single-gap value
![]() $g=2$
(with
$g=2$
(with
![]() $0<p<1$
) and also in the trigonometric limit
$0<p<1$
) and also in the trigonometric limit
![]() $p\to 0$
for arbitrary parameter values
$p\to 0$
for arbitrary parameter values
![]() $g>0$
. The rational limit (
$g>0$
. The rational limit (
![]() $g\to +\infty $
) recovers the spin couplings of the so-called Krawtchouk chain:
$g\to +\infty $
) recovers the spin couplings of the so-called Krawtchouk chain: ![]() . The latter spin chain has been thoroughly studied in the literature as a model for perfect state transfer, cf., for example, [Reference Albanese, Christandl, Datta and EkertA-E04, Reference BoseB07, Reference Bossé and VinetBV17, Reference Chakrabarti and Van der JeugtCV10, Reference Groenland and SchoutensGS18, Reference KayK10, Reference Nikolopoulos, Petrosyan and LambropoulosNPL03, Reference Vinet and ZhedanovVZ12]. As an isotropic
. The latter spin chain has been thoroughly studied in the literature as a model for perfect state transfer, cf., for example, [Reference Albanese, Christandl, Datta and EkertA-E04, Reference BoseB07, Reference Bossé and VinetBV17, Reference Chakrabarti and Van der JeugtCV10, Reference Groenland and SchoutensGS18, Reference KayK10, Reference Nikolopoulos, Petrosyan and LambropoulosNPL03, Reference Vinet and ZhedanovVZ12]. As an isotropic
![]() $XY$
Hamiltonian
$XY$
Hamiltonian
![]() $\boldsymbol {H}^{(m)} $
only exhibits nearest neighbor couplings, which contrasts with the long-range one-dimensional spin models with elliptic couplings found previously by Inozemtsev, cf. [Reference InozemtsevI23, Chapter 3] and [Reference Klabbers and LamersKL22] (and references therein). Let us recall at this point that the two-magnon wave functions for Inozemtsev’s spin chain are given by single-gap Lamé functions, while more generally the n-magnon wave functions are given by eigenfunctions of the corresponding elliptic quantum Calogero–Moser model.
$\boldsymbol {H}^{(m)} $
only exhibits nearest neighbor couplings, which contrasts with the long-range one-dimensional spin models with elliptic couplings found previously by Inozemtsev, cf. [Reference InozemtsevI23, Chapter 3] and [Reference Klabbers and LamersKL22] (and references therein). Let us recall at this point that the two-magnon wave functions for Inozemtsev’s spin chain are given by single-gap Lamé functions, while more generally the n-magnon wave functions are given by eigenfunctions of the corresponding elliptic quantum Calogero–Moser model.
The material is organized as follows. In Section 2, the difference Lamé equation is recalled together with the single-gap difference Lamé wave function stemming from [Reference RuijsenaarsR99c]. At this point, it is pertinent to emphasize that the difference Lamé equation admits various nonequivalent real forms (i.e., Hilbert space formulations) each giving rise to a corresponding spectral theory. In terms of the classification originating from [Reference RuijsenaarsR90]: Here, we are dealing with an example of the (rank-one) compactified elliptic quantum Ruijsenaars–Schneider model whereas [Reference RuijsenaarsR99c] concentrates rather on the more conventional (but at the same time very intricate) noncompact variant(s). As a consequence, the spectral analysis in [Reference RuijsenaarsR99c] does not apply directly to our situation and needs to be adapted. In Section 3, a finite-dimensional system of real solutions of the single-gap difference Lamé equation is isolated. These solutions are both smooth and periodic on the real axis. Upon scaling the period of the elliptic functions such that the difference Lamé equation reduces to a finite-dimensional tridiagonal eigenvalue problem [Reference van Diejen and GörbeDG21], these real solutions provide a complete basis of orthogonal eigenvectors that give rise to explicit formulas for the corresponding eigenvalues. In Section 4, the open inhomogeneous isotropic
![]() $XY$
quantum spin Hamiltonian
$XY$
quantum spin Hamiltonian
![]() $\boldsymbol {H}^{(m)}$
associated with the finite Jacobi matrix under consideration is studied. We compute the n-particle Hamiltonian and construct its eigenfunctions in terms of Slater determinants of single-gap difference Lamé wave functions. Finally, the discussion is closed by connecting the results on the quantum spin chain to those in the literature via trigonometric and rational limits. Readers primarily interested in the spin model are invited to skip straight to Section 4 and skim back over Sections 2 and 3 to pick up some notations and further essentials from the difference Lamé theory when needed.
$\boldsymbol {H}^{(m)}$
associated with the finite Jacobi matrix under consideration is studied. We compute the n-particle Hamiltonian and construct its eigenfunctions in terms of Slater determinants of single-gap difference Lamé wave functions. Finally, the discussion is closed by connecting the results on the quantum spin chain to those in the literature via trigonometric and rational limits. Readers primarily interested in the spin model are invited to skip straight to Section 4 and skim back over Sections 2 and 3 to pick up some notations and further essentials from the difference Lamé theory when needed.
2 Difference Lamé equation
2.1 Elliptic numbers
For
let us recall the definition of the elliptic number associated with
![]() $z\in \mathbb {C}$
(cf. [Reference Gasper and RahmanGR04, Section 1.6]):
$z\in \mathbb {C}$
(cf. [Reference Gasper and RahmanGR04, Section 1.6]):
 $$ \begin{align} [z] = [z;\alpha,p]:= \frac{\vartheta_1 (\frac{\alpha z}{2};p)}{\vartheta_1(\frac{\alpha}{2} ;p)} , \end{align} $$
$$ \begin{align} [z] = [z;\alpha,p]:= \frac{\vartheta_1 (\frac{\alpha z}{2};p)}{\vartheta_1(\frac{\alpha}{2} ;p)} , \end{align} $$
where
![]() $\vartheta _1$
represents the Jacobi theta function [Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClainD-F23, Chapter 20]
$\vartheta _1$
represents the Jacobi theta function [Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClainD-F23, Chapter 20]
 $$ \begin{align} \vartheta_1(z;p)&=2\sum_{k=0}^\infty(-1)^k p^{\big(k+\tfrac{1}{2}\big)^2}\sin(2k+1)z \\ &=2p^{1/4}\sin(z)\prod_{k=1}^\infty(1-p^{2k})(1-2p^{2k}\cos(2z)+p^{4k}). \nonumber \end{align} $$
$$ \begin{align} \vartheta_1(z;p)&=2\sum_{k=0}^\infty(-1)^k p^{\big(k+\tfrac{1}{2}\big)^2}\sin(2k+1)z \\ &=2p^{1/4}\sin(z)\prod_{k=1}^\infty(1-p^{2k})(1-2p^{2k}\cos(2z)+p^{4k}). \nonumber \end{align} $$
All zeros of
![]() $[z;\alpha ,p]$
are simple, and their locus is given by the period lattice
$[z;\alpha ,p]$
are simple, and their locus is given by the period lattice
![]() $\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
with
$\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
with
![]() $ \tau :=\frac {\log p}{\mathrm {i}\pi }$
. We notice that the elliptic numbers are odd in z and quasi-periodic with respect to translations over the periods:
$ \tau :=\frac {\log p}{\mathrm {i}\pi }$
. We notice that the elliptic numbers are odd in z and quasi-periodic with respect to translations over the periods:
For
![]() $\alpha \to 0$
and
$\alpha \to 0$
and
![]() $p\to 0$
, the elliptic numbers degenerate to ordinary complex numbers and their q-deformations, respectively:
$p\to 0$
, the elliptic numbers degenerate to ordinary complex numbers and their q-deformations, respectively:
 $$ \begin{align} \lim_{\alpha \to 0} [z;\alpha,p]=z \quad\text{and}\quad \lim_{p\to 0} [z;\alpha,p]=\frac{\sin ( \frac{\alpha z}{2})}{\sin (\frac{\alpha}{2})}= \frac{q^{\frac{z}{2}}-q^{-\frac{z}{2}}}{q^{\frac{1}{2}}-q^{-\frac{1}{2}}}\ \text{with}\ q:=e^{\mathrm{i}\alpha}. \end{align} $$
$$ \begin{align} \lim_{\alpha \to 0} [z;\alpha,p]=z \quad\text{and}\quad \lim_{p\to 0} [z;\alpha,p]=\frac{\sin ( \frac{\alpha z}{2})}{\sin (\frac{\alpha}{2})}= \frac{q^{\frac{z}{2}}-q^{-\frac{z}{2}}}{q^{\frac{1}{2}}-q^{-\frac{1}{2}}}\ \text{with}\ q:=e^{\mathrm{i}\alpha}. \end{align} $$
2.2 Single-gap wave functions
The difference Lamé equation is an eigenvalue problem for meromorphic functions
![]() $\psi (z)$
on
$\psi (z)$
on
![]() $\mathbb {C}$
of the form [Reference Felder and VarchenkoFV96, Reference Krichever and ZabrodinKZ95, Reference RuijsenaarsR90, Reference RuijsenaarsR99a, Reference RuijsenaarsR99b]:
$\mathbb {C}$
of the form [Reference Felder and VarchenkoFV96, Reference Krichever and ZabrodinKZ95, Reference RuijsenaarsR90, Reference RuijsenaarsR99a, Reference RuijsenaarsR99b]:
where
![]() $g\in \mathbb {C}$
and
$g\in \mathbb {C}$
and ![]() denote the coupling parameter and the eigenvalue, respectively. The following elementary solution of the difference Lamé equation at
denote the coupling parameter and the eigenvalue, respectively. The following elementary solution of the difference Lamé equation at
![]() $g=2$
can be readily gleaned from [Reference RuijsenaarsR99c].
$g=2$
can be readily gleaned from [Reference RuijsenaarsR99c].
Proposition 2.1 (Wave Functions).
For
![]() $-\frac {2\pi }{\alpha }<\xi <\frac {2\pi }{\alpha }$
and
$-\frac {2\pi }{\alpha }<\xi <\frac {2\pi }{\alpha }$
and
![]() $-\frac {\pi \tau }{\mathrm {i}\alpha }< x< \frac {\pi \tau }{\mathrm {i}\alpha }$
, the wave function
$-\frac {\pi \tau }{\mathrm {i}\alpha }< x< \frac {\pi \tau }{\mathrm {i}\alpha }$
, the wave function
 $$ \begin{align} \psi(z;\xi,x) :=\frac{[\mathrm{i}x-z] \exp\big({\frac{\mathrm{i}z}{2} (\frac{\alpha \xi }{2}-\pi) \big)}}{[z+1] [z] [z-1]} \end{align} $$
$$ \begin{align} \psi(z;\xi,x) :=\frac{[\mathrm{i}x-z] \exp\big({\frac{\mathrm{i}z}{2} (\frac{\alpha \xi }{2}-\pi) \big)}}{[z+1] [z] [z-1]} \end{align} $$
provides a meromorphic solution of the difference Lamé equation (2.6) at the single-gap coupling value
![]() $g=2$
with eigenvalue
$g=2$
with eigenvalue
provided the position of the imaginary node
![]() $\mathrm {i}x$
is related to the real-valued spectral parameter
$\mathrm {i}x$
is related to the real-valued spectral parameter
![]() $\xi $
via the nonlinear constraint
$\xi $
via the nonlinear constraint
Proof. If the wave function
![]() $\psi (z;\xi ,x)$
(2.7a) is substituted into the difference Lamé equation (2.6) with
$\psi (z;\xi ,x)$
(2.7a) is substituted into the difference Lamé equation (2.6) with
![]() $g=2$
, then one arrives at following relation upon dividing by
$g=2$
, then one arrives at following relation upon dividing by
![]() $\psi (z;\xi ,x)$
:
$\psi (z;\xi ,x)$
:

The right-hand side is an elliptic function of z with period lattice
![]() $\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
that has at most simple poles congruent to
$\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
that has at most simple poles congruent to
![]() $z=0$
and
$z=0$
and
![]() $z=\mathrm {i}x$
. The constraint (2.7c) is seen to guarantee that the residues at
$z=\mathrm {i}x$
. The constraint (2.7c) is seen to guarantee that the residues at
![]() $z=0$
and
$z=0$
and
![]() $z=\mathrm {i}x$
vanish, so the singularities are in fact removable and the right-hand side is thus a constant function of z. This verifies that
$z=\mathrm {i}x$
vanish, so the singularities are in fact removable and the right-hand side is thus a constant function of z. This verifies that
![]() $\psi (z;\xi ,x)$
(2.7a) satisfies the Lamé equation with
$\psi (z;\xi ,x)$
(2.7a) satisfies the Lamé equation with
![]() $g=2$
provided Equation (2.7c) holds. To compute the corresponding eigenvalue it suffices to evaluate the right-hand side under consideration at
$g=2$
provided Equation (2.7c) holds. To compute the corresponding eigenvalue it suffices to evaluate the right-hand side under consideration at
![]() $z=-1$
:
$z=-1$
:

which readily passes over into Equation (2.7b) when rewriting the exponential factor in terms of x with the aid of Equation (2.7c).
2.3 On the spectral parametrization of the node
The relation stemming from the constraint (2.7c) between the value of the spectral parameter
![]() $\xi $
and the position of the node
$\xi $
and the position of the node
![]() $\mathrm {i}x$
(and therewith the eigenvalue
$\mathrm {i}x$
(and therewith the eigenvalue ![]() ) is determined by the function
) is determined by the function

Proposition 2.2 (Monotonicity).
Upon varying the argument x over the interval
![]() $-\frac {\pi \tau }{\mathrm {i}\alpha }\leq x\leq \frac {\pi \tau }{\mathrm {i}\alpha }$
, the functions
$-\frac {\pi \tau }{\mathrm {i}\alpha }\leq x\leq \frac {\pi \tau }{\mathrm {i}\alpha }$
, the functions ![]() (2.8) and
(2.8) and ![]() (2.7b) strictly increase smoothly from
(2.7b) strictly increase smoothly from ![]() to
to ![]() and from
and from ![]() to
to ![]() , respectively. Moreover, the extremal values are given explicitly by
, respectively. Moreover, the extremal values are given explicitly by
and

with ![]() and
and
![]() $\vartheta _1^\prime (0;p)=2p^{1/4}\prod _{k=1}^\infty (1-p^{2k})^3$
, where
$\vartheta _1^\prime (0;p)=2p^{1/4}\prod _{k=1}^\infty (1-p^{2k})^3$
, where
![]() $\wp (z;2\omega ,2\tilde {\omega })$
denotes the Weierstrass
$\wp (z;2\omega ,2\tilde {\omega })$
denotes the Weierstrass
![]() $\wp $
-function associated with half-periods
$\wp $
-function associated with half-periods
![]() $\omega =\frac {\pi }{\alpha }$
and
$\omega =\frac {\pi }{\alpha }$
and
![]() $\tilde {\omega }=\frac {\pi \tau }{\alpha }$
[Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClainD-F23, Chapter 23].
$\tilde {\omega }=\frac {\pi \tau }{\alpha }$
[Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClainD-F23, Chapter 23].
Proof. For x on the real axis the quotient
![]() $ \frac {[1+\mathrm {i}x]}{[1-\mathrm {i}x]}$
belongs to the unit circle, so the function
$ \frac {[1+\mathrm {i}x]}{[1-\mathrm {i}x]}$
belongs to the unit circle, so the function ![]() is real-valued and odd. The value at
is real-valued and odd. The value at
![]() $x= \frac {\pi \tau }{\mathrm {i}\alpha }$
can be computed via the quasi-periodicity (2.4):
$x= \frac {\pi \tau }{\mathrm {i}\alpha }$
can be computed via the quasi-periodicity (2.4):

To analyze the monotonicity, we first compute the derivative of ![]() for
for
![]() $ -\frac {\pi \tau }{\mathrm {i}\alpha }< x< \frac {\pi \tau }{\mathrm {i}\alpha }$
in terms of Jacobi theta functions:
$ -\frac {\pi \tau }{\mathrm {i}\alpha }< x< \frac {\pi \tau }{\mathrm {i}\alpha }$
in terms of Jacobi theta functions:

which is smooth because the zero loci of the denominators are avoided for x on the real axis. The product representation of the Jacobi theta function (2.3) entails the following series for the logarithmic derivative of the Jacobi theta function [Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClainD-F23, (20.5.10)]
 $$ \begin{align} \frac{\vartheta_1^\prime (z;p)}{\vartheta_1(z;p)}=\cot(z)+4\sin (2z)\sum_{k=1}^\infty \frac{p^{2k}}{1-2 p^{2k}\cos(2z)+p^{4k}}, \end{align} $$
$$ \begin{align} \frac{\vartheta_1^\prime (z;p)}{\vartheta_1(z;p)}=\cot(z)+4\sin (2z)\sum_{k=1}^\infty \frac{p^{2k}}{1-2 p^{2k}\cos(2z)+p^{4k}}, \end{align} $$
which converges uniformly on compacts within the strip
![]() $|\text {Im}(z)| <\pi \, \text {Im}(\tau )=-\mathrm {Log}\, (p)$
. Upon plugging Equation (2.11) into Equation (2.10), one sees that the derivative of
$|\text {Im}(z)| <\pi \, \text {Im}(\tau )=-\mathrm {Log}\, (p)$
. Upon plugging Equation (2.11) into Equation (2.10), one sees that the derivative of ![]() remains positive within the interval
remains positive within the interval
![]() $ -\frac {\pi \tau }{\mathrm {i}\alpha }< x< \frac {\pi \tau }{\mathrm {i}\alpha }$
:
$ -\frac {\pi \tau }{\mathrm {i}\alpha }< x< \frac {\pi \tau }{\mathrm {i}\alpha }$
:

because
![]() $ (1+p^{4k})\cosh (\alpha x) -2p^{2k}\cos \alpha \geq 1+p^{4k}-2p^{2k}=(1-p^{2k})^2>0 $
and
$ (1+p^{4k})\cosh (\alpha x) -2p^{2k}\cos \alpha \geq 1+p^{4k}-2p^{2k}=(1-p^{2k})^2>0 $
and
![]() $\sin \alpha>0$
for
$\sin \alpha>0$
for
![]() $0<\alpha <\pi $
.
$0<\alpha <\pi $
.
Regarding the eigenvalue, it is clear that ![]() (2.7b) constitutes a smooth real-valued function of
(2.7b) constitutes a smooth real-valued function of
![]() $x\in \mathbb {R}$
that is odd, while at the same time being strictly increasing in a neighborhood of
$x\in \mathbb {R}$
that is odd, while at the same time being strictly increasing in a neighborhood of
![]() $x=0$
:
$x=0$
:

To justify the asserted monotonicity globally in the interval
![]() $-\frac {\pi \tau }{\mathrm {i}\alpha }<x<\frac {\pi \tau }{\mathrm {i}\alpha }$
, it therefore suffices to check that
$-\frac {\pi \tau }{\mathrm {i}\alpha }<x<\frac {\pi \tau }{\mathrm {i}\alpha }$
, it therefore suffices to check that
is strictly decreasing for
![]() $0<x<\frac {\pi \tau }{\mathrm {i}\alpha }$
. To this end, we notice that
$0<x<\frac {\pi \tau }{\mathrm {i}\alpha }$
. To this end, we notice that
Indeed, the left-hand side of Equation (2.12) defines an elliptic function of order two in z with period lattice
![]() $\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
; it has zeros congruent to
$\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
; it has zeros congruent to
![]() $z=1$
and
$z=1$
and
![]() $z=-1$
and a double pole congruent to
$z=-1$
and a double pole congruent to
![]() $z=0$
with
$z=0$
with
![]() $\lim _{z\to 0} z^2 \frac { [1+z] [1-z] }{ [z] [-z]}=- \left (\frac {2\vartheta _1(\frac {\alpha }2{};p)}{\alpha \vartheta _1^\prime (0;p)}\right )^2$
. When z moves from
$\lim _{z\to 0} z^2 \frac { [1+z] [1-z] }{ [z] [-z]}=- \left (\frac {2\vartheta _1(\frac {\alpha }2{};p)}{\alpha \vartheta _1^\prime (0;p)}\right )^2$
. When z moves from
![]() $z=0$
to
$z=0$
to
![]() $z=\frac {\pi \tau }{\alpha }$
along the imaginary axis, the Weierstrass
$z=\frac {\pi \tau }{\alpha }$
along the imaginary axis, the Weierstrass
![]() $\wp $
-function increases monotonically from
$\wp $
-function increases monotonically from
![]() $-\infty $
to
$-\infty $
to
![]() $\wp ({\textstyle \frac {\pi \tau }{\alpha };\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha }}) <\wp ({\textstyle \frac {\pi }{\alpha };\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha }}) < \wp ({\textstyle 1 ;\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha }})$
(cf., e.g., [Reference LawdenL89, Chapter 6.11]). Hence, for
$\wp ({\textstyle \frac {\pi \tau }{\alpha };\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha }}) <\wp ({\textstyle \frac {\pi }{\alpha };\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha }}) < \wp ({\textstyle 1 ;\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha }})$
(cf., e.g., [Reference LawdenL89, Chapter 6.11]). Hence, for
![]() $0<x<\frac {\pi \tau }{\mathrm {i}\alpha }$
the value of
$0<x<\frac {\pi \tau }{\mathrm {i}\alpha }$
the value of ![]() decreases monotonically from
decreases monotonically from
![]() $+\infty $
to
$+\infty $
to
![]() $\frac {1}{[2]^2} \left ( \frac {2\vartheta _1(\frac {\alpha }2{};p)}{\alpha \vartheta _1^\prime (0;p)}\right )^2 \Bigl ( \wp (1;\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha })-\wp ( \frac {\pi \tau }{\alpha };\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha })\Bigr )>0$
.
$\frac {1}{[2]^2} \left ( \frac {2\vartheta _1(\frac {\alpha }2{};p)}{\alpha \vartheta _1^\prime (0;p)}\right )^2 \Bigl ( \wp (1;\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha })-\wp ( \frac {\pi \tau }{\alpha };\frac {2\pi }{\alpha },\frac {2\pi \tau }{\alpha })\Bigr )>0$
.
One learns from Proposition 2.2 that for any value of the spectral parameter
![]() $-2(\frac {\pi }{\alpha }-1)\leq \xi \leq 2(\frac {\pi }{\alpha }-1)$
there exists a unique
$-2(\frac {\pi }{\alpha }-1)\leq \xi \leq 2(\frac {\pi }{\alpha }-1)$
there exists a unique
![]() $-\frac {\pi \tau }{\mathrm {i}\alpha }\leq x(\xi )\leq \frac {\pi \tau }{\mathrm {i}\alpha }$
such that
$-\frac {\pi \tau }{\mathrm {i}\alpha }\leq x(\xi )\leq \frac {\pi \tau }{\mathrm {i}\alpha }$
such that
 $$ \begin{align} \frac{2}{\mathrm{i}\alpha} \mathrm{Log} \left( \frac{[1+\mathrm{i}x(\xi)]}{[1-\mathrm{i}x(\xi)]}\right) =\xi, \end{align} $$
$$ \begin{align} \frac{2}{\mathrm{i}\alpha} \mathrm{Log} \left( \frac{[1+\mathrm{i}x(\xi)]}{[1-\mathrm{i}x(\xi)]}\right) =\xi, \end{align} $$
that is,
When combining with Proposition 2.1, this entails the following family of solutions to the difference Lamé equation at
![]() $g=2$
.
$g=2$
.
Corollary 2.3 (Parametrized wave functions).
For
![]() $ -2(\frac {\pi }{\alpha }-1)< \xi < 2(\frac {\pi }{\alpha }-1), $
the single-gap wave function
$ -2(\frac {\pi }{\alpha }-1)< \xi < 2(\frac {\pi }{\alpha }-1), $
the single-gap wave function
![]() $\psi \big (z;\xi ,x(\xi )\big )$
provides a meromorphic solution to the difference Lamé equation (2.6) with
$\psi \big (z;\xi ,x(\xi )\big )$
provides a meromorphic solution to the difference Lamé equation (2.6) with
![]() $g=2$
and eigenvalue
$g=2$
and eigenvalue ![]() .
.
Notice that in Corollary 2.3 the dependence of
![]() $x(\xi )$
(and thus of
$x(\xi )$
(and thus of
![]() $\psi \big (z;\xi ,x(\xi )\big )$
) on the spectral parameter
$\psi \big (z;\xi ,x(\xi )\big )$
) on the spectral parameter
![]() $\xi $
is smooth in view of the inverse function theorem.
$\xi $
is smooth in view of the inverse function theorem.
3 Finite-dimensional reduction
3.1 Smooth periodic wave functions
The wave function in Corollary 2.3 has simple poles in
![]() $\mathbb {C}$
congruent to
$\mathbb {C}$
congruent to
![]() $z=0$
,
$z=0$
,
![]() $z=1$
and
$z=1$
and
![]() $z=-1$
(modulo
$z=-1$
(modulo
![]() $\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
). To get rid of the singularities at
$\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
). To get rid of the singularities at
![]() $z=0$
and
$z=0$
and
![]() $z=\pm 1$
, we extract the even part of the wave function:
$z=\pm 1$
, we extract the even part of the wave function:
 $$ \begin{align} \phi(z;\xi,x)&:= \psi(z;\xi,x)+ \psi(-z;\xi,x) \\ &= \frac{[\mathrm{i}x-z] \exp\big( {\frac{\mathrm{i}z}{2} (\frac{\alpha \xi }{2}-\pi) \big)-[\mathrm{i}x+z] \exp\big( -\frac{\mathrm{i}z}{2} (\frac{\alpha \xi }{2}-\pi) \big)}}{[z+1] [z] [z-1]}. \nonumber \end{align} $$
$$ \begin{align} \phi(z;\xi,x)&:= \psi(z;\xi,x)+ \psi(-z;\xi,x) \\ &= \frac{[\mathrm{i}x-z] \exp\big( {\frac{\mathrm{i}z}{2} (\frac{\alpha \xi }{2}-\pi) \big)-[\mathrm{i}x+z] \exp\big( -\frac{\mathrm{i}z}{2} (\frac{\alpha \xi }{2}-\pi) \big)}}{[z+1] [z] [z-1]}. \nonumber \end{align} $$
Notice that for z on the real axis
![]() $\phi (z;\xi ,x)=2\text {Re} \big ( \psi (z;\xi ,x) \big )$
. At discrete values of the spectral variable of the form
$\phi (z;\xi ,x)=2\text {Re} \big ( \psi (z;\xi ,x) \big )$
. At discrete values of the spectral variable of the form
the even wave function
![]() $\phi \big (z;\xi ,x(\xi )\big )$
becomes periodic or antiperiodic in z with period
$\phi \big (z;\xi ,x(\xi )\big )$
becomes periodic or antiperiodic in z with period
![]() $\frac {2\pi }{\alpha }$
(depending on the parity of k), which gets rid of all singularities on the real axis.
$\frac {2\pi }{\alpha }$
(depending on the parity of k), which gets rid of all singularities on the real axis.
Proposition 3.1 (Smooth periodic wave functions).
(i) For
![]() $-2(\frac {\pi }{\alpha }-1)< \xi < 2(\frac {\pi }{\alpha }-1)$
, the wave function
$-2(\frac {\pi }{\alpha }-1)< \xi < 2(\frac {\pi }{\alpha }-1)$
, the wave function
![]() $\phi \big (z;\xi ,x(\xi )\big )$
solves the difference Lamé equation (2.6) with
$\phi \big (z;\xi ,x(\xi )\big )$
solves the difference Lamé equation (2.6) with
![]() $g=2$
and eigenvalue
$g=2$
and eigenvalue ![]() .
.
(ii) For any integer
![]() $0<k<2(\frac {\pi }{\alpha }-1)$
, the wave function
$0<k<2(\frac {\pi }{\alpha }-1)$
, the wave function
![]() $\phi \big (z;\xi _k,x(\xi _k)\big )$
is (anti)periodic in z with period
$\phi \big (z;\xi _k,x(\xi _k)\big )$
is (anti)periodic in z with period
![]() $\frac {2\pi }{\alpha }$
:
$\frac {2\pi }{\alpha }$
:
(iii) When restricting to the real axis, the (anti)periodic meromorphic wave function
![]() $\phi \big (z;\xi _k,x(\xi _k)\big )$
in part (ii) extends continuously to a smooth function of
$\phi \big (z;\xi _k,x(\xi _k)\big )$
in part (ii) extends continuously to a smooth function of
![]() $z\in \mathbb {R}$
(which subsequently will be denoted by
$z\in \mathbb {R}$
(which subsequently will be denoted by
![]() $\phi \big (z;\xi _k,x(\xi _k)\big )$
as well).
$\phi \big (z;\xi _k,x(\xi _k)\big )$
as well).
Proof. (i) In the situation of Corollary 2.3, it is plain that for z on the real axis
![]() $\phi \big (z;\xi ,x(\xi )\big )=2\text {Re} \big ( \psi \big (z;\xi ,x(\xi )\big ) \big )$
solves the difference Lamé equation with
$\phi \big (z;\xi ,x(\xi )\big )=2\text {Re} \big ( \psi \big (z;\xi ,x(\xi )\big ) \big )$
solves the difference Lamé equation with
![]() $g=2$
and eigenvalue
$g=2$
and eigenvalue ![]() (because the imaginary parts of the coefficients of the difference equation vanish on the real axis). This real meromorphic solution
(because the imaginary parts of the coefficients of the difference equation vanish on the real axis). This real meromorphic solution
![]() $\phi \big (z;\xi ,x(\xi )\big )$
extends in turn from the real axis to the complex plane by analyticity in z.
$\phi \big (z;\xi ,x(\xi )\big )$
extends in turn from the real axis to the complex plane by analyticity in z.
(ii) To ensure that
![]() $\phi \big (z;\xi ,x(\xi )\big )$
is (anti)periodic in z with period
$\phi \big (z;\xi ,x(\xi )\big )$
is (anti)periodic in z with period
![]() $\frac {2\pi }{\alpha }$
it suffices to choose the spectral parameter
$\frac {2\pi }{\alpha }$
it suffices to choose the spectral parameter
![]() $\xi $
such that the exponential factor
$\xi $
such that the exponential factor
![]() $ \exp \big ( \frac {\mathrm {i}z}{2} (\frac {\alpha \xi }{2}-\pi ) \big )$
is (anti-)periodic. This is achieved for
$ \exp \big ( \frac {\mathrm {i}z}{2} (\frac {\alpha \xi }{2}-\pi ) \big )$
is (anti-)periodic. This is achieved for
![]() $\xi \in \frac {2\pi }{\alpha } +2\mathbb {Z}$
. The requirement in Corollary 2.3 that
$\xi \in \frac {2\pi }{\alpha } +2\mathbb {Z}$
. The requirement in Corollary 2.3 that
![]() $-2(\frac {\pi }{\alpha }-1)< \xi < 2(\frac {\pi }{\alpha }-1)$
narrows this down to the spectral values
$-2(\frac {\pi }{\alpha }-1)< \xi < 2(\frac {\pi }{\alpha }-1)$
narrows this down to the spectral values
![]() $\xi _k$
(3.2) with
$\xi _k$
(3.2) with
![]() $0<k<2(\frac {\pi }{\alpha }-1)$
. The value of the sign follows from the observation that
$0<k<2(\frac {\pi }{\alpha }-1)$
. The value of the sign follows from the observation that
![]() $ \exp \big ( \frac {\mathrm {i}z}{2} (\frac {\alpha \xi _k }{2}-\pi ) \big )=(-1)^{k-1}$
at
$ \exp \big ( \frac {\mathrm {i}z}{2} (\frac {\alpha \xi _k }{2}-\pi ) \big )=(-1)^{k-1}$
at
![]() $z=\frac {2\pi }{\alpha }$
.
$z=\frac {2\pi }{\alpha }$
.
(iii) The wave function
![]() $\phi \big (z;\xi ,x(\xi )\big )$
has simple poles on the real axis arising from the denominator at
$\phi \big (z;\xi ,x(\xi )\big )$
has simple poles on the real axis arising from the denominator at
![]() $z=0 \mod \frac {2\pi }{\alpha }\mathbb {Z}$
and
$z=0 \mod \frac {2\pi }{\alpha }\mathbb {Z}$
and
![]() $z=\pm 1\mod \frac {2\pi }{\alpha }\mathbb {Z}$
. Since
$z=\pm 1\mod \frac {2\pi }{\alpha }\mathbb {Z}$
. Since
![]() $\phi \big (z;\xi ,x(\xi )\big )$
is even in z, it is clear that its residue at
$\phi \big (z;\xi ,x(\xi )\big )$
is even in z, it is clear that its residue at
![]() $z=0$
vanishes. The vanishing of the residues of
$z=0$
vanishes. The vanishing of the residues of
![]() $\phi \big (z;\xi ,x(\xi )\big )$
at
$\phi \big (z;\xi ,x(\xi )\big )$
at
![]() $z=\pm 1$
follows in turn via relation (2.7c). By picking the spectral parameter
$z=\pm 1$
follows in turn via relation (2.7c). By picking the spectral parameter
![]() $\xi $
such that
$\xi $
such that
![]() $\phi \big (z;\xi ,x(\xi )\big )$
is (anti-)periodic in z with period
$\phi \big (z;\xi ,x(\xi )\big )$
is (anti-)periodic in z with period
![]() $\frac {2\pi }{\alpha }$
, one guarantees that the residues of all poles on the real axis vanish. In other words, at these spectral values the wave function extends to a smooth function of
$\frac {2\pi }{\alpha }$
, one guarantees that the residues of all poles on the real axis vanish. In other words, at these spectral values the wave function extends to a smooth function of
![]() $z\in \mathbb {R}$
.
$z\in \mathbb {R}$
.
3.2 Truncated discretization
Given
![]() $g>0$
and
$g>0$
and
![]() $m\in \mathbb {Z}_{>1}$
, we will from now on scale the periods by putting
$m\in \mathbb {Z}_{>1}$
, we will from now on scale the periods by putting
 $$ \begin{align} \boxed{\alpha=\frac{2\pi}{2g+m-1} .} \end{align} $$
$$ \begin{align} \boxed{\alpha=\frac{2\pi}{2g+m-1} .} \end{align} $$
It was shown in [Reference van Diejen and GörbeDG21] that then the difference Lamé equation can be truncated onto the space of complex functions supported on
![]() $\{g,g+1,\ldots ,g+m-1\}$
. Indeed, by substituting
$\{g,g+1,\ldots ,g+m-1\}$
. Indeed, by substituting
![]() $z=g+l-1$
in the difference Lamé equation (2.6) and writing
$z=g+l-1$
in the difference Lamé equation (2.6) and writing
![]() $\boxed {\Psi _l:=\psi (g+l-1),}$
one arrives at a finitely truncated discrete Lamé equation of the form
$\boxed {\Psi _l:=\psi (g+l-1),}$
one arrives at a finitely truncated discrete Lamé equation of the form
where the coefficient of
![]() $\Psi _{l+1}$
was simplified by means of the reflection relation
$\Psi _{l+1}$
was simplified by means of the reflection relation
![]() $[\frac {2\pi }{\alpha }-z]=[z]$
(cf. Equation (2.4)). Notice in this connection that the coefficients of
$[\frac {2\pi }{\alpha }-z]=[z]$
(cf. Equation (2.4)). Notice in this connection that the coefficients of
![]() $\Psi _{l+1}$
and of
$\Psi _{l+1}$
and of
![]() $\Psi _{l-1}$
vanish when
$\Psi _{l-1}$
vanish when
![]() $l=m$
and when
$l=m$
and when
![]() $l=1$
, respectively.
$l=1$
, respectively.
Specifically, for
![]() $g=2$
(so
$g=2$
(so
![]() $\alpha =\frac {2\pi }{m+3}$
and
$\alpha =\frac {2\pi }{m+3}$
and
![]() $\Psi _l=\psi (l+1)$
) the truncated discrete Lamé equation amounts to the following m-dimensional tridiagonal eigenvalue problem:
$\Psi _l=\psi (l+1)$
) the truncated discrete Lamé equation amounts to the following m-dimensional tridiagonal eigenvalue problem:
with
 $$ \begin{align} \boldsymbol{L}^{(m)}= \begin{bmatrix} 0 & \frac{[m-1]}{[m+1]} & 0& \cdots & 0\\ \frac{[1]}{[3]} & 0 &\ddots & & \vdots \\ 0 & \frac{[2]}{[4]} & \ddots & \frac{[2]}{[4]} &0\\ \vdots & & \ddots &0 &\frac{[1]}{[3]} \\ 0 & \cdots & 0& \frac{[m-1]}{[m+1]} &0 \end{bmatrix} \quad\text{and}\quad \Psi^{(m)}= \begin{bmatrix} \Psi_1 \\ \Psi_2 \\ \Psi_3 \\ \vdots\\ \vdots \\ \Psi_{m} \end{bmatrix}. \end{align} $$
$$ \begin{align} \boldsymbol{L}^{(m)}= \begin{bmatrix} 0 & \frac{[m-1]}{[m+1]} & 0& \cdots & 0\\ \frac{[1]}{[3]} & 0 &\ddots & & \vdots \\ 0 & \frac{[2]}{[4]} & \ddots & \frac{[2]}{[4]} &0\\ \vdots & & \ddots &0 &\frac{[1]}{[3]} \\ 0 & \cdots & 0& \frac{[m-1]}{[m+1]} &0 \end{bmatrix} \quad\text{and}\quad \Psi^{(m)}= \begin{bmatrix} \Psi_1 \\ \Psi_2 \\ \Psi_3 \\ \vdots\\ \vdots \\ \Psi_{m} \end{bmatrix}. \end{align} $$
We will now show that by restricting the smooth (anti)periodic solutions
![]() $\phi \big (z;\xi _k,x(\xi _k)\big )$
of the difference Lamé equation from Proposition 3.1 to the lattice
$\phi \big (z;\xi _k,x(\xi _k)\big )$
of the difference Lamé equation from Proposition 3.1 to the lattice
![]() $\{2,3,\ldots ,m+1\}$
, one arrives at the spectrum and a corresponding eigenbasis for the matrix
$\{2,3,\ldots ,m+1\}$
, one arrives at the spectrum and a corresponding eigenbasis for the matrix
![]() $\boldsymbol {L}^{(m)}$
(3.6b). To this end, let us write for
$\boldsymbol {L}^{(m)}$
(3.6b). To this end, let us write for
![]() $1\leq l,k\leq m \left (=2(\frac {\pi }{\alpha }-1)-1\right )$
:
$1\leq l,k\leq m \left (=2(\frac {\pi }{\alpha }-1)-1\right )$
:
 $$ \begin{align} \Phi^{(m)}(\xi_k):= \begin{bmatrix} \Phi_1 (\xi_k) \\ \Phi_2 (\xi_k) \\ \vdots\\ \Phi_{m} (\xi_k) \end{bmatrix} \quad\text{with}\quad \Phi_l(\xi_k):=\phi\big(l+1;\xi_k,x(\xi_k)\big), \end{align} $$
$$ \begin{align} \Phi^{(m)}(\xi_k):= \begin{bmatrix} \Phi_1 (\xi_k) \\ \Phi_2 (\xi_k) \\ \vdots\\ \Phi_{m} (\xi_k) \end{bmatrix} \quad\text{with}\quad \Phi_l(\xi_k):=\phi\big(l+1;\xi_k,x(\xi_k)\big), \end{align} $$
where
![]() $\xi _k\stackrel {(3.2),(3.4)}{=}m+1-2k$
.
$\xi _k\stackrel {(3.2),(3.4)}{=}m+1-2k$
.
Theorem 3.2 (Diagonalization of
 $\boldsymbol {L}^{(m)}$
).
$\boldsymbol {L}^{(m)}$
).
(i) The vectors
![]() $ \Phi ^{(m)}(\xi _1),\ldots , \Phi ^{(m)}(\xi _m)$
(3.7) constitute an eigenbasis for
$ \Phi ^{(m)}(\xi _1),\ldots , \Phi ^{(m)}(\xi _m)$
(3.7) constitute an eigenbasis for
![]() $\boldsymbol {L}^{(m)}$
(3.6b) such that
$\boldsymbol {L}^{(m)}$
(3.6b) such that
(ii) The corresponding eigenvalues are evenly distributed around the origin and numbered in decreasing order: ![]() and
and
(where the bound on the spectrum is of the form ![]() ).
).
(iii) The matrix of eigenvectors
![]() $\boldsymbol {\Phi }^{(m)}=\big [ \Phi _l(\xi _k)\big ]_{1\leq l,k\leq m}$
enjoys the following palindromic (anti)symmetries along the rows and columns:
$\boldsymbol {\Phi }^{(m)}=\big [ \Phi _l(\xi _k)\big ]_{1\leq l,k\leq m}$
enjoys the following palindromic (anti)symmetries along the rows and columns:
Proof. (i) Since the matrix
![]() $\boldsymbol {L}^{(m)}$
and the vectors
$\boldsymbol {L}^{(m)}$
and the vectors
![]() $ \Phi ^{(m)}(\xi _k)$
were obtained by restricting the difference Lamé equation and its smooth solutions on the real axis taken from Proposition 3.1, the eigenvalue equations (3.8a) are satisfied manifestly. Furthermore, Proposition 2.2 ensures that the mapping
$ \Phi ^{(m)}(\xi _k)$
were obtained by restricting the difference Lamé equation and its smooth solutions on the real axis taken from Proposition 3.1, the eigenvalue equations (3.8a) are satisfied manifestly. Furthermore, Proposition 2.2 ensures that the mapping ![]() ,
,
![]() $-m-1\leq \xi \leq m+1=2({\textstyle \frac {\pi }{\alpha }}-1)$
is injective, so the eigenvalues
$-m-1\leq \xi \leq m+1=2({\textstyle \frac {\pi }{\alpha }}-1)$
is injective, so the eigenvalues ![]() are all distinct. To confirm that the vectors in question indeed constitute a complete eigenbasis it remains to infer that none of them is equal to the zero vector. To this end, we will check that
are all distinct. To confirm that the vectors in question indeed constitute a complete eigenbasis it remains to infer that none of them is equal to the zero vector. To this end, we will check that
![]() $\Phi _1(\xi _k)=\phi \big (2;\xi _k,x(\xi _k)\big )\neq 0$
for
$\Phi _1(\xi _k)=\phi \big (2;\xi _k,x(\xi _k)\big )\neq 0$
for
![]() $k=1,\ldots ,m$
. Indeed, if
$k=1,\ldots ,m$
. Indeed, if
![]() $\phi (2;\xi ,x)=0$
for
$\phi (2;\xi ,x)=0$
for
![]() $\xi ,x\in \mathbb {C}$
subject to the constraint (2.7c), then we see from (3.1) that
$\xi ,x\in \mathbb {C}$
subject to the constraint (2.7c), then we see from (3.1) that
 $$ \begin{align} \frac{[\mathrm{i}x+2]}{[\mathrm{i}x-2]}=e^{\mathrm{i}\alpha\xi}\stackrel{(2.7\text{c})}{\Longrightarrow} \frac{ [\mathrm{i}x+2] }{[\mathrm{i}x-2] } \frac{ [\mathrm{i}x-1]^2}{[\mathrm{i}x+1]^2}=1. \end{align} $$
$$ \begin{align} \frac{[\mathrm{i}x+2]}{[\mathrm{i}x-2]}=e^{\mathrm{i}\alpha\xi}\stackrel{(2.7\text{c})}{\Longrightarrow} \frac{ [\mathrm{i}x+2] }{[\mathrm{i}x-2] } \frac{ [\mathrm{i}x-1]^2}{[\mathrm{i}x+1]^2}=1. \end{align} $$
The left-hand side of the latter equation is an elliptic function of
![]() $\mathrm {i}x$
of order
$\mathrm {i}x$
of order
![]() $3$
, so (when counting with multiplicity) this equation has three solutions modulo the period lattice
$3$
, so (when counting with multiplicity) this equation has three solutions modulo the period lattice
![]() $\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
. It is readily seen that the identity in fact holds at the three half-periods, so the three solutions are
$\frac {2\pi }{\alpha }\big (\mathbb {Z}+\tau \mathbb {Z}\big )$
. It is readily seen that the identity in fact holds at the three half-periods, so the three solutions are
![]() $\mathrm {i}x=\frac {\pi }{\alpha }$
,
$\mathrm {i}x=\frac {\pi }{\alpha }$
,
![]() $\mathrm {i}x=\frac {\pi }{\alpha }\tau $
and
$\mathrm {i}x=\frac {\pi }{\alpha }\tau $
and
![]() $\mathrm {i}x=\frac {\pi }{\alpha }(1+\tau )$
. In other words, for
$\mathrm {i}x=\frac {\pi }{\alpha }(1+\tau )$
. In other words, for
![]() $-(m+1)<\xi < m+1=2({\textstyle \frac {\pi }{\alpha }}-1)$
the function
$-(m+1)<\xi < m+1=2({\textstyle \frac {\pi }{\alpha }}-1)$
the function
![]() $\phi (2;\xi ,x(\xi ))$
does not vanish (while in the limit
$\phi (2;\xi ,x(\xi ))$
does not vanish (while in the limit
![]() $\xi \to \pm 2({\textstyle \frac {\pi }{\alpha }}-1)\stackrel {\text {Proposition.}~2.2}{\Longrightarrow } x(\xi )\to \pm \frac {\pi \tau }{\mathrm {i}\alpha }$
and thus
$\xi \to \pm 2({\textstyle \frac {\pi }{\alpha }}-1)\stackrel {\text {Proposition.}~2.2}{\Longrightarrow } x(\xi )\to \pm \frac {\pi \tau }{\mathrm {i}\alpha }$
and thus
![]() $\phi (2;\xi ,x(\xi ))\to 0 $
). In particular, one has that
$\phi (2;\xi ,x(\xi ))\to 0 $
). In particular, one has that
![]() $\phi \big (2;\xi _k,x(\xi _k)\big ) \neq 0$
for
$\phi \big (2;\xi _k,x(\xi _k)\big ) \neq 0$
for
![]() $k=1,\ldots ,m$
(while
$k=1,\ldots ,m$
(while
![]() $\lim _{\xi \to \xi _k}\phi \big (2;\xi ,x(\xi )\big ) =0$
if
$\lim _{\xi \to \xi _k}\phi \big (2;\xi ,x(\xi )\big ) =0$
if
![]() $k=0$
or
$k=0$
or
![]() $k=m+1$
).
$k=m+1$
).
(ii) First, since
the ordering of the eigenvalues in (3.8b) is immediate from Proposition 2.2. Secondly, the mapping ![]() is odd in
is odd in
![]() $\xi $
, so the eigenvalues inherit the manifest antisymmetry
$\xi $
, so the eigenvalues inherit the manifest antisymmetry
![]() $ \xi _{m+1-k}=- \xi _k $
.
$ \xi _{m+1-k}=- \xi _k $
.
(iii) Since
![]() $\phi \big (z;\xi _k,x(\xi _k)\big )$
is even in z, the palindromic (anti)symmetry along the columns follows from the (anti)periodicity:
$\phi \big (z;\xi _k,x(\xi _k)\big )$
is even in z, the palindromic (anti)symmetry along the columns follows from the (anti)periodicity:
 $$ \begin{align*} \Phi_{m+1-l} (\xi_k)&\stackrel{(3.7)}{=}\phi \big(m+2-l;\xi_k,x(\xi_k)\big) \stackrel{(3.3)}{=}(-1)^{k-1} \phi \big(-l-1;\xi_k,x(\xi_k)\big) \\ & =(-1)^{k-1} \phi \big(l+1;\xi_k,x(\xi_k)\big) = (-1)^{k-1} \Phi_{l} (\xi_k). \end{align*} $$
$$ \begin{align*} \Phi_{m+1-l} (\xi_k)&\stackrel{(3.7)}{=}\phi \big(m+2-l;\xi_k,x(\xi_k)\big) \stackrel{(3.3)}{=}(-1)^{k-1} \phi \big(-l-1;\xi_k,x(\xi_k)\big) \\ & =(-1)^{k-1} \phi \big(l+1;\xi_k,x(\xi_k)\big) = (-1)^{k-1} \Phi_{l} (\xi_k). \end{align*} $$
The palindromic (anti)symmetry along the rows is verified similarly:
 $$ \begin{align*} \Phi_{l} (\xi_{m+1-k})=\Phi_{l} (-\xi_{k}) &\stackrel{(3.7)}{=} \phi \big(l+1;-\xi_k,-x(\xi_k)\big) \\ & \stackrel{(3.1)}{=} (-1)^{l-1}\phi \big(l+1;\xi_k,x(\xi_k)\big) =(-1)^{l-1} \Phi_{l} (\xi_{k}).\\[-40pt] \end{align*} $$
$$ \begin{align*} \Phi_{l} (\xi_{m+1-k})=\Phi_{l} (-\xi_{k}) &\stackrel{(3.7)}{=} \phi \big(l+1;-\xi_k,-x(\xi_k)\big) \\ & \stackrel{(3.1)}{=} (-1)^{l-1}\phi \big(l+1;\xi_k,x(\xi_k)\big) =(-1)^{l-1} \Phi_{l} (\xi_{k}).\\[-40pt] \end{align*} $$
3.3 Orthogonality
In [Reference van Diejen and GörbeDG21], the solutions of the finitely truncated discrete Lamé equation (3.5) were constructed for
![]() $g>0$
in terms of polynomials on the spectrum. In this context, the Christoffel–Darboux formula gives rise to an orthogonality relation for the eigenfunctions in question. Theorem 3.2 provides for
$g>0$
in terms of polynomials on the spectrum. In this context, the Christoffel–Darboux formula gives rise to an orthogonality relation for the eigenfunctions in question. Theorem 3.2 provides for
![]() $g=2$
: (i) an alternative compact representation for the eigenfunctions in terms of elliptic numbers (i.e., theta functions) and (ii) formulas parametrizing the corresponding eigenvalues explicitly (barring the inversion of
$g=2$
: (i) an alternative compact representation for the eigenfunctions in terms of elliptic numbers (i.e., theta functions) and (ii) formulas parametrizing the corresponding eigenvalues explicitly (barring the inversion of ![]() (2.8)). By applying [Reference van Diejen and GörbeDG21, Proposition 7] in the case
(2.8)). By applying [Reference van Diejen and GörbeDG21, Proposition 7] in the case
![]() $g=2$
, one establishes the following orthogonality relation for the eigenbasis
$g=2$
, one establishes the following orthogonality relation for the eigenbasis
![]() $\Phi ^{(m)}(\xi _k)$
,
$\Phi ^{(m)}(\xi _k)$
,
![]() $k=1,\ldots , m$
.
$k=1,\ldots , m$
.
Proposition 3.3 (Orthogonality relation).
The eigenbasis
![]() $ \Phi ^{(m)}(\xi _1),\ldots , \Phi ^{(m)}(\xi _m)$
(3.7) satisfies the following orthogonality relation:
$ \Phi ^{(m)}(\xi _1),\ldots , \Phi ^{(m)}(\xi _m)$
(3.7) satisfies the following orthogonality relation:
 $$ \begin{align} \sum_{l=1}^m \Phi_l(\xi_k) \Phi_l(\xi_{\tilde{k}})\Delta_l = \begin{cases} \hat{\Delta}_k^{-1}\, \Phi_1^2 (\xi_k) &\text{if}\ \tilde{k}=k, \\ 0&\text{if}\ \tilde{k}\neq k, \end{cases} \end{align} $$
$$ \begin{align} \sum_{l=1}^m \Phi_l(\xi_k) \Phi_l(\xi_{\tilde{k}})\Delta_l = \begin{cases} \hat{\Delta}_k^{-1}\, \Phi_1^2 (\xi_k) &\text{if}\ \tilde{k}=k, \\ 0&\text{if}\ \tilde{k}\neq k, \end{cases} \end{align} $$
where the orthogonality measure is of the following palindromic form
 $$ \begin{align} \Delta_l :=\frac{[l+1]}{[2]} \left[ \begin{matrix} m-1 \\ l-1 \end{matrix} \right] \quad\text{with}\quad \left[ \begin{matrix} m-1 \\ l-1 \end{matrix} \right] := \frac{\prod_{j=1}^{m-1} [j] }{ \prod_{j=1}^{l-1} [j] \prod_{j=1}^{m-l} [j] } \end{align} $$
$$ \begin{align} \Delta_l :=\frac{[l+1]}{[2]} \left[ \begin{matrix} m-1 \\ l-1 \end{matrix} \right] \quad\text{with}\quad \left[ \begin{matrix} m-1 \\ l-1 \end{matrix} \right] := \frac{\prod_{j=1}^{m-1} [j] }{ \prod_{j=1}^{l-1} [j] \prod_{j=1}^{m-l} [j] } \end{align} $$
(so
![]() $\Delta _{m+1-l}=\Delta _l$
), and the quadratic norms factorize in terms of
$\Delta _{m+1-l}=\Delta _l$
), and the quadratic norms factorize in terms of

and
Proof. Proposition 7 of [Reference van Diejen and GörbeDG21] furnishes an orthogonality relation for the eigenvectors of the matrix in [Reference van Diejen and GörbeDG21, Eqs. (2.8a), (2.8b)] with
![]() $g>0$
, where it is assumed that the eigenvectors are normalized such that their first component is equal to
$g>0$
, where it is assumed that the eigenvectors are normalized such that their first component is equal to
![]() $1$
. The asserted orthogonality relation for
$1$
. The asserted orthogonality relation for
![]() $ \Phi ^{(m)}(\xi _1),\ldots , \Phi ^{(m)}(\xi _m)$
readily follows from this proposition upon substituting
$ \Phi ^{(m)}(\xi _1),\ldots , \Phi ^{(m)}(\xi _m)$
readily follows from this proposition upon substituting
![]() $g=2$
,
$g=2$
, ![]() , and accommodating for the current normalization stemming from Equation (3.1).
, and accommodating for the current normalization stemming from Equation (3.1).
4 Isotropic XY chain
4.1 Hamiltonian
Upon assuming that
![]() $\alpha $
is of the form in Equation (3.4) with
$\alpha $
is of the form in Equation (3.4) with
![]() $g=2$
(so
$g=2$
(so
![]() $\alpha =\frac {2\pi }{m+3}$
), we consider the Hamiltonian of an open quantum spin chain on the finite lattice
$\alpha =\frac {2\pi }{m+3}$
), we consider the Hamiltonian of an open quantum spin chain on the finite lattice
![]() $\{ 1,2,\ldots ,m\}$
with positive coupling constants expressed in terms of elliptic integers
$\{ 1,2,\ldots ,m\}$
with positive coupling constants expressed in terms of elliptic integers

This inhomogeneous quantum spin Hamiltonian acts in a
![]() $2^{m}$
-dimensional state space
$2^{m}$
-dimensional state space
 $$ \begin{align} \mathcal{F}^{(m)}=\underbrace{\mathbb{C}^2\otimes\cdots\otimes\mathbb{C}^2}_{m\ \text{times}} \end{align} $$
$$ \begin{align} \mathcal{F}^{(m)}=\underbrace{\mathbb{C}^2\otimes\cdots\otimes\mathbb{C}^2}_{m\ \text{times}} \end{align} $$
that is endowed with the standard sesquilinear inner product determined by
 $$ \begin{align} \langle u_1\otimes\cdots\otimes u_m | v_1\otimes\cdots\otimes v_m \rangle = \prod_{l=1}^m \langle u_l | v_l\rangle , \end{align} $$
$$ \begin{align} \langle u_1\otimes\cdots\otimes u_m | v_1\otimes\cdots\otimes v_m \rangle = \prod_{l=1}^m \langle u_l | v_l\rangle , \end{align} $$
with
 $u_l= \begin {bmatrix}( u_l)_1\\ (u_l)_2\end {bmatrix} \in \mathbb {C}^2 $
,
$u_l= \begin {bmatrix}( u_l)_1\\ (u_l)_2\end {bmatrix} \in \mathbb {C}^2 $
,
 $v_l= \begin {bmatrix}( v_l)_1\\ (v_l)_2\end {bmatrix} \in \mathbb {C}^2 $
and
$v_l= \begin {bmatrix}( v_l)_1\\ (v_l)_2\end {bmatrix} \in \mathbb {C}^2 $
and
![]() $ \langle u_l | v_l\rangle := \overline {( u_l)_1} ( v_l)_1+\overline {( u_l)_2} ( v_l)_2$
. The local spin operators at site l act by means of Pauli matrices:
$ \langle u_l | v_l\rangle := \overline {( u_l)_1} ( v_l)_1+\overline {( u_l)_2} ( v_l)_2$
. The local spin operators at site l act by means of Pauli matrices:
 $$ \begin{align} \sigma_l^{\mathrm{w}}:=\underbrace{I\otimes\cdots\otimes I}_{l-1\ \text{times} }\otimes \sigma^{\mathrm{w}}\otimes\underbrace{ I\otimes \cdots \otimes I}_{m-l\ \text{times}}\qquad (\mathrm{w}\in\{ \mathrm{x},\mathrm{y},\mathrm{z}\} ) , \end{align} $$
$$ \begin{align} \sigma_l^{\mathrm{w}}:=\underbrace{I\otimes\cdots\otimes I}_{l-1\ \text{times} }\otimes \sigma^{\mathrm{w}}\otimes\underbrace{ I\otimes \cdots \otimes I}_{m-l\ \text{times}}\qquad (\mathrm{w}\in\{ \mathrm{x},\mathrm{y},\mathrm{z}\} ) , \end{align} $$
with
 $$ \begin{align} I= \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} \quad \sigma^{\mathrm{x}}= \begin{bmatrix} 0 &1 \\ 1&0 \end{bmatrix} \quad \sigma^{\mathrm{y}}= \begin{bmatrix} 0 &-\mathrm{i} \\ \mathrm{i}&0 \end{bmatrix} \quad \sigma^{\mathrm{z}}= \begin{bmatrix} 1 &0 \\ 0&-1 \end{bmatrix}. \end{align} $$
$$ \begin{align} I= \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} \quad \sigma^{\mathrm{x}}= \begin{bmatrix} 0 &1 \\ 1&0 \end{bmatrix} \quad \sigma^{\mathrm{y}}= \begin{bmatrix} 0 &-\mathrm{i} \\ \mathrm{i}&0 \end{bmatrix} \quad \sigma^{\mathrm{z}}= \begin{bmatrix} 1 &0 \\ 0&-1 \end{bmatrix}. \end{align} $$
Following [Reference Lieb, Schultz and MattisLSM61], the quantum spin Hamiltonian (4.1) can be rewritten in terms of fermionic creation– and annihilation operators (cf., e.g., [Reference WoitW17, Chapter 27]):

where
 $$ \begin{align} c_l^{*} &:=(-1)^{l-1} \underbrace{ \sigma^{\mathrm{z}}\otimes\cdots\otimes \sigma^{\mathrm{z}}}_{l-1\ \text{times} }\otimes \sigma^{+}\otimes\underbrace{ I\otimes \cdots \otimes I}_{m-l\ \text{times}}, \end{align} $$
$$ \begin{align} c_l^{*} &:=(-1)^{l-1} \underbrace{ \sigma^{\mathrm{z}}\otimes\cdots\otimes \sigma^{\mathrm{z}}}_{l-1\ \text{times} }\otimes \sigma^{+}\otimes\underbrace{ I\otimes \cdots \otimes I}_{m-l\ \text{times}}, \end{align} $$
 $$ \begin{align} c_l &:=(-1)^{l-1} \underbrace{ \sigma^{\mathrm{z}}\otimes\cdots\otimes \sigma^{\mathrm{z}}}_{l-1\ \text{times} }\otimes \sigma^{-}\otimes\underbrace{ I\otimes \cdots \otimes I}_{m-l\ \text{times}} , \end{align} $$
$$ \begin{align} c_l &:=(-1)^{l-1} \underbrace{ \sigma^{\mathrm{z}}\otimes\cdots\otimes \sigma^{\mathrm{z}}}_{l-1\ \text{times} }\otimes \sigma^{-}\otimes\underbrace{ I\otimes \cdots \otimes I}_{m-l\ \text{times}} , \end{align} $$
with
 $$ \begin{align} \sigma^{+}=\frac{1}{2}\left( \sigma^{\mathrm{x}} +\mathrm{i} \sigma^{\mathrm{y}} \right) = \begin{bmatrix} 0&1 \\ 0&0 \end{bmatrix} \quad\text{and}\quad \sigma^{-}=\frac{1}{2}\left( \sigma^{\mathrm{x}} -\mathrm{i} \sigma^{\mathrm{y}} \right) =\begin{bmatrix} 0&0 \\ 1&0 \end{bmatrix}. \end{align} $$
$$ \begin{align} \sigma^{+}=\frac{1}{2}\left( \sigma^{\mathrm{x}} +\mathrm{i} \sigma^{\mathrm{y}} \right) = \begin{bmatrix} 0&1 \\ 0&0 \end{bmatrix} \quad\text{and}\quad \sigma^{-}=\frac{1}{2}\left( \sigma^{\mathrm{x}} -\mathrm{i} \sigma^{\mathrm{y}} \right) =\begin{bmatrix} 0&0 \\ 1&0 \end{bmatrix}. \end{align} $$
The fermionic creation – and annihilation operators satisfy the canonical anticommutation relations
where
![]() $\{ a,b\}:=ab+ba$
and
$\{ a,b\}:=ab+ba$
and
![]() $\delta _{l,\tilde {l}}$
represents the Kronecker delta. Moreover, since the coupling constants
$\delta _{l,\tilde {l}}$
represents the Kronecker delta. Moreover, since the coupling constants ![]() are positive and the operators
are positive and the operators
![]() $c_l^{*}$
and
$c_l^{*}$
and
![]() $c_l$
are adjoints in
$c_l$
are adjoints in
![]() $\mathcal {F}^{(m)}$
, that is,
$\mathcal {F}^{(m)}$
, that is,
it is clear that the Hamiltonian
![]() $\boldsymbol {H}^{(m)}$
(4.4a)–(4.4d) is self-adjoint:
$\boldsymbol {H}^{(m)}$
(4.4a)–(4.4d) is self-adjoint:
4.2 n-particle Hamiltonian
Starting from a normalized vacuum vector that is annihilated by
![]() $c_l$
(
$c_l$
(
![]() $l=1,\ldots ,m$
)
$l=1,\ldots ,m$
)
 $$ \begin{align} |\emptyset\rangle := \underbrace{ \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes\cdots \otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix} }_{m\ \text{times}}, \end{align} $$
$$ \begin{align} |\emptyset\rangle := \underbrace{ \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes\cdots \otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix} }_{m\ \text{times}}, \end{align} $$
the standard orthonormal basis for
![]() $\mathcal {F}^{(m)}$
(4.2a), (4.2b) can be generated by acting with fermionic creation operators associated with strict partitions
$\mathcal {F}^{(m)}$
(4.2a), (4.2b) can be generated by acting with fermionic creation operators associated with strict partitions
![]() $\lambda = (\lambda _1,\ldots ,\lambda _n)$
that have bounded row- and column sizes
$\lambda = (\lambda _1,\ldots ,\lambda _n)$
that have bounded row- and column sizes
![]() $\leq m$
:
$\leq m$
:
Here, the parts of the strict partition
![]() $ (\lambda _1,\ldots ,\lambda _n)$
labeling the basis vector
$ (\lambda _1,\ldots ,\lambda _n)$
labeling the basis vector
![]() $|\lambda \rangle $
represent the coordinates of
$|\lambda \rangle $
represent the coordinates of
![]() $n\leq m$
places on the lattice
$n\leq m$
places on the lattice
![]() $\{ 1,2,\ldots ,m\}$
, where in the vaccum vector
$\{ 1,2,\ldots ,m\}$
, where in the vaccum vector
![]() $|\emptyset \rangle $
the local state
$|\emptyset \rangle $
the local state
![]() $ \begin {bmatrix} 0 \\ 1 \end {bmatrix} $
has been flipped to
$ \begin {bmatrix} 0 \\ 1 \end {bmatrix} $
has been flipped to
![]() $ \begin {bmatrix} 1 \\ 0 \end {bmatrix} $
. This gives rise to the following orthogonal decomposition of the state space
$ \begin {bmatrix} 1 \\ 0 \end {bmatrix} $
. This gives rise to the following orthogonal decomposition of the state space
![]() $\mathcal {F}^{(m)}$
in n-particle subspaces:
$\mathcal {F}^{(m)}$
in n-particle subspaces:
 $$ \begin{align} \mathcal{F}^{(m)}= \bigoplus_{n=0}^m \mathcal{F}^{(m,n)} \quad \text{with}\quad \mathcal{F}^{(m,n)}:=\text{Span}_{\mathbb{C}} \{ |\lambda\rangle \mid \lambda\in\Lambda^{(m,n)} \} , \end{align} $$
$$ \begin{align} \mathcal{F}^{(m)}= \bigoplus_{n=0}^m \mathcal{F}^{(m,n)} \quad \text{with}\quad \mathcal{F}^{(m,n)}:=\text{Span}_{\mathbb{C}} \{ |\lambda\rangle \mid \lambda\in\Lambda^{(m,n)} \} , \end{align} $$
where
with the convention that
![]() $\Lambda ^{(m,0)}:=\{ \emptyset \}$
. Notice that the
$\Lambda ^{(m,0)}:=\{ \emptyset \}$
. Notice that the
![]() $\binom {m}{n}$
-dimensional n-particle subspace
$\binom {m}{n}$
-dimensional n-particle subspace
![]() $\mathcal {F}^{(m,n)}$
is stable with respect to the action of
$\mathcal {F}^{(m,n)}$
is stable with respect to the action of
![]() $\boldsymbol {H}^{(m)}$
(4.4a)–(4.4d).
$\boldsymbol {H}^{(m)}$
(4.4a)–(4.4d).
Proposition 4.1 (Matrix elements of the Hamiltonian).
The matrix elements of the quantum spin Hamiltonian
![]() $\boldsymbol {H}^{(m)}$
(4.1) with respect to the standard basis
$\boldsymbol {H}^{(m)}$
(4.1) with respect to the standard basis
![]() $|\lambda \rangle $
(4.7a), (4.7b) read for
$|\lambda \rangle $
(4.7a), (4.7b) read for
![]() $\lambda \in \Lambda ^{(m,n)}$
with
$\lambda \in \Lambda ^{(m,n)}$
with
![]() $0<n<m$
:
$0<n<m$
:

(while
![]() $\boldsymbol {H}^{(m)} |\lambda \rangle =0$
for
$\boldsymbol {H}^{(m)} |\lambda \rangle =0$
for
![]() $\lambda \in \Lambda ^{(m,n)}$
if
$\lambda \in \Lambda ^{(m,n)}$
if
![]() $n=0$
or
$n=0$
or
![]() $n=m$
). Here, the vectors
$n=m$
). Here, the vectors
![]() $e_1,\ldots e_n$
refer to the standard unit basis of
$e_1,\ldots e_n$
refer to the standard unit basis of
![]() $\mathbb {Z}^n$
.
$\mathbb {Z}^n$
.
Proof. Let us act with
![]() $\boldsymbol {H}^{(m)}$
(4.4a)–(4.4d) on
$\boldsymbol {H}^{(m)}$
(4.4a)–(4.4d) on
![]() $|\lambda \rangle $
with
$|\lambda \rangle $
with
![]() $\lambda \in \Lambda ^{(m,n)}$
. For
$\lambda \in \Lambda ^{(m,n)}$
. For
![]() $0<n<m$
and
$0<n<m$
and
![]() $1\leq l< m$
, it is seen from the anticommutation relations (4.5) that the term
$1\leq l< m$
, it is seen from the anticommutation relations (4.5) that the term
vanishes unless
![]() $l\not \in \{\lambda _1,\ldots ,\lambda _n\}$
and
$l\not \in \{\lambda _1,\ldots ,\lambda _n\}$
and
![]() $l+1\in \{\lambda _1,\ldots ,\lambda _n\}$
, that is, unless
$l+1\in \{\lambda _1,\ldots ,\lambda _n\}$
, that is, unless
![]() $\exists 1\leq j\leq n$
such that
$\exists 1\leq j\leq n$
such that
![]() $l=\lambda _j-1$
and
$l=\lambda _j-1$
and
![]() $\lambda _{j+1}<l$
(with the convention that
$\lambda _{j+1}<l$
(with the convention that
![]() $\lambda _{n+1}:=0$
), or equivalently: Unless
$\lambda _{n+1}:=0$
), or equivalently: Unless
![]() $\exists 1\leq j\leq n$
such that
$\exists 1\leq j\leq n$
such that
![]() $l=\lambda _j-1$
and
$l=\lambda _j-1$
and
![]() $\lambda -e_j\in \Lambda ^{(m,n)}$
. In this case, one has that
$\lambda -e_j\in \Lambda ^{(m,n)}$
. In this case, one has that

In the same manner, one deduces that for
![]() $0<n<m$
and
$0<n<m$
and
![]() $1\leq l< m$
the term
$1\leq l< m$
the term ![]() vanishes unless
vanishes unless
![]() $l\in \{\lambda _1,\ldots ,\lambda _n\}$
and
$l\in \{\lambda _1,\ldots ,\lambda _n\}$
and
![]() $l+1\not \in \{\lambda _1,\ldots ,\lambda _n\}$
, that is, unless
$l+1\not \in \{\lambda _1,\ldots ,\lambda _n\}$
, that is, unless
![]() $\exists 1\leq j\leq n$
such that
$\exists 1\leq j\leq n$
such that
![]() $l=\lambda _j$
and
$l=\lambda _j$
and
![]() $\lambda _{j-1}>l+1$
(with the convention that
$\lambda _{j-1}>l+1$
(with the convention that
![]() $\lambda _{0}:=m+1$
), or equivalently: Unless
$\lambda _{0}:=m+1$
), or equivalently: Unless
![]() $\exists 1\leq j\leq n$
such that
$\exists 1\leq j\leq n$
such that
![]() $l=\lambda _j$
and
$l=\lambda _j$
and
![]() $\lambda +e_j\in \Lambda ^{(m,n)}$
. In this case, one has that
$\lambda +e_j\in \Lambda ^{(m,n)}$
. In this case, one has that

Notice that in both cases the relation between the pertinent values of
![]() $1\leq l<m$
and
$1\leq l<m$
and
![]() $1\leq j\leq n$
is one-to-one given
$1\leq j\leq n$
is one-to-one given
![]() $\lambda $
(since our partitions are strict); hence, by summing over all terms from
$\lambda $
(since our partitions are strict); hence, by summing over all terms from
![]() $1\leq l<m$
the asserted formula for the matrix elements in Equation (4.9) follows.
$1\leq l<m$
the asserted formula for the matrix elements in Equation (4.9) follows.
Remark 4.2. In the formulas for the Hamiltonian
![]() $\boldsymbol {H}^{(m)} $
(4.4a)–(4.4c) and for the standard basis
$\boldsymbol {H}^{(m)} $
(4.4a)–(4.4c) and for the standard basis
![]() $|\lambda \rangle $
(4.7a), (4.7b) (as well as in the proof of Proposition 4.1), the fermionic operators
$|\lambda \rangle $
(4.7a), (4.7b) (as well as in the proof of Proposition 4.1), the fermionic operators
![]() $c^{*}_l$
and
$c^{*}_l$
and
![]() $c_l$
can in principle be replaced simply by the spin raising and lowering operators
$c_l$
can in principle be replaced simply by the spin raising and lowering operators
![]() $\sigma ^{+}_l=\sigma ^{\mathrm {x}}_l+\mathrm {i}\sigma ^{\mathrm {y}}_l$
and
$\sigma ^{+}_l=\sigma ^{\mathrm {x}}_l+\mathrm {i}\sigma ^{\mathrm {y}}_l$
and
![]() $\sigma ^{-}_l=\sigma ^{\mathrm {x}}_l-\mathrm {i}\sigma ^{\mathrm {y}}_l$
, respectively. Indeed, in view of the ordering of the parts of the strict partition one has in particular that for any
$\sigma ^{-}_l=\sigma ^{\mathrm {x}}_l-\mathrm {i}\sigma ^{\mathrm {y}}_l$
, respectively. Indeed, in view of the ordering of the parts of the strict partition one has in particular that for any
![]() $\lambda \in \Lambda ^{(m,n)}$
:
$\lambda \in \Lambda ^{(m,n)}$
:
![]() $ c^{*}_{\lambda _n} \cdots c^{*}_{\lambda _2} c^{*}_{\lambda _1} |\emptyset \rangle = \sigma ^{+}_{\lambda _n} \cdots \sigma ^{+}_{\lambda _2} \sigma ^{+}_{\lambda _1} |\emptyset \rangle $
. However, by employing fermionic operators instead it is automatic that all results below apply verbatim to the free-fermion description of the spin model under consideration.
$ c^{*}_{\lambda _n} \cdots c^{*}_{\lambda _2} c^{*}_{\lambda _1} |\emptyset \rangle = \sigma ^{+}_{\lambda _n} \cdots \sigma ^{+}_{\lambda _2} \sigma ^{+}_{\lambda _1} |\emptyset \rangle $
. However, by employing fermionic operators instead it is automatic that all results below apply verbatim to the free-fermion description of the spin model under consideration.
Let
![]() $\ell ^2(\Lambda ^{(m,n)})$
denote the (n-magnon) Hilbert space of complex functions
$\ell ^2(\Lambda ^{(m,n)})$
denote the (n-magnon) Hilbert space of complex functions
![]() $\lambda \stackrel {\Psi }{\mapsto }\Psi _\lambda $
,
$\lambda \stackrel {\Psi }{\mapsto }\Psi _\lambda $
,
![]() $\lambda \in \Lambda ^{(m,n)}$
endowed with the inner product
$\lambda \in \Lambda ^{(m,n)}$
endowed with the inner product
 $$ \begin{align} \langle \tilde\Psi, \Psi\rangle:=\sum_{\lambda\in\Lambda^{(m,n)}} \overline{\tilde\Psi}_\lambda \Psi_\lambda\qquad \big(\forall \Psi,\tilde{\Psi}\in \ell^2(\Lambda^{(m,n)})\big). \end{align} $$
$$ \begin{align} \langle \tilde\Psi, \Psi\rangle:=\sum_{\lambda\in\Lambda^{(m,n)}} \overline{\tilde\Psi}_\lambda \Psi_\lambda\qquad \big(\forall \Psi,\tilde{\Psi}\in \ell^2(\Lambda^{(m,n)})\big). \end{align} $$
It is evident from the orthonormality of the standard basis
![]() $|\lambda \rangle $
,
$|\lambda \rangle $
,
![]() $\lambda \in \Lambda ^{(m,n)}$
that the injection
$\lambda \in \Lambda ^{(m,n)}$
that the injection
![]() $\mathcal {I}^{(m,n)}:\ell ^2(\Lambda ^{(m,n)})\to \mathcal {F}^{(m,n)}$
given by
$\mathcal {I}^{(m,n)}:\ell ^2(\Lambda ^{(m,n)})\to \mathcal {F}^{(m,n)}$
given by
defines an Hilbert-space isomorphism between
![]() $\ell ^2(\Lambda ^{(m,n)})$
and
$\ell ^2(\Lambda ^{(m,n)})$
and
![]() $ \mathcal {F}^{(m,n)}$
.
$ \mathcal {F}^{(m,n)}$
.
Definition 4.1 (n-particle Hamiltonian).
Let us define the n-particle Hamiltonian
![]() $\boldsymbol {H}^{(m,n)}:\ell ^2(\Lambda ^{(m,n)})\to \ell ^2(\Lambda ^{(m,n)})$
as the pull-back of the restriction of the quantum spin Hamiltonian
$\boldsymbol {H}^{(m,n)}:\ell ^2(\Lambda ^{(m,n)})\to \ell ^2(\Lambda ^{(m,n)})$
as the pull-back of the restriction of the quantum spin Hamiltonian
![]() $\boldsymbol {H}^{(m)}$
(4.1) to the n-particle subspace
$\boldsymbol {H}^{(m)}$
(4.1) to the n-particle subspace
![]() $\mathcal {F}^{(m,n)}$
(4.8a), (4.8b) with respect to the isomorphism
$\mathcal {F}^{(m,n)}$
(4.8a), (4.8b) with respect to the isomorphism
![]() $\mathcal {I}^{(m,n)}:\ell ^2(\Lambda ^{(m,n)})\to \mathcal {F}^{(m,n)}$
(4.11):
$\mathcal {I}^{(m,n)}:\ell ^2(\Lambda ^{(m,n)})\to \mathcal {F}^{(m,n)}$
(4.11):
It is clear from this definition that
![]() $\boldsymbol {H}^{(m,n)}$
inherits the self-adjointness of
$\boldsymbol {H}^{(m,n)}$
inherits the self-adjointness of
![]() $\boldsymbol {H}^{(m)}$
. With the aid of Proposition 4.1, we arrive at the following explicit formula for the action of
$\boldsymbol {H}^{(m)}$
. With the aid of Proposition 4.1, we arrive at the following explicit formula for the action of
![]() $\boldsymbol {H}^{(m,n)}$
in
$\boldsymbol {H}^{(m,n)}$
in
![]() $\ell ^2(\Lambda ^{(m,n)})$
.
$\ell ^2(\Lambda ^{(m,n)})$
.
Proposition 4.3 (Action of the n-particle Hamiltonian).
For
![]() $0<n<m$
, one has that
$0<n<m$
, one has that

(
![]() $\forall \Psi \in \ell ^2(\Lambda ^{(m,n)})$
).
$\forall \Psi \in \ell ^2(\Lambda ^{(m,n)})$
).
Proof. Definition 4.1 implies that
![]() $\forall \Psi \in \ell ^2(\Lambda ^{(m,n)})$
:
$\forall \Psi \in \ell ^2(\Lambda ^{(m,n)})$
:
or more explicitly (cf. Equation (4.11)):
 $$ \begin{align} \sum_{\lambda\in\Lambda^{(m,n)}} (\boldsymbol{H}^{(m,n)}\Psi)_\lambda |\lambda\rangle= \boldsymbol{H}^{(m)} \left( \sum_{\lambda\in\Lambda^{(m,n)}} \Psi_\lambda|\lambda\rangle\right). \end{align} $$
$$ \begin{align} \sum_{\lambda\in\Lambda^{(m,n)}} (\boldsymbol{H}^{(m,n)}\Psi)_\lambda |\lambda\rangle= \boldsymbol{H}^{(m)} \left( \sum_{\lambda\in\Lambda^{(m,n)}} \Psi_\lambda|\lambda\rangle\right). \end{align} $$
With the aid of Proposition 4.1 the right-hand side of this intertwining relation is rewritten as

which is equal to

with the convention that
![]() $ |\lambda \pm e_j\rangle =0$
if
$ |\lambda \pm e_j\rangle =0$
if
![]() $\lambda \pm e_j\not \in \Lambda ^{(m,n)}$
. The translations
$\lambda \pm e_j\not \in \Lambda ^{(m,n)}$
. The translations
![]() $\lambda \to \lambda -e_j$
and
$\lambda \to \lambda -e_j$
and
![]() $\lambda \to \lambda +e_j$
recast the respective terms in the form
$\lambda \to \lambda +e_j$
recast the respective terms in the form

with the convention that
![]() $ \Psi _{\lambda \pm e_j}=0$
if
$ \Psi _{\lambda \pm e_j}=0$
if
![]() $\lambda \pm e_j\not \in \Lambda ^{(m,n)}$
. When comparing with the left-hand side of Equation (4.14), the asserted action of
$\lambda \pm e_j\not \in \Lambda ^{(m,n)}$
. When comparing with the left-hand side of Equation (4.14), the asserted action of
![]() $\boldsymbol {H}^{(m,n)}$
in
$\boldsymbol {H}^{(m,n)}$
in
![]() $ \ell ^2(\Lambda ^{(m,n)})$
given by Equation (4.13) follows.
$ \ell ^2(\Lambda ^{(m,n)})$
given by Equation (4.13) follows.
4.3 Spectrum and orthonormal eigenbasis
In the homogeneous case with ![]() , a standard method for diagonalizing
, a standard method for diagonalizing
![]() $\boldsymbol {H}^{(m)} $
(4.4a)–(4.4c) hinges on performing a (discrete) Fourier transform of the fermionic operators. In the inhomogeneous situation with site-dependent coupling constants, this discrete Fourier transform is replaced by the pertinent Bogoliubov transformation stemming from the eigenfunction transform diagonalizing the one-particle Hamiltonian (cf., e.g., [Reference Hamza, Sims and StolzHSS12, Section 4]). Here, we will follow an alternative path, which is based on the observation that Theorem 3.2 and Proposition 3.3 allow for an explicit construction of an orthonormal eigenbasis diagonalizing the n-particle Hamiltonian
$\boldsymbol {H}^{(m)} $
(4.4a)–(4.4c) hinges on performing a (discrete) Fourier transform of the fermionic operators. In the inhomogeneous situation with site-dependent coupling constants, this discrete Fourier transform is replaced by the pertinent Bogoliubov transformation stemming from the eigenfunction transform diagonalizing the one-particle Hamiltonian (cf., e.g., [Reference Hamza, Sims and StolzHSS12, Section 4]). Here, we will follow an alternative path, which is based on the observation that Theorem 3.2 and Proposition 3.3 allow for an explicit construction of an orthonormal eigenbasis diagonalizing the n-particle Hamiltonian
![]() $\boldsymbol {H}^{(m,n)} $
(4.13) in terms of Slater determinants.
$\boldsymbol {H}^{(m,n)} $
(4.13) in terms of Slater determinants.
To this end, some further notation is needed. For any
![]() $\lambda ,\kappa \in \Lambda ^{(m,n)}$
, let us define
$\lambda ,\kappa \in \Lambda ^{(m,n)}$
, let us define
 $$ \begin{align} \Delta^{(m,n)}_\lambda& := \prod_{1\leq j\leq n} \Delta_{\lambda_j}\quad\text{and}\quad \hat{\Delta}^{(m,n)}_\kappa := \prod_{1\leq j\leq n} \hat{\Delta}_{\kappa_j} , \end{align} $$
$$ \begin{align} \Delta^{(m,n)}_\lambda& := \prod_{1\leq j\leq n} \Delta_{\lambda_j}\quad\text{and}\quad \hat{\Delta}^{(m,n)}_\kappa := \prod_{1\leq j\leq n} \hat{\Delta}_{\kappa_j} , \end{align} $$
where (as before)
![]() $\xi _k=\left. 2(\frac {\pi }{\alpha }-1-k) \right |_{\alpha =\frac {2\pi }{m+3}}=m+1-2k$
while
$\xi _k=\left. 2(\frac {\pi }{\alpha }-1-k) \right |_{\alpha =\frac {2\pi }{m+3}}=m+1-2k$
while
![]() $\Delta _l$
and
$\Delta _l$
and
![]() $\hat {\Delta }_k$
are of the form detailed in Proposition 3.3. The corresponding spectrum will be given by eigenvalues of the form
$\hat {\Delta }_k$
are of the form detailed in Proposition 3.3. The corresponding spectrum will be given by eigenvalues of the form

(with ![]() as in Theorem 3.2).
as in Theorem 3.2).
We define the n-particle wave function
![]() $ \Psi ^{(m,n)} \big (\xi ^{(m,n)}_\kappa \big ) \in \ell ^2 (\Lambda ^{(m,n)})$
by means of its values on
$ \Psi ^{(m,n)} \big (\xi ^{(m,n)}_\kappa \big ) \in \ell ^2 (\Lambda ^{(m,n)})$
by means of its values on
![]() $\Lambda ^{(m,n)}$
in terms of the following normalized Slater determinant:
$\Lambda ^{(m,n)}$
in terms of the following normalized Slater determinant:
 $$ \begin{align} \Psi^{(m,n)}_\lambda \big(\xi^{(m,n)}_\kappa\big) :=\sqrt{ \Delta_\lambda^{(m,n)} \hat{\Delta}^{(m,n)}_\kappa } \det \left[ \frac{\Phi_{\lambda_j}(\xi_{\kappa_k})} {\Phi_1 (\xi_{\kappa_k})} \right]_{1\leq j,k\leq n} \end{align} $$
$$ \begin{align} \Psi^{(m,n)}_\lambda \big(\xi^{(m,n)}_\kappa\big) :=\sqrt{ \Delta_\lambda^{(m,n)} \hat{\Delta}^{(m,n)}_\kappa } \det \left[ \frac{\Phi_{\lambda_j}(\xi_{\kappa_k})} {\Phi_1 (\xi_{\kappa_k})} \right]_{1\leq j,k\leq n} \end{align} $$
(with
![]() $\Phi _{1}(\xi _k),\ldots , \Phi _{m}(\xi _k)$
taken from Equation (3.7)). So here and below, when the superscripted dimensions
$\Phi _{1}(\xi _k),\ldots , \Phi _{m}(\xi _k)$
taken from Equation (3.7)). So here and below, when the superscripted dimensions
![]() $(m,n)$
are omitted we are referring to the components of the eigenvectors, the eigenvalues and the weights of the orthogonality measures associated with the truncated difference Lamé matrix
$(m,n)$
are omitted we are referring to the components of the eigenvectors, the eigenvalues and the weights of the orthogonality measures associated with the truncated difference Lamé matrix
![]() $\boldsymbol {L}^{(m)}$
(3.6b) to be imported from Section 3.
$\boldsymbol {L}^{(m)}$
(3.6b) to be imported from Section 3.
Theorem 4.4 (Diagonalization of
 $\boldsymbol {H}^{(m,n)} $
).
$\boldsymbol {H}^{(m,n)} $
).
For
![]() $0<n<m$
, the wave functions
$0<n<m$
, the wave functions
![]() $ \Psi ^{(m,n)} \big (\xi ^{(m,n)}_\kappa \big )$
,
$ \Psi ^{(m,n)} \big (\xi ^{(m,n)}_\kappa \big )$
,
![]() $\kappa \in \Lambda ^{(m,n)}$
constitute and orthogonal eigenbasis diagonalizing
$\kappa \in \Lambda ^{(m,n)}$
constitute and orthogonal eigenbasis diagonalizing
![]() $\boldsymbol {H}^{(m,n)} $
(4.13) in
$\boldsymbol {H}^{(m,n)} $
(4.13) in
![]() $\ell ^2 (\Lambda ^{(m,n)})$
, that is,
$\ell ^2 (\Lambda ^{(m,n)})$
, that is,
![]() $ \forall \kappa ,\tilde {\kappa }\in \Lambda ^{(m,n)}$
:
$ \forall \kappa ,\tilde {\kappa }\in \Lambda ^{(m,n)}$
:
and
 $$ \begin{align} \left\langle \Psi^{(m,n)} \big(\xi^{(m,n)}_\kappa\big), \Psi^{(m,n)} \big(\xi^{(m,n)}_{\tilde{\kappa}}\big)\right\rangle =\begin{cases} 1&\text{if}\ \tilde{\kappa}=\kappa,\\ 0&\text{if}\ \tilde{\kappa}\neq\kappa. \end{cases} \end{align} $$
$$ \begin{align} \left\langle \Psi^{(m,n)} \big(\xi^{(m,n)}_\kappa\big), \Psi^{(m,n)} \big(\xi^{(m,n)}_{\tilde{\kappa}}\big)\right\rangle =\begin{cases} 1&\text{if}\ \tilde{\kappa}=\kappa,\\ 0&\text{if}\ \tilde{\kappa}\neq\kappa. \end{cases} \end{align} $$
Proof. Let us act with
![]() $\boldsymbol {H}^{(m,n)} $
(4.13) on
$\boldsymbol {H}^{(m,n)} $
(4.13) on
![]() $ \Psi ^{(m,n)} \big (\xi ^{(m,n)}_\kappa \big ) $
(4.16), and evaluate the result at
$ \Psi ^{(m,n)} \big (\xi ^{(m,n)}_\kappa \big ) $
(4.16), and evaluate the result at
![]() $\lambda \in \Lambda ^{(m,n)}$
:
$\lambda \in \Lambda ^{(m,n)}$
:

By means of the relations ![]() for
for
![]() $1\leq \lambda _i<m$
and
$1\leq \lambda _i<m$
and ![]() for
for
![]() $1<\lambda _i\leq m$
, the expression in question is rewritten as
$1<\lambda _i\leq m$
, the expression in question is rewritten as
 $$ \begin{align*} =& \sum_{1\leq i\leq n} \det \left[ \Delta_{\lambda_j}^{1/2} \hat{\Delta}_{\kappa_k}^{1/2} \frac{ \big(\frac{[m-\lambda_i]}{[m+2-\lambda_i]} \big)^{\delta_{i,j}} \Phi_{\lambda_j+\delta_{i,j}}(\xi_{\kappa_k})} {\Phi_1 (\xi_{\kappa_k})}\right]_{1\leq j,k\leq n} \\ +& \sum_{1\leq i\leq n} \det \left[ \Delta_{\lambda_j}^{1/2} \hat{\Delta}_{\kappa_k}^{1/2} \frac{ \big(\frac{[\lambda_i-1]}{[\lambda_i+1]} \big)^{\delta_{i,j}} \Phi_{\lambda_j-\delta_{i,j}}(\xi_{\kappa_k})} {\Phi_1 (\xi_{\kappa_k})}\right]_{1\leq j,k\leq n} , \end{align*} $$
$$ \begin{align*} =& \sum_{1\leq i\leq n} \det \left[ \Delta_{\lambda_j}^{1/2} \hat{\Delta}_{\kappa_k}^{1/2} \frac{ \big(\frac{[m-\lambda_i]}{[m+2-\lambda_i]} \big)^{\delta_{i,j}} \Phi_{\lambda_j+\delta_{i,j}}(\xi_{\kappa_k})} {\Phi_1 (\xi_{\kappa_k})}\right]_{1\leq j,k\leq n} \\ +& \sum_{1\leq i\leq n} \det \left[ \Delta_{\lambda_j}^{1/2} \hat{\Delta}_{\kappa_k}^{1/2} \frac{ \big(\frac{[\lambda_i-1]}{[\lambda_i+1]} \big)^{\delta_{i,j}} \Phi_{\lambda_j-\delta_{i,j}}(\xi_{\kappa_k})} {\Phi_1 (\xi_{\kappa_k})}\right]_{1\leq j,k\leq n} , \end{align*} $$
where the restrictions on the summations in i were suppressed in the end since the resulting determinants vanish manifestly for
![]() $\lambda \in \Lambda ^{(n,m)}$
with
$\lambda \in \Lambda ^{(n,m)}$
with
![]() $\lambda +e_i\not \in \Lambda ^{(n,m)}$
or with
$\lambda +e_i\not \in \Lambda ^{(n,m)}$
or with
![]() $\lambda -e_i\not \in \Lambda ^{(n,m)}$
, respectively (either because of a vanishing ith row or because of rows i and
$\lambda -e_i\not \in \Lambda ^{(n,m)}$
, respectively (either because of a vanishing ith row or because of rows i and
![]() $i- 1$
or i and
$i- 1$
or i and
![]() $i+1$
being linearly dependent). Upon exploiting the linearity in the ith row, the determinants can be merged pairwise
$i+1$
being linearly dependent). Upon exploiting the linearity in the ith row, the determinants can be merged pairwise
 $$ \begin{align*} = \sum_{1\leq i\leq n} \det \begin{bmatrix} \frac{ \Delta_{\lambda_j}^{1/2} \hat{\Delta}_{\kappa_k}^{1/2} } {\Phi_1 (\xi_{\kappa_k}) 2^{1-\delta_{i,j}}} \bigg(\big({\textstyle \frac{[m-\lambda_i]}{[m+2-\lambda_i]} }\big)^{\delta_{i,j}} \Phi_{\lambda_j+\delta_{i,j}}(\xi_{\kappa_k}) \qquad \\ \hfill + \big({\textstyle \frac{[\lambda_i-1]}{[\lambda_i+1]} }\big)^{\delta_{i,j}} \Phi_{\lambda_j-\delta_{i,j}}(\xi_{\kappa_k}) \bigg) \end{bmatrix}_{1\leq j,k\leq n} , \end{align*} $$
$$ \begin{align*} = \sum_{1\leq i\leq n} \det \begin{bmatrix} \frac{ \Delta_{\lambda_j}^{1/2} \hat{\Delta}_{\kappa_k}^{1/2} } {\Phi_1 (\xi_{\kappa_k}) 2^{1-\delta_{i,j}}} \bigg(\big({\textstyle \frac{[m-\lambda_i]}{[m+2-\lambda_i]} }\big)^{\delta_{i,j}} \Phi_{\lambda_j+\delta_{i,j}}(\xi_{\kappa_k}) \qquad \\ \hfill + \big({\textstyle \frac{[\lambda_i-1]}{[\lambda_i+1]} }\big)^{\delta_{i,j}} \Phi_{\lambda_j-\delta_{i,j}}(\xi_{\kappa_k}) \bigg) \end{bmatrix}_{1\leq j,k\leq n} , \end{align*} $$
so as to enable invoking of the eigenvalue equations from Theorem 3.2 on each element of the ith row

By first expanding the latter determinants along the ith row and then interchanging the order of the two summations, a comparison of the result with the expansion of the determinant
![]() $ \det \left [ \Delta _{\lambda _j}^{1/2} \hat {\Delta }_{\kappa _k}^{1/2} \frac {\Phi _{\lambda _j} (\xi _{\kappa _k})} {\Phi _1 (\xi _{\kappa _k})} \right ]_{1\leq j,k\leq n} $
along the kth column readily reveals that Equation (4.18) can be rewritten as
$ \det \left [ \Delta _{\lambda _j}^{1/2} \hat {\Delta }_{\kappa _k}^{1/2} \frac {\Phi _{\lambda _j} (\xi _{\kappa _k})} {\Phi _1 (\xi _{\kappa _k})} \right ]_{1\leq j,k\leq n} $
along the kth column readily reveals that Equation (4.18) can be rewritten as

which settles the proof of the eigenvalue equation (4.17a).
The proof of the orthogonality relation (4.17b) hinges in turn on Proposition 3.3 and the Cauchy–Binet formula. Indeed,
![]() $\forall \kappa ,\kappa \in \Lambda ^{(m,n)}$
:
$\forall \kappa ,\kappa \in \Lambda ^{(m,n)}$
:
 $$ \begin{align*} &\left\langle \Psi^{(m,n)} \big(\xi^{(m,n)}_\kappa\big), \Psi^{(m,n)} \big(\xi^{(m,n)}_{\tilde{\kappa}}\big)\right\rangle = \sum_{\lambda\in\Lambda^{(m,n)}} \overline{ \Psi^{(m,n)}_\lambda \big(\xi^{(m,n)}_\kappa\big)} \Psi^{(m,n)}_\lambda \big(\xi^{(m,n)}_{\tilde{\kappa}}\big) \\ &\stackrel{(i)}{=} \sum_{m\geq\lambda_1>\cdots>\lambda_n\geq 1} \det \left[ \hat{\Delta}_{\kappa_j}^{1/2} \frac{\Phi_{\lambda_k}(\xi_{\kappa_j})} {\Phi_1 (\xi_{\kappa_j})} \Delta_{\lambda_k}^{1/2}\right]_{1\leq j,k\leq n} \det \left[ \Delta_{\lambda_j}^{1/2} \frac{\Phi_{\lambda_j}(\xi_{\tilde{\kappa}_k})} {\Phi_1 (\xi_{\tilde{\kappa}_k})} \hat{\Delta}_{\tilde{\kappa}_k}^{1/2} \right]_{1\leq j,k\leq n} \\ &\stackrel{(ii)}{=} \det \left( \left[ \hat{\Delta}_{\kappa_j}^{1/2} \frac{\Phi_{l}(\xi_{\kappa_j})} {\Phi_1 (\xi_{\kappa_j})} \Delta_{l}^{1/2} \right]_{\substack{1\leq j\leq n\\ 1\leq l\leq m}} \left[ \Delta_{l}^{1/2} \frac{\Phi_{l}(\xi_{\tilde{\kappa}_k})} {\Phi_1 (\xi_{\tilde{\kappa}_k})} \hat{\Delta}_{\tilde{\kappa}_k}^{1/2} \right]_{\substack{1\leq l\leq m\\ 1\leq k\leq n}} \right) \\ &\stackrel{(iii)}{=} \det \left[ \frac{ \hat{\Delta}_{\kappa_j}^{1/2} \hat{\Delta}_{\tilde{\kappa}_k}^{1/2} } {\Phi_1 (\xi_{\kappa_j}) \Phi_1 (\xi_{\tilde{\kappa}_k})} \sum_{1\leq l\leq m} \Phi_{l}(\xi_{\kappa_j}) \Phi_{l}(\xi_{\tilde{\kappa}_k} ) \Delta_l \right]_{1\leq j,k\leq n}\\ &\stackrel{(iv)}{=} \det \left[ \delta_{\kappa_j,\tilde{\kappa}_k} \right]_{1\leq j,k\leq n} \stackrel{(v)}{=}\begin{cases} 1&\text{if}\ \kappa=\tilde{\kappa} ,\\ 0&\text{if}\ \kappa\neq\tilde{\kappa}. \end{cases} \end{align*} $$
$$ \begin{align*} &\left\langle \Psi^{(m,n)} \big(\xi^{(m,n)}_\kappa\big), \Psi^{(m,n)} \big(\xi^{(m,n)}_{\tilde{\kappa}}\big)\right\rangle = \sum_{\lambda\in\Lambda^{(m,n)}} \overline{ \Psi^{(m,n)}_\lambda \big(\xi^{(m,n)}_\kappa\big)} \Psi^{(m,n)}_\lambda \big(\xi^{(m,n)}_{\tilde{\kappa}}\big) \\ &\stackrel{(i)}{=} \sum_{m\geq\lambda_1>\cdots>\lambda_n\geq 1} \det \left[ \hat{\Delta}_{\kappa_j}^{1/2} \frac{\Phi_{\lambda_k}(\xi_{\kappa_j})} {\Phi_1 (\xi_{\kappa_j})} \Delta_{\lambda_k}^{1/2}\right]_{1\leq j,k\leq n} \det \left[ \Delta_{\lambda_j}^{1/2} \frac{\Phi_{\lambda_j}(\xi_{\tilde{\kappa}_k})} {\Phi_1 (\xi_{\tilde{\kappa}_k})} \hat{\Delta}_{\tilde{\kappa}_k}^{1/2} \right]_{1\leq j,k\leq n} \\ &\stackrel{(ii)}{=} \det \left( \left[ \hat{\Delta}_{\kappa_j}^{1/2} \frac{\Phi_{l}(\xi_{\kappa_j})} {\Phi_1 (\xi_{\kappa_j})} \Delta_{l}^{1/2} \right]_{\substack{1\leq j\leq n\\ 1\leq l\leq m}} \left[ \Delta_{l}^{1/2} \frac{\Phi_{l}(\xi_{\tilde{\kappa}_k})} {\Phi_1 (\xi_{\tilde{\kappa}_k})} \hat{\Delta}_{\tilde{\kappa}_k}^{1/2} \right]_{\substack{1\leq l\leq m\\ 1\leq k\leq n}} \right) \\ &\stackrel{(iii)}{=} \det \left[ \frac{ \hat{\Delta}_{\kappa_j}^{1/2} \hat{\Delta}_{\tilde{\kappa}_k}^{1/2} } {\Phi_1 (\xi_{\kappa_j}) \Phi_1 (\xi_{\tilde{\kappa}_k})} \sum_{1\leq l\leq m} \Phi_{l}(\xi_{\kappa_j}) \Phi_{l}(\xi_{\tilde{\kappa}_k} ) \Delta_l \right]_{1\leq j,k\leq n}\\ &\stackrel{(iv)}{=} \det \left[ \delta_{\kappa_j,\tilde{\kappa}_k} \right]_{1\leq j,k\leq n} \stackrel{(v)}{=}\begin{cases} 1&\text{if}\ \kappa=\tilde{\kappa} ,\\ 0&\text{if}\ \kappa\neq\tilde{\kappa}. \end{cases} \end{align*} $$
The algorithm to justify the above chain of equalities reads as follows. (i) Use the definitions (4.15b) and (4.16), where the first matrix was replaced by the transposed and the complex conjugation was omitted because all functions are real-valued. (ii) Apply the Cauchy–Binet formula. (iii) Perform the matrix multiplication. (iv) Apply the orthogonality relation of Proposition 3.3. (v) Observe that if
![]() $\kappa _1\neq \tilde {\kappa }_1$
, then either all elements in the first row (if
$\kappa _1\neq \tilde {\kappa }_1$
, then either all elements in the first row (if
![]() $\kappa _1>\tilde {\kappa }_1$
) or all elements in the first column (if
$\kappa _1>\tilde {\kappa }_1$
) or all elements in the first column (if
![]() $\kappa _1<\tilde {\kappa }_1$
) of the matrix in question are equal to zero; next, if
$\kappa _1<\tilde {\kappa }_1$
) of the matrix in question are equal to zero; next, if
![]() $\kappa _1=\tilde {\kappa }_1$
, proceed inductively in the dimension.
$\kappa _1=\tilde {\kappa }_1$
, proceed inductively in the dimension.
The diagonalization of the quantum spin hamiltonian
![]() $\boldsymbol {H}^{(m)}$
is immediate from Theorem 4.4 via the isomorphism (4.11).
$\boldsymbol {H}^{(m)}$
is immediate from Theorem 4.4 via the isomorphism (4.11).
Corollary 4.5 (Diagonalization of
 $\boldsymbol {H}^{(m)} $
).
$\boldsymbol {H}^{(m)} $
).
In addition to the vacuum all-spins-down state
![]() $|\emptyset \rangle $
(4.7a) and the m-particle fully flipped all-spins-up state
$|\emptyset \rangle $
(4.7a) and the m-particle fully flipped all-spins-up state
 $$ \begin{align} |(m,m-1,\ldots,2,1)\rangle=\underbrace{ \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes\cdots \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} }_{m\ \text{times}} , \end{align} $$
$$ \begin{align} |(m,m-1,\ldots,2,1)\rangle=\underbrace{ \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes\cdots \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} }_{m\ \text{times}} , \end{align} $$
which both belong to the kernel of
![]() $\boldsymbol {H}^{(m)}$
(4.1), orthonormal eigenvectors and corresponding eigenvalues diagonalizing our quantum spin Hamiltonian in the state space
$\boldsymbol {H}^{(m)}$
(4.1), orthonormal eigenvectors and corresponding eigenvalues diagonalizing our quantum spin Hamiltonian in the state space
![]() $\mathcal {F}^{(m)}$
(4.2a), (4.2b) are given by
$\mathcal {F}^{(m)}$
(4.2a), (4.2b) are given by
with
![]() $\kappa \in \Lambda ^{(m,n)}$
and
$\kappa \in \Lambda ^{(m,n)}$
and
![]() $0<n<m$
.
$0<n<m$
.
The monotonicity of the eigenvalues in Theorem 3.2 makes it straightforward to read-off the highest – and lowest – eigenvalues of
![]() $\boldsymbol {H}^{(m,n)} $
and
$\boldsymbol {H}^{(m,n)} $
and
![]() $\boldsymbol {H}^{(m)} $
from Theorem 4.4 and Corollary 4.5.
$\boldsymbol {H}^{(m)} $
from Theorem 4.4 and Corollary 4.5.
Corollary 4.6 (Highest – and lowest – eigenvalues).
(i) For
![]() $0<n<m$
the highest and lowest eigenvalues of
$0<n<m$
the highest and lowest eigenvalues of
![]() $\boldsymbol {H}^{(m,n)}$
(4.13) in
$\boldsymbol {H}^{(m,n)}$
(4.13) in
![]() $\ell ^2(\Lambda ^{(m,n)})$
are given by
$\ell ^2(\Lambda ^{(m,n)})$
are given by
and
respectively.
(ii) The highest and lowest eigenvalues of
![]() $\boldsymbol {H}^{(m)}$
(4.1) in
$\boldsymbol {H}^{(m)}$
(4.1) in
![]() $\mathcal {F}^{(m)}$
are given for m odd by
$\mathcal {F}^{(m)}$
are given for m odd by

and

respectively, and for m even by

and

respectively.
Remark 4.7. The all spins up/down states
![]() $|(m,m-1,\ldots ,2,1)\rangle $
and
$|(m,m-1,\ldots ,2,1)\rangle $
and
![]() $|\emptyset \rangle $
are not the only spin states in the kernel of the spin Hamiltonian
$|\emptyset \rangle $
are not the only spin states in the kernel of the spin Hamiltonian
![]() $\boldsymbol {H}^{(m)} $
. Indeed, since the eigenvalues of the truncated difference Lamé matrix
$\boldsymbol {H}^{(m)} $
. Indeed, since the eigenvalues of the truncated difference Lamé matrix
![]() $\boldsymbol {L}^{(m)}$
(3.6b) are distributed symmetrically around the origin (cf. Theorem 3.2), that is,
$\boldsymbol {L}^{(m)}$
(3.6b) are distributed symmetrically around the origin (cf. Theorem 3.2), that is,
it is clear that
![]() $ \boldsymbol {E}^{(m,n)} \big (\xi ^{(m,n)}_\kappa \big )=0$
,
$ \boldsymbol {E}^{(m,n)} \big (\xi ^{(m,n)}_\kappa \big )=0$
,
![]() $ \forall \kappa \in \Lambda ^{(m,n)}$
such that
$ \forall \kappa \in \Lambda ^{(m,n)}$
such that
![]() $\kappa _j+\kappa _{n+1-j}=m+1 $
for
$\kappa _j+\kappa _{n+1-j}=m+1 $
for
![]() $1\leq j \leq \frac {n+1}{2 }$
.
$1\leq j \leq \frac {n+1}{2 }$
.
4.4 On the trigonometric and rational degenerations
The spectral problem for the trigonometric
![]() $p\to 0$
degeneration of the finite discrete Lamé equation (3.5) can be conveniently solved for any
$p\to 0$
degeneration of the finite discrete Lamé equation (3.5) can be conveniently solved for any
![]() $g\in (0,\infty )$
in terms of Rogers’ q-ultraspherical polynomials [Reference van Diejen and GörbeDG21, Section 4.2] (cf. also [Reference RuijsenaarsR90, Section 3C2]). As such, the inhomogeneous isotropic
$g\in (0,\infty )$
in terms of Rogers’ q-ultraspherical polynomials [Reference van Diejen and GörbeDG21, Section 4.2] (cf. also [Reference RuijsenaarsR90, Section 3C2]). As such, the inhomogeneous isotropic
![]() $XY$
chain associated with the pertinent Jacobi matrix works out an example of the exactly solvable quantum spin models stemming from the Askey scheme of (basic) hypergeometric polynomials, cf. [Reference Crampé, Nepomechie and VinetCNV19, Reference Finkel and González-LópezFG20, Reference Genest, Vinet and ZhedanovGVZ16, Reference Grünbaum, Vinet and ZhedanovGVZ13, Reference Jafarov and Van der JeugtJV10, Reference Stoilova and Van der JeugtSV11, Reference Vinet and ZhedanovVZ12]. Indeed, the Hamiltonian of the corresponding trigonometric spin chain is of the form in
$XY$
chain associated with the pertinent Jacobi matrix works out an example of the exactly solvable quantum spin models stemming from the Askey scheme of (basic) hypergeometric polynomials, cf. [Reference Crampé, Nepomechie and VinetCNV19, Reference Finkel and González-LópezFG20, Reference Genest, Vinet and ZhedanovGVZ16, Reference Grünbaum, Vinet and ZhedanovGVZ13, Reference Jafarov and Van der JeugtJV10, Reference Stoilova and Van der JeugtSV11, Reference Vinet and ZhedanovVZ12]. Indeed, the Hamiltonian of the corresponding trigonometric spin chain is of the form in
![]() $\boldsymbol {H}^{(m)}$
(4.1) with (cf. Equation (2.5), (3.4))
$\boldsymbol {H}^{(m)}$
(4.1) with (cf. Equation (2.5), (3.4))

(for any
![]() $g>0$
). Theorem 4.4 and Corollaries 4.5, 4.6 apply verbatim to this case, provided we replace the eigenvalues and eigenvectors of
$g>0$
). Theorem 4.4 and Corollaries 4.5, 4.6 apply verbatim to this case, provided we replace the eigenvalues and eigenvectors of
![]() $\boldsymbol {L}^{(m)}$
(3.6b) stemming from Theorem 3.2 by those drawn from [Reference van Diejen and GörbeDG21, Section 4.2] for the tridiagonal matrix
$\boldsymbol {L}^{(m)}$
(3.6b) stemming from Theorem 3.2 by those drawn from [Reference van Diejen and GörbeDG21, Section 4.2] for the tridiagonal matrix
 $$ \begin{align} \boldsymbol{L}^{(m)}\to \begin{bmatrix} 0 & \frac{[m-1]_q}{[m-1+g]_q} & 0& \cdots & 0\\ \frac{[1]_q}{[1+g]_q} & 0 &\ddots & & \vdots \\ 0 & \frac{[2]_q}{[2+g]_q} & \ddots & \frac{[2]_q}{[2+g]_q} &0\\ \vdots & & \ddots &0 &\frac{[1]_q}{[1+g]_q} \\ 0 & \cdots & 0& \frac{[m-1]_q}{[m-1+g]_q} &0 \end{bmatrix}. \end{align} $$
$$ \begin{align} \boldsymbol{L}^{(m)}\to \begin{bmatrix} 0 & \frac{[m-1]_q}{[m-1+g]_q} & 0& \cdots & 0\\ \frac{[1]_q}{[1+g]_q} & 0 &\ddots & & \vdots \\ 0 & \frac{[2]_q}{[2+g]_q} & \ddots & \frac{[2]_q}{[2+g]_q} &0\\ \vdots & & \ddots &0 &\frac{[1]_q}{[1+g]_q} \\ 0 & \cdots & 0& \frac{[m-1]_q}{[m-1+g]_q} &0 \end{bmatrix}. \end{align} $$
Concretely, this boils down to performing the following substitutions in Equations (4.15a)–(4.15c) and Equation (4.16) so as to adapt the input data for Theorem 4.4 and Corollaries 4.5, 4.6 accordingly:
 $$ \begin{align} \Delta_l\to \frac{[g+l-1]_q}{[g]_q} \left[ \begin{matrix} m-1 \\ l-1 \end{matrix} \right]_{q} \quad\text{with}\quad \left[ \begin{matrix} m-1 \\ l-1 \end{matrix} \right]_q := \frac{\prod_{j=1}^{m-1} [j]_q }{ \prod_{j=1}^{l-1} [j]_q \prod_{j=1}^{m-l} [j]_q } , \end{align} $$
$$ \begin{align} \Delta_l\to \frac{[g+l-1]_q}{[g]_q} \left[ \begin{matrix} m-1 \\ l-1 \end{matrix} \right]_{q} \quad\text{with}\quad \left[ \begin{matrix} m-1 \\ l-1 \end{matrix} \right]_q := \frac{\prod_{j=1}^{m-1} [j]_q }{ \prod_{j=1}^{l-1} [j]_q \prod_{j=1}^{m-l} [j]_q } , \end{align} $$
 $$ \begin{align} \hat{\Delta}_k\to \frac{ \Delta_k }{\mathcal{N}}\quad\text{with}\quad \mathcal{N}:=\sum_{l=1}^m \Delta_l =2 \prod_{1< k < m} \big| q^{\frac{\xi_k}{2}}-q^{-\frac{\xi_k}{2}}\big| , \end{align} $$
$$ \begin{align} \hat{\Delta}_k\to \frac{ \Delta_k }{\mathcal{N}}\quad\text{with}\quad \mathcal{N}:=\sum_{l=1}^m \Delta_l =2 \prod_{1< k < m} \big| q^{\frac{\xi_k}{2}}-q^{-\frac{\xi_k}{2}}\big| , \end{align} $$
and
where
![]() $ C_{l-1}\left (x; q^g | q \right ) $
refers to Rogers’ q-ultraspherical polynomial of degree
$ C_{l-1}\left (x; q^g | q \right ) $
refers to Rogers’ q-ultraspherical polynomial of degree
![]() $l-1$
in
$l-1$
in
![]() $x=\frac {1}{2}(q^{\frac {\xi }{2}}+ q^{-\frac {\xi }{2}})$
[Reference Koekoek, Lesky and SwarttouwKLS10, Chapter 14.10.1] (and the normalization factors are expressed in terms of standard q-Pochhammer symbols).Since the pertinent q-ultraspherical polynomials form a one-parameter subfamily of the q-Racah polynomials [Reference van Diejen and VinetDV98, Section 5.4], in principle the corresponding spin chain is a special instance of the inhomogeneous isotropic
$x=\frac {1}{2}(q^{\frac {\xi }{2}}+ q^{-\frac {\xi }{2}})$
[Reference Koekoek, Lesky and SwarttouwKLS10, Chapter 14.10.1] (and the normalization factors are expressed in terms of standard q-Pochhammer symbols).Since the pertinent q-ultraspherical polynomials form a one-parameter subfamily of the q-Racah polynomials [Reference van Diejen and VinetDV98, Section 5.4], in principle the corresponding spin chain is a special instance of the inhomogeneous isotropic
![]() $XY$
chains proposed in [Reference Jafarov and Van der JeugtJV10, Section 4.4] (at least formally, because here we have that
$XY$
chains proposed in [Reference Jafarov and Van der JeugtJV10, Section 4.4] (at least formally, because here we have that
![]() $|q|=1$
while in [Reference Jafarov and Van der JeugtJV10, Section 4.4] the authors rather pick
$|q|=1$
while in [Reference Jafarov and Van der JeugtJV10, Section 4.4] the authors rather pick
![]() $0<q<1$
). A reminiscent though not identical reduction of the isotropic
$0<q<1$
). A reminiscent though not identical reduction of the isotropic
![]() $XY$
chain associated with the q-Racah polynomials (also in the regime
$XY$
chain associated with the q-Racah polynomials (also in the regime
![]() $0<q<1$
) can be found in [Reference Vinet and ZhedanovVZ12, Section V].
$0<q<1$
) can be found in [Reference Vinet and ZhedanovVZ12, Section V].
Finally, the rational limit
![]() $\alpha \to 0$
corresponds in our picture to the limit
$\alpha \to 0$
corresponds in our picture to the limit
![]() $g\to \infty $
because of the relation (3.4) between the periods and the coupling parameter. After normalizing properly, the finite discrete Lamé equation (3.5) degenerates in this limit to the eigenvalue problem for the celebrated Kac–Sylvester tridiagonal matrix [Reference van Diejen and GörbeDG21, Section 4.1]:
$g\to \infty $
because of the relation (3.4) between the periods and the coupling parameter. After normalizing properly, the finite discrete Lamé equation (3.5) degenerates in this limit to the eigenvalue problem for the celebrated Kac–Sylvester tridiagonal matrix [Reference van Diejen and GörbeDG21, Section 4.1]:
 $$ \begin{align} \boldsymbol{L}^{(m)}\to \begin{bmatrix} 0 & m-1& 0& \cdots & 0\\ 1 & 0 &\ddots & & \vdots \\ 0 &2 & \ddots &2&0\\ \vdots & & \ddots &0 &1 \\ 0 & \cdots & 0&m-1&0 \end{bmatrix}. \end{align} $$
$$ \begin{align} \boldsymbol{L}^{(m)}\to \begin{bmatrix} 0 & m-1& 0& \cdots & 0\\ 1 & 0 &\ddots & & \vdots \\ 0 &2 & \ddots &2&0\\ \vdots & & \ddots &0 &1 \\ 0 & \cdots & 0&m-1&0 \end{bmatrix}. \end{align} $$
The associated inhomogeneous isotropic
![]() $XY$
chain has a Hamiltonian of the form
$XY$
chain has a Hamiltonian of the form
![]() $\boldsymbol {H}^{(m)}$
(4.1) with
$\boldsymbol {H}^{(m)}$
(4.1) with
Hence, this recovers the Krawtchouk chain, a particular inhomogeneous open spin chain that is ubiquitous in the literature as a toy model for the transfer of qubit states through quantum wires, cf., for example, [Reference Albanese, Christandl, Datta and EkertA-E04, Reference BoseB07, Reference Bossé and VinetBV17, Reference Chakrabarti and Van der JeugtCV10, Reference Groenland and SchoutensGS18, Reference KayK10, Reference Nikolopoulos, Petrosyan and LambropoulosNPL03, Reference Vinet and ZhedanovVZ12] and references therein. The corresponding substitutions adapting the formulas of Theorem 4.4 and Corollaries 4.5, 4.6 to the present case read (cf. [Reference van Diejen and GörbeDG21, Section 4.1]):
and
 $$ \begin{align} \Delta_l\to \binom{m-1}{l-1} ,\qquad \hat{\Delta}_k\to \frac{1}{2^{m-1}}\binom{m-1}{k-1} , \end{align} $$
$$ \begin{align} \Delta_l\to \binom{m-1}{l-1} ,\qquad \hat{\Delta}_k\to \frac{1}{2^{m-1}}\binom{m-1}{k-1} , \end{align} $$
where
![]() $ K_{l-1}(x;{\textstyle \frac {1}{2}},m-1)$
denotes the Krawtchouk polynomial of degree
$ K_{l-1}(x;{\textstyle \frac {1}{2}},m-1)$
denotes the Krawtchouk polynomial of degree
![]() $l-1$
in x at the parameter value
$l-1$
in x at the parameter value
![]() $p=\frac {1}{2}$
[Reference Koekoek, Lesky and SwarttouwKLS10, Chapter 9.11].
$p=\frac {1}{2}$
[Reference Koekoek, Lesky and SwarttouwKLS10, Chapter 9.11].
Acknowledgements
Helpful feedback from the anonymous referees is gratefully acknowledged.
Competing interests
The author has no competing interest to declare.
Funding statement
Work supported in part by the Fondo Nacional de Desarrollo Científico y Tecnológico (FONDECYT) Grant # 1210015.