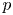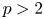1. Introduction and main results
The fractional Laplacian has nowadays become a focus of research due to its extensive applications in describing anomalous diffusions in plasmas, flames propagation and chemical reactions in liquids, population dynamics, geophysical fluid dynamics, see [Reference Caffarelli and Vasseur4, Reference Chen, Li and Ma7, Reference Constantin8] and the references therein. Moreover, it also has important applications in the fields of probability and finance, for example, see [Reference Applebaum1–Reference Bertoin3]. In particular, it can be regarded as the infinitesimal generator of an isotropic stable Lévy diffusion process. To better apply theories of the fractional Laplacian to practice, it is significantly important to make clear its own properties, especially those different from the classical Laplacian operator.
Before listing our main results, we first fix some notations. Let $n\geq 1$![]() , $p\geq 2$
, $p\geq 2$![]() and $0<\sigma <1$
and $0<\sigma <1$![]() . Define the fractional $p$
. Define the fractional $p$![]() -Laplacian $(-\Delta )^{\sigma }_{p}$
-Laplacian $(-\Delta )^{\sigma }_{p}$![]() as follows:
as follows:
where $c_{n,\sigma p}$![]() is a positive constant and $P.V.$
is a positive constant and $P.V.$![]() represents the Cauchy principal value. It is worth pointing out that $(-\Delta )^{\sigma }_{p}$
represents the Cauchy principal value. It is worth pointing out that $(-\Delta )^{\sigma }_{p}$![]() becomes the linear fractional Laplacian operator $(-\Delta )^{\sigma }$
becomes the linear fractional Laplacian operator $(-\Delta )^{\sigma }$![]() if $p=2$
if $p=2$![]() , while it is a nonlinear nonlocal operator if $p>2$
, while it is a nonlinear nonlocal operator if $p>2$![]() . The definition of $(-\Delta )^{\sigma }_{p}u$
. The definition of $(-\Delta )^{\sigma }_{p}u$![]() is valid under the condition that $u\in C^{\sigma p+\alpha }_{loc}(\mathbb {R}^{n})\cap \mathcal {L}_{\sigma p}(\mathbb {R}^{n})$
is valid under the condition that $u\in C^{\sigma p+\alpha }_{loc}(\mathbb {R}^{n})\cap \mathcal {L}_{\sigma p}(\mathbb {R}^{n})$![]() for some $\alpha >0$
for some $\alpha >0$![]() , where $C^{\sigma p+\alpha }_{loc}:=C^{[\sigma p+\alpha ],\sigma p+\alpha -[\sigma p+\alpha ]}_{loc}$
, where $C^{\sigma p+\alpha }_{loc}:=C^{[\sigma p+\alpha ],\sigma p+\alpha -[\sigma p+\alpha ]}_{loc}$![]() with $[\sigma p+\alpha ]$
with $[\sigma p+\alpha ]$![]() denoting the integer part of $\sigma p+\alpha$
denoting the integer part of $\sigma p+\alpha$![]() ,
,
Recently, Du et al. [Reference Du, Jin, Xiong and Yang11] derived the following fact:

In particular, they constructed an example showing that the nonnegative constant $\theta$![]() can be strictly positive, which is different from the classical Laplacian operator. This discrepancy essentially stems from the nonlocal behaviour of the fractional Laplacian operator. Inspired by their proof for the linear fractional Laplacian, in this paper we further overcome the nonlinear difficulty for the fractional $p$
can be strictly positive, which is different from the classical Laplacian operator. This discrepancy essentially stems from the nonlocal behaviour of the fractional Laplacian operator. Inspired by their proof for the linear fractional Laplacian, in this paper we further overcome the nonlinear difficulty for the fractional $p$![]() -Laplacian operator and prove that the above fact also holds for the nonlinear nonlocal operator $(-\Delta )^{\sigma }_{p}$
-Laplacian operator and prove that the above fact also holds for the nonlinear nonlocal operator $(-\Delta )^{\sigma }_{p}$![]() with $p>2$
with $p>2$![]() . Moreover, our result can be extended to more general nonlinear nonlocal operators. The principal result of this paper is stated as follows.
. Moreover, our result can be extended to more general nonlinear nonlocal operators. The principal result of this paper is stated as follows.
Theorem 1.1 Let $n\geq 1$![]() , $p>2$
, $p>2$![]() , $0<\sigma <1$
, $0<\sigma <1$![]() and $\alpha >0$
and $\alpha >0$![]() . Assume that a sequence of nonnegative functions $\{u_{i}\}\subset \mathcal {L}_{\sigma p}(\mathbb {R}^{n})\cap C^{\sigma p+\alpha }_{loc}(\mathbb {R}^{n})$
. Assume that a sequence of nonnegative functions $\{u_{i}\}\subset \mathcal {L}_{\sigma p}(\mathbb {R}^{n})\cap C^{\sigma p+\alpha }_{loc}(\mathbb {R}^{n})$![]() converges in $C_{loc}^{\sigma p+\alpha }(\mathbb {R}^{n})$
converges in $C_{loc}^{\sigma p+\alpha }(\mathbb {R}^{n})$![]() to a function $u\in \mathcal {L}_{\sigma p}(\mathbb {R}^{n})$
to a function $u\in \mathcal {L}_{\sigma p}(\mathbb {R}^{n})$![]() , and $\{(-\Delta )^{\sigma }_{p}u_{i}\}$
, and $\{(-\Delta )^{\sigma }_{p}u_{i}\}$![]() converges pointwisely in $\mathbb {R}^{n}$
converges pointwisely in $\mathbb {R}^{n}$![]() . Then for any $x\in \mathbb {R}^{n}$
. Then for any $x\in \mathbb {R}^{n}$![]() ,
,
where $\theta$![]() is a nonnegative constant given by
is a nonnegative constant given by

Proof. For any fixed $x\in \mathbb {R}^{n}$![]() and $R > > |x|+1$
and $R > > |x|+1$![]() , let
, let

In light of the fact that $u_{i}\rightarrow u$![]() in $C^{\sigma p+\alpha }(B_{2R}(0))$
in $C^{\sigma p+\alpha }(B_{2R}(0))$![]() , we obtain that for each $0<\varepsilon <1$
, we obtain that for each $0<\varepsilon <1$![]() , there exists an integer $N>0$
, there exists an integer $N>0$![]() such that for every $i>N$
such that for every $i>N$![]() ,
,
Define
where $\Phi _{i}(x,\varepsilon )$![]() denotes the integral in $\Phi _{i}(x,R)$
denotes the integral in $\Phi _{i}(x,R)$![]() with the domain $B_{R}(0)$
with the domain $B_{R}(0)$![]() replaced by $B_{\varepsilon }(x)$
replaced by $B_{\varepsilon }(x)$![]() . Using (1.2), we deduce that for $x,y\in B_{2R}(0)$
. Using (1.2), we deduce that for $x,y\in B_{2R}(0)$![]() , $i>N$
, $i>N$![]() ,
,

which yields that
On the other hand, if $\sigma p+\alpha \in (0,1]$![]() , then it follows from (1.2) that
, then it follows from (1.2) that

When $\sigma p+\alpha \in (1,\infty )$![]() , utilizing (1.2) again, it follows from Taylor expansion that
, utilizing (1.2) again, it follows from Taylor expansion that

where we utilized the following element inequality:
By the same argument, we have

Therefore, we obtain that if $\sigma p+\alpha \in (1,\infty )$![]() ,
,

where we utilized the anti-symmetry of $\nabla u(x)(x-y)$![]() and $\nabla u_{i}(x)(x-y)$
and $\nabla u_{i}(x)(x-y)$![]() with regard to the centre $x$
with regard to the centre $x$![]() . Consequently, combining (1.3)–(1.5), we deduce that for every $i>N$
. Consequently, combining (1.3)–(1.5), we deduce that for every $i>N$![]() ,
,

which implies that
Note that $\{(-\Delta )^{\sigma }_{p}u_{i}\}$![]() is a pointwise convergent sequence, we then deduce from (1.1) and (1.6) that
is a pointwise convergent sequence, we then deduce from (1.1) and (1.6) that
Since $u\in \mathcal {L}_{\sigma p}(\mathbb {R}^{n})$![]() and $R > > |x|+1$
and $R > > |x|+1$![]() , then
, then

which yields that
This, in combination with (1.1) and (1.6)–(1.7), leads to that $\lim \limits _{R\rightarrow \infty }\lim \limits _{i\rightarrow \infty }\Psi _{i}(x,R)$![]() exists and is finite,
exists and is finite,
Denote

Then we have

For any given $\varepsilon >0$![]() , it follows from Young's inequality that
, it follows from Young's inequality that
We now divide into three cases to estimate $\mathcal {K}_{2}$![]() and $\mathcal {K}_{3}$
and $\mathcal {K}_{3}$![]() in the following.
in the following.
Case 1. Consider $2< p\leq 3$![]() . Since
. Since

then
Hence it follows from Young's inequality that
Substituting (1.10)–(1.11) into (1.9), we derive
Case 2. Consider the case when $p>3$![]() is an integer. From the binomial theorem and Young's inequality, we have
is an integer. From the binomial theorem and Young's inequality, we have

Using (1.13), we deduce
which implies that

Analogously,
Hence, we have
Utilizing (1.14) and Young's inequality, we obtain

which, in combination with (1.9)–(1.10), gives that
Case 3. Consider the case when $p>3$![]() is not an integer. On one hand, making use of (1.13), we obtain
is not an integer. On one hand, making use of (1.13), we obtain

From Young's inequality, we deduce
Substituting (1.18)–(1.19) into (1.17), it follows that
On the other hand, using (1.13) again, we have

It follows from Young's inequality that
Combining (1.20)–(1.23), we deduce

This, together with (1.20) again, gives that
In light of (1.24), it follows from Young's inequality that


Therefore, substituting (1.10) and (1.25)–(1.26) into (1.9), we derive
Observe that

Since $\lim \limits _{R\rightarrow \infty }\lim \limits _{i\rightarrow \infty }\Psi _{i}(x,R)$![]() exists and is finite, it follows from (1.12), (1.15)–(1.16) and (1.27)–(1.29) that
exists and is finite, it follows from (1.12), (1.15)–(1.16) and (1.27)–(1.29) that

where

Due to the fact that $R > > |x|+1$![]() , we have
, we have
Hence, we deduce

By virtue of the arbitrariness of $\varepsilon$![]() and $\{u_{i}\}$
and $\{u_{i}\}$![]() is nonnegative, we obtain
is nonnegative, we obtain

In order to show that the limit constant $\theta$![]() captured in theorem 1.1 may be positive, we consider a sequence of nonnegative functions in the following. Choose a smooth cut-off function $\eta$
captured in theorem 1.1 may be positive, we consider a sequence of nonnegative functions in the following. Choose a smooth cut-off function $\eta$![]() satisfying that
satisfying that
Then for any $0< s< t$![]() and $j\geq 1$
and $j\geq 1$![]() , define
, define

where $\phi (x)=\eta (|x|-3)$![]() , and $\psi (x)=\eta (|x|-6)$
, and $\psi (x)=\eta (|x|-6)$![]() , $R_{j}=j^{\frac {(t-s)(p-1)}{\sigma p}}\beta ^{\frac {1}{\sigma p}}$
, $R_{j}=j^{\frac {(t-s)(p-1)}{\sigma p}}\beta ^{\frac {1}{\sigma p}}$![]() with
with

Example 1.2 Let $n\geq 1$![]() , $p>2$
, $p>2$![]() and $0<\sigma <1$
and $0<\sigma <1$![]() . If condition (1.31) holds, then we obtain that $v_{j}$
. If condition (1.31) holds, then we obtain that $v_{j}$![]() converges to $1$
converges to $1$![]() in $C^{2}_{loc}(\mathbb {R}^{n})$
in $C^{2}_{loc}(\mathbb {R}^{n})$![]() , and
, and
Remark 1.3 We here would like to point out that the examples constructed in example 1.2 and theorem 2.1 were first given in [Reference Du, Jin, Xiong and Yang11].
Proof. It is easily seen from (1.31) that $v_{j}\in C_{c}^{\infty }(\mathbb {R}^{n})$![]() , $v_{j}\geq 0$
, $v_{j}\geq 0$![]() in $\mathbb {R}^{n}$
in $\mathbb {R}^{n}$![]() , $v_{j}=1$
, $v_{j}=1$![]() in $B_{R_{j}}$
in $B_{R_{j}}$![]() , and $\|v_{j}-1\|_{C^{2}_{loc}}\rightarrow 0$
, and $\|v_{j}-1\|_{C^{2}_{loc}}\rightarrow 0$![]() , as $i\rightarrow \infty$
, as $i\rightarrow \infty$![]() . A direct computation gives that
. A direct computation gives that
For any fixed $x\in \mathbb {R}^{n}$![]() , we have
, we have

where $\beta$![]() is defined by (1.32). This, together with (1.33), gives that
is defined by (1.32). This, together with (1.33), gives that
The proof is complete.
2. Blow-up analysis for the extended fractional Nirenberg problem
The extended fractional Nirenberg problem is equivalent to investigating the following equation:
where $p\geq 2$![]() and $q\in \mathbb {R}$
and $q\in \mathbb {R}$![]() . It has been shown in [Reference Du, Jin, Xiong and Yang11] that there arises blow-up phenomena for the linear fractional Laplacian due to the nonzero constant $\theta$
. It has been shown in [Reference Du, Jin, Xiong and Yang11] that there arises blow-up phenomena for the linear fractional Laplacian due to the nonzero constant $\theta$![]() captured in theorem 1.1. Specially, for $p=2$
captured in theorem 1.1. Specially, for $p=2$![]() , the compactness of solutions to (2.1) will fail in the region where $K$
, the compactness of solutions to (2.1) will fail in the region where $K$![]() is negative. In the following, we follow the proof of theorem 1.3 in [Reference Du, Jin, Xiong and Yang11] and extend the result to the nonlinear case of $p>2$
is negative. In the following, we follow the proof of theorem 1.3 in [Reference Du, Jin, Xiong and Yang11] and extend the result to the nonlinear case of $p>2$![]() . On the other hand, when $K$
. On the other hand, when $K$![]() is positive, Jin et al. [Reference Jin, Li and Xiong12–Reference Jin, Li and Xiong14] derived a priori estimates for the fractional equation (2.1) with $p=2$
is positive, Jin et al. [Reference Jin, Li and Xiong12–Reference Jin, Li and Xiong14] derived a priori estimates for the fractional equation (2.1) with $p=2$![]() .
.
While these above-mentioned works are related to the fractional Nirenberg problem, there is another direction of research to study the classical elliptic equation $-\Delta u=K(x)u^{p}$![]() . When $n=1,2$
. When $n=1,2$![]() and $1< p<\infty$
and $1< p<\infty$![]() , or $n\geq 3$
, or $n\geq 3$![]() and $1< p<\frac {n+2}{n-2}$
and $1< p<\frac {n+2}{n-2}$![]() , $p$
, $p$![]() is called a subcritical Sobolev exponent, while it is the critical Sobolev exponent if $n\geq 3$
is called a subcritical Sobolev exponent, while it is the critical Sobolev exponent if $n\geq 3$![]() and $p=\frac {n+2}{n-2}$
and $p=\frac {n+2}{n-2}$![]() . In particular, the elliptic equation in the case of critical Sobolev exponent corresponds to the Nirenberg problem, which is to seek a new metric conformal to the flat metric on $\mathbb {R}^{n}$
. In particular, the elliptic equation in the case of critical Sobolev exponent corresponds to the Nirenberg problem, which is to seek a new metric conformal to the flat metric on $\mathbb {R}^{n}$![]() so that its scalar curvature is $K(x)$
so that its scalar curvature is $K(x)$![]() . Generally, it needs to establish priori estimates of the solutions for the purpose of obtaining the existence of solutions. We refer to [Reference Gidas and Spruck9, Reference Gidas and Spruck10] for the subcritical case. With regard to the critical case, see [Reference Chang, Gursky and Yang5, Reference Li15, Reference Schoen and Zhang17] for positive functions $K$
. Generally, it needs to establish priori estimates of the solutions for the purpose of obtaining the existence of solutions. We refer to [Reference Gidas and Spruck9, Reference Gidas and Spruck10] for the subcritical case. With regard to the critical case, see [Reference Chang, Gursky and Yang5, Reference Li15, Reference Schoen and Zhang17] for positive functions $K$![]() and [Reference Chen and Li6, Reference Lin16, Reference Zhu18] for $K$
and [Reference Chen and Li6, Reference Lin16, Reference Zhu18] for $K$![]() changing signs, respectively.
changing signs, respectively.
Theorem 2.1 Assume that $n\geq 1$![]() , $p>2$
, $p>2$![]() , $0<\sigma <1$
, $0<\sigma <1$![]() , $q\in \mathbb {R}$
, $q\in \mathbb {R}$![]() and $s>-\frac {\sigma p}{p-1}$
and $s>-\frac {\sigma p}{p-1}$![]() . Then there exist two positive constants $c_{0}=c_{0}(n,\sigma,p,q,s)$
. Then there exist two positive constants $c_{0}=c_{0}(n,\sigma,p,q,s)$![]() and $C_{0}=C_{0}(n,\sigma,p,q,s)$
and $C_{0}=C_{0}(n,\sigma,p,q,s)$![]() , a sequence of functions $\{K_{j}\}\subset C^{\infty }(\mathbb {R}^{n})$
, a sequence of functions $\{K_{j}\}\subset C^{\infty }(\mathbb {R}^{n})$![]() satisfying
satisfying
and a sequence of positive functions $\{u_{j}\}\subset C^{\infty }(\mathbb {R}^{n})$![]() such that
such that
and
Proof. Let $\eta$![]() and $\phi$
and $\phi$![]() be defined in (1.30) and (1.31). For $q\in \mathbb {R}$
be defined in (1.30) and (1.31). For $q\in \mathbb {R}$![]() and $s>-\frac {\sigma p}{p-1}$
and $s>-\frac {\sigma p}{p-1}$![]() , let
, let

where $\varphi (x)=\eta (|x|-R)$![]() and $R=R(n,p,q,\sigma,s,j)>9$
and $R=R(n,p,q,\sigma,s,j)>9$![]() is a sufficiently large constant to be determined later. Then $u_{j}\in C^{\infty }(\mathbb {R}^{n})\cap \mathcal {L}_{\sigma p}(\mathbb {R}^{n})$
is a sufficiently large constant to be determined later. Then $u_{j}\in C^{\infty }(\mathbb {R}^{n})\cap \mathcal {L}_{\sigma p}(\mathbb {R}^{n})$![]() and $u_{j}>0$
and $u_{j}>0$![]() in $\mathbb {R}^{n}$
in $\mathbb {R}^{n}$![]() . Denote
. Denote

Then $K_{j}\in C^{\infty }(\mathbb {R}^{n})$![]() . Moreover, $\{K_{j}\}$
. Moreover, $\{K_{j}\}$![]() satisfies the following properties: there exists four positive constants $C_{i}:=C_{i}(n,\sigma,p)$
satisfies the following properties: there exists four positive constants $C_{i}:=C_{i}(n,\sigma,p)$![]() , $i=1,2,3,4$
, $i=1,2,3,4$![]() , such that for every $j\geq 1$
, such that for every $j\geq 1$![]() ,
,
(K1) $-C_{1}\leq K_{j}(x)\leq -C_{2}$
 , and $\sum \limits ^{3}_{i=1}|\nabla ^{i}K_{j}(x)|\leq C_{3}$
, and $\sum \limits ^{3}_{i=1}|\nabla ^{i}K_{j}(x)|\leq C_{3}$ in $B_{2}$
in $B_{2}$ ;
;(K2) $\nabla ^{2}K_{j}(0)\leq -C_{4}\mathbf {I}_{n}$
 , where $\mathbf {I}_{n}$
, where $\mathbf {I}_{n}$ denotes $n\times n$
denotes $n\times n$ identity matrix.
identity matrix.
We first prove $(\mathbf {K1})$![]() . Observe that
. Observe that

where $\mathcal {A}_{\varphi }(y):=\varphi (y)-1+j^{1-q}\varphi (y)-j^{-q}|y|^{-s}\varphi (y)$![]() . For simplicity, let
. For simplicity, let

A straightforward computation yields that
and
For $x\in B_{2}$![]() , $y\in B_{R}^{c}$
, $y\in B_{R}^{c}$![]() , we have $|x-y|\geq |y|/2$
, we have $|x-y|\geq |y|/2$![]() in virtue of $R>9$
in virtue of $R>9$![]() . Then
. Then

For a sufficiently large $R>9$![]() , we have
, we have
which implies that
Furthermore, after differentiating (2.2), it follows from a similar calculation that

We proceed to verify property $(\bf {K2})$![]() . A simple calculation shows that for $y\in B_{3}^{c}$
. A simple calculation shows that for $y\in B_{3}^{c}$![]() ,
,
Since the integral domain is symmetric, then we see from (2.2) to (2.3) that
If $k=l$![]() , it follows from the radial symmetry of $\phi$
, it follows from the radial symmetry of $\phi$![]() and $\varphi$
and $\varphi$![]() that
that

where we used the fact that $|\mathcal {A}_{\varphi }(y)|^{p-2}\varphi (y)\leq 3$![]() in $B_{R}^{c}$
in $B_{R}^{c}$![]() . That is, property $(\bf {K2})$
. That is, property $(\bf {K2})$![]() holds.
holds.
From the radial symmetry of $u_{j}$![]() with respect to the origin, we know that $K_{j}$
with respect to the origin, we know that $K_{j}$![]() is also radially symmetric. Then we have
is also radially symmetric. Then we have
which, together with $(\bf {K1})$![]() –$(\bf {K2})$
–$(\bf {K2})$![]() , leads to that for $j\geq 1$
, leads to that for $j\geq 1$![]() ,
,
where $e_{1}=(1,0,...,0)\in \mathbb {R}^{n}$![]() , $\varepsilon _{0}:=\varepsilon _{0}(n,p,\sigma )\in (0,1/4)$
, $\varepsilon _{0}:=\varepsilon _{0}(n,p,\sigma )\in (0,1/4)$![]() is a small constant and $c_{1}:=c_{1}(n,p,\sigma )$
is a small constant and $c_{1}:=c_{1}(n,p,\sigma )$![]() is a positive constant.
is a positive constant.
Define
Therefore,
Then combining $(\bf {K1})$![]() and (2.4), we obtain
and (2.4), we obtain
where $\bar {c}=\bar {c}(n,\sigma,p,q,s)$![]() and $\bar {C}=\bar {C}(n,\sigma,p,q,s)$
and $\bar {C}=\bar {C}(n,\sigma,p,q,s)$![]() . Moreover, recalling the definition of $u_{j}$
. Moreover, recalling the definition of $u_{j}$![]() , we have
, we have
The proof is finished.
Data availability statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgements
The author thanks Professor C. X. Miao for his constant encouragement and useful discussions. The author was partially supported by CPSF (2021M700358).
Conflict of interest
None.