We prove that the Christofides algorithm gives a $\frac{4}{3}$ approximation ratio for the special case of traveling salesman problem (TSP) in which the maximum weight in the given graph is at most twice the minimum weight for the odd degree restricted graphs. A graph is odd degree restricted if the number of odd degree vertices in any minimum spanning tree of the given graph is less than $\frac{1}{4}$ times the number of vertices in the graph. We prove that the Christofides algorithm is more efficient (in terms of runtime) than the previous existing algorithms for this special case of the traveling salesman problem. Secondly, we apply the concept of stability of approximation to this special case of traveling salesman problem in order to partition the set of all instances of TSP into an infinite spectrum of classes according to their approximability.

We proceed our work on iterated transductions by studying the closure underunion and composition of some classes of iterated functions. Weanalyze this closure for the classes of length-preservingrational functions, length-preserving subsequential functions andlength-preserving sequential functions with terminal states. All the classes weobtain are equal. We also study the connection with deterministiccontext-sensitive languages.

This paper deals with lower bounds on the approximability of different subproblems of the TravelingSalesman Problem (TSP) which is known not to admit any polynomial time approximation algorithm in general(unless $\mathcal{P}=\mathcal{NP}$ 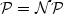). First of all, we present an improved lower bound for the Traveling Salesman Problemwith Triangle Inequality, Delta-TSP for short. Moreover our technique, an extension of the method ofEngebretsen [11], also applies to the case of relaxed and sharpened triangle inequality,respectively, denoted $\Delta_\beta$ 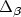-TSP for an appropriate β. In case of theDelta-TSP, we obtain a lowerbound of $\frac{3813}{3812}-\varepsilon$ 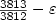on the polynomial-time approximability (for any small $\varepsilon> 0$ 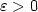), compared to the previous bound of $\frac{5381}{5380}-\varepsilon$ 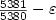in [11]. Incase of the $\Delta_\beta$ 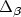-TSP, for the relaxed case ( $\beta> 1$ 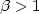) we present a lower bound of $\frac{3803+10\beta}{3804+8\beta}-\varepsilon$ , and for the sharpened triangle inequality( $\frac{1}{2}< \beta< 1$ 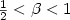), the lower bound is $\frac{7611+10\beta^2+5\beta}{7612+8\beta^2+4\beta}-\varepsilon$ 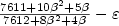. The latter result is of interestespecially since it shows that the TSP is $\mathcal{APX}$ 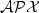-hard even if one comes arbitrarily close to the trivialcase that all edges have the same cost.