Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-04T20:11:35.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation Algorithms for the Traveling Salesman Problem with Range Condition

Published online by Cambridge University Press:  15 April 2002

D. Arun Kumar  and
C. Pandu Rangan
D. Arun Kumar
Affiliation:
Lehrstuhl für Informatik I, RWTH Aachen, 52056 Aachen, Germany Department of Computer-Science, Indian Institute of Technology, Madras 600036, India
C. Pandu Rangan
Affiliation:
Department of Computer-Science, Indian Institute of Technology, Madras 600036, India; ([email protected])
Get access

Abstract

We prove that the Christofides algorithm gives a $\frac{4}{3}$ 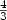approximation ratio for the special case of traveling salesman problem (TSP) in which the maximum weight in the given graph is at most twice the minimum weight for the odd degree restricted graphs. A graph is odd degree restricted if the number of odd degree vertices in any minimum spanning tree of the given graph is less than $\frac{1}{4}$ 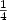times the number of vertices in the graph. We prove that the Christofides algorithm is more efficient (in terms of runtime) than the previous existing algorithms for this special case of the traveling salesman problem. Secondly, we apply the concept of stability of approximation to this special case of traveling salesman problem in order to partition the set of all instances of TSP into an infinite spectrum of classes according to their approximability.

Keywords

Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 34 , Issue 3 , May 2000 , pp. 173 - 181
Copyright
© EDP Sciences, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreae, T. and Bandelt, H.-J., Performance guarantees for approximation algorithms depending on parametrized triangle inequalities. SIAM J. Discrete Math. 8 (1995) 1-16. CrossRef
Bender, M.A. and Chekuri, C., Performance guarantees for the TSP with a parametrized triangle inequality, in Proc. WADS'99. Springer, Lecture Notes in Comput. Sci. 1663 (1999) 80-85. CrossRef
H.-J. Böckenhauer, J. Hromkovic, R. Klasing, S. Seibert and W. Unger, An improved lower bound on the approximability of metric TSP and approximation algorithms for the TSP with sharpened triangle Inequality, in Proc. STACS 2000. Springer, Lecture Notes in Comput. Sci. (to appear).
H.-J. Böckenhauer, J. Hromkovic, R. Klasing, S. Seibert and W. Unger, Towards the Notion of Stability of Approximation Algorithms and the Traveling Salesman Problem, in Electronic Colloquium on Computational Complexity. Report No. 31 (1999).
N. Christofides, Worst-case analysis of a new heuristic for the traveling salesman problem. Technical Report 388, Graduate School of Industrial Administration. Carnegie-Mellon University, Pittsburgh (1976).
J. Edmonds and E.L. Johnson, Matching: A well-solved class of integer linear programs, in Proc. Calgary International conference on Combinatorial Structures and Their Applications. Gordon and Breach (1970) 88-92.
M.R. Garey, R.L. Graham and D.J. Johnson, Some NP-complete geometric problems, in Proc. ACM Symposium on Theory of Computing (1976) 10-22.
Gabow, H.N. and Tarjan, R.E., Faster scaling algorithms for general graph-matching problems. J. ACM 28 (1991) 815-853. CrossRef
Hromkovic, J., Stability of approximation algorithms for hard optimisation problems, in Proc. SOFSEM'99. Springer-Verlag, Lecture Notes in Comput. Sci. 1725 (1999) 29-46. CrossRef
J. Hromkovic, Stability of approximation algorithms and the knapsack problem, in Jewels are forever, edited by J. Karhumäki, H. Maurer and G. Rozenberg. Springer-Verlag (1999) 238-249.
Papadimitriou, C.H., Euclidean TSP is NP-complete. TCS 4 (1977) 237-244. CrossRef
Papadimitriou, C.H. and Yannakakis, M., The Traveling salesman problem with distances one and two. Math. Oper. Res. 18 (1993) 1-11. CrossRef