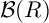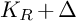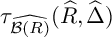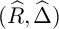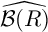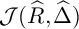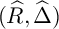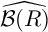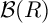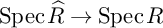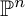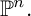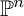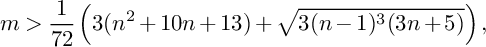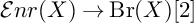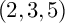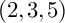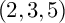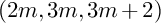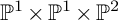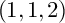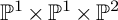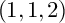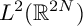Article
BIG COHEN–MACAULAY TEST IDEALS IN EQUAL CHARACTERISTIC ZERO VIA ULTRAPRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2022, pp. 549-575
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERIC LINES IN PROJECTIVE SPACE AND THE KOSZUL PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 06 January 2023, pp. 576-605
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENRIQUES INVOLUTIONS AND BRAUER CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2022, pp. 606-621
-
- Article
- Export citation
CONSTRUCTING MAXIMAL COFINITARY GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2023, pp. 622-651
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINES ON HOLOMORPHIC CONTACT MANIFOLDS AND A GENERALIZATION OF
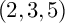 $(2,3,5)$-DISTRIBUTIONS TO HIGHER DIMENSIONS
$(2,3,5)$-DISTRIBUTIONS TO HIGHER DIMENSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2023, pp. 652-668
-
- Article
- Export citation
K-THEORY OF NON-ARCHIMEDEAN RINGS II
- Part of:
-
- Published online by Cambridge University Press:
- 21 February 2023, pp. 669-685
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-STABLE DIVISORS IN
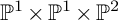 $\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE
$\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE 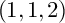 $(1,1,2)$
$(1,1,2)$
- Part of:
-
- Published online by Cambridge University Press:
- 28 April 2023, pp. 686-714
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A BERNSTEIN–SATO POLYNOMIAL OF A MEROMORPHIC FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 06 June 2023, pp. 715-733
-
- Article
- Export citation
TWISTED SHIFT-INVARIANT SYSTEM IN
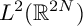 $L^2(\mathbb {R}^{2N})$
$L^2(\mathbb {R}^{2N})$
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2023, pp. 734-767
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
NMJ volume 251 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 September 2023, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
NMJ volume 251 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 September 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation