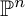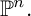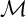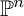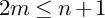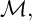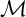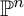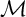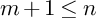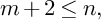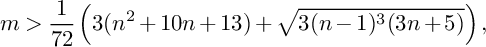1 Introduction
Let
![]() $S=\mathbb {C}[x_0,\ldots ,x_{n}]$
be a polynomial ring, and let J be a graded homogeneous ideal of
$S=\mathbb {C}[x_0,\ldots ,x_{n}]$
be a polynomial ring, and let J be a graded homogeneous ideal of
![]() $S.$
Following Priddy’s work, we say the ring
$S.$
Following Priddy’s work, we say the ring
![]() $R=S/J$
is Koszul if the minimal graded free resolution of the field
$R=S/J$
is Koszul if the minimal graded free resolution of the field
![]() $\mathbb {C}$
over R is linear [Reference Priddy20]. Koszul rings are ubiquitous in commutative algebra. For example, any polynomial ring, all quotients by quadratic monomial ideals, all quadratic complete intersections, the coordinate rings of Grassmannians in their Plücker embedding, and all suitably high Veronese subrings of any standard graded algebra are all Koszul [Reference Fröberg and Backelin15]. Because of the ubiquity of Koszul rings, it is of interest to determine when we can guarantee a coordinate ring will be Koszul. In 1992, Kempf proved the following theorem.
$\mathbb {C}$
over R is linear [Reference Priddy20]. Koszul rings are ubiquitous in commutative algebra. For example, any polynomial ring, all quotients by quadratic monomial ideals, all quadratic complete intersections, the coordinate rings of Grassmannians in their Plücker embedding, and all suitably high Veronese subrings of any standard graded algebra are all Koszul [Reference Fröberg and Backelin15]. Because of the ubiquity of Koszul rings, it is of interest to determine when we can guarantee a coordinate ring will be Koszul. In 1992, Kempf proved the following theorem.
Theorem 1.1 (Kempf [Reference Kempf17, Th. 1])
Let
![]() $\mathcal {P}$
be a collection of p points in
$\mathcal {P}$
be a collection of p points in
![]() $\mathbb {P}^n$
, and let R be the coordinate ring of
$\mathbb {P}^n$
, and let R be the coordinate ring of
![]() $\mathcal {P}.$
If the points of
$\mathcal {P}.$
If the points of
![]() $\mathcal {P}$
are in general linear position and
$\mathcal {P}$
are in general linear position and
![]() $p \leq 2n,$
then R is Koszul.
$p \leq 2n,$
then R is Koszul.
In 2001, Conca, Trung, and Valla extended the theorem to a generic collection of points.
Theorem 1.2. (Conca, Trung, and Valla [Reference Conca, Trung and Valla9, Th. 4.1])
Let
![]() $\mathcal {P}$
be a generic collection of p points in
$\mathcal {P}$
be a generic collection of p points in
![]() $\mathbb {P}^n$
and R the coordinate ring of
$\mathbb {P}^n$
and R the coordinate ring of
![]() $\mathcal {P}.$
Then R is Koszul if and only if
$\mathcal {P}.$
Then R is Koszul if and only if
![]() $p \leq 1 +n + \frac {n^2}{4}.$
$p \leq 1 +n + \frac {n^2}{4}.$
We aim to generalize these theorems to collections of lines. In §2, we review necessary background information and results related to Koszul algebras that we use in the other sections. In §3, we study properties of coordinate rings of collections of lines and how they differ from coordinate rings of collections of points. In particular, we show
Theorem 3.5. Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() $\mathbb {P}^n$
with
$\mathbb {P}^n$
with
![]() $n \geq 3,$
and R be the coordinate ring of
$n \geq 3,$
and R be the coordinate ring of
![]() $\mathcal {M}.$
Then
$\mathcal {M}.$
Then
![]() $\mathrm {reg}_S(R)=\alpha ,$
where
$\mathrm {reg}_S(R)=\alpha ,$
where
![]() $\alpha $
is the smallest nonnegative integer such that
$\alpha $
is the smallest nonnegative integer such that
![]() $\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
$\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
In §4, we prove
Theorem 4.3. Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() $\mathbb {P}^n$
such that
$\mathbb {P}^n$
such that
![]() $m \geq 2,$
and let R be the coordinate ring of
$m \geq 2,$
and let R be the coordinate ring of
![]() $\mathcal {M}.$
$\mathcal {M}.$
-
(a) If m is even and
 $m+1 \leq n,$
then R has a Koszul filtration.
$m+1 \leq n,$
then R has a Koszul filtration. -
(b) If m is odd and
 $m + 2 \leq n,$
then R has a Koszul filtration.
$m + 2 \leq n,$
then R has a Koszul filtration.
In particular, R is Koszul.
Additionally, we show the coordinate ring of a generic collection of five lines in
![]() ${\mathbb {P}}^6$
is Koszul by constructing a Koszul filtration. In §5, we prove
${\mathbb {P}}^6$
is Koszul by constructing a Koszul filtration. In §5, we prove
Theorem 5.2. Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() ${\mathbb {P}}^n$
, and let R be the coordinate ring of
${\mathbb {P}}^n$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
If
$\mathcal {M}.$
If
then R is not Koszul.
Furthermore, there is an exceptional example of a coordinate ring that is not Koszul; if
![]() $\mathcal {M}$
is a collection of three lines in general linear position in
$\mathcal {M}$
is a collection of three lines in general linear position in
![]() $\mathbb {P}^4,$
then the coordinate ring R is not Koszul. In §6, we exhibit a collection of lines that is not a generic collection but the lines are in general linear position, and we give two examples of coordinate rings where each define a generic collection of lines with quadratic defining ideals but for numerical reasons each coordinate ring is not Koszul. We end the document with a table summarizing the results of which coordinates rings are Koszul, which are not Koszul, and which are unknown.
$\mathbb {P}^4,$
then the coordinate ring R is not Koszul. In §6, we exhibit a collection of lines that is not a generic collection but the lines are in general linear position, and we give two examples of coordinate rings where each define a generic collection of lines with quadratic defining ideals but for numerical reasons each coordinate ring is not Koszul. We end the document with a table summarizing the results of which coordinates rings are Koszul, which are not Koszul, and which are unknown.
2 Background
Let
![]() $\mathbb {P}^n$
denote n-dimensional projective space obtained from a
$\mathbb {P}^n$
denote n-dimensional projective space obtained from a
![]() $\mathbb {C}$
-vector space of dimension
$\mathbb {C}$
-vector space of dimension
![]() $n+1$
. A commutative Noetherian
$n+1$
. A commutative Noetherian
![]() $\mathbb {C}$
-algebra R is said to be graded if
$\mathbb {C}$
-algebra R is said to be graded if
![]() $R= \bigoplus _{i \in \mathbb {N}} R_i$
as an Abelian group such that for all nonnegative integers i and j we have
$R= \bigoplus _{i \in \mathbb {N}} R_i$
as an Abelian group such that for all nonnegative integers i and j we have
![]() $R_iR_j \subseteq R_{i+j},$
and is standard graded if
$R_iR_j \subseteq R_{i+j},$
and is standard graded if
![]() $R_0= \mathbb {C}$
and R is generated as a
$R_0= \mathbb {C}$
and R is generated as a
![]() $\mathbb {C}$
-algebra by a finite set of degree
$\mathbb {C}$
-algebra by a finite set of degree
![]() $1$
elements. Additionally, an R-module M is called graded if R is graded and M can be written as
$1$
elements. Additionally, an R-module M is called graded if R is graded and M can be written as
![]() $M= \bigoplus _{i \in \mathbb {N}} M_i$
as an Abelian group such that for all nonnegative integers i and j we have
$M= \bigoplus _{i \in \mathbb {N}} M_i$
as an Abelian group such that for all nonnegative integers i and j we have
![]() $R_iM_j \subseteq M_{i+j}.$
Note each summand
$R_iM_j \subseteq M_{i+j}.$
Note each summand
![]() $R_i$
and
$R_i$
and
![]() $M_i$
is a
$M_i$
is a
![]() $\mathbb {C}$
-vector space of finite dimension. We always assume our rings are standard graded. Let S be the symmetric algebra of
$\mathbb {C}$
-vector space of finite dimension. We always assume our rings are standard graded. Let S be the symmetric algebra of
![]() $R_1$
over
$R_1$
over
![]() $\mathbb {C};$
that is, S is the polynomial ring
$\mathbb {C};$
that is, S is the polynomial ring
![]() $S=\mathbb {C}[x_0,\ldots ,x_n],$
where
$S=\mathbb {C}[x_0,\ldots ,x_n],$
where
![]() $\mathrm {dim}(R_1)=n+1$
and
$\mathrm {dim}(R_1)=n+1$
and
![]() $x_0,\ldots ,x_n$
is a
$x_0,\ldots ,x_n$
is a
![]() $\mathbb {C}$
-basis of
$\mathbb {C}$
-basis of
![]() $R_1.$
We have an induced surjection
$R_1.$
We have an induced surjection
![]() $S \rightarrow R$
of standard graded
$S \rightarrow R$
of standard graded
![]() $\mathbb {C}$
-algebras, and so
$\mathbb {C}$
-algebras, and so
![]() $R \cong S/J,$
where J is a homogenous ideal and the kernel of this map. We say that J defines R and call this ideal J the defining ideal. Denote by
$R \cong S/J,$
where J is a homogenous ideal and the kernel of this map. We say that J defines R and call this ideal J the defining ideal. Denote by
![]() $\mathfrak {m}_R$
the maximal homogeneous ideal of
$\mathfrak {m}_R$
the maximal homogeneous ideal of
![]() $R.$
Except when explicitly said, all rings are graded and Noetherian and all modules are finitely generated. We may view
$R.$
Except when explicitly said, all rings are graded and Noetherian and all modules are finitely generated. We may view
![]() $\mathbb {C}$
as a graded R-module since
$\mathbb {C}$
as a graded R-module since
![]() $\mathbb {C} \cong R/\mathfrak {m}_R.$
The function
$\mathbb {C} \cong R/\mathfrak {m}_R.$
The function
![]() $\mathrm {Hilb}_M:\mathbb {N} \rightarrow \mathbb {N}$
defined by
$\mathrm {Hilb}_M:\mathbb {N} \rightarrow \mathbb {N}$
defined by
![]() $\mathrm {Hilb}_M(d) = \mathrm {dim}_{\mathbb {C}}(M_d)$
is called the Hilbert function of the R-module
$\mathrm {Hilb}_M(d) = \mathrm {dim}_{\mathbb {C}}(M_d)$
is called the Hilbert function of the R-module
![]() $M.$
Furthermore, there exists a unique polynomial
$M.$
Furthermore, there exists a unique polynomial
![]() $\mathrm {HilbP}(d)$
with rational coefficents, called the Hilbert polynomial such that
$\mathrm {HilbP}(d)$
with rational coefficents, called the Hilbert polynomial such that
![]() $\mathrm {HilbP}(d) = \mathrm {Hilb}(d)$
for
$\mathrm {HilbP}(d) = \mathrm {Hilb}(d)$
for
![]() $d \gg 0$
.
$d \gg 0$
.
The minimal graded free resolution
![]() $\textbf {F}$
of an R-module M is an exact sequence of homomorphisms of finitely generated free R-modules
$\textbf {F}$
of an R-module M is an exact sequence of homomorphisms of finitely generated free R-modules
such that
![]() $d_{i-1}d_i = 0$
for all
$d_{i-1}d_i = 0$
for all
![]() $i, M \cong F_0/\mathrm {Im}(d_1),$
and
$i, M \cong F_0/\mathrm {Im}(d_1),$
and
![]() $d_{i+1}(F_{i+1}) \subseteq (x_0,\ldots ,x_n)F_i$
for all
$d_{i+1}(F_{i+1}) \subseteq (x_0,\ldots ,x_n)F_i$
for all
![]() $i \geq 0.$
After choosing bases, we may represent each map in the resolution as a matrix. We can write
$i \geq 0.$
After choosing bases, we may represent each map in the resolution as a matrix. We can write
![]() $F_i = \bigoplus _j R(-j)^{\beta _{i,j}^R(M)},$
where
$F_i = \bigoplus _j R(-j)^{\beta _{i,j}^R(M)},$
where
![]() $R(-j)$
denotes a rank one free module with a generator in degree
$R(-j)$
denotes a rank one free module with a generator in degree
![]() $j,$
and the numbers
$j,$
and the numbers
![]() $\beta _{i,j}^R(M)$
are called the graded Betti numbers of M and are numerical invariants of M. The total Betti numbers of M are defined as
$\beta _{i,j}^R(M)$
are called the graded Betti numbers of M and are numerical invariants of M. The total Betti numbers of M are defined as
![]() $\beta _i^R(M) = \sum _{j} \beta _{i,j}^R(M)$
. When it is clear which module we are speaking about, we will write
$\beta _i^R(M) = \sum _{j} \beta _{i,j}^R(M)$
. When it is clear which module we are speaking about, we will write
![]() $\beta _{i,j}$
and
$\beta _{i,j}$
and
![]() $\beta _i$
to denote the graded Betti numbers and total Betti numbers, respectively. By construction, we have the equalities
$\beta _i$
to denote the graded Betti numbers and total Betti numbers, respectively. By construction, we have the equalities
 $$ \begin{align*} \beta_i^R(M) &= \mathrm{dim}_{\mathbb{C}}\mathrm{Tor}_i^R(M,\mathbb{C}), \\ \beta_{i,j}^R(M) &= \mathrm{dim}_{\mathbb{C}}\mathrm{Tor}_i^R(M,\mathbb{C})_j. \end{align*} $$
$$ \begin{align*} \beta_i^R(M) &= \mathrm{dim}_{\mathbb{C}}\mathrm{Tor}_i^R(M,\mathbb{C}), \\ \beta_{i,j}^R(M) &= \mathrm{dim}_{\mathbb{C}}\mathrm{Tor}_i^R(M,\mathbb{C})_j. \end{align*} $$
Two more invariants of a module are its projective dimension and relative Castelnuovo–Mumford regularity. These invariants are defined for an R-module M as follows:
Both invariants are interesting and measure the growth of the resolution of
![]() $M.$
For instance, if
$M.$
For instance, if
![]() $R=S,$
then by Hilbert’s Syzygy Theorem we are guaranteed that
$R=S,$
then by Hilbert’s Syzygy Theorem we are guaranteed that
![]() $\mathrm {pdim}_S(M) \leq n+1,$
where
$\mathrm {pdim}_S(M) \leq n+1,$
where
![]() $n+1$
is the number of indeterminates of S.
$n+1$
is the number of indeterminates of S.
Certain invariants are related to one another. For example, if
![]() $\mathrm {pdim}_R(M)$
is finite, then the Auslander–Buchsbaum formula relates the projective dimension to the depth of a module (see [Reference Peeva19, Th. 15.3]), where the depth of an R-module M is the length of the largest M-regular sequence consisting of elements of
$\mathrm {pdim}_R(M)$
is finite, then the Auslander–Buchsbaum formula relates the projective dimension to the depth of a module (see [Reference Peeva19, Th. 15.3]), where the depth of an R-module M is the length of the largest M-regular sequence consisting of elements of
![]() $R,$
and is denoted
$R,$
and is denoted
![]() $\mathrm {depth}(M).$
Letting
$\mathrm {depth}(M).$
Letting
![]() $R=S,$
the Auslander–Buchsbaum formula states that the projective dimension and depth of an S-module M are complementary to one another:
$R=S,$
the Auslander–Buchsbaum formula states that the projective dimension and depth of an S-module M are complementary to one another:
The Krull dimension, or dimension, of a ring is the supremum of the lengths k of strictly increasing chains
![]() $P_0 \subset P_1 \subset \ldots \subset P_k$
of prime ideals of
$P_0 \subset P_1 \subset \ldots \subset P_k$
of prime ideals of
![]() $R.$
The dimension of an R-module is denoted
$R.$
The dimension of an R-module is denoted
![]() $\mathrm {dim}(M)$
and is the Krull dimension of the ring
$\mathrm {dim}(M)$
and is the Krull dimension of the ring
![]() $R/I,$
where
$R/I,$
where
![]() $I = \mathrm {Ann}_R(M)$
is the annihilator of
$I = \mathrm {Ann}_R(M)$
is the annihilator of
![]() $M.$
The depth and dimension of a ring have the following properties along a short exact sequence.
$M.$
The depth and dimension of a ring have the following properties along a short exact sequence.
Proposition 2.1. ([Reference Eisenbud11, Cor. 18.6])
Let R be a graded Noetherian ring and suppose that
is an exact sequence of finitely generated graded R-modules. Then
-
(a)
 $\mathrm {depth}(M^{'}) \geq \mathrm {min}\{ \mathrm {depth}(M), \mathrm {depth}(M^{"}) +1 \}, $
$\mathrm {depth}(M^{'}) \geq \mathrm {min}\{ \mathrm {depth}(M), \mathrm {depth}(M^{"}) +1 \}, $
-
(b)
 $\mathrm {depth}(M) \geq \mathrm {min}\{ \mathrm {depth}(M^{'}), \mathrm {depth}(M^{"}) \}, $
$\mathrm {depth}(M) \geq \mathrm {min}\{ \mathrm {depth}(M^{'}), \mathrm {depth}(M^{"}) \}, $
-
(c)
 $\mathrm {depth}(M^{"}) \geq \mathrm {min}\{ \mathrm {depth}(M), \mathrm {depth}(M^{'}) - 1 \}, $
$\mathrm {depth}(M^{"}) \geq \mathrm {min}\{ \mathrm {depth}(M), \mathrm {depth}(M^{'}) - 1 \}, $
-
(d)
 $\mathrm {dim}(M)= \mathrm {max}\{ \mathrm {dim}(M^{"}),\mathrm {dim}(M^{'})\}.$
$\mathrm {dim}(M)= \mathrm {max}\{ \mathrm {dim}(M^{"}),\mathrm {dim}(M^{'})\}.$
Furthermore,
![]() $\mathrm {depth}(M) \leq \mathrm {dim}(M).$
$\mathrm {depth}(M) \leq \mathrm {dim}(M).$
An R-module M is Cohen–Macaulay, if
![]() $\mathrm {depth}(M) = \mathrm {dim}(M).$
Since R is a module over itself, we say R is a Cohen–Macaulay ring if it is a Cohen–Macaulay R-module. Cohen–Macaulay rings have been studied extensively, and the definition is sufficiently general to allow a rich theory with a wealth of examples in algebraic geometry. This notion is a workhorse in commutative algebra, and provides very useful tools and reductions to study rings [Reference Bruns and Herzog6]. For example, if one has a graded Cohen–Macaulay
$\mathrm {depth}(M) = \mathrm {dim}(M).$
Since R is a module over itself, we say R is a Cohen–Macaulay ring if it is a Cohen–Macaulay R-module. Cohen–Macaulay rings have been studied extensively, and the definition is sufficiently general to allow a rich theory with a wealth of examples in algebraic geometry. This notion is a workhorse in commutative algebra, and provides very useful tools and reductions to study rings [Reference Bruns and Herzog6]. For example, if one has a graded Cohen–Macaulay
![]() $\mathbb {C}$
-algebra, then one can take a quotient by generic linear forms to produce an Artinian ring. A reduction of this kind is called an Artinian reduction and provides many useful tools to work with, and almost all homological invariants of the ring are preserved [Reference Migliore and Patnott18]. Unfortunately, we will not be able to use these tools or reductions as the coordinate ring of a generic collection of lines is almost never Cohen–Macaulay, whereas the coordinate ring of a generic collection of points is always Cohen–Macaulay.
$\mathbb {C}$
-algebra, then one can take a quotient by generic linear forms to produce an Artinian ring. A reduction of this kind is called an Artinian reduction and provides many useful tools to work with, and almost all homological invariants of the ring are preserved [Reference Migliore and Patnott18]. Unfortunately, we will not be able to use these tools or reductions as the coordinate ring of a generic collection of lines is almost never Cohen–Macaulay, whereas the coordinate ring of a generic collection of points is always Cohen–Macaulay.
The absolute Castelnuovo–Mumford regularity, or the regularity, is denoted
![]() $\mathrm {reg}_S(M)$
and is the regularity of M as an S-module. There is a cohomological interpretation by local duality [Reference Eisenbud and Goto12]. Set
$\mathrm {reg}_S(M)$
and is the regularity of M as an S-module. There is a cohomological interpretation by local duality [Reference Eisenbud and Goto12]. Set
![]() $H_{\mathfrak {m}_S}^i(M)$
to be the
$H_{\mathfrak {m}_S}^i(M)$
to be the
![]() $i^{th}$
local cohomology module with support in the graded maximal ideal of
$i^{th}$
local cohomology module with support in the graded maximal ideal of
![]() $S.$
One has
$S.$
One has
![]() $H_{\mathfrak {m}_S}^i(M) =0$
if
$H_{\mathfrak {m}_S}^i(M) =0$
if
![]() $i < \mathrm {depth}(M)$
or
$i < \mathrm {depth}(M)$
or
![]() $i> \mathrm {dim}(M)$
and
$i> \mathrm {dim}(M)$
and
In practice, bounding the regularity of M is difficult, since it measures the largest degree of a minimal syzygy of M. We have tools to help the study of the regularity of an S-module.
Proposition 2.2. ([Reference Eisenbud11, Exer. 4C.2, Th. 4.2, and Cor. 4.4])
Suppose that
is an exact sequence of finitely generated graded S-modules. Then
-
(a)
 $\mathrm {reg}_S(M^{'}) \leq \mathrm {max}\{ \mathrm {reg}_S(M), \mathrm {reg}_S(M^{"}) +1 \}, $
$\mathrm {reg}_S(M^{'}) \leq \mathrm {max}\{ \mathrm {reg}_S(M), \mathrm {reg}_S(M^{"}) +1 \}, $
-
(b)
 $\mathrm {reg}_S(M) \leq \mathrm {max}\{ \mathrm {reg}_S(M^{'}), \mathrm {reg}_S(M^{"}) \}, $
$\mathrm {reg}_S(M) \leq \mathrm {max}\{ \mathrm {reg}_S(M^{'}), \mathrm {reg}_S(M^{"}) \}, $
-
(c)
 $\mathrm {reg}_S(M^{"}) \leq \mathrm {max}\{ \mathrm {reg}_S(M), \mathrm {reg}_S(M^{'}) - 1 \}, $
$\mathrm {reg}_S(M^{"}) \leq \mathrm {max}\{ \mathrm {reg}_S(M), \mathrm {reg}_S(M^{'}) - 1 \}, $
and if
![]() $d_0 = \mathrm {min}\{d \, | \, \mathrm {Hilb}(d) = \mathrm {HilbP}(d) \},$
then
$d_0 = \mathrm {min}\{d \, | \, \mathrm {Hilb}(d) = \mathrm {HilbP}(d) \},$
then
![]() $\mathrm {reg}(M) \geq d_0.$
Furthermore, if M is Cohen–Macaulay, then
$\mathrm {reg}(M) \geq d_0.$
Furthermore, if M is Cohen–Macaulay, then
![]() $\mathrm {reg}_S(M) = d_0.$
If M has finite length, then
$\mathrm {reg}_S(M) = d_0.$
If M has finite length, then
![]() $\mathrm {reg}_S(M) = \mathrm {max}\{ d : M_d \neq 0 \}.$
$\mathrm {reg}_S(M) = \mathrm {max}\{ d : M_d \neq 0 \}.$
To study these invariants, we place the graded Betti numbers of a module M into a table, called the Betti table.

The Betti table allows us to determine certain invariants easier; for example, the projective dimension is the length of the table and the regularity is the height of the table.
Denote by
![]() $H_M(t)$
and
$H_M(t)$
and
![]() $P_{M}^{R}(t),$
respectively, the Hilbert series of M and the Poincaré series of an R-module M:
$P_{M}^{R}(t),$
respectively, the Hilbert series of M and the Poincaré series of an R-module M:
 $$ \begin{align*} H_M(t) = \sum_{i \geq 0} \mathrm{Hilb}_M(i) t^i \end{align*} $$
$$ \begin{align*} H_M(t) = \sum_{i \geq 0} \mathrm{Hilb}_M(i) t^i \end{align*} $$
and
 $$ \begin{align*} P_{M}^R(t) = \sum_{i \geq 0} \beta_i^R(M) t^i. \end{align*} $$
$$ \begin{align*} P_{M}^R(t) = \sum_{i \geq 0} \beta_i^R(M) t^i. \end{align*} $$
It is worth observing that since M is finitely generated by homogenous elements of positive degree, the Hilbert series of M is a rational function. A short exact sequence of modules has a property we use extensively in this paper. If we have a short exact sequence of graded S-modules
then
Whenever we use this property, we will refer to it as the additivity property of the Hilbert series.
A standard graded
![]() $\mathbb {C}$
-algebra R is Koszul if
$\mathbb {C}$
-algebra R is Koszul if
![]() $\mathbb {C}$
has a linear R-free resolution; that is,
$\mathbb {C}$
has a linear R-free resolution; that is,
![]() $\beta _{i,j}^R(\mathbb {C}) =0$
for
$\beta _{i,j}^R(\mathbb {C}) =0$
for
![]() $i \neq j$
. Koszul algebras possess remarkable homological properties. For example,
$i \neq j$
. Koszul algebras possess remarkable homological properties. For example,
Theorem 2.3. (Avramov, Eisenbud, and Peeva [Reference Avramov and Eisenbud4, Th. 1] [Reference Avramov and Peeva5, Th. 2])
The following are equivalent:
-
(a) Every finitely generated R-module has finite regularity.
-
(b) The residue field has finite regularity.
-
(c) R is Koszul.
Koszul rings possess other interesting properties as well. Fröberg [Reference Fröberg14] showed that R is Koszul if and only if
![]() $H_R(t)$
and the
$H_R(t)$
and the
![]() $P_{\mathbb {C}}^R(t)$
have the following relationship:
$P_{\mathbb {C}}^R(t)$
have the following relationship:
In general, the Poincaré series of
![]() $\mathbb {C}$
as an R-module can be irrational [Reference Anick1], but if R is Koszul, then Equation (2) tells us the Poincaré series is always rational. So a necessary condition for a coordinate ring R to be Koszul is
$\mathbb {C}$
as an R-module can be irrational [Reference Anick1], but if R is Koszul, then Equation (2) tells us the Poincaré series is always rational. So a necessary condition for a coordinate ring R to be Koszul is
![]() $P_{\mathbb {C}}^R(t) = \frac {1}{H_R(-t)}$
must have nonnegative coefficients in its Maclaurin series. Another necessary condition is that if R is Koszul, then the defining ideal has a minimal generating set of forms of degree at most
$P_{\mathbb {C}}^R(t) = \frac {1}{H_R(-t)}$
must have nonnegative coefficients in its Maclaurin series. Another necessary condition is that if R is Koszul, then the defining ideal has a minimal generating set of forms of degree at most
![]() $2$
. This is easy to see since
$2$
. This is easy to see since
 $$ \begin{align*} \beta_{2,j}^R(\mathbb{C}) = \begin{cases} \beta_{1,j}^S(R), & \text{if }j \neq 2, \\ \beta_{1,2}^S(R) + \binom{n+1}{2}, & \text{if } j=2 \end{cases} \end{align*} $$
$$ \begin{align*} \beta_{2,j}^R(\mathbb{C}) = \begin{cases} \beta_{1,j}^S(R), & \text{if }j \neq 2, \\ \beta_{1,2}^S(R) + \binom{n+1}{2}, & \text{if } j=2 \end{cases} \end{align*} $$
(see [Reference Conca8, Rem. 1.10]). Unfortunately, the converse does not hold, but Fröberg showed that if the defining ideal is generated by monomials of degree at most
![]() $2,$
then R is Koszul.
$2,$
then R is Koszul.
Theorem 2.4. (Fröberg [Reference Fröberg and Backelin15])
If
![]() $R=S/J$
and J is a monomial ideal with each monomial having degree at most
$R=S/J$
and J is a monomial ideal with each monomial having degree at most
![]() $2$
, then R is Koszul.
$2$
, then R is Koszul.
More generally, if J has a Gröbner basis of quadrics in some term order, then R is Koszul. If such a basis exists, we say that R is G-quadratic. More generally, R is LG-quadratic if there is a G-quadratic ring A and a regular sequence of linear forms
![]() $l_1,\ldots ,l_r$
such that
$l_1,\ldots ,l_r$
such that
![]() $R \cong A/(l_1,\ldots ,l_r).$
It is worth noting that every G-quadratic ring is LG-quadratic, and every LG-quadratic ring is Koszul and that all of these implications are strict [Reference Conca8]. We briefly discuss in §6 if coordinate rings of generic collections of lines are G-quadratic or LG-quadratic.
$R \cong A/(l_1,\ldots ,l_r).$
It is worth noting that every G-quadratic ring is LG-quadratic, and every LG-quadratic ring is Koszul and that all of these implications are strict [Reference Conca8]. We briefly discuss in §6 if coordinate rings of generic collections of lines are G-quadratic or LG-quadratic.
We now define a very useful tool in proving rings are Koszul.
Definition 2.5. Let R be a standard graded
![]() $\mathbb {C}$
-algebra. A family
$\mathbb {C}$
-algebra. A family
![]() $\mathcal {F}$
of ideals is said to be a Koszul filtration of R if:
$\mathcal {F}$
of ideals is said to be a Koszul filtration of R if:
-
(a) Every ideal
 $I \in \mathcal {F}$
is generated by linear forms.
$I \in \mathcal {F}$
is generated by linear forms. -
(b) The ideal
 $0$
and the maximal homogeneous ideal
$0$
and the maximal homogeneous ideal
 $\mathfrak {m}_R$
of R belong to
$\mathfrak {m}_R$
of R belong to
 $\mathcal {F}.$
$\mathcal {F}.$
-
(c) For every ideal
 $I \in \mathcal {F}$
different from
$I \in \mathcal {F}$
different from
 $0,$
there exists an ideal
$0,$
there exists an ideal
 $K \in \mathcal {F}$
such that
$K \in \mathcal {F}$
such that
 $K \subset I, I/K$
is cyclic, and
$K \subset I, I/K$
is cyclic, and
 $K : I \in \mathcal {F}.$
$K : I \in \mathcal {F}.$
Conca, Trung, and Valla [Reference Conca, Trung and Valla9] showed that if R has a Koszul filtration, then R is Koszul. In fact, a stronger statement is true.
Proposition 2.6 ([Reference Conca, Trung and Valla9, Prop. 1.2])
Let
![]() $\mathcal {F}$
be a Koszul filtration of
$\mathcal {F}$
be a Koszul filtration of
![]() $R.$
Then
$R.$
Then
![]() $\mathrm {Tor}_i^R(R/J,\mathbb {C})_j=0$
for all
$\mathrm {Tor}_i^R(R/J,\mathbb {C})_j=0$
for all
![]() $i \neq j$
and for all
$i \neq j$
and for all
![]() $J \in {\mathcal {F}}.$
In particular, R is Koszul.
$J \in {\mathcal {F}}.$
In particular, R is Koszul.
Conca, Trung, and Valla construct a Koszul filtration to show certain sets of points in general linear position are Koszul in [Reference Conca, Trung and Valla9]. Since we aim to generalize Theorems 1.1 and 1.2 to collections of lines, we must define what it means for a collection of lines to be generic and what it means for a collection of lines to be in general linear position.
Definition 2.7. Let
![]() $\mathcal {P}$
be a collection of p points in
$\mathcal {P}$
be a collection of p points in
![]() $\mathbb {P}^n$
, and let
$\mathbb {P}^n$
, and let
![]() $\mathcal {M}$
be a collection of m lines in
$\mathcal {M}$
be a collection of m lines in
![]() $\mathbb {P}^n.$
The points of
$\mathbb {P}^n.$
The points of
![]() $\mathcal {P}$
are in general linear position if any s points span a
$\mathcal {P}$
are in general linear position if any s points span a
![]() $\mathbb {P}^{r},$
where
$\mathbb {P}^{r},$
where
![]() $ r = \mathrm {min} \{s-1,n\}.$
Similarly, the lines of
$ r = \mathrm {min} \{s-1,n\}.$
Similarly, the lines of
![]() $\mathcal {M}$
are in general linear position if any s lines span a
$\mathcal {M}$
are in general linear position if any s lines span a
![]() $\mathbb {P}^{r},$
where
$\mathbb {P}^{r},$
where
![]() $ r = \mathrm {min} \{2s-1,n\}.$
A collection of points in
$ r = \mathrm {min} \{2s-1,n\}.$
A collection of points in
![]() $\mathbb {P}^n$
is a generic collection if every linear form in the defining ideal of each point has algebraically independent coefficients over
$\mathbb {P}^n$
is a generic collection if every linear form in the defining ideal of each point has algebraically independent coefficients over
![]() $\mathbb {Q}$
. Similarly, we say a collection of lines is a generic collection if every linear form in the defining ideal of each line has algebraically independent coefficients over
$\mathbb {Q}$
. Similarly, we say a collection of lines is a generic collection if every linear form in the defining ideal of each line has algebraically independent coefficients over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
We can interpret this definition as saying generic collections are sufficiently random since the collection of them forms a dense subset of large parameter space. Furthermore, as one should suspect, a generic collection of lines is in general linear position, since collections of lines in general linear position are characterized by the nonvanishing of certain determinants in the coefficients of the defining linear forms. The converse is not true (see Example 6.1).
Remark 2.8. Suppose
![]() $\mathcal {P}$
is a collection of p points in general linear position in
$\mathcal {P}$
is a collection of p points in general linear position in
![]() $\mathbb {P}^n$
and
$\mathbb {P}^n$
and
![]() $\mathcal {M}$
is a collection of m lines in general linear position in
$\mathcal {M}$
is a collection of m lines in general linear position in
![]() $\mathbb {P}^n.$
The defining ideal for each point is minimally generated by n linear forms and the defining ideal for each line is minimally generated by
$\mathbb {P}^n.$
The defining ideal for each point is minimally generated by n linear forms and the defining ideal for each line is minimally generated by
![]() $n-1$
linear forms. We can see this because a point is an intersection of n hyperplanes and a line is an intersection of
$n-1$
linear forms. We can see this because a point is an intersection of n hyperplanes and a line is an intersection of
![]() $n-1$
hyperplanes. Also, if K is the defining ideal for
$n-1$
hyperplanes. Also, if K is the defining ideal for
![]() $\mathcal {P}$
and J is the defining ideal for
$\mathcal {P}$
and J is the defining ideal for
![]() $\mathcal {M},$
then
$\mathcal {M},$
then
![]() $\mathrm {dim}_{\mathbb {C}}(K_1)=n+1-p$
and
$\mathrm {dim}_{\mathbb {C}}(K_1)=n+1-p$
and
![]() $\mathrm {dim}_{\mathbb {C}}(J_1)=n+1-2m,$
provided either quantity is non-zero.
$\mathrm {dim}_{\mathbb {C}}(J_1)=n+1-2m,$
provided either quantity is non-zero.
3 Properties of coordinate rings of lines
This section aims to establish properties for the coordinate rings of generic collections of lines and collections of lines in general linear position and compare them to the coordinate rings of generic collections of points and collections of points in general linear position. We will see that the significant difference between the two coordinate rings is that the coordinate ring R of a collection of lines in general linear position is never Cohen–Macaulay, unless R is the coordinate ring of a single line, while the coordinate rings of points in general linear position are always Cohen–Macaulay. The lack of the Cohen–Macaulay property presents difficulty since many techniques are not available to us, such as Artinian reductions.
Proposition 3.1. Let
![]() $\mathcal {M}$
be a collection of lines in general linear position in
$\mathcal {M}$
be a collection of lines in general linear position in
![]() $\mathbb {P}^n$
with
$\mathbb {P}^n$
with
![]() $n \geq 3,$
and let R be the coordinate ring of
$n \geq 3,$
and let R be the coordinate ring of
![]() $\mathcal {M}.$
If
$\mathcal {M}.$
If
![]() $|\mathcal {M}|=1$
, then
$|\mathcal {M}|=1$
, then
![]() $\mathrm {pdim}_S(R)=n-1, \mathrm {depth}(R)=2,$
and
$\mathrm {pdim}_S(R)=n-1, \mathrm {depth}(R)=2,$
and
![]() $\mathrm {dim}(R)=2;$
if
$\mathrm {dim}(R)=2;$
if
![]() $|\mathcal {M}| \geq 2,$
then
$|\mathcal {M}| \geq 2,$
then
![]() $\mathrm {pdim}_S(R)=n, \mathrm {depth}(R)=1,$
and
$\mathrm {pdim}_S(R)=n, \mathrm {depth}(R)=1,$
and
![]() $\mathrm {dim}(R)=2$
. In particular, R is Cohen–Macaulay if and only if
$\mathrm {dim}(R)=2$
. In particular, R is Cohen–Macaulay if and only if
![]() $|\mathcal {M}|=1.$
$|\mathcal {M}|=1.$
Proof. We prove the claim by induction on
![]() $|\mathcal {M}|$
. Let
$|\mathcal {M}|$
. Let
![]() $m=|\mathcal {M}|$
and let J be the defining ideal of
$m=|\mathcal {M}|$
and let J be the defining ideal of
![]() $\mathcal {M}$
. If
$\mathcal {M}$
. If
![]() $m=1,$
then by Remark 2.8 the ideal J is minimally generated by
$m=1,$
then by Remark 2.8 the ideal J is minimally generated by
![]() $n-1$
linear forms. So, R is isomorphic to a polynomial ring in two indeterminates. Now, suppose that
$n-1$
linear forms. So, R is isomorphic to a polynomial ring in two indeterminates. Now, suppose that
![]() $m \geq 2,$
and write
$m \geq 2,$
and write
![]() $J = K \cap I,$
where K is the defining ideal for
$J = K \cap I,$
where K is the defining ideal for
![]() $m-1$
lines and I is the defining ideal for the remaining single line. By induction,
$m-1$
lines and I is the defining ideal for the remaining single line. By induction,
![]() $\mathrm {depth}(S/K) \leq 2$
and
$\mathrm {depth}(S/K) \leq 2$
and
![]() $\mathrm {dim}(S/K)=\mathrm {dim}(S/I)=2.$
Furthermore,
$\mathrm {dim}(S/K)=\mathrm {dim}(S/I)=2.$
Furthermore,
![]() $S/(K+I)$
is Artinian, since the variety K defines intersects trivially with the variety I defines. Hence,
$S/(K+I)$
is Artinian, since the variety K defines intersects trivially with the variety I defines. Hence,
![]() $\mathrm {dim}(S/(I+K)) =0.$
So, by Proposition 2.1 the
$\mathrm {dim}(S/(I+K)) =0.$
So, by Proposition 2.1 the
![]() $\mathrm {depth}(S/(I+K))=0.$
$\mathrm {depth}(S/(I+K))=0.$
Using the short exact sequence
and Proposition 2.1, we have two inequalities
and
Regardless if
![]() $\mathrm {depth}(S/K)$
is
$\mathrm {depth}(S/K)$
is
![]() $1$
or
$1$
or
![]() $2,$
our two inequalities yield
$2,$
our two inequalities yield
![]() $\mathrm {depth}(S/J)=1.$
By the Auslander–Buchsbaum formula, we have
$\mathrm {depth}(S/J)=1.$
By the Auslander–Buchsbaum formula, we have
![]() $\mathrm {pdim}_S(S/J)=n.$
Lastly, Proposition 2.1, yields
$\mathrm {pdim}_S(S/J)=n.$
Lastly, Proposition 2.1, yields
![]() $\mathrm {dim}(S/J) =2.$
$\mathrm {dim}(S/J) =2.$
Remark 3.2. We would like to note that when
![]() $n=2, R$
is a hypersurface and so
$n=2, R$
is a hypersurface and so
![]() $\mathrm {pdim}_S(R)=1, \mathrm {depth}(R)=2,$
and
$\mathrm {pdim}_S(R)=1, \mathrm {depth}(R)=2,$
and
![]() $\mathrm {dim}(R)=2.$
Thus, we restrict our attention to the case
$\mathrm {dim}(R)=2.$
Thus, we restrict our attention to the case
![]() $n \geq 3$
. Furthermore, an identical proof shows that if
$n \geq 3$
. Furthermore, an identical proof shows that if
![]() $\mathcal {P}$
is a collection of points in general linear position in
$\mathcal {P}$
is a collection of points in general linear position in
![]() $\mathbb {P}^n$
and R is the coordinate ring of
$\mathbb {P}^n$
and R is the coordinate ring of
![]() $\mathcal {P},$
then
$\mathcal {P},$
then
![]() $\mathrm {pdim}_S(R)=n, \mathrm {depth}(R)=1,$
and
$\mathrm {pdim}_S(R)=n, \mathrm {depth}(R)=1,$
and
![]() $\mathrm {dim}(R)=1.$
Hence, R is Cohen–Macaulay.
$\mathrm {dim}(R)=1.$
Hence, R is Cohen–Macaulay.
In [Reference Conca, Trung and Valla9], Conca, Trung, and Valla used the Hilbert function of points in
![]() $\mathbb {P}^n$
in general linear position to prove the corresponding coordinate ring is Koszul, provided the number of points is at most
$\mathbb {P}^n$
in general linear position to prove the corresponding coordinate ring is Koszul, provided the number of points is at most
![]() $2n+1.$
There is a generalization for the Hilbert function to a generic collection of points. We present both together as a single theorem for completeness, we do not use the Hilbert function for a generic collection of points.
$2n+1.$
There is a generalization for the Hilbert function to a generic collection of points. We present both together as a single theorem for completeness, we do not use the Hilbert function for a generic collection of points.
Theorem 3.3. ([Reference Carlini, Catalisano and Geramita7], [Reference Conca, Trung and Valla9])
Suppose that
![]() $\mathcal {P}$
is a collection of p points in
$\mathcal {P}$
is a collection of p points in
![]() $\mathbb {P}^n.$
If
$\mathbb {P}^n.$
If
![]() $\mathcal {P}$
is a generic collection, or
$\mathcal {P}$
is a generic collection, or
![]() $\mathcal {P}$
is a collection in general linear position with
$\mathcal {P}$
is a collection in general linear position with
![]() $p \leq 2n+1,$
then the Hilbert function of R is
$p \leq 2n+1,$
then the Hilbert function of R is
 $$ \begin{align*} \mathrm{Hilb}_R(d) = \mathrm{min} \left\{ \binom{n+d}{d}, p \right\}. \end{align*} $$
$$ \begin{align*} \mathrm{Hilb}_R(d) = \mathrm{min} \left\{ \binom{n+d}{d}, p \right\}. \end{align*} $$
In particular, if
![]() $p \leq n+1,$
then
$p \leq n+1,$
then
Since we aim to generalize Theorems 1.1 and 1.2, we would like to know the Hilbert series of the coordinate ring of a generic collection of lines. The famous Hartshorne–Hirschowitz Theorem provides an answer.
Theorem 3.4. (Hartshorne–Hirschowitz [Reference Hartshorne and Hirschowitz16])
Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() $\mathbb {P}^n$
, and let R be the coordinate ring of
$\mathbb {P}^n$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
The Hilbert function of R is
$\mathcal {M}.$
The Hilbert function of R is
 $$ \begin{align*}\mathrm{Hilb}_R(d) = \mathrm{min} \Bigg\{\binom{n+d}{d}, m(d+1) \Bigg\}.\end{align*} $$
$$ \begin{align*}\mathrm{Hilb}_R(d) = \mathrm{min} \Bigg\{\binom{n+d}{d}, m(d+1) \Bigg\}.\end{align*} $$
This theorem is very difficult to prove. One could ask if any generalization holds for planes, and unfortunately, this is not known and is an open problem. Interestingly, this theorem allows us to determine the regularity for the coordinate ring R of a generic collection of lines.
Theorem 3.5. Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() $\mathbb {P}^n$
with
$\mathbb {P}^n$
with
![]() $n \geq 3$
, and let R be the coordinate ring of
$n \geq 3$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
Then
$\mathcal {M}.$
Then
![]() $\mathrm {reg}_S(R)=\alpha ,$
where
$\mathrm {reg}_S(R)=\alpha ,$
where
![]() $\alpha $
is the smallest nonnegative integer satisfying
$\alpha $
is the smallest nonnegative integer satisfying
![]() $\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
$\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
Proof. If
![]() $m=1,$
then by Remark 2.8 and a change of basis we can write the defining ideal as
$m=1,$
then by Remark 2.8 and a change of basis we can write the defining ideal as
![]() $J=(x_0,\ldots ,x_{n-2}).$
The coordinate ring R is minimally resolved by the Koszul complex on
$J=(x_0,\ldots ,x_{n-2}).$
The coordinate ring R is minimally resolved by the Koszul complex on
![]() $x_0,\ldots ,x_{n-2}$
. So,
$x_0,\ldots ,x_{n-2}$
. So,
![]() $\mathrm {reg}_S(R)=0,$
and this satisfies the inequality. Suppose that
$\mathrm {reg}_S(R)=0,$
and this satisfies the inequality. Suppose that
![]() $m \geq 2$
and let
$m \geq 2$
and let
![]() $\alpha $
be the smallest nonnegative integer satisfying
$\alpha $
be the smallest nonnegative integer satisfying
![]() $\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
By Theorem 3.4 and Proposition 2.2,
$\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
By Theorem 3.4 and Proposition 2.2,
![]() $\mathrm {reg}_S(R) \geq \alpha .$
$\mathrm {reg}_S(R) \geq \alpha .$
We show the reverse inequality by induction on
![]() $m.$
Let J be the defining ideal for the collection
$m.$
Let J be the defining ideal for the collection
![]() $\mathcal {M}.$
Note, removing a line from a generic collection of lines maintains the generic property for the new collection. Let K be the defining ideal for
$\mathcal {M}.$
Note, removing a line from a generic collection of lines maintains the generic property for the new collection. Let K be the defining ideal for
![]() $m-1$
lines, and let I be the defining ideal for the remaining line such that
$m-1$
lines, and let I be the defining ideal for the remaining line such that
![]() $J = K \cap I.$
By induction
$J = K \cap I.$
By induction
![]() $\mathrm {reg}_S(S/K)=\beta ,$
and
$\mathrm {reg}_S(S/K)=\beta ,$
and
![]() $\beta $
is the smallest nonnegative integer satisfying the inequality
$\beta $
is the smallest nonnegative integer satisfying the inequality
![]() $\binom {n+\beta }{\beta } \geq (m-1)(\beta +1).$
$\binom {n+\beta }{\beta } \geq (m-1)(\beta +1).$
Now, we claim that
![]() $\mathrm {reg}_S(S/K) = \beta \in \{ \alpha , \alpha -1 \}.$
To prove this, we need two inequalities:
$\mathrm {reg}_S(S/K) = \beta \in \{ \alpha , \alpha -1 \}.$
To prove this, we need two inequalities:
![]() $ m-2 \geq \beta $
and
$ m-2 \geq \beta $
and
![]() $\binom {n+\beta }{\beta +1} \geq n(m-1).$
We have the first inequality since
$\binom {n+\beta }{\beta +1} \geq n(m-1).$
We have the first inequality since
 $$ \begin{align*} \binom{n+m-2}{m-2}-(m-1)(m-2+1) &= \frac{(n+m-2)!}{n!(m-2)!} - (m-1)^2 \\ &= \frac{(m+1)!}{3!(m-2)!} - (m-1)^2 \\ &= \frac{(m-3)(m-2)(m-1)}{3!} \\ &\geq 0. \end{align*} $$
$$ \begin{align*} \binom{n+m-2}{m-2}-(m-1)(m-2+1) &= \frac{(n+m-2)!}{n!(m-2)!} - (m-1)^2 \\ &= \frac{(m+1)!}{3!(m-2)!} - (m-1)^2 \\ &= \frac{(m-3)(m-2)(m-1)}{3!} \\ &\geq 0. \end{align*} $$
Thus,
![]() $m-2 \geq \beta .$
We have the second inequality, since by assumption
$m-2 \geq \beta .$
We have the second inequality, since by assumption
 $$ \begin{align*} \binom{n+\beta}{\beta} &\geq (m-1)(\beta+1), \end{align*} $$
$$ \begin{align*} \binom{n+\beta}{\beta} &\geq (m-1)(\beta+1), \end{align*} $$
and rearranging terms gives
 $$ \begin{align*} \binom{n+\beta}{\beta+1} &\geq n(m-1). \end{align*} $$
$$ \begin{align*} \binom{n+\beta}{\beta+1} &\geq n(m-1). \end{align*} $$
These inequalities together yield the following:
 $$ \begin{align*} \binom{n+\beta+1}{\beta+1} &= \binom{n+\beta}{\beta} + \binom{n+\beta}{\beta+1} \\ &\geq (m-1)(\beta+1) + n(m-1) \\ &= (m-1)(\beta+1) + m+(m-1)(n-1) - 1 \\ &\geq (m-1)(\beta+1) + m +(m-1)2 -1 \\ &\geq (m-1)(\beta+1) + m +\beta + 1 \\ &= m (\beta+2). \end{align*} $$
$$ \begin{align*} \binom{n+\beta+1}{\beta+1} &= \binom{n+\beta}{\beta} + \binom{n+\beta}{\beta+1} \\ &\geq (m-1)(\beta+1) + n(m-1) \\ &= (m-1)(\beta+1) + m+(m-1)(n-1) - 1 \\ &\geq (m-1)(\beta+1) + m +(m-1)2 -1 \\ &\geq (m-1)(\beta+1) + m +\beta + 1 \\ &= m (\beta+2). \end{align*} $$
Hence,
![]() $ \beta + 1 \geq \alpha .$
Furthermore, the inequality
$ \beta + 1 \geq \alpha .$
Furthermore, the inequality
 $$ \begin{align*} \binom{n+\beta-1}{\beta-1} < (m-1)(\beta-1+1) \leq m \beta \end{align*} $$
$$ \begin{align*} \binom{n+\beta-1}{\beta-1} < (m-1)(\beta-1+1) \leq m \beta \end{align*} $$
implies that
![]() $ \alpha \geq \beta .$
So,
$ \alpha \geq \beta .$
So,
![]() $\mathrm {reg}_S(S/K) = \beta $
where
$\mathrm {reg}_S(S/K) = \beta $
where
![]() $\beta \in \{ \alpha , \alpha -1 \}.$
$\beta \in \{ \alpha , \alpha -1 \}.$
Consider the short exact sequence
If
![]() $\beta = \alpha ,$
then Theorem 3.4 and the additive property of the Hilbert series yields the following:
$\beta = \alpha ,$
then Theorem 3.4 and the additive property of the Hilbert series yields the following:
 $$ \begin{align*} H_{S/(K+I)}(t) &= \left( H_{S/K}(t) + H_{S/I}(t)\right) - H_{S/J}(t) \\ &= \left(\sum\limits_{k=0}^{\alpha-1} \binom{n+k}{k} t^k + \sum\limits_{k=\alpha}^{\infty} (m-1)(k+1)t^k + \sum\limits_{k=0}^{\infty} (k+1)t^k \right)\\ &\hspace{1cm}- \sum\limits_{k=0}^{\alpha-1} \binom{n+k}{k} t^k - \sum\limits_{k=\alpha}^{\infty} m(k+1)t^k \\ &= \sum_{k=0}^{\alpha-1}(k+1)t^k. \end{align*} $$
$$ \begin{align*} H_{S/(K+I)}(t) &= \left( H_{S/K}(t) + H_{S/I}(t)\right) - H_{S/J}(t) \\ &= \left(\sum\limits_{k=0}^{\alpha-1} \binom{n+k}{k} t^k + \sum\limits_{k=\alpha}^{\infty} (m-1)(k+1)t^k + \sum\limits_{k=0}^{\infty} (k+1)t^k \right)\\ &\hspace{1cm}- \sum\limits_{k=0}^{\alpha-1} \binom{n+k}{k} t^k - \sum\limits_{k=\alpha}^{\infty} m(k+1)t^k \\ &= \sum_{k=0}^{\alpha-1}(k+1)t^k. \end{align*} $$
and similarly if
![]() $\beta = \alpha -1,$
then
$\beta = \alpha -1,$
then
 $$ \begin{align*} H_{S/(K+I)}(t) &= \left( H_{S/K}(t) + H_{S/I}(t)\right) - H_{S/J}(t) \\ &= \left(\sum\limits_{k=0}^{\alpha-2} \binom{n+k}{k} t^k + \sum\limits_{k=\alpha-1}^{\infty} (m-1)(k+1)t^k + \sum\limits_{k=0}^{\infty} (k+1)t^k \right)\\ &\hspace{1cm}- \sum\limits_{k=0}^{\alpha-1} \binom{n+k}{k} t^k - \sum\limits_{k=\alpha}^{\infty} m(k+1)t^k \\ &= \sum_{k=0}^{\alpha-2}(k+1)t^k + \left( m\alpha - \binom{n+\alpha-1}{\alpha-1} \right)t^{\alpha-1}. \end{align*} $$
$$ \begin{align*} H_{S/(K+I)}(t) &= \left( H_{S/K}(t) + H_{S/I}(t)\right) - H_{S/J}(t) \\ &= \left(\sum\limits_{k=0}^{\alpha-2} \binom{n+k}{k} t^k + \sum\limits_{k=\alpha-1}^{\infty} (m-1)(k+1)t^k + \sum\limits_{k=0}^{\infty} (k+1)t^k \right)\\ &\hspace{1cm}- \sum\limits_{k=0}^{\alpha-1} \binom{n+k}{k} t^k - \sum\limits_{k=\alpha}^{\infty} m(k+1)t^k \\ &= \sum_{k=0}^{\alpha-2}(k+1)t^k + \left( m\alpha - \binom{n+\alpha-1}{\alpha-1} \right)t^{\alpha-1}. \end{align*} $$
Note that
![]() $m\alpha - \binom {n+\alpha -1}{\alpha -1}$
is positive since
$m\alpha - \binom {n+\alpha -1}{\alpha -1}$
is positive since
![]() $\alpha $
is the smallest nonnegative integer such that
$\alpha $
is the smallest nonnegative integer such that
![]() $\binom {n+\alpha }{\alpha } \geq m(\alpha +1)$
. So,
$\binom {n+\alpha }{\alpha } \geq m(\alpha +1)$
. So,
![]() $S/(K+I)$
is Artinian. By Proposition 2.2,
$S/(K+I)$
is Artinian. By Proposition 2.2,
![]() $\mathrm {reg}_S(S/(K+I))=\alpha -1.$
Since
$\mathrm {reg}_S(S/(K+I))=\alpha -1.$
Since
![]() $\mathrm {reg}_S(S/K)=\alpha $
or
$\mathrm {reg}_S(S/K)=\alpha $
or
![]() $\mathrm {reg}_S(S/K)=\alpha -1$
and
$\mathrm {reg}_S(S/K)=\alpha -1$
and
![]() $\mathrm {reg}_S(S/I)=0,$
then
$\mathrm {reg}_S(S/I)=0,$
then
![]() $\mathrm {reg}_S(S/J) \leq \alpha $
. Thus,
$\mathrm {reg}_S(S/J) \leq \alpha $
. Thus,
![]() $\mathrm {reg}_S(R)=\alpha .$
$\mathrm {reg}_S(R)=\alpha .$
Remark 3.6. By Proposition 3.1, the coordinate ring R for a generic collection of lines is not Cohen–Macaulay, but
![]() $\mathrm {reg}_S(R) = \alpha ,$
where
$\mathrm {reg}_S(R) = \alpha ,$
where
![]() $\alpha $
is precisely the smallest nonnegative integer where
$\alpha $
is precisely the smallest nonnegative integer where
![]() $\mathrm {Hilb}(d)=\mathrm {HilbP}(d)$
for
$\mathrm {Hilb}(d)=\mathrm {HilbP}(d)$
for
![]() $d \geq \alpha .$
By Proposition 2.2, if a ring is Cohen–Macaulay then the regularity is precisely this number. So, even though we are not Cohen–Macaulay, we do not lose everything in generalizing these theorems.
$d \geq \alpha .$
By Proposition 2.2, if a ring is Cohen–Macaulay then the regularity is precisely this number. So, even though we are not Cohen–Macaulay, we do not lose everything in generalizing these theorems.
Compare the previous result with the following general regularity bound for intersections of ideals generated by linear forms.
Theorem 3.7. (Derksen and Sidman [Reference Derksen and Sidman10, Th. 2.1])
If
 $J = \bigcap \limits _{i=1}^j I_i$
is an ideal of
$J = \bigcap \limits _{i=1}^j I_i$
is an ideal of
![]() $S,$
where each
$S,$
where each
![]() $I_i$
is an ideal generated by linear forms, then
$I_i$
is an ideal generated by linear forms, then
![]() $\mathrm {reg}_S(S/J) \leq j.$
$\mathrm {reg}_S(S/J) \leq j.$
The assumption that R is a coordinate ring of a generic collection of lines tells us the regularity exactly, which is much smaller than the Derksen–Sidman bound for a fixed n. By way of comparison, we compute the following estimate.
Corollary 3.8. Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() $\mathbb {P}^n$
with
$\mathbb {P}^n$
with
![]() $n \geq 3$
, and let R be the coordinate ring of
$n \geq 3$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
Then
$\mathcal {M}.$
Then
Proof. Let
![]() $p(x) = (x+n)\cdots (x+2) - n!m.$
The polynomial
$p(x) = (x+n)\cdots (x+2) - n!m.$
The polynomial
![]() $p(x)$
has a unique positive root by the Intermediate Value Theorem, since the
$p(x)$
has a unique positive root by the Intermediate Value Theorem, since the
![]() $(x+n)\cdots (x+2)$
is increasing on the nonnegative real numbers. Let a be this positive root, and observe that the smallest nonnegative integer
$(x+n)\cdots (x+2)$
is increasing on the nonnegative real numbers. Let a be this positive root, and observe that the smallest nonnegative integer
![]() $\alpha $
satisfying the inequality
$\alpha $
satisfying the inequality
![]() $\binom {n+\alpha }{\alpha } \geq m(\alpha +1)$
is precisely the ceiling of the root
$\binom {n+\alpha }{\alpha } \geq m(\alpha +1)$
is precisely the ceiling of the root
![]() $a.$
$a.$
We now use an inequality of Minkowski (see [Reference Frenkel and Horváth13, (1.5)]). If
![]() $x_k$
and
$x_k$
and
![]() $y_k$
are positive for each
$y_k$
are positive for each
![]() $k,$
then
$k,$
then
 $$ \begin{align*}\sqrt[n-1]{\prod_{k=1}^{n-1} (x_k + y_k)} \geq \sqrt[n-1]{\prod_{k=1}^{n-1} x_k} + \sqrt[n-1]{\prod_{k=1}^{n-1} y_k}. \end{align*} $$
$$ \begin{align*}\sqrt[n-1]{\prod_{k=1}^{n-1} (x_k + y_k)} \geq \sqrt[n-1]{\prod_{k=1}^{n-1} x_k} + \sqrt[n-1]{\prod_{k=1}^{n-1} y_k}. \end{align*} $$
Thus,
 $$ \begin{align*} \sqrt[n-1]{n!m} &= \sqrt[n-1]{ (a+n)\cdots(a+2)} \\ &\geq a + \sqrt[n-1]{n!} \\ \end{align*} $$
$$ \begin{align*} \sqrt[n-1]{n!m} &= \sqrt[n-1]{ (a+n)\cdots(a+2)} \\ &\geq a + \sqrt[n-1]{n!} \\ \end{align*} $$
Therefore,
Taking ceilings gives the inequality.
We would like to note that
![]() $\mathrm {reg}_S(R)$
is roughly asymptotic to the upper bound. Proposition 3.1 and Theorem 3.5 tell us the coordinate ring R of a non-trivial generic collection of lines in
$\mathrm {reg}_S(R)$
is roughly asymptotic to the upper bound. Proposition 3.1 and Theorem 3.5 tell us the coordinate ring R of a non-trivial generic collection of lines in
![]() $\mathbb {P}^n$
is not Cohen–Macaulay,
$\mathbb {P}^n$
is not Cohen–Macaulay,
![]() $\mathrm {pdim}_S(R)=n,$
and the regularity is the smallest nonnegative integer
$\mathrm {pdim}_S(R)=n,$
and the regularity is the smallest nonnegative integer
![]() $\alpha $
satisfying
$\alpha $
satisfying
![]() $\binom {n+\alpha }{\alpha } \geq m(\alpha +1)$
. So, the resolution of R is well-behaved, in the sense that if n is fixed and we allow m to vary we may expect the regularity to be low compared to the number of lines in our collection.
$\binom {n+\alpha }{\alpha } \geq m(\alpha +1)$
. So, the resolution of R is well-behaved, in the sense that if n is fixed and we allow m to vary we may expect the regularity to be low compared to the number of lines in our collection.
4 Koszul filtration for a collection of lines
In this section, we determine when a generic collection of lines, or a collection of lines in general linear position, will yield a Koszul coordinate ring. To this end, most of the work will be in constructing a Koszul filtration in the coordinate ring of a generic collection of lines.
Proposition 4.1. Let
![]() $\mathcal {M}$
be a collection of m lines in general linear position in
$\mathcal {M}$
be a collection of m lines in general linear position in
![]() $\mathbb {P}^n$
, with
$\mathbb {P}^n$
, with
![]() $n\geq 3$
, and let R be the coordinate ring of
$n\geq 3$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
If
$\mathcal {M}.$
If
![]() $n+1 \geq 2m,$
then after a change of basis the defining ideal is minimally generated by monomials of degree at most
$n+1 \geq 2m,$
then after a change of basis the defining ideal is minimally generated by monomials of degree at most
![]() $2.$
Thus, R is Koszul.
$2.$
Thus, R is Koszul.
Proof. We use
![]() $ \widehat {\cdot }$
to denote a term removed from a sequence. Let R be the coordinate ring of
$ \widehat {\cdot }$
to denote a term removed from a sequence. Let R be the coordinate ring of
![]() $\mathcal {M}$
with defining ideal
$\mathcal {M}$
with defining ideal
![]() $J.$
Through a change of basis and Remark 2.8, we may assume the defining ideal for each line has the following form:
$J.$
Through a change of basis and Remark 2.8, we may assume the defining ideal for each line has the following form:
for
![]() $i = 1,\ldots ,m.$
Since every
$i = 1,\ldots ,m.$
Since every
![]() $L_i$
is monomial, so is J. Furthermore, since
$L_i$
is monomial, so is J. Furthermore, since
![]() $n+1 \geq 2m,$
the
$n+1 \geq 2m,$
the
![]() $\mathrm {reg}_S(R) \leq 1.$
Thus, J is generated by monomials of degree at most
$\mathrm {reg}_S(R) \leq 1.$
Thus, J is generated by monomials of degree at most
![]() $2.$
Theorem 2.4 guarantees R is Koszul.
$2.$
Theorem 2.4 guarantees R is Koszul.
Unfortunately, the simplicity of the previous proof does not carry over for larger generic collections of lines. We need a lemma.
Lemma 4.2. Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() $\mathbb {P}^n$
, and let R be the coordinate ring of
$\mathbb {P}^n$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
If
$\mathcal {M}.$
If
![]() $\mathrm {reg}_S(R) = 1$
, then the Hilbert series of R is
$\mathrm {reg}_S(R) = 1$
, then the Hilbert series of R is
 $$ \begin{align*} H_{S/J}(t) = \frac{(1-m)t^2+(m-2)t+1}{(1-t)^2}.\end{align*} $$
$$ \begin{align*} H_{S/J}(t) = \frac{(1-m)t^2+(m-2)t+1}{(1-t)^2}.\end{align*} $$
If
![]() $\mathrm {reg}_S(R) = 2$
, then the Hilbert series of R is
$\mathrm {reg}_S(R) = 2$
, then the Hilbert series of R is
 $$ \begin{align*} H_{S/J}(t) = \frac{(1+n-2m)t^3+(3m-2n-1)t^2+(n-1)t+1}{(1-t)^2}. \end{align*} $$
$$ \begin{align*} H_{S/J}(t) = \frac{(1+n-2m)t^3+(3m-2n-1)t^2+(n-1)t+1}{(1-t)^2}. \end{align*} $$
Proof. By Theorem 3.5, the regularity is the smallest nonnegative integer
![]() $\alpha $
satisfying
$\alpha $
satisfying
![]() $\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
Suppose
$\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
Suppose
![]() $\mathrm {reg}_S(R)=1$
. By Theorem 3.4, the Hilbert series for R is
$\mathrm {reg}_S(R)=1$
. By Theorem 3.4, the Hilbert series for R is
 $$ \begin{align*} H_{R}(t) &= 1 + 2mt + 3mt^2 +4mt^3 + \cdots \\ &= 1 - m\left( \frac{t(t-2)}{(1-t)^2}\right) \\ &= \frac{t^2-2t+1-mt^2+2mt}{(1-t)^2}\\ &= \frac{(1-m)t^2+2(m-1)t+1}{(1-t)^2}. \end{align*} $$
$$ \begin{align*} H_{R}(t) &= 1 + 2mt + 3mt^2 +4mt^3 + \cdots \\ &= 1 - m\left( \frac{t(t-2)}{(1-t)^2}\right) \\ &= \frac{t^2-2t+1-mt^2+2mt}{(1-t)^2}\\ &= \frac{(1-m)t^2+2(m-1)t+1}{(1-t)^2}. \end{align*} $$
Now, suppose
![]() $\mathrm {reg}_S(R)=2$
. By Theorem 3.4, the Hilbert series for R is
$\mathrm {reg}_S(R)=2$
. By Theorem 3.4, the Hilbert series for R is
 $$ \begin{align*} H_{R}(t) &= 1 +(n+1)t + 3mt^2 +4mt^3 + \cdots \\ &= 1+(n+1)t-m\left( \frac{t^2(2t-3)}{(1-t)^2} \right)\\ &= \frac{(n+1)t^3-(2n+1)t^2+(n-1)t+1-2mt^3+3mt^2}{(1-t)^2} \\ &= \frac{(n+1-2m)t^3+(3m-2n-1)t^2+(n-1)t+1}{(1-t)^2}. \end{align*} $$
$$ \begin{align*} H_{R}(t) &= 1 +(n+1)t + 3mt^2 +4mt^3 + \cdots \\ &= 1+(n+1)t-m\left( \frac{t^2(2t-3)}{(1-t)^2} \right)\\ &= \frac{(n+1)t^3-(2n+1)t^2+(n-1)t+1-2mt^3+3mt^2}{(1-t)^2} \\ &= \frac{(n+1-2m)t^3+(3m-2n-1)t^2+(n-1)t+1}{(1-t)^2}. \end{align*} $$
We can now construct a Koszul filtration for the coordinate ring of certain larger generic collections of lines.
Theorem 4.3. Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() $\mathbb {P}^n$
such that
$\mathbb {P}^n$
such that
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $m \geq 3$
, and let R be the coordinate ring of
$m \geq 3$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
$\mathcal {M}.$
-
(a) If m is even and
 $m+1 \leq n,$
then R has a Koszul filtration.
$m+1 \leq n,$
then R has a Koszul filtration. -
(b) If m is odd and
 $m + 2 \leq n,$
then R has a Koszul filtration.
$m + 2 \leq n,$
then R has a Koszul filtration.
In particular, R is Koszul.
Proof. We only prove
![]() $(a)$
due to the length of the proof and note that
$(a)$
due to the length of the proof and note that
![]() $(b)$
is done identically except for the Hilbert series computations. In both cases, we may assume that
$(b)$
is done identically except for the Hilbert series computations. In both cases, we may assume that
![]() $n \leq 2(m-1),$
otherwise Proposition 4.1 and Remark 2.8 prove the claim. By Remark 2.8 and a change of basis, we may assume the defining ideals for our m lines have the following form:
$n \leq 2(m-1),$
otherwise Proposition 4.1 and Remark 2.8 prove the claim. By Remark 2.8 and a change of basis, we may assume the defining ideals for our m lines have the following form:
 $$ \begin{align*} L_1 &= (x_0,\ldots,x_{n-4},x_{n-3},x_{n-2})\\ L_2 &= (x_0,\ldots,x_{n-4},x_{n-1},x_{n})\\ &\hspace{2.5cm}\vdots\\ L_i &= (x_0,\ldots, \widehat{x}_{n-2i+1}, \widehat{x}_{n-2i+2},\ldots,x_{n})\\ &\hspace{2.5cm}\vdots\\ L_k &= (x_0,\ldots, \widehat{x}_{n-2k+1}, \widehat{x}_{n-2k+2},\ldots,x_{n})\\ L_{k+1} &= (l_0,\ldots,l_{n-4},l_{n-3},l_{n-2})\\ L_{k+2} &= (l_0,\ldots,l_{n-4},l_{n-1},l_{n})\\ &\hspace{2.5cm}\vdots\\ L_{k+i} &= (l_0,\ldots, \widehat{l}_{n-2i+1} , \widehat{l}_{n-2i+2},\ldots,l_{n})\\ &\hspace{2.5cm}\vdots\\ L_{2k} &= (l_0,\ldots, \widehat{l}_{n-2k+1}, \widehat{l}_{n-2k+2},\ldots,l_{n}), \end{align*} $$
$$ \begin{align*} L_1 &= (x_0,\ldots,x_{n-4},x_{n-3},x_{n-2})\\ L_2 &= (x_0,\ldots,x_{n-4},x_{n-1},x_{n})\\ &\hspace{2.5cm}\vdots\\ L_i &= (x_0,\ldots, \widehat{x}_{n-2i+1}, \widehat{x}_{n-2i+2},\ldots,x_{n})\\ &\hspace{2.5cm}\vdots\\ L_k &= (x_0,\ldots, \widehat{x}_{n-2k+1}, \widehat{x}_{n-2k+2},\ldots,x_{n})\\ L_{k+1} &= (l_0,\ldots,l_{n-4},l_{n-3},l_{n-2})\\ L_{k+2} &= (l_0,\ldots,l_{n-4},l_{n-1},l_{n})\\ &\hspace{2.5cm}\vdots\\ L_{k+i} &= (l_0,\ldots, \widehat{l}_{n-2i+1} , \widehat{l}_{n-2i+2},\ldots,l_{n})\\ &\hspace{2.5cm}\vdots\\ L_{2k} &= (l_0,\ldots, \widehat{l}_{n-2k+1}, \widehat{l}_{n-2k+2},\ldots,l_{n}), \end{align*} $$
where
![]() $l_i$
are general linear forms in
$l_i$
are general linear forms in
![]() $S.$
Denote the ideals
$S.$
Denote the ideals
 $$ \begin{align*} J = \displaystyle{\bigcap_{i=1}^{2k}} L_i, \hspace{1cm} K = \displaystyle{\bigcap_{i=1}^{k}} L_i, \hspace{1cm} I = \displaystyle{\bigcap_{i=k+1}^{2k}} L_i,\end{align*} $$
$$ \begin{align*} J = \displaystyle{\bigcap_{i=1}^{2k}} L_i, \hspace{1cm} K = \displaystyle{\bigcap_{i=1}^{k}} L_i, \hspace{1cm} I = \displaystyle{\bigcap_{i=k+1}^{2k}} L_i,\end{align*} $$
so that
![]() $J = K \cap I.$
Let
$J = K \cap I.$
Let
![]() $R=S/J;$
to prove that R is Koszul, we will construct a Koszul filtration. To construct the filtration, we need the two Hilbert series
$R=S/J;$
to prove that R is Koszul, we will construct a Koszul filtration. To construct the filtration, we need the two Hilbert series
![]() $H_{\left ( J+(x_0) \right ):(x_1)}(t)$
and
$H_{\left ( J+(x_0) \right ):(x_1)}(t)$
and
![]() $H_{\left ( J+(l_0) \right ):(l_1)}(t).$
We first calculate the former. Observe
$H_{\left ( J+(l_0) \right ):(l_1)}(t).$
We first calculate the former. Observe
![]() $(x_0,x_1) \subseteq L_i$
and
$(x_0,x_1) \subseteq L_i$
and
![]() $(l_0,l_1) \subseteq L_{k+i}$
for
$(l_0,l_1) \subseteq L_{k+i}$
for
![]() $i= 1,\ldots ,k.$
Using the modular law [Reference Atiyah and Macdonald2, Chapter 1], we have the equality
$i= 1,\ldots ,k.$
Using the modular law [Reference Atiyah and Macdonald2, Chapter 1], we have the equality
So, it suffices to determine
![]() $H_{S/((I+(x_0)):(x_1))}(t)$
. To this end, we first calculate
$H_{S/((I+(x_0)):(x_1))}(t)$
. To this end, we first calculate
![]() $H_{S/(I+(x_0,x_1))}(t).$
To do so, we use the short exact sequence
$H_{S/(I+(x_0,x_1))}(t).$
To do so, we use the short exact sequence
 $$ \begin{align*} 0 \rightarrow S/\left( I+(x_0) \right) \cap \left(I+(x_1) \right) &\rightarrow S/\left( I+(x_0)\right) \oplus S/\left(I+(x_1)\right) \\ &\rightarrow S/\left(I+(x_0,x_1)\right) \rightarrow 0. \end{align*} $$
$$ \begin{align*} 0 \rightarrow S/\left( I+(x_0) \right) \cap \left(I+(x_1) \right) &\rightarrow S/\left( I+(x_0)\right) \oplus S/\left(I+(x_1)\right) \\ &\rightarrow S/\left(I+(x_0,x_1)\right) \rightarrow 0. \end{align*} $$
Our assumption
![]() $m+1 \leq n \leq 2(m-1)$
guarantees that
$m+1 \leq n \leq 2(m-1)$
guarantees that
![]() $\mathop {\mathrm {reg}}\nolimits _S(S/I)=1.$
Thus, by Lemma 4.2
$\mathop {\mathrm {reg}}\nolimits _S(S/I)=1.$
Thus, by Lemma 4.2
 $$ \begin{align} H_{S/I}(t) = \frac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}, \end{align} $$
$$ \begin{align} H_{S/I}(t) = \frac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}, \end{align} $$
and since
![]() $x_0$
and
$x_0$
and
![]() $x_1$
are nonzerodivisors on
$x_1$
are nonzerodivisors on
![]() $S/I,$
we have the following two Hilbert series:
$S/I,$
we have the following two Hilbert series:
Furthermore, the coordinate ring
![]() $S/(I+(x_0)) \cap (I+(x_1))$
corresponds precisely to a collection of
$S/(I+(x_0)) \cap (I+(x_1))$
corresponds precisely to a collection of
![]() $2k$
distinct points. These points must necessarily be in general linear position, since by assumption
$2k$
distinct points. These points must necessarily be in general linear position, since by assumption
![]() $2k=m \leq n+1$
and no three are collinear. So, by Theorem 3.3, we have
$2k=m \leq n+1$
and no three are collinear. So, by Theorem 3.3, we have
By the additivity of the Hilbert series
 $$ \begin{align*} H_{S/(I+(x_0,x_1))}(t) &= H_{S/(I+(x_0))}(t) + H_{S/(I+(x_1))}(t) - H_{S/(I+(x_0)) \cap (I+(x_1))}(t) \\ &= 2\left(\frac{(1-k)t^2+2(k-2)t+1}{1-t}\right) - \frac{(2k-1)t+1}{1-t} \\ &= 1+2(k-1)t. \end{align*} $$
$$ \begin{align*} H_{S/(I+(x_0,x_1))}(t) &= H_{S/(I+(x_0))}(t) + H_{S/(I+(x_1))}(t) - H_{S/(I+(x_0)) \cap (I+(x_1))}(t) \\ &= 2\left(\frac{(1-k)t^2+2(k-2)t+1}{1-t}\right) - \frac{(2k-1)t+1}{1-t} \\ &= 1+2(k-1)t. \end{align*} $$
Thus, by the short exact sequence
Equation (3), and the additivity of the Hilbert series
 $$ \begin{align} H_{S/((J+(x_0)):(x_1))}(t) &= H_{S/(I+(x_0)):(x_1)}(t) \\ \nonumber &=\frac{1}{t} \left( H_{S/(I+(x_0))}(t) - H_{S/(I+(x_0,x_1))} \right) \\ \nonumber &= \frac{1}{t} \bigg( \frac{(1-k)t^2+2(k-1)t+1}{1-t} -1-2(k-1)t \bigg) \\ \nonumber &= \frac{(k-1)t+1}{1-t}. \end{align} $$
$$ \begin{align} H_{S/((J+(x_0)):(x_1))}(t) &= H_{S/(I+(x_0)):(x_1)}(t) \\ \nonumber &=\frac{1}{t} \left( H_{S/(I+(x_0))}(t) - H_{S/(I+(x_0,x_1))} \right) \\ \nonumber &= \frac{1}{t} \bigg( \frac{(1-k)t^2+2(k-1)t+1}{1-t} -1-2(k-1)t \bigg) \\ \nonumber &= \frac{(k-1)t+1}{1-t}. \end{align} $$
This gives us our desired Hilbert series. An identical argument and interchanging I with K and
![]() $x_0$
and
$x_0$
and
![]() $x_1$
with
$x_1$
with
![]() $l_0$
and
$l_0$
and
![]() $l_1$
yields
$l_1$
yields
 $$ \begin{align} H_{S/K}(t) = \frac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}, \end{align} $$
$$ \begin{align} H_{S/K}(t) = \frac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}, \end{align} $$
 $$ \begin{align*} \hspace{1.9cm} H_{S/(K+(l_0))}(t) = H_{S/(K+(l_1))}(t) = \frac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}, \end{align*} $$
$$ \begin{align*} \hspace{1.9cm} H_{S/(K+(l_0))}(t) = H_{S/(K+(l_1))}(t) = \frac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}, \end{align*} $$
and
We can now define a Koszul filtration
![]() $\mathcal {F}$
for R. We use
$\mathcal {F}$
for R. We use
![]() $ \overline {\cdot }$
to denote the image of an element of S in
$ \overline {\cdot }$
to denote the image of an element of S in
![]() $R=S/J$
for the remainder of the paper. We have already seen in Equation (5) that
$R=S/J$
for the remainder of the paper. We have already seen in Equation (5) that
 $$ \begin{align*} H_{S/(J+(x_0)):(x_1)}(t) = \frac{(k-1)t+1}{(1-t)} = 1+\sum_{i=1}^{\infty} k t^i.\end{align*} $$
$$ \begin{align*} H_{S/(J+(x_0)):(x_1)}(t) = \frac{(k-1)t+1}{(1-t)} = 1+\sum_{i=1}^{\infty} k t^i.\end{align*} $$
Hence,
![]() $n-k+1$
linearly independent linear forms are in a minimal generating set of
$n-k+1$
linearly independent linear forms are in a minimal generating set of
![]() $(J+(x_0)):(x_1).$
Clearly
$(J+(x_0)):(x_1).$
Clearly
![]() $l_0,\ldots ,l_{n-2k},x_0\in (J+(x_0)):(x_1),$
label
$l_0,\ldots ,l_{n-2k},x_0\in (J+(x_0)):(x_1),$
label
![]() $z_{n-2k+2},\ldots ,z_{n-k}$
as the remaining linear forms from a minimal generating set of
$z_{n-2k+2},\ldots ,z_{n-k}$
as the remaining linear forms from a minimal generating set of
![]() $(J+(x_0)):(x_1).$
Similarly, choose
$(J+(x_0)):(x_1).$
Similarly, choose
![]() $y_i$
from
$y_i$
from
![]() $(J+(l_0)):(l_1)$
so that
$(J+(l_0)):(l_1)$
so that
![]() $x_0,x_1,\ldots ,x_{n-2k},l_0,y_{n-k+2},\ldots ,y_{n-k}$
are linear forms forming a minimal generating set of
$x_0,x_1,\ldots ,x_{n-2k},l_0,y_{n-k+2},\ldots ,y_{n-k}$
are linear forms forming a minimal generating set of
![]() $(J+(l_0)):(l_1).$
$(J+(l_0)):(l_1).$
The set
![]() $\{l_0,\ldots ,l_{n-2k},x_{0},z_{n-2k+1},\ldots ,z_{n-k},x_1\}$
is a linearly independent set over
$\{l_0,\ldots ,l_{n-2k},x_{0},z_{n-2k+1},\ldots ,z_{n-k},x_1\}$
is a linearly independent set over
![]() $S,$
otherwise
$S,$
otherwise
![]() $x_1^2 \in J+(x_0).$
This means
$x_1^2 \in J+(x_0).$
This means
![]() $x_1^2 \in (L_i+(x_0))$
for
$x_1^2 \in (L_i+(x_0))$
for
![]() $i = k+1,\ldots ,2k,$
a contradiction. Similarly,
$i = k+1,\ldots ,2k,$
a contradiction. Similarly,
![]() $\{x_0,\ldots ,x_{n-2k},l_{0},y_{n-2k+1},\ldots ,y_{n-k},l_1\}$
is linearly independent over
$\{x_0,\ldots ,x_{n-2k},l_{0},y_{n-2k+1},\ldots ,y_{n-k},l_1\}$
is linearly independent over
![]() $S.$
Let
$S.$
Let
![]() $w_{n-k+2},\ldots ,w_{n+1},$
and
$w_{n-k+2},\ldots ,w_{n+1},$
and
![]() $u_{n-k+2},\ldots ,u_{n+1}$
be extensions of
$u_{n-k+2},\ldots ,u_{n+1}$
be extensions of
and
to minimal systems of generators of
![]() $\mathfrak {m}_R,$
respectively. Define
$\mathfrak {m}_R,$
respectively. Define
![]() $\mathcal {F}$
as follows:
$\mathcal {F}$
as follows:
 $$ \begin{align*} \mathcal{F} = \begin{cases} 0, ( \overline{x}_0), \hspace{.2cm } ( \overline{x}_0, \overline{x}_1), \hspace{3.3cm} ( \overline{l}_0), \hspace{.2cm} ( \overline{l}_0, \overline{l}_1),\\ \hspace{2cm}\vdots \hspace{5cm}\vdots \\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}), \hspace{2.9cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}),\\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0), \hspace{2.5cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0),\\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2}), \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2}),\\ \hspace{4cm} \vdots \\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}), \\ \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2},\ldots, \overline{z}_{n-k}), \\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}, \overline{l}_{1}), \\ \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2},\ldots, \overline{z}_{n-k}, \overline{x}_{1}),\\ \hspace{4cm}\vdots\\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}, \overline{l}_{1},u_{n-k+2}),\\ \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2}, \ldots, \overline{z}_{n-k}, \overline{x}_{1},w_{n-k+2}),\\ \hspace{4cm}\vdots\\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}, \overline{l}_{1},u_{n-k+2},\ldots,u_{n}),\\ \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2}, \ldots, \overline{z}_{n-k}, \overline{x}_{1},w_{n-k+2},\ldots,w_{n}),\\ \mathfrak{m}_R. \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{F} = \begin{cases} 0, ( \overline{x}_0), \hspace{.2cm } ( \overline{x}_0, \overline{x}_1), \hspace{3.3cm} ( \overline{l}_0), \hspace{.2cm} ( \overline{l}_0, \overline{l}_1),\\ \hspace{2cm}\vdots \hspace{5cm}\vdots \\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}), \hspace{2.9cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}),\\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0), \hspace{2.5cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0),\\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2}), \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2}),\\ \hspace{4cm} \vdots \\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}), \\ \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2},\ldots, \overline{z}_{n-k}), \\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}, \overline{l}_{1}), \\ \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2},\ldots, \overline{z}_{n-k}, \overline{x}_{1}),\\ \hspace{4cm}\vdots\\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}, \overline{l}_{1},u_{n-k+2}),\\ \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2}, \ldots, \overline{z}_{n-k}, \overline{x}_{1},w_{n-k+2}),\\ \hspace{4cm}\vdots\\ ( \overline{x}_0, \overline{x}_1,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}, \overline{l}_{1},u_{n-k+2},\ldots,u_{n}),\\ \hspace{1cm} ( \overline{l}_0, \overline{l}_1,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2}, \ldots, \overline{z}_{n-k}, \overline{x}_{1},w_{n-k+2},\ldots,w_{n}),\\ \mathfrak{m}_R. \end{cases} \end{align*} $$
We now prove
![]() $\mathcal {F}$
is a Koszul filtration. We do this by proving several claims. Throughout the process, we use the inclusion
$\mathcal {F}$
is a Koszul filtration. We do this by proving several claims. Throughout the process, we use the inclusion
![]() $(x_0,x_1) \cap (l_0,l_1) \subseteq J.$
Afterward, we summarize all computed colons and list the claims that prove the calculated colons.
$(x_0,x_1) \cap (l_0,l_1) \subseteq J.$
Afterward, we summarize all computed colons and list the claims that prove the calculated colons.
Claim 4.4. The ideal
![]() $( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1)$
in R has Hilbert series
$( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1)$
in R has Hilbert series
and any ideal P containing this ideal has the property that
![]() $P:(\ell ) = \mathfrak {m}_R,$
where
$P:(\ell ) = \mathfrak {m}_R,$
where
![]() $\ell $
is a linear form not contained in
$\ell $
is a linear form not contained in
![]() $P.$
$P.$
Proof. We begin by observing that our assumption
![]() $m+1 \leq n \leq 2(m-1)$
and Proposition 3.5 yield
$m+1 \leq n \leq 2(m-1)$
and Proposition 3.5 yield
![]() $\mathrm {reg}_S(S/J)=2.$
Thus, by Lemma 4.2
$\mathrm {reg}_S(S/J)=2.$
Thus, by Lemma 4.2
 $$ \begin{align*} H_{S/J}(t) = \frac{(n+1-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2}.\end{align*} $$
$$ \begin{align*} H_{S/J}(t) = \frac{(n+1-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2}.\end{align*} $$
Now,
![]() $L_i:(x_0) = L_i$
for
$L_i:(x_0) = L_i$
for
![]() $i=k+1,\ldots ,2k,$
since
$i=k+1,\ldots ,2k,$
since
![]() $x_0 \notin L_i.$
Thus,
$x_0 \notin L_i.$
Thus,
 $$ \begin{align*}J:(x_0) = \left( \bigcap_{i=1}^{2k} L_i \right) :(x_0) =\bigcap_{i=1}^{2k} \left( L_i :(x_0) \right ) = \bigcap_{i=k+1}^{2k} L_i = I.\end{align*} $$
$$ \begin{align*}J:(x_0) = \left( \bigcap_{i=1}^{2k} L_i \right) :(x_0) =\bigcap_{i=1}^{2k} \left( L_i :(x_0) \right ) = \bigcap_{i=k+1}^{2k} L_i = I.\end{align*} $$
So,
![]() $H_{S/(J:(x_0))}(t)=H_{S/I}(t).$
Using the short exact sequence
$H_{S/(J:(x_0))}(t)=H_{S/I}(t).$
Using the short exact sequence
Equation (4), and the additivity of the Hilbert series yields
 $$ \begin{align*} H_{S/(J+(x_0))}(t) &= H_{S/J}(t)-tH_{S/(J:(x_0)) }(t) \\ &=H_{S/J}(t)-tH_{S/I }(t) \\ &=\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} -t\left( \tfrac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}\right)\\ &= \frac{(n-3k)t^3+(4k-2n+1)t^2+(n-2)t+1}{(1-t)^2}. \end{align*} $$
$$ \begin{align*} H_{S/(J+(x_0))}(t) &= H_{S/J}(t)-tH_{S/(J:(x_0)) }(t) \\ &=H_{S/J}(t)-tH_{S/I }(t) \\ &=\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} -t\left( \tfrac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}\right)\\ &= \frac{(n-3k)t^3+(4k-2n+1)t^2+(n-2)t+1}{(1-t)^2}. \end{align*} $$
Using the short exact sequence
Equation (5), the previous Hilbert series, and the additivity of the Hilbert series yields
 $$ \begin{align*} H_{S/(J+(x_0,x_1))}(t) &= H_{S/(J+(x_0))}(t) - tH_{S/(J+(x_0)):(x_1)}(t) \\ &= \tfrac{(n-3k)t^3+(4k-2n+1)t^2+(n-2)t+1}{(1-t)^2} - t\left( \tfrac{(k-1)t+1}{1-t} \right) \\ &= \frac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}. \end{align*} $$
$$ \begin{align*} H_{S/(J+(x_0,x_1))}(t) &= H_{S/(J+(x_0))}(t) - tH_{S/(J+(x_0)):(x_1)}(t) \\ &= \tfrac{(n-3k)t^3+(4k-2n+1)t^2+(n-2)t+1}{(1-t)^2} - t\left( \tfrac{(k-1)t+1}{1-t} \right) \\ &= \frac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}. \end{align*} $$
Replacing
![]() $x_0$
and
$x_0$
and
![]() $x_1$
with
$x_1$
with
![]() $l_0$
and
$l_0$
and
![]() $l_1$
demonstrates that
$l_1$
demonstrates that
Thus, using the short exact sequence
and the additivity of the Hilbert series yields
 $$ \begin{align*} H_{R/( \overline{x}_0, \overline{x}_1, \overline{l}_0, \overline{l}_1)}(t) &= H_{R/( \overline{x_0}, \overline{x_1})}(t)+H_{R/( \overline{l_0}, \overline{l_1})}(t)-H_{R}(t) \\ \nonumber &= 2\left(\tfrac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}\right) -\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} \\ \nonumber &= \frac{(n-3)t^3+(7-2n)t^2+(n-5)t+1}{(1-t)^2} \\ \nonumber &= 1+(n-3)t. \end{align*} $$
$$ \begin{align*} H_{R/( \overline{x}_0, \overline{x}_1, \overline{l}_0, \overline{l}_1)}(t) &= H_{R/( \overline{x_0}, \overline{x_1})}(t)+H_{R/( \overline{l_0}, \overline{l_1})}(t)-H_{R}(t) \\ \nonumber &= 2\left(\tfrac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}\right) -\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} \\ \nonumber &= \frac{(n-3)t^3+(7-2n)t^2+(n-5)t+1}{(1-t)^2} \\ \nonumber &= 1+(n-3)t. \end{align*} $$
So,
![]() $R_2 \subset ( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1).$
This means that any ideal
$R_2 \subset ( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1).$
This means that any ideal
![]() $P \subset R$
containing the ideal
$P \subset R$
containing the ideal
![]() $( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1)$
has the property that
$( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1)$
has the property that
![]() $P:(\ell ) = \mathfrak {m}_R,$
where
$P:(\ell ) = \mathfrak {m}_R,$
where
![]() $\ell $
is a linear form not contained in P.
$\ell $
is a linear form not contained in P.
Claim 4.5. For
![]() $i = 1,\ldots ,n-2k,$
we have the two Hilbert series
$i = 1,\ldots ,n-2k,$
we have the two Hilbert series
 $$ \begin{align*} H_{R/( \overline{x}_0, \overline{x}_1, \overline{x}_2,\ldots, \overline{x}_i)}(t) &= H_{R/( \overline{l}_0, \overline{l}_1, \overline{l}_2,\ldots, \overline{l}_i)}(t) \\ &=\tfrac{(n-2k-i)t^3+(3k-2n+2i+1)t^2+(n-(i+2))t+1}{(1-t)^2}, \end{align*} $$
$$ \begin{align*} H_{R/( \overline{x}_0, \overline{x}_1, \overline{x}_2,\ldots, \overline{x}_i)}(t) &= H_{R/( \overline{l}_0, \overline{l}_1, \overline{l}_2,\ldots, \overline{l}_i)}(t) \\ &=\tfrac{(n-2k-i)t^3+(3k-2n+2i+1)t^2+(n-(i+2))t+1}{(1-t)^2}, \end{align*} $$
and the two equalities
![]() $J+(x_0,\ldots ,x_{n-2k}) = K,$
and
$J+(x_0,\ldots ,x_{n-2k}) = K,$
and
![]() $J+(l_0,\ldots ,l_{n-2k}) = I.$
$J+(l_0,\ldots ,l_{n-2k}) = I.$
Proof. Adding the linear forms
![]() $x_2,\ldots ,x_i$
to the ideal
$x_2,\ldots ,x_i$
to the ideal
![]() $( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1)$
yields
$( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1)$
yields
for
![]() $i = 2,\ldots ,n-2k$
. Using the short exact sequence
$i = 2,\ldots ,n-2k$
. Using the short exact sequence
and the additivity of the Hilbert series gives
 $$ \begin{align*} H_{R/( \overline{x}_0, \overline{x}_1, \overline{x}_2)}(t) &= H_{R/( \overline{x}_0, \overline{x}_1, \overline{l}_0, \overline{l}_1, \overline{x}_2) }(t) + H_{R}(t)- H_{R/( \overline{l}_0, \overline{l}_1)}(t)\\ &= 1+(n-4)t +\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} \\ &\hspace{3.5cm} -\tfrac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}\\ &=1+(n-4)t+\frac{(2-2k)t^3+(3k-4)t^2+2t}{(1-t)^2} \\ &= \frac{(n-2k-2)t^3+(3k-2n+5)t^2+(n-4)t+1}{(1-t)^2}. \end{align*} $$
$$ \begin{align*} H_{R/( \overline{x}_0, \overline{x}_1, \overline{x}_2)}(t) &= H_{R/( \overline{x}_0, \overline{x}_1, \overline{l}_0, \overline{l}_1, \overline{x}_2) }(t) + H_{R}(t)- H_{R/( \overline{l}_0, \overline{l}_1)}(t)\\ &= 1+(n-4)t +\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} \\ &\hspace{3.5cm} -\tfrac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}\\ &=1+(n-4)t+\frac{(2-2k)t^3+(3k-4)t^2+2t}{(1-t)^2} \\ &= \frac{(n-2k-2)t^3+(3k-2n+5)t^2+(n-4)t+1}{(1-t)^2}. \end{align*} $$
Replacing
![]() $( \overline {x}_0, \overline {x}_1, \overline {x}_2)$
with
$( \overline {x}_0, \overline {x}_1, \overline {x}_2)$
with
![]() $( \overline {x}_0, \overline {x}_1, \overline {x}_2, \overline {x}_3)$
in the above short exact sequence and using the additivity of the Hilbert series yields
$( \overline {x}_0, \overline {x}_1, \overline {x}_2, \overline {x}_3)$
in the above short exact sequence and using the additivity of the Hilbert series yields
 $$ \begin{align*} H_{R/( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3)}(t) &= H_{R/( \overline{x}_0, \overline{x}_1, \overline{l}_0, \overline{l}_1, \overline{x}_2, \overline{x}_3) }(t) + H_{R}(t)- H_{R/( \overline{l}_0, \overline{l}_1)}(t)\\ &= 1+(n-5)t +\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} \\ &\hspace{3.5cm} -\tfrac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}\\ &= 1+(n-5)t + \frac{(2-2k)t^3+(3k-4)t^2+2t}{(1-t)^2} \\ &= \frac{(n-2k-3)t^3+(3k-2n+7)t^2+(n-5)t+1}{(1-t)^2} \end{align*} $$
$$ \begin{align*} H_{R/( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3)}(t) &= H_{R/( \overline{x}_0, \overline{x}_1, \overline{l}_0, \overline{l}_1, \overline{x}_2, \overline{x}_3) }(t) + H_{R}(t)- H_{R/( \overline{l}_0, \overline{l}_1)}(t)\\ &= 1+(n-5)t +\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} \\ &\hspace{3.5cm} -\tfrac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}\\ &= 1+(n-5)t + \frac{(2-2k)t^3+(3k-4)t^2+2t}{(1-t)^2} \\ &= \frac{(n-2k-3)t^3+(3k-2n+7)t^2+(n-5)t+1}{(1-t)^2} \end{align*} $$
By induction,
for
![]() $i =2,\ldots ,n-2k.$
Setting
$i =2,\ldots ,n-2k.$
Setting
![]() $i=n-2k,$
we obtain the Hilbert series
$i=n-2k,$
we obtain the Hilbert series
 $$ \begin{align*} H_{R/( \overline{x}_0,\ldots, \overline{x}_{n-2k})}(t) &= H_{R/( \overline{x}_0, \overline{x}_1, \overline{l}_0, \overline{l}_1, \overline{x}_2,\ldots, \overline{x}_{n-2k}) }(t) \\ \nonumber & \hspace{3cm}+H_{R}(t)- H_{R/( \overline{l}_0, \overline{l}_1)}(t)\\ \nonumber &= 1+(2k-2)t +\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} \\ \nonumber &\hspace{2.9cm} -\tfrac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}\\ \nonumber &= 1+(2k-2)t + \frac{(2-2k)t^3+(3k-4)t^2+2t}{(1-t)^2} \\ \nonumber &= \frac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}. \end{align*} $$
$$ \begin{align*} H_{R/( \overline{x}_0,\ldots, \overline{x}_{n-2k})}(t) &= H_{R/( \overline{x}_0, \overline{x}_1, \overline{l}_0, \overline{l}_1, \overline{x}_2,\ldots, \overline{x}_{n-2k}) }(t) \\ \nonumber & \hspace{3cm}+H_{R}(t)- H_{R/( \overline{l}_0, \overline{l}_1)}(t)\\ \nonumber &= 1+(2k-2)t +\tfrac{(1+n-4k)t^3+(6k-2n-1)t^2+(n-1)t+1}{(1-t)^2} \\ \nonumber &\hspace{2.9cm} -\tfrac{(n-2k-1)t^3+(3k-2n+3)t^2+(n-3)t+1}{(1-t)^2}\\ \nonumber &= 1+(2k-2)t + \frac{(2-2k)t^3+(3k-4)t^2+2t}{(1-t)^2} \\ \nonumber &= \frac{(1-k)t^2+2(k-1)t+1}{(1-t)^2}. \end{align*} $$
Interchanging each
![]() $x_i$
with
$x_i$
with
![]() $l_i$
gives us the other desired Hilbert series.
$l_i$
gives us the other desired Hilbert series.
The Hilbert series in Equation (7) is the same as in Equation (6). Furthermore,
![]() $J+(x_0,\ldots ,x_{n-2k})\subseteq K.$
So, we have that
$J+(x_0,\ldots ,x_{n-2k})\subseteq K.$
So, we have that
![]() $J+(x_0,\ldots ,x_{n-2k})= K$
and interchanging each
$J+(x_0,\ldots ,x_{n-2k})= K$
and interchanging each
![]() $x_i$
with
$x_i$
with
![]() $l_i$
gives us the other equality.
$l_i$
gives us the other equality.
Claim 4.6. We have the equalities
and
for
![]() $i=n-2k+2,\ldots ,n-k.$
Furthermore,
$i=n-2k+2,\ldots ,n-k.$
Furthermore,
and
Proof. We begin by observing
So by Claim 4.4, we conclude that
where
![]() $\alpha \in \{0,1,\ldots ,n-3\}.$
Using the short exact sequence
$\alpha \in \{0,1,\ldots ,n-3\}.$
Using the short exact sequence
 $$ \begin{align} 0 \rightarrow R/(( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}):( \overline{z}_{n-2k+2}))(-1) &\rightarrow R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}) \\ \nonumber& \hspace{-3cm} \rightarrow R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{z}_{n-2k+2}) \rightarrow 0, \end{align} $$
$$ \begin{align} 0 \rightarrow R/(( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}):( \overline{z}_{n-2k+2}))(-1) &\rightarrow R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}) \\ \nonumber& \hspace{-3cm} \rightarrow R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{z}_{n-2k+2}) \rightarrow 0, \end{align} $$
Claim 4.5, and that the fact that
![]() $x_0$
is a nonzerodivisor on
$x_0$
is a nonzerodivisor on
![]() $S/I,$
we obtain
$S/I,$
we obtain
 $$ \begin{align*} H_{R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{z}_{n-2k+2})}(t) &= H_{R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k})}(t) \\ &\hspace{1cm}- tH_{R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}):( \overline{z}_{n-2k+2})}(t) \\ &= \frac{(1-k)t^2+2(k-1)t+1}{(1-t)} - t(1+\alpha t) \\\ &= \frac{\alpha t^3+(2-\alpha-k)t^2+(2k-3)t+1}{(1-t)} \\ &= 1+(2k-2)t+(k-\alpha)t^2 + \sum_{j=3}^{\infty} k t^j. \end{align*} $$
$$ \begin{align*} H_{R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{z}_{n-2k+2})}(t) &= H_{R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k})}(t) \\ &\hspace{1cm}- tH_{R/( \overline{x}_0, \overline{l}_0,\ldots, \overline{l}_{n-2k}):( \overline{z}_{n-2k+2})}(t) \\ &= \frac{(1-k)t^2+2(k-1)t+1}{(1-t)} - t(1+\alpha t) \\\ &= \frac{\alpha t^3+(2-\alpha-k)t^2+(2k-3)t+1}{(1-t)} \\ &= 1+(2k-2)t+(k-\alpha)t^2 + \sum_{j=3}^{\infty} k t^j. \end{align*} $$
We also have the containment
Using Claim 4.5, we obtain the equality
which has Hilbert series computed in Equation (5). Hence,
 $$ \begin{align*} H_{R/(( \overline{l}_0, \overline{l}_{1}, \overline{l}_2,\ldots, \overline{l}_{n-2k}, \overline{x}_0):( \overline{x}_{1}))}(t) &= \frac{(k-1)t+1}{1-t} = 1 + \sum_{j=1}^{\infty} k t^j. \end{align*} $$
$$ \begin{align*} H_{R/(( \overline{l}_0, \overline{l}_{1}, \overline{l}_2,\ldots, \overline{l}_{n-2k}, \overline{x}_0):( \overline{x}_{1}))}(t) &= \frac{(k-1)t+1}{1-t} = 1 + \sum_{j=1}^{\infty} k t^j. \end{align*} $$
Comparing coefficients of
![]() $t^2$
yields
$t^2$
yields
![]() $k \leq k - \alpha ,$
and so
$k \leq k - \alpha ,$
and so
![]() $\alpha =0,$
proving the first equality. We immediately have the equality
$\alpha =0,$
proving the first equality. We immediately have the equality
for each
![]() $i =n-2k+2,\ldots , n-k.$
$i =n-2k+2,\ldots , n-k.$
Notice that setting
![]() $\alpha = 0,$
yields
$\alpha = 0,$
yields
 $$ \begin{align*} H_{R/( \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2})}(t) = \frac{(2-k)t^2+(2k-3)t+1}{(1-t)}. \end{align*} $$
$$ \begin{align*} H_{R/( \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2})}(t) = \frac{(2-k)t^2+(2k-3)t+1}{(1-t)}. \end{align*} $$
Denote
![]() $V_i$
and
$V_i$
and
![]() $V_i'$
to be the ideals
$V_i'$
to be the ideals
and
for
![]() $i = n-2k+2,\ldots ,n-k$
. Replacing the ideals in Equation (8) with the three ideals
$i = n-2k+2,\ldots ,n-k$
. Replacing the ideals in Equation (8) with the three ideals
![]() $V_{n-2k+3},V_{n-2k+2},$
and
$V_{n-2k+3},V_{n-2k+2},$
and
![]() $V_{n-2k+2}:( \overline {z}_{n-2k+3})$
, and using the additivity of the Hilbert series yields
$V_{n-2k+2}:( \overline {z}_{n-2k+3})$
, and using the additivity of the Hilbert series yields
 $$ \begin{align*} H_{R/V_{n-2k+3}}(t) &= H_{R/V_{n-2k+2}}(t) -t H_{R/V_{n-2k+2}:( \overline{z}_{n-2k+3})}(t) \\ &= \frac{(2-k)t^2+(2k-3)t+1}{(1-t)} - t \\ &= \frac{(3-k)t^2+(2k-4)t+1}{(1-t)}. \end{align*} $$
$$ \begin{align*} H_{R/V_{n-2k+3}}(t) &= H_{R/V_{n-2k+2}}(t) -t H_{R/V_{n-2k+2}:( \overline{z}_{n-2k+3})}(t) \\ &= \frac{(2-k)t^2+(2k-3)t+1}{(1-t)} - t \\ &= \frac{(3-k)t^2+(2k-4)t+1}{(1-t)}. \end{align*} $$
Continuing in this fashion gives
 $$ \begin{align*} H_{R/V_{n-k}}(t) &= \frac{(k-1)t+1}{(1-t)}. \end{align*} $$
$$ \begin{align*} H_{R/V_{n-k}}(t) &= \frac{(k-1)t+1}{(1-t)}. \end{align*} $$
So, both
![]() $( \overline {x}_0):( \overline {x}_1)$
and
$( \overline {x}_0):( \overline {x}_1)$
and
![]() $V_{n-k}$
have the same Hilbert series. Furthermore,
$V_{n-k}$
have the same Hilbert series. Furthermore,
![]() $V_{n-k}\subseteq ( \overline {x}_0):( \overline {x}_1).$
So these ideals are in fact equal. Interchanging
$V_{n-k}\subseteq ( \overline {x}_0):( \overline {x}_1).$
So these ideals are in fact equal. Interchanging
![]() $x_0$
and
$x_0$
and
![]() $x_1$
with
$x_1$
with
![]() $l_0$
and
$l_0$
and
![]() $l_1$
yields the remaining equality.
$l_1$
yields the remaining equality.
Claim 4.7. We have the equalities
and
Proof. The two equalities follow immediately since
![]() $(0_R):( \overline {x}_0) \subseteq ( \overline {l}_0,\ldots , \overline {l}_{n-2k})$
and
$(0_R):( \overline {x}_0) \subseteq ( \overline {l}_0,\ldots , \overline {l}_{n-2k})$
and
![]() $(0_R):( \overline {l}_0) \subseteq ( \overline {x}_0,\ldots , \overline {x}_{n-2k})$
and all four ideals have the same Hilbert series by Claim 4.5.
$(0_R):( \overline {l}_0) \subseteq ( \overline {x}_0,\ldots , \overline {x}_{n-2k})$
and all four ideals have the same Hilbert series by Claim 4.5.
Claim 4.8. We have the equality
for
![]() $i=2,\ldots ,n-2k-1.$
$i=2,\ldots ,n-2k-1.$
Proof. Using the short exact sequence
and the Hilbert series from Equation (7), we get
 $$ \begin{align*} H_{R/(( \overline{x}_0,\ldots, \overline{x}_i):( \overline{x}_{i+1}))}(t) &= \frac{1}{t} \Bigg( H_{R/( \overline{x}_0,\ldots, \overline{x}_i)}(t) - H_{R/( \overline{x}_0,\ldots, \overline{x}_i, \overline{x}_{i+1})}(t) \Bigg) \\ &= \frac{1}{t} \bigg( \tfrac{(n-2k-i)t^3+(3k-2n+2i+1)t^2+(n-(i+2))t+1}{(1-t)^2} \\ & \hspace{1cm} -\tfrac{(n-2k-i-1)t^3+(3k-2n+2i+3)t^2+(n-(i+3))t+1}{(1-t)^2}\bigg) \\ &= \frac{t^2-2t+1}{(1-t)^2} \\ &= 1, \end{align*} $$
$$ \begin{align*} H_{R/(( \overline{x}_0,\ldots, \overline{x}_i):( \overline{x}_{i+1}))}(t) &= \frac{1}{t} \Bigg( H_{R/( \overline{x}_0,\ldots, \overline{x}_i)}(t) - H_{R/( \overline{x}_0,\ldots, \overline{x}_i, \overline{x}_{i+1})}(t) \Bigg) \\ &= \frac{1}{t} \bigg( \tfrac{(n-2k-i)t^3+(3k-2n+2i+1)t^2+(n-(i+2))t+1}{(1-t)^2} \\ & \hspace{1cm} -\tfrac{(n-2k-i-1)t^3+(3k-2n+2i+3)t^2+(n-(i+3))t+1}{(1-t)^2}\bigg) \\ &= \frac{t^2-2t+1}{(1-t)^2} \\ &= 1, \end{align*} $$
proving the claim.
Claim 4.9. We have the four equalities
Proof. The equality
follows from the genericity of
![]() $l_0.$
We now aim to show the equality
$l_0.$
We now aim to show the equality
We always have the containment
![]() $V_{n-k} \subseteq V_{n-k}:( \overline {x}_1)$
and by Claim 4.6, we have already determined
$V_{n-k} \subseteq V_{n-k}:( \overline {x}_1)$
and by Claim 4.6, we have already determined
![]() $H_{R/V_{n-k}}(t).$
So, we must only determine
$H_{R/V_{n-k}}(t).$
So, we must only determine
![]() $H_{R/(V_{n-k}:( \overline {x}_1))}(t).$
We aim to use the additivity of the Hilbert series along the short exact sequence
$H_{R/(V_{n-k}:( \overline {x}_1))}(t).$
We aim to use the additivity of the Hilbert series along the short exact sequence
but we first must determine
![]() $H_{R/(V_{n-k}+( \overline {x}_1))}(t).$
By Claim 4.4, adding the linear forms
$H_{R/(V_{n-k}+( \overline {x}_1))}(t).$
By Claim 4.4, adding the linear forms
![]() $ \overline {l}_2,\ldots , \overline {l}_{n-2k}, \overline {z}_{n-2k+2},\ldots , \overline {z}_{n-k}$
to the ideal
$ \overline {l}_2,\ldots , \overline {l}_{n-2k}, \overline {z}_{n-2k+2},\ldots , \overline {z}_{n-k}$
to the ideal
![]() $( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1)$
yields the Hilbert series
$( \overline {x}_0, \overline {x}_1, \overline {l}_0, \overline {l}_1)$
yields the Hilbert series
Using Claim 4.6 and the additivity of the Hilbert series along the short exact sequence (10) yields
 $$ \begin{align*} H_{R/(V_{n-k}:( \overline{x}_1))}(t) &= \frac{1}{t} \Bigg( H_{R/V_{n-k}}(t) -H_{R/(V_{n-k}+( \overline{x}_1))}(t) \Bigg) \\ &= \frac{1}{t}\bigg(\frac{(k-1)t+1}{(1-t)}- (1+(k-1)t)\bigg)\\ &= \frac{(k-1)t+1}{(1-t)}. \end{align*} $$
$$ \begin{align*} H_{R/(V_{n-k}:( \overline{x}_1))}(t) &= \frac{1}{t} \Bigg( H_{R/V_{n-k}}(t) -H_{R/(V_{n-k}+( \overline{x}_1))}(t) \Bigg) \\ &= \frac{1}{t}\bigg(\frac{(k-1)t+1}{(1-t)}- (1+(k-1)t)\bigg)\\ &= \frac{(k-1)t+1}{(1-t)}. \end{align*} $$
Interchanging
![]() $ \overline {x}_0$
and
$ \overline {x}_0$
and
![]() $ \overline {x}_1$
with
$ \overline {x}_1$
with
![]() $ \overline {l}_0$
and
$ \overline {l}_0$
and
![]() $ \overline {l}_1,$
proves the other two equalities.
$ \overline {l}_1,$
proves the other two equalities.
Below is a list of calculated colons with the corresponding justification.
 $$ \begin{align*}\begin{cases} (0):( \overline{x}_0) =( \overline{l}_0,\dots, \overline{l}_{n-2k}), \hspace{1cm} (0):( \overline{l}_0)=( \overline{x}_0,\ldots, \overline{x}_{n-2k}), \hspace{.2cm} 4.7 \\ ( \overline{x}_0):( \overline{x}_1) = ( \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2},\ldots, \overline{z}_{n-k}), \hspace{.2cm} 4.6 \\ \hspace{.3cm} ( \overline{l}_0):( \overline{l}_1)=( \overline{x}_0,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}), \hspace{.2cm} 4.6 \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2,\ldots, \overline{x}_i):( \overline{x}_{i+1})=\mathfrak{m}_R, \hspace{.5cm} i=2,\ldots, n-2k-1, \hspace{.2cm}4.8 \\ \hspace{.5cm} ( \overline{l}_0, \overline{l}_1, \overline{l}_2,\ldots, \overline{l}_i):( \overline{l}_{i+1})=\mathfrak{m}_R, \hspace{.5cm} i=2,\ldots, n-2k-1, \hspace{.2cm}4.8 \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2,\ldots, \overline{x}_{n-2k}):( \overline{l}_{0})=( \overline{l}_0,\ldots, \overline{l}_{n-2k}), \hspace{.2cm} 4.9\\ \hspace{.5cm} ( \overline{l}_0, \overline{l}_1, \overline{l}_2,\ldots, \overline{l}_{n-2k}):( \overline{x}_{0})=( \overline{x}_0,\ldots, \overline{x}_{n-2k}), \hspace{.2cm} 4.9 \\ ( \overline{x}_0,\ldots, \overline{x}_{n-2k}, \overline{l}_0):( \overline{y}_{n-2k+2}) = \mathfrak{m}_R, \hspace{.2cm} 4.6 \\ \hspace{.5cm} ( \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{x}_0):( \overline{z}_{n-2k+2}) = \mathfrak{m}_R, \hspace{.2cm} 4.6 \\ V_{i}':( \overline{y}_{i+1})= \mathfrak{m}_R, \hspace{.3cm} V_{i}:( \overline{z}_{i+1})= \mathfrak{m}_R, \hspace{.1cm} i=n-2k+2,\ldots, n-k-1, \hspace{.2cm} 4.6 \\ \hspace{.3cm} V_{n-k}':( \overline{l}_1)=V_{n-k}',\hspace{.3cm} V_{n-k}:( \overline{x}_1)= V_{n-k}, \hspace{.2cm} 4.9 \\ (V_{n-k}'+( \overline{l}_1)):( \overline{u}_{n-k+1})=\mathfrak{m}_R, \hspace{.3cm} \hspace{.2cm}(V_{n-k}+( \overline{x}_1)):( \overline{w}_{n-k+1})=\mathfrak{m}_R, \hspace{.2cm} 4.4 \\ \hspace{.3cm}(V_{n-k}'+( \overline{l}_1, \overline{u}_{n-k+1},\ldots, \overline{u}_i)):( \overline{u}_{i+1})=\mathfrak{m}_R, \hspace{.01cm} i = n-k+1,\ldots,n-1, \hspace{.2cm} 4.4 \\ (V_{n-k}+( \overline{x}_1, \overline{w}_{n-k+1},\ldots, \overline{w}_i)):( \overline{w}_{i+1})=\mathfrak{m}_R, \hspace{.01cm} i = n-k+1,\ldots,n-1. \hspace{.2cm}4.4 \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} (0):( \overline{x}_0) =( \overline{l}_0,\dots, \overline{l}_{n-2k}), \hspace{1cm} (0):( \overline{l}_0)=( \overline{x}_0,\ldots, \overline{x}_{n-2k}), \hspace{.2cm} 4.7 \\ ( \overline{x}_0):( \overline{x}_1) = ( \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{x}_0, \overline{z}_{n-2k+2},\ldots, \overline{z}_{n-k}), \hspace{.2cm} 4.6 \\ \hspace{.3cm} ( \overline{l}_0):( \overline{l}_1)=( \overline{x}_0,\ldots, \overline{x}_{n-2k}, \overline{l}_0, \overline{y}_{n-2k+2},\ldots, \overline{y}_{n-k}), \hspace{.2cm} 4.6 \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2,\ldots, \overline{x}_i):( \overline{x}_{i+1})=\mathfrak{m}_R, \hspace{.5cm} i=2,\ldots, n-2k-1, \hspace{.2cm}4.8 \\ \hspace{.5cm} ( \overline{l}_0, \overline{l}_1, \overline{l}_2,\ldots, \overline{l}_i):( \overline{l}_{i+1})=\mathfrak{m}_R, \hspace{.5cm} i=2,\ldots, n-2k-1, \hspace{.2cm}4.8 \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2,\ldots, \overline{x}_{n-2k}):( \overline{l}_{0})=( \overline{l}_0,\ldots, \overline{l}_{n-2k}), \hspace{.2cm} 4.9\\ \hspace{.5cm} ( \overline{l}_0, \overline{l}_1, \overline{l}_2,\ldots, \overline{l}_{n-2k}):( \overline{x}_{0})=( \overline{x}_0,\ldots, \overline{x}_{n-2k}), \hspace{.2cm} 4.9 \\ ( \overline{x}_0,\ldots, \overline{x}_{n-2k}, \overline{l}_0):( \overline{y}_{n-2k+2}) = \mathfrak{m}_R, \hspace{.2cm} 4.6 \\ \hspace{.5cm} ( \overline{l}_0,\ldots, \overline{l}_{n-2k}, \overline{x}_0):( \overline{z}_{n-2k+2}) = \mathfrak{m}_R, \hspace{.2cm} 4.6 \\ V_{i}':( \overline{y}_{i+1})= \mathfrak{m}_R, \hspace{.3cm} V_{i}:( \overline{z}_{i+1})= \mathfrak{m}_R, \hspace{.1cm} i=n-2k+2,\ldots, n-k-1, \hspace{.2cm} 4.6 \\ \hspace{.3cm} V_{n-k}':( \overline{l}_1)=V_{n-k}',\hspace{.3cm} V_{n-k}:( \overline{x}_1)= V_{n-k}, \hspace{.2cm} 4.9 \\ (V_{n-k}'+( \overline{l}_1)):( \overline{u}_{n-k+1})=\mathfrak{m}_R, \hspace{.3cm} \hspace{.2cm}(V_{n-k}+( \overline{x}_1)):( \overline{w}_{n-k+1})=\mathfrak{m}_R, \hspace{.2cm} 4.4 \\ \hspace{.3cm}(V_{n-k}'+( \overline{l}_1, \overline{u}_{n-k+1},\ldots, \overline{u}_i)):( \overline{u}_{i+1})=\mathfrak{m}_R, \hspace{.01cm} i = n-k+1,\ldots,n-1, \hspace{.2cm} 4.4 \\ (V_{n-k}+( \overline{x}_1, \overline{w}_{n-k+1},\ldots, \overline{w}_i)):( \overline{w}_{i+1})=\mathfrak{m}_R, \hspace{.01cm} i = n-k+1,\ldots,n-1. \hspace{.2cm}4.4 \end{cases}\end{align*} $$
This completes the proof of Theorem 4.3.
There is at least one example of a coordinate ring with the Koszul property which is not covered by our previous theorem. Let
![]() $\mathcal {M}$
be a generic collection of five lines in
$\mathcal {M}$
be a generic collection of five lines in
![]() $\mathbb {P}^6.$
By Remark 2.8 and a change of basis, we may assume the defining ideals for our five lines have the following form:
$\mathbb {P}^6.$
By Remark 2.8 and a change of basis, we may assume the defining ideals for our five lines have the following form:
 $$ \begin{align*} L_1 &= ( x_0,x_3,x_4,x_5,x_6), \hspace{3.1cm} L_2 = (x_0,x_1,x_4,x_5,x_2+ax_3+x_6), \\ L_3 &= (x_0,x_1,x_2,x_6,x_3+bx_4+x_5), \hspace{1.25cm} L_4 = (x_1,x_2,x_3,x_5,x_0+x_4+x_6), \\ & \hspace{3cm}L_5 = (x_2,x_3,x_4,x_6,x_0+x_1+x_5), \end{align*} $$
$$ \begin{align*} L_1 &= ( x_0,x_3,x_4,x_5,x_6), \hspace{3.1cm} L_2 = (x_0,x_1,x_4,x_5,x_2+ax_3+x_6), \\ L_3 &= (x_0,x_1,x_2,x_6,x_3+bx_4+x_5), \hspace{1.25cm} L_4 = (x_1,x_2,x_3,x_5,x_0+x_4+x_6), \\ & \hspace{3cm}L_5 = (x_2,x_3,x_4,x_6,x_0+x_1+x_5), \end{align*} $$
where
![]() $a,b \in \mathbb {C}$
are algebraically independent over
$a,b \in \mathbb {C}$
are algebraically independent over
![]() $\mathbb {Q}.$
Some further explanation is needed why we may assume our five lines have this form.
$\mathbb {Q}.$
Some further explanation is needed why we may assume our five lines have this form.
By Remark 2.8, the intersection of any triple of the defining ideals of our five lines contains a single linear form in a minimal generating set. Furthermore, the intersection of any pair of defining ideals for our five contains three linear forms in a minimal generating set. Thus, after a change of basis, we may assume
 $$ \begin{align*} L_1 &= ( x_0,x_3,x_4,x_5,x_6), \hspace{1.5cm} L_2 = (x_0,x_1,x_4,x_5,l_0), \\ L_3 &= (x_0,x_1,x_2,x_6,l_1), \hspace{1.6cm} L_4 = (x_1,x_2,x_3,x_5,l_2), \\ & \hspace{2.7cm}L_5 = (x_2,x_3,x_4,x_6,l_3). \end{align*} $$
$$ \begin{align*} L_1 &= ( x_0,x_3,x_4,x_5,x_6), \hspace{1.5cm} L_2 = (x_0,x_1,x_4,x_5,l_0), \\ L_3 &= (x_0,x_1,x_2,x_6,l_1), \hspace{1.6cm} L_4 = (x_1,x_2,x_3,x_5,l_2), \\ & \hspace{2.7cm}L_5 = (x_2,x_3,x_4,x_6,l_3). \end{align*} $$
where the linear forms
![]() $l_0,\ldots ,l_3$
have the form
$l_0,\ldots ,l_3$
have the form
 $$ \begin{align*} l_0 &= c_{0,2}x_2+c_{0,3}x_3+c_{0,6}x_6, \hspace{1cm} l_1 = c_{1,3}x_3+c_{1,4}x_4+c_{1,5}x_5, \\ l_2 &= c_{2,0}x_0+c_{2,4}x_4+c_{2,6}x_6, \hspace{1cm} l_3 = c_{3,0}x_0+c_{3,1}x_1+c_{3,5}x_5. \end{align*} $$
$$ \begin{align*} l_0 &= c_{0,2}x_2+c_{0,3}x_3+c_{0,6}x_6, \hspace{1cm} l_1 = c_{1,3}x_3+c_{1,4}x_4+c_{1,5}x_5, \\ l_2 &= c_{2,0}x_0+c_{2,4}x_4+c_{2,6}x_6, \hspace{1cm} l_3 = c_{3,0}x_0+c_{3,1}x_1+c_{3,5}x_5. \end{align*} $$
It is of no loss to assume these are all monic in certain indeterminates. That is they have the form
 $$ \begin{align*} l_0 &= c_{0,2}x_2+c_{0,3}x_3+x_6, \hspace{1cm} l_1 = x_3+c_{1,4}x_4+c_{1,5}x_5, \\ l_2 &= x_0+c_{2,4}x_4+c_{2,6}x_6, \hspace{1cm} l_3 = c_{3,0}x_0+c_{3,1}x_1+x_5. \end{align*} $$
$$ \begin{align*} l_0 &= c_{0,2}x_2+c_{0,3}x_3+x_6, \hspace{1cm} l_1 = x_3+c_{1,4}x_4+c_{1,5}x_5, \\ l_2 &= x_0+c_{2,4}x_4+c_{2,6}x_6, \hspace{1cm} l_3 = c_{3,0}x_0+c_{3,1}x_1+x_5. \end{align*} $$
Through a change of basis, we may reduce the coefficient on
![]() $x_5$
in
$x_5$
in
![]() $l_1$
to
$l_1$
to
![]() $1,$
and then normalize
$1,$
and then normalize
![]() $l_3$
to be monic in
$l_3$
to be monic in
![]() $x_5;$
then through another change of basis, we may reduce the coefficient on
$x_5;$
then through another change of basis, we may reduce the coefficient on
![]() $x_0$
in
$x_0$
in
![]() $l_3$
to
$l_3$
to
![]() $1,$
and then normalize
$1,$
and then normalize
![]() $l_2$
to be monic in
$l_2$
to be monic in
![]() $x_0;$
then through another change of basis, we may reduce the coefficient on
$x_0;$
then through another change of basis, we may reduce the coefficient on
![]() $x_6$
in
$x_6$
in
![]() $l_2$
to
$l_2$
to
![]() $1,$
and then normalize
$1,$
and then normalize
![]() $l_0$
to be monic in
$l_0$
to be monic in
![]() $x_6;$
then through another change of basis, we may reduce the coefficient on
$x_6;$
then through another change of basis, we may reduce the coefficient on
![]() $x_2$
in
$x_2$
in
![]() $l_0$
to
$l_0$
to
![]() $1;$
then through another change of basis, we may reduce the coefficient on
$1;$
then through another change of basis, we may reduce the coefficient on
![]() $x_4$
in
$x_4$
in
![]() $l_2$
to
$l_2$
to
![]() $1;$
then through another change of basis, we may reduce the coefficient on
$1;$
then through another change of basis, we may reduce the coefficient on
![]() $x_1$
in
$x_1$
in
![]() $l_3$
to
$l_3$
to
![]() $1.$
Ultimately, we obtain
$1.$
Ultimately, we obtain
 $$ \begin{align*} l_0 &= x_2+c_{0,3}x_3+x_6, \hspace{1cm} l_1 = x_3+c_{1,4}x_4+x_5, \\ l_2 &= x_0+x_4+x_6, \hspace{1.6cm} l_3 = x_0+x_1+x_5. \end{align*} $$
$$ \begin{align*} l_0 &= x_2+c_{0,3}x_3+x_6, \hspace{1cm} l_1 = x_3+c_{1,4}x_4+x_5, \\ l_2 &= x_0+x_4+x_6, \hspace{1.6cm} l_3 = x_0+x_1+x_5. \end{align*} $$
Note the order in which we make these reductions is important.
Proposition 4.10. Let
![]() $\mathcal {M}$
be a generic collection of five lines in
$\mathcal {M}$
be a generic collection of five lines in
![]() $\mathbb {P}^6$
, and let R be the coordinate ring. Then R is Koszul.
$\mathbb {P}^6$
, and let R be the coordinate ring. Then R is Koszul.
Proof. After a change of basis, we may represent the defining ideal for our five lines as above. Below is a Koszul filtration
 $$ \begin{align*}\mathcal{F}= \begin{cases} (0_R), ( \overline{x}_0), ( \overline{x}_2), ( \overline{x}_0, \overline{x}_4),( \overline{x}_0, \overline{x}_1),( \overline{x}_2, \overline{x}_3),( \overline{x}_0, \overline{x}_6),( \overline{x}_0, \overline{x}_2, \overline{x}_3),\\ ( \overline{x}_2, \overline{x}_3, \overline{x}_0+ \overline{x}_1+ \overline{x}_4+ \overline{x}_5+ \overline{x}_6),( \overline{x}_0, \overline{x}_4, \overline{x}_5),( \overline{x}_0, \overline{x}_1, \overline{x}_2),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4), ( \overline{x}_0, \overline{x}_1, \overline{x}_4),( \overline{x}_0, \overline{x}_2, \overline{x}_4),( \overline{x}_0, \overline{x}_2, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+b \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5), ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_2+a \overline{x}_3+a \overline{x}_5+ \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_2, \overline{x}_4, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6), ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5), ( \overline{x}_0, \overline{x}_4, \overline{x}_5, \overline{x}_6), ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+b \overline{x}_4+b \overline{x}_6), ( \overline{x}_0, \overline{x}_2, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_3+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b} \overline{x}_5),( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_4+\frac{1}{a} \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+b \overline{x}_4+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_6), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5, \overline{x}_4+ \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_2+ \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6), ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_5), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b} \overline{x}_5), \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_6, \overline{x}_2+a \overline{x}_3+x_6), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_6, \overline{x}_3+ \overline{x}_5), \mathfrak{m}_R. \end{cases}\end{align*} $$
$$ \begin{align*}\mathcal{F}= \begin{cases} (0_R), ( \overline{x}_0), ( \overline{x}_2), ( \overline{x}_0, \overline{x}_4),( \overline{x}_0, \overline{x}_1),( \overline{x}_2, \overline{x}_3),( \overline{x}_0, \overline{x}_6),( \overline{x}_0, \overline{x}_2, \overline{x}_3),\\ ( \overline{x}_2, \overline{x}_3, \overline{x}_0+ \overline{x}_1+ \overline{x}_4+ \overline{x}_5+ \overline{x}_6),( \overline{x}_0, \overline{x}_4, \overline{x}_5),( \overline{x}_0, \overline{x}_1, \overline{x}_2),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4), ( \overline{x}_0, \overline{x}_1, \overline{x}_4),( \overline{x}_0, \overline{x}_2, \overline{x}_4),( \overline{x}_0, \overline{x}_2, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+b \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5), ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_2+a \overline{x}_3+a \overline{x}_5+ \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_2, \overline{x}_4, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6), ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5), ( \overline{x}_0, \overline{x}_4, \overline{x}_5, \overline{x}_6), ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+b \overline{x}_4+b \overline{x}_6), ( \overline{x}_0, \overline{x}_2, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_3+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b} \overline{x}_5),( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_4+\frac{1}{a} \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+b \overline{x}_4+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_6), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5, \overline{x}_4+ \overline{x}_6),( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_2+ \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6), ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_5), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b} \overline{x}_5), \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_6, \overline{x}_2+a \overline{x}_3+x_6), ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_6, \overline{x}_3+ \overline{x}_5), \mathfrak{m}_R. \end{cases}\end{align*} $$
The calculated colons are
 $$ \begin{align*}\begin{cases} (0_R):( \overline{x}_0) = ( \overline{x}_2, \overline{x}_3, \overline{x}_0+ \overline{x}_1+ \overline{x}_4+ \overline{x}_5+ \overline{x}_6),\\ (0_R):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_4, \overline{x}_5), \\ ( \overline{x}_0):( \overline{x}_4) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+b \overline{x}_6),\\ ( \overline{x}_0):( \overline{x}_1) = ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_6), \\ ( \overline{x}_2):( \overline{x}_3) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+\frac{1}{a} \overline{x}_6), \\ ( \overline{x}_0):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_2, \overline{x}_3):( \overline{x}_0)=( \overline{x}_2, \overline{x}_3, \overline{x}_0+ \overline{x}_1+ \overline{x}_4+ \overline{x}_5+ \overline{x}_6), \\ ( \overline{x}_2, \overline{x}_3):( \overline{x}_0+ \overline{x}_1+ \overline{x}_4+ \overline{x}_5+ \overline{x}_6)=( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b} \overline{x}_5), \\ ( \overline{x}_0, \overline{x}_4):( \overline{x}_5) = ( \overline{x}_0, \overline{x}_2, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_3+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5) ( \overline{x}_0, \overline{x}_4):( \overline{x}_3) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_2+a \overline{x}_3+a \overline{x}_5+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1):( \overline{x}_4) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+b \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_4):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_4, \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_6):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_4, \overline{x}_5, \overline{x}_6) ( \overline{x}_0, \overline{x}_1):( \overline{x}_5) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2):( \overline{x}_3+b \overline{x}_4+ \overline{x}_5+b \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2):( \overline{x}_3+b \overline{x}_4+ \overline{x}_5+\frac{1}{a} \overline{x}_6) =( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5, \overline{x}_4+ \overline{x}_6), \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} (0_R):( \overline{x}_0) = ( \overline{x}_2, \overline{x}_3, \overline{x}_0+ \overline{x}_1+ \overline{x}_4+ \overline{x}_5+ \overline{x}_6),\\ (0_R):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_4, \overline{x}_5), \\ ( \overline{x}_0):( \overline{x}_4) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+b \overline{x}_6),\\ ( \overline{x}_0):( \overline{x}_1) = ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_6), \\ ( \overline{x}_2):( \overline{x}_3) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+\frac{1}{a} \overline{x}_6), \\ ( \overline{x}_0):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_2, \overline{x}_3):( \overline{x}_0)=( \overline{x}_2, \overline{x}_3, \overline{x}_0+ \overline{x}_1+ \overline{x}_4+ \overline{x}_5+ \overline{x}_6), \\ ( \overline{x}_2, \overline{x}_3):( \overline{x}_0+ \overline{x}_1+ \overline{x}_4+ \overline{x}_5+ \overline{x}_6)=( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b} \overline{x}_5), \\ ( \overline{x}_0, \overline{x}_4):( \overline{x}_5) = ( \overline{x}_0, \overline{x}_2, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_3+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5) ( \overline{x}_0, \overline{x}_4):( \overline{x}_3) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_2+a \overline{x}_3+a \overline{x}_5+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1):( \overline{x}_4) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3+b \overline{x}_4+ \overline{x}_5+b \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_4):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_4, \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_6):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_4, \overline{x}_5, \overline{x}_6) ( \overline{x}_0, \overline{x}_1):( \overline{x}_5) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2):( \overline{x}_3+b \overline{x}_4+ \overline{x}_5+b \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2):( \overline{x}_3+b \overline{x}_4+ \overline{x}_5+\frac{1}{a} \overline{x}_6) =( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5, \overline{x}_4+ \overline{x}_6), \end{cases}\end{align*} $$
 $$ \begin{align*}\begin{cases} ( \overline{x}_0, \overline{x}_3, \overline{x}_4):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_2+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4):( \overline{x}_5) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_6, \overline{x}_3+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4):( \overline{x}_2+a \overline{x}_3+a \overline{x}_5+ \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_4):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_4+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5, \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_5):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2):( \overline{x}_5) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_4, \overline{x}_5):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_5):( \overline{x}_2+a \overline{x}_3+ \overline{x}_4+ \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_3+b \overline{x}_4+b \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_2, \overline{x}_4, \overline{x}_6):( \overline{x}_1+ \overline{x}_3+ \overline{x}_5) = ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6):( \overline{x}_4+\frac{1}{b} \overline{x}_5 ) = ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_6):( \overline{x}_5 ) = ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6):( \overline{x}_3+b \overline{x}_4+ \overline{x}_5) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_4 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+b \overline{x}_4+bx_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6):( \overline{x}_4 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b} \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_3 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+b \overline{x}_4+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_3+\frac{1}{a} \overline{x}_4+\frac{1}{a} \overline{x}_6)=( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4), \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_3+b \overline{x}_4+\frac{1}{a} \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5, \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5):( \overline{x}_3 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6):( \overline{x}_3+b \overline{x}_4) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5):( \overline{x}_2+a \overline{x}_3+ \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6):( \overline{x}_3 +b \overline{x}_4) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_6, \overline{x}_2+a \overline{x}_3),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_4+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6):( \overline{x}_4 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6):( \overline{x}_3+b \overline{x}_4+ \overline{x}_5) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5):( \overline{x}_3+\frac{1}{a} \overline{x}_6) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5):( \overline{x}_4+ \overline{x}_6) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5):( \overline{x}_2+ \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6):( \overline{x}_1) = ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6):( \overline{x}_1+ \overline{x}_5) = ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b}x_5):( \overline{x}_1)= ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6):( \overline{x}_6)= ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} ( \overline{x}_0, \overline{x}_3, \overline{x}_4):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_2+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4):( \overline{x}_5) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_6, \overline{x}_3+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4):( \overline{x}_2+a \overline{x}_3+a \overline{x}_5+ \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_4):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_4+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5, \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_5):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2):( \overline{x}_5) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_4, \overline{x}_5):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_5):( \overline{x}_2+a \overline{x}_3+ \overline{x}_4+ \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_3+b \overline{x}_4+b \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_6), \\ ( \overline{x}_0, \overline{x}_2, \overline{x}_4, \overline{x}_6):( \overline{x}_1+ \overline{x}_3+ \overline{x}_5) = ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6):( \overline{x}_4+\frac{1}{b} \overline{x}_5 ) = ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_6):( \overline{x}_5 ) = ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6, \overline{x}_1+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6):( \overline{x}_3+b \overline{x}_4+ \overline{x}_5) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_4 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+b \overline{x}_4+bx_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6):( \overline{x}_4 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b} \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_3 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+b \overline{x}_4+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_3+\frac{1}{a} \overline{x}_4+\frac{1}{a} \overline{x}_6)=( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4), \\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_3+b \overline{x}_4+\frac{1}{a} \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5, \overline{x}_4+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5):( \overline{x}_3 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6):( \overline{x}_3+b \overline{x}_4) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5):( \overline{x}_2+a \overline{x}_3+ \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6):( \overline{x}_3 +b \overline{x}_4) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_6, \overline{x}_2+a \overline{x}_3),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5):( \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_5, \overline{x}_3+\frac{1}{a} \overline{x}_4+\frac{1}{a} \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6):( \overline{x}_4 ) = ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6, \overline{x}_3+b \overline{x}_4+ \overline{x}_5),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_6):( \overline{x}_3+b \overline{x}_4+ \overline{x}_5) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_5):( \overline{x}_3+\frac{1}{a} \overline{x}_6) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_3, \overline{x}_5):( \overline{x}_4+ \overline{x}_6) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5):( \overline{x}_2+ \overline{x}_6) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6):( \overline{x}_1) = ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_6):( \overline{x}_1+ \overline{x}_5) = ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_6, \overline{x}_4+\frac{1}{b}x_5):( \overline{x}_1)= ( \overline{x}_0, \overline{x}_2, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6):( \overline{x}_6)= ( \overline{x}_0, \overline{x}_1, \overline{x}_4, \overline{x}_5, \overline{x}_2+a \overline{x}_3+ \overline{x}_6),\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_5, \overline{x}_6, \overline{x}_3+b \overline{x}_4):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6),\end{cases}\end{align*} $$
 $$ \begin{align*}\begin{cases} ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_6):( \overline{x}_3+ \overline{x}_5) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6). \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} ( \overline{x}_0, \overline{x}_1, \overline{x}_2, \overline{x}_4, \overline{x}_6):( \overline{x}_3+ \overline{x}_5) = \mathfrak{m}_R,\\ ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6):( \overline{x}_2) = ( \overline{x}_0, \overline{x}_1, \overline{x}_3, \overline{x}_4, \overline{x}_5, \overline{x}_6). \end{cases}\end{align*} $$
Note that
![]() $|\mathcal {F}|=|57|.$
Every colon is a non-trivial calculation and requires significant effort; the interested reader may find a link to code verifying the filtration at the author’s website (https://www.joshuaandrewrice.com).
$|\mathcal {F}|=|57|.$
Every colon is a non-trivial calculation and requires significant effort; the interested reader may find a link to code verifying the filtration at the author’s website (https://www.joshuaandrewrice.com).
5 Hilbert function obstruction to the Koszul property
In this section, we determine when the coordinate ring of a generic collection of lines is not Koszul. But first, we need a theorem from Complex Analysis.
Theorem 5.1. (Vivanti–Pringsheim [Reference Remmert21, Chap. 8, §1])
Let the power series
![]() $f(z) = \sum a_v z^v$
have positive finite radius of convergence r and suppose that all but finitely many of its coefficients
$f(z) = \sum a_v z^v$
have positive finite radius of convergence r and suppose that all but finitely many of its coefficients
![]() $a_v$
are real and nonnegative. Then
$a_v$
are real and nonnegative. Then
![]() $z = r$
is a singular point of
$z = r$
is a singular point of
![]() $f(z)$
.
$f(z)$
.
Theorem 5.2. Let
![]() $\mathcal {M}$
be a generic collection of m lines in
$\mathcal {M}$
be a generic collection of m lines in
![]() $\mathbb {P}^n$
with
$\mathbb {P}^n$
with
![]() $n \geq 2$
, and let R be the coordinate ring of
$n \geq 2$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
If
$\mathcal {M}.$
If
then R is not Koszul.
Proof. We prove the claim by contradiction. Suppose that
![]() $\mathrm {reg}_S(R) = \alpha .$
Note that by Theorem 3.5,
$\mathrm {reg}_S(R) = \alpha .$
Note that by Theorem 3.5,
![]() $\alpha $
is the smallest nonnegative integer such that
$\alpha $
is the smallest nonnegative integer such that
![]() $\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
We have four cases:
$\binom {n+\alpha }{\alpha } \geq m(\alpha +1).$
We have four cases:
![]() $\alpha =0, \alpha = 1, \alpha =2,$
or
$\alpha =0, \alpha = 1, \alpha =2,$
or
![]() $\alpha \geq 3.$
$\alpha \geq 3.$
-
1. Suppose that
 $\alpha = 0.$
Then a contradiction.
$\alpha = 0.$
Then a contradiction. $$ \begin{align*}1 < \frac{1}{72}\left(3(n^2+10n+13)+\sqrt{3(n-1)^3(3n+5)}\right) < m \leq 1,\end{align*} $$
$$ \begin{align*}1 < \frac{1}{72}\left(3(n^2+10n+13)+\sqrt{3(n-1)^3(3n+5)}\right) < m \leq 1,\end{align*} $$
-
2. If
 $\alpha = 1,$
then
$\alpha = 1,$
then
 $2m \leq n+1,$
and hence a contradiction.
$2m \leq n+1,$
and hence a contradiction. $$ \begin{align*} m &\leq \frac{n+1}{2} < \frac{1}{72}\bigg(3(n^2+10n+13)+\sqrt{3(n-1)^3(3n+5)}\bigg)< m, \hspace{-.8cm} \end{align*} $$
$$ \begin{align*} m &\leq \frac{n+1}{2} < \frac{1}{72}\bigg(3(n^2+10n+13)+\sqrt{3(n-1)^3(3n+5)}\bigg)< m, \hspace{-.8cm} \end{align*} $$
-
3. Now assume that
 $\alpha =2$
and that R is Koszul. By Lemma 4.2, the Hilbert series for R is
$\alpha =2$
and that R is Koszul. By Lemma 4.2, the Hilbert series for R is  $$ \begin{align*} H_R(t) &= \frac{(n+1-2m)t^3+(3m-2n-1)t^2+(n-1)t +1}{ (1-t)^2}. \end{align*} $$
$$ \begin{align*} H_R(t) &= \frac{(n+1-2m)t^3+(3m-2n-1)t^2+(n-1)t +1}{ (1-t)^2}. \end{align*} $$
Thus, by Equation (2),
 $$ \begin{align*}\text{P}_{\mathbb{C}}^R(t) =\frac{1}{\text{H}_R(-t)}=\tfrac{(1+t)^2}{ (2m-n-1)t^3+(3m-2n-1)t^2 +(1-n)t+1}.\end{align*} $$
$$ \begin{align*}\text{P}_{\mathbb{C}}^R(t) =\frac{1}{\text{H}_R(-t)}=\tfrac{(1+t)^2}{ (2m-n-1)t^3+(3m-2n-1)t^2 +(1-n)t+1}.\end{align*} $$
Denote
and note the leading coefficient is positive, since $$ \begin{align*}p(t) =1+(1-n)t+(3m-2n-1)t^2+(2m-n-1)t^3\end{align*} $$
$$ \begin{align*}p(t) =1+(1-n)t+(3m-2n-1)t^2+(2m-n-1)t^3\end{align*} $$
 $n+1 < 2m$
. By the Intermediate Value Theorem
$n+1 < 2m$
. By the Intermediate Value Theorem
 $p(t)$
has a negative zero, since
$p(t)$
has a negative zero, since
 $p(0)=1$
and since
$p(0)=1$
and since $$ \begin{align*} p(-3)=-27m+12n+16 < 0,\end{align*} $$
$$ \begin{align*} p(-3)=-27m+12n+16 < 0,\end{align*} $$
 $n+1 < 2m$
and
$n+1 < 2m$
and
 $1<m.$
So, the radius of convergence r of
$1<m.$
So, the radius of convergence r of
 $P_{\mathbb {C}}^R(t)$
is finite and all the coefficients are positive. So, by Theorem 5.1, r must occur as a singular point of
$P_{\mathbb {C}}^R(t)$
is finite and all the coefficients are positive. So, by Theorem 5.1, r must occur as a singular point of
 $P_{\mathbb {C}}^R(t)$
; meaning that
$P_{\mathbb {C}}^R(t)$
; meaning that
 $p(t)$
must have three real roots and one of them must be positive. Recall that if the discriminant of a cubic polynomial with real coefficients is negative, then the polynomial has two non-real complex roots. Thus, the discriminant of
$p(t)$
must have three real roots and one of them must be positive. Recall that if the discriminant of a cubic polynomial with real coefficients is negative, then the polynomial has two non-real complex roots. Thus, the discriminant of
 $p(t)$
must be nonnegative. The discriminant of
$p(t)$
must be nonnegative. The discriminant of
 $p(t)$
is
$p(t)$
is  $$ \begin{align*} \Delta =-m (108 m^2 - 9 m (n^2 + 10 n + 13) + 4 (n + 2)^3).\end{align*} $$
$$ \begin{align*} \Delta =-m (108 m^2 - 9 m (n^2 + 10 n + 13) + 4 (n + 2)^3).\end{align*} $$
We view the discriminate as a continuous function of
 $m.$
Now, note that the leading term of
$m.$
Now, note that the leading term of
 $\Delta $
is negative. Applying the quadratic formula to the quadratic term above and only considering the larger root of the two yields the following:
$\Delta $
is negative. Applying the quadratic formula to the quadratic term above and only considering the larger root of the two yields the following:  $$ \begin{align*} m &= \dfrac{9(n^2+10n+13) + \sqrt{9^2(n^2+10n+13)^2-4(108)(4)(n+2)^3}}{2(108)} \hspace{-1.3cm} \\ &=\frac{ 3(n^2+10n+13) +\sqrt{9n^4 - 12n^3 - 18n^2 + 36n - 15}}{72} \\ &=\frac{ 3(n^2+10n+13) +\sqrt{3(n-1)^3(3n+5)}}{72}. \end{align*} $$
$$ \begin{align*} m &= \dfrac{9(n^2+10n+13) + \sqrt{9^2(n^2+10n+13)^2-4(108)(4)(n+2)^3}}{2(108)} \hspace{-1.3cm} \\ &=\frac{ 3(n^2+10n+13) +\sqrt{9n^4 - 12n^3 - 18n^2 + 36n - 15}}{72} \\ &=\frac{ 3(n^2+10n+13) +\sqrt{3(n-1)^3(3n+5)}}{72}. \end{align*} $$
Since, we have a unique positive root in the quadratic term and
 $m> 0,$
we may conclude that a contradiction.
$m> 0,$
we may conclude that a contradiction. $$ \begin{align*}m \leq \frac{1}{72}\bigg(3(n^2+10n+13)+\sqrt{3(n-1)^3(3n+5)}\bigg),\end{align*} $$
$$ \begin{align*}m \leq \frac{1}{72}\bigg(3(n^2+10n+13)+\sqrt{3(n-1)^3(3n+5)}\bigg),\end{align*} $$
-
4. Suppose that
 $\alpha \geq 3$
and R is Koszul. By Theorem 3.4, the defining ideal of R contains a form of degree
$\alpha \geq 3$
and R is Koszul. By Theorem 3.4, the defining ideal of R contains a form of degree
 $\alpha $
in a minimal generating set, where
$\alpha $
in a minimal generating set, where
 $\alpha \geq 3$
. Thus, R is not quadratic, a contradiction.
$\alpha \geq 3$
. Thus, R is not quadratic, a contradiction.
Hence, R is not Koszul.
We have at least one exceptional example of a coordinate ring of a generic collection of lines that is not Koszul that the previous theorem does not handle.
Proposition 5.3. Let
![]() $\mathcal {M}$
be a collection of three lines in general linear position in
$\mathcal {M}$
be a collection of three lines in general linear position in
![]() $\mathbb {P}^4$
, and let R be the coordinate ring of
$\mathbb {P}^4$
, and let R be the coordinate ring of
![]() $\mathcal {M}.$
The defining ideal J for R has a cubic in a minimal generating set. Hence, R is not Koszul.
$\mathcal {M}.$
The defining ideal J for R has a cubic in a minimal generating set. Hence, R is not Koszul.
Proof. By Remark 2.8 and a change of basis, we may assume the defining ideals for our three lines have the form
where
![]() $l=x_3+x_4.$
Let J be the defining ideal for R and notice that
$l=x_3+x_4.$
Let J be the defining ideal for R and notice that
![]() $K = L_1 \cap L_2=(x_0,x_1x_2,x_1x_4,x_3x_2,x_3x_4).$
$K = L_1 \cap L_2=(x_0,x_1x_2,x_1x_4,x_3x_2,x_3x_4).$
We have the following ring isomorphism:
 $$ \begin{align*} S/(K+L_3) &= \mathbb{C}[x_0,x_1,x_2,x_3,x_4]/(x_0,x_1,x_2,l,x_3x_4) \\ &\cong \mathbb{C}[x_3,x_4]/(l,x_3x_4) \\ &\cong \mathbb{C}[w]/(w^2). \end{align*} $$
$$ \begin{align*} S/(K+L_3) &= \mathbb{C}[x_0,x_1,x_2,x_3,x_4]/(x_0,x_1,x_2,l,x_3x_4) \\ &\cong \mathbb{C}[x_3,x_4]/(l,x_3x_4) \\ &\cong \mathbb{C}[w]/(w^2). \end{align*} $$
Hence,
 $$ \begin{align*}H_{S/(K+L_3) }(t) = \dfrac{-t^2+1}{1-t} = 1+t.\end{align*} $$
$$ \begin{align*}H_{S/(K+L_3) }(t) = \dfrac{-t^2+1}{1-t} = 1+t.\end{align*} $$
Therefore, by Proposition 2.2, the
![]() $\text {reg}_S(S/(K+L_3)) =1.$
$\text {reg}_S(S/(K+L_3)) =1.$
One checks that the
![]() $\text {reg}_S(S/K) =1.$
Using the short exact sequence
$\text {reg}_S(S/K) =1.$
Using the short exact sequence
and Proposition 2.2 yields
![]() $\text {reg}(S/J) \leq 2.$
So J is generated by forms of degree at most
$\text {reg}(S/J) \leq 2.$
So J is generated by forms of degree at most
![]() $3$
. The previous short exact sequence, Lemma 4.2, and the additivity of the Hilbert series along the previous short exact sequence yields
$3$
. The previous short exact sequence, Lemma 4.2, and the additivity of the Hilbert series along the previous short exact sequence yields
 $$ \begin{align*} H_{S/J}(t) &= H_{S/K}(t) + H_{S/L_3}(t) - H_{S/(K+L_3)}(t) \\ &= \frac{-t^2+2t+1}{(1-t)^2} + \frac{1}{(1-t)^2} - (1+t) \\ &= \frac{-t^3+3t+1}{(1-t)^2} \\ &= 1+5t+9t^2+12t^3 + \cdots. \end{align*} $$
$$ \begin{align*} H_{S/J}(t) &= H_{S/K}(t) + H_{S/L_3}(t) - H_{S/(K+L_3)}(t) \\ &= \frac{-t^2+2t+1}{(1-t)^2} + \frac{1}{(1-t)^2} - (1+t) \\ &= \frac{-t^3+3t+1}{(1-t)^2} \\ &= 1+5t+9t^2+12t^3 + \cdots. \end{align*} $$
Thus, J is generated by six linearly independent quadrics and possibly cubics. The cubic
![]() $x_3x_4l$
is contained in J, but is not contained in the ideal
$x_3x_4l$
is contained in J, but is not contained in the ideal
![]() $(x_0x_1,x_0x_2,x_1x_2,x_1x_4,x_2x_3,x_0l),$
since no term divides
$(x_0x_1,x_0x_2,x_1x_2,x_1x_4,x_2x_3,x_0l),$
since no term divides
![]() $x_3^2x_4.$
Hence, there must be a cubic generator in a minimal generating set of
$x_3^2x_4.$
Hence, there must be a cubic generator in a minimal generating set of
![]() $J.$
Thus, R is not Koszul.
$J.$
Thus, R is not Koszul.
6 Examples
Finally, it is worth observing three examples that have appeared, while studying generic lines.
Example 6.1. There are collections of lines in general linear position that are not generic collections. Consider the four lines in
![]() $\mathbb {P}^3$
:
$\mathbb {P}^3$
:
 $$ \begin{align*} \mathcal{L}_1 &= \{[0:0:\alpha:\beta] : \alpha, \beta \textrm{ not both zero} \}, \\ \mathcal{L}_2 &= \{[\alpha:\beta:0:0] : \alpha, \beta \textrm{ not both zero} \}, \\ \mathcal{L}_3 &=\{ [\alpha : \beta : -\alpha : \beta ] : \alpha, \beta \textrm{ not both zero} \}, \\ \mathcal{L}_4 &= \{[\alpha:-\beta:\alpha:\beta] : \alpha, \beta \textrm{ not both zero}\}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_1 &= \{[0:0:\alpha:\beta] : \alpha, \beta \textrm{ not both zero} \}, \\ \mathcal{L}_2 &= \{[\alpha:\beta:0:0] : \alpha, \beta \textrm{ not both zero} \}, \\ \mathcal{L}_3 &=\{ [\alpha : \beta : -\alpha : \beta ] : \alpha, \beta \textrm{ not both zero} \}, \\ \mathcal{L}_4 &= \{[\alpha:-\beta:\alpha:\beta] : \alpha, \beta \textrm{ not both zero}\}. \end{align*} $$
These lines are in general linear position since every pair spans
![]() $\mathbb {P}^3.$
The four defining ideals in S are
$\mathbb {P}^3.$
The four defining ideals in S are
 $$ \begin{align*} L_1 &= (x_0,x_1), \hspace{3cm} L_2 = (x_2,x_3), \\ L_3 &= (x_0+x_2,x_1-x_3), \hspace{1.3cm} L_4 = (x_0-x_2,x_1+x_3). \end{align*} $$
$$ \begin{align*} L_1 &= (x_0,x_1), \hspace{3cm} L_2 = (x_2,x_3), \\ L_3 &= (x_0+x_2,x_1-x_3), \hspace{1.3cm} L_4 = (x_0-x_2,x_1+x_3). \end{align*} $$
The coordinate ring
![]() $S/J,$
where
$S/J,$
where
![]() $J = \bigcap _{i=1}^4 L_i,$
has the following Hilbert series:
$J = \bigcap _{i=1}^4 L_i,$
has the following Hilbert series:
 $$ \begin{align*}H_{S/J}(t) = \frac{-3t^4+2t^3+2t^2+2t+1}{(1-t)^2} = 1+4t+9t^2+\cdots,\end{align*} $$
$$ \begin{align*}H_{S/J}(t) = \frac{-3t^4+2t^3+2t^2+2t+1}{(1-t)^2} = 1+4t+9t^2+\cdots,\end{align*} $$
whereas, by Theorem 3.4, the coordinate ring R for four generic lines in
![]() $\mathbb {P}^3$
has the following Hilbert series:
$\mathbb {P}^3$
has the following Hilbert series:
 $$ \begin{align*}H_R(t) = \frac{-2t^3+3t^2+2t+1}{(1-t)^2}= 1+4t+10t^2 + \cdots.\end{align*} $$
$$ \begin{align*}H_R(t) = \frac{-2t^3+3t^2+2t+1}{(1-t)^2}= 1+4t+10t^2 + \cdots.\end{align*} $$
So, this is not a generic collection of lines.
Example 6.2. Consider the coordinate ring R for five generic lines in
![]() $\mathbb {P}^5.$
The defining ideal J for R is minimally generated by quadrics and has the following Betti table computed via Macaulay2.
$\mathbb {P}^5.$
The defining ideal J for R is minimally generated by quadrics and has the following Betti table computed via Macaulay2.

The ring R is not Koszul by Theorem 5.2. Furthermore, it is known that if R is Koszul and the defining ideal is generated by g elements, then
![]() $\beta _{i,2i} \leq \binom {g}{i}$
for
$\beta _{i,2i} \leq \binom {g}{i}$
for
![]() $i \in \{2,\ldots ,g\}$
[Reference Avramov, Conca and Iyengar3, Cor. 3.2]. The previous inequality fails for
$i \in \{2,\ldots ,g\}$
[Reference Avramov, Conca and Iyengar3, Cor. 3.2]. The previous inequality fails for
![]() $i=2$
. So, this ring is not Koszul for two numerical reasons.
$i=2$
. So, this ring is not Koszul for two numerical reasons.
Example 6.3. Consider the coordinate ring R for six generic lines in
![]() $\mathbb {P}^6.$
The defining ideal J for R is minimally generated by quadrics and has the following Betti table computed via Macaulay2.
$\mathbb {P}^6.$
The defining ideal J for R is minimally generated by quadrics and has the following Betti table computed via Macaulay2.

The Algebra is not Koszul by Theorem 5.2, and does not fail the aforementioned inequality.
Coordinate rings with defining ideals minimally generated by quadrics are not rare, but the previous two examples are interesting since both fail for identical reasons, and one fails for an additional numerical reason. It would be interesting to determine sufficient reasons why certain numerical conditions fail and others do not. For example, why does
![]() $\beta _{i,2i} \leq \binom {g}{i}$
fail in one of the previous rings but not the other.
$\beta _{i,2i} \leq \binom {g}{i}$
fail in one of the previous rings but not the other.

The Koszul property for the coordinate ring of m generic lines in
![]() $\mathbb {P}^n$
.
$\mathbb {P}^n$
.
Furthermore, we would like to add that our theorems do not cover every coordinate ring R for every generic collection of lines in
![]() $\mathbb {P}^n.$
For the coordinate rings, we could not determine, there is a possibility these rings could be LG-quadratic or G-quadratic. In every possible case computable by Macaulay2, there exists a quadratic monomial ideal whose quotient ring gives the same Hilbert series as
$\mathbb {P}^n.$
For the coordinate rings, we could not determine, there is a possibility these rings could be LG-quadratic or G-quadratic. In every possible case computable by Macaulay2, there exists a quadratic monomial ideal whose quotient ring gives the same Hilbert series as
![]() $R.$
There could even be some change of basis which gives a quadratic Gröbner basis. Furthermore, if we wanted to construct a Koszul filtration in these coordinate rings, then Proposition 4.10 demonstrates that there is no reason we should expect a reasonable filtration unless there is a more efficient change of basis that went unobserved. Below is a table, without
$R.$
There could even be some change of basis which gives a quadratic Gröbner basis. Furthermore, if we wanted to construct a Koszul filtration in these coordinate rings, then Proposition 4.10 demonstrates that there is no reason we should expect a reasonable filtration unless there is a more efficient change of basis that went unobserved. Below is a table, without
![]() $m=1$
,
$m=1$
,
![]() $n=1$
, and
$n=1$
, and
![]() $n=2$
, summarizing our results:
$n=2$
, summarizing our results:
Acknowledgments
The author would like to thank Jason McCullough; you have been a wonderful advisor and mentor for me.
Competing Interests
The author declares none.