Research Article
Mixed cusp forms and parabolic cohomology
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-289
-
- Article
-
- You have access
- Export citation
Invariant submanifolds in flow geometry
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 290-314
-
- Article
-
- You have access
- Export citation
The Dehn function and a regular set of normal forms for R. Thompson's group F
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-328
-
- Article
-
- You have access
- Export citation
Effective measures of irrationality for certain algebraic numbers
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-344
-
- Article
-
- You have access
- Export citation
A new proof of the Macdonald identities for An−1
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-360
-
- Article
-
- You have access
- Export citation
Two-term Edgeworth expansion for M-estimators of a linear regression parameter without Cramér-type conditions and an application to the bootstrap
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 361-370
-
- Article
-
- You have access
- Export citation
On the action of the unitary group on the projective plane over a local field
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 371-397
-
- Article
-
- You have access
- Export citation
Value distribution of certain monomials of algebroid functions
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 398-404
-
- Article
-
- You have access
- Export citation
Algebraic characterizations of locally compact groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-420
-
- Article
-
- You have access
- Export citation
Index
Index
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-422
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 62 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 62 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

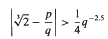 for any non-zero integers
for any non-zero integers  . Some Diophantine consequences are briefly discussed.
. Some Diophantine consequences are briefly discussed.