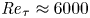1. Introduction
Turbulent flow in circular pipes has always attracted the interest of scientists, owing to its prominent importance in the engineering practice and because of the beautiful simplicity of the set-up. In this respect, the pioneering flow visualizations of Reynolds (Reference Reynolds1883) may be regarded as a milestone for the understanding of turbulent and transitional flows. The most extensive experimental measurements of high-Reynolds-number pipe flows have been carried out in modern times in the Princeton SuperPipe pressurized facility (Zagarola & Smits Reference Zagarola and Smits1998; McKeon, Zagarola & Smits Reference McKeon, Zagarola and Smits2005; Hultmark, Bailey & Smits Reference Hultmark, Bailey and Smits2010). Those investigations have allowed scientists to measure the main flow features such as friction and mean velocity profiles with high precision, and they currently constitute the most comprehensive database for the study of pipe turbulence. However, even the use of specialized microfabricated hot-wire probes could not provide fully reliable information about the viscous and buffer layers at high Reynolds numbers (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012). Additional experimental studies of pipe turbulence have been carried out in the high-Reynolds-number actual flow facility (Hi-Reff), a water tunnel with relatively large diameter, which allows for accurate estimation of friction (Furuichi et al. Reference Furuichi, Terao, Wada and Tsuji2015, Reference Furuichi, Terao, Wada and Tsuji2018). Recently, the Center for International Cooperation in Long Pipe Experiments (CICLoPE) facility of the University of Bologna (Fiorini Reference Fiorini2017; Willert et al. Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017) has been set up, whose large diameter (approximately 1 m) offers a well-established turbulent flow with relatively large viscous scales, thus granting higher spatial resolution. Flows in different facilities seem to have sensibly different properties in terms of friction and mean velocity profiles, which we will comment on.
Numerical simulation of pipe turbulence flow has received less interest than other canonical flows, the plane channel in particular, because of additional difficulties involved with the discrete solution of the Navier–Stokes equations in cylindrical coordinates, with special reference to the treatment of the geometrical singularity at the pipe axis. Early numerical simulations of turbulent pipe flow were carried out by Eggels et al. (Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994), at friction Reynolds number ![]() ${\textit {Re}}_{\tau }=180$ (
${\textit {Re}}_{\tau }=180$ (![]() ${\textit {Re}}_{\tau } = u_{\tau } R / \nu$, with
${\textit {Re}}_{\tau } = u_{\tau } R / \nu$, with ![]() $u_{\tau } = (\tau _w/\rho )^{1/2}$ the friction velocity,
$u_{\tau } = (\tau _w/\rho )^{1/2}$ the friction velocity, ![]() $R$ the pipe radius and
$R$ the pipe radius and ![]() $\nu$ the fluid kinematic viscosity). Effects of drag reduction associated with pipe rotation were later studied by Orlandi & Fatica (Reference Orlandi and Fatica1997). Higher Reynolds numbers (up to
$\nu$ the fluid kinematic viscosity). Effects of drag reduction associated with pipe rotation were later studied by Orlandi & Fatica (Reference Orlandi and Fatica1997). Higher Reynolds numbers (up to ![]() ${\textit {Re}}_{\tau } \approx 1140$) were reached by Wu & Moin (Reference Wu and Moin2008), which first allowed one to observe a near logarithmic layer in the mean velocity profile. Flow visualizations and two-point correlation statistics pointed to the existence of high-speed wavy structures in the pipe core region which are elongated in the axial direction, and whose streamwise and azimuthal dimensions do not change substantially with the Reynolds number, when normalized in outer units. Further follow-up direct numerical simulation (DNS) studies have been carried out by El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013), Chin et al. (Reference Chin, Philip, Klewicki, Ooi and Marusic2014) and Ahn et al. (Reference Ahn, Lee, Jang and Sung2013). At present, the highest Reynolds number in pipe flow (
${\textit {Re}}_{\tau } \approx 1140$) were reached by Wu & Moin (Reference Wu and Moin2008), which first allowed one to observe a near logarithmic layer in the mean velocity profile. Flow visualizations and two-point correlation statistics pointed to the existence of high-speed wavy structures in the pipe core region which are elongated in the axial direction, and whose streamwise and azimuthal dimensions do not change substantially with the Reynolds number, when normalized in outer units. Further follow-up direct numerical simulation (DNS) studies have been carried out by El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013), Chin et al. (Reference Chin, Philip, Klewicki, Ooi and Marusic2014) and Ahn et al. (Reference Ahn, Lee, Jang and Sung2013). At present, the highest Reynolds number in pipe flow (![]() ${\textit {Re}}_{\tau } \approx 3000$) has been reached in the study of Ahn et al. (Reference Ahn, Lee, Lee, Kang and Sung2015). Although no sizeable logarithmic layer is present yet at those conditions, some effects associated with significant scale separation between inner- and outer-scale turbulence were observed, as the presence of a
${\textit {Re}}_{\tau } \approx 3000$) has been reached in the study of Ahn et al. (Reference Ahn, Lee, Lee, Kang and Sung2015). Although no sizeable logarithmic layer is present yet at those conditions, some effects associated with significant scale separation between inner- and outer-scale turbulence were observed, as the presence of a ![]() $k^{-1}$ (
$k^{-1}$ (![]() $k$ being the wavenumber in any wall-parallel direction) power-law ranges in the velocity spectra.
$k$ being the wavenumber in any wall-parallel direction) power-law ranges in the velocity spectra.
Despite inherent limitations in the Reynolds numbers which can be attained, DNS has the advantage over experiments of yielding immediate access to the near-wall region, and of allowing scientists to measure some flow properties, e.g. the turbulence dissipation rate, which can hardly be measured in experiments. Hence, it is generally claimed that DNS data at increasing Reynolds numbers are needed to prove or disprove theoretical claims related to departure (or not) of the statistical properties of wall-bounded turbulence from the universal wall scaling (Cantwell Reference Cantwell2019; Chen & Sreenivasan Reference Chen and Sreenivasan2021; Monkewitz Reference Monkewitz2021). In this paper we thus present DNS data of turbulent flow in a smooth circular pipe at ![]() ${\textit {Re}}_{\tau } \approx 6000$, which is two times higher than the previous state of the art. Relying on the DNS data, we revisit current theoretical inferences and discuss implications about possible trends in the extreme Reynolds number regime.
${\textit {Re}}_{\tau } \approx 6000$, which is two times higher than the previous state of the art. Relying on the DNS data, we revisit current theoretical inferences and discuss implications about possible trends in the extreme Reynolds number regime.
2. The numerical dataset
The code used for DNS is the spin-off of an existing solver previously used to study Rayleigh–Bénard convection in cylindrical containers at extreme Rayleigh numbers (Stevens et al. Reference Stevens, van der Poel, Grossmann and Lohse2013). That code is in turn the evolution of the solver originally developed by Verzicco & Orlandi (Reference Verzicco and Orlandi1996), and used for DNS of pipe flow by Orlandi & Fatica (Reference Orlandi and Fatica1997). A second-order finite-difference discretization of the incompressible Navier–Stokes equations in cylindrical coordinates is used, based on the classical marker-and-cell method (Harlow & Welch Reference Harlow and Welch1965), with staggered arrangement of the flow variables to remove odd–even decoupling phenomena and guarantee discrete conservation of the total kinetic energy in the inviscid flow limit. Uniform volumetric forcing is applied to the axial momentum equation to maintain constant mass flow rate in time. The Poisson equation resulting from enforcement of the divergence-free condition is efficiently solved by double trigonometric expansion in the periodic axial and azimuthal directions, and inversion of tridiagonal matrices in the radial direction (Kim & Moin Reference Kim and Moin1985). An extensive series of previous studies about wall-bounded flows from this group proved that second-order finite-difference discretization yields in practical cases of wall-bounded turbulence results which are by no means inferior in quality to those of pseudospectral methods (e.g. Moin & Verzicco Reference Moin and Verzicco2016; Pirozzoli, Bernardini & Orlandi Reference Pirozzoli, Bernardini and Orlandi2016). A crucial issue is the proper treatment of the polar singularity at the pipe axis. A detailed description of the subject is reported in Verzicco & Orlandi (Reference Verzicco and Orlandi1996), but basically, the radial velocity ![]() $u_r$ in the governing equations is replaced by
$u_r$ in the governing equations is replaced by ![]() $q_r = r u_r$ (
$q_r = r u_r$ (![]() $r$ is the radial space coordinate), which by construction vanishes at the axis. The governing equations are advanced in time by means of a hybrid third-order low-storage Runge–Kutta algorithm, whereby the diffusive terms are handled implicitly, and convective terms in the axial and radial direction are handled explicitly. An important issue in this respect is the convective time step limitation in the azimuthal direction, due to intrinsic shrinking of the cells’ size toward the pipe axis. To alleviate this limitation we rely on implicit treatment of the convective terms in the azimuthal direction (Akselvoll & Moin Reference Akselvoll and Moin1996; Wu & Moin Reference Wu and Moin2008), which enables marching in time with similar time step as in planar domains flow in practical computations. In order to minimize numerical errors associated with implicit time stepping, in the present code explicit and explicit discretizations of the azimuthal convective terms are linearly blended with the radial coordinate, in such a way that near the pipe wall the treatment is fully explicit, and near the pipe axis it is fully implicit. The code was adapted to run on clusters of graphic accelerators (GPUs), using a combination of CUDA Fortran and OpenACC directives, and relying on the CUFFT libraries for efficient execution of fast Fourier transforms (FFTs) (Ruetsch & Fatica Reference Ruetsch and Fatica2014). The DNS were carried out on the Marconi-100 machine based at CINECA (Italy), relying on NVIDIA Volta V100 graphic cards. Specifically, 1024 GPUs were used for DNS-F.
$r$ is the radial space coordinate), which by construction vanishes at the axis. The governing equations are advanced in time by means of a hybrid third-order low-storage Runge–Kutta algorithm, whereby the diffusive terms are handled implicitly, and convective terms in the axial and radial direction are handled explicitly. An important issue in this respect is the convective time step limitation in the azimuthal direction, due to intrinsic shrinking of the cells’ size toward the pipe axis. To alleviate this limitation we rely on implicit treatment of the convective terms in the azimuthal direction (Akselvoll & Moin Reference Akselvoll and Moin1996; Wu & Moin Reference Wu and Moin2008), which enables marching in time with similar time step as in planar domains flow in practical computations. In order to minimize numerical errors associated with implicit time stepping, in the present code explicit and explicit discretizations of the azimuthal convective terms are linearly blended with the radial coordinate, in such a way that near the pipe wall the treatment is fully explicit, and near the pipe axis it is fully implicit. The code was adapted to run on clusters of graphic accelerators (GPUs), using a combination of CUDA Fortran and OpenACC directives, and relying on the CUFFT libraries for efficient execution of fast Fourier transforms (FFTs) (Ruetsch & Fatica Reference Ruetsch and Fatica2014). The DNS were carried out on the Marconi-100 machine based at CINECA (Italy), relying on NVIDIA Volta V100 graphic cards. Specifically, 1024 GPUs were used for DNS-F.
Numerical simulations are carried out with periodic boundary conditions in the axial (![]() $z$) and azimuthal (
$z$) and azimuthal (![]() $\theta$) directions. The velocity field is then controlled by two parameters, namely the bulk Reynolds number (
$\theta$) directions. The velocity field is then controlled by two parameters, namely the bulk Reynolds number (![]() ${\textit {Re}}_b = 2 R u_b / \nu$, with
${\textit {Re}}_b = 2 R u_b / \nu$, with ![]() $R$ the pipe radius,
$R$ the pipe radius, ![]() $u_b$ the fluid bulk velocity and
$u_b$ the fluid bulk velocity and ![]() $\nu$ its kinematic viscosity), and the relative pipe length,
$\nu$ its kinematic viscosity), and the relative pipe length, ![]() $L_z/R$. A list of the main simulations that we have carried out is given in table 1. The mesh resolution is designed based on well-established criteria in the wall turbulence community. In particular, the collocation points are distributed in the wall-normal direction so that approximately 30 points are placed within
$L_z/R$. A list of the main simulations that we have carried out is given in table 1. The mesh resolution is designed based on well-established criteria in the wall turbulence community. In particular, the collocation points are distributed in the wall-normal direction so that approximately 30 points are placed within ![]() $y^+ \le 40$ (
$y^+ \le 40$ (![]() $y=R-r$ is the wall distance, and the
$y=R-r$ is the wall distance, and the ![]() $+$ superscript is used to denote normalization with respect to
$+$ superscript is used to denote normalization with respect to ![]() $u_{\tau }$ and
$u_{\tau }$ and ![]() $\nu$), with the first grid point at
$\nu$), with the first grid point at ![]() $y^+ \approx 0.05$. The mesh is progressively stretched in the outer wall layer in such a way that the mesh spacing is proportional to the local Kolmogorov length scale, which there varies as
$y^+ \approx 0.05$. The mesh is progressively stretched in the outer wall layer in such a way that the mesh spacing is proportional to the local Kolmogorov length scale, which there varies as ![]() $\eta ^+ \approx 0.8 {y^+}^{1/4}$ (Jiménez Reference Jiménez2018), and the radial spacing at the pipe axis is
$\eta ^+ \approx 0.8 {y^+}^{1/4}$ (Jiménez Reference Jiménez2018), and the radial spacing at the pipe axis is ![]() ${\rm \Delta} y^+ \approx 8.8$. Additional details are provided in a specifically focused publication (Pirozzoli & Orlandi Reference Pirozzoli and Orlandi2021). Regarding the axial and azimuthal directions, finite-difference simulations of wall-bounded flows yield grid-independent results as long as
${\rm \Delta} y^+ \approx 8.8$. Additional details are provided in a specifically focused publication (Pirozzoli & Orlandi Reference Pirozzoli and Orlandi2021). Regarding the axial and azimuthal directions, finite-difference simulations of wall-bounded flows yield grid-independent results as long as ![]() ${\rm \Delta} x^+ \approx 10$,
${\rm \Delta} x^+ \approx 10$, ![]() $R^+ {\rm \Delta} \theta \approx 4.5$ (Pirozzoli et al. Reference Pirozzoli, Bernardini and Orlandi2016), hence the associated number of grid points scales as
$R^+ {\rm \Delta} \theta \approx 4.5$ (Pirozzoli et al. Reference Pirozzoli, Bernardini and Orlandi2016), hence the associated number of grid points scales as ![]() $N_z \approx L_z / R \times {\textit {Re}}_{\tau } / 10$,
$N_z \approx L_z / R \times {\textit {Re}}_{\tau } / 10$, ![]() $N_{\theta } \sim 2 {\rm \pi}\times {\textit {Re}}_{\tau } / 4.5$. All DNS have been carried out at Courant–Friedrichs–Lewy (CFL) number close to unity, based on the radial convective time step limitation. The CFL number along the axial direction is typically smaller by a factor two. The time step expressed in wall units (
$N_{\theta } \sim 2 {\rm \pi}\times {\textit {Re}}_{\tau } / 4.5$. All DNS have been carried out at Courant–Friedrichs–Lewy (CFL) number close to unity, based on the radial convective time step limitation. The CFL number along the axial direction is typically smaller by a factor two. The time step expressed in wall units (![]() $\nu / u_{\tau }^2$) ranges from
$\nu / u_{\tau }^2$) ranges from ![]() ${\rm \Delta} t^+ = 0.55$ in DNS-A to
${\rm \Delta} t^+ = 0.55$ in DNS-A to ![]() ${\rm \Delta} t^+ = 0.15$ in DNS-F. According to the established practice (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Ahn et al. Reference Ahn, Lee, Lee, Kang and Sung2015; Lee & Moser Reference Lee and Moser2015), the time intervals used to collect the flow statistics are reported in terms of eddy-turnover times,
${\rm \Delta} t^+ = 0.15$ in DNS-F. According to the established practice (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Ahn et al. Reference Ahn, Lee, Lee, Kang and Sung2015; Lee & Moser Reference Lee and Moser2015), the time intervals used to collect the flow statistics are reported in terms of eddy-turnover times, ![]() $\tau _t = R/u_{\tau }$. For reference, the time window used to collect the flow statistics in DNS-F amounts to approximately 13.1 flow-through times (
$\tau _t = R/u_{\tau }$. For reference, the time window used to collect the flow statistics in DNS-F amounts to approximately 13.1 flow-through times (![]() $L_z/u_b$ time units).
$L_z/u_b$ time units).
Table 1. Flow parameters for DNS of pipe flow. Here ![]() $R$ is the pipe radius;
$R$ is the pipe radius; ![]() $L_z$ is the pipe axial length;
$L_z$ is the pipe axial length; ![]() $N_{\theta }$,
$N_{\theta }$, ![]() $N_r$ and
$N_r$ and ![]() $N_z$ are the number of grid points in the azimuthal, radial and axial directions, respectively;
$N_z$ are the number of grid points in the azimuthal, radial and axial directions, respectively; ![]() ${\textit {Re}}_b = 2 R u_b / \nu$ is the bulk Reynolds number;
${\textit {Re}}_b = 2 R u_b / \nu$ is the bulk Reynolds number; ![]() $\lambda = 8 \tau _w / (\rho u_b^2)$ is the friction factor;
$\lambda = 8 \tau _w / (\rho u_b^2)$ is the friction factor; ![]() ${\textit {Re}}_{\tau } = u_{\tau } R / \nu$ is the friction Reynolds number; T is the time interval used to collect the flow statistics; and
${\textit {Re}}_{\tau } = u_{\tau } R / \nu$ is the friction Reynolds number; T is the time interval used to collect the flow statistics; and ![]() $\tau _t = R/u_{\tau }$ is the eddy turnover time.
$\tau _t = R/u_{\tau }$ is the eddy turnover time.

The sampling errors for some key properties discussed in this paper have been estimated using the method of Russo & Luchini (Reference Russo and Luchini2017), based on an extension of the classical batch means approach. The results of the uncertainty estimation analysis are listed in table 2, where we provide expected values and associated standard deviation for the friction factor (![]() $\,f$), mean centreline velocity (
$\,f$), mean centreline velocity (![]() $U_{{CL}}$), peak axial velocity variance and its position (
$U_{{CL}}$), peak axial velocity variance and its position (![]() $(\left \langle {u_z^2}\right \rangle _{{IP}}$ and
$(\left \langle {u_z^2}\right \rangle _{{IP}}$ and ![]() $y_{{IP}}$, respectively), and the dissipation rate of axial velocity variance (
$y_{{IP}}$, respectively), and the dissipation rate of axial velocity variance (![]() $\epsilon _{{11w}}$). Here and elsewhere, capital letters are used to denote flow properties averaged in the homogeneous spatial directions and in time, brackets denote the averaging operator, and lower-case letters to denote fluctuations from the mean. We find that the sampling error is generally quite limited, being larger in the largest DNS, which have been run for shorter times. In particular, in DNS-F the expected sampling error in friction, centreline velocity and peak velocity variance is approximately
$\epsilon _{{11w}}$). Here and elsewhere, capital letters are used to denote flow properties averaged in the homogeneous spatial directions and in time, brackets denote the averaging operator, and lower-case letters to denote fluctuations from the mean. We find that the sampling error is generally quite limited, being larger in the largest DNS, which have been run for shorter times. In particular, in DNS-F the expected sampling error in friction, centreline velocity and peak velocity variance is approximately ![]() $0.5\,\%$, whereas it is approximately
$0.5\,\%$, whereas it is approximately ![]() $1\,\%$ for the wall dissipation. Additional tests aimed at establishing the effect of axial domain length and grid size have been carried out for the DNS-C flow case, whose results are also reported in table 2. We find that doubling the pipe length yields a change in the basic flow properties of approximately 0.2 %–0.3 %, whereas halving it yields changes of approximately
$1\,\%$ for the wall dissipation. Additional tests aimed at establishing the effect of axial domain length and grid size have been carried out for the DNS-C flow case, whose results are also reported in table 2. We find that doubling the pipe length yields a change in the basic flow properties of approximately 0.2 %–0.3 %, whereas halving it yields changes of approximately ![]() $1\,\%$ in friction and peak velocity variance, and up to
$1\,\%$ in friction and peak velocity variance, and up to ![]() $10\,\%$ in the wall dissipation. Hence, consistent with previous studies (Chin et al. Reference Chin, Ooi, Marusic and Blackburn2010), we believe that the selected pipe length (
$10\,\%$ in the wall dissipation. Hence, consistent with previous studies (Chin et al. Reference Chin, Ooi, Marusic and Blackburn2010), we believe that the selected pipe length (![]() $L_z/R=15$) is representative of an infinitely long pipe, at least for the purposes of the present study. In order to quantify uncertainties associated with numerical discretization, additional simulations have been carried out by doubling the grid points in the azimuthal, radial and axial directions. Based on the data reported in the table, after discarding the short pipe case, we can thus quantify the uncertainty due to numerical discretization and limited pipe length to be approximately
$L_z/R=15$) is representative of an infinitely long pipe, at least for the purposes of the present study. In order to quantify uncertainties associated with numerical discretization, additional simulations have been carried out by doubling the grid points in the azimuthal, radial and axial directions. Based on the data reported in the table, after discarding the short pipe case, we can thus quantify the uncertainty due to numerical discretization and limited pipe length to be approximately ![]() $0.3\,\%$ for the friction coefficient and pipe centreline velocity,
$0.3\,\%$ for the friction coefficient and pipe centreline velocity, ![]() $0.6\,\%$ for the peak velocity variance and
$0.6\,\%$ for the peak velocity variance and ![]() $0.9\,\%$ for the wall dissipation.
$0.9\,\%$ for the wall dissipation.
Table 2. Uncertainty estimation study: mean values of representative quantities and standard deviation of their estimates. Here ![]() $\lambda$ is the friction factor;
$\lambda$ is the friction factor; ![]() $U_{{CL}}^+$ is the mean pipe centreline velocity;
$U_{{CL}}^+$ is the mean pipe centreline velocity; ![]() $\langle u_z^2\rangle ^+_{{IP}}$ is the peak axial velocity variance and
$\langle u_z^2\rangle ^+_{{IP}}$ is the peak axial velocity variance and ![]() $y^+_{{IP}}$ is its distance from the wall; and
$y^+_{{IP}}$ is its distance from the wall; and ![]() $\epsilon ^+_{{11w}}$ is the dissipation rate of
$\epsilon ^+_{{11w}}$ is the dissipation rate of ![]() $\langle u_z^2\rangle$ at the wall.
$\langle u_z^2\rangle$ at the wall.

3. Results
Qualitative information about the structure of the flow field is provided by instantaneous perspective views of the axial velocity field, provided in figure 1. Although finer-scale details are visible at the higher ![]() ${\textit {Re}}$, the flow in the cross-stream planes is always characterized by a limited number of bulges distributed along the azimuthal direction, which closely recall the proper orthogonal decomposition (POD) modes identified by Hellström & Smits (Reference Hellström and Smits2014), and which correspond to alternating intrusions of high-speed fluid from the pipe core and ejections of low-speed fluid from the wall. Streaks are visible in the near-wall cylindrical shells, whose organization has clear association with the cross-stream pattern. Specifically, regardless of the Reynolds number,
${\textit {Re}}$, the flow in the cross-stream planes is always characterized by a limited number of bulges distributed along the azimuthal direction, which closely recall the proper orthogonal decomposition (POD) modes identified by Hellström & Smits (Reference Hellström and Smits2014), and which correspond to alternating intrusions of high-speed fluid from the pipe core and ejections of low-speed fluid from the wall. Streaks are visible in the near-wall cylindrical shells, whose organization has clear association with the cross-stream pattern. Specifically, regardless of the Reynolds number, ![]() $R$-sized low-streaks are observed in association with large-scale ejections, whereas
$R$-sized low-streaks are observed in association with large-scale ejections, whereas ![]() $R$-sized high-speed streaks occur in the presence of large-scale inrush from the core flow. At the same time, smaller streaks scaling in wall units appear, corresponding to buffer-layer ejections/sweeps. Hence, organization of the flow on at least two length scales is apparent here, whose separation increases with
$R$-sized high-speed streaks occur in the presence of large-scale inrush from the core flow. At the same time, smaller streaks scaling in wall units appear, corresponding to buffer-layer ejections/sweeps. Hence, organization of the flow on at least two length scales is apparent here, whose separation increases with ![]() ${\textit {Re}}_{\tau }$.
${\textit {Re}}_{\tau }$.

Figure 1. Instantaneous axial velocity contours (colour scale from blue to red) in turbulent pipe flow as obtained from DNS. Contours are shown on a cross-stream plane and on a near-wall cylindrical shell (![]() $y^+ \approx 15$).
$y^+ \approx 15$).
Mean friction is obviously a parameter of paramount importance as it is related to power expenditure to sustain the flow. In figure 2, we show the friction factor, namely
A correlation generally used for smooth pipes is the Prandtl friction law,
where ![]() $A= \log 10 / (2 k \sqrt {2})$, with
$A= \log 10 / (2 k \sqrt {2})$, with ![]() $k$ being the von Kármán log-law constant. The standard values
$k$ being the von Kármán log-law constant. The standard values ![]() $A=2.0$,
$A=2.0$, ![]() $B=0.8$, were derived by fitting the experimental data of Nikuradse (Reference Nikuradse1933). Reynolds-number-dependent corrections to the standard friction law were introduced by McKeon et al. (Reference McKeon, Zagarola and Smits2005) in order to improve the fitting of the SuperPipe data. Figure 2 shows overall agreement of all DNS and experimental data with the Prandtl law. However, closer scrutiny (see the figure insets) highlights some scatter. Regarding DNS, all datasets overshoot the Prandtl law at low Reynolds number, although to a quite different extent. In fact, the data of Wu & Moin (Reference Wu and Moin2008), El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013) and Chin et al. (Reference Chin, Philip, Klewicki, Ooi and Marusic2014) exceed the theoretical values by up to
$B=0.8$, were derived by fitting the experimental data of Nikuradse (Reference Nikuradse1933). Reynolds-number-dependent corrections to the standard friction law were introduced by McKeon et al. (Reference McKeon, Zagarola and Smits2005) in order to improve the fitting of the SuperPipe data. Figure 2 shows overall agreement of all DNS and experimental data with the Prandtl law. However, closer scrutiny (see the figure insets) highlights some scatter. Regarding DNS, all datasets overshoot the Prandtl law at low Reynolds number, although to a quite different extent. In fact, the data of Wu & Moin (Reference Wu and Moin2008), El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013) and Chin et al. (Reference Chin, Philip, Klewicki, Ooi and Marusic2014) exceed the theoretical values by up to ![]() $4\,\%$, whereas our data tend to be much more consistent with those of Ahn et al. (Reference Ahn, Lee, Lee, Kang and Sung2015). We believe that this difference may be related to different grid resolution in the azimuthal direction, which was
$4\,\%$, whereas our data tend to be much more consistent with those of Ahn et al. (Reference Ahn, Lee, Lee, Kang and Sung2015). We believe that this difference may be related to different grid resolution in the azimuthal direction, which was ![]() $R^+ {\rm \Delta} \theta = 7 - 8$ in those previous studies, and 4–5 in our DNS. Our data in fact show minimal overshoot at low Reynolds number, and consistent undershoot from Prandtl law by approximately
$R^+ {\rm \Delta} \theta = 7 - 8$ in those previous studies, and 4–5 in our DNS. Our data in fact show minimal overshoot at low Reynolds number, and consistent undershoot from Prandtl law by approximately ![]() $2\,\%$. Regarding experiments, SuperPipe data typically tend to lie above the theoretical curve by approximately
$2\,\%$. Regarding experiments, SuperPipe data typically tend to lie above the theoretical curve by approximately ![]() $2\,\%$, whereas the CICLoPE and Hi-Reff data tend to fall short of it. Although the range of data overlap is not extensive, it appears that DNS data tend to be more consistent with the CICLoPE and Hi-Reff data than with other datasets. Fitting the current DNS data with a functional relationship as (3.2), yields
$2\,\%$, whereas the CICLoPE and Hi-Reff data tend to fall short of it. Although the range of data overlap is not extensive, it appears that DNS data tend to be more consistent with the CICLoPE and Hi-Reff data than with other datasets. Fitting the current DNS data with a functional relationship as (3.2), yields ![]() $A \approx 2.102$,
$A \approx 2.102$, ![]() $B \approx 1.148$, with an inferred value of the von Kármán constant of
$B \approx 1.148$, with an inferred value of the von Kármán constant of ![]() $k = 0.387 \pm 0.004$, with uncertainty estimates based on
$k = 0.387 \pm 0.004$, with uncertainty estimates based on ![]() $95\,\%$ confidence bounds from the curve-fitting procedure. This value is extremely close to that suggested by Furuichi et al. (Reference Furuichi, Terao, Wada and Tsuji2018), who reported
$95\,\%$ confidence bounds from the curve-fitting procedure. This value is extremely close to that suggested by Furuichi et al. (Reference Furuichi, Terao, Wada and Tsuji2018), who reported ![]() $k=0.386$ as an average value over a very wide range of Reynolds numbers, and also very close to values reported in boundary layers (Nagib & Chauhan Reference Nagib and Chauhan2009) and channels (Lee & Moser Reference Lee and Moser2015). If this trend is extrapolated, deviations of approximately
$k=0.386$ as an average value over a very wide range of Reynolds numbers, and also very close to values reported in boundary layers (Nagib & Chauhan Reference Nagib and Chauhan2009) and channels (Lee & Moser Reference Lee and Moser2015). If this trend is extrapolated, deviations of approximately ![]() $4\,\%$ from the standard Prandtl law would result at
$4\,\%$ from the standard Prandtl law would result at ![]() ${\textit {Re}}_b = 10^7$.
${\textit {Re}}_b = 10^7$.

Figure 2. Friction factor as a function of bulk Reynolds number, in linear (a) and in semilogarithmic (b) scale. Circles denote present DNS data, other symbols are defined in table 3. The solid line corresponds to the classical Prandtl friction law as given in (3.2), whereas the dashed grey line corresponds to a fit of the DNS data. Relative deviations with respect to the Prandtl friction law are shown in the insets.
Table 3. List of other references for data used in the paper.

The mean velocity profile in turbulent pipes has received extensive attention from theoretical studies, much of the early debate being focused on whether a log law or a power law better fits the experimental results (Barenblatt, Chorin & Prostokishin Reference Barenblatt, Chorin and Prostokishin1997), mainly carried out in the SuperPipe facility (Zagarola & Smits Reference Zagarola and Smits1998; McKeon et al. Reference McKeon, Zagarola and Smits2005). Recent studies have highlighted the need for corrections to the baseline log law in order to accurately describe the velocity profile throughout the log layer into the core part of the flow (Luchini Reference Luchini2017; Cantwell Reference Cantwell2019; Monkewitz Reference Monkewitz2021). In figure 3, we show the series of velocity profiles computed with the present DNS, compared with previous DNS and experimental data. Overall, good agreement is observed across various sources as far as the inner and the overlap regions are concerned, with data gradually approaching a logarithmic distribution, here identified by visual fitting as ![]() $U^+ = 1/k \log y^+ + 4.53$, using the value of
$U^+ = 1/k \log y^+ + 4.53$, using the value of ![]() $k=0.387$ determined from friction data. This is quite close to estimates based on direct fitting of the mean velocity profile in pipe flow (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), which yielded
$k=0.387$ determined from friction data. This is quite close to estimates based on direct fitting of the mean velocity profile in pipe flow (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), which yielded ![]() $U^+ = 1/0.391 \log y^+ + 4.34$. The DNS velocity profiles for
$U^+ = 1/0.391 \log y^+ + 4.34$. The DNS velocity profiles for ![]() ${\textit {Re}}_{\tau } \ge 10^3$ follow this distribution with deviations of no more than
${\textit {Re}}_{\tau } \ge 10^3$ follow this distribution with deviations of no more than ![]() $0.1$ wall units from
$0.1$ wall units from ![]() $y^+ \approx 30$ to
$y^+ \approx 30$ to ![]() $y/R \approx 0.15$, whence the core region develops. Differences with respect to previous DNSs are concentrated in the core region, which seemingly stronger wake in some datasets, including our own, Wu & Moin (Reference Wu and Moin2008) and Ahn et al. (Reference Ahn, Lee, Jang and Sung2013), and weaker in others (El Khoury et al. Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013; Chin et al. Reference Chin, Philip, Klewicki, Ooi and Marusic2014), reflecting previously noted differences in the friction coefficient. Especially satisfactory is the excellent agreement between our DNS-E velocity profile and the data of Ahn et al. (Reference Ahn, Lee, Lee, Kang and Sung2015) at
$y/R \approx 0.15$, whence the core region develops. Differences with respect to previous DNSs are concentrated in the core region, which seemingly stronger wake in some datasets, including our own, Wu & Moin (Reference Wu and Moin2008) and Ahn et al. (Reference Ahn, Lee, Jang and Sung2013), and weaker in others (El Khoury et al. Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013; Chin et al. Reference Chin, Philip, Klewicki, Ooi and Marusic2014), reflecting previously noted differences in the friction coefficient. Especially satisfactory is the excellent agreement between our DNS-E velocity profile and the data of Ahn et al. (Reference Ahn, Lee, Lee, Kang and Sung2015) at ![]() ${\textit {Re}}_{\tau } \approx 3000$. Comparison of our DNS dataset with experimental data also shows overall good agreement, although some differences are quite clear in the core region, in which SuperPipe experiments consistently yield lower
${\textit {Re}}_{\tau } \approx 3000$. Comparison of our DNS dataset with experimental data also shows overall good agreement, although some differences are quite clear in the core region, in which SuperPipe experiments consistently yield lower ![]() $U^+$, which translates into lower friction.
$U^+$, which translates into lower friction.

Figure 3. Inner-scaled mean velocity profiles obtained with our DNS (a), and compared with previous DNS and experiments (b). Deviations from the assumed logarithmic wall law, ![]() $U_{log}^+ = \log y^+ / 0.387 + 4.53$, are highlighted in the inset of panel (a). For greater clarity, profiles in panel (b) are offset in the vertical direction by five wall units steps. Lines denote present DNS data, with colour code as in table 1, and symbols denote data from other authors, as in table 3.
$U_{log}^+ = \log y^+ / 0.387 + 4.53$, are highlighted in the inset of panel (a). For greater clarity, profiles in panel (b) are offset in the vertical direction by five wall units steps. Lines denote present DNS data, with colour code as in table 1, and symbols denote data from other authors, as in table 3.
More refined information on the behaviour of the mean velocity profile can be gained from inspection of the log-law diagnostic function
which is shown in figure 4, and whose constancy would imply the presence of a genuine logarithmic layer in the mean velocity profile. The figure supports universality of the inner-scaled axial velocity for ![]() ${\textit {Re}}_{\tau } \gtrsim 10^3$, up to
${\textit {Re}}_{\tau } \gtrsim 10^3$, up to ![]() $y^+ \approx 100$, where
$y^+ \approx 100$, where ![]() $\varXi$ attains a minimum, and the presence of an outer maximum at
$\varXi$ attains a minimum, and the presence of an outer maximum at ![]() $y/R \approx 0.6$. Between these two sites the distribution is roughly linear, as can be better appreciated in figure 4(b), with nearly constant slope when expressed in outer coordinates. Approximate linear variation of the diagnostic function in channel flow was observed by Jiménez & Moser (Reference Jiménez and Moser2007), who, based on refined overlap arguments expressed by Afzal & Yajnik (Reference Afzal and Yajnik1973), proposed the following fit:
$y/R \approx 0.6$. Between these two sites the distribution is roughly linear, as can be better appreciated in figure 4(b), with nearly constant slope when expressed in outer coordinates. Approximate linear variation of the diagnostic function in channel flow was observed by Jiménez & Moser (Reference Jiménez and Moser2007), who, based on refined overlap arguments expressed by Afzal & Yajnik (Reference Afzal and Yajnik1973), proposed the following fit:
where ![]() $\alpha$,
$\alpha$, ![]() $\beta$ are adjustable constants, and
$\beta$ are adjustable constants, and ![]() $k$ is the von Kármán constant. Here we find that the set of constants
$k$ is the von Kármán constant. Here we find that the set of constants ![]() $k=0.387$,
$k=0.387$, ![]() $\alpha =2.0$,
$\alpha =2.0$, ![]() $\beta =0$, yields overall good approximation of the pipe DNS data. The consequence is that a genuine logarithmic layer would only be attained at infinite Reynolds number. In this respect, SuperPipe data seem to suggest the formation of a plateau at
$\beta =0$, yields overall good approximation of the pipe DNS data. The consequence is that a genuine logarithmic layer would only be attained at infinite Reynolds number. In this respect, SuperPipe data seem to suggest the formation of a plateau at ![]() ${\textit {Re}}_{\tau } \gtrsim 10^4$, although the scatter of points is quite significant. Hence, DNS at higher Reynolds number would be most welcome to confirm or refute our findings, and possibly determine more accurate values of the extended log-law constants in (3.4).
${\textit {Re}}_{\tau } \gtrsim 10^4$, although the scatter of points is quite significant. Hence, DNS at higher Reynolds number would be most welcome to confirm or refute our findings, and possibly determine more accurate values of the extended log-law constants in (3.4).

Figure 4. Log-law diagnostic function as defined in (3.3), expressed as a function of inner-scaled (a) and outer-scaled (b) wall distance. The dashed horizontal line denotes the inverse Kármán constant, ![]() $1/0.387$, and the dash–dotted lines in panel (b) denote the linear fit (3.4), with
$1/0.387$, and the dash–dotted lines in panel (b) denote the linear fit (3.4), with ![]() $k=0.387$,
$k=0.387$, ![]() $\alpha = 2.0$,
$\alpha = 2.0$, ![]() $\beta =0$. Lines denote present DNS data, with colour code as in table 1, and symbols denote SuperPipe data (McKeon et al. Reference McKeon, Zagarola and Smits2005) at
$\beta =0$. Lines denote present DNS data, with colour code as in table 1, and symbols denote SuperPipe data (McKeon et al. Reference McKeon, Zagarola and Smits2005) at ![]() ${\textit {Re}}_{\tau } = 1825, 3328, 6617, 10\,914, 19\,119, 32\,870$.
${\textit {Re}}_{\tau } = 1825, 3328, 6617, 10\,914, 19\,119, 32\,870$.
Comparison with SuperPipe data is presented in outer units in figure 5, limited to the higher ![]() ${\textit {Re}}_{\tau }$ cases. Despite differences in the Reynolds number, the velocity profiles now agree very well, throughout the outer layer. This observation would suggest problems with correct estimation of the friction velocity which, however, seems unlikely both in DNS, in which we independently evaluate friction velocity by computing the wall derivative of the velocity profile and from momentum balance, and in experiments, as measurements of the pressure drop are regarded to have low uncertainty. Hence, reasons for this discrepancy are not known, and additional experiments as those currently carried out in the large CICLoPE facility would be especially useful and welcome. Unfortunately, velocity profiles along the full radial span are not available at the moment for that facility.
${\textit {Re}}_{\tau }$ cases. Despite differences in the Reynolds number, the velocity profiles now agree very well, throughout the outer layer. This observation would suggest problems with correct estimation of the friction velocity which, however, seems unlikely both in DNS, in which we independently evaluate friction velocity by computing the wall derivative of the velocity profile and from momentum balance, and in experiments, as measurements of the pressure drop are regarded to have low uncertainty. Hence, reasons for this discrepancy are not known, and additional experiments as those currently carried out in the large CICLoPE facility would be especially useful and welcome. Unfortunately, velocity profiles along the full radial span are not available at the moment for that facility.

Figure 5. Mean velocity profiles in outer scaling. Data of flow case DNS-E (a) are compared with SuperPipe data at ![]() ${\textit {Re}}_{\tau }=3328$ and
${\textit {Re}}_{\tau }=3328$ and ![]() ${\textit {Re}}_{\tau }=3334$, and data of flow case DNS-F (b) with SuperPipe data at
${\textit {Re}}_{\tau }=3334$, and data of flow case DNS-F (b) with SuperPipe data at ![]() ${\textit {Re}}_{\tau }=5411$ and
${\textit {Re}}_{\tau }=5411$ and ![]() ${\textit {Re}}_{\tau }=6617$.
${\textit {Re}}_{\tau }=6617$.
The structure of the core region is examined in detail in figure 6, where the mean velocity profiles are shown in defect form. Although full outer-layer similarity is not reached at the conditions of our DNS study (also see the inset of figure 3a), scatter across the Reynolds number range and with respect to SuperPipe profiles for ![]() $y/R \ge 0.2$ is no larger than
$y/R \ge 0.2$ is no larger than ![]() $5\,\%$. As suggested by Pirozzoli (Reference Pirozzoli2014), the core velocity profiles can be closely approximated with a simple quadratic function, reflecting near constancy of the eddy viscosity. In particular, we find that the formula
$5\,\%$. As suggested by Pirozzoli (Reference Pirozzoli2014), the core velocity profiles can be closely approximated with a simple quadratic function, reflecting near constancy of the eddy viscosity. In particular, we find that the formula
fits the DNS data with ![]() $C_{{O}} = 8.0$ well, and it smoothly connects at
$C_{{O}} = 8.0$ well, and it smoothly connects at ![]() $y/R \approx 0.2$ with the logarithmic profile expressed in outer form,
$y/R \approx 0.2$ with the logarithmic profile expressed in outer form,
where again ![]() $k=0.387$, and data fitting yields
$k=0.387$, and data fitting yields ![]() $B=0.961$. While, of course, better descriptions of the core velocity profiles are possible based on more elaborate functional relationships (Luchini Reference Luchini2017), the composite profile matching equations (3.5) and (3.6) yields a reasonable representation of the whole outer-layer mean velocity profile within the scatter of available data.
$B=0.961$. While, of course, better descriptions of the core velocity profiles are possible based on more elaborate functional relationships (Luchini Reference Luchini2017), the composite profile matching equations (3.5) and (3.6) yields a reasonable representation of the whole outer-layer mean velocity profile within the scatter of available data.

Figure 6. Defect velocity profiles for DNS and experiments, in linear (a) and semilogarithmic (b) scale. The dashed grey line marks a parabolic fit of the DNS data (![]() $U^+_{{CL}}-U^+ = 8.0 (1-y/R)^2$), and the dashed purple line the outer-layer logarithmic fit
$U^+_{{CL}}-U^+ = 8.0 (1-y/R)^2$), and the dashed purple line the outer-layer logarithmic fit ![]() $U^+_{{CL}}-U^+ = 0.961 - 1/0.387 \log (y/R)$.
$U^+_{{CL}}-U^+ = 0.961 - 1/0.387 \log (y/R)$.
Finer evaluation of similarities and differences between DNS and experiments is provided in figure 7, where we show the mean centreline velocity, ![]() $U_{{CL}}$, normalized by the friction velocity (figure 7a), and by the bulk velocity (figure 7b), as a function of the friction Reynolds number. Consistently with theoretical expectations (e.g. Monkewitz Reference Monkewitz2021), data suggest logarithmic increase with
$U_{{CL}}$, normalized by the friction velocity (figure 7a), and by the bulk velocity (figure 7b), as a function of the friction Reynolds number. Consistently with theoretical expectations (e.g. Monkewitz Reference Monkewitz2021), data suggest logarithmic increase with ![]() ${\textit {Re}}_{\tau }$ according to
${\textit {Re}}_{\tau }$ according to
where we find ![]() $k_{{CL}}=k=0.387$ as for the friction law, and
$k_{{CL}}=k=0.387$ as for the friction law, and ![]() $B_{{CL}}=5.85$. For convenience, the trend of
$B_{{CL}}=5.85$. For convenience, the trend of ![]() $u_b/u_{\tau }$ is also presented, having in fact the same logarithmic growth with
$u_b/u_{\tau }$ is also presented, having in fact the same logarithmic growth with ![]() ${\textit {Re}}_{\tau }$. With some previously noted differences, all pipe flow DNSs seem to exhibit a consistent trend in the accessible range. While the trend is very similar at low Reynolds number, experimental data yield consistently lower values of
${\textit {Re}}_{\tau }$. With some previously noted differences, all pipe flow DNSs seem to exhibit a consistent trend in the accessible range. While the trend is very similar at low Reynolds number, experimental data yield consistently lower values of ![]() $U_{{CL}}^+$, especially those from the SuperPipe. At Reynolds numbers higher than approximately
$U_{{CL}}^+$, especially those from the SuperPipe. At Reynolds numbers higher than approximately ![]() ${\textit {Re}}_{\tau }=10^4$, experiments seem to suggest milder growth rate, although significant differences emerge between the SuperPipe and the Hi-Reff datasets. Hence, whether this is the result of a change of behaviour at high Reynolds number, or some form of shortcoming of experiments, is difficult to say. As a result of the observed identity (or very close vicinity) of the von Kármán constant for the centreline and for the bulk velocity, figure 7(b) highlights that their ratio approaches unity at large
${\textit {Re}}_{\tau }=10^4$, experiments seem to suggest milder growth rate, although significant differences emerge between the SuperPipe and the Hi-Reff datasets. Hence, whether this is the result of a change of behaviour at high Reynolds number, or some form of shortcoming of experiments, is difficult to say. As a result of the observed identity (or very close vicinity) of the von Kármán constant for the centreline and for the bulk velocity, figure 7(b) highlights that their ratio approaches unity at large ![]() ${\textit {Re}}$, supporting the inference that pipe flow asymptotes to plug flow in the infinite-Reynolds-number limit (Pullin, Inoue & Saito Reference Pullin, Inoue and Saito2013). Regarding that study, it is worthwhile noticing that one of the assumptions made in the analysis is that the wall-normal location of the onset of the logarithmic region is either finite, or increases no faster than
${\textit {Re}}$, supporting the inference that pipe flow asymptotes to plug flow in the infinite-Reynolds-number limit (Pullin, Inoue & Saito Reference Pullin, Inoue and Saito2013). Regarding that study, it is worthwhile noticing that one of the assumptions made in the analysis is that the wall-normal location of the onset of the logarithmic region is either finite, or increases no faster than ![]() ${\textit {Re}}_{\tau }$. Interpreting the near-wall minimum of the diagnostic function in figure 4 as the root of the (near) logarithmic layer, our data support that assumption well. Whereas the curvature of the core velocity profile is not changing substantially when expressed in wall units (see figure 6), it would become vanishingly small when expressed in outer units. However, as figure 7(b) suggests, this trend is extremely slow. Interestingly, again despite some scatter, DNS and experiments here seem to indicate a common trend with overall monotonic decrease, perhaps with a ‘bump’ in the range of Reynolds numbers in the low thousands. The DNS data points at the highest Reynolds numbers (DNS-D, DNS-E, DNS-F) now appear to be in good agreement with SuperPipe experiments, which is in line with the previously noted agreement of the outer-scaled mean velocity profiles.
${\textit {Re}}_{\tau }$. Interpreting the near-wall minimum of the diagnostic function in figure 4 as the root of the (near) logarithmic layer, our data support that assumption well. Whereas the curvature of the core velocity profile is not changing substantially when expressed in wall units (see figure 6), it would become vanishingly small when expressed in outer units. However, as figure 7(b) suggests, this trend is extremely slow. Interestingly, again despite some scatter, DNS and experiments here seem to indicate a common trend with overall monotonic decrease, perhaps with a ‘bump’ in the range of Reynolds numbers in the low thousands. The DNS data points at the highest Reynolds numbers (DNS-D, DNS-E, DNS-F) now appear to be in good agreement with SuperPipe experiments, which is in line with the previously noted agreement of the outer-scaled mean velocity profiles.

Figure 7. Mean pipe centreline velocity (![]() $U_{{CL}}$) expressed in inner (a) and in outer (b) units. The dashed grey line corresponds to a fit of the DNS data. The DNS data are shown as circle symbols, and the corresponding logarithmic fits are shown as thick dashed lines. Purple lines and symbols are used for the bulk velocity,
$U_{{CL}}$) expressed in inner (a) and in outer (b) units. The dashed grey line corresponds to a fit of the DNS data. The DNS data are shown as circle symbols, and the corresponding logarithmic fits are shown as thick dashed lines. Purple lines and symbols are used for the bulk velocity, ![]() $u_b$. For the nomenclature of other symbols, refer to table 3.
$u_b$. For the nomenclature of other symbols, refer to table 3.
The distributions of the velocity variances along the coordinate directions are shown in figure 8, in inner scaling. As is now well established (Marusic & Monty Reference Marusic and Monty2019), the longitudinal (![]() $u_z$) and spanwise (
$u_z$) and spanwise (![]() $u_{\theta }$) velocity fluctuations show slow increase with the Reynolds number, with commonly accepted logarithmic growth as after Townsend's attached eddy model (Townsend Reference Townsend1976). On the other hand, the wall-normal velocity fluctuations seem to level off to a maximum value of approximately
$u_{\theta }$) velocity fluctuations show slow increase with the Reynolds number, with commonly accepted logarithmic growth as after Townsend's attached eddy model (Townsend Reference Townsend1976). On the other hand, the wall-normal velocity fluctuations seem to level off to a maximum value of approximately ![]() $1.30$. It is remarkable that the general growth of the longitudinal and spanwise fluctuations is more evident in the outer layer, and in fact it has long been argued about the possible occurrence of a secondary peak of
$1.30$. It is remarkable that the general growth of the longitudinal and spanwise fluctuations is more evident in the outer layer, and in fact it has long been argued about the possible occurrence of a secondary peak of ![]() $\langle u^2_z\rangle$, besides the primary buffer-layer peak. Experiments carried out in the SuperPipe (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012) and CICLoPE (Willert et al. Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017) facilities indeed support the occurrence of such a peak at
$\langle u^2_z\rangle$, besides the primary buffer-layer peak. Experiments carried out in the SuperPipe (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012) and CICLoPE (Willert et al. Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017) facilities indeed support the occurrence of such a peak at ![]() ${\textit {Re}}_{\tau } \gtrsim 10^4$. Whereas DNS data are not at sufficiently high
${\textit {Re}}_{\tau } \gtrsim 10^4$. Whereas DNS data are not at sufficiently high ![]() ${\textit {Re}}_{\tau }$ to show this secondary peak, it appears that in DNS-F the axial velocity variance has attained a nearly horizontal inflectional point at
${\textit {Re}}_{\tau }$ to show this secondary peak, it appears that in DNS-F the axial velocity variance has attained a nearly horizontal inflectional point at ![]() $y^+ \approx 140$. Comparison with the
$y^+ \approx 140$. Comparison with the ![]() ${\textit {Re}}_{\tau } \approx 3000$ DNS of Ahn et al. (Reference Ahn, Lee, Lee, Kang and Sung2015) shows overall good agreement of all turbulence intensities. Comparison with SuperPipe data at
${\textit {Re}}_{\tau } \approx 3000$ DNS of Ahn et al. (Reference Ahn, Lee, Lee, Kang and Sung2015) shows overall good agreement of all turbulence intensities. Comparison with SuperPipe data at ![]() ${\textit {Re}}_{\tau } = 3000$ is also very good, with the exception of the near-wall peak which is likely to be overestimated in experiments. The DNS-F data seem to be well bracketed by SuperPipe and CICLoPE measurements at nearby Reynolds numbers, and also compare very well with experimental data for plane channel flow (Schultz & Flack Reference Schultz and Flack2013).
${\textit {Re}}_{\tau } = 3000$ is also very good, with the exception of the near-wall peak which is likely to be overestimated in experiments. The DNS-F data seem to be well bracketed by SuperPipe and CICLoPE measurements at nearby Reynolds numbers, and also compare very well with experimental data for plane channel flow (Schultz & Flack Reference Schultz and Flack2013).

Figure 8. Distribution of velocity variances (a) and comparison of cases DNS-E, DNS-F with reference DNS and experiments (b). In panel (a), the short dashed lines denote the axial velocity variance (![]() $\langle u_z^2\rangle$), the solid lines denote the radial velocity variance (
$\langle u_z^2\rangle$), the solid lines denote the radial velocity variance (![]() $\langle u_r^2\rangle$), and the long dashed lines denote the azimuthal velocity variance (
$\langle u_r^2\rangle$), and the long dashed lines denote the azimuthal velocity variance (![]() $\langle u_{\theta }^2 \rangle$). For colour codes in DNS data, see table 1, and for nomenclature of symbols, see table 3.
$\langle u_{\theta }^2 \rangle$). For colour codes in DNS data, see table 1, and for nomenclature of symbols, see table 3.
Distributions of the turbulent shear stress are shown in figure 9. As is well established (e.g. Lee & Moser Reference Lee and Moser2015), the shear stress profiles tend to become flatter at higher ![]() ${\textit {Re}}_{\tau }$, the peak value rises towards unity, and its position moves farther from the wall, in inner units. In particular, exploiting mean momentum balance and assuming the presence of a logarithmic layer in the mean axial velocity, the following prediction follows for the position of the turbulent shear stress peak (Afzal Reference Afzal1982):
${\textit {Re}}_{\tau }$, the peak value rises towards unity, and its position moves farther from the wall, in inner units. In particular, exploiting mean momentum balance and assuming the presence of a logarithmic layer in the mean axial velocity, the following prediction follows for the position of the turbulent shear stress peak (Afzal Reference Afzal1982):
which is intermediate between inner and outer scaling. This observation has led some authors to argue about the relevance of a ‘mesolayer’ (e.g. Long & Chen Reference Long and Chen1981; Wei et al. Reference Wei, Fife, Klewicki and McMurtry2005). The asymptotic relationship (3.8) (with ![]() $k=0.387$) is satisfied with good accuracy starting at
$k=0.387$) is satisfied with good accuracy starting at ![]() ${\textit {Re}}_{\tau } \approx 10^3$, reflecting the onset of a near logarithmic layer. Similar results were obtained by Chin et al. (Reference Chin, Philip, Klewicki, Ooi and Marusic2014), by processing the mean velocity profiles obtained in the experiments of Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013).
${\textit {Re}}_{\tau } \approx 10^3$, reflecting the onset of a near logarithmic layer. Similar results were obtained by Chin et al. (Reference Chin, Philip, Klewicki, Ooi and Marusic2014), by processing the mean velocity profiles obtained in the experiments of Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013).

Figure 9. Distributions of turbulent shear stress (a) and its peak position at various ![]() ${\textit {Re}}_{\tau }$ (b). In panel (b) the circles denote the present DNS data, the squares the data of Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013), as processed by Chin et al. (Reference Chin, Philip, Klewicki, Ooi and Marusic2014), and the dashed line the theoretical estimate (3.8). For colour codes in DNS data, see table 1.
${\textit {Re}}_{\tau }$ (b). In panel (b) the circles denote the present DNS data, the squares the data of Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013), as processed by Chin et al. (Reference Chin, Philip, Klewicki, Ooi and Marusic2014), and the dashed line the theoretical estimate (3.8). For colour codes in DNS data, see table 1.
The behaviour of the Reynolds stresses when expressed as a function of the outer-scaled wall distance, which is shown in figure 10, is also of great theoretical interest. In fact, according to the attached-eddy model (Townsend Reference Townsend1976; Marusic & Monty Reference Marusic and Monty2019), the wall-parallel velocity variances are expected to decline logarithmically with the wall distance in the outer layer, hence
where ![]() $A_i$,
$A_i$, ![]() $B_i$ are universal constants. Regarding the axial stress, Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) argued that SuperPipe data at the highest available Reynolds number are best fit with
$B_i$ are universal constants. Regarding the axial stress, Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) argued that SuperPipe data at the highest available Reynolds number are best fit with ![]() $A_1=1.23$,
$A_1=1.23$, ![]() $B_1=1.56$, with a sensible logarithmic layer only emerging at
$B_1=1.56$, with a sensible logarithmic layer only emerging at ![]() ${\textit {Re}}_{\tau } > 10^4$, in the range of wall distances
${\textit {Re}}_{\tau } > 10^4$, in the range of wall distances ![]() $3 {\textit {Re}}_{\tau }^{1/2} \le y^+ \le 0.15 {\textit {Re}}_{\tau }$. The DNS data only show the formation of a near logarithmic layer farther away from the wall, which is not where it is expected from theoretical arguments. Hence, little can be said in this respect. The azimuthal velocity variance, shown in figure 10(b), has a more benign behaviour, and it features clear logarithmic layers even at modest
$3 {\textit {Re}}_{\tau }^{1/2} \le y^+ \le 0.15 {\textit {Re}}_{\tau }$. The DNS data only show the formation of a near logarithmic layer farther away from the wall, which is not where it is expected from theoretical arguments. Hence, little can be said in this respect. The azimuthal velocity variance, shown in figure 10(b), has a more benign behaviour, and it features clear logarithmic layers even at modest ![]() ${\textit {Re}}_{\tau }$. Fitting the DNS data yields
${\textit {Re}}_{\tau }$. Fitting the DNS data yields ![]() $A_3 = 0.40$,
$A_3 = 0.40$, ![]() $B_3 = 1.0$, which is very close to what is found in channels (Bernardini, Pirozzoli & Orlandi Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). Measurements of pipe flow carried out in the CICLoPE facility (Örlü et al. Reference Örlü, Fiorini, Segalini, Bellani, Talamelli and Alfredsson2017) yielded
$B_3 = 1.0$, which is very close to what is found in channels (Bernardini, Pirozzoli & Orlandi Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). Measurements of pipe flow carried out in the CICLoPE facility (Örlü et al. Reference Örlü, Fiorini, Segalini, Bellani, Talamelli and Alfredsson2017) yielded ![]() $A_3 = 0.63$,
$A_3 = 0.63$, ![]() $B_3=1.21$, hence much larger values than in DNS. Possible overestimation of the wall-normal and azimuthal Reynolds stresses was in fact acknowledged by the authors of that paper.
$B_3=1.21$, hence much larger values than in DNS. Possible overestimation of the wall-normal and azimuthal Reynolds stresses was in fact acknowledged by the authors of that paper.

Figure 10. Axial (a) and azimuthal (b) turbulent stresses as a function of outer-scaled wall distance. In panel (a), symbols denote SuperPipe data (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012) at ![]() ${\textit {Re}}_{\tau } = 1985, 3334, 5411, 10\,480, 20\,250, 37\,690$, and the dashed grey line the corresponding fit,
${\textit {Re}}_{\tau } = 1985, 3334, 5411, 10\,480, 20\,250, 37\,690$, and the dashed grey line the corresponding fit, ![]() $\langle u_z^2\rangle = 1.61 - 1.25 \log (y/R)$. In panel (b), the dashed coloured lines denote DNS data of channel flow (Lee & Moser Reference Lee and Moser2015) at
$\langle u_z^2\rangle = 1.61 - 1.25 \log (y/R)$. In panel (b), the dashed coloured lines denote DNS data of channel flow (Lee & Moser Reference Lee and Moser2015) at ![]() ${\textit {Re}}_{\tau } = 550, 1000, 2000, 5200$, and the dashed grey line the fit of the DNS data,
${\textit {Re}}_{\tau } = 550, 1000, 2000, 5200$, and the dashed grey line the fit of the DNS data, ![]() $\langle u_{\theta }^2 \rangle = 1.0 - 0.40 \log (y/R)$. For colour codes in DNS data, see table 1.
$\langle u_{\theta }^2 \rangle = 1.0 - 0.40 \log (y/R)$. For colour codes in DNS data, see table 1.
Quantitative insight into Reynolds number effects is provided by inspection of the amplitude of the inner peak of the axial velocity variance, which we show in figure 11. The general theoretical expectation is that the peak grows logarithmically with ![]() ${\textit {Re}}_{\tau }$ owing to the increasing influence of distant, inactive eddies (Marusic & Monty Reference Marusic and Monty2019). However, some recent experimental results (Willert et al. Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017), and theoretical arguments (Chen & Sreenivasan Reference Chen and Sreenivasan2021), suggest that such growth should eventually saturate. Although the difference between slow logarithmic growth and the attainment of an asymptotic value is quite subtle in practice, the theoretical interest is high, as in the latter case universality of wall scaling would be eventually restored. Within the investigated range of Reynolds numbers, our DNS data in fact support continuing logarithmic increase. Comparison with channel data (Lee & Moser Reference Lee and Moser2015) shows some difference, which might result from stronger geometrical confinement of distant eddies in the pipe geometry. However, differences tend to becomes smaller at higher
${\textit {Re}}_{\tau }$ owing to the increasing influence of distant, inactive eddies (Marusic & Monty Reference Marusic and Monty2019). However, some recent experimental results (Willert et al. Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017), and theoretical arguments (Chen & Sreenivasan Reference Chen and Sreenivasan2021), suggest that such growth should eventually saturate. Although the difference between slow logarithmic growth and the attainment of an asymptotic value is quite subtle in practice, the theoretical interest is high, as in the latter case universality of wall scaling would be eventually restored. Within the investigated range of Reynolds numbers, our DNS data in fact support continuing logarithmic increase. Comparison with channel data (Lee & Moser Reference Lee and Moser2015) shows some difference, which might result from stronger geometrical confinement of distant eddies in the pipe geometry. However, differences tend to becomes smaller at higher ![]() ${\textit {Re}}_{\tau }$. In quantitative terms, we find the slope of logarithmic increase to be approximately
${\textit {Re}}_{\tau }$. In quantitative terms, we find the slope of logarithmic increase to be approximately ![]() $0.67$, a bit steeper than found in channel flow DNS (Lee & Moser Reference Lee and Moser2015, approximately
$0.67$, a bit steeper than found in channel flow DNS (Lee & Moser Reference Lee and Moser2015, approximately ![]() $0.64$), and then suggested from a collection of DNS and experiments (approximately
$0.64$), and then suggested from a collection of DNS and experiments (approximately ![]() $0.63$ (Marusic et al. Reference Marusic, Baars and Hutchins2017)). Experimental data for pipe flow are quite scattered, as SuperPipe experiments yield an unrealistically decreasing trend (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012), particle image velocimetry (known as PIV) measurements taken in the CIPLoPE facility (Willert et al. Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017) suggest saturation of the growth, whereas hot-wire measurements in the same facility support continued logarithmic growth (Fiorini Reference Fiorini2017). The theoretical predictions of Chen & Sreenivasan (Reference Chen and Sreenivasan2021) (see the dashed purple line of figure 11a) seem to conform well with channel flow DNS data and with the experiments of Willert et al. (Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017).
$0.63$ (Marusic et al. Reference Marusic, Baars and Hutchins2017)). Experimental data for pipe flow are quite scattered, as SuperPipe experiments yield an unrealistically decreasing trend (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012), particle image velocimetry (known as PIV) measurements taken in the CIPLoPE facility (Willert et al. Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017) suggest saturation of the growth, whereas hot-wire measurements in the same facility support continued logarithmic growth (Fiorini Reference Fiorini2017). The theoretical predictions of Chen & Sreenivasan (Reference Chen and Sreenivasan2021) (see the dashed purple line of figure 11a) seem to conform well with channel flow DNS data and with the experiments of Willert et al. (Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017).

Figure 11. Magnitude of inner peak of axial velocity variance (a), peak turbulence production (![]() $P_{{PK}}$, red) and wall dissipation of axial velocity variance (
$P_{{PK}}$, red) and wall dissipation of axial velocity variance (![]() $\epsilon _{{11w}}$, black) (b). For colour codes in DNS data, see table 1, and for nomenclature of symbols, see table 3. In panel (a) the dashed grey line marks the DNS data fit,
$\epsilon _{{11w}}$, black) (b). For colour codes in DNS data, see table 1, and for nomenclature of symbols, see table 3. In panel (a) the dashed grey line marks the DNS data fit, ![]() $\langle u^2_z\rangle ^+_{{IP}} = 0.67 \log {\textit {Re}}_{\tau } + 3.3$, the dashed purple line denotes the defect power law of Chen & Sreenivasan (Reference Chen and Sreenivasan2021) and the dash–dotted line the logarithmic law of Marusic, Baars & Hutchins (Reference Marusic, Baars and Hutchins2017),
$\langle u^2_z\rangle ^+_{{IP}} = 0.67 \log {\textit {Re}}_{\tau } + 3.3$, the dashed purple line denotes the defect power law of Chen & Sreenivasan (Reference Chen and Sreenivasan2021) and the dash–dotted line the logarithmic law of Marusic, Baars & Hutchins (Reference Marusic, Baars and Hutchins2017), ![]() $\langle u^2_z\rangle ^+_{{IP}} = 0.63 \log {\textit {Re}}_{\tau } + 3.8$. In panel (b), the dot–dashed and dotted lines denote fits of
$\langle u^2_z\rangle ^+_{{IP}} = 0.63 \log {\textit {Re}}_{\tau } + 3.8$. In panel (b), the dot–dashed and dotted lines denote fits of ![]() $P_{{PK}}$ and
$P_{{PK}}$ and ![]() $\epsilon _{{11w}}$ in their tendency to the respective assumed asymptotic values.
$\epsilon _{{11w}}$ in their tendency to the respective assumed asymptotic values.
While our DNS data cannot be used to directly evaluate the theoretical predictions owing to limited achievable Reynolds number, they can be used to better scrutinize the foundations of the theoretical arguments. The main argument made by Chen & Sreenivasan (Reference Chen and Sreenivasan2021), although not thoroughly justified in our opinion, was that since turbulence kinetic energy production is bounded, the wall dissipation must also stay bounded. Hence, let ![]() $P = - \langle u_z u_r \rangle \text {d} U / \text {d} r$ be the turbulence kinetic energy production rate, and
$P = - \langle u_z u_r \rangle \text {d} U / \text {d} r$ be the turbulence kinetic energy production rate, and ![]() $\epsilon _{11} = \nu \langle | \boldsymbol {\nabla } u_z |^2 \rangle$ be the dissipation rate of the axial velocity variance, those authors first argue that the wall limiting value of
$\epsilon _{11} = \nu \langle | \boldsymbol {\nabla } u_z |^2 \rangle$ be the dissipation rate of the axial velocity variance, those authors first argue that the wall limiting value of ![]() $\epsilon _{11}$ should scale as
$\epsilon _{11}$ should scale as
with ![]() $\beta$ a suitable constant. In figure 11 we explore deviations of
$\beta$ a suitable constant. In figure 11 we explore deviations of ![]() $\epsilon _w$ and of the peak turbulence kinetic energy production, say
$\epsilon _w$ and of the peak turbulence kinetic energy production, say ![]() $P_{{PK}}$, from their asymptotic value, namely
$P_{{PK}}$, from their asymptotic value, namely ![]() $1/4$. According to analytical constraints (Pope Reference Pope2000), we find that production tends to its asymptotic value quite rapidly, as approximately
$1/4$. According to analytical constraints (Pope Reference Pope2000), we find that production tends to its asymptotic value quite rapidly, as approximately ![]() $1/{\textit {Re}}_{\tau }$. Consistent with (3.10), the wall dissipation also tends to
$1/{\textit {Re}}_{\tau }$. Consistent with (3.10), the wall dissipation also tends to ![]() $1/4$, more or less at the predicted rate, thus empirically validating the first assumption. The next argument advocated by Chen & Sreenivasan (Reference Chen and Sreenivasan2021) is that wall balance between viscous diffusion and dissipation and Taylor series expansion of the axial velocity variance near the wall yields
$1/4$, more or less at the predicted rate, thus empirically validating the first assumption. The next argument advocated by Chen & Sreenivasan (Reference Chen and Sreenivasan2021) is that wall balance between viscous diffusion and dissipation and Taylor series expansion of the axial velocity variance near the wall yields
whence, from assumed invariance of the peak location of ![]() $\langle u_z^2 \rangle$ (say,
$\langle u_z^2 \rangle$ (say, ![]() $y_{{IP}}^+$), saturation of growth of the peak velocity variance would follow. Table 2 suggests that this second assumption is in fact violated, as the position of the peak slightly increases with
$y_{{IP}}^+$), saturation of growth of the peak velocity variance would follow. Table 2 suggests that this second assumption is in fact violated, as the position of the peak slightly increases with ![]() ${\textit {Re}}_{\tau }$, with non-negligible effect on the peak variance as it appears in squared form in (3.11). As a consequence, logarithmic growth of the peak velocity variance still holds, at least in the range of Reynolds numbers currently accessible to DNS.
${\textit {Re}}_{\tau }$, with non-negligible effect on the peak variance as it appears in squared form in (3.11). As a consequence, logarithmic growth of the peak velocity variance still holds, at least in the range of Reynolds numbers currently accessible to DNS.
A secondary, outer-layer peak of the axial velocity variance was observed in the SuperPipe experiments of Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012), which relied on nanoscale thermal anemometry probes. Later experiments carried out in the CICLoPE facility (Örlü et al. Reference Örlü, Fiorini, Segalini, Bellani, Talamelli and Alfredsson2017), using custom-made X-wire probes, raised doubts about the existence of a genuine outer peak, and in general prompted further high-quality data to ascertain whether it exists beyond measurement uncertainty. Particle image velocimetry measurements also carried out in the CICLoPE facility (Willert et al. Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017), did show an outer peak that develops and moves away from the inner peak with increasing Reynolds number. Hence, it is clear that this issue is not definitely settled in experiments. Although no distinct outer peak of the axial velocity variance is found at the Reynolds numbers accessed in the present DNS study, it is nevertheless instructive to explore the scaling of the velocity fluctuations in the range of wall distances where the peak is expected to occur. For that purpose, we consider the outer position where the second logarithmic derivative of the velocity variance vanishes, which in the present DNS ranges from ![]() $y^+ \approx 115$ for DNS-A, to
$y^+ \approx 115$ for DNS-A, to ![]() $y^+ \approx 140$ for DNS-F. Weak dependence of the inner-scaled outer peak position on
$y^+ \approx 140$ for DNS-F. Weak dependence of the inner-scaled outer peak position on ![]() ${\textit {Re}}_{\tau }$, although at much higher Reynolds number, was also noticed by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012). The resulting distribution is shown in figure 12. All DNS data fall nicely on a logarithmic fit, and they seem to connect smoothly to the experimental results, whose scatter and uncertainty is expected to be much less than for the inner peak. Experiments indicate a change of behaviour to a shallower logarithmic dependence with slope of approximately
${\textit {Re}}_{\tau }$, although at much higher Reynolds number, was also noticed by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012). The resulting distribution is shown in figure 12. All DNS data fall nicely on a logarithmic fit, and they seem to connect smoothly to the experimental results, whose scatter and uncertainty is expected to be much less than for the inner peak. Experiments indicate a change of behaviour to a shallower logarithmic dependence with slope of approximately ![]() $0.63$ (Pullin et al. Reference Pullin, Inoue and Saito2013; Fiorini Reference Fiorini2017), which would be very close to the growth rate of the inner peak (see figure 11). The figure suggests that verification of this effect would require
$0.63$ (Pullin et al. Reference Pullin, Inoue and Saito2013; Fiorini Reference Fiorini2017), which would be very close to the growth rate of the inner peak (see figure 11). The figure suggests that verification of this effect would require ![]() ${\textit {Re}}_{\tau }$ of approximately
${\textit {Re}}_{\tau }$ of approximately ![]() $10^4$.
$10^4$.

Figure 12. Magnitude of outer peak of axial velocity variance as a function of ![]() ${\textit {Re}}_{\tau }$. Lines and symbols as in tables 1 and 3. The dashed grey line marks the DNS data fit,
${\textit {Re}}_{\tau }$. Lines and symbols as in tables 1 and 3. The dashed grey line marks the DNS data fit, ![]() $\langle u_z^2 \rangle ^+_{OP} = 1.33 \log {\textit {Re}}_{\tau } - 5.61$, and the purple line denotes the logarithmic fit given by Pullin et al. (Reference Pullin, Inoue and Saito2013).
$\langle u_z^2 \rangle ^+_{OP} = 1.33 \log {\textit {Re}}_{\tau } - 5.61$, and the purple line denotes the logarithmic fit given by Pullin et al. (Reference Pullin, Inoue and Saito2013).
As pointed out by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012), the formation and growth of an outer peak of the axial velocity variance has important theoretical and practical implications. From the modelling standpoint, no current Reynolds-averaged Navier–Stokes (RANS) model is capable of predicting non-monotonic behaviour of Reynolds stresses outside the buffer layer. From the fundamental physics standpoint, the presence of an outer peak is suggestive of violation of equilibrium between turbulence production and dissipation. The DNS allows us to substantiate this scenario, and for that purpose in figure 13, we show the relative excess of turbulent kinetic energy production (![]() $P$) over its total dissipation rate, here defined as
$P$) over its total dissipation rate, here defined as ![]() $D = \nu \langle u_i \nabla ^2 u_i\rangle$, which lumps together dissipation rate and viscous diffusion. Data confirm the presence of a near-universal region confined to the buffer layer (say,
$D = \nu \langle u_i \nabla ^2 u_i\rangle$, which lumps together dissipation rate and viscous diffusion. Data confirm the presence of a near-universal region confined to the buffer layer (say, ![]() $8 \lesssim y^+ \lesssim 35$), in which production exceeds dissipation by up to
$8 \lesssim y^+ \lesssim 35$), in which production exceeds dissipation by up to ![]() $40\,\%$. Data also show the onset, starting from DNS-B, of another region farther from the wall with positive unbalance, whose inner limit is constant in inner units, at
$40\,\%$. Data also show the onset, starting from DNS-B, of another region farther from the wall with positive unbalance, whose inner limit is constant in inner units, at ![]() $y^+ = 100$, and whose outer limit tends to become constant at high
$y^+ = 100$, and whose outer limit tends to become constant at high ![]() ${\textit {Re}}_{\tau }$ in outer units, at
${\textit {Re}}_{\tau }$ in outer units, at ![]() $y/R \approx 0.4$. The peak unbalance at high Reynolds number is approximately
$y/R \approx 0.4$. The peak unbalance at high Reynolds number is approximately ![]() $17\,\%$, and its position seems to scale more in inner than in outer units. Turbulence kinetic energy production excess in the presence of a (near) logarithmic mean velocity profile can be interpreted by recalling that only part of the axial velocity fluctuations which are generated correlates with wall-normal velocity fluctuations to yield active motions (Townsend Reference Townsend1976), hence the extra production feeds inactive motions, which do not convey contribution to the turbulent shear stress. This finding clearly indicates that at high enough Reynolds number the outer wall layer becomes a dynamically active part of the flow, having the potential to transfer energy both to the core flow, and towards the wall, in the form of imprinting on the near-wall layer (Marusic & Monty Reference Marusic and Monty2019).
$17\,\%$, and its position seems to scale more in inner than in outer units. Turbulence kinetic energy production excess in the presence of a (near) logarithmic mean velocity profile can be interpreted by recalling that only part of the axial velocity fluctuations which are generated correlates with wall-normal velocity fluctuations to yield active motions (Townsend Reference Townsend1976), hence the extra production feeds inactive motions, which do not convey contribution to the turbulent shear stress. This finding clearly indicates that at high enough Reynolds number the outer wall layer becomes a dynamically active part of the flow, having the potential to transfer energy both to the core flow, and towards the wall, in the form of imprinting on the near-wall layer (Marusic & Monty Reference Marusic and Monty2019).

Figure 13. Excess of turbulence kinetic energy production over dissipation as a function of inner-scaled (a) and outer-scaled (b) wall distance. Lines as in table 1.
4. Concluding comments
Although DNS of wall turbulence is still confined to a moderate range of Reynolds numbers, it is beginning to approach a state in which some typical phenomena of the asymptotically high-![]() ${\textit {Re}}$ emerge. Given its ability to resolve the near-wall layer, DNS lends itself to testing theories of wall turbulence and to in-depth scrutiny of experimental data. In this work, DNS of flow in a smooth pipe has been carried out up to
${\textit {Re}}$ emerge. Given its ability to resolve the near-wall layer, DNS lends itself to testing theories of wall turbulence and to in-depth scrutiny of experimental data. In this work, DNS of flow in a smooth pipe has been carried out up to ![]() ${\textit {Re}}_{\tau } \approx 6000$, which, although still far from what achievable in experimental tests, allows us to uncover a number of interesting issues, in our opinion. First, we have noted that DNS data fall systematically short of the classical Prandtl friction law, by as much as
${\textit {Re}}_{\tau } \approx 6000$, which, although still far from what achievable in experimental tests, allows us to uncover a number of interesting issues, in our opinion. First, we have noted that DNS data fall systematically short of the classical Prandtl friction law, by as much as ![]() $2\,\%$. This evidence is not consistent with data from the SuperPipe facility, although other recent data from the CICLoPE and Hi-Reff facilities seem to yield similar trends. The DNS data fitting suggests that a logarithmic law as (3.2) still holds, however, with a von Kármán constant
$2\,\%$. This evidence is not consistent with data from the SuperPipe facility, although other recent data from the CICLoPE and Hi-Reff facilities seem to yield similar trends. The DNS data fitting suggests that a logarithmic law as (3.2) still holds, however, with a von Kármán constant ![]() $k \approx 0.387$, which matches extremely well the value quoted by Furuichi et al. (Reference Furuichi, Terao, Wada and Tsuji2018), and which would reconcile pipe flow with plane channel and boundary layer flows, thus corroborating claims made by Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013). A logarithmic profile with
$k \approx 0.387$, which matches extremely well the value quoted by Furuichi et al. (Reference Furuichi, Terao, Wada and Tsuji2018), and which would reconcile pipe flow with plane channel and boundary layer flows, thus corroborating claims made by Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013). A logarithmic profile with ![]() $k \approx 0.387$ fits the mean axial velocity distributions for
$k \approx 0.387$ fits the mean axial velocity distributions for ![]() $30 \le y^+ \le 0.15 {\textit {Re}}_{\tau }$ well, although linear deviations are clearly visible, as argued by Afzal & Yajnik (Reference Afzal and Yajnik1973) and Luchini (Reference Luchini2017), which when taken into account yield an excellent representation of the velocity profiles up to
$30 \le y^+ \le 0.15 {\textit {Re}}_{\tau }$ well, although linear deviations are clearly visible, as argued by Afzal & Yajnik (Reference Afzal and Yajnik1973) and Luchini (Reference Luchini2017), which when taken into account yield an excellent representation of the velocity profiles up to ![]() $y/R \approx 0.5$. It is remarkable that the same value of the von Kármán constant also fits the mean centreline velocity distribution well (see figure 7), which is found to grow logarithmically throughout the range of
$y/R \approx 0.5$. It is remarkable that the same value of the von Kármán constant also fits the mean centreline velocity distribution well (see figure 7), which is found to grow logarithmically throughout the range of ![]() ${\textit {Re}}_{\tau }$ under investigation. This finding is quite reasonable as it corroborates that the eventual state of turbulent flow in a pipe should be plug flow, as argued by Pullin et al. (Reference Pullin, Inoue and Saito2013), hence
${\textit {Re}}_{\tau }$ under investigation. This finding is quite reasonable as it corroborates that the eventual state of turbulent flow in a pipe should be plug flow, as argued by Pullin et al. (Reference Pullin, Inoue and Saito2013), hence ![]() $U_{{CL}} \to u_b$ as
$U_{{CL}} \to u_b$ as ![]() ${\textit {Re}}_{\tau } \to \infty$. This would, however, seemingly contrast with recent measurements made in the CICLoPE facility (Nagib et al. Reference Nagib, Monkewitz, Mascotelli, Fiorini, Bellani, Zheng and Talamelli2017), which rather suggest a different von Kármán constant for the bulk and the centreline velocity. Experimental data at
${\textit {Re}}_{\tau } \to \infty$. This would, however, seemingly contrast with recent measurements made in the CICLoPE facility (Nagib et al. Reference Nagib, Monkewitz, Mascotelli, Fiorini, Bellani, Zheng and Talamelli2017), which rather suggest a different von Kármán constant for the bulk and the centreline velocity. Experimental data at ![]() ${\textit {Re}}_{\tau } \gtrsim 10^4$ in fact suggest deviations of
${\textit {Re}}_{\tau } \gtrsim 10^4$ in fact suggest deviations of ![]() $U_{{CL}}^+$ from the logarithmic trend found in DNS, however, this effect requires further confirmation, as data are quite scattered. The core velocity profile is found to be, to a good approximation, parabolic, with curvature which is nearly constant in wall units, and decreasing in outer units.
$U_{{CL}}^+$ from the logarithmic trend found in DNS, however, this effect requires further confirmation, as data are quite scattered. The core velocity profile is found to be, to a good approximation, parabolic, with curvature which is nearly constant in wall units, and decreasing in outer units.
Regarding the velocity fluctuations, we find evidence for continuing logarithmic increase of the inner-peak magnitude with ![]() ${\textit {Re}}_{\tau }$. Some experiments and theoretical arguments would indicate that beyond
${\textit {Re}}_{\tau }$. Some experiments and theoretical arguments would indicate that beyond ![]() ${\textit {Re}}_{\tau } \approx 10^4$ a change of behaviour might occur which, however, is very difficult to quantify. The DNS is probably of little use in this respect, as in order to clearly discern among the various trends,
${\textit {Re}}_{\tau } \approx 10^4$ a change of behaviour might occur which, however, is very difficult to quantify. The DNS is probably of little use in this respect, as in order to clearly discern among the various trends, ![]() ${\textit {Re}}_{\tau }$ in excess of
${\textit {Re}}_{\tau }$ in excess of ![]() $10^5$ are likely to be needed. As predicted by the attached-eddy hypothesis, the wall-parallel velocity variances in the outer layer tend to form logarithmic layers, which are especially evident in the azimuthal velocity. Although we do not find direct evidence for the existence of an outer peak of the axial velocity variance, our results highlight the occurrence of an outer site with substantial turbulence production excess over dissipation, thus contradicting the classical equilibrium hypothesis and likely to yield a distinct peak at
$10^5$ are likely to be needed. As predicted by the attached-eddy hypothesis, the wall-parallel velocity variances in the outer layer tend to form logarithmic layers, which are especially evident in the azimuthal velocity. Although we do not find direct evidence for the existence of an outer peak of the axial velocity variance, our results highlight the occurrence of an outer site with substantial turbulence production excess over dissipation, thus contradicting the classical equilibrium hypothesis and likely to yield a distinct peak at ![]() ${\textit {Re}}_{\tau } \approx 10^4$. Investigating these and other violations of universality of wall turbulence to extrapolate asymptotic behaviours is a formidable challenge for theoreticians in years to come.
${\textit {Re}}_{\tau } \approx 10^4$. Investigating these and other violations of universality of wall turbulence to extrapolate asymptotic behaviours is a formidable challenge for theoreticians in years to come.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2021.727.
Acknowledgements
We acknowledge that the results reported in this paper have been achieved using the PRACE Research Infrastructure resource MARCONI based at CINECA, Casalecchio di Reno, Italy, under project PRACE no. 2019204979. Discussions with A.J. Smits are gratefully acknowledged. We would like to thank P. Luchini and M. Quadrio for providing the code used for the data uncertainty analysis.
Funding
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are openly available at the web page http://newton.dma.uniroma1.it/database/