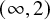1 Introduction
Categories of spans typically appear in algebra and geometry as a convenient way to encode co-and contravariant functorialities (transfer and restriction) and base change isomorphisms between these. For example, span categories of finite G-sets classically appear in representation theory as the indexing categories of Mackey functors [Reference DressDr71]. In the
![]() $\infty $
-categorical setting, spans play an even more significant role because they often provide the only feasible method to organise base change isomorphisms in a homotopy-coherent way. As such, they naturally appear in equivariant homotopy theory (via the theory of spectral Mackey functors [Reference BarwickBa17, Reference NardinNa16]), in motivic homotopy theory [Reference Bachmann and HoyoisBH21] and in higher algebra [Reference CranchCr11, Reference HarpazHa20a, Reference Elmanto and HaugsengEH20].
$\infty $
-categorical setting, spans play an even more significant role because they often provide the only feasible method to organise base change isomorphisms in a homotopy-coherent way. As such, they naturally appear in equivariant homotopy theory (via the theory of spectral Mackey functors [Reference BarwickBa17, Reference NardinNa16]), in motivic homotopy theory [Reference Bachmann and HoyoisBH21] and in higher algebra [Reference CranchCr11, Reference HarpazHa20a, Reference Elmanto and HaugsengEH20].
In each of these cases, one is interested in diagrams indexed by a certain
![]() $\infty $
-category of spans that is constructed informally as follows: from the data of an
$\infty $
-category of spans that is constructed informally as follows: from the data of an
![]() $\infty $
-category X, together with two classes of maps called ingressive (or forwards, denoted
$\infty $
-category X, together with two classes of maps called ingressive (or forwards, denoted
![]() $\rightarrowtail $
) and egressive (or backwards, denoted
$\rightarrowtail $
) and egressive (or backwards, denoted
![]() $\twoheadrightarrow $
), one constructs an
$\twoheadrightarrow $
), one constructs an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Span}(X)$
with the same objects as X and with morphisms from x to y given by spans
$\mathrm {Span}(X)$
with the same objects as X and with morphisms from x to y given by spans

Composition proceeds by pullback of spans, which of course requires that pullbacks of ingressive and egressive maps exist and remain ingressive and egressive. From a geometric point of view, one can think of
![]() $\mathrm {Span}(X)$
as an
$\mathrm {Span}(X)$
as an
![]() $\infty $
-category of (combinatorial) bordisms in
$\infty $
-category of (combinatorial) bordisms in
![]() $X^{{\mathrm {op}}}$
, the two legs of a span giving the two boundary inclusions. As such, span categories also arise in various situations as objects of interest in themselves. Notably, they appear in algebraic K-theory [Reference BarwickBa13, Reference Blumberg, Gepner and TabuadaBGT13] and its hermitian refinements [Reference SchlichtingSc10, CDH+20] via Quillen’s
$X^{{\mathrm {op}}}$
, the two legs of a span giving the two boundary inclusions. As such, span categories also arise in various situations as objects of interest in themselves. Notably, they appear in algebraic K-theory [Reference BarwickBa13, Reference Blumberg, Gepner and TabuadaBGT13] and its hermitian refinements [Reference SchlichtingSc10, CDH+20] via Quillen’s
![]() $\mathcal {Q}$
-construction [Reference QuillenQu73]; see, in particular, [Reference Raptis and SteimleRS19, CDH+20, Reference Hebestreit and SteimleHS21] for works on K-theory where such a geometric perspective on spans is brought to fruition.
$\mathcal {Q}$
-construction [Reference QuillenQu73]; see, in particular, [Reference Raptis and SteimleRS19, CDH+20, Reference Hebestreit and SteimleHS21] for works on K-theory where such a geometric perspective on spans is brought to fruition.
The above informal description of
![]() $\mathrm {Span}(X)$
has been substantiated by Barwick, who constructs an explicit functor sending each adequate triple (of an
$\mathrm {Span}(X)$
has been substantiated by Barwick, who constructs an explicit functor sending each adequate triple (of an
![]() $\infty $
-category X and two classes of maps) to a quasi-category
$\infty $
-category X and two classes of maps) to a quasi-category
![]() $\mathrm {Span}(X)$
[Reference BarwickBa17]. The first purpose of this text is to study some further abstract properties of this construction of span
$\mathrm {Span}(X)$
[Reference BarwickBa17]. The first purpose of this text is to study some further abstract properties of this construction of span
![]() $\infty $
-categories. For example, we give a description of span
$\infty $
-categories. For example, we give a description of span
![]() $\infty $
-categories by a universal property:
$\infty $
-categories by a universal property:
Theorem A. There is an adjoint pair ![]() , where
, where
![]() $\operatorname {\mathrm {Tw}}^{r}(A)$
is the twisted arrow
$\operatorname {\mathrm {Tw}}^{r}(A)$
is the twisted arrow
![]() $\infty $
-category of A with the ingressive and egressive morphisms being those which induce equivalences in the target and source component, respectively.
$\infty $
-category of A with the ingressive and egressive morphisms being those which induce equivalences in the target and source component, respectively.
Here we follow the same notational conventions as in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] and denote the
![]() $\infty $
-category of small
$\infty $
-category of small
![]() $\infty $
-categories by
$\infty $
-categories by
![]() $\mathrm {Cat}$
(and similarly that of
$\mathrm {Cat}$
(and similarly that of
![]() $\infty $
-groupoids by
$\infty $
-groupoids by
![]() $\mathrm {Gpd}$
, etc.). Let us point out that our proof of this result relies on a Segal space construction of span
$\mathrm {Gpd}$
, etc.). Let us point out that our proof of this result relies on a Segal space construction of span
![]() $\infty $
-categories, instead of the point-set approach of Barwick; a slightly different proof was sketched by Raskin in [Reference RaskinRa14]. Theorem A also has a
$\infty $
-categories, instead of the point-set approach of Barwick; a slightly different proof was sketched by Raskin in [Reference RaskinRa14]. Theorem A also has a
![]() $2$
-categorical upgrade, which identifies the diagram
$2$
-categorical upgrade, which identifies the diagram
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {Fun}(A,\mathrm {Span}(X))$
with a span
$\mathrm {Fun}(A,\mathrm {Span}(X))$
with a span
![]() $\infty $
-category of the
$\infty $
-category of the
![]() $\infty $
-category of diagrams
$\infty $
-category of diagrams
![]() $\operatorname {\mathrm {Tw}}^{r}(A) \rightarrow X$
. This statement has already been applied in hermitian K-theory, where it forms the basis for the parametrised algebraic surgery of [Reference Hebestreit and SteimleHS21].
$\operatorname {\mathrm {Tw}}^{r}(A) \rightarrow X$
. This statement has already been applied in hermitian K-theory, where it forms the basis for the parametrised algebraic surgery of [Reference Hebestreit and SteimleHS21].
In addition, we give a description of the ‘universal span category’ (i.e., the cocartesian fibration classified by the functor
![]() $\mathrm {Span}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
):
$\mathrm {Span}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
):
Theorem B. The opposite of the lax under-category ![]() admits the structure of an adequate triple in which a map
admits the structure of an adequate triple in which a map

is egressive if
![]() $\mu \colon y \to f(x)$
is egressive, and ingressive if
$\mu \colon y \to f(x)$
is egressive, and ingressive if
![]() $\mu $
is ingressive and f is an equivalence. The natural map
$\mu $
is ingressive and f is an equivalence. The natural map ![]() extracting the morphisms underlying egressive maps (and inverting those underlying ingressive ones) is then equivalent to the cocartesian fibration classified by
extracting the morphisms underlying egressive maps (and inverting those underlying ingressive ones) is then equivalent to the cocartesian fibration classified by
![]() $\mathrm {Span}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
.
$\mathrm {Span}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
.
As a consequence of Theorem B, we obtain a new proof of the main result of [Reference Barwick, Glasman and NardinBGN18], which asserts that the cocartesian unstraightening of a functor
![]() $F\colon B\rightarrow \mathrm {Cat} $
can be constructed from its cartesian unstraightening via a span construction.
$F\colon B\rightarrow \mathrm {Cat} $
can be constructed from its cartesian unstraightening via a span construction.
Note that the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Span}(X)$
has the following features: the egressive arrows from X are reverted, the ingressive arrows from X are kept and each map factors uniquely as a ‘reverted-egressive’, followed by an ingressive map. This suggests that taking span
$\mathrm {Span}(X)$
has the following features: the egressive arrows from X are reverted, the ingressive arrows from X are kept and each map factors uniquely as a ‘reverted-egressive’, followed by an ingressive map. This suggests that taking span
![]() $\infty $
-categories acts as an involution on adequate triples arising from (orthogonal) factorisation systems. The second part of the paper studies such orthogonal adequate triples, whose egressive and ingressive arrows form a factorisation system and in which all commuting squares of the form
$\infty $
-categories acts as an involution on adequate triples arising from (orthogonal) factorisation systems. The second part of the paper studies such orthogonal adequate triples, whose egressive and ingressive arrows form a factorisation system and in which all commuting squares of the form

are cartesian. Our most significant result about these is the following:
Theorem C. Taking span
![]() $\infty $
-categories gives rise to a
$\infty $
-categories gives rise to a
![]() $C_2$
-action on the full subcategory of orthogonal adequate triples
$C_2$
-action on the full subcategory of orthogonal adequate triples
The simplest example of an orthogonal adequate triple is given by a product
![]() $A\times B$
, with ingressive maps coming from A and egressive maps coming from B. More generally, every cartesian fibration
$A\times B$
, with ingressive maps coming from A and egressive maps coming from B. More generally, every cartesian fibration
![]() $p\colon X\longrightarrow A$
defines the structure of an orthogonal adequate triple on X, for which a map is ingressive if it is p-cartesian and egressive if it is fibrewise (i.e. its image under p is invertible). In fact, every orthogonal adequate triple arises in this way:
$p\colon X\longrightarrow A$
defines the structure of an orthogonal adequate triple on X, for which a map is ingressive if it is p-cartesian and egressive if it is fibrewise (i.e. its image under p is invertible). In fact, every orthogonal adequate triple arises in this way:
Theorem D. An orthogonal factorisation system arises from a cartesian fibration as the cartesian and fibrewise maps if and only if it forms an orthogonal adequate triple. Moreover, this construction restricts to an equivalence between the
![]() $\infty $
-category of orthogonal adequate triples and the
$\infty $
-category of orthogonal adequate triples and the
![]() $\infty $
-category of cartesian fibrations whose fibres have contractible realisation.
$\infty $
-category of cartesian fibrations whose fibres have contractible realisation.
This result extends previous work of Lanari [Reference LanariLa19], who established such a correspondence for pointed cartesian fibrations (i.e., those whose base and total
![]() $\infty $
-category have a terminal object which is preserved by the fibration) and what he calls cartesian factorisation systems. Using the relation between orthogonal adequate triples and cartesian fibrations, the span duality from Theorem C also gives an auto-equivalence of the
$\infty $
-category have a terminal object which is preserved by the fibration) and what he calls cartesian factorisation systems. Using the relation between orthogonal adequate triples and cartesian fibrations, the span duality from Theorem C also gives an auto-equivalence of the
![]() $\infty $
-category of cartesian fibrations. This reduces to the duality functor of Barwick, Glasman and Nardin from [Reference Barwick, Glasman and NardinBGN18].
$\infty $
-category of cartesian fibrations. This reduces to the duality functor of Barwick, Glasman and Nardin from [Reference Barwick, Glasman and NardinBGN18].
Similarly, one can use Theorem C to obtain duality functors for fibrations over a product
![]() $A\times B$
. For example, one can consider maps of orthogonal triples
$A\times B$
. For example, one can consider maps of orthogonal triples
![]() $p=(p_1, p_2)\colon X\longrightarrow A\times B$
such that
$p=(p_1, p_2)\colon X\longrightarrow A\times B$
such that
-
(1) the ingressive maps of X are exactly the p-cartesian lifts of arrows in A,
-
(2)
 $p_2$
is a cocartesian fibration and for any square (1.1) in X where
$p_2$
is a cocartesian fibration and for any square (1.1) in X where
 $x\to y$
is
$x\to y$
is
 $p_1$
-cocartesian, the base change
$p_1$
-cocartesian, the base change
 $x'\longrightarrow y'$
is
$x'\longrightarrow y'$
is
 $p_1$
-cocartesian as well.
$p_1$
-cocartesian as well.
Such maps are called orthofibrations in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], or two-sided fibrations in [Reference Riehl and VerityRV22, Section 7.1], and can be straightened to functors
![]() $A^{{\mathrm {op}}}\times B\longrightarrow \mathrm {Cat} $
, which also correspond to cartesian fibrations over
$A^{{\mathrm {op}}}\times B\longrightarrow \mathrm {Cat} $
, which also correspond to cartesian fibrations over
![]() $A \times B^{\mathrm {op}}$
via unstraightening. Using that
$A \times B^{\mathrm {op}}$
via unstraightening. Using that
![]() ${\mathrm {Span}^{\perp }}$
sends
${\mathrm {Span}^{\perp }}$
sends
![]() $A\times B$
(with the adequate triple structure mentioned above) to
$A\times B$
(with the adequate triple structure mentioned above) to
![]() $A\times B^{{\mathrm {op}}}$
, the dualisation of Theorem C also restricts to an equivalence
$A\times B^{{\mathrm {op}}}$
, the dualisation of Theorem C also restricts to an equivalence
between orthofibrations and cartesian fibrations, taking opposite categories at the level of fibres. There are similar dualities for the various other types of two-variable fibrations considered in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23]; for example, Theorem C also restricts to a duality between curved orthofibrations over
![]() $A\times B$
and op-Gray fibrations over
$A\times B$
and op-Gray fibrations over
![]() $A\times B^{{\mathrm {op}}}$
(see [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] or Section 6 for definitions), which under straightening [Reference LurieLu09b] correspond to
$A\times B^{{\mathrm {op}}}$
(see [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] or Section 6 for definitions), which under straightening [Reference LurieLu09b] correspond to
![]() $2$
-functors out of the Gray tensor product
$2$
-functors out of the Gray tensor product
![]() $B\boxtimes A^{{\mathrm {op}}}$
.
$B\boxtimes A^{{\mathrm {op}}}$
.
Relying on Toën’s equivalence
![]() $\mathrm {Aut}(\mathrm {Cat} ) \simeq C_2$
[Reference ToënTo05], we extend another result from [Reference Barwick, Glasman and NardinBGN18] and show that any composite of dualisations and (un)straightenings as above is uniquely determined by its action on fibres:
$\mathrm {Aut}(\mathrm {Cat} ) \simeq C_2$
[Reference ToënTo05], we extend another result from [Reference Barwick, Glasman and NardinBGN18] and show that any composite of dualisations and (un)straightenings as above is uniquely determined by its action on fibres:
Theorem E. The three functors ![]() given by
given by
have automorphism groups
![]() $*, C_2$
and
$*, C_2$
and
![]() $\ast $
, respectively. The nontrivial automorphism in the middle case is given by post-composition with
$\ast $
, respectively. The nontrivial automorphism in the middle case is given by post-composition with
![]() $(-)^{\mathrm {op}} \colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
. (Here
$(-)^{\mathrm {op}} \colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
. (Here
![]() $\mathbf {Cat}$
denotes the
$\mathbf {Cat}$
denotes the
![]() $(\infty ,2)$
-category of
$(\infty ,2)$
-category of
![]() $\infty $
-categories, as in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23].)
$\infty $
-categories, as in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23].)
For example, this implies that the dualisation equivalence (1.2) arising from Theorem C coincides with the dualisation constructed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] using straightening and unstraightening (though this can also be deduced from Theorem B directly). As an application of this explicit dualisation for two-variable fibrations, we consider the fibrations classified by the enhanced mapping functor
associated to an
![]() $(\infty , 2)$
-category
$(\infty , 2)$
-category
![]() $\mathbf {X}$
with underlying
$\mathbf {X}$
with underlying
![]() $\infty $
-category X. On the one hand, this functor is classified by a cartesian fibration
$\infty $
-category X. On the one hand, this functor is classified by a cartesian fibration
from the oplax twisted arrow
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathbf {X}$
, explicitly constructed in [Reference García and SternAGS23]. We show (Theorem 7.21) that dually (and upon taking opposite categories), this functor also classifies the orthofibration
$\mathbf {X}$
, explicitly constructed in [Reference García and SternAGS23]. We show (Theorem 7.21) that dually (and upon taking opposite categories), this functor also classifies the orthofibration
from the
![]() $\infty $
-category underlying the oplax arrow
$\infty $
-category underlying the oplax arrow
![]() $\infty $
-category, defined using the (in principle unrelated) Gray tensor product of Gagna, Harpaz and Lanari from [Reference Gagna, Harpaz and LanariGHL21]. This is a typical example of an identification of dual fibrations which seems difficult to see by passing through a form of straightening and unstraightening (as in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23]).
$\infty $
-category, defined using the (in principle unrelated) Gray tensor product of Gagna, Harpaz and Lanari from [Reference Gagna, Harpaz and LanariGHL21]. This is a typical example of an identification of dual fibrations which seems difficult to see by passing through a form of straightening and unstraightening (as in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23]).
In a different direction, Theorem E shows that straightening a cartesian fibration over
![]() $A\times B$
to a functor
$A\times B$
to a functor
![]() $A^{\mathrm {op}}\times B^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
is naturally equivalent to straightening it first over A and then over B. This should not be surprising, but deducing it from the definitions does not seem entirely obvious (nevertheless, we provide a second proof as 6.20). As a consequence, we answer a recent question of Clausen:
$A^{\mathrm {op}}\times B^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
is naturally equivalent to straightening it first over A and then over B. This should not be surprising, but deducing it from the definitions does not seem entirely obvious (nevertheless, we provide a second proof as 6.20). As a consequence, we answer a recent question of Clausen:
Corollary F. The Yoneda embedding
![]() $C \hookrightarrow {\mathcal {P}}(C)$
canonically extends to a natural transformation of functors
$C \hookrightarrow {\mathcal {P}}(C)$
canonically extends to a natural transformation of functors ![]() from the inclusion to the composite
from the inclusion to the composite
Again, this result is certainly expected, and we were surprised to learn that it is apparently not contained in the literature. Let us point out that, essentially by definition, the Yoneda embedding does define a natural transformation to the functor ![]() defined using that
defined using that
![]() ${\mathcal {P}}(C)$
is the free cocompletion of C. However, it is not a priori clear that this functor agrees with the one appearing in the corollary in a fashion compatible with the Yoneda embedding (but this follows from the result above as well).
${\mathcal {P}}(C)$
is the free cocompletion of C. However, it is not a priori clear that this functor agrees with the one appearing in the corollary in a fashion compatible with the Yoneda embedding (but this follows from the result above as well).
Remark. Along with [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], this article is part of a recombination of our earlier preprints [Reference HaugsengHa20b] and [Reference Hebestreit, Linskens and NuitenHLN20]. In [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], we described the dualisation of two-variable fibrations, as well as its applications to monoidal and parametrised adjunctions, along the lines of [Reference HaugsengHa20b]; these applications were also discussed in terms of the dualisation functor
![]() ${\mathrm {Span}^{\perp }}$
in [Reference Hebestreit, Linskens and NuitenHLN20] (in particular, Proposition A and Theorem C in there). The results from [Reference Hebestreit, Linskens and NuitenHLN20] concerning span
${\mathrm {Span}^{\perp }}$
in [Reference Hebestreit, Linskens and NuitenHLN20] (in particular, Proposition A and Theorem C in there). The results from [Reference Hebestreit, Linskens and NuitenHLN20] concerning span
![]() $\infty $
-categories and the comparison of various straightening functors for two-variable fibrations (in particular, Theorem B and Corollary D there) are contained in the present paper.
$\infty $
-categories and the comparison of various straightening functors for two-variable fibrations (in particular, Theorem B and Corollary D there) are contained in the present paper.
Organisation
In Section 2, we redevelop Barwick’s theory of span
![]() $\infty $
-categories for adequate triples in terms of complete Segal spaces and then discuss some further properties of the span construction in Section 3. In particular, here we prove Theorem A as Theorem 2.18 and deduce Theorem B as a corollary of Theorem 3.9.
$\infty $
-categories for adequate triples in terms of complete Segal spaces and then discuss some further properties of the span construction in Section 3. In particular, here we prove Theorem A as Theorem 2.18 and deduce Theorem B as a corollary of Theorem 3.9.
We then introduce orthogonal adequate triples in Section 4 and establish Theorem C as Theorem 4.12. The relation between orthogonal adequate triples and fibrations is discussed in Section 5, where Theorem D is proven as Proposition 5.4. In Section 6, we show how Theorem C induces dualities between various types of two-variable fibrations considered in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], we and use this to identify oplax arrow and twisted arrow
![]() $\infty $
-categories as duals in Section 7. We deduce Corollary F in the final Section 8 as Theorem 8.1.
$\infty $
-categories as duals in Section 7. We deduce Corollary F in the final Section 8 as Theorem 8.1.
Finally, the uniqueness of all these dualities (i.e., Theorem E) is derived in Appendix A as Theorem A.1.
Conventions
In order to declutter notation, we will write
![]() $\mathrm {Gpd}, \mathrm {Cat} $
and
$\mathrm {Gpd}, \mathrm {Cat} $
and
![]() $\mathrm {Cat} _2$
for the
$\mathrm {Cat} _2$
for the
![]() $\infty $
-categories of
$\infty $
-categories of
![]() $\infty $
-groupoids (or spaces),
$\infty $
-groupoids (or spaces),
![]() $\infty $
-categories and
$\infty $
-categories and
![]() $(\infty , 2)$
-categories, respectively.
$(\infty , 2)$
-categories, respectively.
The letter
![]() $\iota $
will denote the core of an
$\iota $
will denote the core of an
![]() $\infty $
-category (i.e., the
$\infty $
-category (i.e., the
![]() $\infty $
-groupoid spanned by its equivalences). By a subcategory of an
$\infty $
-groupoid spanned by its equivalences). By a subcategory of an
![]() $\infty $
-category we mean a functor such that the induced morphisms on mapping
$\infty $
-category we mean a functor such that the induced morphisms on mapping
![]() $\infty $
-groupoids and cores are inclusions of path components. A subcategory is full if the functor furthermore induces equivalences on mapping
$\infty $
-groupoids and cores are inclusions of path components. A subcategory is full if the functor furthermore induces equivalences on mapping
![]() $\infty $
-groupoids, while it is wide if the functor induces an equivalence on cores. Similarly, a sub-
$\infty $
-groupoids, while it is wide if the functor induces an equivalence on cores. Similarly, a sub-
![]() $2$
-category of an
$2$
-category of an
![]() $(\infty , 2)$
-category is a functor inducing subcategory inclusions on mapping
$(\infty , 2)$
-category is a functor inducing subcategory inclusions on mapping
![]() $\infty $
-categories and a monomorphism on underlying
$\infty $
-categories and a monomorphism on underlying
![]() $\infty $
-groupoids; we say such a sub-
$\infty $
-groupoids; we say such a sub-
![]() $2$
-category is 1-full if it locally full (i.e., is given by full subcategory inclusions on mapping
$2$
-category is 1-full if it locally full (i.e., is given by full subcategory inclusions on mapping
![]() $\infty $
-categories).
$\infty $
-categories).
Throughout, we shall use small caps such as ![]() to indicate large variants of
to indicate large variants of
![]() $\infty $
-categories and boldface such as
$\infty $
-categories and boldface such as
![]() $\textbf {Cat}$
to denote
$\textbf {Cat}$
to denote
![]() $(\infty ,2)$
-categories. We have also reserved sub- and superscripts on category names to refer to changes on morphisms (e.g.,
$(\infty ,2)$
-categories. We have also reserved sub- and superscripts on category names to refer to changes on morphisms (e.g.,
![]() $\operatorname {\mathrm {Cart}}(A) \subseteq \operatorname {\mathrm {Cart}}^{\mathrm {opl}}(A)$
).
$\operatorname {\mathrm {Cart}}(A) \subseteq \operatorname {\mathrm {Cart}}^{\mathrm {opl}}(A)$
).
We will write
![]() $\operatorname {\mathrm {Ar}}(C)$
for the arrow
$\operatorname {\mathrm {Ar}}(C)$
for the arrow
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fun} ([1],C)$
of an
$\mathrm {Fun} ([1],C)$
of an
![]() $\infty $
-category C, and
$\infty $
-category C, and
![]() $\operatorname {\mathrm {Tw}}^{\ell }(C)$
and
$\operatorname {\mathrm {Tw}}^{\ell }(C)$
and
![]() $\operatorname {\mathrm {Tw}}^{r}(C)$
for the two versions of the twisted arrow category, geared so that the combined source-target map defines a left fibraton in the former, and a right fibration in the latter case; see Example 2.8. Finally, we write
$\operatorname {\mathrm {Tw}}^{r}(C)$
for the two versions of the twisted arrow category, geared so that the combined source-target map defines a left fibraton in the former, and a right fibration in the latter case; see Example 2.8. Finally, we write
![]() $\Lambda _0[2]$
for the span category
$\Lambda _0[2]$
for the span category
![]() $1\leftarrow 0\rightarrow 2$
and
$1\leftarrow 0\rightarrow 2$
and
![]() $\Lambda _2[2]$
for the cospan.
$\Lambda _2[2]$
for the cospan.
2 Adequate triples and
 $\infty $
-categories of spans
$\infty $
-categories of spans
In this section, we will review the theory of adequate triples and their associated span
![]() $\infty $
-categories, as developed by Barwick in [Reference BarwickBa17] under the name effective Burnside
$\infty $
-categories, as developed by Barwick in [Reference BarwickBa17] under the name effective Burnside
![]() $\infty $
-categories. We will use the opportunity to present an alternate viewpoint on the material by translating the assertions along the equivalence between
$\infty $
-categories. We will use the opportunity to present an alternate viewpoint on the material by translating the assertions along the equivalence between
![]() $\infty $
-categories and complete Segal
$\infty $
-categories and complete Segal
![]() $\infty $
-groupoids (i.e., complete Segal spaces). This will allow for simpler proofs with far less explicit combinatorics and will form the basis for our analysis of functors to span
$\infty $
-groupoids (i.e., complete Segal spaces). This will allow for simpler proofs with far less explicit combinatorics and will form the basis for our analysis of functors to span
![]() $\infty $
-categories in the next section.
$\infty $
-categories in the next section.
Since composition in span
![]() $\infty $
-categories proceeds by pullback, one uses the following data as input for span
$\infty $
-categories proceeds by pullback, one uses the following data as input for span
![]() $\infty $
-categories:
$\infty $
-categories:
Definition 2.1. An adequate triple
![]() $(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
consists of an
$(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
consists of an
![]() $\infty $
-category X together with two wide subcategories
$\infty $
-category X together with two wide subcategories
![]() $X_{\mathrm {in}}$
and
$X_{\mathrm {in}}$
and
![]() $X^{\mathrm {eg}}$
, whose morphisms are called ingressive (or forwards, denoted
$X^{\mathrm {eg}}$
, whose morphisms are called ingressive (or forwards, denoted
![]() $\rightarrowtail $
) and egressive (or backwards, denoted
$\rightarrowtail $
) and egressive (or backwards, denoted
![]() $\twoheadrightarrow $
), respectively, such that
$\twoheadrightarrow $
), respectively, such that
-
(1) for any ingressive morphism
 $f \colon y\rightarrowtail x$
and any egressive morphism
$f \colon y\rightarrowtail x$
and any egressive morphism
 $g \colon x'\twoheadrightarrow x$
, there exists a pullback
$g \colon x'\twoheadrightarrow x$
, there exists a pullback 
-
(2) and in any such pullback,
 $f'$
is again ingressive and
$f'$
is again ingressive and
 $g'$
egressive.
$g'$
egressive.
Squares whose horizontal arrows are ingressive and whose vertical arrows are egressive are called ambigressive, and ambigressive cartesian if they are furthermore pullback diagrams. A functor
of adequate triples is given by a functor
![]() $F\colon X\rightarrow Y$
which preserves ambigressive pullbacks. Therefore, we may define
$F\colon X\rightarrow Y$
which preserves ambigressive pullbacks. Therefore, we may define
![]() $\mathrm {AdTrip}$
, the
$\mathrm {AdTrip}$
, the
![]() $\infty $
-category of adequate triples, as the subcategory of
$\infty $
-category of adequate triples, as the subcategory of
![]() $\mathrm {Fun} (\Lambda _2[2],\mathrm {Cat} )$
spanned by the adequate triples and those natural transformations whose evaluation at
$\mathrm {Fun} (\Lambda _2[2],\mathrm {Cat} )$
spanned by the adequate triples and those natural transformations whose evaluation at
![]() $2 \in \Lambda _2[2]$
preserves ambigressive pullback squares.
$2 \in \Lambda _2[2]$
preserves ambigressive pullback squares.
Note that being a natural transformation boils down to preserving ingressive and egressive maps, since these form subcategories. We shall often drop them from notation to avoid cluttering.
Notation 2.2. Given a morphism
![]() $p:Y \rightarrow X$
of adequate triples, we write
$p:Y \rightarrow X$
of adequate triples, we write
![]() $p_{\mathrm {in}}\colon Y_{\mathrm {in}} \rightarrow X_{\mathrm {in}}$
and
$p_{\mathrm {in}}\colon Y_{\mathrm {in}} \rightarrow X_{\mathrm {in}}$
and
![]() $p^{\mathrm {eg}}\colon Y^{\mathrm {eg}} \rightarrow X^{\mathrm {eg}}$
for the restriction of p to ingressives and egressives.
$p^{\mathrm {eg}}\colon Y^{\mathrm {eg}} \rightarrow X^{\mathrm {eg}}$
for the restriction of p to ingressives and egressives.
Example 2.3. Let us record the following immediate examples:
-
(1) For any wide subcategory T of an
 $\infty $
-category S, we have the adequate triples
$\infty $
-category S, we have the adequate triples
 $(S, T, \iota {S})$
and
$(S, T, \iota {S})$
and
 $(S, \iota {S}, T)$
where the ingressives are maps in T and the egressives are equivalences, and vice versa. In particular, for any
$(S, \iota {S}, T)$
where the ingressives are maps in T and the egressives are equivalences, and vice versa. In particular, for any
 $\infty $
-category S, we always have the adequate triples
$\infty $
-category S, we always have the adequate triples
 $(S,S,\iota {S})$
and
$(S,S,\iota {S})$
and
 $(S,\iota {S},S)$
.
$(S,\iota {S},S)$
. -
(2) If S admits all pullbacks, we have the adequate triple
 $(S,S,S)$
where all maps are both egressive and ingressive. This gives rise to a fully faithful embedding
$(S,S,S)$
where all maps are both egressive and ingressive. This gives rise to a fully faithful embedding
 $\mathrm {Cat}^{\mathrm {pb}}\hookrightarrow \mathrm {AdTrip}$
of the subcategory of
$\mathrm {Cat}^{\mathrm {pb}}\hookrightarrow \mathrm {AdTrip}$
of the subcategory of
 $\mathrm {Cat} $
spanned by those
$\mathrm {Cat} $
spanned by those
 $\infty $
-categories which admit pullbacks, and those functors which preserve pullbacks.
$\infty $
-categories which admit pullbacks, and those functors which preserve pullbacks. -
(3) If
 $(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
is an adequate triple, then
$(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
is an adequate triple, then
 $X^{\mathrm {rev}}=(X, X^{\mathrm {eg}}, X_{\mathrm {in}})$
is an adequate triple.
$X^{\mathrm {rev}}=(X, X^{\mathrm {eg}}, X_{\mathrm {in}})$
is an adequate triple.
Lemma 2.4. The
![]() $\infty $
-category of adequate triples admits all limits and one simply computes
$\infty $
-category of adequate triples admits all limits and one simply computes
![]() $\lim \limits \big (X, X_{\mathrm {in}}, X^{\mathrm {eg}}\big )\simeq \big (\lim \limits X, \lim \limits X_{\mathrm {in}}, \lim \limits X^{\mathrm {eg}}\big )$
for every
$\lim \limits \big (X, X_{\mathrm {in}}, X^{\mathrm {eg}}\big )\simeq \big (\lim \limits X, \lim \limits X_{\mathrm {in}}, \lim \limits X^{\mathrm {eg}}\big )$
for every
![]() $X \colon I \rightarrow \mathrm {AdTrip}$
. Likewise,
$X \colon I \rightarrow \mathrm {AdTrip}$
. Likewise,
![]() $\mathrm {AdTrip}$
has filtered colimits given by
$\mathrm {AdTrip}$
has filtered colimits given by ![]() .
.
Proof. Since the limit of a natural wide subcategory inclusion remains a wide subcategory inclusion,
![]() $\big (\lim \limits X, \lim \limits X_{\mathrm {in}}, \lim \limits X^{\mathrm {eg}}\big )$
is indeed a triple of a category together with two wide subcategories (and likewise for filtered colimits). Notice that an ambigressive square in
$\big (\lim \limits X, \lim \limits X_{\mathrm {in}}, \lim \limits X^{\mathrm {eg}}\big )$
is indeed a triple of a category together with two wide subcategories (and likewise for filtered colimits). Notice that an ambigressive square in
![]() $\lim X$
is cartesian if and only if its image in each
$\lim X$
is cartesian if and only if its image in each
![]() $X_i$
is cartesian. Furthermore, a cospan
$X_i$
is cartesian. Furthermore, a cospan
![]() $x\rightarrowtail x'\twoheadleftarrow x"$
in
$x\rightarrowtail x'\twoheadleftarrow x"$
in
![]() $\lim X$
admits an ambigressive pullback if its images in each
$\lim X$
admits an ambigressive pullback if its images in each
![]() $X_i$
do (in this case, those pullbacks assemble into an object of the limit). This implies that
$X_i$
do (in this case, those pullbacks assemble into an object of the limit). This implies that
![]() $\lim X$
is an adequate triple and that a map
$\lim X$
is an adequate triple and that a map
![]() $Z\longrightarrow \lim X$
preserves ambigressive pullback squares if and only each composite
$Z\longrightarrow \lim X$
preserves ambigressive pullback squares if and only each composite
![]() $Z\longrightarrow \lim X\longrightarrow X_i$
does. This implies that the (pointwise) limit in
$Z\longrightarrow \lim X\longrightarrow X_i$
does. This implies that the (pointwise) limit in
![]() $\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
also provides the limit in the subcategory
$\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
also provides the limit in the subcategory
![]() $\mathrm {AdTrip}\hookrightarrow \mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
.
$\mathrm {AdTrip}\hookrightarrow \mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
.
A dual argument applies to the colimit of a filtered diagram. In this case, the image of an ambigressive pullback square in some
![]() $X_i$
under the map
$X_i$
under the map ![]() remains an ambigressive pullback (since at the level of mapping
remains an ambigressive pullback (since at the level of mapping
![]() $\infty $
-groupoids, filtered colimits commute with pullbacks). Conversely, any cospan
$\infty $
-groupoids, filtered colimits commute with pullbacks). Conversely, any cospan
![]() $x\rightarrowtail x'\twoheadleftarrow x"$
in
$x\rightarrowtail x'\twoheadleftarrow x"$
in ![]() arises as the image of a cospan in some
arises as the image of a cospan in some
![]() $X_i$
, whose pullback in
$X_i$
, whose pullback in
![]() $X_i$
then provides the desired ambigressive pullback in
$X_i$
then provides the desired ambigressive pullback in ![]() . It follows that
. It follows that ![]() is an adequate triple and that a map of triples
is an adequate triple and that a map of triples ![]() preserves ambigressive pullback squares if and only if each
preserves ambigressive pullback squares if and only if each ![]() does. This implies that
does. This implies that ![]() is also the colimit in the subcategory
is also the colimit in the subcategory
![]() $\mathrm {AdTrip}\hookrightarrow \mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
.
$\mathrm {AdTrip}\hookrightarrow \mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
.
Lemma 2.5. Let X and Y be two adequate triples and let us write
![]() $\mathrm {Fun} _{\mathrm {AdTrip}}(X,Y)$
for the full subcategory of
$\mathrm {Fun} _{\mathrm {AdTrip}}(X,Y)$
for the full subcategory of
![]() $\mathrm {Fun} (X, Y)$
spanned by the morphisms of adequate triples. Say a natural transformation
$\mathrm {Fun} (X, Y)$
spanned by the morphisms of adequate triples. Say a natural transformation
![]() $\tau \colon F \Rightarrow G$
is ingressive if it is pointwise ingressive in Y and for every egressive
$\tau \colon F \Rightarrow G$
is ingressive if it is pointwise ingressive in Y and for every egressive
![]() $f \colon x \twoheadrightarrow y$
in X, the square
$f \colon x \twoheadrightarrow y$
in X, the square

is cartesian, and analogously for an egressive natural transformation. This endows
![]() $\mathrm {Fun} _{\mathrm {AdTrip}}(X,Y)$
with the structure of an adequate triple, such that the evaluation map
$\mathrm {Fun} _{\mathrm {AdTrip}}(X,Y)$
with the structure of an adequate triple, such that the evaluation map
![]() $\mathrm {Fun} _{\mathrm {AdTrip}}(X,Y)\times X\to Y$
exhibits it as the internal mapping object in
$\mathrm {Fun} _{\mathrm {AdTrip}}(X,Y)\times X\to Y$
exhibits it as the internal mapping object in
![]() $\mathrm {AdTrip}$
. In particular,
$\mathrm {AdTrip}$
. In particular,
![]() $\mathrm {AdTrip}$
is cartesian closed.
$\mathrm {AdTrip}$
is cartesian closed.
Consequently, one obtains a natural equivalence of adequate triples
Proof. The pointwise pullback P of an ingressive and an egressive natural transformation
![]() $F \twoheadrightarrow H \leftarrowtail G$
exists by assumption on Y. To verify that P is indeed a map of adequate triples, note that for an ingressive
$F \twoheadrightarrow H \leftarrowtail G$
exists by assumption on Y. To verify that P is indeed a map of adequate triples, note that for an ingressive
![]() $x \rightarrowtail x'$
, the map
$x \rightarrowtail x'$
, the map
![]() $P(x) \rightarrow P(x')$
participates in the commutative cube
$P(x) \rightarrow P(x')$
participates in the commutative cube

whose front and back face are cartesian by definition of P and whose bottom face is cartesian since
![]() $F \twoheadrightarrow H$
is egressive. Consequently, also the top face is cartesian showing that
$F \twoheadrightarrow H$
is egressive. Consequently, also the top face is cartesian showing that
![]() $P(x) \rightarrow P(x')$
is also ingressive. The argument for the preservation of egressives is the same, and that P preserves ambigressives pullbacks follows directly from the pasting laws.
$P(x) \rightarrow P(x')$
is also ingressive. The argument for the preservation of egressives is the same, and that P preserves ambigressives pullbacks follows directly from the pasting laws.
It is also obvious that the maps
![]() $P \rightarrow G$
and
$P \rightarrow G$
and
![]() $P \rightarrow F$
are pointwise egressive and ingressive, respectively, and the argument above also verifies the second condition in the definition of an egressive transformation, and the argument is dual for the ingressives. In total, this shows that
$P \rightarrow F$
are pointwise egressive and ingressive, respectively, and the argument above also verifies the second condition in the definition of an egressive transformation, and the argument is dual for the ingressives. In total, this shows that
![]() $\mathrm {Fun} _{\mathrm {AdTrip}}(X,Y)$
is an adequate triple.
$\mathrm {Fun} _{\mathrm {AdTrip}}(X,Y)$
is an adequate triple.
To verify the universal property, let Z be a third adequate triple. In suffices to verify that under the equivalence
![]() ${\mathrm {Hom}}_{\mathrm {Cat} }(Z\times X, Y)\simeq {\mathrm {Hom}}_{\mathrm {Cat} }(Z, \mathrm {Fun} (X, Y))$
, a functor
${\mathrm {Hom}}_{\mathrm {Cat} }(Z\times X, Y)\simeq {\mathrm {Hom}}_{\mathrm {Cat} }(Z, \mathrm {Fun} (X, Y))$
, a functor
![]() $F\colon Z\times X\longrightarrow Y$
is a map of adequate triples if and only if the corresponding map
$F\colon Z\times X\longrightarrow Y$
is a map of adequate triples if and only if the corresponding map
![]() $F'\colon Z\longrightarrow \mathrm {Fun} (X, Y)$
takes values in
$F'\colon Z\longrightarrow \mathrm {Fun} (X, Y)$
takes values in
![]() $\mathrm {Fun} _{\mathrm {AdTrip}}(X, Y)$
and determines a map of adequate triples. To see this, note that any ambigressive square in
$\mathrm {Fun} _{\mathrm {AdTrip}}(X, Y)$
and determines a map of adequate triples. To see this, note that any ambigressive square in
![]() $Z\times X$
is uniquely a composite of four types of squares:
$Z\times X$
is uniquely a composite of four types of squares:

Now, F preserving ambigressive (cartesian) squares of the first type is equivalent to
![]() $F'$
taking values in
$F'$
taking values in
![]() $\mathrm {Fun} _{\mathrm {AdTrip}}(X, Y)$
. Preserving the ambigressive (automatically cartesian) squares as in the lower row then corresponds precisely to
$\mathrm {Fun} _{\mathrm {AdTrip}}(X, Y)$
. Preserving the ambigressive (automatically cartesian) squares as in the lower row then corresponds precisely to
![]() $F'\colon Z\longrightarrow \mathrm {Fun} _{\mathrm {AdTrip}}(X, Y)$
preserving ingressive and egressive morphisms. Finally, F preserves the cartesian ambigressive squares as in the upper right corner if and only if
$F'\colon Z\longrightarrow \mathrm {Fun} _{\mathrm {AdTrip}}(X, Y)$
preserving ingressive and egressive morphisms. Finally, F preserves the cartesian ambigressive squares as in the upper right corner if and only if
![]() $F'$
preserves ambigressive pullbacks.
$F'$
preserves ambigressive pullbacks.
One can generate more interesting examples of adequate triples using the following criterion:
Proposition 2.6. Let
![]() $p\colon Y\longrightarrow X$
be a functor and let
$p\colon Y\longrightarrow X$
be a functor and let
![]() $(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
be an adequate triple such that Y has all p-cartesian lifts over
$(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
be an adequate triple such that Y has all p-cartesian lifts over
![]() $X_{\mathrm {in}}$
. Then Y is part of an adequate triple
$X_{\mathrm {in}}$
. Then Y is part of an adequate triple
![]() $\big (Y, Y^{\dagger }, p^{-1}(X^{\mathrm {eg}}))$
, where a map is ingressive if it is p-cartesian and its image is ingressive in X, and egressive if its image under p is. This structure also upgrades p to a map of adequate triples.
$\big (Y, Y^{\dagger }, p^{-1}(X^{\mathrm {eg}}))$
, where a map is ingressive if it is p-cartesian and its image is ingressive in X, and egressive if its image under p is. This structure also upgrades p to a map of adequate triples.
Proof. Consider the left solid cospan in the diagram

with
![]() $x_1\rightarrowtail x_0\twoheadleftarrow x_2$
its image in X under p. By assumption, the right diagram can be completed to an ambigressive pullback in X, and we let
$x_1\rightarrowtail x_0\twoheadleftarrow x_2$
its image in X under p. By assumption, the right diagram can be completed to an ambigressive pullback in X, and we let
![]() $y_3\rightarrowtail y_2$
be a p-cartesian lift of
$y_3\rightarrowtail y_2$
be a p-cartesian lift of
![]() $x_1\times _{x_0} x_2 \rightarrowtail x_2$
. The universal property of p-cartesian maps then implies that there exists a unique map
$x_1\times _{x_0} x_2 \rightarrowtail x_2$
. The universal property of p-cartesian maps then implies that there exists a unique map
![]() $y_3\rightarrow y_1$
which lives over
$y_3\rightarrow y_1$
which lives over
![]() $x_1\times _{x_0} x_2\to x_1$
and makes the left square commute. Note that the left square is ambigressive by definition. To see that it is also a pullback, compute
$x_1\times _{x_0} x_2\to x_1$
and makes the left square commute. Note that the left square is ambigressive by definition. To see that it is also a pullback, compute
 $$ \begin{align*} &\ {\mathrm{Hom}}_Y(y,y_1) \times_{{\mathrm{Hom}}_Y(y,y_0)}{\mathrm{Hom}}_Y(y,y_2) \\ \simeq&\ {\mathrm{Hom}}_X(p(y),x_1) \times_{{\mathrm{Hom}}_X(p(y),x_0)} {\mathrm{Hom}}_Y(y,y_0)\times_{{\mathrm{Hom}}_Y(y,y_0)} {\mathrm{Hom}}_Y(y,y_2) \\ \simeq&\ {\mathrm{Hom}}_X(p(y),x_1) \times_{{\mathrm{Hom}}_X(p(y),x_0)} {\mathrm{Hom}}_Y(p(y),x_2)\times_{{\mathrm{Hom}}_X(p(y),x_2)} {\mathrm{Hom}}_Y(y,y_2) \\ \simeq&\ {\mathrm{Hom}}_X(p(y),x_1 \times_{x_0} x_2) \times_{{\mathrm{Hom}}_X(p(y),x_2)} {\mathrm{Hom}}_Y(y,y_2) \\ \simeq&\ {\mathrm{Hom}}_Y(y,y_3) \end{align*} $$
$$ \begin{align*} &\ {\mathrm{Hom}}_Y(y,y_1) \times_{{\mathrm{Hom}}_Y(y,y_0)}{\mathrm{Hom}}_Y(y,y_2) \\ \simeq&\ {\mathrm{Hom}}_X(p(y),x_1) \times_{{\mathrm{Hom}}_X(p(y),x_0)} {\mathrm{Hom}}_Y(y,y_0)\times_{{\mathrm{Hom}}_Y(y,y_0)} {\mathrm{Hom}}_Y(y,y_2) \\ \simeq&\ {\mathrm{Hom}}_X(p(y),x_1) \times_{{\mathrm{Hom}}_X(p(y),x_0)} {\mathrm{Hom}}_Y(p(y),x_2)\times_{{\mathrm{Hom}}_X(p(y),x_2)} {\mathrm{Hom}}_Y(y,y_2) \\ \simeq&\ {\mathrm{Hom}}_X(p(y),x_1 \times_{x_0} x_2) \times_{{\mathrm{Hom}}_X(p(y),x_2)} {\mathrm{Hom}}_Y(y,y_2) \\ \simeq&\ {\mathrm{Hom}}_Y(y,y_3) \end{align*} $$
for
![]() $y \in Y$
, where the first equivalence uses the universal property of the cartesian edge
$y \in Y$
, where the first equivalence uses the universal property of the cartesian edge
![]() $y_1 \rightarrowtail y_0$
and the last one that of
$y_1 \rightarrowtail y_0$
and the last one that of
![]() $y_3 \rightarrowtail y_2$
. Finally, note that the uniqueness of pullbacks implies that every ambigressive pullback is of this form and is thus clearly preserved by p, which is thus a map of adequate triples.
$y_3 \rightarrowtail y_2$
. Finally, note that the uniqueness of pullbacks implies that every ambigressive pullback is of this form and is thus clearly preserved by p, which is thus a map of adequate triples.
The case of Proposition 2.6 where p is a cartesian fibration admits the following generalisation:
Proposition 2.7. Let
![]() $(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
be an adequate triple,
$(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
be an adequate triple,
![]() $F\colon X^{{\mathrm {op}}}\rightarrow \mathrm {AdTrip}$
a functor and
$F\colon X^{{\mathrm {op}}}\rightarrow \mathrm {AdTrip}$
a functor and
![]() $p\colon Y\longrightarrow X$
its cartesian unstraightening. Then Y has the structure of an adequate triple, in which a map
$p\colon Y\longrightarrow X$
its cartesian unstraightening. Then Y has the structure of an adequate triple, in which a map
![]() $y_1\to y_0$
is egressive if it factors as an egressive morphism in the fibre
$y_1\to y_0$
is egressive if it factors as an egressive morphism in the fibre
![]() $Y_{p(y_1)}\simeq F(p(y_1))$
, followed by a p-cartesian morphism with egressive image in X (and likewise for the ingressives). Furthermore, this structure makes p a map of adequate triples.
$Y_{p(y_1)}\simeq F(p(y_1))$
, followed by a p-cartesian morphism with egressive image in X (and likewise for the ingressives). Furthermore, this structure makes p a map of adequate triples.
An equivalent description of the egressives is given by unstraightening the functor
![]() $X^{\mathrm {op}} \rightarrow \mathrm {AdTrip} \xrightarrow {(-)^{\mathrm {eg}}} \mathrm {Cat} $
and then restricting the arising cartesian fibration to
$X^{\mathrm {op}} \rightarrow \mathrm {AdTrip} \xrightarrow {(-)^{\mathrm {eg}}} \mathrm {Cat} $
and then restricting the arising cartesian fibration to
![]() $X^{\mathrm {eg}}$
, and likewise for the ingressives; this follows immediately from the fact that every map in the domain of a cartesian fibration factors uniquely as a fibrewise followed by a cartesian arrow.
$X^{\mathrm {eg}}$
, and likewise for the ingressives; this follows immediately from the fact that every map in the domain of a cartesian fibration factors uniquely as a fibrewise followed by a cartesian arrow.
Proof. Consider a cospan ![]() where the left arrow is ingressive and the right arrow is egressive in Y. To show that this admits an ambigressive pullback, note that f decomposes into two egressive maps in Y, one contained in a fibre of p and the other p-cartesian (and likewise for
where the left arrow is ingressive and the right arrow is egressive in Y. To show that this admits an ambigressive pullback, note that f decomposes into two egressive maps in Y, one contained in a fibre of p and the other p-cartesian (and likewise for
![]() $y_2\twoheadrightarrow y_0$
). By the pasting lemma for pullbacks, it therefore suffices to show the existence of an ambigressive pullback in the arising special cases.
$y_2\twoheadrightarrow y_0$
). By the pasting lemma for pullbacks, it therefore suffices to show the existence of an ambigressive pullback in the arising special cases.
First, suppose that both f and g are contained in a single fibre
![]() $Y_x\simeq F(x)$
. Since the fibre forms an adequate triple, there exists an ambigressive pullback of f and g within
$Y_x\simeq F(x)$
. Since the fibre forms an adequate triple, there exists an ambigressive pullback of f and g within
![]() $Y_x$
. This square remains a pullback square in Y by [Reference LurieLu09a, Proposition 4.3.1.10] and stays ambigressive by definition.
$Y_x$
. This square remains a pullback square in Y by [Reference LurieLu09a, Proposition 4.3.1.10] and stays ambigressive by definition.
Next, suppose that g is a p-cartesian lift of an egressive arrow. Then Proposition 2.6 implies the existence of a pullback

that maps to an ambigressive pullback in X. It also implies that the left vertical arrow is again p-cartesian and that the upper horizontal one is p-cartesian or fibrewise if f is (the former by switching the roles of ingressives and egressives in 2.6). In both cases, it follows that the square is ambigressive.
The final case (i.e., if f is assumed a p-cartesian lift of an ingressive arrow) follows in the same fashion by again reversing the roles of the egressives and ingressives in Proposition 2.6.
Example 2.8. Let
![]() $(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
be an adequate triple and let
$(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
be an adequate triple and let
![]() $\operatorname {\mathrm {Tw}}^{r}(X)$
be its twisted arrow
$\operatorname {\mathrm {Tw}}^{r}(X)$
be its twisted arrow
![]() $\infty $
-category, with the convention that the source and target define a right fibration. In particular,
$\infty $
-category, with the convention that the source and target define a right fibration. In particular,
![]() $s\colon \operatorname {\mathrm {Tw}}^{r}(X)\longrightarrow X$
is a cartesian fibration and Proposition 2.6 endows
$s\colon \operatorname {\mathrm {Tw}}^{r}(X)\longrightarrow X$
is a cartesian fibration and Proposition 2.6 endows
![]() $\operatorname {\mathrm {Tw}}^{r}(X)$
with the structure of an adequate triple, in which a map
$\operatorname {\mathrm {Tw}}^{r}(X)$
with the structure of an adequate triple, in which a map
![]() $\alpha \longrightarrow \beta $
given by
$\alpha \longrightarrow \beta $
given by

is egressive if f is egressive, and ingressive if f is ingressive and g is an equivalence.
Example 2.9. Let A be an
![]() $\infty $
-category, considered as an adequate triple
$\infty $
-category, considered as an adequate triple
![]() $(A,A,\iota {A})$
with all morphisms ingressive and only the equivalences egressive. Example 2.8 endows
$(A,A,\iota {A})$
with all morphisms ingressive and only the equivalences egressive. Example 2.8 endows
![]() $\operatorname {\mathrm {Tw}}^{r}(A)$
with the structure of an adequate triple, where a morphism is ingressive if its image under
$\operatorname {\mathrm {Tw}}^{r}(A)$
with the structure of an adequate triple, where a morphism is ingressive if its image under
![]() $t\colon \operatorname {\mathrm {Tw}}^{r}(A)\longrightarrow A^{{\mathrm {op}}}$
is an equivalence, and egressive if its image under
$t\colon \operatorname {\mathrm {Tw}}^{r}(A)\longrightarrow A^{{\mathrm {op}}}$
is an equivalence, and egressive if its image under
![]() $s\colon \operatorname {\mathrm {Tw}}^{r}(A)\longrightarrow A$
is an equivalence. This determines a functor
$s\colon \operatorname {\mathrm {Tw}}^{r}(A)\longrightarrow A$
is an equivalence. This determines a functor
![]() $\operatorname {\mathrm {Tw}}^{r} \colon \mathrm {Cat} \longrightarrow \mathrm {AdTrip}$
.
$\operatorname {\mathrm {Tw}}^{r} \colon \mathrm {Cat} \longrightarrow \mathrm {AdTrip}$
.
For the construction of span
![]() $\infty $
-categories, this structure will be of particular interest when A is a simplex. For example,
$\infty $
-categories, this structure will be of particular interest when A is a simplex. For example,
![]() $\operatorname {\mathrm {Tw}}^{r}([2])$
is the poset
$\operatorname {\mathrm {Tw}}^{r}([2])$
is the poset

where the left-pointing arrows are egressive and the right-pointing ones are ingressive. More generally, the ambigressive pullbacks in
![]() $\operatorname {\mathrm {Tw}}^{r}([n])$
are precisely given by the diagrams
$\operatorname {\mathrm {Tw}}^{r}([n])$
are precisely given by the diagrams

for
![]() $i \leq k \leq j \leq l$
.
$i \leq k \leq j \leq l$
.
We next set out to construct Barwick’s functor
sending each adequate triple to its
![]() $\infty $
-category of spans, described informally in the introduction. We will define
$\infty $
-category of spans, described informally in the introduction. We will define
![]() $\mathrm {Span}$
more precisely as a functor into complete Segal
$\mathrm {Span}$
more precisely as a functor into complete Segal
![]() $\infty $
-groupoids. Recall that such functors can be obtained from the following general procedure:
$\infty $
-groupoids. Recall that such functors can be obtained from the following general procedure:
Construction 2.10. Given a functor
![]() $C:D\rightarrow A$
between
$C:D\rightarrow A$
between
![]() $\infty $
-categories, we obtain a ‘singular complex’ functor
$\infty $
-categories, we obtain a ‘singular complex’ functor
![]() $\mathrm {S}_C \colon A \rightarrow {\mathcal {P}}(D)$
with
$\mathrm {S}_C \colon A \rightarrow {\mathcal {P}}(D)$
with
![]() ${\mathcal {P}}(D) = \mathrm {Fun} (D^{\mathrm {op}},\mathrm {Gpd})$
by currying the composition
${\mathcal {P}}(D) = \mathrm {Fun} (D^{\mathrm {op}},\mathrm {Gpd})$
by currying the composition
that is,
![]() $\mathrm {S}_C(X)_d = {\mathrm {Hom}}_A(C(d),X)$
. If A is cocomplete, then
$\mathrm {S}_C(X)_d = {\mathrm {Hom}}_A(C(d),X)$
. If A is cocomplete, then
![]() $\mathrm {S}_C$
is right adjoint to the colimit extension
$\mathrm {S}_C$
is right adjoint to the colimit extension
![]() $|{-}|_C:{\mathcal {P}}(D) \rightarrow A$
; see [Reference LurieLu09a, Proposition 5.2.6.3].
$|{-}|_C:{\mathcal {P}}(D) \rightarrow A$
; see [Reference LurieLu09a, Proposition 5.2.6.3].
For the cosimplicial object
![]() ${\mathbf {\Delta }} \rightarrow \mathrm {Cat} , n \mapsto [n]$
, we obtain in this fashion an adjunction
${\mathbf {\Delta }} \rightarrow \mathrm {Cat} , n \mapsto [n]$
, we obtain in this fashion an adjunction
where
![]() $\mathrm {s}\mathrm {Gpd} = {\mathcal {P}}({\mathbf {\Delta }})$
is the
$\mathrm {s}\mathrm {Gpd} = {\mathcal {P}}({\mathbf {\Delta }})$
is the
![]() $\infty $
-category of simplicial
$\infty $
-category of simplicial
![]() $\infty $
-groupoids. By results of Joyal, Lurie, Rezk and Tierney [Reference Joyal and TierneyJT07, Reference LurieLu09b, Reference RezkRe01], the nerve functor
$\infty $
-groupoids. By results of Joyal, Lurie, Rezk and Tierney [Reference Joyal and TierneyJT07, Reference LurieLu09b, Reference RezkRe01], the nerve functor
![]() $\mathrm {N}$
is fully faithful with essential image the full subcategory of complete Segal objects inside
$\mathrm {N}$
is fully faithful with essential image the full subcategory of complete Segal objects inside
![]() $\mathrm {s}\mathrm {Gpd}$
– that is, those simplicial
$\mathrm {s}\mathrm {Gpd}$
– that is, those simplicial
![]() $\infty $
-groupoids T that satisfy the Segal condition and for which the diagram
$\infty $
-groupoids T that satisfy the Segal condition and for which the diagram

is cartesian; see [Reference RezkRe10, Section 10] for this characterisation of completeness. A general cosimplicial object C in A therefore gives rise to a functor
![]() $A \rightarrow \mathrm {Cat} $
via the composition of
$A \rightarrow \mathrm {Cat} $
via the composition of
![]() $\mathrm {S}_C$
with
$\mathrm {S}_C$
with
![]() $\mathrm {ac}$
. When
$\mathrm {ac}$
. When
![]() $\mathrm {S}_C$
takes values in (complete) Segal
$\mathrm {S}_C$
takes values in (complete) Segal
![]() $\infty $
-groupoids, we have a good understanding of this functor, since there is then no need to localise; this happens precisely when the cosimplicial object C satisfies the dual version of the Segal and completeness conditions.
$\infty $
-groupoids, we have a good understanding of this functor, since there is then no need to localise; this happens precisely when the cosimplicial object C satisfies the dual version of the Segal and completeness conditions.
Example 2.11. Consider the functor
![]() $\mathrm {S}_{B}\colon \mathrm {Cat} \longrightarrow \mathrm {s}\mathrm {Gpd}$
associated to the cosimplicial object
$\mathrm {S}_{B}\colon \mathrm {Cat} \longrightarrow \mathrm {s}\mathrm {Gpd}$
associated to the cosimplicial object
Then
![]() $\mathrm {S}_B(C) \simeq \mathrm {N}\operatorname {\mathrm {Tw}}^{r}(C)$
. This follows from the observation that
$\mathrm {S}_B(C) \simeq \mathrm {N}\operatorname {\mathrm {Tw}}^{r}(C)$
. This follows from the observation that
![]() $\operatorname {\mathrm {Tw}}^{r}$
arises from a right Quillen functor between the Joyal model structures whose left adjoint sends
$\operatorname {\mathrm {Tw}}^{r}$
arises from a right Quillen functor between the Joyal model structures whose left adjoint sends
![]() $[n]$
to
$[n]$
to
![]() $[n]\star [n]^{\mathrm {op}}$
(see [Reference LurieLu17, Section 5.2.1] or [Reference Harpaz, Nuiten and PrasmaHNP17, Proposition 4.13]). In particular,
$[n]\star [n]^{\mathrm {op}}$
(see [Reference LurieLu17, Section 5.2.1] or [Reference Harpaz, Nuiten and PrasmaHNP17, Proposition 4.13]). In particular,
![]() $\mathrm {S}_B$
takes values in complete Segal
$\mathrm {S}_B$
takes values in complete Segal
![]() $\infty $
-groupoids.
$\infty $
-groupoids.
Applying this construction to the functor
![]() $\operatorname {\mathrm {Tw}}^{r}\colon {\mathbf {\Delta }}\longrightarrow \mathrm {AdTrip}$
sending each simplex
$\operatorname {\mathrm {Tw}}^{r}\colon {\mathbf {\Delta }}\longrightarrow \mathrm {AdTrip}$
sending each simplex
![]() $[n]$
to
$[n]$
to
![]() $\operatorname {\mathrm {Tw}}^{r}([n])$
with the structure from Example 2.9, we obtain the following:
$\operatorname {\mathrm {Tw}}^{r}([n])$
with the structure from Example 2.9, we obtain the following:
Definition 2.12. We define
![]() $\mathrm {Span} \colon \mathrm {AdTrip} \rightarrow \mathrm {Cat} $
as the composition
$\mathrm {Span} \colon \mathrm {AdTrip} \rightarrow \mathrm {Cat} $
as the composition
Theorem 2.13 (Barwick)
The essential image of
![]() $\mathrm {S}_{\operatorname {\mathrm {Tw}}^{r}}$
is contained in the complete Segal
$\mathrm {S}_{\operatorname {\mathrm {Tw}}^{r}}$
is contained in the complete Segal
![]() $\infty $
-groupoids. In other words, there is a natural equivalence
$\infty $
-groupoids. In other words, there is a natural equivalence
We will give a new proof of this result (avoiding Barwick’s recourse to a point-set model). Recall also that the category associated to a complete Segal
![]() $\infty $
-groupoid T can be described rather explicitly. For example, the core of
$\infty $
-groupoid T can be described rather explicitly. For example, the core of
![]() $\mathrm {ac}(T)$
is simply given by
$\mathrm {ac}(T)$
is simply given by
![]() $T_0$
, and its morphism
$T_0$
, and its morphism
![]() $\infty $
-groupoids are given by the fibres of
$\infty $
-groupoids are given by the fibres of
![]() $(d_1,d_0) \colon T_1 \rightarrow T_0^2$
. In the case at hand, this gives us the desired description of
$(d_1,d_0) \colon T_1 \rightarrow T_0^2$
. In the case at hand, this gives us the desired description of
![]() $\mathrm {Span}(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
: objects are objects of X, morphisms from x to y are spans
$\mathrm {Span}(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
: objects are objects of X, morphisms from x to y are spans
with the left arrow egressive and the right arrow ingressive, and composition proceeds by pullback of spans. Completeness furthermore implies that
![]() $\iota \mathrm {Span}(X,X_{\mathrm {in}},X^{\mathrm {eg}}) \simeq \iota (X)$
via the degenerate spans consisting of identities. Before we dive into the proof, let us record two immediate properties of the construction, the second of which in particular yields inclusions of subcategories
$\iota \mathrm {Span}(X,X_{\mathrm {in}},X^{\mathrm {eg}}) \simeq \iota (X)$
via the degenerate spans consisting of identities. Before we dive into the proof, let us record two immediate properties of the construction, the second of which in particular yields inclusions of subcategories
when applied to
Lemma 2.14. For an adequate triple
![]() $(X,X_{\mathrm {in}}, X^{\mathrm {eg}})$
with reverse
$(X,X_{\mathrm {in}}, X^{\mathrm {eg}})$
with reverse
![]() $X^{\mathrm {rev}}=(X,X^{\mathrm {eg}},X_{\mathrm {in}})$
as in Example 2.3, there is a natural canonical equivalence
$X^{\mathrm {rev}}=(X,X^{\mathrm {eg}},X_{\mathrm {in}})$
as in Example 2.3, there is a natural canonical equivalence
Proof. For each
![]() $[n]$
, consider
$[n]$
, consider
![]() $\operatorname {\mathrm {Tw}}^{r}([n])$
and
$\operatorname {\mathrm {Tw}}^{r}([n])$
and
![]() $\operatorname {\mathrm {Tw}}^{r}([n]^{{\mathrm {op}}})$
with the structure of an adequate triple as in Example 2.9. There is a natural equivalence of cosimplical adequate triples
$\operatorname {\mathrm {Tw}}^{r}([n]^{{\mathrm {op}}})$
with the structure of an adequate triple as in Example 2.9. There is a natural equivalence of cosimplical adequate triples
![]() $\operatorname {\mathrm {Tw}}^{r}([-]^{{\mathrm {op}}})\simeq \operatorname {\mathrm {Tw}}^{r}([-])^{\mathrm {rev}}$
, sending an object
$\operatorname {\mathrm {Tw}}^{r}([-]^{{\mathrm {op}}})\simeq \operatorname {\mathrm {Tw}}^{r}([-])^{\mathrm {rev}}$
, sending an object
![]() $(i\geq j)$
in
$(i\geq j)$
in
![]() $\operatorname {\mathrm {Tw}}^{r}([n]^{{\mathrm {op}}})$
to the object
$\operatorname {\mathrm {Tw}}^{r}([n]^{{\mathrm {op}}})$
to the object
![]() $(j\leq i)$
in
$(j\leq i)$
in
![]() $\operatorname {\mathrm {Tw}}^{r}([n])$
. This induces a natural equivalence of simplicial objects
$\operatorname {\mathrm {Tw}}^{r}([n])$
. This induces a natural equivalence of simplicial objects
so that the simplicial
![]() $\infty $
-groupoid defining
$\infty $
-groupoid defining
![]() $\mathrm {Span}(X)$
is the reverse of that defining
$\mathrm {Span}(X)$
is the reverse of that defining
![]() $\mathrm {Span}(X^{\mathrm {rev}})$
. The result follows since generally
$\mathrm {Span}(X^{\mathrm {rev}})$
. The result follows since generally
![]() $\mathrm {ac}(T)^{\mathrm {op}} \simeq \mathrm {ac}(T^{\mathrm {rev}})$
as this is true on simplices.
$\mathrm {ac}(T)^{\mathrm {op}} \simeq \mathrm {ac}(T^{\mathrm {rev}})$
as this is true on simplices.
Proposition 2.15. Let
![]() $A \subseteq B$
be a subcategory. Then the triples
$A \subseteq B$
be a subcategory. Then the triples
![]() $(B,A,\iota B)$
and
$(B,A,\iota B)$
and
![]() $(B,\iota B,A)$
are adequate and
$(B,\iota B,A)$
are adequate and
Proof. We shall prove the first claim; the second then follows from 2.14. The triple
![]() $(B,A,\iota B)$
is evidently adequate (cf. Example 2.3). Note that the
$(B,A,\iota B)$
is evidently adequate (cf. Example 2.3). Note that the
![]() $\infty $
-groupoid of functors from an adequate triple
$\infty $
-groupoid of functors from an adequate triple
![]() $(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
into
$(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
into
![]() $(B,A,\iota B)$
is equivalent to the
$(B,A,\iota B)$
is equivalent to the
![]() $\infty $
-groupoid of functors
$\infty $
-groupoid of functors
![]() $X\rightarrow B$
which invert the edges in
$X\rightarrow B$
which invert the edges in
![]() $X^{\mathrm {eg}}$
and take those of
$X^{\mathrm {eg}}$
and take those of
![]() $X_{\mathrm {in}}$
into A. Applying this to
$X_{\mathrm {in}}$
into A. Applying this to
![]() $X=\operatorname {\mathrm {Tw}}^{r}([n])$
shows that the remaining claim is equivalent to the assertion that the source map
$X=\operatorname {\mathrm {Tw}}^{r}([n])$
shows that the remaining claim is equivalent to the assertion that the source map
is a localisation (necessarily at those maps whose source component is an equivalence). This is, in fact, true for all
![]() $\infty $
-categories C in place of
$\infty $
-categories C in place of
![]() $[n]$
, for example, since
$[n]$
, for example, since
![]() $\operatorname {\mathrm {Tw}}^{r}(C) \rightarrow C$
is a cocartesian fibration with contractible fibres (which are always localisations; see Lemma 5.5 below). The localisation property is, however, particularly easy to see when C admits a terminal object. In that case, the source evaluation
$\operatorname {\mathrm {Tw}}^{r}(C) \rightarrow C$
is a cocartesian fibration with contractible fibres (which are always localisations; see Lemma 5.5 below). The localisation property is, however, particularly easy to see when C admits a terminal object. In that case, the source evaluation
![]() $\operatorname {\mathrm {Tw}}^{r}(C) \rightarrow C$
is even a Bousfield localisation, with fully faithful left adjoint sending
$\operatorname {\mathrm {Tw}}^{r}(C) \rightarrow C$
is even a Bousfield localisation, with fully faithful left adjoint sending
![]() $c \mapsto (c \to \ast )$
.
$c \mapsto (c \to \ast )$
.
We now turn to the proof of Theorem 2.13. Instead of following Barwick’s strategy of explicitly filling simplices in a point-set implementation of the above construction, our proof will be a simple adaptation of the argument given in [CDH+20, Section 2.1] for the case of stable
![]() $\infty $
-categories (with all maps ingressive and egressive). In fact, we will prove a slightly stronger statement, which will ultimately allow us to deduce Theorem A. It uses the following definition:
$\infty $
-categories (with all maps ingressive and egressive). In fact, we will prove a slightly stronger statement, which will ultimately allow us to deduce Theorem A. It uses the following definition:
Definition 2.16. Let A be an
![]() $\infty $
-category and X an adequate triple. We write
$\infty $
-category and X an adequate triple. We write
![]() ${\mathrm {Q}}_A(X)$
for the
${\mathrm {Q}}_A(X)$
for the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fun} _{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}(A), X)$
, where
$\mathrm {Fun} _{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}(A), X)$
, where
![]() $\operatorname {\mathrm {Tw}}^{r}(A)$
is the adequate triple from Example 2.9 and denote by
$\operatorname {\mathrm {Tw}}^{r}(A)$
is the adequate triple from Example 2.9 and denote by
![]() ${\mathrm {Q}}\colon \mathrm {Cat}^{{\mathrm {op}}}\times \mathrm {AdTrip}\longrightarrow \mathrm {AdTrip}$
the resulting functor.
${\mathrm {Q}}\colon \mathrm {Cat}^{{\mathrm {op}}}\times \mathrm {AdTrip}\longrightarrow \mathrm {AdTrip}$
the resulting functor.
In particular, each adequate triple X gives rise to a natural simplicial diagram
![]() ${\mathrm {Q}}_{\bullet }(X)$
in
${\mathrm {Q}}_{\bullet }(X)$
in
![]() $\mathrm {Cat} $
.
$\mathrm {Cat} $
.
Lemma 2.17. Let X be an adequate triple. Then the simplicial
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {Q}}_{\bullet }(X)$
satisfies the Segal and completeness conditions; that is, the Segal maps
${\mathrm {Q}}_{\bullet }(X)$
satisfies the Segal and completeness conditions; that is, the Segal maps
are equivalences and

is cartesian.
Note that this immediately implies Theorem 2.13, as
![]() $\iota \colon \mathrm {Cat} \rightarrow \mathrm {Gpd}$
preserves limits.
$\iota \colon \mathrm {Cat} \rightarrow \mathrm {Gpd}$
preserves limits.
Proof. Let
![]() $\mathcal J_n \subseteq \operatorname {\mathrm {Tw}}^{r}([n])$
denote the subposet consisting of those
$\mathcal J_n \subseteq \operatorname {\mathrm {Tw}}^{r}([n])$
denote the subposet consisting of those
![]() $(i \leq j)$
with
$(i \leq j)$
with
![]() $j \leq i+1$
(i.e., the zig-zag along the bottom). Note that
$j \leq i+1$
(i.e., the zig-zag along the bottom). Note that
![]() $\mathcal J_n$
decomposes as an iterated pushout
$\mathcal J_n$
decomposes as an iterated pushout
along the Segal maps; in fact, the nerve
![]() $\mathrm {N}(\mathcal J_n)$
is already the iterated pushout of the nerves
$\mathrm {N}(\mathcal J_n)$
is already the iterated pushout of the nerves
![]() $\mathrm {N}(\operatorname {\mathrm {Tw}}^{r}([1]))$
in simplicial
$\mathrm {N}(\operatorname {\mathrm {Tw}}^{r}([1]))$
in simplicial
![]() $\infty $
-groupoids (see [Reference HaugsengHa18, Proposition 5.13] for a similar argument). The iterated pullback appearing in the Segal condition is therefore equivalent to the full subcategory
$\infty $
-groupoids (see [Reference HaugsengHa18, Proposition 5.13] for a similar argument). The iterated pullback appearing in the Segal condition is therefore equivalent to the full subcategory
![]() $J_n(X)$
of
$J_n(X)$
of
![]() $\mathrm {Fun} (\mathcal J_n,X)$
spanned by those functors taking left-pointing edges in
$\mathrm {Fun} (\mathcal J_n,X)$
spanned by those functors taking left-pointing edges in
![]() $\mathcal J_n$
(i.e., those of the form
$\mathcal J_n$
(i.e., those of the form
![]() $(i \leq i+1) \rightarrow (i \leq i)$
) to ingressives and right-pointing arrows, namely,
$(i \leq i+1) \rightarrow (i \leq i)$
) to ingressives and right-pointing arrows, namely,
![]() $(i \leq i+1) \rightarrow (i+1 \leq i+1)$
, to egressives. Furthermore, this translates the Segal map to the map
$(i \leq i+1) \rightarrow (i+1 \leq i+1)$
, to egressives. Furthermore, this translates the Segal map to the map
![]() ${\mathrm {Q}}_n(X) \rightarrow J_n(X)$
induced by the restriction
${\mathrm {Q}}_n(X) \rightarrow J_n(X)$
induced by the restriction
But from the pointwise formula for Kan extensions, one finds that a diagram
![]() $F \colon \operatorname {\mathrm {Tw}}^{r}([n]) \rightarrow X$
lies in
$F \colon \operatorname {\mathrm {Tw}}^{r}([n]) \rightarrow X$
lies in
![]() ${\mathrm {Q}}_n(X)$
if and only if it is right Kan extended from its restriction to
${\mathrm {Q}}_n(X)$
if and only if it is right Kan extended from its restriction to
![]() $\mathcal J_n$
, which has to lie in
$\mathcal J_n$
, which has to lie in
![]() $J_n$
. The claim now follows from [Reference LurieLu09a, Proposition 4.3.2.15], since right Kan extension from a full subcategory is fully faithful.
$J_n$
. The claim now follows from [Reference LurieLu09a, Proposition 4.3.2.15], since right Kan extension from a full subcategory is fully faithful.
Similarly, for completeness, we first note that the map
![]() $P \rightarrow {\mathrm {Q}}_3(X)$
from the pullback in question to the lower left corner is fully faithful since the degeneracy
$P \rightarrow {\mathrm {Q}}_3(X)$
from the pullback in question to the lower left corner is fully faithful since the degeneracy
![]() ${\mathrm {Q}}_0(X)^2 \rightarrow {\mathrm {Q}}_1(X)^2$
is (as
${\mathrm {Q}}_0(X)^2 \rightarrow {\mathrm {Q}}_1(X)^2$
is (as
![]() $|\operatorname {\mathrm {Tw}}^{r}([1])| \simeq *$
). We claim that its essential image consists exactly of those diagrams whose edges are all equivalences; since also
$|\operatorname {\mathrm {Tw}}^{r}([1])| \simeq *$
). We claim that its essential image consists exactly of those diagrams whose edges are all equivalences; since also
![]() $|\operatorname {\mathrm {Tw}}^{r}([3])| \simeq *$
these are precisely the constant ones, which gives the result. So consider a diagram
$|\operatorname {\mathrm {Tw}}^{r}([3])| \simeq *$
these are precisely the constant ones, which gives the result. So consider a diagram

all of whose squares are (ambigressive) cartesian and such that the four compositions
are equivalences. Then it first follows that, as pullbacks of equivalences, also
![]() $F(0 \leq 3) \rightarrow F(0 \leq 1)$
and
$F(0 \leq 3) \rightarrow F(0 \leq 1)$
and
![]() $F(0 \leq 3) \rightarrow F(2 \leq 3)$
are equivalences and then by two-out-of-six, the entire outer slopes are. But then by commutativity of the larger rectangles, also
$F(0 \leq 3) \rightarrow F(2 \leq 3)$
are equivalences and then by two-out-of-six, the entire outer slopes are. But then by commutativity of the larger rectangles, also
![]() $F(0 \leq 1) \rightarrow F(1 \leq 1)$
and
$F(0 \leq 1) \rightarrow F(1 \leq 1)$
and
![]() $F(2 \leq 3) \rightarrow F(2 \leq 2)$
are equivalences, and then as pullbacks thereof also
$F(2 \leq 3) \rightarrow F(2 \leq 2)$
are equivalences, and then as pullbacks thereof also
![]() $F(0 \leq 2) \rightarrow F(1 \leq 2)$
and
$F(0 \leq 2) \rightarrow F(1 \leq 2)$
and
![]() $F(1 \leq 3) \rightarrow F(1 \leq 2)$
. Finally, this implies that also
$F(1 \leq 3) \rightarrow F(1 \leq 2)$
. Finally, this implies that also
![]() $F(1 \leq 2) \rightarrow F(1 \leq 1)$
and
$F(1 \leq 2) \rightarrow F(1 \leq 1)$
and
![]() $F(1 \leq 2) \rightarrow F(2 \leq 2)$
are equivalences by two-out-of-three.
$F(1 \leq 2) \rightarrow F(2 \leq 2)$
are equivalences by two-out-of-three.
Next we shall describe functors into span
![]() $\infty $
-categories. More precisely, we will show that the equivalence between functors
$\infty $
-categories. More precisely, we will show that the equivalence between functors
![]() $[n]\longrightarrow \mathrm {Span}(X)$
and maps of adequate triples
$[n]\longrightarrow \mathrm {Span}(X)$
and maps of adequate triples
![]() $\operatorname {\mathrm {Tw}}^{r}([n])\longrightarrow X$
from Theorem 2.13 extends to all
$\operatorname {\mathrm {Tw}}^{r}([n])\longrightarrow X$
from Theorem 2.13 extends to all
![]() $\infty $
-categories:
$\infty $
-categories:
Theorem 2.18. The functors ![]() form an adjoint pair. In other words, for each
form an adjoint pair. In other words, for each
![]() $\infty $
-category A and each adequate triple X, there is a natural equivalence
$\infty $
-category A and each adequate triple X, there is a natural equivalence
where
![]() $\operatorname {\mathrm {Tw}}^{r}(A)$
is as in Example 2.9.
$\operatorname {\mathrm {Tw}}^{r}(A)$
is as in Example 2.9.
Remark 2.19. Using a different argument, this result was first sketched by Raskin in [Reference RaskinRa14, Chapter 20]. The resulting description of functors into span categories is, for example, also used in [Reference Hebestreit and SteimleHS21] to perform parametrised surgery on the cobordism
![]() $\infty $
-categories
$\infty $
-categories ![]() from [CDH+20], which are hermitian refinements of
from [CDH+20], which are hermitian refinements of
![]() $\mathrm {Span}(C)$
.
$\mathrm {Span}(C)$
.
Recall from Definition 2.16 that we abbreviate
The theorem will follow readily from the following:
Proposition 2.20. For each adequate triple X, the functor
![]() ${\mathrm {Q}}_{-}(X) \colon \mathrm {Cat}^{\mathrm {op}} \rightarrow \mathrm {Cat} $
preserves limits.
${\mathrm {Q}}_{-}(X) \colon \mathrm {Cat}^{\mathrm {op}} \rightarrow \mathrm {Cat} $
preserves limits.
We will employ the (opposite of the) following criterion:
Lemma 2.21. Let
![]() $f \colon {D} \rightarrow {E}$
be a functor from a small to a cocomplete category, such that the right adjoint in the induced adjunction
$f \colon {D} \rightarrow {E}$
be a functor from a small to a cocomplete category, such that the right adjoint in the induced adjunction
is fully faithful. Then for a functor
![]() $F \colon {E} \rightarrow C$
to another cocomplete category, the following are equivalent:
$F \colon {E} \rightarrow C$
to another cocomplete category, the following are equivalent:
-
(1) F preserves colimits,
-
(2) the natural map
 $|{-}|_{F\circ f} \Longrightarrow F \circ |{-}|_f$
is an equivalence, and
$|{-}|_{F\circ f} \Longrightarrow F \circ |{-}|_f$
is an equivalence, and - (3)
-
(i) the natural map
 $f_!(F\circ f) \Longrightarrow F$
is an equivalence (i.e., F is left Kan extended from its restriction along f), and
$f_!(F\circ f) \Longrightarrow F$
is an equivalence (i.e., F is left Kan extended from its restriction along f), and -
(ii)
 $|{-}|_{F\circ f} \colon {\mathcal {P}}({D}) \rightarrow {C}$
inverts all maps that
$|{-}|_{F\circ f} \colon {\mathcal {P}}({D}) \rightarrow {C}$
inverts all maps that
 $|{-}|_f$
inverts.
$|{-}|_f$
inverts.
-
Applying this to
![]() ${\mathbf {\Delta }} \subset \mathrm {Cat} $
and taking opposites in particular shows that a functor
${\mathbf {\Delta }} \subset \mathrm {Cat} $
and taking opposites in particular shows that a functor
![]() $F \colon \mathrm {Cat}^{\mathrm {op}} \rightarrow {C}$
preserves limits if and only if it is right Kan extended from its restriction along
$F \colon \mathrm {Cat}^{\mathrm {op}} \rightarrow {C}$
preserves limits if and only if it is right Kan extended from its restriction along
![]() ${\mathbf {\Delta }}^{\mathrm {op}} \subset \mathrm {Cat}^{\mathrm {op}}$
and the restriction
${\mathbf {\Delta }}^{\mathrm {op}} \subset \mathrm {Cat}^{\mathrm {op}}$
and the restriction
![]() $F \colon {\mathbf {\Delta }}^{\mathrm {op}} \rightarrow {C}$
is a complete Segal object in
$F \colon {\mathbf {\Delta }}^{\mathrm {op}} \rightarrow {C}$
is a complete Segal object in
![]() ${C}$
. The maps
${C}$
. The maps
encoding the Segal and completeness conditions are (by design) categorical equivalences (i.e., inverted by
![]() $\mathrm {ac}\colon \mathrm {s}\mathrm {Gpd}\rightarrow \mathrm {Cat} $
), proving that if
$\mathrm {ac}\colon \mathrm {s}\mathrm {Gpd}\rightarrow \mathrm {Cat} $
), proving that if
![]() $|{-}|_{F^{\mathrm {op}}} \colon \mathrm {s}\mathrm {Gpd} \rightarrow C^{\mathrm {op}}$
inverts these, then
$|{-}|_{F^{\mathrm {op}}} \colon \mathrm {s}\mathrm {Gpd} \rightarrow C^{\mathrm {op}}$
inverts these, then
![]() $F \colon {\mathbf {\Delta }}^{\mathrm {op}} \rightarrow C$
is a complete Segal object, and the Yoneda lemma reduces the converse to the case
$F \colon {\mathbf {\Delta }}^{\mathrm {op}} \rightarrow C$
is a complete Segal object, and the Yoneda lemma reduces the converse to the case
![]() $C = \mathrm {Gpd}$
, where it follows from the fact that
$C = \mathrm {Gpd}$
, where it follows from the fact that
![]() $|{-}|_{(\mathrm {N} C)^{\mathrm {op}}} \simeq {\mathrm {Hom}}_{\mathrm {Cat} }(\mathrm {ac}({-}),C)$
as (colimit preserving) functors
$|{-}|_{(\mathrm {N} C)^{\mathrm {op}}} \simeq {\mathrm {Hom}}_{\mathrm {Cat} }(\mathrm {ac}({-}),C)$
as (colimit preserving) functors
![]() $\mathrm {s}\mathrm {Gpd} \rightarrow \mathrm {Gpd}^{\mathrm {op}}$
.
$\mathrm {s}\mathrm {Gpd} \rightarrow \mathrm {Gpd}^{\mathrm {op}}$
.
Proof. Let us point out that any colimiting cocone
![]() $G\colon I^{\rhd }\to E$
arises as the image of a colimiting cocone
$G\colon I^{\rhd }\to E$
arises as the image of a colimiting cocone
![]() $G'\colon I^{\rhd }\to \mathcal {P}(D)$
under
$G'\colon I^{\rhd }\to \mathcal {P}(D)$
under
![]() $|{-}|_f$
: indeed, one can take
$|{-}|_f$
: indeed, one can take
![]() $G'$
to be the colimit of the diagram
$G'$
to be the colimit of the diagram
![]() $S_f\circ G_{|I}\colon I\longrightarrow \mathcal {P}(D)$
. Consequently, a functor out of E preserves colimits if and only if its composition with
$S_f\circ G_{|I}\colon I\longrightarrow \mathcal {P}(D)$
. Consequently, a functor out of E preserves colimits if and only if its composition with
![]() $|{-}|_f$
does. Using this, (1)
$|{-}|_f$
does. Using this, (1)
![]() $\Leftrightarrow $
(2) is an immediate consequence of [Reference LurieLu09a, Lemma 5.1.5.5].
$\Leftrightarrow $
(2) is an immediate consequence of [Reference LurieLu09a, Lemma 5.1.5.5].
For (2)
![]() $\Rightarrow $
(3), (ii) follows immediately. To see (i), note that F agrees with the left Kan extension of
$\Rightarrow $
(3), (ii) follows immediately. To see (i), note that F agrees with the left Kan extension of
![]() $|{-}|_{F\circ f} = F \circ |{-}|_f$
along
$|{-}|_{F\circ f} = F \circ |{-}|_f$
along
![]() $|{-}|_f$
, since
$|{-}|_f$
, since
![]() $|{-}|_f$
is a localisation [Reference LurieLu09a, Proposition 5.2.7.12]. In turn,
$|{-}|_f$
is a localisation [Reference LurieLu09a, Proposition 5.2.7.12]. In turn,
![]() $|{-}|_{F\circ f}$
is the left Kan extension of
$|{-}|_{F\circ f}$
is the left Kan extension of
![]() $F\circ f$
along the Yoneda embedding
$F\circ f$
along the Yoneda embedding
![]() $h\colon D\longrightarrow \mathcal {P}(D)$
[Reference LurieLu09a, Lemma 5.1.5.5]. The claim then follows from transitivity of Kan extensions.
$h\colon D\longrightarrow \mathcal {P}(D)$
[Reference LurieLu09a, Lemma 5.1.5.5]. The claim then follows from transitivity of Kan extensions.
Finally, for (3)
![]() $\Rightarrow $
(2), note that (ii) implies that
$\Rightarrow $
(2), note that (ii) implies that
![]() $|{-}|_{F\circ f}$
descends along
$|{-}|_{F\circ f}$
descends along
![]() $|{-}|_f$
to some functor
$|{-}|_f$
to some functor
![]() $G \colon {E} \rightarrow {C}$
, which is then automatically its left Kan extension along
$G \colon {E} \rightarrow {C}$
, which is then automatically its left Kan extension along
![]() $|{-}|_f$
. Part (i) and transitivity of Kan extensions then imply that
$|{-}|_f$
. Part (i) and transitivity of Kan extensions then imply that
![]() $G \simeq F$
, or in other words, that
$G \simeq F$
, or in other words, that
![]() $|{-}|_{F\circ f} \simeq F \circ |{-}|_f$
as desired.
$|{-}|_{F\circ f} \simeq F \circ |{-}|_f$
as desired.
Proof of Proposition 2.20
Since
![]() ${\mathrm {Q}}(X)$
is a complete Segal object in
${\mathrm {Q}}(X)$
is a complete Segal object in
![]() $\mathrm {Cat} $
by Lemma 2.17, we have already shown Item (ii) of Lemma 2.21(3). So we need only show that
$\mathrm {Cat} $
by Lemma 2.17, we have already shown Item (ii) of Lemma 2.21(3). So we need only show that
![]() ${\mathrm {Q}}(X) \colon \mathrm {Cat}^{\mathrm {op}} \rightarrow \mathrm {Cat} $
is right Kan extended from its restriction to
${\mathrm {Q}}(X) \colon \mathrm {Cat}^{\mathrm {op}} \rightarrow \mathrm {Cat} $
is right Kan extended from its restriction to
![]() ${\mathbf {\Delta }}^{\mathrm {op}}$
. By the pointwise formula for Kan extensions, this means that the tautological map
${\mathbf {\Delta }}^{\mathrm {op}}$
. By the pointwise formula for Kan extensions, this means that the tautological map
is an equivalence for all
![]() ${D} \in \mathrm {Cat}$
. The diagram
${D} \in \mathrm {Cat}$
. The diagram
![]() ${\mathbf {\Delta }}/{D} \rightarrow {\mathbf {\Delta }} \hookrightarrow \mathrm {Cat}$
, giving rise to the right-hand side has colimit D and is a typical example of a functor
${\mathbf {\Delta }}/{D} \rightarrow {\mathbf {\Delta }} \hookrightarrow \mathrm {Cat}$
, giving rise to the right-hand side has colimit D and is a typical example of a functor
![]() $F \colon I \rightarrow \mathrm {Cat} $
such that the natural map
$F \colon I \rightarrow \mathrm {Cat} $
such that the natural map
is an equivalence (with both sides evaluating to
![]() $\mathrm {N} {D}$
). We will directly show that
$\mathrm {N} {D}$
). We will directly show that
![]() ${\mathrm {Q}}_{(-)}(X)$
preserves all limits over diagrams with this property.
${\mathrm {Q}}_{(-)}(X)$
preserves all limits over diagrams with this property.
To this end, note that there are natural equivalences of simplicial
![]() $\infty $
-groupoids
$\infty $
-groupoids
In particular, since
![]() $\Delta ^i \star (\Delta ^i)^{\mathrm {op}} \simeq \Delta ^{2i+1}$
is completely compact in
$\Delta ^i \star (\Delta ^i)^{\mathrm {op}} \simeq \Delta ^{2i+1}$
is completely compact in
![]() $\mathrm {s}\mathrm {Gpd}$
, we find an equivalence
$\mathrm {s}\mathrm {Gpd}$
, we find an equivalence
because of (*); let us warn the reader that the above map need not be an equivalence without any assumption on F, as the diagram
![]() $[1] \xleftarrow {0} [0] \xrightarrow {1} [1]$
with pushout
$[1] \xleftarrow {0} [0] \xrightarrow {1} [1]$
with pushout
![]() $[2]$
shows. In the case at hand, it follows that the map
$[2]$
shows. In the case at hand, it follows that the map
is an equivalence.
We have to show that this restricts to an equivalence between the full subcategory ![]() on the left (spanned by morphisms of adequate triples) and
on the left (spanned by morphisms of adequate triples) and
![]() $\lim _{i \in I}{\mathrm {Q}}_{F_i}(X)$
on the right. To this end, notice that any ambigressive pullback square in
$\lim _{i \in I}{\mathrm {Q}}_{F_i}(X)$
on the right. To this end, notice that any ambigressive pullback square in
![]() $\operatorname {\mathrm {Tw}}^{r}(A)$
, say
$\operatorname {\mathrm {Tw}}^{r}(A)$
, say

is contained (up to equivalence) in
![]() $\operatorname {\mathrm {Tw}}^{r}([3])$
for a map
$\operatorname {\mathrm {Tw}}^{r}([3])$
for a map
![]() $[3]\longrightarrow A$
, namely, that given by the string
$[3]\longrightarrow A$
, namely, that given by the string
![]() $a_0 \rightarrow a_1 \rightarrow a_2 \rightarrow a_3$
. Consequently, a functor
$a_0 \rightarrow a_1 \rightarrow a_2 \rightarrow a_3$
. Consequently, a functor
![]() $\operatorname {\mathrm {Tw}}^{r}(A) \rightarrow X$
is a morphism of adequate triples if and only if each restriction
$\operatorname {\mathrm {Tw}}^{r}(A) \rightarrow X$
is a morphism of adequate triples if and only if each restriction
is such. To apply this, note that one has
whenever F satisfies (*), so that a functor ![]() lies in
lies in ![]() if and only if for every
if and only if for every
![]() $j \in I$
and map
$j \in I$
and map
![]() $[3] \rightarrow F_j$
, the composite
$[3] \rightarrow F_j$
, the composite
lies in
![]() ${\mathrm {Q}}_3(X)$
. But this is the case if and only if the functor restricts to an element of
${\mathrm {Q}}_3(X)$
. But this is the case if and only if the functor restricts to an element of
![]() ${\mathrm {Q}}_{F_j}(X)$
for every
${\mathrm {Q}}_{F_j}(X)$
for every
![]() $j \in I$
and thus by definition if and only if it defines an element of
$j \in I$
and thus by definition if and only if it defines an element of
![]() $\lim _{i}{\mathrm {Q}}_{F_i}(X)$
, as desired.
$\lim _{i}{\mathrm {Q}}_{F_i}(X)$
, as desired.
Proof of Theorem 2.18
By Proposition 2.20,
![]() $\iota {\mathrm {Q}}(X) \simeq {\mathrm {Hom}}_{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}(-),X) \colon \mathrm {Cat}^{\mathrm {op}} \rightarrow \mathrm {Gpd}$
preserves limits as does
$\iota {\mathrm {Q}}(X) \simeq {\mathrm {Hom}}_{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}(-),X) \colon \mathrm {Cat}^{\mathrm {op}} \rightarrow \mathrm {Gpd}$
preserves limits as does
![]() ${\mathrm {Hom}}_{\mathrm {Cat} }(-,\mathrm {Span}(X))$
, so by Lemma 2.21, they are both right Kan extended from
${\mathrm {Hom}}_{\mathrm {Cat} }(-,\mathrm {Span}(X))$
, so by Lemma 2.21, they are both right Kan extended from
![]() ${\mathbf {\Delta }}^{\mathrm {op}} \subset \mathrm {Cat}^{\mathrm {op}}$
. Thus, they agree if their restrictions to
${\mathbf {\Delta }}^{\mathrm {op}} \subset \mathrm {Cat}^{\mathrm {op}}$
. Thus, they agree if their restrictions to
![]() ${\mathbf {\Delta }}^{\mathrm {op}}$
agree, which is the case by Theorem 2.13.
${\mathbf {\Delta }}^{\mathrm {op}}$
agree, which is the case by Theorem 2.13.
In fact, one can upgrade Theorem 2.18 to describe the full functor
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fun} (K,\mathrm {Span}(X))$
:
$\mathrm {Fun} (K,\mathrm {Span}(X))$
:
Corollary 2.22. There is a canonical equivalence
natural in
![]() $A \in \mathrm {Cat} $
and
$A \in \mathrm {Cat} $
and
![]() $X \in \mathrm {AdTrip}$
.
$X \in \mathrm {AdTrip}$
.
We warn the reader that this result is misstated as
![]() $\mathrm {Fun} (A,\mathrm {Span}(X)) \simeq {\mathrm {Q}}_A(X)$
in [Reference RaskinRa14, Section 20.9], which is only true on groupoid cores.
$\mathrm {Fun} (A,\mathrm {Span}(X)) \simeq {\mathrm {Q}}_A(X)$
in [Reference RaskinRa14, Section 20.9], which is only true on groupoid cores.
Proof. The left adjoint
![]() $\operatorname {\mathrm {Tw}}^{r}\colon \mathrm {Cat} \rightarrow \mathrm {AdTrip}$
preserves the cartesian product. By adjunction, the right adjoint
$\operatorname {\mathrm {Tw}}^{r}\colon \mathrm {Cat} \rightarrow \mathrm {AdTrip}$
preserves the cartesian product. By adjunction, the right adjoint
![]() $\mathrm {Span} \colon \mathrm {AdTrip} \rightarrow \mathrm {Cat} $
then sends the internal mapping object
$\mathrm {Span} \colon \mathrm {AdTrip} \rightarrow \mathrm {Cat} $
then sends the internal mapping object
![]() ${\mathrm {Q}}_A(X)=\mathrm {Fun} _{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}(A), X)$
from Lemma 2.5 to the internal mapping object
${\mathrm {Q}}_A(X)=\mathrm {Fun} _{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}(A), X)$
from Lemma 2.5 to the internal mapping object
![]() $\mathrm {Fun} (A , \mathrm {Span}(X))$
in
$\mathrm {Fun} (A , \mathrm {Span}(X))$
in
![]() $\mathrm {Cat} $
.
$\mathrm {Cat} $
.
Example 2.23. Since the functors
![]() $s \colon \operatorname {\mathrm {Tw}}^{r}(A) \rightarrow A$
and
$s \colon \operatorname {\mathrm {Tw}}^{r}(A) \rightarrow A$
and
![]() $t \colon \operatorname {\mathrm {Tw}}^{r}(A) \rightarrow A^{\mathrm {op}}$
are localisations, it follows easily from the formula of Corollary 2.22 that the functors
$t \colon \operatorname {\mathrm {Tw}}^{r}(A) \rightarrow A^{\mathrm {op}}$
are localisations, it follows easily from the formula of Corollary 2.22 that the functors
are inclusions of (non-full) subcategories for all
![]() $A \in \mathrm {Cat} $
. Alternatively, this statement can also be reduced to the case
$A \in \mathrm {Cat} $
. Alternatively, this statement can also be reduced to the case
![]() $A=[0]$
(which we recorded before Lemma 2.14) by means of Lemma A.4.
$A=[0]$
(which we recorded before Lemma 2.14) by means of Lemma A.4.
In a different direction, note that even if X admits pullbacks and carries the trivial structure of an adequate triple with all maps ingressive and egressive, the same is typically not true for
![]() ${\mathrm {Q}}_A(X) = \mathrm {Fun} _{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}(A),X)$
; this phenomenon is the basis for the notions of forwards and backwards surgery in [Reference Hebestreit and SteimleHS21].
${\mathrm {Q}}_A(X) = \mathrm {Fun} _{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}(A),X)$
; this phenomenon is the basis for the notions of forwards and backwards surgery in [Reference Hebestreit and SteimleHS21].
3 Cartesian fibrations and
 $\infty $
-categories of spans
$\infty $
-categories of spans
The goal of this section is to describe the cocartesian fibration associated to the functor
![]() $\mathrm {Span} \colon \mathrm {AdTrip} \rightarrow \mathrm {Cat} $
, which is itself given by a certain span
$\mathrm {Span} \colon \mathrm {AdTrip} \rightarrow \mathrm {Cat} $
, which is itself given by a certain span
![]() $\infty $
-category of adequate triples. As a direct application, we will obtain a new and fairly direct proof of the main result of [Reference Barwick, Glasman and NardinBGN18], which identifies the dual cartesian fibration of a cocartesian fibration in terms of a span construction. We shall more generally analyse the interaction of span categories and (co)cartesian fibrations in Section 5 below.
$\infty $
-category of adequate triples. As a direct application, we will obtain a new and fairly direct proof of the main result of [Reference Barwick, Glasman and NardinBGN18], which identifies the dual cartesian fibration of a cocartesian fibration in terms of a span construction. We shall more generally analyse the interaction of span categories and (co)cartesian fibrations in Section 5 below.
To understand (co)cartesian edges in span
![]() $\infty $
-categories, we start by reproducing a criterion due to Barwick. In fact, we provide a proof different from [Reference BarwickBa17] and inspired by the proof of the additivity theorem for Grothendieck–Witt theory in [CDH+20, Section 2.6]; see Example 3.3 for the details of this connection.
$\infty $
-categories, we start by reproducing a criterion due to Barwick. In fact, we provide a proof different from [Reference BarwickBa17] and inspired by the proof of the additivity theorem for Grothendieck–Witt theory in [CDH+20, Section 2.6]; see Example 3.3 for the details of this connection.
Theorem 3.1 (Barwick)
Let
![]() $p\colon Y\rightarrow X$
be a morphism in
$p\colon Y\rightarrow X$
be a morphism in
![]() $\mathrm {AdTrip}$
and let f be an edge in
$\mathrm {AdTrip}$
and let f be an edge in
![]() $X_{\mathrm {in}}$
such that the following conditions hold:
$X_{\mathrm {in}}$
such that the following conditions hold:
-
(1) Every pullback of f along an egressive edge has a lift in
 $Y_{\mathrm {in}}$
which is simultaneously p-cocartesian and
$Y_{\mathrm {in}}$
which is simultaneously p-cocartesian and
 $p_{\mathrm {in}}$
-cocartesian, for any choice of lift of its source.
$p_{\mathrm {in}}$
-cocartesian, for any choice of lift of its source. -
(2) Consider any commutative square
 $\sigma $
in Y
$\sigma $
in Y
such that
 $p(\sigma )$
is an ambigressive pullback in X, the edge
$p(\sigma )$
is an ambigressive pullback in X, the edge
 $g'$
is ingressive, the morphism g is egressive, and the morphism
$g'$
is ingressive, the morphism g is egressive, and the morphism
 $\psi $
is a p-cocartesian and ingressive lift of f. Then
$\psi $
is a p-cocartesian and ingressive lift of f. Then
 $g'$
is p-cocartesian if and only if the square is an ambigressive pullback.
$g'$
is p-cocartesian if and only if the square is an ambigressive pullback.
Then an edge
![]() $x\rightarrow y$
of
$x\rightarrow y$
of
![]() $\mathrm {Span}(Y)$
, represented by a span
$\mathrm {Span}(Y)$
, represented by a span

such that
![]() $\psi $
covers f, is
$\psi $
covers f, is
![]() $\mathrm {Span}(p)$
-cocartesian if
$\mathrm {Span}(p)$
-cocartesian if
![]() $\phi $
is
$\phi $
is
![]() $p^{\mathrm {eg}}$
-cartesian and
$p^{\mathrm {eg}}$
-cartesian and
![]() $\psi $
is p-cocartesian as indicated.
$\psi $
is p-cocartesian as indicated.
Proof. Unwinding definitions, we have to show that for any span ![]() in Y, the solid diagram (ignoring the numbers for a moment)
in Y, the solid diagram (ignoring the numbers for a moment)

admits an essentially unique dashed filling lying over a given entirely solid diagram in
![]() $\mathrm {Span}(X)$
, such that all left-pointing arrows are egressive and all right-pointing arrows ingressive, and the top square is cartesian. We then first observe that the second condition on f (the image of
$\mathrm {Span}(X)$
, such that all left-pointing arrows are egressive and all right-pointing arrows ingressive, and the top square is cartesian. We then first observe that the second condition on f (the image of
![]() $\psi $
in X) implies that for such square in which the arrows
$\psi $
in X) implies that for such square in which the arrows
![]() $w \rightarrow u$
and
$w \rightarrow u$
and
![]() $w \rightarrow \bullet $
are egressive and ingressive, respectively the assertion that the square is cartesian and
$w \rightarrow \bullet $
are egressive and ingressive, respectively the assertion that the square is cartesian and
![]() $\bullet \rightarrow y$
is egressive is equivalent to the assertion that the map
$\bullet \rightarrow y$
is egressive is equivalent to the assertion that the map
![]() $w \rightarrow \bullet $
is p-cocartesian, so we may instead show that there is a unique filler with this property.
$w \rightarrow \bullet $
is p-cocartesian, so we may instead show that there is a unique filler with this property.
We do so by filling the diagram step by step, as indicated by the numbers in the above diagram, essentially uniquely each time:
-
(1) There exists a unique egressive filler because
 $\phi $
is
$\phi $
is
 $p^{\mathrm {eg}}$
-cartesian.
$p^{\mathrm {eg}}$
-cartesian. -
(2) The first assumption on f provides a p-cocartesian left, that is automatically unique and also
 $p_{\mathrm {in}}$
-cocartesian and ingressive.
$p_{\mathrm {in}}$
-cocartesian and ingressive. -
(3) There exists a unique filler making the middle square commute because
 $w \rightarrow \bullet $
is p-cocartesian.
$w \rightarrow \bullet $
is p-cocartesian. -
(4) There is a unique ingressive filler because
 $w\rightarrow \bullet $
is
$w\rightarrow \bullet $
is
 $p_{\mathrm {in}}$
-cocartesian.
$p_{\mathrm {in}}$
-cocartesian.
In the special case where f is an equivalence, the two assumptions are automatic, so we obtain the following:
Corollary 3.2. If
![]() $p\colon Y\rightarrow X$
is a morphism in
$p\colon Y\rightarrow X$
is a morphism in
![]() $\mathrm {AdTrip}$
, then a span in Y of the form
$\mathrm {AdTrip}$
, then a span in Y of the form

represents a
![]() $\mathrm {Span}(p)$
-cocartesian morphism whenever
$\mathrm {Span}(p)$
-cocartesian morphism whenever
![]() $\phi $
is
$\phi $
is
![]() $p^{\mathrm {eg}}$
-cartesian.
$p^{\mathrm {eg}}$
-cartesian.
Remark 3.3. We feel obliged to point out two oversights in the statement of the above result in [Reference BarwickBa17, 12.2 Theorem]:
-
(i) Barwick requires that the edge
 $\phi $
be p-cartesian and not
$\phi $
be p-cartesian and not
 $p^{\mathrm {eg}}$
-cartesian. Our proof above hopefully makes it transparent why this is not enough. For an explicit counterexample, consider
$p^{\mathrm {eg}}$
-cartesian. Our proof above hopefully makes it transparent why this is not enough. For an explicit counterexample, consider
 $X = Y = [1]^2$
with p the identity, where we equip the source with the triple structure with the horizontal maps (and the identities) ingressive and everything but the horizontal maps egressive and the target with the same ingressives but all maps egressive.
$X = Y = [1]^2$
with p the identity, where we equip the source with the triple structure with the horizontal maps (and the identities) ingressive and everything but the horizontal maps egressive and the target with the same ingressives but all maps egressive. -
(ii) As he is working at the point-set level, Barwick has to show that
 $\mathrm {Span}(p)$
is an inner fibration. To this end, he assumes that p is an inner fibration, but in fact requires the stronger assumption that p is an isofibration, as can be seen by lifting a
$\mathrm {Span}(p)$
is an inner fibration. To this end, he assumes that p is an inner fibration, but in fact requires the stronger assumption that p is an isofibration, as can be seen by lifting a
 $2$
-simplex in
$2$
-simplex in
 $\mathrm {Span}(Y)$
of the form
$\mathrm {Span}(Y)$
of the form
where f is some equivalence and all other maps identities.
In order to carry out iterated span constructions as in [Reference Barwick, Glasman and NardinBGN18] at the point-set level, one therefore needs to check that if p is an isofibration, then so is
 $\mathrm {Span}(p)$
. This is indeed the case as a direct consequence of equivalences in span
$\mathrm {Span}(p)$
. This is indeed the case as a direct consequence of equivalences in span
 $\infty $
-categories being precisely the spans of equivalences (which itself follows from the completeness assertion for
$\infty $
-categories being precisely the spans of equivalences (which itself follows from the completeness assertion for
 $\iota {\mathrm {Q}}(X)$
in Lemma 2.17; see also [Reference BarwickBa17, Proposition 3.4]).
$\iota {\mathrm {Q}}(X)$
in Lemma 2.17; see also [Reference BarwickBa17, Proposition 3.4]).
Example 3.4. In particular, in light of the previous remark, let us recount the original purpose of Theorem 3.1 in [Reference BarwickBa17], which is Barwick’s unfurling construction. The input is an adequate triple
![]() $(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
and a functor
$(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
and a functor
![]() $F \colon X^{\mathrm {op}} \rightarrow \mathrm {Cat} $
such that
$F \colon X^{\mathrm {op}} \rightarrow \mathrm {Cat} $
such that
-
(1) for every ingressive
 $f \colon x \rightarrow y$
, the induced functor
$f \colon x \rightarrow y$
, the induced functor
 $f^{*} \colon F(y) \rightarrow F(x)$
admits a left adjoint
$f^{*} \colon F(y) \rightarrow F(x)$
admits a left adjoint
 $f_!$
, and
$f_!$
, and -
(2) the image under F of every ambigressive pullback in X is left-adjointable; that is, given the left square in
the right one commutes via the Beck-Chevalley transformation
 $f_!g^{*} \Rightarrow h^{*}i_!$
.
$f_!g^{*} \Rightarrow h^{*}i_!$
.
The output is an extension of
![]() $F \colon (X^{\mathrm {eg}})^{\mathrm {op}} \rightarrow \mathrm {Cat} $
to a functor
$F \colon (X^{\mathrm {eg}})^{\mathrm {op}} \rightarrow \mathrm {Cat} $
to a functor
![]() $\mathrm {Unf}(F) \colon \mathrm {Span}(X,X_{\mathrm {in}},X^{\mathrm {eg}}) \rightarrow \mathrm {Cat} $
, the unfurling of F, whose additional functoriality is given by the left adjoints to the images of the ingressive edges in X.
$\mathrm {Unf}(F) \colon \mathrm {Span}(X,X_{\mathrm {in}},X^{\mathrm {eg}}) \rightarrow \mathrm {Cat} $
, the unfurling of F, whose additional functoriality is given by the left adjoints to the images of the ingressive edges in X.
It is constructed by considering the cartesian unstraightening
![]() $p \colon Y\rightarrow X$
of F, which carries the structure of an adequate triple with ingressives
$p \colon Y\rightarrow X$
of F, which carries the structure of an adequate triple with ingressives
![]() $p^{-1}(X_{\mathrm {in}})$
and egressives
$p^{-1}(X_{\mathrm {in}})$
and egressives
![]() $Y^{\dagger }$
, the subcategory formed by the p-cartesian lifts of degres in
$Y^{\dagger }$
, the subcategory formed by the p-cartesian lifts of degres in
![]() $X^{\mathrm {eg}}$
, by Proposition 2.6. The claim is that the induced map
$X^{\mathrm {eg}}$
, by Proposition 2.6. The claim is that the induced map
is a cocartesian fibration and that its cocartesian straightening is the desired extension
The first claim follows from an application of Theorem 3.1. Given a span
in X and an element
![]() $c \in F(x) \subseteq Y$
, we can build a
$c \in F(x) \subseteq Y$
, we can build a
![]() $\mathrm {Span}(p)$
-cocartesian lift as follows. Per construction, we can first choose a p-cartesian edge
$\mathrm {Span}(p)$
-cocartesian lift as follows. Per construction, we can first choose a p-cartesian edge
![]() $\phi \colon d \rightarrow c$
covering g. By the first assumption on F and the fibrational characterisation of adjunctions, the edge f then further admits a locally p-cocartesian lift
$\phi \colon d \rightarrow c$
covering g. By the first assumption on F and the fibrational characterisation of adjunctions, the edge f then further admits a locally p-cocartesian lift
![]() $\psi \colon d \rightarrow e$
, which is in fact p-cocartesian by [Reference LurieLu09a, Corollary 5.2.2.4]. Note that this span in Y indeed defines a morphism
$\psi \colon d \rightarrow e$
, which is in fact p-cocartesian by [Reference LurieLu09a, Corollary 5.2.2.4]. Note that this span in Y indeed defines a morphism
![]() $c \rightarrow e$
in
$c \rightarrow e$
in
![]() $\mathrm {Span}(Y, p^{-1}(X_{\mathrm {in}}),p^{\dagger })$
. To see that it is
$\mathrm {Span}(Y, p^{-1}(X_{\mathrm {in}}),p^{\dagger })$
. To see that it is
![]() $\mathrm {Span}(p)$
-cocartesian, we check the conditions of Theorem 3.1. For the first condition, note that all egressive pullbacks of f admit p-cocartesian lifts by the same argument that gives the existence of
$\mathrm {Span}(p)$
-cocartesian, we check the conditions of Theorem 3.1. For the first condition, note that all egressive pullbacks of f admit p-cocartesian lifts by the same argument that gives the existence of
![]() $\phi $
, since such pullbacks are again ingressive. That these lifts are also
$\phi $
, since such pullbacks are again ingressive. That these lifts are also
![]() $p_{\mathrm {in}}$
-cocartesian follows directly from the definition of the ingressives in Y. Next, a square in Y as in the second condition automatically has the form of the solid square
$p_{\mathrm {in}}$
-cocartesian follows directly from the definition of the ingressives in Y. Next, a square in Y as in the second condition automatically has the form of the solid square

if it covers the ambigressive pullback

in X. The dotted map is the Beck-Chevalley transformation, which is an equivalence by the second assumption on F, and the upper right triangle commutes by a simple diagram chase. The task is to show that the large square is an ambigressive pullback if and only if the upper right horizontal map is an equivalence. But if the diagram is ambigressive, the map
![]() $d \rightarrow i_!c$
is by definition p-cartesian, which indeed forces the upper right-hand corner to consist of equivalences. And conversely, if the corner consists of equivalences, then the right-hand composition is cartesian, making the square ambigressive and also forcing it to be cartesian as it covers a cartesian base (see the proof of Proposition 2.6 above for the relevant calculation).
$d \rightarrow i_!c$
is by definition p-cartesian, which indeed forces the upper right-hand corner to consist of equivalences. And conversely, if the corner consists of equivalences, then the right-hand composition is cartesian, making the square ambigressive and also forcing it to be cartesian as it covers a cartesian base (see the proof of Proposition 2.6 above for the relevant calculation).
To apply (the corrected version of) Barwick’s criterion, we finally have to check that
![]() $\phi $
is
$\phi $
is
![]() $p^{\mathrm {eg}}$
-cartesian. But since it is p-cartesian, we are saved by the left-cancellation property of cartesian edges.
$p^{\mathrm {eg}}$
-cartesian. But since it is p-cartesian, we are saved by the left-cancellation property of cartesian edges.
Finally, it remains to check that the composite
agrees with the restriction of F. Unwinding definitions, this composite is given as the cocartesian straightening of
![]() $\mathrm {Span}(Y,p^{-1}(\iota X),Y^{\dagger }) \rightarrow \mathrm {Span}(X,\iota X, X^{\mathrm {eg}})$
and the statement that this is indeed the restriction of F is the main result of [Reference Barwick, Glasman and NardinBGN18], which we shall reprove momentarily in Corollary 3.18 below.
$\mathrm {Span}(Y,p^{-1}(\iota X),Y^{\dagger }) \rightarrow \mathrm {Span}(X,\iota X, X^{\mathrm {eg}})$
and the statement that this is indeed the restriction of F is the main result of [Reference Barwick, Glasman and NardinBGN18], which we shall reprove momentarily in Corollary 3.18 below.
Example 3.5. Suppose that
![]() ${C}$
is stable and consider the target projection
${C}$
is stable and consider the target projection
![]() $p=t \colon \operatorname {\mathrm {Ar}}({C}) \rightarrow {C}$
, regarded as a map of adequate triples with all maps both ingressive and egressive. One readily checks that every edge f in
$p=t \colon \operatorname {\mathrm {Ar}}({C}) \rightarrow {C}$
, regarded as a map of adequate triples with all maps both ingressive and egressive. One readily checks that every edge f in
![]() ${C}$
satisfies the assumptions of Theorem 3.1. It follows that
${C}$
satisfies the assumptions of Theorem 3.1. It follows that
![]() $\mathrm {Span}(\operatorname {\mathrm {Ar}}({C})) \rightarrow \mathrm {Span}({C})$
is a cocartesian fibration for every stable
$\mathrm {Span}(\operatorname {\mathrm {Ar}}({C})) \rightarrow \mathrm {Span}({C})$
is a cocartesian fibration for every stable
![]() ${C}$
, and thus by Lemma 2.14, also a cartesian fibration. Taking classifying
${C}$
, and thus by Lemma 2.14, also a cartesian fibration. Taking classifying
![]() $\infty $
-groupoids (i.e., classifying spaces) preserves pullback squares whose right edge is both a cocartesian and cartesian fibration, as can be shown from Quillen’s Theorem B (see [Reference SteimleSt21, Reference SteinebrunnerSt22] or the proof of [CDH+20, Theorem 2.5.1] for an account in the present language). Therefore, we conclude that
$\infty $
-groupoids (i.e., classifying spaces) preserves pullback squares whose right edge is both a cocartesian and cartesian fibration, as can be shown from Quillen’s Theorem B (see [Reference SteimleSt21, Reference SteinebrunnerSt22] or the proof of [CDH+20, Theorem 2.5.1] for an account in the present language). Therefore, we conclude that
is a fibre sequence. Since
![]() ${\mathcal {K}}({C}) = \Omega |\mathrm {Span}({C})|$
is one possible definition of the algebraic K-space of
${\mathcal {K}}({C}) = \Omega |\mathrm {Span}({C})|$
is one possible definition of the algebraic K-space of
![]() ${C}$
, looping this fibre sequence once recovers Waldhausen’s additivity theorem
${C}$
, looping this fibre sequence once recovers Waldhausen’s additivity theorem
since t is clearly split and
![]() ${\mathcal {K}}({C})$
an
${\mathcal {K}}({C})$
an
![]() ${\mathbb E}_{\infty }$
-group using the direct sum in C. In this way, Proposition 3.1 connects to the discussion of additivity in [CDH+20, Section 2].
${\mathbb E}_{\infty }$
-group using the direct sum in C. In this way, Proposition 3.1 connects to the discussion of additivity in [CDH+20, Section 2].
As a further application of Theorem 3.1, we can identify the cocartesian fibration corresponding to the functor
![]() $\mathrm {Span} \colon \mathrm {AdTrip} \rightarrow \mathrm {Cat} $
. More generally, let X be an
$\mathrm {Span} \colon \mathrm {AdTrip} \rightarrow \mathrm {Cat} $
. More generally, let X be an
![]() $\infty $
-category and consider a diagram of adequate triples
$\infty $
-category and consider a diagram of adequate triples
Writing
![]() $p\colon Y\longrightarrow X$
for the cartesian fibration classified by the underlying functor of F, we can use Proposition 2.7 to endow Y with the structure of an adequate triple:
$p\colon Y\longrightarrow X$
for the cartesian fibration classified by the underlying functor of F, we can use Proposition 2.7 to endow Y with the structure of an adequate triple:
Notation 3.6. By forgetting different pieces of the data, the functor
![]() $F\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {AdTrip}$
gives three diagrams of
$F\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {AdTrip}$
gives three diagrams of
![]() $\infty $
-categories
$\infty $
-categories
![]() $F,F_{\mathrm {in}}$
and
$F,F_{\mathrm {in}}$
and
![]() $F^{\mathrm {eg}}$
, which are classified by three cartesian fibrations
$F^{\mathrm {eg}}$
, which are classified by three cartesian fibrations
respectively, where we generally denote by
the cartesian and cocartesian unstraightening functors, respectively. In our specific situation we further write
![]() $Y_{\mathrm {fw}}, Y_{\mathrm {in}}^{\mathrm {fw}},Y^{\mathrm {eg}}_{\mathrm {fw}}$
for the pullback of
$Y_{\mathrm {fw}}, Y_{\mathrm {in}}^{\mathrm {fw}},Y^{\mathrm {eg}}_{\mathrm {fw}}$
for the pullback of
![]() $Y,Y_{\mathrm {in}},Y^{\mathrm {eg}}$
along
$Y,Y_{\mathrm {in}},Y^{\mathrm {eg}}$
along
![]() $\iota X\rightarrow X$
. Proposition 2.7 then shows that
$\iota X\rightarrow X$
. Proposition 2.7 then shows that
![]() $p\colon Y\longrightarrow X$
is part of a map of adequate triples
$p\colon Y\longrightarrow X$
is part of a map of adequate triples
which gives rise to a map
We will show that this is the cocartesian fibration classifying
![]() $\mathrm {Span} \circ F$
. First we note the following:
$\mathrm {Span} \circ F$
. First we note the following:
Lemma 3.8. The functor
![]() $\mathrm {Span}(p)$
is a cocartesian fibration.
$\mathrm {Span}(p)$
is a cocartesian fibration.
Proof. Corollary 3.2 immediately implies that
![]() $\mathrm {Span}(p)$
is a cocartesian fibration, with cocartesian edges given by spans of the form:
$\mathrm {Span}(p)$
is a cocartesian fibration, with cocartesian edges given by spans of the form: ![]() where
where
![]() $y\rightarrow y'$
is a
$y\rightarrow y'$
is a
![]() $p^{\mathrm {eg}}$
-cartesian edge in Y.
$p^{\mathrm {eg}}$
-cartesian edge in Y.
We will now describe the functor classified by this cocartesian fibration:
Theorem 3.9. Let X be an
![]() $\infty $
-category. Then there exists a natural equivalence
$\infty $
-category. Then there exists a natural equivalence
of functors
![]() $\mathrm {Fun} (X^{\mathrm {op}},\mathrm {AdTrip})\rightarrow \operatorname {\mathrm {Cocart}}(X^{{\mathrm {op}}})$
. In other words, for each
$\mathrm {Fun} (X^{\mathrm {op}},\mathrm {AdTrip})\rightarrow \operatorname {\mathrm {Cocart}}(X^{{\mathrm {op}}})$
. In other words, for each
![]() $F \colon X^{\mathrm {op}} \longrightarrow \mathrm {AdTrip}$
, the induced cocartesian fibration (3.7) is classified by the functor
$F \colon X^{\mathrm {op}} \longrightarrow \mathrm {AdTrip}$
, the induced cocartesian fibration (3.7) is classified by the functor
![]() $\mathrm {Span}\circ F\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
.
$\mathrm {Span}\circ F\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
.
We will use the following description of (co)cartesian unstraightening from [Reference Gepner, Haugseng and NikolausGHN17, Theorem 7.4]:
Theorem 3.10. For a functor
![]() $F\colon B\longrightarrow \mathrm {Cat} $
, there is a natural equivalence
$F\colon B\longrightarrow \mathrm {Cat} $
, there is a natural equivalence
Dually, for a functor
![]() $F\colon B^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
, there is a natural equivalence
$F\colon B^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
, there is a natural equivalence
We will apply this in the setting of 3.6 to compute the cocartesian fibration classified by
![]() $\mathrm {Span}(F)\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
. We find that
$\mathrm {Span}(F)\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
. We find that
![]() $\mathrm {Un}^{\mathrm {cc}}(\mathrm {Span}(F))$
is equivalent to the colimit of the diagram
$\mathrm {Un}^{\mathrm {cc}}(\mathrm {Span}(F))$
is equivalent to the colimit of the diagram
Now note that there are natural equivalences
![]() ${-/}X^{{\mathrm {op}}}\simeq (X{/-})^{{\mathrm {op}}} \simeq \mathrm {Span}(X{/-},\iota (X{/-}),X{/-})$
and recall that
${-/}X^{{\mathrm {op}}}\simeq (X{/-})^{{\mathrm {op}}} \simeq \mathrm {Span}(X{/-},\iota (X{/-}),X{/-})$
and recall that
![]() $\mathrm {Span}$
commutes with products of adequate triples to conclude that this colimit is the same as that of the diagram
$\mathrm {Span}$
commutes with products of adequate triples to conclude that this colimit is the same as that of the diagram
We shall prove Theorem 3.9 by showing that the colimit of the first two functors in this composition is precisely
![]() $Y^{\int }=(Y,Y_{\mathrm {in}}^{\mathrm {fw}},Y^{\mathrm {eg}})$
and that this colimit is preserved by
$Y^{\int }=(Y,Y_{\mathrm {in}}^{\mathrm {fw}},Y^{\mathrm {eg}})$
and that this colimit is preserved by
![]() $\mathrm {Span}$
.
$\mathrm {Span}$
.
We can directly apply the equivalence of Theorem 3.10 to conclude that
where all colimits are taken over
![]() $\operatorname {\mathrm {Tw}}^{r}(X^{{\mathrm {op}}})$
. To exhibit
$\operatorname {\mathrm {Tw}}^{r}(X^{{\mathrm {op}}})$
. To exhibit
![]() $Y_{\mathrm {in}}^{\mathrm {fw}} = Y_{\mathrm {in}}\times _X \iota X$
as a colimit, we need the following lemma:
$Y_{\mathrm {in}}^{\mathrm {fw}} = Y_{\mathrm {in}}\times _X \iota X$
as a colimit, we need the following lemma:
Lemma 3.12. Let
![]() $F\colon B^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
be a functor. Then the functor
$F\colon B^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
be a functor. Then the functor
![]() $\mathrm {Un}^{\mathrm {ct}}(F)\times _B \iota B\longrightarrow \mathrm {Un}^{\mathrm {ct}}(F)$
is naturally equivalent to the functor
$\mathrm {Un}^{\mathrm {ct}}(F)\times _B \iota B\longrightarrow \mathrm {Un}^{\mathrm {ct}}(F)$
is naturally equivalent to the functor
Proof. Consider the full subcategory of
![]() $\mathrm {Fun} \big (\mathrm {Fun} (B^{{\mathrm {op}}}, \mathrm {Cat} ), \mathrm {Cat} \big ){/\mathrm {Un}^{\mathrm {ct}}}$
spanned by those natural transformations
$\mathrm {Fun} \big (\mathrm {Fun} (B^{{\mathrm {op}}}, \mathrm {Cat} ), \mathrm {Cat} \big ){/\mathrm {Un}^{\mathrm {ct}}}$
spanned by those natural transformations
![]() $\Phi \longrightarrow \mathrm {Un}^{\mathrm {ct}}$
with the following two properties:
$\Phi \longrightarrow \mathrm {Un}^{\mathrm {ct}}$
with the following two properties:
-
(1) At the terminal diagram,
 $\Phi (\ast )\longrightarrow \mathrm {Un}^{\mathrm {ct}}(\ast )\simeq B$
exhibits the inclusion of the core of B.
$\Phi (\ast )\longrightarrow \mathrm {Un}^{\mathrm {ct}}(\ast )\simeq B$
exhibits the inclusion of the core of B. -
(2) For each
 $F\colon B^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
, the induced square (3.14)is cartesian.
$F\colon B^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
, the induced square (3.14)is cartesian.
This subcategory is contractible and the natural transformation
![]() $\mathrm {Un}^{\mathrm {ct}}(-)\times _B \iota B\longrightarrow \mathrm {Un}^{\mathrm {ct}}(-)$
is (by definition) an object in there. It will therefore suffice to show that the composite natural transformation
$\mathrm {Un}^{\mathrm {ct}}(-)\times _B \iota B\longrightarrow \mathrm {Un}^{\mathrm {ct}}(-)$
is (by definition) an object in there. It will therefore suffice to show that the composite natural transformation
satisfies conditions (1) and (2) as well.
Let us start by computing
![]() $\Phi (F)$
. To this end, let us write
$\Phi (F)$
. To this end, let us write
![]() $\operatorname {\mathrm {Ar}}(B)_s=\operatorname {\mathrm {Ar}}(B)\times _{B} \iota B$
, where the structure map
$\operatorname {\mathrm {Ar}}(B)_s=\operatorname {\mathrm {Ar}}(B)\times _{B} \iota B$
, where the structure map
![]() $\operatorname {\mathrm {Ar}}(B) \rightarrow B$
is evaluation at the source. Then
$\operatorname {\mathrm {Ar}}(B) \rightarrow B$
is evaluation at the source. Then
![]() $t\colon \operatorname {\mathrm {Ar}}(B)_s\longrightarrow B$
is the left fibration classified by the functor
$t\colon \operatorname {\mathrm {Ar}}(B)_s\longrightarrow B$
is the left fibration classified by the functor
![]() $b\mapsto \iota (B{/b})$
and
$b\mapsto \iota (B{/b})$
and
![]() $s\colon \operatorname {\mathrm {Ar}}(B)_s\longrightarrow \iota B$
admits a fully faithful left adjoint
$s\colon \operatorname {\mathrm {Ar}}(B)_s\longrightarrow \iota B$
admits a fully faithful left adjoint
![]() $\operatorname {\mathrm {cst}}\colon \iota B\hookrightarrow \operatorname {\mathrm {Ar}}(B)_s$
taking degenerate arrows. Let us now consider the following two pullbacks of
$\operatorname {\mathrm {cst}}\colon \iota B\hookrightarrow \operatorname {\mathrm {Ar}}(B)_s$
taking degenerate arrows. Let us now consider the following two pullbacks of
![]() $\infty $
-categories
$\infty $
-categories

as well as the following diagram of
![]() $\infty $
-categories
$\infty $
-categories
Since
![]() $q\colon C\to \operatorname {\mathrm {Tw}}^{r}(B^{{\mathrm {op}}})$
is the left fibration classifying
$q\colon C\to \operatorname {\mathrm {Tw}}^{r}(B^{{\mathrm {op}}})$
is the left fibration classifying
![]() $\iota (B{/-})\colon \operatorname {\mathrm {Tw}}^{r}(B^{{\mathrm {op}}})\to B\to {\mathrm {Gpd}}$
and
$\iota (B{/-})\colon \operatorname {\mathrm {Tw}}^{r}(B^{{\mathrm {op}}})\to B\to {\mathrm {Gpd}}$
and
![]() $F'$
is constant along the fibres of q, the left Kan extension
$F'$
is constant along the fibres of q, the left Kan extension
![]() $q_!F'$
is naturally equivalent to the diagram
$q_!F'$
is naturally equivalent to the diagram
![]() $F(-)\times \iota (B{/-})$
of which we want to compute the colimit [Reference LurieLu09a, Proposition 4.3.3.10]. By transitivity of Kan extensions, it therefore suffices to compute
$F(-)\times \iota (B{/-})$
of which we want to compute the colimit [Reference LurieLu09a, Proposition 4.3.3.10]. By transitivity of Kan extensions, it therefore suffices to compute ![]() .
.
Note that the vertical arrows in the above diagram are all cartesian fibrations, so that the fully faithful inclusion
![]() $D\hookrightarrow C$
admits a (localising) right adjoint [Reference LurieLu09a, Corollary 5.2.7.11]
$D\hookrightarrow C$
admits a (localising) right adjoint [Reference LurieLu09a, Corollary 5.2.7.11]
By construction, the diagram
![]() $F'$
only depended on the first factor
$F'$
only depended on the first factor
![]() $\operatorname {\mathrm {Tw}}^{r}(B^{{\mathrm {op}}})$
; Consequently, it factors as
$\operatorname {\mathrm {Tw}}^{r}(B^{{\mathrm {op}}})$
; Consequently, it factors as
![]() $F'= F"p$
, for some
$F'= F"p$
, for some
![]() $F"\colon D \rightarrow \mathrm {Cat} $
. Because p is a localisation, it is in particular cofinal, so we conclude that
$F"\colon D \rightarrow \mathrm {Cat} $
. Because p is a localisation, it is in particular cofinal, so we conclude that ![]() .
.
Let us first compute the left Kan extension
![]() $\pi _!F"$
of
$\pi _!F"$
of
![]() $F"$
along the cocartesian fibration
$F"$
along the cocartesian fibration
![]() $\pi \colon D\to \iota B$
. We can compute this Kan extension as a colimit over the fibres, which are equivalently the fibres of
$\pi \colon D\to \iota B$
. We can compute this Kan extension as a colimit over the fibres, which are equivalently the fibres of
![]() $t\colon \operatorname {\mathrm {Tw}}^{r}(B^{{\mathrm {op}}})\to B$
. Unravelling the definitions then shows that
$t\colon \operatorname {\mathrm {Tw}}^{r}(B^{{\mathrm {op}}})\to B$
. Unravelling the definitions then shows that
since
![]() $B^{{\mathrm {op}}}/b$
has a terminal object. We conclude that there is a natural equivalence
$B^{{\mathrm {op}}}/b$
has a terminal object. We conclude that there is a natural equivalence
In particular, we see that
![]() $\Phi (\ast )$
is an
$\Phi (\ast )$
is an
![]() $\infty $
-groupoid, so that (1)
$\infty $
-groupoid, so that (1)
![]() $\Phi (\ast )\to B$
is a core inclusion, being a colimit of core inclusions. For (2), note that the vertical maps in (3.14) are cartesian fibrations, so that it suffices to show that the maps on vertical fibres are equivalences. By naturality of the transformation
$\Phi (\ast )\to B$
is a core inclusion, being a colimit of core inclusions. For (2), note that the vertical maps in (3.14) are cartesian fibrations, so that it suffices to show that the maps on vertical fibres are equivalences. By naturality of the transformation
![]() $\Phi \longrightarrow \mathrm {Un}^{\mathrm {ct}}$
in the base B, this map on fibres map is simply the map when
$\Phi \longrightarrow \mathrm {Un}^{\mathrm {ct}}$
in the base B, this map on fibres map is simply the map when
![]() $B=*$
. In this case, the map (3.13) is clearly an equivalence.
$B=*$
. In this case, the map (3.13) is clearly an equivalence.
Proposition 3.15. The diagram
has colimit given by the adequate triple
![]() $Y^{\int }=(Y, Y_{\mathrm {in}}^{\mathrm {fw}}, Y_{\mathrm {eg}})$
.
$Y^{\int }=(Y, Y_{\mathrm {in}}^{\mathrm {fw}}, Y_{\mathrm {eg}})$
.
Proof. The equivalences (3.11) and Lemma 3.12 show that the colimit of
![]() $\Psi $
in
$\Psi $
in
![]() $\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
is given by the triple
$\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
is given by the triple
![]() $Y^{\int }$
. To see that this is also a colimit in the subcategory of adequate triples, it suffices to verify that the following are equivalent for a functor
$Y^{\int }$
. To see that this is also a colimit in the subcategory of adequate triples, it suffices to verify that the following are equivalent for a functor ![]() :
:
-
(1)
 $\phi $
preserves ambigressive pullback squares.
$\phi $
preserves ambigressive pullback squares. -
(2) the composite
 does so for each
does so for each
 $f^{{\mathrm {op}}}\in \operatorname {\mathrm {Tw}}^{r}(X^{{\mathrm {op}}})$
.
$f^{{\mathrm {op}}}\in \operatorname {\mathrm {Tw}}^{r}(X^{{\mathrm {op}}})$
.
Now note that (on underlying
![]() $\infty $
-categories) the map
$\infty $
-categories) the map ![]() can be identified with the functor
can be identified with the functor
![]() $\lambda _f\colon F(x_1)\times X{/x_0}\longrightarrow Y$
sending
$\lambda _f\colon F(x_1)\times X{/x_0}\longrightarrow Y$
sending
![]() $(y, g\colon x_2\to x_0)$
to
$(y, g\colon x_2\to x_0)$
to
![]() $g^{*}f^{*}(y)$
. Because
$g^{*}f^{*}(y)$
. Because
![]() $g^{*}$
is a map of adequate triples for every map g in X,
$g^{*}$
is a map of adequate triples for every map g in X,
![]() $\lambda _f$
is a map of adequate triples, which shows that (1) implies (2).
$\lambda _f$
is a map of adequate triples, which shows that (1) implies (2).
For the converse, note that every ambigressive pullback square in Y can be obtained as a pasting of two types of squares: (a) the pullback of a fibrewise ingressive map along a p-cartesian lift of some
![]() $g\colon x_2\to x_0$
and (b) the pullback of an ingressive and egressive map in a single fibre
$g\colon x_2\to x_0$
and (b) the pullback of an ingressive and egressive map in a single fibre
![]() $Y_{x_0}\simeq F(x_0)$
. It suffices to show that each of these squares is the image of an ambigressive pullback square under some
$Y_{x_0}\simeq F(x_0)$
. It suffices to show that each of these squares is the image of an ambigressive pullback square under some
![]() $\lambda _f$
. For (a), we can take the image under
$\lambda _f$
. For (a), we can take the image under
![]() $\lambda _{\mathrm {id}_{x_0}}$
of the square in
$\lambda _{\mathrm {id}_{x_0}}$
of the square in
![]() $F(x_0)\times X{/x_0}$
formed by an ingressive arrow in
$F(x_0)\times X{/x_0}$
formed by an ingressive arrow in
![]() $F(x_1)$
and the arrow
$F(x_1)$
and the arrow
![]() $g\to \mathrm {id}_{x_0}$
in
$g\to \mathrm {id}_{x_0}$
in
![]() $X/x_0$
. For (b), we simply take the image under
$X/x_0$
. For (b), we simply take the image under
![]() $\lambda _{\mathrm {id}_{x_0}}$
of an ambigressive square in
$\lambda _{\mathrm {id}_{x_0}}$
of an ambigressive square in
![]() $F(x_0)\times \{\mathrm {id}_{x_0}\}$
.
$F(x_0)\times \{\mathrm {id}_{x_0}\}$
.
Applying
![]() $\mathrm {Span}$
to the colimiting cocone of Proposition 3.15, we therefore obtain a natural cocone of the diagram
$\mathrm {Span}$
to the colimiting cocone of Proposition 3.15, we therefore obtain a natural cocone of the diagram
whose tip is the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Span}(Y^{\int })$
. This induces a natural functor
$\mathrm {Span}(Y^{\int })$
. This induces a natural functor
Note that the construction of
![]() $\alpha _F$
is functorial in the diagram F. Applied to the terminal diagram
$\alpha _F$
is functorial in the diagram F. Applied to the terminal diagram
![]() $F=\ast $
, it yields the identity map of
$F=\ast $
, it yields the identity map of
![]() $\mathrm {Span}(X, \iota X, X)$
. Using the identification
$\mathrm {Span}(X, \iota X, X)$
. Using the identification
![]() $\mathrm {Span}(X, \iota X, X) \simeq X^{{\mathrm {op}}}$
from Proposition 2.15, we then obtain the desired natural transformation
$\mathrm {Span}(X, \iota X, X) \simeq X^{{\mathrm {op}}}$
from Proposition 2.15, we then obtain the desired natural transformation
![]() $\alpha \colon \mathrm {Un}^{\mathrm {cc}}(\mathrm {Span}\circ (-)) \Longrightarrow \mathrm {Span}(\mathrm {Un}^{\mathrm {ct}}(-)^{\int })$
between functors
$\alpha \colon \mathrm {Un}^{\mathrm {cc}}(\mathrm {Span}\circ (-)) \Longrightarrow \mathrm {Span}(\mathrm {Un}^{\mathrm {ct}}(-)^{\int })$
between functors
![]() $\mathrm {Fun} (X^{{\mathrm {op}}}, \mathrm {AdTrip})\longrightarrow \mathrm {Cat} {/X^{{\mathrm {op}}}}$
.
$\mathrm {Fun} (X^{{\mathrm {op}}}, \mathrm {AdTrip})\longrightarrow \mathrm {Cat} {/X^{{\mathrm {op}}}}$
.
Lemma 3.16. For each
![]() $F\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {AdTrip}$
, the functor
$F\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {AdTrip}$
, the functor
![]() $\alpha _F$
preserves cocartesian edges over
$\alpha _F$
preserves cocartesian edges over
![]() $X^{\mathrm {op}}$
.
$X^{\mathrm {op}}$
.
Proof. Note that F comes with a natural transformation
![]() $\iota F\longrightarrow F$
, where each
$\iota F\longrightarrow F$
, where each
![]() $\iota F(x)$
comes equipped with the (only possible) adequate triple structure where all morphisms are both ingressive and egressive. Unstraightening, this identifies
$\iota F(x)$
comes equipped with the (only possible) adequate triple structure where all morphisms are both ingressive and egressive. Unstraightening, this identifies
![]() $\mathrm {Un}^{\mathrm {ct}}(\iota F)^{\int }$
with the subcategory of
$\mathrm {Un}^{\mathrm {ct}}(\iota F)^{\int }$
with the subcategory of
![]() $\mathrm {Un}^{\mathrm {ct}}(F)$
on the cartesian arrows, with all arrows egressive and only the equivalences being ingressive.
$\mathrm {Un}^{\mathrm {ct}}(F)$
on the cartesian arrows, with all arrows egressive and only the equivalences being ingressive.
The map
![]() $\iota F\longrightarrow F$
induces a natural transformation
$\iota F\longrightarrow F$
induces a natural transformation
![]() $\iota \mathrm {Span}(F)\simeq \mathrm {Span}(\iota F)\longrightarrow \mathrm {Span}(F)$
, where the first equivalence uses that
$\iota \mathrm {Span}(F)\simeq \mathrm {Span}(\iota F)\longrightarrow \mathrm {Span}(F)$
, where the first equivalence uses that
![]() $\mathrm {Span}(\iota F)\simeq \iota (F)$
(Proposition 2.15). By naturality, we then obtain a commuting diagram
$\mathrm {Span}(\iota F)\simeq \iota (F)$
(Proposition 2.15). By naturality, we then obtain a commuting diagram

The result now follows since both vertical arrows can be identified with the inclusion of the wide subcategory of cocartesian arrows: for the left arrow this is evident and for the right arrow, this follows from our description of
![]() $\mathrm {Un}^{\mathrm {ct}}(\iota F)^{\int }$
and Corollary 3.2.
$\mathrm {Un}^{\mathrm {ct}}(\iota F)^{\int }$
and Corollary 3.2.
Proof of Theorem 3.9
We have seen that
![]() $\alpha $
constitutes a natural transformation between functors into
$\alpha $
constitutes a natural transformation between functors into
![]() $\mathrm {Cat} /X^{{\mathrm {op}}}$
. By Lemma 3.16, the value of
$\mathrm {Cat} /X^{{\mathrm {op}}}$
. By Lemma 3.16, the value of
![]() $\alpha $
at a diagram F is a map between cocartesian fibrations over
$\alpha $
at a diagram F is a map between cocartesian fibrations over
![]() $X^{\mathrm {op}}$
which preserves cocartesian edges. It then suffices to show that
$X^{\mathrm {op}}$
which preserves cocartesian edges. It then suffices to show that
![]() $\alpha _F$
is an equivalence when restricted to every fibre [Reference LurieLu09a, Corollary 2.4.4.4]. Since
$\alpha _F$
is an equivalence when restricted to every fibre [Reference LurieLu09a, Corollary 2.4.4.4]. Since
![]() $\mathrm {Span}$
preserves pullbacks (in particular fibres), we can thus reduce to the case
$\mathrm {Span}$
preserves pullbacks (in particular fibres), we can thus reduce to the case
![]() $X=\ast $
, where the map is equivalent to the identity by inspection.
$X=\ast $
, where the map is equivalent to the identity by inspection.
Remark 3.17. Given a functor
![]() $G\colon X^{\mathrm {op}}\longrightarrow \mathrm {Cat} $
, one way to write down the cartesian fibration encoding it is to write down the cocartesian fibration which classifies
$G\colon X^{\mathrm {op}}\longrightarrow \mathrm {Cat} $
, one way to write down the cartesian fibration encoding it is to write down the cocartesian fibration which classifies
![]() $(-)^{\mathrm {op}}\circ G$
, and then take its opposite. In the case that
$(-)^{\mathrm {op}}\circ G$
, and then take its opposite. In the case that
![]() $G=\mathrm {Span}(F)$
, Lemma 2.14 shows that
$G=\mathrm {Span}(F)$
, Lemma 2.14 shows that
![]() $G^{\mathrm {op}} = \mathrm {Span}(F^{\mathrm {rev}})$
. Therefore, the previous result allows us to describe its cocartesian straightening. Finally, we can again apply Lemma 2.14 to describe the opposite of the result. In total, one finds that
$G^{\mathrm {op}} = \mathrm {Span}(F^{\mathrm {rev}})$
. Therefore, the previous result allows us to describe its cocartesian straightening. Finally, we can again apply Lemma 2.14 to describe the opposite of the result. In total, one finds that
is a cartesian fibration which classifies the functor
![]() $\mathrm {Span}(F)\colon X^{\mathrm {op}}\longrightarrow \mathrm {Cat} $
.
$\mathrm {Span}(F)\colon X^{\mathrm {op}}\longrightarrow \mathrm {Cat} $
.
As a special case, we recover the key insight of [Reference Barwick, Glasman and NardinBGN18].
Corollary 3.18. Let
![]() $p\colon Y \longrightarrow X$
be a cartesian fibration and define
$p\colon Y \longrightarrow X$
be a cartesian fibration and define
![]() $Y^{\vee } \longrightarrow X^{\mathrm {op}}$
to be the functor
$Y^{\vee } \longrightarrow X^{\mathrm {op}}$
to be the functor
where
![]() $Y^{\dagger }$
is the subcategory of p-cartesian morphisms (cf. Proposition 2.6). This gives rise to an equivalence
$Y^{\dagger }$
is the subcategory of p-cartesian morphisms (cf. Proposition 2.6). This gives rise to an equivalence
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}} \colon \operatorname {\mathrm {Cart}}(X)\longrightarrow \operatorname {\mathrm {Cocart}}(X^{\mathrm {op}})$
which fits into a commuting triangle
$\mathrm {S}\mathrm {D}^{\mathrm {cc}} \colon \operatorname {\mathrm {Cart}}(X)\longrightarrow \operatorname {\mathrm {Cocart}}(X^{\mathrm {op}})$
which fits into a commuting triangle

Proof. Note that once we have exhibited the triangle as commutative, the two-out-of-three property will immediately imply that
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}}$
is an equivalence. We will provide a natural equivalence
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}$
is an equivalence. We will provide a natural equivalence
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}}(\mathrm {Un}^{\mathrm {ct}}(F))\longrightarrow \mathrm {Un}^{\mathrm {cc}}(F)$
for functors
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}(\mathrm {Un}^{\mathrm {ct}}(F))\longrightarrow \mathrm {Un}^{\mathrm {cc}}(F)$
for functors
![]() $F\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
. To this end, consider the functor
$F\colon X^{{\mathrm {op}}}\longrightarrow \mathrm {Cat} $
. To this end, consider the functor
![]() $\delta \colon \mathrm {Cat} \longrightarrow \mathrm {AdTrip}$
sending
$\delta \colon \mathrm {Cat} \longrightarrow \mathrm {AdTrip}$
sending
![]() $C\mapsto (C, C, \iota C)$
and note that
$C\mapsto (C, C, \iota C)$
and note that
![]() $\mathrm {Span}\circ \delta \simeq \mathrm {id}$
. One then has natural equivalences
$\mathrm {Span}\circ \delta \simeq \mathrm {id}$
. One then has natural equivalences
where the middle equivalence is Theorem 3.9.
As another special case, we may consider the universal example.
Construction 3.19. Let us define the lax under-category ![]() to be the domain of the cocartesian fibration classifying the functor
to be the domain of the cocartesian fibration classifying the functor
![]() $(-)^{{\mathrm {op}}}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
; see the next remark for a justification. One can identify an object of
$(-)^{{\mathrm {op}}}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
; see the next remark for a justification. One can identify an object of ![]() with a tuple
with a tuple
![]() $(X, x)$
of an adequate triple and an object
$(X, x)$
of an adequate triple and an object
![]() $x\in X$
, and a map
$x\in X$
, and a map
![]() $(X, x)\to (Y, y)$
with a map
$(X, x)\to (Y, y)$
with a map
![]() $f\colon X\to Y$
and a map
$f\colon X\to Y$
and a map
![]() $\mu \colon y\to f(x)$
in Y. We will say that
$\mu \colon y\to f(x)$
in Y. We will say that
![]() $(f, \mu )$
is egressive if
$(f, \mu )$
is egressive if
![]() $\mu $
is egressive, and ingressive if
$\mu $
is egressive, and ingressive if
![]() $\mu $
is ingressive and f is an equivalence.
$\mu $
is ingressive and f is an equivalence.
Remark 3.20. If we write ![]() for the domain of the cocartesian fibration classified by
for the domain of the cocartesian fibration classified by
![]() $(-)^{\mathrm {op}}\colon \mathrm {Cat} \longrightarrow \mathrm {Cat} $
, then
$(-)^{\mathrm {op}}\colon \mathrm {Cat} \longrightarrow \mathrm {Cat} $
, then ![]() . We will show in Section 7 (see specifically Remark 7.22) that
. We will show in Section 7 (see specifically Remark 7.22) that ![]() really is equivalent to the lax under-category, defined a priori via a construction in
really is equivalent to the lax under-category, defined a priori via a construction in
![]() $(\infty ,2)$
-category theory, justifying the notation.
$(\infty ,2)$
-category theory, justifying the notation.
Corollary 3.21. Construction 3.19 defines the structure of an adequate triple on ![]() and the map
and the map
is a cocartesian fibration, classified by the functor
![]() $\mathrm {Span}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
.
$\mathrm {Span}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
.
Proof. Apply Theorem 3.9 to the identity functor on
![]() $\mathrm {AdTrip}$
and observe that the adequate triple structure from 3.6 corresponds precisely to the one from Construction 3.19 under taking opposite categories.
$\mathrm {AdTrip}$
and observe that the adequate triple structure from 3.6 corresponds precisely to the one from Construction 3.19 under taking opposite categories.
Remark 3.22. Applying the conclusions of Remark 3.17, we obtain that if we declare a map
![]() $(f, \mu )$
in
$(f, \mu )$
in ![]() to be ingressive if
to be ingressive if
![]() $\mu $
is ingressive and egressive if
$\mu $
is ingressive and egressive if
![]() $\mu $
is egressive and f is an equivalence, then we obtain a different adequate triple structure on
$\mu $
is egressive and f is an equivalence, then we obtain a different adequate triple structure on ![]() , which gives rise to a cartesian fibration
, which gives rise to a cartesian fibration ![]() , classifying the functor
, classifying the functor
![]() $\mathrm {Span}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
.
$\mathrm {Span}\colon \mathrm {AdTrip}\longrightarrow \mathrm {Cat} $
.
Remark 3.23. In [Reference NardinNa16], Nardin proves that for an orbital
![]() $\infty $
-category T, the T-
$\infty $
-category T, the T-
![]() $\infty $
-category of T-commutative monoids in a T-
$\infty $
-category of T-commutative monoids in a T-
![]() $\infty $
-category C with finite T-products is equivalent to the T-
$\infty $
-category C with finite T-products is equivalent to the T-
![]() $\infty $
-category
$\infty $
-category
![]() $\underline {\mathrm {Fun}}_T^{\times }(\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T),C)$
, where
$\underline {\mathrm {Fun}}_T^{\times }(\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T),C)$
, where
![]() $\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T)$
is a cocartesian fibration whose fibre over
$\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T)$
is a cocartesian fibration whose fibre over
![]() $t\in T$
is equivalent to
$t\in T$
is equivalent to
![]() $\mathrm {Span}((\mathbf {F}_{T}){/t})$
, where
$\mathrm {Span}((\mathbf {F}_{T}){/t})$
, where
![]() $\mathbf {F}_T$
is the finite coproduct completion of T. This indicates that T-commutative monoids are computed by a generalisation of Mackey functors. By inspecting the definition of
$\mathbf {F}_T$
is the finite coproduct completion of T. This indicates that T-commutative monoids are computed by a generalisation of Mackey functors. By inspecting the definition of
![]() $\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T)$
from [Reference NardinNa16, Definition 4.10], one observes that
$\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T)$
from [Reference NardinNa16, Definition 4.10], one observes that
![]() $\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T) = \mathrm {Span}(Y^{\int })$
, where Y is the cartesian unstraightening of the functor underlying
$\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T) = \mathrm {Span}(Y^{\int })$
, where Y is the cartesian unstraightening of the functor underlying
where the functoriality is given by pullback. Therefore, Theorem 3.9 shows that the functoriality of the T-
![]() $\infty $
-category
$\infty $
-category
![]() $\underline {\mathrm {Fun} }_T^{\times }(\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T),C)$
is induced by the standard functoriality of
$\underline {\mathrm {Fun} }_T^{\times }(\underline {\mathbf {A}}^{\mskip -2mu\textit {eff}}(T),C)$
is induced by the standard functoriality of
![]() $\mathrm {Span}(-)$
.
$\mathrm {Span}(-)$
.
4 Orthogonal adequate triples and their duals
Work of Barwick, Glasman and Nardin uses the span category construction from Section 2 to produce an equivalence between cartesian fibrations and cocartesian fibrations of
![]() $\infty $
-categories [Reference Barwick, Glasman and NardinBGN18]. In the previous section, we provided an alternative proof of this fact by exhibiting it as a specific example of a general phenomenon: the cocartesian fibration classifying
$\infty $
-categories [Reference Barwick, Glasman and NardinBGN18]. In the previous section, we provided an alternative proof of this fact by exhibiting it as a specific example of a general phenomenon: the cocartesian fibration classifying
![]() $\mathrm {Span}\circ F$
is given by the span construction applied to a particular adequate triple structure on the cartesian unstraightening of F.
$\mathrm {Span}\circ F$
is given by the span construction applied to a particular adequate triple structure on the cartesian unstraightening of F.
In this section, we will describe a different perspective on this result, which is a priori entirely independent from the discussion of (co)cartesian fibrations. The construction of span
![]() $\infty $
-categories upgrades to an automorphism (of order
$\infty $
-categories upgrades to an automorphism (of order
![]() $2$
) of a certain full subcategory of adequate triples spanned by those triples that we will call orthogonal. In Section 5, we will show how this construction interacts with various notions of (cartesian) fibrations between such orthogonal adequate triples. In particular, we will extend Lanari’s results on the relation between cartesian fibrations and factorisation systems from [Reference LanariLa19] and thus recover the main result from [Reference Barwick, Glasman and NardinBGN18] in a different way.
$2$
) of a certain full subcategory of adequate triples spanned by those triples that we will call orthogonal. In Section 5, we will show how this construction interacts with various notions of (cartesian) fibrations between such orthogonal adequate triples. In particular, we will extend Lanari’s results on the relation between cartesian fibrations and factorisation systems from [Reference LanariLa19] and thus recover the main result from [Reference Barwick, Glasman and NardinBGN18] in a different way.
To define the notion of an orthogonal adequate triple, let us start by briefly recalling Joyal’s notion of a factorisation system on an
![]() $\infty $
-category
$\infty $
-category
![]() ${C}$
(also called an orthogonal factorisation system), following [Reference LurieLu09a, Section 5.2.8]. It consists of two classes of arrows
${C}$
(also called an orthogonal factorisation system), following [Reference LurieLu09a, Section 5.2.8]. It consists of two classes of arrows
![]() ${C}_{l}$
(left) and
${C}_{l}$
(left) and
![]() ${C}_{r}$
(right), denoted
${C}_{r}$
(right), denoted
![]() $\twoheadrightarrow $
and
$\twoheadrightarrow $
and
![]() $\rightarrowtail $
, such that
$\rightarrowtail $
, such that
-
(i) both classes of maps are closed under retracts,
-
(ii) each solid commutative diagram
admits a unique dashed filler whenever
 $f \in {C}_{l}$
and
$f \in {C}_{l}$
and
 $g \in {C}_{r}$
, and
$g \in {C}_{r}$
, and
-
(iii) every map in
 ${C}$
factors as
${C}$
factors as  with
with
 $f \in {C}_{l}$
and
$f \in {C}_{l}$
and
 $g \in {C}_{r}$
.
$g \in {C}_{r}$
.
Let us point out that the notation for the left and right classes is inspired by the notation for the epi-mono factorisation system and is opposite to the convention typically employed for model categories.
Both
![]() ${C}_{l}$
and
${C}_{l}$
and
![]() ${C}_{r}$
then define subcategories of
${C}_{r}$
then define subcategories of
![]() ${C}$
that contain all equivalences and each class uniquely determines the other [Reference LurieLu09a, Proposition 5.2.8.6 & 5.2.8.11].
${C}$
that contain all equivalences and each class uniquely determines the other [Reference LurieLu09a, Proposition 5.2.8.6 & 5.2.8.11].
Remark 4.1. The factorisation in the last item is essentially unique, and this uniqueness is, in fact, equivalent to the first two items [Reference LurieLu09a, Proposition 5.2.8.17]. More precisely, writing
![]() $\mathrm {Fact}(C)\subseteq \mathrm {Fun} ([2], C)$
for the full subcategory of functors sending
$\mathrm {Fact}(C)\subseteq \mathrm {Fun} ([2], C)$
for the full subcategory of functors sending
![]() $0\leq 1$
to
$0\leq 1$
to
![]() ${C}_{l}$
and
${C}_{l}$
and
![]() $1\leq 2$
to
$1\leq 2$
to
![]() ${C}_{r}$
, one has that restriction to the arrow
${C}_{r}$
, one has that restriction to the arrow
![]() $0\leq 2$
defines an equivalence
$0\leq 2$
defines an equivalence
An (essentially unique) section provides a functorial factorisation of morphisms in C.
Definition 4.2. We call an adequate triple
![]() $(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
orthogonal if every ambigressive square in X is cartesian, and the egressives (
$(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
orthogonal if every ambigressive square in X is cartesian, and the egressives (
![]() $\twoheadrightarrow $
) and ingressives (
$\twoheadrightarrow $
) and ingressives (
![]() $\rightarrowtail $
) are the left and right classes, respectively, of an orthogonal factorisation system on X. We denote the full subcategory of orthogonal adequate triples by
$\rightarrowtail $
) are the left and right classes, respectively, of an orthogonal factorisation system on X. We denote the full subcategory of orthogonal adequate triples by
![]() $\mathrm {AdTrip}^{\perp }$
.
$\mathrm {AdTrip}^{\perp }$
.
Remark 4.3. Since every ambigressive square in an orthogonal adequate triple is automatically cartesian, it follows that
![]() $\mathrm {AdTrip}^{\perp }$
is a full subcategory of
$\mathrm {AdTrip}^{\perp }$
is a full subcategory of
![]() $\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
(in contrast to
$\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
(in contrast to
![]() $\mathrm {AdTrip}$
).
$\mathrm {AdTrip}$
).
The simplest examples are
![]() $(A,\iota A,A)$
and
$(A,\iota A,A)$
and
![]() $(A,A,\iota A)$
for any
$(A,A,\iota A)$
for any
![]() $\infty $
-category A. We will generate more interesting examples by means of the following observation, which follows directly from the mapping properties of cartesian edges:
$\infty $
-category A. We will generate more interesting examples by means of the following observation, which follows directly from the mapping properties of cartesian edges:
Proposition 4.4. If X is an orthogonal adequate triple and
![]() $p\colon Y\longrightarrow X$
has all p-cartesian lifts over
$p\colon Y\longrightarrow X$
has all p-cartesian lifts over
![]() $X_{\mathrm {in}}$
, then the adequate triple
$X_{\mathrm {in}}$
, then the adequate triple
![]() $\big (Y, Y^{\dagger }, p^{-1}(X^{\mathrm {eg}}))$
from Proposition 2.6 is again orthogonal.
$\big (Y, Y^{\dagger }, p^{-1}(X^{\mathrm {eg}}))$
from Proposition 2.6 is again orthogonal.
In particular, for a cartesian fibration
![]() $p \colon Y \rightarrow X$
the triple structure on Y with ingressives the p-cartesian edges and egressives the fibrewise maps is orthogonal; in this way, our constructions contain those from [Reference Barwick, Glasman and NardinBGN18].
$p \colon Y \rightarrow X$
the triple structure on Y with ingressives the p-cartesian edges and egressives the fibrewise maps is orthogonal; in this way, our constructions contain those from [Reference Barwick, Glasman and NardinBGN18].
Proof. The fact that any ambigressive square is cartesian follows immediately from the proof of Proposition 2.6. To show that the ingressives and egressives form a factorisation system on Y, let us start by noting that both classes are stable under retracts (for the cartesian morphisms, this uses that they are characterised by a lifting property relative to the base X). Next, consider a commutative square

where
![]() $\phi \in Y^{\mathrm {eg}}$
and
$\phi \in Y^{\mathrm {eg}}$
and
![]() $\psi \in Y_{\mathrm {in}}$
. We need to exhibit a unique dotted arrow making the diagram commute. After applying p, there exists a unique dotted edge in X making the square commute. Since
$\psi \in Y_{\mathrm {in}}$
. We need to exhibit a unique dotted arrow making the diagram commute. After applying p, there exists a unique dotted edge in X making the square commute. Since
![]() $\psi $
is p-cartesian, we find that there is a unique dotted edge in Y which makes the square commute. Finally, given an edge
$\psi $
is p-cartesian, we find that there is a unique dotted edge in Y which makes the square commute. Finally, given an edge
![]() $f\colon x\rightarrow y$
in Y, one can factor
$f\colon x\rightarrow y$
in Y, one can factor
![]() $p(f)=gh$
with
$p(f)=gh$
with
![]() $g\in X_{\mathrm {in}}$
and
$g\in X_{\mathrm {in}}$
and
![]() $h\in X^{\mathrm {eg}}$
. Taking a p-cartesian lift
$h\in X^{\mathrm {eg}}$
. Taking a p-cartesian lift
![]() $g'$
of g, we can factor
$g'$
of g, we can factor
![]() $f= g'h'$
with
$f= g'h'$
with
![]() $h'\in p^{-1}(X^{\mathrm {eg}})$
, so that
$h'\in p^{-1}(X^{\mathrm {eg}})$
, so that
![]() $Y^{\dagger }$
and
$Y^{\dagger }$
and
![]() $p^{-1}(X^{\mathrm {eg}})$
form a factorisation system.
$p^{-1}(X^{\mathrm {eg}})$
form a factorisation system.
Example 4.5. A product
![]() $A\times B$
of two
$A\times B$
of two
![]() $\infty $
-categories admits the structure of an orthogonal adequate triple, denoted
$\infty $
-categories admits the structure of an orthogonal adequate triple, denoted
![]() $(A, B)^{\perp }$
, with ingressives
$(A, B)^{\perp }$
, with ingressives
![]() $A\times \iota B$
and egressives
$A\times \iota B$
and egressives
![]() $\iota A\times B$
.
$\iota A\times B$
.
Example 4.6. Let X be a stable
![]() $\infty $
-category, together with reflective stable subcategories exhibiting X as a recollement [Reference LurieLu17, Definition A.8.1]
$\infty $
-category, together with reflective stable subcategories exhibiting X as a recollement [Reference LurieLu17, Definition A.8.1]

explicitly, this means that
![]() $i^{*}$
and
$i^{*}$
and
![]() $j^{*}$
jointly detect equivalences and
$j^{*}$
jointly detect equivalences and
![]() $j^{*}i_*$
sends every object to the terminal object, but there are several other characterisations; see [CDH+20, Appendix A.2]. In particular, by [CDH+20, Lemma A.2.5],
$j^{*}i_*$
sends every object to the terminal object, but there are several other characterisations; see [CDH+20, Appendix A.2]. In particular, by [CDH+20, Lemma A.2.5],
![]() $i_*$
admits a further right adjoint
$i_*$
admits a further right adjoint
![]() $i^!$
such that
$i^!$
such that
![]() $i_*i^!x\longrightarrow x\longrightarrow j_*j^{*}x$
is a fibre sequence for each
$i_*i^!x\longrightarrow x\longrightarrow j_*j^{*}x$
is a fibre sequence for each
![]() $x\in X$
.
$x\in X$
.
We now claim that X has the structure of an orthogonal adequate triple, in which a map is ingressive or egressive if its image under
![]() $i^!$
or
$i^!$
or
![]() $j^{*}$
is an equivalence, respectively. By [CDH+20, Corollary 2.6.1],
$j^{*}$
is an equivalence, respectively. By [CDH+20, Corollary 2.6.1],
![]() $j^{*}$
is a cartesian fibration with an edge in X being
$j^{*}$
is a cartesian fibration with an edge in X being
![]() $j^{*}$
-cartesian if and only if it is an
$j^{*}$
-cartesian if and only if it is an
![]() $i^!$
-equivalence. Thus, Proposition 4.4 (applied with target
$i^!$
-equivalence. Thus, Proposition 4.4 (applied with target
![]() $(U,U,\iota U)$
) yields the structure of an orthogonal triple on X as desired.
$(U,U,\iota U)$
) yields the structure of an orthogonal triple on X as desired.
Example 4.7. For each
![]() $\infty $
-category A, the source projection
$\infty $
-category A, the source projection
![]() $s\colon \operatorname {\mathrm {Ar}}(A)\longrightarrow A$
is a cartesian fibration. Applying Proposition 4.4 to the triple
$s\colon \operatorname {\mathrm {Ar}}(A)\longrightarrow A$
is a cartesian fibration. Applying Proposition 4.4 to the triple
![]() $(A,A,\iota A)$
, we find that
$(A,A,\iota A)$
, we find that
![]() $\operatorname {\mathrm {Ar}}(A)$
admits the structure of an orthogonal adequate triple in which a map is egressive (ingressive) if its image under the source map
$\operatorname {\mathrm {Ar}}(A)$
admits the structure of an orthogonal adequate triple in which a map is egressive (ingressive) if its image under the source map
![]() $s\colon \operatorname {\mathrm {Ar}}(A)\to A$
(target map
$s\colon \operatorname {\mathrm {Ar}}(A)\to A$
(target map
![]() $t\colon \operatorname {\mathrm {Ar}}(A)\to A$
) is an equivalence. For every
$t\colon \operatorname {\mathrm {Ar}}(A)\to A$
) is an equivalence. For every
![]() $A\to B$
, the induced functor
$A\to B$
, the induced functor
![]() $\operatorname {\mathrm {Ar}}(A)\longrightarrow \operatorname {\mathrm {Ar}}(B)$
preserves ingressive and egressive maps, so that we obtain a functor
$\operatorname {\mathrm {Ar}}(A)\longrightarrow \operatorname {\mathrm {Ar}}(B)$
preserves ingressive and egressive maps, so that we obtain a functor
In fact, Example 4.7 provides the free orthogonal adequate triple generated by A:
Proposition 4.8. The functor
![]() $\operatorname {\mathrm {Ar}}\colon \mathrm {Cat} \longrightarrow \mathrm {AdTrip}^{\perp }$
is the left adjoint to the forgetful functor
$\operatorname {\mathrm {Ar}}\colon \mathrm {Cat} \longrightarrow \mathrm {AdTrip}^{\perp }$
is the left adjoint to the forgetful functor
![]() $\mathrm {AdTrip}^{\perp }\longrightarrow \mathrm {Cat} $
taking underlying
$\mathrm {AdTrip}^{\perp }\longrightarrow \mathrm {Cat} $
taking underlying
![]() $\infty $
-categories. More precisely, the degeneracy map
$\infty $
-categories. More precisely, the degeneracy map
![]() $\operatorname {\mathrm {cst}}\colon A\longrightarrow \operatorname {\mathrm {Ar}}(A)$
provides the unit transformation exhibiting
$\operatorname {\mathrm {cst}}\colon A\longrightarrow \operatorname {\mathrm {Ar}}(A)$
provides the unit transformation exhibiting
![]() $\operatorname {\mathrm {Ar}}$
as the left adjoint to the forgetful functor.
$\operatorname {\mathrm {Ar}}$
as the left adjoint to the forgetful functor.
Proof. It will suffice to define a natural counit map and provide natural homotopies for the triangle identities. Given an adequate triple X, let
![]() $\epsilon _X\colon \operatorname {\mathrm {Ar}}(X)\longrightarrow X$
be the unique functor that fits into a commuting diagram
$\epsilon _X\colon \operatorname {\mathrm {Ar}}(X)\longrightarrow X$
be the unique functor that fits into a commuting diagram

Here, the left vertical functor is the equivalence from Remark 4.1, a section of which provides a functorial egressive-ingressive factorisation. Since all three solid maps are functorial in the adequate triple X, the map
![]() $\epsilon _X$
is functorial in X. Explicitly, the value of
$\epsilon _X$
is functorial in X. Explicitly, the value of
![]() $\epsilon _X$
on a map
$\epsilon _X$
on a map
![]() $\mu \colon f\to g$
in
$\mu \colon f\to g$
in
![]() $\operatorname {\mathrm {Ar}}(X)$
given by the square
$\operatorname {\mathrm {Ar}}(X)$
given by the square

is given by the middle vertical arrow in the unique diagram

From this, we see that
![]() $\epsilon _X$
is a map of adequate triples. Indeed, if
$\epsilon _X$
is a map of adequate triples. Indeed, if
![]() $\mu $
is ingressive (i.e.,
$\mu $
is ingressive (i.e.,
![]() $\mu _1$
is an equivalence), then the middle horizontal map is ingressive by the right cancellation property for ingressives [Reference LurieLu09a, Proposition 5.2.8.6 (3)], and likewise in the egressive case where
$\mu _1$
is an equivalence), then the middle horizontal map is ingressive by the right cancellation property for ingressives [Reference LurieLu09a, Proposition 5.2.8.6 (3)], and likewise in the egressive case where
![]() $\mu _0$
is an equivalence.
$\mu _0$
is an equivalence.
It remains to provide the triangle identities. If X is an adequate triple, then the composite
is evidently naturally equivalent to the identity (using that the functorial factorisation
![]() $\operatorname {\mathrm {Ar}}(X)\to \mathrm {Fact}(X)$
sends degenerate arrows to constant diagrams). Furthermore, for an
$\operatorname {\mathrm {Ar}}(X)\to \mathrm {Fact}(X)$
sends degenerate arrows to constant diagrams). Furthermore, for an
![]() $\infty $
-category A, the composite
$\infty $
-category A, the composite
sends an arrow f to
![]() $f{\stackrel {\sim }{\longrightarrow }} f$
and then applies the ingressive-egressive factorisation to this natural equivalence. This is again naturally equivalent to the identity.
$f{\stackrel {\sim }{\longrightarrow }} f$
and then applies the ingressive-egressive factorisation to this natural equivalence. This is again naturally equivalent to the identity.
Proposition 4.9. For any adequate triple
![]() $(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
, the subcategory inclusions
$(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
, the subcategory inclusions
![]() $(X^{\mathrm {eg}})^{\mathrm {op}}, X_{\mathrm {in}} \to \mathrm {Span}(X)$
from Proposition 2.15 give an orthogonal factorisation system on
$(X^{\mathrm {eg}})^{\mathrm {op}}, X_{\mathrm {in}} \to \mathrm {Span}(X)$
from Proposition 2.15 give an orthogonal factorisation system on
![]() $\mathrm {Span}(X)$
. If the triple
$\mathrm {Span}(X)$
. If the triple
![]() $(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
is furthermore orthogonal, then
$(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
is furthermore orthogonal, then
![]() $(\mathrm {Span}(X), X_{\mathrm {in}}, (X^{\mathrm {eg}})^{{\mathrm {op}}})$
is again an orthogonal adequate triple.
$(\mathrm {Span}(X), X_{\mathrm {in}}, (X^{\mathrm {eg}})^{{\mathrm {op}}})$
is again an orthogonal adequate triple.
Proof. To prove the first claim, we use the criterion from Remark 4.1; that is, we show that the map
is an equivalence. We first observe that this map is an equivalence on cores for all adequate triples. This assertion translates to the statement that the
![]() $\infty $
-groupoid of dotted extensions of the solid diagram
$\infty $
-groupoid of dotted extensions of the solid diagram

is contractible, which is obvious.
To conclude, we now observe that it suffices to show that
is an equivalence for all
![]() $n \geq 0$
(in fact,
$n \geq 0$
(in fact,
![]() $n=1$
suffices, but this will not simplify the argument). But by Corollary 2.22 we can rewrite the target as
$n=1$
suffices, but this will not simplify the argument). But by Corollary 2.22 we can rewrite the target as
Similarly, the source is equivalent to a set of path components in
![]() ${\mathrm {Hom}}_{\mathrm {Cat} }([2],\mathrm {Span}({\mathrm {Q}}_n(X,X_{\mathrm {in}},X^{\mathrm {eg}})))$
, and we claim that it precisely corresponds to
${\mathrm {Hom}}_{\mathrm {Cat} }([2],\mathrm {Span}({\mathrm {Q}}_n(X,X_{\mathrm {in}},X^{\mathrm {eg}})))$
, and we claim that it precisely corresponds to
![]() $\iota \mathrm {Fact}(\mathrm {Span}({\mathrm {Q}}_n(X,X_{\mathrm {in}},X^{\mathrm {eg}})))$
. Thus, the statement on groupoid cores applied to the various
$\iota \mathrm {Fact}(\mathrm {Span}({\mathrm {Q}}_n(X,X_{\mathrm {in}},X^{\mathrm {eg}})))$
. Thus, the statement on groupoid cores applied to the various
![]() ${\mathrm {Q}}_n(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
gives the statement in full. To verify the remaining claim, one unwinds definitions to find both sides spanned by those diagrams
${\mathrm {Q}}_n(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
gives the statement in full. To verify the remaining claim, one unwinds definitions to find both sides spanned by those diagrams
![]() $\operatorname {\mathrm {Tw}}^{r}[n] \times \operatorname {\mathrm {Tw}}^{r}[2] \rightarrow X$
whose restriction along the Segal maps
$\operatorname {\mathrm {Tw}}^{r}[n] \times \operatorname {\mathrm {Tw}}^{r}[2] \rightarrow X$
whose restriction along the Segal maps

has all ambigressively marked squares cartesian and all upwards-pointing maps equivalences.
Now assume the adequate triple
![]() $(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
is orthogonal. To prove that
$(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
is orthogonal. To prove that
![]() $(\mathrm {Span}(X), X_{\mathrm {in}}, (X^{\mathrm {eg}})^{{\mathrm {op}}})$
is adequate, we must show that
$(\mathrm {Span}(X), X_{\mathrm {in}}, (X^{\mathrm {eg}})^{{\mathrm {op}}})$
is adequate, we must show that
![]() $\mathrm {Span}(X)$
admits ambigressive pullbacks. By Lemma 2.14, we may equivalently show that
$\mathrm {Span}(X)$
admits ambigressive pullbacks. By Lemma 2.14, we may equivalently show that
![]() $\mathrm {Span}(X^{\mathrm {rev}})$
admits ambigressive pushouts, which turns out to be notationally slightly more convenient. Let us start by observing that by adjunction, a commuting square in
$\mathrm {Span}(X^{\mathrm {rev}})$
admits ambigressive pushouts, which turns out to be notationally slightly more convenient. Let us start by observing that by adjunction, a commuting square in
![]() $\mathrm {Span}(X^{\mathrm {rev}})$
with horizontal arrows in
$\mathrm {Span}(X^{\mathrm {rev}})$
with horizontal arrows in
![]() $(X_{\mathrm {in}})^{\mathrm {op}}$
and vertical arrows in
$(X_{\mathrm {in}})^{\mathrm {op}}$
and vertical arrows in
![]() $X^{\mathrm {eg}}$
corresponds to a diagram of the form
$X^{\mathrm {eg}}$
corresponds to a diagram of the form

in X, including the dotted arrows, whose top right and bottom left squares are pullbacks (so that the arrows with the blue labels are equivalences as well). Such a diagram is uniquely determined by its solid part (i.e., the left column and top row). Indeed, we can first fill the top right square with equivalences in the vertical direction. Then we can uniquely factor the composite in the bottom left square as an egressive followed by an ingressive edge (the resulting square is cartesian because X is an orthogonal adequate triple). Finally, we fill the right two squares with equivalences as indicated.
We can therefore conclude that the triple
![]() $(\mathrm {Span}(X), X_{\mathrm {in}}, (X^{\mathrm {eg}})^{\mathrm {op}})$
is both adequate and orthogonal as soon as we can show that any diagram as above defines a pushout square in
$(\mathrm {Span}(X), X_{\mathrm {in}}, (X^{\mathrm {eg}})^{\mathrm {op}})$
is both adequate and orthogonal as soon as we can show that any diagram as above defines a pushout square in
![]() $\mathrm {Span}(X^{\mathrm {rev}})$
. This is, however, rather unpleasant to do directly. We shall instead use the fact that pushout squares in an
$\mathrm {Span}(X^{\mathrm {rev}})$
. This is, however, rather unpleasant to do directly. We shall instead use the fact that pushout squares in an
![]() $\infty $
-category
$\infty $
-category
![]() ${C}$
are precisely the cocartesian edges of the source map
${C}$
are precisely the cocartesian edges of the source map
![]() $s \colon \operatorname {\mathrm {Ar}}({C}) \rightarrow {C}$
. Here, we regard the diagram (
$s \colon \operatorname {\mathrm {Ar}}({C}) \rightarrow {C}$
. Here, we regard the diagram (
![]() $\ast $
) as a morphism in
$\ast $
) as a morphism in
![]() $\operatorname {\mathrm {Ar}}(\mathrm {Span}(X^{\mathrm {rev}}))$
from the left vertical span to the right vertical span, so that the top horizontal span is the image of this morphism under s.
$\operatorname {\mathrm {Ar}}(\mathrm {Span}(X^{\mathrm {rev}}))$
from the left vertical span to the right vertical span, so that the top horizontal span is the image of this morphism under s.
By Corollary 2.22, we can identify the functor
![]() $s \colon \operatorname {\mathrm {Ar}}(\mathrm {Span}(X^{\mathrm {rev}})) \rightarrow \mathrm {Span}(X^{\mathrm {rev}})$
with
$s \colon \operatorname {\mathrm {Ar}}(\mathrm {Span}(X^{\mathrm {rev}})) \rightarrow \mathrm {Span}(X^{\mathrm {rev}})$
with
Put into this form, we can apply Barwick’s criterion 3.1 for cocartesian edges, or more precisely Corollary 3.2. It tells us that the diagram (
![]() $\ast $
) defines a
$\ast $
) defines a
![]() $\mathrm {Span}(\mathrm {ev}_{(0 \leq 0)})$
-cocartesian edge if its left-pointing half defines an
$\mathrm {Span}(\mathrm {ev}_{(0 \leq 0)})$
-cocartesian edge if its left-pointing half defines an
![]() $(\mathrm {ev}_{(0\leq 0)})^{\mathrm {eg}}$
-cartesian edge in
$(\mathrm {ev}_{(0\leq 0)})^{\mathrm {eg}}$
-cartesian edge in
![]() ${\mathrm {Q}}_1X^{\mathrm {rev}}$
.
${\mathrm {Q}}_1X^{\mathrm {rev}}$
.
To see that it does, recall from Lemma 2.5 that an edge in
![]() ${\mathrm {Q}}_1X^{\mathrm {rev}} = \mathrm {Fun} _{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}([1]),X^{\mathrm {rev}})$
is egressive if it is pointwise ingressive and its ambigressive square is cartesian. Consider thus the (solid) lifting problem (ignoring the red arrow for a moment)
${\mathrm {Q}}_1X^{\mathrm {rev}} = \mathrm {Fun} _{\mathrm {AdTrip}}(\operatorname {\mathrm {Tw}}^{r}([1]),X^{\mathrm {rev}})$
is egressive if it is pointwise ingressive and its ambigressive square is cartesian. Consider thus the (solid) lifting problem (ignoring the red arrow for a moment)

whose right-hand column is the left half of (
![]() $\ast $
), and whose lower bent rectangle is a pullback. We have to show that it admits a unique dotted filling (whose lower square is then automatically a pullback by pasting).
$\ast $
), and whose lower bent rectangle is a pullback. We have to show that it admits a unique dotted filling (whose lower square is then automatically a pullback by pasting).
Considering the top half of the diagram, there is an essentially unique choice for the upper dotted arrow, because the middle upwards-pointing map is an equivalence, and the composite of ingressives it is itself ingressive. By composition we also obtain the red arrow.
The bottom row of the diagram together with the middle left dot then fit into a diagram

Because the egressives and ingressives in X determine an orthogonal factorisation system, this lifting problem has a unique filler. Moreover, because the right class of an orthogonal factorisation system satisfies right cancellation [Reference LurieLu09a, Proposition 5.2.8.6 (3)], this filler is necessarily ingressive. This provides the necessary lift and concludes the argument.
Definition 4.10. We shall refer to
![]() $(\mathrm {Span}(X), X_{\mathrm {in}}, (X^{\mathrm {eg}})^{\mathrm {op}})$
as the dual of an orthogonal adequate triple
$(\mathrm {Span}(X), X_{\mathrm {in}}, (X^{\mathrm {eg}})^{\mathrm {op}})$
as the dual of an orthogonal adequate triple
![]() $(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
and denote by
$(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
and denote by
![]() ${\mathrm {Span}^{\perp }} \colon \mathrm {AdTrip}^{\perp } \rightarrow \mathrm {AdTrip}^{\perp }$
the resulting functor.
${\mathrm {Span}^{\perp }} \colon \mathrm {AdTrip}^{\perp } \rightarrow \mathrm {AdTrip}^{\perp }$
the resulting functor.
Remark 4.11. Unravelling the proof above, one arrives at the following description of induced maps out of the ambigressive pushouts in
![]() $\mathrm {Span}(X^{\mathrm {rev}})$
from the previous proof. Suppose we are given a commutative square in
$\mathrm {Span}(X^{\mathrm {rev}})$
from the previous proof. Suppose we are given a commutative square in
![]() $\mathrm {Span}(X^{\mathrm {rev}})$
represented by a diagram
$\mathrm {Span}(X^{\mathrm {rev}})$
represented by a diagram

whose lower left and upper right squares are cartesian. Factor the composite
![]() $fg$
into an egressive edge
$fg$
into an egressive edge
![]() $f'$
followed by an ingressive edge
$f'$
followed by an ingressive edge
![]() $g'$
. From the proof above, we learn that the pushout of the two spans starting in the upper left corner is given by the source of
$g'$
. From the proof above, we learn that the pushout of the two spans starting in the upper left corner is given by the source of
![]() $g'$
(or equivalently the target of
$g'$
(or equivalently the target of
![]() $f'$
). The induced map out of it unwinds to the span
$f'$
). The induced map out of it unwinds to the span
where j is the solution of the lifting problem

As a consistency check, note that j is indeed ingressive, as both
![]() $\gamma $
and
$\gamma $
and
![]() $g'$
are.
$g'$
are.
The remainder of this section is dedicated to proving the following result:
Theorem 4.12. The functor
![]() ${\mathrm {Span}^{\perp }}$
is an auto-equivalence of
${\mathrm {Span}^{\perp }}$
is an auto-equivalence of
![]() $\mathrm {AdTrip}^{\perp }$
, which is its own inverse.
$\mathrm {AdTrip}^{\perp }$
, which is its own inverse.
Below in Corollary 5.7, we will upgrade this equivalence to a
![]() $\mathrm {C_{2}}$
-action. In the large, our strategy of proof is the same as that of Barwick, Glasman and Nardin in [Reference Barwick, Glasman and NardinBGN18], who essentially treat the special case corresponding to factorisation systems given by (co)cartesian edges and morphisms lying in a single fibre.
$\mathrm {C_{2}}$
-action. In the large, our strategy of proof is the same as that of Barwick, Glasman and Nardin in [Reference Barwick, Glasman and NardinBGN18], who essentially treat the special case corresponding to factorisation systems given by (co)cartesian edges and morphisms lying in a single fibre.
We have to construct a natural equivalence between
![]() ${\mathrm {Span}^{\perp 2}}={\mathrm {Span}^{\perp }}\circ {\mathrm {Span}^{\perp }}$
and the identity of
${\mathrm {Span}^{\perp 2}}={\mathrm {Span}^{\perp }}\circ {\mathrm {Span}^{\perp }}$
and the identity of
![]() $\mathrm {AdTrip}^{\perp }$
. To do this, let us start by describing the composite
$\mathrm {AdTrip}^{\perp }$
. To do this, let us start by describing the composite
![]() ${\mathrm {Span}^{\perp 2}}$
more explicitly.
${\mathrm {Span}^{\perp 2}}$
more explicitly.
Observation 4.13. Let us write
![]() $\iota {\mathrm {Q}}^{\sharp }\colon \mathrm {s}\mathrm {Gpd}\longrightarrow \mathrm {s}\mathrm {Gpd}$
for the functor sending a simplicial
$\iota {\mathrm {Q}}^{\sharp }\colon \mathrm {s}\mathrm {Gpd}\longrightarrow \mathrm {s}\mathrm {Gpd}$
for the functor sending a simplicial
![]() $\infty $
-groupoid S to the simplicial
$\infty $
-groupoid S to the simplicial
![]() $\infty $
-groupoid given by
$\infty $
-groupoid given by
By the definition of span
![]() $\infty $
-categories (see Lemma 2.17), there is a natural transformation of functors
$\infty $
-categories (see Lemma 2.17), there is a natural transformation of functors
![]() $\mathrm {AdTrip}\longrightarrow \mathrm {s}\mathrm {Gpd}$
$\mathrm {AdTrip}\longrightarrow \mathrm {s}\mathrm {Gpd}$
In every simplicial degree, this is given by the inclusion of path components
Applying this reasoning twice, one sees that for X in
![]() $\mathrm {AdTrip}^{\perp }$
, there is a natural map of simplicial
$\mathrm {AdTrip}^{\perp }$
, there is a natural map of simplicial
![]() $\infty $
-groupoids
$\infty $
-groupoids
which is an inclusion of path components in each degree. To unravel the target of the above map, let us denote by
the twofold iterated twisted arrow
![]() $\infty $
-category of an
$\infty $
-category of an
![]() $\infty $
-category A. We then obtain a natural equivalence
$\infty $
-category A. We then obtain a natural equivalence
 $$ \begin{align*} \iota {\mathrm{Q}}_n^{\sharp}\big(\iota {\mathrm{Q}}^{\sharp}(\mathrm{N} X)\big)&\simeq {\mathrm{Hom}}_{\mathrm{s}\mathrm{Gpd}}\Big(\mathrm{N}\operatorname{\mathrm{Tw}}^{r}([n]), \iota {\mathrm{Q}}^{\sharp}(\mathrm{N} X)\Big)\\ &\simeq \lim_{[m]\in {\mathbf{\Delta}}/\mathrm{N}(\operatorname{\mathrm{Tw}}^{r}[n])} {\mathrm{Hom}}_{\mathrm{s}\mathrm{Gpd}}\big(\mathrm{N}\operatorname{\mathrm{Tw}}^{r}([m]), \mathrm{N} X\big)\\ &\simeq {\mathrm{Hom}}_{\mathrm{s}\mathrm{Gpd}}\big(\mathrm{N}\big(\operatorname{\mathrm{Tw}}^{(2)}([n])\big), \mathrm{N} X\big) \\ &\simeq {\mathrm{Hom}}_{\mathrm{Cat} }(\operatorname{\mathrm{Tw}}^{(2)}([n]), X). \end{align*} $$
$$ \begin{align*} \iota {\mathrm{Q}}_n^{\sharp}\big(\iota {\mathrm{Q}}^{\sharp}(\mathrm{N} X)\big)&\simeq {\mathrm{Hom}}_{\mathrm{s}\mathrm{Gpd}}\Big(\mathrm{N}\operatorname{\mathrm{Tw}}^{r}([n]), \iota {\mathrm{Q}}^{\sharp}(\mathrm{N} X)\Big)\\ &\simeq \lim_{[m]\in {\mathbf{\Delta}}/\mathrm{N}(\operatorname{\mathrm{Tw}}^{r}[n])} {\mathrm{Hom}}_{\mathrm{s}\mathrm{Gpd}}\big(\mathrm{N}\operatorname{\mathrm{Tw}}^{r}([m]), \mathrm{N} X\big)\\ &\simeq {\mathrm{Hom}}_{\mathrm{s}\mathrm{Gpd}}\big(\mathrm{N}\big(\operatorname{\mathrm{Tw}}^{(2)}([n])\big), \mathrm{N} X\big) \\ &\simeq {\mathrm{Hom}}_{\mathrm{Cat} }(\operatorname{\mathrm{Tw}}^{(2)}([n]), X). \end{align*} $$
Here, the third line uses that
![]() $\mathrm {N}\operatorname {\mathrm {Tw}}^{r}(-)$
preserves those colimits of
$\mathrm {N}\operatorname {\mathrm {Tw}}^{r}(-)$
preserves those colimits of
![]() $\infty $
-categories that are preserved by the nerve functor (see the proof of Proposition 2.20). Summarising, we see that there is a map of simplicial
$\infty $
-categories that are preserved by the nerve functor (see the proof of Proposition 2.20). Summarising, we see that there is a map of simplicial
![]() $\infty $
-groupoids, depending functorially on
$\infty $
-groupoids, depending functorially on
![]() $X\in \mathrm {AdTrip}^{\perp }$
, which is a degreewise inclusion of path components
$X\in \mathrm {AdTrip}^{\perp }$
, which is a degreewise inclusion of path components
To identify the essential image of (4.14), let us make the following construction:
Construction 4.15. Note that
![]() $\operatorname {\mathrm {Tw}}^{(2)}([n])$
is equivalent to the poset whose objects are tuples
$\operatorname {\mathrm {Tw}}^{(2)}([n])$
is equivalent to the poset whose objects are tuples
![]() $abcd$
with
$abcd$
with
![]() $0\leq a\leq b\leq c\leq d\leq n$
, corresponding to a map
$0\leq a\leq b\leq c\leq d\leq n$
, corresponding to a map
![]() $(a\leq d)\longrightarrow (b\leq c)$
in
$(a\leq d)\longrightarrow (b\leq c)$
in
![]() $\operatorname {\mathrm {Tw}}^{r}([n])$
. The partial order is then given by
$\operatorname {\mathrm {Tw}}^{r}([n])$
. The partial order is then given by
![]() $abcd\leq a'b'c'd'$
when
$abcd\leq a'b'c'd'$
when
![]() $a \leq a' \leq b' \leq b \leq c \leq c' \leq d' \leq d$
. We define the following four wide subcategories of
$a \leq a' \leq b' \leq b \leq c \leq c' \leq d' \leq d$
. We define the following four wide subcategories of
![]() $\operatorname {\mathrm {Tw}}^{(2)}([n])$
:
$\operatorname {\mathrm {Tw}}^{(2)}([n])$
:
-
(1)
 $\operatorname {\mathrm {Tw}}^{(2)}([n])_1$
is the subcategory spanned by the edges
$\operatorname {\mathrm {Tw}}^{(2)}([n])_1$
is the subcategory spanned by the edges
 $abcd \rightarrow a'bcd$
.
$abcd \rightarrow a'bcd$
. -
(2)
 $\operatorname {\mathrm {Tw}}^{(2)}([n])_2$
is the subcategory spanned by the edges
$\operatorname {\mathrm {Tw}}^{(2)}([n])_2$
is the subcategory spanned by the edges
 $ab'cd \rightarrow abcd$
.
$ab'cd \rightarrow abcd$
. -
(3)
 $\operatorname {\mathrm {Tw}}^{(2)}([n])_3$
is the subcategory spanned by the edges
$\operatorname {\mathrm {Tw}}^{(2)}([n])_3$
is the subcategory spanned by the edges
 $abcd \rightarrow abc'd$
.
$abcd \rightarrow abc'd$
. -
(4)
 $\operatorname {\mathrm {Tw}}^{(2)}([n])_4$
is the subcategory spanned by the edges
$\operatorname {\mathrm {Tw}}^{(2)}([n])_4$
is the subcategory spanned by the edges
 $abcd' \rightarrow abcd$
.
$abcd' \rightarrow abcd$
.
Proposition 4.16. Let
![]() $X\in \mathrm {AdTrip}^{\perp }$
and let
$X\in \mathrm {AdTrip}^{\perp }$
and let
![]() $[n]\in {\mathbf {\Delta }}$
. Then the natural transformation (4.14) identifies the domain with those path components in
$[n]\in {\mathbf {\Delta }}$
. Then the natural transformation (4.14) identifies the domain with those path components in
![]() ${\mathrm {Hom}}_{\mathrm {Cat} }(\operatorname {\mathrm {Tw}}^{(2)}([n]), X)$
consisting of maps
${\mathrm {Hom}}_{\mathrm {Cat} }(\operatorname {\mathrm {Tw}}^{(2)}([n]), X)$
consisting of maps
![]() $f\colon \operatorname {\mathrm {Tw}}^{(2)}([n])\longrightarrow X$
that restrict to
$f\colon \operatorname {\mathrm {Tw}}^{(2)}([n])\longrightarrow X$
that restrict to

Proof. A functor
corresponds by adjunction to a map
![]() $\operatorname {\mathrm {Tw}}^{r}([n])\longrightarrow {\mathrm {Span}^{\perp }}(X)$
of adequate triples – that is, a map of
$\operatorname {\mathrm {Tw}}^{r}([n])\longrightarrow {\mathrm {Span}^{\perp }}(X)$
of adequate triples – that is, a map of
![]() $\infty $
-categories
$\infty $
-categories
![]() $f'\colon \operatorname {\mathrm {Tw}}^{r}([n])\longrightarrow {\mathrm {Span}^{\perp }}(X)$
such that
$f'\colon \operatorname {\mathrm {Tw}}^{r}([n])\longrightarrow {\mathrm {Span}^{\perp }}(X)$
such that
Here, we importantly use that every ambigressive square in the target is automatically a pullback; otherwise, the functor
![]() $f'$
would have to furthermore preserve ambigressive pullbacks. By Theorem 2.18, the map of
$f'$
would have to furthermore preserve ambigressive pullbacks. By Theorem 2.18, the map of
![]() $\infty $
-categories underlying
$\infty $
-categories underlying
![]() $f'$
corresponds itself to a map
$f'$
corresponds itself to a map
![]() $\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n]))\longrightarrow X$
of adequate triples; that is, a map
$\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n]))\longrightarrow X$
of adequate triples; that is, a map
![]() $f"\colon \operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n]))\longrightarrow X$
such that
$f"\colon \operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n]))\longrightarrow X$
such that
Let us now unravel these conditions using the description of
![]() $\operatorname {\mathrm {Tw}}^{(2)}([n])$
from Construction 4.15. Note that, on the one hand,
$\operatorname {\mathrm {Tw}}^{(2)}([n])$
from Construction 4.15. Note that, on the one hand,
![]() $\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n]))_{\mathrm {in}}$
consists of maps of tuples of the form
$\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n]))_{\mathrm {in}}$
consists of maps of tuples of the form
![]() $abcd\leq a'bcd'$
, while
$abcd\leq a'bcd'$
, while
![]() $\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n]))^{\mathrm {eg}}$
consists of maps
$\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n]))^{\mathrm {eg}}$
consists of maps
![]() $abcd\leq ab'c'd$
. On the other hand,
$abcd\leq ab'c'd$
. On the other hand,
![]() $\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n])_{\mathrm {in}})$
consists of maps of the form
$\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n])_{\mathrm {in}})$
consists of maps of the form
![]() $abcc\leq a'b'cc$
and
$abcc\leq a'b'cc$
and
![]() $\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n])^{\mathrm {eg}})$
consists of maps
$\operatorname {\mathrm {Tw}}^{r}(\operatorname {\mathrm {Tw}}^{r}([n])^{\mathrm {eg}})$
consists of maps
![]() $aacd\leq aac'd'$
.
$aacd\leq aac'd'$
.
Furthermore,
![]() ${\mathrm {Span}^{\perp }}(X)_{\mathrm {in}}$
is the subcategory consisting of spans of the form
${\mathrm {Span}^{\perp }}(X)_{\mathrm {in}}$
is the subcategory consisting of spans of the form ![]() , where the right map is in
, where the right map is in
![]() $X_{\mathrm {in}}$
. Similarly,
$X_{\mathrm {in}}$
. Similarly,
![]() ${\mathrm {Span}^{\perp }}(X)^{\mathrm {eg}}$
is the subcategory whose morphisms are spans of the form
${\mathrm {Span}^{\perp }}(X)^{\mathrm {eg}}$
is the subcategory whose morphisms are spans of the form ![]() , where the left map is in
, where the left map is in
![]() $X^{\mathrm {eg}}$
. Combining all this, the above conditions translate as follows:
$X^{\mathrm {eg}}$
. Combining all this, the above conditions translate as follows:
-
(1) Every
 $abcd\leq a'bcd'$
is mapped to
$abcd\leq a'bcd'$
is mapped to
 $X_{\mathrm {in}}$
.
$X_{\mathrm {in}}$
. -
(2) Every
 $abcd\leq ab'c'd$
is mapped to
$abcd\leq ab'c'd$
is mapped to
 $X^{\mathrm {eg}}$
.
$X^{\mathrm {eg}}$
. -
(3) Every
 $abcc\leq a'bcc$
is sent to
$abcc\leq a'bcc$
is sent to
 $X_{\mathrm {in}}$
and every
$X_{\mathrm {in}}$
and every
 $abcc\leq ab'cc$
is sent to an equivalence.
$abcc\leq ab'cc$
is sent to an equivalence. -
(4) Every
 $aacd\leq aac'd$
is sent to
$aacd\leq aac'd$
is sent to
 $X^{\mathrm {eg}}$
and every
$X^{\mathrm {eg}}$
and every
 $aacd\leq aacd'$
is sent to an equivalence.
$aacd\leq aacd'$
is sent to an equivalence.
Note that these conditions are certainly implied by the ones from the proposition. Conversely, given these conditions, the ones from the statement follow: for example, the map
![]() $abcd\leq abcd'$
fits into a square
$abcd\leq abcd'$
fits into a square

The top horizontal arrow is mapped to an equivalence in X by (4), and the vertical arrows are sent to maps over
![]() $X^{\mathrm {eg}}$
by (2). In particular, the bottom arrow maps to
$X^{\mathrm {eg}}$
by (2). In particular, the bottom arrow maps to
![]() $X^{\mathrm {eg}}$
, but also to
$X^{\mathrm {eg}}$
, but also to
![]() $X_{\mathrm {in}}$
by (1). An edge which is in both the left and right part of an orthogonal factorisation system is an equivalence, and therefore,
$X_{\mathrm {in}}$
by (1). An edge which is in both the left and right part of an orthogonal factorisation system is an equivalence, and therefore,
![]() $abcd\leq abcd'$
maps to an equivalence.
$abcd\leq abcd'$
maps to an equivalence.
Let us write
![]() $\mathrm {LTw}^{(2)}([n])$
for the localisation of
$\mathrm {LTw}^{(2)}([n])$
for the localisation of
![]() $\operatorname {\mathrm {Tw}}^{(2)}([n])$
at the classes of maps (2) and (4) and let
$\operatorname {\mathrm {Tw}}^{(2)}([n])$
at the classes of maps (2) and (4) and let
![]() $\mathrm {LTw}^{(2)}([n])_1$
and
$\mathrm {LTw}^{(2)}([n])_1$
and
![]() $\mathrm {LTw}^{(2)}([n])_3$
be its wide subcategories generated by the images of the maps (1) and (3) from Construction 4.15. Since each map in
$\mathrm {LTw}^{(2)}([n])_3$
be its wide subcategories generated by the images of the maps (1) and (3) from Construction 4.15. Since each map in
![]() ${\mathbf {\Delta }}$
induces a map
${\mathbf {\Delta }}$
induces a map
![]() $\operatorname {\mathrm {Tw}}^{(2)}([m])\longrightarrow \operatorname {\mathrm {Tw}}^{(2)}([n])$
preserving these four classes of maps, it follows that the triple of
$\operatorname {\mathrm {Tw}}^{(2)}([m])\longrightarrow \operatorname {\mathrm {Tw}}^{(2)}([n])$
preserving these four classes of maps, it follows that the triple of
![]() $\infty $
-categories
$\infty $
-categories
depends functorially on
![]() $[n]$
. Proposition 4.16 implies that the
$[n]$
. Proposition 4.16 implies that the
![]() $\infty $
-groupoid
$\infty $
-groupoid
![]() $\mathrm {N}({\mathrm {Span}^{\perp 2}}(X))_n$
is naturally equivalent to the
$\mathrm {N}({\mathrm {Span}^{\perp 2}}(X))_n$
is naturally equivalent to the
![]() $\infty $
-groupoid of maps in
$\infty $
-groupoid of maps in
![]() $\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
$\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
We will now identify the localised triples (4.17) more explicitly. To do this, consider the composition
where the first map is the unique natural transformation between the two inclusions
![]() $[k]\rightarrow [k]\star [k]$
of the summands into the join. This induces a natural transformation
$[k]\rightarrow [k]\star [k]$
of the summands into the join. This induces a natural transformation
sending a tuple
![]() $abcd$
in
$abcd$
in
![]() $\operatorname {\mathrm {Tw}}^{(2)}([n])$
to
$\operatorname {\mathrm {Tw}}^{(2)}([n])$
to
![]() $ac$
in
$ac$
in
![]() $\operatorname {\mathrm {Ar}}([n])$
. Recall from Example 4.7 that the arrow category
$\operatorname {\mathrm {Ar}}([n])$
. Recall from Example 4.7 that the arrow category
![]() $\operatorname {\mathrm {Ar}}([n])$
comes equipped with the structure of an adequate triple in which a map is egressive (ingressive) if its image under the source (target) map is an equivalence. The map z then sends the maps (2) and (4) to equivalences, the maps (1) to ingressive arrows and the maps (3) to egressive arrows. Consequently, we obtain a natural transformation of cosimplicial diagrams in
$\operatorname {\mathrm {Ar}}([n])$
comes equipped with the structure of an adequate triple in which a map is egressive (ingressive) if its image under the source (target) map is an equivalence. The map z then sends the maps (2) and (4) to equivalences, the maps (1) to ingressive arrows and the maps (3) to egressive arrows. Consequently, we obtain a natural transformation of cosimplicial diagrams in
![]() $\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
$\mathrm {Fun} (\Lambda _2[2], \mathrm {Cat} )$
Restriction along this diagram of triples then induces a natural map of simplicial
![]() $\infty $
-groupoids
$\infty $
-groupoids
for every
![]() $X\in \mathrm {AdTrip}^{\perp }$
. Here, the first equivalence follows from the fact that
$X\in \mathrm {AdTrip}^{\perp }$
. Here, the first equivalence follows from the fact that
![]() $\operatorname {\mathrm {Ar}}([n])$
is the free orthogonal adequate triple generated by
$\operatorname {\mathrm {Ar}}([n])$
is the free orthogonal adequate triple generated by
![]() $[n]$
, by Proposition 4.8.
$[n]$
, by Proposition 4.8.
Lemma 4.19. For every
![]() $X\in \mathrm {AdTrip}^{\perp }$
, the natural transformation
$X\in \mathrm {AdTrip}^{\perp }$
, the natural transformation
![]() $\zeta $
is an equivalence of complete Segal
$\zeta $
is an equivalence of complete Segal
![]() $\infty $
-groupoids.
$\infty $
-groupoids.
Proof. Since the domain and the target of
![]() $\zeta $
are complete Segal
$\zeta $
are complete Segal
![]() $\infty $
-groupoids,
$\infty $
-groupoids,
![]() $\zeta $
is an equivalence of simplicial
$\zeta $
is an equivalence of simplicial
![]() $\infty $
-groupoids as soon as it induces an equivalence in simplicial degrees
$\infty $
-groupoids as soon as it induces an equivalence in simplicial degrees
![]() $0$
and
$0$
and
![]() $1$
. It therefore suffices to show that the natural transformation (4.18) is an equivalence of triples of
$1$
. It therefore suffices to show that the natural transformation (4.18) is an equivalence of triples of
![]() $\infty $
-categories for
$\infty $
-categories for
![]() $n=0$
or
$n=0$
or
![]() $n=1$
.
$n=1$
.
For
![]() $n=0$
, this is evident since the domain and codomain of (4.18) are both just a point. For
$n=0$
, this is evident since the domain and codomain of (4.18) are both just a point. For
![]() $n=1$
, at the level of the underlying
$n=1$
, at the level of the underlying
![]() $\infty $
-categories, we have to verify that the functor
$\infty $
-categories, we have to verify that the functor
![]() $z\colon \operatorname {\mathrm {Tw}}^{(2)}([1])\longrightarrow \operatorname {\mathrm {Ar}}([1])$
exhibits
$z\colon \operatorname {\mathrm {Tw}}^{(2)}([1])\longrightarrow \operatorname {\mathrm {Ar}}([1])$
exhibits
![]() $\operatorname {\mathrm {Ar}}([1])$
as the localisation of
$\operatorname {\mathrm {Ar}}([1])$
as the localisation of
![]() $\operatorname {\mathrm {Tw}}^{(2)}([1])$
at the maps in
$\operatorname {\mathrm {Tw}}^{(2)}([1])$
at the maps in
![]() $\operatorname {\mathrm {Tw}}^{(2)}([n])_2$
and
$\operatorname {\mathrm {Tw}}^{(2)}([n])_2$
and
![]() $\operatorname {\mathrm {Tw}}^{(2)}([n])_4$
. The map z is given by the map
$\operatorname {\mathrm {Tw}}^{(2)}([n])_4$
. The map z is given by the map
collapsing the two left-pointing arrows. This is manifestly a localisation. Furthermore, under the map z, the noninvertible arrow in
![]() $\operatorname {\mathrm {Tw}}^{r}([1])_1$
(i.e.,
$\operatorname {\mathrm {Tw}}^{r}([1])_1$
(i.e.,
![]() $0111\to 1111$
) is sent to the ingressive
$0111\to 1111$
) is sent to the ingressive
![]() $01\to 11$
and the noninvertible arrow in
$01\to 11$
and the noninvertible arrow in
![]() $\operatorname {\mathrm {Tw}}^{r}([1])_3$
(i.e.,
$\operatorname {\mathrm {Tw}}^{r}([1])_3$
(i.e.,
![]() $0001\to 0011$
) is sent to the egressive
$0001\to 0011$
) is sent to the egressive
![]() $00\to 01$
. We conclude that the map
$00\to 01$
. We conclude that the map
![]() $\mathrm {LTw}^{(2)}([1])\longrightarrow \operatorname {\mathrm {Ar}}([1])$
is an equivalence of (adequate) triples, as desired.
$\mathrm {LTw}^{(2)}([1])\longrightarrow \operatorname {\mathrm {Ar}}([1])$
is an equivalence of (adequate) triples, as desired.
Proof of Theorem 4.12
Lemma 4.19 shows that after post-composing with the forgetful functor
![]() $U\colon \mathrm {AdTrip}\rightarrow \mathrm {Cat} $
, there is a natural equivalence
$U\colon \mathrm {AdTrip}\rightarrow \mathrm {Cat} $
, there is a natural equivalence
It remains to verify that this equivalence on the underlying
![]() $\infty $
-categories also identifies the subcategories of ingressives and egressives. But this is a direct consequence of the naturality of
$\infty $
-categories also identifies the subcategories of ingressives and egressives. But this is a direct consequence of the naturality of
![]() $\zeta $
in
$\zeta $
in
![]() $X\in \mathrm {AdTrip}^{\perp }$
, since the inclusions
$X\in \mathrm {AdTrip}^{\perp }$
, since the inclusions
![]() ${\mathrm {Span}^{\perp 2}}(X)_{\mathrm {in}}\hookrightarrow {\mathrm {Span}^{\perp 2}}(X)\hookleftarrow {\mathrm {Span}^{\perp 2}}(X)^{\mathrm {eg}}$
arise as the functors underlying the maps of adequate triples
${\mathrm {Span}^{\perp 2}}(X)_{\mathrm {in}}\hookrightarrow {\mathrm {Span}^{\perp 2}}(X)\hookleftarrow {\mathrm {Span}^{\perp 2}}(X)^{\mathrm {eg}}$
arise as the functors underlying the maps of adequate triples
and the same for
![]() $X_{\mathrm {in}}\hookrightarrow X\hookleftarrow X^{\mathrm {eg}}$
.
$X_{\mathrm {in}}\hookrightarrow X\hookleftarrow X^{\mathrm {eg}}$
.
5 Cartesian fibrations between orthogonal adequate triples
The purpose of this section is to analyse the interaction between orthogonal adequate triples and cartesian fibrations. In particular, we show that orthogonal adequate triples
![]() $(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
uniquely correspond to cartesian fibrations with contractible fibres, by taking X to
$(X,X_{\mathrm {in}},X^{\mathrm {eg}})$
uniquely correspond to cartesian fibrations with contractible fibres, by taking X to
![]() $X \rightarrow X[(X^{\mathrm {eg}})^{-1}]$
, generalising results of Lanari [Reference LanariLa19]. More generally, we study various kinds of fibrations between adequate triples that are preserved (or exchanged) by the dualisation equivalence from Theorem 4.12. When the base X arises from a product of two
$X \rightarrow X[(X^{\mathrm {eg}})^{-1}]$
, generalising results of Lanari [Reference LanariLa19]. More generally, we study various kinds of fibrations between adequate triples that are preserved (or exchanged) by the dualisation equivalence from Theorem 4.12. When the base X arises from a product of two
![]() $\infty $
-categories (Example 4.5), we can identify these fibrations with the two-variable fibrations studied extensively in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23]; this specialisation will occupy the next section.
$\infty $
-categories (Example 4.5), we can identify these fibrations with the two-variable fibrations studied extensively in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23]; this specialisation will occupy the next section.
The main notion this section will be concerned with is the following:
Definition 5.1. We will say that a map
![]() $p \colon Y \rightarrow X$
of orthogonal adequate triples is an ingressive cartesian fibration if Y admits all p-cartesian lifts over
$p \colon Y \rightarrow X$
of orthogonal adequate triples is an ingressive cartesian fibration if Y admits all p-cartesian lifts over
![]() $X_{\mathrm {in}}$
and these precisely make up
$X_{\mathrm {in}}$
and these precisely make up
![]() $Y_{\mathrm {in}}$
. Given an orthogonal adequate triple X, we will write
$Y_{\mathrm {in}}$
. Given an orthogonal adequate triple X, we will write
![]() $\operatorname {\mathrm {Cart}}_{\mathrm {in}}(X)\subseteq \mathrm {AdTrip}^{\perp }/X$
for the full subcategory on the ingressive cartesian fibrations.
$\operatorname {\mathrm {Cart}}_{\mathrm {in}}(X)\subseteq \mathrm {AdTrip}^{\perp }/X$
for the full subcategory on the ingressive cartesian fibrations.
Observation 5.2. Let us make the following remarks:
-
(1) Let
 $p\colon Y\longrightarrow X$
be an ingressive cartesian fibration. By definition, Y has all p-cartesian lifts over
$p\colon Y\longrightarrow X$
be an ingressive cartesian fibration. By definition, Y has all p-cartesian lifts over
 $X_{\mathrm {in}}$
, and
$X_{\mathrm {in}}$
, and
 $Y_{\mathrm {in}}$
is the wide subcategory on the p-cartesian lifts of ingressive morphisms. Since
$Y_{\mathrm {in}}$
is the wide subcategory on the p-cartesian lifts of ingressive morphisms. Since
 $Y_{\mathrm {in}}$
and
$Y_{\mathrm {in}}$
and
 $Y^{\mathrm {eg}}$
form a factorisation system, this determines
$Y^{\mathrm {eg}}$
form a factorisation system, this determines
 $Y^{\mathrm {eg}}$
uniquely and we find that Y arises exactly from the construction in Proposition 4.4; in particular,
$Y^{\mathrm {eg}}$
uniquely and we find that Y arises exactly from the construction in Proposition 4.4; in particular,
 $Y^{\mathrm {eg}} = p^{-1}(X^{\mathrm {eg}})$
.
$Y^{\mathrm {eg}} = p^{-1}(X^{\mathrm {eg}})$
. -
(2) For a map of orthogonal adequate triples
 $p \colon Y \rightarrow X$
, an ingressive edge g in Y is p-cartesian if and only if it is
$p \colon Y \rightarrow X$
, an ingressive edge g in Y is p-cartesian if and only if it is
 $p_{\mathrm {in}}$
-cartesian, since lifting an arbitrary map
$p_{\mathrm {in}}$
-cartesian, since lifting an arbitrary map
 $f \colon x \rightarrow x'$
in an orthogonal adequate triple along an ingressive
$f \colon x \rightarrow x'$
in an orthogonal adequate triple along an ingressive
 $g \colon z \rightarrow x'$
is equivalent to lifting
$g \colon z \rightarrow x'$
is equivalent to lifting
 $f' \colon w \rightarrow x'$
along g where
$f' \colon w \rightarrow x'$
along g where
 $f = f'h$
is the factorisation of f into an egressive followed by an ingressive.
$f = f'h$
is the factorisation of f into an egressive followed by an ingressive. -
(3) Ingressive cartesian fibrations are stable under pullbacks. In particular, if
 $p\colon Y\longrightarrow X$
is an ingressive cartesian fibration and
$p\colon Y\longrightarrow X$
is an ingressive cartesian fibration and
 $x\in X$
, then the fibre over x carries the structure of an orthogonal adequate triple
$x\in X$
, then the fibre over x carries the structure of an orthogonal adequate triple
 $(Y_x, \iota Y_x, Y_x)$
.
$(Y_x, \iota Y_x, Y_x)$
.
We start with the following partial converse to Proposition 4.4:
Proposition 5.3. Let
![]() $(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
be an orthogonal adequate triple. Then the map
$(X, X_{\mathrm {in}}, X^{\mathrm {eg}})$
be an orthogonal adequate triple. Then the map
is an ingressive cartesian fibration. In other words,
![]() $p \colon X \rightarrow X[(X^{\mathrm {eg}})^{-1}]$
is a cartesian fibration, inverts only the egressives in X, and the ingressive maps in X are precisely the p-cartesian edges.
$p \colon X \rightarrow X[(X^{\mathrm {eg}})^{-1}]$
is a cartesian fibration, inverts only the egressives in X, and the ingressive maps in X are precisely the p-cartesian edges.
Before we dive into the proof, we spell out some consequences. To this end, let us write
![]() $\operatorname {\mathrm {Cart}}$
for the subcategory of
$\operatorname {\mathrm {Cart}}$
for the subcategory of
![]() $\operatorname {\mathrm {Ar}}(\mathrm {Cat} )$
spanned by objects the cartesian fibrations and by morphisms those squares
$\operatorname {\mathrm {Ar}}(\mathrm {Cat} )$
spanned by objects the cartesian fibrations and by morphisms those squares

such that f sends p-cartesian edges to q-cartesian edges. By Proposition 5.3, the assignment
![]() $X\longmapsto (X\rightarrow X[(X^{\mathrm {eg}})^{-1}])$
extends to a functor
$X\longmapsto (X\rightarrow X[(X^{\mathrm {eg}})^{-1}])$
extends to a functor
which is fully faithful by the universal property of a localisation. We claim that the assignment of the orthogonal adequate triple
![]() $(Y,Y^{\dagger }, p^{-1}(\iota S))$
to a cartesian fibration
$(Y,Y^{\dagger }, p^{-1}(\iota S))$
to a cartesian fibration
![]() $p\colon Y\rightarrow S$
defines a right adjoint to
$p\colon Y\rightarrow S$
defines a right adjoint to
![]() $\mathcal {L}^{\mathrm {eg}}$
. Both
$\mathcal {L}^{\mathrm {eg}}$
. Both
are given by those functors
![]() $X \rightarrow Y$
that take ingressives and egressives to p-cartesian and fibrewise maps, respectively.
$X \rightarrow Y$
that take ingressives and egressives to p-cartesian and fibrewise maps, respectively.
Proposition 5.4. The functor
![]() $\mathcal {L}^{\mathrm {eg}}$
restricts to an equivalence between the category
$\mathcal {L}^{\mathrm {eg}}$
restricts to an equivalence between the category
![]() $\mathrm {AdTrip}^{\perp }$
and the full subcategory of
$\mathrm {AdTrip}^{\perp }$
and the full subcategory of
![]() $\operatorname {\mathrm {Cart}}$
spanned by those cartesian fibrations whose fibres all have contractible realisations.
$\operatorname {\mathrm {Cart}}$
spanned by those cartesian fibrations whose fibres all have contractible realisations.
Given the discussion above, this follows immediately from the equivalence between the first and third items in the following:
Lemma 5.5. For a cartesian fibration
![]() $p \colon A \rightarrow B$
, the following conditions are equivalent:
$p \colon A \rightarrow B$
, the following conditions are equivalent:
-
(1) p is a localisation,
-
(2) p is cofinal, and
-
(3) the realisations of the fibres of p are contractible.
Proof. It is generally true that localisations are cofinal (and coinitial). If p is a localisation, it follows straight from the definition of Kan extension as an adjoint to restriction that any functor
![]() $F \colon B \rightarrow C$
is right (and left) Kan extended from its restriction along p and thus has the same colimit as
$F \colon B \rightarrow C$
is right (and left) Kan extended from its restriction along p and thus has the same colimit as
![]() $Fp$
. This proves
$Fp$
. This proves
![]() $(1) \Rightarrow (2)$
.
$(1) \Rightarrow (2)$
.
To see that
![]() $(2) \Leftrightarrow (3)$
, we observe that the inclusion
$(2) \Leftrightarrow (3)$
, we observe that the inclusion
where
![]() $b/p$
denotes the pullback
$b/p$
denotes the pullback
![]() $b/B \times _{B} A$
along p, admits a right adjoint, given by taking
$b/B \times _{B} A$
along p, admits a right adjoint, given by taking
![]() $(a,f \colon b \rightarrow p(a))$
to a p-cartesian lift of f ending at a. Thus,
$(a,f \colon b \rightarrow p(a))$
to a p-cartesian lift of f ending at a. Thus,
![]() $|p^{-1}(b)| \simeq |b/p|$
, whence the claim follows from Joyal’s cofinality criterion [Reference LurieLu09a, Theorem 4.1.3.1].
$|p^{-1}(b)| \simeq |b/p|$
, whence the claim follows from Joyal’s cofinality criterion [Reference LurieLu09a, Theorem 4.1.3.1].
To finally see that
![]() $(3) \Rightarrow (1)$
, consider for some
$(3) \Rightarrow (1)$
, consider for some
![]() $\infty $
-category C the functor
$\infty $
-category C the functor
where the superscript on the right denotes those functors inverting all maps that p inverts. We have to show that
![]() $p^{*}$
is an equivalence. We first claim that it has a right adjoint
$p^{*}$
is an equivalence. We first claim that it has a right adjoint
![]() $p_*$
. By [Reference LurieLu09a, 4.3.3.7], this will follow from
$p_*$
. By [Reference LurieLu09a, 4.3.3.7], this will follow from
admitting a limit for every
![]() $b \in B$
and
$b \in B$
and
![]() $F \colon A \rightarrow C$
that inverts the fibrewise maps. But as we just discussed above, the inclusion
$F \colon A \rightarrow C$
that inverts the fibrewise maps. But as we just discussed above, the inclusion
![]() $p^{-1}(b) \subseteq b/p$
admits a right adjoint and is thus coinitial, so we may instead consider
$p^{-1}(b) \subseteq b/p$
admits a right adjoint and is thus coinitial, so we may instead consider
which factors through the localisation
![]() $p^{-1}(b) \rightarrow |p^{-1}(b)|$
since F inverts all fibrewise maps by assumption. Thus, the assumption
$p^{-1}(b) \rightarrow |p^{-1}(b)|$
since F inverts all fibrewise maps by assumption. Thus, the assumption
![]() $|p^{-1}(b)| \simeq *$
implies that
$|p^{-1}(b)| \simeq *$
implies that
![]() $F(a)$
is a limit of the above diagram for any
$F(a)$
is a limit of the above diagram for any
![]() $a \in p^{-1}(b)$
. It also follows from the formula for the adjoint as a right Kan extension that the unit and counit of the adjunction
$a \in p^{-1}(b)$
. It also follows from the formula for the adjoint as a right Kan extension that the unit and counit of the adjunction
![]() $(p^{*},p_*)$
are equivalences, as desired.
$(p^{*},p_*)$
are equivalences, as desired.
Example 5.6. A cartesian fibration
![]() $p\colon X\rightarrow S$
is called pointed if both X and S have a terminal object and p preserves it. In [Reference LanariLa19], Lanari shows that the
$p\colon X\rightarrow S$
is called pointed if both X and S have a terminal object and p preserves it. In [Reference LanariLa19], Lanari shows that the
![]() $\infty $
-category of pointed cartesian fibrations is equivalent to a certain subcategory of factorisation systems (he calls them cartesian).
$\infty $
-category of pointed cartesian fibrations is equivalent to a certain subcategory of factorisation systems (he calls them cartesian).
To see the relationship between this equivalence and ours, note that every fibre
![]() $X_s$
of a pointed cartesian fibration admits a final object, given by the source x of a cartesian edge
$X_s$
of a pointed cartesian fibration admits a final object, given by the source x of a cartesian edge
![]() $x \rightarrow \ast $
, which lies over the unique map
$x \rightarrow \ast $
, which lies over the unique map
![]() $s \rightarrow \ast $
in S. Therefore, the fibre of pointed cartesian fibrations have contractible realisations, and we conclude that our equivalence extends that of [Reference LanariLa19].
$s \rightarrow \ast $
in S. Therefore, the fibre of pointed cartesian fibrations have contractible realisations, and we conclude that our equivalence extends that of [Reference LanariLa19].
In fact, in the case of pointed cartesian fibrations, Lemma 5.5 can be sharpened. It is easy to check that assigning to some
![]() $s \in S$
the source x of a cartesian lift
$s \in S$
the source x of a cartesian lift
![]() $x \rightarrow \ast $
of
$x \rightarrow \ast $
of
![]() $s \rightarrow \ast $
defines a right adjoint to p, so that any pointed cartesian fibration is, in fact, a left Bousfield localisation. As a typical application, one finds that an exact functor between stable
$s \rightarrow \ast $
defines a right adjoint to p, so that any pointed cartesian fibration is, in fact, a left Bousfield localisation. As a typical application, one finds that an exact functor between stable
![]() $\infty $
-categories is a cartesian fibration if and only if it is a right split Verdier projection (in the language of [CDH+20, Appendix A]), and both a cartesian and a cocartesian fibration if and only if it participates (as
$\infty $
-categories is a cartesian fibration if and only if it is a right split Verdier projection (in the language of [CDH+20, Appendix A]), and both a cartesian and a cocartesian fibration if and only if it participates (as
![]() $j^{*}$
) in a stable recollement as in Example 4.6.
$j^{*}$
) in a stable recollement as in Example 4.6.
Corollary 5.7. The self-equivalence
![]() ${\mathrm {Span}^{\perp }}$
upgrades to a
${\mathrm {Span}^{\perp }}$
upgrades to a
![]() $\mathrm {C}_2$
-action on
$\mathrm {C}_2$
-action on
![]() $\mathrm {AdTrip}^{\perp }$
.
$\mathrm {AdTrip}^{\perp }$
.
Proof. According to Corollary 3.18 above, the embedding
![]() $\mathcal {L}^{\mathrm {eg}} \colon \mathrm {AdTrip}^{\perp } \rightarrow \operatorname {\mathrm {Cart}}$
from Proposition 5.4 translates
$\mathcal {L}^{\mathrm {eg}} \colon \mathrm {AdTrip}^{\perp } \rightarrow \operatorname {\mathrm {Cart}}$
from Proposition 5.4 translates
![]() ${\mathrm {Span}^{\perp }}$
to the functor that takes a cartesian fibration to its fibrewise opposite (defined via straightening, postcomposing with
${\mathrm {Span}^{\perp }}$
to the functor that takes a cartesian fibration to its fibrewise opposite (defined via straightening, postcomposing with
![]() $(-)^{\mathrm {op}} \colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
, and then unstraightening). Since
$(-)^{\mathrm {op}} \colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
, and then unstraightening). Since
![]() $\mathrm {Aut}(\mathrm {Cat} ) \simeq \mathrm {C}_2$
by Toën’s theorem [Reference ToënTo05], this latter operation defines a
$\mathrm {Aut}(\mathrm {Cat} ) \simeq \mathrm {C}_2$
by Toën’s theorem [Reference ToënTo05], this latter operation defines a
![]() $\mathrm {C}_2$
-action, and hence, so does the former.
$\mathrm {C}_2$
-action, and hence, so does the former.
It would be interesting to provide a more direct construction of the coherences for this
![]() $\mathrm {C}_2$
-action that does not rely on the (un)straightening equivalence, but we have not pursued this.
$\mathrm {C}_2$
-action that does not rely on the (un)straightening equivalence, but we have not pursued this.
As another consequence, we obtain the following description of free cartesian fibrations, a generalisation of which was already proven by different means in [Reference Gepner, Haugseng and NikolausGHN17]:
Corollary 5.8. Consider the functor
![]() $\operatorname {\mathrm {Cart}}\longrightarrow \mathrm {Cat} $
sending a cartesian fibration
$\operatorname {\mathrm {Cart}}\longrightarrow \mathrm {Cat} $
sending a cartesian fibration
![]() $p\colon Y\to X$
to its domain Y. This functor admits a left adjoint sending A to the cartesian fibration
$p\colon Y\to X$
to its domain Y. This functor admits a left adjoint sending A to the cartesian fibration
![]() $s\colon \operatorname {\mathrm {Ar}}(A)\to A$
.
$s\colon \operatorname {\mathrm {Ar}}(A)\to A$
.
Proof. The forgetful functor factors as
![]() $\operatorname {\mathrm {Cart}}\longrightarrow \mathrm {AdTrip}^{\perp }\longrightarrow \mathrm {Cat} $
. The first functor has left adjoint
$\operatorname {\mathrm {Cart}}\longrightarrow \mathrm {AdTrip}^{\perp }\longrightarrow \mathrm {Cat} $
. The first functor has left adjoint
![]() $\mathcal {L}^{\mathrm {eg}}$
by Proposition 5.4, and the second has left adjoint
$\mathcal {L}^{\mathrm {eg}}$
by Proposition 5.4, and the second has left adjoint
![]() $\operatorname {\mathrm {Ar}}$
by Proposition 4.8. The composite precisely sends A to
$\operatorname {\mathrm {Ar}}$
by Proposition 4.8. The composite precisely sends A to
![]() $s\colon \operatorname {\mathrm {Ar}}(A)\longrightarrow A$
, since this has contractible fibres and the associated orthogonal triple structure on
$s\colon \operatorname {\mathrm {Ar}}(A)\longrightarrow A$
, since this has contractible fibres and the associated orthogonal triple structure on
![]() $\operatorname {\mathrm {Ar}}(A)$
is precisely that from Example 4.7.
$\operatorname {\mathrm {Ar}}(A)$
is precisely that from Example 4.7.
We now come to the proof of Proposition 5.3.
Proof of Proposition 5.3
Let us start by recalling the model for
![]() $X[(X^{\mathrm {eg}})^{-1}]$
given by the relative Rezk nerve [Reference Mazel-GeeMG19]. For each
$X[(X^{\mathrm {eg}})^{-1}]$
given by the relative Rezk nerve [Reference Mazel-GeeMG19]. For each
![]() $[n]$
, let us write
$[n]$
, let us write
for the subcategory of all functors
![]() $[n]\longrightarrow X$
and natural transformations which are pointwise egressive. The core of this
$[n]\longrightarrow X$
and natural transformations which are pointwise egressive. The core of this
![]() $\infty $
-category is simply
$\infty $
-category is simply
![]() ${\mathrm {Hom}}_{\mathrm {Cat} }([n], X)$
. Taking geometric realisations, we then obtain a map of simplicial
${\mathrm {Hom}}_{\mathrm {Cat} }([n], X)$
. Taking geometric realisations, we then obtain a map of simplicial
![]() $\infty $
-groupoids
$\infty $
-groupoids
such that the induced map on associated
![]() $\infty $
-categories is the localisation
$\infty $
-categories is the localisation
![]() $X\longrightarrow X[(X^{\mathrm {eg}})^{-1}]$
.
$X\longrightarrow X[(X^{\mathrm {eg}})^{-1}]$
.
We are now going to give a smaller description of
![]() $\big |\mathrm {N}^{\mathrm {rel}}(X)\big |$
, which will show in particular that it already satisfies the Segal condition (so that the associated
$\big |\mathrm {N}^{\mathrm {rel}}(X)\big |$
, which will show in particular that it already satisfies the Segal condition (so that the associated
![]() $\infty $
-category is just its completion). To this end, consider the full subcategories
$\infty $
-category is just its completion). To this end, consider the full subcategories
whose objects are functors
![]() $[n]\longrightarrow X$
with values in
$[n]\longrightarrow X$
with values in
![]() $X_{\mathrm {in}}$
. For each
$X_{\mathrm {in}}$
. For each
![]() $\alpha \in \mathrm {N}^{\mathrm {rel}}(X)(n)$
, there exists an initial
$\alpha \in \mathrm {N}^{\mathrm {rel}}(X)(n)$
, there exists an initial
![]() $\tilde {\alpha }$
in
$\tilde {\alpha }$
in
![]() $\mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)(n)$
equipped with a map from
$\mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)(n)$
equipped with a map from
![]() $\alpha $
, given by the unique factorisation (starting at the end)
$\alpha $
, given by the unique factorisation (starting at the end)

It follows that each inclusion
![]() $\mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)(n)\hookrightarrow \mathrm {N}^{\mathrm {rel}}(X)(n)$
admits a left adjoint. We thus obtain a diagram of simplicial categories
$\mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)(n)\hookrightarrow \mathrm {N}^{\mathrm {rel}}(X)(n)$
admits a left adjoint. We thus obtain a diagram of simplicial categories

where the objects on the left and on the right are simplicial
![]() $\infty $
-groupoids and the right vertical map is an equivalence, since it is given in each simplicial degree by the geometric realisation of a right adjoint functor.
$\infty $
-groupoids and the right vertical map is an equivalence, since it is given in each simplicial degree by the geometric realisation of a right adjoint functor.
The simplicial
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)$
satisfies the Segal conditions. The equivalence
$\mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)$
satisfies the Segal conditions. The equivalence
![]() $\mathrm {Fun} ([n], X)\simeq \mathrm {Fun} ([1], X)\times _{X}\dots \times _X \mathrm {Fun} ([1], X)$
restricts to an equivalence of
$\mathrm {Fun} ([n], X)\simeq \mathrm {Fun} ([1], X)\times _{X}\dots \times _X \mathrm {Fun} ([1], X)$
restricts to an equivalence of
![]() $\infty $
-categories
$\infty $
-categories
Here, the pullbacks are taken along the source and target functors. The target functor
is both a left fibration (since each
![]() $\rightarrowtail \twoheadrightarrow $
fits into a unique ambigressive square) and a right fibration (since ingressive maps can be pulled back along egressive maps). This implies that the pullbacks along t in (5.10) induce pullbacks after taking realisations (see again [Reference SteimleSt21, Reference SteinebrunnerSt22] or the proof of [CDH+20, Theorem 2.5.1] for the more (co)cartesian version of this assertion), so that the equivalent simplicial
$\rightarrowtail \twoheadrightarrow $
fits into a unique ambigressive square) and a right fibration (since ingressive maps can be pulled back along egressive maps). This implies that the pullbacks along t in (5.10) induce pullbacks after taking realisations (see again [Reference SteimleSt21, Reference SteinebrunnerSt22] or the proof of [CDH+20, Theorem 2.5.1] for the more (co)cartesian version of this assertion), so that the equivalent simplicial
![]() $\infty $
-groupoids on the right in (5.9) also satisfy the Segal conditions.
$\infty $
-groupoids on the right in (5.9) also satisfy the Segal conditions.
We will use this description of
![]() $X[(X^{\mathrm {eg}})^{-1}]$
in terms of
$X[(X^{\mathrm {eg}})^{-1}]$
in terms of
![]() $\mathrm {N}^{\mathrm {rel}}_{\mathrm {in}}(X)$
to identify its over-categories. To this end, recall that for any Segal
$\mathrm {N}^{\mathrm {rel}}_{\mathrm {in}}(X)$
to identify its over-categories. To this end, recall that for any Segal
![]() $\infty $
-groupoid S and
$\infty $
-groupoid S and
![]() $s\in S(0)$
, the simplicial
$s\in S(0)$
, the simplicial
![]() $\infty $
-groupoid
$\infty $
-groupoid
is again a Segal
![]() $\infty $
-groupoid, such that the associated
$\infty $
-groupoid, such that the associated
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {ac}(S/s)\simeq \mathrm {ac}(S)/s$
is a model for the over-category of s [CDH+20, Lemma 2.4.7]. Let us now take an object
$\mathrm {ac}(S/s)\simeq \mathrm {ac}(S)/s$
is a model for the over-category of s [CDH+20, Lemma 2.4.7]. Let us now take an object
![]() $x\in X$
and consider the maps of simplicial
$x\in X$
and consider the maps of simplicial
![]() $\infty $
-groupoids induced by the top row in (5.9)
$\infty $
-groupoids induced by the top row in (5.9)
Here, the middle term is given by first taking (5.12) at the level of simplicial
![]() $\infty $
-categories and then taking realisations. Unraveling the definitions, the simplicial
$\infty $
-categories and then taking realisations. Unraveling the definitions, the simplicial
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {N}^{\mathrm {rel}}_{\mathrm {in}}(X)/x$
is given in degree n by the
$\mathrm {N}^{\mathrm {rel}}_{\mathrm {in}}(X)/x$
is given in degree n by the
![]() $\infty $
-category with objects
$\infty $
-category with objects
![]() $\alpha (0)\rightarrowtail \dots \rightarrowtail \alpha (n)\rightarrowtail x$
and morphisms
$\alpha (0)\rightarrowtail \dots \rightarrowtail \alpha (n)\rightarrowtail x$
and morphisms

Since the ingressives and egressives form a factorisation system, all vertical maps are equivalences. Consequently, the first map in (5.13) is an equivalence (even before taking geometric realisations). In addition, since the target map (5.11) is a Kan fibration, so is the map
![]() $\mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)([n+1])\longrightarrow \mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)(\{n+1\})$
(being a composite of its base changes). It follows that the pullbacks (5.12) are preserved under taking classifying
$\mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)([n+1])\longrightarrow \mathrm {N}_{\mathrm {in}}^{\mathrm {rel}}(X)(\{n+1\})$
(being a composite of its base changes). It follows that the pullbacks (5.12) are preserved under taking classifying
![]() $\infty $
-groupoids, so that the second map in (5.13) is an equivalence. Since
$\infty $
-groupoids, so that the second map in (5.13) is an equivalence. Since
![]() $\big |\mathrm {N}^{\mathrm {rel}}_{\mathrm {in}}(X)\big |$
has associated
$\big |\mathrm {N}^{\mathrm {rel}}_{\mathrm {in}}(X)\big |$
has associated
![]() $\infty $
-category
$\infty $
-category
![]() $X[(X^{\mathrm {eg}})^{-1}]$
, the associated
$X[(X^{\mathrm {eg}})^{-1}]$
, the associated
![]() $\infty $
-category of
$\infty $
-category of
![]() $\big |\mathrm {N}^{\mathrm {rel}}_{\mathrm {in}}(X)\big |/x$
is
$\big |\mathrm {N}^{\mathrm {rel}}_{\mathrm {in}}(X)\big |/x$
is
![]() $X[(X^{\mathrm {eg}})^{-1}]/p(x)$
.
$X[(X^{\mathrm {eg}})^{-1}]/p(x)$
.
All in all, we have therefore found that for each object
![]() $x\in X$
, the composite functor
$x\in X$
, the composite functor
is an equivalence. Under this equivalence, the functor p is identified with the functor
![]() $X/x\longrightarrow X_{\mathrm {in}}/x$
sending each
$X/x\longrightarrow X_{\mathrm {in}}/x$
sending each
![]() $y\to x$
to the ingressive part
$y\to x$
to the ingressive part
![]() $y'\rightarrowtail x$
of its functorial egressive-ingressive factorisation. This functor admits a fully faithful right adjoint, whose essential image is given by the ingressive maps to x. By [Reference Ayala and FrancisAF20, Lemma 2.16], this implies that p is a cartesian fibration and that an arrow in X is p-cartesian if and only if it is ingressive.
$y'\rightarrowtail x$
of its functorial egressive-ingressive factorisation. This functor admits a fully faithful right adjoint, whose essential image is given by the ingressive maps to x. By [Reference Ayala and FrancisAF20, Lemma 2.16], this implies that p is a cartesian fibration and that an arrow in X is p-cartesian if and only if it is ingressive.
In particular, we can apply Proposition 4.4 to obtain an orthogonal triple structure on X whose ingressives are the p-cartesian arrows and whose egressives are the maps that are inverted by p. Since the first class coincides with
![]() $X_{\mathrm {in}}$
, the second class coincides with
$X_{\mathrm {in}}$
, the second class coincides with
![]() $X^{\mathrm {eg}}$
.
$X^{\mathrm {eg}}$
.
We now turn to more restrictive types of fibrations between orthogonal triples:
Definition 5.14. An ingressive cartesian fibration
![]() $p\colon Y\longrightarrow X$
is said to be
$p\colon Y\longrightarrow X$
is said to be
-
(1) an op-Gray fibration if
 $p^{\mathrm {eg}}\colon Y^{\mathrm {eg}}\longrightarrow X^{\mathrm {eg}}$
is a cartesian fibration, and
$p^{\mathrm {eg}}\colon Y^{\mathrm {eg}}\longrightarrow X^{\mathrm {eg}}$
is a cartesian fibration, and -
(2) a curved orthofibration if
 $p^{\mathrm {eg}}\colon Y^{\mathrm {eg}}\longrightarrow X^{\mathrm {eg}}$
is a cocartesian fibration.
$p^{\mathrm {eg}}\colon Y^{\mathrm {eg}}\longrightarrow X^{\mathrm {eg}}$
is a cocartesian fibration.
For X an orthogonal adequate triple, we will write
![]() $\mathrm {CrvOrtho}(X), \mathrm {OpGray}(X)$
for the subcategories of
$\mathrm {CrvOrtho}(X), \mathrm {OpGray}(X)$
for the subcategories of
![]() $\operatorname {\mathrm {Cart}}_{\mathrm {in}}(X)$
spanned by the curved orthofibrations and op-Gray fibrations, and maps between them preserving (in addition)
$\operatorname {\mathrm {Cart}}_{\mathrm {in}}(X)$
spanned by the curved orthofibrations and op-Gray fibrations, and maps between them preserving (in addition)
![]() $p^{\mathrm {eg}}$
-(co)cartesian morphisms.
$p^{\mathrm {eg}}$
-(co)cartesian morphisms.
Remark 5.15. To avoid confusion, we would like to explicitly mention that while arrows with the decoration
![]() $\twoheadrightarrow $
denoted cartesian edges in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], with our conventions it is exactly the ingressive edges in Y which are all p-cartesian, and that the egressive edges are almost never all p-cartesian.
$\twoheadrightarrow $
denoted cartesian edges in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], with our conventions it is exactly the ingressive edges in Y which are all p-cartesian, and that the egressive edges are almost never all p-cartesian.
The naming schema above is inspired by the definitions of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23]. We will show in Section 6 that in the case
![]() $X= (A\times B,A\times \iota B,\iota A \times B)$
, the definitions above reduce to the corresponding objects of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23].
$X= (A\times B,A\times \iota B,\iota A \times B)$
, the definitions above reduce to the corresponding objects of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23].
Note that, on the one hand,
![]() $\operatorname {\mathrm {Cart}}_{\mathrm {in}}(A,A,\iota A)$
is simply the
$\operatorname {\mathrm {Cart}}_{\mathrm {in}}(A,A,\iota A)$
is simply the
![]() $\infty $
-category of cartesian fibrations over A, as are the two subcategories
$\infty $
-category of cartesian fibrations over A, as are the two subcategories
![]() $\mathrm {CrvOrtho}$
and
$\mathrm {CrvOrtho}$
and
![]() $\mathrm {OpGray}$
in this case. On the other hand,
$\mathrm {OpGray}$
in this case. On the other hand,
![]() $\operatorname {\mathrm {Cart}}_{\mathrm {in}}(A,\iota A,A)$
is just
$\operatorname {\mathrm {Cart}}_{\mathrm {in}}(A,\iota A,A)$
is just
![]() $\mathrm {Cat} /A$
, while
$\mathrm {Cat} /A$
, while
![]() $\mathrm {OpGray}(A,\iota A,A) = \operatorname {\mathrm {Cart}}(A)$
and
$\mathrm {OpGray}(A,\iota A,A) = \operatorname {\mathrm {Cart}}(A)$
and
![]() $\mathrm {CrvOrtho}(A,\iota A,A) = \mathrm {Cocart}(A)$
.
$\mathrm {CrvOrtho}(A,\iota A,A) = \mathrm {Cocart}(A)$
.
One can informally think about an op-Gray fibration over X as encoding a lax functor from X to
![]() $\mathrm {Cat} $
, which is strong on
$\mathrm {Cat} $
, which is strong on
![]() $2$
-simplices in
$2$
-simplices in
![]() $X_{\mathrm {in}}$
or
$X_{\mathrm {in}}$
or
![]() $X^{\mathrm {eg}}$
, as well as
$X^{\mathrm {eg}}$
, as well as
![]() $2$
-simplices of the form
$2$
-simplices of the form
![]() $x_0\twoheadrightarrow x_1 \rightarrowtail x_2$
. This is substantiated (using the scaled straightening construction of Lurie [Reference LurieLu09b]) by the following observation:
$x_0\twoheadrightarrow x_1 \rightarrowtail x_2$
. This is substantiated (using the scaled straightening construction of Lurie [Reference LurieLu09b]) by the following observation:
Lemma 5.16. An op-Gray fibration
![]() $p\colon Y\longrightarrow X$
is, in particular, a locally cartesian fibration. Furthermore, for each
$p\colon Y\longrightarrow X$
is, in particular, a locally cartesian fibration. Furthermore, for each
![]() $2$
-simplex
$2$
-simplex
![]() $\sigma \colon [2]\longrightarrow X$
arising from the composition of an ingressive and an egressive map
$\sigma \colon [2]\longrightarrow X$
arising from the composition of an ingressive and an egressive map
![]() $x_0\twoheadrightarrow x_1\rightarrowtail x_2$
, the restriction
$x_0\twoheadrightarrow x_1\rightarrowtail x_2$
, the restriction
![]() $\sigma ^{*}(p)\colon \sigma ^{*}Y\longrightarrow [2]$
is a cartesian fibration.
$\sigma ^{*}(p)\colon \sigma ^{*}Y\longrightarrow [2]$
is a cartesian fibration.
Proof. Note that the second part implies that p is a locally cartesian fibration since every morphism in X fits into a
![]() $2$
-simplex
$2$
-simplex
![]() $\sigma $
as indicated. To see that
$\sigma $
as indicated. To see that
![]() $\sigma ^{*}(p)$
is a cartesian fibration, one simply notes that it admits enough cartesian lifts of
$\sigma ^{*}(p)$
is a cartesian fibration, one simply notes that it admits enough cartesian lifts of
![]() $x_1\rightarrowtail x_2$
(since p does) and locally cartesian lifts over
$x_1\rightarrowtail x_2$
(since p does) and locally cartesian lifts over
![]() $x_0\twoheadrightarrow x_1$
.
$x_0\twoheadrightarrow x_1$
.
Lemma 5.17. Let
![]() $p\colon Y\longrightarrow X$
be an op-Gray fibration between orthogonal adequate triples. Then the following are equivalent:
$p\colon Y\longrightarrow X$
be an op-Gray fibration between orthogonal adequate triples. Then the following are equivalent:
-
(1) The underlying functor
 $p\colon Y\longrightarrow X$
is a cartesian fibration.
$p\colon Y\longrightarrow X$
is a cartesian fibration. -
(2) For every ambigressive square
(5.18)in which
 $f'$
is
$f'$
is
 $p^{\mathrm {eg}}$
-cartesian, f is
$p^{\mathrm {eg}}$
-cartesian, f is
 $p^{\mathrm {eg}}$
-cartesian as well.
$p^{\mathrm {eg}}$
-cartesian as well.
Proof. Assuming (1), the uniqueness of cartesian lifts implies that an egressive morphism in Y is
![]() $p^{\mathrm {eg}}$
-cartesian if and only if it is p-cartesian. Except for
$p^{\mathrm {eg}}$
-cartesian if and only if it is p-cartesian. Except for
![]() $f'$
, all arrows in the square (5.18) are therefore p-cartesian, which implies that
$f'$
, all arrows in the square (5.18) are therefore p-cartesian, which implies that
![]() $f'$
is p-cartesian as well.
$f'$
is p-cartesian as well.
For the converse, Lemma 5.16 already asserts that p is a locally cartesian fibration. It then suffices to verify that locally p-cartesian morphisms are closed under composition. To this end, let f and g be two composable locally p-cartesian morphisms in Y and consider the diagram

Here, the two triangles factor f and g into an egressive followed by an ingressive morphism; Lemma 5.16 shows that the maps
![]() $f_1, f_2, g_1$
and
$f_1, f_2, g_1$
and
![]() $g_2$
are all locally p-cartesian. The top right square is obtained by factoring the down-right composite into an egressive, followed by an ingressive map. Condition (2) then implies that all individual arrows depicted in the above picture are locally p-cartesian (and the horizontal ones are p-cartesian). Since
$g_2$
are all locally p-cartesian. The top right square is obtained by factoring the down-right composite into an egressive, followed by an ingressive map. Condition (2) then implies that all individual arrows depicted in the above picture are locally p-cartesian (and the horizontal ones are p-cartesian). Since
![]() $p^{\mathrm {eg}}$
was a cartesian fibration, the top composite is then locally p-cartesian, and since the right vertical composite is p-cartesian, the composite
$p^{\mathrm {eg}}$
was a cartesian fibration, the top composite is then locally p-cartesian, and since the right vertical composite is p-cartesian, the composite
![]() $gf$
is locally p-cartesian as well.
$gf$
is locally p-cartesian as well.
Definition 5.19. We will say that a map
![]() $p\colon Y\longrightarrow X$
of orthogonal adequate triples is a cartesian fibration if it is an op-Gray fibration satisfying the equivalent conditions of Lemma 5.17. Dually, a curved orthofibration is called an orthofibration if for each ambigressive square (5.18) in which f is
$p\colon Y\longrightarrow X$
of orthogonal adequate triples is a cartesian fibration if it is an op-Gray fibration satisfying the equivalent conditions of Lemma 5.17. Dually, a curved orthofibration is called an orthofibration if for each ambigressive square (5.18) in which f is
![]() $p^{\mathrm {eg}}$
-cocartesian,
$p^{\mathrm {eg}}$
-cocartesian,
![]() $f'$
is
$f'$
is
![]() $p^{\mathrm {eg}}$
-cocartesian as well.
$p^{\mathrm {eg}}$
-cocartesian as well.
Let us write
![]() $\operatorname {\mathrm {Cart}}(X)\subseteq \mathrm {OpGray}(X)$
and
$\operatorname {\mathrm {Cart}}(X)\subseteq \mathrm {OpGray}(X)$
and
![]() $\operatorname {\mathrm {Ortho}}(X)\subseteq \mathrm {CrvOrtho}(X)$
for the full subcategories on cartesian and orthofibrations; this notation is justified by the following observation:
$\operatorname {\mathrm {Ortho}}(X)\subseteq \mathrm {CrvOrtho}(X)$
for the full subcategories on cartesian and orthofibrations; this notation is justified by the following observation:
Observation 5.20. Note that the datum of a cartesian fibration of orthogonal adequate triples
![]() $p\colon Y\longrightarrow X$
is equivalent to that of a cartesian fibration between the underlying
$p\colon Y\longrightarrow X$
is equivalent to that of a cartesian fibration between the underlying
![]() $\infty $
-categories. In addition, a map in
$\infty $
-categories. In addition, a map in
![]() $\operatorname {\mathrm {Cart}}(X)$
is required to preserve cartesian lifts over ingressive and egressive maps in X; since every map in X factors into an egressive map followed by an ingressive one, it follows that the maps in
$\operatorname {\mathrm {Cart}}(X)$
is required to preserve cartesian lifts over ingressive and egressive maps in X; since every map in X factors into an egressive map followed by an ingressive one, it follows that the maps in
![]() $\operatorname {\mathrm {Cart}}(X)$
preserve all cartesian arrows. In other words,
$\operatorname {\mathrm {Cart}}(X)$
preserve all cartesian arrows. In other words,
![]() $\operatorname {\mathrm {Cart}}(X)$
is simply equivalent to the
$\operatorname {\mathrm {Cart}}(X)$
is simply equivalent to the
![]() $\infty $
-category of cartesian fibrations over the underlying
$\infty $
-category of cartesian fibrations over the underlying
![]() $\infty $
-category of X.
$\infty $
-category of X.
The main result about these various types of fibration is that they behave well under dualisation:
Theorem 5.21. Let X be an orthogonal adequate triple. Then the natural equivalence
restricts to natural equivalences
 $$ \begin{align*} \operatorname{\mathrm{Cart}}_{\mathrm{in}}(X)&\simeq \operatorname{\mathrm{Cart}}_{\mathrm{in}}({\mathrm{Span}^{\perp}}(X))\\ \mathrm{OpGray}(X)&\simeq \mathrm{CrvOrtho}({\mathrm{Span}^{\perp}}(X))\\ \operatorname{\mathrm{Cart}}(X)& \simeq \operatorname{\mathrm{Ortho}}({\mathrm{Span}^{\perp}}(X)). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Cart}}_{\mathrm{in}}(X)&\simeq \operatorname{\mathrm{Cart}}_{\mathrm{in}}({\mathrm{Span}^{\perp}}(X))\\ \mathrm{OpGray}(X)&\simeq \mathrm{CrvOrtho}({\mathrm{Span}^{\perp}}(X))\\ \operatorname{\mathrm{Cart}}(X)& \simeq \operatorname{\mathrm{Ortho}}({\mathrm{Span}^{\perp}}(X)). \end{align*} $$
Furthermore, for each fibration
![]() $p\colon Y\longrightarrow X$
, the dual fibration
$p\colon Y\longrightarrow X$
, the dual fibration
![]() ${\mathrm {Span}^{\perp }}(Y)\longrightarrow {\mathrm {Span}^{\perp }}(X)$
has fibres given by the opposites of the fibres of p.
${\mathrm {Span}^{\perp }}(Y)\longrightarrow {\mathrm {Span}^{\perp }}(X)$
has fibres given by the opposites of the fibres of p.
In the simple case
![]() $X = (A, A, \iota A)$
, this result specialises to the statement that taking span categories for the adequate triple structure given by the cartesian and fibrewise maps provides an equivalence
$X = (A, A, \iota A)$
, this result specialises to the statement that taking span categories for the adequate triple structure given by the cartesian and fibrewise maps provides an equivalence
sending a cartesian fibration to the cartesian fibration with opposite fibres. Postcomposing with the equivalence
![]() $\operatorname {\mathrm {Cart}}(A)\simeq \operatorname {\mathrm {Cocart}}(A^{{\mathrm {op}}})$
sending
$\operatorname {\mathrm {Cart}}(A)\simeq \operatorname {\mathrm {Cocart}}(A^{{\mathrm {op}}})$
sending
![]() $Y\longrightarrow A$
to
$Y\longrightarrow A$
to
![]() $Y^{{\mathrm {op}}}\longrightarrow A^{{\mathrm {op}}}$
, we obtain the equivalence first established by Barwick, Glasman and Nardin [Reference Barwick, Glasman and NardinBGN18, Theorem 1.4]. Note that by Lemma 2.14, this composite equivalence coincides with the equivalence obtained by first exchanging the ingressive and egressive maps and then applying the equivalence from Corollary 3.18.
$Y^{{\mathrm {op}}}\longrightarrow A^{{\mathrm {op}}}$
, we obtain the equivalence first established by Barwick, Glasman and Nardin [Reference Barwick, Glasman and NardinBGN18, Theorem 1.4]. Note that by Lemma 2.14, this composite equivalence coincides with the equivalence obtained by first exchanging the ingressive and egressive maps and then applying the equivalence from Corollary 3.18.
In the case
![]() $X= (A,\iota A, A)$
, however, the result simply specialises to the equivalence
$X= (A,\iota A, A)$
, however, the result simply specialises to the equivalence
given by taking opposites. In the case of a general X, our equivalence combines these two extremes, as we shall discuss in the case of two-variable fibrations from [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] in the next section.
Proof. Note that naturality of these equivalences follows directly from
![]() ${\mathrm {Span}^{\perp }}$
being a functor and taking over-categories being natural in the base.
${\mathrm {Span}^{\perp }}$
being a functor and taking over-categories being natural in the base.
Let us start with the first equivalence. Since
![]() ${\mathrm {Span}^{\perp }}$
is its own inverse, it suffices to verify that for an ingressive cartesian fibration
${\mathrm {Span}^{\perp }}$
is its own inverse, it suffices to verify that for an ingressive cartesian fibration
![]() $p\colon Y\longrightarrow X$
, the dual map
$p\colon Y\longrightarrow X$
, the dual map
![]() $q = {\mathrm {Span}^{\perp }}(p)\colon {\mathrm {Span}^{\perp }}(Y)\longrightarrow {\mathrm {Span}^{\perp }}(X)$
is an ingressive cartesian fibration. Recall that an ingressive map in
$q = {\mathrm {Span}^{\perp }}(p)\colon {\mathrm {Span}^{\perp }}(Y)\longrightarrow {\mathrm {Span}^{\perp }}(X)$
is an ingressive cartesian fibration. Recall that an ingressive map in
![]() ${\mathrm {Span}^{\perp }}(Y)$
is given by a span
${\mathrm {Span}^{\perp }}(Y)$
is given by a span
![]() $y_{11}{\xleftarrow {\sim }} y_{01} \rightarrowtail y_{00}$
in Y.
$y_{11}{\xleftarrow {\sim }} y_{01} \rightarrowtail y_{00}$
in Y.
To see that q is an ingressive fibration, it suffices to verify that all such spans define q-cartesian edges in
![]() $\mathrm {Span}(Y)$
, since there are then clearly enough cartesian lifts of edges in
$\mathrm {Span}(Y)$
, since there are then clearly enough cartesian lifts of edges in
![]() $X_{\mathrm {in}}$
. Equivalently, this means that the reverse span
$X_{\mathrm {in}}$
. Equivalently, this means that the reverse span
![]() $y_{00}\leftarrowtail y_{01}{\stackrel {\sim }{\longrightarrow }} y_{11}$
defines a
$y_{00}\leftarrowtail y_{01}{\stackrel {\sim }{\longrightarrow }} y_{11}$
defines a
![]() $q^{{\mathrm {op}}}$
-cocartesian arrow. We can identify the opposite map
$q^{{\mathrm {op}}}$
-cocartesian arrow. We can identify the opposite map
![]() $q^{{\mathrm {op}}}\colon \mathrm {Span}(Y)^{{\mathrm {op}}}\longrightarrow \mathrm {Span}(X)^{{\mathrm {op}}}$
with
$q^{{\mathrm {op}}}\colon \mathrm {Span}(Y)^{{\mathrm {op}}}\longrightarrow \mathrm {Span}(X)^{{\mathrm {op}}}$
with
![]() $\mathrm {Span}(p^{\mathrm {rev}})\colon \mathrm {Span}(Y^{\mathrm {rev}})\longrightarrow \mathrm {Span}(X^{\mathrm {rev}})$
(that is, we exchange the roles of the ingressive and egressive maps). The reverse span is then
$\mathrm {Span}(p^{\mathrm {rev}})\colon \mathrm {Span}(Y^{\mathrm {rev}})\longrightarrow \mathrm {Span}(X^{\mathrm {rev}})$
(that is, we exchange the roles of the ingressive and egressive maps). The reverse span is then
![]() $\mathrm {Span}(p^{\mathrm {rev}})$
-cocartesian by Corollary 3.2.
$\mathrm {Span}(p^{\mathrm {rev}})$
-cocartesian by Corollary 3.2.
To see the second equivalence, we observe that given any
![]() $p\colon Y\longrightarrow X$
in
$p\colon Y\longrightarrow X$
in
![]() $\operatorname {\mathrm {Cart}}_{\mathrm {in}}(X)$
, the functor
$\operatorname {\mathrm {Cart}}_{\mathrm {in}}(X)$
, the functor
![]() $q^{\mathrm {eg}}\colon {\mathrm {Span}^{\perp }}(Y)^{\mathrm {eg}}\longrightarrow {\mathrm {Span}^{\perp }}(X)^{\mathrm {eg}}$
is equivalent to the opposite of
$q^{\mathrm {eg}}\colon {\mathrm {Span}^{\perp }}(Y)^{\mathrm {eg}}\longrightarrow {\mathrm {Span}^{\perp }}(X)^{\mathrm {eg}}$
is equivalent to the opposite of
![]() $p^{\mathrm {eg}}\colon Y^{\mathrm {eg}}\longrightarrow X^{\mathrm {eg}}$
. This immediately implies that
$p^{\mathrm {eg}}\colon Y^{\mathrm {eg}}\longrightarrow X^{\mathrm {eg}}$
. This immediately implies that
![]() ${\mathrm {Span}^{\perp }}$
exchanges curved orthofibrations and op-Gray fibrations and furthermore preserves maps between them that preserve (co)cartesian ingressive arrows.
${\mathrm {Span}^{\perp }}$
exchanges curved orthofibrations and op-Gray fibrations and furthermore preserves maps between them that preserve (co)cartesian ingressive arrows.
For the third equivalence, recall from Proposition 4.9 that an ambigressive square in
![]() ${\mathrm {Span}^{\perp }}(Y)$
corresponds to a diagram of the form
${\mathrm {Span}^{\perp }}(Y)$
corresponds to a diagram of the form

in Y. Suppose p is a cartesian fibration. The left span defines a
![]() $q^{\mathrm {eg}}$
-cocartesian arrow if and only if
$q^{\mathrm {eg}}$
-cocartesian arrow if and only if
![]() $\alpha $
is
$\alpha $
is
![]() $p^{\mathrm {eg}}$
-cartesian. This immediately implies that
$p^{\mathrm {eg}}$
-cartesian. This immediately implies that
![]() $\beta $
is also
$\beta $
is also
![]() $p^{\mathrm {eg}}$
-cartesian. Finally, the top right square is cartesian, and therefore, we conclude by 5.17 that
$p^{\mathrm {eg}}$
-cartesian. Finally, the top right square is cartesian, and therefore, we conclude by 5.17 that
![]() $\gamma $
is also
$\gamma $
is also
![]() $p^{\mathrm {eg}}$
-cartesian, so that the right vertical span is
$p^{\mathrm {eg}}$
-cartesian, so that the right vertical span is
![]() $q^{\mathrm {eg}}$
-cartesian. This implies by definition that q is an orthofibration of orthogonal triples. A dual argument (again using 5.17) shows that the dual of an orthofibration is a cartesian fibration.
$q^{\mathrm {eg}}$
-cartesian. This implies by definition that q is an orthofibration of orthogonal triples. A dual argument (again using 5.17) shows that the dual of an orthofibration is a cartesian fibration.
Finally, for the statement about fibres, note that
![]() ${\mathrm {Span}^{\perp }}$
(being an equivalence) preserves fibres (i.e., pullbacks along a map (of orthogonal adequate triples)
${\mathrm {Span}^{\perp }}$
(being an equivalence) preserves fibres (i.e., pullbacks along a map (of orthogonal adequate triples)
![]() $\ast \longrightarrow X$
). Observation 5.2 then implies that the fibre of
$\ast \longrightarrow X$
). Observation 5.2 then implies that the fibre of
![]() ${\mathrm {Span}^{\perp }}(Y)\longrightarrow {\mathrm {Span}^{\perp }}(X)$
over a point x is given by
${\mathrm {Span}^{\perp }}(Y)\longrightarrow {\mathrm {Span}^{\perp }}(X)$
over a point x is given by
![]() ${\mathrm {Span}^{\perp }}(Y_x, \iota Y_x, Y_x)$
, whose underlying category is equivalent to
${\mathrm {Span}^{\perp }}(Y_x, \iota Y_x, Y_x)$
, whose underlying category is equivalent to
![]() $Y_x^{{\mathrm {op}}}$
by Proposition 2.15.
$Y_x^{{\mathrm {op}}}$
by Proposition 2.15.
6 Dualisation and straightening of two-variable fibrations
The purpose of this section is to use the results of the previous section to dualise and straighten various kinds of fibrations over a product of
![]() $\infty $
-categories. The first part essentially consists of specialising Theorem 5.21 to the case where X is the particular orthogonal triple
$\infty $
-categories. The first part essentially consists of specialising Theorem 5.21 to the case where X is the particular orthogonal triple
associated to a product of two
![]() $\infty $
-categories. We will find that the various fibrations defined over
$\infty $
-categories. We will find that the various fibrations defined over
![]() $(A,B)^{\perp }$
in the previous section recover a subset of the fibrations which we considered in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23].
$(A,B)^{\perp }$
in the previous section recover a subset of the fibrations which we considered in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23].
In particular, we will extend the explicit description of dual (co)cartesian fibrations to the situation of curved ortho- and Gray fibrations. As an application, we give an explicit description of parametrised adjoints from [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], extending previous work of Torii [Reference ToriiTo20].
Let us start by making the various types of fibrations of orthogonal adequate triples
![]() $p\colon Y\longrightarrow (A, B)^{\perp }$
appearing in Section 5 more explicit. Recall that for all these fibrations, the structure of an adequate triple on Y is uniquely determined by the underlying functor (see Observation 5.2)
$p\colon Y\longrightarrow (A, B)^{\perp }$
appearing in Section 5 more explicit. Recall that for all these fibrations, the structure of an adequate triple on Y is uniquely determined by the underlying functor (see Observation 5.2)
By Proposition 4.4, such p determines an ingressive cartesian fibration if and only if all (ingressive) arrows in
![]() $A\times \iota B$
have enough cartesian lifts. By [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Corollary 2.2.2] or [Reference LurieLu09a, Proposition 2.4.1.3(3)], this is equivalent to
$A\times \iota B$
have enough cartesian lifts. By [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Corollary 2.2.2] or [Reference LurieLu09a, Proposition 2.4.1.3(3)], this is equivalent to

defining a map of cartesian fibrations over A preserving cartesian arrows. In particular, each
![]() $\alpha \colon a\longrightarrow a'$
in A gives rise to a cartesian transport functor
$\alpha \colon a\longrightarrow a'$
in A gives rise to a cartesian transport functor
![]() $\alpha ^{*}\colon Y_{a'}\longrightarrow Y_a$
between the fibres of
$\alpha ^{*}\colon Y_{a'}\longrightarrow Y_a$
between the fibres of
![]() $p_1$
. Following [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], let us write
$p_1$
. Following [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], let us write
![]() $\operatorname {\mathrm {LCart}}(A, B)$
for the
$\operatorname {\mathrm {LCart}}(A, B)$
for the
![]() $\infty $
-category of
$\infty $
-category of
![]() $p\colon Y\longrightarrow A\times B$
having p-cartesian lifts over
$p\colon Y\longrightarrow A\times B$
having p-cartesian lifts over
![]() $A\times \iota B$
and maps preserving such p-cartesian lifts. In these terms, we have the following:
$A\times \iota B$
and maps preserving such p-cartesian lifts. In these terms, we have the following:
Observation 6.1. There are natural equivalences of
![]() $\infty $
-categories
$\infty $
-categories
Remark 6.2. There is an evident analogue
![]() $\operatorname {\mathrm {LCocart}}(A, B)$
consisting of
$\operatorname {\mathrm {LCocart}}(A, B)$
consisting of
![]() $p\colon Y\longrightarrow A\times B$
having p-cocartesian lifts over
$p\colon Y\longrightarrow A\times B$
having p-cocartesian lifts over
![]() $A\times \iota B$
. This
$A\times \iota B$
. This
![]() $\infty $
-category does not have a good interpretation in terms of adequate triples; one can typically not equip Y with the natural structure of an adequate triple.
$\infty $
-category does not have a good interpretation in terms of adequate triples; one can typically not equip Y with the natural structure of an adequate triple.
Lemma 6.3. Let
![]() $p=(p_1, p_2)\colon Y\longrightarrow A\times B$
be a map in
$p=(p_1, p_2)\colon Y\longrightarrow A\times B$
be a map in
![]() $\operatorname {\mathrm {LCart}}(A, B)$
. Then p defines the following:
$\operatorname {\mathrm {LCart}}(A, B)$
. Then p defines the following:
-
(1) an op-Gray fibration in the sense of Definition 5.14 if and only if for each
 $a\in A$
, the map
$a\in A$
, the map
 $p_2\colon Y_a\longrightarrow Y\longrightarrow B$
from the fibre of
$p_2\colon Y_a\longrightarrow Y\longrightarrow B$
from the fibre of
 $p_1$
is a cartesian fibration.
$p_1$
is a cartesian fibration. -
(2) a curved orthofibration in the sense of Definition 5.14 if and only if for each
 $a\in A$
, the map
$a\in A$
, the map
 $p_2\colon Y_a\longrightarrow Y\longrightarrow B$
from the fibre of
$p_2\colon Y_a\longrightarrow Y\longrightarrow B$
from the fibre of
 $p_1$
is a cocartesian fibration.
$p_1$
is a cocartesian fibration.
Proof. Observe that the map
![]() $Y^{\mathrm {eg}}\longrightarrow ((A, B)^{\perp })^{\mathrm {eg}}$
is simply given by the restriction of
$Y^{\mathrm {eg}}\longrightarrow ((A, B)^{\perp })^{\mathrm {eg}}$
is simply given by the restriction of
![]() $p\colon Y\longrightarrow A\times B$
to
$p\colon Y\longrightarrow A\times B$
to
![]() $\iota A\times B$
. It follows from [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Remark 2.2.9] that this restriction to
$\iota A\times B$
. It follows from [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Remark 2.2.9] that this restriction to
![]() $\iota A\times B$
is a (co)cartesian fibration if and only if for each
$\iota A\times B$
is a (co)cartesian fibration if and only if for each
![]() $a\in A$
, the restriction
$a\in A$
, the restriction
![]() $p_a\colon Y_a\longrightarrow \{a\}\times B$
of p is a (co)cartesian fibration. Finally, note that
$p_a\colon Y_a\longrightarrow \{a\}\times B$
of p is a (co)cartesian fibration. Finally, note that
![]() $p_a$
can be identified with
$p_a$
can be identified with
![]() $p_2$
(restricted to the fibre
$p_2$
(restricted to the fibre
![]() $Y_a$
).
$Y_a$
).
Definition 6.4. Let us denote by
![]() $\mathrm {CrvOrtho}(A, B)$
the subcategory of
$\mathrm {CrvOrtho}(A, B)$
the subcategory of
![]() $\mathrm {Cat} /A\times B$
whose objects are curved orthofibrations and whose morphisms are maps preserving locally p-cartesian morphisms over
$\mathrm {Cat} /A\times B$
whose objects are curved orthofibrations and whose morphisms are maps preserving locally p-cartesian morphisms over
![]() $A\times \iota B$
and locally p-cocartesian morphisms over
$A\times \iota B$
and locally p-cocartesian morphisms over
![]() $\iota A\times B$
. We define
$\iota A\times B$
. We define
![]() $\mathrm {OpGray}(A, B)$
similarly.
$\mathrm {OpGray}(A, B)$
similarly.
We then immediately find the following:
Corollary 6.5. There are natural equivalences

Remark 6.6. As one may expect, the notion of a Gray fibration
![]() $p\colon Y\longrightarrow A\times B$
was introduced in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] as the opposite of an op-Gray fibration; that is, there is an equivalence
$p\colon Y\longrightarrow A\times B$
was introduced in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] as the opposite of an op-Gray fibration; that is, there is an equivalence
In particular,
![]() $\mathrm {Gray}(A, B)$
is a certain subcategory of
$\mathrm {Gray}(A, B)$
is a certain subcategory of
![]() $\operatorname {\mathrm {LCocart}}(A, B)$
. As in Remark 6.2, it does not have a good analogue for general orthogonal adequate triples.
$\operatorname {\mathrm {LCocart}}(A, B)$
. As in Remark 6.2, it does not have a good analogue for general orthogonal adequate triples.
Remark 6.7. In [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 2], we recorded various other ways to recognise (op-)Gray fibrations and curved orthofibrations. For example,
![]() $(p_1, p_2)\colon Y\longrightarrow A\times B$
is a curved orthofibration if
$(p_1, p_2)\colon Y\longrightarrow A\times B$
is a curved orthofibration if
![]() $p_1$
is a cartesian fibration and
$p_1$
is a cartesian fibration and
![]() $p_2$
is a cocartesian fibration [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 2.3.3]; that is,
$p_2$
is a cocartesian fibration [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 2.3.3]; that is,
Lemma 6.8. A map
![]() $p=(p_1, p_2)\colon Y\longrightarrow A\times B$
is an orthofibration in the sense of Definition 5.19 if and only if it is a curved orthofibration and for each map
$p=(p_1, p_2)\colon Y\longrightarrow A\times B$
is an orthofibration in the sense of Definition 5.19 if and only if it is a curved orthofibration and for each map
![]() $\alpha \colon a\longrightarrow a'$
, the cartesian transport functor
$\alpha \colon a\longrightarrow a'$
, the cartesian transport functor
![]() $\alpha ^{*}\colon Y_{a'}\longrightarrow Y_{a}$
preserves
$\alpha ^{*}\colon Y_{a'}\longrightarrow Y_{a}$
preserves
![]() $p_2$
-cocartesian arrows.
$p_2$
-cocartesian arrows.
Proof. Let us start by noting that an arrow in some fibre
![]() $Y_a\subseteq Y$
is
$Y_a\subseteq Y$
is
![]() $p_2$
-cocartesian if and only if it defines a cocartesian arrow for the base change of p to
$p_2$
-cocartesian if and only if it defines a cocartesian arrow for the base change of p to
![]() $\iota A\times B$
; see [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Corollary 2.2.7]. This base change coincides with
$\iota A\times B$
; see [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Corollary 2.2.7]. This base change coincides with
![]() $p^{\mathrm {eg}}\colon Y^{\mathrm {eg}}\longrightarrow ((A\times B)^{\perp })^{\mathrm {eg}}$
, so an arrow in
$p^{\mathrm {eg}}\colon Y^{\mathrm {eg}}\longrightarrow ((A\times B)^{\perp })^{\mathrm {eg}}$
, so an arrow in
![]() $Y_a$
is
$Y_a$
is
![]() $p_2$
-cocartesian if and only if it defines a
$p_2$
-cocartesian if and only if it defines a
![]() $p^{\mathrm {eg}}$
-cocartesian arrow.
$p^{\mathrm {eg}}$
-cocartesian arrow.
Using this, it follows that
![]() $\alpha ^{*}$
preserves
$\alpha ^{*}$
preserves
![]() $p_2$
-cocartesian arrows if and only if the following holds: for each square in Y
$p_2$
-cocartesian arrows if and only if the following holds: for each square in Y

in which the vertical arrows are p-cartesian and the bottom horizontal arrow is
![]() $p_{\mathrm {in}}$
-cocartesian, the top horizontal arrow is
$p_{\mathrm {in}}$
-cocartesian, the top horizontal arrow is
![]() $p_2$
-cocartesian. This is precisely the condition of Definition 5.19, since the ambigressive squares in Y are precisely squares of the above form whose vertical maps are p-cartesian.
$p_2$
-cocartesian. This is precisely the condition of Definition 5.19, since the ambigressive squares in Y are precisely squares of the above form whose vertical maps are p-cartesian.
Lemma 6.8 asserts that the notion of an orthofibration as defined in Definition 5.19 agrees (over
![]() $X=A\times B$
) with the notion of an orthofibration employed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] (see, in particular, [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 2.3.11]). Writing
$X=A\times B$
) with the notion of an orthofibration employed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] (see, in particular, [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 2.3.11]). Writing
![]() $\operatorname {\mathrm {Ortho}}(A, B)\subseteq \mathrm {CrvOrtho}(A, B)$
for the full subcategory spanned by the orthofibrations, we therefore obtain the following:
$\operatorname {\mathrm {Ortho}}(A, B)\subseteq \mathrm {CrvOrtho}(A, B)$
for the full subcategory spanned by the orthofibrations, we therefore obtain the following:
Corollary 6.9. There are natural equivalences of
![]() $\infty $
-categories
$\infty $
-categories
All in all, we have found that over the orthogonal triple
![]() $(A, B)^{\perp }=(A\times B, A\times \iota B, \iota A\times B)$
, the
$(A, B)^{\perp }=(A\times B, A\times \iota B, \iota A\times B)$
, the
![]() $\infty $
-categories of fibrations introduced in Section 5 coincide with those appearing under the same name in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23].
$\infty $
-categories of fibrations introduced in Section 5 coincide with those appearing under the same name in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23].
We will now unravel the content of the dualisation equivalence from Theorem 5.21 over the base
![]() $X=(A, B)^{\perp }$
. To this end, let us start with the following observation:
$X=(A, B)^{\perp }$
. To this end, let us start with the following observation:
Lemma 6.10. Let A and B be two
![]() $\infty $
-categories. Then there is an equivalence of orthogonal adequate triples
$\infty $
-categories. Then there is an equivalence of orthogonal adequate triples
Proof. Note that
![]() $(A, B)^{\perp }$
decomposes as a product of the triples
$(A, B)^{\perp }$
decomposes as a product of the triples
![]() $(A,A,\iota A)$
and
$(A,A,\iota A)$
and
![]() $(B,\iota B, B)$
, both of which are evidently orthogonal and adequate (and both these properties are preserved under taking products). Since the span construction preserves products, being a right adjoint, the claim follows from Proposition 2.15.
$(B,\iota B, B)$
, both of which are evidently orthogonal and adequate (and both these properties are preserved under taking products). Since the span construction preserves products, being a right adjoint, the claim follows from Proposition 2.15.
Consequently, Theorem 5.21 provides equivalences between certain types of fibrations over
![]() $A\times B$
and
$A\times B$
and
![]() $A\times B^{\mathrm {op}}$
, respectively. Recall from Theorem 5.21 that these equivalences take opposite categories at the level of fibres. To conform with the conventions of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], we will therefore compose the equivalences of Theorem 5.21 with taking opposites, resulting in the following:
$A\times B^{\mathrm {op}}$
, respectively. Recall from Theorem 5.21 that these equivalences take opposite categories at the level of fibres. To conform with the conventions of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], we will therefore compose the equivalences of Theorem 5.21 with taking opposites, resulting in the following:
Definition 6.11. For
![]() $\infty $
-categories A and B, we define functors
$\infty $
-categories A and B, we define functors

using the identifications from Observation 6.1 and Lemma 6.10.
Using Theorem 5.21 and the identifications Corollary 6.5 from Corollary 6.9, we then immediately find the following:
Corollary 6.12. The functor
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}} \colon \operatorname {\mathrm {LCart}}(A, B) \rightarrow \operatorname {\mathrm {LCocart}}(A^{{\mathrm {op}}}, B)$
is an equivalence with inverse
$\mathrm {S}\mathrm {D}^{\mathrm {cc}} \colon \operatorname {\mathrm {LCart}}(A, B) \rightarrow \operatorname {\mathrm {LCocart}}(A^{{\mathrm {op}}}, B)$
is an equivalence with inverse
![]() $\mathrm {S}\mathrm {D}^{\mathrm {ct}}$
and restricts to equivalences
$\mathrm {S}\mathrm {D}^{\mathrm {ct}}$
and restricts to equivalences
natural in
![]() $A, B \in \mathrm {Cat} $
. For
$A, B \in \mathrm {Cat} $
. For
![]() $A=*$
, and thus in particular on fibres, this equivalence restricts to the identity.
$A=*$
, and thus in particular on fibres, this equivalence restricts to the identity.
Remark 6.13. For a map
![]() $p \colon Y \rightarrow A \times B$
in
$p \colon Y \rightarrow A \times B$
in
![]() $\operatorname {\mathrm {LCart}}(A, B)$
, the dual fibration
$\operatorname {\mathrm {LCart}}(A, B)$
, the dual fibration
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}}(p)\colon \mathrm {S}\mathrm {D}^{\mathrm {cc}}(Y)\longrightarrow A^{{\mathrm {op}}}\times B$
is given explicitly as follows. The objects of
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}(p)\colon \mathrm {S}\mathrm {D}^{\mathrm {cc}}(Y)\longrightarrow A^{{\mathrm {op}}}\times B$
is given explicitly as follows. The objects of
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}}(Y)$
are the same as those of Y, and a morphism from y to
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}(Y)$
are the same as those of Y, and a morphism from y to
![]() $y'$
is given by a span
$y'$
is given by a span

where the left map
![]() $z\rightarrow y$
is p-cartesian. Dually, for a map
$z\rightarrow y$
is p-cartesian. Dually, for a map
![]() $q \colon X \rightarrow A \times B$
in
$q \colon X \rightarrow A \times B$
in
![]() $\operatorname {\mathrm {LCocart}}(A,B)$
, we find
$\operatorname {\mathrm {LCocart}}(A,B)$
, we find
![]() $\mathrm {S}\mathrm {D}^{\mathrm {ct}}(Y) \rightarrow A^{\mathrm {op}} \times B$
has morphisms from y to
$\mathrm {S}\mathrm {D}^{\mathrm {ct}}(Y) \rightarrow A^{\mathrm {op}} \times B$
has morphisms from y to
![]() $y'$
given by diagrams
$y'$
given by diagrams

where the right map
![]() $y' \rightarrow z$
is q-cocartesian.
$y' \rightarrow z$
is q-cocartesian.
Taking
![]() $B=\ast $
, Corollary 6.12 reproduces the dualisation equivalence between cartesian fibrations over A and cocartesian fibrations over
$B=\ast $
, Corollary 6.12 reproduces the dualisation equivalence between cartesian fibrations over A and cocartesian fibrations over
![]() $A^{{\mathrm {op}}}$
from [Reference Barwick, Glasman and NardinBGN18], which their main result shows is equivalent (naturally in A and B) to
$A^{{\mathrm {op}}}$
from [Reference Barwick, Glasman and NardinBGN18], which their main result shows is equivalent (naturally in A and B) to
we gave a more direct proof of this fact as Theorem 3.18 above (it also follows from the unicity results from Appendix A). In [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 2.5], we extended this procedure to an equivalence
by straightening in one variable. We deduce the following:
Corollary 6.14. The functors
agree with the equivalences
![]() $\mathrm {D}^{\mathrm {cc}}$
and
$\mathrm {D}^{\mathrm {cc}}$
and
![]() $\mathrm {D}^{\mathrm {ct}}$
constructed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 2.5].
$\mathrm {D}^{\mathrm {ct}}$
constructed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 2.5].
Proof. Essentially by construction, the two diagrams

commute naturally in A and B. Here, the bottom copy of
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}}$
arises from Definition 6.11 by taking
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}$
arises from Definition 6.11 by taking
![]() $B=\ast $
. Since the vertical maps are equivalences, the agreement of the two functors in the one-variable case implies that in the two-variable case.
$B=\ast $
. Since the vertical maps are equivalences, the agreement of the two functors in the one-variable case implies that in the two-variable case.
Example 6.15. As an example, consider the dual of the bifibration
![]() $(s,t)\colon \operatorname {\mathrm {Ar}}(X)\longrightarrow X\times X$
; see [Reference LurieLu09a, Corollary 2.4.7.11], which, in particular, defines an object in
$(s,t)\colon \operatorname {\mathrm {Ar}}(X)\longrightarrow X\times X$
; see [Reference LurieLu09a, Corollary 2.4.7.11], which, in particular, defines an object in
![]() $\operatorname {\mathrm {Ortho}}(X,X)$
. We claim that the functor from Definition 6.11 sends this to
$\operatorname {\mathrm {Ortho}}(X,X)$
. We claim that the functor from Definition 6.11 sends this to
Let us mention that an analogous identification
is a direct consequence of [Reference Haugseng, Melani and SafronovHMS22, Corollary A.2.5], the argument of which is based on the universal property of twisted arrow
![]() $\infty $
-categories from [Reference LurieLu17, Corollary 5.2.1.22]. In the (current) absence of a similar universal property for twisted arrow
$\infty $
-categories from [Reference LurieLu17, Corollary 5.2.1.22]. In the (current) absence of a similar universal property for twisted arrow
![]() $\infty $
-categories of
$\infty $
-categories of
![]() $(\infty ,2)$
-categories, such a proof does not generalise to this more general situation. The present example should be considered a warm-up for Section 7 below, where we provide this extension using the span model for dual fibrations.
$(\infty ,2)$
-categories, such a proof does not generalise to this more general situation. The present example should be considered a warm-up for Section 7 below, where we provide this extension using the span model for dual fibrations.
Now for the proof: Unravelling the definitions, we find that
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}}$
is given by the opposite of the associated
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}$
is given by the opposite of the associated
![]() $\infty $
-category of a certain simplicial
$\infty $
-category of a certain simplicial
![]() $\infty $
-groupoid
$\infty $
-groupoid
![]() $\Phi $
, where
$\Phi $
, where
![]() $\Phi _n$
is given by the
$\Phi _n$
is given by the
![]() $\infty $
-groupoid of diagrams
$\infty $
-groupoid of diagrams
![]() $\phi \colon \operatorname {\mathrm {Tw}}^{r}([n])\times [1] \longrightarrow X$
that take edges in
$\phi \colon \operatorname {\mathrm {Tw}}^{r}([n])\times [1] \longrightarrow X$
that take edges in
![]() $\operatorname {\mathrm {Tw}}^{r}([n])^{\mathrm {eg}}\times \{0\}$
and
$\operatorname {\mathrm {Tw}}^{r}([n])^{\mathrm {eg}}\times \{0\}$
and
![]() $\operatorname {\mathrm {Tw}}^{r}([n])_{\mathrm {in}}\times \{1\}$
to equivalences. We now claim that the localisation of
$\operatorname {\mathrm {Tw}}^{r}([n])_{\mathrm {in}}\times \{1\}$
to equivalences. We now claim that the localisation of
![]() $\operatorname {\mathrm {Tw}}^{r}([n])\times [1]$
at these subcategories is naturally equivalent to
$\operatorname {\mathrm {Tw}}^{r}([n])\times [1]$
at these subcategories is naturally equivalent to ![]() via the map
via the map

where we have used subscripts to indicate join factors. Restriction along this map then shows that
![]() $\mathrm {ac} (\Phi ) \simeq \operatorname {\mathrm {Tw}}^{r}(X),$
and so
$\mathrm {ac} (\Phi ) \simeq \operatorname {\mathrm {Tw}}^{r}(X),$
and so
![]() $\mathrm {ac} (\Phi )^{\mathrm {op}} \simeq \operatorname {\mathrm {Tw}}^{\ell }(X)$
, as required. One can also check that this equivalence lives over
$\mathrm {ac} (\Phi )^{\mathrm {op}} \simeq \operatorname {\mathrm {Tw}}^{\ell }(X)$
, as required. One can also check that this equivalence lives over
![]() $X^{\mathrm {op}}\times X$
.
$X^{\mathrm {op}}\times X$
.
To see the claim, we note that both restrictions
![]() $\operatorname {\mathrm {Tw}}^{r}([n]) \times \{\epsilon \} \rightarrow X$
of a diagram
$\operatorname {\mathrm {Tw}}^{r}([n]) \times \{\epsilon \} \rightarrow X$
of a diagram
![]() $\phi $
as considered above take all squares in
$\phi $
as considered above take all squares in
![]() $\operatorname {\mathrm {Tw}}^{r}([n])$
to pushout squares in X (namely, ones in which two opposite edges are equivalences). Using the pointwise formula for left Kan extensions, one readily checks that
$\operatorname {\mathrm {Tw}}^{r}([n])$
to pushout squares in X (namely, ones in which two opposite edges are equivalences). Using the pointwise formula for left Kan extensions, one readily checks that
![]() $\phi \colon \operatorname {\mathrm {Tw}}^{r}([n]) \times [1] \rightarrow X$
is then left Kan extended from the subposet
$\phi \colon \operatorname {\mathrm {Tw}}^{r}([n]) \times [1] \rightarrow X$
is then left Kan extended from the subposet
![]() $\mathcal J_n \times [1]$
, where
$\mathcal J_n \times [1]$
, where
![]() $\mathcal J_n$
is the arch along the top of
$\mathcal J_n$
is the arch along the top of
![]() $\operatorname {\mathrm {Tw}}^{r}([n])$
consisting of all
$\operatorname {\mathrm {Tw}}^{r}([n])$
consisting of all
![]() $(i \leq j)$
with
$(i \leq j)$
with
![]() $i=0$
or
$i=0$
or
![]() $j=n$
. It follows that the inclusion
$j=n$
. It follows that the inclusion
![]() $\mathcal J_n \times [1] \rightarrow \operatorname {\mathrm {Tw}}^{r}([n]) \times [1]$
induces an equivalence upon localisation.
$\mathcal J_n \times [1] \rightarrow \operatorname {\mathrm {Tw}}^{r}([n]) \times [1]$
induces an equivalence upon localisation.
Now note that
![]() $\mathcal J_n$
consists of two copies of
$\mathcal J_n$
consists of two copies of
![]() $[n]$
glued along the initial vertex. The claim then follows from the fact that the localisation of
$[n]$
glued along the initial vertex. The claim then follows from the fact that the localisation of
![]() $[n] \times [1]$
at
$[n] \times [1]$
at
![]() $[n] \times \{1\}$
is given by
$[n] \times \{1\}$
is given by
![]() $[n+1]$
and likewise for the localisation at
$[n+1]$
and likewise for the localisation at
![]() $[n] \times \{0\}$
; this realises the localisation of
$[n] \times \{0\}$
; this realises the localisation of
![]() $\mathcal J_n$
as the pushout of
$\mathcal J_n$
as the pushout of
![]() $[n+1]$
and
$[n+1]$
and
![]() $[1+n]$
along
$[1+n]$
along
![]() $[1]$
, embedded into the former as the terminal segment, and into the latter as the initial one. Finally, observe that the localisation map
$[1]$
, embedded into the former as the terminal segment, and into the latter as the initial one. Finally, observe that the localisation map ![]() just described is indeed the restriction of (*).
just described is indeed the restriction of (*).
We can also use the identification of
![]() $\mathrm {D}^{\mathrm {cc}}$
and the functor
$\mathrm {D}^{\mathrm {cc}}$
and the functor
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}}$
from Definition 6.11 to describe the fibrewise adjoints constructed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 3.1] more explicitly. For this, we need to recall some notation from [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 3]. Fix a parametrised left adjoint
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}$
from Definition 6.11 to describe the fibrewise adjoints constructed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 3.1] more explicitly. For this, we need to recall some notation from [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 3]. Fix a parametrised left adjoint

(i.e., a map between two cartesian fibrations (though not necessarily preserving cartesian edges)) such that the restrictions
![]() $L_b\colon D_b\longrightarrow C_b$
to the fibres admit right adjoints
$L_b\colon D_b\longrightarrow C_b$
to the fibres admit right adjoints
![]() $R_b\colon C_b \longrightarrow D_b$
. In [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], we constructed from this data a diagram
$R_b\colon C_b \longrightarrow D_b$
. In [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23], we constructed from this data a diagram

such that R restricts to the functors
![]() $R_b$
under the identifications
$R_b$
under the identifications
![]() $\mathrm {D}^{\mathrm {cc}}(p)_b \simeq D_p$
and
$\mathrm {D}^{\mathrm {cc}}(p)_b \simeq D_p$
and
![]() $\mathrm {D}^{\mathrm {cc}}(q)_b \simeq C_b$
arising from the naturality of
$\mathrm {D}^{\mathrm {cc}}(q)_b \simeq C_b$
arising from the naturality of
![]() $\mathrm {D}^{\mathrm {cc}}$
and showed that this gives an equivalence between the
$\mathrm {D}^{\mathrm {cc}}$
and showed that this gives an equivalence between the
![]() $(\infty ,2)$
-category of parametrised left adjoints and that of parametrised right adjoints (after taking opposites appropriately). One can use the equivalence
$(\infty ,2)$
-category of parametrised left adjoints and that of parametrised right adjoints (after taking opposites appropriately). One can use the equivalence
![]() $\mathrm {S}\mathrm {D}^{\mathrm {cc}} \simeq \mathrm {D}^{\mathrm {cc}}$
to give an explicit description of the functor R; see also [Reference ToriiTo20, Section 3.1] for a point-set variant of this construction of fibrewise adjoints.
$\mathrm {S}\mathrm {D}^{\mathrm {cc}} \simeq \mathrm {D}^{\mathrm {cc}}$
to give an explicit description of the functor R; see also [Reference ToriiTo20, Section 3.1] for a point-set variant of this construction of fibrewise adjoints.
To formulate the statement, observe that for each
![]() $\beta \colon b'\to b$
, the left adjoints
$\beta \colon b'\to b$
, the left adjoints
![]() $L_b$
and
$L_b$
and
![]() $L_b'$
and the cartesian transport functors of p and q are related by a natural transformation
$L_b'$
and the cartesian transport functors of p and q are related by a natural transformation
![]() $\lambda _{\beta }\colon L_{b'}\beta ^{*}\to \beta ^{*}L_b$
. We then have the following:
$\lambda _{\beta }\colon L_{b'}\beta ^{*}\to \beta ^{*}L_b$
. We then have the following:
Proposition 6.16. For a parametrised left adjoint L, the associated parametrised right adjoint

can be described as follows:
-
• For an object
 $y_b$
in the fibre
$y_b$
in the fibre
 $\mathrm {S}\mathrm {D}^{\mathrm {cc}}(q)_b\simeq C_b$
over
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}(q)_b\simeq C_b$
over
 $b\in B$
, one has
$b\in B$
, one has
 $R(y_b)\simeq R_b(y_b)$
.
$R(y_b)\simeq R_b(y_b)$
. -
• For a map
 $\beta \colon b'\to b$
in B, the functor R is given on morphisms over
$\beta \colon b'\to b$
in B, the functor R is given on morphisms over
 $\beta ^{{\mathrm {op}}}$
in
$\beta ^{{\mathrm {op}}}$
in
 $\mathrm {S}\mathrm {D}^{\mathrm {cc}}(q)$
by Here, the left-pointing arrows are cartesian lifts of
$\mathrm {S}\mathrm {D}^{\mathrm {cc}}(q)$
by Here, the left-pointing arrows are cartesian lifts of
 $\beta $
in C and D, and the right-pointing arrows are fibrewise over
$\beta $
in C and D, and the right-pointing arrows are fibrewise over
 $b'$
, with g given by the (fibrewise) adjoint to (6.17)
$b'$
, with g given by the (fibrewise) adjoint to (6.17)
Proof. A direct construction of R can be carried out exactly as in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Theorem 3.1.11], so we will be brief. Applying cocartesian unstraightening to the functor L yields a curved orthofibration
![]() $\pi \colon X\longrightarrow B\times [1]$
. Since L admits fibrewise right adjoints, this map is an op-Gray fibration as well. Applying the span dualisation from Corollary 6.12 to this op-Gray fibration yields a curved orthofibration
$\pi \colon X\longrightarrow B\times [1]$
. Since L admits fibrewise right adjoints, this map is an op-Gray fibration as well. Applying the span dualisation from Corollary 6.12 to this op-Gray fibration yields a curved orthofibration
![]() $\mathrm {S}\mathrm {D}^{\mathrm {ct}}(\pi )\colon \mathrm {S}\mathrm {D}^{\mathrm {ct}}(X)\longrightarrow [1]\times B^{{\mathrm {op}}}$
, which can be straightened over
$\mathrm {S}\mathrm {D}^{\mathrm {ct}}(\pi )\colon \mathrm {S}\mathrm {D}^{\mathrm {ct}}(X)\longrightarrow [1]\times B^{{\mathrm {op}}}$
, which can be straightened over
![]() $[1]$
to yield the desired functor R.
$[1]$
to yield the desired functor R.
Let us now describe the behaviour of R on arrows (and hence also on objects). Note that the functor R arises from cartesian transport in
![]() $\mathrm {S}\mathrm {D}^{\mathrm {ct}}(\pi )\colon \mathrm {S}\mathrm {D}^{\mathrm {ct}}(X)\longrightarrow [1]\times B^{{\mathrm {op}}}$
in the direction of
$\mathrm {S}\mathrm {D}^{\mathrm {ct}}(\pi )\colon \mathrm {S}\mathrm {D}^{\mathrm {ct}}(X)\longrightarrow [1]\times B^{{\mathrm {op}}}$
in the direction of
![]() $[1]$
. Consequently, it suffices to understand those squares in
$[1]$
. Consequently, it suffices to understand those squares in
![]() $\mathrm {S}\mathrm {D}^{\mathrm {ct}}(\pi )$
whose vertical maps are cartesian lifts of the map in
$\mathrm {S}\mathrm {D}^{\mathrm {ct}}(\pi )$
whose vertical maps are cartesian lifts of the map in
![]() $[1]$
and whose horizontal maps cover an arrow
$[1]$
and whose horizontal maps cover an arrow
![]() $\beta ^{{\mathrm {op}}}$
in
$\beta ^{{\mathrm {op}}}$
in
![]() $B^{{\mathrm {op}}}$
. Like in the proof of Theorem 5.21, unraveling the definitions shows that such a square in
$B^{{\mathrm {op}}}$
. Like in the proof of Theorem 5.21, unraveling the definitions shows that such a square in
![]() $\mathrm {S}\mathrm {D}^{\mathrm {ct}}(X)$
corresponds to a diagram in the domain of
$\mathrm {S}\mathrm {D}^{\mathrm {ct}}(X)$
corresponds to a diagram in the domain of
![]() $\pi \colon X\longrightarrow B\times [1]$
of the form
$\pi \colon X\longrightarrow B\times [1]$
of the form

where the top right and bottom left squares are (cartesian) ambigressive in X. In particular, the left-pointing arrows are all
![]() $\pi $
-cartesian lifts of
$\pi $
-cartesian lifts of
![]() $\beta $
. Let us explain the rest of the diagram in more detail. For the left and right vertical spans to describe cartesian arrows in
$\beta $
. Let us explain the rest of the diagram in more detail. For the left and right vertical spans to describe cartesian arrows in
![]() $\mathrm {S}\mathrm {D}^{\mathrm {ct}}(X)$
, one needs their upwards-pointing leg to be an equivalence (as indicated) and their downwards-pointing leg to define a cartesian arrow for the map
$\mathrm {S}\mathrm {D}^{\mathrm {ct}}(X)$
, one needs their upwards-pointing leg to be an equivalence (as indicated) and their downwards-pointing leg to define a cartesian arrow for the map
![]() $\pi _b\colon X_b\longrightarrow \{b\}\times [1]$
. Because each
$\pi _b\colon X_b\longrightarrow \{b\}\times [1]$
. Because each
![]() $\pi _b$
is both a cocartesian and a cartesian fibration classifying the adjoint pair
$\pi _b$
is both a cocartesian and a cartesian fibration classifying the adjoint pair
![]() $(L_b, R_b)$
, the objects in the middle row are then given by
$(L_b, R_b)$
, the objects in the middle row are then given by
![]() $R_b(x), \beta ^{*}R_b(x)$
and
$R_b(x), \beta ^{*}R_b(x)$
and
![]() $R_{b'}(y)$
. Finally, the right vertical square is entirely contained in the fibre
$R_{b'}(y)$
. Finally, the right vertical square is entirely contained in the fibre
![]() $X_{b'}$
. Since
$X_{b'}$
. Since
![]() $R_{b'}(y)\longrightarrow y$
was
$R_{b'}(y)\longrightarrow y$
was
![]() $\pi _{b'}$
-cartesian, the map g is therefore the unique one making the square commute.
$\pi _{b'}$
-cartesian, the map g is therefore the unique one making the square commute.
It now remains to verify that we can indeed take g to be the adjoint to (6.17). This follows from an analysis very similar to [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 3.2.7]. In fact, when f is the identity, the adjoint to (6.17) is precisely the mate of
![]() $\lambda _{\beta }$
; In this case, [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 3.2.7] precisely asserts that the mate makes the bottom right square commute.
$\lambda _{\beta }$
; In this case, [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 3.2.7] precisely asserts that the mate makes the bottom right square commute.
Finally, we will use Corollary 6.12 to identify various ways of straightening orthofibrations.
Proposition 6.18. The four equivalences given by

and
are pairwise equivalent, naturally in
![]() $A, B\in \mathrm {Cat} $
.
$A, B\in \mathrm {Cat} $
.
Definition 6.19. We shall refer to any of the functors above as the orthocartesian (un)straightening equivalence, in formulae
For example, we learn from Example 6.15 that
which we will generalise to (op)lax arrow categories of
![]() $(\infty ,2)$
-categories in the next section.
$(\infty ,2)$
-categories in the next section.
We shall give a fairly direct comparison between the four equivalences above in the present section, but there could be more ways of straightening an orthofibration. For example, in [Reference StevensonSt18], Stevenson produced an equivalence
by comparing both sides to a model category of correspondences. In order to settle such coherence questions once and for all, we take another cue from [Reference Barwick, Glasman and NardinBGN18] and show in the appendix that any equivalence as in the statement of Proposition 6.18 that is natural in the input categories and restricts to the identity for
![]() $A=*=B$
agrees with that above (in an essentially unique fashion). We also include similar statements for curved orthofibrations and bifibrations, in particular settling the comparison with Stevenson’s construction.
$A=*=B$
agrees with that above (in an essentially unique fashion). We also include similar statements for curved orthofibrations and bifibrations, in particular settling the comparison with Stevenson’s construction.
For the direct proof (and also the naturality of the Yoneda embedding), we need the following:
Lemma 6.20. The three functors
are pairwise equivalent.
Proof. We again use the formula
from [Reference Gepner, Haugseng and NikolausGHN17]. Using
![]() $ \operatorname {\mathrm {Tw}}^{r}(A \times B) = \operatorname {\mathrm {Tw}}^{r}(A) \times \operatorname {\mathrm {Tw}}^{r}(B)$
and
$ \operatorname {\mathrm {Tw}}^{r}(A \times B) = \operatorname {\mathrm {Tw}}^{r}(A) \times \operatorname {\mathrm {Tw}}^{r}(B)$
and
![]() $(A \times B)_{-/} = A_{-/} \times B_{-/}$
and the fact that colimits over a product can (naturally in the indexing categories) be computed in two steps, we find that this colimit agrees with that of
$(A \times B)_{-/} = A_{-/} \times B_{-/}$
and the fact that colimits over a product can (naturally in the indexing categories) be computed in two steps, we find that this colimit agrees with that of
where the first functor is curried from
![]() $\Phi _F$
; that is, it takes
$\Phi _F$
; that is, it takes
![]() $f \colon x \rightarrow y \in \operatorname {\mathrm {Tw}}^{r}(B)$
to
$f \colon x \rightarrow y \in \operatorname {\mathrm {Tw}}^{r}(B)$
to
But the colimit of this functor is naturally equivalent to the unstraightening of
![]() $F(-,x) \times B_{y/} \colon A \rightarrow \mathrm {Cat} $
, so in total,
$F(-,x) \times B_{y/} \colon A \rightarrow \mathrm {Cat} $
, so in total,
![]() $\mathrm {Un}^{\mathrm {cc}}(F)$
is naturally identified with
$\mathrm {Un}^{\mathrm {cc}}(F)$
is naturally identified with
which is itself unstraightening over B; here, we regard
![]() $\mathrm {Un}^{\mathrm {cc}}_A$
as the functor
$\mathrm {Un}^{\mathrm {cc}}_A$
as the functor
by forgetting the map to A. In total, this process identifies
as the composite
as desired.
Proof of Proposition 6.18
Recall that
![]() $\mathrm {D}^{\mathrm {cc}}$
is defined as the composite
$\mathrm {D}^{\mathrm {cc}}$
is defined as the composite
Thus, Lemma 6.20 immediately identifies the functors
and
and the argument for the first and fourth functors is dual. To compare the first composite with
we observe that the diagram

commutes essentially by construction (whereas this does not seem clear from the construction for
![]() $\mathrm {D}^{\mathrm {ct}}$
). It now follows from Corollary 6.14 that
$\mathrm {D}^{\mathrm {ct}}$
). It now follows from Corollary 6.14 that
![]() $\mathrm {D}^{\mathrm {cc}} \colon \operatorname {\mathrm {Ortho}}(A,B) \rightarrow \operatorname {\mathrm {Cocart}}(A^{{\mathrm {op}}} \times B)$
agrees with
$\mathrm {D}^{\mathrm {cc}} \colon \operatorname {\mathrm {Ortho}}(A,B) \rightarrow \operatorname {\mathrm {Cocart}}(A^{{\mathrm {op}}} \times B)$
agrees with
whence the result follows from Corollary 3.18.
Remark 6.21.
-
(1) Straightening of bifibrations is also discussed in detail in [Reference Heine, Lopez-Avila and SpitzweckHLAS16, Section 5], [Reference Haugseng, Melani and SafronovHMS22, Appendix A] and [CDH+23, Section 7.1], in each case by choosing one of the last two equivalences from 6.18 as the definition. For example, the stable
 $\infty $
-category underlying the Poincaré
$\infty $
-category underlying the Poincaré
 $\infty $
-category
$\infty $
-category  from [CDH+23, Section 7.3] is simply the orthocartesian unstraightening of
from [CDH+23, Section 7.3] is simply the orthocartesian unstraightening of  in the language of the present paper.
in the language of the present paper. -
(2) The equivalence
constructed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Section 5.2] by definition restricts to the composite $$\begin{align*}\mathrm{Gray}(A,B)\simeq \mathrm{Fun} (A \boxtimes B,\mathrm{Cat} )\end{align*}$$
see [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Remark 5.2.10]. As another consequence of (the dual of) Corollary 6.20, we obtain that our straightening equivalence for Gray fibrations extends the usual one for cocartesian fibrations over
$$\begin{align*}\mathrm{Gray}(A,B)\simeq \mathrm{Fun} (A \boxtimes B,\mathrm{Cat} )\end{align*}$$
see [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Remark 5.2.10]. As another consequence of (the dual of) Corollary 6.20, we obtain that our straightening equivalence for Gray fibrations extends the usual one for cocartesian fibrations over $$\begin{align*}\operatorname{\mathrm{Cocart}}(A \times B) \xrightarrow{\mathrm{Str}^{\mathrm{cc}}} \mathrm{Fun} (A, \operatorname{\mathrm{Cocart}}(B)) \xrightarrow{\mathrm{Str}^{\mathrm{cc}}} \mathrm{Fun} (A \times B, \mathrm{Cat} );\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Cocart}}(A \times B) \xrightarrow{\mathrm{Str}^{\mathrm{cc}}} \mathrm{Fun} (A, \operatorname{\mathrm{Cocart}}(B)) \xrightarrow{\mathrm{Str}^{\mathrm{cc}}} \mathrm{Fun} (A \times B, \mathrm{Cat} );\end{align*}$$
 $A \times B$
.
$A \times B$
.
7 (Op)lax arrow and twisted arrow
 $\infty $
-categories
$\infty $
-categories
In this section, we will discuss an application of the dualisation procedure from Corollary 6.12 which extends Example 6.15. The duality between the arrow and twisted arrow category of an
![]() $\infty $
-category X extends to a duality between the oplax arrow and twisted arrow category of an
$\infty $
-category X extends to a duality between the oplax arrow and twisted arrow category of an
![]() $(\infty , 2)$
-category
$(\infty , 2)$
-category
![]() $\mathbf {X}$
. More precisely, the oplax twisted arrow category of
$\mathbf {X}$
. More precisely, the oplax twisted arrow category of
![]() $\mathbf {X}$
$\mathbf {X}$
is introduced in work of Abellán García and Stern [Reference García and SternAGS23] as an explicit model for the cartesian fibration classified by the enriched mapping functor of
![]() $\mathbf {X}$
(restricted to its underlying
$\mathbf {X}$
(restricted to its underlying
![]() $(\infty , 1)$
-category X)
$(\infty , 1)$
-category X)
We will show that the enriched mapping functor also classifies the orthofibration
from the
![]() $(\infty , 1)$
-category underlying the oplax arrow category, defined using the (a priori unrelated) Gray tensor product of Gagna, Harpaz and Lanari from [Reference Gagna, Harpaz and LanariGHL21].
$(\infty , 1)$
-category underlying the oplax arrow category, defined using the (a priori unrelated) Gray tensor product of Gagna, Harpaz and Lanari from [Reference Gagna, Harpaz and LanariGHL21].
Since the oplax twisted arrow category and the Gray tensor product are both defined using the model for
![]() $(\infty ,2)$
-categories given by scaled simplicial sets [Reference LurieLu09b], we will start with a minimalistic review of these.
$(\infty ,2)$
-categories given by scaled simplicial sets [Reference LurieLu09b], we will start with a minimalistic review of these.
Notation 7.1. Recall that a scaled simplicial set is a pair
![]() $(\mathbf {X}, S)$
consisting of a simplicial set
$(\mathbf {X}, S)$
consisting of a simplicial set
![]() $\mathbf {X}$
and a subset
$\mathbf {X}$
and a subset
![]() $S\subseteq \mathbf {X}_2$
of
$S\subseteq \mathbf {X}_2$
of
![]() $2$
-simplices that are called thin. The category
$2$
-simplices that are called thin. The category
![]() $\mathrm {sSet}^{\mathrm {sc}}$
of scaled simplicial sets carries a model structure in which the cofibrations are the monomorphisms, which is related to the model category
$\mathrm {sSet}^{\mathrm {sc}}$
of scaled simplicial sets carries a model structure in which the cofibrations are the monomorphisms, which is related to the model category
![]() $\mathrm {Cat} (\mathrm {sSet}^{+})$
of categories enriched in marked simplicial sets (with the categorical model structure) by a Quillen equivalence
$\mathrm {Cat} (\mathrm {sSet}^{+})$
of categories enriched in marked simplicial sets (with the categorical model structure) by a Quillen equivalence ![]() [Reference LurieLu09b, Theorem 4.2.7]. We define the
[Reference LurieLu09b, Theorem 4.2.7]. We define the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Cat} _2$
of
$\mathrm {Cat} _2$
of
![]() $(\infty ,2)$
-categories as the
$(\infty ,2)$
-categories as the
![]() $\infty $
-category associated to any of these two Quillen equivalent model categories (or any of the other standard models, cf. [Reference LurieLu09b, Theorem 0.0.3]).
$\infty $
-category associated to any of these two Quillen equivalent model categories (or any of the other standard models, cf. [Reference LurieLu09b, Theorem 0.0.3]).
Notation 7.2. For a simplicial set X, we write
![]() $X^{\sharp }$
for the associated scaled simplicial set in which every
$X^{\sharp }$
for the associated scaled simplicial set in which every
![]() $2$
-simplex is thin. This determines a left Quillen functor
$2$
-simplex is thin. This determines a left Quillen functor
![]() $(-)^{\sharp }\colon {\mathrm {sSet}} \longrightarrow \mathrm {sSet}^{\mathrm {sc}}$
, where
$(-)^{\sharp }\colon {\mathrm {sSet}} \longrightarrow \mathrm {sSet}^{\mathrm {sc}}$
, where
![]() $\mathrm {sSet}$
is equipped with the Joyal model structure. Its right adjoint sends a scaled simplicial set
$\mathrm {sSet}$
is equipped with the Joyal model structure. Its right adjoint sends a scaled simplicial set
![]() $(\mathbf {X}, S)$
to the sub-simplicial set of X spanned by the thin
$(\mathbf {X}, S)$
to the sub-simplicial set of X spanned by the thin
![]() $2$
-simplices. At the level of
$2$
-simplices. At the level of
![]() $\infty $
-categories, this induces the fully faithful inclusion
$\infty $
-categories, this induces the fully faithful inclusion
![]() $\mathrm {Cat} \hookrightarrow \mathrm {Cat} _2$
of
$\mathrm {Cat} \hookrightarrow \mathrm {Cat} _2$
of
![]() $(\infty , 1)$
-categories into
$(\infty , 1)$
-categories into
![]() $(\infty , 2)$
-categories, together with its right adjoint sending an
$(\infty , 2)$
-categories, together with its right adjoint sending an
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathbf {X}$
to its underlying
$\mathbf {X}$
to its underlying
![]() $(\infty , 1)$
-category X.
$(\infty , 1)$
-category X.
To manipulate simple diagrams in
![]() $(\infty ,2)$
-categories, such as lax commuting squares and triangles, let us recall from [Reference Barwick and Schommer-PriesBSP21] that a gaunt
$(\infty ,2)$
-categories, such as lax commuting squares and triangles, let us recall from [Reference Barwick and Schommer-PriesBSP21] that a gaunt
![]() $2$
-category is a strict
$2$
-category is a strict
![]() $2$
-category whose only invertible
$2$
-category whose only invertible
![]() $1$
- and
$1$
- and
![]() $2$
-cells are the identities. For example, a gaunt
$2$
-cells are the identities. For example, a gaunt
![]() $1$
-category A gives rise to a gaunt
$1$
-category A gives rise to a gaunt
![]() $2$
-category
$2$
-category
![]() $[1]_A$
with
$[1]_A$
with
Every gaunt
![]() $2$
-category determines an object in
$2$
-category determines an object in
![]() $\mathrm {Cat} (\mathrm {sSet}^{+})$
by taking the nerves of its mapping categories (with degenerate marking), and this determines a fully faithful functor
$\mathrm {Cat} (\mathrm {sSet}^{+})$
by taking the nerves of its mapping categories (with degenerate marking), and this determines a fully faithful functor
![]() $\mathrm {Gaunt}_2\hookrightarrow \mathrm {Cat}_2$
from the (ordinary) category of gaunt
$\mathrm {Gaunt}_2\hookrightarrow \mathrm {Cat}_2$
from the (ordinary) category of gaunt
![]() $2$
-categories into the
$2$
-categories into the
![]() $\infty $
-category of
$\infty $
-category of
![]() $(\infty , 2)$
-categories, with essential image given by the
$(\infty , 2)$
-categories, with essential image given by the
![]() $0$
-truncated objects [Reference Barwick and Schommer-PriesBSP21, Corollary 12.3]. To decompose diagrams indexed by gaunt
$0$
-truncated objects [Reference Barwick and Schommer-PriesBSP21, Corollary 12.3]. To decompose diagrams indexed by gaunt
![]() $2$
-categories into simpler ones, let us record the following:
$2$
-categories into simpler ones, let us record the following:
Proposition 7.3. The inclusion
![]() $\mathrm {Gaunt}_2\hookrightarrow \mathrm {Cat} _2$
preserves coproducts and the following pushouts:
$\mathrm {Gaunt}_2\hookrightarrow \mathrm {Cat} _2$
preserves coproducts and the following pushouts:
-
(1) Pushouts of the form
 $[1]_A \longleftarrow \{i\}\xrightarrow {x} \mathbf {X}$
for
$[1]_A \longleftarrow \{i\}\xrightarrow {x} \mathbf {X}$
for
 $i=0, 1$
.
$i=0, 1$
. -
(2) Pushouts of the form
 $[2]\xleftarrow {\partial ^1} [1]{\stackrel {\gamma }{\longrightarrow }} \mathbf {X}$
, freely adding a factorisation
$[2]\xleftarrow {\partial ^1} [1]{\stackrel {\gamma }{\longrightarrow }} \mathbf {X}$
, freely adding a factorisation
 $\gamma =\alpha \beta $
.
$\gamma =\alpha \beta $
. -
(3) Pushouts of the form
 $[1]_{[1]} \longleftarrow [1]_{\{i\}}{\stackrel {\gamma }{\longrightarrow }} \mathbf {X}$
for
$[1]_{[1]} \longleftarrow [1]_{\{i\}}{\stackrel {\gamma }{\longrightarrow }} \mathbf {X}$
for
 $i=0, 1$
, where
$i=0, 1$
, where
 $\gamma \colon x\to y$
is an arrow in
$\gamma \colon x\to y$
is an arrow in
 $\mathbf {X}$
such that x has no nontrivial incoming arrows and y has no nontrivial outgoing arrows.
$\mathbf {X}$
such that x has no nontrivial incoming arrows and y has no nontrivial outgoing arrows.
Proof. Let us first give explicit descriptions of these three types of strict pushouts in
![]() $\mathrm {Cat} ({\mathrm {sSet}}^{+})$
, for an arbitrary marked simplicial category
$\mathrm {Cat} ({\mathrm {sSet}}^{+})$
, for an arbitrary marked simplicial category
![]() $\mathbf {X}$
. These will show that when
$\mathbf {X}$
. These will show that when
![]() $\mathbf {X}$
arises from a gaunt
$\mathbf {X}$
arises from a gaunt
![]() $2$
-category, then so does the pushout
$2$
-category, then so does the pushout
![]() $\mathbf {X}'$
.
$\mathbf {X}'$
.
Case (1): We only treat the pushout along
![]() $\{0\}\longrightarrow [1]_A$
. The pushout
$\{0\}\longrightarrow [1]_A$
. The pushout
![]() $\mathbf {X}'$
contains
$\mathbf {X}'$
contains
![]() $\mathbf {X}$
as a full subcategory, together with a new object z, so that for any object
$\mathbf {X}$
as a full subcategory, together with a new object z, so that for any object
![]() $u\in \mathbf {X}$
,
$u\in \mathbf {X}$
,
Composition is defined by acting on the right factor of
![]() $A\times {\mathrm {Hom}}_{\mathbf {X}}(u, x)$
. Case (2): The pushout
$A\times {\mathrm {Hom}}_{\mathbf {X}}(u, x)$
. Case (2): The pushout
![]() $\mathbf {X}'$
then freely adds a factorisation
$\mathbf {X}'$
then freely adds a factorisation
![]() $\gamma =\alpha \beta $
, where
$\gamma =\alpha \beta $
, where
![]() $\alpha $
has source x,
$\alpha $
has source x,
![]() $\beta $
has target y, and they have a new object z as common target and source, respectively. More precisely,
$\beta $
has target y, and they have a new object z as common target and source, respectively. More precisely,
![]() $\mathbf {X}'$
has one additional object z and mapping categories
$\mathbf {X}'$
has one additional object z and mapping categories
 $$ \begin{align*} {\mathrm{Hom}}_{\mathbf{X}'}(u, v)& ={\mathrm{Hom}}_{\mathbf{X}}(u, v), & {\mathrm{Hom}}_{\mathbf{X}'}(u, z)&=\alpha\cdot {\mathrm{Hom}}_{\mathbf{X}}(u, x),\\ {\mathrm{Hom}}_{\mathbf{X}'}(z, v)&={\mathrm{Hom}}_{\mathbf{X}}(y, v)\cdot \beta, & {\mathrm{Hom}}_{\mathbf{X}'}(z, z) &= \{\mathrm{id}_z\}\sqcup \alpha\cdot {\mathrm{Hom}}_{\mathbf{X}}(y, x)\cdot \beta \end{align*} $$
$$ \begin{align*} {\mathrm{Hom}}_{\mathbf{X}'}(u, v)& ={\mathrm{Hom}}_{\mathbf{X}}(u, v), & {\mathrm{Hom}}_{\mathbf{X}'}(u, z)&=\alpha\cdot {\mathrm{Hom}}_{\mathbf{X}}(u, x),\\ {\mathrm{Hom}}_{\mathbf{X}'}(z, v)&={\mathrm{Hom}}_{\mathbf{X}}(y, v)\cdot \beta, & {\mathrm{Hom}}_{\mathbf{X}'}(z, z) &= \{\mathrm{id}_z\}\sqcup \alpha\cdot {\mathrm{Hom}}_{\mathbf{X}}(y, x)\cdot \beta \end{align*} $$
for
![]() $u, v\in \mathbf {X}$
. Here, the notation
$u, v\in \mathbf {X}$
. Here, the notation
![]() $\alpha \cdot {\mathrm {Hom}}_{\mathbf {X}}(u, x)$
indicates that
$\alpha \cdot {\mathrm {Hom}}_{\mathbf {X}}(u, x)$
indicates that
![]() $\alpha \circ (-)\colon {\mathrm {Hom}}_{\mathbf {X}}(u, x)\longrightarrow {\mathrm {Hom}}_{\mathbf {X}'}(u, z)$
is an isomorphism for all
$\alpha \circ (-)\colon {\mathrm {Hom}}_{\mathbf {X}}(u, x)\longrightarrow {\mathrm {Hom}}_{\mathbf {X}'}(u, z)$
is an isomorphism for all
![]() $u\in \mathbf {X}$
. The composition is then the evident one, using the (formal) relation that
$u\in \mathbf {X}$
. The composition is then the evident one, using the (formal) relation that
![]() $\alpha \beta =\gamma $
.
$\alpha \beta =\gamma $
.
Case (3): The pushout
![]() $\mathbf {X}'$
has the same objects and mapping categories as
$\mathbf {X}'$
has the same objects and mapping categories as
![]() $\mathbf {X}$
, except for
$\mathbf {X}$
, except for
![]() ${\mathrm {Hom}}_{\mathbf {X}'}(x, y)$
, which is given by a (homotopy) pushout
${\mathrm {Hom}}_{\mathbf {X}'}(x, y)$
, which is given by a (homotopy) pushout
![]() $[1]\longleftarrow \{i\}\longrightarrow {\mathrm {Hom}}_{\mathbf {X}}(x, y)$
. Note that when
$[1]\longleftarrow \{i\}\longrightarrow {\mathrm {Hom}}_{\mathbf {X}}(x, y)$
. Note that when
![]() ${\mathrm {Hom}}_{\mathbf {X}}(x, y)$
is the nerve of a gaunt
${\mathrm {Hom}}_{\mathbf {X}}(x, y)$
is the nerve of a gaunt
![]() $1$
-category, this pushout of marked simplicial sets is weakly equivalent to the nerve of a gaunt
$1$
-category, this pushout of marked simplicial sets is weakly equivalent to the nerve of a gaunt
![]() $1$
-category (essentially by Case (1)).
$1$
-category (essentially by Case (1)).
It remains to show that the above (strict) pushouts also model the pushout in the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Cat} _2$
. From the above descriptions, one sees that a Dwyer–Kan equivalence of marked simplicial categories
$\mathrm {Cat} _2$
. From the above descriptions, one sees that a Dwyer–Kan equivalence of marked simplicial categories
![]() $\mathbf {X}\longrightarrow \mathbf {Y}$
induces a Dwyer–Kan equivalence between the resulting pushouts. It clearly induces weak equivalences on mapping objects, and since we add at most one extra object, it remains essentially surjective on homotopy categories. Since
$\mathbf {X}\longrightarrow \mathbf {Y}$
induces a Dwyer–Kan equivalence between the resulting pushouts. It clearly induces weak equivalences on mapping objects, and since we add at most one extra object, it remains essentially surjective on homotopy categories. Since
![]() $\mathrm {Cat} ({\mathrm {sSet}}^{+})$
is left proper [Reference LurieLu09a, Proposition A.3.2.4], this means that the above pushouts are all homotopy pushouts, and the result follows.
$\mathrm {Cat} ({\mathrm {sSet}}^{+})$
is left proper [Reference LurieLu09a, Proposition A.3.2.4], this means that the above pushouts are all homotopy pushouts, and the result follows.
The
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Cat} _2$
admits a closed (non-symmetric) monoidal structure given by the (oplax) Gray tensor product
$\mathrm {Cat} _2$
admits a closed (non-symmetric) monoidal structure given by the (oplax) Gray tensor product
![]() $\boxtimes $
. The Gray tensor product is induced by a Quillen bifunctor
$\boxtimes $
. The Gray tensor product is induced by a Quillen bifunctor
![]() $\boxtimes \colon {\mathrm {sSet}}^{\mathrm {sc}}\times {\mathrm {sSet}}^{\mathrm {sc}}\longrightarrow {\mathrm {sSet}}^{\mathrm {sc}}$
. The scaled simplicial set
$\boxtimes \colon {\mathrm {sSet}}^{\mathrm {sc}}\times {\mathrm {sSet}}^{\mathrm {sc}}\longrightarrow {\mathrm {sSet}}^{\mathrm {sc}}$
. The scaled simplicial set
![]() $(\mathbf {X},S)\boxtimes (\mathbf {Y},T)$
equals
$(\mathbf {X},S)\boxtimes (\mathbf {Y},T)$
equals
![]() $(\mathbf {X}\times \mathbf {Y},S\boxtimes T),$
where a
$(\mathbf {X}\times \mathbf {Y},S\boxtimes T),$
where a
![]() $2$
-simplex
$2$
-simplex
![]() $(\sigma ,\sigma ')$
is in
$(\sigma ,\sigma ')$
is in
![]() $S\boxtimes T$
if the following conditions hold:
$S\boxtimes T$
if the following conditions hold:
-
(1)
 $(\sigma ,\sigma ')\in S\times T$
,
$(\sigma ,\sigma ')\in S\times T$
, -
(2)
 $\sigma $
factors through
$\sigma $
factors through
 $\Delta ^{2}\rightarrow \Delta ^{\{1,2\}}$
or
$\Delta ^{2}\rightarrow \Delta ^{\{1,2\}}$
or
 $\sigma '$
factors through
$\sigma '$
factors through
 $\Delta ^{2}\rightarrow \Delta ^{\{0,1\}}$
.
$\Delta ^{2}\rightarrow \Delta ^{\{0,1\}}$
.
See [Reference Gagna, Harpaz and LanariGHL21] for the details of this construction. Furthermore, by [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 5.1.9], its value on the pair
![]() $([m], [n])$
is naturally equivalent to the expected (gaunt)
$([m], [n])$
is naturally equivalent to the expected (gaunt)
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category

The internal mapping objects induced by the Gray tensor product via
are by definition the
![]() $(\infty ,2)$
-categories of
$(\infty ,2)$
-categories of
![]() $2$
-functors and (op)lax natural transformations between them; see [Reference HaugsengHa21, Definition 3.9].
$2$
-functors and (op)lax natural transformations between them; see [Reference HaugsengHa21, Definition 3.9].
Let us now describe the complete Segal
![]() $\infty $
-groupoid models for the fibrations
$\infty $
-groupoid models for the fibrations
associated to an
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathbf {X}$
. We will start with the oplax arrow
$\mathbf {X}$
. We will start with the oplax arrow
![]() $\infty $
-category.
$\infty $
-category.
Definition 7.5. Let
![]() $\mathbf {X}$
be a
$\mathbf {X}$
be a
![]() $(\infty ,2)$
-category. The oplax arrow
$(\infty ,2)$
-category. The oplax arrow
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
is the
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
is the
![]() $\infty $
-category underlying the oplax functor
$\infty $
-category underlying the oplax functor
![]() $\infty $
-category
$\infty $
-category
![]() $\mathbf {Ar}^{\mathrm {opl}}(\mathbf {X})=\mathbf {Fun}^{\mathrm {opl}}\big ([1], \mathbf {X}\big )$
.
$\mathbf {Ar}^{\mathrm {opl}}(\mathbf {X})=\mathbf {Fun}^{\mathrm {opl}}\big ([1], \mathbf {X}\big )$
.
Informally,
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
is the
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
is the
![]() $\infty $
-category with objects given by arrows of
$\infty $
-category with objects given by arrows of
![]() $\mathbf {X}$
, such that morphisms from f to g are given by oplax commuting squares:
$\mathbf {X}$
, such that morphisms from f to g are given by oplax commuting squares:

More precisely,
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
can be characterised in terms of the Gray tensor product by the natural equivalence
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
can be characterised in terms of the Gray tensor product by the natural equivalence
Example 7.6. If
![]() $\mathbf {X}$
is a gaunt
$\mathbf {X}$
is a gaunt
![]() $2$
-category (i.e., a
$2$
-category (i.e., a
![]() $0$
-truncated object in
$0$
-truncated object in
![]() $\mathrm {Cat} _2$
), then the above natural equivalence becomes a natural bijection of sets. It follows that
$\mathrm {Cat} _2$
), then the above natural equivalence becomes a natural bijection of sets. It follows that
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
is a gaunt
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
is a gaunt
![]() $1$
-category (i.e., a strict category without nontrivial isomorphisms), and from the description (7.4) of the Gray tensor product, one sees that it coincides with the classical oplax arrow category of
$1$
-category (i.e., a strict category without nontrivial isomorphisms), and from the description (7.4) of the Gray tensor product, one sees that it coincides with the classical oplax arrow category of
![]() $\mathbf {X}$
.
$\mathbf {X}$
.
Remark 7.7. Of course, the lax arrow category
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {lax}}(\mathbf {X})$
is defined by a similar universal property:
$\operatorname {\mathrm {Ar}}^{\mathrm {lax}}(\mathbf {X})$
is defined by a similar universal property:
The description of the Gray tensor product of simplices (7.4) shows that for any simplex
![]() $[m]$
, there is a natural equivalence of gaunt
$[m]$
, there is a natural equivalence of gaunt
![]() $2$
-categories
$2$
-categories
![]() $[1]\boxtimes ([m]^{{\mathrm {op}}})\simeq \big ([m]\boxtimes [1]^{{\mathrm {op}}}\big )^{{\mathrm {op}}}$
. By adjunction, this determines a natural equivalence
$[1]\boxtimes ([m]^{{\mathrm {op}}})\simeq \big ([m]\boxtimes [1]^{{\mathrm {op}}}\big )^{{\mathrm {op}}}$
. By adjunction, this determines a natural equivalence
where
![]() $\mathbf {X}^{1-{\mathrm {op}}}$
has only the directions of the
$\mathbf {X}^{1-{\mathrm {op}}}$
has only the directions of the
![]() $1$
-morphisms inverted. On objects, this equivalence sends an arrow in
$1$
-morphisms inverted. On objects, this equivalence sends an arrow in
![]() $\mathbf {X}$
to the opposite arrow in
$\mathbf {X}$
to the opposite arrow in
![]() $\mathbf {X}^{1-{\mathrm {op}}}$
.
$\mathbf {X}^{1-{\mathrm {op}}}$
.
Proposition 7.9. Suppose
![]() $\mathbf {X}$
is an
$\mathbf {X}$
is an
![]() $(\infty ,2)$
-category. Then the functor
$(\infty ,2)$
-category. Then the functor
is an orthofibration where an edge
![]() $\sigma $
, given by an oplax square
$\sigma $
, given by an oplax square

over
![]() $\iota X\times X$
is cocartesian if and only if
$\iota X\times X$
is cocartesian if and only if
![]() $\rho $
is invertible, and similarly, an edge over
$\rho $
is invertible, and similarly, an edge over
![]() $ X\times \iota X$
is cartesian if and only if
$ X\times \iota X$
is cartesian if and only if
![]() $\rho $
is invertible. More formally, a morphism
$\rho $
is invertible. More formally, a morphism
![]() $\sigma :[1]\boxtimes [1] \rightarrow \mathbf {X}$
over
$\sigma :[1]\boxtimes [1] \rightarrow \mathbf {X}$
over
![]() $\iota X\times X$
(resp.
$\iota X\times X$
(resp.
![]() $ X\times \iota X$
) is cocartesian (resp. cartesian) if and only if it factors through the 2-functor
$ X\times \iota X$
) is cocartesian (resp. cartesian) if and only if it factors through the 2-functor
![]() $[1]\boxtimes [1]\rightarrow [1]\times [1]$
.
$[1]\boxtimes [1]\rightarrow [1]\times [1]$
.
Proof. Let us first show that a square
![]() $\sigma \colon [1]\times [1]\longrightarrow \mathbf {X}$
(i.e., a square
$\sigma \colon [1]\times [1]\longrightarrow \mathbf {X}$
(i.e., a square
![]() $\sigma $
for which
$\sigma $
for which
![]() $\rho $
is an equivalence), corresponding to an arrow in
$\rho $
is an equivalence), corresponding to an arrow in
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
living over
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
living over
![]() $\iota X\times X$
, is cocartesian. To see this, consider the following two equivalent unique lifting problems:
$\iota X\times X$
, is cocartesian. To see this, consider the following two equivalent unique lifting problems:

where
![]() $\Lambda _0[2]$
is the
$\Lambda _0[2]$
is the
![]() $\infty $
-category
$\infty $
-category
![]() $1 \leftarrow 0 \rightarrow 2$
. Using the explicit description of the Gray tensor product of simplices of (7.4), the right vertical map is the inclusion of the sub-
$1 \leftarrow 0 \rightarrow 2$
. Using the explicit description of the Gray tensor product of simplices of (7.4), the right vertical map is the inclusion of the sub-
![]() $(\infty ,2)$
-category of
$(\infty ,2)$
-category of
![]() $[2]\boxtimes [1]$
given by
$[2]\boxtimes [1]$
given by

Now suppose that the morphism
![]() $0\leq 1$
in
$0\leq 1$
in
![]() $\Lambda _0[2]$
projects to
$\Lambda _0[2]$
projects to
![]() $\iota X\times X$
and the corresponding map
$\iota X\times X$
and the corresponding map
![]() $[1]\boxtimes [1]\longrightarrow \mathbf {X}$
factors over
$[1]\boxtimes [1]\longrightarrow \mathbf {X}$
factors over
![]() $[1]\times [1]$
. This means that in the above diagram, the left oplax square commutes and that
$[1]\times [1]$
. This means that in the above diagram, the left oplax square commutes and that
![]() $00\longrightarrow 10$
is an equivalence. The
$00\longrightarrow 10$
is an equivalence. The
![]() $\infty $
-groupoid of such diagrams is given by the
$\infty $
-groupoid of such diagrams is given by the
![]() $\infty $
-groupoid of 2-functors from the
$\infty $
-groupoid of 2-functors from the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category

to
![]() $\mathbf {X}$
, where the left triangle commutes. For example, this follows by decomposing the 2-category before as a pushout in
$\mathbf {X}$
, where the left triangle commutes. For example, this follows by decomposing the 2-category before as a pushout in
![]() $\mathrm {Cat} _{2}$
using Proposition 7.3 and then observing that the 2-category
$\mathrm {Cat} _{2}$
using Proposition 7.3 and then observing that the 2-category

is equivalent to
![]() $[1]$
. A similar argument shows that the
$[1]$
. A similar argument shows that the
![]() $\infty $
-groupoid of diagrams
$\infty $
-groupoid of diagrams
![]() $[2]\boxtimes [1] \rightarrow \mathbf {X}$
such that the morphism
$[2]\boxtimes [1] \rightarrow \mathbf {X}$
such that the morphism
![]() $0\leq 1$
in
$0\leq 1$
in
![]() $[2]$
projects to
$[2]$
projects to
![]() $\iota X\times X$
and the corresponding map
$\iota X\times X$
and the corresponding map
![]() $[1]\boxtimes [1]\longrightarrow \mathbf {X}$
factors over
$[1]\boxtimes [1]\longrightarrow \mathbf {X}$
factors over
![]() $[1]\times [1]$
is also equivalent to the
$[1]\times [1]$
is also equivalent to the
![]() $\infty $
-groupoid of 2-functors from the
$\infty $
-groupoid of 2-functors from the
![]() $(\infty ,2)$
-category above to
$(\infty ,2)$
-category above to
![]() $\mathbf {X}$
. The functor
$\mathbf {X}$
. The functor
 $$\begin{align*}{\mathrm{Hom}}_{\mathrm{Cat} _2}\big([2]\boxtimes [1],\mathbf{X}\big)\longrightarrow {\mathrm{Hom}}_{\mathrm{Cat} _2}\big(\Lambda_0[2]\boxtimes [1]\coprod\limits_{\Lambda_0[2]\times \{0, 1\}} [2]\times \{0, 1\},\mathbf{X}\big) \end{align*}$$
$$\begin{align*}{\mathrm{Hom}}_{\mathrm{Cat} _2}\big([2]\boxtimes [1],\mathbf{X}\big)\longrightarrow {\mathrm{Hom}}_{\mathrm{Cat} _2}\big(\Lambda_0[2]\boxtimes [1]\coprod\limits_{\Lambda_0[2]\times \{0, 1\}} [2]\times \{0, 1\},\mathbf{X}\big) \end{align*}$$
lives over the restriction to
![]() $[0,1]\boxtimes [1]$
. By the previous argument, taking fibres over
$[0,1]\boxtimes [1]$
. By the previous argument, taking fibres over
![]() $\sigma $
, we obtain an equivalence, and so we conclude that
$\sigma $
, we obtain an equivalence, and so we conclude that
![]() $\sigma $
is a cocartesian edge.
$\sigma $
is a cocartesian edge.
Next, note that for any arrow in
![]() $\iota X\times X$
and a lift of its domain, there exists an
$\iota X\times X$
and a lift of its domain, there exists an
![]() $(s, t)$
-cocartesian lift
$(s, t)$
-cocartesian lift
![]() $\sigma \colon [1]\times [1]\rightarrow \mathbf {X}$
and that lifts of this form are closed under equivalence. This shows both that there are enough
$\sigma \colon [1]\times [1]\rightarrow \mathbf {X}$
and that lifts of this form are closed under equivalence. This shows both that there are enough
![]() $(s,t)$
-cocartesian edges over
$(s,t)$
-cocartesian edges over
![]() $\iota X\times X$
, and that, up to equivalence, all
$\iota X\times X$
, and that, up to equivalence, all
![]() $(s, t)$
-cocartesian lifts over
$(s, t)$
-cocartesian lifts over
![]() $\iota X\times X$
are of the form asserted in the proposition.
$\iota X\times X$
are of the form asserted in the proposition.
A dual argument proves the existence and form of
![]() $(s, t)$
-cartesian arrows over
$(s, t)$
-cartesian arrows over
![]() $X\times \iota X$
. It follows that
$X\times \iota X$
. It follows that
![]() $(s, t)$
is a curved orthofibration in the sense of Definition 6.4.
$(s, t)$
is a curved orthofibration in the sense of Definition 6.4.
To show that
![]() $(s,t)$
is an orthofibration, consider
$(s,t)$
is an orthofibration, consider
![]() $\alpha \colon a'\longrightarrow a$
,
$\alpha \colon a'\longrightarrow a$
,
![]() $\beta \colon b\longrightarrow b'$
and let
$\beta \colon b\longrightarrow b'$
and let
![]() $f\colon a\longrightarrow b$
be an object in the fibre
$f\colon a\longrightarrow b$
be an object in the fibre
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})_{(a, b)}$
. We have to show that the interpolating edge associated to this data is an equivalence. Because interpolating edges are unique, we may equivalently exhibit a commutative square in
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})_{(a, b)}$
. We have to show that the interpolating edge associated to this data is an equivalence. Because interpolating edges are unique, we may equivalently exhibit a commutative square in
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
living over the square
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
living over the square

whose bottom left corner is f and whose horizontal and vertical morphisms are cocartesian and cartesian, respectively; indeed, in this case, the interpolating edge is the identity on
![]() $\beta f \alpha $
in
$\beta f \alpha $
in
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
. Such a square is given by the following cube in
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
. Such a square is given by the following cube in
![]() $\mathbf {X}$
$\mathbf {X}$

in which all faces commute.
Let us now introduce the model for the enhanced twisted arrow
![]() $\infty $
-category given in [Reference García and SternAGS23], which is constructed via the model of scaled simplicial sets.
$\infty $
-category given in [Reference García and SternAGS23], which is constructed via the model of scaled simplicial sets.
Notation 7.10. In the following, we will denote the image of
![]() $i\in \Delta ^n$
under the inclusion
$i\in \Delta ^n$
under the inclusion ![]() by i and the image of
by i and the image of
![]() $j\in \Delta ^{n,{\mathrm {op}}}$
under the inclusion of
$j\in \Delta ^{n,{\mathrm {op}}}$
under the inclusion of ![]() by
by
![]() $\bar {j}$
.
$\bar {j}$
.
Definition 7.11. Consider the cosimplicial object
sending each n to the join ![]() , where a 2-simplex
, where a 2-simplex ![]() is thin if one of the following conditions holds:
is thin if one of the following conditions holds:
-
(i)
 $\sigma $
is degenerate,
$\sigma $
is degenerate, -
(ii)
 $\sigma $
is contained totally in either
$\sigma $
is contained totally in either
 $\Delta ^n$
or
$\Delta ^n$
or
 $\Delta ^{n,{\mathrm {op}}}$
,
$\Delta ^{n,{\mathrm {op}}}$
, -
(iii)
 $\sigma = \Delta ^{\{i,j,\bar {k}\}}$
for
$\sigma = \Delta ^{\{i,j,\bar {k}\}}$
for
 $i< j \leq k$
, or
$i< j \leq k$
, or -
(iv)
 $\sigma = \Delta ^{\{k,\bar {j},\bar {i}\}}$
for
$\sigma = \Delta ^{\{k,\bar {j},\bar {i}\}}$
for
 $i < j \leq k$
.
$i < j \leq k$
.
The functor
![]() $\kappa _{r}$
induces a functor
$\kappa _{r}$
induces a functor
![]() $\operatorname {\mathrm {Tw}}^{r}=S_{\kappa _{r}}\colon {\mathrm {sSet}}^{\mathrm {sc}}\longrightarrow {\mathrm {sSet}}$
from scaled simplicial sets to simplicial sets such that
$\operatorname {\mathrm {Tw}}^{r}=S_{\kappa _{r}}\colon {\mathrm {sSet}}^{\mathrm {sc}}\longrightarrow {\mathrm {sSet}}$
from scaled simplicial sets to simplicial sets such that ![]() . We enhance this to a functor with values in marked simplicial sets by declaring an edge in
. We enhance this to a functor with values in marked simplicial sets by declaring an edge in
![]() $\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}, S)$
to be marked if it arises from a totally thin diagram
$\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}, S)$
to be marked if it arises from a totally thin diagram ![]() and write
and write
for the resulting functor. Note that the two inclusions ![]() induce a map
induce a map
![]() $\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}, S)\rightarrow X\times X^{{\mathrm {op}}}$
.
$\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}, S)\rightarrow X\times X^{{\mathrm {op}}}$
.
Theorem 7.12 (Abellán García, Stern)
Let
![]() $p\colon (\mathbf {Y}, T)\longrightarrow (\mathbf {X}, S)$
be a fibration between fibrant scaled simplicial sets. Then the map
$p\colon (\mathbf {Y}, T)\longrightarrow (\mathbf {X}, S)$
be a fibration between fibrant scaled simplicial sets. Then the map
is a fibration between fibrant objects in the cartesian model structure on
![]() $({\mathrm {sSet}}^{+}){/Y\times Y^{{\mathrm {op}}}}$
(where all arrows in
$({\mathrm {sSet}}^{+}){/Y\times Y^{{\mathrm {op}}}}$
(where all arrows in
![]() $X\times X^{{\mathrm {op}}}$
and
$X\times X^{{\mathrm {op}}}$
and
![]() $Y\times Y^{{\mathrm {op}}}$
are marked).
$Y\times Y^{{\mathrm {op}}}$
are marked).
For each fibrant scaled simplicial set
![]() $(\mathbf {X}, S)$
, the cartesian fibration
$(\mathbf {X}, S)$
, the cartesian fibration
![]() $\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}, S)\longrightarrow X\times X^{{\mathrm {op}}}$
is classified by the functor
$\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}, S)\longrightarrow X\times X^{{\mathrm {op}}}$
is classified by the functor
![]() ${\mathrm {Hom}}_{\mathbf {X}}\colon X^{{\mathrm {op}}}\times X\longrightarrow \mathrm {Cat} $
.
${\mathrm {Hom}}_{\mathbf {X}}\colon X^{{\mathrm {op}}}\times X\longrightarrow \mathrm {Cat} $
.
Proof. For the first part, it suffices to verify that
![]() $\operatorname {\mathrm {Tw}}^{r}_+(\mathbf {Y}, T)\longrightarrow \operatorname {\mathrm {Tw}}^{r}_+(\mathbf {X}, S)\times _{X\times X^{\mathrm {op}}} Y\times Y^{{\mathrm {op}}}$
has the right lifting property with respect to all marked anodyne maps [Reference LurieLu17, Proposition B.2.7]. Let us write L for the left adjoint of
$\operatorname {\mathrm {Tw}}^{r}_+(\mathbf {Y}, T)\longrightarrow \operatorname {\mathrm {Tw}}^{r}_+(\mathbf {X}, S)\times _{X\times X^{\mathrm {op}}} Y\times Y^{{\mathrm {op}}}$
has the right lifting property with respect to all marked anodyne maps [Reference LurieLu17, Proposition B.2.7]. Let us write L for the left adjoint of
![]() $\operatorname {\mathrm {Tw}}^{r}_+$
and note that for each marked simplicial set
$\operatorname {\mathrm {Tw}}^{r}_+$
and note that for each marked simplicial set
![]() $(A, E)$
, there is a natural map
$(A, E)$
, there is a natural map
![]() $A^{\sharp }\amalg A^{{\mathrm {op}}, \sharp }\longrightarrow L(A, E)$
, such that mapping into
$A^{\sharp }\amalg A^{{\mathrm {op}}, \sharp }\longrightarrow L(A, E)$
, such that mapping into
![]() $(\mathbf {X},S)$
, we obtain the value of the canonical projection
$(\mathbf {X},S)$
, we obtain the value of the canonical projection
![]() $\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}, S)\longrightarrow X\times X^{{\mathrm {op}}}$
on
$\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}, S)\longrightarrow X\times X^{{\mathrm {op}}}$
on
![]() $(A,E)$
. The desired right lifting property now follows from the fact that for each (generating) marked anodyne map
$(A,E)$
. The desired right lifting property now follows from the fact that for each (generating) marked anodyne map
![]() $(A, E)\longrightarrow (B, F)$
, the map
$(A, E)\longrightarrow (B, F)$
, the map
is a scaled anodyne map [Reference García and SternAGS23, Lemma 2.9 and 2.10]. The second part of the theorem is [Reference García and SternAGS23, Theorem 3.3].
Corollary 7.13. The functor
![]() $\operatorname {\mathrm {Tw}}^{r}\colon {\mathrm {sSet}}^{\mathrm {sc}}\longrightarrow {\mathrm {sSet}}$
is a right Quillen functor, where
$\operatorname {\mathrm {Tw}}^{r}\colon {\mathrm {sSet}}^{\mathrm {sc}}\longrightarrow {\mathrm {sSet}}$
is a right Quillen functor, where
![]() ${\mathrm {sSet}}$
is endowed with the Joyal model structure.
${\mathrm {sSet}}$
is endowed with the Joyal model structure.
Proof. The left adjoint to
![]() $\operatorname {\mathrm {Tw}}^{r}$
preserves cofibrations, which are simply monomorphisms. Furthermore, Theorem 7.12 implies that the map
$\operatorname {\mathrm {Tw}}^{r}$
preserves cofibrations, which are simply monomorphisms. Furthermore, Theorem 7.12 implies that the map
is a composite of fibrations in the cartesian model structure. Since fibrations in the cartesian model structure are, in particular, categorical fibrations [Reference LurieLu09a, Proposition 3.1.5.3], we conclude that
![]() $\operatorname {\mathrm {Tw}}^{r}$
sends fibrations between fibrant scaled simplicial sets to categorical fibrations between quasicategories. This suffices by [Reference JoyalJo08, Proposition E.2.14].
$\operatorname {\mathrm {Tw}}^{r}$
sends fibrations between fibrant scaled simplicial sets to categorical fibrations between quasicategories. This suffices by [Reference JoyalJo08, Proposition E.2.14].
Definition 7.14. The right Quillen functor from Corollary 7.13 induces a right adjoint functor of
![]() $\infty $
-categories which we will denote
$\infty $
-categories which we will denote
![]() $\operatorname {\mathrm {Tw}}^{r}\colon \mathrm {Cat} _2\longrightarrow \mathrm {Cat} $
and refer to as taking the oplax twisted arrow
$\operatorname {\mathrm {Tw}}^{r}\colon \mathrm {Cat} _2\longrightarrow \mathrm {Cat} $
and refer to as taking the oplax twisted arrow
![]() $\infty $
-category.
$\infty $
-category.
To compare with the oplax arrow category, it will be convenient to give a slightly different presentation of
![]() $\operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
in terms of Segal
$\operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
in terms of Segal
![]() $\infty $
-groupoids (which a posteriori does not make use of scaled simplicial sets). To this end, let us make the following observation:
$\infty $
-groupoids (which a posteriori does not make use of scaled simplicial sets). To this end, let us make the following observation:
Definition 7.15. Let us write ![]() for the gaunt
for the gaunt
![]() $2$
-category informally depicted as
$2$
-category informally depicted as

More precisely, the categories ![]() and
and ![]() are a point if
are a point if
![]() $i\leq j$
and empty otherwise, and
$i\leq j$
and empty otherwise, and ![]() is the poset of integers
is the poset of integers
![]() $\max (i, j)\leq '\leq n$
, ordered by size. We will refer to these integers as heights. The composition maps preserve these heights. One readily verifies that this defines a functor
$\max (i, j)\leq '\leq n$
, ordered by size. We will refer to these integers as heights. The composition maps preserve these heights. One readily verifies that this defines a functor
![]() ${\mathbf {\Delta }}\longrightarrow \mathrm {Gaunt}_2\subseteq \mathrm {Cat} _2$
.
${\mathbf {\Delta }}\longrightarrow \mathrm {Gaunt}_2\subseteq \mathrm {Cat} _2$
.
Lemma 7.16. For each n, there is a natural equivalence between ![]() and the
and the
![]() $(\infty ,2)$
-category presented by the scaled simplicial set
$(\infty ,2)$
-category presented by the scaled simplicial set ![]() .
.
Proof. We will provide a natural weak equivalence of cosimplicial diagrams in
![]() $\mathrm {Cat} ({\mathrm {sSet}}^{+})$
$\mathrm {Cat} ({\mathrm {sSet}}^{+})$
where the target is viewed as a marked simplicially enriched category by taking nerves of the mapping categories.
Unraveling the definitions, ![]() is given as follows. Its objects are the objects of the poset
is given as follows. Its objects are the objects of the poset
![]() $0\leq \dots \leq n\leq \overline {n}\leq \dots \leq \overline {0}$
. Given two such objects
$0\leq \dots \leq n\leq \overline {n}\leq \dots \leq \overline {0}$
. Given two such objects
![]() $a, b$
, the simplicial set
$a, b$
, the simplicial set
![]() ${\mathrm {Hom}}(a, b)$
is the nerve of the poset of chains
${\mathrm {Hom}}(a, b)$
is the nerve of the poset of chains
![]() $a=x_0\leq x_1\leq \dots \leq x_l=b$
, ordered by inclusion. Within (the nerve of) this poset of chains, the following arrows are marked:
$a=x_0\leq x_1\leq \dots \leq x_l=b$
, ordered by inclusion. Within (the nerve of) this poset of chains, the following arrows are marked:
-
(a) if
 $a=i$
and
$a=i$
and
 $b=j$
are both contained in the first half or if
$b=j$
are both contained in the first half or if
 $a=\overline {i}$
and
$a=\overline {i}$
and
 $b=\overline {j}$
are both contained in the second half, then all inclusions of chains are marked.
$b=\overline {j}$
are both contained in the second half, then all inclusions of chains are marked. -
(b) for
 $a=i$
and
$a=i$
and
 $b=\overline {j}$
, let us define the height of a chain
$b=\overline {j}$
, let us define the height of a chain
 $\sigma \colon i=x_0\leq x_1\leq \dots \leq x_l=\overline {j}$
to be the largest number k such that either k or
$\sigma \colon i=x_0\leq x_1\leq \dots \leq x_l=\overline {j}$
to be the largest number k such that either k or
 $\overline {k}$
is contained in
$\overline {k}$
is contained in
 $\sigma $
. Then an inclusion of chains is marked if it does not change the height.
$\sigma $
. Then an inclusion of chains is marked if it does not change the height.
The map
![]() $\phi $
is then given by the identity on objects and on (nerves of) mapping categories it (a) either sends all chains to the point or (b) takes the height of a chain. It suffices to verify that these maps between mapping categories are exactly the localisations at the marked arrows. This is evident in case (a), since the poset of chains is either empty or a cube (hence contractible). In case (b), the functor sending a chain to its height has a fully faithful right adjoint, sending each height k to the maximal chain
$\phi $
is then given by the identity on objects and on (nerves of) mapping categories it (a) either sends all chains to the point or (b) takes the height of a chain. It suffices to verify that these maps between mapping categories are exactly the localisations at the marked arrows. This is evident in case (a), since the poset of chains is either empty or a cube (hence contractible). In case (b), the functor sending a chain to its height has a fully faithful right adjoint, sending each height k to the maximal chain
![]() $i\leq i+1\leq \dots \leq k-1\leq k\leq \overline {k}\leq \overline {k-1}\leq \dots \leq \overline {j+1}\leq \overline {j}$
.
$i\leq i+1\leq \dots \leq k-1\leq k\leq \overline {k}\leq \overline {k-1}\leq \dots \leq \overline {j+1}\leq \overline {j}$
.
Corollary 7.17. Let
![]() $\mathbf {X}$
be an
$\mathbf {X}$
be an
![]() $(\infty ,2)$
-category. Then the simplicial
$(\infty ,2)$
-category. Then the simplicial
![]() $\infty $
-groupoid
$\infty $
-groupoid
is a complete Segal
![]() $\infty $
-groupoid, whose associated
$\infty $
-groupoid, whose associated
![]() $\infty $
-category is naturally equivalent to
$\infty $
-category is naturally equivalent to
![]() $\operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
.
$\operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
.
Proof. Corollary 7.13 and Lemma 7.16 identify the simplicial
![]() $\infty $
-groupoid
$\infty $
-groupoid ![]() with
with
![]() $\mathrm {N}(\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}))$
.
$\mathrm {N}(\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}))$
.
We will now compute the image of
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
under the dualisation functor
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})$
under the dualisation functor
and show it is equivalent to the functor
Recall that
![]() $\mathrm {S}\mathrm {D}^{\mathrm {ct}}$
is given as the composite of
$\mathrm {S}\mathrm {D}^{\mathrm {ct}}$
is given as the composite of
![]() $(-)^{\mathrm {op}}$
and
$(-)^{\mathrm {op}}$
and
![]() ${\mathrm {Span}^{\perp }}$
. Since Remark 7.7 identifies the opposite of the oplax arrow category of
${\mathrm {Span}^{\perp }}$
. Since Remark 7.7 identifies the opposite of the oplax arrow category of
![]() $\mathbf {X}$
with the lax arrow category of
$\mathbf {X}$
with the lax arrow category of
![]() $\mathbf {X}^{1-{\mathrm {op}}}$
, we find that the dual of
$\mathbf {X}^{1-{\mathrm {op}}}$
, we find that the dual of
![]() $(s, t)\colon \operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})\longrightarrow X\times X$
is given by
$(s, t)\colon \operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X})\longrightarrow X\times X$
is given by
Unwinding definitions, we find that
![]() $\mathcal {D}$
is the associated
$\mathcal {D}$
is the associated
![]() $\infty $
-category of the complete Segal
$\infty $
-category of the complete Segal
![]() $\infty $
-groupoid given in level n by the sub-
$\infty $
-groupoid given in level n by the sub-
![]() $\infty $
-groupoid of
$\infty $
-groupoid of
spanned by the functors
which send
-
(i)
 $\operatorname {\mathrm {Tw}}^{r}([n])_{\mathrm {in}} \boxtimes \{1\}$
to
$\operatorname {\mathrm {Tw}}^{r}([n])_{\mathrm {in}} \boxtimes \{1\}$
to
 $\iota {X^{\mathrm {op}}}$
,
$\iota {X^{\mathrm {op}}}$
, -
(ii)
 $\operatorname {\mathrm {Tw}}^{r}([n])^{\mathrm {eg}} \boxtimes \{0\}$
to
$\operatorname {\mathrm {Tw}}^{r}([n])^{\mathrm {eg}} \boxtimes \{0\}$
to
 $\iota {X^{\mathrm {op}}}$
, and
$\iota {X^{\mathrm {op}}}$
, and -
(iii) every 2-morphism
 $\sigma \subseteq \operatorname {\mathrm {Tw}}^{r}([n])_{\mathrm {in}} \boxtimes [1]$
to an invertible 2-morphism in
$\sigma \subseteq \operatorname {\mathrm {Tw}}^{r}([n])_{\mathrm {in}} \boxtimes [1]$
to an invertible 2-morphism in
 $\mathbf {X}$
.
$\mathbf {X}$
.
This is, of course, naturally equivalent to the
![]() $\infty $
-groupoid of functors
$\infty $
-groupoid of functors
![]() $f\colon \big (\operatorname {\mathrm {Tw}}^{r}([n])\boxtimes [1]\big )^{1-{\mathrm {op}}} \longrightarrow \mathbf {X}$
satisfying analogous conditions. To obtain a functor
$f\colon \big (\operatorname {\mathrm {Tw}}^{r}([n])\boxtimes [1]\big )^{1-{\mathrm {op}}} \longrightarrow \mathbf {X}$
satisfying analogous conditions. To obtain a functor
![]() $\mathcal {D}\rightarrow \operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
, we will write down a natural transformation of cosimplicial objects in
$\mathcal {D}\rightarrow \operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
, we will write down a natural transformation of cosimplicial objects in
![]() $\mathrm {Cat} _2$
$\mathrm {Cat} _2$
We will produce this map at the level of scaled simplicial sets, using that for a scaled simplicial set
![]() $(\mathbf {Y}',T)$
modeling
$(\mathbf {Y}',T)$
modeling
![]() $\mathbf {Y}$
, the opposite
$\mathbf {Y}$
, the opposite
![]() $\mathbf {Y}^{1-{\mathrm {op}}}$
is modelled by
$\mathbf {Y}^{1-{\mathrm {op}}}$
is modelled by
![]() $((\mathbf {Y}')^{{\mathrm {op}}}, T)$
. Let us therefore define
$((\mathbf {Y}')^{{\mathrm {op}}}, T)$
. Let us therefore define

exactly as in Example 6.15. By inspection, this defines a map of scaled simplicial sets. For example,
![]() $\phi _n(\sigma ,\sigma ') = \Delta ^{\{i,j,\bar {k}\}}$
for
$\phi _n(\sigma ,\sigma ') = \Delta ^{\{i,j,\bar {k}\}}$
for
![]() $i\leq j\leq k$
when
$i\leq j\leq k$
when
![]() $\sigma '$
equals
$\sigma '$
equals
![]() $s_1\colon \Delta ^{2}\rightarrow \Delta ^{\{0,1\}}$
. By definition, this is thin in
$s_1\colon \Delta ^{2}\rightarrow \Delta ^{\{0,1\}}$
. By definition, this is thin in ![]() . Similarly, one can readily show that the image of the other thin simplicies is thin. We conclude that the
. Similarly, one can readily show that the image of the other thin simplicies is thin. We conclude that the
![]() $\phi _n$
determine a natural transformation of cosimplicial objects in
$\phi _n$
determine a natural transformation of cosimplicial objects in
![]() ${\mathrm {sSet}}^{\mathrm {sc}}$
.
${\mathrm {sSet}}^{\mathrm {sc}}$
.
Example 7.18. Let us describe the induced map ![]() in
in
![]() $\mathrm {Cat} _2$
a bit more precisely in the case
$\mathrm {Cat} _2$
a bit more precisely in the case
![]() $n=1$
. In this case, the domain is the pushout in
$n=1$
. In this case, the domain is the pushout in
![]() $\mathrm {Cat} _2$
of two lax squares along a common
$\mathrm {Cat} _2$
of two lax squares along a common
![]() $1$
-morphism, which is a gaunt
$1$
-morphism, which is a gaunt
![]() $2$
-category by Proposition 7.3. In particular, the domain and codomain of
$2$
-category by Proposition 7.3. In particular, the domain and codomain of
![]() $\phi _1$
are gaunt
$\phi _1$
are gaunt
![]() $2$
-categories, and the map
$2$
-categories, and the map
![]() $\phi _1$
is then given by the strict
$\phi _1$
is then given by the strict
![]() $2$
-functor
$2$
-functor

obtained by collapsing the
![]() $1$
- and
$1$
- and
![]() $2$
-morphisms marked by
$2$
-morphisms marked by
![]() $\sim $
. To see that this agrees with the description of
$\sim $
. To see that this agrees with the description of
![]() $\phi _1$
in terms of scaled simplicial sets, it suffices to note that this strict
$\phi _1$
in terms of scaled simplicial sets, it suffices to note that this strict
![]() $2$
-functor is uniquely determined by its values on objects and
$2$
-functor is uniquely determined by its values on objects and
![]() $1$
-morphisms.
$1$
-morphisms.
Remark 7.20. More generally, since ![]() is a gaunt
is a gaunt
![]() $2$
-category,
$2$
-category,
![]() $\phi _n$
is adjoint to a (strict) functor
$\phi _n$
is adjoint to a (strict) functor ![]() into its strict oplax arrow category (see Example 7.6). This functor sends each
into its strict oplax arrow category (see Example 7.6). This functor sends each
![]() $(i\leq j)$
in
$(i\leq j)$
in
![]() $\operatorname {\mathrm {Tw}}^{r}([n])$
to the arrow
$\operatorname {\mathrm {Tw}}^{r}([n])$
to the arrow
![]() $j\to \overline {i}$
in
$j\to \overline {i}$
in ![]() of minimal height.
of minimal height.
For each
![]() $\mathbf {X}$
, the maps
$\mathbf {X}$
, the maps
![]() $\phi _n$
induce a natural transformation of simplicial
$\phi _n$
induce a natural transformation of simplicial
![]() $\infty $
-groupoids
$\infty $
-groupoids
which, after taking associated
![]() $\infty $
-categories, gives a functor
$\infty $
-categories, gives a functor
![]() $\Phi \colon \mathcal {D}\rightarrow \operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
which evidently commutes with the canonical functors to
$\Phi \colon \mathcal {D}\rightarrow \operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
which evidently commutes with the canonical functors to
![]() $X\times X^{\mathrm {op}}$
.
$X\times X^{\mathrm {op}}$
.
Theorem 7.21. The functor
is an equivalence of
![]() $\infty $
-categories. Consequently, the orthofibration
$\infty $
-categories. Consequently, the orthofibration
![]() $(s,t)\colon \operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X}) \rightarrow X \times X$
classifies the mapping
$(s,t)\colon \operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X}) \rightarrow X \times X$
classifies the mapping
![]() $\infty $
-category functor
$\infty $
-category functor
Proof. Given the first part of the theorem, the second part follows from Corollary 6.14 and Theorem 7.12. Because both sides of the equivalence are the associated
![]() $\infty $
-category of Segal
$\infty $
-category of Segal
![]() $\infty $
-groupoids, and the functor is induced by a natural transformation of Segal
$\infty $
-groupoids, and the functor is induced by a natural transformation of Segal
![]() $\infty $
-groupoids, it suffices to prove that
$\infty $
-groupoids, it suffices to prove that
![]() $\Phi _0$
and
$\Phi _0$
and
![]() $\Phi _1$
are equivalences of
$\Phi _1$
are equivalences of
![]() $\infty $
-groupoids. Note that the map
$\infty $
-groupoids. Note that the map
![]() $\phi _0$
is simply the identity on
$\phi _0$
is simply the identity on
![]() $[1]$
, so that
$[1]$
, so that
![]() $\Phi _0$
is certainly an equivalence.
$\Phi _0$
is certainly an equivalence.
To see that
![]() $\Phi _1$
is an equivalence, note that its domain
$\Phi _1$
is an equivalence, note that its domain
![]() $\mathrm {N}(\mathcal {D})_1$
is the
$\mathrm {N}(\mathcal {D})_1$
is the
![]() $\infty $
-groupoid of
$\infty $
-groupoid of
![]() $2$
-functors from the gaunt
$2$
-functors from the gaunt
![]() $2$
-category
$2$
-category
![]() $(\operatorname {\mathrm {Tw}}^{r}([1])\times [1])^{{\mathrm {op}}}$
$(\operatorname {\mathrm {Tw}}^{r}([1])\times [1])^{{\mathrm {op}}}$

sending the marked
![]() $1$
- and
$1$
- and
![]() $2$
-cells to equivalences in
$2$
-cells to equivalences in
![]() $\mathbf {X}$
. It therefore suffices to verify that the functor
$\mathbf {X}$
. It therefore suffices to verify that the functor
![]() $\phi _1$
(7.19) is the universal functor of
$\phi _1$
(7.19) is the universal functor of
![]() $(\infty ,2)$
-categories that collapses these marked morphisms and
$(\infty ,2)$
-categories that collapses these marked morphisms and
![]() $2$
-morphisms.
$2$
-morphisms.
To see this, we observe that the above gaunt
![]() $2$
-category can be obtained by ‘cell attachments’, along the lines of the following picture:
$2$
-category can be obtained by ‘cell attachments’, along the lines of the following picture:

Here, we start from the middle vertical arrow and attach the bottom horizontal arrows, then the 2-cells and finally the factorisations over
![]() $00$
and
$00$
and
![]() $11$
. Each step is given by a pushout of gaunt
$11$
. Each step is given by a pushout of gaunt
![]() $2$
-categories as described in Proposition 7.3 (which is hence also a pushout in
$2$
-categories as described in Proposition 7.3 (which is hence also a pushout in
![]() $\mathrm {Cat} _2$
).
$\mathrm {Cat} _2$
).
For each pushout where we add a marked cell, collapsing the resulting cell in
![]() $\mathrm {Cat} _2$
simply has the result of not adding a cell at all. Consequently, the
$\mathrm {Cat} _2$
simply has the result of not adding a cell at all. Consequently, the
![]() $(\infty ,2)$
-category obtained from
$(\infty ,2)$
-category obtained from
![]() $(\operatorname {\mathrm {Tw}}^{r}([1])\times [1])^{{\mathrm {op}}}$
by collapsing the marked cells is the gaunt
$(\operatorname {\mathrm {Tw}}^{r}([1])\times [1])^{{\mathrm {op}}}$
by collapsing the marked cells is the gaunt
![]() $2$
-category obtained by performing only those cell attachments where no marked cell was added. The result of this is then precisely
$2$
-category obtained by performing only those cell attachments where no marked cell was added. The result of this is then precisely ![]() , and the collapsing map is precisely
, and the collapsing map is precisely
![]() $\phi _1$
.
$\phi _1$
.
Remark 7.22. Note that the functor
![]() ${\mathrm {Hom}}_{\textbf {Cat}}(*,-)\colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
is equivalent to the identity on
${\mathrm {Hom}}_{\textbf {Cat}}(*,-)\colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
is equivalent to the identity on
![]() $\mathrm {Cat} $
. Therefore, we conclude immediately from the previous theorem that the functor
$\mathrm {Cat} $
. Therefore, we conclude immediately from the previous theorem that the functor
is a model for the universal cocartesian fibration (i.e., the cocartesian fibration which classifies the identity on
![]() $\mathrm {Cat} $
). The fibre of
$\mathrm {Cat} $
). The fibre of
![]() $s\colon \operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\textbf {Cat})\rightarrow \mathrm {Cat} $
over
$s\colon \operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\textbf {Cat})\rightarrow \mathrm {Cat} $
over
![]() $*$
is one definition for the oplax slice category
$*$
is one definition for the oplax slice category
![]() $*/\!/^{\mathrm {opl}} \,\mathrm {Cat} $
, and the previous theorem therefore gives one way to make precise the statement that the forgetful functor
$*/\!/^{\mathrm {opl}} \,\mathrm {Cat} $
, and the previous theorem therefore gives one way to make precise the statement that the forgetful functor
![]() $*/\!/^{\mathrm {opl}} \,\mathrm {Cat} \rightarrow \mathrm {Cat} $
is the universal cocartesian fibration.
$*/\!/^{\mathrm {opl}} \,\mathrm {Cat} \rightarrow \mathrm {Cat} $
is the universal cocartesian fibration.
The universal cartesian fibration has a similar description. Indeed, by Remark 7.7, the functor
is equivalent to
Again by Theorem 7.21, this classifies the enhanced mapping functor of
![]() $\mathbf {X}^{1-{\mathrm {op}}}$
, which is equivalent to the functor
$\mathbf {X}^{1-{\mathrm {op}}}$
, which is equivalent to the functor
Applying this in the case
![]() $\mathbf {X} = \textbf {Cat}$
, we obtain that the functor
$\mathbf {X} = \textbf {Cat}$
, we obtain that the functor
is a cartesian fibration which classifies the identity on
![]() $\mathrm {Cat} $
. Because the fibre of
$\mathrm {Cat} $
. Because the fibre of
![]() $t\colon \operatorname {\mathrm {Ar}}^{\mathrm {lax}}(\textbf {Cat})\rightarrow \mathrm {Cat} $
over
$t\colon \operatorname {\mathrm {Ar}}^{\mathrm {lax}}(\textbf {Cat})\rightarrow \mathrm {Cat} $
over
![]() $\{*\}$
is one definition for the lax over-category, this makes precise the statement that
$\{*\}$
is one definition for the lax over-category, this makes precise the statement that ![]() is the universal cartesian fibration.
is the universal cartesian fibration.
Remark 7.23. Let us also briefly discuss the cocartesian fibration encoding the enhanced mapping functor of an
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathbf {X}$
. Just as for
$\mathbf {X}$
. Just as for
![]() $\infty $
-categories, it is given by a version of the left twisted arrow
$\infty $
-categories, it is given by a version of the left twisted arrow
![]() $\infty $
-category. However, simply taking the opposite of
$\infty $
-category. However, simply taking the opposite of
![]() $\operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
, as one does for
$\operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
, as one does for
![]() $\infty $
-categories, would also apply
$\infty $
-categories, would also apply
![]() $(-)^{{\mathrm {op}}}$
to the fibres. Therefore, we instead consider the simplicial object
$(-)^{{\mathrm {op}}}$
to the fibres. Therefore, we instead consider the simplicial object
![]() $\kappa _{l} = (\kappa _{r})^{\mathrm {rev},2-{\mathrm {op}}}$
in
$\kappa _{l} = (\kappa _{r})^{\mathrm {rev},2-{\mathrm {op}}}$
in
![]() $\mathrm {Cat} _{2}$
obtained from that defining
$\mathrm {Cat} _{2}$
obtained from that defining
![]() $\operatorname {\mathrm {Tw}}^{r}$
by reversing the simplicial direction and taking opposites for
$\operatorname {\mathrm {Tw}}^{r}$
by reversing the simplicial direction and taking opposites for
![]() $2$
-morphisms at each level and define
$2$
-morphisms at each level and define
![]() $\operatorname {\mathrm {Tw}}^{\ell }(\mathbf {X})= S_{\kappa _{l}}(\mathbf {X})$
. By direct inspection, one then finds
$\operatorname {\mathrm {Tw}}^{\ell }(\mathbf {X})= S_{\kappa _{l}}(\mathbf {X})$
. By direct inspection, one then finds
![]() $\operatorname {\mathrm {Tw}}^{\ell }(\mathbf {X}) \simeq \operatorname {\mathrm {Tw}}^{r}(\mathbf {X}^{2-{\mathrm {op}}})^{{\mathrm {op}}}$
. In particular, it follows from Theorem 7.12 that
$\operatorname {\mathrm {Tw}}^{\ell }(\mathbf {X}) \simeq \operatorname {\mathrm {Tw}}^{r}(\mathbf {X}^{2-{\mathrm {op}}})^{{\mathrm {op}}}$
. In particular, it follows from Theorem 7.12 that
is a cocartesian fibration, which classifies the composition
We claim this composite is the enhanced mapping functor of
![]() $\mathbf X$
. One way to see this is to note that the functor
$\mathbf X$
. One way to see this is to note that the functor
![]() $(-)^{2-{\mathrm {op}}}\colon \mathrm {Cat} _2\rightarrow \mathrm {Cat} _2$
is modelled on categories enriched in marked simplicial sets (which we used to define the enhanced mapping functor) by changing the enrichment via
$(-)^{2-{\mathrm {op}}}\colon \mathrm {Cat} _2\rightarrow \mathrm {Cat} _2$
is modelled on categories enriched in marked simplicial sets (which we used to define the enhanced mapping functor) by changing the enrichment via
![]() $(-)^{{\mathrm {op}}}\colon {\mathrm {sSet}}_{+}\rightarrow {\mathrm {sSet}}_{+}$
. Let us remark that the model of scaled simplicial sets does not seem to admit a simple implementation of reversing
$(-)^{{\mathrm {op}}}\colon {\mathrm {sSet}}_{+}\rightarrow {\mathrm {sSet}}_{+}$
. Let us remark that the model of scaled simplicial sets does not seem to admit a simple implementation of reversing
![]() $2$
-morphisms, so, in particular, we do not know of a simplicial object in scaled simplicial sets giving rise to
$2$
-morphisms, so, in particular, we do not know of a simplicial object in scaled simplicial sets giving rise to
![]() $\kappa ^{\mathrm {rev},2-{\mathrm {op}}}$
, and consequently also no explicit model for
$\kappa ^{\mathrm {rev},2-{\mathrm {op}}}$
, and consequently also no explicit model for
![]() $\operatorname {\mathrm {Tw}}^{\ell }(\mathbf {X})$
as a scaled simplicial set even if
$\operatorname {\mathrm {Tw}}^{\ell }(\mathbf {X})$
as a scaled simplicial set even if
![]() $\mathbf {X}$
is given as such. Nevertheless, applying the equivalence of Lemma 7.16, one can write down a cosimplicial diagram of gaunt
$\mathbf {X}$
is given as such. Nevertheless, applying the equivalence of Lemma 7.16, one can write down a cosimplicial diagram of gaunt
![]() $2$
-categories equivalent to
$2$
-categories equivalent to
![]() $\kappa _{l}$
.
$\kappa _{l}$
.
Note also that
![]() $\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}^{1-{\mathrm {op}}}) \simeq \operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
as cartesian fibrations over
$\operatorname {\mathrm {Tw}}^{r}(\mathbf {X}^{1-{\mathrm {op}}}) \simeq \operatorname {\mathrm {Tw}}^{r}(\mathbf {X})$
as cartesian fibrations over
![]() $X\times X^{\mathrm {op}}$
, since
$X\times X^{\mathrm {op}}$
, since
![]() $(\kappa _{r})^{1-{\mathrm {op}}}\simeq \kappa _{r}$
.
$(\kappa _{r})^{1-{\mathrm {op}}}\simeq \kappa _{r}$
.
Remark 7.24. For the sake of completeness, let us also mention the behaviour of
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}$
and
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}$
and
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {lax}}$
under the two kinds of taking opposites. Recall that we have already seen in (7.8) that
$\operatorname {\mathrm {Ar}}^{\mathrm {lax}}$
under the two kinds of taking opposites. Recall that we have already seen in (7.8) that
![]() $\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X}^{1-{\mathrm {op}}}) \simeq \operatorname {\mathrm {Ar}}^{\mathrm {lax}}(\mathbf {X})^{{\mathrm {op}}}$
. We are left to note
$\operatorname {\mathrm {Ar}}^{\mathrm {opl}}(\mathbf {X}^{1-{\mathrm {op}}}) \simeq \operatorname {\mathrm {Ar}}^{\mathrm {lax}}(\mathbf {X})^{{\mathrm {op}}}$
. We are left to note
To see this, observe that both are orthofibrations over
![]() $X \times X$
and that the functors
$X \times X$
and that the functors
![]() $X^{{\mathrm {op}}} \times X \rightarrow \mathrm {Cat} $
which both classify are equivalent by Theorem 7.21 and the corresponding statements for the twisted arrow
$X^{{\mathrm {op}}} \times X \rightarrow \mathrm {Cat} $
which both classify are equivalent by Theorem 7.21 and the corresponding statements for the twisted arrow
![]() $\infty $
-categories.
$\infty $
-categories.
8 Naturality of the Yoneda embedding
In this short final section, we deduce the following result as an application of Lemma 6.20:
Theorem 8.1. The Yoneda embedding
![]() ${A} \rightarrow {\mathcal {P}}({A})$
canonically extends to a natural transformation of functors
${A} \rightarrow {\mathcal {P}}({A})$
canonically extends to a natural transformation of functors
![]() $\mathrm {Cat} \rightarrow $
Cat
from the inclusion to the composite
$\mathrm {Cat} \rightarrow $
Cat
from the inclusion to the composite
Remark 8.2. As our model of the equivalence ![]() , we take the equivalence of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Theorem 3.1.11]. Intuitively, it acts as the identity on objects and sends a left adjoint
, we take the equivalence of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Theorem 3.1.11]. Intuitively, it acts as the identity on objects and sends a left adjoint
![]() $L\colon C\rightarrow D$
to a choice of right adjoint
$L\colon C\rightarrow D$
to a choice of right adjoint
![]() $R\colon D\rightarrow C$
.
$R\colon D\rightarrow C$
.
Remark 8.3. This question was recently posed to the second author (among others) by D. Clausen during a visit to the University of Copenhagen, as it can be used to simplify a number of arguments in [Reference Clausen and JansenCØJ21, Section 2] and appears missing from the literature so far. It is a lucky accident that our methods answer it.
Let us also mention that, building on Theorem 8.1, Ben Moshe and Schlank have recently upgraded the monoidal (and modal) versions of the Yoneda embedding to natural transformations as well; see [Reference Moshe and SchlankBMS21, Theorem D].
Before giving a proof of Theorem 8.1, let us briefly comment on related results that already appear in the literature. First, the characterisation of
![]() ${\mathcal {P}}({A})$
as the free cocompletion of
${\mathcal {P}}({A})$
as the free cocompletion of
![]() ${A}$
[Reference LurieLu09a, Section 5.1.5] implies that the assignment
${A}$
[Reference LurieLu09a, Section 5.1.5] implies that the assignment
![]() ${A} \mapsto {\mathcal {P}}({A})$
extends to a functor equipped with a natural transformation
${A} \mapsto {\mathcal {P}}({A})$
extends to a functor equipped with a natural transformation
![]() ${A}\longrightarrow {\mathcal {P}}({A})$
given pointwise by the Yoneda embedding (essentially by construction). However, it is not a priori clear that this second functor agrees with the one described in Theorem 8.1; let us write
${A}\longrightarrow {\mathcal {P}}({A})$
given pointwise by the Yoneda embedding (essentially by construction). However, it is not a priori clear that this second functor agrees with the one described in Theorem 8.1; let us write
![]() ${\mathcal {P}}_{\mathrm {free}}$
and
${\mathcal {P}}_{\mathrm {free}}$
and
![]() ${\mathcal {P}}_{\mathrm {Kan}}$
to distinguish these two functorialities, the first being the functoriality via the free cocompletion and the second the functoriality of the statement.
${\mathcal {P}}_{\mathrm {Kan}}$
to distinguish these two functorialities, the first being the functoriality via the free cocompletion and the second the functoriality of the statement.
Without considering the naturality of the Yoneda embedding, one can produce a natural equivalence
![]() ${\mathcal {P}}_{\mathrm {free}}\simeq {\mathcal {P}}_{\mathrm {Kan}}$
as follows. Both of these functors are easily checked to factor as
${\mathcal {P}}_{\mathrm {free}}\simeq {\mathcal {P}}_{\mathrm {Kan}}$
as follows. Both of these functors are easily checked to factor as
where the second term denotes the
![]() $\infty $
-category of small idempotent complete
$\infty $
-category of small idempotent complete
![]() $\infty $
-categories (and the first functor idempotent completion), and the third term the
$\infty $
-categories (and the first functor idempotent completion), and the third term the
![]() $\infty $
-category of cocomplete
$\infty $
-category of cocomplete
![]() $\infty $
-categories admitting a set of completely compact objects that jointly detect equivalences, and functors among them preserving both colimits and completely compact objects. By an argument analogous to [Reference LurieLu09a, Proposition 5.5.7.8],
$\infty $
-categories admitting a set of completely compact objects that jointly detect equivalences, and functors among them preserving both colimits and completely compact objects. By an argument analogous to [Reference LurieLu09a, Proposition 5.5.7.8],
![]() ${\mathcal {P}}_{\mathrm {free}}$
is an equivalence between the middle two terms. Since
${\mathcal {P}}_{\mathrm {free}}$
is an equivalence between the middle two terms. Since
![]() ${\mathcal {P}}_{\mathrm {free}}$
and
${\mathcal {P}}_{\mathrm {free}}$
and
![]() ${\mathcal {P}}_{\mathrm {Kan}}$
are homotopic on individual morphism
${\mathcal {P}}_{\mathrm {Kan}}$
are homotopic on individual morphism
![]() $\infty $
-groupoids [Reference LurieLu09a, Proposition 5.2.6.3], the same follows for
$\infty $
-groupoids [Reference LurieLu09a, Proposition 5.2.6.3], the same follows for
![]() ${\mathcal {P}}_{\mathrm {Kan}}$
. But by a minor modification of Toën’s theorem [Reference ToënTo05],
${\mathcal {P}}_{\mathrm {Kan}}$
. But by a minor modification of Toën’s theorem [Reference ToënTo05],
![]() $\mathrm {Cat}^{\natural }$
has a discrete automorphism
$\mathrm {Cat}^{\natural }$
has a discrete automorphism
![]() $\infty $
-groupoid consisting of two objects (the identity and op), whence there is a unique natural equivalence between
$\infty $
-groupoid consisting of two objects (the identity and op), whence there is a unique natural equivalence between
![]() ${\mathcal {P}}_{\mathrm {free}}$
and
${\mathcal {P}}_{\mathrm {free}}$
and
![]() ${\mathcal {P}}_{\mathrm {Kan}}$
.
${\mathcal {P}}_{\mathrm {Kan}}$
.
To conclude that the Yoneda embedding extends to a natural transformation as in Theorem 8.1, it thus remains to verify that this equivalence is given pointwise by the identity of
![]() ${\mathcal {P}}({A})$
; the trouble is that this latter identification is not clear.
${\mathcal {P}}({A})$
; the trouble is that this latter identification is not clear.
After this paper appeared, a proof of Theorem 8.1 along the lines just sketched was completed by Ramzi, with the additional input being a nifty rigidity result for the identity functor on
![]() $\mathrm {Cat} $
; see [Reference RamziRa23, Theorem 2.2].
$\mathrm {Cat} $
; see [Reference RamziRa23, Theorem 2.2].
Proof of Theorem 8.1
Recall that for any
![]() $\infty $
-category
$\infty $
-category
![]() ${A}$
, the Yoneda embedding
${A}$
, the Yoneda embedding
![]() ${A} \rightarrow {\mathcal {P}}({A})$
is defined as the adjoint of the functor
${A} \rightarrow {\mathcal {P}}({A})$
is defined as the adjoint of the functor
![]() ${\mathrm {Hom}}_{{A}} \colon {A}^{\mathrm {op}} \times {A} \rightarrow \mathrm {Gpd}$
, which in turn is given by the cocartesian unstraightening of
${\mathrm {Hom}}_{{A}} \colon {A}^{\mathrm {op}} \times {A} \rightarrow \mathrm {Gpd}$
, which in turn is given by the cocartesian unstraightening of
![]() $\operatorname {\mathrm {Tw}}^{\ell }({A}) \rightarrow {A}^{\mathrm {op}} \times {A}$
. The definition of the twisted arrow category makes this left fibration functorial in
$\operatorname {\mathrm {Tw}}^{\ell }({A}) \rightarrow {A}^{\mathrm {op}} \times {A}$
. The definition of the twisted arrow category makes this left fibration functorial in
![]() ${A}$
. More precisely, we can consider the pullback square
${A}$
. More precisely, we can consider the pullback square

and note that
![]() $\operatorname {\mathrm {Tw}}^{\ell }$
defines a functor from
$\operatorname {\mathrm {Tw}}^{\ell }$
defines a functor from
![]() $\mathrm {Cat} $
to the full subcategory of
$\mathrm {Cat} $
to the full subcategory of
![]() $F\subset E$
spanned by the left fibrations. Note that F is the cartesian unstraightening of the functor
$F\subset E$
spanned by the left fibrations. Note that F is the cartesian unstraightening of the functor
![]() $({A}, {B}) \mapsto \mathrm {LFib}({A}^{\mathrm {op}} \times {B})$
, where the functoriality is in pullback. There are equivalences
$({A}, {B}) \mapsto \mathrm {LFib}({A}^{\mathrm {op}} \times {B})$
, where the functoriality is in pullback. There are equivalences
which are natural in the input
![]() $\infty $
-categories (where the contravariant functoriality on
$\infty $
-categories (where the contravariant functoriality on
![]() $\mathcal {P}(-)$
is given by precomposition). Writing
$\mathcal {P}(-)$
is given by precomposition). Writing ![]() for the functor sending
for the functor sending
![]() $({A}, {B})\mapsto \mathrm {Fun} ({B},{\mathcal {P}}({A}))$
, we therefore obtain a functor
$({A}, {B})\mapsto \mathrm {Fun} ({B},{\mathcal {P}}({A}))$
, we therefore obtain a functor
On objects, this takes an
![]() $\infty $
-category
$\infty $
-category
![]() ${A}$
to its Yoneda embedding, and on morphisms, it witnesses the lax commutativity of the diagrams
${A}$
to its Yoneda embedding, and on morphisms, it witnesses the lax commutativity of the diagrams

given pointwise by the maps
![]() ${\mathrm {Hom}}_{{A}}(-,c) \longrightarrow {\mathrm {Hom}}_{{B}}\big (f(-),f(c)\big )$
. It therefore contains all the requisite data for a natural transformation
${\mathrm {Hom}}_{{A}}(-,c) \longrightarrow {\mathrm {Hom}}_{{B}}\big (f(-),f(c)\big )$
. It therefore contains all the requisite data for a natural transformation
![]() ${A}\longrightarrow {\mathcal {P}}({A})$
as in the statement.
${A}\longrightarrow {\mathcal {P}}({A})$
as in the statement.
To extract the desired natural transformation, curry
![]() $\mathcal F$
into a functor
$\mathcal F$
into a functor
Now observe that this functor takes values in the subcategory of ![]() spanned by functors to
spanned by functors to ![]() with left adjointable squares as morphisms. Via cartesian unstraightening, this
with left adjointable squares as morphisms. Via cartesian unstraightening, this
![]() $\infty $
-category is equivalent to
$\infty $
-category is equivalent to ![]() , the intersection the two subcategories
, the intersection the two subcategories ![]() and
and ![]() in the over-
in the over-
![]() $\infty $
-category
$\infty $
-category ![]() . Via cocartesian unstraightening, it is then also equivalent to the subcategory of
. Via cocartesian unstraightening, it is then also equivalent to the subcategory of ![]() spanned by functors into
spanned by functors into ![]() and right adjointable squares.
and right adjointable squares.
Applying these equivalences to
![]() $\mathcal F$
results in a functor
$\mathcal F$
results in a functor
![]() ${\mathcal {G}}$
in
${\mathcal {G}}$
in
which still has
![]() ${\mathcal {G}}({B}, {A}) \simeq \mathrm {Fun} ({B},{\mathcal {P}}({A}))$
, but now the functoriality in the
${\mathcal {G}}({B}, {A}) \simeq \mathrm {Fun} ({B},{\mathcal {P}}({A}))$
, but now the functoriality in the
![]() ${A}$
-variable is by the left adjoint to restriction (i.e., by left Kan extension).
${A}$
-variable is by the left adjoint to restriction (i.e., by left Kan extension).
Let
![]() $\mathrm {Un}^{\mathrm {oc}}({\mathcal {G}})\longrightarrow \mathrm {Cat} \times \mathrm {Cat} $
be the orthocartesian unstraightening of
$\mathrm {Un}^{\mathrm {oc}}({\mathcal {G}})\longrightarrow \mathrm {Cat} \times \mathrm {Cat} $
be the orthocartesian unstraightening of
![]() ${\mathcal {G}}$
. We claim that there is a canonical equivalence
${\mathcal {G}}$
. We claim that there is a canonical equivalence
![]() $\mathrm {Un}^{\mathrm {ct}}(\mathcal F) \simeq \mathrm {Un}^{\mathrm {oc}}({\mathcal {G}})$
. To this end, invoke Corollary 6.20 to write the cartesian unstraightening functor as
$\mathrm {Un}^{\mathrm {ct}}(\mathcal F) \simeq \mathrm {Un}^{\mathrm {oc}}({\mathcal {G}})$
. To this end, invoke Corollary 6.20 to write the cartesian unstraightening functor as
and the orthocartesian one as
But now by definition,
![]() ${\mathcal {G}}$
and
${\mathcal {G}}$
and
![]() $\mathcal F$
have the same image in
$\mathcal F$
have the same image in ![]() , viewed as a subcategory of
, viewed as a subcategory of ![]() and
and ![]() , respectively. This gives the claim that
, respectively. This gives the claim that
![]() $\mathrm {Un}^{\mathrm {ct}}(\mathcal F) \simeq \mathrm {Un}^{\mathrm {oc}}({\mathcal {G}})$
.
$\mathrm {Un}^{\mathrm {ct}}(\mathcal F) \simeq \mathrm {Un}^{\mathrm {oc}}({\mathcal {G}})$
.
The resulting functor
again takes
![]() ${A}$
to its Yoneda embedding, but this time morphisms witness lax commuting squares
${A}$
to its Yoneda embedding, but this time morphisms witness lax commuting squares

But by [Reference LurieLu09a, Proposition 5.2.6.3] (or rather the second step of its proof), the natural transformation
![]() $\mu $
is an equivalence (i.e., the diagram actually commutes).
$\mu $
is an equivalence (i.e., the diagram actually commutes).
Armed with this information, consider the diagram

whose top right corner is the oplax arrow
![]() $\infty $
-category
$\infty $
-category ![]() of large
of large
![]() $\infty $
-categories by Theorem 7.21. Via the inclusion
$\infty $
-categories by Theorem 7.21. Via the inclusion ![]() , it contains the actual arrow
, it contains the actual arrow
![]() $\infty $
-category
$\infty $
-category ![]() as a wide subcategory, and by the previous observation, the composite
as a wide subcategory, and by the previous observation, the composite
actually takes values in this subcategory. The resulting functor ![]() is then the natural transformation we set out to construct.
is then the natural transformation we set out to construct.
A Uniqueness of straightening and dualisation
To resolve coherence questions surrounding the dualisation and straightening equivalences once and for all, we will prove a rigidity result in this appendix, implying that any two ways of straightening or dualising a two-variable fibration are naturally equivalent; namely, we compute the automorphism groups of the functors

following ideas of [Reference Barwick, Glasman and NardinBGN18], who treated the case of a single variable. Here,
![]() $\boxtimes $
denotes the Gray tensor product (see Section 7), and
$\boxtimes $
denotes the Gray tensor product (see Section 7), and
![]() $\mathrm {Fun} (A\boxtimes B,\textbf {Cat})$
denotes the
$\mathrm {Fun} (A\boxtimes B,\textbf {Cat})$
denotes the
![]() $\infty $
-category of functors from the
$\infty $
-category of functors from the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $A\boxtimes B$
to the
$A\boxtimes B$
to the
![]() $(\infty ,2)$
-category of
$(\infty ,2)$
-category of
![]() $\infty $
-categories. By [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, 5.2.9], the functor
$\infty $
-categories. By [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, 5.2.9], the functor
![]() $\mathcal {F}_{\mathrm {Gray}}$
is equivalent to the functor
$\mathcal {F}_{\mathrm {Gray}}$
is equivalent to the functor
![]() $\mathrm {Gray}(-,-)$
which sends a pair
$\mathrm {Gray}(-,-)$
which sends a pair
![]() $(A,B)$
to the
$(A,B)$
to the
![]() $\infty $
-category of Gray fibrations over
$\infty $
-category of Gray fibrations over
![]() $A\times B$
(see Remark 6.6).
$A\times B$
(see Remark 6.6).
Before we describe the result of our calculations, note that the functor
![]() $\mathcal {F}$
carries a natural action of the group
$\mathcal {F}$
carries a natural action of the group
![]() $\mathrm {Aut}(\mathrm {Cat} )$
, acting pointwise on
$\mathrm {Aut}(\mathrm {Cat} )$
, acting pointwise on
![]() $\mathrm {Fun} (A\times B, \mathrm {Cat} )$
by postcomposition. When evaluated at
$\mathrm {Fun} (A\times B, \mathrm {Cat} )$
by postcomposition. When evaluated at
![]() $([0], [0])\in \mathrm {Cat}^{\times 2}$
, this simply gives the canonical action of
$([0], [0])\in \mathrm {Cat}^{\times 2}$
, this simply gives the canonical action of
![]() $\mathrm {Aut}(\mathrm {Cat} )$
on
$\mathrm {Aut}(\mathrm {Cat} )$
on
![]() $\mathrm {Cat} $
. By a theorem of Toën,
$\mathrm {Cat} $
. By a theorem of Toën,
![]() $\mathrm {Aut}(\mathrm {Cat} )$
is discrete with two path components, corresponding to the identity and
$\mathrm {Aut}(\mathrm {Cat} )$
is discrete with two path components, corresponding to the identity and
![]() $(-)^{\mathrm {op}} \colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
[Reference ToënTo05]. Our goal will be to prove the following:
$(-)^{\mathrm {op}} \colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
[Reference ToënTo05]. Our goal will be to prove the following:
Theorem A.1. Acting by postcomposition and evaluation at
![]() $([0],[0]) \in \mathrm {Cat}^{\times 2}$
determines inverse equivalences
$([0],[0]) \in \mathrm {Cat}^{\times 2}$
determines inverse equivalences
In particular,
![]() $\mathrm {Aut}(\mathcal {F})$
is discrete with
$\mathrm {Aut}(\mathcal {F})$
is discrete with
![]() $\pi _0\mathrm {Aut}(\mathcal {F}) = \mathbb Z/2$
having its nontrivial element induced by postcomposition with
$\pi _0\mathrm {Aut}(\mathcal {F}) = \mathbb Z/2$
having its nontrivial element induced by postcomposition with
![]() $(-)^{\mathrm {op}} \colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
. Furthermore,
$(-)^{\mathrm {op}} \colon \mathrm {Cat} \rightarrow \mathrm {Cat} $
. Furthermore,
![]() $\mathrm {Aut}(\mathcal {F}_{{\mathrm {Gpd}} })\simeq \ast $
and
$\mathrm {Aut}(\mathcal {F}_{{\mathrm {Gpd}} })\simeq \ast $
and
![]() $\mathrm {Aut}(\mathcal {F}_{\mathrm {Gray}})\simeq \ast $
.
$\mathrm {Aut}(\mathcal {F}_{\mathrm {Gray}})\simeq \ast $
.
Remark A.2. Orthocartesian (un)straightening restricts to a natural (un)straightening equivalence
![]() $\mathrm {Str}^{\mathrm {bi}}\colon \operatorname {\mathrm {Bifib}} \longrightarrow \mathcal {F}_{{\mathrm {Gpd}} }$
for bifibrations by [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, 2.3.15]. Theorem A.1 implies that the equivalence
$\mathrm {Str}^{\mathrm {bi}}\colon \operatorname {\mathrm {Bifib}} \longrightarrow \mathcal {F}_{{\mathrm {Gpd}} }$
for bifibrations by [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, 2.3.15]. Theorem A.1 implies that the equivalence
![]() $\mathrm {Str}^{\mathrm {bi}}$
in fact agrees with the equivalence from [Reference StevensonSt18], provided the latter is natural. This can be verified using the techniques of [Reference Gepner, Haugseng and NikolausGHN17, Appendix A]; we refrain from working out further details, as we do not need the statement.
$\mathrm {Str}^{\mathrm {bi}}$
in fact agrees with the equivalence from [Reference StevensonSt18], provided the latter is natural. This can be verified using the techniques of [Reference Gepner, Haugseng and NikolausGHN17, Appendix A]; we refrain from working out further details, as we do not need the statement.
Remark A.3. As mentioned, the analogue of Theorem A.1 for the functor
![]() $A \mapsto \mathrm {Fun} (A,\mathrm {Cat} )$
is one step in the proof of [Reference Barwick, Glasman and NardinBGN18, Theorem 1.4], and our proof below follows their strategy in the large. There is, however, one crucial difference: Barwick, Glasman and Nardin use Yoneda’s lemma to deduce that the automorphisms of the functor
$A \mapsto \mathrm {Fun} (A,\mathrm {Cat} )$
is one step in the proof of [Reference Barwick, Glasman and NardinBGN18, Theorem 1.4], and our proof below follows their strategy in the large. There is, however, one crucial difference: Barwick, Glasman and Nardin use Yoneda’s lemma to deduce that the automorphisms of the functor
are given by
![]() $\mathrm {Aut}(\mathrm {Cat} )$
. This suffices to establish the analogue of Theorem A.1 after taking
$\mathrm {Aut}(\mathrm {Cat} )$
. This suffices to establish the analogue of Theorem A.1 after taking
![]() $\infty $
-groupoid cores, but it is unclear to us how to obtain the actual statement from this information.
$\infty $
-groupoid cores, but it is unclear to us how to obtain the actual statement from this information.
By contrast, our more elaborate proof of Theorem A.1 below also makes use of intermediate steps of Toën’s results (and the strategy applies equally well in the situation of [Reference Barwick, Glasman and NardinBGN18]).
In the proof, we will make use of two tangential results. For the first, recall that
![]() $f\colon A\to B$
is called a faithful functor if each
$f\colon A\to B$
is called a faithful functor if each
![]() ${\mathrm {Hom}}_A(a, b)\to {\mathrm {Hom}}_B(f(a), f(b))$
is an inclusion of path components, or equivalently, if
${\mathrm {Hom}}_A(a, b)\to {\mathrm {Hom}}_B(f(a), f(b))$
is an inclusion of path components, or equivalently, if
![]() $\mathrm {h} f$
is faithful and the commutative square
$\mathrm {h} f$
is faithful and the commutative square

is cartesian.
Lemma A.4. If
![]() $f \colon {A} \longrightarrow {B}$
is faithful, then the diagram
$f \colon {A} \longrightarrow {B}$
is faithful, then the diagram

is cartesian and, in particular,
![]() $f_* \colon \mathrm {Fun} ({C},{A}) \longrightarrow \mathrm {Fun} ({C},{B})$
is again faithful for any
$f_* \colon \mathrm {Fun} ({C},{A}) \longrightarrow \mathrm {Fun} ({C},{B})$
is again faithful for any
![]() ${C} \in \mathrm {Cat} $
. If, furthermore, the restriction
${C} \in \mathrm {Cat} $
. If, furthermore, the restriction
![]() $\iota ({A}) \rightarrow \iota ({B})$
is an inclusion of path components, then so is
$\iota ({A}) \rightarrow \iota ({B})$
is an inclusion of path components, then so is
Remark A.5. Note that the functor
is not usually an equivalence, so the square of the lemma does not agree with the square

which is cartesian if and only if
![]() $f_*$
is faithful.
$f_*$
is faithful.
Proof of Lemma A.4
The first assertion is immediate from
![]() $\mathrm {Fun} (\mathrm {h} {C}, \mathrm {h}{B}) \simeq \mathrm {Fun} ({C},\mathrm {h}{B})$
and the analogous assertion for
$\mathrm {Fun} (\mathrm {h} {C}, \mathrm {h}{B}) \simeq \mathrm {Fun} ({C},\mathrm {h}{B})$
and the analogous assertion for
![]() ${A}$
in place of
${A}$
in place of
![]() ${B}$
. The second assertion then follows, since the lower horizontal functor is clearly faithful, and faithful functors are closed under pullback. This is most easily seen from the characterisation that all induced maps on morphism complexes have empty or contractible fibres, which is evidently stable under pullback. The third statement similarly follows from the analogue for ordinary categories by applying cores to the diagram of the lemma.
${B}$
. The second assertion then follows, since the lower horizontal functor is clearly faithful, and faithful functors are closed under pullback. This is most easily seen from the characterisation that all induced maps on morphism complexes have empty or contractible fibres, which is evidently stable under pullback. The third statement similarly follows from the analogue for ordinary categories by applying cores to the diagram of the lemma.
In the following, recall that a full subcategory
![]() $I\hookrightarrow C$
is said to be dense if the restricted Yoneda embedding
$I\hookrightarrow C$
is said to be dense if the restricted Yoneda embedding
![]() $C\longrightarrow {\mathcal {P}}(I)$
is fully faithful, or equivalently, if for each
$C\longrightarrow {\mathcal {P}}(I)$
is fully faithful, or equivalently, if for each
![]() $c\in C$
, the canonical map
$c\in C$
, the canonical map ![]() in C is an equivalence.
in C is an equivalence.
Lemma A.6. Let
![]() $\mathbf {X}$
be an
$\mathbf {X}$
be an
![]() $(\infty ,2)$
-category and
$(\infty ,2)$
-category and
![]() $\mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
the
$\mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
the
![]() $\infty $
-category of
$\infty $
-category of
![]() $2$
-functors
$2$
-functors
![]() $\mathbf {X}\longrightarrow \mathbf {Cat}$
. For each
$\mathbf {X}\longrightarrow \mathbf {Cat}$
. For each
![]() $x\in \mathbf {X}$
and
$x\in \mathbf {X}$
and
![]() $A\in \mathrm {Cat} $
, there exists an object
$A\in \mathrm {Cat} $
, there exists an object
![]() $h_{x, A}\in \mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
with the universal property
$h_{x, A}\in \mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
with the universal property
The full subcategory
![]() ${\mathbf {\Delta }}_{\mathbf {X}}\subseteq \mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
spanned by all
${\mathbf {\Delta }}_{\mathbf {X}}\subseteq \mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
spanned by all
![]() $h_{x, [k]}$
with
$h_{x, [k]}$
with
![]() $x\in \mathbf {X}$
and
$x\in \mathbf {X}$
and
![]() $k\geq 0$
then forms a dense subcategory.
$k\geq 0$
then forms a dense subcategory.
Observation A.8. For any functor
![]() $f\colon \mathbf {X}\longrightarrow \mathbf {Y}$
, let
$f\colon \mathbf {X}\longrightarrow \mathbf {Y}$
, let
![]() $f_!\colon \mathrm {Fun} (\mathbf {X}, \mathbf {Cat})\longrightarrow \mathrm {Fun} (\mathbf {Y}, \mathbf {Cat})$
be the left adjoint to the restriction functor. By the universal property (A.7), this sends
$f_!\colon \mathrm {Fun} (\mathbf {X}, \mathbf {Cat})\longrightarrow \mathrm {Fun} (\mathbf {Y}, \mathbf {Cat})$
be the left adjoint to the restriction functor. By the universal property (A.7), this sends
![]() $h_{x, A}$
to
$h_{x, A}$
to
![]() $h_{f(x), A}$
and hence restricts to
$h_{f(x), A}$
and hence restricts to
![]() $f_!\colon {\mathbf {\Delta }}_{\mathbf {X}}\longrightarrow {\mathbf {\Delta }}_{\mathbf {Y}}$
.
$f_!\colon {\mathbf {\Delta }}_{\mathbf {X}}\longrightarrow {\mathbf {\Delta }}_{\mathbf {Y}}$
.
Proof. Let us start by observing that by the enriched Yoneda lemma [Reference HinichHi20, Proposition 6.2.7], these universal functors
![]() $h_{x, A}$
indeed exist and are given by
$h_{x, A}$
indeed exist and are given by
Moreover, Hinich’s results show that the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
can be described as that of
$\mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
can be described as that of
![]() $\mathbf {X}$
-modules in
$\mathbf {X}$
-modules in
![]() $\mathrm {Cat} $
(in the sense of algebras for a many-object module
$\mathrm {Cat} $
(in the sense of algebras for a many-object module
![]() $\infty $
-operad whose underlying many-object algebra is the
$\infty $
-operad whose underlying many-object algebra is the
![]() $\mathrm {Cat} $
-enriched
$\mathrm {Cat} $
-enriched
![]() $\infty $
-category
$\infty $
-category
![]() $\mathbf {X}$
). From this description, it follows that
$\mathbf {X}$
). From this description, it follows that
![]() $\mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
admits all colimits, and so the inclusion
$\mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
admits all colimits, and so the inclusion
![]() $j\colon {\mathbf {\Delta }}_{\mathbf {X}}\hookrightarrow \mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
induces an adjoint pair
$j\colon {\mathbf {\Delta }}_{\mathbf {X}}\hookrightarrow \mathrm {Fun} (\mathbf {X}, \mathbf {Cat})$
induces an adjoint pair ![]() and we have to verify that the counit map
and we have to verify that the counit map
is an equivalence for all F. We will prove this in increasing levels of generality.
First, suppose that
![]() $F=h_{y, A}$
. In this case, we claim that there is a cofinal functor
$F=h_{y, A}$
. In this case, we claim that there is a cofinal functor
![]() $h_y\colon {\mathbf {\Delta }}/A\longrightarrow {\mathbf {\Delta }}_{\mathbf {X}}/h_{y, A}$
sending each
$h_y\colon {\mathbf {\Delta }}/A\longrightarrow {\mathbf {\Delta }}_{\mathbf {X}}/h_{y, A}$
sending each
![]() $[k]\to A$
to
$[k]\to A$
to
![]() $h_{y, [k]}\longrightarrow h_{y, A}$
. The result then follows from the fact that
$h_{y, [k]}\longrightarrow h_{y, A}$
. The result then follows from the fact that
![]() $A\longmapsto h_{y, A}$
preserves colimits and that
$A\longmapsto h_{y, A}$
preserves colimits and that ![]() . To see that
. To see that
![]() $h_y$
is indeed cofinal, it suffices to verify that the natural map
$h_y$
is indeed cofinal, it suffices to verify that the natural map
is an equivalence. From the universal property (A.7) and the explicit formula (A.9) for
![]() $h_{y, A}$
, one sees that this map is equivalent to
$h_{y, A}$
, one sees that this map is equivalent to
Taking the constant factor
![]() ${\mathrm {Hom}}_{\mathrm {Cat} }\big ([n], {\mathrm {Hom}}_{\mathbf {X}}(y, x)\big )$
out of the colimit, one sees that this is an equivalence since
${\mathrm {Hom}}_{\mathrm {Cat} }\big ([n], {\mathrm {Hom}}_{\mathbf {X}}(y, x)\big )$
out of the colimit, one sees that this is an equivalence since
![]() ${\mathbf {\Delta }}\hookrightarrow \mathrm {Cat} $
is a dense subcategory [Reference RezkRe01].
${\mathbf {\Delta }}\hookrightarrow \mathrm {Cat} $
is a dense subcategory [Reference RezkRe01].
Next, note that the class of F for which (A.10) is an equivalence is closed under all colimits that are preserved by
![]() $j^{*}$
. For example, one easily sees from the universal property (A.7) that
$j^{*}$
. For example, one easily sees from the universal property (A.7) that
![]() $j^{*}$
preserves all coproducts.
$j^{*}$
preserves all coproducts.
To conclude, we now write each functor F as the geometric realisation of a bar construction. More precisely, let us fix a set S and an essentially surjective functor
![]() $f\colon S\longrightarrow \mathbf {X}$
. The description of
$f\colon S\longrightarrow \mathbf {X}$
. The description of
![]() $\mathrm {Fun} (\mathbf {X}, \mathrm {Cat} )$
as modules then gives a free/forgetful adjunction
$\mathrm {Fun} (\mathbf {X}, \mathrm {Cat} )$
as modules then gives a free/forgetful adjunction
where
![]() $f^{*}$
evaluates at each object in S. Note that
$f^{*}$
evaluates at each object in S. Note that
![]() $f^{*}$
preserves all limits and colimits and detects equivalences, so that
$f^{*}$
preserves all limits and colimits and detects equivalences, so that
![]() $(f_!, f^{*})$
is a monadic adjunction. The left adjoint
$(f_!, f^{*})$
is a monadic adjunction. The left adjoint
![]() $f_!$
sends each
$f_!$
sends each
![]() $(A_s)_{s\in S}\in \mathrm {Cat} $
to
$(A_s)_{s\in S}\in \mathrm {Cat} $
to
![]() $\coprod _{s\in S} h_{s, A_s}$
.
$\coprod _{s\in S} h_{s, A_s}$
.
Any
![]() $F\colon \mathbf {X}\longrightarrow \mathbf {Cat}$
can now be written as the geometric realisation
$F\colon \mathbf {X}\longrightarrow \mathbf {Cat}$
can now be written as the geometric realisation
![]() $F\simeq |B_{\bullet }|$
, where
$F\simeq |B_{\bullet }|$
, where
![]() $B_{\bullet }=\mathrm {Bar}(f_!, f^{*}f_!, f^{*}F)$
is the usual bar resolution of F for the monadic adjunction (A.11). The functor
$B_{\bullet }=\mathrm {Bar}(f_!, f^{*}f_!, f^{*}F)$
is the usual bar resolution of F for the monadic adjunction (A.11). The functor
![]() $j^{*}$
preserves these geometric realisations (i.e., for any
$j^{*}$
preserves these geometric realisations (i.e., for any
![]() $x\in \mathbf {X}$
and
$x\in \mathbf {X}$
and
![]() $k\geq 0$
, the map
$k\geq 0$
, the map
![]() $\big |{\mathrm {Hom}}_{\mathrm {Cat}}([k], B_{\bullet }(x)\big )\big |\longrightarrow {\mathrm {Hom}}_{\mathrm {Cat}}\big ([k], F(x)\big )$
is an equivalence). Indeed, up to equivalence, we may take
$\big |{\mathrm {Hom}}_{\mathrm {Cat}}([k], B_{\bullet }(x)\big )\big |\longrightarrow {\mathrm {Hom}}_{\mathrm {Cat}}\big ([k], F(x)\big )$
is an equivalence). Indeed, up to equivalence, we may take
![]() $x=f(s)$
, in which case this follows from the augmented simplicial object
$x=f(s)$
, in which case this follows from the augmented simplicial object
![]() $f^{*}B_{\bullet }\to f^{*}F$
having extra degeneracies [Reference LurieLu17, Example 4.7.2.7]. Since each term in the bar construction is a coproduct of functors of the form
$f^{*}B_{\bullet }\to f^{*}F$
having extra degeneracies [Reference LurieLu17, Example 4.7.2.7]. Since each term in the bar construction is a coproduct of functors of the form
![]() $h_{f(s), A}$
, for which we have already verified that the counit map (A.10) is an equivalence, it follows that (A.10) is an equivalence for F as well.
$h_{f(s), A}$
, for which we have already verified that the counit map (A.10) is an equivalence, it follows that (A.10) is an equivalence for F as well.
Proof of Theorem A.1
We will spell out the case of
![]() $\mathcal {F}$
and discuss the modifications required for
$\mathcal {F}$
and discuss the modifications required for
![]() $\mathcal {F}_{{\mathrm {Gpd}} }$
and
$\mathcal {F}_{{\mathrm {Gpd}} }$
and
![]() $\mathcal {F}_{\mathrm {Gray}}$
at the end of the proof.
$\mathcal {F}_{\mathrm {Gray}}$
at the end of the proof.
Step 1: reducing to simplices
Recall that precomposition with the localisation
![]() $\mathrm {ac}\colon \mathrm {s}\mathrm {Gpd} \rightarrow \mathrm {Cat} $
gives a fully faithful embedding
$\mathrm {ac}\colon \mathrm {s}\mathrm {Gpd} \rightarrow \mathrm {Cat} $
gives a fully faithful embedding
for any
![]() $\infty $
-category
$\infty $
-category
![]() ${X}$
. Since
${X}$
. Since
![]() $\mathrm {ac}$
preserves colimits, this inclusion furthermore preserves the property of commuting with small limits in each variable separately, and on the right, the full subcategory spanned by such functors is equivalent to
$\mathrm {ac}$
preserves colimits, this inclusion furthermore preserves the property of commuting with small limits in each variable separately, and on the right, the full subcategory spanned by such functors is equivalent to
![]() $\mathrm {Fun} ({\mathbf {\Delta }}^{\mathrm {op}} \times {\mathbf {\Delta }}^{\mathrm {op}},{X})$
. Since
$\mathrm {Fun} ({\mathbf {\Delta }}^{\mathrm {op}} \times {\mathbf {\Delta }}^{\mathrm {op}},{X})$
. Since ![]() does indeed preserve small limits in each variable, we find that
does indeed preserve small limits in each variable, we find that
![]() $\mathrm {Aut}(\mathcal {F})$
agrees with the automorphisms of the (large) bisimplicial
$\mathrm {Aut}(\mathcal {F})$
agrees with the automorphisms of the (large) bisimplicial
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {F}_{|{\mathbf {\Delta }}^2}$
given by
$\mathcal {F}_{|{\mathbf {\Delta }}^2}$
given by
![]() $(n,m) \mapsto \mathrm {Fun} ([n] \times [m],\mathrm {Cat} )$
, with functoriality arising from restriction.
$(n,m) \mapsto \mathrm {Fun} ([n] \times [m],\mathrm {Cat} )$
, with functoriality arising from restriction.
Step 2: restricting to generators
Note that
![]() $\mathcal {F}_{|{\mathbf {\Delta }}^2}$
takes values in the subcategory
$\mathcal {F}_{|{\mathbf {\Delta }}^2}$
takes values in the subcategory
![]() $\mathrm {Pr}^{\mathrm {R}}$
of
$\mathrm {Pr}^{\mathrm {R}}$
of ![]() consisting of presentable
consisting of presentable
![]() $\infty $
-categories and right adjoint functors. Although the inclusion
$\infty $
-categories and right adjoint functors. Although the inclusion ![]() is not fully faithful, it does induce a fully faithful map on
is not fully faithful, it does induce a fully faithful map on
![]() $\infty $
-groupoid cores, and by Lemma A.4, this feature persists to simplicial objects. We may therefore compute the automorphisms of
$\infty $
-groupoid cores, and by Lemma A.4, this feature persists to simplicial objects. We may therefore compute the automorphisms of
![]() $\mathcal {F}_{|{\mathbf {\Delta }}^2}$
as a bisimplicial object in
$\mathcal {F}_{|{\mathbf {\Delta }}^2}$
as a bisimplicial object in
![]() $\mathrm {Pr}^{\mathrm {R}}$
instead.
$\mathrm {Pr}^{\mathrm {R}}$
instead.
From the equivalence
![]() $\mathrm {Pr}^{\mathrm {R}} \simeq (\mathrm {Pr}^{\mathrm {L}})^{\mathrm {op}}$
, given by taking adjoints, we find
$\mathrm {Pr}^{\mathrm {R}} \simeq (\mathrm {Pr}^{\mathrm {L}})^{\mathrm {op}}$
, given by taking adjoints, we find
By another application of Lemma A.4, it follows that
![]() $\mathrm {Aut}(\mathcal {F}_{|{\mathbf {\Delta }}^2})\simeq \mathrm {Aut}({\mathcal {G}})$
, where
$\mathrm {Aut}(\mathcal {F}_{|{\mathbf {\Delta }}^2})\simeq \mathrm {Aut}({\mathcal {G}})$
, where
![]() ${\mathcal {G}}$
denotes the (large) bicosimplicial
${\mathcal {G}}$
denotes the (large) bicosimplicial
![]() $\infty $
-category
$\infty $
-category
with functoriality arising by left Kan extension.
Now consider the dense subcategories
![]() $\mathcal {H}(n, m)={\mathbf {\Delta }}_{[n]\times [m]}\subseteq \mathcal {G}(n, m)$
from Lemma A.6. By Observation A.8, every induced map on homotopy categories
$\mathcal {H}(n, m)={\mathbf {\Delta }}_{[n]\times [m]}\subseteq \mathcal {G}(n, m)$
from Lemma A.6. By Observation A.8, every induced map on homotopy categories
![]() $\mathrm {h}{\mathcal {G}}(n,m) \rightarrow \mathrm {h}{\mathcal {G}}(n',m')$
carries
$\mathrm {h}{\mathcal {G}}(n,m) \rightarrow \mathrm {h}{\mathcal {G}}(n',m')$
carries
![]() $\mathrm {h} {\mathcal {H}}(n,m)$
into
$\mathrm {h} {\mathcal {H}}(n,m)$
into
![]() $\mathrm {h} {\mathcal {H}}(n',m')$
. In fact,
$\mathrm {h} {\mathcal {H}}(n',m')$
. In fact,
![]() ${\mathcal {H}}(n, m)$
coincides with the full subcategory spanned by the images of
${\mathcal {H}}(n, m)$
coincides with the full subcategory spanned by the images of
![]() ${\mathbf {\Delta }}\subseteq \mathrm {Cat} =\mathcal {G}(0, 0)$
under all structure maps
${\mathbf {\Delta }}\subseteq \mathrm {Cat} =\mathcal {G}(0, 0)$
under all structure maps
![]() $\mathcal {G}(0, 0)\to {\mathcal {G}}(n, m)$
. Since there are pullbacks
$\mathcal {G}(0, 0)\to {\mathcal {G}}(n, m)$
. Since there are pullbacks

it follows from the functoriality of pullbacks that the
![]() ${\mathcal {H}}(n,m)$
assemble into a functor
${\mathcal {H}}(n,m)$
assemble into a functor
![]() $\mathbf {\Delta }^{2} \rightarrow \mathrm {Cat} $
equipped with a natural transformation
$\mathbf {\Delta }^{2} \rightarrow \mathrm {Cat} $
equipped with a natural transformation
![]() ${\mathcal {H}} \rightarrow {\mathcal {G}}$
.
${\mathcal {H}} \rightarrow {\mathcal {G}}$
.
Let us now consider the induced maps
We claim that both are inclusions of path components. To see this, note that the universal property of
![]() ${\mathcal {P}}(\mathcal {H}(n, m))$
as the free cocompletion of
${\mathcal {P}}(\mathcal {H}(n, m))$
as the free cocompletion of
![]() $\mathcal {H}(n, m)$
produces a natural transformation
$\mathcal {H}(n, m)$
produces a natural transformation
![]() ${\mathcal {P}}(\mathcal {H})\longrightarrow {\mathcal {G}}$
. By Lemma A.6, this exhibits each
${\mathcal {P}}(\mathcal {H})\longrightarrow {\mathcal {G}}$
. By Lemma A.6, this exhibits each
![]() ${\mathcal {G}}(n,m)$
as a (left Bousfield) localisation of
${\mathcal {G}}(n,m)$
as a (left Bousfield) localisation of
![]() ${\mathcal {P}}({\mathcal {H}}(n,m))$
for each
${\mathcal {P}}({\mathcal {H}}(n,m))$
for each
![]() $(n,m) \in {\mathbf {\Delta }}^2$
. Consequently, writing out the terms as
$(n,m) \in {\mathbf {\Delta }}^2$
. Consequently, writing out the terms as
![]() $\infty $
-groupoids of natural transformations and applying [Reference Gepner, Haugseng and NikolausGHN17, Proposition 5.1], we find
$\infty $
-groupoids of natural transformations and applying [Reference Gepner, Haugseng and NikolausGHN17, Proposition 5.1], we find

where the limits run over
![]() $[f \colon (n,m) \rightarrow (n',m')] \in \operatorname {\mathrm {Tw}}^{r}({\mathbf {\Delta }} \times {\mathbf {\Delta }})$
. The second term is a set of path components in the third; indeed, this is so before taking limits, so that the fibre over a point in the target is the limit of a diagram only taking values
$[f \colon (n,m) \rightarrow (n',m')] \in \operatorname {\mathrm {Tw}}^{r}({\mathbf {\Delta }} \times {\mathbf {\Delta }})$
. The second term is a set of path components in the third; indeed, this is so before taking limits, so that the fibre over a point in the target is the limit of a diagram only taking values
![]() $\emptyset $
and
$\emptyset $
and
![]() $\ast $
, and thus also either empty or contractible itself. Similarly, we find
$\ast $
, and thus also either empty or contractible itself. Similarly, we find

Now notice that any automorphism
![]() $\varphi $
of
$\varphi $
of
![]() ${\mathcal {G}}$
preserves the sub-diagram
${\mathcal {G}}$
preserves the sub-diagram
![]() ${\mathcal {H}}$
. Indeed, the induced automorphism on
${\mathcal {H}}$
. Indeed, the induced automorphism on
![]() ${\mathcal {G}}(0,0) = \mathrm {Cat} $
preserves the full subcategory
${\mathcal {G}}(0,0) = \mathrm {Cat} $
preserves the full subcategory
![]() ${\mathbf {\Delta }} \subset \mathrm {Cat} $
by [Reference LurieLu09b, Corollary 4.4.11 & Proposition 4.4.13] and naturality with respect to left Kan extension and then implies that
${\mathbf {\Delta }} \subset \mathrm {Cat} $
by [Reference LurieLu09b, Corollary 4.4.11 & Proposition 4.4.13] and naturality with respect to left Kan extension and then implies that
![]() $\varphi $
preserves the full subcategory
$\varphi $
preserves the full subcategory
![]() ${\mathcal {H}}(n,m) \subset {\mathcal {G}}(n,m)$
as well. The inclusions of path components above therefore refine to inclusions of path components
${\mathcal {H}}(n,m) \subset {\mathcal {G}}(n,m)$
as well. The inclusions of path components above therefore refine to inclusions of path components
In particular, the claim that
![]() $\mathrm {Aut}({\mathcal {G}}, {\mathcal {G}})$
is discrete with two components will follow from the analogous statement for
$\mathrm {Aut}({\mathcal {G}}, {\mathcal {G}})$
is discrete with two components will follow from the analogous statement for
![]() ${\mathcal {H}}$
.
${\mathcal {H}}$
.
Step 3: automorphism group of the generators
Recall that
![]() ${\mathcal {H}}(n, m)$
is spanned by the functors
${\mathcal {H}}(n, m)$
is spanned by the functors
![]() $h_{(i, j), [k]}$
for
$h_{(i, j), [k]}$
for
![]() $(i, j)\in [n]\times [m]$
and
$(i, j)\in [n]\times [m]$
and
![]() $k\geq 0$
, defined by the universal property (A.7) or by the explicit formula (A.9). The latter formula reduces to
$k\geq 0$
, defined by the universal property (A.7) or by the explicit formula (A.9). The latter formula reduces to
 $$\begin{align*}h_{(i, j), [k]}\colon [n] \times [m] \longrightarrow \mathrm{Cat} , \quad (a,b) \longmapsto \begin{cases} [k] & a \geq i, b \geq j \\ \emptyset & \text{otherwise}. \end{cases}\end{align*}$$
$$\begin{align*}h_{(i, j), [k]}\colon [n] \times [m] \longrightarrow \mathrm{Cat} , \quad (a,b) \longmapsto \begin{cases} [k] & a \geq i, b \geq j \\ \emptyset & \text{otherwise}. \end{cases}\end{align*}$$
Combined with (A.7), one sees that the mapping
![]() $\infty $
-groupoids between such functors are discrete and that there are equivalences
$\infty $
-groupoids between such functors are discrete and that there are equivalences
In particular, the
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathcal {H}(n, m)$
are 0-truncated (i.e., equivalent to ordinary categories with discrete core); one can use this to conclude that the above equivalence is natural in
$\mathcal {H}(n, m)$
are 0-truncated (i.e., equivalent to ordinary categories with discrete core); one can use this to conclude that the above equivalence is natural in
![]() $(n, m)$
(which is now a property, rather than a structure), for the obvious functoriality on the left leaving
$(n, m)$
(which is now a property, rather than a structure), for the obvious functoriality on the left leaving
![]() ${\mathbf {\Delta }}$
fixed.
${\mathbf {\Delta }}$
fixed.
Since all
![]() $\mathcal {H}(n, m)$
are
$\mathcal {H}(n, m)$
are
![]() $0$
-truncated,
$0$
-truncated,
![]() $\mathcal {H}$
is a
$\mathcal {H}$
is a
![]() $0$
-truncated object in the
$0$
-truncated object in the
![]() $\infty $
-category of bicosimplicial
$\infty $
-category of bicosimplicial
![]() $\infty $
-categories, and
$\infty $
-categories, and
![]() $\mathrm {Aut}(\mathcal {H})$
is discrete. Furthermore, any automorphism of
$\mathrm {Aut}(\mathcal {H})$
is discrete. Furthermore, any automorphism of
![]() ${\mathcal {H}}$
induces one on
${\mathcal {H}}$
induces one on
![]() ${\mathcal {H}}(0,0) = {\mathbf {\Delta }}$
, and this restriction determines the entire transformation: The composite
${\mathcal {H}}(0,0) = {\mathbf {\Delta }}$
, and this restriction determines the entire transformation: The composite
is determined by naturality for the codegeneracy map
![]() $(n,m) \rightarrow (0,0)$
and the composite
$(n,m) \rightarrow (0,0)$
and the composite
by naturality with respect to the boundary maps
![]() $(0,0) \rightarrow (n,m)$
. Thus,
$(0,0) \rightarrow (n,m)$
. Thus,
as desired.
The other two cases
To conclude, we briefly describe the modifications to be made to the above argument to prove that
![]() $\mathcal {F}_{{\mathrm {Gpd}} }$
and
$\mathcal {F}_{{\mathrm {Gpd}} }$
and
![]() $\mathcal {F}_{\mathrm {Gray}}$
have trivial automorphism groups.
$\mathcal {F}_{\mathrm {Gray}}$
have trivial automorphism groups.
For
![]() $\mathcal {F}_{{\mathrm {Gpd}} }$
, we repeat the entire argument, but in Step 2 we use the natural subcategory
$\mathcal {F}_{{\mathrm {Gpd}} }$
, we repeat the entire argument, but in Step 2 we use the natural subcategory
![]() $\mathcal {H}_{{\mathrm {Gpd}} }(n, m)\subseteq \mathrm {Fun} ([n]\times [m], {\mathrm {Gpd}} )$
of diagrams of
$\mathcal {H}_{{\mathrm {Gpd}} }(n, m)\subseteq \mathrm {Fun} ([n]\times [m], {\mathrm {Gpd}} )$
of diagrams of
![]() $\infty $
-groupoids given by left Kan extensions along
$\infty $
-groupoids given by left Kan extensions along
![]() $(i, j)\colon [0]\longrightarrow [n]\times [m]$
of the constant diagram on the point. One then identifies the diagram
$(i, j)\colon [0]\longrightarrow [n]\times [m]$
of the constant diagram on the point. One then identifies the diagram
![]() $\mathcal {H}_{{\mathrm {Gpd}}}$
, with functoriality by left Kan extension, with the obvious diagram sending
$\mathcal {H}_{{\mathrm {Gpd}}}$
, with functoriality by left Kan extension, with the obvious diagram sending
![]() $(n, m)\mapsto [n]^{{\mathrm {op}}}\times [m]^{\mathrm {op}}$
. This has trivial automorphisms.
$(n, m)\mapsto [n]^{{\mathrm {op}}}\times [m]^{\mathrm {op}}$
. This has trivial automorphisms.
For
![]() $\mathcal {F}_{\mathrm {Gray}}$
, one uses the dense subcategories
$\mathcal {F}_{\mathrm {Gray}}$
, one uses the dense subcategories
![]() $\mathcal {H}_{\mathrm {Gray}}(n, m)={\mathbf {\Delta }}_{[n]\boxtimes [m]}\subseteq \mathrm {Fun} ([n]\boxtimes [m], \mathbf {Cat}).$
Again, these full subcategories can also be characterised as those spanned by the essential images of
$\mathcal {H}_{\mathrm {Gray}}(n, m)={\mathbf {\Delta }}_{[n]\boxtimes [m]}\subseteq \mathrm {Fun} ([n]\boxtimes [m], \mathbf {Cat}).$
Again, these full subcategories can also be characterised as those spanned by the essential images of
![]() ${\mathbf {\Delta }}$
under all structure maps
${\mathbf {\Delta }}$
under all structure maps
![]() ${\mathcal {G}}_{\mathrm {Gray}}(0, 0)\to {\mathcal {G}}_{\mathrm {Gray}}(n, m)$
. Formula (A.9) shows that the object
${\mathcal {G}}_{\mathrm {Gray}}(0, 0)\to {\mathcal {G}}_{\mathrm {Gray}}(n, m)$
. Formula (A.9) shows that the object
![]() $h_{(i, j), [k]}$
in
$h_{(i, j), [k]}$
in
![]() $\mathcal {H}_{\mathrm {Gray}}(n, m)$
is given by the
$\mathcal {H}_{\mathrm {Gray}}(n, m)$
is given by the
![]() $2$
-functor
$2$
-functor
The explicit description of the Gray tensor product (7.4) (see [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23, Proposition 5.1.9]) identifies the mapping
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {Hom}}_{[n]\boxtimes [m]}((i, j), (a, b))$
with the poset of maximal chains from
${\mathrm {Hom}}_{[n]\boxtimes [m]}((i, j), (a, b))$
with the poset of maximal chains from
![]() $(i, j)$
to
$(i, j)$
to
![]() $(a, b)$
in the grid
$(a, b)$
in the grid
![]() $[n]\times [m]$
, ordered using that for each square, ‘right-after-down’ is smaller than ‘down-after-right’. Using this and the equivalence (A.7) to compute mapping
$[n]\times [m]$
, ordered using that for each square, ‘right-after-down’ is smaller than ‘down-after-right’. Using this and the equivalence (A.7) to compute mapping
![]() $\infty $
-groupoids, one readily sees that each
$\infty $
-groupoids, one readily sees that each
![]() $\mathcal {H}_{\mathrm {Gray}}(n, m)$
is a
$\mathcal {H}_{\mathrm {Gray}}(n, m)$
is a
![]() $0$
-truncated
$0$
-truncated
![]() $\infty $
-category. This already implies that
$\infty $
-category. This already implies that
![]() $\mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}})$
is discrete, so it remains to verify that it has only one component.
$\mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}})$
is discrete, so it remains to verify that it has only one component.
To see this, consider the fully faithful functor (which we only need for gaunt
![]() $2$
-categories)
$2$
-categories)
defined as follows: for each
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathbf {C}$
and
$\mathbf {C}$
and
![]() $[k]\in {\mathbf {\Delta }}$
, let
$[k]\in {\mathbf {\Delta }}$
, let
![]() $\Phi (\mathbf {C})_k$
be the
$\Phi (\mathbf {C})_k$
be the
![]() $\infty $
-category obtained by applying the monoidal functor
$\infty $
-category obtained by applying the monoidal functor
![]() ${\mathrm {Hom}}_{\mathrm {Cat} }([k], -)\colon \mathrm {Cat} \longrightarrow {\mathrm {Gpd}}$
to each mapping object. By naturality in
${\mathrm {Hom}}_{\mathrm {Cat} }([k], -)\colon \mathrm {Cat} \longrightarrow {\mathrm {Gpd}}$
to each mapping object. By naturality in
![]() $[k]$
, this defines a simplicial diagram of
$[k]$
, this defines a simplicial diagram of
![]() $\infty $
-categories, whose underlying simplicial diagram of
$\infty $
-categories, whose underlying simplicial diagram of
![]() $\infty $
-groupoids of objects is constant; we define
$\infty $
-groupoids of objects is constant; we define
![]() $\Phi (\mathbf {C})\longrightarrow {\mathbf {\Delta }}$
to be the cartesian unstraightening of this simplicial diagram of
$\Phi (\mathbf {C})\longrightarrow {\mathbf {\Delta }}$
to be the cartesian unstraightening of this simplicial diagram of
![]() $\infty $
-categories. Unraveling the definitions then shows that the codegeneracy map
$\infty $
-categories. Unraveling the definitions then shows that the codegeneracy map
![]() $\mathcal {H}_{\mathrm {Gray}}(n, m)\longrightarrow \mathcal {H}_{\mathrm {Gray}}(0, 0)\cong {\mathbf {\Delta }}$
can be identified with the cartesian fibration between
$\mathcal {H}_{\mathrm {Gray}}(n, m)\longrightarrow \mathcal {H}_{\mathrm {Gray}}(0, 0)\cong {\mathbf {\Delta }}$
can be identified with the cartesian fibration between
![]() $0$
-truncated
$0$
-truncated
![]() $\infty $
-categories
$\infty $
-categories
![]() $\Phi ([n]\boxtimes [m])\longrightarrow {\mathbf {\Delta }}$
(naturally in
$\Phi ([n]\boxtimes [m])\longrightarrow {\mathbf {\Delta }}$
(naturally in
![]() $[n]$
and
$[n]$
and
![]() $[m]$
).
$[m]$
).
Let us now consider the map of sets
![]() $\mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}})\longrightarrow \mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}}(0, 0))$
restricting an automorphism
$\mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}})\longrightarrow \mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}}(0, 0))$
restricting an automorphism
![]() $\varphi $
of
$\varphi $
of
![]() $\mathcal {H}_{\mathrm {Gray}}$
to the component
$\mathcal {H}_{\mathrm {Gray}}$
to the component
![]() $\varphi _{0, 0}$
. For an automorphism
$\varphi _{0, 0}$
. For an automorphism
![]() $\psi $
of
$\psi $
of
![]() $\mathcal {H}_{\mathrm {Gray}}(0, 0)$
, the fibre
$\mathcal {H}_{\mathrm {Gray}}(0, 0)$
, the fibre
![]() $\mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}})_{\psi }$
can be identified with the set of isomorphisms
$\mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}})_{\psi }$
can be identified with the set of isomorphisms
of bicosimplicial diagrams in the over-
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Cat} /\mathcal {H}_{\mathrm {Gray}}(0, 0)$
. By the above discussion,
$\mathrm {Cat} /\mathcal {H}_{\mathrm {Gray}}(0, 0)$
. By the above discussion,
![]() $\mathcal {H}$
actually determines a cosimplicial diagram in the subcategory
$\mathcal {H}$
actually determines a cosimplicial diagram in the subcategory
![]() $\operatorname {\mathrm {Cart}}(\mathcal {H}_{\mathrm {Gray}}(0, 0))\subseteq \mathrm {Cat} /\mathcal {H}_{\mathrm {Gray}}(0, 0)$
. By Lemma A.4, it then suffices to compute the sets of isomorphisms
$\operatorname {\mathrm {Cart}}(\mathcal {H}_{\mathrm {Gray}}(0, 0))\subseteq \mathrm {Cat} /\mathcal {H}_{\mathrm {Gray}}(0, 0)$
. By Lemma A.4, it then suffices to compute the sets of isomorphisms
![]() $\mathcal {H}_{\mathrm {Gray}}\longrightarrow \psi ^{*}\mathcal {H}_{\mathrm {Gray}}$
within
$\mathcal {H}_{\mathrm {Gray}}\longrightarrow \psi ^{*}\mathcal {H}_{\mathrm {Gray}}$
within
![]() $\operatorname {\mathrm {Cart}}(\mathcal {H}_{\mathrm {Gray}}(0, 0))$
.
$\operatorname {\mathrm {Cart}}(\mathcal {H}_{\mathrm {Gray}}(0, 0))$
.
Identifying
![]() $\mathcal {H}(0, 0)\cong {\mathbf {\Delta }}$
, it now suffices to compute the set of isomorphisms of bicosimplicial diagrams in
$\mathcal {H}(0, 0)\cong {\mathbf {\Delta }}$
, it now suffices to compute the set of isomorphisms of bicosimplicial diagrams in
![]() $\operatorname {\mathrm {Cart}}({\mathbf {\Delta }})$
$\operatorname {\mathrm {Cart}}({\mathbf {\Delta }})$
for all
![]() $\psi \in \mathrm {Aut}({\mathbf {\Delta }})\cong \{\mathrm {id}, {\mathrm {op}}\}$
. Since
$\psi \in \mathrm {Aut}({\mathbf {\Delta }})\cong \{\mathrm {id}, {\mathrm {op}}\}$
. Since
![]() $\Phi \colon \mathrm {Cat}_2\longrightarrow \operatorname {\mathrm {Cart}}({\mathbf {\Delta }})$
is fully faithful (at least on gaunt
$\Phi \colon \mathrm {Cat}_2\longrightarrow \operatorname {\mathrm {Cart}}({\mathbf {\Delta }})$
is fully faithful (at least on gaunt
![]() $2$
-categories), this comes down to computing the sets of natural isomorphisms
$2$
-categories), this comes down to computing the sets of natural isomorphisms
Since such isomorphisms are determined by their behaviour on objects, compatibility with the vertex inclusions shows that there is a unique natural
![]() $\varphi $
(the identity) and no natural
$\varphi $
(the identity) and no natural
![]() $\varphi '$
. We conclude that
$\varphi '$
. We conclude that
![]() $\mathrm {Aut}(F_{\mathrm {Gray}})\subseteq \mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}})\simeq \ast $
.
$\mathrm {Aut}(F_{\mathrm {Gray}})\subseteq \mathrm {Aut}(\mathcal {H}_{\mathrm {Gray}})\simeq \ast $
.
Acknowledgements
It is a pleasure to thank Dustin Clausen, Emanuele Dotto, Yonatan Harpaz, Gijsbert Scheltus Karel Sebastiaan Heuts, Corina Keller, Achim Krause, Markus Land, Denis Nardin, Thomas Nikolaus, Stefan Schwede, Wolfgang Steimle and Lior Yanovski for several very useful discussions. We further thank Shaul Barkan and Jan Steinebrunner for pointing out an omission in the verification of orthogonality for the factorisation system on span categories in the original version of this paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
During the preparation of this text, FH and SL were members of the Hausdorff Center for Mathematics at the University of Bonn funded by the German Research Foundation (DFG), and FH was furthermore a member of the cluster ‘Mathematics Münster: Dynamics-Geometry-Structure’ at the University of Münster under grant nos. EXC 2047 and EXC 2044, respectively. FH would also like to thank the Mittag-Leffler Institute for its hospitality during the research program ‘Higher Algebraic Structures in Algebra, Topology and Geometry’, supported by the Swedish Research Council (VR) under grant no. 2016-06596. FH and JN were further supported by the European Research Council (ERC) through the grants ‘Moduli Spaces, Manifolds and Arithmetic’, grant no. 682922, and ‘Derived Symplectic Geometry and Applications’, grant no. 768679, respectively. SL was supported by the DFG Schwerpunktprogramm 1786 ‘Homotopy Theory and Algebraic Geometry’ (project ID SCHW 860/1-1).