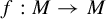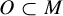1. Introduction
In this paper, we consider a family of systems which is called pointwise hyperbolic, introduced by Chen, Hu, and Zhou in [Reference Chen, Hu and Zhou10], and we construct countable Markov partition with a finite-to-one almost everywhere induced coding for it. A pointwise hyperbolic diffeomorphism
![]() $f:M\rightarrow M$
is different from the uniformly hyperbolic situation since the expansion and contraction depend on points. If the system is defined on an open invariant subset
$f:M\rightarrow M$
is different from the uniformly hyperbolic situation since the expansion and contraction depend on points. If the system is defined on an open invariant subset
![]() $O\subset M$
, as stated in [Reference Chen, Hu and Zhou10], hyperbolicity may not be uniform near the boundary of O. Under some additional conditions (see [Reference Chen, Hu and Zhou10, Assumptions U and S]), the authors proved that such a system has unstable and stable manifolds over any orbit with initial value
$O\subset M$
, as stated in [Reference Chen, Hu and Zhou10], hyperbolicity may not be uniform near the boundary of O. Under some additional conditions (see [Reference Chen, Hu and Zhou10, Assumptions U and S]), the authors proved that such a system has unstable and stable manifolds over any orbit with initial value
![]() $x\in O$
. As applications, they give two examples, the almost Anosov diffeomorphisms [Reference Hu and Young15] and gentle perturbations of Katok’s map [Reference Katok17], and show that under certain conditions, the requirements given in Assumptions U and S can be verified. For more details, see [Reference Chen, Hu and Zhou10].
$x\in O$
. As applications, they give two examples, the almost Anosov diffeomorphisms [Reference Hu and Young15] and gentle perturbations of Katok’s map [Reference Katok17], and show that under certain conditions, the requirements given in Assumptions U and S can be verified. For more details, see [Reference Chen, Hu and Zhou10].
In 2013, Sarig constructed countable Markov partitions with full topological entropy for
![]() $C^{1+\alpha } (0<\alpha <1)$
closed surface diffeomorphisms [Reference Sarig22]. His method has been proven to be successful for other classes of systems. Here are some of the recent developments: surface maps with singularities [Reference Lima and Matheus20],
$C^{1+\alpha } (0<\alpha <1)$
closed surface diffeomorphisms [Reference Sarig22]. His method has been proven to be successful for other classes of systems. Here are some of the recent developments: surface maps with singularities [Reference Lima and Matheus20],
![]() $C^{1+\alpha }$
closed manifolds diffeomorphisms in dimension
$C^{1+\alpha }$
closed manifolds diffeomorphisms in dimension
![]() $d\geq 2$
[Reference Ben Ovadia6], non-invertible and/or singular maps [Reference Araujo, Lima and Poletti4, Reference Lima18], and injective semi-conjugacies [Reference Buzzi9]. A comprehensive survey on the construction of Markov partitions for non-uniformly hyperbolic systems can be found in [Reference Lima19].
$d\geq 2$
[Reference Ben Ovadia6], non-invertible and/or singular maps [Reference Araujo, Lima and Poletti4, Reference Lima18], and injective semi-conjugacies [Reference Buzzi9]. A comprehensive survey on the construction of Markov partitions for non-uniformly hyperbolic systems can be found in [Reference Lima19].
As pointed out in [Reference Ben Ovadia7], the key engine that allows Sarig’s methods to be applied to more suitable adaptations and generalizations is the Pesin theory. For a fixed constant
![]() $\chi>0$
and a non-uniformly hyperbolic orbit, Pesin’s idea [Reference Barreira and Pesin5] was to construct local charts to represent the action of the differential as a small perturbation of a hyperbolic matrix. After the local change of coordinates, although the domain of the chart is no longer uniform in size, as it is in the uniformly hyperbolic situation, this approach produces uniform estimates in charts, that is, one contracts in rate at most
$\chi>0$
and a non-uniformly hyperbolic orbit, Pesin’s idea [Reference Barreira and Pesin5] was to construct local charts to represent the action of the differential as a small perturbation of a hyperbolic matrix. After the local change of coordinates, although the domain of the chart is no longer uniform in size, as it is in the uniformly hyperbolic situation, this approach produces uniform estimates in charts, that is, one contracts in rate at most
![]() $e^{-\chi }$
, and one expands at least
$e^{-\chi }$
, and one expands at least
![]() $e^{\chi }$
. Thanks to these uniform estimates in charts, one can carry out Pesin’s unstable and stable manifold theorem over a chain (no longer than an orbit), which is then used in Sarig’s and subsequent work mentioned above to construct a coding for big classes of systems.
$e^{\chi }$
. Thanks to these uniform estimates in charts, one can carry out Pesin’s unstable and stable manifold theorem over a chain (no longer than an orbit), which is then used in Sarig’s and subsequent work mentioned above to construct a coding for big classes of systems.
Unfortunately, similar to 0-summable points considered in [Reference Ben Ovadia7, Definition 2.1], the orbits in pointwise hyperbolic systems may not be the
![]() $\chi $
-hyperbolic ones mentioned above since hyperbolicity may become weak near
$\chi $
-hyperbolic ones mentioned above since hyperbolicity may become weak near
![]() $\partial O$
. An extreme case is an almost Anosov diffeomorphism on the two-dimensional torus studied in [Reference Hu13, Reference Hu and Young15], where the orbit spends almost all the time near the boundary of O for almost every initial point in the sense of Lebesgue measure. Therefore, the estimates in charts may not be held uniform over an orbit. To construct unstable manifolds, in [Reference Chen, Hu and Zhou10], they require a prior condition that the expansion of the map along unstable directions is stronger than the rates of the point moving away from the boundary [Reference Chen, Hu and Zhou10, Assumption U(ii)].
$\partial O$
. An extreme case is an almost Anosov diffeomorphism on the two-dimensional torus studied in [Reference Hu13, Reference Hu and Young15], where the orbit spends almost all the time near the boundary of O for almost every initial point in the sense of Lebesgue measure. Therefore, the estimates in charts may not be held uniform over an orbit. To construct unstable manifolds, in [Reference Chen, Hu and Zhou10], they require a prior condition that the expansion of the map along unstable directions is stronger than the rates of the point moving away from the boundary [Reference Chen, Hu and Zhou10, Assumption U(ii)].
Since a chain or a pseudo-orbit is an orbit up to small errors at each iteration, a slightly stronger assumption (see Assumption US(ii) and (iii) in §2) than [Reference Chen, Hu and Zhou10, Assumptions U(ii) and S(ii)] is indeed necessary if we construct unstable manifolds over the recurrent-pointwise-pseudo-orbit we introduce in Definition 5.1 of §5. However, Assumption US(i) is weaker than [Reference Chen, Hu and Zhou10, Assumptions U(i) and S(i)] since they constructed unstable manifolds along the orbit of f and thus they required the assumption of pointwise dominated splitting. At the same time, the Assumption US(ii) and (iii) we require in this paper were designed to be sufficiently lax that allows us to cover the examples considered in [Reference Chen, Hu and Zhou10].
The paper is organized as follows. In §2, we give definitions and statements of the main results. The results apply to counting the number of closed orbits for pointwise hyperbolic diffeomorphism f under certain pointwise hyperbolic conditions (Assumption US) and regularity assumption (Assumption R). In §3, we represent the dynamics as a small perturbation of a pointwise hyperbolic block-form matrix in a suitable (varying) size of a neighborhood in tangent space (rather than Euclidean space as was done in [Reference Sarig22]) and estimate some inequalities for the ratio of two adjacent neighborhoods under the action of f. Since the charts no longer have uniform estimates (the orbits may have
![]() $0$
Lyapunov exponents), we need to find a suitable definition for admissible manifolds on which the graph transform is operable over some suitable edge, this is the content of §4. Section 5 is devoted to the construction of local unstable and stable manifolds over the recurrent-pointwise-pseudo-orbits, which are the limit points of compositions of a graph transform acting on admissible manifolds. Finally, in §6, we show how to employ the shadowing theory of a recurrent-pointwise-pseudo-orbit to construct a Markov partition which induces a finite-to-one almost everywhere coding for pointwise hyperbolic systems on open regions O satisfying Assumptions US and R.
$0$
Lyapunov exponents), we need to find a suitable definition for admissible manifolds on which the graph transform is operable over some suitable edge, this is the content of §4. Section 5 is devoted to the construction of local unstable and stable manifolds over the recurrent-pointwise-pseudo-orbits, which are the limit points of compositions of a graph transform acting on admissible manifolds. Finally, in §6, we show how to employ the shadowing theory of a recurrent-pointwise-pseudo-orbit to construct a Markov partition which induces a finite-to-one almost everywhere coding for pointwise hyperbolic systems on open regions O satisfying Assumptions US and R.
Although our coding works on some examples, the question of whether or not there is an example to clarify the results of the present paper are not included in the work of [Reference Ben Ovadia7], which is an interesting and unresolved question so far. In [Reference Ben Ovadia7, Theorem 8.3 and Corollary 8.4], Ben Ovadia shows that if an almost Anosov diffeomorphisms defined in a two-dimensional torus is topologically transitive and the contraction rates along the stable direction are smaller than 1 even at indifferent fixed point p, then it is 0-summable for every
![]() $x\neq p$
, and moreover it is codable. Note that the example of almost Anosov diffeomorphisms in this paper is not necessarily topologically transitive and the contraction rates can reach 1 at p. However, this does not mean that our example includes the former, because near p, the rates in the expansion direction are not limited in [Reference Ben Ovadia7, Definition 8.2(3)], but we require the rates of expansion to be greater than the distance from the point to p (see Assumption US(ii)). We mention that there are non-uniformly contracting maps satisfying Assumption US(iii) in a subset of an open invariant set with every point near p that is not summable. For details, see Example 2.1 in §2.
$x\neq p$
, and moreover it is codable. Note that the example of almost Anosov diffeomorphisms in this paper is not necessarily topologically transitive and the contraction rates can reach 1 at p. However, this does not mean that our example includes the former, because near p, the rates in the expansion direction are not limited in [Reference Ben Ovadia7, Definition 8.2(3)], but we require the rates of expansion to be greater than the distance from the point to p (see Assumption US(ii)). We mention that there are non-uniformly contracting maps satisfying Assumption US(iii) in a subset of an open invariant set with every point near p that is not summable. For details, see Example 2.1 in §2.
2. Definition and statements of results
Let M be a
![]() $C^{\infty }$
connected compact Riemannian manifold with dimension
$C^{\infty }$
connected compact Riemannian manifold with dimension
![]() $d\geq 2$
, and
$d\geq 2$
, and
![]() $O \subset~M$
an open connected subset of M. We will always assume that the diameter of M is smaller than one (just multiply the metric by a small constant).
$O \subset~M$
an open connected subset of M. We will always assume that the diameter of M is smaller than one (just multiply the metric by a small constant).
Let
![]() $f: M \rightarrow M$
be a
$f: M \rightarrow M$
be a
![]() $C^{1+\alpha }$
diffeomorphism (
$C^{1+\alpha }$
diffeomorphism (
![]() $\alpha>0$
) such that
$\alpha>0$
) such that
![]() $f(O)=O$
. Denote by
$f(O)=O$
. Denote by
![]() $\|D_{x} f\|$
and
$\|D_{x} f\|$
and
![]() $m(D_{x} f)$
the norm and the minimal norm of
$m(D_{x} f)$
the norm and the minimal norm of
![]() $D_{x} f$
, respectively. Note that we have
$D_{x} f$
, respectively. Note that we have
![]() $m(D_{x} f)=\|D_{f(x)} f^{-1}\|^{-1}$
.
$m(D_{x} f)=\|D_{f(x)} f^{-1}\|^{-1}$
.
Definition 2.1. The
![]() $C^{1+\alpha }$
diffeomorphism (
$C^{1+\alpha }$
diffeomorphism (
![]() $\alpha>0$
) f is called a pointwise hyperbolic on an invariant set
$\alpha>0$
) f is called a pointwise hyperbolic on an invariant set
![]() $O \subset M$
if there exist two continuous functions
$O \subset M$
if there exist two continuous functions
![]() $\unicode{x3bb} ^{u}, \unicode{x3bb} ^{s}: O \rightarrow \mathbb {R}_{+}$
with
$\unicode{x3bb} ^{u}, \unicode{x3bb} ^{s}: O \rightarrow \mathbb {R}_{+}$
with
![]() $\unicode{x3bb} ^{s}(x)<1<\unicode{x3bb} ^{u}(x)$
for any
$\unicode{x3bb} ^{s}(x)<1<\unicode{x3bb} ^{u}(x)$
for any
![]() $x\in O$
, and an invariant decomposition
$x\in O$
, and an invariant decomposition
![]() $T_{O} M=E^{u} \oplus E^{s}$
such that for any
$T_{O} M=E^{u} \oplus E^{s}$
such that for any
![]() $x \in O$
,
$x \in O$
,
 $$ \begin{align*} \begin{aligned} &\unicode{x3bb}^{u}(x) \leqslant m(D_{x} f|_{E^{u}(x)}), \\ &\|D_{x} f|_{E^{s}(x)}\| \leqslant \unicode{x3bb}^{s}(x), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\unicode{x3bb}^{u}(x) \leqslant m(D_{x} f|_{E^{u}(x)}), \\ &\|D_{x} f|_{E^{s}(x)}\| \leqslant \unicode{x3bb}^{s}(x), \end{aligned} \end{align*} $$
where
![]() $E_{x}^{u}$
and
$E_{x}^{u}$
and
![]() $E_{x}^{s}$
are called unstable and stable subspaces, respectively.
$E_{x}^{s}$
are called unstable and stable subspaces, respectively.
Remark 2.1. Although it is possible that
![]() $m(D_{x} f|_{E^{u}(x)}) \rightarrow 1$
or
$m(D_{x} f|_{E^{u}(x)}) \rightarrow 1$
or
![]() $\|D_{x} f|_{E^{s}(x)}\| \rightarrow 1$
as
$\|D_{x} f|_{E^{s}(x)}\| \rightarrow 1$
as
![]() $x \rightarrow \partial O$
, hyperbolicity is uniform when restricted to any compact set contained in O because of continuity of
$x \rightarrow \partial O$
, hyperbolicity is uniform when restricted to any compact set contained in O because of continuity of
![]() $\unicode{x3bb} ^{u}(x)$
and
$\unicode{x3bb} ^{u}(x)$
and
![]() $\unicode{x3bb} ^{s}(x)$
.
$\unicode{x3bb} ^{s}(x)$
.
The following Assumption US is motivated by [Reference Chen, Hu and Zhou10, Assumptions U and S].
Assumption US.
-
(i) The distributions
 $E^{u}$
and
$E^{u}$
and
 $E^{s}$
are continuous.
$E^{s}$
are continuous. -
(ii) (U-boundary control) There exist
 $r_0^u, \beta ^u>0, \gamma ^u>{\max } \{1, \beta ^u / \alpha \}$
,
$r_0^u, \beta ^u>0, \gamma ^u>{\max } \{1, \beta ^u / \alpha \}$
,
 $0<\kappa ^u<1$
, and
$0<\kappa ^u<1$
, and
 $C^u>1$
such that for any
$C^u>1$
such that for any
 $x \in O$
satisfying
$x \in O$
satisfying
 $d(x, \partial O) \leqslant r_0^u$
, we have
$d(x, \partial O) \leqslant r_0^u$
, we have  $$ \begin{align*} m(D f|_{E^{u}(x)})^{\kappa^u}-1 \geqslant C^u {\max} \bigg\{d(x, \partial O)^{\beta^u},\bigg(\frac{d(f(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^u}-1\bigg\}.\end{align*} $$
$$ \begin{align*} m(D f|_{E^{u}(x)})^{\kappa^u}-1 \geqslant C^u {\max} \bigg\{d(x, \partial O)^{\beta^u},\bigg(\frac{d(f(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^u}-1\bigg\}.\end{align*} $$
-
(iii) (S-boundary control) There exist
 $r^s_0, \beta ^s>0, \gamma ^s>{\max } \{1, \beta ^s / \alpha \}$
,
$r^s_0, \beta ^s>0, \gamma ^s>{\max } \{1, \beta ^s / \alpha \}$
,
 $0<\kappa ^s<1$
, and
$0<\kappa ^s<1$
, and
 $C^s>1$
such that for any
$C^s>1$
such that for any
 $x \in O$
satisfying
$x \in O$
satisfying
 $d(x, \partial O) \leqslant r^s_0$
, we have
$d(x, \partial O) \leqslant r^s_0$
, we have  $$ \begin{align*} m(D f^{-1}|_{E^{s}(x)})^{\kappa^s}-1 \geqslant C^s {\max} \bigg\{d(x, \partial O)^{\beta^s},\bigg(\frac{d(f^{-1}(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^s}-1\bigg\}. \end{align*} $$
$$ \begin{align*} m(D f^{-1}|_{E^{s}(x)})^{\kappa^s}-1 \geqslant C^s {\max} \bigg\{d(x, \partial O)^{\beta^s},\bigg(\frac{d(f^{-1}(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^s}-1\bigg\}. \end{align*} $$
Remark 2.2. Assumption US(i) is a corollary of [Reference Chen, Hu and Zhou10, Assumption U(i)], see [Reference Chen, Hu and Zhou10, Lemma 3.1]. It is therefore weaker than the latter.
Remark 2.3. Near the boundary, the forward images of u-admissible manifolds defined in Definition 4.2 grow essentially
![]() $m(D_{x} f|_{E^{u}(x)})\rightarrow 1$
as
$m(D_{x} f|_{E^{u}(x)})\rightarrow 1$
as
![]() $x \rightarrow \partial O$
, that is, the hyperbolicity may become weak. A priori, the ratio of size of u-admissible manifolds
$x \rightarrow \partial O$
, that is, the hyperbolicity may become weak. A priori, the ratio of size of u-admissible manifolds
![]() $({d(f(x), \partial O)}/{d(x, \partial O)})^{\gamma ^u}$
may be bigger and far from 1. Fortunately, this is not the case in our setting: Assumption US(ii) means that near the boundary, the expansion rates along the unstable direction are stronger than the ratio of size along the orbit which is near the boundary. Therefore, Assumption US(ii) is required for the unstable manifold theorem (Proposition 5.2(1)) since the size of local unstable manifolds can be recovered under the forward iteration of f when orbits are near the boundary of O.
$({d(f(x), \partial O)}/{d(x, \partial O)})^{\gamma ^u}$
may be bigger and far from 1. Fortunately, this is not the case in our setting: Assumption US(ii) means that near the boundary, the expansion rates along the unstable direction are stronger than the ratio of size along the orbit which is near the boundary. Therefore, Assumption US(ii) is required for the unstable manifold theorem (Proposition 5.2(1)) since the size of local unstable manifolds can be recovered under the forward iteration of f when orbits are near the boundary of O.
Assumption US is similar to the boundary condition control in [Reference Chen, Hu and Zhou10, Assumptions U and S]. The additional requirements of
![]() $\kappa ^u$
and
$\kappa ^u$
and
![]() $\kappa ^s$
were designed to recover the local unstable and stable manifolds, but also sufficiently lax that allow us to cover the examples considered in [Reference Chen, Hu and Zhou10]. It is needed since the local unstable and stable manifold in this paper are constructed over the recurrent-pointwise-pseudo-orbit defined in Definition 5.1 rather than an orbit of f as done in [Reference Chen, Hu and Zhou10]. In fact, under certain conditions (see [Reference Chen, Hu and Zhou10, Assumptions A and K]), for the almost Anosov diffeomorphisms and gentle perturbations of Katok’s map, we can take
$\kappa ^s$
were designed to recover the local unstable and stable manifolds, but also sufficiently lax that allow us to cover the examples considered in [Reference Chen, Hu and Zhou10]. It is needed since the local unstable and stable manifold in this paper are constructed over the recurrent-pointwise-pseudo-orbit defined in Definition 5.1 rather than an orbit of f as done in [Reference Chen, Hu and Zhou10]. In fact, under certain conditions (see [Reference Chen, Hu and Zhou10, Assumptions A and K]), for the almost Anosov diffeomorphisms and gentle perturbations of Katok’s map, we can take
![]() $({n+2\delta })/({n+3\delta })<\kappa ^t<1$
and
$({n+2\delta })/({n+3\delta })<\kappa ^t<1$
and
![]() $({2\alpha +1})/({2\alpha +1.5})<\kappa ^t<1$
, respectively, where
$({2\alpha +1})/({2\alpha +1.5})<\kappa ^t<1$
, respectively, where
![]() $t=u,s$
. For more details, see [Reference Chen, Hu and Zhou10, Theorems D and E].
$t=u,s$
. For more details, see [Reference Chen, Hu and Zhou10, Theorems D and E].
Given
![]() $a,b>0$
, we write
$a,b>0$
, we write
![]() $a\wedge b:=\min \{a,b\}$
,
$a\wedge b:=\min \{a,b\}$
,
![]() $a\vee b:={\max }\{a,b\}$
. The next assumption is on the regularity of f.
$a\vee b:={\max }\{a,b\}$
. The next assumption is on the regularity of f.
Assumption R.
![]() $\alpha>({\beta }/{\gamma }) $
, where
$\alpha>({\beta }/{\gamma }) $
, where
![]() $\gamma =\gamma ^u\wedge \gamma ^s$
,
$\gamma =\gamma ^u\wedge \gamma ^s$
,
![]() $\beta =\beta ^u\vee \beta ^s$
.
$\beta =\beta ^u\vee \beta ^s$
.
Remark 2.4. This is stronger than
![]() $\gamma ^u>{\max } \{1, \beta ^u / \alpha \}$
together with
$\gamma ^u>{\max } \{1, \beta ^u / \alpha \}$
together with
![]() $\gamma ^s>{\max } \{1, \beta ^s / \alpha \}$
given in Assumption US(ii) and (iii). However, at the end of the proof of [Reference Chen, Hu and Zhou10, Theorems D and E], we can see that for almost Anosov diffeomorphisms and Katok’s map with gentle perturbations, the authors took
$\gamma ^s>{\max } \{1, \beta ^s / \alpha \}$
given in Assumption US(ii) and (iii). However, at the end of the proof of [Reference Chen, Hu and Zhou10, Theorems D and E], we can see that for almost Anosov diffeomorphisms and Katok’s map with gentle perturbations, the authors took
![]() $\alpha =n\geq 2, \beta ^u=n+\delta , \gamma ^u=n+2\delta $
where
$\alpha =n\geq 2, \beta ^u=n+\delta , \gamma ^u=n+2\delta $
where
![]() $\delta \in (0,1/3)$
and
$\delta \in (0,1/3)$
and
![]() $\alpha \geq 2, \beta ^u=2\alpha +1/2, \gamma ^u=2\alpha +1$
, respectively. Because of symmetry between the expression of the mapping and its inverse, we can take
$\alpha \geq 2, \beta ^u=2\alpha +1/2, \gamma ^u=2\alpha +1$
, respectively. Because of symmetry between the expression of the mapping and its inverse, we can take
![]() $\beta ^s=\beta ^u, \gamma ^s=\gamma ^u$
. Therefore,
$\beta ^s=\beta ^u, \gamma ^s=\gamma ^u$
. Therefore,
![]() ${\alpha \geq 2}$
selected in [Reference Chen, Hu and Zhou10, Theorems D and E] is enough for Assumption R.
${\alpha \geq 2}$
selected in [Reference Chen, Hu and Zhou10, Theorems D and E] is enough for Assumption R.
We now give a non-uniformly contracting map satisfying Assumption US(iii) in a subset of O which is unsummable in the sense of [Reference Ben Ovadia7, Definition 2.1]: a point
![]() $x \in M$
is called summable if its tangent space decomposes uniquely into
$x \in M$
is called summable if its tangent space decomposes uniquely into
![]() $T_x M=H^s(x) \oplus H^u(x)$
where
$T_x M=H^s(x) \oplus H^u(x)$
where
![]() $\text {for all } \xi ^s \in H^s(x), \xi ^u \in H^u(x)$
,
$\text {for all } \xi ^s \in H^s(x), \xi ^u \in H^u(x)$
,
We mention that contrary to the present work, the distribution
![]() $H^s(x) \oplus H^u(x)$
is usually not more than just measurable.
$H^s(x) \oplus H^u(x)$
is usually not more than just measurable.
Example 2.1. For simplicity, let us consider a
![]() $C^{1+\alpha } (\alpha =2k, k\in \mathbb {N}_+)$
diffeomorphism f of a two-dimensional closed (compact without boundary) connected smooth Riemannian manifold M that has a fixed point p. Suppose f is a non-uniformly contracting map on
$C^{1+\alpha } (\alpha =2k, k\in \mathbb {N}_+)$
diffeomorphism f of a two-dimensional closed (compact without boundary) connected smooth Riemannian manifold M that has a fixed point p. Suppose f is a non-uniformly contracting map on
![]() $O=M/{p}$
and that there exist a neighborhood U of p and a local coordinate system
$O=M/{p}$
and that there exist a neighborhood U of p and a local coordinate system
![]() $(x, y)$
with
$(x, y)$
with
![]() $p = (0, 0)$
. We assume further that on U, f has the form
$p = (0, 0)$
. We assume further that on U, f has the form
where
![]() $\varepsilon _1>0$
.
$\varepsilon _1>0$
.
Denote
![]() $z=(x,y)$
. From
$z=(x,y)$
. From
 $$ \begin{align*} D_z f=\left(\begin{array}{@{}ll@{}} 1-(1+\alpha)x^\alpha & 0 \\ -\varepsilon_1\alpha yx^{\alpha-1} & 1-\varepsilon_1x^\alpha \end{array}\right)\!, \end{align*} $$
$$ \begin{align*} D_z f=\left(\begin{array}{@{}ll@{}} 1-(1+\alpha)x^\alpha & 0 \\ -\varepsilon_1\alpha yx^{\alpha-1} & 1-\varepsilon_1x^\alpha \end{array}\right)\!, \end{align*} $$
it is easy to verify that if
![]() $z\in U$
, we have
$z\in U$
, we have
 $$ \begin{align*} \begin{aligned} D_{z} f^{-1}&=\left(\begin{array}{@{}ll@{}} 1+(1+\alpha)x^\alpha+O(x^{\alpha+1}) & 0\\ \varepsilon_1\alpha yx^{\alpha-1}+yO(x^{2\alpha-1}) & 1+\varepsilon_1x^\alpha+O(x^{\alpha+1}) \end{array}\right)\!. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} D_{z} f^{-1}&=\left(\begin{array}{@{}ll@{}} 1+(1+\alpha)x^\alpha+O(x^{\alpha+1}) & 0\\ \varepsilon_1\alpha yx^{\alpha-1}+yO(x^{2\alpha-1}) & 1+\varepsilon_1x^\alpha+O(x^{\alpha+1}) \end{array}\right)\!. \end{aligned} \end{align*} $$
Now let us consider a subset of U:
Claim 1. If
![]() $\varepsilon _1>1$
, then there exist
$\varepsilon _1>1$
, then there exist
![]() $r^s_0, \beta ^s>0, \gamma ^s>{\max } \{1, \beta ^s / \alpha \}$
,
$r^s_0, \beta ^s>0, \gamma ^s>{\max } \{1, \beta ^s / \alpha \}$
,
![]() $0<\kappa ^s<1$
, and
$0<\kappa ^s<1$
, and
![]() $C^s>1$
such that for any
$C^s>1$
such that for any
![]() $z \in U_1$
satisfying
$z \in U_1$
satisfying
![]() $\|z\| \leqslant r^s_0$
, we have
$\|z\| \leqslant r^s_0$
, we have
 $$ \begin{align*} m(D_zf^{-1})^{\kappa^s}-1 \geqslant C^s {\max} \bigg\{\|z\|^{\beta^s},\bigg(\frac{\|f^{-1}(z)\|}{\|z\|}\bigg)^{\gamma^s}-1\bigg\}. \end{align*} $$
$$ \begin{align*} m(D_zf^{-1})^{\kappa^s}-1 \geqslant C^s {\max} \bigg\{\|z\|^{\beta^s},\bigg(\frac{\|f^{-1}(z)\|}{\|z\|}\bigg)^{\gamma^s}-1\bigg\}. \end{align*} $$
Proof of Claim 1
Note that if
![]() $z \in U_1$
, we get
$z \in U_1$
, we get
 $$ \begin{align*} \begin{aligned} D_{z} f^{-1}&=\left(\begin{array}{@{}ll@{}} 1+(1+\alpha)x^\alpha+O(x^{\alpha+1}) & 0\\ O(|x|^{\alpha+\varepsilon_2-1}) & 1+\varepsilon_1x^\alpha+O(x^{\alpha+1}) \end{array}\right)\!, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} D_{z} f^{-1}&=\left(\begin{array}{@{}ll@{}} 1+(1+\alpha)x^\alpha+O(x^{\alpha+1}) & 0\\ O(|x|^{\alpha+\varepsilon_2-1}) & 1+\varepsilon_1x^\alpha+O(x^{\alpha+1}) \end{array}\right)\!, \end{aligned} \end{align*} $$
and thus
![]() $m(D_zf^{-1})^{\kappa ^s}-1=\varepsilon _1\kappa ^sx^\alpha +O(|x|^{\alpha +2(\varepsilon _2-1)})$
.
$m(D_zf^{-1})^{\kappa ^s}-1=\varepsilon _1\kappa ^sx^\alpha +O(|x|^{\alpha +2(\varepsilon _2-1)})$
.
It is easy to see that
One can choose
![]() $r^s_0$
small enough such that
$r^s_0$
small enough such that
![]() $f^{-1}(z)\in U$
for any
$f^{-1}(z)\in U$
for any
![]() $z \in U_1$
satisfying
$z \in U_1$
satisfying
![]() $\|z\| \leqslant r^s_0$
, and therefore
$\|z\| \leqslant r^s_0$
, and therefore
Let us compute
 $$ \begin{align*} \begin{aligned} C^s\bigg[\bigg(\frac{\|f^{-1}(z)\|}{\|z\|}\bigg)^{\gamma^s}-1\bigg]&=C^s\bigg[\bigg(\frac{\|f^{-1}(z)\|}{\|z\|}\bigg)^{\gamma^s}-1\bigg]\notag\\ &=C^s\bigg[\bigg(\frac{x^2+2x^{2+\alpha}+y^2+O(|x|^{\alpha+\min\{2\varepsilon_2,3\}})}{x^2+y^2}\bigg)^{\gamma^s/2}-1\bigg]\notag\\ &=C^s\gamma^s\frac{2x^{2+\alpha}+O(|x|^{\alpha+\min\{2\varepsilon_2,3\}})}{2(x^2+y^2)}\notag\\ &\leq C^s\gamma^sx^{\alpha}+O(|x|^{\alpha+\min\{2\varepsilon_2-2,1\}}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} C^s\bigg[\bigg(\frac{\|f^{-1}(z)\|}{\|z\|}\bigg)^{\gamma^s}-1\bigg]&=C^s\bigg[\bigg(\frac{\|f^{-1}(z)\|}{\|z\|}\bigg)^{\gamma^s}-1\bigg]\notag\\ &=C^s\bigg[\bigg(\frac{x^2+2x^{2+\alpha}+y^2+O(|x|^{\alpha+\min\{2\varepsilon_2,3\}})}{x^2+y^2}\bigg)^{\gamma^s/2}-1\bigg]\notag\\ &=C^s\gamma^s\frac{2x^{2+\alpha}+O(|x|^{\alpha+\min\{2\varepsilon_2,3\}})}{2(x^2+y^2)}\notag\\ &\leq C^s\gamma^sx^{\alpha}+O(|x|^{\alpha+\min\{2\varepsilon_2-2,1\}}). \end{aligned} \end{align*} $$
Hence, we get
 $$ \begin{align*} m(D_zf^{-1})^{\kappa^s}-1 \geqslant C^s {\max} \bigg\{\|z\|^{\beta^s},\bigg(\frac{\|f^{-1}(z)\|}{\|z\|}\bigg)^{\gamma^s}-1\bigg\}, \end{align*} $$
$$ \begin{align*} m(D_zf^{-1})^{\kappa^s}-1 \geqslant C^s {\max} \bigg\{\|z\|^{\beta^s},\bigg(\frac{\|f^{-1}(z)\|}{\|z\|}\bigg)^{\gamma^s}-1\bigg\}, \end{align*} $$
where
![]() $1/\sqrt {\varepsilon _1}<\kappa ^s<1$
,
$1/\sqrt {\varepsilon _1}<\kappa ^s<1$
,
![]() $1<C^s=\gamma ^s<\sqrt [4]{\varepsilon _1}$
, and
$1<C^s=\gamma ^s<\sqrt [4]{\varepsilon _1}$
, and
![]() $\alpha <\beta ^s<\alpha \gamma ^s$
.
$\alpha <\beta ^s<\alpha \gamma ^s$
.
Claim 2.
If
![]() $\varepsilon _1<({\alpha }/{2})+1$
, then
$\varepsilon _1<({\alpha }/{2})+1$
, then
![]() $\sum _{m \geq 0}\|D_z f^m({\partial }/{\partial y})\|^2=\infty $
for all
$\sum _{m \geq 0}\|D_z f^m({\partial }/{\partial y})\|^2=\infty $
for all
![]() $z\in U$
, where
$z\in U$
, where
![]() $({\partial }/{\partial y})=(0,1)^T$
.
$({\partial }/{\partial y})=(0,1)^T$
.
Proof of Claim 2
Denote
![]() $z_m=(x_m,y_m):=f^m(z)$
. Notice that
$z_m=(x_m,y_m):=f^m(z)$
. Notice that
![]() $z_m\in U$
for all
$z_m\in U$
for all
![]() $z\in U$
. By using induction, we get for all
$z\in U$
. By using induction, we get for all
![]() $m\geq 1$
that
$m\geq 1$
that
where
![]() $g(x_m)=(({1-\varepsilon _1x^\alpha _m})/({1-x^\alpha _m}))g(x_{m-1})$
and
$g(x_m)=(({1-\varepsilon _1x^\alpha _m})/({1-x^\alpha _m}))g(x_{m-1})$
and
![]() $g(x)=({1-\varepsilon _1x^\alpha })/({x-x^{\alpha +1}})$
.
$g(x)=({1-\varepsilon _1x^\alpha })/({x-x^{\alpha +1}})$
.
Clearly,
![]() $x_{m-1}=x_{m}+x^{\alpha +1}_{m}+O(x^{\alpha +1}_{m})$
for all
$x_{m-1}=x_{m}+x^{\alpha +1}_{m}+O(x^{\alpha +1}_{m})$
for all
![]() $m\geq 1$
since
$m\geq 1$
since
![]() $z_m\in U$
for all
$z_m\in U$
for all
![]() $z\in U$
, so by [Reference Hu and Vaienti14, Lemma 3.1], for all large m, we have
$z\in U$
, so by [Reference Hu and Vaienti14, Lemma 3.1], for all large m, we have
 $$ \begin{align*} |x_m|=\bigg(\frac{1}{\alpha(m+k)}\bigg)^{1/\alpha}+O\bigg(\frac{1}{m^{\theta}}\bigg) \end{align*} $$
$$ \begin{align*} |x_m|=\bigg(\frac{1}{\alpha(m+k)}\bigg)^{1/\alpha}+O\bigg(\frac{1}{m^{\theta}}\bigg) \end{align*} $$
for some integer k, where
![]() $\theta>1/\alpha $
.
$\theta>1/\alpha $
.
Now it is easy to get
 $$ \begin{align*} \begin{aligned} &\lim_{m\rightarrow\infty}m\bigg(\frac{\|D_z f^m({\partial}/{\partial y})\|^2}{\|D_z f^{m+1}({\partial}/{\partial y})\|^2}-1\bigg)\notag\\ &\quad=\lim_{m\rightarrow\infty}m\bigg(\frac{g(x_{m-1})^2x_m^2}{g(x_m)^2x_{m+1}^2}-1\bigg)\notag\\ &\quad=\frac{2(\varepsilon_1-1)}{\alpha}\notag\\ &\quad<1. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\lim_{m\rightarrow\infty}m\bigg(\frac{\|D_z f^m({\partial}/{\partial y})\|^2}{\|D_z f^{m+1}({\partial}/{\partial y})\|^2}-1\bigg)\notag\\ &\quad=\lim_{m\rightarrow\infty}m\bigg(\frac{g(x_{m-1})^2x_m^2}{g(x_m)^2x_{m+1}^2}-1\bigg)\notag\\ &\quad=\frac{2(\varepsilon_1-1)}{\alpha}\notag\\ &\quad<1. \end{aligned} \end{align*} $$
Therefore,
![]() $\sum _{m \geq 0}\|D_z f^m({\partial }/{\partial y})\|^2=\infty $
from Raabe’s test. This concludes Claim 2.
$\sum _{m \geq 0}\|D_z f^m({\partial }/{\partial y})\|^2=\infty $
from Raabe’s test. This concludes Claim 2.
In §6, we show how Assumptions US and R for pointwise hyperbolic diffeomorphism f on O are sufficient for the construction of a Markov partition. The conclusion is the existence of a symbolic model for f. Let us give the definitions in the general situation.
Let
![]() $\widehat {\mathscr {G}}=(\widehat {V}, \widehat {E})$
be a directed graph with a countable collection of vertices
$\widehat {\mathscr {G}}=(\widehat {V}, \widehat {E})$
be a directed graph with a countable collection of vertices
![]() $\widehat {V}$
such that every vertex has at least one edge coming in and at least one edge coming out, that is, for each
$\widehat {V}$
such that every vertex has at least one edge coming in and at least one edge coming out, that is, for each
![]() $v\in \widehat {V}$
, there are
$v\in \widehat {V}$
, there are
![]() $u,w\in \widehat {V}$
and a path
$u,w\in \widehat {V}$
and a path
![]() $u\rightarrow v\rightarrow w$
which is made up of two edges. The topological Markov shift (TMS) associated to
$u\rightarrow v\rightarrow w$
which is made up of two edges. The topological Markov shift (TMS) associated to
![]() $\widehat {\mathscr {G}}$
is the pair
$\widehat {\mathscr {G}}$
is the pair
![]() $(\widehat {\Sigma },\widehat {\sigma })$
which is the set
$(\widehat {\Sigma },\widehat {\sigma })$
which is the set
equipped with the left-shift
![]() $\widehat {\sigma }: \widehat {\Sigma } \rightarrow \widehat {\Sigma }$
,
$\widehat {\sigma }: \widehat {\Sigma } \rightarrow \widehat {\Sigma }$
,
![]() $\widehat {\sigma }(\{v_{n}\}_{n \in \mathbb {Z}})=\{v_{n+1}\}_{n \in \mathbb {Z}}$
. An element of
$\widehat {\sigma }(\{v_{n}\}_{n \in \mathbb {Z}})=\{v_{n+1}\}_{n \in \mathbb {Z}}$
. An element of
![]() $\widehat {\Sigma }$
is denoted by
$\widehat {\Sigma }$
is denoted by
![]() $\underline {v}=\{v_{n}\}_{n \in \mathbb {Z}}$
for the sake of simplicity. We endow
$\underline {v}=\{v_{n}\}_{n \in \mathbb {Z}}$
for the sake of simplicity. We endow
![]() $\widehat {\Sigma }$
with the distance
$\widehat {\Sigma }$
with the distance
![]() $d(\underline {v}, \underline {w}):=\exp [-\min \{|n|: n \in \mathbb {Z}$
such that
$d(\underline {v}, \underline {w}):=\exp [-\min \{|n|: n \in \mathbb {Z}$
such that
![]() $v_{n} \neq w_{n}\}]$
. With this metric,
$v_{n} \neq w_{n}\}]$
. With this metric,
![]() $\widehat {\Sigma }$
is a complete separable metric space. Recall that
$\widehat {\Sigma }$
is a complete separable metric space. Recall that
![]() $\widehat {\Sigma }$
is compact if and only if
$\widehat {\Sigma }$
is compact if and only if
![]() $\widehat {\mathscr {G}}$
is finite. Additionally,
$\widehat {\mathscr {G}}$
is finite. Additionally,
![]() $\widehat {\Sigma }$
is locally compact if and only if every vertex of
$\widehat {\Sigma }$
is locally compact if and only if every vertex of
![]() $\widehat {\mathscr {G}}$
has finite ingoing and outgoing degree.
$\widehat {\mathscr {G}}$
has finite ingoing and outgoing degree.
Let
![]() $\widehat {\Sigma }^{\#}$
be the recurrent set of
$\widehat {\Sigma }^{\#}$
be the recurrent set of
![]() $\widehat {\Sigma }$
which is due to Sarig [Reference Sarig22]:
$\widehat {\Sigma }$
which is due to Sarig [Reference Sarig22]:
 $$ \begin{align*} \widehat{\Sigma}^{\#}:=\{\underline{v}\in\widehat{\Sigma}:&\text{ there exists } u,w\in \widehat{V},\text{ there exists } n_k,m_k\uparrow\infty\\ & \text{ such that}\ v_{n_k}=u\ \text{and}\ v_{-m_k}=w \text{ for all } k\in \mathbb{Z}\}. \end{align*} $$
$$ \begin{align*} \widehat{\Sigma}^{\#}:=\{\underline{v}\in\widehat{\Sigma}:&\text{ there exists } u,w\in \widehat{V},\text{ there exists } n_k,m_k\uparrow\infty\\ & \text{ such that}\ v_{n_k}=u\ \text{and}\ v_{-m_k}=w \text{ for all } k\in \mathbb{Z}\}. \end{align*} $$
By the Poincaré recurrence theorem, every
![]() $\widehat {\sigma }$
-invariant probability measure is carried by
$\widehat {\sigma }$
-invariant probability measure is carried by
![]() $\widehat {\Sigma }^{\#}$
. Furthermore, every periodic point of
$\widehat {\Sigma }^{\#}$
. Furthermore, every periodic point of
![]() $\widehat {\sigma }$
is in
$\widehat {\sigma }$
is in
![]() $\widehat {\Sigma }^{\#}$
. Notice that when V is finite,
$\widehat {\Sigma }^{\#}$
. Notice that when V is finite,
![]() $\widehat {\Sigma }^{\#}=\widehat {\Sigma }$
.
$\widehat {\Sigma }^{\#}=\widehat {\Sigma }$
.
Let
![]() $\widehat {M}$
be a Riemannian manifold and
$\widehat {M}$
be a Riemannian manifold and
![]() $\widehat {f}: \widehat {M} \rightarrow \widehat {M}$
be a diffeomorphism.
$\widehat {f}: \widehat {M} \rightarrow \widehat {M}$
be a diffeomorphism.
Definition 2.2. A symbolic model for
![]() $\widehat {f}$
is a triple
$\widehat {f}$
is a triple
![]() $(\widehat {\Sigma }^{\#}, \widehat {\sigma }, \widehat {\pi })$
satisfying:
$(\widehat {\Sigma }^{\#}, \widehat {\sigma }, \widehat {\pi })$
satisfying:
-
(1)
 $(\widehat {\Sigma }^{\#}, \widehat {\sigma })$
is a recurrent TMS;
$(\widehat {\Sigma }^{\#}, \widehat {\sigma })$
is a recurrent TMS; -
(2)
 $\widehat {\pi }: \widehat {\Sigma }^{\#} \rightarrow \widehat {\pi }(\widehat {\Sigma }^{\#})\subset \widehat {M}$
is continuous and finite-to-one;
$\widehat {\pi }: \widehat {\Sigma }^{\#} \rightarrow \widehat {\pi }(\widehat {\Sigma }^{\#})\subset \widehat {M}$
is continuous and finite-to-one; -
(3)
 $\widehat {\pi } \circ \widehat {\sigma }=\widehat {f} \circ \widehat {\pi }$
on
$\widehat {\pi } \circ \widehat {\sigma }=\widehat {f} \circ \widehat {\pi }$
on
 $\widehat {\Sigma }^{\#}$
.
$\widehat {\Sigma }^{\#}$
.
In contrast to the notion of a symbolic model of uniform and non-uniform hyperbolic systems, which requires the map
![]() $\widehat {\pi }$
to define in the whole of
$\widehat {\pi }$
to define in the whole of
![]() $\widehat {\Sigma }$
, the notion here assumes not necessarily in
$\widehat {\Sigma }$
, the notion here assumes not necessarily in
![]() $\widehat {\Sigma }$
, but in a recurrent subset
$\widehat {\Sigma }$
, but in a recurrent subset
![]() $\widehat {\Sigma }^{\#}$
. Intuitively, a diffeomorphism can have many symbolic models. Roughly speaking, an acceptable symbolic model is one for which
$\widehat {\Sigma }^{\#}$
. Intuitively, a diffeomorphism can have many symbolic models. Roughly speaking, an acceptable symbolic model is one for which
![]() $\widehat {\pi }(\widehat {\Sigma }^{\#})$
(rather than
$\widehat {\pi }(\widehat {\Sigma }^{\#})$
(rather than
![]() $\widehat {\pi }(\widehat {\Sigma })$
) contains a subset where
$\widehat {\pi }(\widehat {\Sigma })$
) contains a subset where
![]() $\widehat {f}$
displays chaotic dynamics. For us, this occurs when
$\widehat {f}$
displays chaotic dynamics. For us, this occurs when
![]() $\widehat {f}=f$
is pointwise hyperbolic on an open invariant subset
$\widehat {f}=f$
is pointwise hyperbolic on an open invariant subset
![]() $O\subset M$
satisfying Assumptions US and R.
$O\subset M$
satisfying Assumptions US and R.
We assume the metric on M is taken in such a way that for any
![]() $x\in O$
,
$x\in O$
,
![]() $E^u(x)$
and
$E^u(x)$
and
![]() $E^s(x)$
are pairwise orthogonal [Reference Chen, Hu and Zhou10].
$E^s(x)$
are pairwise orthogonal [Reference Chen, Hu and Zhou10].
Theorem 2.1. Let f be a pointwise hyperbolic diffeomorphism on an invariant set
![]() $O \subset M$
, and suppose it satisfies Assumptions US and R, then f possesses a symbolic model
$O \subset M$
, and suppose it satisfies Assumptions US and R, then f possesses a symbolic model
![]() $(\widehat {\Sigma }^{\#}, \widehat {\sigma }, \widehat {\pi })$
. More precisely, there is a set
$(\widehat {\Sigma }^{\#}, \widehat {\sigma }, \widehat {\pi })$
. More precisely, there is a set
![]() $O^{\#}\subset O$
, a locally compact countable topological Markov shift
$O^{\#}\subset O$
, a locally compact countable topological Markov shift
![]() $(\widehat {\Sigma }, \widehat {\sigma })$
, and a continuous map
$(\widehat {\Sigma }, \widehat {\sigma })$
, and a continuous map
![]() $\widehat {\pi }:\widehat {\Sigma }^{\#}\rightarrow O $
such that:
$\widehat {\pi }:\widehat {\Sigma }^{\#}\rightarrow O $
such that:
-
(1)
 $\widehat {\pi } \circ \widehat {\sigma }|_{\widehat {\Sigma }^{\#}}=f \circ \widehat {\pi }$
;
$\widehat {\pi } \circ \widehat {\sigma }|_{\widehat {\Sigma }^{\#}}=f \circ \widehat {\pi }$
; -
(2)
 $\mu (O^{\#})=\mu (O)$
for every finite f-invariant measure
$\mu (O^{\#})=\mu (O)$
for every finite f-invariant measure
 $\mu $
;
$\mu $
; -
(3)
 $\widehat {\pi }: \widehat {\Sigma }^{\#}\rightarrow O^{\#}$
is a finite-to-one surjective map.
$\widehat {\pi }: \widehat {\Sigma }^{\#}\rightarrow O^{\#}$
is a finite-to-one surjective map.
In fact, the subset
![]() $O^{\#}\subset O$
in Theorem 2.1 is given by
$O^{\#}\subset O$
in Theorem 2.1 is given by
By the Poincaré recurrence theorem, if
![]() $\mu $
is an f-invariant probability measure supported on O, then it is supported on
$\mu $
is an f-invariant probability measure supported on O, then it is supported on
![]() $O^{\#}$
.
$O^{\#}$
.
We stress the argument in the proof of Theorem 2.1(3) providing more details on the number of the
![]() $\widehat {\pi }$
-pre-image, and traditionally refer to the following theorem which precisely characterizes the loss of injectivity of
$\widehat {\pi }$
-pre-image, and traditionally refer to the following theorem which precisely characterizes the loss of injectivity of
![]() $\widehat {\pi }$
.
$\widehat {\pi }$
.
Theorem 2.2. For
![]() $(\widehat {\Sigma }^{\#}, \widehat {\sigma }, \widehat {\pi })$
given by Theorem 2.1, denote the set of vertices of
$(\widehat {\Sigma }^{\#}, \widehat {\sigma }, \widehat {\pi })$
given by Theorem 2.1, denote the set of vertices of
![]() $\widehat {\Sigma }$
by
$\widehat {\Sigma }$
by
![]() $\widehat {V}$
. Then there exists a function
$\widehat {V}$
. Then there exists a function
![]() $N:\widehat {V}\rightarrow \mathbb {N}$
such that for every
$N:\widehat {V}\rightarrow \mathbb {N}$
such that for every
![]() $x\in O^{\#}$
which can be written as
$x\in O^{\#}$
which can be written as
![]() $x=\widehat {\pi }(\underline {v})$
with
$x=\widehat {\pi }(\underline {v})$
with
![]() $v_n=u$
for infinitely many
$v_n=u$
for infinitely many
![]() $n>0$
, and
$n>0$
, and
![]() $v_n=w$
for infinitely many
$v_n=w$
for infinitely many
![]() $n<0$
, we have
$n<0$
, we have
Set
![]() $P_n(f):=|\{x\in M:f^n(x)=x\}|$
and let
$P_n(f):=|\{x\in M:f^n(x)=x\}|$
and let
![]() $h_{\mathrm {top}}(f,O):=\sup \{h_{\mathrm {\mathrm {top}}}(f,\mathscr {O}): \mathscr {O}\ \textit {finite} \textit {open cover of } O\}$
denote the topological entropy of
$h_{\mathrm {top}}(f,O):=\sup \{h_{\mathrm {\mathrm {top}}}(f,\mathscr {O}): \mathscr {O}\ \textit {finite} \textit {open cover of } O\}$
denote the topological entropy of
![]() $f|_O$
, where the supremum runs over all finite open covers of O. As an application, when
$f|_O$
, where the supremum runs over all finite open covers of O. As an application, when
![]() $f|_O$
has an ergodic measure of maximal entropy
$f|_O$
has an ergodic measure of maximal entropy
![]() $\mu $
satisfying
$\mu $
satisfying
![]() $h_{\mu }(f|_O)=h_{\mathrm {top}}(f,O)$
, where
$h_{\mu }(f|_O)=h_{\mathrm {top}}(f,O)$
, where
![]() $h_{\mu }(f|_O)$
is the Kolmogorov–Sinai entropy of
$h_{\mu }(f|_O)$
is the Kolmogorov–Sinai entropy of
![]() $f|_O$
-invariant probability measure
$f|_O$
-invariant probability measure
![]() $\mu $
, we have the following consequence.
$\mu $
, we have the following consequence.
Corollary 2.1. Under the assumptions in Theorem 2.1, suppose that
![]() $f|_O$
has an ergodic measure of maximal entropy, then
$f|_O$
has an ergodic measure of maximal entropy, then
![]() $\text {there exists } C>0$
and
$\text {there exists } C>0$
and
![]() $p\in \mathbb {N}$
such that f has at least
$p\in \mathbb {N}$
such that f has at least
![]() $Ce^{pnh_{\mathrm {top}}(f,O)}$
periodic points of period
$Ce^{pnh_{\mathrm {top}}(f,O)}$
periodic points of period
![]() $pn$
for all
$pn$
for all
![]() $n\in \mathbb {N}$
, that is,
$n\in \mathbb {N}$
, that is,
Proof. The proof follows the arguments in [Reference Sarig22, Theorem 1.1], we provide some details.
Write
![]() $\widehat {\Sigma }=\widehat {\Sigma }(\widehat {\mathscr {G}})$
and let
$\widehat {\Sigma }=\widehat {\Sigma }(\widehat {\mathscr {G}})$
and let
![]() $\mu $
be an ergodic measure of maximal entropy for
$\mu $
be an ergodic measure of maximal entropy for
![]() $f|_O$
. Proceeding as in [Reference Sarig22, §13], we can lift
$f|_O$
. Proceeding as in [Reference Sarig22, §13], we can lift
![]() $\mu $
to an ergodic measure of maximal entropy
$\mu $
to an ergodic measure of maximal entropy
![]() $\widehat {\mu }$
for
$\widehat {\mu }$
for
![]() $\widehat {\sigma }$
via
$\widehat {\sigma }$
via
 $$ \begin{align} \widehat{\mu}=\int_{O} \frac{1}{|\widehat{\pi}^{-1}(x)|}\bigg(\sum_{\underline{v} \in \widehat{\pi}^{-1}(x)} \delta_{\underline{v}}\bigg)\, d \mu(x), \end{align} $$
$$ \begin{align} \widehat{\mu}=\int_{O} \frac{1}{|\widehat{\pi}^{-1}(x)|}\bigg(\sum_{\underline{v} \in \widehat{\pi}^{-1}(x)} \delta_{\underline{v}}\bigg)\, d \mu(x), \end{align} $$
such that
![]() $h_{\widehat {\mu }}(\widehat {\sigma })=h_{\mu }(f|_O)$
.
$h_{\widehat {\mu }}(\widehat {\sigma })=h_{\mu }(f|_O)$
.
By [Reference Gurevich11, Reference Gurevich12],
![]() $\widehat {\mu }$
is supported on a subset
$\widehat {\mu }$
is supported on a subset
![]() $\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime )\subset \widehat {\Sigma }(\widehat {\mathscr {G}})$
, where the smaller TMS
$\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime )\subset \widehat {\Sigma }(\widehat {\mathscr {G}})$
, where the smaller TMS
![]() $(\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ),\widehat {\sigma })$
is topologically transitive. For a topologically transitive TMS with countable many vertexes, Gurevič [Reference Gurevich11, Reference Gurevich12] showed a good estimate on
$(\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ),\widehat {\sigma })$
is topologically transitive. For a topologically transitive TMS with countable many vertexes, Gurevič [Reference Gurevich11, Reference Gurevich12] showed a good estimate on
![]() $\mathrm {Per}_n(\widehat {\sigma })$
: a topologically transitive TMS
$\mathrm {Per}_n(\widehat {\sigma })$
: a topologically transitive TMS
![]() $(\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ),\widehat {\sigma })$
admits at most one measure of maximal entropy
$(\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ),\widehat {\sigma })$
admits at most one measure of maximal entropy
![]() $h_{\max }(\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ))$
, and such a measure exists if and only if
$h_{\max }(\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ))$
, and such a measure exists if and only if
![]() $\text {there exists } p\in \mathbb {N}$
such that for every vertex
$\text {there exists } p\in \mathbb {N}$
such that for every vertex
![]() $v\in \widehat {\mathscr {G}}^\prime $
,
$v\in \widehat {\mathscr {G}}^\prime $
,
![]() $\text {there exists } C_v\geq 1$
, such that
$\text {there exists } C_v\geq 1$
, such that
 $$ \begin{align*} C_v^{-1}\leq\frac{\mathrm{Per}_{pn}(\widehat{\sigma}|_{\widehat{\Sigma}(\widehat{\mathscr{G}}^\prime)},v)}{e^{pnh_{\max}( \widehat{\Sigma}(\widehat{\mathscr{G}}^\prime))}}\leq C_v \end{align*} $$
$$ \begin{align*} C_v^{-1}\leq\frac{\mathrm{Per}_{pn}(\widehat{\sigma}|_{\widehat{\Sigma}(\widehat{\mathscr{G}}^\prime)},v)}{e^{pnh_{\max}( \widehat{\Sigma}(\widehat{\mathscr{G}}^\prime))}}\leq C_v \end{align*} $$
for all
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
 $$ \begin{align*} &h_{\max}(\widehat{\Sigma}(\widehat{\mathscr{G}}^\prime)):=h_{\max}(\widehat{\sigma})\\ &\quad={\max}\{h_{\nu}(\widehat{\sigma}): \nu \text{ is } \widehat{\sigma}\text{-invariant Borel probability measure on } \widehat{\Sigma}(\widehat{\mathscr{G}}^\prime)\}, \end{align*} $$
$$ \begin{align*} &h_{\max}(\widehat{\Sigma}(\widehat{\mathscr{G}}^\prime)):=h_{\max}(\widehat{\sigma})\\ &\quad={\max}\{h_{\nu}(\widehat{\sigma}): \nu \text{ is } \widehat{\sigma}\text{-invariant Borel probability measure on } \widehat{\Sigma}(\widehat{\mathscr{G}}^\prime)\}, \end{align*} $$
and
From Theorem 2.1(1) and (3), every periodic point in
![]() $\{\underline {v}\in \widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ): v_0=v, \widehat {\sigma }^n(\underline {v})=\underline {v}\}\subset \widehat {\Sigma }^{\#}$
is mapped by
$\{\underline {v}\in \widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ): v_0=v, \widehat {\sigma }^n(\underline {v})=\underline {v}\}\subset \widehat {\Sigma }^{\#}$
is mapped by
![]() $\widehat {\pi }$
to a periodic point of the same period in O. By Theorem 2.2, this mapping is at most
$\widehat {\pi }$
to a periodic point of the same period in O. By Theorem 2.2, this mapping is at most
![]() $N(v)^2$
-to-one. Therefore, for any
$N(v)^2$
-to-one. Therefore, for any
![]() $v\in \widehat {\mathscr {G}}^\prime $
and all
$v\in \widehat {\mathscr {G}}^\prime $
and all
![]() $n\geq 1$
,
$n\geq 1$
,
Finally, by assumption and construction,
![]() ${h_{\max }(\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ){\kern-1pt}){\kern-1.2pt}={\kern-1.2pt}h_{\widehat {\mu }}(\widehat {\sigma }){\kern-1.2pt}={\kern-1.2pt}h_{\mu }(f|_O{\kern-1pt}){\kern-1.2pt}={\kern-1.2pt}h_{\mathrm {top}} (f{\kern-1pt},{\kern-1.5pt}O)}$
. Therefore, we have
${h_{\max }(\widehat {\Sigma }(\widehat {\mathscr {G}}^\prime ){\kern-1pt}){\kern-1.2pt}={\kern-1.2pt}h_{\widehat {\mu }}(\widehat {\sigma }){\kern-1.2pt}={\kern-1.2pt}h_{\mu }(f|_O{\kern-1pt}){\kern-1.2pt}={\kern-1.2pt}h_{\mathrm {top}} (f{\kern-1pt},{\kern-1.5pt}O)}$
. Therefore, we have
Remark 2.5. It should be noted that the reverse of the second inequality in equation (2.3) above might not hold, because
![]() $\widehat {\pi }$
may not code trajectories inside
$\widehat {\pi }$
may not code trajectories inside
![]() $O/O^{\#}$
. A wealth of diffeomorphisms such that the growth rate of
$O/O^{\#}$
. A wealth of diffeomorphisms such that the growth rate of
![]() $P_{n}(f)$
is superexponential can be found in [Reference Kaloshin16].
$P_{n}(f)$
is superexponential can be found in [Reference Kaloshin16].
Notational convention and standing assumption. From now on, f will be a pointwise hyperbolic on an open invariant subset O of a connected compact smooth Riemannian manifold of dimension greater than 1, and satisfies Assumptions US and R.
Suppose P is a property. The statement ‘for all
![]() $\varepsilon $
, small enough P holds’ means ‘
$\varepsilon $
, small enough P holds’ means ‘
![]() $\text {there exists } \varepsilon _0>0$
which only depends on f, M,
$\text {there exists } \varepsilon _0>0$
which only depends on f, M,
![]() $C_{1-4}$
(see Lemma 4.1), and the parameters given by Assumption US(ii) and (iii) such that for all
$C_{1-4}$
(see Lemma 4.1), and the parameters given by Assumption US(ii) and (iii) such that for all
![]() $0<\varepsilon <\varepsilon _0$
, P holds’.
$0<\varepsilon <\varepsilon _0$
, P holds’.
3. Linearization up to small errors
In this section, we will show that
![]() $F_{x,y}:=\exp _y^{-1}\circ f\circ \exp _x$
is a small perturbation of a hyperbolic block-form matrix for any
$F_{x,y}:=\exp _y^{-1}\circ f\circ \exp _x$
is a small perturbation of a hyperbolic block-form matrix for any
![]() $x,y\in O$
such that
$x,y\in O$
such that
![]() $F_{x,y}$
is well defined and
$F_{x,y}$
is well defined and
![]() $d(f(x), y)$
small enough. First, we denote some constants and introduce two main functions, the
$d(f(x), y)$
small enough. First, we denote some constants and introduce two main functions, the
![]() $\varepsilon (x)$
and
$\varepsilon (x)$
and
![]() $Q(x)$
, which will be used many times throughout the paper.
$Q(x)$
, which will be used many times throughout the paper.
Denote
![]() $r_0=r_0^u\wedge r_0^s$
, where
$r_0=r_0^u\wedge r_0^s$
, where
![]() $r_0^u$
and
$r_0^u$
and
![]() $r_0^s$
are given by Assumption US. Let
$r_0^s$
are given by Assumption US. Let
here
is a compact subset of O since M is compact. Observe that
![]() $C_0>1$
as hyperbolicity is uniform in
$C_0>1$
as hyperbolicity is uniform in
![]() $O(r_0)$
.
$O(r_0)$
.
Fix a small parameter
![]() $\varepsilon>0$
(how small depends on a finite number of inequalities that
$\varepsilon>0$
(how small depends on a finite number of inequalities that
![]() $\varepsilon $
has to satisfy). For
$\varepsilon $
has to satisfy). For
![]() $x\in O$
, set
$x\in O$
, set
where
![]() $\beta =\beta ^u\vee \beta ^s$
as in Assumption R. We start with a basic lemma.
$\beta =\beta ^u\vee \beta ^s$
as in Assumption R. We start with a basic lemma.
Lemma 3.1. For all
![]() $\varepsilon $
small enough and for every
$\varepsilon $
small enough and for every
![]() $x\in O$
,
$x\in O$
,
where
![]() $C=C^u\wedge C^s$
and
$C=C^u\wedge C^s$
and
![]() $\kappa =\kappa ^u\vee \kappa ^s$
.
$\kappa =\kappa ^u\vee \kappa ^s$
.
Proof. Our first constraint on
![]() $\varepsilon $
is that it has to be small so that
$\varepsilon $
is that it has to be small so that
 $$ \begin{align*} 0<\varepsilon\leq\min \bigg\{\frac{C_0^\kappa-1}{Cr_0^\beta},1 \bigg\}. \end{align*} $$
$$ \begin{align*} 0<\varepsilon\leq\min \bigg\{\frac{C_0^\kappa-1}{Cr_0^\beta},1 \bigg\}. \end{align*} $$
Recall that the diameter of M is smaller than
![]() $1$
. There are the following two cases.
$1$
. There are the following two cases.
Case 1.
![]() $\varepsilon (x)\hspace{-0.5pt}=\hspace{-0.5pt}\varepsilon r_0^\beta $
. In this case, we note that
$\varepsilon (x)\hspace{-0.5pt}=\hspace{-0.5pt}\varepsilon r_0^\beta $
. In this case, we note that
![]() $x\hspace{-1pt}\in\hspace{-1pt} O(r_0)$
and
$x\hspace{-1pt}\in\hspace{-1pt} O(r_0)$
and
![]() $1\hspace{-1pt}<\hspace{-1pt}C_0\hspace{-1pt}\leq\hspace{-1pt} \min \{m(D f|_{E^{u}(x)}), m(D f^{-1}|_{E^{s}(x)})\}$
. Therefore,
$1\hspace{-1pt}<\hspace{-1pt}C_0\hspace{-1pt}\leq\hspace{-1pt} \min \{m(D f|_{E^{u}(x)}), m(D f^{-1}|_{E^{s}(x)})\}$
. Therefore,
Case 2.
![]() $ \varepsilon (x)=\varepsilon d(x,\partial O)^\beta $
. Now we have
$ \varepsilon (x)=\varepsilon d(x,\partial O)^\beta $
. Now we have
![]() $d(x,\partial O)\leq r_0$
. Since
$d(x,\partial O)\leq r_0$
. Since
![]() $\beta =\beta ^u\vee \beta ^s$
,
$\beta =\beta ^u\vee \beta ^s$
,
![]() $C=C^u\wedge C^s$
, and
$C=C^u\wedge C^s$
, and
![]() $\kappa =\kappa ^u\vee \kappa ^s$
, the required inequality is an immediate result of Assumption US(ii) and (iii).
$\kappa =\kappa ^u\vee \kappa ^s$
, the required inequality is an immediate result of Assumption US(ii) and (iii).
Now we fix another parameter
![]() $0<\delta <\min \{1,\alpha -{\beta }/{\gamma }\}$
, which is well defined from Assumption R. Setting
$0<\delta <\min \{1,\alpha -{\beta }/{\gamma }\}$
, which is well defined from Assumption R. Setting
note that
![]() $Q(x)^{\alpha -\delta }\leq \varepsilon \varepsilon (x)$
because
$Q(x)^{\alpha -\delta }\leq \varepsilon \varepsilon (x)$
because
![]() $(\alpha -\delta )\gamma>\beta $
and
$(\alpha -\delta )\gamma>\beta $
and
![]() $Q(x)\leq d(x,\partial O)$
for
$Q(x)\leq d(x,\partial O)$
for
![]() $\gamma>1$
when
$\gamma>1$
when
![]() $0<\varepsilon <1$
.
$0<\varepsilon <1$
.
Lemma 3.2. The following holds for all
![]() $\varepsilon $
small enough. For every
$\varepsilon $
small enough. For every
![]() $x\in O$
, we have
$x\in O$
, we have
and
A similar statement holds for
![]() $f^{-1}$
.
$f^{-1}$
.
Proof. We give the proofs for equations (3.5) and (3.6). The proofs for
![]() $f^{-1}$
are almost identical, the major change being the substitution of
$f^{-1}$
are almost identical, the major change being the substitution of
![]() $f^{-1}$
for f.
$f^{-1}$
for f.
For the companion inequality in equation (3.5), there are four cases. It is worth pointing out that Case 2 is the most interesting, since it is the case where both x and
![]() $f(x)$
are close to
$f(x)$
are close to
![]() $\partial O$
, and hence there is little hyperbolicity.
$\partial O$
, and hence there is little hyperbolicity.
Case 1.
![]() $Q(x)=Q(f(x))=\varepsilon ^{{2}/({\alpha -\delta })}r_0^\gamma $
. In this case, equation (3.5) is straightforward since for any
$Q(x)=Q(f(x))=\varepsilon ^{{2}/({\alpha -\delta })}r_0^\gamma $
. In this case, equation (3.5) is straightforward since for any
![]() $x\in O$
,
$x\in O$
,
Case 2.
![]() $Q(x)=\varepsilon ^{{2}/({\alpha -\delta })}d(x, \partial O)^\gamma $
and
$Q(x)=\varepsilon ^{{2}/({\alpha -\delta })}d(x, \partial O)^\gamma $
and
![]() $Q(f(x))=\varepsilon ^{{2}/({\alpha -\delta })}d(f(x), \partial O)^\gamma $
. Equivalently,
$Q(f(x))=\varepsilon ^{{2}/({\alpha -\delta })}d(f(x), \partial O)^\gamma $
. Equivalently,
![]() $d(x, \partial O) \leq r_0\leq r_0^u$
and
$d(x, \partial O) \leq r_0\leq r_0^u$
and
![]() $d(f(x), \partial O) \leq r_0\leq r_0^s$
. Taking Assumption US(ii) and (iii) into consideration, we find in this case that
$d(f(x), \partial O) \leq r_0\leq r_0^s$
. Taking Assumption US(ii) and (iii) into consideration, we find in this case that
 $$ \begin{align*} \bigg(\frac{d(f(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^u}\leq\frac{1}{C^u}(m(D f|_{E^{u}(x)})^{\kappa^u}-1)+1 \end{align*} $$
$$ \begin{align*} \bigg(\frac{d(f(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^u}\leq\frac{1}{C^u}(m(D f|_{E^{u}(x)})^{\kappa^u}-1)+1 \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} \bigg(\frac{d(x, \partial O)}{d(f(x), \partial O)}\bigg)^{\gamma^s}&\leq\frac{1}{C^s}(m(D f^{-1}|_{E^{s}(f(x))})^{\kappa^s}-1)+1\notag\\ &=\frac{1}{C^s}(\|Df_{E^{s}(x)}\|^{-\kappa^s}-1)+1, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \bigg(\frac{d(x, \partial O)}{d(f(x), \partial O)}\bigg)^{\gamma^s}&\leq\frac{1}{C^s}(m(D f^{-1}|_{E^{s}(f(x))})^{\kappa^s}-1)+1\notag\\ &=\frac{1}{C^s}(\|Df_{E^{s}(x)}\|^{-\kappa^s}-1)+1, \end{aligned} \end{align*} $$
where in the last equality, we used that
![]() $m(D f^{-1}|_{E^{s}(f(x))})^{\kappa ^s}=\|D f|_{E^{s}(x)}\|^{-\kappa ^s}$
.
$m(D f^{-1}|_{E^{s}(f(x))})^{\kappa ^s}=\|D f|_{E^{s}(x)}\|^{-\kappa ^s}$
.
If
![]() $({d(f(x),\partial O)}/{d(x,\partial O)})\geq 1$
, on the one hand,
$({d(f(x),\partial O)}/{d(x,\partial O)})\geq 1$
, on the one hand,
 $$ \begin{align*} \frac{Q(f(x))}{Q(x)}=\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma>1\geq\frac{C}{\|Df|_{E^s(x)}\|^{-\kappa}+(C-1)}. \end{align*} $$
$$ \begin{align*} \frac{Q(f(x))}{Q(x)}=\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma>1\geq\frac{C}{\|Df|_{E^s(x)}\|^{-\kappa}+(C-1)}. \end{align*} $$
On the other hand, since
![]() $\gamma \leq \gamma ^u$
,
$\gamma \leq \gamma ^u$
,
![]() $C\leq C^u$
,
$C\leq C^u$
,
![]() $\kappa ^u\leq \kappa $
, we have
$\kappa ^u\leq \kappa $
, we have
 $$ \begin{align*} \begin{aligned} \frac{Q(f(x))}{Q(x)}&=\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma\notag\\ &\leq\bigg(\frac{d(f(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^u}\notag\\ &\leq\frac{1}{C^u}(m(D f|_{E^{u}(x)})^{\kappa^u}-1)+1\notag\\ &\leq\frac{1}{C}(m(D f|_{E^{u}(x)})^{\kappa}-1)+1. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{Q(f(x))}{Q(x)}&=\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma\notag\\ &\leq\bigg(\frac{d(f(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^u}\notag\\ &\leq\frac{1}{C^u}(m(D f|_{E^{u}(x)})^{\kappa^u}-1)+1\notag\\ &\leq\frac{1}{C}(m(D f|_{E^{u}(x)})^{\kappa}-1)+1. \end{aligned} \end{align*} $$
Therefore, the companion inequality in equation (3.5) holds when
![]() $({d(f(x),\partial O)}/ {d(x,\partial O)})\geq 1$
in Case 2.
$({d(f(x),\partial O)}/ {d(x,\partial O)})\geq 1$
in Case 2.
Now if
![]() $0<({d(f(x),\partial O)}/{d(x,\partial O)})\leq 1$
, then
$0<({d(f(x),\partial O)}/{d(x,\partial O)})\leq 1$
, then
Using
![]() $\gamma \leq \gamma ^s$
,
$\gamma \leq \gamma ^s$
,
![]() $C\leq C^s$
,
$C\leq C^s$
,
![]() $\kappa ^s\leq \kappa $
, we obtain
$\kappa ^s\leq \kappa $
, we obtain
 $$ \begin{align*} \begin{aligned} \frac{Q(f(x))}{Q(x)}&=\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma\notag\\ &\geq\bigg(\frac{d(f(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^s}\notag\\ &\geq\bigg[\frac{1}{C^s}(\|Df_{E^{s}(x)}\|^{-\kappa^s}-1)+1\bigg]^{-1}\notag\\ &\geq\bigg[\frac{1}{C}(\|Df_{E^{s}(x)}\|^{-\kappa}-1)+1\bigg]^{-1}\notag\\ &=\frac{C}{\|Df|_{E^s(x)}\|^{-\kappa}+(C-1)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{Q(f(x))}{Q(x)}&=\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma\notag\\ &\geq\bigg(\frac{d(f(x), \partial O)}{d(x, \partial O)}\bigg)^{\gamma^s}\notag\\ &\geq\bigg[\frac{1}{C^s}(\|Df_{E^{s}(x)}\|^{-\kappa^s}-1)+1\bigg]^{-1}\notag\\ &\geq\bigg[\frac{1}{C}(\|Df_{E^{s}(x)}\|^{-\kappa}-1)+1\bigg]^{-1}\notag\\ &=\frac{C}{\|Df|_{E^s(x)}\|^{-\kappa}+(C-1)}. \end{aligned} \end{align*} $$
This completes the proof of equation (3.5) in Case 2.
Case 3.
![]() $Q(x)=\varepsilon ^{{2}/({\alpha -\delta })}d(x, \partial O)^\gamma $
and
$Q(x)=\varepsilon ^{{2}/({\alpha -\delta })}d(x, \partial O)^\gamma $
and
![]() $Q(f(x))=\varepsilon ^{{2}/({\alpha -\delta })}r_0^\gamma $
. Now
$Q(f(x))=\varepsilon ^{{2}/({\alpha -\delta })}r_0^\gamma $
. Now
![]() $d(x, \partial O)^\gamma \leq r_0^\gamma \leq d(f(x), \partial O)^\gamma $
, so it follows that
$d(x, \partial O)^\gamma \leq r_0^\gamma \leq d(f(x), \partial O)^\gamma $
, so it follows that
 $$ \begin{align*} \frac{Q(f(x))}{Q(x)}=\frac{r_0^\gamma}{d(x, \partial O)^\gamma}\geq1\geq\frac{C}{\|Df|_{E^s(x)}\|^{-\kappa}+(C-1)}. \end{align*} $$
$$ \begin{align*} \frac{Q(f(x))}{Q(x)}=\frac{r_0^\gamma}{d(x, \partial O)^\gamma}\geq1\geq\frac{C}{\|Df|_{E^s(x)}\|^{-\kappa}+(C-1)}. \end{align*} $$
In this case, since
![]() $d(x, \partial O)\leq r_0^u$
and
$d(x, \partial O)\leq r_0^u$
and
![]() $({d(f(x),\partial O)}/{d(x,\partial O)})\geq 1$
, we have
$({d(f(x),\partial O)}/{d(x,\partial O)})\geq 1$
, we have
 $$ \begin{align*} \begin{aligned} \frac{Q(f(x))}{Q(x)}&\leq\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma\notag\\ &\leq\frac{1}{C}(m(D f|_{E^{u}(x)})^{\kappa}-1)+1 \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{Q(f(x))}{Q(x)}&\leq\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma\notag\\ &\leq\frac{1}{C}(m(D f|_{E^{u}(x)})^{\kappa}-1)+1 \end{aligned} \end{align*} $$
as in Case 2 when
![]() $({d(f(x),\partial O)}{d(x,\partial O)})\geq 1$
.
$({d(f(x),\partial O)}{d(x,\partial O)})\geq 1$
.
Case 4.
![]() $Q(x)=\varepsilon ^{{2}/({\alpha -\delta })}r_0^\gamma $
and
$Q(x)=\varepsilon ^{{2}/({\alpha -\delta })}r_0^\gamma $
and
![]() $Q(f(x))=\varepsilon ^{{2}/({\alpha -\delta })}d(f(x), \partial O)^\gamma $
. In this case,
$Q(f(x))=\varepsilon ^{{2}/({\alpha -\delta })}d(f(x), \partial O)^\gamma $
. In this case,
![]() $d(f(x), \partial O)^\gamma \leq r_0^\gamma \leq d(x, \partial O)^\gamma $
, then
$d(f(x), \partial O)^\gamma \leq r_0^\gamma \leq d(x, \partial O)^\gamma $
, then
 $$ \begin{align*} \frac{Q(f(x))}{Q(x)}=\frac{d(f(x), \partial O)^\gamma}{r_0^\gamma}\leq1\leq\frac{1}{C}(m(D f|_{E^{u}(x)})^{\kappa}-1)+1. \end{align*} $$
$$ \begin{align*} \frac{Q(f(x))}{Q(x)}=\frac{d(f(x), \partial O)^\gamma}{r_0^\gamma}\leq1\leq\frac{1}{C}(m(D f|_{E^{u}(x)})^{\kappa}-1)+1. \end{align*} $$
Notice that
![]() $d(f(x), \partial O)\leq r_0^s$
and
$d(f(x), \partial O)\leq r_0^s$
and
![]() $0<({d(f(x),\partial O)}/{d(x,\partial O)})\leq 1$
, so we obtain
$0<({d(f(x),\partial O)}/{d(x,\partial O)})\leq 1$
, so we obtain
 $$ \begin{align*} \begin{aligned} \frac{Q(f(x))}{Q(x)}&\geq\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma\notag\\ &\geq\frac{C}{\|Df|_{E^s(x)}\|^{-\kappa}+(C-1)} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{Q(f(x))}{Q(x)}&\geq\bigg(\frac{d(f(x),\partial O)}{d(x,\partial O)}\bigg)^\gamma\notag\\ &\geq\frac{C}{\|Df|_{E^s(x)}\|^{-\kappa}+(C-1)} \end{aligned} \end{align*} $$
as in Case 2 when
![]() $0<({d(f(x),\partial O)}/{d(x,\partial O)})\leq 1$
.
$0<({d(f(x),\partial O)}/{d(x,\partial O)})\leq 1$
.
Hence, the companion inequality in equation (3.5) is proved. From Lemma 3.1, it remains to show that
![]() $C\varepsilon (x)\leq 1-\|Df|_{E^s(x)}\|^{\kappa }$
for small
$C\varepsilon (x)\leq 1-\|Df|_{E^s(x)}\|^{\kappa }$
for small
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
 $$ \begin{align*} 0<\varepsilon\leq\min\bigg\{1,\frac{C_0^\kappa-1}{Cr_0^\beta},\frac{1-C_0^{-\kappa}}{Cr_0^\beta}, \frac{1}{A_s^\beta(C^f)^{\kappa^s}}\bigg\}, \end{align*} $$
$$ \begin{align*} 0<\varepsilon\leq\min\bigg\{1,\frac{C_0^\kappa-1}{Cr_0^\beta},\frac{1-C_0^{-\kappa}}{Cr_0^\beta}, \frac{1}{A_s^\beta(C^f)^{\kappa^s}}\bigg\}, \end{align*} $$
where
![]() $A_s:=[({1}/{C^s})((C^f)^{\kappa ^s}-1)+1]^{1/\gamma ^s}>1$
and
$A_s:=[({1}/{C^s})((C^f)^{\kappa ^s}-1)+1]^{1/\gamma ^s}>1$
and
![]() $C^f:={\max }_{x\in M}\{{\max }\{\|D_xf\|, \|D_x f^{-1}\|\}\}$
.
$C^f:={\max }_{x\in M}\{{\max }\{\|D_xf\|, \|D_x f^{-1}\|\}\}$
.
For any
![]() $x\in O$
,
$x\in O$
,
![]() $f(x)\in O$
, there are the following two cases.
$f(x)\in O$
, there are the following two cases.
Case 1.
![]() $\varepsilon (f(x))=\varepsilon r_0^\beta $
. In this case, observe that
$\varepsilon (f(x))=\varepsilon r_0^\beta $
. In this case, observe that
![]() $f(x)\in O(r_0)$
, so using equation (3.1), we get
$f(x)\in O(r_0)$
, so using equation (3.1), we get
and hence
Case 2.
![]() $\varepsilon (f(x))=\varepsilon d(f(x),\partial O)^\beta $
. Now
$\varepsilon (f(x))=\varepsilon d(f(x),\partial O)^\beta $
. Now
![]() $d(f(x),\partial O)\leq r_0^s$
, and from Assumption US(iii), we find
$d(f(x),\partial O)\leq r_0^s$
, and from Assumption US(iii), we find
 $$ \begin{align*} \bigg(\frac{d(x, \partial O)}{d(f(x), \partial O)}\bigg)^{\beta}\leq A_s^\beta \end{align*} $$
$$ \begin{align*} \bigg(\frac{d(x, \partial O)}{d(f(x), \partial O)}\bigg)^{\beta}\leq A_s^\beta \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} C^s d(f(x),\partial O)^{\beta^s}&\leq m(Df^{-1}|_{E^s(f(x))})^{\kappa^s}(1- m(Df^{-1}|_{E^s(f(x))})^{-\kappa^s})\notag\\ &=m(Df^{-1}|_{E^s(f(x))})^{\kappa^s}(1- \|D f|_{E^{s}(x)}\|^{\kappa^s})\notag\\ &\leq(C^f)^{\kappa^s}(1-\|D f|_{E^{s}(x)}\|^{\kappa^s}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} C^s d(f(x),\partial O)^{\beta^s}&\leq m(Df^{-1}|_{E^s(f(x))})^{\kappa^s}(1- m(Df^{-1}|_{E^s(f(x))})^{-\kappa^s})\notag\\ &=m(Df^{-1}|_{E^s(f(x))})^{\kappa^s}(1- \|D f|_{E^{s}(x)}\|^{\kappa^s})\notag\\ &\leq(C^f)^{\kappa^s}(1-\|D f|_{E^{s}(x)}\|^{\kappa^s}). \end{aligned} \end{align*} $$
Therefore, we obtain that
 $$ \begin{align*} \begin{aligned} C\varepsilon(x)&\leq \varepsilon C d(x,\partial O)^\beta\notag\\ &\leq\varepsilon A_s^\beta C^sd(f(x), \partial O)^\beta\notag\\ &\leq \varepsilon A_s^\beta(C^f)^{\kappa^s} (1-\|D f|_{E^{s}(x)}\|^{\kappa^s})\notag\\ &\leq 1-\|D f|_{E^{s}(x)}\|^{\kappa}. \end{aligned}\\[-35pt] \end{align*} $$
$$ \begin{align*} \begin{aligned} C\varepsilon(x)&\leq \varepsilon C d(x,\partial O)^\beta\notag\\ &\leq\varepsilon A_s^\beta C^sd(f(x), \partial O)^\beta\notag\\ &\leq \varepsilon A_s^\beta(C^f)^{\kappa^s} (1-\|D f|_{E^{s}(x)}\|^{\kappa^s})\notag\\ &\leq 1-\|D f|_{E^{s}(x)}\|^{\kappa}. \end{aligned}\\[-35pt] \end{align*} $$
Before we begin, recall the following basic fact from Riemannian geometry: since M is compact, there exist
![]() $r(M),\rho (M)>0$
such that for every
$r(M),\rho (M)>0$
such that for every
![]() $z\in M$
, the exponential map
$z\in M$
, the exponential map
![]() $\exp _z$
maps
$\exp _z$
maps
![]() $T_zM(r(M)):=\{v\in T_zM:\|v\|< r(M)\}$
diffeomorphically (that is,
$T_zM(r(M)):=\{v\in T_zM:\|v\|< r(M)\}$
diffeomorphically (that is,
![]() $\exp _z$
is a bijective
$\exp _z$
is a bijective
![]() $C^\infty $
map whose
$C^\infty $
map whose
![]() $\exp _z^{-1}$
is also
$\exp _z^{-1}$
is also
![]() $C^\infty $
) onto a neighborhood of
$C^\infty $
) onto a neighborhood of
![]() $B(z,\rho (M)):=\{y\in M:d(y,z)< \rho (M)\}$
in a 2-bi-Lipschitz way.
$B(z,\rho (M)):=\{y\in M:d(y,z)< \rho (M)\}$
in a 2-bi-Lipschitz way.
For any
![]() $x\in O$
, let
$x\in O$
, let
![]() $B_x^u(Q(x))$
and
$B_x^u(Q(x))$
and
![]() $B_x^s(Q(x))$
denote the closed balls of radius
$B_x^s(Q(x))$
denote the closed balls of radius
![]() $Q(x)$
about the origin in
$Q(x)$
about the origin in
![]() $E^u(x)$
and
$E^u(x)$
and
![]() $E^s(x)$
, respectively. Denote the
$E^s(x)$
, respectively. Denote the
![]() $Q(x)$
-square centered at x by
$Q(x)$
-square centered at x by
Fix
![]() $\varepsilon>0$
small enough such that
$\varepsilon>0$
small enough such that
![]() $Q(x)<\min \{{r(M)}/{\sqrt {2}},{\rho (M)}/{2\sqrt {2}}\}$
, and
$Q(x)<\min \{{r(M)}/{\sqrt {2}},{\rho (M)}/{2\sqrt {2}}\}$
, and
![]() $\exp _x$
maps
$\exp _x$
maps
![]() $S_x\hspace{-1pt}\subset\hspace{-1pt} T_xM(r(M))$
diffeomorphically into a subset of
$S_x\hspace{-1pt}\subset\hspace{-1pt} T_xM(r(M))$
diffeomorphically into a subset of
![]() $B(x,2\sqrt {2}Q(x))\hspace{-1pt}\subset\hspace{-1pt} B(x,\rho (M))$
. It fol lows that
$B(x,2\sqrt {2}Q(x))\hspace{-1pt}\subset\hspace{-1pt} B(x,\rho (M))$
. It fol lows that
![]() $f\hspace{-0.5pt}\circ\hspace{-0.5pt} \exp _x$
maps
$f\hspace{-0.5pt}\circ\hspace{-0.5pt} \exp _x$
maps
![]() $S_x C^{1+\alpha }$
diffeomorphically into a subset of
$S_x C^{1+\alpha }$
diffeomorphically into a subset of
![]() $B(f(x),2\sqrt {2}C^fQ(x))$
. Moreover, if necessary, choosing a smaller
$B(f(x),2\sqrt {2}C^fQ(x))$
. Moreover, if necessary, choosing a smaller
![]() $\varepsilon $
such that
$\varepsilon $
such that
![]() $Q(x)<({\rho (M)}/{2\sqrt {2}C^f})$
, then for
$Q(x)<({\rho (M)}/{2\sqrt {2}C^f})$
, then for
![]() $y\in O$
satisfying
$y\in O$
satisfying
![]() $d(f(x),y)<\rho (M)-2\sqrt {2}C^fQ(x)$
,
$d(f(x),y)<\rho (M)-2\sqrt {2}C^fQ(x)$
,
![]() $f\circ \exp _x$
maps
$f\circ \exp _x$
maps
![]() $S_x C^{1+\alpha }$
diffeomorphically into
$S_x C^{1+\alpha }$
diffeomorphically into
![]() $B(f(x),2\sqrt {2}C^fQ(x))\subset B(y,d(y,f(x))+2\sqrt {2}C^fQ(x))$
, which is a subset of
$B(f(x),2\sqrt {2}C^fQ(x))\subset B(y,d(y,f(x))+2\sqrt {2}C^fQ(x))$
, which is a subset of
![]() $B(y,\rho (M))$
. Since
$B(y,\rho (M))$
. Since
![]() $\exp ^{-1}_y$
is a diffeomorphism on
$\exp ^{-1}_y$
is a diffeomorphism on
![]() $B(y,\rho (M))$
, the map
$B(y,\rho (M))$
, the map
![]() $F_{x,y}: S_x \rightarrow T_{y}M$
defined by
$F_{x,y}: S_x \rightarrow T_{y}M$
defined by
is well defined and a
![]() $C^{1+\alpha }$
diffeomorphism onto its image.
$C^{1+\alpha }$
diffeomorphism onto its image.
For
![]() $x\in O$
, denote by
$x\in O$
, denote by
![]() $P_x^u$
and
$P_x^u$
and
![]() $P_x^s$
the projections from
$P_x^s$
the projections from
![]() $T_xM$
to
$T_xM$
to
![]() $E^u(x)$
and
$E^u(x)$
and
![]() $E^s(x)$
, respectively. Whenever
$E^s(x)$
, respectively. Whenever
![]() $F_{x,y}$
is defined, with respect to
$F_{x,y}$
is defined, with respect to
![]() $E^u\oplus E^s$
, we have
$E^u\oplus E^s$
, we have
 $$ \begin{align} D_0F_{x,y}=\left(\begin{array}{@{}cc@{}} D^{uu}_{x,y} & D^{us}_{x,y} \\ D^{su}_{x,y} & D^{ss}_{x,y} \\ \end{array}\right)\!, \end{align} $$
$$ \begin{align} D_0F_{x,y}=\left(\begin{array}{@{}cc@{}} D^{uu}_{x,y} & D^{us}_{x,y} \\ D^{su}_{x,y} & D^{ss}_{x,y} \\ \end{array}\right)\!, \end{align} $$
where
![]() $D^{\tau t}_{x,y}=P_y^{\tau }\circ D_{f(x)}\exp ^{-1}_y\circ D_xf|_{E^t(x)}:B_x^t(Q(x))\rightarrow E^\tau (y)$
,
$D^{\tau t}_{x,y}=P_y^{\tau }\circ D_{f(x)}\exp ^{-1}_y\circ D_xf|_{E^t(x)}:B_x^t(Q(x))\rightarrow E^\tau (y)$
,
![]() $\tau ,t=u,s$
.
$\tau ,t=u,s$
.
We write
![]() $F_{x,y}|_{S_x}=D_0F_{x,y}+\phi _{x,y}$
in the form
$F_{x,y}|_{S_x}=D_0F_{x,y}+\phi _{x,y}$
in the form
 $$ \begin{align} &F_{x,y}(v_x^u,v_x^s)\nonumber\\ &\quad=(D^{uu}_{x,y}(v_x^u)+D^{us}_{x,y}(v_x^s)+\phi^u_{x,y}(v_x^u,v_x^s), D^{ss}_{x,y}(v_x^s)+D^{su}_{x,y}(v_x^u)+\phi^s_{x,y}(v_x^u,v_x^s)) \end{align} $$
$$ \begin{align} &F_{x,y}(v_x^u,v_x^s)\nonumber\\ &\quad=(D^{uu}_{x,y}(v_x^u)+D^{us}_{x,y}(v_x^s)+\phi^u_{x,y}(v_x^u,v_x^s), D^{ss}_{x,y}(v_x^s)+D^{su}_{x,y}(v_x^u)+\phi^s_{x,y}(v_x^u,v_x^s)) \end{align} $$
under the basis
![]() $(E^u,E^s)$
for all
$(E^u,E^s)$
for all
![]() $v_x=(v_x^u,v_x^s)\in S_x$
. Note that
$v_x=(v_x^u,v_x^s)\in S_x$
. Note that
![]() $\|\phi _{x,y}(0)\|=d(f(x),y)$
and
$\|\phi _{x,y}(0)\|=d(f(x),y)$
and
![]() $D_0\phi _{x,y}=0$
.
$D_0\phi _{x,y}=0$
.
Since the distribution
![]() $E^u$
is continuous under Assumption US(i), for
$E^u$
is continuous under Assumption US(i), for
![]() $\varepsilon>0$
small enough and any
$\varepsilon>0$
small enough and any
![]() $x\in O$
, there exists a local monotone function
$x\in O$
, there exists a local monotone function
![]() $\delta ^u(\cdot ): (0,\varepsilon (x)]\rightarrow (0, \rho (M)-2\sqrt {2}C^fQ(x))$
in the sense that
$\delta ^u(\cdot ): (0,\varepsilon (x)]\rightarrow (0, \rho (M)-2\sqrt {2}C^fQ(x))$
in the sense that
![]() $\delta ^u(a)\leq \delta ^u(b)$
if
$\delta ^u(a)\leq \delta ^u(b)$
if
![]() $0<a\leq b\leq \varepsilon (x)$
such that for all
$0<a\leq b\leq \varepsilon (x)$
such that for all
![]() $y\in B(f(x),\delta ^u(\varepsilon (x)))$
, we have
$y\in B(f(x),\delta ^u(\varepsilon (x)))$
, we have
Similarly, we have
By the same reason, for any
![]() $y\in O$
and any
$y\in O$
and any
![]() $x\in B(f^{-1}(y),\delta ^s(\varepsilon (y))$
, where
$x\in B(f^{-1}(y),\delta ^s(\varepsilon (y))$
, where
![]() $\delta ^s(\varepsilon (y))$
is defined analogous to
$\delta ^s(\varepsilon (y))$
is defined analogous to
![]() $\delta ^u(\varepsilon (x))$
, by considering
$\delta ^u(\varepsilon (x))$
, by considering
![]() $F_{x,y}^{-1}=\exp _{x}^{-1} \circ f^{-1} \circ \exp _y$
instead of
$F_{x,y}^{-1}=\exp _{x}^{-1} \circ f^{-1} \circ \exp _y$
instead of
![]() $F_{x,y}$
, we can get that
$F_{x,y}$
, we can get that
![]() $F_{x,y}^{-1}$
is well defined and a
$F_{x,y}^{-1}$
is well defined and a
![]() $C^{1+\alpha }$
diffeomorphism from
$C^{1+\alpha }$
diffeomorphism from
![]() $S_y$
onto its image, also to get four similar inequalities like equations (3.11) and (3.12).
$S_y$
onto its image, also to get four similar inequalities like equations (3.11) and (3.12).
Proposition 3.1. The following holds for all
![]() $\varepsilon>0$
small enough. For all
$\varepsilon>0$
small enough. For all
![]() $x\in O$
, there is a local monotone function
$x\in O$
, there is a local monotone function
![]() $0<\delta ^u(\varepsilon (x))<\varepsilon \varepsilon (x)$
such that for
$0<\delta ^u(\varepsilon (x))<\varepsilon \varepsilon (x)$
such that for
![]() $y\in O$
satisfying
$y\in O$
satisfying
![]() $d(f(x),y)<\delta ^u(\varepsilon (x))$
,
$d(f(x),y)<\delta ^u(\varepsilon (x))$
,
![]() $F_{x,y}|_{S_x}=D_0F_{x,y}+\phi _{x,y}$
can be put in the form
$F_{x,y}|_{S_x}=D_0F_{x,y}+\phi _{x,y}$
can be put in the form
 $$ \begin{align*}&F_{x,y}(v_x^u,v_x^s)\\ &\quad=(D^{uu}_{x,y}(v_x^u)+D^{us}_{x,y}(v_x^s)+\phi^u_{x,y}(v_x^u,v_x^s),D^{ss}_{x,y}(v_x^s)+D^{su}_{x,y}(v_x^u)+\phi^s_{x,y}(v_x^u,v_x^s))\end{align*} $$
$$ \begin{align*}&F_{x,y}(v_x^u,v_x^s)\\ &\quad=(D^{uu}_{x,y}(v_x^u)+D^{us}_{x,y}(v_x^s)+\phi^u_{x,y}(v_x^u,v_x^s),D^{ss}_{x,y}(v_x^s)+D^{su}_{x,y}(v_x^u)+\phi^s_{x,y}(v_x^u,v_x^s))\end{align*} $$
under the basis
![]() $(E^u,E^s)$
for all
$(E^u,E^s)$
for all
![]() $v_x=(v_x^u,v_x^s)\in S_x$
, where
$v_x=(v_x^u,v_x^s)\in S_x$
, where
![]() $\phi _{x,y}:=(\phi ^u_{x,y},\phi ^s_{x,y})$
satisfies:
$\phi _{x,y}:=(\phi ^u_{x,y},\phi ^s_{x,y})$
satisfies:
-
(1)
 $\|\phi _{x,y}(0)\|=d(f(x),y)$
;
$\|\phi _{x,y}(0)\|=d(f(x),y)$
; -
(2)
 $\|D\phi _{x,y}\|_{C^0}\leq \varepsilon \varepsilon (x)$
;
$\|D\phi _{x,y}\|_{C^0}\leq \varepsilon \varepsilon (x)$
; -
(3)
 $\|D_v\phi _{x,y}-D_w\phi _{x,y}\|\leq \varepsilon \varepsilon (x)\|v-w\|^{\delta /2}$
for all
$\|D_v\phi _{x,y}-D_w\phi _{x,y}\|\leq \varepsilon \varepsilon (x)\|v-w\|^{\delta /2}$
for all
 $v,w\in S_x$
.
$v,w\in S_x$
.
A similar statement holds for
![]() $F_{x,y}^{-1}=\exp _{x}^{-1} \circ f^{-1} \circ \exp _y$
defined on
$F_{x,y}^{-1}=\exp _{x}^{-1} \circ f^{-1} \circ \exp _y$
defined on
![]() $S_{y}$
for all
$S_{y}$
for all
![]() $x\in B(f^{-1}(y),\delta ^s(\varepsilon (y)))$
.
$x\in B(f^{-1}(y),\delta ^s(\varepsilon (y)))$
.
Proof. Since
![]() $F_{x,y}$
is
$F_{x,y}$
is
![]() $C^{1+\alpha }$
, there is
$C^{1+\alpha }$
, there is
![]() $ \hat {C}>0$
such that for any
$ \hat {C}>0$
such that for any
![]() $v,w\in S_{x}$
,
$v,w\in S_{x}$
,
Fix
![]() $\varepsilon>0$
small enough so that
$\varepsilon>0$
small enough so that
 $$ \begin{align*} \varepsilon^{{\delta}/({\alpha-\delta})}\leq\min\bigg\{1,\frac{1}{(2\sqrt{2})^{\alpha-{\delta}/{2}}\hat{C}}\bigg\}. \end{align*} $$
$$ \begin{align*} \varepsilon^{{\delta}/({\alpha-\delta})}\leq\min\bigg\{1,\frac{1}{(2\sqrt{2})^{\alpha-{\delta}/{2}}\hat{C}}\bigg\}. \end{align*} $$
Part (1) is free and part (2) is a special case of part (3) when
![]() $w=0$
since
$w=0$
since
![]() $D_0\phi _{x,y}=0$
. Then what we need to check is property (3).
$D_0\phi _{x,y}=0$
. Then what we need to check is property (3).
In fact, we have
 $$ \begin{align*} \begin{aligned} \|D_v\phi_{x,y}-D_w\phi_{x,y}\|&=\|D_vF_{x,y}-D_wF_{x,y}\|\notag\\ &\leq \hat{C}\|v-w\|^{\alpha-{\delta}/{2}}\|v-w\|^{\delta/2}\notag\\ &\leq (2\sqrt{2})^{\alpha-{\delta}/{2}}\hat{C}Q(x)^{\delta/2} Q(x)^{\alpha-\delta}\|v-w\|^{\delta/2}\notag\\ &\leq (2\sqrt{2})^{\alpha-{\delta}/{2}}\hat{C}\varepsilon^{{\delta}/({\alpha-\delta})}\cdot\varepsilon\varepsilon(x)\|v-w\|^{\delta/2}\notag\\ &\leq \varepsilon\varepsilon(x)\|v-w\|^{\delta/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|D_v\phi_{x,y}-D_w\phi_{x,y}\|&=\|D_vF_{x,y}-D_wF_{x,y}\|\notag\\ &\leq \hat{C}\|v-w\|^{\alpha-{\delta}/{2}}\|v-w\|^{\delta/2}\notag\\ &\leq (2\sqrt{2})^{\alpha-{\delta}/{2}}\hat{C}Q(x)^{\delta/2} Q(x)^{\alpha-\delta}\|v-w\|^{\delta/2}\notag\\ &\leq (2\sqrt{2})^{\alpha-{\delta}/{2}}\hat{C}\varepsilon^{{\delta}/({\alpha-\delta})}\cdot\varepsilon\varepsilon(x)\|v-w\|^{\delta/2}\notag\\ &\leq \varepsilon\varepsilon(x)\|v-w\|^{\delta/2}. \end{aligned} \end{align*} $$
By considering
![]() $f^{-1}$
in the charts
$f^{-1}$
in the charts
![]() $\exp _y$
of point y and
$\exp _y$
of point y and
![]() $\exp _x^{-1}$
of
$\exp _x^{-1}$
of
![]() $f^{-1}(y)$
when x is near
$f^{-1}(y)$
when x is near
![]() $f^{-1}(y)$
, we can apply a similar treatment to
$f^{-1}(y)$
, we can apply a similar treatment to
![]() $F_{x,y}^{-1}$
. The details are left to the reader.
$F_{x,y}^{-1}$
. The details are left to the reader.
4. Admissible manifolds and graph transform along the edge
In this section, denote
![]() $t:= u,s$
. As usual, we give the canonical definition of t-manifolds first.
$t:= u,s$
. As usual, we give the canonical definition of t-manifolds first.
Definition 4.1. Suppose
![]() $x\in O$
.
$x\in O$
.
-
(1) A u-manifold at x is a manifold
 $V_x^{u}= \exp _{x}\{(v^u,\sigma _x^u(v^u))\in T_xM:\|v^u\| \leq Q (x)\}\subset M$
, where
$V_x^{u}= \exp _{x}\{(v^u,\sigma _x^u(v^u))\in T_xM:\|v^u\| \leq Q (x)\}\subset M$
, where
 $\sigma ^u:B_x^u(Q(x)) \rightarrow E^s(x)$
is a
$\sigma ^u:B_x^u(Q(x)) \rightarrow E^s(x)$
is a
 $C^{1+\delta /2}$
function such that
$C^{1+\delta /2}$
function such that
 $\|\sigma _x^u\|_{C^0}\leq Q(x)$
.
$\|\sigma _x^u\|_{C^0}\leq Q(x)$
. -
(2) Similarly, an s-manifold at x is a manifold
 $V_x^{s}=\exp _{x}\{(\sigma ^s_x(v^s),v^s):\|v^s\| \leq Q(x)\}$
where
$V_x^{s}=\exp _{x}\{(\sigma ^s_x(v^s),v^s):\|v^s\| \leq Q(x)\}$
where
 $\sigma ^s_x:B_x^s(Q(x)) \rightarrow E^u(x)$
is a
$\sigma ^s_x:B_x^s(Q(x)) \rightarrow E^u(x)$
is a
 $C^{1+\delta /2}$
function such that
$C^{1+\delta /2}$
function such that
 $\|\sigma _x^s\|_{C^0}\leq Q(x)$
.
$\|\sigma _x^s\|_{C^0}\leq Q(x)$
.
Thus, every t-manifold at x is contained in
![]() $\exp _{x}(S_x)$
. For any
$\exp _{x}(S_x)$
. For any
![]() $x\in O$
, we call
$x\in O$
, we call
![]() $\sigma ^t_x$
the representing functions of
$\sigma ^t_x$
the representing functions of
![]() $V_x^{t}$
.
$V_x^{t}$
.
Among the t-manifolds, we are interested in those that can eventually represent unstable and stable manifolds, and for that, we require some extra conditions on the representing functions. We call them admissible manifolds.
Definition 4.2. For any
![]() $x\in O$
, a t-admissible manifold at x is a t-manifold
$x\in O$
, a t-admissible manifold at x is a t-manifold
![]() $V_x^{t}$
where the representing function
$V_x^{t}$
where the representing function
![]() $\sigma ^t_x$
satisfies the following three conditions:
$\sigma ^t_x$
satisfies the following three conditions:
-
(AM1)
 $\|\sigma _x^t(0)\| \leq 10^{-3}Q(x)$
;
$\|\sigma _x^t(0)\| \leq 10^{-3}Q(x)$
; -
(AM2)
 $\|D\sigma _x^t\|_{C^0} \leq \sqrt {\varepsilon }$
;
$\|D\sigma _x^t\|_{C^0} \leq \sqrt {\varepsilon }$
; -
(AM3)
 $\|D\sigma _x^t\|_{C^{\delta /2}}:=\|D\sigma _x^t\|_{C^{0}}+\operatorname {Hol}_{\delta /2}(D\sigma ^t_x) \leq \tfrac 12$
, with norms taken in
$\|D\sigma _x^t\|_{C^{\delta /2}}:=\|D\sigma _x^t\|_{C^{0}}+\operatorname {Hol}_{\delta /2}(D\sigma ^t_x) \leq \tfrac 12$
, with norms taken in
 $B_x^t(Q(x))$
.
$B_x^t(Q(x))$
.
Observe that the upper bound of
![]() $\|\sigma _x^t(0)\|$
is linear in
$\|\sigma _x^t(0)\|$
is linear in
![]() $Q(x)$
, while the estimate on the derivative of a representing function is constant in our setting rather than of the order of
$Q(x)$
, while the estimate on the derivative of a representing function is constant in our setting rather than of the order of
![]() $Q(x)^{\delta /2}$
as in [Reference Sarig22, Definition 4.8]. This distinction will be clear when we start to establish an estimate in the graph transform along the edge (Definition 4.4).
$Q(x)^{\delta /2}$
as in [Reference Sarig22, Definition 4.8]. This distinction will be clear when we start to establish an estimate in the graph transform along the edge (Definition 4.4).
Let
![]() $\mathscr {V}_{x}^t$
be the space of all t-admissible manifolds at
$\mathscr {V}_{x}^t$
be the space of all t-admissible manifolds at
![]() $x\in O$
. We introduce two metrics on
$x\in O$
. We introduce two metrics on
![]() $\mathscr {V}_{x}^{t}$
as follows: for
$\mathscr {V}_{x}^{t}$
as follows: for
![]() $V^t_{1}, V^t_{2} \in \mathscr {V}_x^{t}$
with representing functions
$V^t_{1}, V^t_{2} \in \mathscr {V}_x^{t}$
with representing functions
![]() $\sigma ^t_{1}, \sigma ^t_{2}$
, respectively, put
$\sigma ^t_{1}, \sigma ^t_{2}$
, respectively, put
where
 $$ \begin{align*} \|\sigma^t_{1}-\sigma^t_{2}\|_{C^{0}}&={\max}_{v_x\in B_x^t(Q(x))}\|\sigma^t_{1}(v_x)-\sigma^t_{2}(v_x)\|,\\ \|\sigma^t_{1}-\sigma^t_{2}\|_{C^{1}}&=\|\sigma^t_{1}-\sigma^t_{2}\|_{C^{0}}+\|D\sigma^t_{1}-D\sigma^t_{2}\|_{C^{0}}, \end{align*} $$
$$ \begin{align*} \|\sigma^t_{1}-\sigma^t_{2}\|_{C^{0}}&={\max}_{v_x\in B_x^t(Q(x))}\|\sigma^t_{1}(v_x)-\sigma^t_{2}(v_x)\|,\\ \|\sigma^t_{1}-\sigma^t_{2}\|_{C^{1}}&=\|\sigma^t_{1}-\sigma^t_{2}\|_{C^{0}}+\|D\sigma^t_{1}-D\sigma^t_{2}\|_{C^{0}}, \end{align*} $$
and
If
![]() $\varepsilon>0$
is small enough, from conditions (AM1) and (AM2), we have
$\varepsilon>0$
is small enough, from conditions (AM1) and (AM2), we have
![]() $\|\sigma _x^t\|_{C^0}\leq Q(x)$
, because for all
$\|\sigma _x^t\|_{C^0}\leq Q(x)$
, because for all
![]() $v_x\in B_x^t(Q(x))$
,
$v_x\in B_x^t(Q(x))$
,
 $$ \begin{align} \|\sigma_x^t(v_x)\|&\leq\|\sigma_x^t(0)\|+\operatorname{Lip}(\sigma_x^t)\|v_x\| \leq 10^{-3}Q(x)\nonumber\\ &\quad+\sqrt{\varepsilon}\|v_x\| \leq(10^{-3}+\sqrt{\varepsilon})Q(x)<10^{-2}Q(x), \end{align} $$
$$ \begin{align} \|\sigma_x^t(v_x)\|&\leq\|\sigma_x^t(0)\|+\operatorname{Lip}(\sigma_x^t)\|v_x\| \leq 10^{-3}Q(x)\nonumber\\ &\quad+\sqrt{\varepsilon}\|v_x\| \leq(10^{-3}+\sqrt{\varepsilon})Q(x)<10^{-2}Q(x), \end{align} $$
where in the last inequality, we require
![]() $\varepsilon>0$
to be small. In particular,
$\varepsilon>0$
to be small. In particular,
![]() $\sigma _x^u$
maps the ball
$\sigma _x^u$
maps the ball
![]() $B_x^u(10^{-2}Q(x))$
into
$B_x^u(10^{-2}Q(x))$
into
![]() $B_x^s(10^{-2}Q(x))$
, and maps
$B_x^s(10^{-2}Q(x))$
, and maps
![]() $B_x^u(Q(x))$
into
$B_x^u(Q(x))$
into
![]() $B_x^s(Q(x))$
.
$B_x^s(Q(x))$
.
Proposition 4.1. For every
![]() $x\in O$
, the following holds for
$x\in O$
, the following holds for
![]() $\varepsilon>0$
small enough. For every
$\varepsilon>0$
small enough. For every
![]() $V_x^{u} \in \mathscr {V}_x^{u}$
and
$V_x^{u} \in \mathscr {V}_x^{u}$
and
![]() $V_x^{s} \in \mathscr {V}_x^{s}$
, the following hold:
$V_x^{s} \in \mathscr {V}_x^{s}$
, the following hold:
-
(1)
 $V_x^{u}$
and
$V_x^{u}$
and
 $V_x^{s}$
intersect at a single point
$V_x^{s}$
intersect at a single point
 $P=P(V_x^{u},V_x^{s}):=\exp _{x}(w)\in O$
, and
$P=P(V_x^{u},V_x^{s}):=\exp _{x}(w)\in O$
, and
 $\|w\|\leq 50^{-1}Q(x)$
;
$\|w\|\leq 50^{-1}Q(x)$
; -
(2) P is a Lipschitz function of
 $(V_x^u,V_x^s)$
, with Lipschitz constant less than
$(V_x^u,V_x^s)$
, with Lipschitz constant less than
 ${2}/({1-\sqrt {\varepsilon }})$
.
${2}/({1-\sqrt {\varepsilon }})$
.
Proof. We follow the same strategy of [Reference Sarig22, Proposition 4.11].
(1) To prove the non-emptiness of
![]() $V_x^{u}\cap V_x^{s}$
, we fix
$V_x^{u}\cap V_x^{s}$
, we fix
![]() $V_x^{t}$
with representing function
$V_x^{t}$
with representing function
![]() $\sigma _x^t$
. From a pedagogical perspective, the ideas of the proof are very simple. If we suppose the intersections of
$\sigma _x^t$
. From a pedagogical perspective, the ideas of the proof are very simple. If we suppose the intersections of
![]() $V_x^{u}$
and
$V_x^{u}$
and
![]() $V_x^{s}$
are non-empty, it corresponds to points
$V_x^{s}$
are non-empty, it corresponds to points
![]() $(v^u,v^s)$
that satisfy
$(v^u,v^s)$
that satisfy
![]() $\exp _x(v^u,\sigma _x^u(v^u))=\exp _x(\sigma _x^s(v^s),v^s)$
, so it is the solution of the equation:
$\exp _x(v^u,\sigma _x^u(v^u))=\exp _x(\sigma _x^s(v^s),v^s)$
, so it is the solution of the equation:
 $$ \begin{align*} \begin{cases} v^u=\sigma_x^s(v^s), \\ v^s=\sigma_x^u(v^u). \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} v^u=\sigma_x^s(v^s), \\ v^s=\sigma_x^u(v^u). \end{cases} \end{align*} $$
Hence, the trick of the proof is to find the fixed points of
![]() $\sigma _x^s \circ \sigma _x^u$
on
$\sigma _x^s \circ \sigma _x^u$
on
![]() $B_x^u(Q(x))$
.
$B_x^u(Q(x))$
.
We first note that
![]() $\sigma _x^s \circ \sigma _x^u$
maps the ball
$\sigma _x^s \circ \sigma _x^u$
maps the ball
![]() $B_x^u(10^{-2}Q(x))$
into itself from equation (4.1) if
$B_x^u(10^{-2}Q(x))$
into itself from equation (4.1) if
![]() $\varepsilon>0$
is small enough. It follows that
$\varepsilon>0$
is small enough. It follows that
![]() $\sigma _x^s \circ \sigma _x^u$
is an
$\sigma _x^s \circ \sigma _x^u$
is an
![]() $\varepsilon $
-contraction of
$\varepsilon $
-contraction of
![]() $B_x^u(10^{-2}Q(x))$
into itself. Indeed, from condition (AM2), we have
$B_x^u(10^{-2}Q(x))$
into itself. Indeed, from condition (AM2), we have
![]() $\|D(\sigma _x^s\hspace{-0.5pt} \circ\hspace{-0.5pt} \sigma _x^u)\|_{C^0}\hspace{-0.5pt}\leq\hspace{-0.5pt} \|D\sigma _x^s\|_{C^0}\|D\sigma _x^u\|_{C^0}\hspace{-0.5pt}\leq\hspace{-0.5pt} \varepsilon $
. By the Banach fixed point theorem,
$\|D(\sigma _x^s\hspace{-0.5pt} \circ\hspace{-0.5pt} \sigma _x^u)\|_{C^0}\hspace{-0.5pt}\leq\hspace{-0.5pt} \|D\sigma _x^s\|_{C^0}\|D\sigma _x^u\|_{C^0}\hspace{-0.5pt}\leq\hspace{-0.5pt} \varepsilon $
. By the Banach fixed point theorem,
![]() $\sigma _x^s \circ \sigma _x^u$
has a unique fixed point:
$\sigma _x^s \circ \sigma _x^u$
has a unique fixed point:
![]() $(\sigma _x^s \circ \sigma _x^u)(v_0^u)=v_0^u,$
where
$(\sigma _x^s \circ \sigma _x^u)(v_0^u)=v_0^u,$
where
![]() $v_0^u\in B_x^u(10^{-2}Q(x))$
.
$v_0^u\in B_x^u(10^{-2}Q(x))$
.
Let
![]() $v_0^s:=\sigma _x^u(v_0^u)$
,
$v_0^s:=\sigma _x^u(v_0^u)$
,
![]() $w:=(v_0^u,v_0^s)$
, then
$w:=(v_0^u,v_0^s)$
, then
![]() $V_x^{u}$
intersects
$V_x^{u}$
intersects
![]() $V_x^{s}$
at
$V_x^{s}$
at
![]() $P:=\exp _{x}(w)$
. Indeed,
$P:=\exp _{x}(w)$
. Indeed,
![]() $P \in V_x^{u}$
is evident because
$P \in V_x^{u}$
is evident because
![]() $v_0^s=\sigma _x^u(v_0^u)$
and
$v_0^s=\sigma _x^u(v_0^u)$
and
![]() $\|v_0^u\| \leq 10^{-2} Q(x)<Q(x).$
Since
$\|v_0^u\| \leq 10^{-2} Q(x)<Q(x).$
Since
![]() $v_0^u=(\sigma _x^s \circ \sigma _x^u)(v_0^u)=\sigma _x^s (v_0^s)$
and
$v_0^u=(\sigma _x^s \circ \sigma _x^u)(v_0^u)=\sigma _x^s (v_0^s)$
and
we have
![]() $P \in V_x^{s}$
. Moreover, we also see that
$P \in V_x^{s}$
. Moreover, we also see that
![]() $\|w\|\leq \|v_0^u\|+\|v_0^s\| \leq 50^{-1} Q(x)<d(x,\partial O)$
, and thus
$\|w\|\leq \|v_0^u\|+\|v_0^s\| \leq 50^{-1} Q(x)<d(x,\partial O)$
, and thus
![]() $P\in O$
.
$P\in O$
.
To prove the uniqueness in the bigger ball
![]() $B_x^u(Q(x))$
, we note that
$B_x^u(Q(x))$
, we note that
![]() $\sigma _x^s \circ \sigma _x^u$
maps
$\sigma _x^s \circ \sigma _x^u$
maps
![]() $B_x^u(Q(x))$
into itself if
$B_x^u(Q(x))$
into itself if
![]() $\varepsilon>0$
is small enough, and the same calculation as above shows that such a map has a unique fixed point even in
$\varepsilon>0$
is small enough, and the same calculation as above shows that such a map has a unique fixed point even in
![]() $B_x^u(Q(x))$
.
$B_x^u(Q(x))$
.
(2) Now we verify that P is a Lipschitz function of
![]() $V_x^{u}, V_x^{s}$
. For every
$V_x^{u}, V_x^{s}$
. For every
![]() $x\in O$
, suppose
$x\in O$
, suppose
![]() $V_{i}^{t}\in \mathscr {V}_x^{t}$
are represented by
$V_{i}^{t}\in \mathscr {V}_x^{t}$
are represented by
![]() $\sigma ^t_{i}$
,
$\sigma ^t_{i}$
,
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $P_{i}=\exp _{x}(w_i)=\exp _{x}(v^u_{i}, v^s_{i})$
denote the intersection points of
$P_{i}=\exp _{x}(w_i)=\exp _{x}(v^u_{i}, v^s_{i})$
denote the intersection points of
![]() $V_{i}^{u} \cap V_{i}^{s}$
. We saw above that
$V_{i}^{u} \cap V_{i}^{s}$
. We saw above that
![]() $v^s_{i}=\sigma ^u_{i}(v^u_{i})$
and that
$v^s_{i}=\sigma ^u_{i}(v^u_{i})$
and that
![]() $v^u_{i}=\sigma ^s_{i}(v^s_{i})$
because
$v^u_{i}=\sigma ^s_{i}(v^s_{i})$
because
![]() $v^u_{i}$
is a fixed point of
$v^u_{i}$
is a fixed point of
![]() $\sigma ^s_{i}\circ \sigma ^u_{i}$
.
$\sigma ^s_{i}\circ \sigma ^u_{i}$
.
Since
![]() $\exp _x$
is 2-Lipschitz, this gives that
$\exp _x$
is 2-Lipschitz, this gives that
![]() $d(P_1,P_2)\leq 2\|w_1-w_2\|$
. We have
$d(P_1,P_2)\leq 2\|w_1-w_2\|$
. We have
 $$ \begin{align*} \|w_1-w_2\|&\leq\|v^u_1-v^u_2\|+\|v^s_1-v^s_2\|\notag\\ &=\|\sigma_1^s(v^s_1)-\sigma_2^s(v^s_2)\|+\|\sigma_1^u(v^u_1)-\sigma_2^u(v^u_2)\|\notag\\ &\leq\|\sigma_1^s(v^s_1)-\sigma_1^s(v^s_2)\|+\|\sigma_1^s(v^s_2)-\sigma_2^s(v^s_2)\|\\&\quad+\|\sigma_1^u(v^u_1)-\sigma_1^u(v^u_2)\|+\|\sigma_1^u(v^u_2)-\sigma_2^u(v^u_2)\|\notag\\ &\leq\sqrt{\varepsilon}(\|v^s_1-v^s_2\|+\|v^u_1-v^u_2\|)+\|\sigma_1^s-\sigma_2^s\|_{C^0}+\|\sigma_1^u-\sigma_2^u\|_{C^0}. \end{align*} $$
$$ \begin{align*} \|w_1-w_2\|&\leq\|v^u_1-v^u_2\|+\|v^s_1-v^s_2\|\notag\\ &=\|\sigma_1^s(v^s_1)-\sigma_2^s(v^s_2)\|+\|\sigma_1^u(v^u_1)-\sigma_2^u(v^u_2)\|\notag\\ &\leq\|\sigma_1^s(v^s_1)-\sigma_1^s(v^s_2)\|+\|\sigma_1^s(v^s_2)-\sigma_2^s(v^s_2)\|\\&\quad+\|\sigma_1^u(v^u_1)-\sigma_1^u(v^u_2)\|+\|\sigma_1^u(v^u_2)-\sigma_2^u(v^u_2)\|\notag\\ &\leq\sqrt{\varepsilon}(\|v^s_1-v^s_2\|+\|v^u_1-v^u_2\|)+\|\sigma_1^s-\sigma_2^s\|_{C^0}+\|\sigma_1^u-\sigma_2^u\|_{C^0}. \end{align*} $$
Therefore, we conclude that
 $$ \begin{align*} \begin{aligned} d(P_1,P_2)&\leq2( \|v^u_1-v^u_2\|+\|v^s_1-v^s_2\|)\notag\\ &\leq\frac{2}{1-\sqrt{\varepsilon}}(d_{C^0}(V^u_1,V^u_2)+d_{C^0}(V^s_1,V^s_2)). \end{aligned}\\[-43pt] \end{align*} $$
$$ \begin{align*} \begin{aligned} d(P_1,P_2)&\leq2( \|v^u_1-v^u_2\|+\|v^s_1-v^s_2\|)\notag\\ &\leq\frac{2}{1-\sqrt{\varepsilon}}(d_{C^0}(V^u_1,V^u_2)+d_{C^0}(V^s_1,V^s_2)). \end{aligned}\\[-43pt] \end{align*} $$
Although the spaces
![]() $\mathscr {V}^{t}$
and the action of f or
$\mathscr {V}^{t}$
and the action of f or
![]() $f^{-1}$
are hard to work with due to the nonlinearity, from the definition of admissible manifold, through the inverse of the exponential map, the action of f or
$f^{-1}$
are hard to work with due to the nonlinearity, from the definition of admissible manifold, through the inverse of the exponential map, the action of f or
![]() $f^{-1}$
on an admissible manifold can be locally lifted to the tangent space. For example, for the action of f, if
$f^{-1}$
on an admissible manifold can be locally lifted to the tangent space. For example, for the action of f, if
![]() $V_x^u$
is a u-admissible manifold at x, then
$V_x^u$
is a u-admissible manifold at x, then
![]() $f(V_x^u)=\exp _{y}\{F_{x,y}(v_x^u,\sigma ^u_x(v_x^u)):\|v_x^u\|\leq Q(x)\}$
if
$f(V_x^u)=\exp _{y}\{F_{x,y}(v_x^u,\sigma ^u_x(v_x^u)):\|v_x^u\|\leq Q(x)\}$
if
![]() $d(f(x),y)<\delta ^u(\varepsilon (x))$
, where
$d(f(x),y)<\delta ^u(\varepsilon (x))$
, where
![]() $\delta ^u(\cdot )$
is given by Proposition 3.1. To prove that
$\delta ^u(\cdot )$
is given by Proposition 3.1. To prove that
![]() $f(V_x^u)$
contains a u-admissible manifold
$f(V_x^u)$
contains a u-admissible manifold
![]() $V_y^u$
at y, we write
$V_y^u$
at y, we write
![]() $F_{x,y}|_{S_x}=D_0F_{x,y}+\phi _{x,y}$
in the form
$F_{x,y}|_{S_x}=D_0F_{x,y}+\phi _{x,y}$
in the form
where
 $$ \begin{align} G_{x,y}^{\sigma^u_x}(\cdot):&=D^{uu}_{x,y}(\cdot)+D^{us}_{x,y}\circ\sigma_x^u(\cdot)+\phi^u_{x,y}(\cdot,\sigma_x^u(\cdot)),\notag\\ L_{x,y}^{\sigma^u_x}(\cdot):&=D^{ss}_{x,y}\circ\sigma_x^u(\cdot)+D^{su}_{x,y}(\cdot)+\phi^s_{x,y}(\cdot,\sigma_x^u(\cdot)). \end{align} $$
$$ \begin{align} G_{x,y}^{\sigma^u_x}(\cdot):&=D^{uu}_{x,y}(\cdot)+D^{us}_{x,y}\circ\sigma_x^u(\cdot)+\phi^u_{x,y}(\cdot,\sigma_x^u(\cdot)),\notag\\ L_{x,y}^{\sigma^u_x}(\cdot):&=D^{ss}_{x,y}\circ\sigma_x^u(\cdot)+D^{su}_{x,y}(\cdot)+\phi^s_{x,y}(\cdot,\sigma_x^u(\cdot)). \end{align} $$
If
![]() $B_y^u(Q(y))\subset G_{x,y}^{\sigma ^u_x}(B_x^u(Q(x)))$
and
$B_y^u(Q(y))\subset G_{x,y}^{\sigma ^u_x}(B_x^u(Q(x)))$
and
![]() $G_{x,y}^{\sigma ^u_x}$
is injective, we can define
$G_{x,y}^{\sigma ^u_x}$
is injective, we can define
![]() $\sigma _y^u:=L_{x,y}^{\sigma _x^u}\circ (G_{x,y}^{\sigma _x^u})^{-1}$
, and we have
$\sigma _y^u:=L_{x,y}^{\sigma _x^u}\circ (G_{x,y}^{\sigma _x^u})^{-1}$
, and we have
 $$ \begin{align*} \begin{aligned} f(V_x^u)&=\exp_{y}\{(G_{x,y}^{\sigma_x^u}(v_x^u),\ L_{x,y}^{\sigma_x^u}\circ(G_{x,y}^{\sigma_x^u})^{-1}\circ G_{x,y}^{\sigma_x^u}(v_x^u)):\|v_x^u\|\leq Q(x)\}\notag\\ &\supset\exp_y\{(v_y^u,\sigma_y^u(v_y^u)):\|v_y^u\|\leq Q(y)\}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} f(V_x^u)&=\exp_{y}\{(G_{x,y}^{\sigma_x^u}(v_x^u),\ L_{x,y}^{\sigma_x^u}\circ(G_{x,y}^{\sigma_x^u})^{-1}\circ G_{x,y}^{\sigma_x^u}(v_x^u)):\|v_x^u\|\leq Q(x)\}\notag\\ &\supset\exp_y\{(v_y^u,\sigma_y^u(v_y^u)):\|v_y^u\|\leq Q(y)\}, \end{aligned} \end{align*} $$
that is,
![]() $f(V_x^u)$
contains a u-admissible manifold
$f(V_x^u)$
contains a u-admissible manifold
![]() $V_y^u=\exp _y\{(v_y^u,\sigma _y^u(v_y^u)):\|v_y^u\|\leq Q(y)\}$
when
$V_y^u=\exp _y\{(v_y^u,\sigma _y^u(v_y^u)):\|v_y^u\|\leq Q(y)\}$
when
![]() $\sigma _y^u$
satisfies properties (AM1)–(AM3). If
$\sigma _y^u$
satisfies properties (AM1)–(AM3). If
![]() $V_y^u$
obtained in this way is unique, then the graph transform
$V_y^u$
obtained in this way is unique, then the graph transform
![]() $\mathscr {F}_{x,y}^{u}$
(see Definition 4.4 below) sends a u-admissible manifold at x with representing function
$\mathscr {F}_{x,y}^{u}$
(see Definition 4.4 below) sends a u-admissible manifold at x with representing function
![]() $\sigma _x^u$
to a u-admissible manifold at y whose graph of the representing function
$\sigma _x^u$
to a u-admissible manifold at y whose graph of the representing function
![]() $\sigma _y^u$
is contained in the action of
$\sigma _y^u$
is contained in the action of
![]() $F_{x,y}$
on the graph of
$F_{x,y}$
on the graph of
![]() $\sigma _x^u$
.
$\sigma _x^u$
.
Similarly, when
![]() $d(f^{-1}(y), x)<\delta ^s(\varepsilon (y))$
, the case of
$d(f^{-1}(y), x)<\delta ^s(\varepsilon (y))$
, the case of
![]() $f^{-1}(V_y^s)$
is symmetric and the corresponding graph transform
$f^{-1}(V_y^s)$
is symmetric and the corresponding graph transform
![]() $\mathscr {F}_{x,y}^{s}$
maps an s-admissible manifold at y to an s-admissible manifold at x.
$\mathscr {F}_{x,y}^{s}$
maps an s-admissible manifold at y to an s-admissible manifold at x.
We start with a definition and a basic lemma which will be used many times throughout the paper.
Definition 4.3. For
![]() $x,y\in O$
, the edge
$x,y\in O$
, the edge
![]() $x\rightarrow y$
means
$x\rightarrow y$
means
Lemma 4.1. Fix any positive constants
![]() $C_1, C_2, C_3, C_4$
, and suppose
$C_1, C_2, C_3, C_4$
, and suppose
![]() $x\rightarrow y$
. If
$x\rightarrow y$
. If
![]() $\varepsilon>0$
is small enough, we have:
$\varepsilon>0$
is small enough, we have:
-
(1)
 $C_1Q(y)+d(f(x),y)\leq C_1Q(x)(m(Df|_{E^u(x)})^\kappa -C_2\varepsilon \varepsilon (x))$
;
$C_1Q(y)+d(f(x),y)\leq C_1Q(x)(m(Df|_{E^u(x)})^\kappa -C_2\varepsilon \varepsilon (x))$
; -
(2)
 $C_3Q(y)-d(f(x),y)\geq C_3Q(x)(\|Df|_{E^s(x)}\|^\kappa +C_4\varepsilon \varepsilon (x))$
.
$C_3Q(y)-d(f(x),y)\geq C_3Q(x)(\|Df|_{E^s(x)}\|^\kappa +C_4\varepsilon \varepsilon (x))$
.
A similar statement holds for
![]() $f^{-1}$
.
$f^{-1}$
.
Proof. We give the proof for part (1), the proof of part (2) follows in a similar manner and is left to the reader.
First, we fix
 $$ \begin{align*} 0<\varepsilon\leq\min\bigg\{1,\frac{1}{\gamma-1},(2\gamma C_1)^{-({\alpha-\delta})/{2}}, \bigg(\frac{C_1}{2}\bigg)^{({\alpha-\delta})/{4}}, \frac{C-1}{1+C_2}\bigg\}. \end{align*} $$
$$ \begin{align*} 0<\varepsilon\leq\min\bigg\{1,\frac{1}{\gamma-1},(2\gamma C_1)^{-({\alpha-\delta})/{2}}, \bigg(\frac{C_1}{2}\bigg)^{({\alpha-\delta})/{4}}, \frac{C-1}{1+C_2}\bigg\}. \end{align*} $$
Since
![]() $d(f(x),y)<\delta ^u(\varepsilon (x))Q(x)^2Q(f(x))$
, we have
$d(f(x),y)<\delta ^u(\varepsilon (x))Q(x)^2Q(f(x))$
, we have
![]() $({d(f(x),y)}/{d(f(x),\partial O)})<\delta ^u(\varepsilon (x))Q(x)^2<\varepsilon $
. By the fact that
$({d(f(x),y)}/{d(f(x),\partial O)})<\delta ^u(\varepsilon (x))Q(x)^2<\varepsilon $
. By the fact that
![]() $(1+a)^\gamma \leq 1+2\gamma a$
if
$(1+a)^\gamma \leq 1+2\gamma a$
if
![]() $0<a\leq ({1}/({\gamma -1}))$
, we obtain
$0<a\leq ({1}/({\gamma -1}))$
, we obtain
 $$ \begin{align*} \begin{aligned} Q(y)&\leq\varepsilon^{{2}/({\alpha-\delta})}\min\{r_0^\gamma,(d(f(x),\partial O)+d(y,f(x)))^\gamma\}\notag\\ &\leq\varepsilon^{{2}/({\alpha-\delta})}\min\bigg\{r_0^\gamma,d(f(x),\partial O)^\gamma\bigg(1+2\gamma\frac{d(y,f(x))}{d(f(x),\partial O)}\bigg)\bigg\}\notag\\ &\leq Q(f(x))+2\gamma\varepsilon^{{2}/({\alpha-\delta})}d(y,f(x))\notag\\ &\leq Q(f(x))+ \frac{d(y,f(x))}{C_1}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} Q(y)&\leq\varepsilon^{{2}/({\alpha-\delta})}\min\{r_0^\gamma,(d(f(x),\partial O)+d(y,f(x)))^\gamma\}\notag\\ &\leq\varepsilon^{{2}/({\alpha-\delta})}\min\bigg\{r_0^\gamma,d(f(x),\partial O)^\gamma\bigg(1+2\gamma\frac{d(y,f(x))}{d(f(x),\partial O)}\bigg)\bigg\}\notag\\ &\leq Q(f(x))+2\gamma\varepsilon^{{2}/({\alpha-\delta})}d(y,f(x))\notag\\ &\leq Q(f(x))+ \frac{d(y,f(x))}{C_1}. \end{aligned} \end{align*} $$
Recall that
![]() $0<\delta ^u(\varepsilon (x))<\varepsilon \varepsilon (x)$
in Proposition 3.1 and using Lemma 3.2, we have
$0<\delta ^u(\varepsilon (x))<\varepsilon \varepsilon (x)$
in Proposition 3.1 and using Lemma 3.2, we have
 $$ \begin{align*} \begin{aligned} &\frac{C_1Q(y)+d(f(x),y)+C_1C_2\varepsilon\varepsilon(x)Q(x)}{C_1Q(x)}\\ &\quad\leq\frac{Q(f(x))}{Q(x)}+\frac{2d(y,f(x))}{C_1Q(x)}+C_2\varepsilon\varepsilon(x)\notag\\ &\quad\leq\frac{Q(f(x))}{Q(x)}+\frac{2}{C_1}\varepsilon^{{4}/({\alpha-\delta})}\delta^u(\varepsilon(x))+C_2\varepsilon\varepsilon(x)\notag\\ &\quad\leq \frac{1}{C}(m(Df|_{E^u(x)})^\kappa-1)+1+(1+C_2)\varepsilon\varepsilon(x)\notag\\ &\quad\leq \frac{1}{C}(m(Df|_{E^u(x)})^\kappa-1)+1+\frac{C-1}{C}(m(Df|_{E^u(x)})^\kappa-1)\notag\\ &\quad=m(Df|_{E^u(x)})^\kappa, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\frac{C_1Q(y)+d(f(x),y)+C_1C_2\varepsilon\varepsilon(x)Q(x)}{C_1Q(x)}\\ &\quad\leq\frac{Q(f(x))}{Q(x)}+\frac{2d(y,f(x))}{C_1Q(x)}+C_2\varepsilon\varepsilon(x)\notag\\ &\quad\leq\frac{Q(f(x))}{Q(x)}+\frac{2}{C_1}\varepsilon^{{4}/({\alpha-\delta})}\delta^u(\varepsilon(x))+C_2\varepsilon\varepsilon(x)\notag\\ &\quad\leq \frac{1}{C}(m(Df|_{E^u(x)})^\kappa-1)+1+(1+C_2)\varepsilon\varepsilon(x)\notag\\ &\quad\leq \frac{1}{C}(m(Df|_{E^u(x)})^\kappa-1)+1+\frac{C-1}{C}(m(Df|_{E^u(x)})^\kappa-1)\notag\\ &\quad=m(Df|_{E^u(x)})^\kappa, \end{aligned} \end{align*} $$
proving part (1).
Proposition 4.2. The following hold for all
![]() $\varepsilon>0$
small enough. Suppose
$\varepsilon>0$
small enough. Suppose
![]() $x\rightarrow y$
, then:
$x\rightarrow y$
, then:
-
(1) the map
 $G_{x,y}^{\sigma _x^u}:B_x^u(Q(x))\rightarrow E^u(y)$
defined by
$G_{x,y}^{\sigma _x^u}:B_x^u(Q(x))\rightarrow E^u(y)$
defined by  $$ \begin{align*}&G_{x,y}^{\sigma_x^u}(v^u_x)\\ &\quad=D_{x,y}^{uu}(v^u_x)+D_{x,y}^{us}\circ\sigma^u_x(v^u_x)+\phi_{x,y}^u(v^u_x,\sigma^u_x(v^u_x))\quad \text{for all } v^u_x\in B_x^u(Q(x)),\end{align*} $$
$$ \begin{align*}&G_{x,y}^{\sigma_x^u}(v^u_x)\\ &\quad=D_{x,y}^{uu}(v^u_x)+D_{x,y}^{us}\circ\sigma^u_x(v^u_x)+\phi_{x,y}^u(v^u_x,\sigma^u_x(v^u_x))\quad \text{for all } v^u_x\in B_x^u(Q(x)),\end{align*} $$
is injective, and
 $G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))\supset B_y^u(Q(y))$
;
$G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))\supset B_y^u(Q(y))$
; -
(2) the map
 $\sigma _y^u:=L_{x,y}^{\sigma _x^u}\circ (G_{x,y}^{\sigma _x^u})^{-1}$
defined on
$\sigma _y^u:=L_{x,y}^{\sigma _x^u}\circ (G_{x,y}^{\sigma _x^u})^{-1}$
defined on
 $G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
satisfies properties (AM1)–(AM3), where the map
$G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
satisfies properties (AM1)–(AM3), where the map
 $L_{x,y}^{\sigma ^u_x}:B_x^u(Q(x))\rightarrow E^u(y)$
is defined by
$L_{x,y}^{\sigma ^u_x}:B_x^u(Q(x))\rightarrow E^u(y)$
is defined by  $$ \begin{align*}L_{x,y}^{\sigma^u_x}(v^u_x)&:=D^{ss}_{x,y}\circ\sigma_x^u(v^u_x)\\ &\quad+D^{su}_{x,y}(v^u_x)+\phi^s_{x,y}(v^u_x,\sigma_x^u(v^u_x))\quad \text{for all } v^u_x\in B_x^u(Q(x)).\end{align*} $$
$$ \begin{align*}L_{x,y}^{\sigma^u_x}(v^u_x)&:=D^{ss}_{x,y}\circ\sigma_x^u(v^u_x)\\ &\quad+D^{su}_{x,y}(v^u_x)+\phi^s_{x,y}(v^u_x,\sigma_x^u(v^u_x))\quad \text{for all } v^u_x\in B_x^u(Q(x)).\end{align*} $$
The symmetric statement holds for
 $F_{x,y}^{-1}$
.
$F_{x,y}^{-1}$
.
Proof. The proof is a straightforward adaption of arguments in [Reference Sarig22, Proposition 4.12]. We give the proof in the case of
![]() $F_{x,y}$
. The case of
$F_{x,y}$
. The case of
![]() $F_{x,y}^{-1}$
is symmetric.
$F_{x,y}^{-1}$
is symmetric.
(1) The well-defined nature of
![]() $(G_{x,y}^{\sigma _x^u})^{-1}$
is a consequence of the expansion property of
$(G_{x,y}^{\sigma _x^u})^{-1}$
is a consequence of the expansion property of
![]() $Df|_{E^u(x)}$
. For every
$Df|_{E^u(x)}$
. For every
![]() $v_x^u\in B_x^u(Q(x))$
, by property (AM2), we know that
$v_x^u\in B_x^u(Q(x))$
, by property (AM2), we know that
![]() $\|D_{v_x^u}{\sigma ^u_x}\|\leq 1$
if
$\|D_{v_x^u}{\sigma ^u_x}\|\leq 1$
if
![]() $0<\varepsilon \leq \min \{1,{C}/{4}\}$
. Therefore, from Proposition 3.1(2) and Lemma 3.1, we have
$0<\varepsilon \leq \min \{1,{C}/{4}\}$
. Therefore, from Proposition 3.1(2) and Lemma 3.1, we have
 $$ \begin{align*} \begin{aligned} \|D_{v_x^u}G_{x,y}^{\sigma^u_x}\|&\geq m(D_{x,y}^{uu})-\|D_{x,y}^{us}\|\ \|D_{v_x^u}{\sigma^u_x}\|-\|D_{(v_x^u,\sigma^u_x(v_x^u))}\phi^u_{x,y}\|(1+\|D_{v_x^u}{\sigma^u_x}\|)\notag\\ &\geq m(Df|_{E^{u}(x)})-\varepsilon\varepsilon(x)-\varepsilon\varepsilon(x)-2\varepsilon\varepsilon(x)\notag\\ &\geq m(Df|_{E^{u}(x)})^\kappa-4\varepsilon\varepsilon(x)>1. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|D_{v_x^u}G_{x,y}^{\sigma^u_x}\|&\geq m(D_{x,y}^{uu})-\|D_{x,y}^{us}\|\ \|D_{v_x^u}{\sigma^u_x}\|-\|D_{(v_x^u,\sigma^u_x(v_x^u))}\phi^u_{x,y}\|(1+\|D_{v_x^u}{\sigma^u_x}\|)\notag\\ &\geq m(Df|_{E^{u}(x)})-\varepsilon\varepsilon(x)-\varepsilon\varepsilon(x)-2\varepsilon\varepsilon(x)\notag\\ &\geq m(Df|_{E^{u}(x)})^\kappa-4\varepsilon\varepsilon(x)>1. \end{aligned} \end{align*} $$
It follows that
![]() $G_{x,y}^{\sigma ^u_x}$
is
$G_{x,y}^{\sigma ^u_x}$
is
![]() $[m(Df|_{E^{u}(x)})-4\varepsilon \varepsilon (x)]$
-expanding and hence one-to-one, and
$[m(Df|_{E^{u}(x)})-4\varepsilon \varepsilon (x)]$
-expanding and hence one-to-one, and
![]() $(G_{x,y}^{\sigma _x^u})^{-1}$
is well defined on
$(G_{x,y}^{\sigma _x^u})^{-1}$
is well defined on
![]() $G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
.
$G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
.
By invariance of the domain, to prove
![]() $G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))\supset B_y^u(Q(y))$
, the problem reduces to show that
$G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))\supset B_y^u(Q(y))$
, the problem reduces to show that
for any
![]() $v_x^u\in \partial B_x^u(Q(x))$
.
$v_x^u\in \partial B_x^u(Q(x))$
.
According to
 $$ \begin{align*} \begin{aligned} \|G_{x,y}^{\sigma^u_x}(0)\|&=\|D_{x,y}^{us}\circ\sigma^u_x(0)+\phi^u_{x,y}(0,\sigma^u_x(0))\|\notag\\ &\leq\|D_{x,y}^{us}\|\ \|\sigma^u_x(0)\|+\|\phi_{x,y}(0,0)\|+\operatorname{Lip}(\phi_{x,y})\|\sigma^u_x(0)\|,\\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|G_{x,y}^{\sigma^u_x}(0)\|&=\|D_{x,y}^{us}\circ\sigma^u_x(0)+\phi^u_{x,y}(0,\sigma^u_x(0))\|\notag\\ &\leq\|D_{x,y}^{us}\|\ \|\sigma^u_x(0)\|+\|\phi_{x,y}(0,0)\|+\operatorname{Lip}(\phi_{x,y})\|\sigma^u_x(0)\|,\\ \end{aligned} \end{align*} $$
by property (AM1) and Proposition 3.1(2), we have
In particular, using Lemma 4.1 for
![]() $C_1=1, C_2=5$
, and the fact that
$C_1=1, C_2=5$
, and the fact that
![]() $G_{x,y}^{\sigma ^u_x}$
is
$G_{x,y}^{\sigma ^u_x}$
is
![]() $[m(Df|_{E^{u}(x)})-4\varepsilon \varepsilon (x)]$
-expanding, we have that for any
$[m(Df|_{E^{u}(x)})-4\varepsilon \varepsilon (x)]$
-expanding, we have that for any
![]() $v_x^u\in \partial B_x^u(Q(x))$
,
$v_x^u\in \partial B_x^u(Q(x))$
,
 $$ \begin{align*} \begin{aligned} \|G_{x,y}^{\sigma^u_x}(v_x^u)\|&\geq \|G_{x,y}^{\sigma^u_x}(v_x^u)-G_{x,y}^{\sigma^u_x}(0)\|-\|G_{x,y}^{\sigma^u_x}(0)\|\notag\\ &\geq (m(Df|_{E^{u}(x)})-4\varepsilon\varepsilon(x))Q(x)-2\varepsilon\varepsilon(x)\times 10^{-3}Q(x)-d(f(x),y)\notag\\ &\geq (m(Df|_{E^{u}(x)})^\kappa-5\varepsilon\varepsilon(x))Q(x)-d(f(x),y)\notag\\ &\geq Q(y). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|G_{x,y}^{\sigma^u_x}(v_x^u)\|&\geq \|G_{x,y}^{\sigma^u_x}(v_x^u)-G_{x,y}^{\sigma^u_x}(0)\|-\|G_{x,y}^{\sigma^u_x}(0)\|\notag\\ &\geq (m(Df|_{E^{u}(x)})-4\varepsilon\varepsilon(x))Q(x)-2\varepsilon\varepsilon(x)\times 10^{-3}Q(x)-d(f(x),y)\notag\\ &\geq (m(Df|_{E^{u}(x)})^\kappa-5\varepsilon\varepsilon(x))Q(x)-d(f(x),y)\notag\\ &\geq Q(y). \end{aligned} \end{align*} $$
(2) We first prove
![]() $\sigma ^u_y$
satisfies property (AM1). Denote
$\sigma ^u_y$
satisfies property (AM1). Denote
![]() $v_{0x}^u:=(G_{x,y}^{\sigma ^u_x})^{-1}(0)$
, since
$v_{0x}^u:=(G_{x,y}^{\sigma ^u_x})^{-1}(0)$
, since
![]() $G_{x,y}^{\sigma ^u_x}$
is
$G_{x,y}^{\sigma ^u_x}$
is
![]() $[m(Df|_{E^{u}(x)})-4\varepsilon \varepsilon (x)]$
-expanding on
$[m(Df|_{E^{u}(x)})-4\varepsilon \varepsilon (x)]$
-expanding on
![]() $B_x^u(Q(x))$
, in particular,
$B_x^u(Q(x))$
, in particular,
By equation (4.4), we have
 $$ \begin{align*} \begin{aligned} \|v_{0x}^u\|&=\|(G_{x,y}^{\sigma^u_x})^{-1}(0)-(G_{x,y}^{\sigma^u_x})^{-1}\circ G_{x,y}^{\sigma^u_x}(0)\|\notag\\ &\leq\|D(G_{x,y}^{\sigma^u_x})^{-1})\|_{C^0}\|G_{x,y}^{\sigma^u_x}(0)\|\notag\\ &\leq2\varepsilon\varepsilon(x)\times 10^{-3}Q(x)+d(f(x),y)\notag\\ &\leq3\varepsilon\varepsilon(x)\times 10^{-3}Q(x). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|v_{0x}^u\|&=\|(G_{x,y}^{\sigma^u_x})^{-1}(0)-(G_{x,y}^{\sigma^u_x})^{-1}\circ G_{x,y}^{\sigma^u_x}(0)\|\notag\\ &\leq\|D(G_{x,y}^{\sigma^u_x})^{-1})\|_{C^0}\|G_{x,y}^{\sigma^u_x}(0)\|\notag\\ &\leq2\varepsilon\varepsilon(x)\times 10^{-3}Q(x)+d(f(x),y)\notag\\ &\leq3\varepsilon\varepsilon(x)\times 10^{-3}Q(x). \end{aligned} \end{align*} $$
Note that from equation (3.6) of Lemma 3.2, it follows that
![]() $\|D_{x,y}^{ss}\|\leq \|Df|_{E^s(x)}\|^\kappa +\varepsilon \varepsilon (x)\leq 1$
if
$\|D_{x,y}^{ss}\|\leq \|Df|_{E^s(x)}\|^\kappa +\varepsilon \varepsilon (x)\leq 1$
if
![]() $0<\varepsilon \leq \min \{1,C\}$
. According to properties (AM1), (AM2), and Lemma 4.1 for
$0<\varepsilon \leq \min \{1,C\}$
. According to properties (AM1), (AM2), and Lemma 4.1 for
![]() $C_3=10^{-3}, C_4=13$
, we obtain
$C_3=10^{-3}, C_4=13$
, we obtain
 $$ \begin{align*} \begin{aligned} \|\sigma^u_y(0)\|&=\|L_{x,y}^{\sigma_x^u}(v_{0x}^u)\|\notag\\ &=\|D_{x,y}^{ss}\circ\sigma_x^u(v_{0x}^u)+D_{x,y}^{su}(v_{0x}^u)+ \phi_{x,y}^s(v_{0x}^u,\sigma_x^u(v_{0x}^u))\|\notag\\ &\leq\|D_{x,y}^{ss}\|(\|\sigma_x^u(0)\|+\operatorname{Lip}(\sigma_x^u)\|v_{0x}^u\|)+\|D_{x,y}^{su}\|\ \|v_{0x}^u\|+ \|\phi_{x,y}^s(0,0)\|\\&\quad+\operatorname{Lip}(\phi^s_{x,y})(1+\operatorname{Lip}(\sigma_x^u))\|v_{0x}^u\|\notag\\ &\leq(\|Df|_{E^s(x)}\|^\kappa+\varepsilon\varepsilon(x))10^{-3}Q(x)+12\varepsilon\varepsilon(x)\times 10^{-3}Q(x)+d(f(x),y)\notag\\ &\leq 10^{-3}Q(y), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\sigma^u_y(0)\|&=\|L_{x,y}^{\sigma_x^u}(v_{0x}^u)\|\notag\\ &=\|D_{x,y}^{ss}\circ\sigma_x^u(v_{0x}^u)+D_{x,y}^{su}(v_{0x}^u)+ \phi_{x,y}^s(v_{0x}^u,\sigma_x^u(v_{0x}^u))\|\notag\\ &\leq\|D_{x,y}^{ss}\|(\|\sigma_x^u(0)\|+\operatorname{Lip}(\sigma_x^u)\|v_{0x}^u\|)+\|D_{x,y}^{su}\|\ \|v_{0x}^u\|+ \|\phi_{x,y}^s(0,0)\|\\&\quad+\operatorname{Lip}(\phi^s_{x,y})(1+\operatorname{Lip}(\sigma_x^u))\|v_{0x}^u\|\notag\\ &\leq(\|Df|_{E^s(x)}\|^\kappa+\varepsilon\varepsilon(x))10^{-3}Q(x)+12\varepsilon\varepsilon(x)\times 10^{-3}Q(x)+d(f(x),y)\notag\\ &\leq 10^{-3}Q(y), \end{aligned} \end{align*} $$
proving property (AM1).
Next we prove
![]() $\|D\sigma ^u_y\|_{C^0}\leq \sqrt {\varepsilon }$
, where the norm is taken in
$\|D\sigma ^u_y\|_{C^0}\leq \sqrt {\varepsilon }$
, where the norm is taken in
![]() $G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
.
$G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
.
For all
![]() $v_y^u\in G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
,
$v_y^u\in G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
,
![]() $v_x^u=(G_{x,y}^{\sigma _x^u})^{-1}(v_y^u)\in B_x^u(Q(x))$
. Thanks to
$v_x^u=(G_{x,y}^{\sigma _x^u})^{-1}(v_y^u)\in B_x^u(Q(x))$
. Thanks to
![]() $\|D_{v_y^u} (G_{x,y}^{\sigma ^u_x})^{-1})\|<1$
, property (AM2) is easy to be verified from
$\|D_{v_y^u} (G_{x,y}^{\sigma ^u_x})^{-1})\|<1$
, property (AM2) is easy to be verified from
 $$ \begin{align*} \begin{aligned} \|D_{v_y^u}\sigma^u_y\|&=\|D_{x,y}^{ss}\cdot D_{v_{x}^u}\sigma_x^u\cdot D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}+D_{x,y}^{su}\cdot D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\\&\quad+ D_{v_{x}^u}\phi_{x,y}^s\cdot D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|\notag\\ &\leq\|D_{x,y}^{ss}\|\ \|D\sigma_x^u\|_{C^0}+3\varepsilon\varepsilon(x)\notag\\ &\leq\|Df|_{E^s(x)}\|\sqrt{\varepsilon}+4\varepsilon\varepsilon(x)\notag\\ &\leq\sqrt{\varepsilon} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|D_{v_y^u}\sigma^u_y\|&=\|D_{x,y}^{ss}\cdot D_{v_{x}^u}\sigma_x^u\cdot D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}+D_{x,y}^{su}\cdot D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\\&\quad+ D_{v_{x}^u}\phi_{x,y}^s\cdot D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|\notag\\ &\leq\|D_{x,y}^{ss}\|\ \|D\sigma_x^u\|_{C^0}+3\varepsilon\varepsilon(x)\notag\\ &\leq\|Df|_{E^s(x)}\|\sqrt{\varepsilon}+4\varepsilon\varepsilon(x)\notag\\ &\leq\sqrt{\varepsilon} \end{aligned} \end{align*} $$
if
![]() $0<\varepsilon \leq \min \{1,({C}/{4})^2\}$
.
$0<\varepsilon \leq \min \{1,({C}/{4})^2\}$
.
Finally, we have to show that
![]() $\sigma ^u_y$
satisfies property (AM3) also. From
$\sigma ^u_y$
satisfies property (AM3) also. From
we have
 $$ \begin{align*} \begin{aligned} \|D\sigma_y^u\|_{C^{\delta/2}}&=\|(D^{ss}_{x,y}\cdot D\sigma_x^u+D^{su}_{x,y} +D\phi^s_{x,y})\cdot D(G_{x,y}^{\sigma_x^u})^{-1}\|_{C^{\delta/2}}\notag\\ &\leq(\|D^{ss}_{x,y}\|\cdot \|D\sigma_x^u\|_{C^{\delta/2}}+\|D^{su}_{x,y}\|+2\|D\phi_{x,y}\|_{C^{\delta/2}(S_x)}) \|D(G_{x,y}^{\sigma_x^u})^{-1}\|_{C^{\delta/2}}.\notag\\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|D\sigma_y^u\|_{C^{\delta/2}}&=\|(D^{ss}_{x,y}\cdot D\sigma_x^u+D^{su}_{x,y} +D\phi^s_{x,y})\cdot D(G_{x,y}^{\sigma_x^u})^{-1}\|_{C^{\delta/2}}\notag\\ &\leq(\|D^{ss}_{x,y}\|\cdot \|D\sigma_x^u\|_{C^{\delta/2}}+\|D^{su}_{x,y}\|+2\|D\phi_{x,y}\|_{C^{\delta/2}(S_x)}) \|D(G_{x,y}^{\sigma_x^u})^{-1}\|_{C^{\delta/2}}.\notag\\ \end{aligned} \end{align*} $$
Claim.
If
![]() $\varepsilon>0$
is small enough,
$\varepsilon>0$
is small enough,
![]() $\|D(G^{\sigma _x^u}_{x,y})^{-1}\|_{C^{\delta /2}}<1$
.
$\|D(G^{\sigma _x^u}_{x,y})^{-1}\|_{C^{\delta /2}}<1$
.
Proof of Claim
For
![]() $v_y^u,w_y^u\in G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
, notice that
$v_y^u,w_y^u\in G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
, notice that
![]() $D_{v_y^u}(G_{x,y}^{\sigma _x^u})^{-1}\cdot D_{v_x^u}G_{x,y}^{\sigma _x^u}$
and
$D_{v_y^u}(G_{x,y}^{\sigma _x^u})^{-1}\cdot D_{v_x^u}G_{x,y}^{\sigma _x^u}$
and
![]() $D_{w_x^u}G_{x,y}^{\sigma _x^u}\cdot D_{w_y^u}(G_{x,y}^{\sigma _x^u})^{-1}$
are identity maps, where
$D_{w_x^u}G_{x,y}^{\sigma _x^u}\cdot D_{w_y^u}(G_{x,y}^{\sigma _x^u})^{-1}$
are identity maps, where
![]() $v_y^u=G_{x,y}^{\sigma _x^u}(v_x^u)$
,
$v_y^u=G_{x,y}^{\sigma _x^u}(v_x^u)$
,
![]() $w_x^u=(G_{x,y}^{\sigma _x^u})^{-1}(w_y^u)$
. Thus, we have
$w_x^u=(G_{x,y}^{\sigma _x^u})^{-1}(w_y^u)$
. Thus, we have
 $$ \begin{align*} \begin{aligned} &\|D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}-D_{w_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|\notag\\ &\quad=\|D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\cdot(D_{w_x^u}G_{x,y}^{\sigma_x^u}-D_{v_x^u}G_{x,y}^{\sigma_x^u})\cdot D_{w_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|\notag\\ &\quad=\|D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\cdot(D_{x,y}^{us}D_{w_x^u}\sigma_x^u+D_{w_x^u}\phi_{x,y}^u\\&\qquad-D_{x,y}^{us}D_{v_x^u}\sigma_x^u-D_{v_x^u}\phi_{x,y}^u)\cdot D_{w_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}-D_{w_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|\notag\\ &\quad=\|D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\cdot(D_{w_x^u}G_{x,y}^{\sigma_x^u}-D_{v_x^u}G_{x,y}^{\sigma_x^u})\cdot D_{w_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|\notag\\ &\quad=\|D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\cdot(D_{x,y}^{us}D_{w_x^u}\sigma_x^u+D_{w_x^u}\phi_{x,y}^u\\&\qquad-D_{x,y}^{us}D_{v_x^u}\sigma_x^u-D_{v_x^u}\phi_{x,y}^u)\cdot D_{w_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|. \end{aligned} \end{align*} $$
First, to estimate
![]() $\|D_{w_x^u}\phi _{x,y}^u-D_{v_x^u}\phi _{x,y}^u\|$
in parentheses, a little manipulation is needed. If
$\|D_{w_x^u}\phi _{x,y}^u-D_{v_x^u}\phi _{x,y}^u\|$
in parentheses, a little manipulation is needed. If
![]() $0<\varepsilon \leq 1$
, by property (AM3) and Proposition 3.1(3), we can get
$0<\varepsilon \leq 1$
, by property (AM3) and Proposition 3.1(3), we can get
 $$ \begin{align*} \begin{aligned} &\|D_{w_x^u}\phi^u_{x,y}(\cdot,\sigma_x^u(\cdot))-D_{v_x^u}\phi^u_{x,y}(\cdot,\sigma_x^u(\cdot))\|\notag\\ &\quad=\left\|D_{(w_x^u,\sigma_x^u(w_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{w_x^u}\sigma_x^u \end{array}\right]-D_{(v_x^u,\sigma_x^u(v_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_x^u}\sigma_x^u \end{array}\right]\right\|\notag\\ &\quad\leq\left\|D_{(w_x^u,\sigma_x^u(w_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{w_x^u}\sigma_x^u \end{array}\right]-D_{(w_x^u,\sigma_x^u(w_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_x^u}\sigma_x^u \end{array}\right]\right\|\notag\\ &\qquad+\left\|D_{(w_x^u,\sigma_x^u(w_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_x^u}\sigma_x^u \end{array}\right]-D_{(v_x^u,\sigma_x^u(v_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_x^u}\sigma_x^u \end{array}\right]\right\|\notag\\ &\quad\leq\frac{\varepsilon\varepsilon(x)}{2}\|w_x^u-v_x^u\|^{\delta/2}+4\varepsilon\varepsilon(x)\|w_x^u-v_x^u\|^{\delta/2}\notag\\ &\quad=\frac{9\varepsilon\varepsilon(x)}{2}\|w_x^u-v_x^u\|^{\delta/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{w_x^u}\phi^u_{x,y}(\cdot,\sigma_x^u(\cdot))-D_{v_x^u}\phi^u_{x,y}(\cdot,\sigma_x^u(\cdot))\|\notag\\ &\quad=\left\|D_{(w_x^u,\sigma_x^u(w_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{w_x^u}\sigma_x^u \end{array}\right]-D_{(v_x^u,\sigma_x^u(v_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_x^u}\sigma_x^u \end{array}\right]\right\|\notag\\ &\quad\leq\left\|D_{(w_x^u,\sigma_x^u(w_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{w_x^u}\sigma_x^u \end{array}\right]-D_{(w_x^u,\sigma_x^u(w_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_x^u}\sigma_x^u \end{array}\right]\right\|\notag\\ &\qquad+\left\|D_{(w_x^u,\sigma_x^u(w_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_x^u}\sigma_x^u \end{array}\right]-D_{(v_x^u,\sigma_x^u(v_x^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_x^u}\sigma_x^u \end{array}\right]\right\|\notag\\ &\quad\leq\frac{\varepsilon\varepsilon(x)}{2}\|w_x^u-v_x^u\|^{\delta/2}+4\varepsilon\varepsilon(x)\|w_x^u-v_x^u\|^{\delta/2}\notag\\ &\quad=\frac{9\varepsilon\varepsilon(x)}{2}\|w_x^u-v_x^u\|^{\delta/2}. \end{aligned} \end{align*} $$
For the rest in the parentheses, from property (AM3), we find
therefore, we obtain that
 $$ \begin{align*} \begin{aligned} &\|D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}-D_{w_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|\notag\\ &\quad\leq \|D(G_{x,y}^{\sigma_x^u})^{-1}\|^2_{C^0}\ 5\varepsilon\varepsilon(x)\|w_x^u-v_x^u\|^{\delta/2}\notag\\ &\quad\leq 5\varepsilon\varepsilon(x)\|D(G_{x,y}^{\sigma_x^u})^{-1}\|^{2+{\delta}/{2}}_{C^0}\|w_y^u-v_y^u\|^{\delta/2} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_y^u}(G_{x,y}^{\sigma_x^u})^{-1}-D_{w_y^u}(G_{x,y}^{\sigma_x^u})^{-1}\|\notag\\ &\quad\leq \|D(G_{x,y}^{\sigma_x^u})^{-1}\|^2_{C^0}\ 5\varepsilon\varepsilon(x)\|w_x^u-v_x^u\|^{\delta/2}\notag\\ &\quad\leq 5\varepsilon\varepsilon(x)\|D(G_{x,y}^{\sigma_x^u})^{-1}\|^{2+{\delta}/{2}}_{C^0}\|w_y^u-v_y^u\|^{\delta/2} \end{aligned} \end{align*} $$
or
Using
![]() $G_{x,y}^{\sigma ^u_x}$
is
$G_{x,y}^{\sigma ^u_x}$
is
![]() $[m(Df|_{E^{u}(x)})-4\varepsilon \varepsilon (x)]$
-expanding again, that is,
$[m(Df|_{E^{u}(x)})-4\varepsilon \varepsilon (x)]$
-expanding again, that is,
 $$ \begin{align*} \|D(G_{x,y}^{\sigma^u_x})^{-1}\|_{C^0}\leq\frac{1}{m(Df|_{E^{u}(x)})-4\varepsilon\varepsilon(x)}, \end{align*} $$
$$ \begin{align*} \|D(G_{x,y}^{\sigma^u_x})^{-1}\|_{C^0}\leq\frac{1}{m(Df|_{E^{u}(x)})-4\varepsilon\varepsilon(x)}, \end{align*} $$
we get finally
 $$ \begin{align*} \begin{aligned} \|D(G^{\sigma_x^u}_{x,y})^{-1}\|_{C^{\delta/2}}&=\|D(G^{\sigma_x^u}_{x,y})^{-1}\|_{C^0}+ \operatorname{Hol}_{\delta/2}(D(G^{\sigma_x^u}_{x,y})^{-1})\notag\\ &\leq\frac{1}{m(Df|_{E^{u}(x)})-4\varepsilon\varepsilon(x)}+5\varepsilon\varepsilon(x)\notag\\ &<1 \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|D(G^{\sigma_x^u}_{x,y})^{-1}\|_{C^{\delta/2}}&=\|D(G^{\sigma_x^u}_{x,y})^{-1}\|_{C^0}+ \operatorname{Hol}_{\delta/2}(D(G^{\sigma_x^u}_{x,y})^{-1})\notag\\ &\leq\frac{1}{m(Df|_{E^{u}(x)})-4\varepsilon\varepsilon(x)}+5\varepsilon\varepsilon(x)\notag\\ &<1 \end{aligned} \end{align*} $$
if
![]() $0<\varepsilon <\min \{1,{C}/{5(C^f+4)}\}$
. This completes the proof of the claim.
$0<\varepsilon <\min \{1,{C}/{5(C^f+4)}\}$
. This completes the proof of the claim.
We are now turning to the proof of
![]() $\|D\sigma _y^u\|_{C^{\delta /2}}\leq \tfrac 12$
. From Proposition 3.1(2) and (3), we have
$\|D\sigma _y^u\|_{C^{\delta /2}}\leq \tfrac 12$
. From Proposition 3.1(2) and (3), we have
![]() $\|D\phi _{x,y}\|_{C^{\delta /2}(S_x)}\leq 2\varepsilon \varepsilon (x)$
. By using equation (3.6) of Lemma 3.2 and combining with the claim above, we obtain that
$\|D\phi _{x,y}\|_{C^{\delta /2}(S_x)}\leq 2\varepsilon \varepsilon (x)$
. By using equation (3.6) of Lemma 3.2 and combining with the claim above, we obtain that
 $$ \begin{align*} \begin{aligned} \|D\sigma_y^u\|_{C^{\delta/2}}&\leq(\|D^{ss}_{x,y}\|\cdot \|D\sigma_x^u\|_{C^{\delta/2}}+\|D^{su}_{x,y}\|+2\|D\phi_{x,y}\|_{C^{\delta/2}(S_x)}) \|D(G_{x,y}^{\sigma_x^u})^{-1}\|_{C^{\delta/2}}\notag\\ &\leq\|D^{ss}_{x,y}\|\cdot \|D\sigma_x^u\|_{C^{\delta/2}}+\|D^{su}_{x,y}\|+2\|D\phi_{x,y}\|_{C^{\delta/2}(S_x)}\notag\\ &\leq\tfrac{1}{2}(\|Df|_{E^s(x)}\|+\varepsilon\varepsilon(x))+5\varepsilon\varepsilon(x)\notag\\ &\leq \tfrac{1}{2} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|D\sigma_y^u\|_{C^{\delta/2}}&\leq(\|D^{ss}_{x,y}\|\cdot \|D\sigma_x^u\|_{C^{\delta/2}}+\|D^{su}_{x,y}\|+2\|D\phi_{x,y}\|_{C^{\delta/2}(S_x)}) \|D(G_{x,y}^{\sigma_x^u})^{-1}\|_{C^{\delta/2}}\notag\\ &\leq\|D^{ss}_{x,y}\|\cdot \|D\sigma_x^u\|_{C^{\delta/2}}+\|D^{su}_{x,y}\|+2\|D\phi_{x,y}\|_{C^{\delta/2}(S_x)}\notag\\ &\leq\tfrac{1}{2}(\|Df|_{E^s(x)}\|+\varepsilon\varepsilon(x))+5\varepsilon\varepsilon(x)\notag\\ &\leq \tfrac{1}{2} \end{aligned} \end{align*} $$
when
![]() $0<\varepsilon \leq \min \{1, {C}/{11}\}$
, and the proof of this proposition is completed.
$0<\varepsilon \leq \min \{1, {C}/{11}\}$
, and the proof of this proposition is completed.
As has been said, since
and
![]() $G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))\supset B_y^u(Q(y))$
, Proposition 4.2 above shows that
$G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))\supset B_y^u(Q(y))$
, Proposition 4.2 above shows that
![]() $f(V_x^u)$
restricts to a unique u-admissible manifold
$f(V_x^u)$
restricts to a unique u-admissible manifold
![]() $\widehat {V}_y^u$
at y, where
$\widehat {V}_y^u$
at y, where
Thus, we can summarize what we have proved as the following definition which is well defined for
![]() $\varepsilon>0$
small enough.
$\varepsilon>0$
small enough.
Definition 4.4. Suppose
![]() $x\rightarrow y$
.
$x\rightarrow y$
.
-
(1) The unstable graph transform
 $\mathscr {F}_{x,y}^{u}: \mathscr {V}_x^{u} \rightarrow \mathscr {V}_y^{u} $
is the map that sends
$\mathscr {F}_{x,y}^{u}: \mathscr {V}_x^{u} \rightarrow \mathscr {V}_y^{u} $
is the map that sends
 $V_x^{u} \in \mathscr {V}_x^{u}$
to the unique
$V_x^{u} \in \mathscr {V}_x^{u}$
to the unique
 $\mathscr {F}_{x,y}^{u}[V_x^{u}] \in \mathscr {V}_y^{u}$
with representing function
$\mathscr {F}_{x,y}^{u}[V_x^{u}] \in \mathscr {V}_y^{u}$
with representing function
 $\sigma _y^u$
such that
$\sigma _y^u$
such that
 $\mathscr {F}_{x,y}^{u}[V_x^{u}]=\exp _{y}\{(v^u, \sigma _y^u(v^u)):\|v^u\| \leq Q(y)\}\subset f(V_x^{u})$
.
$\mathscr {F}_{x,y}^{u}[V_x^{u}]=\exp _{y}\{(v^u, \sigma _y^u(v^u)):\|v^u\| \leq Q(y)\}\subset f(V_x^{u})$
. -
(2) The stable graph transform
 $\mathscr {F}_{x,y}^{s}: \mathscr {V}_y^{s} \rightarrow \mathscr {V}_x^{s} $
is the map that sends
$\mathscr {F}_{x,y}^{s}: \mathscr {V}_y^{s} \rightarrow \mathscr {V}_x^{s} $
is the map that sends
 $V_y^{s} \in \mathscr {V}_x^{s}$
to the unique
$V_y^{s} \in \mathscr {V}_x^{s}$
to the unique
 $\mathscr {F}_{x,y}^{s}[V_y^{s}] \in \mathscr {V}_x^{s}$
with representing function
$\mathscr {F}_{x,y}^{s}[V_y^{s}] \in \mathscr {V}_x^{s}$
with representing function
 $\sigma _x^s$
such that
$\sigma _x^s$
such that
 $\mathscr {F}_{x,y}^{s}[V_{y}^{s}]=\exp _{x}\{(\sigma _x^s(v^s), v^s):\|v^s\| \leq Q(x)\}\subset f^{-1}(V_y^{s})$
.
$\mathscr {F}_{x,y}^{s}[V_{y}^{s}]=\exp _{x}\{(\sigma _x^s(v^s), v^s):\|v^s\| \leq Q(x)\}\subset f^{-1}(V_y^{s})$
.
Corollary 4.1. The following holds for
![]() $\varepsilon>0$
small enough. Suppose
$\varepsilon>0$
small enough. Suppose
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
![]() $V_x^u\in \mathscr {V}_{x}^u$
. Then:
$V_x^u\in \mathscr {V}_{x}^u$
. Then:
-
(1) if
 $V_x^u$
is represented by the function
$V_x^u$
is represented by the function
 $\sigma ^u_x$
and
$\sigma ^u_x$
and
 $p:=\exp _x(0,\sigma ^u_x(0))$
, then
$p:=\exp _x(0,\sigma ^u_x(0))$
, then
 $f(p)\in \mathscr {F}_{x,y}^{u}[V_x^u]$
;
$f(p)\in \mathscr {F}_{x,y}^{u}[V_x^u]$
; -
(2)
 $f(V_x^u)$
intersects any
$f(V_x^u)$
intersects any
 $V_y^s\in \mathscr {V}_{y}^s$
at a unique point.
$V_y^s\in \mathscr {V}_{y}^s$
at a unique point.
Similar statements hold for the
![]() $f^{-1}$
-image of an s-admissible manifold at y.
$f^{-1}$
-image of an s-admissible manifold at y.
Proof.
-
(1) Since
 $\mathscr {F}_{x,y}^{u}[V_x^u]=\exp _{y}\{(v_y^u,\sigma _y^u(v_y^u)):\|v_y^u\|\leq Q(y)\}$
, it suffices to check that or check
$\mathscr {F}_{x,y}^{u}[V_x^u]=\exp _{y}\{(v_y^u,\sigma _y^u(v_y^u)):\|v_y^u\|\leq Q(y)\}$
, it suffices to check that or check $$ \begin{align*} F_{x,y}(0,\sigma^u_x(0))=(G_{x,y}^{\sigma_x^u}(0),L_{x,y}^{\sigma_x^u}(0))\in\{(v_y^u,\sigma_y^u(v_y^u)):\|v_y^u\|\leq Q(y)\}, \end{align*} $$
$$ \begin{align*} F_{x,y}(0,\sigma^u_x(0))=(G_{x,y}^{\sigma_x^u}(0),L_{x,y}^{\sigma_x^u}(0))\in\{(v_y^u,\sigma_y^u(v_y^u)):\|v_y^u\|\leq Q(y)\}, \end{align*} $$
 $\|G_{x,y}^{\sigma _x^u}(0)\|\leq Q(y)$
, which is straightforward.
$\|G_{x,y}^{\sigma _x^u}(0)\|\leq Q(y)$
, which is straightforward.
-
(2) For any
 $V_y^s\in \mathscr {V}_{y}^s$
with the representing function
$V_y^s\in \mathscr {V}_{y}^s$
with the representing function
 $\sigma _y^s$
, by Proposition 4.1(1),
$\sigma _y^s$
, by Proposition 4.1(1),
 $\mathscr {F}_{x,y}^{u}[V_x^u]$
and
$\mathscr {F}_{x,y}^{u}[V_x^u]$
and
 $V_y^s$
intersect at a single point. According to Definition 4.4,
$V_y^s$
intersect at a single point. According to Definition 4.4,
 $f(V_x^u)$
contains a u-manifold
$f(V_x^u)$
contains a u-manifold
 $\mathscr {F}_{x,y}^{u}[V_x^u]\in \mathscr {V}_{y}^u$
; therefore,
$\mathscr {F}_{x,y}^{u}[V_x^u]\in \mathscr {V}_{y}^u$
; therefore,
 $f(V_x^u)$
and
$f(V_x^u)$
and
 $V_y^s$
intersect at least at one point.
$V_y^s$
intersect at least at one point.
Since
with
![]() $\operatorname {Lip}(\sigma _y^u)\leq \sqrt {\varepsilon }$
, by the Kirszbraun theorem, we can extend
$\operatorname {Lip}(\sigma _y^u)\leq \sqrt {\varepsilon }$
, by the Kirszbraun theorem, we can extend
![]() $\sigma _y^s$
to a Lipschitz function
$\sigma _y^s$
to a Lipschitz function
![]() $\tilde {\sigma }_y^s$
on
$\tilde {\sigma }_y^s$
on
![]() $G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
with
$G_{x,y}^{\sigma _x^u}(B_x^u(Q(x)))$
with
![]() $\operatorname {Lip}(\tilde {\sigma }_y^s)=\operatorname {Lip}(\sigma _y^s)\leq \sqrt {\varepsilon }$
. The extension represents a Lipschitz manifold
$\operatorname {Lip}(\tilde {\sigma }_y^s)=\operatorname {Lip}(\sigma _y^s)\leq \sqrt {\varepsilon }$
. The extension represents a Lipschitz manifold
![]() $\tilde {V}_y^s\supset V_y^s$
. Hence, the proof is quite similar to that given earlier in Proposition 4.1(1) to conclude that
$\tilde {V}_y^s\supset V_y^s$
. Hence, the proof is quite similar to that given earlier in Proposition 4.1(1) to conclude that
![]() $f(V_x^u)\cap \tilde {V}_y^s$
consists of a single point and so is omitted.
$f(V_x^u)\cap \tilde {V}_y^s$
consists of a single point and so is omitted.
Proposition 4.3. If
![]() $\varepsilon>0$
is small enough, then the following hold. Suppose
$\varepsilon>0$
is small enough, then the following hold. Suppose
![]() $x\rightarrow y$
, if
$x\rightarrow y$
, if
![]() $V^u_{1}, V^u_{2} \in \mathscr {V}_x^u$
, we have:
$V^u_{1}, V^u_{2} \in \mathscr {V}_x^u$
, we have:
-
(1)
 $d_{C^{0}}(\mathscr {F}^u_{x,y}(V^u_{1}), \mathscr {F}^u_{x,y}(V^u_{2})) \leq \|Df|_{E^s(x)}\|^{1/2} d_{C^{0}}(V^u_{1}, V^u_{2})$
;
$d_{C^{0}}(\mathscr {F}^u_{x,y}(V^u_{1}), \mathscr {F}^u_{x,y}(V^u_{2})) \leq \|Df|_{E^s(x)}\|^{1/2} d_{C^{0}}(V^u_{1}, V^u_{2})$
; -
(2)
 $d_{C^{1}}(\mathscr {F}^u_{x,y}(V^u_{1}), \mathscr {F}^u_{x,y}(V^u_{2})) \leq \|Df|_{E^s(x)}\|^{1/2} (d_{C^{1}}(V^u_{1}, V^u_{2})+d_{C^{0}}(V^u_{1}, V^u_{2})^{\delta /2})$
.
$d_{C^{1}}(\mathscr {F}^u_{x,y}(V^u_{1}), \mathscr {F}^u_{x,y}(V^u_{2})) \leq \|Df|_{E^s(x)}\|^{1/2} (d_{C^{1}}(V^u_{1}, V^u_{2})+d_{C^{0}}(V^u_{1}, V^u_{2})^{\delta /2})$
.
Similar statements hold for
![]() $\mathscr {F}^s_{x,y}$
.
$\mathscr {F}^s_{x,y}$
.
Proof. The proof is similar to the proof of [Reference Sarig22, Proposition 4.14]. We prove the proposition for
![]() $\mathscr {F}^u_{x,y}$
and leave the case of
$\mathscr {F}^u_{x,y}$
and leave the case of
![]() $\mathscr {F}^s_{x,y}$
to the reader.
$\mathscr {F}^s_{x,y}$
to the reader.
Let
![]() $V_{1}, V_{2}$
with representing functions
$V_{1}, V_{2}$
with representing functions
![]() $\sigma _{1}, \sigma _{2}$
, and let
$\sigma _{1}, \sigma _{2}$
, and let
![]() $\tilde {\sigma }_{1}, \tilde {\sigma }_{2}$
be the representing functions of
$\tilde {\sigma }_{1}, \tilde {\sigma }_{2}$
be the representing functions of
![]() $\mathscr {F}^u_{x,y}(V_{1}), \mathscr {F}^u_{x,y}(V_{2}),$
that is,
$\mathscr {F}^u_{x,y}(V_{1}), \mathscr {F}^u_{x,y}(V_{2}),$
that is,
![]() $\tilde {\sigma }_{i}=L^{\sigma _i}_{x,y}\circ (G^{\sigma _i}_{x,y})^{-1}|_{B_y^u(Q(y))}$
,
$\tilde {\sigma }_{i}=L^{\sigma _i}_{x,y}\circ (G^{\sigma _i}_{x,y})^{-1}|_{B_y^u(Q(y))}$
,
![]() $i=1,2$
.
$i=1,2$
.
(1) For any
![]() $v_y^u\in B_y^u(Q(y))$
, denote
$v_y^u\in B_y^u(Q(y))$
, denote
![]() $v_{1x}^u=(G^{\sigma _1}_{x,y})^{-1}(v_y^u)$
,
$v_{1x}^u=(G^{\sigma _1}_{x,y})^{-1}(v_y^u)$
,
![]() $v_{2x}^u=(G^{\sigma _2}_{x,y})^{-1}(v_y^u)$
. Some tedious manipulation yields
$v_{2x}^u=(G^{\sigma _2}_{x,y})^{-1}(v_y^u)$
. Some tedious manipulation yields
 $$ \begin{align*} \begin{aligned} &\|\tilde{\sigma}_{1}(v_y^u)-\tilde{\sigma}_{2}(v_y^u)\|=\|\tilde{\sigma}_{1}\circ G^{\sigma_1}_{x,y}(v_{1x}^u)-\tilde{\sigma}_{2}\circ G^{\sigma_1}_{x,y}(v_{1x}^u)\|\notag\\ &\quad\leq\|\tilde{\sigma}_{1}\circ G^{\sigma_1}_{x,y}(v_{1x}^u)-\tilde{\sigma}_{2}\circ G^{\sigma_2}_{x,y}(v_{1x}^u)\|+\|\tilde{\sigma}_{2}\circ G^{\sigma_2}_{x,y}(v_{1x}^u)-\tilde{\sigma}_{2}\circ G^{\sigma_1}_{x,y}(v_{1x}^u)\|\notag\\ &\quad\leq\|D_{x,y}^{ss}(\sigma_1(v_{1x}^u)-\sigma_2(v_{1x}^u))\|+\|\phi_{x,y}^s(v_{1x}^u,\sigma_1(v_{1x}^u))-\phi_{x,y}^s(v_{1x}^u,\sigma_2(v_{1x}^u))\|\\&\qquad+\operatorname{Lip}(\tilde{\sigma}_{2}) \|G^{\sigma_2}_{x,y}(v_{1x}^u)-G^{\sigma_1}_{x,y}(v_{1x}^u)\|\notag \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|\tilde{\sigma}_{1}(v_y^u)-\tilde{\sigma}_{2}(v_y^u)\|=\|\tilde{\sigma}_{1}\circ G^{\sigma_1}_{x,y}(v_{1x}^u)-\tilde{\sigma}_{2}\circ G^{\sigma_1}_{x,y}(v_{1x}^u)\|\notag\\ &\quad\leq\|\tilde{\sigma}_{1}\circ G^{\sigma_1}_{x,y}(v_{1x}^u)-\tilde{\sigma}_{2}\circ G^{\sigma_2}_{x,y}(v_{1x}^u)\|+\|\tilde{\sigma}_{2}\circ G^{\sigma_2}_{x,y}(v_{1x}^u)-\tilde{\sigma}_{2}\circ G^{\sigma_1}_{x,y}(v_{1x}^u)\|\notag\\ &\quad\leq\|D_{x,y}^{ss}(\sigma_1(v_{1x}^u)-\sigma_2(v_{1x}^u))\|+\|\phi_{x,y}^s(v_{1x}^u,\sigma_1(v_{1x}^u))-\phi_{x,y}^s(v_{1x}^u,\sigma_2(v_{1x}^u))\|\\&\qquad+\operatorname{Lip}(\tilde{\sigma}_{2}) \|G^{\sigma_2}_{x,y}(v_{1x}^u)-G^{\sigma_1}_{x,y}(v_{1x}^u)\|\notag \end{aligned} \end{align*} $$
 $$ \begin{align*} \begin{aligned} &\qquad+\operatorname{Lip}(\phi_{x,y})) \|\sigma_2(v_{1x}^u)-\sigma_1(v_{1x}^u)\|\notag\\ &\quad\leq(\|D_{x,y}^{ss}\|+\|D_{x,y}^{us}\|+ 2\operatorname{Lip}(\phi_{x,y}))\|\sigma_2(v_{1x}^u)-\sigma_1(v_{1x}^u)\|\notag\\ &\quad\leq(\|Df|_{E^s(x)}\|+6\varepsilon\varepsilon(x))\|\sigma_2(v_{1x}^u)-\sigma_1(v_{1x}^u)\|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\qquad+\operatorname{Lip}(\phi_{x,y})) \|\sigma_2(v_{1x}^u)-\sigma_1(v_{1x}^u)\|\notag\\ &\quad\leq(\|D_{x,y}^{ss}\|+\|D_{x,y}^{us}\|+ 2\operatorname{Lip}(\phi_{x,y}))\|\sigma_2(v_{1x}^u)-\sigma_1(v_{1x}^u)\|\notag\\ &\quad\leq(\|Df|_{E^s(x)}\|+6\varepsilon\varepsilon(x))\|\sigma_2(v_{1x}^u)-\sigma_1(v_{1x}^u)\|. \end{aligned} \end{align*} $$
We remind the reader that
![]() $C\varepsilon (x)\leq 1-\|Df|_{E^s(x)}\|^\kappa \leq 1-\|Df|_{E^s(x)}\|$
and introduce a new constant
$C\varepsilon (x)\leq 1-\|Df|_{E^s(x)}\|^\kappa \leq 1-\|Df|_{E^s(x)}\|$
and introduce a new constant
 $$ \begin{align} a:=\inf_{x\in O}\frac{\|Df|_{E^s(x)}\|^{1/2}-\|Df|_{E^s(x)}\|}{1-\|Df|_{E^s(x)}\|}>0, \end{align} $$
$$ \begin{align} a:=\inf_{x\in O}\frac{\|Df|_{E^s(x)}\|^{1/2}-\|Df|_{E^s(x)}\|}{1-\|Df|_{E^s(x)}\|}>0, \end{align} $$
then if
![]() $0<\varepsilon \leq ({aC}/{6})$
, we get finally
$0<\varepsilon \leq ({aC}/{6})$
, we get finally
 $$ \begin{align*} \begin{aligned} \|\tilde{\sigma}_{1}-\tilde{\sigma}_{2}\|_{C^0}&\leq(\|Df|_{E^s(x)}\|+aC\varepsilon(x))\|\sigma_{1}-\sigma_{2}\|_{C^0}\notag\\ &\leq\|Df|_{E^s(x)}\|^{1/2}\|\sigma_{1}-\sigma_{2}\|_{C^0}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\tilde{\sigma}_{1}-\tilde{\sigma}_{2}\|_{C^0}&\leq(\|Df|_{E^s(x)}\|+aC\varepsilon(x))\|\sigma_{1}-\sigma_{2}\|_{C^0}\notag\\ &\leq\|Df|_{E^s(x)}\|^{1/2}\|\sigma_{1}-\sigma_{2}\|_{C^0}. \end{aligned} \end{align*} $$
(2) In view of part (1), our task now is to estimate
![]() $\|D\tilde {\sigma }_{1}- D\tilde {\sigma }_{2}\|_{C^{0}}$
in terms of
$\|D\tilde {\sigma }_{1}- D\tilde {\sigma }_{2}\|_{C^{0}}$
in terms of
![]() $\|D\sigma _{1}-D\sigma _{2}\|_{C^{0}}$
and
$\|D\sigma _{1}-D\sigma _{2}\|_{C^{0}}$
and
![]() $\|\sigma _{1}-\sigma _{2}\|_{C^{0}}^{\delta /2}$
. We will show that
$\|\sigma _{1}-\sigma _{2}\|_{C^{0}}^{\delta /2}$
. We will show that
 $$ \begin{align*} \begin{aligned} &\|D\tilde{\sigma}_{1}-D\tilde{\sigma}_{2}\|_{C^0}\notag\\ &\quad\leq(\|Df|_{E^s(x)}\|+3\varepsilon\varepsilon(x))\|D\sigma_1-D\sigma_2\|_{C^0} +\tfrac{1}{2}(\|Df|_{E^s(x)}\|+25\varepsilon\varepsilon(x))\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D\tilde{\sigma}_{1}-D\tilde{\sigma}_{2}\|_{C^0}\notag\\ &\quad\leq(\|Df|_{E^s(x)}\|+3\varepsilon\varepsilon(x))\|D\sigma_1-D\sigma_2\|_{C^0} +\tfrac{1}{2}(\|Df|_{E^s(x)}\|+25\varepsilon\varepsilon(x))\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}. \end{aligned} \end{align*} $$
For any
![]() $v_y^u\in B_y^u(Q(y))$
, let
$v_y^u\in B_y^u(Q(y))$
, let
![]() $v_{ix}^u=(G^{\sigma _i}_{x,y})^{-1}(v_y^u)$
as part (1), where
$v_{ix}^u=(G^{\sigma _i}_{x,y})^{-1}(v_y^u)$
as part (1), where
![]() $i=1,2$
. We have
$i=1,2$
. We have
 $$ \begin{align*} \begin{aligned} &\|D_{v_y^u}\tilde{\sigma}_{1}-D_{v_y^u}\tilde{\sigma}_{2}\|\notag\\ &\quad=\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1} -D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\\ &\qquad+\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\qquad+\|D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_y^u}\tilde{\sigma}_{1}-D_{v_y^u}\tilde{\sigma}_{2}\|\notag\\ &\quad=\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1} -D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\\ &\qquad+\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\qquad+\|D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|, \end{aligned} \end{align*} $$
so we need to estimate each term above. We divide our proof of part (2) into four steps.
First, note that the last term is easy to estimate because
![]() $\|D(G_{x,y}^{\sigma _2})^{-1}\|<1$
and
$\|D(G_{x,y}^{\sigma _2})^{-1}\|<1$
and
![]() $L_{x,y}^{\sigma _1}(\cdot )=D^{ss}_{x,y}\circ \sigma _1(\cdot )+D^{su}_{x,y}(\cdot )+\phi ^s_{x,y}(\cdot ,\sigma _1(\cdot ))$
,
$L_{x,y}^{\sigma _1}(\cdot )=D^{ss}_{x,y}\circ \sigma _1(\cdot )+D^{su}_{x,y}(\cdot )+\phi ^s_{x,y}(\cdot ,\sigma _1(\cdot ))$
,
 $$ \begin{align*} \begin{aligned} &\|D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq \|D_{v_{2x}^u}L^{\sigma_1}_{x,y} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\|\notag\\ &\quad\leq\|D^{ss}_{x,y}\|\cdot\|D_{v_{2x}^u}\sigma_1-D_{v_{2x}^u}\sigma_2\| +\|D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))-D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_2(\cdot))\|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq \|D_{v_{2x}^u}L^{\sigma_1}_{x,y} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\|\notag\\ &\quad\leq\|D^{ss}_{x,y}\|\cdot\|D_{v_{2x}^u}\sigma_1-D_{v_{2x}^u}\sigma_2\| +\|D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))-D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_2(\cdot))\|. \end{aligned} \end{align*} $$
However, if
![]() $0<\varepsilon \leq 1$
, using Proposition 3.1(2), (3), and property (AM3), we get
$0<\varepsilon \leq 1$
, using Proposition 3.1(2), (3), and property (AM3), we get
 $$ \begin{align*} \begin{aligned} &\|D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))-D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_2(\cdot))\|\notag\\ &\quad=\left\|D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]-D_{(v_{2x}^u,\sigma_2(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_2 \end{array}\right]\right\|\notag \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))-D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_2(\cdot))\|\notag\\ &\quad=\left\|D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]-D_{(v_{2x}^u,\sigma_2(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_2 \end{array}\right]\right\|\notag \end{aligned} \end{align*} $$
 $$ \begin{align*} \begin{aligned} &\quad\leq\left\|D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]-D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_2 \end{array}\right]\right\|\notag\\ &\qquad+\left\|D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_2 \end{array}\right]-D_{(v_{2x}^u,\sigma_2(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_2 \end{array}\right]\right\|\notag\\ &\quad\leq\varepsilon\varepsilon(x)\|D\sigma_1-D\sigma_2\|_{C^0}+4\varepsilon\varepsilon(x)\|\sigma_1-\sigma_2\|^{\delta/2}_{C^0}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\quad\leq\left\|D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]-D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_2 \end{array}\right]\right\|\notag\\ &\qquad+\left\|D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_2 \end{array}\right]-D_{(v_{2x}^u,\sigma_2(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_2 \end{array}\right]\right\|\notag\\ &\quad\leq\varepsilon\varepsilon(x)\|D\sigma_1-D\sigma_2\|_{C^0}+4\varepsilon\varepsilon(x)\|\sigma_1-\sigma_2\|^{\delta/2}_{C^0}. \end{aligned} \end{align*} $$
Consequently, we infer that the last term satisfies
 $$ \begin{align} &\|D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq(\|Df|_{E^s(x)}\|+2\varepsilon\varepsilon(x))\|D\sigma_1-D\sigma_2\|_{C^0}+4\varepsilon\varepsilon(x)\|\sigma_1-\sigma_2\|^{\delta/2}_{C^0}. \end{align} $$
$$ \begin{align} &\|D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_2}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq(\|Df|_{E^s(x)}\|+2\varepsilon\varepsilon(x))\|D\sigma_1-D\sigma_2\|_{C^0}+4\varepsilon\varepsilon(x)\|\sigma_1-\sigma_2\|^{\delta/2}_{C^0}. \end{align} $$
The next thing to do is to estimate the second term:
 $$ \begin{align*} \begin{aligned} &\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}-D_{v_{2x}^u}L^{\sigma_1}_{x,y}\|\notag\\ &\quad\leq\|D^{ss}_{x,y}\|\cdot\|D_{v_{1x}^u}\sigma_1-D_{v_{2x}^u}\sigma_1\| +\|D_{v_{1x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))-D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))\|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}-D_{v_{2x}^u}L^{\sigma_1}_{x,y}\|\notag\\ &\quad\leq\|D^{ss}_{x,y}\|\cdot\|D_{v_{1x}^u}\sigma_1-D_{v_{2x}^u}\sigma_1\| +\|D_{v_{1x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))-D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))\|. \end{aligned} \end{align*} $$
Similarly, if
![]() $0<\varepsilon \leq 1$
, using Proposition 3.1(2), (3), and property (AM3), we have
$0<\varepsilon \leq 1$
, using Proposition 3.1(2), (3), and property (AM3), we have
 $$ \begin{align*} \begin{aligned} &\|D_{v_{1x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))-D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))\|\notag\\ &\quad=\left\|D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]-D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\quad\leq\left\|D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]-D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\qquad+\left\|D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]-D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\quad\leq\frac{\varepsilon\varepsilon(x)}{2}\|v_{1x}^u-v_{2x}^u\|^{\delta/2}+2\varepsilon\varepsilon(x)\|v_{1x}^u-v_{2x}^u\|^{\delta/2}\notag\\ &\quad=\frac{5\varepsilon\varepsilon(x)}{2}\|v_{1x}^u-v_{2x}^u\|^{\delta/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_{1x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))-D_{v_{2x}^u}\phi^s_{x,y}(\cdot,\sigma_1(\cdot))\|\notag\\ &\quad=\left\|D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]-D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\quad\leq\left\|D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]-D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\qquad+\left\|D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]-D_{(v_{2x}^u,\sigma_1(v_{2x}^u))}\phi^s_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{2x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\quad\leq\frac{\varepsilon\varepsilon(x)}{2}\|v_{1x}^u-v_{2x}^u\|^{\delta/2}+2\varepsilon\varepsilon(x)\|v_{1x}^u-v_{2x}^u\|^{\delta/2}\notag\\ &\quad=\frac{5\varepsilon\varepsilon(x)}{2}\|v_{1x}^u-v_{2x}^u\|^{\delta/2}. \end{aligned} \end{align*} $$
Due to
![]() $G_{x,y}^{\sigma _i}(\cdot )=D_{x,y}^{uu}(\cdot )+D_{x,y}^{us}\sigma _i(\cdot )+\phi _{x,y}^u(\cdot ,\sigma _i(\cdot ))$
, we obtain
$G_{x,y}^{\sigma _i}(\cdot )=D_{x,y}^{uu}(\cdot )+D_{x,y}^{us}\sigma _i(\cdot )+\phi _{x,y}^u(\cdot ,\sigma _i(\cdot ))$
, we obtain
 $$ \begin{align} \|v_{1x}^u-v_{2x}^u\|&=\|(G^{\sigma_1}_{x,y})^{-1}(v_y^u)-(G^{\sigma_2}_{x,y})^{-1}(v_y^u)\|\notag\\ &=\|(G^{\sigma_1}_{x,y})^{-1}\circ (G^{\sigma_2}_{x,y}\circ(G^{\sigma_2}_{x,y})^{-1}(v_y^u))-(G^{\sigma_1}_{x,y})^{-1}\circ(G^{\sigma_1}_{x,y}\circ(G^{\sigma_2}_{x,y})^{-1}(v_y^u))\|\notag\\ &\leq\|D(G^{\sigma_1}_{x,y})^{-1}\|_{C^0}\|G^{\sigma_2}_{x,y}(v_{2x}^u)-G^{\sigma_1}_{x,y}(v_{2x}^u)\|\notag\\ &\leq\|D_{x,y}^{us}\|\ \|\sigma_2(v_{2x}^u)-\sigma_1(v_{2x}^u)\|+\operatorname{Lip}(\phi_{x,y})\|\sigma_2(v_{2x}^u)-\sigma_1(v_{2x}^u)\|\notag\\ &\leq2\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}\notag\\ &\leq\|\sigma_2-\sigma_1\|_{C^0}.\end{align} $$
$$ \begin{align} \|v_{1x}^u-v_{2x}^u\|&=\|(G^{\sigma_1}_{x,y})^{-1}(v_y^u)-(G^{\sigma_2}_{x,y})^{-1}(v_y^u)\|\notag\\ &=\|(G^{\sigma_1}_{x,y})^{-1}\circ (G^{\sigma_2}_{x,y}\circ(G^{\sigma_2}_{x,y})^{-1}(v_y^u))-(G^{\sigma_1}_{x,y})^{-1}\circ(G^{\sigma_1}_{x,y}\circ(G^{\sigma_2}_{x,y})^{-1}(v_y^u))\|\notag\\ &\leq\|D(G^{\sigma_1}_{x,y})^{-1}\|_{C^0}\|G^{\sigma_2}_{x,y}(v_{2x}^u)-G^{\sigma_1}_{x,y}(v_{2x}^u)\|\notag\\ &\leq\|D_{x,y}^{us}\|\ \|\sigma_2(v_{2x}^u)-\sigma_1(v_{2x}^u)\|+\operatorname{Lip}(\phi_{x,y})\|\sigma_2(v_{2x}^u)-\sigma_1(v_{2x}^u)\|\notag\\ &\leq2\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}\notag\\ &\leq\|\sigma_2-\sigma_1\|_{C^0}.\end{align} $$
Hence, the second term is estimated as
 $$ \begin{align} &\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\circ D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_1}_{x,y}\circ D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D^{ss}_{x,y}\|\cdot\frac{1}{2}\|v_{1x}^u-v_{2x}^u\|^{\delta/2}+\frac{5\varepsilon\varepsilon(x)}{2}\|v_{1x}^u-v_{2x}^u\|^{\delta/2}\notag\\ &\quad\leq(\tfrac{1}{2}\|Df|_{E^s(x)}\|+3\varepsilon\varepsilon(x))\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}. \end{align} $$
$$ \begin{align} &\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\circ D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1} -D_{v_{2x}^u}L^{\sigma_1}_{x,y}\circ D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D^{ss}_{x,y}\|\cdot\frac{1}{2}\|v_{1x}^u-v_{2x}^u\|^{\delta/2}+\frac{5\varepsilon\varepsilon(x)}{2}\|v_{1x}^u-v_{2x}^u\|^{\delta/2}\notag\\ &\quad\leq(\tfrac{1}{2}\|Df|_{E^s(x)}\|+3\varepsilon\varepsilon(x))\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}. \end{align} $$
Another step in the proof of part (2) is to establish an estimate of the first term. Since
![]() $\|D_{v_{1x}^u}L^{\sigma _1}_{x,y}\|<1$
and
$\|D_{v_{1x}^u}L^{\sigma _1}_{x,y}\|<1$
and
![]() $\|D_{v_y^u}(G^{\sigma _i}_{x,y})^{-1}\|<1$
,
$\|D_{v_y^u}(G^{\sigma _i}_{x,y})^{-1}\|<1$
,
![]() $i=1,2$
, we have
$i=1,2$
, we have
 $$ \begin{align*} \begin{aligned} &\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1} -D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1}-D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad=\|D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1}(D_{v_{2x}^u}G^{\sigma_2}_{x,y}-D_{v_{1x}^u}G^{\sigma_1}_{x,y})D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_{2x}^u}G^{\sigma_2}_{x,y}-D_{v_{1x}^u}G^{\sigma_2}_{x,y}\|+\|D_{v_{1x}^u}G^{\sigma_2}_{x,y}-D_{v_{1x}^u}G^{\sigma_1}_{x,y}\|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1} -D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1}-D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad=\|D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1}(D_{v_{2x}^u}G^{\sigma_2}_{x,y}-D_{v_{1x}^u}G^{\sigma_1}_{x,y})D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_{2x}^u}G^{\sigma_2}_{x,y}-D_{v_{1x}^u}G^{\sigma_2}_{x,y}\|+\|D_{v_{1x}^u}G^{\sigma_2}_{x,y}-D_{v_{1x}^u}G^{\sigma_1}_{x,y}\|. \end{aligned} \end{align*} $$
From the proof in property (AM3) of Proposition 4.2 and equation (4.7) above, we obtain that
At the same time, if
![]() $0<\varepsilon \leq 1$
, using Proposition 3.1(2), (3), and property (AM3), we get
$0<\varepsilon \leq 1$
, using Proposition 3.1(2), (3), and property (AM3), we get
 $$ \begin{align*} \begin{aligned} &\|D_{v_{1x}^u}\phi^u_{x,y}(\cdot,\sigma_2(\cdot))-D_{v_{1x}^u}\phi^u_{x,y}(\cdot,\sigma_1(\cdot))\|\notag\\ &\quad=\left\|D_{(v_{1x}^u,\sigma_2(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_2 \end{array}\right]-D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\quad\leq\left\|D_{(v_{1x}^u,\sigma_2(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_2 \end{array}\right]-D_{(v_{1x}^u,\sigma_2(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\qquad+\left\|D_{(v_{1x}^u,\sigma_2(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]-D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\quad\leq\varepsilon\varepsilon(x)\|D\sigma_2-D\sigma_1\|_{C^0}+2\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D_{v_{1x}^u}\phi^u_{x,y}(\cdot,\sigma_2(\cdot))-D_{v_{1x}^u}\phi^u_{x,y}(\cdot,\sigma_1(\cdot))\|\notag\\ &\quad=\left\|D_{(v_{1x}^u,\sigma_2(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_2 \end{array}\right]-D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\quad\leq\left\|D_{(v_{1x}^u,\sigma_2(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_2 \end{array}\right]-D_{(v_{1x}^u,\sigma_2(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\qquad+\left\|D_{(v_{1x}^u,\sigma_2(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]-D_{(v_{1x}^u,\sigma_1(v_{1x}^u))}\phi^u_{x,y}\left[\begin{array}{@{}c@{}} I \\ D_{v_{1x}^u}\sigma_1 \end{array}\right]\right\|\notag\\ &\quad\leq\varepsilon\varepsilon(x)\|D\sigma_2-D\sigma_1\|_{C^0}+2\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}. \end{aligned} \end{align*} $$
Hence, by using property (AM3) and equation (4.7) again, we get for this term that
 $$ \begin{align} &\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1} -D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_{2x}^u}G^{\sigma_2}_{x,y}-D_{v_{1x}^u}G^{\sigma_2}_{x,y}\|+\|D_{x,y}^{us}D_{v_{1x}^u}\sigma_2-D_{x,y}^{us}D_{v_{1x}^u}\sigma_2\|\notag\\ &\qquad+\|D_{v_{1x}^u}\phi^u_{x,y}(\cdot,\sigma_2(\cdot))-D_{v_{1x}^u}\phi^u_{x,y}(\cdot,\sigma_1(\cdot))\|\notag\\ &\quad\leq5\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|^{\delta/2}+\tfrac{1}{2}\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\qquad+\varepsilon\varepsilon(x)\|D\sigma_2-D\sigma_1\|_{C^0}+2\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\quad=\varepsilon\varepsilon(x)\|D\sigma_2-D\sigma_1\|_{C^0}+\frac{15}{2}\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}. \end{align} $$
$$ \begin{align} &\|D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_1}_{x,y})^{-1} -D_{v_{1x}^u}L^{\sigma_1}_{x,y}\cdot D_{v_y^u}(G^{\sigma_2}_{x,y})^{-1}\|\notag\\ &\quad\leq\|D_{v_{2x}^u}G^{\sigma_2}_{x,y}-D_{v_{1x}^u}G^{\sigma_2}_{x,y}\|+\|D_{x,y}^{us}D_{v_{1x}^u}\sigma_2-D_{x,y}^{us}D_{v_{1x}^u}\sigma_2\|\notag\\ &\qquad+\|D_{v_{1x}^u}\phi^u_{x,y}(\cdot,\sigma_2(\cdot))-D_{v_{1x}^u}\phi^u_{x,y}(\cdot,\sigma_1(\cdot))\|\notag\\ &\quad\leq5\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|^{\delta/2}+\tfrac{1}{2}\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\qquad+\varepsilon\varepsilon(x)\|D\sigma_2-D\sigma_1\|_{C^0}+2\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\quad=\varepsilon\varepsilon(x)\|D\sigma_2-D\sigma_1\|_{C^0}+\frac{15}{2}\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}. \end{align} $$
Finally, plugging all estimates in equations (4.6), (4.8), and (4.9) together, it holds that
 $$ \begin{align*} \begin{aligned} &\|D\tilde{\sigma}_{1}-D\tilde{\sigma}_{2}\|_{C^0}\notag\\ &\quad\leq\varepsilon\varepsilon(x)\|D\sigma_2-D\sigma_1\|_{C^0}+\frac{15}{2}\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\qquad+\big(\tfrac{1}{2}\|Df|_{E^s(x)}\|+3\varepsilon\varepsilon(x)\big)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\qquad+(\|Df|_{E^s(x)}\|+2\varepsilon\varepsilon(x))\|D\sigma_1-D\sigma_2\|_{C^0}+4\varepsilon\varepsilon(x)\|\sigma_1-\sigma_2\|^{\delta/2}_{C^0}\notag\\ &\quad\leq(\|Df|_{E^s(x)}\|+3\varepsilon\varepsilon(x))\|D\sigma_1-D\sigma_2\|_{C^0} +\frac{1}{2}(\|Df|_{E^s(x)}\|+29\varepsilon\varepsilon(x))\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\quad\leq\|Df|_{E^s(x)}\|^{1/2}(\|D\sigma_1-D\sigma_2\|_{C^0}+\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|D\tilde{\sigma}_{1}-D\tilde{\sigma}_{2}\|_{C^0}\notag\\ &\quad\leq\varepsilon\varepsilon(x)\|D\sigma_2-D\sigma_1\|_{C^0}+\frac{15}{2}\varepsilon\varepsilon(x)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\qquad+\big(\tfrac{1}{2}\|Df|_{E^s(x)}\|+3\varepsilon\varepsilon(x)\big)\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\qquad+(\|Df|_{E^s(x)}\|+2\varepsilon\varepsilon(x))\|D\sigma_1-D\sigma_2\|_{C^0}+4\varepsilon\varepsilon(x)\|\sigma_1-\sigma_2\|^{\delta/2}_{C^0}\notag\\ &\quad\leq(\|Df|_{E^s(x)}\|+3\varepsilon\varepsilon(x))\|D\sigma_1-D\sigma_2\|_{C^0} +\frac{1}{2}(\|Df|_{E^s(x)}\|+29\varepsilon\varepsilon(x))\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}\notag\\ &\quad\leq\|Df|_{E^s(x)}\|^{1/2}(\|D\sigma_1-D\sigma_2\|_{C^0}+\|\sigma_2-\sigma_1\|_{C^0}^{\delta/2}) \end{aligned} \end{align*} $$
if
![]() $0<\varepsilon \leq \min \{1,{aC}/{29}\}$
, where a is defined in equation (4.5). With the estimates of part (1), we conclude finally that
$0<\varepsilon \leq \min \{1,{aC}/{29}\}$
, where a is defined in equation (4.5). With the estimates of part (1), we conclude finally that
proving part (2).
5. Shadowing lemma and an infinite-to-one coding for f
Since O is second countable, we would like to replace O by a countable subset
![]() $\mathscr {A}$
which will be used to construct the set of vertices of a directed graph related to the dynamics of f.
$\mathscr {A}$
which will be used to construct the set of vertices of a directed graph related to the dynamics of f.
Proposition 5.1. For all
![]() $\varepsilon>0$
sufficiently small, there exists a countable subset
$\varepsilon>0$
sufficiently small, there exists a countable subset
![]() $\mathscr {A}\subset O$
with the following properties.
$\mathscr {A}\subset O$
with the following properties.
-
(1) Discreteness: for all
 $r>0$
, the set
$r>0$
, the set
 $\{x \in \mathscr {A}: d(x,\partial O)\geq r\}$
is finite.
$\{x \in \mathscr {A}: d(x,\partial O)\geq r\}$
is finite. -
(2) Sufficiency: for every
 $x \in O$
, there is a sequence
$x \in O$
, there is a sequence
 $\{x_n\}_{n\in \mathbb {Z}}$
in
$\{x_n\}_{n\in \mathbb {Z}}$
in
 $\mathscr {A}$
such that for every
$\mathscr {A}$
such that for every
 $n\in \mathbb {Z}$
:
$n\in \mathbb {Z}$
:-
(a)
 $e^{-\beta \varepsilon }\leq ({\varepsilon (f^n(x))}/{\varepsilon (x_n)})\leq e^{\beta \varepsilon }$
and
$e^{-\beta \varepsilon }\leq ({\varepsilon (f^n(x))}/{\varepsilon (x_n)})\leq e^{\beta \varepsilon }$
and
 $e^{-\gamma \varepsilon }\leq ({Q(f^n(x))}/{Q(x_n)})\leq e^{\gamma \varepsilon }$
;
$e^{-\gamma \varepsilon }\leq ({Q(f^n(x))}/{Q(x_n)})\leq e^{\gamma \varepsilon }$
; -
(b)
 $x_n\rightarrow x_{n+1}$
.
$x_n\rightarrow x_{n+1}$
.
-
Proof. Fix a countable subset
![]() $\mathscr {A}$
of O such that
$\mathscr {A}$
of O such that
where
![]() $r(z)=\varepsilon \min \{\delta ^u(\varepsilon \cdot \varepsilon (z)),\delta ^s(\varepsilon \cdot \varepsilon (z))\}\cdot Q(z)^2\cdot \min \{Q(f(z)),Q(f^{-1}(z))\}$
.
$r(z)=\varepsilon \min \{\delta ^u(\varepsilon \cdot \varepsilon (z)),\delta ^s(\varepsilon \cdot \varepsilon (z))\}\cdot Q(z)^2\cdot \min \{Q(f(z)),Q(f^{-1}(z))\}$
.
(1) For all
![]() $r>0$
, since
$r>0$
, since
![]() $O(r)=\{x\in O: d(x,\partial O)\geq r\}$
is compact, if necessary, we can remove some elements of
$O(r)=\{x\in O: d(x,\partial O)\geq r\}$
is compact, if necessary, we can remove some elements of
![]() $\mathscr {A}$
in
$\mathscr {A}$
in
![]() $O(r)$
to make the set
$O(r)$
to make the set
![]() $\{x \in \mathscr {A}: d(x,\partial O)\geq r\}$
finite and maintain the above denseness assumption.
$\{x \in \mathscr {A}: d(x,\partial O)\geq r\}$
finite and maintain the above denseness assumption.
(2) As mentioned above, we can fix a countable subset
![]() $\mathscr {A}$
of O such that
$\mathscr {A}$
of O such that
![]() $O=\bigcup _{z\in \mathscr {A}}B(z,r(z))$
and satisfying discreteness. For every
$O=\bigcup _{z\in \mathscr {A}}B(z,r(z))$
and satisfying discreteness. For every
![]() $x\in O$
and any
$x\in O$
and any
![]() $n\in \mathbb {Z}$
, since
$n\in \mathbb {Z}$
, since
![]() $f^n(x)\in O$
, there exist
$f^n(x)\in O$
, there exist
![]() $\{x_n\}_{n\in \mathbb {Z}}\in \mathscr {A}^{\mathbb {Z}}$
such that
$\{x_n\}_{n\in \mathbb {Z}}\in \mathscr {A}^{\mathbb {Z}}$
such that
![]() $d(f^n(x),x_{n})\leq r(x_n)$
for all
$d(f^n(x),x_{n})\leq r(x_n)$
for all
![]() $n\in \mathbb {Z}$
. For
$n\in \mathbb {Z}$
. For
![]() $\varepsilon>0$
sufficiently small, since
$\varepsilon>0$
sufficiently small, since
![]() $r(x_n)\leq ({\varepsilon }/{2}) Q(x_n)\leq ({\varepsilon }/{2}) d(x_n,\partial O)$
, it follows that
$r(x_n)\leq ({\varepsilon }/{2}) Q(x_n)\leq ({\varepsilon }/{2}) d(x_n,\partial O)$
, it follows that
 $$ \begin{align*} \begin{aligned} d(f^n(x),\partial O)&\leq d(f^n(x),x_n)+d(x_n,\partial O) \notag\\ &\leq e^\varepsilon d(x_n,\partial O), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(f^n(x),\partial O)&\leq d(f^n(x),x_n)+d(x_n,\partial O) \notag\\ &\leq e^\varepsilon d(x_n,\partial O), \end{aligned} \end{align*} $$
and hence
Analogously, from
![]() $d(f^n(x),\partial O)\geq d(x_n,\partial O)-d(f^n(x),x_n)\geq e^{-\varepsilon } d(x_n,\partial O)$
, we have
$d(f^n(x),\partial O)\geq d(x_n,\partial O)-d(f^n(x),x_n)\geq e^{-\varepsilon } d(x_n,\partial O)$
, we have
Therefore, we obtain
![]() $e^{-\beta \varepsilon }\leq {\varepsilon (f^n(x))}/{\varepsilon (x_n)}\leq e^{\beta \varepsilon }$
and
$e^{-\beta \varepsilon }\leq {\varepsilon (f^n(x))}/{\varepsilon (x_n)}\leq e^{\beta \varepsilon }$
and
![]() $e^{-\gamma \varepsilon }\leq {Q(f^n(x))}/{Q(x_n)}\leq e^{\gamma \varepsilon }$
if
$e^{-\gamma \varepsilon }\leq {Q(f^n(x))}/{Q(x_n)}\leq e^{\gamma \varepsilon }$
if
![]() $\varepsilon>0$
is small enough. It remains to prove part (b).
$\varepsilon>0$
is small enough. It remains to prove part (b).
First we claim that
where
![]() $A_u:=[({1}/{C^u})((C^f)^{\kappa ^u}-1)+1]^{1/\gamma ^u}>1$
.
$A_u:=[({1}/{C^u})((C^f)^{\kappa ^u}-1)+1]^{1/\gamma ^u}>1$
.
In practice, by using
![]() $e^{-\varepsilon }\leq ({d(f^n(x),\partial O)}/{d(x_n,\partial O)})\leq e^{\varepsilon }$
, equation (5.1) holds in the case
$e^{-\varepsilon }\leq ({d(f^n(x),\partial O)}/{d(x_n,\partial O)})\leq e^{\varepsilon }$
, equation (5.1) holds in the case
![]() $\varepsilon (f^n(x))=\varepsilon r_0^\beta $
since
$\varepsilon (f^n(x))=\varepsilon r_0^\beta $
since
 $$ \begin{align*} \begin{aligned} \varepsilon(x_{n+1})&\leq\varepsilon r_0^\beta\notag\\ &\leq\varepsilon d(f^n(x),\partial O)^\beta\notag\\ &\leq\varepsilon e^{\beta\varepsilon} d(x_n,\partial O)^\beta, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \varepsilon(x_{n+1})&\leq\varepsilon r_0^\beta\notag\\ &\leq\varepsilon d(f^n(x),\partial O)^\beta\notag\\ &\leq\varepsilon e^{\beta\varepsilon} d(x_n,\partial O)^\beta, \end{aligned} \end{align*} $$
which implies that
![]() $\varepsilon (x_{n+1})\leq A_u^\beta e^{2\beta \varepsilon }\varepsilon (x_n)$
when
$\varepsilon (x_{n+1})\leq A_u^\beta e^{2\beta \varepsilon }\varepsilon (x_n)$
when
![]() $0<\varepsilon \leq A_u^\beta $
.
$0<\varepsilon \leq A_u^\beta $
.
However, if
![]() $\varepsilon (f^n(x))=\varepsilon d(f^n(x),\partial O)^\beta $
, from Assumption US(ii) and
$\varepsilon (f^n(x))=\varepsilon d(f^n(x),\partial O)^\beta $
, from Assumption US(ii) and
![]() $e^{-\varepsilon }\leq ({d(f^n(x),\partial O)}/{d(x_n,\partial O)})\leq e^{\varepsilon }$
again, we obtain for all
$e^{-\varepsilon }\leq ({d(f^n(x),\partial O)}/{d(x_n,\partial O)})\leq e^{\varepsilon }$
again, we obtain for all
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
 $$ \begin{align*} \begin{aligned} d(x_{n+1},\partial O)&\leq e^{\varepsilon} d(f^{n+1}(x),\partial O)\notag\\ &\leq A_ue^\varepsilon d(f^n(x),\partial O)\notag\\ &\leq A_ue^{2\varepsilon} d(x_n,\partial O). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(x_{n+1},\partial O)&\leq e^{\varepsilon} d(f^{n+1}(x),\partial O)\notag\\ &\leq A_ue^\varepsilon d(f^n(x),\partial O)\notag\\ &\leq A_ue^{2\varepsilon} d(x_n,\partial O). \end{aligned} \end{align*} $$
Then
![]() $\varepsilon (x_{n+1})\leq A_u^\beta e^{2\beta \varepsilon }\varepsilon (x_n)$
, which completes the proof of the claim.
$\varepsilon (x_{n+1})\leq A_u^\beta e^{2\beta \varepsilon }\varepsilon (x_n)$
, which completes the proof of the claim.
Denote
![]() $A:=({1}/{C})((C^f)^{\kappa }-1)+1>1$
, and according to property (a) and equation (3.5) of Lemma 3.2, we get for all
$A:=({1}/{C})((C^f)^{\kappa }-1)+1>1$
, and according to property (a) and equation (3.5) of Lemma 3.2, we get for all
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
 $$ \begin{align} Q(x_{n+1})&\leq e^{\gamma\varepsilon} Q(f^{n+1}(x))\notag\\ &\leq Ae^{\gamma\varepsilon} Q(f^n(x))\notag\\ &\leq Ae^{2\gamma\varepsilon} Q(x_n), \end{align} $$
$$ \begin{align} Q(x_{n+1})&\leq e^{\gamma\varepsilon} Q(f^{n+1}(x))\notag\\ &\leq Ae^{\gamma\varepsilon} Q(f^n(x))\notag\\ &\leq Ae^{2\gamma\varepsilon} Q(x_n), \end{align} $$
and
 $$ \begin{align} Q(f(x_{n+1}))&\leq A Q(x_{n+1})\notag\\ &\leq A^2e^{2\gamma\varepsilon} Q(x_n)\notag\\ &\leq A^3e^{2\gamma\varepsilon} Q(f(x_n)). \end{align} $$
$$ \begin{align} Q(f(x_{n+1}))&\leq A Q(x_{n+1})\notag\\ &\leq A^2e^{2\gamma\varepsilon} Q(x_n)\notag\\ &\leq A^3e^{2\gamma\varepsilon} Q(f(x_n)). \end{align} $$
Combining equations (5.1), (5.2), and (5.3), we have
 $$ \begin{align*} \begin{aligned} d(f^{n+1}(x),x_{n+1})&\leq r(x_{n+1})\notag\\ &\leq\varepsilon\delta^u(\varepsilon\varepsilon(x_{n+1})) Q(x_{n+1})^2Q(f(x_{n+1}))\notag\\ \end{aligned}\end{align*} $$
$$ \begin{align*} \begin{aligned} d(f^{n+1}(x),x_{n+1})&\leq r(x_{n+1})\notag\\ &\leq\varepsilon\delta^u(\varepsilon\varepsilon(x_{n+1})) Q(x_{n+1})^2Q(f(x_{n+1}))\notag\\ \end{aligned}\end{align*} $$
 $$ \begin{align*} \begin{aligned} &\leq\varepsilon\delta^u(\varepsilon A_u^\beta e^{2\beta\varepsilon}\varepsilon(x_n))\cdot A^2e^{4\gamma\varepsilon}Q(x_n)^2\cdot A^3e^{2\gamma\varepsilon}Q(f(x_n))\notag\\ &=A^5 \cdot \varepsilon e^{6\gamma\varepsilon}\delta^u(A_u^\beta\cdot \varepsilon e^{2\beta\varepsilon}\varepsilon(x_n)) Q(x_n)^2Q(f(x_n)). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\leq\varepsilon\delta^u(\varepsilon A_u^\beta e^{2\beta\varepsilon}\varepsilon(x_n))\cdot A^2e^{4\gamma\varepsilon}Q(x_n)^2\cdot A^3e^{2\gamma\varepsilon}Q(f(x_n))\notag\\ &=A^5 \cdot \varepsilon e^{6\gamma\varepsilon}\delta^u(A_u^\beta\cdot \varepsilon e^{2\beta\varepsilon}\varepsilon(x_n)) Q(x_n)^2Q(f(x_n)). \end{aligned} \end{align*} $$
Now we can verify the half of
![]() $x_n\rightarrow x_{n+1}$
for all
$x_n\rightarrow x_{n+1}$
for all
![]() $n\in \mathbb {Z}$
from the local monotonicity of
$n\in \mathbb {Z}$
from the local monotonicity of
![]() $\delta ^u(\cdot )$
if
$\delta ^u(\cdot )$
if
![]() $\varepsilon>0$
is small enough. In fact,
$\varepsilon>0$
is small enough. In fact,
 $$ \begin{align*} \begin{aligned} d(f(x_n),x_{n+1})&\leq d(f(x_n),f^{n+1}(x))+d(f^{n+1}(x),x_{n+1}) \notag\\ &\leq C^fd(x_n,f^n(x))+d(f^{n+1}(x),x_{n+1})\notag\\ &\leq\varepsilon[C^f\delta^u(\varepsilon\varepsilon(x_n))+A^5\cdot e^{6\gamma\varepsilon}\delta^u(A_u^\beta\cdot \varepsilon e^{2\beta\varepsilon}\varepsilon(x_n))]Q(x_n)^2Q(f(x_n))\notag\\ &\leq\delta^u(\varepsilon(x_n))Q(x_n)^2Q(f(x_n)), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(f(x_n),x_{n+1})&\leq d(f(x_n),f^{n+1}(x))+d(f^{n+1}(x),x_{n+1}) \notag\\ &\leq C^fd(x_n,f^n(x))+d(f^{n+1}(x),x_{n+1})\notag\\ &\leq\varepsilon[C^f\delta^u(\varepsilon\varepsilon(x_n))+A^5\cdot e^{6\gamma\varepsilon}\delta^u(A_u^\beta\cdot \varepsilon e^{2\beta\varepsilon}\varepsilon(x_n))]Q(x_n)^2Q(f(x_n))\notag\\ &\leq\delta^u(\varepsilon(x_n))Q(x_n)^2Q(f(x_n)), \end{aligned} \end{align*} $$
where the last inequality holds if
![]() $0<\varepsilon \leq \min \{1,{1}/{A_u^\beta e^{2\beta }},{1}/({C^f+A^5 e^{6\gamma }})\}$
.
$0<\varepsilon \leq \min \{1,{1}/{A_u^\beta e^{2\beta }},{1}/({C^f+A^5 e^{6\gamma }})\}$
.
Similarly, we can perform as above to conclude that
if
![]() $\varepsilon>0$
is small enough.
$\varepsilon>0$
is small enough.
Therefore,
![]() $x_n\rightarrow x_{n+1}$
for all
$x_n\rightarrow x_{n+1}$
for all
![]() $n\in \mathbb {Z}$
when
$n\in \mathbb {Z}$
when
![]() $\varepsilon>0$
is small enough. The proof is completed.
$\varepsilon>0$
is small enough. The proof is completed.
Let
![]() $\mathscr {G}=(V,E)$
be the directed graph with vertex set
$\mathscr {G}=(V,E)$
be the directed graph with vertex set
![]() $V=\mathscr {A}$
and edge set
$V=\mathscr {A}$
and edge set
![]() $E= \{x\rightarrow y:x,y\in V\}$
, with
$E= \{x\rightarrow y:x,y\in V\}$
, with
![]() $x\rightarrow y$
defined in Definition 4.3 for
$x\rightarrow y$
defined in Definition 4.3 for
![]() $x,y\in V$
. This is a countable directed graph. Every vertex of
$x,y\in V$
. This is a countable directed graph. Every vertex of
![]() $\mathscr {G}$
has finite degree if
$\mathscr {G}$
has finite degree if
![]() $\varepsilon>0$
is small enough. In fact, for every
$\varepsilon>0$
is small enough. In fact, for every
![]() $x\in V$
, if
$x\in V$
, if
![]() $y\in V$
satisfies
$y\in V$
satisfies
![]() $x\rightarrow y$
, we have
$x\rightarrow y$
, we have
 $$ \begin{align*} \begin{aligned} d(y,\partial O)&\geq d(f(x),\partial O)-d(y,f(x)) \notag\\ &\geq d(f(x),\partial O)-\frac{\varepsilon}{2} d(f(x),\partial O)\notag\\ &\geq e^{-\varepsilon} d(f(x),\partial O)\notag\\ &\geq A_ue^{-\varepsilon} d(x,\partial O), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(y,\partial O)&\geq d(f(x),\partial O)-d(y,f(x)) \notag\\ &\geq d(f(x),\partial O)-\frac{\varepsilon}{2} d(f(x),\partial O)\notag\\ &\geq e^{-\varepsilon} d(f(x),\partial O)\notag\\ &\geq A_ue^{-\varepsilon} d(x,\partial O), \end{aligned} \end{align*} $$
and from the discreteness of V (Proposition 5.1(1)), there are only finitely many
![]() $y\in V$
such that
$y\in V$
such that
![]() $x\rightarrow y$
.
$x\rightarrow y$
.
We define
![]() $\Sigma :=\Sigma (\mathscr {G})$
to be the set of
$\Sigma :=\Sigma (\mathscr {G})$
to be the set of
![]() $\mathbb {Z}$
-indexed paths on
$\mathbb {Z}$
-indexed paths on
![]() $\mathscr {G}$
:
$\mathscr {G}$
:
An element of
![]() $\Sigma $
is denoted by
$\Sigma $
is denoted by
![]() $\underline {x}:=\{x_n\}_{n\in \mathbb {Z}}$
. We equip
$\underline {x}:=\{x_n\}_{n\in \mathbb {Z}}$
. We equip
![]() $\Sigma $
with the metric
$\Sigma $
with the metric
![]() $d(\underline {x},\underline {y})=\exp [-\min \{|n|:n\in \mathbb {Z}\ \text {such that}\ x_n\neq y_n\}]$
and the action of the left shift map
$d(\underline {x},\underline {y})=\exp [-\min \{|n|:n\in \mathbb {Z}\ \text {such that}\ x_n\neq y_n\}]$
and the action of the left shift map
![]() $\sigma :\Sigma \rightarrow \Sigma , \sigma :\{x_n\}_{n\in \mathbb {Z}}\mapsto \{x_{n+1}\}_{n\in \mathbb {Z}}$
as before. Therefore, we get a TMS
$\sigma :\Sigma \rightarrow \Sigma , \sigma :\{x_n\}_{n\in \mathbb {Z}}\mapsto \{x_{n+1}\}_{n\in \mathbb {Z}}$
as before. Therefore, we get a TMS
![]() $(\Sigma ,\sigma )$
, it is locally compact since every vertex of
$(\Sigma ,\sigma )$
, it is locally compact since every vertex of
![]() $\mathscr {G}$
has finite degree.
$\mathscr {G}$
has finite degree.
Let
![]() $\Sigma ^{\#}$
denote the recurrent set of
$\Sigma ^{\#}$
denote the recurrent set of
![]() $\Sigma $
, defined by
$\Sigma $
, defined by
 $$ \begin{align*} \Sigma^{\#}:=\{\underline{x}\in\Sigma:\text{there exists } x,y\in V,&\text{there exists } n_k,m_k\uparrow\infty \text{ such that }\ x_{n_k}=x\\ \quad\text{and}\ x_{-m_k}=y \text{ for all } k\in \mathbb{Z}\}. \end{align*} $$
$$ \begin{align*} \Sigma^{\#}:=\{\underline{x}\in\Sigma:\text{there exists } x,y\in V,&\text{there exists } n_k,m_k\uparrow\infty \text{ such that }\ x_{n_k}=x\\ \quad\text{and}\ x_{-m_k}=y \text{ for all } k\in \mathbb{Z}\}. \end{align*} $$
By the Poincaré recurrence theorem, every
![]() $\sigma $
-invariant probability measure gives
$\sigma $
-invariant probability measure gives
![]() $\Sigma ^{\#}$
full measure.
$\Sigma ^{\#}$
full measure.
Definition 5.1. An
![]() $\varepsilon $
-recurrent-pointwise-pseudo-orbit (or
$\varepsilon $
-recurrent-pointwise-pseudo-orbit (or
![]() $\varepsilon $
-rppo for short) in O is a sequence
$\varepsilon $
-rppo for short) in O is a sequence
![]() $\underline {x}=\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
.
$\underline {x}=\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
.
Along an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
, we can construct the local unstable and stable manifolds at
$\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
, we can construct the local unstable and stable manifolds at
![]() $x_0$
since the pointwise dominated splitting holds for the property of recurrence. The ideas are simple. Let
$x_0$
since the pointwise dominated splitting holds for the property of recurrence. The ideas are simple. Let
![]() $\{V^{(n)}\}_{n=0}^\infty $
denote a sequence of t-manifolds at
$\{V^{(n)}\}_{n=0}^\infty $
denote a sequence of t-manifolds at
![]() $x_0$
. We say that
$x_0$
. We say that
![]() $V^{(n)}$
converges to a t-manifold V at
$V^{(n)}$
converges to a t-manifold V at
![]() $x_0$
if
$x_0$
if
where
![]() $\sigma ^{(n)}$
and
$\sigma ^{(n)}$
and
![]() $\sigma $
are the representing functions of
$\sigma $
are the representing functions of
![]() $V^{(n)}$
and V, respectively.
$V^{(n)}$
and V, respectively.
Call a sequence
![]() $\underline {x}^+=\{x_n\}_{n\geq 0}$
a positive
$\underline {x}^+=\{x_n\}_{n\geq 0}$
a positive
![]() $\varepsilon $
-rppo if
$\varepsilon $
-rppo if
![]() $x_n\rightarrow x_{n+1}$
for all
$x_n\rightarrow x_{n+1}$
for all
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\{x_n\}_{n\geq 0}$
has constant subsequence. Similarly, a negative
$\{x_n\}_{n\geq 0}$
has constant subsequence. Similarly, a negative
![]() $\varepsilon $
-rppo is a sequence
$\varepsilon $
-rppo is a sequence
![]() $\underline {x}^-=\{x_{-n}\}_{n\geq 0}$
such that
$\underline {x}^-=\{x_{-n}\}_{n\geq 0}$
such that
![]() $x_{-n}\rightarrow x_{-n+1}$
for all
$x_{-n}\rightarrow x_{-n+1}$
for all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\{x_{-n}\}_{n\geq 0}$
has constant subsequence.
$\{x_{-n}\}_{n\geq 0}$
has constant subsequence.
For any
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $V_{-n}^{u}$
be a u-admissible manifold at
$V_{-n}^{u}$
be a u-admissible manifold at
![]() $x_{-n}$
. The unstable graph transform along
$x_{-n}$
. The unstable graph transform along
![]() $x_{-n} \rightarrow x_{-n+1}$
maps
$x_{-n} \rightarrow x_{-n+1}$
maps
![]() $V_{-n}^{u}$
to a u-admissible manifold at
$V_{-n}^{u}$
to a u-admissible manifold at
![]() $x_{-n+1}$
, which we denote by
$x_{-n+1}$
, which we denote by
![]() $\mathscr {F}_{-n,-n+1}^u[V^u_{-n}]$
. Another application of the unstable graph transform, this time relative to
$\mathscr {F}_{-n,-n+1}^u[V^u_{-n}]$
. Another application of the unstable graph transform, this time relative to
![]() $x_{-n+1} \rightarrow x_{-n+2}$
, maps
$x_{-n+1} \rightarrow x_{-n+2}$
, maps
![]() $\mathscr {F}_{-n,-n+1}^u[V_{-n}]\in \mathscr {V}_{-n+1}^u$
to a u-admissible manifold at
$\mathscr {F}_{-n,-n+1}^u[V_{-n}]\in \mathscr {V}_{-n+1}^u$
to a u-admissible manifold at
![]() $x_{-n+2}$
, which we denote by
$x_{-n+2}$
, which we denote by
![]() $\mathscr {F}_{-n+1,-n+2}^u\circ \mathscr {F}_{-n,-n+1}^u[V^u_{-n}]$
. Continuing this way, we eventually reach a u-admissible manifold at
$\mathscr {F}_{-n+1,-n+2}^u\circ \mathscr {F}_{-n,-n+1}^u[V^u_{-n}]$
. Continuing this way, we eventually reach a u-admissible manifold at
![]() $x_{0}$
which we denote by
$x_{0}$
which we denote by
![]() $\mathscr {F}_{-1,0}^u\circ \cdots \circ \mathscr {F}_{-n+1,-n+2}^u\circ \mathscr {F}_{-n,-n+1}^u[V^u_{-n}]$
. If this limit converges to a u-admissible manifold as
$\mathscr {F}_{-1,0}^u\circ \cdots \circ \mathscr {F}_{-n+1,-n+2}^u\circ \mathscr {F}_{-n,-n+1}^u[V^u_{-n}]$
. If this limit converges to a u-admissible manifold as
![]() $n\rightarrow \infty $
, we call it a local unstable manifold of a negative
$n\rightarrow \infty $
, we call it a local unstable manifold of a negative
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}^-$
. Similarly, any s-admissible manifold
$\underline {x}^-$
. Similarly, any s-admissible manifold
![]() $V^s_{n}$
at
$V^s_{n}$
at
![]() $x_{n}$
is mapped by n applications of a stable graph transform
$x_{n}$
is mapped by n applications of a stable graph transform
![]() $\mathscr {F}^{s}$
to an s-admissible manifold
$\mathscr {F}^{s}$
to an s-admissible manifold
![]() $\mathscr {F}_{0,1}^s\circ \cdots \circ \mathscr {F}_{n-2,n-1}^s\circ \mathscr {F}_{n-1,n}^s[V^s_{n}]$
at
$\mathscr {F}_{0,1}^s\circ \cdots \circ \mathscr {F}_{n-2,n-1}^s\circ \mathscr {F}_{n-1,n}^s[V^s_{n}]$
at
![]() $x_{0}$
. We call it a local stable manifold of a positive
$x_{0}$
. We call it a local stable manifold of a positive
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}^+$
if this limit converges to an s-admissible manifold as
$\underline {x}^+$
if this limit converges to an s-admissible manifold as
![]() $n\rightarrow \infty $
. Set
$n\rightarrow \infty $
. Set
and
Proposition 5.2. The following holds for all
![]() $\varepsilon>0$
small enough. Suppose
$\varepsilon>0$
small enough. Suppose
![]() $\{x_n\}_{n\in \mathbb {Z}}$
is an
$\{x_n\}_{n\in \mathbb {Z}}$
is an
![]() $\varepsilon $
-rppo, and choose arbitrary u-admissible manifolds
$\varepsilon $
-rppo, and choose arbitrary u-admissible manifolds
![]() $V_{-n}^{u}$
at
$V_{-n}^{u}$
at
![]() $x_{-n}$
and arbitrary s-admissible manifolds
$x_{-n}$
and arbitrary s-admissible manifolds
![]() $V_{n}^{s}$
at
$V_{n}^{s}$
at
![]() $x_{n}$
for
$x_{n}$
for
![]() $n\geq 0$
. Then:
$n\geq 0$
. Then:
-
(1)
 $V^{u}(\underline {x}^-)$
is a u-admissible manifold at
$V^{u}(\underline {x}^-)$
is a u-admissible manifold at
 $x_0$
, and
$x_0$
, and
 $V^{s}(\underline {x}^+)$
is an s-admissible manifold at
$V^{s}(\underline {x}^+)$
is an s-admissible manifold at
 $x_0$
;
$x_0$
; -
(2)
 $f^{-1}[V^{u}(\{x_{-n}\}_{n\geq 0})] \subset V^{u}(\{x_{-n-1}\}_{n\geq 0})$
and
$f^{-1}[V^{u}(\{x_{-n}\}_{n\geq 0})] \subset V^{u}(\{x_{-n-1}\}_{n\geq 0})$
and
 $f[V^{s}(\{x_{n}\}_{n\geq 0})] \subset V^{s}(\{x_{n+1}\}_{n\geq 0})$
;
$f[V^{s}(\{x_{n}\}_{n\geq 0})] \subset V^{s}(\{x_{n+1}\}_{n\geq 0})$
; -
(3) if
 $y,z\in V^{u}(\underline {x}^-)$
, then for all
$y,z\in V^{u}(\underline {x}^-)$
, then for all
 $k\geq 0$
, Similarly, if
$k\geq 0$
, Similarly, if $$ \begin{align*} d(f^{-k}(y),f^{-k}(z))\leq8Q(x_0)\prod_{i=0}^{k-1}\|Df^{-1}|_{E^u(x_{-i})}\|^{1/2}. \end{align*} $$
$$ \begin{align*} d(f^{-k}(y),f^{-k}(z))\leq8Q(x_0)\prod_{i=0}^{k-1}\|Df^{-1}|_{E^u(x_{-i})}\|^{1/2}. \end{align*} $$
 $y,z\in V^{s}(\underline {x}^+)$
, for all
$y,z\in V^{s}(\underline {x}^+)$
, for all
 $k\geq 0$
, we have
$k\geq 0$
, we have  $$ \begin{align*} d(f^{k}(y),f^{k}(z))\leq8Q(x_0)\prod_{i=0}^{k-1}\|Df|_{E^s(x_i)}\|^{1/2}; \end{align*} $$
$$ \begin{align*} d(f^{k}(y),f^{k}(z))\leq8Q(x_0)\prod_{i=0}^{k-1}\|Df|_{E^s(x_i)}\|^{1/2}; \end{align*} $$
-
(4) we have the following respective shadowing property along the negative and positive direction:
 $$ \begin{align*} \begin{aligned} &V^{u}(\underline{x}^-)=\{x\in\exp_{x_0}(S_{x_0}) \text{ for all } k\geq0, f^{-k}(x)\in\exp_{x_{-k}}(S_{x_{-k}})\},\\ &V^{s}(\underline{x}^+)=\{x\in\exp_{x_0}(S_{x_0}) \text{ for all } k\geq0, f^{k}(x)\in\exp_{x_{k}}(S_{x_{k}})\};\\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &V^{u}(\underline{x}^-)=\{x\in\exp_{x_0}(S_{x_0}) \text{ for all } k\geq0, f^{-k}(x)\in\exp_{x_{-k}}(S_{x_{-k}})\},\\ &V^{s}(\underline{x}^+)=\{x\in\exp_{x_0}(S_{x_0}) \text{ for all } k\geq0, f^{k}(x)\in\exp_{x_{k}}(S_{x_{k}})\};\\ \end{aligned} \end{align*} $$
-
(5) if
 $\{x_n\}_{n \in \mathbb {Z}}, \{y_n\}_{n \in \mathbb {Z}}\in \Sigma ^{\#}$
satisfy
$\{x_n\}_{n \in \mathbb {Z}}, \{y_n\}_{n \in \mathbb {Z}}\in \Sigma ^{\#}$
satisfy
 $x_i=y_i$
for
$x_i=y_i$
for
 $i=-N,\ldots , N$
, then
$i=-N,\ldots , N$
, then  $$ \begin{align*} d_{C^1}(V^{u}(\underline{x}^-), V^{u}(\underline{y}^-)) &\leq 2(N+1) \prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|^{\delta/4},\\[3pt] d_{C^1}(V^{s}(\underline{x}^+), V^{s}(\underline{y}^+)) &\leq 2(N+1) \prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|^{\delta/4}. \end{align*} $$
$$ \begin{align*} d_{C^1}(V^{u}(\underline{x}^-), V^{u}(\underline{y}^-)) &\leq 2(N+1) \prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|^{\delta/4},\\[3pt] d_{C^1}(V^{s}(\underline{x}^+), V^{s}(\underline{y}^+)) &\leq 2(N+1) \prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|^{\delta/4}. \end{align*} $$
Remark 5.1. Unlike in [Reference Sarig22, Proposition 4.15], since the recurrence might be very slow, the convergence of
![]() $\prod _{i=1}^{N}\|Df|_{E^s(x_{-i})}\|$
or
$\prod _{i=1}^{N}\|Df|_{E^s(x_{-i})}\|$
or
![]() $\prod _{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|$
to zero might be very slow and hence the continuity of maps
$\prod _{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|$
to zero might be very slow and hence the continuity of maps
![]() $\{x_n\}_{n \in \mathbb {Z}} \mapsto V^{u}(\underline {x}^-),V^{s}(\underline {x}^+)$
are not guaranteed by Assumptions US and R.
$\{x_n\}_{n \in \mathbb {Z}} \mapsto V^{u}(\underline {x}^-),V^{s}(\underline {x}^+)$
are not guaranteed by Assumptions US and R.
Proof. The proof is quite similar to the proof of [Reference Sarig22, Proposition 4.15]. We treat the case of u-admissible manifolds and s-admissible manifolds in the proof of items (1,2,4,5) and (3), respectively. By suitable modification to the proof, all the other cases are similar in its opposite direction.
(1) We divide our proof into three steps. First, we verify that if the limit exists, then it is independent of the choice of
![]() $V_{-n}^{u}$
. Since
$V_{-n}^{u}$
. Since
![]() $\mathscr {F}_{-1,0}^{u} \circ \cdots \circ \mathscr {F}_{-n, -n+1}^{u}[V^u_{-n}]$
is a u-admissible manifold at
$\mathscr {F}_{-1,0}^{u} \circ \cdots \circ \mathscr {F}_{-n, -n+1}^{u}[V^u_{-n}]$
is a u-admissible manifold at
![]() $x_{0}$
, by using Proposition 4.3, for any other choice of u-admissible manifolds
$x_{0}$
, by using Proposition 4.3, for any other choice of u-admissible manifolds
![]() $W_{-n}^{u}$
at
$W_{-n}^{u}$
at
![]() $ x_{-n}$
, we have
$ x_{-n}$
, we have
 $$ \begin{align*} \begin{aligned} &d_{C^{0}}(\mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u}[V^u_{-n}], \mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u}[W^u_{-n}])\notag\\ &\quad\leq\prod_{i=1}^n \|Df|_{E^s(x_{-i})}\|^{1/2}d_{C^{0}}(V^u_{-n},W^u_{-n})\notag\\ &\quad\leq\prod_{i=1}^n \|Df|_{E^s(x_{-i})}\|^{1/2}\underset{n \rightarrow \infty}{\longrightarrow}0, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &d_{C^{0}}(\mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u}[V^u_{-n}], \mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u}[W^u_{-n}])\notag\\ &\quad\leq\prod_{i=1}^n \|Df|_{E^s(x_{-i})}\|^{1/2}d_{C^{0}}(V^u_{-n},W^u_{-n})\notag\\ &\quad\leq\prod_{i=1}^n \|Df|_{E^s(x_{-i})}\|^{1/2}\underset{n \rightarrow \infty}{\longrightarrow}0, \end{aligned} \end{align*} $$
since
![]() $d_{C^{0}}(V^u_{-n},W^u_{-n})\leq 2Q(x_{-n})<1$
if
$d_{C^{0}}(V^u_{-n},W^u_{-n})\leq 2Q(x_{-n})<1$
if
![]() $\varepsilon>0$
is small enough and
$\varepsilon>0$
is small enough and
![]() $\{x_{-n}\}_{n\geq 0}$
have constant subsequence. Thus, if the limit exists, then it is independent of
$\{x_{-n}\}_{n\geq 0}$
have constant subsequence. Thus, if the limit exists, then it is independent of
![]() $V_{-n}^{u}$
.
$V_{-n}^{u}$
.
The next thing to do is to prove that the limit exists. For every
![]() $m>n $
, we have
$m>n $
, we have
 $$ \begin{align*} \begin{aligned} &d_{C^{0}}(\mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u}[V^u_{-n}], \mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-m, -m+1}^{u}[V^u_{-m}])\notag\\ &\quad\leq\prod_{i=1}^n \|Df|_{E^s(x_{-i})}\|^{1/2}d_{C^{0}}(V^u_{-n},\mathscr{F}_{-n-1,-n}^{u} \circ \cdots \circ \mathscr{F}_{-m, -m+1}^{u}[V^u_{-m}])\notag\\ &\quad\leq\prod_{i=1}^n \|Df|_{E^s(x_{-i})}\|^{1/2}\underset{n \rightarrow \infty}{\longrightarrow}0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &d_{C^{0}}(\mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u}[V^u_{-n}], \mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-m, -m+1}^{u}[V^u_{-m}])\notag\\ &\quad\leq\prod_{i=1}^n \|Df|_{E^s(x_{-i})}\|^{1/2}d_{C^{0}}(V^u_{-n},\mathscr{F}_{-n-1,-n}^{u} \circ \cdots \circ \mathscr{F}_{-m, -m+1}^{u}[V^u_{-m}])\notag\\ &\quad\leq\prod_{i=1}^n \|Df|_{E^s(x_{-i})}\|^{1/2}\underset{n \rightarrow \infty}{\longrightarrow}0. \end{aligned} \end{align*} $$
Hence,
![]() $\{\mathscr {F}_{-1,0}^{u} \circ \cdots \circ \mathscr {F}_{-n, -n+1}^{u}[V^u_{-n}]\}_{n\geq 1}$
is a Cauchy sequence and therefore converges.
$\{\mathscr {F}_{-1,0}^{u} \circ \cdots \circ \mathscr {F}_{-n, -n+1}^{u}[V^u_{-n}]\}_{n\geq 1}$
is a Cauchy sequence and therefore converges.
Finally, we have to show the admissibility of the limit. Since
![]() $\mathscr {F}_{-1,0}^{u} \circ \cdots \circ \mathscr {F}_{-n, -n+1}^{u}[V^u_{-n}] \underset {n \rightarrow \infty }{\longrightarrow } V^{u}[\{x_{-n}\}_{n\geq 0}]$
, we have
$\mathscr {F}_{-1,0}^{u} \circ \cdots \circ \mathscr {F}_{-n, -n+1}^{u}[V^u_{-n}] \underset {n \rightarrow \infty }{\longrightarrow } V^{u}[\{x_{-n}\}_{n\geq 0}]$
, we have
![]() $\sigma ^{(n)} \underset {n \rightarrow \infty }{\longrightarrow } \sigma $
uniformly on
$\sigma ^{(n)} \underset {n \rightarrow \infty }{\longrightarrow } \sigma $
uniformly on
![]() $B_{x_0}^u(Q(x_0))$
, where
$B_{x_0}^u(Q(x_0))$
, where
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma ^{(n)}$
represent
$\sigma ^{(n)}$
represent
![]() $V^{u}[\{x_{-n}\}_{n\geq 0}]$
and
$V^{u}[\{x_{-n}\}_{n\geq 0}]$
and
![]() $\mathscr {F}_{-1,0}^{u} \circ \cdots \circ \mathscr {F}_{-n, -n+1}^{u}[V^u_{-n}]$
, respectively.
$\mathscr {F}_{-1,0}^{u} \circ \cdots \circ \mathscr {F}_{-n, -n+1}^{u}[V^u_{-n}]$
, respectively.
Due to property (AM3), that is,
![]() $\operatorname {Hol}_{\delta /2}(D\sigma ^{(n)})\leq \tfrac 12$
and
$\operatorname {Hol}_{\delta /2}(D\sigma ^{(n)})\leq \tfrac 12$
and
![]() $\|D\sigma ^{(n)}\|_{C^0}\leq \tfrac 12$
, by the Arzelà–Ascoli theorem,
$\|D\sigma ^{(n)}\|_{C^0}\leq \tfrac 12$
, by the Arzelà–Ascoli theorem,
![]() $\text {there exists } n_{k} \uparrow \infty $
such that
$\text {there exists } n_{k} \uparrow \infty $
such that
![]() $D\sigma ^{(n_k)}\underset {k \rightarrow \infty }{\longrightarrow } \omega $
uniformly where
$D\sigma ^{(n_k)}\underset {k \rightarrow \infty }{\longrightarrow } \omega $
uniformly where
![]() $\|\omega \|_{C^{\delta /2}} \leq \tfrac 12$
. Thus, for any
$\|\omega \|_{C^{\delta /2}} \leq \tfrac 12$
. Thus, for any
![]() $v\in B_{x_0}^u(Q(x_0))$
,
$v\in B_{x_0}^u(Q(x_0))$
,
 $$ \begin{align*}\sigma^{(n_k)}(v)=\sigma^{(n_k)}(0)+\int_0^1 D_{\unicode{x3bb} v}\sigma^{(n_k)}\cdot vd\unicode{x3bb}\underset{k \rightarrow \infty}{\longrightarrow} \sigma(0)+\int_0^1 \omega(\unicode{x3bb} v)\cdot vd\unicode{x3bb}\end{align*} $$
$$ \begin{align*}\sigma^{(n_k)}(v)=\sigma^{(n_k)}(0)+\int_0^1 D_{\unicode{x3bb} v}\sigma^{(n_k)}\cdot vd\unicode{x3bb}\underset{k \rightarrow \infty}{\longrightarrow} \sigma(0)+\int_0^1 \omega(\unicode{x3bb} v)\cdot vd\unicode{x3bb}\end{align*} $$
and hence
![]() $\sigma $
is differentiable, and
$\sigma $
is differentiable, and
![]() $D\sigma =\omega $
. We also see that
$D\sigma =\omega $
. We also see that
![]() $\{D\sigma ^{(n)}\}$
can only have one limit point. Consequently,
$\{D\sigma ^{(n)}\}$
can only have one limit point. Consequently,
![]() $D\sigma ^{(n)}\underset {n \rightarrow \infty }{\longrightarrow } D\sigma $
uniformly. It follows that
$D\sigma ^{(n)}\underset {n \rightarrow \infty }{\longrightarrow } D\sigma $
uniformly. It follows that
![]() $\|\sigma (0)\| \leq 10^{-3}Q(x_0)$
,
$\|\sigma (0)\| \leq 10^{-3}Q(x_0)$
,
![]() $\|D\sigma \|_{C^0} \leq \sqrt {\varepsilon }$
, and
$\|D\sigma \|_{C^0} \leq \sqrt {\varepsilon }$
, and
![]() $\|D\sigma \|_{C^{\delta /2}}\leq \tfrac 12$
; hence the u-admissibility of
$\|D\sigma \|_{C^{\delta /2}}\leq \tfrac 12$
; hence the u-admissibility of
![]() $V^{u}(\underline {x}^-)$
.
$V^{u}(\underline {x}^-)$
.
(2) By the continuity of
![]() $\mathscr {F}_{-1,0}^{u}$
and the definition of
$\mathscr {F}_{-1,0}^{u}$
and the definition of
![]() $\mathscr {F}_{-1,0}^{u}$
, we have
$\mathscr {F}_{-1,0}^{u}$
, we have
 $$ \begin{align*} \begin{aligned} V^{u}(\{x_{-n}\}_{n\geq0})&=\lim _{n \rightarrow\infty}(\mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u})[V^u_{-n}]\notag\\ &=\mathscr{F}_{-1,0}^{u}\Big[\lim _{n \rightarrow\infty}(\mathscr{F}_{-2,-1}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u})[V^u_{-n}]\Big]\notag\\ &=\mathscr{F}_{-1,0}^{u}[ V^{u}(\{x_{-n-1}\}_{n\geq0})]\notag\\ &\subset f[ V^{u}(\{x_{-n-1}\}_{n\geq0})]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} V^{u}(\{x_{-n}\}_{n\geq0})&=\lim _{n \rightarrow\infty}(\mathscr{F}_{-1,0}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u})[V^u_{-n}]\notag\\ &=\mathscr{F}_{-1,0}^{u}\Big[\lim _{n \rightarrow\infty}(\mathscr{F}_{-2,-1}^{u} \circ \cdots \circ \mathscr{F}_{-n, -n+1}^{u})[V^u_{-n}]\Big]\notag\\ &=\mathscr{F}_{-1,0}^{u}[ V^{u}(\{x_{-n-1}\}_{n\geq0})]\notag\\ &\subset f[ V^{u}(\{x_{-n-1}\}_{n\geq0})]. \end{aligned} \end{align*} $$
(3) We write
and
Admissibility implies that
![]() $\|\sigma ^s_k(0)\| \leq 10^{-3} Q(x_k)$
and
$\|\sigma ^s_k(0)\| \leq 10^{-3} Q(x_k)$
and
![]() $Lip(\sigma ^s_k)\leq \sqrt {\varepsilon }$
for all
$Lip(\sigma ^s_k)\leq \sqrt {\varepsilon }$
for all
![]() $k\geq 0$
.
$k\geq 0$
.
By part (2),
![]() $f^{k}[V^s(\{x_{n}\}_{n\geq 0})]\subset V^{s}(\{x_{n+k}\}_{n\geq 0}) \subset \exp _{x_k}(S_{x_k})$
for all
$f^{k}[V^s(\{x_{n}\}_{n\geq 0})]\subset V^{s}(\{x_{n+k}\}_{n\geq 0}) \subset \exp _{x_k}(S_{x_k})$
for all
![]() $k \geq 0$
. Therefore, for any
$k \geq 0$
. Therefore, for any
![]() $y, z \in V^s(\{x_{n}\}_{n\geq 0})$
, one can write
$y, z \in V^s(\{x_{n}\}_{n\geq 0})$
, one can write
![]() $f^{k}(y)=\exp _{x_{k}}(\sigma ^s_k(v^s_k), v^s_k)$
and
$f^{k}(y)=\exp _{x_{k}}(\sigma ^s_k(v^s_k), v^s_k)$
and
![]() $f^{k}(z)=\exp _{x_k}(\sigma ^s_k(w^s_k), w^s_k)$
.
$f^{k}(z)=\exp _{x_k}(\sigma ^s_k(w^s_k), w^s_k)$
.
For all
![]() $k \geq 0$
, since the exponential map has Lipschitz constant less than two, we get
$k \geq 0$
, since the exponential map has Lipschitz constant less than two, we get
 $$ \begin{align*} \begin{aligned} d(f^{k}(y),f^{k}(z))&\leq2(\|v^s_{k}-w^s_{k}\|+\mathrm{Lip}(\sigma^s_{k})\|v^s_{k}-w^s_{k}\|)\notag\\ &\leq4\|v^s_{k}-w^s_{k}\| \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(f^{k}(y),f^{k}(z))&\leq2(\|v^s_{k}-w^s_{k}\|+\mathrm{Lip}(\sigma^s_{k})\|v^s_{k}-w^s_{k}\|)\notag\\ &\leq4\|v^s_{k}-w^s_{k}\| \end{aligned} \end{align*} $$
if
![]() $0<\varepsilon \leq 1$
.
$0<\varepsilon \leq 1$
.
Notice that
 $$ \begin{align*} (\sigma^s_{k}(v^s_{k}), v^s_{k})&=F_{x_{k-1},x_{k}}(\sigma^s_{k-1}(v^s_{k-1}), v^s_{k-1})\quad \text{and}\quad (\sigma^s_{k}(w^s_{k}), w^s_{k})\\&=F_{x_{k-1},x_{k}}(\sigma^s_{k-1}(w^s_{k-1}), w^s_{k-1}), \end{align*} $$
$$ \begin{align*} (\sigma^s_{k}(v^s_{k}), v^s_{k})&=F_{x_{k-1},x_{k}}(\sigma^s_{k-1}(v^s_{k-1}), v^s_{k-1})\quad \text{and}\quad (\sigma^s_{k}(w^s_{k}), w^s_{k})\\&=F_{x_{k-1},x_{k}}(\sigma^s_{k-1}(w^s_{k-1}), w^s_{k-1}), \end{align*} $$
or in the s-direction,
and
So we have
 $$ \begin{align*} \begin{aligned} \tfrac{1}{4}d(f^{k}(y),f^{k}(z))&\leq\|v^s_{k}-w^s_{k}\|\notag\\ &\leq(\|D^{ss}_{x_{k-1},x_{k}}\|+\|D^{su}_{x_{k-1},x_{k}}\|+2\operatorname{Lip}(\phi^s_{x_{k-1},x_{k}}) )\|v^s_{k-1}-w^s_{k-1}\|\notag\\ &\leq\|Df|_{E^s(x_{k-1})}\|^{1/2}\|v^s_{k-1}-w^s_{k-1}\| \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \tfrac{1}{4}d(f^{k}(y),f^{k}(z))&\leq\|v^s_{k}-w^s_{k}\|\notag\\ &\leq(\|D^{ss}_{x_{k-1},x_{k}}\|+\|D^{su}_{x_{k-1},x_{k}}\|+2\operatorname{Lip}(\phi^s_{x_{k-1},x_{k}}) )\|v^s_{k-1}-w^s_{k-1}\|\notag\\ &\leq\|Df|_{E^s(x_{k-1})}\|^{1/2}\|v^s_{k-1}-w^s_{k-1}\| \end{aligned} \end{align*} $$
as at the end of the proof of Proposition 4.3(1). Thus,
 $$ \begin{align*} \begin{aligned} d(f^{k}(y),f^{k}(z))&\leq4\prod_{i=0}^{k-1}\|Df|_{E^s(x_i)}\|^{1/2}\|v^s_0-w^s_0\|\notag\\ &\leq8Q(x_0)\prod_{i=0}^{k-1}\|Df|_{E^s(x_i)}\|^{1/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(f^{k}(y),f^{k}(z))&\leq4\prod_{i=0}^{k-1}\|Df|_{E^s(x_i)}\|^{1/2}\|v^s_0-w^s_0\|\notag\\ &\leq8Q(x_0)\prod_{i=0}^{k-1}\|Df|_{E^s(x_i)}\|^{1/2}. \end{aligned} \end{align*} $$
(4) The inclusion
![]() $\subseteq $
is trivial. In fact, notice that
$\subseteq $
is trivial. In fact, notice that
![]() $V^{u}(\underline {x}^-)$
is a u-admissible manifold at
$V^{u}(\underline {x}^-)$
is a u-admissible manifold at
![]() $x_0$
, it is contained in
$x_0$
, it is contained in
![]() $\exp _{x_0}(S_{x_0})$
, that is, for every
$\exp _{x_0}(S_{x_0})$
, that is, for every
![]() $x\in V^{u}(\underline {x}^-)$
,
$x\in V^{u}(\underline {x}^-)$
,
![]() $x\in \exp _{x_0}(S_{x_0})$
. By part (2), for every
$x\in \exp _{x_0}(S_{x_0})$
. By part (2), for every
![]() $k \geq 0$
,
$k \geq 0$
,
because
![]() $V^{u}(\{x_{-n-k}\}_{n \geq 0})$
is a u-admissible manifold at
$V^{u}(\{x_{-n-k}\}_{n \geq 0})$
is a u-admissible manifold at
![]() $x_{-k}$
. We have
$x_{-k}$
. We have
![]() $\subseteq $
.
$\subseteq $
.
Now we prove
![]() $\supseteq $
. An outline of the proof of this inclusion is as follows. For every point x satisfying
$\supseteq $
. An outline of the proof of this inclusion is as follows. For every point x satisfying
![]() $f^{-k}(x)\in \exp _{x_{-k}}(S_{x_{-k}})$
for all
$f^{-k}(x)\in \exp _{x_{-k}}(S_{x_{-k}})$
for all
![]() $k \geq 0$
, write
$k \geq 0$
, write
![]() $x=\exp _{x_{0}}(v^u_{0}, v^s_{0})$
. We show that
$x=\exp _{x_{0}}(v^u_{0}, v^s_{0})$
. We show that
![]() $x \in V^{u}(\{x_{-n}\}_{n\geq 0})$
by proving that
$x \in V^{u}(\{x_{-n}\}_{n\geq 0})$
by proving that
![]() $v^s_{0}=\sigma ^u(v^u_{0})$
, where
$v^s_{0}=\sigma ^u(v^u_{0})$
, where
![]() $\sigma ^u$
is the function which represents
$\sigma ^u$
is the function which represents
![]() $V^{u}(\{x_{-n}\}_{n\geq 0})$
.
$V^{u}(\{x_{-n}\}_{n\geq 0})$
.
Introduce for this purpose the point
![]() $\bar {x}=\exp _{x_{0}}(\bar {v}^u_{0}, \bar {v}^s_{0})\in V^{u}(\{x_{-n}\}_{n\geq 0})$
, where
$\bar {x}=\exp _{x_{0}}(\bar {v}^u_{0}, \bar {v}^s_{0})\in V^{u}(\{x_{-n}\}_{n\geq 0})$
, where
![]() $\bar {v}^u_{0}=v^u_{0}$
and
$\bar {v}^u_{0}=v^u_{0}$
and
![]() $\bar {v}^s_{0}=\sigma ^u(\bar {v}^u_{0})$
. Our task now is to prove
$\bar {v}^s_{0}=\sigma ^u(\bar {v}^u_{0})$
. Our task now is to prove
![]() $\bar {v}^s_{0}=v^s_{0}$
.
$\bar {v}^s_{0}=v^s_{0}$
.
For every
![]() $k \geq 0$
, write
$k \geq 0$
, write
where
![]() $\|v^u_{-k}\|,\|v^s_{-k}\|,\|\bar {v}^u_{-k}\|,\|\bar {v}^u_{-k}\| \leq Q(x_{-k})$
for all
$\|v^u_{-k}\|,\|v^s_{-k}\|,\|\bar {v}^u_{-k}\|,\|\bar {v}^u_{-k}\| \leq Q(x_{-k})$
for all
![]() $k \geq 0$
.
$k \geq 0$
.
By Proposition 3.1 in its version for
![]() $f^{-1}$
, for every
$f^{-1}$
, for every
![]() $k \geq 0, F_{x_{-k-1}x_{-k}}^{-1}=\exp _{x_{-k-1}}^{-1} \circ f^{-1} \circ \exp _{x_{-k}}$
can be put in the form
$k \geq 0, F_{x_{-k-1}x_{-k}}^{-1}=\exp _{x_{-k-1}}^{-1} \circ f^{-1} \circ \exp _{x_{-k}}$
can be put in the form
 $$ \begin{align*} \begin{aligned} &F^{-1}_{x_{-k-1},x_{-k}}(v_{-k}^u,v_{-k}^s)\notag\\ &\quad=(\bar{D}^{uu}_{x_{-k},x_{-k-1}}(v_{-k}^u)+\bar{D}^{us}_{x_{-k},x_{-k-1}}(v_{-k}^s) +\bar{\phi}^u_{x_{-k},x_{-k-1}}(v_{-k}^u,v_{-k}^s), \bar{D}^{ss}_{x_{-k},x_{-k-1}}(v_{-k}^s)\\&\qquad+\bar{D}^{su}_{x_{-k},x_{-k-1}}(v_{-k}^u)+\bar{\phi}^s_{x_{-k},x_{-k-1}}(v_{-k}^u,v_{-k}^s)) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &F^{-1}_{x_{-k-1},x_{-k}}(v_{-k}^u,v_{-k}^s)\notag\\ &\quad=(\bar{D}^{uu}_{x_{-k},x_{-k-1}}(v_{-k}^u)+\bar{D}^{us}_{x_{-k},x_{-k-1}}(v_{-k}^s) +\bar{\phi}^u_{x_{-k},x_{-k-1}}(v_{-k}^u,v_{-k}^s), \bar{D}^{ss}_{x_{-k},x_{-k-1}}(v_{-k}^s)\\&\qquad+\bar{D}^{su}_{x_{-k},x_{-k-1}}(v_{-k}^u)+\bar{\phi}^s_{x_{-k},x_{-k-1}}(v_{-k}^u,v_{-k}^s)) \end{aligned} \end{align*} $$
under the basis
![]() $(E^u,E^s)$
for all
$(E^u,E^s)$
for all
![]() $v_{-k}=(v_{-k}^u,v_{-k}^s)\in S_{x_{-k}}$
, where
$v_{-k}=(v_{-k}^u,v_{-k}^s)\in S_{x_{-k}}$
, where
 $$ \begin{align*}\bar{D}^{\tau t}_{x_{-k},x_{-k-1}}&=P_{x_{-k-1}}^{\tau}\circ D_{f^{-1}(x_{-k})}\exp^{-1}_{x_{-k-1}}\circ D_{x_{-k}}f^{-1}|_{E^t(x_{-k})}:B_{x_{-k}}^t(Q(x_{-k}))\\&\quad\rightarrow E^\tau(x_{-k-1}), \tau,t=u,s.\end{align*} $$
$$ \begin{align*}\bar{D}^{\tau t}_{x_{-k},x_{-k-1}}&=P_{x_{-k-1}}^{\tau}\circ D_{f^{-1}(x_{-k})}\exp^{-1}_{x_{-k-1}}\circ D_{x_{-k}}f^{-1}|_{E^t(x_{-k})}:B_{x_{-k}}^t(Q(x_{-k}))\\&\quad\rightarrow E^\tau(x_{-k-1}), \tau,t=u,s.\end{align*} $$
Since
![]() $d(f^{-1}(x_{-k}), x_{-k-1})<\delta ^s(\varepsilon (x_{-k}))$
, in the s-direction, we have
$d(f^{-1}(x_{-k}), x_{-k-1})<\delta ^s(\varepsilon (x_{-k}))$
, in the s-direction, we have
While in the u-direction, we have
and moreover,
where
![]() $\bar {\phi }=(\bar {\phi }^u,\bar {\phi }^s)$
.
$\bar {\phi }=(\bar {\phi }^u,\bar {\phi }^s)$
.
Let
![]() $\Delta v^u_{-k}:=v^u_{-k}-\bar {v}^u_{-k}$
and
$\Delta v^u_{-k}:=v^u_{-k}-\bar {v}^u_{-k}$
and
![]() $\Delta v^s_{-k}:=v^s_{-k}-\bar {v}^s_{-k}$
. Observe that for every
$\Delta v^s_{-k}:=v^s_{-k}-\bar {v}^s_{-k}$
. Observe that for every
![]() $k \geq 0$
,
$k \geq 0$
,
![]() $(v^u_{-k-1}, v^s_{-k-1})=F_{x_{-k-1}x_{-k}}^{-1}(v^u_{-k}, v^s_{-k})$
, and
$(v^u_{-k-1}, v^s_{-k-1})=F_{x_{-k-1}x_{-k}}^{-1}(v^u_{-k}, v^s_{-k})$
, and
![]() $(\bar {v}^u_{-k-1}, \bar {v}^s_{-k-1})=F_{x_{-k-1}x_{-k}}^{-1}{ }(\bar {v}^u_{-k}, \bar {v}^s_{-k})$
, we have
$(\bar {v}^u_{-k-1}, \bar {v}^s_{-k-1})=F_{x_{-k-1}x_{-k}}^{-1}{ }(\bar {v}^u_{-k}, \bar {v}^s_{-k})$
, we have
 $$ \begin{align*} \begin{aligned} \|\Delta v^u_{-k-1}\|&\leq\|\bar{D}^{uu}_{x_{-k},x_{-k-1}}\|\cdot \|\Delta v_{-k}^u\|+\|\bar{D}^{us}_{x_{-k},x_{-k-1}}\|\cdot \|\Delta v_{-k}^s\|\\ &\quad+\operatorname{Lip}(\bar{\phi}^u_{x_{-k},x_{-k-1}})(\|\Delta v_{-k}^u\|+\|\Delta v_{-k}^s\|)\notag\\ &\leq(\|Df^{-1}|_{E^u(x_{-k})}\|+2\varepsilon\varepsilon(x_{-k}))\|\Delta v^u_{-k}\|+2\varepsilon\varepsilon(x_{-k})\|\Delta v^s_{-k}\| \notag \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\Delta v^u_{-k-1}\|&\leq\|\bar{D}^{uu}_{x_{-k},x_{-k-1}}\|\cdot \|\Delta v_{-k}^u\|+\|\bar{D}^{us}_{x_{-k},x_{-k-1}}\|\cdot \|\Delta v_{-k}^s\|\\ &\quad+\operatorname{Lip}(\bar{\phi}^u_{x_{-k},x_{-k-1}})(\|\Delta v_{-k}^u\|+\|\Delta v_{-k}^s\|)\notag\\ &\leq(\|Df^{-1}|_{E^u(x_{-k})}\|+2\varepsilon\varepsilon(x_{-k}))\|\Delta v^u_{-k}\|+2\varepsilon\varepsilon(x_{-k})\|\Delta v^s_{-k}\| \notag \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} \|\Delta v^s_{-k-1}\|&\geq m(\bar{D}^{ss}_{x_{-k},x_{-k-1}})\|\Delta v_{-k}^s\|-\|\bar{D}^{su}_{x_{-k},x_{-k-1}}\|\cdot \|\Delta v_{-k}^u\|\\ &\quad-\operatorname{Lip}(\bar{\phi}^s_{x_{-k},x_{-k-1}})(\|\Delta v_{-k}^u\|+\|\Delta v_{-k}^s\|)\notag\\ &\geq (m(Df^{-1}|_{E^s(x_{-k})})-2\varepsilon\varepsilon(x_{-k}))\|\Delta v^s_{-k}\|-2\varepsilon\varepsilon(x_{-k})\|\Delta v^u_{-k}\|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\Delta v^s_{-k-1}\|&\geq m(\bar{D}^{ss}_{x_{-k},x_{-k-1}})\|\Delta v_{-k}^s\|-\|\bar{D}^{su}_{x_{-k},x_{-k-1}}\|\cdot \|\Delta v_{-k}^u\|\\ &\quad-\operatorname{Lip}(\bar{\phi}^s_{x_{-k},x_{-k-1}})(\|\Delta v_{-k}^u\|+\|\Delta v_{-k}^s\|)\notag\\ &\geq (m(Df^{-1}|_{E^s(x_{-k})})-2\varepsilon\varepsilon(x_{-k}))\|\Delta v^s_{-k}\|-2\varepsilon\varepsilon(x_{-k})\|\Delta v^u_{-k}\|. \end{aligned} \end{align*} $$
We claim that an easy induction gives
![]() $\|\Delta v^u_{-k}\|\leq \|\Delta v^s_{-k}\| \leq \|\Delta v^s_{-k-1}\|$
for all
$\|\Delta v^u_{-k}\|\leq \|\Delta v^s_{-k}\| \leq \|\Delta v^s_{-k-1}\|$
for all
![]() $k\geq 0$
. In fact, for
$k\geq 0$
. In fact, for
![]() $k=0$
, this is because
$k=0$
, this is because
![]() $\|\Delta v^u_{0}\|=0$
by definition and
$\|\Delta v^u_{0}\|=0$
by definition and
![]() $C\varepsilon \varepsilon (x_{-k})\leq m(Df^{-1}|_{E^s(x_{-k})})-1$
if
$C\varepsilon \varepsilon (x_{-k})\leq m(Df^{-1}|_{E^s(x_{-k})})-1$
if
![]() $\varepsilon>0$
is small enough from Lemma 3.1. Assume by induction that
$\varepsilon>0$
is small enough from Lemma 3.1. Assume by induction that
![]() $\|\Delta v^u_{-k}\|\leq \|\Delta v^s_{-k}\| \leq \|\Delta v^s_{-k-1}\|$
. Notice that
$\|\Delta v^u_{-k}\|\leq \|\Delta v^s_{-k}\| \leq \|\Delta v^s_{-k-1}\|$
. Notice that
![]() $C\varepsilon (x_{-k})\leq 1-\|Df^{-1}|_{E^u(x_{-k})}\|$
from the case
$C\varepsilon (x_{-k})\leq 1-\|Df^{-1}|_{E^u(x_{-k})}\|$
from the case
![]() $f^{-1}$
of Lemma 3.2, and choosing a smaller
$f^{-1}$
of Lemma 3.2, and choosing a smaller
![]() $\varepsilon $
if necessary such that
$\varepsilon $
if necessary such that
![]() $\varepsilon \leq \min \{1,{C}/{4}\}$
, then we have
$\varepsilon \leq \min \{1,{C}/{4}\}$
, then we have
 $$ \begin{align*} \begin{aligned} \|\Delta v^u_{-k-1}\| &\leq (\|Df^{-1}|_{E^u(x_{-k})}\|+2\varepsilon\varepsilon(x_{-k}))\|\Delta v^u_{-k}\|+2\varepsilon\varepsilon(x_{-k})\|\Delta v^s_{-k}\|\notag\\ & \leq(\|Df^{-1}|_{E^u(x_{-k})}\|+4\varepsilon\varepsilon(x_{-k}))\|\Delta v^s_{-k}\|\leq \|\Delta v^s_{-k}\| \leq \|\Delta v^s_{-k-1}\| \\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\Delta v^u_{-k-1}\| &\leq (\|Df^{-1}|_{E^u(x_{-k})}\|+2\varepsilon\varepsilon(x_{-k}))\|\Delta v^u_{-k}\|+2\varepsilon\varepsilon(x_{-k})\|\Delta v^s_{-k}\|\notag\\ & \leq(\|Df^{-1}|_{E^u(x_{-k})}\|+4\varepsilon\varepsilon(x_{-k}))\|\Delta v^s_{-k}\|\leq \|\Delta v^s_{-k}\| \leq \|\Delta v^s_{-k-1}\| \\ \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} \|\Delta v^s_{-k-2}\| &\geq (m(Df^{-1}|_{E^s(x_{-k-1})})-2\varepsilon\varepsilon(x_{-k-1}))\|\Delta v^s_{-k-1}\|-2\varepsilon\varepsilon(x_{-k-1})\|\Delta v^u_{-k-1}\|\notag\\ &\geq(m(Df^{-1}|_{E^s(x_{-k-1})})-4\varepsilon\varepsilon(x_{-k-1})) \|\Delta v^s_{-k-1}\|\geq \|\Delta v^s_{-k-1}\|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\Delta v^s_{-k-2}\| &\geq (m(Df^{-1}|_{E^s(x_{-k-1})})-2\varepsilon\varepsilon(x_{-k-1}))\|\Delta v^s_{-k-1}\|-2\varepsilon\varepsilon(x_{-k-1})\|\Delta v^u_{-k-1}\|\notag\\ &\geq(m(Df^{-1}|_{E^s(x_{-k-1})})-4\varepsilon\varepsilon(x_{-k-1})) \|\Delta v^s_{-k-1}\|\geq \|\Delta v^s_{-k-1}\|. \end{aligned} \end{align*} $$
Hence, the claim is verified.
We now return to the proof of this part. If we introduce a new constant
 $$ \begin{align*} b:=\inf_{x\in O}\frac{m(Df^{-1}|_{E^s(x)})-m(Df^{-1}|_{E^s(x)})^{1/2}}{m(Df^{-1}|_{E^s(x)})-1}>0, \end{align*} $$
$$ \begin{align*} b:=\inf_{x\in O}\frac{m(Df^{-1}|_{E^s(x)})-m(Df^{-1}|_{E^s(x)})^{1/2}}{m(Df^{-1}|_{E^s(x)})-1}>0, \end{align*} $$
and choosing a smaller
![]() $\varepsilon $
if necessary such that
$\varepsilon $
if necessary such that
![]() $0<\varepsilon \leq ({bC}/{4})$
, then by Assumption US(iii), we see that
$0<\varepsilon \leq ({bC}/{4})$
, then by Assumption US(iii), we see that
 $$ \begin{align*} \begin{aligned} \|\Delta v^s_{-k-2}\|&\geq(m(Df^{-1}|_{E^s(x_{-k-1})})-bC\varepsilon(x_{-k-1}))\|\Delta v^s_{-k-1}\|\notag\\ &\geq m(Df^{-1}|_{E^s(x_{-k-1})})^{1/2}\|\Delta v^s_{-k-1}\|\notag \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\Delta v^s_{-k-2}\|&\geq(m(Df^{-1}|_{E^s(x_{-k-1})})-bC\varepsilon(x_{-k-1}))\|\Delta v^s_{-k-1}\|\notag\\ &\geq m(Df^{-1}|_{E^s(x_{-k-1})})^{1/2}\|\Delta v^s_{-k-1}\|\notag \end{aligned} \end{align*} $$
for all
![]() $k\geq 0$
. Therefore, we get
$k\geq 0$
. Therefore, we get
![]() $\|\Delta v^s_{-k}\| \geq \prod _{i=0}^{k-1} m(Df^{-1}|_{E^s(x_{-i})})^{1/2} \|\Delta v^s_{0}\| $
and hence either
$\|\Delta v^s_{-k}\| \geq \prod _{i=0}^{k-1} m(Df^{-1}|_{E^s(x_{-i})})^{1/2} \|\Delta v^s_{0}\| $
and hence either
![]() $\|\Delta v^s_{0}\|=0$
or
$\|\Delta v^s_{0}\|=0$
or
![]() $\|\Delta v^s_{-k}\| \underset {k \rightarrow \infty }{\longrightarrow } \infty .$
However,
$\|\Delta v^s_{-k}\| \underset {k \rightarrow \infty }{\longrightarrow } \infty .$
However,
![]() $\|\Delta v^s_{-k}\|=\|v^s_{-k}-\bar {v}^s_{-k}\| \leq 2Q(x_{-k})<2$
, so
$\|\Delta v^s_{-k}\|=\|v^s_{-k}-\bar {v}^s_{-k}\| \leq 2Q(x_{-k})<2$
, so
![]() $\|\Delta v^s_{0}\|=0 .$
Recall that
$\|\Delta v^s_{0}\|=0 .$
Recall that
![]() $\Delta v^s_{0}=v^s_{0}-\bar {v}^s_{0}$
, we have
$\Delta v^s_{0}=v^s_{0}-\bar {v}^s_{0}$
, we have
![]() $v^s_{0}=\bar {v}^s_{0}$
and then
$v^s_{0}=\bar {v}^s_{0}$
and then
![]() $v^s_0=\bar {v}^s_0=\sigma ^u(\bar {v}^u_0)=\sigma ^u(v^u_0)$
by definition. Thus,
$v^s_0=\bar {v}^s_0=\sigma ^u(\bar {v}^u_0)=\sigma ^u(v^u_0)$
by definition. Thus,
![]() $x=\exp _{x_0}(v^u_0, \sigma ^u(v^u_0)) \in V^{u}(\{x_{-n}\}_{n\geq 0})$
.
$x=\exp _{x_0}(v^u_0, \sigma ^u(v^u_0)) \in V^{u}(\{x_{-n}\}_{n\geq 0})$
.
(5) Given
![]() $n>N$
, let
$n>N$
, let
![]() $V_{-n}^{u}$
be a u-admissible manifold at
$V_{-n}^{u}$
be a u-admissible manifold at
![]() $x_{-n}$
and let
$x_{-n}$
and let
![]() $W_{-n}^u$
be a u-admissible manifold at
$W_{-n}^u$
be a u-admissible manifold at
![]() $y_{-n}$
. For the sake of simplicity in notation, let
$y_{-n}$
. For the sake of simplicity in notation, let
![]() $\mathscr {F}_{u}^{\ell }(V_{-n}^{u})$
(respectively
$\mathscr {F}_{u}^{\ell }(V_{-n}^{u})$
(respectively
![]() $\mathscr {F}_{u}^{\ell }(W_{-n}^{u}))$
denote the result of applying
$\mathscr {F}_{u}^{\ell }(W_{-n}^{u}))$
denote the result of applying
![]() $\mathscr {F}^{u}_{\cdot ,\cdot } \ell $
times to
$\mathscr {F}^{u}_{\cdot ,\cdot } \ell $
times to
![]() $V_{-n}^u$
using the path
$V_{-n}^u$
using the path
![]() $x_{-n} \rightarrow \cdots \rightarrow x_{-n+\ell }$
(respectively using
$x_{-n} \rightarrow \cdots \rightarrow x_{-n+\ell }$
(respectively using
![]() $y_{-n} \rightarrow \cdots \rightarrow y_{-n+\ell }$
).
$y_{-n} \rightarrow \cdots \rightarrow y_{-n+\ell }$
).
Here,
![]() $\mathscr {F}_{u}^{n-N}(V_{-n}^{u})$
and
$\mathscr {F}_{u}^{n-N}(V_{-n}^{u})$
and
![]() $\mathscr {F}_{u}^{n-N}(W_{-n}^{u})$
are u-admissible manifolds at
$\mathscr {F}_{u}^{n-N}(W_{-n}^{u})$
are u-admissible manifolds at
![]() $x_{-N}$
and
$x_{-N}$
and
![]() $y_{-N}$
, respectively. Let
$y_{-N}$
, respectively. Let
![]() $\sigma _{-N}, \widetilde {\sigma }_{-N}$
be their representing functions. Admissibility implies that
$\sigma _{-N}, \widetilde {\sigma }_{-N}$
be their representing functions. Admissibility implies that
 $$ \begin{align*} \begin{aligned} &\|\sigma_{-N}-\widetilde{\sigma}_{-N}\|_{C^0} \leq\|\sigma_{-N}\|_{C^0}+\|\widetilde{\sigma}_{-N}\|_{C^0}\leq2 Q(x_{-N})<1, \\ &\|D\sigma_{-N}-D\widetilde{\sigma}_{-N}\|_{C^0} \leq\|D\sigma_{-N}\|_{C^0}+\|D\widetilde{\sigma}_{-N}\|_{C^0}\leq2 \sqrt{\varepsilon}<1 \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\|\sigma_{-N}-\widetilde{\sigma}_{-N}\|_{C^0} \leq\|\sigma_{-N}\|_{C^0}+\|\widetilde{\sigma}_{-N}\|_{C^0}\leq2 Q(x_{-N})<1, \\ &\|D\sigma_{-N}-D\widetilde{\sigma}_{-N}\|_{C^0} \leq\|D\sigma_{-N}\|_{C^0}+\|D\widetilde{\sigma}_{-N}\|_{C^0}\leq2 \sqrt{\varepsilon}<1 \end{aligned} \end{align*} $$
if
![]() $\varepsilon $
is small enough.
$\varepsilon $
is small enough.
For every
![]() $0\leq k\leq N$
, represent
$0\leq k\leq N$
, represent
![]() $\mathscr {F}_{u}^{n-k}[V_{-n}^{u}]$
and
$\mathscr {F}_{u}^{n-k}[V_{-n}^{u}]$
and
![]() $\mathscr {F}_{u}^{n-k}[W_{-n}^{u}]$
by functions
$\mathscr {F}_{u}^{n-k}[W_{-n}^{u}]$
by functions
![]() $\sigma _{-k}$
and
$\sigma _{-k}$
and
![]() $\widetilde {\sigma }_{-k}$
, respectively. By Proposition 4.3, we have
$\widetilde {\sigma }_{-k}$
, respectively. By Proposition 4.3, we have
and
Iterating equation (5.4), from
![]() $k=N$
and going down, we get
$k=N$
and going down, we get
 $$ \begin{align*} \begin{aligned} \|\sigma_{-k}-\widetilde{\sigma}_{-k}\|_{C^0} &\leq\|Df|_{E^s(x_{-k-1})}\|^{1/2}\|\sigma_{-k-1}-\widetilde{\sigma}_{-k-1}\|_{C^0}\notag\\ &\leq\prod^{N}_{i=k+1}\|Df|_{E^s(x_{-i})}\|^{1/2}\|\sigma_{-N}-\widetilde{\sigma}_{-N}\|_{C^0}\notag\\ &\leq\prod^{N}_{i=k+1}\|Df|_{E^s(x_{-i})}\|^{1/2}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\sigma_{-k}-\widetilde{\sigma}_{-k}\|_{C^0} &\leq\|Df|_{E^s(x_{-k-1})}\|^{1/2}\|\sigma_{-k-1}-\widetilde{\sigma}_{-k-1}\|_{C^0}\notag\\ &\leq\prod^{N}_{i=k+1}\|Df|_{E^s(x_{-i})}\|^{1/2}\|\sigma_{-N}-\widetilde{\sigma}_{-N}\|_{C^0}\notag\\ &\leq\prod^{N}_{i=k+1}\|Df|_{E^s(x_{-i})}\|^{1/2}, \end{aligned} \end{align*} $$
and hence
![]() $d_{C^0}(\mathscr {F}_{u}^{n}[V_{-n}^{u}], \mathscr {F}_{u}^{n}[W_{-n}^{u}]) \leq \prod ^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}$
. Passing to the limit
$d_{C^0}(\mathscr {F}_{u}^{n}[V_{-n}^{u}], \mathscr {F}_{u}^{n}[W_{-n}^{u}]) \leq \prod ^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}$
. Passing to the limit
![]() ${n \rightarrow \infty }$
, we obtain
${n \rightarrow \infty }$
, we obtain
 $$ \begin{align*} d_{C^0}(V^{u}(\{x_{-n}\}_{n\geq0}), V^{u}(\{y_{-n}\}_{n\geq0})) \leq \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}. \end{align*} $$
$$ \begin{align*} d_{C^0}(V^{u}(\{x_{-n}\}_{n\geq0}), V^{u}(\{y_{-n}\}_{n\geq0})) \leq \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}. \end{align*} $$
Apply
![]() $\|\sigma _{-k}-\widetilde {\sigma }_{-k}\|_{C^0} \leq \prod ^{N}_{i=k+1}\|Df|_{E^s(x_{-i})}\|^{1/2}$
to equation (5.5), and set
$\|\sigma _{-k}-\widetilde {\sigma }_{-k}\|_{C^0} \leq \prod ^{N}_{i=k+1}\|Df|_{E^s(x_{-i})}\|^{1/2}$
to equation (5.5), and set
![]() $c_{-k}:=\|D\sigma _{-k}-D\widetilde {\sigma }_{-k}\|_{C^0}$
for every
$c_{-k}:=\|D\sigma _{-k}-D\widetilde {\sigma }_{-k}\|_{C^0}$
for every
![]() $0\leq k\leq N$
. Then
$0\leq k\leq N$
. Then
![]() $c_{-k+1} \leq \|Df|_{E^s(x_{-k})}\|^{1/2}(c_{-k}+2\prod ^{N}_{i=k+1} \|Df|_{E^s(x_{-i})}\|^{\delta /4} )$
for every
$c_{-k+1} \leq \|Df|_{E^s(x_{-k})}\|^{1/2}(c_{-k}+2\prod ^{N}_{i=k+1} \|Df|_{E^s(x_{-i})}\|^{\delta /4} )$
for every
![]() $0\leq k\leq N$
. Now an easy induction gives that for every
$0\leq k\leq N$
. Now an easy induction gives that for every
![]() $0 \leq k \leq N$
,
$0 \leq k \leq N$
,
 $$ \begin{align*} \begin{aligned} c_0 &\leq \prod^{k}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2} c_{-k}+2\times\bigg[\prod^{k}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}\cdot\prod^{N}_{i=k+1}\|Df|_{E^s(x_{-i})}\|^{\delta/4}\notag\\ &\quad+\prod^{k-1}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}\cdot\prod^{N}_{i=k}\|Df|_{E^s(x_{-i})}\|^{\delta/4} +\cdots+\|Df|_{E^s(x_{-1})}\|^{1/2}\\ &\quad\times\prod^{N}_{i=2}\|Df|_{E^s(x_{-i})}\|^{\delta/4}\bigg]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} c_0 &\leq \prod^{k}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2} c_{-k}+2\times\bigg[\prod^{k}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}\cdot\prod^{N}_{i=k+1}\|Df|_{E^s(x_{-i})}\|^{\delta/4}\notag\\ &\quad+\prod^{k-1}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}\cdot\prod^{N}_{i=k}\|Df|_{E^s(x_{-i})}\|^{\delta/4} +\cdots+\|Df|_{E^s(x_{-1})}\|^{1/2}\\ &\quad\times\prod^{N}_{i=2}\|Df|_{E^s(x_{-i})}\|^{\delta/4}\bigg]. \end{aligned} \end{align*} $$
We now take
![]() $k=N$
, paying attention to the inequalities
$k=N$
, paying attention to the inequalities
![]() $\|Df|_{E^s(x_{-i})}\|^{1/2} \leq \|Df|_{E^s(x_{-i})}\|^{\delta /4}$
for all
$\|Df|_{E^s(x_{-i})}\|^{1/2} \leq \|Df|_{E^s(x_{-i})}\|^{\delta /4}$
for all
![]() $i=1,\ldots ,N$
since
$i=1,\ldots ,N$
since
![]() $0<\delta <\min \{1,\alpha -{\beta }/{\gamma }\}$
and noting that
$0<\delta <\min \{1,\alpha -{\beta }/{\gamma }\}$
and noting that
![]() $c_{-N} \leq 1$
, we have
$c_{-N} \leq 1$
, we have
 $$ \begin{align*} c_{0} \leq \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}+2 N \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{\delta/4}<(2 N+1) \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{\delta/4}. \end{align*} $$
$$ \begin{align*} c_{0} \leq \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{1/2}+2 N \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{\delta/4}<(2 N+1) \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{\delta/4}. \end{align*} $$
Immediately, it follows that
![]() $d_{C^1}(\mathscr {F}^n_{u}[V_{-n}^{u}], \mathscr {F}^n_{u}[W^u_{-n}]) \kern1pt{\leq}\kern1pt 2(N+1) \prod ^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{\delta /4}$
. In part (1), we saw that
$d_{C^1}(\mathscr {F}^n_{u}[V_{-n}^{u}], \mathscr {F}^n_{u}[W^u_{-n}]) \kern1pt{\leq}\kern1pt 2(N+1) \prod ^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{\delta /4}$
. In part (1), we saw that
![]() $\mathscr {F}^n_{u}[V_{-n}^{u}]$
and
$\mathscr {F}^n_{u}[V_{-n}^{u}]$
and
![]() $\mathscr {F}_{u}^{n}[W_{-n}^{u}]$
converge to
$\mathscr {F}_{u}^{n}[W_{-n}^{u}]$
converge to
![]() $V^{u}(\{x_{-n}\}_{n \geq 0})$
and
$V^{u}(\{x_{-n}\}_{n \geq 0})$
and
![]() $V^{u}(\{y_{-n}\}_{n \geq 0})$
in
$V^{u}(\{y_{-n}\}_{n \geq 0})$
in
![]() $C^{1}$
, respectively. If we pass to the limit as
$C^{1}$
, respectively. If we pass to the limit as
![]() $n \rightarrow \infty $
, finally we get
$n \rightarrow \infty $
, finally we get
 $$ \begin{align*}d_{C^1}(V^{u}(\{x_{-n}\}_{n \geq 0}), V^{u}(\{y_{-n}\}_{n \geq 0})) \leq 2(N+1) \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{\delta/4}.\\[-50pt] \end{align*} $$
$$ \begin{align*}d_{C^1}(V^{u}(\{x_{-n}\}_{n \geq 0}), V^{u}(\{y_{-n}\}_{n \geq 0})) \leq 2(N+1) \prod^{N}_{i=1}\|Df|_{E^s(x_{-i})}\|^{\delta/4}.\\[-50pt] \end{align*} $$
We will see that Proposition 5.2 ensures that every
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}\in \Sigma ^{\#}$
is associated to a unique point.
$\underline {x}\in \Sigma ^{\#}$
is associated to a unique point.
Definition 5.2. We say that an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}\in \Sigma ^{\#}$
in O shadows a point
$\underline {x}\in \Sigma ^{\#}$
in O shadows a point
![]() $x \in O$
when
$x \in O$
when
![]() ${f^{n}(x)\in \exp _{x_n}(S_{x_n})}$
for all
${f^{n}(x)\in \exp _{x_n}(S_{x_n})}$
for all
![]() $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
.
The following lemma is the so called the shadowing lemma, which is at the heart in the proof of Theorem 5.1. The general idea is similar to what Sarig does in [Reference Sarig22, §4.3].
Lemma 5.1. Every
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}\in \Sigma ^{\#}$
in O shadows a unique point
$\underline {x}\in \Sigma ^{\#}$
in O shadows a unique point
![]() $x \in O$
.
$x \in O$
.
Proof. Let
![]() $\underline {x}\in \Sigma ^{\#}$
be an
$\underline {x}\in \Sigma ^{\#}$
be an
![]() $\varepsilon $
-rppo. From Proposition 4.1(1), there is a singleton set
$\varepsilon $
-rppo. From Proposition 4.1(1), there is a singleton set
![]() ${\{x\}:=V^u(\underline {x}^-)\cap V^s(\underline {x}^+)\subset O}$
, we claim that
${\{x\}:=V^u(\underline {x}^-)\cap V^s(\underline {x}^+)\subset O}$
, we claim that
![]() $\underline {x}$
shadows x and
$\underline {x}$
shadows x and
![]() $x\in O$
. By Proposition 5.2(2), for all
$x\in O$
. By Proposition 5.2(2), for all
![]() $k\geq 0$
, we have
$k\geq 0$
, we have
and
that is,
![]() $f^{k}(x)\in \exp _{x_k}(S_{x_k})$
for all
$f^{k}(x)\in \exp _{x_k}(S_{x_k})$
for all
![]() $k \in \mathbb {Z}$
, and hence
$k \in \mathbb {Z}$
, and hence
![]() $\underline {x}$
shadows x.
$\underline {x}$
shadows x.
If
![]() $y\in O$
is any other point shadowed by
$y\in O$
is any other point shadowed by
![]() $\underline {x}$
, according to Definition 5.2 and Proposition 5.2(4), it must lie in
$\underline {x}$
, according to Definition 5.2 and Proposition 5.2(4), it must lie in
![]() $V^u(\underline {x}^-)\cap V^s(\underline {x}^+)=\{x\}$
.
$V^u(\underline {x}^-)\cap V^s(\underline {x}^+)=\{x\}$
.
For every
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}\in \Sigma ^{\#}$
, let
$\underline {x}\in \Sigma ^{\#}$
, let
![]() $\pi :\Sigma ^{\#}\rightarrow O$
be defined by
$\pi :\Sigma ^{\#}\rightarrow O$
be defined by
By the shadowing lemma in Lemma 5.1,
![]() $\pi (\underline {x})$
is the shadowed point of
$\pi (\underline {x})$
is the shadowed point of
![]() $\underline {x}$
, and the uniqueness guarantees that
$\underline {x}$
, and the uniqueness guarantees that
![]() $\pi $
is well defined for every element of
$\pi $
is well defined for every element of
![]() $\Sigma ^{\#}$
.
$\Sigma ^{\#}$
.
Here are the main properties of the triple
![]() $(\Sigma ^{\#},\sigma ,\pi )$
.
$(\Sigma ^{\#},\sigma ,\pi )$
.
Theorem 5.1. The following hold for all
![]() $\varepsilon>0$
small enough.
$\varepsilon>0$
small enough.
-
(1)
 $\pi \circ \sigma =f\circ \pi $
on
$\pi \circ \sigma =f\circ \pi $
on
 $\Sigma ^{\#}$
.
$\Sigma ^{\#}$
. -
(2)
 $\pi (\Sigma ^\#)=O^{\#}$
.
$\pi (\Sigma ^\#)=O^{\#}$
. -
(3)
 $\pi :\Sigma ^\#\rightarrow O$
is continuous. More specifically, if
$\pi :\Sigma ^\#\rightarrow O$
is continuous. More specifically, if
 $\underline {x}=\{x_n\}_{n \in \mathbb {Z}}, \underline {y}=\{y_n\}_{n \in \mathbb {Z}}\in \Sigma ^{\#}$
satisfy
$\underline {x}=\{x_n\}_{n \in \mathbb {Z}}, \underline {y}=\{y_n\}_{n \in \mathbb {Z}}\in \Sigma ^{\#}$
satisfy
 $x_i=y_i$
for
$x_i=y_i$
for
 $i=-N,\ldots , N$
, then
$i=-N,\ldots , N$
, then  $$ \begin{align*} d(\pi(\underline{x}),\pi(\underline{y})) \leq 6 \bigg[\prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|^{1/2}+\prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|^{1/2}\bigg]. \end{align*} $$
$$ \begin{align*} d(\pi(\underline{x}),\pi(\underline{y})) \leq 6 \bigg[\prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|^{1/2}+\prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|^{1/2}\bigg]. \end{align*} $$
Remark 5.2.
![]() $(\Sigma ^{\#},\sigma ,\pi )$
is not a symbolic model for f, since
$(\Sigma ^{\#},\sigma ,\pi )$
is not a symbolic model for f, since
![]() $\pi $
is usually infinite-to-one.
$\pi $
is usually infinite-to-one.
Proof. (1) Notice that for all
![]() $\underline {x}\in \Sigma ^{\#}$
, from the shadowing lemma in Lemma 5.1 and Definition 5.2, we can denote
$\underline {x}\in \Sigma ^{\#}$
, from the shadowing lemma in Lemma 5.1 and Definition 5.2, we can denote
![]() $x=\pi (\underline {x})$
which satisfies
$x=\pi (\underline {x})$
which satisfies
![]() $f^{n}(f\circ \pi (\underline {x}))=f^{n+1}(x)\in \exp _{x_{n+1}}(S_{x_{n+1}})$
for all
$f^{n}(f\circ \pi (\underline {x}))=f^{n+1}(x)\in \exp _{x_{n+1}}(S_{x_{n+1}})$
for all
![]() $n \in \mathbb {Z}$
. However, since
$n \in \mathbb {Z}$
. However, since
![]() $\sigma (\underline {x})=\{x_{n+1}\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
, using the shadowing lemma in Lemma 5.1 again, we can denote
$\sigma (\underline {x})=\{x_{n+1}\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
, using the shadowing lemma in Lemma 5.1 again, we can denote
![]() $y=\pi \circ \sigma (\underline {x})$
which satisfies
$y=\pi \circ \sigma (\underline {x})$
which satisfies
![]() $f^{n}(\pi \circ \sigma (\underline {x}))=f^{n}(y)\in \exp _{x_{n+1}}(S_{x_{n+1}})$
for all
$f^{n}(\pi \circ \sigma (\underline {x}))=f^{n}(y)\in \exp _{x_{n+1}}(S_{x_{n+1}})$
for all
![]() $n \in \mathbb {Z}$
by Definition 5.2 again. From the uniqueness of the shadowing point,
$n \in \mathbb {Z}$
by Definition 5.2 again. From the uniqueness of the shadowing point,
![]() $y=f(x)$
, that is,
$y=f(x)$
, that is,
![]() $\pi \circ \sigma (\underline {x})=f\circ \pi (\underline {x})$
for all
$\pi \circ \sigma (\underline {x})=f\circ \pi (\underline {x})$
for all
![]() $\underline {x}\in \Sigma ^{\#}$
.
$\underline {x}\in \Sigma ^{\#}$
.
(2) First we prove
![]() $\pi (\Sigma ^\#)\supset O^{\#}$
. For every
$\pi (\Sigma ^\#)\supset O^{\#}$
. For every
![]() $x\in O^{\#}\subset O$
, looking closely into the proof of Proposition 5.1(2), we see that there exists a sequence
$x\in O^{\#}\subset O$
, looking closely into the proof of Proposition 5.1(2), we see that there exists a sequence
![]() $\{x_n\}_{n\in \mathbb {Z}}\in \Sigma $
that satisfies
$\{x_n\}_{n\in \mathbb {Z}}\in \Sigma $
that satisfies
![]() $d(f^n(x),x_n)<\varepsilon Q(x_n)$
and
$d(f^n(x),x_n)<\varepsilon Q(x_n)$
and
![]() $d(x_n,\partial O)\geq e^{-\varepsilon }d(f^n(x),\partial O)$
for all
$d(x_n,\partial O)\geq e^{-\varepsilon }d(f^n(x),\partial O)$
for all
![]() $n\in \mathbb {Z}$
. By the definition of
$n\in \mathbb {Z}$
. By the definition of
![]() $O^{\#}$
,
$O^{\#}$
,
![]() $d(x_n,\partial O)\geq e^{-\varepsilon }d(f^n(x),\partial O)$
means there exist sequences
$d(x_n,\partial O)\geq e^{-\varepsilon }d(f^n(x),\partial O)$
means there exist sequences
![]() $n_k,m_k\uparrow \infty $
for which
$n_k,m_k\uparrow \infty $
for which
![]() $d(x_{n_k},\partial O)$
and
$d(x_{n_k},\partial O)$
and
![]() $d(x_{-m_k},\partial O)$
are bounded away from zero. By the discreteness of
$d(x_{-m_k},\partial O)$
are bounded away from zero. By the discreteness of
![]() $\mathscr {A}$
(Proposition 5.1(1)),
$\mathscr {A}$
(Proposition 5.1(1)),
![]() $x_n$
must repeat some symbol infinitely often in the past and (possibly a different symbol) in the future, that is,
$x_n$
must repeat some symbol infinitely often in the past and (possibly a different symbol) in the future, that is,
![]() $\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
. Since
$\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
. Since
![]() $d(f^n(x),x_n)<\varepsilon Q(x_n)$
, that is,
$d(f^n(x),x_n)<\varepsilon Q(x_n)$
, that is,
![]() $f^n(x)\in \exp _{x_n}(T_{x_n}M(\varepsilon Q(x_n)))\subset \exp _{x_n}(S_{x_n})$
if
$f^n(x)\in \exp _{x_n}(T_{x_n}M(\varepsilon Q(x_n)))\subset \exp _{x_n}(S_{x_n})$
if
![]() $\varepsilon>0$
is small enough, from the uniqueness of the shadowing point, we have
$\varepsilon>0$
is small enough, from the uniqueness of the shadowing point, we have
![]() $x=\pi (\{x_n\}_{n\in \mathbb {Z}})\in \pi (\Sigma ^{\#})$
for all
$x=\pi (\{x_n\}_{n\in \mathbb {Z}})\in \pi (\Sigma ^{\#})$
for all
![]() $n\in \mathbb {Z}$
. Thus, we get
$n\in \mathbb {Z}$
. Thus, we get
![]() $\pi (\Sigma ^\#)\supset O^{\#}$
.
$\pi (\Sigma ^\#)\supset O^{\#}$
.
In the opposite direction, for every
![]() $\underline {x}=\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
, the shadowing lemma in Lemma 5.1 claims there is a unique
$\underline {x}=\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
, the shadowing lemma in Lemma 5.1 claims there is a unique
![]() $x\in O$
such that
$x\in O$
such that
![]() $x=\pi (\underline {x})$
. Since
$x=\pi (\underline {x})$
. Since
![]() $d(f^n(x),x_n)\leq ({1}/{50})Q(x_n)\leq ({1}/{50})d(x_n,\partial O)$
from Proposition 4.1(1), we have
$d(f^n(x),x_n)\leq ({1}/{50})Q(x_n)\leq ({1}/{50})d(x_n,\partial O)$
from Proposition 4.1(1), we have
and then
![]() $x\in O^{\#}$
. Therefore,
$x\in O^{\#}$
. Therefore,
![]() $\pi (\Sigma ^\#)\subset O^{\#}$
.
$\pi (\Sigma ^\#)\subset O^{\#}$
.
(3) Write
![]() $\{\pi (\underline {x})\}=V^u(\underline {x}^-)\cap V^s(\underline {x}^+)$
,
$\{\pi (\underline {x})\}=V^u(\underline {x}^-)\cap V^s(\underline {x}^+)$
,
![]() $\{\pi (\underline {y})\}=V^u(\underline {y}^-)\cap V^s(\underline {y}^+)$
. From Propositions 4.1(2), 4.3(1), and using induction, we have
$\{\pi (\underline {y})\}=V^u(\underline {y}^-)\cap V^s(\underline {y}^+)$
. From Propositions 4.1(2), 4.3(1), and using induction, we have
 $$ \begin{align*} \begin{aligned} d(\pi(\underline{x}),\pi(\underline{y})) &\leq \frac{2}{1-\sqrt{\varepsilon}}[d_{C^0}(V^u(\underline{x}^-),V^u(\underline{y}^-))+d_{C^0}(V^s(\underline{x}^+),V^s(\underline{y}^+))]\notag\\ &\leq \frac{2}{1-\sqrt{\varepsilon}} \bigg[\prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|^{1/2}+\prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|^{1/2}\bigg]\notag\\ &\leq 6 \bigg[\prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|^{1/2}+\prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|^{1/2}\bigg] \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(\pi(\underline{x}),\pi(\underline{y})) &\leq \frac{2}{1-\sqrt{\varepsilon}}[d_{C^0}(V^u(\underline{x}^-),V^u(\underline{y}^-))+d_{C^0}(V^s(\underline{x}^+),V^s(\underline{y}^+))]\notag\\ &\leq \frac{2}{1-\sqrt{\varepsilon}} \bigg[\prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|^{1/2}+\prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|^{1/2}\bigg]\notag\\ &\leq 6 \bigg[\prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|^{1/2}+\prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|^{1/2}\bigg] \end{aligned} \end{align*} $$
if
![]() $0<\varepsilon \leq \tfrac 19$
.
$0<\varepsilon \leq \tfrac 19$
.
Finally, the continuity is obvious since
 $$ \begin{align*} \lim_{N\rightarrow\infty}\prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|=\lim_{N\rightarrow\infty}\prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|=0.\\[-48pt] \end{align*} $$
$$ \begin{align*} \lim_{N\rightarrow\infty}\prod_{i=1}^{N}\|Df|_{E^s(x_{-i})}\|=\lim_{N\rightarrow\infty}\prod_{i=1}^{N}\|Df^{-1}|_{E^u(x_{i})}\|=0.\\[-48pt] \end{align*} $$
6. Markov partitions and symbolic dynamics
Let
![]() $(\Sigma ,\sigma )$
be the TMS constructed in §5, and let
$(\Sigma ,\sigma )$
be the TMS constructed in §5, and let
![]() $\pi :\Sigma ^{\#}\rightarrow O$
as defined in equation (5.6). In what follows, we use Theorem 5.1 to construct a cover of
$\pi :\Sigma ^{\#}\rightarrow O$
as defined in equation (5.6). In what follows, we use Theorem 5.1 to construct a cover of
![]() $O^{\#}$
that is locally finite and satisfies a (symbolic) Markov property.
$O^{\#}$
that is locally finite and satisfies a (symbolic) Markov property.
Definition 6.1. Call
![]() $\mathscr {Z}:=\{Z(z): z \in \mathscr {A}\}$
the Markov cover, where
$\mathscr {Z}:=\{Z(z): z \in \mathscr {A}\}$
the Markov cover, where
In other words,
![]() $\mathscr {Z}$
is the family defined by the natural partition of
$\mathscr {Z}$
is the family defined by the natural partition of
![]() $\Sigma ^{\#}$
into a cylinder at the zeroth position. Although every element
$\Sigma ^{\#}$
into a cylinder at the zeroth position. Although every element
![]() $Z(z)$
of
$Z(z)$
of
![]() $\mathscr {Z}$
is a subset of the much smaller set
$\mathscr {Z}$
is a subset of the much smaller set
![]() $\exp _z(T_zM({2}/{50}Q(z)))$
(Proposition 4.1(1)), it is a cover of
$\exp _z(T_zM({2}/{50}Q(z)))$
(Proposition 4.1(1)), it is a cover of
![]() $O^{\#}$
since
$O^{\#}$
since
Thus,
![]() $O=\bigcup _{Z\in \mathscr {Z}}Z\ \text {mod}\ \mu $
for every f-invariant probability measure
$O=\bigcup _{Z\in \mathscr {Z}}Z\ \text {mod}\ \mu $
for every f-invariant probability measure
![]() $\mu $
supported on O.
$\mu $
supported on O.
Suppose
![]() $x \in Z(z) \in \mathscr {Z}$
, then
$x \in Z(z) \in \mathscr {Z}$
, then
![]() $\text {there exists } \underline {x} \in \Sigma ^{\#}$
such that
$\text {there exists } \underline {x} \in \Sigma ^{\#}$
such that
![]() $x_{0}=z$
and
$x_{0}=z$
and
![]() $\pi (\underline {x})=x$
. Associated to
$\pi (\underline {x})=x$
. Associated to
![]() $\underline {x}$
are two admissible manifolds at
$\underline {x}$
are two admissible manifolds at
![]() $z: V^{u}(\underline {x}^-)$
and
$z: V^{u}(\underline {x}^-)$
and
![]() $V^{s}(\underline {x}^+)$
. The following proposition says that these manifolds do not depend on the choice of
$V^{s}(\underline {x}^+)$
. The following proposition says that these manifolds do not depend on the choice of
![]() $\underline {x}:$
if
$\underline {x}:$
if
![]() $\underline {y} \in \Sigma ^{\#}$
is another
$\underline {y} \in \Sigma ^{\#}$
is another
![]() $\varepsilon $
-rppo such that
$\varepsilon $
-rppo such that
![]() $y_{0}=z$
and
$y_{0}=z$
and
![]() $\pi (\underline {y})=x$
, then
$\pi (\underline {y})=x$
, then
which allows us to define invariant fibers inside each
![]() $Z \in \mathscr {Z}$
(see Definition 6.4).
$Z \in \mathscr {Z}$
(see Definition 6.4).
Proposition 6.1. For any
![]() $\underline {x},\underline {y}\in \Sigma ^{\#}$
such that
$\underline {x},\underline {y}\in \Sigma ^{\#}$
such that
![]() $x_0=y_0$
and
$x_0=y_0$
and
![]() $\pi (\underline {x})=\pi (\underline {y})=x$
, we have
$\pi (\underline {x})=\pi (\underline {y})=x$
, we have
Proof. As proven in [Reference Sarig22, Proposition 6.4], we show the proposition for
![]() $V^{s}$
by dividing our proof into three claims, and leave the case of
$V^{s}$
by dividing our proof into three claims, and leave the case of
![]() $V^{u}$
to the reader. Suppose
$V^{u}$
to the reader. Suppose
![]() $\varepsilon>0$
is small enough.
$\varepsilon>0$
is small enough.
Claim 1.
![]() $f^{k}[ V^{s}(\underline {y}^+)] \subseteq \exp _{y_k}[B_{y_k}^u(\tfrac 18Q(y_k))\oplus B_{y_k}^s(\tfrac 18Q(y_k))]$
for all k large enough.
$f^{k}[ V^{s}(\underline {y}^+)] \subseteq \exp _{y_k}[B_{y_k}^u(\tfrac 18Q(y_k))\oplus B_{y_k}^s(\tfrac 18Q(y_k))]$
for all k large enough.
Proof of Claim 1
Recall that by Proposition 5.2(2), for all
![]() $k \geq 0$
, we have
$k \geq 0$
, we have
where
![]() $\sigma ^s_k$
is the function which represents s-admissible manifold
$\sigma ^s_k$
is the function which represents s-admissible manifold
![]() $V^{s}(\{y_{n+k}\}_{n\geq 0})$
at
$V^{s}(\{y_{n+k}\}_{n\geq 0})$
at
![]() $y_k$
for all
$y_k$
for all
![]() $k\geq 0$
. Hence, for any
$k\geq 0$
. Hence, for any
![]() $y \in V^{s}(\underline {y}^+)$
, one can write
$y \in V^{s}(\underline {y}^+)$
, one can write
![]() $f^{k}(y)=\exp _{y_{k}}(\sigma ^s_k(v^s_k), v^s_k)$
,
$f^{k}(y)=\exp _{y_{k}}(\sigma ^s_k(v^s_k), v^s_k)$
,
![]() $\|v^s_k\|\leq Q(y_k)$
.
$\|v^s_k\|\leq Q(y_k)$
.
Notice that
![]() $(\sigma ^s_{k}(v^s_{k}), v^s_{k})=F_{y_{k-1},y_{k}}(\sigma ^s_{k-1}(v^s_{k-1}), v^s_{k-1})$
, or in the s-direction,
$(\sigma ^s_{k}(v^s_{k}), v^s_{k})=F_{y_{k-1},y_{k}}(\sigma ^s_{k-1}(v^s_{k-1}), v^s_{k-1})$
, or in the s-direction,
Using equations (4.1), (3.12), and
![]() $\|\phi ^s_{y_{k-1},y_{k}}(0,0)\|\leq \varepsilon \varepsilon (y_{k-1})Q(y_{k-1})$
, it follows that
$\|\phi ^s_{y_{k-1},y_{k}}(0,0)\|\leq \varepsilon \varepsilon (y_{k-1})Q(y_{k-1})$
, it follows that
 $$ \begin{align*} \begin{aligned} \|v^s_{k}\|&\leq\|D^{ss}_{y_{k-1},y_{k}}\|\ \|v^s_{k-1}\|+\|D^{su}_{y_{k-1},y_{k}}\|\ \|\sigma_{k-1}^s(v^s_{k-1})\|+\|\phi^s_{y_{k-1},y_{k}}(0,0)\|\\&\quad+\operatorname{Lip}(\phi^s_{y_{k-1},y_{k}}) (\|\sigma_{k-1}^s(v^s_{k-1})\|+\|v^s_{k-1}\|))\notag\\ &\leq(\|Df|_{E^s(y_{k-1})}\|+4\varepsilon\varepsilon(y_{k-1}))\|v^s_{k-1}\|+2\varepsilon\varepsilon(y_{k-1})Q(y_{k-1}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|v^s_{k}\|&\leq\|D^{ss}_{y_{k-1},y_{k}}\|\ \|v^s_{k-1}\|+\|D^{su}_{y_{k-1},y_{k}}\|\ \|\sigma_{k-1}^s(v^s_{k-1})\|+\|\phi^s_{y_{k-1},y_{k}}(0,0)\|\\&\quad+\operatorname{Lip}(\phi^s_{y_{k-1},y_{k}}) (\|\sigma_{k-1}^s(v^s_{k-1})\|+\|v^s_{k-1}\|))\notag\\ &\leq(\|Df|_{E^s(y_{k-1})}\|+4\varepsilon\varepsilon(y_{k-1}))\|v^s_{k-1}\|+2\varepsilon\varepsilon(y_{k-1})Q(y_{k-1}). \end{aligned} \end{align*} $$
We see that
![]() $\|v^s_{k}\| \leq a_{k}$
where
$\|v^s_{k}\| \leq a_{k}$
where
![]() $a_{k}$
is defined inductively by
$a_{k}$
is defined inductively by
We claim that
![]() $a_{k}\leq \tfrac 18 Q(y_k)$
for some
$a_{k}\leq \tfrac 18 Q(y_k)$
for some
![]() $k\geq 0$
. If the assertion would not hold, then
$k\geq 0$
. If the assertion would not hold, then
![]() ${Q(y_k) < 8 a_{k}}$
for all
${Q(y_k) < 8 a_{k}}$
for all
![]() $k\geq 0$
, and hence
$k\geq 0$
, and hence
![]() $a_{k} <(\|Df|_{E^s(y_{k-1})}\|+20\varepsilon \varepsilon (y_{k-1})) a_{k-1}$
for all
$a_{k} <(\|Df|_{E^s(y_{k-1})}\|+20\varepsilon \varepsilon (y_{k-1})) a_{k-1}$
for all
![]() $k\geq 0$
, which implies that
$k\geq 0$
, which implies that
 $$ \begin{align*} a_{k}<\prod_{i=0}^{k-1}(\|Df|_{E^s(y_i)}\|+20\varepsilon\varepsilon(y_i)) a_{0}. \end{align*} $$
$$ \begin{align*} a_{k}<\prod_{i=0}^{k-1}(\|Df|_{E^s(y_i)}\|+20\varepsilon\varepsilon(y_i)) a_{0}. \end{align*} $$
Fix
![]() $\kappa <\kappa _1<1$
, and introduce a new constant
$\kappa <\kappa _1<1$
, and introduce a new constant
![]() $c_1$
associated to
$c_1$
associated to
![]() $\kappa _1$
given by
$\kappa _1$
given by
 $$ \begin{align*} c_1:=\inf_{x\in O}\frac{\|Df|_{E^s(x)}\|^{\kappa_1}-\|Df|_{E^s(x)}\|}{1-\|Df|_{E^s(x)}\|}>0, \end{align*} $$
$$ \begin{align*} c_1:=\inf_{x\in O}\frac{\|Df|_{E^s(x)}\|^{\kappa_1}-\|Df|_{E^s(x)}\|}{1-\|Df|_{E^s(x)}\|}>0, \end{align*} $$
then if
![]() $0<\varepsilon \leq ({c_1C}/{20})$
, we get
$0<\varepsilon \leq ({c_1C}/{20})$
, we get
 $$ \begin{align*} a_{k}<\prod_{i=0}^{k-1}\|Df|_{E^s(y_i)}\|^{\kappa_1} a_{0}. \end{align*} $$
$$ \begin{align*} a_{k}<\prod_{i=0}^{k-1}\|Df|_{E^s(y_i)}\|^{\kappa_1} a_{0}. \end{align*} $$
Whereas by assumption,
![]() $a_{k}> \tfrac 18 Q(y_k)$
for all
$a_{k}> \tfrac 18 Q(y_k)$
for all
![]() $k\geq 0$
. Since
$k\geq 0$
. Since
![]() $y_{k-1}\rightarrow y_k$
, from Lemma 4.1 in the case
$y_{k-1}\rightarrow y_k$
, from Lemma 4.1 in the case
![]() $C_3=C_4=1$
, we obtain
$C_3=C_4=1$
, we obtain
 $$ \begin{align*} \begin{aligned} Q(y_k)&> Q(y_k)-d(f(y_{k-1}),y_k)\notag\\ &\geq(\|Df|_{E^s(y_{k-1})}\|^\kappa+\varepsilon\varepsilon(y_{k-1}))Q(y_{k-1})\notag\\ &> \|Df|_{E^s(y_{k-1})}\|^\kappa Q(y_{k-1}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} Q(y_k)&> Q(y_k)-d(f(y_{k-1}),y_k)\notag\\ &\geq(\|Df|_{E^s(y_{k-1})}\|^\kappa+\varepsilon\varepsilon(y_{k-1}))Q(y_{k-1})\notag\\ &> \|Df|_{E^s(y_{k-1})}\|^\kappa Q(y_{k-1}). \end{aligned} \end{align*} $$
Therefore,
 $$ \begin{align*} \begin{aligned} a_{k}> \tfrac{1}{8}Q(y_k)&>\tfrac{1}{8}\|Df|_{E^s(y_{k-1})}\|^\kappa Q(y_{k-1})\notag\\ &>\frac{1}{8}\prod_{i=0}^{k-1}\|Df|_{E^s(y_{i})}\|^\kappa a_0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} a_{k}> \tfrac{1}{8}Q(y_k)&>\tfrac{1}{8}\|Df|_{E^s(y_{k-1})}\|^\kappa Q(y_{k-1})\notag\\ &>\frac{1}{8}\prod_{i=0}^{k-1}\|Df|_{E^s(y_{i})}\|^\kappa a_0. \end{aligned} \end{align*} $$
Combining with the above, we have
 $$ \begin{align*} \frac{1}{8}\leq \prod_{i=0}^{k-1}\|Df|_{E^s(y_{i})}\|^{\kappa_1-\kappa}\underset{k \rightarrow \infty}{\longrightarrow} 0, \end{align*} $$
$$ \begin{align*} \frac{1}{8}\leq \prod_{i=0}^{k-1}\|Df|_{E^s(y_{i})}\|^{\kappa_1-\kappa}\underset{k \rightarrow \infty}{\longrightarrow} 0, \end{align*} $$
which is a contradiction. Consequently, we infer that
![]() $\text {there exists } k_0\geq 0$
such that
$\text {there exists } k_0\geq 0$
such that
![]() ${a_{k_0}\leq \tfrac 18Q(y_{k_0})}$
.
${a_{k_0}\leq \tfrac 18Q(y_{k_0})}$
.
Moreover, we have
![]() $a_{k}\leq \tfrac 18Q(y_k)$
for all k large enough by using induction. In fact, suppose that the inequality is true for
$a_{k}\leq \tfrac 18Q(y_k)$
for all k large enough by using induction. In fact, suppose that the inequality is true for
![]() $k-1$
, we have by the definition of
$k-1$
, we have by the definition of
![]() $a_k$
that
$a_k$
that
 $$ \begin{align*} \begin{aligned} a_{k}&\leq(\|Df|_{E^s(y_{k-1})}\|+4\varepsilon\varepsilon(y_{k-1}))\tfrac{1}{8}Q(y_{k-1})+2\varepsilon\varepsilon(y_{k-1})Q(y_{k-1})\notag\\ &\leq(\|Df|_{E^s(y_{k-1})}\|+20\varepsilon\varepsilon(y_{k-1}))\tfrac{1}{8}Q(y_{k-1})\notag\\ &\leq\|Df|_{E^s(y_{k-1})}\|^{\kappa_1}\tfrac{1}{8}Q(y_{k-1})\notag\\ &\leq\|Df|_{E^s(y_{k-1})}\|^{\kappa}\tfrac{1}{8}Q(y_{k-1})\notag\\ &\leq\tfrac{1}{8}Q(y_k). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} a_{k}&\leq(\|Df|_{E^s(y_{k-1})}\|+4\varepsilon\varepsilon(y_{k-1}))\tfrac{1}{8}Q(y_{k-1})+2\varepsilon\varepsilon(y_{k-1})Q(y_{k-1})\notag\\ &\leq(\|Df|_{E^s(y_{k-1})}\|+20\varepsilon\varepsilon(y_{k-1}))\tfrac{1}{8}Q(y_{k-1})\notag\\ &\leq\|Df|_{E^s(y_{k-1})}\|^{\kappa_1}\tfrac{1}{8}Q(y_{k-1})\notag\\ &\leq\|Df|_{E^s(y_{k-1})}\|^{\kappa}\tfrac{1}{8}Q(y_{k-1})\notag\\ &\leq\tfrac{1}{8}Q(y_k). \end{aligned} \end{align*} $$
Thus,
![]() $a_{k}\leq \tfrac 18Q(y_k)$
for all k large enough.
$a_{k}\leq \tfrac 18Q(y_k)$
for all k large enough.
In particular,
![]() $\|v^s_k\|\leq \tfrac 18Q(y_k)$
for all k large enough. Since
$\|v^s_k\|\leq \tfrac 18Q(y_k)$
for all k large enough. Since
![]() $\|\sigma ^s_{k}(v^s_{k})\| \leq \|\sigma ^s_{k}(0)\|+\operatorname {Lip}(\sigma ^s_{k})\|v^s_{k}\|<(10^{-3}+\sqrt {\varepsilon }) Q(y_k)\leq \tfrac 18Q(y_k)$
, if
$\|\sigma ^s_{k}(v^s_{k})\| \leq \|\sigma ^s_{k}(0)\|+\operatorname {Lip}(\sigma ^s_{k})\|v^s_{k}\|<(10^{-3}+\sqrt {\varepsilon }) Q(y_k)\leq \tfrac 18Q(y_k)$
, if
![]() $\varepsilon $
is small enough, we have
$\varepsilon $
is small enough, we have
 $$ \begin{align*} f^{k}[ V^{s}(\underline{y}^+)] \subseteq \exp_{y_k}\bigg[B_{y_k}^u\bigg(\frac{1}{8}Q(y_k)\bigg)\oplus B_{y_k}^s\bigg(\frac{1}{8}Q(y_k)\bigg)\bigg] \end{align*} $$
$$ \begin{align*} f^{k}[ V^{s}(\underline{y}^+)] \subseteq \exp_{y_k}\bigg[B_{y_k}^u\bigg(\frac{1}{8}Q(y_k)\bigg)\oplus B_{y_k}^s\bigg(\frac{1}{8}Q(y_k)\bigg)\bigg] \end{align*} $$
for all k large enough.
Claim 2.
![]() $f^{k}[ V^{s}(\underline {y}^+)] \subseteq \exp _{x_k}(S_{x_k})$
for all k large enough.
$f^{k}[ V^{s}(\underline {y}^+)] \subseteq \exp _{x_k}(S_{x_k})$
for all k large enough.
Proof of Claim 2
For any
![]() $y\in V^{s}(\underline {y}^+)$
, since
$y\in V^{s}(\underline {y}^+)$
, since
![]() $\pi (\underline {x})=\pi (\underline {y})=x$
, from Proposition 4.1(1), we get
$\pi (\underline {x})=\pi (\underline {y})=x$
, from Proposition 4.1(1), we get
and hence
![]() $d(f^k(y),x_k)\leq d(f^k(y),y_k)+d(y_k,x_k)<\rho (M)$
and we have
$d(f^k(y),x_k)\leq d(f^k(y),y_k)+d(y_k,x_k)<\rho (M)$
and we have
![]() $f^k(y)\in B(x_k, \rho (M))$
. Now for
$f^k(y)\in B(x_k, \rho (M))$
. Now for
![]() $k>0$
large enough, by Claim 1, we have
$k>0$
large enough, by Claim 1, we have
 $$ \begin{align*} \begin{aligned} \|\!\exp_{x_k}^{-1}f^k(y)\|&\leq\|\!\exp_{y_k}^{-1}f^k(y)\|+d(y_k,x_k)\notag\\ &\leq\frac{1}{4}Q(y_k)+\frac{1}{50}Q(x_k)+\frac{1}{50}Q(y_k)\notag\\ &\leq\tfrac{1}{4}(2Q(y_k)+Q(x_k)). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\!\exp_{x_k}^{-1}f^k(y)\|&\leq\|\!\exp_{y_k}^{-1}f^k(y)\|+d(y_k,x_k)\notag\\ &\leq\frac{1}{4}Q(y_k)+\frac{1}{50}Q(x_k)+\frac{1}{50}Q(y_k)\notag\\ &\leq\tfrac{1}{4}(2Q(y_k)+Q(x_k)). \end{aligned} \end{align*} $$
Note that
![]() $Q(x_k)\leq \varepsilon ^{{2}/({\alpha -\delta })}d(x_k,\partial O)$
, then
$Q(x_k)\leq \varepsilon ^{{2}/({\alpha -\delta })}d(x_k,\partial O)$
, then
 $$ \begin{align*} \begin{aligned} d(f^k(x),\partial O)&\leq d(x_k,\partial O)+d(x_k,f^k(x))\notag\\ &\leq d(x_k,\partial O)+\frac{1}{50}Q(x_k)\notag\\ &\leq e^{\varepsilon^{{2}/({\alpha-\delta})}}d(x_k,\partial O) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(f^k(x),\partial O)&\leq d(x_k,\partial O)+d(x_k,f^k(x))\notag\\ &\leq d(x_k,\partial O)+\frac{1}{50}Q(x_k)\notag\\ &\leq e^{\varepsilon^{{2}/({\alpha-\delta})}}d(x_k,\partial O) \end{aligned} \end{align*} $$
and we have
![]() $Q(f^k(x))\leq e^{\gamma \varepsilon ^{{2}/({\alpha -\delta }})} Q(x_k)$
.
$Q(f^k(x))\leq e^{\gamma \varepsilon ^{{2}/({\alpha -\delta }})} Q(x_k)$
.
Similarly, from
 $$ \begin{align*} \begin{aligned} d(f^k(x),\partial O)&\geq d(y_k,\partial O)-d(y_k,f^k(x))\notag\\ &\geq d(y_k,\partial O)-\frac{1}{50}Q(y_k)\notag\\ &\geq e^{-\varepsilon^{{2}/({\alpha-\delta})}}d(y_k,\partial O), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(f^k(x),\partial O)&\geq d(y_k,\partial O)-d(y_k,f^k(x))\notag\\ &\geq d(y_k,\partial O)-\frac{1}{50}Q(y_k)\notag\\ &\geq e^{-\varepsilon^{{2}/({\alpha-\delta})}}d(y_k,\partial O), \end{aligned} \end{align*} $$
we have
![]() $Q(f^k(x))\geq e^{-\gamma \varepsilon ^{{2}/({\alpha -\delta })}} Q(y_k)$
. Thus, we arrive at two useful inequalities:
$Q(f^k(x))\geq e^{-\gamma \varepsilon ^{{2}/({\alpha -\delta })}} Q(y_k)$
. Thus, we arrive at two useful inequalities:
and
This leads to
 $$ \begin{align*} \begin{aligned} \|\!\exp_{x_k}^{-1}f^k(y)\|&\leq\tfrac{1}{4}(2Q(y_k)+Q(x_k))\notag\\ &\leq\tfrac{1}{4}(2e^{2\gamma\varepsilon^{{2}/({\alpha-\delta})}}+1)Q(x_k)\notag\\ &\leq Q(x_k) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|\!\exp_{x_k}^{-1}f^k(y)\|&\leq\tfrac{1}{4}(2Q(y_k)+Q(x_k))\notag\\ &\leq\tfrac{1}{4}(2e^{2\gamma\varepsilon^{{2}/({\alpha-\delta})}}+1)Q(x_k)\notag\\ &\leq Q(x_k) \end{aligned} \end{align*} $$
if k is large enough and
![]() $0<\varepsilon \leq (({\log 3-\log 2})/{2\gamma })^{({\alpha -\delta })/{2}}$
.
$0<\varepsilon \leq (({\log 3-\log 2})/{2\gamma })^{({\alpha -\delta })/{2}}$
.
It is now obvious that the claim holds since we have assumed as in [Reference Chen, Hu and Zhou10] that the metric on M is taken in such a way that for any
![]() $x\in O$
,
$x\in O$
,
![]() $E^u(x)$
and
$E^u(x)$
and
![]() $E^s(x)$
are pairwise orthogonal, we thus prove
$E^s(x)$
are pairwise orthogonal, we thus prove
for all k large enough.
Claim 3.
![]() $V^{s}(\underline {x}^+)=V^{s}(\underline {y}^+)$
.
$V^{s}(\underline {x}^+)=V^{s}(\underline {y}^+)$
.
Proof of Claim 3
The proof of this claim is made exactly as in [Reference Ben Ovadia6, Claim 3 on p. 102] by using Claims 1 and 2.
This completes the proof of Proposition 6.1.
Definition 6.2. Suppose
![]() $Z=Z(z)\in \mathscr {Z}$
. For any
$Z=Z(z)\in \mathscr {Z}$
. For any
![]() $x \in Z$
, the local unstable manifold through x is defined by
$x \in Z$
, the local unstable manifold through x is defined by
![]() $V^u(x,Z):=V^{u}(\underline {x}^-)$
for some (any)
$V^u(x,Z):=V^{u}(\underline {x}^-)$
for some (any)
![]() $\underline {x}=\{x_{n}\}_{n \in \mathbb {Z}} \in \Sigma ^{\#}$
such that
$\underline {x}=\{x_{n}\}_{n \in \mathbb {Z}} \in \Sigma ^{\#}$
such that
![]() $\pi (\underline {x})=x$
and
$\pi (\underline {x})=x$
and
![]() $x_{0}=z$
. Similarly, the local stable manifold through x is defined by
$x_{0}=z$
. Similarly, the local stable manifold through x is defined by
![]() $V^s(x,Z):=V^{s}(\underline {x}^+)$
for some (any)
$V^s(x,Z):=V^{s}(\underline {x}^+)$
for some (any)
![]() $\underline {x}=\{x_{n}\}_{n \in \mathbb {Z}} \in \Sigma ^{\#}$
such that
$\underline {x}=\{x_{n}\}_{n \in \mathbb {Z}} \in \Sigma ^{\#}$
such that
![]() $\pi (\underline {x})=x$
and
$\pi (\underline {x})=x$
and
![]() $x_{0}=z$
.
$x_{0}=z$
.
By Proposition 6.1, the definitions above do not depend on the choice of
![]() $\underline {x}$
. Since
$\underline {x}$
. Since
![]() $\bigcup _{Z\in \mathscr {Z}}Z=O^{\#}$
, we only construct locally unstable/stable manifolds on
$\bigcup _{Z\in \mathscr {Z}}Z=O^{\#}$
, we only construct locally unstable/stable manifolds on
![]() $O^{\#}$
rather than O as done in [Reference Chen, Hu and Zhou10].
$O^{\#}$
rather than O as done in [Reference Chen, Hu and Zhou10].
Theorem 6.1. For every
![]() $Z\in \mathscr {Z}$
,
$Z\in \mathscr {Z}$
,
![]() $|\{Z^\prime \in \mathscr {Z}: Z^\prime \cap Z\neq \varnothing \}|<\infty $
.
$|\{Z^\prime \in \mathscr {Z}: Z^\prime \cap Z\neq \varnothing \}|<\infty $
.
Proof. Fix some
![]() $Z=Z(z)\in \mathscr {Z}$
. If
$Z=Z(z)\in \mathscr {Z}$
. If
![]() $Z^\prime =Z^\prime (z^\prime )$
intersects Z, then there must exist two
$Z^\prime =Z^\prime (z^\prime )$
intersects Z, then there must exist two
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x},\underline {y}\in \Sigma ^{\#}$
such that
$\underline {x},\underline {y}\in \Sigma ^{\#}$
such that
![]() $x_0=z$
,
$x_0=z$
,
![]() $y_0=z^\prime $
, and
$y_0=z^\prime $
, and
![]() $\pi (\underline {x})=\pi (\underline {y})$
. From equation (6.1), we have
$\pi (\underline {x})=\pi (\underline {y})$
. From equation (6.1), we have
It follows that
![]() $Z^\prime $
belongs to
$Z^\prime $
belongs to
![]() $\{Z^\prime (z^\prime ):z^\prime \in \mathscr {A}, d(z^\prime ,\partial O)\geq e^{-2\varepsilon ^{{2}/({\alpha -\delta })}}d(z,\partial O)\}$
. This set is finite because of the discreteness of
$\{Z^\prime (z^\prime ):z^\prime \in \mathscr {A}, d(z^\prime ,\partial O)\geq e^{-2\varepsilon ^{{2}/({\alpha -\delta })}}d(z,\partial O)\}$
. This set is finite because of the discreteness of
![]() $\mathscr {A}$
(Proposition 5.1(1)).
$\mathscr {A}$
(Proposition 5.1(1)).
Proposition 6.2. Suppose
![]() $Z \in \mathscr {Z}$
, then for any
$Z \in \mathscr {Z}$
, then for any
![]() $x, y \in Z, V^{u}(x, Z)$
and
$x, y \in Z, V^{u}(x, Z)$
and
![]() $V^{s}(y, Z)$
intersect at a unique point z, and
$V^{s}(y, Z)$
intersect at a unique point z, and
![]() $z \in Z$
.
$z \in Z$
.
Proof. It follows from Proposition 4.1(1), proved as in [Reference Sarig22, Proposition 10.5].
Definition 6.3. The Smale bracket of two points
![]() $x, y \in Z \in \mathscr {Z}$
is the unique point
$x, y \in Z \in \mathscr {Z}$
is the unique point
![]() $[x, y]_{Z} \in V^{u}(x, Z) \cap V^{s}(y, Z)$
.
$[x, y]_{Z} \in V^{u}(x, Z) \cap V^{s}(y, Z)$
.
Lemma 6.1. If
![]() $x,y\in Z\in \mathscr {Z}$
, then
$x,y\in Z\in \mathscr {Z}$
, then
Proof. Write
![]() $Z=Z(z)$
where
$Z=Z(z)$
where
![]() $z\in \mathscr {A}$
. There are two
$z\in \mathscr {A}$
. There are two
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x},\underline {y}\in \Sigma ^{\#}$
such that
$\underline {x},\underline {y}\in \Sigma ^{\#}$
such that
![]() $x_0=y_0=z$
,
$x_0=y_0=z$
,
![]() $\pi (\underline {x})=x, \pi (\underline {y})=y$
, and so that
$\pi (\underline {x})=x, \pi (\underline {y})=y$
, and so that
It holds that
![]() $\{[x,y]_Z\}=V^u(\underline {x}^-)\cap V^s(\underline {y}^+)=\{\pi (\underline {z})\}\subset Z(z)$
, where
$\{[x,y]_Z\}=V^u(\underline {x}^-)\cap V^s(\underline {y}^+)=\{\pi (\underline {z})\}\subset Z(z)$
, where
![]() $z_0=z$
, and
$z_0=z$
, and
 $$ \begin{align*} z_n=\begin{cases} x_n, & n \leq 0, \\ y_n, & n\geq0, \end{cases}\in\Sigma^{\#}. \end{align*} $$
$$ \begin{align*} z_n=\begin{cases} x_n, & n \leq 0, \\ y_n, & n\geq0, \end{cases}\in\Sigma^{\#}. \end{align*} $$
By Definition 6.2,
and
Lemma 6.2. Suppose
![]() $x, y \in Z(z_{0})$
, and
$x, y \in Z(z_{0})$
, and
![]() $f(x), f(y) \in Z(z_{1})$
. If
$f(x), f(y) \in Z(z_{1})$
. If
![]() $z_{0} \rightarrow z_{1}$
, then
$z_{0} \rightarrow z_{1}$
, then
![]() $f([x, y]_{Z(z_{0})})=[f(x), f(y)]_{Z(z_{1})}$
.
$f([x, y]_{Z(z_{0})})=[f(x), f(y)]_{Z(z_{1})}$
.
Despite the definition of staying in window [Reference Sarig22, Definitions 6.1 and 6.2] and the conclusion that any two local stable manifolds either coincide or are disjoint [Reference Sarig22, Proposition 6.4], which are used in the proof of Lemma 6.2 above in [Reference Sarig22, Lemma 10.7], we can still circumvent the problem just by using the weaker Proposition 6.1 above to prove the conclusion, and we will see that this conclusion is just from the Markov structure of
![]() $\Sigma ^{\#}$
.
$\Sigma ^{\#}$
.
Proof. Compared with the proof of [Reference Sarig22, Lemma 10.7], the difference is in the proof of
![]() $f[V^s(y,Z(z_0))]\subset V^s(f(y),Z(z_1))$
and
$f[V^s(y,Z(z_0))]\subset V^s(f(y),Z(z_1))$
and
![]() $f[V^u(x,Z(z_0))]\supset V^u(f(x),Z(z_1))$
. We give the details of the first half, the other half is proved in the same way.
$f[V^u(x,Z(z_0))]\supset V^u(f(x),Z(z_1))$
. We give the details of the first half, the other half is proved in the same way.
Since
![]() $V^s_{z_1}:=V^s(f(y),Z(z_1))=V^s(\{x_{n+1}\}_{n\geq 0})$
for any
$V^s_{z_1}:=V^s(f(y),Z(z_1))=V^s(\{x_{n+1}\}_{n\geq 0})$
for any
![]() $\{x_{n+1}\}_{n\geq 0}\in \Sigma ^{\#}$
such that
$\{x_{n+1}\}_{n\geq 0}\in \Sigma ^{\#}$
such that
![]() $x_0=z_0$
,
$x_0=z_0$
,
![]() $x_1=z_1$
, and
$x_1=z_1$
, and
![]() $\pi (\{x_{n+1}\}_{n\in \mathbb {Z}})=f(y)$
, it is an s-admissible manifold at
$\pi (\{x_{n+1}\}_{n\in \mathbb {Z}})=f(y)$
, it is an s-admissible manifold at
![]() $z_1$
. By Definition 4.4,
$z_1$
. By Definition 4.4,
![]() $\mathscr {F}_{z_0,z_1}^s[V^s_{z_1}]$
is the unique s-admissible manifold at
$\mathscr {F}_{z_0,z_1}^s[V^s_{z_1}]$
is the unique s-admissible manifold at
![]() $z_0$
contained in
$z_0$
contained in
![]() $f^{-1}(V^s_{z_1})$
, and thus our problem reduces to prove
$f^{-1}(V^s_{z_1})$
, and thus our problem reduces to prove
![]() $V^s(y,Z(z_0))=\mathscr {F}_{z_0,z_1}^s[V^s_{z_1}]$
.
$V^s(y,Z(z_0))=\mathscr {F}_{z_0,z_1}^s[V^s_{z_1}]$
.
According to Theorem 5.1(1) and (2),
![]() $\mathscr {F}_{z_0,z_1}^s[V^s_{z_1}]=V^s(\{x_{n}\}_{n\geq 0})$
, where
$\mathscr {F}_{z_0,z_1}^s[V^s_{z_1}]=V^s(\{x_{n}\}_{n\geq 0})$
, where
![]() $x_0=z_0$
and
$x_0=z_0$
and
![]() $\pi (\{x_{n}\}_{n\in \mathbb {Z}})=y$
since the shadowing point is unique. Notice that
$\pi (\{x_{n}\}_{n\in \mathbb {Z}})=y$
since the shadowing point is unique. Notice that
![]() $V^s(y,Z(z_0))=V^s(\{y_{n}\}_{n\geq 0})$
for any
$V^s(y,Z(z_0))=V^s(\{y_{n}\}_{n\geq 0})$
for any
![]() $\{y_{n}\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
such that
$\{y_{n}\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
such that
![]() $y_0=z_0$
, and
$y_0=z_0$
, and
![]() $\pi (\{y_{n}\}_{n\in \mathbb {Z}})=y$
, from Proposition 6.1, so we have
$\pi (\{y_{n}\}_{n\in \mathbb {Z}})=y$
, from Proposition 6.1, so we have
![]() $V^s(y,Z(z_0))=V^s(\{y_{n}\}_{n\geq 0})=V^s(\{x_{n}\}_{n\geq 0})=\mathscr {F}_{z_0,z_1}^s[V^s_{z_1}]$
.
$V^s(y,Z(z_0))=V^s(\{y_{n}\}_{n\geq 0})=V^s(\{x_{n}\}_{n\geq 0})=\mathscr {F}_{z_0,z_1}^s[V^s_{z_1}]$
.
Definition 6.4. For any
![]() $x\in Z\in \mathscr {Z}$
, the u-fiber of x inside Z is defined as
$x\in Z\in \mathscr {Z}$
, the u-fiber of x inside Z is defined as
![]() $W^{u}(x, Z):=V^u(x,Z)\cap Z$
, and the s-fiber of x inside Z is defined as
$W^{u}(x, Z):=V^u(x,Z)\cap Z$
, and the s-fiber of x inside Z is defined as
![]() $W^{s}(x, Z):=V^s(x,Z)\cap Z$
.
$W^{s}(x, Z):=V^s(x,Z)\cap Z$
.
Obviously, since
![]() $V^{u}(x, Z)\cap V^{s}(y, Z)\subset Z$
, Proposition 6.2 and Lemma 6.1 hold for an
$V^{u}(x, Z)\cap V^{s}(y, Z)\subset Z$
, Proposition 6.2 and Lemma 6.1 hold for an
![]() $u/s$
-fiber also, that is,
$u/s$
-fiber also, that is,
![]() $W^{u}(x, Z)\cap W^{s}(y, Z)=V^{u}(x, Z)\cap V^{s}(y, Z)$
, and
$W^{u}(x, Z)\cap W^{s}(y, Z)=V^{u}(x, Z)\cap V^{s}(y, Z)$
, and
if
![]() $x,y\in Z\in \mathscr {Z}$
.
$x,y\in Z\in \mathscr {Z}$
.
Proposition 6.3. Suppose
![]() $Z\in \mathscr {Z}$
. For any
$Z\in \mathscr {Z}$
. For any
![]() $x,y\in Z$
,
$x,y\in Z$
,
![]() $W^{u}(x, Z)$
and
$W^{u}(x, Z)$
and
![]() $W^{u}(y, Z)$
are either equal or they are disjoint. Similarly for
$W^{u}(y, Z)$
are either equal or they are disjoint. Similarly for
![]() $W^{s}(x, Z)$
and
$W^{s}(x, Z)$
and
![]() $W^{s}(y, Z)$
.
$W^{s}(y, Z)$
.
Proof. We prove the proposition for a u-fiber and leave the case of an s-fiber to the reader.
For any
![]() $x,y\in Z$
, assume that
$x,y\in Z$
, assume that
![]() $W^{u}(x, Z)\cap W^{u}(y, Z)\neq \varnothing $
. Let
$W^{u}(x, Z)\cap W^{u}(y, Z)\neq \varnothing $
. Let
![]() $z\in W^{u}(x, Z)\cap W^{u}(y, Z)\subset Z$
. Since
$z\in W^{u}(x, Z)\cap W^{u}(y, Z)\subset Z$
. Since
![]() $x,z\in Z$
,
$x,z\in Z$
,
![]() $\{[x,z]_Z\}$
is well defined and equal to
$\{[x,z]_Z\}$
is well defined and equal to
![]() $W^{u}(x, Z)\cap W^{s}(z, Z)$
, notice that
$W^{u}(x, Z)\cap W^{s}(z, Z)$
, notice that
![]() $z\in W^{u}(x, Z)\cap W^{s}(z, Z)$
, and thus
$z\in W^{u}(x, Z)\cap W^{s}(z, Z)$
, and thus
By Lemma 6.1, we have
![]() $W^{u}(z, Z)=W^{u}([x,z]_Z, Z)=W^{u}(x, Z)$
.
$W^{u}(z, Z)=W^{u}([x,z]_Z, Z)=W^{u}(x, Z)$
.
Similarly,
![]() $W^{u}(z, Z)=W^{u}(y, Z)$
. Hence,
$W^{u}(z, Z)=W^{u}(y, Z)$
. Hence,
![]() $W^{u}(x, Z)=W^{u}(y, Z)$
.
$W^{u}(x, Z)=W^{u}(y, Z)$
.
The following proposition states the symbolic Markov property of a
![]() $u/s$
-fiber, which also follows from the Markov structure of
$u/s$
-fiber, which also follows from the Markov structure of
![]() $\Sigma ^{\#}$
.
$\Sigma ^{\#}$
.
Proposition 6.4. If
![]() $x=\pi (\underline {x})$
where
$x=\pi (\underline {x})$
where
![]() $\underline {x}=\{x_{n}\}_{n \in \mathbb {Z}} \in \Sigma ^{\#}$
, then
$\underline {x}=\{x_{n}\}_{n \in \mathbb {Z}} \in \Sigma ^{\#}$
, then
Proof. The proof is the same as in [Reference Sarig22, Proposition 10.9]. We prove the inclusion for the s-fiber. The case of the u-fiber follows by symmetry.
By Definitions 6.4 and 6.2,
![]() $W^{s}(x, Z(x_{0})) \subset V^{s}(x, Z(x_{0})) = V^{s}(\{x_{n}\}_{n \geq 0})$
. Using Proposition 5.2(2), we have
$W^{s}(x, Z(x_{0})) \subset V^{s}(x, Z(x_{0})) = V^{s}(\{x_{n}\}_{n \geq 0})$
. Using Proposition 5.2(2), we have
the last manifold is equal to
![]() $V^{s}(f(x), Z(x_{1}))$
since
$V^{s}(f(x), Z(x_{1}))$
since
![]() $\{x_{n+1}\}_{n \geq 0}\in \Sigma ^{\#}$
satisfies
$\{x_{n+1}\}_{n \geq 0}\in \Sigma ^{\#}$
satisfies
![]() $x_{0+1}=x_1$
and
$x_{0+1}=x_1$
and
Therefore,
![]() $f[W^{s}(x, Z(x_{0}))] \subset V^{s}(f(x), Z(x_{1}))$
.
$f[W^{s}(x, Z(x_{0}))] \subset V^{s}(f(x), Z(x_{1}))$
.
Suppose
![]() $y\in W^{s}(x, Z(x_{0}))$
. Since
$y\in W^{s}(x, Z(x_{0}))$
. Since
![]() $y\in Z(x_{0})$
, there exists an
$y\in Z(x_{0})$
, there exists an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {y}\in \Sigma ^{\#}$
such that
$\underline {y}\in \Sigma ^{\#}$
such that
![]() $y_0=x_0$
and
$y_0=x_0$
and
![]() $\pi (\underline {y})=y$
. From
$\pi (\underline {y})=y$
. From
![]() $y,x\in Z(x_{0})$
, we know that
$y,x\in Z(x_{0})$
, we know that
![]() $\{[y,x]_{Z(x_0)}\}$
is well defined and equal to
$\{[y,x]_{Z(x_0)}\}$
is well defined and equal to
![]() $V^u(\underline {y}^-)\cap V^s(\underline {x}^+)$
. However,
$V^u(\underline {y}^-)\cap V^s(\underline {x}^+)$
. However,
![]() $y\in V^{s}(x, Z(x_0))=V^{s}(\underline {x}^+)$
and
$y\in V^{s}(x, Z(x_0))=V^{s}(\underline {x}^+)$
and
![]() $y=\pi (\underline {y})$
implies that
$y=\pi (\underline {y})$
implies that
![]() $y\in V^u(\underline {y}^-)\cap V^s(\underline {x}^+)$
, and thus
$y\in V^u(\underline {y}^-)\cap V^s(\underline {x}^+)$
, and thus
where
![]() $z_0=x_0$
, and
$z_0=x_0$
, and
 $$ \begin{align*} z_n=\begin{cases} y_n, & n \leq 0, \\ x_n, & n\geq0, \end{cases}\in\Sigma^{\#}. \end{align*} $$
$$ \begin{align*} z_n=\begin{cases} y_n, & n \leq 0, \\ x_n, & n\geq0, \end{cases}\in\Sigma^{\#}. \end{align*} $$
Therefore,
![]() $f(y)\in Z(x_1)$
since
$f(y)\in Z(x_1)$
since
![]() $\{z_{n+1}\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
satisfies
$\{z_{n+1}\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
satisfies
![]() $z_{0+1}=z_1=x_1$
and
$z_{0+1}=z_1=x_1$
and
Lemma 6.3. Suppose
![]() $Z,Z^{\prime }\in \mathscr {Z}$
and
$Z,Z^{\prime }\in \mathscr {Z}$
and
![]() $Z\cap Z^{\prime }\neq \varnothing $
.
$Z\cap Z^{\prime }\neq \varnothing $
.
-
(1) If
 $Z=Z(z)$
and
$Z=Z(z)$
and
 $Z^{\prime }=Z^{\prime }(z^{\prime })$
, where
$Z^{\prime }=Z^{\prime }(z^{\prime })$
, where
 $z,z^{\prime }\in \mathscr {A}$
, then
$z,z^{\prime }\in \mathscr {A}$
, then
 $Z\subset \exp _{z^{\prime }}(S_{z^{\prime }})$
.
$Z\subset \exp _{z^{\prime }}(S_{z^{\prime }})$
. -
(2) For any
 $x\in Z\cap Z^{\prime }$
,
$x\in Z\cap Z^{\prime }$
,
 $W^u(x,Z)\subset V^u(x,Z^{\prime })$
and
$W^u(x,Z)\subset V^u(x,Z^{\prime })$
and
 $W^s(x,Z)\subset V^s(x,Z^{\prime })$
.
$W^s(x,Z)\subset V^s(x,Z^{\prime })$
.
Proof. We follow a similar strategy in [Reference Sarig22, Lemma 10.10].
(1) Note that by Proposition 4.1(1),
 $$ \begin{align*} \begin{aligned} Z(z)\subset\exp_z\bigg(T_zM\bigg(\frac{2}{50}Q(z)\bigg)\bigg)\subset B\bigg(z,\frac{4}{50}Q(z)\bigg)\subset B\bigg(z^{\prime},\frac{4}{50}Q(z)+d(z,z^{\prime})\bigg). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} Z(z)\subset\exp_z\bigg(T_zM\bigg(\frac{2}{50}Q(z)\bigg)\bigg)\subset B\bigg(z,\frac{4}{50}Q(z)\bigg)\subset B\bigg(z^{\prime},\frac{4}{50}Q(z)+d(z,z^{\prime})\bigg). \end{aligned} \end{align*} $$
Fix some
![]() $x\in Z\cap Z^\prime \subset O$
, so from equation (6.2), we have
$x\in Z\cap Z^\prime \subset O$
, so from equation (6.2), we have
and
 $$ \begin{align*} \begin{aligned} \frac{4}{50}Q(z)+d(z,z')&\leq\frac{5}{50}Q(z)+\frac{1}{50}Q(z^{\prime})\notag\\ &\leq\bigg(\frac{5}{50}e^{2\gamma\varepsilon^{{2}/({\alpha-\delta})}}+\frac{1}{50}\bigg)Q(z^{\prime})\notag\\ &\leq\frac{16}{50}Q(z^{\prime}) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{4}{50}Q(z)+d(z,z')&\leq\frac{5}{50}Q(z)+\frac{1}{50}Q(z^{\prime})\notag\\ &\leq\bigg(\frac{5}{50}e^{2\gamma\varepsilon^{{2}/({\alpha-\delta})}}+\frac{1}{50}\bigg)Q(z^{\prime})\notag\\ &\leq\frac{16}{50}Q(z^{\prime}) \end{aligned} \end{align*} $$
if
![]() $0<\varepsilon \leq ({\log 3}/{2\gamma })^{({\alpha -\delta })/{2}}$
.
$0<\varepsilon \leq ({\log 3}/{2\gamma })^{({\alpha -\delta })/{2}}$
.
Therefore,
 $$ \begin{align*} Z(z)\subset B\bigg(z^{\prime},\frac{4}{50}Q(z)+d(z,z^{\prime})\bigg)\subset B\bigg(z^{\prime},\frac{8}{25}Q(z^{\prime})\bigg)\subset\exp_{z^{\prime}}(S_{z^{\prime}}). \end{align*} $$
$$ \begin{align*} Z(z)\subset B\bigg(z^{\prime},\frac{4}{50}Q(z)+d(z,z^{\prime})\bigg)\subset B\bigg(z^{\prime},\frac{8}{25}Q(z^{\prime})\bigg)\subset\exp_{z^{\prime}}(S_{z^{\prime}}). \end{align*} $$
(2) We show that
![]() $W^{s}(x, Z) \subset V^{s}(x, Z^{\prime })$
. The case of the u-direction follows by symmetry.
$W^{s}(x, Z) \subset V^{s}(x, Z^{\prime })$
. The case of the u-direction follows by symmetry.
Since
![]() $x\in Z(z)\cap Z^\prime (z^\prime )$
, we can write
$x\in Z(z)\cap Z^\prime (z^\prime )$
, we can write
![]() $x=\pi (\underline {x})$
where
$x=\pi (\underline {x})$
where
![]() $\underline {x}\in \Sigma ^{\#}$
,
$\underline {x}\in \Sigma ^{\#}$
,
![]() $x_0=z$
, and
$x_0=z$
, and
![]() $x=\pi (\underline {y})$
, where
$x=\pi (\underline {y})$
, where
![]() $\underline {y}\in \Sigma ^{\#}$
,
$\underline {y}\in \Sigma ^{\#}$
,
![]() $y_0=z^\prime $
. Observe that for all
$y_0=z^\prime $
. Observe that for all
![]() $k\in \mathbb {Z}$
,
$k\in \mathbb {Z}$
,
![]() $f^{k}(x)=f^k(\pi (\underline {x}))=\pi (\sigma ^k(\underline {x}))\in Z(x_{k})$
, we have
$f^{k}(x)=f^k(\pi (\underline {x}))=\pi (\sigma ^k(\underline {x}))\in Z(x_{k})$
, we have
![]() $f^{k}(x)\in Z(x_{k})$
. Similarly, since
$f^{k}(x)\in Z(x_{k})$
. Similarly, since
![]() $f^{k}(x)=f^k(\pi (\underline {y}))=\pi (\sigma ^k(\underline {y}))\in Z^\prime (y_{k})$
, we have
$f^{k}(x)=f^k(\pi (\underline {y}))=\pi (\sigma ^k(\underline {y}))\in Z^\prime (y_{k})$
, we have
![]() $f^{k}(x)\in Z^\prime (y_{k})$
, and hence
$f^{k}(x)\in Z^\prime (y_{k})$
, and hence
![]() $f^{k}(x)\in Z(x_{k})\cap Z^\prime (y_{k})$
. By the first part of the lemma,
$f^{k}(x)\in Z(x_{k})\cap Z^\prime (y_{k})$
. By the first part of the lemma,
![]() $Z(x_{k}) \subset \exp _{y_{k}}(S_{y_k})$
.
$Z(x_{k}) \subset \exp _{y_{k}}(S_{y_k})$
.
Since
![]() $x=\pi (\underline {x})$
and
$x=\pi (\underline {x})$
and
![]() $Z(z)=Z(x_0)$
, we have by the symbolic Markov property of an s-fiber iterated forward k times
$Z(z)=Z(x_0)$
, we have by the symbolic Markov property of an s-fiber iterated forward k times
for all
![]() $k \geq 0$
. By Proposition 5.2(4),
$k \geq 0$
. By Proposition 5.2(4),
![]() $W^{s}(x, Z) \subset V^{s}(\underline {y}^+) = V^{s}(x, Z^{\prime })$
.
$W^{s}(x, Z) \subset V^{s}(\underline {y}^+) = V^{s}(x, Z^{\prime })$
.
The next step to do in the construction of a Markov partition is to refine
![]() $\mathscr {Z}$
to destroy its non-trivial intersections. The result will be a partition of
$\mathscr {Z}$
to destroy its non-trivial intersections. The result will be a partition of
![]() $O^{\#}$
by sets with the (geometrical) Markov property. This method is the so called Bowen–Sinai refinement procedure, first developed by Sinai and Bowen for finite covers [Reference Bowen8, Reference Sinai23, Reference Sinai24], and also works for countable covers satisfying the local finiteness property [Reference Sarig22, §11].
$O^{\#}$
by sets with the (geometrical) Markov property. This method is the so called Bowen–Sinai refinement procedure, first developed by Sinai and Bowen for finite covers [Reference Bowen8, Reference Sinai23, Reference Sinai24], and also works for countable covers satisfying the local finiteness property [Reference Sarig22, §11].
Write
![]() $\mathscr {Z}=\{Z_1,Z_2,\ldots \}$
. Following [Reference Bowen8, Reference Sarig22], we define a partition of
$\mathscr {Z}=\{Z_1,Z_2,\ldots \}$
. Following [Reference Bowen8, Reference Sarig22], we define a partition of
![]() $Z_{i}$
such that for every
$Z_{i}$
such that for every
![]() $Z_{i}, Z_{j} \in \mathscr {Z}$
,
$Z_{i}, Z_{j} \in \mathscr {Z}$
,
 $$ \begin{align*} \begin{aligned} T_{i j}^{u s} &:=\{x \in Z_{i}: W^{u}(x, Z_{i}) \cap Z_{j} \neq \varnothing, W^{s}(x, Z_{i}) \cap Z_{j} \neq \varnothing\}, \\ T_{i j}^{u \varnothing}&: =\{x \in Z_{i}: W^{u}(x, Z_{i}) \cap Z_{j} \neq \varnothing, W^{s}(x, Z_{i}) \cap Z_{j}=\varnothing\}, \\ T_{i j}^{\varnothing s}&: =\{x \in Z_{i}: W^{u}(x, Z_{i}) \cap Z_{j}=\varnothing, W^{s}(x, Z_{i}) \cap Z_{j} \neq \varnothing\}, \\ T_{i j}^{\varnothing \varnothing}&: =\{x \in Z_{i}: W^{u}(x, Z_{i}) \cap Z_{j}=\varnothing, W^{s}(x, Z_{i}) \cap Z_{j}=\varnothing\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} T_{i j}^{u s} &:=\{x \in Z_{i}: W^{u}(x, Z_{i}) \cap Z_{j} \neq \varnothing, W^{s}(x, Z_{i}) \cap Z_{j} \neq \varnothing\}, \\ T_{i j}^{u \varnothing}&: =\{x \in Z_{i}: W^{u}(x, Z_{i}) \cap Z_{j} \neq \varnothing, W^{s}(x, Z_{i}) \cap Z_{j}=\varnothing\}, \\ T_{i j}^{\varnothing s}&: =\{x \in Z_{i}: W^{u}(x, Z_{i}) \cap Z_{j}=\varnothing, W^{s}(x, Z_{i}) \cap Z_{j} \neq \varnothing\}, \\ T_{i j}^{\varnothing \varnothing}&: =\{x \in Z_{i}: W^{u}(x, Z_{i}) \cap Z_{j}=\varnothing, W^{s}(x, Z_{i}) \cap Z_{j}=\varnothing\}. \end{aligned} \end{align*} $$
Let
![]() $\mathscr {T}:=\{T_{i j}^{\alpha \beta }: i, j \in \mathbb {N}, Z_{i} \cap Z_{j} \neq \varnothing , \alpha \in \{u, \varnothing \}, \beta \in \{s, \varnothing \}\}$
.
$\mathscr {T}:=\{T_{i j}^{\alpha \beta }: i, j \in \mathbb {N}, Z_{i} \cap Z_{j} \neq \varnothing , \alpha \in \{u, \varnothing \}, \beta \in \{s, \varnothing \}\}$
.
Clearly,
![]() $T_{i i}^{u s}=Z_{i}$
; therefore,
$T_{i i}^{u s}=Z_{i}$
; therefore,
![]() $\mathscr {T}$
covers the same set as
$\mathscr {T}$
covers the same set as
![]() $\mathscr {Z}$
, namely
$\mathscr {Z}$
, namely
![]() $\pi (\Sigma ^{\#})=O^{\#}$
. Using Proposition 6.3 and Lemma 6.3(2) above, we prove that
$\pi (\Sigma ^{\#})=O^{\#}$
. Using Proposition 6.3 and Lemma 6.3(2) above, we prove that
![]() $T_{i j}^{u s}=Z_{i} \cap Z_{j}$
as in [Reference Sarig22, p. 386].
$T_{i j}^{u s}=Z_{i} \cap Z_{j}$
as in [Reference Sarig22, p. 386].
Definition 6.5. For every
![]() $x\in \pi (\Sigma ^{\#})=O^{\#}$
, let
$x\in \pi (\Sigma ^{\#})=O^{\#}$
, let
 $R(x):=\underset {{\substack {T \in \mathscr {T} \\ x\in T}}}{\bigcap T}$
and set
$R(x):=\underset {{\substack {T \in \mathscr {T} \\ x\in T}}}{\bigcap T}$
and set
![]() $\mathscr {R}:=\{R(x): x\in O^{\#}\}$
.
$\mathscr {R}:=\{R(x): x\in O^{\#}\}$
.
Proposition 6.5.
![]() $\mathscr {R}$
is a countable pairwise disjoint cover of
$\mathscr {R}$
is a countable pairwise disjoint cover of
![]() $O^{\#}$
.
$O^{\#}$
.
An outline of the proof of this proposition is as follows, the details of which we omit. Proceeding as in [Reference Sarig22, Proposition 11.2], first, from the locally finite property of
![]() $\mathscr {Z}$
(Theorem 6.1),
$\mathscr {Z}$
(Theorem 6.1),
![]() $R(x)$
is a finite intersection of elements of
$R(x)$
is a finite intersection of elements of
![]() $\mathscr {T}$
, that is, for every
$\mathscr {T}$
, that is, for every
![]() $R\in \mathscr {R}$
,
$R\in \mathscr {R}$
,
![]() $|\{Z\in \mathscr {Z}:Z\supset R\}|<\infty $
. Second, since
$|\{Z\in \mathscr {Z}:Z\supset R\}|<\infty $
. Second, since
![]() $\mathscr {T}$
is countable and the fact that
$\mathscr {T}$
is countable and the fact that
![]() $T_{i i}^{u s}=Z_{i}$
, we conclude that
$T_{i i}^{u s}=Z_{i}$
, we conclude that
![]() $\mathscr {R}$
is a countable cover of
$\mathscr {R}$
is a countable cover of
![]() $O^{\#}$
, that is,
$O^{\#}$
, that is,
![]() $\underset {R\in \mathscr {R}}\bigcup R=O^{\#}$
. Moreover, it is a countable pairwise disjoint cover of
$\underset {R\in \mathscr {R}}\bigcup R=O^{\#}$
. Moreover, it is a countable pairwise disjoint cover of
![]() $O^{\#}$
. The key point to destroy the non-trivial intersection is to prove that
$O^{\#}$
. The key point to destroy the non-trivial intersection is to prove that
![]() $R(x)$
is the equivalence class of x for the following equivalence relation on
$R(x)$
is the equivalence class of x for the following equivalence relation on
![]() $O^{\#}$
: for every
$O^{\#}$
: for every
![]() $x, y\in O^{\#}$
, define
$x, y\in O^{\#}$
, define
 $$ \begin{align*} x \sim y \text { if and only if } \text{ for all } Z, Z^{\prime} \in \mathscr{Z}, \quad\left(\begin{array}{@{}rll@{}} x \in Z & \Leftrightarrow & y \in Z, \\ W^{u}(x, Z) \cap Z^{\prime} \neq \varnothing & \Leftrightarrow & W^{u}(y, Z) \cap Z^{\prime} \neq \varnothing, \\ W^{s}(x, Z) \cap Z^{\prime} \neq \varnothing & \Leftrightarrow & W^{s}(y, Z) \cap Z^{\prime} \neq \varnothing \end{array}\right)\!. \end{align*} $$
$$ \begin{align*} x \sim y \text { if and only if } \text{ for all } Z, Z^{\prime} \in \mathscr{Z}, \quad\left(\begin{array}{@{}rll@{}} x \in Z & \Leftrightarrow & y \in Z, \\ W^{u}(x, Z) \cap Z^{\prime} \neq \varnothing & \Leftrightarrow & W^{u}(y, Z) \cap Z^{\prime} \neq \varnothing, \\ W^{s}(x, Z) \cap Z^{\prime} \neq \varnothing & \Leftrightarrow & W^{s}(y, Z) \cap Z^{\prime} \neq \varnothing \end{array}\right)\!. \end{align*} $$
So for every
![]() $x, y \in \underset {R\in \mathscr {R}}\bigcup R=O^{\#}$
, either
$x, y \in \underset {R\in \mathscr {R}}\bigcup R=O^{\#}$
, either
![]() $R(x)=R(y)$
or
$R(x)=R(y)$
or
![]() $R(x) \cap R(y)=\varnothing $
. Thus,
$R(x) \cap R(y)=\varnothing $
. Thus,
![]() $\mathscr {R}$
is a Bowen–Sinai refinement of
$\mathscr {R}$
is a Bowen–Sinai refinement of
![]() $\mathscr {Z}$
. For more details, see [Reference Sarig22, Proposition 11.2].
$\mathscr {Z}$
. For more details, see [Reference Sarig22, Proposition 11.2].
By Definition 6.5 and the local finiteness property of
![]() $\mathscr {Z}$
, the following inclusion relation and local finiteness properties for
$\mathscr {Z}$
, the following inclusion relation and local finiteness properties for
![]() $\mathscr {R}$
are proved exactly as in [Reference Sarig22, Lemma 11.3].
$\mathscr {R}$
are proved exactly as in [Reference Sarig22, Lemma 11.3].
Lemma 6.4.
![]() $\mathscr {R}$
is a locally finite refinement of
$\mathscr {R}$
is a locally finite refinement of
![]() $\mathscr {Z}$
:
$\mathscr {Z}$
:
-
(1) for every
 $R \in \mathscr {R}$
and
$R \in \mathscr {R}$
and
 $Z\in \mathscr {Z}$
, if
$Z\in \mathscr {Z}$
, if
 $R\cap Z\neq \varnothing $
, then
$R\cap Z\neq \varnothing $
, then
 $R\subset Z$
;
$R\subset Z$
; -
(2) for every
 $Z \in \mathscr {Z}, |\{R \in \mathscr {R}: R \subset Z\}|<\infty $
;
$Z \in \mathscr {Z}, |\{R \in \mathscr {R}: R \subset Z\}|<\infty $
; -
(3) for every
 $R\in \mathscr {R}$
,
$R\in \mathscr {R}$
,
 $|\{Z\in \mathscr {Z}:Z\supset R\}|<\infty $
.
$|\{Z\in \mathscr {Z}:Z\supset R\}|<\infty $
.
Now we follow [Reference Sarig22, §11] to show that
![]() $\mathscr {R}$
is a Markov partition in the sense of Sinai [Reference Sinai24].
$\mathscr {R}$
is a Markov partition in the sense of Sinai [Reference Sinai24].
Definition 6.6. For any
![]() $R \in \mathscr {R}$
and
$R \in \mathscr {R}$
and
![]() $x\in R$
, we define the u-fiber and s-fiber of
$x\in R$
, we define the u-fiber and s-fiber of
![]() $x \textit {inside }R$
respectively by
$x \textit {inside }R$
respectively by
 $$ \begin{align*} W^{u}(x, R):=\bigcap_{\substack{ T_{i j}^{\alpha \beta} \in \mathscr{T} \\ T_{i j}^{\alpha \beta} \supset R}} W^{u}(x, Z_{i}) \cap T_{i j}^{\alpha \beta}\quad \text{and}\quad W^{s}(x, R):=\bigcap_{\substack{T_{i j}^{\alpha \beta} \in \mathscr{T} \\ T_{i j}^{\alpha \beta} \supset R}} W^{s}(x, Z_{i}) \cap T_{i j}^{\alpha \beta}. \end{align*} $$
$$ \begin{align*} W^{u}(x, R):=\bigcap_{\substack{ T_{i j}^{\alpha \beta} \in \mathscr{T} \\ T_{i j}^{\alpha \beta} \supset R}} W^{u}(x, Z_{i}) \cap T_{i j}^{\alpha \beta}\quad \text{and}\quad W^{s}(x, R):=\bigcap_{\substack{T_{i j}^{\alpha \beta} \in \mathscr{T} \\ T_{i j}^{\alpha \beta} \supset R}} W^{s}(x, Z_{i}) \cap T_{i j}^{\alpha \beta}. \end{align*} $$
Proposition 6.3 implies that any two u-fibers (s-fibers) either coincide or are disjoint: suppose
![]() $R \in \mathscr {R}$
and
$R \in \mathscr {R}$
and
![]() $x,y\in R$
, either
$x,y\in R$
, either
![]() $W^{u}(x, R)$
,
$W^{u}(x, R)$
,
![]() $W^{u}(y, R)$
are equal or they are disjoint, and similarly for
$W^{u}(y, R)$
are equal or they are disjoint, and similarly for
![]() $W^{s}(x, R)$
and
$W^{s}(x, R)$
and
![]() $W^{s}(y, R)$
. The proof is straightforward as in [Reference Sarig22, Proposition 11.5(2)].
$W^{s}(y, R)$
. The proof is straightforward as in [Reference Sarig22, Proposition 11.5(2)].
Proposition 6.6. Suppose
![]() $R \in \mathscr {R}$
and
$R \in \mathscr {R}$
and
![]() $x,y\in R$
.
$x,y\in R$
.
-
(1)
 $W^u(x,R),W^s(x, R)\subset R$
and
$W^u(x,R),W^s(x, R)\subset R$
and
 $W^u(x,R)\cap W^s(x, R)={x}$
.
$W^u(x,R)\cap W^s(x, R)={x}$
. -
(2) The intersection
 $W^{u}(x, R) \cap W^{s}(y, R)$
consists of a single point and this point belongs to R. Denote it by
$W^{u}(x, R) \cap W^{s}(y, R)$
consists of a single point and this point belongs to R. Denote it by
 $[x, y]_{R}$
and call the Smale bracket of
$[x, y]_{R}$
and call the Smale bracket of
 $x,y$
in R.
$x,y$
in R. -
(3) Markov property: let
 $R_{0}, R_{1} \in \mathscr {R}$
. If
$R_{0}, R_{1} \in \mathscr {R}$
. If
 $x \in R_{0}$
and
$x \in R_{0}$
and
 $f(x) \in R_{1}$
, then
$f(x) \in R_{1}$
, then  $$ \begin{align*} f(W^{s}(x, R_{0})) \subset W^{s}(f(x), R_{1}) \quad\text{and}\quad f^{-1}(W^{u}(f(x), R_{1})) \subset W^{u}(x, R_{0}). \end{align*} $$
$$ \begin{align*} f(W^{s}(x, R_{0})) \subset W^{s}(f(x), R_{1}) \quad\text{and}\quad f^{-1}(W^{u}(f(x), R_{1})) \subset W^{u}(x, R_{0}). \end{align*} $$
Proof. Part (1) is proved exactly as in [Reference Sarig22, Proposition 11.5(1)]. Using Proposition 6.3, part (2) is a standard result which can be found in [Reference Sarig22, Proposition 11.5(3)]. Along the proof, we also obtain that
![]() $[x, y]_{R}=[x, y]_{Z}$
for every
$[x, y]_{R}=[x, y]_{Z}$
for every
![]() $x,y\in R$
and all
$x,y\in R$
and all
![]() $Z\in \mathscr {Z}$
containing R. Finally, part (3) is the heart to obtain a Markov partition which is proved as in [Reference Sarig22, Proposition 11.7], using Propositions 6.3, 6.4, and Lemmas 6.2, 6.3(2), and the equality
$Z\in \mathscr {Z}$
containing R. Finally, part (3) is the heart to obtain a Markov partition which is proved as in [Reference Sarig22, Proposition 11.7], using Propositions 6.3, 6.4, and Lemmas 6.2, 6.3(2), and the equality
![]() $[x, y]_{R}=[x, y]_{Z}$
holds for every
$[x, y]_{R}=[x, y]_{Z}$
holds for every
![]() $x,y\in R$
and every
$x,y\in R$
and every
![]() $Z\in \mathscr {Z}$
containing R.
$Z\in \mathscr {Z}$
containing R.
We now construct a new symbolic coding of f, which is a symbolic model of f generated by the Markov partition
![]() $\mathscr {R}$
that satisfies Theorem 2.1. Let
$\mathscr {R}$
that satisfies Theorem 2.1. Let
![]() $\widehat {\mathscr {G}}=(\widehat {V}, \widehat {E})$
be the directed graph with vertex set
$\widehat {\mathscr {G}}=(\widehat {V}, \widehat {E})$
be the directed graph with vertex set
![]() $\widehat {V}=\mathscr {R}$
and edge set
$\widehat {V}=\mathscr {R}$
and edge set
![]() $\widehat {E}=\{R_1 \rightarrow R_2: R_1, R_2 \in \mathscr {R}$
such that
$\widehat {E}=\{R_1 \rightarrow R_2: R_1, R_2 \in \mathscr {R}$
such that
![]() ${R_1 \cap f^{-1}R_2 \neq \varnothing \}}$
. This is also a countable directed graph, and every vertex has finite degree because for every
${R_1 \cap f^{-1}R_2 \neq \varnothing \}}$
. This is also a countable directed graph, and every vertex has finite degree because for every
![]() $R_0\in \mathscr {R}$
, if
$R_0\in \mathscr {R}$
, if
![]() $R_1\in \mathscr {R}$
satisfies
$R_1\in \mathscr {R}$
satisfies
![]() $R_0\rightarrow R_1$
, by Definition 6.5 and the local finiteness property (Lemma 6.4(3)) for
$R_0\rightarrow R_1$
, by Definition 6.5 and the local finiteness property (Lemma 6.4(3)) for
![]() $\mathscr {R}$
, there are finite points of
$\mathscr {R}$
, there are finite points of
![]() $\mathscr {A}$
, say z such that
$\mathscr {A}$
, say z such that
![]() ${R_0\subset Z(z)}$
. Since
${R_0\subset Z(z)}$
. Since
![]() $R_0\rightarrow R_1$
, we can take
$R_0\rightarrow R_1$
, we can take
![]() $x\in R_0\cap f^{-1}(R_1)\subset Z(z)$
, there exist by Definition 6.1 an
$x\in R_0\cap f^{-1}(R_1)\subset Z(z)$
, there exist by Definition 6.1 an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}\in \Sigma ^{\#}$
such that
$\underline {x}\in \Sigma ^{\#}$
such that
![]() $x_0=z$
and
$x_0=z$
and
![]() $\pi (\underline {x})=x$
. Then
$\pi (\underline {x})=x$
. Then
![]() $f(x)\in R_1\cap Z(x_1)$
and from the inclusion relation (Lemma 6.4(1)) for
$f(x)\in R_1\cap Z(x_1)$
and from the inclusion relation (Lemma 6.4(1)) for
![]() $\mathscr {R}$
,
$\mathscr {R}$
,
![]() $R_1\subset Z(x_1)$
and such
$R_1\subset Z(x_1)$
and such
![]() $R_1$
is finite (Lemma 6.4(2)) since
$R_1$
is finite (Lemma 6.4(2)) since
![]() $Z(x_1)$
is finite for fixed
$Z(x_1)$
is finite for fixed
![]() $R_0$
(Lemma 6.4(3)). Therefore,
$R_0$
(Lemma 6.4(3)). Therefore,
 $$ \begin{align*} |\{R_1\in\mathscr{R}:R_0\rightarrow R_1\}|\leq\underset{{\substack{z\in\mathscr{A} \\ Z(z)\supset R_0}}}\sum\underset{{\substack{z^\prime\in\mathscr{A} \\ z\rightarrow z^{\prime}}}}\sum|\{R_1\in\mathscr{R}:R_1\subset Z(z^\prime)\}|<\infty. \end{align*} $$
$$ \begin{align*} |\{R_1\in\mathscr{R}:R_0\rightarrow R_1\}|\leq\underset{{\substack{z\in\mathscr{A} \\ Z(z)\supset R_0}}}\sum\underset{{\substack{z^\prime\in\mathscr{A} \\ z\rightarrow z^{\prime}}}}\sum|\{R_1\in\mathscr{R}:R_1\subset Z(z^\prime)\}|<\infty. \end{align*} $$
Let
![]() $(\widehat {\Sigma }, \widehat {\sigma })$
be the TMS induced by
$(\widehat {\Sigma }, \widehat {\sigma })$
be the TMS induced by
![]() $\widehat {\mathscr {G}}$
:
$\widehat {\mathscr {G}}$
:
where the
![]() $\widehat {\sigma }$
is the left shift and the element of
$\widehat {\sigma }$
is the left shift and the element of
![]() $\widehat {\Sigma }$
is denoted by
$\widehat {\Sigma }$
is denoted by
![]() $\underline {R}:=\{R_n\}_{n\in \mathbb {Z}}$
. We equip
$\underline {R}:=\{R_n\}_{n\in \mathbb {Z}}$
. We equip
![]() $\widehat {\Sigma }$
with the metric
$\widehat {\Sigma }$
with the metric
![]() $d(\underline {R},\underline {S}) = \exp [-\min \{|n| : n\in \mathbb {Z}\ \text {such that}\ R_n\neq S_n\}]$
as before. Since every vertex of
$d(\underline {R},\underline {S}) = \exp [-\min \{|n| : n\in \mathbb {Z}\ \text {such that}\ R_n\neq S_n\}]$
as before. Since every vertex of
![]() $\widehat {\mathscr {G}}$
has finite degree,
$\widehat {\mathscr {G}}$
has finite degree,
![]() $\widehat {\Sigma }$
is locally compact. Define as before
$\widehat {\Sigma }$
is locally compact. Define as before
 $$ \begin{align*} {\widehat{\Sigma}}^{\#}:=\{\underline{R}\in \widehat{\Sigma}: &\text{ there exists } R,S\in \mathscr{R}, \text{there exists } n_k,m_k\uparrow\infty \\& \text{ such that}\ R_{n_k}=R\ \text{and}\ R_{-m_k}=S \text{ for all } k\in \mathbb{Z}\}. \end{align*} $$
$$ \begin{align*} {\widehat{\Sigma}}^{\#}:=\{\underline{R}\in \widehat{\Sigma}: &\text{ there exists } R,S\in \mathscr{R}, \text{there exists } n_k,m_k\uparrow\infty \\& \text{ such that}\ R_{n_k}=R\ \text{and}\ R_{-m_k}=S \text{ for all } k\in \mathbb{Z}\}. \end{align*} $$
Again by the Poincaré recurrence theorem, every
![]() $\widehat {\sigma }-$
invariant probability measure gives
$\widehat {\sigma }-$
invariant probability measure gives
![]() $\widehat {\Sigma }^{\#}$
full measure. Furthermore, every periodic point of
$\widehat {\Sigma }^{\#}$
full measure. Furthermore, every periodic point of
![]() $\widehat {\sigma }$
is in
$\widehat {\sigma }$
is in
![]() ${\widehat {\Sigma }}^{\#}$
.
${\widehat {\Sigma }}^{\#}$
.
For
![]() $n \in \mathbb {Z}$
and a path
$n \in \mathbb {Z}$
and a path
![]() $R_{-n} \rightarrow \cdots \rightarrow R_{n}$
on
$R_{-n} \rightarrow \cdots \rightarrow R_{n}$
on
![]() $\widehat {\mathscr {G}}$
,
$\widehat {\mathscr {G}}$
,
![]() $\bigcap _{i=-n}^{n}f^{-i}(R_i) \neq \varnothing $
. This follows by induction, using the Markov property of
$\bigcap _{i=-n}^{n}f^{-i}(R_i) \neq \varnothing $
. This follows by induction, using the Markov property of
![]() $\mathscr {R}$
(Proposition 6.6(3)), as done originally by Adler, Weiss, and Sinai [Reference Adler and Weiss1, Reference Adler and Weiss3, Reference Sinai23, Reference Sinai24]. For more details, see [Reference Sarig22, Lemma 12.1].
$\mathscr {R}$
(Proposition 6.6(3)), as done originally by Adler, Weiss, and Sinai [Reference Adler and Weiss1, Reference Adler and Weiss3, Reference Sinai23, Reference Sinai24]. For more details, see [Reference Sarig22, Lemma 12.1].
Lemma 6.5. For every finite path
![]() $R_{-n} \rightarrow \cdots \rightarrow R_{n}$
on
$R_{-n} \rightarrow \cdots \rightarrow R_{n}$
on
![]() $\widehat {\mathscr {G}}$
, there exists an
$\widehat {\mathscr {G}}$
, there exists an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}=\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
such that for every
$\underline {x}=\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
such that for every
![]() $i=-n,\ldots ,n$
,
$i=-n,\ldots ,n$
,
![]() $R_i\subset Z(x_i)$
, and
$R_i\subset Z(x_i)$
, and
 $$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-n}^{n}f^{-i}(R_i)\kern-1.2pt\bigg)\kern-1.2pt\leq 8Q(x_n)\prod_{j=1}^{n}\|Df^{-1}|_{E^u(x_{j})}\|^{1/2}+8Q(x_{-n})\kern-1pt\prod_{j=1}^{n}\|Df|_{E^s(x_{-j})}\|^{1/2}. \end{align*} $$
$$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-n}^{n}f^{-i}(R_i)\kern-1.2pt\bigg)\kern-1.2pt\leq 8Q(x_n)\prod_{j=1}^{n}\|Df^{-1}|_{E^u(x_{j})}\|^{1/2}+8Q(x_{-n})\kern-1pt\prod_{j=1}^{n}\|Df|_{E^s(x_{-j})}\|^{1/2}. \end{align*} $$
Moreover, for every
![]() $\underline {R}=\{R_n\}_{n\in \mathbb {Z}}\in {\widehat {\Sigma }}^{\#}$
, we have
$\underline {R}=\{R_n\}_{n\in \mathbb {Z}}\in {\widehat {\Sigma }}^{\#}$
, we have
 $$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-N}^{N}f^{-i}(R_i)\bigg)\underset{N \rightarrow \infty}{\longrightarrow}0. \end{align*} $$
$$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-N}^{N}f^{-i}(R_i)\bigg)\underset{N \rightarrow \infty}{\longrightarrow}0. \end{align*} $$
Proof. Fix
![]() $x,y\in \bigcap _{i=-n}^{n}f^{-i}(R_i)$
. By Definition 6.5, we can pick some
$x,y\in \bigcap _{i=-n}^{n}f^{-i}(R_i)$
. By Definition 6.5, we can pick some
![]() $z\in \mathscr {A}$
such that
$z\in \mathscr {A}$
such that
![]() $R_0\subset Z(z)\in \mathscr {Z}$
. Since
$R_0\subset Z(z)\in \mathscr {Z}$
. Since
![]() $x\in R_0\subset Z(z)$
, there exists by Definition 6.1 an
$x\in R_0\subset Z(z)$
, there exists by Definition 6.1 an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}\in \Sigma ^{\#}$
such that
$\underline {x}\in \Sigma ^{\#}$
such that
![]() $x_0=z$
,
$x_0=z$
,
![]() $\pi (\underline {x})=x$
. From
$\pi (\underline {x})=x$
. From
![]() $f^i(x)=f^i\circ \pi (\underline {x})=\pi \circ \sigma ^i(\underline {x})\in Z(x_i)$
and
$f^i(x)=f^i\circ \pi (\underline {x})=\pi \circ \sigma ^i(\underline {x})\in Z(x_i)$
and
![]() $f^i(x)\in R_i$
, we have
$f^i(x)\in R_i$
, we have
![]() $f^i(x)\in R_i\cap Z(x_i)$
for all
$f^i(x)\in R_i\cap Z(x_i)$
for all
![]() $i=-n,\ldots ,n$
. So we have
$i=-n,\ldots ,n$
. So we have
![]() $R_i\subset Z(x_i)$
by inclusion relation Lemma 6.4(1) for all
$R_i\subset Z(x_i)$
by inclusion relation Lemma 6.4(1) for all
![]() $i=-n,\ldots ,n$
. It follows that
$i=-n,\ldots ,n$
. It follows that
 $$ \begin{align*} \bigcap_{i=-n}^{n}f^{-i}(R_i)\subset \bigcap_{i=-n}^{n}f^{-i}[Z(x_i)], \end{align*} $$
$$ \begin{align*} \bigcap_{i=-n}^{n}f^{-i}(R_i)\subset \bigcap_{i=-n}^{n}f^{-i}[Z(x_i)], \end{align*} $$
and hence
![]() $y\in \bigcap _{i=-n}^{n}f^{-i}[Z(x_i)]\subset Z(x_0)$
.
$y\in \bigcap _{i=-n}^{n}f^{-i}[Z(x_i)]\subset Z(x_0)$
.
Since
![]() $x,y\in Z(x_0)$
, we can let
$x,y\in Z(x_0)$
, we can let
![]() $z^\prime :=[x,y]_{Z(x_0)}\in Z(x_0)$
. Notice that
$z^\prime :=[x,y]_{Z(x_0)}\in Z(x_0)$
. Notice that
![]() $f^i(x), f^i(y)\in Z(x_i)$
for all
$f^i(x), f^i(y)\in Z(x_i)$
for all
![]() $i=-n,\ldots ,n$
and
$i=-n,\ldots ,n$
and
![]() $x_0\rightarrow \cdots \rightarrow x_n$
, we have by Lemma 6.2 iterated forward n times
$x_0\rightarrow \cdots \rightarrow x_n$
, we have by Lemma 6.2 iterated forward n times
 $$ \begin{align*} \begin{aligned} f^n(z^\prime)&=f^n([x,y]_{Z(x_0)})\notag\\ &=f^{n-1}([f(x),f(y)]_{Z(x_1)})\notag\\ &=\cdots=[f^n(x),f^n(y)]_{Z(x_n)}\notag\\ &=V^u(f^n(x),Z(x_n))\cap V^s(f^n(y),Z(x_n)), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} f^n(z^\prime)&=f^n([x,y]_{Z(x_0)})\notag\\ &=f^{n-1}([f(x),f(y)]_{Z(x_1)})\notag\\ &=\cdots=[f^n(x),f^n(y)]_{Z(x_n)}\notag\\ &=V^u(f^n(x),Z(x_n))\cap V^s(f^n(y),Z(x_n)), \end{aligned} \end{align*} $$
and thus
![]() $f^n(z^\prime )\in V^u(f^n(x),Z(x_n))=V^u(\{x_{-k+n}\}_{k\geq 0})$
.
$f^n(z^\prime )\in V^u(f^n(x),Z(x_n))=V^u(\{x_{-k+n}\}_{k\geq 0})$
.
Similarly, since
![]() $x_{-n}\rightarrow \cdots \rightarrow x_0$
, we have by Lemma 6.2 iterated backward n times
$x_{-n}\rightarrow \cdots \rightarrow x_0$
, we have by Lemma 6.2 iterated backward n times
 $$ \begin{align*} \begin{aligned} f^{-n}(z^\prime)&=f^{-n}([x,y]_{Z(x_0)})\notag\\ &=f^{-n+1}([f^{-1}(x),f^{-1}(y)]_{Z(x_{-1})})\notag\\ &=\cdots=[f^{-n}(x),f^{-n}(y)]_{Z(x_{-n})}\notag\\ &=V^u(f^{-n}(x),Z(x_{-n}))\cap V^s(f^{-n}(y),Z(x_{-n})), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} f^{-n}(z^\prime)&=f^{-n}([x,y]_{Z(x_0)})\notag\\ &=f^{-n+1}([f^{-1}(x),f^{-1}(y)]_{Z(x_{-1})})\notag\\ &=\cdots=[f^{-n}(x),f^{-n}(y)]_{Z(x_{-n})}\notag\\ &=V^u(f^{-n}(x),Z(x_{-n}))\cap V^s(f^{-n}(y),Z(x_{-n})), \end{aligned} \end{align*} $$
and thus
![]() $f^{-n}(z^\prime )\in V^s(f^{-n}(y),Z(x_{-n}))=V^s(\{x_{k-n}\}_{k\geq 0})$
.
$f^{-n}(z^\prime )\in V^s(f^{-n}(y),Z(x_{-n}))=V^s(\{x_{k-n}\}_{k\geq 0})$
.
Now using Proposition 5.2(3), for
![]() $x,y\in \bigcap _{i=-n}^{n}f^{-i}(R_i)$
, we have
$x,y\in \bigcap _{i=-n}^{n}f^{-i}(R_i)$
, we have
 $$ \begin{align*} \begin{aligned} d(x,y)&\leq d(x,z^\prime)+d(z^\prime,y)\notag\\ &=d(f^{-n}(f^n(x)),f^{-n}(f^n(z^\prime)))+d(f^{n}(f^{-n}(z^\prime)),f^{n}(f^{-n}(y)))\notag\\ &\leq 8Q(x_n)\prod_{i=0}^{n-1}\|Df^{-1}|_{E^u(x_{-i+n})}\|^{1/2}+8Q(x_{-n})\prod_{i=0}^{n-1}\|Df|_{E^s(x_{i-n})}\|^{1/2}\notag\\ &= 8Q(x_n)\prod_{j=1}^{n}\|Df^{-1}|_{E^u(x_{j})}\|^{1/2}+8Q(x_{-n})\prod_{j=1}^{n}\|Df|_{E^s(x_{-j})}\|^{1/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(x,y)&\leq d(x,z^\prime)+d(z^\prime,y)\notag\\ &=d(f^{-n}(f^n(x)),f^{-n}(f^n(z^\prime)))+d(f^{n}(f^{-n}(z^\prime)),f^{n}(f^{-n}(y)))\notag\\ &\leq 8Q(x_n)\prod_{i=0}^{n-1}\|Df^{-1}|_{E^u(x_{-i+n})}\|^{1/2}+8Q(x_{-n})\prod_{i=0}^{n-1}\|Df|_{E^s(x_{i-n})}\|^{1/2}\notag\\ &= 8Q(x_n)\prod_{j=1}^{n}\|Df^{-1}|_{E^u(x_{j})}\|^{1/2}+8Q(x_{-n})\prod_{j=1}^{n}\|Df|_{E^s(x_{-j})}\|^{1/2}. \end{aligned} \end{align*} $$
Therefore, for every finite path
![]() $R_{-n} \rightarrow \cdots \rightarrow R_{n}$
on
$R_{-n} \rightarrow \cdots \rightarrow R_{n}$
on
![]() $\widehat {\mathscr {G}}$
, there exists an
$\widehat {\mathscr {G}}$
, there exists an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}=\{x_n\}_{n\in \mathbb {Z}}$
such that
$\underline {x}=\{x_n\}_{n\in \mathbb {Z}}$
such that
 $$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-n}^{n}f^{-i}(R_i)\kern-1pt\bigg)\kern-1.3pt\leq8Q(x_n)\prod_{j=1}^{n}\|Df^{-1}|_{E^u(x_{j})}\|^{1/2}+8Q(x_{-n})\prod_{j=1}^{n}\|Df|_{E^s(x_{-j})}\|^{1/2}. \end{align*} $$
$$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-n}^{n}f^{-i}(R_i)\kern-1pt\bigg)\kern-1.3pt\leq8Q(x_n)\prod_{j=1}^{n}\|Df^{-1}|_{E^u(x_{j})}\|^{1/2}+8Q(x_{-n})\prod_{j=1}^{n}\|Df|_{E^s(x_{-j})}\|^{1/2}. \end{align*} $$
Finally, if
![]() $\underline {R}=\{R_n\}_{n\in \mathbb {Z}}\in {\widehat {\Sigma }}^{\#}$
, then
$\underline {R}=\{R_n\}_{n\in \mathbb {Z}}\in {\widehat {\Sigma }}^{\#}$
, then
![]() $\text {there exists } R\in \mathscr {R}$
, such that
$\text {there exists } R\in \mathscr {R}$
, such that
![]() $R_m=R$
for infinitely many
$R_m=R$
for infinitely many
![]() $m>0$
. From Lemma 6.4(3), for this R,
$m>0$
. From Lemma 6.4(3), for this R,
![]() $|\{Z\in \mathscr {Z}:Z\supset R\}|$
is finite, so by the pigeonhole principle,
$|\{Z\in \mathscr {Z}:Z\supset R\}|$
is finite, so by the pigeonhole principle,
![]() $\text {there exists } \bar {x}\in \mathscr {A}$
, such that
$\text {there exists } \bar {x}\in \mathscr {A}$
, such that
![]() $x_m=\bar {x}$
for infinitely many
$x_m=\bar {x}$
for infinitely many
![]() $m>0$
. Similarly,
$m>0$
. Similarly,
![]() $\text {there exists } \bar {y}\in \mathscr {A}$
, such that
$\text {there exists } \bar {y}\in \mathscr {A}$
, such that
![]() $x_m=\bar {y}$
for infinitely many
$x_m=\bar {y}$
for infinitely many
![]() $m<0$
. Thus, for every
$m<0$
. Thus, for every
![]() $\underline {R}\in {\widehat {\Sigma }}^{\#}$
, there exists an
$\underline {R}\in {\widehat {\Sigma }}^{\#}$
, there exists an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}=\{x_n\}_{n\in \mathbb {Z}}$
such that
$\underline {x}=\{x_n\}_{n\in \mathbb {Z}}$
such that
 $$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-N}^{N}f^{-i}(R_i)\bigg)\leq8Q(x_N)\prod_{j=1}^{N}\|Df^{-1}|_{E^u(x_{j})}\|^{1/2}+8Q(x_{-N})\prod_{j=1}^{N}\|Df|_{E^s(x_{-j})}\|^{1/2} \end{align*} $$
$$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-N}^{N}f^{-i}(R_i)\bigg)\leq8Q(x_N)\prod_{j=1}^{N}\|Df^{-1}|_{E^u(x_{j})}\|^{1/2}+8Q(x_{-N})\prod_{j=1}^{N}\|Df|_{E^s(x_{-j})}\|^{1/2} \end{align*} $$
holds for every
![]() $N\geq 1$
. So we have
$N\geq 1$
. So we have
 $$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-N}^{N}f^{-i}(R_i)\bigg)\underset{N \rightarrow \infty}{\longrightarrow}0.\\[-46pt] \end{align*} $$
$$ \begin{align*} \mathrm{diam}\bigg(\bigcap_{i=-N}^{N}f^{-i}(R_i)\bigg)\underset{N \rightarrow \infty}{\longrightarrow}0.\\[-46pt] \end{align*} $$
For every
![]() $\underline {R}\in \widehat {\Sigma }^{\#}$
, let
$\underline {R}\in \widehat {\Sigma }^{\#}$
, let
![]() $\widehat {\pi }: \widehat {\Sigma }^{\#}\rightarrow O$
be defined by
$\widehat {\pi }: \widehat {\Sigma }^{\#}\rightarrow O$
be defined by
 $$ \begin{align*} \{\widehat{\pi}(\underline{R})\}:=\bigcap_{n \geq 0} \overline{\bigcap_{i=-n}^{n}f^{-i}(R_i)}. \end{align*} $$
$$ \begin{align*} \{\widehat{\pi}(\underline{R})\}:=\bigcap_{n \geq 0} \overline{\bigcap_{i=-n}^{n}f^{-i}(R_i)}. \end{align*} $$
Here,
![]() $\widehat {\pi }$
is well defined because
$\widehat {\pi }$
is well defined because
![]() $\overline {\bigcap _{i=-n}^{n}f^{-i}(R_i)}$
is a non-empty compact subset of M whose diameters tend to zero as
$\overline {\bigcap _{i=-n}^{n}f^{-i}(R_i)}$
is a non-empty compact subset of M whose diameters tend to zero as
![]() $n\rightarrow \infty $
and the intersection
$n\rightarrow \infty $
and the intersection
![]() $\bigcap _{n \geq 0} \overline {\bigcap _{i=-n}^{n}f^{-i}(R_i)}$
is a singleton.
$\bigcap _{n \geq 0} \overline {\bigcap _{i=-n}^{n}f^{-i}(R_i)}$
is a singleton.
It is worthy to point out that we take the closures of
![]() $\bigcap _{i=-n}^{n}f^{-i}(R_i)$
because the
$\bigcap _{i=-n}^{n}f^{-i}(R_i)$
because the
![]() $R_i$
terms are not necessarily closed. A priori, the image of
$R_i$
terms are not necessarily closed. A priori, the image of
![]() $\widehat {\pi }$
on
$\widehat {\pi }$
on
![]() ${\widehat {\Sigma }}^{\#}$
could be bigger than
${\widehat {\Sigma }}^{\#}$
could be bigger than
![]() $\pi (\Sigma ^{\#})=O^{\#}$
. Fortunately, this is not the case for Theorem 2.1(3), or see the proof of the following Theorem 6.2(3).
$\pi (\Sigma ^{\#})=O^{\#}$
. Fortunately, this is not the case for Theorem 2.1(3), or see the proof of the following Theorem 6.2(3).
The triple
![]() $(\widehat {\Sigma }^{\#}, \widehat {\sigma }, \widehat {\pi })$
is the one that satisfies Theorem 2.1, where the non-injectivity of
$(\widehat {\Sigma }^{\#}, \widehat {\sigma }, \widehat {\pi })$
is the one that satisfies Theorem 2.1, where the non-injectivity of
![]() $\widehat {\pi }$
is analyzed using the following notion of affiliation, which was introduced by Sarig [Reference Sarig22, §12.3].
$\widehat {\pi }$
is analyzed using the following notion of affiliation, which was introduced by Sarig [Reference Sarig22, §12.3].
Definition 6.7.
![]() $R,R^\prime \in \mathscr {R}$
are called affiliated if there exist
$R,R^\prime \in \mathscr {R}$
are called affiliated if there exist
![]() $Z,Z^\prime \in \mathscr {Z}$
such that
$Z,Z^\prime \in \mathscr {Z}$
such that
![]() $Z\supset R$
,
$Z\supset R$
,
![]() $Z^\prime \supset R^\prime $
, and
$Z^\prime \supset R^\prime $
, and
![]() $Z\cap Z^\prime \neq \varnothing $
. If this occurs, we write
$Z\cap Z^\prime \neq \varnothing $
. If this occurs, we write
![]() $R\sim R^\prime $
.
$R\sim R^\prime $
.
For
![]() $R\in \mathscr {R}$
, define
$R\in \mathscr {R}$
, define
![]() $N(R):=\{(R^\prime , z)\in \mathscr {R}\times \mathscr {A}:R^\prime \sim R\ \text {and}\ Z(z)\supset R^\prime \}$
. By the local-finiteness of
$N(R):=\{(R^\prime , z)\in \mathscr {R}\times \mathscr {A}:R^\prime \sim R\ \text {and}\ Z(z)\supset R^\prime \}$
. By the local-finiteness of
![]() $\mathscr {Z}$
, and Lemma 6.4(2) and (3),
$\mathscr {Z}$
, and Lemma 6.4(2) and (3),
![]() $N(R)$
is finite. See the proof of [Reference Sarig22, Lemma 12.7].
$N(R)$
is finite. See the proof of [Reference Sarig22, Lemma 12.7].
Definition 6.8. We say that
![]() $\underline {R}\approx \underline {R}^\prime $
if
$\underline {R}\approx \underline {R}^\prime $
if
![]() $R_n\sim R_n^\prime $
for all
$R_n\sim R_n^\prime $
for all
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
Lemma 6.6. If
![]() $\underline {R},\underline {R}^\prime \in {\widehat {\Sigma }}^{\#}$
and
$\underline {R},\underline {R}^\prime \in {\widehat {\Sigma }}^{\#}$
and
![]() $\widehat {\pi }(\underline {R})=\widehat {\pi }(\underline {R}^\prime )$
, then
$\widehat {\pi }(\underline {R})=\widehat {\pi }(\underline {R}^\prime )$
, then
![]() $\underline {R}\approx \underline {R}^\prime $
.
$\underline {R}\approx \underline {R}^\prime $
.
Proof. Suppose
![]() $\underline {R}=\{R_n\}_{n\in \mathbb {Z}}\in {\widehat {\Sigma }}^{\#}$
. By Definition 6.5, we can pick some
$\underline {R}=\{R_n\}_{n\in \mathbb {Z}}\in {\widehat {\Sigma }}^{\#}$
. By Definition 6.5, we can pick some
![]() $x_0\in \mathscr {A}$
such that
$x_0\in \mathscr {A}$
such that
![]() $R_0\subset Z(x_0)\in \mathscr {Z}$
. Since
$R_0\subset Z(x_0)\in \mathscr {Z}$
. Since
![]() $R_0\rightarrow R_1$
, there exists a point
$R_0\rightarrow R_1$
, there exists a point
![]() $x\in R_0\cap f^{-1}(R_1)\subset Z(x_0)$
. So there exists by Definition 6.1 an
$x\in R_0\cap f^{-1}(R_1)\subset Z(x_0)$
. So there exists by Definition 6.1 an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}^{\prime }\in \Sigma ^{\#}$
such that
$\underline {x}^{\prime }\in \Sigma ^{\#}$
such that
![]() $x_0^\prime =x_0$
,
$x_0^\prime =x_0$
,
![]() $\pi (\underline {x}^{\prime })=x$
. Then
$\pi (\underline {x}^{\prime })=x$
. Then
![]() $f(x)\in R_1\cap Z(x_1^\prime )$
. From Lemma 6.4(1), we have
$f(x)\in R_1\cap Z(x_1^\prime )$
. From Lemma 6.4(1), we have
![]() $R_1\subset Z(x_1^\prime )$
. Set
$R_1\subset Z(x_1^\prime )$
. Set
![]() $x_1=x_1^\prime $
, so we get
$x_1=x_1^\prime $
, so we get
![]() $x_0\rightarrow x_1$
. Inductively forwards, one can proceed this construction to give us a path
$x_0\rightarrow x_1$
. Inductively forwards, one can proceed this construction to give us a path
![]() $x_0\rightarrow \cdots \rightarrow x_n$
on
$x_0\rightarrow \cdots \rightarrow x_n$
on
![]() $\Sigma $
satisfies
$\Sigma $
satisfies
![]() $R_n\subset Z(x_n)$
for every
$R_n\subset Z(x_n)$
for every
![]() $n\geq 0$
. Similarly, repeating the procedure inductively backwards gives us another path
$n\geq 0$
. Similarly, repeating the procedure inductively backwards gives us another path
![]() $x_{-n}\rightarrow \cdots \rightarrow x_0$
on
$x_{-n}\rightarrow \cdots \rightarrow x_0$
on
![]() $\Sigma $
satisfies
$\Sigma $
satisfies
![]() $R_{-n}\subset Z(x_{-n})$
for every
$R_{-n}\subset Z(x_{-n})$
for every
![]() $n\geq 0$
. Therefore, this procedure gives us a sequence
$n\geq 0$
. Therefore, this procedure gives us a sequence
![]() ${\{x_n\}_{n\in \mathbb {Z}}\in \Sigma} $
. We claim that
${\{x_n\}_{n\in \mathbb {Z}}\in \Sigma} $
. We claim that
![]() $\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
for
$\{x_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
for
![]() $\underline {R}\in {\widehat {\Sigma }}^{\#}$
.
$\underline {R}\in {\widehat {\Sigma }}^{\#}$
.
In fact, since
![]() $\underline {R}\in {\widehat {\Sigma }}^{\#}$
,
$\underline {R}\in {\widehat {\Sigma }}^{\#}$
,
![]() $\text {there exists } R\in \mathscr {R}$
, such that
$\text {there exists } R\in \mathscr {R}$
, such that
![]() $R_m=R$
for infinitely many
$R_m=R$
for infinitely many
![]() ${m>0}$
. From Lemma 6.4(3), for this R,
${m>0}$
. From Lemma 6.4(3), for this R,
![]() $|\{Z\in \mathscr {Z}:Z\supset R\}|$
is finite, so by the pigeonhole principle,
$|\{Z\in \mathscr {Z}:Z\supset R\}|$
is finite, so by the pigeonhole principle,
![]() $\text {there exists } z\in \mathscr {A}$
, such that
$\text {there exists } z\in \mathscr {A}$
, such that
![]() $x_m=z$
for infinitely many
$x_m=z$
for infinitely many
![]() $m>0$
. Similarly,
$m>0$
. Similarly,
![]() $\text { there exists } z^\prime \in \mathscr {A}$
, such that
$\text { there exists } z^\prime \in \mathscr {A}$
, such that
![]() $x_m=z^\prime $
for infinitely many
$x_m=z^\prime $
for infinitely many
![]() $m<0$
. Thus, we construct an
$m<0$
. Thus, we construct an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}\in \Sigma ^{\#}$
for
$\underline {x}\in \Sigma ^{\#}$
for
![]() $\underline {R}\in {\widehat {\Sigma }}^{\#}$
such that
$\underline {R}\in {\widehat {\Sigma }}^{\#}$
such that
 $$ \begin{align*} z:=\widehat{\pi}(\underline{R})\in\bigcap_{n \geq 0} \overline{\bigcap_{i=-n}^{n}f^{-i}(Z(x_i))}, \end{align*} $$
$$ \begin{align*} z:=\widehat{\pi}(\underline{R})\in\bigcap_{n \geq 0} \overline{\bigcap_{i=-n}^{n}f^{-i}(Z(x_i))}, \end{align*} $$
that is,
![]() $f^n(z)\in \overline {Z(x_n)}$
for all
$f^n(z)\in \overline {Z(x_n)}$
for all
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
Recall that every element
![]() $Z(x_n)$
is a subset of the much smaller set
$Z(x_n)$
is a subset of the much smaller set
![]() $\exp _{x_n}(T_{x_n}M({2}/{50} Q(x_n)))$
(Proposition 4.1(1)), we have
$\exp _{x_n}(T_{x_n}M({2}/{50} Q(x_n)))$
(Proposition 4.1(1)), we have
![]() $d(f^n(z),x_n)\leq \mathrm {diam}(\overline {Z(x_n)})=\mathrm {diam}(Z(x_n))\leq \tfrac 12Q(x_n)$
and then
$d(f^n(z),x_n)\leq \mathrm {diam}(\overline {Z(x_n)})=\mathrm {diam}(Z(x_n))\leq \tfrac 12Q(x_n)$
and then
![]() $f^{n}(z)\in \exp _{x_n}(S_{x_n})$
for all
$f^{n}(z)\in \exp _{x_n}(S_{x_n})$
for all
![]() $n \in \mathbb {Z}$
. By Definition 5.2 and the shadowing lemma (Lemma 5.1),
$n \in \mathbb {Z}$
. By Definition 5.2 and the shadowing lemma (Lemma 5.1),
![]() $\pi (\underline {x})=z=\widehat {\pi }(\underline {R})$
.
$\pi (\underline {x})=z=\widehat {\pi }(\underline {R})$
.
Analogously, for
![]() $\underline {R}^\prime \in {\widehat {\Sigma }}^{\#}$
, there exist
$\underline {R}^\prime \in {\widehat {\Sigma }}^{\#}$
, there exist
![]() $\{y_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
such that
$\{y_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
such that
![]() $\pi (\underline {y})=\widehat {\pi }(\underline {R})$
. Since
$\pi (\underline {y})=\widehat {\pi }(\underline {R})$
. Since
![]() $\widehat {\pi }(\underline {R})=\widehat {\pi }(\underline {R}^\prime )=z$
, we have for every
$\widehat {\pi }(\underline {R})=\widehat {\pi }(\underline {R}^\prime )=z$
, we have for every
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
![]() $f^n(z)=\pi \circ \sigma ^n(\underline {x})=\pi \circ \sigma ^n(\underline {y})$
and so
$f^n(z)=\pi \circ \sigma ^n(\underline {x})=\pi \circ \sigma ^n(\underline {y})$
and so
![]() $f^n(z)\in Z(x_n)\cap Z(y_n)$
, proving that
$f^n(z)\in Z(x_n)\cap Z(y_n)$
, proving that
![]() $R_n\sim R_n^\prime $
for all
$R_n\sim R_n^\prime $
for all
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
Theorem 6.2. The following holds for all
![]() $\varepsilon>0$
small enough.
$\varepsilon>0$
small enough.
-
(1)
 $\widehat {\pi } \circ \widehat {\sigma }=f \circ \widehat {\pi }$
on
$\widehat {\pi } \circ \widehat {\sigma }=f \circ \widehat {\pi }$
on
 $\widehat {\Sigma }^{\#}$
.
$\widehat {\Sigma }^{\#}$
. -
(2)
 $\widehat {\pi }: \widehat {\Sigma }^{\#} \rightarrow O$
is continuous.
$\widehat {\pi }: \widehat {\Sigma }^{\#} \rightarrow O$
is continuous. -
(3)
 $\widehat {\pi }|_{\widehat {\Sigma }^{\#}}: \widehat {\Sigma }^{\#}\rightarrow O^{\#}$
is a finite-to-one surjective map.
$\widehat {\pi }|_{\widehat {\Sigma }^{\#}}: \widehat {\Sigma }^{\#}\rightarrow O^{\#}$
is a finite-to-one surjective map.
Proof. (1) For any
![]() $\underline {R}\in \widehat {\Sigma }^{\#}$
, because f is a homeomorphism, we have
$\underline {R}\in \widehat {\Sigma }^{\#}$
, because f is a homeomorphism, we have
 $$ \begin{align*} \begin{aligned} \{\widehat{\pi} \circ \widehat{\sigma}(\underline{R})\}&=\bigg\{\bigcap_{n=0}^{\infty}\overline{f^n(R_{-n+1})\cap\cdots\cap f^{-n}(R_{n+1})}\bigg\}=\bigg\{\bigcap_{n=0}^{\infty}\overline{\bigcap_{i=-n}^{n}f^{-i}(R_{i+1})}\bigg\}\notag\\ &\supset\bigg\{\bigcap_{n=0}^{\infty}\overline{\bigcap_{i=-n-2}^{n}f^{-(i+1)+1}(R_{i+1})}\bigg\}=\bigg\{f\bigg(\bigcap_{n=0}^{\infty}\overline{\bigcap_{i=-n-2}^{n}f^{-(i+1)}(R_{i+1})}\bigg)\bigg\}\notag\\ &=\bigg\{f\bigg(\bigcap_{n=0}^{\infty}\overline{\bigcap_{j=-n-1}^{n+1}f^{-j}(R_j)}\bigg)\bigg\}=\{f\circ\widehat{\pi}(\underline{R})\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \{\widehat{\pi} \circ \widehat{\sigma}(\underline{R})\}&=\bigg\{\bigcap_{n=0}^{\infty}\overline{f^n(R_{-n+1})\cap\cdots\cap f^{-n}(R_{n+1})}\bigg\}=\bigg\{\bigcap_{n=0}^{\infty}\overline{\bigcap_{i=-n}^{n}f^{-i}(R_{i+1})}\bigg\}\notag\\ &\supset\bigg\{\bigcap_{n=0}^{\infty}\overline{\bigcap_{i=-n-2}^{n}f^{-(i+1)+1}(R_{i+1})}\bigg\}=\bigg\{f\bigg(\bigcap_{n=0}^{\infty}\overline{\bigcap_{i=-n-2}^{n}f^{-(i+1)}(R_{i+1})}\bigg)\bigg\}\notag\\ &=\bigg\{f\bigg(\bigcap_{n=0}^{\infty}\overline{\bigcap_{j=-n-1}^{n+1}f^{-j}(R_j)}\bigg)\bigg\}=\{f\circ\widehat{\pi}(\underline{R})\}. \end{aligned} \end{align*} $$
(2) If otherwise, then there is a
![]() $\xi>0$
so that for every
$\xi>0$
so that for every
![]() $N>0$
, one can find
$N>0$
, one can find
![]() $\underline {R}^{(N)}, \underline {S}^{(N)}\in \widehat {\Sigma }^{\#}$
with
$\underline {R}^{(N)}, \underline {S}^{(N)}\in \widehat {\Sigma }^{\#}$
with
![]() $R^{(N)}_i=S^{(N)}_i$
for all
$R^{(N)}_i=S^{(N)}_i$
for all
![]() $i=-N,\ldots , N$
, but
$i=-N,\ldots , N$
, but
![]() $d(\widehat {\pi }(\underline {R}^{(N)}),\widehat {\pi }(\underline {S}^{(N)}))\geq \xi $
. However, notice that
$d(\widehat {\pi }(\underline {R}^{(N)}),\widehat {\pi }(\underline {S}^{(N)}))\geq \xi $
. However, notice that
![]() $\widehat {\pi }(\underline {R}^{(N)}), \widehat {\pi }(\underline {S}^{(N)})\in \overline {\bigcap _{i=-N}^{N}f^{-i}(R^{(N)}_i)}$
, and hence by Lemma 6.5, there exists an
$\widehat {\pi }(\underline {R}^{(N)}), \widehat {\pi }(\underline {S}^{(N)})\in \overline {\bigcap _{i=-N}^{N}f^{-i}(R^{(N)}_i)}$
, and hence by Lemma 6.5, there exists an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}=\{x^{(N)}_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
such that
$\underline {x}=\{x^{(N)}_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
such that
 $$ \begin{align*} \begin{aligned} &d(\widehat{\pi}(\underline{R}^{(N)}),\widehat{\pi}(\underline{S}^{(N)}))\\&\quad\leq \mathrm{diam}\bigg(\overline{\bigcap_{i=-N}^{N}f^{-i}(R^{(N)}_i)}\bigg)\notag\\ &\quad=\mathrm{diam}(\bigcap_{i=-N}^{N}f^{-i}(R^{(N)}_i))\notag\\ &\quad\leq8Q(x^{(N)}_N)\prod_{j=1}^{N}\|Df^{-1}|_{E^u(x^{(N)}_{j})}\|^{1/2}+8Q(x^{(N)}_{-N})\prod_{j=1}^{N}\|Df|_{E^s(x^{(N)}_{-j})}\|^{1/2}\underset{N \rightarrow \infty}{\longrightarrow}0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &d(\widehat{\pi}(\underline{R}^{(N)}),\widehat{\pi}(\underline{S}^{(N)}))\\&\quad\leq \mathrm{diam}\bigg(\overline{\bigcap_{i=-N}^{N}f^{-i}(R^{(N)}_i)}\bigg)\notag\\ &\quad=\mathrm{diam}(\bigcap_{i=-N}^{N}f^{-i}(R^{(N)}_i))\notag\\ &\quad\leq8Q(x^{(N)}_N)\prod_{j=1}^{N}\|Df^{-1}|_{E^u(x^{(N)}_{j})}\|^{1/2}+8Q(x^{(N)}_{-N})\prod_{j=1}^{N}\|Df|_{E^s(x^{(N)}_{-j})}\|^{1/2}\underset{N \rightarrow \infty}{\longrightarrow}0. \end{aligned} \end{align*} $$
This leads to a contradiction.
(3) We first prove that
![]() $O^{\#}= \widehat {\pi }({\widehat {\Sigma }^{\#}})$
. The proof of
$O^{\#}= \widehat {\pi }({\widehat {\Sigma }^{\#}})$
. The proof of
![]() $O^{\#}\subset \widehat {\pi }({\widehat {\Sigma }^{\#}})$
is the same as [Reference Sarig22, Theorem 12.5(3)]. So it suffices to establish the opposite direction
$O^{\#}\subset \widehat {\pi }({\widehat {\Sigma }^{\#}})$
is the same as [Reference Sarig22, Theorem 12.5(3)]. So it suffices to establish the opposite direction
![]() $O^{\#}\supset \widehat {\pi }({\widehat {\Sigma }^{\#}})$
.
$O^{\#}\supset \widehat {\pi }({\widehat {\Sigma }^{\#}})$
.
Suppose
![]() $\underline {R}=\{R_n\}_{n\in \mathbb {Z}}\in {\widehat {\Sigma }}^{\#}$
, proceeding as in the proof of Lemma 6.6, we can construct an
$\underline {R}=\{R_n\}_{n\in \mathbb {Z}}\in {\widehat {\Sigma }}^{\#}$
, proceeding as in the proof of Lemma 6.6, we can construct an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}\in \Sigma ^{\#}$
for
$\underline {x}\in \Sigma ^{\#}$
for
![]() $\underline {R}\in {\widehat {\Sigma }}^{\#}$
such that
$\underline {R}\in {\widehat {\Sigma }}^{\#}$
such that
 $$ \begin{align*} z:=\widehat{\pi}(\underline{R})\in\bigcap_{n \geq 0} \overline{\bigcap_{i=-n}^{n}f^{-i}(Z(x_i))}, \end{align*} $$
$$ \begin{align*} z:=\widehat{\pi}(\underline{R})\in\bigcap_{n \geq 0} \overline{\bigcap_{i=-n}^{n}f^{-i}(Z(x_i))}, \end{align*} $$
that is,
![]() $f^n(z)\in \overline {Z(x_n)}$
for all
$f^n(z)\in \overline {Z(x_n)}$
for all
![]() $n\in \mathbb {Z}$
. Therefore,
$n\in \mathbb {Z}$
. Therefore,
![]() $d(f^n(z),x_n)\leq \mathrm {diam}(\overline {Z(x_n)})=\mathrm {diam}(Z(x_n)) \leq \tfrac 12Q(x_n)\leq \tfrac 12d(x_n,\partial O)$
, and we have
$d(f^n(z),x_n)\leq \mathrm {diam}(\overline {Z(x_n)})=\mathrm {diam}(Z(x_n)) \leq \tfrac 12Q(x_n)\leq \tfrac 12d(x_n,\partial O)$
, and we have
Thus,
![]() $z\in O^{\#}$
, that is,
$z\in O^{\#}$
, that is,
![]() $\widehat {\pi }({\widehat {\Sigma }^{\#}})\subset O^{\#}$
.
$\widehat {\pi }({\widehat {\Sigma }^{\#}})\subset O^{\#}$
.
Finally, we prove
![]() $\widehat {\pi }|_{\widehat {\Sigma }^{\#}}$
is finite-to-one. The proof is an adaptation of [Reference Lima and Sarig21, Theorem 5.6(5)] and [Reference Ben Ovadia6] to our context. The original proof [Reference Sarig22, Theorem 12.8] has a small error that was corrected in [Reference Lima and Sarig21].
$\widehat {\pi }|_{\widehat {\Sigma }^{\#}}$
is finite-to-one. The proof is an adaptation of [Reference Lima and Sarig21, Theorem 5.6(5)] and [Reference Ben Ovadia6] to our context. The original proof [Reference Sarig22, Theorem 12.8] has a small error that was corrected in [Reference Lima and Sarig21].
Suppose
![]() $x\in O^{\#}$
, since
$x\in O^{\#}$
, since
![]() $\widehat {\pi }({\widehat {\Sigma }^{\#}})=O^{\#}$
, x has a
$\widehat {\pi }({\widehat {\Sigma }^{\#}})=O^{\#}$
, x has a
![]() $\widehat {\pi }$
-preimage
$\widehat {\pi }$
-preimage
![]() $\underline {R}\in {\widehat {\Sigma }^{\#}}$
such that
$\underline {R}\in {\widehat {\Sigma }^{\#}}$
such that
![]() $R_n=R$
for infinitely many positive n and
$R_n=R$
for infinitely many positive n and
![]() $R_n=S$
for infinitely many negative n. Let
$R_n=S$
for infinitely many negative n. Let
![]() $N:=N(R)N(S)$
and suppose by way of contradiction that there are
$N:=N(R)N(S)$
and suppose by way of contradiction that there are
![]() $N+1$
different
$N+1$
different
![]() $\underline {R}^{(0)},\underline {R}^{(1)},\ldots , \underline {R}^{(N)}\in {\widehat {\Sigma }^{\#}}$
with
$\underline {R}^{(0)},\underline {R}^{(1)},\ldots , \underline {R}^{(N)}\in {\widehat {\Sigma }^{\#}}$
with
![]() $\underline {R}^{(0)}=\underline {R}$
and
$\underline {R}^{(0)}=\underline {R}$
and
![]() $\widehat {\pi }(\underline {R}^{(m)})=x$
for all
$\widehat {\pi }(\underline {R}^{(m)})=x$
for all
![]() $m=0,1,\ldots ,N$
. As produced in the proof of Lemma 6.6, we can construct for each
$m=0,1,\ldots ,N$
. As produced in the proof of Lemma 6.6, we can construct for each
![]() $\underline {R}^{(m)}$
an
$\underline {R}^{(m)}$
an
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {x}^{(m)}\in \Sigma ^{\#}$
such that
$\underline {x}^{(m)}\in \Sigma ^{\#}$
such that
![]() $\pi (\underline {x}^{(m)})=\widehat {\pi }(\underline {R}^{(m)})=x$
, and
$\pi (\underline {x}^{(m)})=\widehat {\pi }(\underline {R}^{(m)})=x$
, and
![]() $R^{(m)}_n\subset Z(x^{(m)}_n)$
for all
$R^{(m)}_n\subset Z(x^{(m)}_n)$
for all
![]() $n\in \mathbb {Z}$
and all
$n\in \mathbb {Z}$
and all
![]() $m=0,1,\ldots ,N$
.
$m=0,1,\ldots ,N$
.
Since the sequences
![]() $\{\underline {R}^{(m)}\}_{m=0}^N$
are distinct, there exists some
$\{\underline {R}^{(m)}\}_{m=0}^N$
are distinct, there exists some
![]() $n_0>0$
such that
$n_0>0$
such that
Denote by
![]() $n^{+}$
the first
$n^{+}$
the first
![]() $n\geq n_0$
such that
$n\geq n_0$
such that
![]() $R_n=R$
, and by
$R_n=R$
, and by
![]() $n^{-}$
, the first
$n^{-}$
, the first
![]() $n\leq -n_0$
such that
$n\leq -n_0$
such that
![]() $R_n=S$
. Lemma 6.6 implies that there are at most
$R_n=S$
. Lemma 6.6 implies that there are at most
![]() $N=N(R)N(S)$
distinct choices of quadruple
$N=N(R)N(S)$
distinct choices of quadruple
![]() $(R_{n^{+}}^{(m)},x_{n^{+}}^{(m)};R_{n^{-}}^{(m)},x_{n^{-}}^{(m)} )$
for m. By the pigeonhole principle, there are
$(R_{n^{+}}^{(m)},x_{n^{+}}^{(m)};R_{n^{-}}^{(m)},x_{n^{-}}^{(m)} )$
for m. By the pigeonhole principle, there are
![]() $0\leq k,l\leq N$
with
$0\leq k,l\leq N$
with
![]() $k\neq l$
such that
$k\neq l$
such that
![]() $(R,x_{n^+,R}):=(R_{n^{+}}^{(k)},x_{n^{+}}^{(k)})=(R_{n^{+}}^{(l)},x_{n^{+}}^{(l)})$
,
$(R,x_{n^+,R}):=(R_{n^{+}}^{(k)},x_{n^{+}}^{(k)})=(R_{n^{+}}^{(l)},x_{n^{+}}^{(l)})$
,
![]() $(S,x_{n^-,S}):=(R_{n^{-}}^{(k)},x_{n^{-}}^{(k)})=(R_{n^{-}}^{(l)},x_{n^{-}}^{(l)})$
, and
$(S,x_{n^-,S}):=(R_{n^{-}}^{(k)},x_{n^{-}}^{(k)})=(R_{n^{-}}^{(l)},x_{n^{-}}^{(l)})$
, and
Now we apply the diamond argument [Reference Adler2, Lemma 6.7] to finish the proof of part (3). Fix
![]() $x\in \bigcap _{i=n^-}^{n^+}f^{-i}(R_i^{(k)})$
,
$x\in \bigcap _{i=n^-}^{n^+}f^{-i}(R_i^{(k)})$
,
![]() $y\in \bigcap _{i=n^-}^{n^+}f^{-i}(R_i^{(l)})$
, and define
$y\in \bigcap _{i=n^-}^{n^+}f^{-i}(R_i^{(l)})$
, and define
![]() $z_1,z_2$
by the equalities
$z_1,z_2$
by the equalities
These points are uniquely defined by Proposition 6.6(2) since
![]() $f^{n^+}(x),f^{n^+}(y)\in R_{n^{+}}^{(k)}=R_{n^{+}}^{(l)}=R$
,
$f^{n^+}(x),f^{n^+}(y)\in R_{n^{+}}^{(k)}=R_{n^{+}}^{(l)}=R$
,
![]() $f^{n^-}(x),f^{n^-}(y)\in R_{n^{-}}^{(k)}=R_{n^{-}}^{(l)}=S$
. We will obtain a contradiction once we show that
$f^{n^-}(x),f^{n^-}(y)\in R_{n^{-}}^{(k)}=R_{n^{-}}^{(l)}=S$
. We will obtain a contradiction once we show that
![]() $z_1\neq z_2$
and
$z_1\neq z_2$
and
![]() $z_1= z_2$
.
$z_1= z_2$
.
First, note that
![]() $\{f^{n^+}(z_1)\}=W^u(f^{n^+}(x),R_{n^{+}}^{(k)})\cap W^s(f^{n^+}(y),R_{n^{+}}^{(l)})\subset W^u(f^{n^+}(x), R_{n^{+}}^{(k)})$
, by the Markov property (Proposition 6.6(3)), we have
$\{f^{n^+}(z_1)\}=W^u(f^{n^+}(x),R_{n^{+}}^{(k)})\cap W^s(f^{n^+}(y),R_{n^{+}}^{(l)})\subset W^u(f^{n^+}(x), R_{n^{+}}^{(k)})$
, by the Markov property (Proposition 6.6(3)), we have
![]() $z_1\in \bigcap _{i=n^-}^{n^+}f^{-i}(R_i^{(k)})$
. Similarly, since
$z_1\in \bigcap _{i=n^-}^{n^+}f^{-i}(R_i^{(k)})$
. Similarly, since
![]() $\{f^{n^-}(z_2)\}=W^u(f^{n^-}(x),R_{n^{-}}^{(k)})\cap W^s(f^{n^-}(y),R_{n^{-}}^{(l)})\subset W^s(f^{n^-}(y),R_{n^{-}}^{(l)})$
, we have
$\{f^{n^-}(z_2)\}=W^u(f^{n^-}(x),R_{n^{-}}^{(k)})\cap W^s(f^{n^-}(y),R_{n^{-}}^{(l)})\subset W^s(f^{n^-}(y),R_{n^{-}}^{(l)})$
, we have
![]() $z_2\in \bigcap _{i=n^-}^{n^+}f^{-i}(R_i^{(l)})$
. Therefore, we get
$z_2\in \bigcap _{i=n^-}^{n^+}f^{-i}(R_i^{(l)})$
. Therefore, we get
![]() $z_1\neq z_2$
for
$z_1\neq z_2$
for
![]() $(R_{n^{-}}^{(k)},\ldots , R_{n^{+}}^{(k)})\neq (R_{n^{-}}^{(l)},\ldots ,R_{n^{+}}^{(l)} )$
.
$(R_{n^{-}}^{(k)},\ldots , R_{n^{+}}^{(k)})\neq (R_{n^{-}}^{(l)},\ldots ,R_{n^{+}}^{(l)} )$
.
We now show that
![]() $z_1= z_2$
. Since
$z_1= z_2$
. Since
![]() $f^{n^+}(z_1)\in R\subset Z(x_{n^+,R})$
and
$f^{n^+}(z_1)\in R\subset Z(x_{n^+,R})$
and
![]() $f^{n^-}(z_2)\in S\subset Z(x_{n^-,S})$
, there are
$f^{n^-}(z_2)\in S\subset Z(x_{n^-,S})$
, there are
![]() $\underline {x}=\{x_n\}_{n\in \mathbb {Z}}, \underline {y}=\{y_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
with
$\underline {x}=\{x_n\}_{n\in \mathbb {Z}}, \underline {y}=\{y_n\}_{n\in \mathbb {Z}}\in \Sigma ^{\#}$
with
![]() $x_{n^+}=x_{n^+,R}, y_{n^-}=x_{n^-,S}$
such that
$x_{n^+}=x_{n^+,R}, y_{n^-}=x_{n^-,S}$
such that
![]() $z_1=\pi (\underline {x})$
,
$z_1=\pi (\underline {x})$
,
![]() $z_2=\pi (\underline {y})$
. Define
$z_2=\pi (\underline {y})$
. Define
![]() $\underline {z}^\prime =\{z_n^\prime \}_{n\in \mathbb {Z}}\in \Sigma $
by
$\underline {z}^\prime =\{z_n^\prime \}_{n\in \mathbb {Z}}\in \Sigma $
by
 $$ \begin{align*} z^\prime_n=\begin{cases} y_n, & n \leq n^-, \\ x^{(k)}_n, & n^-\leq n\leq n^+,\\ x_n, & n\geq n^+.\\ \end{cases} \end{align*} $$
$$ \begin{align*} z^\prime_n=\begin{cases} y_n, & n \leq n^-, \\ x^{(k)}_n, & n^-\leq n\leq n^+,\\ x_n, & n\geq n^+.\\ \end{cases} \end{align*} $$
Since both
![]() $\underline {x}, \underline {y}\in \Sigma ^{\#}$
, also
$\underline {x}, \underline {y}\in \Sigma ^{\#}$
, also
![]() $\underline {z}^\prime \in \Sigma ^{\#}$
. We claim that
$\underline {z}^\prime \in \Sigma ^{\#}$
. We claim that
![]() $z_1=\pi (\underline {z}^\prime )=z_2$
.
$z_1=\pi (\underline {z}^\prime )=z_2$
.
In practice, note again that from
![]() $f^{n^+}(z_1)\in W^u(f^{n^+}(x),R_{n^{+}}^{(k)})$
and the Markov property (Proposition 6.6(3)), we have
$f^{n^+}(z_1)\in W^u(f^{n^+}(x),R_{n^{+}}^{(k)})$
and the Markov property (Proposition 6.6(3)), we have
![]() $f^{n^-}(z_1)\in W^u(f^{n^-}(x),R_{n^{-}}^{(k)})$
. Naturally,
$f^{n^-}(z_1)\in W^u(f^{n^-}(x),R_{n^{-}}^{(k)})$
. Naturally,
![]() $f^{n^-}(z_2)\in W^u(f^{n^-}(x),R_{n^{-}}^{(k)})$
. Hence, we have by Definition 6.6,
$f^{n^-}(z_2)\in W^u(f^{n^-}(x),R_{n^{-}}^{(k)})$
. Hence, we have by Definition 6.6,
By the symbolic Markov property (Proposition 6.4), for all
![]() $n\leq n^-$
, Proposition 5.2(2) and (4) imply that
$n\leq n^-$
, Proposition 5.2(2) and (4) imply that
Similarly, we obtain that for all
![]() $n\geq n^+$
,
$n\geq n^+$
,
The next thing is to fix
![]() $n^-\leq n\leq n^+$
. Observe that we have
$n^-\leq n\leq n^+$
. Observe that we have
![]() $f^{n}(z_1), f^{n}(z_2)\in R_n^{(k)}\cup R_n^{(l)}\subset Z(x_n^{(k)})\cup Z(x_n^{(l)})$
. Since
$f^{n}(z_1), f^{n}(z_2)\in R_n^{(k)}\cup R_n^{(l)}\subset Z(x_n^{(k)})\cup Z(x_n^{(l)})$
. Since
![]() $\pi (\underline {x}^{(k)})=\pi (\underline {x}^{(l)})=x$
, we get
$\pi (\underline {x}^{(k)})=\pi (\underline {x}^{(l)})=x$
, we get
![]() $f^n(x)\in Z(x_n^{(k)})\cap Z(x_n^{(l)})$
. Then Lemma 6.3(1) implies that
$f^n(x)\in Z(x_n^{(k)})\cap Z(x_n^{(l)})$
. Then Lemma 6.3(1) implies that
![]() $Z(x_n^{(k)})\cup Z(x_n^{(l)})\subset \exp _{x_n^{(k)}}(S_{x_n^{(k)}})$
. Recalling
$Z(x_n^{(k)})\cup Z(x_n^{(l)})\subset \exp _{x_n^{(k)}}(S_{x_n^{(k)}})$
. Recalling
![]() $x_n^{(k)}=z^\prime _n$
for all
$x_n^{(k)}=z^\prime _n$
for all
![]() $n^-\leq n\leq n^+$
, therefore,
$n^-\leq n\leq n^+$
, therefore,
In conclusion, for this
![]() $\varepsilon $
-rppo
$\varepsilon $
-rppo
![]() $\underline {z}^\prime \in \Sigma ^{\#}$
,
$\underline {z}^\prime \in \Sigma ^{\#}$
,
![]() $f^{n}(z_1), f^{n}(z_2)\in \exp _{z^\prime _{n}}(S_{z^\prime _{n}})$
for all
$f^{n}(z_1), f^{n}(z_2)\in \exp _{z^\prime _{n}}(S_{z^\prime _{n}})$
for all
![]() $n\in \mathbb {Z}$
. By the uniqueness of shadowing point,
$n\in \mathbb {Z}$
. By the uniqueness of shadowing point,
![]() $z_1=z_2$
. This leads to a contradiction.
$z_1=z_2$
. This leads to a contradiction.
Acknowledgements
We are grateful to Professor Huyi Hu and the anonymous referees for useful comments and suggestions. The second author is the corresponding author. This work is supported by NSFC (Grant No. 11871120,12071082) and Natural Science Foundation of Chongqing (Grant No. cstc2021jcyj-msxmX0299).