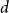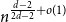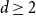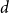Twin-width of sparse random graphs

Abstract

We show that the twin-width of every $n$-vertex $d$-regular graph is at most $n^{\frac{d-2}{2d-2}+o(1)}$ for any fixed integer $d \geq 2$ and that almost all $d$-regular graphs attain this bound. More generally, we obtain bounds on the twin-width of sparse Erdős–Renyi and regular random graphs, complementing the bounds in the denser regime due to Ahn, Chakraborti, Hendrey, Kim, and Oum.

1. Introduction

The twin-width $\textrm{tww}(G)$ of a graph $G$ is a parameter recently introduced by Bonnet, Kim, Thomassé, and Watrigant [6]. ¹ Twin-width has received a lot of attention largely due to its algorithmic applications, as it is shown in [6] that any first-order formula can be evaluated in linear time on graphs in a given class of bounded twin-width, given a witness certifying that twin-width is bounded. Structured graph classes such as proper minor closed graph classes and classes of bounded clique-width or rank-width have bounded twin-width. Meanwhile, a counting argument can be used to show that there exist $3$ -regular graphs of unbounded twin-width [5].

Bounds on the twin-width of general graphs were first considered by Ahn, Hendrey, Kim, and Oum [3], who have shown that $\textrm{tww}(G) \leq \left (\frac{1}{2}+o(1)\right )n$ and that

(1) \begin{align} \textrm{tww}(G) \leq \left (1 + o(1)\right ) \sqrt{3m} \end{align}

for every graph $G$ with $n$ vertices and $m$ edges. They have also started investigating the twin-width of random graphs $G(n,p)$ . This investigation was continued in [1] where it was shown that with high probability the twin-width of $G(n,p)$ is $\Theta (n \sqrt{p})$ for $726\log n/n\,\leq \,p\,\leq \,1/2$ , i.e. (1) is tight up to a constant factor in this regime. Meanwhile, already in [3] it was shown that if $p \lt c/n$ for fixed $c\lt 1$ then the twin-width of $G(n,p)$ is at most two. These results left open the question of determining the typical twin-width of $G(n,p)$ for the range $1/n \lt p = o(\log n/n )$ . As one of the contributions of this paper, we almost fully resolve this question (see Theorem1.3).

We also consider the twin-width of random $d$ -regular $n$ -vertex graphs for $d = o (\log n)$ . Prior to our work, very little was known even in the case $d=3$ . As mentioned above, $3$ -regular graphs have unbounded twin-width, but the counting argument only gives a lower bound which is triply logarithmic in the number of vertices. Meanwhile, the best prior upper bound on the twin-width of $n$ -vertex $3$ -regular graphs was of the order $O\!\left(\sqrt{n}\right)$ as above. In this paper, we precisely determine the maximum twin-width among all $n$ -vertex $3$ -regular graphs as $n^{\frac{1}{4}+o(1)}$ and show that $\textrm{tww}(G) = n^{1/4 + o(1)}$ for almost all $n$ -vertex $3$ -regular graphs $G$ . These results generalize to $d$ -regular graphs, determining precisely the asymptotics for the maximum twin-width of $n$ -vertex $d$ -regular graphs for any $d$ .

Theorem 1.1. If $d \geq 2$ is an integer, then

\begin{align*} \textrm {tww}(G) \leq n^{\frac {d-2}{2d-2}+ o(1)} \end{align*}

for every $n$ -vertex $d$ -regular graph $G$ . Moreover, the inequality holds with equality for almost all $n$ -vertex $d$ -regular graphs.

More generally, for various sparse random graph models we show that the twin-width is typically polynomial in the number of vertices, with the exponent governed by the maximum average degree of the graph.

Recall that the maximum average degree of a graph $G$ , denoted by $\textrm{mad}(G)$ , is defined as the maximum average degree of subgraphs of $G$ , i.e.

\begin{align*}\textrm {mad}(G) = \max _{H \subseteq G, {\textsf {v}}(H)\gt 0}\frac {2{\textsf {e}}(H)}{{\textsf {v}}(H)}.\end{align*}

(We denote the number of vertices and edges of a graph $H$ by ${\textsf{v}}(H)$ and ${\textsf{e}}(H)$ , respectively.)

Let us first state a special case of our most general result for Erdős–Renyi random graphs with constant average degree.

Theorem 1.2. For every $c \gt 1$ there exists $\rho = \rho (c) \gt 2c$ such that with high probability

\begin{align*} \textrm {mad}\left (G\left (n,\frac {c}{n}\right )\right )=(1+o(1))\rho \qquad \mathrm {and} \qquad \textrm {tww}\left (G\left (n,\frac {c}{n}\right )\right ) = n^{\frac {\rho -2}{2\rho -2}+ o(1)}. \end{align*}

Our most general result gives estimates of the typical twin-width for several models of sparse random graphs with average degree bounded from below away from one. It extends Theorems1.1 and 1.2 as well as giving tighter bounds on the error terms.

Theorem 1.3. Fix $\varepsilon \gt 0$ . Let $G$ be a random $n$ -vertex graph obtained using any of the following models:

• • $G$ is a uniformly random $d$ -regular graph on $n$ vertices with $2 \lt d \lt \frac{1}{5}\log n$ ,

• • $G$ is a uniformly random graph on $n$ vertices and $m$ edges with $(1+\varepsilon )n \leq m \leq \frac{1}{11}n\log n$ , or

• • $G$ is a random graph $G(n,p)$ with $\frac{1+\varepsilon }{n} \leq p \leq \frac{1}{12}\frac{\log n}{n}$ .

Then, with high probability, we have

(2) \begin{align} n^{\frac{d-2}{2d-2} }\cdot \Omega _{\varepsilon }\left ( \frac{d}{\sqrt{\log n}}\right ) \leq \textrm{tww}(G) \leq n^{\frac{d-2}{2d-2}} \cdot e^{O_{\varepsilon }\left (d^{-1}\sqrt{\log n}\cdot{\log \log n} +\log d\right )}, \end{align}

where $d = \textrm{mad}(G)$ .

Our results, in particular, answer a question of Sylvester [12] whether $\textrm{tww}(G)=\Theta\!\left(\sqrt{{\textsf{e}}(G)}\right)$ with high probability for sparse Erdős–Renyi random graphs and random cubic graphs. By Theorem1.3 the answer is negative for random $d$ -regular graphs with $d=o\!\left(\frac{\log n}{n \log \log n}\right)$ and for $G(n,p)$ with $p = o\!\left(\frac{\log n}{n \log \log n}\right)$ and the answer is positive for $p = \Omega\! \left(\frac{\log n}{n}\right)$ .

For an $n$ -vertex graph $G$ denote $\frac{\log \textrm{tww}(G)}{\log n}$ by $a(G)$ for brevity, i.e. $\textrm{tww}(G)=n^{a(G)}$ . It follows from the results of [1, 3] that $a(G(n,p)) = o(1)$ when $p = \frac{1-o(1)}{n}$ , and $a(G(n,p)) = \frac{1}{2} - o(1)$ when $p = \Omega\!\left(\frac{\log n}{n}\right)$ and $p=\frac{1}{n^{1-o(1)}}$ . Theorem1.3 establishes the asymptotics of $a(G(n,p))$ and $\frac{1}{2}-a(G(n,p))$ in most of the intermediate range, i.e. for $ \frac{1+o(1)}{n} \leq p \leq o\!\left (\frac{\log n}{n \log \log n}\right )$ .

We finish the introduction by briefly and informally describing the techniques we use to prove Theorems1.1, 1.2 and 1.3. To obtain the upper bounds on twin-width of a graph $G$ , we map the vertices of $G$ to random sequences over some alphabet so that the images of far away vertices are independent and uniformly distributed over the set of all sequences, while the images of neighbours share a fair amount of information. This yields a homomorphism from the original graph to a structured and appropriately sparse graph $H$ , allowing us to bound the twin-width of $G$ in terms of the twin-width of $H$ . We then finish by bounding the twin-width of the more structured graph $H$ . We prove the upper bounds in Section 2.

Our proofs of lower bounds on the twin-width rely on counting, which as far as we know remains the only successful technique for establishing superconstant lower bounds on the twin-width of graphs with constant maximum degree. As a new ingredient to facilitate counting arguments, we show that for every graph $G$ with twin-width at most $w$ and any $K \leq{\textsf{v}}(G)$ , $G$ is a spanning subgraph of a “fairly balanced” blowup of some $(w+\Delta (G))$ -degenerate graph on $K$ vertices. We prove the lower bounds in Section 3.

Preliminaries, basic definitions and notation

We mostly use standard graph theoretical notation. Let $G$ be a graph and $X\subseteq V(G)$ . We denote by $\Delta (G)$ the maximum degree of $G$ , by $G[X]$ the subgraph of $G$ induced by $X$ , and by $G\setminus X$ the graph $G[V(G)\setminus X]$ (if $X=\{v\}$ , we write $G \setminus v$ ).

Let $[n] = \{1,2,\ldots, n\}$ . If $S$ and $T$ are sets, $\boldsymbol{v}=(s_1,s_2,\ldots, s_r) \in S^r$ is a sequence of elements of $S$ , and $f\,:\,S \to T$ is map, let $f(\boldsymbol{v}) \,:\!=\,\left(f(s_1),f(s_2),\ldots, f( s_r)\right) \in T^r.$

It will be convenient for us to work with a somewhat atypical notion of homomorphism, where we allow adjacent vertices to be mapped to the same vertex. Explicitly, for graphs $G$ and $H$ we say that a map $\phi \, :\, V(G) \to V(H)$ is a homomorphism from $G$ to $H$ if for every $uv \in E(G)$ we either have $\phi (u)\phi (v) \in E(H)$ or $\phi (u) = \phi (v)$ .

Next let us elaborate on the relationship between Theorems1.1, 1.2 and 1.3. The error terms in (2) are of the form $n^{o(1)}$ in the setting covered by the theorem and so Theorem1.3 implies Theorems1.1 and 1.2 except

• • the upper bound in Theorem1.1 needs to hold for all $n$ -vertex $d$ -regular graphs not just almost all such graphs, and

• • Theorem1.2 postulates concentration of $\textrm{mad}(G(n,p))$ for $p=c/n$ and constant $c$ , i.e. the existence of $\rho (c)$ such that $\textrm{mad}(G(n,c/n)) = (1+o(1))\rho (c)$ with high probability. Anantharam and Salez establish existence of such a $\rho$ in [4] and show that $\rho$ can be found as a fixed point of a certain distributional fixed-point equation, as was conjectured earlier by Hajek [7]. Thus by the results from [4], Theorem1.2 is implied by Theorem1.3.

Finally, it is well-known that the random graph $G(n,p)$ with high probability has $m = p\binom{n}{2} + o(\sqrt{p}n \log n)$ edges, and for fixed $m$ every graph with $V(G)=[n]$ and ${\textsf{e}}(G)=m$ has the same probability in $G(n,p)$ . Thus, if (2) holds for any value of $m = p\binom{n}{2} \pm o(\sqrt{p}n \log n)$ with high probability (independent of the choice of $m$ ), then it holds with high probability for $G(n,p)$ . It follows that the conclusion of Theorem1.3 for $G(n,p)$ follows from its conclusion for uniformly random graphs on $n$ vertices and $m$ edges.

Thus Theorems1.1, 1.2 and 1.3 follow from the next two theorems, which we prove in Sections 2 and 3, respectively.

Theorem 1.4. [Upper bounds]

1. (i) If $G$ is an $n$ -vertex, $d$ -regular graph with $d \gt 2$ , then

   (3) \begin{align} \textrm{tww}(G) \leq n^{\frac{d-2}{2d-2}} \cdot e^{O\left (d^{-1}\sqrt{\log n}\cdot{\log \log n} +\log d\right )}. \end{align}

2. (ii) Let $\varepsilon \gt 0$ be fixed. If $G$ is a uniformly random graph on $n$ vertices and $m$ edges with $m \geq (1+\varepsilon )n$ and $d = \textrm{mad}(G)$ , then ( 3 ) holds with high probability.

Theorem 1.5. [Lower bounds] If $G$ is either

1. (i) a uniformly random $n$ -vertex, $d$ -regular graph with $2 \lt d \lt \frac{1}{5}\log n$ , or

2. (ii) a uniformly random graph on $n$ vertices and $m$ edges where $(1+\varepsilon )n \leq m \leq \frac{1}{11}n\log n$ and $d = \textrm{mad}(G)$ ,

then with high probability

(4) \begin{align} \textrm{tww}(G) \geq n^{\frac{d-2}{2d-2} }\cdot \Omega \left ( \frac{d}{\sqrt{\log n}}\right ). \end{align}

The time has come to define twin-width, or rather a substitute of it that we will work with. A contraction sequence from a graph $G$ to a graph $H$ is a sequence of graphs $(G=G_1,G_2,\ldots, G_k=H)$ such that for each $i \in [k-1]$ the graph $G_{i+1}$ is obtained from $G_i$ by identifying two vertices. That is, for some pair of distinct vertices $u,v \in G_i$ the graph $G_{i+1}$ is obtained from $G_i \setminus \{u, v\}$ by adding a new vertex $w$ such that $wx \in E(G_{i+1})$ if and only if $ux \in E(G_i)$ or $vx \in E(G_i)$ . We say that a contraction sequence $(G_1,G_2,\ldots, G_k)$ is a $w$ -contraction sequence for some positive integer $w$ if $\Delta (G_i) \leq w$ for every $i \in [k]$ , and this sequence is a contraction sequence for the graph $G_1$ if ${\textsf{v}}(G_k)=1$ .

Finally, we define the sparse twin-width of a graph $G$ , denotes by $\textrm{stww}(G)$ , as the minimum positive integer $w$ such that there exists a $w$ -contraction sequence for $G$ . That is, $\textrm{stww}(G)$ is the minimum $w$ such that we can reduce $G$ to a one-vertex graph via a sequence of pairwise vertex identifications such that the degrees of all the vertices throughout this process are at most $w$ .

The twin-width $\textrm{tww}(G)$ is defined similarly to the sparse twin-width, but using a notion of trigraphs. In particular, the twin-width of $G$ is the minimum over contraction sequences $(G=G_1,G_2,\ldots )$ for $G$ of a parameter that is upper bounded by $\max _{i}\Delta (G_i)$ . For every graph $G$ , we have

(5) \begin{align} \max \{\textrm{tww}(G),\Delta (G)\} \leq \textrm{stww}(G) \leq \textrm{tww}(G) + \Delta (G), \end{align}

where the inequality $\textrm{tww}(G) \leq \textrm{stww}(G)$ follows from the partial description of $\textrm{tww}(G)$ above, and the inequality $\textrm{stww}(G) \leq \textrm{tww}(G) + \Delta (G)$ is implicit in [[5], Lemma 7.1].

The maximum degree $\Delta (G)$ is much smaller than the estimates given on $\textrm{tww}(G)$ in Theorems1.4 and 1.5 and those estimates remain true even if $\textrm{tww}(G)$ is rescaled by a constant factor. Thus by (5) it suffices to prove these theorems with $\textrm{tww}(G)$ replaced by $\textrm{stww}(G)$ , and that is what we will do, working from now on almost exclusively with the notion of sparse twin-width.

2. Upper bounds

In this section we prove Theorem1.4, establishing the upper bounds in our main results.

We start by expanding on the description of our methods in the introduction and giving a sketch of a proof of an upper bound of $n^{\frac{1}{3}+ o(1)}$ on the sparse twin-width of $n$ -vertex $3$ -regular graphs. While this bound is weaker than the tight bound $n^{\frac{1}{4}+ o(1)}$ , which we will end up proving, it already substantially improves on the previously known bounds and illustrates the main steps of the approach implemented in this section.

Let $G$ be an $n$ -vertex $3$ -regular graph. Let $\ell = \left (\frac{1}{6}+o(1)\right )\log _2 n$ be an integer. For each $v \in V(G)$ , let the label $f(v) \in \{0,1\}^{\ell }$ be chosen uniformly at random among all $2^{\ell }$ distinct $\{0,1\}$ -sequences of length $\ell$ . If $u_1,u_2,u_3$ are the neighbours of $v$ , we define

\begin{align*}\phi (v) = \begin {pmatrix} f(v) \\ f(u_1) \\ f(u_2) \\ f(u_3) \end {pmatrix} \in \{0,1\}^{4 \times \ell }.\end{align*}

In particular, $\phi (v)$ is uniformly distributed among the $2^{4\ell }= n^{\frac{2}{3}+o(1)}$ matrices of size $4 \times \ell$ with $\{0,1\}$ values. Furthermore, if $uv \in E(G)$ then $\phi (u)$ and $\phi (v)$ have (at least) two rows in common, although not in the same positions. Thus if $H=H(\ell )$ is the graph with all possible such $4 \times \ell$ matrices as vertices and an edge between any two matrices sharing at least two rows in this way, then $\phi$ is a homomorphism from $G$ to $H$ , and we can obtain a contraction sequence from $G$ to $H$ by arbitrarily identifying pairs of vertices of $G$ with the same image, until we obtain a subgraph of $H$ . As the dependencies between values of $\phi$ are only local, it is not hard to believe (and will be shown later in a more general and technical setting) that the number of preimages of every vertex of $H$ is typically close to the expected value $n^{\frac{1}{3}+o(1)}$ and so we can choose $\phi$ so that the total degree of vertices identified into a single one in this process is $n^{\frac{1}{3}+o(1)}$ , i.e. our contraction sequence from $G$ to $H$ is an $n^{\frac{1}{3}+o(1)}$ -contraction sequence. To show that $\textrm{stww}(G) \leq n^{\frac{1}{3}+o(1)}$ it remains to extend this sequence to an $n^{\frac{1}{3}+o(1)}$ -contraction sequence for $G$ , i.e. to obtain an $n^{\frac{1}{3}+o(1)}$ -contraction sequence for $H$ .

To accomplish this final step note that $\Delta (H(\ell )) = n^{\frac{1}{3}+o(1)}$ and that there exists a natural homomorphism from $H(\ell )$ to $H(\ell -1)$ by deleting the final column of each matrix. As in the previous paragraph, we can convert the homomorphism in to an $n^{\frac{1}{3}+o(1)}$ -contraction sequence from $H(\ell )$ to $H(\ell -1)$ , and repeating this process eventually extend this sequence to an $n^{\frac{1}{3}+o(1)}$ -contraction sequence for $H$ .

This finishes the sketch.

We proceed to tighten and generalize the steps presented above. The next three lemmas lay down the groundwork which will allow us to obtain a random map $\phi$ from the vertices of a sparse graph $G$ to a set of matrices in a way similar to the above so that the neighbours share as much information as possible, but far away vertices share none. If a graph corresponds to a digraph with maximum outdegree one, it is possible to obtain such $\phi$ with neighbours sharing almost all the information (see Lemma2.2). In general, we obtain $\phi$ by decomposing $G$ into such digraphs.

Lemma 2.1. If $G$ is a graph and $a,b\in \mathbb{N}$ are such that $a\geq b$ and $ \frac{a}{b} \geq \frac{1}{2} \textrm{mad}(G)$ , then there exist spanning subgraphs $G_1,\ldots, G_a$ of $G$ , each of which admits an orientation with maximum outdegree one, such that each edge of $G$ belongs to exactly $b$ of them.

Proof. Let $G=(V,E)$ , and consider the following auxiliary bipartite graph $H$ . The bipartition of $H$ consists of the two sets $V \times [a]$ and $E\times [b]$ , and there exists an edge between vertices $(v,i)\in V\times [a]$ and $(e,j) \in E\times [b]$ if $v$ and $e$ are incident in $G$ . We now claim that $H$ admits a matching that covers $E\times [b]$ , and to prove this we use Hall’s theorem. So consider any subset $X\subseteq E\times [b]$ . Let $F \subseteq E$ be the projection of $X$ to the first coordinate, and let $A\subseteq V$ be the set of vertices in $G$ that touch at least one edge in $F$ . Since $\textrm{mad}(G)\le \frac{2a}{b}$ , we have $|F|\le \frac{a}{b}\cdot |A|$ . Furthermore, it follows directly by definition of $H$ that $N_H(X)=A\times [a]$ . Thus, we have $|N_H(X)|=|A|\cdot a\ge b \cdot |F|\ge |X|$ , where we used that $X\subseteq F \times [b]$ in the last inequality. Thus, Hall’s condition is satisfied and we indeed find a matching $M$ in $H$ that covers every vertex in $E\times [b]$ . For $i=1,\ldots, a$ , define $E_i \,:\!=\,\{(u,v)\:|\:\exists t\in [b]\,:\, (u,i)\text{ is matched to }(uv,t)\text{ in }M\}$ . It is readily verified that $D_i \,:\!=\,(V,E_i)$ is a digraph of maximum out-degree at most $1$ , and its underlying graph $G_i$ is a subgraph of $G$ . The fact that $M$ covers every vertex in $E\times [b]$ now directly implies that every edge $e$ of $G$ belongs to exactly $b$ of the graphs $G_1,\ldots, G_a$ , as desired.

In the next lemma we construct homomorphisms from graphs that admit an orientation with maximum outdegree one (which we will obtain from Lemma2.1) to a certain explicit family of sparse graphs, which will serve as building blocks of the homomorphism we will use to bound $\textrm{stww}(G)$ .

We now define this graph family. Let $S$ be a (possibly infinite) set. We say that two sequences $(s_1,s_2,\ldots, s_r)$ and $(s^{\prime}_1,s^{\prime}_2,\ldots, s^{\prime}_r)$ of the same length $r$ are close if they contain a common subsequence of length $r-1$ , that is if there exist indices $i$ and $j$ such that

\begin{align*}(s_1,s_2,\ldots, s_{i-1},s_{i+1},\ldots, s_r) = (s^{\prime}_1,s^{\prime}_2,\ldots, s^{\prime}_{j-1},s^{\prime}_{j+1},\ldots, s^{\prime}_r).\end{align*}

Let $\Gamma =\Gamma (S,r)$ be a graph with $V(\Gamma )=S^{r}$ such that two sequences are adjacent in $\Gamma$ if and only if they are close. Let $\Gamma _*(S,r)$ be the induced subgraph of $\Gamma$ with vertex set restricted to the set of sequences in which each element of $S$ appears at most once.

Lemma 2.2. If $G$ is a graph which admits an orientation with maximum outdegree at most one, then for every positive integer $r$ there exists a set $S$ and a homomorphism $\phi$ from $G$ to $\Gamma _*(S,r)$ such that for every pair of vertices $u,v\in V(G)$ , if the sequences $\phi (u)$ and $\phi (v)$ share a common element, then the distance between $u$ and $v$ in $G$ is at most $2r-2$ .

Proof. It suffices to prove the lemma for connected graphs $G$ . Indeed, if $G$ is a union of two vertex disjoint graphs non-null graphs $G_1$ and $G_2$ , we may inductively assume that for $i=1,2$ there exist homomorhisms $\phi _i \,:\, V(G_i) \to \Gamma _*(S_i,r)$ satisfying the conditions of the lemma for $G_i$ . Further, we may assume without loss of generality that $S_1 \cap S_2 = \emptyset$ . If $\phi \,:\, V(G) \to \Gamma _*(S_1 \cup S_2,r)$ is defined so that $\phi |_{V(G_i)}=\phi _i$ for $i=1,2$ , then $\phi$ is as desired.

Hence we assume that $G$ is connected and that the edges of $G$ are directed so that every vertex has at most one outneighbour. Then $G$ contains a unique directed cycle $C$ or exactly one vertex with no outneighbours.

Let $S=V(G)\cup \{s_1,\ldots, s_r\}$ , where $\{s_1,\ldots, s_r\}$ is an arbitrary set disjoint from $V(G)$ . For each vertex $v$ , let $v=v_1, v_2,\ldots, v_t$ be the vertices of the unique longest directed path starting at $v$ , and let $f(v)=\min (t, r)$ . Now set $\phi (v) \,:\!=\,(v_1,\ldots, v_{f(v)},s_1,\ldots, s_{r-f(v)})$ . Observe that if $(v,w)$ is a directed edge, then the substring obtained by deleting $v_1$ from $\phi (v)$ can be obtained from $\phi (w)$ either by deleting the final element of $\phi (w)$ or by deleting $v$ from $\phi (w)$ . Additionally, if $v$ and $w$ share an element then they share an element in $V(G)$ , and so the distance between them is at most $2r-2$ . Thus $\phi$ is a homorphism satisfying the lemma.

Next we formalize the arguments used to bound twinwidth via homomorphisms sketched at the beginning of the section, starting with the following simple lemma.

Lemma 2.3. If $G,H$ are graphs and $\phi$ is a homomorphism from $G$ to $H$ , then

(6) \begin{align} \textrm{stww}(G) \leq \max \!\left\{\textrm{stww}(H), m\Delta (G)\right\}, \end{align}

where $m \,:\!=\, \max _{v \in V(H)}|\phi ^{-1}(v)|$ .

Proof. It suffices to show that there exists a $m\Delta (G)$ -contraction sequence from $G$ to a subgraph of $H$ , as we can then extend it to a $\max \{\textrm{stww}(H), m\Delta (G)\}$ -contraction sequence for $G$ using the $\textrm{stww}(H)$ -contraction sequence for $H$ . We obtain such a sequence by repeatedly identifying the vertices in $\phi ^{-1}(v)$ into a single vertex for every $v$ in $V(H)$ . At any step of this process each vertex of the intermediate graph $G_i$ has been obtained by identification of at most $m$ vertices of $G$ and so has degree at most $m\Delta (G)$ .

Next we define a certain technical product of the graphs $\Gamma (S,r)$ defined above to which we will map our graph $G$ and bound its twin-width. For positive integers $q \geq 2$ , $r_1,\ldots, r_a,$ and $b,$ let $\Pi =\Pi (r_1,r_2,\ldots, r_a;b,q)$ be the graph with

\begin{align*}V(\Pi ) = \left\{(v_1,v_2,\ldots, v_a) \: | \: v_i \in [q]^{r_i}\right\}\end{align*}

where two vertices $\boldsymbol{v}=(v_1,v_2,\ldots, v_a)$ and $\boldsymbol{u}=(u_1,u_2,\ldots, u_a)$ are adjacent if there exists a set of $b$ components of $\boldsymbol{u}$ which are close to the corresponding components of $\boldsymbol{v}$ , that is if there exists $I \subseteq [a]$ with $|I|=b$ such that for each $i \in I$ either $u_iv_i \in E(\Gamma ([q],r_i))$ or $u_i=v_i$ .

Lemma 2.4. If $a,b,q,r,r_1,\ldots, r_a\in \mathbb{N}$ are such that $a \geq b$ , $q\geq 2$ and $r_1,\ldots, r_a \leq r$ , then

(7) \begin{align} \textrm{stww}(\Pi (r_1,r_2,\ldots, r_a;b,q)) \leq r^{2b} a^b q^{ar-b(r-1)+1}. \end{align}

Proof. Let $\Pi =\Pi (r_1,r_2,\ldots, r_a;\,b,q)$ . First, we bound $\Delta (\Pi )$ . Given $\boldsymbol{u}=(u_1,u_2,\ldots, u_a) \in V(\Pi )$ we can enumerate its neighbours as follows. There are $\binom{a}{b} \lt a^b$ ways of choosing a set $I \subseteq [a]$ with $|I|=b$ such that the components with indices in $I$ in the neighbour are close to the corresponding components of $\boldsymbol{u}$ . For each $i \in I$ there are at most $q r^2$ ways of choosing the entries of this row in the neighbour, as there are at most $r^2$ ways of choosing the shared subsequences, and at most $q$ ways of choosing the remaining entry. Finally, there are at most $q^r$ ways of choosing entries of each remaining row, yielding an upper bound $a^b \times (qr^2)^b \times (q^r)^{a-b}$ on the number of neighbours of $\boldsymbol{u}$ . Thus

(8) \begin{align} \Delta (\Pi ) \leq r^{2b} a^b q^{ar-b(r-1)} \end{align}

We now prove the lemma by induction on $\sum _{i=1}^a r_i$ using (8) and Lemma2.3. The base case, when $r_i=1$ for every $i \in [a]$ , is trivial, as $\textrm{stww}(\Pi )\le{\textsf{v}}(\Pi )=q^a\lt r^{2b}a^bq^{ar-b(r-1)+1}$ in this case.

For the induction step assume without loss of generality that $r_1 \geq 2$ . Let $\psi \,:\, [q]^{r_1} \to [q]^{r_1-1}$ be a map erasing the last component, i.e. $\psi ((x_1,\ldots, x_{r_1-1},x_{r_1})) = (x_1,\ldots, x_{r_1-1})$ .

Note that $\psi$ maps pairs of close sequences to close ones. Indeed, if deleting the $i$ -th component of $(x_1,\ldots, x_{r_1-1},x_{r_1})$ and $j$ -th component of $(y_1,\ldots, y_{r_1-1},y_{r_1})$ yields the same sequence, then deleting $i^{\prime}$ -th component of $(x_1,\ldots, x_{r_1-1})$ and $j^{\prime}$ -th component of $(y_1,\ldots, y_{r_1-1})$ yields the same sequence, where $i^{\prime}= \min (i, r-1)$ and $j^{\prime}=\min (j, r-1)$ . Equivalently, $\psi$ is a homomorphism from $\Gamma ([q],r_1)$ to $\Gamma ([q],r_1-1).$

Let $\Pi ^{\prime} = \Pi (r_1-1,r_2,\ldots, r_a;\,b,q)$ and let $\phi \,:\, V(\Pi ) \to V(\Pi ^{\prime})$ be defined by $ \phi ((u_1,u_2,\ldots, u_a))=(\psi (u_1),u_2,\ldots, u_a)$ , i.e. $\phi$ erases the last entry of the first component of each vertex of $\Pi$ . It is easily seen from the definitions that $\phi$ is a homomorphism from $\Pi$ to $\Pi ^{\prime}$ and $|\phi ^{-1}(\boldsymbol{v})|=q$ for every $\boldsymbol{v} \in V(\Pi ^{\prime})$ . Thus by (8), Lemma2.3 applied to $\phi$ , and the induction hypothesis applied to $\Pi ^{\prime}$ we have

\begin{align*} \textrm{stww}(\Pi ) \leq \max \!\left\{\textrm{stww}(\Pi ^{\prime}), q \Delta (\Pi ) \right\} \leq r^{2b} a^b q^{ar-b(r-1)+1}, \end{align*}

and (7) holds.

For the next steps in the proof we need the following rather loose variant of the Chernoff bound.

If $X$ be a sum of independent random variables taking values in $\{0,1\}$ , then

(9) \begin{align} \mathbb{P}[X \gt c] \leq e^{-c/3} \end{align}

for every $c \geq 3\textrm{E}[X].$

This inequality follows from a more standard form of the Chernoff bound (see e.g. [[10], Theorem 2.3])

(10) \begin{align} \mathbb{P}\!\left[X \gt (1+\delta )\textrm{E}[X]\right] \leq e^{-\frac{\delta }{2 +\delta }\mathbb{E}[X]} \end{align}

for every $\delta \geq 0$ applied with $c=(1+\delta )\mathbb{E}[X]$ , as $\frac{\delta }{2 +\delta } \geq \frac{1}{3}(1+\delta )$ for $\delta \geq 2$ .

We will also use the Hajnal–Szemerédi theorem on the existence of equitable colourings in graphs with a given maximum degree.

Theorem 2.5 ([8]). If $G$ is a graph and $k\in \mathbb{N}$ such that $k\geq \Delta (G)+1$ , then $V(G)$ can be partitioned into independent sets $V_1,\ldots, V_k$ such that $|V_i| \leq \frac{{\textsf{v}}(G)}{k}+1$ .

Applying Theorem2.5 to the $\ell$ -th power of $G$ we obtain the following.

Corollary 2.6. If $G$ is a graph and $\ell, k\in \mathbb{N}$ are such that $k \geq (\Delta (G))^{\ell }+1$ , then $V(G)$ can be partitioned into sets $V_1,\ldots, V_k$ such that $|V_i| \leq \frac{{\textsf{v}}(G)}{k}+1$ and the distance between any pair of distinct vertices of $V_i$ in $G$ is at least $\ell +1$ in $G$ .

Proof. Let $G_*$ be the graph with $V(G_*)=V(G)$ such that two vertices of $G_*$ are adjacent if the distance between them in $G$ is at most $\ell$ . Then $\Delta (G_*) \leq (\Delta (G))^{\ell }$ , and so the corollary follows from Theorem2.5 applied to $G_*$ .

Our next lemma gives an upper bound on the sparse twin-width of a graph in terms of several parameters, which we optimize in a subsequent lemma to get the upper bounds in our main results.

Lemma 2.7. If $G$ is a graph and $a,b,q,r\in \mathbb{N}$ are such that $a\geq b$ , $ \frac{a}{b} \geq \frac{1}{2} \textrm{mad}(G)$ , $q\geq 2$ and

(11) \begin{align} {\textsf{v}}(G) \geq 6ra\cdot q^{ar+1}(\Delta (G))^{2r}, \end{align}

then

(12) \begin{align} \textrm{stww}(G) \leq \max \left \{ r^{2b} a^b q^{ar-b(r-1)+1}, \frac{4}{q^{ar}}{\textsf{v}}(G)\Delta (G)\right \}. \end{align}

Proof. By Lemma2.1 there exist spanning subgraphs $G_1,\ldots, G_a$ of $G$ , each of which admits an orientation with maximum outdegree one, such that each edge of $G$ belongs to at least $b$ of them. By Lemma2.2 for each $i \in [a]$ there exists a set $S_i$ and a homomorphism $\psi _i$ from $G_i$ to $\Gamma _*(S_i,r)$ such that for every pair of vertices $u,v$ , if the sequences $\psi _i(u)$ and $\psi _i(v)$ share a common element, then the distance between $u$ and $v$ in $G$ is at most $2r-2$ .

Let $\Pi = \Pi (r_1, r_2, \dots, r_a ; b,q)$ , where $r_i=r$ for all $i\in [a]$ . We define a random map $\phi \,:\, V(G) \to V(\Pi )$ as follows. For each $i \in [a]$ , we independently choose a random map $\pi _i\,:\, S_i \to [q]$ , with the values of each individual $\pi _i$ chosen uniformly and independently at random. Then, let

\begin{align*}\phi (v) \,:\!=\, \left(\pi _1(\psi _1(v)),\pi _2(\psi _2(v)), \ldots, \pi _a(\psi _a(v))\right)\end{align*}

for every $v\in V(G)$ , where we are abusing notation by denoting by $\pi _i(\psi _i(v))$ the element of $[q]^r$ obtained from $\psi _i(v)$ by applying $\pi _i$ component-wise. Note that given that $\psi _i$ is a homomorphism and by definition of $\Gamma _*(S_i,r)$ , if $uv \in E(G_i)$ then $\psi _i(u)$ and $\psi _i(v)$ are close, and so $\pi _i(\psi _i(v))$ and $\pi _i(\psi _i(u))$ are also close. As each edge of $G$ belongs to at least $b$ subgraphs $G_i$ it follows that $\phi$ is a homomorphism from $G$ to $\Pi$ , since adjacency in $\Pi$ is defined by having at least $b$ components which are close. As the components of $\psi _i(v)$ are distinct, $\pi _i(\psi _i(v))$ is uniformly distributed on $[q]^r$ . Indeed, by definition of $\pi _i$ for every $(s_1,\ldots, s_r) \in S_i^r$ such that $s_1,\ldots, s_r$ are pairwise-distinct and every $q_1,\ldots, q_r \in [q]^r$ we have

\begin{align*} \mathbb {P}\!\left[\wedge _{i=1}^r(\pi _i(s_i)=q_i)\right] = \prod _{i=1}^r\mathbb {P}\!\left[\pi _i(s_i)=q_i\right] = \frac {1}{q^r} .\end{align*}

As the maps $\pi _i$ are chosen independently, for each $v \in V(G)$ its image $\phi (v)$ is uniformly distributed on $[q]^r \times [q]^r \times \ldots [q]^{r}=V(\Pi )$ .

Note that if $\Delta (G) \leq 1$ then $\textrm{stww}(G) \leq \Delta (G)$ and the lemma trivially holds. Thus we assume $\Delta (G) \geq 2$ .

Let $k=(\Delta (G))^{2r-2}+1 \leq \Delta (G)^{2r-1}$ . By Corollary2.6, the vertex set of $G$ can be partitioned into sets $V_1,\ldots, V_k$ such that for every $i\in [k]$ , $|V_i| \leq \frac{{\textsf{v}}(G)}{k}+1$ and the distance between any pair of distinct vertices of $V_i$ in $G$ is at least $2r-1$ in $G$ . Thus for any pair of distinct vertices $u,v \in V_i$ , the sequences $\psi _j(u)$ and $\psi _j(v)$ are disjoint for every $j\in [a]$ . It follows that for each $i \in [k]$ the random variables $\{\phi (v)\}_{v \in V_i}$ are mutually independent.

We will bound $\textrm{stww}(G)$ by applying Lemma2.3 to $\phi$ chosen so that

\begin{align*}m(\phi ) \,:\!=\, \max _{\boldsymbol {u} \in V(\Pi )}|\phi ^{-1}(\boldsymbol {u})|\end{align*}

is as small as possible. Let

\begin{align*}c = \frac {3}{{\textsf {v}}(\Pi )}\left (\frac {{\textsf {v}}(G)}{k}+1\right ) .\end{align*}

Recalling that $\phi (v)$ is uniformly distributed on $V(\Pi )$ for every $v\in V(G)$ , we have that $\mathbb{E}[|\phi ^{-1}(\boldsymbol{u}) \cap V_i|] = \frac{|V_i|}{{\textsf{v}}(\Pi )} \leq c/3$ for every $\boldsymbol{u} \in V(\Pi )$ and $i \in [k]$ . Thus

\begin{align*} \mathbb {P}[|\phi ^{-1}(\boldsymbol {u}) \cap V_i| \gt c] \leq e^{-c/3} \end{align*}

by the Chernoff bound (9). It follows from the union bound that $ \mathbb{P}[|\psi ^{-1}(\boldsymbol{u}) | \gt kc] \leq ke^{-c/3}$ for every $\boldsymbol{u} \in V(\Pi )$ , and so $ \mathbb{P}[m(\phi ) \leq kc] \geq 1-{\textsf{v}}(\Pi ) ke^{-c/3}.$ Using (11) we have

\begin{align*} \log \left (k{\textsf{v}}(\Pi ) e^{-c/3} \right ) & = \log k + ar\log q - \frac{1}{{\textsf{v}}(\Pi )}\left (\frac{{\textsf{v}}(G)}{k}+1\right ) \\ &\leq 3r \Delta (G) + q ar -\frac{{\textsf{v}}(G)}{ q^{ar}\Delta (G)^{2r-1}} \\ &\leq 3r \Delta (G) + q ar -4qar\Delta (G) \\ &\lt 0. \end{align*}

Thus with positive probability we have $ m(\phi ) \leq kc = \frac{3}{{\textsf{v}}(\Pi )} \left ({\textsf{v}}(G)+k\right ) \leq 4 \frac{{\textsf{v}}(G)}{q^{ar}}$ . Applying Lemma2.3 to $\phi$ and using Lemma2.4 to bound $\textrm{stww}(\Pi )$ gives

\begin{align*}\textrm {stww}(G) \leq \max \{\textrm {stww}(\Pi ), kc\Delta (G)\} \leq \max \left \{ r^{2b} a^b q^{ar-b(r-1)+1}, \frac {4}{q^{ar}}{\textsf {v}}(G)\Delta (G)\right \},\end{align*}

as desired.

The following lemma is obtained from Lemma2.7 by optimizing the choice of parameters.

Lemma 2.8. Let $G$ be a graph and let $d \,:\!=\, \textrm{mad}(G)$ and $\ell \,:\!=\, \log{\textsf{v}}(G)$ . If

(13) \begin{align} 2 + \ell ^{-1/6} \leq d \leq \frac{\ell }{30 \log \ell }\qquad \mathrm{ and} \qquad \log (\Delta (G)) \leq \ell ^{1/6}, \end{align}

then

(14) \begin{align} \textrm{stww}(G) \leq \Delta (G) \cdot ({\textsf{v}}(G))^{\frac{d-2}{2d-2}} \cdot e^{O(d^{-1} \ell ^{1/2} \log \ell +\log d)}. \end{align}

Proof. Let $b \,:\!=\, \left \lceil \frac{\ell ^{1/2}}{d\log \ell } \right \rceil$ , $a \,:\!=\, \lceil \frac{db}{2} \rceil \leq db$ , $r \,:\!=\, \left \lfloor \frac{\ell }{2db \log \ell } \right \rfloor$ . First note that

(15) \begin{align} r & \leq \frac{\ell }{2d \log \ell \cdot \frac{\ell ^{1/2}}{d\log \ell }} \leq \ell ^{1/2}, \qquad \mathrm{and} \end{align}

(16) \begin{align} ar &\leq db \cdot \frac{\ell }{2db\log \ell } \leq \frac{\ell }{2\log \ell } . \end{align}

Let $\kappa \,:\!=\, \frac{\ell }{(2a-b)r}$ , i.e. ${\textsf{v}}(G)= e^{\kappa (2a-b)r}$ . Finally, let $q \,:\!=\,\lceil e^{\kappa } \rceil \leq e^\kappa + 1 \leq 2 e^{\kappa }$ .

Our goal is to apply Lemma2.7, but first let us estimate $\kappa$ . For the lower bound we have

\begin{align*} \kappa \geq \frac{\ell }{2ar} \stackrel{(16)}{\geq } \frac{\ell }{2\frac{\ell }{2\log \ell }} = \log \ell . \end{align*}

Thus

(17) \begin{align} ar\log \left (\frac{q}{e^{\kappa }}\right ) \leq ar\!\left(\log (1+e^{-\kappa })\right) \leq are^{-\kappa } \leq \frac{ar}{\ell } \stackrel{(16)}{\leq } 1, \end{align}

and so

(18) \begin{align} q^{ar} = \left (\frac{q}{e^{\kappa }}\right )^{ar} \cdot e^{\kappa a r} \stackrel{(17)}{\leq } e^{\kappa ar +1}. \end{align}

Similarly for the upper bound on $\kappa$ , assuming ${\textsf{v}}(G)$ , and thus $\ell$ , are large enough, we have

\begin{align*} \frac{\ell }{\kappa } & = (2a-b)r \geq (d-1)br \\&\geq (d-1)b \left ( \frac{\ell }{2db \log \ell } -1\right ) \geq \frac{d-1}{2d} \frac{\ell }{ \log \ell } - bd \\ &\geq \frac{1}{4} \frac{\ell }{ \log \ell }- \left (\frac{\ell ^{1/2}}{d\log \ell } + 1\right )d \geq \frac{1}{6} \frac{\ell }{ \log \ell }, \end{align*}

where the last inequality uses that $d\leq \frac{\ell }{30\log \ell }$ and that $\ell$ is large. Thus we have

(19) \begin{align} \kappa \leq 6\log \ell . \end{align}

Next, we verify that (11) holds. As $a \geq bd/2$ implies $b \leq 2a/d$ and $\frac{a}{2a-b}$ is increasing in $b$ , we have

(20) \begin{align} e^{\kappa ar} \leq ({\textsf{v}}(G))^{\frac{a}{2a-b}} \leq ({\textsf{v}}(G))^{\frac{a}{2a-2a/d}} = ({\textsf{v}}(G))^{\frac{d}{2d-2}}. \end{align}

We have that

\begin{align*} 6 ra \cdot q^{ar+1}(\Delta (G))^{2r} & \stackrel{(15)}{\leq } 6 ra \cdot q^{ar+1}(\Delta (G))^{2\ell ^{1/2}}\\ & \stackrel{(18)}{\leq } 6 \cdot ra \cdot q \cdot e^{\kappa ar +1}(\Delta (G))^{2\ell ^{1/2}}\\ & \stackrel{(20)}{\leq } 6e\cdot ra\cdot q \cdot ({\textsf{v}}(G))^{\frac{d}{2d-2}}\cdot (\Delta (G))^{2\ell ^{1/2}}\\ & \stackrel{(16)}{\leq } 6e\cdot q \cdot \frac{\ell }{2\log \ell } \cdot ({\textsf{v}}(G))^{\frac{d}{2d-2}}\cdot (\Delta (G))^{2\ell ^{1/2}}\\ &\leq 12 e \cdot e^{\kappa } \cdot \frac{\ell }{2\log \ell } \cdot ({\textsf{v}}(G))^{\frac{d}{2d-2}} \cdot (\Delta (G))^{2 \ell ^{1/2}}\\ & \stackrel{(19)}{\leq } \ell ^{7} \cdot ({\textsf{v}}(G))^{\frac{d}{2d-2}} \cdot (\Delta (G))^{2 \ell ^{1/2}}, \end{align*}

where the last inequality holds for $\log \ell \geq 6e$ , and so to verify (11) it suffices to show that

(21) \begin{align} \ell ^{7} \cdot (\Delta (G))^{2 \ell ^{1/2}} \leq ({\textsf{v}}(G))^{\frac{d-2}{2d-2}}. \end{align}

By (13) and since $\frac{d-2}{2d-2}$ is increasing in $d$ we have

\begin{align*} \frac {d-2}{2d-2} \geq \frac {\ell ^{-1/6}}{2 + 2\ell ^{-1/6}} \geq \frac {1}{4}\ell ^{-1/6} \end{align*}

and therefore

\begin{align*} 7\log \ell + 2 \ell ^{1/2} \log \Delta (G) \stackrel{(13)}{\leq } 7\log \ell + 2 \ell ^{2/3} \leq \frac{1}{4}\ell ^{5/6} \leq \frac{d-2}{2d-2} \ell, \end{align*}

where the second inequality holds for $\ell$ large enough. Exponentiating the above we obtain (21).

Thus (11) holds and so (12) holds by Lemma2.7. As ${\textsf{v}}(G) \leq q^{(2a-b)r}$ , we have

\begin{align*} \textrm{stww}(G) & \leq \max \left \{ r^{2b} a^b q^{ar-b(r-1)+1}, \frac{4}{q^{ar}}{\textsf{v}}(G)\Delta (G)\right \} \\ &\leq 4r^{2b} a^b q^{b+1}\Delta (G) q^{(a-b)r} \\ &= \left (\Delta (G) \cdot ({\textsf{v}}(G))^{\frac{d-2}{2d-2}} \right ) \cdot \left ( 4 (r^{2b} a^b e^{\kappa (b+1)}) \cdot \left (\frac{q}{e^\kappa }\right )^{(a-b)r+b+1} \cdot \frac{e^{\kappa (a-b)r}}{({\textsf{v}}(G))^{\frac{d-2}{2d-2}}}\right ). \end{align*}

Thus to verify (14) it remains to show that

(22) \begin{align} 4 (r^{2b} a^b e^{\kappa (b+1)}) \cdot \left (\frac{q}{e^\kappa }\right )^{(a-b)r+b+1} \cdot \frac{e^{\kappa (a-b)r}}{({\textsf{v}}(G))^{\frac{d-2}{2d-2}}} = e^{O(d^{-1} \ell ^{1/2}\log \ell + \log d)}. \end{align}

We prove (22) by showing that the logarithms of the terms on the left side are of the form $O(d^{-1} \ell ^{1/2}\log \ell + \log d)$ , starting with the last:

\begin{align*} \log \left (\frac{e^{\kappa (a-b)r}}{({\textsf{v}}(G))^{\frac{d-2}{2d-2}}}\right ) &= \left ((a-b)r - \frac{d-2}{2d-2}(2a-b)r\right )\kappa \\ &=\left (\frac{2}{2d-2}a-\frac{d}{2d-2}b\right ) \kappa r\\ &\leq \left (\frac{2}{2d-2}\left (\frac{db}{2}+1\right )-\frac{d}{2d-2}b\right ) \kappa r \\ &= \frac{\kappa r}{d-1} = O\left (\frac{\log \ell \cdot \ell ^{1/2}}{d}\right ), \end{align*}

where the last estimate uses (15) and (19). For the second term, using that $r\geq 2$ for sufficiently large $\ell$ , we get

\begin{align*}\log \left (\left (\frac {q}{e^\kappa }\right )^{(a-b)r+b+1}\right ) \leq ar\log \left (\frac {q}{e^{\kappa }}\right ) \stackrel {(17)}{\leq } 1.\end{align*}

Finally, for the first term,

(23) \begin{align} \log \left (r^{2b} a^b e^{\kappa (b+1)} \right ) = b \cdot O\!\left( \log r + \log d + \log b + \kappa \right) = b \cdot O\!\left(\log d + \log \ell \right). \end{align}

If $d \leq \frac{\ell ^{1/2}}{\log \ell }$ then $\log d = O( \log \ell )$ and $b = O\!\left( \frac{\ell ^{1/2}}{d\log \ell }\right)$ and so the expression in (23) has the form $O\!\left( d^{-1}\ell ^{1/2}\right)$ as desired. Otherwise, $b=1$ and $\log \ell = O(\log d)$ and so the expression in (23) has the form $O(\log d)$ . This yields the desired bound for the first term in (22), and so (14) holds.

Theorem1.4, which we restate for convenience, readily follows from Lemma2.8.

Proof. Let $G$ be an $n$ -vertex graph, $\ell \,:\!=\,\log n$ and $d \,:\!=\, \textrm{mad}(G)$ .

If $d = \Omega (\frac{\ell }{\log \log \ell })$ then by (1) we have

\begin{align*}\textrm {tww}(G) = O\!\left(\sqrt {dn}\right) = n^{\frac {d-2}{2d-2}} O\!\left(\sqrt {d}\cdot n^{\frac {1}{2d-2}}\right) = n^{\frac {d-2}{2d-2}} e^{O\left (\frac {\ell }{d} + \log d\right )} = n^{\frac {d-2}{2d-2}} e^{O( \log d)}.\end{align*}

Thus (3) holds, and so we may assume that $d \leq \frac{\ell }{30 \log \ell }$ . As it suffices to establish (3) when $n$ is sufficiently large (and sufficiently large as a function of $\varepsilon$ in (ii)), we assume from now on that $\ell$ is large enough to satisfy subsequent inequalities. In particular, we can assume $\ell ^{-1/6} \leq \varepsilon /2$ in (ii), and so that $d \geq 2 + \ell ^{-1/6}$ .

Given $2 + \ell ^{-1/6} \leq d \leq \frac{\ell }{30 \log \ell }$ , (3) follows from Lemma2.8 and (5), as long as

(24) \begin{align} \log\!\left(\Delta (G)\right) \leq \ell ^{1/6} \qquad \mathrm{and} \qquad \log \Delta (G) = O\!\left(d^{-1}\ell ^{1/2}\log \ell + \log d\right). \end{align}

Clearly, (24) holds in (i) as $\Delta (G) = d$ in this case.

It remains to verify that (24) holds with high probability if $G$ is as in (ii). It is well known and is an easy consequence of Chernoff type bounds that $\Delta (G) = O (\ell \frac{m}{n}) = O(\ell d)$ with high probability, and so $\log \Delta (G) = O(\log \ell )$ with high probability. Thus (24) holds with high probability as $d^{-1}\ell ^{1/2}\log \ell + \log d \geq \frac{1}{2}\log \ell$ (which can be easily seen by splitting into cases $d\geq l^{1/2}$ and $d\leq l^{1/2}$ ).

3. Lower bounds

In this section we prove Theorem1.5, establishing the lower bounds in our main results.

We start by showing that for every graph $G$ with $\textrm{stww}(G) \leq w$ we can divide the vertices of $G$ into roughly equal parts, close to any prescribed size, so that identifying all vertices in each part yields a graph with average degree close to $w$ . As mentioned in the introduction, this fact will be the basis of our counting argument.

If $G$ is a graph and $\mathcal P$ is a partition of $V(G)$ , we define the quotient graph $G/\mathcal P$ as the graph on vertex set $\mathcal P$ in which distinct $P_1,P_2\in \mathcal P$ are adjacent if and only if there exists at least one edge in $G$ between a vertex in $P_1$ and a vertex in $P_2$ . If $X\subseteq V(G)$ , we denote by $\mathcal P-X$ the partition of $G\setminus X$ obtained by restricting each part of $\mathcal P$ to $V(G)\setminus X$ . We say $G$ is $w$ -degenerate if every subgraph of $G$ contains a vertex of degree at most $w$ .

Lemma 3.1. If $G$ is a graph and $K\lt{\textsf{v}}(G)$ is an integer, then there exists a partition $\mathcal P$ of $V(G)$ such that $|\mathcal P| \leq K$ , $|P| \leq \frac{2{\textsf{v}}(G)}{K}$ for every $P \in \mathcal{P}$ and $G/\mathcal P$ is $\textrm{stww}(G)$ -degenerate.

Proof. Let $n \,:\!=\,{\textsf{v}}(G)$ and $w \,:\!=\,\textrm{stww}(G)$ . Let $\mathcal P_1,\dots, \mathcal P_n$ be the sequence of partitions of $V(G)$ such that

1. 1. $|\mathcal{P}_i|=n-i+1$ for every $i\in [n]$ ,

2. 2. $\mathcal{P}_{i+1}$ is a coarsening of $\mathcal{P}_i$ for every $i\in [n-1]$ , and

3. 3. $G=G/\mathcal{P}_1,G/\mathcal{P}_2,\ldots, G/\mathcal{P}_n$ is a $w$ -contraction sequence for $G$ ,

which exists by definition of $\textrm{stww}(G)$ and contraction sequences.

We define a partition $\mathcal P=(P_1,\dots, P_k)$ for some $k \leq K$ recursively as follows. Suppose we have already defined $P_1,\dots, P_{r-1}$ . Let $X_{r-1}=P_1\cup \dots \cup P_{r-1}$ . If $V(G)\setminus X_{r-1}=\emptyset$ , we let $k=r-1$ . Otherwise, we wish to define $P_r$ .

Let $i_r$ be the minimum index $i\leq n$ such that $\mathcal P_{i} -X_{r-1}$ contains a part of size at least $\frac{{\textsf{v}}(G)}{K}$ and let $P_r$ be any such part. If no such index $i$ exists, let $i_r=n$ and set $P_r=V(G)\setminus X_{r-1}$ . Note that in the latter case, $P_r$ is the sole part of $\mathcal P_n-X_{r-1}$ , so we have $k=r$ and $|P_k|\lt \frac{{\textsf{v}}(G)}{K}$ .

We now show that $\mathcal{P}=(P_1,\dots, P_k)$ satisfies the requirements of the lemma. Clearly $\mathcal P$ is a partition of $G$ . We have $|P_r| \geq \frac{{\textsf{v}}(G)}{K}$ for $r \in [k-1]$ and $P_k \neq \emptyset$ . Thus ${\textsf{v}}(G) = \sum _{r=1}^{k}|P_r| \gt (k-1) \frac{{\textsf{v}}(G)}{K}$ , thus $|\mathcal P| = k \leq K$ as desired.

Next we show that $|P_r| \leq \frac{2{\textsf{v}}(G)}{K}$ for every $r\in [k]$ . As noted above this holds for $r=k$ and so we assume $r\lt k$ . Then $|P_r| \geq \frac{{\textsf{v}}(G)}{K} \gt 1$ and so $i_r\gt 1$ , and $P_r$ was chosen as a part of $\mathcal P_{i_r} -X_{r-1}$ of size at least $\frac{{\textsf{v}}(G)}{K}$ . As $P_r$ is a union of at most two parts of $\mathcal P_{i_r-1} -X_{r-1}$ , and each part of $\mathcal P_{i_r-1} -X_{r-1}$ has size less than $\frac{{\textsf{v}}(G)}{K}$ by the choice of $i_r$ , it follows that $|P_r| \leq \frac{2{\textsf{v}}(G)}{K}$ , as desired.

We now claim that $G/\mathcal P$ is $w$ -degenerate. It suffices to show that for every $r\in [k-1]$ , there are at most $w$ parts among $P_{r+1},\dots, P_{k}$ with neighbours in $P_r$ . Indeed, $P_r=P^{\prime}_r-X_{r-1}$ for some $P^{\prime}_r \in \mathcal{P}_{i_r}$ . As $G / \mathcal{P}_{i_r}$ has maximum degree at most $w$ , there are parts $\hat P_1,\hat P_2,\ldots, \hat P_s\in \mathcal{P}_{i_r}$ for some $s \leq w$ such that every neighbour of $P_r$ in $G-X_{r-1}$ belongs to one of them. As $i_r \leq i_{r+1} \leq \ldots \leq i_k$ , each part $\hat P_j$ intersects at most one of $P_{r+1},\dots, P_{k}$ , implying the claim.

This concludes the proof of the lemma.

In estimates below we frequently use the following standard bounds on binomial coefficients:

(25) \begin{align} \binom{n}{m} \leq \left (\frac{en}{m}\right )^m \end{align}

for all integer $n \geq m \gt 0$ .

Lemma 3.2. There exists $C_0 \gt 0$ satisfying the following. For every $0 \lt \varepsilon \leq 1/3$ , there exists $n_0\in \mathbb{N}$ such that for all $n,m\in \mathbb{N}$ satisfying $n \geq n_0$ and

(26) \begin{align} (1 + \varepsilon )n \leq m \leq \frac{1}{10}n{\log n} \end{align}

there are at most $ \left (C_0\varepsilon \frac{n^2}{m}\right )^{m}$ graphs $G$ with $V(G)=[n]$ , ${\textsf{e}}(G)=m$ and

\begin{align*}\textrm {stww}(G) \leq \varepsilon d \left (\frac {n}{\log n}\right )^{\frac {d-2}{2d-2}},\end{align*}

where $d= \frac{2m}{n}.$

Proof. Set $C_0 \,:\!=\,24000$ . Let $\varepsilon$ be given.

Choose $n_0$ large enough such that $\frac{\varepsilon }{2}\left (\frac{n_0}{\log n_0}\right )^{\frac{\varepsilon }{2+4\varepsilon }}\geq 1$ , and further such that $\frac{2}{d}+\frac{4d}{\log n} \leq 1$ for every $n,d$ such that $n\ge n_0$ and $2+2\varepsilon \leq d \leq \frac{1}{5}\log n$ .

Let $n,m,d$ be as in the statement.

Let $w \,:\!=\, \left \lfloor \varepsilon d \left (\frac{ n}{\log n}\right )^{\frac{d-2}{2d-2}} \right \rfloor$ and $K \,:\!=\,\left \lfloor \frac{d^2n}{w\log n}\right \rfloor$ .

By our choice of $n_0$ , we can ensure that

(27) \begin{align} w\geq \frac{\varepsilon }{2} d \left (\frac{ n}{\log n}\right )^{\frac{d-2}{2d-2}} \ge d \end{align}

and thus $K\le \frac{dn}{\log n}\le \frac{n}{5}\lt n$ . Furthermore, as $w\lt d\frac{n}{\log n}$ we have that $\frac{d^2n}{w\log n}\geq d\gt 2$ and so

(28) \begin{align} K\gt \frac{d^2n}{2w\log n}. \end{align}

By Lemma3.1, if $G$ is a graph with $V(G)=[n]$ and $\textrm{stww}(G) \leq w$ , then there exists a partition $\mathcal{P}=(P_1,\ldots, P_K)$ of $[n]$ such that $|P_i| \leq \frac{2n}{K}$ for every $i \in K$ and $G/\mathcal P$ is $w$ -degenerate. We wish to compute the number of graphs $G$ for which this is possible.

For a given partition $\mathcal P=(P_1,\ldots, P_K)$ of $[n]$ and $F \subseteq \binom{[K]}{2}$ , let $E(\mathcal{P},F)$ be the set of all $\{u,v\} \in [n]^2$ such that either $u,v \in P_i$ for some $i \in [K],$ or $u \in P_i$ and $v \in P_j$ for some $\{i,j\} \in F$ . In other words, $E(\mathcal{P},F)$ is the set of possible edges for a graph $G$ on $[n]$ if $E(G/\mathcal P)\subseteq F$ (writing $V(G/\mathcal P)=[K]$ for simplicity).

Let $N$ be the number of graphs $G$ with $V(G)=[n]$ , ${\textsf{e}}(G)=m$ and $\textrm{stww}(G) \leq w$ . Every such graph $G$ is determined by the choice of a partition $\mathcal{P}$ of $[n]$ with $|\mathcal{P}|=K$ , a set $F \subseteq \binom{[K]}{2}$ with $|F|=wK$ (since it follows from degeneracy that ${\textsf{e}}(G/\mathcal P) \leq wK$ ) and a choice of $E(G) \subseteq E(\mathcal{P},F)$ with $|E(G)|=m$ .

There are at most $K^n$ choices of $\mathcal{P}$ .

The number of choices of $F$ is upper bounded by

(29) \begin{align} \binom{\binom{K}{2}}{wK} &\stackrel{(25)}{\leq } \left (\frac{eK}{w}\right )^{wK} \stackrel{(28)}{\leq } \left (\frac{ed^2n}{w^2\log n}\right )^{\frac{d^2 n}{\log n}} \stackrel{(27)}{\leq }\left (\frac{ed^2n}{ \frac{\varepsilon ^2}{4} d^2 \left (\frac{ n}{\log n}\right )^{\frac{2d-4}{2d-2}} \log n}\right )^{\frac{d^2 n}{\log n}} \nonumber \\ &\leq \left (\frac{4e}{\varepsilon ^2}\right )^{\frac{d^2 n}{\log n}} n^{\frac{d^2 n}{(d-1)\log n}} =\left (\frac{4e}{\varepsilon ^2}\right )^{\frac{2dm}{\log n}} e^{\frac{2dm}{d-1}} \leq e^{4m}\cdot \left (\frac{4e}{\varepsilon ^2}\right )^{\frac{2d m}{\log n}} \end{align}

Finally, using that

\begin{align*}|E(\mathcal {P},F)| = \sum _{\{i,j\}\in F}|P_i||P_j| + \sum _{i \in [K]}\binom {|P_i|}{2} \leq (|F|+K)\left (\frac {2n}{K}\right )^2= K(w+1)\left (\frac {2n}{K}\right )^2\leq \frac {8wn^2}{K},\end{align*}

the number of choices of $E(G) \subseteq E(\mathcal{P},F)$ with $|E(G)|=m$ is upper bounded by

(30) \begin{align} \binom{|E(\mathcal{P},F)|}{m} \stackrel{(25)}{\leq } \left (\frac{e\frac{8wn^2}{K}}{m}\right )^{m} = \left (\frac{16ewn}{dK}\right )^{m}. \end{align}

Combining the upper bounds (29) and (30) on the number of choices of $F$ and $E(G) \subseteq E(\mathcal{P},F)$ , respectively, we obtain

\begin{align*} N^{\frac{1}{m}} &\leq K^{2/d} \cdot e^{4} \left (\frac{4e}{\varepsilon ^2}\right )^{\frac{2d}{\log n}} \cdot \frac{16ewn}{dK}\\ &= 16 e^5 \cdot (4e)^{\frac{2d}{\log n}}\cdot \varepsilon ^{-\frac{4d}{\log n}} \cdot K^{2/d-1}\cdot w \cdot \frac{n}{d}\\ &\stackrel{(26), (28)}{\leq } 8 e^5 \cdot (4e)^{\frac{2\cdot \frac{1}{5}\log n}{\log n}}\cdot \varepsilon ^{-\frac{4d}{\log n}}\cdot \left (\frac{2w\log n}{d^2 n}\right )^{\frac{d-2}{d}}\cdot w \cdot \frac{n^2}{m}\\ &\leq 16 e^5 \cdot (4e)^{\frac{2}{5}}\cdot \varepsilon ^{-\frac{4d}{\log n}} \cdot \left (\frac{\log n}{ n}\right )^{\frac{d-2}{d}}\cdot d^{-\frac{2d-4}{d}}\cdot w^{\frac{2d-2}{d}} \cdot \frac{n^2}{m}\\ &\leq 8000\cdot \varepsilon ^{-\frac{4d}{\log n}} \cdot \left (\frac{\log n}{ n}\right )^{\frac{d-2}{d}}\cdot d^{-\frac{2d-4}{d}}\cdot \left (\varepsilon d \left (\frac{ n}{\log n}\right )^{\frac{d-2}{2d-2}}\right )^{\frac{2d-2}{d}} \cdot \frac{n^2}{m}\\ &= 8000\cdot \varepsilon ^{2-\left (\frac{2}{d}+\frac{4d}{\log n}\right )} \cdot d^{\frac{2}{d}}\cdot \frac{n^2}{m}\\ &\leq 24000\cdot \varepsilon \cdot \frac{n^2}{m}=C_0\cdot \varepsilon \cdot \frac{n^2}{m}, \end{align*}

the last inequality following from our choice of $n_0$ .

This concludes the proof of the lemma.

Lemma3.2 immediately implies the desired lower bounds on the sparse twin-width of $d$ -regular graphs, when combined with the following rather loose estimate of the number of $n$ -vertex $d$ -regular graphs, which is implied for example by a much more precise and general result of McKay and Wormald [11].

Theorem 3.3 (see [11]). There exists $C_1 \gt 0$ such that for all $n,d$ such that $d \leq \log n$ and $dn$ is even there are at least $(C_1\frac{n}{d})^{\frac{dn}{2}}$ $d$ -regular graphs $G$ with $V(G)=[n]$ .

We now derive Theorem1.5 (i), which we restate here as a corollary, from Lemma3.2 and Theorem3.3.

Corollary 3.4 (Theorem1.5 (i)). There exists $\varepsilon \gt 0$ such that if $G$ is a uniformly random $n$ -vertex, $d$ -regular graph with $2 \lt d \lt \frac{1}{5}\log n$ , then

\begin{align*}\textrm {stww}(G) \geq \varepsilon \frac {d}{\sqrt {\log n}}n^{\frac {d-2}{2d-2}}\end{align*}

with high probability.

Proof. Let $\varepsilon \,:\!=\, \frac{C_1}{3 C_0}$ , where $C_0$ and $C_1$ are the constants satisfying the conditions of Lemma3.2 and Theorem3.3, respectively. We may suppose that $n\geq n_0$ , where $n_0$ is obtained from Lemma3.2, depending on $\varepsilon$ . Let $w \,:\!=\, \varepsilon \frac{d}{\sqrt{\log n}}n^{\frac{d-2}{2d-2} }.$ Then by Lemma3.2 there are at most

\begin{align*}\left (C_0\varepsilon \frac {2n}{d}\right )^{\frac {dn}{2}}\end{align*}

$d$ -regular graphs on $n$ -vertices with $\textrm{stww}(G) \lt w$ , and by Theorem3.3 it follows that the probability that $\textrm{stww}(G) \lt w$ is at most

\begin{align*} \left (C_0\varepsilon \frac {2n}{d}\right )^{\frac {dn}{2}} / \left (C_1\frac {n}{d}\right )^{\frac {dn}{2}} = \left (\frac {2C_0\varepsilon }{C_1}\right )^{\frac {dn}{2}} = \left (\frac {2}{3}\right )^{\frac {dn}{2}}\leq \left (\frac {2}{3}\right )^n\xrightarrow {n\rightarrow \infty } 0.\end{align*}

Thus $\textrm{stww}(G)\geq w$ w.h.p., as desired.

It remains to prove Theorem1.5 (ii). This requires more preparation, as in this setting we will not be applying Lemma3.2 to $G$ itself, but to the subgraph of $G$ attaining the maximum average degree. First, we will need to ensure that this subgraph is not too small.

Let $\mathcal{G}_{n,m}$ denote the set of all graphs $G$ with $V(G)=[n]$ and ${\textsf{e}}(G)=m$ . We say that a graph $G$ with $n$ vertices and $m$ edges is $\alpha$ -balanced if ${\textsf{e}}(G[X]) \leq \frac{m}{n}|X|$ for every $X \subseteq [n]$ with $|X| \leq \alpha (n-1)$ .

Lemma 3.5. If $0\lt \varepsilon \lt \frac{1}{10}$ , $\alpha = \frac{1}{4}e^{-\frac{4}{\varepsilon }}$ and $n,m\in \mathbb{N}$ are such that $(1+\varepsilon )n\leq m\leq \frac{n^2}{8}$ , almost all graphs in $\mathcal{G}_{n,m}$ are $\alpha$ -balanced.

Proof. Given the upper bound on $m$ , we may assume that $n$ is large enough such that $\binom{n}{2}-m\geq \frac{\binom{n}{2}}{e}$ (and $n\geq e^2+1$ ).

We start with an auxiliary computation. Let $d \,:\!=\, \frac{m}{n}\geq 1+\varepsilon$ and let

\begin{align*}f(x) \,:\!=\, e^{(2d+1)x} \left (\frac {x-1}{n-1}\right )^{(d-1)x}. \end{align*}

Note that for $2 \leq x \leq \alpha (n-1)$ , we have

\begin{align*} \frac{f(x+1)}{f(x)} &= e^{2d+1}\left (\frac{x}{x-1}\right )^{(d-1)x}\left (\frac{x}{n-1}\right )^{d-1} \leq e^{2d+1}4^{d-1}\alpha ^{d-1}=e^3 \!\left(4e^2\alpha \right)^{d-1}\\ &=e^3\!\left(e^{-\frac{4}{\varepsilon }+2}\right)^{d-1} \leq e^3\!\left(e^{-\frac{4}{\varepsilon }+2}\right)^{\varepsilon } =e^{2\varepsilon -1}\leq \frac{1}{2}, \end{align*}

where for the first inequality sign, we used that $\left(\frac{x}{x-1}\right)^x$ is monotonically decreasing for $x\gt 1$ and that $x\ge 2$ . It follows that $f(x) \leq f(2)2^{2-x}$ for all integers $2 \leq x \leq \alpha (n-1)$ .

Moving on to the main proof, for $X \subseteq [n]$ let $\mathcal{B}(X)$ denote the set of all graphs $G \in \mathcal{G}_{n,m}$ such that ${\textsf{e}}(G[X]) \gt d|X|$ . Let $x \,:\!=\, |X|$ and $k \,:\!=\, \lceil dx \rceil$ . Then

(31) \begin{align} |\mathcal{B}(X)| \leq \binom{\binom{x}{2}}{k} \binom{\binom{n}{2}}{m-k}, \end{align}

as there are at most $\binom{\binom{x}{2}}{k}$ ways of choosing $k$ edges of $G[X]$ and at most $\binom{\binom{n}{2}}{m-k}$ choices for the remaining edges. Thus

\begin{align*} \frac{|\mathcal{B}(X)|}{|\mathcal{G}_{n,m}|} &\leq \frac{\binom{\binom{x}{2}}{k} \binom{\binom{n}{2}}{m-k}}{\binom{\binom{n}{2}}{m}} = \binom{\binom{x}{2}}{k}\frac{ \frac{\binom{n}{2}!}{(m-k)!\left (\binom{n}{2}-(m-k)\right )!}}{\frac{\binom{n}{2}!}{m!\left (\binom{n}{2}-m\right )!}}\\ &= \binom{\binom{x}{2}}{k} \frac{m(m-1)\dots (m-k+1)}{\left (\binom{n}{2}-m+k\right )\left (\binom{n}{2}-m+k-1\right )\dots \left (\binom{n}{2}-m+1\right )}\\ &\leq \left (\frac{e\binom{x}{2}}{k}\right )^k \frac{m^k}{\left (\binom{n}{2}-m\right )^k} \leq \left (\frac{e\binom{x}{2}}{dx} \cdot \frac{dn}{\binom{n}{2}/e}\right )^k\\ &= \left (\frac{e^2 (x-1)}{n-1}\right )^k \leq \left (\frac{e^2 (x-1)}{n-1}\right )^{dx}. \end{align*}

We upper bound the proportion of graphs in $\mathcal{G}_{n,m}$ which are not $\alpha$ -balanced by

\begin{align*} \sum _{X \subseteq [n], 0 \lt |X| \lt \alpha n} &\frac{|\mathcal{B}(X)|}{|\mathcal{G}_{n,dn}|} \leq \sum _{1 \leq x \lt \alpha n} \binom{n}{x}\left (\frac{e^2(x-1)}{(n-1)}\right )^{dx} \leq \sum _{2 \leq x \lt \alpha n}\left (\frac{en}{x}\right )^{x}\left (\frac{e^2(x-1)}{(n-1)}\right )^{dx} \\ &\leq \sum _{2 \leq x \lt \alpha n} e^{(2d+1)x} \left (\frac{x-1}{n-1}\right )^{(d-1)x} = \sum _{2 \leq x \lt \alpha n} f(x) \leq f(2) \sum _{2 \leq x \lt \alpha n} 2^{2-x} \\ &\leq 2 f(2) = \frac{2e^{2(2d+1)}}{(n-1)^{2(d-1)}}=2e^6\left (\frac{e^2}{(n-1)}\right )^{2(d-1)} \leq 2e^6\left (\frac{e^2}{(n-1)}\right )^{2\varepsilon }. \end{align*}

As the last term tends to $0$ as $n \to \infty$ the lemma follows.

The next lemma states that there is no large part of $G$ which is too dense, which will allow us to apply Lemma3.2.

Lemma 3.6. Let $\alpha \gt 0$ and let $n,m\in \mathbb{N}$ be such that $n \leq m \leq \frac{1}{11}n\log n$ . If $G$ is a uniformly random graph in $\mathcal G_{n,m}$ , then with high probability for every set $X\subseteq [n]$ with $|X|\geq \alpha n+1$ we have

(32) \begin{align} {\textsf{e}}(G[X])\leq \frac{1}{10}|X|\log |X|. \end{align}

Proof. We may first suppose that $n$ is large enough such that $\alpha n\geq 3$ .

Say a graph $G$ with vertex set $[n]$ has property (*) if (32) holds for every $X\subseteq [n]$ with $|X|\geq \alpha n+1$ .

We first claim that if $G$ is a random graph $G(n,p)$ , with $p=\frac{m}{\binom{n}{2}}$ , then (*) holds.

Let $X\subseteq [n]$ such that $|X|\geq \max (\alpha n+1,3)$ be fixed and $x=|X|$ . Then, ${\textsf{e}}(G[X])$ is a sum of independent binomial variables (one for each possible edge). We have $\mathbb{E}[{\textsf{e}}(G[X])]=p\cdot \binom{x}{2}=\frac{m\cdot \binom{x}{2}}{\binom{n}{2}}= \frac{mx(x-1)}{n(n-1)}$ .

Note that the function $\frac{\log x}{x}$ is monotone decreasing for $x\geq e$ . In particular, as $x\leq n$ , $\frac{\log x}{x}\geq \frac{\log n}{n}$ . Let $f_1(n)$ and $f_2(n)$ be two functions, such that $n f_1(n)\leq m\leq n f_2(n)$ ; we will have to consider two different regimes. However we will always have $f_2(n)\leq \frac{1}{11}\log n$ , and so $\frac{\log n}{10f_2(n)}\gt 1$ . We then have that

\begin{align*} \frac{1}{10}x\log x &= \frac{1}{10}\cdot \frac{\log x}{x}x^2 \geq \frac{1}{10}\cdot \frac{\log n}{n}x^2\cdot \frac{m}{n f_2(n)} =\frac{\log n}{10 f_2(n)}\cdot \frac{mx^2}{n^2}\\ &\geq \frac{\log n}{10 f_2(n)}\cdot \frac{mx(x-1)}{n(n-1)} =\left (1+\left (\frac{\log n}{10 f_2(n)}-1\right )\right )\mathbb{E}[{\textsf{e}}(G[X])]. \end{align*}

Hence, by the Chernoff bound (10),

\begin{align*} \mathbb{P}\left [{\textsf{e}}(G[X])\geq \frac{1}{10}x\log x\right ] &\leq \mathbb{P}\left [{\textsf{e}}(G[X])\geq \left (1+\left (\frac{\log n}{10 f_2(n)}-1\right )\right )\mathbb{E}[{\textsf{e}}(G[X])]\right ]\\ &\leq \exp \left (-\frac{\left (\frac{\log n}{10 f_2(n)}-1\right )^2}{2+\left (\frac{\log n}{10 f_2(n)}-1\right )}\cdot \frac{mx(x-1)}{n(n-1)}\right )\\ &\leq \exp \left (-\frac{\left (\frac{\log n}{10 f_2(n)}-1\right )^2}{1+\frac{\log n}{10 f_2(n)}}\cdot \frac{n f_1(n)\cdot (\alpha n)^2}{n^2}\right )\\ &\lt \exp \left (-\alpha ^2\frac{\left (\frac{\log n}{10 f_2(n)}-1\right )^2}{\frac{\log n}{5 f_2(n)}}f_1(n) \cdot n \right ). \end{align*}

If $n\leq m\leq n\sqrt{\log n}$ , i.e. $f_1(n)=1$ and $f_2(n)=\sqrt{\log n}$ , then this value becomes

\begin{align*}\exp \left (-\alpha ^2\frac {\left (\frac {\log n}{10 \sqrt {\log n}}-1\right )^2}{\frac {\log n}{10 \sqrt {\log n}}}n\right ) =\exp \left (-\frac {\alpha ^2}{10}\left (\sqrt {\log n}-20+\frac {100}{\sqrt {\log n}}\right )n\right )\ll 2^{-n}.\end{align*}

Otherwise, if $n\sqrt{\log n}\leq m\leq \frac{1}{11}n\log n$ , i.e. $f_1(n)=\sqrt{\log n}$ and $f_2(n)=\frac{1}{11}\log n$ , then this value becomes

\begin{align*}\exp \left (-\alpha ^2\frac {\left (\frac {\log n}{10 \cdot \frac {1}{11}\log n}-1\right )^2}{\frac {\log n}{5 \cdot \frac {1}{11}\log n}}\sqrt {\log n}\cdot n \right ) =\exp \left (-\frac {\alpha ^2}{220}\sqrt {\log n} \cdot n\right )\ll 2^{-n}.\end{align*}

Given that are at most $2^n$ possible choices of $X$ , in all cases the probability that there is some $X$ with $|X|\geq \alpha n+1$ for which (32) does not hold converges to $0$ as $n\rightarrow \infty$ . This completes the proof of the claim.

We now show the statement when $G$ is uniformly chosen in $\mathcal G_{n,m}$ with a coupling argument.

Let $G(n,p,m)$ denote the random graph distribution defined by conditioning $G(n,p)$ on having at least $m$ edges. The number of edges of $G(n,p)$ follows a binomial distribution with parameters $B(\binom{n}{2},p)$ . It is well-known (see [9], for instance) that when the mean of a binomial distribution is an integer, it is also equal to the median. In particular, for our previous choice $p=\frac{m}{\binom{n}{2}}$ ,

\begin{align*}\mathbb {P}({\textsf {e}}(G(n,p)\geq m)\geq \frac {1}{2}.\end{align*}

It thus also holds that if $G$ is a random graph $G(n,p,m)$ , with high probability (*) holds.

Let $G$ and $G^{\prime}$ be random graphs obtained using the following process. $G^{\prime}$ will have distribution $G(n,p,m)$ , and $G$ will be chosen as a uniformly random subgraph of $G^{\prime}$ with exactly $m$ edges. It is immediate by symmetry that $G$ is a uniformly random graph in $\mathcal G_{n,m}$ . Furthermore, $E(G)\subseteq E(G^{\prime})$ and so ${\textsf{e}}(G[X])\leq{\textsf{e}}(G^{\prime}[X])$ for any $X\subseteq [n]$ . As (*) holds with high probability for $G^{\prime}$ , it thus follows that with high probability (*) holds for $G$ . This concludes the proof of the statement.

We are now ready to start the proof of Theorem1.5 (ii), which we restate here with $\textrm{tww}$ replaced by $\textrm{stww}$ , which is equivalent to the original statement by (5), as $\Delta (G)$ is logarithmic in ${\textsf{v}}(G)$ in the regime covered by Theorem1.5 (ii) with high probability, while the claimed bound on $\textrm{tww}$ is polynomial in ${\textsf{v}}(G)$ .

Theorem 3.7 (Theorem1.5 (ii)). For every $\varepsilon \gt 0$ there exists $\delta \gt 0$ such that for all $n,m\in \mathbb{N}$ such that $(1+\varepsilon )n \leq m \leq \frac{1}{11}n\log n$ the following holds. If $G$ is a uniformly random graph in $\mathcal G_{n,m}$ , then with high probability we have

(33) \begin{align} \textrm{stww}(G) \geq \delta \frac{d}{\sqrt{\log n}}n^{\frac{d-2}{2d-2} }, \end{align}

where $d = \textrm{mad}(G)$ .

Proof. W.l.o.g. suppose $\varepsilon \lt 0.1$ , let $\alpha = \frac{1}{4}e^{-\frac{4}{\varepsilon }}$ and let $C_0$ be as in Lemma3.2. We show that $\delta = \frac{\alpha ^{3/2} 4^{-2/\alpha }}{24C_0}$ satisfies the theorem. We may suppose that $n$ is sufficiently large such that $\alpha (n-1) \geq \frac{\alpha }{2}n$ , $\binom{n}{2}-m\geq n^2/3$ , which is possible given the upper bound on $m$ , and $\alpha (n-1)\geq n_0$ , where $n_0$ is obtained from Lemma3.2.

Let $S(X,m^{\prime})$ be the set of all graphs in $\mathcal G_{n,m}$ such that ${\textsf{e}}(G[X])=m^{\prime}$ and $X$ is a maximal subset of $[n]$ satisfying $\textrm{mad}(G)=\frac{2{\textsf{e}}(G[X])}{|X|}$ , i.e. such that $\textrm{mad}(G)$ is the average degree of $G[X]$ . Note that $\textrm{mad}(G)\geq \frac{2e(G)}{{\textsf{v}}(G)}=\frac{2m}{n}$ .

By Lemma3.5, with high probability every $X\subseteq [n]$ with $|X|\leq \alpha (n-1)$ is such that ${\textsf{e}}(G[X])\leq \frac{m}{n}|X|$ . In particular, for such an $X$ , $\frac{2{\textsf{e}}(G[X])}{|X|}\leq \frac{2m}{n}\leq \textrm{mad}(G)$ . Hence, no such $X$ has average degree greater than that of the entire graph $G$ . Hence, with high probability $G$ has a set $X\subseteq [n]$ which attains the maximum average degree and has size $|X|\geq \alpha (n-1)$ .

On the other hand, Lemma3.6 states that with high probability every set $X$ with $|X|\geq \alpha (n-1)$ is such that ${\textsf{e}}(G[X])\leq \frac{1}{10}|X|\log |X|$ .

Hence, with high probability $G$ belongs to some set $S(X,m^{\prime})$ where $|X| \geq \alpha (n-1)$ and $m^{\prime}\leq \frac{1}{10}|X|\log |X|$ . Furthermore, as $X$ attains the maximum average degree, then $\frac{2m^{\prime}}{|X|}\geq \frac{2m}{n}$ and so $m^{\prime}\geq \frac{m}{n}|X|\geq (1+\varepsilon )|X|$ .

Let $w \,:\!=\, \delta \frac{d}{\sqrt{\log n}}n^{\frac{d-2}{2d-2} }$ . Let $N(X,m^{\prime})$ be the number of graphs $G \in S(X,m^{\prime})$ with $\textrm{stww}(G) \leq w$ . As there are at most $2^n$ choices of $X$ and $o(2^n)$ choices of $m^{\prime}$ , to prove the theorem it suffices to show that for any $X$ and $m^{\prime}$ as above we have

(34) \begin{align} 4^n N(X,m^{\prime}) =o( |\mathcal G_{n,m}|). \end{align}

Let $x \,:\!=\,|X|$ and $\varepsilon ^{\prime} \,:\!=\,\frac{2\delta }{\alpha ^{1/2}}$ . Note that

\begin{align*}\varepsilon ^{\prime}=\frac {\alpha \cdot 4^{-2/\alpha }}{12C_0}\lt \alpha =\frac {1}{4}e^{-\frac {4}{\varepsilon }}\lt \varepsilon .\end{align*}

As $n\geq x \geq \alpha (n-1) \geq \frac{\alpha }{2}n$ , we have

\begin{align*}\varepsilon ^{\prime} d\left (\frac {x}{\log x}\right )^{\frac {d-2}{2d-2}} \geq \varepsilon ^{\prime} \sqrt {\frac {\alpha }{2}} \cdot \frac {d}{\sqrt {\log n}} n^{\frac {d-2}{2d-2}} \geq w.\end{align*}

Hence, as $\textrm{stww}(G) \leq w$ we have $\textrm{stww}(G[X]) \leq w \leq \varepsilon ^{\prime} \left (\frac{x}{\log x}\right )^{\frac{d-2}{2d-2}}$ . Given that $x\geq \alpha (n-1)\geq n_0$ and $(1+\varepsilon ^{\prime})x\leq (1+\varepsilon )x\leq m^{\prime}\leq \frac{1}{10}x\log x$ , by Lemma3.2 there are at most $\left (C_0 \varepsilon ^{\prime} \frac{x^2}{m^{\prime}}\right )^{m^{\prime}}$ possible choices of for the subgraph $G[X]$ such that $G \in S(X,m^{\prime})$ and $\textrm{tww}(G) \leq w$ . There are also at most $\binom{\binom{n}{2}-\binom{x}{2}}{m-m^{\prime}}\leq \binom{\binom{n}{2}}{m-m^{\prime}}$ choices for the remaining edges of $G$ . It follows that

\begin{align*} N(X,m^{\prime}) \leq \left (C_0 \varepsilon ^{\prime} \frac {x^2}{m^{\prime}}\right )^{m^{\prime}}\binom {\binom {n}{2}-\binom {x}{2}}{m-m^{\prime}}.\end{align*}

Using $m \leq \frac{n}{x}m^{\prime} \leq \frac{2}{\alpha }m^{\prime}$ , we obtain

\begin{align*} &\left (\frac{4^nN(X,m^{\prime})}{|G_{n,m}|}\right )^{1/m^{\prime}} \leq 4^{n/m^{\prime}} C_0 \cdot \varepsilon ^{\prime} \cdot \frac{x^2}{m^{\prime}} \left (\frac{\binom{\binom{n}{2}}{m-m^{\prime}}}{\binom{\binom{n}{2}}{m}}\right )^{1/m^{\prime}} \\ & \leq 4^{m/m^{\prime}} C_0 \cdot \frac{2\delta }{\alpha ^{1/2}} \cdot \frac{x^2}{m^{\prime}} \left (\frac{\frac{\binom{n}{2}!}{(m-m^{\prime})!\left (\binom{n}{2}-(m-m^{\prime})\right )!}}{\frac{\binom{n}{2}!}{m!\left (\binom{n}{2}-m\right )!}}\right )^{1/m^{\prime}} \\ & \leq 4^{m/m^{\prime}} C_0 \cdot \frac{2\delta }{\alpha ^{1/2}} \cdot \frac{x^2}{m^{\prime}} \left (\frac{m(m-1)\dots (m-m^{\prime}+1)}{\left (\binom{n}{2}-m+m^{\prime}\right )\left (\binom{n}{2}-m+m^{\prime}-1\right )\dots \left (\binom{n}{2}-m+1\right )}\right )^{1/m^{\prime}} \\ &\leq 4^{2/\alpha } C_0 \cdot \frac{2\delta }{\alpha ^{1/2}} \cdot \frac{x^2}{m^{\prime}}\cdot \frac{m}{\binom{n}{2}-m} \leq 4^{2/\alpha } C_0 \cdot \frac{2\delta }{\alpha ^{1/2}} \cdot \frac{m}{m^{\prime}} \cdot \frac{x^2}{n^2/3} \\ &\leq \delta \cdot \frac{12}{\alpha ^{3/2}} \cdot 4^{2/\alpha } \cdot C_0 \leq 1/2, \end{align*}

implying (34) as desired. This concludes the proof of the theorem.

4. Concluding remarks

We have established bounds on the twin-width of sparse graphs in terms of their maximum average degree (see e.g. Lemma2.8) and have shown that these bounds are essentially tight for random graphs and random regular graphs. In combination with the previously known results, our bounds, in particular, asymptotically determine $\log \textrm{tww}(G(n,p))$ for $\frac{1 + \varepsilon (n)}{n} \leq p \leq 1 - \frac{1 + \varepsilon (n)}{n}$ for some function $\varepsilon (n)$ sufficiently slowly approaching zero.

The regime in which $\textrm{tww}(G(n,p))$ remains least understood is the critical window $p=\frac{1+o(1)}{n}$ . A related open question is to find optimal bounds on the twin-width of $n$ -vertex graphs with maximum average degree $2 + \varepsilon (n)$ , where $\varepsilon (n)$ quickly approaches zero. Such graphs structurally resemble long subdivisions, and the twin-width of subdivisions has been investigated before in [5] and [2]. It is tempting to extend our result to this setting, but substantial technical difficulties, in particular, involving the treatment of large degree vertices, remain.